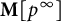1 Introduction
When studying degenerations of abelian varieties, one is led to Kato’s theory of finite Kummer flat group log schemes and log p-divisible groups (see [Reference Kato12] and [Reference Zhao26, Appendix]Footnote
1
for a brief account of finite Kummer flat group log schemes). For instance, by a theorem of Kato (see [Reference Zhao28, Theorem 1.3]), the p-divisible group of a semistable abelian variety over a complete discrete valuation field extends to a log p-divisible group over the corresponding discrete valuation ring. In this article, we will expand on some ideas developed in [Reference Kato12] and connect them with the theory of log
![]() $1$
-motives and log abelian varieties.
$1$
-motives and log abelian varieties.
Let S be an fs log scheme endowed with a suitable global chart, whose underlying scheme is the spectrum of a Noetherian Henselian local ring with positive residue characteristic p. When studying finite Kummer flat group log schemes over S, one key point is to understand extensions of classical finite étale group schemes by classical finite flat group schemes over S in a logarithmic category (see [Reference Zhao26, the paragraph before Theorem A.3] for an explanation of this). In [Reference Kato12, Theorem 3.3] (see also Theorem 3.8), Kato gives a description of such an extension in terms of a classical extension together with a certain monodromy datum. We call such extensions standard (see Definition 3.1).
As a corollary of Kato’s theorem (Theorem 3.8), one then also gets a description of the extensions of a classical étale p-divisible group by a classical p-divisible group over S (see Theorem 3.13). After presenting the basic objects in Section 2, we then in Section 3 present a complete proof to Kato’s theorem following Kato’s approach. In the procedure, we explore Kato’s idea further and define the notion of a standard extension of a classical finite étale group scheme (resp. classical étale p-divisible group) by a classical finite flat group scheme (resp. classical p-divisible group) (see Definition 3.1 [resp. Definition 3.12]). Then Kato’s results amount to saying that, over a Noetherian Henselian local fs log scheme admitting a global chart, any extension of a classical finite étale group scheme (resp. classical étale p-divisible group) by a classical finite flat group scheme (resp. classical p-divisible group) is always standard. Over a general base, we get the following.
Theorem (See Theorem 3.11)
Let S be a locally Noetherian fs log scheme, and let G be a finite Kummer flat group log scheme over S, which is an extension of a classical finite étale group scheme by a classical finite flat group scheme. Then G is a standard extension étale locally on S.
Moreover, as an application of Kato’s results, we can prove the following theorem for objects in the category
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
, which consists of log p-divisible groups whose dual is also a log p-divisible group. This is analogous to the formal smoothness of classical p-divisible groups (see [Reference Messing16, Chapter II 3.3.13]).
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
, which consists of log p-divisible groups whose dual is also a log p-divisible group. This is analogous to the formal smoothness of classical p-divisible groups (see [Reference Messing16, Chapter II 3.3.13]).
Theorem (See Theorem 3.16)
Let S be a locally Noetherian fs log scheme on which p is locally nilpotent, and let H be a log p-divisible group over S, which lies in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. Then H is formally log smooth, i.e., for any strict closed square-zero thickening
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. Then H is formally log smooth, i.e., for any strict closed square-zero thickening
![]() $T_0\hookrightarrow T$
in
$T_0\hookrightarrow T$
in
![]() $(\mathrm {fs}/S)$
, any element of
$(\mathrm {fs}/S)$
, any element of
![]() $H(T_0)$
can be lifted to an element of
$H(T_0)$
can be lifted to an element of
![]() $H(T)$
étale locally on T.
$H(T)$
étale locally on T.
In Section 4, we study the finite Kummer flat group log scheme
for a log 1-motive
![]() $\mathbf {M}=[Y\xrightarrow {u}G_{\mathrm {log}}]$
over a locally Noetherian fs log scheme S, as well as the log p-divisible group
$\mathbf {M}=[Y\xrightarrow {u}G_{\mathrm {log}}]$
over a locally Noetherian fs log scheme S, as well as the log p-divisible group
![]() $\mathbf {M}[p^{\infty }]:=\varinjlim _n T_{p^n}(\mathbf {M})$
of
$\mathbf {M}[p^{\infty }]:=\varinjlim _n T_{p^n}(\mathbf {M})$
of
![]() $\mathbf {M}$
. Let T be the torus part of G, and let X be the character group of T. The composition
$\mathbf {M}$
. Let T be the torus part of G, and let X be the character group of T. The composition
gives rise to a pairing
![]() $\langle -,-\rangle :X\times Y\to \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}}$
(see [Reference Kajiwara, Kato and Nakayama8, Section 2.3]). We call this pairing the monodromy pairing of
$\langle -,-\rangle :X\times Y\to \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}}$
(see [Reference Kajiwara, Kato and Nakayama8, Section 2.3]). We call this pairing the monodromy pairing of
![]() $\mathbf {M}$
. In Proposition 4.7, we show that étale locally the monodromy pairing of
$\mathbf {M}$
. In Proposition 4.7, we show that étale locally the monodromy pairing of
![]() $\mathbf {M}$
gives rise to a canonical pseudo-monodromy of
$\mathbf {M}$
gives rise to a canonical pseudo-monodromy of
![]() $T_n(\mathbf {M})$
, as well as of
$T_n(\mathbf {M})$
, as well as of
![]() $\mathbf {M}[p^{\infty }]$
.
$\mathbf {M}[p^{\infty }]$
.
In Section 5, we turn to the Serre–Tate theorem for log abelian varieties with constant degeneration.
Theorem (see Theorem 5.14)
Let
![]() $S_{0}$
be a locally Noetherian fs log scheme on which p is locally nilpotent, and let
$S_{0}$
be a locally Noetherian fs log scheme on which p is locally nilpotent, and let
![]() $S_{0}\subset S$
be a strict infinitesimal thickening of fs log schemes. Let
$S_{0}\subset S$
be a strict infinitesimal thickening of fs log schemes. Let
![]() $A_{0}$
be a log abelian variety with constant degeneration over
$A_{0}$
be a log abelian variety with constant degeneration over
![]() $S_{0}$
. Let
$S_{0}$
. Let
![]() $\mathrm {Def}_{A_{0}}(S)$
be the category of pairs
$\mathrm {Def}_{A_{0}}(S)$
be the category of pairs
![]() $(A, \phi )$
where A is log abelian variety over S, and
$(A, \phi )$
where A is log abelian variety over S, and
![]() $\phi :A_{S_{0}}\xrightarrow {\cong }A_{0}$
is an isomorphism. Similarly, let
$\phi :A_{S_{0}}\xrightarrow {\cong }A_{0}$
is an isomorphism. Similarly, let
![]() $\mathrm {Def}_{A_{0}[p^{\infty }]}(S)$
be the category of pairs
$\mathrm {Def}_{A_{0}[p^{\infty }]}(S)$
be the category of pairs
![]() $(H, \psi )$
, where H is a log p-divisible group over S, with an identification
$(H, \psi )$
, where H is a log p-divisible group over S, with an identification
![]() $\psi :H_{S_{0}}\xrightarrow {\cong } A_{0}[p^{\infty }]$
.
$\psi :H_{S_{0}}\xrightarrow {\cong } A_{0}[p^{\infty }]$
.
Then the functor
![]() $A\mapsto A[p^{\infty }]$
, taking a log abelian variety over S to its associated log p-divisible group, induces an equivalence of categories
$A\mapsto A[p^{\infty }]$
, taking a log abelian variety over S to its associated log p-divisible group, induces an equivalence of categories
For this, we follow Drinfeld’s approach for abelian varieties as in [Reference Katz15, Section 1]. The key point here is to verify the hypothesis about formal (log) smoothness from [Reference Katz15, Lemma 1.1.3] for log p-divisible groups in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
and log abelian varieties with constant degeneration.
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
and log abelian varieties with constant degeneration.
The above theorem can also be regarded as a Serre–Tate theorem for pointwise polarizable log 1-motives. There is also a Serre–Tate theorem for classical
![]() $1$
-motives over local Artin rings, which is the main theorem of [Reference Bertapelle and Mazzari4].
$1$
-motives over local Artin rings, which is the main theorem of [Reference Bertapelle and Mazzari4].
2 Finite Kummer flat group log schemes and log p-divisible groups
2.1 Kummer log topologies
Unless otherwise stated, we always denote by S a locally Noetherian fs log scheme. By log structure, we always mean log structure on the classical étale site. We denote by
![]() $(\mathrm {fs}/S)$
the category of fs log schemes over S. We recall the Kummer log flat topology and the Kummer log étale topology on
$(\mathrm {fs}/S)$
the category of fs log schemes over S. We recall the Kummer log flat topology and the Kummer log étale topology on
![]() $(\mathrm {fs}/S)$
(see [Reference Kato13, Definition 2.3] or [Reference Nizioł20, Definition 2.13]).
$(\mathrm {fs}/S)$
(see [Reference Kato13, Definition 2.3] or [Reference Nizioł20, Definition 2.13]).
Definition 2.1 For
![]() $U\in (\mathrm {fs}/S)$
, a family of morphisms
$U\in (\mathrm {fs}/S)$
, a family of morphisms
![]() $\{U_i\xrightarrow {f_i} U\}$
is called a Kummer log flat cover (resp. Kummer log étale cover), if the following are satisfied.
$\{U_i\xrightarrow {f_i} U\}$
is called a Kummer log flat cover (resp. Kummer log étale cover), if the following are satisfied.
-
(1) Each
 $f_i$
is log flat (resp. log étale) and of Kummer type, and its underlying map of schemes is locally of finite presentation.
$f_i$
is log flat (resp. log étale) and of Kummer type, and its underlying map of schemes is locally of finite presentation. -
(2) The family is set-theoretically surjective, i.e.,
 $U=\bigcup _if_i(U_i)$
.
$U=\bigcup _if_i(U_i)$
.
The Kummer log flat topology (resp. Kummer log étale topology) on
![]() $(\mathrm {fs}/S)$
is the Grothendieck topology given by the Kummer log flat cover (resp. Kummer log étale cover) on
$(\mathrm {fs}/S)$
is the Grothendieck topology given by the Kummer log flat cover (resp. Kummer log étale cover) on
![]() $(\mathrm {fs}/S)$
. We will sometimes call the Kummer log flat (resp. Kummer log étale) topology simply the Kummer flat (resp. Kummer étale) topology, and denote the resulting site by
$(\mathrm {fs}/S)$
. We will sometimes call the Kummer log flat (resp. Kummer log étale) topology simply the Kummer flat (resp. Kummer étale) topology, and denote the resulting site by
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
(resp.
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
(resp.
![]() $(\mathrm {fs}/S)_{\mathrm {k\acute {e}t}}$
).
$(\mathrm {fs}/S)_{\mathrm {k\acute {e}t}}$
).
To see that these are indeed Grothendieck topology, we refer to [Reference Kato13, Section 2] and [Reference Nizioł20, Section 2].
By taking the strict flat covers, i.e., families of strict morphisms whose underlying maps of schemes form flat covers of schemes, one gets the classical flat site on
![]() $(\mathrm {fs}/S)$
, denoted by
$(\mathrm {fs}/S)$
, denoted by
![]() $(\mathrm {fs}/S)_{\mathrm {fl}}$
. Similarly, one also gets the classical étale site on
$(\mathrm {fs}/S)_{\mathrm {fl}}$
. Similarly, one also gets the classical étale site on
![]() $(\mathrm {fs}/S)$
, denoted by
$(\mathrm {fs}/S)$
, denoted by
![]() $(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
. We have a natural “forgetful” map of sites
$(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
. We have a natural “forgetful” map of sites
There is of course the étale version of the above forgetful map of sites, but we do not need it in this article. In order to shorten formulas, we will mostly abbreviate
![]() $(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
(resp.
$(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
(resp.
![]() $(\mathrm {fs}/S)_{\mathrm {k\acute {e}t}}$
, resp.
$(\mathrm {fs}/S)_{\mathrm {k\acute {e}t}}$
, resp.
![]() $(\mathrm {fs}/S)_{\mathrm {fl}}$
, resp.
$(\mathrm {fs}/S)_{\mathrm {fl}}$
, resp.
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
) as
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
) as
![]() $S_{\mathrm {\acute {e}t}}$
(resp.
$S_{\mathrm {\acute {e}t}}$
(resp.
![]() $S_{\mathrm {k\acute {e}t}}$
, resp.
$S_{\mathrm {k\acute {e}t}}$
, resp.
![]() $S_{\mathrm {fl}}$
, resp.
$S_{\mathrm {fl}}$
, resp.
![]() $S_{\mathrm {kfl}}$
).
$S_{\mathrm {kfl}}$
).
Definition 2.2 Kato’s multiplicative group (or the log multiplicative group)
![]() $\mathbb {G}_{\mathrm {m,log}}$
is the sheaf on
$\mathbb {G}_{\mathrm {m,log}}$
is the sheaf on
![]() $S_{\mathrm {\acute {e}t}}$
defined by
$S_{\mathrm {\acute {e}t}}$
defined by
![]() $\mathbb {G}_{\mathrm {m,log}}(U)=\Gamma (U,M^{\mathrm {gp}}_U)$
for any
$\mathbb {G}_{\mathrm {m,log}}(U)=\Gamma (U,M^{\mathrm {gp}}_U)$
for any
![]() $U\in (\mathrm {fs}/S)$
, where
$U\in (\mathrm {fs}/S)$
, where
![]() $M_U$
denotes the log structure of U and
$M_U$
denotes the log structure of U and
![]() $M^{\mathrm {gp}}_U$
denotes the group envelope of
$M^{\mathrm {gp}}_U$
denotes the group envelope of
![]() $M_U$
.
$M_U$
.
The étale sheaf
![]() $\mathbb {G}_{\mathrm {m,log}}$
is also a sheaf on
$\mathbb {G}_{\mathrm {m,log}}$
is also a sheaf on
![]() $S_{\mathrm {kfl}}$
(see [Reference Kato13, Theorem 3.2] or [Reference Nizioł20, Corollary 2.22]).
$S_{\mathrm {kfl}}$
(see [Reference Kato13, Theorem 3.2] or [Reference Nizioł20, Corollary 2.22]).
By convention, for any sheaf of abelian groups F on
![]() $S_{\mathrm {kfl}}$
and a subgroup sheaf G of F on
$S_{\mathrm {kfl}}$
and a subgroup sheaf G of F on
![]() $S_{\mathrm {kfl}}$
, we denote by
$S_{\mathrm {kfl}}$
, we denote by
![]() $(F/G)_{S_{\mathrm {\acute {e}t}}}$
(resp.
$(F/G)_{S_{\mathrm {\acute {e}t}}}$
(resp.
![]() $(F/G)_{S_{\mathrm {fl}}}$
, resp.
$(F/G)_{S_{\mathrm {fl}}}$
, resp.
![]() $(F/G)_{S_{\mathrm {k\acute {e}t}}}$
) the quotient sheaf on
$(F/G)_{S_{\mathrm {k\acute {e}t}}}$
) the quotient sheaf on
![]() $S_{\mathrm {\acute {e}t}}$
(resp.
$S_{\mathrm {\acute {e}t}}$
(resp.
![]() $S_{\mathrm {fl}}$
, resp.
$S_{\mathrm {fl}}$
, resp.
![]() $S_{\mathrm {k\acute {e}t}}$
), while
$S_{\mathrm {k\acute {e}t}}$
), while
![]() $F/G$
denotes the quotient sheaf on
$F/G$
denotes the quotient sheaf on
![]() $S_{\mathrm {kfl}}$
.
$S_{\mathrm {kfl}}$
.
2.2 Finite Kummer flat group log schemes and log p-divisible groups
Definition 2.3 The category
![]() $(\mathrm {fin}/S)_{\mathrm {c}}$
is the full subcategory of the category of sheaves of abelian groups over
$(\mathrm {fin}/S)_{\mathrm {c}}$
is the full subcategory of the category of sheaves of abelian groups over
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
consisting of objects which are representable by a classical finite flat group scheme over S. Here, classical means that the log structure of the representing log scheme is induced from S.
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
consisting of objects which are representable by a classical finite flat group scheme over S. Here, classical means that the log structure of the representing log scheme is induced from S.
The category
![]() $(\mathrm {fin}/S)_{\mathrm {f}}$
is the full subcategory of the category of sheaves of abelian groups over
$(\mathrm {fin}/S)_{\mathrm {f}}$
is the full subcategory of the category of sheaves of abelian groups over
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
consisting of objects which are representable by a classical finite flat group scheme over a Kummer log flat cover of S. For
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
consisting of objects which are representable by a classical finite flat group scheme over a Kummer log flat cover of S. For
![]() $F\in (\mathrm {fin}/S)_{\mathrm {f}}$
, let
$F\in (\mathrm {fin}/S)_{\mathrm {f}}$
, let
![]() $U\rightarrow S$
be a Kummer log flat cover of S such that
$U\rightarrow S$
be a Kummer log flat cover of S such that
![]() $F_U:=F\times _S U\in (\mathrm {fin}/U)_{\mathrm {c}}$
. Then the rank of F is defined to be the rank of
$F_U:=F\times _S U\in (\mathrm {fin}/U)_{\mathrm {c}}$
. Then the rank of F is defined to be the rank of
![]() $F_U$
over U.
$F_U$
over U.
The category
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
is the full subcategory of
$(\mathrm {fin}/S)_{\mathrm {r}}$
is the full subcategory of
![]() $(\mathrm {fin}/S)_{\mathrm {f}}$
consisting of objects which are representable by a log scheme over S.
$(\mathrm {fin}/S)_{\mathrm {f}}$
consisting of objects which are representable by a log scheme over S.
Let
![]() $F\in (\mathrm {fin}/S)_{\mathrm {f}}$
, and the Cartier dual of F is the sheaf
$F\in (\mathrm {fin}/S)_{\mathrm {f}}$
, and the Cartier dual of F is the sheaf
![]() $F^*:=\mathcal {H}om_{S_{\mathrm {kfl}}}(F,\mathbb {G}_{\mathrm {m}})$
. By the definition of
$F^*:=\mathcal {H}om_{S_{\mathrm {kfl}}}(F,\mathbb {G}_{\mathrm {m}})$
. By the definition of
![]() $(\mathrm {fin}/S)_{\mathrm {f}}$
, it is clear that
$(\mathrm {fin}/S)_{\mathrm {f}}$
, it is clear that
![]() $F^*\in (\mathrm {fin}/S)_{\mathrm {f}}$
.
$F^*\in (\mathrm {fin}/S)_{\mathrm {f}}$
.
The category
![]() $(\mathrm {fin}/S)_{\mathrm {d}}$
is the full subcategory of
$(\mathrm {fin}/S)_{\mathrm {d}}$
is the full subcategory of
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
consisting of objects whose Cartier dual also lies in
$(\mathrm {fin}/S)_{\mathrm {r}}$
consisting of objects whose Cartier dual also lies in
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
.
$(\mathrm {fin}/S)_{\mathrm {r}}$
.
The category
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
also has an alternative description as follows.
$(\mathrm {fin}/S)_{\mathrm {r}}$
also has an alternative description as follows.
Proposition 2.4 Let G be a sheaf of abelian groups on
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
. Then we have
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
. Then we have
![]() $G\in (\mathrm {fin}/S)_{\mathrm {r}}$
if and only if G satisfies the following condition.
$G\in (\mathrm {fin}/S)_{\mathrm {r}}$
if and only if G satisfies the following condition.
-
(⋆) G is representable by an fs log scheme such that the structure morphism
 $G\to S$
is Kummer log flat and its underlying morphism of schemes is finite.
$G\to S$
is Kummer log flat and its underlying morphism of schemes is finite.
Proof Assume that G satisfied the condition (
![]() $\star $
). We want to show that
$\star $
). We want to show that
![]() $G\in (\mathrm {fin}/S)_{\mathrm {r}}$
. As the problem is classically étale local on S, we can assume that S is quasi-compact and that the log structure on S admits a global chart. Moreover, if S is quasi-compact, so is G. Hence, by [Reference Kato13, Theorem 2.7(2)], there is a Kummer log flat cover
$G\in (\mathrm {fin}/S)_{\mathrm {r}}$
. As the problem is classically étale local on S, we can assume that S is quasi-compact and that the log structure on S admits a global chart. Moreover, if S is quasi-compact, so is G. Hence, by [Reference Kato13, Theorem 2.7(2)], there is a Kummer log flat cover
![]() $S'\to S$
such that
$S'\to S$
such that
![]() $G_{S'}\to S'$
is strict. By [Reference Kato and Saito14, Lemma 4.3.1], the morphism
$G_{S'}\to S'$
is strict. By [Reference Kato and Saito14, Lemma 4.3.1], the morphism
![]() $G_{S'}\to S'$
is classically flat. The underlying morphism of schemes of
$G_{S'}\to S'$
is classically flat. The underlying morphism of schemes of
![]() $G_{S'}\to S'$
is also finite by [Reference Nakayama19, 1.10]. Hence,
$G_{S'}\to S'$
is also finite by [Reference Nakayama19, 1.10]. Hence,
![]() $G_{S'}\to S'$
is a classical finite flat group scheme over
$G_{S'}\to S'$
is a classical finite flat group scheme over
![]() $S'$
. It follows that
$S'$
. It follows that
![]() $G\in (\mathrm {fin}/S)_{\mathrm {r}}$
.
$G\in (\mathrm {fin}/S)_{\mathrm {r}}$
.
Conversely, assume that
![]() $G\in (\mathrm {fin}/S)_{\mathrm {r}}$
, i.e., there is a Kummer log flat cover
$G\in (\mathrm {fin}/S)_{\mathrm {r}}$
, i.e., there is a Kummer log flat cover
![]() $S'\to S$
such that
$S'\to S$
such that
![]() $G_{S'}\to S'$
is a classical finite flat group scheme. The property of being log-flat descends along Kummer log flat covers of the base, by [Reference Illusie, Nakayama and Tsuji7, Theorem 0.1]. Hence, G is log flat over S. Moreover, by [Reference Kato13, Proposition 2.7(1)],
$G_{S'}\to S'$
is a classical finite flat group scheme. The property of being log-flat descends along Kummer log flat covers of the base, by [Reference Illusie, Nakayama and Tsuji7, Theorem 0.1]. Hence, G is log flat over S. Moreover, by [Reference Kato13, Proposition 2.7(1)],
![]() $G\to S$
is of Kummer type. To finish the proof, we are left with showing that the underlying map of schemes of
$G\to S$
is of Kummer type. To finish the proof, we are left with showing that the underlying map of schemes of
![]() $G\to S$
is finite, which follows from Proposition C.2.Footnote
2
$G\to S$
is finite, which follows from Proposition C.2.Footnote
2
Definition 2.5 Due to Proposition 2.4, we call an object of
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
a finite Kummer log flat group log scheme, or simply finite Kummer flat group log scheme, or even a finite kfl group log scheme.
$(\mathrm {fin}/S)_{\mathrm {r}}$
a finite Kummer log flat group log scheme, or simply finite Kummer flat group log scheme, or even a finite kfl group log scheme.
Definition 2.6 Let p be a prime number. A log p-divisible group over S is a sheaf of abelian groups G on
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
satisfying:
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
satisfying:
-
(1)
 $G=\varinjlim _{n}G_n$
with
$G=\varinjlim _{n}G_n$
with
 $G_n:=\mathrm {ker}(p^n:G\rightarrow G)$
;
$G_n:=\mathrm {ker}(p^n:G\rightarrow G)$
; -
(2)
 $p:G\rightarrow G$
is surjective;
$p:G\rightarrow G$
is surjective; -
(3)
 $G_n\in (\mathrm {fin}/S)_{\mathrm {r}}$
for any
$G_n\in (\mathrm {fin}/S)_{\mathrm {r}}$
for any
 $n> 0$
.
$n> 0$
.
We denote the category of log p-divisible groups over S by
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
. The full subcategory of
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
. The full subcategory of
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
consisting of objects G with
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
consisting of objects G with
![]() $G_n\in (\mathrm {fin}/S)_{\mathrm {d}}$
for
$G_n\in (\mathrm {fin}/S)_{\mathrm {d}}$
for
![]() $n>0$
will be denoted by
$n>0$
will be denoted by
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. A log p-divisible group G with
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. A log p-divisible group G with
![]() $G_n\in (\mathrm {fin}/S)_{\mathrm {c}}$
for
$G_n\in (\mathrm {fin}/S)_{\mathrm {c}}$
for
![]() $n>0$
is clearly just a classical p-divisible group, and we denote the full subcategory of
$n>0$
is clearly just a classical p-divisible group, and we denote the full subcategory of
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
consisting of classical p-divisible groups by
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
consisting of classical p-divisible groups by
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
.
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
.
Remark 2.7. In Definition 2.6, one can replace the condition (3) by simply requiring
![]() $G_1\in (\mathrm {fin}/S)_{\mathrm {r}}$
. This follows from the fact that the category
$G_1\in (\mathrm {fin}/S)_{\mathrm {r}}$
. This follows from the fact that the category
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
is closed under extension in the category of sheaves of abelian groups on
$(\mathrm {fin}/S)_{\mathrm {r}}$
is closed under extension in the category of sheaves of abelian groups on
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
(see [Reference Zhao26, Proposition A.1]). Similarly, a log p-divisible group G lies in
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
(see [Reference Zhao26, Proposition A.1]). Similarly, a log p-divisible group G lies in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
if
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
if
![]() $G_1\in (\mathrm {fin}/S)_{\mathrm {d}}$
; this also follows from [Reference Zhao26, Proposition A.1]. Note that the corresponding statement for
$G_1\in (\mathrm {fin}/S)_{\mathrm {d}}$
; this also follows from [Reference Zhao26, Proposition A.1]. Note that the corresponding statement for
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
does not hold.
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
does not hold.
3 Kato’s classification theorem of log p-divisible groups
3.1 Standard extensions of log finite flat group objects
In this subsection, we further assume that S admits a global chart
![]() $P\rightarrow M_S$
with P an fs monoid. Throughout the article, if Q is a monoid, we also denote by Q the constant sheaf associated with Q.
$P\rightarrow M_S$
with P an fs monoid. Throughout the article, if Q is a monoid, we also denote by Q the constant sheaf associated with Q.
Let
![]() $F"\in (\mathrm {fin}/S)_{\mathrm {c}}$
be étale, let
$F"\in (\mathrm {fin}/S)_{\mathrm {c}}$
be étale, let
![]() $F'\in (\mathrm {fin}/S)_{\mathrm {c}}$
, and let n be a positive integer which kills both
$F'\in (\mathrm {fin}/S)_{\mathrm {c}}$
, and let n be a positive integer which kills both
![]() $F'$
and
$F'$
and
![]() $F"$
. We denote by
$F"$
. We denote by
the category of extensions of
![]() $F"$
by
$F"$
by
![]() $F'$
in
$F'$
in
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
(resp.
$(\mathrm {fin}/S)_{\mathrm {r}}$
(resp.
![]() $(\mathrm {fin}/S)_{\mathrm {c}}$
). Let
$(\mathrm {fin}/S)_{\mathrm {c}}$
). Let
![]() $F"(1):=F"\otimes _{{\mathbb Z}/n{\mathbb Z}}{\mathbb Z}/n{\mathbb Z}(1)$
, and we denote by
$F"(1):=F"\otimes _{{\mathbb Z}/n{\mathbb Z}}{\mathbb Z}/n{\mathbb Z}(1)$
, and we denote by
the discrete category associated with the set
![]() $\mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. There is a natural functor
$\mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. There is a natural functor
constructed as follows.
First, we construct a functor
For every element
![]() $a\in P^{\mathrm {gp}}$
, let
$a\in P^{\mathrm {gp}}$
, let
![]() $\mathbf {M}_a$
be the log 1-motive
$\mathbf {M}_a$
be the log 1-motive
![]() $[{\mathbb Z}\xrightarrow {1\mapsto a}\mathbb {G}_{\mathrm {m,log}}]$
. Then
$[{\mathbb Z}\xrightarrow {1\mapsto a}\mathbb {G}_{\mathrm {m,log}}]$
. Then
![]() $E_a:=H^{-1}(\mathbf {M}_a\otimes ^{L}_{{\mathbb Z}}{\mathbb Z}/n{\mathbb Z})$
fits into a short exact sequence
$E_a:=H^{-1}(\mathbf {M}_a\otimes ^{L}_{{\mathbb Z}}{\mathbb Z}/n{\mathbb Z})$
fits into a short exact sequence
which splits Kummer flat locally. Hence, we get another short exact sequence
after tensoring with
![]() $F"$
. For any
$F"$
. For any
![]() $N\in \mathrm {Hom}_S(F"(1),F')$
, we define
$N\in \mathrm {Hom}_S(F"(1),F')$
, we define
![]() $\Phi _2(N\otimes a)$
as the pushout
$\Phi _2(N\otimes a)$
as the pushout
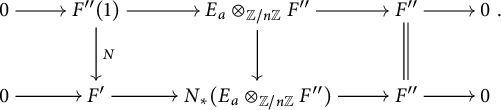
Now, for any
![]() $\beta =\sum _iN_i\otimes a_i\in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, we define
$\beta =\sum _iN_i\otimes a_i\in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, we define
![]() $\Phi _2(\beta )\in \mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')$
as the Baer sum of the extensions
$\Phi _2(\beta )\in \mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')$
as the Baer sum of the extensions
![]() $\Phi _2(N_i\otimes a_i)$
. Now the functor
$\Phi _2(N_i\otimes a_i)$
. Now the functor
![]() $\Phi $
is defined as
$\Phi $
is defined as
for
![]() $F^{\mathrm {cl}}\in \mathfrak {Ext}_{S_{\mathrm {fl}}}(F",F')$
and
$F^{\mathrm {cl}}\in \mathfrak {Ext}_{S_{\mathrm {fl}}}(F",F')$
and
![]() $\beta \in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. Here, the sum
$\beta \in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. Here, the sum
![]() $+_{\mathrm {Baer}}$
denotes the Baer sum.
$+_{\mathrm {Baer}}$
denotes the Baer sum.
Definition 3.1 An extension F of
![]() $F"$
by
$F"$
by
![]() $F'$
in the category
$F'$
in the category
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
is called standard with respect to the given chart, if it lies in the essential image of the functor
$(\mathrm {fin}/S)_{\mathrm {r}}$
is called standard with respect to the given chart, if it lies in the essential image of the functor
![]() $\Phi $
. We denote by
$\Phi $
. We denote by
![]() $\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')_{\mathrm {std}}$
the full subcategory of
$\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')_{\mathrm {std}}$
the full subcategory of
![]() $\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')$
consisting of standard extensions. Then the functor
$\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')$
consisting of standard extensions. Then the functor
![]() $\Phi $
induces a functor
$\Phi $
induces a functor
For any
![]() $F=\Phi (F^{\mathrm {cl}},\beta )$
in
$F=\Phi (F^{\mathrm {cl}},\beta )$
in
![]() $\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')_{\mathrm {std}}$
, we call
$\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')_{\mathrm {std}}$
, we call
![]() $\beta $
a pseudo-monodromy of the extension F. If the functor above is an equivalence of categories, we call
$\beta $
a pseudo-monodromy of the extension F. If the functor above is an equivalence of categories, we call
![]() $\beta $
a monodromy of F.
$\beta $
a monodromy of F.
In general, not every extension is standard, and a standard extension F admits more than one pseudo-monodromy. The name pseudo-monodromy comes from the fact that, for arbitrary charts, the decompositions one gets might be strange. In particular, a purely classical group scheme might have nonzero pseudo-monodromy.
Now we are going to investigate the essential image of the functor
![]() $\Phi $
.
$\Phi $
.
Given an element
![]() $0\rightarrow F'\rightarrow F\rightarrow F"\rightarrow 0$
in
$0\rightarrow F'\rightarrow F\rightarrow F"\rightarrow 0$
in
![]() $\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')$
, applying the direct image functor
$\mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')$
, applying the direct image functor
![]() $\varepsilon _*$
, we get a long exact sequence
$\varepsilon _*$
, we get a long exact sequence
Note that if
![]() $F=\Phi (F^{\mathrm {cl}}, \beta )$
, we have
$F=\Phi (F^{\mathrm {cl}}, \beta )$
, we have
![]() $\delta _{F^{\mathrm {cl}}}=0$
, so the connecting map
$\delta _{F^{\mathrm {cl}}}=0$
, so the connecting map
![]() $\delta _{F}$
only depends on
$\delta _{F}$
only depends on
![]() $\beta $
. By [Reference Nizioł20, Theorem 3.12] or [Reference Kato13, Theorem 4.1], we have
$\beta $
. By [Reference Nizioł20, Theorem 3.12] or [Reference Kato13, Theorem 4.1], we have
with
Note that
![]() $W=\mathcal {H}om_{S}({\mathbb Z}/n{\mathbb Z}(1),F')$
, since
$W=\mathcal {H}om_{S}({\mathbb Z}/n{\mathbb Z}(1),F')$
, since
![]() $F'$
is n-torsion. Then the homomorphism
$F'$
is n-torsion. Then the homomorphism
![]() $\delta _F$
can be rewritten as
$\delta _F$
can be rewritten as
![]() $\delta _F: F"\rightarrow W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
, which is an element of the group
$\delta _F: F"\rightarrow W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
, which is an element of the group
![]() $\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}})$
. At the same time, the chart
$\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}})$
. At the same time, the chart
![]() $P\rightarrow M_S$
induces a canonical homomorphism
$P\rightarrow M_S$
induces a canonical homomorphism
![]() $\gamma _{P}:P^{\mathrm {gp}}\rightarrow (\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
, where
$\gamma _{P}:P^{\mathrm {gp}}\rightarrow (\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
, where
![]() $P^{\mathrm {gp}}$
denotes the group envelope of the monoid P. Therefore, we have a canonical homomorphism
$P^{\mathrm {gp}}$
denotes the group envelope of the monoid P. Therefore, we have a canonical homomorphism
Remark 3.2. In [Reference Kato12, Section 3.7],
is simply replaced by
without further explanation. From the authors’ point of view, this is not completely correct, as
![]() $(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
is not constant, even in the Henselian local case. This is one reason why we present a complete treatment to Kato’s Theorem 3.8.
$(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
is not constant, even in the Henselian local case. This is one reason why we present a complete treatment to Kato’s Theorem 3.8.
We have a canonical identification
Lemma 3.3 Let
![]() $\beta \in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, and let
$\beta \in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, and let
![]() $F_{\beta }:=\Phi _2(\beta )$
. Applying the functor
$F_{\beta }:=\Phi _2(\beta )$
. Applying the functor
![]() $\varepsilon _*$
to the short exact sequence
$\varepsilon _*$
to the short exact sequence
![]() $0\rightarrow F'\rightarrow F_{\beta }\rightarrow F"\rightarrow 0$
gives rise to a long exact sequence
$0\rightarrow F'\rightarrow F_{\beta }\rightarrow F"\rightarrow 0$
gives rise to a long exact sequence
![]() $0\rightarrow F'\rightarrow F_{\beta }\rightarrow F"\xrightarrow {\delta _{F_{\beta }}}R^1\varepsilon _*F'$
. Let
$0\rightarrow F'\rightarrow F_{\beta }\rightarrow F"\xrightarrow {\delta _{F_{\beta }}}R^1\varepsilon _*F'$
. Let
![]() $\bar {\delta }_{F_{\beta }}$
be the homomorphism corresponding to
$\bar {\delta }_{F_{\beta }}$
be the homomorphism corresponding to
![]() $\beta $
under the canonical identification (3.7). Then the homomorphism
$\beta $
under the canonical identification (3.7). Then the homomorphism
![]() $\delta _{F_{\beta }}$
factors as
$\delta _{F_{\beta }}$
factors as
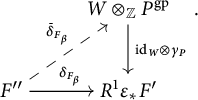
Proof It suffices to consider the case
![]() $\beta =N\otimes a\in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
.
$\beta =N\otimes a\in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
.
We abbreviate
![]() $(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
as
$(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
as
![]() $\mathcal {G}$
in order to shorten formulas. Applying the functor
$\mathcal {G}$
in order to shorten formulas. Applying the functor
![]() $\varepsilon _*$
to the short exact sequence
$\varepsilon _*$
to the short exact sequence
we get a map
Applying the functor
![]() $\varepsilon _*$
to
$\varepsilon _*$
to
![]() $0\rightarrow F"(1)\rightarrow E_a\otimes _{{\mathbb Z}/n{\mathbb Z}} F"\rightarrow F"\rightarrow 0$
, we get another map
$0\rightarrow F"(1)\rightarrow E_a\otimes _{{\mathbb Z}/n{\mathbb Z}} F"\rightarrow F"\rightarrow 0$
, we get another map
The map
![]() $\delta _{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
is identical to the map
$\delta _{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
is identical to the map
![]() $\delta _{E_{a}}\otimes 1_{F"}$
. Applying the functor
$\delta _{E_{a}}\otimes 1_{F"}$
. Applying the functor
![]() $\varepsilon _*$
to the commutative diagram (3.3), we get the following commutative diagram:
$\varepsilon _*$
to the commutative diagram (3.3), we get the following commutative diagram:
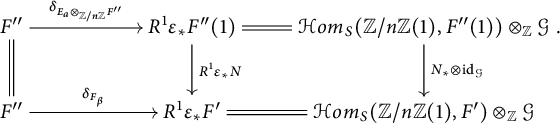
It is clear that
![]() $\delta _{E_{a}}$
factors through
$\delta _{E_{a}}$
factors through
Therefore,
![]() $\delta _{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
factors through
$\delta _{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
factors through
where
![]() $\bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
is defined as the map
$\bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
is defined as the map
![]() $\bar {\delta }_{E_{a}}\otimes 1_{F"}$
. We can rewrite
$\bar {\delta }_{E_{a}}\otimes 1_{F"}$
. We can rewrite
![]() $\bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
as
$\bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
as
We have an obvious commutative diagram
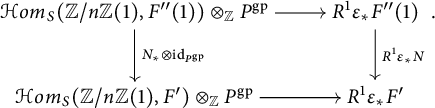
It follows that
![]() $\delta _{F_{\beta }}$
factors through
$\delta _{F_{\beta }}$
factors through
![]() $\bar {\delta }_{F_{\beta }}:=(N_*\otimes \mathrm {id}_{P^{\mathrm {gp}}})\circ \bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
. This finishes the proof.
$\bar {\delta }_{F_{\beta }}:=(N_*\otimes \mathrm {id}_{P^{\mathrm {gp}}})\circ \bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
. This finishes the proof.
Remark 3.4. In the proof of Lemma 3.3, the map
corresponds to
and
![]() ${\mathbb Z}\rightarrow P^{\mathrm {gp}},1\mapsto a$
. Therefore,
${\mathbb Z}\rightarrow P^{\mathrm {gp}},1\mapsto a$
. Therefore,
![]() $(N_*\otimes \mathrm {id}_{P^{\mathrm {gp}}})\circ \bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
is nothing but
$(N_*\otimes \mathrm {id}_{P^{\mathrm {gp}}})\circ \bar {\delta }_{E_{a}\otimes _{{\mathbb Z}/n{\mathbb Z}} F"}$
is nothing but
Proposition 3.5 Let F be an extension of
![]() $F"$
by
$F"$
by
![]() $F'$
in the category
$F'$
in the category
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
. Then F is a standard extension with respect to the given chart if and only if the homomorphism
$(\mathrm {fin}/S)_{\mathrm {r}}$
. Then F is a standard extension with respect to the given chart if and only if the homomorphism
![]() $\delta _F$
from (3.5) factors
$\delta _F$
from (3.5) factors
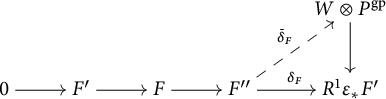
through the canonical homomorphism
![]() $W\otimes P^{\mathrm {gp}}\rightarrow W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}=R^1\varepsilon _*F'$
.
$W\otimes P^{\mathrm {gp}}\rightarrow W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}=R^1\varepsilon _*F'$
.
Proof The “only-if” part follows from Lemma 3.3 easily. Now we assume that
![]() $\delta _F$
has a factorization as above. We want to express F as a standard extension.
$\delta _F$
has a factorization as above. We want to express F as a standard extension.
First, we digress to investigate the behavior of the map (3.9) with respect to Baer sums. Let
![]() $F_1$
and
$F_1$
and
![]() $F_2$
be two extensions of
$F_2$
be two extensions of
![]() $F"$
by
$F"$
by
![]() $F'$
. The following commutative diagram
$F'$
. The following commutative diagram
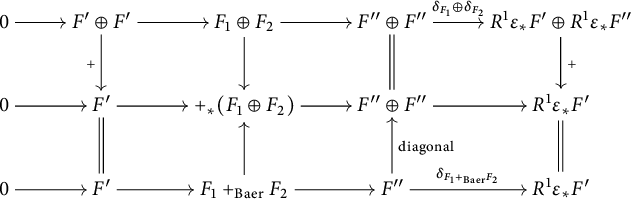
implies that
![]() $\delta _{F_1+_{\mathrm {Baer}}F_2}=\delta _{F_1}+\delta _{F_2}$
, i.e., the formation of
$\delta _{F_1+_{\mathrm {Baer}}F_2}=\delta _{F_1}+\delta _{F_2}$
, i.e., the formation of
![]() $\delta _{-}$
is compatible with the Baer sum.
$\delta _{-}$
is compatible with the Baer sum.
Now we go back to the proof of the proposition. By abuse of notation, we use the same notation
![]() $\bar {\delta }_{F}$
for the element in
$\bar {\delta }_{F}$
for the element in
![]() $\mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
corresponding to
$\mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
corresponding to
![]() $\bar {\delta }_{F}$
in
$\bar {\delta }_{F}$
in
![]() $\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})$
. Let
$\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})$
. Let
![]() $F_{\bar {\delta }_F}:=\Phi _2(\bar {\delta }_F)$
, and let
$F_{\bar {\delta }_F}:=\Phi _2(\bar {\delta }_F)$
, and let
![]() $F^{\mathrm {cl}}:=F-_{\mathrm {Baer}}F_{\bar {\delta }_F}$
. By Lemma 3.3, the connection map
$F^{\mathrm {cl}}:=F-_{\mathrm {Baer}}F_{\bar {\delta }_F}$
. By Lemma 3.3, the connection map
![]() $F"\rightarrow R^1\varepsilon _*F'$
for
$F"\rightarrow R^1\varepsilon _*F'$
for
![]() $F^{\mathrm {cl}}$
is
$F^{\mathrm {cl}}$
is
![]() $\delta _F-\delta _F=0$
. Therefore,
$\delta _F-\delta _F=0$
. Therefore,
![]() $F^{\mathrm {cl}}$
lies in
$F^{\mathrm {cl}}$
lies in
![]() $\mathfrak {Ext}_{S_{\mathrm {fl}}}(F",F')$
, and
$\mathfrak {Ext}_{S_{\mathrm {fl}}}(F",F')$
, and
![]() $F=F^{\mathrm {cl}}+_{\mathrm {Baer}}F_{\bar {\delta }_F}=F^{\mathrm {cl}}+_{\mathrm {Baer}}\Phi _2(\bar {\delta }_F)$
is standard with respect to the given chart.
$F=F^{\mathrm {cl}}+_{\mathrm {Baer}}F_{\bar {\delta }_F}=F^{\mathrm {cl}}+_{\mathrm {Baer}}\Phi _2(\bar {\delta }_F)$
is standard with respect to the given chart.
By Proposition 3.5, it is clear that the homomorphism
induced by
![]() $\gamma _{P}:P^{\mathrm {gp}}\rightarrow (\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
is important for understanding standard extensions.
$\gamma _{P}:P^{\mathrm {gp}}\rightarrow (\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
is important for understanding standard extensions.
For any
![]() $U\in (\mathrm {fs}/S)$
, both
$U\in (\mathrm {fs}/S)$
, both
![]() $P^{\mathrm {gp}}$
and
$P^{\mathrm {gp}}$
and
![]() $(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
are constructible
$(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
are constructible
![]() ${\mathbb Z}$
-modules on the small étale site of U (see [Reference Olsson22, Lemma 3.5(ii)]). By [Reference Milne17, Chapter V, Remark 1.7(e)] and Lemma A.1, the sheaf
${\mathbb Z}$
-modules on the small étale site of U (see [Reference Olsson22, Lemma 3.5(ii)]). By [Reference Milne17, Chapter V, Remark 1.7(e)] and Lemma A.1, the sheaf
![]() $W=\mathcal {H}om_S({\mathbb Z}/n{\mathbb Z}(1),F')$
is a constructible
$W=\mathcal {H}om_S({\mathbb Z}/n{\mathbb Z}(1),F')$
is a constructible
![]() ${\mathbb Z}$
-module for the étale topology. By [24, Tag 095I], the tensor product of W and
${\mathbb Z}$
-module for the étale topology. By [24, Tag 095I], the tensor product of W and
![]() $P^{\mathrm {gp}}$
for the étale topology is a constructible
$P^{\mathrm {gp}}$
for the étale topology is a constructible
![]() ${\mathbb Z}$
-module; hence, it is representable by an algebraic space by [Reference Artin, Grothendieck and Verdier2, Exposé IX, Proposition 2.7], and therefore automatically a sheaf on
${\mathbb Z}$
-module; hence, it is representable by an algebraic space by [Reference Artin, Grothendieck and Verdier2, Exposé IX, Proposition 2.7], and therefore automatically a sheaf on
![]() $(\mathrm {fs}/S)_{\mathrm {fl}}$
. It follows that the tensor product
$(\mathrm {fs}/S)_{\mathrm {fl}}$
. It follows that the tensor product
![]() $W\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
on
$W\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
on
![]() $(\mathrm {fs}/S)_{\mathrm {fl}}$
coincides with the corresponding tensor product for the étale topology. So we do not have to distinguish for which topology we take the tensor product of W and
$(\mathrm {fs}/S)_{\mathrm {fl}}$
coincides with the corresponding tensor product for the étale topology. So we do not have to distinguish for which topology we take the tensor product of W and
![]() $P^{\mathrm {gp}}$
, and just simply write
$P^{\mathrm {gp}}$
, and just simply write
![]() $W\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. We have similar result for
$W\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. We have similar result for
![]() $W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
.
$W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
.
Recall that the log structure in this article is defined in the étale topology. Let
![]() $M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
be the quotient on the small étale site of S. Since
$M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
be the quotient on the small étale site of S. Since
![]() $F"$
is étale locally constant, the homomorphism
$F"$
is étale locally constant, the homomorphism
![]() $\alpha $
is identified with
$\alpha $
is identified with
in which the Hom-groups are taken in the small étale site of S. By abuse of notation, we denote this homomorphism also by
![]() $\alpha $
.
$\alpha $
.
The chart
![]() $P\rightarrow M_S$
induces a canonical epimorphism
$P\rightarrow M_S$
induces a canonical epimorphism
![]() $P^{\mathrm {gp}}\rightarrow M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
. Let K be the kernel of this homomorphism. We then get a short exact sequence
$P^{\mathrm {gp}}\rightarrow M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
. Let K be the kernel of this homomorphism. We then get a short exact sequence
of sheaves on the small étale site of S. Since the stalks of K,
![]() $P^{\mathrm {gp}}$
, and
$P^{\mathrm {gp}}$
, and
![]() $M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
are free abelian groups, the canonical sequence
$M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
are free abelian groups, the canonical sequence
is exact on all stalks at geometric points of S. It follows that the sequence itself is exact.
Now, applying the functor
![]() $\mathrm {Hom}_S(F",-)$
to (3.9), we get another exact sequence
$\mathrm {Hom}_S(F",-)$
to (3.9), we get another exact sequence
Proposition 3.6 Let the notation and the assumptions be as above.
-
(1) Assume that
 $\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}K)=0$
, i.e., the map
$\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}K)=0$
, i.e., the map
 $\alpha $
from (3.10) is injective. Then the functor (3.4) is an equivalence of categories.
$\alpha $
from (3.10) is injective. Then the functor (3.4) is an equivalence of categories. $$\begin{align*}\Phi_{\mathrm{std}}:\mathfrak{Ext}_{S_{\mathrm{fl}}}(F",F')\times \mathfrak{Hom}(F"(1),F')\otimes_{{\mathbb Z}}P^{\mathrm{gp}}\rightarrow \mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F')_{\mathrm{std}}\end{align*}$$
$$\begin{align*}\Phi_{\mathrm{std}}:\mathfrak{Ext}_{S_{\mathrm{fl}}}(F",F')\times \mathfrak{Hom}(F"(1),F')\otimes_{{\mathbb Z}}P^{\mathrm{gp}}\rightarrow \mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F')_{\mathrm{std}}\end{align*}$$
-
(2) Assume that
 $\alpha $
is an isomorphism. Then whence the functor
$\alpha $
is an isomorphism. Then whence the functor $$ \begin{align*}\mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F')_{\mathrm{std}}=\mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F'),\end{align*} $$
$$ \begin{align*}\mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F')_{\mathrm{std}}=\mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F'),\end{align*} $$
 $\Phi $
(3.1) is an equivalence of categories.
$\Phi $
(3.1) is an equivalence of categories.
Proof We claim that
![]() $\Phi _{\mathrm {std}}$
admits a quasi-inverse, given by
$\Phi _{\mathrm {std}}$
admits a quasi-inverse, given by
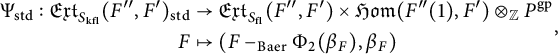 $$ \begin{align} \begin{aligned} \Psi_{\mathrm{std}}:\mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F')_{\mathrm{std}}&\rightarrow \mathfrak{Ext}_{S_{\mathrm{fl}}}(F",F')\times \mathfrak{Hom}(F"(1),F')\otimes_{{\mathbb Z}}P^{\mathrm{gp}} \\ F&\mapsto (F-_{\mathrm{Baer}}\Phi_2(\beta_F),\beta_F) \end{aligned}, \end{align} $$
$$ \begin{align} \begin{aligned} \Psi_{\mathrm{std}}:\mathfrak{Ext}_{S_{\mathrm{kfl}}}(F",F')_{\mathrm{std}}&\rightarrow \mathfrak{Ext}_{S_{\mathrm{fl}}}(F",F')\times \mathfrak{Hom}(F"(1),F')\otimes_{{\mathbb Z}}P^{\mathrm{gp}} \\ F&\mapsto (F-_{\mathrm{Baer}}\Phi_2(\beta_F),\beta_F) \end{aligned}, \end{align} $$
where
![]() $\beta _F$
, under the identification
$\beta _F$
, under the identification
corresponds to
![]() $\bar {\delta }_F$
, which is the unique lift of the connecting map
$\bar {\delta }_F$
, which is the unique lift of the connecting map
![]() $\delta _F:F"\rightarrow R^1\varepsilon _*F'$
of F. Note that the uniqueness of
$\delta _F:F"\rightarrow R^1\varepsilon _*F'$
of F. Note that the uniqueness of
![]() $\beta _F$
, which amounts to the uniqueness of
$\beta _F$
, which amounts to the uniqueness of
![]() $\bar {\delta }_F$
, is guaranteed by
$\bar {\delta }_F$
, is guaranteed by
![]() $\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}K)=0$
.
$\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}K)=0$
.
Since the functor (3.4) is clearly essentially surjective, it suffices to show that
![]() $\Psi _{\mathrm {std}}\circ \Phi _{\mathrm {std}}=1$
.
$\Psi _{\mathrm {std}}\circ \Phi _{\mathrm {std}}=1$
.
By Lemma 3.3, for
![]() $F=\Phi _2(\beta )$
with
$F=\Phi _2(\beta )$
with
![]() $\beta \in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, we have
$\beta \in \mathrm {Hom}_S(F"(1),F')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, we have
![]() $\beta _F=\beta $
. Hence, for any
$\beta _F=\beta $
. Hence, for any
![]() $F\in \mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')_{\mathrm {std}}$
, we have
$F\in \mathfrak {Ext}_{S_{\mathrm {kfl}}}(F",F')_{\mathrm {std}}$
, we have
This implies that the direct image of the short exact sequence
remains exact; therefore,
![]() $F-_{\mathrm {Baer}}\Phi _2(\beta _F)$
is indeed classical. We also have
$F-_{\mathrm {Baer}}\Phi _2(\beta _F)$
is indeed classical. We also have
This proves part (1).
For (2), note that under the assumption that
![]() $\alpha $
is an isomorphism, every extension of
$\alpha $
is an isomorphism, every extension of
![]() $F"$
by
$F"$
by
![]() $F'$
is standard with respect to the given chart by Proposition 3.5. So part (2) follows from part (1).
$F'$
is standard with respect to the given chart by Proposition 3.5. So part (2) follows from part (1).
Lemma 3.7 Assume that the underlying scheme of S is
![]() $\mathop {\mathrm {Spec}} A$
with A a Noetherian Henselian local ring, and S admits a global chart
$\mathop {\mathrm {Spec}} A$
with A a Noetherian Henselian local ring, and S admits a global chart
![]() $P\rightarrow M_S$
such that the induced map
$P\rightarrow M_S$
such that the induced map
![]() $P\rightarrow M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism for the closed point s of S. Then the canonical homomorphism
$P\rightarrow M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism for the closed point s of S. Then the canonical homomorphism
![]() $\alpha $
(3.8) is an isomorphism, so the group
$\alpha $
(3.8) is an isomorphism, so the group
![]() $\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}})$
can canonically be identified with the group
$\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}})$
can canonically be identified with the group
Proof It suffices to prove that the map
![]() $\alpha $
from (3.10) is an isomorphism. Then the result follows from
$\alpha $
from (3.10) is an isomorphism. Then the result follows from
![]() $P^{\mathrm {gp}}\cong {\mathbb Z}^r$
for some
$P^{\mathrm {gp}}\cong {\mathbb Z}^r$
for some
![]() $r\in {\mathbb N}$
.
$r\in {\mathbb N}$
.
We first deal with the case that the finite étale group scheme
![]() $F"$
is constant. Then, for any sheaf G on the small étale site of S, the group
$F"$
is constant. Then, for any sheaf G on the small étale site of S, the group
![]() $\mathrm {Hom}_S(F",G)$
is determined by the group
$\mathrm {Hom}_S(F",G)$
is determined by the group
![]() $\mathrm {Hom}(F"(S),G(S))$
. On the other hand, we have
$\mathrm {Hom}(F"(S),G(S))$
. On the other hand, we have
![]() $\Gamma (S,G)=\Gamma (s,G|_s)$
by Gabber’s theorem (see [24, Tag 09ZI]). This implies that the exact sequence
$\Gamma (S,G)=\Gamma (s,G|_s)$
by Gabber’s theorem (see [24, Tag 09ZI]). This implies that the exact sequence
can be identified with the exact sequence
where
![]() $(-)|_s$
denotes the pullback from the small étale site of S to that of s. By the property of the given chart
$(-)|_s$
denotes the pullback from the small étale site of S to that of s. By the property of the given chart
![]() $P\rightarrow M_S$
, we have
$P\rightarrow M_S$
, we have
![]() $P^{\mathrm {gp}}|_s\cong (M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times })|_s$
. It follows that the map
$P^{\mathrm {gp}}|_s\cong (M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times })|_s$
. It follows that the map
![]() $\beta $
is an isomorphism. Therefore, the map
$\beta $
is an isomorphism. Therefore, the map
![]() $\alpha $
is an isomorphism.
$\alpha $
is an isomorphism.
In general, choose a finite étale cover
![]() $\tilde {S}=\mathop {\mathrm {Spec}} \tilde {A}\rightarrow \mathop {\mathrm {Spec}} A$
with
$\tilde {S}=\mathop {\mathrm {Spec}} \tilde {A}\rightarrow \mathop {\mathrm {Spec}} A$
with
![]() $\tilde {A}$
Henselian local, such that
$\tilde {A}$
Henselian local, such that
![]() $F"|_{\tilde {S}}$
is a constant group scheme. Let
$F"|_{\tilde {S}}$
is a constant group scheme. Let
Then
![]() $\tilde {f}:=f\times _S\tilde {S}$
lifts to a unique
$\tilde {f}:=f\times _S\tilde {S}$
lifts to a unique
![]() $\tilde {g}\in \mathrm {Hom}_{\tilde {S}}(F",W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})$
by the previous case. Since
$\tilde {g}\in \mathrm {Hom}_{\tilde {S}}(F",W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})$
by the previous case. Since
![]() $\tilde {S}\times _S\tilde {S}$
is a disjoint union of Henselian local schemes which are finite étale over
$\tilde {S}\times _S\tilde {S}$
is a disjoint union of Henselian local schemes which are finite étale over
![]() $\tilde {S}$
, we have
$\tilde {S}$
, we have
![]() $p_1^*\tilde {g}=p_2^*\tilde {g}$
by the previous case again, where
$p_1^*\tilde {g}=p_2^*\tilde {g}$
by the previous case again, where
![]() $p_1$
and
$p_1$
and
![]() $p_2$
are the projections from
$p_2$
are the projections from
![]() $\tilde {S}\times _S\tilde {S}$
to its two factors. It follows that
$\tilde {S}\times _S\tilde {S}$
to its two factors. It follows that
![]() $\tilde {g}$
descends to a unique element of
$\tilde {g}$
descends to a unique element of
![]() $\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})$
. This finishes the proof.
$\mathrm {Hom}_S(F",W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})$
. This finishes the proof.
Theorem 3.8 (Kato)
Let the assumptions be as in Lemma 3.7. Then
and the functor (3.1)
is an equivalence of categories with inverse (3.11)
3.2 The connected-étale sequence
Assume that
![]() $S=\mathop {\mathrm {Spec}}(R)$
is a local Henselian ring with residue characteristic p. The results in this section are all due to Kato, and we will only sketch the proofs.
$S=\mathop {\mathrm {Spec}}(R)$
is a local Henselian ring with residue characteristic p. The results in this section are all due to Kato, and we will only sketch the proofs.
For any
![]() $G\in (\mathrm {fin}/S)_{\mathrm {f}}$
, there is a unique exact sequence
$G\in (\mathrm {fin}/S)_{\mathrm {f}}$
, there is a unique exact sequence
which restricts to the usual connected-étale sequence over any finite Kummer log flat cover, over which G becomes a classical flat group scheme. To get this, one can descend the usual connected-étale sequence from some cover over which G is classical (the sequence descends because it is unique and compatible with base change).
One now has the following result.
Proposition 3.9 Let
![]() $G\in (\mathrm {fin}/S)_{\mathrm {d}}$
. Assume that the residue characteristic p is positive, and G is killed by a power of p. Then
$G\in (\mathrm {fin}/S)_{\mathrm {d}}$
. Assume that the residue characteristic p is positive, and G is killed by a power of p. Then
![]() $G^{\circ }$
and
$G^{\circ }$
and
![]() $G^{\mathrm {\acute {e}t}}$
are classical finite flat group schemes.
$G^{\mathrm {\acute {e}t}}$
are classical finite flat group schemes.
Proof One has to show that a connected finite kfl log group scheme
![]() $f:H\to S$
is classical. For this, one looks at the unit map
$f:H\to S$
is classical. For this, one looks at the unit map
![]() $e:S\to H$
, and sees that for any geometric point
$e:S\to H$
, and sees that for any geometric point
![]() $\bar {s}$
of S, one gets that the identity factors as
$\bar {s}$
of S, one gets that the identity factors as
Using that
![]() $H\to S$
is Kummer, one concludes that
$H\to S$
is Kummer, one concludes that
![]() $f^{-1}(M_{S}/\mathcal {O}^{\times }_{S})\to M_{H}/\mathcal {O}^{\times }_{H}$
is an isomorphism.
$f^{-1}(M_{S}/\mathcal {O}^{\times }_{S})\to M_{H}/\mathcal {O}^{\times }_{H}$
is an isomorphism.
From this, it then follows that
![]() $G^{\circ }$
is classical. As the dual
$G^{\circ }$
is classical. As the dual
![]() $(G^{\mathrm {\acute {e}t}})^{D}$
of
$(G^{\mathrm {\acute {e}t}})^{D}$
of
![]() $G^{\mathrm {\acute {e}t}}$
is representable by assumption and clearly connected, it is classical. Hence,
$G^{\mathrm {\acute {e}t}}$
is representable by assumption and clearly connected, it is classical. Hence,
![]() $G^{\mathrm {\acute {e}t}}$
is classical as well.
$G^{\mathrm {\acute {e}t}}$
is classical as well.
Recall the following definition. Let Z be an fs log scheme, and let z be a point of Z. A chart
![]() $P\to M_Z$
of Z is called neat at z, if the induced map
$P\to M_Z$
of Z is called neat at z, if the induced map
![]() $P\xrightarrow {\cong }M_{Z,\bar {z}}/\mathcal {O}_{Z,\bar {z}}^{\times }$
is an isomorphism (see [Reference Ogus21, Chapter II, Definition 2.3.1]). Neat charts exist étale locally by [Reference Ogus21, Chapter II, Proposition 2.3.7].
$P\xrightarrow {\cong }M_{Z,\bar {z}}/\mathcal {O}_{Z,\bar {z}}^{\times }$
is an isomorphism (see [Reference Ogus21, Chapter II, Definition 2.3.1]). Neat charts exist étale locally by [Reference Ogus21, Chapter II, Proposition 2.3.7].
We also denote by
![]() $(\mathrm {fin}/S)^{p}_{\mathrm {d}}$
the subcategory of
$(\mathrm {fin}/S)^{p}_{\mathrm {d}}$
the subcategory of
![]() $(\mathrm {fin}/S)_{\mathrm {d}}$
whose objects are p-power torsion. Using Theorem 3.8, one then gets the following corollary.
$(\mathrm {fin}/S)_{\mathrm {d}}$
whose objects are p-power torsion. Using Theorem 3.8, one then gets the following corollary.
Corollary 3.10 Assume that
![]() $P\to M_S$
is a neat chart and that the residue characteristic p is positive. Then there is an equivalence of categories between
$P\to M_S$
is a neat chart and that the residue characteristic p is positive. Then there is an equivalence of categories between
![]() $(\mathrm {fin}/S)^{p}_{\mathrm {d}}$
and the category of pairs
$(\mathrm {fin}/S)^{p}_{\mathrm {d}}$
and the category of pairs
![]() $(G^{\mathrm {cl}}, N)$
, where
$(G^{\mathrm {cl}}, N)$
, where
![]() $G^{\mathrm {cl}}$
is a classical extension of
$G^{\mathrm {cl}}$
is a classical extension of
![]() $G^{\mathrm {\acute {e}t}}$
by
$G^{\mathrm {\acute {e}t}}$
by
![]() $G^{\circ }$
, and
$G^{\circ }$
, and
![]() $N\in \mathrm {Hom}(G^{\mathrm {\acute {e}t}}(1), G^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
.
$N\in \mathrm {Hom}(G^{\mathrm {\acute {e}t}}(1), G^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
.
3.3 Extensions are always standard étale locally
In the previous section, we studied standard extensions of classical finite flat group schemes after fixing a chart on the base. In this section, we show that any extension of one classical finite étale group scheme by another classical finite flat group scheme is always étale locally standard with respect to a suitable chosen local chart.
Theorem 3.11 Let S be an fs log scheme whose underlying scheme is locally Noetherian. Let
![]() $F',F"\in (\mathrm {fin}/S)_{\mathrm {c}}$
with
$F',F"\in (\mathrm {fin}/S)_{\mathrm {c}}$
with
![]() $F"$
étale, and let
$F"$
étale, and let
![]() $F\in (\mathrm {fin}/S)_{\mathrm {r}}$
be an extension of
$F\in (\mathrm {fin}/S)_{\mathrm {r}}$
be an extension of
![]() $F"$
by
$F"$
by
![]() $F'$
. Then, for any
$F'$
. Then, for any
![]() $s\in S$
, there exists an étale neighborhood
$s\in S$
, there exists an étale neighborhood
![]() $\tilde {S}$
of s such that the log structure of S admits a chart
$\tilde {S}$
of s such that the log structure of S admits a chart
![]() $P_{\tilde {S}}\to M_{\tilde {S}}=(M_S)|_{\tilde {S}}$
on
$P_{\tilde {S}}\to M_{\tilde {S}}=(M_S)|_{\tilde {S}}$
on
![]() $\tilde {S}$
with P an fs monoid, and F is standard with respect to this chart.
$\tilde {S}$
with P an fs monoid, and F is standard with respect to this chart.
Proof By shrinking S étale locally if necessary, we assume that S admits a chart
![]() $P\to M_S$
such that the induced map
$P\to M_S$
such that the induced map
![]() $P\to M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism. We adopt the notation from Section 3.1. By Proposition 3.5, we are left with lifting
$P\to M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism. We adopt the notation from Section 3.1. By Proposition 3.5, we are left with lifting
to a homomorphism
![]() $\bar {\delta }_F:F"\to W\otimes _{\mathbb Z} P^{\mathrm {gp}}$
étale locally around s.
$\bar {\delta }_F:F"\to W\otimes _{\mathbb Z} P^{\mathrm {gp}}$
étale locally around s.
The short exact sequence (3.10) extends to a longer exact sequence
The local-to-global extension spectral sequence gives rise to an exact sequence
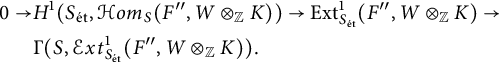 $$ \begin{align*} 0\rightarrow &H^1(S_{\mathrm{\acute{e}t}},\mathcal{H}om_S(F",W\otimes_{{\mathbb Z}}K))\rightarrow \mathrm{Ext}^1_{S_{\mathrm{\acute{e}t}}}(F",W\otimes_{{\mathbb Z}}K)\rightarrow \\ &\Gamma(S,\mathcal{E}xt^1_{S_{\mathrm{\acute{e}t}}}(F",W\otimes_{{\mathbb Z}}K)). \end{align*} $$
$$ \begin{align*} 0\rightarrow &H^1(S_{\mathrm{\acute{e}t}},\mathcal{H}om_S(F",W\otimes_{{\mathbb Z}}K))\rightarrow \mathrm{Ext}^1_{S_{\mathrm{\acute{e}t}}}(F",W\otimes_{{\mathbb Z}}K)\rightarrow \\ &\Gamma(S,\mathcal{E}xt^1_{S_{\mathrm{\acute{e}t}}}(F",W\otimes_{{\mathbb Z}}K)). \end{align*} $$
We claim that
![]() $\gamma (\delta _F)$
has trivial image in
$\gamma (\delta _F)$
has trivial image in
![]() $\Gamma (S,\mathcal {E}xt^1_{S_{\mathrm {\acute {e}t}}}(F",W\otimes _{{\mathbb Z}}K))$
. It suffices to show that
$\Gamma (S,\mathcal {E}xt^1_{S_{\mathrm {\acute {e}t}}}(F",W\otimes _{{\mathbb Z}}K))$
. It suffices to show that
![]() $\gamma (\delta _F)$
vanishes at all stalks of
$\gamma (\delta _F)$
vanishes at all stalks of
![]() $\mathcal {E}xt^1_{S_{\mathrm {\acute {e}t}}}(F",W\otimes _{{\mathbb Z}}K)$
. Let t be any point of S with
$\mathcal {E}xt^1_{S_{\mathrm {\acute {e}t}}}(F",W\otimes _{{\mathbb Z}}K)$
. Let t be any point of S with
![]() $\bar {t}$
a geometric point above t, and let
$\bar {t}$
a geometric point above t, and let
![]() $S_{\bar {t}}$
be the strict Henselization of S at
$S_{\bar {t}}$
be the strict Henselization of S at
![]() $\bar {t}$
. Pulling back the short exact sequence (3.9) to
$\bar {t}$
. Pulling back the short exact sequence (3.9) to
![]() $S_{\bar {t}}$
and then taking global section, we get a short exact sequence
$S_{\bar {t}}$
and then taking global section, we get a short exact sequence
By [24, Tag 09ZH], this exact sequence can be identified with the short exact sequence
Now, over the geometric point
![]() $\bar {t}$
, the epimorphism
$\bar {t}$
, the epimorphism
![]() $P^{\mathrm {gp}}\to M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
admits a section. It follows that the epimorphism
$P^{\mathrm {gp}}\to M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }$
admits a section. It follows that the epimorphism
![]() $\Gamma (S_{\bar {t}},W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})\rightarrow \Gamma (S_{\bar {t}},W\otimes _{{\mathbb Z}}(M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }))$
also admits a section. This forces the homomorphism
$\Gamma (S_{\bar {t}},W\otimes _{{\mathbb Z}}P^{\mathrm {gp}})\rightarrow \Gamma (S_{\bar {t}},W\otimes _{{\mathbb Z}}(M_S^{\mathrm {gp}}/\mathcal {O}_S^{\times }))$
also admits a section. This forces the homomorphism
to be surjective. It follows that the stalk of
![]() $\gamma (\delta _F)$
at
$\gamma (\delta _F)$
at
![]() $\bar {t}$
vanishes.
$\bar {t}$
vanishes.
Now we see that
![]() $\gamma (\delta _F)$
lies in the subgroup
$\gamma (\delta _F)$
lies in the subgroup
![]() $H^1(S,\mathcal {H}om_S(F",W\otimes _{{\mathbb Z}}K))$
of
$H^1(S,\mathcal {H}om_S(F",W\otimes _{{\mathbb Z}}K))$
of
![]() $\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}(F",W\otimes _{{\mathbb Z}}K)$
. Hence, passing to an étale cover of S,
$\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}(F",W\otimes _{{\mathbb Z}}K)$
. Hence, passing to an étale cover of S,
![]() $\gamma (\delta _F)$
vanishes; in other words,
$\gamma (\delta _F)$
vanishes; in other words,
![]() $\delta _F$
lifts to a homomorphism
$\delta _F$
lifts to a homomorphism
![]() $\bar {\delta }_F:F"\to W\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
after passing to a suitable étale cover of S. This finishes the proof.
$\bar {\delta }_F:F"\to W\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
after passing to a suitable étale cover of S. This finishes the proof.
3.4 Standard extensions of log p-divisible groups
First, we assume that S admits a global chart
![]() $P\rightarrow M_S$
with P an fs monoid.
$P\rightarrow M_S$
with P an fs monoid.
Let
![]() $H'=\varinjlim _{n}H^{\prime }_n$
,
$H'=\varinjlim _{n}H^{\prime }_n$
,
![]() $H"=\varinjlim _{n}H^{\prime \prime }_n$
be two objects in
$H"=\varinjlim _{n}H^{\prime \prime }_n$
be two objects in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
, and we assume that
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
, and we assume that
![]() $H"$
is étale. We denote by
$H"$
is étale. We denote by
the category of extensions of
![]() $H"$
by
$H"$
by
![]() $H'$
in
$H'$
in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
(resp. (
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
(resp. (
![]() $p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
). Let
$p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
). Let
and we denote by
the discrete category associated with the set
![]() $\mathrm {Hom}_S(H"(1),H')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. Let
$\mathrm {Hom}_S(H"(1),H')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. Let
and
![]() $\beta \in \mathfrak {Hom}(H"(1),H')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. The element
$\beta \in \mathfrak {Hom}(H"(1),H')\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
. The element
![]() $\beta $
induces a compatible system
$\beta $
induces a compatible system
We apply the functor (3.1) to the pair
![]() $(H_n^{\mathrm {cl}},\beta _n)$
for each
$(H_n^{\mathrm {cl}},\beta _n)$
for each
![]() $n\geq 1$
and change the notation for the functor (3.1) (resp. (3.2)) from
$n\geq 1$
and change the notation for the functor (3.1) (resp. (3.2)) from
![]() $\Phi $
(resp.
$\Phi $
(resp.
![]() $\Phi _2$
) to
$\Phi _2$
) to
![]() $\Phi ^n$
(resp.
$\Phi ^n$
(resp.
![]() $\Phi _2^n$
) in order to indicate its relation with
$\Phi _2^n$
) in order to indicate its relation with
![]() $(H_n^{\mathrm {cl}},\beta _n)$
. Then we get a compatible system
$(H_n^{\mathrm {cl}},\beta _n)$
. Then we get a compatible system
![]() $\{\Phi ^n(H_n^{\mathrm {cl}},\beta _n)\}_n$
with
$\{\Phi ^n(H_n^{\mathrm {cl}},\beta _n)\}_n$
with
Note that
![]() $\Phi _2(\beta ):=\varinjlim _n\Phi _2^n(\beta _n)$
is an object of
$\Phi _2(\beta ):=\varinjlim _n\Phi _2^n(\beta _n)$
is an object of
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
. Therefore,
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
. Therefore,
lies in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
. We denote
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
. We denote
![]() $\varinjlim _n\Phi ^n(H_n^{\mathrm {cl}},\beta _n)$
by
$\varinjlim _n\Phi ^n(H_n^{\mathrm {cl}},\beta _n)$
by
![]() $\Phi (H^{\mathrm {cl}},\beta )$
. The association of
$\Phi (H^{\mathrm {cl}},\beta )$
. The association of
![]() $\Phi (H^{\mathrm {cl}},\beta )$
with the pair
$\Phi (H^{\mathrm {cl}},\beta )$
with the pair
![]() $(H^{\mathrm {cl}},\beta )$
gives rise to a functor
$(H^{\mathrm {cl}},\beta )$
gives rise to a functor
Note that we use the same notation for both the functor (3.12) and the functor (3.1), but the potential confusion between the two functors can be cleared in the context.
Definition 3.12 Let
![]() $H',H"\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
with
$H',H"\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
with
![]() $H"$
étale. An extension H of
$H"$
étale. An extension H of
![]() $H"$
by
$H"$
by
![]() $H'$
in the category
$H'$
in the category
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
is called standard with respect to the given chart
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {r}}$
is called standard with respect to the given chart
![]() $P\rightarrow M_S$
, if it lies in the essential image of the functor (3.12). We denote by
$P\rightarrow M_S$
, if it lies in the essential image of the functor (3.12). We denote by
![]() $\mathfrak {Ext}_{S_{\mathrm {kfl}}}(H",H')_{\mathrm {std}}$
the full subcategory of
$\mathfrak {Ext}_{S_{\mathrm {kfl}}}(H",H')_{\mathrm {std}}$
the full subcategory of
![]() $\mathfrak {Ext}_{S_{\mathrm {kfl}}}(H",H')$
consisting of the standard extensions, and the functor (3.12) induces a functor
$\mathfrak {Ext}_{S_{\mathrm {kfl}}}(H",H')$
consisting of the standard extensions, and the functor (3.12) induces a functor
If
![]() $H\cong \Phi (H^{\mathrm {cl}},\beta )$
, we call
$H\cong \Phi (H^{\mathrm {cl}},\beta )$
, we call
![]() $\beta $
a pseudo-monodromy of H with respect to the given chart
$\beta $
a pseudo-monodromy of H with respect to the given chart
![]() $P\rightarrow M_S$
. If the functor (3.13) is an equivalence, the pseudo-monodromy
$P\rightarrow M_S$
. If the functor (3.13) is an equivalence, the pseudo-monodromy
![]() $\beta $
is uniquely determined. In this case, we call
$\beta $
is uniquely determined. In this case, we call
![]() $\beta $
the monodromy of H with respect to the given chart
$\beta $
the monodromy of H with respect to the given chart
![]() $P\to M_S$
.
$P\to M_S$
.
Theorem 3.13 (Kato)
Let S be an fs log scheme whose underlying scheme is
![]() $\mathop {\mathrm {Spec}} A$
for a Noetherian Henselian local ring A, and let
$\mathop {\mathrm {Spec}} A$
for a Noetherian Henselian local ring A, and let
![]() $P\rightarrow M_S$
be a global chart such that the induced map
$P\rightarrow M_S$
be a global chart such that the induced map
![]() $P\rightarrow M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism for the closed point s of S. Let
$P\rightarrow M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism for the closed point s of S. Let
![]() $H',H"\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
with
$H',H"\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {c}}$
with
![]() $H"$
étale. Then the functor
$H"$
étale. Then the functor
from (3.12) is an equivalence of categories.
Proof This follows from the equivalences on the finite levels (see Theorem 3.8).
Let S be as in Theorem 3.13, and we further assume that the residue characteristic p is positive. Assume that
![]() $H\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. Similarly to Section 3.2, there is an exact connected-étale sequence
$H\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. Similarly to Section 3.2, there is an exact connected-étale sequence
where
![]() $H^{\circ }$
(resp.
$H^{\circ }$
(resp.
![]() $H^{\mathrm {\acute {e}t}}$
) is a connected (resp. étale) classical p-divisible group. This one gets by observing that the connected-étale sequences for the finite levels are compatible with the transition maps. Using this and Corollary 3.10, one gets a complete classification of log-p-divisible groups in
$H^{\mathrm {\acute {e}t}}$
) is a connected (resp. étale) classical p-divisible group. This one gets by observing that the connected-étale sequences for the finite levels are compatible with the transition maps. Using this and Corollary 3.10, one gets a complete classification of log-p-divisible groups in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
.
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
.
Corollary 3.14 (Kato)
Let S be an fs log scheme whose underlying scheme is
![]() $\mathop {\mathrm {Spec}} A$
for a Noetherian Henselian local ring A with residue characteristic
$\mathop {\mathrm {Spec}} A$
for a Noetherian Henselian local ring A with residue characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $P\rightarrow M_S$
be a global chart such that the induced map
$P\rightarrow M_S$
be a global chart such that the induced map
![]() $P\rightarrow M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}$
is an isomorphism for the closed point s of S. Then any
$P\rightarrow M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}$
is an isomorphism for the closed point s of S. Then any
![]() $H\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
is constructed out of a unique object in
$H\in (p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
is constructed out of a unique object in
from the equivalence of categories (3.12).
Remark 3.15. Let S be a general fs log scheme whose underlying scheme is locally Noetherian, and let
![]() $H=(H_n)_n$
be extension of an étale classical p-divisible group
$H=(H_n)_n$
be extension of an étale classical p-divisible group
![]() $H"$
by another classical p-divisible group
$H"$
by another classical p-divisible group
![]() $H'$
. For each n, we can make
$H'$
. For each n, we can make
![]() $H_n$
standard étale locally on S by Theorem 3.11. With some more effort, we can make all
$H_n$
standard étale locally on S by Theorem 3.11. With some more effort, we can make all
![]() $H_n$
standard at the same time over some étale neighborhood of any point
$H_n$
standard at the same time over some étale neighborhood of any point
![]() $s\in S$
. However, it is not clear to the authors how to construct a compatible system of monodromies at all levels.
$s\in S$
. However, it is not clear to the authors how to construct a compatible system of monodromies at all levels.
We can, however, use the theorem to prove that log p-divisible groups are formally log smooth.
Theorem 3.16 Let S be a locally Noetherian fs log scheme on which p is locally nilpotent, and let H be a log p-divisible group over S, which lies in
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. Then H is formally log smooth, i.e., for any strict closed square-zero thickening
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
. Then H is formally log smooth, i.e., for any strict closed square-zero thickening
![]() $T_0\hookrightarrow T$
in
$T_0\hookrightarrow T$
in
![]() $(\mathrm {fs}/S)$
, any element of
$(\mathrm {fs}/S)$
, any element of
![]() $H(T_0)$
can be lifted to an element of
$H(T_0)$
can be lifted to an element of
![]() $H(T)$
étale locally on T.
$H(T)$
étale locally on T.
Proof We may assume that T is affine. Now we work locally around a geometric point
![]() $\bar {t}$
of T. Let
$\bar {t}$
of T. Let
![]() $\overline {T}$
be the spectrum of the étale stalk of the structure sheaf
$\overline {T}$
be the spectrum of the étale stalk of the structure sheaf
![]() $\mathcal {O}_{T, \bar {t}}$
, which is a strict Henselian local ring. Then
$\mathcal {O}_{T, \bar {t}}$
, which is a strict Henselian local ring. Then
![]() $\overline {T}=\varprojlim _{(V,\bar {t})} V$
is the limit along the étale neighborhoods of
$\overline {T}=\varprojlim _{(V,\bar {t})} V$
is the limit along the étale neighborhoods of
![]() $\bar {t}$
. Now
$\bar {t}$
. Now
![]() $H=\varinjlim H_{n}$
, where
$H=\varinjlim H_{n}$
, where
![]() $H_{n}$
are finite kfl log group schemes. So the
$H_{n}$
are finite kfl log group schemes. So the
![]() $H_{n}$
are in particular of finite presentation and therefore limit preserving functors. Here, on the étale neighborhoods, we put the log structure that is induced from the log structure on T. Hence, we get
$H_{n}$
are in particular of finite presentation and therefore limit preserving functors. Here, on the étale neighborhoods, we put the log structure that is induced from the log structure on T. Hence, we get
 $$ \begin{align*} H(\overline{T}) & = \varinjlim_{n}H_{n}(\overline{T})\\ & = \varinjlim_{n}H_{n}(\varprojlim V)\\ &= \varinjlim_{n}\varinjlim_{V}H_{n}(V)\\ & = \varinjlim_{V}H(V). \end{align*} $$
$$ \begin{align*} H(\overline{T}) & = \varinjlim_{n}H_{n}(\overline{T})\\ & = \varinjlim_{n}H_{n}(\varprojlim V)\\ &= \varinjlim_{n}\varinjlim_{V}H_{n}(V)\\ & = \varinjlim_{V}H(V). \end{align*} $$
Here, the first equality is due to quasi-compactness of
![]() $\overline {T}$
and the last equality follows formally since colimits commute with colimits. In particular, any section of
$\overline {T}$
and the last equality follows formally since colimits commute with colimits. In particular, any section of
![]() $H(\overline {T})$
extends to an étale neighborhood.
$H(\overline {T})$
extends to an étale neighborhood.
From this, we see that we can assume that T is strict Henselian local. Further, by replacing H by
![]() $H\times _ST$
, we may work with the base T. It suffices to prove the surjectivity of the map
$H\times _ST$
, we may work with the base T. It suffices to prove the surjectivity of the map
![]() $H(T)\to H(T_0)$
.
$H(T)\to H(T_0)$
.
Fix a neat chart P of
![]() $\mathcal {M}_{T}$
, such that
$\mathcal {M}_{T}$
, such that
![]() $P\cong M_{T,\bar {t}}/\mathcal {O}_{T,\bar {t}}^{\times }=M_{T_{0},\bar {t}}/\mathcal {O}_{T_{0},\bar {t}}^{\times }$
, where now
$P\cong M_{T,\bar {t}}/\mathcal {O}_{T,\bar {t}}^{\times }=M_{T_{0},\bar {t}}/\mathcal {O}_{T_{0},\bar {t}}^{\times }$
, where now
![]() $\bar {t}$
denotes the closed point of T. Now let
$\bar {t}$
denotes the closed point of T. Now let
![]() $0\to H^{\circ }\to H\to H^{\mathrm {\acute {e}t}}\to 0$
be the connected-étale sequence of H, and we have that
$0\to H^{\circ }\to H\to H^{\mathrm {\acute {e}t}}\to 0$
be the connected-étale sequence of H, and we have that
![]() $H^{\circ }$
and
$H^{\circ }$
and
![]() $H^{\mathrm {\acute {e}t}}$
are classical. By Corollary 3.14, H admits a decomposition
$H^{\mathrm {\acute {e}t}}$
are classical. By Corollary 3.14, H admits a decomposition
![]() $H_{T}=H^{\mathrm {cl}}+_{\mathrm {Baer}} H^{N}$
into the Baer sum of a classical p-divisible group
$H_{T}=H^{\mathrm {cl}}+_{\mathrm {Baer}} H^{N}$
into the Baer sum of a classical p-divisible group
![]() $H^{\mathrm {cl}}\in \mathfrak {Ext}_{S_{\mathrm {fl}}}(H^{\mathrm {\acute {e}t}}, H^{\circ })$
and a log p-divisible group
$H^{\mathrm {cl}}\in \mathfrak {Ext}_{S_{\mathrm {fl}}}(H^{\mathrm {\acute {e}t}}, H^{\circ })$
and a log p-divisible group
![]() $H^{N}$
constructed out of the monodromy
$H^{N}$
constructed out of the monodromy
![]() $N\in \mathfrak {Hom}(H^{\mathrm {\acute {e}t}}(1), H^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
of H. We have the following canonical commutative diagram
$N\in \mathfrak {Hom}(H^{\mathrm {\acute {e}t}}(1), H^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
of H. We have the following canonical commutative diagram
with exact rows. Since both
![]() $H^{\circ }$
and
$H^{\circ }$
and
![]() $H^{\mathrm {\acute {e}t}}$
are classically formally smooth by [Reference Messing16, Chapter II, 3.3.13], both
$H^{\mathrm {\acute {e}t}}$
are classically formally smooth by [Reference Messing16, Chapter II, 3.3.13], both
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
are surjective. Moreover, since
$\gamma $
are surjective. Moreover, since
![]() $H^{\mathrm {\acute {e}t}}$
is étale,
$H^{\mathrm {\acute {e}t}}$
is étale,
![]() $\gamma $
is even an isomorphism. To show the surjectivity of
$\gamma $
is even an isomorphism. To show the surjectivity of
![]() $\beta $
, it suffices to show that the restriction
$\beta $
, it suffices to show that the restriction
![]() $\lambda \vert _{\mathrm {im}(\delta )}$
of
$\lambda \vert _{\mathrm {im}(\delta )}$
of
![]() $\lambda $
to
$\lambda $
to
![]() $\mathrm {im}(\delta )$
is injective by the five lemma.
$\mathrm {im}(\delta )$
is injective by the five lemma.
Let
![]() $\varepsilon :(\mathrm {fs}/T)_{\mathrm {kfl}}\rightarrow (\mathrm {fs}/T)_{\mathrm {fl}}$
be the canonical forgetful map between the two sites. By Proposition D.1, the choice of P also provides a splitting
$\varepsilon :(\mathrm {fs}/T)_{\mathrm {kfl}}\rightarrow (\mathrm {fs}/T)_{\mathrm {fl}}$
be the canonical forgetful map between the two sites. By Proposition D.1, the choice of P also provides a splitting
For all
![]() $n\geq 1$
, the sheaf
$n\geq 1$
, the sheaf
![]() $\mathcal {H}om_T({\mathbb Z}/p^n{\mathbb Z}(1),H^{\circ }_n)$
is representable by an étale group scheme over T by Lemma A.1. Thus, we have
$\mathcal {H}om_T({\mathbb Z}/p^n{\mathbb Z}(1),H^{\circ }_n)$
is representable by an étale group scheme over T by Lemma A.1. Thus, we have
Therefore, the map
![]() $\lambda $
is injective on
$\lambda $
is injective on
![]() $\mathrm {Hom}_T(\mathbb {Z}_{p}(1), H^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
.
$\mathrm {Hom}_T(\mathbb {Z}_{p}(1), H^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
.
Recall that we have
![]() $H=H^{\mathrm {cl}}+_{\mathrm {Baer}}H^N$
. Let
$H=H^{\mathrm {cl}}+_{\mathrm {Baer}}H^N$
. Let
![]() $\mathrm {pr}_{\mathrm {cl}}$
(resp.
$\mathrm {pr}_{\mathrm {cl}}$
(resp.
![]() $\mathrm {pr}_N$
) be the projection from
$\mathrm {pr}_N$
) be the projection from
![]() $H^{\mathrm {cl}}$
(resp.
$H^{\mathrm {cl}}$
(resp.
![]() $H^N$
) to
$H^N$
) to
![]() $H^{\mathrm {\acute {e}t}}$
. For any
$H^{\mathrm {\acute {e}t}}$
. For any
![]() $x\in H^{\mathrm {\acute {e}t}}(T)$
,
$x\in H^{\mathrm {\acute {e}t}}(T)$
,
![]() $\delta (x)$
can be represented by the sum of the two torsors
$\delta (x)$
can be represented by the sum of the two torsors
![]() $\mathrm {pr}_{\mathrm {cl}}^{-1}(x)\in H^1_{\mathrm {fl}}(T,H^{\circ })$
and
$\mathrm {pr}_{\mathrm {cl}}^{-1}(x)\in H^1_{\mathrm {fl}}(T,H^{\circ })$
and
![]() $\mathrm {pr}_N^{-1}(x)\in H^1_{\mathrm {kfl}}(T,H^{\circ })$
, and this sum is the direct decomposition with respect to (3.14). Let x be such that
$\mathrm {pr}_N^{-1}(x)\in H^1_{\mathrm {kfl}}(T,H^{\circ })$
, and this sum is the direct decomposition with respect to (3.14). Let x be such that
![]() $\delta (x)\in \mathrm {ker}(\lambda )$
. Since
$\delta (x)\in \mathrm {ker}(\lambda )$
. Since
![]() $\lambda $
is injective on
$\lambda $
is injective on
![]() $\mathrm {Hom}_T(\mathbb {Z}_{p}(1), H^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, it follows that
$\mathrm {Hom}_T(\mathbb {Z}_{p}(1), H^{\circ })\otimes _{{\mathbb Z}}P^{\mathrm {gp}}$
, it follows that
![]() $\delta (x)$
is represented by its classical part
$\delta (x)$
is represented by its classical part
![]() $\mathrm {pr}_{\mathrm {cl}}^{-1}(x)$
, and
$\mathrm {pr}_{\mathrm {cl}}^{-1}(x)$
, and
![]() $0=\lambda (\delta (x))=\lambda (\mathrm {pr}_{\mathrm {cl}}^{-1}(x))$
. Since
$0=\lambda (\delta (x))=\lambda (\mathrm {pr}_{\mathrm {cl}}^{-1}(x))$
. Since
![]() $H^{\mathrm {cl}}$
is formally smooth by [Reference Messing16, Chapter II, 3.3.13], the homomorphism
$H^{\mathrm {cl}}$
is formally smooth by [Reference Messing16, Chapter II, 3.3.13], the homomorphism
![]() $\beta ^{\mathrm {cl}}$
in the diagram
$\beta ^{\mathrm {cl}}$
in the diagram
is surjective. An easy diagram chasing tells us that
![]() $\delta (x)=\delta ^{\mathrm {cl}}(x)$
is trivial (here the bijectivity of
$\delta (x)=\delta ^{\mathrm {cl}}(x)$
is trivial (here the bijectivity of
![]() $\gamma $
is used). Hence,
$\gamma $
is used). Hence,
![]() $\lambda \vert _{\mathrm {im}(\delta )}$
is injective. This finishes the proof.
$\lambda \vert _{\mathrm {im}(\delta )}$
is injective. This finishes the proof.
4 Log
 $p$
-divisible groups associated with log 1-motives
$p$
-divisible groups associated with log 1-motives
In this section, we want to study the finite Kummer flat group log schemes associated with log
![]() $1$
-motives. In this case, we will see that the splittings (in the sense of the previous section) are induced from the monodromy pairings of log 1-motives (see Definition 4.1).
$1$
-motives. In this case, we will see that the splittings (in the sense of the previous section) are induced from the monodromy pairings of log 1-motives (see Definition 4.1).
Let S be an fs log scheme with its underlying scheme locally Noetherian. Let G be an extension of an abelian scheme by a torus T, and let
![]() $G_{\mathrm {log}}$
be the pushout of G in the category of sheaves of abelian groups on
$G_{\mathrm {log}}$
be the pushout of G in the category of sheaves of abelian groups on
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
along the log-enlargement
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
along the log-enlargement
![]() $T\to T_{\mathrm {log}}$
. Here,
$T\to T_{\mathrm {log}}$
. Here,
![]() $T_{\mathrm {log}}=\mathcal {H}om(X, \mathbb {G}_{\mathrm {m,log}})$
with X the character sheaf of the torus T. Then a log 1-motive
$T_{\mathrm {log}}=\mathcal {H}om(X, \mathbb {G}_{\mathrm {m,log}})$
with X the character sheaf of the torus T. Then a log 1-motive
![]() $\mathbf {M}=[Y\xrightarrow {u} G_{\mathrm {log}}]$
over S is a morphism of commutative group sheaves, where Y is a lattice, i.e., an étale locally finite free abelian group sheaf. See [Reference Kajiwara, Kato and Nakayama8, Definition 2.2] for the details about log 1-motives. Note that
$\mathbf {M}=[Y\xrightarrow {u} G_{\mathrm {log}}]$
over S is a morphism of commutative group sheaves, where Y is a lattice, i.e., an étale locally finite free abelian group sheaf. See [Reference Kajiwara, Kato and Nakayama8, Definition 2.2] for the details about log 1-motives. Note that
![]() $G_{\mathrm {log}}$
in [Reference Kajiwara, Kato and Nakayama8] is defined on the site
$G_{\mathrm {log}}$
in [Reference Kajiwara, Kato and Nakayama8] is defined on the site
![]() $(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
, and agrees with ours by [Reference Zhao26, Proposition 2.1].
$(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
, and agrees with ours by [Reference Zhao26, Proposition 2.1].
The composition
corresponds to a pairing
Definition 4.1 We call the pairing
![]() $\langle -,-\rangle _{\mathbf {M}}$
the monodromy pairing of the log 1-motive
$\langle -,-\rangle _{\mathbf {M}}$
the monodromy pairing of the log 1-motive
![]() $\mathbf {M}$
.
$\mathbf {M}$
.
Proposition 4.2 Suppose G is an extension of an abelian scheme B by a torus T over the underlying scheme of S. Then étale locally on S we have a decomposition
![]() $u=u_1+u_2$
, where
$u=u_1+u_2$
, where
![]() $u_i:Y\rightarrow G_{\mathrm {log}}$
for
$u_i:Y\rightarrow G_{\mathrm {log}}$
for
![]() $i=1,2$
, such that
$i=1,2$
, such that
![]() $u_1$
factorizes as
$u_1$
factorizes as
![]() $Y\rightarrow G\hookrightarrow G_{\mathrm {log}}$
and
$Y\rightarrow G\hookrightarrow G_{\mathrm {log}}$
and
![]() $u_2$
factorizes as
$u_2$
factorizes as
![]() $Y\rightarrow T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
.
$Y\rightarrow T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
.
Proof Let
![]() $\bar {u}$
be the composition
$\bar {u}$
be the composition
The short exact sequence
![]() $0\rightarrow T\rightarrow T_{\mathrm {log}}\rightarrow (T_{\mathrm {log}}/T)_{S_{\mathrm {\acute {e}t}}}\rightarrow 0$
gives rise to an exact sequence
$0\rightarrow T\rightarrow T_{\mathrm {log}}\rightarrow (T_{\mathrm {log}}/T)_{S_{\mathrm {\acute {e}t}}}\rightarrow 0$
gives rise to an exact sequence
Étale locally,
![]() $\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}(Y,T)=\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}({\mathbb Z}^r,\mathbb {G}_{\mathrm {m}}^t)=\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}({\mathbb Z},\mathbb {G}_{\mathrm {m}})^{rt}\cong \mathrm {Pic}(S)^{rt}$
. Since a line bundle is Zariski locally trivial,
$\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}(Y,T)=\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}({\mathbb Z}^r,\mathbb {G}_{\mathrm {m}}^t)=\mathrm {Ext}^1_{S_{\mathrm {\acute {e}t}}}({\mathbb Z},\mathbb {G}_{\mathrm {m}})^{rt}\cong \mathrm {Pic}(S)^{rt}$
. Since a line bundle is Zariski locally trivial,
![]() $\delta (\bar {u})$
is zero étale locally on S. It follows that there exists
$\delta (\bar {u})$
is zero étale locally on S. It follows that there exists
![]() $u_2\in \mathrm {Hom}_S(Y,T_{\mathrm {log}})$
lifting
$u_2\in \mathrm {Hom}_S(Y,T_{\mathrm {log}})$
lifting
![]() $\bar {u}$
étale locally on S. Let
$\bar {u}$
étale locally on S. Let
![]() $u_1:=u-u_2$
as a homomorphism from Y to
$u_1:=u-u_2$
as a homomorphism from Y to
![]() $G_{\mathrm {log}}$
, and it is easy to see that
$G_{\mathrm {log}}$
, and it is easy to see that
![]() $u_1$
factors through G. This finishes the proof.
$u_1$
factors through G. This finishes the proof.
Proposition 4.3 Assume that S admits a global chart
![]() $\alpha :P\rightarrow M_S$
, where P is an fs monoid. Any bilinear map
$\alpha :P\rightarrow M_S$
, where P is an fs monoid. Any bilinear map
![]() $\langle -,-\rangle :X\times Y\rightarrow P^{\mathrm {gp}}_S$
which lifts the monodromy pairing
$\langle -,-\rangle :X\times Y\rightarrow P^{\mathrm {gp}}_S$
which lifts the monodromy pairing
![]() $\langle -,-\rangle _{\mathbf {M}}$
of
$\langle -,-\rangle _{\mathbf {M}}$
of
![]() $\mathbf {M}$
, gives rise to a splitting
$\mathbf {M}$
, gives rise to a splitting
![]() $u=u_{1}+u_{2}$
, where
$u=u_{1}+u_{2}$
, where
![]() $u_2:Y\rightarrow T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
is the map induced by
$u_2:Y\rightarrow T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
is the map induced by
![]() $\langle -,-\rangle $
and
$\langle -,-\rangle $
and
![]() $u_1=u-u_2:Y\rightarrow G_{\mathrm {log}}$
factors through
$u_1=u-u_2:Y\rightarrow G_{\mathrm {log}}$
factors through
![]() $G\hookrightarrow G_{\mathrm {log}}$
.
$G\hookrightarrow G_{\mathrm {log}}$
.
And, such a bilinear map always exists étale locally.
Proof The chart
![]() $\alpha :P\rightarrow M_S$
gives rise to a pushout diagram
$\alpha :P\rightarrow M_S$
gives rise to a pushout diagram
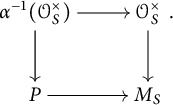
Since taking group envelope commutes with colimits, we get another pushout diagram
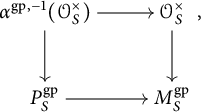
where
![]() $\alpha ^{gp}:P^{\mathrm {gp}}_S\rightarrow M^{\mathrm {gp}}_S$
denotes the homomorphism induced from
$\alpha ^{gp}:P^{\mathrm {gp}}_S\rightarrow M^{\mathrm {gp}}_S$
denotes the homomorphism induced from
![]() $\alpha $
. This pushout diagram gives a short exact sequence
$\alpha $
. This pushout diagram gives a short exact sequence
on the small étale site of S with
![]() $\overline {M}^{\mathrm {gp}}_S:=M^{\mathrm {gp}}_S/\mathcal {O}_S^{\times }$
. Applying
$\overline {M}^{\mathrm {gp}}_S:=M^{\mathrm {gp}}_S/\mathcal {O}_S^{\times }$
. Applying
![]() $\mathrm {Hom}_{S_{\mathrm {\acute {e}t}}}(Y\otimes _{{\mathbb Z}}X,-)$
to this short exact sequence, we get an exact sequence
$\mathrm {Hom}_{S_{\mathrm {\acute {e}t}}}(Y\otimes _{{\mathbb Z}}X,-)$
to this short exact sequence, we get an exact sequence
Let
![]() $\bar {\gamma }:Y\otimes _{{\mathbb Z}}X\rightarrow (\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {\acute {e}t}}}$
be the homomorphism induced by the canonical pairing. Since both X and Y are étale locally constant, the map
$\bar {\gamma }:Y\otimes _{{\mathbb Z}}X\rightarrow (\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {\acute {e}t}}}$
be the homomorphism induced by the canonical pairing. Since both X and Y are étale locally constant, the map
![]() $\bar {\gamma }$
is determined by its induced map
$\bar {\gamma }$
is determined by its induced map
![]() $Y\otimes _{{\mathbb Z}}X\rightarrow \overline {M}^{\mathrm {gp}}_S$
, which we still denote by
$Y\otimes _{{\mathbb Z}}X\rightarrow \overline {M}^{\mathrm {gp}}_S$
, which we still denote by
![]() $\bar {\gamma }$
by abuse of notation. Since
$\bar {\gamma }$
by abuse of notation. Since
the element
![]() $\delta (\bar {\gamma })$
is étale locally trivial on S. Therefore, étale locally on S the map
$\delta (\bar {\gamma })$
is étale locally trivial on S. Therefore, étale locally on S the map
![]() $\bar {\gamma }$
lifts to a homomorphism
$\bar {\gamma }$
lifts to a homomorphism
![]() $\gamma :Y\otimes _{{\mathbb Z}}X\rightarrow P^{\mathrm {gp}}_S$
. The map
$\gamma :Y\otimes _{{\mathbb Z}}X\rightarrow P^{\mathrm {gp}}_S$
. The map
![]() $\gamma $
gives rise to a homomorphism
$\gamma $
gives rise to a homomorphism
![]() $Y\otimes _{{\mathbb Z}}X\rightarrow \mathbb {G}_{\mathrm {m,log}}$
which corresponds to a homomorphism
$Y\otimes _{{\mathbb Z}}X\rightarrow \mathbb {G}_{\mathrm {m,log}}$
which corresponds to a homomorphism
![]() $u_2:Y\rightarrow T_{\mathrm {log}}$
. Obviously,
$u_2:Y\rightarrow T_{\mathrm {log}}$
. Obviously,
![]() $u_2$
lifts
$u_2$
lifts
![]() $\bar {u}$
. Let
$\bar {u}$
. Let
![]() $u_1:=u-u_2$
, and we have that
$u_1:=u-u_2$
, and we have that
![]() $u_1$
factors through
$u_1$
factors through
![]() $G\hookrightarrow G_{\mathrm {log}}$
. This finishes the proof.
$G\hookrightarrow G_{\mathrm {log}}$
. This finishes the proof.
Definition 4.4 For any positive integer n, let
Proposition 4.5 Let S be a locally Noetherian fs log scheme, let
![]() $M=[Y\xrightarrow {u}G_{\mathrm {log}}]$
be a log 1-motive over S, and let n be a positive integer. Then we have the following.
$M=[Y\xrightarrow {u}G_{\mathrm {log}}]$
be a log 1-motive over S, and let n be a positive integer. Then we have the following.
-
(1)
 $T_n(M)$
fits into the following exact sequence of sheaves of abelian groups on
$T_n(M)$
fits into the following exact sequence of sheaves of abelian groups on $$ \begin{align*}0\rightarrow G[n]\rightarrow T_n(\mathbf{M})\rightarrow Y/nY\rightarrow0\end{align*} $$
$$ \begin{align*}0\rightarrow G[n]\rightarrow T_n(\mathbf{M})\rightarrow Y/nY\rightarrow0\end{align*} $$
 $(\mathrm {fs}/S)_{\mathrm {kfl}}$
.
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
.
-
(2)
 $T_n(\mathbf {M})\in (\mathrm {fin}/S)_{\mathrm {d}}$
.
$T_n(\mathbf {M})\in (\mathrm {fin}/S)_{\mathrm {d}}$
. -
(3) Let m be another positive integer. Then the map
 $T_{mn}(\mathbf {M})\rightarrow T_{n}(\mathbf {M})$
induced by
$T_{mn}(\mathbf {M})\rightarrow T_{n}(\mathbf {M})$
induced by
 ${\mathbb Z}/mn{\mathbb Z}\xrightarrow {m}{\mathbb Z}/n{\mathbb Z}$
is surjective.
${\mathbb Z}/mn{\mathbb Z}\xrightarrow {m}{\mathbb Z}/n{\mathbb Z}$
is surjective.
Proof The map
![]() $Y\xrightarrow {n}Y$
is clearly injective. Consider the following commutative diagram
$Y\xrightarrow {n}Y$
is clearly injective. Consider the following commutative diagram
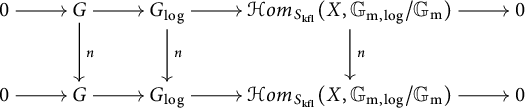
with exact rows. By [Reference Kato13, Proposition 4.2], we also have the following commutative diagram with exact rows:
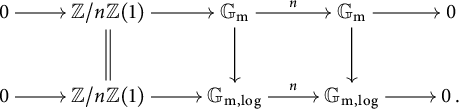
From the last diagram, one sees that
is an isomorphism. Moreover,
![]() $G\xrightarrow {n}G$
is surjective, so we get that
$G\xrightarrow {n}G$
is surjective, so we get that
![]() $G[n]\cong G_{\mathrm {log}}[n]$
and that
$G[n]\cong G_{\mathrm {log}}[n]$
and that
![]() $G_{\mathrm {log}}\xrightarrow {n}G_{\mathrm {log}}$
is surjective. By [Reference Raynaud23, Section 3.1], we get a short exact sequence
$G_{\mathrm {log}}\xrightarrow {n}G_{\mathrm {log}}$
is surjective. By [Reference Raynaud23, Section 3.1], we get a short exact sequence
This finishes the proof of part (1).
For part (2), note that by [Reference Kato12, Proposition 2.3] and the short exact sequence from part (1), we have that
![]() $T_n(\mathbf {M})\in (\mathrm {fin}/S)_{\mathrm {r}}$
. Let
$T_n(\mathbf {M})\in (\mathrm {fin}/S)_{\mathrm {r}}$
. Let
![]() $\mathbf {M}^{\vee }$
be the dual log 1-motive of
$\mathbf {M}^{\vee }$
be the dual log 1-motive of
![]() $\mathbf {M}$
(see [Reference Kajiwara, Kato and Nakayama8, Section 2.7]). Then we can identify the Cartier dual of
$\mathbf {M}$
(see [Reference Kajiwara, Kato and Nakayama8, Section 2.7]). Then we can identify the Cartier dual of
![]() $T_n(\mathbf {M})$
with
$T_n(\mathbf {M})$
with
![]() $T_n(\mathbf {M}^{\vee })$
. Since we also have
$T_n(\mathbf {M}^{\vee })$
. Since we also have
![]() $T_n(\mathbf {M}^{\vee })\in (\mathrm {fin}/S)_{\mathrm {r}}$
, we get
$T_n(\mathbf {M}^{\vee })\in (\mathrm {fin}/S)_{\mathrm {r}}$
, we get
![]() $T_n(\mathbf {M})\in (\mathrm {fin}/S)_{\mathrm {d}}$
.
$T_n(\mathbf {M})\in (\mathrm {fin}/S)_{\mathrm {d}}$
.
Part (3) is clearly true for the two log 1-motives
![]() $[Y\rightarrow 0]$
and
$[Y\rightarrow 0]$
and
![]() $[0\rightarrow G_{\mathrm {log}}]$
. It follows that it also holds for
$[0\rightarrow G_{\mathrm {log}}]$
. It follows that it also holds for
![]() $\mathbf {M}$
.
$\mathbf {M}$
.
Definition 4.6 By Proposition 4.5,
is an object of
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
, and we call it the log p-divisible group associated with
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
, and we call it the log p-divisible group associated with
![]() $\mathbf {M}$
.
$\mathbf {M}$
.
Proposition 4.7 Assume that S admits a global chart
![]() $\alpha :P\rightarrow M_S$
, where P is an fs monoid. Let
$\alpha :P\rightarrow M_S$
, where P is an fs monoid. Let
![]() $\mathbf {M}=[Y\xrightarrow {u} G_{\mathrm {log}}]$
be a log 1-motive over S, such that X and Y are constant. Let n be a positive integer.
$\mathbf {M}=[Y\xrightarrow {u} G_{\mathrm {log}}]$
be a log 1-motive over S, such that X and Y are constant. Let n be a positive integer.
Assume further that there exists a bilinear map as in Proposition 4.3
such that the homomorphism
![]() $u_2:Y\xrightarrow {\beta } T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
, which is induced from the pairing
$u_2:Y\xrightarrow {\beta } T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
, which is induced from the pairing
![]() $\langle -,-\rangle $
, gives rise to a decomposition
$\langle -,-\rangle $
, gives rise to a decomposition
![]() $u=u_1+u_2$
with
$u=u_1+u_2$
with
![]() $u_1:Y\xrightarrow {\alpha } G\hookrightarrow G_{\mathrm {log}}$
. Then we have the following.
$u_1:Y\xrightarrow {\alpha } G\hookrightarrow G_{\mathrm {log}}$
. Then we have the following.
-
(1)
 $T_n(\mathbf {M})$
is a standard extension of
$T_n(\mathbf {M})$
is a standard extension of
 $Y/nY$
by
$Y/nY$
by
 $G[n]$
with respect to the given chart.
$G[n]$
with respect to the given chart. -
(2) Let
 $f_1,\ldots ,f_m$
(resp.
$f_1,\ldots ,f_m$
(resp.
 $e_1,\ldots ,e_r$
) be a basis of X (resp. Y), and let
$e_1,\ldots ,e_r$
) be a basis of X (resp. Y), and let
 $f_1^*,\ldots ,f_m^*$
(resp.
$f_1^*,\ldots ,f_m^*$
(resp.
 $e_1^*,\ldots ,e_r^*$
) be the corresponding dual basis of
$e_1^*,\ldots ,e_r^*$
) be the corresponding dual basis of
 $X^*=\mathrm {Hom}_{{\mathbb Z}}(X,{\mathbb Z})$
(resp.
$X^*=\mathrm {Hom}_{{\mathbb Z}}(X,{\mathbb Z})$
(resp.
 $Y^*=\mathrm {Hom}_{{\mathbb Z}}(Y,{\mathbb Z})$
). The pairing
$Y^*=\mathrm {Hom}_{{\mathbb Z}}(Y,{\mathbb Z})$
). The pairing
 $\langle , \rangle :X\times Y\rightarrow P^{\mathrm {gp}}_S$
gives rise to a canonical pseudo-monodromy of
$\langle , \rangle :X\times Y\rightarrow P^{\mathrm {gp}}_S$
gives rise to a canonical pseudo-monodromy of
 $T_n(M)$
, namely the element
$T_n(M)$
, namely the element
 $\sum _{i,j}\delta _{ij}\otimes \langle f_i,e_j\rangle $
in the group Here,
$\sum _{i,j}\delta _{ij}\otimes \langle f_i,e_j\rangle $
in the group Here, $$\begin{align*}\mathrm{Hom}_S(Y/nY(1),T[n])\otimes P^{\mathrm{gp}}=\mathrm{Hom}_S(X/nX,Y^*/nY^*)\otimes P^{\mathrm{gp}}.\end{align*}$$
$$\begin{align*}\mathrm{Hom}_S(Y/nY(1),T[n])\otimes P^{\mathrm{gp}}=\mathrm{Hom}_S(X/nX,Y^*/nY^*)\otimes P^{\mathrm{gp}}.\end{align*}$$
 $\delta _{ij}$
denotes the map
$\delta _{ij}$
denotes the map
 $\bar {f}_k\mapsto \begin {cases}0, &\text {if } k\neq i, \\ \bar {e}_j^*, &\text {if } k=i. \end {cases}$
$\bar {f}_k\mapsto \begin {cases}0, &\text {if } k\neq i, \\ \bar {e}_j^*, &\text {if } k=i. \end {cases}$
-
(3) For varying n, the pseudo-monodromies from (2) are compatible with each other.
Proof Let
![]() $\mathbf {M}_1:=[Y\xrightarrow {u_1} G_{\mathrm {log}}]$
,
$\mathbf {M}_1:=[Y\xrightarrow {u_1} G_{\mathrm {log}}]$
,
![]() $\mathbf {M}_{\alpha }:=[Y\xrightarrow {\alpha } G]$
,
$\mathbf {M}_{\alpha }:=[Y\xrightarrow {\alpha } G]$
,
![]() $M_2=[Y\xrightarrow {u_2} G_{\mathrm {log}}]$
, and
$M_2=[Y\xrightarrow {u_2} G_{\mathrm {log}}]$
, and
![]() $\mathbf {M}_{\beta }:= [Y\xrightarrow {\beta } T_{\mathrm {log}}]$
. Then
$\mathbf {M}_{\beta }:= [Y\xrightarrow {\beta } T_{\mathrm {log}}]$
. Then
![]() $T_n(\mathbf {M}_1)$
is canonically isomorphic to
$T_n(\mathbf {M}_1)$
is canonically isomorphic to
![]() $T_n(\mathbf {M}_{\alpha })$
,
$T_n(\mathbf {M}_{\alpha })$
,
![]() $T_n(M_2)$
is given by the pushout of
$T_n(M_2)$
is given by the pushout of
![]() $T_n(M_{\beta })$
along the canonical map
$T_n(M_{\beta })$
along the canonical map
![]() $T[n]\hookrightarrow G[n]$
, and
$T[n]\hookrightarrow G[n]$
, and
![]() $T_n(\mathbf {M})=T_n(\mathbf {M}_1)+_{\mathrm {Baer}}T_n(\mathbf {M}_2)$
. Since
$T_n(\mathbf {M})=T_n(\mathbf {M}_1)+_{\mathrm {Baer}}T_n(\mathbf {M}_2)$
. Since
![]() $T_n(\mathbf {M}_1)=T_n(\mathbf {M}_{\alpha })\in (\mathrm {fin}/S)_{\mathrm {c}}$
, we are reduced to show that
$T_n(\mathbf {M}_1)=T_n(\mathbf {M}_{\alpha })\in (\mathrm {fin}/S)_{\mathrm {c}}$
, we are reduced to show that
![]() $T_n(\mathbf {M}_2)$
is a standard extension of
$T_n(\mathbf {M}_2)$
is a standard extension of
![]() $Y/nY$
by
$Y/nY$
by
![]() $G[n]$
.
$G[n]$
.
We first deal with the case that
![]() $G=T$
. Applying the functor
$G=T$
. Applying the functor
![]() $\varepsilon _*$
to the short exact sequence
$\varepsilon _*$
to the short exact sequence
![]() $0\rightarrow T[n]\rightarrow T_n(\mathbf {M}_2)\rightarrow Y/nY\rightarrow 0$
on
$0\rightarrow T[n]\rightarrow T_n(\mathbf {M}_2)\rightarrow Y/nY\rightarrow 0$
on
![]() $(\mathrm {fs}/S)_{\mathrm {kfl}}$
, we get a long exact sequence
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
, we get a long exact sequence
on
![]() $(\mathrm {fs}/S)_{\mathrm {fl}}$
. For any
$(\mathrm {fs}/S)_{\mathrm {fl}}$
. For any
![]() $1\leq j\leq r$
,
$1\leq j\leq r$
,
![]() $\delta (\bar {e}_j)$
is represented by the
$\delta (\bar {e}_j)$
is represented by the
![]() $T[n]$
-torsor
$T[n]$
-torsor
Let
![]() $\bar {u}$
be the composition
$\bar {u}$
be the composition
![]() $Y\xrightarrow {u_2}T_{\mathrm {log}}\rightarrow T_{\mathrm {log}}/T\cong \mathcal {H}om_{S_{\mathrm {kfl}}}(X,\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})$
. Then
$Y\xrightarrow {u_2}T_{\mathrm {log}}\rightarrow T_{\mathrm {log}}/T\cong \mathcal {H}om_{S_{\mathrm {kfl}}}(X,\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})$
. Then
![]() $\bar {u}(e_j)(f_i)=p_{ij}$
, where
$\bar {u}(e_j)(f_i)=p_{ij}$
, where
![]() $p_{ij}\in P^{\mathrm {gp}}$
is such that
$p_{ij}\in P^{\mathrm {gp}}$
is such that
![]() $\langle f_i,e_j\rangle =p_{ij}$
for each
$\langle f_i,e_j\rangle =p_{ij}$
for each
![]() $1\leq i\leq m$
. Therefore, under the identification
$1\leq i\leq m$
. Therefore, under the identification
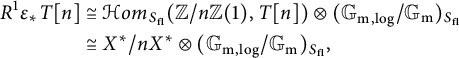 $$ \begin{align*} R^1\varepsilon_*T[n]&\cong\mathcal{H}om_{S_{\mathrm{fl}}}({\mathbb Z}/n{\mathbb Z}(1),T[n])\otimes (\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{fl}}} \\&\cong X^*/nX^*\otimes (\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{fl}}}, \end{align*} $$
$$ \begin{align*} R^1\varepsilon_*T[n]&\cong\mathcal{H}om_{S_{\mathrm{fl}}}({\mathbb Z}/n{\mathbb Z}(1),T[n])\otimes (\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{fl}}} \\&\cong X^*/nX^*\otimes (\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{fl}}}, \end{align*} $$
we have
![]() $\delta (\bar {e}_j)=\sum _{i=1}^m\bar {f}_i^*\otimes p_{ij}$
. It follows that
$\delta (\bar {e}_j)=\sum _{i=1}^m\bar {f}_i^*\otimes p_{ij}$
. It follows that
![]() $\delta $
can be lifted canonically to a homomorphism
$\delta $
can be lifted canonically to a homomorphism
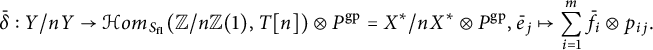 $$ \begin{align*}\bar{\delta}:Y/nY\rightarrow \mathcal{H}om_{S_{\mathrm{fl}}}({\mathbb Z}/n{\mathbb Z}(1),T[n])\otimes P^{\mathrm{gp}}=X^*/nX^*\otimes P^{\mathrm{gp}},\bar{e}_j\mapsto\sum_{i=1}^m\bar{f}_i\otimes p_{ij}.\end{align*} $$
$$ \begin{align*}\bar{\delta}:Y/nY\rightarrow \mathcal{H}om_{S_{\mathrm{fl}}}({\mathbb Z}/n{\mathbb Z}(1),T[n])\otimes P^{\mathrm{gp}}=X^*/nX^*\otimes P^{\mathrm{gp}},\bar{e}_j\mapsto\sum_{i=1}^m\bar{f}_i\otimes p_{ij}.\end{align*} $$
Therefore,
![]() $T_n(\mathbf {M}_2)$
is standard with respect to the given chart by Proposition 3.5.
$T_n(\mathbf {M}_2)$
is standard with respect to the given chart by Proposition 3.5.
In general, applying the functor
![]() $\varepsilon _*$
to the pushout diagram
$\varepsilon _*$
to the pushout diagram
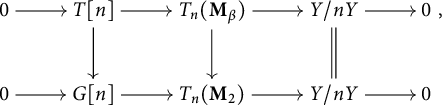
we get the following commutative diagram
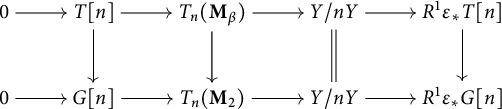
with exact rows. Therefore, we are reduced to the case
![]() $G=T$
by Proposition 3.5. This finishes the proof of part (1). The searched canonical pseudo-monodromy in part (2) is given by the canonical lift
$G=T$
by Proposition 3.5. This finishes the proof of part (1). The searched canonical pseudo-monodromy in part (2) is given by the canonical lift
![]() $\bar {\delta }$
of the map
$\bar {\delta }$
of the map
![]() $\delta $
. The compatibility in part (3) is clear from the construction of the canonical pseudo-monodromy.
$\delta $
. The compatibility in part (3) is clear from the construction of the canonical pseudo-monodromy.
Remark 4.8. If we have a decomposition of
![]() $\mathbf {M}$
into
$\mathbf {M}$
into
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
as above, it is easy to see that for any
$u_{2}$
as above, it is easy to see that for any
![]() $n\geq 1$
, we also get a decomposition
$n\geq 1$
, we also get a decomposition
![]() $T_{n}(\mathbf {M})=T_{n}(u_{1})+_{\mathrm {Baer}} T_{n}(u_{2})$
, where
$T_{n}(\mathbf {M})=T_{n}(u_{1})+_{\mathrm {Baer}} T_{n}(u_{2})$
, where
![]() $T_{n}(u_{1})$
is classical. The proposition shows that this decomposition is the same as the one obtained from the proof of Proposition 3.5, if one uses the lift
$T_{n}(u_{1})$
is classical. The proposition shows that this decomposition is the same as the one obtained from the proof of Proposition 3.5, if one uses the lift
of
![]() $Y/nY\to R^1\varepsilon _*G[n]$
.
$Y/nY\to R^1\varepsilon _*G[n]$
.
Assume that the underlying scheme of S is the spectrum of a Henselian local ring R and
![]() $P\to M_S$
is a global chart which is neat at the closed point s of S. By the same argument as in Lemma 3.7, we have
$P\to M_S$
is a global chart which is neat at the closed point s of S. By the same argument as in Lemma 3.7, we have
therefore, the lifting of the canonical pairing is uniquely determined by the choice of the chart, and, further, the pure log part
![]() $u_2:Y\to T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
is uniquely determined by the choice of the chart. When R is further a complete discrete valuation ring, choosing a uniformizer determines a neat chart, and therefore determines a decomposition
$u_2:Y\to T_{\mathrm {log}}\hookrightarrow G_{\mathrm {log}}$
is uniquely determined by the choice of the chart. When R is further a complete discrete valuation ring, choosing a uniformizer determines a neat chart, and therefore determines a decomposition
![]() $u=u_1+u_2$
. Such a determination is compatible with Raynaud’s decomposition of strict 1-motives over
$u=u_1+u_2$
. Such a determination is compatible with Raynaud’s decomposition of strict 1-motives over
![]() $\mathrm {Frac}(R)$
with integral geometric monodromy (see [Reference Raynaud23, Corollary 4.5.1] and [Reference Zhao28, Section 4.2]). In the case of a DVR endowed with its canonical log structure, the compatibility with the work of Kato has also already been treated in [Reference Bertapelle, Candilera and Cristante3].
$\mathrm {Frac}(R)$
with integral geometric monodromy (see [Reference Raynaud23, Corollary 4.5.1] and [Reference Zhao28, Section 4.2]). In the case of a DVR endowed with its canonical log structure, the compatibility with the work of Kato has also already been treated in [Reference Bertapelle, Candilera and Cristante3].
5 The Serre–Tate theorem for log abelian varieties with constant degeneration
In this section, we want to show how one can adapt Drinfeld’s proof of the classical Serre–Tate theorem to the situation of log abelian varieties with constant degeneration using the results from the previous sections.
5.1 Log abelian varieties with constant degeneration
We first recall the notion of a log abelian variety with constant degeneration from [Reference Kajiwara, Kato and Nakayama8, Section 3]. Let S be an fs log scheme. Let
![]() $\mathbf {M}=[Y\xrightarrow {u} G_{\mathrm {log}}]$
be a log 1-motive over S with its dual log 1-motive
$\mathbf {M}=[Y\xrightarrow {u} G_{\mathrm {log}}]$
be a log 1-motive over S with its dual log 1-motive
![]() $\mathbf {M}^*=[X\xrightarrow {u^*} G^{*}_{\mathrm {log}} ]$
. Consider the subsheaf
$\mathbf {M}^*=[X\xrightarrow {u^*} G^{*}_{\mathrm {log}} ]$
. Consider the subsheaf
of
![]() $\mathcal {H}om(X, \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})$
on the site
$\mathcal {H}om(X, \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})$
on the site
![]() $(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
, whose sections over
$(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
, whose sections over
![]() $V\in (\mathrm {fs}/S)$
are defined to be
$V\in (\mathrm {fs}/S)$
are defined to be
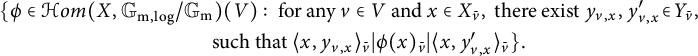 $$ \begin{align*} &\{ \phi\in \mathcal{H}om(X, \mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})(V) : \textrm{ for any } v\in V \textrm{ and } x\in X_{\bar{v}}, \textrm{ there exist } y_{v, x}, y_{v, x}'{\kern-1.5pt}\in{\kern-1.5pt} Y_{\bar{v}},\\&\kern100pt\textrm{ such that } \langle x,y_{v, x}\rangle_{\bar{v}} \vert \phi(x)_{\bar{v}} \vert \langle x,y^{\prime}_{v, x}\rangle_{\bar{v}} \}. \end{align*} $$
$$ \begin{align*} &\{ \phi\in \mathcal{H}om(X, \mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})(V) : \textrm{ for any } v\in V \textrm{ and } x\in X_{\bar{v}}, \textrm{ there exist } y_{v, x}, y_{v, x}'{\kern-1.5pt}\in{\kern-1.5pt} Y_{\bar{v}},\\&\kern100pt\textrm{ such that } \langle x,y_{v, x}\rangle_{\bar{v}} \vert \phi(x)_{\bar{v}} \vert \langle x,y^{\prime}_{v, x}\rangle_{\bar{v}} \}. \end{align*} $$
Here,
![]() $\langle - , - \rangle :X\times Y\to \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}}$
denotes the monodromy pairing of M. We then define
$\langle - , - \rangle :X\times Y\to \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}}$
denotes the monodromy pairing of M. We then define
![]() $G_{\mathrm {log}}^{(Y)}$
as the preimage of
$G_{\mathrm {log}}^{(Y)}$
as the preimage of
![]() $\mathcal {H}om(X, \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y)}$
under the natural map
$\mathcal {H}om(X, \mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y)}$
under the natural map
A log abelian variety with constant degeneration over S is defined to be a sheaf of abelian groups on
![]() $(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
, which is isomorphic to
$(\mathrm {fs}/S)_{\mathrm {\acute {e}t}}$
, which is isomorphic to
![]() $G_{\mathrm {log}}^{(Y)}/Y$
for a pointwise polarizable log 1-motive
$G_{\mathrm {log}}^{(Y)}/Y$
for a pointwise polarizable log 1-motive
![]() $[Y\xrightarrow {u} G_{\mathrm {log}}]$
. For the notion of being pointwise polarizable for a log 1-motive, we refer to [Reference Kajiwara, Kato and Nakayama8, Definition 2.8]. One of the main results of [Reference Kajiwara, Kato and Nakayama8] is then the following.
$[Y\xrightarrow {u} G_{\mathrm {log}}]$
. For the notion of being pointwise polarizable for a log 1-motive, we refer to [Reference Kajiwara, Kato and Nakayama8, Definition 2.8]. One of the main results of [Reference Kajiwara, Kato and Nakayama8] is then the following.
Theorem 5.1 [Reference Kajiwara, Kato and Nakayama8, Theorem 3.4]
The association
defines an equivalence of categories from pointwise polarizable log 1-motives over S to log abelian varieties with constant degeneration over S.
Remark 5.2. Pointwise polarizable log
![]() $1$
-motives satisfy effective étale descent. For this, assume that
$1$
-motives satisfy effective étale descent. For this, assume that
![]() $\tilde {S}\to S$
is étale and
$\tilde {S}\to S$
is étale and
![]() $[\tilde {u}:\tilde {Y}\to \tilde {G}_{\mathrm {log}}]$
is a pointwise polarizable log
$[\tilde {u}:\tilde {Y}\to \tilde {G}_{\mathrm {log}}]$
is a pointwise polarizable log
![]() $1$
-motive on
$1$
-motive on
![]() $\tilde {S}$
, with a gluing datum on
$\tilde {S}$
, with a gluing datum on
![]() $\tilde {S}\times _{S}\tilde {S}$
. Then, by [Reference Kajiwara, Kato and Nakayama8, Proposition 2.5], one also gets a descent datum on the group scheme
$\tilde {S}\times _{S}\tilde {S}$
. Then, by [Reference Kajiwara, Kato and Nakayama8, Proposition 2.5], one also gets a descent datum on the group scheme
![]() $\tilde {G}$
, which is an extension of an abelian scheme by a torus. Hence,
$\tilde {G}$
, which is an extension of an abelian scheme by a torus. Hence,
![]() $\tilde {G}$
descends to such an extension G over S. Moreover,
$\tilde {G}$
descends to such an extension G over S. Moreover,
![]() $\tilde {Y}$
also descends to some Y over S and then
$\tilde {Y}$
also descends to some Y over S and then
![]() $\tilde {u}$
glues to a morphism
$\tilde {u}$
glues to a morphism
![]() $[u:Y\to G_{\mathrm {log}}]$
. By the definition of being pointwise polarizable, u is still pointwise polarizable.
$[u:Y\to G_{\mathrm {log}}]$
. By the definition of being pointwise polarizable, u is still pointwise polarizable.
By this, one then also gets effective étale descent for log abelian varieties with constant degeneration.
First, we remark that the log p-divisible group of a log abelian variety with constant degeneration coincides with the one coming from the log 1-motive.
Lemma 5.3 Let A be a weak log abelian variety with constant degeneration over S (see [Reference Kajiwara, Kato and Nakayama9, Section 1.7]). By [Reference Kajiwara, Kato and Nakayama9, Section 1.7], there exists an admissible and nondegenerate log 1-motive
![]() $\mathbf {M}=[Y\rightarrow G_{\mathrm {log}}]$
such that
$\mathbf {M}=[Y\rightarrow G_{\mathrm {log}}]$
such that
![]() $A=G_{\mathrm {log}}^{(Y)}/Y$
. Then we have the following.
$A=G_{\mathrm {log}}^{(Y)}/Y$
. Then we have the following.
-
(1) For any positive integer n,
 $A[n]$
is canonically identified with
$A[n]$
is canonically identified with
 $T_n(\mathbf {M})$
.
$T_n(\mathbf {M})$
. -
(2)
 $A[p^{\infty }]:=\bigcup _{n>0}A[p^n]$
is canonically identified with
$A[p^{\infty }]:=\bigcup _{n>0}A[p^n]$
is canonically identified with
 $\mathbf {M}[p^{\infty }]$
.
$\mathbf {M}[p^{\infty }]$
.
Proof Consider the following two commutative diagrams
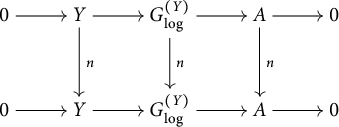
and
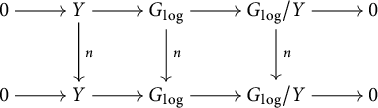
with exact rows. By Lemma [Reference Zhao26, Lemma 3.2], we have that
![]() $G_{\mathrm {log}}^{(Y)}\xrightarrow {n}G_{\mathrm {log}}^{(Y)}$
is surjective with kernel
$G_{\mathrm {log}}^{(Y)}\xrightarrow {n}G_{\mathrm {log}}^{(Y)}$
is surjective with kernel
![]() $G[n]$
. We also have that
$G[n]$
. We also have that
![]() $G_{\mathrm {log}}\xrightarrow {n}G_{\mathrm {log}}$
is surjective with kernel
$G_{\mathrm {log}}\xrightarrow {n}G_{\mathrm {log}}$
is surjective with kernel
![]() $G[n]$
. It follows that
$G[n]$
. It follows that
![]() $A[n]$
and
$A[n]$
and
![]() $(G_{\mathrm {log}}/Y)[n]$
fit into the following commutative diagram
$(G_{\mathrm {log}}/Y)[n]$
fit into the following commutative diagram
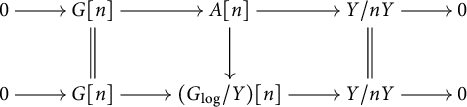
with exact rows. Hence,
![]() $A[n]$
is canonically identified with
$A[n]$
is canonically identified with
![]() $(G_{\mathrm {log}}/Y)[n]$
. The canonical quasi-isomorphism
$(G_{\mathrm {log}}/Y)[n]$
. The canonical quasi-isomorphism
gives rise to canonical isomorphism
![]() $T_n(\mathbf {M})\cong (G_{\mathrm {log}}/Y)[n]$
. It follows that
$T_n(\mathbf {M})\cong (G_{\mathrm {log}}/Y)[n]$
. It follows that
![]() $A[n]$
is canonically identified with
$A[n]$
is canonically identified with
![]() $T_n(\mathbf {M})$
.
$T_n(\mathbf {M})$
.
Lemma 5.4 Let
![]() $F_1\in (\mathrm {fin}/S)_{\mathrm {c}}$
, and let
$F_1\in (\mathrm {fin}/S)_{\mathrm {c}}$
, and let
![]() $F_2$
be a subobject of
$F_2$
be a subobject of
![]() $F_1$
in
$F_1$
in
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
. Then we have
$(\mathrm {fin}/S)_{\mathrm {r}}$
. Then we have
![]() $F_2\in (\mathrm {fin}/S)_{\mathrm {c}}$
. In other words, the category
$F_2\in (\mathrm {fin}/S)_{\mathrm {c}}$
. In other words, the category
![]() $(\mathrm {fin}/S)_{\mathrm {c}}$
is closed under subobjects in
$(\mathrm {fin}/S)_{\mathrm {c}}$
is closed under subobjects in
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
.
$(\mathrm {fin}/S)_{\mathrm {r}}$
.
Proof We need to show that the log scheme representing
![]() $F_2$
has log structure induced from S. This can be verified on each fiber over S. Hence, we are reduced to the case that S is a log point, which is [Reference Zhao26, Lemma 3.1]
$F_2$
has log structure induced from S. This can be verified on each fiber over S. Hence, we are reduced to the case that S is a log point, which is [Reference Zhao26, Lemma 3.1]
The following lemma generalizes [Reference Zhao26, Lemma 3.2].
Lemma 5.5 Let
![]() $\mathbf {M}=[Y\rightarrow G_{\mathrm {log}}],\mathbf {M}'=[Y'\rightarrow G^{\prime }_{\mathrm {log}}]$
be two nondegenerate log 1-motives over S,
$\mathbf {M}=[Y\rightarrow G_{\mathrm {log}}],\mathbf {M}'=[Y'\rightarrow G^{\prime }_{\mathrm {log}}]$
be two nondegenerate log 1-motives over S,
![]() $(f_{-1},f_0):\mathbf {M}\rightarrow \mathbf {M}'$
a homomorphism of log 1-motives, and
$(f_{-1},f_0):\mathbf {M}\rightarrow \mathbf {M}'$
a homomorphism of log 1-motives, and
![]() $f_{\mathrm {c}}:G\rightarrow G'$
the map induced by
$f_{\mathrm {c}}:G\rightarrow G'$
the map induced by
![]() $f_0$
. Let X (resp.
$f_0$
. Let X (resp.
![]() $X'$
) be the character group of the torus part T (resp.
$X'$
) be the character group of the torus part T (resp.
![]() $T'$
) of G (resp.
$T'$
) of G (resp.
![]() $G'$
),
$G'$
),
![]() $\mathcal {Q}$
(resp.
$\mathcal {Q}$
(resp.
![]() $\mathcal {Q}'$
) the sheaf
$\mathcal {Q}'$
) the sheaf
![]() $\mathcal {H}om(X,\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y)}$
(resp.
$\mathcal {H}om(X,\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y)}$
(resp.
![]() $\mathcal {H}om(X',\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y')}$
),
$\mathcal {H}om(X',\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y')}$
),
![]() $f_{\mathrm {l}}:X'\rightarrow X$
the map induced by
$f_{\mathrm {l}}:X'\rightarrow X$
the map induced by
![]() $f_{\mathrm {c}}$
, and
$f_{\mathrm {c}}$
, and
![]() $\tilde {f}_{\mathrm {d}}:\mathcal {Q}\rightarrow \mathcal {Q}'$
the map induced by
$\tilde {f}_{\mathrm {d}}:\mathcal {Q}\rightarrow \mathcal {Q}'$
the map induced by
![]() $f_{\mathrm {l}}$
. If
$f_{\mathrm {l}}$
. If
![]() $f_{\mathrm {c}}$
is an isogeny, then the map
$f_{\mathrm {c}}$
is an isogeny, then the map
![]() $\tilde {f}:G_{\mathrm {log}}^{(Y)}\rightarrow G^{\prime (Y')}_{\mathrm {log}}$
induced by
$\tilde {f}:G_{\mathrm {log}}^{(Y)}\rightarrow G^{\prime (Y')}_{\mathrm {log}}$
induced by
![]() $(f_{-1},f_0)$
is surjective with kernel
$(f_{-1},f_0)$
is surjective with kernel
![]() $\mathrm {Ker}(f_{\mathrm {c}})$
, and the map
$\mathrm {Ker}(f_{\mathrm {c}})$
, and the map
![]() $\tilde {f}_{\mathrm {d}}$
is bijective.
$\tilde {f}_{\mathrm {d}}$
is bijective.
Proof Without loss of generality, we may assume that the underlying scheme of S is Noetherian. Then the proof of [Reference Zhao26, Lemma 3.2] works also here.
The following proposition generalizes [Reference Zhao26, Proposition 3.2].
Proposition 5.6 Let A be a log abelian variety with constant degeneration over S, and let
![]() $F\in (\mathrm {fin}/S)_{\mathrm {r}}$
be a subgroup sheaf of A. Let n be a positive integer which kills F, and let
$F\in (\mathrm {fin}/S)_{\mathrm {r}}$
be a subgroup sheaf of A. Let n be a positive integer which kills F, and let
![]() $\mathbf {M}=[Y\xrightarrow {u}G_{\mathrm {log}}]$
be the pointwise polarizable log 1-motive corresponding to A. Let
$\mathbf {M}=[Y\xrightarrow {u}G_{\mathrm {log}}]$
be the pointwise polarizable log 1-motive corresponding to A. Let
![]() $F':=\mathrm {ker}(F\to A[n]\to Y/nY)$
and
$F':=\mathrm {ker}(F\to A[n]\to Y/nY)$
and
![]() $F":=F/F'$
. Assume that
$F":=F/F'$
. Assume that
![]() $F'\in (\mathrm {fin}/S)_{\mathrm {r}}$
. Then:
$F'\in (\mathrm {fin}/S)_{\mathrm {r}}$
. Then:
-
(1) Both
 $F'$
and
$F'$
and
 $F"$
lie in
$F"$
lie in
 $(\mathrm {fin}/S)_{\mathrm {c}}$
.
$(\mathrm {fin}/S)_{\mathrm {c}}$
. -
(2) There exist a pointwise polarizable log 1-motive
 $\mathbf {M}'=[Y'\xrightarrow {u'}G^{\prime }_{\mathrm {log}}]$
and a morphism
$\mathbf {M}'=[Y'\xrightarrow {u'}G^{\prime }_{\mathrm {log}}]$
and a morphism
 $(f_{-1},f_0):\mathbf {M}\to \mathbf {M}'$
such that
$(f_{-1},f_0):\mathbf {M}\to \mathbf {M}'$
such that
 $F'=\mathrm {ker}(G\xrightarrow {f_{\mathrm {c}}}G')$
and
$F'=\mathrm {ker}(G\xrightarrow {f_{\mathrm {c}}}G')$
and
 $F"\cong Y'/Y$
.
$F"\cong Y'/Y$
. -
(3) The morphism
 $(f_{-1},f_0)$
induces an isogeny
$(f_{-1},f_0)$
induces an isogeny
 $A\to A'$
of log abelian varieties with constant degeneration with kernel F, where
$A\to A'$
of log abelian varieties with constant degeneration with kernel F, where
 $A'$
is the one associated with
$A'$
is the one associated with
 $\mathbf {M}'$
.
$\mathbf {M}'$
.
Proof The proof is very similar to the proof of [Reference Zhao26, Proposition 3.2]. By construction,
![]() $F'$
and
$F'$
and
![]() $F"$
fit into the following commutative diagram:
$F"$
fit into the following commutative diagram:
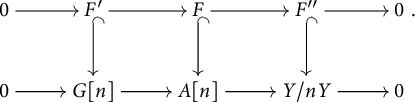
Then part (1) follows from Lemma 5.4, using that
![]() $G[n]$
and
$G[n]$
and
![]() $Y/nY$
are classical.
$Y/nY$
are classical.
For part (2), let E be the pullback of
![]() $G_{\mathrm {log}}^{(Y)}$
along
$G_{\mathrm {log}}^{(Y)}$
along
![]() $F\subset A$
$F\subset A$
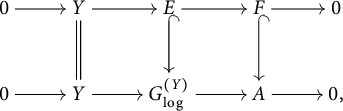
and let
![]() $E_{\mathrm {tor}}$
be the torsion subsheaf of E and
$E_{\mathrm {tor}}$
be the torsion subsheaf of E and
![]() $Y'=E/E_{\mathrm {tor}}$
. Now,
$Y'=E/E_{\mathrm {tor}}$
. Now,
is torsion-free and
![]() $E_{\mathrm {tor}}$
maps into G. Therefore, we have
$E_{\mathrm {tor}}$
maps into G. Therefore, we have
![]() $E_{\mathrm {tor}}=F'$
and
$E_{\mathrm {tor}}=F'$
and
![]() $Y'/Y=F"\subset Y/nY$
, and
$Y'/Y=F"\subset Y/nY$
, and
![]() $Y'$
is étale locally constant. Let
$Y'$
is étale locally constant. Let
![]() $G':=G/E_{\mathrm {tor}}=G/F'$
. Then the inclusion
$G':=G/E_{\mathrm {tor}}=G/F'$
. Then the inclusion
![]() $E\hookrightarrow G_{\mathrm {log}}^{(Y)}\hookrightarrow G_{\mathrm {log}}$
yields a homomorphism
$E\hookrightarrow G_{\mathrm {log}}^{(Y)}\hookrightarrow G_{\mathrm {log}}$
yields a homomorphism
![]() $Y'\rightarrow G_{\mathrm {log}}/F'=G^{\prime }_{\mathrm {log}}$
by taking the quotients by
$Y'\rightarrow G_{\mathrm {log}}/F'=G^{\prime }_{\mathrm {log}}$
by taking the quotients by
![]() $F'$
. In this way, we get a log 1-motive
$F'$
. In this way, we get a log 1-motive
![]() $\mathbf {M}':=[Y'\xrightarrow {u'} G^{\prime }_{\mathrm {log}}]$
together with a homomorphism
$\mathbf {M}':=[Y'\xrightarrow {u'} G^{\prime }_{\mathrm {log}}]$
together with a homomorphism
To show that
![]() $\mathbf {M}'$
is pointwise polarizable, we may assume that S is a log point with its underlying field separably closed. The existence of a polarization in this case is shown in the proof of [Reference Zhao26, Proposition 3.2]. Let now
$\mathbf {M}'$
is pointwise polarizable, we may assume that S is a log point with its underlying field separably closed. The existence of a polarization in this case is shown in the proof of [Reference Zhao26, Proposition 3.2]. Let now
![]() $A'$
be the log abelian variety with constant degeneration associated with
$A'$
be the log abelian variety with constant degeneration associated with
![]() $\mathbf {M}'$
. Then, by [Reference Kajiwara, Kato and Nakayama8, Theorem 3.4], the homomorphism
$\mathbf {M}'$
. Then, by [Reference Kajiwara, Kato and Nakayama8, Theorem 3.4], the homomorphism
![]() $(f_{-1},f_0)$
gives rise to a homomorphism
$(f_{-1},f_0)$
gives rise to a homomorphism
![]() $f:A\rightarrow A'$
of log abelian varieties with constant degeneration, which fits into a commutative diagram
$f:A\rightarrow A'$
of log abelian varieties with constant degeneration, which fits into a commutative diagram
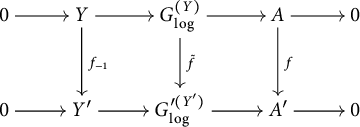
with exact rows. It then follows from Lemma 5.5 that f is an isogeny with kernel F.
5.2 Serre–Tate theorem
In this subsection, we closely follow [Reference Katz15].
Let R be a ring which is killed by an integer
![]() $N\geq 1$
, and let I be an ideal of R satisfying
$N\geq 1$
, and let I be an ideal of R satisfying
![]() $I^{v+1}=0$
. Let S be an fs log scheme with its underlying scheme
$I^{v+1}=0$
. Let S be an fs log scheme with its underlying scheme
![]() $\mathop {\mathrm {Spec}} R$
,
$\mathop {\mathrm {Spec}} R$
,
![]() $(\mathrm {fs}/S)$
the category of fs log schemes over S, and
$(\mathrm {fs}/S)$
the category of fs log schemes over S, and
![]() $(\mathrm {fsAff}/S)$
the full subcategory of
$(\mathrm {fsAff}/S)$
the full subcategory of
![]() $(\mathrm {fs}/S)$
consisting of fs log schemes whose underlying scheme is affine. We denote
$(\mathrm {fs}/S)$
consisting of fs log schemes whose underlying scheme is affine. We denote
![]() $R/I$
(resp.
$R/I$
(resp.
![]() $\mathop {\mathrm {Spec}}(R/I)$
) by
$\mathop {\mathrm {Spec}}(R/I)$
) by
![]() $R_0$
(resp.
$R_0$
(resp.
![]() $S_0$
), and we endow
$S_0$
), and we endow
![]() $S_0$
with the induced log structure from S.
$S_0$
with the induced log structure from S.
Definition 5.7 Let G be a functor from
![]() $(\mathrm {fsAff}/S)$
to the category of abelian groups. The subgroup functor
$(\mathrm {fsAff}/S)$
to the category of abelian groups. The subgroup functor
![]() $G_I$
of G is defined by
$G_I$
of G is defined by
for
![]() $U\in (\mathrm {fsAff}/S)$
, where
$U\in (\mathrm {fsAff}/S)$
, where
![]() $U\otimes _RR_0$
is endowed with the induced log structure from U.
$U\otimes _RR_0$
is endowed with the induced log structure from U.
The subgroup functor
![]() $\hat {G}$
of G is defined by
$\hat {G}$
of G is defined by
for
![]() $U\in (\mathrm {fsAff}/S)$
, where
$U\in (\mathrm {fsAff}/S)$
, where
![]() $U^{\mathrm {red}}$
is the reduced closed subscheme of U endowed with the induced log structure from U.
$U^{\mathrm {red}}$
is the reduced closed subscheme of U endowed with the induced log structure from U.
Lemma 5.8 Let G be a commutative formal Lie group over R, and we endow G with the log structure induced from S. Then the subgroup functor
![]() $G_I$
is killed by
$G_I$
is killed by
![]() $N^v$
.
$N^v$
.
Proof See [Reference Katz15, Lemma 1.1.1].
Lemma 5.9 Let G be a sheaf of abelian groups on
![]() $(\mathrm {fs}/S)_{\mathrm {{kfl}}}$
such that
$(\mathrm {fs}/S)_{\mathrm {{kfl}}}$
such that
![]() $\hat {G}$
is Kummer log flat locally representable by a classical formal Lie group over R. Then
$\hat {G}$
is Kummer log flat locally representable by a classical formal Lie group over R. Then
![]() $N^v$
kills
$N^v$
kills
![]() $G_I$
.
$G_I$
.
Proof See [Reference Katz15, Lemma 1.1.2].
Lemma 5.10 Let G and H be two sheaves of abelian groups on
![]() $(\mathrm {fs}/S)_{\mathrm {{kfl}}}$
such that:
$(\mathrm {fs}/S)_{\mathrm {{kfl}}}$
such that:
-
(a) G is N-divisible.
-
(b)
 $\hat {H}$
is Kummer log flat locally representable by a classical formal Lie group.
$\hat {H}$
is Kummer log flat locally representable by a classical formal Lie group. -
(c) H is formally log smooth.
Let
![]() $G_0$
(resp.
$G_0$
(resp.
![]() $H_0$
) denote the pullback of G (resp. H) to
$H_0$
) denote the pullback of G (resp. H) to
![]() $(\mathrm {fs}/S_0)_{\mathrm {{kfl}}}$
. Then we have:
$(\mathrm {fs}/S_0)_{\mathrm {{kfl}}}$
. Then we have:
-
(1) The groups
 $\mathrm {Hom}_S(G,H)$
and
$\mathrm {Hom}_S(G,H)$
and
 $\mathrm {Hom}_{S_0}(G_0,H_0)$
have no N-torsion.
$\mathrm {Hom}_{S_0}(G_0,H_0)$
have no N-torsion. -
(2) The natural map “reduction mod I”
 $\mathrm {Hom}_S(G,H)\rightarrow \mathrm {Hom}_{S_0}(G_0,H_0)$
is injective.
$\mathrm {Hom}_S(G,H)\rightarrow \mathrm {Hom}_{S_0}(G_0,H_0)$
is injective. -
(3) For any homomorphism
 $f_0:G_0\rightarrow H_0$
, there exists a unique homomorphism
$f_0:G_0\rightarrow H_0$
, there exists a unique homomorphism
 $"N^vf":G\rightarrow H$
which lifts
$"N^vf":G\rightarrow H$
which lifts
 $N^vf_0$
.
$N^vf_0$
. -
(4) In order that a homomorphism
 $f_0:G_0\rightarrow H_0$
lifts to a (necessarily unique) homomorphism
$f_0:G_0\rightarrow H_0$
lifts to a (necessarily unique) homomorphism
 $f:G\rightarrow H$
, it is necessary and sufficient that the homomorphism
$f:G\rightarrow H$
, it is necessary and sufficient that the homomorphism
 $"N^vf":G\rightarrow H$
annihilates the subgroup
$"N^vf":G\rightarrow H$
annihilates the subgroup
 $G[N^v]:=\mathrm {ker}(G\xrightarrow {N^v}G)$
of G.
$G[N^v]:=\mathrm {ker}(G\xrightarrow {N^v}G)$
of G.
Proof Properties (1), (2), and (4) follow from Lemma 5.9 just as in [Reference Katz15, Lemma 1.1.3]. Only (3) requires a bit more care. Let T be an fs log scheme over S, and let
![]() $T_{0}$
be the closed subscheme defined by I together with the induced log structure from T. We will construct a map
$T_{0}$
be the closed subscheme defined by I together with the induced log structure from T. We will construct a map
![]() $G(T)\to H(T)$
lifting
$G(T)\to H(T)$
lifting
![]() $N^{v}f_{0}$
and its uniqueness will follow from (2).
$N^{v}f_{0}$
and its uniqueness will follow from (2).
For any
![]() $t\in G(T)$
, let
$t\in G(T)$
, let
![]() $t_{0}\in G(T_{0})$
be its reduction mod I. Then, by formal log smoothness of H, there is an étale cover
$t_{0}\in G(T_{0})$
be its reduction mod I. Then, by formal log smoothness of H, there is an étale cover
![]() $\tilde {T}\to T$
such that the image of
$\tilde {T}\to T$
such that the image of
![]() $f_{0}(t_{0})$
in
$f_{0}(t_{0})$
in
![]() $H(\tilde {T}_{0})$
lifts to some element
$H(\tilde {T}_{0})$
lifts to some element
![]() $\tilde {h}\in H(\tilde {T})$
. Now
$\tilde {h}\in H(\tilde {T})$
. Now
![]() $N^{v}\tilde {h}$
is unique, so, in particular, on the overlap
$N^{v}\tilde {h}$
is unique, so, in particular, on the overlap
![]() $\tilde {T}\times _{T} \tilde {T}$
, we have
$\tilde {T}\times _{T} \tilde {T}$
, we have
![]() $\mathrm {pr}_{1}^{*}(N^{v}\tilde {h})=\mathrm {pr}_{2}^{*}(N^{v}\tilde {h})$
. Hence,
$\mathrm {pr}_{1}^{*}(N^{v}\tilde {h})=\mathrm {pr}_{2}^{*}(N^{v}\tilde {h})$
. Hence,
![]() $N^{v}\tilde {h}$
descends to a unique
$N^{v}\tilde {h}$
descends to a unique
![]() $h\in H(T)$
. One readily checks that this construction is natural in T.
$h\in H(T)$
. One readily checks that this construction is natural in T.
Now let N be
![]() $p^r$
for a prime number p and a positive integer r. Let A be a log abelian variety with constant degeneration over S, and
$p^r$
for a prime number p and a positive integer r. Let A be a log abelian variety with constant degeneration over S, and
![]() $A[p^{\infty }]$
the log p-divisible group associated with A. We are going to show that both A and
$A[p^{\infty }]$
the log p-divisible group associated with A. We are going to show that both A and
![]() $A[p^{\infty }]$
satisfy the conditions (a)–(c) from Lemma 5.10.
$A[p^{\infty }]$
satisfy the conditions (a)–(c) from Lemma 5.10.
Proposition 5.11 The conditions (a)–(c) from Lemma 5.10 hold for A.
Proof The multiplication by n map
![]() $n_A:A\rightarrow A$
is an isogeny by [Reference Zhao27, Corollary 2.1] for any positive integer n. In particular, A is p-divisible.
$n_A:A\rightarrow A$
is an isogeny by [Reference Zhao27, Corollary 2.1] for any positive integer n. In particular, A is p-divisible.
By [Reference Kajiwara, Kato and Nakayama9, Theorem 4.1], A is log smooth over S. In particular, it is formally log smooth over S.
We are left with checking the condition (b). Assume that
![]() $A\cong G_{\mathrm {log}}^{(Y)}/Y$
for a pointwise polarizable log 1-motive
$A\cong G_{\mathrm {log}}^{(Y)}/Y$
for a pointwise polarizable log 1-motive
![]() $[Y\to G_{\mathrm {log}}]$
over S. By [Reference Zhao26, Theorem 2.1], A fits into the following short exact sequence
$[Y\to G_{\mathrm {log}}]$
over S. By [Reference Zhao26, Theorem 2.1], A fits into the following short exact sequence
of sheaves of abelian groups over
![]() $(\mathrm {fs}/S)_{\mathrm {{kfl}}}$
. We abbreviate
$(\mathrm {fs}/S)_{\mathrm {{kfl}}}$
. We abbreviate
![]() $\mathcal {H}om_S(X,\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y)}$
as
$\mathcal {H}om_S(X,\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})^{(Y)}$
as
![]() $\mathcal {Q}$
. Let
$\mathcal {Q}$
. Let
![]() $U\in (\mathrm {fsAff}/S)$
, and we have the following two commutative diagrams
$U\in (\mathrm {fsAff}/S)$
, and we have the following two commutative diagrams

and
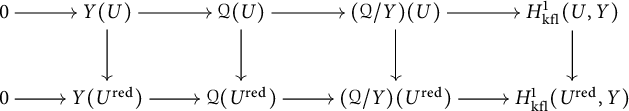
with exact rows. By [Reference Zhao26, Lemma 2.4]Footnote
3
, we have
![]() $H^1_{\mathrm {kfl}}(U,Y)\cong H^1_{\mathrm {fl}}(U,Y)$
and
$H^1_{\mathrm {kfl}}(U,Y)\cong H^1_{\mathrm {fl}}(U,Y)$
and
![]() $H^1_{\mathrm {kfl}}(U^{\mathrm {red}},Y)\cong H^1_{\mathrm {fl}}(U^{\mathrm {red}},Y)$
. Since Y is a smooth group scheme over S, we further get
$H^1_{\mathrm {kfl}}(U^{\mathrm {red}},Y)\cong H^1_{\mathrm {fl}}(U^{\mathrm {red}},Y)$
. Since Y is a smooth group scheme over S, we further get
![]() $H^1_{\mathrm {fl}}(U,Y)\cong H^1_{\mathrm {\acute {e}t}}(U,Y)$
and
$H^1_{\mathrm {fl}}(U,Y)\cong H^1_{\mathrm {\acute {e}t}}(U,Y)$
and
![]() $H^1_{\mathrm {fl}}(U^{\mathrm {red}},Y)\cong H^1_{\mathrm {\acute {e}t}}(U^{\mathrm {red}},Y)$
. Since the small étale site of U and the small étale site of
$H^1_{\mathrm {fl}}(U^{\mathrm {red}},Y)\cong H^1_{\mathrm {\acute {e}t}}(U^{\mathrm {red}},Y)$
. Since the small étale site of U and the small étale site of
![]() $U^{\mathrm {red}}$
are equivalent, we get
$U^{\mathrm {red}}$
are equivalent, we get
![]() $H^1_{\mathrm {\acute {e}t}}(U,Y)\cong H^1_{\mathrm {\acute {e}t}}(U^{\mathrm {red}},Y)$
and
$H^1_{\mathrm {\acute {e}t}}(U,Y)\cong H^1_{\mathrm {\acute {e}t}}(U^{\mathrm {red}},Y)$
and
![]() $Y(U)\cong Y(U^{\mathrm {red}})$
. Hence, the left vertical map and the right vertical map of (5.3) are both isomorphisms. Since the formation of
$Y(U)\cong Y(U^{\mathrm {red}})$
. Hence, the left vertical map and the right vertical map of (5.3) are both isomorphisms. Since the formation of
![]() $\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}}$
is compatible with strict base change of log schemes, we get that the canonical map
$\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}}$
is compatible with strict base change of log schemes, we get that the canonical map
![]() $\mathcal {Q}(U)\rightarrow \mathcal {Q}(U^{\mathrm {red}})$
is an isomorphism. Applying the five lemma to (5.3), we get that the canonical map
$\mathcal {Q}(U)\rightarrow \mathcal {Q}(U^{\mathrm {red}})$
is an isomorphism. Applying the five lemma to (5.3), we get that the canonical map
![]() $\mathcal {Q}/Y(U)\rightarrow \mathcal {Q}/Y(U^{\mathrm {red}})$
is injective. By diagram (5.2), we have that the canonical map
$\mathcal {Q}/Y(U)\rightarrow \mathcal {Q}/Y(U^{\mathrm {red}})$
is injective. By diagram (5.2), we have that the canonical map
![]() $\hat {G}(U)\rightarrow \hat {A}(U)$
is an isomorphism. Since
$\hat {G}(U)\rightarrow \hat {A}(U)$
is an isomorphism. Since
![]() $\hat {G}$
is representable by a formal Lie group, so is
$\hat {G}$
is representable by a formal Lie group, so is
![]() $\hat {A}$
.
$\hat {A}$
.
Proposition 5.12 Let
![]() $S_0$
be an fs log scheme where p is locally nilpotent. Let
$S_0$
be an fs log scheme where p is locally nilpotent. Let
![]() $\mathbf {M}_0=[Y_0\to G_{0,\mathrm {log}}]$
be a log 1-motive over
$\mathbf {M}_0=[Y_0\to G_{0,\mathrm {log}}]$
be a log 1-motive over
![]() $S_0$
. Let
$S_0$
. Let
![]() $S_0\to S$
be strict closed immersion of fs log schemes defined by a nilpotent sheaf of ideals, and let H be a log p-divisible group over S such that
$S_0\to S$
be strict closed immersion of fs log schemes defined by a nilpotent sheaf of ideals, and let H be a log p-divisible group over S such that
![]() $H_0:=H\times _SS_0= \mathbf {M}_0[p^{\infty }]$
. Then
$H_0:=H\times _SS_0= \mathbf {M}_0[p^{\infty }]$
. Then
![]() $\hat {H}_0$
(resp.
$\hat {H}_0$
(resp.
![]() $\hat {H}$
) is locally a formal Lie group over
$\hat {H}$
) is locally a formal Lie group over
![]() $S_0$
(resp. over S).
$S_0$
(resp. over S).
Proof The log p-divisible group
![]() $H_0$
fits into a short exact sequence
$H_0$
fits into a short exact sequence
Since
![]() $Y_0\otimes _Z{\mathbb Q}_p/{\mathbb Z}_p$
is classical étale, the subgroup functor
$Y_0\otimes _Z{\mathbb Q}_p/{\mathbb Z}_p$
is classical étale, the subgroup functor
![]() $\hat {H}_0$
of
$\hat {H}_0$
of
![]() $H_0$
coincides with
$H_0$
coincides with
![]() $\hat {G}_0=\widehat {G_0[p^{\infty }]}$
which is locally a formal Lie group.
$\hat {G}_0=\widehat {G_0[p^{\infty }]}$
which is locally a formal Lie group.
Since the small étale site of
![]() $S_0$
is equivalent to the small étale site of S,
$S_0$
is equivalent to the small étale site of S,
![]() $Y_0$
extends to a locally constant sheaf Y over S. Let
$Y_0$
extends to a locally constant sheaf Y over S. Let
![]() $H_n:=H[p^n]$
and
$H_n:=H[p^n]$
and
![]() $H_{0,n}:=H_0[p^n]$
. Consider the commutative diagram
$H_{0,n}:=H_0[p^n]$
. Consider the commutative diagram
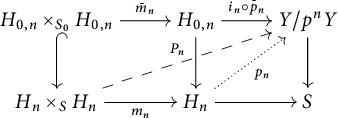
of solids arrows, where
![]() $\bar {m}_n$
(resp.
$\bar {m}_n$
(resp.
![]() $m_n$
) is the group law of
$m_n$
) is the group law of
![]() $H_{0,n}$
(resp.
$H_{0,n}$
(resp.
![]() $H_n$
),
$H_n$
),
![]() $\bar {p}_n$
is the composition
$\bar {p}_n$
is the composition
![]() $H_{0,n}=T_{p^n}(\mathbf {M}_0)\to Y_0/p^nY_0$
, and
$H_{0,n}=T_{p^n}(\mathbf {M}_0)\to Y_0/p^nY_0$
, and
![]() $i_n$
is the closed immersion
$i_n$
is the closed immersion
![]() $Y_0/p^nY_0\hookrightarrow Y/p^nY$
. Since
$Y_0/p^nY_0\hookrightarrow Y/p^nY$
. Since
![]() $Y/p^nY$
is log étale (in fact even classical étale) over S and
$Y/p^nY$
is log étale (in fact even classical étale) over S and
![]() $H_{0,n}\to H_n$
is a strict closed immersion defined by a nilpotent ideal,
$H_{0,n}\to H_n$
is a strict closed immersion defined by a nilpotent ideal,
![]() $i_n\circ \bar {p}_n$
and
$i_n\circ \bar {p}_n$
and
![]() $i_n\circ \bar {p}_n\circ \bar {m}_n$
lift to unique maps
$i_n\circ \bar {p}_n\circ \bar {m}_n$
lift to unique maps
![]() $p_n$
and
$p_n$
and
![]() $P_n$
, respectively, such that the diagram remains commutative. Let
$P_n$
, respectively, such that the diagram remains commutative. Let
![]() $\mu _n$
be the group law of
$\mu _n$
be the group law of
![]() $Y/p^nY$
. Since
$Y/p^nY$
. Since
![]() $(i_n\circ \bar {\mu }_n)\circ \bar {p}_n\times \bar {p}_n=(i_n\circ \bar {p}_n)\circ \bar {m}_n$
, the outer square of the commutative diagram
$(i_n\circ \bar {\mu }_n)\circ \bar {p}_n\times \bar {p}_n=(i_n\circ \bar {p}_n)\circ \bar {m}_n$
, the outer square of the commutative diagram
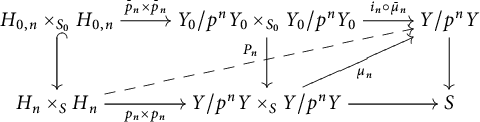
of solid arrows coincides with the outer square of the last diagram. Therefore, the map
![]() $P_n$
from last diagram is also the unique lifting of
$P_n$
from last diagram is also the unique lifting of
![]() $(i_n\circ \bar {\mu }_n)\circ \bar {p}_n\times \bar {p}_n$
such that the diagram remains commutative. It follows that
$(i_n\circ \bar {\mu }_n)\circ \bar {p}_n\times \bar {p}_n$
such that the diagram remains commutative. It follows that
![]() $\mu _n\circ (p_n\times p_n)=P_n=p_n\circ m_n$
. Therefore,
$\mu _n\circ (p_n\times p_n)=P_n=p_n\circ m_n$
. Therefore,
![]() $p_n$
is a homomorphism of group log schemes. By the uniqueness of
$p_n$
is a homomorphism of group log schemes. By the uniqueness of
![]() $p_n$
, it is also clear that
$p_n$
, it is also clear that
![]() $(p_n)_{n\geq 1}$
gives rise to a homomorphism
$(p_n)_{n\geq 1}$
gives rise to a homomorphism
Let
![]() $H^{\prime }_n:=\mathrm {ker}(H_n\xrightarrow {p_n}Y/p^nY)$
. Clearly,
$H^{\prime }_n:=\mathrm {ker}(H_n\xrightarrow {p_n}Y/p^nY)$
. Clearly,
![]() $H^{\prime }_n$
is representable. Since
$H^{\prime }_n$
is representable. Since
![]() $S_0\to S$
is a strict nil immersion and
$S_0\to S$
is a strict nil immersion and
![]() $H^{\prime }_n$
is strict over S. Since
$H^{\prime }_n$
is strict over S. Since
![]() $G_0[p^n]$
is classically flat, in particular log flat,
$G_0[p^n]$
is classically flat, in particular log flat,
![]() $(p_n)_0$
is log flat over
$(p_n)_0$
is log flat over
![]() $S_0$
by descent. Since
$S_0$
by descent. Since
![]() $H_n$
is log flat over S,
$H_n$
is log flat over S,
![]() $p_n$
is log flat by Corollary B.2. Hence,
$p_n$
is log flat by Corollary B.2. Hence,
![]() $H_n'=\mathrm {ker}(p_n)$
is log flat. Since it is also strict over S, it is even classically flat. Moreover,
$H_n'=\mathrm {ker}(p_n)$
is log flat. Since it is also strict over S, it is even classically flat. Moreover,
![]() $H_n'\to S$
agrees with
$H_n'\to S$
agrees with
where Z denotes the fiber product of
![]() $H_n\rightarrow Y/p^nY\xleftarrow {e} S$
in the category of schemes. The first map is finite by [Reference Ogus21, Chapter III, Corollary 2.1.6]. Since the unit section e of
$H_n\rightarrow Y/p^nY\xleftarrow {e} S$
in the category of schemes. The first map is finite by [Reference Ogus21, Chapter III, Corollary 2.1.6]. Since the unit section e of
![]() $Y/p^nY$
is a closed immersion, the second map is also finite. The last map is finite by Proposition 2.4. It follows that
$Y/p^nY$
is a closed immersion, the second map is also finite. The last map is finite by Proposition 2.4. It follows that
![]() $H_n'\in (\mathrm {fin}/S)_{\mathrm {c}}$
.
$H_n'\in (\mathrm {fin}/S)_{\mathrm {c}}$
.
Thus, we get a classical p-divisible group
![]() $H':=\varinjlim _nH^{\prime }_n$
such that
$H':=\varinjlim _nH^{\prime }_n$
such that
![]() $H'\times _SS_0=G_0[p^{\infty }]$
. Using the exact sequence
$H'\times _SS_0=G_0[p^{\infty }]$
. Using the exact sequence
we get that
![]() $\hat {H}=\hat {H'}$
is locally a formal Lie group.
$\hat {H}=\hat {H'}$
is locally a formal Lie group.
Proposition 5.13 Let
![]() $S_0$
, S,
$S_0$
, S,
![]() $H_0$
, and H be as in Proposition 5.12. Then
$H_0$
, and H be as in Proposition 5.12. Then
![]() $H_0$
and H satisfy the conditions (a)–(c) from Lemma 5.10.
$H_0$
and H satisfy the conditions (a)–(c) from Lemma 5.10.
Proof Condition (a) is trivial, condition (b) follows from Proposition 5.12, and condition (c) follows from Theorem 3.16.
We denote by
![]() $\mathrm {LAVwCD}_S$
the category of log abelian varieties with constant degeneration over S, and by
$\mathrm {LAVwCD}_S$
the category of log abelian varieties with constant degeneration over S, and by
![]() $\mathrm {Def}(S,S_0)$
the category of triples
$\mathrm {Def}(S,S_0)$
the category of triples
consisting of a log abelian variety with constant degeneration
![]() $A_0$
over
$A_0$
over
![]() $S_0$
, an object H of
$S_0$
, an object H of
![]() $(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
, and an isomorphism
$(p\text {-div}/S)^{\mathrm {log}}_{\mathrm {d}}$
, and an isomorphism
![]() $\varepsilon :H_0\xrightarrow {\cong }A_0[p^{\infty }]$
of log p-divisible groups over
$\varepsilon :H_0\xrightarrow {\cong }A_0[p^{\infty }]$
of log p-divisible groups over
![]() $S_0$
.
$S_0$
.
Theorem 5.14 (Serre–Tate for LAVwCD)
Let
![]() $R,R_0,S,S_0,I, N$
, and v be as in the beginning of this subsection. We further assume that N is a power of a prime number p. Then the canonical functor
$R,R_0,S,S_0,I, N$
, and v be as in the beginning of this subsection. We further assume that N is a power of a prime number p. Then the canonical functor
where
![]() $A_0$
denotes the base change of A to
$A_0$
denotes the base change of A to
![]() $S_0$
, is an equivalence of categories.
$S_0$
, is an equivalence of categories.
Proof Step 1: Full faithfulness. Let
![]() $A, A'$
be log abelian varieties over S,
$A, A'$
be log abelian varieties over S,
![]() $f_{p^{\infty }}:A[p^{\infty }]\rightarrow A'[p^{\infty }]$
a homomorphism of log p-divisible groups over S, and
$f_{p^{\infty }}:A[p^{\infty }]\rightarrow A'[p^{\infty }]$
a homomorphism of log p-divisible groups over S, and
![]() $f_0:A_0\rightarrow A^{\prime }_0$
a homomorphism of log abelian varieties over
$f_0:A_0\rightarrow A^{\prime }_0$
a homomorphism of log abelian varieties over
![]() $S_0$
such that
$S_0$
such that
![]() $f_0[p^{\infty }]$
coincides with
$f_0[p^{\infty }]$
coincides with
![]() $f_{p^{\infty }}\times _SS_0$
. To finish the proof of full faithfulness, it suffices to show that there exists a unique homomorphism
$f_{p^{\infty }}\times _SS_0$
. To finish the proof of full faithfulness, it suffices to show that there exists a unique homomorphism
![]() $f:A\rightarrow A'$
which induces both
$f:A\rightarrow A'$
which induces both
![]() $f_{p^{\infty }}$
and
$f_{p^{\infty }}$
and
![]() $f_0$
. The uniqueness follows easily from Proposition 5.11 and Lemma 5.10(2).
$f_0$
. The uniqueness follows easily from Proposition 5.11 and Lemma 5.10(2).
To construct the homomorphism f, consider the canonical lifting
![]() $"N^vf\text{"}:A\rightarrow A'$
of
$"N^vf\text{"}:A\rightarrow A'$
of
![]() $N^vf_0$
guaranteed by Lemma 5.10(3). Since
$N^vf_0$
guaranteed by Lemma 5.10(3). Since
![]() $"N^vf\text{"}$
lifts
$"N^vf\text{"}$
lifts
![]() $N^vf_0$
, the induced map
$N^vf_0$
, the induced map
![]() $"N^vf\text{"}[p^{\infty }]$
on log p-divisible groups lifts
$"N^vf\text{"}[p^{\infty }]$
on log p-divisible groups lifts
![]() $N^v(f_0[p^{\infty }])$
. By part (2) of Lemma 5.10, we have
$N^v(f_0[p^{\infty }])$
. By part (2) of Lemma 5.10, we have
![]() $"N^vf\text{"}[p^{\infty }]=N^vf_{p^{\infty }}$
. Hence,
$"N^vf\text{"}[p^{\infty }]=N^vf_{p^{\infty }}$
. Hence,
![]() $"N^vf \text{"}$
kills
$"N^vf \text{"}$
kills
![]() $A[N^v]$
. By part (4) of Lemma 5.10, there exists a homomorphism
$A[N^v]$
. By part (4) of Lemma 5.10, there exists a homomorphism
![]() $f:A\rightarrow A'$
lifting
$f:A\rightarrow A'$
lifting
![]() $f_0$
such that
$f_0$
such that
![]() $"N^vf\text{"}=N^vf$
. Since f lifting
$"N^vf\text{"}=N^vf$
. Since f lifting
![]() $f_0$
implies
$f_0$
implies
![]() $f[p^{\infty }]$
lifting
$f[p^{\infty }]$
lifting
![]() $f_0[p^{\infty }]$
, we get
$f_0[p^{\infty }]$
, we get
![]() $f[p^{\infty }]=f_{p^{\infty }}$
again by part (2) of Lemma 5.10. This finishes the proof of the full faithfulness.
$f[p^{\infty }]=f_{p^{\infty }}$
again by part (2) of Lemma 5.10. This finishes the proof of the full faithfulness.
Step 2: Essential surjectivity. Let
![]() $(A_0,H,\alpha _{0})$
be an object of
$(A_0,H,\alpha _{0})$
be an object of
![]() $\mathrm {Def}(S,S_0)$
, and we look for a log abelian variety A which gives rise to
$\mathrm {Def}(S,S_0)$
, and we look for a log abelian variety A which gives rise to
![]() $(A_0,H,\alpha _{0})$
up to isomorphism. By [Reference Kajiwara, Kato and Nakayama10, Theorem 1.6] and [Reference Kato11, Corollary 3.11],
$(A_0,H,\alpha _{0})$
up to isomorphism. By [Reference Kajiwara, Kato and Nakayama10, Theorem 1.6] and [Reference Kato11, Corollary 3.11],
![]() $A_0$
lifts to a log abelian variety with constant degeneration
$A_0$
lifts to a log abelian variety with constant degeneration
![]() $A'$
over S. The isomorphism
$A'$
over S. The isomorphism
of log abelian varieties over
![]() $S_0$
induces an isomorphism
$S_0$
induces an isomorphism
of log p-divisible groups over
![]() $S_0$
. By part (3) of Lemma 5.8,
$S_0$
. By part (3) of Lemma 5.8,
![]() $N^v\alpha _0[p^{\infty }]$
has a unique lifting to a homomorphism
$N^v\alpha _0[p^{\infty }]$
has a unique lifting to a homomorphism
of log p-divisible groups over S. The same procedure applied to
![]() $\beta _0:=\alpha _0^{-1}$
, and we get a homomorphism
$\beta _0:=\alpha _0^{-1}$
, and we get a homomorphism
of log p-divisible groups over S. Since the composition
![]() $(N^v\beta _0[p^{\infty }])\circ (N^v\alpha _0[p^{\infty }])$
(resp.
$(N^v\beta _0[p^{\infty }])\circ (N^v\alpha _0[p^{\infty }])$
(resp.
![]() $(N^v\alpha _0[p^{\infty }])\circ (N^v\beta _0[p^{\infty }])$
) is the multiplication by
$(N^v\alpha _0[p^{\infty }])\circ (N^v\beta _0[p^{\infty }])$
) is the multiplication by
![]() $N^{2v}$
map on
$N^{2v}$
map on
![]() $A^{\prime }_0[p^{\infty }]$
(resp.
$A^{\prime }_0[p^{\infty }]$
(resp.
![]() $H_0$
), the composition
$H_0$
), the composition
![]() $\text{"}N^v\beta [p^{\infty }]\text{"}\circ "N^v\alpha [p^{\infty }]\text{"}$
(resp.
$\text{"}N^v\beta [p^{\infty }]\text{"}\circ "N^v\alpha [p^{\infty }]\text{"}$
(resp.
![]() $"N^v\alpha [p^{\infty }]\text{"}\circ "N^v\beta [p^{\infty }]\text{"}$
) is the multiplication by
$"N^v\alpha [p^{\infty }]\text{"}\circ "N^v\beta [p^{\infty }]\text{"}$
) is the multiplication by
![]() $N^{2v}$
map on
$N^{2v}$
map on
![]() $A'[p^{\infty }]$
(resp. H). Let
$A'[p^{\infty }]$
(resp. H). Let
![]() $K:=\mathrm {ker}("N^v\alpha [p^{\infty }]\text{"})$
and
$K:=\mathrm {ker}("N^v\alpha [p^{\infty }]\text{"})$
and
![]() $Q:=\mathrm {ker}("N^v\beta [p^{\infty }]\text{"})$
. Thus, we get a short exact sequence
$Q:=\mathrm {ker}("N^v\beta [p^{\infty }]\text{"})$
. Thus, we get a short exact sequence
using the kernel–cokernel exact sequences for the compositions
and
Claim
![]() $K=\mathrm {ker}("N^v\alpha [p^{\infty }]\text{"})$
lies in
$K=\mathrm {ker}("N^v\alpha [p^{\infty }]\text{"})$
lies in
![]() $(\mathrm {fin}/S)_{\mathrm {r}}$
.
$(\mathrm {fin}/S)_{\mathrm {r}}$
.
Since K is also the kernel of
![]() $A'[N^{2v}]\to H[N^{2v}]$
, it is representable by an fs log scheme. Clearly, both
$A'[N^{2v}]\to H[N^{2v}]$
, it is representable by an fs log scheme. Clearly, both
![]() $K_0:=K\times _SS_0$
and
$K_0:=K\times _SS_0$
and
![]() $Q_0:=Q\times _SS_0$
lie in
$Q_0:=Q\times _SS_0$
lie in
![]() $(\mathrm {fin}/S_0)_{\mathrm {r}}$
. Then
$(\mathrm {fin}/S_0)_{\mathrm {r}}$
. Then
![]() $u_0:A^{\prime }_0[N^{2v}]\to Q_0$
as a
$u_0:A^{\prime }_0[N^{2v}]\to Q_0$
as a
![]() $K_0$
-torsor is log flat by Kummer log flat descent (see [Reference Illusie, Nakayama and Tsuji7, Theorem 0.1]). By the log flatness of
$K_0$
-torsor is log flat by Kummer log flat descent (see [Reference Illusie, Nakayama and Tsuji7, Theorem 0.1]). By the log flatness of
![]() $A'[N^{2v}]\to S$
and Corollary B.2, u is log flat. From this, it then follows that K is log flat over S. Moreover, the Kummer property extends to infinitesimal lifts by Lemma 5.15. Therefore, K is also of Kummer type over S. Being the kernel of
$A'[N^{2v}]\to S$
and Corollary B.2, u is log flat. From this, it then follows that K is log flat over S. Moreover, the Kummer property extends to infinitesimal lifts by Lemma 5.15. Therefore, K is also of Kummer type over S. Being the kernel of
![]() $A'[N^{2v}]\to H[N^{2v}]$
, the group K is also finite over S, by the same argument as in the proof of the finiteness of the group
$A'[N^{2v}]\to H[N^{2v}]$
, the group K is also finite over S, by the same argument as in the proof of the finiteness of the group
![]() $H_n'$
in the proof of Proposition 5.12. But then, K being finite Kummer log flat over S, one has
$H_n'$
in the proof of Proposition 5.12. But then, K being finite Kummer log flat over S, one has
![]() $K\in (\mathrm {fin}/S)_{\mathrm {r}}$
(see Proposition 2.4). This finishes the proof of the claim.
$K\in (\mathrm {fin}/S)_{\mathrm {r}}$
(see Proposition 2.4). This finishes the proof of the claim.
Let
![]() $[Y\to G_{\mathrm {log}}]$
be the log 1-motive corresponding to
$[Y\to G_{\mathrm {log}}]$
be the log 1-motive corresponding to
![]() $A'$
. Let
$A'$
. Let
Since
![]() $K_0=\mathrm {ker}(N^v\alpha _0[p^{\infty }])=A^{\prime }_0[N^v]$
, we have
$K_0=\mathrm {ker}(N^v\alpha _0[p^{\infty }])=A^{\prime }_0[N^v]$
, we have
Replacing u by
![]() $K\to Y/N^{2v}Y$
and K by
$K\to Y/N^{2v}Y$
and K by
![]() $K'$
, the same proof as that of the claim implies that
$K'$
, the same proof as that of the claim implies that
![]() $K'\in (\mathrm {fin}/S)_{\mathrm {r}}$
. Now, applying Proposition 5.6, we get that
$K'\in (\mathrm {fin}/S)_{\mathrm {r}}$
. Now, applying Proposition 5.6, we get that
![]() $A'\to A'/K$
is an isogeny of log abelian varieties with constant degeneration with kernel K. Let
$A'\to A'/K$
is an isogeny of log abelian varieties with constant degeneration with kernel K. Let
![]() $A:=A'/K$
. Apparently,
$A:=A'/K$
. Apparently,
and
![]() $"N^v\alpha [p^{\infty }]\text{"}$
induces an isomorphism
$"N^v\alpha [p^{\infty }]\text{"}$
induces an isomorphism
![]() $A[p^{\infty }]\xrightarrow {\cong }H$
. This finishes the proof of the essential surjectivity.
$A[p^{\infty }]\xrightarrow {\cong }H$
. This finishes the proof of the essential surjectivity.
In the proof above, we have used the following lemma.
Lemma 5.15 Assume that
![]() $S_{0}\subset S$
is a strict nilpotent thickening of fs log schemes, and let
$S_{0}\subset S$
is a strict nilpotent thickening of fs log schemes, and let
![]() $f:X\to Y$
be a morphism of fs log schemes over S, such that
$f:X\to Y$
be a morphism of fs log schemes over S, such that
![]() $f_{0}=f\times _{S} S_{0}$
is Kummer. Then f is also Kummer.
$f_{0}=f\times _{S} S_{0}$
is Kummer. Then f is also Kummer.
Proof For any log scheme Z, we denote
![]() $M_Z/\mathcal {O}_Z^{\times }$
by
$M_Z/\mathcal {O}_Z^{\times }$
by
![]() $\overline {M}_Z$
.
$\overline {M}_Z$
.
Let x be any point of X, and let
![]() $y=f(x)$
. It suffices to show that the canonical map
$y=f(x)$
. It suffices to show that the canonical map
![]() $\overline {M}_{Y,\bar {y}}\to \overline {M}_{X,\bar {x}}$
of fs monoids is Kummer. Let
$\overline {M}_{Y,\bar {y}}\to \overline {M}_{X,\bar {x}}$
of fs monoids is Kummer. Let
![]() $X_0:=X\times _SS_0$
and
$X_0:=X\times _SS_0$
and
![]() $Y_0:=Y\times _SS_0$
. Consider the following commutative diagram
$Y_0:=Y\times _SS_0$
. Consider the following commutative diagram
with horizontal maps strict. This square induces another commutative square
Since
![]() $f_0$
is Kummer, the left vertical map in the above square is Kummer. If follows that the right vertical map is also Kummer.
$f_0$
is Kummer, the left vertical map in the above square is Kummer. If follows that the right vertical map is also Kummer.
A A lemma on finite flat group schemes
Lemma A.1 Let S be a scheme, F a finite flat group scheme over S which is of multiplicative type, and
![]() $F'$
a finite flat group scheme over S. Then the fppf sheaf
$F'$
a finite flat group scheme over S. Then the fppf sheaf
![]() $H:=\mathcal {H}om_S(F,F')$
is representable by an étale quasi-finite separated group scheme over S.
$H:=\mathcal {H}om_S(F,F')$
is representable by an étale quasi-finite separated group scheme over S.
Proof Let
![]() $0\rightarrow F'\rightarrow G_1\rightarrow G_2\rightarrow 0$
be the canonical smooth resolution of
$0\rightarrow F'\rightarrow G_1\rightarrow G_2\rightarrow 0$
be the canonical smooth resolution of
![]() $F'$
with
$F'$
with
![]() $G_1,G_2$
affine smooth group schemes over S (see [Reference Milne18, Theorem A.5]). Then we have an exact sequence
$G_1,G_2$
affine smooth group schemes over S (see [Reference Milne18, Theorem A.5]). Then we have an exact sequence
of fppf sheaves of abelian groups over S. By [Reference Artin, Demazure, Grothendieck, Raynaud and Serre1, Exposé XI, Corollary 4.2], the sheaves
![]() $\mathcal {H}om_S(F,G_i)$
, for
$\mathcal {H}om_S(F,G_i)$
, for
![]() $i=1,2$
, are representable by smooth separated group schemes over S. Hence,
$i=1,2$
, are representable by smooth separated group schemes over S. Hence,
![]() $H=\mathcal {H}om_S(F,F')$
is the kernel of a morphism of representable sheaves and thus representable itself. Let n be a positive integer which kills F. We then have
$H=\mathcal {H}om_S(F,F')$
is the kernel of a morphism of representable sheaves and thus representable itself. Let n be a positive integer which kills F. We then have
where
![]() $\mathcal {H}om_S(F,G_i)[n]$
denotes the n-torsion subgroup scheme of
$\mathcal {H}om_S(F,G_i)[n]$
denotes the n-torsion subgroup scheme of
![]() $\mathcal {H}om_S(F,G_i)$
. The fibers of the group scheme
$\mathcal {H}om_S(F,G_i)$
. The fibers of the group scheme
![]() $\mathcal {H}om_S(F,G_i)$
over S are finite by the structure theorem [Reference Artin, Demazure, Grothendieck, Raynaud and Serre1, Exposé XVII, Theorem 7.2.1] of commutative group schemes and [Reference Artin, Demazure, Grothendieck, Raynaud and Serre1, Exposé XVII, Proposition 2.4]. It follows that the group schemes
$\mathcal {H}om_S(F,G_i)$
over S are finite by the structure theorem [Reference Artin, Demazure, Grothendieck, Raynaud and Serre1, Exposé XVII, Theorem 7.2.1] of commutative group schemes and [Reference Artin, Demazure, Grothendieck, Raynaud and Serre1, Exposé XVII, Proposition 2.4]. It follows that the group schemes
![]() $\mathcal {H}om_S(F,G_i)$
, for
$\mathcal {H}om_S(F,G_i)$
, for
![]() $i=1,2$
, are étale and quasi-finite over S. By [Reference Dieudonné and Grothendieck5, Corollary 17.3.5],
$i=1,2$
, are étale and quasi-finite over S. By [Reference Dieudonné and Grothendieck5, Corollary 17.3.5],
![]() $\alpha $
is étale. It is also separated. It follows that H is étale separated and quasi-finite. This finishes the proof.
$\alpha $
is étale. It is also separated. It follows that H is étale separated and quasi-finite. This finishes the proof.
B Fiberwise flatness for algebraic stacks
Lemma B.1 Let
![]() $\mathcal {S}$
be a locally Noetherian algebraic stack. Let
$\mathcal {S}$
be a locally Noetherian algebraic stack. Let
![]() $f:\mathcal {X}\to \mathcal {Y}$
be a 1-morphism of locally Noetherian algebraic stacks over
$f:\mathcal {X}\to \mathcal {Y}$
be a 1-morphism of locally Noetherian algebraic stacks over
![]() $\mathcal {S}$
, where
$\mathcal {S}$
, where
![]() $\mathcal {X}$
is flat over
$\mathcal {X}$
is flat over
![]() $\mathcal {S}$
. Assume that
$\mathcal {S}$
. Assume that
![]() $f_{s}:\mathcal {X}_{s}\to \mathcal {Y}_{s}$
is flat for all points (valued in fields)
$f_{s}:\mathcal {X}_{s}\to \mathcal {Y}_{s}$
is flat for all points (valued in fields)
![]() $s:\mathop {\mathrm {Spec}}(k(s))\to \mathcal {S}$
. Then f is flat.
$s:\mathop {\mathrm {Spec}}(k(s))\to \mathcal {S}$
. Then f is flat.
Proof As being locally Noetherian and flatness of a morphism are local for the smooth topology, everything reduces to the case of schemes, where the relevant statement is [24, Tag 039D].
More precisely, we have a commutative diagram
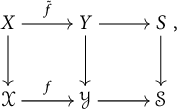
where the vertical morphisms are smooth covers by locally Noetherian schemes. We then let
![]() $s':\mathop {\mathrm {Spec}}(k(s))\to S$
be a point of S. It maps to a point s of
$s':\mathop {\mathrm {Spec}}(k(s))\to S$
be a point of S. It maps to a point s of
![]() $\mathcal {S}$
. We then get a commutative diagram
$\mathcal {S}$
. We then get a commutative diagram
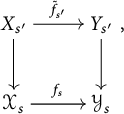
where again the vertical maps are smooth coverings by schemes. Now
![]() $f_{s}$
is flat by assumption. But this is the same thing as saying that
$f_{s}$
is flat by assumption. But this is the same thing as saying that
![]() $\tilde {f}_{s'}$
is flat (see, for example, [24, Tag 06FN] and note that flatness is local on the source and the target). Hence,
$\tilde {f}_{s'}$
is flat (see, for example, [24, Tag 06FN] and note that flatness is local on the source and the target). Hence,
![]() $\tilde {f}_{s'}$
is flat for all
$\tilde {f}_{s'}$
is flat for all
![]() $s'\in S$
. So, by the fiberwise flatness criterion for schemes,
$s'\in S$
. So, by the fiberwise flatness criterion for schemes,
![]() $\tilde {f}$
is flat as well. This, in turn, implies that f is flat.
$\tilde {f}$
is flat as well. This, in turn, implies that f is flat.
Corollary B.2 Let
![]() $S_0$
be a Noetherian fs log scheme, and let
$S_0$
be a Noetherian fs log scheme, and let
![]() $S_0\to S$
be a strict closed immersion defined by a nilpotent sheaf of ideals I. Let
$S_0\to S$
be a strict closed immersion defined by a nilpotent sheaf of ideals I. Let
![]() $f:G\to H$
be a morphism of Noetherian fs log schemes over S with
$f:G\to H$
be a morphism of Noetherian fs log schemes over S with
![]() $G\to S$
log flat. Assume that
$G\to S$
log flat. Assume that
![]() $f_0:=f\times _SS_0:G_0\to H_0$
is log flat. Then f is log flat.
$f_0:=f\times _SS_0:G_0\to H_0$
is log flat. Then f is log flat.
Proof Consider the following diagram of algebraic stacks:
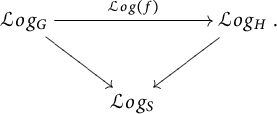
Here, if Z is a log scheme,
![]() $\mathcal {L}og_{Z}$
denotes the stack of log structures introduced in [Reference Olsson22, Section 1]. It is an algebraic stack. If Z is locally Noetherian, then so is
$\mathcal {L}og_{Z}$
denotes the stack of log structures introduced in [Reference Olsson22, Section 1]. It is an algebraic stack. If Z is locally Noetherian, then so is
![]() $\mathcal {L}og_Z$
(by [Reference Olsson22, Corollary 5.25]). Furthermore, a morphism
$\mathcal {L}og_Z$
(by [Reference Olsson22, Corollary 5.25]). Furthermore, a morphism
![]() $f:Z\to Z'$
of fine log schemes is log flat if and only if the induced morphism
$f:Z\to Z'$
of fine log schemes is log flat if and only if the induced morphism
![]() $\mathcal {L}og(f):\mathcal {L}og_{Z}\to \mathcal {L}og_{Z'}$
is flat (see [Reference Olsson22, Theorem 4.6 and Remark 4.7]).
$\mathcal {L}og(f):\mathcal {L}og_{Z}\to \mathcal {L}og_{Z'}$
is flat (see [Reference Olsson22, Theorem 4.6 and Remark 4.7]).
Moreover, by [Reference Olsson22, Proposition 3.20], the diagram above reduces modulo I to
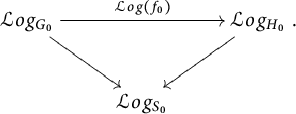
Now, as
![]() $f_{0}$
is log flat,
$f_{0}$
is log flat,
![]() $\mathcal {L}og(f_{0})$
is flat. Thus, by the fiberwise flatness criterion for algebraic stacks (see Lemma B.1),
$\mathcal {L}og(f_{0})$
is flat. Thus, by the fiberwise flatness criterion for algebraic stacks (see Lemma B.1),
![]() $\mathcal {L}og(f)$
is flat as well, which means that f is log flat.
$\mathcal {L}og(f)$
is flat as well, which means that f is log flat.
C Kummer log flat descent of finiteness
Following [Reference Nakayama19, Definition 1.9], we say a morphism
![]() $f:X\to S$
of fs log scheme is finite (resp. quasi-finite, resp. separated, resp. proper, resp. universally closed, resp. locally of finite presentation, surjective), if the underlying morphism of schemes is so.
$f:X\to S$
of fs log scheme is finite (resp. quasi-finite, resp. separated, resp. proper, resp. universally closed, resp. locally of finite presentation, surjective), if the underlying morphism of schemes is so.
Remark C.1. According to [Reference Olsson22, Lemma 4.8],
![]() $f:X\to S$
is locally of finite presentation if and only if the induced morphism
$f:X\to S$
is locally of finite presentation if and only if the induced morphism
![]() $\mathcal {L}og(f):\mathcal {L}og_X\to \mathcal {L}og_S$
of algebraic stacks is locally of finite presentation, where
$\mathcal {L}og(f):\mathcal {L}og_X\to \mathcal {L}og_S$
of algebraic stacks is locally of finite presentation, where
![]() $\mathcal {L}og_T$
, for a log scheme T, is the stack of log structures as in [Reference Olsson22, Section 1].
$\mathcal {L}og_T$
, for a log scheme T, is the stack of log structures as in [Reference Olsson22, Section 1].
By [24, Tag 02LA], the finiteness of morphisms of schemes descends in the fpqc topology. According to [Reference Kato13, Theorem 7.1], the descent of the finiteness of morphisms of fs log schemes in the Kummer flat topology has been shown in Tani’s thesis [Reference Tani25]. However, the thesis is in Japanese, so we present a proof here.
Let
![]() $X\to S$
and
$X\to S$
and
![]() $T\to S$
be two morphisms of fs log schemes. We denote by
$T\to S$
be two morphisms of fs log schemes. We denote by
![]() $\mathring {X}\times _{\mathring {S}}\mathring {T}$
the fiber product of the underlying schemes. Note that in this article
$\mathring {X}\times _{\mathring {S}}\mathring {T}$
the fiber product of the underlying schemes. Note that in this article
![]() $X\times _ST$
denotes the fiber product in the category of fs log schemes.
$X\times _ST$
denotes the fiber product in the category of fs log schemes.
Proposition C.2 Let
![]() $f:X\to S$
be a morphism of fs log schemes, and let
$f:X\to S$
be a morphism of fs log schemes, and let
![]() $g:S'\to S$
be a Kummer log flat cover (see Definition 2.1). Let
$g:S'\to S$
be a Kummer log flat cover (see Definition 2.1). Let
![]() $f':X':=X\times _SS'\rightarrow S'$
be the base change of f. Then f is finite if and only if
$f':X':=X\times _SS'\rightarrow S'$
be the base change of f. Then f is finite if and only if
![]() $f'$
is finite.
$f'$
is finite.
Proof If f is finite, so is
![]() $f'$
by [Reference Nakayama19, Section 1.10].
$f'$
by [Reference Nakayama19, Section 1.10].
Conversely, assume that
![]() $f'$
is finite. To show that f is finite, we need to show that f is (1) quasi-finite, (2) universally closed, (3) separated, and (4) of finite type.
$f'$
is finite. To show that f is finite, we need to show that f is (1) quasi-finite, (2) universally closed, (3) separated, and (4) of finite type.
(1) The quasi-finiteness of f follows from Nakayama’s “fourth point lemma” (see [Reference Nakayama19, Section 2.2.2]) and the finiteness of
![]() $f'$
.
$f'$
.
(2) To show that f is universally closed, it suffices to show that for any strict morphism
![]() $U\to S$
, the base change
$U\to S$
, the base change
![]() $X\times _SU\to U$
is closed. Consider the following diagram
$X\times _SU\to U$
is closed. Consider the following diagram
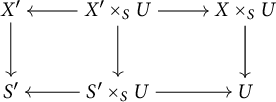
with the two squares Cartesian. Since
![]() $X'\to S'$
is universally closed and
$X'\to S'$
is universally closed and
![]() $S'\times _SU\to S'$
is strict, the map
$S'\times _SU\to S'$
is strict, the map
![]() $X'\times _SU\to S'\times _SU$
is closed. Since
$X'\times _SU\to S'\times _SU$
is closed. Since
![]() $S'\to S$
is a Kummer log flat cover, so are
$S'\to S$
is a Kummer log flat cover, so are
![]() $S'\times _SU\to U$
and
$S'\times _SU\to U$
and
![]() $X'\times _SU\to X\times _SU$
. By [Reference Kato13, Proposition 2.5], the underlying topological maps of
$X'\times _SU\to X\times _SU$
. By [Reference Kato13, Proposition 2.5], the underlying topological maps of
![]() $S'\times _SU\to U$
and
$S'\times _SU\to U$
and
![]() $X'\times _SU\to X\times _SU$
are open and surjective.
$X'\times _SU\to X\times _SU$
are open and surjective.
Let
![]() $(\mathrm {logSch}/S)$
be the category of log schemes over S, and let
$(\mathrm {logSch}/S)$
be the category of log schemes over S, and let
![]() $(\mathrm {int}/S)$
be the full subcategory consisting of integral log schemes over S. Recall that
$(\mathrm {int}/S)$
be the full subcategory consisting of integral log schemes over S. Recall that
![]() $(\mathrm {fs}/S)$
is the full subcategory consisting of fs log schemes over S. We denote by Z the fiber product of
$(\mathrm {fs}/S)$
is the full subcategory consisting of fs log schemes over S. We denote by Z the fiber product of
![]() $S'\times _SU$
and
$S'\times _SU$
and
![]() $X\times _SU$
over U in
$X\times _SU$
over U in
![]() $(\mathrm {logSch}/S)$
. Then the integral log scheme
$(\mathrm {logSch}/S)$
. Then the integral log scheme
![]() $Z^{\mathrm {int}}$
associated with Z is the fiber product of
$Z^{\mathrm {int}}$
associated with Z is the fiber product of
![]() $S'\times _SU$
and
$S'\times _SU$
and
![]() $X\times _SU$
over U in
$X\times _SU$
over U in
![]() $(\mathrm {int}/S)$
, and the fs log scheme
$(\mathrm {int}/S)$
, and the fs log scheme
![]() $Z^{\mathrm {fs}}:=(Z^{\mathrm {int}})^{\mathrm {sat}}$
associated with
$Z^{\mathrm {fs}}:=(Z^{\mathrm {int}})^{\mathrm {sat}}$
associated with
![]() $Z^{\mathrm {int}}$
is the fiber product of
$Z^{\mathrm {int}}$
is the fiber product of
![]() $S'\times _SU$
and
$S'\times _SU$
and
![]() $X\times _SU$
over U in
$X\times _SU$
over U in
![]() $(\mathrm {fs}/S)$
(see [Reference Ogus21, Chapter III, Proposition 2.1.5 and Corollary 2.1.6]). Note that the fiber product
$(\mathrm {fs}/S)$
(see [Reference Ogus21, Chapter III, Proposition 2.1.5 and Corollary 2.1.6]). Note that the fiber product
![]() $Z^{\mathrm {fs}}$
of
$Z^{\mathrm {fs}}$
of
![]() $S'\times _SU$
and
$S'\times _SU$
and
![]() $X\times _SU$
over U in
$X\times _SU$
over U in
![]() $(\mathrm {fs}/S)$
is nothing but the fiber product
$(\mathrm {fs}/S)$
is nothing but the fiber product
![]() $X'\times _SU$
(in
$X'\times _SU$
(in
![]() $(\mathrm {fs}/S)$
). The map
$(\mathrm {fs}/S)$
). The map
![]() $X'\times _S U=Z^{\mathrm {fs}}\to Z^{\mathrm {int}}$
is finite and surjective by [Reference Ogus21, Chapter III, Proposition 2.1.5(2)], and the map
$X'\times _S U=Z^{\mathrm {fs}}\to Z^{\mathrm {int}}$
is finite and surjective by [Reference Ogus21, Chapter III, Proposition 2.1.5(2)], and the map
![]() $Z^{\mathrm {int}}\to Z$
is a nil immersion by [Reference Ogus21, Chapter III, Corollary 2.2.4]. Now we put the information useful for us in the following commutative diagram
$Z^{\mathrm {int}}\to Z$
is a nil immersion by [Reference Ogus21, Chapter III, Corollary 2.2.4]. Now we put the information useful for us in the following commutative diagram
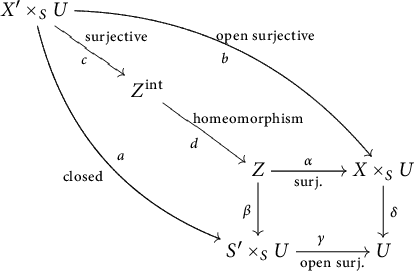
of topological spaces. To prove that
![]() $X\times _SU\to U$
is closed, it suffices to show that
$X\times _SU\to U$
is closed, it suffices to show that
![]() $\delta (V)$
is closed for any closed subset V of
$\delta (V)$
is closed for any closed subset V of
![]() $X\times _SU$
. Since c is surjective, one can check that
$X\times _SU$
. Since c is surjective, one can check that
![]() $\beta (\alpha ^{-1}(V))=a(b^{-1}(V))$
. Since the map a is closed, the set
$\beta (\alpha ^{-1}(V))=a(b^{-1}(V))$
. Since the map a is closed, the set
![]() $\beta (\alpha ^{-1}(V))$
is closed. Since
$\beta (\alpha ^{-1}(V))$
is closed. Since
![]() $\alpha $
is surjective, one sees that
$\alpha $
is surjective, one sees that
![]() $\delta (V)=\gamma (\beta (\alpha ^{-1}(V)))$
. By the Cartesian property of the inner square in the category of schemes, one sees that
$\delta (V)=\gamma (\beta (\alpha ^{-1}(V)))$
. By the Cartesian property of the inner square in the category of schemes, one sees that
![]() $\gamma ^{-1}(\delta (V))=\beta (\alpha ^{-1}(V))$
by [Reference Görtz and Wedhorn6, Lemma 4.28]. Since
$\gamma ^{-1}(\delta (V))=\beta (\alpha ^{-1}(V))$
by [Reference Görtz and Wedhorn6, Lemma 4.28]. Since
![]() $\gamma $
is open and
$\gamma $
is open and
![]() $\beta (\alpha ^{-1}(V))$
is closed, we get that
$\beta (\alpha ^{-1}(V))$
is closed, we get that
![]() $\delta (V)$
is closed.
$\delta (V)$
is closed.
(3) Let
![]() $\Delta _{X'/S'}:X'\rightarrow X'\times _{S'}X'$
(resp.
$\Delta _{X'/S'}:X'\rightarrow X'\times _{S'}X'$
(resp.
![]() $\Delta _{\mathring {X}'/\mathring {S}'}:\mathring {X}'\rightarrow \mathring {X}'\times _{\mathring {S}'}\mathring {X}'$
) be the diagonal map in the category of fs log schemes (resp. category of schemes). Similarly for
$\Delta _{\mathring {X}'/\mathring {S}'}:\mathring {X}'\rightarrow \mathring {X}'\times _{\mathring {S}'}\mathring {X}'$
) be the diagonal map in the category of fs log schemes (resp. category of schemes). Similarly for
![]() $\Delta _{X/S}$
and
$\Delta _{X/S}$
and
![]() $\Delta _{\mathring {X}/\mathring {S}}$
. We have
$\Delta _{\mathring {X}/\mathring {S}}$
. We have
![]() $X'\times _{S'}X'=(X\times _SX)\times _SS'$
(resp.
$X'\times _{S'}X'=(X\times _SX)\times _SS'$
(resp.
![]() $\mathring {X}'\times _{\mathring {S}'}\mathring {X}'=(\mathring {X}\times _{\mathring {S}}\mathring {X})\times _{\mathring {S}}\mathring {S}'$
) and
$\mathring {X}'\times _{\mathring {S}'}\mathring {X}'=(\mathring {X}\times _{\mathring {S}}\mathring {X})\times _{\mathring {S}}\mathring {S}'$
) and
![]() $\Delta _{X'/S'}=\Delta _{X/S}\times _SS'$
(resp.
$\Delta _{X'/S'}=\Delta _{X/S}\times _SS'$
(resp.
![]() $\Delta _{\mathring {X}'/\mathring {S}'}=\Delta _{\mathring {X}/\mathring {S}}\times _{\mathring {S}}\mathring {S}'$
). In the commutative diagram
$\Delta _{\mathring {X}'/\mathring {S}'}=\Delta _{\mathring {X}/\mathring {S}}\times _{\mathring {S}}\mathring {S}'$
). In the commutative diagram
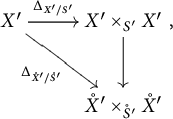
the map
![]() $\Delta _{\mathring {X}'/\mathring {S}'}$
is a closed immersion by the separatedness of
$\Delta _{\mathring {X}'/\mathring {S}'}$
is a closed immersion by the separatedness of
![]() $X'\to S'$
, the map
$X'\to S'$
, the map
![]() $X'\times _{S'}X'\to \mathring {X}'\times _{\mathring {S}'}\mathring {X}'$
is finite by [Reference Nakayama19, Section 1.10]; hence,
$X'\times _{S'}X'\to \mathring {X}'\times _{\mathring {S}'}\mathring {X}'$
is finite by [Reference Nakayama19, Section 1.10]; hence,
![]() $\Delta _{X'/S'}$
is a closed immersion. In particular,
$\Delta _{X'/S'}$
is a closed immersion. In particular,
![]() $\Delta _{X'/S'}$
is universally closed. By the descent of universal closeness along Kummer log flat covers from the last part, we have that
$\Delta _{X'/S'}$
is universally closed. By the descent of universal closeness along Kummer log flat covers from the last part, we have that
![]() $\Delta _{X/S}$
is universally closed. The finite morphism
$\Delta _{X/S}$
is universally closed. The finite morphism
![]() $X\times _SX\to \mathring {X}\times _{\mathring {S}}\mathring {X}$
is clearly universally closed; hence,
$X\times _SX\to \mathring {X}\times _{\mathring {S}}\mathring {X}$
is clearly universally closed; hence,
![]() $\Delta _{\mathring {X}/\mathring {S}}$
as the composition
$\Delta _{\mathring {X}/\mathring {S}}$
as the composition
![]() $X\xrightarrow {\Delta _{X/S}} X\times _SX\to \mathring {X}\times _{\mathring {S}}\mathring {X}$
is also universally closed. By [24, Tag 01KJ],
$X\xrightarrow {\Delta _{X/S}} X\times _SX\to \mathring {X}\times _{\mathring {S}}\mathring {X}$
is also universally closed. By [24, Tag 01KJ],
![]() $\Delta _{\mathring {X}/\mathring {S}}$
is an immersion. It follows that
$\Delta _{\mathring {X}/\mathring {S}}$
is an immersion. It follows that
![]() $\Delta _{\mathring {X}/\mathring {S}}$
is a closed immersion, i.e., X is separated over S.
$\Delta _{\mathring {X}/\mathring {S}}$
is a closed immersion, i.e., X is separated over S.
(4) By [24, Tag 04XU], the universally closed map
![]() $f:X\to S$
is quasi-compact. Thus, to show that f is of finite type, it suffices to show that it is locally of finite type. By [24, Tag 02KX], being locally of finite type is local on the target for the fppf topology. Therefore, we may assume that the Kummer log flat cover g is as in the local situation of [Reference Illusie, Nakayama and Tsuji7, Proposition 1.3], i.e., g admits a chart
$f:X\to S$
is quasi-compact. Thus, to show that f is of finite type, it suffices to show that it is locally of finite type. By [24, Tag 02KX], being locally of finite type is local on the target for the fppf topology. Therefore, we may assume that the Kummer log flat cover g is as in the local situation of [Reference Illusie, Nakayama and Tsuji7, Proposition 1.3], i.e., g admits a chart
![]() $(Q\to M_{S'},P\to M_S, P\xrightarrow {h} Q)$
with P, Q fs monoids, and h Kummer, and thus g admits a factorization
$(Q\to M_{S'},P\to M_S, P\xrightarrow {h} Q)$
with P, Q fs monoids, and h Kummer, and thus g admits a factorization
![]() $S'\xrightarrow {g_1} S"\xrightarrow {g_2} S$
of g with
$S'\xrightarrow {g_1} S"\xrightarrow {g_2} S$
of g with
![]() $S":=S\times _{\mathop {\mathrm {Spec}}{\mathbb Z}[P]}\mathop {\mathrm {Spec}}{\mathbb Z}[Q]$
and
$S":=S\times _{\mathop {\mathrm {Spec}}{\mathbb Z}[P]}\mathop {\mathrm {Spec}}{\mathbb Z}[Q]$
and
![]() $g_1$
a classical fppf cover. Consider the following diagram
$g_1$
a classical fppf cover. Consider the following diagram
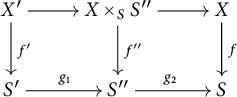
with the two small squares Cartesian. Since
![]() $f'$
is of finite type, so is
$f'$
is of finite type, so is
![]() $f"$
by [24, Tag 02KZ]. By [Reference Illusie, Nakayama and Tsuji7, Lemma 2.1],
$f"$
by [24, Tag 02KZ]. By [Reference Illusie, Nakayama and Tsuji7, Lemma 2.1],
![]() $g_2$
satisfies the condition on the base change map in [Reference Illusie, Nakayama and Tsuji7, Lemma 2.3]. From this, we further get that f is locally of finite type. This finishes the proof.
$g_2$
satisfies the condition on the base change map in [Reference Illusie, Nakayama and Tsuji7, Lemma 2.3]. From this, we further get that f is locally of finite type. This finishes the proof.
D Decomposition of Kummer log flat torsors under classical finite flat group schemes over Henselian local base
Let S be a locally Noetherian fs log scheme, and let
![]() $\varepsilon :(\mathrm {fs}/S)_{\mathrm {kfl}}\to (\mathrm {fs}/S)_{\mathrm {fl}}$
be the forgetful map between these two sites. Let G be a finite flat group scheme over the underlying scheme of S, and we endow it with the induced log structure from S. The Leray spectral sequence
$\varepsilon :(\mathrm {fs}/S)_{\mathrm {kfl}}\to (\mathrm {fs}/S)_{\mathrm {fl}}$
be the forgetful map between these two sites. Let G be a finite flat group scheme over the underlying scheme of S, and we endow it with the induced log structure from S. The Leray spectral sequence
![]() $H^i_{\mathrm {fl}}(S,R^j\varepsilon _*G)\Rightarrow H^{i+j}_{\mathrm {kfl}}(S,G)$
gives rise to an exact sequence
$H^i_{\mathrm {fl}}(S,R^j\varepsilon _*G)\Rightarrow H^{i+j}_{\mathrm {kfl}}(S,G)$
gives rise to an exact sequence
Proposition D.1 Assume that the underlying scheme of S is the spectrum of a Henselian local ring and that the log structure of S admits a chart
![]() $P\to M_S$
for an fs monoid P such that the induced map
$P\to M_S$
for an fs monoid P such that the induced map
![]() $P\to M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism, where s denotes the closed point of S. Then we have the following.
$P\to M_{S,\bar {s}}/\mathcal {O}_{S,\bar {s}}^{\times }$
is an isomorphism, where s denotes the closed point of S. Then we have the following.
-
(1) Let n be a positive integer which kills G. Then
 $$ \begin{align*} H^0_{\mathrm{fl}}(S,R^1\varepsilon_*G)=&H^0_{\mathrm{fl}}(S,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}(\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{fl}}}) \\ =&\mathrm{Hom}_S(\mathbb Z/n\mathbb Z(1),G)\otimes_{\mathbb Z}P^{\mathrm{gp}}. \end{align*} $$
$$ \begin{align*} H^0_{\mathrm{fl}}(S,R^1\varepsilon_*G)=&H^0_{\mathrm{fl}}(S,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}(\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{fl}}}) \\ =&\mathrm{Hom}_S(\mathbb Z/n\mathbb Z(1),G)\otimes_{\mathbb Z}P^{\mathrm{gp}}. \end{align*} $$
-
(2) The short exact sequence
 $0\to {\mathbb Z}/n{\mathbb Z}(1)\to \mathbb {G}_{\mathrm {m,log}}\xrightarrow {n}\mathbb {G}_{\mathrm {m,log}}\to 0$
on
$0\to {\mathbb Z}/n{\mathbb Z}(1)\to \mathbb {G}_{\mathrm {m,log}}\xrightarrow {n}\mathbb {G}_{\mathrm {m,log}}\to 0$
on
 $(\mathrm {fs}/S)_{\mathrm {kfl}}$
gives rise to a canonical map
$(\mathrm {fs}/S)_{\mathrm {kfl}}$
gives rise to a canonical map
 $\delta :H^0_{\mathrm {kfl}}(S,\mathbb {G}_{\mathrm {m,log}})\to H^1_{\mathrm {kfl}}(S,{\mathbb Z}/n{\mathbb Z}(1))$
. For any
$\delta :H^0_{\mathrm {kfl}}(S,\mathbb {G}_{\mathrm {m,log}})\to H^1_{\mathrm {kfl}}(S,{\mathbb Z}/n{\mathbb Z}(1))$
. For any
 $a\in P^{\mathrm {gp}}$
, let
$a\in P^{\mathrm {gp}}$
, let
 $T_a$
denote the Kummer log flat
$T_a$
denote the Kummer log flat
 ${\mathbb Z}/n{\mathbb Z}(1)$
-torsor over S given by
${\mathbb Z}/n{\mathbb Z}(1)$
-torsor over S given by
 $\delta (a)$
. Then the map
$\delta (a)$
. Then the map
 $\alpha $
from the exact sequence (D.1) admits a canonical section given by
$\alpha $
from the exact sequence (D.1) admits a canonical section given by  $$ \begin{align*}\beta:\mathrm{Hom}_S(\mathbb Z/n\mathbb Z(1),G)\otimes_{\mathbb Z}P^{\mathrm{gp}}\to H^{1}_{\mathrm{kfl}}(S,G),\quad h\otimes_{{\mathbb Z}}a\mapsto h_*T_a.\end{align*} $$
$$ \begin{align*}\beta:\mathrm{Hom}_S(\mathbb Z/n\mathbb Z(1),G)\otimes_{\mathbb Z}P^{\mathrm{gp}}\to H^{1}_{\mathrm{kfl}}(S,G),\quad h\otimes_{{\mathbb Z}}a\mapsto h_*T_a.\end{align*} $$
-
(3) We have a canonical (after having fixed P) decomposition
(D.2) $$ \begin{align} H^{1}_{\mathrm{kfl}}(S,G)\cong H^{1}_{\mathrm{fl}}(S,G)\oplus \mathrm{Hom}_S(\mathbb Z/n\mathbb Z(1),G)\otimes_{\mathbb Z}P^{\mathrm{gp}}. \end{align} $$
$$ \begin{align} H^{1}_{\mathrm{kfl}}(S,G)\cong H^{1}_{\mathrm{fl}}(S,G)\oplus \mathrm{Hom}_S(\mathbb Z/n\mathbb Z(1),G)\otimes_{\mathbb Z}P^{\mathrm{gp}}. \end{align} $$
Proof (1) Let
![]() $\mathcal {G}:=(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
. By Kato’s theorem (see [Reference Kato13, Theorem 4.1] or [Reference Nizioł20, Theorem 3.12]), we have an isomorphism
$\mathcal {G}:=(\mathbb {G}_{\mathrm {m,log}}/\mathbb {G}_{\mathrm {m}})_{S_{\mathrm {fl}}}$
. By Kato’s theorem (see [Reference Kato13, Theorem 4.1] or [Reference Nizioł20, Theorem 3.12]), we have an isomorphism
which is locally given by the map
![]() $\beta $
(see [Reference Kato13, Section 4.3]). Consider the following canonical commutative diagram:
$\beta $
(see [Reference Kato13, Section 4.3]). Consider the following canonical commutative diagram:

By [24, Tag 09ZI], we have
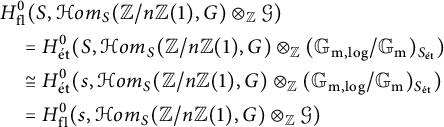 $$ \begin{align*} &H^0_{\mathrm{fl}}(S,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}\mathcal{G}) \\ & \quad =H^0_{\mathrm{\acute{e}t}}(S,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}(\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{\acute{e}t}}}) \\ & \quad \cong H^0_{\mathrm{\acute{e}t}}(s,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}(\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{\acute{e}t}}}) \\ & \quad =H^0_{\mathrm{fl}}(s,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}\mathcal{G}) \end{align*} $$
$$ \begin{align*} &H^0_{\mathrm{fl}}(S,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}\mathcal{G}) \\ & \quad =H^0_{\mathrm{\acute{e}t}}(S,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}(\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{\acute{e}t}}}) \\ & \quad \cong H^0_{\mathrm{\acute{e}t}}(s,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}(\mathbb{G}_{\mathrm{m,log}}/\mathbb{G}_{\mathrm{m}})_{S_{\mathrm{\acute{e}t}}}) \\ & \quad =H^0_{\mathrm{fl}}(s,\mathcal{H}om_S({\mathbb Z}/n{\mathbb Z}(1),G)\otimes_{{\mathbb Z}}\mathcal{G}) \end{align*} $$
and
Let k be the residue field of S. The property of the given chart forces the induced log structure on s to be the one associated with
 $P\mapsto k,p\mapsto \begin {cases}0,&\text { if } p\neq 0, \\ 1,&\text {otherwise.}\end {cases}$
Hence, the lower horizontal map in (D.4) is clearly an isomorphism. Then part (1) follows from the commutative diagram (D.4).
$P\mapsto k,p\mapsto \begin {cases}0,&\text { if } p\neq 0, \\ 1,&\text {otherwise.}\end {cases}$
Hence, the lower horizontal map in (D.4) is clearly an isomorphism. Then part (1) follows from the commutative diagram (D.4).
(2) Since the map
![]() $\gamma $
from (D.3) is locally constructed in the same way as
$\gamma $
from (D.3) is locally constructed in the same way as
![]() $\beta $
, the diagram
$\beta $
, the diagram
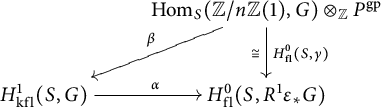
is commutative. Therefore,
![]() $\beta $
is a section to
$\beta $
is a section to
![]() $\alpha $
after the identification
$\alpha $
after the identification
![]() $H^0_{\mathrm {fl}}(S,\gamma )$
.
$H^0_{\mathrm {fl}}(S,\gamma )$
.
Part (3) follows from part (2) and the exact sequence (D.1).
Acknowledgment
The second-named author thanks Professor Ulrich Görtz for very helpful discussions and the Deutsche Arberitsgemeinschaft Kleine AG 2018 “Deformationen abelscher Varietäten,” from which he has benefited a lot. We wish to thank the anonymous referees for very helpful suggestions for improvements.