Satellite gravity and the mass balance of the antarctic ice sheet

Abstract

Changes in the Earth’s gravity field with time have important applications to a broad range of disciplines. Any process that involves a large enough horizontal redistribution of mass, either within the Earth or on or above its surface, is potentially detectable. In particular, when ice sheets grow or shrink, gravity changes as mass is redistributed in the solid earth and between the oceans and the ice sheets. The sources of global sea-level rise (about 2 mm a⁻¹ over the last century) and in particular the contribution of the Antarctic ice sheet thereto are not well understood. Gravity measurements can help to diminish this uncertainty.

The technology currently exists to measure gravity with high accuracy by a dual-satellite mission in which the distance between the satellites is precisely monitored. We estimate from recent studies that temporal changes in the gravity field as determined by a satellite gravity mission lasting 5 years at an orbital height of 400 km would be sensitive to changes in the overall mass of the Antarctic ice sheet to a precision corresponding to better than 0.01 mm a⁻¹ of sea-level change. However, the effects of three other phenomena that could each produce a temporally varying gravity signal with characteristics comparable to that caused by a change in Antarctic ice—postglacial rebound, inter-annual variability in snowfall, and atmospheric pressure trends — also need to be evaluated. Postglacial rebound could be partly separated from ice-mass changes with the aid of global positioning system campaigns and numerical models of rebound that use improved determinations of mantle viscosity also provided by the gravity mission. Determination of inter-annual ice-mass changes will be aided by measurements of moisture-flux divergence around the perimeters of the ice sheets and direct observations of inter-annual changes by the gravity satellite itself. The removal of pressure effects over Antarctica will become more effective as the number of automatic weather stations in the interior of the continent increases.

Even after corrections are made for these factors, the uncertainties they cause limit the accuracy in the détermination of the contribution of the Antarctic ice sheet to sea-level change to about 0.5 mm a⁻¹. However, there is a strong complementarity between gravity measurements and the surface-height measurements that will be produced by NASA’s laser altimeter mission early next century. Together, they should be able to determine that contribution to an accuracy of about 0.1 mm a⁻¹.

Introduction

The mass of the inland Antarctic ice sheet (i.e. the grounded portion; Fig. 1) varies temporally through the exchange of water with the oceans. It gains mass only by snowfall on its surface; the moisture source is evaporation from the oceans. Mass is lost to the ocean primarily by solid flow across the margins of the inland ice, i.e. across the grounding line, and secondarily by excess melting and liquid water runoff. Thus, the measurement of the total change in mass of the ice on land is a direct (though partial) measure of the change of water mass in the oceans. Currently, the large-scale mass balance of the Antarctic ice sheet is poorly known. Estimates of the Antarctic contribution to the observed global sea-level rise during this century are in the range 0 ± 1.4 mm a⁻¹ (Warrick and others, 1996); not even the sign is known. This corresponds to the yearly addition or removal of a layer of water 40 mm thick, spread over the ice sheet, i.e. some 25% of the annual average input of ~ 150 mm a⁻¹ personal communication from D.H Bromwich,1997) (hereafter we express changes in the ice sheet in mm a⁻¹; “water equivalent” is to be understood).

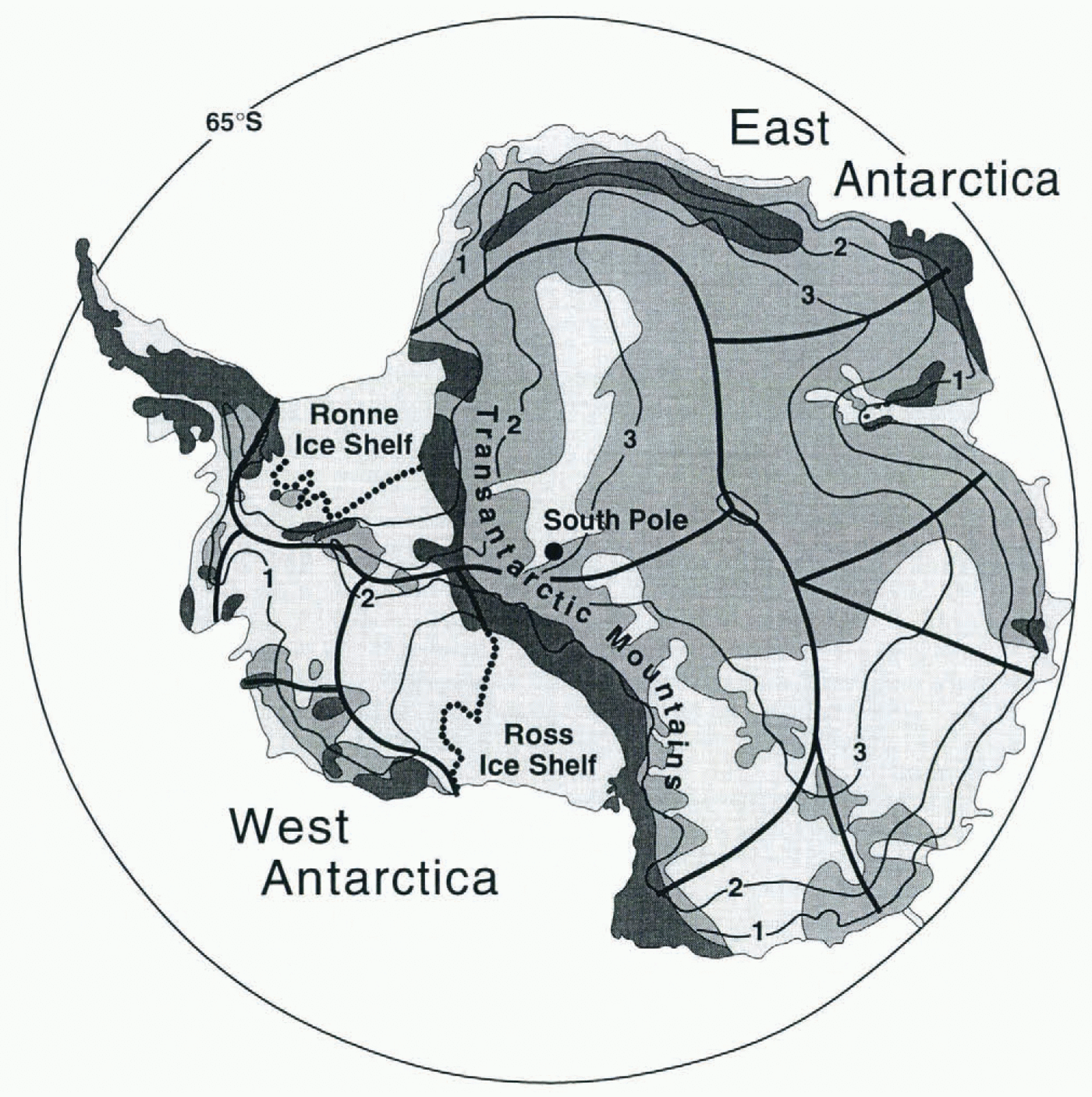
Fig. 1. Map of the inland (grounded) ice sheet of Antarctica, showing surface elevations (black contour lines; heights in km), mountainous regions (dark gray) and sections of the ice sheet where the bed is above (medium gray) and below (light gray) sea level. The heavy black lines divide the principal drainage systems. The grounding lines of the Ross and Filchner-Ronne Ice Shelves are designated by the black dotted lines.

Satellite Gravity Measurements

There are at least three major advantages of satellite gravity measurements for large-scale mass-balance studies. The first is that since gravity depends simply on mass, changes in gravity provide a direct measure of ice-mass balance that is independent of the mean density of the ice sheet, which can change with time. Secondly, gravity integrates spatially, thus obviating the huge difficulty that glaciologists face in extrapolating results from field studies in a few areas to much larger regions, especially to an entire ice sheet. Thirdly, satellite gravity rapidly provides a measure of ice-sheet mass at a particular epoch; repeated measurements at later limes yield mass changes over well-defined time intervals. Therein lies a limitation of the technique also: any result would be representative of the ice sheet for only the relatively brief duration of the satellite mission.

The U.S. National Research Council recently completed a study on satellite gravity that includes an examination of its value for studying glaciers and ice sheets (USNRC, 1997). This paper is based on the findings of that report, to which we contributed. In that report several different gravity-mission scenarios, involving different instrumental concepts, were examined. Here, we will consider only one of those concepts, known as “satellite-to-satellite tracking” (SST). In this scheme, differential orbital perturbations arc measured by placing two satellites in the same orbit, separated from each other by a few hundred kilometers, so that in effect one satellite “chases” the other. A microwave link between the two satellites is used to measure the line-of-sight range rate (time derivative of the inter-satellite distance), which, in turn, provides information on the gravitational accelerations acting on the two satellites. We choose this single scheme not only to simplify the discussion, but also because it is the basic concept of the gravity recovery and climate experiment (GRACE), recently accepted by NASA as one of the two initial missions for its Earth System Science Pathfinder program. We further assume that the orbital height is 400 km and that the mission lasts for 5 years.

Our purpose here is to assess what changes in the mass of the Antarctic ice sheet would be detectable by such a satellite gravity mission. The outer bounds of the Antarctic contribution to sea-level change (±1.4 mm a⁻¹) cited above correspond to a change in height of the Antarctic geoid of about 2.2 mm a⁻¹. However, that is not a convenient form in which to make a sensitivity comparison. Instead, the spherical harmonic components of the geoidal perturbation caused by a particular distribution of mass change were estimated and compared with the estimated measurement errors for the SST mission. (A number of simplifying assumptions about the errors to be expected in the measurements were made to permit their analytical evaluation. Further details can be found in the USNRC (1997) report. From the harmonic components it is possible to calculate the sensitivity of the gravity mission to mass layers distributed evenly on surface squares of different lateral dimensions (Fig. 2). Approximating Antarctica by a square about 3500 km on a side, we estimate from Figure 2 that the assumed SST mission would be sensitive to changes in the overall mass of the Antarctic ice sheet to an astonishing accuracy of 0.1 mm a⁻¹, i.e. only 3μma⁻¹ of sea-level rise! It would be nice to think that all problems of Antarctic ice-sheet mass balance would thereby be solved. Unfortunately, there are major ambiguities in interpreting the gravity-signals over the ice sheet, that limit the accuracy of the mass-balance determinations.

Fig. 2. Sensitivity to variations in the thickness of a square disk of water vs size of the square for an SST satellite gravity mission at an altitude of 400 km. The solid line refers to the detection of the average change over 5 years, used to evaluate the secular trend, whereas the dashed line refers So the detection of a single-year change, used to evaluate the inter-annual variations in mass input.

Ambiguities

These problems have to do with separating the effects of ice-sheet changes from those arising from (a) isostatic rebound, (b) inter-annual variations in snow accumulation rates, and (c) inter-annual variations in mean atmospheric pressure. The sizes of these effects are discussed in turn below and summarized in Table 1.

Table 1. Magnitudes of various processes, in terms of mean effects on Antarctica and on sea level, together with the sensitivity of an SST satellite gravity mission

Isostatic rebound

It is particularly difficult in Antarctica to distinguish between effects of present-day changes in ice-sheet mass and effects of the Earth’s viscoelastic response to changes in ice mass over the past few hundred to several thousand years. For example, the top panel of Figure 3 shows the secular change in the geoid that would be caused by an increase in Antarctic ice, uniformly distributed over the ice sheet (the rate of thickness was chosen to be consistent with a global sea-level fall of 1 mm a⁻¹. The middle panel of Figure 3 shows the secular change in the geoid caused by the Earth’s isostatic adjustment to a thinning of the ice sheet over the last 4000 years, at a rate equivalent to a steady 1 mm a⁻¹ rise in sea level, using the viscoelastic Green’s functions of Dazhong and Wahr (1995) (the viscosity parameters are given in the figure caption). Note that the results in these two panels have similar spatial patterns and amplitudes that are not greatly different.

Fig. 3. The estimated secular in the geoid, in mm a⁻¹, from; (top) a uniform increase in ice over Antarctica, with a rate of thickness change corresponding to a 1mm a⁻¹ fall in global sea level; (middle)the viscoelastic response of the solid earth to a uniform rate of decrease in Antarctic ice during the last 1000years, with a rate of thickness change corresponding to a 1 mm a⁻¹ rise in sea level, assuming upper-mantle viscosity = 10²¹ P_as, and lower-mantle viscosity — 10²² P_as; and (bottom) the earth’s viscoelastic response to the late-Pleistocene deglaciation of Antarctica, assuming ice model ICE3G (Tushingham and Peltier, 1991) and the same viscosity profile used in the middle panel.

In principle, one could correct for the isostatic uplift by-measuring it on exposed rock. Although most of Antarctica is ice-covered, there are many exposures in the extensive Transantarctic Mountains, which cut through the continent from the Atlantic to the Pacific (Fig. 1). Hence, continuous global positioning system (GPS) measurements at selected sites along the Transantarctic Mountains (and elsewhere) to determine uplift rates would be a valuable undertaking (James and Ivins, 1995). Accuracies on the order of 1 mm a⁻¹ in the vertical component should be attainable with 5 years of continuous GPS measurements (for this estimate we assume that accuracies in the vertical are about 10 mm averaged over every 2 weeks, and that the errors are not notably correlated from one 2 week period to another). Repeatabilities of about 2 mm a⁻¹ for GPS measurements in Antarctica are already being reported (Dietrich and others, 1997; Hothem and others, 1997) and an appropriate network in the Transantarctic Mountains is being established Raymond and others, 1997). An accuracy of 1 mm a⁻¹ in the rate of vertical crustal deformation corresponds to an uncertainty in the secular gravity signal that is equivalent to about 4 mm a⁻¹ of ice removal or growth, or about 0.12 mm a⁻¹ of global sea-level rise. The problem is, however, that crustal uplift rates measured for the Transantarctic Mountains, which occupy only a small fraction of the total area of Antarctica, are unlikely to be representative of the average uplift rates for the entire continent. It is thus probable that the best use of such GPS measurements would be to help constrain models of the rebound, which would then be used to remove the effects at all locations.

Constraints on rebound models are necessary because they alone, in their current state of development, would not suffice to solve the problem. Uncertainties in the Earth’s viscosity profile and in the time evolution of the Antarctic ice sheet could lead to errors in the rebound solutions that are large enough to degrade estimates of present-day ice-sheet changes significantly. We have attempted to quantify this degradation, as follows. We used the approach described by Dazhong and Wahr (1995) to compute viscoelastic Green’s functions for various plausible mantle-viscosity profiles. We convolved those Green’s functions with different space-time distributions of the Antarctic ice sheet, thus generating a suite of possible geoid signals caused by isostatic rebound. The difference between these signals is an estimate of the error in rebound models. We took differences between pairs of estimated geoid signals, and fitted to each difference a hypothetical present-day change in Antarctic ice thickness that would cause it. The results indicate the possible effects of errors in the rebound model on the solutions for present-day changes in the ice sheet. We find, for example, that uncertainties in the current rebound models are likely to correspond to uncertainties on the order of 30 mm a⁻¹ in present-day ice, which is equivalent to about 1 mm a⁻¹ of global sea-level change.

At first glance, this result suggests that a gravity mission alone would not improve the global sea-level-change estimates of Warrick and others (1996). However, it is likely that a dedicated gravity mission will lead to a solution for secular changes in the gravity field over Canada (resulting from the disappearance of the Laurentide ice sheet) that would greatly improve knowledge of the earth’s viscosity profile, particularly in the lower mantle (USNRC, 1997). Upper-mantle viscosity would be less well constrained, and could conceivably be somewhat different under Antarctica than under Canada. However, errors in the upper-mantle-viscosity model would have their largest impact on the gravity-field at relatively short wavelengths. As such, they are likely to be less of a problem for learning about present-day changes in ice than are lower-mantle errors. Thus, we assume that after the gravity mission has been in place for a number of years, the main source of uncertainty in the Antarctic viscoelastic change would be the time evolution of the Antarctic ice sheet itself. We estimated ibis uncertainty by taking differences between geoid signals caused by different models of isostatic rebound, as described above, except that when taking differences between two models in this case, we kept the viscosity profile fixed while varying the ice-sheet history.

Estimates of the contribution of shrinkage of the Antarctic ice sheet to sea-level rise since the Late Glacial Maximum were reviewed by Clark and others (1996), who suggested that there may be a convergence of estimates to within a range of about 15 20 m. However, that range does not include the estimates made by Peltier and his associates for either the ICE3G model (26 m; Tushingham and Peltier, 1991) or the 1CE4G model (22 m; Peltier. 1994). Consequently, to be conservative, we have adopted a somewhat broader range within which we assume the actual value probably lies: 20±5 m. We do not extend our range to include the 35 m estimate of Nakada and Lambeck (1988), which we find unreasonably large on glaciological grounds: even a fully developed ice sheet that extends to the edge of the continental shelf around the continent would contain only enough ice to lower sea level by 25 m or less (Hughes and others 1981: Huybrechts, 1990). There is disagreement also over the timing of the major production of melt water from tile Antarctic; Clark and others (1996), for example, place the principal contribution at about 14000 BP, whereas Peltier (1991) believes it came only about 11000 years ago. Again, to be conservative, we have adopted a 3000 year uncertainty in the timing of the mass loss from Antarctica. We have also allowed for the possibility that the ice mass has been changing over the last few hundred to few thousand years (the middle panel of Figure 3 shows an example).

The present-day viscoelastic uplift rate depends on the earth’s viscosity profile. If the lower-mantle viscosity turns out to be 5 × 10²¹P_as or smaller, the uncertainty in the Antarctic contribution to present-day sea-level rise would be on the order of 0.6 mm a⁻¹, with about equal contributions from uncertainties in the Pleistocene ice history and in estimates of what the mass balance might have been over the past several hundred to several thousand years. At larger values of lower-mantle viscosity (e.g. 20 × 10²¹ P_as or greater), the Earth would respond more slowly to past changes in ice, and the total uncertainty might be reduced to 0.3 mm a⁻¹ or smaller.

In either case, constraints from GPS measurements on exposed rock would reduce the uncertainty further, to about ± 0.2 mm a⁻¹. Uncertainty estimates this small would indeed lead to improved estimates of the Antarctic contributions to sea-level change.

Snow accumulation rates

The second interpretation difficulty arises from the consideration of inter-annual variations in the snow accumulation rate on the ice-sheet surface. Here the problem is not in determining the change in mass of the ice sheet, but in distinguishing between changes in the mass of the solid ice, which can only occur by ice-dynamic processes with time-scales in decades to millennia and which, consequently, are of the most interest in terms of secular changes in sea level, and ephemeral changes associated with a few years of higher-than-normal or lower-than-normal snowfall rates. Inter-annual variability will result in changes in ice-sheet mass over the lifetime of a satellite mission that are not related to the long-term (i.e. centennial-scale) balance. Thus it interferes with the evaluation of long-term changes from a relatively short mission. We therefore assume, for evaluation purposes, that the long-term changes are “contaminated” by shorter-term variability, producing a “pseudo-secular” effect.

To estimate the magnitude of this effect we employ (he analysis of Van der Veen (1993). We consider the inter-annual variations in accumulation rate to be randomly distributed in time; we must assume a standard deviation for the inter-annual variation of annual accumulation rates. It is not well known how large the average variability in snowfall might be over an entire ice sheet, but on a more local scale an average inter-annual variability of 25% has been estimated (Giovinetto, 1964); that is (he figure we will adopt for all of Antarctica (i.e. 45 mm a⁻¹). We also assume a 5 year mission for all our calculai ions. We then find from Van der Veen’s (1993) analysis (Fig. 4) that if we were to detect an average growth or shrinkage rate in mass that was 25% of the inter-annual variation in the accumulation rate, there would be a 70% chance that it was a “real”’ (i.e. long-term) change. Thus, if the variability in accumulation rate is treated as an error source, the 1σ uncertainty (68% probability) is about 25% of the inter-annual variability, or 6% of die accumulation rate. So, for a mean accumulation rate of 150 mm a⁻¹ over t he entire tee sheet, we find an uncertainty in the secular mass change arising from the inter-annual variability of about 9 mm a⁻¹ (0.3 mm a⁻¹ in sea level). This is a very rough estimate, but it suffices to show lhal the error source is important.

Fig. 4. Probability that a thickness change (water equivalent) of an ice sheet, observed over several years, is due to stochastic fluctuations in the mass input. The thickness change is normalized by the standard deviation (with respect to time) of the annual accumulation rate, i.e. the inter-annual variability, The number of years of measurement is indicated next to each curve. From Van der Veen (1993).

There are two ways actually to measure the inter-annual differences, The first is by the calculation of broadly averaged snowfall rates from convergence of the atmospheric moisture flux across the boundaries of the ice sheet, which is determined from the small number of surface stations making regular rawinsonde observations and supplemented by satellite-based soundings of water vapor and winds. Meteorologists hope that by the year 2000 the total input can be known to 10% (personal communications from D. H. Bromwich, 1996 and W. F. Budd, 1996), although difficulties remain (personal communication from D. H. Bromwich, 1997). Furthermore, the uncertainties would be to a large extent systematic, i.e. not varying year-to-year. Thus the error in the inter-annual differences would be less than 10%; if it were half that, the error would be about 10 mm a⁻¹ (0.3 mm a⁻¹ in sea level), i.e. about the same as the uncertainty cited above. Thus, while not perhaps significantly reducing the uncertainty from this source, the meteorological measurements will give a valuable estimate of its size.

Secondly, the gravity measurements themselves can help determine the inter-annual variations, at least for the period of the mission. According to our calculations (Fig. 2) the SST mission could, in principle, resolve these thickness variations to an accuracy of about 0.4 mm. In actuality, the accuracy will be less, because the gravity signal of the ice sheet is contaminated by the signal from the surrounding ocean. We estimate, using an annually varying geoid predicted from oceanic general-circulation data (USNRG, 1997), that the oceanic effects would limit die accuracy in determining inter-annual changes in snowfall to about 2 mm (0.07 mm of sea level). This would represent a great improvement over current methods of determining changes in snowfall over time, but would not directly improve the estimate of the “pseudo-secular” change.

Atmospheric pressure

The third problem arises from the fact that the gravity satellite will measure the mass of the atmosphere, as well as the masses of the ice sheet and the solid earth. The mean atmospheric pressure on the ice-sheet surface (which reflects the overlying mass) must be determined from measurements at only a small number of points; consequently there may be considerable error in evaluating annual averages. Part of this could be a relatively static error, nearly constant through time, so it would not notably affect a calculation of secular change rates. However, there still remains a random-error component, which is also on the order of 1 or 2 mbar (about equal in mass to 10–20 mm of ice or 0.3 0.6 mm of sea-level equivalent on annual averages (personal communication from D. H. Bromwich, 1997), and hence presumably is on the order of 1 mbar (10 mm of ice; 0.3 mm of sea level) with respect to an estimate of the secular change rate based on a 5 year time series. The uncertainties in mean pressures can best be reduced by continuing to extend the number of automatic weather stations (AWSs) over the Antarctic surface and assuring that data from them are used in calculations of the mean pressure (there were about 80 AWSs and nearly 40 occupied stations as of the Antarctic “FROST” Project in 1994–95, but their distribution was very uneven, leaving major gaps in the coverage of the continent (Turner and others, 1996)).

Complementarity with Glas

From the discussion of ambiguities we conclude that a satellite gravity mission, together with available (or soon-to-be-available) ancillary information, can lead to a determination of the Antarctic contribution to sea-level change with an accuracy on the order of 0.5 mm a⁻¹. Calculations of mass balance will become dramatically more accurate when on-going changes in the height of the ice sheet are determined separately using laser altimeter measurements from an orbiting satellite, specifically, one carrying NASA’s planned Geoscience Laser Altimeter System (GLAS), which is scheduled for launch in 2001. For a given mass increase, the surface-height changes for isostatic uplift, changes in solid ice and changes in snow accumulation at the surface would be in the ratio of 1: 3.5:10, respectively, because 1 he source of mass change in each of those cases is characterized by a different mean density. If the cause of mass change were in the atmosphere, there would be no change in height at all (the response of the ice to pressure fluctuations is negligible). It follows that simultaneous measurements of change in height and change in gravity should, in principle, make it possible to distinguish between different causes of mass change. NASA’s planned laser-altimeter mission, carrying GLAS in a 94° orbit with a nominal lifetime of 4 years, is designed to detect mean surface-height changes to better than 10 mm a⁻¹; an accuracy of a few mm a⁻¹ in mean height change over large areas will probably be attained. An accuracy of 3 mm a⁻¹, combined with the satellite gravity measurements, would make it possible to calculate the contribution of the ice sheet to sea-level change at the O.1 mm a⁻¹ level. Neither satellite gravity nor satellite laser altimetry has that capability alone: the two types of measurement are strongly complementary. (The laser altimeter measurements are subject to most of the same uncertainties about causes as the gravity measurements, but with different sensitivities. Without better knowledge of the isostatic-rebound and snowfall-variation effects, such as can be obtained using satellite gravity, the GLAS-based estimates of the ice-sheet contributions to sea level would probably be accurate to a few tenths of a millimeter per year.)

Drainage Systems within Ice Sheets

The Antarctic ice sheet is, of course, a complex composite of individual drainage systems or basins, some of which are characterized by fast-moving, low-gradient ice streams bordered by slowly flowing ice, some by large outlet glaciers through peripheral mountain ranges, and some by broad expanses of open sheet flow with only small, local glaciers. From a direct societal standpoint, the total mass balance of the ice on land may be the most relevant quantity to measure, but, from a glaciological standpoint, it is at least as important to measure the mass changes in individual drainage systems within the ice sheets, because they are the basic dynamic units; the dynamic behavior of a particular drainage system may be nearly independent of the dynamic behavior of even its nearest neighbors. Glaciologists can learn how to predict future changes in ice-sheet mass balance only by understanding the dynamics of these basic units.

The ice sheet is so large, and satellite gravity so sensitive, that a gravity mission can provide a valuable approach to the study of subdivisions like individual drainage systems, as well as entire ice sheets. For example, the mass of ice in the large drainage system that empties into the east side of the Ross Ice Shelf, West Antarctica (Fig. 1) is suspected to have fluctuated dramatically in the past because of unstable dynamic behavior, including a rapid retreat at the end of the last ice age that may be continuing at present, albeit at a reduced rate. Secular changes in the thickness of this drainage system could be tens of millimeters per year. We see from Figure 2 that the assumed SST mission could determine the secular change in mass of this region (approximated by a square 600km on a side) to an accuracy of about 4 mm a⁻¹ (in sea level), or the order of 10% of the possible imbalance. The determination of secular changes in the masses of this and other large drainage systems would allow models of ice-sheet dynamics to be tested.

The same problems arise with interpretation of gravity changes over a drainage system as with changes over the encompassing ice sheet as a whole, and the same approaches to alleviating those problems mostly apply. There is a special situation with respect to isostatic rebound, however. Isostatic rebound models that incorporate the results of analyses of ice-sheet dynamics, such as those based on the ICE3G and ICE4G models of Tushingham and Peltier (1991) and Peltier (1994), show an isostatic rebound rate on the cast side of the Ross Ice Shelf that is much greater than the Antarctic average because of the major modeled ice-sheet retreat there at the end of the last ice age (Peltier, 1995). Modeled rebound rates are greater than 10 mm a⁻¹ over a wide area, and the maximum rate is over 15 mm a⁻¹ (the pattern is the same as for the geoidal change shown in the bottom panel of Figure 3). It is no coincidence that the highest modeled uplift rates are focused on the regions where the greatest likelihood of rapid change from a glaciological perspective exists today; the same high glaciological sensitivity that is of concern today presumably led to large changes in ice mass in these areas in the past. As a rebound rate of 15 mm a⁻¹ is gravitationally equivalent to an ice-thickness change of about 60 mm a⁻¹, even a large glaciological imbalance could be obscured by ongoing isostatic uplift.

Since the Transantarctic Mountains cut through the region showing large modeled uplift rates, GPS surveys in those mountains of the type recommended above would provide an excellent check on the models. Furthermore, since the rates of change that might be attributed to either changing ice mass or isostalic rebound are so large, this region is particularly well suited to testing by comparing results from a gravity satellite with those from a laser-altimeter satellite.

Conclusions

The measurement and interpretation of changes in Antarctica is a complex issue, given the complex nature of the phenomena involved: secular changes in ice-sheet mass, postglacial rebound, inter-annual variability in snowfall, and the effect of atmospheric pressure trends, (a) Postglacial rebound could be partly separated from ice changes by combining measurements from a network of GPS receivers on the land surface with numerical models of rebound that use improved determinations of mantle viscosity provided by the gravity mission, (b) Separation of the pseudo-secular effect of the inter-annual mass changes from true secular changes will be aided by calculations of mass input lo the ice s h eel from atmospheric moisture-flux divergences and by the direct observations of inter-annual changes by the gravity satellite, (c) The removal of pressure effects over Antarctica will become more effective as the number of AWSs in the interior of the continent increases, (d) Gravity measurements will be most effective in combination with the observations planned for NASA’s laser-altimeter mission. By combining results from the two missions, an accuracy of 0.1 mm a⁻¹ in the determination of the contribution of the Antarctic ice sheet to sea-level change should be attainable.

In addition, satellite gravity measurements are capable of yielding valuable information about the mass balance of individual drainage systems within the Antarctic ice sheet. Glaciologists will find such information highly useful for testing models of ice dynamics, which are essential to the prediction of future sea-level change.