12 - The Influence of Nanoporosity on the Behavior of Carbon-Bearing Fluids

Summary

A new finding over the past decade is the stability – and even potential synthesis – of hydrocarbons at depth in Earth. Of course, this has been a highly controversial area of research for decades, but recent evidence has been obtained from natural orogenic geological settings, thermodynamic simulations, and observations of seafloor samples. This chapter reviews this new evidence while highlighting the importance of the physical state of C-O-H fluids contained in rocks on the transport of alkanes like methane, propane, and octane, the impact of pore space and fracture confinement on fluid reactivity, and how reactivity under confinement varies from bulk fluid properties.

12.1 Introduction

Porosity and permeability are key variables linking the origin, form, movement, and quantity of carbon-bearing fluids that collectively dictate the physical and chemical evolution of fluid–gas–rock systems.¹ The distribution of pores, pore volume, and their connectedness vary widely, depending on the Earth material, its geologic context, and its history. The general tendency is for porosity and permeability to decrease with increasing depth, along with pore size and/or fracture aperture width. Exceptions involve zones of deformation (e.g. fault or shear zones), regions bounding magma emplacement and subduction zones. Pores or fractures display three-dimensional hierarchical structures, exhibiting variable connectivity defining the pore and/or fracture network.^2–5 This network structure and topology control: (1) internal pore volumes, mineral phases, and potentially reactive surfaces accessible to fluids, aqueous solutions, volatiles, inclusions, etc.^6–8; and (2) diffusive path lengths, tortuosity, and the predominance of advective or diffusive transport.^9–12 For solids dominated by finer networks, transport is dominated by slow advection and/or diffusion.^13–16

Despite the extensive spatial and temporal scales over which fluid–mineral interactions can occur in geologic systems, interfacial phenomena including fluids at mineral surfaces or contained within buried interfaces such as pores, pore throats, grain boundaries, micro-fractures, and dislocations (Figure 12.1) impact the nature of multiphase flow and reactive transport in geologic systems.^{13, 17–21} Complexity in fluid–mineral systems takes many forms, including the interaction of dissolved constituents in water, wetting films on mineral surfaces, adsorption of dissolved and volatile species, the initiation of reactions, and transport of mobile species.^22–24 Direct observations and modeling of physical (transport) and chemical properties (reactivity) and associated interactions are challenging when considering the smallest length scales typical of pore and fracture features and their extended three-dimensional network structures.^{25, 26}

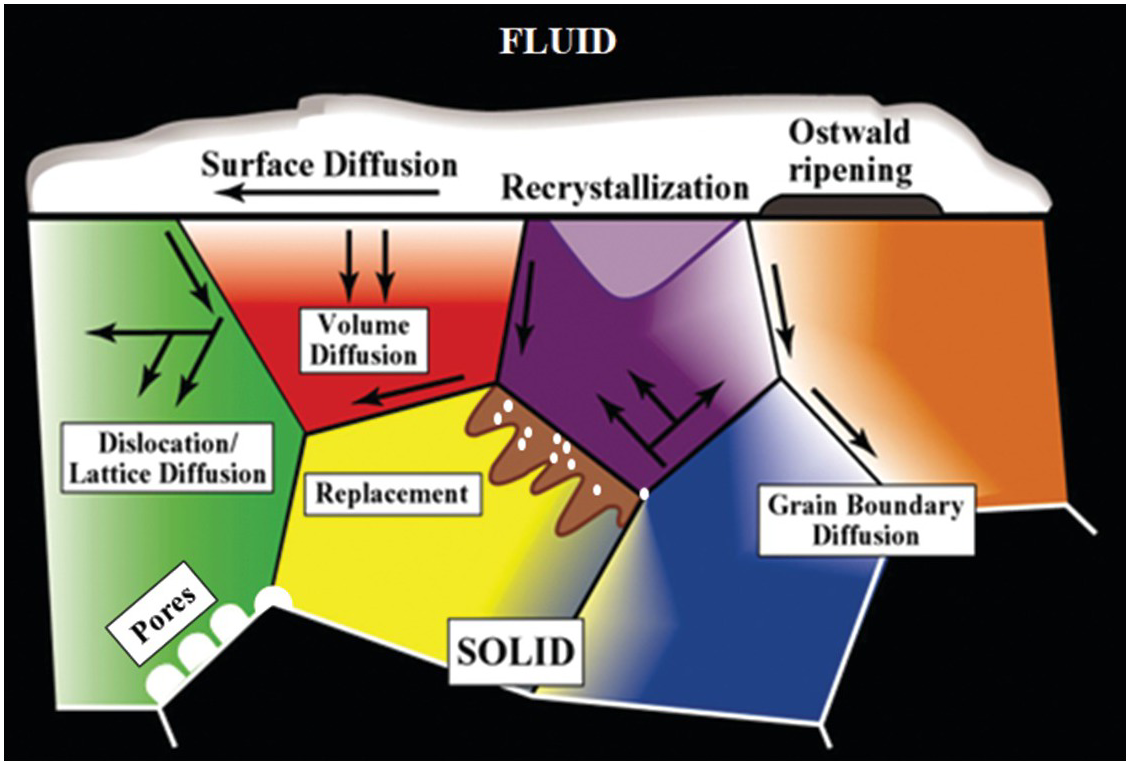
Figure 12.1 Schematic illustration of the various mass transfer and diffusion processes that can control the behavior of fluids and dissolved species in a heterogeneous crystalline matrix.

The various void types and their evolution during reaction with fluids are critically important factors controlling the distribution of the fluid-accessible pore volume, flow dynamics, fluid retention, chemical reactivity, and contaminant species transport.^27–32 While fracture-dominated flow can be volumetrically dominant in shallow crustal settings or in zones of deformation,^33–38 there is a continuum of coupled reaction–transport phenomena at length scales from fractures to the smallest nanopores. Nanoscale pores may interconnect larger volumes, act as pore throats, and play an important role in fracture initiation. Diffusion of chemical constituents from pore fluids along grain boundaries and into solids may drive the textural and chemical evolution of geologic media.^38–41

There is general agreement that the collective structure and properties of bulk fluids are altered by solid substrates, confinement between two mineral surfaces, or in narrow pores due to the interplay of the intrinsic length scales of the fluid molecules and the length scale of fluid–solid (i.e. confinement) interactions.^{22, 42–45} The combined effect of confinement and intermolecular forces, which vary among different mineral systems, results in unique (and poorly constrained) perturbations to a wide range of thermodynamic and transport parameters, generally different from those observed in the bulk phase.^46–51 Also impactful is the degree of randomness of the matrix, geometry, surface composition (e.g. silicates, carbonates, organic matter (OM)), fractal nature of the pores, and connectivity of the pore network.⁵²

It has also been hypothesized that chemical reactions in pores smaller than 100 nm may be different from those in larger pores because of: (1) confinement-induced changes in fluid properties and associated solutes (e.g. electrolytes, scCO₂, CH₄)⁵³; (2) shifts in thermodynamic equilibrium composition^54–56; and (3) overlapping electric double layers and surface curvature, distribution of preferential adsorption sites, surface charge, and counterion behavior.⁵⁷ The question as to whether surface chemical processes (e.g. ionization, complexation, adsorption) in nanopores differ from those in macropores (>100 nm) remains largely unresolved. Compounding this is the formidable challenge in characterizing the structure and dynamics of fluid species within internal pore or fracture networks.¹³ Predictions on the direction and magnitude of changes in chemical reactions have not been thoroughly explored, despite the fact that the large surface area contributed by smaller pores can make them extremely significant in fluid–rock interactions.^{6–8, 58}

This chapter seeks to show how the structure of nanoconfined fluids is responsible for a variety of effects relevant to the origin, form, movement, and quantity of carbon-bearing fluids. “Form” is related to the molecular structure of confined fluids, which includes segregation of molecular species across the pore. In Section 12.3, we discuss how form is related to “movement,” which is reflected by the diffusion and transport mechanisms of confined fluids. In Section 12.4, we discuss how form relates to “quantity” (i.e. the solubility of gases in confined fluids). In Section 12.5, we discuss how form is related to “origin,” restricted to the reactivity of nanoconfined fluids.

The richness and complexity of fluid behavior (e.g. phase transitions, molecular orientation and relaxation, diffusion, adsorption, wetting, capillary condensation, etc.) in confined geometries underscores the need to adopt a multidisciplinary approach. In concert with molecular simulations, there is a robust set of experimental approaches used to directly or indirectly probe the behavior of fluids at interfaces or in nanopore confinement. The reader is referred to our previous research²² and to a number of excellent reviews on molecular dynamics (MD)^{50, 55, 59–64} and experimental methods and outcomes.^65–71

12.2 Nanopore Earth Materials and Fluids

12.2.1 Nanopore Features

Porosity and permeability are key variables that link the thermal, hydrologic, geomechanical, and geochemical behavior exhibited by most, if not all, fluid–rock systems. In general, there is a strong positive correlation between porosity and permeability in many porous and fractured geologic media (see Nelson⁷² for sedimentary rocks and Ingebritsen et al.⁷³ for crystalline rocks). What is truly remarkable is the extraordinary range in measured permeability (some 16 orders of magnitude), from as high as 10^–7 m² (10⁵ Darcy) for well-sorted gravel to as low as 10^–23 m² (sub-nano Darcy) in crystalline rocks, mudstones (shale), fault gouges, and halide deposits.^{38, 74} An assortment of measurements (e.g. deep borehole, core-scale flooding, geophysical) indicates that both porosity and permeability tend to decrease with increasing depth. For example, permeability measurements of core obtained from the Kola superdeep well (11.4–12.0 km) range from 10^–17 to 10^–22 m², depending on the effective confining pressure.⁷⁵ In a series of seminal papers, Ingebritsen and Manning^76–78 described the permeability of continental crust as a function of depth in the context of specific geologic settings. They demonstrated that permeabilities decreased rapidly through the brittle portion of the crust to values between 10^–14 and 10^–16 m² at a depth of approximately 10 km. Below this depth through the brittle–ductile transition zone (~10–15 km) extending to depths of roughly 25 km, the permeability becomes more constant with depth, ranging between 10^–16 and 10^–18 m².

Norton and Knapp³⁹ documented the porosity of numerous crystalline rocks and classified pores (fractures) into three broad categories: flow, diffuse, and residual (isolated). Of these, the first two are relevant to the nature of the permeability regimes, in that the smaller, sometimes dead-ended diffuse pores and pore throats contribute to the chemistry of the larger, throughgoing connected pores and fractures (i.e. flow porosity). The diffuse porosity estimates identified by Norton and Knapp³⁹ for volcanic and crystalline rocks range from 0.01% to 10%. Bredehoeft and Norton⁷⁹ expanded on this by providing estimates of permeability for fractured igneous and metamorphic rocks that range from 10^–12 to 10^–16 m², and for unfractured equivalents ranging from 10^–17 to 10^–20 m². Anovitz and Cole^{80, 81} surveyed the many techniques used to quantify pore features (e.g. advanced electron microscopy, X-ray, and neutron scattering) and indicated that the range in pore size measured in rocks (sedimentary, igneous, and metamorphic) can vary by approximately eight orders of magnitude from the nanometer scale to the millimeter scale.

General nanoscale features observed in many rocks include intergranular or interparticle (Figure 12.2a, c, and d) versus intraparticle porosity (Figure 12.2b, e, and f). The latter pore type is frequently the result of dissolution–precipitation processes and is typically less well connected to the flow porosity compared to intergranular porosity involving grain-to-grain contacts of two different phases known as interphase boundaries or grain boundaries, defined as the interface of two grains of the same phase. The intergranular pore type is thought to control transport in very tight rocks, especially those encountered deeper in the crust and mantle. As Wark and Watson⁸² point out, the premise is that rocks below the brittle–ductile transition (>12 km for continental crust) cannot sustain a fracture network system, and thus fluids – especially at low-volume fractions – must reside in intergranular pores. Intergranular fluids, however, will flow only if the pores (i.e. grain boundaries in this case) are interconnected. Fluid flow may be a misnomer when discussing very deep-seated rocks. The width of space between grains in very deep crustal and mantle rocks (e.g. olivine-rich mantle) has been a source of debate for many years. Marquardt and Faul⁴¹ provided an excellent summary of the structure and composition of olivine grain boundaries and conclude that the width is on the order of 1 nm or less (Figure 12.3a). At this reduced dimension, fluid mobility takes the form of grain boundary diffusion, which can be several orders of magnitude greater than volume (lattice) diffusion through minerals, but many orders of magnitude slower than advective flow.^83–85 Nevertheless, fluids do penetrate these spatially restricted domains, as evidenced by dissolution, grain boundary migration, and phase alteration (e.g. olivine conversion to serpentine) (Figure 12.3b). High-resolution transmission electron microscopy reveals that some olivine-rich rocks like the San Carlos olivine also display amorphous films that are 1–2 nm wide between olivine grains thought to be remnant melt.⁸⁶

Figure 12.2 Transmission electron microscopy images of different nanoscale pores. (a) St. Peter sandstone, Wisconsin; (b) illite from Utica shale, Ohio; (c) basalt clast, Costa Rica; (d) Hueco limestone, north Mexico; (e) organic embedded in clay, Utica shale, Ohio; (f) experimental hydrothermal replacement of adularia by albite, 600°C, 200 MPa.

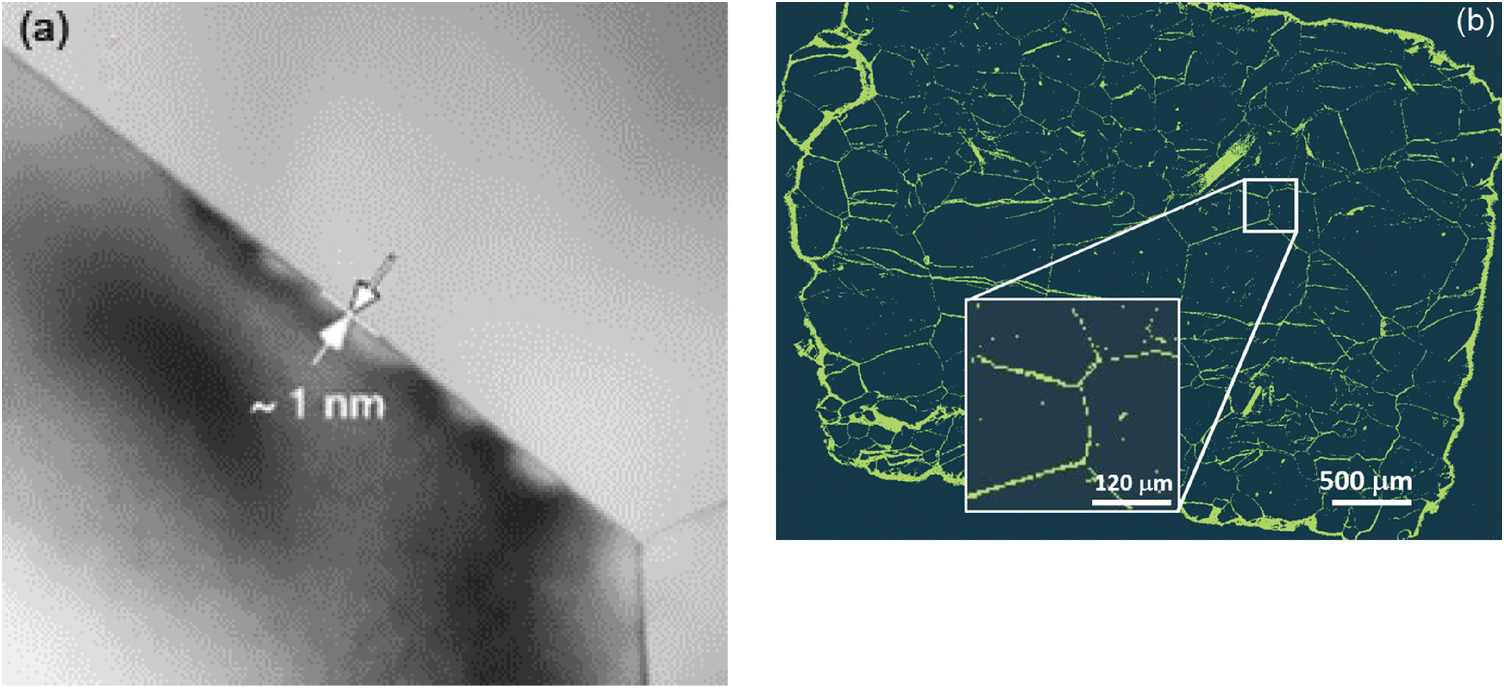
Figure 12.3 (a) High-resolution transmission electron microscopy image of the San Carlos olivine grain boundary and triple junction (from Marquardt and Faul⁴¹). Note the estimated grain boundary width of ~1 nm. (b) Balsam Gap dunite showing the extent of fluid infiltration and serpentinization along olivine grain boundaries, hydrothermally treated at 300°C, 200 MPa.

Reprinted with permission from Marquardt K, Faul UH. The structure and composition of olivine grain boundaries: 40 years of studies, status and current developments. Phys Chem Miner 2018; 45: 139–172.⁴¹ Copyright 2018 Physics and Chemistry of Minerals.

The presence of nanoscale pores and fractures seems to be widespread in Earth materials and may be extremely significant for controlling fluid accessibility in deep-seated crustal and upper-mantle rocks depending on the extent of pore network connectivity. Pores may be either slit-like or cylindrical in shape and can exist along grain boundaries, at the contact of unlike grains (interphase boundaries), or entirely within a given phase. In simplest terms, the pore surface compositions are dominated by silica or silicates, oxides, clay, carbonate, and, where present, OM of varying thermal maturity. As we discuss below, it is at the dimensions of a few nanometers to tens of nanometers that fluid properties deviate significantly from those of the bulk fluids.

12.2.2 Fluid Properties Affected by Nanoconfinement

It has been reported that the collective structure and properties of bulk fluids are altered by confinement between two surfaces or in narrow pores due to the interplay of the intrinsic length scales of the fluid and the length scale due to confinement.^87–89 For example, melting/freezing of water is affected by confinement in geomaterials,^{90, 91} and confined fluids can be liquid at the thermodynamic conditions (pressure and temperature) at which the correspondent bulk fluids are gaseous. It has also been shown that confinement can promote new phases that simply do not exist in the bulk.⁹² This has been an area of particular interest to those who investigate the properties of water. It has been demonstrated that confined water can be prevented from freezing at conditions well inside the “no-man’s land.”⁹³ It is possible that similar effects will also be observed for carbon-bearing fluids, although perhaps the high temperature in the subsurface will prevent the formation of exotic phases. In point of fact, almost any fluid property is influenced by nanoconfinement to a varying degree: thermophysical (e.g. density, phase behavior, dielectric constant, compressibility), transport (e.g. diffusion, shear), dynamical motion (translational, rotational, vibrational, and librational), and interfacial interactions (e.g. adsorption, wetting, solubility) are expected to be strongly dependent upon confinement.

12.3 Form and Movement: Transport Mechanisms under Nanoconfinement

The main mechanisms responsible for fluid transport are convective motion and molecular diffusion. When the pore size becomes of the order of magnitude of fluid molecules (i.e. in nanopores), diffusion can become the dominant mechanism. Because in the subsurface many pores are in this size regime, it is important to understand the mechanisms by which molecular diffusion can take place in nanopores. In this section, we discuss how the structure of confined fluids (form) affects their transport (movement). We focus on fluid mixtures. The studies summarized here are selected primarily from the body of work produced by the authors. Future investigations will stress the wide applicability of our extrapolations.

As a first example, we refer to Chiavazzo et al.,⁹⁴ who used computer simulation to investigate water transport in “nanoconfined geometries” (i.e. within nanopores, around nanoparticles, carbon nanotubes, and proteins). Almost 60 cases were considered, some being obtained from the literature. The results, reproduced in Figure 12.4, were interpreted using a general phenomenological relationship:

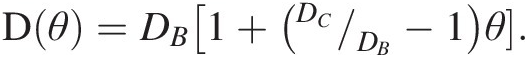$D\left(\theta \right)=D_B\left(1+\left(\frac{D_C}{D_B}-1\right)\theta \right).$(12.1)

In (12.1), D is the overall self-diffusion coefficient of water calculated in the various systems and D_C and D_B are the self-diffusion coefficients estimated for confined and bulk water, respectively. According to this relationship, D was found to scale linearly with the ratio θ between “surface” and total water volumes. The “surface” water volume is a measure of the interfacial region where water molecules are in contact with the confining material. As the pore width decreases, the amount of “surface” versus total volume increases.

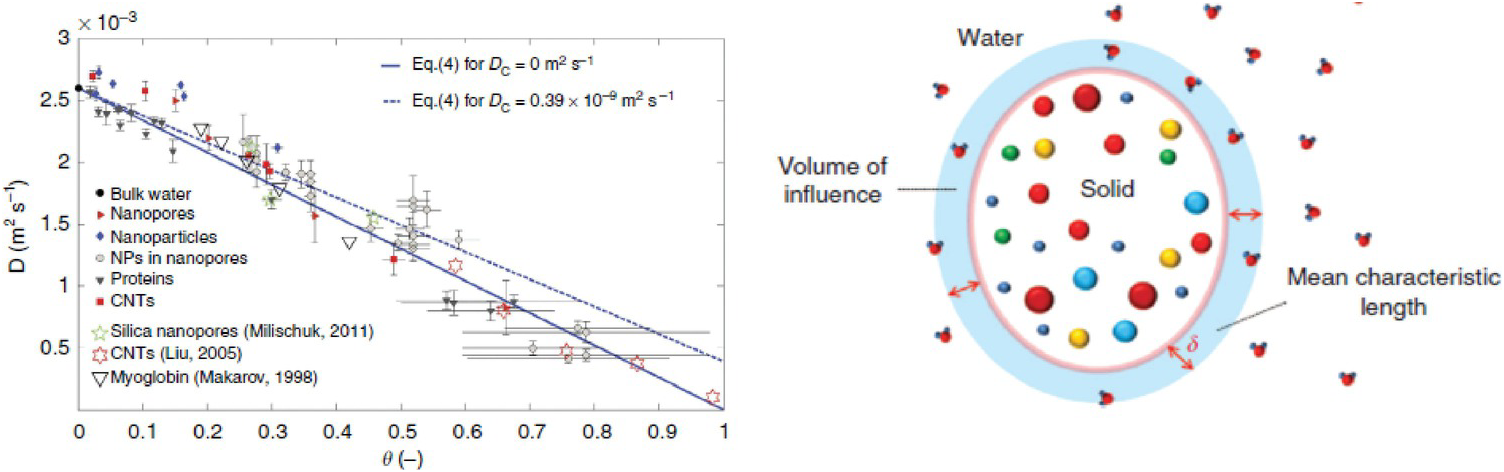
Figure 12.4 (Left) Self-diffusion coefficient for nanoconfined water as a function of the ratio θ between “surface” and total water volumes. The image contains simulation results for many systems. (Right) Schematic illustrating the region of influence of a solid substrate on an interfacial fluid.

Figure reproduced from Chiavazzo E, Fasano M, Asinari P, Decuzzi P. Scaling behaviour for the water transport in nanoconfined geometries. Nat Commun 2014; 5: 3565.⁹⁴ Permission granted from Creative Commons https://creativecommons.org/licenses/by/3.0.

12.3.1 Steric Effects Enhance Surface versus Pore Diffusion

When fluid molecules are confined within nanopores, they can experience a strong attraction to the pore surfaces (e.g. via hydrogen bonds). It is possible that the molecules strongly adsorbed on a surface show very slow diffusion parallel to the surface (i.e. surface diffusion). This is because to move from one adsorption site to an adjacent one, the fluid molecules need to be released from one strong interaction. Hopping mechanisms can be observed, in which one molecule hops from one preferential adsorption site to the next. As the adsorption energy becomes stronger, the frequency of such hops lowers, and diffusion is delayed. If the preferential adsorption sites are so close to each other that hopping is not necessary, it is possible to observe sliding.⁹⁵ It is generally assumed that surface diffusion is slower than that near the pore center (i.e. “pore diffusion”). For a pure fluid, as the pore size decreases, the contribution of surface diffusion increases compared to that of surface diffusion, as shown in Figure 12.4 in the case of water.

However, we also know that the opposite situation can also arise. Phan et al.⁴⁴ considered a fluid mixture composed of ethanol and water inside a slit-shaped alumina nanopore of width 1 nm. The pore surface exposed a high density of –OH groups. Equilibrium studies on a flat surface⁴³ showed that water preferentially adsorbs on the alumina substrate and displaces ethanol molecules, should these be present on the surface. When the pore is of 1 nm, the physical state of the system, depending on composition, can present one layer of water on each of the two pore surfaces, with ethanol near the pore center. The pore width is so narrow that steric effects hinder the diffusion of ethanol near the pore center, while water surface diffusion is possible. This effect disappears when the pore width increases. A detailed analysis of the trajectories of the confined water molecules showed that the diffusion of water is characterized by hops. Such hops are from one adsorption site to another one on the surface across the pore volume. This mechanism becomes hindered as the pore width increases because the water molecules would have to transport across a large region filled with ethanol. In this example, increasing pore width delays water surface diffusion while allowing faster ethanol pore diffusion.

Complementary experimental investigations are difficult because it is hard to differentiate between molecules that are adsorbed on the surface from those that accumulate near the pore center. Some experimental results, however, suggest that, in some cases, surface diffusion can be the dominant transport mechanism. For example, Kim et al.⁹⁶ synthesized “silylated” mesoporous silica membranes. The chemical functionalization made the pore surfaces more attractive for ethanol than for water. Once exposed to water–ethanol liquid mixtures, ethanol permeated the membranes much faster than water, suggesting that surface diffusion became an important mechanism of transport. Ge et al.⁹⁷ used zeolites to enhance polymer-based composite membranes. The zeolites preferentially attracted water, and separation factors of ~10,000 were achieved in water-removal pervaporation processes (i.e. water permeated these membranes much faster than ethanol). For completeness, it should be remembered that the permeability of a membrane is equal to the product of the diffusion coefficient of the fluid through the membrane and the amount adsorbed. Thus, enhanced diffusion might not be the only mechanism responsible for the results just discussed.

12.3.2 Molecular Lubrication Enhances Pore Diffusion

Even in the absence of preferential adsorption sites where nonspecific attractive interactions lead to an accumulation of fluids near pore surfaces, it is generally expected that the diffusion of the fluid molecules in a nano- to meso-pore is slower than that in the bulk. For example, the enhanced fluid density near the pore walls leads to more frequent fluid–fluid and fluid–pore collisions, which reduce the mean free path and the diffusion coefficient. This expectation is demonstrated, for example, by quasielastic neutron scattering (QENS) experiments conducted for ethane in the gas phase. When ethane was confined in two SiO₂ pore-glass materials with pore sizes 11.1 and 41.5 nm, the self-diffusion coefficient was found to be a factor of ~4 slower compared to that measured for bulk ethane at similar temperature–pressure conditions.⁹⁸

If these results are due to the fluid accumulation near the pore interface, then it might be possible to enhance the fluid diffusion by adding small amounts of another fluid that preferentially adsorbs on the solid substrate. For example, Le et al.^{99, 100} simulated systems containing a hydrocarbon (either butane or octane) and CO₂ in a silica slit-shaped pore of width ~2 nm. CO₂ formed molecularly thin layers on the pore surfaces, while the hydrocarbon filled the pore. At low dosages, CO₂ enhanced hydrocarbon diffusion. These computational results were confirmed by Gautam et al.¹⁰¹ and Patankar et al.,⁹⁸ who used QENS to study the diffusion of propane and ethane in mesoporous SiO₂, respectively, in the presence of CO₂. The ethane experiments, conducted at different temperatures, showed that the activation energy of diffusion decreased in the presence of CO₂ by a factor of ~2 compared to data obtained for pure ethane, which was consistent with the simulations. Others also reported that CO₂ enhanced the diffusion of hydrocarbons through different porous materials.^{99, 101, 102}

12.3.3 Molecular Hurdles Due to Strong Fluid–Fluid Interactions

The enhanced diffusion discussed in Section 12.3.2 is due to the preferential adsorption of CO₂ to the pore surface, but one can ask whether similar observations are possible when a fluid other than CO₂, also strongly attracted to the pore surface, is used. One such fluid could be water. Gautam et al.¹⁰³ used QENS to probe whether this was the case. The system used contained propane and D₂O in silica-based, cylindrical pores of diameter ~1.5 nm. The experimental results showed that the propane diffusion was depressed, rather than enhanced, by D₂O. Le et al.¹⁰⁴ conducted MD simulations for a system mimicking the experimental one. The results showed that although water molecules are strongly adsorbed on the pore surface, the pores have such a narrow diameter and the water–water interactions are so strong that water molecules form molecular bridges across the pore volume. These bridges hinder propane diffusion. Simulation snapshots illustrating the phenomenon are shown in Figure 12.5.

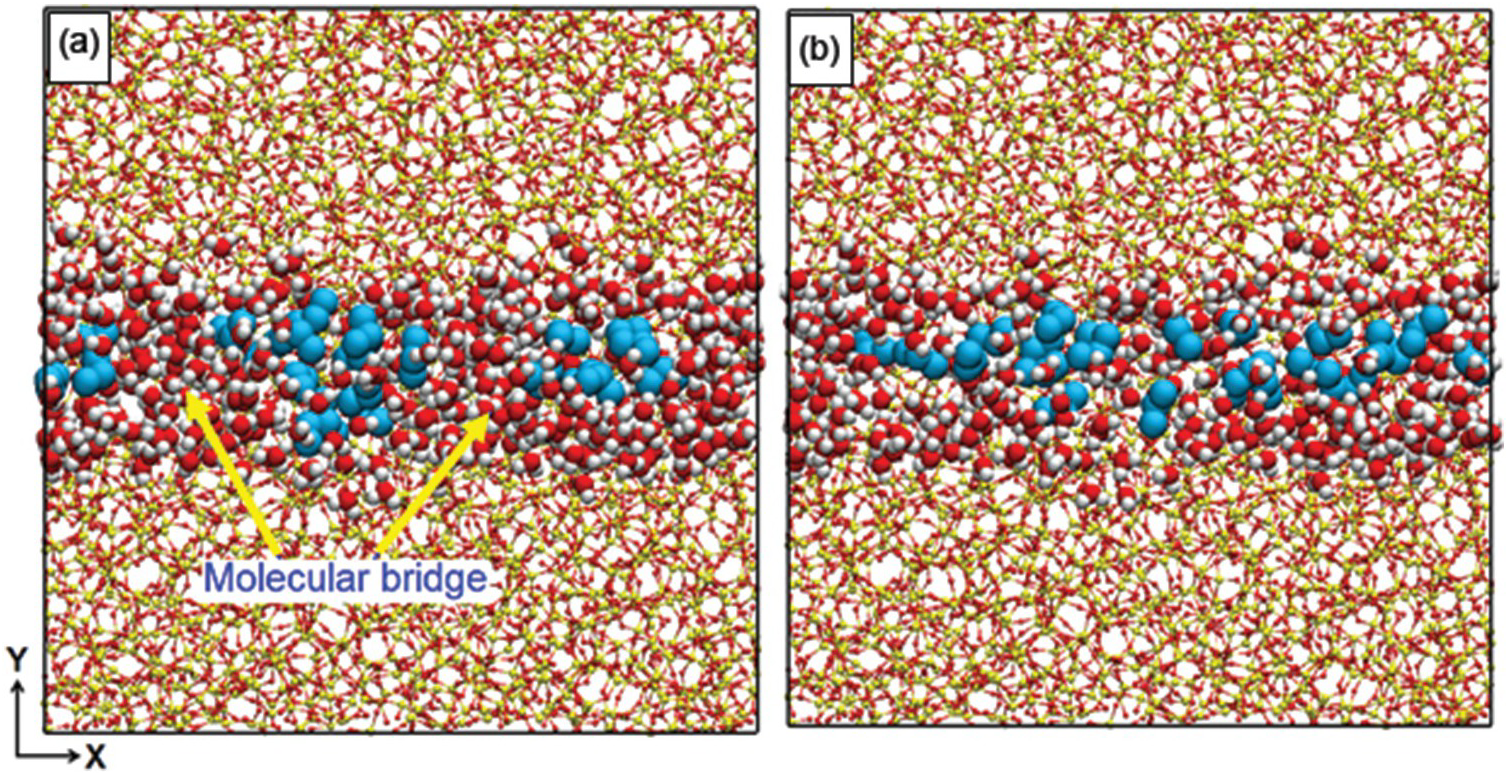
Figure 12.5 Simulation snapshots representing the effect of water molecular bridges (red and white spheres) on the transport of propane (cyan spheres) diffusing through a cylindrical pore carved out of amorphous silica (red and yellow spheres connected by lines). In (a), the water bridges hinder the transport at higher water/gas ratios (≥17), while in (b), the bridges are dissociated and propane diffusion is faster at lower water/gas ratios (≤12).

Reprinted with permission from Le TTB, Striolo A, Gautam S, Cole DR. Propane–water mixtures confined within cylindrical silica nanopores: structural and dynamical properties probed by molecular dynamics. Langmuir 2017; 33: 11310–11320.¹⁰⁴ Copyright 2017 American Chemical Society.

The formation of water bridges was also found to delay methane transport across slit-shaped muscovite pores. Ho and Striolo¹⁰⁵ found that methane convective transport within slit-shaped pores carved out of muscovite and partially filled with water is strongly dependent on the relative orientation of the water bridges and that of imposed motion. When the water bridges are perpendicular to the direction of motion, methane transport is regulated by the movement of water, which adheres to the pore surface. When the water bridges are parallel to the direction of motion, fast methane transport is observed.

Phenomena such as those just described are expected to be important when low-solubility or immiscible fluids are simultaneously present within a pore, and they are relevant for the production of shale gas, in which water is often used as the fracturing fluid. Many studies have addressed how methane could escape kerogen. These studies could be relevant for systems in which pores are extremely heterogeneous in geometry and of comparable size to the fluid molecules.

12.3.4 Transport of Guest Molecules in Confined Fluids

It is worth discussing the relation between the structure of fluids in confined water and their transport. Phan et al.¹⁰⁶ simulated the transport of a mixture mimicking natural gas (ethane, methane, and H₂S) through nanopores filled with water. The results show that H₂S permeates the pores much faster than the other compounds and that ethane is too large to permeate the hydrated pores. Bui et al.¹⁰⁷ extended the study to consider different porous materials. In the left-hand panel of Figure 12.6, we report the self-diffusion coefficient estimated for water in various nanopores: confinement reduces the self-diffusion of water, consistent with Figure 12.4. For reference, MD simulations yield a self-diffusion coefficient for bulk liquid water of ~28 × 10^–10 m²/s.¹⁰⁸ The results in Figure 12.6 also show that the chemical properties of the minerals are important: all the pores considered have the same width and the simulation temperature is constant, yet the water self-diffusion coefficient varies by a factor of ~2. In the right-hand panel of Figure 12.6, we report the self-diffusion coefficients estimated for aqueous methane confined in the water-bearing pores considered in the left-hand panel of Figure 12.6. There is a correlation between the self-diffusion coefficient of water and that of aqueous methane, but there are also deviations. Bui et al.¹⁰⁷ highlighted the fact that the diffusion of aqueous methane in calcite nanopores can be anisotropic (the diffusion along the x-axis of the pore is about three times faster than that along the y-axis). For completeness, it is worth pointing out that anisotropic diffusion of hydrocarbons had been previously reported in nanopores carved out of calcite by Franco et al.,¹⁰⁹ suggesting that the surface structure of this solid material indeed affects the transport of the guest molecules.

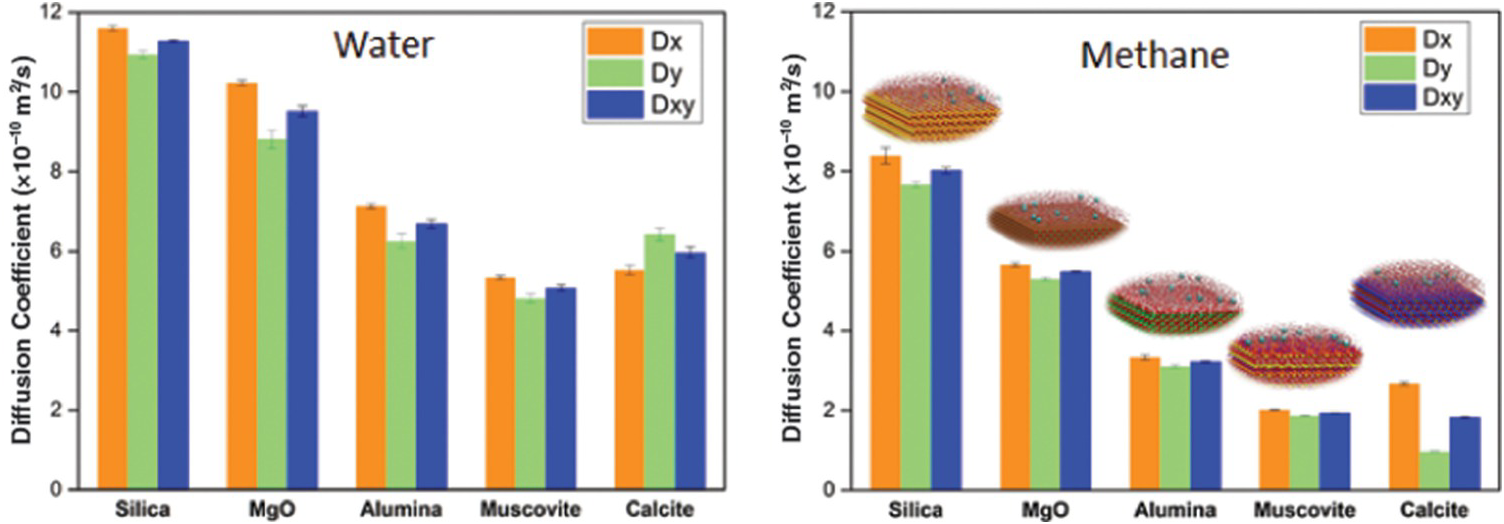
Figure 12.6 (Left) Self-diffusion coefficient for water in slit-shaped pores of width 1 nm carved out of different minerals at the same temperature. (Right) Self-diffusion coefficient for methane molecules dissolved in confined water. The results distinguish the diffusion coefficients along two perpendicular directions. While the self-diffusion coefficient for water is for the most part isotropic, that of aqueous methane in calcite pores is highly anisotropic, with transport along the x-axis being much faster than that along the y-axis.

Reprinted with permission from Bui T, Phan A, Cole DR, Striolo A. Transport mechanism of guest methane in water-filled nanopores. J Phys Chem C 2017; 121: 15675–15686.¹⁰⁷ Copyright 2017 American Chemical Society.

12.3.5 Transport of Aqueous Electrolytes in Narrow Pores

Argyris et al.¹¹⁰ and Ho et al.¹¹¹ attempted to quantify the mobility of aqueous electrolytes at low concentration within narrow slit-shaped pores. The goal was to quantify potential differences in the mobility of Cs⁺ and Na⁺ ions, which have the same valence but significantly different size. The aqueous solutions were electrostatically balanced by Cl^– ions. These MD simulations were conducted at similar conditions (1 M ionic strength, ambient temperature). The cristobalite silica pores were slit-shaped, with widths of ~1.2 nm. The surface chemistry was manipulated to replicate different pH scenarios. The results were quantified in terms of the self-diffusion coefficients of the electrolytes in the direction parallel to the pore surface. A strong correlation was observed between the preferential position of an ion in the direction perpendicular to the pore surface and its mobility. This correlation was interpreted based on prior results^{112, 113} that revealed that the mobility of interfacial water strongly depends on the distance from the solid substrate, as well as on the protonation state of the surface. The results concerning ion mobility are summarized in Figure 12.7.

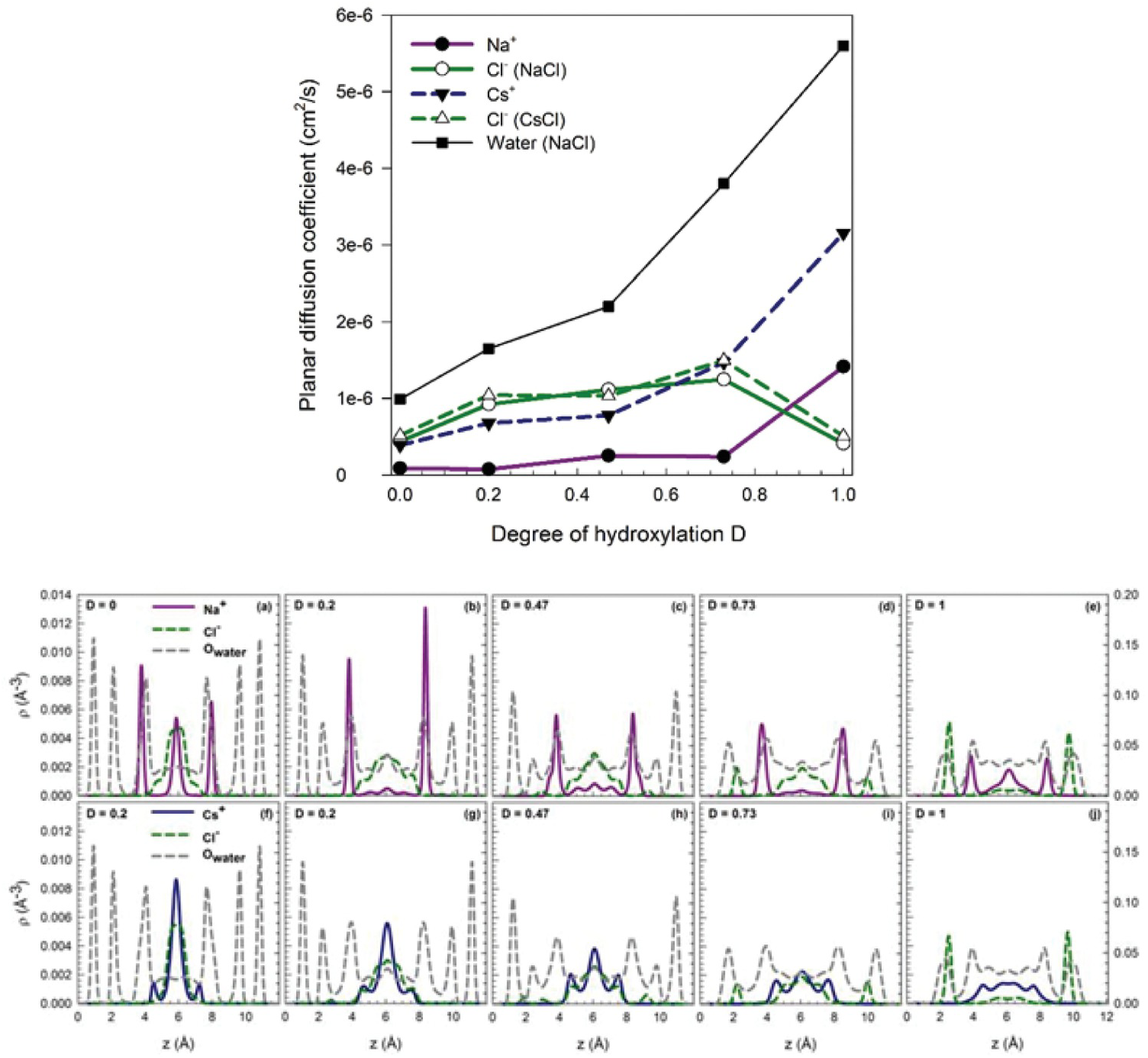
Figure 12.7 (Top) Self-diffusion coefficient estimated for different aqueous electrolytes and water in slit-shaped pores as a function of the degree of protonation D (D=0 in panel (a); D=0.2 in (b); D=0.47 in (c); D=0.73 in (d); and (D=1 in (e)). In all systems, Cs⁺ ions are more mobile than Na⁺ ions. (Bottom) Density profiles in the direction perpendicular to the solid substrate, with the same degree of protonation as in Top panels (panels f-j). The density profiles discriminate NaCl and CsCl systems. In general, the Cs⁺ ions accumulate near the centers of the pores, while Na⁺ ions are more closely associated with the pore surfaces. Because the molecular mobility depends on the distance from the surface, slower near the surface, the preferential distribution correlates with the ionic mobility.

Reprinted with permission from Ho TA, Argyris D, Cole DR, Striolo A. Aqueous NaCl and CsCl solutions confined in crystalline slit-shaped silica nanopores of varying degree of protonation. Langmuir 2012; 28: 1256–1266.¹¹¹ Copyright 2012 American Chemical Society.

It is worth stressing that the results depend strongly on the properties of the pore surface. In fact, MD simulations by Rotenberg et al.¹¹⁴ have shown how Cs⁺ ions tend to accumulate near clay surfaces, presumably because of the difference in surface charge. Because of the importance of preferential adsorption sites (e.g. see the recent contribution by Loganathan and Kalinichev¹¹⁵), which include pore edges, and because of the practical importance of quantifying ion migrations in the subsurface, advanced force fields are being developed to enhance the reliability of atomistic simulations,^116–118 and various approaches are being developed to include hydrodynamics and multiscale properties in the calculations.^119–122

12.4 Form and Quantity: Confinement Effects on Solubility

To estimate the amounts of fluids present in the subsurface, one approach could be first to estimate the volume available (i.e. the accessible pore space) and then to use our understanding of bulk fluids to estimate the amount of fluids in such a volume at the subsurface pressure–temperature conditions. This approach is reasonable as long as the fluid behavior in the bulk is consistent with that in the subsurface, which it is for larger pores (>100 nm). In this section, we discuss the effects nanopores have on the structure of fluids (“form”) that deviate markedly from the bulk. One property affected strongly by nanoconfinement is solubility. Another property of importance concerns the behavior of aqueous electrolytes in confinement. Because confinement alters the dynamics of water molecules, could it be that the dielectric constant of water in the deep subsurface differs strongly from that known in the bulk? Should this be the case, what are the implications regarding our still limited understanding of aqueous electrolytes in the subsurface?

12.4.1 Volatile Gas Solubility in Confined Liquids

Several studies reported an enhanced solubility of gases in liquids confined in small pores,^{123, 124} a phenomenon referred to as “oversolubility.” Luzar and Bratko¹²⁵ reported 5–10-fold enhancements of N₂ and O₂ solubility in water in 38–43‑Å hydrophobic pores. Experiments support these estimates. Pera-Titus et al.¹²⁶ studied the solubility of H₂ in CHCl₃, CCl₄, n-hexane, ethanol, and water within γ-alumina, silica, and MCM-41 and found that H₂ solubility was enhanced by up to 15 times when the pore size was <15 nm. Rakotovao et al.¹²⁷ confirmed these results using ¹H nuclear magnetic resonance (NMR).

According to Ho et al.,¹²³ oversolubility could be due to: (1) more favorable interactions between solute and solid than between solvent and solid, favoring solute adsorption close to the pore walls; (2) the pore being partially filled, resulting in a gas–solvent interface; and (3) adsorption of the gas being favored in regions of low solvent densities due to layering. Gadikota et al.¹²⁸ showed that solute size and the presence of salt in confined water are also important in modulating the dissolution of various gases in confined water. Using both experiments and simulations, these authors demonstrated greater solubility for CO₂ and Ar in Na-montmorillonite compared to bulk water, whereas confinement reduced CH₄. Gadikota et al.¹²⁸ analyzed the contributions to the free energy of solvation due to cavity formation and affinity to the water-filled pore. The free energy change due to cavity formation was found to be generally positive (i.e. it introduces a barrier to solubility), while the enthalpic contribution is generally favorable to solubilization. Both effects depend on the size of the gas molecule.

Phan et al.¹²⁹ revealed approximately one order of magnitude higher solubility of methane in water confined in a partially filled 1 nm-wide silica pore. Methane molecules accumulated in narrow regions within the pores, where water molecular density was low. It was found that water molecules surrounding the guest methane were organized in hydrogen-bonded structures resembling gas hydrates. However, because of steric constraints, these clathrates were not stable. Phan et al.¹³⁰ also considered other 1‑nm slit-pore systems (MgO, Al₂O₃). The results demonstrated that methane solubility in confined water strongly depends on the confining material (Figure 12.8) because the molecular structure of confined water differs markedly within the three pore types. A direct correlation was observed between methane diffusion coefficients and water molecular density fluctuations.

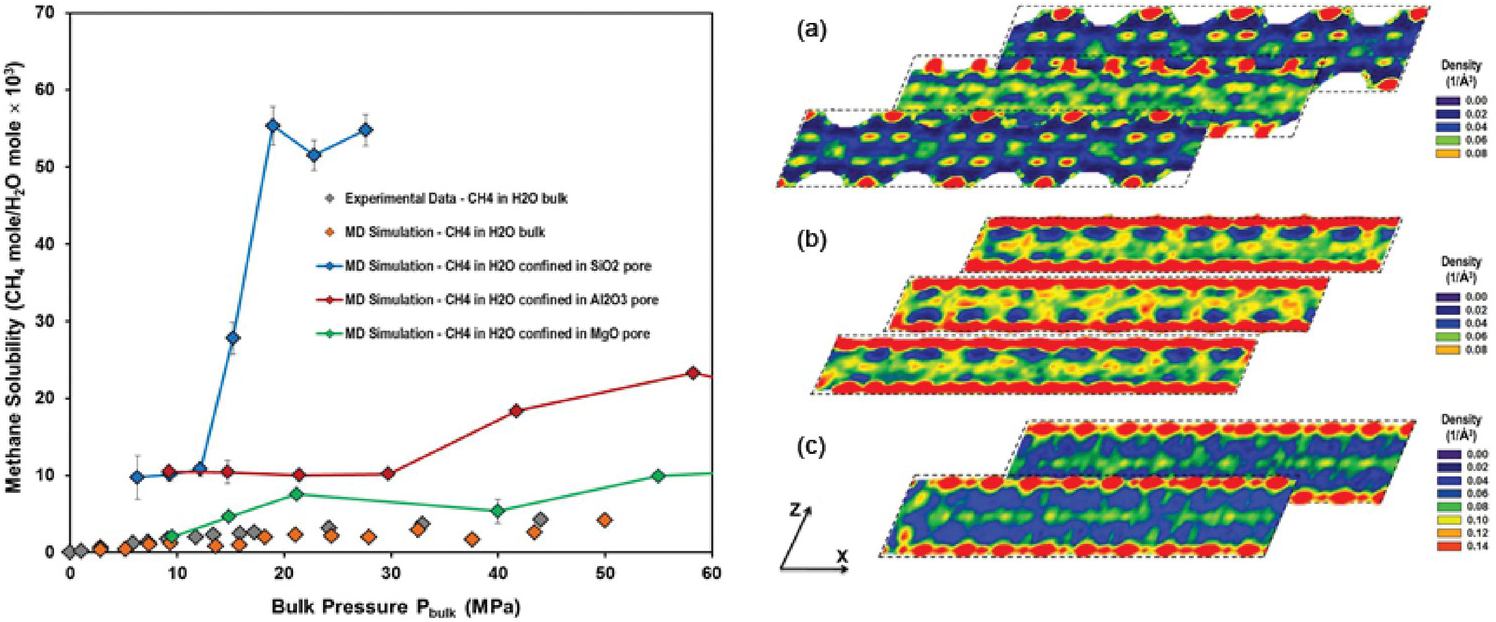
Figure 12.8 (Left) Methane solubility in confined water as a function of bulk pressure in MPa – SiO₂ blue, Al₂O₃ red, MgO green. Simulated bulk solubility of methane in liquid water at 298 K from Sakamaki et al.¹³¹ (Right) Variability for in-plane density distributions of water oxygen in layers parallel to the x–z plane at several locations along the y-axis within (a) SiO₂, (b) Al₂O₃, and (c) MgO. The results are for pores containing only water. Densities are expressed in number of molecules per cubic Å.

Reprinted with permission from Phan A, Cole DR, Striolo A. Factors governing the behaviour of aqueous methane in narrow pores. Philos Trans A Math Phys Eng Sci 2015; 374: 20150019.¹³⁰ Copyright and usage: the authors.

These observations are in contrast to those by Badmos et al.,¹³² who estimated, using molecular dynamics, the solubility of H₂S in water confined in silica nanopores at 313 K. The simulation results suggested that confinement reduces the H₂S solubility in water and that the solubility increases with increasing pore size. These results are due to perturbations on the coordination of water molecules around H₂S due to confinement. The perturbations are stronger in the narrowest pores considered. These results are qualitatively consistent with those reported for aqueous NaCl reported by Malani et al.¹³³ This group reported a lower NaCl solubility in water confined within graphene nanopores. However, NaCl is a salt, and therefore it is likely that the mechanisms responsible for the reduced solubility of H₂S and NaCl in confined water are due to different interfacial processes.

The interest in geologic CO₂ sequestration resulted in numerous studies on the form and movement of CO₂ through porous networks, chiefly focusing on montmorillonite. Bowers et al.¹³⁴ studied the incorporation of supercritical CO₂ in smectite by in situ ¹³C and ²³Na magic angle spinning NMR. They observed line broadening in the ¹³CO₂ resonance at 90°C and 50 bar CO₂ pressure for Na-hectorite, consistent with CO₂ pressure in the interlayers. Kirkpatrick et al.¹³⁵ reviewed efforts using NMR and molecular modeling to explore mineral surfaces and interlayer filling by H₂O, cations, anions, CO₂, and natural OM in swelling clays. In addition to entering the interlayer, there is evidence that CO₂ dissolves in the confined water. Schaef et al.¹³⁶ used NMR, x-ray diffraction and Monte Carlo simulation to explore the intercalation of dry supercritical CO₂ into three swelling clays in which Na, NH₄, or Cs occupied the interlayer. In the absence of water, CO₂ did enter the NH₄ and Cs clays, but was excluded from the Na clay. A weak intercalation of CH₄ has been observed for smectites,¹³⁷ but is more pronounced for 4‑nm weakly hydrated silica pores, as demonstrated by Ok et al.¹³⁸

12.4.2 Aqueous Electrolytes in Confinement

The effect of nanoconfinement on the transport of aqueous electrolytes has been briefly summarized in Section 12.3.5. It is possible that, because confinement affects the structure and dynamics of confined water, it indirectly affects the solubility of electrolytes. For molecular simulations to reliably predict the properties of confined electrolytes, it is important that adequate force fields describe the interactions between water, electrolytes, and pore constituents, as well as all the cross-interactions between these components.^{139, 140} The reliability of the force fields used to describe the electrolytes depends on the model chosen to simulate water, and it is essential to tune the ion–ion interactions if one seeks to replicate the experimental salt solubility.^{141, 142} Svoboda and Lísal¹⁴⁰ recently employed the grand canonical Monte Carlo algorithm to predict the solubility of NaCl in montmorillonite pores. The simulations were conducted at 365 K and 275 bar. At these conditions, the simulation models implemented (SPC/E model for water) predict a saturation NaCl concentration in water of 3.14 mol/kg,¹³⁹ which underestimates the experimental value of 6.1 mol/kg.¹⁴³ The pore widths considered ranged from 1.0 to 3.2 nm, and they were simulated in equilibrium with saturated bulk aqueous NaCl solutions. The results show that the concentrations of the adsorbed ions in the nanopores are lower than in the bulk aqueous system and decrease as the pore width narrows. Moucka et al.¹³⁹ used simulations to compare the aqueous solubility of NaCl in Na-montmorillonite and pyrophyllite pores of the same width. They were able to distinguish the ionic solubility near the center of the pore, where the properties are similar to those found in bulk water, and those near the pore surfaces, where the properties are significantly different from those found in bulk water. As the pore width decreases, the contribution of the region near to the pore surface increases compared to that of the fluids near the pore center, and consequently the NaCl solubility strongly decreases compared to that observed in bulk water. In addition to structural effects, one could attempt to explain these observations based on the changes in the dielectric constant of water due to confinement, discussed below.

12.4.3 Dielectric Constant of Nanoconfined Water

The dielectric properties of water and electrolytes in nanopores are still poorly constrained for most substrates relevant to the subsurface. According to Renou et al.,¹⁴⁴ the static dielectric constant (ε) characterizes the capacity of a material to transmit an electric field and controls the charge migration and dipole reorientation. Compared to other fluids types, bulk water has a high ε due to the strong bonds between hydrogen and oxygen as well as hydrogen bonding between water molecules. This large ε means that ionic substances tend to dissociate in water, yielding ionic solutions. Thus, the water ε is essential to understanding the solvation of ions and their transport. For example, Sverjensky et al.¹⁴⁵ extracted from the research of Pan et al.¹⁴⁶ the theoretical estimates of the water dielectric constant at extreme pressures and temperatures to calculate the solubility of quartz and corundum to 600 MPa and 1200°C. This effort indicates that ε ranges from as low as ~2 at 1200°C and 100 PMa to ~80 for ambient conditions.

Of interest to this chapter is how much of an effect nanoconfinement might have on ε, and further, how this change might impact mineral solubility. In confinement or near interfaces, ε is no longer a simple scalar quantity, but it becomes tensorial. The radial component of water ε_⊥ is fundamentally important to the solvation and transport of ions, in contrast to the axial component (ε_ll), which is important for transport behavior along the pore wall. However, there are conflicting results with respect to the magnitude of the ε values. For example, a number of MD studies have demonstrated a local interfacial increase in the axial (tangential) component of the dielectric constant (ε_ll) relative to the bulk water value and to values exhibited by the radial ε_⊥.^147–149 An enhanced ε_ll was also predicted in other studies that addressed the role of cylindrical silica and carbon nanopores.^{144, 149–151} Conversely, values for the radial ε_⊥ tend to be equal to or much less than the bulk ε. This anisotropy is most pronounced in hydrophobic pores.

Unlike the increase of the axial dielectric permittivity near the pore wall noted above, Renou et al.¹⁴⁴ observed a significant decrease in ε_ll relative to the ambient bulk water value with increasing surface charge density using MD. More recently, Fumagalli et al.¹⁵² observed anomalously low ε (approaching 1) of confined water that was two to three molecules thick in dielectric imaging experiments involving graphene and boron nitrite. Similarly, Zhu et al.¹⁵³ reported on the anomalous behavior of ε for aqueous solutions of NaCl of varying concentration (0–1.5 M) confined in a 2.4‑nm diameter cylindrical silica pore (Figure 12.9). They noted that the dielectric constant profile near the surface correlates with that of the water density. Using classical MD simulations, Zhu et al.¹⁵³ demonstrated: (1) a marked anisotropy between ε_ll and ε_⊥; (2) that the values for ε_ll decrease relative to those of pure water, but show enhancement near the pore wall; and (3) that ε_⊥ shows a nonlinear NaCl concentration dependency. Renou et al.¹⁵⁴ addressed the structural and dielectric behavior of confined NaCl, NaI, MgCl₂, and Na₂SO₄ (1 M concentration) in nanoporous hydrophilic 1.2‑nm silica pores. They also reported a dielectric anisotropy of confined water and an unusual increase in the radial component of permittivity (ε_⊥) of confined solutions.

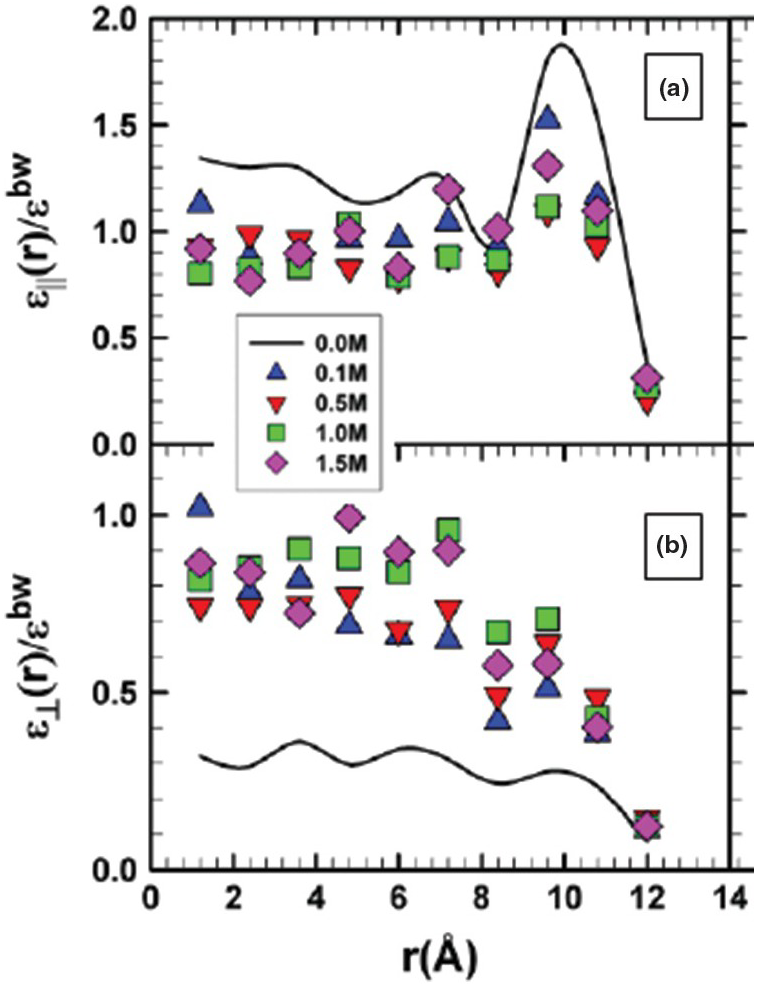
Figure 12.9 Profiles of the ratios of ε_ll (a) and ε_⊥ (b) for NaCl solutions of varying concentrations confined in 2.4‑nm diameter cylindrical SiO₂ pores to the dielectric constant of bulk water (ε^bw).

Reprinted with permission from Zhu H, Ghoufi A, Szymczyk A, Balannec B, Morineau D. Anomalous dielectric behavior of nanoconfined electrolytic solutions. Phys Rev Lett 2012; 109: 107801.¹⁵³ Copyright 2012 American Physical Society.

It is notable that the range of dielectric constant values reported for water confined in nanopores encompasses the range of ε values estimated for bulk water from ambient to extreme conditions. This suggests the distinct possibility that the bulk values for ε currently used to estimate fluid properties in the subsurface might not be appropriate, especially for pores such as those illustrated in Figures 12.2 and 12.3. We lack a comprehensive assessment of ε for nanoconfined environments relevant to subsurface conditions (i.e. at elevated pressure and temperature with widely varying solution compositions) and a quantification of whether these “local” effects yield important consequences on, for example, salt solubility and other important observables.

12.5 Form and Origin: Confinement Effects on Reactivity

12.5.1 General Concept

In this section, we address the reactivity of carbon-bearing fluids and how confinement can affect their behavior. Based on thermodynamic arguments, Shock¹⁵⁵ predicted that, in the subsurface, the most common form of fluid carbon would be that of CO₂, not CH₄. This prediction was based on the analysis of the thermodynamic equilibrium of the reaction:

CO₂ + 4H₂ ↔ CH₄ + 2H₂O.

${\mathrm{CO}}_2+4H_2\leftrightarrow {\mathrm{CH}}_4+2H_{2}O.$(12.2)

The equilibrium was assessed based on the expected pH as buffered by the rocks. However, nanoconfinement could potentially affect fluid reactivity via three main mechanisms: (1) the closeness of the rock surfaces provides catalytic sites that speed up some reaction pathways, thus affecting the kinetics of the reactions; (2) the confinement is so restrictive that some of the reactants or the products are either not able to react or are not allowed to escape from the porous matrix; and (3) the preferential adsorption of some of the fluid components onto the rock surface can affect the overall equilibrium composition via a molecular-level application of Le Chatelier’s principle. The first of these three scenarios concerns kinetic effects. We only note that some olivines contain Ni, Co, and/or Cr, which could act as catalysts to increase the rate of chemical reactions, including the oxidation of CH₄ to CO₂.¹⁵⁶

12.5.2 Methanation of Carbon Dioxide

Using reactive ensemble Monte Carlo simulation, Le et al.¹⁵⁷ explored whether confinement could alter the bulk expectations regarding reaction (12.2). In particular, they tested whether the preferential adsorption of either CO₂ or H₂O on the pore surface could affect the equilibrium conversion of CO₂ to CH₄. The system simulated represented a nanoporous matrix in contact with a larger microfracture occupied by the bulk fluid. Water, hydrogen, carbon dioxide, and methane were free to exchange between the nanopores and the microfracture and to react within the various environments. The microfracture was large enough to provide a “bulk” system. The conceptual framework is summarized in Figure 12.10.

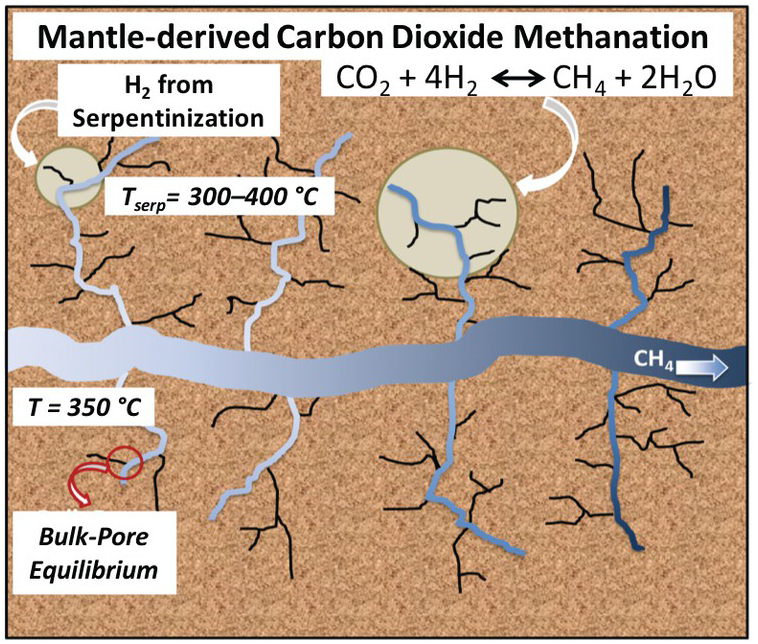
Figure 12.10 Schematic for a possible carbon dioxide methanation process. Within oceanic crust, mantle-derived melt is emplaced at shallow depths and heats the ultramafic ocean crust driving seawater circulation along natural fractures and microfractures where serpentinization reactions take place. The H₂ produced could come into contact with carbon dioxide derived from the mantle.

Reprinted with permission from Le T, Striolo A, Turner CH, Cole DR. Confinement effects on carbon dioxide methanation: a novel mechanism for abiotic methane formation. Sci Rep 2017; 7: 9021.¹⁵⁷

Le et al.¹⁵⁷ generated slit-shaped pores (1 and 2 nm) carved out of β-cristobalite silica. The results showed that the thermodynamic equilibrium composition shifted toward methane production, suggesting that thermal hydrocarbon synthesis near hydrothermal vents and deeper in the magma-hydrothermal system is possible. The results showed strong dependency of the reaction equilibrium conversions, X_CO2$X_{{\mathrm{CO}}_2}$, on nanopore size, nanopore chemistry, and nanopore morphology. All conditions that enhance water adsorption (i.e. increasing pore hydrophilicity or surface roughness) resulted in an enhancement of reaction yield. Representative results for 1‑nm pores are shown in Figure 12.11, where the composition in the bulk phase (left-hand panels) is compared to that within the pores (right-hand panels). In situations in which the pore space is dominant compared to the bulk space, it is conceivable that the overall system composition strongly deviates from bulk expectations.

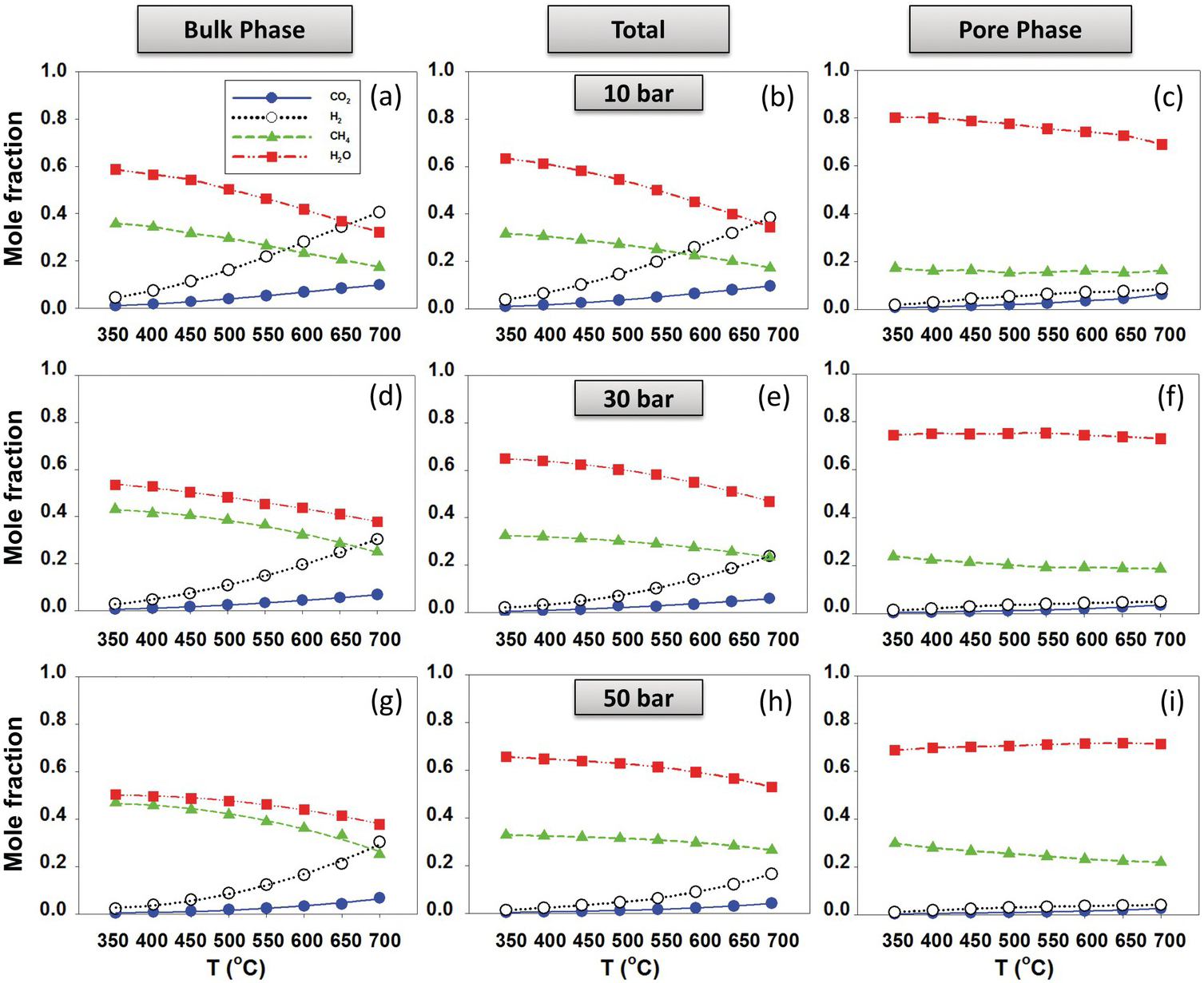
Figure 12.11 Product fraction of CO₂ methanation (reaction (12.1)) for the (a, d, and g) bulk phase and (c, f, and i) pore phase in equilibrium with each other at different temperatures and pressures. (b), (e), and (h) show total molecular fractions.

Reprinted with permission from Le T, Striolo A, Turner CH, Cole DR. Confinement effects on carbon dioxide methanation: a novel mechanism for abiotic methane formation. Sci Rep 2017; 7: 9021.¹⁵⁷

These results could contribute to an important scientific debate focusing on the possibility of the abiotic synthesis of hydrocarbons during oceanic crust–seawater interactions, which could reshape the core hypotheses of the origin of life.^{158, 159}

12.6 Summary and Opportunities

Exploring the behavior of complex geofluids confined in micro- and meso-porous networks provides the foundation for quantifying geologically relevant systems where mass and energy exchange occur. Nanoconfinement in porous systems gives rise to rich behavior that results from the interplay of geometrical restriction imposed by different pore features (size, geometry, chemical composition, etc.), the interaction between the porous material and the fluid, and the nature of the confined fluid itself. Fluid structure (or “form”) affects most if not all fundamental properties of interest. Since nanopores affect structure, they impact movement, reactivity (“origin”), and quantity. While in relatively large mesopores fluid “movement” might occur at different timescales as a function of location in the pore, greater geometric confinement can lead to severely constrained motion, such as the molecular diffusion mechanisms discussed in Section 12.3. Within a given porous matrix, timescales of motion of confined fluids can exhibit interesting dependencies on the molecular size and concentration of the confining fluid, such as the levitation effect of confined hydrocarbons or anomalous pressure dependence on gas dynamics in mesoporous media.

Water and associated dissolved constituents, as a confined fluid, exhibit very rich structural and dynamical behavior due to the effects of hydrogen bonding, compounded by the other effects identified above. All of these effects lead to a wide variety of length and time scales relevant to the study of confined fluids and as such require a variety of experimental and computational tools for a thorough study of the behavior of geologically relevant confined fluids. The techniques that probe the behavior of confined fluids at the molecular level depend heavily on the interpretation of the measured data and as such can be prone to subjective bias. Therefore, if possible, it is advantageous to look at each solid–fluid system from different perspectives, both experimental and computational. Much progress is expected when synergistic approaches are implemented. For example, one obvious next step would be the detailed experimental and computational investigation of the structural properties of fluid mixtures in increasingly realistic systems. This includes complex fluid mixtures, as well as porous materials that are heterogeneous and better representative of the subsurface. Once these analyses are obtained, one should challenge the mechanisms discussed in Sections 12.3 and 12.4. A second target of opportunity pertains to whether the presence of ions and associated hydration affect the transport and accumulation of hydrocarbons in nanoporous matrices. The presence of concentrated salts disrupts water structure, slows down its dynamics, and alters the water free energy landscape, which impacts transport of guest molecules.^{106, 130} Clearly, how one fluid component invades and displaces and/or competes with another for surface sites will have a profound effect on these types of transport mechanisms. The dielectric properties of water and aqueous systems under nanoconfinement are poorly constrained for Earth-relevant systems. Recent studies have exhibited a wide range of values that are not always in agreement.

Finally, we point to the effects of confinement on the equilibrium composition of reactive systems. The results summarized in Section 12.5 suggest that thermogenic methane production could be enhanced by nanoconfinement, albeit within a specific window of pressure–temperature–composition conditions. To quantify whether those simulation results are relevant across a broader temperature and pressure landscape, a few research questions remain to be addressed, in particular:

1. 1. Will the CO₂ methanation reaction encounter kinetic barriers within the pores or will the pore surfaces provide active sites for catalyzing the reaction?

2. 2. How much nanopore volume in the subsurface is needed for achieving levels of methane production that are relevant for hydrocarbons synthesis?

3. 3. Can these insights be reproduced by experiments?

Future studies could be implemented to address these and related questions and to quantify how these phenomena affect the carbon cycle.

Acknowledgments

AS acknowledges financial support from the European Union via the Marie Curie Career Integration Grant No. 2013-CIG-631435, as well as from the European Union’s Horizon 2020 research and innovation program under Grant No. 640979 and Grant No. 764810. DC was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences under grant DE-SC0006878. DC and AS both receive partial funding from the Sloan Foundation-funded Deep Carbon Observatory. Special thanks to Ms. Tran Le for her help in assembling the reference list.

Questions for the Classroom

1. Are nanopores observed in all Earth materials? How are these observed? What are their shapes, sizes, and distributions? Is there a correlation between these properties and depth?

2. Discuss quantitatively how confinement affects the thermophysical properties of a fluid, whether pure or a mixture. Discuss the effects due to strong pore–fluid interactions and how changing the pore width affects these outcomes. Discuss in particular such effects with respect to solubility, reactivity, phase equilibria, and melting.

3. Discuss the differences between surface and pore diffusion. What are the mechanisms responsible for each and when is surface diffusion expected to dominate over pore diffusion in determining the overall fluid transport across a porous material? What mechanisms become dominant as the pore size becomes comparable to the size of a fluid molecule?

4. How does the presence of a pore affect the reactivity of a fluid? Distinguish between kinetic and thermodynamic effects.