Introduction
Glacier-dammed lakes can release their water suddenly, causing a so-called outburst flood or ‘jökulhlaup’ (e.g. Reference BjörnssonBjörnsson, 1998). They represent a severe threat in many mountain ranges and have caused major destruction in historical time (e.g. Reference HaeberliHaeberli, 1983; Reference Richardson and ReynoldsRichardson and Reynolds, 2000; Reference BjörnssonBjörnsson, 2002; Reference Raymond, Wegmann and FunkRaymond and others, 2003). Discharge at the glacier tongue may increase by more than an order of magnitude (e.g. Reference BjörnssonBjörnsson, 1992). High water pressure gives rise to extensive perturbations of the glacial drainage system and of the dynamics of the ice mass (Reference Röthlisberger, Lang, Gurnell and ClarkRöthlisberger and Lang, 1987).
Glacier outburst floods have been addressed empirically and theoretically. Reference Clague and MathewsClague and Mathews (1973) proposed a widely known empirical relation to predict peak discharge, indicative of the hazard potential, from lake volume. Further studies elaborated on this relation (Reference Costa, Baker, Kochel and PattonCosta, 1988; Reference Walder and CostaWalder and Costa, 1996; Reference Ng and BjörnssonNg and Björnsson, 2003). Theory postulates that the drainage of glacier-dammed lakes can be controlled by two different processes: (1) the classical Röthlisberger-channel enlargement (Reference RöthlisbergerRöthlisberger, 1972; Reference NyeNye, 1976), inducing a gradually rising limb of the hydrograph; and (2) flotation of the ice dam, producing a sharp and sudden runoff peak (e.g. Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others, 2004). Based on these theories many attempts have been made to simulate glacier-dammed lake outburst events numerically (e.g. Reference NyeNye, 1976; Reference Spring and HutterSpring and Hutter, 1981; Reference ClarkeClarke, 1982, 2003; Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others, 2004). Only a few theories exist that focus on the initiation of drainage (e.g. Reference FowlerFowler, 1999).
Data about glacier-dammed lake outbursts are sparse and our understanding is incomplete owing to the complex nature of these events. Many of the processes involved are only partially known. Exceptional datasets exist for Grímsvötn, Iceland, (Reference BjörnssonBjörnsson, 1988, 1998, Reference Björnsson2002) and Hidden Creek Lake, Kennicott Glacier, Alaska (Reference AndersonAnderson and others, 2003, Reference Anderson, Walder, Anderson, Trabant and Fountain2005; Reference WalderWalder and others, 2005, 2006). The project on Gornergletsche, Switzerland, presented in this paper is the first integrated study of a lake outburst event in the Alps.
Our project investigates the outburst events of an ice-marginal lake, Gornersee, that forms annually in spring and drains in summer. The present study deals with the hydrological part of the outbursts. Various studies have been carried out on Gornergletscher focusing on glacial hydrology (Reference RöthlisbergerRöthlisberger, 1972; Reference EllistonElliston, 1973; Reference CollinsCollins, 1979; Reference Aschwanden and LeibundgutAschwanden and Leibundgut, 1982; Reference CollinsCollins, 1986; Reference Iken, Fabri and FunkIken and others, 1996). Gornergletscher is particularly suitable for a hydrological study of glacier-dammed lake outburst events, due to the long time series of discharge measurements at the terminus of more than three decades and the long-term climate records available in the vicinity. Additionally, observations of lake drainage by Reference Bezinge, Perreten and SchaferBezinge and others (1973) in the 1950s and 1960s provide the possibility of an assessment of glacier floods over more than half a century.
This paper consists of two parts: an analysis of the 50 year time series of the annual lake outburst events including trends in flood timing and drainage volume, and an analysis of detailed field investigations performed in 2004 and 2005.
In order to separate the outburst component of the discharge hydrograph from the melt/precipitation component we perform a hydrograph separation using a coupled melt–runoff model (Reference HockHock, 1999). This is necessary for Gornergletscher since background discharge is relatively large during the outbursts. By calculating hourly discharge in the period 1970–2005 we are able to derive timings and drainage volumes of the annual outburst events. Data from the extensive field campaigns in 2004 and 2005 allow an integrated investigation of the processes involved in the drainage event focusing on short timescales, providing a unique opportunity for a comprehensive study of glacier-dammed lake outbursts. For both years we compute the water volume impounded in the lake, the lake outflow and the drainage hydrograph at the glacier terminus. The hydrographs are interpreted with respect to water-pressure records in boreholes and ice motion. We detect different initiation mechanisms of the glacier outburst flood and infer water storage processes during the drainage event.
Field Site
Gornergletscher is the second largest glacier in the Alps (Fig. 1). It consists of several tributaries and covers an area of ~60 km2. The glacier spans an elevation range from 2200 to 4600 m a.s.l. Most parts of the glacial system are temperate. The main tributary, however, Grenzgletscher, accumulates cold firn at altitudes higher than 4000 m a.s.l. (Reference SuterSuter, 2002). The cold ice reappears on the flat glacier tongue, which extends 5 km further downstream from the lake, causing a polythermal regime (Reference HaeberliHaeberli, 1976). Radio-echo soundings and borehole temperature measurements indicate that the base of the glacier is temperate, and thus does not inhibit water flow (personal communication from O. Eisen, 2006). The maximum ice thickness is 450 m (Reference HussHuss, 2005) and the main glacial valley is slightly overdeepened (Fig. 2b).

Fig. 1. Map of the ablation area of Gornergletscher. Dots mark two boreholes, and crosses indicate the position of four stakes for ice motion measurement. Debris-covered ice is shaded grey. The central flowline used for the profiles in Figure 2 is shown.

Fig. 2. (a) Schematic profile of the evolution of Gornersee in the past few decades. The glacier surface for 1931 is based on a digitized map of the official Swiss topographic survey; for 1960 on unpublished material of Grande Dixence, SA; and for 1982 and 2003 on evaluated aerial photographs (Reference Bauder, Funk and HussBauder and others, in press). (b) Longitudinal profile of the tongue of Gornergletscher. Bed topography is obtained from radioecho soundings. Two boreholes and four stake locations are indicated.
Gornersee is situated in a deep basin at the confluence of two tributaries (Figs 1 and 2). Significant changes of glacier geometry during the past century caused shifts in lake location and volume (Fig. 2a). The lake usually starts to fill in May and drains annually between June and August (Reference Bezinge, Perreten and SchaferBezinge and others, 1973). Each year 1–5 × 106m3 of meltwater are impounded by the lake. Often, the lake is filled to the maximum level beyond which supraglacial outflow occurs at the start of the drainage. However, it has also been known to drain earlier (Reference Bezinge, Perreten and SchaferBezinge and others, 1973; personal communication from H. Röthlisberger, 2005). In 2004 we observed a supraglacial outflow for a few days before water left the basin subglacially. The duration of the lake drainage is 2–7 days. The peak discharges during the outburst events measured at the glacier terminus reach 20–50 m3 s−1, of which (as calculated in this study) 40–75% is lake water. In the first half of the 20th century, flood intensities of more than 100 m3s−1were reported, regularly causing severe damage in the valley of Zermatt (Reference Raymond, Wegmann and FunkRaymond and others, 2003).
Field Campaigns and Methods
Data collection and field methods
A gauging station operated by Grande Dixence hydropower company, and situated 1 km from the glacier snout, has recorded hourly discharge since 1970 (Fig. 1). Long-term climate data since 1982 are provided at hourly resolution by the weather station of MeteoSchweiz, Zermatt (1638 m a.s.l.) 5 km from the glacier terminus. For the period 1970–81 we used sub-daily data from a weather station at Grächen (1550 m a.s.l.) 25 km down-valley from Gornergletscher. During the field studies in 2004 and 2005 we operated an automatic weather station (AWS) at 2650 m a.s.l., that measured ventilated air temperature and precipitation at 30 min intervals at the northern margin of Gornergletscher (Fig. 1). A network of up to 30 stakes was maintained and ablation readings were taken at intervals of 1–3 weeks. In April 2004, the water equivalent of the snow cover was determined at several positions. An automatic camera on Gornergrat provides daily photographs to map the extent of snow cover and monitor the lake evolution. Digital elevation models (DEMs) of the glacier surface topography were derived from aerial photographs for 1982, 2003, 2004 and 2005 (Bauder and others, in press). We installed pressure transducers in the lake in 2004 and 2005, recording the water depth every 10 min. Surface ice motion was continuously monitored both by differential GPS (global positioning system) at 3 hour intervals, and a theodolite surveying 30 stakes hourly, providing a distributed picture of ice motion. In both years we drilled several boreholes to the glacier bed using a hot-water drilling system. In the boreholes, we recorded water pressure and englacial temperature and conducted measurements of vertical strain with magnetic rings. Tracer injections were carried out and seismic activity was monitored.
Hydrograph separation
The discharge of lake outburst events is superimposed on melt/precipitation induced runoff variations. Since the latter, in contrast to previous studies (e.g. Reference BjörnssonBjörnsson, 1998; Reference AndersonAnderson and others, 2003), are not negligible in the case of the Gornersee outburst floods, it is necessary to conduct a hydrograph separation. We apply a distributed temperature-index melt model coupled to a linear-reservoir runoff model (Reference HockHock, 1999) to compute hourly discharge from the catchment of Gornergletscher. The model and its calibration are described in the Appendix. By subtracting simulated melt/precipitation induced discharge from discharge measured at the gauging station we extract the outburst component of the hydrograph (Fig. 3).

Fig. 3. (a) Measured and simulated hourly discharge of Gornergletscher during summer 2004. The lake drainage event is eyecatching. (b,c) Periods marked with bars in (a) are shown in detail: 29 May–13 June (b) and 21 July–5 August (c). Temperature (T) and precipitation (P) are shown for comparison.
The analysis of the drainage events of Gornersee consists of two stages. Firstly, discharge in all years with available runoff data (1970–2005) was simulated using the calibrated melt-runoff model. Thus, based on the difference between measured and modeled discharge, the timing of the drainage event could be identified for every year of the 35 year period considered. Secondly, the model was re-calibrated for every year over a period of 25 days around the drainage event. An initial snow cover for this reduced period was generated with a model run starting in October of the previous year, providing information about hibernal snow accumulation. By re-calibrating the model, an individual parameter combination was found for each year that maximized agreement between modeled and measured discharge before, after and, thus, presumably during the outburst. This enables the determination of outburst volume, peak lake discharge, and timing and flood duration with optimal accuracy. Estimates of drainage volume and timing between 1950 and 1970 by Reference Bezinge, Perreten and SchaferBezinge and others (1973) were combined with our new 35 year data series.
The measured and simulated quantities have two sources of uncertainty: (1) errors in the runoff measurements (estimated as ±5%) and (2) modeling uncertainties. The accuracy of the model is difficult to judge during the outburst floods as no experimental validation is possible in this period. Therefore, the potential errors were estimated arbitrarily for every year, mainly based on model performance before and after the outburst event. The occurrence of heavy rainfall events during the flood influences the quality of the model results in a negative way and was also considered. We estimate an error of between ±5% and ±30% of both drainage volume and peak lake discharge for individual years.
Lake bathymetry and meltwater input
As a more extended database exists for 2004 and 2005, we are able to determine the bathymetry of the lake basin from highly resolved DEMs derived from aerial photographs taken immediately after the drainage for both years. By combining lake level measurements and bathymetry we calculate lake volume. Errors may arise due to floating icebergs or partial flotation of the ice dam. These uncertainties are minor and are not incorporated in the computation. They contribute to an estimated uncertainty of lake volume of ±5%.
For water-balance considerations we simulate the meltwater input into the lake for the pre-drainage periods of 2004 and 2005 with the melt-runoff model (see Appendix). The catchment basin of the glacier-dammed lake has an extent of 8.6 km2. We define it as the surface watershed. To model runoff from the lake catchment basin we use the parameters calibrated for the entire glacial system.
Results
Lake outburst events, 1950–2005
We identified significant drainage events in every year since 1970, except for 1984, 1991 and 1995. Figure 4a presents the evolution of the lake outburst timing, showing an obvious trend. Between 1950 and 2005 a shift of about 2 months has been observed, moving the expected date of the event from late August to late June. In contrast, the temporal evolution of drainage volume does not show a uniform trend. In addition to the year-to-year variability, long-term fluctuations of drainage volumes also occurred (Fig. 4b). Since only very limited direct observations exist from the past, we do not know to what extent the volume fluctuations are caused by changing lake basin geometry or different filling levels of the lake.

Fig. 4. (a) Evolution of lake outburst timing. The dots correspond to the date of the peak discharge. In 1984, 1991 and 1995 no drainage events could be found. Vertical bars (after 1970) show the duration of the drainage event. (b) Evolution of drainage volume. Error bars indicate the uncertainty range of the calculated values.
We find a power-law relation between peak lake discharge Q max (m3s−1) and drained volume V (106m3) as proposed by Reference Clague and MathewsClague and Mathews (1973) in the form
with constant k = 10 and exponent b = 2/3 yielding the best fit for the drainage events of Gornersee (r 2 = 0.61, n = 33). Considering the range of drainage volumes involved, which is much lower than in previous studies (Reference Clague and MathewsClague and Mathews, 1973; Reference Walder and CostaWalder and Costa, 1996), the two variables show a strong correlation (Fig. 5). The peak lake discharges of the analyzed drainage events of Gornersee are lower than those predicted by the Clague–Mathews relation. However, the proportionality, Q max ∝ V 2/3, seems applicable to Gornersee.

Fig. 5. Log–log plot of drainage volumes and peak lake discharges for the outburst events 1970–2005. The relation Q max ∝ V 2/3 is shown, corresponding to the Clague–Mathews formula with a constant of k = 10 (r 2 = 0.61, n = 33).
Outburst events, 2004 and 2005
Lake filling
The glacier-dammed lake reached a maximum volume of (4 ± 0.2) × 106 m3 in 2004 and (1.3 ± 0.1) × 106m3 in 2005. The maximum water volume stored in the lake varies greatly between the years, although the lake basin size was nearly the same. In 2004, the cumulative modeled lake input and the measurements of lake volume agree well (Fig. 6). In 2005 the simulated cumulative meltwater input matches the measured lake volume well until 2 June. Afterwards lake volume rises at a slower rate (Fig. 6). Based on these considerations we suggest that a leak was opened 1 week prior to the beginning of the lake outburst in 2005.

Fig. 6. Temporal evolution of water volume stored in Gornersee in 2004 and 2005 (solid lines). Dotted lines correspond to the cumulative modeled input of meltwater into the lake basin. The hypsometric relation between lake level and water volume in 2004 is shown in the inset.
Lake outflow and river flood hydrographs
In this section we analyze two types of hydrographs. The ‘lake outflow hydrograph’ describes the discharge from the lake, and the ‘river flood hydrograph’ refers to the discharge at the glacier terminus that solely results from the outburst. The hydrographs are defined as:
Comparison of the hydrographs provides information about the modification of the flood wave during its passage through the glacial system. Unfortunately, in 2004 an iceberg buried the pressure transducer in the lake 4 days after the initiation of the outburst and terminated the measurements.
As shown in Figure 7d, the lake outflow hydrographs for 2004 and 2005 display significantly different shapes. In 2004 a rapid rise of lake outflow is observed, reaching its peak 2 days after the start. In contrast, the drainage event in 2005 is characterized by a progressive increase of lake outflow followed by an abrupt termination. Furthermore, the lake outflow hydrograph reveals fluctuations with amplitudes of ~1 m3 s−1 (Fig. 7d, right). The hydrograph reaches its maxima in the morning and its minima in the afternoon, behaving anticyclically to water pressure in the glacial system. The lake outflow peaks at 17 m3 s−1 in 2004 and at 10 m3 s−1 in 2005.

Fig. 7. Compilation of measurements and simulations around the drainage events of 2004 (left) and 2005 (right). (a) Temperature (T) and precipitation (P); (b) measured and simulated discharge at the gauging station; (c) measured and simulated lake volume; (d) lake outflow hydrograph; (e) river flood hydrograph; (f) water pressure in boreholes (BH430, BH1) reaching the glacier bed; (g) sub- or englacially stored lake water; (h) uplift of glacier surface at stake 14 (GPS measurement); (i) uplift of glacier surface at stakes 34, 24 and 12 surveyed by theodolite. Note that for (b), (c) and (f) the scales differ between 2004 and 2005. All data have hourly resolution, except the GPS measurements which are 3 hourly. Thin vertical lines correspond to the start of lake outflow (I), the arrival of lake water at the tongue (II), the culmination of the flood (III) and its termination (IV).
In 2004 and 2005, runoff at the glacier terminus before and after the drainage event is modeled well (Fig. 7b). By integrating the river flood hydrograph a drainage volume of (5.7 ± 0.5) × 106 m3 is determined for 2004, which differs by 1.7 × 106 m3 from the lake volume derived from bathymetry. The flood duration was 7 days. During this time 0.9 x 106 m3 of water flows into the lake and contributes to the drainage volume; this leaves 0.8 × 106 m3 unaccounted for. The peak discharge at the glacier terminus was 38 m3s−1, of which 25 ± 3 m3 s−1 did not originate from surface melt or precipitation (Fig. 7e, left). Unlike the lake outflow hydrograph, the river flood hydrograph increases over a time-span of almost 5 days and culminates 3 days after the maximum of lake outflow. This indicates significant internal storage of lake water in the glacier. The main part of the flood ends with a sudden drop in runoff. However, for 2 days after the apparent termination of the drainage event, discharge remains significantly greater than can be explained by melt and rainfall processes (Fig. 7b, left).
In 2005, we determined a drainage volume of (1.5 ± 0.2) × 106 m3 over a period of 5 days. The peak discharge was 20 m3 s−1, with a contribution of 12 ± 1.5 m3 s−1 from the lake. The flood at the glacier terminus starts more than 3 days after the onset of lake evacuation and culminates within 2.5 days (Fig. 7e, right).
The temporal evolution of lake water storage in the glacial system is determined from the cumulated difference between the lake outflow and the river flood hydrograph (Fig. 7g). In 2004 a fast accumulation of water in the glacial system is computed, reaching a maximum of 1.5 × 106m3. The temporary storage of lake water amounts to 0.7 × 106 m3 in 2005. In 2004 a ‘negative storage’ of 0.8 × 106m3 results by the end of the glacier flood (Fig. 7d, e and g, left). This value lies beyond errors of the modeling procedure and the measurements and is due to the fact that the drainage volume is significantly larger than the lake volume. The negative storage implies that water stored prior to the drainage event in the glacial system is released. Such a process was not observed in 2005, when the temporary storage of lake water drops to zero by the end of the flood.
Water pressure and ice surface uplift
Water pressure is recorded in boreholes BH430 and BH1 at distances of 1 km from the lake (Figs 1 and 2). During the flood, water pressure remains close to flotation level in 2004 and 2005, with reduced diurnal amplitudes (Fig. 7f). The end of the lake drainage is marked in both years by a significant drop of 30–40% of the water column in the boreholes, coinciding with a simultaneous decrease in discharge at the glacier terminus (Fig. 7e and f). After the flood, the diurnal water-pressure minima are significantly lower than before, indicating a more efficient drainage system.
Vertical uplift at stake 14 on the central flowline is measured by GPS and shows a clear signal during the flood event (Fig. 7h). The accuracy of the records is ±0.3 cm (Reference Sugiyama and GudmundssonSugiyama and Gudmundsson, 2004). The glacier surface was lifted by as much as 20 cm at this location compared to pre-drainage conditions. To show the spatial distribution of surface uplift we also present results of the theodolite survey at chosen stakes along the central flowline (Fig. 7i). Reference Gudmundsson, Bassi, Vonmoos, Bauder, Fischer and FunkGudmundsson and others (2000) estimate an accuracy of ±5 cm for single data points in the z direction measured by theodolite. By filtering, the error can be reduced to a third of this value. The ice motion data show that a glacier surface uplift of 2–20 cm occurred along the central flowline of Gornergletscher with a maximum at stake 14. An interesting aspect is the similar temporal evolution of the uplift curve (Fig. 7h and i) and the lake water storage in both 2004 and 2005 (Fig. 7g).
Discussion
Decadal trends
Analysis of the lake drainage events of Gornersee from 1950–2005 indicates trends in lake outburst timing and large variations in the drainage volume (Fig. 4). Several processes may be the cause of these findings. Rapid shrinkage of ice volume and glacier extent took place in recent decades due to climate change (Fig. 2b). It is likely that these modifications of glacier geometry influence lake drainage. The position of Gornersee moved westwards out of a tributary valley accompanied by a decrease in ice thickness in the central parts of the glacier (Fig. 2a).
Timing of outburst
A shift in lake outburst timing of 70 days is observed since 1950 (Fig. 4a). We can only speculate about the driving factors of this significant trend. To investigate the possible influence of an earlier start of the melting season and thus earlier filling of the lake we conducted additional model simulations. They show a slight trend towards more melting in late spring and early summer. However, this change can only explain shifts in timing of a few days.
For our calculations, the size of the lake catchment area was kept fixed for all years. It is probable that fluctuations in the extent of the catchment basin due to changes in glacier geometry occurred during the past few decades. Assuming that the catchment basin has remained at its current extent over the past 35 years, the results of the model simulations indicate that more meltwater was produced when the drainage event occurred than was impounded in the lake at that time. Based on these findings we suggest that the catchment area of the lake has increased during the past three decades, causing an earlier filling of Gornersee. A contribution of this effect on the observed trend in the outburst timing is likely, but its relative importance is difficult to estimate.
The hydraulic gradient, Δh, is given by the elevation difference, Δz (lake level – glacier terminus), divided by the length of the drainage path, Δx. In 1970 Δh was 0.09; it had dropped to 0.07 in 2000. Reference ClarkeClarke (2003) demonstrated a major influence of the location of the seal on timing as well as on magnitude of the flood. The changes in glacier geometry around the lake are considerable (Fig. 2a). Although we do not know the exact position of the seal for all past glacier geometries, a shift may have occurred, influencing the timing of the outburst event.
Drainage volume
A maximum in drainage volumes was observed in the early 1970s and a significant minimum occurred in the 1980s (Fig. 4b). In the 1990s the data reveal a more variable pattern of flood magnitude than before, with either quite large or small floods. There is no correlation between drainage volume and the timing of the lake outburst. The volume of the lake is subject to substantial long-term changes which are attributed to fluctuations in glacier geometry (Fig. 2a). For 1982 a potential lake basin size of about 2 × 106 m3 is determined from a DEM. However, drainage volumes ~6 × 106 m3 at the end of the 1960s suggest that a much greater amount could have been stored in the lake basin at that time. This is supported by photographs and descriptions (Reference Bezinge, Perreten and SchaferBezinge and others, 1973; unpublished material, Grands Dixence, SA). The glacier retreat in 1995–2005 favored a rapid enlargement of the ice-marginal basin, mainly due to calving. We suspect the geometry change in the lake basin is not the sole reason for the variations in drainage volume. In particular, the interannual fluctuations may be caused by different initiation mechanisms leading to the lake draining subglacially, either partially filled (as observed in 2005) or after an antecedent supraglacial outflow (2004).
Volume–peak-discharge relation
Several empirical studies confirm the exponent b = 2/3 in the power-law relation (Equation (1)) between Q max and V (Reference Clague and MathewsClague and Mathews, 1973; Reference Costa, Baker, Kochel and PattonCosta, 1988; Reference Desloges, Jones and RickerDesloges and others, 1989; Reference Walder and CostaWalder and Costa, 1996). The constant, k, varies between the studies, from 46 to 113. These values originate from analyses of different lake systems and not multiple outbursts of one lake. Reference Ng and BjörnssonNg and Björnsson (2003) developed a theoretical approach to shed light on the background of the Clague–Mathews relation. For the incomplete drainage of Grímsvötn they predict an exponent, b, of 1–2, corresponding well with observations for the same lake (Reference BjörnssonBjörnsson, 1992). The exponent b = 2/3 seems to be a combined result due to effects of different system sizes and geometries and the conditions at flood initiation (Reference Ng and BjörnssonNg and Björnsson, 2003).
Our relation between Q max and V satisfies the proportionality proposed by Reference Clague and MathewsClague and Mathews (1973) and is in line with the other empirical studies, although we consider only a single lake. However, bearing in mind the dramatic changes in both glacier and lake geometry in the past century, it is hardly possible to speak of the ‘same’ lake during the entire period (Fig. 2a). The peak discharges of Gornersee are small compared to other lakes. The value of k (Equation (1)) is nearly one order of magnitude lower than in the previous studies (Reference Clague and MathewsClague and Mathews, 1973; Reference Costa, Baker, Kochel and PattonCosta, 1988; Reference Desloges, Jones and RickerDesloges and others, 1989; Reference Walder and CostaWalder and Costa, 1996). This may be caused by the setting of Gornergletscher. The ice extending downstream of the lake has a thickness of more than 400m and the bed is overdeepened. It is not known to what extent the polythermal character of the ice influences the lake outburst mechanism. It remains puzzling that in the first half of the 19th century much higher flood magnitudes, estimated indirectly from observations, were reported, although the lake basin was never significantly larger than it is at present (Wilhelm, 1967; Reference Bezinge, Perreten and SchaferBezinge and others, 1973).
By analyzing a 50 year time series of annual lake outburst events, the complexity and diversity of the jökulhlaup system becomes evident. The data from 2004 and 2005 illustrate that there can be various triggering mechanisms of an outburst event for the same lake. The year-to-year variability in drainage volume in the past decades is remarkable.
Drainage events of 2004 and 2005
Initiation mechanisms
The datasets of 2004 and 2005 show some similarities as well as significant differences. The outburst events differ greatly in terms of lake volume, drainage volume, peak lake discharge (by a factor of 2–4) and timing. However, the patterns of water-pressure fluctuations and ice motion on the central flowline of the glacier downstream of the lake are similar in both years (Fig. 7f, h and i). Also the river flood hydrographs at the glacier terminus exhibit a gradually rising limb and a sharp termination (Fig. 7e). In contrast, the lake outflow hydrographs differ remarkably, hinting at different flood initiation mechanisms. In 2005 a progressive increase in lake outflow (Fig. 7d, right) suggests a classical enlargement of Röthlisberger channels as proposed by Reference NyeNye (1976). The abrupt flood initiation in 2004 could indicate a temporary flotation of the ice dam near the lake. This claim is supported by the observation of short-term uplifts of the ice dam, up to 3 m during the main drainage phase (Reference Sugiyama, Bauder, Weiss and FunkSugiyama and others, 2007).
Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others (2004) present a model of glacial hydrology incorporating a subglacial water sheet interacting with a nascent chanelized system. The lake outflow hydrograph of 2004 suggests similar processes (Fig. 7d, left). In the first stage of the drainage event the ice dam was lifted, causing lake outflow to increase rapidly. The slight increase in lake outflow measured after the first culmination suggests channel enlargement as the second phase of the lake drainage. Due to the breakdown of the pressure transducer in 2004, the further course of the lake outflow hydrograph is unknown. From the bathymetry, however, we know the water volume left in the lake basin at that time. The termination of lake water input into the glacial system coincides, most probably, with the rapid loss of hydraulic head at borehole BH430 (Fig. 7f, left). To evacuate the remaining lake water after the termination of the measurement, a constant lake outflow would have to be 13 ± 3m3 s−1 for the period without data. Thus, a second culmination of the lake outflow hydrograph (Fig. 7d, left) does not seem implausible.
Leakage of the lake
The start of the 2005 outburst event merits further comment. It was one of the earliest since 1950, starting when the lake was filled to less than a third of its potential volume. After 2 June 2005, the time series for the measured lake volume and the cumulative simulated lake input diverge (Fig. 8b). In 2005 the discharge modeling was performed with the same parameters and boundary conditions as in 2004, when good agreement between model and field data was achieved. The simulated lake input from 2 June 2005 until the start of the lake drainage on 10 June is more than twice as great as the measured input. Inaccuracies in the runoff modeling procedure are not able to explain this discrepancy. Two reasons could account for the divergence. Firstly, there is a slowly expanding leak in the dam of Gornersee; secondly, the subglacial drainage system has changed in such a way that water no longer enters the lake, but benefits from new subglacial pathways directing the meltwater directly downglacier. Stagnations or drops in the lake level would support the hypothesis of a leak. In fact, the measured lake volume slightly decreases during nighttime in the days preceding the flood (inset in Fig. 8b). The leakage is very limited. It ceases almost completely during daytime and attains about 0.7 m3 s−1 in periods of low water pressure in the glacial drainage system (inset in Fig. 8c). Model sensitivity tests showed that this observation is not an artefact of the melt-runoff model. For more than 1 week the leak does not grow substantially. On 10 June, lake outflow starts to increase overnight, provoking a progressive rise in the minimal water pressure at borehole BH430 (Fig. 8b and c).

Fig. 8. (a) Hourly air temperature at AWS. (b) Filling of the lake in 2005 in comparison with water-pressure fluctuations in borehole BH430. The solid line indicates the measured evolution of lake volume and the dashed line the cumulative simulated melt in the lake catchment basin. Bars mark the timing of lake outflow. The inset shows the lake volume enlarged during the period of leakage. Thin vertical lines correspond to midnight. (c) Lake outflow hydrograph with the period of the leakage enlarged in the inset. Local outflow maxima occur between 0300 and 0600 h local standard time.
In Figure 8b the water pressure recorded in borehole BH430 shows the transition of a ‘winter drainage system’ to a well-developed ‘summer drainage system’ with pronounced diurnal amplitudes (Reference Schuler, Fischer, Sterr, Hock and GudmundssonSchuler and others, 2002). The position of the transition from an inefficient to an efficient drainage system slowly moves up-glacier, as observed in dye-tracing experiments (VAW/ETH Zürich, unpublished data). The transition at BH430 takes place 2 days before the melt-runoff model fails to explain the volume stored in the lake (Fig. 8b). It seems plausible that leakage starts once an efficient drainage system has developed close to the lake.
Internal water storage
Water storage plays an important role in glacial hydrology and is manifested in various processes (Reference Schuler, Fischer, Sterr, Hock and GudmundssonSchuler and others, 2002; Reference Jansson, Hock and SchneiderJansson and others, 2003). Storage of water in the glacial system can occur in subglacial cavities (e.g. Reference Iken, Fabri and FunkIken and others, 1996) or englacially in channels or voids (e.g. Reference Fountain and WalderFountain and Walder, 1998). Drainage events of glacier-dammed lakes are excellent subjects for the study of water storage processes in glaciers as large perturbations of the drainage system occur.
Associated with the strong drainage event of 2004, we observe a period of enhanced runoff for 2 days after the abrupt drop in discharge forming a hydrograph ‘tail’ (Fig. 7e, left). In this period a volume of approximately 0.8 × 106m3 of water is released that cannot be due to melt or rainfall. This value lies above the uncertainties of model and measurement. This feature may yield an explanation for the considerable difference between lake volume (determined by bathymetry of the lake basin) and drainage volume (integration of the river flood hydrograph). We suggest that the additional water recorded at the glacier terminus during the flood results from water storage in the glacial system prior to the lake drainage event. Presumably, this water is released during the 2 days after the main phase of the outburst event, benefiting from the well-developed drainage pathways. Reference AndersonAnderson and others (2003) report a similar hydrograph tail for Kennicott Glacier and explained it by the presence of a floated part of the ice dam and its dampening effect with lower water pressures.
Compared to the total lake volume, temporary storage of lake water in the glacial system during the drainage event reaches proportions of 38% (2004) and 54% (2005), emphasizing the importance of this storage term. The uplifts of the glacier surface of up to 20 cm follow the evolution of the storage curve (Fig. 7g–i). Obviously, glacier surface uplift and lake water storage are closely related. However, when distributing the temporarily stored flood water uniformly over the total area downstream of the lake, the storage water column corresponds to 35 cm in 2004 and to 17 cm in 2005.
Uplift of the glacier surface can be due to (1) vertical straining, (2) sliding over an inclined bed or (3) cavity formation at the bed (Reference Sugiyama and GudmundssonSugiyama and Gudmundsson, 2004). The measurements of vertical strain show no stretching signal during the outburst events (VAW/ETH Zürich, unpublished data). The inclination of the bedrock underneath the tongue of Gornergletscher is small, so (2) is excluded. This leaves cavity formation to be responsible for the observed surface uplifts. The glacier surface elevation returns to its starting point after the termination of the flood, which supports our assumption.
In Figure 9, water pressures in BH430 (2004) and BH1 (2005) are plotted, normalized to flotation level pressure, versus en- and subglacial lake water storage. The pressure data are smoothed using a 24 hour running mean. We obtain a hysteresis of storage that reveals some interesting aspects. The findings of Reference Hubbard, Sharp, Willis, Willis, Nielsen and SmartHubbard and others (1995) on Haut Glacier d’Arolla, Switzerland, help in interpreting our observations. With a dense network of boreholes, they succeeded in showing two different pressure regimes at the glacier bed. Water pressure around an efficient drainage channel reacts immediately to external meltwater input, whereas the variations in hydraulic head decrease sideways. The hydraulic gradient between hydraulically well-connected and unconnected parts of the glacier bed changes direction in the course of a day (Reference Hubbard, Sharp, Willis, Willis, Nielsen and SmartHubbard and others, 1995).

Fig. 9. Hysteresis between water pressure, normalized to flotation level, and en- and subglacial lake water storage for 2004 (solid line) and 2005 (dashed line). Arrows indicate the direction of time.
At the beginning of the drainage events in both 2004 and 2005, water level in a borehole, well connected to the main drainage system, increases abruptly as shown in Figure 9. Due to the limited amount of englacial voids in the zone of high water pressure, the potential to store water is minimal. However, the storage increases abruptly near overburden pressure. We attribute this to a partial detachment of the glacier from its bed, allowing the water to penetrate into subglacial cavities sideways from the main drainage channels. Thus, the pressure perturbations spread into regions hydraulically unconnected with the efficient drainage system under normal conditions. Storage at the bed and in englacial voids in these parts of the glacier increases. The internal lake water storage increases by roughly 1 × 106m3 in 2004, when the water column is at flotation level. In 2005, by contrast, the hydraulic head starts to decrease soon after reaching flotation level due to the smaller lake volume. The hysteresis curves have comparable slopes in 2004 and 2005. This indicates that similar processes contribute to internal storage in both years. However, the pressure perturbation seems to spread over a wider area of the glacier in 2004.
More water is stored in the glacial system during decreasing than during increasing water pressures. After the end of lake water input, stored water slowly flows back from englacial voids and subglacial cavities into the main drainage system. Then the pressure is lower than before the outburst event owing to the channel enlargement during flood conditions.
As discussed above, surface uplift is mainly due to cavity formation at the bed. The measured surface-elevation changes during the outburst events are not sufficient to accommodate the sub- or englacially stored lake water, even with the unlikely assumption of a uniform distribution of lake water. We conclude that only parts of the stored water penetrate into subglacial cavities and that the rest is stored in englacial voids or in water pockets that are not detectable by measurements of ice motion.
The importance of englacial voids
Based on our data of glacier surface uplift, subglacial storage alone cannot account for the additional water volume in the glacial system. Therefore, we attribute a particular importance to englacial voids. The volumetric content of englacial voids was quantified as 0.5% by Reference Copland, Harbor, Gordon and SharpCopland and others (1997) using borehole-video methods in a temperate alpine glacier. On Gornergletscher we also observed englacial voids and crevasses with a borehole video camera.
Here we combine our data of water input into the glacial system (lake outflow hydrograph), water output (river flood hydrograph), glacier surface uplift and water pressure records and attempt to estimate an integrated void ratio, r v, for the ice downstream of the lake. This is defined as the ratio between the volume of englacial voids and the total ice volume, and is calculated as follows:
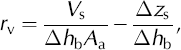
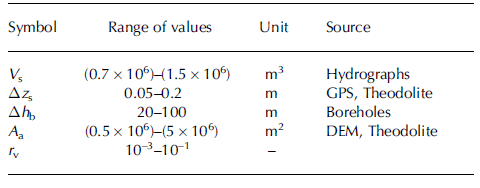
where V s is the stored lake water volume, Δh b the change of water column height, A a the area of the glacier bed accessible to water storage and Δz s the glacier surface uplift. We estimated possible ranges for the values of all quantities. Although V s is well known from the data, we cannot be sure about the representativity of the point-based measurements for Δh b and Δz s. We recorded Δh b in boreholes connected to the main drainage system. However, an important part of the storage seems to take place in hydraulically unconnected parts of the ice mass, as could be inferred from the hysteresis of storage (Fig. 9). There, smaller pressure variations, Δh b, are expected (Reference Hubbard, Sharp, Willis, Willis, Nielsen and SmartHubbard and others, 1995). We measured Δz s using GPS and theodolite in 2004 and 2005 (Fig. 7h and i). The amounts of uplift are not uniformly distributed and lie between 2 and 20 cm (Reference WeissWeiss, 2005). This demonstrates the inhomogeneity of surface elevation change in reaction to the flood. A quantity difficult to estimate is A a. If we presume the drainage takes place in one or a few discrete drainage channels with the pressure perturbations spreading out from these, the accessible area, A a, for water storage should be less than the total subglacial area downstream of the lake. We calculate the void ratio r v for a reasonable range of input data (Table 1) and obtain a value of r v = 0.1–10%. Our estimates imply that the amount of englacial voids is not negligible.
Table 1. Estimated ranges of input data for the calculation of the void ratio, r v
Conclusions
This study investigates the annual drainage events of an ice- marginal lake, Gornersee, in detail. Using a distributed temperature-index model coupled to a linear-reservoir runoff model, we simulate glacial discharge due to melt and precipitation in hourly resolution. We can extract lake drainage hydrographs from measured runoff at the glacier terminus and determine outburst timing, lake volume and peak lake discharge.
Since 1950 the lake has been draining progressively earlier in the course of the year. The drainage volumes show remarkable long-term and interannual fluctuations. The relation between peak lake discharge and drainage volume follows the proportionality Q max ∝ V 2/3 proposed by Reference Clague and MathewsClague and Mathews (1973), but exhibits a lower constant, k, leading to reduced runoff peaks during the flood events.
Extensive field measurements around the drainage events of 2004 and 2005 provide the data for an integrative assessment of the outburst of Gornersee. We detected two different drainage mechanisms, a temporary flotation of the ice dam in 2004 and classical channel enlargement in 2005 after a leakage over 8 days. Lake outflow hydrographs differ greatly between 2004 and 2005. During the passage of the flood wave through the glacier, however, these differences are blurred and a canonical drainage hydrograph is recorded at the tongue in both years. Water pressure and glacier surface motion show a close interrelation to the lake drainage characteristics. Temporary storage of lake water in the glacial system causes uplifts of up to 20 cm at the glacier surface with a similar temporal evolution. In 2004 a large amount of water stored sub- or englacially prior to the drainage event was released during the 2 days after the outburst.
The detailed datasets of 2 years, and the analysis of the annual outbursts of the past few decades, prove that, even for an individual system, a variety of different processes are involved which alter the character of the drainage with varying degrees of importance. This study shows the need for an integrative assessment of glacier-dammed lake floods to better understand the nature of these events.
Acknowledgements
The project was funded by the Swiss National Science Foundation, grant No. 200021-103882/1. R. Hock is Royal Swedish Academy of Science Research Fellow supported by a grant from the Knut Wallenberg Foundation. We are grateful to many members of VAW/ETH Zürich who helped with data acquisition and fieldwork. Grande Dixence SA provided the discharge data and MeteoSchweiz made climate data available for Zermatt and Grächen. H. Bösch processed aerial photographs for 1982, 2003, 2004 and 2005. S. Sugiyama provided the GPS data. T. Schuler and O. Eisen made valuable comments on the manuscript. S. Braun-Clarke edited the English. Together with constructive comments by the scientific editor J. Walder, reviews by R. Bingham, P. Jansson and an anonymous reviewer improved the paper.
Appendix
Melt and Discharge Modeling
A distributed temperature-index melt-accumulation model coupled to a linear-reservoir discharge model (Reference HockHock, 1999) is used to compute hourly meltwater production and runoff from the catchment of Gornergletscher. It elaborates on classical models using degree-day factors by varying these as a function of potential clear-sky radiation in order to account for the effects of slope, aspect and shading. The model has been shown (Reference HockHock, 1999) to be capable of reproducing the large diurnal runoff amplitudes typical of glacier discharge regimes, although driven only by air temperature and precipitation data. Surface melt rates, M, are computed by:

where F M denotes a melt factor, r snow/ice are radiation factors for snow and ice and I is the potential direct solar radiation (Table 2). Reduced melt rates over debris-covered surfaces are accounted for.
Table 2. Optimized parameters of the distributed temperature-index model on Gornergletscher obtained from the calibration period (April–September 2004)

The surface characteristics (snow/ice) were either modeled using an initial distribution of winter snow cover (1970–2003), or prescribed by weekly evaluation of photographs from an automatic camera (2004 and 2005).
The air temperature and precipitation at every gridcell are calculated using constant gradients with altitude. In this model approach, correction factors account for rain gauge under-catch errors and increased losses in the case of solid precipitation. A threshold temperature distinguishes snow from rainfall (Reference HockHock, 1999).
To derive hydrographs of glacial discharge, the melt model is coupled to a simple runoff model which routes meltwater through the glacier using a linear-reservoir approach (Reference Baker, Escher-Vetter, Moser, Oerter and ReinwarthBaker and others, 1982; Reference Hock and NoetzliHock and Noetzli, 1997). Melt- and rainwater are distributed to three water reservoirs – ice, firn and snow – according to the surface characteristics of the gridcell where the water originates. The firn reservoir is defined as the area above 3500 m a.s.l. The reservoirs are characterized by different retention constants, c i, which need to be calibrated. The model is based on the assumption that discharge, Qi (t), from reservoir i is proportional to the stored water volume, Vi (t):
The constants, ci , correspond to the mean residence time of water in reservoir i and have values of hours to days (Table 2).
The climatic constraints are obtained from comparison of overlapping periods of the weather data (dT/dz, dP/dz) or from the literature (precipitation corrections, threshold liquid–solid precipitation; Reference HockHock, 1999; Reference SchwarbSchwarb, 2000; see Table 2). Melt parameters (F M, r ice, r snow) and runoff parameters (c ice, c firn, c snow) are obtained from calibration. The parameters are chosen to achieve maximum agreement between three types of data providing optimal constraint of the model: (1) simulated and measured melt at ablation stakes, (2) simulated and measured hourly discharge and (3) simulated and observed snowline retreat. We choose the ablation season 2004 as the calibration period because of the existing extensive data, and 2005 as the validation period. Two different parameter sets were calibrated, based on the meteorological input data (temperature and precipitation) of the AWS (2004, 2005) and the weather stations at Zermatt and Grächen (1970–2003).
At all ablation stake locations good agreement between field data and model results is achieved for the calibration period. Measured and simulated runoff during the melt season 2004 (April to September) agree well (Fig. 3). To judge the model performance we use the R 2 efficiency criterion (Reference Nash and SutcliffeNash and Sutcliffe, 1970) defined as

with Q measured the measured and Q simulated the simulated discharge. For 2004 (2005) R 2 is 0.91 (0.73) with weather input data from the AWS, and 0.88 (0.79) with data from Zermatt and Grächen, respectively. Simulated snowlines were compared with the automatic camera photographs and good agreement was obtained (Reference HussHuss, 2005).













