Hyperbolically embedded subgroups and quasi-isometries of pairs

Abstract

We give technical conditions for a quasi-isometry of pairs to preserve a subgroup being hyperbolically embedded. We consider applications to the quasi-isometry and commensurability invariance of acylindrical hyperbolicity of finitely generated groups.

1 Introduction

A group G is acylindrically hyperbolic if it admits a nonelementary, acylindrical action on a hyperbolic space. An alternative characterization is that G is acylindrically hyperbolic if and only if G contains a hyperbolically embedded subgroup H, denoted $H\hookrightarrow _h G$ , and we will give a characterization from [13] in Proposition 3.1.

The class of acylindrically hyperbolic groups generalizes the classes of nonelementary hyperbolic and relatively hyperbolic groups while sharing many similar properties [17]. In spite of this, there are still foundational questions that remain open, for instance, it is known that a group being hyperbolic or relatively hyperbolic is invariant under quasi-isometry [8, 9], but the corresponding question for acylindrical hyperbolicity is still open.

Question 1.1 [17, Question 2.20(a)]

Is the class of finitely generated acylindrically hyperbolic groups closed under quasi-isometry?

Some partial results are known, for instance, acylindrical hyperbolicity passes to finite-index subgroups and is preserved by quotienting out a finite normal subgroup [15]. If the group is ${\mathcal {A}}{\mathcal {H}}$ -accessible, then acylindrical hyperbolicity can be passed to finite extensions [16]. The property of being ${\mathcal {A}}{\mathcal {H}}$ -accessible also passes to finite-index overgroups [3]. However, not every finitely presented acylindrically hyperbolic group is ${\mathcal {A}}{\mathcal {H}}$ -accessible [1, Theorem 2.18]. Some experts in the field do not expect a complete positive answer to Question 1.1.

This article relies on the notion of quasi-isometry of pairs, and our results provide technical conditions to ensure that a quasi-isometry of pairs carries the property of being a hyperbolically embedded subgroup.

Definition 1.1 (Quasi-isometry of pairs)

Let X and Y be metric spaces, and let $\mathcal {A}$ and $\mathcal {B}$ be collections of subspaces of X and Y, respectively. A quasi-isometry $q\colon X\to Y$ is a quasi-isometry of pairs $q\colon (X,\mathcal {A}) \to (Y,\mathcal {B})$ if there is $M>0$ :

1. (1) For any $A\in \mathcal {A}$ , the set $\{ B\in \mathcal {B} \colon \operatorname {\mathrm {\mathsf {hdist}}}_Y(q(A), B) <M \}$ is nonempty.

2. (2) For any $B\in \mathcal {B}$ , the set $\{ A\in \mathcal {A} \colon \operatorname {\mathrm {\mathsf {hdist}}}_Y(q(A), B) <M \}$ is nonempty.

In this case, if $q\colon X \to Y$ is an $(L,C)$ -quasi-isometry, then $q\colon (X, \mathcal {A})\to (Y,\mathcal {B})$ is called an $(L,C,M)$ -quasi-isometry. If there is a quasi-isometry of pairs $(X,\mathcal {A}) \to (Y,\mathcal {B})$ , we say that $(X,\mathcal {A})$ and $(Y,\mathcal {B})$ are quasi-isometric pairs.

We specialize the previous definition to the case of finitely generated groups with finite collections of subgroups as follows.

Definition 1.2 (Quasi-isometry of group pairs)

Consider two pairs $(G, \mathcal {P})$ and $(H, \mathcal {Q})$ where G and H are finitely generated groups with chosen word metrics $\operatorname {\mathrm {\mathsf {dist}}}_G$ and $\operatorname {\mathrm {\mathsf {dist}}}_H$ . Denote the Hausdorff distance between subsets of H by $\operatorname {\mathrm {\mathsf {hdist}}}_H$ . An $(L,C)$ -quasi-isometry $q\colon G \to H$ is an $(L,C,M)$ -quasi-isometry of pairs $q\colon (G, \mathcal {P})\to (H, \mathcal {Q})$ if the relation

$$ \begin{align*} \dot{q} = \{ (A, B)\in G/\mathcal{P} \times H/\mathcal{Q} \colon \operatorname{\mathrm{\mathsf{hdist}}}_H(q(A), B) <M \} \end{align*} $$

satisfies that the projections into $G/\mathcal {P}$ and $H/\mathcal {Q}$ are surjective.

Example 1.1 (Quasi-isometry of pairs and finite extensions)

Let H be a finite index normal subgroup of finitely generated group G, and let ${\mathcal {Q}}$ be a finite collection of subgroups of H. Then the inclusion $(H,{\mathcal {Q}}) \hookrightarrow (G,{\mathcal {Q}})$ is a quasi-isometry of pairs if the collection $\{hQh^{-1} \colon h\in H \text { and } Q\in {\mathcal {Q}}\}$ is invariant under conjugation by G (see Proposition 4.1).

Recall that the commensurator of a subgroup P of a group G is the subgroup

$$\begin{align*}Comm_G(P)=\{g\in G \colon P\cap gPg^{-1} \text{ is a finite index subgroup of } P \text{ and } gPg^{-1}\}. \end{align*}$$

Definition 1.3 (Refinements)

Let ${\mathcal {P}}$ be a collection of subgroups of group G. A refinement ${\mathcal {P}}^\ast $ of ${\mathcal {P}}$ is a set of representatives of conjugacy classes of the collection of subgroups

$$\begin{align*}\{\operatorname{{\mathrm{Comm}}}_G(gPg^{-1}) \colon P\in{\mathcal{P}} \text{ and } g\in G \}. \end{align*}$$

Example 1.2 (Refinements and qi of pairs)

Let ${\mathcal {Q}}$ be a finite collection of subgroups of a finitely generated group H, and let ${\mathcal {Q}}^\ast $ be a refinement. If each $Q\in {\mathcal {Q}}$ is finite index in $\operatorname {{\mathrm {Comm}}}_H(Q)$ , then the identity map on G is a quasi-isometry of pairs $(H,{\mathcal {Q}})\to (H,{\mathcal {Q}}^\ast )$ .

Example 1.3 (Refinements and finite extensions)

Let A be a group, let $\mathcal {H}$ be an almost malnormal collection of infinite subgroups, and let $F\leq \mathsf {Aut}(A)$ be a finite subgroup. If F acts freely on $\mathcal {H}$ and $\mathcal {H}_F$ is a collection of representatives of F-orbits in $\mathcal {H}$ , then a refinement of $\mathcal {H}$ in $A\rtimes F$ is $\mathcal {H}_F$ .

Definition 1.4 (Reduced collections)

A collection of subgroups ${\mathcal {P}}$ of a group G is reduced if for any $P,Q\in {\mathcal {P}}$ and $g\in G$ , if P and $gQg^{-1}$ are commensurable, then $P=Q$ and $g\in P$ .

Our first result, Theorem A, describes a strategy to obtain positive results to Question 1.1. For a group G with a generating set S, let $\Gamma (G,S)$ denote the corresponding Cayley graph (see Definition 2.3).

Theorem A (Theorem 3.1)

Let $q\colon G\to H$ be a quasi-isometry of finitely generated groups, let ${\mathcal {P}}$ and ${\mathcal {Q}}$ be finite collections of subgroups of G and H, respectively, and let S and T be (not necessarily finite) generating sets of G and H, respectively. Suppose that:

1. (1) $q\colon (G,{\mathcal {P}}) \to (H,{\mathcal {Q}})$ is a quasi-isometry of pairs and

2. (2) $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry.

The following statements hold:

1. (1) If ${\mathcal {P}}$ and ${\mathcal {Q}}$ are reduced collections in G and H, respectively, then ${\mathcal {P}}\hookrightarrow _h (G,S)$ if and only if ${\mathcal {Q}}\hookrightarrow _h (G,T)$ .

2. (2) If ${\mathcal {Q}}$ contains only infinite subgroups and ${\mathcal {Q}}\hookrightarrow _h (H,T)$ , then ${\mathcal {P}}^*\hookrightarrow _h (G,S)$ .

1.1 Qi-characteristic collections

The first numbered hypothesis of Theorem A raises the following general problem: Given a finite collection of subgroups ${\mathcal {Q}}$ of a group H and a quasi-isometry $q\colon G\to H$ of finitely generated groups, is there a collection ${\mathcal {P}}$ of subgroups of G such that $q\colon (G,{\mathcal {P}})\to (H,{\mathcal {Q}})$ is a quasi-isometry of pairs?

This problem was studied in [14] where the notion of qi-characteristic collection is introduced and it is proved that if the collection ${\mathcal {Q}}$ is qi-characteristic in H, then any quasi-isometry of finitely generated groups induces a collection ${\mathcal {P}}$ .

Definition 1.5 (Qi-characteristic [14])

A collection of subgroups $\mathcal {P}$ of a finitely generated group G is quasi-isometrically characteristic (or shorter qi-characteristic) if $\mathcal {P}$ is finite; each $P\in \mathcal {P}$ has finite index in its commensurator; and for every $L\geq 1$ and $C\geq 0$ , there is $M=M(G, \mathcal {P}, L,C)\geq 0$ such that every $(L,C)$ -quasi-isometry $q\colon G\to G$ is an $(L,C,M)$ -quasi-isometry of pairs $q\colon (G,\mathcal {P})\to (G,\mathcal {P})$ .

Example 1.4. The argument by Behrstock, Druţu, and Mosher proving quasi-isometric rigidity of relative hyperbolicity with respect to nonrelatively hyperbolic groups (NRH groups) shows that if H is hyperbolic group relative to a collection ${\mathcal {Q}}$ of NRH subgroups, then ${\mathcal {Q}}$ is qi-characteristic [4, Theorems 4.1 and 4.8]. Another example is provided by mapping class groups. Ruling out a few surfaces of low complexity, any self-quasi-isometry of the mapping class group is at uniform distance from left multiplication by an element of the group (see the work of Behrstock, Kleiner, Minsky, and Mosher [6, Theorem 1.1]). As a consequence, the hyperbolically embedded (virtually cyclic) subgroup generated by a pseudo-Anosov is qi-characteristic. More generally, any finite collection of subgroups of such mapping class groups are qi-characteristic.

Corollary B Let G and H be finitely generated groups, let T be a generating set of H, let ${\mathcal {Q}}$ be a finite collection of subgroups of H such that ${\mathcal {Q}}\hookrightarrow _h (H,T)$ , and let $q\colon G \to H$ be a quasi-isometry. If:

1. (1) ${\mathcal {Q}}$ is a qi-characteristic collection of subgroups of H and

2. (2) there is a generating set $S\subset G$ such that $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry,

then there is a finite collection ${\mathcal {P}}$ of subgroups of G such that ${\mathcal {P}}\hookrightarrow _h (G,S)$ and $q\colon (G,{\mathcal {P}}) \to (H,{\mathcal {Q}})$ is a quasi-isometry of pairs.

Proof Without loss of generality, assume that all subgroups in ${\mathcal {Q}}$ are proper infinite subgroups. Note that removing finite subgroups from ${\mathcal {Q}}$ preserves being qi-characteristic and that ${\mathcal {Q}}\hookrightarrow _h (H,T)$ . On the other hand, if ${\mathcal {Q}}$ contains H, then the theorem is trivial by taking ${\mathcal {P}}$ the collection that contains only G and S any finite generating set of G. Since ${\mathcal {Q}}$ is qi-characteristic, the quasi-isometry $q\colon G\to H$ induces a finite collection ${\mathcal {P}}$ such that $q\colon (G,{\mathcal {P}})\to (H,{\mathcal {Q}})$ is a quasi-isometry of pairs, and this is precisely [14, Theorem 1.1]. Then the second statement of Theorem A and ${\mathcal {Q}}\hookrightarrow _h (H,T)$ imply that ${\mathcal {P}}^\ast \hookrightarrow _h (G,S)$ .

1.2 Uniform quasi-actions

The second numbered hypothesis of Theorem A raises the problem: Given a group H with a generating set T and a quasi-isometry $q\colon G\to H$ of finitely generated groups, is there a generating set $S\subset G$ such that $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry of Cayley graphs?

We show that a positive answer to this question is equivalent to asking that the quasi-action of G on H induced by q is T-uniform in the following sense (see Proposition C).

Definition 1.6 (Uniform induced quasi-action)

Let G and H be finitely generated groups, and let $q\colon G\to H$ be a quasi-isometry with quasi-inverse $\bar q$ . Let $T\subset H$ be a generating set (possibly infinite). We say that the quasi-action of G on H induced by q is uniform with respect to T if there are constants $L\geq 1$ , $C\geq 0$ such that, for each ${g\in G}$ , the function $q_g\colon H\to H$ given by $q_g(h)= q(g\cdot \bar q(h))$ is an $(L,C)$ -quasi-isometry $q_g\colon \Gamma (H,T)\to \Gamma (H,T)$ .

Example 1.5 (Uniform quasi-action and finite extensions)

Let H be a finite index normal subgroup of finitely generated group G, and let T be a generating set of H invariant under conjugation by G. The G-action by conjugation on H preserves the word metric induced by T. On the other hand, any transversal R of H in G induces a quasi-isometry $q\colon G \to H$ given by $q(hg)=h$ for $h\in H$ and $g\in R$ . In this case, the quasi-action of G on H induced by q is uniform with respect to T (see Lemma 2.1).

Proposition C (Proposition 2.1)

Let G and H be groups with finite generating sets $S_0$ and $T_0$ , and let $q\colon \Gamma (G,S_0) \to \Gamma (H,T_0)$ be a quasi-isometry. Let $T\subset H$ containing $T_0$ . The following statements are equivalent:

1. (1) The quasi-action of G on H induced by q is uniform with respect to T.

2. (2) There is $S\subset G$ containing $S_0$ such that $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry.

Corollary D Let G and H be finitely generated groups with finite collections of infinite subgroups ${\mathcal {P}}$ and ${\mathcal {Q}}$ , respectively. Suppose that $q\colon (G,{\mathcal {P}}) \to (H,{\mathcal {Q}})$ is a quasi-isometry of pairs inducing a T-uniform quasi-action of G on H. If ${\mathcal {Q}}\hookrightarrow _h(H,T)$ , then ${\mathcal {P}}^\ast \hookrightarrow _h G$ .

Proof Since the quasi-action of G on H induced by q is T-uniform, Proposition C implies that there is a generating set S of G such that $q\colon \Gamma (G, S) \to \Gamma (H,T)$ is a quasi-isometry. Then the second statement of Theorem A and ${\mathcal {Q}}\hookrightarrow _h (H,T)$ imply that ${\mathcal {P}}^\ast \hookrightarrow _h (G,S)$ .

Let us remark that for this last corollary, in the case that T is finite, then there is a finite $S\subset G$ such that $\mathcal {P} \hookrightarrow _h (G, S)$ ; this case is implied by the results on quasi-isometric rigidity of relative hyperbolicity in [4].

1.3 Finite extensions

The following application is a particular instance of Theorem 4.1 in the main body of the article.

Theorem E (Theorem 4.1)

Let H be a finite index normal subgroup of a finitely generated group G, and let ${\mathcal {Q}}$ be a finite collection of infinite subgroups of H such that ${\mathcal {Q}}\hookrightarrow _h (H,T)$ . Suppose that:

1. (1) The set T is invariant under conjugation by G.

2. (2) The collection $\{hQh^{-1} \colon h\in H \text { and } Q\in {\mathcal {Q}}\}$ is invariant under conjugation by G.

If ${\mathcal {Q}}^*$ is a refinement of ${\mathcal {Q}}$ in G, then ${\mathcal {Q}}^*\hookrightarrow _h G$ .

Example 1.6. Let $G= \langle a,b,t \colon tat^{-1}=b,\ t^2=1 \rangle \cong F_2\rtimes \mathbb {Z}_2$ , let $H=\langle a,b\rangle $ , and let ${{\mathcal {Q}}=\{ \langle a\rangle , \langle b\rangle \}}$ . Note that ${\mathcal {Q}}\hookrightarrow _h H$ , and, for instance, one can take ${\mathcal {Q}}^\ast = \{\langle a \rangle \}$ and observe that ${\mathcal {Q}}^* \hookrightarrow _h G$ . In contrast, for ${\mathcal {Q}}_0=\{ \langle a \rangle \} \hookrightarrow _h H$ , the theorem does not apply since the conjugates of $\langle a\rangle $ in H are not invariant under conjugation by elements of G.

The next result illustrates concrete examples where Theorem E applies.

Theorem F (Theorem 5.1)

Let A be a finitely generated group with a (not necessarily finite) generating set T, and let $\mathcal {H}$ be a finite collection of infinite subgroups such that $\mathcal {H}\hookrightarrow _h (A,T)$ . If $F\leq \mathsf {Aut}(A)$ is finite, T and $\mathcal {H}$ are F-invariant, and the F-action on $\mathcal {H}$ is free, then ${\mathcal {H}}_F\hookrightarrow _h(A\rtimes F,T\cup F)$ where ${\mathcal {H}}_F$ is collection of representatives of F-orbits in ${\mathcal {H}}$ .

Example 1.7. Let with each $B_i$ isomorphic to a fixed finitely generated group B. Let $F=\mathbb {Z}_n$ act on A by cyclically permuting the copies of B. Consider the generating set of A given by $T=\bigcup _{i=1}^nB_i\backslash \{1\}$ , then T is F-invariant. Now, the collection ${\mathcal {H}}=\{B_1,\dots ,B_n\}$ is hyperbolically embedded into $(A,T)$ and F acts freely by conjugation on ${\mathcal {H}}$ . All of the hypotheses of the previous theorem have been verified, so we conclude that $B_1\hookrightarrow _h(A\rtimes F,T\cup F)$ .

1.4 Organization

The rest of the article is divided into five sections. Section 2 is on quasi-actions; it contains the proof of Proposition C as well as some corollaries. The proof of Theorem A is the content of Section 3. Then Sections 4 and 5 contain the proofs of Theorems E and F, respectively. Finally , Section 6 contains some questions and discussion about related to the results in this article and the definition of a quasi-isometry of pairs.

2 Uniform quasi-actions

Definition 2.1 (Uniform quasi-action)

Let G be a group, and let X be a metric space. Let $\mathsf {QI(X)}$ denote the set of quasi-isometries $X\to X$ . A function $G\to \mathsf {QI(X)}$ , $g\mapsto f_g$ , is a quasi-action if there is $K\geq 0$ such that for any $g_1,g_2\in G$ :

1. (1) the map $f_{g_1g_2}$ is at distance at most K from the map $f_{g_1}\circ f_{g_2}$ in the $L_\infty $ -distance and

2. (2) the map $f_{g_1}\circ f_{g_1^{-1}}$ is at distance at most K from the identity.

The quasi-action $G\to \mathsf {QI}(X)$ is uniform if there are constants $L\geq 1$ and $C\geq 0$ such that, for any $g\in G$ , the map $f_g$ is an $(L,C)$ -quasi-isometry.

It is well known that a quasi-isometry $q\colon G\to H$ of finitely generated groups induces a uniform quasi-action of G on H:

Definition 2.2 (Uniform quasi-action induced by a quasi-isometry)

Let G be a group with a word metric induced by a finite generating set, let X be a metric space, and let $q\colon G \to X $ and $\bar q\colon X \to G$ be $(L_0,C_0)$ -quasi-isometries such that $q\circ \bar q$ and $\bar q\circ q$ are at distance less than $C_0$ from the identity maps on X and G, respectively. For $g\in G$ , let

$$\begin{align*}L_g\colon G\to G, \qquad x\mapsto gx, \end{align*}$$

and let

$$\begin{align*}q_g\colon X\to X,\qquad q_g= q \circ \mathbf{g}\circ\bar q. \end{align*}$$

It is an exercise to verify that there are constants $L\geq 1$ and $C\geq 0$ such that:

• • For $g\in G$ , $q_g\colon X\to X$ is an $(L,C)$ -quasi-isometry.

• • (G quasi-acts on X) For $g_1,g_2\in G$ , the map $q_{g_1g_2}$ is at distance at most C from the map $q_{g_1}\circ q_{g_2}$ , and the map $q_{g_1}\circ q_{g_1^{-1}}$ is at distance at most C from the identity.

• • (G acts $C_0$ -transitively on X) For every $x ,y\in X$ , there is $g\in G$ such that $\operatorname {\mathrm {\mathsf {dist}}}_G(x, q_g(y))\leq C$ .

The map $G\to \mathsf {QI}(X)$ given by $g\mapsto q_g$ is called the uniform quasi-action of G on X induced by q and $\bar q$ .

Remark 2.1 (Equivalence of Definitions 1.6 and 2.2)

In the context of Definition 1.6, if the induced quasi-action of G on H is uniform with respect to T, then $G\to \mathsf {QI}(\Gamma (H,T))$ given by $g\mapsto q_q$ is a uniform quasi-action in the sense of Definition 2.2. Indeed, since T contains a finite generating set of H, there is $M>0$ such that $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T)}\leq M\operatorname {\mathrm {\mathsf {dist}}}_{(H,T_0)}$ . Hence, if two functions $H\to H$ are at finite $L_\infty $ -distance with respect to $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T_0)}$ , then the same holds for $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T)}$ .

Definition 2.3 (Cayley graph)

Let G be a group with a generating set S. The Cayley graph $\Gamma (G,S)$ of G with respect to S is the G-graph with vertex set G and edge set $\{ \{g, gs\}\colon g\in G,\ s\in S \}$ .

Proposition 2.1 (Proposition C)

Let G and H be groups with finite generating sets $S_0$ and $T_0$ , and let $q\colon \Gamma (G,S_0) \to \Gamma (H,T_0)$ be a quasi-isometry. Let $T\subset H$ containing $T_0$ . The following statements are equivalent:

1. (1) The quasi-action of G on H induced by q is uniform with respect to T.

2. (2) There is $S\subset G$ containing $S_0$ such that $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry.

Proof That the second statement implies the first one is immediate. Conversely, suppose that q and $\bar q$ are $(L_0,C_0)$ -quasi-isometries $\Gamma (G,S_0)\to \Gamma (H,T_0)$ and $\Gamma (H,T_0)\to \Gamma (G,S_0)$ , respectively. Without loss of generality, assume that $q(e)=e$ and $\bar q(e)=e$ where e denotes the identity in each corresponding group.

Let $K_0=L_0+C_0+1$ and define

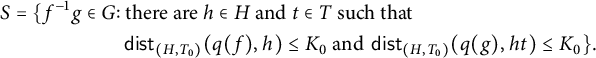$$\begin{align*}\begin{aligned} S= \{ f^{-1}g \in G \colon & \text{ there are } h\in H \text{ and } t\in T \text{ such that } \\ & \operatorname{\mathrm{\mathsf{dist}}}_{(H, T_0)}(q(f),h)\leq K_0 \text{ and } \operatorname{\mathrm{\mathsf{dist}}}_{(H,T_0)}(q(g),ht)\leq K_0 \}. \end{aligned} \end{align*}$$

Note that $S_0\subset S$ since $q\colon \Gamma (G,S_0)\to \Gamma (H,T_0)$ is an $(L_0,C_0)$ -quasi-isometry. In particular, S is a generating set of G.

Let $L_1\geq 1$ and $C_1\geq 0$ be such that the G-action on H induced by q is $(L_1,C_1)$ -uniform with respect to T. In particular, for every $g\in G$ , the function $q_g\colon H\to H$ is an $(L_1,C_1)$ -quasi-isometry $\Gamma (H,T) \to \Gamma (H,T)$ .

Now, we prove that if the induced quasi-action of G on H is uniform with respect to T, then $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry. Observe that every vertex of $\Gamma (H,T)$ is at distance at most $C_0$ from $q(G)$ with respect to $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T_0)}$ and hence with respect to $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T)}$ . Below, we prove inequalities (2.1) and (2.2), which will conclude proof.

Claim There is constant $\bar L$ such that

(2.1) $$ \begin{align} \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(a),q(b)) \leq \bar L\operatorname{\mathrm{\mathsf{dist}}}_{(G,S)}(a,b), \end{align} $$

for any $a,b\in G$ .

Proof of claim

Let $s\in S$ . Then there are $f,g\in G$ , $h\in H$ , and $t\in T$ such that $s=f^{-1}g$ and

$$\begin{align*}\operatorname{\mathrm{\mathsf{dist}}}_{(H,T_0)}(q(f),h)\leq K_0,\quad \operatorname{\mathrm{\mathsf{dist}}}_{(H,T_0)}(q(g),ht)\leq K_0.\end{align*}$$

It follows that

$$\begin{align*}\operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q_f(e),q_g(e))= \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(f),q(g))\leq 2K_0+1.\end{align*}$$

Since the quasi-action of G on $\Gamma (H,T)$ is $(L_1,C_1)$ -uniform, the previous inequality implies that

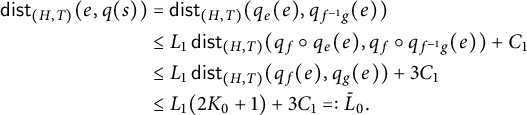$$\begin{align*}\begin{aligned} \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(e,q(s)) &= \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q_e(e),q_{f^{-1}g}(e)) \\ & \leq L_1\operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q_f\circ q_e(e),q_f\circ q_{f^{-1}g}(e))+ C_1\\ & \leq L_1\operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q_f(e), q_{g}(e))+ 3C_1\\ & \leq L_1(2K_0+1)+3C_1=:\bar L_0. \end{aligned} \end{align*}$$

For any $g\in G$ and $s\in S$ , we have that

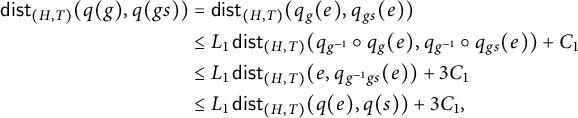$$ \begin{align*} \begin{aligned} \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(g),q(gs)) & = \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q_{g}(e), q_{gs}(e)) \\ &\leq L_1 \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q_{g^{-1}}\circ q_{g}(e), q_{g^{-1}}\circ q_{gs}(e)) + C_1 \\ &\leq L_1\operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(e, q_{g^{-1}gs}(e)) +3C_1\\ & \leq L_1\operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(e),q(s)) + 3C_1, \end{aligned} \end{align*} $$

and hence

$$\begin{align*}\operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(g),q(gs)) \leq \operatorname{\mathrm{\mathsf{dist}}}_{(H,T_0)}(q(g),q(gs)) \leq \bar L, \end{align*}$$

where $\bar L= L_1(\bar L_0)+3C_1$ . If $a,b\in G$ and $[u_0,\ldots , u_\ell ]$ is a geodesic in $\Gamma (G,S)$ from a to b, then the triangle inequality implies inequality (2.1).

Claim For any $a,b\in G$ , we have

(2.2) $$ \begin{align} \operatorname{\mathrm{\mathsf{dist}}}_{(G,S)}(a,b)\leq \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(a),q(b)). \end{align} $$

Proof of claim

Suppose that $[h_0,\ldots ,h_\ell ]$ is a geodesic in $\Gamma (H,T)$ from $q(a)$ to $q(b)$ . Since $q\colon \Gamma (G,S_0)\to \Gamma (H,T_0)$ is an $(L_0,C_0)$ -quasi-isometry, for each i, there is $g_i\in G$ such that $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T_0)}(q(g_i),h_i)\leq C_0$ . Let $g_0=a$ and $g_\ell =b$ . Observe that $g_i^{-1}g_{i+1}\in S$ for $0\leq i<\ell $ , and hence $\operatorname {\mathrm {\mathsf {dist}}}_{(G,S)}(g_i,g_{i+1})\leq 1$ . Now, $[g_0, \ldots , g_\ell ]$ is a path in $\Gamma (G,S)$ from a to b and therefore $\operatorname {\mathrm {\mathsf {dist}}}_{(G,S)}(a,b)\leq \operatorname {\mathrm {\mathsf {dist}}}_{(H,T)}(q(a),q(b))$ proving inequality (2.2).

Corollary 2.1 Let G and H be groups with finite generating sets $S_0$ and $T_0$ . Let $q\colon G\to H$ be a group homomorphism which is also an $(L_0,C_0)$ -quasi-isometry $q\colon \Gamma (G,S_0) \to \Gamma (H,T_0)$ . If $T\subset H$ contains $T_0$ , then there is $S\subset G$ containing $S_0$ such that $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry.

Proof Let $\bar q\colon H\to G$ be a quasi-inverse of q and, by increasing $L_0$ and $C_0$ if necessary, assume that $\bar q\colon \Gamma (H,T_0) \to \Gamma (G, S_0)$ is an $(L_0,C_0)$ -quasi-isometry. Moreover, suppose $q\circ \bar q$ and $\bar q\circ q$ are at distance at most $C_0$ from the corresponding identity maps with respect to $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T_0)}$ and $\operatorname {\mathrm {\mathsf {dist}}}_{(G,S_0)}$ . Note that for any $g\in G$ ,

$$\begin{align*}q_g (h) = q(g \cdot \bar q (h))=q(g) \cdot q (\bar q (h)). \end{align*}$$

Hence, $q_g$ is a $(1,C_0)$ -quasi-isometry since it is the composition of $q \circ \bar q$ followed by the isometry given by multiplication on the left by $q(g)$ . Then the proof concludes by invoking Proposition 2.1.

The following result is the particular case of Corollary 2.1 in which H is a finite index subgroup of G. In this case, one can give a more algebraic description of the generating set S. The proof follows the same lines as the previous argument modulo Lemma 2.1.

Proposition 2.2 Let H be a finite index normal subgroup of a finitely generated group G. Let T be a generating set of H, let R be a right transversal of H in G, and let $S=T\cup R$ . If the G-action by conjugation on H is a uniform quasi-action on $\Gamma (H,T)$ , then the inclusion $\Gamma (H,T) \hookrightarrow \Gamma (G,S)$ is a quasi-isometry.

We divert the proof of the proposition after the following lemma.

Lemma 2.1 Let H be a finite index normal subgroup of a finitely generated group G. Let T be a generating set of H containing a finite generating set $T_0$ , let R be transversal of H in G, let $S_0$ be a finite generating set of G, and let $q\colon \Gamma (G,S_0)\to \Gamma (H,T_0)$ be the quasi-isometry defined by $q(hg)=h$ for $h\in H$ and $g\in R$ . The following statements are equivalent:

1. (1) The G-action by conjugation on H is a uniform quasi-action on $\Gamma (H,T)$ .

2. (2) The quasi-action of G on H induced by q is uniform with respect to T.

Proof Take as the quasi-inverse of q the inclusion $H\hookrightarrow G$ . For $h\in H$ , let ${L_h\colon H\to H}$ be given by $L_h(x)=hx$ , i.e., multiplication on the left. Note that $L_h\colon \Gamma (H,T)\to \Gamma (H,T)$ is an isometry for every $h\in H$ .

Let $g\in G$ and suppose that $g=h_*g_*$ where $h_*\in H$ and $g_*\in R$ . Then

$$\begin{align*}q_g(h)=q(gh)=q(ghg^{-1}h_*g_*)=ghg^{-1}h_*=h_*g_*hg_*^{-1}h_*^{-1}h_*=h_*g_*hg_*^{-1}\end{align*}$$

and hence

$$\begin{align*}q_g = L_{h_*}\circ \textrm{Ad}({g_*}),\end{align*}$$

where $\textrm {Ad}(g_*)$ is conjugation by $g_*$ . It follows $q_g\colon \Gamma (H,T)\to \Gamma (H,T)$ is an $(L,C)$ -quasi-isometry for all $g\in G$ if and only if $\textrm {Ad}({g_*}) \colon \Gamma (H,T)\to \Gamma (H,T)$ is an $(L,C)$ -quasi-isometry for all $g_*\in R$ . In particular, the first statement implies the second by Remark 2.1, and the second statement implies the first since the constants L and C hold for all conjugations.

Proof [Proof of Proposition 2.2.]

Let $T_0 \subset T$ be a finite generating set of H, and let $S_0=T_0\cup R$ . Note that $S_0$ is a finite generating set of G. Then $q\colon \Gamma (G,S_0)\to \Gamma (H,T_0)$ is an $(L_0,C_0)$ quasi-isometry for some $L_0\geq 1$ and $C_0\geq 0$ , and the quasi-inverse $\bar q$ can be taken as the inclusion $\Gamma (H,T_0)\hookrightarrow \Gamma (G,S_0)$ .

Observe that, in $\Gamma (G,S)$ , the vertices $g=hr$ and $q(g)=h$ are adjacent since ${r\in S}$ . Therefore, if $[v_0,\ldots ,v_\ell ]$ is a geodesic path in $\Gamma (H,T)$ from $q(a)$ to $q(b)$ , then $[a, v_0,\ldots ,v_\ell ,b]$ is a path in $\Gamma (G,S)$ from a to b, and hence

$$\begin{align*}\operatorname{\mathrm{\mathsf{dist}}}_{(G,S)}(a,b) \leq \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(a),q(b))+2. \end{align*}$$

We now prove the other inequality. Since the G-action on H by conjugation is a uniform quasi-action on $\Gamma (H,T)$ , Lemma 2.1 implies that the quasi-action of G on H induced by q is $(L_1,C_1)$ -uniform with respect to T, for some $L_1\geq 1$ and $C_1\geq 0$ .

Let $K_0=L_0+C_0+1$ . Observe that

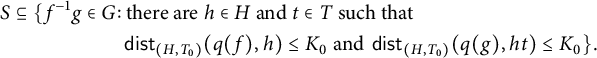$$\begin{align*}\begin{aligned} S \subseteq \{ f^{-1}g \in G \colon & \text{ there are } h\in H \text{ and } t\in T \text{ such that } \\ & \operatorname{\mathrm{\mathsf{dist}}}_{(H, T_0)}(q(f),h)\leq K_0 \text{ and } \operatorname{\mathrm{\mathsf{dist}}}_{(H,T_0)}(q(g),ht)\leq K_0 \}. \end{aligned} \end{align*}$$

Indeed, let $s\in S=T\cup R$ , and there are two cases. First, if $s\in T$ , let $f=h=e$ and $g=t=s$ , and second, if $s\in R$ , let $f=h=e$ , $g=s$ , and t be any element of $T_0$ . Then, exactly as in the first claim in the proof of Proposition 2.1, one defines a constant $\bar L=\bar L(L_1,C_1,K_0)$ and deduces the inequality

(2.3) $$ \begin{align} \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(a),q(b)) \leq \bar L\operatorname{\mathrm{\mathsf{dist}}}_{(G,S)}(a,b). \end{align} $$

It remains to show that

(2.4) $$ \begin{align} \operatorname{\mathrm{\mathsf{dist}}}_{(G,S)}(a,b)\leq \operatorname{\mathrm{\mathsf{dist}}}_{(H,T)}(q(a),q(b))+2, \end{align} $$

for any $a,b\in G$ , concluding the proof. This is clear since $\Gamma (H,T)$ is a subgraph of $\Gamma (G,T)$ and $\operatorname {\mathrm {\mathsf {dist}}}_{G,S}(g,q(g))\leq 1$ for any $g\in G$ .

The following example by Minasyan and Osin illustrates the need for the hypothesis relating to the conjugation action in Corollary 2.2.

Example 2.1 [16]

Let $H=\langle a,b \rangle $ be the free group of rank 2, let $G=\langle a,b,t \colon tat^{-1}\,{=}\,b, t^2=e \rangle $ , let $T=\{b,a,a^{-1},a^2,a^{-2},\ldots \}$ , and let $S=T\cup \{t\}$ . The inclusion $\Gamma (H,T) \to \Gamma (G,S)$ is not a quasi-isometry. Indeed, in G, we have $ta^nt^{-1}=b^n$ , and hence $\operatorname {\mathrm {\mathsf {dist}}}_{(G,S)}(e,b^n)=3$ , but $\operatorname {\mathrm {\mathsf {dist}}}_{(H,T)}(e,b^n)=n$ for every n. In particular, the map $\Gamma (H,T)\to \Gamma (H,T)$ given by $h\mapsto tht^{-1}$ is not a quasi-isometry, and hence the G-action on H by conjugation is not an action by quasi-isometries.

3 Quasi-isometries and hyperbolically embedded subgroups

In this section, we will prove Theorem A. The theorem is obtained by putting together a simple characterization of hyperbolically embedded subgroups in terms of coned-off Cayley graphs which appeared in the work of Rashid and the second author (see [13, Propositions 1.5 and 5.8]), some results about quasi-isometries of pairs from [11], and some basic facts about hyperbolically embedded subgroups from [7]. Below, we state these results and then we discuss the proof of Theorem 3.1.

Definition 3.1 (Reduced collections)

A collection of subgroups ${\mathcal {Q}}$ of a group H is reduced if for any $P,Q\in {\mathcal {Q}}$ and $g\in H$ , if P and $gQg^{-1}$ are commensurable subgroups, then $P=Q$ and $g\in P$ .

Remark 3.1. An almost malnormal collection is reduced.

Definition 3.2 (Fine)

Let $\Gamma $ be a graph, and let v be a vertex of $\Gamma $ . Let

$$ \begin{align*} T_v \Gamma = \{w \in V(\Gamma) \mid \{v,w\}\in E(\Gamma)\} \end{align*} $$

denote the set of the vertices adjacent to v. For $x,y \in T_v \Gamma $ , the angle metric $\angle _v (x,y)$ is the length of the shortest path in the graph $\Gamma \setminus \{v\}$ between x and y, with $\angle _v (x,y) = \infty $ if there is no such path. The graph $\Gamma $ is fine at v if $(T_v \Gamma ,\angle _v)$ is a locally finite metric space. The graph $\Gamma $ is fine at $C \subseteq V(\Gamma )$ if $\Gamma $ is fine at v for all $v \in C$ .

Definition 3.3 (Coned-off Cayley graph)

Let G be a group, let ${\mathcal {P}}$ be an arbitrary collection of subgroups of G, and let S be a subset of G. Denote by $G/{\mathcal {P}}$ the set of all cosets $gP$ with $g\in G$ and $P\in {\mathcal P}$ . The coned-off Cayley graph of G with respect to ${\mathcal {P}}$ is the graph $\hat \Gamma (G,{\mathcal {P}},S)$ with vertex set $G\cup G/{\mathcal {P}}$ and edges are of the following type:

• • $\{g,gs\}$ for $s\in S$ and

• • $\{x, gP\}$ for $g\in G$ , $P\in {\mathcal {P}}$ , and $x\in gP$ .

We call vertices of the form $gP$ cone points.

Proposition 3.1 [13]

Let ${\mathcal {P}}$ be a collection of infinite subgroups of G, and let S be a subset of G. Then ${\mathcal {P}} \hookrightarrow _h (G,S) $ if and only if the Coned-off Cayley graph $\hat {\Gamma }(G,{\mathcal {P}},S)$ is a connected hyperbolic graph which is fine at every cone vertex.

Proposition 3.2 [11, Proposition 5.6]

Let G and H be groups, let $S\subset G$ and $T\subset H$ , and let $S_0\subset S$ and $T_0\subset T$ be finite generating sets of G and H, respectively. Consider collections ${\mathcal P}$ and $\mathcal Q$ of subgroups of G and H, respectively. Let $q\colon G\to H$ be a function.

Suppose that q is a quasi-isometry $\Gamma (G,S) \to \Gamma (H,T)$ , is a quasi-isometry of pairs $(G, \mathcal {P},S_0)\to (H, \mathcal {Q},T_0)$ , and $\dot {q}$ is a bijection $G/{\mathcal {P}} \to H/{\mathcal {Q}}$ .

1. (1) Let $\hat q = q\cup \dot {q}$ , then $\hat q$ is a quasi-isometry $\hat \Gamma (G,{\mathcal {P}}, S) \to \hat \Gamma (H,{\mathcal {Q}}, T)$ .

2. (2) If $\hat \Gamma (H,{\mathcal {Q}}, T)$ is fine at cone vertices, then $\hat \Gamma (G,{\mathcal {P}}, S)$ is fine at cone vertices.

3. (3) If ${\mathcal {Q}}\hookrightarrow _h(H,T)$ , then ${\mathcal {P}}\hookrightarrow _h(G,S)$ .

Items (1) and (2) of Proposition 3.2 are taken from [11, Proposition 5.6], and the last item is a direct consequence of Proposition 3.1.

Proposition 3.3 [11, Proposition 5.12]

Let $q\colon (G, \mathcal {P})\to (H, \mathcal {Q})$ be an $(L,C,M)$ -quasi-isometry of pairs. Then:

1. (1) $\dot {q}$ is a surjective function $G/{\mathcal {P}} \to H/{\mathcal {Q}}$ if ${\mathcal {Q}}$ is reduced.

2. (2) $\dot {q}$ is a bijection $G/{\mathcal {P}} \to H/{\mathcal {Q}}$ if ${\mathcal {P}}$ and ${\mathcal {Q}}$ are reduced.

Proposition 3.4 [11, Proposition 6.2]

Let ${\mathcal {P}}^\ast $ be a refinement of a finite collection of subgroups ${\mathcal {P}}$ of a finitely generated group G. If P is a finite index subgroup of $\operatorname {{\mathrm {Comm}}}_G(P)$ for every $P\in {\mathcal {P}}$ , then $(G,{\mathcal {P}})$ and $(G,{\mathcal {P}}^*)$ are quasi-isometric pairs via the identity map on G.

Proposition 3.5 [11, Proposition 6.7]

Let $q\colon (G, \mathcal {P})\to (H, \mathcal {Q})$ be a quasi-isometry of pairs. If ${\mathcal {Q}}$ is an almost malnormal finite collection of infinite subgroups and ${\mathcal {P}}$ is a finite collection, then any refinement ${\mathcal {P}}^*$ of ${\mathcal {P}}$ is almost malnormal.

Proposition 3.6 [7, Proposition 4.33]

Let ${\mathcal {P}}$ be a collection of subgroups of a group G. If ${\mathcal {P}}\hookrightarrow _h G$ , then ${\mathcal {P}}$ is an almost malnormal collection.

We are now ready to prove Theorem A.

Theorem 3.1 (Theorem A)

Let $q\colon G\to H$ be a quasi-isometry of finitely generated groups, let ${\mathcal {P}}$ and ${\mathcal {Q}}$ be finite collections of subgroups of G and H, respectively, and let S and T be (not necessarily finite) generating sets of G and H, respectively. Suppose that:

1. (1) $q\colon (G,{\mathcal {P}}) \to (H,{\mathcal {Q}})$ is a quasi-isometry of pairs and

2. (2) $q\colon \Gamma (G,S) \to \Gamma (H,T)$ is a quasi-isometry.

The following statements hold:

1. (1) If ${\mathcal {P}}$ and ${\mathcal {Q}}$ are reduced collections in G and H, respectively, then ${\mathcal {P}}\hookrightarrow _h (G,S)$ if and only if ${\mathcal {Q}}\hookrightarrow _h (H,T)$ .

2. (2) If ${\mathcal {Q}}$ contains only infinite subgroups and ${\mathcal {Q}}\hookrightarrow _h (H,T)$ , then ${\mathcal {P}}^*\hookrightarrow _h (G,S)$ .

Proof For the first statement, since ${\mathcal {P}}$ and ${\mathcal {Q}}$ are reduced, Proposition 3.3 implies that $\dot q\colon G/{\mathcal {P}} \to H/{\mathcal {Q}}$ is a bijection. Then Proposition 3.2 implies that $\hat \Gamma (G,{\mathcal {P}},S)$ is hyperbolic and fine at cone vertices if and only if $\hat \Gamma (H,{\mathcal {Q}},T)$ is hyperbolic and fine at cone vertices. Then Proposition 3.1 concludes the proof of the first statement.

The second statement is a consequence of the first statement as follows. That ${\mathcal {Q}}\hookrightarrow _h H$ implies that ${\mathcal {Q}}$ is an almost malnormal collection of subgroups in H (see Proposition 3.6). It follows that ${\mathcal {Q}}$ is reduced in H. Then, since ${\mathcal {Q}}$ contains only infinite subgroups, Proposition 3.5 implies that ${\mathcal {P}}^\ast $ is reduced. By Proposition 3.4, $q\colon (G,{\mathcal {P}}^\ast )\to (H,{\mathcal {Q}})$ is a quasi-isometry of pairs. Then ${\mathcal {Q}}\hookrightarrow _h H$ and the first statement of the proposition imply that ${\mathcal {P}}^\ast \hookrightarrow (G,S)$ .

4 Hyperbolically embedded subgroups and commensurability

In this section, we prove Theorem E. The argument uses the following proposition, which is a strengthening of [14, Proposition 2.15]. It essentially follows from the proof in the cited article, but we have included the proof for the convenience of the reader.

Proposition 4.1 Let H be a finite index subgroup of a finitely generated group G, and let $\mathcal {Q}$ be a finite collection of subgroups of H. The following statements are equivalent:

1. (1) The inclusion $H\hookrightarrow G$ is a quasi-isometry of pairs $(H,\mathcal {Q}) \hookrightarrow (G, \mathcal {Q})$ .

2. (2) For any $Q\in \mathcal {Q}$ and $g\in G$ , there is $Q'\in \mathcal {Q}$ and $h\in H$ such that ${\operatorname {\mathrm {\mathsf {hdist}}}_G(gQ , hQ')<\infty} $ .

Proof That (1) implies (2) is trivial. Assume statement (2). Since H is a finite index subgroup of the finitely generated group G, assume that $H\hookrightarrow G$ is an $(L,C)$ quasi-isometry. Since H is finite index in G, and $\mathcal {Q}$ is a finite collection, the H-action on $G/\mathcal {Q}$ has finitely many orbits. For $gQ\in G/\mathcal {Q}$ , let

$$\begin{align*}\operatorname{\mathrm{\mathsf{hdist}}}_G(gQ, H/\mathcal{Q}):= \min\left\{\operatorname{\mathrm{\mathsf{hdist}}}_G(gQ, hQ') \colon hQ'\in H/\mathcal{Q} \right\}\!. \end{align*}$$

Let $\mathcal {R}$ be a finite collection of orbit representatives of the H-action on $G/\mathcal {Q}$ . By hypothesis, for $gQ \in \mathcal {R}$ , there is $h Q'\in H/ \mathcal {Q}$ such that $\operatorname {\mathrm {\mathsf {hdist}}}(gQ,hQ')<\infty $ and therefore

$$\begin{align*}M = \max\{\operatorname{\mathrm{\mathsf{hdist}}}_G(gQ,H/\mathcal{Q}) \colon gQ \in \mathcal{R}\} <\infty \end{align*}$$

is a well-defined integer since $\mathcal {R}$ is a finite set. Since the subset $H/\mathcal {Q}$ of $G/\mathcal {Q}$ is H-invariant,

$$\begin{align*}\operatorname{\mathrm{\mathsf{hdist}}}_G(gQ, H/\mathcal{Q}) = \operatorname{\mathrm{\mathsf{hdist}}}_G(hgQ, H/\mathcal{Q}) \end{align*}$$

for every $gQ\in \mathcal {R}$ and $h\in H$ . Since $\mathcal {R}$ is a collection of representatives of orbits of $G/\mathcal {Q}$ ,

$$\begin{align*}\operatorname{\mathrm{\mathsf{hdist}}}_G(gQ, H/\mathcal{Q}) \leq M \end{align*}$$

for every $gQ \in G/ \mathcal {Q}$ . Hence, $(H, \mathcal {Q}) \hookrightarrow (G, \mathcal {Q})$ is an $(L,C,M)$ quasi-isometry of pairs.

Remark 4.1. Let G be a group, and let T and S generating sets with finite symmetric difference. Then the identity map on G is a quasi-isometry $\Gamma (G,T) \to \Gamma (G,S)$ .

Theorem 4.1 (Theorem E)

Let H be a finite index normal subgroup of a finitely generated group G, and let ${\mathcal {Q}}$ be a finite collection of infinite subgroups of H such that ${\mathcal {Q}}\hookrightarrow _h (H,T)$ . Suppose that:

1. (1) The G-action by conjugation on H is a uniform quasi-action on $\Gamma (H,T)$ .

2. (2) The collection $\{hQh^{-1} \colon h\in H \text { and } Q\in {\mathcal {Q}}\}$ is invariant under conjugation by G.

If ${\mathcal {Q}}^*$ is a refinement of ${\mathcal {Q}}$ in G and R is a transversal of H in G, then ${\mathcal {Q}}^*\hookrightarrow _h (G, T\cup R)$ .

Proof Since H is finitely generated, by adding a finitely many elements, we can assume that T generates H. Note that this preserves ${\mathcal {Q}}\hookrightarrow _h (H,T)$ by [7, Corollary 4.27], and the quasi-isometry type of $\Gamma (H,T)$ by Remark 4.1. Under this assumption, the conclusion will follow from the second statement of Theorem 3.1 applied to the quasi-isometry of finitely generated groups given by the inclusion $H\hookrightarrow G$ .

Since ${\mathcal {Q}}\hookrightarrow _h (H,T)$ , ${\mathcal {Q}}$ is an almost malnormal collection (see Proposition 3.6). The assumption that ${\mathcal {Q}}$ consists only of infinite subgroups implies that for any $Q\in {\mathcal {Q}}$ ,

$$\begin{align*}Q=\operatorname{{\mathrm{Comm}}}_H(Q)=\operatorname{{\mathrm{Comm}}}_G(Q)\cap H. \end{align*}$$

Since H is finite index in G, we have that Q is finite index in $\operatorname {{\mathrm {Comm}}}_G(Q)$ . Then Proposition 3.4 implies that the identity map on G is a quasi-isometry of pairs $(G,{\mathcal {Q}}) \xrightarrow {}(G,{\mathcal {Q}}^\ast )$ . On the other hand, since the collection $\{hQh^{-1}\colon h\in H \text { and} Q\in {\mathcal {Q}}\}$ is invariant under conjugation by elements of G, we have for any $g\in G$ and $Q\in {\mathcal {Q}}$ there is $h\in H$ such that $gQg^{-1}=hQ'h^{-1}$ and hence

$$\begin{align*}\operatorname{\mathrm{\mathsf{hdist}}}_G(gQ,hQ')\leq \operatorname{\mathrm{\mathsf{hdist}}}_G(gQ,Q^g)+ \operatorname{\mathrm{\mathsf{hdist}}}_G(Q^g,(Q')^h)+ \operatorname{\mathrm{\mathsf{hdist}}}((Q')^h,hQ')<\infty.\end{align*}$$

Proposition 4.1 implies that $H\hookrightarrow G$ is a quasi-isometry of pairs $(H,{\mathcal {Q}})\to (G,{\mathcal {Q}})$ . It follows that $H\hookrightarrow G$ is a quasi-isometry of pairs $(H,{\mathcal {Q}}) \to (G,{\mathcal {Q}}^\ast )$ as it is the composition $(H,{\mathcal {Q}})\hookrightarrow (G,{\mathcal {Q}}) \xrightarrow {}(G,{\mathcal {Q}}^\ast )$ . Let R be a transversal of H in G, and let ${S=T\cup R}$ . Since the G-action by conjugation on H is uniform on $\Gamma (H,T)$ , Proposition 2.2 implies that $H\hookrightarrow G$ is a quasi-isometry $\Gamma (H,T) \to (G,S)$ . The hypothesis of Theorem 3.1 has been verified, and therefore ${\mathcal {Q}}\hookrightarrow _h (H,T)$ implies ${\mathcal {Q}}^*\hookrightarrow _h (G,S)$ .

5 Semidirect products and hyperbolically embedded subgroups

In this section, we will prove Theorem F about semidirect products. The hypothesis of the following proposition and theorem reflects the issues posed by the example of Minasyan and Osin (Example 2.1).

Proposition 5.1 Let A be a group with (not necessarily finite) generating set T, let $\mathcal {H}$ be a collection of subgroups, and let $F\leq \mathsf {Aut}(A)$ be a finite subgroup. Suppose that T and $\mathcal {H}$ are F-invariant and that the F-action on $\mathcal {H}$ is free. Let ${\mathcal {H}}_F$ be a collection of representatives of F-orbits in ${\mathcal {H}}$ . Then the inclusion $A\hookrightarrow A\rtimes F$ induces:

1. (1) a quasi-isometry $\Gamma (A,T) \to \Gamma (A\rtimes F, T\cup F)$ and

2. (2) if A is finitely generated, a quasi-isometry of pairs $(A,\mathcal {H}) \to (A\rtimes F,\mathcal {H}_F)$ .

Proof To prove the first statement, let $S=T\cup F$ and let $\operatorname {\mathrm {\mathsf {dist}}}_{T}$ and $\operatorname {\mathrm {\mathsf {dist}}}_S$ be the word metrics on A and $A\rtimes F$ induced by T and S, respectively. Let $q \colon A \hookrightarrow A\rtimes F$ be the inclusion, and let $\bar q\colon A\rtimes F \to A$ be such that for $a\in A$ and $f\in F$ , $\bar q(af)=a$ . Note that $\bar q$ is a well-defined A-equivariant map since each element of $A\rtimes F$ can be expressed as a product $af$ in a unique way. Observe that $\bar q\circ q$ is the identity on A, and $q\circ \bar q$ is at distance 1 from the identity map on $A\rtimes F$ with respect to $\operatorname {\mathrm {\mathsf {dist}}}_S$ . Since the Cayley graph $\Gamma (A,T)$ is a subgraph of $\Gamma (A\rtimes F, T\cup F)$ , it is immediate that for any $u,v\in A$ , $\operatorname {\mathrm {\mathsf {dist}}}_S(q(u),q(v))\leq \operatorname {\mathrm {\mathsf {dist}}}_T(u,v)$ . To conclude the proof of the statement, we show that for any $u,v\in A\rtimes F$ , $\operatorname {\mathrm {\mathsf {dist}}}_T(\bar q(u),\bar q(v))\leq \operatorname {\mathrm {\mathsf {dist}}}_S(u,v)$ . Note that it is enough to consider the case that $\operatorname {\mathrm {\mathsf {dist}}}_S(u,v)=1$ . Let $w_1,w_2\in A\rtimes F$ such that $\operatorname {\mathrm {\mathsf {dist}}}_S(w_1,w_2)=1$ . Then $w_1=a_1f_1$ and $w_2=a_2f_2$ and $\bar q(w_i)=a_i$ . It follows that $g=(a_1f_1)^{-1}a_2f_2\in T\cup F$ . Observe that

$$\begin{align*}g= f_1^{-1}a_1^{-1}a_2f_2=(a_1^{-1})^{f_1^{-1}}f_1^{-1}a_2f_2=(a_1^{-1})^{f_1^{-1}}a_2^{f_1^{-1}}f_1^{-1} f_2=(a_1^{-1}a_2)^{f_1^{-1}}f_1^{-1}f_2\in T\cup F. \end{align*}$$

There are two cases, either $g\in T$ or $g\in F$ , since $T\cap F=\emptyset $ . We regard $T\cup F$ and F as a subset and a subgroup of $A\rtimes F$ , respectively. If $g\in T$ , then $f_1=f_2$ and hence $(a_1^{-1}a_2)^{f_1^{-1}} \in T$ ; since T is F-invariant, $a_1$ and $a_2$ are adjacent in $\Gamma $ , and hence $\operatorname {\mathrm {\mathsf {dist}}}_T(\bar q(w_1), \bar q(w_2))=1$ . If $g\in F$ , then $a_1=a_2$ and hence $\operatorname {\mathrm {\mathsf {dist}}}_T(\bar q(w_1), \bar q(w_2))=0$ .

For the second statement, suppose that A is finitely generated and let $\operatorname {\mathrm {\mathsf {dist}}}$ denote word metric on $A\rtimes F$ induced by finite generating set, and let $\operatorname {\mathrm {\mathsf {hdist}}}_{A\rtimes F}$ be the induced Hausdorff distance. Let $M=\max _{f\in F}\operatorname {\mathrm {\mathsf {dist}}}(1, f)$ . Since the inclusion $A\hookrightarrow A\rtimes F$ is a quasi-isometry of finitely generated groups and ${\mathcal {H}}_F \subset {\mathcal {H}}$ , it is enough to prove that for any $H\in {\mathcal {H}}$ , there is a left coset in $(A\rtimes F)/{\mathcal {H}}_F$ at Haudorff distance at most M in $A\rtimes F$ . Let $H\in {\mathcal {H}}$ . Since the F-action on ${\mathcal {H}}$ by conjugation is free, there is a unique $f\in F$ and a unique $K\in {\mathcal {H}}_F$ such that $H=fKf^{-1}$ . Observe that

$$\begin{align*}\operatorname{\mathrm{\mathsf{hdist}}}(H, fK) = \operatorname{\mathrm{\mathsf{hdist}}}(fKf^{-1}, fK) \leq \operatorname{\mathrm{\mathsf{dist}}}(1, f^{-1}) \leq M, \end{align*}$$

and this completes the proof.

Theorem 5.1 (Theorem F)

Let A be a finitely generated group with (not necessarily finite) generating set T, and let ${\mathcal {H}}$ be a finite collection of infinite subgroups such that $\mathcal {H}\hookrightarrow _h (A,T)$ . If $F\leq \mathsf {Aut}(A)$ is finite, T and ${\mathcal {H}}$ are F-invariant, and the F-action on $\mathcal {H}$ is free, then ${\mathcal {H}}_F\hookrightarrow _h(A\rtimes F,T\cup F)$ , where ${\mathcal {H}}_F$ is collection of representatives of F-orbits in ${\mathcal {H}}$ .

Proof By Proposition 5.1, the inclusion $A\hookrightarrow A\rtimes F$ induces a quasi-isometry $\Gamma (A,T) \to \Gamma (A\rtimes F, T\cup F)$ , and a quasi-isometry of pairs $(A,{\mathcal {H}}) \to (A\rtimes F, {\mathcal {H}}_F)$ . Since ${\mathcal {H}}\hookrightarrow _h A$ , the collection ${\mathcal {H}}$ is almost malnormal in A; then the assumption that F acts freely on $\mathcal {H}$ implies that a refinement of ${\mathcal {H}}$ in $A\rtimes F$ is $\mathcal {H}_F$ , and this was observed in Example 1.3. Since ${\mathcal {H}}$ contains only infinite subgroups and ${\mathcal {H}}\hookrightarrow _h A$ , Theorem 3.1 implies that ${\mathcal {H}}_F \hookrightarrow _h (A\rtimes F, T\cup F)$ .

6 Concluding remarks

A positive answer to the following question would allow us to drop the first hypothesis of Theorem A for the relevant groups.

Question 6.1. Let G be a finitely generated NRH acylindrically hyperbolic group. Does G contain a qi-characteristic collection of hyperbolically embedded subgroups?

It is possible that ${\mathcal {A}}{\mathcal {H}}$ -accessibility as defined in [1] may be necessary for a positive answer to Question 6.1. Note that this property does not always hold (see [2]).

It is tempting to weaken the definition of a quasi-isometry of pairs $q\colon (G,{\mathcal {P}})\to (H,{\mathcal {Q}})$ to remove the uniform constant M bounding the Hausdorff distances on the cosets and instead ask the relation

$$\begin{align*}\dot{q}=\{(A,B)\in G/{\mathcal{P}}\times H/{\mathcal{Q}} : \operatorname{\mathrm{\mathsf{hdist}}}_H(q(A),B)<\infty\}\end{align*}$$

satisfies that the projections into $G/{\mathcal {P}}$ and $H/{\mathcal {Q}}$ are surjective. We shall call the map q in this modified definition an almost quasi-isometry of pairs following [10, Section 5].

Indeed, there is work of Margolis [12] where the main theorems do not require this additional hypothesis. However, Margolis shows that the hypotheses assumed in the main results of loc. cit. in fact imply that such a constant M exists (see [12, Theorem 4.1]). Note that our results in this article rely on the existence of a constant M—primarily due to the use of [11, Proposition 5.6]. Thus, we raise the following question.

Question 6.2. Let G and H be finitely generated groups with finite collections of subgroups ${\mathcal {P}}$ and ${\mathcal {Q}}$ , respectively. When is an $(L,C)$ -almost quasi-isometry of pairs $q\colon (G,{\mathcal {P}})\to (H,{\mathcal {Q}})$ an $(L,C,M)$ -quasi-isometry of pairs?

Motivated by results of [5], the referee of the article suggested that it might be interesting to investigate other relaxations of the definition of a quasi-isometry of pairs (Defintion 1.1), for example, in the sense that the image of every element of the collection $\mathcal {A}$ lies at uniform Hausdorff distance of the union of finitely many elements in the collection $\mathcal {B}$ . Having a more general notion could allow a broader strategy toward tackling Question 1.1 based on the methods in this article.