The Dawes Review 2: Nucleosynthesis and Stellar Yields of Low- and Intermediate-Mass Single Stars

Abstract

The chemical evolution of the Universe is governed by the chemical yields from stars, which in turn are determined primarily by the initial stellar mass. Even stars as low as 0.9 M_⊙ can, at low metallicity, contribute to the chemical evolution of elements. Stars less massive than about 10 M_⊙ experience recurrent mixing events that can significantly change the surface composition of the envelope, with observed enrichments in carbon, nitrogen, fluorine, and heavy elements synthesized by the slow neutron capture process (the s-process). Low- and intermediate-mass stars release their nucleosynthesis products through stellar outflows or winds, in contrast to massive stars that explode as core-collapse supernovae. Here we review the stellar evolution and nucleosynthesis for single stars up to ~ 10 M_⊙ from the main sequence through to the tip of the asymptotic giant branch (AGB). We include a discussion of the main uncertainties that affect theoretical calculations and review the latest observational data, which are used to constrain uncertain details of the stellar models. We finish with a review of the stellar yields available for stars less massive than about 10 M_⊙ and discuss efforts by various groups to address these issues and provide homogeneous yields for low- and intermediate-mass stars covering a broad range of metallicities.

The Dawes Reviews are substantial reviews of topical areas in astronomy, published by authors of international standing at the invitation of the PASA Editorial Board. The reviews recognise William Dawes (1762–1836), second lieutenant in the Royal Marines and the astronomer on the First Fleet. Dawes was not only an accomplished astronomer, but spoke five languages, had a keen interest in botany, mineralogy, engineering, cartography and music, compiled the first Aboriginal-English dictionary, and was an outspoken opponent of slavery.

1 INTRODUCTION

Stars with initial masses between about 0.8 and 10 M_⊙ dominate the stellar population in our Milky Way Galaxy. This mass interval spans a huge range in stellar lifetimes, from the longest lived low-mass stars, that have existed for as long as our Galaxy (≈ 1.2 × 10¹⁰ years) to the most massive of this range, whose lives are over in the blink of a cosmic eye (≲ 20 million years). These stars are numerous because of the shape of the initial mass function which peaks at ≈ 1 M_⊙. Their importance is underlined by that fact that they experience a diversity of rich nucleosynthesis, making them crucial contributors to the chemical evolution of elements in our Universe (e.g., Travaglio et al. 2001a; Romano et al. 2010; Kobayashi, Karakas, & Umeda 2011b). When these stars evolve they lose mass through strong stellar outflows or winds and it has been estimated that they have produced nearly 90% of the dust injected into the interstellar medium (ISM) of our Galaxy, with massive stars accounting for the rest (Sloan et al. 2008). Furthermore, galaxies dominated by intermediate-age stellar populations have a significant fraction of their starlight emitted by low- and intermediate-mass stars, especially when they evolve off the main sequence to the giant branches (Mouhcine & Lançon 2002; Maraston 2005; Maraston et al. 2006; Tonini et al. 2009; Melbourne et al. 2012).

For low- and intermediate-mass stars the most important nucleosynthesis occurs when the stars reach the giant branches. It is during the ascent of the red giant branch (RGB) that the first dredge-up occurs. This changes the surface composition by mixing to the surface material from the interior that has been exposed to partial hydrogen (H) burning. It is also on the upper part of the RGB where extra mixing processes occur in the envelopes of low-mass giants. These are processes not included in traditional calculations which assume convection is the only mixing mechanism present. Such processes may include meridional circulation, shear mixing, and various hydrodynamic and magnetic mixing processes. Empirically we know that something occurs that results in further products of H-burning nucleosynthesis becoming visible at the surface.

The more massive stars in our selected mass range will also experience a second dredge-up, which occurs following core helium (He) exhaustion as the star begins its ascent of the giant branch for the second time, now called the asymptotic giant branch, or AGB. It is on the AGB where we expect the largest changes to the surface composition. These are driven by a complex interplay of nucleosynthesis and mixing. The nucleosynthesis is driven by thermal instabilities in the He-burning shell, known as shell flashes or thermal pulses. The products of this burning, mostly carbon, may be mixed to the stellar surface by recurrent convective mixing episodes. These mixing episodes can occur after each thermal pulse and are known as third dredge-up events.

Thermal pulses are responsible for a large variety of stellar spectral types. Stars begin their lives with an atmosphere that is oxygen rich, in the sense that the ratio of the number of carbon to oxygen atoms n(C)/n(O) is less than unity. Recurring third dredge-up on the AGB can add enough carbon to the envelope that the star becomes carbon rich with n(C)/n(O) ⩾ 1, hence becoming a ‘carbon star’ (or C star). There are many different types of C stars including both intrinsic, meaning that they result from internal evolution (as described above, e.g., C(N) stars) or extrinsic, where it is mass transfer from a close binary C star that produces n(C)/n(O) ⩾ 1 in a star that is not sufficiently evolved to have thermal pulses itself (e.g., CH stars and dwarf C stars; Wallerstein & Knapp 1998). It is also the third dredge-up that mixes to the surface the heavy elements such as barium and lead that are produced by the slow neutron capture process (the s-process). This can result in S-stars, barium stars, and technetium-rich stars (Wallerstein & Knapp 1998). Strong stellar winds then expel this enriched material into the ISM, where it can contribute to the next generation of star formation.

Intermediate-mass AGB stars may also experience hot bottom burning (HBB), where the bottom of the convective envelope penetrates into the top of the H-burning shell. Proton-capture nucleosynthesis occurs at the base of the mixed envelope (Blöcker & Schoenberner 1991; Lattanzio 1992; Boothroyd, Sackmann, & Wasserburg 1995). Third dredge-up operates alongside HBB and this can lead to some interesting results, such as substantial production of primary nitrogen, together with other hydrogen-burning products including sodium and aluminium.

The short lifetime of those AGB stars that experience HBB (τ ≲ 100Myr) has implicated them as potential polluters of Galactic globular clusters (GCs), which show abundance trends consistent with hot H burning (Gratton, Sneden, & Carretta 2004; Gratton, Carretta, & Bragaglia 2012; Prantzos, Charbonnel, & Iliadis 2007). The ability of detailed models to match the observed abundance trend depends on highly uncertain assumptions about the treatment of convection and mass loss in stellar models (e.g., Fenner et al. 2004; Karakas et al. 2006a; Ventura & D’Antona 2009).

Not so long ago there was a belief that if you were interested in the chemical evolution of the Galaxy, or indeed the Universe, then all you needed was yields from core-collapse supernovae (SNe), and perhaps Type I supernovae (e.g., Timmes, Woosley, & Weaver 1995). But with an increased understanding of the breadth and depth of nucleosynthesis in AGB stars has come clear evidence that the picture is simply incomplete without them. It has been shown by Kobayashi et al. (2011b) that AGB models are essential to reproduce the solar system abundances of carbon, nitrogen, and the neutron-rich isotopes of oxygen and neon. Similarly, Renda et al. (2004) and Kobayashi et al. (2011a) showed the importance of AGB stars for fluorine. Fenner et al. (2004) performed a similar study for magnesium, highlighting the contribution from intermediate-mass AGB stars of low metallicity to the chemical evolution of ²⁵Mg and ²⁶Mg. The importance of AGB stars to understanding the composition anomalies seen in globular clusters is just another reason why they are of such interest to contemporary astrophysics.

1.1 Definitions and overview of evolution

We will here be concerned with stars with masses between about 0.8 and 10 M_⊙. Stars more massive than this proceed through all nuclear burning phases and end their lives as core-collapse supernovae. While these massive stars are relatively rare they inject considerable energy and nucleosynthesis products into the galaxy per event. For this reason they are extremely important when considering the evolution of galaxies. Their remnants are either neutron stars or black holes (for the evolution and nucleosynthesis of massive stars we refer the reader to Langer 2012; Nomoto, Kobayashi, & Tominaga 2013).

Stars that will become AGB stars begin their journey with core H and He burning (and possibly C burning on the ‘super-AGB’; see below), before they lose their outer envelopes to a stellar wind during the AGB phase of stellar evolution. It is convenient to define mass ranges according to the evolutionary behaviour the stars will experience. The exact numerical values will, of course, depend on the star’s composition and possibly other effects (such as rotation, which we ignore for now).

The definitions we will use are given below and shown in Figure 1 for solar metallicity. A reduction in the global stellar metallicity will shift the borders introduced here to a lower mass (e.g., core C burning will ignite at about 7 M_⊙ at Z = 10^{− 4} instead of about 8 M_⊙ at Z = Z _⊙ ≈ 0.014). We introduce some new nomenclature in this diagram, while maintaining the definitions of ‘low’ and ‘intermediate’ mass as given in the existing literature.

Figure 1. Schematic showing how stellar mass determines the main nuclear burning phases at solar metallicity, as well as the fate of the final remnant. This defines the different mass intervals we will deal with in this paper. Note that the borders are often not well determined theoretically, depending on details such as mass loss and the implementation of mixing, for example. This is particularly true for the borders around the region of the electron-capture supernovae. Likewise, all numbers are rough estimates, and depend on composition in addition to details of the modelling process.

1.1.1 The lowest mass stars

We define the ‘lowest mass stars’ as those that burn H in their core but take part in no further (significant) nuclear burning processes.

1.1.2 The low-mass stars

We have defined ‘low-mass stars’ to be those with initial masses between about 0.8 and 2 M_⊙ which experience He ignition under degenerate conditions, known as the core He flash (Demarque & Mengel 1971; Despain 1981; Deupree 1984; Dearborn, Lattanzio, & Eggleton 2006; Mocák et al. 2009). Stars more massive than this succeed in igniting He gently. These low-mass stars will experience core He burning and then all but the least massive of these will go on to the AGB (without an appreciable second dredge-up), ending their lives as C-O white dwarfs (WDs, see Figure 1).

1.1.3 The intermediate-mass stars

We then enter the domain of ‘intermediate-mass stars’, a name well known in the literature. Here we have broken this mass range into three distinct sub-classes, based on C ignition and their final fate. We will only use these new names when the sub-divisions are important, otherwise we simply call them ‘intermediate-mass stars’.

1.1.4 The lower intermediate mass stars

These stars are not sufficiently massive to ignite the C in their core, which is now composed primarily of C and O following He burning. We say the star is of ‘lower intermediate mass’, being about 2 − 7 M_⊙. These stars will proceed to the AGB following core He exhaustion, and the more massive of them will experience the second dredge-up as they begin their ascent of the AGB. They will end their lives as C–O white dwarfs.

1.1.5 The middle intermediate mass stars

At slightly higher masses we find C ignites (off centre) under degenerate conditions. We have defined these stars as ‘middle intermediate-mass stars’. These stars go on to experience thermal pulses on what is called the ‘super-AGB’; they are distinguished from genuine massive stars by the fact that they do not experience further nuclear burning in their cores. Super-AGB stars were first studied by Icko Iben and collaborators (e.g., Ritossa, Garcia-Berro, & Iben 1996), and their final fate depends on the competition between mass loss and core growth. If they lose their envelope before the core reaches the Chandrasekhar mass, as is the usual case, then the result is an O–Ne white dwarf.

1.1.6 The massive intermediate mass stars

If, on the other hand, the core grows to exceed the Chandrasekhar mass then these stars may end their lives as electron-capture supernovae. Stars in this very narrow mass range (perhaps less than 0.5 M_⊙) we shall call ‘massive intermediate-mass stars’.

It is still unclear what fraction of super-AGB stars explode as electron-capture supernovae, the details being dependent on uncertain input physics and implementation choices (Poelarends et al. 2008). The existence of massive white dwarfs (Gänsicke et al. 2010), with masses above the C–O core limit of ≈ 1.1 M_⊙ lends some support to the scenario that at least some fraction evade exploding as supernovae. The super-AGB stars that do explode as electron-capture supernovae have been proposed as a potential site for the formation of heavy elements via the rapid neutron capture process (the r-process; Wanajo et al. 2009; Wanajo, Janka, & Müller 2011). A review of this field is therefore particularly timely as we are only now becoming aware of the nucleosynthesis outcomes of super-AGB stars and their progeny (Siess 2010; Doherty et al. 2014a, 2014b).

1.1.7 The massive stars

Stars with masses greater than about 10 M_⊙ we call ‘massive stars’ and these will proceed through Ne/O burning and beyond, and end their lives as iron core collapse supernovae. Note that there is a rich variety of outcomes possible, depending on the way one models mixing and other processes, and we do not show all of the different sub-cases here. We have tried to maintain the existing definitions in the literature, while adding some divisions that we think are useful. We also reserve the use of the word ‘massive’ for those stars that end their lives as supernovae, being either ‘massive intermediate stars’ in the case of electron-capture supernovae, or the traditional ‘massive stars’ for the case of iron core-collapse supernovae.

1.2 Stellar yield calculations

Stellar yields are an essential ingredient of chemical evolution models. Prior to 2001, the only stellar yields available for low- and intermediate-mass stars were for synthetic AGB evolution models or from a combination of detailed and synthetic models (van den Hoek & Groenewegen 1997; Forestini & Charbonnel 1997; Marigo 2001; Izzard et al. 2004).

Synthetic AGB models are generally calculated by constructing fitting formulae to the results of detailed models, rather than by solving the equations of stellar evolution. This approach was originally motivated by the linear core-mass versus luminosity relation noted by Paczyński (1970). It was soon realised that many other important descriptors and properties of AGB evolution could be similarly parameterised, saving the huge effort that goes into a fully consistent solution of the equations of stellar evolution, with all of the important input physics that is required (opacities, equations of state, thermonuclear reaction rates, convective mixing, etc.). These models can be used to examine rapidly the effect of variations in some stellar physics or model inputs. One must remember of course that there is no feedback on the structure. Any change that would alter the stellar structure such that the parameterised relations also change is not going to be included in the results. Nevertheless, even within this limitation there are many uses for synthetic models. Further, we are now starting to see the next generation of synthetic codes. These sophisticated codes are more like hybrids, combining parameterised evolution with detailed envelope integrations. An example is the Colibri code of Marigo et al. (2013).

With the growth of cluster computing it is now common to have access to thousands of CPU nodes. It is possible for stellar models of many different masses and compositions to be calculated in detail on modern computer clusters. In this way we can obtain results from detailed models in reasonable times. The first stellar yields from detailed AGB models were published by Ventura et al. (2001) and Herwig (2004b) but for limited ranges of masses and/or metallicities. The first stellar yields for a large range of masses, and metallicities from detailed AGB models were published by Karakas & Lattanzio (2007), with an update by Karakas (2010). In Section 5 we provide an updated list of the latest AGB stellar yields that are available in the literature.

In Figure 2 and in what follows we show stellar evolutionary sequences that were computed using the Mount Stromlo/Monash Stellar Structure code. This code has undergone various revisions and updates over the past decades (e.g., Lattanzio 1986, 1989, 1991; Frost & Lattanzio 1996b; Karakas & Lattanzio 2007; Campbell & Lattanzio 2008; Karakas, Campbell, & Stancliffe 2010; Karakas, García-Hernández, & Lugaro 2012). We will highlight particular improvements that affect the nucleosynthesis in Section 3. We note that the stellar evolutionary sequences described here are calculated using a reduced nuclear network that includes only H, He, C, N, and O. The wealth of data on abundances from stars necessitates the inclusion of more nuclear species. Most of these are involved in reactions that produce negligible energy (e.g., the higher order H burning Ne–Na and Mg–Al reactions; Arnould, Goriely, & Jorissen 1999). For this reason, a post-processing nucleosynthesis code is usually sufficient, provided there is no feedback on the structure from the reactions not included in the evolutionary calculations. This is indeed usually the case.

Figure 2. A Hertzsprung–Russell (HR) diagram showing the evolutionary tracks for masses of 1, 2, 3, and 6 M_⊙ with a global metallicity of Z = 0.02. The evolutionary tracks show the evolution from the ZAMS through to the start of thermally-pulsing AGB. The thermally-pulsing phase has been removed for clarity. The location of the tip of the RGB is indicated by the asterisk.

We take the results from our evolutionary calculations and use them as input for our post-processing nucleosynthesis code Monsoon (Cannon 1993; Frost et al. 1998a) in order to calculate the abundances of many elements and isotopes (for a selection of recent papers we refer the interested reader to Campbell & Lattanzio 2008; Lugaro et al. 2012; Kamath, Karakas, & Wood 2012; Karakas et al. 2012; Shingles & Karakas 2013; Doherty et al. 2014a). In Monsoon we require initial abundances (usually scaled solar) along with nuclear reaction rates and β-decay lifetimes, and include time-dependent convection using an advective algorithm. We couple the nuclear burning with convective mixing in relevant regions of the star. It is important to remember that the results presented here depend on the input physics and numerical procedure, with different codes sometimes finding different results. For example, the inclusion of core overshoot during the main sequence and core He-burning will lower the upper mass limit for a C–O core AGB star from ≈ 8 M_⊙ to ≈ 6 M_⊙ (e.g., Bertelli et al. 1986a, 1986b; Lattanzio et al. 1991; Bressan et al. 1993; Fagotto et al. 1994).

The most recent reviews of AGB evolution and nucleosynthesis include Busso, Gallino, & Wasserburg (1999), with a focus on nucleosynthesis and the operation of the s-process, and Herwig (2005), who reviewed the evolution and nucleosynthesis of AGB stars in general, including a discussion of multi-dimensional hydrodynamical simulations relevant to AGB star evolution. Since 2005 there have been many advances, including insights into AGB mass loss provided by the Spitzer and Herschel Space Observatories, new theoretical models of AGB stars covering a wide range of masses and compositions, and the publication of stellar yields from detailed AGB star models. In this review we focus on theoretical models of low- and intermediate-mass stars and in particular on recent progress in calculating AGB yields. Not only are yields needed for chemical evolution modelling but they are also needed to interpret the wealth of observational data coming from current surveys such as SkyMapper (Keller et al. 2007) and SEGUE (Yanny et al. 2009), which are geared toward discovering metal-poor stars in the Galactic halo. Future surveys and instruments (e.g., the GAIA-ESO survey, HERMES on the AAT, APOGEE, LAMOST) will also require accurate stellar yields from stars in all mass ranges in order to disentangle the Galactic substructure revealed through chemical tagging (Freeman & Bland-Hawthorn 2002).

Finally we note that, as we will discuss in Section 2.2.4, there is compelling evidence for some form of mixing on the RGB that is needed to explain the abundances seen at the tip of the RGB. The standard models simply fail in this regard. While the number of isotopes affected is reasonably small (e.g., ³He, ⁷Li, ¹³C) it is essential to include the effect of this mixing in order to properly model the chemical evolution of those few isotopes. Usually, a set of stellar yields is calculated based on standard models, which we know are wrong because they fail to match the observed abundances along the RGB.

2 EVOLUTION AND NUCLEOSYNTHESIS PRIOR TO THE ASYMPTOTIC GIANT BRANCH

2.1 Illustrative examples

In the following we describe the evolution and nucleosynthesis for representative low- and intermediate-mass stars. All have a metallicity Z = 0.02 ¹ . According to the most recent solar abundances from Asplund et al. (2009) the global solar metallicity is Z = 0.0142, which makes these models slightly super solar, with a [Fe/H] = + 0.14 ² .

To illustrate the evolution of low- and intermediate-mass stars we use new stellar evolutionary sequences with masses between 1 and 8 M_⊙ and Z = 0.02 calculated with the same version of the Mt Stromlo/Monash Stellar Structure code described in Kamath et al. (2012). Within this grid of models, the divide between low-mass stellar evolution and intermediate is at about 2 M_⊙, as we discuss below. These models will also introduce the basic principles of the evolution of all stars that evolve up to the AGB. The theoretical evolutionary tracks for a sample of these models are shown in Figure 2 and include all evolutionary phases from the zero age main sequence through to the AGB.

All stars begin their nuclear-burning life on the main sequence, where fusion converts H to He in the stellar core. The majority of a star’s nuclear-burning life is spent on the main sequence, which is why most stars in the night sky and most stars in a typical colour-magnitude diagram are in this phase of stellar evolution.

The 1 M_⊙ model in Figure 2 burns H on the main sequence via the pp chains. In contrast, the models with M ⩾ 2 M_⊙ shown in Figure 2 mostly burn H in the core via CNO cycling. The higher temperature dependence of the CNO cycles, with a rate roughly ∝T ^{16 − 20} (compared to a rate approximately ∝T ⁴ for the pp chains at Z = 0.02), produces a steep energy generation rate and results in the formation of a convective core. It is convenient to divide the zero-age main sequence (ZAMS) into an ‘upper’ and ‘lower’ main sequence, which is reflected in slightly different mass-radius and mass-luminosity relationships for these two regions. The division between the two is instructive: stars on the lower main sequence have convective envelopes, radiative cores, and are primarily powered by the pp chains. Conversely, stars on the upper main sequence show radiative envelopes, convective cores, and are powered primarily through the CN (and ON) cycles. The dividing mass between the upper and lower main sequence is at about 1.2 M_⊙ for Z = 0.02.

The larger a star’s mass the larger is its gravity. Hence it requires a substantial pressure gradient to maintain hydrostatic equilibrium. The central pressure is therefore higher and in turn so is the temperature. This means that more massive stars burn at much higher luminosities and given that fusing four protons into one ⁴He nucleus produces a constant amount of energy, then the duration of the H burning phase must be correspondingly lower as the stellar mass increases. From a quick inspection of Figure 2 it is clear that the 6 M_⊙ model is much brighter on the main sequence than the 2 M_⊙ model by almost two orders of magnitude. Core H exhaustion takes place after approximately 1 × 10⁹ years (or 1 Gyr) for the 2 M_⊙ model but only 53 million years for the 6 M_⊙ model.

Following core H exhaustion the core contracts and the star crosses the Hertzsprung Gap. Nuclear burning is now established in a shell surrounding the contracting ⁴He core. Simultaneously, the outer layers expand and cool and as a consequence become convective, due to an increase in the opacity at lower temperatures. The star runs up against the Hayashi limit, where the coolest envelope solution corresponds to complete convection. The star cannot cool further and it begins its rise up the giant branch while the convective envelope grows deeper and deeper (in mass). This is shown in Figure 3 for the 1 M_⊙ model. This deepening of the convective envelope leads to mixing of the outer envelope with regions that have experienced some nuclear processing, with the result that the products of H burning are mixed to the surface. This is called the ‘first dredge-up’, hereafter FDU.

Figure 3. First dredge-up in the 1 M_⊙, Z = 0.02 model. The left panel shows the HR diagram and the right panel shows the luminosity as a function of the mass position of the inner edge of the convective envelope. We can clearly see that the envelope begins to deepen just as the star leaves the main sequence, and reaches its deepest extent on the RGB, marking the end of FDU. Further evolution sees the star reverse its evolution and descend the RGB briefly before resuming the climb. This corresponds to the observed bump in the luminosity function of stellar clusters (see text for details).

The star is now very big (up to ~ 100 times its radius on the main sequence) but most of the mass in the core is within a small fraction of the total radius. A consequence of this is that the outer layers are only tenuously held onto the star and can be lost through an outflow of gas called a stellar wind. At present we do not know how much mass is lost during the ascent of the RGB. This may be perhaps as much as 30% of the star’s total mass for the lowest mass stars that spend the longest time on the RGB. Kepler data for metal-rich old open clusters have provided some constraints, with the amount of mass lost on the RGB estimated to be less than results from applying the commonly used Reimer’s mass-loss prescription (Reimers 1975; Kudritzki & Reimers 1978; Miglio et al. 2012). While there are refinements to the Reimer’s mass-loss law (Catelan 2000; Schröder & Cuntz 2005, 2007) we are still lacking a detailed understanding of the physical mechanism responsible for mass loss on the RGB.

During the ascent of the RGB our low- and intermediate-mass stars experience the FDU, which we will address in detail in Section 2.2. Simultaneously, the He core continues to contract and heat and in the case of low-mass stars becomes electron degenerate. Neutrino energy losses become important, and since they are highly dependent on density, they dominate in the centre. This produces a cooling and can cause the mass location of the temperature maximum to move outward. The RGB lifetime is terminated when the necessary temperatures for central He ignition are reached, at about 100 million K. For our low-mass stars the triple alpha reactions are ignited at the point of maximum temperature and under degenerate conditions (Despain 1981; Deupree 1984).

The electron degenerate equation of state results in the temperature and density being essentially decoupled. When He does begin to fuse into C, the energy released does not go into expansion but stays as thermal energy, raising the temperature of the plasma locally. This leads to a much higher burning rate and a runaway result, leading to a violent and explosive He ignition that is known as the ‘core He flash’.

The maximum initial mass for the core He-flash to occur is about 2.1 M_⊙ at Z = 0.02 using the new grid of models presented here, which include no convective overshoot (similar to the models of Karakas, Lattanzio, & Pols 2002, where the maximum mass is at about 2.25 M_⊙). This is the dividing line between low- and intermediate-mass stars. In contrast, models which include overshooting from the convective H-burning core find that this division occurs at a lower mass of M ≈ 1.6 M_⊙ (Bertelli et al. 1986a).

For intermediate-mass stars, the cores are not degenerate and He is ignited under quiescent conditions. These stars often do not proceed as far up the RGB as do low-mass stars, prior to He ignition. As a consequence their RGB phase is shorter and the FDU phase can be terminated relatively early for these more massive stars. This has consequences for colour-magnitude diagrams and is demonstrated in Figure 2. For example, the 2 M_⊙ model has a long RGB lifetime of ≈ 200 × 10⁶ years or 200 Myr. This means that while the minimum effective temperature attained by the 2 M_⊙ red-giant model is less (T _eff ≈ 3 600 K) than the 6 M_⊙ model (T _eff ≈ 4 100 K), the peak RGB luminosity is similar, at log ₁₀(L/L_⊙) ≈ 3.2. This means that old low-mass RGB populations are observable out to great distances (e.g., Galactic GCs and dwarf spheroidal galaxies, which are dominated by old low-mass stars). Note the contrast to the 3 M_⊙ model, which has a peak RGB luminosity that is more than 10 times lower, at only 140 L_⊙ (due to ignition of He under non-degenerate conditions).

Following core He ignition the star settles down to a period of central He burning, where He burns in a convective core and H in a shell, which provides most of the luminosity. The Coulomb repulsion is larger for He than for H and more particle (kinetic) energy is required to sustain the triple-alpha process. This then requires that the temperature is higher for He burning. Note also that about a factor of 10 less energy is produced by the triple alpha process per gram of fuel than during H burning. The overall result is the core He burning phase is shorter than the main sequence. For example, for the 2 M_⊙ model core He burning lasts 124 Myr (a figure of about 100 Myr is typical for low-mass stars), compared to ≈ 13 Myrs for the 6 M_⊙ model. Helium burning increases the content of ¹²C, which in turn increases the abundance of ¹⁶O from the reaction ¹²C(α, γ)¹⁶O.

The details of He burning are subject to uncertainties that are all too often ignored or dismissed. We have known for decades that the fusion of He into C and O produces a discontinuity in the opacity at the edge of the convective core (Castellani, Giannone, & Renzini 1971a). This means that there is an acceleration at the edge of the core. In other words there is no neutrally stable point which would be the edge of the core if one were using the Schwarzschild or Ledoux criterion for determining the borders of convective regions. The result is that the convective core grows with time. The next complication is that the variation of temperature and density is such that there is a local minimum in the radiative gradient in the convective region and this causes the region to split into a convective core and a ‘semi-convective’ region (Castellani, Giannone, & Renzini 1971b).

This semi-convection extends the duration of the core He burning phase by mixing more fuel into the core. Star counts in clusters clearly show that observations require this extension to the core He burning phase, and models constructed without semi-convection are a poor match (Buzzoni et al. 1983; Buonanno, Corsi, & Fusi Pecci 1985).

There is yet another complication that arises as the star approaches the exhaustion of its core He supply. Theoretical models show that as the He content decreases, the convective core is unstable to rapid growth into the semi-convective region. This results in ‘breathing pulses’ of the convective core (Gingold 1976; Castellani et al. 1985). These mix more He into the core and further extend the lifetime in this phase. While this behaviour shows many of the signs of a numerical instability, an analytic study by Sweigart & Demarque (1973) showed that there is a genuine physical basis for the instability, and indeed verified that it should only occur when the central He mass fraction reduces below about 0.12. Nevertheless, appealing again to star counts as a proxy for timescales, the data seem to argue against the reality of these pulses (Renzini & Fusi Pecci 1988; Caputo et al. 1989, but see also Campbell et al. 2013).

This leaves us in the most unsatisfactory position. We have an instability shown by models, which theory can explain and indeed argues to be real, but that the data do not support. Further, we have no obvious way to calculate through this phase in a way that removes the breathing pulses (although see Dorman & Rood 1993). What is worse is that the details of the evolution through this phase determine the size of the He exhausted core and the position of the H-burning shell as the star arrives on the early AGB. The star must now rapidly adopt the structure of a thermally-pulsing AGB star, by which we mean that burning shells will burn through the fuel profile resulting from the earlier evolution until they reach the thermally-pulsing AGB structure. This results in removing some of the uncertainty in the structure that exists at the end of core He burning. But it is still true that the subsequent evolution on the AGB is critically dependent on the core size which is poorly understood because of uncertainties during the prior core He burning phase.

Following exhaustion of the core He supply, low- and intermediate-mass stars proceed toward the red giant branch, now called the ‘asymptotic giant branch’ because the colour-magnitude diagrams of old clusters show this population seemingly joining the first giant branch almost asymptotically. A better name may have been the less commonly used ‘second giant branch’, but AGB is now well establi-shed.

For stars more massive than about 4 M_⊙ (depending on the composition) or with H-exhausted core masses ≳ 0.8 M_⊙ the convective envelope extends quite some distance into the H-exhausted region. It usually reaches deeper than during the FDU (e.g., Boothroyd & Sackmann 1999). This event is called the ‘second dredge-up’, hereafter SDU. In both cases (FDU and SDU) we are mixing to the surface the products of H burning, so qualitatively the changes are similar. However, there are substantial quantitative differences, as we discuss below in Section 2.2.

2.2 First dredge-up

We have outlined the evolution of low- and intermediate-mass stars above. Now we look in more detail at the first and second dredge-up prior to the thermally-pulsing AGB. Figure 4 shows the different dredge-up processes that stars experience as a function of their mass. It also shows the rough qualitative changes in surface abundances that result.

Figure 4. A schematic diagram showing the mass dependence of the different dredge-up, mixing, and nucleosynthesis events. The species most affected are also indicated. The lower mass limits for the onset of the SDU, third dredge up, and HBB depend on metallicity and we show approximate values for Z = 0.02. Note that the ‘extra-mixing’ band has a very uncertain upper mass-limit, because the mechanism of the mixing is at present unknown.

2.2.1 Abundance changes due to FDU

The material mixed to the envelope by the FDU has been subjected to partial H burning, which means it is still mostly H but with some added ⁴He and the products of CN cycling. Figure 5 shows the situation for a 2 M_⊙ model. The upper panel shows the abundance profile after the star has departed the main sequence and prior to the FDU. We have plotted the major species and some selected species involved in the CNO cycles. The lower panel is taken at the time of the maximum depth of the convective envelope. The timescale for convective mixing is much shorter than the evolution timescale so mixing essentially homogenises the region instantly, as far as we are concerned.

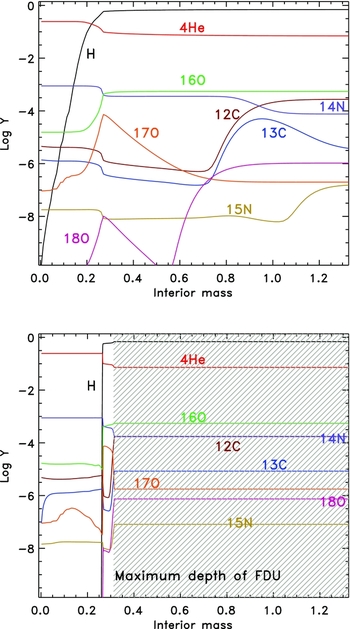
Figure 5. Composition profiles from the 2 M_⊙, Z = 0.02 model. The top panel illustrates the interior composition after the main sequence and before the FDU takes place, showing mostly CNO isotopes. The lower panel shows the composition at the deepest extent of the FDU (0.31 M_⊙), where the shaded region is the convective envelope. Surface abundance changes after the FDU include: a reduction in the C/O ratio from 0.50 to 0.33, in the ¹²C/¹³C ratio from 86.5 to 20.5, an increase in the isotopic ratio of ¹⁴N/¹⁵N from 472 to 2 188, a decrease in ¹⁶O/¹⁷O from 2 765 to 266, and an increase in ¹⁶O/¹⁸O from 524 to 740. Elemental abundances also change: [C/Fe] decreases by about 0.20, [N/Fe] increases by about 0.4, and [Na/Fe] increases by about 0.1. The helium abundance increases by ΔY ≈ 0.012.

Typical surface abundance changes from FDU are an increase in the ⁴He abundance by ΔY ≈ 0.03 (in mass fraction), a decrease in the ¹²C abundance by about 30%, and an increase in the ¹⁴N and ¹³C abundances. In Table 1 we provide the predicted post-FDU and SDU values for model stars with masses between 1 and 8 M_⊙ at Z = 0.02. We include the He mass fraction, Y, the isotopic ratios of C, N, and O, and the mass fraction of Na.

Table 1. Predicted post-FDU and SDU values for model stars with masses between 1 and 8 M_⊙ at Z = 0.02. We include the helium mass fraction, Y, the isotopic ratios of carbon, nitrogen, and oxygen, and the mass fraction of sodium. Initial values are given in the first row.

The C isotopic ratio is a very useful tracer of stellar evolution and nucleosynthesis in low- and intermediate-mass stars. First, this is because the ¹²C/¹³C ratio is one of the few isotopic ratios that can be readily derived from stellar spectra which means that there are large samples of stars for comparison to theoretical calculations (e.g., Gilroy & Brown 1991; Gratton et al. 2000; Smiljanic et al. 2009; Mikolaitis et al. 2010; Tautvaišienė et al. 2013). Second, the C isotope ratio is predicted to vary significantly at the surface as a result of the FDU (and SDU) as shown in Figure 6 and in Table 1. This figure shows that the number ratio of ¹²C/¹³C drops from its initial value (typically about 89 for the Sun) to lie between 18 and 26 (see also Charbonnel 1994; Boothroyd & Sackmann 1999). Comparisons for intermediate-mass stars are in relatively good agreement with the observations, to within ~ 25% (El Eid 1994; Charbonnel 1994; Boothroyd & Sackmann 1999; Santrich, Pereira, & Drake 2013). But the agreement found at low luminosities is not seen further up the RGB (e.g., Charbonnel 1995), as discussed in Section 2.2.4.

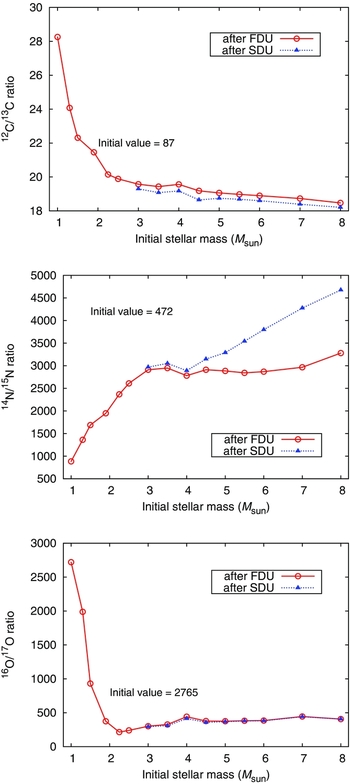
Figure 6. Surface abundance predictions from Z = 0.02 models showing the ratio (by number) of ¹²C/¹³C, ¹⁴N/¹⁵N, and ¹⁶O/¹⁷O after the first dredge-up (red solid line) and second dredge-up (blue dotted line).

In Figure 7 we show the innermost mass layer reached by the convective envelope during FDU (solid lines) and SDU (dashed lines) as a function of the initial stellar mass and metallicity. The deepest FDU occurs in the Z = 0.02 models at approximately 2.5 M_⊙ with a strong metallicity dependence for models with masses over about 3 M_⊙ (Boothroyd & Sackmann 1999). In contrast there is little difference in the depth of the second dredge-up for models with ≳ 3.5 M_⊙ regardless of metallicity. In even lower metallicity intermediate-mass stars, the RGB phase is skipped altogether because core He burning is ignited before the model star reaches the RGB so that the first change to the surface composition is actually due to the second dredge-up.

Figure 7. Innermost mass layer reached by the convective envelope during the first dredge-up (solid lines) and second dredge-up (dashed lines) as a function of the initial stellar mass and metallicity. The mass co-ordinate on the y-axis is given as a fraction of the total stellar mass (M _du/M ₀)—from Karakas (2003).

One check on the models concerns the predictions for O isotopes. Broadly, the CNO cycles produce ¹⁷O but significantly destroy ¹⁸O, with the result that the FDU should increase the observed ratio of ¹⁷O/¹⁶O and decrease the observed ratio of ¹⁸O/¹⁶O (e.g., Table 1 and Dearborn 1992). Spectroscopic data, where available, seem to agree reasonably well with the FDU predictions (Dearborn 1992; Boothroyd, Sackmann, & Wasserburg 1994), but see also Section 2.2.4.

The effect of the first dredge-up on other elements (besides lithium, which we discuss in Section 2.4 below) is relatively minor. It is worth noting that there is some dispute about the status of sodium. Figure 8 shows that sodium is not predicted to be significantly enhanced in low-mass stars by the FDU or by extra-mixing processes (Charbonnel & Lagarde 2010) at disk metallicities. This agrees with El Eid & Champagne (1995) who find modest enhancements in low mass (0.1 dex) and intermediate mass (0.2 – 0.3 dex) stars. Observations are in general agreement with models with masses ≳ 2 M_⊙, where enhancements of up to [Na/Fe] ≲ 0.3 are found in stars up to 8 M_⊙ at Z = 0.02 (Figure 8). This result is confirmed by observations that show only mild enhancements of [Na/Fe] ≲ +0.2 (Hamdani et al. 2000; Smiljanic et al. 2009). But this is in contradiction with other studies showing typical overabundances of + 0.5 (Bragaglia et al. 2001; Jacobson, Friel, & Pilachowski 2007; Schuler, King, & The 2009). The reasons for the conflicting results are not well understood; we refer to Smiljanic (2012) for a detailed discussion of observational uncertainties.

Figure 8. Predicted [Na/Fe] after the FDU and SDU for the Z = 0.02 models.

2.2.2 The onset of FDU

Theoretical models must confront observations for us to verify that they are reliable or identify where they need improvements. In the current context there are two related comparisons to be made: the expected nucleosynthesis, which we addressed above, and the structural aspects. In this section we look at the predictions for the location of the start of FDU and in the next section we compare the observed location of the bump in the luminosity function to theoretical models.

During the evolution up the giant branch there are three significant points, as illustrated in Figure 3:

• • the luminosity at which the surface abundances start to change;

• • the maximum depth of the FDU;

• • the luminosity of the bump.

Note that these are not independent—the maximum depth of the FDU determines where the abundance discontinuity occurs, and that determines the position of the bump. Similarly, the resulting compositions are dependent on the depth of the FDU and we are not free to adjust that without consequences for both the observed abundances and the location of the bump.

The obvious question is how closely do these points match the observations? Perhaps the best place to look is in star clusters, as usual. Gilroy & Brown (1991) found that the ratios of C/N and ¹²C/¹³C at the onset of the FDU matched the models quite well, as reported in Charbonnel (1994). Mishenina et al. (2006) also looked at C/N and various other species, and the data again seem to match models for the onset of the FDU. Of course the onset is very rapid and the data are sparse. This is also seen in the study by Chanamé, Pinsonneault, & Terndrup (2005) who found that the C isotopic ratio in M67 fitted the models rather well (see their Figures 13 and 14). For field giants (with − 2 < [Fe/H] < −1) the data are not so good, with mostly lower limits for ¹²C/¹³C making it hard to identify the exact onset of the FDU (see Chanamé et al. 2005, Figure 16). Better data over a larger range in luminosity in many clusters are needed to check that the models are not diverging from reality at this early stage in the evolution.

2.2.3 The bump in the luminosity function

We now move to an analysis of the luminosity function (LF) bump. There is much more literature here, dating back to Sweigart (1978) where it was shown that the bump reduced in size and appeared at higher luminosities as either the He content increased or the metallicity decreased. Indeed, at low metallicity (say [Fe/H] ≲ −1.6) it can be hard to identify the LF bump, and Fusi Pecci et al. (1990) combined data for the GCs M92, M15, and NGC 5466 so that they could reliably identify the bump in these clusters (all of similar metallicity). Their conclusion, based on a study of 11 clusters, was that the theoretical position of the bump was 0.4 mag too bright.

The next part of the long history of this topic was the study by Cassisi & Salaris (1997) with newer models who concluded that there was no discrepancy within the theoretical uncertainty. Idealised models show a discontinuity in composition at the mass where the convective envelope reached its maximum inward extent. But in reality this discontinuity is likely to be a steep profile, with a gradient determined by many things, such as the details of mixing at the bottom of the convective envelope. It is likely that gravity waves and the possibility of partial overshoot would smooth this profile through entrainment, and Cassisi, Salaris, & Bono (2002) showed that such uncertainties do cause a small shift in the position of the bump but they are unlikely to be significant.

Riello et al. (2003) looked at 54 Galactic GCs and found good agreement between theory and observation, both for the position of the bump itself as well as the number of stars (i.e., evolutionary timescales) in the bump region. The only caveat was that for low metallicities there seemed to be a discrepancy but it was hard to quantify due to the low number of stars available. A Monte Carlo study by Bjork & Chaboyer (2006) concluded that the difference between theory and observation was no larger than the uncertainties in both of those quantities. In what seems to be emerging as a consensus, Di Cecco et al. (2010) found that the metal-poor clusters showed a discrepancy of about 0.4 mag, and that variations in CNO and α-elements (e.g., O, Mg, Si, Ti) did not improve the situation. These authors did point out that the position of the bump is sensitive to the He content and since we now believe that there are multiple populations in most GCs, this is going to cause a spread in the position of the LF bump.

It would appear that a reasonable conclusion is that the theoretical models are in good agreement, while perhaps being about 0.2 mag too bright (Cassisi et al. 2011), except for the metal-poor regime where the discrepancy may be doubled to 0.4 mag, although this is plagued by the bump being small and harder to observe. Nataf et al. (2013) find evidence for a second parameter, other than metallicity, being involved. In their study of 72 globular clusters there were some that did not fit the models well, and this was almost certainly due to the presence of multiple populations. This reminds us again that quantitative studies must include these different populations and that this could be the source of some of the discrepancies found in the literature.

The obvious way to decrease the luminosity of the bump is to include some overshooting inward from the bottom of the convective envelope. This will push the envelope deeper and will shift the LF bump to lower luminosities. Of course this deeper mixing alters the predictions of the FDU; however it appears that there is a saturation of composition changes such that the small increase needed in the depth of the FDU does not produce an observable difference in the envelope abundances (Kamath et al. 2012; Angelou 2013, private communication).

2.2.4 The need for extra-mixing

We have seen that the predictions for FDU are largely in agreement with the observations. However when we look at higher luminosities we find that something has changed the abundances beyond the values predicted from FDU. Standard models do not predict any further changes on the RGB once FDU is complete. Something must be occurring in real stars that is not predicted by the models.

For low-mass stars the predicted trend of the post-FDU ¹²C/¹³C ratio is a rapid decrease with increasing initial mass as illustrated in Figure 6. Yet this does not agree with the observed trend. For example, observations of the ¹²C/¹³C ratio in open metal-rich clusters reveal values of ≲ 20, sometimes ≲ 10 (e.g., Gilroy 1989; Smiljanic et al. 2009; Mikolaitis et al. 2010) well below the predicted values of ≈ 25 − 30. The deviation between theory and observation is even more striking in metal-poor field stars and in giants in GCs (e.g., Pilachowski et al. 1996; Gratton et al. 2000, 2004; Cohen, Briley, & Stetson 2005; Origlia, Valenti, & Rich 2008; Valenti, Origlia, & Rich 2011).

The observed trend is in the same direction as the FDU: i.e., as if we are mixing in more material that has been processed by CN cycling, so that ¹²C decreases just as ¹³C and ¹⁴N increase. Indeed, in some GCs we see a clear decrease in [C/Fe] with increasing luminosity on the RGB (see Angelou et al. 2011, 2012, and references therein). If some form of mixing can connect the hot region at the top of the H-burning shell with the convective envelope then the results of the burning can be seen at the surface. These observations have been interpreted as evidence for extra mixing taking place between the base of the convective envelope and the H shell.

Further evidence comes from observations of the fragile element Li (Pilachowski, Sneden, & Booth 1993; Lind et al. 2009) which essentially drops at the FDU to the predicted value of A(Li) ≈ 1 ³ , but for higher luminosities decreases to much lower abundances of A(Li) ≈ 0 to − 1. Again, this can be explained by exposing the envelope material to higher temperatures, where Li is destroyed. So just as for the C isotopes the observations argue for some form of extra mixing to join the envelope to the region of the H-burning shell (see also Section 2.4).

We discussed O isotopes earlier as a diagnostic of the FDU. Although these ratios may not be so easy to determine spectroscopically, the science of meteorite grain analysis (for reviews see Zinner 1998; Lodders & Amari 2005) offers beautiful data on O isotopic ratios from Al₂O₃ grains. We expect that these grains would be expelled from the star during periods of mass loss and would primarily sample the tip of the RGB or the AGB. Some of these data show good agreement with predictions for the FDU, while a second group clearly require further ¹⁸O destruction. This can be provided by the deep-mixing models of Wasserburg, Boothroyd, & Sackmann (1995) and Nollett, Busso, & Wasserburg (2003). Hence pre-solar grains contain further evidence for the existence of some kind of extra mixing on the RGB.

We note here that a case has been made for some similar form of mixing in AGB envelopes as we discuss later in Section 4.3.

2.2.5 The ³He problem

Another piece of evidence for deep-mixing concerns the stellar yield of ³He, as discussed recently by Lagarde et al. (2011, 2012). We now have good constraints on the primordial abundance of ³He, from updated Big Bang Nucleosynthesis calculations together with WMAP data. The currently accepted value is ³He/H = 1.00 ± 0.07 × 10^{− 5} according to Cyburt, Fields, & Olive (2008) and ³He/H = 1.04 ± 0.04 × 10^{− 5} according to Coc et al. (2004). This is within a factor of two or three of the best estimates of the local value in the present interstellar medium of ³He/H = 2.4 ± 0.7 × 10^{− 5} according to Gloeckler & Geiss (1996), a value also in agreement with the measurements in Galactic HII regions by Bania, Rood, & Balser (2002). This indicates a very slow growth of the ³He content over the Galaxy’s lifetime.

However, the evolution of low-mass stars predicts that they produce copious amounts of ³He. This isotope is produced by the pp chains and when the stars reach the giant branches their stellar winds carry the ³He into the interstellar medium. Current models for the chemical evolution of the Galaxy, using standard yields for ³He, predict that the local interstellar medium should show ³He/H ≈ 5 × 10^{− 5} (Lagarde et al. 2012) which is about twice the observed value.

It has long been recognised that one way to solve this problem is to change the yield of ³He in low-mass stars to almost zero (Charbonnel 1995). In this case the build up of ³He over the lifetime of the Galaxy will be much slower. One way to decrease the yield of ³He is to destroy it in the star on the RGB while the extra mixing is taking place. We discuss this further in Section 2.3.

2.3 Non-convective mixing processes on the first giant branch

2.3.1 The onset of extra mixing

So where does the extra-mixing begin and what can it be? Observations generally indicate that the conflict between theory and observation does not arise until the star has reached the luminosity of the bump in the LF. This is beautifully demonstrated in the Li data from Lind et al. (2009) which we reproduce in Figure 9 together with a theoretical calculation for a model of the appropriate mass and composition for NGC 6397 (Angelou 2013, private communication). The left panel shows the measured A(Li) values for the stars as a function of magnitude. The near constant values until M_V ≈ 3.3 are perfectly consistent with the models. It is at this luminosity that the convective envelope starts to penetrate into regions that have burnt ⁷Li, diluting the surface ⁷Li content. This stops when the envelope reaches its maximum extent, near M_V ≈ 1.5. Then there is a sharp decrease in the Li abundance once the luminosity reaches M_V ≈ 0, which roughly corresponds to the point where the H shell has reached the discontinuity left behind by FDU (see right panel). This is the same position as the bump in the LF. Note that there is a small discrepancy between the models and the data, as shown in the figure and as discussed in Section 2.2.3.

Figure 9. Observed behaviour of Li in stars in NGC 6397, from Lind et al. (2009), and as modelled by Angelou et al. (in preparation). The leftmost panel shows A(Li) = log ₁₀(Li/H) + 12 plotted against luminosity for NGC 6397. Moving to the right the next panel shows the HR diagram for the same stars. The next panel to the right shows the inner edge of the convective envelope in a model of a typical red-giant star in NGC 6397. The rightmost panel shows the resulting predictions for A(Li) using thermohaline mixing and C = 120 (see Section 2.3.4). Grey lines identify the positions on the RGB where the major mixing events take place. Dotted red lines identify these with the theoretical predictions in the rightmost panels.

This is the common understanding—that the deep mixing begins once the advancing H shell removes the abundance discontinuity left behind by the FDU. The reason for this is that one expects that gradients in the composition can inhibit mixing (Kippenhahn & Weigert 1990) and once they are removed by burning then the mixing is free to develop. It was Mestel (1953) who first proposed that for a large enough molecular weight gradient one could effectively have a barrier to mixing (see also Chanamé et al. 2005). This simple theory, combined with the very close alignment of the beginning of the extra mixing and the LF bump, has led to the two being thought synonymous. However we do note that there are discrepancies with this idea. For example it has been pointed out by many authors that there is a serious problem with the metal-poor GC M92 (Chanamé et al. 2005; Angelou et al. 2012). Here the data show a clear decrease in [C/Fe] with increasing luminosity on the RGB (Bellman et al. 2001; Smith & Martell 2003), starting at M_V ≈ 1–2. The problem is that the decrease begins well before the bump in the LF, which Martell, Smith, & Briley (2008) place at M_V ≈ −0.5. This is a substantial disagreement. A similar disagreement was noted by Angelou et al. (2012) for M15 although possibly not for NGC 5466, despite all three clusters having a very similar [Fe/H] of ≈ − 2.

To be sure that we cannot dismiss this disagreement lightly, there is also the work by Drake et al. (2011) on λ Andromeda, a mildly metal-poor ([Fe/H] ≈ −0.5) first ascent giant star that is believed to have recently completed its FDU. It is not yet bright enough for the H shell to have reached the abundance discontinuity left by the FDU, but it shows ¹²C/¹³C ≲ 20, which is below the prediction for the FDU and more in line with the value expected after extra mixing has been operating for some time. We know λ Andromeda is a binary so we cannot rule out contamination from a companion. But finding a companion that can produce the required envelope composition is not trivial. Drake et al. (2011) also give the case of a similar star, 29 Draconis, thus arguing further that these exceptions are not necessarily the result of some unusual evolution. The problem demands further study because the discrepancy concerns fundamental stellar physics.

2.3.2 Rotation

It is well known that rotating stars cannot simultaneously maintain hydrostatic and thermal equilibrium, because surfaces of constant pressure (oblate spheroids) are no longer surfaces of constant temperature. Dynamical motions develop that are known as ‘meridional circulation’ and which cause mixing of chemical species. It is not our intention to provide a review of rotation in a stellar context. There are many far more qualified for such a task and we refer the reader to Heger, Langer, & Woosley (2000), Tassoul (2007), Maeder & Meynet (2010), and the series of 11 papers by Tassoul and Tassoul, ending with Tassoul & Tassoul (1995). Note that most studies that discuss the impact of rotation on stellar evolution often ignore magnetic fields. Magnetic fields likely play an important role in the removal of angular momentum from stars as they evolve (e.g., through stellar winds; Gallet & Bouvier 2013; Mathis 2013; Cohen & Drake 2014).

Most of the literature on rotating stars concerns massive stars because they rotate faster than low- and intermediate-mass stars. Nevertheless, there is a substantial history of calculations relevant to our subject. Sweigart & Mengel (1979) were the first to attempt to explain the observed extra mixing with meridional circulation. Later advances in the theory of rotation and chemical transport (Kawaler 1988; Zahn 1992; Maeder & Zahn 1998) led to more sophisticated models for the evolution of rotating low- and intermediate-mass stars (Palacios et al. 2003, 2006).

With specific regard to the extra mixing problem on the RGB, Palacios et al. (2006) found that the best rotating models did not produce enough mixing to explain the decrease seen in the ¹²C/¹³C ratio on the upper RGB, above the bump in the LF. This is essentially the same result as found by Chanamé et al. (2005) and Charbonnel & Lagarde (2010). Although one can never dismiss the possibility that a better understanding of rotation and related instabilities may solve the problem, the current belief is that rotating models do not reproduce the observations of RGB stars.

2.3.3 Parameterised models

With the failure of rotation to provide a solution to extra mixing on the RGB, the investigation naturally fell to phenomenological models of the mixing. One main method used is to set up a conveyor belt of material that mixes to a specified depth and at a specified rate. An alternative is to solve the diffusion equation for a specified diffusion co-efficient D, which may be specified by a particular formula or a specified value.

It is common in these models to specify the depth of mixing in terms of the difference in temperature between the bottom of the mixed region and some reference temperature in the H shell. The rates of mixing are sometimes given as mass fluxes and sometimes as a speed. These are usually assumed constant on the RGB, although some models include prescriptions for variation. In any event, there is no reason to believe that the depth or mixing rate is really constant. (Note also that a constant mass flux requires a varying mixing speed during evolution along the RGB, and vice versa!).

Smith & Tout (1992) showed that such simplified models could reproduce the decrease of [C/Fe] seen along the RGB of GCs, provided an appropriate choice was made for the depth and rate of mixing. More sophisticated calculations within a similar paradigm are provided by Boothroyd et al. (1994, 1995), Wasserburg et al. (1995), Langer & Hoffman (1995), Sackmann & Boothroyd (1999), Nollett et al. (2003), Denissenkov & Tout (2000), Denissenkov, Chaboyer, & Li (2006), and Palmerini et al. (2009).

In summary, these models showed that for ‘reasonable’ values of the free parameters one could indeed reproduce the observations for the C and O isotopic ratios, the decrease in A(Li), the variation of [C/Fe] with luminosity, and also destroy most of the ³He traditionally produced by low-mass stars.

2.3.4 Thermohaline mixing

The phenomenon of thermohaline mixing is not new, having appeared in the astrophysics literature many decades ago (e.g., Ulrich 1972). What is new is the discovery by Eggleton, Dearborn, & Lattanzio (2006) that it may be the cause of the extra mixing that is required on the RGB. We outline here the pros and cons of the mechanism.

The name ‘thermohaline mixing’ comes from its widespread occurrence in salt water. Cool water sinks while warm water rises. However warm water can hold more salt, making it denser. This means it is possible to find regions where warm, salty, denser water sits atop cool, fresh, less dense water. The subsequent development of these layers depends on the relative timescales for the two diffusion processes acting in the upper layer—the diffusion of heat and the diffusion of salt. For this reason the situation is often called ‘doubly diffusive mixing’. In this case the heat diffuses more quickly than the salt so the denser material starts to form long ‘salt fingers’ that penetrate downwards into the cool, fresh water. Figure 10 shows a simple example of this form of instability.

Figure 10. A simple experiment in thermohaline mixing that can be performed in the kitchen. Here some blue dye has been added to the warm, salty water to make the resulting salt fingers stand out more clearly. This experiment was performed by E. Glebbeek and R. Izzard, whom we thank for the picture.

We sometimes have an analogous situation in stars. Consider the core He flash. The nuclear burning begins at the position of the maximum temperature, which is off-centre due to neutrino losses. This fusion produces ¹²C which has a higher molecular weight μ than the almost pure ⁴He interior to the ignition point. We have warm, high μ material sitting atop cool, lower μ material. We expect some mixing based on the relative timescales for the heat diffusion and the chemical mixing. Indeed, this region is Rayleigh–Taylor unstable but stable according to the Schwarzschild or Ledoux criteria (Grossman, Narayan, & Arnett 1993). This was in fact one of the first cases considered in the stellar context (Ulrich 1972) although it seems likely that hydrodynamical effects will wipe out this μ inversion before the thermohaline mixing can act (Dearborn et al. 2006; Mocák et al. 2009, 2010). Another common application is mass transfer in a binary system, where nuclearly processed material (of high μ) is dumped on the envelope of an unevolved companion, which is mostly H (Stancliffe & Glebbeek 2008).

One rather nice way of viewing the various mixing mechanisms in stars is given in Figure 11, based on Figure 2 of Grossman & Taam (1996). In the left panel we give the various stability criteria and the types of mixing that result, while the right panel also shows typical mixing speeds. In both panels the Schwarzschild stability criterion is given by the red line, and it predicts convection to the right of this red line. The blue line is the Ledoux criterion, with convection expected above the blue line. The green lines show expected velocities in the convective regions, while the brown lines show the dramatically reduced velocities expected for thermohaline or semi-convective mixing. For a general hydrodynamic formulation that includes both thermohaline mixing and semi-convection we refer the reader to Spiegel (1972) and Grossman et al. (1993), and the series of papers by Canuto (Canuto 2011a, 2011b, 2011c, 2011d, 2011e).

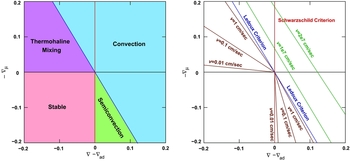
Figure 11. These diagrams show the main stability criteria for stellar models, the expected kind of mixing, and typical velocities. The left panel shows the Schwarzschild criterion as a red line, with convection expected to the right of the red line. The Ledoux criterion is the blue line, with convection expected above this line. The green region shows where the material is stable according to the Ledoux criterion but unstable according to the Schwarzschild criterion: this is semiconvection. The magenta region shows that although formally stable, mixing can occur if the gradient of the molecular weight is negative. The bottom left region is stable with no mixing. The right panel repeats the two stability criteria and also gives typical velocities in the convective regime (green lines) as well as the thermohaline and semi-convective regions (the brown lines). This figure is based on Figure 2 in Grossman & Taam (1996).

Ulrich (1972) developed a one-dimensional theory for thermohaline mixing that was cast in the form of a diffusion co-efficient for use in stellar evolution calculations. This assumed a perfect gas equation of state but was later generalised by Kippenhahn, Ruschenplatt, & Thomas (1980). These two formulations are identical and rely on a single parameter C which is related to the assumed aspect ratio α of the resulting fingers via C = 8/3π²α² (Charbonnel & Zahn 2007b).

The relevance of thermohaline mixing for our purposes follows from the work of Eggleton et al. (2006). They found that a μ inversion developed naturally during the evolution along the RGB. During main sequence evolution a low-mass star produces ³He at relatively low temperatures as a result of the pp chains. At higher temperatures, closer to the centre, the ³He is destroyed efficiently by other reactions in the pp chains. This situation is shown in the left panel of Figure 12, which shows the profile of ³He when the star leaves the main sequence. The abundance of ³He begins very low in the centre, rises to a maximum about mid-way out (in mass) and then drops back to the initial abundance at the surface. When the FDU begins it homogenises the composition profile, as we have seen earlier and as shown in the right panel of Figure 12, and this mixes a significant amount of ³He in the stellar envelope. When the H shell approaches the abundance discontinuity left by the FDU the first reaction to occur at a significant rate is the destruction of ³He, which is at an abundance that is orders of magnitude higher than the equilibrium value for a region involved in H burning. The specific reaction is

Figure 12. Abundance profiles in a 0.8 M_⊙ model with Z = 0.00015 (see also Figure 9). The left panel shows a time just after core hydrogen exhaustion and the right panel shows the situation soon after the maximum inward penetration of the convective envelope. At this time the hydrogen burning shell is at m(r) ≈ 0.31 M_⊙ and the convective envelope has homogenised all abundances beyond m(r) ≈ 0.36 M_⊙. The initial ³He profile has been homogenised throughout the mixed region, resulting in an increase in the surface value, which is then returned to the interstellar medium through winds, unless some extra-mixing process can destroy it first.

\begin{equation*}\centerline{$^3$He\ $ +\, ^3$He\ $ \rightarrow$\ $^4$He\ $ + $\ $2$p,} \end{equation*}

which completes the fusion of He. This reaction is unusual in that it actually increases the number of particles per volume, starting with two particles and producing three. The mass is the same and the reaction reduces μ locally. This is a very small effect, and it is usually swamped by the other fusion reactions that occur in a H-burning region. But here, this is the fastest reaction and it rapidly produces a μ inversion. This should initiate mixing. Further, it occurs just as the H shell approaches the discontinuity in the composition left behind by the FDU, i.e., it occurs just at the position of the LF bump, in accord with (most) observations. This mechanism has many attractive features because it is based on well-known physics, occurs in all low-mass stars, and occurs at the required position on the RGB (Charbonnel & Zahn 2007b; Eggleton, Dearborn, & Lattanzio 2008).

Having identified a mechanism it remains to determine how to model it. Eggleton et al. (2006, 2008) preferred to try to determine a mixing speed from first principles, and try to apply that in a phenomenological way. Charbonnel & Zahn (2007b) preferred to use the existing theory of Ulrich (1972) and Kippenhahn et al. (1980). Both groups found that the mechanism had the desired features, in that it began to alter the surface abundances at the required observed magnitude, it reduced the C isotope ratio to the lower values observed, and it destroyed almost all of the ³He produced in the star, thus reconciling the predicted yields of ³He with observations (Eggleton et al. 2006; Lagarde et al. 2011, 2012), provided the free parameter C was taken to be C ≈ 1 000. Further, mixing reduced the A(Li) values as required by observation and it also showed the correct variation in behaviour with metallicity, i.e., the final ¹²C/¹³C ratios were lower for lower metallicity (Eggleton et al. 2008; Charbonnel & Lagarde 2010).

An extensive study of thermohaline mixing within rotating stars was performed by Charbonnel & Lagarde (2010). They found that thermohaline mixing was far more efficient at mixing than meridional circulation, a result also found by Cantiello & Langer (2010). Note that the latter authors did not find that thermohaline mixing was able to reproduce the observed abundance changes on the RGB, but this is entirely due to their choice of a substantially lower value of the free parameter C (see also Wachlin, Miller Bertolami, & Althaus 2011). Cantiello & Langer (2010) also showed that thermohaline mixing can continue during core He burning as well as on the AGB, and Stancliffe et al. (2009) found that it was able to reproduce most of the observed properties of both C-normal and C-rich stars, for the ‘canonical’ value of C ≈ 1 000.

The interaction between rotation and thermohaline mixing is a subtle thing, yet both Charbonnel & Lagarde (2010) and Cantiello & Langer (2010) treated this crudely, by simply adding the separate diffusion coefficients. This is unlikely to be correct and one can easily imagine a situation where rotation, or any horizontal turbulence, could decrease the efficiency or even remove the thermohaline mixing altogether. Indeed a later study by Maeder et al. (2013) showed that simple addition of the coefficients was not correct and these authors provide a formalism for simultaneously including multiple processes. Calculations using this scheme have not yet appeared in the literature.

For a more detailed comparison of predictions with data, Angelou et al. (2011, 2012) decided to investigate the variation of [C/Fe] with absolute magnitude in GCs. The C isotopic ratio saturates quickly on the RGB, whereas [C/Fe] and [N/Fe] continue to vary along the RGB, providing information on the mixing over a wide range of luminosity. They found good agreement with the thermohaline mixing mechanism, again provided C ≈ 1 000, although they also noted that standard models failed to match the FDU found in the more metal-poor GCs, such as M92. This is not a failure of the thermohaline mixing paradigm but of the standard theory itself (as discussed earlier in Section 2.3.1).

Clearly the value of the free parameter C is crucial. On the one hand, it is gratifying that so many observational constraints are matched by a value of C ≈ 1 000. However, the value is not favoured a priori by some authors. We have seen that within the formalism of the idealised one-dimensional theory of Ulrich (1972) and Kippenhahn et al. (1980), the value of C is related to the aspect ratio α of the assumed ‘fingers’ doing the mixing, with C = 8/3π²α². If the mixing is more ‘blob-like’ than ‘finger-like’ then α ≈ 1 and C ≈ 20 rather than 1 000. This was the case preferred by Kippenhahn et al. (1980), in fact, whereas Ulrich (1972) preferred fingers with α ≈ 5 leading to C ≈ 700, much closer to the value of 1 000 that seems to fit so many constraints. We would caution against a literal interpretation of the aspect ratio and finger-like nature of the mixing. The one-dimensional theory is very idealised and we feel it is perhaps wise to remember that the diffusion equation is a convenient, rather than accurate, description of the mixing.

Even if we assume that the mechanism identified by Eggleton et al. (2006) is the one driving extra mixing, it is unsatisfactory having an idealised, yet approximate, theory that still contains a free parameter. We need a detailed hydrodynamical understanding of the process. Studies along these lines have begun but a discussion of that would take us far afield from our main aim in this paper. We refer the reader to the following papers for details: Denissenkov, Pinsonneault, & MacGregor (2009), Denissenkov (2010), Denissenkov & Merryfield (2011), Traxler, Garaud, & Stellmach (2011), Rosenblum et al. (2011), Mirouh et al. (2012), and Brown, Garaud, & Stellmach (2013). Let us summarise by saying that the models predict more blob-like structures, with low values of α and C values too small to match the observations. The stellar regime is difficult for simulations to model accurately and the final word is not yet written on the subject.

To summarise, thermohaline mixing occurs naturally at the appropriate magnitude on the RGB and it provides the right sort of mixing to solve many of the abundance problems seen on the RGB, as well as the ³He problem. One area where the thermohaline mechanism is open to criticism is its prediction that low-mass stars should almost completely destroy ³He and yet there are known planetary nebulae (PNe) with large amounts (i.e., consistent with the standard models) of ³He present, as pointed out by Balser, Rood, & Bania (2007, see also Guzman-Ramirez et al. 2013) immediately after the paper by Eggleton et al. (2006). Charbonnel & Zahn (2007a) suggested that perhaps an explanation could be related to magnetic fields and identified the few percent of stars that do not show decreased C isotopic ratios with the descendants of Ap stars. They showed that remnant fields of order 10⁴ – 10⁵ Gauss, as expected from Ap stars when they become giants, are enough to inhibit thermohaline mixing.

2.3.5 Magnetic fields and other mechanisms

Despite its many appealing features, thermohaline mixing still suffers from at least one major problem: hydrodynamical models do not support the value of C required to match the observations. This leads to the search for other mechanisms.

One obvious contender is magnetic fields (Busso et al. 2007) produced by differential rotation just below the convective envelope. This can produce a toroidal field and mixing by magnetic buoyancy has been investigated by various authors (e.g., Nordhaus et al. 2008; Denissenkov et al. 2009).

In contrast, Denissenkov & Tout (2000) suggested that a combination of meridional circulation and turbulent diffusion could produce the required mixing. These authors found that the rotation rates required were reasonable but we note that the best models of rotating stars at present do not produce enough mixing.

2.4 Lithium

The behaviour of lithium is complex and deserves a special mention. The main isotope of lithium, ⁷Li, is destroyed by H burning at relatively low temperatures (T ≳ 2.5 × 10⁶ K or 2.5 MK) and as such is observed to be depleted during the pre-main sequence phase (see, for example, Yee & Jensen 2010; Eggenberger et al. 2012; Jeffries et al. 2013). The FDU acts to further reduce the surface lithium abundance through dilution with material that has had its lithium previously destroyed. It then appears to be further destroyed by extra mixing above the bump on the RGB. The behaviour of Li in the GC NGC 6397 was discussed earlier in Section 2.3 and is shown in Figure 9.

The situation with Li is complicated by the existence of Li-rich K-giants (Charbonnel & Balachandran 2000; Kumar, Reddy, & Lambert 2011; Monaco et al. 2011). Approximately 1% of giants show an enhancement of Li, sometimes a large enhancement to values greater than found on the main sequence (say A(Li) > 2.4). While some studies argue that these Li-rich giants are distributed all along the RGB, others find them clustered predominantly near the bump. Palacios, Charbonnel, & Forestini (2001) suggested that meridional circulation could lead to a ‘Li-flash’ that produces large amounts of Li that are only present for a short time, making the Li-rich stars themselves relatively rare. Lithium production was found in the parameterised calculations of extra mixing by Sackmann & Boothroyd (1999), for the case where the mixing (as measured by a mass flux in their case) was fast enough. Denissenkov & Herwig (2004) also found that Li could be produced through sufficiently rapid mixing. Within the approximation of diffusive mixing, they found that a value of D ≈ 10⁹ cm²s^{− 1} is required to explain the usual abundance changes beyond the bump on the RGB, but a value about 100 times larger was shown to produce Li.

It seems natural that if the Li-rich stars really are created at all points along the RGB then the cause is most likely external to the star. If this requires an increase in the diffusion coefficient then something like a binary interaction or the engulfing of a planet due to the growth of the stellar envelope may be involved (Siess & Livio 1999a, 1999b; Denissenkov & Herwig 2004; Carlberg, Majewski, & Arras 2009; Carlberg et al. 2010).

Kumar et al. (2011) argue that in fact the Li-rich giants are predominantly clump stars, involved in core He burning. They argue that the Li may be produced at the tip of the giant branch at the core flash, and then given the longer evolutionary timescales for core He burning, the stars appear to be clustered around the clump (at a similar luminosity to the bump). In addition to the cases noted above that produce Li, we note here that some implementations of thermohaline mixing also produce Li at the tip of the giant branch and that there is evidence for Li-rich stars at this phase of the evolution (Alcalá et al. 2011).

2.5 Second dredge-up

We have seen that following core He exhaustion the star begins to ascend the AGB. If the mass is above about 4 M_⊙ then the model will experience the SDU where the convective envelope grows into the stellar interior. In contrast to the FDU, the SDU goes deeper and mixes material exposed to complete H burning. The main changes are listed in Table 1 and include a substantial increase in the He content by up to ΔY ≈ 0.1 as well as an increase in the ¹⁴N/¹⁵N ratio and the ²³Na abundance (Figure 6).

This huge increase in He is one of the reasons why intermediate-mass AGB stars have been implicated in the origin of the multiple populations observed in Galactic GCs (D’Antona et al. 2002; Norris 2004; Piotto et al. 2005). Increases in He and changes to the composition of the light elements C, N, and O are the most likely cause of the multiple main sequence, sub-giant, and giant branches observed in all clusters that have Hubble Space Telescope photometry (e.g., for 47 Tucanae, NGC 6397, NGC 2808, M22; Milone et al. 2012a, 2012b, 2012c; Piotto et al. 2012).

Figure 6 illustrates the effect of the SDU on the abundance of intermediate-mass stars of solar metallicity. Figure 7 shows that the depth reached by the SDU is approximately the same for all the 5 and 6 M_⊙ models, regardless of the initial metallicity (Boothroyd & Sackmann 1999). The effect of the SDU on other elements is small. Boothroyd et al. (1994) showed that the O isotope ratios are essentially unchanged. Small decreases in the surface abundance of fluorine may occur by at most 10% and sodium is predicted to increase by up to a factor of ≈ 2 at the surface of intermediate-mass stars that experience the SDU (e.g., Figure 8; El Eid & Champagne 1995; Forestini & Charbonnel 1997).

2.6 Variations at low metallicity

2.6.1 Curtailing first dredge-up

At metallicities of [Fe/H] ≲ −1, the evolution of post main sequence stars begins to significantly differ to that found in disk or near-solar metallicity stars. For intermediate-mass stars the necessary central temperatures for core He burning are reached while the star crosses the Hertzsprung gap. This means that the star will ignite He before evolving up the RGB and as a consequence will not experience the FDU (e.g., Boothroyd & Sackmann 1999; Marigo et al. 2001). In Figure 13 we show evolutionary tracks for models of 3 M_⊙ at a metallicity of Z = 0.02 and Z = 0.0001, respectively. The lower metallicity model skips the RGB altogether. At a metallicity of Z = 0.001 or [Fe/H] ≈ −1.2 the upper mass limit that experiences the FDU is 3 M_⊙, by a metallicity of Z = 0.0001 or [Fe/H] ≈ −2.3, this mass has been reduced to 2.25 M_⊙, and even at that mass the maximum extent of the convective envelope only reaches a depth of ≈ 1 M_⊙ from the centre (compared to a Z = 0.02 model of 2.25 M_⊙ where the FDU reaches a depth of ≈ 0.35 M_⊙ from the stellar centre). Because the lower metallicity model is hotter and has a larger core during the main sequence the FDU still causes a 30% drop in the surface C abundance (compared to a drop of 36% for the Z = 0.02 model). For intermediate-mass stars that do not experience a FDU, the second dredge-up event, which takes place during the early ascent of the AGB, is the first mixing episode that changes the surface composition (Boothroyd & Sackmann 1999; Chieffi et al. 2001; Marigo et al. 2001; Karakas & Lattanzio 2007; Campbell & Lattanzio 2008).

Figure 13. Hertzsprung–Russell (HR) diagram showing the evolutionary tracks for 3 M_⊙ models of Z = 0.02 (black solid line) and Z = 0.0001 (red dashed line). The low-metallicity model is hotter and brighter at all evolutionary stages and does not experience a RGB phase or the first dredge-up.

2.6.2 The core helium flash

Metallicity has an important consequence for stars that experience the core He flash. Evolution at lower metallicities is hotter, owing to a lower opacity. This means that the stars experience a shorter time on the RGB before reaching temperatures for core He ignition and therefore do not become as electron degenerate. This means that the maximum mass for the core He flash decreases with decreasing Z (Marigo et al. 2001). We mentioned previously that at solar metallicity the maximum mass for the core He flash is 2.1 M_⊙, whereas at [Fe/H] = − 2.3 the maximum mass is 1.75 M_⊙, with the 2 M_⊙ model experiencing a fairly quiescent He ignition with only a moderate peak in the He luminosity (Karakas & Lattanzio 2007; Karakas 2010).

There is now a fairly extensive literature on multi-dimensional studies of the core He flash (Deupree 1984, 1986; Deupree & Wallace 1987; Deupree 1996; Dearborn et al. 2006; Mocák et al. 2009). Early results from two-dimensional hydrodynamic simulations (Deupree & Wallace 1987) suggest that the flash could be a relatively quiescent or violent hydrodynamic event, depending on the degeneracy of the stellar model. Deupree (1996) finds for low-mass solar composition models, using improved but still uncertain input physics, that the core flash is not a violent hydrodynamic event and that there is no mixing between the flash-driven H-exhausted core and the envelope at this metallicity. More recent multi-dimensional hydrodynamic simulations of the core He flash in metal-free stars find that the He-burning convection zone moves across the entropy barrier and reaches the H-rich layers (Mocák et al. 2010; Mocák, Siess, & Müller 2011).

For the present we assume that stars experiencing the core He flash do not mix any products into their envelope. This is in accord with standard models and the observations do not disagree. We do note that this is not necessarily true at lower metallicity, as we discuss in the next section.

2.6.3 Proton ingestion episodes

The low entropy barrier between the He- and H-rich layer can lead to the He flash-driven convective region penetrating the inner edge of the (now extinguished) H-burning shell. If this happens, protons will be ingested into the hot core during the core He flash. If enough protons are ingested, a concurrent secondary flash may occur that is powered by H burning and gives rise to further nucleosynthesis in the core. The subsequent dredge-up of matter enriches the stellar surface with large amounts of He, C, N, and even possibly heavy elements synthesised by the s process. There has been an extensive number of studies of the core He flash and resulting nucleosynthesis in low-mass, very metal-poor stars (e.g., D’Antona & Mazzitelli 1982; Fujimoto, Iben, & Hollowell 1990; Hollowell, Iben, & Fujimoto 1990; Schlattl et al. 2001; Picardi et al. 2004; Weiss et al. 2004; Suda, Fujimoto, & Itoh 2007; Campbell & Lattanzio 2008; Suda & Fujimoto 2010; Campbell, Lugaro, & Karakas 2010). The details of the input physics used in the calculations clearly matter, where the low-mass Z = 0 models of Siess, Livio, & Lattanzio (2002) find no mixing between the flash-driven convective region and the overlying H-rich layers. It has been known for some time that the treatment of the core He flash in one-dimensional stellar evolutionary codes is approximate at best, owing to the fact that the core He flash is a multi-dimensional phenomenon (Deupree 1996; Mocák et al. 2011). We deal more extensively with this in Section 3.8.

3 EVOLUTION AND NUCLEOSYNTHESIS DURING THE ASYMPTOTIC GIANT BRANCH

The mass of the H-exhausted core (hereafter core mass) at the end of core He-burning is the prime determinant of many important features of AGB evolution including luminosity and nucleosynthesis (e.g., Dominguez et al. 1999; Imbriani et al. 2001; Straniero et al. 2003b; Ekström et al. 2012; Halabi, El Eid, & Champagne 2012; Valle et al. 2013). When the star begins to ascend the AGB the core becomes increasingly electron degenerate and the star’s energy output is mostly provided by He burning, which proceeds through the material outside the C–O core as a thin He-burning shell is established. In intermediate-mass stars the H shell is extinguished, which allows the inward movement of the convective envelope and the SDU. It is at this time that middle and massive intermediate-mass stars ignite C in the C–O core, which results in an O–Ne core prior to the start of the thermally-pulsing phase. While the evolution of AGB stars with O–Ne cores (super-AGB stars) is qualitatively similar to C–O core AGB stars, we discuss these objects separately in Section 3.9.

The He shell thins as the star evolves up the AGB and eventually becomes thermally unstable. At the first thermal instability of the He shell (also known as a ‘thermal pulse’ or ‘shell flash’) the star is said to have entered the thermally-pulsing-AGB (or TP-AGB) phase. The evolution along the AGB prior to the first instability is referred to as the early AGB phase. The structure of an AGB star, illustrated in Figure 14, is qualitatively the same for all masses. We now focus on the thermally-pulsing AGB phase of evolution, which alters the surface abundances of the models in two distinct and important ways. The first is through the operation of the third dredge-up (TDU), which can occur periodically after each thermal pulse and is the mechanism for turning (single) stars into C-rich stars. The second mechanism is hot bottom burning.

Figure 14. Schematic structure of an AGB star showing the electron-degenerate core surrounded by a helium-burning shell above the core, and a hydrogen-burning shell below the deep convective envelope. The burning shells are separated by an intershell region rich in helium (~ 75%) and carbon (~ 22%), with some oxygen and ²²Ne. A super-AGB star has an O–Ne degenerate core otherwise the qualitative schematic structure remains the same. From Karakas, Lattanzio, & Pols (2002). Click on the image to run an animation of a pulse cycle.

3.1 The thermally-pulsing asymptotic giant branch

Here we briefly review the main features of AGB evolution. Previous reviews include Iben (1991), Frost & Lattanzio (1996a), Wood (1997), Busso et al. (1999), and more recently Herwig (2005).

The thermally-pulsing AGB phase of evolution is characterised by relatively long periods of quiescent H-shell burning, known as the interpulse phase, interrupted by instabilities of the He-burning shell. Helium burning is ignited at the base of the He-rich intershell region (see Figure 14), which is composed of material exposed to previous He-shell flashes plus the ashes of H-shell burning which have accumulated over the previous interpulse phase. The He shell burns fiercely and can produce ≳ 10⁸ L_⊙ for a short time. Figure 15 shows the luminosities of the H and He shells, along with the surface luminosity for a 6 M_⊙, Z = 0.02 model star during the first 10 thermal pulses. This figure illustrates the beginning of the TP-AGB phase where the strength of thermal pulses grows with time owing to the overall contraction of the H-exhausted core, which leads to hotter, more electron degenerate conditions in the burning shells. For the 6 M_⊙ model shown in Figure 15 the luminosity produced by the He shell is already ≈ 10⁶ L_⊙ by the third thermal pulse, a figure that grows to over 4 × 10⁸ L_⊙ by the final thermal pulses.

Figure 15. Evolution of the luminosities and core masses (in solar units) for a 6 M_⊙, Z = 0.02 model during the start of the TP-AGB. Each panel shows the evolution during the first 10 thermal pulses. Panel (a) shows the surface (or radiated) luminosity (black solid line), H-burning shell luminosity (blue dot-dashed line), and He-burning shell luminosity (red dashed line). Panel (b) shows the masses of the H-exhausted core (black solid line), He-exhausted core (red dashed line), and the inner edge of the convective envelope (blue dot-dashed line).

The energy produced by the flash powers a convective region which begins in the He-burning shell and extends almost all the way to the H-burning shell. This has the effect of homogenising abundances in this region. In Figure 16 we show the flash-driven convective regions in the intershell during the first five thermal pulses of the 6 M_⊙, Z = 0.02 model. The teardrop-shaped green pockets represent flash-driven convection, which lasts for ≲ 10² years, depending on the core mass. Convection in the intershell retreats once the energy from the thermal pulse starts to die down, in what is referred to as the power down phase. During power down, the huge amount of energy produced by the thermal pulse does not reach the stellar surface but goes into expanding the star, which cools the material outwards of the He shell and shuts off the H shell. The power down phase is seen in the decrease of the H-shell luminosity in Figure 15. Note that while the H-shell luminosity drops by many orders of magnitude, the surface luminosity is only seen to dip by about 10% during the expansion stage.

Figure 16. Convective regions for the 6 M_⊙, Z = 0.02 model during the first five thermal pulses. The x-axis is nucleosynthesis time-step number, which is a proxy for time. For each model, along the x-axis, a green dot represents a convective mass shell and a magenta dot is a radiative shell. The dense magenta regions mark the H and He shells. The teardrop-shaped pockets correspond to the flash-driven convective region that extends over most of the intershell. These have the effect of homogenising the abundances within the intershell. For this model, the duration of the convective zones is about 25 years and the interpulse periods about ≈ 4000 years.

The cooling of these inner layers leads to an increase in the stellar opacity, which allows the base of the outer convective envelope to move inwards in mass, interior to the erstwhile H-burning shell, and to regions previously mixed by intershell convection. Hence material from the interior, which has been exposed to He burning, is mixed into the envelope where it can be observed at the surface. This phase is known as third dredge-up and may occur after each thermal pulse.

In Figure 15 we show the evolution of the masses of the H-exhausted core, of the He-exhausted core, and of the inner edge of the convective envelope for the 6 M_⊙, Z = 0.02 model during the first 10 thermal pulses. By the third thermal pulse we can see a small temporary decrease in the mass of the H-exhausted core, which is seen more clearly in Figure 16. The decrease is caused by the TDU, where the inner edge of the convective envelope penetrates into the top layers of the He intershell. This mixes H into a H-poor region, reducing the mass of the core while mixing the products of H and He nucleosynthesis into the envelope. Following the third dredge-up, the star contracts, the H-burning shell is re-ignited and the star enters a new interpulse phase. The cycle of interpulse–thermal pulse–power down–dredge-up may occur many times on the AGB, depending on the initial mass, composition, and mass-loss rate. For the 6 M_⊙, Z = 0.02 model, this cycle occurs 42 times before the model experienced convergence problems of the type discussed by Lau et al. (2012) and calculations were terminated.

In summary, the AGB evolutionary cycle can be broken down into four distinct phases (Iben 1981):

1. 1. Thermal pulse, which is when the He shell burns brightly producing ≲ 10⁸ L_⊙ for a short time (≈ 10² years). The energy drives a convective zone in the He intershell.

2. 2. The power down phase when the He shell dies down. The enormous amount of energy from the thermal pulse drives an expansion of the whole star and the H shell is extinguished.

3. 3. Third dredge-up phase, which is when the outer convective envelope may move inwards into regions previously mixed by flash-driven convection. Carbon and other He-burning products are mixed to the stellar surface.

4. 4. The interpulse phase is the relatively long (≈ 10⁴ years) phase in between thermal pulses where the H shell provides most of the surface luminosity.

3.2 Hot bottom burning

It has been known for some time that intermediate-mass stars over about 5 M_⊙ develop deep convective envelopes with very high temperatures at the base, allowing for nuclear burning and some energy generation (Scalo, Despain, & Ulrich 1975; Lattanzio 1992; Lattanzio et al. 1996). In fact, what happens is that the bottom of the convective envelope is situated near the top of the H-burning shell. The observational evidence that HBB is occurring in intermediate-mass AGB stars came from the lack of optically-bright C-rich stars in the Magellanic Clouds (Wood, Bessell, & Fox 1983). Many of these luminous, O-rich stars were later found to be rich in lithium (Smith & Lambert 1989, Smith & Lambert 1990a; Plez, Smith, & Lambert 1993). The first detailed calculations were made in the early 1990’s by Blöcker & Schoenberner (1991) and Lattanzio (1992). Boothroyd, Sackmann, & Ahern (1993) found that HBB prevents the formation of a C-rich atmosphere by burning ¹²C into ¹⁴N thus providing a mechanism for the lack of bright C-stars in the Magellanic Clouds.

HBB can dramatically alter the surface composition. This is because the temperature in a thin region at the very base of the envelope, hereafter T _bce, can exceed 50 × 10⁶K (50 MK), which is hot enough for activation of the CNO cycle and also the Ne-Na and Mg-Al chains (if the temperature is high enough). In the most massive, lowest metallicity AGB models, and super-AGB models, the temperature can exceed 100 MK (e.g., Karakas & Lattanzio 2007; Ventura et al. 2013; Doherty et al. 2014a).

The convective envelopes of AGB stars are well mixed, with a convective turnover time of about 1 year, which means that the whole envelope will be exposed to the hot region at least 1 000 times per interpulse period. In Figure 17 we show the evolution of the temperature at the base of the convective envelope for the 6 M_⊙, Z = 0.02 model. The temperature reaches a peak of 82 MK at the 28th thermal pulse, before decreasing to below 20 MK, at which point HBB has been shut off. The decrease in temperature is caused by mass loss, which slowly erodes the envelope. The minimum envelope mass required to support HBB is about 1 M_⊙, depending on the metallicity.

Figure 17. The evolution of the temperature at the base of the convective envelope in the 6 M_⊙, Z = 0.02 model.

3.2.1 Dredge-up, HBB and the brightest C stars

Third dredge-up can continue after the cessation of HBB, which allows the C abundance to increase instead of being burnt to N. The envelope mass is relatively small at this stage (≲ 1 M_⊙), which means that dilution is also lower. It is possible the star will become C-rich at the very tip of the AGB where C/O ⩾ 1 (Frost et al. 1998a), depending on the number of TDU episodes after the end of HBB and the O abundance in the envelope (noting that some O can also be destroyed by HBB). van Loon, Zijlstra, & Groenewegen (1999b) presented observational evidence that supports this scenario, finding a sample of very luminous, dust-obscured AGB stars in the Magellanic Clouds. The existence of very bright, C-rich AGB stars is also evidence that stars in this mass range experience TDU, at least down to the metallicities of the Magellanic Clouds.

3.2.2 The core-mass vs. luminosity relation

The surface luminosity will reach a maximum value during the interpulse and this is reached just before the onset of the next thermal pulse. Paczyński (1970) was the first to derive a linear relationship between the maximum surface luminosity during the quiescent interpulse phase and the H-exhausted core mass:

(1) \begin{equation} L / {\rm L}_{\odot }= 59250 \, ( M_{\rm H}/{\rm M}_{\odot }- 0.522 ). \end{equation}

Paczyński’s calculations infer that there is a maximum luminosity an AGB model can have of 52 021 L_⊙, determined by the maximum possible core mass of ≈ 1.4 M_⊙. Subsequent calculations of intermediate-mass AGB stars revealed that hot bottom burning can violate the conditions of the core-mass luminosity relationship (Blöcker & Schoenberner 1991; Lattanzio 1992; Boothroyd & Sackmann 1992) and that an AGB model can have luminosities larger than predicted by Paczyński. The core-mass luminosity relationship on the AGB is also a key ingredient in a synthetic AGB model because it determines many fundamental features of AGB evolution including the growth of the H-exhausted core with time. The most accurate fits to the core-mass luminosity relationship are those that include a correction for the extra luminosity provided by HBB (Wagenhuber & Groenewegen 1998; Izzard et al. 2004, 2006). In Figure 18 we show the core-mass luminosity relationship for a selection of models at Z = 0.02. HBB occurs in models with M ⩾ 4.5 M_⊙ at Z = 0.02 and we can see for these models that the luminosity strongly increases with core mass before peaking and then declining. The decline is caused by mass loss, which reduces the temperature at the base of the convective envelope and in turn the luminosity from the CN cycle. In comparison, the lower mass AGB models do not experience HBB and show a reasonably linear core-mass luminosity relationship.

Figure 18. The core-mass versus luminosity relationship for a selection of Z = 0.02 models between 2 M_⊙ and 7 M_⊙. The models with M ⩾ 4.5 M_⊙ have hot bottom burning and deviate from the Paczyński relation, shown by the solid black line.

3.3 Third dredge-up

The chemical enrichment at the surface of AGB stars is governed by the TDU mixing event that follows a thermal pulse. TDU is responsible for the largest changes to the surface composition of low-mass AGB stars and has important consequences for nucleosynthesis in intermediate-mass AGB stars as well owing to the production of primary C which is converted to primary N by HBB.

3.3.1 The dredge-up parameter

If there is dredge-up, then a fraction of the outer-most part of the H-exhausted core will be mixed into the envelope according to

(2) \begin{equation} \lambda = \frac{\Delta M_{\rm dredge}}{\Delta M_{\rm core}}, \end{equation}

where λ is the third dredge-up efficiency parameter, ΔM _dredge is the mass mixed into the envelope, and ΔM _core is the amount by which the H-exhausted core increases over the previous interpulse phase; see Figure 19. From the above definition, when λ = 1, the core mass does not grow from pulse to pulse but remains constant. The value of λ depends on physical parameters such as the core mass and metallicity of the star. Exactly how λ depends on these quantities is unknown and reflects our lack of understanding about how convection operates in stellar interiors. Different stellar codes predict different behaviour, a point we will come back to in Section 4.1. Note that there is no a priori reason why λ cannot exceed unity.

Figure 19. The definition of λ, shown schematically, where the x–axis represents time and the y–axis represents the mass of the H-exhausted core.

So in summary, AGB nucleosynthesis depends on

1. 1. λ, the efficiency of third dredge-up;

2. 2. M ^min _c, the minimum core mass at which the TDU begins; this determines how many TDU episodes will occur before mass loss removes the envelope;

3. 3. the size of the convective envelope, which sets the level of dilution of each TDU episode;

4. 4. the mass of the He intershell.

Karakas et al. (2002) provided the first parameterisation of λ and M ^min _c as functions of the total mass, envelope mass, and metallicity (see also Straniero et al. 2003a). The general trend is that λ increases with increasing stellar mass, at a given Z. The parameter λ also increases with decreasing metallicity, at a given mass (e.g., Boothroyd & Sackmann 1988). Naively, this means that it should be easier to make C stars in lower metallicity or higher mass models. But there is also a second reason why C stars are more easily made at lower metallicity. Carbon production is a primary product of the triple-α process, and hence the C intershell abundance does not depend on the global metallicity, Z. In a low-metallicity star the amount of C added per pulse is roughly independent of metallicity, whereas the amount of O that must be overcome to produce C > O is lower. So fewer pulses are required to make a C star. This is true even for α-enhanced compositions where [O/Fe] ≈ +0.4. As we note, stars of lower metallicity are predicted to have deeper dredge-up which accelerates the effect further. Both mechanisms act to make C-stars easier to form at lower metallicities.

For intermediate-mass stars the situation is more complex. Even though the calculations of Karakas et al. (2002) predict larger values of λ, the effect of TDU is mitigated by the mass of the He intershell which is approximately a factor of 10 smaller in intermediate-mass AGB stars compared to AGB stars of lower mass. This means that even if λ ≈ 0.9, the amount of material added to the envelope per TDU event (λ × ΔM _core) is smaller by about an order of magnitude. Second, the mass of the convective envelope is large in intermediate-mass stars, which means that the material will be more diluted. Finally, HBB will act to prevent the formation of C-rich luminous AGB stars at the highest metallicities (e.g., Karakas et al. 2012), which is in agreement with observations of O-rich luminous AGB stars in our Galaxy (García-Hernández et al. 2006, 2013). So even though the conventional wisdom is that C-star production does not happen at intermediate-mass for the above reason, calculations of low-metallicity (Z ⩽ 0.001) intermediate-mass stars suggest that C-star formation will occur before HBB ceases (Herwig 2004a, 2004b; Karakas 2010; Lugaro et al. 2012; Fishlock, Karakas, & Stancliffe 2014; Straniero, Cristallo, & Piersanti 2014). This is driven by the combination of primary C production plus the effect of HBB destroying some O.

It is important to know if the stellar models are providing an accurate description of the efficiency of mixing in AGB stars. For example, the models of Karakas et al. (2002) do not predict any TDU for models less than 2 M_⊙ at Z = 0.02 and quite efficient TDU for models of intermediate mass. While it is notoriously difficult to determine the masses of stars in our Galaxy, observations suggest that the minimum initial stellar mass for C-star formation is ≈ 1.5 M_⊙ (Wallerstein & Knapp 1998). The Large and Small Magellanic Clouds (LMC, SMC, respectively) are the closest satellite galaxies of our Milky Way and they both have thousands of known C stars (Frogel, Mould, & Blanco 1990; Groenewegen 2004). We know the distances to these two galaxies reasonably well, enabling us to construct C-star luminosity functions (CSLFs).

3.3.2 The carbon star luminosity function and other observational constraints

Is it possible to constrain the efficiency of third dredge-up by using the CSLF of the LMC and the SMC? That the stellar luminosity on the AGB is a nearly linear function of the H-exhausted core mass (e.g., Equation (1) and Figure 18) has stimulated the development of synthetic AGB evolution models, as a quick way of simulating populations of AGB stars. The main observational constraint which models must face is the CSLF for the Magellanic Clouds.

Synthetic AGB evolution calculations performed by Groenewegen & de Jong (1993) and Marigo, Bressan, & Chiosi (1996) treat λ as a constant free parameter, calibrated by comparison with the CSLF. Synthetic AGB calculations designed to reproduce the CSLF in the LMC and SMC require an average λ = 0.5 and λ = 0.65 respectively, and M ^min _c ≈ 0.58 M_⊙ (Groenewegen & de Jong 1993; Marigo, Girardi, & Bressan 1999; Izzard et al. 2004; Marigo & Girardi 2007). The values for M ^min _c are lower than found in detailed models by e.g., Karakas et al. (2002) and shown in Figure 20 and the synthetic best fit values for λ are higher than those found for the low-mass AGB models that become C-rich (e.g., λ ≲ 0.4 in Figure 20) unless considerable overshoot is applied (e.g., Herwig 2000; Cristallo et al. 2009; Weiss & Ferguson 2009).

Figure 20. The minimum core mass for TDU (upper panel) and the maximum value of λ plotted against initial mass for the Z = 0.008 models from Karakas et al. (2002). Only models with M ⩾ 1.9 M_⊙ become C-rich. Figure taken from Karakas et al. (2002).

Stancliffe, Izzard, & Tout (2005) were able to reproduce the CSLF of the LMC by computing AGB models without convective overshoot using the Cambridge STARS code, which predicts deeper TDU at smaller core masses than Straniero et al. (1997) or Karakas et al. (2002). However, the CSLF in the SMC cannot be reproduced from detailed STARS models, indicating that the problem is not yet fully solved.

Star clusters are ideal sites to constrain the TDU in AGB stars as they contain stars of similar age and metallicity. Open clusters of solar metallicity in the Milky Way Galaxy can be used to study the TDU and the growth of the core using observations of white dwarf masses in comparison to theoretical models (Kalirai, Marigo, & Tremblay 2014). Star clusters in the Magellanic Clouds in particular prove very valuable as they span a wide range of age, which enables us to study the evolution of stars with masses around 1.5 to 5 M_⊙ (e.g., Girardi et al. 1995; Girardi, Rubele, & Kerber 2009; Maceroni et al. 2002; Mucciarelli et al. 2006; Mackey et al. 2008; Milone et al. 2009).

The clusters NGC 1978 and NGC 1846 in the LMC have been the subject of much study owing to the availability of accurate estimates of AGB structural parameters such as pulsation masses, effective temperatures, and luminosity. Kamath et al. (2010) obtained (current day) pulsation masses for NGC 1978 (and the SMC cluster NGC 419), while Lebzelter & Wood (2007) obtained masses for the LMC cluster NGC 1846. Abundance studies have also been done (Ferraro et al. 2006; Mucciarelli et al. 2008; Lebzelter et al. 2008; Lederer et al. 2009), along with attempts to explain the observed C and O abundances for NGC 1978 and NGC 1846 using stellar evolution models (Lebzelter et al. 2008; Lederer et al. 2009).

Kamath et al. (2012) presented stellar models for AGB stars in NGC 1978, NGC 1846, and NGC 419 with the aim of constraining the TDU and mass loss on the AGB. The stellar evolution models were constrained to reflect the observed AGB pulsation mass, cluster metallicity, giant branch effective temperature, M-type to C-type transition luminosity, and the AGB-tip luminosity. A major finding from the study by Kamath et al. (2012) is that a large amount of convective overshoot (up to 3 pressure scale heights) is required at the base of the convective envelope during third dredge-up in order to get the correct O-rich to C-rich transition luminosity. Such large overshoot leads to λ values in the range 0.66 to 0.82 for the best fitting models. The first shell flashes with dredge-up occur for core masses of M ^min _c ≈ 0.56 − 0.58 M_⊙. These values are much closer to the those values above suggested by synthetic AGB models to fit CSLFs and suggest that considerable convective overshoot occurs in low-mass AGB stars (see also studies by Herwig et al. 1997; Herwig 2000; Cristallo et al. 2009; Weiss & Ferguson 2009; Karakas et al. 2010).

It is important to note that this overshoot is measured from the formal Schwarzschild boundary. We know that this point is unstable to growth, but it does form a convenient position from which to measure the required amount of overshoot. Knowing the Schwarzschild boundary to be unstable has motivated some authors to implement an algorithm to try to search for a neutrally stable point (e.g., Lattanzio 1986). We note that this was not able to reproduce the observations in Kamath et al. (2012), and further mixing was required (although the required depth was not compared to the position of the neutral point).

The large spread in the amount of overshoot required to match the observations could be telling us that is not the best way to quantify the required deeper mixing. It may indicate a mass dependence, with lower masses requiring deeper mixing. It is good to remember that although we call this ‘overshoot’ because it is mixing beyond the Schwarzschild boundary, we are not identifying the cause of the deeper mixing as ‘convective overshoot’ in the usual sense, that is to say, the mixing caused by conservation of momentum in the moving gas, which causes it to cross the point of zero acceleration (the Schwarzschild boundary). Rather, we mean any process that mixes beyond the Schwarzschild border.

3.4 Nucleosynthesis during asymptotic giant branch evolution

Thermal pulses and dredge-up may occur many times during the TP-AGB phase. Each TDU episode mixes ¹²C from the He intershell into the envelope and this has the effect of slowly increasing the C/O ratio of the surface, illustrated in Figure 21 for models of 3 M_⊙ and 6 M_⊙ at Z = 0.02. Repeated TDU episodes can explain the transition from M-type (C/O ≈ 0.5, similar to the Sun) to C-type stars:

(3) \begin{equation} {\rm M} \rightarrow {\rm MS} \rightarrow {\rm S} \rightarrow {\rm SC} \rightarrow {\rm C}, \end{equation}

where SC-type stars have C/O of approximately unity, and C-type stars have C/O > 1 by definition (Wallerstein & Knapp 1998).

Figure 21. The surface C/O ratio as a function of thermal pulse number for (a) a 3 M_⊙, Z = 0.02 model AGB star, and (b) a 6 M_⊙, Z = 0.02 model. The lower mass 3 M_⊙ model does not experience HBB and becomes C-rich. In contrast, efficient HBB occurs for the 6 M_⊙ model and the C/O ratio never reaches unity. The C/O ratio is given by number, and the initial abundance is the solar ratio at C/O = 0.506.

Many C stars also have surface enrichments of heavy elements synthesised by the s-process (e.g., Zr, Y, Sr, Ba, Tc; Smith & Lambert 1986; Smith, Lambert, & McWilliam 1987; Smith & Lambert 1990b; Abia et al. 2002). The element technetium has no stable isotopes. The presence of this radioactive element in AGB star spectra is a particularly important indicator of ‘recent’ s-process nucleosynthesis and mixing (Merrill 1952; Little-Marenin & Little 1979; Smith & Lambert 1988; Vanture et al. 1991; Van Eck & Jorissen 1999; Lebzelter & Hron 2003; Vanture et al. 2007; Uttenthaler 2013). This is because the half-life of ⁹⁹Tc (the isotope produced by the s-process) is 210 000 years, much shorter than the main-sequence lifetime of low-mass stars.

While C and s-process elements are the most obvious and easily verifiable examples of He-shell nucleosynthesis and TDU, there are other elements that are produced during thermal pulses including F, Na, ²²Ne, and the neutron-rich Mg isotopes. Some of these isotopes are synthesised through a combination of H burning and He burning (e.g., Na). Hot bottom burning occurs in the most massive AGB stars and the main observable product of H burning is N which is produced by the CNO cycles, although other H-burning products may also be made (e.g., Na, Al etc.). The stellar yields of intermediate-mass AGB stars are strongly dependent on the complex interplay between HBB and TDU, as TDU is a supplier of primary C and ²²Ne. Overall, the TP-AGB gives rise to a combination of H and He-processed material that is expelled by the star as its envelope is lost through stellar winds.

3.5 Nucleosynthesis via thermal pulses

A He-shell flash produces heat and mixing throughout the intershell region, which is composed mostly of the ashes of H-shell burning (≈ 98% ⁴He and 2% ¹⁴N). The two main He-burning reactions are:

1. 1. the triple-alpha process: effectively 3 ⁴He → ¹²C; the main source of energy during thermal pulses;

2. 2. the ¹²C(α, γ)¹⁶O reaction, which requires a reservoir of ¹²C for efficient activation; this reaction produces negligible energy during shell flashes.

During a thermal pulse some of the ⁴He in the shell is converted into ¹²C by partial He burning, leaving the composition of the well-mixed intershell approximately 70% – 75% ⁴He (by mass), 20% – 25% ¹²C and a few percent ¹⁶O (e.g., Figure 14). These approximate numbers reflect the intershell composition of canonical stellar evolution models without overshoot into the C–O core. The inclusion of overshoot into the core increases the intershell composition of ¹²C and ¹⁶O as discussed in Herwig (2000) and Section 3.5.3. There is a few percent (by mass) of ²²Ne and trace amounts of other species including ¹⁷O, ²³Na, ²⁵Mg, ²⁶Mg, and ¹⁹F. Sodium and ²⁷Al are produced by H-burning during the preceding interpulse phase but are not destroyed by α-capture reactions during the thermal pulse. The exact composition of the He intershell after a thermal pulse depends on the mass and composition of the He shell before the pulse, the duration of the shell flash, as well as the peak temperature and density under which the burning takes place. These quantities in turn depend on the stellar mass and metallicity. The core contracts with time along the AGB which means that the thermodynamic conditions of the He shell become somewhat more extreme toward the end of the TP-AGB compared to the beginning (e.g., higher temperatures and densities resulting from a thinner, slightly more electron-degenerate shell).

3.5.1 The carbon isotopic ratio: ¹²C/¹³C

The C isotope ratio ¹²C/¹³C is a useful probe of AGB nucleosynthesis. Dredge-up increases the amount of ¹²C, so the ratio will increase from ¹²C/¹³C ≈ 10 − 20 at the tip of the RGB to between 30 and > 100, depending on the number of TDU episodes and the initial mass. For the 3 M_⊙ model star the predicted ¹²C/¹³C ratio goes from ≈ 20 before the AGB to 119 at the tip of the AGB.

The ¹²C/¹³C ratio has been observed in samples of C-rich AGB stars (Lambert et al. 1986; Abia & Isern 1997) as well as PNe (Palla et al. 2000; Rubin et al. 2004). The C isotopic composition of pre-solar mainstream silicon carbide (SiC) grains, which are assumed to form in the extended envelopes of C-rich AGB stars, show a well-defined distribution where 40 ≲ ¹²C/¹³C ≲ 100, which matches the ratios observed in C(N) stars (e.g., Zinner 1998).

The ¹²C/¹³C ratios are difficult to measure in PNe, with values spanning the range from ~ 4, the equilibrium value of the CN cycle, to upper limits of ≈ 38 (Palla et al. 2000, 2002; Rubin et al. 2004). These ratios are, in general, lower than measured in C-rich AGB stars and lower than found in pre-solar SiC grains and suggest efficient mixing of H-burning material with the observed nebula. Atacama large millimeter/sub-millimeter array (ALMA) observations of R Sculptoris however show the surprising result that the ¹²C/¹³C ratio at the stellar photosphere is much lower, at 19, compared to the ratio obtained in the present-day mass loss (≳ 60; Vlemmings et al. 2013). These authors speculate that the lower C isotopic ratio is due to an embedded source of UV-radiation that is primarily photo-dissociating the ¹³CO molecule. This suggests that we need to be wary of the ratios obtained from PNe, where the star is a strong UV source illuminating the nebula.

The C and N abundances predicted by models do not match those observed in AGB stars (e.g., Lambert et al. 1986; Abia & Isern 1997; Milam, Woolf, & Ziurys 2009). In particular the observed ¹²C/¹³C ratios are lower than predicted by standard AGB models (e.g., Forestini & Charbonnel 1997; Cristallo et al. 2009; Karakas 2010). For example, standard AGB models predict that by the time C/O ⩾ 1 then ¹²C/¹³C ⩾ 80, which is already close to the upper limit observed in AGB stars or measured in SiC grains.

It is possible to match the observed N and C isotopic ratios by artificially lowering the ¹²C/¹³C ratio at the tip of the RGB to values observed in RGB stars (Kahane et al. 2000; Lebzelter et al. 2008; Karakas et al. 2010; Kamath et al. 2012). By adopting a ¹²C/¹³C ratio of 12 at the tip of the RGB, Kahane et al. (2000) found that they could match the observed ¹²C/¹³C ratio of 45 for CW Leo. Similarly Karakas et al. (2010) were able to reproduce the observed ¹²C/¹³C ratios for most of the Galactic C-rich stars. Whereas most C-rich AGB stars have ¹²C/¹³C ratios between about 30 and 80, there is a small number with ¹²C/¹³C ratios below 30 (e.g., Lambert et al. 1986; Abia & Isern 1997) that cannot be explained using the method above. That is, for a minimum ¹²C/¹³C ratio of 10 at the tip of the RGB the minimum predicted value at the tip of the AGB is about 30 (depending on mass and composition). A value lower than this will require some form of extra mixing on the AGB.

3.5.2 Nitrogen isotopic ratios

Nitrogen isotopic measurements have been made for a small number of evolved stars. Measurements were made for the cool C star IRC + 10216, where the ¹⁴N/¹⁵N ratio was estimated at > 4 400 (Guelin et al. 1995; Kahane et al. 2000). A tentative value of ≈ 150 was made for the J-type star Y CVn (Olson & Richter 1979), and lower limits (along with two detections) were obtained in eight C stars and two proto-PNe (Wannier et al. 1991). In this last study six of the lower limits (> 500) were significantly larger than the ratio found in giant molecular clouds (330). Note that the Wannier et al. (1991) ¹⁴N/¹⁵N abundance ratio for Y CVn is 70, and for IRC + 10216 it is 5 300.

The most recent measurements by Hedrosa et al. (2013) were made for a selection of AGB stars of type C, SC, and J, where J-type C stars are defined mainly by their low ¹²C/¹³C ratio and by the absence of s-process elements (Wallerstein & Knapp 1998). While almost all the data for C-type AGB stars show ¹⁴N/¹⁵N ≳ 1 000, a few C-type AGB stars have N isotopic values close to solar. These are difficult to reconcile with current models because known mixing events either increase the ¹⁴N/¹⁵N ratio by mixing with regions that have experienced H burning (e.g., FDU, SDU with typical values shown in Table 1 and extra mixing) or leave it largely unchanged because the material mixed to the surface is not primarily from H-burning regions (e.g., TDU). Furthermore, some of the SC type AGB stars, which are defined by having C/O ≈ 1, and presumably on an evolutionary path that takes them from M-type (O-rich) to C-type (C-rich) should have N isotopic ratios similar to C-type AGB stars. Instead, Hedrosa et al. (2013) find the SC-type AGB stars to be ¹⁵N-rich (with ¹⁴N/¹⁵N ≲ 1 000), regardless of their C isotopic ratios. The reason for this deviation between SC and C-type AGB stars is unclear and difficult to understand from a theoretical viewpoint. Furthermore, the J-type stars, whose origin is already a mystery, show ¹⁴N/¹⁵N ratios ≲ 1 000. The origin of the ¹⁵N enrichments is not clear but the only way that this isotope can be produced in low-mass AGB stars is via the CNO cycle reaction ¹⁸O(p,α)¹⁵N, which can take place in the He-burning shell provided there is a supply of protons (as discussed below in the context of F production).

3.5.3 The intershell oxygen abundance

The short duration of thermal pulses and the low C content of the region means that the ¹²C(α, γ)¹⁶O reaction produces negligible energy and does not produce much ¹⁶O. Canonical stellar evolution calculations of AGB stars find ¹⁶O intershell compositions of ≲ 2% (by mass, e.g., Boothroyd & Sackmann 1988; Karakas et al. 2010). Here by ‘canonical’ we are referring to model calculations with no convective overshoot of the flash-driven convective pocket into the C–O core. Herwig (2000) does include convective overshoot at the inner border of the flash driven convective zone and finds that some C and O from the C–O core is mixed into the intershell. This has the effect of increasing the C and O intershell abundances to up to ≈ 40% and 20%, respectively. The inclusion of such overshoot means that the oxygen stellar yields from low-mass AGB stars may become significant (Pignatari et al. 2013). We discuss this further in Section 3.5.7.

3.5.4 Fluorine

Fluorine is produced through a complex series of reactions as outlined in detail by Forestini et al. (1992), Mowlavi, Jorissen, & Arnould (1996), Mowlavi, Jorissen, & Arnould (1998) and more recently by Lugaro et al. (2004). The main reaction pathway involves the production of ¹⁵N which is burnt to ¹⁹F via ¹⁵N(α,γ)¹⁹F. The difficulty here is in making ¹⁵N which is destroyed by proton captures in the CNO cycles, which means that the composition of the He shell before a thermal pulse will be almost devoid of this isotope. If protons can be produced by secondary reactions (e.g., ¹⁴N(n,p)¹²C which itself requires free neutrons) then the CNO chain reaction ¹⁸O(p,α)¹⁵N can make ¹⁵N. Because F is produced in the He intershell the composition in the envelope correlates with the abundance of C and s-process elements, as shown in Figure 22 (for C).

Figure 22. The C/O ratio versus the [F/Fe] abundance at the surface of a 3 M_⊙, Z = 0.02 AGB model. Other products of helium nucleosynthesis include ²²Ne, and the final ²²Ne/Ne ratio in this model increases to ≈ 0.4 from 0.068 initially. The total Ne abundance increases from log ε(Ne) = log ₁₀(Ne/H) + 12 = 8.11 at the main sequence to 8.33 at the tip of the AGB where He/H = 0.119, C/O = 1.74 (shown in Figure 21), ¹²C/¹³C = 119, ¹⁴N/¹⁵N ≈ 2 500, and N/O = 0.40.

Fluorine has been observed in AGB stars in our Galaxy and in Local Group Galaxies (Jorissen, Smith, & Lambert 1992; Lebzelter et al. 2008; Abia et al. 2009, 2010), PG 1159 post-AGB stars and PNe (Werner, Rauch, & Kruk 2005; Otsuka et al. 2008), and in barium stars (Alves-Brito et al. 2011), which are hypothesised to have received their C and Ba through mass transfer from a previous AGB companion.

The observations of Jorissen et al. (1992) revealed F abundances that were much higher than model predictions (Forestini et al. 1992; Lugaro et al. 2004; Karakas et al. 2008), especially for the SC-type AGB stars with C/O ≈ 1. A re-analysis of the F abundance in three Galactic AGB stars (TX Psc, AQ Sgr, and R Scl) by Abia et al. (2010) revealed the cause of the discrepancy to be the model atmospheres used in the original analysis, which did not properly take into account blending with C-bearing molecules. The new abundances are up to 0.8 dex lower, bringing the models into agreement with the observations. Observations of F in the C-rich AGB stars in the LMC cluster NGC 1846 however show a discrepancy with models (Lebzelter et al. 2008; Kamath et al. 2012), with the observed F abundance increasing more strongly with the C/O ratio than in the theoretical model. While observations of F in extra-galactic C stars show most of the stars to be F rich, the models over predict the amount of C relative to the observations; see Abia et al. (2011), who also suggested possible solutions including the hypothesis that most of the C might be trapped in dust grains.

3.5.5 Other species in the intershell

There is a wealth of other He-burning products produced as a consequence of thermal pulses including ¹⁹F, ²²Ne, ²³Na, ²⁵Mg, ²⁶Mg, and ²⁷Al (Forestini & Charbonnel 1997; Mowlavi 1999b; Herwig 2000; Karakas & Lattanzio 2003a, 2003b; Lugaro et al. 2004; Cristallo et al. 2009; Karakas 2010; Cristallo et al. 2011). The isotope ²²Ne is produced by the reaction ¹⁴N(α, γ)¹⁸F, where ¹⁸F β-decays to ¹⁸O allowing for the reaction ¹⁸O(α, γ)²²Ne. The composition of ²²Ne in the intershell is fairly high, at ≈ 2%. This is because the abundant ¹⁴N is completely converted into ²²Ne during a thermal pulse. The ²²Ne abundance is predicted to increase by almost an order of magnitude (~ 1 dex) in some AGB models (Karakas & Lattanzio 2003a). If the ²²Ne abundance exceeds or is equal to the ²⁰Ne abundance we should expect an observable enhancement in the elemental Ne composition. The intershell is also enriched in ²³Na and ²⁷Al. Na and ²⁷Al are not He-burning products but are synthesised in the H shell during the previous interpulse. Unlike other H-burning products (e.g., ¹⁴N) these are left unburnt by the subsequent TP and mixed into the envelope by the next TDU episode.

3.5.6 Heavy magnesium isotopes

If the peak temperature of the thermal pulse exceeds 300 × 10⁶ K, the neutron-rich Mg isotopes, ²⁵Mg and ²⁶Mg, can be synthesised by the ²²Ne(α, n)²⁵Mg and ²²Ne(α, γ)²⁶Mg reactions. These two ²²Ne + α reactions have similar although uncertain rates at He-shell burning temperatures (Angulo et al. 1999; Karakas et al. 2006b; Longland, Iliadis, & Karakas 2012; Wiescher, Käppeler, & Langanke 2012). Owing to the relatively high temperatures required for these two reactions, they are predicted to occur efficiently in intermediate-mass AGB stars with masses greater than about 4 M_⊙ depending on metallicity (Karakas & Lattanzio 2003b; Karakas et al. 2006b). The He intershell of lower mass AGB stars will only reach 300 MK during the last few thermal pulses (if at all). This means that the ²²Ne(α, n)²⁵Mg reaction is only marginally activated near the end of the AGB. The ²²Ne(α, n)²⁵Mg is particularly important because it produces free neutrons that can be captured by iron-peak elements enabling the s-process (Iben 1975; Wiescher et al. 2012). It is the dominant neutron-producing reaction in the He and C-burning regions of massive stars (The, El Eid, & Meyer 2007; Heil et al. 2008; Pignatari et al. 2010) and the dominant neutron source in intermediate-mass AGB stars (García-Hernández et al. 2006; Karakas et al. 2012). We will come back to this reaction when we discuss s-process nucleosynthesis in Section 3.7.

3.5.7 Planetary nebulae and post-AGB stars

Comparisons to observations of AGB stars and their progeny can be made for many of the species considered so far. Comparisons with Ne measured in PG 1159 stars reveal good agreement with ²²Ne intershell abundances found in standard models (Werner & Wolff 1999). Neon abundances can be reliably measured in PNe so observations of these objects can be used as a probe of AGB nucleosynthesis. A correlation is observed to exist between the Ne/H and O/H abundance in PNe in the Galaxy, LMC, SMC and M31, within a small but probably real spread (Kaler 1978; Aller & Czyzak 1983; Henry 1989; Dopita et al. 1997; Stasińska, Richer, & McCall 1998; Leisy & Dennefeld 2006; Stanghellini et al. 2000, 2006; Bernard-Salas et al. 2008). While AGB models can produce considerable ²²Ne which results in an overall increase in the elemental Ne abundance, this is predicted to occur in only a narrow mass range and the overall agreement with the observations is good (Marigo 2001; Karakas & Lattanzio 2003a; Henry et al. 2012; Shingles & Karakas 2013).

We can compare AGB predictions to the surface abundance observations of PG 1159-type post-AGB stars, which are thought to be in transition from central stars of PNe to white dwarfs (Werner et al. 2009). These H-deficient objects are quite rare, with only about two dozen known, and their atmospheres are mostly composed of He, C, and O (Werner & Rauch 1994; Werner & Herwig 2006; Jahn et al. 2007; Werner et al. 2009). Spectroscopic observations of the PG 1159 central stars reveal O mass fractions as high as 20% (e.g., Werner & Herwig 2006) clearly at odds with standard stellar models. Spectroscopic observations of Ne and F reveal abundances consistent with the models (Werner & Wolff 1999; Werner et al. 2005). The diffusive convective overshooting models of Herwig (2000) have intershell abundances that are consistent with the abundance patterns observed in PG 1159 central stars (see also, e.g., Miller Bertolami & Althaus 2006; Althaus et al. 2009), as discussed in Section 3.5.3. The degenerate thermal pulses found by Frost, Lattanzio, & Wood (1998b) may have a similar effect. In this case, deep third dredge-up following the degenerate pulse can mix material from the C–O core into the envelope, enhancing the envelope in ¹⁶O.

There is other observational evidence for increased O intershell content. The high [O/Fe] abundances measured in post-AGB stars in the Galaxy and Magellanic Clouds are difficult to reconcile with standard O intershell abundances of 2% or less (Van Winckel & Reyniers 2000; De Smedt et al. 2012). In particular the low-metallicity SMC post-AGB star J004441.04-732136.4 has a [Fe/H] ≈ −1.3, a low C/O ratio of 1.9, combined with a high [O/Fe] ≈ 1.10. These numbers cannot be explained by canonical stellar evolution models as discussed in De Smedt et al. (2012), which produce very high C/O ratios ≈ 20 at this low metallicity. One way to reconcile the models and observations would be through changing the O intershell abundances. Further evidence for non-standard intershell compositions comes from the O isotope ratios measured in evolved red giant stars (see discussion in Karakas et al. 2010), which show an increase in the ¹⁶O/¹⁷O and ¹⁶O/¹⁸O ratios with evolution along the AGB. The C/O and ¹²C/¹³C ratios measured in the C-rich AGB stars in NGC 1978 are also difficult to reconcile with standard models and require higher O intershell compositions of 15% (Kamath et al. 2012). One source of uncertainty in these conclusions is the large error bars present in the O isotopic data measured by Harris, Lambert, and collaborators (Harris et al. 1983; Harris & Lambert 1984; Harris, Lambert, & Smith 1985a, 1985b; Harris et al. 1987; Smith & Lambert 1990b).

3.6 Nucleosynthesis from hot bottom burning

H-burning occurs primarily via the CNO cycles but also via the Ne–Na and Mg–Al chains if the temperature is high enough. In this section we summarise the main H-burning reactions and their products and review the results of HBB that are predicted to be observed at the surface of intermediate-mass AGB stars.

3.6.1 C, N, and O

In Section 2.2.1 we discussed the CNO cycle in the context of FDU abundance changes. During HBB the temperatures at the base of the convective envelope are higher than in the H shell during the first ascent of the giant branch, reaching T _bce ≳ 100 MK in the lowest metallicity, massive AGB stars (with C–O and O–Ne cores, e.g., Karakas & Lattanzio 2007; Ventura & D’Antona 2009; Siess 2010; Doherty et al. 2014a). While these high temperatures are normally associated with He burning, the density at the base of the envelope is only a few grams cm^{− 3}, much lower than in the H shell and other H-burning regions (e.g., the central density in the Sun is ρ_⊙ ≈ 160 gram cm^{− 3}; at the base of the H shell the typical densities during the interpulse are ≈ 30 − 40 gram cm^{− 3} in an intermediate-mass AGB star). This means that higher temperatures are required for nucleosynthesis and energy production than in a typical H-burning environment and also partly explains why HBB is more efficient at lower metallicities where the stars are more compact.

During HBB the CN cycle, which results in an increase in the abundance of ¹³C and ¹⁴N from the destruction of other CNO species, comes into equilibrium quickly. The isotopes ¹²C and ¹⁵N are first destroyed by the CN cycle and later the oxygen isotopes ¹⁶O and ¹⁸O are also destroyed to produce ¹⁴N. The abundance of ¹⁷O can be enhanced by the CNO bi-cycle, depending on the uncertain rates of the ¹⁷O + p branching reactions whereas ¹⁹F is destroyed (e.g., Angulo et al. 1999; Arnould et al. 1999; Iliadis et al. 2010).

In Figure 21(b) we show the evolution of the C/O ratio at the surface of a 6 M_⊙, Z = 0.02 model with HBB. The C/O ratio stays below unity for the entire TP-AGB phase and only starts to increase from C/O ≲ 0.1 during the final eight thermal pulses, which is when HBB starts to shut down owing to the erosion of the envelope by mass loss. By the final calculated thermal pulse the C/O ratio is just above the starting (solar) value of 0.5. The evolution of the ¹²C/¹³C ratio and elemental N abundance in Figure 23 also demonstrates efficient activation of the CNO cycles. The ¹²C/¹³C ratio behaves similarly to the C/O ratio and stays close to the equilibrium value of ≈ 3 for much of the TP-AGB. The N abundance is seen to increase by almost an order of magnitude, more than would be allowed if the initial C + N + O was consumed to produce ¹⁴N. This is because primary ¹²C is mixed from the intershell by the TDU into the envelope, where it is converted into N. Note also that the ¹⁴N/¹⁵N ratio during the TP-AGB is ≳ 10 000, reaching essentially the CN cycle equilibrium value. The O isotopic ratios also evolve, where the ¹⁶O/¹⁷O ratio increases with evolution to a final value of ≈ 465 whereas the ¹⁶O/¹⁸O ratio increases to above 10⁶ as almost all of the available ¹⁸O is destroyed. The elemental O abundance in the 6 M_⊙ model only decreases however by ≈ 0.06 dex.

Figure 23. The evolution of the ¹²C/¹³C ratio and the nitrogen elemental abundance at the surface of the 6 M_⊙, Z = 0.02 model during the TP-AGB. The ratio is given by number and the abundance of nitrogen is in units of log ₁₀(Y), where Y = X/A and X is mass fraction and A is atomic mass.

3.6.2 Ne, Na, Mg, and Al

In the left part of Figure 24 we show the reactions of the Ne–Na chain (Rolfs & Rodney 1988; Arnould et al. 1999), where unstable isotopes are denoted by dashed circles. The main result of the Ne–Na chain is the production of ²³Na at the expense of the Ne isotopes, primarily ²²Ne but also ²¹Ne, which is the rarest neon isotope. The production of Na by the Ne–Na chain was examined in detail by Mowlavi (1999b), who predicted that AGB stars could play an integral role in the chemical evolution of Na in the Galaxy.

Figure 24. Reactions of the Ne–Na and Mg–Al chains. Unstable isotopes are denoted by dashed circles. From Karakas & Lattanzio (2003a) and based on a similar figure in Arnould et al. (1999).

The dominant ²⁰Ne is not significantly altered by H-shell burning, but the destruction of ²³Na at temperatures over 90 MK can lead to a slight enhancement in the ²⁰Ne abundance. The rate of ²³Na destruction is important for determining Na yields (e.g., Iliadis et al. 2001; Izzard et al. 2007). Whether there is leakage out of the Ne-Na chain into the Mg-Al chain depends on the relative rates of the uncertain ²³Na(p,α)²⁰Ne and ²³Na(p,γ)²⁴Mg reactions. Hale et al. (2004) presented revised rates of both of these reactions and found them to be faster than previous estimates (e.g., Angulo et al. 1999; Iliadis et al. 2001) which had a significant impact on Na yields from AGB stars as we discuss in Section 5.

Magnesium and aluminium are altered in the H-burning shell via the activation of the Mg–Al chain, whose reactions are shown on the right-hand side of Figure 24. This series of reactions involves the radioactive nuclide ²⁶Al which has a ground state ²⁶Al _g with a half-life of τ_1/2 = 700 000 years along with a short-lived (τ_1/2 = 6.35 s) isomeric state ²⁶Al _m . These have to be considered as separate species since they are out of thermal equilibrium at the relevant temperatures (Arnould et al. 1999). Hereafter, when we refer to ²⁶Al we are referring to the ground-state, ²⁶Al _g .

The first isotope in the Mg–Al chain to be affected is ²⁵Mg, which is burnt to ²⁶Al. The β-decay lifetime of ²⁶Al relative to proton capture generally favours proton capture within the H-burning shell. This produces the unstable ²⁷Si which quickly β-decays (with a lifetime on the order of a few seconds) to ²⁷Al. The abundance of ²⁶Mg is enhanced by the β-decay of ²⁶Al in the H-shell ashes. Proton capture on ²⁴Mg requires higher temperatures than those required for the other reactions in the Mg–Al chain but model predictions (e.g., Figure 25) suggest that this dominant isotope can be efficiently destroyed by HBB.

Figure 25. The evolution of various species involved in the Ne–Na and Mg–Al chains at the surface of the 6 M_⊙, Z = 0.02 model (upper panel) and 6 M_⊙, Z = 0.004 model (lower panel) during the TP-AGB. Time on the x-axis is scaled such that t = 0 is the time at the first thermal pulse. Abundances on the y-axis are in units of log ₁₀ Y, where Y = X/A, where X is mass fraction and A is atomic mass. Both calculations used the same set of of reaction rates and scaled solar abundances. The 6 M_⊙, Z = 0.004 model has been described previously in Karakas (2010).

In Figure 25 we show the evolution of various isotopes involved in the Ne–Na and Mg–Al chains at the surface of two models of 6 M_⊙. The upper panel shows the predicted nucleosynthesis for the 6 M_⊙, Z = 0.02 model we have been describing so far, which has a peak T _bce of 82 MK. The lower panel shows results from a 6 M_⊙, Z = 0.004 model which has a peak T _bce of 95 MK. While the CNO isotopes for the 6 M_⊙, Z = 0.02 model (Figure 23) clearly show the effects of HBB on the predicted surface abundances, the abundances of heavier isotopes show only marginal activation of the Ne–Na and Mg–Al chains. Most of the increase in ²²Ne, ²⁵Mg, and ²⁶Mg is from the TDU bringing He-shell burning products to the surface. The slight increase in ²⁷Al ([Al/Fe] ≈ 0.1 at the tip of the AGB) is mostly from Al produced in the H shell and mixed to the surface by the TDU and not from HBB. Sodium barely increases from the post-SDU value. In contrast, the lower metallicity 6 M_⊙ model, which is not only hotter but more compact, shows considerable destruction of ²⁴Mg, an increase in ²⁶Al which can only come from H burning and the Mg–Al chains, and variations in ²⁵Mg and ²⁶Mg consistent with HBB. Sodium initially increases before being destroyed again by proton-capture reactions.

There is a paucity of observational evidence for constraining stellar models of intermediate-mass stars during their TP-AGB phase. This is partly because there are few stars found at the AGB-luminosity limit near M _bol ≈ −7 but also because of the complexity of the model atmospheres required for the interpretation of the spectra. Evolved intermediate-mass AGB stars are long-period pulsators with low effective temperatures, which means that the dynamics of the atmosphere must be taken into consideration (McSaveney et al. 2007). The few observations of stars in our Galaxy suggest that most of them, even the optically obscured stars, are O-rich and s-process-rich which points to both efficient HBB and TDU (Wood et al. 1983; García-Hernández et al. 2006, 2013). In the Magellanic Clouds, most of the bright AGB stars are also O-rich but some dust-obscured objects are also C-rich as we have already noted.

The study by McSaveney et al. (2007) obtained abundances for a small sample of bright AGB stars for comparison to theoretical models. The observations of C, N, and O were a relatively good match to stellar evolution models but no observed enrichments were found for Na and Al. We note that the latest nuclear reaction rates suggest much lower Na production than previously calculated (Karakas 2010) so perhaps this is not surprising. Al production is also predicted to be highly metallicity dependent with little production in AGB stars with [Fe/H] ≳ −0.7 (Ventura et al. 2013).

Predictions such as those presented here (or by others, e.g., Ventura et al. 2013) that intermediate-mass AGB stars result in nucleosynthesis variations in the Ne, Na, Mg, and Al isotopes are particularly useful for comparison to GC abundance anomalies. All well-studied GCs show star-to-star abundance variations in C, N, O, F, and Na, and some show variations in Mg, Al, and Si (e.g., Gratton et al. 2004, 2012; Carretta et al. 2009; Yong et al. 2013, and references therein) and only a few GCs show variations in iron-peak and heavy elements (e.g., ω Cen and M22 Norris & Da Costa 1995; Johnson et al. 2008; Da Costa & Marino 2011). The lack of star-to-star variations in Fe and Eu have led to the conclusion that core-collapse supernovae did not play a role in the self enrichment of these systems and have suggested an important contribution from intermediate-mass AGB stars. Globular cluster star abundances show C and N are anti-correlated with each other, as are O and Na, and (sometimes) Mg and Al. That is the pattern expected if H burning at relatively high temperatures has caused the observed abundance patterns (Prantzos et al. 2007).

At the highest HBB temperatures, breakout of the Mg–Al cycle can occur via the ²⁷Al(p,γ)²⁸Si reaction. If this occurs then we would expect to see correlations between enhanced Al and Si (Ventura, Carini, & D’Antona 2011). Yong et al. (2008) find that N abundances in the giant stars of the GC NGC 6752 are positively correlated with Si, Al, and Na, indicating breakout of the Mg–Al chain. Carretta et al. (2009) also find a spread in the Si abundances of the GCs NGC 6752 (see also Yong et al. 2013) and NGC 2808, and a positive correlation between Al and Si. Models by Ventura et al. (2011) show that the most Al-enriched models are also enriched in Si so it seems that hot H burning can produce such a trend, even if the site of the proton-capture nucleosynthesis in GCs is still unknown.

It is possible to obtain isotopic ratios for Mg by using the MgH line (Guelin et al. 1995; Shetrone 1996a, 1996b; Gay & Lambert 2000; Kahane et al. 2000; Yong et al. 2003a; Yong, Lambert, & Ivans 2003b; Yong, Aoki, & Lambert 2006; Da Costa, Norris, & Yong 2013). The Mg isotopic ratios therefore become an important probe of the site of the nucleosynthesis that has added to the chemical enrichment of GC systems. The GCs show an intriguing trend: the stars that are considered normal or ‘not polluted’ are (relatively) O-rich and Na-poor, and sometimes Mg-rich and Al-poor. These stars show a near solar Mg isotopic ratio. The stars that are considered ‘polluted’ show O-depletions and sometimes Mg-depletions, are rich in Na and sometimes Al. For those globular clusters that do show stars with variations in Mg and Al we find that ²⁴Mg is depleted at the expense of ²⁶Mg with essentially no star-to-star variations in ²⁵Mg (e.g., Da Costa et al. 2013).

In Figure 26 we show the evolution of the Mg isotopes at the surface of a 6 M_⊙, Z = 0.004 ([Fe/H] ≈ −0.7) AGB model. The metallicity of this model matches some of the stars in ω Cen studied by Da Costa et al. (2013) and the sole M 71 star analysed by Yong et al. (2006), and may help reveal a trend with metallicity. If we focus just on ω Cen, then at all metallicities the stars show approximately solar ratios for ²⁵Mg/Mg ≈ 0.1 (e.g., Figure 9 in Da Costa et al. 2013). In contrast, ²⁴Mg/Mg shows a decrease with [Fe/H], while ²⁶Mg/Mg shows an increase, with the most extreme cases showing ²⁴Mg/Mg ≈ 0.5 and ²⁶Mg/Mg ≈ 0.4 at [Fe/H] ≈ −1.5. At the metallicity of the 6 M_⊙ AGB model shown in Figure 26, all observed ratios are again approximately solar, in disagreement with model predictions.

Figure 26. The evolution of stable Mg isotopes at the surface of the 6 M_⊙, Z = 0.004 model during the TP-AGB. Time on the x-axis is scaled such that t = 0 is the time at the first thermal pulse. Abundances on the y-axis are scaled to the total Mg composition, Y( ⁱ Mg)/{Y(²⁴Mg) + Y(²⁵Mg) + Y(²⁶Mg)}, where Y = X/A, where X is mass fraction and A is atomic mass. The initial Mg isotopic ratios on the main sequence are solar: ²⁴Mg/²⁵Mg = 7.89 and ²⁴Mg/²⁶Mg = 7.17 (e.g. Asplund et al. 2009). By the tip of the TP-AGB, the model ratios are ²⁴Mg/²⁵Mg = 0.11 and ²⁴Mg/²⁶Mg = 0.14 indicating that most of the ²⁴Mg has been destroyed by proton captures.

What is particularly unusual about these observed abundance ratios is: (1) at the low metallicities of the GC stars examined to date, chemical evolution models suggest a dominant contribution from core-collapse supernovae that produce mostly ²⁴Mg and there should be almost no ²⁵Mg or ²⁶Mg (e.g., Kobayashi et al. 2011b). That is, the normal stars should be completely dominated by ²⁴Mg (about 97% of the total Mg) and not show a solar Mg isotopic ratio. (2) H burning in AGB stars or massive stars, regardless of the stellar evolution code used, struggles to explain these isotopic ratios and unchanging ²⁵Mg abundances without resorting to variations in reaction rates (Fenner et al. 2004; Herwig 2004b; Decressin, Charbonnel, & Meynet 2007; de Mink et al. 2009; Ventura & D’Antona 2009). Parametric models can explain the observed abundances but provide few clues as to the physical site responsible (Prantzos et al. 2007). We note that reaction rates involving the Mg and Al species are quite uncertain and the new reaction rates presented by Straniero et al. (2013) may help resolve the issue.

3.6.3 Lithium

The discovery that the brightest AGB stars are rich in Li (Smith & Lambert 1989, 1990a; Plez et al. 1993; García-Hernández et al. 2013) gave further credibility to the idea that HBB was actually occurring in intermediate-mass AGB stars. The production of ⁷Li is thought to occur via the Cameron–Fowler mechanism (Cameron & Fowler 1971): Some ³He, created earlier in the evolution (during central H-burning), captures an α-particle to create ⁷Be. The ⁷Be can either (1) capture a proton to complete the ppIII chain, or (2) capture an electron to produce ⁷Li. Whether the ⁷Be follows path (1) or path (2) depends critically on the temperature of the region. Owing to efficient mixing in the convective envelope, some of the ⁷Be is mixed into a cooler region which prevents proton capture. The ⁷Be will undergo electron capture instead, producing ⁷Li. The ⁷Li is also subject to proton capture and is eventually mixed into the hot temperature region and subsequently destroyed. Once the envelope is depleted in ³He, ⁷Li production stops. In Figure 27 we illustrate the evolution of ⁷Li at the surface of a 6 M_⊙, Z = 0.02 model during the TP-AGB. The Li-rich phase occurs when the abundance of Li exceeds log ε(Li) ≳ 2 and lasts for ~ 200 000 years for the 6 M_⊙, Z = 0.02 model shown in Figure 27.

Figure 27. The surface abundance of ⁷Li during the TP-AGB phase for a 6 M_⊙, Z = 0.02 model. The units on the y-axis are log ₁₀(n(Li)/n(H) + 12) and time on the x-axis is scaled such that t = 0 is the beginning of the TP-AGB. The lithium-rich phase lasts for about 200 000 years.

Some approximation to time-dependent mixing is required to produce ⁷Li in a HBB calculation because the nuclear timescale for the reactions involved in the Cameron–Fowler mechanism is similar to the convective turnover timescale (see Figure 2 in Boothroyd & Sackmann 1992). Stellar evolution calculations usually use the diffusion equation to approximate mixing in stellar interiors, although we warn that this is only an approximation and that mixing is advective rather than diffusive.

Stellar evolution models are able to account for the magnitude of the Li-enrichment observed in intermediate-mass AGB stars, even though there are considerable modelling uncertainties (van Raai et al. 2012; García-Hernández et al. 2013). Ventura, D’Antona, & Mazzitelli (2000) were able to use the Li-rich phase of bright intermediate-mass AGB stars in the Magellanic Clouds as a constraint of mass-loss rates, which are a highly uncertain but important ingredient in stellar evolution modelling. Ventura et al. (2000) concluded that large mass-loss rates of 10^{− 4} M_⊙/year are required to fit the observations of Li-rich AGB stars in the Magellanic Clouds. Using the Blöcker mass-loss rate (Blöcker 1995), they were able to constrain the η _r parameter to ≈ 0.01, where higher values of ⩾ 0.05 lead to too high mass-loss rates when compared to the population of optically visible luminous, Li-rich AGB stars in the Magellanic Clouds.

3.6.4 Type I planetary nebulae

Type I PNe are defined as a separate class based on both abundances and morphology. Peimbert & Torres-Peimbert (1987) originally defined Type I PNe to have He/H > 0.125, N/O > 0.5 and to show, in general, bipolar morphologies (Peimbert 1978; Peimbert & Torres-Peimbert 1987; Peimbert 1990). Kingsburgh & Barlow (1994) propose a modified N threshold (N/O > 0.8) based on nuclear processing constraints and find that Type I PNe constitute about 16% of their sample. This fraction is close to the fraction of bipolar PNe found by Manchado (2003), at 17%. The bipolars are more or less the same as the Type Is, with an average N/O = 1.3. Note that selection effects are uncertain and can be substantial (e.g., not accounting for selection effects, roughly 23% of the PNe are Type I in the sample of Sterling & Dinerstein 2008).

Type I PNe are associated with a younger, metal-rich population that evolved from initial stellar masses of 2 – 8 M_⊙ (Peimbert 1990; Corradi & Schwarz 1995; Peña, Rechy-García, & García-Rojas 2013). The origin of Type I PNe has been associated with intermediate-mass stars experien-cing HBB (Vassiliadis et al. 1996) but the large number of Type I objects (roughly 17%), combined with the very short post-AGB crossing time for M ⩾ 4 M_⊙ stars (e.g., Bloecker 1995) suggest that the initial progenitor masses are closer to 3 M_⊙.

Standard AGB models of ≈ 3 M_⊙ do not produce the high He/H and N/O ratios that are typical of Type I PNe (e.g., Figure 22). While some Type I PNe may be associated with binary evolution owing to the high frequency of Type I objects associated with non-spherical/elliptical morphologies (e.g., Shaw et al. 2006; Stanghellini & Haywood 2010) some fraction of the Type I PNe will have evolved as essentially single stars. Rotation rates peak in main sequence stars of ≳ 3 M_⊙ and it has been suggested that rotationally induced mixing on the main sequence could be one mechanism to increase the post-FDU He and N abundance (Karakas et al. 2009; Lagarde et al. 2012; Miszalski et al. 2012; Stasińska et al. 2013).

3.7 The slow neutron capture process

Most heavy nuclei with atomic masses greater than A > 56 are formed by neutron addition onto abundant Fe-peak elements. The solar abundance distribution shown in Figure 28 is characterised by peaks that can be explained by:

1. 1. the slow neutron capture process, the s-process;

   

   Figure 28. Solar abundance distribution using data from Asplund et al. (2009). The main features of the abundance distribution include the hydrogen (proton number, Z = 1) and helium peaks, resulting from Big Bang nucleosynthesis, followed by the gorge separating helium from carbon where the light elements lithium, beryllium, and boron reside. From carbon there is a continuous decrease to scandium followed by the iron peak and then a gentle downwards slope to the elements predominantly produced by neutron captures. These include elements heavier than zinc and are highlighted in blue. Proton numbers are also given for a selection of elements.

2. 2. the rapid neutron capture process, the r-process.

The seminal papers by Burbidge, Burbidge, Fowler, & Hoyle (1957) and Cameron (1957) laid down the foundations for these processes and Wallerstein et al. (1997) provides an updated review (see also the reviews by Meyer 1994; Busso et al. 1999; Herwig 2005; Lattanzio & Lugaro 2005; Käppeler et al. 2011).

During the r-process neutron densities as high as N _n ≳ 10²⁰ neutrons cm^{− 3} are produced. This means that the timescales for neutron capture are much faster than β-decay rates. The r-process will produce isotopes essentially up to the neutron drip line. These isotopes then decay to stable, neutron-rich isotopes once the neutron flux is gone. Given the extreme conditions required for the r-process, it has been hypothesised to occur during supernovae explosions (Fryer et al. 2006; Wanajo et al. 2009, 2011; Arcones, Janka, & Scheck 2007; Arcones & Montes 2011; Winteler et al. 2012) but other sites have also been proposed including colliding neutron stars (Argast et al. 2004; Korobkin et al. 2012), and black hole/neutron star mergers (Surman et al. 2008). We refer to Meyer (1994), Arnould, Goriely, & Takahashi (2007), and Thielemann et al. (2011) for further details.

For the rest of this section we will concern ourselves with the s-process, which occurs under conditions of relatively low neutron densities (N _n ≲ 10⁸ neutrons cm^{− 3}). In Figure 29 we show the typical path of the s-process through a section of the chart of the nuclides around the Zr to Ru region. During the s-process the timescale for neutron capture is slower, in general, than the β-decay rate of unstable isotopes. In Figure 29 we can see that when neutrons reach a relatively short-lived isotope, such as ⁹⁵Zr with a half-life of approximately 64 days, the isotope will have time to decay to ⁹⁵Mo instead of capturing another neutron. The s-process will therefore produce isotopes along the valley of β-stability and is responsible for the production of roughly half of all elements heavier than Fe.

Figure 29. Schematic showing the Zr to Ru region of the chart of the nuclides. Neutron number increases along the x-axis and proton number on the y-axis. Unstable isotopes are shown as white squares with the half-life of the ground state. Stable isotopes are shown in colour with the solar-system percentage shown (not all isotopes are shown, so the total may not sum to 100). The typical s-process path that results from neutron densities typical of the ¹³C(α,n)¹⁶O neutron source is shown by the thick blue line. Under these conditions, the isotope ⁹⁶Zr is not reached by the s-process and is an r-process only isotope (in blue). Similarly, the isotope ⁹⁶Mo is an s-only isotope (in yellow) because it is shielded from the r-process by ⁹⁶Zr. The isotopes that are not reached by neutron capture are shown in pink and are produced either by proton addition or spallation under extreme conditions. The unstable isotope ⁹⁹Tc is on the main s-process path.

While it is common to characterise elements as being produced by one of the neutron-capture processes (e.g., Eu is an r-process element), we stress that most heavy elements are produced in part by both the s- and the r-processes. However, there are some isotopes that are only produced by the s-process (e.g., ⁹⁶Mo in Figure 29) because of shielding from the r-process, while some neutron-rich isotopes cannot be easily reached by the s-process (e.g., ⁹⁶Zr). Some proton-rich heavy isotopes cannot be reached by either the s- or r-process and are usually rare in nature and a small component of the total elemental fraction. Examples include ^{92, 94}Mo, shown in Figure 29, which together make up 24% of elemental Mo in the solar system. Arlandini et al. (1999) used detailed AGB stellar models to provide a breakdown of the solar system isotopic abundance distribution according to an origin in either the r- or s-process (their Table 2; see similar breakdowns by Goriely 1999; Travaglio et al. 2004; Simmerer et al. 2004; Sneden, Cowan, & Gallino 2008). Examples of elements where the solar-system abundance fraction is mainly produced by the s-process include Sr, Y, Zr, Ba, La, and Pb, where 91% of solar-system Pb was produced in the s-process (Table 3 in Travaglio et al. 2001a). Similarly some elements such as Ag, Xe, Eu are predominantly produced by the r-process (e.g., 97% of solar-system Eu, see Sneden et al. 2008).

Table 2. List of AGB yields available. We only include detailed AGB evolutionary studies that include yields; not just surface abundance predictions, and we include studies with more than one mass. We list the range of masses and metallicities for each study and we note if they include s-process element predictions.

^a Yields for six metallicities are provided with the range noted in the table.

^b Yields for nine metallicities are provided with the range noted in the table.

^c Downloadable tables are surface abundance predictions, yields are given in their Table 4.

In Figure 28 we show the distribution of elements in our solar system using the latest set of solar abundances from Asplund et al. (2009). We have highlighted elements heavier than Fe in blue, and an examination of this figure shows peaks around Sr, Ba, and Pb (corresponding to atomic masses 88, 137, 207 respectively). These elements are dominated by nuclei with a magic number of neutrons (n = 50, 82, 126). Note that for lighter elements there are also peaks at n = 2, 8, 20, and 28. A nucleus composed of a magic number of protons and a magic number of neutrons is very stable and considered to be ‘doubly magic’. Examples include ¹⁶O with 8 protons and 8 neutrons, and ²⁰⁸Pb, with 82 protons and 126 neutrons. Supernovae produce a considerable amount of ⁵⁶Ni, which is doubly magic with 28 protons and 28 neutrons and eventually decays to ⁵⁶Fe and is the cause of the Fe-peak seen in Figure 28. The stability of nuclei with a magic number of nucleons follows from the closed shells in the quantum mechanical model of the nucleus (Mayer 1950). In practice, nuclei with a magic number of neutrons are more stable against neutron capture than surrounding nuclei because of their low neutron capture cross sections. These nuclei act as bottlenecks and are consequently seen as s-process peaks in the abundance distribution.

Theoretically there are two main astrophysical ‘sites’ of the s-process in nature. The first are AGB stars, which are observationally and theoretically confirmed as factories for the production of heavy elements. The first evidence that stars and not the Big Bang are responsible for the production of elements heavier than Fe came from observations by Merrill (1952) of radioactive Tc in red giant stars. The second main s-process site is massive stars, where the s-process occurs during core He burning and in the convective C-burning shell, prior to the supernova explosion (The, El Eid, & Meyer 2000; The et al. 2007; Pignatari et al. 2010; Frischknecht, Hirschi, & Thielemann 2012). We will concentrate on the s-process occurring in AGB stars.

3.7.1 Neutron sources in AGB stars

Neutron capture processes require a source of free neutrons, given that neutrons are unstable and decay in about 15 minutes. There are two important neutron sources available during He-shell burning in AGB stars:

1. 1. ¹⁴N(α, γ)¹⁸F(β⁺ ν)¹⁸O(α, γ)²²Ne(α, n)²⁵Mg.

2. 2. ¹²C(p, γ)¹³N(β⁺ ν)¹³C(α, n)¹⁶O.

The ²²Ne(α, n)²⁵Mg reaction was first identified as a neutron source for AGB stars by Cameron (1960). The intershell region is rich in ¹⁴N from CNO cycling and during a thermal pulse ¹⁴N can suffer successive α captures to produce ²²Ne. If the temperature exceeds 300 × 10⁶ K, ²²Ne starts to capture α particles to produce ²⁵Mg and ²⁶Mg in almost equal proportions. Neutrons are released by the ²²Ne(α, n)²⁵Mg reaction during convective thermal pulses. Given the high temperatures required for the ²²Ne(α, n)²⁵Mg to operate efficiently, it is theoretically predicted to be effective in AGB stars with initial masses ≳ 4 M_⊙.

The observational data for the s-process mainly comes from ‘intrinsic’ low-mass AGB stars and their progeny, with initial progenitor masses ≲ 4 M_⊙. The ²²Ne(α, n)²⁵Mg is not efficient in these stars and requires operation of the ¹³C(α, n)¹⁶O neutron source instead. Observations come from stars with spectral types M, S, SC, C(N), post-AGB stars, and planetary nebulae (Smith & Lambert 1986; Vanture et al. 1991; Abia et al. 2001, 2002; Abia, de Laverny, & Wahlin 2008; Van Winckel & Reyniers 2000; Reyniers et al. 2007; Sterling & Dinerstein 2008; van Aarle et al. 2013). Extrinsic s-process rich objects also provide a wealth of observational data and include barium and CH-type stars, carbon-enhanced metal-poor (CEMP) stars, dwarf C stars, and some planetary nebulae (Luck & Bond 1991; Allen & Barbuy 2006a, 2006b; Allen & Porto de Mello 2007; Suda et al. 2008, 2011; Masseron et al. 2010; Pereira, Gallino, & Bisterzo 2012; Miszalski et al. 2013). These observations are consistent with theoretical models covering a broad range in metallicity and mass (e.g., Hollowell & Iben 1988; Gallino et al. 1998; Goriely & Mowlavi 2000; Busso et al. 2001; Lugaro et al. 2003; Karakas, Lugaro, & Gallino 2007; Karakas et al. 2009; Cristallo et al. 2009, 2011; Karakas & Lugaro 2010; Bisterzo et al. 2010, 2011, 2012; Lugaro et al. 2012; Pignatari et al. 2013).

Efficient activation of the ¹³C(α, n)¹⁶O reaction requires some ¹³C to be present in the intershell. CNO cycling during the previous interpulse phase leaves a small amount of ¹³C but not enough to account for the s-process enrichments of AGB stars (e.g., Gallino et al. 1998; Karakas et al. 2007). For the ¹³C neutron source to produce enough neutrons to feed the s-process there has to be an additional source of ¹³C. This requires the operation of both proton and α-capture reactions in the He intershell, a region normally devoid of protons.

If some protons are mixed from the convective envelope into the top layers of the He intershell then these protons will react with the abundant ¹²C to produce ¹³C via the CN cycle reactions: ¹²C(p,γ)¹³N(β⁺ ν)¹³C (Iben & Renzini 1982b). This results in a thin layer rich in ¹³C and ¹⁴N known as the ‘¹³C pocket’ (Iben & Renzini 1982a). Straniero et al. (1995) discovered that the ¹³C nuclei then burn via (α,n) reactions in radiative conditions before the onset of the next thermal pulse. The neutrons are released in the ¹³C pocket, and the s-process occurs between thermal pulses in the same layers where the ¹³C was produced. When the next convective thermal pulse occurs, it ingests this s-element rich layer, mixing it over the intershell.

It does appear that there is a dichotomy in models of the s-process in AGB stars. This arises because low-mass models do not reach temperatures high enough to activate the ²²Ne source and as a consequence the ¹³C neutron source is dominant. At a metallicity of Z = 0.02 the mass at which the importance of the two neutron sources switch is ≃ 4 M_⊙ (Goriely & Siess 2004). This dichotomy has important implications for the yields of s-process elements produced by AGB stars of different mass ranges.

The ¹³C and the ²²Ne neutron sources produce s-process abundance distributions that are very different from each other. There are two main reasons for this. The first is that the ¹³C source operates over long timescales (≈ 10³ years), which means that the time integrated neutron fluxes are high even if the peak neutron densities are lower (≲ 10⁷ neutrons cm^{− 3}) than for the ²²Ne source (Busso et al. 2001). This means the s-process can reach isotopes beyond the first s-peak at Sr–Y–Zr to Ba and Pb (Gallino et al. 1998). It is for this reason that the ¹³C source is responsible for the production of the bulk of the s-process elements in low-mass AGB stars reaching, as mentioned above, up to Pb at low metallicities (Gallino et al. 1998). In contrast, the ²²Ne source operates on timescales of ≈ 10 years and even though the peak neutron densities are high (up to 10¹⁵ neutrons cm^{− 3}) the time integrated neutron fluxes are low and the s-process will not, in general, reach beyond the first s-process peak.

The second reason for the difference in the predicted distribution is that branching points on the s-process path are activated by the ²²Ne source (Abia et al. 2001; van Raai et al. 2012; Karakas et al. 2012). For example, the amount of Rb produced during the s-process depends on the probability of the two unstable nuclei ⁸⁵Kr and ⁸⁶Rb capturing a neutron before decaying. These two isotopes therefore act as ‘branching points’ and the probability of this occurring depends on the local neutron density (Beer & Macklin 1989). When the ²²Ne source is active, branching points at ⁸⁵Kr and ⁸⁶Rb are open and ⁸⁷Rb is produced. In particular, more Rb is produced relative to Sr (or Y or Zr). In constrast, during the operation of the ¹³C neutron source these branching points are not efficiently activated and the ratio of Rb to Sr (or Y or Zr) remains less than unity.

3.7.2 The formation of ¹³C pockets

For the ¹³C(α, n)¹⁶O reaction to occur efficiently, some partial mixing is required at the border between the H-rich envelope and the C-rich intershell. This mixing pushes protons into a C-rich region suitable for the production of ¹³C. It is important that there are not too many protons mixed into this region because then the CN cycle goes to completion, producing ¹⁴N rather than ¹³C. Now ¹⁴N is a neutron poison, which means that it is an efficient neutron absorber and will change the resulting abundance distribution. In the region of the pocket where ¹⁴N is more abundant than ¹³C, no s-process nucleosynthesis occurs because of the dominance of the ¹⁴N(n,p)¹⁴C reaction over neutron captures by Fe-seed nuclei and their progeny.

In the intermediate-mass AGB stars that experience HBB, the formation of a ¹³C pocket may be inhibited by proton captures occurring at the hot base of the convective envelope during the TDU, which produces ¹⁴N and not ¹³C (Goriely & Siess 2004). Extremely deep TDU may also inhibit the activation of the ¹³C(α,n)¹⁶O reaction by penetrating into regions of the stellar core with a low abundance of He (Herwig 2004a). Furthermore, a lack of Tc in the spectra of intermediate-mass AGB stars that are rich in Rb is observational evidence that ¹³C pocket formation is inhibited (García-Hernández et al. 2013).

The details of how the ¹³C pocket forms and its shape and extent in mass in the He intershell are still unknown. These are serious uncertainties and mostly arise from our inability to accurately model convection in stars (Busso et al. 1999). Various mechanisms have been proposed including partial mixing from convective overshoot (Herwig 2000; Cristallo et al. 2009, 2011), rotation (Herwig, Langer, & Lugaro 2003; Piersanti, Cristallo, & Straniero 2013), and gravity waves (Denissenkov & Tout 2003).

Progress will come from continued three-dimensional hydrodynamical simulations of the interface between the envelope and the intershell of AGB stars. The first simulations by Herwig et al. (2006) have provided some insight into the nature of convection during thermal pulses but are still too crude in spatial resolution, and cover such a small amount of star time that we are still very limited in any insights into the nature of ¹³C pocket formation in low-mass AGB stars.

Models that include artificial ¹³C pockets produce s-process abundance distributions that fit the observational data reasonably well. Free parameters allow us to adjust the features of the mixing zone (e.g., the shape of the ¹³C profile and its extent in mass) in order to match the observations (Goriely & Mowlavi 2000; Cristallo et al. 2009; Bisterzo et al. 2010; Kamath et al. 2012; Lugaro et al. 2012). Some of the best observational constraints come from post-AGB stars, where the higher photospheric temperatures allow for more accurate abundance determinations. Observations suggest that stochastic variations in the size of the ¹³C pocket in AGB stars are present. Bonačić Marinović et al. (2007a) find that Galactic disk objects are reproduced by a spread of a factor of two or three in the effectiveness of the ¹³C pocket, lower than that found by Busso et al. (2001), who needed a spread of a factor of about 20. Comparisons to lower metallicity post-AGB stars infer spreads of a factor of 3 – 6 (Bonačić Marinović et al. 2007b; De Smedt et al. 2012), while comparison to even lower metallicity CEMP stars require spreads of up to a factor of 10 or more (Bisterzo et al. 2012; Lugaro et al. 2012).

In summary, there is observational evidence that a spread in effectiveness of the ¹³C pocket is needed in theoretical models, but there is no consensus on how large that spread actually is. This problem indicates a significant lack of understanding of the mechanism(s) responsible for the formation of ¹³C pockets in AGB stars. In Section 4.5 we discuss other uncertainties related to the modelling of the s-process in AGB stars such as stellar rotation.

3.7.3 The s-process in low-mass AGB stars

We first define the s-process indices light ‘ls’ and heavy ‘hs’. We choose the three main elements belonging to the first s-process peak Sr, Y, and Zr to define [ls/Fe]=([Sr/Fe]+[Y/Fe]+[Zr/Fe])/3, and three main elements belonging to the second s-process peak Ba, La, and Ce to define [hs/Fe]=([Ba/Fe]+[La/Fe]+[Ce/Fe])/3. These are chosen because data for these elements are often available in observational compilations, e.g., CEMP stars (see the SAGA database and other compilations; Suda et al. 2008, 2011; Frebel 2010; Masseron et al. 2010).

The ‘intrinsic’ ratios [hs/ls] and [Pb/hs] reflect ratios of elements only produced by AGB stars, differing from, e.g., [C/Fe] and [Ba/Fe], because Fe is not produced during AGB nucleosynthesis. These intrinsic ratios move away from their initial solar values towards their s-process values after a small number of thermal pulses in low-mass AGB models (in intermediate-mass models this is not necessarily the case owing to the large dilution of the envelope). The intrinsic ratios are, in a first approximation, independent of stellar modelling uncertainties that affect comparison to the observations including TDU, mass loss, stellar lifetime, and accretion and mixing processes on a binary companion. Instead, they mostly constrain the nucleosynthesis occurring in the deep layers of the star.

We have seen that some partial mixing is assumed to produce a ¹³C pocket that provides the neutrons for low-mass stars. Some authors add a partially mixed region by parameterising an overshoot zone where the mixing velocity falls to zero (Herwig 2000; Cristallo et al. 2009, 2011). The models by Bisterzo et al. (2010) instead artificially introduce a ¹³C pocket into a post-processing code. The details of the pocket are free parameters and kept constant from pulse by pulse. Starting from a ‘standard case’ first adopted by Gallino et al. (1998) in order to match the s-process main component, Bisterzo et al. (2010) multiply or divide the ¹³C and ¹⁴N abundances in the pocket by different factors.

In our calculations the inclusion of the ¹³C pocket was made artificially during the post-processing by forcing the code to mix a small amount of protons from the envelope into the intershell (e.g., Karakas et al. 2007; Lugaro et al. 2012). We assume that the proton abundance in the intershell decreases monotonically from the envelope value of ≃ 0.7 to a minimum value of 10^{− 4} at a given point in mass located at M _mix below the base of the envelope. This method is described in detail in Lugaro et al. (2012) and is very similar to that used by Goriely & Mowlavi (2000). The protons are subsequently captured by ¹²C to form a ¹³C-rich layer during the next interpulse, where the ¹³C pocket is much less than M _mix and is typically about 1/10th the mass of the intershell region. In the calculations shown in Figures 30 and 31 we set M _mix = 2 × 10^{− 3} M_⊙ and this value is held constant for each TDU episode. For further details on our method for introducing ¹³C pockets we refer to Lugaro et al. (2004), Karakas (2010), Karakas et al. (2007), and Kamath et al. (2012).

Figure 30. Average abundance in the stellar wind (in [X/Fe]) for elements heavier than iron for AGB models of 2.5 M_⊙ at two different metallicities: Z = 0.0001 using data published in Lugaro et al. (2012), and new predictions for the Z = 0.02 model. In both models the same size partially mixed zone is inserted into the post-processing nucleosynthesis calculations to produce a ¹³C pocket (see text for details). The average abundance is calculated from the integrated yield of mass expelled into the interstellar medium over the model star’s lifetime.

Figure 31. Average abundance predicted in the ejected wind (in [X/Fe]) for elements heavier than iron for AGB models of 2 M_⊙ and 6 M_⊙ at a metallicity of Z = 0.0001 ([Fe/H] = − 2.3) using data published in Lugaro et al. (2012). No ¹³C pocket is included in the 6 M_⊙ model, while we set M _mix = 2 × 10^{− 3} M_⊙ in the 2 M_⊙ case (see Section 3.7.3 for details).

In Figure 30 we show s-process predictions from models of 2.5 M_⊙ at two different metallicities: [Fe/H] = − 2.3 and [Fe/H] = 0.0. In both models we manually add a ¹³C pocket into the top layers of the He intershell at the deepest extent of each TDU episode, as discussed above. The operation of the ¹³C(α,n)¹⁶O reaction produces [hs/ls] ⩾ 0 for low-mass AGB models, regardless of metallicity and the size of the ¹³C pocket. For example, for the 2.5 M_⊙ models shown in Figure 30 the average [hs/ls] in the ejected wind is 0.20 and 0.58, for the Z = 0.02 and Z = 0.0001 models, respectively. Figure 30 illustrates that the initial metallicity has a strong impact on s-process abundance predictions, with significantly more Pb produced at lower metallicity.

The metallicity dependence arises because (most of) the ¹³C nuclei needed for the ¹³C(α,n)¹⁶O are produced from the H and He initially present in the model star, which is fused into ¹²C and then to ¹³C. That is to say that it is a primary neutron source, and is essentially independent of the metallicity of the star, or in other words, largely independent of [Fe/H]. These neutrons are captured on the heavy-element seeds, whose number is roughly proportional to [Fe/H], which is again roughly proportional to the metallicity Z.

This means that the number of time-integrated neutron captures from the ¹³C source is proportional to ¹³C/Z (Clayton 1988). Thus there are more neutron captures, producing heavier elements, for stars of lower [Fe/H] (Busso et al. 2001). This property allowed Gallino et al. (1998) to predict the existence of low-metallicity Pb-rich stars, which was confirmed by observations of Pb-rich CEMP stars (Van Eck et al. 2001, 2003). Note that for our 2.5 M_⊙ examples, the [Pb/hs] ratio in the ejected stellar wind is − 0.36 for the Z = 0.02 model and increases to 0.76 for the Z = 0.0001 model. Here we have focused on predictions for AGB models with [Fe/H] ≳ −2.5; lower metallicity AGB models will be discussed in Section 3.8.

3.7.4 The s-process in intermediate-mass AGB stars

Wood et al. (1983) noted that the brightest, O-rich AGB stars in the Magellanic Clouds exhibit strong molecular bands of ZrO, indicating that the atmospheres of these stars are enriched in the s-process element Zr. García-Hernández et al. (2006) and García-Hernández et al. (2009) identified several bright, O-rich Galactic and Magellanic Cloud AGB stars with significant enrichments of the neutron-capture element Rb. These observations support the prediction that efficient TDU and HBB has occurred in these stars (García-Hernández et al. 2007).

An enrichment in the element Rb over the elements Sr, Y, and Zr is an important clue that points toward the efficient operation of the ²²Ne(α,n)²⁵Mg neutron source in intermediate-mass AGB stars (Truran & Iben 1977; Cosner, Iben, & Truran 1980; Lambert et al. 1995; Abia et al. 2001; van Raai et al. 2012). Under conditions of high neutron densities two branching points open that allow Rb to be synthesised (van Raai et al. 2012). At N _n = 5 × 10⁸ n/cm³, ≈ 86% of the neutron flux goes through ⁸⁵Kr allowing for ⁸⁵Kr(n, γ)⁸⁶Kr(n, γ)⁸⁷Kr that decays to ⁸⁷Rb. Note that ⁸⁷Rb has a magic number of neutrons and the probability to capture neutrons is extremely low. Also, high neutron densities allow neutrons to bypass the branching point at ⁸⁵Kr and ⁸⁶Rb, allowing for the chain ⁸⁶Rb(n, γ)⁸⁷Rb. For this reason, the elemental ratios of Rb/Sr and Rb/Zr are indicators of the neutron densities, and have been used as evidence that the ¹³C(α, n)¹⁶O reaction is the major neutron source in low-mass AGB stars (Lambert et al. 1995; Abia et al. 2001).

In Figure 31 we show the predicted s-process abundance pattern from a 6 M_⊙, Z = 0.0001 AGB model alongside predictions from a low-mass 2 M_⊙, Z = 0.0001 AGB model. The predictions for the 6 M_⊙ model are typical of intermediate-mass AGB stars and the operation of the ²²Ne neutron source in that elements at the first peak around Rb dominate over elements at the second peak, around Ba. This is in contrast to the s-process abundance pattern from the 2 M_⊙ model, which is typical of the ¹³C neutron source operating in a low-mass, low-metallicity AGB model in that it produces significant amounts of Sr, Ba, and Pb, where the average ejected [Pb/Fe] ≈ 3.2 (see also Figure 30).

The 6 M_⊙ model produces considerable Rb, where the average [Rb/Fe] = 1.60 in the ejected wind, higher than the neighbouring [Sr/Fe] = 1.4, which gives [Sr/Rb] < 0. The s-process indicators, [hs/ls] and [Pb/hs] are negative (− 0.38 and − 0.50, respectively for the 6 M_⊙, Z = 0.0001 model), indicating that elements at the first s-process peak around Rb-Sr-Y-Zr are predominantly produced. Figure 31 highlights why it is important to have s-process yields covering a large range in mass, not just metallicity as shown in Figure 30.

There are few model predictions of s-process nucleosynthesis from intermediate-mass AGB stars, in contrast to the situation for lower mass AGB stars. This is partly because the models experience many thermal pulses and computations involving hundreds of isotopes are particularly time-consuming. It is also because there are few observational constraints that there is much debate as to the occurrence (or not) of the TDU in intermediate-mass AGB stars.

The s-process predictions published for intermediate-mass stars include the following works: Goriely & Siess (2004), who studied the interplay between hot TDU episodes and the s-process as a function of mass; Karakas et al. (2009), who provided predictions up to the first s-process peak for comparison to Type I PNe; Lugaro et al. (2012) who provided predictions for a mass grid (M = 1 to 6 M_⊙) at Z = 0.0001 (or [Fe/H] ≈ −2.3); Karakas et al. (2012) who extended the study to Z = 0.02 for comparison to the Galactic OH/IR sample; D’Orazi et al. (2013) who presented new predictions for comparison to globular cluster stars; Pignatari et al. (2013) who provided NuGrid s-process predictions from a 5 M_⊙ model at two metallicities (Z = 0.02, 0.01); and Straniero et al. (2014) who provide predictions for 4, 5, and 6 M_⊙ models at one metallicity (Z = 0.0003 and [α/Fe] = + 0.5). The models by Pignatari et al. (2013) are calculated with the MESA stellar evolution code ⁴ and include convective overshoot into the C–O core and consequently have higher peak temperatures than canonical models without such overshoot.

3.8 Proton ingestion episodes: PIEs

Stellar evolution at low metallicity presents a new phenomenon, which we have briefly discussed in Section 2.6.3. We saw that during the core flash in very low metallicity models ([Fe/H] ≲ −3) we can find contact between the flash-driven convective region, which is rich in He, and the H-rich envelope. There are two reasons why this happens preferentially in lower metallicity stars: first, the core flash is ignited far off centre, and relatively close to the H-rich envelope. Second, there is normally a substantial entropy gradient that acts to keep these two regions separated. But at lower metallicity this gradient is greatly reduced, enabling the two convective regions to make contact. This results in H-rich material being mixed down to temperatures where He is burning almost explosively, at T ≳ 100MK. There are many names for these events in the literature, some quite convoluted. We follow Campbell & Lattanzio (2008) and refer generically to these events as ‘proton ingestion episodes’ or PIEs. We shall define two different kinds below. We note in passing that three-dimensional simulations show that turbulent entrainment of material could produce similar PIEs at higher metallicities (Mocák et al. 2008, 2009) although this is not found in simple one-dimensional models.

It was realised some time ago that PIEs may arise in the evolution of low-mass and low-metallicity stars (D’Antona & Mazzitelli 1982; Fujimoto et al. 1990; Hollowell et al. 1990; Cassisi, Castellani, & Tornambe 1996). Later work studied how such events depended on the numerical details (Schlattl et al. 2001) and the possibility of explaining some of the abundances seen in CEMP stars (Hollowell et al. 1990; Fujimoto, Ikeda, & Iben 2000; Chieffi et al. 2001; Schlattl et al. 2001, 2002; Picardi et al. 2004; Weiss et al. 2004; Suda et al. 2004; Lau, Stancliffe, & Tout 2009) including possible s-process nucleosynthesis (Goriely & Siess 2001).

A PIE is defined as any event that mixes protons into a very hot region, typically at temperatures where He burns, or is already burning. These naturally occur during a He flash which drives strong convection. They could be He-core flashes or even He-shell flashes on the AGB. When the H is exposed to very high temperatures it produces a secondary ‘H-flash’ and a PIE results in a ‘dual-flash’ event: a He-flash rapidly followed by the initiation of a H-flash. Although both are defined as PIEs, Campbell & Lattanzio (2008) distinguish between them according to whether the initiating He flash is a result of a core flash or an AGB shell flash: hence we have dual core flashes (DCFs) and dual shell flashes (DSFs).

Note that PIEs are also seen in the ‘late hot flasher’ scenario (Sweigart 1997; Brown et al. 2001; Cassisi et al. 2003) and the ‘born-again’ or ‘(very) late thermal pulse’ scenario for explaining objects like Sakurai’s Object (Iben et al. 1983; Asplund et al. 1997; Herwig et al. 1999). We do not discuss these phenomena here, but we remind the reader that the essential physics is the same, involving dredge-up of CNO-processed material to the surface and even neutron captures, as we discuss below. For a comparison of nucleosynthesis predictions in very late thermal pulses and data from pre-solar grain analysis see Fujiya et al. (2013) and Jadhav et al. (2013).

The largest uncertainty with calculating the evolution during a PIE is how to handle the convective mixing. This must be done in a time-dependent way because the convective turnover timescale is close to the burning timescale for H at the high temperatures found during a PIE. Usually convective mixing is approximated by solving a diffusion equation, and usually in one dimension. Within this approximation the diffusion coefficient D is naively given by $\frac{1}{3} v l$ where v is the velocity of the blob and l is its mean-free-path. These values are normally taken from the Mixing-Length Theory (MLT). The results are to be taken with all of the caveats that come with a literal interpretation of this phenomenological theory. Note that one of the assumptions of the MLT is that nuclear burning is negligible in the blob of gas, and this is clearly untrue in the present case.

Within the one-dimensional diffusive mixing approximation the protons are mixed down to a region where they burn fiercely and generate essentially as much energy as the He-burning reactions, which initiated the convection in the first place. This leads to a split in the convective zone: two separate convective burning shells develop, the inner one burning He and the outer burning H, with the two separated by an initially narrow radiative region. Clearly the details of this process will depend on how one calculates the burning and mixing, and that is essentially a three-dimensional process as we expect burning plumes to develop, rather than strict spherical symmetry. Fortunately, multi-dimensional hydrodynamical simulations have progressed to the stage where exploratory calculations are possible (to see simulations of normal shell flash convection see Herwig et al. 2006). We will discuss this further below in Section 3.8.4.

3.8.1 Overview of one-dimensional PIEs

Most calculations of PIEs have been done within the paradigm of one-dimensional models using the diffusion approximation for mixing (for some recent calculations see Campbell & Lattanzio 2008; Cristallo et al. 2009; Lau et al. 2009; Campbell et al. 2010; Suda & Fujimoto 2010). Following the PIE, dredge-up mixes the products of H and He burning to the stellar surface, and the surface layers of the models are dramatically enriched in ¹²C and ¹⁴N. One of the motivations for the study of such events initially was that they share some of the characteristics of CEMP stars (see references given above). Although there has been a reasonable number of calculations of such events, most authors have stopped their calculations after the PIE rather than go to the end of the star’s evolution. It is only if that is done that we can determine the yields for such stars (see Section 3.8.3). Until we have reliable calculations of PIEs, it will be hard to provide improved yields for stars undergoing PIEs.

Campbell & Lattanzio (2008) calculated the complete evolution for low and zero metallicity stars of low mass, through to the end of the AGB phase, so that they included the PIEs, third dredge-up, and HBB. They were able to delimit regions in mass and metallicity space where specific nucleosynthesis events dominates. For example, the DCF dominate the nucleosynthesis for M ≲ 1.5 M_⊙ and [Fe/H] ≲ −5. For higher metallicities, in the same mass range, the DSF dominates. Increasing the mass allows for the TDU and HBB to become active, and dominate the production of elements. For [Fe/H] ≳ −4 (with a slight mass dependence) the DSF does not occur and normal AGB evolution results. The various regions are shown in Figure 32 taken from Campbell & Lattanzio (2008). Note that uncertainties in the location of convective borders, in particular, have a substantial effect on the borders of the various regimes shown in the figure. Nevertheless, the agreement with a similar plot in Fujimoto et al. (2000) is very good.

Figure 32. Models calculated by Campbell & Lattanzio (2008) in the [Fe/H]-mass plane. Red crosses represent models where the DCF dominates the nucleosynthesis. Filled blue triangles show where DSFs dominate. Open blue circles indicate models that experience DSFs, although they are not the dominant event for those models. Green filled circles are used where TDU and HBB on the AGB dominate the nucleosynthesis occurring. The models for Z = 0 are plotted at the position of [Fe/H] = −8.

3.8.2 One-dimensional PIEs and the i-process

With protons and ¹²C in abundance one may expect neutrons to be present, provided by the ¹³C neutron source. This indeed is the case, with calculations showing a ‘neutron super-burst’ when convection engulfs the long H tail left behind by the H shell (Fujimoto et al. 2000; Iwamoto et al. 2004; Campbell et al. 2010). This tail is longer than normal because of the very low metallicity in these stars, which means that the pp chains (showing a relatively low temperature dependence) play a significant role in the H burning, and the shell is more extended than is the case when there are enough catalysts for efficient CNO cycling (which has a much higher temperature dependence). During the peak of the burst we find neutron densities as high as 10¹⁵ neutrons cm^{− 3} (Cristallo et al. 2009; Campbell et al. 2010; Herwig et al. 2011).

Similar, but not identical, results were found by Cruz, Serenelli, & Weiss (2013) and Bertolli et al. (2013). The neutron densities are higher than expected for the s-process, but well short of what is needed for the r-process. These neutron exposure events have been called the i-process, for ‘intermediate’ neutron capture. These stars are of great interest to those trying to understand the CEMP-r/s stars, which show evidence of neutron capture nucleosynthesis that lies between the s- and r-process extremes (Lugaro, Campbell, & de Mink 2009; Lugaro et al. 2012; Bisterzo et al. 2012; Bertolli et al. 2013). The patterns predicted by the models do a reasonably good job of matching the observations, assuming that the observed CEMP-r/s stars result from mass transfer in a binary (with appropriate dilution). The fit is not perfect, however, with too much Ba (Campbell et al. 2010) and N (Cruz et al. 2013) produced to match HE1327-2326. Clearly the field is ripe for further study, but see caveats concerning one-dimensional models below. For a study of the (not insignificant) impact of nuclear uncertainties, see Bertolli et al. (2013).

3.8.3 Yields from one-dimensional PIEs

To the best of our knowledge, the only yields available at present for the complete evolution of low-mass stars, including PIEs and later AGB phases, are those given by Campbell & Lattanzio (2008) and Iwamoto (2009). One reason for the dearth of such calculations is the legitimate question over the validity of the one-dimensional and MLT approximations used in most calculations. Further there is the question of mass-loss rates for low metallicity stars, although this is mitigated somewhat by the fact that dredge-up events produce substantial contamination of the envelope during the star’s evolution. We are only now beginning to develop hydrodynamical models that may be used for guidance in such cases.

3.8.4 Multi-dimensional PIE calculations

Since PIEs clearly challenge the assumptions used in most one-dimensional stellar models, they have been the subject of various multi-dimensional hydrodynamical calculations. Extra motivation for this is the work of Herwig (2001) who showed that he could match the observed evolutionary timescale of Sakurai’s Object if the convective timescale during the PIE was about 30 to 100 times slower than predicted from the MLT.

The simulations performed with the Djehuty code by Stancliffe et al. (2011) found significant inhomogeneities in the mixing process (see also Herwig et al. 2011), with plumes of H mixed all the way down to the CO core where they burned rapidly. These calculations showed no sign of the split into two convective zones that is a universal feature of one-dimensional MLT calculations. Similarly, Mocák et al. (2010) found that a calculation that started with a split convective zone soon showed merging into one zone. The final word is yet to be spoken, but a significant step forward was made by Herwig et al. (2013). They found an initial period showing one deep convective region, but that this soon developed an entropy step that seems to divide two mixing zones within a single convective zone. The mixing between the zones seems to be inefficient but not negligible. Indeed, they may later separate, but we cannot be sure because the three-dimensional simulations covered only a relatively short simulation time of ~ 10 hours. It is noteworthy that Herwig et al. (2011) found that such a history of mixed regions was able to match the nucleosynthesis of Sakurai’s Object and that these new results are also in agreement with the convection constraints imposed by the evolutionary timescale of Sakurai’s Object.

It is a common result from these hydrodynamical models that the radial velocities of the material are significantly higher than found in the MLT, by factors of 20 – 30. Whereas MLT predicts velocities of a few km s^{− 1} the simulations show spherically averaged values of 10 – 20 km s^{− 1} with individual plumes reaching even higher velocities at times (Stancliffe et al. 2011; Herwig et al. 2011). This seems to contradict the one-dimensional models of Herwig (2001) who could only match the observed evolutionary timescale of Sakurai’s object by decreasing the MLT mixing efficiency by factors of 30 – 100. But this need not be the case. Reducing the convective efficiency places the H-burning closer to the surface, where the response time to thermal perturbations is shorter. This was found to occur in the simulations of Herwig et al. (2013), who found the position of the split in the convective zone matched the location found by the one-dimensional code using the reduced convective efficiency. Further, Herwig et al. (2011) showed that if there was a single mixed zone for the first ~ 900 minutes of the simulation, before the split into two zones occurs, then the simulation was able to match the observed abundances also.

In summary, it appears the PIEs are crucial events in the nucleosynthesis of low mass, low metallicity stars. They may be involved in explaining some of the observations of CEMP stars. However, we should have some serious concerns about the reliability of the one-dimensional models during this phase. Although the deviations in temperature from spherical symmetry are small (Stancliffe et al. 2011) there are substantial inhomogeneities in the composition in the mixed regions. The details of the PIE and how (and if) the resulting convective zone splits into two require much further work. Significant work has been done but we are only at the beginning, and are still restricted by numerical resolution. Indeed, to the best of our knowledge there is only one calculation that has shown convergence of results with increasing resolution (Woodward, Herwig, & Lin 2013), which is crucial for these studies. Most calculations are almost certainly limited by resolution in a way that has not been quantified. The fact that these numerical simulations can only cover a few hours of star time is another concern: we need to be confident that the behaviour seen is representative of the behaviour of the star over longer timescales. Much work remains to be done, but at least it has started.

3.9 Beyond the AGB: Super-AGB stars

Stars in a relatively narrow mass range will ignite C off-centre under degenerate conditions. These stars will experience thermal pulses on the ‘super-AGB’. The upper mass limit for this range is set by those stars that go on to burn Ne and heavier species, ending with an iron core and dying as a core-collapse supernova (these are the traditional ‘massive’ stars). In the nomenclature introduced in this paper the super-AGB stars are the middle intermediate and massive intermediate stars, as shown in Figure 1.

These stars are particularly difficult to calculate for many reasons, including high sensitivity to spatial and temporal resolution, a large number of thermal pulses (hundreds to thousands), and dramatically different final fates (electron-capture supernova or white dwarf) depending on the uncertain mass loss and its importance compared to core growth. The first studies of the evolution of super-AGB stars were by Garcia-Berro & Iben (1994), Ritossa et al. (1996), Garcia-Berro, Ritossa, & Iben (1997), Iben, Ritossa, & Garcia-Berro (1997), and Ritossa, García-Berro, & Iben (1999). These early calculations ignored mass loss and looked only at solar compositions, as is entirely appropriate for the first explorations. In the last decade researchers have extended the investigations to cover a wide range of metallicities, now that computers have enabled us to face the difficult computational task these stars present. There has been an increasing number of studies of super-AGB stars in recent years (Gil-Pons & García-Berro 2002; Gil-Pons et al. 2005; Gil-Pons, Gutiérrez, & García-Berro 2007; Siess 2007; Poelarends et al. 2008; Ventura & D’Antona 2009, 2010; Doherty et al. 2010; Ventura & D’Antona 2011; Ventura et al. 2011; Karakas et al. 2012; Herwig et al. 2012; Doherty et al. 2014a; Gil-Pons et al. 2013; Ventura et al. 2013; Jones et al. 2013; Doherty et al. 2014b).

3.9.1 Super-AGB evolution

These calculations all agree qualitatively on the evolution of super-AGB stars, although there are substantial and important quantitative differences. The stars ignite C off-centre when the temperature reaches 600 – 650 MK, and develop a convective shell reaching outward from the ignition point. After this C burning dies down and contraction resumes, secondary convective zones develop and the C burning eventually reaches the centre where it ceases before consuming all of the C, leaving a mass fraction of C of around 1%. Carbon burning continues just outside the inner core generating more convective flashes when regions of high C content are traversed. At the completion of C burning we are left with an O–Ne core surrounded by an inactive C–O shell, as well as He- and H-burning shells and the large convective envelope.

Quantitative details are harder to agree upon. This is mostly due to uncertainties in how to treat convection and semiconvection, as much during the core He burning phase as during C burning. It is the size of the C–O core at the end of He burning that is the prime determinant of super-AGB evolution during C burning. For a comparison between different codes and the resulting differences in evolution, and critical mass boundaries (see Figure 1) we refer to Poelarends et al. (2008) and Doherty et al. (2010).

During, or soon after, core C burning (which need not go to completion) the star will experience second dredge-up. This relatively simple event is much more complicated in the case of super-AGB stars. Sometimes, usually in the more massive models, we find ‘corrosive’ SDU, where the convection extends inward of the He-burning shell with the result that it dredges C (and sometimes O) to the surface (Doherty et al. 2014a; Gil-Pons et al. 2013). Similarly we can find ‘dredge-out’ episodes, first encountered by Ritossa et al. (1996), where H diffuses into a He-burning convective zone. This mixes the H to extreme temperatures, resulting in a H flash. Thus these dredge-out events are another form of proton-ingestion episode (Campbell & Lattanzio 2008). As expected, the details of these events, and even their occurrence or not, depend on the previous evolution, especially the mass of the core, and how the borders of convection are treated.

Once the super-AGB stars settle on the TP-AGB their evolution is similar to other intermediate-mass AGB stars, showing recurring thermal pulses and HBB, with the usual associated nucleosynthesis. The differences here are that the thermal pulses are not very strong, reaching typically L _He ≃ 10⁶L_⊙ for models without much dredge-up (e.g., Siess 2007, 2010), compared with values more like 10⁸L_⊙ where there is deep dredge-up in lower mass C–O core AGB stars. These pulses have short duration, and the flash-driven convective pocket is only in existence for about 6 – 12 months. The pulses repeat every 100 years or so with the result that the expected number of pulses can be hundreds to thousands, depending on the uncertain mass-loss rate. For this reason most of the calculations to date do not cover the full evolution, but only a few pulses at the start of the TP-AGB. Detailed models of the full super-AGB evolution include Pumo, D’Antona, & Ventura (2008), Siess (2010), Karakas et al. (2012), Gil-Pons et al. (2013), Ventura et al. (2013), and Doherty et al. (2014a, 2014b).

Note that all authors find convergence difficulties near the end of the evolution of intermediate-mass AGB stars. Lau et al. (2012) attribute this to the opacity bump produced by Fe, which has also been noted in models of Wolf-Rayet stars by Petrovic, Pols, & Langer (2006) (but not, apparently, by Dray et al. 2003). The convergence problem is believed due to the disappearance of a hydrostatic solution for large core masses, when a region of super-Eddington luminosity develops (Wood & Faulkner 1986). Exactly how the star responds to this is uncertain. Lau et al. (2012) show that there is not enough energy available to eject the envelope so after some dynamical motion the envelope may again settle on the star and further evolution may occur. For this reason Doherty et al. (2014a) and Gil-Pons et al. (2013) provide yields for two cases: (a) assuming the envelope is ejected with the composition it had when the instability developed, and (b) assuming that pulses similar to the last few continue until the envelope is removed by the stellar wind. Reality is likely to lie somewhere between these two extremes.

3.9.2 Third dredge-up

One area that requires further study is the occurrence, or not, of third dredge-up in super-AGB stars. Siess (2010) and Ventura & D’Antona (2011) find no dredge-up in their detailed models, whereas Karakas et al. (2012), Doherty et al. (2014a), and Gil-Pons et al. (2013) do find reasonably efficient TDU. This is again a sensitive function of mixing details and how the numerical calculations are performed (Frost & Lattanzio 1996b). In any event, even if TDU is very efficient, as measured by the dredge-up parameter λ, it is unlikely to be very important for most species, because of the masses involved.

In a typical low to intermediate-mass AGB star the intershell region contains a mass within a factor of two of m _is ≈ 0.01 M_⊙ and the increase in core mass between thermal pulses is similar with ΔM_c ≈ 0.01 M_⊙. Compare these with typical values found for super-AGB stars, which are at least two orders of magnitude smaller: m _is ≈ 10^{− 4} M_⊙, and ΔM _c ≈ 10^{− 4} − 10^{− 5} M_⊙. Hence dredging up such a small amount, albeit over many pulses, has only a small effect on surface abundances. The total amount dredged to the surface is usually less than ≈ 0.1 M_⊙ (Doherty et al. 2014a). This has a negligible effect, especially when one considers that this material is diluted in a much larger envelope than is the case for lower mass AGB stars.

3.9.3 Super-AGB nucleosynthesis

The nucleosynthesis in super-AGB stars is again qualitatively similar to that in their lower mass AGB star siblings. Here the intershell is very hot, where temperatures can reach well above 400 MK, depending on the initial mass and metallicity. This results in substantial s-processing with α-captures on ²²Ne providing the neutron source. If the TDU proceeds as in the models of Doherty et al. (2014a) then we expect this material to be mixed to the surface. The sizes of the regions involved, however, are small and from a chemical evolution viewpoint any species that is primarily produced by dredge-up is unlikely to be substantially produced by super-AGB stars. (Note that this is not true at very low metallicity, where the small amount of heavy elements added to the surface can be a significant perturbation on the original content.)

The other main nucleosynthesis pathway for AGB and super-AGB stars is HBB. Indeed, for super-AGB stars the temperature at the bottom of the convective envelope can exceed 100 MK which is high enough for substantial and extensive H burning. We expect CNO cycling, in near equilibrium conditions, as well as the more exotic Ne–Na and Mg–Al chains to be very active.

Detailed calculations by Siess (2010) conclude that these stars may produce significant amounts of ¹³C, ¹⁴N, ¹⁷O, ²²Ne, ²³Na, ^{25, 26}Mg, ²⁶Al, and ⁶⁰Fe. These results were confirmed by Doherty et al. (2014a, 2014b), and Gil-Pons et al. (2013), who present yields for super-AGB stars (see also Ventura et al. 2013).

It is because of their strong HBB that these stars have been discussed frequently as being implicated in explaining the chemical compositions of globular clusters. There is an extensive literature on the problem (Cottrell & Da Costa 1981; Pumo et al. 2008; Ventura & D’Antona 2009, 2010; D’Ercole et al. 2010; D’Ercole, D’Antona, & Vesperini 2011; Ventura & D’Antona 2011; Ventura et al. 2011; D’Ercole et al. 2012; D’Antona et al. 2012; Ventura et al. 2012, 2013; Doherty et al. 2014b). Although super-AGB stars qualitatively have many of the required properties for the polluters of GCs, there are still substantial difficulties, and one has to tune many inputs to get models that are close to the observations. While super-AGB stars may be involved in the GC abundance problems, they are not apparently the magic bullet.

3.10 Final fates of AGB and super-AGB stars

The most massive AGB stars, the lower intermediate mass stars, will end their lives as C–O white dwarfs (Althaus et al. 2010). The super-AGB stars, however, produce a richer variety of remnants (e.g., Jones et al. 2013). At the lower mass limit of stars that ignite C, the ignition is in the outermost layers, and does not proceed to the centre. This leads to a class of hybrid white dwarfs that we refer to as CO(Ne)s. In these stars a C–O core is surrounded by a shell of 0.1–0.4 M_⊙ that has seen C burning and is mostly O and Ne. We note that the 8 M_⊙, Z = 0.02 model presented here is an example of a CO(Ne)-core model, and these are also found by other authors (Heger 2013, private communication; Ventura & D’Antona 2011; Denissenkov et al. 2013a). Stars with more massive cores will undergo off-centre Ne ignition with convective flashes (Ritossa et al. 1999; Eldridge & Tout 2004).

Following core He-exhaustion, most of the middle and massive intermediate-mass stars have core masses that exceed the Chandrasekhar mass, which we take to be M _Ch = 1.37 M_⊙ as determined by Miyaji et al. (1980), Hillebrandt, Nomoto, & Wolff (1984), and Nomoto (1984). The core masses we find are typically 2 – 2.5 M_⊙. Following the SDU (or dredge-out, if it occurs) the core mass is reduced to below the critical Chandrasekhar value. The final fate of these stars is crucially dependent on SDU and dredge-out, for if these do not reduce their core mass to below M _Ch then the star will continue on through the various nuclear burning stages and explode as an iron core-collapse supernova; i.e., as a true massive star. If the core mass is reduced sufficiently by SDU or dredge-out then the fate depends on the competition between core growth and mass loss. If the former dominates and the core reaches M _Ch then an electron-capture supernova will result. If mass loss keeps the mass below the critical value then the star ends as an O–Ne WD.

The existence of massive WDs in the Galaxy with oxygen-rich atmospheres (Gänsicke et al. 2010) lends credence to the idea that at least some of the super-AGB stars avoid core-collapse supernova explosions. Furthermore, there is evidence that some classical novae explode in a binary where the compact companion is an O–Ne WD (e.g., Jose & Hernanz 1998; Denissenkov et al. 2013b).

Figure 33 is taken from Doherty et al. (in preparation) and shows the predicted fate for models in the AGB and super-AGB mass range. We note that these results are in reasonably good agreement with other authors (Siess 2007; Poelarends et al. 2008) given the sensitivity inherent in the calculations. We find the electron-capture supernovae comprise just a few percent of all supernovae in the metallicity range Z = 0.02 to 10^{− 4}.

Figure 33. Predicted final fates for the super-AGB mass range, as a function of metallicity Z. CC-SN refers to core collapse supernovae and EC-SN refers to electron capture supernovae. The regions of C–O, CO(Ne) and O–Ne white dwarfs are also indicated. See text for details.

4 MAJOR UNCERTAINTIES

The evolution and nucleosynthesis of low-mass and intermediate-mass stars is significantly affected by numerical modelling uncertainties as well as uncertainties in the input physics. Here we review the main uncertainties affecting AGB model calculations including convection, which affects the occurrence and efficiency of TDU, and mass loss, which determines the AGB lifetime. We also comment on uncertainties affecting s-process element predictions.

4.1 Convection and the third dredge-up

Dealing with convection in stellar interiors is one of the major problems of stellar evolution modelling. There are two main ways that convection affects AGB evolution and nucleosynthesis. The first is through the way stellar evolution codes treat the interface between radiative and convective regions within a stellar model (Frost & Lattanzio 1996b; Mowlavi 1999a). The second is how the temperature gradient affects the energy transport in the convective regions.

4.1.1 Determining the borders of convection

We know from observations that AGB stars experience third dredge-up. We unambiguously observe C and Tc-rich AGB stars but we still (after 40 years) do not know at which initial stellar mass that dredge-up begins. Circumstantial evidence suggests that the minimum mass be about 1.5 M_⊙ in the Galaxy (e.g., Wallerstein & Knapp 1998) but theoretical models mostly struggle to obtain enough TDU at this stellar mass without the inclusion of some form of convective overshoot (Herwig et al. 1997; Mowlavi 1999a; Herwig 2000; Cristallo et al. 2009; Karakas et al. 2010; Kamath et al. 2012).

Observations of external galaxies such as the LMC, SMC, and dwarf spheroidal galaxies show higher numbers of C-stars than in our Galaxy (e.g., Zijlstra et al. 2006; Sloan et al. 2008, 2012), which is evidence that it is easier to obtain TDU at lower metallicities, for a given mass. On the other hand, Boyer et al. (2013) found a lack of C stars in the inner metal-rich region of M31, indicating that there is a metallicity ceiling for the operation of TDU. Stellar evolution codes qualitatively agree with these observations.

The main problem for calculating TDU is how we determine the border between a convective and radiative region. Applying the Schwarzschild criterion for convection (∇_rad > ∇_ad) is too simplistic because while the accelerations of blobs at this border is zero, the velocities may be finite. This suggests that some overshoot is inevitable and to be expected. The question then is how much?

While the amount of convective overshoot can be constrained by considering various observations (Herwig 2000; Cristallo et al. 2009; Weiss & Ferguson 2009; Kamath et al. 2012), this provides little insight into the actual physics occurring in convective envelopes, given the numerical differences between the various stellar evolution codes. The fact that Kamath et al. (2012) found such a diversity in the amount of overshoot required to match observations may indicate that this is not the best way to characterise the depth of mixing required.

The problem of determining convective borders in stellar interiors is surely also linked to the question of ¹³C pocket formation, which can be formed by the inclusion of a partially mixed overshoot region, for example. Uncertainties not only include the formation mechanism but also the size of the pocket in the He intershell as well as the shape. When more protons are added the resultant ¹³C pocket is accompanied by a sizeable ¹⁴N pocket, which acts as an efficient neutron absorber and suppresses the s-process.

The way forward is to consider multi-dimensional simulations which unfortunately have not yet advanced sufficiently to answer the problem of overshoot or ¹³C pocket formation.

4.1.2 Structural changes from convection

The second important way that convection affects models is the substantial effect on the structure of AGB convective envelopes. The treatment of convection in stellar envelopes determines surface properties such as the luminosity and effective temperature and it has an impact on the efficiency of hot bottom burning (Ventura & D’Antona 2005a). The most commonly used treatment of convection is the MLT which has a free parameter, the mixing-length parameter α, which is usually set by calibrating a 1 M_⊙, Z = Z _⊙ stellar model to the Sun’s present day radius. The parameter α is then assumed to remain constant throughout the star’s evolution, with the same value used for all masses and metallicities.

However, AGB stars have very different envelope structures to the shallow convection zone found in our Sun. There is no good reason why the value of α required to fit a standard solar model is appropriate for AGB stars. Furthermore Lebzelter & Wood (2007) found evidence for α to increase with evolution along the AGB, which suggests that α need not be constant. Increasing α leads to shallower temperature gradients which produces higher luminosities and stronger burning in intermediate-mass AGB stars (Ventura & D’Antona 2005a). Convective models other than the MLT are also used, such as the Full Spectrum of Turbulence (Ventura et al. 1998; Mazzitelli, D’Antona, & Ventura 1999) applied by, e.g., Ventura & D’Antona (2005a).

4.2 Mass loss

Dealing with the extent and temporal variation of mass loss in AGB stars is one of the main uncertainties in stellar modelling (Blöcker 1995; Habing 1996; Ventura & D’Antona 2005b). This is because the mass-loss rates of AGB stars are very uncertain and difficult to determine from observations without a priori assumptions about dust mass and type, and/or radiative transfer modelling (e.g., Bedijn 1988; Vassiliadis & Wood 1993; Habing 1996; van Loon et al. 1999a; Groenewegen et al. 2009a, 2009b; Lagadec & Zijlstra 2008; Lagadec et al. 2010; Guandalini 2010; De Beck et al. 2010; Riebel et al. 2012). Mass loss on the AGB determines the AGB lifetime and the number of thermal pulses experienced by TP-AGB models. This then limits the number of TDU episodes and the duration of HBB; and hence determines the level of chemical enrichment expected from a population of AGB stellar models at a given metallicity.

In order to calculate stellar yields, mass loss has to be included in the calculation of AGB models. The available prescriptions are simple, parameterised formulae that result in mass being removed from the envelope smoothly in time, in contrast to observations which suggest that AGB mass loss in real stars is clumpy and asymmetric (e.g., Meixner et al. 1998; Dinh-V-Trung & Lim 2008; Olofsson et al. 2010; Wittkowski et al. 2011; Paladini et al. 2012; Lombaert et al. 2013).

The upper part of the AGB in particular is dominated by continuously increasing mass loss (Habing 1996). Observations indicate rates increase from 10^{− 7} M_⊙ year^{− 1} for short period Mira variables to ≈ 10^{− 4} M_⊙ year^{− 1} for luminous long-period variables including OH/IR stars and Miras (Groenewegen et al. 2009a; Justtanont et al. 2013). These winds are most likely dust and shock driven (Winters et al. 2003), which leads to the star becoming completely enshrouded by dust and visible predominantly in the infra-red (Habing 1996; Uttenthaler 2013).

One of the biggest uncertainties is the rate of mass loss from low-metallicity AGB stars. Based on theoretical calculations, Mattsson et al. (2008) conclude that low-metallicity C stars have similar mass-loss rates to their metal-rich counterparts. Observations showed that mass-loss rates in low metallicity C-rich AGB stars in nearby galaxies are of a similar magnitude to AGB stars in our Galaxy (e.g., Sloan et al. 2009; Lagadec et al. 2009).

The most widely used prescriptions in AGB evolutionary calculations include the Vassiliadis & Wood (1993) mass-loss law, based on empirical observations of mass-loss rates in C and O-rich AGB stars in the Galaxy and Magellanic Clouds; the Blöcker (1995) formula, based on dynamical calculations of the atmospheres of Mira-like stars; and the Reimer’s mass-loss prescription (Reimers 1975; Kudritzki & Reimers 1978), even though it was originally derived for first ascent giant stars and does not predict a superwind (Groenewegen 2012). Both the Blöcker (1995) and Reimers (1975) rates depend on an uncertain parameter η which typically takes values from 0.01 to 10 (Ventura et al. 2000; Straniero et al. 1997; Karakas 2010). Ventura et al. (2000) found η = 0.01 by calibrating their intermediate-mass AGB models to Li abundances in the LMC.

Other mass-loss prescriptions for AGB stars are available (e.g., Bedijn 1988; Arndt, Fleischer, & Sedlmayr 1997; Wachter et al. 2002; van Loon et al. 2005; Wachter et al. 2008; Mattsson, Wahlin, & Höfner 2010). Some of these prescriptions are specifically for C-rich stars e.g., Arndt et al. (1997) and Wachter et al. (2002) and are not appropriate for bright intermediate-mass AGB stars. The theoretical mass-loss rates from Mattsson et al. (2010) for solar-metallicity C stars are available as a FORTRAN routine that can be coupled to a stellar evolution code.

4.3 Extra mixing in AGB stars

A case has been made for some form of slow non-convective mixing to operate in AGB envelopes, in an analogous situation to the extra mixing operating in first giant branch envelopes (Sections 2.2.4 and 2.3).

The evidence for deep mixing on the AGB comes mainly from O and Al isotope ratios measured in pre-solar oxide grains, which support the existence of such extra mixing in low-mass (M ≲ 1.3 M_⊙) AGB stars (Busso et al. 2010; Palmerini et al. 2009, 2011). The C isotopic ratios measured in AGB stars span a large range, from very low ¹²C/¹³C ratios of ≈ 4 to a maximum of about 100 (Lambert et al. 1986; Abia & Isern 1997). The sample by Lambert et al. (1986) has an average value of 58 (without the J-type C stars whose origin is unknown). The range of ¹²C/¹³C ratios in AGB stars is similar to that measured in mainstream pre-solar silicon carbide grains, with values between 40 ≲ ¹²C/¹³C ≲ 100 with an average ¹²C/¹³C ≈ 60 (Zinner 1998). The lowest values of the ¹²C/¹³C ratio in AGB stars suggest that some small fraction of Galactic disk C-rich AGB stars experience extra mixing. In Section 3.5.1 we summarise the C isotope predictions from AGB models, including the range expected when extra mixing occurs on the first gaint branch.

Carbon-enhanced metal-poor stars that are s-process rich presumably received their C, N and s-process enrichments from a previous AGB companion and their ¹²C/¹³C ratios are therefore an indicator of extra mixing and nucleosynthesis in the AGB star. The ¹²C/¹³C ratio has been measured in CEMP stars covering a range of evolutionary phase, from turn-off stars through to giants. Figure 7 from Stancliffe et al. (2009) illustrates the observed C isotopic ratios of unevolved (log g ⩾ 3) CEMP stars are ≲ 10 (e.g., Cohen et al. 2004; Sivarani et al. 2006; Jonsell et al. 2006; Aoki et al. 2007; Beers et al. 2007; Lucatello et al. 2011). Such low observed ratios are difficult to reconcile with standard AGB nucleosynthesis models, which produce very high ¹²C/¹³C ratios (> 10³) at low metallicity (e.g., Karakas 2010; Cristallo et al. 2011; Lugaro et al. 2012). Such low ¹²C/¹³C ratios could reveal a metallicity dependence to the extra-mixing occurring in AGB envelopes.

Nitrogen abundances of CEMP stars also show a spread that is not easily explained by canonical models as shown by the population synthesis study by Izzard et al. (2009). Stancliffe (2010) studied thermohaline mixing in low-metallicity AGB models and found it not strong enough to explain the low C isotopic ratios. Clearly additional mixing – whatever the mechanism – is required in low-metallicity AGB envelopes, but the need for extra mixing in solar-metallicity C-rich AGB stars is more ambiguous as discussed in detail by Karakas et al. (2010, but see Busso et al. 2010).

4.4 Low-temperature opacities

In recent years there has been considerable effort put into developing accurate low-temperature molecular opacity tables for stellar evolution calculations. The opacity tables of Alexander & Ferguson (1994) and later Ferguson et al. (2005) included the first detailed treatment of the inclusion of molecules to the total opacity at temperatures where T ≲ 10⁴ K. These tables were only available for solar or scaled-solar abundance mixtures. As we have seen, AGB stars experience multiple mixing episodes that alter their envelope compositions, such that the stars may become C and N-rich and in some cases, the envelope C/O ratio can exceed unity.

Marigo (2002) showed that at the transition from C/O < 1 to C/O ⩾ 1 the dominant source of molecular opacity changes from oxygen-bearing molecules to C-bearing molecules. In AGB stellar models, this change in opacity leads to a sudden decrease in the effective temperature and subsequent expansion in radius. These changes to the stellar structure cause an increase in the rate of mass loss. Marigo (2002) showed that this resulted in shorter AGB lifetimes and therefore smaller stellar yields. AGB models with HBB can also deplete C and O (while producing N), which causes changes to the stellar structure and nucleosynthesis (Weiss & Ferguson 2009; Ventura & Marigo 2009, 2010; Fishlock et al. 2014). Despite claims to the contrary, Constantino et al. (2014) showed that there was no threshold in [Fe/H] below which the composition dependent molecular opacities would not produce significant changes. It is therefore necessary to use low-temperature molecular opacity tables that follow the change in C, N, and C/O ratio with time at all masses and compositions.

Besides the scaled-solar tables from Ferguson et al. (2005), other tables currently available for stellar evolutionary calculations are: (1) Lederer & Aringer (2009), who account for an enhancement of C and N compared to the initial abundance for various metallicities, and (2) Marigo & Aringer (2009), who provide the ÆSOPUS on-line downloadable tables ⁵ . These tables are available for essentially arbitrary variations in C, N, and C/O (including enhancements and depletions) for whatever metallicity desired and for various choices of the solar composition.

4.5 The s-process

While the formation mechanism of the ¹³C pocket is still the main uncertainty in the s-process models, there are a number of further problems associated with the s-process scenario discussed previously in Section 3.7.

Lugaro et al. (2012) identified four different regimes of neutron captures that can occur in theoretical AGB models including: (1) the ²²Ne(α,n)²⁵Mg source operates during convective thermal pulses, (2) the ¹³C(α,n)¹⁶O reaction burns under radiative conditions, with the ¹³C produced via the inclusion of a ¹³C pocket, (3) the ¹³C(α,n)¹⁶O reaction burns under convective conditions during a thermal pulse, with the ¹³C produced via the inclusion of a ¹³C pocket, and (4) the ¹³C(α,n)¹⁶O reaction operates under convective conditions with the ¹³C produced via the ingestion of a small number of protons from the tail of the H shell during the thermal pulse.

The mass range at which these regimes occur is model dependent as described in Lugaro et al. (2012). At the metallicity considered in that study (Z = 0.0001) proton ingestion (Regime 4) dominates the s-process abundance predictions at the lowest masses (M ⩽ 1 M_⊙ at Z = 0.0001) when no (or small) ¹³C pockets are present. Proton ingestion is expected to be more important at even lower metallicities, although the mass and metallicity range where proton ingestion occurs is still very uncertain and may occur at solar metallicities under specific conditions (e.g., Sakurai’s Object). Again, the problem comes down to the treatment of convection and convective borders in stars. The first multi-dimensional studies are becoming available to guide the one-dimensional models (Stancliffe et al. 2011; Herwig et al. 2011, 2013).

For the first few pulses in low-mass stars, the temperature in the intershell is not large enough for efficient radiative burning of the ¹³C. Hence Regime 3, where all or most of the ¹³C is burnt under convective conditions during the next thermal pulse is possibly a common occurrence during the first few thermal pulses for all low-mass AGB stars of ≲ 2 M_⊙, regardless of Z (see also Cristallo et al. 2009; Lugaro et al. 2012). The main result of Regime 3 is that the overall neutron exposure (i.e., total number of free neutrons) decreases owing to ingestion of the neutron poison ¹⁴N alongside the ¹³C from the H-shell ashes. Also during Regime 3 the neutron density increases owing to the short timescale of thermal pulses (order 10² years) relative to radiative burning during the interpulse (≈ 10⁴ years).

The occurrence of ¹³C ingestion during thermal pulses is strongly connected to the uncertainties related to the onset of TDU in the lowest-mass AGB stars (e.g., the initial stellar mass for the onset of the TDU at a given Z, the efficiency of TDU as a function of stellar mass, core mass, metallicity; Frost & Lattanzio 1996b; Straniero et al. 1997; Mowlavi 1999a; Karakas et al. 2002; Stancliffe & Jeffery 2007; Karakas et al. 2010).

If stars as low as ≈ 1.2 M_⊙ experience TDU at solar metallicities then we expect Regime 3 to be dominant in these stars for the first few thermal pulses, before the He shell region has heated up to sufficient temperature to ignite ¹³C(α,n)¹⁶O under radiative conditions. If these stars only experience a few TDU episodes, then this regime will dominate the stellar yields of s-process elements.

All stars rotate but the effect of rotation on stellar structure in general, and the s-process in particular, is still poorly known. The angular velocity profile inside AGB stars may produce a strong shear instability between the contracting core and the expanding envelope. Unlike the (partial) mixing postulated to come from overshoot during TDU, this shear layer does not disappear at the end of TDU. This is expected to result in continuous mixing of protons into the top layers of the He intershell, resulting in the complete operation of the CN cycle and the production of a higher abundance of the neutron-poison ¹⁴N instead of ¹³C. This has been shown to lower the neutron exposure and suppress the formation of s-process elements (Herwig et al. 2003; Piersanti et al. 2013). The effect of magnetic fields (Suijs et al. 2008) and gravity waves may modify the angular momentum in the star and reduce the mixing between core and envelope but has not been considered in detailed stellar evolution models so far.

We have mentioned convective overshoot at the bottom of the thermal pulse in the context of O intershell abundances. Such overshoot can lead to increased temperatures and the activation of the ²²Ne neutron source at lower initial stellar mass than canonical models with no overshoot. While it has been shown for a 3 M_⊙ star that such overshoot produces Zr isotopic ratios inconsistent with those measured in stardust grains (Lugaro et al. 2003), other observations such as oxygen in post-AGB stars suggest that such overshoot occurs. While the first s-process yields from models with overshoot into the C–O core are becoming available (Pignatari et al. 2013) a comprehensive study on the effect of such overshoot on the s-process is still lacking.

4.6 Binary evolution

Most stars (roughly 60%) exist in binary or multiple systems (Duquennoy & Mayor 1991). Not all stars in binary systems (or higher order multiples) will be close enough to interact and hence they will evolve essentially as single stars. The fate of these stars and their contribution to the enrichment of the Galaxy is determined by their initial mass and metallicity. For binary stars that are close enough to interact, there are many more variables that determine the type of interaction including the orbital parameters of the system and the mass ratio between the two stars.

Possible interactions include mass transfer via Roche Lobe Overflow (RLOF), which can lead to a common envelope and possible stellar merger. For example, the warm R-type C stars are all single stars which has led various authors to propose that they must be the result of stellar mergers (McClure 1997b; Izzard et al. 2007). If the stars do not merge during the common envelope phase the orbital period will be dramatically shortened, allowing for later mass transfer. The details of common envelope evolution are complex and not well understood (e.g., Taam & Ricker 2010).

Regardless of the final outcome of the common envelope, the evolution of the two stars will be significantly altered from a single stellar evolution channel. Common envelopes may truncate the evolution of the more massive star on the first giant branch, which means it will never become an AGB star. Clearly the nucleosynthesis yields will be significantly altered from the expectations from single stellar evolution (Izzard 2004; Izzard et al. 2006).

Interactions can come in other forms. For example if one of the stars is on the AGB and has a strong wind, then some of that wind may be transferred to the companion. That wind may then contain the products of AGB nucleosynthesis, which will later be observed on the surface of the lower mass companion. Stellar wind accretion is thought to be the dominant mechanism to produce barium and CH-type stars (McClure 1983; McClure & Woodsworth 1990; McClure 1997a; Boffin & Jorissen 1988; Han et al. 1995; Karakas, Tout, & Lattanzio 2000; Izzard, Dermine, & Church 2010; Miszalski et al. 2013), as well as carbon and nitrogen-enhanced metal-poor stars (Beers & Christlieb 2005; Lucatello et al. 2005; Izzard et al. 2009; Pols et al. 2012; Abate et al. 2013).

5 CHEMICAL ENRICHMENT FROM AGB STARS

Stellar yields are a key ingredient in models of the chemical evolution of galaxies and stellar systems (Tinsley 1980; Gibson 1997; Romano et al. 2010; Nomoto et al. 2013). Core collapse supernova explosions release vast quantities of α-elements (e.g., O, Mg, Si, Ti) and Fe-peak elements into the Galaxy on relatively short timescales (≲ 10⁷ years). Classical nova explosions (Romano & Matteucci 2003; Romano et al. 2010) and rapidly rotating massive stars may also be an important source of C, N, and heavy elements at the earliest times (Chiappini, Matteucci, & Meynet 2003; Chiappini et al. 2006; Hirschi 2007; Frischknecht et al. 2012).

Binary systems that explode as Type Ia supernovae are also responsible for producing substantial metals, mostly in the form of Fe (e.g., Seitenzahl et al. 2010), although Type Ia explosions typically take place on much longer timescales from a few hundred million years to a few gigayears (Matteucci & Greggio 1986). There is evidence that galaxies had a small number of prompt Type Ia explosions, which take place on much shorter timescales of ≈ 100 Myr since the beginning of star formation (Bonaparte et al. 2013). Together, massive stars, that explode as Type II supernovae, and Type Ia supernovae dominate the chemical evolution of many elements and for this reason AGB stars were until recently largely ignored in models of chemical enrichment (Matteucci & Francois 1989; Timmes et al. 1995; Gibson 1997; Kobayashi et al. 2006).

However, low- and intermediate-mass stars are a common inhabitant of galaxies and stellar systems and produce a copious amount of the gas and dust seen in the interstellar medium. In the last decade there has been considerable progress in our understanding of the nucleosynthesis of AGB stars. We now know that they produce considerable amounts of C, N, F, Na, the neutron-rich isotopes of Ne, Mg, as well as Na, Al, and heavy elements produced by the s-process. For a complete picture of the chemical evolution of galaxies, stellar yields from low- and intermediate-mass stars must be included.

5.1 Stellar yields from AGB stars

Renzini & Voli (1981) produced the first set of stellar yields from low- to intermediate-mass stars. These CNO yields were calculated with a fully synthetic evolutionary algorithm, which included HBB, TDU, and mass loss via the Reimers (1975) formula. Further contributions using synthetic AGB models have been made by Marigo et al. (1996), van den Hoek & Groenewegen (1997), Marigo (2001), Izzard et al. (2004), and Gavilán, Buell, & Mollá (2005). The biggest difference between the recent calculations listed above and those of Renzini & Voli (1981) is in the improved parameterisations of the AGB phase of evolution, based on detailed models with improved input physics. The latest synthetic models also use parameterisations that depend on the initial metallicity, which is something that Renzini & Voli’s calculation did not do.

The increasing speed of modern computers means that the problem of running large grids of stellar models becomes time consuming, rather than impossible. There are now various compilations in the literature for yields from detailed AGB stellar models. Table 2 compiles these yields along with the mass and metallicity range, tells if they include predictions for s-process elements, and if downloadable yield tables are provided.

There are other studies of low- and intermediate-mass stars that include stellar yields but are not included in Table 2 for the following reasons. Stancliffe & Jeffery (2007) perform a detailed study of the uncertainties affecting yields of low-mass AGB stars but only at one mass (1.5 M_⊙, Z = 0.008). Church et al. (2009) present full s-process yields but also only for one mass (3 M_⊙, Z = 0.02). We include only the most recent stellar yield predictions calculated by Ventura and collaborators from 2013 and 2014. Earlier calculations (e.g., Ventura et al. 2001; Ventura, D’Antona, & Mazzitelli 2002; Ventura & D’Antona 2008, 2009; Ventura & Marigo 2009; Ventura & D’Antona 2011) either use older input physics or cover a smaller range in mass and metallicity. There are also many papers that include surface abundances predictions for AGB models (a highly incomplete list includes the following examples: Kahane et al. 2000; Chieffi et al. 2001; Abia et al. 2002; Lebzelter et al. 2008; Weiss & Ferguson 2009; Campbell et al. 2010; Bisterzo et al. 2010; Kamath et al. 2012; D’Orazi et al. 2013) but not stellar yields; these are not included in Table 2.

The yields from Lagarde et al. (2011) are not included in Table 2 because they only include one isotope, ³He, although for a grid of low- and intermediate-mass models covering a large range in metallicity. Charbonnel & Lagarde (2010) examine the effects of extra mixing and rotation on the light-element yields of model stars up to 4 M_⊙ but only provide yields for ⁷Li; we therefore do not include these in Table 2.

There are fewer yields for low-metallicity AGB stars below [Fe/H] ⩽ −3 because of the difficulty of calculating the stellar evolution owing to the added complexity of proton ingestion episodes and mixing during the core He flash. Iwamoto (2009) and Campbell & Lattanzio (2008) present yields for low-metallicity AGB stars of [Fe/H] ⩽ −3, and Gil-Pons et al. (2013) provide surface abundance predictions for intermediate-mass AGB and super-AGB stars at Z = 10^{− 5} between M = 4 to 9 M_⊙. Chieffi et al. (2001) present calculations of Z = 0 intermediate-mass (4 – 8 M_⊙) AGB stars but no tabulated yields. No yields of s-process elements are available from very low-metallicity AGB models at the present (although see Campbell et al. 2010; Cruz et al. 2013).

Ideally, chemical evolution modellers would like a self-consistent set of AGB stellar yields covering a range in mass from ≈ 0.8 M_⊙ to the limit for core collapse supernovae, ≈ 10 M_⊙, for a broad range of metallicities, and for all elements from H through to Bi. In this context, none of the AGB yield sets mentioned is complete.

Some of these studies provide yields for a limited number of masses but for all elements up to bismuth (e.g., Cristallo et al. 2011; Pignatari et al. 2013). The yields by Siess (2010), Doherty et al. (2014a, 2014b), and Ventura et al. (2013) focus on light elements (up to Fe) for the mass range of stars that become super-AGB stars. The largest grid of detailed stellar yields for low- and intermediate-mass AGB stars in terms of the range of masses (1 – 6 M_⊙), metallicities (Z = 0.0001, 0.004, 0.008, 0.02), and number of species (light elements up to Fe) is still Karakas (2010) but the yields of Ventura et al. (2013) cover almost the same range of masses, elements and metallicities (but not including solar).

5.2 Summary of elements produced by low and intermediate-mass stars

The stellar yields shown here are calculated according to

(4) \begin{equation} M_{\rm i} = \int _{0}^{\tau } \left[ X(i) - X_{0} (i)\right] \frac{d M}{dt} dt, \end{equation}

where M_i is the yield of species i (in solar masses), dM/dt is the current mass-loss rate, X(i) and X ₀(i) refer to the current and initial mass fraction of species i, and τ is the total lifetime of the stellar model. The yield can be negative, in the case where the element is destroyed, and positive if it is produced.

5.2.1 Lithium

It is still an open question whether low- and intermediate-mass stars contribute to the production of ⁷Li in the Galaxy (Romano et al. 2001; Travaglio et al. 2001b; Prantzos 2012). Prantzos (2012) concluded that primordial nucleosynthesis can produce at most only about 30% of the solar Li and that stellar sources (red giants, AGB stars, novae) must be responsible for at least half. Current stellar yields of Li from AGB stars do not support this production. The stellar yields by e.g., Karakas (2010) show that only a narrow mass range of intermediate-mass AGB stars produce more Li than they destroy. This occurs when the Li produced from HBB takes place at the period of highest mass loss. At Z = 0.02 this occurs at ≈ 5 M_⊙. Super-AGB stars are also a possible source of Li (Ventura & D’Antona 2010; Ventura et al. 2013; Siess 2010; Doherty et al. 2014a).

There are many uncertainties involved in the production of ⁷Li in AGB models, including the mass-loss rates and the treatment of convective mixing (Ventura & D’Antona 2005a, 2005b; Iwamoto 2009). The stellar Li content initially rises dramatically from production through the Cameron-Fowler mechanism, but it then decreases slowly as the Li is cycled through the hot bottom of the envelope, resulting in its gradual destruction. Mass-loss rates for AGB stars, such as the formulae given by Vassiliadis & Wood (1993) and Blöcker (1995), have a superwind phase which occurs during the final few thermal pulses. The superwind phase results in a period of rapid mass loss, and most of the convective envelope is lost during this time. Thus the composition of the envelope at the start of the superwind phase critically determines the contribution that AGB stars make to the enrichment of the interstellar medium. By adjusting the mass-loss formula, one can manipulate the Li yield. In Figure 27 most of the ⁷Li has been destroyed by the time the superwind phase starts. Other factors that may influence the yields of Li include the presence of a binary companion, rotation, and the efficiency of extra mixing on the first and asymptotic giant branches (Charbonnel & Lagarde 2010; Lagarde et al. 2012).

5.2.2 Carbon, nitrogen, oxygen

AGB stars are one of the most important sources of ¹²C in the Galaxy. An estimate of the contribution of ¹²C from AGB stars suggests that they produce roughly one third of the Galaxy’s inventory of ¹²C, providing roughly the same amount as core-collapse supernovae and Wolf-Rayet stars (Dray et al. 2003). These quantitative estimates are hindered by uncertainties in the depth and onset of the third dredge-up. Figure 34 shows yields from Karakas (2010) for ¹²C, ¹⁴N, ¹⁷O, and ¹⁹F for two metallicities. At Z = 0.02 production is dominated by models of about 3 M_⊙, with no C production for models below about 2.5 M_⊙. While it is difficult to determine masses for Galactic C stars, estimates point to stars with initial masses as low as about 1.5 M_⊙ (Wallerstein & Knapp 1998) for the Galaxy. This suggests that C production is underestimated in the yields by Karakas (2010).

Figure 34. Stellar yields of ¹²C, ¹⁴N, ¹⁷O, and ¹⁹F as a function of the initial mass for models of Z = 0.02 (left-hand panels) and Z = 0.0001 (right-hand panels) from Karakas (2010). The solid line and open circles show results for the updated yields; the dashed line and closed circles show results from Karakas & Lattanzio (2007). The updated yields from Karakas (2010) use scaled-solar abundances, whereas the yields from Karakas & Lattanzio (2007) used non-solar C, N, and O to reflect the composition of the LMC and SMC. Reaction rates were also updated, which mostly affected ¹⁹F and ²³Na. Also, we used Reimer’s mass loss on the AGB in the M ⩾ 3 M_⊙, Z = 0.0001 models from Karakas (2010), whereas in Karakas & Lattanzio (2007) we used Vassiliadis & Wood (1993) on the AGB.

The isotopes ¹³C and ¹⁴N are produced by the CNO cycles and mixed to the surface by first and second dredge-up prior to the AGB, and by HBB during the AGB. Figure 34 shows that the yields of N are dominated by intermediate-mass stars that experience HBB (see also Frost et al. 1998a; Chieffi et al. 2001; Pols et al. 2012). Chemical evolution models with AGB yields show that low-metallicity intermediate-mass stars play an essential role in the production of N along with massive rotating stars (e.g., Fenner et al. 2004; Romano et al. 2010; Kobayashi et al. 2011b).

Canonical AGB models do not produce substantial quantities of elemental O and stellar yields from such models are generally negligible, except at the lowest metallicities (e.g., at Z ⩽ 10^{− 4} Karakas & Lattanzio 2007; Campbell & Lattanzio 2008; Karakas 2010; Cristallo et al. 2011). Intermediate-mass stars of low metallicity can destroy a significant amount of ¹⁶O by HBB such that the surface oxgyen abundance decreases by 0.5 – 1.0 dex, depending on the stellar model (Ventura et al. 2013). The stellar yields by Pignatari et al. (2013), which include diffusive convective overshoot into the C–O core, suggest that low-mass AGB stars may be an important source of ¹⁶O in the Universe. Chemical evolution models that use these yields are needed to test the idea.

The only O isotope produced by canonical models is ¹⁷O which is produced by the CNO cycle during HBB. Kobayashi et al. (2011b) examined the evolution of the isotopic ¹⁶O/¹⁷O and ¹⁶O/¹⁸O ratios taking into account the contributions from Type II SNe and AGB stars. It was found that while the solar ¹⁶O/¹⁸O ratio is well matched by current yields, the present-day ratio for ¹⁶O/¹⁷O was too low, indicating an over-production of ¹⁷O by AGB models. This may put constraints on the rates of the ¹⁷O + p reactions, which are uncertain at stellar energies (e.g., Chafa et al. 2007; Sergi et al. 2010).

5.2.3 Fluorine

The cosmic origin of fluorine is not yet completely understood. Core collapse supernovae (Woosley & Weaver 1995) and stellar winds from Wolf Rayet stars (Meynet & Arnould 2000) are both predicted to release F-enriched material into the ISM, alongside AGB stars (Renda et al. 2004). Observationally, AGB stars and their progeny (e.g., post-AGB stars, planetary nebulae) are the only confirmed site of F production (Jorissen et al. 1992; Werner et al. 2005; Zhang & Liu 2005; Pandey 2006; Schuler et al. 2007; Abia et al. 2010; Lucatello et al. 2011), with no clear indication for enhanced F abundances resulting from the ν-process in a region shaped by past SNe (Federman et al. 2005). Recio-Blanco et al. (2012) noted that AGB stars are likely the dominant source of F in the cool main-sequence dwarfs they observed in the solar neighbourhood.

Figure 34 shows that F production is coupled with C production. Observations also show a clear correlation between [F/O] content and C/O in AGB stars (Jorissen et al. 1992, and Figure 22). The stellar yields follow a similar function in mass and metallicity space. This means that the uncertainties that are the most significant for C similarly affect F, although with the added complication that the reaction rates involved in F production in the He shell are rather uncertain as discussed in Section 3.5.

Kobayashi et al. (2011a) provide the most recent estimates of the chemical evolution of F using updated AGB yields as well as the latest ν-process yields from core-collapse SNe (see also Sánchez-Blázquez et al. 2012). The model by Kobayashi et al. (2011a) was able to reproduce the F abundances observed in field stars covering a range of metallicities, with SNe dominating production at the lowest metallicities (here using O as the tracer, [O/H] ≲ −1.2), followed by a rapid increase from AGB stars at around [O/H] ≈ −0.5.

5.2.4 From neon to iron

The yields of elemental Ne from AGB stars are generally small, except in the case when substantial ²²Ne is produced during thermal pulses (Karakas & Lattanzio 2003a). Kobayashi et al. (2011b) found that the contribution of AGB stars was essential for matching the solar Ne isotopic ratios (see also Gibson, Fenner, & Kiessling 2005). Without AGB stars the contribution from SNe dominate and produce too much ²⁰Ne relative to the neutron-rich ²¹Ne and ²²Ne.

Intermediate-mass AGB stars produce some Na via the Ne–Na chain (Forestini & Charbonnel 1997; Mowlavi 1999b; Ventura et al. 2013), although production is highly dependent on the uncertain rates of the ²³Na + p reactions (Hale et al. 2004; Izzard et al. 2007). The AGB models used by Fenner et al. (2004) produced copious sodium and led to much larger [Na/Fe] abundances compared to observations of globular cluster stars (see also Gibson 2007). The stellar models in Karakas (2010) produced between ~ 6 to 30 times less Na compared to the stellar models in Karakas & Lattanzio (2007) as a result of using updated reaction rates. Figure 35 shows the difference for the Z = 0.004 models. Using the updated yields from Karakas (2010), Kobayashi et al. (2011b) found that AGB stars do not noticeably affect the chemical evolution of Na in the Milky Way Galaxy.

Figure 35. Stellar yields of ²³Na as a function of the initial mass for models of Z = 0.004. The solid line and open circles show results from Karakas (2010), while the dashed line and closed circles show results from Karakas & Lattanzio (2007).

The yields of Na and Al from AGB stars are also critically dependent on model assumptions and in particular on the convective model and temperature structure of the envelope (Ventura & D’Antona 2005a). While the Na and Al yields of Karakas (2010) are reasonably small, the yields from Ventura et al. (2013) suggest that intermediate-mass AGB and super-AGB stars may be substantial producers of Na and Al at low metallicities (Ventura et al. 2011).

The neutron-rich isotopes of Mg are produced by intermediate-mass AGB stars alongside core collapse SNe. The amounts of ²⁵Mg and ²⁶Mg produced by low-metallicity intermediate-mass AGB stars can be enough to affect the galactic chemical evolution of these isotopes. Fenner et al. (2003) found that the contribution of AGB stars was essential to explain the Mg isotopic ratios observed in cool evolved field stars (Gay & Lambert 2000; Yong et al. 2003b). Kobayashi et al. (2011b) noted that their chemical evolution model predicted higher than present-day solar ratios for ²⁴Mg/^{25, 26}Mg using yields from AGB stars and SNe and concluded that AGB stars (or some other source, such as Wolf Rayet stars) need to produce more ²⁵Mg and ²⁶Mg.

Phosphorus and Sc can also be produced in small quantities by AGB stars as a consequence of neutron captures in the He intershell (Smith et al. 1987; Karakas et al. 2012). Most of the other intermediate-mass elements including Si, Cl, Ar, K, Mn are not significantly produced by AGB nucleosynthesis except for small isotopic shifts caused by neutron captures (Karakas et al. 2009). The predicted isotopic shifts, which include increases in the neutron-rich ^{29, 30}Si, can be compared to measurements of the Si isotopes in pre-solar silicon carbide grains. We refer to Lugaro et al. (1999) and references therein for details (see also Zinner et al. 2006; Zinner 2008; Lewis et al. 2013).

5.2.5 Heavy elements produced by the s-process

The contribution from AGB stars is crucial to understand the origin and evolution of elements heavier than iron. About half of all heavy elements are produced by the s-process, and most of those elements are produced by AGB stars. One current uncertainty is the Galactic epoch at which AGB stars begin contributing toward the bulk Galactic chemical evolution of elements. Simmerer et al. (2004) suggested this epoch occurred around [Fe/H] ≳ −1, but that AGB stars can contribute inhomogeneously (locally) from [Fe/H] ≳ −3. This is also the metallicity at which CEMP stars with s-process elements become more common, compared to the CEMP stars without neutron-capture element overabundances, which dominate at lower metallicities (Beers & Christlieb 2005; Sneden et al. 2008; Frebel & Norris 2013).

Unfortunately, stellar yields from AGB stars that include predictions for heavy elements are even more incomplete than for light elements. The yields by Cristallo et al. (2011) include a complete network of elements to Bi for masses to 3 M_⊙, these were extended to 4, 5, and 6 M_⊙ AGB models for one metallicity (Z = 0.0003) by Straniero et al. (2014); Pignatari et al. (2013) include yields for three AGB masses at two metallicities (Z = 0.01 and 0.02); and Fishlock et al. (2014, submitted) present yields for M = 1 to 7 M_⊙ at one metallicity, Z = 0.001. Lugaro et al. (2012) present tables of stellar abundance predictions as a function of thermal pulse number from models from 0.9 to 6 M_⊙ for only one metallicity (Z = 0.0001 or [Fe/H] = − 2.3). The predictions from Lugaro et al. (2012) are not included in Table 2 because integrated yields are not provided.

For super-AGB stars the situation is even worse. The only s-process calculations currently published are for a single 9 M_⊙, Z = 0.02 model in Karakas et al. (2012) and only for a limited nuclear network up to Mo. No yield tables were included with that study. Wanajo et al. (2011) calculate r-process yields from electron-capture SNe, which have evolved from super-AGB stars with massive O–Ne cores.

There have been various chemical evolution models that focus on the evolution of the neutron-capture elements and the contribution of AGB stars (e.g., Raiteri et al. 1999; Travaglio et al. 1999, 2001a, 2004; Fenner et al. 2006; Serminato et al. 2009; Hansen et al. 2013). In these models, the yields of s-process elements are included by extrapolating from the existing models, especially for intermediate-mass AGB stars where there are no or few existing theoretical predictions.

We comment on the production of s-process elements from intermediate-mass AGB stars. While the contribution from low-mass AGB stars to the chemical evolution of Ba and Pb is well supported by models and observations (Travaglio et al. 2001a), the contribution from intermediate-mass AGB stars has for some time been seen as minimal. For example, Travaglio et al. (2004) estimate that intermediate-mass stars contribute ≈ 8%, 6%, 6%, 1%, and 5% toward the solar-system composition of Sr, Y, Zr, Nb, and Mo, respectively. However, observational evidence suggests that intermediate-mass AGB stars produce substantial amounts of Rb (García-Hernández et al. 2006). Chemical evolution models are required, with a complete set of intermediate-mass and super-AGB yields, to quantitatively assess the impact of intermediate-mass stars on the chemical evolution of Rb.

We finish with a discussion of another uncertainty on stellar yield predictions: the effect of helium enrichment. Karakas et al. (2014) study the effect of helium enrichment on AGB evolution and nucleosynthesis for two masses (M = 1.7, 2.36 M_⊙) at two metallicities appropriate for the GC ω Centauri (Z = 0.0003, 0.0006, which is roughly [Fe/H] ≈ −1.8 and − 1.4, respectively). An increase of ΔY = 0.10 at a given mass decreases the yields of C by up to ≈ 60%, of F by up to 80%, and the yields of the s-process elements Ba and La by ≈ 45%. The main reason is that an increase of ΔY = 0.10 leads to roughly a factor of 3 decrease in the amount of dredged up material during the AGB. The lifetimes of He-enriched models are significantly shorter than their counterparts with primordial He content, which means that they will contribute to the chemical evolution of a system sooner.

It may not be enough to simply evolve grids of stellar evolutionary sequences covering a range in mass and metallicity. Variations in the helium mass fraction have a significant impact on the stellar yields and may be an important third parameter. This reminds us of the days before the primordial He abundance was determined, and stellar models were typically published with a spread of Y values.

6 SUMMARY AND OUTLOOK

Stellar yields are a key ingredient in chemical evolution models. Low- and intermediate-mass stars are an integral part of galaxies and help shape their evolution, gas and dust content, as well as their integrated light. Even stars as low as 0.9 M_⊙ can, at low metallicity, contribute to the chemical evolution of elements. The days of only considering supernovae are over. However, for low- and intermediate-mass stars to be included, theoretical predictions from stars covering a large range in mass and metallicity need to be calculated.

In this review we have discussed the various mixing processes that affect the surface composition and yields of stars less massive than about 10 M_⊙. These recurrent mixing events can significantly change the surface composition of the envelope, with the richest nucleosynthesis occurring during the AGB phase of evolution. AGB stars are observed to show enrichments in C, N, F, and heavy elements synthesised by the s-process. AGB stars release their nucleosynthesis products through stellar outflows or winds, in contrast to massive stars that explode as core-collapse SNe.

Supercomputers have allowed the calculation of stellar yields from detailed (but still single!) AGB models covering large ranges in mass and composition. While significant progress has been made over the past decade, there are still crucial gaps, especially for elements produced by the s-process for all mass and metallicity ranges. This is mostly because many nuclear species (on the order of hundreds) are required to accurately model the s-process and the computational time required is still significant (e.g., months of supercomputer time on a single CPU is required for an intermediate-mass AGB model of low metallicity).

Gaps in our knowledge are also apparent for AGB stars of very low metallicity (e.g., [Fe/H] ⩽ −3). More theoretical effort is needed to address these gaps, especially because current and new surveys (e.g., SEGUE, GALAH, APOGEE, and GAIA-ESO) will provide spectra of hundreds of thousands of stars in all regions of our Milky Way Galaxy including in the metal-poor halo. These huge surveys are going to drive dramatic improvements in the reliability of stellar models, by providing data that show inconsistencies and errors in our current understanding. Detailed nucleosynthesis models of AGB stars and SNe at low metallicity will be required in order to disentangle their history or to provide insight into the nature of the Galaxy at the earliest times.

Many significant uncertainties affect the stellar yield calculations, such as convection and mass loss, and these in turn affect the accuracy and reliability of chemical evolution model predictions. Convection has proven to be a persistent problem in one-dimensional stellar evolution calculations. While we have better observations with which to constrain convection and convective borders in AGB models to calibrate any given stellar evolution code, we are only slowly improving our understanding of the physics of convection in stellar interiors (Meakin & Arnett 2007; Arnett, Meakin, & Young 2009; Viallet et al. 2013).

The Spitzer Space Telescope has provided important insight into the nature of mass loss in evolved stars. We have learnt that mass-loss rates are not necessarily smaller at low metallicity owing to the copious dredge-up of primary C. We also presumably have a better understanding of the theory of mass loss, at least for C-rich AGB stars and progress is being made for O-rich AGB stars as well.

Non-standard physics such as rotation and thermohaline mixing are now starting to be included in stellar evolutionary calculations and the first yields are appearing, albeit only for a small number of isotopes. Chemical evolution calculations using these yields show the importance of these physical phenomena on the evolution of light species such as ³He, ⁷Li, and the C isotopes. Ideally these calculations should be extended to include all species affected by extra mixing.

Where will we be in the next 5 to 20 years? Future effort must go into understanding how convection operates in stellar interiors. This is singly the most important and crucial uncertainty and one that requires multi-dimensional calculations on supercomputers. Advances driven by supercomputers will reveal insights into the nature of ¹³C pocket formation in low-mass AGB stars as well as help solve the puzzle of the O abundances observed in post-AGB stars (e.g., is there really overshoot into the C–O core?). We still have some way to go to unravel these puzzles!

Supercomputers will also help drive advances in our understanding of rotation and magnetic fields in stellar interiors, as well as non-convective extra mixing processes. While progress has been made in understanding how thermohaline mixing operates in red giant envelopes, we still do not know if thermohaline mixing is efficient in AGB stars. Some form of non-convective mixing is needed to drive changes that we know occur in the envelopes of low-metallicity AGB stars (e.g., low-observed ¹²C/¹³C ratios compared to AGB yields).

The greatest understanding of mass loss from evolved stars will be driven by observations from e.g., ALMA and James Webb Space Telescope (JWST). ALMA is already starting to probe the clumpy nature of mass loss from evolved stars and supergiants. While thermonuclear reaction rates are probably the least of our worries for low- and intermediate-mass stars, we know that some key rates (e.g., those that destroy ²³Na and the neutron-producing reactions) are still highly uncertain and can effect stellar yields. New experimental facilities such as the Facility for Rare Isotope Beams being built at the University of Michigan will provide new experimental data.

Stellar yields from populations of binaries covering a range of metallicities are desperately needed. Most stars are in binaries and many will interact. The interactions can lead to dramatic outcomes such as Type Ia SNe, which play an essential role in chemical evolution (and cosmology), but also less energetic outcomes such as novae, symbiotic stars, barium and CH stars, and CEMP stars. Binary evolution will also change the yields from a single stellar population but exactly how still needs to be determined.

In the next 10 years there will be an explosion of new stellar abundance data driven by new surveys and instruments (e.g., the GALAH survey using High Efficiency and Resolution Multi-Element Spectograph (HERMES) on the Anglo-Australian Telescope (AAT), the GAIA-ESO survey, Large Sky Area Multi-Object Fibre Spectroscopic Telescope (LAMOST), APOGEE etc.). These data will help answer big questions facing astronomy including how stars evolve and produce elements and how the elements are ejected to enrich the Universe, as well as questions related to the formation and evolution of galaxies. These tremendous investments in astronomical infrastructure will pay the largest dividends when augmented by complementary theoretical and modelling research.