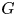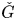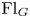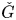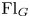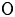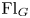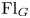1. Introduction
1.1 Reminder about the work of [Reference Arkhipov and BezrukavnikovAB09]
1.1.1
Let ![]() $G$ be a reductive group over an algebraically closed field
$G$ be a reductive group over an algebraically closed field ![]() $\mathsf {k}$. Fix a pair (
$\mathsf {k}$. Fix a pair (![]() $B$,
$B$, ![]() $B^-$) of opposite Borel subgroups, and denote by
$B^-$) of opposite Borel subgroups, and denote by ![]() $N$ and
$N$ and ![]() $N^-$ their unipotent radicals, respectively. Denote by
$N^-$ their unipotent radicals, respectively. Denote by ![]() $\mathcal {K}=\mathsf {k}(\!(t)\!)$ the field of Laurent series and by
$\mathcal {K}=\mathsf {k}(\!(t)\!)$ the field of Laurent series and by ![]() $\mathcal {O}=\mathsf {k}[\![t]\!]$ the ring of formal power series. We denote by
$\mathcal {O}=\mathsf {k}[\![t]\!]$ the ring of formal power series. We denote by ![]() $G(\mathcal {K})$ the loop group of
$G(\mathcal {K})$ the loop group of ![]() $G$, by
$G$, by ![]() $I$ the Iwahori subgroup, and by
$I$ the Iwahori subgroup, and by ![]() ${\operatorname {Fl}}_G:= G(\mathcal {K})/I$ the affine flags. In this section, we assume
${\operatorname {Fl}}_G:= G(\mathcal {K})/I$ the affine flags. In this section, we assume ![]() $\mathsf {k}=\mathbb {C}$.
$\mathsf {k}=\mathbb {C}$.
It is known that the category of D-modules on ![]() ${\operatorname {Fl}}_G$, with certain equivariance properties, can be realized in terms of the category of representations of the Langlands dual group
${\operatorname {Fl}}_G$, with certain equivariance properties, can be realized in terms of the category of representations of the Langlands dual group ![]() $\check {G}$.
$\check {G}$.
An important equivariance condition is the Whittaker condition. Denote by ![]() $N(\mathcal {K})$ the loop group of
$N(\mathcal {K})$ the loop group of ![]() $N$. We refer to the category of Whittaker D-modules on
$N$. We refer to the category of Whittaker D-modules on ![]() ${\operatorname {Fl}}_G$ as the (DG) category of D-modules on
${\operatorname {Fl}}_G$ as the (DG) category of D-modules on ![]() ${\operatorname {Fl}}_G$ which are
${\operatorname {Fl}}_G$ which are ![]() $N(\mathcal {K})$-equivariant against a non-degenerate character
$N(\mathcal {K})$-equivariant against a non-degenerate character ![]() $\chi$. We denote it by
$\chi$. We denote it by ![]() $\operatorname {Whit}(\operatorname {D-mod}({\operatorname {Fl}}_G))$. A well-known result of Arkhipov and Bezrukavnikov [Reference Arkhipov and BezrukavnikovAB09] states that there is an equivalence of categories
$\operatorname {Whit}(\operatorname {D-mod}({\operatorname {Fl}}_G))$. A well-known result of Arkhipov and Bezrukavnikov [Reference Arkhipov and BezrukavnikovAB09] states that there is an equivalence of categories
In the above formula, ![]() $\tilde {\mathcal {N}}:= T^*(\check {G}/\check {B})$ is the Springer resolution of the nilpotent cone, and
$\tilde {\mathcal {N}}:= T^*(\check {G}/\check {B})$ is the Springer resolution of the nilpotent cone, and ![]() $\operatorname {QCoh}(\tilde {\mathcal {N}}/\check {G})$ is the (DG) category of
$\operatorname {QCoh}(\tilde {\mathcal {N}}/\check {G})$ is the (DG) category of ![]() $\check {G}$-equivariant quasi-coherent sheaves on
$\check {G}$-equivariant quasi-coherent sheaves on ![]() $\tilde {\mathcal {N}}$.
$\tilde {\mathcal {N}}$.
It is natural to consider the following question.
Question 1 What is the deformed version of (1.1.1)?
1.1.2
It is expected that (1.1.1) deforms over the space of levels, i.e. the space of Weyl group-invariant symmetric bilinear forms on ![]() $\Lambda$. Here
$\Lambda$. Here ![]() $\Lambda$ is the coweight lattice of
$\Lambda$ is the coweight lattice of ![]() $G$.
$G$.
The left-hand side of (1.1.1) admits a naturally defined level-parameterized deformation. Namely, a level ![]() $\kappa$ gives rise to a twisting, and we can consider
$\kappa$ gives rise to a twisting, and we can consider ![]() $\kappa$-twisted D-modules on
$\kappa$-twisted D-modules on ![]() ${\operatorname {Fl}}_G$. Then
${\operatorname {Fl}}_G$. Then ![]() $\operatorname {Whit}(\operatorname {D-mod}_{\kappa }({\operatorname {Fl}}_G))$, the category of
$\operatorname {Whit}(\operatorname {D-mod}_{\kappa }({\operatorname {Fl}}_G))$, the category of ![]() $\kappa$-twisted Whittaker D-modules on
$\kappa$-twisted Whittaker D-modules on ![]() ${\operatorname {Fl}}_G$, is defined as the category of
${\operatorname {Fl}}_G$, is defined as the category of ![]() $(N(\mathcal {K}),\chi )$-equivariant
$(N(\mathcal {K}),\chi )$-equivariant ![]() $\kappa$-twisted D-modules on
$\kappa$-twisted D-modules on ![]() ${\operatorname {Fl}}_G$.
${\operatorname {Fl}}_G$.
The deformation of the right-hand side of (1.1.1) is not obvious. In order to present it, we rewrite ![]() $\tilde {\mathcal {N}}/\check {G}$ as
$\tilde {\mathcal {N}}/\check {G}$ as ![]() $\check {\mathfrak {n}}/\check {B}$. Here
$\check {\mathfrak {n}}/\check {B}$. Here ![]() $\check {\mathfrak {n}}$ is the Lie algebra of the unipotent radical
$\check {\mathfrak {n}}$ is the Lie algebra of the unipotent radical ![]() $\check {N}$ of
$\check {N}$ of ![]() $\check {B}$, and the action of
$\check {B}$, and the action of ![]() $\check {B}$ on
$\check {B}$ on ![]() $\check {\mathfrak {n}}$ is the adjoint action.
$\check {\mathfrak {n}}$ is the adjoint action.
A quasi-coherent sheaf on ![]() $\check {\mathfrak {n}}/\check {B}$ is a
$\check {\mathfrak {n}}/\check {B}$ is a ![]() $\mathcal {O}(\check {\mathfrak {n}})$-module with a compatible action of
$\mathcal {O}(\check {\mathfrak {n}})$-module with a compatible action of ![]() $\check {B}$. It can be regarded as a
$\check {B}$. It can be regarded as a ![]() $\Lambda$-graded vector space with compatible actions of
$\Lambda$-graded vector space with compatible actions of ![]() $\mathop {\operatorname {\rm Sym}}(\check {\mathfrak {n}}^-)$ and
$\mathop {\operatorname {\rm Sym}}(\check {\mathfrak {n}}^-)$ and ![]() $U(\check {\mathfrak {n}})$, with the locally nilpotent condition. The universal enveloping algebra
$U(\check {\mathfrak {n}})$, with the locally nilpotent condition. The universal enveloping algebra ![]() $U(\check {\mathfrak {n}})$ naturally deforms. Namely, the Lusztig quantum group
$U(\check {\mathfrak {n}})$ naturally deforms. Namely, the Lusztig quantum group ![]() $U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ provides a deformation of
$U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ provides a deformation of ![]() $U(\check {\mathfrak {n}})$ over the space of levels. Here the relation between the level
$U(\check {\mathfrak {n}})$ over the space of levels. Here the relation between the level ![]() $\kappa$ and the quantum parameter
$\kappa$ and the quantum parameter
is given by ![]() $q(\lambda )= \exp (\pi i\cdot \kappa (\lambda,\lambda ))$ for
$q(\lambda )= \exp (\pi i\cdot \kappa (\lambda,\lambda ))$ for ![]() $\lambda \in \Lambda$. Note that
$\lambda \in \Lambda$. Note that ![]() $\mathop {\operatorname {\rm Sym}}(\check {\mathfrak {n}}^-)$ is the graded dual of
$\mathop {\operatorname {\rm Sym}}(\check {\mathfrak {n}}^-)$ is the graded dual of ![]() $U(\check {\mathfrak {n}})$, so the graded dual of
$U(\check {\mathfrak {n}})$, so the graded dual of ![]() $U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ provides a deformation of
$U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ provides a deformation of ![]() $\mathop {\operatorname {\rm Sym}}(\check {\mathfrak {n}}^-)$ over the space of levels.
$\mathop {\operatorname {\rm Sym}}(\check {\mathfrak {n}}^-)$ over the space of levels.
From this point of view, the right-hand side of (1.1.1) has a deformation. It is given by the category of representations of a certain quantum group, whose positive part is the Lusztig quantum group ![]() $U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ and the negative part is the De Concini–Kac quantum group
$U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ and the negative part is the De Concini–Kac quantum group ![]() $U^{\rm DK}_{\rm q}(\check {\mathfrak {n}}^-)$ (i.e. the graded dual of the Lusztig quantum group). It is exactly the category of representations of the mixed quantum group introduced by Gaitsgory in [Reference GaitsgoryGai21a, § 5.3], which is denoted by
$U^{\rm DK}_{\rm q}(\check {\mathfrak {n}}^-)$ (i.e. the graded dual of the Lusztig quantum group). It is exactly the category of representations of the mixed quantum group introduced by Gaitsgory in [Reference GaitsgoryGai21a, § 5.3], which is denoted by ![]() ${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}_{\rm q}(\check {G})$.
${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}_{\rm q}(\check {G})$.
Now it is natural to ask the following question.
Question 2 Is there an equivalence
1.2 Main theorem of this paper
The weak version of the main theorem (Theorem 3.3.2) says that, when ![]() $q$ avoids small torsion (see § 3.3.1), there exists a t-exact equivalence of categories between
$q$ avoids small torsion (see § 3.3.1), there exists a t-exact equivalence of categories between ![]() $\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ and
$\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ and ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$. Furthermore, both
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$. Furthermore, both ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ and
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ and ![]() $\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ acquire structures of highest weight categories,Footnote 1 and the equivalence functor preserves highest weight category structure.
$\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ acquire structures of highest weight categories,Footnote 1 and the equivalence functor preserves highest weight category structure.
However, Theorem 6.4.8, the strong version of the main theorem, proves a more general statement, where we do not need to assume that the base field of schemes is ![]() $\mathbb {C}$ and the sheaf category is the category of D-modules.
$\mathbb {C}$ and the sheaf category is the category of D-modules.
Let ![]() $\mathsf {k}$ denote the base field of schemes, and let
$\mathsf {k}$ denote the base field of schemes, and let ![]() $\mathsf {e}$ denote the coefficients field of sheaves. Note that (1.1.2) only makes sense when
$\mathsf {e}$ denote the coefficients field of sheaves. Note that (1.1.2) only makes sense when ![]() $\mathsf {k}=\mathsf {e}=\mathbb {C}$, otherwise we cannot define D-modules and the mixed quantum group simultaneously. In this case,
$\mathsf {k}=\mathsf {e}=\mathbb {C}$, otherwise we cannot define D-modules and the mixed quantum group simultaneously. In this case, ![]() ${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$ can be realized as the category of factorization modules [Reference GaitsgoryGai21b] over a factorization algebra
${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$ can be realized as the category of factorization modules [Reference GaitsgoryGai21b] over a factorization algebra ![]() $\Omega _{\rm q}^{{L,'}}$. Instead of working with
$\Omega _{\rm q}^{{L,'}}$. Instead of working with ![]() ${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$, we compare
${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$, we compare ![]() $\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ with this factorization module category.
$\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ with this factorization module category.
The advantage of using factorization modules lies in the fact that the statement involving factorization modules is geometric (i.e. motivic). Rather than D-modules, we can also consider factorization modules in the settings of the ![]() $\ell$-adic sheaves and the constructible sheaves with arbitrary coefficients
$\ell$-adic sheaves and the constructible sheaves with arbitrary coefficients ![]() $\mathsf {e}$.
$\mathsf {e}$.
Theorem 6.4.8 claims that there is a t-exact equivalence of highest weight categories
In the above formula:
–
 $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G)$ is the category of twisted Whittaker sheaves on
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G)$ is the category of twisted Whittaker sheaves on  ${\operatorname {Fl}}_G$;
${\operatorname {Fl}}_G$;–
 $\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$ is the category of factorization modules over
$\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$ is the category of factorization modules over  $\Omega _{\rm q}^{{\rm L},\prime }$.
$\Omega _{\rm q}^{{\rm L},\prime }$.
This theorem holds in a greater generality: in addition to D-modules, it is true for all the sheaves contexts listed in § 1.6.1 and any ![]() $q$.
$q$.
1.3 Other motivations
In this section, we provide motivations for Theorem 3.3.2 other than those coming from the work of [Reference Arkhipov and BezrukavnikovAB09]. We assume ![]() $\mathsf {k}=\mathsf {e}=\mathbb {C}$ in this section.
$\mathsf {k}=\mathsf {e}=\mathbb {C}$ in this section.
1.3.1 Fundamental local equivalence
Another main idea that motivates this work comes from the quantum local Langlands conjecture. We explain it in this section.
In [Reference GaitsgoryGai18b], Gaitsgory proposed a very general conjecture of the quantum Langlands program.
Consider the category ![]() $\operatorname {D-mod}_\kappa (G(\mathcal {K}))$ of
$\operatorname {D-mod}_\kappa (G(\mathcal {K}))$ of ![]() $\kappa$-twisted D-modules on the loop group
$\kappa$-twisted D-modules on the loop group ![]() $G(\mathcal {K})$. The group structure on
$G(\mathcal {K})$. The group structure on ![]() $G(\mathcal {K})$ induces a monoidal structure on this category. We denote by
$G(\mathcal {K})$ induces a monoidal structure on this category. We denote by ![]() $G(\mathcal {K}){\operatorname {-mod}}_\kappa$ the 2-category of module categories over this monoidal category. The quantum local Langlands conjecture asserts the following equivalences.
$G(\mathcal {K}){\operatorname {-mod}}_\kappa$ the 2-category of module categories over this monoidal category. The quantum local Langlands conjecture asserts the following equivalences.
Conjecture 1
(1) There is an equivalence of categories,
(1.3.1)Here \begin{equation} G(\mathcal{K}){\operatorname{-mod}}_{-\kappa}\simeq \check{G}(\mathcal{K}){\operatorname{-mod}}_{\check{\kappa}}. \end{equation}
\begin{equation} G(\mathcal{K}){\operatorname{-mod}}_{-\kappa}\simeq \check{G}(\mathcal{K}){\operatorname{-mod}}_{\check{\kappa}}. \end{equation} $\check {\kappa }$ denotes the dual level of
$\check {\kappa }$ denotes the dual level of  $\kappa$ (see [Reference Gaitsgory and LysenkoGL19, 0.1.1]).
$\kappa$ (see [Reference Gaitsgory and LysenkoGL19, 0.1.1]).(2) If
 $\mathcal {C}\in G(\mathcal {K}){\operatorname {-mod}}_{-\kappa }$ goes to
$\mathcal {C}\in G(\mathcal {K}){\operatorname {-mod}}_{-\kappa }$ goes to  $\check {\mathcal {C}}\in \check {G}(\mathcal {K}){\operatorname {-mod}}_{\check {\kappa }}$ under the equivalence (1.3.1), then their Iwahori strong invariants [Reference BeraldoBer17, § 4] are equivalent
(1.3.2)
$\check {\mathcal {C}}\in \check {G}(\mathcal {K}){\operatorname {-mod}}_{\check {\kappa }}$ under the equivalence (1.3.1), then their Iwahori strong invariants [Reference BeraldoBer17, § 4] are equivalent
(1.3.2) \begin{equation} \mathcal{C}^{I}\simeq \check{\mathcal{C}}^{\check{I}}. \end{equation}
\begin{equation} \mathcal{C}^{I}\simeq \check{\mathcal{C}}^{\check{I}}. \end{equation}Namely, the category of
 $\operatorname {D-mod}_{-\kappa }(G(\mathcal {K}))$-equivariant functors from
$\operatorname {D-mod}_{-\kappa }(G(\mathcal {K}))$-equivariant functors from  $\operatorname {D-mod}_{-\kappa }({\operatorname {Fl}}_G))$ to
$\operatorname {D-mod}_{-\kappa }({\operatorname {Fl}}_G))$ to  $\mathcal {C}$, is equivalent to the category of
$\mathcal {C}$, is equivalent to the category of  $\operatorname {D-mod}_{\check {\kappa }}(\check {G}(\mathcal {K}))$-equivariant functors from
$\operatorname {D-mod}_{\check {\kappa }}(\check {G}(\mathcal {K}))$-equivariant functors from  $\operatorname {D-mod}_{\check {\kappa }}({\operatorname {Fl}}_{\check {G}})$ to
$\operatorname {D-mod}_{\check {\kappa }}({\operatorname {Fl}}_{\check {G}})$ to  $\check {\mathcal {C}}$.
$\check {\mathcal {C}}$.
Conjectural 1 is supposed to be characterized by the property that it intertwines the Whittaker model and the Kac–Moody model. The functor sending ![]() $\mathcal {C}\in G(\mathcal {K}){\operatorname {-mod}}_{-\kappa }$ to its Whittaker model is co-represented by
$\mathcal {C}\in G(\mathcal {K}){\operatorname {-mod}}_{-\kappa }$ to its Whittaker model is co-represented by ![]() $\operatorname {D-mod}_{-\kappa }(G(\mathcal {K})/N(\mathcal {K}),\chi )$. The functor sending
$\operatorname {D-mod}_{-\kappa }(G(\mathcal {K})/N(\mathcal {K}),\chi )$. The functor sending ![]() $\check {\mathcal {C}}\in \check {G}(\mathcal {K}){\operatorname {-mod}}_{\check {\kappa }}$ to its Kac–Moody model is co-represented by the category of Kac–Moody representations
$\check {\mathcal {C}}\in \check {G}(\mathcal {K}){\operatorname {-mod}}_{\check {\kappa }}$ to its Kac–Moody model is co-represented by the category of Kac–Moody representations ![]() $\hat {\check {\mathfrak {g}}}_{\check {\kappa }}{\operatorname {-mod}}$. Hence,
$\hat {\check {\mathfrak {g}}}_{\check {\kappa }}{\operatorname {-mod}}$. Hence,
under the equivalence (1.3.1).
By applying property (2) of Conjecture 1 to (1.3.3), we arrive the following conjectural equivalence,Footnote 2 which was proposed by Gaitsgory and Lurie [Reference GaitsgoryGai16, Conjecture 3.11].
Conjecture 2 (Iwahori fundamental local equivalence)
There is an equivalence of categories
Here ![]() $\hat {\check {\mathfrak {g}}}_{\check {\kappa }}{\operatorname {-mod}}^{\check {I}}$ denotes the category of Iwahori-integrable Kac–Moody representations.
$\hat {\check {\mathfrak {g}}}_{\check {\kappa }}{\operatorname {-mod}}^{\check {I}}$ denotes the category of Iwahori-integrable Kac–Moody representations.
In the upcoming paper [Reference Chen and FuCF21] of Chen and Fu, the authors prove that ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is equivalent to
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is equivalent to ![]() $\hat {\check {\mathfrak {g}}}_{\check {\kappa }}{\operatorname {-mod}}^{\check {I}}$. Hence, the combination of our papers provides a new proof of Conjecture 2.
$\hat {\check {\mathfrak {g}}}_{\check {\kappa }}{\operatorname {-mod}}^{\check {I}}$. Hence, the combination of our papers provides a new proof of Conjecture 2.
1.3.2 Relation with Kazhdan–Lusztig
By [Reference Kazhdan and LusztigKL93, Reference Kazhdan and LusztigKL94], ![]() ${\operatorname {Rep}}_{\rm q}(\check {G})$, the category of representations of the quantum group, is equivalent to the category of
${\operatorname {Rep}}_{\rm q}(\check {G})$, the category of representations of the quantum group, is equivalent to the category of ![]() $\check {G}(\mathcal {O})$-integrable Kac–Moody representations. Furthermore, by [Reference Campbell, Dhillon and RaskinCDR21], the latter is equivalent to the twisted Whittaker category on the affine Grassmannian
$\check {G}(\mathcal {O})$-integrable Kac–Moody representations. Furthermore, by [Reference Campbell, Dhillon and RaskinCDR21], the latter is equivalent to the twisted Whittaker category on the affine Grassmannian ![]() ${\operatorname {Gr}}_G:= G(\mathcal {K})/G(\mathcal {O})$. Hence, there is an equivalence of categories
${\operatorname {Gr}}_G:= G(\mathcal {K})/G(\mathcal {O})$. Hence, there is an equivalence of categories
Theorem 3.3.2 provides a tamely ramified version of the above equivalence of categories.
1.3.3 BGG Category  $\mathsf {O}$
$\mathsf {O}$
When ![]() $q$ is generic, the Lusztig quantum group
$q$ is generic, the Lusztig quantum group ![]() $U_{\rm q}^{\rm L}(\check {\mathfrak {n}}^-)$ is naturally isomorphic to the De Concini–Kac quantum group
$U_{\rm q}^{\rm L}(\check {\mathfrak {n}}^-)$ is naturally isomorphic to the De Concini–Kac quantum group ![]() $U_{\rm q}^{\rm DK}(\check {\mathfrak {n}}^-)$. In particular, the category
$U_{\rm q}^{\rm DK}(\check {\mathfrak {n}}^-)$. In particular, the category ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is equivalent to the quantum category
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is equivalent to the quantum category ![]() $\mathsf {O}$ in [Reference Bernstein, Gelfand and GelfandBGG71] when
$\mathsf {O}$ in [Reference Bernstein, Gelfand and GelfandBGG71] when ![]() $q$ is generic. Thus, in this case, Theorem 3.3.2 gives a geometric realization of the quantum category
$q$ is generic. Thus, in this case, Theorem 3.3.2 gives a geometric realization of the quantum category ![]() $\mathsf {O}$.
$\mathsf {O}$.
In the case of root of unity, the category ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is different from the quantum category
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is different from the quantum category ![]() $\mathsf {O}$. For example, the standard objects (i.e. Verma modules) and costandard objects (i.e. co-Verma modules) of
$\mathsf {O}$. For example, the standard objects (i.e. Verma modules) and costandard objects (i.e. co-Verma modules) of ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ are no longer of finite length. Nevertheless,
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ are no longer of finite length. Nevertheless, ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is still a highest weight category. The comparison of the highest weight category structures of
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is still a highest weight category. The comparison of the highest weight category structures of ![]() ${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}_{\rm q}(\check {G})$ and
${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}_{\rm q}(\check {G})$ and ![]() $\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ plays an important role in our proof.
$\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ plays an important role in our proof.
1.3.4 Casselman–Shalika theorem
The original Casselman–Shalika theorem interprets the values of the spherical Whittaker function as characters of the irreducible representations of the Langlands dual group.
Let ![]() ${\operatorname {Bun}}_N$ be the algebraic stack classifying principal
${\operatorname {Bun}}_N$ be the algebraic stack classifying principal ![]() $N$-bundles on a smooth connected projective curve
$N$-bundles on a smooth connected projective curve ![]() $X$. In [Reference Frenkel, Gaitsgory and VilonenFGV01], the authors proved a generalization of the geometric Casselman–Shalika formula. It interprets the category of representations of the Langlands dual group as Whittaker D-modules (equivalently,
$X$. In [Reference Frenkel, Gaitsgory and VilonenFGV01], the authors proved a generalization of the geometric Casselman–Shalika formula. It interprets the category of representations of the Langlands dual group as Whittaker D-modules (equivalently, ![]() $\ell$-adic sheaves) on
$\ell$-adic sheaves) on ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}$, where the algebraic stack
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}$, where the algebraic stack ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}$ denotes the Drinfeld compactification of
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}$ denotes the Drinfeld compactification of ![]() ${\operatorname {Bun}}_N$ with a possible pole at a fixed point
${\operatorname {Bun}}_N$ with a possible pole at a fixed point ![]() $x$ (see § 7.1 for definition).
$x$ (see § 7.1 for definition).
By a local–global comparison, [Reference Frenkel, Gaitsgory and VilonenFGV01] actually proves that (1.3.5) is an equivalence when ![]() $q=1$.
$q=1$.
The geometric Casselman–Shalika formula gives us a hint of how to construct a functor to relate the category of Whittaker sheaves to the category of representations. Namely, the ‘integration’ of a Whittaker D-module along ![]() $G(\mathcal {O})$-orbits (or
$G(\mathcal {O})$-orbits (or ![]() $N^-(\mathcal {K})$-orbits) encodes representation-theoretic information. The construction of the functor
$N^-(\mathcal {K})$-orbits) encodes representation-theoretic information. The construction of the functor ![]() $F^{\rm L}$ (see § 6.4 for a definition) is inspired by this idea and Raskin's thesis [Reference RaskinRas14].
$F^{\rm L}$ (see § 6.4 for a definition) is inspired by this idea and Raskin's thesis [Reference RaskinRas14].
1.3.5 Small quantum groups
In [Reference Gaitsgory and LysenkoGL19], a geometric realization of the category of representations of the small quantum groups was studied. In [Reference Gaitsgory and LysenkoGL19], it was proved that the category of Hecke-eigensheaves of the twisted Whittaker categories on ![]() ${\operatorname {Gr}}_G$, is equivalent to the same category of representations of the small quantum groups. Our work has adopted the strategy developed in [Reference Gaitsgory and LysenkoGL19]. This method originated from [Reference GaitsgoryGai08, Reference Bezrukavnikov, Finkelberg and SchechtmanBFS98, Reference Frenkel, Gaitsgory and VilonenFGV01], and has proven to be a powerful method in geometric representation theory. The recent work of Braverman, Finkelberg, and Travkin on the Gaiotto conjecture for
${\operatorname {Gr}}_G$, is equivalent to the same category of representations of the small quantum groups. Our work has adopted the strategy developed in [Reference Gaitsgory and LysenkoGL19]. This method originated from [Reference GaitsgoryGai08, Reference Bezrukavnikov, Finkelberg and SchechtmanBFS98, Reference Frenkel, Gaitsgory and VilonenFGV01], and has proven to be a powerful method in geometric representation theory. The recent work of Braverman, Finkelberg, and Travkin on the Gaiotto conjecture for ![]() ${\mathop {\operatorname {\rm GL}}}(N-1\,|\,N)$ (see [Reference Braverman, Finkelberg and TravkinBFT21]), the work of Travkin and the present author on the Gaiotto conjecture for
${\mathop {\operatorname {\rm GL}}}(N-1\,|\,N)$ (see [Reference Braverman, Finkelberg and TravkinBFT21]), the work of Travkin and the present author on the Gaiotto conjecture for ![]() ${\mathop {\operatorname {\rm GL}}}(M\,|\,N)$, and the Iwahori Gaiotto conjecture also use this strategy.
${\mathop {\operatorname {\rm GL}}}(M\,|\,N)$, and the Iwahori Gaiotto conjecture also use this strategy.
The small quantum group is very similar to the mixed quantum group: both of the categories of their representations ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm small}}}}(\check {G})$ and
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm small}}}}(\check {G})$ and ![]() ${\operatorname {Rep}}^{\mathop {\operatorname {\rm mxd}}}_{\rm q}(\check {G})$ can be realized as categories of factorization modules. In particular, the method used in [Reference Gaitsgory and LysenkoGL19] indicates to us a strategy to prove Theorem 3.3.2 and offers us models for the constructions of the functors and stacks used in our paper. For example, the key step of the proof of our main theorem is to use the local–global equivalence of Whittaker categories and then prove the theorem in the global case. This idea comes from [Reference Gaitsgory and LysenkoGL19].
${\operatorname {Rep}}^{\mathop {\operatorname {\rm mxd}}}_{\rm q}(\check {G})$ can be realized as categories of factorization modules. In particular, the method used in [Reference Gaitsgory and LysenkoGL19] indicates to us a strategy to prove Theorem 3.3.2 and offers us models for the constructions of the functors and stacks used in our paper. For example, the key step of the proof of our main theorem is to use the local–global equivalence of Whittaker categories and then prove the theorem in the global case. This idea comes from [Reference Gaitsgory and LysenkoGL19].
In our case, there are some technical difficulties caused by the additional Iwahori structure. For example, in [Reference Gaitsgory and LysenkoGL19], standard objects of ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Gr}}_G)$ are defined as
$\operatorname {Whit}_{\rm q}({\operatorname {Gr}}_G)$ are defined as ![]() $!$-pushforward of the unique irreducible twisted Whittaker sheaf supported on a single relevant
$!$-pushforward of the unique irreducible twisted Whittaker sheaf supported on a single relevant ![]() $N(\mathcal {K})$-orbit and costandard objects are
$N(\mathcal {K})$-orbit and costandard objects are ![]() $*$-pushforward of that irreducible Whittaker sheaf. In our case, since co-Verma modules of
$*$-pushforward of that irreducible Whittaker sheaf. In our case, since co-Verma modules of ![]() ${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$ are not compact, it is impossible to define standard objects and costandard objects similar to [Reference Gaitsgory and LysenkoGL19] such that they match Verma modules and co-Verma modules in
${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$ are not compact, it is impossible to define standard objects and costandard objects similar to [Reference Gaitsgory and LysenkoGL19] such that they match Verma modules and co-Verma modules in ![]() ${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$. Instead, we define standard objects by
${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$. Instead, we define standard objects by ![]() $!$-Whittaker averaging of ‘Wakimoto sheaves’ which are twisted and Iwahori equivariant against a character. However, this definition does not make sense because (classical) Wakimoto sheaves are Iwahori-equivariant and only defined in the non-twisted case. We need to extend the definition of Wakimoto sheaves to the twisted and
$!$-Whittaker averaging of ‘Wakimoto sheaves’ which are twisted and Iwahori equivariant against a character. However, this definition does not make sense because (classical) Wakimoto sheaves are Iwahori-equivariant and only defined in the non-twisted case. We need to extend the definition of Wakimoto sheaves to the twisted and ![]() $(I, b_\lambda )$-equivariant case. Here
$(I, b_\lambda )$-equivariant case. Here ![]() $b_\lambda$ is a character of the Iwahori subgroup.
$b_\lambda$ is a character of the Iwahori subgroup.
1.4 Strategy of the proof
The idea of proving Theorem 3.3.2 is to compare both sides with a factorization category. In [Reference GaitsgoryGai20], the author proved that ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ can be realized as the category of factorization modules on the configuration space over a factorization algebra
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ can be realized as the category of factorization modules on the configuration space over a factorization algebra ![]() $\Omega _{\rm q}^{\rm L}$ (see Definition 4.2.2) in the D-module setting. Therefore, we need to construct an equivalence between
$\Omega _{\rm q}^{\rm L}$ (see Definition 4.2.2) in the D-module setting. Therefore, we need to construct an equivalence between ![]() $\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ and
$\operatorname {Whit}(\operatorname {D-mod}_\kappa ({\operatorname {Fl}}_G))$ and ![]() $\Omega _{\rm q}^{\rm L}\text {-}{\operatorname {FactMod}}$.
$\Omega _{\rm q}^{\rm L}\text {-}{\operatorname {FactMod}}$.
A naive attempt is to use the pullback–pushforward functor ![]() $F^{\rm DK}$,Footnote 3 namely, we
$F^{\rm DK}$,Footnote 3 namely, we ![]() $!$-pullback Whittaker D-modules on
$!$-pullback Whittaker D-modules on ![]() ${\operatorname {Fl}}_G$ to an Iwahori version Zastava space and then take
${\operatorname {Fl}}_G$ to an Iwahori version Zastava space and then take ![]() $*$-pushforward to the configuration space. However, the image of
$*$-pushforward to the configuration space. However, the image of ![]() $F^{\rm DK}$ does not have a
$F^{\rm DK}$ does not have a ![]() $\Omega _{\rm q}^{\rm L}$-factorization module structure (except when
$\Omega _{\rm q}^{\rm L}$-factorization module structure (except when ![]() $\kappa$ is generic). For a coweight
$\kappa$ is generic). For a coweight ![]() $\lambda$, the
$\lambda$, the ![]() $\lambda$-component of this functor is given by
$\lambda$-component of this functor is given by
Here ![]() $j_*(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ denotes the
$j_*(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ denotes the ![]() $*$-extension of the dualizing D-module on the
$*$-extension of the dualizing D-module on the ![]() $N^-(\mathcal {K})$-orbit of
$N^-(\mathcal {K})$-orbit of ![]() $t^\lambda \in {\operatorname {Fl}}_G$.
$t^\lambda \in {\operatorname {Fl}}_G$.
The functor ![]() $F^{\rm L}$ used in this paper is a modification of
$F^{\rm L}$ used in this paper is a modification of ![]() $F^{\rm DK}$. The
$F^{\rm DK}$. The ![]() $\lambda$-component of
$\lambda$-component of ![]() $F^{\rm L}$ is given by
$F^{\rm L}$ is given by
Here ![]() $j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ denotes the
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ denotes the ![]() $!$-extension of the dualizing D-module on the
$!$-extension of the dualizing D-module on the ![]() $N^-(\mathcal {K})$-orbit of
$N^-(\mathcal {K})$-orbit of ![]() $t^\lambda \in {\operatorname {Fl}}_G$.
$t^\lambda \in {\operatorname {Fl}}_G$.
We show that ![]() $F^{\rm L}$ factors through
$F^{\rm L}$ factors through ![]() $\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$ (Proposition 6.4.7), and there is
$\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$ (Proposition 6.4.7), and there is ![]() $\Omega _{\rm q}^{{\rm L},\prime }\simeq \Omega _{\rm q}^{\rm L}$ if
$\Omega _{\rm q}^{{\rm L},\prime }\simeq \Omega _{\rm q}^{\rm L}$ if ![]() $q$ avoids small torsion. Theorem 6.4.8 claims that
$q$ avoids small torsion. Theorem 6.4.8 claims that ![]() $F^{\rm L}$ induces an equivalence between the Whittaker category on
$F^{\rm L}$ induces an equivalence between the Whittaker category on ![]() ${\operatorname {Fl}}_G$ and the category of factorization modules over
${\operatorname {Fl}}_G$ and the category of factorization modules over ![]() $\Omega _{\rm q}^{{\rm L},\prime }$.
$\Omega _{\rm q}^{{\rm L},\prime }$.
To prove that ![]() $F^{\rm L}$ is an equivalence, we use some tautological arguments about highest weight categories. That is to say, we construct standards and costandards of both sides, prove that
$F^{\rm L}$ is an equivalence, we use some tautological arguments about highest weight categories. That is to say, we construct standards and costandards of both sides, prove that ![]() $F^{\rm L}$ preserves them and induces an isomorphism of Hom spaces.
$F^{\rm L}$ preserves them and induces an isomorphism of Hom spaces.
The compatibility of costandards is more or less trivial. It follows by a direct calculation of ![]() $!$-stalks of
$!$-stalks of ![]() $F^{\rm L}$ (Corollary 6.5.5). The claim of fully faithfulness of
$F^{\rm L}$ (Corollary 6.5.5). The claim of fully faithfulness of ![]() $F^{\rm L}$ follows from a calculation of Hom spaces, and the latter reduces to the problem of compatibility of standards (Proposition 6.6.2). However, since the calculation of
$F^{\rm L}$ follows from a calculation of Hom spaces, and the latter reduces to the problem of compatibility of standards (Proposition 6.6.2). However, since the calculation of ![]() $*$-stalks is difficult (seems impossible), the proof of the compatibility of standards is not tautological at all. It is the main difficulty of the proof.
$*$-stalks is difficult (seems impossible), the proof of the compatibility of standards is not tautological at all. It is the main difficulty of the proof.
The method to overcome this difficulty is to define a duality functor to transfer the calculation of ![]() $*$-stalks to a calculation of
$*$-stalks to a calculation of ![]() $!$-stalks. This duality functor is not tautological. Since the Whittaker category used in this paper is defined as a category of invariants, its dual category is a category of coinvariants in nature. By a theorem of Raskin (see [Reference RaskinRas21, Theorem 2.1.1]), we can identify the invariant-Whittaker category as the coinvariant-Whittaker category. Hence, this duality functor can be defined.
$!$-stalks. This duality functor is not tautological. Since the Whittaker category used in this paper is defined as a category of invariants, its dual category is a category of coinvariants in nature. By a theorem of Raskin (see [Reference RaskinRas21, Theorem 2.1.1]), we can identify the invariant-Whittaker category as the coinvariant-Whittaker category. Hence, this duality functor can be defined.
We need to prove that this duality functor intertwines ![]() $F^{\rm L}$ and
$F^{\rm L}$ and ![]() $F^{\rm DK}$. Following [Reference GaitsgoryGai20], we can identify the (local) Whittaker category with the global Whittaker category. By translating the problem into the global Whittaker category defined on a Drinfeld compactification, we need to prove that the Verdier duality functor intertwines the global functors corresponding to
$F^{\rm DK}$. Following [Reference GaitsgoryGai20], we can identify the (local) Whittaker category with the global Whittaker category. By translating the problem into the global Whittaker category defined on a Drinfeld compactification, we need to prove that the Verdier duality functor intertwines the global functors corresponding to ![]() $F^{\rm L}$ and
$F^{\rm L}$ and ![]() $F^{\rm DK}$ (Theorem 8.2.2). According to the constructions, we need to compare a
$F^{\rm DK}$ (Theorem 8.2.2). According to the constructions, we need to compare a ![]() $!$-tensor product and a
$!$-tensor product and a ![]() $*$-tensor product. We solve this problem by using a universally locally acyclic property.
$*$-tensor product. We solve this problem by using a universally locally acyclic property.
1.5 Organization of the paper
(1) In § 2, we introduce some prestacks and gerbes used in this paper.
(2) In § 3, we explain the definitions of the Whittaker category on
 ${\operatorname {Fl}}_G$ and
${\operatorname {Fl}}_G$ and  ${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$. Then we state Theorem 3.3.2.
${\operatorname {Rep}}_{\rm q}^{\mathop {\operatorname {\rm mxd}}}(\check {G})$. Then we state Theorem 3.3.2.(3) In § 4, we review factorization algebras and factorization modules. We replace Theorem 3.3.2 by an equivalent statement: Theorem 4.3.1.
(4) In § 5, we study standards and duality functor of the Whittaker category, and show that standards compactly generate the Whittaker category.
(5) In § 6, we construct a functor
 $F^{\rm L}$ which goes from the Whittaker side to the factorization side. We show that
$F^{\rm L}$ which goes from the Whittaker side to the factorization side. We show that  $F^{\rm L}$ is an equivalence functor modulo Proposition 6.6.2 which is about the comparison of standards.
$F^{\rm L}$ is an equivalence functor modulo Proposition 6.6.2 which is about the comparison of standards.(6) In § 7, the global Whittaker category is defined. By using the global Whittaker category, we reduce Proposition 6.6.2 to 7.6.6 where we can use a universally locally acyclic property.
1.6 Generality of our results
1.6.1 Sheaf theories
Let ![]() $\mathsf {k}$,
$\mathsf {k}$, ![]() $\mathsf {e}$ be algebraically closed fields, and
$\mathsf {e}$ be algebraically closed fields, and ![]() $\text {char}(\mathsf {e})=0$. The strong version of our main result (Theorem 6.4.8) is true for any of the sheaf theories listed in [Reference Gaitsgory and LysenkoGL19, § 0.8.8].
$\text {char}(\mathsf {e})=0$. The strong version of our main result (Theorem 6.4.8) is true for any of the sheaf theories listed in [Reference Gaitsgory and LysenkoGL19, § 0.8.8].
(1) (de Rham) Schemes are defined over
 $\mathsf {k}$ (assume
$\mathsf {k}$ (assume  $\text {char}(\mathsf {k})=0$ here) and the sheaf category is the category of D-modules, or the ind-completion of the category of holonomic D-modules, or the ind-completion of the category of regular holonomic D-modules.
$\text {char}(\mathsf {k})=0$ here) and the sheaf category is the category of D-modules, or the ind-completion of the category of holonomic D-modules, or the ind-completion of the category of regular holonomic D-modules.(2) (Betti) Schemes are defined over
 $\mathbb {C}$ and the sheaf category is the ind-completion of the category of constructible sheaves with respect to the classical topology with coefficients
$\mathbb {C}$ and the sheaf category is the ind-completion of the category of constructible sheaves with respect to the classical topology with coefficients  $\mathsf {e}$.
$\mathsf {e}$.(3) (
 $\ell$-adic) Schemes are defined over
$\ell$-adic) Schemes are defined over  $\mathsf {k}$ and the sheaf category is the ind-completion of the category of constructible
$\mathsf {k}$ and the sheaf category is the ind-completion of the category of constructible  $\bar {\mathbb {Q}}_\ell$-adic sheaves. Here
$\bar {\mathbb {Q}}_\ell$-adic sheaves. Here  $\mathsf {e}=\bar {\mathbb {Q}}_\ell$.
$\mathsf {e}=\bar {\mathbb {Q}}_\ell$.
We denote by ![]() $\operatorname {Shv}$ any sheaf theory listed above.
$\operatorname {Shv}$ any sheaf theory listed above.
Note that the Whittaker category is not always well-defined for the sheaf theories above, such as the Betti setting and the ![]() $\ell$-adic setting on schemes defined over a field
$\ell$-adic setting on schemes defined over a field ![]() $\mathsf {k}$ of characteristic 0. In these cases, neither the exponential D-module nor the Artin–Schreier sheaf makes sense, so we are not allowed to talk about
$\mathsf {k}$ of characteristic 0. In these cases, neither the exponential D-module nor the Artin–Schreier sheaf makes sense, so we are not allowed to talk about ![]() $(N(\mathcal {K}),\chi )$-equivariant sheaves. We need to replace the Whittaker category by the Kirillov model [Reference GaitsgoryGai21a, Appendix A] in Theorem 6.4.8. However, applying the Lefschetz principle and Riemann–Hilbert correspondence, the proof for these cases can be easily reduced to the setting of regular holonomic D-modules. In order to simplify the notation and not get distracted, we only focus on the sheaf theories such that the Whittaker category makes sense.
$(N(\mathcal {K}),\chi )$-equivariant sheaves. We need to replace the Whittaker category by the Kirillov model [Reference GaitsgoryGai21a, Appendix A] in Theorem 6.4.8. However, applying the Lefschetz principle and Riemann–Hilbert correspondence, the proof for these cases can be easily reduced to the setting of regular holonomic D-modules. In order to simplify the notation and not get distracted, we only focus on the sheaf theories such that the Whittaker category makes sense.
1.6.2 Deformation parameters
In the general case, we need to use gerbes to twist a sheaf category. Given a gerbe ![]() $\mathcal {G}$ with respect to the multiplicative group
$\mathcal {G}$ with respect to the multiplicative group ![]() $\mathsf {e}^\times$, one can twist a sheaf category with coefficients in
$\mathsf {e}^\times$, one can twist a sheaf category with coefficients in ![]() $\mathsf {e}$. We refer the reader to [Reference Gaitsgory and LysenkoGL18, § 1.7] for the definition of the category of
$\mathsf {e}$. We refer the reader to [Reference Gaitsgory and LysenkoGL18, § 1.7] for the definition of the category of ![]() $\mathcal {G}$-twisted sheaves.
$\mathcal {G}$-twisted sheaves.
Let us be more precise about which kind of gerbes are used in different sheaf theories. In the Betti setting and ![]() $\ell$-adic setting, we use the gerbes with respect to the torsion multiplicative group
$\ell$-adic setting, we use the gerbes with respect to the torsion multiplicative group ![]() $\mathsf {e}^{\mathsf {torsion},\times }$ (see [Reference Gaitsgory and LysenkoGL18, § 1.3]). In the D-module setting, we use the tame gerbes [Reference ZhaoZha20, § 3.3].
$\mathsf {e}^{\mathsf {torsion},\times }$ (see [Reference Gaitsgory and LysenkoGL18, § 1.3]). In the D-module setting, we use the tame gerbes [Reference ZhaoZha20, § 3.3].
If readers are not familiar with how to twist a sheaf category with a gerbe, we advise to think about the case of D-modules, and ![]() $G$ is a simple and simply connected group over
$G$ is a simple and simply connected group over ![]() $\mathbb {C}$. In this case, the twisting parameter
$\mathbb {C}$. In this case, the twisting parameter ![]() $q$ is just a non-zero complex number. Twisted D-modules on
$q$ is just a non-zero complex number. Twisted D-modules on ![]() ${\operatorname {Fl}}_G$ are those D-modules on the canonical line bundle of
${\operatorname {Fl}}_G$ are those D-modules on the canonical line bundle of ![]() ${\operatorname {Fl}}_G$ which are
${\operatorname {Fl}}_G$ which are ![]() $\mathbb {G}_m$-monodromic along the fiber with the monodromy
$\mathbb {G}_m$-monodromic along the fiber with the monodromy ![]() $q^2$. This restriction of generality does not mean we lose the main interest of this paper.
$q^2$. This restriction of generality does not mean we lose the main interest of this paper.
1.7 Conventions and notation
In the main body of the paper, to simplify, we assume that ![]() $G$ is a reductive group defined over any algebraically closed field
$G$ is a reductive group defined over any algebraically closed field ![]() $\mathsf {k}$, and the derived subgroup
$\mathsf {k}$, and the derived subgroup ![]() $[G,G]$ is simply connected. Let
$[G,G]$ is simply connected. Let ![]() $T:= B^-\cap B$ be the Cartan subgroup of
$T:= B^-\cap B$ be the Cartan subgroup of ![]() $G$.
$G$.
We denote by ![]() $\Lambda$ the coweight lattice of
$\Lambda$ the coweight lattice of ![]() $G$ and by
$G$ and by ![]() $\check {\Lambda }$ the weight lattice. Let
$\check {\Lambda }$ the weight lattice. Let ![]() $\Lambda ^{\text {{neg}}}$ be the semi-group spanned by negative simple coroots. Its inverse is denoted by
$\Lambda ^{\text {{neg}}}$ be the semi-group spanned by negative simple coroots. Its inverse is denoted by ![]() $\Lambda ^{\text {pos}}$. Set
$\Lambda ^{\text {pos}}$. Set ![]() $\Lambda ^+$ (respectively,
$\Lambda ^+$ (respectively, ![]() $\check {\Lambda }^+$) the semi-group of dominant coweights (respectively, dominant weights),
$\check {\Lambda }^+$) the semi-group of dominant coweights (respectively, dominant weights), ![]() $\Delta$ the root system of
$\Delta$ the root system of ![]() $\check {G}$, and
$\check {G}$, and ![]() $\alpha _1, \alpha _2, \ldots, \alpha _r$ the simple coroots. Let
$\alpha _1, \alpha _2, \ldots, \alpha _r$ the simple coroots. Let ![]() $W$ denote the finite Weyl group and
$W$ denote the finite Weyl group and ![]() $W^{{\operatorname {ext}}}$ denote the extended affine Weyl group.
$W^{{\operatorname {ext}}}$ denote the extended affine Weyl group.
The theory of sheaves ‘![]() $\operatorname {Shv}$’ on infinite-dimensional schemes (also prestacks) used in this paper is developed in [Reference BeraldoBer17], [Reference Gaitsgory and RozenblyumGR17a], [Reference Gaitsgory and RozenblyumGR17b], [Reference RaskinRas], etc. When we talk about the Whittaker category, we assume that we are in the D-module setting or the
$\operatorname {Shv}$’ on infinite-dimensional schemes (also prestacks) used in this paper is developed in [Reference BeraldoBer17], [Reference Gaitsgory and RozenblyumGR17a], [Reference Gaitsgory and RozenblyumGR17b], [Reference RaskinRas], etc. When we talk about the Whittaker category, we assume that we are in the D-module setting or the ![]() $\ell$-adic setting.
$\ell$-adic setting.
In this paper, the categories considered are cocomplete ![]() $\mathsf {e}$-linear DG-categories (see [Reference Gaitsgory and RozenblyumGR17a, Chapter 1, § 10]). We need the theory of higher categories developed in [Reference LurieLur17] and [Reference LurieLur09] in this paper.
$\mathsf {e}$-linear DG-categories (see [Reference Gaitsgory and RozenblyumGR17a, Chapter 1, § 10]). We need the theory of higher categories developed in [Reference LurieLur17] and [Reference LurieLur09] in this paper.
Let ![]() ${\rm Vect}$ be the
${\rm Vect}$ be the ![]() $(\infty,1)$-category of complexes of vector spaces over
$(\infty,1)$-category of complexes of vector spaces over ![]() $\mathsf {e}$. Given a category
$\mathsf {e}$. Given a category ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $c_1, c_2\in \mathcal {C}$, we denote by
$c_1, c_2\in \mathcal {C}$, we denote by ![]() $\mathcal {H}om_{\mathcal {C}}(c_1, c_2)\in {\rm Vect}$ the Hom space of
$\mathcal {H}om_{\mathcal {C}}(c_1, c_2)\in {\rm Vect}$ the Hom space of ![]() $c_1$ and
$c_1$ and ![]() $c_2$, and denote by
$c_2$, and denote by ![]() ${\mathop {\operatorname {\rm Hom}}}_{\mathcal {C}}(c_1, c_2):= H^0(\mathcal {H}om_{\mathcal {C}}(c_1, c_2))$.
${\mathop {\operatorname {\rm Hom}}}_{\mathcal {C}}(c_1, c_2):= H^0(\mathcal {H}om_{\mathcal {C}}(c_1, c_2))$.
2. Geometric preparation
In this section, we define some basic geometric objects used in this paper. First of all, we recall the definitions of Ran space and Configuration space (§§ 2.1 and 2.2), and then review the definitions of Ran-ified (or Beilinson–Drinfeld) affine flags and affine Grassmannian in § 2.3. In § 2.4, we explain the gerbes used in this paper.
2.1 Ran space
The Ran space is important for us, since it is naturally factorizable. We need factorization prestacks over ![]() ${\mathop {\operatorname {\rm Ran}}}$ to perform our construction of the equivalence in Theorem 3.3.2.
${\mathop {\operatorname {\rm Ran}}}$ to perform our construction of the equivalence in Theorem 3.3.2.
Let ![]() $X$ be a smooth connected projective curve defined over
$X$ be a smooth connected projective curve defined over ![]() $\mathsf {k}$.
$\mathsf {k}$.
Definition 2.1.1 The Ran space ![]() ${\mathop {\operatorname {\rm Ran}}}:={\mathop {\operatorname {\rm Ran}}}_X$ is defined as the prestack whose
${\mathop {\operatorname {\rm Ran}}}:={\mathop {\operatorname {\rm Ran}}}_X$ is defined as the prestack whose ![]() $S$-points classify non-empty finite sets
$S$-points classify non-empty finite sets ![]() $\mathcal {I}$ of
$\mathcal {I}$ of ![]() $\operatorname {Maps}(S, X)$ for any affine scheme
$\operatorname {Maps}(S, X)$ for any affine scheme ![]() $S$ over
$S$ over ![]() $\mathsf {k}$.
$\mathsf {k}$.
We denote by ![]() $({\mathop {\operatorname {\rm Ran}}}\times {\mathop {\operatorname {\rm Ran}}})_{\rm disj}$ the open sub-prestack of
$({\mathop {\operatorname {\rm Ran}}}\times {\mathop {\operatorname {\rm Ran}}})_{\rm disj}$ the open sub-prestack of ![]() ${\mathop {\operatorname {\rm Ran}}}\times {\mathop {\operatorname {\rm Ran}}}$ with disjoint support condition.
${\mathop {\operatorname {\rm Ran}}}\times {\mathop {\operatorname {\rm Ran}}}$ with disjoint support condition.
The Ran space admits a (non-unital) semi-group structure by taking union
Let ![]() $\mathcal {D}_{\mathcal {I}}$ be the formal completion of
$\mathcal {D}_{\mathcal {I}}$ be the formal completion of ![]() $S\times X$ along the graph of
$S\times X$ along the graph of ![]() $\mathcal {I}$, and denote by
$\mathcal {I}$, and denote by ![]() $\overset {\circ }{\mathcal {D}}_{\mathcal {I}}$ the open subscheme of
$\overset {\circ }{\mathcal {D}}_{\mathcal {I}}$ the open subscheme of ![]() $\mathcal {D}_{\mathcal {I}}$ obtained by removing the graph of
$\mathcal {D}_{\mathcal {I}}$ obtained by removing the graph of ![]() $\mathcal {I}$.
$\mathcal {I}$.
Definition 2.1.2 For any affine scheme ![]() $S$, the
$S$, the ![]() $S$-points of
$S$-points of ![]() ${\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}$ classify the triples
${\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}$ classify the triples ![]() $(\mathcal {I}, \mathcal {P}_T,\alpha )$, where
$(\mathcal {I}, \mathcal {P}_T,\alpha )$, where ![]() $\mathcal {I}\in {\mathop {\operatorname {\rm Ran}}}(S)$,
$\mathcal {I}\in {\mathop {\operatorname {\rm Ran}}}(S)$, ![]() $\mathcal {P}_T$ is a
$\mathcal {P}_T$ is a ![]() $T$-bundle on
$T$-bundle on ![]() $\mathcal {D}_{\mathcal {I}}$,
$\mathcal {D}_{\mathcal {I}}$, ![]() $\alpha$ is an isomorphism of
$\alpha$ is an isomorphism of ![]() $\mathcal {P}_T$ with the trivial
$\mathcal {P}_T$ with the trivial ![]() $T$-bundle
$T$-bundle ![]() $\mathcal {P}^0_T$ on
$\mathcal {P}^0_T$ on ![]() $\overset {\circ }{\mathcal {D}}_{\mathcal {I}}$.
$\overset {\circ }{\mathcal {D}}_{\mathcal {I}}$.
The prestack ![]() ${\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}$ is called the Beilinson–Drinfeld (i.e. Ran-ified) affine Grassmannian [Reference Beilinson, Drinfeld, de Monvel and MarchenkoBD96, § 5.3.11].
${\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}$ is called the Beilinson–Drinfeld (i.e. Ran-ified) affine Grassmannian [Reference Beilinson, Drinfeld, de Monvel and MarchenkoBD96, § 5.3.11].
Remark 2.1.3 By the Beauville–Laszlo theorem [Reference Beauville and LaszloBL95], we can require that ![]() $\mathcal {P}_T$ is a
$\mathcal {P}_T$ is a ![]() $T$-bundle on
$T$-bundle on ![]() $S\times X$, and
$S\times X$, and ![]() $\alpha$ is an isomorphism of
$\alpha$ is an isomorphism of ![]() $\mathcal {P}_T$ with
$\mathcal {P}_T$ with ![]() $\mathcal {P}^0_T$ on the complement of the graph of
$\mathcal {P}^0_T$ on the complement of the graph of ![]() $\mathcal {I}$. The resulting prestack is the same.
$\mathcal {I}$. The resulting prestack is the same.
The important note here is that ![]() ${\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}$ is factorizable over
${\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}$ is factorizable over ![]() ${\mathop {\operatorname {\rm Ran}}}$. Namely, we have an isomorphism
${\mathop {\operatorname {\rm Ran}}}$. Namely, we have an isomorphism
with higher homotopy coherence (see [Reference Gaitsgory and LysenkoGL19, § 5.1.2]).
Inside ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$, there is a closed factorization sub-prestack denoted by
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$, there is a closed factorization sub-prestack denoted by ![]() ${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ (see [Reference Gaitsgory and LysenkoGL19, 4.6.2]).
${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ (see [Reference Gaitsgory and LysenkoGL19, 4.6.2]).
Definition 2.1.4 If ![]() $G$ is semi-simple and simply connected, then a
$G$ is semi-simple and simply connected, then a ![]() $S$-point
$S$-point ![]() $(\mathcal {I}, \mathcal {P}_T,\alpha )$ of
$(\mathcal {I}, \mathcal {P}_T,\alpha )$ of ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ is in
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ is in ![]() ${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ if
${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ if
– for any dominant weight
 $\check {\lambda } \in \check {\Lambda }^+$, the meromorphic map of the line bundles on
$\check {\lambda } \in \check {\Lambda }^+$, the meromorphic map of the line bundles on  $S\times X$
(2.1.3)induced by
$S\times X$
(2.1.3)induced by \begin{equation} \check{\lambda}(\mathcal{P}_T) \to\check{\lambda}(\mathcal{P}^0_T ) \end{equation}
\begin{equation} \check{\lambda}(\mathcal{P}_T) \to\check{\lambda}(\mathcal{P}^0_T ) \end{equation} $\alpha$, is regular;
$\alpha$, is regular;– for any point
 $s \in S$ and any element
$s \in S$ and any element  $i \in \mathcal {I}$, there exists at least one
$i \in \mathcal {I}$, there exists at least one  $\check {\lambda } \in \check {\Lambda }^+$, such that (2.1.3) has a zero at the point
$\check {\lambda } \in \check {\Lambda }^+$, such that (2.1.3) has a zero at the point  $s\to S \overset {i}{\to } X$.
$s\to S \overset {i}{\to } X$.
For general reductive group ![]() $G$, we define
$G$, we define ![]() ${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ as
${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ as ![]() ${\operatorname {Gr}}^{\text {neg}}_{T^{sc}, {\mathop {\operatorname {\rm Ran}}}}$, where
${\operatorname {Gr}}^{\text {neg}}_{T^{sc}, {\mathop {\operatorname {\rm Ran}}}}$, where ![]() $T^{sc}$ is the Cartan subgroup of the simply connected cover of
$T^{sc}$ is the Cartan subgroup of the simply connected cover of ![]() $[G,G]$.
$[G,G]$.
2.1.5
We also need the Ran space with a marked point.
Definition 2.1.6 Fix ![]() $x\in X$. We denote by
$x\in X$. We denote by ![]() ${\mathop {\operatorname {\rm Ran}}}_{x}:={\mathop {\operatorname {\rm Ran}}}_{X,x}$ the prestack whose
${\mathop {\operatorname {\rm Ran}}}_{x}:={\mathop {\operatorname {\rm Ran}}}_{X,x}$ the prestack whose ![]() $S$-points classify non-empty sets
$S$-points classify non-empty sets ![]() $\mathcal {I}$ of
$\mathcal {I}$ of ![]() $\operatorname {Maps}(S, X)$ with a distinguished element
$\operatorname {Maps}(S, X)$ with a distinguished element ![]() $\widetilde {x}$, where
$\widetilde {x}$, where ![]() $\widetilde {x}$ denotes the constant map
$\widetilde {x}$ denotes the constant map ![]() $\widetilde {x}: S\to x\to X$.
$\widetilde {x}: S\to x\to X$.
Taking union defines a map
It equips ![]() ${\mathop {\operatorname {\rm Ran}}}_{x}$ with a structure of module space over
${\mathop {\operatorname {\rm Ran}}}_{x}$ with a structure of module space over ![]() ${\mathop {\operatorname {\rm Ran}}}$.
${\mathop {\operatorname {\rm Ran}}}$.
Let ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}$ be
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}$ be ![]() ${\mathop {\operatorname {\rm Ran}}}_x\underset {{\mathop {\operatorname {\rm Ran}}}}{\times }{\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$. It has a closed sub-prestack
${\mathop {\operatorname {\rm Ran}}}_x\underset {{\mathop {\operatorname {\rm Ran}}}}{\times }{\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$. It has a closed sub-prestack ![]() $({\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$.
$({\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$.
Definition 2.1.7 For any affine scheme ![]() $S$, a
$S$, a ![]() $S$-point
$S$-point ![]() $(\mathcal {I}, \mathcal {P}_T,\alpha )$ of
$(\mathcal {I}, \mathcal {P}_T,\alpha )$ of ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}$ belongs to the sub-prestack
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}$ belongs to the sub-prestack ![]() $({\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$, if there exists a
$({\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$, if there exists a ![]() $T$-bundle
$T$-bundle ![]() $\mathcal {P}_{T,1}$ on
$\mathcal {P}_{T,1}$ on ![]() $S \times X$ and an isomorphism
$S \times X$ and an isomorphism
such that the resulting point ![]() $(\mathcal {I}, \mathcal {P}_{T,1},\alpha \circ \alpha ')$ of
$(\mathcal {I}, \mathcal {P}_{T,1},\alpha \circ \alpha ')$ of ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}$ belongs to
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}$ belongs to ![]() ${\mathop {\operatorname {\rm Ran}}}_x\mathop {\times }_{{\mathop {\operatorname {\rm Ran}}}}{\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$.
${\mathop {\operatorname {\rm Ran}}}_x\mathop {\times }_{{\mathop {\operatorname {\rm Ran}}}}{\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$.
2.2 Configuration spaces
Definition 2.2.1 The configuration space ![]() ${\mathop {\operatorname {\rm Conf}}}:={\mathop {\operatorname {\rm Conf}}}(X, \Lambda ^{\text {neg}})$ is defined as the scheme classifying colored divisors of
${\mathop {\operatorname {\rm Conf}}}:={\mathop {\operatorname {\rm Conf}}}(X, \Lambda ^{\text {neg}})$ is defined as the scheme classifying colored divisors of ![]() $X$ with coefficients in
$X$ with coefficients in ![]() $\Lambda ^{\text {neg}}\setminus \{0\}$, i.e. it classifies
$\Lambda ^{\text {neg}}\setminus \{0\}$, i.e. it classifies
2.2.2 Connected components
Connected components of ![]() ${\mathop {\operatorname {\rm Conf}}}$ are indexed by
${\mathop {\operatorname {\rm Conf}}}$ are indexed by ![]() $\Lambda ^{\text {neg}}\setminus \{0\}$,
$\Lambda ^{\text {neg}}\setminus \{0\}$,
Here ![]() ${\mathop {\operatorname {\rm Conf}}}^\lambda$ denotes the subscheme of
${\mathop {\operatorname {\rm Conf}}}^\lambda$ denotes the subscheme of ![]() ${\mathop {\operatorname {\rm Conf}}}$ where we require the total degree of
${\mathop {\operatorname {\rm Conf}}}$ where we require the total degree of ![]() $D$ in (2.2.1) (i.e.
$D$ in (2.2.1) (i.e. ![]() $\sum _k \lambda _k$) to be
$\sum _k \lambda _k$) to be ![]() $\lambda$. If
$\lambda$. If ![]() $\lambda =-\sum _i n_i\cdot \alpha _i$, then
$\lambda =-\sum _i n_i\cdot \alpha _i$, then ![]() ${{\mathop {\operatorname {\rm Conf}}}^\lambda }$ is isomorphic to
${{\mathop {\operatorname {\rm Conf}}}^\lambda }$ is isomorphic to ![]() $\prod _i {X^{(n_i)}}$, where
$\prod _i {X^{(n_i)}}$, where ![]() ${X^{(n_i)}}$ classifies unordered
${X^{(n_i)}}$ classifies unordered ![]() $n_i$ points in
$n_i$ points in ![]() $X$.
$X$.
Similar to the Ran space, ![]() ${\mathop {\operatorname {\rm Conf}}}$ is equipped with a structure of non-unital commutative semi-group. There is a map
${\mathop {\operatorname {\rm Conf}}}$ is equipped with a structure of non-unital commutative semi-group. There is a map
If we restrict this map to the open subscheme ![]() $({\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}})_{\rm disj}$ with disjoint support condition, then it is étale.
$({\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}})_{\rm disj}$ with disjoint support condition, then it is étale.
Configuration space is essentially the same as ![]() ${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$. The following lemma is from [Reference Gaitsgory and LysenkoGL19, Lemma 4.6.4].
${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$. The following lemma is from [Reference Gaitsgory and LysenkoGL19, Lemma 4.6.4].
Lemma 2.2.3 Evaluation on fundamental weights gives rise to a morphism
It induces an isomorphism of the sheafifications in the topology generated by finite surjective maps.
In particular, (2.2.3) induces an equivalence between categories of gerbes on ![]() ${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ and
${\operatorname {Gr}}^{\text {neg}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ and ![]() ${\mathop {\operatorname {\rm Conf}}}$. Furthermore, it induces an equivalence of corresponding categories of twisted sheaves.
${\mathop {\operatorname {\rm Conf}}}$. Furthermore, it induces an equivalence of corresponding categories of twisted sheaves.
2.2.4
Similarly, we define the configuration space with a marked point.
Definition 2.2.5 Fix ![]() $x\in X$. We denote by
$x\in X$. We denote by ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ the ind-scheme classifying the colored divisors on
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ the ind-scheme classifying the colored divisors on ![]() $X$ with
$X$ with ![]() $\Lambda$-coefficient
$\Lambda$-coefficient
such that ![]() $\lambda _k\in \Lambda ^{\text {neg}}$,
$\lambda _k\in \Lambda ^{\text {neg}}$, ![]() $\lambda _x\in \Lambda$ and
$\lambda _x\in \Lambda$ and ![]() $x_k\neq x$.
$x_k\neq x$.
Regard ![]() ${\mathop {\operatorname {\rm Conf}}}$ as a (non-unital) algebra in the category of prestacks, the addition map
${\mathop {\operatorname {\rm Conf}}}$ as a (non-unital) algebra in the category of prestacks, the addition map
gives ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ a module structure over
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ a module structure over ![]() ${\mathop {\operatorname {\rm Conf}}}$.
${\mathop {\operatorname {\rm Conf}}}$.
If we restrict ![]() $\operatorname {add}_{{\mathop {\operatorname {\rm Conf}}}_x}$ to
$\operatorname {add}_{{\mathop {\operatorname {\rm Conf}}}_x}$ to ![]() $({\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})_{\rm disj}$, the open ind-scheme with disjoint support condition, then it is étale. In particular,
$({\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})_{\rm disj}$, the open ind-scheme with disjoint support condition, then it is étale. In particular, ![]() $\operatorname {add}_{{\mathop {\operatorname {\rm Conf}}}_x}^!\simeq \operatorname {add}_{{\mathop {\operatorname {\rm Conf}}}_x}^*$ on
$\operatorname {add}_{{\mathop {\operatorname {\rm Conf}}}_x}^!\simeq \operatorname {add}_{{\mathop {\operatorname {\rm Conf}}}_x}^*$ on ![]() $({\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})_{\rm disj}$.
$({\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})_{\rm disj}$.
Similar to (2.2.3), there is a map of prestacks
Lemma 2.2.6 [Reference Gaitsgory and LysenkoGL19, 4.6.7]
The morphism (2.2.6) induces an isomorphism of the sheafifications in the topology generated by finite surjective maps.
2.3 Ran-ified  ${\operatorname {Fl}}$ and
${\operatorname {Fl}}$ and  ${\operatorname {Gr}}$
${\operatorname {Gr}}$
The Beilinson–Drinfeld affine Grassmannian ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ is similarly defined as
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ is similarly defined as ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ (only replace
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}$ (only replace ![]() $T$-bundles by
$T$-bundles by ![]() $G$-bundles in the definition). By adding an Iwahori structure at
$G$-bundles in the definition). By adding an Iwahori structure at ![]() $x$, we arrive the definition of the Beilinson–Drinfeld affine flags.
$x$, we arrive the definition of the Beilinson–Drinfeld affine flags.
Definition 2.3.1 We define ![]() ${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}$ as the prestack whose
${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}$ as the prestack whose ![]() $S$-points classify the quadruples
$S$-points classify the quadruples ![]() $(\mathcal {I}, \mathcal {P}_G, \alpha, \epsilon )$, where
$(\mathcal {I}, \mathcal {P}_G, \alpha, \epsilon )$, where ![]() $(\mathcal {I}, \mathcal {P}_G, \alpha )\in {\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}(S)$, and
$(\mathcal {I}, \mathcal {P}_G, \alpha )\in {\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}(S)$, and ![]() $\epsilon$ is a
$\epsilon$ is a ![]() $B$-reduction of
$B$-reduction of ![]() $\mathcal {P}_G$ over
$\mathcal {P}_G$ over ![]() $S\times x$.
$S\times x$.
An important feature of ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ is that it is factorizable over
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ is that it is factorizable over ![]() ${\mathop {\operatorname {\rm Ran}}}$. That is to say, we have an isomorphism
${\mathop {\operatorname {\rm Ran}}}$. That is to say, we have an isomorphism
with higher homotopy coherence.
Here ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ is a factorization module space over
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ is a factorization module space over ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$, i.e. for any non-empty set with a distinguished point
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$, i.e. for any non-empty set with a distinguished point ![]() $(*\in {{\mathcal {I}}})$, there is an isomorphism
$(*\in {{\mathcal {I}}})$, there is an isomorphism
with higher homotopy coherence.
2.4 Gerbes used in this paper
In the Betti setting and the ![]() $\ell$-adic setting, we let
$\ell$-adic setting, we let ![]() $\mathcal {G}^G$ be a factorization
$\mathcal {G}^G$ be a factorization ![]() $\mathsf {e}^{\mathsf {torsion},\times }$-gerbe on
$\mathsf {e}^{\mathsf {torsion},\times }$-gerbe on ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$, which is compatible with the factorization structure on
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$, which is compatible with the factorization structure on ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ (see (2.3.1)). It is defined in [Reference Gaitsgory and LysenkoGL18, § 2.4], and is called metaplectic parameter. In the D-module setting, we should require
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ (see (2.3.1)). It is defined in [Reference Gaitsgory and LysenkoGL18, § 2.4], and is called metaplectic parameter. In the D-module setting, we should require ![]() $\mathcal {G}^G$ to be a tame factorization gerbe on
$\mathcal {G}^G$ to be a tame factorization gerbe on ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ defined in [Reference ZhaoZha20, § 3.3]. In this section, we explain how to get gerbes on some prestacks from
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ defined in [Reference ZhaoZha20, § 3.3]. In this section, we explain how to get gerbes on some prestacks from ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}$.
${\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}$.
2.4.1 Gerbe on the Hecke prestack
We denote by ![]() $\mathit{\mathcal{H}\kern-.2ex ecke}_G$ the Hecke prestack which classifies the data:
$\mathit{\mathcal{H}\kern-.2ex ecke}_G$ the Hecke prestack which classifies the data: ![]() $(\mathcal {P}_{G,1}, \mathcal {P}_{G,2}, \alpha )$, where
$(\mathcal {P}_{G,1}, \mathcal {P}_{G,2}, \alpha )$, where ![]() $\mathcal {P}_{G,1}$ and
$\mathcal {P}_{G,1}$ and ![]() $\mathcal {P}_{G,2}$ are
$\mathcal {P}_{G,2}$ are ![]() $G$-bundles on
$G$-bundles on ![]() $X$ and
$X$ and ![]() $\alpha$ is an isomorphism of
$\alpha$ is an isomorphism of ![]() $\mathcal {P}_{G,1}$ and
$\mathcal {P}_{G,1}$ and ![]() $\mathcal {P}_{G,2}$ over
$\mathcal {P}_{G,2}$ over ![]() $X\setminus x$,
$X\setminus x$, ![]() $\alpha : \mathcal {P}_{G,1}|_{X\setminus x}\simeq \mathcal {P}_{G,2}|_{X\setminus x}$. Then by the
$\alpha : \mathcal {P}_{G,1}|_{X\setminus x}\simeq \mathcal {P}_{G,2}|_{X\setminus x}$. Then by the ![]() $G(\mathcal {O})$-equivariance of
$G(\mathcal {O})$-equivariance of ![]() $\mathcal {G}^G$ (see [Reference Gaitsgory and LysenkoGL18, § 7.3]),
$\mathcal {G}^G$ (see [Reference Gaitsgory and LysenkoGL18, § 7.3]), ![]() $\mathcal {G}^G$ gives rise to a gerbe on the Hecke prestack. We denote the descent gerbe on
$\mathcal {G}^G$ gives rise to a gerbe on the Hecke prestack. We denote the descent gerbe on ![]() $\mathit{\mathcal{H}\kern-.2ex ecke}_G$ by
$\mathit{\mathcal{H}\kern-.2ex ecke}_G$ by ![]() $\mathcal {G}^G_{\mathit{\mathcal{H}\kern-.2ex ecke}}$.
$\mathcal {G}^G_{\mathit{\mathcal{H}\kern-.2ex ecke}}$.
2.4.2  $\omega ^\rho$-twisted prestacks
$\omega ^\rho$-twisted prestacks
Fix a square root of the canonical line bundle ![]() $\omega$ on
$\omega$ on ![]() $X$ and denote it by
$X$ and denote it by ![]() $\omega ^{\otimes \frac {1}{2}}$. We define
$\omega ^{\otimes \frac {1}{2}}$. We define ![]() $\omega ^\rho$ as the
$\omega ^\rho$ as the ![]() $T$-bundle induced from
$T$-bundle induced from ![]() $\omega ^{\otimes \frac {1}{2}}$ by the morphism of group schemes
$\omega ^{\otimes \frac {1}{2}}$ by the morphism of group schemes
Here ![]() $\rho$ is the sum of all fundamental coweights.
$\rho$ is the sum of all fundamental coweights.
If we replace the trivial ![]() $G$-bundle
$G$-bundle ![]() $\mathcal {P}_G^0$ by the
$\mathcal {P}_G^0$ by the ![]() $G$-bundle
$G$-bundle ![]() $\mathcal {P}_G^{\omega }:=\omega ^\rho \overset {T}{\times }G$ in the definition of
$\mathcal {P}_G^{\omega }:=\omega ^\rho \overset {T}{\times }G$ in the definition of ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$, we will obtain the
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$, we will obtain the ![]() $\omega ^\rho$-twisted Beilinson–Drinfeld affine Grassmannian. Let us denote it by
$\omega ^\rho$-twisted Beilinson–Drinfeld affine Grassmannian. Let us denote it by ![]() ${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}}$. It is still a factorization prestack over
${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}}$. It is still a factorization prestack over ![]() ${\mathop {\operatorname {\rm Ran}}}$. Similarly, we can also define
${\mathop {\operatorname {\rm Ran}}}$. Similarly, we can also define ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$,
${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$, ![]() ${\operatorname {Gr}}_{G}^{\omega ^\rho }$,
${\operatorname {Gr}}_{G}^{\omega ^\rho }$, ![]() ${\operatorname {Fl}}_{G}^{\omega ^\rho }$,
${\operatorname {Fl}}_{G}^{\omega ^\rho }$, ![]() $G(\mathcal {K})^{\omega ^\rho }$,
$G(\mathcal {K})^{\omega ^\rho }$, ![]() $N(\mathcal {K})^{\omega ^\rho }$,
$N(\mathcal {K})^{\omega ^\rho }$, ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$,
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$, ![]() $({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho })^{\text {neg}}$,
$({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho })^{\text {neg}}$, ![]() $({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$, etc. Similar to the classical affine flags and affine Grassmannian, we have
$({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$, etc. Similar to the classical affine flags and affine Grassmannian, we have
and
Here ![]() $I^{\omega ^\rho }$ and
$I^{\omega ^\rho }$ and ![]() $G(\mathcal {O})^{\omega ^\rho }$ are
$G(\mathcal {O})^{\omega ^\rho }$ are ![]() $\omega ^\rho$-twisted version of
$\omega ^\rho$-twisted version of ![]() $I$ and
$I$ and ![]() $G(\mathcal {O})$, respectively.
$G(\mathcal {O})$, respectively.
2.4.3 Gerbes on  ${\operatorname {Fl}}^{\omega ^\rho }_G$ and
${\operatorname {Fl}}^{\omega ^\rho }_G$ and  ${\operatorname {Gr}}^{\omega ^\rho }_G$
${\operatorname {Gr}}^{\omega ^\rho }_G$
By definition, taking ![]() $\mathcal {P}_{G,2}$ to be
$\mathcal {P}_{G,2}$ to be ![]() $\mathcal {P}_G^{\omega }$ defines a map
$\mathcal {P}_G^{\omega }$ defines a map ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\to \mathit{\mathcal{H}\kern-.2ex ecke}_G$. The pullback of
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\to \mathit{\mathcal{H}\kern-.2ex ecke}_G$. The pullback of ![]() $\mathcal {G}^G_{\mathit{\mathcal{H}\kern-.2ex ecke}}$ along this map is a factorization gerbe on
$\mathcal {G}^G_{\mathit{\mathcal{H}\kern-.2ex ecke}}$ along this map is a factorization gerbe on ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. With some abuse of notation, we denote it by
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. With some abuse of notation, we denote it by ![]() $\mathcal {G}^G$. Its pullback to
$\mathcal {G}^G$. Its pullback to ![]() ${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ (respectively,
${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ (respectively, ![]() ${\operatorname {Fl}}_{G}^{\omega ^\rho }$,
${\operatorname {Fl}}_{G}^{\omega ^\rho }$, ![]() ${\operatorname {Gr}}_{G}^{\omega ^\rho }$,
${\operatorname {Gr}}_{G}^{\omega ^\rho }$, ![]() $G(\mathcal {K})^{\omega ^\rho }$, etc.) is also denoted by
$G(\mathcal {K})^{\omega ^\rho }$, etc.) is also denoted by ![]() $\mathcal {G}^G$.
$\mathcal {G}^G$.
By [Reference Gaitsgory and LysenkoGL18, Proposition 7.2.5], the pullback of ![]() $\mathcal {G}^G$ along
$\mathcal {G}^G$ along ![]() $G(\mathcal {K})^{\omega ^\rho }\to {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ is a multiplicative gerbe, i.e.
$G(\mathcal {K})^{\omega ^\rho }\to {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ is a multiplicative gerbe, i.e.
Here ![]() $m$ denotes the multiplication map
$m$ denotes the multiplication map
In particular, the gerbes ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Fl}}_{G}^{\omega ^\rho }$ and
${\operatorname {Fl}}_{G}^{\omega ^\rho }$ and ![]() ${\operatorname {Gr}}_{G}^{\omega ^\rho }$ are equivariant with respect to the action of
${\operatorname {Gr}}_{G}^{\omega ^\rho }$ are equivariant with respect to the action of ![]() $G(\mathcal {K})^{\omega ^\rho }$ against the gerbe
$G(\mathcal {K})^{\omega ^\rho }$ against the gerbe ![]() $\mathcal {G}^G$.
$\mathcal {G}^G$.
2.4.4 Gerbe on  ${\mathop {\operatorname {\rm Conf}}}$
${\mathop {\operatorname {\rm Conf}}}$
Replace ![]() $G$ by
$G$ by ![]() $B$ in the definition of
$B$ in the definition of ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$, one can define a factorization prestack
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$, one can define a factorization prestack ![]() ${\operatorname {Gr}}_{B, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. Consider the following diagram of prestacks.
${\operatorname {Gr}}_{B, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. Consider the following diagram of prestacks.

The pullback of ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$ along the left morphism gives a factorization gerbe on
${\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$ along the left morphism gives a factorization gerbe on ![]() ${\operatorname {Gr}}_{B, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. By [Reference Gaitsgory and LysenkoGL18, § 5.1], this factorization gerbe descends to a factorization gerbe on
${\operatorname {Gr}}_{B, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. By [Reference Gaitsgory and LysenkoGL18, § 5.1], this factorization gerbe descends to a factorization gerbe on ![]() ${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. We denote the resulting gerbe by
${\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$. We denote the resulting gerbe by ![]() $\mathcal {G}^T$.
$\mathcal {G}^T$.
By constructions similar to (2.2.3) and (2.2.6), we have maps
and
By (a tiny modification of) Lemmas 2.2.3 and 2.2.6, (2.4.3) and (2.4.4) induce equivalences of gerbes on the Beilinson–Drinfeld affine Grassmannians and Configuration spaces. Hence, we can descend the factorization gerbe ![]() $\mathcal {G}^T$ on
$\mathcal {G}^T$ on ![]() $({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho })^{\text {neg}}$ (respectively,
$({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho })^{\text {neg}}$ (respectively, ![]() $({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$) to a gerbe
$({\operatorname {Gr}}_{T, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$) to a gerbe ![]() $\mathcal {G}^\Lambda$ on
$\mathcal {G}^\Lambda$ on ![]() ${\mathop {\operatorname {\rm Conf}}}$ (respectively,
${\mathop {\operatorname {\rm Conf}}}$ (respectively, ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$). Note that the above maps are compatible with the factorization structures, the gerbes on
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$). Note that the above maps are compatible with the factorization structures, the gerbes on ![]() ${\mathop {\operatorname {\rm Conf}}}$ and
${\mathop {\operatorname {\rm Conf}}}$ and ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ are factorizable.
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ are factorizable.
Following [Reference Gaitsgory and LysenkoGL18, § 4.2], we can get a quadratic form
from a factorization gerbe ![]() $\mathcal {G}^\Lambda$ on
$\mathcal {G}^\Lambda$ on ![]() ${\mathop {\operatorname {\rm Conf}}}$ in the D-module setting. In the Betti setting and the
${\mathop {\operatorname {\rm Conf}}}$ in the D-module setting. In the Betti setting and the ![]() $\ell$-adic setting,
$\ell$-adic setting, ![]() $q$ takes value in
$q$ takes value in ![]() $\mathsf {e}^{\mathsf {torsion},\times }(-1):= {\rm colim}_n {\mathop {\operatorname {\rm Hom}}}(\mu _n, \mathsf {e}^{\mathsf {torsion},\times })$.
$\mathsf {e}^{\mathsf {torsion},\times }(-1):= {\rm colim}_n {\mathop {\operatorname {\rm Hom}}}(\mu _n, \mathsf {e}^{\mathsf {torsion},\times })$.
2.4.5 Gerbe on  ${\operatorname {Bun}}_G$
${\operatorname {Bun}}_G$
Let ![]() ${\operatorname {Bun}}_G$ denote the algebraic stack classifying principal
${\operatorname {Bun}}_G$ denote the algebraic stack classifying principal ![]() $G$-bundles on
$G$-bundles on ![]() $X$. It is shown in [Reference Gaitsgory and LysenkoGL18] that any factorization gerbe on
$X$. It is shown in [Reference Gaitsgory and LysenkoGL18] that any factorization gerbe on ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ descends to a gerbe on
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}$ descends to a gerbe on ![]() ${\operatorname {Bun}}_G$. We also denote the resulting gerbe on
${\operatorname {Bun}}_G$. We also denote the resulting gerbe on ![]() ${\operatorname {Bun}}_G$ by
${\operatorname {Bun}}_G$ by ![]() $\mathcal {G}^G$.
$\mathcal {G}^G$.
Remark 2.4.6 The pullback of ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Bun}}_G$ along
${\operatorname {Bun}}_G$ along
is the gerbe ![]() $\mathcal {G}^G$ defined in § 2.4.3 tensored with the fiber
$\mathcal {G}^G$ defined in § 2.4.3 tensored with the fiber ![]() $\mathcal {G}^G|_{\omega ^\rho \in {\operatorname {Bun}}_G}$.
$\mathcal {G}^G|_{\omega ^\rho \in {\operatorname {Bun}}_G}$.
3. Statement of the main theorem
In this section, we introduce two sides of Theorem 3.3.2 explicitly:
(1) the category of Whittaker sheaves on affine flags (§ 3.1);
(2) the category of representations of the mixed quantum group (§ 3.2).
3.1 Definition of Whittaker category (through invariants)
In § 2.4.2, we have already defined ![]() $\omega ^\rho$-twisted prestacks. These objects have an advantage over the non-twisted prestacks: we can define the non-degenerate character
$\omega ^\rho$-twisted prestacks. These objects have an advantage over the non-twisted prestacks: we can define the non-degenerate character ![]() $\chi$ of
$\chi$ of ![]() $N(\mathcal {K})^{\omega ^\rho }$ and Whittaker sheaves on
$N(\mathcal {K})^{\omega ^\rho }$ and Whittaker sheaves on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G}$ canonically. In the rest of this paper, we consider the
${\operatorname {Fl}}^{\omega ^\rho }_{G}$ canonically. In the rest of this paper, we consider the ![]() $\omega ^\rho$-twisted affine flags
$\omega ^\rho$-twisted affine flags ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ and related geometric objects. One can show that the Whittaker category on
${\operatorname {Fl}}_G^{\omega ^\rho }$ and related geometric objects. One can show that the Whittaker category on ![]() ${\operatorname {Fl}}_G$ and the corresponding category on
${\operatorname {Fl}}_G$ and the corresponding category on ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ are equivalent.
${\operatorname {Fl}}_G^{\omega ^\rho }$ are equivalent.
Consider a non-degenerate character of ![]() $N(\mathcal {K})^{\omega ^\rho }$,
$N(\mathcal {K})^{\omega ^\rho }$,
The pullback of the exponential D-module along ![]() $\chi$ is a character D-module, we denote this character D-module by the same notation
$\chi$ is a character D-module, we denote this character D-module by the same notation ![]() $\chi$. In the
$\chi$. In the ![]() $\ell$-adic case, we use the Artin–Schreier sheaf instead of the exponential D-module here.
$\ell$-adic case, we use the Artin–Schreier sheaf instead of the exponential D-module here.
Definition 3.1.1 We define the Whittaker category on affine flags as
Here ![]() $q$ is the quadratic form associated with
$q$ is the quadratic form associated with ![]() $\mathcal {G}^G$ (see (2.4.5)).
$\mathcal {G}^G$ (see (2.4.5)).
3.1.2
We note that Definition 3.1.1 involves taking invariants with respect to an ind-pro-group scheme, we need to be more precise about this definition.
Write ![]() $N(\mathcal {K})^{\omega ^\rho }$ as
$N(\mathcal {K})^{\omega ^\rho }$ as
where ![]() $N_k:= \text {Ad}_{t^{-k\rho }}N(\mathcal {O})^{\omega ^\rho }$.
$N_k:= \text {Ad}_{t^{-k\rho }}N(\mathcal {O})^{\omega ^\rho }$.
First, by [Reference BeraldoBer17, § 4.4.3], we have
Fix a natural number ![]() $k\geq 0$. By (3.1.4), we only need to define
$k\geq 0$. By (3.1.4), we only need to define ![]() $\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}^{\omega ^\rho }_G)^{N_k,\chi }$.
$\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}^{\omega ^\rho }_G)^{N_k,\chi }$.
Since ![]() ${\operatorname {Fl}}^{\omega ^\rho }_G$ is an ind-scheme, we can write
${\operatorname {Fl}}^{\omega ^\rho }_G$ is an ind-scheme, we can write ![]() ${\operatorname {Fl}}^{\omega ^\rho }_G$ as a colimit of finite-dimensional schemes
${\operatorname {Fl}}^{\omega ^\rho }_G$ as a colimit of finite-dimensional schemes ![]() $Y_i$. Furthermore, we can assume that each
$Y_i$. Furthermore, we can assume that each ![]() $Y_i$ is
$Y_i$ is ![]() $N_k$-invariants. Then by
$N_k$-invariants. Then by
we have
We note that ![]() $N_k$ is a pro-scheme of finite type, we can write it as
$N_k$ is a pro-scheme of finite type, we can write it as
such that each ![]() $N^l_k$ is a finite-dimensional unipotent group scheme and the action of
$N^l_k$ is a finite-dimensional unipotent group scheme and the action of ![]() $N_k$ on
$N_k$ on ![]() $Y_i$ factors through
$Y_i$ factors through ![]() $N^l_k$. Finally, we define
$N^l_k$. Finally, we define
Since for any ![]() $l'\geq l$, the kernel of
$l'\geq l$, the kernel of ![]() $N_k^{l'}\to N_k^{l}$ is unipotent, the above definition is independent of the choice of
$N_k^{l'}\to N_k^{l}$ is unipotent, the above definition is independent of the choice of ![]() $N_k^l$.
$N_k^l$.
3.1.3 Averaging functors
Denote by
the fully faithful forgetful functor.
It admits a (partially defined) left adjoint functor ![]() $\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$. Since
$\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$. Since ![]() $\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$ is a (partially defined) left adjoint functor, it commutes with filtered colimits. In contrast, the right adjoint functor
$\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$ is a (partially defined) left adjoint functor, it commutes with filtered colimits. In contrast, the right adjoint functor ![]() $\operatorname {Av}_*^{N(\mathcal {K})^{\omega ^\rho },\chi }$ of
$\operatorname {Av}_*^{N(\mathcal {K})^{\omega ^\rho },\chi }$ of ![]() $\operatorname {oblv}_{N(\mathcal {K})^{\omega ^\rho },\chi }$ is discontinuous.
$\operatorname {oblv}_{N(\mathcal {K})^{\omega ^\rho },\chi }$ is discontinuous.
With the ind-pro-group scheme presentation (3.1.3) of ![]() $N(\mathcal {K})^{\omega ^\rho }$, we may write
$N(\mathcal {K})^{\omega ^\rho }$, we may write ![]() $\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$ more precisely,
$\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$ more precisely,
If ![]() $\operatorname {Av}_!^{N_k,\chi }(\mathcal {F})$ can be defined for any
$\operatorname {Av}_!^{N_k,\chi }(\mathcal {F})$ can be defined for any ![]() $k$, then
$k$, then ![]() $\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(\mathcal {F})$ can be defined by taking colimit. In particular,
$\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(\mathcal {F})$ can be defined by taking colimit. In particular, ![]() $\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$ can be defined in the
$\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }$ can be defined in the ![]() $\ell$-adic setting and for ind-holonomic D-modules in the D-module setting.
$\ell$-adic setting and for ind-holonomic D-modules in the D-module setting.
3.2 Mixed quantum groups
The quantum group used in this paper is not the classical quantum group. It is neither the Lusztig quantum group nor its graded dual. It is a combination of these two quantum groups: the positive part is the Lusztig quantum group ![]() $U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ and the negative part is the graded dual of it (i.e. the De Concini–Kac quantum group
$U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ and the negative part is the graded dual of it (i.e. the De Concini–Kac quantum group ![]() $U^{\rm DK}_{\rm q}(\check {\mathfrak {n}}^-)$).
$U^{\rm DK}_{\rm q}(\check {\mathfrak {n}}^-)$).
3.2.1 Mixed representation category
Let ![]() ${\rm Vect}_{\rm q}^\Lambda$ denote
${\rm Vect}_{\rm q}^\Lambda$ denote ![]() ${\operatorname {Rep}}_{\rm q}(\check {T})$, the braided monoidal category of
${\operatorname {Rep}}_{\rm q}(\check {T})$, the braided monoidal category of ![]() $\mathsf {e}$-representations of the quantum torus
$\mathsf {e}$-representations of the quantum torus ![]() $\check {T}$. We denote by
$\check {T}$. We denote by ![]() $U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}}$ the ind-completion of the derived category of finite-dimensional
$U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}}$ the ind-completion of the derived category of finite-dimensional ![]() $U_{\rm q}^{\rm L}(\check {\mathfrak {n}})$-modules in
$U_{\rm q}^{\rm L}(\check {\mathfrak {n}})$-modules in ![]() ${\rm Vect}_{\rm q}^\Lambda$.
${\rm Vect}_{\rm q}^\Lambda$.
Definition 3.2.2 The category ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is defined as
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is defined as ![]() $Z_{{\rm Dr}, {\rm Vect}^\Lambda _{\rm q}}(U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}})$, which is the relative Drinfeld center of
$Z_{{\rm Dr}, {\rm Vect}^\Lambda _{\rm q}}(U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}})$, which is the relative Drinfeld center of ![]() $U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}}$ with respect to
$U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}}$ with respect to ![]() ${\rm Vect}_{\rm q}^\Lambda$ (see [Reference Gaitsgory and LysenkoGL19, 27.2]).
${\rm Vect}_{\rm q}^\Lambda$ (see [Reference Gaitsgory and LysenkoGL19, 27.2]).
Remark 3.2.3 At abelian category level, an object in ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is a
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ is a ![]() $\Lambda$-graded vector space with actions of
$\Lambda$-graded vector space with actions of ![]() $U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ (with the locally nilpotent condition) and
$U^{\rm L}_{\rm q}(\check {\mathfrak {n}})$ (with the locally nilpotent condition) and ![]() $U^{\rm DK}_{\rm q}(\check {\mathfrak {n}}^-)$.
$U^{\rm DK}_{\rm q}(\check {\mathfrak {n}}^-)$.
3.2.4 Verma modules
We denote by ![]() $\operatorname {ind}_{L\to Dr}$ the left adjoint functor of the forgetful functor from
$\operatorname {ind}_{L\to Dr}$ the left adjoint functor of the forgetful functor from ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ to
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ to ![]() $U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}}$, and by
$U_{\rm q}^{\rm L}(\check {\mathfrak {n}}){\operatorname {-mod}}^{\mathsf {loc.nil}}$, and by ![]() $\operatorname {coind}_{\rm DK\to Dr}$ the right adjoint functor of the forgetful functor from
$\operatorname {coind}_{\rm DK\to Dr}$ the right adjoint functor of the forgetful functor from ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ to
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ to ![]() $U_{\rm q}^{\rm DK}(\check {\mathfrak {n}}^-){\operatorname {-mod}}$. For
$U_{\rm q}^{\rm DK}(\check {\mathfrak {n}}^-){\operatorname {-mod}}$. For ![]() $\lambda \in \Lambda$, we define Verma modules and co-Verma modules in
$\lambda \in \Lambda$, we define Verma modules and co-Verma modules in ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ as
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ as
Here ![]() $\mathsf {e}^\lambda$ denotes the one-dimensional representation of
$\mathsf {e}^\lambda$ denotes the one-dimensional representation of ![]() $U_{\rm q}^{\rm L}(\check {\mathfrak {n}})$ (or
$U_{\rm q}^{\rm L}(\check {\mathfrak {n}})$ (or ![]() $U_{\rm q}^{\rm DK}(\check {\mathfrak {n}}^-)$) in
$U_{\rm q}^{\rm DK}(\check {\mathfrak {n}}^-)$) in ![]() ${\rm Vect}_{\rm q}^\Lambda$, where the action of the torus corresponds to
${\rm Vect}_{\rm q}^\Lambda$, where the action of the torus corresponds to ![]() $\lambda$ and the action of the unipotent group is trivial.
$\lambda$ and the action of the unipotent group is trivial.
Following [Reference GaitsgoryGai21a, 5.3.2], we have
 \[ \mathcal{H}om_{{\operatorname{Rep}}_{\rm q}^{{\mathop{\operatorname{\rm mxd}}}}(\check{G})}(V_\lambda^{{\mathop{\operatorname{\rm mxd}}}}, V_\mu^{{\mathop{\operatorname{\rm mxd}}}, \vee})= \left\{\begin{aligned}\! \mathsf{e},\quad \text{if } \lambda=\mu,\\ 0,\quad \text{if } \lambda\neq\mu. \end{aligned}\right. \]
\[ \mathcal{H}om_{{\operatorname{Rep}}_{\rm q}^{{\mathop{\operatorname{\rm mxd}}}}(\check{G})}(V_\lambda^{{\mathop{\operatorname{\rm mxd}}}}, V_\mu^{{\mathop{\operatorname{\rm mxd}}}, \vee})= \left\{\begin{aligned}\! \mathsf{e},\quad \text{if } \lambda=\mu,\\ 0,\quad \text{if } \lambda\neq\mu. \end{aligned}\right. \]
Furthermore, by construction, the objects ![]() $V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ are compact and compactly generate
$V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ are compact and compactly generate ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$. Thus, there is a highest weight structure of
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$. Thus, there is a highest weight structure of ![]() ${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ with standard objects
${\operatorname {Rep}}_{\rm q}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ with standard objects ![]() $V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ and costandard objects
$V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ and costandard objects ![]() $V_\mu ^{{\mathop {\operatorname {\rm mxd}}}, \vee }$.
$V_\mu ^{{\mathop {\operatorname {\rm mxd}}}, \vee }$.
3.3 Statement of Theorem 3.3.2
3.3.1 Avoid small torsion
A quadratic form ![]() $q$ avoids small torsion ([Reference GaitsgoryGai21b, 1.1.5], [Reference LusztigLus10, 35.1.2 (a)]) if for any long coroot
$q$ avoids small torsion ([Reference GaitsgoryGai21b, 1.1.5], [Reference LusztigLus10, 35.1.2 (a)]) if for any long coroot ![]() $\alpha _l$ of a simple factor of
$\alpha _l$ of a simple factor of ![]() $G$, there is
$G$, there is
where ![]() $d_G = 1, 2, 3$ is the lacing number (i.e. the maximal number of edges in the Dynkin diagram).
$d_G = 1, 2, 3$ is the lacing number (i.e. the maximal number of edges in the Dynkin diagram).
Theorem 3.3.2 In the setting of D-modules, when ![]() $q$ avoids small torsion, there exists a
$q$ avoids small torsion, there exists a ![]() $t$-exact equivalence of highest weight categories
$t$-exact equivalence of highest weight categories
3.3.3 Highest weight category structure
In § 5.5, we define a collection of standard objects ![]() $\Delta _\lambda$ in
$\Delta _\lambda$ in ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ indexed by
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ indexed by ![]() $\Lambda$. They are given by
$\Lambda$. They are given by ![]() $!$-averaging the Wakimoto sheaves. In addition, we define a collection of costandard objects
$!$-averaging the Wakimoto sheaves. In addition, we define a collection of costandard objects ![]() $\nabla _\lambda \in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$. We show that Verma modules
$\nabla _\lambda \in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$. We show that Verma modules ![]() $V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ and
$V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ and ![]() $\Delta _\lambda$ match under the equivalence (3.3.1) and similarly for costandards.
$\Delta _\lambda$ match under the equivalence (3.3.1) and similarly for costandards.
3.3.4 t-structure
The equivalence (3.3.1) is an equivalence at the derived level. We define a t-structure on ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ in § 5.6 (see Definition 5.6.2) using
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ in § 5.6 (see Definition 5.6.2) using ![]() $\Delta _\lambda$, and we show that it is compatible with the tautological t-structure on
$\Delta _\lambda$, and we show that it is compatible with the tautological t-structure on ![]() ${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}_{\rm q}(\check {G})$ under the equivalence.
${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}_{\rm q}(\check {G})$ under the equivalence.
4. Factorization algebra and factorization module
Since [Reference Bezrukavnikov, Finkelberg and SchechtmanBFS98], it is known that the category of modules over a Hopf algebra can be realized as the category of factorization modules over a factorization algebra. In this section, we review factorization modules and factorization algebras, and give an equivalent expression of Theorem 3.3.2 with factorization modules.
4.1 Factorization algebras and factorization modules
Definition 4.1.1 We call a twisted sheaf ![]() $\Omega \in \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}})$ factorization algebra on
$\Omega \in \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}})$ factorization algebra on ![]() ${\mathop {\operatorname {\rm Conf}}}$ if it is compatible with the factorization property of
${\mathop {\operatorname {\rm Conf}}}$ if it is compatible with the factorization property of ![]() ${\mathop {\operatorname {\rm Conf}}}$, i.e. there is an isomorphism
${\mathop {\operatorname {\rm Conf}}}$, i.e. there is an isomorphism
with higher homotopy coherence.
The above definition makes sense in the ![]() $\mathcal {G}^\Lambda$-twisted case because
$\mathcal {G}^\Lambda$-twisted case because
It is easy to see that the Verdier dual of a factorization algebra is also a factorization algebra.
4.1.2
Given a factorization algebra ![]() $\Omega$ on
$\Omega$ on ![]() ${\mathop {\operatorname {\rm Conf}}}$, we can consider its module category on
${\mathop {\operatorname {\rm Conf}}}$, we can consider its module category on ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$.
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$.
Definition 4.1.3 We call a twisted sheaf ![]() $\mathcal {M}\in \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$ factorization module over
$\mathcal {M}\in \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$ factorization module over ![]() $\Omega$ if it is compatible with the factorization structure of
$\Omega$ if it is compatible with the factorization structure of ![]() $\Omega$, i.e. there is an isomorphism
$\Omega$, i.e. there is an isomorphism
with higher homotopy coherence.
We denote by ![]() $\Omega \text {-}{\operatorname {FactMod}}$ the category of factorization modules over
$\Omega \text {-}{\operatorname {FactMod}}$ the category of factorization modules over ![]() $\Omega$.
$\Omega$.
4.1.4 Structure of  $\Omega {\text {-}}{\operatorname {FactMod}}$
$\Omega {\text {-}}{\operatorname {FactMod}}$
Given ![]() $\lambda \in \Lambda$, let
$\lambda \in \Lambda$, let ![]() ${\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}$ be the locally closed subscheme of
${\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}$ be the locally closed subscheme of ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ consisting of the points
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ consisting of the points ![]() $D= \lambda \cdot x+\sum \lambda _i\cdot x_i$ such that
$D= \lambda \cdot x+\sum \lambda _i\cdot x_i$ such that ![]() $\lambda _i\in \Lambda ^{\text {neg}}\ \text {and}\ x_i\neq x\ \forall i$.
$\lambda _i\in \Lambda ^{\text {neg}}\ \text {and}\ x_i\neq x\ \forall i$.
The restriction of (2.2.5) to ![]() ${\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}$ induces a map
${\mathop {\operatorname {\rm Conf}}}\times {\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}$ induces a map
We call ![]() ${\check {\mathcal {M}}}{}\in \operatorname {Shv}_{{\mathcal {G}}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x})$ a factorization module over
${\check {\mathcal {M}}}{}\in \operatorname {Shv}_{{\mathcal {G}}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x})$ a factorization module over ![]() $\Omega$, if there is
$\Omega$, if there is
We denote by ![]() $\Omega {\text {-}}{\operatorname {FactMod}}_{=\lambda }$ the category of factorization modules on
$\Omega {\text {-}}{\operatorname {FactMod}}_{=\lambda }$ the category of factorization modules on ![]() ${\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}$ over
${\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}$ over ![]() $\Omega$.
$\Omega$.
Let ![]() $\mathcal {G}^\Lambda |_{\lambda \cdot x}$ be the fiber of
$\mathcal {G}^\Lambda |_{\lambda \cdot x}$ be the fiber of ![]() $\mathcal {G}^\Lambda$ at
$\mathcal {G}^\Lambda$ at ![]() $\lambda \cdot x$. The following lemma is from [Reference Gaitsgory and LysenkoGL19, Lemma 5.3.5].
$\lambda \cdot x$. The following lemma is from [Reference Gaitsgory and LysenkoGL19, Lemma 5.3.5].
Lemma 4.1.5 Taking ![]() $!$-stalks at
$!$-stalks at ![]() $\lambda \cdot x$ defines a
$\lambda \cdot x$ defines a ![]() $t$-exact equivalence
$t$-exact equivalence
Here ![]() ${\rm Vect}_{\mathcal {G}^\Lambda |_{\lambda \cdot x}}$ denotes the category of
${\rm Vect}_{\mathcal {G}^\Lambda |_{\lambda \cdot x}}$ denotes the category of ![]() $\mathcal {G}|_{\lambda \cdot x}$-twisted vector spaces.
$\mathcal {G}|_{\lambda \cdot x}$-twisted vector spaces.
Definition 4.1.6 Assume that ![]() $\Omega$ is in the heart of
$\Omega$ is in the heart of ![]() $\operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}})$. Consider the perverseFootnote 4 generator of
$\operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}})$. Consider the perverseFootnote 4 generator of ![]() $\Omega {\text {-}}{\operatorname {FactMod}}_{=\lambda }$, and we denote its
$\Omega {\text {-}}{\operatorname {FactMod}}_{=\lambda }$, and we denote its ![]() $*$ (respectively,
$*$ (respectively, ![]() $!$)-pushforward along the locally closed embedding
$!$)-pushforward along the locally closed embedding
by ![]() $\nabla _{\lambda, \Omega }$ (respectively,
$\nabla _{\lambda, \Omega }$ (respectively, ![]() $\Delta _{\lambda, \Omega }$).
$\Delta _{\lambda, \Omega }$).
Here ![]() $\nabla _{\lambda, \Omega }$ is called the costandard object of
$\nabla _{\lambda, \Omega }$ is called the costandard object of ![]() $\Omega {\text {-}}{\operatorname {FactMod}}$ and
$\Omega {\text {-}}{\operatorname {FactMod}}$ and ![]() $\Delta _{\lambda, \Omega }$ is called the standard object.
$\Delta _{\lambda, \Omega }$ is called the standard object.
By definition, standard objects ![]() $\Delta _{\lambda, \Omega }$ are compact and generate
$\Delta _{\lambda, \Omega }$ are compact and generate ![]() $\Omega {\text {-}}{\operatorname {FactMod}}$. Standard objects
$\Omega {\text {-}}{\operatorname {FactMod}}$. Standard objects ![]() $\Delta _{\lambda, \Omega }$ and costandard objects
$\Delta _{\lambda, \Omega }$ and costandard objects ![]() $\nabla _{\lambda, \Omega }$ are perverse.
$\nabla _{\lambda, \Omega }$ are perverse.
4.1.7
The Verdier duality functor is well-defined for both ![]() $\Delta _{\lambda, \Omega }$ and
$\Delta _{\lambda, \Omega }$ and ![]() $\nabla _{\lambda, \Omega }$. Furthermore, we have
$\nabla _{\lambda, \Omega }$. Furthermore, we have
Here ![]() $\Delta _{\lambda, \Omega }\in \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$ and
$\Delta _{\lambda, \Omega }\in \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$ and ![]() $\nabla _{\lambda, \mathbb {D}^{{\mathop {\operatorname {\rm Verdier}}}}(\Omega )}\in \operatorname {Shv}_{(\mathcal {G}^\Lambda )^{-1}}({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$.
$\nabla _{\lambda, \mathbb {D}^{{\mathop {\operatorname {\rm Verdier}}}}(\Omega )}\in \operatorname {Shv}_{(\mathcal {G}^\Lambda )^{-1}}({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$.
By definition, ![]() $\Delta _{\lambda, \Omega }$ and
$\Delta _{\lambda, \Omega }$ and ![]() $\nabla _{\mu, \Omega }$ satisfy the following orthogonality property.
$\nabla _{\mu, \Omega }$ satisfy the following orthogonality property.
Lemma 4.1.8 For ![]() $\lambda,\mu \in \Lambda$, we have
$\lambda,\mu \in \Lambda$, we have
 \[ \mathcal{H}om_{\Omega{\text{-}}{\operatorname{FactMod}}}(\Delta_{\lambda,\Omega}, \nabla_{\mu, \Omega})= \left\{\begin{aligned} \mathsf{e},\quad \text{if}\ \lambda=\mu,\\ 0, \quad \text{if}\ \lambda\neq\mu. \end{aligned}\right. \]
\[ \mathcal{H}om_{\Omega{\text{-}}{\operatorname{FactMod}}}(\Delta_{\lambda,\Omega}, \nabla_{\mu, \Omega})= \left\{\begin{aligned} \mathsf{e},\quad \text{if}\ \lambda=\mu,\\ 0, \quad \text{if}\ \lambda\neq\mu. \end{aligned}\right. \]
Proof. It follows from the adjointness of ![]() $!$-pushforward and
$!$-pushforward and ![]() $!$-pullback along the locally closed embedding
$!$-pullback along the locally closed embedding ![]() ${\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}\to {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$, and Lemma 4.1.5.
${\mathop {\operatorname {\rm Conf}}}_{=\lambda \cdot x}\to {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$, and Lemma 4.1.5.
4.1.9
The tautological t-structure on ![]() $\operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$ gives a t-structure on
$\operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$ gives a t-structure on ![]() $\Omega {\text {-}}{\operatorname {FactMod}}$. In fact, by [Reference Gaitsgory and LysenkoGL19, Proposition 5.4.2], we can describe this t-structure on
$\Omega {\text {-}}{\operatorname {FactMod}}$. In fact, by [Reference Gaitsgory and LysenkoGL19, Proposition 5.4.2], we can describe this t-structure on ![]() $\Omega {\text {-}}{\operatorname {FactMod}}$ by
$\Omega {\text {-}}{\operatorname {FactMod}}$ by ![]() $\Delta _{\lambda,\Omega }$. To be more precise, an
$\Delta _{\lambda,\Omega }$. To be more precise, an ![]() $\Omega$-factorization module
$\Omega$-factorization module ![]() $\mathcal {M}$ is coconnective as a twisted sheaf if and only if for any
$\mathcal {M}$ is coconnective as a twisted sheaf if and only if for any ![]() $\lambda \in \Lambda$,
$\lambda \in \Lambda$,
4.2 An explicit description of  $\Omega _{\rm q}^{\rm L}$
$\Omega _{\rm q}^{\rm L}$
In this section, we recall the factorization algebra ![]() $\Omega _{\rm q}^{\rm L}$ given in [Reference GaitsgoryGai21b, § 2.3]. It is the category of modules over this factorization algebra that is expected to be equivalent to the Whittaker category on affine flags.
$\Omega _{\rm q}^{\rm L}$ given in [Reference GaitsgoryGai21b, § 2.3]. It is the category of modules over this factorization algebra that is expected to be equivalent to the Whittaker category on affine flags.
Here ![]() ${\mathop {\operatorname {\rm Conf}}}$ has an open subscheme
${\mathop {\operatorname {\rm Conf}}}$ has an open subscheme ![]() $\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$ removing all diagonals. A point
$\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$ removing all diagonals. A point ![]() $D= \mathop {\sum }_k \lambda _k\cdot x_k$ belongs to
$D= \mathop {\sum }_k \lambda _k\cdot x_k$ belongs to ![]() $\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$ if and only if the coefficient of any point
$\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$ if and only if the coefficient of any point ![]() $x_k$ is a negative coroot. If
$x_k$ is a negative coroot. If ![]() $\lambda =-\sum _i n_i\cdot \alpha _i$, then the
$\lambda =-\sum _i n_i\cdot \alpha _i$, then the ![]() $\lambda$ connected component
$\lambda$ connected component ![]() $\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}^\lambda }$ is isomorphic to
$\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}^\lambda }$ is isomorphic to ![]() $\prod _i \overset {\circ }{X^{(n_i)}}$. Here
$\prod _i \overset {\circ }{X^{(n_i)}}$. Here ![]() $\overset {\circ }{X^{(n_i)}}$ classifies unordered
$\overset {\circ }{X^{(n_i)}}$ classifies unordered ![]() $n_i$ different points in
$n_i$ different points in ![]() $X$.
$X$.
Following [Reference Gaitsgory and LysenkoGL19, § 17.1.2], ![]() $\mathcal {G}^\Lambda |_{\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}}$ is canonically trivialized. In particular,
$\mathcal {G}^\Lambda |_{\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}}$ is canonically trivialized. In particular,
The product of sign local systems on each ![]() $\overset {\circ }{X^{(n_i)}}$ gives rise to a factorization algebra on
$\overset {\circ }{X^{(n_i)}}$ gives rise to a factorization algebra on ![]() $\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$. Under the equivalence (4.2.1), it can be regarded as a twisted factorization algebra on
$\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$. Under the equivalence (4.2.1), it can be regarded as a twisted factorization algebra on ![]() $\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$. We denote it by
$\overset {\circ }{{\mathop {\operatorname {\rm Conf}}}}$. We denote it by ![]() $\overset {\circ }{\Omega }_{\rm q}$, where
$\overset {\circ }{\Omega }_{\rm q}$, where ![]() $q$ is the quadratic form in (2.4.5).
$q$ is the quadratic form in (2.4.5).
4.2.1
By factorization (i.e. (4.1.1)), we only need to indicate how to extend ![]() $\Omega ^{\rm L}_{\rm q}$ from its restriction on
$\Omega ^{\rm L}_{\rm q}$ from its restriction on ![]() ${\mathop {\operatorname {\rm Conf}}}^\lambda \setminus X$ to
${\mathop {\operatorname {\rm Conf}}}^\lambda \setminus X$ to ![]() ${\mathop {\operatorname {\rm Conf}}}^\lambda$, for any
${\mathop {\operatorname {\rm Conf}}}^\lambda$, for any ![]() $\lambda \in \Lambda ^{\text {neg}}\setminus \{0\}$. Here
$\lambda \in \Lambda ^{\text {neg}}\setminus \{0\}$. Here ![]() $X$ embeds into
$X$ embeds into ![]() ${\mathop {\operatorname {\rm Conf}}}^\lambda$ by assigning
${\mathop {\operatorname {\rm Conf}}}^\lambda$ by assigning ![]() $x$ to
$x$ to ![]() $\lambda \cdot x$.
$\lambda \cdot x$.
We denote by ![]() $\jmath _\lambda$ the open embedding from
$\jmath _\lambda$ the open embedding from ![]() ${\mathop {\operatorname {\rm Conf}}}^{\lambda }\setminus X$ to
${\mathop {\operatorname {\rm Conf}}}^{\lambda }\setminus X$ to ![]() ${\mathop {\operatorname {\rm Conf}}}^\lambda$ and by
${\mathop {\operatorname {\rm Conf}}}^\lambda$ and by ![]() $l$ the length function of the Weyl group.
$l$ the length function of the Weyl group.
Definition 4.2.2 The factorization algebra ![]() $\Omega ^{\rm L}_{\rm q}$ is defined inductively as follows.
$\Omega ^{\rm L}_{\rm q}$ is defined inductively as follows.
(1) If
 $\lambda = w(\rho )-\rho$ and
$\lambda = w(\rho )-\rho$ and  $l(w)=2$, then
$l(w)=2$, then
 \[ \jmath_{\lambda,!}\circ \jmath_\lambda^!(\Omega^{\rm L}_{\rm q})\overset{\sim}{\longrightarrow} \Omega^{\rm L}_{\rm q}. \]
\[ \jmath_{\lambda,!}\circ \jmath_\lambda^!(\Omega^{\rm L}_{\rm q})\overset{\sim}{\longrightarrow} \Omega^{\rm L}_{\rm q}. \]
(2) If
 $\lambda = w(\rho )-\rho$ and
$\lambda = w(\rho )-\rho$ and  $l(w)\leq 3$,
$l(w)\leq 3$,
 \[ H^0(\jmath_{\lambda,!}\circ \jmath_\lambda^!(\Omega^{\rm L}_{\rm q}))\simeq \Omega^{\rm L}_{\rm q}. \]
\[ H^0(\jmath_{\lambda,!}\circ \jmath_\lambda^!(\Omega^{\rm L}_{\rm q}))\simeq \Omega^{\rm L}_{\rm q}. \]
(3) If
 $\lambda$ is not of the form
$\lambda$ is not of the form  $w(\rho )-\rho$, then
$w(\rho )-\rho$, then
 \[ \Omega^{\rm L}_{\rm q}\simeq \jmath_{\lambda, !*}\circ \jmath_\lambda^!(\Omega^{\rm L}_{\rm q}). \]
\[ \Omega^{\rm L}_{\rm q}\simeq \jmath_{\lambda, !*}\circ \jmath_\lambda^!(\Omega^{\rm L}_{\rm q}). \]
The following lemma is indicated in [Reference Gaitsgory and LysenkoGL19, § 29], see [Reference Chen and FuCF21, Theorem 1.2.1] for a precise statement and proof.
Lemma 4.2.3 In the D-module setting and the Betti setting, there is
Furthermore, under the above equivalence, ![]() $V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ (respectively,
$V_\lambda ^{{\mathop {\operatorname {\rm mxd}}}}$ (respectively, ![]() $V_\lambda ^{{\mathop {\operatorname {\rm mxd}}},\vee }$) corresponds to
$V_\lambda ^{{\mathop {\operatorname {\rm mxd}}},\vee }$) corresponds to ![]() $\Delta _{\lambda, \Omega _{\rm q}^{\rm L}}$ (respectively,
$\Delta _{\lambda, \Omega _{\rm q}^{\rm L}}$ (respectively, ![]() $\nabla _{\lambda, \Omega _{\rm q}^{\rm L}}$).
$\nabla _{\lambda, \Omega _{\rm q}^{\rm L}}$).
Proof. By Lefschetz principle and Riemann–Hilbert correspondence, we only need to prove the claim in the setting of constructible sheaves with coefficients in ![]() $\mathbb {C}$ in classical topology.
$\mathbb {C}$ in classical topology.
Following [Reference Gaitsgory and LysenkoGL19, § 29.5.1], one can associate a factorization algebra with a Hopf algebra ![]() $A$. Furthermore, the relative Drinfeld center of
$A$. Furthermore, the relative Drinfeld center of ![]() $A$-mod is equivalent to the category of factorization modules over the corresponding factorization algebra. Applying it to our case, there is an equivalence of categories
$A$-mod is equivalent to the category of factorization modules over the corresponding factorization algebra. Applying it to our case, there is an equivalence of categories
Here ![]() $\Omega _{q, \text {quant}}^{\rm L}$ denotes the
$\Omega _{q, \text {quant}}^{\rm L}$ denotes the ![]() $\mathcal {G}^\Lambda$-twisted factorization algebra associated with
$\mathcal {G}^\Lambda$-twisted factorization algebra associated with ![]() $U_{\rm q}^{\rm L}(\check {\mathfrak {n}})$ for a certain factorization algebra.
$U_{\rm q}^{\rm L}(\check {\mathfrak {n}})$ for a certain factorization algebra.
However, by the Verdier dual of [Reference GaitsgoryGai21b, § 2.3.8, Theorem 3.6.2], there is ![]() $\Omega _{q, \text {quant}}^{\rm L}\simeq \Omega ^{\rm L}_{\rm q}$.
$\Omega _{q, \text {quant}}^{\rm L}\simeq \Omega ^{\rm L}_{\rm q}$.
4.3 Restatement of Theorem 3.3.2
The following theorem is equivalent to Theorem 3.3.2.
Theorem 4.3.1 In the setting of D-modules, when ![]() $q$ avoids small torsion, there is a functor
$q$ avoids small torsion, there is a functor ![]() $F^{\rm L}$ which establishes a t-exactFootnote 5 equivalence
$F^{\rm L}$ which establishes a t-exactFootnote 5 equivalence
and preserves standard objects and costandard objects.
}
Remark 4.3.2 The above theorem holds in the Betti setting if we replace the Whittaker category by the Kirillov model.
5. Standard object and duality of Whittaker category
The principal goal of this section is to construct standard objects of ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ (§ 5.5) and define the duality functor of
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ (§ 5.5) and define the duality functor of ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ using a lemma from [Reference RaskinRas21] (§ 5.7). They play an important role in the proof of our main theorem.
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)$ using a lemma from [Reference RaskinRas21] (§ 5.7). They play an important role in the proof of our main theorem.
5.1 Relevant orbits
To study ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$, we should first study when a
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$, we should first study when a ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbit admits non-zero Whittaker sheaves support on it.
$N(\mathcal {K})^{\omega ^\rho }$-orbit admits non-zero Whittaker sheaves support on it.
It is known that the ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbits in
$N(\mathcal {K})^{\omega ^\rho }$-orbits in ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ are indexed by the extended affine Weyl group
${\operatorname {Fl}}_G^{\omega ^\rho }$ are indexed by the extended affine Weyl group ![]() $W^{{\operatorname {ext}}}:= W\ltimes \Lambda$. For any
$W^{{\operatorname {ext}}}:= W\ltimes \Lambda$. For any ![]() $\widetilde {w}\in W^{{\operatorname {ext}}}$, we denote by
$\widetilde {w}\in W^{{\operatorname {ext}}}$, we denote by ![]() $S_{{\operatorname {Fl}}}^{\widetilde {w}}$ the
$S_{{\operatorname {Fl}}}^{\widetilde {w}}$ the ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbit in
$N(\mathcal {K})^{\omega ^\rho }$-orbit in ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ of
${\operatorname {Fl}}_G^{\omega ^\rho }$ of ![]() $\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho }$. Let
$\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho }$. Let ![]() $\overline {S}_{{\operatorname {Fl}}}^{\widetilde {w}}$ denote the closure of
$\overline {S}_{{\operatorname {Fl}}}^{\widetilde {w}}$ denote the closure of ![]() $S_{{\operatorname {Fl}}}^{\widetilde {w}}$ in
$S_{{\operatorname {Fl}}}^{\widetilde {w}}$ in ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$.
${\operatorname {Fl}}_G^{\omega ^\rho }$.
The orbits which admit non-zero ![]() $\mathcal {G}^G$-twisted Whittaker sheaves are called relevant orbits. Since
$\mathcal {G}^G$-twisted Whittaker sheaves are called relevant orbits. Since ![]() $N(\mathcal {K})^{\omega ^\rho }$ is ind-pro-unipotent and
$N(\mathcal {K})^{\omega ^\rho }$ is ind-pro-unipotent and ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ is
${\operatorname {Fl}}_G^{\omega ^\rho }$ is ![]() $\mathcal {G}^G$-equivariant with respect to the action of
$\mathcal {G}^G$-equivariant with respect to the action of ![]() $G(\mathcal {K})^{\omega ^\rho }$, the gerbe
$G(\mathcal {K})^{\omega ^\rho }$, the gerbe ![]() $\mathcal {G}^G$ on any single
$\mathcal {G}^G$ on any single ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbit admits a
$N(\mathcal {K})^{\omega ^\rho }$-orbit admits a ![]() $N(\mathcal {K})^{\omega ^\rho }$-equivariant trivialization. As a result, the necessary and sufficient condition for a
$N(\mathcal {K})^{\omega ^\rho }$-equivariant trivialization. As a result, the necessary and sufficient condition for a ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbit
$N(\mathcal {K})^{\omega ^\rho }$-orbit ![]() ${S}^{\widetilde {w}}_{{\operatorname {Fl}}}$ to be relevant is that it is relevant in the non-twisted case. Namely,
${S}^{\widetilde {w}}_{{\operatorname {Fl}}}$ to be relevant is that it is relevant in the non-twisted case. Namely,
Definition 5.1.1 Given an element ![]() $\widetilde {w}\in W^{{\operatorname {ext}}}$, we denote by
$\widetilde {w}\in W^{{\operatorname {ext}}}$, we denote by ![]() $l(\widetilde {w})$ the dimension of its Iwahori orbit in the affine flags (or the length of
$l(\widetilde {w})$ the dimension of its Iwahori orbit in the affine flags (or the length of ![]() $\widetilde {w}$). To be more precise, if
$\widetilde {w}$). To be more precise, if ![]() $\widetilde {w}=t^\lambda w$, then
$\widetilde {w}=t^\lambda w$, then
Proposition 5.1.2 A ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbit
$N(\mathcal {K})^{\omega ^\rho }$-orbit ![]() $S_{{\operatorname {Fl}}}^{\widetilde {w}}\subset {\operatorname {Fl}}^{\omega ^\rho }_G$ is relevant if and only if
$S_{{\operatorname {Fl}}}^{\widetilde {w}}\subset {\operatorname {Fl}}^{\omega ^\rho }_G$ is relevant if and only if ![]() $t^\rho \widetilde {w}$ is the maximal length element in the left coset
$t^\rho \widetilde {w}$ is the maximal length element in the left coset ![]() $Wt^\rho \widetilde {w}\subset W^{{\operatorname {ext}}}$.
$Wt^\rho \widetilde {w}\subset W^{{\operatorname {ext}}}$.
In particular, for any dominant coweight ![]() $\lambda \in \Lambda ^+$,
$\lambda \in \Lambda ^+$, ![]() $t^\lambda \in W^{\operatorname {ext}}$ is relevant.
$t^\lambda \in W^{\operatorname {ext}}$ is relevant.
Proof. Denote by
the set of the roots of ![]() $G(\mathcal {K})^{\omega ^\rho }$ corresponding to
$G(\mathcal {K})^{\omega ^\rho }$ corresponding to ![]() $I^{\omega ^\rho }$. Here
$I^{\omega ^\rho }$. Here ![]() $\delta$ is the positive imaginary root generator. We denote by
$\delta$ is the positive imaginary root generator. We denote by ![]() $\check {\Delta }^+$ (respectively,
$\check {\Delta }^+$ (respectively, ![]() $\check {\Pi }^+$) the set of positive (respectively, positive simple) roots of
$\check {\Pi }^+$) the set of positive (respectively, positive simple) roots of ![]() $G$.
$G$.
If the ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbit of
$N(\mathcal {K})^{\omega ^\rho }$-orbit of ![]() $\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho }\in {\operatorname {Fl}}_G^{\omega ^\rho }$ is relevant, we need the formula (5.1.1) to hold. By a straightforward calculation
$\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho }\in {\operatorname {Fl}}_G^{\omega ^\rho }$ is relevant, we need the formula (5.1.1) to hold. By a straightforward calculation
 \begin{align} & {\mathop{\operatorname{\rm Stab}}}_{N(\mathcal{K})^{\omega^\rho}}(\widetilde{w}\cdot I^{\omega^\rho}/I^{\omega^\rho})= \widetilde{w}I^{\omega^\rho} \widetilde{w}^{-1}\cap N(\mathcal{K})^{\omega^\rho}\subset {\mathop{\operatorname{\rm Ker}}}(\chi) \nonumber\\ &\quad \Leftrightarrow \widetilde{w}({\widetilde{\check{\Delta}}}^+)\cap (\check{\Pi}^+-\delta)=\emptyset \nonumber\\ &\quad \Leftrightarrow \widetilde{w}({\widetilde{\check{\Delta}}}^+)\cap t^{-\rho}(\check{\Pi}^+)=\emptyset \nonumber\\ &\quad \Leftrightarrow t^{\rho}\widetilde{w}({\widetilde{\check{\Delta}}}^+)\cap \check{\Pi}^+=\emptyset \nonumber\\ &\quad \Leftrightarrow -\{\check{\Pi}^+\}\subset t^{\rho}\widetilde{w}({\widetilde{\check{\Delta}}}^+) \nonumber\\ &\quad \Leftrightarrow \widetilde{w}^{-1}t^{-\rho}(\check{\Delta}^+)< 0. \end{align}
\begin{align} & {\mathop{\operatorname{\rm Stab}}}_{N(\mathcal{K})^{\omega^\rho}}(\widetilde{w}\cdot I^{\omega^\rho}/I^{\omega^\rho})= \widetilde{w}I^{\omega^\rho} \widetilde{w}^{-1}\cap N(\mathcal{K})^{\omega^\rho}\subset {\mathop{\operatorname{\rm Ker}}}(\chi) \nonumber\\ &\quad \Leftrightarrow \widetilde{w}({\widetilde{\check{\Delta}}}^+)\cap (\check{\Pi}^+-\delta)=\emptyset \nonumber\\ &\quad \Leftrightarrow \widetilde{w}({\widetilde{\check{\Delta}}}^+)\cap t^{-\rho}(\check{\Pi}^+)=\emptyset \nonumber\\ &\quad \Leftrightarrow t^{\rho}\widetilde{w}({\widetilde{\check{\Delta}}}^+)\cap \check{\Pi}^+=\emptyset \nonumber\\ &\quad \Leftrightarrow -\{\check{\Pi}^+\}\subset t^{\rho}\widetilde{w}({\widetilde{\check{\Delta}}}^+) \nonumber\\ &\quad \Leftrightarrow \widetilde{w}^{-1}t^{-\rho}(\check{\Delta}^+)< 0. \end{align}
According to [Reference KacKac90, Lemma 3.11 a.], it means that for any simple reflection ![]() $r_i$ of
$r_i$ of ![]() $W$, there is
$W$, there is ![]() $l(\widetilde {w}^{-1} t^{-\rho } r_i)\leq l(\widetilde {w}^{-1} t^{-\rho })$. We conclude that for any simple reflection
$l(\widetilde {w}^{-1} t^{-\rho } r_i)\leq l(\widetilde {w}^{-1} t^{-\rho })$. We conclude that for any simple reflection ![]() $r_i$ of
$r_i$ of ![]() $W$, there is
$W$, there is ![]() $l(r_i t^{\rho } \widetilde {w})\leq l(t^{\rho } \widetilde {w})$. It means
$l(r_i t^{\rho } \widetilde {w})\leq l(t^{\rho } \widetilde {w})$. It means ![]() $t^{\rho } \widetilde {w}$ is the unique maximal length element in
$t^{\rho } \widetilde {w}$ is the unique maximal length element in ![]() $W t^{\rho } \widetilde {w}\subset W^{{\operatorname {ext}}}$.
$W t^{\rho } \widetilde {w}\subset W^{{\operatorname {ext}}}$.
Remark 5.1.3 Relevant orbits of ![]() ${\operatorname {Fl}}_G$ are naturally indexed
${\operatorname {Fl}}_G$ are naturally indexed ![]() $\Lambda$. One can check that
$\Lambda$. One can check that
 \begin{equation} \begin{aligned} \phi: W^{{\operatorname{ext}}}\to W^{{\operatorname{ext}}}\\ \widetilde{w}\mapsto t^{-\rho} \widetilde{w}_l, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \phi: W^{{\operatorname{ext}}}\to W^{{\operatorname{ext}}}\\ \widetilde{w}\mapsto t^{-\rho} \widetilde{w}_l, \end{aligned} \end{equation}
induces a bijection between ![]() $\Lambda$ and the set
$\Lambda$ and the set ![]() $\{\widetilde {w},\ \widetilde {w}\ \text {is relevant}\}$. Here
$\{\widetilde {w},\ \widetilde {w}\ \text {is relevant}\}$. Here ![]() $\widetilde {w}_l$ denotes the unique maximal length element in the left coset
$\widetilde {w}_l$ denotes the unique maximal length element in the left coset ![]() $W\widetilde {w}$. For example, if
$W\widetilde {w}$. For example, if ![]() $\widetilde {w}=t^0$, then
$\widetilde {w}=t^0$, then ![]() $\phi (\widetilde {w})= t^{-\rho }w_0$; if
$\phi (\widetilde {w})= t^{-\rho }w_0$; if ![]() $\widetilde {w}=t^{\rho +\lambda }$ and
$\widetilde {w}=t^{\rho +\lambda }$ and ![]() $\lambda$ is dominant, then
$\lambda$ is dominant, then ![]() $\phi (\widetilde {w})= t^\lambda$.
$\phi (\widetilde {w})= t^\lambda$.
Proposition 5.1.4 The category of twisted Whittaker sheaves on ![]() $S^{\widetilde {w}}_{{\operatorname {Fl}}}$ is equivalent to
$S^{\widetilde {w}}_{{\operatorname {Fl}}}$ is equivalent to ![]() ${\rm Vect}$ or
${\rm Vect}$ or ![]() $0$ depends on if
$0$ depends on if ![]() $\widetilde {w}$ is relevant or not, i.e.
$\widetilde {w}$ is relevant or not, i.e.
Proof. There is a ![]() $N(\mathcal {K})^{\omega ^\rho }$-equivariant trivialization of
$N(\mathcal {K})^{\omega ^\rho }$-equivariant trivialization of ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() $S_{{\operatorname {Fl}}}^{\widetilde {w}}$, we have
$S_{{\operatorname {Fl}}}^{\widetilde {w}}$, we have ![]() $\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\widetilde {w}})\simeq \operatorname {Whit}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$. Since
$\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\widetilde {w}})\simeq \operatorname {Whit}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$. Since ![]() ${\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })$ is a connected pro-unipotent group,
${\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })$ is a connected pro-unipotent group, ![]() $\operatorname {Whit}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$ is a full subcategory of
$\operatorname {Whit}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$ is a full subcategory of ![]() $\operatorname {Shv}^{N(\mathcal {K})^{\omega ^\rho },\chi }(N(\mathcal {K})^{\omega ^\rho })$. The latter category is equivalent to
$\operatorname {Shv}^{N(\mathcal {K})^{\omega ^\rho },\chi }(N(\mathcal {K})^{\omega ^\rho })$. The latter category is equivalent to ![]() ${\rm Vect}$, we only need to show that the fully faithful embedding
${\rm Vect}$, we only need to show that the fully faithful embedding
is actually an equivalence if ![]() $\widetilde {w}$ is relevant and is
$\widetilde {w}$ is relevant and is ![]() $0$ otherwise.
$0$ otherwise.
If ![]() $\widetilde {w}$ is relevant,
$\widetilde {w}$ is relevant, ![]() ${\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })\subset {\mathop {\operatorname {\rm Ker}}} (\chi )$, so any Whittaker sheaf on
${\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })\subset {\mathop {\operatorname {\rm Ker}}} (\chi )$, so any Whittaker sheaf on ![]() $N(\mathcal {K})^{\omega ^\rho }$ descends to a Whittaker sheaf on
$N(\mathcal {K})^{\omega ^\rho }$ descends to a Whittaker sheaf on ![]() $S_{{\operatorname {Fl}}}^{\widetilde {w}}\simeq N(\mathcal {K})^{\omega ^\rho }/ {\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })$. If
$S_{{\operatorname {Fl}}}^{\widetilde {w}}\simeq N(\mathcal {K})^{\omega ^\rho }/ {\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })$. If ![]() $\widetilde {w}$ is not relevant, we should prove that for any
$\widetilde {w}$ is not relevant, we should prove that for any ![]() $\mathcal {F}\in \operatorname {Whit}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$, there is
$\mathcal {F}\in \operatorname {Whit}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$, there is ![]() $\mathcal {F}=0$. Since the action of
$\mathcal {F}=0$. Since the action of ![]() $N(\mathcal {K})^{\omega ^\rho }$ is transitive, we only need to show that the stalk of
$N(\mathcal {K})^{\omega ^\rho }$ is transitive, we only need to show that the stalk of ![]() $\mathcal {F}$ is
$\mathcal {F}$ is ![]() $0$ at
$0$ at ![]() $\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho }$. It follows immediately from the fact that this fiber is equivariant with respect to
$\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho }$. It follows immediately from the fact that this fiber is equivariant with respect to ![]() ${\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })$ against a non-trivial character.
${\mathop {\operatorname {\rm Stab}}}_{N(\mathcal {K})^{\omega ^\rho }}(\widetilde {w}\cdot I^{\omega ^\rho }/I^{\omega ^\rho })$ against a non-trivial character.
Definition 5.1.5 Assume that ![]() $\widetilde {w}$ is relevant, we define
$\widetilde {w}$ is relevant, we define
and
where ![]() $j_{{\widetilde {w}}, {\operatorname {Fl}}}$ is the locally closed embedding
$j_{{\widetilde {w}}, {\operatorname {Fl}}}$ is the locally closed embedding
They are defined up to tensoring by a line, i.e. depending on the trivialization of ![]() ${\mathcal {G}}^G$ at
${\mathcal {G}}^G$ at ![]() $\widetilde {w}\in {\operatorname {Fl}}_G^{\omega ^{\rho }}$.
$\widetilde {w}\in {\operatorname {Fl}}_G^{\omega ^{\rho }}$.
Remark 5.1.6 Here the superscript ‘![]() ${{\mathop {\operatorname {\rm ver}}}}$’ means Verma. We expect, under Conjecture 2,
${{\mathop {\operatorname {\rm ver}}}}$’ means Verma. We expect, under Conjecture 2, ![]() $\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}\}$ correspond to Verma modules in the category of modules over Kac–Moody Lie algebra.
$\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}\}$ correspond to Verma modules in the category of modules over Kac–Moody Lie algebra.
The object ![]() $\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is the
$\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is the ![]() $!$-pushforward of the generator of
$!$-pushforward of the generator of ![]() $\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$, and
$\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$, and ![]() $\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is the
$\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is the ![]() $*$-pushforward of the generator of
$*$-pushforward of the generator of ![]() $\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$. They have the following properties.
$\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\widetilde {w}})$. They have the following properties.
Proposition 5.1.7 We have:
(1)
 $\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \widetilde {w}\ \text {is relevant}\}$ (respectively,
$\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \widetilde {w}\ \text {is relevant}\}$ (respectively,  $\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \widetilde {w}\ \text {is relevant}\}$) compactly generate
$\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \widetilde {w}\ \text {is relevant}\}$) compactly generate  $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$;
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$;(2)
 \[ \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_{\widetilde{w}}^{{\mathop{\operatorname{\rm ver}}}}, \nabla_{\widetilde{w}'}^{{\mathop{\operatorname{\rm ver}}}})\simeq\left\{\begin{aligned} 0,\quad \text{if}\ \widetilde{w}\neq \widetilde{w}',\\ \mathsf{e},\quad \text{if}\ \widetilde{w}= \widetilde{w}'. \end{aligned}\right. \]
\[ \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_{\widetilde{w}}^{{\mathop{\operatorname{\rm ver}}}}, \nabla_{\widetilde{w}'}^{{\mathop{\operatorname{\rm ver}}}})\simeq\left\{\begin{aligned} 0,\quad \text{if}\ \widetilde{w}\neq \widetilde{w}',\\ \mathsf{e},\quad \text{if}\ \widetilde{w}= \widetilde{w}'. \end{aligned}\right. \]
Proof. Since ![]() $j_{\widetilde {w}, {\operatorname {Fl}},!}$ is the left adjoint functor of a continuous functor (i.e.
$j_{\widetilde {w}, {\operatorname {Fl}},!}$ is the left adjoint functor of a continuous functor (i.e. ![]() $j^!_{\widetilde {w}, {\operatorname {Fl}}}$), it preserves compactness. In particular,
$j^!_{\widetilde {w}, {\operatorname {Fl}}}$), it preserves compactness. In particular, ![]() $\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is compact. Note that for
$\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is compact. Note that for ![]() $\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G)$,
$\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G)$, ![]() $\mathcal {H}om_{\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })}(\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \mathcal {F})$ is isomorphic to the
$\mathcal {H}om_{\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })}(\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \mathcal {F})$ is isomorphic to the ![]() $!$-stalks of
$!$-stalks of ![]() $\mathcal {F}$ at
$\mathcal {F}$ at ![]() $\widetilde {w}$ up to a shift. Hence, if
$\widetilde {w}$ up to a shift. Hence, if ![]() $\mathcal {H}om_{\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })}(\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \mathcal {F})=0$ for any relevant
$\mathcal {H}om_{\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })}(\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \mathcal {F})=0$ for any relevant ![]() $\widetilde {w}$, then
$\widetilde {w}$, then ![]() $\mathcal {F}=0$.
$\mathcal {F}=0$.
To show the claim for ![]() $\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \widetilde {w}\ \text {is relevant}\}$, note that the closure of any
$\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}, \widetilde {w}\ \text {is relevant}\}$, note that the closure of any ![]() $N(\mathcal {K})^{\omega ^\rho }$-orbit in
$N(\mathcal {K})^{\omega ^\rho }$-orbit in ![]() ${\operatorname {Fl}}^{\omega ^\rho }_G$ only contains finite many relevant orbits. Hence, any
${\operatorname {Fl}}^{\omega ^\rho }_G$ only contains finite many relevant orbits. Hence, any ![]() $\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is a finite extension of objects in
$\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is a finite extension of objects in ![]() $\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}[k], \widetilde {w}\ \text {is relevant}, k\in \mathbb {Z}\}$. In particular,
$\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}[k], \widetilde {w}\ \text {is relevant}, k\in \mathbb {Z}\}$. In particular, ![]() $\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is compact. Similarly, any
$\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is compact. Similarly, any ![]() $\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is a finite extension of objects in
$\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ is a finite extension of objects in ![]() $\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}[k], \widetilde {w}\ \text {is relevant}, k\in \mathbb {Z}\}$. Hence, the objects
$\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}[k], \widetilde {w}\ \text {is relevant}, k\in \mathbb {Z}\}$. Hence, the objects ![]() $\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ compactly generate
$\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ compactly generate ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ as the objects
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ as the objects ![]() $\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ do.
$\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}$ do.
Claim (2) directly follows from the adjointness of ![]() $!$-pushforward and
$!$-pushforward and ![]() $!$-pullback, and Proposition 5.1.4.
$!$-pullback, and Proposition 5.1.4.
As a corollary, an object ![]() $\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ is compact if and only if
$\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ is compact if and only if ![]() $\mathcal {F}$ is supported on finitely many
$\mathcal {F}$ is supported on finitely many ![]() ${S}^{\widetilde {w}}_{{\operatorname {Fl}}}$, and its restriction is compact in
${S}^{\widetilde {w}}_{{\operatorname {Fl}}}$, and its restriction is compact in ![]() $\operatorname {Whit}_{\rm q}({S}_{{\operatorname {Fl}}}^{\widetilde {w}})$, for any
$\operatorname {Whit}_{\rm q}({S}_{{\operatorname {Fl}}}^{\widetilde {w}})$, for any ![]() $\widetilde {w}$.
$\widetilde {w}$.
Remark 5.1.8 We can define a highest weight category structure on ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ with standards
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ with standards ![]() $\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}\}$ and costandards
$\{\Delta _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}\}$ and costandards ![]() $\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}\}$. It is the highest weight category structure in [Reference Campbell, Dhillon and RaskinCDR21]. However, it is different from that used in this paper. For generic
$\{\nabla _{\widetilde {w}}^{{\mathop {\operatorname {\rm ver}}}}\}$. It is the highest weight category structure in [Reference Campbell, Dhillon and RaskinCDR21]. However, it is different from that used in this paper. For generic ![]() $q$, we expect that they are essentially the same (up to a convolution).
$q$, we expect that they are essentially the same (up to a convolution).
5.2 Right equivariant sheaf
Recall the main theorem of [Reference Arkhipov and BezrukavnikovAB09],
It is not only an equivalence of plain categories, but also compatible with highest weight category structures on both sides. The standard objects in ![]() ${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ are Verma modules
${\operatorname {Rep}}^{{\mathop {\operatorname {\rm mxd}}}}(\check {G})$ are Verma modules ![]() $V^{{\mathop {\operatorname {\rm mxd}}}}_\lambda$ and the standard objects in
$V^{{\mathop {\operatorname {\rm mxd}}}}_\lambda$ and the standard objects in ![]() $\operatorname {Whit}({\operatorname {Fl}}_G)$ are given by the !-averaging of the BMWFootnote 6 sheaves
$\operatorname {Whit}({\operatorname {Fl}}_G)$ are given by the !-averaging of the BMWFootnote 6 sheaves ![]() ${{J}}_\lambda$ (i.e. Wakimoto sheaves). Hence, in the twisted case, we need to define the twisted BMW sheaves
${{J}}_\lambda$ (i.e. Wakimoto sheaves). Hence, in the twisted case, we need to define the twisted BMW sheaves ![]() ${{J}}_\lambda$ and use them to define standard objects
${{J}}_\lambda$ and use them to define standard objects ![]() $\Delta _\lambda$ in
$\Delta _\lambda$ in ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ by
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ by ![]() $!$-averaging.
$!$-averaging.
5.2.1
Let ![]() $I^0$ be the unipotent radical of the
$I^0$ be the unipotent radical of the ![]() $\omega ^\rho$-twisted Iwahori subgroup
$\omega ^\rho$-twisted Iwahori subgroup ![]() $I^{\omega ^\rho }$, and let
$I^{\omega ^\rho }$, and let ![]() $T^{\omega ^\rho }$ be
$T^{\omega ^\rho }$ be ![]() $I^{\omega ^\rho }/I^0$. When there is no twisting,
$I^{\omega ^\rho }/I^0$. When there is no twisting, ![]() ${{J}}_\lambda$ is Iwahori-equivariant. However, there are ‘much fewer’ Iwahori-equivariant objects in the twisted case.
${{J}}_\lambda$ is Iwahori-equivariant. However, there are ‘much fewer’ Iwahori-equivariant objects in the twisted case.
Indeed, since ![]() $I^0$ is pro-unipotent, there is a unique (up to a non-canonical isomorphism)
$I^0$ is pro-unipotent, there is a unique (up to a non-canonical isomorphism) ![]() $I^0$-equivariant trivialization of the gerbe
$I^0$-equivariant trivialization of the gerbe ![]() $\mathcal {G}^G$ on any Iwahori orbit
$\mathcal {G}^G$ on any Iwahori orbit
of ![]() ${\operatorname {Fl}}^{\omega ^\rho }_G$. In the twisted case, the
${\operatorname {Fl}}^{\omega ^\rho }_G$. In the twisted case, the ![]() $I^0$-equivariant trivialization of
$I^0$-equivariant trivialization of ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Fl}}_G^{\widetilde {w}}$ is not necessarily Iwahori-equivariant. Instead, it is equivariant with respect to a certain character of
${\operatorname {Fl}}_G^{\widetilde {w}}$ is not necessarily Iwahori-equivariant. Instead, it is equivariant with respect to a certain character of ![]() $T^{\omega ^\rho }$. For example, when the quadratic form
$T^{\omega ^\rho }$. For example, when the quadratic form ![]() $q$ is generic, there is no
$q$ is generic, there is no ![]() $I^{\omega ^\rho }$-equivariant sheaf on
$I^{\omega ^\rho }$-equivariant sheaf on ![]() ${\operatorname {Fl}}_G^{t^\lambda w}$ unless
${\operatorname {Fl}}_G^{t^\lambda w}$ unless ![]() $\lambda =0$.
$\lambda =0$.
The solution to fix this problem is to consider ![]() $I^0$-equivariant sheaves on
$I^0$-equivariant sheaves on ![]() $\widetilde {{\operatorname {Fl}}}:=G(\mathcal {K})^{\omega ^\rho }/I^0$, rather than Iwahori-equivariant sheaves on
$\widetilde {{\operatorname {Fl}}}:=G(\mathcal {K})^{\omega ^\rho }/I^0$, rather than Iwahori-equivariant sheaves on ![]() ${\operatorname {Fl}}_G$.
${\operatorname {Fl}}_G$.
5.2.2
The exact sequence
is split. Hence, we may consider the right action of ![]() $T^{\omega ^\rho }$ on
$T^{\omega ^\rho }$ on ![]() $\widetilde {{\operatorname {Fl}}}:=G(\mathcal {K})^{\omega ^\rho }/I^0$. In order to define BMW sheaves in the twisted case, we need to consider sheaves on
$\widetilde {{\operatorname {Fl}}}:=G(\mathcal {K})^{\omega ^\rho }/I^0$. In order to define BMW sheaves in the twisted case, we need to consider sheaves on ![]() $\widetilde {{\operatorname {Fl}}}$ which are right
$\widetilde {{\operatorname {Fl}}}$ which are right ![]() $T^{\omega ^\rho }$-equivariant against a character. This idea appears in [Reference BezrukavnikovBez16] and [Reference Lusztig and YunLY20].
$T^{\omega ^\rho }$-equivariant against a character. This idea appears in [Reference BezrukavnikovBez16] and [Reference Lusztig and YunLY20].
Let ![]() $b(-,-)$ be the symmetric bilinear form associated with the quadratic form
$b(-,-)$ be the symmetric bilinear form associated with the quadratic form ![]() $q$, i.e. in the D-module setting,
$q$, i.e. in the D-module setting,
in the Betti setting and the ![]() $\ell$-adic setting,
$\ell$-adic setting,
In the D-module setting (respectively, Betti setting and ![]() $\ell$-adic setting), we denote by
$\ell$-adic setting), we denote by
the associated character of ![]() $T^{\omega ^\rho }$. With some abuse of notation, we denote by
$T^{\omega ^\rho }$. With some abuse of notation, we denote by ![]() $b_\lambda$ the associated Kummer sheaf on
$b_\lambda$ the associated Kummer sheaf on ![]() $T^{\omega ^\rho }$. Its pullback to
$T^{\omega ^\rho }$. Its pullback to ![]() $I^{\omega ^\rho }$ is also denoted by
$I^{\omega ^\rho }$ is also denoted by ![]() $b_\lambda$.
$b_\lambda$.
Definition 5.2.3 We define
as the category of left ![]() $(I^{\omega ^\rho },b_\lambda )$-equivariant and right
$(I^{\omega ^\rho },b_\lambda )$-equivariant and right ![]() $(T^{\omega ^\rho },b_\mu )$-equivariant twisted sheaves on
$(T^{\omega ^\rho },b_\mu )$-equivariant twisted sheaves on ![]() $\widetilde {{\operatorname {Fl}}}$.
$\widetilde {{\operatorname {Fl}}}$.
Similarly, we define
as the category of left ![]() $I^0$-equivariant and right
$I^0$-equivariant and right ![]() $(T^{\omega ^\rho },b_\mu )$-equivariant twisted sheaves on
$(T^{\omega ^\rho },b_\mu )$-equivariant twisted sheaves on ![]() $\widetilde {{\operatorname {Fl}}}$.
$\widetilde {{\operatorname {Fl}}}$.
When ![]() $\mu =0$, we omit
$\mu =0$, we omit ![]() $\mu$ in the notation. In this case, we can realize right
$\mu$ in the notation. In this case, we can realize right ![]() $T^{\omega ^\rho }$-equivariant objects on
$T^{\omega ^\rho }$-equivariant objects on ![]() $\widetilde {{\operatorname {Fl}}}$ as objects on
$\widetilde {{\operatorname {Fl}}}$ as objects on ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$.
${\operatorname {Fl}}_G^{\omega ^\rho }$.
Let ![]() $\widetilde {{\operatorname {Fl}}}^{\widetilde {w}}$ be the preimage of
$\widetilde {{\operatorname {Fl}}}^{\widetilde {w}}$ be the preimage of ![]() ${{\operatorname {Fl}}}^{\widetilde {w}}_G$ in
${{\operatorname {Fl}}}^{\widetilde {w}}_G$ in ![]() $\widetilde {{\operatorname {Fl}}}$. We have equivalences
$\widetilde {{\operatorname {Fl}}}$. We have equivalences
 \begin{align*}
\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{{\operatorname{Fl}}}^{\widetilde{w}})_{\mu}^{I^0}&\simeq
\operatorname{Shv}_{\mathcal{G}^G}((\widetilde{w}I^{\omega^\rho}/I^0)/T^{\omega^\rho},
b_\mu)\simeq
\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{w}I^{\omega^\rho}/I^{\omega^\rho},
b_\mu)\\&\simeq
\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{w}T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},
b_\mu). \end{align*}
\begin{align*}
\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{{\operatorname{Fl}}}^{\widetilde{w}})_{\mu}^{I^0}&\simeq
\operatorname{Shv}_{\mathcal{G}^G}((\widetilde{w}I^{\omega^\rho}/I^0)/T^{\omega^\rho},
b_\mu)\simeq
\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{w}I^{\omega^\rho}/I^{\omega^\rho},
b_\mu)\\&\simeq
\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{w}T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},
b_\mu). \end{align*}
Given an identification of ![]() $\operatorname {Shv}_{\mathcal {G}^G}(\widetilde {w}T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }, b_\mu )$ with
$\operatorname {Shv}_{\mathcal {G}^G}(\widetilde {w}T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }, b_\mu )$ with ![]() ${\rm Vect}$ which preserves the cohomological degree of
${\rm Vect}$ which preserves the cohomological degree of ![]() $!$-fiber, we denote by
$!$-fiber, we denote by ![]() $(c_{\widetilde {w}})_{\mu }$ the twisted sheaf on
$(c_{\widetilde {w}})_{\mu }$ the twisted sheaf on ![]() $\widetilde {{\operatorname {Fl}}}^{\widetilde {w}}$ corresponding to
$\widetilde {{\operatorname {Fl}}}^{\widetilde {w}}$ corresponding to ![]() $\mathsf {e}\in {\rm Vect}$. Different identifications will change the resulting twisted sheaf
$\mathsf {e}\in {\rm Vect}$. Different identifications will change the resulting twisted sheaf ![]() $(c_{\widetilde {w}})_{\mu }$ by tensoring by a line in cohomological degree
$(c_{\widetilde {w}})_{\mu }$ by tensoring by a line in cohomological degree ![]() $0$, so we can regard
$0$, so we can regard ![]() $(c_{\widetilde {w}})_{\mu }$ as an object defined up to tensoring by a line.
$(c_{\widetilde {w}})_{\mu }$ as an object defined up to tensoring by a line.
Remark 5.2.4 In the case ![]() $\mu =0$,
$\mu =0$, ![]() $\operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}}^{\widetilde {w}})_{\mu }^{I^0}\simeq \operatorname {Shv}_{\mathcal {G}^G}({{\operatorname {Fl}}^{\widetilde {w}}_G})^{I^0}\simeq \operatorname {Shv}({{\operatorname {Fl}}^{\widetilde {w}}_G})^{I^0}$, and
$\operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}}^{\widetilde {w}})_{\mu }^{I^0}\simeq \operatorname {Shv}_{\mathcal {G}^G}({{\operatorname {Fl}}^{\widetilde {w}}_G})^{I^0}\simeq \operatorname {Shv}({{\operatorname {Fl}}^{\widetilde {w}}_G})^{I^0}$, and ![]() $(c_{\widetilde {w}})_{\mu }=c_{\widetilde {w}}$ is just the (twisted) dualizing sheaf on
$(c_{\widetilde {w}})_{\mu }=c_{\widetilde {w}}$ is just the (twisted) dualizing sheaf on ![]() ${\operatorname {Fl}}_G^{\widetilde {w}}$ with respect to the unique (up to a non-canonical isomorphism)
${\operatorname {Fl}}_G^{\widetilde {w}}$ with respect to the unique (up to a non-canonical isomorphism) ![]() $I^0$-equivariant trivialization on
$I^0$-equivariant trivialization on ![]() ${{\operatorname {Fl}}^{\widetilde {w}}_G}$.
${{\operatorname {Fl}}^{\widetilde {w}}_G}$.
Definition 5.2.5 Let ![]() $({{J}}_{\widetilde {w},!})_{\mu }$ (respectively,
$({{J}}_{\widetilde {w},!})_{\mu }$ (respectively, ![]() $({{J}}_{\widetilde {w},*})_{\mu })$ be the ! (respectively, *)-extension of
$({{J}}_{\widetilde {w},*})_{\mu })$ be the ! (respectively, *)-extension of ![]() $(c_{\widetilde {w}})_{\mu }[{-}l(\widetilde {w})]$ along the locally closed embedding
$(c_{\widetilde {w}})_{\mu }[{-}l(\widetilde {w})]$ along the locally closed embedding
5.3 Convolution product
Denote by
the natural projection from ![]() $G(\mathcal {K})^{\omega ^\rho }$ to
$G(\mathcal {K})^{\omega ^\rho }$ to ![]() $\widetilde {{\operatorname {Fl}}}$.
$\widetilde {{\operatorname {Fl}}}$.
For a right ![]() $(I^{\omega ^\rho }, b_\lambda )$-equivariant sheaf
$(I^{\omega ^\rho }, b_\lambda )$-equivariant sheaf ![]() $\mathcal {F}_1\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_\lambda$ and a left
$\mathcal {F}_1\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_\lambda$ and a left ![]() $(I^{\omega ^\rho }, b_\lambda )$-equivariant and right
$(I^{\omega ^\rho }, b_\lambda )$-equivariant and right ![]() $(I^{\omega ^\rho }, b_\eta )$-equivariant sheaf
$(I^{\omega ^\rho }, b_\eta )$-equivariant sheaf ![]() $\mathcal {F}_2\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})^{I,\lambda }_{\eta }$. Consider the following diagram.
$\mathcal {F}_2\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})^{I,\lambda }_{\eta }$. Consider the following diagram.
Since the equivariant conditions translate to the descent condition, the external product ![]() $\widetilde {\pi }^!(\mathcal {F}_1)\boxtimes \mathcal {F}_2$ on
$\widetilde {\pi }^!(\mathcal {F}_1)\boxtimes \mathcal {F}_2$ on ![]() $G(\mathcal {K})^{\omega ^\rho }\times \widetilde {{\operatorname {Fl}}}$ descends to a twisted sheaf
$G(\mathcal {K})^{\omega ^\rho }\times \widetilde {{\operatorname {Fl}}}$ descends to a twisted sheaf ![]() $\widetilde {\pi }^!(\mathcal {F}_1)\widetilde {\boxtimes } \mathcal {F}_2$ on
$\widetilde {\pi }^!(\mathcal {F}_1)\widetilde {\boxtimes } \mathcal {F}_2$ on ![]() $G(\mathcal {K})^{\omega ^\rho }\mathop {\times }^I \widetilde {{\operatorname {Fl}}}$, such that
$G(\mathcal {K})^{\omega ^\rho }\mathop {\times }^I \widetilde {{\operatorname {Fl}}}$, such that
By the multiplicative property of ![]() $\mathcal {G}^G$, the pullback of
$\mathcal {G}^G$, the pullback of ![]() $\mathcal {G}^G$ along the multiplication map
$\mathcal {G}^G$ along the multiplication map
is ![]() $\mathcal {G}^G\boxtimes \mathcal {G}^G$. In particular, the pushforward of a
$\mathcal {G}^G\boxtimes \mathcal {G}^G$. In particular, the pushforward of a ![]() $\mathcal {G}^G\boxtimes \mathcal {G}^G$-twisted sheaf along the multiplication map is
$\mathcal {G}^G\boxtimes \mathcal {G}^G$-twisted sheaf along the multiplication map is ![]() $\mathcal {G}^G$-twisted.
$\mathcal {G}^G$-twisted.
Definition 5.3.1 Set
Remark 5.3.2 Since ![]() $m$ is (ind-)proper, it does not matter whether we consider
$m$ is (ind-)proper, it does not matter whether we consider ![]() $!$- or
$!$- or ![]() $*$-pushforward of
$*$-pushforward of ![]() $m$.
$m$.
We denote by ![]() $\overline {\widetilde {w}}$ the image of
$\overline {\widetilde {w}}$ the image of ![]() $\widetilde {w}$ under the first projection
$\widetilde {w}$ under the first projection ![]() $W^{{\operatorname {ext}}}= \Lambda \rtimes W\to \Lambda$. For
$W^{{\operatorname {ext}}}= \Lambda \rtimes W\to \Lambda$. For ![]() $\widetilde {w}=t^\lambda w\in W^{{\operatorname {ext}}}$,
$\widetilde {w}=t^\lambda w\in W^{{\operatorname {ext}}}$, ![]() $\overline {\widetilde {w}}=\lambda$.
$\overline {\widetilde {w}}=\lambda$.
Remark 5.3.3 We have that ![]() $({{J}}_{\widetilde {w},?})_{\mu }$ (? = ! or *) is left
$({{J}}_{\widetilde {w},?})_{\mu }$ (? = ! or *) is left ![]() $(I^{\omega ^\rho }, b_{\overline {\widetilde {w}t^\mu }})$-equivariant and right
$(I^{\omega ^\rho }, b_{\overline {\widetilde {w}t^\mu }})$-equivariant and right ![]() $(T^{\omega ^\rho }, b_\mu )$-equivariant.
$(T^{\omega ^\rho }, b_\mu )$-equivariant.
In order to define the twisted BMW sheaf for any coweight ![]() $\lambda \in \Lambda$, we need the following lemma which is an analog of [Reference Arkhipov and BezrukavnikovAB09, Lemma 8] and [Reference Lusztig and YunLY20, Lemmas 3.4 and 3.5].
$\lambda \in \Lambda$, we need the following lemma which is an analog of [Reference Arkhipov and BezrukavnikovAB09, Lemma 8] and [Reference Lusztig and YunLY20, Lemmas 3.4 and 3.5].
Lemma 5.3.4 For ![]() $\widetilde {w}, \widetilde {w}'\in W^{{\operatorname {ext}}}$ and
$\widetilde {w}, \widetilde {w}'\in W^{{\operatorname {ext}}}$ and ![]() $\mu \in \Lambda$, if
$\mu \in \Lambda$, if ![]() $l(\widetilde {w}\widetilde {w}')=l(\widetilde {w})+l(\widetilde {w}')$, then:
$l(\widetilde {w}\widetilde {w}')=l(\widetilde {w})+l(\widetilde {w}')$, then:
(1)
 \[ ({{J}}_{\widetilde{w},!})_{\overline{\widetilde{w}'t^\mu}}\star ({{J}}_{\widetilde{w}',!})_{\mu}\simeq ({{J}}_{\widetilde{w}\widetilde{w}',!})_{\mu}, \]
\[ ({{J}}_{\widetilde{w},!})_{\overline{\widetilde{w}'t^\mu}}\star ({{J}}_{\widetilde{w}',!})_{\mu}\simeq ({{J}}_{\widetilde{w}\widetilde{w}',!})_{\mu}, \]
 \[ ({{J}}_{\widetilde{w},*})_{\overline{\widetilde{w}'t^\mu}}\star ({{J}}_{\widetilde{w}',*})_{\mu}\simeq ({{J}}_{\widetilde{w}\widetilde{w}',*})_{\mu}; \]
\[ ({{J}}_{\widetilde{w},*})_{\overline{\widetilde{w}'t^\mu}}\star ({{J}}_{\widetilde{w}',*})_{\mu}\simeq ({{J}}_{\widetilde{w}\widetilde{w}',*})_{\mu}; \]
(2)
 $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }\simeq ({{J}}_0)_\mu \simeq ({{J}}_{\widetilde {w},*})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},!})_{\mu }$.
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }\simeq ({{J}}_0)_\mu \simeq ({{J}}_{\widetilde {w},*})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},!})_{\mu }$.
Proof. The proof is similar to the non-twisted case. Here we sketch the proof.
For part (1), we only prove the first claim, the second one follows from the same argument.
By the Cartan decomposition of ![]() $G(\mathcal {K})^{\omega ^\rho }$ by the Iwahori subgroup
$G(\mathcal {K})^{\omega ^\rho }$ by the Iwahori subgroup ![]() $I^{\omega ^\rho }$, the multiplication map
$I^{\omega ^\rho }$, the multiplication map
is an isomorphism after restricting to ![]() $I^{\omega ^\rho } \widetilde {w} I^{\omega ^\rho }\mathop {\times }^{I^{\omega ^\rho }} I^{\omega ^\rho } \widetilde {w}' I^{\omega ^\rho }/I^0\to I^{\omega ^\rho } \widetilde {w}\widetilde {w}'I^{\omega ^\rho }/I^0$. Note that the trivializations of gerbes on both sides are compatible. Now the first assertion follows from the fact that both
$I^{\omega ^\rho } \widetilde {w} I^{\omega ^\rho }\mathop {\times }^{I^{\omega ^\rho }} I^{\omega ^\rho } \widetilde {w}' I^{\omega ^\rho }/I^0\to I^{\omega ^\rho } \widetilde {w}\widetilde {w}'I^{\omega ^\rho }/I^0$. Note that the trivializations of gerbes on both sides are compatible. Now the first assertion follows from the fact that both ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}'t^\mu }}\star ({{J}}_{\widetilde {w}',!})_{\mu }$ and
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}'t^\mu }}\star ({{J}}_{\widetilde {w}',!})_{\mu }$ and ![]() $({{J}}_{\widetilde {w}\widetilde {w}',!})_{\mu }$ have zero
$({{J}}_{\widetilde {w}\widetilde {w}',!})_{\mu }$ have zero ![]() $*$-stalks outside
$*$-stalks outside ![]() $I^{\omega ^\rho } \widetilde {w}\widetilde {w}'I^{\omega ^\rho }/I^{\omega ^\rho }\subset {\operatorname {Fl}}_G^{\omega ^\rho }$.
$I^{\omega ^\rho } \widetilde {w}\widetilde {w}'I^{\omega ^\rho }/I^{\omega ^\rho }\subset {\operatorname {Fl}}_G^{\omega ^\rho }$.
To prove part (2), by part (1), we can reduce the question to the case when ![]() $\widetilde {w}$ is a simple reflection. In this case,
$\widetilde {w}$ is a simple reflection. In this case, ![]() $\overline {I^{\omega ^\rho } \widetilde {w}I^{\omega ^\rho }/I^{\omega ^\rho }}\subset {\operatorname {Fl}}_G^{\omega ^\rho }$ is isomorphic to
$\overline {I^{\omega ^\rho } \widetilde {w}I^{\omega ^\rho }/I^{\omega ^\rho }}\subset {\operatorname {Fl}}_G^{\omega ^\rho }$ is isomorphic to ![]() $\mathbb {P}^1$.
$\mathbb {P}^1$.
The support of ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ is contained in
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ is contained in ![]() $\overline {I^{\omega ^\rho }\widetilde {w}I^{\omega ^\rho }\cdot I^{\omega ^\rho } \widetilde {w}^{-1}I^{\omega ^\rho }/I^0}$, which is equal to the disjoint union
$\overline {I^{\omega ^\rho }\widetilde {w}I^{\omega ^\rho }\cdot I^{\omega ^\rho } \widetilde {w}^{-1}I^{\omega ^\rho }/I^0}$, which is equal to the disjoint union ![]() $I^{\omega ^\rho }\widetilde {w}I^{\omega ^\rho }/I^0\sqcup I^{\omega ^\rho }/I^0$. By the equivariance property of
$I^{\omega ^\rho }\widetilde {w}I^{\omega ^\rho }/I^0\sqcup I^{\omega ^\rho }/I^0$. By the equivariance property of ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$, we should prove that the
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$, we should prove that the ![]() $!$-stalks of
$!$-stalks of ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ is zero at
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ is zero at ![]() $\widetilde {w}$ and is
$\widetilde {w}$ and is ![]() $\mathsf {e}$ at
$\mathsf {e}$ at ![]() $1$.
$1$.
For ![]() $g_0\in G(\mathcal {K})^{\omega ^\rho }$, taking pushforward along the map
$g_0\in G(\mathcal {K})^{\omega ^\rho }$, taking pushforward along the map ![]() $G(\mathcal {K})^{\omega ^\rho }\to G(\mathcal {K})^{\omega ^\rho }: g\mapsto g_0g^{-1}$ induces a functor
$G(\mathcal {K})^{\omega ^\rho }\to G(\mathcal {K})^{\omega ^\rho }: g\mapsto g_0g^{-1}$ induces a functor
where ![]() $\mathcal {G}_{g_0}^G$ denotes the fiber of
$\mathcal {G}_{g_0}^G$ denotes the fiber of ![]() $\mathcal {G}^G$ at
$\mathcal {G}^G$ at ![]() $g_0$.
$g_0$.
Note that ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^! \iota _{g^0}(({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ is right
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^! \iota _{g^0}(({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ is right ![]() $T^{\omega ^\rho }$-equivariant, so it descends to a twisted sheaf on
$T^{\omega ^\rho }$-equivariant, so it descends to a twisted sheaf on ![]() ${{\operatorname {Fl}}}_G^{\omega ^\rho }$. We denote the resulting sheaf by the same notation.
${{\operatorname {Fl}}}_G^{\omega ^\rho }$. We denote the resulting sheaf by the same notation.
The projection of ![]() $g_0$ in
$g_0$ in ![]() $G(\mathcal {K})^{\omega ^\rho }/I^0$ is denoted by
$G(\mathcal {K})^{\omega ^\rho }/I^0$ is denoted by ![]() $\bar {g}_0$. The preimage of
$\bar {g}_0$. The preimage of ![]() $\bar {g}_0$ along (5.3.3) is identified with
$\bar {g}_0$ along (5.3.3) is identified with ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ via the composition of the first projection map
${\operatorname {Fl}}_G^{\omega ^\rho }$ via the composition of the first projection map ![]() $p_1: G(\mathcal {K})^{\omega ^\rho }\mathop {\times }^{I^{\omega ^\rho }} G(\mathcal {K})^{\omega ^\rho }/I^0\to G(\mathcal {K})^{\omega ^\rho }/I^0$ and
$p_1: G(\mathcal {K})^{\omega ^\rho }\mathop {\times }^{I^{\omega ^\rho }} G(\mathcal {K})^{\omega ^\rho }/I^0\to G(\mathcal {K})^{\omega ^\rho }/I^0$ and ![]() $G(\mathcal {K})^{\omega ^\rho }/I^0\to G(\mathcal {K})^{\omega ^\rho }/I^{\omega ^\rho }$.
$G(\mathcal {K})^{\omega ^\rho }/I^0\to G(\mathcal {K})^{\omega ^\rho }/I^{\omega ^\rho }$.
Under this identification, the ![]() $!$-restriction of
$!$-restriction of ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ to the preimage of
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ to the preimage of ![]() $\bar {g}_0$ is identified with
$\bar {g}_0$ is identified with
By the base change theorem, the ![]() $!$-stalks of
$!$-stalks of ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ at the point
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ at the point ![]() $\bar {g}_0$ is isomorphic to
$\bar {g}_0$ is isomorphic to
In particular, the ![]() $!$-stalks of
$!$-stalks of ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ at
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\star ({{J}}_{\widetilde {w}^{-1},*})_{\mu }$ at ![]() $\widetilde {w}$ is isomorphic to
$\widetilde {w}$ is isomorphic to
Under the identification ![]() $\overline {I^{\omega ^\rho } \widetilde {w} I^{\omega ^\rho }/I^{\omega ^\rho }}\simeq \mathbb {P}^1$,
$\overline {I^{\omega ^\rho } \widetilde {w} I^{\omega ^\rho }/I^{\omega ^\rho }}\simeq \mathbb {P}^1$, ![]() $({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^! \iota _{\widetilde {w}}({}_{}({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ is identified with the
$({{J}}_{\widetilde {w},!})_{\overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^! \iota _{\widetilde {w}}({}_{}({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ is identified with the ![]() $*$-extension from a
$*$-extension from a ![]() $\mathbb {G}_m$-equivariant (with respect to certain Kummer sheaf) sheaf on
$\mathbb {G}_m$-equivariant (with respect to certain Kummer sheaf) sheaf on ![]() $\mathbb {G}_m:= \mathbb {P}^1\setminus \{0,\infty \}$ to
$\mathbb {G}_m:= \mathbb {P}^1\setminus \{0,\infty \}$ to ![]() $\mathbb {A}^1:=\mathbb {P}^1\setminus \{\infty \}$, and then
$\mathbb {A}^1:=\mathbb {P}^1\setminus \{\infty \}$, and then ![]() $!$-pushforward to
$!$-pushforward to ![]() $\mathbb {P}^1$. By Braden's theorem (see [Reference Drinfeld and GaitsgoryDG14, Proposition 3.2.2]), its cohomology equals its
$\mathbb {P}^1$. By Braden's theorem (see [Reference Drinfeld and GaitsgoryDG14, Proposition 3.2.2]), its cohomology equals its ![]() $*$-stalks at
$*$-stalks at ![]() $\infty$, which equals zero.
$\infty$, which equals zero.
Over the point ![]() $1\in {\operatorname {Fl}}_G^{\omega ^\rho }$, the
$1\in {\operatorname {Fl}}_G^{\omega ^\rho }$, the ![]() $!$-stalks can be calculated by
$!$-stalks can be calculated by
Note that the restriction of ![]() $({{J}}_{\widetilde {w},!})_{ \overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^!\iota _{1}({}_{ }({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ to
$({{J}}_{\widetilde {w},!})_{ \overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^!\iota _{1}({}_{ }({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ to ![]() $\mathbb {A}^1$ is isomorphic to the constant object. By the projection formula,
$\mathbb {A}^1$ is isomorphic to the constant object. By the projection formula, ![]() $({{J}}_{\widetilde {w},!})_{ \overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^!\iota _{\widetilde {w}}({}_{ }({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ is the
$({{J}}_{\widetilde {w},!})_{ \overline {\widetilde {w}^{-1}\mu }}\mathop {\otimes }^!\iota _{\widetilde {w}}({}_{ }({{J}}_{\widetilde {w}^{-1},*})_{\mu })$ is the ![]() $*$-pushforward of the constant sheaf on
$*$-pushforward of the constant sheaf on ![]() $\mathbb {A}^1$, and its cohomology is
$\mathbb {A}^1$, and its cohomology is ![]() $\mathsf {e}$.
$\mathsf {e}$.
5.4 Twisted BMW sheaf
With the preparation given in the last several sections, finally, we can construct the BMW sheaves in the twisted cases.
Definition 5.4.1 Given ![]() $\lambda \in \Lambda$, such that
$\lambda \in \Lambda$, such that ![]() $\lambda =\lambda _1-\lambda _2, \lambda _1, \lambda _2\in \Lambda ^+$. We define the twisted BMW sheaf
$\lambda =\lambda _1-\lambda _2, \lambda _1, \lambda _2\in \Lambda ^+$. We define the twisted BMW sheaf ![]() $({{J}}_\lambda )_{\mu }\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_{\mu }$ as
$({{J}}_\lambda )_{\mu }\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_{\mu }$ as
Similarly, we define the dual BMW sheaf as
They are well-defined up to tensoring by a line in degree ![]() $0$, and according to Lemma 5.3.4, the definitions are independent of choices of
$0$, and according to Lemma 5.3.4, the definitions are independent of choices of ![]() $\lambda _1, \lambda _2$.
$\lambda _1, \lambda _2$.
Remark 5.4.2 To be more precise, they are determined by ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}(t^\lambda T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho },b_\mu )\simeq {\rm Vect}$ (equivalently, an identification
$\operatorname {Shv}_{{\mathcal {G}}^G}(t^\lambda T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho },b_\mu )\simeq {\rm Vect}$ (equivalently, an identification ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}(t^{\lambda _1}T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho },b_{-\lambda _2+\mu })\otimes \operatorname {Shv}_{{\mathcal {G}}^G}(t^{-\lambda _2}T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }, b_\mu )\simeq {\rm Vect}$), since there is a canonical equivalence
$\operatorname {Shv}_{{\mathcal {G}}^G}(t^{\lambda _1}T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho },b_{-\lambda _2+\mu })\otimes \operatorname {Shv}_{{\mathcal {G}}^G}(t^{-\lambda _2}T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }, b_\mu )\simeq {\rm Vect}$), since there is a canonical equivalence
 \begin{align*}
&\operatorname{Shv}_{{\mathcal{G}}^G}(t^{\lambda_1}T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},b_{-\lambda_2+\mu})\otimes
\operatorname{Shv}_{{\mathcal{G}}^G}(t^{-\lambda_2}T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},b_\mu)\\&\quad \simeq
\operatorname{Shv}_{{\mathcal{G}}^G}(t^\lambda
T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},b_\mu). \end{align*}
\begin{align*}
&\operatorname{Shv}_{{\mathcal{G}}^G}(t^{\lambda_1}T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},b_{-\lambda_2+\mu})\otimes
\operatorname{Shv}_{{\mathcal{G}}^G}(t^{-\lambda_2}T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},b_\mu)\\&\quad \simeq
\operatorname{Shv}_{{\mathcal{G}}^G}(t^\lambda
T({\mathcal{O}})^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho},b_\mu). \end{align*}
The identification determines the right-hand side of (5.4.1) (respectively, (5.4.2)), and there are canonical isomorphisms between ![]() $({{J}}_{\lambda _1,!})_{-\lambda _2+\mu }\star ({{J}}_{-\lambda _2,*})_\mu$ (respectively,
$({{J}}_{\lambda _1,!})_{-\lambda _2+\mu }\star ({{J}}_{-\lambda _2,*})_\mu$ (respectively, ![]() $({{J}}_{\lambda _{1,*}})_{-\lambda _2+\mu }\star ({{J}}_{-\lambda _{2,!}})_\mu$) for different
$({{J}}_{\lambda _{1,*}})_{-\lambda _2+\mu }\star ({{J}}_{-\lambda _{2,!}})_\mu$) for different ![]() $\lambda _1,\lambda _2$.
$\lambda _1,\lambda _2$.
When ![]() $\mu =0$, we omit the subscript
$\mu =0$, we omit the subscript ![]() $\mu$ in
$\mu$ in ![]() $({{J}}_\lambda )_{\mu }$ and
$({{J}}_\lambda )_{\mu }$ and ![]() $({{J}}_\lambda ^{\mathbb {D}})_\mu$.
$({{J}}_\lambda ^{\mathbb {D}})_\mu$.
By Lemma 5.3.4, twisted BMW sheaves admit a convolution product
5.5 Standards and costandards
Definition 5.5.1 Given an identification ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}(t^\lambda T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho })\simeq {\rm Vect}$ as before, i.e. a trivialization of
$\operatorname {Shv}_{{\mathcal {G}}^G}(t^\lambda T({\mathcal {O}})^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho })\simeq {\rm Vect}$ as before, i.e. a trivialization of ![]() ${\mathcal {G}}^G|_{t^\lambda \in {\operatorname {Fl}}}$, we define
${\mathcal {G}}^G|_{t^\lambda \in {\operatorname {Fl}}}$, we define
and
where ![]() ${\rm Av}_*^{\rm ren}$ is the renormalized averaging functor
${\rm Av}_*^{\rm ren}$ is the renormalized averaging functor
![]() $\operatorname {Av}_*^{N_k,\chi }$ is the
$\operatorname {Av}_*^{N_k,\chi }$ is the ![]() $*$-averaging functor with respect to
$*$-averaging functor with respect to ![]() $(N_k, \chi )$ (see § 3.1.2) and
$(N_k, \chi )$ (see § 3.1.2) and ![]() $l_{k,k'}$ is the line of
$l_{k,k'}$ is the line of ![]() $*$-fiber of the dualizing sheaf of
$*$-fiber of the dualizing sheaf of ![]() $N_{k'}/N_k$ at
$N_{k'}/N_k$ at ![]() $1$ for
$1$ for ![]() $k'\geq k$. Furthermore, up to a shift,
$k'\geq k$. Furthermore, up to a shift, ![]() $({{J}}_{\mu,*})_{\lambda -\mu }\mathop {\star }{{J}}_{\lambda -\mu,*}$ is the
$({{J}}_{\mu,*})_{\lambda -\mu }\mathop {\star }{{J}}_{\lambda -\mu,*}$ is the ![]() $(N({\mathcal {O}})^{\omega ^\rho }$,
$(N({\mathcal {O}})^{\omega ^\rho }$, ![]() $*)$-averaging of the
$*)$-averaging of the ![]() $*$-extension of the twisted dualizing sheaf on
$*$-extension of the twisted dualizing sheaf on ![]() ${\rm Ad}_{\mu }I^{\omega ^\rho }t^\lambda I^{\omega ^\rho }/I^{\omega ^\rho }$ with respect to the unique
${\rm Ad}_{\mu }I^{\omega ^\rho }t^\lambda I^{\omega ^\rho }/I^{\omega ^\rho }$ with respect to the unique ![]() ${\rm Ad}_{\mu }I^0$-equivariant trivialization. If we further require
${\rm Ad}_{\mu }I^0$-equivariant trivialization. If we further require ![]() $\mu _2-\mu _1\in \Lambda ^+$, we have
$\mu _2-\mu _1\in \Lambda ^+$, we have ![]() ${\rm Ad}_{\mu _1}I^{\omega ^\rho }t^\lambda I^{\omega ^\rho }/I^{\omega ^\rho }\subset {\rm Ad}_{\mu _2}I^{\omega ^\rho }t^\lambda I^{\omega ^\rho }/I^{\omega ^\rho }$. The transition maps between
${\rm Ad}_{\mu _1}I^{\omega ^\rho }t^\lambda I^{\omega ^\rho }/I^{\omega ^\rho }\subset {\rm Ad}_{\mu _2}I^{\omega ^\rho }t^\lambda I^{\omega ^\rho }/I^{\omega ^\rho }$. The transition maps between ![]() $({{J}}_{\mu,*})_{\lambda -\mu }\mathop {\star }{{J}}_{\lambda -\mu,*}$ are obtained from natural maps between the dualizing sheaves.
$({{J}}_{\mu,*})_{\lambda -\mu }\mathop {\star }{{J}}_{\lambda -\mu,*}$ are obtained from natural maps between the dualizing sheaves.
Similar to twisted BMW sheaves, we also regard ![]() $\Delta _\lambda$ and
$\Delta _\lambda$ and ![]() $\nabla _\lambda$ as objects which are well-defined up to tensoring by a line in degree
$\nabla _\lambda$ as objects which are well-defined up to tensoring by a line in degree ![]() $0$, i.e. depend on the choice of identifications. We call
$0$, i.e. depend on the choice of identifications. We call ![]() $\{\Delta _\lambda,\ \lambda \in \Lambda \}$ standard objects of
$\{\Delta _\lambda,\ \lambda \in \Lambda \}$ standard objects of ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ and
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ and ![]() $\{\nabla _\lambda,\ \lambda \in \Lambda \}$ costandard objects.
$\{\nabla _\lambda,\ \lambda \in \Lambda \}$ costandard objects.
Proposition 5.5.2 The standard objects ![]() $\{\Delta _\lambda, \lambda \in \Lambda \}$ are a collection of compact generators of
$\{\Delta _\lambda, \lambda \in \Lambda \}$ are a collection of compact generators of ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$.
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$.
Proof. Taking convolution with BMW sheaf is invertible, in particular, it preserves compactness. Since ![]() $\Delta _\lambda \simeq \operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }({{J}}_\lambda )\simeq \operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(({{J}}_0)_\lambda )\star {{J}}_\lambda$ and
$\Delta _\lambda \simeq \operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }({{J}}_\lambda )\simeq \operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(({{J}}_0)_\lambda )\star {{J}}_\lambda$ and ![]() $\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(({{J}}_0)_\lambda )$ is compact, the standard object
$\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(({{J}}_0)_\lambda )$ is compact, the standard object ![]() $\Delta _\lambda$ is compact.
$\Delta _\lambda$ is compact.
By an analysis of the support of the convolution product, one proves that ![]() ${\mathop {\operatorname {\rm supp}}}(\Delta _\lambda )= \overline {S}^{\phi (\rho +\lambda )}_{{\operatorname {Fl}}}$. According to [Reference BezrukavnikovBez06, Lemma 11], we have
${\mathop {\operatorname {\rm supp}}}(\Delta _\lambda )= \overline {S}^{\phi (\rho +\lambda )}_{{\operatorname {Fl}}}$. According to [Reference BezrukavnikovBez06, Lemma 11], we have
Now the proposition directly follows from the fact that ![]() $\operatorname {rank}(\Delta _{\phi (\rho +\lambda )}^{{\mathop {\operatorname {\rm ver}}}}|_{{S}^{\phi (\rho +\lambda )}_{{\operatorname {Fl}}}})=1$ (i.e.
$\operatorname {rank}(\Delta _{\phi (\rho +\lambda )}^{{\mathop {\operatorname {\rm ver}}}}|_{{S}^{\phi (\rho +\lambda )}_{{\operatorname {Fl}}}})=1$ (i.e. ![]() $\Delta _{\phi (\rho +\lambda )}^{{\mathop {\operatorname {\rm ver}}}}|_{{S}^{\phi (\rho +\lambda )}_{{\operatorname {Fl}}}}$ is the generator of
$\Delta _{\phi (\rho +\lambda )}^{{\mathop {\operatorname {\rm ver}}}}|_{{S}^{\phi (\rho +\lambda )}_{{\operatorname {Fl}}}}$ is the generator of ![]() $\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\phi (\rho +\lambda )})\simeq {\rm Vect}$).
$\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}}}^{\phi (\rho +\lambda )})\simeq {\rm Vect}$).
The standards ![]() $\Delta _\lambda$ and costandards
$\Delta _\lambda$ and costandards ![]() $\nabla _\mu$ satisfy the orthogonality property.
$\nabla _\mu$ satisfy the orthogonality property.
Proposition 5.5.3 We have
 \begin{equation} \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \nabla_\mu) \simeq\left\{\begin{aligned} 0,\quad \text{if}\ \lambda\neq \mu, \\ \mathsf{e},\quad \text{if}\ \lambda=\mu. \end{aligned}\right. \end{equation}
\begin{equation} \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \nabla_\mu) \simeq\left\{\begin{aligned} 0,\quad \text{if}\ \lambda\neq \mu, \\ \mathsf{e},\quad \text{if}\ \lambda=\mu. \end{aligned}\right. \end{equation}Proof. We have
 \begin{align} & \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \nabla_\mu) \nonumber\\ &\quad \simeq\mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}({{J}}_\lambda), \operatorname{Av}_*^{\rm ren}\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+}(({{J}}_{\alpha,*})_{\mu-\alpha}\mathop{\star}{{J}}_{\mu-\alpha,*})) \nonumber\\ &\quad \simeq\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+} \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}({{J}}_\lambda), \operatorname{Av}_*^{\rm ren}(({{J}}_{\alpha,*})_{\mu-\alpha}\mathop{\star}{{J}}_{\mu-\alpha,*})) \nonumber\\ &\quad \simeq\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+} \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_{\mu-\alpha}}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi} ({{J}}_\lambda\star ({{J}}_{\alpha-\mu,!})_{\mu-\alpha}),\operatorname{Av}_*^{\rm ren}(({{J}}_{\alpha,*})_{\mu-\alpha}, \nonumber\\ & \mathop{\star}{{J}}_{\mu-\alpha,*}\star ({{J}}_{\alpha-\mu,!})_{\mu-\alpha}) \nonumber\\ &\quad \simeq\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+} \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_{\mu-\alpha}}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi} (({{J}}_{\lambda+\alpha-\mu,!})_{\mu-\alpha}),\operatorname{Av}_*^{\rm ren}(({{J}}_{\alpha,*})_{\mu-\alpha})) \end{align}
\begin{align} & \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \nabla_\mu) \nonumber\\ &\quad \simeq\mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}({{J}}_\lambda), \operatorname{Av}_*^{\rm ren}\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+}(({{J}}_{\alpha,*})_{\mu-\alpha}\mathop{\star}{{J}}_{\mu-\alpha,*})) \nonumber\\ &\quad \simeq\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+} \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}({{J}}_\lambda), \operatorname{Av}_*^{\rm ren}(({{J}}_{\alpha,*})_{\mu-\alpha}\mathop{\star}{{J}}_{\mu-\alpha,*})) \nonumber\\ &\quad \simeq\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+} \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_{\mu-\alpha}}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi} ({{J}}_\lambda\star ({{J}}_{\alpha-\mu,!})_{\mu-\alpha}),\operatorname{Av}_*^{\rm ren}(({{J}}_{\alpha,*})_{\mu-\alpha}, \nonumber\\ & \mathop{\star}{{J}}_{\mu-\alpha,*}\star ({{J}}_{\alpha-\mu,!})_{\mu-\alpha}) \nonumber\\ &\quad \simeq\mathop{{\rm colim}}_{\alpha{,\alpha-\mu}\in \Lambda^+} \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_{\mu-\alpha}}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi} (({{J}}_{\lambda+\alpha-\mu,!})_{\mu-\alpha}),\operatorname{Av}_*^{\rm ren}(({{J}}_{\alpha,*})_{\mu-\alpha})) \end{align}By the following lemma (Lemma 5.5.4), the above colimit is isomorphic to
Up to tensoring by a line, we denote by ![]() $(\delta _{\lambda +\alpha -\mu })_{\mu -\alpha }\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_{\mu -\alpha }$ (respectively,
$(\delta _{\lambda +\alpha -\mu })_{\mu -\alpha }\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_{\mu -\alpha }$ (respectively, ![]() $(\delta _{\alpha })_{\mu -\alpha }\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_{\mu -\alpha }$) the
$(\delta _{\alpha })_{\mu -\alpha }\in \operatorname {Shv}_{\mathcal {G}^G}(\widetilde {{\operatorname {Fl}}})_{\mu -\alpha }$) the ![]() $!$ (equivalently,
$!$ (equivalently, ![]() $*$)-extension of the Kummer sheaf corresponding to
$*$)-extension of the Kummer sheaf corresponding to ![]() $\mu -\alpha$ on
$\mu -\alpha$ on ![]() $\widetilde {{\operatorname {Fl}}}\mathop {\times }_{{\operatorname {Fl}}_G}t^{\lambda +\alpha -\mu }$ (respectively,
$\widetilde {{\operatorname {Fl}}}\mathop {\times }_{{\operatorname {Fl}}_G}t^{\lambda +\alpha -\mu }$ (respectively, ![]() $\widetilde {{\operatorname {Fl}}}\mathop {\times }_{{\operatorname {Fl}}_G}t^\alpha$) to
$\widetilde {{\operatorname {Fl}}}\mathop {\times }_{{\operatorname {Fl}}_G}t^\alpha$) to ![]() $\widetilde {{\operatorname {Fl}}}$.
$\widetilde {{\operatorname {Fl}}}$.
Here ![]() $\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(\delta _{\lambda +\alpha -\mu })_{\mu -\alpha }[\langle \mu -\lambda -\alpha, 2\check {\rho }\rangle ]$ is the
$\operatorname {Av}_!^{N(\mathcal {K})^{\omega ^\rho },\chi }(\delta _{\lambda +\alpha -\mu })_{\mu -\alpha }[\langle \mu -\lambda -\alpha, 2\check {\rho }\rangle ]$ is the ![]() $!$-extension of the generator of
$!$-extension of the generator of ![]() $\operatorname {Whit}_{\rm q}(S^{\lambda +\alpha -\mu }_{\widetilde {{\operatorname {Fl}}}})_{\mu -\alpha }$ to
$\operatorname {Whit}_{\rm q}(S^{\lambda +\alpha -\mu }_{\widetilde {{\operatorname {Fl}}}})_{\mu -\alpha }$ to ![]() $\widetilde {{\operatorname {Fl}}}$, and
$\widetilde {{\operatorname {Fl}}}$, and ![]() $\operatorname {Av}_*^{\rm ren}(\delta _{\alpha })_{\mu -\alpha }[\langle \alpha, 2\check {\rho }\rangle ]$ is the
$\operatorname {Av}_*^{\rm ren}(\delta _{\alpha })_{\mu -\alpha }[\langle \alpha, 2\check {\rho }\rangle ]$ is the ![]() $*$-extension of the generator of
$*$-extension of the generator of ![]() $\operatorname {Whit}_{\rm q}(S^{\lambda +\alpha -\mu }_{\widetilde {{\operatorname {Fl}}}})_{\mu -\alpha }$ to
$\operatorname {Whit}_{\rm q}(S^{\lambda +\alpha -\mu }_{\widetilde {{\operatorname {Fl}}}})_{\mu -\alpha }$ to ![]() $\widetilde {{\operatorname {Fl}}}$. Hence, by adjointness, we have (5.5.5) is
$\widetilde {{\operatorname {Fl}}}$. Hence, by adjointness, we have (5.5.5) is ![]() $\mathsf {e}$ if
$\mathsf {e}$ if ![]() $\lambda =\mu$ and is
$\lambda =\mu$ and is ![]() $0$ otherwise.
$0$ otherwise.
Lemma 5.5.4 For ![]() $\lambda \in \Lambda ^+$,
$\lambda \in \Lambda ^+$, ![]() $\mu \in \Lambda$, we have:
$\mu \in \Lambda$, we have:
(1)
 \[ \operatorname{Av}_*^{\rm ren}((\delta_\lambda)_\mu)[\langle\lambda,2\check{\rho}\rangle]\simeq \operatorname{Av}_*^{\rm ren}(({{J}}_{\lambda,*})_{\mu}); \]
\[ \operatorname{Av}_*^{\rm ren}((\delta_\lambda)_\mu)[\langle\lambda,2\check{\rho}\rangle]\simeq \operatorname{Av}_*^{\rm ren}(({{J}}_{\lambda,*})_{\mu}); \]
(2)
 \[ \operatorname{Av}^{N(\mathcal{K})^{\omega^\rho},\chi}_!((\delta_\lambda)_\mu) [-\langle\lambda,2\check{\rho}\rangle]\simeq \operatorname{Av}^{N(\mathcal{K})^{\omega^\rho},\chi}_!(({{J}}_{\lambda,!})_{\mu}). \]
\[ \operatorname{Av}^{N(\mathcal{K})^{\omega^\rho},\chi}_!((\delta_\lambda)_\mu) [-\langle\lambda,2\check{\rho}\rangle]\simeq \operatorname{Av}^{N(\mathcal{K})^{\omega^\rho},\chi}_!(({{J}}_{\lambda,!})_{\mu}). \]
Proof. For part (1), note that if ![]() $\lambda$ is dominant, then
$\lambda$ is dominant, then ![]() $N(\mathcal {K})^{\omega ^\rho }t^\lambda I^{\omega ^\rho }=N(\mathcal {K})^{\omega ^\rho }I^{\omega ^\rho } t^\lambda I^{\omega ^\rho }$. Hence, both sheaves in (1) are
$N(\mathcal {K})^{\omega ^\rho }t^\lambda I^{\omega ^\rho }=N(\mathcal {K})^{\omega ^\rho }I^{\omega ^\rho } t^\lambda I^{\omega ^\rho }$. Hence, both sheaves in (1) are ![]() $*$-extensions from their restrictions on
$*$-extensions from their restrictions on ![]() $S^\lambda _{\widetilde {{\operatorname {Fl}}}}\subset \widetilde {{\operatorname {Fl}}}$. As they are
$S^\lambda _{\widetilde {{\operatorname {Fl}}}}\subset \widetilde {{\operatorname {Fl}}}$. As they are ![]() $(N(\mathcal {K})^{\omega ^\rho },\chi )$-equivariant, we only need to prove that their
$(N(\mathcal {K})^{\omega ^\rho },\chi )$-equivariant, we only need to prove that their ![]() $!$-stalks at any lift of
$!$-stalks at any lift of ![]() $t^\lambda \in \widetilde {{\operatorname {Fl}}}$ coincide. It follows from the constructions that the
$t^\lambda \in \widetilde {{\operatorname {Fl}}}$ coincide. It follows from the constructions that the ![]() $!$-stalks of both sides are isomorphic to
$!$-stalks of both sides are isomorphic to ![]() $\mathsf {e}[-\langle \lambda,2\check {\rho }\rangle ]$.
$\mathsf {e}[-\langle \lambda,2\check {\rho }\rangle ]$.
The proof of the second claim is absolutely similar.
Remark 5.5.5 In particular, if ![]() $\lambda$ is dominant, there is an isomorphism
$\lambda$ is dominant, there is an isomorphism
5.6 t-structure on Whittaker category
Recall the following lemma in [Reference Beligiannis and ReitenBR07].
Lemma 5.6.1 Let ![]() $\mathcal {C}$ be a compactly generated category with compact generators
$\mathcal {C}$ be a compactly generated category with compact generators ![]() $\{c_i\}$, then there is a t-structure given by
$\{c_i\}$, then there is a t-structure given by
In particular, we define a new t-structure (different from that from the tautological t-structure on ![]() $\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$) on
$\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$) on ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ by the compact generators
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ by the compact generators ![]() $\Delta _\lambda$, i.e. we have the following.
$\Delta _\lambda$, i.e. we have the following.
Definition 5.6.2 We have ![]() $\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })^{\geq 0}$ if and only if
$\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })^{\geq 0}$ if and only if
After we have proved our main theorem, we show that ![]() $\Delta _\lambda$ and
$\Delta _\lambda$ and ![]() $\nabla _\lambda$ are in the heart of this t-structure (see Corollary 6.6.3). Furthermore,
$\nabla _\lambda$ are in the heart of this t-structure (see Corollary 6.6.3). Furthermore, ![]() $\Delta _\lambda$ and
$\Delta _\lambda$ and ![]() $\nabla _\lambda$ are of finite length for all
$\nabla _\lambda$ are of finite length for all ![]() $\lambda \in \Lambda$ if and only if
$\lambda \in \Lambda$ if and only if ![]() $q$ is generic. When
$q$ is generic. When ![]() $q$ is a root of unity, costandard objects and irreducible objects are not even compact, but standard objects are still compact.
$q$ is a root of unity, costandard objects and irreducible objects are not even compact, but standard objects are still compact.
5.7 Coinvariants
By considering the coinvariant-Whittaker category, we can obtain the definition of the Verdier duality functor for ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$.
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$.
Definition 5.7.1 We define ![]() $\operatorname {Whit}_{q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}$ as the quotient DG-category of
$\operatorname {Whit}_{q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}$ as the quotient DG-category of ![]() $\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$ by the full subcategory generated by
$\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$ by the full subcategory generated by
![]() $\text {for all}\ \mathcal {F}\in \operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })\ \text {and}\ k\in \mathbb {Z}$.
$\text {for all}\ \mathcal {F}\in \operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })\ \text {and}\ k\in \mathbb {Z}$.
5.7.2
The functor ![]() $\operatorname {Av}_*^{\rm ren}$ (see (5.5.3)) maps all morphisms of the form (5.7.1) to isomorphisms. In particular, it induces a functor
$\operatorname {Av}_*^{\rm ren}$ (see (5.5.3)) maps all morphisms of the form (5.7.1) to isomorphisms. In particular, it induces a functor ![]() $\operatorname {Av}_*^{\rm ren}$ from
$\operatorname {Av}_*^{\rm ren}$ from ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}$ to
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}$ to ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$. The following lemma is proved in [Reference RaskinRas21, Theorem 2.1.1].
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$. The following lemma is proved in [Reference RaskinRas21, Theorem 2.1.1].
Lemma 5.7.3 The functor
is an equivalence of categories.
5.7.4
For a DG-category ![]() $\mathcal {C}$, we denote by
$\mathcal {C}$, we denote by ![]() $\mathcal {C}^\vee$ the dual category of
$\mathcal {C}^\vee$ the dual category of ![]() $\mathcal {C}$ if it is dualizable. By definition, it is given by the DG-category of functors
$\mathcal {C}$ if it is dualizable. By definition, it is given by the DG-category of functors ![]() ${\mathop {\operatorname {\rm Funct}}}(\mathcal {C}, {\rm Vect})$. Since
${\mathop {\operatorname {\rm Funct}}}(\mathcal {C}, {\rm Vect})$. Since ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ is compactly generated and any compactly generated category is dualizable,
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ is compactly generated and any compactly generated category is dualizable, ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ is dualizable. By Lemma 5.7.3,
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ is dualizable. By Lemma 5.7.3, ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}$ is also dualizable.
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}$ is also dualizable.
By definition, ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}^\vee$ is the full subcategory of
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}^\vee$ is the full subcategory of ![]() $\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$ spanned by the functors
$\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$ spanned by the functors
 $$\begin{gather} \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho})\to {\rm Vect} \nonumber\\ \mathcal{F}\mapsto \langle \mathcal{F}, \mathcal{F}_0\rangle, \end{gather}$$
$$\begin{gather} \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho})\to {\rm Vect} \nonumber\\ \mathcal{F}\mapsto \langle \mathcal{F}, \mathcal{F}_0\rangle, \end{gather}$$
such that for any ![]() $\mathcal {F}\in \operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$ and
$\mathcal {F}\in \operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$ and ![]() $k$,
$k$,
that is,
In other words, we require ![]() $\operatorname {Av}_*^{N_k,\chi }(\mathcal {F}^0)\simeq \mathcal {F}^0$ for any
$\operatorname {Av}_*^{N_k,\chi }(\mathcal {F}^0)\simeq \mathcal {F}^0$ for any ![]() $k$. Hence, the duality functor
$k$. Hence, the duality functor
 \begin{equation} \begin{aligned} \operatorname{Shv}_{(\mathcal{G}^G)^{-1}}({\operatorname{Fl}}_G^{\omega^\rho}) & \simeq \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho})^\vee,\\ \mathcal{F}_0 & \mapsto (\mathcal{F}\mapsto \langle \mathcal{F}, \mathcal{F}_0\rangle). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \operatorname{Shv}_{(\mathcal{G}^G)^{-1}}({\operatorname{Fl}}_G^{\omega^\rho}) & \simeq \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho})^\vee,\\ \mathcal{F}_0 & \mapsto (\mathcal{F}\mapsto \langle \mathcal{F}, \mathcal{F}_0\rangle). \end{aligned} \end{equation}induces an equivalence of full subcategories
Definition 5.7.5 The Verdier duality functor for Whittaker sheaves is defined as the composition of functors
In particular, it defines an equivalence of subcategories generated by compact objects.
The dual of the standard object ![]() $\Delta _\lambda$ can be described by the dual BMW sheaf
$\Delta _\lambda$ can be described by the dual BMW sheaf ![]() ${{J}}_\lambda ^{\mathbb {D}}$.
${{J}}_\lambda ^{\mathbb {D}}$.
Proposition 5.7.6 For any ![]() $\lambda \in \Lambda$,
$\lambda \in \Lambda$, ![]() $\Delta _\lambda \in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$, we have
$\Delta _\lambda \in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$, we have
Proof. The object ![]() $\Delta _\lambda$ corresponds to the functor
$\Delta _\lambda$ corresponds to the functor
 \begin{equation} \begin{aligned} \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho}) & \to {\rm Vect}\\ \mathcal{F} & \mapsto \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \mathcal{F}) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho}) & \to {\rm Vect}\\ \mathcal{F} & \mapsto \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \mathcal{F}) \end{aligned} \end{equation}
in ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$. By definition, its image under
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$. By definition, its image under ![]() $(\operatorname {Av}_*^{\rm ren})^\vee$ is the functor
$(\operatorname {Av}_*^{\rm ren})^\vee$ is the functor
 \begin{equation} \begin{aligned} \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})_{co} & \to {\rm Vect}\\ \mathcal{F}' & \mapsto \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \operatorname{Av}_*^{\rm ren}(\mathcal{F}')). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})_{co} & \to {\rm Vect}\\ \mathcal{F}' & \mapsto \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \operatorname{Av}_*^{\rm ren}(\mathcal{F}')). \end{aligned} \end{equation}Using the adjointness, there is
Note that ![]() ${{J}}_\lambda$ goes to
${{J}}_\lambda$ goes to ![]() ${{J}}_\lambda ^{\mathbb {D}}$ under the equivalence
${{J}}_\lambda ^{\mathbb {D}}$ under the equivalence ![]() $(\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho }))^\vee \simeq \operatorname {Shv}_{(\mathcal {G}^G)^{-1}}({\operatorname {Fl}}_G^{\omega ^\rho })$, we have
$(\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho }))^\vee \simeq \operatorname {Shv}_{(\mathcal {G}^G)^{-1}}({\operatorname {Fl}}_G^{\omega ^\rho })$, we have ![]() $\mathcal {H}om_{\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })}({{J}}_\lambda, \operatorname {Av}_*^{\rm ren}(\mathcal {F}')) \simeq \langle \operatorname {Av}_*^{\rm ren}(\mathcal {F}'), {{J}}_{\lambda }^{\mathbb {D}}\rangle$.
$\mathcal {H}om_{\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })}({{J}}_\lambda, \operatorname {Av}_*^{\rm ren}(\mathcal {F}')) \simeq \langle \operatorname {Av}_*^{\rm ren}(\mathcal {F}'), {{J}}_{\lambda }^{\mathbb {D}}\rangle$.
Thus, by regarding ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}^\vee$ as a subcategory of
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })_{co}^\vee$ as a subcategory of ![]() $\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$, the image of
$\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$, the image of ![]() $\Delta _\lambda$ in
$\Delta _\lambda$ in ![]() $\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$ can be realized as
$\operatorname {Shv}_{\mathcal {G}^G}({\operatorname {Fl}}_G^{\omega ^\rho })^\vee$ can be realized as
 \begin{equation} \begin{aligned} \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho}) & \to {\rm Vect}\\ \mathcal{F} & \mapsto \langle \operatorname{Av}_*^{\rm ren}(\mathcal{F}), {{J}}_{\lambda}^{\mathbb{D}}\rangle. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho}) & \to {\rm Vect}\\ \mathcal{F} & \mapsto \langle \operatorname{Av}_*^{\rm ren}(\mathcal{F}), {{J}}_{\lambda}^{\mathbb{D}}\rangle. \end{aligned} \end{equation}Since there is an isomorphism
![]() $(\operatorname {Av}_*^{\rm ren})^\vee (\Delta _\lambda )$ is the functor
$(\operatorname {Av}_*^{\rm ren})^\vee (\Delta _\lambda )$ is the functor
 \begin{equation} \begin{aligned} \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho}) & \to {\rm Vect}\\ \mathcal{F} & \mapsto \langle \mathcal{F}, \operatorname{Av}_*^{\rm ren}({{J}}_{\lambda}^{\mathbb{D}})\rangle. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_G^{\omega^\rho}) & \to {\rm Vect}\\ \mathcal{F} & \mapsto \langle \mathcal{F}, \operatorname{Av}_*^{\rm ren}({{J}}_{\lambda}^{\mathbb{D}})\rangle. \end{aligned} \end{equation}
By the construction of (5.7.5), the image of ![]() $(\operatorname {Av}_*^{\rm ren})^\vee (\Delta _\lambda )$ under (5.7.5) is
$(\operatorname {Av}_*^{\rm ren})^\vee (\Delta _\lambda )$ under (5.7.5) is ![]() $\operatorname {Av}_*^{\rm ren}({{J}}_{\lambda }^{\mathbb {D}})$.
$\operatorname {Av}_*^{\rm ren}({{J}}_{\lambda }^{\mathbb {D}})$.
6. The functor to the category of factorization modules
In this section, we will construct the functor from the twisted Whittaker category to ![]() $\Omega _{\rm q}^{\rm L}\text {-}{\operatorname {FactMod}}$ mimicking the constructions in [Reference Gaitsgory and LysenkoGL19]. That is to say, [Reference Gaitsgory and LysenkoGL19] uses the Jacquet functor, which is the pullback–pushforward functor along
$\Omega _{\rm q}^{\rm L}\text {-}{\operatorname {FactMod}}$ mimicking the constructions in [Reference Gaitsgory and LysenkoGL19]. That is to say, [Reference Gaitsgory and LysenkoGL19] uses the Jacquet functor, which is the pullback–pushforward functor along ![]() ${\operatorname {Gr}}_G\longleftarrow {\operatorname {Gr}}_{B^-}\longrightarrow {\operatorname {Gr}}_T$.Footnote 7 We construct an Iwahori Jacquet functor.
${\operatorname {Gr}}_G\longleftarrow {\operatorname {Gr}}_{B^-}\longrightarrow {\operatorname {Gr}}_T$.Footnote 7 We construct an Iwahori Jacquet functor.
In brief, our Iwahori Jacquet functor is an adaptation of the pullback–pushforward functor ![]() $\operatorname {Whit}({\operatorname {Fl}}_G)\longrightarrow \operatorname {Shv}({\operatorname {Gr}}_T)$ of the following diagram.
$\operatorname {Whit}({\operatorname {Fl}}_G)\longrightarrow \operatorname {Shv}({\operatorname {Gr}}_T)$ of the following diagram.

Here, ![]() ${\operatorname {Fl}}^1_{B^-}$ is substack of
${\operatorname {Fl}}^1_{B^-}$ is substack of
where we require the ![]() $B^-$-bundle and the Iwahori structure to be transversal at
$B^-$-bundle and the Iwahori structure to be transversal at ![]() $x$. The
$x$. The ![]() $\lambda$-component of this functor is
$\lambda$-component of this functor is ![]() $H({\operatorname {Fl}}_G, j_*(\omega _{S_{{\operatorname {Fl}}}^{-,\lambda }})\overset {!}{\otimes }-)$. In fact, the
$H({\operatorname {Fl}}_G, j_*(\omega _{S_{{\operatorname {Fl}}}^{-,\lambda }})\overset {!}{\otimes }-)$. In fact, the ![]() $\lambda$-component of functor constructed in this section is
$\lambda$-component of functor constructed in this section is ![]() $H({\operatorname {Fl}}_G, j_!(\omega _{S_{{\operatorname {Fl}}}^{-,\lambda }})\overset {!}{\otimes }-)$.
$H({\operatorname {Fl}}_G, j_!(\omega _{S_{{\operatorname {Fl}}}^{-,\lambda }})\overset {!}{\otimes }-)$.
The organization of this section is as follows.
In § 6.1, we will construct a closed sub-prestack ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ of the Beilinson–Drinfeld affine flags
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ of the Beilinson–Drinfeld affine flags ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$. Lemma 6.1.12 ensures that we can regard a Whittaker sheaf on
${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$. Lemma 6.1.12 ensures that we can regard a Whittaker sheaf on ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ as a Whittaker sheaf on
${\operatorname {Fl}}_G^{\omega ^\rho }$ as a Whittaker sheaf on ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ with factorization property.
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ with factorization property.
In § 6.2, we introduce the configuration version affine flags which is important for the construction of the functor.
In § 6.4, we construct the functor ![]() $F^{\rm L}$ that appeared in Theorem 4.3.1. We also construct another closely related functor
$F^{\rm L}$ that appeared in Theorem 4.3.1. We also construct another closely related functor ![]() $F^{\rm DK}$ in this section.
$F^{\rm DK}$ in this section.
In § 6.5, we describe the functors defined in the previous section by calculating the ![]() $!$-stalks of
$!$-stalks of ![]() $F^{\rm L}$ and
$F^{\rm L}$ and ![]() $F^{\rm DK}$ at
$F^{\rm DK}$ at ![]() $\lambda \cdot x\in {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$.
$\lambda \cdot x\in {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$.
In § 6.6, we prove the main theorem of this paper modulo Proposition 6.6.2.
6.1 Whittaker category on  ${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$
${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$
6.1.1
Recall that we defined the Beilinson–Drinfeld affine flags ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ in §§ 2.3 and 2.4.2. The idea of the construction of the functor
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ in §§ 2.3 and 2.4.2. The idea of the construction of the functor ![]() $F^{\rm L}$ is to regard a twisted Whittaker sheaf on
$F^{\rm L}$ is to regard a twisted Whittaker sheaf on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_G$ as a twisted Whittaker sheaf on
${\operatorname {Fl}}^{\omega ^\rho }_G$ as a twisted Whittaker sheaf on ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ (and
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ (and ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }\!$), and then pushforward along the projection to
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }\!$), and then pushforward along the projection to ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$. Let us start by explaining the definition of Whittaker sheaves on
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$. Let us start by explaining the definition of Whittaker sheaves on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$.
${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$.
Let ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ (respectively,
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ (respectively, ![]() $N(\mathcal {O})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}\!$) be Ran-ified loop group of
$N(\mathcal {O})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}\!$) be Ran-ified loop group of ![]() $N$. It is the prestack classifying the data
$N$. It is the prestack classifying the data ![]() $(\mathcal {I}, \alpha )$, where
$(\mathcal {I}, \alpha )$, where ![]() $\mathcal {I}\in {\mathop {\operatorname {\rm Ran}}}(S)$ and
$\mathcal {I}\in {\mathop {\operatorname {\rm Ran}}}(S)$ and ![]() $\alpha$ is an automorphism of
$\alpha$ is an automorphism of ![]() $\omega ^\rho \overset {T}{\times } B$ on
$\omega ^\rho \overset {T}{\times } B$ on ![]() $\overset {\circ }{\mathcal {D}}_{\mathcal {I}}$ (respectively,
$\overset {\circ }{\mathcal {D}}_{\mathcal {I}}$ (respectively, ![]() ${\mathcal {D}}_{\mathcal {I}}$), which is compatible with the identification of
${\mathcal {D}}_{\mathcal {I}}$), which is compatible with the identification of ![]() $\omega ^\rho$. Similarly, one can define
$\omega ^\rho$. Similarly, one can define ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ and
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ and ![]() $N(\mathcal {O})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$.
$N(\mathcal {O})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$.
We define a character
 \begin{align} & \chi_{{\mathop{\operatorname{\rm Ran}}}_x}: N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}\to N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}/[N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}, N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}]\to \omega^r_{{\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{K}) \nonumber\\ &\quad \overset{\text{sum}}{\longrightarrow} \omega_{{\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{K}) \overset{\text{residue}}{\longrightarrow} \mathbb{G}_a \end{align}
\begin{align} & \chi_{{\mathop{\operatorname{\rm Ran}}}_x}: N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}\to N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}/[N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}, N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}]\to \omega^r_{{\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{K}) \nonumber\\ &\quad \overset{\text{sum}}{\longrightarrow} \omega_{{\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{K}) \overset{\text{residue}}{\longrightarrow} \mathbb{G}_a \end{align}
of ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$. Similarly, we can define a character
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$. Similarly, we can define a character
of ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$.
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$.
For ![]() $\bar {x}=\{x_1, x_2, \ldots, x_n\}\in {\mathop {\operatorname {\rm Ran}}}$, we denote by
$\bar {x}=\{x_1, x_2, \ldots, x_n\}\in {\mathop {\operatorname {\rm Ran}}}$, we denote by ![]() $\chi _{\bar {x}}$ the restriction of
$\chi _{\bar {x}}$ the restriction of ![]() $\chi _{{\mathop {\operatorname {\rm Ran}}}}$ to
$\chi _{{\mathop {\operatorname {\rm Ran}}}}$ to ![]() $N(\mathcal {K})^{\omega ^\rho }_{\bar {x}}:= N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}\underset {{\mathop {\operatorname {\rm Ran}}}}{\times }\{\bar {x}\}$. Note that the character
$N(\mathcal {K})^{\omega ^\rho }_{\bar {x}}:= N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}\underset {{\mathop {\operatorname {\rm Ran}}}}{\times }\{\bar {x}\}$. Note that the character ![]() $\chi$ of
$\chi$ of ![]() $N(\mathcal {K})^{\omega ^\rho }_{{x}}$ in (3.1.1) equals
$N(\mathcal {K})^{\omega ^\rho }_{{x}}$ in (3.1.1) equals ![]() $\chi _x$ here.
$\chi _x$ here.
6.1.2
Left multiplication gives an action of ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ on
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ on ![]() ${\operatorname {Gr}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}}$, and an action of
${\operatorname {Gr}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}}$, and an action of ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ on
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}_x}$. Following [Reference Gaitsgory and LysenkoGL18, Proposition 7.2.5], the pullback of
${\operatorname {Fl}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}_x}$. Following [Reference Gaitsgory and LysenkoGL18, Proposition 7.2.5], the pullback of ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ (see § 2.4) to
${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ (see § 2.4) to ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ is a multiplicative gerbe, in particular, the gerbe
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ is a multiplicative gerbe, in particular, the gerbe ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ is equivariant with respect to
${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ is equivariant with respect to ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ against
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ against ![]() $\mathcal {G}^G$. Since
$\mathcal {G}^G$. Since ![]() $N$ is unipotent,
$N$ is unipotent, ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ is an ind-pro-affine space over
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$ is an ind-pro-affine space over ![]() ${\mathop {\operatorname {\rm Ran}}}_x$. There is a canonical trivialization of
${\mathop {\operatorname {\rm Ran}}}_x$. There is a canonical trivialization of ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$. Hence, the gerbe
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$. Hence, the gerbe ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ is equivariant with respect to the action of
${\operatorname {Fl}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}_x}$ is equivariant with respect to the action of ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$. In particular, we may consider the category of
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}$. In particular, we may consider the category of ![]() $(N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x},\chi _{{\mathop {\operatorname {\rm Ran}}}_x}\!)$-equivariant sheaves.
$(N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x},\chi _{{\mathop {\operatorname {\rm Ran}}}_x}\!)$-equivariant sheaves.
Definition 6.1.3 We define
6.1.4
Now we define a closed ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$-invariant subspace
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$-invariant subspace ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}\subset {\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$.
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}\subset {\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$.
Definition 6.1.5 A point ![]() $(\mathcal {I},\mathcal {P}_G,\alpha,\epsilon )\in {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$ belongs to
$(\mathcal {I},\mathcal {P}_G,\alpha,\epsilon )\in {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$ belongs to ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ if and only if for any dominant weight
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ if and only if for any dominant weight ![]() $\check {\lambda }\in \check {\Lambda }^+$, the composite meromorphic map
$\check {\lambda }\in \check {\Lambda }^+$, the composite meromorphic map
is regular on ![]() $X\setminus x$. Here
$X\setminus x$. Here ![]() $\mathcal {V}_{\mathcal {P}_G}^{\check {\lambda }}$ (respectively,
$\mathcal {V}_{\mathcal {P}_G}^{\check {\lambda }}$ (respectively, ![]() $\mathcal {V}_{\mathcal {P}_G^\omega }^{\check {\lambda }}$) is defined as the vector bundle associated with
$\mathcal {V}_{\mathcal {P}_G^\omega }^{\check {\lambda }}$) is defined as the vector bundle associated with ![]() $\mathcal {P}_G$ (respectively,
$\mathcal {P}_G$ (respectively, ![]() $\mathcal {P}_G^{\omega }:= \omega ^\rho \overset {T}{\times }G$) with fiber the Weyl module
$\mathcal {P}_G^{\omega }:= \omega ^\rho \overset {T}{\times }G$) with fiber the Weyl module ![]() $\mathcal {V}_G^{\check {\lambda }}$. The first map is the map mapping to the highest weight vector, and the second map is induced by
$\mathcal {V}_G^{\check {\lambda }}$. The first map is the map mapping to the highest weight vector, and the second map is induced by ![]() $\alpha$.
$\alpha$.
Definition 6.1.6 A point ![]() $(\mathcal {I},\mathcal {P}_G, \alpha )\in {\operatorname {Gr}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}}$ belongs to
$(\mathcal {I},\mathcal {P}_G, \alpha )\in {\operatorname {Gr}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}}$ belongs to ![]() $\overline {S}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}^0$, if for any dominant weight
$\overline {S}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}^0$, if for any dominant weight ![]() $\check {\lambda }\in \check {\Lambda }^+$, the composite meromorphic map
$\check {\lambda }\in \check {\Lambda }^+$, the composite meromorphic map
is regular on ![]() $X$.
$X$.
If we require that ![]() $\kappa ^{\check {\lambda }}$ in (6.1.4) is injective on
$\kappa ^{\check {\lambda }}$ in (6.1.4) is injective on ![]() $X$ for any
$X$ for any ![]() $\check {\lambda }\in \check {\Lambda }^+$, the resulting prestack
$\check {\lambda }\in \check {\Lambda }^+$, the resulting prestack ![]() $S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ is the unique open dense
$S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ is the unique open dense ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$-orbit in
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$-orbit in ![]() $\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$.
$\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$.
6.1.7 Factorization property
Following the argument in the proof of [Reference Braverman, Finkelberg, Gaitsgory and MirkovićBFGM02, Proposition 2.4], we can prove that the prestacks defined above satisfy the following factorization property.
Lemma 6.1.8 We have that:
(1)
 $\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ is a factorization prestack, i.e. there is a canonical isomorphism of prestacks
(6.1.5)
$\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ is a factorization prestack, i.e. there is a canonical isomorphism of prestacks
(6.1.5) \begin{equation} \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}} ({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}})_{\rm disj}\simeq \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times \overline{S}^0_{ {\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}} ({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}})_{\rm disj}; \end{equation}
\begin{equation} \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}} ({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}})_{\rm disj}\simeq \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times \overline{S}^0_{ {\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}} ({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}})_{\rm disj}; \end{equation}(2)
 $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$ factorizes with respect to
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$ factorizes with respect to  $\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$, i.e. there is a canonical isomorphism of prestacks
(6.1.6)
$\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$, i.e. there is a canonical isomorphism of prestacks
(6.1.6) \begin{equation} \begin{aligned} (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}_x} ({\mathop{\operatorname{\rm Ran}}}\mathop{\times}{\mathop{\operatorname{\rm Ran}}}_{x})_{\rm disj}\\ \simeq & \\ \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}_x} ({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}_{ x})_{\rm disj}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}_x} ({\mathop{\operatorname{\rm Ran}}}\mathop{\times}{\mathop{\operatorname{\rm Ran}}}_{x})_{\rm disj}\\ \simeq & \\ \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}_x} ({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}_{ x})_{\rm disj}. \end{aligned} \end{equation}
6.1.9
Let ![]() ${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ (respectively,
${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ (respectively, ![]() ${\operatorname {Gr}}_{G,x_i}^{\omega ^\rho }$) denote the fiber of
${\operatorname {Gr}}_{G,x_i}^{\omega ^\rho }$) denote the fiber of ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ (respectively,
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ (respectively, ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$) over
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$) over ![]() $x$ (respectively,
$x$ (respectively, ![]() $x_i$), it is isomorphic to
$x_i$), it is isomorphic to ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ (respectively,
${\operatorname {Fl}}_G^{\omega ^\rho }$ (respectively, ![]() ${\operatorname {Gr}}_G^{\omega ^\rho }$) by choosing a uniformizer. Denote by
${\operatorname {Gr}}_G^{\omega ^\rho }$) by choosing a uniformizer. Denote by ![]() $\overline {S}^0_{{\operatorname {Gr}}, x_i}$ the closure of the
$\overline {S}^0_{{\operatorname {Gr}}, x_i}$ the closure of the ![]() $N(\mathcal {K})_{x_i}^{\omega ^\rho }$-orbit of
$N(\mathcal {K})_{x_i}^{\omega ^\rho }$-orbit of ![]() $t^0\in {\operatorname {Gr}}^{\omega ^\rho }_{G,x_i}$.
$t^0\in {\operatorname {Gr}}^{\omega ^\rho }_{G,x_i}$.
By definition, the fiber of ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_{x}})_{\infty \cdot x}$ over the point
$(\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_{x}})_{\infty \cdot x}$ over the point ![]() ${{\mathcal {I}}}=\{x,x_1,x_2,\ldots,x_k\}\in {\mathop {\operatorname {\rm Ran}}}_{x}$ is isomorphic to the product
${{\mathcal {I}}}=\{x,x_1,x_2,\ldots,x_k\}\in {\mathop {\operatorname {\rm Ran}}}_{x}$ is isomorphic to the product ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G,x}\times \prod _{i=1}^k \overline {S}_{{\operatorname {Gr}}, x_i}^{0}$, and the fiber of
${\operatorname {Fl}}^{\omega ^\rho }_{G,x}\times \prod _{i=1}^k \overline {S}_{{\operatorname {Gr}}, x_i}^{0}$, and the fiber of ![]() $\overline {S}^0_{{\mathop {\operatorname {\rm Ran}}},{\operatorname {Gr}}}$ over the point
$\overline {S}^0_{{\mathop {\operatorname {\rm Ran}}},{\operatorname {Gr}}}$ over the point ![]() ${{\mathcal {I}}}=\{x_1,x_2,\ldots,x_k\}\in {\mathop {\operatorname {\rm Ran}}}$ is isomorphic to
${{\mathcal {I}}}=\{x_1,x_2,\ldots,x_k\}\in {\mathop {\operatorname {\rm Ran}}}$ is isomorphic to ![]() $\prod _{i=1}^k \overline {S}^0_{{\operatorname {Gr}}, x_i}$.
$\prod _{i=1}^k \overline {S}^0_{{\operatorname {Gr}}, x_i}$.
6.1.10 Relation with  $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$
Consider the product space ![]() ${\mathop {\operatorname {\rm Ran}}}_{x}\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$. The
${\mathop {\operatorname {\rm Ran}}}_{x}\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$. The ![]() $N(\mathcal {K})^{\omega ^\rho }_x$ action on the second factor gives a
$N(\mathcal {K})^{\omega ^\rho }_x$ action on the second factor gives a ![]() $N(\mathcal {K})^{\omega ^\rho }_x$-action on
$N(\mathcal {K})^{\omega ^\rho }_x$-action on ![]() ${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$. The pullback of the gerbe
${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$. The pullback of the gerbe ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G,x}$ to
${\operatorname {Fl}}^{\omega ^\rho }_{G,x}$ to ![]() ${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$ is still
${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$ is still ![]() $N(\mathcal {K})^{\omega ^\rho }_x$-equivariant, hence we can consider the Whittaker category on
$N(\mathcal {K})^{\omega ^\rho }_x$-equivariant, hence we can consider the Whittaker category on ![]() ${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$,
${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$,
There is a closed embedding
which sends ![]() $\mathcal {I}\in {\mathop {\operatorname {\rm Ran}}}_x, (\mathcal {P}_G, \alpha, \epsilon )\in {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ to
$\mathcal {I}\in {\mathop {\operatorname {\rm Ran}}}_x, (\mathcal {P}_G, \alpha, \epsilon )\in {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ to ![]() $(\mathcal {I}, \mathcal {P}_G, \alpha, \epsilon )\in (\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_{x}})_{\infty \cdot x}$. Similarly, we have
$(\mathcal {I}, \mathcal {P}_G, \alpha, \epsilon )\in (\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_{x}})_{\infty \cdot x}$. Similarly, we have
The ![]() $!$-pullback along the projection
$!$-pullback along the projection
gives rise to a functor
By definition, ![]() $\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}$ commutes with
$\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}$ commutes with ![]() $N(\mathcal {K})_x^{\omega ^\rho }$-actions, so
$N(\mathcal {K})_x^{\omega ^\rho }$-actions, so ![]() $\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}^!$ induces a functor between the corresponding Whittaker categories
$\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}^!$ induces a functor between the corresponding Whittaker categories
6.1.11
Consider the pullback functor along (6.1.8)
We claim that this map induces a functor between the corresponding Whittaker categories
Indeed, consider the closed subgroup ![]() $N'$ in
$N'$ in ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ whose fiber over a point
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ whose fiber over a point ![]() $\{x, x_1,x_2,\ldots,x_k\} \in {\mathop {\operatorname {\rm Ran}}}_x$ is given by
$\{x, x_1,x_2,\ldots,x_k\} \in {\mathop {\operatorname {\rm Ran}}}_x$ is given by ![]() $N(\mathcal {K})_x^{\omega ^\rho }\times \prod _{i=1}^k N(\mathcal {O})_{x_i}^{\omega ^\rho }$. Restriction to
$N(\mathcal {K})_x^{\omega ^\rho }\times \prod _{i=1}^k N(\mathcal {O})_{x_i}^{\omega ^\rho }$. Restriction to ![]() $x$ gives a projection
$x$ gives a projection
The map (6.1.8) is compatible with ![]() $N'$-action, where the action of
$N'$-action, where the action of ![]() $N'$ on
$N'$ on ![]() ${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ is given by the projection (6.1.13) and the action of
${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ is given by the projection (6.1.13) and the action of ![]() $N(\mathcal {K})^{\omega ^\rho }_x$ on
$N(\mathcal {K})^{\omega ^\rho }_x$ on ![]() ${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$. Since the kernel of the projection (6.1.13) is pro-unipotent, the forgetful functor
${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$. Since the kernel of the projection (6.1.13) is pro-unipotent, the forgetful functor
is an equivalence. Hence, ![]() $\operatorname {unit}^!$ induces a functor
$\operatorname {unit}^!$ induces a functor
 \begin{align} \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_{x}}\!)_{\infty \cdot x})^{N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}, \chi_{{\mathop{\operatorname{\rm Ran}}}_x}} &\to \operatorname{Shv}_{\mathcal{G}^G}({\mathop{\operatorname{\rm Ran}}}_x\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N',\chi} \nonumber\\ &\simeq \operatorname{Shv}_{\mathcal{G}^G}({\mathop{\operatorname{\rm Ran}}}_x\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N(\mathcal{K})_x^{\omega^\rho},\chi}, \end{align}
\begin{align} \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_{x}}\!)_{\infty \cdot x})^{N(\mathcal{K})^{\omega^\rho}_{{\mathop{\operatorname{\rm Ran}}}_x}, \chi_{{\mathop{\operatorname{\rm Ran}}}_x}} &\to \operatorname{Shv}_{\mathcal{G}^G}({\mathop{\operatorname{\rm Ran}}}_x\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N',\chi} \nonumber\\ &\simeq \operatorname{Shv}_{\mathcal{G}^G}({\mathop{\operatorname{\rm Ran}}}_x\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N(\mathcal{K})_x^{\omega^\rho},\chi}, \end{align}that is,
Similarly, we can define
According to [Reference GaitsgoryGai20, Theorem 6.2.5], the functor (6.1.16) is an equivalence. By an argument similar to [Reference GaitsgoryGai20, §§ 6.2–6.6], we can prove the following lemma.
Lemma 6.1.12 The functor (6.1.15) is an equivalence.
Proof. We only sketch the proof.
Given a finite set ![]() ${\mathfrak {I}}$ with a distinguished point, let
${\mathfrak {I}}$ with a distinguished point, let ![]() $X^{{\mathfrak {I}}}_x$ be the subspace of
$X^{{\mathfrak {I}}}_x$ be the subspace of ![]() $X^{{\mathfrak {I}}}$ such that the coordinate indexed by the distinguished point is
$X^{{\mathfrak {I}}}$ such that the coordinate indexed by the distinguished point is ![]() $x$. Note that
$x$. Note that ![]() ${\mathop {\operatorname {\rm Ran}}}_x={\rm colim} X^{{\mathfrak {I}}}_x$, and we can define
${\mathop {\operatorname {\rm Ran}}}_x={\rm colim} X^{{\mathfrak {I}}}_x$, and we can define ![]() $\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_{x}})_{\infty \cdot x})$ and
$\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_{x}})_{\infty \cdot x})$ and ![]() $\operatorname {Whit}_{\rm q}(X^{{\mathfrak {I}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ similarly.
$\operatorname {Whit}_{\rm q}(X^{{\mathfrak {I}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ similarly.
It is sufficient to show that ![]() $\operatorname {unit}_{{\mathfrak {I}}}^!: \operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_{x}})_{\infty \cdot x}\!)\to \operatorname {Whit}_{\rm q}(X^{{\mathfrak {I}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ is an equivalence for any finite set
$\operatorname {unit}_{{\mathfrak {I}}}^!: \operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_{x}})_{\infty \cdot x}\!)\to \operatorname {Whit}_{\rm q}(X^{{\mathfrak {I}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ is an equivalence for any finite set ![]() ${\mathfrak {I}}$ with a distinguished point, then the desired property follows by taking limit. For any such
${\mathfrak {I}}$ with a distinguished point, then the desired property follows by taking limit. For any such ![]() ${\mathfrak {I}}$, one can give
${\mathfrak {I}}$, one can give ![]() $X^{{\mathfrak {I}}}_x$ a stratification
$X^{{\mathfrak {I}}}_x$ a stratification ![]() $\{X^{{\mathfrak {B}}}_x\}$ according to the collision of points. Note that there is
$\{X^{{\mathfrak {B}}}_x\}$ according to the collision of points. Note that there is ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {B}}}_{x}}\!)_{\infty \cdot x}\simeq (((X-x)^k-\text {Diag})\underset {{\mathop {\operatorname {\rm Ran}}}}{\times } \overline {S}^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}})\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$, where
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {B}}}_{x}}\!)_{\infty \cdot x}\simeq (((X-x)^k-\text {Diag})\underset {{\mathop {\operatorname {\rm Ran}}}}{\times } \overline {S}^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}})\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$, where ![]() $k$ is the number of different elements in
$k$ is the number of different elements in ![]() ${\mathfrak {B}}$ without the element containing the distinguished point. Thus, we have
${\mathfrak {B}}$ without the element containing the distinguished point. Thus, we have
 \begin{align} \operatorname{Whit}_{\rm q}((\overline{S}^{w_0}_{{\operatorname{Fl}}, X^{{\mathfrak{B}}}_{x}}\!)_{\infty \cdot x}) &\simeq \operatorname{Shv}_{{\mathcal{G}}^G}((((X-x)^k-\text{Diag})\underset{{\mathop{\operatorname{\rm Ran}}}}{\times} \overline{S}^0_{{\operatorname{Gr}},{\mathop{\operatorname{\rm Ran}}}})\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N({\mathcal{K}})^{\omega^\rho}_{X^{{\mathfrak{B}}}_x},\chi_{{{\mathfrak{B}}}}} \nonumber\\ &\simeq\operatorname{Shv}_{{\mathcal{G}}^G}((((X-x)^k-\text{Diag})\underset{{\mathop{\operatorname{\rm Ran}}}}{\times} {S}^0_{{\operatorname{Gr}},{\mathop{\operatorname{\rm Ran}}}})\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N({\mathcal{K}})^{\omega^\rho}_{X^{{\mathfrak{B}}}_x},\chi_{{{\mathfrak{B}}}}} \nonumber\\ &\simeq \operatorname{Shv}_{{\mathcal{G}}^G}((((X-x)^k-\text{Diag}))\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N({\mathcal{K}})_x^{\omega^\rho},\chi_x} \simeq \operatorname{Whit}_{\rm q}(X^{{\mathfrak{B}}}_{x}\times {\operatorname{Fl}}_{G,x}^{\omega^\rho}). \end{align}
\begin{align} \operatorname{Whit}_{\rm q}((\overline{S}^{w_0}_{{\operatorname{Fl}}, X^{{\mathfrak{B}}}_{x}}\!)_{\infty \cdot x}) &\simeq \operatorname{Shv}_{{\mathcal{G}}^G}((((X-x)^k-\text{Diag})\underset{{\mathop{\operatorname{\rm Ran}}}}{\times} \overline{S}^0_{{\operatorname{Gr}},{\mathop{\operatorname{\rm Ran}}}})\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N({\mathcal{K}})^{\omega^\rho}_{X^{{\mathfrak{B}}}_x},\chi_{{{\mathfrak{B}}}}} \nonumber\\ &\simeq\operatorname{Shv}_{{\mathcal{G}}^G}((((X-x)^k-\text{Diag})\underset{{\mathop{\operatorname{\rm Ran}}}}{\times} {S}^0_{{\operatorname{Gr}},{\mathop{\operatorname{\rm Ran}}}})\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N({\mathcal{K}})^{\omega^\rho}_{X^{{\mathfrak{B}}}_x},\chi_{{{\mathfrak{B}}}}} \nonumber\\ &\simeq \operatorname{Shv}_{{\mathcal{G}}^G}((((X-x)^k-\text{Diag}))\times {\operatorname{Fl}}_{G,x}^{\omega^\rho})^{N({\mathcal{K}})_x^{\omega^\rho},\chi_x} \simeq \operatorname{Whit}_{\rm q}(X^{{\mathfrak{B}}}_{x}\times {\operatorname{Fl}}_{G,x}^{\omega^\rho}). \end{align}
Here, the second equivalence follows from the fact that ![]() $\overline {S}^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}\backslash {S}^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}$ does not carry non-zero Whittaker sheaf, and the third equivalence follows from
$\overline {S}^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}\backslash {S}^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}$ does not carry non-zero Whittaker sheaf, and the third equivalence follows from ![]() $N({\mathcal {K}})^{\omega ^\rho }_{X^{{\mathfrak {B}}}_x}\simeq (((X-x)^k-\text {Diag})\underset {{\mathop {\operatorname {\rm Ran}}}}{\times } N({\mathcal {K}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}})\times N({\mathcal {K}})_x^{\omega ^\rho }$. It implies that the restriction
$N({\mathcal {K}})^{\omega ^\rho }_{X^{{\mathfrak {B}}}_x}\simeq (((X-x)^k-\text {Diag})\underset {{\mathop {\operatorname {\rm Ran}}}}{\times } N({\mathcal {K}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}})\times N({\mathcal {K}})_x^{\omega ^\rho }$. It implies that the restriction ![]() $\operatorname {unit}_{{\mathfrak {B}}}^!:\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {B}}}_{x}}\!)_{\infty \cdot x})\to \operatorname {Whit}_{\rm q}(X^{{\mathfrak {B}}}_{x}\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ is an equivalence.
$\operatorname {unit}_{{\mathfrak {B}}}^!:\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {B}}}_{x}}\!)_{\infty \cdot x})\to \operatorname {Whit}_{\rm q}(X^{{\mathfrak {B}}}_{x}\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ is an equivalence.
In particular, ![]() $\operatorname {unit}^!_{{\mathfrak {I}}}$ is conservative, and we only need to construct the left adjoint functor
$\operatorname {unit}^!_{{\mathfrak {I}}}$ is conservative, and we only need to construct the left adjoint functor ![]() $(\operatorname {unit}^!_{{\mathfrak {I}}})^{\rm L}$ such that
$(\operatorname {unit}^!_{{\mathfrak {I}}})^{\rm L}$ such that ![]() ${\mathop {\operatorname {\rm Id}}}\to \operatorname {unit}^!_{{\mathfrak {I}}}\circ (\operatorname {unit}^!_{{\mathfrak {I}}})^{\rm L}$ is an isomorphism.
${\mathop {\operatorname {\rm Id}}}\to \operatorname {unit}^!_{{\mathfrak {I}}}\circ (\operatorname {unit}^!_{{\mathfrak {I}}})^{\rm L}$ is an isomorphism.
For ![]() $n\geq 0$, let
$n\geq 0$, let ![]() $I_{n}:= {\rm Ad}_{-n\rho }(G({\mathcal {O}})^{\omega ^\rho }\underset {G({\mathcal {O}}/t^n{\mathcal {O}})^{\omega ^\rho }}{\times }N({\mathcal {O}}/t^n{\mathcal {O}})^{\omega ^\rho })$. There is a canonical way to extend the character
$I_{n}:= {\rm Ad}_{-n\rho }(G({\mathcal {O}})^{\omega ^\rho }\underset {G({\mathcal {O}}/t^n{\mathcal {O}})^{\omega ^\rho }}{\times }N({\mathcal {O}}/t^n{\mathcal {O}})^{\omega ^\rho })$. There is a canonical way to extend the character ![]() $\chi |_{I_n\cap N({\mathcal {K}})^{\omega ^\rho }}$ to
$\chi |_{I_n\cap N({\mathcal {K}})^{\omega ^\rho }}$ to ![]() $I_n$ such that it is trivial on the negative part (i.e.
$I_n$ such that it is trivial on the negative part (i.e. ![]() $B^-({\mathcal {O}})\cap I_n$), we still use the same notation
$B^-({\mathcal {O}})\cap I_n$), we still use the same notation ![]() $\chi$.
$\chi$.
A quite non-trivial result of [Reference RaskinRas, Theorem 2.7.1] says that the left adjoint ![]() $\operatorname {Av}_!^{N({\mathcal {K}})^{\omega ^\rho },\chi _x}$ is well-defined for any
$\operatorname {Av}_!^{N({\mathcal {K}})^{\omega ^\rho },\chi _x}$ is well-defined for any ![]() $(I_n,\chi _x)$-equivariant sheaf. With the same proof, one can show that
$(I_n,\chi _x)$-equivariant sheaf. With the same proof, one can show that ![]() $\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined for any
$\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined for any ![]() $(I_n',\chi _x)$-equivariant sheaf on
$(I_n',\chi _x)$-equivariant sheaf on ![]() ${\operatorname {Fl}}_{G,X^{{\mathfrak {I}}}_x}^{\omega ^\rho }$. Here,
${\operatorname {Fl}}_{G,X^{{\mathfrak {I}}}_x}^{\omega ^\rho }$. Here, ![]() $I_n'\subset G({\mathcal {K}})^{\omega ^\rho }_{{\mathfrak {I}}}$ is the subgroup whose fiber over
$I_n'\subset G({\mathcal {K}})^{\omega ^\rho }_{{\mathfrak {I}}}$ is the subgroup whose fiber over ![]() $\{x,x_1,x_2,\ldots,x_n\}$ is
$\{x,x_1,x_2,\ldots,x_n\}$ is ![]() $I_n\times \prod _{i=1}^n G({\mathcal {O}})^{\omega ^\rho }_{x_i}$, and
$I_n\times \prod _{i=1}^n G({\mathcal {O}})^{\omega ^\rho }_{x_i}$, and ![]() $\chi _{{\mathfrak {I}}}$ is the character given by the map
$\chi _{{\mathfrak {I}}}$ is the character given by the map ![]() $I_n'\to I_n\overset {\chi }{\to }{\mathbb {G}}_a$.
$I_n'\to I_n\overset {\chi }{\to }{\mathbb {G}}_a$.
To construct the left adjoint functor ![]() $(\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ of
$(\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ of ![]() $\operatorname {unit}_{{\mathfrak {I}}}^!$, we should prove that
$\operatorname {unit}_{{\mathfrak {I}}}^!$, we should prove that ![]() $\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined on the image of the composition
$\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined on the image of the composition
Then, ![]() $(\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ is given by the composition of the above functor and
$(\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ is given by the composition of the above functor and ![]() $\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$.
$\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$.
Note that the category ![]() $\operatorname {Whit}_{\rm q}(X^{{\mathfrak {I}}}_{x}\times {\operatorname {Fl}}_G^{\omega ^\rho })$ is generated by applying
$\operatorname {Whit}_{\rm q}(X^{{\mathfrak {I}}}_{x}\times {\operatorname {Fl}}_G^{\omega ^\rho })$ is generated by applying ![]() $\operatorname {Av}_!^{N({\mathcal {K}})^{\omega ^\rho },\chi _x}$ to
$\operatorname {Av}_!^{N({\mathcal {K}})^{\omega ^\rho },\chi _x}$ to ![]() $(I_n,\chi _x)$-equivariant objects on
$(I_n,\chi _x)$-equivariant objects on ![]() $X^{{\mathfrak {I}}}_{x}\times {\operatorname {Fl}}_G^{\omega ^\rho }$. Thus, we only need to show that
$X^{{\mathfrak {I}}}_{x}\times {\operatorname {Fl}}_G^{\omega ^\rho }$. Thus, we only need to show that ![]() $\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined on the image of
$\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined on the image of
Furthermore, note that ![]() $\operatorname {unit}_{{\mathfrak {I}}}:X^{{\mathfrak {I}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }\to (\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_{x}})_{\infty \cdot x}$ is
$\operatorname {unit}_{{\mathfrak {I}}}:X^{{\mathfrak {I}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }\to (\overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_{x}})_{\infty \cdot x}$ is ![]() $I_n'$-invariant, where
$I_n'$-invariant, where ![]() $I_n'$ acts on
$I_n'$ acts on ![]() $X^{{\mathfrak {I}}}_{x}\times {\operatorname {Fl}}_G^{\omega ^\rho }$ via
$X^{{\mathfrak {I}}}_{x}\times {\operatorname {Fl}}_G^{\omega ^\rho }$ via ![]() $I_n'\to I_n$. In particular, the image of (6.1.18) is
$I_n'\to I_n$. In particular, the image of (6.1.18) is ![]() $({I_n',\chi _x})$-equivariant, and
$({I_n',\chi _x})$-equivariant, and ![]() $\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined for those equivariant sheaves.
$\operatorname {Av}_!^{N({\mathcal {K}})_{{{\mathfrak {I}}}}^{\omega ^\rho },\chi _{{\mathfrak {I}}}}$ is well-defined for those equivariant sheaves.
Finally, by repeating the same argument as in [Reference GaitsgoryGai20, § 6.5] we can prove that the functor ![]() $(\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ satisfies the desired property, i.e.
$(\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ satisfies the desired property, i.e. ![]() ${\mathop {\operatorname {\rm Id}}}\to \operatorname {unit}_{{\mathfrak {I}}}^!\circ (\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ is an isomorphism.
${\mathop {\operatorname {\rm Id}}}\to \operatorname {unit}_{{\mathfrak {I}}}^!\circ (\operatorname {unit}_{{\mathfrak {I}}}^!)^{\rm L}$ is an isomorphism.
Definition 6.1.13 For ![]() $\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$, we denote by
$\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$, we denote by ![]() $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ the Whittaker sheaf on
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ the Whittaker sheaf on ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$ corresponding to
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$ corresponding to ![]() $\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}^!(\mathcal {F})$ under the equivalence (6.1.15).
$\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}^!(\mathcal {F})$ under the equivalence (6.1.15).
Using the fiber description of ![]() $(\overline {S}^0_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_{x}}\!)_{\infty \cdot x}$ in § 6.1.9, we can describe
$(\overline {S}^0_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_{x}}\!)_{\infty \cdot x}$ in § 6.1.9, we can describe ![]() $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ more explicitly. Namely, the restriction of
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ more explicitly. Namely, the restriction of ![]() $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ to
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ to ![]() ${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ is
${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ is ![]() $\mathcal {F}$, and its restriction to
$\mathcal {F}$, and its restriction to ![]() $\overline {S}^0_{{\operatorname {Gr}}, x_i}$ is the generator of
$\overline {S}^0_{{\operatorname {Gr}}, x_i}$ is the generator of ![]() $\operatorname {Whit}_{\rm q}(\overline {S}^0_{{\operatorname {Gr}}, x_i}\!)$.
$\operatorname {Whit}_{\rm q}(\overline {S}^0_{{\operatorname {Gr}}, x_i}\!)$.
Definition 6.1.14 Let ![]() ${\rm Vac}$ denote the Whittaker sheaf on
${\rm Vac}$ denote the Whittaker sheaf on ![]() $\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ which is uniquely characterized by the property that its !-pullback to
$\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ which is uniquely characterized by the property that its !-pullback to ![]() ${\mathop {\operatorname {\rm Ran}}}$ via the canonical section
${\mathop {\operatorname {\rm Ran}}}$ via the canonical section
 \begin{equation} \begin{aligned} s_{{\mathop{\operatorname{\rm Ran}}}}: {\mathop{\operatorname{\rm Ran}}}\to \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\\ \mathcal{I}\mapsto (\mathcal{I}, \mathcal{P}_G^{\omega}, {\rm id}) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} s_{{\mathop{\operatorname{\rm Ran}}}}: {\mathop{\operatorname{\rm Ran}}}\to \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\\ \mathcal{I}\mapsto (\mathcal{I}, \mathcal{P}_G^{\omega}, {\rm id}) \end{aligned} \end{equation}
is the dualizing sheaf on ![]() ${\mathop {\operatorname {\rm Ran}}}$, i.e.
${\mathop {\operatorname {\rm Ran}}}$, i.e. ![]() $s_{{\mathop {\operatorname {\rm Ran}}}}^!({\rm Vac})\simeq \omega _{{\mathop {\operatorname {\rm Ran}}}}$.
$s_{{\mathop {\operatorname {\rm Ran}}}}^!({\rm Vac})\simeq \omega _{{\mathop {\operatorname {\rm Ran}}}}$.
It is important that ![]() ${\rm Vac}$ and
${\rm Vac}$ and ![]() $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ satisfy the following factorization properties:
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ satisfy the following factorization properties:
Corollary 6.1.15
(1)
 ${\rm Vac}$ is a factorization algebra on
${\rm Vac}$ is a factorization algebra on  $\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$, i.e. there is a canonical isomorphism
which is compatible with (6.1.5);
$\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$, i.e. there is a canonical isomorphism
which is compatible with (6.1.5); \[ {\rm Vac}\boxtimes {\rm Vac}|_{(\overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}})_{\rm disj}}\simeq {\rm Vac}|_{\overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\underset{{\mathop{\operatorname{\rm Ran}}}}{\times} ({\mathop{\operatorname{\rm Ran}}}\times{\mathop{\operatorname{\rm Ran}}})_{\rm disj}}, \]
\[ {\rm Vac}\boxtimes {\rm Vac}|_{(\overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}})_{\rm disj}}\simeq {\rm Vac}|_{\overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\underset{{\mathop{\operatorname{\rm Ran}}}}{\times} ({\mathop{\operatorname{\rm Ran}}}\times{\mathop{\operatorname{\rm Ran}}})_{\rm disj}}, \]
(2)
 $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})\in \operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_{x}})_{\infty \cdot x})$ is a factorization module over
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})\in \operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_{x}})_{\infty \cdot x})$ is a factorization module over  ${\rm Vac}$, i.e. there is a canonical isomorphism
${\rm Vac}$, i.e. there is a canonical isomorphism
 \[ {\rm Vac}\boxtimes \operatorname{sprd}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{F})|_{(\overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_{x}}\!)_{\infty \cdot x}\!)_{\rm disj}} \]
\[ {\rm Vac}\boxtimes \operatorname{sprd}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{F})|_{(\overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Ran}}}}\times (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_{x}}\!)_{\infty \cdot x}\!)_{\rm disj}} \]
 \[ \simeq \]
which is compatible with (6.1.6).
\[ \simeq \]
which is compatible with (6.1.6). \[ \operatorname{sprd}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{F})|_{(\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_{x}})_{\infty \cdot x}) \underset{{\mathop{\operatorname{\rm Ran}}}_{ x}}{\times}({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}_{ x})_{\rm disj}}, \]
\[ \operatorname{sprd}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}(\mathcal{F})|_{(\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_{x}})_{\infty \cdot x}) \underset{{\mathop{\operatorname{\rm Ran}}}_{ x}}{\times}({\mathop{\operatorname{\rm Ran}}}\times {\mathop{\operatorname{\rm Ran}}}_{ x})_{\rm disj}}, \]
Proof. Part (1) is [Reference Gaitsgory and LysenkoGL19, Theorem 8.4.6 (a)]. We only show part (2).
It is known that for any ![]() $x\in \overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}\setminus S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$, we have
$x\in \overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}\setminus S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$, we have
It implies ![]() $\operatorname {Whit}_{\rm q}(\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}\setminus S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}})=0$. In particular,
$\operatorname {Whit}_{\rm q}(\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}\setminus S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}})=0$. In particular,
Since ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ acts transitively on
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ acts transitively on ![]() $S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ over
$S^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}$ over ![]() ${\mathop {\operatorname {\rm Ran}}}$ and
${\mathop {\operatorname {\rm Ran}}}$ and ![]() $N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ is ind-pro-unipotent, taking
$N(\mathcal {K})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}}$ is ind-pro-unipotent, taking ![]() $!$-stalks along
$!$-stalks along ![]() $s_{{\mathop {\operatorname {\rm Ran}}}}$ induces an equivalence of categories
$s_{{\mathop {\operatorname {\rm Ran}}}}$ induces an equivalence of categories
Consider the following commutative diagram.

By Lemma 6.1.12, we need to prove
which follows from the facts that ![]() $\operatorname {unit}^!(\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F}))\simeq \omega _{{\mathop {\operatorname {\rm Ran}}}_x}\boxtimes \mathcal {F}$, and the (twisted) sheaf
$\operatorname {unit}^!(\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F}))\simeq \omega _{{\mathop {\operatorname {\rm Ran}}}_x}\boxtimes \mathcal {F}$, and the (twisted) sheaf ![]() $\omega _{{\mathop {\operatorname {\rm Ran}}}_x}$ on
$\omega _{{\mathop {\operatorname {\rm Ran}}}_x}$ on ![]() ${\mathop {\operatorname {\rm Ran}}}_x$ factorizes with respect to
${\mathop {\operatorname {\rm Ran}}}_x$ factorizes with respect to ![]() $\omega _{{\mathop {\operatorname {\rm Ran}}}}$, i.e. we have
$\omega _{{\mathop {\operatorname {\rm Ran}}}}$, i.e. we have
6.2 Configuration version of  ${\operatorname {Gr}}_G^{\omega ^\rho }$ and
${\operatorname {Gr}}_G^{\omega ^\rho }$ and  ${\operatorname {Fl}}_G^{\omega ^\rho }$
${\operatorname {Fl}}_G^{\omega ^\rho }$
The most important prestacks in this paper are constructed in this section. They are analogs of the constructions in [Reference Gaitsgory and LysenkoGL19]. The target of the functor ![]() $F^{\rm L}$ lives on
$F^{\rm L}$ lives on ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$. Hence, it is convenient to consider prestacks over the configuration space. In this section, we explain the configuration version
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$. Hence, it is convenient to consider prestacks over the configuration space. In this section, we explain the configuration version ![]() ${\operatorname {Gr}}_G^{\omega ^\rho }$ and
${\operatorname {Gr}}_G^{\omega ^\rho }$ and ![]() ${\operatorname {Fl}}_G^{\omega ^\rho }$ and related factorization prestacks.
${\operatorname {Fl}}_G^{\omega ^\rho }$ and related factorization prestacks.
Definition 6.2.1 Let ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$ (respectively,
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$ (respectively, ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$) be the prestack over
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$) be the prestack over ![]() ${\mathop {\operatorname {\rm Conf}}}$ (respectively,
${\mathop {\operatorname {\rm Conf}}}$ (respectively, ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$) which classifies the data
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$) which classifies the data ![]() $(D, \mathcal {P}_G, \alpha )$ (respectively,
$(D, \mathcal {P}_G, \alpha )$ (respectively, ![]() $(D, \mathcal {P}_G, \alpha, \epsilon )$), here
$(D, \mathcal {P}_G, \alpha, \epsilon )$), here ![]() $D\in {\mathop {\operatorname {\rm Conf}}}$ (respectively,
$D\in {\mathop {\operatorname {\rm Conf}}}$ (respectively, ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}\!$),
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}\!$), ![]() $\mathcal {P}_G\in {\operatorname {Bun}}_G,\ \alpha :\mathcal {P}_G|_{X\setminus {\mathop {\operatorname {\rm supp}}}(D)}\simeq \mathcal {P}_G^{\omega }|_{X\setminus {\mathop {\operatorname {\rm supp}}}(D)}$, and
$\mathcal {P}_G\in {\operatorname {Bun}}_G,\ \alpha :\mathcal {P}_G|_{X\setminus {\mathop {\operatorname {\rm supp}}}(D)}\simeq \mathcal {P}_G^{\omega }|_{X\setminus {\mathop {\operatorname {\rm supp}}}(D)}$, and ![]() $\epsilon$ is a
$\epsilon$ is a ![]() $B$-reduction of
$B$-reduction of ![]() $\mathcal {P}_G$ at
$\mathcal {P}_G$ at ![]() $x$.
$x$.
Similarly, we can define the configuration analog of ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$,
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$, ![]() $N(\mathcal {O})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$,
$N(\mathcal {O})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$, ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$,
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$, ![]() $N(\mathcal {O})_{{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$, etc. We denote the resulting prestacks by
$N(\mathcal {O})_{{\mathop {\operatorname {\rm Ran}}}_{x}}^{\omega ^\rho }$, etc. We denote the resulting prestacks by ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$,
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$, ![]() $N(\mathcal {O})_{{\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$,
$N(\mathcal {O})_{{\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$, ![]() $N(\mathcal {K})_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$, and
$N(\mathcal {K})_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$, and ![]() $N(\mathcal {O})_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$, respectively.
$N(\mathcal {O})_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$, respectively.
6.2.2
Note that
As a result, the gerbe ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}}$ gives a gerbe on
${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Ran}}}}$ gives a gerbe on ![]() ${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Conf}}}}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}} ({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}})^{\text {neg}}$. By Lemma 2.2.3, it descends to a gerbe on
${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Conf}}}}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}} ({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}})^{\text {neg}}$. By Lemma 2.2.3, it descends to a gerbe on ![]() ${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Conf}}}}$. We still denote it by
${\operatorname {Gr}}^{\omega ^\rho }_{G, {\mathop {\operatorname {\rm Conf}}}}$. We still denote it by ![]() $\mathcal {G}^G$. Similarly, we can define gerbes on other prestacks in Definition 6.2.1.
$\mathcal {G}^G$. Similarly, we can define gerbes on other prestacks in Definition 6.2.1.
To define the functor ![]() $F^{\rm L}$, we need to define two sub-prestacks of
$F^{\rm L}$, we need to define two sub-prestacks of ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$: one carries Whittaker sheaves, and the other one carries the kernel. The former space is given by
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$: one carries Whittaker sheaves, and the other one carries the kernel. The former space is given by ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$, and the latter is
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$, and the latter is ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
$S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
Definition 6.2.3 Denote by ![]() $\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ the closed sub-prestack of
$\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ the closed sub-prestack of ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$ such that the maps
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$ such that the maps ![]() $\kappa ^{\check {\lambda }}$ in (6.1.4) extend to regular maps on
$\kappa ^{\check {\lambda }}$ in (6.1.4) extend to regular maps on ![]() $X$ and satisfy the Plücker relations.
$X$ and satisfy the Plücker relations.
We denote by ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$ the closed sub-prestack of
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$ the closed sub-prestack of ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$ such that the maps
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$ such that the maps ![]() $\kappa ^{\check {\lambda }}$ in (6.1.3) are regular on
$\kappa ^{\check {\lambda }}$ in (6.1.3) are regular on ![]() $X\setminus x$ and satisfy Plücker relations.
$X\setminus x$ and satisfy Plücker relations.
Definition 6.2.4 Let ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ (respectively,
$S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ (respectively, ![]() $\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$) denote the prestack classifying the data
$\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$) denote the prestack classifying the data ![]() $(D, \mathcal {P}_G, \alpha )$, such that for any
$(D, \mathcal {P}_G, \alpha )$, such that for any ![]() $\check {\lambda }$ dominant, the induced map
$\check {\lambda }$ dominant, the induced map
which is a priori defined on ![]() $X\setminus {\mathop {\operatorname {\rm supp}}}(D)$, extends to a surjective (respectively, regular) map on the whole curve
$X\setminus {\mathop {\operatorname {\rm supp}}}(D)$, extends to a surjective (respectively, regular) map on the whole curve ![]() $X$ and satisfies the Plücker relations. Here
$X$ and satisfies the Plücker relations. Here ![]() $'\mathcal {V}_{\mathcal {P}_G}^{\check {\lambda }}$ (respectively,
$'\mathcal {V}_{\mathcal {P}_G}^{\check {\lambda }}$ (respectively, ![]() $'\mathcal {V}_{\mathcal {P}_G^\omega }^{\check {\lambda }}$) is the vector bundle associated with
$'\mathcal {V}_{\mathcal {P}_G^\omega }^{\check {\lambda }}$) is the vector bundle associated with ![]() $\mathcal {P}_G$ (respectively,
$\mathcal {P}_G$ (respectively, ![]() $\mathcal {P}_G^{\omega }= \omega ^\rho \overset {T}{\times }G$) with fiber the dual Weyl module
$\mathcal {P}_G^{\omega }= \omega ^\rho \overset {T}{\times }G$) with fiber the dual Weyl module ![]() $'\mathcal {V}_G^{\check {\lambda }}$. The first map is induced by
$'\mathcal {V}_G^{\check {\lambda }}$. The first map is induced by ![]() $\alpha$ and the second map is the map mapping to the highest weight vector.
$\alpha$ and the second map is the map mapping to the highest weight vector.
Let ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ (respectively,
$S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ (respectively, ![]() $\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$) denote the prestack classifying the data from
$\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$) denote the prestack classifying the data from ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ (respectively,
$S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ (respectively, ![]() $\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$) plus a
$\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$) plus a ![]() $B$-reduction of
$B$-reduction of ![]() $\mathcal {P}_G$ at
$\mathcal {P}_G$ at ![]() $x$.
$x$.
The fiber of ![]() ${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$ (respectively,
${\operatorname {Fl}}_{G, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$ (respectively, ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$) over the point (2.2.4) (respectively, (2.2.1)) is canonically isomorphic to
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho }$) over the point (2.2.4) (respectively, (2.2.1)) is canonically isomorphic to
 $$\begin{gather}\bigg(\text{respectively,}\ \prod_{1\leq i\leq k} {\operatorname{Gr}}_{G,x_i}^{\omega^\rho}\bigg) \end{gather}$$
$$\begin{gather}\bigg(\text{respectively,}\ \prod_{1\leq i\leq k} {\operatorname{Gr}}_{G,x_i}^{\omega^\rho}\bigg) \end{gather}$$6.2.5 Factorization property
Similar to Lemma 6.1.8, ![]() $\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ and
$\overline {S}^0_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ and ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$ are factorizable. That is to say,
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$ are factorizable. That is to say,
 \begin{equation} \begin{aligned} \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}\\ & \simeq\\ \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}\\ & \simeq\\ \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}, \end{aligned} \end{equation}and
 \begin{equation} \begin{aligned} (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\mathop{\times}{\mathop{\operatorname{\rm Conf}}}_{x})_{\rm disj}\\ & \simeq\\ \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{x})_{\rm disj}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\mathop{\times}{\mathop{\operatorname{\rm Conf}}}_{x})_{\rm disj}\\ & \simeq\\ \overline{S}^0_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{x})_{\rm disj}. \end{aligned} \end{equation} Furthermore, ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ is a factorization prestack,
$S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ is a factorization prestack, ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is factorizable with respect to
$S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is factorizable with respect to ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$.
$S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$.
6.2.6 Relative position
The prestack ![]() $S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ admits a stratification given by the relative position of the
$S^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ admits a stratification given by the relative position of the ![]() $B$-reduction given by
$B$-reduction given by ![]() $\epsilon$ and the
$\epsilon$ and the ![]() $B^-$-reduction given by the morphisms
$B^-$-reduction given by the morphisms ![]() $\{\kappa ^{{-,\check {\lambda }}}\}$. To be more precise, the morphisms
$\{\kappa ^{{-,\check {\lambda }}}\}$. To be more precise, the morphisms ![]() $\{\kappa ^{-,\check {\lambda }}\}$ are surjective, so they induce a
$\{\kappa ^{-,\check {\lambda }}\}$ are surjective, so they induce a ![]() $B^-$-reduction of
$B^-$-reduction of ![]() $\mathcal {P}_G$ at
$\mathcal {P}_G$ at ![]() $x$, i.e. we have a map
$x$, i.e. we have a map
given by sending a point ![]() $(D, \mathcal {P}_G, \alpha, \epsilon )$ of
$(D, \mathcal {P}_G, \alpha, \epsilon )$ of ![]() $S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ to
$S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ to ![]() $\mathcal {P}_G$ and its
$\mathcal {P}_G$ and its ![]() $B^-$-reduction at
$B^-$-reduction at ![]() $x$ induced by
$x$ induced by ![]() $\{\kappa ^{-,\check {\lambda }}\}$. In addition,
$\{\kappa ^{-,\check {\lambda }}\}$. In addition, ![]() $\epsilon$ also gives a map
$\epsilon$ also gives a map
Note that their compositions with the functors of inductions to ![]() $G$-bundles coincide, so we have a map of relative position
$G$-bundles coincide, so we have a map of relative position
The Bruhat decomposition gives a double coset decomposition of ![]() $(B^-,B)$ in
$(B^-,B)$ in ![]() $G$ and it induces a stratification of
$G$ and it induces a stratification of ![]() $B^-\backslash G/B$. We denote by
$B^-\backslash G/B$. We denote by ![]() ${\operatorname {Br}}^w\subset B^-\backslash G/B$ the Bruhat cell corresponding to
${\operatorname {Br}}^w\subset B^-\backslash G/B$ the Bruhat cell corresponding to ![]() $B^-wB$.
$B^-wB$.
Definition 6.2.7 For ![]() $w\in W$, let us denote by
$w\in W$, let us denote by ![]() $S^{-,w, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ the preimage of
$S^{-,w, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ the preimage of ![]() ${\operatorname {Br}}^w$ in
${\operatorname {Br}}^w$ in ![]() $S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$. In particular,
$S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$. In particular, ![]() $S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is open dense in
$S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is open dense in ![]() $S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
$S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
Similar to Lemma 6.1.8, the prestacks ![]() $S^{-,w, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ and
$S^{-,w, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ and ![]() $S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ (and their closures in
$S^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ (and their closures in ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$) factorize with respect to
${\operatorname {Fl}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$) factorize with respect to ![]() $S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ (respectively,
$S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ (respectively, ![]() $\overline {S}^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$), i.e.
$\overline {S}^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$), i.e.
 \begin{equation} \begin{aligned} S^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\\ & \simeq\\ S^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}} \times S^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} S^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\\ & \simeq\\ S^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}} \times S^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj} \end{aligned} \end{equation} \begin{equation} \begin{aligned} \text{(respectively,}\ \overline{S}^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\\ & \simeq\\ \overline{S}^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\text{).} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \text{(respectively,}\ \overline{S}^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\\ & \simeq\\ \overline{S}^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^{-,w, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\text{).} \end{aligned} \end{equation}6.2.8 Description of fibers
The fiber of ![]() $S^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ over the point
$S^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ over the point ![]() $D= \lambda _x\cdot x+ \mathop {\sum }_i \lambda _i\cdot x_i\in {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ is canonically isomorphic to
$D= \lambda _x\cdot x+ \mathop {\sum }_i \lambda _i\cdot x_i\in {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ is canonically isomorphic to
Here ![]() $S^{-,t^{\lambda _x} w}_{{\operatorname {Fl}},x}\subset {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$ denotes the
$S^{-,t^{\lambda _x} w}_{{\operatorname {Fl}},x}\subset {\operatorname {Fl}}^{\omega ^\rho }_{G,x}$ denotes the ![]() $N^-(\mathcal {K})^{\omega ^\rho }$-orbit of
$N^-(\mathcal {K})^{\omega ^\rho }$-orbit of ![]() $t^{\lambda _x} w\in {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$, and
$t^{\lambda _x} w\in {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$, and ![]() $S^{-,\lambda _i}_{{\operatorname {Gr}},x_i}\subset {\operatorname {Gr}}^{\omega ^\rho }_{G,x}$ denotes the
$S^{-,\lambda _i}_{{\operatorname {Gr}},x_i}\subset {\operatorname {Gr}}^{\omega ^\rho }_{G,x}$ denotes the ![]() $N^-(\mathcal {K})^{\omega ^\rho }$-orbit of
$N^-(\mathcal {K})^{\omega ^\rho }$-orbit of ![]() $t^{\lambda _i} \in {\operatorname {Gr}}_{G, x_i}^{\omega ^\rho }$.
$t^{\lambda _i} \in {\operatorname {Gr}}_{G, x_i}^{\omega ^\rho }$.
Remark 6.2.9 The above identification of the fiber is compatible with that given in (6.2.2).
6.3 Semi-infinite sheaf on  $S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$
$S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$
In Appendix A, we review the theory of semi-infinite sheaves on affine flags. In this section, we use it to define the ![]() $!$-extension semi-infinite sheaf on
$!$-extension semi-infinite sheaf on ![]() $S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
$S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
Consider the sub-prestack ![]() $\overline {S}^{-, 1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ of
$\overline {S}^{-, 1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ of ![]() ${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$, which classifies the data
${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$, which classifies the data ![]() $({\mathcal {I}}, \mathcal {P}_G, \alpha, \epsilon )$, such that for any
$({\mathcal {I}}, \mathcal {P}_G, \alpha, \epsilon )$, such that for any ![]() $\check {\lambda }$ dominant, the induced map
$\check {\lambda }$ dominant, the induced map
which is a priori defined on ![]() $X-{\mathcal {I}}$, extends to a regular map on the whole curve
$X-{\mathcal {I}}$, extends to a regular map on the whole curve ![]() $X$ and satisfies the Plücker relations. We let
$X$ and satisfies the Plücker relations. We let ![]() ${S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ be the substack where we require that the extended map
${S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ be the substack where we require that the extended map ![]() $\kappa ^{-,\check {\lambda }}$ to be surjective and the induced
$\kappa ^{-,\check {\lambda }}$ to be surjective and the induced ![]() $B^-$-bundle and
$B^-$-bundle and ![]() $\epsilon$ to be transversal at
$\epsilon$ to be transversal at ![]() $x$.
$x$.
The restriction of ![]() $({\mathcal {G}}^G)^{-1}$ to
$({\mathcal {G}}^G)^{-1}$ to ![]() ${S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ is canonically trivialized, we denote by
${S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ is canonically trivialized, we denote by ![]() $\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}$ the
$\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}$ the ![]() $({\mathcal {G}}^G)^{-1}$-twisted dualizing sheaf on
$({\mathcal {G}}^G)^{-1}$-twisted dualizing sheaf on ![]() ${S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$. According to Proposition A.1.5, the
${S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$. According to Proposition A.1.5, the ![]() $!$-extension is well-defined for
$!$-extension is well-defined for ![]() $\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}$, and we denote it by
$\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}$, and we denote it by ![]() $j_!(\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}\!)$.
$j_!(\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}\!)$.
6.3.1
The twisted dualizing sheaf ![]() $\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}$ and its
$\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}$ and its ![]() $!$-extension
$!$-extension ![]() $j_!(\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}\!)$ naturally acquire
$j_!(\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}\!)$ naturally acquire ![]() $T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$-equivariant structures, and
$T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$-equivariant structures, and ![]() $({\mathcal {G}}^G)^{-1}$ is
$({\mathcal {G}}^G)^{-1}$ is ![]() $T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$-equivariant, we can think
$T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$-equivariant, we can think ![]() $j_!(\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}\!)$ as a sheaf on
$j_!(\omega _{{S}^{-,1}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}}\!)$ as a sheaf on ![]() $T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash \overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}$. In particular, the construction of
$T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash \overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}$. In particular, the construction of ![]() $j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ admits a
$j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ admits a ![]() $T$-twisted construction.
$T$-twisted construction.
That is to say, given a prestack ![]() ${\mathcal {Y}}$ with a map
${\mathcal {Y}}$ with a map ![]() ${\mathcal {Y}}\longrightarrow T({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}\backslash {\mathop {\operatorname {\rm Ran}}}_x$, we consider the fiber product
${\mathcal {Y}}\longrightarrow T({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}\backslash {\mathop {\operatorname {\rm Ran}}}_x$, we consider the fiber product
We let ![]() $({}_{{\mathcal {Y}}}{\mathcal {G}}^G)^{-1}$ be the pullback of the descent gerbe on
$({}_{{\mathcal {Y}}}{\mathcal {G}}^G)^{-1}$ be the pullback of the descent gerbe on ![]() $T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ and
$T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ and ![]() ${}_{{\mathcal {Y}}}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ be the
${}_{{\mathcal {Y}}}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ be the ![]() $!$-pullback of
$!$-pullback of ![]() $j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ along the projection
$j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ along the projection
6.3.2
Let ![]() ${\mathcal {Y}}=({\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$, we have the following identification
${\mathcal {Y}}=({\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$, we have the following identification
Under the above identification, the preimage of ![]() $T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}$ under (6.3.2) is identified with the product
$T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}$ under (6.3.2) is identified with the product ![]() ${S}^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}} ({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}^{\text {neg}}$. In addition, the gerbe
${S}^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}} ({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}^{\text {neg}}$. In addition, the gerbe ![]() $({}_{{\mathcal {Y}}}{\mathcal {G}}^G)^{-1}$ on
$({}_{{\mathcal {Y}}}{\mathcal {G}}^G)^{-1}$ on ![]() ${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}} ({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}^{\text {neg}}$ is identified with the ratio gerbe
${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}} ({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}^{\text {neg}}$ is identified with the ratio gerbe
Since ![]() $({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}^{\text {neg}}\longrightarrow {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ is an isomorphism in
$({\operatorname {Gr}}^{\omega ^\rho }_{T, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}^{\text {neg}}\longrightarrow {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$ is an isomorphism in ![]() $h$-topology, the gerbes and the corresponding categories of twisted sheaves on
$h$-topology, the gerbes and the corresponding categories of twisted sheaves on ![]() ${}_{{\mathcal {Y}}}{\operatorname {Fl}}$ and
${}_{{\mathcal {Y}}}{\operatorname {Fl}}$ and ![]() ${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$ are the same.
${\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }$ are the same.
Definition 6.3.3 We denote the sheaf corresponding to ![]() ${}_{{\mathcal {Y}}}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ by
${}_{{\mathcal {Y}}}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ by ![]() $j_!({\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)\in \operatorname {Shv}_{{\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}}({\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }\!)$. Its restriction to
$j_!({\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)\in \operatorname {Shv}_{{\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}}({\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{\omega ^\rho }\!)$. Its restriction to ![]() $S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is the dualizing sheaf under the canonical trivialization of
$S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is the dualizing sheaf under the canonical trivialization of ![]() ${\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}|_{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}$.
${\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}|_{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}$.
6.3.4
The above constructions also work for affine Grassmannian. To be more precise, let ![]() $j_!(\omega _{S_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0}})\in \operatorname {Shv}_{({\mathcal {G}}^G)^{-1}}(\overline {S}_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0})$ be the
$j_!(\omega _{S_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0}})\in \operatorname {Shv}_{({\mathcal {G}}^G)^{-1}}(\overline {S}_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0})$ be the ![]() $!$-extension of the dualizing sheaf on
$!$-extension of the dualizing sheaf on ![]() ${S_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0}}$ (which is defined similarly as
${S_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0}}$ (which is defined similarly as ![]() ${S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}$, but without the Iwahori structure). Given
${S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}$, but without the Iwahori structure). Given ![]() ${\mathcal {Y}}:=({\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho })^{\text {neg}}\longrightarrow T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\backslash {\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$, we can also define a twisted sheaf
${\mathcal {Y}}:=({\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho })^{\text {neg}}\longrightarrow T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\backslash {\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$, we can also define a twisted sheaf ![]() $j_!({\omega _{S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}})\in \operatorname {Shv}_{{\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}}({\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho })$ which corresponds to
$j_!({\omega _{S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}})\in \operatorname {Shv}_{{\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}}({\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Conf}}}}^{\omega ^\rho })$ which corresponds to ![]() ${}_{{\mathcal {Y}}}j_!(\omega _{S^{-,0}_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}}\!)$.
${}_{{\mathcal {Y}}}j_!(\omega _{S^{-,0}_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}}\!)$.
Using the fact that ![]() $j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ is factorizable with respect to
$j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ is factorizable with respect to ![]() $j_!(\omega _{S_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0}}\!)$, and pulling-back along
$j_!(\omega _{S_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}^{-,0}}\!)$, and pulling-back along ![]() ${}_{{\mathcal {Y}}}{\operatorname {Fl}}\longrightarrow T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ and
${}_{{\mathcal {Y}}}{\operatorname {Fl}}\longrightarrow T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }\backslash {\operatorname {Fl}}_{G,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ and ![]() ${}_{{\mathcal {Y}}}{\operatorname {Gr}}\longrightarrow T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\backslash {\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$ preserve factorization structures, we conclude that
${}_{{\mathcal {Y}}}{\operatorname {Gr}}\longrightarrow T({\mathcal {O}})_{{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\backslash {\operatorname {Gr}}_{G,{\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }$ preserve factorization structures, we conclude that ![]() $j_!({\omega _{S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}}\!)$ and
$j_!({\omega _{S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}}\!)$ and ![]() $j_!({\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)$ satisfy the factorization properties.
$j_!({\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)$ satisfy the factorization properties.
That is to say, ![]() $j_!(S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}})$ is a factorization algebra,
$j_!(S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}})$ is a factorization algebra,
 \begin{align} & j_!(\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}}\!)|_{\overline{S}^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}} \nonumber\\ &\quad \simeq j_!(\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}})\boxtimes j_!(\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}})|_{\overline{S}^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}}, \end{align}
\begin{align} & j_!(\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}}\!)|_{\overline{S}^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}} \nonumber\\ &\quad \simeq j_!(\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}})\boxtimes j_!(\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}})|_{\overline{S}^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}})_{\rm disj}}, \end{align}
and ![]() $j_!(\omega _{S^{-,1,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ factorizes with respect to
$j_!(\omega _{S^{-,1,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ factorizes with respect to ![]() $j_!(\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}\!)$, i.e.
$j_!(\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}\!)$, i.e.
 \begin{align} & j_!(\omega_{S^{-,1,{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}\!)|_{\overline{S}^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}\mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}} \nonumber\\ &\quad \simeq j_!(\omega_{S^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}})\boxtimes j_!(\omega_{S^{-,1,{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}\!)|_{\overline{S}^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}}. \end{align}
\begin{align} & j_!(\omega_{S^{-,1,{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}\!)|_{\overline{S}^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}\mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}} \nonumber\\ &\quad \simeq j_!(\omega_{S^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}})\boxtimes j_!(\omega_{S^{-,1,{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}\!)|_{\overline{S}^{-,{\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}\times \overline{S}^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}}. \end{align}6.4 Constructions of functors
In this section, we define the functor ![]() $F^{\rm L}: \operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)\to \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$, which is used in Theorem 4.3.1.
$F^{\rm L}: \operatorname {Whit}_{\rm q}({\operatorname {Fl}}^{\omega ^\rho }_G)\to \operatorname {Shv}_{\mathcal {G}^\Lambda }({\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x})$, which is used in Theorem 4.3.1.
To start with, let us summarize the prestacks defined in previous sections of this paper in the following diagram.

The morphism ![]() $\operatorname {unit}: {\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }\to (\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$ is given by (6.1.8).
$\operatorname {unit}: {\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }\to (\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x}$ is given by (6.1.8).
6.4.1 Construction of  $F^{\rm L}$
$F^{\rm L}$
We can construct ![]() $F^{\rm L}$ via the following steps.
$F^{\rm L}$ via the following steps.
(1) Given a twisted Whittaker sheaf
 $\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$, first of all, we !-pullback it to
$\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$, first of all, we !-pullback it to  ${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ along the morphism
${\mathop {\operatorname {\rm Ran}}}_x\times {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ along the morphism  $\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}$. By Lemma 6.1.12, it gives rise to a twisted Whittaker sheaf
$\operatorname {pr}_{{\mathop {\operatorname {\rm Ran}}}_x}$. By Lemma 6.1.12, it gives rise to a twisted Whittaker sheaf  $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ on
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ on  $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$.
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$.(2) Consider the image of
 $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ under the following functor
The first functor above is given by
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ under the following functor
The first functor above is given by \begin{align*} & \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x})\to \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}_x} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)^{\text{neg}}_{\infty \cdot x})\\ &\quad \simeq \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}\!)_{\infty \cdot x} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)^{\text{neg}}_{\infty \cdot x}) \simeq \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}\!)_{\infty \cdot x}). \end{align*}
\begin{align*} & \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x})\to \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}_x} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)^{\text{neg}}_{\infty \cdot x})\\ &\quad \simeq \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}\!)_{\infty \cdot x} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)^{\text{neg}}_{\infty \cdot x}) \simeq \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}\!)_{\infty \cdot x}). \end{align*}
 $!$-pullback. The second follows from the isomorphism
The third is given by Lemma 2.2.6. We denote the resulting sheaf by
$!$-pullback. The second follows from the isomorphism
The third is given by Lemma 2.2.6. We denote the resulting sheaf by \[ (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}_x} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty\cdot x}^{\text{neg}}\simeq (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty\cdot x} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x}^{\text{neg}}. \]
\[ (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x}\mathop{\times}_{{\mathop{\operatorname{\rm Ran}}}_x} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty\cdot x}^{\text{neg}}\simeq (\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty\cdot x} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\operatorname{Gr}}^{\omega^\rho}_{T, {\mathop{\operatorname{\rm Ran}}}_x}\!)_{\infty \cdot x}^{\text{neg}}. \]
 $\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})$.
(6.4.2)
$\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})$.
(6.4.2) \begin{equation} \operatorname{sprd}_{{\operatorname{Fl}}}: \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})\to \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x}). \end{equation}
\begin{equation} \operatorname{sprd}_{{\operatorname{Fl}}}: \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})\to \operatorname{Shv}_{\mathcal{G}^G}((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x}). \end{equation}(3) Take
 $!$-tensor product of
$!$-tensor product of  $\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})$ with the semi-infinite
$\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})$ with the semi-infinite  $!$-extension sheaf
$!$-extension sheaf  $j_!(\omega _{S_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, 1,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ defined in § 6.2.
$j_!(\omega _{S_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, 1,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ defined in § 6.2.(4) Then take
 $!$ (or, equivalently, take
$!$ (or, equivalently, take  $*$)-pushforward along the projection
$*$)-pushforward along the projection  $v_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ with cohomology shift
$v_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ with cohomology shift  $\langle \lambda, 2\check {\rho } \rangle$ on the connected component
$\langle \lambda, 2\check {\rho } \rangle$ on the connected component  ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^\lambda$ of
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^\lambda$ of  ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$.
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}$.
Definition 6.4.2 To summarize, the functor
is defined as
where the shift ![]() $[\deg ]$ equals
$[\deg ]$ equals ![]() $\langle \lambda, 2\check {\rho } \rangle$ on the connected component
$\langle \lambda, 2\check {\rho } \rangle$ on the connected component ![]() ${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^\lambda$.
${\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^\lambda$.
Remark 6.4.3 The resulting sheaf ![]() $F^{\rm L}(\mathcal {F})$ is
$F^{\rm L}(\mathcal {F})$ is ![]() $\mathcal {G}^\Lambda$-twisted. Indeed,
$\mathcal {G}^\Lambda$-twisted. Indeed, ![]() $\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})\in \operatorname {Shv}_{\mathcal {G}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x})$ and
$\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})\in \operatorname {Shv}_{\mathcal {G}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x})$ and ![]() $j_!({\omega _{S^{-,{1,} {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)\in \operatorname {Shv}_{\mathcal {G}^{G, T, {\mathop {\operatorname {\rm ratio}}}}}(\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)$. Note that
$j_!({\omega _{S^{-,{1,} {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)\in \operatorname {Shv}_{\mathcal {G}^{G, T, {\mathop {\operatorname {\rm ratio}}}}}(\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)$. Note that ![]() $\mathcal {G}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$ is the quotient of
$\mathcal {G}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$ is the quotient of ![]() $\mathcal {G}^G$ by
$\mathcal {G}^G$ by ![]() $\mathcal {G}^\Lambda$. Hence, the tensor product of the sheaf
$\mathcal {G}^\Lambda$. Hence, the tensor product of the sheaf ![]() $\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})\in \operatorname {Shv}_{\mathcal {G}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x})$ and the sheaf
$\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})\in \operatorname {Shv}_{\mathcal {G}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x})$ and the sheaf ![]() $j_!({\omega _{S^{-,{1,} {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)\in \operatorname {Shv}_{\mathcal {G}^{G, T, {\mathop {\operatorname {\rm ratio}}}}}(\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)$ is
$j_!({\omega _{S^{-,{1,} {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)\in \operatorname {Shv}_{\mathcal {G}^{G, T, {\mathop {\operatorname {\rm ratio}}}}}(\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)$ is ![]() ${\mathcal {G}^\Lambda }$-twisted.
${\mathcal {G}^\Lambda }$-twisted.
6.4.4 Construction of  $F^{\rm L}_{{\operatorname {Gr}}}$
$F^{\rm L}_{{\operatorname {Gr}}}$
Similarly, we consider the following diagram.

By applying the same steps (1) and (2) as in the above construction (with a tiny modification: replace affine flags by the affine Grassmannian), we get a functor
Definition 6.4.5 The functor
is defined as
Recall that ![]() $\operatorname {Whit}_{\rm q}(\overline {S}^0_{{\operatorname {Gr}}})\simeq \operatorname {Whit}_{\rm q}(S^0_{{\operatorname {Gr}}})\simeq {\rm Vect}$, hence, there exists a unique irreducible Whittaker sheaf on
$\operatorname {Whit}_{\rm q}(\overline {S}^0_{{\operatorname {Gr}}})\simeq \operatorname {Whit}_{\rm q}(S^0_{{\operatorname {Gr}}})\simeq {\rm Vect}$, hence, there exists a unique irreducible Whittaker sheaf on ![]() $\overline {S}^0_{{\operatorname {Gr}}}$. We denote it by
$\overline {S}^0_{{\operatorname {Gr}}}$. We denote it by ![]() $\mathcal {F}_0$. Set
$\mathcal {F}_0$. Set ![]() $\Omega _{\rm q}^{{\rm L},\prime }:= F^{\rm L}_{{\operatorname {Gr}}}(\mathcal {F}_0)$. The following lemma is proved in [Reference GaitsgoryGai21b, Theorem 6.2.5].
$\Omega _{\rm q}^{{\rm L},\prime }:= F^{\rm L}_{{\operatorname {Gr}}}(\mathcal {F}_0)$. The following lemma is proved in [Reference GaitsgoryGai21b, Theorem 6.2.5].
Lemma 6.4.6 In the setting of D-modules, when ![]() $q$ avoids small torsion, there is an isomorphism of factorization algebras
$q$ avoids small torsion, there is an isomorphism of factorization algebras ![]() $\Omega _{\rm q}^{{\rm L},\prime }\simeq \Omega _{\rm q}^{\rm L}$.
$\Omega _{\rm q}^{{\rm L},\prime }\simeq \Omega _{\rm q}^{\rm L}$.
Proposition 6.4.7 Given any ![]() $\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$,
$\mathcal {F}\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$, ![]() $F^{\rm L}(\mathcal {F})$ has a naturally defined
$F^{\rm L}(\mathcal {F})$ has a naturally defined ![]() $\Omega _{\rm q}^{{\rm L},\prime }$-factorization module structure.
$\Omega _{\rm q}^{{\rm L},\prime }$-factorization module structure.
Proof. By the factorization property of ![]() $\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$,
$\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$, ![]() $\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$,
$\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$, ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$, and
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}$, and ![]() $\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ (see (6.2.4), (6.2.5), (6.2.9), and (6.2.10)), we obtain that the prestack
$\overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ (see (6.2.4), (6.2.5), (6.2.9), and (6.2.10)), we obtain that the prestack ![]() $\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ is factorizable, and the prestack
$\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ is factorizable, and the prestack ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is a factorization module space with respect to
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})_{\infty \cdot x}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is a factorization module space with respect to ![]() $\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$. Note that
$\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$. Note that ![]() $v_{{\mathop {\operatorname {\rm Conf}}}}$ and
$v_{{\mathop {\operatorname {\rm Conf}}}}$ and ![]() $v_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ are compatible with the factorization structures on
$v_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ are compatible with the factorization structures on ![]() $\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ and
$\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}$ and ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)_{\infty \cdot x}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$, hence, it suffices to show that
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)_{\infty \cdot x}\cap \overline {S}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$, hence, it suffices to show that
factorizes with respect to ![]() $\operatorname {sprd}_{{\operatorname {Gr}}}(\mathcal {F}_0)|_{(\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}})}\overset {!}{\otimes } j_!({\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}}\!)$.
$\operatorname {sprd}_{{\operatorname {Gr}}}(\mathcal {F}_0)|_{(\overline {S}^{0}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}})}\overset {!}{\otimes } j_!({\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}}\!)$.
According to Corollary 6.1.15, the Whittaker sheaf ![]() $\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ on
$\operatorname {sprd}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}(\mathcal {F})$ on ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ factorizes with respect to the factorization algebra
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ factorizes with respect to the factorization algebra ![]() ${\rm Vac}$. Since the
${\rm Vac}$. Since the ![]() $!$-pullback from
$!$-pullback from ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ to
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x}$ to ![]() $(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)_{\infty \cdot x}$ is compatible with the factorization structure and
$(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}\!)_{\infty \cdot x}$ is compatible with the factorization structure and ![]() $\operatorname {sprd}_{{\operatorname {Gr}}}(\mathcal {F}_0)$ is exactly the pullback of
$\operatorname {sprd}_{{\operatorname {Gr}}}(\mathcal {F}_0)$ is exactly the pullback of ![]() ${\rm Vac}$, we obtain that
${\rm Vac}$, we obtain that ![]() $\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})$ is a factorization module over
$\operatorname {sprd}_{{\operatorname {Fl}}}(\mathcal {F})$ is a factorization module over ![]() $\operatorname {sprd}_{{\operatorname {Gr}}}(\mathcal {F}_0)$.
$\operatorname {sprd}_{{\operatorname {Gr}}}(\mathcal {F}_0)$.
By (6.3.6), ![]() $j_!(\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ factorizes with respect to
$j_!(\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ factorizes with respect to ![]() $j_!(\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}})$.
$j_!(\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}})$.
Now Proposition 6.4.7 follows from the fact that the tensor product of factorization modules is a factorization module over the tensor product of the corresponding factorization algebras.
The functor ![]() $F^{\rm L}$ defined in (6.4.3) factors through
$F^{\rm L}$ defined in (6.4.3) factors through ![]() $\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$. We also denote by
$\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$. We also denote by ![]() $F^{\rm L}$ the resulting functor
$F^{\rm L}$ the resulting functor
Of course, Theorem 4.3.1 can be deduced from the following stronger statement.
Theorem 6.4.8 For any ![]() $q$, the functor
$q$, the functor ![]() $F^{\rm L}$ in (6.4.7) is a t-exact equivalence that preserves standards and costandards.
$F^{\rm L}$ in (6.4.7) is a t-exact equivalence that preserves standards and costandards.
6.4.9
By constructions similar to ![]() $F^{\rm L}$ and
$F^{\rm L}$ and ![]() $F^{\rm L}_{{\operatorname {Gr}}}$, if we replace the semi-infinite
$F^{\rm L}_{{\operatorname {Gr}}}$, if we replace the semi-infinite ![]() $!$-extension sheaves
$!$-extension sheaves ![]() $j_!({\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}}\!)$ and
$j_!({\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}}\!)$ and ![]() $j_!({\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)$ by the semi-infinite
$j_!({\omega _{S^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}}\!)$ by the semi-infinite ![]() $*$-extension sheaves, then we can define the following functors.
$*$-extension sheaves, then we can define the following functors.
Definition 6.4.10 We have
 \begin{equation} \begin{aligned} F^{\rm DK}: \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})\\ \mathcal{F} & \to v_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}, *}(\operatorname{sprd}_{{\operatorname{Fl}}}(\mathcal{F})|_{(\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x})_{\infty \cdot x}} \overset{!}{\otimes} j_*({\omega_{S^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}}))[\deg], \end{aligned} \end{equation}
\begin{equation} \begin{aligned} F^{\rm DK}: \operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})\\ \mathcal{F} & \to v_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}, *}(\operatorname{sprd}_{{\operatorname{Fl}}}(\mathcal{F})|_{(\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x})_{\infty \cdot x}} \overset{!}{\otimes} j_*({\omega_{S^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}}))[\deg], \end{aligned} \end{equation} \begin{equation} \begin{aligned} F^{\rm DK}_{{\operatorname{Gr}}}: \operatorname{Whit}_{\rm q}(\overline{S}^0_{{\operatorname{Gr}}}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}})\\ \mathcal{F} & \to v_{{\operatorname{Gr}},*}(\operatorname{sprd}_{{\operatorname{Gr}}}(\mathcal{F})|_{(\overline{S}^{0}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}})} \overset{!}{\otimes} j_*({\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}}}))[\deg]. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} F^{\rm DK}_{{\operatorname{Gr}}}: \operatorname{Whit}_{\rm q}(\overline{S}^0_{{\operatorname{Gr}}}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}})\\ \mathcal{F} & \to v_{{\operatorname{Gr}},*}(\operatorname{sprd}_{{\operatorname{Gr}}}(\mathcal{F})|_{(\overline{S}^{0}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}})} \overset{!}{\otimes} j_*({\omega_{S^{-, {\mathop{\operatorname{\rm Conf}}}}_{{\operatorname{Gr}}, {\mathop{\operatorname{\rm Conf}}}}}}))[\deg]. \end{aligned} \end{equation} Similarly, we define ![]() $\Omega _{\rm q}^{{\rm DK},\prime }:= F^{\rm DK}_{{\operatorname {Gr}}}(\mathcal {F}_0)$. When
$\Omega _{\rm q}^{{\rm DK},\prime }:= F^{\rm DK}_{{\operatorname {Gr}}}(\mathcal {F}_0)$. When ![]() $q$ avoids small torsion, we have
$q$ avoids small torsion, we have ![]() $\Omega _{\rm q}^{{\rm DK},\prime }\simeq \Omega _{\rm q}^{\rm DK}$ (see [Reference GaitsgoryGai21b, Theorem 3.6.2]). By the same proof as that of Proposition 6.4.7, we have the following result.
$\Omega _{\rm q}^{{\rm DK},\prime }\simeq \Omega _{\rm q}^{\rm DK}$ (see [Reference GaitsgoryGai21b, Theorem 3.6.2]). By the same proof as that of Proposition 6.4.7, we have the following result.
Proposition 6.4.11 ![]() $F^{\rm DK}$ factors through
$F^{\rm DK}$ factors through ![]() $\Omega _{\rm q}^{{\rm DK},\prime }\text {-}{\operatorname {FactMod}}$, i.e. it gives rise to a functor
$\Omega _{\rm q}^{{\rm DK},\prime }\text {-}{\operatorname {FactMod}}$, i.e. it gives rise to a functor
6.5 Calculation of the  $!$-stalks of
$!$-stalks of  $F^{\rm L}$ and
$F^{\rm L}$ and  $F^{\rm DK}$
$F^{\rm DK}$
By Lemma 4.1.5, in the category of ![]() $\Omega {\text {-}}{\operatorname {FactMod}}$, the standard object
$\Omega {\text {-}}{\operatorname {FactMod}}$, the standard object ![]() $\Delta _{\lambda, \Omega }$ is always uniquely characterized by the requirement that its
$\Delta _{\lambda, \Omega }$ is always uniquely characterized by the requirement that its ![]() $*$-stalks at
$*$-stalks at ![]() $\mu \cdot x, \mu \in \Lambda$ is
$\mu \cdot x, \mu \in \Lambda$ is ![]() $\mathsf {e}$ if
$\mathsf {e}$ if ![]() $\lambda =\mu$ and
$\lambda =\mu$ and ![]() $0$ otherwise, and the costandard object
$0$ otherwise, and the costandard object ![]() $\nabla _{\lambda, \Omega }$ is uniquely characterized by the requirement that its
$\nabla _{\lambda, \Omega }$ is uniquely characterized by the requirement that its ![]() $!$-stalks at
$!$-stalks at ![]() $\mu \cdot x, \mu \in \Lambda$ is
$\mu \cdot x, \mu \in \Lambda$ is ![]() $\mathsf {e}$ if
$\mathsf {e}$ if ![]() $\lambda =\mu$ and
$\lambda =\mu$ and ![]() $0$ otherwise. Hence, in order to prove that
$0$ otherwise. Hence, in order to prove that ![]() $F^{\rm L}$ sends standard objects to standard objects, costandard objects to costandard objects, we only need to find an explicit expression of the
$F^{\rm L}$ sends standard objects to standard objects, costandard objects to costandard objects, we only need to find an explicit expression of the ![]() $!$-stalks and
$!$-stalks and ![]() $*$-stalks of the image of
$*$-stalks of the image of ![]() $F^{\rm L}$.
$F^{\rm L}$.
The theory of sheaves on prestack is friendly with taking ![]() $!$-stalks. There are two reasons for this: the first is that the
$!$-stalks. There are two reasons for this: the first is that the ![]() $!$-pullback functor is always well-defined, the second is that we have a base change theorem for
$!$-pullback functor is always well-defined, the second is that we have a base change theorem for ![]() $!$-pullback (see [Reference Gaitsgory and RozenblyumGR17b, Corollary 3.1.4]), hence, the calculation will be much easier than the calculation of
$!$-pullback (see [Reference Gaitsgory and RozenblyumGR17b, Corollary 3.1.4]), hence, the calculation will be much easier than the calculation of ![]() $*$-stalks.
$*$-stalks.
In this section, we give an explicit formula (Proposition 6.5.2) for the ![]() $!$-stalks of
$!$-stalks of ![]() $F^{\rm L}$ and
$F^{\rm L}$ and ![]() $F^{\rm DK}$ at
$F^{\rm DK}$ at ![]() $\lambda \cdot x$.
$\lambda \cdot x$.
6.5.1
Consider the following Cartesian diagram.

Choosing a trivialization of the fiber of ![]() $\mathcal {G}^\Lambda$ at
$\mathcal {G}^\Lambda$ at ![]() $\lambda \cdot x$. By the base change theorem [Reference Gaitsgory and RozenblyumGR17b, Corollary 3.1.4], we have
$\lambda \cdot x$. By the base change theorem [Reference Gaitsgory and RozenblyumGR17b, Corollary 3.1.4], we have
 \begin{align} i_{\lambda}^!(F^{\rm L}(\mathcal{F}))&\simeq i_{\lambda}^{!}\circ v_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x},*} (\operatorname{sprd}_{{\operatorname{Fl}}}(\mathcal{F})|_{((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x})} \overset{!}{\otimes} j_!({\omega_{S^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}}\!)) [\langle \lambda, 2\check{\rho}\rangle] \nonumber\\ &\simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, i_{\lambda, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}^{!}(\operatorname{sprd}_{{\operatorname{Fl}}}(\mathcal{F})) \mathop{\otimes}^! i_{\lambda, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}^{-, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x},!} (j_!({\omega_{S^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}}\!)) [\langle \lambda, 2\check{\rho}\rangle]). \end{align}
\begin{align} i_{\lambda}^!(F^{\rm L}(\mathcal{F}))&\simeq i_{\lambda}^{!}\circ v_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x},*} (\operatorname{sprd}_{{\operatorname{Fl}}}(\mathcal{F})|_{((\overline{S}^{w_0}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}})_{\infty \cdot x})} \overset{!}{\otimes} j_!({\omega_{S^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}}\!)) [\langle \lambda, 2\check{\rho}\rangle] \nonumber\\ &\simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, i_{\lambda, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}^{!}(\operatorname{sprd}_{{\operatorname{Fl}}}(\mathcal{F})) \mathop{\otimes}^! i_{\lambda, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}^{-, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x},!} (j_!({\omega_{S^{-,1, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}}}}\!)) [\langle \lambda, 2\check{\rho}\rangle]). \end{align}In the above formula:
–
 $i_{\lambda, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ denotes the embedding of
$i_{\lambda, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ denotes the embedding of  $\overline {S}^{-, \lambda }_{{\operatorname {Fl}},x}$ into
$\overline {S}^{-, \lambda }_{{\operatorname {Fl}},x}$ into  $\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$;
$\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$;–
 $i_{\lambda, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ denotes the embedding of
$i_{\lambda, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ denotes the embedding of  ${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ into
${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ into  $\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
$\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$.
First, by the construction (6.4.2), there is
Second, by Corollary A.2.9, we have a base change theorem for ![]() $!$-pushforward and
$!$-pushforward and ![]() $!$-pullback for semi-infinite sheaves. Namely, there is an isomorphism
$!$-pullback for semi-infinite sheaves. Namely, there is an isomorphism
Here, ![]() $\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }}$ denotes the
$\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }}$ denotes the ![]() $({\mathcal {G}}^G)^{-1}\otimes {\mathcal {G}}^\Lambda |_{\lambda \cdot x}$- twisted dualizing sheaf on
$({\mathcal {G}}^G)^{-1}\otimes {\mathcal {G}}^\Lambda |_{\lambda \cdot x}$- twisted dualizing sheaf on ![]() $S_{{\operatorname {Fl}},x}^{-,\lambda }$ and
$S_{{\operatorname {Fl}},x}^{-,\lambda }$ and ![]() $j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ denotes its
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ denotes its ![]() $!$-pushforward to
$!$-pushforward to ![]() $\overline {S}_{{\operatorname {Fl}},x}^{-,\lambda }$. By choosing a trivialization of the fiber
$\overline {S}_{{\operatorname {Fl}},x}^{-,\lambda }$. By choosing a trivialization of the fiber ![]() ${\mathcal {G}}^\Lambda |_{\lambda \cdot x}$ (which is equivalent to choosing a trivialization of
${\mathcal {G}}^\Lambda |_{\lambda \cdot x}$ (which is equivalent to choosing a trivialization of ![]() ${\mathcal {G}}^G|_{t^\lambda \in {\operatorname {Fl}}}$), we can think
${\mathcal {G}}^G|_{t^\lambda \in {\operatorname {Fl}}}$), we can think ![]() $j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ as the
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ as the ![]() $!$-extension of the
$!$-extension of the ![]() $({\mathcal {G}}^G)^{-1}$- twisted dualizing sheaf on
$({\mathcal {G}}^G)^{-1}$- twisted dualizing sheaf on ![]() $S_{{\operatorname {Fl}},x}^{-,\lambda }$ under the unique
$S_{{\operatorname {Fl}},x}^{-,\lambda }$ under the unique ![]() $N^-({\mathcal {K}})^{\omega ^\rho }_x$-equivariant trivialization.
$N^-({\mathcal {K}})^{\omega ^\rho }_x$-equivariant trivialization.
From the above observations, we deduce the following proposition.
Proposition 6.5.2 Choosing a trivialization of ![]() $\mathcal {G}^\Lambda |_{\lambda \cdot x}$, there exists an isomorphism
$\mathcal {G}^\Lambda |_{\lambda \cdot x}$, there exists an isomorphism
Similarly, we have the following proposition.
Proposition 6.5.3 Choosing a trivialization of ![]() $\mathcal {G}^\Lambda |_{\lambda \cdot x}$, there exists an isomorphism
$\mathcal {G}^\Lambda |_{\lambda \cdot x}$, there exists an isomorphism
6.5.4
The following corollary relates the functor ![]() $i_\lambda ^!(F^{\rm L})$ with the standard objects that we constructed in Definition 5.5.1.
$i_\lambda ^!(F^{\rm L})$ with the standard objects that we constructed in Definition 5.5.1.
Corollary 6.5.5 Given ![]() $\lambda \in \Lambda$ and a trivialization of
$\lambda \in \Lambda$ and a trivialization of ![]() $\mathcal {G}^\Lambda |_{\lambda \cdot x}$, there exists an isomorphism
$\mathcal {G}^\Lambda |_{\lambda \cdot x}$, there exists an isomorphism
Proof. According to Proposition 6.5.2, we have to prove
By the assumption, ![]() $\mathcal {F}$ is
$\mathcal {F}$ is ![]() $(N(\mathcal {K})_x^{\omega ^\rho }, \chi )$-equivariant. In particular, it is
$(N(\mathcal {K})_x^{\omega ^\rho }, \chi )$-equivariant. In particular, it is ![]() $(N(\mathcal {O})_x^{\omega ^\rho }, \chi )$-equivariant.
$(N(\mathcal {O})_x^{\omega ^\rho }, \chi )$-equivariant.
Note that ![]() $\chi |_{N(\mathcal {O})_x^{\omega ^\rho }}$ is trivial, we have
$\chi |_{N(\mathcal {O})_x^{\omega ^\rho }}$ is trivial, we have
By Proposition 6.5.6, we have
According to the construction of the convolution product in § 5.3, it is isomorphic to the ![]() $!$-stalks of the convolution product
$!$-stalks of the convolution product ![]() $\mathcal {F}\star ({{J}}_{-\lambda }\!)_{\lambda }$ at
$\mathcal {F}\star ({{J}}_{-\lambda }\!)_{\lambda }$ at ![]() $t^0\in \widetilde {{\operatorname {Fl}}}$. Furthermore, there exist isomorphisms
$t^0\in \widetilde {{\operatorname {Fl}}}$. Furthermore, there exist isomorphisms
 \begin{align*} & \mathcal{H}om_{\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{{\operatorname{Fl}}})_{\lambda}} ((\delta_0)_{\lambda}, \mathcal{F}\star ({{J}}_{-\lambda})_{\lambda}\!)\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_\lambda}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} ((\delta_0)_{\lambda}), \mathcal{F}\star ({{J}}_{-\lambda})_\lambda)\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_\lambda}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} (({{J}}_0)_\lambda), \mathcal{F}\star ({{J}}_{-\lambda})_\lambda)\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({{\operatorname{Fl}}_G^{\omega^\rho}})}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} (({{J}}_0)_\lambda)\star {{J}}_\lambda, \mathcal{F})\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({{\operatorname{Fl}}_G^{\omega^\rho}})}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} ({{J}}_\lambda), \mathcal{F})\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \mathcal{F}). \end{align*}
\begin{align*} & \mathcal{H}om_{\operatorname{Shv}_{\mathcal{G}^G}(\widetilde{{\operatorname{Fl}}})_{\lambda}} ((\delta_0)_{\lambda}, \mathcal{F}\star ({{J}}_{-\lambda})_{\lambda}\!)\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_\lambda}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} ((\delta_0)_{\lambda}), \mathcal{F}\star ({{J}}_{-\lambda})_\lambda)\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}(\widetilde{{\operatorname{Fl}}})_\lambda}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} (({{J}}_0)_\lambda), \mathcal{F}\star ({{J}}_{-\lambda})_\lambda)\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({{\operatorname{Fl}}_G^{\omega^\rho}})}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} (({{J}}_0)_\lambda)\star {{J}}_\lambda, \mathcal{F})\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({{\operatorname{Fl}}_G^{\omega^\rho}})}(\operatorname{Av}_!^{N(\mathcal{K}), \chi} ({{J}}_\lambda), \mathcal{F})\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_G^{\omega^\rho})}(\Delta_\lambda, \mathcal{F}). \end{align*}
Proposition 6.5.6 Given ![]() $\lambda \in \Lambda$, there is an isomorphism
$\lambda \in \Lambda$, there is an isomorphism
Proof. We regard ![]() $j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ as a
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ as a ![]() $({\mathcal {G}}^G)^{-1}$-twisted sheaf. Thus, it is the
$({\mathcal {G}}^G)^{-1}$-twisted sheaf. Thus, it is the ![]() $!$-extension of the
$!$-extension of the ![]() $({\mathcal {G}}^G)^{-1}$-twisted dualizing sheaf on
$({\mathcal {G}}^G)^{-1}$-twisted dualizing sheaf on ![]() $S_{{\operatorname {Fl}},x}^{-,\lambda }$ under the unique (up to a choice of trivialization of
$S_{{\operatorname {Fl}},x}^{-,\lambda }$ under the unique (up to a choice of trivialization of ![]() $({\mathcal {G}}^G)^{-1}|_{t^\lambda \in {\operatorname {Fl}}}$)
$({\mathcal {G}}^G)^{-1}|_{t^\lambda \in {\operatorname {Fl}}}$) ![]() $N^-({\mathcal {K}})^{\omega ^\rho }_x$-equivariant trivialization.
$N^-({\mathcal {K}})^{\omega ^\rho }_x$-equivariant trivialization.
Assuming ![]() $\alpha$ to be very dominant, we have
$\alpha$ to be very dominant, we have ![]() $t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }\subset N^-({\mathcal {K}})^{\omega ^\rho } t^{\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$, and
$t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }\subset N^-({\mathcal {K}})^{\omega ^\rho } t^{\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$, and ![]() $t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }=t^\alpha N^-(t{\mathcal {O}})^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$. Here,
$t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }=t^\alpha N^-(t{\mathcal {O}})^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$. Here, ![]() $N^-(t{\mathcal {O}})^{\omega ^\rho }$ denotes the negative part of
$N^-(t{\mathcal {O}})^{\omega ^\rho }$ denotes the negative part of ![]() $I^{\omega ^\rho }$.
$I^{\omega ^\rho }$.
Since ![]() $I^0$ is pro-unipotent, the twisting
$I^0$ is pro-unipotent, the twisting ![]() $({\mathcal {G}}^G)^{-1}$ on
$({\mathcal {G}}^G)^{-1}$ on ![]() $I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }=I^{0} t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ has a unique (up to a choice of trivialization of
$I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }=I^{0} t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ has a unique (up to a choice of trivialization of ![]() $({\mathcal {G}}^G)^{-1}|_{t^{-\alpha +\lambda }\in {\operatorname {Fl}}}$)
$({\mathcal {G}}^G)^{-1}|_{t^{-\alpha +\lambda }\in {\operatorname {Fl}}}$) ![]() $I^0$-equivariant trivialization. By definition,
$I^0$-equivariant trivialization. By definition, ![]() $J_{-\alpha +\lambda,!}$ is the
$J_{-\alpha +\lambda,!}$ is the ![]() $!$-extension of the
$!$-extension of the ![]() $({\mathcal {G}}^G)^{-1}$-twisted constant perverse sheaf on
$({\mathcal {G}}^G)^{-1}$-twisted constant perverse sheaf on ![]() $I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ with respect to this trivialization.
$I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ with respect to this trivialization.
Given an element ![]() $g\in G({\mathcal {K}})^{\omega ^\rho }$ and a trivialization of
$g\in G({\mathcal {K}})^{\omega ^\rho }$ and a trivialization of ![]() $({\mathcal {G}}^G)^{-1}|_g$, we can define the left transition functor
$({\mathcal {G}}^G)^{-1}|_g$, we can define the left transition functor ![]() $g\cdot -:\operatorname {Shv}_{({\mathcal {G}}^G)^{-1}}({\operatorname {Fl}}_G^{\omega ^\rho })\to \operatorname {Shv}_{({\mathcal {G}}^G)^{-1}}({\operatorname {Fl}}_G^{\omega ^\rho })$. Now, we choose a trivialization of
$g\cdot -:\operatorname {Shv}_{({\mathcal {G}}^G)^{-1}}({\operatorname {Fl}}_G^{\omega ^\rho })\to \operatorname {Shv}_{({\mathcal {G}}^G)^{-1}}({\operatorname {Fl}}_G^{\omega ^\rho })$. Now, we choose a trivialization of ![]() $({\mathcal {G}}^G)^{-1}$ at
$({\mathcal {G}}^G)^{-1}$ at ![]() $t^\alpha \in T^{\omega ^\rho }({\mathcal {K}})$ such that it matches the chosen trivializations
$t^\alpha \in T^{\omega ^\rho }({\mathcal {K}})$ such that it matches the chosen trivializations ![]() $({\mathcal {G}}^G)^{-1}|_{t^{-\alpha +\lambda }\in {\operatorname {Fl}}}$ and
$({\mathcal {G}}^G)^{-1}|_{t^{-\alpha +\lambda }\in {\operatorname {Fl}}}$ and ![]() $({\mathcal {G}}^G)^{-1}|_{t^\lambda \in {\operatorname {Fl}}}$ under the isomorphism
$({\mathcal {G}}^G)^{-1}|_{t^\lambda \in {\operatorname {Fl}}}$ under the isomorphism ![]() $({\mathcal {G}}^G)^{-1}|_{t^\alpha \in G({\mathcal {K}})}\otimes ({\mathcal {G}}^G)^{-1}|_{t^{-\alpha +\lambda }\in {\operatorname {Fl}}}\simeq ({\mathcal {G}}^G)^{-1}|_{t^\lambda \in {\operatorname {Fl}}}$.
$({\mathcal {G}}^G)^{-1}|_{t^\alpha \in G({\mathcal {K}})}\otimes ({\mathcal {G}}^G)^{-1}|_{t^{-\alpha +\lambda }\in {\operatorname {Fl}}}\simeq ({\mathcal {G}}^G)^{-1}|_{t^\lambda \in {\operatorname {Fl}}}$.
Left-multiplying with ![]() $t^\alpha$, the
$t^\alpha$, the ![]() $I^0$-equivariant trivialization on
$I^0$-equivariant trivialization on ![]() $I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ becomes the unique
$I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ becomes the unique ![]() ${\rm Ad}_{\alpha }I^0$-equivariant trivialization on
${\rm Ad}_{\alpha }I^0$-equivariant trivialization on ![]() $t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$.Footnote 8 It coincides with the restriction of the unique
$t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$.Footnote 8 It coincides with the restriction of the unique ![]() $N^-({\mathcal {K}})^{\omega ^\rho }$-equivariant trivialization on
$N^-({\mathcal {K}})^{\omega ^\rho }$-equivariant trivialization on ![]() $N^-({\mathcal {K}})^{\omega ^\rho } t^{\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ (since different trivializations differ by a tame local system on the affine space
$N^-({\mathcal {K}})^{\omega ^\rho } t^{\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ (since different trivializations differ by a tame local system on the affine space ![]() $t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$, which has to be trivial). In particular,
$t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$, which has to be trivial). In particular, ![]() $t^\alpha {{J}}_{-\alpha +\lambda,!}$ exactly coincides with the
$t^\alpha {{J}}_{-\alpha +\lambda,!}$ exactly coincides with the ![]() $!$-extension of the
$!$-extension of the ![]() $!$-restriction of
$!$-restriction of ![]() $j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ on
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$ on ![]() $t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ up to a shift by
$t^\alpha I^{\omega ^\rho } t^{-\alpha +\lambda } I^{\omega ^\rho }/I^{\omega ^\rho }$ up to a shift by ![]() $\langle \alpha -\lambda, 2\check {\rho }\rangle$. The adjointness of
$\langle \alpha -\lambda, 2\check {\rho }\rangle$. The adjointness of ![]() $!$-pushforward and
$!$-pushforward and ![]() $!$-pullback gives rise to transition maps between
$!$-pullback gives rise to transition maps between ![]() $t^\alpha {{J}}_{-\alpha +\lambda,!}[\langle \alpha -\lambda, 2\check {\rho }\rangle ]$.
$t^\alpha {{J}}_{-\alpha +\lambda,!}[\langle \alpha -\lambda, 2\check {\rho }\rangle ]$.
Now we write ![]() $j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})[\langle \lambda, 2\check {\rho }\rangle ]$ as
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})[\langle \lambda, 2\check {\rho }\rangle ]$ as ![]() $\mathop {{\rm colim}}_{{\alpha,}\alpha -\lambda \in \Lambda ^+} t^\alpha {{J}}_{-\alpha +\lambda,!}[\langle \alpha, 2\check {\rho }\rangle ]$. Note that
$\mathop {{\rm colim}}_{{\alpha,}\alpha -\lambda \in \Lambda ^+} t^\alpha {{J}}_{-\alpha +\lambda,!}[\langle \alpha, 2\check {\rho }\rangle ]$. Note that ![]() ${{J}}_{-\alpha +\lambda,!}$ is
${{J}}_{-\alpha +\lambda,!}$ is ![]() $I^0$-equivariant and
$I^0$-equivariant and ![]() $T$-equivariant with respect to a character
$T$-equivariant with respect to a character ![]() $b_{-\lambda +\alpha }$. For such a sheaf
$b_{-\lambda +\alpha }$. For such a sheaf ![]() $\mathcal {F}$, we have
$\mathcal {F}$, we have
Indeed, for any such a ![]() $({\mathcal {G}}^G)^{-1}$-twisted sheaf
$({\mathcal {G}}^G)^{-1}$-twisted sheaf ![]() ${\mathcal {F}}$, taking
${\mathcal {F}}$, taking ![]() $*$-averaging of
$*$-averaging of ![]() $t^\alpha \cdot {\mathcal {F}}$ with respect to
$t^\alpha \cdot {\mathcal {F}}$ with respect to ![]() $N(\mathcal {O})^{\omega ^\rho }$ is given by taking the convolution of
$N(\mathcal {O})^{\omega ^\rho }$ is given by taking the convolution of ![]() ${\mathcal {F}}$ with the
${\mathcal {F}}$ with the ![]() $*$-extension of the twisted constant sheaf on
$*$-extension of the twisted constant sheaf on ![]() $N(\mathcal {O})^{\omega ^\rho } t^\alpha$. Since
$N(\mathcal {O})^{\omega ^\rho } t^\alpha$. Since ![]() ${\mathcal {F}}$ is
${\mathcal {F}}$ is ![]() $(I^{\omega ^\rho }, b_{-\lambda +\alpha })$-equivariant, we can first take right
$(I^{\omega ^\rho }, b_{-\lambda +\alpha })$-equivariant, we can first take right ![]() $(I^{\omega ^\rho }, b_{-\lambda +\alpha })$-averaging of the constant sheaf on
$(I^{\omega ^\rho }, b_{-\lambda +\alpha })$-averaging of the constant sheaf on ![]() $N(\mathcal {O})^{\omega ^\rho } t^\alpha$ and then take the convolution with
$N(\mathcal {O})^{\omega ^\rho } t^\alpha$ and then take the convolution with ![]() ${\mathcal {F}}$ after descending along
${\mathcal {F}}$ after descending along ![]() $G({\mathcal {K}})^{\omega ^\rho }\times {\operatorname {Fl}}_G^{\omega ^\rho }\longrightarrow G({\mathcal {K}})^{\omega ^\rho }\overset {I^{\omega ^\rho }}{\times } {\operatorname {Fl}}_G^{\omega ^\rho }$. Up to a shift, the right
$G({\mathcal {K}})^{\omega ^\rho }\times {\operatorname {Fl}}_G^{\omega ^\rho }\longrightarrow G({\mathcal {K}})^{\omega ^\rho }\overset {I^{\omega ^\rho }}{\times } {\operatorname {Fl}}_G^{\omega ^\rho }$. Up to a shift, the right ![]() $(I^{\omega ^\rho }, b_{-\lambda +\alpha })$-averaging of the constant sheaf on
$(I^{\omega ^\rho }, b_{-\lambda +\alpha })$-averaging of the constant sheaf on ![]() $N(\mathcal {O})^{\omega ^\rho } t^\alpha$ is isomorphic to the pullback of
$N(\mathcal {O})^{\omega ^\rho } t^\alpha$ is isomorphic to the pullback of ![]() $(J_{\alpha,*})_{-\lambda +\alpha }$.
$(J_{\alpha,*})_{-\lambda +\alpha }$.
Thus, there is
Here we use the fact that ![]() $\operatorname {Av}^{N(\mathcal {O})^{\omega ^\rho }}_*$ commutes with colimits.
$\operatorname {Av}^{N(\mathcal {O})^{\omega ^\rho }}_*$ commutes with colimits.
Similarly, we can calculate ![]() $N(\mathcal {O})^{\omega ^\rho }$-averaging of
$N(\mathcal {O})^{\omega ^\rho }$-averaging of ![]() $j_*(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$.
$j_*(\omega _{S_{{\operatorname {Fl}},x}^{-,\lambda }})$.
Proposition 6.5.7 For ![]() $\lambda \in \Lambda$, we have
$\lambda \in \Lambda$, we have
6.6 Proof of Theorem 3.3.2 modulo Proposition 6.6.2
This section is devoted to the proof of Theorem 4.3.1 using Proposition 6.6.2.
First of all, let us check the compatibility of costandard objects under ![]() $F^{\rm L}$.
$F^{\rm L}$.
Proposition 6.6.1 For any ![]() $\lambda \in \Lambda$, there is an isomorphism
$\lambda \in \Lambda$, there is an isomorphism
Proof. By the isomorphism (6.5.5), there is
Now the claim follows from Proposition 5.5.3.
Then we prove Theorem 6.4.8 with the help of the following proposition. In particular, by Lemma 6.4.6, we actually prove Theorem 4.3.1 (= Theorem 3.3.2).
Proposition 6.6.2 For ![]() $\lambda \in \Lambda$, the functor
$\lambda \in \Lambda$, the functor
sends standards to standards, i.e.
Proof of Theorem 6.4.8 To prove the fully faithfulness of ![]() $F^{\rm L}$, we need to prove that the following map is an isomorphism
$F^{\rm L}$, we need to prove that the following map is an isomorphism
for any ![]() $\mathcal {F}_1, \mathcal {F}_2\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$.
$\mathcal {F}_1, \mathcal {F}_2\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$.
Since the standards ![]() $\{\Delta _\lambda, \lambda \in \Lambda \}$ generate the category
$\{\Delta _\lambda, \lambda \in \Lambda \}$ generate the category ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ by cohomology shifts, colimits and extensions, it is sufficient to prove
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ by cohomology shifts, colimits and extensions, it is sufficient to prove
for any ![]() $\mathcal {F}_2\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$
$\mathcal {F}_2\in \operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$
Fix a ![]() $\Delta _{\lambda }$. Since both
$\Delta _{\lambda }$. Since both ![]() $\Delta _\lambda$ and
$\Delta _\lambda$ and ![]() $F^{\rm L}(\Delta _\lambda )=\Delta _{\lambda,\Omega _{\rm q}^{{\rm L},\prime }}$ are compact, we only need to construct a collection of compact generators
$F^{\rm L}(\Delta _\lambda )=\Delta _{\lambda,\Omega _{\rm q}^{{\rm L},\prime }}$ are compact, we only need to construct a collection of compact generators ![]() $\{\Delta '_{\lambda, \widetilde {w}}, \widetilde {w}\ \text {relevant}\}$ of
$\{\Delta '_{\lambda, \widetilde {w}}, \widetilde {w}\ \text {relevant}\}$ of ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ and prove that
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ and prove that ![]() $F^{\rm L}$ induces an isomorphism (6.6.2) if
$F^{\rm L}$ induces an isomorphism (6.6.2) if ![]() ${\mathcal {F}}_2= \Delta '_{\lambda, \widetilde {w}}$.
${\mathcal {F}}_2= \Delta '_{\lambda, \widetilde {w}}$.
Without loss of generality, we can assume that ![]() $\lambda$ is dominant, the construction of
$\lambda$ is dominant, the construction of ![]() $\Delta '_{\lambda, \widetilde {w}}$ for general
$\Delta '_{\lambda, \widetilde {w}}$ for general ![]() $\lambda$ follows by taking the convolution with twisted BMW sheaf.
$\lambda$ follows by taking the convolution with twisted BMW sheaf.
In this case, we let ![]() $\Delta '_{\lambda, \widetilde {w}}=\Delta _\lambda$ if
$\Delta '_{\lambda, \widetilde {w}}=\Delta _\lambda$ if ![]() $\widetilde {w}=t^\lambda$, and
$\widetilde {w}=t^\lambda$, and ![]() $\Delta '_{\lambda, \widetilde {w}}=\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\widetilde {w}}$ if
$\Delta '_{\lambda, \widetilde {w}}=\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\widetilde {w}}$ if ![]() $\widetilde {w}\neq t^\lambda$. It is not hard to see that they form a collection of compact generators. Indeed, according to Proposition 5.1.7,
$\widetilde {w}\neq t^\lambda$. It is not hard to see that they form a collection of compact generators. Indeed, according to Proposition 5.1.7, ![]() $\{\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\widetilde {w}}, \widetilde {w} \text {relevant}\}$ is a collection of compact generators. Furthermore,
$\{\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\widetilde {w}}, \widetilde {w} \text {relevant}\}$ is a collection of compact generators. Furthermore, ![]() $\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\lambda }$ is a finite extension of
$\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\lambda }$ is a finite extension of ![]() $\Delta _{\lambda,\lambda }'=\Delta _{\lambda }$ and
$\Delta _{\lambda,\lambda }'=\Delta _{\lambda }$ and ![]() $\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\widetilde {w}}$, for
$\nabla ^{{\mathop {\operatorname {\rm ver}}}}_{\widetilde {w}}$, for ![]() $\widetilde {w}\neq t^\lambda$.
$\widetilde {w}\neq t^\lambda$.
If ![]() $\widetilde {w}\neq t^\lambda$, by Corollary 6.5.5 and Proposition 6.6.2, we have
$\widetilde {w}\neq t^\lambda$, by Corollary 6.5.5 and Proposition 6.6.2, we have ![]() $\mathcal {H}om_{\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })}(\Delta _{\lambda },\mathcal {F}_2)$
$\mathcal {H}om_{\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })}(\Delta _{\lambda },\mathcal {F}_2)$ ![]() $=i_\lambda ^! (F^{\rm L}(\mathcal {F}_2))=\mathcal {H}om_{\Omega _{q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}}(F^{\rm L}(\Delta _{\lambda }),F^{\rm L}(\mathcal {F}_2))=0$. The map (6.6.2) has to be
$=i_\lambda ^! (F^{\rm L}(\mathcal {F}_2))=\mathcal {H}om_{\Omega _{q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}}(F^{\rm L}(\Delta _{\lambda }),F^{\rm L}(\mathcal {F}_2))=0$. The map (6.6.2) has to be ![]() $0$.
$0$.
If ![]() $\widetilde {w}= t^\lambda$, by Proposition 6.6.2, both sides of (6.6.2) are
$\widetilde {w}= t^\lambda$, by Proposition 6.6.2, both sides of (6.6.2) are ![]() $\mathsf {e}$, the map (6.6.2) is an isomorphism since
$\mathsf {e}$, the map (6.6.2) is an isomorphism since ![]() $F^{\rm L}$ sends
$F^{\rm L}$ sends ![]() ${\rm id}$ to
${\rm id}$ to ![]() ${\rm id}$.
${\rm id}$.
Then, we note that standards ![]() $\{\Delta _{\lambda, \Omega _{\rm q}^{{\rm L},\prime }}\}$ generate the category
$\{\Delta _{\lambda, \Omega _{\rm q}^{{\rm L},\prime }}\}$ generate the category ![]() $\Omega _{q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$ under cohomology shifts, extensions, and colimits, and the functor
$\Omega _{q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$ under cohomology shifts, extensions, and colimits, and the functor ![]() $F^{\rm L}$ is compatible with cohomology shift, extensions, and colimits. Hence,
$F^{\rm L}$ is compatible with cohomology shift, extensions, and colimits. Hence, ![]() $F^{\rm L}$ is essentially surjective by Proposition 6.6.2.
$F^{\rm L}$ is essentially surjective by Proposition 6.6.2.
To prove the t-exactness of ![]() $F^{\rm L}$, note that according to (3.3.1) and (4.1.5), t-structures on both sides are defined by the ’Hom’ with standard objects. According to Proposition 6.6.2, the functor
$F^{\rm L}$, note that according to (3.3.1) and (4.1.5), t-structures on both sides are defined by the ’Hom’ with standard objects. According to Proposition 6.6.2, the functor ![]() $F^{\rm L}$ preserves standards. Hence,
$F^{\rm L}$ preserves standards. Hence, ![]() $F^{\rm L}$ is t-exact.
$F^{\rm L}$ is t-exact.
Corollary 6.6.3 The objects ![]() $\Delta _\lambda$ and
$\Delta _\lambda$ and ![]() $\nabla _\lambda$ are in the heart of
$\nabla _\lambda$ are in the heart of ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$.
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$.
Proof. Note that ![]() $F^{\rm L}$ preserves standards and costandards, and
$F^{\rm L}$ preserves standards and costandards, and ![]() $F^{\rm L}$ is t-exact, we only need to prove that
$F^{\rm L}$ is t-exact, we only need to prove that ![]() $\Delta _{\lambda, \Omega _{\rm q}^{{\rm L},\prime }}$ and
$\Delta _{\lambda, \Omega _{\rm q}^{{\rm L},\prime }}$ and ![]() $\nabla _{\lambda, \Omega _{\rm q}^{{\rm L},\prime }}$ are in the heart of the t-structure on
$\nabla _{\lambda, \Omega _{\rm q}^{{\rm L},\prime }}$ are in the heart of the t-structure on ![]() $\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$. The later claim follows from the fact that
$\Omega _{\rm q}^{{\rm L},\prime }\text {-}{\operatorname {FactMod}}$. The later claim follows from the fact that ![]() $\Omega _{\rm q}^{\rm L}$ is perverse, and all standard objects and costandards in
$\Omega _{\rm q}^{\rm L}$ is perverse, and all standard objects and costandards in ![]() $\Omega {\text {-}}{\operatorname {FactMod}}$ are perverse if
$\Omega {\text {-}}{\operatorname {FactMod}}$ are perverse if ![]() $\Omega$ is perverse.
$\Omega$ is perverse.
The proof of Proposition 6.6.2 is hard. It occupies the rest of the paper and is finally given in § 8.3.
7. Global Whittaker category
From now on, we focus on the proof of Proposition 6.6.2. As we noted before, it is very hard to calculate ![]() $*$-stalks. Luckily, we can use duality functor to transfer the calculation of
$*$-stalks. Luckily, we can use duality functor to transfer the calculation of ![]() $*$-stalks to a calculation of
$*$-stalks to a calculation of ![]() $!$-stalks. To make the calculation possible, we introduce the global counterparts of the category
$!$-stalks. To make the calculation possible, we introduce the global counterparts of the category ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ and the functor
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_G^{\omega ^\rho })$ and the functor ![]() $F^{\rm L}$. In this section, our aim is to transfer Proposition 6.6.2 to 7.6.6 by the local–global comparison.
$F^{\rm L}$. In this section, our aim is to transfer Proposition 6.6.2 to 7.6.6 by the local–global comparison.
7.1 Drinfeld compactifications
Fix ![]() $x\in X$. The Drinfeld compactification is introduced in [Reference Braverman and GaitsgoryBG02, § 1]. In this section, we define the Whittaker category on the (Iwahori version) Drinfeld compactification.
$x\in X$. The Drinfeld compactification is introduced in [Reference Braverman and GaitsgoryBG02, § 1]. In this section, we define the Whittaker category on the (Iwahori version) Drinfeld compactification.
Definition 7.1.1 Let ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ be the stack classifying the triples
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ be the stack classifying the triples ![]() $(\mathcal {P}_G,\{\kappa ^{\check {\lambda }}, \check {\lambda }\in \Lambda ^+\}, \epsilon )$, where
$(\mathcal {P}_G,\{\kappa ^{\check {\lambda }}, \check {\lambda }\in \Lambda ^+\}, \epsilon )$, where ![]() $\mathcal {P}_G\in {\operatorname {Bun}}_G$,
$\mathcal {P}_G\in {\operatorname {Bun}}_G$, ![]() $\{\kappa ^{\check {\lambda }}, \check {\lambda }\in \Lambda ^+\}$ is a family of morphisms of coherent sheaves
$\{\kappa ^{\check {\lambda }}, \check {\lambda }\in \Lambda ^+\}$ is a family of morphisms of coherent sheaves
which satisfy the Plücker relations, such that it is regular over ![]() $X\setminus x$, and
$X\setminus x$, and ![]() $\epsilon$ is a
$\epsilon$ is a ![]() $B$-reduction of
$B$-reduction of ![]() $\mathcal {P}_G$ at
$\mathcal {P}_G$ at ![]() $x$.
$x$.
If we omit the Iwahori structure (i.e. ![]() $\epsilon$) at
$\epsilon$) at ![]() $x$ and ask
$x$ and ask ![]() $\kappa ^{\check {\lambda }}$ to be defined and regular on the whole curve
$\kappa ^{\check {\lambda }}$ to be defined and regular on the whole curve ![]() $X$ for any dominant weight
$X$ for any dominant weight ![]() $\check {\lambda }$, we denote the resulting algebraic stack by
$\check {\lambda }$, we denote the resulting algebraic stack by ![]() $\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$.
$\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$.
7.1.2
Note that there is a projection map from ![]() ${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ to
${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ to ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$,
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$,
This morphism sends ![]() $(\mathcal {P}_G, \alpha,\epsilon )\in {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ to
$(\mathcal {P}_G, \alpha,\epsilon )\in {\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ to ![]() $(\mathcal {P}_G, \{\kappa ^{\check {\lambda }}, \check {\lambda }\in \check {\Lambda }^+\}, \epsilon )$. Here
$(\mathcal {P}_G, \{\kappa ^{\check {\lambda }}, \check {\lambda }\in \check {\Lambda }^+\}, \epsilon )$. Here ![]() $\kappa ^{\check {\lambda }}$ is induced from
$\kappa ^{\check {\lambda }}$ is induced from ![]() $\alpha$, i.e. for any dominant weight
$\alpha$, i.e. for any dominant weight ![]() $\check {\lambda }$,
$\check {\lambda }$,
Similarly, by omitting ![]() $\epsilon$, we have a projection map from
$\epsilon$, we have a projection map from ![]() $\overline {S}^0_{{\operatorname {Gr}}}$ to
$\overline {S}^0_{{\operatorname {Gr}}}$ to ![]() $\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$,
$\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$,
7.1.3
Here ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ and
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ and ![]() $\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$ project to
$\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$ project to ![]() ${\operatorname {Bun}}_G$. By taking the ratio of pullback of
${\operatorname {Bun}}_G$. By taking the ratio of pullback of ![]() $\mathcal {G}^G$ on
$\mathcal {G}^G$ on ![]() ${\operatorname {Bun}}_G$ and the fiber
${\operatorname {Bun}}_G$ and the fiber ![]() $\mathcal {G}^G|_{\mathcal {P}_G^{\omega ^\rho }\in {\operatorname {Bun}}_G}$, we get gerbes on
$\mathcal {G}^G|_{\mathcal {P}_G^{\omega ^\rho }\in {\operatorname {Bun}}_G}$, we get gerbes on ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ and
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ and ![]() $\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$. We denote the resulting the gerbes by
$\overline {{\operatorname {Bun}}_N^{\omega ^\rho }}$. We denote the resulting the gerbes by ![]() $\mathcal {G}^G$. By constructions in § 2.4, their pullbacks along the projections (7.1.1) and (7.1.2) are isomorphic to the same-named gerbes on
$\mathcal {G}^G$. By constructions in § 2.4, their pullbacks along the projections (7.1.1) and (7.1.2) are isomorphic to the same-named gerbes on ![]() ${\operatorname {Fl}}_{G}^{\omega ^\rho }$ and
${\operatorname {Fl}}_{G}^{\omega ^\rho }$ and ![]() ${\operatorname {Gr}}_G^{\omega ^\rho }$.
${\operatorname {Gr}}_G^{\omega ^\rho }$.
7.2 Global Whittaker category
In [Reference Frenkel, Gaitsgory and VilonenFGV01], the authors defined the category ![]() $\operatorname {Whit}_{q}(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})$. We can define the twisted Whittaker category on
$\operatorname {Whit}_{q}(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})$. We can define the twisted Whittaker category on ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ similarly.
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ similarly.
Given a point ![]() $\bar {y}=\{y_1, y_2,\ldots, y_n\}$ in
$\bar {y}=\{y_1, y_2,\ldots, y_n\}$ in ![]() ${\mathop {\operatorname {\rm Ran}}}$, which is disjoint from
${\mathop {\operatorname {\rm Ran}}}$, which is disjoint from ![]() $x$, i.e.
$x$, i.e. ![]() $x\neq y_i$ for any
$x\neq y_i$ for any ![]() $i$.
$i$.
Definition 7.2.1 We define ![]() $((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ as the open substack of
$((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ as the open substack of ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$, such that for any dominant weight
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$, such that for any dominant weight ![]() $\check {\lambda }$, the map
$\check {\lambda }$, the map ![]() $\kappa ^{\check {\lambda }}$ is injective on the fiber over any point
$\kappa ^{\check {\lambda }}$ is injective on the fiber over any point ![]() $y_i\in \bar {y}$.
$y_i\in \bar {y}$.
Since ![]() $\{\kappa ^{\check {\lambda }}, \lambda \in \Lambda ^+\}$ are injective bundle maps near
$\{\kappa ^{\check {\lambda }}, \lambda \in \Lambda ^+\}$ are injective bundle maps near ![]() $\bar {y}$, they give rise to a
$\bar {y}$, they give rise to a ![]() $N^{\omega ^\rho }$-reduction of
$N^{\omega ^\rho }$-reduction of ![]() $\mathcal {P}_G$ near
$\mathcal {P}_G$ near ![]() $\bar {y}$, which means there exists a
$\bar {y}$, which means there exists a ![]() $B$-bundle
$B$-bundle ![]() $\mathcal {P}_B$ on the disk
$\mathcal {P}_B$ on the disk ![]() $\mathcal {D}_{\bar {y}}$, such that
$\mathcal {D}_{\bar {y}}$, such that
and ![]() $\beta _{\bar {y}}^T: \mathcal {P}_B\mathop {\times }^B T\simeq \omega ^\rho$.
$\beta _{\bar {y}}^T: \mathcal {P}_B\mathop {\times }^B T\simeq \omega ^\rho$.
Similar to [Reference GaitsgoryGai08, § 2.3], we construct a ![]() $N(\mathcal {O})_{\bar {y}}^{\omega ^\rho }$-principal bundle
$N(\mathcal {O})_{\bar {y}}^{\omega ^\rho }$-principal bundle ![]() $_{\bar {y}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ over the stack
$_{\bar {y}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ over the stack ![]() $((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$. This bundle classifies data from
$((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$. This bundle classifies data from ![]() $((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ plus a choice of identification of the
$((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ plus a choice of identification of the ![]() $B$-bundle
$B$-bundle ![]() $\mathcal {P}_B|_{\mathcal {D}_{\bar {y}}}$ with the
$\mathcal {P}_B|_{\mathcal {D}_{\bar {y}}}$ with the ![]() $B$-bundle induced from
$B$-bundle induced from ![]() $\omega ^\rho$, such that it is compatible with
$\omega ^\rho$, such that it is compatible with ![]() $\beta _{\bar {y}}^T$.
$\beta _{\bar {y}}^T$.
By a standard gluing procedure (see [Reference Frenkel, Gaitsgory and VilonenFGV01, Lemma 3.2.7]), we can extend the ![]() $N(\mathcal {O})_{\bar {y}}^{\omega ^\rho }$-action on
$N(\mathcal {O})_{\bar {y}}^{\omega ^\rho }$-action on ![]() $_{\bar {y}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ to an action of
$_{\bar {y}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ to an action of ![]() $N(\mathcal {K})_{\bar {y}}^{\omega ^\rho }$.
$N(\mathcal {K})_{\bar {y}}^{\omega ^\rho }$.
Definition 7.2.2 A twisted Whittaker sheaf on ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ is a twisted sheaf on
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ is a twisted sheaf on ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ such that its pullback to
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ such that its pullback to ![]() ${}_{\bar {y}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ is
${}_{\bar {y}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})_{{\rm good}\ {\rm at}\ \bar {y}}$ is ![]() $(N(\mathcal {K})^{\omega ^\rho }_{\bar {y}}, {-}\chi _{\bar {y}})$-equivariant for any
$(N(\mathcal {K})^{\omega ^\rho }_{\bar {y}}, {-}\chi _{\bar {y}})$-equivariant for any ![]() $\bar {y}$ disjoint with
$\bar {y}$ disjoint with ![]() $x$. We denote the category of
$x$. We denote the category of ![]() $\mathcal {G}^G$-twisted Whittaker sheaf on
$\mathcal {G}^G$-twisted Whittaker sheaf on ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ by
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x}$ by ![]() $\operatorname {Whit}_{q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$.
$\operatorname {Whit}_{q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$.
Applying the method of the proof of [Reference GaitsgoryGai20, Theorem 5.2.2], we have the following.
Lemma 7.2.3 We have:
is an equivalence of categories; and
is an equivalence of categories.
We denote by ![]() $\Delta _{{\mathop {\operatorname {\rm glob}}}}^{\lambda }$ the twisted sheaf
$\Delta _{{\mathop {\operatorname {\rm glob}}}}^{\lambda }$ the twisted sheaf ![]() $\pi _{{\operatorname {Fl}},x}^!(\Delta _\lambda )[d_g]$, where
$\pi _{{\operatorname {Fl}},x}^!(\Delta _\lambda )[d_g]$, where ![]() $d_g:= \dim ({\operatorname {Bun}}_N^{\omega ^\rho })$.
$d_g:= \dim ({\operatorname {Bun}}_N^{\omega ^\rho })$.
Remark 7.2.4 Although the local Whittaker categories are equivalent to the global Whittaker categories, we have to use both of them in this paper: we use the local Whittaker category to show the factorization property, and we use the global Whittaker category to show prove Proposition 6.6.2.
7.2.5 Proof of Lemma 7.2.3
The second claim of Lemma 7.2.3 is the statement of [Reference GaitsgoryGai20, Theorem 5.2.2]. To be self-contained, we prove the first claim.
First, we give the algebraic ind-stack ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$ a stratification. By definition, the algebraic ind-stack
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$ a stratification. By definition, the algebraic ind-stack ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$ classifies the data of points
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$ classifies the data of points ![]() $({\mathcal {P}}_G, \sigma, \epsilon )$, where
$({\mathcal {P}}_G, \sigma, \epsilon )$, where ![]() ${\mathcal {P}}_G$ is a
${\mathcal {P}}_G$ is a ![]() $G$-bundle on
$G$-bundle on ![]() $X$,
$X$, ![]() $\sigma$ is a section of
$\sigma$ is a section of ![]() $X-x$ in
$X-x$ in ![]() $T\backslash \overline {N\backslash G}^{{\operatorname {aff}}}\overset {G}{\times } {\mathcal {P}}_G$ which generically lies in
$T\backslash \overline {N\backslash G}^{{\operatorname {aff}}}\overset {G}{\times } {\mathcal {P}}_G$ which generically lies in ![]() ${T\backslash (N\backslash G)}\overset {G}{\times } {\mathcal {P}}_G$, such that the induced map to
${T\backslash (N\backslash G)}\overset {G}{\times } {\mathcal {P}}_G$, such that the induced map to ![]() $T\backslash {\operatorname {pt}}$ is given by
$T\backslash {\operatorname {pt}}$ is given by ![]() $\omega ^{\rho }$, and
$\omega ^{\rho }$, and ![]() $\epsilon$ is a
$\epsilon$ is a ![]() $B$-reduction of
$B$-reduction of ![]() ${\mathcal {P}}_G$ at
${\mathcal {P}}_G$ at ![]() $x$.
$x$.
According to [Reference ZhuZhu16, Lemma 1.3.7], we can trivialize ![]() ${\mathcal {P}}_G$ on the formal disc
${\mathcal {P}}_G$ on the formal disc ![]() ${\mathcal {D}}_x$. Furthermore, we can choose an isomorphism
${\mathcal {D}}_x$. Furthermore, we can choose an isomorphism ![]() ${\mathcal {P}}_G|_{{\mathcal {D}}_x}\overset {\phi }{\simeq } {\mathcal {P}}_G^\omega$, such that the Iwahori structure
${\mathcal {P}}_G|_{{\mathcal {D}}_x}\overset {\phi }{\simeq } {\mathcal {P}}_G^\omega$, such that the Iwahori structure ![]() $\epsilon$ goes to
$\epsilon$ goes to ![]() $\omega ^\rho \overset {T}{\times } B|_x$ under this isomorphism.
$\omega ^\rho \overset {T}{\times } B|_x$ under this isomorphism.
For any geometric point in ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$, taking the restriction of
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$, taking the restriction of ![]() $\sigma$ to
$\sigma$ to ![]() $\overset {\circ }{{\mathcal {D}}}_x$, we obtain a map
$\overset {\circ }{{\mathcal {D}}}_x$, we obtain a map ![]() $\sigma |_{\overset {\circ }{{\mathcal {D}}}_x}:\overset {\circ }{{\mathcal {D}}}_x \to T\backslash (N\backslash G)\overset {G}{\times }{\mathcal {P}}_G\simeq T\backslash (N\backslash G)\overset {G}{\times }{\mathcal {P}}^{\omega }_G$, such that the induced map to
$\sigma |_{\overset {\circ }{{\mathcal {D}}}_x}:\overset {\circ }{{\mathcal {D}}}_x \to T\backslash (N\backslash G)\overset {G}{\times }{\mathcal {P}}_G\simeq T\backslash (N\backslash G)\overset {G}{\times }{\mathcal {P}}^{\omega }_G$, such that the induced map to ![]() $T\backslash {\operatorname {pt}}$ is given by
$T\backslash {\operatorname {pt}}$ is given by ![]() $\omega ^\rho$. It gives rise to a point in
$\omega ^\rho$. It gives rise to a point in ![]() $(N\backslash G)^{\omega ^\rho }({\mathcal {K}})$. In addition, different identifications
$(N\backslash G)^{\omega ^\rho }({\mathcal {K}})$. In addition, different identifications ![]() $\phi$ preserving the
$\phi$ preserving the ![]() $B$-reduction structure at
$B$-reduction structure at ![]() $x$ differ by a multiplication by Iwahori
$x$ differ by a multiplication by Iwahori ![]() $I^{\omega ^\rho }$. Hence, for any geometric point in
$I^{\omega ^\rho }$. Hence, for any geometric point in ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$, we can obtain a point in
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}'$, we can obtain a point in ![]() $|(N\backslash G)^{\omega ^\rho }({\mathcal {K}})/I^{\omega ^\rho }|=|N({\mathcal {K}})^{\omega ^\rho }\backslash {\operatorname {Fl}}_G^{\omega ^\rho }|=W^{{\operatorname {ext}}}$.
$|(N\backslash G)^{\omega ^\rho }({\mathcal {K}})/I^{\omega ^\rho }|=|N({\mathcal {K}})^{\omega ^\rho }\backslash {\operatorname {Fl}}_G^{\omega ^\rho }|=W^{{\operatorname {ext}}}$.
For any ![]() $t^\lambda w\in W^{{\operatorname {ext}}}$, we denote the corresponding locally closed substack by
$t^\lambda w\in W^{{\operatorname {ext}}}$, we denote the corresponding locally closed substack by ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w$. It has an open substack
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w$. It has an open substack ![]() $({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w$ where we require
$({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w$ where we require ![]() $\kappa ^{\check {\lambda }}$ to be injective on
$\kappa ^{\check {\lambda }}$ to be injective on ![]() $X-x$.
$X-x$.
The projection ![]() $\pi _{{\operatorname {Fl}}, x}$ induces a map for each stratum:
$\pi _{{\operatorname {Fl}}, x}$ induces a map for each stratum:
We claim that ![]() $\pi _{{\operatorname {Fl}},x}^!$ induces a strata-wise equivalence, i.e.
$\pi _{{\operatorname {Fl}},x}^!$ induces a strata-wise equivalence, i.e.
First, using the same proof as [Reference Frenkel, Gaitsgory and VilonenFGV01, Lemma 6.2.8], one can show that ![]() $(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w- ({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w$ does not carry non-zero Whittaker sheaf.
$(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w- ({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w$ does not carry non-zero Whittaker sheaf.
Furthermore, there is an isomorphism of stacks
where ![]() $N^{\omega ^\rho }_{X-x}$ is the mapping space
$N^{\omega ^\rho }_{X-x}$ is the mapping space ![]() $X-x\longrightarrow N^{\omega ^\rho }$ and the right-hand side of (7.2.3) is understood as the fpqc (equivalently, étale) sheafification of the prestack quotient.
$X-x\longrightarrow N^{\omega ^\rho }$ and the right-hand side of (7.2.3) is understood as the fpqc (equivalently, étale) sheafification of the prestack quotient.
In addition, for any geometric point ![]() $\bar {y}=\{y_1, y_2, \ldots, y_n\}\in {\mathop {\operatorname {\rm Ran}}}_{X-x}$, we have
$\bar {y}=\{y_1, y_2, \ldots, y_n\}\in {\mathop {\operatorname {\rm Ran}}}_{X-x}$, we have
 \begin{equation} ({{\operatorname{Bun}}_N^{\omega^\rho}})_{=\lambda\cdot x, {\rm good}\ {\rm at}\ \bar{y}}^w\simeq ({{\operatorname{Bun}}_N^{\omega^\rho}})_{=\lambda\cdot x}^w\simeq N^{\omega^\rho}_{X-\bar{y}-x}\backslash \prod_{i=1}^{n} S^0_{{\operatorname{Gr}}, y_i}\times S^{t^\lambda w}_{{\operatorname{Fl}},x}, \end{equation}
\begin{equation} ({{\operatorname{Bun}}_N^{\omega^\rho}})_{=\lambda\cdot x, {\rm good}\ {\rm at}\ \bar{y}}^w\simeq ({{\operatorname{Bun}}_N^{\omega^\rho}})_{=\lambda\cdot x}^w\simeq N^{\omega^\rho}_{X-\bar{y}-x}\backslash \prod_{i=1}^{n} S^0_{{\operatorname{Gr}}, y_i}\times S^{t^\lambda w}_{{\operatorname{Fl}},x}, \end{equation}
where ![]() $N^{\omega ^\rho }_{X-\bar {y}-x}$ acts on
$N^{\omega ^\rho }_{X-\bar {y}-x}$ acts on ![]() $\prod _{i=1}^{n} S^0_{{\operatorname {Gr}}, y_i}\times S^{t^\lambda w}_{{\operatorname {Fl}},x}$ diagonally.
$\prod _{i=1}^{n} S^0_{{\operatorname {Gr}}, y_i}\times S^{t^\lambda w}_{{\operatorname {Fl}},x}$ diagonally.
It follows immediately that
 \begin{equation} {}_{\bar{y}}({{\operatorname{Bun}}_N^{\omega^\rho}})_{=\lambda\cdot x, {\rm good}\ {\rm at}\ \bar{y}}^w \simeq N^{\omega^\rho}_{X-\bar{y}-x}\backslash \prod_{i=1}^{n} N({\mathcal{K}})_{y_i}^{\omega^\rho} \times S^{t^\lambda w}_{{\operatorname{Fl}},x}, \end{equation}
\begin{equation} {}_{\bar{y}}({{\operatorname{Bun}}_N^{\omega^\rho}})_{=\lambda\cdot x, {\rm good}\ {\rm at}\ \bar{y}}^w \simeq N^{\omega^\rho}_{X-\bar{y}-x}\backslash \prod_{i=1}^{n} N({\mathcal{K}})_{y_i}^{\omega^\rho} \times S^{t^\lambda w}_{{\operatorname{Fl}},x}, \end{equation}
and the ![]() $(N({\mathcal {K}})^{\omega ^\rho }_{\bar {y}},-\chi _{\bar {y}})$-equivariant twisted D-modules on
$(N({\mathcal {K}})^{\omega ^\rho }_{\bar {y}},-\chi _{\bar {y}})$-equivariant twisted D-modules on ![]() ${}_{\bar {y}}({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x,{\rm \ good\ at\ }\bar {y}}^w$ are exactly those twisted D-modules on
${}_{\bar {y}}({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x,{\rm \ good\ at\ }\bar {y}}^w$ are exactly those twisted D-modules on ![]() $S^{t^\lambda w}_{{\operatorname {Fl}},x}$ which are
$S^{t^\lambda w}_{{\operatorname {Fl}},x}$ which are ![]() $(N^{\omega ^\rho }_{X-\bar {y}-x}, \chi _{x})$-equivariant.
$(N^{\omega ^\rho }_{X-\bar {y}-x}, \chi _{x})$-equivariant.
Now, the strata-wise equivalence follows from
To prove Lemma 7.2.3, it is sufficient to show that ![]() $\pi ^!_{{\operatorname {Fl}},x}$ induces a functor between the Whittaker categories and is fully faithful. (Then, the essentially surjective property follows from
$\pi ^!_{{\operatorname {Fl}},x}$ induces a functor between the Whittaker categories and is fully faithful. (Then, the essentially surjective property follows from ![]() $\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ is generated by
$\operatorname {Whit}_{\rm q}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$ is generated by ![]() $*$-extensions of objects in
$*$-extensions of objects in ![]() $\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}},x}^{t^\lambda w}$)).
$\operatorname {Whit}_{\rm q}(S_{{\operatorname {Fl}},x}^{t^\lambda w}$)).
The functor ![]() $\pi _{{\operatorname {Fl}},x}^!$ sends any global Whittaker sheaf to local Whittaker sheaf:
$\pi _{{\operatorname {Fl}},x}^!$ sends any global Whittaker sheaf to local Whittaker sheaf: ![]() $\operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$ is generated by
$\operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$ is generated by ![]() $*$-extensions of objects in
$*$-extensions of objects in ![]() $\operatorname {Whit}_{\rm q}({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w)$, and
$\operatorname {Whit}_{\rm q}({{\operatorname {Bun}}_N^{\omega ^\rho }})_{=\lambda \cdot x}^w)$, and ![]() $\pi ^!_{{\operatorname {Fl}},x}$ sends any such sheaf to a local Whittaker sheaf, then using the fact that the local Whittaker category is a full cocomplete subcategory of
$\pi ^!_{{\operatorname {Fl}},x}$ sends any such sheaf to a local Whittaker sheaf, then using the fact that the local Whittaker category is a full cocomplete subcategory of ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$, we obtain that
$\operatorname {Shv}_{{\mathcal {G}}^G}({\operatorname {Fl}}_{G,x}^{\omega ^\rho })$, we obtain that ![]() $\pi ^!_{{\operatorname {Fl}},x}$ sends any global Whittaker sheaf to a local Whittaker sheaf.
$\pi ^!_{{\operatorname {Fl}},x}$ sends any global Whittaker sheaf to a local Whittaker sheaf.
Consider the following commutative diagram.

Since ![]() ${\mathop {\operatorname {\rm Ran}}}_x$ is contractible (see [Reference GaitsgoryGai13, Theorem 1.6.5] and [Reference Beilinson and DrinfeldBD04, Proposition 4.3.3]), we only need to show that the
${\mathop {\operatorname {\rm Ran}}}_x$ is contractible (see [Reference GaitsgoryGai13, Theorem 1.6.5] and [Reference Beilinson and DrinfeldBD04, Proposition 4.3.3]), we only need to show that the ![]() $!$-pullback along the right-hand side induces a fully faithful embedding:
$!$-pullback along the right-hand side induces a fully faithful embedding:
According to Lemma 6.1.12, there is ![]() $\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})\simeq \operatorname {Whit}_{\rm q}({\mathop {\operatorname {\rm Ran}}}_{X,x}\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x})$. Thus, we only need to show
$\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})\simeq \operatorname {Whit}_{\rm q}({\mathop {\operatorname {\rm Ran}}}_{X,x}\times {\operatorname {Fl}}^{\omega ^\rho }_{G,x})$. Thus, we only need to show ![]() $\pi _{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_{X,x}}: \operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')\to \operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})$ is fully faithful. Note that
$\pi _{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_{X,x}}: \operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')\to \operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})$ is fully faithful. Note that ![]() $\operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$ and
$\operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$ and ![]() $\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x})$ are full subcategories of
$\operatorname {Whit}_{\rm q}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}\!)_{\infty \cdot x})$ are full subcategories of ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$ and
$\operatorname {Shv}_{{\mathcal {G}}^G}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')$ and ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})$, respectively. We only need to prove
$\operatorname {Shv}_{{\mathcal {G}}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})$, respectively. We only need to prove ![]() $\pi _{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_{X,x}}:\operatorname {Shv}_{{\mathcal {G}}^G}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}') \longrightarrow \operatorname {Shv}_{{\mathcal {G}}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})$ is fully faithful.
$\pi _{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_{X,x}}:\operatorname {Shv}_{{\mathcal {G}}^G}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}') \longrightarrow \operatorname {Shv}_{{\mathcal {G}}^G}((\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x})_{\infty \cdot x})$ is fully faithful.
Denote by ![]() ${\operatorname {Bun}}_G^{N, \text {gen}}$ the stack which classifies principal
${\operatorname {Bun}}_G^{N, \text {gen}}$ the stack which classifies principal ![]() $G$-bundles on
$G$-bundles on ![]() $X$ with a generic
$X$ with a generic ![]() $N^{\omega ^\rho }$-reduction. Consider the following Cartesian diagram.
$N^{\omega ^\rho }$-reduction. Consider the following Cartesian diagram.

Now the desired fully faithfulness follows from the fact that ![]() ${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\longrightarrow {\operatorname {Bun}}_G^{N, \text {gen}}$ is universally homologically contractible [Reference GaitsgoryGai22, Theorem A.1.10].
${\operatorname {Gr}}_{G, {\mathop {\operatorname {\rm Ran}}}}^{\omega ^\rho }\longrightarrow {\operatorname {Bun}}_G^{N, \text {gen}}$ is universally homologically contractible [Reference GaitsgoryGai22, Theorem A.1.10].
7.3 Global semi-infinite !-extension sheaf
Before we define global functors corresponding to the functors ![]() $F^{\rm L}$ and
$F^{\rm L}$ and ![]() $F^{\rm DK}$, we should construct the global analog of the semi-infinite sheaves
$F^{\rm DK}$, we should construct the global analog of the semi-infinite sheaves ![]() $j_!(\omega _{S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}\!)$,
$j_!(\omega _{S^{-,{\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}}\!)$, ![]() $j_!(\omega _{S^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ defined in § 6.2.
$j_!(\omega _{S^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)$ defined in § 6.2.
Definition 7.3.1 We denote by ![]() ${\operatorname {Bun}}_{B^-}'$ the algebraic stack classifying
${\operatorname {Bun}}_{B^-}'$ the algebraic stack classifying ![]() $B^-$-bundles on
$B^-$-bundles on ![]() $X$ plus a
$X$ plus a ![]() $B$-reduction of the induced
$B$-reduction of the induced ![]() $G$-bundle at the point
$G$-bundle at the point ![]() $x$. In other words, it is the fiber product of
$x$. In other words, it is the fiber product of ![]() ${\operatorname {Bun}}_{B^-}$ with the classifying stack of
${\operatorname {Bun}}_{B^-}$ with the classifying stack of ![]() $B$ over the classifying stack of
$B$ over the classifying stack of ![]() $G$.
$G$.
We define ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}'$ as the Drinfeld compactification of
$\overline {{\operatorname {Bun}}}{}_{B^-}'$ as the Drinfeld compactification of ![]() ${\operatorname {Bun}}_{B^-}'$. It classifies the quadruples
${\operatorname {Bun}}_{B^-}'$. It classifies the quadruples ![]() $\{\mathcal {P}_T, \mathcal {P}_G, \{\kappa ^{-, \check {\lambda }}, \check {\lambda }\in \Lambda ^+\},\epsilon \}$, where
$\{\mathcal {P}_T, \mathcal {P}_G, \{\kappa ^{-, \check {\lambda }}, \check {\lambda }\in \Lambda ^+\},\epsilon \}$, where ![]() $\mathcal {P}_T\in {\operatorname {Bun}}_T$ is a
$\mathcal {P}_T\in {\operatorname {Bun}}_T$ is a ![]() $T$-bundle on
$T$-bundle on ![]() $X$,
$X$, ![]() $\mathcal {P}_G$ is a
$\mathcal {P}_G$ is a ![]() $G$-bundle on
$G$-bundle on ![]() $X$ and
$X$ and
is a collection of morphisms which are regular on ![]() $X$ and satisfy the Plücker relations.
$X$ and satisfy the Plücker relations.
By omitting the Iwahori structure ![]() $\epsilon$, we get the Drinfeld compactification
$\epsilon$, we get the Drinfeld compactification ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}$ of
$\overline {{\operatorname {Bun}}}{}_{B^-}$ of ![]() ${\operatorname {Bun}}_{B^-}$.
${\operatorname {Bun}}_{B^-}$.
Remark 7.3.2 If we require ![]() $\kappa ^{-.\check {\lambda }}$ to be surjective in the definition of
$\kappa ^{-.\check {\lambda }}$ to be surjective in the definition of ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}'$ (respectively,
$\overline {{\operatorname {Bun}}}{}_{B^-}'$ (respectively, ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}$), the resulting stack is
$\overline {{\operatorname {Bun}}}{}_{B^-}$), the resulting stack is ![]() ${{\operatorname {Bun}}}_{B^-}'$ (respectively,
${{\operatorname {Bun}}}_{B^-}'$ (respectively, ![]() ${\operatorname {Bun}}_{B^-}$).
${\operatorname {Bun}}_{B^-}$).
Definition 7.3.3 We define the gerbe ![]() $\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$ on
$\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$ on ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}$ (respectively,
$\overline {{\operatorname {Bun}}}{}_{B^-}$ (respectively, ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}'$) as
$\overline {{\operatorname {Bun}}}{}_{B^-}'$) as ![]() $(\mathcal {G}^G)^{-1}\otimes (\mathcal {G}^T)$.
$(\mathcal {G}^G)^{-1}\otimes (\mathcal {G}^T)$.
Here ![]() ${\operatorname {Bun}}_{B^-}'$ has a relative position map
${\operatorname {Bun}}_{B^-}'$ has a relative position map
We denote the preimage of the Bruhat cell ![]() ${\operatorname {Br}}^w\subset B^-\backslash G/B$ in
${\operatorname {Br}}^w\subset B^-\backslash G/B$ in ![]() ${\operatorname {Bun}}_{B^-}'$ by
${\operatorname {Bun}}_{B^-}'$ by ![]() ${\operatorname {Bun}}_{B^-}^w$,
${\operatorname {Bun}}_{B^-}^w$, ![]() $w\in W$. For convenience, we denote by
$w\in W$. For convenience, we denote by ![]() ${\operatorname {Bun}}_{B^-}^{\prime \prime }$ the stack
${\operatorname {Bun}}_{B^-}^{\prime \prime }$ the stack ![]() ${\operatorname {Bun}}_{B^-}^{1}$.
${\operatorname {Bun}}_{B^-}^{1}$.
By the definitions of ![]() $\mathcal {G}^G$ and
$\mathcal {G}^G$ and ![]() $\mathcal {G}^T$ in § 2.4, we see that the gerbe
$\mathcal {G}^T$ in § 2.4, we see that the gerbe ![]() $\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$ is canonically trivial on
$\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$ is canonically trivial on ![]() ${\operatorname {Bun}}_{B^-}''\subset \overline {{\operatorname {Bun}}}{}_{B^-}'$ and
${\operatorname {Bun}}_{B^-}''\subset \overline {{\operatorname {Bun}}}{}_{B^-}'$ and ![]() ${\operatorname {Bun}}_{B^-}\subset \overline {{\operatorname {Bun}}}{}_{B^-}$. Hence, the categories of
${\operatorname {Bun}}_{B^-}\subset \overline {{\operatorname {Bun}}}{}_{B^-}$. Hence, the categories of ![]() $\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$-twisted sheaves on
$\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$-twisted sheaves on ![]() ${\operatorname {Bun}}_{B^-}''$ and
${\operatorname {Bun}}_{B^-}''$ and ![]() ${\operatorname {Bun}}_{B^-}$ are equivalent to the categories of non-twisted sheaves on the corresponding stacks. In particular, we can consider the constant sheaf in the twisted case.
${\operatorname {Bun}}_{B^-}$ are equivalent to the categories of non-twisted sheaves on the corresponding stacks. In particular, we can consider the constant sheaf in the twisted case.
Definition 7.3.4 We denote by ![]() $j^-_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ (respectively,
$j^-_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ (respectively, ![]() $j^-_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}$) the
$j^-_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}$) the ![]() $!$-extension of the
$!$-extension of the ![]() $\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$-twisted perverse constant sheaf on
$\mathcal {G}_{{\mathop {\operatorname {\rm glob}}}}^{G, T, {\mathop {\operatorname {\rm ratio}}}}$-twisted perverse constant sheaf on ![]() ${\operatorname {Bun}}_{B^-}''$ (respectively,
${\operatorname {Bun}}_{B^-}''$ (respectively, ![]() ${\operatorname {Bun}}_{B^-}\!$) to
${\operatorname {Bun}}_{B^-}\!$) to ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}'$ (respectively,
$\overline {{\operatorname {Bun}}}{}_{B^-}'$ (respectively, ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}\!$).
$\overline {{\operatorname {Bun}}}{}_{B^-}\!$).
7.4 Zastava spaces
Zastava spaces are introduced in [Reference Finkelberg and MirkovićFM99]. They play an important role in our global construction of the functor. Let us recall the definitions of the Zastava space and related stacks in this section.
Definition 7.4.1 We define the compactified Zastava space ![]() $\bar {Z}_{{\operatorname {Gr}}}$ and Zastava space
$\bar {Z}_{{\operatorname {Gr}}}$ and Zastava space ![]() ${Z}_{{\operatorname {Gr}}}$ as
${Z}_{{\operatorname {Gr}}}$ as
 \[ \begin{aligned} \bar{Z}_{{\operatorname{Gr}}}:=\overline{{\operatorname{Bun}}_N^{\omega^\rho}}\mathop{\times'}_{{\operatorname{Bun}}_G} \overline{{\operatorname{Bun}}}{}_{B^-},\\ {Z}_{{\operatorname{Gr}}}:=\overline{{\operatorname{Bun}}_N^{\omega^\rho}}\mathop{\times'}_{{\operatorname{Bun}}_G} {{\operatorname{Bun}}}_{B^-}, \end{aligned} \]
\[ \begin{aligned} \bar{Z}_{{\operatorname{Gr}}}:=\overline{{\operatorname{Bun}}_N^{\omega^\rho}}\mathop{\times'}_{{\operatorname{Bun}}_G} \overline{{\operatorname{Bun}}}{}_{B^-},\\ {Z}_{{\operatorname{Gr}}}:=\overline{{\operatorname{Bun}}_N^{\omega^\rho}}\mathop{\times'}_{{\operatorname{Bun}}_G} {{\operatorname{Bun}}}_{B^-}, \end{aligned} \]
where ![]() $\times '$ means the open substack of the fiber product such that the composition of
$\times '$ means the open substack of the fiber product such that the composition of ![]() $\kappa ^{\check {\lambda }}$ and
$\kappa ^{\check {\lambda }}$ and ![]() $\kappa ^{-, \check {\lambda }}$ is non-zero for any dominant weight
$\kappa ^{-, \check {\lambda }}$ is non-zero for any dominant weight ![]() $\check {\lambda }$.
$\check {\lambda }$.
Definition 7.4.2 Similarly, we define the affine flags version of Zastava spaces as
 \begin{equation} \begin{aligned} (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}:=\overline{({\operatorname{Bun}}_N^{\omega^\rho})}'_{\infty\cdot x} \mathop{\times'}_{{\operatorname{Bun}}_G'} \overline{{\operatorname{Bun}}}{}_{B^-}',\\ ({Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}:=\overline{({\operatorname{Bun}}_N^{\omega^\rho})}'_{\infty\cdot x} \mathop{\times'}_{{\operatorname{Bun}}_G'} {{\operatorname{Bun}}_{B^-}^{\prime \prime}}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}:=\overline{({\operatorname{Bun}}_N^{\omega^\rho})}'_{\infty\cdot x} \mathop{\times'}_{{\operatorname{Bun}}_G'} \overline{{\operatorname{Bun}}}{}_{B^-}',\\ ({Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}:=\overline{({\operatorname{Bun}}_N^{\omega^\rho})}'_{\infty\cdot x} \mathop{\times'}_{{\operatorname{Bun}}_G'} {{\operatorname{Bun}}_{B^-}^{\prime \prime}}. \end{aligned} \end{equation} Since we assume that ![]() $[G,G]$ is simply-connected, taking zeros of the composition of
$[G,G]$ is simply-connected, taking zeros of the composition of ![]() $\kappa ^{\check {\lambda }}$ and
$\kappa ^{\check {\lambda }}$ and ![]() $\kappa ^{-,\check {\lambda }}$ gives ind-proper maps
$\kappa ^{-,\check {\lambda }}$ gives ind-proper maps
and
By [Reference Braverman, Finkelberg, Gaitsgory and MirkovićBFGM02, § 2.3], the Zastava spaces satisfy the factorization property.
Lemma 7.4.3 There exists isomorphisms
and
 \begin{equation} \begin{aligned} (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\\ & \simeq\\ (\bar{Z}_{{\operatorname{Gr}}}\times (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}) & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}\\ & \simeq\\ (\bar{Z}_{{\operatorname{Gr}}}\times (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}) & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})_{\rm disj}. \end{aligned} \end{equation}7.5 Construction of global functors
Let us consider the following diagram.

Definition 7.5.1 We define global functors ![]() $F_{{\mathop {\operatorname {\rm glob}}}}^{\rm L}$ and
$F_{{\mathop {\operatorname {\rm glob}}}}^{\rm L}$ and ![]() $F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$ as
$F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$ as
 \begin{equation} \begin{aligned} F^{\rm L}_{{\mathop{\operatorname{\rm glob}}}}: \operatorname{Whit}_{q}((\overline{{\operatorname{Bun}}_N^{\omega^\rho}})'_{\infty\cdot x}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})\\ \mathcal{F} & \mapsto v_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{\prime ,!}(\mathcal{F})\mathop{\otimes}^{!} \bar{\mathfrak{p}}_Z^{\prime ,!} (j^-_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}} [\dim {\operatorname{Bun}}_G'])), \end{aligned} \end{equation}
\begin{equation} \begin{aligned} F^{\rm L}_{{\mathop{\operatorname{\rm glob}}}}: \operatorname{Whit}_{q}((\overline{{\operatorname{Bun}}_N^{\omega^\rho}})'_{\infty\cdot x}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})\\ \mathcal{F} & \mapsto v_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{\prime ,!}(\mathcal{F})\mathop{\otimes}^{!} \bar{\mathfrak{p}}_Z^{\prime ,!} (j^-_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}} [\dim {\operatorname{Bun}}_G'])), \end{aligned} \end{equation}and
 \begin{equation} \begin{aligned} F^{\rm DK}_{{\mathop{\operatorname{\rm glob}}}}: \operatorname{Whit}_{q}((\overline{{\operatorname{Bun}}_N^{\omega^\rho}})'_{\infty\cdot x}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})\\ \mathcal{F} & \mapsto v_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{\prime ,!}(\mathcal{F}) \mathop{\otimes}^{!}\bar{\mathfrak{p}}_Z^{\prime ,!} (j^-_{*, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}[\dim {\operatorname{Bun}}_G'])). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} F^{\rm DK}_{{\mathop{\operatorname{\rm glob}}}}: \operatorname{Whit}_{q}((\overline{{\operatorname{Bun}}_N^{\omega^\rho}})'_{\infty\cdot x}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x})\\ \mathcal{F} & \mapsto v_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{\prime ,!}(\mathcal{F}) \mathop{\otimes}^{!}\bar{\mathfrak{p}}_Z^{\prime ,!} (j^-_{*, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}[\dim {\operatorname{Bun}}_G'])). \end{aligned} \end{equation}Similarly, we consider the following diagram without the Iwahori structures.

Definition 7.5.2 We define functors ![]() $F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}$ and
$F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}$ and ![]() $F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}(\mathcal {F})$ as
$F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}(\mathcal {F})$ as
 \begin{equation} \begin{aligned} F^{\rm L}_{{\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}: \operatorname{Whit}_{q}(\overline{{\operatorname{Bun}}_N^{\omega^\rho}}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}})\\ \mathcal{F} & \mapsto v_{{\operatorname{Gr}},{\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{!}(\mathcal{F})\mathop{\otimes}^{!} \bar{\mathfrak{p}}_Z^{!} (j^-_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}[\dim {\operatorname{Bun}}_G])), \end{aligned} \end{equation}
\begin{equation} \begin{aligned} F^{\rm L}_{{\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}: \operatorname{Whit}_{q}(\overline{{\operatorname{Bun}}_N^{\omega^\rho}}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}})\\ \mathcal{F} & \mapsto v_{{\operatorname{Gr}},{\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{!}(\mathcal{F})\mathop{\otimes}^{!} \bar{\mathfrak{p}}_Z^{!} (j^-_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}[\dim {\operatorname{Bun}}_G])), \end{aligned} \end{equation}and
 \begin{equation} \begin{aligned} F^{\rm DK}_{{\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}: \operatorname{Whit}_{q}(\overline{{\operatorname{Bun}}_N^{\omega^\rho}}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}})\\ \mathcal{F} & \mapsto v_{{\operatorname{Gr}},{\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{!}(\mathcal{F})\mathop{\otimes}^{!} \bar{\mathfrak{p}}_Z^{!} (j^-_{*, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}[\dim {\operatorname{Bun}}_G])). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} F^{\rm DK}_{{\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}: \operatorname{Whit}_{q}(\overline{{\operatorname{Bun}}_N^{\omega^\rho}}) & \to \operatorname{Shv}_{\mathcal{G}^\Lambda}({\mathop{\operatorname{\rm Conf}}})\\ \mathcal{F} & \mapsto v_{{\operatorname{Gr}},{\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{!}(\mathcal{F})\mathop{\otimes}^{!} \bar{\mathfrak{p}}_Z^{!} (j^-_{*, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Gr}}}[\dim {\operatorname{Bun}}_G])). \end{aligned} \end{equation}7.6 Comparison between local–global functors
7.6.1
Recall that in § 6.3, we define a ![]() ${{\mathcal {Y}}}$-parametrized prestack
${{\mathcal {Y}}}$-parametrized prestack ![]() ${}_{{\mathcal {Y}}}{\operatorname {Fl}}$, for any prestack
${}_{{\mathcal {Y}}}{\operatorname {Fl}}$, for any prestack ![]() ${\mathcal {Y}}$ with a map to
${\mathcal {Y}}$ with a map to ![]() $T({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}\backslash {\mathop {\operatorname {\rm Ran}}}_x$. Now, we consider two cases:
$T({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}\backslash {\mathop {\operatorname {\rm Ran}}}_x$. Now, we consider two cases: ![]() ${\mathcal {Y}}=({\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$ and
${\mathcal {Y}}=({\operatorname {Gr}}_{T,{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho })_{\infty \cdot x}^{\text {neg}}$ and ![]() ${\mathcal {Y}}={\operatorname {Bun}}_T\times {\mathop {\operatorname {\rm Ran}}}_x$. We denote the resulting prestacks by
${\mathcal {Y}}={\operatorname {Bun}}_T\times {\mathop {\operatorname {\rm Ran}}}_x$. We denote the resulting prestacks by ![]() ${}_{{\operatorname {Gr}}_T}{\operatorname {Fl}}$ and
${}_{{\operatorname {Gr}}_T}{\operatorname {Fl}}$ and ![]() ${}_{{\operatorname {Bun}}_T}{\operatorname {Fl}}$, respectively.
${}_{{\operatorname {Bun}}_T}{\operatorname {Fl}}$, respectively.
Note that the restriction of ![]() ${\mathcal {G}}^G$ on
${\mathcal {G}}^G$ on ![]() ${\operatorname {Bun}}_{B^-}':={\operatorname {Bun}}_{B^-}\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B$ is canonically identified with
${\operatorname {Bun}}_{B^-}':={\operatorname {Bun}}_{B^-}\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B$ is canonically identified with ![]() ${\mathcal {G}}^T$, which implies that
${\mathcal {G}}^T$, which implies that ![]() ${\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}$ on
${\mathcal {G}}^{G,T,{\mathop {\operatorname {\rm ratio}}}}$ on ![]() ${\operatorname {Bun}}_{B^-}'$ is canonically trivial. Let
${\operatorname {Bun}}_{B^-}'$ is canonically trivial. Let ![]() $j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^-\in \operatorname {Shv}_{(({\mathcal {G}})^{G,T,{\mathop {\operatorname {\rm ratio}}}})^{-1}}(\overline {{\operatorname {Bun}}}_{B^-}')$ be the
$j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^-\in \operatorname {Shv}_{(({\mathcal {G}})^{G,T,{\mathop {\operatorname {\rm ratio}}}})^{-1}}(\overline {{\operatorname {Bun}}}_{B^-}')$ be the ![]() $!$-extension of the (twisted) constant perverse on
$!$-extension of the (twisted) constant perverse on ![]() ${\operatorname {Bun}}_{B^-}'$.
${\operatorname {Bun}}_{B^-}'$.
The algebraic stack ![]() $\overline {{\operatorname {Bun}}}_{B^-}'$ is an algebraic stack over
$\overline {{\operatorname {Bun}}}_{B^-}'$ is an algebraic stack over ![]() ${\operatorname {Bun}}_T$ and can be regarded as a
${\operatorname {Bun}}_T$ and can be regarded as a ![]() $T$-twisted construction of
$T$-twisted construction of ![]() $(\overline {{\operatorname {Bun}}}_{N^-}^{\omega ^\rho })^{1}$ (the negative analog of
$(\overline {{\operatorname {Bun}}}_{N^-}^{\omega ^\rho })^{1}$ (the negative analog of ![]() $(\overline {{\operatorname {Bun}}}_{N}^{\omega ^\rho })^{w_0}$ in § A). In other words, it is a stack over
$(\overline {{\operatorname {Bun}}}_{N}^{\omega ^\rho })^{w_0}$ in § A). In other words, it is a stack over ![]() ${\operatorname {Bun}}_T$ and the fiber over
${\operatorname {Bun}}_T$ and the fiber over ![]() ${\mathcal {P}}_T$ is the
${\mathcal {P}}_T$ is the ![]() ${\mathcal {P}}_T$-twisted
${\mathcal {P}}_T$-twisted ![]() $(\overline {{\operatorname {Bun}}}_{N^-}^{\omega ^\rho })^{1}$. We have a natural projection
$(\overline {{\operatorname {Bun}}}_{N^-}^{\omega ^\rho })^{1}$. We have a natural projection
A relative version of the proof of Lemma A.2.1 yields the following lemma.
Lemma 7.6.2
Furthermore, by definition, the ![]() $!$-pullback of
$!$-pullback of ![]() ${}_{{\operatorname {Bun}}_T}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ along
${}_{{\operatorname {Bun}}_T}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$ along ![]() ${}_{{\operatorname {Gr}}_T}{\operatorname {Fl}}\longrightarrow {}_{{\operatorname {Bun}}_T}{\operatorname {Fl}}$ goes to
${}_{{\operatorname {Gr}}_T}{\operatorname {Fl}}\longrightarrow {}_{{\operatorname {Bun}}_T}{\operatorname {Fl}}$ goes to ![]() ${}_{{\operatorname {Gr}}_T}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$. This implies the following lemma
${}_{{\operatorname {Gr}}_T}j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{-,1}}\!)$. This implies the following lemma
Lemma 7.6.3 We have
where ![]() $\pi _{S_{{\mathop {\operatorname {\rm Conf}}}}\to {\operatorname {Bun}}_B}$ is the natural projection from
$\pi _{S_{{\mathop {\operatorname {\rm Conf}}}}\to {\operatorname {Bun}}_B}$ is the natural projection from ![]() $\overline {S}^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ to
$\overline {S}^{-,1, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ to ![]() $\overline {{\operatorname {Bun}}}'_{B^-}$.
$\overline {{\operatorname {Bun}}}'_{B^-}$.
With the preparations above, we prove the following proposition, which is the analog of [Reference Gaitsgory and LysenkoGL19, Proposition 20.3.4] in the affine flags case.
Lemma 7.6.4 We have
and
Proof. The Zastava space ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ is isomorphic to
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ is isomorphic to ![]() $(\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{w_0})_{\infty \cdot x}\cap (\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})$ (see [Reference Gaitsgory and LysenkoGL19, Proposition 20.2.2]). Under this identification,
$(\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{w_0})_{\infty \cdot x}\cap (\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}})$ (see [Reference Gaitsgory and LysenkoGL19, Proposition 20.2.2]). Under this identification, ![]() $v_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is identified with
$v_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}$ is identified with ![]() $v_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}$.
$v_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}$.
Now the lemma follows from the following two facts.
– The
 $!$-pullback of
$!$-pullback of  $j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^-[\dim {\operatorname {Bun}}_G']$ along
$j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^-[\dim {\operatorname {Bun}}_G']$ along  $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}\to \overline {{\operatorname {Bun}}}{}_{B^-}'$ is isomorphic to the sheaf
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}\to \overline {{\operatorname {Bun}}}{}_{B^-}'$ is isomorphic to the sheaf  $j_!(\omega _{S_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)[\deg +d_g]|_{(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}}$.
$j_!(\omega _{S_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{-,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}}\!)[\deg +d_g]|_{(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}}$.– The sheaf
 $\operatorname {sprd}_{{\operatorname {Fl}}}\circ \pi _{{\operatorname {Fl}},x}^!(\mathcal {F})$ is isomorphic to the
$\operatorname {sprd}_{{\operatorname {Fl}}}\circ \pi _{{\operatorname {Fl}},x}^!(\mathcal {F})$ is isomorphic to the  $!$-pullback of
$!$-pullback of  $\mathcal {F}$ along
$\mathcal {F}$ along  $(\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{w_0})_{\infty \cdot x}\to (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })_{\infty \cdot x}$.
$(\overline {S}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}^{w_0})_{\infty \cdot x}\to (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })_{\infty \cdot x}$.
The first fact follows from Lemma 7.6.3, and the second follows from Lemma 7.2.3.
Similarly, by a local–global comparison, one can prove that
and
Here ![]() $\mathcal {F}_{\emptyset }$ is the unique irreducible object in
$\mathcal {F}_{\emptyset }$ is the unique irreducible object in ![]() $\operatorname {Whit}_{q}(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})$.
$\operatorname {Whit}_{q}(\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})$.
Remark 7.6.5 A priori, it is not easy at all to show that ![]() $F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}}$ factors through a category of factorization modules and the image of
$F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}}$ factors through a category of factorization modules and the image of ![]() $\mathcal {F}_\emptyset$ under
$\mathcal {F}_\emptyset$ under ![]() $F^{\rm L}_{{\mathop {\operatorname {\rm glob}}},{\operatorname {Gr}}}$ admits a factorization algebra structure. It is the reason why we have to start from the local Whittaker category and construct Ran-ified affine flags in preceding sections.
$F^{\rm L}_{{\mathop {\operatorname {\rm glob}}},{\operatorname {Gr}}}$ admits a factorization algebra structure. It is the reason why we have to start from the local Whittaker category and construct Ran-ified affine flags in preceding sections.
By Lemma 7.6.4, to prove Proposition 6.6.2, we only need to prove the following proposition.
Proposition 7.6.6 For any ![]() $\lambda \in \Lambda$, there exists an isomorphism
$\lambda \in \Lambda$, there exists an isomorphism
8. Proof of Proposition 7.6.6: duality
In this section, we study the relationship between ![]() $F_{{\mathop {\operatorname {\rm glob}}}}^{{\rm L}}$ and
$F_{{\mathop {\operatorname {\rm glob}}}}^{{\rm L}}$ and ![]() $F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$. We want to prove that
$F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$. We want to prove that ![]() $F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}}$ and
$F^{\rm L}_{{\mathop {\operatorname {\rm glob}}}}$ and ![]() $F^{\rm DK}_{{\mathop {\operatorname {\rm glob}}}}$ are Verdier dual to each other
$F^{\rm DK}_{{\mathop {\operatorname {\rm glob}}}}$ are Verdier dual to each other
The method is given by reducing the above isomorphism to some stack where we can apply the universally locally acyclic property (ULA).
8.1 Universally locally acyclic
In [Reference Braverman and GaitsgoryBG02, § 5], the authors introduced the notion of ULA.Footnote 9 Roughly speaking, a sheaf is ULA with respect to a morphism if its singular support over each fiber is the same. The following lemma (it is straightforward from the definition in [Reference Braverman and GaitsgoryBG02, § 5.1.2]) explains why the notion of ULA is important.
Lemma 8.1.1 For algebraic stacks ![]() $\mathcal {X}, \mathcal {Y}$ and
$\mathcal {X}, \mathcal {Y}$ and ![]() $\mathcal {W}$, consider the following Cartesian diagram of algebraic stacks.
$\mathcal {W}$, consider the following Cartesian diagram of algebraic stacks.

Given ![]() $\mathcal {F}_1\in \operatorname {Shv}(\mathcal {X}),\mathcal {F}_2\in \operatorname {Shv}(\mathcal {Y})$. If we assume that
$\mathcal {F}_1\in \operatorname {Shv}(\mathcal {X}),\mathcal {F}_2\in \operatorname {Shv}(\mathcal {Y})$. If we assume that ![]() $\mathcal {F}_1$ is ULA with respect to
$\mathcal {F}_1$ is ULA with respect to ![]() $q_2$ and
$q_2$ and ![]() $\mathcal {W}$ is smooth and of dimension
$\mathcal {W}$ is smooth and of dimension ![]() $d$, then the following canonical map (see [Reference Braverman and GaitsgoryBG02, § 5.1])
$d$, then the following canonical map (see [Reference Braverman and GaitsgoryBG02, § 5.1])
is an isomorphism.
8.2 Duality of  $F_{{\mathop {\operatorname {\rm glob}}}}^{\rm L}$ and
$F_{{\mathop {\operatorname {\rm glob}}}}^{\rm L}$ and  $F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$
$F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$
We denote by ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}^{\prime, \lambda }$ the substack of
$\overline {{\operatorname {Bun}}}{}_{B^-}^{\prime, \lambda }$ the substack of ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}'$ such that the degree of the
$\overline {{\operatorname {Bun}}}{}_{B^-}'$ such that the degree of the ![]() $T$-bundle is
$T$-bundle is ![]() $-\lambda +(2g-2)\rho$, and denote by
$-\lambda +(2g-2)\rho$, and denote by ![]() $\overline {{\operatorname {Bun}}}_{B^-, \leq \mu }^{\prime,\lambda }$ the open substack of
$\overline {{\operatorname {Bun}}}_{B^-, \leq \mu }^{\prime,\lambda }$ the open substack of ![]() $\overline {{\operatorname {Bun}}}{}_{B^-}^{\prime, \lambda }$ such that the total order of degeneracy of the generalized
$\overline {{\operatorname {Bun}}}{}_{B^-}^{\prime, \lambda }$ such that the total order of degeneracy of the generalized ![]() $B^-$-reductions is no more than
$B^-$-reductions is no more than ![]() $\mu$.
$\mu$.
The following lemma is a tiny modification of [Reference CampbellCam19, Propsoition 4.1.1] (see [Reference YangYan21] for a detailed proof).
Lemma 8.2.1 There exists an integer ![]() $d$ which depends only on the genus of
$d$ which depends only on the genus of ![]() $X$, such that, for any
$X$, such that, for any ![]() $\mu \in \Lambda ^{\text {pos}}$, and
$\mu \in \Lambda ^{\text {pos}}$, and ![]() $\lambda \in \Lambda$ satisfying the condition (X): for any
$\lambda \in \Lambda$ satisfying the condition (X): for any ![]() $0\leq \mu '\leq \mu$,
$0\leq \mu '\leq \mu$,
the restriction of ![]() $j^{-}_{!,{\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ to
$j^{-}_{!,{\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ to ![]() $\overline {{\operatorname {Bun}}}_{B^-, \leq \mu }^{\prime,\lambda }$ is ULA with respect to the natural projection
$\overline {{\operatorname {Bun}}}_{B^-, \leq \mu }^{\prime,\lambda }$ is ULA with respect to the natural projection
In this section, we prove the following theorem using Lemma 8.2.1.
Theorem 8.2.2 We have that ![]() $F_{{\mathop {\operatorname {\rm glob}}}}^{\rm L}$ and
$F_{{\mathop {\operatorname {\rm glob}}}}^{\rm L}$ and ![]() $F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$ are Verdier dual to each other, i.e.
$F_{{\mathop {\operatorname {\rm glob}}}}^{\rm DK}$ are Verdier dual to each other, i.e.
The proof of Theorem 8.2.2 follows a standard factorization argument that has been used in various references such as [Reference Gaitsgory and NadlerGN10, § 16.4], [Reference GaitsgoryGai18a, Proof of Proposition 3.6.5], [Reference Gaitsgory and LysenkoGL19, § 21.2], etc.
8.2.3 Step I
We want to prove that the natural transformation
 \[ \begin{aligned} \mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}(v_{{\operatorname{Fl}},{\mathop{\operatorname{\rm glob}}},!}(\bar{\mathfrak{q}}_Z^{!}(\mathcal{F}) \mathop{\otimes}^{!} & \bar{\mathfrak{p}}_Z^{!} (j^{-}_{*, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}[\dim {\operatorname{Bun}}_G'])))\\ \downarrow & \\ v_{{\operatorname{Fl}},{\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{!}(\mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}(\mathcal{F})) \mathop{\otimes}^{!} & \bar{\mathfrak{p}}_Z^{!} (j^{-}_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}[\dim {\operatorname{Bun}}_G'])), \end{aligned} \]
\[ \begin{aligned} \mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}(v_{{\operatorname{Fl}},{\mathop{\operatorname{\rm glob}}},!}(\bar{\mathfrak{q}}_Z^{!}(\mathcal{F}) \mathop{\otimes}^{!} & \bar{\mathfrak{p}}_Z^{!} (j^{-}_{*, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}[\dim {\operatorname{Bun}}_G'])))\\ \downarrow & \\ v_{{\operatorname{Fl}},{\mathop{\operatorname{\rm glob}}}, !}(\bar{\mathfrak{q}}_Z^{!}(\mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}(\mathcal{F})) \mathop{\otimes}^{!} & \bar{\mathfrak{p}}_Z^{!} (j^{-}_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}[\dim {\operatorname{Bun}}_G'])), \end{aligned} \]
which is obtained in [Reference Braverman and GaitsgoryBG02, § 5.1] is an isomorphism for any locally compact object ![]() $\mathcal {F}\in \operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')^{\rm loc.c}$.
$\mathcal {F}\in \operatorname {Whit}_{\rm q}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')^{\rm loc.c}$.
By definition, ![]() $v_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}$ is ind-proper, hence, it suffices to prove
$v_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}$ is ind-proper, hence, it suffices to prove
We only need to prove
for any ![]() $\mathcal {F}\in \operatorname {Whit}_{q^{-1}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')^{\rm loc.c}$. Since
$\mathcal {F}\in \operatorname {Whit}_{q^{-1}}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})_{\infty \cdot x}')^{\rm loc.c}$. Since ![]() $j^{-}_{*, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ and
$j^{-}_{*, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ and ![]() $j^{-}_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ are dual to each other, we should prove
$j^{-}_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ are dual to each other, we should prove
This indicates to us that we should use Lemma 8.1.1. That is to say, if we can prove that ![]() $j^{-}_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ is ULA with respect to the projection morphism (8.2.1), then (8.2.3) follows from Lemma 8.1.1. But, in fact, we do not need such a strong property. We can recover the isomorphism (8.2.3) by factorization property from its restriction to an open subset.
$j^{-}_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Fl}}}$ is ULA with respect to the projection morphism (8.2.1), then (8.2.3) follows from Lemma 8.1.1. But, in fact, we do not need such a strong property. We can recover the isomorphism (8.2.3) by factorization property from its restriction to an open subset.
Definition 8.2.4 Denote by ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda, \leq \mu }$ the preimage of
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda, \leq \mu }$ the preimage of ![]() $\overline {{\operatorname {Bun}}}_{B^-, \leq \mu }^{\prime,\lambda }$ in
$\overline {{\operatorname {Bun}}}_{B^-, \leq \mu }^{\prime,\lambda }$ in ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ under the projection morphism
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ under the projection morphism ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}\to \overline {{\operatorname {Bun}}}{}_{B^-}'$. Note that
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}\to \overline {{\operatorname {Bun}}}{}_{B^-}'$. Note that ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda, \leq \mu }$ is open in
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda, \leq \mu }$ is open in ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ for any
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ for any ![]() $\lambda \in \Lambda, \mu \in \Lambda ^{\text {pos}}$.
$\lambda \in \Lambda, \mu \in \Lambda ^{\text {pos}}$.
Combine Lemma 8.1.1 with Lemma 8.2.1, we obtain the following corollary.
Corollary 8.2.5 If ![]() $\lambda$,
$\lambda$, ![]() $\mu$ satisfy condition (X), then the natural transformation (8.2.3) is an isomorphism on
$\mu$ satisfy condition (X), then the natural transformation (8.2.3) is an isomorphism on ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda, \leq \mu }$, for any twisted sheaf
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda, \leq \mu }$, for any twisted sheaf ![]() $\mathcal {F}\in \operatorname {Shv}_{\mathcal {G}^G}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})$.
$\mathcal {F}\in \operatorname {Shv}_{\mathcal {G}^G}((\overline {{\operatorname {Bun}}_N^{\omega ^\rho }})'_{\infty \cdot x})$.
We set
then by the corollary above, (8.2.3) is an isomorphism on ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^s$.
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^s$.
8.2.6 Step II
Now we want to extend this isomorphism to the whole affine flags Zastava space ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ via the factorization properties.
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ via the factorization properties.
We denote by ![]() $\bar {Z}_{{\operatorname {Gr}}}^{\lambda }$ the fiber product
$\bar {Z}_{{\operatorname {Gr}}}^{\lambda }$ the fiber product
Similarly, we denote by ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda }$ the fiber product
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda }$ the fiber product ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^{\lambda }$.
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^{\lambda }$.
By Proposition 7.4.3, the affine flags Zastava space ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ is a factorization module space with respect to
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$ is a factorization module space with respect to ![]() $\bar {Z}_{{\operatorname {Gr}}}$. Note that the factorization structure is compatible with degree, i.e.
$\bar {Z}_{{\operatorname {Gr}}}$. Note that the factorization structure is compatible with degree, i.e.
 \begin{equation} \begin{aligned} \bar{Z}_{{\operatorname{Gr}}}^{\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}\\ & \simeq\\ (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1+\lambda_2}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \bar{Z}_{{\operatorname{Gr}}}^{\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}\\ & \simeq\\ (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1+\lambda_2}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}. \end{aligned} \end{equation}
Denote by ![]() ${Z}_{{\operatorname {Gr}}}^{\circ }:= {\operatorname {Bun}}_N^{\omega ^\rho }\times ' {\operatorname {Bun}}_{B^-}$. Taking the restriction of (8.2.5), we get the following map
${Z}_{{\operatorname {Gr}}}^{\circ }:= {\operatorname {Bun}}_N^{\omega ^\rho }\times ' {\operatorname {Bun}}_{B^-}$. Taking the restriction of (8.2.5), we get the following map
 \begin{equation} \begin{aligned} {Z}_{{\operatorname{Gr}}}^{\circ,\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}\\ & \downarrow\\ (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_1+\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} {Z}_{{\operatorname{Gr}}}^{\circ,\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}\\ & \downarrow\\ (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2} & \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_1+\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}. \end{aligned} \end{equation} We note that for any point in ![]() $Z_{{\operatorname {Gr}}}^{\circ,\lambda _1}$, the
$Z_{{\operatorname {Gr}}}^{\circ,\lambda _1}$, the ![]() $B^-$-structure is genuine (non-degenerate). As a result, given an arbitrary point
$B^-$-structure is genuine (non-degenerate). As a result, given an arbitrary point ![]() $z_2\in (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ and arbitrary point
$z_2\in (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ and arbitrary point ![]() $z_1$ in
$z_1$ in ![]() $Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}$, the corresponding object on the right-hand side of (8.2.6) has the same order of degeneracy of generalized
$Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}$, the corresponding object on the right-hand side of (8.2.6) has the same order of degeneracy of generalized ![]() $B^-$-bundle as
$B^-$-bundle as ![]() $z_2$.
$z_2$.
8.2.7
Here ![]() $Z_{{\operatorname {Gr}}}^{\circ,\lambda _1}\mathop {\times }(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}^{\lambda _1}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^{\lambda _2}} ({\mathop {\operatorname {\rm Conf}}}^{\lambda _1}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^{\lambda _2})_{\rm disj}$ admits two smooth morphisms to
$Z_{{\operatorname {Gr}}}^{\circ,\lambda _1}\mathop {\times }(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}\mathop {\times }_{{\mathop {\operatorname {\rm Conf}}}^{\lambda _1}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^{\lambda _2}} ({\mathop {\operatorname {\rm Conf}}}^{\lambda _1}\times {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}^{\lambda _2})_{\rm disj}$ admits two smooth morphisms to ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$:
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$:
– one is given by the projection to
 $(\bar {Z}_{{\operatorname {Fl}},x})^{\lambda _2}_{\infty \cdot x}$
(8.2.7)
$(\bar {Z}_{{\operatorname {Fl}},x})^{\lambda _2}_{\infty \cdot x}$
(8.2.7) \begin{equation} r_1^{\lambda_1}: Z_{{\operatorname{Gr}}}^{\circ,\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}\to (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2}; \end{equation}
\begin{equation} r_1^{\lambda_1}: Z_{{\operatorname{Gr}}}^{\circ,\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj}\to (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2}; \end{equation}– another one is given by the factorization map (8.2.6) composed with the projection to
 $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$
(8.2.8)
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$
(8.2.8) \begin{align} & r_2^{\lambda_1}: Z_{{\operatorname{Gr}}}^{\circ,\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj} \nonumber\\ &\quad \overset{\text{(8.2.6)}}{\longrightarrow}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1+\lambda_2}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj} \nonumber\\ &\quad \to (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2}. \end{align}
\begin{align} & r_2^{\lambda_1}: Z_{{\operatorname{Gr}}}^{\circ,\lambda_1}\mathop{\times}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_2} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj} \nonumber\\ &\quad \overset{\text{(8.2.6)}}{\longrightarrow}(\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2} \mathop{\times}_{{\mathop{\operatorname{\rm Conf}}}^{\lambda_1+\lambda_2}_{\infty\cdot x}} ({\mathop{\operatorname{\rm Conf}}}^{\lambda_1}\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\lambda_2})_{\rm disj} \nonumber\\ &\quad \to (\bar{Z}_{{\operatorname{Fl}},x})_{\infty \cdot x}^{\lambda_1+\lambda_2}. \end{align}
The key observation for the proof of Theorem 8.2.2 is
– for any
 $\mu \in \Lambda ^{\text {pos}}$,
$\mu \in \Lambda ^{\text {pos}}$,  $\lambda _1\in \Lambda ^{\text {neg}}$, and
$\lambda _1\in \Lambda ^{\text {neg}}$, and  $\lambda _2\in \Lambda$, we can take an open subset
$\lambda _2\in \Lambda$, we can take an open subset  $(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ of
$(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ of  $Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ whose image under
$Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ whose image under  $r_2^{\lambda _1}$ lies in
$r_2^{\lambda _1}$ lies in  $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^s$, and if we let
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^s$, and if we let  $\lambda _1$ and
$\lambda _1$ and  $\mu$ vary, the collection of stacks
$\mu$ vary, the collection of stacks  $\{(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }, \mu \in \Lambda ^{\text {pos}}, \lambda _1\in \Lambda ^{\text {neg}} \}$ gives a smooth cover of
$\{(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }, \mu \in \Lambda ^{\text {pos}}, \lambda _1\in \Lambda ^{\text {neg}} \}$ gives a smooth cover of  $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ by the map
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ by the map  $r_1^{\lambda _1}$.
$r_1^{\lambda _1}$.
Now let us explain the construction of ![]() $(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$.
$(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$.
Definition 8.2.8 Given ![]() $\mu \in \Lambda ^{\text {pos}}$,
$\mu \in \Lambda ^{\text {pos}}$, ![]() $\lambda _1\in \Lambda ^{\text {neg}}$, and
$\lambda _1\in \Lambda ^{\text {neg}}$, and ![]() $\lambda _2\in \Lambda$, a point of
$\lambda _2\in \Lambda$, a point of ![]() $(Z_{{\operatorname {Gr}}}^{\circ,\lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\rm disj}$ belongs to
$(Z_{{\operatorname {Gr}}}^{\circ,\lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\rm disj}$ belongs to ![]() $(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ if and only if:
$(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ if and only if:
(1) the order of degeneracy of the generalized
 $B^-$-structure is no more than
$B^-$-structure is no more than  $\mu$;
$\mu$;(2)
 $\lambda :=\lambda _1+\lambda _2$ and
$\lambda :=\lambda _1+\lambda _2$ and  $\mu$ satisfy condition (X).
$\mu$ satisfy condition (X).
If we allow ![]() $\lambda _1$ and
$\lambda _1$ and ![]() $\mu$ to vary, the collection of
$\mu$ to vary, the collection of ![]() $(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ forms a smooth cover of
$(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ forms a smooth cover of ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ by
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ by ![]() $r_1^{\lambda _1}$. The claim (8.2.3) is local in smooth topology, so we only need to prove that the
$r_1^{\lambda _1}$. The claim (8.2.3) is local in smooth topology, so we only need to prove that the ![]() $!$-pullback of the morphism (8.2.3) to
$!$-pullback of the morphism (8.2.3) to ![]() $(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ along
$(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ along ![]() $r_1^{\lambda _1}$ is an isomorphism.
$r_1^{\lambda _1}$ is an isomorphism.
By the same argument as [Reference GaitsgoryGai18a, § 3.9], we can see that the pullbacks of the morphism (8.2.3) along ![]() $r_1^{\lambda _1}$ and
$r_1^{\lambda _1}$ and ![]() $r_2^{\lambda _1}$ differ by a
$r_2^{\lambda _1}$ differ by a ![]() $lisse$ local system. To be more precise, by factorization property, the
$lisse$ local system. To be more precise, by factorization property, the ![]() $!$-pullback of the restriction of (8.2.3) on
$!$-pullback of the restriction of (8.2.3) on ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _1+\lambda _2}$ along
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _1+\lambda _2}$ along ![]() $r_2^{\lambda _1}$ is given by the restriction of the external product of
$r_2^{\lambda _1}$ is given by the restriction of the external product of ![]() $\bar {\mathfrak {q}}_Z^{!}(\mathcal {F}_\emptyset )\mathop {\otimes }^{!} \bar {\mathfrak {p}}_Z^{!} (j^-_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}[\dim {\operatorname {Bun}}_G])$ and (8.2.3). On the other hand, the
$\bar {\mathfrak {q}}_Z^{!}(\mathcal {F}_\emptyset )\mathop {\otimes }^{!} \bar {\mathfrak {p}}_Z^{!} (j^-_{!, {\mathop {\operatorname {\rm glob}}}, {\operatorname {Gr}}}[\dim {\operatorname {Bun}}_G])$ and (8.2.3). On the other hand, the ![]() $!$-pullback of (8.2.3) along
$!$-pullback of (8.2.3) along ![]() $r_1^{\lambda _1}$ is given by the restriction of the external product of the dualizing sheaf on
$r_1^{\lambda _1}$ is given by the restriction of the external product of the dualizing sheaf on ![]() $Z^{\circ,\lambda _1}_{{\operatorname {Gr}}}$ and (8.2.3).
$Z^{\circ,\lambda _1}_{{\operatorname {Gr}}}$ and (8.2.3).
Hence, we only need to prove that the pullback of (8.2.3) along ![]() $r_2^{\lambda _1}$ is an isomorphism when restricted to
$r_2^{\lambda _1}$ is an isomorphism when restricted to ![]() $(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$.
$(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$.
By Corollary 8.2.5, we know that our claim is true on
Hence, the pullback of the morphism (8.2.3) to the open subset ![]() $(r_2^{\lambda _1})^{-1}((\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{s,\lambda _1+\lambda _2})$ in
$(r_2^{\lambda _1})^{-1}((\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{s,\lambda _1+\lambda _2})$ in ![]() $Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ is still an isomorphism. Now the claim follows from the fact that
$Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2}$ is still an isomorphism. Now the claim follows from the fact that ![]() $(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ is contained in
$(Z_{{\operatorname {Gr}}}^{\circ, \lambda _1}\times (\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{\lambda _2})_{\mu }$ is contained in ![]() $(r_2^{\lambda _1})^{-1}((\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{s,\lambda _1+\lambda _2})$ by our choice of
$(r_2^{\lambda _1})^{-1}((\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}^{s,\lambda _1+\lambda _2})$ by our choice of ![]() $\lambda _1,\lambda _2$ and
$\lambda _1,\lambda _2$ and ![]() $\mu$.
$\mu$.
Thus, we have proved Theorem 8.2.2.
8.3 Proof of Proposition 7.6.6
We define ![]() $\widetilde {\nabla }_{\lambda, {\mathop {\operatorname {\rm glob}}}}$ to be the Verdier dual of
$\widetilde {\nabla }_{\lambda, {\mathop {\operatorname {\rm glob}}}}$ to be the Verdier dual of ![]() $\Delta _{\lambda, {\mathop {\operatorname {\rm glob}}}}$.
$\Delta _{\lambda, {\mathop {\operatorname {\rm glob}}}}$.
Proposition 8.3.1 There is an isomorphism
Proof. In order to simplify the notation, we omit the twisting notation here.
According to Lemma 7.6.4, we have ![]() $F^{\rm DK}\simeq F^{\rm DK}_{{\mathop {\operatorname {\rm glob}}}}\circ \pi _{{\operatorname {Fl}},x}[d_g]$. Furthermore, since the Verdier duality functor commutes with
$F^{\rm DK}\simeq F^{\rm DK}_{{\mathop {\operatorname {\rm glob}}}}\circ \pi _{{\operatorname {Fl}},x}[d_g]$. Furthermore, since the Verdier duality functor commutes with ![]() $\pi _{{\operatorname {Fl}},x}[d_g]$, we only need to prove that the image of
$\pi _{{\operatorname {Fl}},x}[d_g]$, we only need to prove that the image of ![]() $\widetilde {\nabla }_\lambda := \mathbb {D}^{{\mathop {\operatorname {\rm Verdier}}}}(\Delta _\lambda )$ under the functor
$\widetilde {\nabla }_\lambda := \mathbb {D}^{{\mathop {\operatorname {\rm Verdier}}}}(\Delta _\lambda )$ under the functor ![]() $F^{\rm DK}$ is isomorphic to
$F^{\rm DK}$ is isomorphic to ![]() $\nabla _{\lambda, \Omega _{q}^{{\rm DK}, \prime }}$.
$\nabla _{\lambda, \Omega _{q}^{{\rm DK}, \prime }}$.
Proposition 5.7.6 asserts that the twisted sheaf ![]() $\widetilde {\nabla }_\lambda \simeq \mathbb {D}^{{\mathop {\operatorname {\rm Verdier}}}}(\Delta _\lambda )$ is isomorphic to
$\widetilde {\nabla }_\lambda \simeq \mathbb {D}^{{\mathop {\operatorname {\rm Verdier}}}}(\Delta _\lambda )$ is isomorphic to ![]() $\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}})$. By Corollary 6.5.3, in order to show the proposition, it suffices to show
$\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}})$. By Corollary 6.5.3, in order to show the proposition, it suffices to show
if ![]() $\lambda \neq \mu$, and
$\lambda \neq \mu$, and
if ![]() $\lambda =\mu$.
$\lambda =\mu$.
Note that ![]() $\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}})$ is compact, so it is supported on finitely many
$\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}})$ is compact, so it is supported on finitely many ![]() $N({\mathcal {K}})^{\omega ^\rho }$-orbits in
$N({\mathcal {K}})^{\omega ^\rho }$-orbits in ![]() ${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$. Furthermore, the intersection
${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$. Furthermore, the intersection ![]() $S_{{\operatorname {Fl}},x}^{t^\lambda w}\cap S_{{\operatorname {Fl}},x}^{-,\mu }$ is of finite type for any
$S_{{\operatorname {Fl}},x}^{t^\lambda w}\cap S_{{\operatorname {Fl}},x}^{-,\mu }$ is of finite type for any ![]() $t^\lambda w$ and
$t^\lambda w$ and ![]() $\mu$ (since it is the central fiber of a finite type scheme
$\mu$ (since it is the central fiber of a finite type scheme ![]() $({\operatorname {Bun}}_N^{\omega ^\rho })_{=\lambda \cdot x}^{w}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\prime \prime,\mu }$ over
$({\operatorname {Bun}}_N^{\omega ^\rho })_{=\lambda \cdot x}^{w}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\prime \prime,\mu }$ over ![]() $\mu \cdot x\in {\mathop {\operatorname {\rm Conf}}}^\mu _{\leq \lambda \cdot x}$). This implies that there exists a very dominant
$\mu \cdot x\in {\mathop {\operatorname {\rm Conf}}}^\mu _{\leq \lambda \cdot x}$). This implies that there exists a very dominant ![]() $\eta$ such that
$\eta$ such that ![]() ${\mathop {\operatorname {\rm supp}}}(\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}}))\cap t^{\eta }I^{\omega ^\rho } t^{-\eta +\mu }I^{\omega ^\rho }/I^{\omega ^\rho }= {\mathop {\operatorname {\rm supp}}}(\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}}))\cap S_{{\operatorname {Fl}},x}^{-,\mu }.$ Let
${\mathop {\operatorname {\rm supp}}}(\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}}))\cap t^{\eta }I^{\omega ^\rho } t^{-\eta +\mu }I^{\omega ^\rho }/I^{\omega ^\rho }= {\mathop {\operatorname {\rm supp}}}(\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}}))\cap S_{{\operatorname {Fl}},x}^{-,\mu }.$ Let ![]() $t^\eta {\operatorname {Fl}}^{{-\eta +\mu }}:=t^{\eta }I^{\omega ^\rho } t^{-\eta +\mu }I^{\omega ^\rho }/I^{\omega ^\rho }$, and denote
$t^\eta {\operatorname {Fl}}^{{-\eta +\mu }}:=t^{\eta }I^{\omega ^\rho } t^{-\eta +\mu }I^{\omega ^\rho }/I^{\omega ^\rho }$, and denote ![]() $j_*(\omega _{t^\eta {\operatorname {Fl}}^{{-\eta +\mu }}})$ as the
$j_*(\omega _{t^\eta {\operatorname {Fl}}^{{-\eta +\mu }}})$ as the ![]() $*$-extension of the twisted dualizing sheaf on
$*$-extension of the twisted dualizing sheaf on ![]() $t^\eta {\operatorname {Fl}}^{{-\eta +\mu }}$.
$t^\eta {\operatorname {Fl}}^{{-\eta +\mu }}$.
Since ![]() $\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}})$ is
$\operatorname {Av}_*^{\rm ren}({{J}}_\lambda ^{\mathbb {D}})$ is ![]() $N(\mathcal {O})^{\omega ^\rho }$-equivariant, we have
$N(\mathcal {O})^{\omega ^\rho }$-equivariant, we have
 \begin{align} & H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \mathop{\otimes}^! j_{*}(\omega_{S^{-, \mu}_{{\operatorname{Fl}},x}})[\langle\mu, 2\check{\rho}\rangle]) \nonumber\\ &\quad \simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \mathop{\otimes}^! j_*(\omega_{t^\eta{\operatorname{Fl}}^{{-\eta+\mu}}})[\langle\mu, 2\check{\rho}\rangle]) \nonumber\\ &\quad \simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \mathop{\otimes}^! \operatorname{Av}_*^{N(\mathcal{O})^{\omega^\rho}}(j_{*}(\omega_{t^\eta{\operatorname{Fl}}^{{-\eta+\mu}}}) [\langle\mu, 2\check{\rho}\rangle])) \nonumber\\ &\quad \simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \overset{!}{\otimes} {{J}}_{\eta,*}\star {{J}}_{-\eta+\mu,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} (\delta_0, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}})\star {{J}}_{\eta-\mu,*}\star {{J}}_{-\eta,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} ({{J}}_{\eta,!}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}})\star {{J}}_{\eta-\mu,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} (\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}({{J}}_{\eta,!}), \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}})\star {{J}}_{\eta-\mu,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho})}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi} ({{J}}_{\eta,!}), \operatorname{Av}_*^{\rm ren}({{J}}_{\lambda+\eta-\mu}^{\mathbb{D}})) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} (\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}(\delta_{\eta,!})[-\langle\eta,2\check{\rho}\rangle], \operatorname{Av}_*^{\rm ren}(\delta_{\lambda+\eta-\mu})[\langle\lambda+\eta-\mu,2\check{\rho}\rangle]). \end{align}
\begin{align} & H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \mathop{\otimes}^! j_{*}(\omega_{S^{-, \mu}_{{\operatorname{Fl}},x}})[\langle\mu, 2\check{\rho}\rangle]) \nonumber\\ &\quad \simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \mathop{\otimes}^! j_*(\omega_{t^\eta{\operatorname{Fl}}^{{-\eta+\mu}}})[\langle\mu, 2\check{\rho}\rangle]) \nonumber\\ &\quad \simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \mathop{\otimes}^! \operatorname{Av}_*^{N(\mathcal{O})^{\omega^\rho}}(j_{*}(\omega_{t^\eta{\operatorname{Fl}}^{{-\eta+\mu}}}) [\langle\mu, 2\check{\rho}\rangle])) \nonumber\\ &\quad \simeq H({\operatorname{Fl}}_{G,x}^{\omega^\rho}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}}) \overset{!}{\otimes} {{J}}_{\eta,*}\star {{J}}_{-\eta+\mu,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} (\delta_0, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}})\star {{J}}_{\eta-\mu,*}\star {{J}}_{-\eta,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Shv}_{\mathcal{G}^G}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} ({{J}}_{\eta,!}, \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}})\star {{J}}_{\eta-\mu,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} (\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}({{J}}_{\eta,!}), \operatorname{Av}_*^{\rm ren}({{J}}_\lambda^{\mathbb{D}})\star {{J}}_{\eta-\mu,*}) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho})}(\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi} ({{J}}_{\eta,!}), \operatorname{Av}_*^{\rm ren}({{J}}_{\lambda+\eta-\mu}^{\mathbb{D}})) \nonumber\\ &\quad \simeq \mathcal{H}om_{\operatorname{Whit}_{\rm q}({\operatorname{Fl}}_{G,x}^{\omega^\rho})} (\operatorname{Av}_!^{N(\mathcal{K})^{\omega^\rho},\chi}(\delta_{\eta,!})[-\langle\eta,2\check{\rho}\rangle], \operatorname{Av}_*^{\rm ren}(\delta_{\lambda+\eta-\mu})[\langle\lambda+\eta-\mu,2\check{\rho}\rangle]). \end{align} And the latter space is ![]() $0$ if
$0$ if ![]() $\lambda \neq \mu$ and is
$\lambda \neq \mu$ and is ![]() $\mathsf {e}$ if
$\mathsf {e}$ if ![]() $\lambda =\mu$.
$\lambda =\mu$.
Combining Proposition 8.3.1 with (4.1.4), there is an isomorphism
Now Proposition 7.6.6 follows directly.
Proof of Proposition 7.6.6 According to Theorem 8.2.2, there is
 \begin{align*} F_{{\mathop{\operatorname{\rm glob}}}}^{\rm L}(\Delta_{\lambda, {\mathop{\operatorname{\rm glob}}}})&\simeq F_{{\mathop{\operatorname{\rm glob}}}}^{\rm L}(\mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}} (\widetilde{\nabla}_{\lambda, {\mathop{\operatorname{\rm glob}}}}))\\ &\simeq \mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}F_{{\mathop{\operatorname{\rm glob}}}}^{\rm DK}(\widetilde{\nabla}_{\lambda, {\mathop{\operatorname{\rm glob}}}})\\ &\simeq\mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}(\nabla_{\lambda, \Omega_{q^{-1}}^{{\rm DK},\prime}})\\ &\simeq \Delta_{\lambda, \Omega_{\rm q}^{{\rm L},\prime}}. \end{align*}
\begin{align*} F_{{\mathop{\operatorname{\rm glob}}}}^{\rm L}(\Delta_{\lambda, {\mathop{\operatorname{\rm glob}}}})&\simeq F_{{\mathop{\operatorname{\rm glob}}}}^{\rm L}(\mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}} (\widetilde{\nabla}_{\lambda, {\mathop{\operatorname{\rm glob}}}}))\\ &\simeq \mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}F_{{\mathop{\operatorname{\rm glob}}}}^{\rm DK}(\widetilde{\nabla}_{\lambda, {\mathop{\operatorname{\rm glob}}}})\\ &\simeq\mathbb{D}^{{\mathop{\operatorname{\rm Verdier}}}}(\nabla_{\lambda, \Omega_{q^{-1}}^{{\rm DK},\prime}})\\ &\simeq \Delta_{\lambda, \Omega_{\rm q}^{{\rm L},\prime}}. \end{align*}
Acknowledgements
This paper is part of the author's PhD thesis which was defended in June 2020. The author thanks Dennis Gaitsgory for suggesting this subject and also deeply thanks him for his guidance. Without his help, the author could not have finished this study. The author thanks Sergey Lysenko for helpful discussions and comments on the paper. The author also thanks Michael Finkelberg, Lin Chen, and Yuchen Fu for their careful reading and detailed suggestions about writing and organizing this paper. Without their help, this article would be far less well-written. The author thanks Yifei Zhao for explaining his work [Reference ZhaoZha20]. The author thanks the anonymous referee for pointing out mistakes and gaps in the former version and constructive comments, which made this paper more complete. The author also thanks Sam Raskin, Peng Zheng, Qiao Zhou, Zicheng Qian, Roman Travkin, Jonathan Wise, Justin Campbell, Lizao Ye, Simon Riche, Christoph Baerligea, and Mihai Pavel for their help.
Conflicts of Interest
None.
Appendix A. Semi-infinite sheaves on affine flags
To be self-contained, we review the theory of semi-infinite sheaves developed in [Reference GaitsgoryGai18a] and [Reference GaitsgoryGai22] and provide additional details. Our goal is to supply the necessary materials for the ![]() $!$-extension semi-infinite sheaves
$!$-extension semi-infinite sheaves ![]() $j_!(\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}})$ and
$j_!(\omega _{S^{-, {\mathop {\operatorname {\rm Conf}}}}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Conf}}}}})$ and ![]() $j_!(\omega _{S^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}})$ in § 6.2.
$j_!(\omega _{S^{-,w,{\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Conf}}}_{\infty \cdot x}}})$ in § 6.2.
To simplify the notation, we consider the semi-infinite sheaves on ![]() $N({\mathcal {K}})$-orbit, whereas in the main content, we consider semi-infinite sheaves on
$N({\mathcal {K}})$-orbit, whereas in the main content, we consider semi-infinite sheaves on ![]() $N^-({\mathcal {K}})$-orbit.
$N^-({\mathcal {K}})$-orbit.
A.1 Existence of  $!$-extension semi-infinite sheaf
$!$-extension semi-infinite sheaf
Recall the prestack ![]() ${S}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}^0$ defined in Definition 6.1.6. Since
${S}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}^0$ defined in Definition 6.1.6. Since ![]() $\kappa ^{\check {\lambda }}$ is injective for any
$\kappa ^{\check {\lambda }}$ is injective for any ![]() $\check {\lambda }$, the collection of maps {
$\check {\lambda }$, the collection of maps {![]() $\kappa ^{\check {\lambda }}$} determines a
$\kappa ^{\check {\lambda }}$} determines a ![]() $N^{\omega ^\rho }$-reduction (in particular, a
$N^{\omega ^\rho }$-reduction (in particular, a ![]() $B$-reduction) of
$B$-reduction) of ![]() ${\mathcal {P}}_G$ at
${\mathcal {P}}_G$ at ![]() $x\in X$. The fiber product
$x\in X$. The fiber product ![]() $S_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}:={S}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}^0\underset {{\operatorname {pt}}/G}{\times } {\operatorname {pt}}/B$ admits a relative position map to
$S_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}:={S}_{{\operatorname {Gr}}, {\mathop {\operatorname {\rm Ran}}}}^0\underset {{\operatorname {pt}}/G}{\times } {\operatorname {pt}}/B$ admits a relative position map to ![]() ${\operatorname {pt}}/B\underset {{\operatorname {pt}}/G}{\times }{{\operatorname {pt}}/B}\simeq B\backslash G/B$. For any
${\operatorname {pt}}/B\underset {{\operatorname {pt}}/G}{\times }{{\operatorname {pt}}/B}\simeq B\backslash G/B$. For any ![]() $w\in W$, let
$w\in W$, let ![]() $S^w_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ be the preimage of the Bruhat cell
$S^w_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ be the preimage of the Bruhat cell ![]() $B\backslash BwB/B$ under the above relative position map.
$B\backslash BwB/B$ under the above relative position map.
A.1.1
Now, we define the ![]() $!$-extension of semi-infinite sheaves on
$!$-extension of semi-infinite sheaves on ![]() $S^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$. Similar constructions work for
$S^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$. Similar constructions work for ![]() $S^w_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ and
$S^w_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ and ![]() $S^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}$ as well.
$S^0_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}$ as well.
Denote ![]() $\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ as the closure of
$\overline {S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ as the closure of ![]() ${S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ in
${S}^{w_0}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ in ![]() ${\operatorname {Fl}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}_x}$, it is isomorphic to
${\operatorname {Fl}}^{\omega ^\rho }_{G,{\mathop {\operatorname {\rm Ran}}}_x}$, it is isomorphic to ![]() $\overline {S}^{0}_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B$. If
$\overline {S}^{0}_{{\operatorname {Gr}},{\mathop {\operatorname {\rm Ran}}}}\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B$. If ![]() $\lambda \in \Lambda ^{\text {neg}}$, let
$\lambda \in \Lambda ^{\text {neg}}$, let ![]() $({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset \subset {\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x$ be the subspace such that
$({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset \subset {\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x$ be the subspace such that ![]() $(D,\mathcal {I})\in {\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x$ belongs to
$(D,\mathcal {I})\in {\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x$ belongs to ![]() $({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset$ if and only if
$({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset$ if and only if ![]() ${\mathop {\operatorname {\rm supp}}}(D)\subset \mathcal {I}$.
${\mathop {\operatorname {\rm supp}}}(D)\subset \mathcal {I}$.
Let ![]() $\preccurlyeq$ be the semi-infinite Bruhat order. For any
$\preccurlyeq$ be the semi-infinite Bruhat order. For any ![]() $t^\lambda w \preccurlyeq w_0$, we define
$t^\lambda w \preccurlyeq w_0$, we define
as the sub-prestack such that the map ![]() $\kappa ^{\check {\lambda }}$ induced by
$\kappa ^{\check {\lambda }}$ induced by ![]() $\alpha$ extends to an injective map
$\alpha$ extends to an injective map
on ![]() $X$, and the relative position of the resulting
$X$, and the relative position of the resulting ![]() $B$-reduction at
$B$-reduction at ![]() $x$ and the Iwahori structure
$x$ and the Iwahori structure ![]() $\epsilon$ is
$\epsilon$ is ![]() $w$.
$w$.
For any such ![]() $S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$, the map
$S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$, the map
is a locally closed embedding, and ![]() $\{S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}, t^\lambda w\preccurlyeq w_0\}$ gives rise to a stratification of
$\{S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}, t^\lambda w\preccurlyeq w_0\}$ gives rise to a stratification of ![]() $\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$.
$\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$.
The projection ![]() $p^{t^\lambda w}: S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\to ({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset$ has a section
$p^{t^\lambda w}: S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}\to ({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset$ has a section ![]() $s^{t^\lambda w}:({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset \to S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ which sends
$s^{t^\lambda w}:({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset \to S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ which sends ![]() $(D, {\mathcal {I}})$ to
$(D, {\mathcal {I}})$ to ![]() $(D,{\mathcal {I}}, {\mathcal {P}}_G, \alpha, \epsilon )$, where
$(D,{\mathcal {I}}, {\mathcal {P}}_G, \alpha, \epsilon )$, where ![]() ${\mathcal {P}}_G= \omega ^\rho (-D)\overset {T}{\times }G$,
${\mathcal {P}}_G= \omega ^\rho (-D)\overset {T}{\times }G$, ![]() $\alpha$ is given by the identification of
$\alpha$ is given by the identification of ![]() $\omega ^\rho (-D)$ and
$\omega ^\rho (-D)$ and ![]() $\omega ^\rho$ on
$\omega ^\rho$ on ![]() $X-{\mathcal {I}}$, and
$X-{\mathcal {I}}$, and ![]() $\epsilon$ is given by
$\epsilon$ is given by ![]() $\omega ^\rho (-D)|_x\overset {T}{\times }wB$.
$\omega ^\rho (-D)|_x\overset {T}{\times }wB$.
Definition A.1.2 We define the semi-infinite category ![]() ${\rm {SI}}^{\preccurlyeq w_0}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}:= \operatorname {Shv}_{{\mathcal {G}}^G}(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})^{N({\mathcal {K}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }}$ and
${\rm {SI}}^{\preccurlyeq w_0}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}:= \operatorname {Shv}_{{\mathcal {G}}^G}(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})^{N({\mathcal {K}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }}$ and ![]() ${\rm {SI}}^{=t^\lambda w}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}:= \operatorname {Shv}_{{\mathcal {G}}^G}({S}^{t^\lambda w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})^{N({\mathcal {K}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }}$.
${\rm {SI}}^{=t^\lambda w}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}:= \operatorname {Shv}_{{\mathcal {G}}^G}({S}^{t^\lambda w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})^{N({\mathcal {K}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }}$.
One can check that the pullback ![]() ${\mathcal {G}}^G$ along (A.1.3) is canonically identified with the pullback of
${\mathcal {G}}^G$ along (A.1.3) is canonically identified with the pullback of ![]() ${\mathcal {G}}^\Lambda$ along
${\mathcal {G}}^\Lambda$ along
In particular, we define
 \begin{equation} \begin{aligned} (s^{t^\lambda w})^!: {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^{=t^\lambda w}\longrightarrow \operatorname{Shv}_{{\mathcal{G}}^\Lambda}(({\mathop{\operatorname{\rm Conf}}}^\lambda\times {\mathop{\operatorname{\rm Ran}}}_x)^\subset),\\ (p^{t^\lambda w})^!: \operatorname{Shv}_{{\mathcal{G}}^\Lambda}(({\mathop{\operatorname{\rm Conf}}}^\lambda\times {\mathop{\operatorname{\rm Ran}}}_x)^\subset)\longrightarrow {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^{=t^\lambda w}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} (s^{t^\lambda w})^!: {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^{=t^\lambda w}\longrightarrow \operatorname{Shv}_{{\mathcal{G}}^\Lambda}(({\mathop{\operatorname{\rm Conf}}}^\lambda\times {\mathop{\operatorname{\rm Ran}}}_x)^\subset),\\ (p^{t^\lambda w})^!: \operatorname{Shv}_{{\mathcal{G}}^\Lambda}(({\mathop{\operatorname{\rm Conf}}}^\lambda\times {\mathop{\operatorname{\rm Ran}}}_x)^\subset)\longrightarrow {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^{=t^\lambda w}. \end{aligned} \end{equation}
Here, we use the observation that ![]() $(p^{t^\lambda w})^!:\operatorname {Shv}_{{\mathcal {G}}^\Lambda }(({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset )\longrightarrow \operatorname {Shv}_{{\mathcal {G}}^G}({S}^{t^\lambda w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})$ factors through the full subcategory
$(p^{t^\lambda w})^!:\operatorname {Shv}_{{\mathcal {G}}^\Lambda }(({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset )\longrightarrow \operatorname {Shv}_{{\mathcal {G}}^G}({S}^{t^\lambda w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})$ factors through the full subcategory ![]() ${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$.
${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$.
Since ![]() $({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset \underset {{\mathop {\operatorname {\rm Ran}}}_x}{\times }N({\mathcal {K}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ acts transitively on
$({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^\subset \underset {{\mathop {\operatorname {\rm Ran}}}_x}{\times }N({\mathcal {K}})_{{\mathop {\operatorname {\rm Ran}}}_x}^{\omega ^\rho }$ acts transitively on ![]() $S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ and is (ind-pro-)unipotent, the functors in (A.1.5) are equivalences. Furthermore, we have the following.
$S^{t^{\lambda }w}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ and is (ind-pro-)unipotent, the functors in (A.1.5) are equivalences. Furthermore, we have the following.
Lemma A.1.3 We have ![]() $({\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w})^{T({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}}=0$ if
$({\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w})^{T({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Ran}}}_x}}=0$ if ![]() $\lambda \notin \Lambda ^\sharp$. Here,
$\lambda \notin \Lambda ^\sharp$. Here, ![]() $\Lambda ^\sharp$ denotes the kernel of the bilinear form
$\Lambda ^\sharp$ denotes the kernel of the bilinear form ![]() $b$ (i.e.
$b$ (i.e. ![]() $b_\lambda$ is trivial).
$b_\lambda$ is trivial).
Proof. By the factorization property, we only consider the point case ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}(S^{-,t^\lambda w}_{{\operatorname {Fl}},x})^{N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }} \simeq \operatorname {Shv}_{{\mathcal {G}}^\Lambda |_{\lambda \cdot x}}({\operatorname {pt}})^{T({\mathcal {O}})^{\omega ^\rho }}$. According to [Reference Gaitsgory and LysenkoGL18, § 7.5], the
$\operatorname {Shv}_{{\mathcal {G}}^G}(S^{-,t^\lambda w}_{{\operatorname {Fl}},x})^{N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }} \simeq \operatorname {Shv}_{{\mathcal {G}}^\Lambda |_{\lambda \cdot x}}({\operatorname {pt}})^{T({\mathcal {O}})^{\omega ^\rho }}$. According to [Reference Gaitsgory and LysenkoGL18, § 7.5], the ![]() $T({\mathcal {O}})^{\omega ^\rho }$-equivariance structure on the fiber
$T({\mathcal {O}})^{\omega ^\rho }$-equivariance structure on the fiber ![]() ${\mathcal {G}}^\Lambda |_{\lambda \cdot x}$ corresponds to the character
${\mathcal {G}}^\Lambda |_{\lambda \cdot x}$ corresponds to the character ![]() $b_\lambda$. In particular, it is trivial only if
$b_\lambda$. In particular, it is trivial only if ![]() $\lambda \in \Lambda ^\sharp$.
$\lambda \in \Lambda ^\sharp$.
A.1.4
With the preparations above, we prove the following.
Proposition A.1.5 The left adjoint functor of ![]() $(i^{t^\lambda w})^!:{\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{\preccurlyeq w_0}\longrightarrow {\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$ is well-defined.
$(i^{t^\lambda w})^!:{\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{\preccurlyeq w_0}\longrightarrow {\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$ is well-defined.
Proof. By considering the dual category, it is equivalent to proving that ![]() $(i^{t^\lambda w})^*$ exists, which is further equivalent to the following:
$(i^{t^\lambda w})^*$ exists, which is further equivalent to the following:
(i) for any finite set
 ${\mathfrak {I}}$ with a distinguished point, the functor
(A.1.6)exists, where
${\mathfrak {I}}$ with a distinguished point, the functor
(A.1.6)exists, where \begin{equation} (i^{t^\lambda w}_{{\mathfrak{I}}})^*: {\rm{SI}}_{q,{\operatorname{Fl}}, X^{\mathfrak{I}}_x}^{\preccurlyeq w_0}\longrightarrow {\rm{SI}}_{q,{\operatorname{Fl}}, X^{\mathfrak{I}}_x}^{=t^\lambda w} \end{equation}
\begin{equation} (i^{t^\lambda w}_{{\mathfrak{I}}})^*: {\rm{SI}}_{q,{\operatorname{Fl}}, X^{\mathfrak{I}}_x}^{\preccurlyeq w_0}\longrightarrow {\rm{SI}}_{q,{\operatorname{Fl}}, X^{\mathfrak{I}}_x}^{=t^\lambda w} \end{equation} ${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}$ (respectively,
${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}$ (respectively,  ${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{=t^\lambda w}\!$) is the base change of
${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{=t^\lambda w}\!$) is the base change of  ${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{\preccurlyeq w_0}$ (respectively,
${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{\preccurlyeq w_0}$ (respectively,  ${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}\!$) along
${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}\!$) along  $X^{\mathfrak {I}}_x\to {\mathop {\operatorname {\rm Ran}}}_x$;
$X^{\mathfrak {I}}_x\to {\mathop {\operatorname {\rm Ran}}}_x$;(ii) for any surjection preserving the distinguished point
 $\phi : {\mathfrak {I}}\to {\mathfrak {J}}$, denote
$\phi : {\mathfrak {I}}\to {\mathfrak {J}}$, denote  $\Delta _\phi : X^{\mathfrak {J}}_x\hookrightarrow X^{\mathfrak {I}}_x$ the corresponding diagonal embedding. The natural transformation
(A.1.7)is an isomorphism.
$\Delta _\phi : X^{\mathfrak {J}}_x\hookrightarrow X^{\mathfrak {I}}_x$ the corresponding diagonal embedding. The natural transformation
(A.1.7)is an isomorphism. \begin{equation} (i^{t^\lambda w}_{{\mathfrak{J}}})^*\circ \Delta_\phi^!\longrightarrow \Delta_\phi^!\circ (i^{t^\lambda w}_{{\mathfrak{I}}})^* \end{equation}
\begin{equation} (i^{t^\lambda w}_{{\mathfrak{J}}})^*\circ \Delta_\phi^!\longrightarrow \Delta_\phi^!\circ (i^{t^\lambda w}_{{\mathfrak{I}}})^* \end{equation}
Once the above two points are proven, we obtain the desired functor by passing to the limit.
The category ![]() ${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}$ admits a block decomposition according to different characters of
${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}$ admits a block decomposition according to different characters of ![]() $T$ indexed by
$T$ indexed by ![]() $\Lambda /\Lambda ^\sharp$. To show the existence of adjoint functor, it is sufficient to show in the block. We assume
$\Lambda /\Lambda ^\sharp$. To show the existence of adjoint functor, it is sufficient to show in the block. We assume ![]() $\lambda \in \Lambda ^\sharp$, and prove parts (i) and (ii) for
$\lambda \in \Lambda ^\sharp$, and prove parts (i) and (ii) for ![]() $T$-monodromic objects in
$T$-monodromic objects in ![]() ${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}$.
${\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}$.
In this case, (i) and (ii) are corollaries of the Braden theorem in [Reference Drinfeld and GaitsgoryDG14, Theorem 3.1.6].
Similar to the construction of ![]() ${S}^{t^\lambda w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}$, we can define
${S}^{t^\lambda w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}$, we can define ![]() ${S}^{-, t^\lambda w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}$. Let
${S}^{-, t^\lambda w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}$. Let ![]() $s_{{\mathfrak {I}}}^{-,t^\lambda w}:({\mathop {\operatorname {\rm Conf}}}^\lambda \times X^{{\mathfrak {I}}}_x)^\subset \to S^{-,t^{\lambda }w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x} , i_{{\mathfrak {I}}}^{-,t^\lambda w}: S^{-,t^{\lambda }w}_{{\operatorname {Fl}}},$
$s_{{\mathfrak {I}}}^{-,t^\lambda w}:({\mathop {\operatorname {\rm Conf}}}^\lambda \times X^{{\mathfrak {I}}}_x)^\subset \to S^{-,t^{\lambda }w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x} , i_{{\mathfrak {I}}}^{-,t^\lambda w}: S^{-,t^{\lambda }w}_{{\operatorname {Fl}}},$ ![]() ${X^{{\mathfrak {I}}}_x}\cap \overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x} \to \overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}, \text {and } p_{{\mathfrak {I}}}^{-,t^\lambda w}:S^{-,t^{\lambda }w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}\to ({\mathop {\operatorname {\rm Conf}}}^\lambda \times X^{{\mathfrak {I}}}_x)^\subset$ denote the corresponding maps.
${X^{{\mathfrak {I}}}_x}\cap \overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x} \to \overline {S}^{w_0}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}, \text {and } p_{{\mathfrak {I}}}^{-,t^\lambda w}:S^{-,t^{\lambda }w}_{{\operatorname {Fl}}, X^{{\mathfrak {I}}}_x}\to ({\mathop {\operatorname {\rm Conf}}}^\lambda \times X^{{\mathfrak {I}}}_x)^\subset$ denote the corresponding maps.
Consider the ![]() ${\mathbb {G}}_m$-action on the fiber of
${\mathbb {G}}_m$-action on the fiber of ![]() $\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ via
$\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$ via ![]() ${\mathbb {G}}_m\overset {2\rho }{\longrightarrow } T\curvearrowright \overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$. In our specific case, the Braden theorem says that the functors
${\mathbb {G}}_m\overset {2\rho }{\longrightarrow } T\curvearrowright \overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$. In our specific case, the Braden theorem says that the functors ![]() $(s_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (i_{{\mathfrak {I}}}^{t^\lambda w})^*$ and
$(s_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (i_{{\mathfrak {I}}}^{t^\lambda w})^*$ and ![]() $(s_{{\mathfrak {I}}}^{-,t^\lambda w})^*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!$ are well-defined for
$(s_{{\mathfrak {I}}}^{-,t^\lambda w})^*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!$ are well-defined for ![]() ${\mathbb {G}}_m$-monodromic D-modules on
${\mathbb {G}}_m$-monodromic D-modules on ![]() $\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$, and are canonically isomorphic. In addition,
$\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}$, and are canonically isomorphic. In addition, ![]() $(s_{{\mathfrak {I}}}^{-,t^\lambda w})^*= (p_{{\mathfrak {I}}}^{-,t^\lambda w})_*$ for
$(s_{{\mathfrak {I}}}^{-,t^\lambda w})^*= (p_{{\mathfrak {I}}}^{-,t^\lambda w})_*$ for ![]() ${\mathbb {G}}_m$-monodromic D-modules.
${\mathbb {G}}_m$-monodromic D-modules.
Since (A.1.5) are equivalences, we have ![]() $(i_{{\mathfrak {I}}}^{t^\lambda w})^*=(p_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (s_{{\mathfrak {I}}}^{-,t^\lambda w})^*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!$
$(i_{{\mathfrak {I}}}^{t^\lambda w})^*=(p_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (s_{{\mathfrak {I}}}^{-,t^\lambda w})^*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!$ ![]() $=(p_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (p_{{\mathfrak {I}}}^{-,t^\lambda w})_*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!: {\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}\longrightarrow {\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{=t^\lambda w}$. This implies part (i) immediately. For part (ii), we observe that the
$=(p_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (p_{{\mathfrak {I}}}^{-,t^\lambda w})_*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!: {\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{\preccurlyeq w_0}\longrightarrow {\rm {SI}}_{q,{\operatorname {Fl}}, X^{\mathfrak {I}}_x}^{=t^\lambda w}$. This implies part (i) immediately. For part (ii), we observe that the ![]() $!$-pullback and
$!$-pullback and ![]() $*$-pushforward satisfy base-change, in particular
$*$-pushforward satisfy base-change, in particular ![]() $(p_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (p_{{\mathfrak {I}}}^{-,t^\lambda w})_*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!$ commutes with taking
$(p_{{\mathfrak {I}}}^{t^\lambda w})^!\circ (p_{{\mathfrak {I}}}^{-,t^\lambda w})_*\circ (i_{{\mathfrak {I}}}^{-,t^\lambda w})^!$ commutes with taking ![]() $!$-restriction to the diagonal.
$!$-restriction to the diagonal.
A.2 Local–global comparison
Recall the substack ![]() $({\operatorname {Bun}}_N^{\omega ^\rho })_{=\lambda \cdot x}^w$ of
$({\operatorname {Bun}}_N^{\omega ^\rho })_{=\lambda \cdot x}^w$ of ![]() $\overline {({\operatorname {Bun}}_N^{\omega ^\rho })}'_{\infty \cdot x}$ in § 7.2.5. In this section, we focus on the
$\overline {({\operatorname {Bun}}_N^{\omega ^\rho })}'_{\infty \cdot x}$ in § 7.2.5. In this section, we focus on the ![]() $!$-extension of the constant D-module on
$!$-extension of the constant D-module on ![]() $({\operatorname {Bun}}_N^{\omega ^\rho })^{w_0}:=({\operatorname {Bun}}_N^{\omega ^\rho })_{=0\cdot x}^{w_0}$.
$({\operatorname {Bun}}_N^{\omega ^\rho })^{w_0}:=({\operatorname {Bun}}_N^{\omega ^\rho })_{=0\cdot x}^{w_0}$.
The restriction of ![]() ${\mathcal {G}}^G$ to
${\mathcal {G}}^G$ to ![]() $({\operatorname {Bun}}_N^{\omega ^\rho })^{w_0}$ is canonically trivialized. Let
$({\operatorname {Bun}}_N^{\omega ^\rho })^{w_0}$ is canonically trivialized. Let ![]() $j_{!, glob, {\operatorname {Fl}}}^N$ be the
$j_{!, glob, {\operatorname {Fl}}}^N$ be the ![]() $!$-extension of the twisted constant sheaf on
$!$-extension of the twisted constant sheaf on ![]() $({\operatorname {Bun}}_N^{\omega ^\rho })^{w_0}$, it is well-defined since the constant sheaf is holonomic. In this section, we aim to prove the following.
$({\operatorname {Bun}}_N^{\omega ^\rho })^{w_0}$, it is well-defined since the constant sheaf is holonomic. In this section, we aim to prove the following.
Lemma A.2.1 Pulling-back along ![]() $\pi _{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}: \overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}\hookrightarrow (\overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}\!)_{\infty \cdot x}\longrightarrow \overline {({\operatorname {Bun}}_N^{\omega ^\rho }\!)}'_{\infty \cdot x}$ induces an isomorphism of semi-infinite sheaves
$\pi _{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}: \overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}\hookrightarrow (\overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}\!)_{\infty \cdot x}\longrightarrow \overline {({\operatorname {Bun}}_N^{\omega ^\rho }\!)}'_{\infty \cdot x}$ induces an isomorphism of semi-infinite sheaves
A.2.2
Let ![]() ${\operatorname {Bun}}_B^w$ be the preimage of the Bruhat cell
${\operatorname {Bun}}_B^w$ be the preimage of the Bruhat cell ![]() $B\backslash BwB/B$ under
$B\backslash BwB/B$ under ![]() ${\operatorname {Bun}}_B':= {\operatorname {Bun}}_B\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B\longrightarrow B\backslash G/B$.
${\operatorname {Bun}}_B':= {\operatorname {Bun}}_B\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B\longrightarrow B\backslash G/B$.
For any ![]() $t^\lambda w\preccurlyeq w_0$, we define
$t^\lambda w\preccurlyeq w_0$, we define
where the map ![]() ${\mathop {\operatorname {\rm Conf}}}^\lambda \longrightarrow {\operatorname {Bun}}_T$ is given by
${\mathop {\operatorname {\rm Conf}}}^\lambda \longrightarrow {\operatorname {Bun}}_T$ is given by ![]() $D\mapsto \omega ^\rho (-D)$.
$D\mapsto \omega ^\rho (-D)$.
Let ![]() $i^{t^\lambda w}_{{\mathop {\operatorname {\rm glob}}}}$ be the locally closed embedding
$i^{t^\lambda w}_{{\mathop {\operatorname {\rm glob}}}}$ be the locally closed embedding
which sends ![]() $({\mathcal {P}}_B, \epsilon, D)$ to
$({\mathcal {P}}_B, \epsilon, D)$ to ![]() $({\mathcal {P}}_G, \{\kappa ^{\check {\lambda }}\}, \epsilon )$. Here,
$({\mathcal {P}}_G, \{\kappa ^{\check {\lambda }}\}, \epsilon )$. Here, ![]() ${\mathcal {P}}_G= {\mathcal {P}}_B\overset {B}{\times } G$, and
${\mathcal {P}}_G= {\mathcal {P}}_B\overset {B}{\times } G$, and ![]() $\kappa ^{\check {\lambda }}: (\omega ^{{1}/{2}})^{\langle \check {\lambda }, 2\rho \rangle }\longrightarrow {\mathcal {V}}^{\check {\lambda }}_{{\mathcal {P}}_G}$ is given by
$\kappa ^{\check {\lambda }}: (\omega ^{{1}/{2}})^{\langle \check {\lambda }, 2\rho \rangle }\longrightarrow {\mathcal {V}}^{\check {\lambda }}_{{\mathcal {P}}_G}$ is given by ![]() $(\omega ^{{1}/{2}})^{\langle \check {\lambda }, 2\rho \rangle }\hookrightarrow (\omega ^{{1}/{2}})^{\langle \check {\lambda }, 2\rho \rangle }(-\langle \check {\lambda }, D\rangle )\longrightarrow {\mathcal {V}}^{\check {\lambda }}_{{\mathcal {P}}_G}$.
$(\omega ^{{1}/{2}})^{\langle \check {\lambda }, 2\rho \rangle }\hookrightarrow (\omega ^{{1}/{2}})^{\langle \check {\lambda }, 2\rho \rangle }(-\langle \check {\lambda }, D\rangle )\longrightarrow {\mathcal {V}}^{\check {\lambda }}_{{\mathcal {P}}_G}$.
The map ![]() $i^{t^\lambda w}$ factors through
$i^{t^\lambda w}$ factors through ![]() $(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N\!)^{w_0}:= \overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B$. The collection
$(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N\!)^{w_0}:= \overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\underset {{\operatorname {pt}}/G}{\times }{\operatorname {pt}}/B$. The collection ![]() $\{({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w}, t^\lambda w\preccurlyeq w_0\}$ gives rise to a stratification of
$\{({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w}, t^\lambda w\preccurlyeq w_0\}$ gives rise to a stratification of ![]() $(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N\!)^{w_0}$.
$(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N\!)^{w_0}$.
Furthermore, the following lemmas follow from definitions.
Lemma A.2.3 The diagram

is Cartesian.
Lemma A.2.4 The morphism
is identified with
Here, ![]() $p^{t^\lambda w}_{{\mathop {\operatorname {\rm glob}}}}: ({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w}={\operatorname {Bun}}_B^w\underset {{\operatorname {Bun}}_T}{\times } {\mathop {\operatorname {\rm Conf}}}^\lambda {\longrightarrow } {\mathop {\operatorname {\rm Conf}}}^\lambda$ is the projection.
$p^{t^\lambda w}_{{\mathop {\operatorname {\rm glob}}}}: ({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w}={\operatorname {Bun}}_B^w\underset {{\operatorname {Bun}}_T}{\times } {\mathop {\operatorname {\rm Conf}}}^\lambda {\longrightarrow } {\mathop {\operatorname {\rm Conf}}}^\lambda$ is the projection.
Similar to Definition 7.2.2, if we erase the character ![]() $\chi$, we can define the global semi-infinite sheaf category
$\chi$, we can define the global semi-infinite sheaf category ![]() ${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}$ on
${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}$ on ![]() $\overline {({\operatorname {Bun}}_N^{\omega ^\rho })}'_{\infty \cdot x}$. We denote by
$\overline {({\operatorname {Bun}}_N^{\omega ^\rho })}'_{\infty \cdot x}$. We denote by ![]() ${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}^{\preccurlyeq w_0}$ and
${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}^{\preccurlyeq w_0}$ and ![]() ${\rm {SI}}_{q, {\operatorname {Fl}},{\mathop {\operatorname {\rm glob}}}}^{=t^\lambda w}$ the corresponding categories on
${\rm {SI}}_{q, {\operatorname {Fl}},{\mathop {\operatorname {\rm glob}}}}^{=t^\lambda w}$ the corresponding categories on ![]() $(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N\!)^{w_0}$ and
$(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N\!)^{w_0}$ and ![]() $({\operatorname {Bun}}_N^{\omega ^\rho }\!)^{t^\lambda w}$, respectively.
$({\operatorname {Bun}}_N^{\omega ^\rho }\!)^{t^\lambda w}$, respectively.
Since the equivariance property is against a unipotent groupoid, the global semi-infinite sheaf category is a full subcategory of the category of D-modules. The pushforward and pullback functors for plain D-modules give rise to the corresponding functors for semi-infinite D-modules. That is to say, we have the following functors:
 \begin{align*} i^{t^\lambda w}_{{\mathop{\operatorname{\rm glob}}},!}: {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{=t^\lambda w}\rightleftharpoons &{\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{\preccurlyeq w_0}: i^{t^\lambda w,!}_{{\mathop{\operatorname{\rm glob}}}}\\ i^{t^\lambda w,*}_{{\mathop{\operatorname{\rm glob}}}}: {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{\preccurlyeq w_0}\rightleftharpoons &{\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{=t^\lambda w}: i^{t^\lambda w}_{{\mathop{\operatorname{\rm glob}}},*}. \end{align*}
\begin{align*} i^{t^\lambda w}_{{\mathop{\operatorname{\rm glob}}},!}: {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{=t^\lambda w}\rightleftharpoons &{\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{\preccurlyeq w_0}: i^{t^\lambda w,!}_{{\mathop{\operatorname{\rm glob}}}}\\ i^{t^\lambda w,*}_{{\mathop{\operatorname{\rm glob}}}}: {\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{\preccurlyeq w_0}\rightleftharpoons &{\rm{SI}}_{q,{\operatorname{Fl}}, {\mathop{\operatorname{\rm glob}}}}^{=t^\lambda w}: i^{t^\lambda w}_{{\mathop{\operatorname{\rm glob}}},*}. \end{align*}
One can check that the full subcategory ![]() ${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}^{=t^\lambda w}\subset \operatorname {Shv}_{{\mathcal {G}}^G}(({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w})$ coincides with the image of the fully faithful functor
${\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}^{=t^\lambda w}\subset \operatorname {Shv}_{{\mathcal {G}}^G}(({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w})$ coincides with the image of the fully faithful functor ![]() $p^{t^\lambda w,!}_{{\mathop {\operatorname {\rm glob}}}}: \operatorname {Shv}_{{\mathcal {G}}^\Lambda }({\mathop {\operatorname {\rm Conf}}}^\lambda )\longrightarrow \operatorname {Shv}_{{\mathcal {G}}^G}(({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w})$. Thus, for any object
$p^{t^\lambda w,!}_{{\mathop {\operatorname {\rm glob}}}}: \operatorname {Shv}_{{\mathcal {G}}^\Lambda }({\mathop {\operatorname {\rm Conf}}}^\lambda )\longrightarrow \operatorname {Shv}_{{\mathcal {G}}^G}(({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w})$. Thus, for any object ![]() ${\mathcal {F}}\in {\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}^{\preccurlyeq w_0}$, its restriction to the strata
${\mathcal {F}}\in {\rm {SI}}_{q,{\operatorname {Fl}}, {\mathop {\operatorname {\rm glob}}}}^{\preccurlyeq w_0}$, its restriction to the strata ![]() $({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w}$ is the
$({\operatorname {Bun}}_N^{\omega ^\rho })^{t^\lambda w}$ is the ![]() $!$-pullback of a
$!$-pullback of a ![]() ${\mathcal {G}}^\Lambda$-twisted sheaf on
${\mathcal {G}}^\Lambda$-twisted sheaf on ![]() ${\mathop {\operatorname {\rm Conf}}}^\Lambda$. Combined with Lemmas A.2.3 and A.2.4,
${\mathop {\operatorname {\rm Conf}}}^\Lambda$. Combined with Lemmas A.2.3 and A.2.4, ![]() $i^{t^\lambda w,!}\circ \pi ^!_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}({\mathcal {F}})$ lies in the full subcategory
$i^{t^\lambda w,!}\circ \pi ^!_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}({\mathcal {F}})$ lies in the full subcategory ![]() $\operatorname {Shv}_{{\mathcal {G}}^\Lambda }(({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^{\subset })\simeq {\rm {SI}}_{q, {\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$. Note that for any object
$\operatorname {Shv}_{{\mathcal {G}}^\Lambda }(({\mathop {\operatorname {\rm Conf}}}^\lambda \times {\mathop {\operatorname {\rm Ran}}}_x)^{\subset })\simeq {\rm {SI}}_{q, {\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$. Note that for any object ![]() ${\mathcal {F}}$ in
${\mathcal {F}}$ in ![]() $\operatorname {Shv}_{{\mathcal {G}}^G}(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})$, it belongs to
$\operatorname {Shv}_{{\mathcal {G}}^G}(\overline {S}^{w_0}_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x})$, it belongs to ![]() ${\rm {SI}}^{\preccurlyeq w_0}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ if and only if
${\rm {SI}}^{\preccurlyeq w_0}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$ if and only if ![]() $i^{t^\lambda w,!}({\mathcal {F}})\in {\rm {SI}}_{q, {\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$ for any
$i^{t^\lambda w,!}({\mathcal {F}})\in {\rm {SI}}_{q, {\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}^{=t^\lambda w}$ for any ![]() $t^\lambda w$. In particular,
$t^\lambda w$. In particular, ![]() $\pi ^!_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}({\mathcal {F}})\in {\rm {SI}}^{\preccurlyeq w_0}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$.Footnote 10
$\pi ^!_{{\operatorname {Fl}}, {\mathop {\operatorname {\rm Ran}}}_x}({\mathcal {F}})\in {\rm {SI}}^{\preccurlyeq w_0}_{q,{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}$.Footnote 10
In order to prove Lemma A.2.1, we need to show for any ![]() $t^\lambda w\preccurlyeq w_0$, we have
$t^\lambda w\preccurlyeq w_0$, we have
It is sufficient to use the Braden theorem again. Recall that ![]() $(s^{t^\lambda w})^!$ in (A.1.5) is an equivalence, the equation (A.2.4) equals
$(s^{t^\lambda w})^!$ in (A.1.5) is an equivalence, the equation (A.2.4) equals
In addition, there is an action of ![]() $T$ on
$T$ on ![]() $(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N)^{w_0}$ given by the adjoint action of
$(\overline {{\operatorname {Bun}}}^{\omega ^\rho }_N)^{w_0}$ given by the adjoint action of ![]() $T$ on
$T$ on ![]() $N$, which is compatible with the
$N$, which is compatible with the ![]() $T$-action on the fiber of
$T$-action on the fiber of ![]() $\overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}$. In particular, since
$\overline {S}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}$. In particular, since ![]() $j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$ is
$j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$ is ![]() $T$-monodromic, the sheaf
$T$-monodromic, the sheaf ![]() $\pi ^!_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)$ is
$\pi ^!_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)$ is ![]() $T$-monodromic. In particular, (A.2.4) is true if
$T$-monodromic. In particular, (A.2.4) is true if ![]() $\lambda \notin \Lambda ^\sharp$.
$\lambda \notin \Lambda ^\sharp$.
If ![]() $\lambda \in \Lambda ^\sharp$, using the Braden theorem, we have
$\lambda \in \Lambda ^\sharp$, using the Braden theorem, we have
 \begin{align} (s^{t^\lambda w})^!\circ (i^{t^\lambda w})^*\circ \pi_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^! (j_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}^N) &= (s^{-,t^\lambda w})^*\circ (i^{-,t^\lambda w})^!\circ \pi_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^! (j_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}^N) \nonumber\\ &=(p^{-,t^\lambda w})_*\circ (i^{-,t^\lambda w})^! \circ\pi_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^! (j_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}^N). \end{align}
\begin{align} (s^{t^\lambda w})^!\circ (i^{t^\lambda w})^*\circ \pi_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^! (j_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}^N) &= (s^{-,t^\lambda w})^*\circ (i^{-,t^\lambda w})^!\circ \pi_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^! (j_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}^N) \nonumber\\ &=(p^{-,t^\lambda w})_*\circ (i^{-,t^\lambda w})^! \circ\pi_{{\operatorname{Fl}}, {\mathop{\operatorname{\rm Ran}}}_x}^! (j_{!, {\mathop{\operatorname{\rm glob}}}, {\operatorname{Fl}}}^N). \end{align} Let ![]() ${\operatorname {Bun}}_{B^-}^{\lambda, w}$ be the algebraic substack of
${\operatorname {Bun}}_{B^-}^{\lambda, w}$ be the algebraic substack of ![]() ${\operatorname {Bun}}_{B^-}'$ such that the degree of the induced
${\operatorname {Bun}}_{B^-}'$ such that the degree of the induced ![]() $T$-bundle is
$T$-bundle is ![]() $-\lambda +(2-2g)\rho$ and the relative position of the
$-\lambda +(2-2g)\rho$ and the relative position of the ![]() $B^-$-bundle and the Iwahori structure at
$B^-$-bundle and the Iwahori structure at ![]() $x$ is
$x$ is ![]() $w$. We denote by
$w$. We denote by ![]() $(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}$ the sub-Zastava space of
$(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}$ the sub-Zastava space of ![]() $(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$. It has a projection
$(\bar {Z}_{{\operatorname {Fl}},x})_{\infty \cdot x}$. It has a projection ![]() $v^{\lambda, w}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm glob}}}}$ to
$v^{\lambda, w}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm glob}}}}$ to ![]() ${\mathop {\operatorname {\rm Conf}}}^\lambda$, and we denote by
${\mathop {\operatorname {\rm Conf}}}^\lambda$, and we denote by ![]() $s_{{\mathop {\operatorname {\rm glob}}}}^{t^\lambda w}: {\mathop {\operatorname {\rm Conf}}}^\lambda \to (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}$ its section.
$s_{{\mathop {\operatorname {\rm glob}}}}^{t^\lambda w}: {\mathop {\operatorname {\rm Conf}}}^\lambda \to (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}$ its section.
Lemma A.2.5 In the following, the upper diagram is commutative and the lower diagram is Cartesian.

In addition, pulling-back the gerbe ![]() ${\mathcal {G}}^G$ along
${\mathcal {G}}^G$ along
is canonically isomorphic to the pullback of the gerbe ![]() ${\mathcal {G}}^\Lambda$ along
${\mathcal {G}}^\Lambda$ along
Using the above lemma, we obtain
 \begin{align} & (A.2.6)=pr^{\lambda}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Ran}}},*}\circ ({\mathop{\operatorname{\rm Id}}}\times pr^\lambda)^!\circ \bar{{\mathfrak{q}}}_Z'^!(j_{!,{\mathop{\operatorname{\rm glob}}},{\operatorname{Fl}}}^N) \nonumber\\ &\quad \underset{\text{Base change}}{=}(pr^\lambda)^!\circ v^{\lambda, w}_{{\operatorname{Fl}},{\mathop{\operatorname{\rm glob}}},*}\circ \bar{{\mathfrak{q}}}_Z'^! (j_{!,{\mathop{\operatorname{\rm glob}}},{\operatorname{Fl}}}^N) \nonumber\\ &\quad \underset{\text{Braden theorem}}{=}(pr^\lambda)^!\circ (s_{{\mathop{\operatorname{\rm glob}}}}^{t^\lambda w})^* \circ \bar{{\mathfrak{q}}}_Z'^! (j_{!,{\mathop{\operatorname{\rm glob}}},{\operatorname{Fl}}}^N). \end{align}
\begin{align} & (A.2.6)=pr^{\lambda}_{{\mathop{\operatorname{\rm Conf}}}\times {\mathop{\operatorname{\rm Ran}}},*}\circ ({\mathop{\operatorname{\rm Id}}}\times pr^\lambda)^!\circ \bar{{\mathfrak{q}}}_Z'^!(j_{!,{\mathop{\operatorname{\rm glob}}},{\operatorname{Fl}}}^N) \nonumber\\ &\quad \underset{\text{Base change}}{=}(pr^\lambda)^!\circ v^{\lambda, w}_{{\operatorname{Fl}},{\mathop{\operatorname{\rm glob}}},*}\circ \bar{{\mathfrak{q}}}_Z'^! (j_{!,{\mathop{\operatorname{\rm glob}}},{\operatorname{Fl}}}^N) \nonumber\\ &\quad \underset{\text{Braden theorem}}{=}(pr^\lambda)^!\circ (s_{{\mathop{\operatorname{\rm glob}}}}^{t^\lambda w})^* \circ \bar{{\mathfrak{q}}}_Z'^! (j_{!,{\mathop{\operatorname{\rm glob}}},{\operatorname{Fl}}}^N). \end{align}It remains to show
In the affine Grassmannian case, it is well-known that the ![]() $!$-pullback from the Drinfeld compactification to the Zastava space sends
$!$-pullback from the Drinfeld compactification to the Zastava space sends ![]() $!$-extension (respectively, IC) sheaf on
$!$-extension (respectively, IC) sheaf on ![]() $(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })_{\infty \cdot x}$ to
$(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })_{\infty \cdot x}$ to ![]() $!$-extension (respectively, IC) sheaf on the Zastava space. The analogous result also holds in the affine flags case.
$!$-extension (respectively, IC) sheaf on the Zastava space. The analogous result also holds in the affine flags case.
Proposition A.2.6 Up to a cohomological shift, there is
Here, ![]() $j_!(c_{({{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}})$ is the shifted
$j_!(c_{({{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}})$ is the shifted ![]() $!$-extension of the (twisted) constant sheaf on the open Zastava space
$!$-extension of the (twisted) constant sheaf on the open Zastava space ![]() ${({{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}}$.
${({{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}}$.
Proof. The proof adapts a similar argument of § 8.2.3–8.2.7. Here, we sketch the proof.
We fix a ![]() $\mu$, and let
$\mu$, and let ![]() $\lambda$ be very anti-dominant. Taking projection defines a map
$\lambda$ be very anti-dominant. Taking projection defines a map
The factorization structure gives another map, i.e. composing the factorization map
 \begin{align} & (({{\operatorname{Bun}}}_N^{\omega^\rho}\underset{{\operatorname{Bun}}_G}{\times'} {\operatorname{Bun}}_{B^-}^{\mu}) \times((\overline{{\operatorname{Bun}}}_N^{\omega^\rho})^{ w_0}\underset{{\operatorname{Bun}}_G'}{\times'} {\operatorname{Bun}}_{B^-}^{\lambda, w}))_{\rm disj} \nonumber\\ &\quad \longrightarrow (\overline{{\operatorname{Bun}}}_N^{\omega^\rho})^{ w_0}\underset{{\operatorname{Bun}}_G'}{\times'} {\operatorname{Bun}}_{B^-}^{\mu+\lambda, w}\underset{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\mu+\lambda}}{\times} ({\mathop{\operatorname{\rm Conf}}}^\mu\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^\lambda)_{\rm disj} \end{align}
\begin{align} & (({{\operatorname{Bun}}}_N^{\omega^\rho}\underset{{\operatorname{Bun}}_G}{\times'} {\operatorname{Bun}}_{B^-}^{\mu}) \times((\overline{{\operatorname{Bun}}}_N^{\omega^\rho})^{ w_0}\underset{{\operatorname{Bun}}_G'}{\times'} {\operatorname{Bun}}_{B^-}^{\lambda, w}))_{\rm disj} \nonumber\\ &\quad \longrightarrow (\overline{{\operatorname{Bun}}}_N^{\omega^\rho})^{ w_0}\underset{{\operatorname{Bun}}_G'}{\times'} {\operatorname{Bun}}_{B^-}^{\mu+\lambda, w}\underset{{\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^{\mu+\lambda}}{\times} ({\mathop{\operatorname{\rm Conf}}}^\mu\times {\mathop{\operatorname{\rm Conf}}}_{\infty\cdot x}^\lambda)_{\rm disj} \end{align}with the projection
gives a map ![]() $r_2$.
$r_2$.
Furthermore, the images of both maps land in the open subspace ![]() $((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}\subset (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu$, where we impose the condition that the generalized
$((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}\subset (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu$, where we impose the condition that the generalized ![]() $N^{\omega ^\rho }$-structure is genuine at the support of the point in
$N^{\omega ^\rho }$-structure is genuine at the support of the point in ![]() ${\mathop {\operatorname {\rm Conf}}}^\mu$.
${\mathop {\operatorname {\rm Conf}}}^\mu$.
Similar to § 7.2, one can define a ![]() $N({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$-bundle
$N({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$-bundle ![]() $((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )^{{\rm level}}_{{\rm good}}$ on
$((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )^{{\rm level}}_{{\rm good}}$ on ![]() $((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}$, and the action of
$((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}$, and the action of ![]() $N({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$ extends to an action of
$N({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$ extends to an action of ![]() $N({\mathcal {K}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$. One can check that further compositions of
$N({\mathcal {K}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$. One can check that further compositions of ![]() $r_1, r_2$ with the projection
$r_1, r_2$ with the projection
are the same if ![]() $N'$ is a large enough sub-pro-group of
$N'$ is a large enough sub-pro-group of ![]() $N({\mathcal {K}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$ which contains
$N({\mathcal {K}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$ which contains ![]() $N({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$.
$N({\mathcal {O}})^{\omega ^\rho }_{{\mathop {\operatorname {\rm Conf}}}^\mu }$.
To prove (A.2.9), since the composition of ![]() $r_1$ and the projection to
$r_1$ and the projection to ![]() $(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}$ is surjective, we need to prove that the
$(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}$ is surjective, we need to prove that the ![]() $!$-pullback of the
$!$-pullback of the ![]() $!$-extension sheaf on
$!$-extension sheaf on ![]() $(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}$ along
$(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}$ along ![]() $(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu \longrightarrow (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}$ and
$(\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu \longrightarrow (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}$ and ![]() $r_1$ is the
$r_1$ is the ![]() $!$-extension sheaf on
$!$-extension sheaf on ![]() $(({{\operatorname {Bun}}}_N^{\omega ^\rho }\underset {{\operatorname {Bun}}_G}{\times '} {\operatorname {Bun}}_{B^-}^{\mu })\times ((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}))_{\rm disj}$.
$(({{\operatorname {Bun}}}_N^{\omega ^\rho }\underset {{\operatorname {Bun}}_G}{\times '} {\operatorname {Bun}}_{B^-}^{\mu })\times ((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}))_{\rm disj}$.
By the identification of composed maps ![]() $r_1, r_2$ with projection (A.2.13), it is equivalent to proving that the
$r_1, r_2$ with projection (A.2.13), it is equivalent to proving that the ![]() $!$-pullback of the
$!$-pullback of the ![]() $!$-extension sheaf on
$!$-extension sheaf on ![]() $((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}$ along
$((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}$ along ![]() $r_2$ is the
$r_2$ is the ![]() $!$-extension sheaf on
$!$-extension sheaf on ![]() $(({{\operatorname {Bun}}}_N^{\omega ^\rho }\underset {{\operatorname {Bun}}_G}{\times '} {\operatorname {Bun}}_{B^-}^{\mu })\times ((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}))_{\rm disj}$.
$(({{\operatorname {Bun}}}_N^{\omega ^\rho }\underset {{\operatorname {Bun}}_G}{\times '} {\operatorname {Bun}}_{B^-}^{\mu })\times ((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}))_{\rm disj}$.
Since the ![]() $!$-extension sheaf on
$!$-extension sheaf on ![]() $((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}$ is the
$((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}$ is the ![]() $!$-pullback of
$!$-pullback of ![]() $j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$, we only need to show that the
$j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$, we only need to show that the ![]() $!$-pullback of
$!$-pullback of ![]() $j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$ along
$j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$ along ![]() $((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}\longrightarrow (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}$ and
$((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}\longrightarrow (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}$ and ![]() $r_2$ is the
$r_2$ is the ![]() $!$-extension sheaf. Now, it follows that if
$!$-extension sheaf. Now, it follows that if ![]() $\lambda +\mu$ is anti-dominant enough, the composed map of
$\lambda +\mu$ is anti-dominant enough, the composed map of ![]() $r_2$ and
$r_2$ and ![]() $((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}\longrightarrow (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}$ is smooth.
$((\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}\times {\mathop {\operatorname {\rm Conf}}}^\mu )_{{\rm good}}\longrightarrow (\overline {{\operatorname {Bun}}}_N^{\omega ^\rho }\!)^{ w_0}$ is smooth.
Now, the desired isomorphism (A.2.8) follows immediately, since the image of ![]() $s^{t^\lambda w}_{{\mathop {\operatorname {\rm glob}}}}$ lies in the complement of
$s^{t^\lambda w}_{{\mathop {\operatorname {\rm glob}}}}$ lies in the complement of ![]() ${({{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}}$.
${({{\operatorname {Bun}}}_N^{\omega ^\rho })^{ w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}}$.
A.2.7 Comparison between  $j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$ and
$j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N$ and  $j_!(\omega _{S_{{\operatorname {Fl}},x}^{w_0}}\!\!)$
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{w_0}}\!\!)$
Let ![]() $\omega _{S^{w_0}_{{\operatorname {Fl}}}}$ be the twisted dualizing sheaf on
$\omega _{S^{w_0}_{{\operatorname {Fl}}}}$ be the twisted dualizing sheaf on ![]() $S^{w_0}_{{\operatorname {Fl}}}$ under the canonical trivialization of
$S^{w_0}_{{\operatorname {Fl}}}$ under the canonical trivialization of ![]() ${\mathcal {G}}^G$ on
${\mathcal {G}}^G$ on ![]() $S^{w_0}_{{\operatorname {Fl}}}$. In this section, we prove the following.
$S^{w_0}_{{\operatorname {Fl}}}$. In this section, we prove the following.
Lemma A.2.8 We have ![]() $\pi _{{\operatorname {Fl}},x}^!(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)[d_g]\simeq j_!(\omega _{S^{w_0}_{{\operatorname {Fl}}}})$.
$\pi _{{\operatorname {Fl}},x}^!(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)[d_g]\simeq j_!(\omega _{S^{w_0}_{{\operatorname {Fl}}}})$.
Proof. Similar to the Ran case, ![]() $\pi _{{\operatorname {Fl}},x}^!(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)$ is also
$\pi _{{\operatorname {Fl}},x}^!(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)$ is also ![]() $N({\mathcal {K}})^{\omega ^\rho }_{x}$-equivariant and
$N({\mathcal {K}})^{\omega ^\rho }_{x}$-equivariant and ![]() $T$-equivariant. Thus, we can use the Braden theorem once again.
$T$-equivariant. Thus, we can use the Braden theorem once again.
Recall the notation ![]() $j_{t^\lambda w,{\operatorname {Fl}}}: S_{{\operatorname {Fl}}}^{t^\lambda w}\longrightarrow {\operatorname {Fl}}_G^{\omega ^\rho }$ in Definition 5.1.5, and let us denote by
$j_{t^\lambda w,{\operatorname {Fl}}}: S_{{\operatorname {Fl}}}^{t^\lambda w}\longrightarrow {\operatorname {Fl}}_G^{\omega ^\rho }$ in Definition 5.1.5, and let us denote by ![]() $i_x^{t^\lambda w}$ the closed embedding
$i_x^{t^\lambda w}$ the closed embedding ![]() ${\operatorname {pt}}=\{t^\lambda w\}\hookrightarrow S_{{\operatorname {Fl}},x}^{t^\lambda w}$. According to Proposition 5.1.4, we only need to prove
${\operatorname {pt}}=\{t^\lambda w\}\hookrightarrow S_{{\operatorname {Fl}},x}^{t^\lambda w}$. According to Proposition 5.1.4, we only need to prove
if ![]() $t^\lambda w\neq 1$. If
$t^\lambda w\neq 1$. If ![]() $\lambda \notin \Lambda ^\sharp$, it is true since semi-infinite sheaves on
$\lambda \notin \Lambda ^\sharp$, it is true since semi-infinite sheaves on ![]() $S^{t^\lambda w}_{{\operatorname {Fl}},x}$ is not
$S^{t^\lambda w}_{{\operatorname {Fl}},x}$ is not ![]() $T$-monodromic (to be more precise, it has a different
$T$-monodromic (to be more precise, it has a different ![]() $T$-monodromy structure from
$T$-monodromy structure from ![]() $\pi _{{\operatorname {Fl}},x}^!(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)$).
$\pi _{{\operatorname {Fl}},x}^!(j_{!,{\mathop {\operatorname {\rm glob}}},{\operatorname {Fl}}}^N)$).
Assume ![]() $\lambda \in \Lambda ^\sharp$. By the Braden theorem,
$\lambda \in \Lambda ^\sharp$. By the Braden theorem,
By base change and Proposition A.2.6, (A.2.15) is just the shifted ![]() $!$-fiber of the sheaf
$!$-fiber of the sheaf ![]() $v^{\lambda, w}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm glob}}},*}\circ j_!(c_{({{\operatorname {Bun}}}_N^{\omega ^\rho })^{w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}})$ at
$v^{\lambda, w}_{{\operatorname {Fl}},{\mathop {\operatorname {\rm glob}}},*}\circ j_!(c_{({{\operatorname {Bun}}}_N^{\omega ^\rho })^{w_0}\underset {{\operatorname {Bun}}_G'}{\times '} {\operatorname {Bun}}_{B^-}^{\lambda, w}})$ at ![]() $t^\lambda \cdot x\in {\mathop {\operatorname {\rm Conf}}}^\lambda _x$. Using the Braden theorem again, we have
$t^\lambda \cdot x\in {\mathop {\operatorname {\rm Conf}}}^\lambda _x$. Using the Braden theorem again, we have
As a combination of Lemmas A.2.1 and A.2.8, we obtain
Corollary A.2.9 The ![]() $!$-restriction of
$!$-restriction of ![]() $j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}}\!)$ to
$j_!(\omega _{S_{{\operatorname {Fl}},{\mathop {\operatorname {\rm Ran}}}_x}^{w_0}}\!)$ to ![]() ${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ is isomorphic to
${\operatorname {Fl}}_{G,x}^{\omega ^\rho }$ is isomorphic to ![]() $j_!(\omega _{S_{{\operatorname {Fl}},x}^{w_0}}\!)$.
$j_!(\omega _{S_{{\operatorname {Fl}},x}^{w_0}}\!)$.
Appendix B. Semi-infinite equivalence vs Iwahori equivalence
In the untwisted case, it is known that for a category ![]() $\mathcal {C}$ with a strong action of
$\mathcal {C}$ with a strong action of ![]() $G({\mathcal {K}})^{\omega ^\rho }$, and any
$G({\mathcal {K}})^{\omega ^\rho }$, and any ![]() $\lambda,\mu \in \Lambda$, the following functors are equivalences:
$\lambda,\mu \in \Lambda$, the following functors are equivalences:
 \begin{equation} \begin{gathered} \mathcal{C}^{{\rm Ad}_{\lambda}I^{\omega^\rho}}\overset{\operatorname{oblv}}{\longrightarrow} \mathcal{C}^{T({\mathcal{O}})^{\omega^\rho}}\overset{\operatorname{Av}_*^{{\rm Ad}_{\mu}I^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho}}}{\longrightarrow} \mathcal{C}^{{\rm Ad}_{\mu} I^{\omega^\rho}}\\ \mathcal{C}^{I^{\omega^\rho}}\overset{\operatorname{Av}_!^{N^-({\mathcal{K}})^{\omega^\rho}}}{\simeq} \mathcal{C}^{N^-({\mathcal{K}})^{\omega^\rho}T({\mathcal{O}})^{\omega^\rho}}. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \mathcal{C}^{{\rm Ad}_{\lambda}I^{\omega^\rho}}\overset{\operatorname{oblv}}{\longrightarrow} \mathcal{C}^{T({\mathcal{O}})^{\omega^\rho}}\overset{\operatorname{Av}_*^{{\rm Ad}_{\mu}I^{\omega^\rho}/T({\mathcal{O}})^{\omega^\rho}}}{\longrightarrow} \mathcal{C}^{{\rm Ad}_{\mu} I^{\omega^\rho}}\\ \mathcal{C}^{I^{\omega^\rho}}\overset{\operatorname{Av}_!^{N^-({\mathcal{K}})^{\omega^\rho}}}{\simeq} \mathcal{C}^{N^-({\mathcal{K}})^{\omega^\rho}T({\mathcal{O}})^{\omega^\rho}}. \end{gathered} \end{equation}The first is implicit in [Reference Arkhipov and BezrukavnikovAB09, Lemma 8] and the second is proved in [Reference RaskinRas14, Theorem 17.2.1, Corollary 17.2.3].Footnote 11 For self-completeness, we prove the metaplectic version of the above equivalence with a similar proof as in [Reference RaskinRas14] and [Reference GaitsgoryGai18a, Proposition 5.2.2].
Proposition B.0.1 For a category ![]() $\mathcal {C}$ with a strong action of
$\mathcal {C}$ with a strong action of ![]() $(\operatorname {Shv}_{{\mathcal {G}}^G}(G({\mathcal {K}})^{\omega ^\rho }),\star )$, and any
$(\operatorname {Shv}_{{\mathcal {G}}^G}(G({\mathcal {K}})^{\omega ^\rho }),\star )$, and any ![]() $\lambda,\mu \in \Lambda$, the functors in (B.0.1) are still equivalences.
$\lambda,\mu \in \Lambda$, the functors in (B.0.1) are still equivalences.
Proof. Let us first consider the first claim.
The gerbe ![]() ${\mathcal {G}}^G$ on
${\mathcal {G}}^G$ on ![]() $G({\mathcal {K}})^{\omega ^\rho }$ has a canonical trivialization on
$G({\mathcal {K}})^{\omega ^\rho }$ has a canonical trivialization on ![]() $T({\mathcal {O}})^{\omega ^\rho }$, which canonically extends to
$T({\mathcal {O}})^{\omega ^\rho }$, which canonically extends to ![]() ${\rm Ad}_{\mu } I^{\omega ^\rho }$ preserving the multiplication structure. We consider the constant sheaf on
${\rm Ad}_{\mu } I^{\omega ^\rho }$ preserving the multiplication structure. We consider the constant sheaf on ![]() ${\rm Ad}_{\mu } I^{\omega ^\rho }$ under this trivialization, denoted by
${\rm Ad}_{\mu } I^{\omega ^\rho }$ under this trivialization, denoted by ![]() $c_{{\rm Ad}_{\mu } I^{\omega ^\rho }}$. By definition,
$c_{{\rm Ad}_{\mu } I^{\omega ^\rho }}$. By definition, ![]() $\operatorname {Av}_*^{{\rm Ad}_{\mu }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$ is given by
$\operatorname {Av}_*^{{\rm Ad}_{\mu }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$ is given by ![]() $c_{{\rm Ad}_{\mu } I^{\omega ^\rho }}\overset {T({\mathcal {O}})^{\omega ^\rho }}{\times } {\mathcal {F}}$ for any
$c_{{\rm Ad}_{\mu } I^{\omega ^\rho }}\overset {T({\mathcal {O}})^{\omega ^\rho }}{\times } {\mathcal {F}}$ for any ![]() ${\rm Ad}_\lambda I^{\omega ^\rho }$-equivariant object
${\rm Ad}_\lambda I^{\omega ^\rho }$-equivariant object ![]() ${\mathcal {F}}\in \mathcal {C}$.
${\mathcal {F}}\in \mathcal {C}$.
Choose a trivialization of ![]() ${\mathcal {G}}^G$ at
${\mathcal {G}}^G$ at ![]() $t^{-\lambda }\in G({\mathcal {K}})^{\omega ^\rho }$, which determines a left transition functor
$t^{-\lambda }\in G({\mathcal {K}})^{\omega ^\rho }$, which determines a left transition functor ![]() $t^{-\lambda }\cdot -:\operatorname {Shv}_{{\mathcal {G}}^G}({\operatorname {Fl}}_G^{\omega ^\rho })\to \operatorname {Shv}_{{\mathcal {G}}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$. Applying this functor to
$t^{-\lambda }\cdot -:\operatorname {Shv}_{{\mathcal {G}}^G}({\operatorname {Fl}}_G^{\omega ^\rho })\to \operatorname {Shv}_{{\mathcal {G}}^G}({\operatorname {Fl}}_G^{\omega ^\rho })$. Applying this functor to ![]() ${\mathcal {F}}$, we obtain an
${\mathcal {F}}$, we obtain an ![]() $I^0$-equivariant
$I^0$-equivariant ![]() ${\mathcal {G}}^G$-twisted sheaf. However, note that conjugating the trivialization on
${\mathcal {G}}^G$-twisted sheaf. However, note that conjugating the trivialization on ![]() $T({\mathcal {O}})^{\omega ^\rho }$ by
$T({\mathcal {O}})^{\omega ^\rho }$ by ![]() $t^{-\lambda }$ will change the trivialization by a character sheaf
$t^{-\lambda }$ will change the trivialization by a character sheaf ![]() $b_{-\lambda }$ on
$b_{-\lambda }$ on ![]() $T({\mathcal {O}})^{\omega ^\rho }$. So,
$T({\mathcal {O}})^{\omega ^\rho }$. So, ![]() $t^{-\lambda } {\mathcal {F}}$ is
$t^{-\lambda } {\mathcal {F}}$ is ![]() $(I^{\omega ^\rho }, b_{-\lambda })$-equivariant.
$(I^{\omega ^\rho }, b_{-\lambda })$-equivariant.
Similarly, if we choose a trivialization of ![]() ${\mathcal {G}}^G$ at
${\mathcal {G}}^G$ at ![]() $t^{-\mu }\in G({\mathcal {K}})^{\omega ^\rho }$, it determines a transition functor
$t^{-\mu }\in G({\mathcal {K}})^{\omega ^\rho }$, it determines a transition functor ![]() $t^{-\mu }\cdot -$. Let
$t^{-\mu }\cdot -$. Let ![]() $c_{I^{\omega ^\rho } t^{-\mu }}:= t^{-\mu }\cdot c_{{\rm Ad}_{\mu } I^{\omega ^\rho }}$. We have
$c_{I^{\omega ^\rho } t^{-\mu }}:= t^{-\mu }\cdot c_{{\rm Ad}_{\mu } I^{\omega ^\rho }}$. We have
Since ![]() $t^{-\lambda } {\mathcal {F}}$ is
$t^{-\lambda } {\mathcal {F}}$ is ![]() $I^0$-equivariant, we can take right
$I^0$-equivariant, we can take right ![]() $I^0$-averaging of
$I^0$-averaging of ![]() $c_{I^{\omega ^\rho } t^{-\mu }} t^{\lambda }\in \operatorname {Shv}_{{\mathcal {G}}^G}(G({\mathcal {K}})^{\omega ^\rho })$ before taking convolution. Up to a shift, it is isomorphic to the pullback of
$c_{I^{\omega ^\rho } t^{-\mu }} t^{\lambda }\in \operatorname {Shv}_{{\mathcal {G}}^G}(G({\mathcal {K}})^{\omega ^\rho })$ before taking convolution. Up to a shift, it is isomorphic to the pullback of ![]() $(J_{-\mu +\lambda,*})_{-\lambda }$ along
$(J_{-\mu +\lambda,*})_{-\lambda }$ along ![]() $G({\mathcal {K}})^{\omega ^\rho }\longrightarrow \widetilde {{\operatorname {Fl}}}$.
$G({\mathcal {K}})^{\omega ^\rho }\longrightarrow \widetilde {{\operatorname {Fl}}}$.
In conclusion, we obtain that, up to a shift, ![]() $\operatorname {Av}_*^{{\rm Ad}_{\mu }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$ is given by
$\operatorname {Av}_*^{{\rm Ad}_{\mu }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$ is given by ![]() $t^{\mu } (J_{-\mu +\lambda,*})_{-\lambda } \overset {I}{\star } t^{-\lambda }{\mathcal {F}}$. The functor
$t^{\mu } (J_{-\mu +\lambda,*})_{-\lambda } \overset {I}{\star } t^{-\lambda }{\mathcal {F}}$. The functor ![]() $t^{\mu } (J_{-\mu +\lambda,*})_{-\lambda } \overset {I}{\star } t^{-\lambda }\cdot -$ is an equivalence since transitions and convolution with twisted BMW sheaves are equivalences.
$t^{\mu } (J_{-\mu +\lambda,*})_{-\lambda } \overset {I}{\star } t^{-\lambda }\cdot -$ is an equivalence since transitions and convolution with twisted BMW sheaves are equivalences.
Now, we prove the second claim.
First, we need to prove that ![]() $\operatorname {Av}_!^{N^-({\mathcal {K}})^{\omega ^\rho }}({\mathcal {F}})$ is well-defined for
$\operatorname {Av}_!^{N^-({\mathcal {K}})^{\omega ^\rho }}({\mathcal {F}})$ is well-defined for ![]() ${\mathcal {F}}$ in the image of
${\mathcal {F}}$ in the image of ![]() $\mathcal {C}^{I^{\omega ^\rho }}\longrightarrow \mathcal {C}$. We only need to prove
$\mathcal {C}^{I^{\omega ^\rho }}\longrightarrow \mathcal {C}$. We only need to prove ![]() $\operatorname {Av}_!^{{\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$ exits for any dominant
$\operatorname {Av}_!^{{\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$ exits for any dominant ![]() $\alpha$, and then
$\alpha$, and then ![]() $\operatorname {Av}_!^{N^-({\mathcal {K}})^{\omega ^\rho }}({\mathcal {F}})= {\rm colim} \operatorname {Av}_!^{{\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$. Since
$\operatorname {Av}_!^{N^-({\mathcal {K}})^{\omega ^\rho }}({\mathcal {F}})= {\rm colim} \operatorname {Av}_!^{{\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$. Since ![]() ${\rm Ad}_{\alpha }I^{\omega ^\rho }={\rm Ad}_{\alpha }N({\mathcal {O}})^{\omega ^\rho } \cdot T({\mathcal {O}})^{\omega ^\rho }\cdot {\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }$, and
${\rm Ad}_{\alpha }I^{\omega ^\rho }={\rm Ad}_{\alpha }N({\mathcal {O}})^{\omega ^\rho } \cdot T({\mathcal {O}})^{\omega ^\rho }\cdot {\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }$, and ![]() ${\rm Ad}_{\alpha }N({\mathcal {O}})^{\omega ^\rho }\subset I^{\omega ^\rho }$, we obtain that for
${\rm Ad}_{\alpha }N({\mathcal {O}})^{\omega ^\rho }\subset I^{\omega ^\rho }$, we obtain that for ![]() ${\mathcal {F}}$ lies in the image of
${\mathcal {F}}$ lies in the image of ![]() $\mathcal {C}^{I^{\omega ^\rho }}\longrightarrow \mathcal {C}$, we have
$\mathcal {C}^{I^{\omega ^\rho }}\longrightarrow \mathcal {C}$, we have ![]() $\operatorname {Av}_!^{{\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})\simeq \operatorname {Av}_!^{{\rm Ad}_{\alpha }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$. The latter exists and is the left adjoint functor of the equivalence functor
$\operatorname {Av}_!^{{\rm Ad}_{\alpha }N^-(t{\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})\simeq \operatorname {Av}_!^{{\rm Ad}_{\alpha }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$. The latter exists and is the left adjoint functor of the equivalence functor ![]() $\mathcal {C}^{{\rm Ad}_{\alpha } I^{\omega ^\rho }}\overset {\operatorname {oblv}}{\longrightarrow }\mathcal {C}^{T({\mathcal {O}})^{\omega ^\rho }}\overset {\operatorname {Av}_*^{I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}}{\longrightarrow }\mathcal {C}^{I^{\omega ^\rho }}$.
$\mathcal {C}^{{\rm Ad}_{\alpha } I^{\omega ^\rho }}\overset {\operatorname {oblv}}{\longrightarrow }\mathcal {C}^{T({\mathcal {O}})^{\omega ^\rho }}\overset {\operatorname {Av}_*^{I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}}{\longrightarrow }\mathcal {C}^{I^{\omega ^\rho }}$.
To be more precise, for ![]() ${\mathcal {F}}$ lies in the image of
${\mathcal {F}}$ lies in the image of ![]() $\mathcal {C}^{I^{\omega ^\rho }}\longrightarrow \mathcal {C}$,
$\mathcal {C}^{I^{\omega ^\rho }}\longrightarrow \mathcal {C}$,
In particular, there is
We note that the functor ![]() $\operatorname {Av}_!^{N^-({\mathcal {K}})^{\omega ^\rho }}: \mathcal {C}^{I^{\omega ^\rho }}{\longrightarrow } \mathcal {C}^{N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }}$ is the left adjoint functor of
$\operatorname {Av}_!^{N^-({\mathcal {K}})^{\omega ^\rho }}: \mathcal {C}^{I^{\omega ^\rho }}{\longrightarrow } \mathcal {C}^{N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }}$ is the left adjoint functor of ![]() $\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}: \mathcal {C}^{N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }}\longrightarrow \mathcal {C}^{I^{\omega ^\rho }}$. Thus, it remains to show
$\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}: \mathcal {C}^{N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }}\longrightarrow \mathcal {C}^{I^{\omega ^\rho }}$. Thus, it remains to show ![]() $\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}$ is conservative, i.e. if
$\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}$ is conservative, i.e. if ![]() $\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})=0$ and
$\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})=0$ and ![]() ${\mathcal {F}}$ is
${\mathcal {F}}$ is ![]() $N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }$-equivariant, then
$N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }$-equivariant, then ![]() $\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})=0$ implies
$\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})=0$ implies ![]() ${\mathcal {F}}=0$.
${\mathcal {F}}=0$.
Indeed, since ![]() $N^-(t{\mathcal {O}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }=\bigcap _{\alpha \in \Lambda ^+} I^{\omega ^\rho }\cap {\rm Ad}_{\alpha }I^{\omega ^\rho }$, we have
$N^-(t{\mathcal {O}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }=\bigcap _{\alpha \in \Lambda ^+} I^{\omega ^\rho }\cap {\rm Ad}_{\alpha }I^{\omega ^\rho }$, we have ![]() ${\mathcal {F}}=\operatorname {Av}_*^{N^-({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})= {\rm colim} \operatorname {Av}_*^{I^{\omega ^\rho }\cap {\rm Ad}_{\alpha }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$. In particular, if
${\mathcal {F}}=\operatorname {Av}_*^{N^-({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})= {\rm colim} \operatorname {Av}_*^{I^{\omega ^\rho }\cap {\rm Ad}_{\alpha }I^{\omega ^\rho }/T({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})$. In particular, if ![]() ${\mathcal {F}}\neq 0$, there exists a very dominant
${\mathcal {F}}\neq 0$, there exists a very dominant ![]() $\alpha$, such that
$\alpha$, such that
Using the fact that ![]() ${\mathcal {F}}$ is
${\mathcal {F}}$ is ![]() $N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }$-equivariant, we have
$N^-({\mathcal {K}})^{\omega ^\rho }T({\mathcal {O}})^{\omega ^\rho }$-equivariant, we have
The latter is an ![]() ${\rm Ad}_{\alpha }I^{\omega ^\rho }$-equivariant object.
${\rm Ad}_{\alpha }I^{\omega ^\rho }$-equivariant object.
Now, note that
the desired property ![]() $\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})\neq 0$ follows from
$\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})\neq 0$ follows from ![]() $\operatorname {Av}_*^{{\rm Ad}_{\alpha }N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})\neq 0$ and the fact that
$\operatorname {Av}_*^{{\rm Ad}_{\alpha }N({\mathcal {O}})^{\omega ^\rho }}({\mathcal {F}})\neq 0$ and the fact that ![]() $\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}: \mathcal {C}^{{\rm Ad}_{\alpha }I^{\omega ^\rho }}\longrightarrow \mathcal {C}^{I^{\omega ^\rho }}$ is an equivalence (the first claim of (B.0.1)).
$\operatorname {Av}_*^{N({\mathcal {O}})^{\omega ^\rho }}: \mathcal {C}^{{\rm Ad}_{\alpha }I^{\omega ^\rho }}\longrightarrow \mathcal {C}^{I^{\omega ^\rho }}$ is an equivalence (the first claim of (B.0.1)).