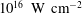1. Introduction
Inertial fusion energy (IFE) is based on high compression[Reference Nuckolls, Wood, Thiessen and Zimmermann1–Reference Mima, Murakami, Nakai, Eliezer, Eliezer and Mima3]. The reasoning is that it is energetically cheaper to compress rather than to heat and the nuclear reactions are proportional to the density squared. IFE of deuterium–tritium (DT) requires high compression (![]() ${>}1000$) and, in particular, the aneutronic fusion[Reference Martinez Val, Eliezer, Piera and Velarde4–Reference Son and Fish6] of proton–boron11 needs extremely high compression (
${>}1000$) and, in particular, the aneutronic fusion[Reference Martinez Val, Eliezer, Piera and Velarde4–Reference Son and Fish6] of proton–boron11 needs extremely high compression (![]() ${>}10\, 000$). The high compression is achieved by shock waves and the accumulation of matter during stagnation of the implosion of the target shell.
${>}10\, 000$). The high compression is achieved by shock waves and the accumulation of matter during stagnation of the implosion of the target shell.
Shock waves in laser plasma interactions[Reference Eliezer7] have played an important role in the study of IFE. In 1974 the first direct observation of a laser-driven shock wave was reported[Reference Van Kessel and Sigel8]. A planar solid hydrogen target was irradiated with a 10 J, 5 ns, Nd laser and a pressure of approximately 2 Mbar was measured. Twenty years after this experiment, the Nova laser from Livermore created a pressure of ![]() $750\pm 200$ Mbar[Reference Cauble, Phillion, Hoover, Holmes, Kilkenny and Lee9]. This was achieved in a collision between two gold foils, where the flyer (Au foil) was accelerated by a high intensity X-ray flux created by the laser–plasma interaction.
$750\pm 200$ Mbar[Reference Cauble, Phillion, Hoover, Holmes, Kilkenny and Lee9]. This was achieved in a collision between two gold foils, where the flyer (Au foil) was accelerated by a high intensity X-ray flux created by the laser–plasma interaction.
In order to achieve nuclear fusion ignition, a mega-joule (MJ) laser with a few nanoseconds pulse duration has been constructed in the USA[Reference Moses10]. The central spark ignition of DT is expected in the near future. In this scheme the target and the driver pulse shape are designed in such a way that only a spark at the centre of the compressed fuel is heated and ignited[Reference Lindl11, Reference Atzeni and Meyer-ter-Vehn12]. The rest of the fuel is heated by ![]() $\alpha $ particles produced in the DT reactions.
$\alpha $ particles produced in the DT reactions.
In order to ignite a DT target with significantly less than a few MJ of energy, it was suggested[Reference Basov, Guskov and Feoktistov13, Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason14] to separate the drivers that compress the target from those that heat the target. This idea is called fast ignition (FI), and triggers not in a central spark, but in a secondary interaction of an igniting driver of a very short duration, such as a multi-Petawatt (PW) laser beam. The PW laser is supposed to form a channel for a few picoseconds in the plasma atmosphere and to ignite a part of the fuel at the stagnation point of the implosion. For this purpose it is estimated that ignition requires of the order of a few tens of kilo-joule of laser energy for a duration of approximately 10 ps with an irradiance of the order of ![]() $10^{20}\ \mathrm{W\ cm}^{-2}$. The FI problem is that the laser pulse does not penetrate directly into the compressed target, which has an electron density of the order of
$10^{20}\ \mathrm{W\ cm}^{-2}$. The FI problem is that the laser pulse does not penetrate directly into the compressed target, which has an electron density of the order of ![]() $10^{24}\ \mathrm{cm}^{-3}$. Therefore many schemes of FI have been suggested: (1) the laser energy is converted into electrons that ignite the target[Reference Norreys, Allot, Clarke, Colliers, Neely, Rose, Zepf, Santala, Bell, Krushelnick, Dangor, Woolsey, Evans, Habara, Norimatsu and Kodama15]. (2) The laser energy is converted into protons that ignite the target[Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell16]. (3) Since the heating in the previous proposals is not confined and furthermore it is necessary to avoid preheating, a gold cone[Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama and Zepf17] (Au density/solid DT density
$10^{24}\ \mathrm{cm}^{-3}$. Therefore many schemes of FI have been suggested: (1) the laser energy is converted into electrons that ignite the target[Reference Norreys, Allot, Clarke, Colliers, Neely, Rose, Zepf, Santala, Bell, Krushelnick, Dangor, Woolsey, Evans, Habara, Norimatsu and Kodama15]. (2) The laser energy is converted into protons that ignite the target[Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell16]. (3) Since the heating in the previous proposals is not confined and furthermore it is necessary to avoid preheating, a gold cone[Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama and Zepf17] (Au density/solid DT density ![]() ${\sim }100$) is stuck in the spherical pellet. (4) FI is induced by plasma jets[Reference Martinez Val and Piera18] that are induced by the same laser system that compresses the pellet. (5) The FI is achieved by a plasma flow created from a thin exploding pusher foil[Reference Caruso and Strangio19, Reference Guskov20]. (6) Plasma blocks for FI have also been suggested[Reference Lalousis, Foldes and Hora21, Reference Lalousis, Hora, Eliezer, Martinez Val, Moustaizis, Miley and Mourou22]. (7) Murakami et al. [Reference Murakami, Nagatomo, Azechi, Ogando, Perlado and Eliezer23] revived the old idea of impact fusion with the help of the cone. (8) The use of clusters[Reference Eliezer, Martinez Val and Deutsch24] was also suggested to ignite the compressed pellet. (9) Furthermore, the use of an extra laser-induced shock wave created by the same lasers that compressed the target in order to ignite the target was suggested[Reference Betti, Zhou, Anderson, Perkins, Theobald and Sokolov25]. (10) Alternatively the FI shock wave from a laser-accelerated impact foil[Reference Eliezer and Martinez Val26, Reference Eliezer and Pinhasi27] was proposed. The shock wave ignition schemes are actually based on heating by collision of two shock waves using tailored laser pulses that had already been suggested[Reference Jackel, Saltzmann, Krumbein and Eliezer28] even before the idea of FI was explicitly published[Reference Basov, Guskov and Feoktistov13, Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason14].
${\sim }100$) is stuck in the spherical pellet. (4) FI is induced by plasma jets[Reference Martinez Val and Piera18] that are induced by the same laser system that compresses the pellet. (5) The FI is achieved by a plasma flow created from a thin exploding pusher foil[Reference Caruso and Strangio19, Reference Guskov20]. (6) Plasma blocks for FI have also been suggested[Reference Lalousis, Foldes and Hora21, Reference Lalousis, Hora, Eliezer, Martinez Val, Moustaizis, Miley and Mourou22]. (7) Murakami et al. [Reference Murakami, Nagatomo, Azechi, Ogando, Perlado and Eliezer23] revived the old idea of impact fusion with the help of the cone. (8) The use of clusters[Reference Eliezer, Martinez Val and Deutsch24] was also suggested to ignite the compressed pellet. (9) Furthermore, the use of an extra laser-induced shock wave created by the same lasers that compressed the target in order to ignite the target was suggested[Reference Betti, Zhou, Anderson, Perkins, Theobald and Sokolov25]. (10) Alternatively the FI shock wave from a laser-accelerated impact foil[Reference Eliezer and Martinez Val26, Reference Eliezer and Pinhasi27] was proposed. The shock wave ignition schemes are actually based on heating by collision of two shock waves using tailored laser pulses that had already been suggested[Reference Jackel, Saltzmann, Krumbein and Eliezer28] even before the idea of FI was explicitly published[Reference Basov, Guskov and Feoktistov13, Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason14].
It is well known that the interaction of a high power laser (HPL) with a planar target creates a one dimensional (1D) shock wave[Reference Fortov and Lomonosov29, Reference Eliezer, McKenna, Neely, Bingham and Jaroszynski30]. The theoretical basis for laser-induced shock waves analysed and measured experimentally so far is based on plasma ablation. For laser intensities in the range ![]() $10^{12}\ \mathrm{W\ cm}^{-2}<I_{\mathrm{L}}<10^{16}\ \mathrm{W\ cm}^{-2}$ and nanosecond pulse durations a hot plasma is created. This plasma exerts a high pressure on the surrounding material, leading to the formation of an intense shock wave moving into the interior of the target. The momentum of the out-flowing plasma balances the momentum imparted to the compressed medium behind the shock front, similar to a rocket effect.
$10^{12}\ \mathrm{W\ cm}^{-2}<I_{\mathrm{L}}<10^{16}\ \mathrm{W\ cm}^{-2}$ and nanosecond pulse durations a hot plasma is created. This plasma exerts a high pressure on the surrounding material, leading to the formation of an intense shock wave moving into the interior of the target. The momentum of the out-flowing plasma balances the momentum imparted to the compressed medium behind the shock front, similar to a rocket effect.
For ![]() $I_{\mathrm{L}} < 10^{16}\ \mathrm{W\ cm}^{-2}$ the ablation pressure is dominant. For
$I_{\mathrm{L}} < 10^{16}\ \mathrm{W\ cm}^{-2}$ the ablation pressure is dominant. For ![]() ${I}_{\mathrm{L}}>10^{16}\ \mathrm{W\ cm}^{-2}$ the radiation pressure is the dominant pressure at the solid–vacuum interface and the ablation pressure is negligible. In this last case the ponderomotive force drives the shock wave. For laser irradiances
${I}_{\mathrm{L}}>10^{16}\ \mathrm{W\ cm}^{-2}$ the radiation pressure is the dominant pressure at the solid–vacuum interface and the ablation pressure is negligible. In this last case the ponderomotive force drives the shock wave. For laser irradiances ![]() ${I}_{\mathrm{L}} > 10^{21}\ \mathrm{W\ cm}^{-2}$ one gets a relativistic laser-induced shock wave[Reference Eliezer, Nissim, Raicher and Martinez Val31]. The theoretical foundation of relativistic shock waves is based on relativistic hydrodynamics[Reference Landau and Lifshitz32] and is first analysed by Taub[Reference Taub33]. Relativistic shock waves may be of importance in intense stellar explosions or in collisions of extremely high energy nuclear particles. Furthermore, relativistic shock waves may be a new route for FI nuclear fusion.
${I}_{\mathrm{L}} > 10^{21}\ \mathrm{W\ cm}^{-2}$ one gets a relativistic laser-induced shock wave[Reference Eliezer, Nissim, Raicher and Martinez Val31]. The theoretical foundation of relativistic shock waves is based on relativistic hydrodynamics[Reference Landau and Lifshitz32] and is first analysed by Taub[Reference Taub33]. Relativistic shock waves may be of importance in intense stellar explosions or in collisions of extremely high energy nuclear particles. Furthermore, relativistic shock waves may be a new route for FI nuclear fusion.
In Section 2 the formalism of relativistic shock waves is given for further consideration. In Section 3 the laser-induced shock wave equations are explicitly written and solved numerically without approximation for the first time. In a recent publication[Reference Eliezer, Nissim, Raicher and Martinez Val31] the solution is given only for very strong relativistic shocks, whereas in this paper the transition between relativistic and nonrelativistic laser-induced shock waves is obtained. It turns out that this transition domain is important and relevant for the FI scheme as described in Section 4. The paper is concluded with a short summary and discussion.
2. Relativistic shock waves
The relativistic 1D (or non-relativistic[Reference Zeldovich and Raizer34]) shock wave is described by five variables: the particle density ![]() $n$ (or the density
$n$ (or the density ![]() $\rho ={Mn}$, where
$\rho ={Mn}$, where ![]() $M$ is the particle mass), the pressure
$M$ is the particle mass), the pressure ![]() $P$, the energy density
$P$, the energy density ![]() $e$, the shock wave velocity
$e$, the shock wave velocity ![]() ${u}_{\mathrm{s}}$, and the particle flow velocity
${u}_{\mathrm{s}}$, and the particle flow velocity ![]() ${u}_{\mathrm{p}}$, assuming that we know the initial condition of the target:
${u}_{\mathrm{p}}$, assuming that we know the initial condition of the target: ![]() ${n}_{\mathrm{0}}$ (or
${n}_{\mathrm{0}}$ (or ![]() $\rho _{\mathrm{0}}$),
$\rho _{\mathrm{0}}$), ![]() ${P}_{\mathrm{0}}$,
${P}_{\mathrm{0}}$, ![]() ${e}_{\mathrm{0}}$, and the particle flow velocity
${e}_{\mathrm{0}}$, and the particle flow velocity ![]() ${u}_{\mathrm{0}}$, before the shock arrival. The four equations relating the shock wave variables are the three Hugoniot relations describing the conservation laws of energy, momentum, and particles, and the equation of state[Reference Eliezer, Ghatak and Hora35, Reference Eliezer and Ricci36] connecting the thermodynamic variables of the state under consideration. In order to solve the problem an extra equation is required, which in our case we derive from a laser–plasma interaction model.
${u}_{\mathrm{0}}$, before the shock arrival. The four equations relating the shock wave variables are the three Hugoniot relations describing the conservation laws of energy, momentum, and particles, and the equation of state[Reference Eliezer, Ghatak and Hora35, Reference Eliezer and Ricci36] connecting the thermodynamic variables of the state under consideration. In order to solve the problem an extra equation is required, which in our case we derive from a laser–plasma interaction model.
The relativistic hydrodynamic starting point is the energy momentum 4-tensor ![]() ${T}_{\mu \nu }$ given by
${T}_{\mu \nu }$ given by
![]() ${U}_{\mu }\ ({\mu }= 0, 1, 2, 3)$ is the dimensionless 4-velocity, where the subscript 0 indicates the time component and subscripts 1, 2, and 3 indicate the space
${U}_{\mu }\ ({\mu }= 0, 1, 2, 3)$ is the dimensionless 4-velocity, where the subscript 0 indicates the time component and subscripts 1, 2, and 3 indicate the space ![]() $x,y$, and
$x,y$, and ![]() $z$ components, respectively, and
$z$ components, respectively, and ![]() $g_{{\mu \nu }}$ is the metric tensor,
$g_{{\mu \nu }}$ is the metric tensor,
 $$\begin{eqnarray} & {u}_{{\mu } } =cU_{{\mu }} = ({\gamma c,\gamma {v}_{1} ,\gamma {v}_{2} ,\gamma {v}_{3}}), \\ &{g}_{{\mu \nu } } :{ g}_{00} =-1, {g}_{11} ={g}_{22} ={g}_{33} =1,{g}_{{\mu \nu } } =0\mbox { if }~{\mu } \ne \mathrm {\nu } ,\label {eq2} \\ &\gamma =\frac {1}{\sqrt {1-\beta ^{2}} };\quad \beta = \frac {{v}}{c};\quad {v}=\sqrt {{v}_{1}^{2}+{v}_{2} ^{2}+{v}_{3}^{2}}, \end{eqnarray}$$
$$\begin{eqnarray} & {u}_{{\mu } } =cU_{{\mu }} = ({\gamma c,\gamma {v}_{1} ,\gamma {v}_{2} ,\gamma {v}_{3}}), \\ &{g}_{{\mu \nu } } :{ g}_{00} =-1, {g}_{11} ={g}_{22} ={g}_{33} =1,{g}_{{\mu \nu } } =0\mbox { if }~{\mu } \ne \mathrm {\nu } ,\label {eq2} \\ &\gamma =\frac {1}{\sqrt {1-\beta ^{2}} };\quad \beta = \frac {{v}}{c};\quad {v}=\sqrt {{v}_{1}^{2}+{v}_{2} ^{2}+{v}_{3}^{2}}, \end{eqnarray}$$ $$\begin{eqnarray} \begin{array}{c} T_{00} =\gamma ^{2} ({e+P})-P\\ T_{0i} =T_{i0} =-\gamma ^{2} ({e+P}) \left ({\frac {{v}_{\mathrm {i}} }{c}} \right )\quad \mbox { for } i=1,2,3 \label {eq3}\\ T_{ij} =\gamma ^{2} ({e+P})\left ({\frac {{v}_{\mathrm {i}} }{c}} \right )\left ({\frac {{v}_{j} }{c}} \right )+P\delta _{ij} \quad \mbox { for } i,j=1,2,3. \end{array} \end{eqnarray}$$
$$\begin{eqnarray} \begin{array}{c} T_{00} =\gamma ^{2} ({e+P})-P\\ T_{0i} =T_{i0} =-\gamma ^{2} ({e+P}) \left ({\frac {{v}_{\mathrm {i}} }{c}} \right )\quad \mbox { for } i=1,2,3 \label {eq3}\\ T_{ij} =\gamma ^{2} ({e+P})\left ({\frac {{v}_{\mathrm {i}} }{c}} \right )\left ({\frac {{v}_{j} }{c}} \right )+P\delta _{ij} \quad \mbox { for } i,j=1,2,3. \end{array} \end{eqnarray}$$ In our 1D model one has for the velocity vector ![]() $\mathbf{v} = (v,0,0)$ and the Lorentz transformation is
$\mathbf{v} = (v,0,0)$ and the Lorentz transformation is
 $$\begin{equation} \label {eq4} \mbox {Lorentz transformation}=\left ({{\begin{array}{@{}*{20}c} \gamma & {-\gamma \beta } & 0 & 0 \\ {-\gamma \beta } & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} }} \right ). \end{equation}$$
$$\begin{equation} \label {eq4} \mbox {Lorentz transformation}=\left ({{\begin{array}{@{}*{20}c} \gamma & {-\gamma \beta } & 0 & 0 \\ {-\gamma \beta } & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} }} \right ). \end{equation}$$Energy–momentum conservation, particle number conservation, and the equation of state (EOS) are given accordingly (Einstein summation is assumed from 0 to 3 for identical indices)
 $$\begin{equation} \label {eq5} \begin{array}{c} \displaystyle \frac {\partial T_{{\mu } }^{\mathrm {\nu } } }{\partial x^{\nu }}\equiv \partial _{\nu } T_{{\mu } }^{\mathrm {\nu } } =0\quad \mbox { for }~{\mu } =0,1,2,3\\ \displaystyle \frac {\partial (nU^{{\mu } })}{\partial x^{{\mu } }}\equiv \partial _{{\mu } } ({nU^{{\mu }}})=0\\ P = P (e,n). \end{array} \end{equation}$$
$$\begin{equation} \label {eq5} \begin{array}{c} \displaystyle \frac {\partial T_{{\mu } }^{\mathrm {\nu } } }{\partial x^{\nu }}\equiv \partial _{\nu } T_{{\mu } }^{\mathrm {\nu } } =0\quad \mbox { for }~{\mu } =0,1,2,3\\ \displaystyle \frac {\partial (nU^{{\mu } })}{\partial x^{{\mu } }}\equiv \partial _{{\mu } } ({nU^{{\mu }}})=0\\ P = P (e,n). \end{array} \end{equation}$$ We use equations (1), (3) and (5) for the conservation of energy density flux ![]() $c[T_{\mathrm{0x}}]_{0} =c[T_{\mathrm{0x}}]_{\mathrm{1}}$, the conservation of momentum density flux
$c[T_{\mathrm{0x}}]_{0} =c[T_{\mathrm{0x}}]_{\mathrm{1}}$, the conservation of momentum density flux ![]() $[T_{\mathrm{xx}}]_{0} =[T_{\mathrm{xx}}]_{1}$, and the conservation of particle number flux
$[T_{\mathrm{xx}}]_{0} =[T_{\mathrm{xx}}]_{1}$, and the conservation of particle number flux ![]() $[nU_{\mathrm{x}}]_{0} = [nU_{\mathrm{x}}]_{1}$ along the shock wave singularity, with the subscripts 0 and 1 respectively denoting the domains before and after shock arrival, to obtain the following equations
$[nU_{\mathrm{x}}]_{0} = [nU_{\mathrm{x}}]_{1}$ along the shock wave singularity, with the subscripts 0 and 1 respectively denoting the domains before and after shock arrival, to obtain the following equations
 $$\begin{equation} \label {eq6} \begin{array}{c} \gamma _{0}^{2}\beta _{0} ({e_{0}+P_{0}})=\gamma _{1} ^{2}\beta _{1} ({e_{1} +P_{1} })\\ \gamma _{0}^{2}\beta _{0}^{2}({e_{0} +P_{0} })+P_{0} =\gamma _{1}^{2}\beta _{1}^{2}({e_{1} +P_{1} })+P_{1}\\ \gamma _{0} \beta _{0} n_{0} =\gamma _{1} \beta _{1} n_{1}, \end{array} \end{equation}$$
$$\begin{equation} \label {eq6} \begin{array}{c} \gamma _{0}^{2}\beta _{0} ({e_{0}+P_{0}})=\gamma _{1} ^{2}\beta _{1} ({e_{1} +P_{1} })\\ \gamma _{0}^{2}\beta _{0}^{2}({e_{0} +P_{0} })+P_{0} =\gamma _{1}^{2}\beta _{1}^{2}({e_{1} +P_{1} })+P_{1}\\ \gamma _{0} \beta _{0} n_{0} =\gamma _{1} \beta _{1} n_{1}, \end{array} \end{equation}$$ where ![]() $\gamma _{\mathrm{i}}$ and
$\gamma _{\mathrm{i}}$ and ![]() $\beta _{\mathrm{i}}=v_{\mathrm{i}}/c$ for the domains 0 and 1 are defined in equation (2), where
$\beta _{\mathrm{i}}=v_{\mathrm{i}}/c$ for the domains 0 and 1 are defined in equation (2), where ![]() $v_{0}$ and
$v_{0}$ and ![]() $v_{1}$ are the inflow and outflow onto the shock wave singularity. Figure 1 describes the fluid flow velocities
$v_{1}$ are the inflow and outflow onto the shock wave singularity. Figure 1 describes the fluid flow velocities ![]() $v_{0}$ and
$v_{0}$ and ![]() $v_{1}$ as seen in the shock wave singularity frame of reference
$v_{1}$ as seen in the shock wave singularity frame of reference ![]() $S_1$ and the shock wave velocity
$S_1$ and the shock wave velocity ![]() $u_{\mathrm{s1}}$ and the particle flow velocities
$u_{\mathrm{s1}}$ and the particle flow velocities ![]() $u_{\mathrm{p1}}$ and
$u_{\mathrm{p1}}$ and ![]() $u_{\mathrm{p0}}= u_{0}$ as seen in the laboratory frame of reference.
$u_{\mathrm{p0}}= u_{0}$ as seen in the laboratory frame of reference.
From equations (6) the velocities ![]() $v_{0}$ and
$v_{0}$ and ![]() $v_{1}$ are obtained
$v_{1}$ are obtained
 $$\begin{equation} \label {eq7} \begin{array}{l} \frac {{v}_{0} }{c}\equiv \beta _{0} =\sqrt {\frac {({P_{1} -P_{0} } )({e_{1} +P_{0} } )}{({e_{1} -e_{0} } )({e_{0} +P_{1} } )}} \\ \frac {{v}_{1} }{c}\equiv \beta _{1} =\sqrt {\frac {({P_{1} -P_{0} } )({e_{0} +P_{1} } )}{({e_{1} -e_{0} } )({e_{1} +P_{0}})}}, \end{array} \end{equation}$$
$$\begin{equation} \label {eq7} \begin{array}{l} \frac {{v}_{0} }{c}\equiv \beta _{0} =\sqrt {\frac {({P_{1} -P_{0} } )({e_{1} +P_{0} } )}{({e_{1} -e_{0} } )({e_{0} +P_{1} } )}} \\ \frac {{v}_{1} }{c}\equiv \beta _{1} =\sqrt {\frac {({P_{1} -P_{0} } )({e_{0} +P_{1} } )}{({e_{1} -e_{0} } )({e_{1} +P_{0}})}}, \end{array} \end{equation}$$and the relativistic Hugoniot equation is derived[Reference Taub33],
 $$\begin{eqnarray} && \frac {({e_{1} +P_{1} } )^{2}}{n_{1}^{2}}-\frac {({e_{0} +P_{0} } )^{2}}{n_{0}^{2}} \\ && \quad = ({P_{1} -P_{0} } ) \left [{\frac {({e_{0} +P_{0} } )}{n_{0}^{2}}+\frac {({e_{1} +P_{1} } )}{n_{1}^{2}}}\right ]. \label {eq8} \end{eqnarray}$$
$$\begin{eqnarray} && \frac {({e_{1} +P_{1} } )^{2}}{n_{1}^{2}}-\frac {({e_{0} +P_{0} } )^{2}}{n_{0}^{2}} \\ && \quad = ({P_{1} -P_{0} } ) \left [{\frac {({e_{0} +P_{0} } )}{n_{0}^{2}}+\frac {({e_{1} +P_{1} } )}{n_{1}^{2}}}\right ]. \label {eq8} \end{eqnarray}$$ Assuming that in the laboratory the target is initially at rest, ![]() $u_{\mathrm{0}} = 0$, the shock wave velocity
$u_{\mathrm{0}} = 0$, the shock wave velocity ![]() $u_{\mathrm{s}}$ and the particle flow velocity
$u_{\mathrm{s}}$ and the particle flow velocity ![]() $u_{\mathrm{p}}$ in the laboratory frame of reference are related to the flow velocities
$u_{\mathrm{p}}$ in the laboratory frame of reference are related to the flow velocities ![]() $v_{\mathrm{0}}$ and
$v_{\mathrm{0}}$ and ![]() $v_{\mathrm{1}}$ in the shock wave rest frame of reference by
$v_{\mathrm{1}}$ in the shock wave rest frame of reference by
The EOS taken here in order to calculate the shock wave parameters is the ideal gas EOS
where ![]() $\Gamma $ is the specific heat ratio and
$\Gamma $ is the specific heat ratio and ![]() $v_{0}$ and
$v_{0}$ and ![]() $v_{\mathrm{1}}$ are given in equations (7) .
$v_{\mathrm{1}}$ are given in equations (7) .

Figure 1. The fluid flow velocities ![]() $v_{0}$ and
$v_{0}$ and ![]() $v_{1}$ as seen in the shock wave singularity frame of reference
$v_{1}$ as seen in the shock wave singularity frame of reference ![]() $S_1$ and the shock wave velocity
$S_1$ and the shock wave velocity ![]() $u_{\mathrm{s1}}$ and the particle flow velocities
$u_{\mathrm{s1}}$ and the particle flow velocities ![]() $u_{\mathrm{p1}}$ and
$u_{\mathrm{p1}}$ and ![]() $u_{\mathrm{p0}}= u_{0}$ as seen in the laboratory frame of reference.
$u_{\mathrm{p0}}= u_{0}$ as seen in the laboratory frame of reference.
3. Laser-induced shock waves
This paper analyses the shock wave created in a planar target by the ponderomotive force induced by very high laser irradiance. In this domain of laser intensities the force acts on the electrons that are accelerated and the ions that follow accordingly. This model describes our piston model[Reference Eliezer and Hora37, Reference Eliezer, Nissim, Martinez Val, Mima and Hora38] as summarized schematically in Figure 2: Figure 2(a) shows the capacitor model for laser irradiances ![]() $I_{\mathrm{L}}$, where the ponderomotive force dominates the interaction. In Figure 2(b) the system of the negative and positive layers is called a double layer (DL),
$I_{\mathrm{L}}$, where the ponderomotive force dominates the interaction. In Figure 2(b) the system of the negative and positive layers is called a double layer (DL), ![]() $n_{\mathrm{e}}$ and
$n_{\mathrm{e}}$ and ![]() $n_{\mathrm{i}}$ are the electron and ion densities respectively,
$n_{\mathrm{i}}$ are the electron and ion densities respectively, ![]() $E_{\mathrm{x}}$ is the electric field,
$E_{\mathrm{x}}$ is the electric field, ![]() $\lambda _{\mathrm{DL}}$ is the distance between the positive and negative DL charges, and
$\lambda _{\mathrm{DL}}$ is the distance between the positive and negative DL charges, and ![]() $\delta $ is the solid density skin depth of the foil. The DL is geometrically followed by a neutral plasma where the electric field decays within a skin depth and a shock wave is created. The shock wave description in the laboratory frame of reference is given in Figure 2(c). This DL acts as a piston driving a shock wave[Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou39, Reference Eliezer, Martinez Val and Pinhasi40]. This model is supported in the literature by particle in cell (PIC) simulation[Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou39, Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima41] and independently by hydrodynamic two-fluid simulations[Reference Lalousis, Foldes and Hora21, Reference Lalousis, Hora, Eliezer, Martinez Val, Moustaizis, Miley and Mourou22, Reference Hora, Lalousis and Eliezer42]. The relativistic shock wave parameters, such as compression, pressure, shock wave and particle flow velocities, and temperature are calculated here for any compression
$\delta $ is the solid density skin depth of the foil. The DL is geometrically followed by a neutral plasma where the electric field decays within a skin depth and a shock wave is created. The shock wave description in the laboratory frame of reference is given in Figure 2(c). This DL acts as a piston driving a shock wave[Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou39, Reference Eliezer, Martinez Val and Pinhasi40]. This model is supported in the literature by particle in cell (PIC) simulation[Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou39, Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima41] and independently by hydrodynamic two-fluid simulations[Reference Lalousis, Foldes and Hora21, Reference Lalousis, Hora, Eliezer, Martinez Val, Moustaizis, Miley and Mourou22, Reference Hora, Lalousis and Eliezer42]. The relativistic shock wave parameters, such as compression, pressure, shock wave and particle flow velocities, and temperature are calculated here for any compression ![]() $\kappa = \rho /\rho _{\mathrm{0}} > 1$ for the first time in the context of relativistic hydrodynamics. In a recent previous paper this was solved only for
$\kappa = \rho /\rho _{\mathrm{0}} > 1$ for the first time in the context of relativistic hydrodynamics. In a recent previous paper this was solved only for ![]() $\kappa = \rho /\rho _{\mathrm{0}}> 4$ with
$\kappa = \rho /\rho _{\mathrm{0}}> 4$ with ![]() $\Gamma = 5/3$.
$\Gamma = 5/3$.

Figure 2. (a) The capacitor model for laser irradiances ![]() $I_{\mathrm{L}}$ where the ponderomotive force dominates the interaction. (b) The parameters that define our capacitor model:
$I_{\mathrm{L}}$ where the ponderomotive force dominates the interaction. (b) The parameters that define our capacitor model: ![]() $n_{\mathrm{e}}$ and
$n_{\mathrm{e}}$ and ![]() $n_{\mathrm{i}}$ are the electron and ion densities accordingly,
$n_{\mathrm{i}}$ are the electron and ion densities accordingly, ![]() $E_{\mathrm{x}}$ is the electric field,
$E_{\mathrm{x}}$ is the electric field, ![]() $\lambda _{\mathrm{DL}}$ is the distance between the positive and negative DL charges. The DL is geometrically followed by a neutral plasma where the electric field decays within a skin depth
$\lambda _{\mathrm{DL}}$ is the distance between the positive and negative DL charges. The DL is geometrically followed by a neutral plasma where the electric field decays within a skin depth ![]() $\delta $ and a shock wave is created. (c) The shock wave description in the piston model.
$\delta $ and a shock wave is created. (c) The shock wave description in the piston model.
For ![]() $I_{\mathrm{L}}<10^{16}\ \mathrm{W\ cm}^{-2}$ the ablation pressure
$I_{\mathrm{L}}<10^{16}\ \mathrm{W\ cm}^{-2}$ the ablation pressure ![]() $P_{\mathrm{a}}$ is dominant and scales with the laser irradiance
$P_{\mathrm{a}}$ is dominant and scales with the laser irradiance ![]() $I_{\mathrm{L}}$ like
$I_{\mathrm{L}}$ like ![]() $P_{\mathrm{a }} \sim I_{\mathrm{L}}^{\mathrm{\alpha }}$, where
$P_{\mathrm{a }} \sim I_{\mathrm{L}}^{\mathrm{\alpha }}$, where ![]() $\alpha $ is of the order of 2/3 in a 1D model[Reference Eliezer7]. For
$\alpha $ is of the order of 2/3 in a 1D model[Reference Eliezer7]. For ![]() $I_{\mathrm{L}} > 10^{16}\ \mathrm{W\ cm}^{\mathrm{-2}}$ the radiation pressure is the dominant pressure at the solid–vacuum interface and the ablation pressure is negligible. In this last case the ponderomotive force drives the shock wave. The equations forrelativistic hydrodynamics with the ideal gas EOS in the laboratory frame of reference are
$I_{\mathrm{L}} > 10^{16}\ \mathrm{W\ cm}^{\mathrm{-2}}$ the radiation pressure is the dominant pressure at the solid–vacuum interface and the ablation pressure is negligible. In this last case the ponderomotive force drives the shock wave. The equations forrelativistic hydrodynamics with the ideal gas EOS in the laboratory frame of reference are
 $$\begin{equation} \label {eq11} \begin{array}{l} \;\; (\mathrm {i})\mbox { }\frac {u_{{\rm p1}} }{c}=\sqrt {\frac {({P_{1} -P_{0} } )({e_{1} -e_{0} } )}{({e_{0} +P_{1} } )({e_{1} +P_{0} } )}} \\ \;\; (\mathrm {ii})\mbox { }\frac {u_{{\rm s1}} }{c}=\sqrt {\frac {({P_{1} -P_{0} } )({e_{1} +P_{0} } )}{({e_{1} -e_{0} } )({e_{0} +P_{1} })}} \\ \;\;(\mathrm {iii})\mbox { }\frac {({e_{1} +P_{1} } )^{2}}{\rho _{1} ^{2}}-\frac {({e_{0} +P_{0} })^{2}}{\rho _{0}^{2}} \\ \qquad =({P_{1} -P_{0} } )\left [{\frac {({e_{0} +P_{0} } )}{\rho _{0}^{2}}+\frac {({e_{1} +P_{1} } )}{\rho _{1}^{2}}} \right ] \\ \left . {\begin{array}{l} (\mathrm {iv}) \\ (\mathrm {v}) \\ \end{array}}\!\!\right \} e_{j} =\rho _{j} c^{2}+\frac {P_{j} }{\Gamma -1}; j=0,1. \end{array} \end{equation}$$
$$\begin{equation} \label {eq11} \begin{array}{l} \;\; (\mathrm {i})\mbox { }\frac {u_{{\rm p1}} }{c}=\sqrt {\frac {({P_{1} -P_{0} } )({e_{1} -e_{0} } )}{({e_{0} +P_{1} } )({e_{1} +P_{0} } )}} \\ \;\; (\mathrm {ii})\mbox { }\frac {u_{{\rm s1}} }{c}=\sqrt {\frac {({P_{1} -P_{0} } )({e_{1} +P_{0} } )}{({e_{1} -e_{0} } )({e_{0} +P_{1} })}} \\ \;\;(\mathrm {iii})\mbox { }\frac {({e_{1} +P_{1} } )^{2}}{\rho _{1} ^{2}}-\frac {({e_{0} +P_{0} })^{2}}{\rho _{0}^{2}} \\ \qquad =({P_{1} -P_{0} } )\left [{\frac {({e_{0} +P_{0} } )}{\rho _{0}^{2}}+\frac {({e_{1} +P_{1} } )}{\rho _{1}^{2}}} \right ] \\ \left . {\begin{array}{l} (\mathrm {iv}) \\ (\mathrm {v}) \\ \end{array}}\!\!\right \} e_{j} =\rho _{j} c^{2}+\frac {P_{j} }{\Gamma -1}; j=0,1. \end{array} \end{equation}$$We have to solve these five equations together with our piston model equation[Reference Eliezer, Nissim, Raicher and Martinez Val31, Reference Eliezer, Nissim, Martinez Val, Mima and Hora38].
Equations (11) and (12) describe six equations with six unknowns: ![]() $u_{\mathrm{s}}$,
$u_{\mathrm{s}}$, ![]() $u_{\mathrm{p1}}$,
$u_{\mathrm{p1}}$, ![]() $P_{\mathrm{1}}$,
$P_{\mathrm{1}}$, ![]() $\rho _{\mathrm{1}}$,
$\rho _{\mathrm{1}}$, ![]() $e_{1}$, and
$e_{1}$, and ![]() $e_{0}$, assuming that we know
$e_{0}$, assuming that we know ![]() $I_{\mathrm{L}}$,
$I_{\mathrm{L}}$, ![]() $\rho _{0}$,
$\rho _{0}$, ![]() $P_{0}$,
$P_{0}$, ![]() $\Gamma $, and
$\Gamma $, and ![]() $u_{\mathrm{o}}=0$. We take the ideal gas EOS with
$u_{\mathrm{o}}=0$. We take the ideal gas EOS with ![]() $\Gamma = 5/3$. The calculations are conveniently done in the dimensionless units defined by
$\Gamma = 5/3$. The calculations are conveniently done in the dimensionless units defined by
 $$\begin{eqnarray} \label {eq13} \Pi _{\mathrm {L}} &\equiv & \frac {I_{\mathrm {L}} }{\rho _{0} c^{3}}; \quad \kappa \equiv \frac {\rho _{1} }{\rho _{0} }; \\ \kappa _{0} &\equiv & \frac {\Gamma +1}{\Gamma -1}; \quad \Pi =\frac {P_{1} }{\rho _{0} c^{2}}; \quad \Pi _{0} =\frac {P_{0} }{\rho _{0} c^{2}}. \end{eqnarray}$$
$$\begin{eqnarray} \label {eq13} \Pi _{\mathrm {L}} &\equiv & \frac {I_{\mathrm {L}} }{\rho _{0} c^{3}}; \quad \kappa \equiv \frac {\rho _{1} }{\rho _{0} }; \\ \kappa _{0} &\equiv & \frac {\Gamma +1}{\Gamma -1}; \quad \Pi =\frac {P_{1} }{\rho _{0} c^{2}}; \quad \Pi _{0} =\frac {P_{0} }{\rho _{0} c^{2}}. \end{eqnarray}$$ $$\begin{eqnarray} \frac {P_{0} }{P_{1} }&=&\frac {\Pi _{0} }{\Pi }={\rm {\bf 0}} \\ &\Rightarrow & \left \{ {\begin{array}{@{}l@{}} \Pi =-B ({\Pi _{0} =0})=\frac { ({\Gamma -1} )^{2}}{\Gamma }\kappa ({\kappa -\kappa _{0}}) \\ \kappa \equiv \frac {\rho _{1} }{\rho _{0} }\ge \kappa _{0}, \end{array}} \right .\label {eq14} \end{eqnarray}$$
$$\begin{eqnarray} \frac {P_{0} }{P_{1} }&=&\frac {\Pi _{0} }{\Pi }={\rm {\bf 0}} \\ &\Rightarrow & \left \{ {\begin{array}{@{}l@{}} \Pi =-B ({\Pi _{0} =0})=\frac { ({\Gamma -1} )^{2}}{\Gamma }\kappa ({\kappa -\kappa _{0}}) \\ \kappa \equiv \frac {\rho _{1} }{\rho _{0} }\ge \kappa _{0}, \end{array}} \right .\label {eq14} \end{eqnarray}$$ $$\begin{equation} \label {eq15} \begin{array}{l} \frac {P_{0} }{P_{1} }=\frac {\Pi _{0} }{\Pi }\ne {\rm {\bf 0}} \Rightarrow \left \{ {\begin{array}{l} \Pi ^{2}+B\Pi +C=0 \\ \kappa \equiv \frac {\rho _{1} }{\rho _{0} }\ge 1 \end{array}} \right . \\ \Pi = (\textstyle \frac {1}{2}) \left ({-B\pm \sqrt {B^{2}-4C} } \right ) \\ B=\frac {({\Gamma -1})^{2}}{\Gamma }({\kappa _{0} \kappa -\kappa ^{2}})+\Pi _{0} ({\Gamma -1})({1-\kappa ^{2}}) \\ \mbox {C} = \frac {({\Gamma -1})^{2}}{\Gamma }({\kappa -\kappa _{0} \kappa ^{2}} )\mbox { }\Pi _{0} -\kappa ^{2}\Pi _{0}^{2}. \end{array} \end{equation}$$
$$\begin{equation} \label {eq15} \begin{array}{l} \frac {P_{0} }{P_{1} }=\frac {\Pi _{0} }{\Pi }\ne {\rm {\bf 0}} \Rightarrow \left \{ {\begin{array}{l} \Pi ^{2}+B\Pi +C=0 \\ \kappa \equiv \frac {\rho _{1} }{\rho _{0} }\ge 1 \end{array}} \right . \\ \Pi = (\textstyle \frac {1}{2}) \left ({-B\pm \sqrt {B^{2}-4C} } \right ) \\ B=\frac {({\Gamma -1})^{2}}{\Gamma }({\kappa _{0} \kappa -\kappa ^{2}})+\Pi _{0} ({\Gamma -1})({1-\kappa ^{2}}) \\ \mbox {C} = \frac {({\Gamma -1})^{2}}{\Gamma }({\kappa -\kappa _{0} \kappa ^{2}} )\mbox { }\Pi _{0} -\kappa ^{2}\Pi _{0}^{2}. \end{array} \end{equation}$$ The compression ![]() $\kappa $ as a function of the dimensionless pressure
$\kappa $ as a function of the dimensionless pressure ![]() $\Pi = P_{1}/(\rho _{0}c^{2})$ is given in Figure 3 for
$\Pi = P_{1}/(\rho _{0}c^{2})$ is given in Figure 3 for ![]() $\kappa _{0} = 4 (\Gamma =5/3)$. Although
$\kappa _{0} = 4 (\Gamma =5/3)$. Although ![]() $P_{\mathrm{0}}/P_{1}$ is extremely small one cannot neglect it in the very near vicinity of
$P_{\mathrm{0}}/P_{1}$ is extremely small one cannot neglect it in the very near vicinity of ![]() $\kappa _{0}$ and in this domain one has to solve equation (15) numerically. Furthermore, in order to see the transition between the relativistic and nonrelativistic approximations (see appendix A) one has to solve the relativistic equations with equation (15) in order to see transition effects such as the one shown in Figure 3. However for
$\kappa _{0}$ and in this domain one has to solve equation (15) numerically. Furthermore, in order to see the transition between the relativistic and nonrelativistic approximations (see appendix A) one has to solve the relativistic equations with equation (15) in order to see transition effects such as the one shown in Figure 3. However for ![]() $\kappa > \kappa _{0}$, for (
$\kappa > \kappa _{0}$, for (![]() $\kappa -\kappa _{0})/\kappa _{0} > 10^{-3}$, the approximation of equation (14) is very good for calculating the shock wave variables as a function of the dimensionless laser irradiance
$\kappa -\kappa _{0})/\kappa _{0} > 10^{-3}$, the approximation of equation (14) is very good for calculating the shock wave variables as a function of the dimensionless laser irradiance ![]() $\Pi _{\mathrm{L}}$.
$\Pi _{\mathrm{L}}$.

Figure 3. The compression ![]() $\kappa = \rho /\rho _{0}$ as a function of the shock wave dimensionless pressure
$\kappa = \rho /\rho _{0}$ as a function of the shock wave dimensionless pressure ![]() $\Pi = P/(\rho _{0}c^{2})$. The numerical values are obtained for
$\Pi = P/(\rho _{0}c^{2})$. The numerical values are obtained for ![]() $\Gamma = 5/3$.
$\Gamma = 5/3$.

Figure 4. The dimensionless shock wave pressure ![]() $\Pi =P/(\rho _{0}c^{2})$ versus the dimensionless laser irradiance
$\Pi =P/(\rho _{0}c^{2})$ versus the dimensionless laser irradiance ![]() $\Pi _{\mathrm{L}} = I_{\mathrm{L}}/(\rho _{\mathrm{0}}c^{\mathrm{3}})$ in the range 10
$\Pi _{\mathrm{L}} = I_{\mathrm{L}}/(\rho _{\mathrm{0}}c^{\mathrm{3}})$ in the range 10![]() $^{\mathrm{-4}} < \Pi _{\mathrm{L}} < 1$. For a better understanding of this graph the inserted table shows numerical values in the range
$^{\mathrm{-4}} < \Pi _{\mathrm{L}} < 1$. For a better understanding of this graph the inserted table shows numerical values in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$.
$10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$.

Figure 5. The dimensionless shock wave velocity ![]() $u_{\mathrm{s}}/c$ and the particle velocity
$u_{\mathrm{s}}/c$ and the particle velocity ![]() $u _{\mathrm{p}}/c$ in the laboratory frame of reference versus the dimensionless laser irradiance
$u _{\mathrm{p}}/c$ in the laboratory frame of reference versus the dimensionless laser irradiance ![]() $\Pi _{\mathrm{L}} = I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range
$\Pi _{\mathrm{L}} = I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range ![]() $10^{-4} <\Pi _{\mathrm{L}} < 1$. For a better understanding of this graph the inserted tables show numerical values in the range
$10^{-4} <\Pi _{\mathrm{L}} < 1$. For a better understanding of this graph the inserted tables show numerical values in the range ![]() $10^{-4}< \Pi _{\mathrm{L}} < 10^{-2}$.
$10^{-4}< \Pi _{\mathrm{L}} < 10^{-2}$.
The numerical solutions of equations (11) and (12) are shown in Figures 4 and 5. Figure 4 gives the dimensionless shock wave pressure ![]() $\Pi =P_{1}/(\rho _{0}c^{2})$ versus the dimensionless laser irradiance
$\Pi =P_{1}/(\rho _{0}c^{2})$ versus the dimensionless laser irradiance ![]() $\Pi _{\mathrm{L}} =I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range
$\Pi _{\mathrm{L}} =I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 1$. For a better understanding of this graph and for the practical proposal in the next section, the inserted table shows numerical values in the range
$10^{-4} < \Pi _{\mathrm{L}} < 1$. For a better understanding of this graph and for the practical proposal in the next section, the inserted table shows numerical values in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$. Figure 5 describes the dimensionless shock wave velocity
$10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$. Figure 5 describes the dimensionless shock wave velocity ![]() $u_{\mathrm{s}}/c$ and the particle velocity
$u_{\mathrm{s}}/c$ and the particle velocity ![]() $u_{\mathrm{p}}/c$ in the laboratory frame of reference versus the dimensionless laser irradiance
$u_{\mathrm{p}}/c$ in the laboratory frame of reference versus the dimensionless laser irradiance ![]() $\Pi _{\mathrm{L}} = I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range
$\Pi _{\mathrm{L}} = I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 1$ while the inserted table shows numerical values in the range
$10^{-4} < \Pi _{\mathrm{L}} < 1$ while the inserted table shows numerical values in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$. As a numerical example we take a target (liquid DT) with initial density
$10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$. As a numerical example we take a target (liquid DT) with initial density ![]() $\rho _{0}=0.2\ \mathrm{g\ cm}^{-3}$ irradiated by a laser with intensity
$\rho _{0}=0.2\ \mathrm{g\ cm}^{-3}$ irradiated by a laser with intensity ![]() $I_{\mathrm{L}} = 5 \times 10^{22}\ \mathrm{W\ cm}^{-2}$, namely
$I_{\mathrm{L}} = 5 \times 10^{22}\ \mathrm{W\ cm}^{-2}$, namely ![]() $\Pi _{\mathrm{L}}= 9.26 \times 10^{-2}$. In this case our relativistic equations yield a compression
$\Pi _{\mathrm{L}}= 9.26 \times 10^{-2}$. In this case our relativistic equations yield a compression ![]() $\kappa =\rho /\rho _{0} = 4.09$, a pressure
$\kappa =\rho /\rho _{0} = 4.09$, a pressure ![]() $P = 2\times 10^{13}$ bar, a shock wave velocity
$P = 2\times 10^{13}$ bar, a shock wave velocity ![]() $u_{\mathrm{s}}= 0.35c$ and a particle velocity
$u_{\mathrm{s}}= 0.35c$ and a particle velocity ![]() $u_{\mathrm{p}} = 0.27c$, where
$u_{\mathrm{p}} = 0.27c$, where ![]() $c$ is the speed of light.
$c$ is the speed of light.
The relativistic speed of sound ![]() $c_{\mathrm{S}}$ for an ideal gas EOS is
$c_{\mathrm{S}}$ for an ideal gas EOS is
In the shocked medium the characteristic velocity of a disturbance from the piston to the shock wave front, equal to the rarefaction wave in the shocked medium ![]() $c_{\mathrm{rw}}$, is given by
$c_{\mathrm{rw}}$, is given by
Figures 6(a) and 6(b) respectively describe the speed of sound in units of the speed of light, ![]() $c_{\mathrm{S}}/c$, and the ratio of shock velocity to the rarefaction velocity,
$c_{\mathrm{S}}/c$, and the ratio of shock velocity to the rarefaction velocity, ![]() $u_{\mathrm{s}}/ c_{\mathrm{rw}}$ as a function of the dimensionless laser irradiance
$u_{\mathrm{s}}/ c_{\mathrm{rw}}$ as a function of the dimensionless laser irradiance ![]() $\Pi _{\mathrm{L}}= I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range
$\Pi _{\mathrm{L}}= I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 1$. The inserted tables show numerical values in the range
$10^{-4} < \Pi _{\mathrm{L}} < 1$. The inserted tables show numerical values in the range ![]() $10^{\mathrm{-4}} < \Pi _{\mathrm{L}} < 10^{-2}$.
$10^{\mathrm{-4}} < \Pi _{\mathrm{L}} < 10^{-2}$.
We now analyse the temperature problem. The partial pressures of an ideal gas that contains electrons and ions with appropriate densities ![]() $n_{\mathrm{e}}$ and
$n_{\mathrm{e}}$ and ![]() $n_{\mathrm{i}}$ and temperatures
$n_{\mathrm{i}}$ and temperatures ![]() $T_{\mathrm{e}}$ and
$T_{\mathrm{e}}$ and ![]() $T_{\mathrm{i}}$ are
$T_{\mathrm{i}}$ are ![]() $P_{\mathrm{e}}$ and
$P_{\mathrm{e}}$ and ![]() $P_{\mathrm{i}}$, and can be described by
$P_{\mathrm{i}}$, and can be described by
If the associated photons in this system are in thermal equilibrium then a radiation temperature ![]() $T_{\mathrm{r}}$ can be defined, with a radiation pressure
$T_{\mathrm{r}}$ can be defined, with a radiation pressure ![]() $P_{\mathrm{r}}$ given by[Reference Eliezer, Ghatak and Hora35]
$P_{\mathrm{r}}$ given by[Reference Eliezer, Ghatak and Hora35]
For a plasma in local thermal equilibrium satisfying ![]() $T_{\mathrm{e}} = T_{\mathrm{i}} = T_{\mathrm{r}} =T$, where the ions have an ionization
$T_{\mathrm{e}} = T_{\mathrm{i}} = T_{\mathrm{r}} =T$, where the ions have an ionization ![]() $Z$ and an atomic number
$Z$ and an atomic number ![]() $A$, implying a ion mass of
$A$, implying a ion mass of ![]() $Am_{\mathrm{p}}$, where
$Am_{\mathrm{p}}$, where ![]() $m_{\mathrm{p}}$ is the proton mass, the plasma pressure is given by
$m_{\mathrm{p}}$ is the proton mass, the plasma pressure is given by
If the ion density satisfies
then the radiation pressure is dominant and the temperature is given by
It is conceivable to assume that electrons and ions are in thermal equilibrium, i.e., ![]() $T_{\mathrm{e}}= T_{\mathrm{i}}$, however the shocked area is not optically thick for the energetic photons. In this case the energetic photons created by bremsstrahlung leave the system, implying
$T_{\mathrm{e}}= T_{\mathrm{i}}$, however the shocked area is not optically thick for the energetic photons. In this case the energetic photons created by bremsstrahlung leave the system, implying ![]() $T_{\mathrm{r}} \ll T_{\mathrm{e}}$, or one can have a situation where radiation temperature is not defined at all. Therefore if the photon radiation in equation (19) is negligible then one has
$T_{\mathrm{r}} \ll T_{\mathrm{e}}$, or one can have a situation where radiation temperature is not defined at all. Therefore if the photon radiation in equation (19) is negligible then one has
Therefore in general we can write that the plasma temperature is constrained to the following range

Figure 6. The speed of sound ![]() $c_{\mathrm{S}}$ is given in units of the speed of light
$c_{\mathrm{S}}$ is given in units of the speed of light ![]() $c$ in (a) and the ratio of the shock velocity to the rarefaction velocity,
$c$ in (a) and the ratio of the shock velocity to the rarefaction velocity, ![]() $u_{\mathrm{S}}/c_{\mathrm{rw}}$ is shown in (b) as function of the dimensionless laser irradiance
$u_{\mathrm{S}}/c_{\mathrm{rw}}$ is shown in (b) as function of the dimensionless laser irradiance ![]() $\Pi _{\mathrm{L}}=I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range
$\Pi _{\mathrm{L}}=I_{\mathrm{L}}/(\rho _{0}c^{3})$ in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 1$. The inserted tables show numerical values in the range
$10^{-4} < \Pi _{\mathrm{L}} < 1$. The inserted tables show numerical values in the range ![]() $10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$.
$10^{-4} < \Pi _{\mathrm{L}} < 10^{-2}$.

Figure 7. The FI scheme suggested in this paper. As a numerical example an initial pellet with radius ![]() $R_{0} =1\ \mathrm{mm}$ and DT fuel of density
$R_{0} =1\ \mathrm{mm}$ and DT fuel of density ![]() $0.2\ \mathrm{g\ cm}^{-3}$ with thickness
$0.2\ \mathrm{g\ cm}^{-3}$ with thickness ![]() $0.1\ \mathrm{mm}$ (i.e., an aspect ratio of 10) is compressed to a density of
$0.1\ \mathrm{mm}$ (i.e., an aspect ratio of 10) is compressed to a density of ![]() $\rho _{0}=10^{3}\ \mathrm{g\ cm}^{-3}$ by nanosecond lasers with a radius of
$\rho _{0}=10^{3}\ \mathrm{g\ cm}^{-3}$ by nanosecond lasers with a radius of ![]() $67\ {\mu \mathrm{m}}$. The picosecond fast igniter laser with a
$67\ {\mu \mathrm{m}}$. The picosecond fast igniter laser with a ![]() $7.2\ {\mu \mathrm{m}}$ beam diameter creates a shock wave pulse with a thickness of
$7.2\ {\mu \mathrm{m}}$ beam diameter creates a shock wave pulse with a thickness of ![]() $0.72\ {\mu }\mathrm{m}$ and can be considered a 1D shock wave to a reasonable approximation.
$0.72\ {\mu }\mathrm{m}$ and can be considered a 1D shock wave to a reasonable approximation.
Taking the example given above for liquid DT with ![]() $A = 2.5, Z = 1, m_{\mathrm{p}}= 938.3\ \mathrm{MeV}/c^{2}$ and initial density
$A = 2.5, Z = 1, m_{\mathrm{p}}= 938.3\ \mathrm{MeV}/c^{2}$ and initial density ![]() $\rho = 0.2\ \mathrm{g\ cm}^{-3}$ irradiated by a laser with intensity
$\rho = 0.2\ \mathrm{g\ cm}^{-3}$ irradiated by a laser with intensity ![]() $I_{\mathrm{L}}= 5 \times 10^{22}\ \mathrm{W\ cm}^{-2}$, namely
$I_{\mathrm{L}}= 5 \times 10^{22}\ \mathrm{W\ cm}^{-2}$, namely ![]() $\Pi _{\mathrm{L}}=9.26 \times 10^{-2}$, we get
$\Pi _{\mathrm{L}}=9.26 \times 10^{-2}$, we get ![]() $\Pi = 0.11, \kappa =4.09$ and a temperature in the range
$\Pi = 0.11, \kappa =4.09$ and a temperature in the range ![]() $26.2\ \mathrm{keV} < k_{\mathrm{B}}T < 31.6\ \mathrm{MeV}$. However, for
$26.2\ \mathrm{keV} < k_{\mathrm{B}}T < 31.6\ \mathrm{MeV}$. However, for ![]() $k_{\mathrm{B}}T > 1\ \mathrm{MeV}$ we have electron–positron pair production[Reference Di Piazza, Muller, Hatsagortsyan and Keitel43, Reference Ruffini, Vereshchagin and Xue44] and new physics is required here for the temperature calculations. It is out of the scope of this paper to analyse this exotic case here.
$k_{\mathrm{B}}T > 1\ \mathrm{MeV}$ we have electron–positron pair production[Reference Di Piazza, Muller, Hatsagortsyan and Keitel43, Reference Ruffini, Vereshchagin and Xue44] and new physics is required here for the temperature calculations. It is out of the scope of this paper to analyse this exotic case here.
4. An ultrafast ignition solution to the energy problem
In order to solve the energy problem of future generations scientists have considered using controlled nuclear fusion energy. One of the approaches is the well-known inertial confinement fusion driven by HPLs where the physics is based on compressing and igniting rather than confining the fuel[Reference Nuckolls, Wood, Thiessen and Zimmermann1, Reference Velarde and Carpintero-Santamaria2]. In order to ignite the fuel with less energy it was suggested to separate the drivers that compress the target from whose that ignite the target[Reference Basov, Guskov and Feoktistov13, Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason14]. First the fuel is compressed, then a second driver ignites a small part of the fuel while the alpha particles created in the DT interaction heat the rest of the target. This idea is called FI. The problem with FI is that the laser pulse does not penetrate directly into the compressed target; therefore many alternative schemes have been suggested[Reference Guskov45].
The laser solution of the energy problem requires very sophisticated high power laser science and engineering (HPLSE). In a recent paper[Reference Bodner, Schmitt and Sethian46] the various HPLSE optimizations and design constraints for a laser fusion power plant are beautifully summarized and analysed. From the many possible proposals to solve the energy problem with HPLs we consider three criteria for choosing the best candidate (present or future): (i) Understanding the physics. In HPL–target interactions there are many scientific problems not yet fully understood, such as laser–plasma instabilities, hydrodynamic instabilities, equations of state, nonlinear transport issues, non-local thermodynamic equilibrium, even neglecting energy conservation! (ii) Engineering simplicity. The IFE project is extremely complicated technologically and therefore a major effort is required in choosing the laser system, target design, etc., from all possible proposals by physicists. Technological simplicity must be seriously taken into account. For example, IFE requires ![]() $10^{8}$ or more laser shots per year; therefore complicated target designs (such as inserting a golden cone inside a pellet) are not realistic. (iii) Last, but not least, IFE is supposed to be economically practical. This implies the required gain, defined as the nuclear energy output divided by the laser input per shot, be larger than 100 and that the cost of a target should not be more expensive than 0.1 US$.
$10^{8}$ or more laser shots per year; therefore complicated target designs (such as inserting a golden cone inside a pellet) are not realistic. (iii) Last, but not least, IFE is supposed to be economically practical. This implies the required gain, defined as the nuclear energy output divided by the laser input per shot, be larger than 100 and that the cost of a target should not be more expensive than 0.1 US$.
Taking into account these three criteria it looks as though: (a) direct drive is simpler than indirect drive. (b) FI needs significantly less energy (approximately 0.3 MJ instead of 3 MJ). Therefore direct drive FI has the potential to be the best route to achieve nuclear fusion as an energy source. (c) From all presently known FI schemes the simplest FI seems to be by means of an ‘extra shock’ wave. We suggest a novel shock wave ignition scheme requiring less energy (in comparison with the present shock wave ignition scheme[Reference Betti, Zhou, Anderson, Perkins, Theobald and Sokolov25]) and free of laser–plasma instabilities (no more than ![]() $I_{\mathrm{L}}\lambda _{\mathrm{L}}^{2}=10^{\mathrm{14}}\ (\mathrm{W\ cm}^{-2})\mu \mathrm{m}^{2}$ in the laser compression pulses). In this proposal the ignition shock wave is created by a high irradiance laser and the shock wave is induced by a ponderomotive force in the intermediate domain between the relativistic and non-relativistic hydrodynamics. For this case the relativistic shock wave formalism has to be considered as developed in our previous section. We call our scheme ultrafast, since the laser pulse duration for the ignition process is significantly smaller, by one to two orders of magnitude.
$I_{\mathrm{L}}\lambda _{\mathrm{L}}^{2}=10^{\mathrm{14}}\ (\mathrm{W\ cm}^{-2})\mu \mathrm{m}^{2}$ in the laser compression pulses). In this proposal the ignition shock wave is created by a high irradiance laser and the shock wave is induced by a ponderomotive force in the intermediate domain between the relativistic and non-relativistic hydrodynamics. For this case the relativistic shock wave formalism has to be considered as developed in our previous section. We call our scheme ultrafast, since the laser pulse duration for the ignition process is significantly smaller, by one to two orders of magnitude.
The shock wave ignition criteria for DT nuclear fuel are
For the DT fusion one has ![]() $A = 2.5$ and
$A = 2.5$ and ![]() $Z = 1$, therefore equation (23) for
$Z = 1$, therefore equation (23) for ![]() $10\ \mathrm{keV}$ temperatures and a compression of
$10\ \mathrm{keV}$ temperatures and a compression of ![]() $\kappa = 4$ implies a minimum dimensionless pressure
$\kappa = 4$ implies a minimum dimensionless pressure ![]() $\Pi _{\mathrm{min}}= 3.4 \times 10^{-5}$. According to our solution the dimensionless laser irradiance satisfies
$\Pi _{\mathrm{min}}= 3.4 \times 10^{-5}$. According to our solution the dimensionless laser irradiance satisfies ![]() $\Pi _{\mathrm{L}} > \Pi _{\mathrm{L,min}}= 1.8\times 10^{-5}$.
$\Pi _{\mathrm{L}} > \Pi _{\mathrm{L,min}}= 1.8\times 10^{-5}$. ![]() $\Pi _{\mathrm{min}}$ and
$\Pi _{\mathrm{min}}$ and ![]() $\kappa = 4$ imply a minimum shock velocity and particle velocity
$\kappa = 4$ imply a minimum shock velocity and particle velocity ![]() $u_{\mathrm{s}}/c =0.59 \times 10^{-2}$ and
$u_{\mathrm{s}}/c =0.59 \times 10^{-2}$ and ![]() $u_{\mathrm{p}}/c = 0.44 \times 10^{-2}$ respectively. Using these values in equation (25)
$u_{\mathrm{p}}/c = 0.44 \times 10^{-2}$ respectively. Using these values in equation (25)![]() $_{\mathrm{(i)}}$, one gets a laser pulse duration of
$_{\mathrm{(i)}}$, one gets a laser pulse duration of ![]() $\tau _{\mathrm{L}}= 1.6\ \mathrm{ps}$. Assuming a pre-compression of
$\tau _{\mathrm{L}}= 1.6\ \mathrm{ps}$. Assuming a pre-compression of ![]() $\rho _{\mathrm{o}}= 10^{\mathrm{3}}\ \mathrm{g\ cm}^{-3}$, the
$\rho _{\mathrm{o}}= 10^{\mathrm{3}}\ \mathrm{g\ cm}^{-3}$, the ![]() $\Pi _{\mathrm{L,min}} = 1.8\times 10^{-5}$ requires
$\Pi _{\mathrm{L,min}} = 1.8\times 10^{-5}$ requires ![]() $I_{\mathrm{L}}=4.8 \times 10^{\mathrm{22}}\ \mathrm{W\ cm}^{\mathrm{-2}}$. The shock wave thickness turn out to be
$I_{\mathrm{L}}=4.8 \times 10^{\mathrm{22}}\ \mathrm{W\ cm}^{\mathrm{-2}}$. The shock wave thickness turn out to be ![]() $l_{\mathrm{s}} = (u_{\mathrm{s}} - u_{\mathrm{p}})\tau _{\mathrm{L}} =0.72\ \mu \mathrm{m}$. In order to have a 1D shock wave to a reasonable approximation we require a laser focal spot radius
$l_{\mathrm{s}} = (u_{\mathrm{s}} - u_{\mathrm{p}})\tau _{\mathrm{L}} =0.72\ \mu \mathrm{m}$. In order to have a 1D shock wave to a reasonable approximation we require a laser focal spot radius ![]() $R_{\mathrm{L}} = 5 l_{\mathrm{s}}$, implying a laser cross section of
$R_{\mathrm{L}} = 5 l_{\mathrm{s}}$, implying a laser cross section of ![]() $S = \pi R_{\mathrm{L}}^{2} = 4.0 \times 10^{-7}\ \mathrm{cm}^{2}$. In this case the laser energy
$S = \pi R_{\mathrm{L}}^{2} = 4.0 \times 10^{-7}\ \mathrm{cm}^{2}$. In this case the laser energy ![]() $W_{\mathrm{L}}$ and power
$W_{\mathrm{L}}$ and power ![]() $P_{\mathrm{L}}$ are 30 kJ and 19 PW respectively. This example was taken to describe our concept in Figure 7. As a numerical example in this figure we take an initial pellet with radius
$P_{\mathrm{L}}$ are 30 kJ and 19 PW respectively. This example was taken to describe our concept in Figure 7. As a numerical example in this figure we take an initial pellet with radius ![]() $R_{0} =1\ \mathrm{mm}$ and a DT fuel of density
$R_{0} =1\ \mathrm{mm}$ and a DT fuel of density ![]() $0.2\ \mathrm{g\ cm}^{-3}$ with thickness 0.1 mm (i.e., an aspect ratio of 10) that is compressed to a density of
$0.2\ \mathrm{g\ cm}^{-3}$ with thickness 0.1 mm (i.e., an aspect ratio of 10) that is compressed to a density of ![]() $\rho _{0} =10^{3}\ \mathrm{g\ cm}^{-3}$ (with a radius of
$\rho _{0} =10^{3}\ \mathrm{g\ cm}^{-3}$ (with a radius of ![]() $67\ \mu \mathrm{m}$) by the nanosecond lasers. The picosecond fast igniter laser with a
$67\ \mu \mathrm{m}$) by the nanosecond lasers. The picosecond fast igniter laser with a ![]() $7.2\ \mu \mathrm{m}$ in diameter creates a shock wave pulse with a thickness of
$7.2\ \mu \mathrm{m}$ in diameter creates a shock wave pulse with a thickness of ![]() $0.72\ \mu \mathrm{m}$, which can be consider a 1D shock wave to a reasonably good approximation. The compressed pellet has a radius much larger than
$0.72\ \mu \mathrm{m}$, which can be consider a 1D shock wave to a reasonably good approximation. The compressed pellet has a radius much larger than ![]() $\sqrt{S}\gg l_{\mathrm{s}}$ in order to have a 1D shock wave. In Table 1 we show how larger values of
$\sqrt{S}\gg l_{\mathrm{s}}$ in order to have a 1D shock wave. In Table 1 we show how larger values of ![]() $\Pi _{\mathrm{L}}$ change the laser and shock wave parameters.
$\Pi _{\mathrm{L}}$ change the laser and shock wave parameters.
Table 1. The laser is defined by its irradiance ![]() $I_{\mathrm{L}}$, pulse duration
$I_{\mathrm{L}}$, pulse duration ![]() $\tau _{\mathrm{L}}$, energy W
$\tau _{\mathrm{L}}$, energy W![]() $_{\mathrm{L}}$ and power P
$_{\mathrm{L}}$ and power P![]() $_{\mathrm{L}}$. This laser creates a shock wave with a compression
$_{\mathrm{L}}$. This laser creates a shock wave with a compression ![]() $\kappa $ in a pre-compressed target with an initial density
$\kappa $ in a pre-compressed target with an initial density ![]() $\rho _{0} $. The shock wave thickness
$\rho _{0} $. The shock wave thickness ![]() $(= (u_{\mathrm{s}}-u_{\mathrm{p}})\tau _{\mathrm{L}}$, where
$(= (u_{\mathrm{s}}-u_{\mathrm{p}})\tau _{\mathrm{L}}$, where ![]() $u_{\mathrm{s}}$ and
$u_{\mathrm{s}}$ and ![]() $u_{\mathrm{p}}$ are the shock wave velocity and the particle velocity respectively) and its cross section are
$u_{\mathrm{p}}$ are the shock wave velocity and the particle velocity respectively) and its cross section are ![]() $l_{\mathrm{s}}$ and
$l_{\mathrm{s}}$ and ![]() $S$, respectively, satisfying
$S$, respectively, satisfying ![]() $\sqrt{S}\gg l_{\mathrm{s}}$ in order to have a 1D shock wave.
$\sqrt{S}\gg l_{\mathrm{s}}$ in order to have a 1D shock wave.

The compression of a typical pellet as discussed in the literature[Reference Atzeni and Meyer-ter-Vehn12, Reference Eliezer, Murakami and Martinez Val47] requires between 100 and 300 kJ of energy, depending on the EOS, target design and the final required density. The FI in our case needs approximately 30 kJ of energy. Such a laser is under development and may be available in the near future.
5. Summary and discussion
Recently[Reference Eliezer, Nissim, Raicher and Martinez Val31] it was suggested that relativistic shock waves with a shock wave velocity of more than 50% light speed can be created in the laboratory with HPLs which are recently under development. In this paper we discuss two novel ideas. The first is the transition domain between the relativistic and non-relativistic laser-induced shock waves. The second is the use of this transition domain for shock-wave-induced ultrafast ignition of a pre-compressed target. The laser parameters for these purposes are calculated and the main advantages of this scheme are described. The many laser beams with few nanosecond pulses that compresses the target do not require ![]() $I_{\mathrm{L}}\lambda _{\mathrm{L}}^{2}= 10^{\mathrm{15}}\ \mathrm{W\ cm}^{-2}\ \mu \mathrm{m}^{2}$ as in the previously proposed shock wave ignition scheme[Reference Betti, Zhou, Anderson, Perkins, Theobald and Sokolov25], thus disturbing laser plasma instabilities do not occur. Furthermore, in the present scheme less energy is required in the main laser pulses where a picosecond laser with very high power (
$I_{\mathrm{L}}\lambda _{\mathrm{L}}^{2}= 10^{\mathrm{15}}\ \mathrm{W\ cm}^{-2}\ \mu \mathrm{m}^{2}$ as in the previously proposed shock wave ignition scheme[Reference Betti, Zhou, Anderson, Perkins, Theobald and Sokolov25], thus disturbing laser plasma instabilities do not occur. Furthermore, in the present scheme less energy is required in the main laser pulses where a picosecond laser with very high power (![]() $\sim $30 PW) is required for the ultrafast ignition with the shock wave in the intermediate domain between the relativistic and non-relativistic hydrodynamics.
$\sim $30 PW) is required for the ultrafast ignition with the shock wave in the intermediate domain between the relativistic and non-relativistic hydrodynamics.
Presently existing petawatt lasers (see appendix B) might be used to start relativistic experimental research in the laboratory. Recent and future developments of HPLs in the multi-petawatt domain could be important for relativistic shock waves in the laboratory with pressures of ![]() $10^{15}$ atmospheres or energy densities of the order of
$10^{15}$ atmospheres or energy densities of the order of ![]() $10^{14}\ \mathrm{J\ cm}^{-3}$. Such pressures or energy densities have been suggested so far only in astrophysical objects.
$10^{14}\ \mathrm{J\ cm}^{-3}$. Such pressures or energy densities have been suggested so far only in astrophysical objects.
The ultrafast ignition scheme suggested in this paper appears advantageous in comparison with the many FI proposals, as given in our introduction section. It is based on the following merit criteria: (i) Understanding the physics, (ii) Engineering simplicity, and (iii) Economically practical. We think that shock wave FI is the best choice and the model suggested here between the relativistic and non-relativistic domain has significant advantages and should be taken seriously into account.
Finally we must mention a very recent FI proposal[Reference Weng, Murakami, Azechi, Wang, Tasoko, Chen, Sheng, Mulser, Yu and Shen48] using a laser system similar to our laser parameters estimated in Section 4. In particular this scheme requires a temporally tailored pulse with an energy of 65 kJ of duration 1.48 ps with a maximum intensity of ![]() $4\times 10^{22}\ \mathrm{W\ cm}^{-2}$. This model is based on the use of a hole–boring[Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou39, Reference Max and Perkins49, Reference Pukhov and Meyer-ter-Vehn50] phenomenon that enables the HPL beam to penetrate beyond the critical density. As early as 1971 it was analytically calculated[Reference Max and Perkins49] that the condition for a laser to propagate in non-uniform plasma with an electron density
$4\times 10^{22}\ \mathrm{W\ cm}^{-2}$. This model is based on the use of a hole–boring[Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou39, Reference Max and Perkins49, Reference Pukhov and Meyer-ter-Vehn50] phenomenon that enables the HPL beam to penetrate beyond the critical density. As early as 1971 it was analytically calculated[Reference Max and Perkins49] that the condition for a laser to propagate in non-uniform plasma with an electron density ![]() $n_{\mathrm{e}}$ and density gradient scale length
$n_{\mathrm{e}}$ and density gradient scale length ![]() $L_{\mathrm{n}}$ beyond the electron critical density
$L_{\mathrm{n}}$ beyond the electron critical density ![]() $n_{\mathrm{c}}$ is given by
$n_{\mathrm{c}}$ is given by
 $$\begin{equation} \label {eq26} \begin{array}{l} \frac {1}{4\pi }\left ({\frac {L_{\mathrm {n}} }{\lambda _{\mathrm {L}} }} \right )\left ({\frac {n_{\mathrm {c}} }{n_{\mathrm {e}} }} \right )^{2}a^{2}>1 \\ a\equiv \frac {eE_{\mathrm {L}} \lambda _{\mathrm {L}}}{2\pi m_{\mathrm {e}} c^{2}}\approx 840\left [{I_{\mathrm {L}} \lambda _{\mathrm {L}}^{2}/10^{24}\left ({\frac {W\cdot \mu \mathrm {m}^{2}}{\mathrm {cm}^{2}}} \right )} \right ]^{1/2}. \end{array} \end{equation}$$
$$\begin{equation} \label {eq26} \begin{array}{l} \frac {1}{4\pi }\left ({\frac {L_{\mathrm {n}} }{\lambda _{\mathrm {L}} }} \right )\left ({\frac {n_{\mathrm {c}} }{n_{\mathrm {e}} }} \right )^{2}a^{2}>1 \\ a\equiv \frac {eE_{\mathrm {L}} \lambda _{\mathrm {L}}}{2\pi m_{\mathrm {e}} c^{2}}\approx 840\left [{I_{\mathrm {L}} \lambda _{\mathrm {L}}^{2}/10^{24}\left ({\frac {W\cdot \mu \mathrm {m}^{2}}{\mathrm {cm}^{2}}} \right )} \right ]^{1/2}. \end{array} \end{equation}$$ PIC simulations[Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou39, Reference Weng, Murakami, Azechi, Wang, Tasoko, Chen, Sheng, Mulser, Yu and Shen48, Reference Pukhov and Meyer-ter-Vehn50] derived ![]() $L_{\mathrm{n}} \sim 20\lambda _{\mathrm{L}}$, implying a laser penetration up to approximately
$L_{\mathrm{n}} \sim 20\lambda _{\mathrm{L}}$, implying a laser penetration up to approximately ![]() $10^{24}\ \mathrm{cm}^{\mathrm{-3}}$ for a one micron wavelength laser with an intensity
$10^{24}\ \mathrm{cm}^{\mathrm{-3}}$ for a one micron wavelength laser with an intensity ![]() $I_{\mathrm{L}}=5\times 10^{22}\ \mathrm{W\ cm}^{-2}$. The quasi mono-energetic ions[Reference Weng, Murakami, Azechi, Wang, Tasoko, Chen, Sheng, Mulser, Yu and Shen48] generated by the tailored laser pulses penetrate beyond this density to ignite the pre-compressed pellet. The in situ accelerated ions are the driver of FI.
$I_{\mathrm{L}}=5\times 10^{22}\ \mathrm{W\ cm}^{-2}$. The quasi mono-energetic ions[Reference Weng, Murakami, Azechi, Wang, Tasoko, Chen, Sheng, Mulser, Yu and Shen48] generated by the tailored laser pulses penetrate beyond this density to ignite the pre-compressed pellet. The in situ accelerated ions are the driver of FI.
In our model the laser-induced relativistic shock wave induces the ignition. The preliminary compressed fusion target for ICF is usually spherically symmetric and the density increases very rapidly towards the core of the target when our shock wave model is applied as described in Figure 7. As long as the thickness of the shock wave ![]() $l_{\mathrm{s}}$ is much smaller than the density gradient
$l_{\mathrm{s}}$ is much smaller than the density gradient ![]() $L_{\mathrm{n}}$, i.e.,
$L_{\mathrm{n}}$, i.e., ![]() $L_{\mathrm{n}} \gg l_{\mathrm{s}}$, we can assume that the target is uniform in the shock wave domain. Looking at our Table 1 one gets
$L_{\mathrm{n}} \gg l_{\mathrm{s}}$, we can assume that the target is uniform in the shock wave domain. Looking at our Table 1 one gets ![]() $l_{\mathrm{s}} \sim 1\ \mu \mathrm{m}$, which is much smaller than the density gradient
$l_{\mathrm{s}} \sim 1\ \mu \mathrm{m}$, which is much smaller than the density gradient ![]() $L_{\mathrm{n}} \sim 20\lambda _{\mathrm{L}}$ derived in PIC simulations[Reference Weng, Murakami, Azechi, Wang, Tasoko, Chen, Sheng, Mulser, Yu and Shen48, Reference Pukhov and Meyer-ter-Vehn50].
$L_{\mathrm{n}} \sim 20\lambda _{\mathrm{L}}$ derived in PIC simulations[Reference Weng, Murakami, Azechi, Wang, Tasoko, Chen, Sheng, Mulser, Yu and Shen48, Reference Pukhov and Meyer-ter-Vehn50].
The solution suggested in this paper, like all other solutions to the energy problem, is extremely difficult scientifically, and a lot of money and enormous optimism is required for a positive solution. HPLSE is complex, complicated but possible. If civilization is to survive we need large new sources of energy. To quote Mark Twain (1835–1910): ‘And what is a man without energy? Nothing – nothing at all’.
Appendix A For convenience we write the nonrelativistic Hugoniot equations and the ideal gas EOS:
 $$\begin{equation} \label {eq27} \begin{array}{l} \;\; \mbox {(i) } u_{{\rm p1}} = [{P_{1} -P_{0} }]^{1/2}\left ({\frac {1}{\rho _{0} }-\frac {1}{\rho _{1} }} \right )^{1/2} \\ \\ \;\; \mbox {(ii) }u_{{\rm s}} =\left ({\frac {1}{\rho _{0} }} \right )\frac {[{P_{1} -P_{0}}]^{1/2}}{\left ({\frac {1}{\rho _{0} }-\frac {1}{\rho _{1} }} \right )^{1/2}} \\ \\ \;\; \mbox {(iii) }E_{1} -E_{0} =\left ({\frac {1}{2}} \right ) [{P_{1} +P_{0}}]\left ({\frac {1}{\rho _{0} }-\frac {1}{\rho _{1} }} \right ) \\ \left . {\begin{array}{l} \mbox {(iv)} \\ \mbox {(v)} \end{array}} \right \} \mbox { }E_{j} =\left ({\frac {1}{\Gamma -1}} \right )\left ({\frac {P_{j} }{\rho _{j} }} \right )\quad \mbox { for }j=0,1. \end{array} \end{equation}$$
$$\begin{equation} \label {eq27} \begin{array}{l} \;\; \mbox {(i) } u_{{\rm p1}} = [{P_{1} -P_{0} }]^{1/2}\left ({\frac {1}{\rho _{0} }-\frac {1}{\rho _{1} }} \right )^{1/2} \\ \\ \;\; \mbox {(ii) }u_{{\rm s}} =\left ({\frac {1}{\rho _{0} }} \right )\frac {[{P_{1} -P_{0}}]^{1/2}}{\left ({\frac {1}{\rho _{0} }-\frac {1}{\rho _{1} }} \right )^{1/2}} \\ \\ \;\; \mbox {(iii) }E_{1} -E_{0} =\left ({\frac {1}{2}} \right ) [{P_{1} +P_{0}}]\left ({\frac {1}{\rho _{0} }-\frac {1}{\rho _{1} }} \right ) \\ \left . {\begin{array}{l} \mbox {(iv)} \\ \mbox {(v)} \end{array}} \right \} \mbox { }E_{j} =\left ({\frac {1}{\Gamma -1}} \right )\left ({\frac {P_{j} }{\rho _{j} }} \right )\quad \mbox { for }j=0,1. \end{array} \end{equation}$$ The equations are obtained from the relativistic equations (11) by using ![]() $e = \rho c^{2}+\rho E, P$ and
$e = \rho c^{2}+\rho E, P$ and ![]() $\rho E$ are much smaller than
$\rho E$ are much smaller than ![]() $\rho c^{2}$ and
$\rho c^{2}$ and ![]() $v/c \ll 1$.
$v/c \ll 1$.
In this appendix we give a list of petawatt lasers that are in use in different laboratories at the end of the year 2013. The following data are not officially confirmed – however, this was used in the literature and conferences according to our knowledge.
USA
Michigan University, Ann Arbor: 10J/30fs
Texas University, Austin: 186J/167fs
Berkeley National Laboratory: 40J/40fs
Rochester University, Rochester: 1 kJ/1ps
LLNL, Livermore: 600J/500fs
CHINA
Beijing National Laboratory: 32J/28fs
Shanghai Institute of Optics and Fine Mechanics: 35J/27fs
EUROPE
Central Laser Facility, UK: 500J/500fs & 15J/30fs
Jena, Germany: 120J/120fs
GSI Darmstadt, Germany: 500J/500fs
JAPAN
Osaka University: 500J/500fs
KOREA
Gwangju University: 34J/30fs