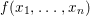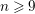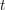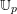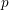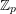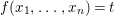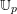1 Introduction
Let
![]() $A=(a_{i,j})_{1\leqslant i,j\leqslant n}$
be a symmetric integral matrix with
$A=(a_{i,j})_{1\leqslant i,j\leqslant n}$
be a symmetric integral matrix with
![]() $n\geqslant 4$
. In other words,
$n\geqslant 4$
. In other words,
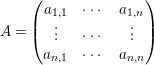 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}a_{1,1} & \cdots \, & a_{1,n}\\ \vdots & \cdots \, & \vdots \\ a_{n,1} & \cdots \, & a_{n,n}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}a_{1,1} & \cdots \, & a_{1,n}\\ \vdots & \cdots \, & \vdots \\ a_{n,1} & \cdots \, & a_{n,n}\end{array}\right)\end{eqnarray}$$
with
![]() $a_{i,j}=a_{j,i}\in \mathbb{Z}$
for all
$a_{i,j}=a_{j,i}\in \mathbb{Z}$
for all
![]() $1\leqslant i<j\leqslant n$
. Let
$1\leqslant i<j\leqslant n$
. Let
![]() $f(x_{1},\ldots ,x_{n})$
be the quadratic form defined as
$f(x_{1},\ldots ,x_{n})$
be the quadratic form defined as
Let
![]() $t$
be an integer. We call
$t$
be an integer. We call
![]() $f$
regular if
$f$
regular if
![]() $A$
is invertible. For regular indefinite quadratic forms with
$A$
is invertible. For regular indefinite quadratic forms with
![]() $n\geqslant 4$
, the well-known Hasse principle asserts that
$n\geqslant 4$
, the well-known Hasse principle asserts that
![]() $f(x_{1},\ldots ,x_{n})=t$
has integer solutions if and only if
$f(x_{1},\ldots ,x_{n})=t$
has integer solutions if and only if
![]() $f(x_{1},\ldots ,x_{n})=t$
has local solutions.
$f(x_{1},\ldots ,x_{n})=t$
has local solutions.
In this paper, we consider the equation
![]() $f(x_{1},\ldots ,x_{n})=t$
, where
$f(x_{1},\ldots ,x_{n})=t$
, where
![]() $x_{1},\ldots ,x_{n}$
are prime variables. It is expected that
$x_{1},\ldots ,x_{n}$
are prime variables. It is expected that
![]() $f(x_{1},\ldots ,x_{n})=t$
has solutions with
$f(x_{1},\ldots ,x_{n})=t$
has solutions with
![]() $x_{1},\ldots ,x_{n}$
primes if there are suitable local solutions. The classical theorem of Hua [Reference Hua7] deals with diagonal quadratic forms in five prime variables. In particular, every sufficiently large integer, congruent to 5 modulo 24, can be represented as a sum of five squares of primes. Recently, Liu [Reference Liu9] handled a wide class of quadratic forms
$x_{1},\ldots ,x_{n}$
primes if there are suitable local solutions. The classical theorem of Hua [Reference Hua7] deals with diagonal quadratic forms in five prime variables. In particular, every sufficiently large integer, congruent to 5 modulo 24, can be represented as a sum of five squares of primes. Recently, Liu [Reference Liu9] handled a wide class of quadratic forms
![]() $f$
with 10 or more prime variables. The general quadratic form in prime variables (or in dense sets) was recently investigated by Cook and Magyar [Reference Cook and Magyar3], and by Keil [Reference Keil8]. In particular, Cook and Magyar [Reference Cook and Magyar3] handled all regular quadratic forms in 21 or more prime variables, while the work of Keil [Reference Keil8] can deal with all regular quadratic forms in 17 or more variables. It involves only five prime variables for diagonal quadratic equation due to the effective mean value theorem. This is similar to the problem concerning Diophantine equations for cubic forms. The works of Baker [Reference Baker1], Vaughan [Reference Vaughan10, Reference Vaughan11] and Wooley [Reference Wooley13, Reference Wooley14] can deal with the diagonal cubic equation in seven variables. However, more variables are involved for general cubic forms. One can refer to the works of Heath-Brown [Reference Heath-Brown4, Reference Heath-Brown5] and Hooley [Reference Hooley6] for general cubic forms.
$f$
with 10 or more prime variables. The general quadratic form in prime variables (or in dense sets) was recently investigated by Cook and Magyar [Reference Cook and Magyar3], and by Keil [Reference Keil8]. In particular, Cook and Magyar [Reference Cook and Magyar3] handled all regular quadratic forms in 21 or more prime variables, while the work of Keil [Reference Keil8] can deal with all regular quadratic forms in 17 or more variables. It involves only five prime variables for diagonal quadratic equation due to the effective mean value theorem. This is similar to the problem concerning Diophantine equations for cubic forms. The works of Baker [Reference Baker1], Vaughan [Reference Vaughan10, Reference Vaughan11] and Wooley [Reference Wooley13, Reference Wooley14] can deal with the diagonal cubic equation in seven variables. However, more variables are involved for general cubic forms. One can refer to the works of Heath-Brown [Reference Heath-Brown4, Reference Heath-Brown5] and Hooley [Reference Hooley6] for general cubic forms.
The purpose of this paper is to investigate general regular quadratic forms in nine or more prime variables. We define
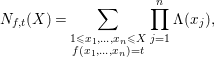 $$\begin{eqnarray}N_{f,t}(X)=\mathop{\sum }_{\substack{ 1\leqslant x_{1},\ldots ,x_{n}\leqslant X \\ f(x_{1},\ldots ,x_{n})=t}}\mathop{\prod }_{j=1}^{n}{\rm\Lambda}(x_{j}),\end{eqnarray}$$
$$\begin{eqnarray}N_{f,t}(X)=\mathop{\sum }_{\substack{ 1\leqslant x_{1},\ldots ,x_{n}\leqslant X \\ f(x_{1},\ldots ,x_{n})=t}}\mathop{\prod }_{j=1}^{n}{\rm\Lambda}(x_{j}),\end{eqnarray}$$
where
![]() ${\rm\Lambda}(\cdot )$
is the von Mangoldt function. Our main result is the following.
${\rm\Lambda}(\cdot )$
is the von Mangoldt function. Our main result is the following.
Theorem 1.1. Suppose that
![]() $f(x_{1},\ldots ,x_{n})$
is a regular integral quadratic form with
$f(x_{1},\ldots ,x_{n})$
is a regular integral quadratic form with
![]() $n\geqslant 9$
, and that
$n\geqslant 9$
, and that
![]() $t\in \mathbb{Z}$
. Let
$t\in \mathbb{Z}$
. Let
![]() $\mathfrak{S}(f,t)$
and
$\mathfrak{S}(f,t)$
and
![]() $\mathfrak{I}_{f,t}(X)$
be defined in (3.11) and (3.13), respectively. Suppose that
$\mathfrak{I}_{f,t}(X)$
be defined in (3.11) and (3.13), respectively. Suppose that
![]() $K$
is an arbitrary large real number. Then we have
$K$
is an arbitrary large real number. Then we have
where the implied constant depends on
![]() $f$
and
$f$
and
![]() $K$
.
$K$
.
Denote by
![]() $\mathbb{P}$
the set of all prime numbers. For a prime
$\mathbb{P}$
the set of all prime numbers. For a prime
![]() $p\in \mathbb{P}$
, we use
$p\in \mathbb{P}$
, we use
![]() $\mathbb{Z}_{p}$
to denote the ring of
$\mathbb{Z}_{p}$
to denote the ring of
![]() $p$
-adic integers. Then we use
$p$
-adic integers. Then we use
![]() $\mathbb{U}_{p}$
to denote the set of
$\mathbb{U}_{p}$
to denote the set of
![]() $p$
-adic units in
$p$
-adic units in
![]() $\mathbb{Z}_{p}$
. The general local to global conjecture of Bourgain–Gamburd–Sarnak [Reference Bourgain, Gamburd and Sarnak2] asserts that
$\mathbb{Z}_{p}$
. The general local to global conjecture of Bourgain–Gamburd–Sarnak [Reference Bourgain, Gamburd and Sarnak2] asserts that
![]() $f(x_{1},\ldots ,x_{n})=t$
has prime solutions provided that there are local solutions in
$f(x_{1},\ldots ,x_{n})=t$
has prime solutions provided that there are local solutions in
![]() $\mathbb{U}_{p}$
for all
$\mathbb{U}_{p}$
for all
![]() $p\in \mathbb{P}$
. Liu [Reference Liu9, Theorem 1.1] verified this conjecture for a wide class of regular indefinite integral quadratic forms with ten or more variables. Theorem 1.1 has the following consequence improving upon Liu [Reference Liu9, Theorem 1.1].
$p\in \mathbb{P}$
. Liu [Reference Liu9, Theorem 1.1] verified this conjecture for a wide class of regular indefinite integral quadratic forms with ten or more variables. Theorem 1.1 has the following consequence improving upon Liu [Reference Liu9, Theorem 1.1].
Theorem 1.2. Let
![]() $f(x_{1},\ldots ,x_{n})$
be a regular indefinite integral quadratic form with
$f(x_{1},\ldots ,x_{n})$
be a regular indefinite integral quadratic form with
![]() $n\geqslant 9$
, and let
$n\geqslant 9$
, and let
![]() $t\in \mathbb{Z}$
. Then
$t\in \mathbb{Z}$
. Then
![]() $f(x_{1},\ldots ,x_{n})=t$
has prime solutions if we have the following two conditions:
$f(x_{1},\ldots ,x_{n})=t$
has prime solutions if we have the following two conditions:
-
(i) there are real solutions in
 $\mathbb{R}^{+}$
, and
$\mathbb{R}^{+}$
, and -
(ii) there are local solutions in
 $\mathbb{U}_{p}$
for all prime
$\mathbb{U}_{p}$
for all prime
 $p$
.
$p$
.
We define
![]() $N_{f,t}^{\ast }(X)$
to be the number of prime solutions to
$N_{f,t}^{\ast }(X)$
to be the number of prime solutions to
![]() $f(p_{1},\ldots ,p_{n})=t$
with
$f(p_{1},\ldots ,p_{n})=t$
with
![]() $1\leqslant p_{1},\ldots ,p_{n}\leqslant X$
. Suppose that
$1\leqslant p_{1},\ldots ,p_{n}\leqslant X$
. Suppose that
![]() $f$
is regular with
$f$
is regular with
![]() $n\geqslant 9$
. Actually, in view of Theorem 1.1, one has
$n\geqslant 9$
. Actually, in view of Theorem 1.1, one has
![]() $N_{f,t}^{\ast }(X)\gg _{f,t}X^{n-2}\log ^{-n}X$
for sufficiently large
$N_{f,t}^{\ast }(X)\gg _{f,t}X^{n-2}\log ^{-n}X$
for sufficiently large
![]() $X$
if the conditions (i) and (ii) in Theorem 1.2 hold.
$X$
if the conditions (i) and (ii) in Theorem 1.2 hold.
Theorem 1.2 covers all regular indefinite integral quadratic forms in nine prime variables. The
![]() $O$
-constant in the asymptotic formula (1.3) is independent of
$O$
-constant in the asymptotic formula (1.3) is independent of
![]() $t$
. Therefore, Theorem 1.1 can be applied to definite quadratic forms. In particular, if
$t$
. Therefore, Theorem 1.1 can be applied to definite quadratic forms. In particular, if
![]() $f(x_{1},\ldots ,x_{n})$
is a positive definite integral quadratic form with
$f(x_{1},\ldots ,x_{n})$
is a positive definite integral quadratic form with
![]() $n\geqslant 9$
, then there exist
$n\geqslant 9$
, then there exist
![]() $r,q\in \mathbb{N}$
so that all sufficiently large natural numbers
$r,q\in \mathbb{N}$
so that all sufficiently large natural numbers
![]() $N$
, congruent to
$N$
, congruent to
![]() $r$
modulo
$r$
modulo
![]() $q$
, can be represented as
$q$
, can be represented as
![]() $N=f(p_{1},\ldots ,p_{n})$
, where
$N=f(p_{1},\ldots ,p_{n})$
, where
![]() $p_{1},\ldots ,p_{n}$
are prime numbers.
$p_{1},\ldots ,p_{n}$
are prime numbers.
The method in this paper can also be applied to refine Keil [Reference Keil8, Theorem 1.1]. In particular, one may obtain a variant of Keil [Reference Keil8, Theorem 1.1] for a wide class of quadratic forms in nine variables.
2 Notations
As usual, we write
![]() $e(z)$
for
$e(z)$
for
![]() $e^{2{\it\pi}iz}$
. Throughout we assume that
$e^{2{\it\pi}iz}$
. Throughout we assume that
![]() $X$
is sufficiently large. Let
$X$
is sufficiently large. Let
![]() $L=\log X$
. We use
$L=\log X$
. We use
![]() $\ll$
and
$\ll$
and
![]() $\gg$
to denote Vinogradov’s well-known notations, while the implied constants may depend on the form
$\gg$
to denote Vinogradov’s well-known notations, while the implied constants may depend on the form
![]() $f$
. Denote by
$f$
. Denote by
![]() ${\it\phi}(q)$
Euler’s totient function.
${\it\phi}(q)$
Euler’s totient function.
For a set
![]() ${\mathcal{S}}$
in a field
${\mathcal{S}}$
in a field
![]() $\mathbb{F}$
, we define
$\mathbb{F}$
, we define
We use
![]() $M_{m,n}({\mathcal{S}})$
to denote the set of
$M_{m,n}({\mathcal{S}})$
to denote the set of
![]() $m$
by
$m$
by
![]() $n$
matrixes
$n$
matrixes
and
![]() $GL_{n}({\mathcal{S}})$
to denote the set of invertible matrixes of order
$GL_{n}({\mathcal{S}})$
to denote the set of invertible matrixes of order
![]() $n$
$n$
respectively. We define the off-diagonal rank of
![]() $A$
as
$A$
as
where
In other words,
![]() $\text{rank}_{\text{off}}(A)$
is the maximal rank of a submatrix in
$\text{rank}_{\text{off}}(A)$
is the maximal rank of a submatrix in
![]() $A$
, which does not contain any diagonal entries. For
$A$
, which does not contain any diagonal entries. For
![]() $\mathbf{x}=(x_{1},\ldots ,x_{n})^{T}\in \mathbb{N}^{n}$
, we write
$\mathbf{x}=(x_{1},\ldots ,x_{n})^{T}\in \mathbb{N}^{n}$
, we write
For
![]() $\mathbf{x}=(x_{1},\ldots ,x_{n})^{T}\in \mathbb{Z}^{n}$
, we also use the notation
$\mathbf{x}=(x_{1},\ldots ,x_{n})^{T}\in \mathbb{Z}^{n}$
, we also use the notation
![]() ${\mathcal{A}}(\mathbf{x})$
to indicate that the argument
${\mathcal{A}}(\mathbf{x})$
to indicate that the argument
![]() ${\mathcal{A}}(x_{j})$
holds for all
${\mathcal{A}}(x_{j})$
holds for all
![]() $1\leqslant j\leqslant s$
. The meaning will be clear from the text. For example, we use
$1\leqslant j\leqslant s$
. The meaning will be clear from the text. For example, we use
![]() $1\leqslant \mathbf{x}\leqslant X$
and
$1\leqslant \mathbf{x}\leqslant X$
and
![]() $|\mathbf{x}|\leqslant X$
to denote
$|\mathbf{x}|\leqslant X$
to denote
![]() $1\leqslant x_{j}\leqslant X$
for
$1\leqslant x_{j}\leqslant X$
for
![]() $1\leqslant j\leqslant n$
and
$1\leqslant j\leqslant n$
and
![]() $|x_{j}|\leqslant X$
for
$|x_{j}|\leqslant X$
for
![]() $1\leqslant j\leqslant n$
, respectively.
$1\leqslant j\leqslant n$
, respectively.
In order to apply the circle method, we introduce the exponential sum
where
![]() $A$
is defined in (1.1). We define
$A$
is defined in (1.1). We define
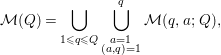 $$\begin{eqnarray}{\mathcal{M}}(Q)=\mathop{\bigcup }_{1\leqslant q\leqslant Q}\mathop{\bigcup }_{\substack{ a=1 \\ (a,q)=1}}^{q}{\mathcal{M}}(q,a;Q),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}(Q)=\mathop{\bigcup }_{1\leqslant q\leqslant Q}\mathop{\bigcup }_{\substack{ a=1 \\ (a,q)=1}}^{q}{\mathcal{M}}(q,a;Q),\end{eqnarray}$$
where
The intervals
![]() ${\mathcal{M}}(q,a;Q)$
are pairwise disjoint for
${\mathcal{M}}(q,a;Q)$
are pairwise disjoint for
![]() $1\leqslant a\leqslant q\leqslant Q$
and
$1\leqslant a\leqslant q\leqslant Q$
and
![]() $(a,q)=1$
provided that
$(a,q)=1$
provided that
![]() $Q\leqslant X/2$
. For
$Q\leqslant X/2$
. For
![]() $Q\leqslant X/2$
, we set
$Q\leqslant X/2$
, we set
Now we introduce the major arcs defined as
where
![]() $K$
is a sufficiently large constant throughout this paper. Then we define the minor arcs as
$K$
is a sufficiently large constant throughout this paper. Then we define the minor arcs as
3 The contribution from the major arcs
For
![]() $q\in \mathbb{N}$
and
$q\in \mathbb{N}$
and
![]() $(a,q)=1$
, we define
$(a,q)=1$
, we define
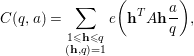 $$\begin{eqnarray}C(q,a)=\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant q \\ (\mathbf{h},q)=1}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{q}\bigg),\end{eqnarray}$$
$$\begin{eqnarray}C(q,a)=\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant q \\ (\mathbf{h},q)=1}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{q}\bigg),\end{eqnarray}$$
where
![]() $A$
is given by (1.1). Throughout, we assume that
$A$
is given by (1.1). Throughout, we assume that
![]() $f$
is connected to
$f$
is connected to
![]() $A$
given by (1.1) and (1.2). Let
$A$
given by (1.1) and (1.2). Let
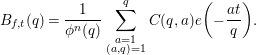 $$\begin{eqnarray}B_{f,t}(q)=\frac{1}{{\it\phi}^{n}(q)}\mathop{\sum }_{\substack{ a=1 \\ (a,q)=1}}^{q}C(q,a)e\bigg(-\frac{at}{q}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}B_{f,t}(q)=\frac{1}{{\it\phi}^{n}(q)}\mathop{\sum }_{\substack{ a=1 \\ (a,q)=1}}^{q}C(q,a)e\bigg(-\frac{at}{q}\bigg).\end{eqnarray}$$
Concerning
![]() $B_{f,t}(q)$
, we have the following multiplicative property.
$B_{f,t}(q)$
, we have the following multiplicative property.
Lemma 3.1. The arithmetic function
![]() $B_{f,t}(q)$
is multiplicative.
$B_{f,t}(q)$
is multiplicative.
Proof. The desired conclusion can be proved by changing variables. ◻
Lemma 3.2. Suppose that
![]() $A$
is invertible. For any prime
$A$
is invertible. For any prime
![]() $p$
, there exists
$p$
, there exists
![]() ${\it\gamma}_{p}={\it\gamma}_{p}(f,t)$
such that
${\it\gamma}_{p}={\it\gamma}_{p}(f,t)$
such that
![]() $B_{f,t}(p^{k})=0$
for all
$B_{f,t}(p^{k})=0$
for all
![]() $k>{\it\gamma}_{p}$
. Moreover, if
$k>{\it\gamma}_{p}$
. Moreover, if
![]() $p\nmid 2\det (A)$
, then we have
$p\nmid 2\det (A)$
, then we have
![]() ${\it\gamma}_{p}=1$
.
${\it\gamma}_{p}=1$
.
Proof. Throughout this proof, we assume that
![]() $(a,p)=1$
. We first deal with the case
$(a,p)=1$
. We first deal with the case
![]() $p\geqslant 3$
. We claim that if
$p\geqslant 3$
. We claim that if
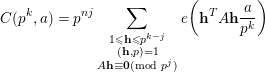 $$\begin{eqnarray}C(p^{k},a)=p^{nj}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg)\end{eqnarray}$$
$$\begin{eqnarray}C(p^{k},a)=p^{nj}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg)\end{eqnarray}$$
for some
![]() $j\leqslant (k-2)/2$
, then
$j\leqslant (k-2)/2$
, then
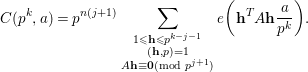 $$\begin{eqnarray}C(p^{k},a)=p^{n(j+1)}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j+1})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}C(p^{k},a)=p^{n(j+1)}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j+1})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg).\end{eqnarray}$$
Indeed, by changing variables, we obtain from (3.3) that
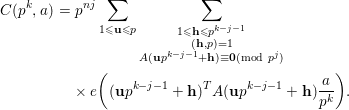 $$\begin{eqnarray}\displaystyle C(p^{k},a) & = & \displaystyle p^{nj}\mathop{\sum }_{1\leqslant \mathbf{u}\leqslant p}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A(\mathbf{u}p^{k-j-1}+\mathbf{h})\equiv \mathbf{0}(\text{mod}~p^{j})}}\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg((\mathbf{u}p^{k-j-1}+\mathbf{h})^{T}A(\mathbf{u}p^{k-j-1}+\mathbf{h})\frac{a}{p^{k}}\bigg).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C(p^{k},a) & = & \displaystyle p^{nj}\mathop{\sum }_{1\leqslant \mathbf{u}\leqslant p}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A(\mathbf{u}p^{k-j-1}+\mathbf{h})\equiv \mathbf{0}(\text{mod}~p^{j})}}\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg((\mathbf{u}p^{k-j-1}+\mathbf{h})^{T}A(\mathbf{u}p^{k-j-1}+\mathbf{h})\frac{a}{p^{k}}\bigg).\nonumber\end{eqnarray}$$
It follows from
![]() $j\leqslant (k-2)/2$
that
$j\leqslant (k-2)/2$
that
![]() $j\leqslant k-j-1$
and
$j\leqslant k-j-1$
and
![]() $k\leqslant 2(k-j-1)$
. Thus we deduce that
$k\leqslant 2(k-j-1)$
. Thus we deduce that
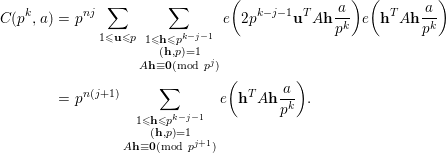 $$\begin{eqnarray}\displaystyle C(p^{k},a) & = & \displaystyle p^{nj}\mathop{\sum }_{1\leqslant \mathbf{u}\leqslant p}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j})}}e\bigg(2p^{k-j-1}\mathbf{u}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg)e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle p^{n(j+1)}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j+1})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C(p^{k},a) & = & \displaystyle p^{nj}\mathop{\sum }_{1\leqslant \mathbf{u}\leqslant p}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j})}}e\bigg(2p^{k-j-1}\mathbf{u}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg)e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle p^{n(j+1)}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-j-1} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{j+1})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg).\nonumber\end{eqnarray}$$
This establishes the desired claim, and therefore we arrive at
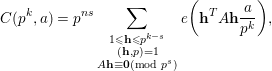 $$\begin{eqnarray}C(p^{k},a)=p^{ns}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-s} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{s})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg),\end{eqnarray}$$
$$\begin{eqnarray}C(p^{k},a)=p^{ns}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{k-s} \\ (\mathbf{h},p)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{s})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p^{k}}\bigg),\end{eqnarray}$$
where
![]() $s=\lfloor k/2\rfloor$
. There exists
$s=\lfloor k/2\rfloor$
. There exists
![]() $P\in GL_{n}(\mathbb{Z}_{p})$
with
$P\in GL_{n}(\mathbb{Z}_{p})$
with
![]() $\det (P)=1$
such that
$\det (P)=1$
such that
![]() $P^{T}AP=D=\text{diag}\{d_{1},\ldots ,d_{n}\}$
with
$P^{T}AP=D=\text{diag}\{d_{1},\ldots ,d_{n}\}$
with
![]() $d_{1},\ldots ,d_{n}\in \mathbb{Z}_{p}$
. Note that
$d_{1},\ldots ,d_{n}\in \mathbb{Z}_{p}$
. Note that
![]() $A$
is invertible, one has
$A$
is invertible, one has
![]() $d_{1}\cdots d_{n}\not =0$
. In particular, we can choose
$d_{1}\cdots d_{n}\not =0$
. In particular, we can choose
![]() $r\in \mathbb{N}$
such that
$r\in \mathbb{N}$
such that
![]() $p^{r}\nmid d_{j}$
for all
$p^{r}\nmid d_{j}$
for all
![]() $1\leqslant j\leqslant n$
. The condition
$1\leqslant j\leqslant n$
. The condition
![]() $A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{s})$
implies
$A\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{s})$
implies
![]() $DP\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{s})$
. If
$DP\mathbf{h}\equiv \mathbf{0}(\text{mod}~p^{s})$
. If
![]() $s\geqslant r$
, then
$s\geqslant r$
, then
![]() $P\mathbf{h}\equiv \mathbf{0}(\text{mod}~p)$
. So we obtain
$P\mathbf{h}\equiv \mathbf{0}(\text{mod}~p)$
. So we obtain
![]() $\mathbf{h}\equiv \mathbf{0}(\text{mod}~p)$
, which is a contradiction to the condition
$\mathbf{h}\equiv \mathbf{0}(\text{mod}~p)$
, which is a contradiction to the condition
![]() $(\mathbf{h},p)=1$
. Therefore, we conclude that
$(\mathbf{h},p)=1$
. Therefore, we conclude that
Moreover, when
![]() $p\nmid 2\det (A)$
, we can take
$p\nmid 2\det (A)$
, we can take
![]() $r=1$
in (3.6).
$r=1$
in (3.6).
For
![]() $p=2$
, the above argument is still valid with minor modifications. We now claim that if
$p=2$
, the above argument is still valid with minor modifications. We now claim that if
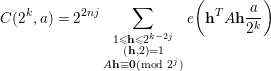 $$\begin{eqnarray}C(2^{k},a)=2^{2nj}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant 2^{k-2j} \\ (\mathbf{h},2)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~2^{j})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{2^{k}}\bigg)\end{eqnarray}$$
$$\begin{eqnarray}C(2^{k},a)=2^{2nj}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant 2^{k-2j} \\ (\mathbf{h},2)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~2^{j})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{2^{k}}\bigg)\end{eqnarray}$$
for some
![]() $j\leqslant (k-4)/4$
, then
$j\leqslant (k-4)/4$
, then
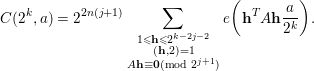 $$\begin{eqnarray}C(2^{k},a)=2^{2n(j+1)}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant 2^{k-2j-2} \\ (\mathbf{h},2)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~2^{j+1})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{2^{k}}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}C(2^{k},a)=2^{2n(j+1)}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant 2^{k-2j-2} \\ (\mathbf{h},2)=1 \\ A\mathbf{h}\equiv \mathbf{0}(\text{mod}~2^{j+1})}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{2^{k}}\bigg).\end{eqnarray}$$
This claim can be established by changing variables
![]() $\mathbf{h}=\mathbf{u}2^{k-2j-2}+\mathbf{v}$
with
$\mathbf{h}=\mathbf{u}2^{k-2j-2}+\mathbf{v}$
with
![]() $\mathbf{u}(\text{mod}~2^{2})$
and
$\mathbf{u}(\text{mod}~2^{2})$
and
![]() $\mathbf{v}(\text{mod}~2^{k-2j-2})$
. The argument leading to (3.6) implies that there exists
$\mathbf{v}(\text{mod}~2^{k-2j-2})$
. The argument leading to (3.6) implies that there exists
![]() $k_{0}$
such that
$k_{0}$
such that
The desired conclusion follows from (3.2), (3.6) and (3.9).◻
Lemma 3.3. Let
![]() $B_{f,t}(q)$
be defined as (3.2). If
$B_{f,t}(q)$
be defined as (3.2). If
![]() $A$
is invertible and
$A$
is invertible and
![]() $n\geqslant 5$
, then
$n\geqslant 5$
, then
Proof. In view of Lemma 3.2, it suffices to prove
for
![]() $p\nmid 2\det (A)$
and
$p\nmid 2\det (A)$
and
![]() $(a,p)=1$
. Note that
$(a,p)=1$
. Note that
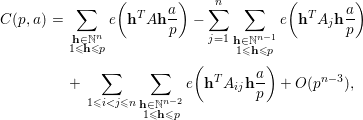 $$\begin{eqnarray}\displaystyle C(p,a) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{n} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p}\bigg)-\mathop{\sum }_{j=1}^{n}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{n-1} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}A_{j}\mathbf{h}\frac{a}{p}\bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i<j\leqslant n}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{n-2} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}A_{ij}\mathbf{h}\frac{a}{p}\bigg)+O(p^{n-3}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C(p,a) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{n} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}A\mathbf{h}\frac{a}{p}\bigg)-\mathop{\sum }_{j=1}^{n}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{n-1} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}A_{j}\mathbf{h}\frac{a}{p}\bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i<j\leqslant n}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{n-2} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}A_{ij}\mathbf{h}\frac{a}{p}\bigg)+O(p^{n-3}),\nonumber\end{eqnarray}$$
where
![]() $A_{j}$
denotes the submatrix of
$A_{j}$
denotes the submatrix of
![]() $A$
by deleting the
$A$
by deleting the
![]() $j$
th row and
$j$
th row and
![]() $j$
th column, and
$j$
th column, and
![]() $A_{ij}$
denotes the submatrix of
$A_{ij}$
denotes the submatrix of
![]() $A_{j}$
by deleting the
$A_{j}$
by deleting the
![]() $i$
th row and
$i$
th row and
![]() $i$
th column. For complete Gauss sums, we have
$i$
th column. For complete Gauss sums, we have
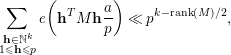 $$\begin{eqnarray}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{k} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}M\mathbf{h}\frac{a}{p}\bigg)\ll p^{k-\text{rank}(M)/2},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{N}^{k} \\ 1\leqslant \mathbf{h}\leqslant p}}e\bigg(\mathbf{h}^{T}M\mathbf{h}\frac{a}{p}\bigg)\ll p^{k-\text{rank}(M)/2},\end{eqnarray}$$
where the implied constant depends on the square matrix
![]() $M$
. The estimate (3.10) follows by observing that
$M$
. The estimate (3.10) follows by observing that
![]() $\text{rank}(A_{j})\geqslant 3$
and
$\text{rank}(A_{j})\geqslant 3$
and
![]() $\text{rank}(A_{ij})\geqslant 1$
. We complete the proof.◻
$\text{rank}(A_{ij})\geqslant 1$
. We complete the proof.◻
Now we introduce the singular series
![]() $\mathfrak{S}(f,t)$
defined as
$\mathfrak{S}(f,t)$
defined as
where
![]() $B_{f,t}(q)$
is given by (3.2). From Lemmas 3.2 and 3.3, we conclude the following result.
$B_{f,t}(q)$
is given by (3.2). From Lemmas 3.2 and 3.3, we conclude the following result.
Lemma 3.4. Suppose that
![]() $A$
is invertible and
$A$
is invertible and
![]() $n\geqslant 5$
. Then the singular series
$n\geqslant 5$
. Then the singular series
![]() $\mathfrak{S}(f,t)$
is absolutely convergent, and
$\mathfrak{S}(f,t)$
is absolutely convergent, and
where the local densities
![]() ${\it\chi}_{p}(f,t)$
are defined as
${\it\chi}_{p}(f,t)$
are defined as
Moreover, if
![]() $f(x_{1},\ldots ,x_{n})=t$
has local solutions in
$f(x_{1},\ldots ,x_{n})=t$
has local solutions in
![]() $\mathbb{U}_{p}$
for all prime
$\mathbb{U}_{p}$
for all prime
![]() $p$
, then one has
$p$
, then one has
Proof. It suffices to explain
![]() $\mathfrak{S}(f,t)\gg 1$
provided that
$\mathfrak{S}(f,t)\gg 1$
provided that
![]() $f(x_{1},\ldots ,x_{n})=t$
has local solutions in
$f(x_{1},\ldots ,x_{n})=t$
has local solutions in
![]() $\mathbb{U}_{p}$
for all prime
$\mathbb{U}_{p}$
for all prime
![]() $p$
. Indeed, in view of Lemma 3.3, one has
$p$
. Indeed, in view of Lemma 3.3, one has
![]() $\prod _{p\geqslant p_{0}}{\it\chi}_{p}(f,t)\gg 1$
for some
$\prod _{p\geqslant p_{0}}{\it\chi}_{p}(f,t)\gg 1$
for some
![]() $p_{0}$
. When
$p_{0}$
. When
![]() $p<p_{0}$
, by Lemma 3.2, for some
$p<p_{0}$
, by Lemma 3.2, for some
![]() ${\it\gamma}={\it\gamma}_{p}$
we have
${\it\gamma}={\it\gamma}_{p}$
we have
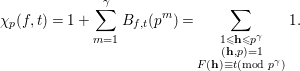 $$\begin{eqnarray}{\it\chi}_{p}(f,t)=1+\mathop{\sum }_{m=1}^{{\it\gamma}}B_{f,t}(p^{m})=\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{{\it\gamma}} \\ (\mathbf{h},p)=1 \\ F(\mathbf{h})\equiv t(\text{mod}~p^{{\it\gamma}})}}1.\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}_{p}(f,t)=1+\mathop{\sum }_{m=1}^{{\it\gamma}}B_{f,t}(p^{m})=\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant p^{{\it\gamma}} \\ (\mathbf{h},p)=1 \\ F(\mathbf{h})\equiv t(\text{mod}~p^{{\it\gamma}})}}1.\end{eqnarray}$$
Since
![]() $f(x_{1},\ldots ,x_{n})=t$
has local solutions in
$f(x_{1},\ldots ,x_{n})=t$
has local solutions in
![]() $\mathbb{U}_{p}$
, one has
$\mathbb{U}_{p}$
, one has
![]() ${\it\chi}_{p}(f,t)>0$
. This concludes that
${\it\chi}_{p}(f,t)>0$
. This concludes that
![]() $\mathop{\prod }_{p}{\it\chi}_{p}(f,t)\gg 1$
.◻
$\mathop{\prod }_{p}{\it\chi}_{p}(f,t)\gg 1$
.◻
Remark 3.5. We point out that in view of the proof of Lemmas 3.2–3.3, one has
where
![]() $q_{1}$
is square-free and
$q_{1}$
is square-free and
![]() $(2,q_{1}q_{2})=(q_{1},q_{2})=1$
. In particular, the singular series is absolutely convergent if
$(2,q_{1}q_{2})=(q_{1},q_{2})=1$
. In particular, the singular series is absolutely convergent if
![]() $\text{rank}(A)\geqslant 5$
. Therefore, the condition that
$\text{rank}(A)\geqslant 5$
. Therefore, the condition that
![]() $f$
is regular with
$f$
is regular with
![]() $n\geqslant 9$
in our Theorem 1.1 can be replaced by
$n\geqslant 9$
in our Theorem 1.1 can be replaced by
![]() $\text{rank}(A)\geqslant 9$
.
$\text{rank}(A)\geqslant 9$
.
We define
Since
![]() $I({\it\beta})\ll X^{n}(1+X^{2}|{\it\beta}|)^{-2}$
for
$I({\it\beta})\ll X^{n}(1+X^{2}|{\it\beta}|)^{-2}$
for
![]() $\text{rank}(A)\geqslant 5$
, we introduce the singular integral
$\text{rank}(A)\geqslant 5$
, we introduce the singular integral
where
![]() $f(\mathbf{x})=\mathbf{x}^{T}A\mathbf{x}$
. Note that
$f(\mathbf{x})=\mathbf{x}^{T}A\mathbf{x}$
. Note that
![]() $\mathfrak{I}_{f,t}(X)\gg _{f,t}X^{n-2}$
if
$\mathfrak{I}_{f,t}(X)\gg _{f,t}X^{n-2}$
if
![]() $f(x_{1},\ldots ,x_{n})$
is indefinite and
$f(x_{1},\ldots ,x_{n})$
is indefinite and
![]() $f(x_{1},\ldots ,x_{n})=t$
has positive real solutions.
$f(x_{1},\ldots ,x_{n})=t$
has positive real solutions.
Lemma 3.6. Let
![]() $t\in \mathbb{Z}$
, and let
$t\in \mathbb{Z}$
, and let
where
![]() $A\in M_{n,n}(\mathbb{Z})$
is a symmetric matrix with
$A\in M_{n,n}(\mathbb{Z})$
is a symmetric matrix with
![]() $\text{rank}(A)\geqslant 5$
. Then one has
$\text{rank}(A)\geqslant 5$
. Then one has
Proof. We write
![]() $f(\mathbf{x})$
for
$f(\mathbf{x})$
for
![]() $\mathbf{x}^{T}A\mathbf{x}$
. By the definition of
$\mathbf{x}^{T}A\mathbf{x}$
. By the definition of
![]() $\mathfrak{M}$
, one has
$\mathfrak{M}$
, one has
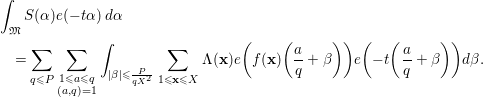 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{M}}S({\it\alpha})e(-t{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{q\leqslant P}\mathop{\sum }_{\substack{ 1\leqslant a\leqslant q \\ (a,q)=1}}\int _{|{\it\beta}|\leqslant \frac{P}{qX^{2}}}\mathop{\sum }_{1\leqslant \mathbf{x}\leqslant X}{\rm\Lambda}(\mathbf{x})e\bigg(f(\mathbf{x})\bigg(\frac{a}{q}+{\it\beta}\bigg)\bigg)e\bigg(-t\bigg(\frac{a}{q}+{\it\beta}\bigg)\bigg)d{\it\beta}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{M}}S({\it\alpha})e(-t{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{q\leqslant P}\mathop{\sum }_{\substack{ 1\leqslant a\leqslant q \\ (a,q)=1}}\int _{|{\it\beta}|\leqslant \frac{P}{qX^{2}}}\mathop{\sum }_{1\leqslant \mathbf{x}\leqslant X}{\rm\Lambda}(\mathbf{x})e\bigg(f(\mathbf{x})\bigg(\frac{a}{q}+{\it\beta}\bigg)\bigg)e\bigg(-t\bigg(\frac{a}{q}+{\it\beta}\bigg)\bigg)d{\it\beta}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We introduce the congruence condition to deduce that
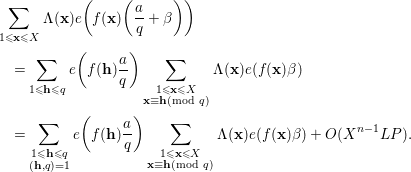 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{x}\leqslant X}{\rm\Lambda}(\mathbf{x})e\bigg(f(\mathbf{x})\bigg(\frac{a}{q}+{\it\beta}\bigg)\bigg)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{1\leqslant \mathbf{h}\leqslant q}e\bigg(f(\mathbf{h})\frac{a}{q}\bigg)\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ \mathbf{x}\equiv \mathbf{h}(\text{mod}~q)}}{\rm\Lambda}(\mathbf{x})e(f(\mathbf{x}){\it\beta})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant q \\ (\mathbf{h},q)=1}}e\bigg(f(\mathbf{h})\frac{a}{q}\bigg)\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ \mathbf{x}\equiv \mathbf{h}(\text{mod}~q)}}{\rm\Lambda}(\mathbf{x})e(f(\mathbf{x}){\it\beta})+O(X^{n-1}LP).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{x}\leqslant X}{\rm\Lambda}(\mathbf{x})e\bigg(f(\mathbf{x})\bigg(\frac{a}{q}+{\it\beta}\bigg)\bigg)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{1\leqslant \mathbf{h}\leqslant q}e\bigg(f(\mathbf{h})\frac{a}{q}\bigg)\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ \mathbf{x}\equiv \mathbf{h}(\text{mod}~q)}}{\rm\Lambda}(\mathbf{x})e(f(\mathbf{x}){\it\beta})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ 1\leqslant \mathbf{h}\leqslant q \\ (\mathbf{h},q)=1}}e\bigg(f(\mathbf{h})\frac{a}{q}\bigg)\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ \mathbf{x}\equiv \mathbf{h}(\text{mod}~q)}}{\rm\Lambda}(\mathbf{x})e(f(\mathbf{x}){\it\beta})+O(X^{n-1}LP).\nonumber\end{eqnarray}$$
Since
![]() $q\leqslant P=L^{K}$
, the Siegel–Walfisz theorem together with summation by parts will imply for
$q\leqslant P=L^{K}$
, the Siegel–Walfisz theorem together with summation by parts will imply for
![]() $(\mathbf{h},q)=1$
that
$(\mathbf{h},q)=1$
that
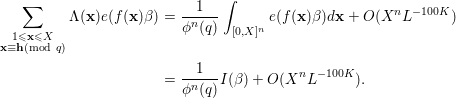 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ \mathbf{x}\equiv \mathbf{h}(\text{mod}~q)}}{\rm\Lambda}(\mathbf{x})e(f(\mathbf{x}){\it\beta}) & = & \displaystyle \frac{1}{{\it\phi}^{n}(q)}\int _{[0,X]^{n}}e(f(\mathbf{x}){\it\beta})d\mathbf{x}+O(X^{n}L^{-100K})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{{\it\phi}^{n}(q)}I({\it\beta})+O(X^{n}L^{-100K}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ \mathbf{x}\equiv \mathbf{h}(\text{mod}~q)}}{\rm\Lambda}(\mathbf{x})e(f(\mathbf{x}){\it\beta}) & = & \displaystyle \frac{1}{{\it\phi}^{n}(q)}\int _{[0,X]^{n}}e(f(\mathbf{x}){\it\beta})d\mathbf{x}+O(X^{n}L^{-100K})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{{\it\phi}^{n}(q)}I({\it\beta})+O(X^{n}L^{-100K}).\nonumber\end{eqnarray}$$
It follows from above
By putting (3.16) into (3.15), we obtain
It follows from
![]() $I({\it\beta})\ll X^{n}(1+X^{2}|{\it\beta}|)^{-2}$
that
$I({\it\beta})\ll X^{n}(1+X^{2}|{\it\beta}|)^{-2}$
that
and
Combining (3.17)–(3.19) together with Remark 3.5, we conclude
The proof of Lemma 3.6 is complete. ◻
4 Estimates for exponential sums
Lemma 4.1. Let
![]() $\{{\it\xi}_{z}\}$
be a sequence satisfying
$\{{\it\xi}_{z}\}$
be a sequence satisfying
![]() $|{\it\xi}_{z}|\leqslant 1$
. Then one has
$|{\it\xi}_{z}|\leqslant 1$
. Then one has
Proof. We expand the square to deduce that
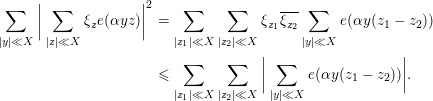 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{|y|\ll X}\bigg|\mathop{\sum }_{|z|\ll X}{\it\xi}_{z}e({\it\alpha}yz)\bigg|^{2} & = & \displaystyle \mathop{\sum }_{|z_{1}|\ll X}\mathop{\sum }_{|z_{2}|\ll X}{\it\xi}_{z_{1}}\overline{{\it\xi}_{z_{2}}}\mathop{\sum }_{|y|\ll X}e({\it\alpha}y(z_{1}-z_{2}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{|z_{1}|\ll X}\mathop{\sum }_{|z_{2}|\ll X}\bigg|\mathop{\sum }_{|y|\ll X}e({\it\alpha}y(z_{1}-z_{2}))\bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{|y|\ll X}\bigg|\mathop{\sum }_{|z|\ll X}{\it\xi}_{z}e({\it\alpha}yz)\bigg|^{2} & = & \displaystyle \mathop{\sum }_{|z_{1}|\ll X}\mathop{\sum }_{|z_{2}|\ll X}{\it\xi}_{z_{1}}\overline{{\it\xi}_{z_{2}}}\mathop{\sum }_{|y|\ll X}e({\it\alpha}y(z_{1}-z_{2}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{|z_{1}|\ll X}\mathop{\sum }_{|z_{2}|\ll X}\bigg|\mathop{\sum }_{|y|\ll X}e({\it\alpha}y(z_{1}-z_{2}))\bigg|.\nonumber\end{eqnarray}$$
By changing variables, one can obtain
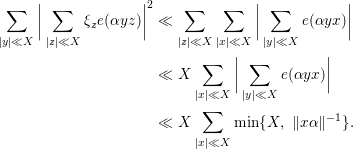 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{|y|\ll X}\bigg|\mathop{\sum }_{|z|\ll X}{\it\xi}_{z}e({\it\alpha}yz)\bigg|^{2} & \ll & \displaystyle \mathop{\sum }_{|z|\ll X}\mathop{\sum }_{|x|\ll X}\bigg|\mathop{\sum }_{|y|\ll X}e({\it\alpha}yx)\bigg|\nonumber\\ \displaystyle & \ll & \displaystyle X\mathop{\sum }_{|x|\ll X}\bigg|\mathop{\sum }_{|y|\ll X}e({\it\alpha}yx)\bigg|\nonumber\\ \displaystyle & \ll & \displaystyle X\mathop{\sum }_{|x|\ll X}\min \{X,~\Vert x{\it\alpha}\Vert ^{-1}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{|y|\ll X}\bigg|\mathop{\sum }_{|z|\ll X}{\it\xi}_{z}e({\it\alpha}yz)\bigg|^{2} & \ll & \displaystyle \mathop{\sum }_{|z|\ll X}\mathop{\sum }_{|x|\ll X}\bigg|\mathop{\sum }_{|y|\ll X}e({\it\alpha}yx)\bigg|\nonumber\\ \displaystyle & \ll & \displaystyle X\mathop{\sum }_{|x|\ll X}\bigg|\mathop{\sum }_{|y|\ll X}e({\it\alpha}yx)\bigg|\nonumber\\ \displaystyle & \ll & \displaystyle X\mathop{\sum }_{|x|\ll X}\min \{X,~\Vert x{\it\alpha}\Vert ^{-1}\}.\nonumber\end{eqnarray}$$
We complete the proof.◻
Lemma 4.2. For
![]() ${\it\alpha}\in \mathfrak{m}(Q)$
, one has
${\it\alpha}\in \mathfrak{m}(Q)$
, one has
Proof. For
![]() ${\it\alpha}\in \mathfrak{m}(Q)$
, there exist
${\it\alpha}\in \mathfrak{m}(Q)$
, there exist
![]() $a$
and
$a$
and
![]() $q$
such that
$q$
such that
![]() $1\leqslant a\leqslant q\leqslant 2Q$
,
$1\leqslant a\leqslant q\leqslant 2Q$
,
![]() $(a,q)=1$
and
$(a,q)=1$
and
![]() $|{\it\alpha}-a/q|\leqslant 2Q(qX^{2})^{-1}$
. By a variant of Vaughan [Reference Vaughan12, Lemma 2.2] (see also Exercise 2 in Chapter 2 [Reference Vaughan12]), one has
$|{\it\alpha}-a/q|\leqslant 2Q(qX^{2})^{-1}$
. By a variant of Vaughan [Reference Vaughan12, Lemma 2.2] (see also Exercise 2 in Chapter 2 [Reference Vaughan12]), one has
Since
![]() ${\it\alpha}\in \mathfrak{m}(Q)$
, one has either
${\it\alpha}\in \mathfrak{m}(Q)$
, one has either
![]() $q>Q$
or
$q>Q$
or
![]() $|{\it\alpha}-a/q|>Q(qX^{2})^{-1}$
. Then the desired estimate follows immediately.◻
$|{\it\alpha}-a/q|>Q(qX^{2})^{-1}$
. Then the desired estimate follows immediately.◻
Lemma 4.3. Let
![]() ${\it\alpha}\in \mathfrak{m}$
and
${\it\alpha}\in \mathfrak{m}$
and
![]() ${\it\beta}\in \mathbb{R}$
. For
${\it\beta}\in \mathbb{R}$
. For
![]() $d\in \mathbb{Q}$
, we define
$d\in \mathbb{Q}$
, we define
If
![]() $d\not =0$
, then one has
$d\not =0$
, then one has
where the implied constant depends only on
![]() $d$
and
$d$
and
![]() $K$
.
$K$
.
Proof. The result is essentially classical. In particular, the method used to handle
![]() $\sum _{1\leqslant x\leqslant X}{\rm\Lambda}(x)e({\it\alpha}x^{2})$
can be modified to establish the desired conclusion. We only explain that the implied constant is independent of
$\sum _{1\leqslant x\leqslant X}{\rm\Lambda}(x)e({\it\alpha}x^{2})$
can be modified to establish the desired conclusion. We only explain that the implied constant is independent of
![]() ${\it\beta}$
. By Vaughan’s identity, we essentially consider two types of exponential sums
${\it\beta}$
. By Vaughan’s identity, we essentially consider two types of exponential sums
and
By Cauchy’s inequality, to handle the summation (4.3), it suffices to deal with
One can apply the differencing argument to the summation of the type
![]() $\sum _{x}e({\it\alpha}^{\prime }x^{2}+x{\it\beta}^{\prime })$
as follows
$\sum _{x}e({\it\alpha}^{\prime }x^{2}+x{\it\beta}^{\prime })$
as follows
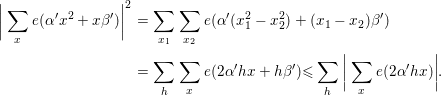 $$\begin{eqnarray}\displaystyle \bigg|\mathop{\sum }_{x}e({\it\alpha}^{\prime }x^{2}+x{\it\beta}^{\prime })\bigg|^{2} & = & \displaystyle \mathop{\sum }_{x_{1}}\mathop{\sum }_{x_{2}}e({\it\alpha}^{\prime }(x_{1}^{2}-x_{2}^{2})+(x_{1}-x_{2}){\it\beta}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{h}\mathop{\sum }_{x}e(2{\it\alpha}^{\prime }hx+h{\it\beta}^{\prime })\leqslant \mathop{\sum }_{h}\bigg|\mathop{\sum }_{x}e(2{\it\alpha}^{\prime }hx)\bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bigg|\mathop{\sum }_{x}e({\it\alpha}^{\prime }x^{2}+x{\it\beta}^{\prime })\bigg|^{2} & = & \displaystyle \mathop{\sum }_{x_{1}}\mathop{\sum }_{x_{2}}e({\it\alpha}^{\prime }(x_{1}^{2}-x_{2}^{2})+(x_{1}-x_{2}){\it\beta}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{h}\mathop{\sum }_{x}e(2{\it\alpha}^{\prime }hx+h{\it\beta}^{\prime })\leqslant \mathop{\sum }_{h}\bigg|\mathop{\sum }_{x}e(2{\it\alpha}^{\prime }hx)\bigg|.\nonumber\end{eqnarray}$$
This leads to the fact that the estimate (4.1) is uniformly for
![]() ${\it\beta}$
.◻
${\it\beta}$
.◻
Lemma 4.4. Let
![]() ${\it\alpha}\in \mathfrak{m}(Q)$
. Suppose that
${\it\alpha}\in \mathfrak{m}(Q)$
. Suppose that
![]() $A$
is in the form
$A$
is in the form
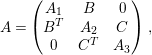 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & B & 0\\ B^{T} & A_{2} & C\\ 0 & C^{T} & A_{3}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & B & 0\\ B^{T} & A_{2} & C\\ 0 & C^{T} & A_{3}\end{array}\right),\end{eqnarray}$$
where
![]() $\text{rank}(B)\geqslant 3$
and
$\text{rank}(B)\geqslant 3$
and
![]() $\text{rank}(C)\geqslant 2$
. Then we have
$\text{rank}(C)\geqslant 2$
. Then we have
Remark 4.5. In view of the proof, the estimate (4.5) still holds provided that
![]() $\text{rank}(B)+\text{rank}(C)\geqslant 5$
.
$\text{rank}(B)+\text{rank}(C)\geqslant 5$
.
Proof. By (4.4), we can write
![]() $S({\it\alpha})$
in the form
$S({\it\alpha})$
in the form
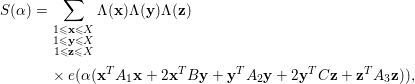 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}+\mathbf{y}^{T}A_{2}\mathbf{y}+2\mathbf{y}^{T}C\mathbf{z}+\mathbf{z}^{T}A_{3}\mathbf{z})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}+\mathbf{y}^{T}A_{2}\mathbf{y}+2\mathbf{y}^{T}C\mathbf{z}+\mathbf{z}^{T}A_{3}\mathbf{z})),\nonumber\end{eqnarray}$$
where
![]() $\mathbf{x}\in \mathbb{N}^{r}$
,
$\mathbf{x}\in \mathbb{N}^{r}$
,
![]() $\mathbf{y}\in \mathbb{N}^{s}$
and
$\mathbf{y}\in \mathbb{N}^{s}$
and
![]() $\mathbf{z}\in \mathbb{N}^{t}$
. Then we have
$\mathbf{z}\in \mathbb{N}^{t}$
. Then we have
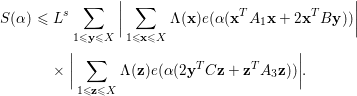 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & {\leqslant} & \displaystyle L^{s}\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X}}{\rm\Lambda}(\mathbf{x})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}))\bigg|\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{z})e({\it\alpha}(2\mathbf{y}^{T}C\mathbf{z}+\mathbf{z}^{T}A_{3}\mathbf{z}))\bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & {\leqslant} & \displaystyle L^{s}\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X}}{\rm\Lambda}(\mathbf{x})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}))\bigg|\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{z})e({\it\alpha}(2\mathbf{y}^{T}C\mathbf{z}+\mathbf{z}^{T}A_{3}\mathbf{z}))\bigg|.\nonumber\end{eqnarray}$$
By Cauchy’s inequality, we obtain
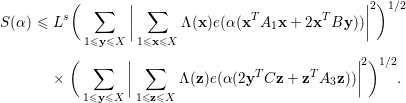 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & {\leqslant} & \displaystyle L^{s}\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X}}{\rm\Lambda}(\mathbf{x})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}))\bigg|^{2}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{z})e({\it\alpha}(2\mathbf{y}^{T}C\mathbf{z}+\mathbf{z}^{T}A_{3}\mathbf{z}))\bigg|^{2}\bigg)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & {\leqslant} & \displaystyle L^{s}\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X}}{\rm\Lambda}(\mathbf{x})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}))\bigg|^{2}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{z})e({\it\alpha}(2\mathbf{y}^{T}C\mathbf{z}+\mathbf{z}^{T}A_{3}\mathbf{z}))\bigg|^{2}\bigg)^{1/2}.\end{eqnarray}$$
We deduce by expanding the square that
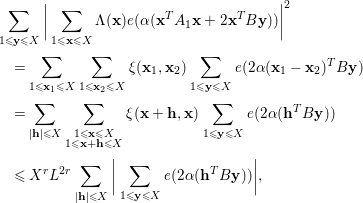 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X}}{\rm\Lambda}(\mathbf{x})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}))\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}_{1}\leqslant X}}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}_{2}\leqslant X}}{\it\xi}(\mathbf{x}_{1},\mathbf{x}_{2})\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2{\it\alpha}(\mathbf{x}_{1}-\mathbf{x}_{2})^{T}B\mathbf{y})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ 1\leqslant \mathbf{x}+\mathbf{h}\leqslant X}}{\it\xi}(\mathbf{x}+\mathbf{h},\mathbf{x})\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2{\it\alpha}(\mathbf{h}^{T}B\mathbf{y}))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,X^{r}L^{2r}\mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2{\it\alpha}(\mathbf{h}^{T}B\mathbf{y}))\bigg|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}\bigg|\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X}}{\rm\Lambda}(\mathbf{x})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}))\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}_{1}\leqslant X}}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}_{2}\leqslant X}}{\it\xi}(\mathbf{x}_{1},\mathbf{x}_{2})\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2{\it\alpha}(\mathbf{x}_{1}-\mathbf{x}_{2})^{T}B\mathbf{y})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\mathop{\sum }_{\substack{ 1\leqslant \mathbf{x}\leqslant X \\ 1\leqslant \mathbf{x}+\mathbf{h}\leqslant X}}{\it\xi}(\mathbf{x}+\mathbf{h},\mathbf{x})\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2{\it\alpha}(\mathbf{h}^{T}B\mathbf{y}))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,X^{r}L^{2r}\mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2{\it\alpha}(\mathbf{h}^{T}B\mathbf{y}))\bigg|,\nonumber\end{eqnarray}$$
where
![]() ${\it\xi}(\mathbf{x}_{1},\mathbf{x}_{2})$
is defined as
${\it\xi}(\mathbf{x}_{1},\mathbf{x}_{2})$
is defined as
We write
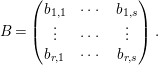 $$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}b_{1,1} & \cdots \, & b_{1,s}\\ \vdots & \cdots \, & \vdots \\ b_{r,1} & \cdots \, & b_{r,s}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}b_{1,1} & \cdots \, & b_{1,s}\\ \vdots & \cdots \, & \vdots \\ b_{r,1} & \cdots \, & b_{r,s}\end{array}\right).\end{eqnarray}$$
Since
![]() $\text{rank}(B)\geqslant 3$
, without loss of generality, we assume that
$\text{rank}(B)\geqslant 3$
, without loss of generality, we assume that
![]() $\text{rank}(B_{0})=3$
, where
$\text{rank}(B_{0})=3$
, where
![]() $B_{0}=(b_{i,j})_{1\leqslant i,j\leqslant 3}$
. Let
$B_{0}=(b_{i,j})_{1\leqslant i,j\leqslant 3}$
. Let
![]() $B^{\prime }=(b_{i,j})_{4\leqslant i\leqslant r,1\leqslant j\leqslant 3}$
. Then one has
$B^{\prime }=(b_{i,j})_{4\leqslant i\leqslant r,1\leqslant j\leqslant 3}$
. Then one has
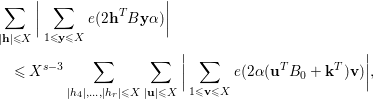 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2\mathbf{h}^{T}B\mathbf{y}{\it\alpha})\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,X^{s-3}\mathop{\sum }_{|h_{4}|,\ldots ,|h_{r}|\leqslant X}\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{v}\leqslant X}e(2{\it\alpha}(\mathbf{u}^{T}B_{0}+\mathbf{k}^{T})\mathbf{v})\bigg|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2\mathbf{h}^{T}B\mathbf{y}{\it\alpha})\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,X^{s-3}\mathop{\sum }_{|h_{4}|,\ldots ,|h_{r}|\leqslant X}\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{v}\leqslant X}e(2{\it\alpha}(\mathbf{u}^{T}B_{0}+\mathbf{k}^{T})\mathbf{v})\bigg|,\nonumber\end{eqnarray}$$
where
![]() $\mathbf{u}^{T}=(h_{1},h_{2},h_{3})$
,
$\mathbf{u}^{T}=(h_{1},h_{2},h_{3})$
,
![]() $\mathbf{v}^{T}=(y_{1},y_{2},y_{3})$
and
$\mathbf{v}^{T}=(y_{1},y_{2},y_{3})$
and
![]() $\mathbf{k}^{T}=(h_{4},\ldots ,h_{r})B^{\prime }$
. By changing variables
$\mathbf{k}^{T}=(h_{4},\ldots ,h_{r})B^{\prime }$
. By changing variables
![]() $\mathbf{x}^{T}=2(\mathbf{u}^{T}B_{0}+\mathbf{k}^{T})$
, we obtain
$\mathbf{x}^{T}=2(\mathbf{u}^{T}B_{0}+\mathbf{k}^{T})$
, we obtain
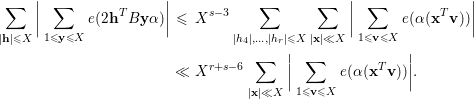 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2\mathbf{h}^{T}B\mathbf{y}{\it\alpha})\bigg| & {\leqslant} & \displaystyle X^{s-3}\mathop{\sum }_{|h_{4}|,\ldots ,|h_{r}|\leqslant X}\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{v}\leqslant X}e({\it\alpha}(\mathbf{x}^{T}\mathbf{v}))\bigg|\nonumber\\ \displaystyle & \ll & \displaystyle X^{r+s-6}\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{v}\leqslant X}e({\it\alpha}(\mathbf{x}^{T}\mathbf{v}))\bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e(2\mathbf{h}^{T}B\mathbf{y}{\it\alpha})\bigg| & {\leqslant} & \displaystyle X^{s-3}\mathop{\sum }_{|h_{4}|,\ldots ,|h_{r}|\leqslant X}\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{v}\leqslant X}e({\it\alpha}(\mathbf{x}^{T}\mathbf{v}))\bigg|\nonumber\\ \displaystyle & \ll & \displaystyle X^{r+s-6}\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{v}\leqslant X}e({\it\alpha}(\mathbf{x}^{T}\mathbf{v}))\bigg|.\nonumber\end{eqnarray}$$
We apply Lemma 4.2 to conclude that
and therefore,
Similar to (4.7), we can prove
Lemma 4.6. Suppose that
![]() $A$
is in the form (4.4) with
$A$
is in the form (4.4) with
![]() $\text{rank}(B)\geqslant 3$
and
$\text{rank}(B)\geqslant 3$
and
![]() $\text{rank}(C)\geqslant 2$
. Then we have
$\text{rank}(C)\geqslant 2$
. Then we have
Proof. By Dirichlet’s approximation theorem, for any
![]() ${\it\alpha}\in [X^{-1},1+X^{-1}]$
, there exist
${\it\alpha}\in [X^{-1},1+X^{-1}]$
, there exist
![]() $a$
and
$a$
and
![]() $q$
with
$q$
with
![]() $1\leqslant a\leqslant q\leqslant X$
and
$1\leqslant a\leqslant q\leqslant X$
and
![]() $(a,q)=1$
such that
$(a,q)=1$
such that
![]() $|{\it\alpha}-a/q|\leqslant (qX)^{-1}$
. Thus the desired conclusion follows from Lemma 4.4 by the dyadic argument.◻
$|{\it\alpha}-a/q|\leqslant (qX)^{-1}$
. Thus the desired conclusion follows from Lemma 4.4 by the dyadic argument.◻
5 Quadratic forms with off-diagonal rank
 ${\leqslant}3$
${\leqslant}3$
Proposition 5.1. Let
![]() $A$
be given by (1.1), and let
$A$
be given by (1.1), and let
![]() $S({\it\alpha})$
be defined in (2.5). Suppose that
$S({\it\alpha})$
be defined in (2.5). Suppose that
![]() $\text{rank}(A)\geqslant 9$
and
$\text{rank}(A)\geqslant 9$
and
![]() $\text{rank}_{\text{off}}(A)\leqslant 3$
. Then we have
$\text{rank}_{\text{off}}(A)\leqslant 3$
. Then we have
where the implied constant depends on
![]() $A$
and
$A$
and
![]() $K$
.
$K$
.
From now on, we assume throughout Section 5 that
![]() $\text{rank}(A)\geqslant 9$
and
$\text{rank}(A)\geqslant 9$
and
where
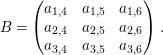 $$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}a_{1,4} & a_{1,5} & a_{1,6}\\ a_{2,4} & a_{2,5} & a_{2,6}\\ a_{3,4} & a_{3,5} & a_{3,6}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}a_{1,4} & a_{1,5} & a_{1,6}\\ a_{2,4} & a_{2,5} & a_{2,6}\\ a_{3,4} & a_{3,5} & a_{3,6}\end{array}\right).\end{eqnarray}$$
Then we introduce
![]() $B_{1},B_{2},B_{3}\in M_{3,n-4}(\mathbb{Z})$
defined as
$B_{1},B_{2},B_{3}\in M_{3,n-4}(\mathbb{Z})$
defined as
 $$\begin{eqnarray}\displaystyle B_{1} & = & \displaystyle \left(\begin{array}{@{}cccccc@{}}a_{1,5} & a_{1,6} & a_{1,7} & a_{1,8} & \cdots \, & a_{1,n}\\ a_{2,5} & a_{2,6} & a_{2,7} & a_{2,8} & \cdots \, & a_{2,n}\\ a_{3,5} & a_{3,6} & a_{3,7} & a_{3,8} & \cdots \, & a_{3,n}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{1} & = & \displaystyle \left(\begin{array}{@{}cccccc@{}}a_{1,5} & a_{1,6} & a_{1,7} & a_{1,8} & \cdots \, & a_{1,n}\\ a_{2,5} & a_{2,6} & a_{2,7} & a_{2,8} & \cdots \, & a_{2,n}\\ a_{3,5} & a_{3,6} & a_{3,7} & a_{3,8} & \cdots \, & a_{3,n}\end{array}\right),\end{eqnarray}$$
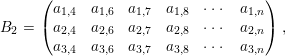 $$\begin{eqnarray}\displaystyle B_{2} & = & \displaystyle \left(\begin{array}{@{}cccccc@{}}a_{1,4} & a_{1,6} & a_{1,7} & a_{1,8} & \cdots \, & a_{1,n}\\ a_{2,4} & a_{2,6} & a_{2,7} & a_{2,8} & \cdots \, & a_{2,n}\\ a_{3,4} & a_{3,6} & a_{3,7} & a_{3,8} & \cdots \, & a_{3,n}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{2} & = & \displaystyle \left(\begin{array}{@{}cccccc@{}}a_{1,4} & a_{1,6} & a_{1,7} & a_{1,8} & \cdots \, & a_{1,n}\\ a_{2,4} & a_{2,6} & a_{2,7} & a_{2,8} & \cdots \, & a_{2,n}\\ a_{3,4} & a_{3,6} & a_{3,7} & a_{3,8} & \cdots \, & a_{3,n}\end{array}\right),\end{eqnarray}$$
and
 $$\begin{eqnarray}B_{3}=\left(\begin{array}{@{}cccccc@{}}a_{1,4} & a_{1,5} & a_{1,7} & a_{1,8} & \cdots \, & a_{1,n}\\ a_{2,4} & a_{2,5} & a_{2,7} & a_{2,8} & \cdots \, & a_{2,n}\\ a_{3,4} & a_{3,5} & a_{3,7} & a_{3,8} & \cdots \, & a_{3,n}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}B_{3}=\left(\begin{array}{@{}cccccc@{}}a_{1,4} & a_{1,5} & a_{1,7} & a_{1,8} & \cdots \, & a_{1,n}\\ a_{2,4} & a_{2,5} & a_{2,7} & a_{2,8} & \cdots \, & a_{2,n}\\ a_{3,4} & a_{3,5} & a_{3,7} & a_{3,8} & \cdots \, & a_{3,n}\end{array}\right).\end{eqnarray}$$
Subject to the assumption (5.1), we have the following.
Lemma 5.2. If
![]() $\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=2$
, then one has
$\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=2$
, then one has
Lemma 5.3. If
![]() $\text{rank}(B_{1})=\text{rank}(B_{2})=2$
and
$\text{rank}(B_{1})=\text{rank}(B_{2})=2$
and
![]() $\text{rank}(B_{3})=3$
, then one has
$\text{rank}(B_{3})=3$
, then one has
Lemma 5.4. If
![]() $\text{rank}(B_{1})=2$
and
$\text{rank}(B_{1})=2$
and
![]() $\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then one has
$\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then one has
Lemma 5.5. If
![]() $\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then one has
$\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then one has
Remark for the Proof of Proposition 5.1.
If
![]() $\text{rank}_{\text{off}}(A)=0$
, then
$\text{rank}_{\text{off}}(A)=0$
, then
![]() $A$
is a diagonal matrix and the conclusion is classical. When
$A$
is a diagonal matrix and the conclusion is classical. When
![]() $\text{rank}_{\text{off}}(A)=3$
, our conclusion follows from Lemmas 5.2–5.5 immediately. The method applied to establish Lemmas 5.2–5.5 can also be used to deal with the case
$\text{rank}_{\text{off}}(A)=3$
, our conclusion follows from Lemmas 5.2–5.5 immediately. The method applied to establish Lemmas 5.2–5.5 can also be used to deal with the case
![]() $1\leqslant \text{rank}_{\text{off}}(A)\leqslant 2$
. Indeed, the proof of Proposition 5.1 under the condition
$1\leqslant \text{rank}_{\text{off}}(A)\leqslant 2$
. Indeed, the proof of Proposition 5.1 under the condition
![]() $1\leqslant \text{rank}_{\text{off}}(A)\leqslant 2$
is easier, and we omit the details. Therefore, our main task is to establish Lemmas 5.2–5.5.
$1\leqslant \text{rank}_{\text{off}}(A)\leqslant 2$
is easier, and we omit the details. Therefore, our main task is to establish Lemmas 5.2–5.5.
Lemma 5.6. Let
![]() $C\in M_{n,n}(\mathbb{Q})$
be a symmetric matrix, and let
$C\in M_{n,n}(\mathbb{Q})$
be a symmetric matrix, and let
![]() $H\in M_{n,k}(\mathbb{Q})$
. For
$H\in M_{n,k}(\mathbb{Q})$
. For
![]() ${\it\alpha}\in \mathbb{R}$
and
${\it\alpha}\in \mathbb{R}$
and
![]() ${\bf\beta}\in \mathbb{R}^{k}$
, we define
${\bf\beta}\in \mathbb{R}^{k}$
, we define
where
![]() ${\mathcal{X}}\subset \mathbb{Z}^{n}$
is a finite subset of
${\mathcal{X}}\subset \mathbb{Z}^{n}$
is a finite subset of
![]() $\mathbb{Z}^{n}$
. Let
$\mathbb{Z}^{n}$
. Let
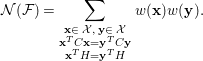 $$\begin{eqnarray}{\mathcal{N}}({\mathcal{F}})=\mathop{\sum }_{\substack{ \mathbf{x}\in \,{\mathcal{X}},\,\mathbf{y}\in \,{\mathcal{X}} \\ \mathbf{x}^{T}C\mathbf{x}=\mathbf{y}^{T}C\mathbf{y} \\ \mathbf{x}^{T}H=\mathbf{y}^{T}H}}w(\mathbf{x})w(\mathbf{y}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}({\mathcal{F}})=\mathop{\sum }_{\substack{ \mathbf{x}\in \,{\mathcal{X}},\,\mathbf{y}\in \,{\mathcal{X}} \\ \mathbf{x}^{T}C\mathbf{x}=\mathbf{y}^{T}C\mathbf{y} \\ \mathbf{x}^{T}H=\mathbf{y}^{T}H}}w(\mathbf{x})w(\mathbf{y}).\end{eqnarray}$$
Then we have
where the implied constant may depend on
![]() $C$
and
$C$
and
![]() $H$
.
$H$
.
Proof. We can choose a natural number
![]() $h\in \mathbb{N}$
such that
$h\in \mathbb{N}$
such that
![]() $hC\in M_{n,n}(\mathbb{Z})$
and
$hC\in M_{n,n}(\mathbb{Z})$
and
![]() $hH\in M_{n,k}(\mathbb{Z})$
. Then we deduce that
$hH\in M_{n,k}(\mathbb{Z})$
. Then we deduce that
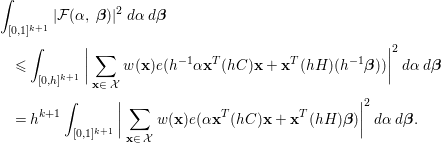 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{k+1}}|{\mathcal{F}}({\it\alpha},\,{\bf\beta})|^{2}\,d{\it\alpha}\,d{\bf\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{[0,h]^{k+1}}\bigg|\mathop{\sum }_{\mathbf{x}\in \,{\mathcal{X}}}w(\mathbf{x})e(h^{-1}{\it\alpha}\mathbf{x}^{T}(hC)\mathbf{x}+\mathbf{x}^{T}(hH)(h^{-1}{\bf\beta}))\bigg|^{2}\,d{\it\alpha}\,d{\bf\beta}\nonumber\\ \displaystyle & & \displaystyle \quad =h^{k+1}\int _{[0,1]^{k+1}}\bigg|\mathop{\sum }_{\mathbf{x}\in \,{\mathcal{X}}}w(\mathbf{x})e({\it\alpha}\mathbf{x}^{T}(hC)\mathbf{x}+\mathbf{x}^{T}(hH){\bf\beta})\bigg|^{2}\,d{\it\alpha}\,d{\bf\beta}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{k+1}}|{\mathcal{F}}({\it\alpha},\,{\bf\beta})|^{2}\,d{\it\alpha}\,d{\bf\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{[0,h]^{k+1}}\bigg|\mathop{\sum }_{\mathbf{x}\in \,{\mathcal{X}}}w(\mathbf{x})e(h^{-1}{\it\alpha}\mathbf{x}^{T}(hC)\mathbf{x}+\mathbf{x}^{T}(hH)(h^{-1}{\bf\beta}))\bigg|^{2}\,d{\it\alpha}\,d{\bf\beta}\nonumber\\ \displaystyle & & \displaystyle \quad =h^{k+1}\int _{[0,1]^{k+1}}\bigg|\mathop{\sum }_{\mathbf{x}\in \,{\mathcal{X}}}w(\mathbf{x})e({\it\alpha}\mathbf{x}^{T}(hC)\mathbf{x}+\mathbf{x}^{T}(hH){\bf\beta})\bigg|^{2}\,d{\it\alpha}\,d{\bf\beta}.\nonumber\end{eqnarray}$$
By orthogonality, we have
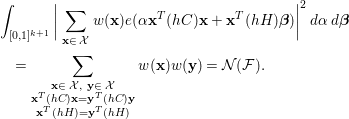 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{k+1}}\bigg|\mathop{\sum }_{\mathbf{x}\in \,{\mathcal{X}}}w(\mathbf{x})e({\it\alpha}\mathbf{x}^{T}(hC)\mathbf{x}+\mathbf{x}^{T}(hH){\bf\beta})\bigg|^{2}\,d{\it\alpha}\,d{\bf\beta}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ \mathbf{x}\in \,{\mathcal{X}},~\mathbf{y}\in \,{\mathcal{X}} \\ \mathbf{x}^{T}(hC)\mathbf{x}=\mathbf{y}^{T}(hC)\mathbf{y} \\ \mathbf{x}^{T}(hH)=\mathbf{y}^{T}(hH)}}w(\mathbf{x})w(\mathbf{y})={\mathcal{N}}({\mathcal{F}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{k+1}}\bigg|\mathop{\sum }_{\mathbf{x}\in \,{\mathcal{X}}}w(\mathbf{x})e({\it\alpha}\mathbf{x}^{T}(hC)\mathbf{x}+\mathbf{x}^{T}(hH){\bf\beta})\bigg|^{2}\,d{\it\alpha}\,d{\bf\beta}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ \mathbf{x}\in \,{\mathcal{X}},~\mathbf{y}\in \,{\mathcal{X}} \\ \mathbf{x}^{T}(hC)\mathbf{x}=\mathbf{y}^{T}(hC)\mathbf{y} \\ \mathbf{x}^{T}(hH)=\mathbf{y}^{T}(hH)}}w(\mathbf{x})w(\mathbf{y})={\mathcal{N}}({\mathcal{F}}).\nonumber\end{eqnarray}$$
Therefore, one obtains
and this completes the proof. ◻
Lemma 5.7. Let
![]() $C\in M_{n,n}(\mathbb{Q})$
be a symmetric matrix, and let
$C\in M_{n,n}(\mathbb{Q})$
be a symmetric matrix, and let
![]() $H\in M_{n,k}(\mathbb{Q})$
. We have
$H\in M_{n,k}(\mathbb{Q})$
. We have
where
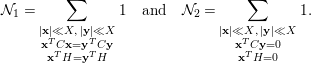 $$\begin{eqnarray}{\mathcal{N}}_{1}=\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X,\,|\mathbf{y}|\ll X \\ \mathbf{x}^{T}C\mathbf{x}=\mathbf{y}^{T}C\mathbf{y} \\ \mathbf{x}^{T}H=\mathbf{y}^{T}H}}1\quad \text{and}\quad {\mathcal{N}}_{2}=\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X,\,|\mathbf{y}|\ll X \\ \mathbf{x}^{T}C\mathbf{y}=0 \\ \mathbf{x}^{T}H=0}}1.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}_{1}=\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X,\,|\mathbf{y}|\ll X \\ \mathbf{x}^{T}C\mathbf{x}=\mathbf{y}^{T}C\mathbf{y} \\ \mathbf{x}^{T}H=\mathbf{y}^{T}H}}1\quad \text{and}\quad {\mathcal{N}}_{2}=\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X,\,|\mathbf{y}|\ll X \\ \mathbf{x}^{T}C\mathbf{y}=0 \\ \mathbf{x}^{T}H=0}}1.\end{eqnarray}$$
Proof. By changing variables
![]() $\mathbf{x}-\mathbf{y}=\mathbf{h}$
and
$\mathbf{x}-\mathbf{y}=\mathbf{h}$
and
![]() $\mathbf{x}+\mathbf{y}=\mathbf{z}$
, the desired conclusion follows immediately.◻
$\mathbf{x}+\mathbf{y}=\mathbf{z}$
, the desired conclusion follows immediately.◻
The following result is well known.
Lemma 5.8. Let
![]() $C\in M_{k,m}(\mathbb{Q})$
. If
$C\in M_{k,m}(\mathbb{Q})$
. If
![]() $\text{rank}(C)\geqslant 2$
, then one has
$\text{rank}(C)\geqslant 2$
, then one has
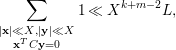 $$\begin{eqnarray}\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X,|\mathbf{y}|\ll X \\ \mathbf{x}^{T}C\mathbf{y}=0}}1\ll X^{k+m-2}L,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ |\mathbf{x}|\ll X,|\mathbf{y}|\ll X \\ \mathbf{x}^{T}C\mathbf{y}=0}}1\ll X^{k+m-2}L,\end{eqnarray}$$
where the implied constant depends on the matrix
![]() $C$
.
$C$
.
5.1 Proof of Lemma 5.2
Lemma 5.9. If
![]() $\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=2$
, then we can write
$\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=2$
, then we can write
![]() $A$
in the form
$A$
in the form
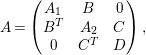 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & B & 0\\ B^{T} & A_{2} & C\\ 0 & C^{T} & D\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & B & 0\\ B^{T} & A_{2} & C\\ 0 & C^{T} & D\end{array}\right),\end{eqnarray}$$
where
![]() $B\in GL_{3}(\mathbb{Z})$
,
$B\in GL_{3}(\mathbb{Z})$
,
![]() $C\in M_{3,n-6}(\mathbb{Z})$
and
$C\in M_{3,n-6}(\mathbb{Z})$
and
![]() $D=\text{diag}\{d_{1},\ldots ,d_{n-6}\}$
is a diagonal matrix.
$D=\text{diag}\{d_{1},\ldots ,d_{n-6}\}$
is a diagonal matrix.
Proof. We write for
![]() $1\leqslant j\leqslant n-3$
that
$1\leqslant j\leqslant n-3$
that
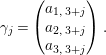 $$\begin{eqnarray}{\it\gamma}_{j}=\left(\begin{array}{@{}c@{}}a_{1,\,3+j}\\ a_{2,\,3+j}\\ a_{3,\,3+j}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}{\it\gamma}_{j}=\left(\begin{array}{@{}c@{}}a_{1,\,3+j}\\ a_{2,\,3+j}\\ a_{3,\,3+j}\end{array}\right).\end{eqnarray}$$
Since
![]() $B=({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Z})$
,
$B=({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Z})$
,
![]() ${\it\gamma}_{1}$
,
${\it\gamma}_{1}$
,
![]() ${\it\gamma}_{2}$
and
${\it\gamma}_{2}$
and
![]() ${\it\gamma}_{3}$
are linearly independent. For any
${\it\gamma}_{3}$
are linearly independent. For any
![]() $4\leqslant j\leqslant n-3$
, one has
$4\leqslant j\leqslant n-3$
, one has
![]() $\text{rank}({\it\gamma}_{2},{\it\gamma}_{3},{\it\gamma}_{j})\leqslant \text{rank}(B_{1})=2$
. Therefore, we obtain
$\text{rank}({\it\gamma}_{2},{\it\gamma}_{3},{\it\gamma}_{j})\leqslant \text{rank}(B_{1})=2$
. Therefore, we obtain
![]() ${\it\gamma}_{j}\in <{\it\gamma}_{2},{\it\gamma}_{3}>$
. Similarly, one has
${\it\gamma}_{j}\in <{\it\gamma}_{2},{\it\gamma}_{3}>$
. Similarly, one has
![]() ${\it\gamma}_{j}\in <{\it\gamma}_{1},{\it\gamma}_{3}>$
and
${\it\gamma}_{j}\in <{\it\gamma}_{1},{\it\gamma}_{3}>$
and
![]() ${\it\gamma}_{j}\in <{\it\gamma}_{1},{\it\gamma}_{2}>$
. Then we can conclude that
${\it\gamma}_{j}\in <{\it\gamma}_{1},{\it\gamma}_{2}>$
. Then we can conclude that
![]() ${\it\gamma}_{j}=0$
for
${\it\gamma}_{j}=0$
for
![]() $4\leqslant j\leqslant n-3$
.
$4\leqslant j\leqslant n-3$
.
For
![]() $7\leqslant i<j\leqslant n$
, we write
$7\leqslant i<j\leqslant n$
, we write
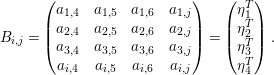 $$\begin{eqnarray}B_{i,j}=\left(\begin{array}{@{}cccc@{}}a_{1,4} & a_{1,5} & a_{1,6} & a_{1,j}\\ a_{2,4} & a_{2,5} & a_{2,6} & a_{2,j}\\ a_{3,4} & a_{3,5} & a_{3,6} & a_{3,j}\\ a_{i,4} & a_{i,5} & a_{i,6} & a_{i,j}\end{array}\right)=\left(\begin{array}{@{}c@{}}{\it\eta}_{1}^{T}\\ {\it\eta}_{2}^{T}\\ {\it\eta}_{3}^{T}\\ {\it\eta}_{4}^{T}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}B_{i,j}=\left(\begin{array}{@{}cccc@{}}a_{1,4} & a_{1,5} & a_{1,6} & a_{1,j}\\ a_{2,4} & a_{2,5} & a_{2,6} & a_{2,j}\\ a_{3,4} & a_{3,5} & a_{3,6} & a_{3,j}\\ a_{i,4} & a_{i,5} & a_{i,6} & a_{i,j}\end{array}\right)=\left(\begin{array}{@{}c@{}}{\it\eta}_{1}^{T}\\ {\it\eta}_{2}^{T}\\ {\it\eta}_{3}^{T}\\ {\it\eta}_{4}^{T}\end{array}\right).\end{eqnarray}$$
Since
![]() $3\leqslant \text{rank}(B_{i,j})\leqslant \text{rank}_{\text{off}}(A)=3$
, we conclude that
$3\leqslant \text{rank}(B_{i,j})\leqslant \text{rank}_{\text{off}}(A)=3$
, we conclude that
![]() ${\it\eta}_{4}^{T}$
can be linearly represented by
${\it\eta}_{4}^{T}$
can be linearly represented by
![]() ${\it\eta}_{1}^{T}$
,
${\it\eta}_{1}^{T}$
,
![]() ${\it\eta}_{2}^{T}$
and
${\it\eta}_{2}^{T}$
and
![]() ${\it\eta}_{3}^{T}$
. Then we obtain
${\it\eta}_{3}^{T}$
. Then we obtain
![]() $a_{i,j}=0$
due to
$a_{i,j}=0$
due to
![]() $a_{1,j}=a_{2,j}=a_{3,j}=0$
. Therefore, the matrix
$a_{1,j}=a_{2,j}=a_{3,j}=0$
. Therefore, the matrix
![]() $A$
is in the form (5.6). We complete the proof.◻
$A$
is in the form (5.6). We complete the proof.◻
Proof of Lemma 5.2.
By Lemma 5.9, we have
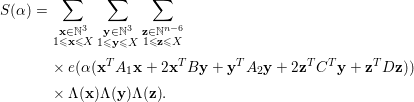 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-6} \\ 1\leqslant \mathbf{z}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}+\mathbf{y}^{T}A_{2}\mathbf{y}+2\mathbf{z}^{T}C^{T}\mathbf{y}+\mathbf{z}^{T}D\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-6} \\ 1\leqslant \mathbf{z}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}B\mathbf{y}+\mathbf{y}^{T}A_{2}\mathbf{y}+2\mathbf{z}^{T}C^{T}\mathbf{y}+\mathbf{z}^{T}D\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z}).\nonumber\end{eqnarray}$$
By orthogonality, we have
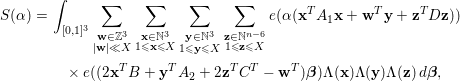 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{\substack{ \mathbf{w}\in \mathbb{Z}^{3} \\ |\mathbf{w}|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-6} \\ 1\leqslant \mathbf{z}\leqslant X}}e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{w}^{T}\mathbf{y}+\mathbf{z}^{T}D\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e((2\mathbf{x}^{T}B+\mathbf{y}^{T}A_{2}+2\mathbf{z}^{T}C^{T}-\mathbf{w}^{T}){\bf\beta}){\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\,d{\bf\beta},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{\substack{ \mathbf{w}\in \mathbb{Z}^{3} \\ |\mathbf{w}|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-6} \\ 1\leqslant \mathbf{z}\leqslant X}}e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{w}^{T}\mathbf{y}+\mathbf{z}^{T}D\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e((2\mathbf{x}^{T}B+\mathbf{y}^{T}A_{2}+2\mathbf{z}^{T}C^{T}-\mathbf{w}^{T}){\bf\beta}){\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\,d{\bf\beta},\nonumber\end{eqnarray}$$
where
![]() ${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
and we use
${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
and we use
![]() $d{\bf\beta}$
to denote
$d{\bf\beta}$
to denote
![]() $d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. We define
$d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. We define
and
where
![]() ${\it\xi}_{j}=(a_{4,6+j},a_{5,6+j},a_{6,6+j})^{T}$
for
${\it\xi}_{j}=(a_{4,6+j},a_{5,6+j},a_{6,6+j})^{T}$
for
![]() $1\leqslant j\leqslant n-6$
. On writing
$1\leqslant j\leqslant n-6$
. On writing
![]() $I_{3}=(\mathbf{e}_{1},\mathbf{e}_{2},\mathbf{e}_{3})$
, we introduce
$I_{3}=(\mathbf{e}_{1},\mathbf{e}_{2},\mathbf{e}_{3})$
, we introduce
where
![]() ${\it\gamma}_{j}^{T}=(a_{3+j,4},a_{3+j,5},a_{3+j,6})$
for
${\it\gamma}_{j}^{T}=(a_{3+j,4},a_{3+j,5},a_{3+j,6})$
for
![]() $1\leqslant j\leqslant 3$
. With above notations, we have
$1\leqslant j\leqslant 3$
. With above notations, we have
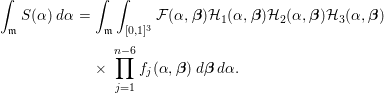 $$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}S({\it\alpha})\,d{\it\alpha} & = & \displaystyle \int _{\mathfrak{m}}\int _{[0,1]^{3}}{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{n-6}f_{j}({\it\alpha},{\bf\beta})\,d{\bf\beta}\,d{\it\alpha}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}S({\it\alpha})\,d{\it\alpha} & = & \displaystyle \int _{\mathfrak{m}}\int _{[0,1]^{3}}{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{n-6}f_{j}({\it\alpha},{\bf\beta})\,d{\bf\beta}\,d{\it\alpha}.\nonumber\end{eqnarray}$$
Therefore, one has the following inequality
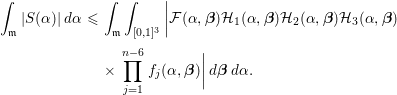 $$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \int _{\mathfrak{m}}\int _{[0,1]^{3}}\bigg|{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{n-6}f_{j}({\it\alpha},{\bf\beta})\bigg|\,d{\bf\beta}\,d{\it\alpha}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \int _{\mathfrak{m}}\int _{[0,1]^{3}}\bigg|{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{n-6}f_{j}({\it\alpha},{\bf\beta})\bigg|\,d{\bf\beta}\,d{\it\alpha}.\end{eqnarray}$$
We first consider the case
![]() $\text{rank}(D)\geqslant 3$
. Without loss of generality, we assume
$\text{rank}(D)\geqslant 3$
. Without loss of generality, we assume
![]() $d_{1}d_{2}d_{3}\not =0$
. By (5.8) and the Cauchy–Schwarz inequality, one has
$d_{1}d_{2}d_{3}\not =0$
. By (5.8) and the Cauchy–Schwarz inequality, one has
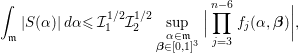 $$\begin{eqnarray}\int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha}\leqslant \,{\mathcal{I}}_{1}^{1/2}{\mathcal{I}}_{2}^{1/2}\sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\Big|\mathop{\prod }_{j=3}^{n-6}f_{j}({\it\alpha},{\bf\beta})\bigg|,\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha}\leqslant \,{\mathcal{I}}_{1}^{1/2}{\mathcal{I}}_{2}^{1/2}\sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\Big|\mathop{\prod }_{j=3}^{n-6}f_{j}({\it\alpha},{\bf\beta})\bigg|,\end{eqnarray}$$
where
and
By Lemmas 5.6 and 5.7, one has
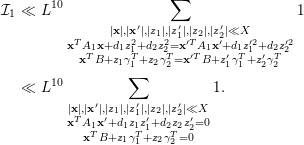 $$\begin{eqnarray}\displaystyle {\mathcal{I}}_{1} & \ll & \displaystyle L^{10}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}+d_{1}z_{1}^{2}+d_{2}z_{2}^{2}=\mathbf{x}^{\prime T}A_{1}\mathbf{x}^{\prime }+d_{1}z_{1}^{\prime 2}+d_{2}z_{2}^{\prime 2} \\ \mathbf{x}^{T}B+z_{1}{\it\gamma}_{1}^{T}+z_{2}{\it\gamma}_{2}^{T}=\mathbf{x}^{\prime T}B+z_{1}^{\prime }{\it\gamma}_{1}^{T}+z_{2}^{\prime }{\it\gamma}_{2}^{T}}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{10}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+d_{1}z_{1}z_{1}^{\prime }+d_{2}z_{2}z_{2}^{\prime }=0 \\ \mathbf{x}^{T}B+z_{1}{\it\gamma}_{1}^{T}+z_{2}{\it\gamma}_{2}^{T}=0}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{I}}_{1} & \ll & \displaystyle L^{10}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}+d_{1}z_{1}^{2}+d_{2}z_{2}^{2}=\mathbf{x}^{\prime T}A_{1}\mathbf{x}^{\prime }+d_{1}z_{1}^{\prime 2}+d_{2}z_{2}^{\prime 2} \\ \mathbf{x}^{T}B+z_{1}{\it\gamma}_{1}^{T}+z_{2}{\it\gamma}_{2}^{T}=\mathbf{x}^{\prime T}B+z_{1}^{\prime }{\it\gamma}_{1}^{T}+z_{2}^{\prime }{\it\gamma}_{2}^{T}}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{10}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+d_{1}z_{1}z_{1}^{\prime }+d_{2}z_{2}z_{2}^{\prime }=0 \\ \mathbf{x}^{T}B+z_{1}{\it\gamma}_{1}^{T}+z_{2}{\it\gamma}_{2}^{T}=0}}1.\nonumber\end{eqnarray}$$
Since
![]() $B$
is invertible, we obtain
$B$
is invertible, we obtain
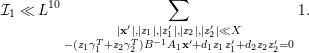 $$\begin{eqnarray}{\mathcal{I}}_{1}\ll L^{10}\mathop{\sum }_{\substack{ |\mathbf{x}^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|\ll X \\ -(z_{1}{\it\gamma}_{1}^{T}+z_{2}{\it\gamma}_{2}^{T})B^{-1}A_{1}\mathbf{x}^{\prime }+d_{1}z_{1}z_{1}^{\prime }+d_{2}z_{2}z_{2}^{\prime }=0}}1.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{1}\ll L^{10}\mathop{\sum }_{\substack{ |\mathbf{x}^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|\ll X \\ -(z_{1}{\it\gamma}_{1}^{T}+z_{2}{\it\gamma}_{2}^{T})B^{-1}A_{1}\mathbf{x}^{\prime }+d_{1}z_{1}z_{1}^{\prime }+d_{2}z_{2}z_{2}^{\prime }=0}}1.\end{eqnarray}$$
Then we conclude from Lemma 5.8 that
It follows from Lemmas 5.6–5.7 that
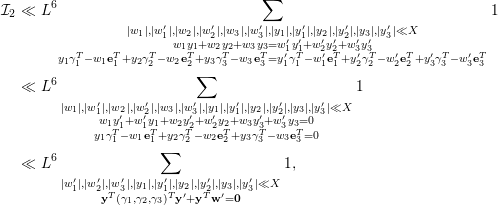 $$\begin{eqnarray}\displaystyle {\mathcal{I}}_{2} & \ll & \displaystyle L^{6}\!\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|w_{3}|,|w_{3}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|y_{3}|,|y_{3}^{\prime }|\ll X \\ w_{1}y_{1}+w_{2}y_{2}+w_{3}y_{3}=w_{1}^{\prime }y_{1}^{\prime }+w_{2}^{\prime }y_{2}^{\prime }+w_{3}^{\prime }y_{3}^{\prime } \\ y_{1}{\it\gamma}_{1}^{T}-w_{1}\mathbf{e}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{2}\mathbf{e}_{2}^{T}+y_{3}{\it\gamma}_{3}^{T}-w_{3}\mathbf{e}_{3}^{T}=y_{1}^{\prime }{\it\gamma}_{1}^{T}-w_{1}^{\prime }\mathbf{e}_{1}^{T}+y_{2}^{\prime }{\it\gamma}_{2}^{T}-w_{2}^{\prime }\mathbf{e}_{2}^{T}+y_{3}^{\prime }{\it\gamma}_{3}^{T}-w_{3}^{\prime }\mathbf{e}_{3}^{T}}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|w_{3}|,|w_{3}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|y_{3}|,|y_{3}^{\prime }|\ll X \\ w_{1}y_{1}^{\prime }+w_{1}^{\prime }y_{1}+w_{2}y_{2}^{\prime }+w_{2}^{\prime }y_{2}+w_{3}y_{3}^{\prime }+w_{3}^{\prime }y_{3}=0 \\ y_{1}{\it\gamma}_{1}^{T}-w_{1}\mathbf{e}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{2}\mathbf{e}_{2}^{T}+y_{3}{\it\gamma}_{3}^{T}-w_{3}\mathbf{e}_{3}^{T}=0}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |w_{1}^{\prime }|,|w_{2}^{\prime }|,|w_{3}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|y_{3}|,|y_{3}^{\prime }|\ll X \\ \mathbf{y}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})^{T}\mathbf{y}^{\prime }+\mathbf{y}^{T}\mathbf{w}^{\prime }=\mathbf{0}}}1,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{I}}_{2} & \ll & \displaystyle L^{6}\!\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|w_{3}|,|w_{3}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|y_{3}|,|y_{3}^{\prime }|\ll X \\ w_{1}y_{1}+w_{2}y_{2}+w_{3}y_{3}=w_{1}^{\prime }y_{1}^{\prime }+w_{2}^{\prime }y_{2}^{\prime }+w_{3}^{\prime }y_{3}^{\prime } \\ y_{1}{\it\gamma}_{1}^{T}-w_{1}\mathbf{e}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{2}\mathbf{e}_{2}^{T}+y_{3}{\it\gamma}_{3}^{T}-w_{3}\mathbf{e}_{3}^{T}=y_{1}^{\prime }{\it\gamma}_{1}^{T}-w_{1}^{\prime }\mathbf{e}_{1}^{T}+y_{2}^{\prime }{\it\gamma}_{2}^{T}-w_{2}^{\prime }\mathbf{e}_{2}^{T}+y_{3}^{\prime }{\it\gamma}_{3}^{T}-w_{3}^{\prime }\mathbf{e}_{3}^{T}}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|w_{3}|,|w_{3}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|y_{3}|,|y_{3}^{\prime }|\ll X \\ w_{1}y_{1}^{\prime }+w_{1}^{\prime }y_{1}+w_{2}y_{2}^{\prime }+w_{2}^{\prime }y_{2}+w_{3}y_{3}^{\prime }+w_{3}^{\prime }y_{3}=0 \\ y_{1}{\it\gamma}_{1}^{T}-w_{1}\mathbf{e}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{2}\mathbf{e}_{2}^{T}+y_{3}{\it\gamma}_{3}^{T}-w_{3}\mathbf{e}_{3}^{T}=0}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |w_{1}^{\prime }|,|w_{2}^{\prime }|,|w_{3}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|y_{3}|,|y_{3}^{\prime }|\ll X \\ \mathbf{y}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})^{T}\mathbf{y}^{\prime }+\mathbf{y}^{T}\mathbf{w}^{\prime }=\mathbf{0}}}1,\nonumber\end{eqnarray}$$
where
![]() $\mathbf{y}=(y_{1},y_{2},y_{3})^{T}$
,
$\mathbf{y}=(y_{1},y_{2},y_{3})^{T}$
,
![]() $\mathbf{y}^{\prime }=(y_{1}^{\prime },y_{2}^{\prime },y_{3}^{\prime })^{T}$
and
$\mathbf{y}^{\prime }=(y_{1}^{\prime },y_{2}^{\prime },y_{3}^{\prime })^{T}$
and
![]() $\mathbf{w}^{\prime }=(w_{1}^{\prime },w_{2}^{\prime },w_{3}^{\prime })^{T}$
. Then by Lemma 5.8, we have
$\mathbf{w}^{\prime }=(w_{1}^{\prime },w_{2}^{\prime },w_{3}^{\prime })^{T}$
. Then by Lemma 5.8, we have
Since
![]() $d_{3}\not =0$
, we obtain by Lemma 4.3
$d_{3}\not =0$
, we obtain by Lemma 4.3
and thereby
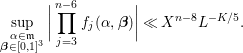 $$\begin{eqnarray}\sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{j=3}^{n-6}f_{j}({\it\alpha},{\bf\beta})\bigg|\ll X^{n-8}L^{-K/5}.\end{eqnarray}$$
$$\begin{eqnarray}\sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{j=3}^{n-6}f_{j}({\it\alpha},{\bf\beta})\bigg|\ll X^{n-8}L^{-K/5}.\end{eqnarray}$$
Now we conclude from (5.9), (5.12)–(5.14) that
Next we consider the case
![]() $1\leqslant \text{rank}(D)\leqslant 2$
. Without loss of generality, we suppose that
$1\leqslant \text{rank}(D)\leqslant 2$
. Without loss of generality, we suppose that
![]() $d_{1}\not =0$
and
$d_{1}\not =0$
and
![]() $d_{k}=0$
for
$d_{k}=0$
for
![]() $3\leqslant k\leqslant n$
. Since
$3\leqslant k\leqslant n$
. Since
![]() $\text{rank}(A)\geqslant 9$
, there exists
$\text{rank}(A)\geqslant 9$
, there exists
![]() $k$
with
$k$
with
![]() $3\leqslant k\leqslant n-6$
such that
$3\leqslant k\leqslant n-6$
such that
![]() ${\it\xi}_{k}\not =0\in \mathbb{Z}^{3}$
. Then we can find
${\it\xi}_{k}\not =0\in \mathbb{Z}^{3}$
. Then we can find
![]() $i,j$
with
$i,j$
with
![]() $1\leqslant i<j\leqslant 3$
so that
$1\leqslant i<j\leqslant 3$
so that
![]() $\text{rank}(\mathbf{e}_{i},\mathbf{e}_{j},{\it\xi}_{k})=3$
. Without loss of generality, we can assume that
$\text{rank}(\mathbf{e}_{i},\mathbf{e}_{j},{\it\xi}_{k})=3$
. Without loss of generality, we can assume that
![]() $i=1,j=2$
and
$i=1,j=2$
and
![]() $k=3$
. One has
$k=3$
. One has
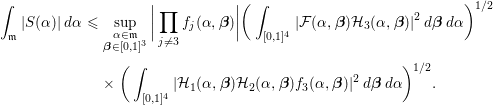 $$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{j\not =3}f_{j}({\it\alpha},{\bf\beta})\bigg|\bigg(\int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}|{\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta})f_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{j\not =3}f_{j}({\it\alpha},{\bf\beta})\bigg|\bigg(\int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}|{\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta})f_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}.\nonumber\end{eqnarray}$$
We deduce from Lemmas 5.6–5.7 that
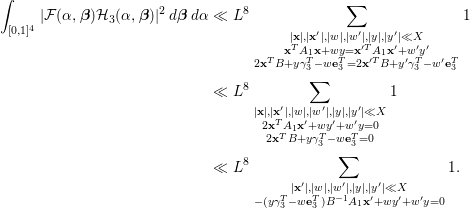 $$\begin{eqnarray}\displaystyle \int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha} & \ll & \displaystyle L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|w|,|w^{\prime }|,|y|,|y^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}+wy={\mathbf{x}^{\prime }}^{T}A_{1}\mathbf{x}^{\prime }+w^{\prime }y^{\prime } \\ 2\mathbf{x}^{T}B+y{\it\gamma}_{3}^{T}-w\mathbf{e}_{3}^{T}=2{\mathbf{x}^{\prime }}^{T}B+y^{\prime }{\it\gamma}_{3}^{T}-w^{\prime }\mathbf{e}_{3}^{T}}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|w|,|w^{\prime }|,|y|,|y^{\prime }|\ll X \\ 2\mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+wy^{\prime }+w^{\prime }y=0 \\ 2\mathbf{x}^{T}B+y{\it\gamma}_{3}^{T}-w\mathbf{e}_{3}^{T}=0}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}^{\prime }|,|w|,|w^{\prime }|,|y|,|y^{\prime }|\ll X \\ -(y{\it\gamma}_{3}^{T}-w\mathbf{e}_{3}^{T})B^{-1}A_{1}\mathbf{x}^{\prime }+wy^{\prime }+w^{\prime }y=0}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta}){\mathcal{H}}_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha} & \ll & \displaystyle L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|w|,|w^{\prime }|,|y|,|y^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}+wy={\mathbf{x}^{\prime }}^{T}A_{1}\mathbf{x}^{\prime }+w^{\prime }y^{\prime } \\ 2\mathbf{x}^{T}B+y{\it\gamma}_{3}^{T}-w\mathbf{e}_{3}^{T}=2{\mathbf{x}^{\prime }}^{T}B+y^{\prime }{\it\gamma}_{3}^{T}-w^{\prime }\mathbf{e}_{3}^{T}}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|w|,|w^{\prime }|,|y|,|y^{\prime }|\ll X \\ 2\mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+wy^{\prime }+w^{\prime }y=0 \\ 2\mathbf{x}^{T}B+y{\it\gamma}_{3}^{T}-w\mathbf{e}_{3}^{T}=0}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}^{\prime }|,|w|,|w^{\prime }|,|y|,|y^{\prime }|\ll X \\ -(y{\it\gamma}_{3}^{T}-w\mathbf{e}_{3}^{T})B^{-1}A_{1}\mathbf{x}^{\prime }+wy^{\prime }+w^{\prime }y=0}}1.\nonumber\end{eqnarray}$$
Then by Lemma 5.8, one has
We deduce from Lemmas 5.6–5.7 again that
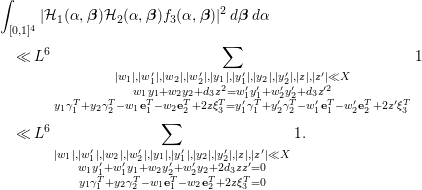 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{4}}|{\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta})f_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{6}\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|z|,|z^{\prime }|\ll X \\ w_{1}y_{1}+w_{2}y_{2}+d_{3}z^{2}=w_{1}^{\prime }y_{1}^{\prime }+w_{2}^{\prime }y_{2}^{\prime }+d_{3}{z^{\prime }}^{2} \\ y_{1}{\it\gamma}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{1}\mathbf{e}_{1}^{T}-w_{2}\mathbf{e}_{2}^{T}+2z{\it\xi}_{3}^{T}=y_{1}^{\prime }{\it\gamma}_{1}^{T}+y_{2}^{\prime }{\it\gamma}_{2}^{T}-w_{1}^{\prime }\mathbf{e}_{1}^{T}-w_{2}^{\prime }\mathbf{e}_{2}^{T}+2z^{\prime }{\it\xi}_{3}^{T}}}1\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{6}\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|z|,|z^{\prime }|\ll X \\ w_{1}y_{1}^{\prime }+w_{1}^{\prime }y_{1}+w_{2}y_{2}^{\prime }+w_{2}^{\prime }y_{2}+2d_{3}zz^{\prime }=0 \\ y_{1}{\it\gamma}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{1}\mathbf{e}_{1}^{T}-w_{2}\mathbf{e}_{2}^{T}+2z{\it\xi}_{3}^{T}=0}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{4}}|{\mathcal{H}}_{1}({\it\alpha},{\bf\beta}){\mathcal{H}}_{2}({\it\alpha},{\bf\beta})f_{3}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{6}\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|z|,|z^{\prime }|\ll X \\ w_{1}y_{1}+w_{2}y_{2}+d_{3}z^{2}=w_{1}^{\prime }y_{1}^{\prime }+w_{2}^{\prime }y_{2}^{\prime }+d_{3}{z^{\prime }}^{2} \\ y_{1}{\it\gamma}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{1}\mathbf{e}_{1}^{T}-w_{2}\mathbf{e}_{2}^{T}+2z{\it\xi}_{3}^{T}=y_{1}^{\prime }{\it\gamma}_{1}^{T}+y_{2}^{\prime }{\it\gamma}_{2}^{T}-w_{1}^{\prime }\mathbf{e}_{1}^{T}-w_{2}^{\prime }\mathbf{e}_{2}^{T}+2z^{\prime }{\it\xi}_{3}^{T}}}1\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{6}\mathop{\sum }_{\substack{ |w_{1}|,|w_{1}^{\prime }|,|w_{2}|,|w_{2}^{\prime }|,|y_{1}|,|y_{1}^{\prime }|,|y_{2}|,|y_{2}^{\prime }|,|z|,|z^{\prime }|\ll X \\ w_{1}y_{1}^{\prime }+w_{1}^{\prime }y_{1}+w_{2}y_{2}^{\prime }+w_{2}^{\prime }y_{2}+2d_{3}zz^{\prime }=0 \\ y_{1}{\it\gamma}_{1}^{T}+y_{2}{\it\gamma}_{2}^{T}-w_{1}\mathbf{e}_{1}^{T}-w_{2}\mathbf{e}_{2}^{T}+2z{\it\xi}_{3}^{T}=0}}1.\nonumber\end{eqnarray}$$
On applying
![]() $\text{rank}(\mathbf{e}_{1},\mathbf{e}_{2},{\it\xi}_{3})=3$
and Lemma 5.8, we obtain
$\text{rank}(\mathbf{e}_{1},\mathbf{e}_{2},{\it\xi}_{3})=3$
and Lemma 5.8, we obtain
It follows from Lemma 4.3 that
Then we conclude from (5.15)–(5.17) that
Now it suffices to assume
![]() $D=0$
. Then the matrix
$D=0$
. Then the matrix
![]() $A$
is in the form
$A$
is in the form
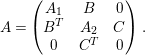 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & B & 0\\ B^{T} & A_{2} & C\\ 0 & C^{T} & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & B & 0\\ B^{T} & A_{2} & C\\ 0 & C^{T} & 0\end{array}\right).\end{eqnarray}$$
It follows from
![]() $\text{rank}(A)\geqslant 9$
that
$\text{rank}(A)\geqslant 9$
that
![]() $\text{rank}(C)\geqslant 3$
. By Lemma 4.6,
$\text{rank}(C)\geqslant 3$
. By Lemma 4.6,
This completes the proof of Lemma 5.2.
5.2 Proof of Lemma 5.3
Lemma 5.10. If
![]() $\text{rank}(B_{1})=\text{rank}(B_{2})=2$
and
$\text{rank}(B_{1})=\text{rank}(B_{2})=2$
and
![]() $\text{rank}(B_{3})=3$
, then the symmetric integral matrix
$\text{rank}(B_{3})=3$
, then the symmetric integral matrix
![]() $A$
can be written in the form
$A$
can be written in the form
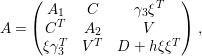 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & C & {\it\gamma}_{3}{\it\xi}^{T}\\ C^{T} & A_{2} & V\\ {\it\xi}{\it\gamma}_{3}^{T} & V^{T} & D+h{\it\xi}{\it\xi}^{T}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & C & {\it\gamma}_{3}{\it\xi}^{T}\\ C^{T} & A_{2} & V\\ {\it\xi}{\it\gamma}_{3}^{T} & V^{T} & D+h{\it\xi}{\it\xi}^{T}\end{array}\right),\end{eqnarray}$$
where
![]() $C=({\it\gamma}_{1},{\it\gamma}_{2})\in M_{3,2}(\mathbb{Z})$
,
$C=({\it\gamma}_{1},{\it\gamma}_{2})\in M_{3,2}(\mathbb{Z})$
,
![]() ${\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
${\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
![]() ${\it\xi}\in \mathbb{Z}^{n-5}$
,
${\it\xi}\in \mathbb{Z}^{n-5}$
,
![]() $V\in M_{2,n-5}(\mathbb{Z})$
,
$V\in M_{2,n-5}(\mathbb{Z})$
,
![]() $h\in \mathbb{Q}$
and
$h\in \mathbb{Q}$
and
![]() $D=\text{diag}\{d_{1},\ldots ,d_{n-5}\}\in M_{n-5,n-5}(\mathbb{Q})$
is a diagonal matrix. Moreover, one has
$D=\text{diag}\{d_{1},\ldots ,d_{n-5}\}\in M_{n-5,n-5}(\mathbb{Q})$
is a diagonal matrix. Moreover, one has
![]() $({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Q})$
.
$({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Q})$
.
Proof. Let us write
 $$\begin{eqnarray}{\it\gamma}_{j}^{\prime }=\left(\begin{array}{@{}c@{}}a_{1,\,3+j}\\ a_{2,\,3+j}\\ a_{3,\,3+j}\end{array}\right)\quad \text{for }1\leqslant j\leqslant n-3.\end{eqnarray}$$
$$\begin{eqnarray}{\it\gamma}_{j}^{\prime }=\left(\begin{array}{@{}c@{}}a_{1,\,3+j}\\ a_{2,\,3+j}\\ a_{3,\,3+j}\end{array}\right)\quad \text{for }1\leqslant j\leqslant n-3.\end{eqnarray}$$
Since
![]() $\text{rank}({\it\gamma}_{1}^{\prime },{\it\gamma}_{2}^{\prime },{\it\gamma}_{3}^{\prime })=\text{rank}(B)=3$
, we conclude that
$\text{rank}({\it\gamma}_{1}^{\prime },{\it\gamma}_{2}^{\prime },{\it\gamma}_{3}^{\prime })=\text{rank}(B)=3$
, we conclude that
![]() ${\it\gamma}_{1}^{\prime }$
,
${\it\gamma}_{1}^{\prime }$
,
![]() ${\it\gamma}_{2}^{\prime }$
and
${\it\gamma}_{2}^{\prime }$
and
![]() ${\it\gamma}_{3}^{\prime }$
are linearly independent. For any
${\it\gamma}_{3}^{\prime }$
are linearly independent. For any
![]() $4\leqslant j\leqslant n-3$
, we deduce from
$4\leqslant j\leqslant n-3$
, we deduce from
![]() $\text{rank}(B_{1})=\text{rank}(B_{2})=2$
that
$\text{rank}(B_{1})=\text{rank}(B_{2})=2$
that
![]() ${\it\gamma}_{j}^{\prime }\in <{\it\gamma}_{2}^{\prime },{\it\gamma}_{3}^{\prime }>\cap <{\it\gamma}_{1}^{\prime },{\it\gamma}_{3}^{\prime }>=<{\it\gamma}_{3}^{\prime }>$
. Therefore, we can write
${\it\gamma}_{j}^{\prime }\in <{\it\gamma}_{2}^{\prime },{\it\gamma}_{3}^{\prime }>\cap <{\it\gamma}_{1}^{\prime },{\it\gamma}_{3}^{\prime }>=<{\it\gamma}_{3}^{\prime }>$
. Therefore, we can write
![]() $A$
in the form
$A$
in the form
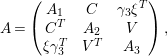 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & C & {\it\gamma}_{3}{\it\xi}^{T}\\ C^{T} & A_{2} & V\\ {\it\xi}{\it\gamma}_{3}^{T} & V^{T} & A_{3}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & C & {\it\gamma}_{3}{\it\xi}^{T}\\ C^{T} & A_{2} & V\\ {\it\xi}{\it\gamma}_{3}^{T} & V^{T} & A_{3}\end{array}\right),\end{eqnarray}$$
where
![]() $C=({\it\gamma}_{1},{\it\gamma}_{2})\in M_{3,2}(\mathbb{Z})$
,
$C=({\it\gamma}_{1},{\it\gamma}_{2})\in M_{3,2}(\mathbb{Z})$
,
![]() ${\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
${\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
![]() ${\it\xi}\in \mathbb{Z}^{n-5}$
,
${\it\xi}\in \mathbb{Z}^{n-5}$
,
![]() $V\in M_{2,n-5}(\mathbb{Z})$
and
$V\in M_{2,n-5}(\mathbb{Z})$
and
![]() $A_{3}\in M_{n-5,n-5}(\mathbb{Q})$
.
$A_{3}\in M_{n-5,n-5}(\mathbb{Q})$
.
For
![]() $6\leqslant j\leqslant n$
. we define
$6\leqslant j\leqslant n$
. we define
![]() ${\it\eta}_{j}^{T}=(a_{j,4},\ldots ,a_{j,j-1},a_{j,j+1},\ldots ,a_{j,n})^{T}\in \mathbb{Z}^{n-4}$
. Then we set
${\it\eta}_{j}^{T}=(a_{j,4},\ldots ,a_{j,j-1},a_{j,j+1},\ldots ,a_{j,n})^{T}\in \mathbb{Z}^{n-4}$
. Then we set
![]() ${\it\theta}_{i,j}^{T}=(a_{i,4},\ldots ,a_{i,j-1},a_{i,j+1},\ldots ,a_{i,n})^{T}\in \mathbb{Z}^{n-4}$
for
${\it\theta}_{i,j}^{T}=(a_{i,4},\ldots ,a_{i,j-1},a_{i,j+1},\ldots ,a_{i,n})^{T}\in \mathbb{Z}^{n-4}$
for
![]() $1\leqslant i\leqslant 3$
. Since
$1\leqslant i\leqslant 3$
. Since
![]() $\text{rank}_{\text{off}}(A)=\text{rank}(B)=\text{rank}(B_{3})=3$
,
$\text{rank}_{\text{off}}(A)=\text{rank}(B)=\text{rank}(B_{3})=3$
,
![]() ${\it\eta}_{j}$
can be linearly represented by
${\it\eta}_{j}$
can be linearly represented by
![]() ${\it\theta}_{1,j}$
,
${\it\theta}_{1,j}$
,
![]() ${\it\theta}_{2,j}$
and
${\it\theta}_{2,j}$
and
![]() ${\it\theta}_{3,j}$
. Let
${\it\theta}_{3,j}$
. Let
Then one can choose
![]() $a_{j,j}^{\prime }\in \mathbb{Q}$
such that
$a_{j,j}^{\prime }\in \mathbb{Q}$
such that
![]() $(a_{j,4},\ldots ,a_{j,j-1},a_{j,j}^{\prime },a_{j,j+1},\ldots ,a_{j,n})$
is linearly represented by
$(a_{j,4},\ldots ,a_{j,j-1},a_{j,j}^{\prime },a_{j,j+1},\ldots ,a_{j,n})$
is linearly represented by
![]() ${\it\theta}_{1}$
,
${\it\theta}_{1}$
,
![]() ${\it\theta}_{2}$
and
${\it\theta}_{2}$
and
![]() ${\it\theta}_{3}$
. We consider
${\it\theta}_{3}$
. We consider
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{3}^{\prime }$
defined as
$A_{3}^{\prime }$
defined as
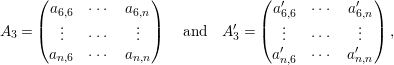 $$\begin{eqnarray}A_{3}=\left(\begin{array}{@{}ccc@{}}a_{6,6} & \cdots \, & a_{6,n}\\ \vdots & \cdots \, & \vdots \\ a_{n,6} & \cdots \, & a_{n,n}\end{array}\right)\quad \text{and}\quad A_{3}^{\prime }=\left(\begin{array}{@{}ccc@{}}a_{6,6}^{\prime } & \cdots \, & a_{6,n}^{\prime }\\ \vdots & \cdots \, & \vdots \\ a_{n,6}^{\prime } & \cdots \, & a_{n,n}^{\prime }\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A_{3}=\left(\begin{array}{@{}ccc@{}}a_{6,6} & \cdots \, & a_{6,n}\\ \vdots & \cdots \, & \vdots \\ a_{n,6} & \cdots \, & a_{n,n}\end{array}\right)\quad \text{and}\quad A_{3}^{\prime }=\left(\begin{array}{@{}ccc@{}}a_{6,6}^{\prime } & \cdots \, & a_{6,n}^{\prime }\\ \vdots & \cdots \, & \vdots \\ a_{n,6}^{\prime } & \cdots \, & a_{n,n}^{\prime }\end{array}\right),\end{eqnarray}$$
where
![]() $a_{i,j}^{\prime }=a_{i,j}$
for
$a_{i,j}^{\prime }=a_{i,j}$
for
![]() $6\leqslant i\not =j\leqslant n$
. Since
$6\leqslant i\not =j\leqslant n$
. Since
![]() $A_{3}^{\prime }$
is symmetric, we conclude from above that
$A_{3}^{\prime }$
is symmetric, we conclude from above that
![]() $A_{3}^{\prime }=h{\it\xi}{\it\xi}^{T}$
for some
$A_{3}^{\prime }=h{\it\xi}{\it\xi}^{T}$
for some
![]() $h\in \mathbb{Q}$
. The proof is completed by noting that
$h\in \mathbb{Q}$
. The proof is completed by noting that
![]() $D=A_{3}-A_{3}^{\prime }$
is a diagonal matrix.◻
$D=A_{3}-A_{3}^{\prime }$
is a diagonal matrix.◻
Proof of Lemma 5.3.
One can deduce from Lemma 5.10 that
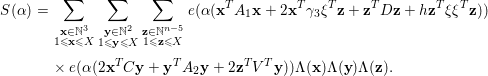 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{2} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-5} \\ 1\leqslant \mathbf{z}\leqslant X}}e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}{\it\gamma}_{3}{\it\xi}^{T}\mathbf{z}+\mathbf{z}^{T}D\mathbf{z}+h\mathbf{z}^{T}{\it\xi}{\it\xi}^{T}\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}C\mathbf{y}+\mathbf{y}^{T}A_{2}\mathbf{y}+2\mathbf{z}^{T}V^{T}\mathbf{y})){\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{2} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-5} \\ 1\leqslant \mathbf{z}\leqslant X}}e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}{\it\gamma}_{3}{\it\xi}^{T}\mathbf{z}+\mathbf{z}^{T}D\mathbf{z}+h\mathbf{z}^{T}{\it\xi}{\it\xi}^{T}\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}C\mathbf{y}+\mathbf{y}^{T}A_{2}\mathbf{y}+2\mathbf{z}^{T}V^{T}\mathbf{y})){\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z}).\nonumber\end{eqnarray}$$
We introduce new variables
![]() $\mathbf{w}\in \mathbb{Z}^{2}$
and
$\mathbf{w}\in \mathbb{Z}^{2}$
and
![]() $s\in \mathbb{Z}$
to replace
$s\in \mathbb{Z}$
to replace
![]() $2\mathbf{x}^{T}C+\mathbf{y}^{T}A_{2}+2\mathbf{z}^{T}V^{T}$
and
$2\mathbf{x}^{T}C+\mathbf{y}^{T}A_{2}+2\mathbf{z}^{T}V^{T}$
and
![]() ${\it\xi}^{T}\mathbf{z}$
, respectively. Therefore, we have
${\it\xi}^{T}\mathbf{z}$
, respectively. Therefore, we have
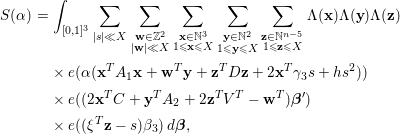 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{|s|\ll X}\mathop{\sum }_{\substack{ \mathbf{w}\in \mathbb{Z}^{2} \\ |\mathbf{w}|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{2} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-5} \\ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{w}^{T}\mathbf{y}+\mathbf{z}^{T}D\mathbf{z}+2\mathbf{x}^{T}{\it\gamma}_{3}s+hs^{2}))\nonumber\\ \displaystyle & & \displaystyle \times \,e((2\mathbf{x}^{T}C+\mathbf{y}^{T}A_{2}+2\mathbf{z}^{T}V^{T}-\mathbf{w}^{T}){\bf\beta}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,e(({\it\xi}^{T}\mathbf{z}-s){\it\beta}_{3})\,d{\bf\beta},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{|s|\ll X}\mathop{\sum }_{\substack{ \mathbf{w}\in \mathbb{Z}^{2} \\ |\mathbf{w}|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{2} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-5} \\ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{w}^{T}\mathbf{y}+\mathbf{z}^{T}D\mathbf{z}+2\mathbf{x}^{T}{\it\gamma}_{3}s+hs^{2}))\nonumber\\ \displaystyle & & \displaystyle \times \,e((2\mathbf{x}^{T}C+\mathbf{y}^{T}A_{2}+2\mathbf{z}^{T}V^{T}-\mathbf{w}^{T}){\bf\beta}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,e(({\it\xi}^{T}\mathbf{z}-s){\it\beta}_{3})\,d{\bf\beta},\nonumber\end{eqnarray}$$
where
![]() ${\bf\beta}^{\prime }=({\it\beta}_{1},{\it\beta}_{2})^{T}$
,
${\bf\beta}^{\prime }=({\it\beta}_{1},{\it\beta}_{2})^{T}$
,
![]() ${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
and
${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
and
![]() $d{\bf\beta}=d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. We define
$d{\bf\beta}=d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. We define
On writing
![]() $I_{2}=(\mathbf{e}_{1},\mathbf{e}_{2})$
, we introduce
$I_{2}=(\mathbf{e}_{1},\mathbf{e}_{2})$
, we introduce
where
![]() ${\it\rho}_{j}=(a_{3+j,4},a_{3+j,5})^{T}$
for
${\it\rho}_{j}=(a_{3+j,4},a_{3+j,5})^{T}$
for
![]() $1\leqslant j\leqslant 2$
. Let
$1\leqslant j\leqslant 2$
. Let
![]() ${\it\xi}=({\it\epsilon}_{1},\ldots ,{\it\epsilon}_{n-5})^{T}$
. Then we define
${\it\xi}=({\it\epsilon}_{1},\ldots ,{\it\epsilon}_{n-5})^{T}$
. Then we define
where
![]() $V=({\it\upsilon}_{1},\ldots ,{\it\upsilon}_{n-5})$
with
$V=({\it\upsilon}_{1},\ldots ,{\it\upsilon}_{n-5})$
with
![]() ${\it\upsilon}_{j}=(a_{4,5+j},a_{5,5+j})^{T}$
for
${\it\upsilon}_{j}=(a_{4,5+j},a_{5,5+j})^{T}$
for
![]() $1\leqslant j\leqslant n-5$
. With above notations, we obtain
$1\leqslant j\leqslant n-5$
. With above notations, we obtain
Let
and
By (5.19) and the Cauchy–Schwarz inequality, one has for
![]() $i\not =j$
that
$i\not =j$
that
One can deduce by Lemmas 5.6 and 5.7 that
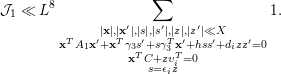 $$\begin{eqnarray}{\mathcal{J}}_{1}\ll L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+s{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+hss^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}C+z{\it\upsilon}_{i}^{T}=0 \\ s={\it\epsilon}_{i}z}}1.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}_{1}\ll L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+s{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+hss^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}C+z{\it\upsilon}_{i}^{T}=0 \\ s={\it\epsilon}_{i}z}}1.\end{eqnarray}$$
Note that
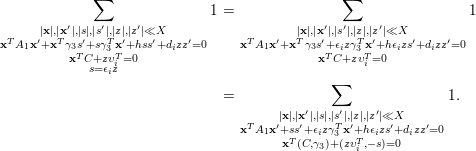 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+s{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+hss^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}C+z{\it\upsilon}_{i}^{T}=0 \\ s={\it\epsilon}_{i}z}}1 & = & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+{\it\epsilon}_{i}z{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+h{\it\epsilon}_{i}zs^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}C+z{\it\upsilon}_{i}^{T}=0}}1\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+ss^{\prime }+{\it\epsilon}_{i}z{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+h{\it\epsilon}_{i}zs^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}(C,{\it\gamma}_{3})+(z{\it\upsilon}_{i}^{T},-s)=0}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+s{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+hss^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}C+z{\it\upsilon}_{i}^{T}=0 \\ s={\it\epsilon}_{i}z}}1 & = & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+{\it\epsilon}_{i}z{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+h{\it\epsilon}_{i}zs^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}C+z{\it\upsilon}_{i}^{T}=0}}1\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|z|,|z^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+ss^{\prime }+{\it\epsilon}_{i}z{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+h{\it\epsilon}_{i}zs^{\prime }+d_{i}zz^{\prime }=0 \\ \mathbf{x}^{T}(C,{\it\gamma}_{3})+(z{\it\upsilon}_{i}^{T},-s)=0}}1.\nonumber\end{eqnarray}$$
Recalling
![]() $\text{rank}(C,{\it\gamma}_{3})=3$
, one can replace
$\text{rank}(C,{\it\gamma}_{3})=3$
, one can replace
![]() $\mathbf{x}$
by
$\mathbf{x}$
by
![]() $-(z{\it\upsilon}_{i}^{T},-s)(C,{\it\gamma}_{3})^{-1}$
. Therefore, by Lemma 5.8, one has
$-(z{\it\upsilon}_{i}^{T},-s)(C,{\it\gamma}_{3})^{-1}$
. Therefore, by Lemma 5.8, one has
The argument leading to (5.16) also implies
Now we are able to handle the case
![]() $\text{rank}(D)\geqslant 2$
. Since
$\text{rank}(D)\geqslant 2$
. Since
![]() $\text{rank}(B_{3})=3$
, one has
$\text{rank}(B_{3})=3$
, one has
![]() ${\it\epsilon}_{l}\not =0$
for some
${\it\epsilon}_{l}\not =0$
for some
![]() $l$
satisfying
$l$
satisfying
![]() $2\leqslant l\leqslant n-5$
. We may assume
$2\leqslant l\leqslant n-5$
. We may assume
![]() ${\it\epsilon}_{2}\not =0$
. We also have
${\it\epsilon}_{2}\not =0$
. We also have
![]() ${\it\epsilon}_{1}\not =0$
due to
${\it\epsilon}_{1}\not =0$
due to
![]() $\text{rank}(B)=3$
. If
$\text{rank}(B)=3$
. If
![]() $d_{l}\not =0$
for some
$d_{l}\not =0$
for some
![]() $l\geqslant 3$
, then we can find
$l\geqslant 3$
, then we can find
![]() $i,j,k$
pairwise distinct so that
$i,j,k$
pairwise distinct so that
![]() ${\it\epsilon}_{j}\not =0$
and
${\it\epsilon}_{j}\not =0$
and
![]() $d_{i}d_{k}\not =0$
. If
$d_{i}d_{k}\not =0$
. If
![]() $d_{1}d_{2}\not =0$
and
$d_{1}d_{2}\not =0$
and
![]() ${\it\epsilon}_{j}\not =0$
for some
${\it\epsilon}_{j}\not =0$
for some
![]() $j\geqslant 3$
, then we can also find
$j\geqslant 3$
, then we can also find
![]() $i,j,k$
pairwise distinct so that
$i,j,k$
pairwise distinct so that
![]() ${\it\epsilon}_{j}\not =0$
and
${\it\epsilon}_{j}\not =0$
and
![]() $d_{i}d_{k}\not =0$
. In these cases, we can conclude from (5.20)–(5.22) that
$d_{i}d_{k}\not =0$
. In these cases, we can conclude from (5.20)–(5.22) that
Next we assume
![]() $d_{l}={\it\epsilon}_{l}=0$
for all
$d_{l}={\it\epsilon}_{l}=0$
for all
![]() $l\geqslant 3$
. Then we can represent
$l\geqslant 3$
. Then we can represent
![]() $A$
in the form
$A$
in the form
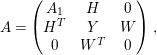 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & H & 0\\ H^{T} & Y & W\\ 0 & W^{T} & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & H & 0\\ H^{T} & Y & W\\ 0 & W^{T} & 0\end{array}\right),\end{eqnarray}$$
where
![]() $H\in M_{3,4}(\mathbb{Z})$
,
$H\in M_{3,4}(\mathbb{Z})$
,
![]() $Y\in M_{4,4}(\mathbb{Z})$
and
$Y\in M_{4,4}(\mathbb{Z})$
and
![]() $W\in M_{4,n-7}(\mathbb{Z})$
. It follows from
$W\in M_{4,n-7}(\mathbb{Z})$
. It follows from
![]() $\text{rank}(B)=3$
and
$\text{rank}(B)=3$
and
![]() $\text{rank}(A)\geqslant 9$
that
$\text{rank}(A)\geqslant 9$
that
![]() $\text{rank}(H)\geqslant 3$
and
$\text{rank}(H)\geqslant 3$
and
![]() $\text{rank}(W)\geqslant 2$
. We apply Lemma 4.6 to conclude
$\text{rank}(W)\geqslant 2$
. We apply Lemma 4.6 to conclude
We are left to handle the case
![]() $\text{rank}(D)\leqslant 1$
. Since
$\text{rank}(D)\leqslant 1$
. Since
![]() $\text{rank}(D)+\text{rank}(V)+1+5\geqslant \text{rank}(A)\geqslant 9$
, we obtain
$\text{rank}(D)+\text{rank}(V)+1+5\geqslant \text{rank}(A)\geqslant 9$
, we obtain
![]() $\text{rank}(D)\geqslant 1$
. Therefore,
$\text{rank}(D)\geqslant 1$
. Therefore,
![]() $\text{rank}(D)=1$
. We have
$\text{rank}(D)=1$
. We have
where
and
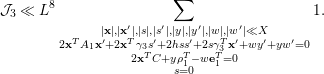 $$\begin{eqnarray}{\mathcal{J}}_{3}\ll L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|y|,|y^{\prime }|,|w|,|w^{\prime }|\ll X \\ 2\mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+2\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+2hss^{\prime }+2s{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+wy^{\prime }+yw^{\prime }=0 \\ 2\mathbf{x}^{T}C+y{\it\rho}_{1}^{T}-w\mathbf{e}_{1}^{T}=0 \\ s=0}}1.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}_{3}\ll L^{8}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|s|,|s^{\prime }|,|y|,|y^{\prime }|,|w|,|w^{\prime }|\ll X \\ 2\mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+2\mathbf{x}^{T}{\it\gamma}_{3}s^{\prime }+2hss^{\prime }+2s{\it\gamma}_{3}^{T}\mathbf{x}^{\prime }+wy^{\prime }+yw^{\prime }=0 \\ 2\mathbf{x}^{T}C+y{\it\rho}_{1}^{T}-w\mathbf{e}_{1}^{T}=0 \\ s=0}}1.\end{eqnarray}$$
Since
![]() $\text{rank}(C)\geqslant 3$
, we can represent two of
$\text{rank}(C)\geqslant 3$
, we can represent two of
![]() $x_{1},x_{2},x_{3}$
(say
$x_{1},x_{2},x_{3}$
(say
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
) in terms of
$x_{2}$
) in terms of
![]() $x_{3}$
,
$x_{3}$
,
![]() $y$
and
$y$
and
![]() $w$
. Then by Lemma 5.8, one has
$w$
. Then by Lemma 5.8, one has
We deduce from Lemma 5.10 that
![]() $\text{rank}\left(\begin{array}{@{}c@{}}{\it\xi}^{T}\\ V\end{array}\right)\geqslant \text{rank}(A)-5-\text{rank}(D)\geqslant 3$
. Therefore, there exist distinct
$\text{rank}\left(\begin{array}{@{}c@{}}{\it\xi}^{T}\\ V\end{array}\right)\geqslant \text{rank}(A)-5-\text{rank}(D)\geqslant 3$
. Therefore, there exist distinct
![]() $i,j,k,s$
such that
$i,j,k,s$
such that
![]() $\text{rank}\left(\begin{array}{@{}ccc@{}}{\it\upsilon}_{i}^{T} & {\it\upsilon}_{j}^{T} & {\it\upsilon}_{k}^{T}\\ {\it\epsilon}_{i} & {\it\epsilon}_{j} & {\it\epsilon}_{k}\end{array}\right)=3$
and
$\text{rank}\left(\begin{array}{@{}ccc@{}}{\it\upsilon}_{i}^{T} & {\it\upsilon}_{j}^{T} & {\it\upsilon}_{k}^{T}\\ {\it\epsilon}_{i} & {\it\epsilon}_{j} & {\it\epsilon}_{k}\end{array}\right)=3$
and
![]() $d_{s}\not =0$
. By Lemmas 5.6–5.7, we also have
$d_{s}\not =0$
. By Lemmas 5.6–5.7, we also have
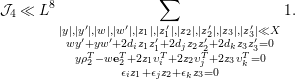 $$\begin{eqnarray}{\mathcal{J}}_{4}\ll L^{8}\mathop{\sum }_{\substack{ |y|,|y^{\prime }|,|w|,|w^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|,|z_{3}|,|z_{3}^{\prime }|\ll X \\ wy^{\prime }+yw^{\prime }+2d_{i}z_{1}z_{1}^{\prime }+2d_{j}z_{2}z_{2}^{\prime }+2d_{k}z_{3}z_{3}^{\prime }=0 \\ y{\it\rho}_{2}^{T}-w\mathbf{e}_{2}^{T}+2z_{1}{\it\upsilon}_{i}^{T}+2z_{2}{\it\upsilon}_{j}^{T}+2z_{3}{\it\upsilon}_{k}^{T}=0 \\ {\it\epsilon}_{i}z_{1}+{\it\epsilon}_{j}z_{2}+{\it\epsilon}_{k}z_{3}=0}}1.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}_{4}\ll L^{8}\mathop{\sum }_{\substack{ |y|,|y^{\prime }|,|w|,|w^{\prime }|,|z_{1}|,|z_{1}^{\prime }|,|z_{2}|,|z_{2}^{\prime }|,|z_{3}|,|z_{3}^{\prime }|\ll X \\ wy^{\prime }+yw^{\prime }+2d_{i}z_{1}z_{1}^{\prime }+2d_{j}z_{2}z_{2}^{\prime }+2d_{k}z_{3}z_{3}^{\prime }=0 \\ y{\it\rho}_{2}^{T}-w\mathbf{e}_{2}^{T}+2z_{1}{\it\upsilon}_{i}^{T}+2z_{2}{\it\upsilon}_{j}^{T}+2z_{3}{\it\upsilon}_{k}^{T}=0 \\ {\it\epsilon}_{i}z_{1}+{\it\epsilon}_{j}z_{2}+{\it\epsilon}_{k}z_{3}=0}}1.\end{eqnarray}$$
Hence we can replace
![]() $z_{1},z_{2}$
and
$z_{1},z_{2}$
and
![]() $z_{3}$
by linear functions of
$z_{3}$
by linear functions of
![]() $y$
and
$y$
and
![]() $w$
, and it follows that
$w$
, and it follows that
Hence we can obtain again that
The proof of Lemma 5.3 is finished.
5.3 Proof of Lemma 5.4
The proof of Lemma 5.10 can be modified to establish the following result. The detail of the proof is omitted.
Lemma 5.11. If
![]() $\text{rank}(B_{1})=2$
and
$\text{rank}(B_{1})=2$
and
![]() $\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then we can write
$\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then we can write
![]() $A$
in the form
$A$
in the form
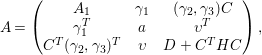 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & {\it\gamma}_{1} & ({\it\gamma}_{2},{\it\gamma}_{3})C\\ {\it\gamma}_{1}^{T} & a & {\it\upsilon}^{T}\\ C^{T}({\it\gamma}_{2},{\it\gamma}_{3})^{T} & {\it\upsilon} & D+C^{T}HC\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}A_{1} & {\it\gamma}_{1} & ({\it\gamma}_{2},{\it\gamma}_{3})C\\ {\it\gamma}_{1}^{T} & a & {\it\upsilon}^{T}\\ C^{T}({\it\gamma}_{2},{\it\gamma}_{3})^{T} & {\it\upsilon} & D+C^{T}HC\end{array}\right),\end{eqnarray}$$
where
![]() ${\it\gamma}_{1}\in \mathbb{Z}^{3}$
,
${\it\gamma}_{1}\in \mathbb{Z}^{3}$
,
![]() ${\it\gamma}_{2},{\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
${\it\gamma}_{2},{\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
![]() $C\in M_{2,n-4}(\mathbb{Z})$
,
$C\in M_{2,n-4}(\mathbb{Z})$
,
![]() $a\in \mathbb{Z}$
,
$a\in \mathbb{Z}$
,
![]() ${\it\upsilon}\in \mathbb{Z}^{n-4}$
,
${\it\upsilon}\in \mathbb{Z}^{n-4}$
,
![]() $H\in M_{2,2}(\mathbb{Q})$
and
$H\in M_{2,2}(\mathbb{Q})$
and
![]() $D=\text{diag}\{d_{1},\ldots ,d_{n-4}\}\in M_{n-4,n-4}(\mathbb{Q})$
is a diagonal matrix. Moreover, one has
$D=\text{diag}\{d_{1},\ldots ,d_{n-4}\}\in M_{n-4,n-4}(\mathbb{Q})$
is a diagonal matrix. Moreover, one has
![]() $({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Q})$
.
$({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Q})$
.
Lemma 5.12. Let
![]() $A$
be given by (5.26). We write
$A$
be given by (5.26). We write
Let
Under the conditions in Lemma 5.11, one can find pairwise distinct
![]() $i,j,k,u$
with
$i,j,k,u$
with
![]() $1\leqslant i,j,k,u\leqslant n-4$
such that at least one of the following two statements holds: (i)
$1\leqslant i,j,k,u\leqslant n-4$
such that at least one of the following two statements holds: (i)
![]() $\text{rank}(R_{i,j,k})=3$
and
$\text{rank}(R_{i,j,k})=3$
and
![]() $d_{u}\not =0$
; (ii)
$d_{u}\not =0$
; (ii)
![]() $\text{rank}({\it\xi}_{i},{\it\xi}_{j})=2$
and
$\text{rank}({\it\xi}_{i},{\it\xi}_{j})=2$
and
![]() $d_{k}d_{u}\not =0$
.
$d_{k}d_{u}\not =0$
.
Proof. It follows from
![]() $9\leqslant \text{rank}(A)\leqslant \text{rank}(D)+\text{rank}({\it\upsilon})+\text{rank}(C)+4$
that
$9\leqslant \text{rank}(A)\leqslant \text{rank}(D)+\text{rank}({\it\upsilon})+\text{rank}(C)+4$
that
![]() $\text{rank}(D)\geqslant 2$
. If
$\text{rank}(D)\geqslant 2$
. If
![]() $\text{rank}(D)=2$
, say
$\text{rank}(D)=2$
, say
![]() $d_{1}d_{2}\not =0$
, then
$d_{1}d_{2}\not =0$
, then
![]() $\text{rank}(R)\geqslant 3$
, where
$\text{rank}(R)\geqslant 3$
, where
Then statement (i) holds. Next we assume
![]() $\text{rank}(D)\geqslant 3$
. Note that
$\text{rank}(D)\geqslant 3$
. Note that
![]() $\text{rank}({\it\xi}_{1},{\it\xi}_{2})=2$
due to
$\text{rank}({\it\xi}_{1},{\it\xi}_{2})=2$
due to
![]() $\text{rank}(B)=3$
. If
$\text{rank}(B)=3$
. If
![]() $d_{r}d_{s}\not =0$
for some
$d_{r}d_{s}\not =0$
for some
![]() $r>s\geqslant 3$
, then statement (ii) follows by choosing
$r>s\geqslant 3$
, then statement (ii) follows by choosing
![]() $i=1,j=2,k=r$
and
$i=1,j=2,k=r$
and
![]() $u=s$
. Therefore, we now assume that
$u=s$
. Therefore, we now assume that
![]() $\text{rank}(D)=3$
and
$\text{rank}(D)=3$
and
![]() $d_{1}d_{2}\not =0$
. Without loss of generality, we suppose that
$d_{1}d_{2}\not =0$
. Without loss of generality, we suppose that
![]() $d_{3}\not =0$
and
$d_{3}\not =0$
and
![]() $d_{s}=0(4\leqslant s\leqslant n-4)$
. We consider
$d_{s}=0(4\leqslant s\leqslant n-4)$
. We consider
![]() $\text{rank}({\it\xi}_{1},{\it\xi}_{s})$
and
$\text{rank}({\it\xi}_{1},{\it\xi}_{s})$
and
![]() $\text{rank}({\it\xi}_{2},{\it\xi}_{s})$
for
$\text{rank}({\it\xi}_{2},{\it\xi}_{s})$
for
![]() $4\leqslant s\leqslant n-4$
. If
$4\leqslant s\leqslant n-4$
. If
![]() $\text{rank}({\it\xi}_{1},{\it\xi}_{s})=2$
for some
$\text{rank}({\it\xi}_{1},{\it\xi}_{s})=2$
for some
![]() $s$
with
$s$
with
![]() $4\leqslant s\leqslant n-4$
, then one can choose
$4\leqslant s\leqslant n-4$
, then one can choose
![]() $i=1$
,
$i=1$
,
![]() $j=s$
$j=s$
![]() $k=2$
and
$k=2$
and
![]() $u=3$
to establish statement (ii). Similarly, statement (ii) follows if
$u=3$
to establish statement (ii). Similarly, statement (ii) follows if
![]() $\text{rank}({\it\xi}_{2},{\it\xi}_{s})=2$
for some
$\text{rank}({\it\xi}_{2},{\it\xi}_{s})=2$
for some
![]() $s$
with
$s$
with
![]() $4\leqslant s\leqslant n-4$
. Thus it remains to consider the case
$4\leqslant s\leqslant n-4$
. Thus it remains to consider the case
![]() $\text{rank}({\it\xi}_{1},{\it\xi}_{s})=\text{rank}({\it\xi}_{2},{\it\xi}_{s})=1$
for
$\text{rank}({\it\xi}_{1},{\it\xi}_{s})=\text{rank}({\it\xi}_{2},{\it\xi}_{s})=1$
for
![]() $4\leqslant s\leqslant n-4$
. However, it follows from
$4\leqslant s\leqslant n-4$
. However, it follows from
![]() $\text{rank}({\it\xi}_{1},{\it\xi}_{2})=\text{rank}({\it\xi}_{1},{\it\xi}_{2},{\it\xi}_{s})=2$
that
$\text{rank}({\it\xi}_{1},{\it\xi}_{2})=\text{rank}({\it\xi}_{1},{\it\xi}_{2},{\it\xi}_{s})=2$
that
![]() ${\it\xi}_{s}=0$
, and this is contradictory to the condition
${\it\xi}_{s}=0$
, and this is contradictory to the condition
![]() $\text{rank}(A)\geqslant 9$
. We complete the proof of Lemma 5.12.◻
$\text{rank}(A)\geqslant 9$
. We complete the proof of Lemma 5.12.◻
Proof of Lemma 5.4.
We deduce from Lemma 5.11 that
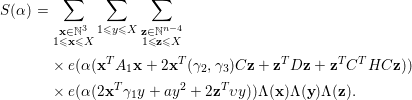 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ 1\leqslant y\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-4} \\ 1\leqslant \mathbf{z}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})C\mathbf{z}+\mathbf{z}^{T}D\mathbf{z}+\mathbf{z}^{T}C^{T}HC\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}{\it\gamma}_{1}y+ay^{2}+2\mathbf{z}^{T}{\it\upsilon}y)){\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ 1\leqslant y\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-4} \\ 1\leqslant \mathbf{z}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})C\mathbf{z}+\mathbf{z}^{T}D\mathbf{z}+\mathbf{z}^{T}C^{T}HC\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}{\it\gamma}_{1}y+ay^{2}+2\mathbf{z}^{T}{\it\upsilon}y)){\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z}).\nonumber\end{eqnarray}$$
We introduce new variables
![]() $w\in \mathbb{Z}$
and
$w\in \mathbb{Z}$
and
![]() $\mathbf{h}\in \mathbb{Z}^{2}$
to replace
$\mathbf{h}\in \mathbb{Z}^{2}$
to replace
![]() $2\mathbf{x}^{T}{\it\gamma}_{1}+ay+2\mathbf{z}^{T}{\it\upsilon}^{T}$
and
$2\mathbf{x}^{T}{\it\gamma}_{1}+ay+2\mathbf{z}^{T}{\it\upsilon}^{T}$
and
![]() $C\mathbf{z}$
, respectively. Therefore, we have
$C\mathbf{z}$
, respectively. Therefore, we have
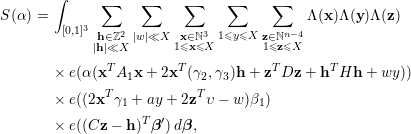 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{Z}^{2} \\ |\mathbf{h}|\ll X}}\mathop{\sum }_{\substack{ |w|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{1\leqslant y\leqslant X}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-4} \\ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}+\mathbf{z}^{T}D\mathbf{z}+\mathbf{h}^{T}H\mathbf{h}+wy))\nonumber\\ \displaystyle & & \displaystyle \times \,e((2\mathbf{x}^{T}{\it\gamma}_{1}+ay+2\mathbf{z}^{T}{\it\upsilon}-w){\it\beta}_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,e((C\mathbf{z}-\mathbf{h})^{T}{\bf\beta}^{\prime })\,d{\bf\beta},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{Z}^{2} \\ |\mathbf{h}|\ll X}}\mathop{\sum }_{\substack{ |w|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{1\leqslant y\leqslant X}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{N}^{n-4} \\ 1\leqslant \mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{z})\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}+\mathbf{z}^{T}D\mathbf{z}+\mathbf{h}^{T}H\mathbf{h}+wy))\nonumber\\ \displaystyle & & \displaystyle \times \,e((2\mathbf{x}^{T}{\it\gamma}_{1}+ay+2\mathbf{z}^{T}{\it\upsilon}-w){\it\beta}_{1})\nonumber\\ \displaystyle & & \displaystyle \times \,e((C\mathbf{z}-\mathbf{h})^{T}{\bf\beta}^{\prime })\,d{\bf\beta},\nonumber\end{eqnarray}$$
where
![]() ${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
,
${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
,
![]() ${\bf\beta}^{\prime }=({\it\beta}_{2},{\it\beta}_{3})^{T}$
and
${\bf\beta}^{\prime }=({\it\beta}_{2},{\it\beta}_{3})^{T}$
and
![]() $d{\bf\beta}=d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. Now we introduce
$d{\bf\beta}=d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. Now we introduce
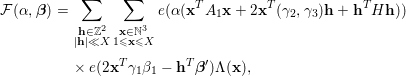 $$\begin{eqnarray}\displaystyle {\mathcal{F}}({\it\alpha},{\bf\beta}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{Z}^{2} \\ |\mathbf{h}|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}+\mathbf{h}^{T}H\mathbf{h}))\nonumber\\ \displaystyle & & \displaystyle \times \,e(2\mathbf{x}^{T}{\it\gamma}_{1}{\it\beta}_{1}-\mathbf{h}^{T}{\bf\beta}^{\prime }){\rm\Lambda}(\mathbf{x}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}({\it\alpha},{\bf\beta}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{h}\in \mathbb{Z}^{2} \\ |\mathbf{h}|\ll X}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+2\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}+\mathbf{h}^{T}H\mathbf{h}))\nonumber\\ \displaystyle & & \displaystyle \times \,e(2\mathbf{x}^{T}{\it\gamma}_{1}{\it\beta}_{1}-\mathbf{h}^{T}{\bf\beta}^{\prime }){\rm\Lambda}(\mathbf{x}),\nonumber\end{eqnarray}$$
and
On recalling notations in (5.27), we define
Then we obtain from above
One can deduce from Lemmas 5.6 and 5.7 that
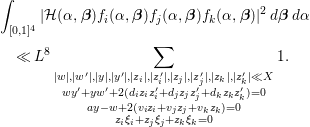 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{4}}|{\mathcal{H}}({\it\alpha},{\bf\beta})f_{i}({\it\alpha},{\bf\beta})f_{j}({\it\alpha},{\bf\beta})f_{k}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{8}\mathop{\sum }_{\substack{ |w|,|w^{\prime }|,|y|,|y^{\prime }|,|z_{i}|,|z_{i}^{\prime }|,|z_{j}|,|z_{j}^{\prime }|,|z_{k}|,|z_{k}^{\prime }|\ll X \\ wy^{\prime }+yw^{\prime }+2(d_{i}z_{i}z_{i}^{\prime }+d_{j}z_{j}z_{j}^{\prime }+d_{k}z_{k}z_{k}^{\prime })=0 \\ ay-w+2(v_{i}z_{i}+v_{j}z_{j}+v_{k}z_{k})=0 \\ z_{i}{\it\xi}_{i}+z_{j}{\it\xi}_{j}+z_{k}{\it\xi}_{k}=0}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[0,1]^{4}}|{\mathcal{H}}({\it\alpha},{\bf\beta})f_{i}({\it\alpha},{\bf\beta})f_{j}({\it\alpha},{\bf\beta})f_{k}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{8}\mathop{\sum }_{\substack{ |w|,|w^{\prime }|,|y|,|y^{\prime }|,|z_{i}|,|z_{i}^{\prime }|,|z_{j}|,|z_{j}^{\prime }|,|z_{k}|,|z_{k}^{\prime }|\ll X \\ wy^{\prime }+yw^{\prime }+2(d_{i}z_{i}z_{i}^{\prime }+d_{j}z_{j}z_{j}^{\prime }+d_{k}z_{k}z_{k}^{\prime })=0 \\ ay-w+2(v_{i}z_{i}+v_{j}z_{j}+v_{k}z_{k})=0 \\ z_{i}{\it\xi}_{i}+z_{j}{\it\xi}_{j}+z_{k}{\it\xi}_{k}=0}}1.\nonumber\end{eqnarray}$$
If
![]() $\text{rank}(R_{i,j,k})=3$
, then we can represent
$\text{rank}(R_{i,j,k})=3$
, then we can represent
![]() $z_{i},z_{j}$
and
$z_{i},z_{j}$
and
![]() $z_{k}$
by linear functions of
$z_{k}$
by linear functions of
![]() $y$
and
$y$
and
![]() $w$
. Then by Lemma 5.8,
$w$
. Then by Lemma 5.8,
If
![]() $\text{rank}({\it\xi}_{i},{\it\xi}_{j})=2$
, then we can represent
$\text{rank}({\it\xi}_{i},{\it\xi}_{j})=2$
, then we can represent
![]() $z_{i},z_{j}$
and
$z_{i},z_{j}$
and
![]() $w$
by linear functions of
$w$
by linear functions of
![]() $y$
and
$y$
and
![]() $z_{k}$
. Then we obtain by Lemma 5.8 again
$z_{k}$
. Then we obtain by Lemma 5.8 again
provided that
![]() $d_{k}\not =0$
. By Lemmas 5.6–5.7, we can obtain
$d_{k}\not =0$
. By Lemmas 5.6–5.7, we can obtain
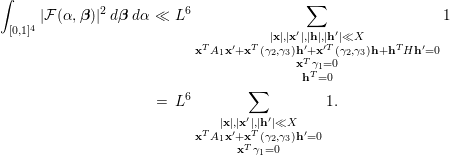 $$\begin{eqnarray}\displaystyle \int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha} & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|\mathbf{h}|,|\mathbf{h}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}^{\prime }+{\mathbf{x}^{\prime }}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}+\mathbf{h}^{T}H\mathbf{h}^{\prime }=0 \\ \mathbf{x}^{T}{\it\gamma}_{1}=0 \\ \mathbf{h}^{T}=0}}1\nonumber\\ \displaystyle & = & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|\mathbf{h}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}^{\prime }=0 \\ \mathbf{x}^{T}{\it\gamma}_{1}=0}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha} & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|\mathbf{h}|,|\mathbf{h}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}^{\prime }+{\mathbf{x}^{\prime }}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}+\mathbf{h}^{T}H\mathbf{h}^{\prime }=0 \\ \mathbf{x}^{T}{\it\gamma}_{1}=0 \\ \mathbf{h}^{T}=0}}1\nonumber\\ \displaystyle & = & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|\mathbf{h}^{\prime }|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{x}^{T}({\it\gamma}_{2},{\it\gamma}_{3})\mathbf{h}^{\prime }=0 \\ \mathbf{x}^{T}{\it\gamma}_{1}=0}}1.\nonumber\end{eqnarray}$$
Then we deduce that
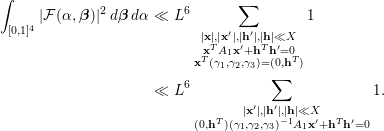 $$\begin{eqnarray}\displaystyle \int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha} & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|\mathbf{h}^{\prime }|,|\mathbf{h}|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{h}^{T}\mathbf{h}^{\prime }=0 \\ \mathbf{x}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})=(0,\mathbf{h}^{T})}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}^{\prime }|,|\mathbf{h}^{\prime }|,|\mathbf{h}|\ll X \\ (0,\mathbf{h}^{T})({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})^{-1}A_{1}\mathbf{x}^{\prime }+\mathbf{h}^{T}\mathbf{h}^{\prime }=0}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha} & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}|,|\mathbf{x}^{\prime }|,|\mathbf{h}^{\prime }|,|\mathbf{h}|\ll X \\ \mathbf{x}^{T}A_{1}\mathbf{x}^{\prime }+\mathbf{h}^{T}\mathbf{h}^{\prime }=0 \\ \mathbf{x}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})=(0,\mathbf{h}^{T})}}1\nonumber\\ \displaystyle & \ll & \displaystyle L^{6}\mathop{\sum }_{\substack{ |\mathbf{x}^{\prime }|,|\mathbf{h}^{\prime }|,|\mathbf{h}|\ll X \\ (0,\mathbf{h}^{T})({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})^{-1}A_{1}\mathbf{x}^{\prime }+\mathbf{h}^{T}\mathbf{h}^{\prime }=0}}1.\nonumber\end{eqnarray}$$
On invoking Lemma 5.8, we arrive at
If
![]() $1\leqslant i,j,k\leqslant n-4$
are pairwise distinct, then one has by (5.29) and the Cauchy–Schwarz inequality
$1\leqslant i,j,k\leqslant n-4$
are pairwise distinct, then one has by (5.29) and the Cauchy–Schwarz inequality
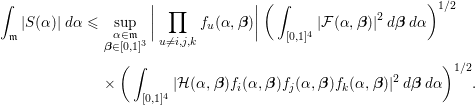 $$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{u\not =i,j,k}f_{u}({\it\alpha},{\bf\beta})\bigg|\,\bigg(\int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}|{\mathcal{H}}({\it\alpha},{\bf\beta})f_{i}({\it\alpha},{\bf\beta})f_{j}({\it\alpha},{\bf\beta})f_{k}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{u\not =i,j,k}f_{u}({\it\alpha},{\bf\beta})\bigg|\,\bigg(\int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}|{\mathcal{H}}({\it\alpha},{\bf\beta})f_{i}({\it\alpha},{\bf\beta})f_{j}({\it\alpha},{\bf\beta})f_{k}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}.\nonumber\end{eqnarray}$$
Now it follows from above together with Lemmas 4.3 and 5.12 that
We complete the proof of Lemma 5.4.
5.4 Proof of Lemma 5.5
Similar to Lemmas 5.9–5.11, we also have the following result.
Lemma 5.13. If
![]() $\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then we can write
$\text{rank}(B_{1})=\text{rank}(B_{2})=\text{rank}(B_{3})=3$
, then we can write
![]() $A$
in the form
$A$
in the form
where
![]() $C\in M_{3,n-3}(\mathbb{Z})$
,
$C\in M_{3,n-3}(\mathbb{Z})$
,
![]() ${\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
${\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3}\in \mathbb{Q}^{3}$
,
![]() $H\in M_{3,3}(\mathbb{Q})$
and
$H\in M_{3,3}(\mathbb{Q})$
and
![]() $D=\text{diag}\{d_{1},\ldots ,d_{n-3}\}\in M_{n-3,n-3}(\mathbb{Q})$
is a diagonal matrix. Furthermore, we have
$D=\text{diag}\{d_{1},\ldots ,d_{n-3}\}\in M_{n-3,n-3}(\mathbb{Q})$
is a diagonal matrix. Furthermore, we have
![]() $({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Q})$
.
$({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\in GL_{3}(\mathbb{Q})$
.
Lemma 5.14. Let
![]() $A$
be given by (5.30) satisfying the conditions in Lemma 5.13. We write
$A$
be given by (5.30) satisfying the conditions in Lemma 5.13. We write
Then we can find pairwise distinct
![]() $u_{j}(1\leqslant j\leqslant 6)$
with
$u_{j}(1\leqslant j\leqslant 6)$
with
![]() $1\leqslant u_{1},u_{2},u_{3},u_{4},u_{5},u_{6}\leqslant n-3$
so that
$1\leqslant u_{1},u_{2},u_{3},u_{4},u_{5},u_{6}\leqslant n-3$
so that
![]() $\text{rank}({\it\xi}_{u_{1}},{\it\xi}_{u_{2}},{\it\xi}_{u_{3}})=3$
and
$\text{rank}({\it\xi}_{u_{1}},{\it\xi}_{u_{2}},{\it\xi}_{u_{3}})=3$
and
![]() $d_{u_{4}}d_{u_{5}}d_{u_{6}}\not =0$
.
$d_{u_{4}}d_{u_{5}}d_{u_{6}}\not =0$
.
Proof. It follows from
![]() $\text{rank}(A)\geqslant 9$
that
$\text{rank}(A)\geqslant 9$
that
![]() $\text{rank}(D)\geqslant 3$
. If
$\text{rank}(D)\geqslant 3$
. If
![]() $\text{rank}(D)=3$
, then we may assume that
$\text{rank}(D)=3$
, then we may assume that
![]() $d_{1}d_{2}d_{3}\not =0$
and
$d_{1}d_{2}d_{3}\not =0$
and
![]() $d_{j}=0$
for
$d_{j}=0$
for
![]() $j\geqslant 4$
. Thus
$j\geqslant 4$
. Thus
![]() $\text{rank}({\it\xi}_{4},\ldots ,{\it\xi}_{n-3})=3$
, and the desired conclusion follows. Next we assume
$\text{rank}({\it\xi}_{4},\ldots ,{\it\xi}_{n-3})=3$
, and the desired conclusion follows. Next we assume
![]() $\text{rank}(D)\geqslant 4$
. Since
$\text{rank}(D)\geqslant 4$
. Since
![]() $\text{rank}({\it\xi}_{1},{\it\xi}_{2},{\it\xi}_{3})=3$
, the desired conclusion follows again if there are distinct
$\text{rank}({\it\xi}_{1},{\it\xi}_{2},{\it\xi}_{3})=3$
, the desired conclusion follows again if there are distinct
![]() $k_{1},k_{2}$
and
$k_{1},k_{2}$
and
![]() $k_{3}$
such that
$k_{3}$
such that
![]() $d_{k_{1}}d_{k_{2}}d_{k_{3}}\not =0$
and
$d_{k_{1}}d_{k_{2}}d_{k_{3}}\not =0$
and
![]() $k_{1},k_{2},k_{3}\geqslant 4$
. Thus we now assume that for any distinct
$k_{1},k_{2},k_{3}\geqslant 4$
. Thus we now assume that for any distinct
![]() $k_{1},k_{2},k_{3}\geqslant 4$
, one has
$k_{1},k_{2},k_{3}\geqslant 4$
, one has
![]() $d_{k_{1}}d_{k_{2}}d_{k_{3}}=0$
. This yields
$d_{k_{1}}d_{k_{2}}d_{k_{3}}=0$
. This yields
![]() $\text{rank}(D)\leqslant 5$
. We first consider the case
$\text{rank}(D)\leqslant 5$
. We first consider the case
![]() $\text{rank}(D)=4$
. There are at least two distinct
$\text{rank}(D)=4$
. There are at least two distinct
![]() $j_{1},j_{2}\leqslant 3$
such that
$j_{1},j_{2}\leqslant 3$
such that
![]() $d_{j_{1}}d_{j_{2}}\not =0$
. Suppose that
$d_{j_{1}}d_{j_{2}}\not =0$
. Suppose that
![]() $d_{s_{i}}=0$
for
$d_{s_{i}}=0$
for
![]() $1\leqslant i\leqslant n-7$
. Then the rank of
$1\leqslant i\leqslant n-7$
. Then the rank of
![]() $\{{\it\xi}_{s_{i}}\}_{1\leqslant i\leqslant n-7}$
is at least 2, say
$\{{\it\xi}_{s_{i}}\}_{1\leqslant i\leqslant n-7}$
is at least 2, say
![]() $\text{rank}({\it\xi}_{s_{1}},{\it\xi}_{s_{2}})=2$
. Since
$\text{rank}({\it\xi}_{s_{1}},{\it\xi}_{s_{2}})=2$
. Since
![]() $\text{rank}({\it\xi}_{1},{\it\xi}_{2},{\it\xi}_{3})=3$
, we can find
$\text{rank}({\it\xi}_{1},{\it\xi}_{2},{\it\xi}_{3})=3$
, we can find
![]() $j$
with
$j$
with
![]() $1\leqslant j\leqslant 3$
such that
$1\leqslant j\leqslant 3$
such that
![]() $\text{rank}({\it\xi}_{j},{\it\xi}_{s_{1}},{\it\xi}_{s_{2}})=3$
. The desired conclusion follows easily by choosing
$\text{rank}({\it\xi}_{j},{\it\xi}_{s_{1}},{\it\xi}_{s_{2}})=3$
. The desired conclusion follows easily by choosing
![]() $u_{1}=j$
,
$u_{1}=j$
,
![]() $u_{2}=s_{1}$
and
$u_{2}=s_{1}$
and
![]() $u_{3}=s_{2}$
. Now we consider the case
$u_{3}=s_{2}$
. Now we consider the case
![]() $\text{rank}(D)=5$
, and we may assume that
$\text{rank}(D)=5$
, and we may assume that
![]() $d_{1}d_{2}d_{3}d_{4}d_{5}\not =0$
and
$d_{1}d_{2}d_{3}d_{4}d_{5}\not =0$
and
![]() $d_{r}=0$
for
$d_{r}=0$
for
![]() $r\geqslant 6$
. Since
$r\geqslant 6$
. Since
![]() $\text{rank}(A)\geqslant 9$
, there exist
$\text{rank}(A)\geqslant 9$
, there exist
![]() $r\geqslant 6$
(say
$r\geqslant 6$
(say
![]() $r=6$
) such that
$r=6$
) such that
![]() ${\it\xi}_{r}\not =0$
. Then one can choose
${\it\xi}_{r}\not =0$
. Then one can choose
![]() $j_{1},j_{2}\leqslant 3$
so that
$j_{1},j_{2}\leqslant 3$
so that
![]() $\text{rank}({\it\xi}_{j_{1}},{\it\xi}_{j_{2}},{\it\xi}_{6})=3$
. The desired conclusion follows by choosing
$\text{rank}({\it\xi}_{j_{1}},{\it\xi}_{j_{2}},{\it\xi}_{6})=3$
. The desired conclusion follows by choosing
![]() $u_{1}=j_{1}$
,
$u_{1}=j_{1}$
,
![]() $u_{2}=j_{2}$
and
$u_{2}=j_{2}$
and
![]() $u_{3}=6$
. The proof of Lemma 5.14 is completed.◻
$u_{3}=6$
. The proof of Lemma 5.14 is completed.◻
Proof of Lemma 5.5.
We apply Lemma 5.13 to conclude that
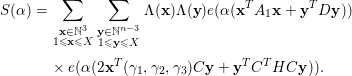 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{n-3} \\ 1\leqslant \mathbf{y}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{y}^{T}D\mathbf{y}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})C\mathbf{y}+\mathbf{y}^{T}C^{T}HC\mathbf{y})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{n-3} \\ 1\leqslant \mathbf{y}\leqslant X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{y}^{T}D\mathbf{y}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})C\mathbf{y}+\mathbf{y}^{T}C^{T}HC\mathbf{y})).\nonumber\end{eqnarray}$$
By orthogonality, one has
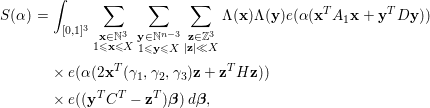 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{n-3} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{Z}^{3} \\ |\mathbf{z}|\ll X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{y}^{T}D\mathbf{y}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\mathbf{z}+\mathbf{z}^{T}H\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,e((\mathbf{y}^{T}C^{T}-\mathbf{z}^{T}){\bf\beta})\,d{\bf\beta},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \int _{[0,1]^{3}}\mathop{\sum }_{\substack{ \mathbf{x}\in \mathbb{N}^{3} \\ 1\leqslant \mathbf{x}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{y}\in \mathbb{N}^{n-3} \\ 1\leqslant \mathbf{y}\leqslant X}}\mathop{\sum }_{\substack{ \mathbf{z}\in \mathbb{Z}^{3} \\ |\mathbf{z}|\ll X}}{\rm\Lambda}(\mathbf{x}){\rm\Lambda}(\mathbf{y})e({\it\alpha}(\mathbf{x}^{T}A_{1}\mathbf{x}+\mathbf{y}^{T}D\mathbf{y}))\nonumber\\ \displaystyle & & \displaystyle \times \,e({\it\alpha}(2\mathbf{x}^{T}({\it\gamma}_{1},{\it\gamma}_{2},{\it\gamma}_{3})\mathbf{z}+\mathbf{z}^{T}H\mathbf{z}))\nonumber\\ \displaystyle & & \displaystyle \times \,e((\mathbf{y}^{T}C^{T}-\mathbf{z}^{T}){\bf\beta})\,d{\bf\beta},\nonumber\end{eqnarray}$$
where
![]() ${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
and
${\bf\beta}=({\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3})^{T}$
and
![]() $d{\bf\beta}=d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. Now we introduce
$d{\bf\beta}=d{\it\beta}_{1}\,d{\it\beta}_{2}\,d{\it\beta}_{3}$
. Now we introduce
and
where
![]() ${\it\xi}_{1},\ldots ,{\it\xi}_{n-3}$
is given by (5.31). We conclude from above
${\it\xi}_{1},\ldots ,{\it\xi}_{n-3}$
is given by (5.31). We conclude from above
One applying Lemmas 5.6–5.8, we can easily establish
provided that
![]() $\text{rank}({\it\xi}_{u_{1}},{\it\xi}_{u_{2}},{\it\xi}_{u_{3}})=3$
and
$\text{rank}({\it\xi}_{u_{1}},{\it\xi}_{u_{2}},{\it\xi}_{u_{3}})=3$
and
![]() $d_{u_{4}}d_{u_{5}}\not =0$
. Similarly, we also have
$d_{u_{4}}d_{u_{5}}\not =0$
. Similarly, we also have
By (5.32) and the Cauchy–Schwarz inequality, one has for distinct
![]() $u_{1},u_{2},u_{3},u_{4}$
and
$u_{1},u_{2},u_{3},u_{4}$
and
![]() $u_{5}$
that
$u_{5}$
that
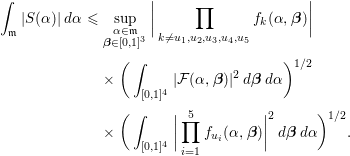 $$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{k\not =u_{1},u_{2},u_{3},u_{4},u_{5}}f_{k}({\it\alpha},{\bf\beta})\bigg|\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}\bigg|\mathop{\prod }_{i=1}^{5}f_{u_{i}}({\it\alpha},{\bf\beta})\bigg|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \sup _{\substack{ {\it\alpha}\in \mathfrak{m} \\ {\bf\beta}\in [0,1]^{3}}}\bigg|\mathop{\prod }_{k\not =u_{1},u_{2},u_{3},u_{4},u_{5}}f_{k}({\it\alpha},{\bf\beta})\bigg|\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}|{\mathcal{F}}({\it\alpha},{\bf\beta})|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\int _{[0,1]^{4}}\bigg|\mathop{\prod }_{i=1}^{5}f_{u_{i}}({\it\alpha},{\bf\beta})\bigg|^{2}\,d{\bf\beta}\,d{\it\alpha}\bigg)^{1/2}.\end{eqnarray}$$
Combining (5.33)–(5.35), Lemma 4.3 and Lemma 5.14, one has
The proof of Lemma 5.5 is finished.
6 Quadratic forms with off-diagonal rank
 ${\geqslant}4$
${\geqslant}4$
Proposition 6.1. Let
![]() $A$
be defined in (1.1), and let
$A$
be defined in (1.1), and let
![]() $S({\it\alpha})$
be defined in (2.5). We write
$S({\it\alpha})$
be defined in (2.5). We write
 $$\begin{eqnarray}G=\left(\begin{array}{@{}ccc@{}}a_{1,5} & \cdots \, & a_{1,9}\\ \vdots & \cdots \, & \vdots \\ a_{5,5} & \cdots \, & a_{5,9}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}G=\left(\begin{array}{@{}ccc@{}}a_{1,5} & \cdots \, & a_{1,9}\\ \vdots & \cdots \, & \vdots \\ a_{5,5} & \cdots \, & a_{5,9}\end{array}\right).\end{eqnarray}$$
Suppose that
![]() $\det (G)\not =0$
. Then we have
$\det (G)\not =0$
. Then we have
where the implied constant depends on
![]() $A$
and
$A$
and
![]() $K$
.
$K$
.
Throughout this section, we shall assume that the matrix
![]() $G$
given by (6.1) is invertible.
$G$
given by (6.1) is invertible.
Lemma 6.2. Let
![]() ${\it\tau}\not =0$
be a real number. Then we have
${\it\tau}\not =0$
be a real number. Then we have
where the implied constant depends on
![]() ${\it\tau}$
.
${\it\tau}$
.
Proof. Without loss of generality, we assume that
![]() $0<|{\it\tau}|\leqslant 1$
. Thus
$0<|{\it\tau}|\leqslant 1$
. Thus
![]() $|{\it\tau}({\it\alpha}-{\it\beta})|\leqslant 1$
. We introduce
$|{\it\tau}({\it\alpha}-{\it\beta})|\leqslant 1$
. We introduce
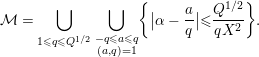 $$\begin{eqnarray}{\mathcal{M}}=\mathop{\bigcup }_{1\leqslant q\leqslant Q^{1/2}}\mathop{\bigcup }_{\substack{ -q\leqslant a\leqslant q \\ (a,q)=1}}\biggl\{\big|{\it\alpha}-\frac{a}{q}\big|\leqslant \frac{Q^{1/2}}{qX^{2}}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}=\mathop{\bigcup }_{1\leqslant q\leqslant Q^{1/2}}\mathop{\bigcup }_{\substack{ -q\leqslant a\leqslant q \\ (a,q)=1}}\biggl\{\big|{\it\alpha}-\frac{a}{q}\big|\leqslant \frac{Q^{1/2}}{qX^{2}}\biggr\}.\end{eqnarray}$$
By Dirichlet’s approximation theorem, there exist
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
![]() $q\in \mathbb{N}$
with
$q\in \mathbb{N}$
with
![]() $(a,q)=1$
,
$(a,q)=1$
,
![]() $1\leqslant q\leqslant X^{2}Q^{-1/2}$
and
$1\leqslant q\leqslant X^{2}Q^{-1/2}$
and
![]() $|{\it\tau}({\it\alpha}-{\it\beta})-a/q|\leqslant Q^{1/2}(qX^{2})^{-1}$
. Since
$|{\it\tau}({\it\alpha}-{\it\beta})-a/q|\leqslant Q^{1/2}(qX^{2})^{-1}$
. Since
![]() $|{\it\tau}({\it\alpha}-{\it\beta})|\leqslant 1$
, one has
$|{\it\tau}({\it\alpha}-{\it\beta})|\leqslant 1$
, one has
![]() $-q\leqslant a\leqslant q$
. If
$-q\leqslant a\leqslant q$
. If
![]() ${\it\tau}({\it\alpha}-{\it\beta})\not \in {\mathcal{M}}$
, then
${\it\tau}({\it\alpha}-{\it\beta})\not \in {\mathcal{M}}$
, then
![]() $q>Q^{1/2}$
. By Vaughan [Reference Vaughan12, Lemma 2.2],
$q>Q^{1/2}$
. By Vaughan [Reference Vaughan12, Lemma 2.2],
Therefore, we obtain
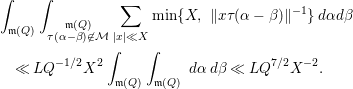 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}\int _{\substack{ \mathfrak{m}(Q) \\ {\it\tau}({\it\alpha}-{\it\beta})\not \in {\mathcal{M}}}}\mathop{\sum }_{|x|\ll X}\min \{X,~\Vert x{\it\tau}({\it\alpha}-{\it\beta})\Vert ^{-1}\}\,d{\it\alpha}d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \ll LQ^{-1/2}X^{2}\int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\,d{\it\alpha}\,d{\it\beta}\ll LQ^{7/2}X^{-2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}\int _{\substack{ \mathfrak{m}(Q) \\ {\it\tau}({\it\alpha}-{\it\beta})\not \in {\mathcal{M}}}}\mathop{\sum }_{|x|\ll X}\min \{X,~\Vert x{\it\tau}({\it\alpha}-{\it\beta})\Vert ^{-1}\}\,d{\it\alpha}d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \ll LQ^{-1/2}X^{2}\int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\,d{\it\alpha}\,d{\it\beta}\ll LQ^{7/2}X^{-2}.\nonumber\end{eqnarray}$$
When
![]() ${\it\tau}({\it\alpha}-{\it\beta})\in {\mathcal{M}}$
, we apply the trivial bound to the summation over
${\it\tau}({\it\alpha}-{\it\beta})\in {\mathcal{M}}$
, we apply the trivial bound to the summation over
![]() $x$
to deduce that
$x$
to deduce that
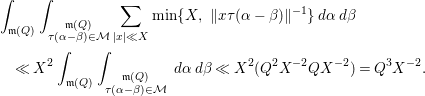 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}\int _{\substack{ \mathfrak{m}(Q) \\ {\it\tau}({\it\alpha}-{\it\beta})\in {\mathcal{M}}}}\mathop{\sum }_{|x|\ll X}\min \{X,~\Vert x{\it\tau}({\it\alpha}-{\it\beta})\Vert ^{-1}\}\,d{\it\alpha}\,d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \ll X^{2}\int _{\mathfrak{m}(Q)}\int _{\substack{ \mathfrak{m}(Q) \\ {\it\tau}({\it\alpha}-{\it\beta})\in {\mathcal{M}}}}\,d{\it\alpha}\,d{\it\beta}\ll X^{2}(Q^{2}X^{-2}QX^{-2})=Q^{3}X^{-2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}\int _{\substack{ \mathfrak{m}(Q) \\ {\it\tau}({\it\alpha}-{\it\beta})\in {\mathcal{M}}}}\mathop{\sum }_{|x|\ll X}\min \{X,~\Vert x{\it\tau}({\it\alpha}-{\it\beta})\Vert ^{-1}\}\,d{\it\alpha}\,d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \ll X^{2}\int _{\mathfrak{m}(Q)}\int _{\substack{ \mathfrak{m}(Q) \\ {\it\tau}({\it\alpha}-{\it\beta})\in {\mathcal{M}}}}\,d{\it\alpha}\,d{\it\beta}\ll X^{2}(Q^{2}X^{-2}QX^{-2})=Q^{3}X^{-2}.\nonumber\end{eqnarray}$$
The desired conclusion follows from above immediately. ◻
To introduce the next lemma, we define
For
![]() $\mathbf{v}=(v_{1},\ldots ,v_{5})\in \mathbb{Z}^{5}$
and
$\mathbf{v}=(v_{1},\ldots ,v_{5})\in \mathbb{Z}^{5}$
and
![]() $G$
given by (6.1), we write
$G$
given by (6.1), we write
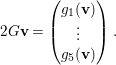 $$\begin{eqnarray}2G\mathbf{v}=\left(\begin{array}{@{}c@{}}g_{1}(\mathbf{v})\\ \vdots \\ g_{5}(\mathbf{v})\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}2G\mathbf{v}=\left(\begin{array}{@{}c@{}}g_{1}(\mathbf{v})\\ \vdots \\ g_{5}(\mathbf{v})\end{array}\right).\end{eqnarray}$$
Lemma 6.3. One has
where
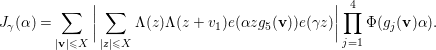 $$\begin{eqnarray}J_{{\it\gamma}}({\it\alpha})=\mathop{\sum }_{|\mathbf{v}|\leqslant X}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+v_{1})e({\it\alpha}zg_{5}(\mathbf{v}))e({\it\gamma}z)\bigg|\mathop{\prod }_{j=1}^{4}{\rm\Phi}(g_{j}(\mathbf{v}){\it\alpha}).\end{eqnarray}$$
$$\begin{eqnarray}J_{{\it\gamma}}({\it\alpha})=\mathop{\sum }_{|\mathbf{v}|\leqslant X}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+v_{1})e({\it\alpha}zg_{5}(\mathbf{v}))e({\it\gamma}z)\bigg|\mathop{\prod }_{j=1}^{4}{\rm\Phi}(g_{j}(\mathbf{v}){\it\alpha}).\end{eqnarray}$$
Proof. Let
 $$\begin{eqnarray}\displaystyle r(\mathbf{y}) & = & \displaystyle \mathop{\sum }_{i=1}^{4}\mathop{\sum }_{j=1}^{4}a_{i,j}y_{i}y_{j},\quad q(\mathbf{z})=\mathop{\sum }_{i=5}^{9}\mathop{\sum }_{j=5}^{9}a_{i,j}z_{i}z_{j}\quad \text{and}\quad \nonumber\\ \displaystyle p(\mathbf{w}) & = & \displaystyle \mathop{\sum }_{i=10}^{n}\mathop{\sum }_{j=10}^{n}a_{i,j}w_{i}w_{j}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r(\mathbf{y}) & = & \displaystyle \mathop{\sum }_{i=1}^{4}\mathop{\sum }_{j=1}^{4}a_{i,j}y_{i}y_{j},\quad q(\mathbf{z})=\mathop{\sum }_{i=5}^{9}\mathop{\sum }_{j=5}^{9}a_{i,j}z_{i}z_{j}\quad \text{and}\quad \nonumber\\ \displaystyle p(\mathbf{w}) & = & \displaystyle \mathop{\sum }_{i=10}^{n}\mathop{\sum }_{j=10}^{n}a_{i,j}w_{i}w_{j}.\nonumber\end{eqnarray}$$
We set
Then
![]() $f$
can be written in the form
$f$
can be written in the form
where
![]() $\mathbf{z}=(z_{1},\ldots ,z_{5})$
,
$\mathbf{z}=(z_{1},\ldots ,z_{5})$
,
![]() $\mathbf{y}=(y_{1},\ldots ,y_{4})$
,
$\mathbf{y}=(y_{1},\ldots ,y_{4})$
,
![]() $\mathbf{w}=(w_{1},\ldots ,w_{n-9})$
. Note that
$\mathbf{w}=(w_{1},\ldots ,w_{n-9})$
. Note that
![]() $\mathbf{y}^{T}B\mathbf{w}+\mathbf{z}^{T}C\mathbf{w}+p(\mathbf{w})$
vanishes if
$\mathbf{y}^{T}B\mathbf{w}+\mathbf{z}^{T}C\mathbf{w}+p(\mathbf{w})$
vanishes if
![]() $n=9$
. Therefore, one has
$n=9$
. Therefore, one has
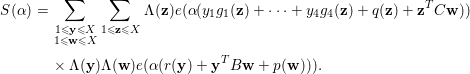 $$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\mathop{\sum }_{1\leqslant \mathbf{z}\leqslant X}{\rm\Lambda}(\mathbf{z})e({\it\alpha}(y_{1}g_{1}(\mathbf{z})+\cdots +y_{4}g_{4}(\mathbf{z})+q(\mathbf{z})+\mathbf{z}^{T}C\mathbf{w}))\nonumber\\ \displaystyle & & \displaystyle \times \,{\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{w})e({\it\alpha}(r(\mathbf{y})+\mathbf{y}^{T}B\mathbf{w}+p(\mathbf{w}))).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\mathop{\sum }_{1\leqslant \mathbf{z}\leqslant X}{\rm\Lambda}(\mathbf{z})e({\it\alpha}(y_{1}g_{1}(\mathbf{z})+\cdots +y_{4}g_{4}(\mathbf{z})+q(\mathbf{z})+\mathbf{z}^{T}C\mathbf{w}))\nonumber\\ \displaystyle & & \displaystyle \times \,{\rm\Lambda}(\mathbf{y}){\rm\Lambda}(\mathbf{w})e({\it\alpha}(r(\mathbf{y})+\mathbf{y}^{T}B\mathbf{w}+p(\mathbf{w}))).\nonumber\end{eqnarray}$$
By Cauchy’s inequality,
where
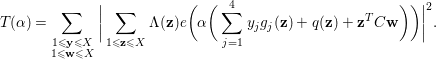 $$\begin{eqnarray}T({\it\alpha})=\mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{z}\leqslant X}{\rm\Lambda}(\mathbf{z})e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{z})+q(\mathbf{z})+\mathbf{z}^{T}C\mathbf{w}\bigg)\bigg)\bigg|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}T({\it\alpha})=\mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\bigg|\mathop{\sum }_{1\leqslant \mathbf{z}\leqslant X}{\rm\Lambda}(\mathbf{z})e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{z})+q(\mathbf{z})+\mathbf{z}^{T}C\mathbf{w}\bigg)\bigg)\bigg|^{2}.\end{eqnarray}$$
Then we deduce that
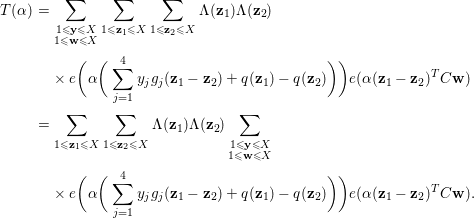 $$\begin{eqnarray}\displaystyle T({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\mathop{\sum }_{1\leqslant \mathbf{z}_{1}\leqslant X}\mathop{\sum }_{1\leqslant \mathbf{z}_{2}\leqslant X}{\rm\Lambda}(\mathbf{z}_{1}){\rm\Lambda}(\mathbf{z}_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{z}_{1}-\mathbf{z}_{2})+q(\mathbf{z}_{1})-q(\mathbf{z}_{2})\bigg)\bigg)e({\it\alpha}(\mathbf{z}_{1}-\mathbf{z}_{2})^{T}C\mathbf{w})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{z}_{1}\leqslant X}\mathop{\sum }_{1\leqslant \mathbf{z}_{2}\leqslant X}{\rm\Lambda}(\mathbf{z}_{1}){\rm\Lambda}(\mathbf{z}_{2})\mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{z}_{1}-\mathbf{z}_{2})+q(\mathbf{z}_{1})-q(\mathbf{z}_{2})\bigg)\bigg)e({\it\alpha}(\mathbf{z}_{1}-\mathbf{z}_{2})^{T}C\mathbf{w}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\mathop{\sum }_{1\leqslant \mathbf{z}_{1}\leqslant X}\mathop{\sum }_{1\leqslant \mathbf{z}_{2}\leqslant X}{\rm\Lambda}(\mathbf{z}_{1}){\rm\Lambda}(\mathbf{z}_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{z}_{1}-\mathbf{z}_{2})+q(\mathbf{z}_{1})-q(\mathbf{z}_{2})\bigg)\bigg)e({\it\alpha}(\mathbf{z}_{1}-\mathbf{z}_{2})^{T}C\mathbf{w})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{z}_{1}\leqslant X}\mathop{\sum }_{1\leqslant \mathbf{z}_{2}\leqslant X}{\rm\Lambda}(\mathbf{z}_{1}){\rm\Lambda}(\mathbf{z}_{2})\mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{z}_{1}-\mathbf{z}_{2})+q(\mathbf{z}_{1})-q(\mathbf{z}_{2})\bigg)\bigg)e({\it\alpha}(\mathbf{z}_{1}-\mathbf{z}_{2})^{T}C\mathbf{w}).\nonumber\end{eqnarray}$$
By changing variables
![]() $\mathbf{z}_{1}=\mathbf{z}_{2}+\mathbf{v}$
, we have
$\mathbf{z}_{1}=\mathbf{z}_{2}+\mathbf{v}$
, we have
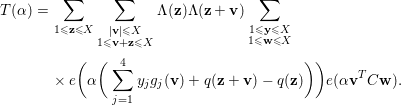 $$\begin{eqnarray}\displaystyle T({\it\alpha}) & = & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{z}\leqslant X}\mathop{\sum }_{\substack{ |\mathbf{v}|\leqslant X \\ 1\leqslant \mathbf{v}+\mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{z}){\rm\Lambda}(\mathbf{z}+\mathbf{v})\mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{v})+q(\mathbf{z}+\mathbf{v})-q(\mathbf{z})\bigg)\bigg)e({\it\alpha}\mathbf{v}^{T}C\mathbf{w}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T({\it\alpha}) & = & \displaystyle \mathop{\sum }_{1\leqslant \mathbf{z}\leqslant X}\mathop{\sum }_{\substack{ |\mathbf{v}|\leqslant X \\ 1\leqslant \mathbf{v}+\mathbf{z}\leqslant X}}{\rm\Lambda}(\mathbf{z}){\rm\Lambda}(\mathbf{z}+\mathbf{v})\mathop{\sum }_{\substack{ 1\leqslant \mathbf{y}\leqslant X \\ 1\leqslant \mathbf{w}\leqslant X}}\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg({\it\alpha}\bigg(\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{v})+q(\mathbf{z}+\mathbf{v})-q(\mathbf{z})\bigg)\bigg)e({\it\alpha}\mathbf{v}^{T}C\mathbf{w}).\nonumber\end{eqnarray}$$
We exchange the summation over
![]() $\mathbf{z}$
and the summation over
$\mathbf{z}$
and the summation over
![]() $\mathbf{v}$
to obtain
$\mathbf{v}$
to obtain
where
and
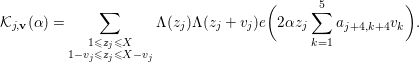 $$\begin{eqnarray}{\mathcal{K}}_{j,\mathbf{v}}({\it\alpha})=\mathop{\sum }_{\substack{ 1\leqslant z_{j}\leqslant X \\ 1-v_{j}\leqslant z_{j}\leqslant X-v_{j}}}{\rm\Lambda}(z_{j}){\rm\Lambda}(z_{j}+v_{j})e\bigg(2{\it\alpha}z_{j}\mathop{\sum }_{k=1}^{5}a_{j+4,k+4}v_{k}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}_{j,\mathbf{v}}({\it\alpha})=\mathop{\sum }_{\substack{ 1\leqslant z_{j}\leqslant X \\ 1-v_{j}\leqslant z_{j}\leqslant X-v_{j}}}{\rm\Lambda}(z_{j}){\rm\Lambda}(z_{j}+v_{j})e\bigg(2{\it\alpha}z_{j}\mathop{\sum }_{k=1}^{5}a_{j+4,k+4}v_{k}\bigg).\end{eqnarray}$$
The range of
![]() $z_{j}$
in summation (6.7) depends on
$z_{j}$
in summation (6.7) depends on
![]() $v_{j}$
. We first follow the standard argument (see for example the argument around (15) in [Reference Wooley15]) to remove the dependence on
$v_{j}$
. We first follow the standard argument (see for example the argument around (15) in [Reference Wooley15]) to remove the dependence on
![]() $v_{j}$
. We write
$v_{j}$
. We write
and
Then we deduce from (6.7)–(6.9) that
On substituting (6.10) into (6.6), we obtain
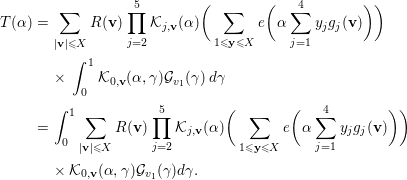 $$\begin{eqnarray}\displaystyle T({\it\alpha}) & = & \displaystyle \mathop{\sum }_{|\mathbf{v}|\leqslant X}R(\mathbf{v})\mathop{\prod }_{j=2}^{5}{\mathcal{K}}_{j,\mathbf{v}}({\it\alpha})\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e\bigg({\it\alpha}\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{v})\bigg)\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{0}^{1}{\mathcal{K}}_{0,\mathbf{v}}({\it\alpha},{\it\gamma}){\mathcal{G}}_{v_{1}}({\it\gamma})\,d{\it\gamma}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\mathop{\sum }_{|\mathbf{v}|\leqslant X}R(\mathbf{v})\mathop{\prod }_{j=2}^{5}{\mathcal{K}}_{j,\mathbf{v}}({\it\alpha})\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e\bigg({\it\alpha}\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{v})\bigg)\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{K}}_{0,\mathbf{v}}({\it\alpha},{\it\gamma}){\mathcal{G}}_{v_{1}}({\it\gamma})d{\it\gamma}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T({\it\alpha}) & = & \displaystyle \mathop{\sum }_{|\mathbf{v}|\leqslant X}R(\mathbf{v})\mathop{\prod }_{j=2}^{5}{\mathcal{K}}_{j,\mathbf{v}}({\it\alpha})\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e\bigg({\it\alpha}\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{v})\bigg)\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{0}^{1}{\mathcal{K}}_{0,\mathbf{v}}({\it\alpha},{\it\gamma}){\mathcal{G}}_{v_{1}}({\it\gamma})\,d{\it\gamma}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\mathop{\sum }_{|\mathbf{v}|\leqslant X}R(\mathbf{v})\mathop{\prod }_{j=2}^{5}{\mathcal{K}}_{j,\mathbf{v}}({\it\alpha})\bigg(\mathop{\sum }_{1\leqslant \mathbf{y}\leqslant X}e\bigg({\it\alpha}\mathop{\sum }_{j=1}^{4}y_{j}g_{j}(\mathbf{v})\bigg)\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{K}}_{0,\mathbf{v}}({\it\alpha},{\it\gamma}){\mathcal{G}}_{v_{1}}({\it\gamma})d{\it\gamma}.\nonumber\end{eqnarray}$$
Then we conclude that
By putting (6.11) into (6.5), one has
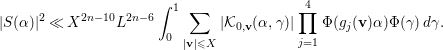 $$\begin{eqnarray}|S({\it\alpha})|^{2}\ll X^{2n-10}L^{2n-6}\int _{0}^{1}\mathop{\sum }_{|\mathbf{v}|\leqslant X}|{\mathcal{K}}_{0,\mathbf{v}}({\it\alpha},{\it\gamma})|\mathop{\prod }_{j=1}^{4}{\rm\Phi}(g_{j}(\mathbf{v}){\it\alpha}){\rm\Phi}({\it\gamma})\,d{\it\gamma}.\end{eqnarray}$$
$$\begin{eqnarray}|S({\it\alpha})|^{2}\ll X^{2n-10}L^{2n-6}\int _{0}^{1}\mathop{\sum }_{|\mathbf{v}|\leqslant X}|{\mathcal{K}}_{0,\mathbf{v}}({\it\alpha},{\it\gamma})|\mathop{\prod }_{j=1}^{4}{\rm\Phi}(g_{j}(\mathbf{v}){\it\alpha}){\rm\Phi}({\it\gamma})\,d{\it\gamma}.\end{eqnarray}$$
Therefore,
The proof is completed. ◻
Lemma 6.4. Let
![]() $J_{{\it\gamma}}({\it\alpha})$
be defined in (6.4). Then one has uniformly for
$J_{{\it\gamma}}({\it\alpha})$
be defined in (6.4). Then one has uniformly for
![]() ${\it\gamma}\in [0,1]$
that
${\it\gamma}\in [0,1]$
that
Proof. We deduce by changing variables
![]() $\mathbf{h}=2G\mathbf{v}$
that
$\mathbf{h}=2G\mathbf{v}$
that
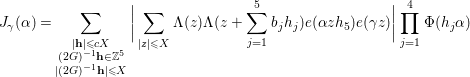 $$\begin{eqnarray}J_{{\it\gamma}}({\it\alpha})=\mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant cX \\ (2G)^{-1}\mathbf{h}\in \mathbb{Z}^{5} \\ |(2G)^{-1}\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+\mathop{\sum }_{j=1}^{5}b_{j}h_{j})e({\it\alpha}zh_{5})e({\it\gamma}z)\bigg|\mathop{\prod }_{j=1}^{4}{\rm\Phi}(h_{j}{\it\alpha})\end{eqnarray}$$
$$\begin{eqnarray}J_{{\it\gamma}}({\it\alpha})=\mathop{\sum }_{\substack{ |\mathbf{h}|\leqslant cX \\ (2G)^{-1}\mathbf{h}\in \mathbb{Z}^{5} \\ |(2G)^{-1}\mathbf{h}|\leqslant X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+\mathop{\sum }_{j=1}^{5}b_{j}h_{j})e({\it\alpha}zh_{5})e({\it\gamma}z)\bigg|\mathop{\prod }_{j=1}^{4}{\rm\Phi}(h_{j}{\it\alpha})\end{eqnarray}$$
for some constants
![]() $c,b_{1},\ldots ,b_{5}$
depending only on
$c,b_{1},\ldots ,b_{5}$
depending only on
![]() $G$
. We point out that
$G$
. We point out that
![]() $b_{1},\ldots ,b_{5}$
are rational numbers, and we extend the domain of function
$b_{1},\ldots ,b_{5}$
are rational numbers, and we extend the domain of function
![]() ${\rm\Lambda}(x)$
by taking
${\rm\Lambda}(x)$
by taking
![]() ${\rm\Lambda}(x)=0$
if
${\rm\Lambda}(x)=0$
if
![]() $x\in \mathbb{Q}\setminus \mathbb{N}$
. Then we have
$x\in \mathbb{Q}\setminus \mathbb{N}$
. Then we have
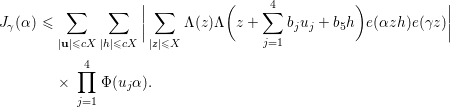 $$\begin{eqnarray}\displaystyle J_{{\it\gamma}}({\it\alpha}) & {\leqslant} & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}{\it\alpha}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{{\it\gamma}}({\it\alpha}) & {\leqslant} & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}{\it\alpha}).\nonumber\end{eqnarray}$$
We first handle the easier case
![]() $b_{5}=0$
. In this case, we can easily obtain a nontrivial estimate for the summation over
$b_{5}=0$
. In this case, we can easily obtain a nontrivial estimate for the summation over
![]() $h$
. By Cauchy’s inequality and Lemma 4.1, one has
$h$
. By Cauchy’s inequality and Lemma 4.1, one has
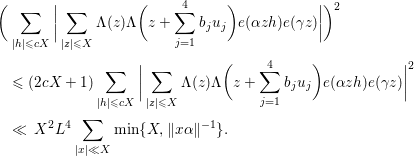 $$\begin{eqnarray}\displaystyle & & \displaystyle \bigg(\mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\bigg)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,(2cX+1)\mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \,X^{2}L^{4}\mathop{\sum }_{|x|\ll X}\min \{X,\Vert x{\it\alpha}\Vert ^{-1}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \bigg(\mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\bigg)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,(2cX+1)\mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \,X^{2}L^{4}\mathop{\sum }_{|x|\ll X}\min \{X,\Vert x{\it\alpha}\Vert ^{-1}\}.\nonumber\end{eqnarray}$$
For
![]() ${\it\alpha}\in \mathfrak{m}(Q)$
, we apply Lemma 4.2 to deduce from above
${\it\alpha}\in \mathfrak{m}(Q)$
, we apply Lemma 4.2 to deduce from above
Then for
![]() ${\it\alpha}\in \mathfrak{m}(Q)$
, we obtain
${\it\alpha}\in \mathfrak{m}(Q)$
, we obtain
and thereby
provided that
![]() $b_{5}=0$
. From now on, we assume
$b_{5}=0$
. From now on, we assume
![]() $b_{5}\not =0$
. Then we have
$b_{5}\not =0$
. Then we have
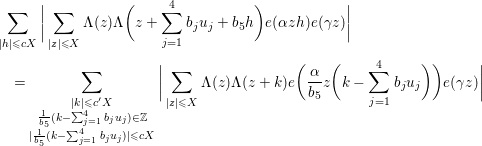 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X \\ \frac{1}{b_{5}}(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j})\in \mathbb{Z} \\ |\frac{1}{b_{5}}(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j})|\leqslant cX}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X \\ \frac{1}{b_{5}}(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j})\in \mathbb{Z} \\ |\frac{1}{b_{5}}(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j})|\leqslant cX}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|\nonumber\end{eqnarray}$$
for some constant
![]() $c^{\prime }$
depending only on
$c^{\prime }$
depending only on
![]() $b_{1},\ldots ,b_{5}$
and
$b_{1},\ldots ,b_{5}$
and
![]() $c$
. Therefore, one has
$c$
. Therefore, one has
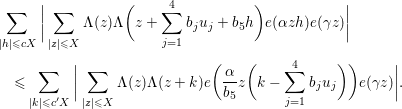 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|.\nonumber\end{eqnarray}$$
We apply Cauchy’s inequality to deduce that
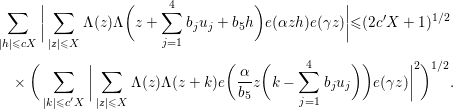 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\leqslant (2c^{\prime }X+1)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg(\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|^{2}\bigg)^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|h|\leqslant cX}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}\bigg(z+\mathop{\sum }_{j=1}^{4}b_{j}u_{j}+b_{5}h\bigg)e({\it\alpha}zh)e({\it\gamma}z)\bigg|\leqslant (2c^{\prime }X+1)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg(\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|^{2}\bigg)^{1/2}.\nonumber\end{eqnarray}$$
We apply Cauchy’s inequality again to obtain
where
![]() ${\rm\Xi}_{{\it\gamma}}({\it\alpha})$
is defined as
${\rm\Xi}_{{\it\gamma}}({\it\alpha})$
is defined as
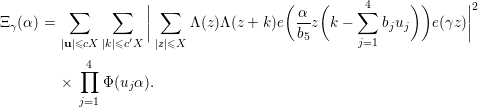 $$\begin{eqnarray}\displaystyle {\rm\Xi}_{{\it\gamma}}({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}{\it\alpha}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Xi}_{{\it\gamma}}({\it\alpha}) & = & \displaystyle \mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\mathop{\sum }_{|z|\leqslant X}{\rm\Lambda}(z){\rm\Lambda}(z+k)e\bigg(\frac{{\it\alpha}}{b_{5}}z\bigg(k-\mathop{\sum }_{j=1}^{4}b_{j}u_{j}\bigg)\bigg)e({\it\gamma}z)\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}{\it\alpha}).\nonumber\end{eqnarray}$$
By Lemma 4.2,
Therefore, we have
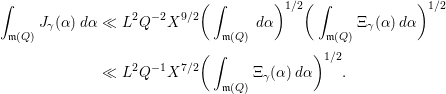 $$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}(Q)}J_{{\it\gamma}}({\it\alpha})\,d{\it\alpha} & \ll & \displaystyle L^{2}Q^{-2}X^{9/2}\bigg(\int _{\mathfrak{m}(Q)}\,d{\it\alpha}\bigg)^{1/2}\bigg(\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle L^{2}Q^{-1}X^{7/2}\bigg(\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\bigg)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}(Q)}J_{{\it\gamma}}({\it\alpha})\,d{\it\alpha} & \ll & \displaystyle L^{2}Q^{-2}X^{9/2}\bigg(\int _{\mathfrak{m}(Q)}\,d{\it\alpha}\bigg)^{1/2}\bigg(\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle L^{2}Q^{-1}X^{7/2}\bigg(\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\bigg)^{1/2}.\end{eqnarray}$$
Now it suffices to estimate
![]() $\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}$
. We observe
$\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}$
. We observe
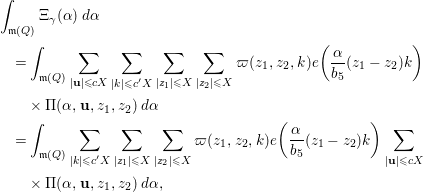 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathfrak{m}(Q)}\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}{\it\varpi}(z_{1},z_{2},k)e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathfrak{m}(Q)}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}{\it\varpi}(z_{1},z_{2},k)e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathfrak{m}(Q)}\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}{\it\varpi}(z_{1},z_{2},k)e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathfrak{m}(Q)}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}{\it\varpi}(z_{1},z_{2},k)e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha},\nonumber\end{eqnarray}$$
where
and
We exchange the order of summation and integration to conclude that
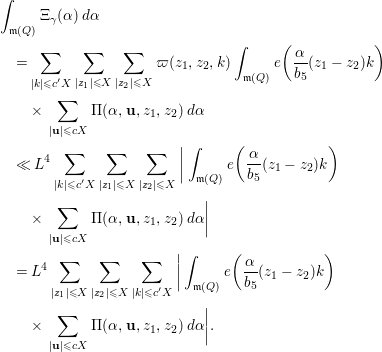 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}{\it\varpi}(z_{1},z_{2},k)\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{4}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad =L^{4}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}{\it\varpi}(z_{1},z_{2},k)\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{4}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad =L^{4}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|.\nonumber\end{eqnarray}$$
Then the Cauchy–Schwarz inequality implies
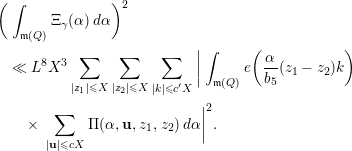 $$\begin{eqnarray}\displaystyle & & \displaystyle \bigg(\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\bigg)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{8}X^{3}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \bigg(\int _{\mathfrak{m}(Q)}{\rm\Xi}_{{\it\gamma}}({\it\alpha})\,d{\it\alpha}\bigg)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{8}X^{3}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}.\end{eqnarray}$$
Now we apply the method developed by the author [Reference Zhao16] to deduce that
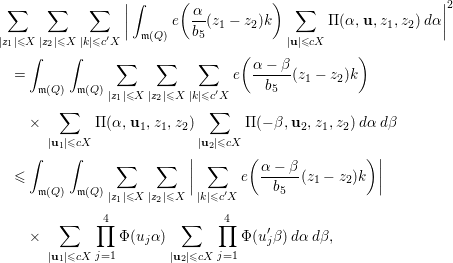 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}e\bigg(\frac{{\it\alpha}-{\it\beta}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}_{1}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u}_{1},z_{1},z_{2})\mathop{\sum }_{\substack{ |\mathbf{u}_{2}|\leqslant cX}}{\rm\Pi}(-{\it\beta},\mathbf{u}_{2},z_{1},z_{2})\,d{\it\alpha}\,d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\bigg|\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}e\bigg(\frac{{\it\alpha}-{\it\beta}}{b_{5}}(z_{1}-z_{2})k\bigg)\bigg|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}_{1}|\leqslant cX}}\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}{\it\alpha})\mathop{\sum }_{\substack{ |\mathbf{u}_{2}|\leqslant cX}}\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}^{\prime }{\it\beta})\,d{\it\alpha}\,d{\it\beta},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}e\bigg(\frac{{\it\alpha}-{\it\beta}}{b_{5}}(z_{1}-z_{2})k\bigg)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}_{1}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u}_{1},z_{1},z_{2})\mathop{\sum }_{\substack{ |\mathbf{u}_{2}|\leqslant cX}}{\rm\Pi}(-{\it\beta},\mathbf{u}_{2},z_{1},z_{2})\,d{\it\alpha}\,d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\bigg|\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}e\bigg(\frac{{\it\alpha}-{\it\beta}}{b_{5}}(z_{1}-z_{2})k\bigg)\bigg|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ |\mathbf{u}_{1}|\leqslant cX}}\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}{\it\alpha})\mathop{\sum }_{\substack{ |\mathbf{u}_{2}|\leqslant cX}}\mathop{\prod }_{j=1}^{4}{\rm\Phi}(u_{j}^{\prime }{\it\beta})\,d{\it\alpha}\,d{\it\beta},\nonumber\end{eqnarray}$$
where
![]() $\mathbf{u}_{1}=(u_{1},\ldots ,u_{4})^{T}\in \mathbb{Z}^{4}$
and
$\mathbf{u}_{1}=(u_{1},\ldots ,u_{4})^{T}\in \mathbb{Z}^{4}$
and
![]() $\mathbf{u}_{2}=(u_{1}^{\prime },\ldots ,u_{4}^{\prime })^{T}\in \mathbb{Z}^{4}$
. Therefore, we obtain by Lemma 4.2
$\mathbf{u}_{2}=(u_{1}^{\prime },\ldots ,u_{4}^{\prime })^{T}\in \mathbb{Z}^{4}$
. Therefore, we obtain by Lemma 4.2
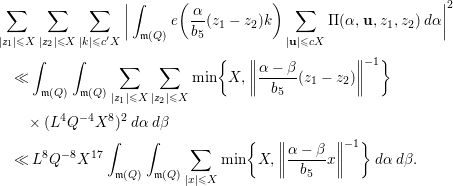 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\min \biggl\{X,\biggl\|\frac{{\it\alpha}-{\it\beta}}{b_{5}}(z_{1}-z_{2})\biggr\|^{-1}\biggr\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(L^{4}Q^{-4}X^{8})^{2}\,d{\it\alpha}\,d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{8}Q^{-8}X^{17}\int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|x|\leqslant X}\min \biggl\{X,\biggl\|\frac{{\it\alpha}-{\it\beta}}{b_{5}}x\biggr\|^{-1}\biggr\}\,d{\it\alpha}\,d{\it\beta}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\min \biggl\{X,\biggl\|\frac{{\it\alpha}-{\it\beta}}{b_{5}}(z_{1}-z_{2})\biggr\|^{-1}\biggr\}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(L^{4}Q^{-4}X^{8})^{2}\,d{\it\alpha}\,d{\it\beta}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{8}Q^{-8}X^{17}\int _{\mathfrak{m}(Q)}\int _{\mathfrak{m}(Q)}\mathop{\sum }_{|x|\leqslant X}\min \biggl\{X,\biggl\|\frac{{\it\alpha}-{\it\beta}}{b_{5}}x\biggr\|^{-1}\biggr\}\,d{\it\alpha}\,d{\it\beta}.\nonumber\end{eqnarray}$$
Then we conclude from Lemma 6.2 that
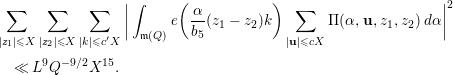 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{9}Q^{-9/2}X^{15}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|z_{1}|\leqslant X}\mathop{\sum }_{|z_{2}|\leqslant X}\mathop{\sum }_{\substack{ |k|\leqslant c^{\prime }X}}\bigg|\int _{\mathfrak{m}(Q)}e\bigg(\frac{{\it\alpha}}{b_{5}}(z_{1}-z_{2})k\bigg)\mathop{\sum }_{\substack{ |\mathbf{u}|\leqslant cX}}{\rm\Pi}({\it\alpha},\mathbf{u},z_{1},z_{2})\,d{\it\alpha}\bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll L^{9}Q^{-9/2}X^{15}.\end{eqnarray}$$
By substituting (6.16) into (6.13), we obtain
provided that
![]() $b_{5}\not =0$
.
$b_{5}\not =0$
.
We complete the proof in view of the argument around (6.12) and (6.17).◻
Lemma 6.5. One has
Proof. By Cauchy’s inequality,
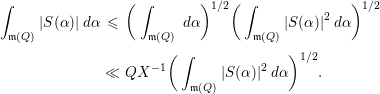 $$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}(Q)}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \bigg(\int _{\mathfrak{m}(Q)}\,d{\it\alpha}\bigg)^{1/2}\bigg(\int _{\mathfrak{m}(Q)}|S({\it\alpha})|^{2}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle QX^{-1}\bigg(\int _{\mathfrak{m}(Q)}|S({\it\alpha})|^{2}\,d{\it\alpha}\bigg)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathfrak{m}(Q)}|S({\it\alpha})|\,d{\it\alpha} & {\leqslant} & \displaystyle \bigg(\int _{\mathfrak{m}(Q)}\,d{\it\alpha}\bigg)^{1/2}\bigg(\int _{\mathfrak{m}(Q)}|S({\it\alpha})|^{2}\,d{\it\alpha}\bigg)^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle QX^{-1}\bigg(\int _{\mathfrak{m}(Q)}|S({\it\alpha})|^{2}\,d{\it\alpha}\bigg)^{1/2}.\end{eqnarray}$$
It follows from Lemmas 6.3–6.4 that
We finish Section 6 by pointing out that Proposition 6.1 follows from Lemma 6.5 by the dyadic argument.
7 The Proof of Theorem 1.1
By orthogonality, we have
Recalling the definitions of
![]() $\mathfrak{M}$
and
$\mathfrak{M}$
and
![]() $\mathfrak{m}$
in (2.8) and (2.9), we have
$\mathfrak{m}$
in (2.8) and (2.9), we have
In light of Lemma 3.6, to establish the asymptotic formula (1.3), it suffices to prove
In view of Proposition 6.1 and the work of Liu [Reference Liu9] (see also Remark of Lemma 4.4), the estimate (7.2) holds if there exists an invertible matrix
 $$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}a_{i_{1},j_{1}} & \cdots \, & a_{i_{5},j_{5}}\\ \vdots & \cdots \, & \vdots \\ a_{i_{5},j_{1}} & \cdots \, & a_{i_{5},j_{5}}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}a_{i_{1},j_{1}} & \cdots \, & a_{i_{5},j_{5}}\\ \vdots & \cdots \, & \vdots \\ a_{i_{5},j_{1}} & \cdots \, & a_{i_{5},j_{5}}\end{array}\right)\end{eqnarray}$$
with
Next we assume
![]() $\text{rank}(B)\leqslant 4$
for all
$\text{rank}(B)\leqslant 4$
for all
![]() $B=(a_{i_{k},j_{l}})_{1\leqslant k,l\leqslant 5}$
satisfying
$B=(a_{i_{k},j_{l}})_{1\leqslant k,l\leqslant 5}$
satisfying
![]() $|\{i_{1},\ldots ,i_{5}\}\cap \{j_{1},\ldots ,j_{5}\}|\leqslant 1$
. This yields
$|\{i_{1},\ldots ,i_{5}\}\cap \{j_{1},\ldots ,j_{5}\}|\leqslant 1$
. This yields
![]() $\text{rank}_{\text{off}}(A)\leqslant 4$
. By Proposition 5.1, we can establish (7.2) again if
$\text{rank}_{\text{off}}(A)\leqslant 4$
. By Proposition 5.1, we can establish (7.2) again if
![]() $\text{rank}_{\text{off}}(A)\leqslant 3$
. It remains to consider the case
$\text{rank}_{\text{off}}(A)\leqslant 3$
. It remains to consider the case
![]() $\text{rank}_{\text{off}}(A)=4$
. Without loss of generality, we assume that
$\text{rank}_{\text{off}}(A)=4$
. Without loss of generality, we assume that
![]() $\text{rank}(C)=4$
, where
$\text{rank}(C)=4$
, where
 $$\begin{eqnarray}C=\left(\begin{array}{@{}cccc@{}}a_{1,5} & a_{1,6} & a_{1,7} & a_{1,8}\\ a_{2,5} & a_{2,6} & a_{2,7} & a_{2,8}\\ a_{3,5} & a_{3,6} & a_{3,7} & a_{3,8}\\ a_{4,5} & a_{4,6} & a_{4,7} & a_{4,8}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}C=\left(\begin{array}{@{}cccc@{}}a_{1,5} & a_{1,6} & a_{1,7} & a_{1,8}\\ a_{2,5} & a_{2,6} & a_{2,7} & a_{2,8}\\ a_{3,5} & a_{3,6} & a_{3,7} & a_{3,8}\\ a_{4,5} & a_{4,6} & a_{4,7} & a_{4,8}\end{array}\right).\end{eqnarray}$$
Let
![]() ${\it\gamma}_{j}=(a_{j,5},\ldots ,a_{j,n})^{T}\in \mathbb{Z}^{n-4}$
for
${\it\gamma}_{j}=(a_{j,5},\ldots ,a_{j,n})^{T}\in \mathbb{Z}^{n-4}$
for
![]() $1\leqslant j\leqslant n$
. Then
$1\leqslant j\leqslant n$
. Then
![]() ${\it\gamma}_{1}$
,
${\it\gamma}_{1}$
,
![]() ${\it\gamma}_{2}$
,
${\it\gamma}_{2}$
,
![]() ${\it\gamma}_{3}$
and
${\it\gamma}_{3}$
and
![]() ${\it\gamma}_{4}$
are linear independent due to
${\it\gamma}_{4}$
are linear independent due to
![]() $\text{rank}(C)=4$
. For
$\text{rank}(C)=4$
. For
![]() $5\leqslant k\leqslant n$
, we consider
$5\leqslant k\leqslant n$
, we consider
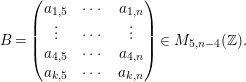 $$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}a_{1,5} & \cdots \, & a_{1,n}\\ \vdots & \cdots \, & \vdots \\ a_{4,5} & \cdots \, & a_{4,n}\\ a_{k,5} & \cdots \, & a_{k,n}\end{array}\right)\in M_{5,n-4}(\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}}a_{1,5} & \cdots \, & a_{1,n}\\ \vdots & \cdots \, & \vdots \\ a_{4,5} & \cdots \, & a_{4,n}\\ a_{k,5} & \cdots \, & a_{k,n}\end{array}\right)\in M_{5,n-4}(\mathbb{Z}).\end{eqnarray}$$
According to our assumption, one has
![]() $\text{rank}(B)\leqslant 4$
. Then we conclude from above that
$\text{rank}(B)\leqslant 4$
. Then we conclude from above that
![]() ${\it\gamma}_{k}$
can be linear represented by
${\it\gamma}_{k}$
can be linear represented by
![]() ${\it\gamma}_{1}$
,
${\it\gamma}_{1}$
,
![]() ${\it\gamma}_{2}$
,
${\it\gamma}_{2}$
,
![]() ${\it\gamma}_{3}$
and
${\it\gamma}_{3}$
and
![]() ${\it\gamma}_{4}$
. Therefore, one has
${\it\gamma}_{4}$
. Therefore, one has
![]() $\text{rank}(H)=4$
, where
$\text{rank}(H)=4$
, where
 $$\begin{eqnarray}H=\left(\begin{array}{@{}ccc@{}}a_{1,5} & \cdots \, & a_{1,n}\\ \vdots & \cdots \, & \vdots \\ a_{n,5} & \cdots \, & a_{n,n}\end{array}\right)\in M_{n,n-4}(\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}H=\left(\begin{array}{@{}ccc@{}}a_{1,5} & \cdots \, & a_{1,n}\\ \vdots & \cdots \, & \vdots \\ a_{n,5} & \cdots \, & a_{n,n}\end{array}\right)\in M_{n,n-4}(\mathbb{Z}).\end{eqnarray}$$
We obtain
![]() $\text{rank}(A)\leqslant \text{rank}(H)+4\leqslant 8$
. This is contradictory to the condition that
$\text{rank}(A)\leqslant \text{rank}(H)+4\leqslant 8$
. This is contradictory to the condition that
![]() $\text{rank}(A)\geqslant 9$
. Therefore, we complete the proof of Theorem 1.1.
$\text{rank}(A)\geqslant 9$
. Therefore, we complete the proof of Theorem 1.1.