The Strength–Density Relationship for Dry Snow

Abstract

A linear relationship between strength and density is a characteristic feature of deposited snow. This relationship is explained theoretically in the case of old dry snow in ternis of the theory of sintering. The discontinuity in the relationship at a density of about 0.4 g./cm³ is considered to mark a transition point below which the snow densifies primarily by rearranement of the grains and the strength increases by the growth of existing bonds, and above which densification occurs by volume diffusion and the strength increases primarily by the creation of new bonds. Experimental evidence to support these ideas is presented.

Une relation linéaire entre la solidité et la densité est une caractéristique d’une neige de dépôt. Cette relation est expliquée théoriquement dans le cas d’un névé sec en termes de la théorie du frittage. La discontinuité dans cette relation pour une densité d’environ 0,4 g/cm³ est considérée comme marquant un point de transition en-dessous duquel la neige augmente sa densité avant tout par un réarrangement des grains et la solidité augmente par la croissance des liaisons existantes, et au-dessus duquel la densification a lieu par diffusion volumétrique et la solidité augmente avant tout par la création de nouvelles liaisons. Les résultats d’expérience supportent ces idées.

Zusammenfassung

Eines der charakteristischen Merkmale einer natürlichen Schneedecke ist ein linearer Zusammenhang zwischen Festigkeit und Dichte. Dieser Zusammenhang wird für den Fall von trockenem Altschnee als Sinterungsphänomen theoretisch erklärt. Die lineare Funktion zeigt eine Diskontinuität bei einer Dichte von etwa 0,4 g/cm³. Darunter vollzieht sich die Dichtezunahme vorwiegend durch Umgruppierung der Firnkörner, während die Festigkeit durcit das Wachstum vorhandener Brücken zunimmt. Darüber erfolgt die Dichtezunahme durch Volumdiffusion und die Festigkeitszunahme durch Bildung neuer Brücken. Experimentelles Beweismaterial für diese Annahmen wird vorgelegt.

Introduction

Measurements of the strength and density of deposited snow show that these two quantities are linearly related over a fairly wide range of densities. For example, Butkovich (1958) found this to be the case for naturally compacted high-density snow taken from the no-meIt zone of the northern Greenland ice sheet (Fig. 1). There is a discontinuity in the relationship, however, at a density of about 0.4 g./cm³, below this value the strength falls off less sharply with decreasing density. A theoretical explanation for the linear strength-density relationship in the case of old dry snow is presented in this paper.

Fig. 1. Strength-density measurements on snow samples taken from an Arctic glacier (from Butkouich, 1958)

Strength and Density of Firn

Dry snow of density between about 0.4 and 0.6 g./cm³ may be represented by a compact of ice grains which are fairly uniform in size. In this case, under appropriate conditions, the variations of the strength and density of the snow with time are described by the theories of Hobbs (1965) and Hobbs and Radke (1967).

Hobbs (1965) assumed that the strength of old snow is proportional to the area of contact between the grains. Now the radius x between two spheres of ice of radius r which have sintered together for time t at a constant temperature is given by (Hobbs and Mason, 1964)

(1)

where B is a temperature-dependent term. Hence the variation of the strength S of old snow with time should be given by

(2)

The validity of Equation (2) is supported by the experimental measurements of several workers (Jellinek, 1959; Nakaya, 1959; Wuori, 1963) which show that the strength of a compact of ice spheres does increase as the two-fifths power of the age of the compact. Hobbs and Radke (1967) have shown that, even in the absence of temperature gradients or overburden pressure, snow can density by volume diffusion in the ice, and in this case the decrease ΔV in the volume of a given mass of old snow is given by

(3)

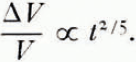
From Equation (3) the density ρ of the snow at time t may be written as

(4)

It can be seen from Equations (2) and (4) that the strength and density of old snow have the same time dependence and should therefore be linearly related, as found experimentally. However, if the strength of snow were determined solely by the growth of existing bonds between the grains, and the densification proceeded entirely by volume diffusion, a discontinuity in the strength-density relationship at about 0.4 g./cm.³ would not occur. It is necessary, therefore, to take a closer look at the relationship between the strength and density of snow, although it will be possible to do this only in a semi-quantitative manner.

We will assume that the strength of a sample of snow is proportional to the total area of the ice bonds in a cross-section through the sample, that is, to the number of bonds and to their individual cross-sectional areas. In loosely packed snow, significant densification can occur due to the rearrangement of the grains in the sample. In fact, the density can increase to about 0.55 g./cm.³ by this means. In the initial stages of the rearrangement of grains, a rather large increase in the density occurs to produce a relatively small increase in the number of new bonds. The increase in strength with density is therefore rather slow at this stage. As the sample approaches the random close-packed configuration, further densification occurs by volume diffusion at the points of contact between the grains. The porosity of a random close-packed array is almost twice that of the close-packed or rhombohedral arrangement; therefore, in the former case the number of bonds which a particular particle has with its neighbours should be about one-half the maximum possible number. It is also reasonable to assume that in the random close packing the distances between near neighbours which are not in contact are uniformly distributed. Hence, as old snow densifies by volume diffusion and the centre-centre distances between grains decreases, the number of new bonds that are formed should be approximately proportional to the amount of densification; that is, to t ^2/5. The strength and densification of the compact should therefore increase as t ^2/5 in a region around the critical density (0.55 g./cm.³).

On the basis of the above argument we consider the discontinuity in the strength-density relationship at about 0.4. g./cm.³ marks a transition point. Below this point the density of the dry snow increases primarily by repacking of the grains, and the increase in strength is dominated by the growth of existing bonds. In a region above this transition point, however, densification occurs by volume diffusion and the creation of new bonds becomes the major factor in determining the strength of the snow. At still higher densities the growth of existing bonds become once again the major mechanism for increasing the strength of the snow.

The above conclusion is supported by some recent experimental results obtained by Ramseier and Keeler (1966). These workers measured the compressive strengths of two samples of snow as a function of time, one sample being allowed to sinter in air and the other in silicone oil. Both samples were initially at the critical density. The rate at which the sample in air increased in strength was found to be about one hundred times greater than the rate at which the sample in silicone oil increased in strength. Now Hobbs and Radke (1967) have shown that the time required to increase the size of the neck between two ice spheres situated in silicone oil by a given amount is only ten times greater than in air, while the rate of densification of a compact of ice spheres in silicone oil is about the same as that in air. This means that the rate of increase in the areas of existing ice bonds in a compact should be a factor of about 2.5 less in silicone oil than in air. In view of this result it is clear that the two orders of magnitude reduction in the rate of increase in the strength of a sample of fire in silicone oil cannot be due primarily to the reduction in the rate of growth of the existing bonds. It must, therefore, be due to the failure to create new bonds during sintering in silicone oil. This last fact has been pointed out previously by Hobbs and Radke (1967) who found that if two ice spheres are covered in silicone oil and then pushed together, actual physical contact between the spheres does not take place. Hence, in silicone oil the increase in strength of a sample of snow must be due to the growth of existing bonds only. This result, together with the experimental observations of Ramseier and Keeler (1966), supports the conclusion reached above that in the neighbourhood of the initial density the creation of new bonds is the important factor in determining the increase in the strength of old snow.

Before concluding this discussion it is interesting to note that Wuori (1963) found that sintering at high temperatures increases the rate of hardening of snow, but lower temperatures generally produce greater ultimate hardness. In view of the linear relationship between strength and density, this result implies that the rate of increase in the density of snow is greater at high temperatures, but low temperatures produce greater ultimate density. The theory for the densification of firn developed by Hobbs and Radke (1967) predicts that more densification of firn should occur in a given time at higher temperatures than at lower temperatures, but the theory does not predict that greater densities are ultimately attained at low temperatures. However, the experimental results obtained by these workers are in agreement with Wuori’s observations, for Hobbs and Radke observed there was a definite decrease in the slope with increasing temperature. This can be seen in Figure 2 where the experimental results are shown for −2.5°C. and −26.5°C. For the period of time over which measurements were taken, the firn at −2.5°C. had less volume than the same mass of firn at −26.5°C. If the results are extrapolated to longer times, however, it is found that the firn at −26.5°C. should achieve the smaller volume, and therefore the greater density after a period of about 10 days.

Fig. 2. Experimental measurements on the densification of fins at two different temperatures (from Hobbs and Radke, 1967)

Acknowledgements

This research was supported by the Atmospheric Sciences Section, National Science Foundation, NSF GP−3809 and NSF 11–2769.