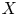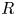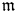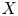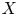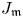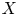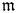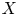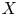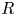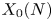Introduction
Let ![]() $R$ be a discrete valuation ring, with field of fractions
$R$ be a discrete valuation ring, with field of fractions ![]() $F$ and residue field
$F$ and residue field ![]() $k$. Let
$k$. Let ![]() $\mathcal {X}$ be a regular scheme, proper and flat over
$\mathcal {X}$ be a regular scheme, proper and flat over ![]() $S=\operatorname {Spec} R$, whose generic fibre
$S=\operatorname {Spec} R$, whose generic fibre ![]() $X=\mathcal {X}_F$ is a smooth curve. In [Reference RaynaudRay70] Raynaud describes the relationship between the Néron model of the Jacobian
$X=\mathcal {X}_F$ is a smooth curve. In [Reference RaynaudRay70] Raynaud describes the relationship between the Néron model of the Jacobian ![]() $J=\operatorname {Pic}^0_{X/F}$ of
$J=\operatorname {Pic}^0_{X/F}$ of ![]() $X$ and the relative Picard functor
$X$ and the relative Picard functor ![]() $P=\operatorname {Pic}_{\mathcal {X}/S}$. The aim of this paper is twofold: first, to extend Raynaud's results to the generalized Jacobian
$P=\operatorname {Pic}_{\mathcal {X}/S}$. The aim of this paper is twofold: first, to extend Raynaud's results to the generalized Jacobian ![]() $J_\mathfrak {m}$ of
$J_\mathfrak {m}$ of ![]() $X$ with respect to a reduced modulus
$X$ with respect to a reduced modulus ![]() $\mathfrak {m}$; and, second, to apply these results to compute the component and character groups of the Néron models of generalized Jacobians attached to modular curves and moduli supported on cusps.
$\mathfrak {m}$; and, second, to apply these results to compute the component and character groups of the Néron models of generalized Jacobians attached to modular curves and moduli supported on cusps.
Our motivation for this work arises from applications to the arithmetic of modular forms, the point being that just as the arithmetic of cusp forms of weight ![]() $2$ on a congruence subgroup of
$2$ on a congruence subgroup of ![]() $\operatorname {SL}(2,\mathbb {Z})$ is controlled by the Jacobian of the associated complete modular curve, so the arithmetic of the space of holomorphic modular forms on the same group is controlled by a suitable generalized Jacobian. Raynaud's results have been used extensively to study the arithmetic of cusp forms of weight
$\operatorname {SL}(2,\mathbb {Z})$ is controlled by the Jacobian of the associated complete modular curve, so the arithmetic of the space of holomorphic modular forms on the same group is controlled by a suitable generalized Jacobian. Raynaud's results have been used extensively to study the arithmetic of cusp forms of weight ![]() $2$ and their associated Galois representations, for example, in [Reference MazurMaz77, Reference Mazur and WilesMW84, Reference RibetRib88, Reference RibetRib90]. In future work we plan to give arithmetic applications of the results obtained here. We note that generalized modular Jacobians with cuspidal modulus have been considered by Gross [Reference GrossGro12], Yamazaki and Yang [Reference Yamazaki and YangYY16], Bruinier and Li [Reference Bruinier and LiBL16], Wei and Yamazaki [Reference Wei and YamazakiWY19], and Iranzo [Reference IranzoIra21]. Another point of view, using
$2$ and their associated Galois representations, for example, in [Reference MazurMaz77, Reference Mazur and WilesMW84, Reference RibetRib88, Reference RibetRib90]. In future work we plan to give arithmetic applications of the results obtained here. We note that generalized modular Jacobians with cuspidal modulus have been considered by Gross [Reference GrossGro12], Yamazaki and Yang [Reference Yamazaki and YangYY16], Bruinier and Li [Reference Bruinier and LiBL16], Wei and Yamazaki [Reference Wei and YamazakiWY19], and Iranzo [Reference IranzoIra21]. Another point of view, using ![]() $1$-motives rather than generalized Jacobians (see also § 1.7 below), has been investigated by Lecouturier [Reference LecouturierLec21].
$1$-motives rather than generalized Jacobians (see also § 1.7 below), has been investigated by Lecouturier [Reference LecouturierLec21].
Before describing our main results, we briefly recall from [Reference RaynaudRay70] the results of Raynaud on Jacobians. To simplify the discussion, we assume for the rest of this introduction that ![]() $R$ is Henselian,
$R$ is Henselian, ![]() $k$ is algebraically closed, and that the greatest common divisor of the multiplicities of the irreducible components of the fibre
$k$ is algebraically closed, and that the greatest common divisor of the multiplicities of the irreducible components of the fibre ![]() $\mathcal {X}_s$ at the closed point
$\mathcal {X}_s$ at the closed point ![]() $s=\operatorname {Spec} k$ is
$s=\operatorname {Spec} k$ is ![]() $1$. (We review Raynaud's theory in §§ 2.2–3 in greater detail and under less restrictive hypotheses.) Under these hypotheses, [Reference RaynaudRay70, (8.2.1)] shows that
$1$. (We review Raynaud's theory in §§ 2.2–3 in greater detail and under less restrictive hypotheses.) Under these hypotheses, [Reference RaynaudRay70, (8.2.1)] shows that ![]() $P$ is represented by a smooth group scheme over
$P$ is represented by a smooth group scheme over ![]() $S$, and there is a canonical morphism of group schemes
$S$, and there is a canonical morphism of group schemes ![]() $\deg \colon P \to \mathbb {Z}$, which maps a line bundle to its total degree along the fibres of
$\deg \colon P \to \mathbb {Z}$, which maps a line bundle to its total degree along the fibres of ![]() $\mathcal {X}/S$. The open and closed subgroup scheme
$\mathcal {X}/S$. The open and closed subgroup scheme ![]() $P'=\ker (\deg )$ then has
$P'=\ker (\deg )$ then has ![]() $J$ as its generic fibre.
$J$ as its generic fibre.
Let ![]() $r$ be the number of irreducible components of
$r$ be the number of irreducible components of ![]() $\mathcal {X}_s$. If
$\mathcal {X}_s$. If ![]() $r>1$, then
$r>1$, then ![]() $P$ is not separated over
$P$ is not separated over ![]() $S$. Indeed, if
$S$. Indeed, if ![]() $Y\subset \mathcal {X}_s^\mathrm {red}$ is an irreducible component, viewed as a reduced divisor on
$Y\subset \mathcal {X}_s^\mathrm {red}$ is an irreducible component, viewed as a reduced divisor on ![]() $\mathcal {X}$, then the line bundle
$\mathcal {X}$, then the line bundle ![]() $\mathcal {O}_\mathcal {X}(Y)$ represents an element of
$\mathcal {O}_\mathcal {X}(Y)$ represents an element of ![]() $P'(S)$, nonzero if
$P'(S)$, nonzero if ![]() $r>1$, whose image in
$r>1$, whose image in ![]() $P'(F)$ vanishes. The closure
$P'(F)$ vanishes. The closure ![]() $E\subset P'$ of the zero section is then an étale (but not separated)
$E\subset P'$ of the zero section is then an étale (but not separated) ![]() $S$-group scheme, whose generic fibre is trivial, and whose special fibre is isomorphic to
$S$-group scheme, whose generic fibre is trivial, and whose special fibre is isomorphic to ![]() $\mathbb {Z}^{r-1}$, generated by the classes of the bundles
$\mathbb {Z}^{r-1}$, generated by the classes of the bundles ![]() $\mathcal {O}_\mathcal {X}(Y)$ restricted to
$\mathcal {O}_\mathcal {X}(Y)$ restricted to ![]() $\mathcal {X}_s$. Raynaud shows the following.
$\mathcal {X}_s$. Raynaud shows the following.
(i) The maximal separated quotient
 $P'/E$ is the Néron model
$P'/E$ is the Néron model  $\mathcal {J}$ of
$\mathcal {J}$ of  $J$.
$J$.(ii) The identity component
 $\mathcal {J}_s^0$ of the special fibre of
$\mathcal {J}_s^0$ of the special fibre of  $\mathcal {J}$ is canonically isomorphic to the Picard scheme
$\mathcal {J}$ is canonically isomorphic to the Picard scheme  $\operatorname {Pic}_{\mathcal {X}_s/k}^0$.
$\operatorname {Pic}_{\mathcal {X}_s/k}^0$.(iii) Let
 $\mathcal {J}_s^{0,\mathrm {lin}}$ be the maximal connected affine subgroup scheme of
$\mathcal {J}_s^{0,\mathrm {lin}}$ be the maximal connected affine subgroup scheme of  $\mathcal {J}_s^0$; its character group
$\mathcal {J}_s^0$; its character group  $\mathbb {X}(J_s) := \operatorname {Hom}_k(\mathcal {J}_s^{0,\mathrm {lin}},\mathbb {G}_{\mathrm {m}})$ is canonically isomorphic to
$\mathbb {X}(J_s) := \operatorname {Hom}_k(\mathcal {J}_s^{0,\mathrm {lin}},\mathbb {G}_{\mathrm {m}})$ is canonically isomorphic to  $H_1(\widetilde{\Gamma} _{\mathcal {X}_s},\mathbb {Z})$, the integral homology of the extended dual graph
$H_1(\widetilde{\Gamma} _{\mathcal {X}_s},\mathbb {Z})$, the integral homology of the extended dual graph  $\widetilde{\Gamma} _{\mathcal {X}_s}$ of the singular curve
$\widetilde{\Gamma} _{\mathcal {X}_s}$ of the singular curve  $\mathcal {X}_s$ (we recall the definition in § 1.2).
$\mathcal {X}_s$ (we recall the definition in § 1.2).(iv) The component group
 $\Phi (J) := \mathcal {J}_s/\mathcal {J}_s^0$ is canonically isomorphic to the homology of the complex
where
$\Phi (J) := \mathcal {J}_s/\mathcal {J}_s^0$ is canonically isomorphic to the homology of the complex
where \[ \mathbb{Z}[C] \to \mathbb{Z}^C \to \mathbb{Z}, \]
\[ \mathbb{Z}[C] \to \mathbb{Z}^C \to \mathbb{Z}, \]
 $C$ is the set of irreducible components
$C$ is the set of irreducible components  $Y\subset \mathcal {X}_s^\mathrm {red}$, the first map is given by the intersection pairing
$Y\subset \mathcal {X}_s^\mathrm {red}$, the first map is given by the intersection pairing  $C\times C \to \mathbb {Z}$ on
$C\times C \to \mathbb {Z}$ on  $\mathcal {X}$, and the second by
$\mathcal {X}$, and the second by  $(m_Y\!)_Y\mapsto \sum _Y \delta _Ym_Y$, where
$(m_Y\!)_Y\mapsto \sum _Y \delta _Ym_Y$, where  $\delta _Y$ is the multiplicity of
$\delta _Y$ is the multiplicity of  $Y$ in the fibre.
$Y$ in the fibre.
In the special case where ![]() $\mathcal {X}_s$ is a reduced divisor on
$\mathcal {X}_s$ is a reduced divisor on ![]() $\mathcal {X}$ with normal crossings, statements (iii) and (iv) become:
$\mathcal {X}$ with normal crossings, statements (iii) and (iv) become:
(iii′)
 $\operatorname {Hom}_k(\mathcal {J}_s^{0,\mathrm {lin}},\mathbb {G}_{\mathrm {m}})\simeq H_1(\Gamma _{\mathcal {X}_s},\mathbb {Z})$, where
$\operatorname {Hom}_k(\mathcal {J}_s^{0,\mathrm {lin}},\mathbb {G}_{\mathrm {m}})\simeq H_1(\Gamma _{\mathcal {X}_s},\mathbb {Z})$, where  $\Gamma _{\mathcal {X}_s}$ is the reduced dual graph of
$\Gamma _{\mathcal {X}_s}$ is the reduced dual graph of  $\mathcal {X}_s$, whose vertex set is
$\mathcal {X}_s$, whose vertex set is  $C$ and edge set is
$C$ and edge set is  $\mathcal {X}_s^\mathrm {sing}$;
$\mathcal {X}_s^\mathrm {sing}$;(iv′)
 $\Phi (J)\simeq \operatorname {coker}(\square \colon \mathbb {Z}[C] \to \mathbb {Z}[C]_0 )$, where
$\Phi (J)\simeq \operatorname {coker}(\square \colon \mathbb {Z}[C] \to \mathbb {Z}[C]_0 )$, where  $\square$ is the Laplacian of the graph
$\square$ is the Laplacian of the graph  $\Gamma _{\mathcal {X}_s}$, which is the endomorphism of
$\Gamma _{\mathcal {X}_s}$, which is the endomorphism of  $\mathbb {Z}[C]$ taking a vertex
$\mathbb {Z}[C]$ taking a vertex  $v\in C$ to
$v\in C$ to  $\sum (v)-(v')$, where the sum is taken over all edges joining
$\sum (v)-(v')$, where the sum is taken over all edges joining  $v$ to an adjacent vertex
$v$ to an adjacent vertex  $v'$.
$v'$.
Now let ![]() $\mathfrak {m}$ be a modulus (effective divisor) on
$\mathfrak {m}$ be a modulus (effective divisor) on ![]() $X$. Then one has [Reference RosenlichtRos54, Reference SerreSer84] the generalized Jacobian
$X$. Then one has [Reference RosenlichtRos54, Reference SerreSer84] the generalized Jacobian ![]() $J_\mathfrak {m}$ of
$J_\mathfrak {m}$ of ![]() $X$ relative to
$X$ relative to ![]() $\mathfrak {m}$, which is an extension of
$\mathfrak {m}$, which is an extension of ![]() $J$ by a commutative connected linear group
$J$ by a commutative connected linear group ![]() $H$. Assume that
$H$. Assume that ![]() $\mathfrak {m}=\sum _{i\in I}(x_i)$ is a sum of distinct points, whose residue fields
$\mathfrak {m}=\sum _{i\in I}(x_i)$ is a sum of distinct points, whose residue fields ![]() $F_i$ are all separable over
$F_i$ are all separable over ![]() $F$. This is equivalent to assuming that
$F$. This is equivalent to assuming that ![]() $H$ is a torus. Then by the results of Raynaud [Reference Bosch, Lütkebohmert and RaynaudBLR90, Ch. 10],
$H$ is a torus. Then by the results of Raynaud [Reference Bosch, Lütkebohmert and RaynaudBLR90, Ch. 10], ![]() $J_\mathfrak {m}$ has a Néron model
$J_\mathfrak {m}$ has a Néron model ![]() $\mathcal {J}_\mathfrak {m}$, which is a smooth separated group scheme over
$\mathcal {J}_\mathfrak {m}$, which is a smooth separated group scheme over ![]() $S$, not necessarily of finite type, with generic fibre
$S$, not necessarily of finite type, with generic fibre ![]() $J_\mathfrak {m}$ and satisfying the Néron universal property. (In the terminology of [Reference Bosch, Lütkebohmert and RaynaudBLR90],
$J_\mathfrak {m}$ and satisfying the Néron universal property. (In the terminology of [Reference Bosch, Lütkebohmert and RaynaudBLR90], ![]() $\mathcal {J}_\mathfrak {m}$ is a Néron lft-model.) We obtain results analogous to results (i)–(iv
$\mathcal {J}_\mathfrak {m}$ is a Néron lft-model.) We obtain results analogous to results (i)–(iv![]() ${}'$) for
${}'$) for ![]() $\mathcal {J}_\mathfrak {m}$. Specifically, let
$\mathcal {J}_\mathfrak {m}$. Specifically, let ![]() $R_i$ be the integral closure of
$R_i$ be the integral closure of ![]() $R$ in
$R$ in ![]() $F_i$, and
$F_i$, and ![]() $\Sigma _s$ be the disjoint union of the
$\Sigma _s$ be the disjoint union of the ![]() $\operatorname {Spec}( R_i\otimes _Rk)$,
$\operatorname {Spec}( R_i\otimes _Rk)$, ![]() $i\in I$. The inclusion of the set of points
$i\in I$. The inclusion of the set of points ![]() $x_i$ in
$x_i$ in ![]() $X$ gives a morphism
$X$ gives a morphism ![]() $\Sigma _s\to \mathcal {X}_s$. We show the following.
$\Sigma _s\to \mathcal {X}_s$. We show the following.
(i) There exists a smooth
 $S$-group scheme
$S$-group scheme  $P_\mathfrak {m}$, parametrizing equivalence classes of line bundles on
$P_\mathfrak {m}$, parametrizing equivalence classes of line bundles on  $\mathcal {X}$ with a trivialization at each
$\mathcal {X}$ with a trivialization at each  $x_i$, and
$x_i$, and  $\mathcal {J}_\mathfrak {m}$ is the maximal separated quotient of
$\mathcal {J}_\mathfrak {m}$ is the maximal separated quotient of  $P_\mathfrak {m}'=\ker (\deg \colon P_\mathfrak {m} \to \mathbb {Z})$ (Theorems 1.15 and 1.16).
$P_\mathfrak {m}'=\ker (\deg \colon P_\mathfrak {m} \to \mathbb {Z})$ (Theorems 1.15 and 1.16).(ii) The identity component
 $\mathcal {J}_{\mathfrak {m},s}^0$ of the special fibre of
$\mathcal {J}_{\mathfrak {m},s}^0$ of the special fibre of  $\mathcal {J}_\mathfrak {m}$ is canonically isomorphic to
$\mathcal {J}_\mathfrak {m}$ is canonically isomorphic to  $\operatorname {Pic}_{(\mathcal {X}_s,\Sigma _s)/k}^0$, the generalized Picard scheme classifying line bundles on
$\operatorname {Pic}_{(\mathcal {X}_s,\Sigma _s)/k}^0$, the generalized Picard scheme classifying line bundles on  $\mathcal {X}_s$ of degree zero on each irreducible component, together with a trivialization of the pullback to
$\mathcal {X}_s$ of degree zero on each irreducible component, together with a trivialization of the pullback to  $\Sigma _s$ (Corollary 1.18(a)).
$\Sigma _s$ (Corollary 1.18(a)).(iii) The character group
 $\operatorname {Hom}_k(\mathcal {J}_{\mathfrak {m},s}^{0,\mathrm {lin}},\mathbb {G}_{\mathrm {m}})$ is the integral homology of an extended graph
$\operatorname {Hom}_k(\mathcal {J}_{\mathfrak {m},s}^{0,\mathrm {lin}},\mathbb {G}_{\mathrm {m}})$ is the integral homology of an extended graph  $\widetilde{\Gamma} _{\mathcal {X}_s,\Sigma }$, depending only on the combinatorics of the components of
$\widetilde{\Gamma} _{\mathcal {X}_s,\Sigma }$, depending only on the combinatorics of the components of  $\mathcal {X}_s$ and the reductions
$\mathcal {X}_s$ and the reductions  $\bar x_i\in \mathcal {X}_s$ of the points
$\bar x_i\in \mathcal {X}_s$ of the points  $x_i$ (Corollary 1.18(b)).
$x_i$ (Corollary 1.18(b)).(iv) The component group
 $\Phi (J_\mathfrak {m})=\mathcal {J}_{\mathfrak {m},s}/\mathcal {J}_{\mathfrak {m}.s}^0$, which is an abelian group of finite type (not necessarily finite), is isomorphic to the homology of the complex (1.6.4)
(Theorem 1.19).
$\Phi (J_\mathfrak {m})=\mathcal {J}_{\mathfrak {m},s}/\mathcal {J}_{\mathfrak {m}.s}^0$, which is an abelian group of finite type (not necessarily finite), is isomorphic to the homology of the complex (1.6.4)
(Theorem 1.19). \[ \mathbb{Z}[C] \oplus \mathbb{Z} \to \mathbb{Z}^C \oplus \mathbb{Z}^I \to \mathbb{Z} \]
\[ \mathbb{Z}[C] \oplus \mathbb{Z} \to \mathbb{Z}^C \oplus \mathbb{Z}^I \to \mathbb{Z} \]
If ![]() $\mathcal {X}_s$ is a reduced divisor with normal crossings, and the points
$\mathcal {X}_s$ is a reduced divisor with normal crossings, and the points ![]() $x_i$ are
$x_i$ are ![]() $F$-rational, then the character and component groups have simple descriptions in terms of the homology and Laplacian of a generalized reduced dual graph (Corollary 1.20).
$F$-rational, then the character and component groups have simple descriptions in terms of the homology and Laplacian of a generalized reduced dual graph (Corollary 1.20).
We then apply these results to a modular curve ![]() $X_0(N)$ and a modulus
$X_0(N)$ and a modulus ![]() $\mathfrak {m}$ supported on the cusps. If
$\mathfrak {m}$ supported on the cusps. If ![]() $p>3$ is a prime exactly dividing
$p>3$ is a prime exactly dividing ![]() $N$, we compute the character and component groups, together with the action of the Hecke operators on them. In particular, if
$N$, we compute the character and component groups, together with the action of the Hecke operators on them. In particular, if ![]() $N=p$ and
$N=p$ and ![]() $\mathfrak {m}=(\infty )+(0)$ is the sum of the two cusps of
$\mathfrak {m}=(\infty )+(0)$ is the sum of the two cusps of ![]() $X_0(p)$, then the component group is infinite cyclic, with
$X_0(p)$, then the component group is infinite cyclic, with ![]() $T_\ell$ acting by
$T_\ell$ acting by ![]() $\ell +1$ for
$\ell +1$ for ![]() $\ell \ne p$, and the representation of the full Hecke algebra on the character group is given by the classical Brandt matrices. We also compute the component group for
$\ell \ne p$, and the representation of the full Hecke algebra on the character group is given by the classical Brandt matrices. We also compute the component group for ![]() $N=p^2$, which for the full cuspidal modulus is free of rank
$N=p^2$, which for the full cuspidal modulus is free of rank ![]() $2$.
$2$.
There has been considerable interest in ‘Jacobians of graphs’; for example, Lorenzini [Reference LorenziniLor89, Reference LorenziniLor91], Bacher, de la Harpe, and Nagnibeda [Reference Bacher, de la Harpe and NagnibedaBdlHN97] and Baker and Norine [Reference Baker and NorineBN07]. Our results here on ![]() $\Phi (J_\mathfrak {m})$ suggest that there is also a theory of ‘generalized Jacobians of graphs’. We investigate this in a future paper.
$\Phi (J_\mathfrak {m})$ suggest that there is also a theory of ‘generalized Jacobians of graphs’. We investigate this in a future paper.
Let us briefly describe the contents of the rest of the paper. In § 1, we prove our results on Néron models of generalized Jacobians. Although not needed for the applications we have in mind, we decided to work in a very general setting (in particular, there are no conditions imposed on the base ring). Sections 1.1–1.3 review well-known facts about Néron models, Weil restriction, and Picard schemes of singular curves, as well as some of Raynaud's results from [Reference RaynaudRay70].
In §§ 1.4 and 1.5 we describe the structure of the generalized Picard scheme of a singular curve with respect to a modulus, and discuss its functoriality. The main results on the Néron models of generalized Jacobian are contained in § 1.6. In the following two sections we explain the relation with ![]() $1$-motives, and describe some of the behaviour of the Néron model of
$1$-motives, and describe some of the behaviour of the Néron model of ![]() $J_\mathfrak {m}$ under correspondences.
$J_\mathfrak {m}$ under correspondences.
In § 2 we apply our results to the modular curves ![]() $X_0(N)$ and cuspidal moduli, computing in several cases the component and characters groups of the reduction of the Néron model modulo a prime
$X_0(N)$ and cuspidal moduli, computing in several cases the component and characters groups of the reduction of the Néron model modulo a prime ![]() $p>3$.
$p>3$.
We describe some prior work on these topics. If the points ![]() $(x_i)$ are
$(x_i)$ are ![]() $F$-rational and their closures in
$F$-rational and their closures in ![]() $\mathcal {X}$ are disjoint, then by identifying them, one obtains a singular relative curve
$\mathcal {X}$ are disjoint, then by identifying them, one obtains a singular relative curve ![]() $\mathcal {X}/\mathfrak {m}$ which is semifactorial. Some of our results in this case are then subsumed by the works [Reference OrecchiaOre17a, Reference OrecchiaOre17b, Reference PépinPép13] on Picard schemes of semifactorial curves. In [Reference OverkampOve21], Overkamp proves general results on the existence of Néron models of Picard schemes of singular curves. Finally, Suzuki [Reference SuzukiSuz19] has defined Néron models of
$\mathcal {X}/\mathfrak {m}$ which is semifactorial. Some of our results in this case are then subsumed by the works [Reference OrecchiaOre17a, Reference OrecchiaOre17b, Reference PépinPép13] on Picard schemes of semifactorial curves. In [Reference OverkampOve21], Overkamp proves general results on the existence of Néron models of Picard schemes of singular curves. Finally, Suzuki [Reference SuzukiSuz19] has defined Néron models of ![]() $1$-motives and studied their duality properties and component groups. We discuss its relation with the present work in § 1.7.
$1$-motives and studied their duality properties and component groups. We discuss its relation with the present work in § 1.7.
Notation
Throughout the paper, unless otherwise stated, ![]() $R$ will denote a discrete valuation ring with field of fractions
$R$ will denote a discrete valuation ring with field of fractions ![]() $F$, uniformizer
$F$, uniformizer ![]() $\varpi$, and residue field
$\varpi$, and residue field ![]() $k$. Except where stated otherwise, we make no further hypotheses on
$k$. Except where stated otherwise, we make no further hypotheses on ![]() $R$ or
$R$ or ![]() $k$. We write
$k$. We write ![]() $p = \max (1, \mathrm {char}(k))$ for the characteristic exponent of
$p = \max (1, \mathrm {char}(k))$ for the characteristic exponent of ![]() $k$. We put
$k$. We put ![]() $S = \operatorname {Spec} R$ and denote by
$S = \operatorname {Spec} R$ and denote by ![]() $s$ its closed point. Let
$s$ its closed point. Let ![]() $R^{\mathrm {sh}}$ be a strict henselization of
$R^{\mathrm {sh}}$ be a strict henselization of ![]() $R$, and
$R$, and ![]() $F^{\mathrm {sh}}$ its field of fractions. Write
$F^{\mathrm {sh}}$ its field of fractions. Write ![]() $k^\mathrm {sep}$ for the residue field of
$k^\mathrm {sep}$ for the residue field of ![]() $R^{\mathrm {sh}}$ (a separable closure of
$R^{\mathrm {sh}}$ (a separable closure of ![]() $k$), and
$k$), and ![]() $\bar s$ for its spectrum. We write
$\bar s$ for its spectrum. We write ![]() $(Sm/S)$ for the category of essentially smooth
$(Sm/S)$ for the category of essentially smooth ![]() $S$-schemes, and
$S$-schemes, and ![]() $(Sm/S)_\mathrm {\acute et}$ for its étale site. For a scheme
$(Sm/S)_\mathrm {\acute et}$ for its étale site. For a scheme ![]() $X$, we write
$X$, we write ![]() $\kappa (x)$ for the residue field at a point
$\kappa (x)$ for the residue field at a point ![]() $x\in X$, and if
$x\in X$, and if ![]() $X$ is irreducible,
$X$ is irreducible, ![]() $\kappa (X)$ for the residue field of the generic point of
$\kappa (X)$ for the residue field of the generic point of ![]() $X$. All group schemes considered in this paper will be commutative. We frequently identify étale group schemes over a field with their associated Galois modules.
$X$. All group schemes considered in this paper will be commutative. We frequently identify étale group schemes over a field with their associated Galois modules.
If ![]() $S$ is a finite set we write
$S$ is a finite set we write ![]() $\mathbb {Z}[S]$ for the free abelian group on
$\mathbb {Z}[S]$ for the free abelian group on ![]() $S$ and
$S$ and ![]() $\mathbb {Z}[S]_0$ for the kernel of the degree map
$\mathbb {Z}[S]_0$ for the kernel of the degree map ![]() $\mathbb {Z}[S] \to \mathbb {Z}$,
$\mathbb {Z}[S] \to \mathbb {Z}$, ![]() $s \mapsto 1$ for
$s \mapsto 1$ for ![]() $s\in S$.
$s\in S$.
1. Néron models of generalized Jacobians
1.1 Preliminaries
In this section we collect together properties of Néron models and Weil restriction of scalars. Most of these may be found in [Reference Bosch, Lütkebohmert and RaynaudBLR90], especially Chapter 10.
Recall that if ![]() $G/F$ is a smooth group scheme of finite type, then a Néron model for
$G/F$ is a smooth group scheme of finite type, then a Néron model for ![]() $G$ is a smooth separated group scheme
$G$ is a smooth separated group scheme ![]() $\mathcal {G}/S$ with generic fibre
$\mathcal {G}/S$ with generic fibre ![]() $G$, such that for every smooth
$G$, such that for every smooth ![]() $S$-scheme
$S$-scheme ![]() $S'$, the canonical map
$S'$, the canonical map ![]() $\mathcal {G}(S') \to \mathcal {G}(S'_F)=G(S'_F)$ is bijective. If
$\mathcal {G}(S') \to \mathcal {G}(S'_F)=G(S'_F)$ is bijective. If ![]() $\mathcal {G}$ exists, it is unique up to unique isomorphism. (In [Reference Bosch, Lütkebohmert and RaynaudBLR90] these are called Néron lft-models.) The identity component
$\mathcal {G}$ exists, it is unique up to unique isomorphism. (In [Reference Bosch, Lütkebohmert and RaynaudBLR90] these are called Néron lft-models.) The identity component ![]() $\mathcal {G}^0$ of
$\mathcal {G}^0$ of ![]() $\mathcal {G}$ is a smooth group scheme of finite type. The formation of Néron models commutes with strict henselization and completion of the base ring
$\mathcal {G}$ is a smooth group scheme of finite type. The formation of Néron models commutes with strict henselization and completion of the base ring ![]() $R$. If
$R$. If ![]() $G \otimes _F \widehat {F}^{\mathrm {sh}}$ does not contain a copy of
$G \otimes _F \widehat {F}^{\mathrm {sh}}$ does not contain a copy of ![]() $\mathbb {G}_{\mathrm a}$, then
$\mathbb {G}_{\mathrm a}$, then ![]() $G$ has a Néron model [Reference Bosch, Lütkebohmert and RaynaudBLR90, 10.2 Thm.2]. (More generally, this holds if
$G$ has a Néron model [Reference Bosch, Lütkebohmert and RaynaudBLR90, 10.2 Thm.2]. (More generally, this holds if ![]() $S$ is merely a semilocal Dedekind scheme.) We write
$S$ is merely a semilocal Dedekind scheme.) We write ![]() $\Phi (G)$ for the component group
$\Phi (G)$ for the component group ![]() $(\mathcal {G}_s/\mathcal {G}_s^0)(k^\mathrm {sep})$. If
$(\mathcal {G}_s/\mathcal {G}_s^0)(k^\mathrm {sep})$. If ![]() $k$ is perfect, then by Chevalley's theorem [Reference ConradCon02]
$k$ is perfect, then by Chevalley's theorem [Reference ConradCon02] ![]() $\mathcal {G}_s$ has a unique maximal connected affine smooth subgroup scheme
$\mathcal {G}_s$ has a unique maximal connected affine smooth subgroup scheme ![]() $\mathcal {G}_s^{0,\mathrm {lin}}$, and we then write
$\mathcal {G}_s^{0,\mathrm {lin}}$, and we then write ![]() $\mathbb {X}(G)$ for the character group
$\mathbb {X}(G)$ for the character group ![]() $\operatorname {Hom}(\mathcal {G}_s^{0,\mathrm {lin}}\otimes _k\bar k,\mathbb {G}_{\mathrm {m}})$, a finite free
$\operatorname {Hom}(\mathcal {G}_s^{0,\mathrm {lin}}\otimes _k\bar k,\mathbb {G}_{\mathrm {m}})$, a finite free ![]() $\mathbb {Z}$-module with a continuous action of
$\mathbb {Z}$-module with a continuous action of ![]() $\operatorname {Gal}(\bar k/k)$.
$\operatorname {Gal}(\bar k/k)$.
Let ![]() $0 \to G_1 \to G_2 \to G_3 \to 0$ be an exact sequence of smooth connected
$0 \to G_1 \to G_2 \to G_3 \to 0$ be an exact sequence of smooth connected ![]() $F$-groups which have Néron models
$F$-groups which have Néron models ![]() $\mathcal {G}_i$. Consider the complexes
$\mathcal {G}_i$. Consider the complexes
The following two exactness results are a restatement of [Reference ChaiCha00, Remark (4.8)(a)], with the same proof, which we give for the reader's convenience.
Lemma 1.1 Suppose that the induced map ![]() $\mathcal {G}_2 \to \mathcal {G}_3$ is a surjection of sheaves for the smooth topology. Then:
$\mathcal {G}_2 \to \mathcal {G}_3$ is a surjection of sheaves for the smooth topology. Then:
Proof. (a) Since locally for the smooth topology the morphism ![]() $\mathcal {G}_2 \to \mathcal {G}_3$ of group schemes has a section, it is evidently surjective. Let
$\mathcal {G}_2 \to \mathcal {G}_3$ of group schemes has a section, it is evidently surjective. Let ![]() $\mathcal {G}'$ denote its kernel. By [Reference Liu and LorenziniLL01, Lemma 4.3(b)],
$\mathcal {G}'$ denote its kernel. By [Reference Liu and LorenziniLL01, Lemma 4.3(b)], ![]() $\mathcal {G}'$ is smooth. The canonical morphism
$\mathcal {G}'$ is smooth. The canonical morphism ![]() $\mathcal {G}_1 \to \mathcal {G}_2$ factors though a morphism
$\mathcal {G}_1 \to \mathcal {G}_2$ factors though a morphism ![]() $\gamma \colon \mathcal {G}_1 \to \mathcal {G}'$ which is the identity on generic fibres, and since
$\gamma \colon \mathcal {G}_1 \to \mathcal {G}'$ which is the identity on generic fibres, and since ![]() $\mathcal {G}_1$ is a Néron model, there is a morphism
$\mathcal {G}_1$ is a Néron model, there is a morphism ![]() $\delta \colon \mathcal {G}' \to \mathcal {G}_1$ which is the identity on generic fibres. As
$\delta \colon \mathcal {G}' \to \mathcal {G}_1$ which is the identity on generic fibres. As ![]() $\mathcal {G}_1$ and
$\mathcal {G}_1$ and ![]() $\mathcal {G}'$ are separated over
$\mathcal {G}'$ are separated over ![]() $S$,
$S$, ![]() $\gamma$ and
$\gamma$ and ![]() $\delta$ are mutually inverse isomorphisms.
$\delta$ are mutually inverse isomorphisms.
(b) The map ![]() $\mathcal {G}_2^0 \to \mathcal {G}_3^0$ is surjective, so we have an exact sequence
$\mathcal {G}_2^0 \to \mathcal {G}_3^0$ is surjective, so we have an exact sequence
in which each term is of finite type over ![]() $S$. Hence,
$S$. Hence, ![]() $\mathcal {G}_{1,s}^0$ has finite index in
$\mathcal {G}_{1,s}^0$ has finite index in ![]() $\mathcal {G}_{1,s} \cap \mathcal {G}_{2,s}^0$, and since
$\mathcal {G}_{1,s} \cap \mathcal {G}_{2,s}^0$, and since ![]() $\Phi (G_1)$ is torsion-free we have
$\Phi (G_1)$ is torsion-free we have ![]() $\mathcal {G}_1 \cap \mathcal {G}_2^0 = \mathcal {G}_1^0$. Thus, (1.1.2) and therefore also (1.1.3) are exact.
$\mathcal {G}_1 \cap \mathcal {G}_2^0 = \mathcal {G}_1^0$. Thus, (1.1.2) and therefore also (1.1.3) are exact.
Corollary 1.2 Suppose that ![]() $G_1$ is a product of tori of the form
$G_1$ is a product of tori of the form ![]() $\mathcal {R}_{F'/F} T$, where
$\mathcal {R}_{F'/F} T$, where ![]() $F'/F$ is finite separable,
$F'/F$ is finite separable, ![]() $T$ is an
$T$ is an ![]() $F'$-torus which splits over an unramified extension, and
$F'$-torus which splits over an unramified extension, and ![]() $\mathcal {R}_{F'/F}$ is Weil restriction of scalars. Then (1.1.1)–(1.1.3) are exact.
$\mathcal {R}_{F'/F}$ is Weil restriction of scalars. Then (1.1.1)–(1.1.3) are exact.
Proof. Replacing ![]() $R$ by
$R$ by ![]() $R^{\mathrm {sh}}$, we may assume that each
$R^{\mathrm {sh}}$, we may assume that each ![]() $T/F'$ is split. According to [Reference Bosch and XarlesBX96, 4.2], [Reference ChaiCha00, (4.5)], one then has
$T/F'$ is split. According to [Reference Bosch and XarlesBX96, 4.2], [Reference ChaiCha00, (4.5)], one then has ![]() $R^1j_{\mathrm {sm}\,*} G_1 = 0$, where
$R^1j_{\mathrm {sm}\,*} G_1 = 0$, where ![]() $j_\mathrm {sm} \colon (\operatorname {Spec} F )_\mathrm {sm} \to S_\mathrm {sm}$ is the inclusion of small smooth sites. Therefore,
$j_\mathrm {sm} \colon (\operatorname {Spec} F )_\mathrm {sm} \to S_\mathrm {sm}$ is the inclusion of small smooth sites. Therefore, ![]() $\mathcal {G}_2 \to \mathcal {G}_3$ is surjective as a map of sheaves on
$\mathcal {G}_2 \to \mathcal {G}_3$ is surjective as a map of sheaves on ![]() $S_\mathrm {sm}$. By Proposition 1.4(a) below,
$S_\mathrm {sm}$. By Proposition 1.4(a) below, ![]() $\Phi (G_1)$ is torsion-free, so everything follows from the lemma.
$\Phi (G_1)$ is torsion-free, so everything follows from the lemma.
We will need the following minor generalization of a result from [Reference Bosch, Lütkebohmert and RaynaudBLR90].
Proposition 1.3 Let
be an exact sequence of smooth ![]() $S$-group schemes. If
$S$-group schemes. If ![]() $\mathcal {G}_1$ and
$\mathcal {G}_1$ and ![]() $\mathcal {G}_3$ are the Néron models of their generic fibres, the same is true for
$\mathcal {G}_3$ are the Néron models of their generic fibres, the same is true for ![]() $\mathcal {G}_2$.
$\mathcal {G}_2$.
Proof. This follows by the same argument as in the proof of § 7.5, Proposition 1(b) in [Reference Bosch, Lütkebohmert and RaynaudBLR90] (middle of p. 185), using the criterion of § 10.1, Proposition 2.
From [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 7.6] we recall basic properties of Weil restriction. Let ![]() $Z'/Z$ be a finite flat morphism of finite presentation. If
$Z'/Z$ be a finite flat morphism of finite presentation. If ![]() $Y$ is a quasiprojective
$Y$ is a quasiprojective ![]() $Z'$-scheme, then the Weil restriction
$Z'$-scheme, then the Weil restriction ![]() $\mathcal {R}_{Z'/Z} Y$ exists, and is characterized by its functor of points
$\mathcal {R}_{Z'/Z} Y$ exists, and is characterized by its functor of points ![]() $\mathcal {R}_{Z'/Z}Y(-) = Y(- \times _Z Z')$. If
$\mathcal {R}_{Z'/Z}Y(-) = Y(- \times _Z Z')$. If ![]() $Y$ is smooth over
$Y$ is smooth over ![]() $Z'$, then
$Z'$, then ![]() $\mathcal {R}_{Z'/Z} Y$ is smooth over
$\mathcal {R}_{Z'/Z} Y$ is smooth over ![]() $Z$. If
$Z$. If ![]() $Y \to X$ is a closed immersion of quasiprojective
$Y \to X$ is a closed immersion of quasiprojective ![]() $Z'$-schemes, then
$Z'$-schemes, then ![]() $\mathcal {R}_{Z'/Z} Y \to \mathcal {R}_{Z'/Z} X$ is a closed immersion. If
$\mathcal {R}_{Z'/Z} Y \to \mathcal {R}_{Z'/Z} X$ is a closed immersion. If ![]() $Z' \to Z$ is surjective and
$Z' \to Z$ is surjective and ![]() $Y$ is a quasiprojective
$Y$ is a quasiprojective ![]() $Z$-scheme, then the canonical map
$Z$-scheme, then the canonical map ![]() $Y \to \mathcal {R}_{Z'/Z} (Y \times _Z Z')$ is a closed immersion.
$Y \to \mathcal {R}_{Z'/Z} (Y \times _Z Z')$ is a closed immersion.
Now let ![]() $k$ be a field,
$k$ be a field, ![]() $k'$ a finite
$k'$ a finite ![]() $k$-algebra, and
$k$-algebra, and ![]() $k''$ a finite flat
$k''$ a finite flat ![]() $k'$-algebra. Let
$k'$-algebra. Let ![]() $Y$ be a quasiprojective
$Y$ be a quasiprojective ![]() $k$-scheme. There is then a canonical map
$k$-scheme. There is then a canonical map
We may write ![]() $k' = k_1' \times k_2'$ where
$k' = k_1' \times k_2'$ where ![]() $\operatorname {Spec} k_1'\subset \operatorname {Spec} k'$ is the image of
$\operatorname {Spec} k_1'\subset \operatorname {Spec} k'$ is the image of ![]() $\operatorname {Spec} k''$ (and
$\operatorname {Spec} k''$ (and ![]() $k_2'$ is possibly zero). The morphism
$k_2'$ is possibly zero). The morphism ![]() $g$ then factors
$g$ then factors
 \begin{align*} \mathcal{R}_{k'/k} (Y
\otimes_k k' ) &= \mathcal{R}_{k_1'/k} (Y \otimes_k k_1' )
\times_{\operatorname{Spec} k} \mathcal{R}_{k_2'/k} (Y
\otimes_k k_2') \\ &\xrightarrow{\mathrm{pr}_1}\mathcal{R}_{k_1'/k} (Y \otimes_k k_1' ) \to
\mathcal{R}_{k_1'/k} \mathcal{R}_{k''/k_1'} (Y \otimes_k
k'' ) = \mathcal{R}_{k''/k} (Y \otimes_k k'' )
\end{align*}
\begin{align*} \mathcal{R}_{k'/k} (Y
\otimes_k k' ) &= \mathcal{R}_{k_1'/k} (Y \otimes_k k_1' )
\times_{\operatorname{Spec} k} \mathcal{R}_{k_2'/k} (Y
\otimes_k k_2') \\ &\xrightarrow{\mathrm{pr}_1}\mathcal{R}_{k_1'/k} (Y \otimes_k k_1' ) \to
\mathcal{R}_{k_1'/k} \mathcal{R}_{k''/k_1'} (Y \otimes_k
k'' ) = \mathcal{R}_{k''/k} (Y \otimes_k k'' )
\end{align*}
and the second arrow is a closed immersion. In particular, if ![]() $Y$ is a smooth
$Y$ is a smooth ![]() $k$-group, then
$k$-group, then ![]() $g$ is a surjection onto a closed subgroup scheme, and its cokernel is smooth.
$g$ is a surjection onto a closed subgroup scheme, and its cokernel is smooth.
Let ![]() $k$ be a field and
$k$ be a field and ![]() $k'$ a finite
$k'$ a finite ![]() $k$-algebra. Then
$k$-algebra. Then ![]() $\mathcal {R}_{k'/k}\mathbb {G}_{\mathrm {m}}$ is a connected smooth
$\mathcal {R}_{k'/k}\mathbb {G}_{\mathrm {m}}$ is a connected smooth ![]() $k$-group scheme of finite type. It is a torus if and only if
$k$-group scheme of finite type. It is a torus if and only if ![]() $k'/k$ is étale.
$k'/k$ is étale.
We return to Néron models. Recall that the multiplicative group ![]() $\mathbb {G}_{\mathrm {m}}/F$ has a Néron model
$\mathbb {G}_{\mathrm {m}}/F$ has a Néron model ![]() $\mathcal {G}_\mathrm {m} /S$, whose special fibre is
$\mathcal {G}_\mathrm {m} /S$, whose special fibre is ![]() $\mathbb {G}_{\mathrm {m}} \times \mathbb {Z}$. It fits into an exact sequence of group schemes
$\mathbb {G}_{\mathrm {m}} \times \mathbb {Z}$. It fits into an exact sequence of group schemes
where on ![]() $R$-points
$R$-points ![]() $v_F$ is the normalized valuation
$v_F$ is the normalized valuation ![]() $v_F \colon \mathcal {G}_\mathrm {m} (R) = F^\times \to \mkern -15mu\to \mathbb {Z}$.
$v_F \colon \mathcal {G}_\mathrm {m} (R) = F^\times \to \mkern -15mu\to \mathbb {Z}$.
Let ![]() $F'$ be a finite étale
$F'$ be a finite étale ![]() $F$-algebra,
$F$-algebra, ![]() $R' \subset F'$ the normalization of
$R' \subset F'$ the normalization of ![]() $R$ in
$R$ in ![]() $F'$,
$F'$, ![]() $S' = \operatorname {Spec} R'$. Let
$S' = \operatorname {Spec} R'$. Let ![]() $F' \otimes _F F^{\mathrm {sh}} = \prod _{i\in I} F_i$, where the fields
$F' \otimes _F F^{\mathrm {sh}} = \prod _{i\in I} F_i$, where the fields ![]() $F_i$ are totally ramified extensions of
$F_i$ are totally ramified extensions of ![]() $F^{\mathrm {sh}}$, of degrees
$F^{\mathrm {sh}}$, of degrees ![]() $e_i p^{s_i}$, where
$e_i p^{s_i}$, where ![]() $p^{s_i}$ is the degree of the (purely inseparable) residue class extension.
$p^{s_i}$ is the degree of the (purely inseparable) residue class extension.
Proposition 1.4
(a) The Néron model of
 $\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}}$ is
$\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}}$ is  $\mathcal {R}_{S'/S}\mathcal {G}_\mathrm {m}$, and the product of the valuations
(1.1.4)induces an isomorphism
$\mathcal {R}_{S'/S}\mathcal {G}_\mathrm {m}$, and the product of the valuations
(1.1.4)induces an isomorphism \begin{equation} \mathcal{R}_{S'/S}\mathcal{G}_\mathrm{m}(F^{\mathrm{sh}})=\prod_{i\in I} F_i^\times \xrightarrow{(v_{F_i})} \mathbb{Z}^I \end{equation}(1.1.5)
\begin{equation} \mathcal{R}_{S'/S}\mathcal{G}_\mathrm{m}(F^{\mathrm{sh}})=\prod_{i\in I} F_i^\times \xrightarrow{(v_{F_i})} \mathbb{Z}^I \end{equation}(1.1.5) \begin{equation} \Phi(\mathcal{R}_{F'/F}\mathbb{G}_{\mathrm{m}})=\pi_0((\mathcal{R}_{S'/S}\mathcal{G}_\mathrm{m})_s) \xrightarrow{\ \sim\ } \mathbb{Z}^I. \end{equation}
\begin{equation} \Phi(\mathcal{R}_{F'/F}\mathbb{G}_{\mathrm{m}})=\pi_0((\mathcal{R}_{S'/S}\mathcal{G}_\mathrm{m})_s) \xrightarrow{\ \sim\ } \mathbb{Z}^I. \end{equation}(b) The adjunction map
 $\mathcal {G}_\mathrm {m} \to \mathcal {R}_{S'/S}\mathcal {G}_\mathrm {m}$ is a closed immersion, and its cokernel is the Néron model of
$\mathcal {G}_\mathrm {m} \to \mathcal {R}_{S'/S}\mathcal {G}_\mathrm {m}$ is a closed immersion, and its cokernel is the Néron model of  $(\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})/\mathbb {G}_{\mathrm {m}}$, inducing a isomorphism
$(\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})/\mathbb {G}_{\mathrm {m}}$, inducing a isomorphism
 \[ \Phi((\mathcal{R}_{F'/F}\mathbb{G}_{\mathrm{m}})/\mathbb{G}_{\mathrm{m}}) \xrightarrow{\ \sim\ } \operatorname{coker}(e=(e_i)\colon \mathbb{Z}\to\mathbb{Z}^I). \]
\[ \Phi((\mathcal{R}_{F'/F}\mathbb{G}_{\mathrm{m}})/\mathbb{G}_{\mathrm{m}}) \xrightarrow{\ \sim\ } \operatorname{coker}(e=(e_i)\colon \mathbb{Z}\to\mathbb{Z}^I). \]
Here we use ![]() $\mathcal {G}_\mathrm {m}$ to denote also the Néron model of
$\mathcal {G}_\mathrm {m}$ to denote also the Néron model of ![]() $\mathbb {G}_{\mathrm {m}}$ over the semilocal base
$\mathbb {G}_{\mathrm {m}}$ over the semilocal base ![]() $S'$.
$S'$.
Proof. (a) The first statement follows from [Reference Bosch, Lütkebohmert and RaynaudBLR90, Propositions 10.1/4 and 6]. For the second, replacing ![]() $F$ by
$F$ by ![]() $F^{\mathrm {sh}}$ we are reduced to the case of a totally ramified field extension
$F^{\mathrm {sh}}$ we are reduced to the case of a totally ramified field extension ![]() $F'/F$. Then as
$F'/F$. Then as ![]() $\mathcal {G}_{{\mathrm m},s}\simeq \mathbb {G}_{\mathrm m,s}\times \mathbb {Z}$, we have
$\mathcal {G}_{{\mathrm m},s}\simeq \mathbb {G}_{\mathrm m,s}\times \mathbb {Z}$, we have ![]() $(\mathcal {R}_{S'/S}\mathcal {G}_\mathrm {m})_s = \mathcal {R}_{R'\otimes k/k}\mathbb {G}_{\mathrm {m}} \times \mathcal {R}_{R'\otimes k/k}\mathbb {Z}$. As the first factor is connected, and the second is
$(\mathcal {R}_{S'/S}\mathcal {G}_\mathrm {m})_s = \mathcal {R}_{R'\otimes k/k}\mathbb {G}_{\mathrm {m}} \times \mathcal {R}_{R'\otimes k/k}\mathbb {Z}$. As the first factor is connected, and the second is ![]() $\mathbb {Z}$ (since
$\mathbb {Z}$ (since ![]() $R'\otimes k/k$ is radicial) we get
$R'\otimes k/k$ is radicial) we get ![]() $\Phi (\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})\simeq \mathbb {Z}$, and the fact that this isomorphism is given by the valuation follows from [Reference Bosch, Lütkebohmert and RaynaudBLR90, 1.1/Proposition 7].
$\Phi (\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})\simeq \mathbb {Z}$, and the fact that this isomorphism is given by the valuation follows from [Reference Bosch, Lütkebohmert and RaynaudBLR90, 1.1/Proposition 7].
(b) By Corollary 1.2, the exact sequence ![]() $0\to \mathbb {G}_{\mathrm {m}}\to \mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}} \to (\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})/\mathbb {G}_{\mathrm {m}}\to 0$ gives rise to exact sequences of Néron models and component groups. It is therefore enough to show that the map
$0\to \mathbb {G}_{\mathrm {m}}\to \mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}} \to (\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})/\mathbb {G}_{\mathrm {m}}\to 0$ gives rise to exact sequences of Néron models and component groups. It is therefore enough to show that the map ![]() $\Phi (\mathbb {G}_{\mathrm {m}})=\mathbb {Z} \to \Phi (\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})=\mathbb {Z}^I$ is equal to
$\Phi (\mathbb {G}_{\mathrm {m}})=\mathbb {Z} \to \Phi (\mathcal {R}_{F'/F}\mathbb {G}_{\mathrm {m}})=\mathbb {Z}^I$ is equal to ![]() $e$. Replacing
$e$. Replacing ![]() $F$ by
$F$ by ![]() $F^{\mathrm {sh}}$ again, we are reduced to the case when
$F^{\mathrm {sh}}$ again, we are reduced to the case when ![]() $F'/F$ is a totally ramified field extension of degree
$F'/F$ is a totally ramified field extension of degree ![]() $ep^s$ with residue degree
$ep^s$ with residue degree ![]() $p^s$. Then by part (a) we have a commutative square
$p^s$. Then by part (a) we have a commutative square

proving the result.
1.2 Graphs and Picard schemes of singular curves
In this section we work over an arbitrary field ![]() $k$. By a curve over
$k$. By a curve over ![]() $k$ we shall mean a
$k$ we shall mean a ![]() $k$-scheme
$k$-scheme ![]() $X$ of finite type which is equidimensional of dimension 1 and Cohen–Macaulay (i.e. has no embedded points). Let
$X$ of finite type which is equidimensional of dimension 1 and Cohen–Macaulay (i.e. has no embedded points). Let ![]() $\{X_j\}$ be the irreducible components of
$\{X_j\}$ be the irreducible components of ![]() $X$, and
$X$, and ![]() $\eta _j$ the generic point of
$\eta _j$ the generic point of ![]() $X_j$. The local ring
$X_j$. The local ring ![]() $\mathcal {O}_{X,\eta _j}$ is Artinian, and following Raynaud [Reference RaynaudRay70, (6.1.1) and (8.1.1)] we write
$\mathcal {O}_{X,\eta _j}$ is Artinian, and following Raynaud [Reference RaynaudRay70, (6.1.1) and (8.1.1)] we write ![]() $d_j$ for its length, and
$d_j$ for its length, and ![]() $\delta _j$ for the total multiplicity of
$\delta _j$ for the total multiplicity of ![]() $X_j$ in
$X_j$ in ![]() $X$. If
$X$. If ![]() $k'/k$ is a radicial closure of
$k'/k$ is a radicial closure of ![]() $k$, and
$k$, and ![]() $\eta '_j\in X\otimes k'$ is the point lying over
$\eta '_j\in X\otimes k'$ is the point lying over ![]() $\eta _j$, then
$\eta _j$, then ![]() $\delta _j$ equals the length of the local ring of
$\delta _j$ equals the length of the local ring of ![]() $\eta '_j$. Moreover,
$\eta '_j$. Moreover, ![]() $\delta _j = d_j[\kappa (\eta _j)\cap k' : k]=d_jp^{n_j}$ for some
$\delta _j = d_j[\kappa (\eta _j)\cap k' : k]=d_jp^{n_j}$ for some ![]() $n_j\ge 0$.
$n_j\ge 0$.
Until the end of this section, ![]() $k$ denotes an algebraically closed field. We review the well-known description of the toric part of the Picard scheme of a singular curve over
$k$ denotes an algebraically closed field. We review the well-known description of the toric part of the Picard scheme of a singular curve over ![]() $k$.
$k$.
Let ![]() $Y/k$ be a reduced proper curve, and
$Y/k$ be a reduced proper curve, and ![]() $Y^\mathrm {sing}\subset Y(k)$ its set of singular points. Write
$Y^\mathrm {sing}\subset Y(k)$ its set of singular points. Write ![]() $\phi \colon \widetilde Y \to Y$ for its normalization. Define sets
$\phi \colon \widetilde Y \to Y$ for its normalization. Define sets
We have maps
where ![]() $\psi$ maps
$\psi$ maps ![]() $x\in B$ to the connected component of
$x\in B$ to the connected component of ![]() $\widetilde Y$ containing it.
$\widetilde Y$ containing it.
The extended graph ![]() $\widetilde{\Gamma} _Y = (\widetilde V,\widetilde E)$ of
$\widetilde{\Gamma} _Y = (\widetilde V,\widetilde E)$ of ![]() $Y$ is the graph with vertices
$Y$ is the graph with vertices ![]() $\widetilde V$ and edges
$\widetilde V$ and edges ![]() $\widetilde E$, where:
$\widetilde E$, where:
–
 $\widetilde V= A\sqcup C$,
$\widetilde V= A\sqcup C$,  $\widetilde E = B$;
$\widetilde E = B$;– the endpoints of an edge
 $b\in B$ are
$b\in B$ are  $\phi (b)\in A$ and
$\phi (b)\in A$ and  $\psi (b)\in C$.
$\psi (b)\in C$.
The graph ![]() $\widetilde{\Gamma} _Y$ is bipartite, and therefore has a canonical structure of directed graph, by directing the edge
$\widetilde{\Gamma} _Y$ is bipartite, and therefore has a canonical structure of directed graph, by directing the edge ![]() $b$ so that its source is
$b$ so that its source is ![]() $\phi (b)$.
$\phi (b)$.
Suppose ![]() $Y$ only has double points (meaning that if
$Y$ only has double points (meaning that if ![]() $y\in Y^\mathrm {sing}$ then
$y\in Y^\mathrm {sing}$ then ![]() $\phi ^{-1}(y)$ has exactly two elements). The reduced graph
$\phi ^{-1}(y)$ has exactly two elements). The reduced graph ![]() $\Gamma _Y=(V,E)$ is the undirected graph (possibly with multiple edges and loops) whose vertex set is
$\Gamma _Y=(V,E)$ is the undirected graph (possibly with multiple edges and loops) whose vertex set is ![]() $V=\pi _0(\widetilde Y)$ and edge set is
$V=\pi _0(\widetilde Y)$ and edge set is ![]() $E=Y^\mathrm {sing}$. It is obtained from
$E=Y^\mathrm {sing}$. It is obtained from ![]() $\tilde \Gamma _Y$ by, for each vertex
$\tilde \Gamma _Y$ by, for each vertex ![]() $v\in A$, deleting
$v\in A$, deleting ![]() $v$ and replacing the two edges incident to
$v$ and replacing the two edges incident to ![]() $v$ with a single edge. There is a canonical homeomorphism between the geometric realizations of
$v$ with a single edge. There is a canonical homeomorphism between the geometric realizations of ![]() $\widetilde{\Gamma} _Y$ and
$\widetilde{\Gamma} _Y$ and ![]() $\Gamma _Y$, under which
$\Gamma _Y$, under which ![]() $v\in A$ is mapped to the midpoint of the replacing edge. If
$v\in A$ is mapped to the midpoint of the replacing edge. If ![]() $Y/k$ is a proper curve, not necessarily reduced, we define
$Y/k$ is a proper curve, not necessarily reduced, we define ![]() $\widetilde{\Gamma} _Y=\widetilde{\Gamma} _{Y^\mathrm {red}}$,
$\widetilde{\Gamma} _Y=\widetilde{\Gamma} _{Y^\mathrm {red}}$, ![]() $\Gamma _Y=\Gamma _{Y^\mathrm {red}}$, where
$\Gamma _Y=\Gamma _{Y^\mathrm {red}}$, where ![]() $Y^\mathrm {red}\subset Y$ is the reduced subscheme.
$Y^\mathrm {red}\subset Y$ is the reduced subscheme.
Let ![]() $G=\operatorname {Pic}^0_Y$ be the identity component of the Picard scheme of
$G=\operatorname {Pic}^0_Y$ be the identity component of the Picard scheme of ![]() $Y$. It is a smooth group scheme of finite type over
$Y$. It is a smooth group scheme of finite type over ![]() $k$, classifying line bundles on
$k$, classifying line bundles on ![]() $Y$ whose restriction to each irreducible component has degree zero. The filtration of
$Y$ whose restriction to each irreducible component has degree zero. The filtration of ![]() $G$ by its linear and unipotent subgroups is described as follows.
$G$ by its linear and unipotent subgroups is described as follows.
Let ![]() $Y'\to Y$ be the ‘seminormalization’ of
$Y'\to Y$ be the ‘seminormalization’ of ![]() $Y$, which is obtained from
$Y$, which is obtained from ![]() $Y$ by replacing its singularities with singularities which are étale locally isomorphic to the union of coordinate axes in
$Y$ by replacing its singularities with singularities which are étale locally isomorphic to the union of coordinate axes in ![]() $\mathbb {A}^N_k$. The normalization map factors into a pair of finite morphisms
$\mathbb {A}^N_k$. The normalization map factors into a pair of finite morphisms ![]() $\widetilde Y \overset {\phi '}\to Y' \to Y$. These give rise to a commutative diagram, whose rows are exact:
$\widetilde Y \overset {\phi '}\to Y' \to Y$. These give rise to a commutative diagram, whose rows are exact:

(where ![]() $G^\mathrm {unip}$ is the maximal connected unipotent subgroup of
$G^\mathrm {unip}$ is the maximal connected unipotent subgroup of ![]() $G$) giving an isomorphism
$G$) giving an isomorphism ![]() $\ker \phi ^{\prime *}\simeq G^\mathrm {tor}=G^\mathrm {lin}/G^\mathrm {unip}$ by the snake lemma.
$\ker \phi ^{\prime *}\simeq G^\mathrm {tor}=G^\mathrm {lin}/G^\mathrm {unip}$ by the snake lemma.
To give a line bundle on ![]() $Y'$ is equivalent to giving a line bundle on
$Y'$ is equivalent to giving a line bundle on ![]() $\widetilde Y$ together with descent data for
$\widetilde Y$ together with descent data for ![]() $\phi '\colon \widetilde Y\to Y'$, so the toric part
$\phi '\colon \widetilde Y\to Y'$, so the toric part ![]() $G^\mathrm {tor}$ classifies trivial line bundles on
$G^\mathrm {tor}$ classifies trivial line bundles on ![]() $\widetilde Y$ equipped with descent data to
$\widetilde Y$ equipped with descent data to ![]() $Y'$. For the trivial bundle
$Y'$. For the trivial bundle ![]() $\mathcal {O}_{\widetilde Y}$, to give such descent data is equivalent to giving, for each singular point
$\mathcal {O}_{\widetilde Y}$, to give such descent data is equivalent to giving, for each singular point ![]() $y\in Y$, an element of
$y\in Y$, an element of ![]() $(k^\times )^{\phi ^{-1}(y)}/k^\times$. The automorphism group of
$(k^\times )^{\phi ^{-1}(y)}/k^\times$. The automorphism group of ![]() $\mathcal {O}_{\widetilde Y}$ is
$\mathcal {O}_{\widetilde Y}$ is ![]() $(k^\times )^{\pi _0(\widetilde Y)}$. Hence,
$(k^\times )^{\pi _0(\widetilde Y)}$. Hence, ![]() $G^\mathrm {tor}$ is canonically
$G^\mathrm {tor}$ is canonically
Here ![]() $\mathbb {G}_{\mathrm {m}}^{\pi _0(\widetilde Y)}$ acts on
$\mathbb {G}_{\mathrm {m}}^{\pi _0(\widetilde Y)}$ acts on ![]() $\mathbb {G}_{\mathrm {m}}^{\phi ^{-1}(y)}$ by the dual of the map
$\mathbb {G}_{\mathrm {m}}^{\phi ^{-1}(y)}$ by the dual of the map ![]() $\phi ^{-1}(y)\subset \widetilde Y(k)\overset \psi \to \pi _0(Y)$ associating to
$\phi ^{-1}(y)\subset \widetilde Y(k)\overset \psi \to \pi _0(Y)$ associating to ![]() $x\in \widetilde Y$ the connected component of
$x\in \widetilde Y$ the connected component of ![]() $\widetilde Y$ containing it. The character group of
$\widetilde Y$ containing it. The character group of ![]() $G^\mathrm {tor}$ is therefore the kernel of the map
$G^\mathrm {tor}$ is therefore the kernel of the map
which (after replacing ![]() $\phi$ with
$\phi$ with ![]() $-\phi$) is the chain complex of
$-\phi$) is the chain complex of ![]() $\widetilde{\Gamma} _Y$. This gives the formula [Reference Deligne and RapoportDR73, I.3]
$\widetilde{\Gamma} _Y$. This gives the formula [Reference Deligne and RapoportDR73, I.3]
Suppose now that ![]() $Y$ is a proper curve over
$Y$ is a proper curve over ![]() $k$, not necessarily reduced. The map
$k$, not necessarily reduced. The map ![]() $\operatorname {Pic}^0_Y \to \operatorname {Pic}^0_{Y^\mathrm {red}}$ is an epimorphism, and its kernel is a connected unipotent group scheme, so (1.2.1) remains valid.
$\operatorname {Pic}^0_Y \to \operatorname {Pic}^0_{Y^\mathrm {red}}$ is an epimorphism, and its kernel is a connected unipotent group scheme, so (1.2.1) remains valid.
If ![]() $k$ is merely assumed to be perfect, (1.2.1) holds as an isomorphism of
$k$ is merely assumed to be perfect, (1.2.1) holds as an isomorphism of ![]() $\operatorname {Gal}(\bar k/k)$-modules.
$\operatorname {Gal}(\bar k/k)$-modules.
If ![]() $Y$ only has double points with distinct branches, then by the homeomorphism
$Y$ only has double points with distinct branches, then by the homeomorphism ![]() $\widetilde{\Gamma} _Y\to \Gamma _Y$ we obtain the formula
$\widetilde{\Gamma} _Y\to \Gamma _Y$ we obtain the formula
1.3 The Néron model of  $J$
$J$
In preparation for § 1.6, we review in more detail the results of Raynaud. We will follow mainly the notation of [Reference RaynaudRay70] (see also [Reference Bosch, Lütkebohmert and RaynaudBLR90], where the notation is slightly different).
We consider a proper flat morphism ![]() $\mathcal {X} \to S=\operatorname {Spec} R$, satisfying the following hypotheses (H1)–(H3).
$\mathcal {X} \to S=\operatorname {Spec} R$, satisfying the following hypotheses (H1)–(H3).
(H1) The generic fibre
 $X := \mathcal {X}_F$ is a smooth geometrically connected curve over
$X := \mathcal {X}_F$ is a smooth geometrically connected curve over  $F$ (in particular,
$F$ (in particular,  $\Gamma (\mathcal {X},\mathcal {O}_\mathcal {X})=R$).
$\Gamma (\mathcal {X},\mathcal {O}_\mathcal {X})=R$).(H2) The scheme
 $\mathcal {X}$ is regular.
$\mathcal {X}$ is regular.
Let the irreducible components of ![]() $\mathcal {X}_s$ be indexed by the set
$\mathcal {X}_s$ be indexed by the set ![]() $C$, and for
$C$, and for ![]() $j\in C$, let
$j\in C$, let ![]() $\mathcal {X}_j\subset \mathcal {X}_s$ be the scheme-theoretic closure of the corresponding maximal point of
$\mathcal {X}_j\subset \mathcal {X}_s$ be the scheme-theoretic closure of the corresponding maximal point of ![]() $\mathcal {X}_s$,
$\mathcal {X}_s$, ![]() $\delta _j=p^{n_j}d_j$ its total multiplicity (§ 1.2), and
$\delta _j=p^{n_j}d_j$ its total multiplicity (§ 1.2), and ![]() $Y_j= \mathcal {X}_j^\mathrm {red}$. Define
$Y_j= \mathcal {X}_j^\mathrm {red}$. Define ![]() $\delta =\gcd \{\delta _j\}$,
$\delta =\gcd \{\delta _j\}$, ![]() $d=\gcd \{d_j\}$.
$d=\gcd \{d_j\}$.
(H3) We have
 $(\delta,p)=1$.
$(\delta,p)=1$.
Hypotheses (H1) and (H2) imply that Raynaud's condition ![]() $(\mathrm N)^*$ is satisfied [Reference RaynaudRay70, (6.1.4)]. Hypothesis (H1) is not particularly restrictive, since one may always reduce to this case using Stein factorization. In the presence of hypotheses (H1) and (H2), hypothesis (H3) implies that
$(\mathrm N)^*$ is satisfied [Reference RaynaudRay70, (6.1.4)]. Hypothesis (H1) is not particularly restrictive, since one may always reduce to this case using Stein factorization. In the presence of hypotheses (H1) and (H2), hypothesis (H3) implies that ![]() $\mathcal {X}/S$ is cohomologically flat (equivalently, that
$\mathcal {X}/S$ is cohomologically flat (equivalently, that ![]() $\Gamma (\mathcal {X}_s,\mathcal {O}_{\mathcal {X}_s})=k$), by [Reference RaynaudRay70, (7.2.1)].
$\Gamma (\mathcal {X}_s,\mathcal {O}_{\mathcal {X}_s})=k$), by [Reference RaynaudRay70, (7.2.1)].
Let ![]() $J=\operatorname {Pic}^0_{X/F}$ be the Jacobian variety of
$J=\operatorname {Pic}^0_{X/F}$ be the Jacobian variety of ![]() $X$, and let
$X$, and let ![]() $\mathcal {J}$ be the Néron model of
$\mathcal {J}$ be the Néron model of ![]() $J$.
$J$.
The relative Picard functor ![]() $P=\operatorname {Pic}_{\mathcal {X}/S}$ is the sheafification (for the fppf topology) of the functor on the category of
$P=\operatorname {Pic}_{\mathcal {X}/S}$ is the sheafification (for the fppf topology) of the functor on the category of ![]() $S$-schemes
$S$-schemes
There is a morphism of abelian sheaves ![]() $\deg \colon P \to \mathbb {Z}$ which takes a line bundle to its total degree along the fibres, and
$\deg \colon P \to \mathbb {Z}$ which takes a line bundle to its total degree along the fibres, and ![]() $P'\subset P$ denotes its kernel. By [Reference RaynaudRay70, (5.2) and (2.3.2)],
$P'\subset P$ denotes its kernel. By [Reference RaynaudRay70, (5.2) and (2.3.2)], ![]() $P$ and
$P$ and ![]() $P'$ are formally smooth algebraic spaces over
$P'$ are formally smooth algebraic spaces over ![]() $S$, and the closure
$S$, and the closure ![]() $E\subset P$ of the zero section is an étale algebraic space over
$E\subset P$ of the zero section is an étale algebraic space over ![]() $S$, contained in
$S$, contained in ![]() $P'$. The maximal separated quotient
$P'$. The maximal separated quotient ![]() $Q=P/E$ is a smooth separated
$Q=P/E$ is a smooth separated ![]() $S$-group scheme, and the subgroup
$S$-group scheme, and the subgroup ![]() $Q'=P'/E$ is the closure in
$Q'=P'/E$ is the closure in ![]() $Q$ of the identity component
$Q$ of the identity component ![]() $Q^0$ (proof of [Reference RaynaudRay70, (8.1.2)(iii)]). One also has the subgroup
$Q^0$ (proof of [Reference RaynaudRay70, (8.1.2)(iii)]). One also has the subgroup ![]() $Q^\tau \subset Q$, which is the inverse image of the torsion subgroup of
$Q^\tau \subset Q$, which is the inverse image of the torsion subgroup of ![]() $Q/Q^0$. As
$Q/Q^0$. As ![]() $\mathcal {X}$ is regular, condition d) of [Reference RaynaudRay70, (8.1.2)] holds, and so
$\mathcal {X}$ is regular, condition d) of [Reference RaynaudRay70, (8.1.2)] holds, and so ![]() $Q^\tau$ is closed in
$Q^\tau$ is closed in ![]() $Q$. By definition
$Q$. By definition ![]() $\deg (Q^\tau )=0$, and therefore
$\deg (Q^\tau )=0$, and therefore ![]() $Q'=Q^\tau$. Therefore, [Reference RaynaudRay70, (8.1.2) and (8.1.4)(b)] imply that
$Q'=Q^\tau$. Therefore, [Reference RaynaudRay70, (8.1.2) and (8.1.4)(b)] imply that ![]() $\mathcal {J}=Q'=P'/E$.
$\mathcal {J}=Q'=P'/E$.
(If hypothesis (H3) is not satisfied, then ![]() $P$ is in general not representable, but it still has a maximal separated quotient
$P$ is in general not representable, but it still has a maximal separated quotient ![]() $Q$ which is a smooth separated
$Q$ which is a smooth separated ![]() $S$-group scheme [Reference RaynaudRay70, (4.1.1)]. If moreover
$S$-group scheme [Reference RaynaudRay70, (4.1.1)]. If moreover ![]() $k$ is perfect, then
$k$ is perfect, then ![]() $Q'$ again equals
$Q'$ again equals ![]() $\mathcal {J}$ (see [Reference RaynaudRay70, (8.1.4)(a)]).)
$\mathcal {J}$ (see [Reference RaynaudRay70, (8.1.4)(a)]).)
Let ![]() $P_s^0$ be the identity component of
$P_s^0$ be the identity component of ![]() $P_s$. We have
$P_s$. We have ![]() $P_s^0=\operatorname {Pic}^0_{\mathcal {X}_s/k}$, the identity component of the Picard scheme of
$P_s^0=\operatorname {Pic}^0_{\mathcal {X}_s/k}$, the identity component of the Picard scheme of ![]() $\mathcal {X}_s$. By [Reference RaynaudRay70, (6.4.1)(3)], the intersection
$\mathcal {X}_s$. By [Reference RaynaudRay70, (6.4.1)(3)], the intersection ![]() $P^0_s\cap E_s$ is a constant group scheme over
$P^0_s\cap E_s$ is a constant group scheme over ![]() $k$, cyclic of order
$k$, cyclic of order ![]() $d$, generated by the class of the line bundle
$d$, generated by the class of the line bundle ![]() $\mathcal {L}'=\mathcal {O}(\sum _j(d_j/d)Y_j)$. (Because
$\mathcal {L}'=\mathcal {O}(\sum _j(d_j/d)Y_j)$. (Because ![]() $\mathcal {X}$ is regular, the integers
$\mathcal {X}$ is regular, the integers ![]() $d$ and
$d$ and ![]() $d'$ (see [Reference RaynaudRay70, (6.1.11)(3)]) are equal.) Therefore,
$d'$ (see [Reference RaynaudRay70, (6.1.11)(3)]) are equal.) Therefore, ![]() $\mathcal {J}_s^0$ is canonically isomorphic to
$\mathcal {J}_s^0$ is canonically isomorphic to ![]() $\operatorname {Pic}^0_{\mathcal {X}_s/k}/\langle \mathcal {L}'\rangle$ and, in particular, if
$\operatorname {Pic}^0_{\mathcal {X}_s/k}/\langle \mathcal {L}'\rangle$ and, in particular, if ![]() $d=1$, then
$d=1$, then ![]() $\mathcal {J}_s^0=\operatorname {Pic}^0_{\mathcal {X}_s/k}$.
$\mathcal {J}_s^0=\operatorname {Pic}^0_{\mathcal {X}_s/k}$.
Suppose that ![]() $k$ is perfect and
$k$ is perfect and ![]() $d=1$. Combining the above with the discussion in § 2.2, we then have an isomorphism of
$d=1$. Combining the above with the discussion in § 2.2, we then have an isomorphism of ![]() $\operatorname {Gal}(\bar k/k)$-modules
$\operatorname {Gal}(\bar k/k)$-modules
Finally, we recall the description of the component group. First suppose that ![]() $R$ is strictly Henselian (
$R$ is strictly Henselian (![]() $k$ not necessarily perfect). Then [Reference RaynaudRay70, (8.1.2)] shows that the component group
$k$ not necessarily perfect). Then [Reference RaynaudRay70, (8.1.2)] shows that the component group ![]() $\Phi (J)=\mathcal {J}_s/\mathcal {J}_s^0$ is computed as follows: by the above,
$\Phi (J)=\mathcal {J}_s/\mathcal {J}_s^0$ is computed as follows: by the above, ![]() $\Phi (J)= Q'_s/Q^0_s$ is the cokernel of the map
$\Phi (J)= Q'_s/Q^0_s$ is the cokernel of the map
One has an isomorphism
Let ![]() $D\subset \operatorname {Div}\mathcal {X}$ be the group of Cartier divisors supported in the special fibre, and
$D\subset \operatorname {Div}\mathcal {X}$ be the group of Cartier divisors supported in the special fibre, and ![]() $D_0\subset D$ the subgroup of principal divisors. By [Reference RaynaudRay70, (6.1.3)] one has
$D_0\subset D$ the subgroup of principal divisors. By [Reference RaynaudRay70, (6.1.3)] one has ![]() $E_s=D/D_0$. As
$E_s=D/D_0$. As ![]() $\mathcal {X}$ is regular and
$\mathcal {X}$ is regular and ![]() $R=\Gamma (\mathcal {X},\mathcal {O}_\mathcal {X})$,
$R=\Gamma (\mathcal {X},\mathcal {O}_\mathcal {X})$, ![]() $D$ is freely generated by the set of reduced components
$D$ is freely generated by the set of reduced components ![]() $\{Y_j\}$, and
$\{Y_j\}$, and ![]() $D_0$ is the subgroup generated by the divisor
$D_0$ is the subgroup generated by the divisor ![]() $(\varpi )$ of the special fibre. The complex of [Reference RaynaudRay70, (8.1.2)(i)] then becomes
$(\varpi )$ of the special fibre. The complex of [Reference RaynaudRay70, (8.1.2)(i)] then becomes
where the maps are
 \begin{align} i(1) &= \sum_{j \in C}d_j (j) , \nonumber\\ a(\ell) &= \bigg(\frac1{\delta_j}\deg\mathcal{O}_{\mathcal{X}}(Y_\ell)|_{Y_j} \bigg)_{j\in C} = \bigg(\frac1{p^{n_j}}(Y_j.Y_\ell)\bigg)_{j\in C} \quad (\ell\in C) , \nonumber\\ b(m) &= \sum_{j\in C}\delta_jm_j, \quad{m=(m_j)\in \mathbb{Z}^C,} \end{align}
\begin{align} i(1) &= \sum_{j \in C}d_j (j) , \nonumber\\ a(\ell) &= \bigg(\frac1{\delta_j}\deg\mathcal{O}_{\mathcal{X}}(Y_\ell)|_{Y_j} \bigg)_{j\in C} = \bigg(\frac1{p^{n_j}}(Y_j.Y_\ell)\bigg)_{j\in C} \quad (\ell\in C) , \nonumber\\ b(m) &= \sum_{j\in C}\delta_jm_j, \quad{m=(m_j)\in \mathbb{Z}^C,} \end{align}
and ![]() $\Phi (J)=\ker (b)/\operatorname {im}(a)$.
$\Phi (J)=\ker (b)/\operatorname {im}(a)$.
If ![]() $\mathcal {X}$ is semistable (meaning that
$\mathcal {X}$ is semistable (meaning that ![]() $\mathcal {X}_s$ is smooth over
$\mathcal {X}_s$ is smooth over ![]() $k$ apart from double points with distinct tangents), then both the character group and component group can be described in terms of the reduced graph
$k$ apart from double points with distinct tangents), then both the character group and component group can be described in terms of the reduced graph ![]() $\Gamma _{\mathcal {X}_s}$. The character group equals the homology of
$\Gamma _{\mathcal {X}_s}$. The character group equals the homology of ![]() $\Gamma _{\mathcal {X}_s}$. The map
$\Gamma _{\mathcal {X}_s}$. The map ![]() $a\colon \mathbb {Z}[C] \to \ker (b)=\mathbb {Z}^{C,0}\subset \mathbb {Z}^C$ is, after identifying
$a\colon \mathbb {Z}[C] \to \ker (b)=\mathbb {Z}^{C,0}\subset \mathbb {Z}^C$ is, after identifying ![]() $\mathbb {Z}[C]$ with
$\mathbb {Z}[C]$ with ![]() $\mathbb {Z}^C$, the Laplacian of the graph
$\mathbb {Z}^C$, the Laplacian of the graph ![]() $\Gamma _{\mathcal {X}_s}$, which takes a vertex
$\Gamma _{\mathcal {X}_s}$, which takes a vertex ![]() $v\in C$ to
$v\in C$ to ![]() $\sum (v)- (v')\in \mathbb {Z}[C]_0$, the sum taken over all edges joining
$\sum (v)- (v')\in \mathbb {Z}[C]_0$, the sum taken over all edges joining ![]() $v$ to an adjacent vertex
$v$ to an adjacent vertex ![]() $v'$.
$v'$.
In general, we have an isomorphism of ![]() $\operatorname {Gal}(\bar k/k)$-modules
$\operatorname {Gal}(\bar k/k)$-modules ![]() $\Phi (J) =\ker (b)/\operatorname {im}(a)$, where
$\Phi (J) =\ker (b)/\operatorname {im}(a)$, where ![]() $a$,
$a$, ![]() $b$ are the maps in the complex (1.3.1) for the base change
$b$ are the maps in the complex (1.3.1) for the base change ![]() $\mathcal {X}\otimes _R R^{\mathrm {sh}}$.
$\mathcal {X}\otimes _R R^{\mathrm {sh}}$.
1.4 Generalized Picard schemes of singular curves
Let ![]() $k$ be a field, and
$k$ be a field, and ![]() $Y/k$ a proper curve (in the sense of § 1.2). Write
$Y/k$ a proper curve (in the sense of § 1.2). Write ![]() $k'$ for the
$k'$ for the ![]() $k$-algebra
$k$-algebra ![]() $\Gamma (Y,\mathcal {O}_Y)$. By a generalized modulus on
$\Gamma (Y,\mathcal {O}_Y)$. By a generalized modulus on ![]() $Y$ we mean a morphism of
$Y$ we mean a morphism of ![]() $k$-schemes
$k$-schemes ![]() $\Sigma \to Y$, where
$\Sigma \to Y$, where ![]() $\Sigma$ is a finite
$\Sigma$ is a finite ![]() $k$-scheme, flat over
$k$-scheme, flat over ![]() $\operatorname {Spec} k'$.
$\operatorname {Spec} k'$.
Lemma 1.5 Let ![]() $g\colon \Sigma \to Y$ be a generalized modulus. Suppose that
$g\colon \Sigma \to Y$ be a generalized modulus. Suppose that ![]() $g(\Sigma )$ meets each connected component of
$g(\Sigma )$ meets each connected component of ![]() $Y$. Then
$Y$. Then ![]() $(\Sigma, g)$ is a rigidifierFootnote 1 of
$(\Sigma, g)$ is a rigidifierFootnote 1 of ![]() $\operatorname {Pic}_{X/k}$, in the sense of [Reference RaynaudRay70, (2.1.1)]
$\operatorname {Pic}_{X/k}$, in the sense of [Reference RaynaudRay70, (2.1.1)]
Proof. For ![]() $(\Sigma, g)$ to be a rigidifier, it is necessary and sufficient that for every
$(\Sigma, g)$ to be a rigidifier, it is necessary and sufficient that for every ![]() $k$-algebra
$k$-algebra ![]() $A$, the map
$A$, the map ![]() $g^* \colon \Gamma (Y \otimes _k A, \mathcal {O}_{Y\otimes A}) \to \Gamma (\Sigma \otimes A, \mathcal {O}_{\Sigma \otimes A})$ is injective. As
$g^* \colon \Gamma (Y \otimes _k A, \mathcal {O}_{Y\otimes A}) \to \Gamma (\Sigma \otimes A, \mathcal {O}_{\Sigma \otimes A})$ is injective. As ![]() $k$ is a field it is enough to show this for
$k$ is a field it is enough to show this for ![]() $A = k$, and this holds since by hypothesis
$A = k$, and this holds since by hypothesis ![]() $\Sigma /k'$ is faithfully flat.
$\Sigma /k'$ is faithfully flat.
We define ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}$ to be the scheme classifying line bundles on
$\operatorname {Pic}_{(Y,\Sigma )/k}$ to be the scheme classifying line bundles on ![]() $Y$ together with a trivialization of the pullback to
$Y$ together with a trivialization of the pullback to ![]() $\Sigma$. Precisely, consider the functor
$\Sigma$. Precisely, consider the functor ![]() $\mathcal {F}$ which to a
$\mathcal {F}$ which to a ![]() $k$-scheme
$k$-scheme ![]() $S$ associates the set of equivalence classes of pairs
$S$ associates the set of equivalence classes of pairs ![]() $(\mathcal {L},\alpha )$, where
$(\mathcal {L},\alpha )$, where ![]() $\mathcal {L}$ is a line bundle on
$\mathcal {L}$ is a line bundle on ![]() $Y\times S$ and
$Y\times S$ and ![]() $\alpha \colon \mathcal {O}_{\Sigma \times S} \xrightarrow \sim (g\times \mathrm {id}_S)^*\mathcal {L}$ is a trivialization, and where pairs
$\alpha \colon \mathcal {O}_{\Sigma \times S} \xrightarrow \sim (g\times \mathrm {id}_S)^*\mathcal {L}$ is a trivialization, and where pairs ![]() $(\mathcal {L},\alpha )$,
$(\mathcal {L},\alpha )$, ![]() $(\mathcal {L}',\alpha ')$ are equivalent if there exists an isomorphism
$(\mathcal {L}',\alpha ')$ are equivalent if there exists an isomorphism ![]() $\sigma \colon \mathcal {L} \xrightarrow \sim \mathcal {L}'$ such that
$\sigma \colon \mathcal {L} \xrightarrow \sim \mathcal {L}'$ such that ![]() $\alpha '=g^*(\sigma )\circ \alpha$.
$\alpha '=g^*(\sigma )\circ \alpha$.
Let ![]() $Y = Y_1 \sqcup Y_2$ where
$Y = Y_1 \sqcup Y_2$ where ![]() $g(\Sigma )$ is disjoint from
$g(\Sigma )$ is disjoint from ![]() $Y_2$ and meets each connected component of
$Y_2$ and meets each connected component of ![]() $Y_1$. If
$Y_1$. If ![]() $Y_2 = \emptyset$, then by Lemma 1.5 we are in the situation of [Reference RaynaudRay70, § 2], and
$Y_2 = \emptyset$, then by Lemma 1.5 we are in the situation of [Reference RaynaudRay70, § 2], and ![]() $\mathcal {F}$ is a sheaf for the fppf topology which we denote
$\mathcal {F}$ is a sheaf for the fppf topology which we denote ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}$. In general, we define
$\operatorname {Pic}_{(Y,\Sigma )/k}$. In general, we define ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}$ to be the sheafification of
$\operatorname {Pic}_{(Y,\Sigma )/k}$ to be the sheafification of ![]() $\mathcal {F}$ for the fppf topology. Obviously
$\mathcal {F}$ for the fppf topology. Obviously ![]() $\operatorname {Pic}_{(Y,\Sigma )/k} = \operatorname {Pic}_{(Y_1 ,\Sigma )/k} \times _k \operatorname {Pic}_{Y_2/k}$. Put
$\operatorname {Pic}_{(Y,\Sigma )/k} = \operatorname {Pic}_{(Y_1 ,\Sigma )/k} \times _k \operatorname {Pic}_{Y_2/k}$. Put ![]() $k' = k_1 \times k_2$ where
$k' = k_1 \times k_2$ where ![]() $k_i = \Gamma (Y_i , \mathcal {O}_{Y_i} )$. From [Reference RaynaudRay70] we then obtain the following.
$k_i = \Gamma (Y_i , \mathcal {O}_{Y_i} )$. From [Reference RaynaudRay70] we then obtain the following.
Proposition 1.6 The functor ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}$ is represented by a smooth
$\operatorname {Pic}_{(Y,\Sigma )/k}$ is represented by a smooth ![]() $k$-group scheme, and there is an exact sequence of smooth group schemes
$k$-group scheme, and there is an exact sequence of smooth group schemes
where
Proof. From (2.1.2), (2.4.1), and (2.4.3) of [Reference RaynaudRay70] we get the representability of ![]() $\operatorname {Pic}_{(Y_1 ,\Sigma )/k}$ along with an exact sequence
$\operatorname {Pic}_{(Y_1 ,\Sigma )/k}$ along with an exact sequence
of smooth group schemes (since, in this setting, Raynaud's ![]() $\Gamma _X^*$ and
$\Gamma _X^*$ and ![]() $\Gamma _R^*$ are just
$\Gamma _R^*$ are just ![]() $\mathcal {R}_{k_1/k} \mathbb {G}_{\mathrm {m}}$ and
$\mathcal {R}_{k_1/k} \mathbb {G}_{\mathrm {m}}$ and ![]() $\mathcal {R}_{\Sigma /k}\mathbb {G}_{\mathrm {m}}$). By § 1.1, the quotient
$\mathcal {R}_{\Sigma /k}\mathbb {G}_{\mathrm {m}}$). By § 1.1, the quotient ![]() $H$ is a smooth group scheme, and taking products with
$H$ is a smooth group scheme, and taking products with ![]() $\operatorname {Pic}_{Y_2/k}$ gives the result.
$\operatorname {Pic}_{Y_2/k}$ gives the result.
Let ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}^0$ denote the inverse image of
$\operatorname {Pic}_{(Y,\Sigma )/k}^0$ denote the inverse image of ![]() $\operatorname {Pic}_{Y/k}^0$ (classifying line bundles which are of degree zero on every irreducible component of
$\operatorname {Pic}_{Y/k}^0$ (classifying line bundles which are of degree zero on every irreducible component of ![]() $Y$). Then
$Y$). Then ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}^0$ is a smooth connected
$\operatorname {Pic}_{(Y,\Sigma )/k}^0$ is a smooth connected ![]() $k$-group scheme of finite type.
$k$-group scheme of finite type.
Example 1.7 Suppose ![]() $Y$ is smooth over
$Y$ is smooth over ![]() $k$ and absolutely irreducible, and that
$k$ and absolutely irreducible, and that ![]() $\Sigma \to Y$ is a closed immersion. Then the image of
$\Sigma \to Y$ is a closed immersion. Then the image of ![]() $\Sigma$ is an effective divisor
$\Sigma$ is an effective divisor ![]() $\mathfrak {m}=\sum m_i(y_i)$ for points
$\mathfrak {m}=\sum m_i(y_i)$ for points ![]() $y_i\in Y(k)$. In this case
$y_i\in Y(k)$. In this case ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}^0$ is none other than the classical [Reference RosenlichtRos54, Reference SerreSer84] generalized Jacobian
$\operatorname {Pic}_{(Y,\Sigma )/k}^0$ is none other than the classical [Reference RosenlichtRos54, Reference SerreSer84] generalized Jacobian ![]() $J_{\mathfrak {m}}(Y)$ of
$J_{\mathfrak {m}}(Y)$ of ![]() $Y$. The isomorphism
$Y$. The isomorphism ![]() $J_\mathfrak {m}(Y) \xrightarrow \sim \operatorname {Pic}^0_{(Y,\Sigma )/k}$ is given on
$J_\mathfrak {m}(Y) \xrightarrow \sim \operatorname {Pic}^0_{(Y,\Sigma )/k}$ is given on ![]() $k$-points by mapping the class of a divisor
$k$-points by mapping the class of a divisor ![]() $D\in \operatorname {Div}^0(Y\smallsetminus \Sigma )$ to the class of the pair
$D\in \operatorname {Div}^0(Y\smallsetminus \Sigma )$ to the class of the pair ![]() $(\mathcal {O}_Y(D),\alpha _{\mathrm {triv}})$, where
$(\mathcal {O}_Y(D),\alpha _{\mathrm {triv}})$, where ![]() $\alpha _{\mathrm {triv}}$ is the canonical trivialization
$\alpha _{\mathrm {triv}}$ is the canonical trivialization ![]() $\mathcal {O}_{\Sigma } \xrightarrow \sim \mathcal {O}_Y|_\Sigma =\mathcal {O}_Y(D)|_\Sigma$.
$\mathcal {O}_{\Sigma } \xrightarrow \sim \mathcal {O}_Y|_\Sigma =\mathcal {O}_Y(D)|_\Sigma$.
Let ![]() $k$ be perfect. Then
$k$ be perfect. Then ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}^0$ has a maximal connected affine subgroup
$\operatorname {Pic}_{(Y,\Sigma )/k}^0$ has a maximal connected affine subgroup ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}^{0,\mathrm {lin}}$ which is a linear group, and its character group has the following combinatorial description, generalizing § 1.2.
$\operatorname {Pic}_{(Y,\Sigma )/k}^{0,\mathrm {lin}}$ which is a linear group, and its character group has the following combinatorial description, generalizing § 1.2.
First suppose that ![]() $k$ is algebraically closed, and that
$k$ is algebraically closed, and that ![]() $Y$,
$Y$, ![]() $\Sigma$ are reduced. As in § 1.2, let
$\Sigma$ are reduced. As in § 1.2, let ![]() $\phi \colon \widetilde Y \to Y$ be the normalization, and define
$\phi \colon \widetilde Y \to Y$ be the normalization, and define ![]() $A=Y^\mathrm {sing}$,
$A=Y^\mathrm {sing}$, ![]() $B=\phi ^{-1}(A)$,
$B=\phi ^{-1}(A)$, ![]() $C=\pi _0(\widetilde Y)$. Decompose
$C=\pi _0(\widetilde Y)$. Decompose ![]() $\Sigma =\Sigma ^\mathrm {sing}\sqcup \Sigma ^\mathrm {reg}$, where
$\Sigma =\Sigma ^\mathrm {sing}\sqcup \Sigma ^\mathrm {reg}$, where ![]() $z\in \Sigma ^\mathrm {sing}$ (respectively,
$z\in \Sigma ^\mathrm {sing}$ (respectively, ![]() $\Sigma ^\mathrm {reg}$) if
$\Sigma ^\mathrm {reg}$) if ![]() $g(z)$ is a singular (respectively, smooth) point of
$g(z)$ is a singular (respectively, smooth) point of ![]() $Y$. There are maps
$Y$. There are maps

where ![]() $\phi$,
$\phi$, ![]() $\psi$ are as before,
$\psi$ are as before, ![]() $\lambda$ is the restriction of
$\lambda$ is the restriction of ![]() $g$ to
$g$ to ![]() $\Sigma ^\mathrm {sing}$, and
$\Sigma ^\mathrm {sing}$, and ![]() $\theta (z)$ is the component of
$\theta (z)$ is the component of ![]() $\widetilde Y$ containing
$\widetilde Y$ containing ![]() $g(z)$.
$g(z)$.
Define the extended graph of ![]() $(Y,\Sigma )$ to be the directed graph
$(Y,\Sigma )$ to be the directed graph ![]() $\widetilde{\Gamma} _{Y,\Sigma }$ obtained by adding to the graph
$\widetilde{\Gamma} _{Y,\Sigma }$ obtained by adding to the graph ![]() $\widetilde{\Gamma} _Y$:
$\widetilde{\Gamma} _Y$:
– a single vertex
 $v_0$;
$v_0$;– for each
 $z\in \Sigma ^\mathrm {sing}$, an edge from
$z\in \Sigma ^\mathrm {sing}$, an edge from  $v_0$ to the vertex
$v_0$ to the vertex  $\lambda (z)\in A\subset V(\widetilde{\Gamma} _Y)$;
$\lambda (z)\in A\subset V(\widetilde{\Gamma} _Y)$;– for each
 $z\in \Sigma ^\mathrm {reg}$, an edge from
$z\in \Sigma ^\mathrm {reg}$, an edge from  $v_0$ to the vertex
$v_0$ to the vertex  $\theta (z)\in C\subset V(\widetilde{\Gamma} _Y)$.
$\theta (z)\in C\subset V(\widetilde{\Gamma} _Y)$.
If ![]() $Y$ only has double points and
$Y$ only has double points and ![]() $\Sigma =\Sigma ^\mathrm {reg}$, then we may likewise define the reduced graph
$\Sigma =\Sigma ^\mathrm {reg}$, then we may likewise define the reduced graph ![]() $\Gamma _{Y,\Sigma }$, which is the undirected graph obtained by adding to
$\Gamma _{Y,\Sigma }$, which is the undirected graph obtained by adding to ![]() $\Gamma _Y$ a single vertex
$\Gamma _Y$ a single vertex ![]() $v_0$ and, for each
$v_0$ and, for each ![]() $z\in \Sigma$, an edge joining
$z\in \Sigma$, an edge joining ![]() $v_0$ to
$v_0$ to ![]() $\theta (z)\in C=V(\Gamma _Y)$. As before, the geometric realizations of
$\theta (z)\in C=V(\Gamma _Y)$. As before, the geometric realizations of ![]() $\widetilde{\Gamma} _{Y,\Sigma }$ and
$\widetilde{\Gamma} _{Y,\Sigma }$ and ![]() $\Gamma _{Y,\Sigma }$ are canonically homeomorphic.
$\Gamma _{Y,\Sigma }$ are canonically homeomorphic.
For arbitrary perfect ![]() $k$ and proper curve
$k$ and proper curve ![]() $Y$, we define
$Y$, we define ![]() $\widetilde{\Gamma} _{Y,\Sigma }$,
$\widetilde{\Gamma} _{Y,\Sigma }$, ![]() $\Gamma _{Y,\Sigma }$ to be the graphs attached to the curve with modulus
$\Gamma _{Y,\Sigma }$ to be the graphs attached to the curve with modulus ![]() $(Y^\mathrm {red}\otimes \bar k, \Sigma ^\mathrm {red}\otimes \bar k)$, which are graphs with a continuous action of
$(Y^\mathrm {red}\otimes \bar k, \Sigma ^\mathrm {red}\otimes \bar k)$, which are graphs with a continuous action of ![]() $\operatorname {Gal}(\bar k/k)$.
$\operatorname {Gal}(\bar k/k)$.
Proposition 1.8
(a) The character group
 $\operatorname {Hom}(\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k},\mathbb {G}_{\mathrm {m}})$ is canonically isomorphic, as a
$\operatorname {Hom}(\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k},\mathbb {G}_{\mathrm {m}})$ is canonically isomorphic, as a  $\operatorname {Gal}(\bar k/k)$-module, to
$\operatorname {Gal}(\bar k/k)$-module, to  $H_1(\widetilde{\Gamma} _{Y,\Sigma },\mathbb {Z})$.
$H_1(\widetilde{\Gamma} _{Y,\Sigma },\mathbb {Z})$.(b) If
 $Y^\mathrm {red}$ has only double points, then
$Y^\mathrm {red}$ has only double points, then  $\operatorname {Hom}(\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k},\mathbb {G}_{\mathrm {m}})\simeq H_1(\Gamma _{Y,\Sigma },\mathbb {Z})$.
$\operatorname {Hom}(\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k},\mathbb {G}_{\mathrm {m}})\simeq H_1(\Gamma _{Y,\Sigma },\mathbb {Z})$.
Proof. We may assume that ![]() $k$ is algebraically closed; the Galois equivariance of the isomorphisms will be clear from the construction. By the homeomorphism between the extended and reduced graphs, it suffices to prove part (a).
$k$ is algebraically closed; the Galois equivariance of the isomorphisms will be clear from the construction. By the homeomorphism between the extended and reduced graphs, it suffices to prove part (a).
The map ![]() $g^\mathrm {red}\colon \Sigma ^\mathrm {red} \to Y^\mathrm {red}$ is a reduced modulus, and the obvious morphism induced by pullback
$g^\mathrm {red}\colon \Sigma ^\mathrm {red} \to Y^\mathrm {red}$ is a reduced modulus, and the obvious morphism induced by pullback
has unipotent kernel, since the same is true for the maps ![]() $\mathcal {R}_{\Sigma /k}\mathbb {G}_{\mathrm {m}}\to \mathcal {R}_{\Sigma ^\mathrm {red}/k}\mathbb {G}_{\mathrm {m}}$ and
$\mathcal {R}_{\Sigma /k}\mathbb {G}_{\mathrm {m}}\to \mathcal {R}_{\Sigma ^\mathrm {red}/k}\mathbb {G}_{\mathrm {m}}$ and ![]() $\operatorname {Pic}_{Y/k}^0 \to \operatorname {Pic}_{Y^\mathrm {red}/k}^0$. Thus, the character group of
$\operatorname {Pic}_{Y/k}^0 \to \operatorname {Pic}_{Y^\mathrm {red}/k}^0$. Thus, the character group of ![]() $\operatorname {Pic}_{(Y,\Sigma )/k}^{0,\mathrm {lin}}$ is unchanged by passing to reduced subschemes; hence, we may assume that both
$\operatorname {Pic}_{(Y,\Sigma )/k}^{0,\mathrm {lin}}$ is unchanged by passing to reduced subschemes; hence, we may assume that both ![]() $Y$ and
$Y$ and ![]() $\Sigma$ are reduced. Next, let
$\Sigma$ are reduced. Next, let ![]() $Y'\to Y$ be the seminormalization. Then as
$Y'\to Y$ be the seminormalization. Then as ![]() $\Sigma$ is reduced,
$\Sigma$ is reduced, ![]() $\Sigma \to Y$ factors uniquely through
$\Sigma \to Y$ factors uniquely through ![]() $Y'$, and the resulting map
$Y'$, and the resulting map
has unipotent kernel. Therefore, we may assume in addition that ![]() $Y$ is seminormal. Finally, normalization induces an exact sequence
$Y$ is seminormal. Finally, normalization induces an exact sequence
where ![]() $G$ classifies equivalence classes of pairs
$G$ classifies equivalence classes of pairs ![]() $(\mathcal {L},\beta )$, where
$(\mathcal {L},\beta )$, where ![]() $\mathcal {L}$ is a line bundle on
$\mathcal {L}$ is a line bundle on ![]() $Y$ whose pullback to
$Y$ whose pullback to ![]() $\tilde Y$ is trivial, and
$\tilde Y$ is trivial, and ![]() $\beta$ is a trivialization of the pullback of
$\beta$ is a trivialization of the pullback of ![]() $\mathcal {L}$ to
$\mathcal {L}$ to ![]() $\Sigma$. There is a surjective map
$\Sigma$. There is a surjective map
given as follows: a tuple
determines:
(i) for every
 $y\in A$, and any
$y\in A$, and any  $x$,
$x$,  $x'\in \phi ^{-1}(y)$, isomorphisms
$x'\in \phi ^{-1}(y)$, isomorphisms  $a_x^{-1}a_{x'} \colon x^*\mathcal {O}_{\tilde Y}=k \xrightarrow \sim k=x^{\prime *}\mathcal {O}_{\tilde Y}$ satisfying the cocycle condition and, thus, a descent of
$a_x^{-1}a_{x'} \colon x^*\mathcal {O}_{\tilde Y}=k \xrightarrow \sim k=x^{\prime *}\mathcal {O}_{\tilde Y}$ satisfying the cocycle condition and, thus, a descent of  $\mathcal {O}_{\tilde Y}$ to a line bundle
$\mathcal {O}_{\tilde Y}$ to a line bundle  $\mathcal {L}$ on
$\mathcal {L}$ on  $Y$;
$Y$;(ii) for every
 $z\in \Sigma ^\mathrm {sing}$, and every
$z\in \Sigma ^\mathrm {sing}$, and every  $x\in \phi ^{-1}(g(z))$, a trivialization
$x\in \phi ^{-1}(g(z))$, a trivialization  $b_za_x^{-1}\colon k\xrightarrow \sim k=x^*\mathcal {O}_{\tilde Y}$; these trivializations are compatible with the descent data (i) and therefore give trivializations
$b_za_x^{-1}\colon k\xrightarrow \sim k=x^*\mathcal {O}_{\tilde Y}$; these trivializations are compatible with the descent data (i) and therefore give trivializations  $k\xrightarrow \sim z^*\mathcal {L}$ for every
$k\xrightarrow \sim z^*\mathcal {L}$ for every  $z\in \Sigma ^\mathrm {sing}$;
$z\in \Sigma ^\mathrm {sing}$;(iii) for every
 $z\in \Sigma ^\mathrm {reg}$, a trivialization
$z\in \Sigma ^\mathrm {reg}$, a trivialization  $k\xrightarrow \sim z^*\mathcal {L}=k$ given by multiplication by
$k\xrightarrow \sim z^*\mathcal {L}=k$ given by multiplication by  $c_z$.
$c_z$.
What is the kernel of the map (1.4.3)? Fix ![]() $y\in A$. Then multiplying
$y\in A$. Then multiplying ![]() $a_x$, for
$a_x$, for ![]() $x\in \phi ^{-1}(y)$, and
$x\in \phi ^{-1}(y)$, and ![]() $b_z$, for
$b_z$, for ![]() $z \in \Sigma ^\mathrm {sing}$ such that
$z \in \Sigma ^\mathrm {sing}$ such that ![]() $g(z)=y$, by a common element of
$g(z)=y$, by a common element of ![]() $k^\times$ does not change the descent data (i) or the trivialization (ii), so we obtain the same
$k^\times$ does not change the descent data (i) or the trivialization (ii), so we obtain the same ![]() $(\mathcal {L},\beta )$. The equivalence relation on pairs is realized by the automorphism group
$(\mathcal {L},\beta )$. The equivalence relation on pairs is realized by the automorphism group ![]() $\mathbb {G}_{\mathrm {m}}^C$ of
$\mathbb {G}_{\mathrm {m}}^C$ of ![]() $\phi ^*\mathcal {L}=\mathcal {O}_{\tilde Y}$, which acts on tuples by
$\phi ^*\mathcal {L}=\mathcal {O}_{\tilde Y}$, which acts on tuples by
Therefore, ![]() $G$ is the torus whose character group is the kernel of the map
$G$ is the torus whose character group is the kernel of the map
with matrix
The homology complex of ![]() $\widetilde{\Gamma} _{Y,\Sigma }$ is
$\widetilde{\Gamma} _{Y,\Sigma }$ is
with differential given by the matrix
 \[ \begin{bmatrix} \psi & 0 & \theta \\ -\phi & \lambda & 0 \\ 0 & -\varepsilon & -\varepsilon \end{bmatrix}, \]
\[ \begin{bmatrix} \psi & 0 & \theta \\ -\phi & \lambda & 0 \\ 0 & -\varepsilon & -\varepsilon \end{bmatrix}, \]
where ![]() $\varepsilon \colon \mathbb {Z}[\Sigma ^?] \to \mathbb {Z}$ is the augmentation
$\varepsilon \colon \mathbb {Z}[\Sigma ^?] \to \mathbb {Z}$ is the augmentation ![]() $z\mapsto 1$, for
$z\mapsto 1$, for ![]() $z\in \Sigma ^?$,
$z\in \Sigma ^?$, ![]() $?\in \{\mathrm {reg},\mathrm {sing}\}$. There is an obvious map from the complex (1.4.5) to the complex (1.4.4) which induces an isomorphism on kernels. Since
$?\in \{\mathrm {reg},\mathrm {sing}\}$. There is an obvious map from the complex (1.4.5) to the complex (1.4.4) which induces an isomorphism on kernels. Since ![]() $G$ is by (1.4.2) the maximal multiplicative quotient of
$G$ is by (1.4.2) the maximal multiplicative quotient of ![]() $\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}$, this gives the isomorphism (a). The construction is Galois equivariant by transport of structure.
$\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}$, this gives the isomorphism (a). The construction is Galois equivariant by transport of structure.
1.5 Functoriality I
Let ![]() $g\colon \Sigma \to Y$,
$g\colon \Sigma \to Y$, ![]() $g'\colon \Sigma ' \to Y'$ be generalized moduli on proper curves over
$g'\colon \Sigma ' \to Y'$ be generalized moduli on proper curves over ![]() $k$ as in the previous section, and suppose we have finite morphisms
$k$ as in the previous section, and suppose we have finite morphisms ![]() $f$,
$f$, ![]() $f_\Sigma$ fitting into the following commutative diagram.
$f_\Sigma$ fitting into the following commutative diagram.

Then there is an associated pullback morphism
taking a pair ![]() $(\mathcal {L}, \alpha \colon \mathcal {O}_\Sigma \xrightarrow \sim g^*\mathcal {L})$ to the pair
$(\mathcal {L}, \alpha \colon \mathcal {O}_\Sigma \xrightarrow \sim g^*\mathcal {L})$ to the pair
which we will simply denote by ![]() $f^*$ if no confusion can arise.
$f^*$ if no confusion can arise.
To define pushforward, consider the following commutative diagram.

We assume that ![]() $f$ is flat, and that
$f$ is flat, and that ![]() $h$ is a closed immersion whose ideal sheaf
$h$ is a closed immersion whose ideal sheaf ![]() $\mathcal {I}$ is nilpotent and satisfies
$\mathcal {I}$ is nilpotent and satisfies
We may then define a morphism ![]() $f_* =(f,\Sigma )_* \colon \operatorname {Pic}_{(Y',\Sigma ')/k} \to \operatorname {Pic}_{(Y,\Sigma )/k}$ by
$f_* =(f,\Sigma )_* \colon \operatorname {Pic}_{(Y',\Sigma ')/k} \to \operatorname {Pic}_{(Y,\Sigma )/k}$ by ![]() $f_*\colon (\mathcal {L}',\alpha ') \mapsto (\mathcal {L},\alpha )$, where
$f_*\colon (\mathcal {L}',\alpha ') \mapsto (\mathcal {L},\alpha )$, where ![]() $\mathcal {L}=\mathcal {N}_f(\mathcal {L}')$, the norm of
$\mathcal {L}=\mathcal {N}_f(\mathcal {L}')$, the norm of ![]() $\mathcal {L}'$ (see [Reference GrothendieckGro61, 6.5]) and
$\mathcal {L}'$ (see [Reference GrothendieckGro61, 6.5]) and ![]() $\alpha$ is given as follows: if
$\alpha$ is given as follows: if ![]() $\mathcal {I}=0$ is zero, then (1.5.1) is Cartesian, and
$\mathcal {I}=0$ is zero, then (1.5.1) is Cartesian, and ![]() $\alpha$ is the composite
$\alpha$ is the composite
(the second isomorphism given by [Reference GrothendieckGro61, (6.5.8)]). In general, ![]() $\alpha '\colon \mathcal {O}_{\Sigma '} \xrightarrow \sim g^{\prime *}\mathcal {L}'$ can at least locally be extended to an isomorphism
$\alpha '\colon \mathcal {O}_{\Sigma '} \xrightarrow \sim g^{\prime *}\mathcal {L}'$ can at least locally be extended to an isomorphism ![]() $\alpha '' \colon \mathcal {O}_{\Sigma \times _YY'} \xrightarrow \sim \mathrm {pr}_2^*\mathcal {L}'$, well-defined up to local sections of
$\alpha '' \colon \mathcal {O}_{\Sigma \times _YY'} \xrightarrow \sim \mathrm {pr}_2^*\mathcal {L}'$, well-defined up to local sections of ![]() $1+\mathcal {I}$. Taking norms, we then get a well-defined global isomorphism
$1+\mathcal {I}$. Taking norms, we then get a well-defined global isomorphism ![]() $\alpha =\mathcal {N}_{\Sigma \times _Y Y'/\Sigma }(\alpha '')\colon \mathcal {O}_\Sigma \xrightarrow \sim g^*\mathcal {L}$.
$\alpha =\mathcal {N}_{\Sigma \times _Y Y'/\Sigma }(\alpha '')\colon \mathcal {O}_\Sigma \xrightarrow \sim g^*\mathcal {L}$.
The maps ![]() $f^*$,
$f^*$, ![]() $f_*$ preserve
$f_*$ preserve ![]() $\operatorname {Pic}^0$ in all cases.
$\operatorname {Pic}^0$ in all cases.
Example 1.9 Suppose that ![]() $Y$,
$Y$, ![]() $Y'$ are smooth over
$Y'$ are smooth over ![]() $k$ and absolutely irreducible, and that
$k$ and absolutely irreducible, and that ![]() $\Sigma \subset Y$,
$\Sigma \subset Y$, ![]() $\Sigma '\subset Y'$ are closed subschemes defined by reduced moduli
$\Sigma '\subset Y'$ are closed subschemes defined by reduced moduli ![]() $\mathfrak {m}$,
$\mathfrak {m}$, ![]() $\mathfrak {m}'$. Let
$\mathfrak {m}'$. Let ![]() $J_\mathfrak {m}=\operatorname {Pic}^0_{(Y,\Sigma )/k}$,
$J_\mathfrak {m}=\operatorname {Pic}^0_{(Y,\Sigma )/k}$, ![]() $J'_{\mathfrak {m}'}=\operatorname {Pic}^0_{(Y',\Sigma ')/k}$, be the associated generalized Jacobians. Let
$J'_{\mathfrak {m}'}=\operatorname {Pic}^0_{(Y',\Sigma ')/k}$, be the associated generalized Jacobians. Let ![]() $f\colon Y' \to Y$ be a finite morphism with
$f\colon Y' \to Y$ be a finite morphism with ![]() $f^{-1}(\Sigma )^{\mathrm {red}}=\Sigma '$. Then (1.5.2) holds and, therefore, we get morphisms
$f^{-1}(\Sigma )^{\mathrm {red}}=\Sigma '$. Then (1.5.2) holds and, therefore, we get morphisms
If ![]() $f'\colon Y' \to Y$ is another finite morphism with
$f'\colon Y' \to Y$ is another finite morphism with ![]() $f^{\prime -1}(\Sigma )\supset \Sigma '$, then we get an induced endomorphism
$f^{\prime -1}(\Sigma )\supset \Sigma '$, then we get an induced endomorphism ![]() $f_*f^{\prime *}\colon J_\mathfrak {m} \to J_\mathfrak {m}$, compatible with the usual correspondence action on
$f_*f^{\prime *}\colon J_\mathfrak {m} \to J_\mathfrak {m}$, compatible with the usual correspondence action on ![]() $J$ (pullback along
$J$ (pullback along ![]() $f'$ followed by norm with respect to
$f'$ followed by norm with respect to ![]() $f$). For later reference, we will say that the modulus
$f$). For later reference, we will say that the modulus ![]() $\mathfrak {m}$ is stable under the correspondence
$\mathfrak {m}$ is stable under the correspondence ![]() $f_*f^{\prime *}$.
$f_*f^{\prime *}$.
Returning to the general case, assume that ![]() $k$ is algebraically closed, that
$k$ is algebraically closed, that ![]() $f$ is flat and that (1.5.2) holds. Write
$f$ is flat and that (1.5.2) holds. Write
for the character groups of the linear parts of the generalized Picard schemes. Then ![]() $f^*$,
$f^*$, ![]() $f_*$ induce by functoriality homomorphisms
$f_*$ induce by functoriality homomorphisms
By Proposition 1.8 and (1.4.4) we have canonical isomorphisms
 \begin{align*} \mathbb{X} &=\ker\bigg( \begin{bmatrix} \psi & 0 & \theta \\ \phi & \lambda & 0\end{bmatrix} \colon \mathbb{Z}[B] \oplus \mathbb{Z}[\Sigma^\mathrm{sing}] \oplus \mathbb{Z}[\Sigma^\mathrm{reg}] \to \mathbb{Z}[C] \oplus \mathbb{Z}[A] \bigg)\\ &= H_1(\widetilde\Gamma_{Y,\Sigma},\mathbb{Z}), \end{align*}
\begin{align*} \mathbb{X} &=\ker\bigg( \begin{bmatrix} \psi & 0 & \theta \\ \phi & \lambda & 0\end{bmatrix} \colon \mathbb{Z}[B] \oplus \mathbb{Z}[\Sigma^\mathrm{sing}] \oplus \mathbb{Z}[\Sigma^\mathrm{reg}] \to \mathbb{Z}[C] \oplus \mathbb{Z}[A] \bigg)\\ &= H_1(\widetilde\Gamma_{Y,\Sigma},\mathbb{Z}), \end{align*}
where ![]() $A=(Y^\mathrm {red})^{\mathrm {sing}}$,
$A=(Y^\mathrm {red})^{\mathrm {sing}}$, ![]() $B=\phi ^{-1}(A)$,
$B=\phi ^{-1}(A)$, ![]() $C=\pi _0(\widetilde Y)$, and similarly for
$C=\pi _0(\widetilde Y)$, and similarly for ![]() $\mathbb {X}'$. We now describe the maps (1.5.3) combinatorially, under further hypotheses. Let
$\mathbb {X}'$. We now describe the maps (1.5.3) combinatorially, under further hypotheses. Let ![]() $A'$,
$A'$, ![]() $B'$,
$B'$, ![]() $C'$ denote the corresponding sets for
$C'$ denote the corresponding sets for ![]() $Y'$, and assume the following.
$Y'$, and assume the following.
Hypotheses 1.10
(i)
 $f^{-1}(A)=A'$, and
$f^{-1}(A)=A'$, and  $f$ is étale at each point of
$f$ is étale at each point of  $A'$;
$A'$;(ii)
 $\Sigma ^\mathrm {sing}=\emptyset =\Sigma ^{\prime \mathrm {sing}}$, and
$\Sigma ^\mathrm {sing}=\emptyset =\Sigma ^{\prime \mathrm {sing}}$, and  $\Sigma$,
$\Sigma$,  $\Sigma '$ are reduced;
$\Sigma '$ are reduced;(iii)
 $\Sigma '=f^{-1}(\Sigma )^\mathrm {red}$.
$\Sigma '=f^{-1}(\Sigma )^\mathrm {red}$.
Hypotheses 1.10(ii) and (iii) together imply that (1.5.2) is satisfied. Then ![]() $f$ induces maps
$f$ induces maps ![]() $A'\to A$,
$A'\to A$, ![]() $B'\to B$,
$B'\to B$, ![]() $C'\to C$ which we also denote by
$C'\to C$ which we also denote by ![]() $f$. The diagram
$f$. The diagram

commutes, and so we have the following commutative square.

Proposition 1.11 Assume Hypotheses 1.10. The homomorphism ![]() $\mathbb {X}(f^*)$ is induced by the vertical maps in (1.5.5).
$\mathbb {X}(f^*)$ is induced by the vertical maps in (1.5.5).
Proof. We first observe that we may assume that Y and ![]() $Y'$ are reduced and seminormal. Indeed, the description of the character groups
$Y'$ are reduced and seminormal. Indeed, the description of the character groups ![]() $\mathbb {X}$ and
$\mathbb {X}$ and ![]() $\mathbb {X}'$ is unchanged after replacing the curves by their seminormalizations. It remains to verify that the induced map on seminormalizations
$\mathbb {X}'$ is unchanged after replacing the curves by their seminormalizations. It remains to verify that the induced map on seminormalizations ![]() $f^{\mathrm {sn}} \colon Y^{\prime \mathrm {sn}} \to Y^{\mathrm {sn}}$ is flat. But
$f^{\mathrm {sn}} \colon Y^{\prime \mathrm {sn}} \to Y^{\mathrm {sn}}$ is flat. But ![]() $Y^{\mathrm {sn}}\smallsetminus A = Y^{\mathrm {red}}\smallsetminus A$ is smooth, and so the restriction of
$Y^{\mathrm {sn}}\smallsetminus A = Y^{\mathrm {red}}\smallsetminus A$ is smooth, and so the restriction of ![]() $f^{\mathrm {sn}}$ to
$f^{\mathrm {sn}}$ to ![]() $Y^{\prime \mathrm {sn}}\smallsetminus A'$ is automatically flat. By hypothesis, there is a neighbourhood
$Y^{\prime \mathrm {sn}}\smallsetminus A'$ is automatically flat. By hypothesis, there is a neighbourhood ![]() $U\subset Y$ of
$U\subset Y$ of ![]() $A$ such that
$A$ such that ![]() $f \colon U':= f^{-1}(U) \to U$ is étale. Then by [Reference Greco and TraversoGT80, Proposition 5.1], we have a Cartesian square
$f \colon U':= f^{-1}(U) \to U$ is étale. Then by [Reference Greco and TraversoGT80, Proposition 5.1], we have a Cartesian square

and, in particular, ![]() $f^{\mathrm {sn}}$ restricted to
$f^{\mathrm {sn}}$ restricted to ![]() $U^{\prime \mathrm {sn}}$ is étale.
$U^{\prime \mathrm {sn}}$ is étale.
We now compute the dual map ![]() $f^* \colon \operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k} \to \operatorname {Pic}^{0,\mathrm {lin}}_{(Y',\Sigma ')/k}$ which is a morphism of tori (since we are assuming that
$f^* \colon \operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k} \to \operatorname {Pic}^{0,\mathrm {lin}}_{(Y',\Sigma ')/k}$ which is a morphism of tori (since we are assuming that ![]() $Y$ and
$Y$ and ![]() $Y'$ are seminormal and
$Y'$ are seminormal and ![]() $\Sigma$,
$\Sigma$, ![]() $\Sigma '$ are reduced). As explained in § 1.4, a
$\Sigma '$ are reduced). As explained in § 1.4, a ![]() $k$-point of
$k$-point of ![]() $\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}$ is represented by a pair
$\operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}$ is represented by a pair ![]() $((a_x)_{x\in B},(c_z)_{z\in \Sigma }) \in (k^\times )^B\times (k^\times )^\Sigma$, where
$((a_x)_{x\in B},(c_z)_{z\in \Sigma }) \in (k^\times )^B\times (k^\times )^\Sigma$, where ![]() $(a_x)$ determines descent data for
$(a_x)$ determines descent data for ![]() $\mathcal {O}_{\widetilde Y}$ with respect to the normalization morphism
$\mathcal {O}_{\widetilde Y}$ with respect to the normalization morphism ![]() $\phi \colon \widetilde Y \to Y$, and
$\phi \colon \widetilde Y \to Y$, and ![]() $(c_z)$ determines trivializations
$(c_z)$ determines trivializations ![]() $\times c_z\colon k\xrightarrow {\sim }k=z^*\mathcal {O}_{\widetilde Y}$ which descend to a rigidification along
$\times c_z\colon k\xrightarrow {\sim }k=z^*\mathcal {O}_{\widetilde Y}$ which descend to a rigidification along ![]() $\Sigma$ of the descended line bundle.
$\Sigma$ of the descended line bundle.
Let ![]() $a'_{x'}=a_{f(x')}$ (
$a'_{x'}=a_{f(x')}$ (![]() $x'\in B'$) and
$x'\in B'$) and ![]() $c'_{z'}=c_{f(z')}$ (
$c'_{z'}=c_{f(z')}$ (![]() $z'\in \Sigma '$). Then if
$z'\in \Sigma '$). Then if ![]() $(\mathcal {L},\alpha ) \in \operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}(k)$ is represented by the pair
$(\mathcal {L},\alpha ) \in \operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}(k)$ is represented by the pair ![]() $((a_x), (c_z))$, the pullback
$((a_x), (c_z))$, the pullback ![]() $f^*(\mathcal {L},\alpha )$ is represented by
$f^*(\mathcal {L},\alpha )$ is represented by ![]() $((a'_{x'}),(c'_{z'}))$. The obvious map
$((a'_{x'}),(c'_{z'}))$. The obvious map
is induced by ![]() $f\colon C'\to C$ and, therefore,
$f\colon C'\to C$ and, therefore, ![]() $\mathbb {X}(f^*)$ is induced by the vertical maps
$\mathbb {X}(f^*)$ is induced by the vertical maps ![]() $f$ in (1.5.5) as required.
$f$ in (1.5.5) as required.
We now compute ![]() $\mathbb {X}(f_*)$ assuming Hypotheses 1.10. Let
$\mathbb {X}(f_*)$ assuming Hypotheses 1.10. Let
 \[ f^*\colon \begin{cases} \mathbb{Z}[\Sigma] \to \mathbb{Z}[\Sigma'] & \\ \mathbb{Z}[A] \to \mathbb{Z}[A'] & \\ \mathbb{Z}[B] \to \mathbb{Z}[B'] & \end{cases} \]
\[ f^*\colon \begin{cases} \mathbb{Z}[\Sigma] \to \mathbb{Z}[\Sigma'] & \\ \mathbb{Z}[A] \to \mathbb{Z}[A'] & \\ \mathbb{Z}[B] \to \mathbb{Z}[B'] & \end{cases} \]
be the inverse image maps on divisors. By Hypothesis 1.10(i), this means that if ![]() $x\in A$ or
$x\in A$ or ![]() $x\in B$, then
$x\in B$, then ![]() $f^*\colon (x) \mapsto \sum _{f(x')=x}(x')$, and if
$f^*\colon (x) \mapsto \sum _{f(x')=x}(x')$, and if ![]() $z\in \Sigma$, then
$z\in \Sigma$, then
where ![]() $r_{z'/z}$ is the ramification degree of
$r_{z'/z}$ is the ramification degree of ![]() $f$ at
$f$ at ![]() $z'$. Finally, define
$z'$. Finally, define ![]() $f^*\colon \mathbb {Z}[C] \to \mathbb {Z}[C']$ by
$f^*\colon \mathbb {Z}[C] \to \mathbb {Z}[C']$ by
where ![]() $Z\subset \widetilde Y$,
$Z\subset \widetilde Y$, ![]() $Z'\subset \widetilde Y'$ are connected components. These maps fit into the following diagram.
$Z'\subset \widetilde Y'$ are connected components. These maps fit into the following diagram.

Proposition 1.12 Assume Hypotheses 1.10. The diagram (1.5.6) commutes, and the vertical maps induce the homomorphism ![]() $\mathbb {X}(f_*)\colon \mathbb {X} \to \mathbb {X}'$.
$\mathbb {X}(f_*)\colon \mathbb {X} \to \mathbb {X}'$.
Proof. As in Proposition 1.11, we may assume that ![]() $Y$ and
$Y$ and ![]() $Y'$ are seminormal. Consider again the dual map of tori
$Y'$ are seminormal. Consider again the dual map of tori ![]() $f^*\colon \operatorname {Pic}^{0,\mathrm {lin}}_{(Y',\Sigma ')/k} \to \operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}$. Let
$f^*\colon \operatorname {Pic}^{0,\mathrm {lin}}_{(Y',\Sigma ')/k} \to \operatorname {Pic}^{0,\mathrm {lin}}_{(Y,\Sigma )/k}$. Let ![]() $(\mathcal {L}',\alpha ')\in \operatorname {Pic}^{0,\mathrm {lin}}_{(Y',\Sigma ')/k}(k)$, represented by the pair
$(\mathcal {L}',\alpha ')\in \operatorname {Pic}^{0,\mathrm {lin}}_{(Y',\Sigma ')/k}(k)$, represented by the pair ![]() $((a'_{x'})_{x'\in B'}, (c'_{z'})_{z'\in \Sigma '})$. Since
$((a'_{x'})_{x'\in B'}, (c'_{z'})_{z'\in \Sigma '})$. Since ![]() $f$ is étale at
$f$ is étale at ![]() $B'$, the normalized map
$B'$, the normalized map ![]() $\tilde f \colon \widetilde Y'\to \widetilde Y$ induces a norm homomorphism
$\tilde f \colon \widetilde Y'\to \widetilde Y$ induces a norm homomorphism
which equals the homomorphism ![]() $f_! \colon (k^\times )^{B'} \to (k^\times )^{B}$ given by
$f_! \colon (k^\times )^{B'} \to (k^\times )^{B}$ given by
The analogous statement holds for
Since ![]() $f$ is étale at
$f$ is étale at ![]() $A'$, the square
$A'$, the square

is Cartesian and, therefore,
Next, we consider the rigidification ![]() $\alpha '\colon \mathcal {O}_{\Sigma '} \xrightarrow \sim g^{\prime *}\mathcal {L}=g^{\prime *}\mathcal {O}_{\widetilde Y}=\mathcal {O}_{\Sigma '}$ given by multiplication by
$\alpha '\colon \mathcal {O}_{\Sigma '} \xrightarrow \sim g^{\prime *}\mathcal {L}=g^{\prime *}\mathcal {O}_{\widetilde Y}=\mathcal {O}_{\Sigma '}$ given by multiplication by ![]() $(c'_{z'}) \in (k^\times )^{\Sigma '}$. Let
$(c'_{z'}) \in (k^\times )^{\Sigma '}$. Let ![]() $\Sigma '' =f^{-1}(\Sigma )$ be the scheme-theoretic inverse image of
$\Sigma '' =f^{-1}(\Sigma )$ be the scheme-theoretic inverse image of ![]() $\Sigma$. Then
$\Sigma$. Then ![]() $\Sigma ''=\coprod _{z'\in \Sigma '} \tilde z'$ say, where
$\Sigma ''=\coprod _{z'\in \Sigma '} \tilde z'$ say, where ![]() $\tilde z'\simeq \operatorname {Spec} k[t]/(t^{r_{z'/z}})$. According to the discussion preceding Example 1.9, to compute
$\tilde z'\simeq \operatorname {Spec} k[t]/(t^{r_{z'/z}})$. According to the discussion preceding Example 1.9, to compute ![]() $f_*(\mathcal {L}',\alpha ')$ we need to extend
$f_*(\mathcal {L}',\alpha ')$ we need to extend ![]() $\alpha '$ to a rigidification
$\alpha '$ to a rigidification
and we may as well take ![]() $\alpha ''$ to be the sum of the maps
$\alpha ''$ to be the sum of the maps ![]() $\mathcal {O}_{\tilde z'} \xrightarrow \sim \mathcal {O}_{\tilde z'}$ given by multiplication by
$\mathcal {O}_{\tilde z'} \xrightarrow \sim \mathcal {O}_{\tilde z'}$ given by multiplication by ![]() $c'_{z'}$. Then
$c'_{z'}$. Then ![]() $\mathcal {N}(\alpha '')\colon \mathcal {O}_\Sigma \xrightarrow \sim \mathcal {O}_\Sigma$ is multiplication by
$\mathcal {N}(\alpha '')\colon \mathcal {O}_\Sigma \xrightarrow \sim \mathcal {O}_\Sigma$ is multiplication by ![]() $(c_z)=\hat f_!(c'_{z'})$, where
$(c_z)=\hat f_!(c'_{z'})$, where ![]() $\hat f_!\colon (k^\times )^{\Sigma '} \to (k^\times )^\Sigma$ is the map
$\hat f_!\colon (k^\times )^{\Sigma '} \to (k^\times )^\Sigma$ is the map
whose dual is the map ![]() $f^*\colon \mathbb {Z}[\Sigma '] \to \mathbb {Z}[\Sigma ]$ defined above.
$f^*\colon \mathbb {Z}[\Sigma '] \to \mathbb {Z}[\Sigma ]$ defined above.
Finally, we need to compute the action of ![]() $\operatorname {Aut} \mathcal {O}_{\widetilde Y'}=(k^\times )^{C'}$. From § 1.4 we know that
$\operatorname {Aut} \mathcal {O}_{\widetilde Y'}=(k^\times )^{C'}$. From § 1.4 we know that ![]() $d'\in (k^\times )^{C'}$ maps
$d'\in (k^\times )^{C'}$ maps ![]() $((a'_{x'})_{x'\in B'}, (c'_{z'})_{z'\in \Sigma '})$ to
$((a'_{x'})_{x'\in B'}, (c'_{z'})_{z'\in \Sigma '})$ to ![]() $((d'_{\psi '(x')}a'_{x'}), (d'_{\theta '(z')}c'_{z'}))$, which under the norm maps to
$((d'_{\psi '(x')}a'_{x'}), (d'_{\theta '(z')}c'_{z'}))$, which under the norm maps to
 \begin{equation} \bigg( \bigg(\prod_{\tilde f(x')=x} d'_{\psi'(x')}a'_{x'}\bigg)_{x\in B}, \bigg(\prod_{\tilde f(z')=z} (d'_{\theta'(z')}c'_{z'})^{r_{z'/z}}\bigg)_{z\in \Sigma} \bigg). \end{equation}
\begin{equation} \bigg( \bigg(\prod_{\tilde f(x')=x} d'_{\psi'(x')}a'_{x'}\bigg)_{x\in B}, \bigg(\prod_{\tilde f(z')=z} (d'_{\theta'(z')}c'_{z'})^{r_{z'/z}}\bigg)_{z\in \Sigma} \bigg). \end{equation}
Let ![]() $x\in B$ be fixed. Then if
$x\in B$ be fixed. Then if ![]() $Z=\psi (x)\in C$ is the component containing
$Z=\psi (x)\in C$ is the component containing ![]() $x$, and
$x$, and ![]() $Z'\in C'$ is a component of
$Z'\in C'$ is a component of ![]() $\widetilde Y'$ lying over
$\widetilde Y'$ lying over ![]() $Z$, the set
$Z$, the set ![]() $f^{-1}(x)\cap Z'$ has cardinality
$f^{-1}(x)\cap Z'$ has cardinality ![]() $[\kappa (Z'):\kappa (Z)]$, since
$[\kappa (Z'):\kappa (Z)]$, since ![]() $f$ is étale at
$f$ is étale at ![]() $f^{-1}(x)$. Therefore,
$f^{-1}(x)$. Therefore,
 \[ \prod_{\tilde f(x')=x} d'_{\psi'(x')} = \prod_{\substack{Z'\in C'\\ f(Z')=\psi(x)}} (d'_{Z'})^{[\kappa(Z'):\kappa(Z)]}. \]
\[ \prod_{\tilde f(x')=x} d'_{\psi'(x')} = \prod_{\substack{Z'\in C'\\ f(Z')=\psi(x)}} (d'_{Z'})^{[\kappa(Z'):\kappa(Z)]}. \]
Similarly, let ![]() $z\in \Sigma$ be fixed, and
$z\in \Sigma$ be fixed, and ![]() $Z=\theta (z)\in C$ the component of
$Z=\theta (z)\in C$ the component of ![]() $\widetilde Y$ containing it. Then if
$\widetilde Y$ containing it. Then if ![]() $Z'\in C'$ is a component of
$Z'\in C'$ is a component of ![]() $\widetilde Y'$ lying over
$\widetilde Y'$ lying over ![]() $Z$,
$Z$,
and, therefore,
 \[ \prod_{\tilde f(z')=z} (d'_{\theta'(z')})^{r_{z'/z}} = \prod_{\substack{Z'\in C'\\ f(Z')=\theta(z)}} (d'_{Z'})^{[\kappa(Z'):\kappa(Z)]}. \]
\[ \prod_{\tilde f(z')=z} (d'_{\theta'(z')})^{r_{z'/z}} = \prod_{\substack{Z'\in C'\\ f(Z')=\theta(z)}} (d'_{Z'})^{[\kappa(Z'):\kappa(Z)]}. \]
In other words, the pair (1.5.7) equals
where
 \[ d_Z = \prod_{\substack{Z'\in C'\\ f(Z')=Z}} (d'_{Z'})^{[\kappa(Z'):\kappa(Z)]}. \]
\[ d_Z = \prod_{\substack{Z'\in C'\\ f(Z')=Z}} (d'_{Z'})^{[\kappa(Z'):\kappa(Z)]}. \]
The dual of this map ![]() $d'\mapsto d$ is therefore the homomorphism
$d'\mapsto d$ is therefore the homomorphism ![]() $f^*\colon \mathbb {Z}[C] \to \mathbb {Z}[C']$ defined above.
$f^*\colon \mathbb {Z}[C] \to \mathbb {Z}[C']$ defined above.
1.6 Generalized Jacobians over discrete valuation rings
We resume the notations and hypotheses of § 1.3. Let ![]() $(x_i)_{i\in I}$ be a nonempty finite family of distinct closed points of
$(x_i)_{i\in I}$ be a nonempty finite family of distinct closed points of ![]() $X$, whose residue fields
$X$, whose residue fields ![]() $F_i$ are separable over
$F_i$ are separable over ![]() $F$. Let
$F$. Let ![]() $\mathfrak {m}=\sum _{i\in I}(x_i)$ be the associated modulus on
$\mathfrak {m}=\sum _{i\in I}(x_i)$ be the associated modulus on ![]() $X$, and let
$X$, and let ![]() $J_\mathfrak {m}=\operatorname {Pic}^0_{(X,\mathfrak {m})/F}$ be the generalized Jacobian of
$J_\mathfrak {m}=\operatorname {Pic}^0_{(X,\mathfrak {m})/F}$ be the generalized Jacobian of ![]() $X$ with respect to
$X$ with respect to ![]() $\mathfrak {m}$. The semiabelian variety
$\mathfrak {m}$. The semiabelian variety ![]() $J_\mathfrak {m}$ is an extension of
$J_\mathfrak {m}$ is an extension of ![]() $J$ by the torus
$J$ by the torus
 \[ T_\mathfrak{m}=\bigg(\prod_{i\in I} \mathcal{R}_{F_i/F}\mathbb{G}_{\mathrm{m}}\bigg)/ \mathbb{G}_{\mathrm{m}}. \]
\[ T_\mathfrak{m}=\bigg(\prod_{i\in I} \mathcal{R}_{F_i/F}\mathbb{G}_{\mathrm{m}}\bigg)/ \mathbb{G}_{\mathrm{m}}. \]
Write ![]() $\mathcal {J}_\mathfrak {m}$ for the Néron model of
$\mathcal {J}_\mathfrak {m}$ for the Néron model of ![]() $J_\mathfrak {m}$.
$J_\mathfrak {m}$.
Let ![]() $R_i$ be the integral closure of
$R_i$ be the integral closure of ![]() $R$ in
$R$ in ![]() $F_i$. Then the inclusion of the points
$F_i$. Then the inclusion of the points ![]() $(x_i)$ in
$(x_i)$ in ![]() $X$ extends to a unique morphism
$X$ extends to a unique morphism
As ![]() $\Gamma (\mathcal {X}_s, \mathcal {O}_{\mathcal {X}_s} ) = k$, the special fibre
$\Gamma (\mathcal {X}_s, \mathcal {O}_{\mathcal {X}_s} ) = k$, the special fibre ![]() $g_s \colon \Sigma _s \to \mathcal {X}_s$ is a generalized modulus, in the sense of the previous section. By Proposition 1.4(b) the Néron model
$g_s \colon \Sigma _s \to \mathcal {X}_s$ is a generalized modulus, in the sense of the previous section. By Proposition 1.4(b) the Néron model ![]() $\mathcal {T}_\mathfrak {m}$ of
$\mathcal {T}_\mathfrak {m}$ of ![]() $T_\mathfrak {m}$ equals
$T_\mathfrak {m}$ equals ![]() $(\mathcal {R}_{\Sigma /S} \mathcal {G}_\mathrm {m} )/\mathcal {G}_\mathrm {m}$, and its identity subgroup is
$(\mathcal {R}_{\Sigma /S} \mathcal {G}_\mathrm {m} )/\mathcal {G}_\mathrm {m}$, and its identity subgroup is ![]() $\mathcal {T}_\mathfrak {m}^0 = (\mathcal {R}_{\Sigma /S}\mathbb {G}_{\mathrm {m}} )/\mathbb {G}_{\mathrm {m}}$.
$\mathcal {T}_\mathfrak {m}^0 = (\mathcal {R}_{\Sigma /S}\mathbb {G}_{\mathrm {m}} )/\mathbb {G}_{\mathrm {m}}$.
Lemma 1.13 The pair ![]() $(\Sigma, g)$ is a rigidifier [Reference RaynaudRay70, (2.1.1)] of
$(\Sigma, g)$ is a rigidifier [Reference RaynaudRay70, (2.1.1)] of ![]() $\operatorname {Pic}_{\mathcal {X}/S}$.
$\operatorname {Pic}_{\mathcal {X}/S}$.
Proof. Let ![]() $S'$ be any
$S'$ be any ![]() $S$-scheme. Since
$S$-scheme. Since ![]() $\mathcal {X}/S$ is cohomologically flat and
$\mathcal {X}/S$ is cohomologically flat and ![]() $\Sigma$ is flat over
$\Sigma$ is flat over ![]() $S$, we have
$S$, we have
As ![]() $\Sigma$ is nonempty,
$\Sigma$ is nonempty, ![]() $R \to \Gamma (\Sigma, \mathcal {O}_\Sigma )$ is a split injection of
$R \to \Gamma (\Sigma, \mathcal {O}_\Sigma )$ is a split injection of ![]() $R$-modules, and therefore
$R$-modules, and therefore ![]() $\Gamma (\mathcal {X} \times _S S', \mathcal {O}_{\mathcal {X}\times _S S'}) \to \Gamma (\Sigma \times _S S', \mathcal {O}_{\Sigma \times _S S'})$ is injective.
$\Gamma (\mathcal {X} \times _S S', \mathcal {O}_{\mathcal {X}\times _S S'}) \to \Gamma (\Sigma \times _S S', \mathcal {O}_{\Sigma \times _S S'})$ is injective.
Let ![]() $P_\Sigma$ denote the rigidified Picard functor of [Reference RaynaudRay70, (2.1)]: for any
$P_\Sigma$ denote the rigidified Picard functor of [Reference RaynaudRay70, (2.1)]: for any ![]() $S$-scheme
$S$-scheme ![]() $S'$,
$S'$, ![]() $P_\Sigma (S')$ is the group of equivalence classes of pairs
$P_\Sigma (S')$ is the group of equivalence classes of pairs ![]() $(\mathcal {L}, \alpha )$, where
$(\mathcal {L}, \alpha )$, where ![]() $\mathcal {L}$ is a line bundle on
$\mathcal {L}$ is a line bundle on ![]() $\mathcal {X} \times _S S'$, and
$\mathcal {X} \times _S S'$, and ![]() $\alpha \colon \mathcal {O}_{\Sigma \times _SS'}\xrightarrow \sim (g \times \mathrm {id}_{S'})^* \mathcal {L}$ is a trivialization. Pairs
$\alpha \colon \mathcal {O}_{\Sigma \times _SS'}\xrightarrow \sim (g \times \mathrm {id}_{S'})^* \mathcal {L}$ is a trivialization. Pairs ![]() $(\mathcal {L}, \alpha )$ and
$(\mathcal {L}, \alpha )$ and ![]() $(\mathcal {L}', \alpha ')$ are equivalent if there exists an isomorphism
$(\mathcal {L}', \alpha ')$ are equivalent if there exists an isomorphism ![]() $\sigma \colon \mathcal {L} \xrightarrow \sim \mathcal {L}'$ such that
$\sigma \colon \mathcal {L} \xrightarrow \sim \mathcal {L}'$ such that ![]() $\alpha ' = (g \times \mathrm {id}_{S'})^*(\sigma ) \circ \alpha$. By [Reference RaynaudRay70, (2.3.1–2)],
$\alpha ' = (g \times \mathrm {id}_{S'})^*(\sigma ) \circ \alpha$. By [Reference RaynaudRay70, (2.3.1–2)], ![]() $P_\Sigma$ is a smooth algebraic space in groups over
$P_\Sigma$ is a smooth algebraic space in groups over ![]() $S$, and we have an exact sequence of algebraic spaces in groups [Reference RaynaudRay70, (2.4.1)]
$S$, and we have an exact sequence of algebraic spaces in groups [Reference RaynaudRay70, (2.4.1)]
where ![]() $r$ is the ‘forget the rigidification’ functor. (Since
$r$ is the ‘forget the rigidification’ functor. (Since ![]() $\mathcal {X}/S$ is cohomologically flat and
$\mathcal {X}/S$ is cohomologically flat and ![]() $f_*\mathcal {O}_\mathcal {X}=\mathcal {O}_S$, one has
$f_*\mathcal {O}_\mathcal {X}=\mathcal {O}_S$, one has ![]() $\Gamma _X^*=\mathbb {G}_{\mathrm {m}}$.) If
$\Gamma _X^*=\mathbb {G}_{\mathrm {m}}$.) If ![]() $S$ is strictly Henselian,
$S$ is strictly Henselian, ![]() $P_\Sigma$ is a scheme; indeed,
$P_\Sigma$ is a scheme; indeed, ![]() $P$ is a scheme, and
$P$ is a scheme, and ![]() $\mathcal {T}_\mathfrak {m}^0$ is affine, so by flat descent for affine schemes [Stacks, tag 0245], the
$\mathcal {T}_\mathfrak {m}^0$ is affine, so by flat descent for affine schemes [Stacks, tag 0245], the ![]() $\mathcal {T}_\mathfrak {m}^0$-torsor
$\mathcal {T}_\mathfrak {m}^0$-torsor ![]() $P_\Sigma$ over
$P_\Sigma$ over ![]() $P$ is representable.
$P$ is representable.
Define the sheaf ![]() $P_\mathfrak {m}$ to be the following pushout of fppf sheaves.
$P_\mathfrak {m}$ to be the following pushout of fppf sheaves.

Explicitly, ![]() $P_\mathfrak {m}$ is the sheafification of the functor on
$P_\mathfrak {m}$ is the sheafification of the functor on ![]() $S$-schemes
$S$-schemes
where ![]() $\mathcal {T}_\mathfrak {m}^0(S')$ acts on the product by
$\mathcal {T}_\mathfrak {m}^0(S')$ acts on the product by ![]() $a(b, c) = (ab, a^{-1}c)$.
$a(b, c) = (ab, a^{-1}c)$.
Proposition 1.14 The sheaf ![]() $P_\mathfrak {m}$ is a smooth algebraic space in groups over
$P_\mathfrak {m}$ is a smooth algebraic space in groups over ![]() $S$. If
$S$. If ![]() $S$ is strictly Henselian,
$S$ is strictly Henselian, ![]() $P_\mathfrak {m}$ is represented by a smooth
$P_\mathfrak {m}$ is represented by a smooth ![]() $S$-group scheme.
$S$-group scheme.
Proof. We have an exact sequence ![]() $0 \to \mathcal {T}_\mathfrak {m}^0 \to \mathcal {T}_\mathfrak {m} \xrightarrow {\pi } s_* \Phi (T) \to 0$ of
$0 \to \mathcal {T}_\mathfrak {m}^0 \to \mathcal {T}_\mathfrak {m} \xrightarrow {\pi } s_* \Phi (T) \to 0$ of ![]() $S$-group schemes. For
$S$-group schemes. For ![]() $h \in \Phi (T) = (s_*\Phi (T))(S)$, let
$h \in \Phi (T) = (s_*\Phi (T))(S)$, let ![]() $U_h = \pi ^{-1}(h)$, an affine open subscheme of
$U_h = \pi ^{-1}(h)$, an affine open subscheme of ![]() $\mathcal {T}_\mathfrak {m}$. Then
$\mathcal {T}_\mathfrak {m}$. Then ![]() $\mathcal {T}_\mathfrak {m}$ is the union of the
$\mathcal {T}_\mathfrak {m}$ is the union of the ![]() $U_h$, glued along their generic fibres. If
$U_h$, glued along their generic fibres. If ![]() $\hat h \in \mathcal {T}_\mathfrak {m}(S) = T(F)$ is any lift of
$\hat h \in \mathcal {T}_\mathfrak {m}(S) = T(F)$ is any lift of ![]() $h$, then
$h$, then ![]() $U_h$ is the translate of
$U_h$ is the translate of ![]() $\mathcal {T}_\mathfrak {m}^0$ by
$\mathcal {T}_\mathfrak {m}^0$ by ![]() $\hat h$. Therefore,
$\hat h$. Therefore, ![]() $P_\mathfrak {m}$ is the union of copies of
$P_\mathfrak {m}$ is the union of copies of ![]() $P_\Sigma$ indexed by
$P_\Sigma$ indexed by ![]() $\Phi (T)$, glued along their generic fibres by the isomorphism given by translation by
$\Phi (T)$, glued along their generic fibres by the isomorphism given by translation by ![]() $\hat h \in P_\Sigma (F)$, and the result follows from the corresponding statement for
$\hat h \in P_\Sigma (F)$, and the result follows from the corresponding statement for ![]() $P_\Sigma$.
$P_\Sigma$.
This result implies that ![]() $P_\mathfrak {m}$ is determined by its restriction to
$P_\mathfrak {m}$ is determined by its restriction to ![]() $(Sm/S)$, the category of essentially smooth
$(Sm/S)$, the category of essentially smooth ![]() $S$-schemes. We can describe this functor explicitly. Let
$S$-schemes. We can describe this functor explicitly. Let ![]() $\mathcal {F}^*$ be the functor on
$\mathcal {F}^*$ be the functor on ![]() $(Sm/S)$ whose value on
$(Sm/S)$ whose value on ![]() $S'$ is the group of equivalence classes of pairs
$S'$ is the group of equivalence classes of pairs ![]() $(\mathcal {L}, \beta = (\beta _i )_{i\in I})$, where
$(\mathcal {L}, \beta = (\beta _i )_{i\in I})$, where ![]() $\mathcal {L}$ is a line bundle on
$\mathcal {L}$ is a line bundle on ![]() $\mathcal {X} \times _S S'$ and for each
$\mathcal {X} \times _S S'$ and for each ![]() $i \in I$,
$i \in I$, ![]() $\beta _i \colon \mathcal {O}_{S'} \otimes _R F_i \xrightarrow \sim (x_i \times \mathrm {id}_{S'})^*\mathcal {L}$ is a trivialization of
$\beta _i \colon \mathcal {O}_{S'} \otimes _R F_i \xrightarrow \sim (x_i \times \mathrm {id}_{S'})^*\mathcal {L}$ is a trivialization of ![]() $\mathcal {L}$ at
$\mathcal {L}$ at ![]() $x_i \times _S S'$. Pairs
$x_i \times _S S'$. Pairs ![]() $(\mathcal {L}, \beta )$ and
$(\mathcal {L}, \beta )$ and ![]() $(\mathcal {L}', \beta ')$ are equivalent if there exists an isomorphism
$(\mathcal {L}', \beta ')$ are equivalent if there exists an isomorphism ![]() $\sigma \colon \mathcal {L} \xrightarrow \sim \mathcal {L}'$ and some
$\sigma \colon \mathcal {L} \xrightarrow \sim \mathcal {L}'$ and some ![]() $u \in \mathcal {O}^\times (S'\otimes _R F)$ such that for every
$u \in \mathcal {O}^\times (S'\otimes _R F)$ such that for every ![]() $i$ the following diagram commutes.
$i$ the following diagram commutes.

Note that ![]() $u$ is uniquely determined by
$u$ is uniquely determined by ![]() $\sigma$. If
$\sigma$. If ![]() $S' \in (Sm/S)$ is actually an
$S' \in (Sm/S)$ is actually an ![]() $F$-scheme, then giving a pair
$F$-scheme, then giving a pair ![]() $(u, \sigma )$ is the same as giving an isomorphism
$(u, \sigma )$ is the same as giving an isomorphism ![]() $(\mathcal {L}, \beta ) \xrightarrow \sim (\mathcal {L}', \beta ')$, since we can absorb
$(\mathcal {L}, \beta ) \xrightarrow \sim (\mathcal {L}', \beta ')$, since we can absorb ![]() $u$ into
$u$ into ![]() $\sigma$ and, therefore, the restrictions of
$\sigma$ and, therefore, the restrictions of ![]() $\mathcal {F}^*$ and
$\mathcal {F}^*$ and ![]() $P_\Sigma$ to
$P_\Sigma$ to ![]() $(Sm/F)$ are equal.
$(Sm/F)$ are equal.
Theorem 1.15 The restriction of ![]() $P_\mathfrak {m}$ to
$P_\mathfrak {m}$ to ![]() $(Sm/S)_\mathrm {\acute et}$ is the sheafification for the étale topology of the presheaf
$(Sm/S)_\mathrm {\acute et}$ is the sheafification for the étale topology of the presheaf ![]() $\mathcal {F}^*$.
$\mathcal {F}^*$.
Proof. We have an exact sequence of fppf sheaves
where the map ![]() $\psi$ on
$\psi$ on ![]() $S'$-valued points is given by
$S'$-valued points is given by
By definition, ![]() $P_\mathfrak {m}$ is the cokernel of
$P_\mathfrak {m}$ is the cokernel of ![]() $\psi$ in the category of fppf sheaves. As the coimage of
$\psi$ in the category of fppf sheaves. As the coimage of ![]() $\psi$ is a smooth
$\psi$ is a smooth ![]() $S$-group scheme,
$S$-group scheme, ![]() $P_\mathfrak {m}$ is also the cokernel of
$P_\mathfrak {m}$ is also the cokernel of ![]() $\psi$ in the category of étale sheaves. Let
$\psi$ in the category of étale sheaves. Let ![]() $S' \in (Sm/S)$ and consider the map
$S' \in (Sm/S)$ and consider the map
given as follows: let ![]() $(\mathcal {L}, \alpha )$ represent an element of
$(\mathcal {L}, \alpha )$ represent an element of ![]() $P_\Sigma (S')$ and
$P_\Sigma (S')$ and ![]() $v \in \mathbb {G}_{\mathrm {m}} (\Sigma _F \times _S S' )$. We map the pair
$v \in \mathbb {G}_{\mathrm {m}} (\Sigma _F \times _S S' )$. We map the pair ![]() $((\mathcal {L}, \alpha ), v)$ to the equivalence class of
$((\mathcal {L}, \alpha ), v)$ to the equivalence class of ![]() $(\mathcal {L}, \beta )$, where
$(\mathcal {L}, \beta )$, where ![]() $\beta = \alpha \otimes v \colon \mathcal {O}_{\Sigma \times S' \otimes F}\xrightarrow \sim (g \times \mathrm {id}_{S' \otimes F} )^* \mathcal {L}$. It is easy to see that this is well-defined and functorial, and that the resulting sequence of presheaves on
$\beta = \alpha \otimes v \colon \mathcal {O}_{\Sigma \times S' \otimes F}\xrightarrow \sim (g \times \mathrm {id}_{S' \otimes F} )^* \mathcal {L}$. It is easy to see that this is well-defined and functorial, and that the resulting sequence of presheaves on ![]() $(Sm/S)$
$(Sm/S)$
is exact. Moreover, for any ![]() $(\mathcal {L}, \beta ) \in \mathcal {F}^* (S' )$, there exists a Zariski cover
$(\mathcal {L}, \beta ) \in \mathcal {F}^* (S' )$, there exists a Zariski cover ![]() $S'' \to S'$ such that
$S'' \to S'$ such that ![]() $(\mathcal {L}, \beta )|_{S''}$ is in the image of
$(\mathcal {L}, \beta )|_{S''}$ is in the image of ![]() $\phi _{S''}$. The result follows.
$\phi _{S''}$. The result follows.
Let ![]() $E_\mathfrak {m}$ denote the closure in
$E_\mathfrak {m}$ denote the closure in ![]() $P_\mathfrak {m}$ of the zero section. It is contained in
$P_\mathfrak {m}$ of the zero section. It is contained in
Theorem 1.16
(a) The map
 $r'$ (1.6.1) induces an isomorphism
$r'$ (1.6.1) induces an isomorphism  $E_\mathfrak {m} \xrightarrow \sim E$.
$E_\mathfrak {m} \xrightarrow \sim E$.(b) The quotient
 $P_\mathfrak {m}' /E_\mathfrak {m}$ is represented by the Néron model
$P_\mathfrak {m}' /E_\mathfrak {m}$ is represented by the Néron model  $\mathcal {J}_\mathfrak {m}$ of
$\mathcal {J}_\mathfrak {m}$ of  $J_\mathfrak {m}$.
$J_\mathfrak {m}$.(c) There is an exact sequence of Néron models
 \[ 0 \to \mathcal{T}_\mathfrak{m} \to \mathcal{J}_\mathfrak{m} \to \mathcal{J} \to 0. \]
\[ 0 \to \mathcal{T}_\mathfrak{m} \to \mathcal{J}_\mathfrak{m} \to \mathcal{J} \to 0. \]
(d) Assume that S is strictly Henselian. Then there is a canonical isomorphism
where \[ P_{\mathfrak{m},s} /P_{\mathfrak{m},s}^0 \xrightarrow\sim \mathbb{Z}^C \oplus \mathbb{Z}^I /e\mathbb{Z}, \]
\[ P_{\mathfrak{m},s} /P_{\mathfrak{m},s}^0 \xrightarrow\sim \mathbb{Z}^C \oplus \mathbb{Z}^I /e\mathbb{Z}, \]
 $e = (e_i) \colon \mathbb {Z} \to \mathbb {Z}^I$ is as in Proposition 1.4.
$e = (e_i) \colon \mathbb {Z} \to \mathbb {Z}^I$ is as in Proposition 1.4.
The analogue of assertion (a) need not hold for ![]() $P_\Sigma$: see Example 1.17 after the proof.
$P_\Sigma$: see Example 1.17 after the proof.
Proof. (a) By [Reference RaynaudRay70, (3.3.5)] and Proposition 1.14, ![]() $E_\mathfrak {m}$ is an étale algebraic space in groups over
$E_\mathfrak {m}$ is an étale algebraic space in groups over ![]() $S$. We may therefore compute it by restriction to
$S$. We may therefore compute it by restriction to ![]() $(Sm/S)_\mathrm {\acute et}$, using the description of Theorem 1.15, and we may also assume that
$(Sm/S)_\mathrm {\acute et}$, using the description of Theorem 1.15, and we may also assume that ![]() $S$ is strictly Henselian. In this case, from § 1.3 we have that
$S$ is strictly Henselian. In this case, from § 1.3 we have that ![]() $E(S)$ is generated by the classes of the line bundles
$E(S)$ is generated by the classes of the line bundles ![]() $\mathcal {O}_\mathcal {X} (Y_j )$. Let
$\mathcal {O}_\mathcal {X} (Y_j )$. Let ![]() $\beta _{\mathrm {triv}} = (\beta _{\mathrm {triv},i} )$ be the trivial rigidification of the generic fibre
$\beta _{\mathrm {triv}} = (\beta _{\mathrm {triv},i} )$ be the trivial rigidification of the generic fibre ![]() $\mathcal {O}_\mathcal {X} (Y_j )_F = \mathcal {O}_X$ at
$\mathcal {O}_\mathcal {X} (Y_j )_F = \mathcal {O}_X$ at ![]() $(x_i)$. Then
$(x_i)$. Then ![]() $E_\mathfrak {m}$ is generated by the equivalence classes of pairs
$E_\mathfrak {m}$ is generated by the equivalence classes of pairs ![]() $(\mathcal {O}_\mathcal {X} (Y_j ),\beta _{\mathrm {triv}})$, and therefore
$(\mathcal {O}_\mathcal {X} (Y_j ),\beta _{\mathrm {triv}})$, and therefore ![]() $E_\mathfrak {m} \simeq E$.
$E_\mathfrak {m} \simeq E$.
(b),(c) We now have an exact sequence
of smooth separated ![]() $S$-algebraic spaces in groups, which are therefore separated
$S$-algebraic spaces in groups, which are therefore separated ![]() $S$-group schemes [Reference RaynaudRay70, (3.3.1)], whose generic fibre is the sequence
$S$-group schemes [Reference RaynaudRay70, (3.3.1)], whose generic fibre is the sequence ![]() $0 \to T_\mathfrak {m} \to J_\mathfrak {m} \to J \to 0$. As
$0 \to T_\mathfrak {m} \to J_\mathfrak {m} \to J \to 0$. As ![]() $\mathcal {T}_\mathfrak {m}$ and
$\mathcal {T}_\mathfrak {m}$ and ![]() $P'/E$ are the Néron models of
$P'/E$ are the Néron models of ![]() $T$ and
$T$ and ![]() $J$, the result follows from Proposition 1.3.
$J$, the result follows from Proposition 1.3.
(d) From § 1.1, ![]() $\mathcal {T}_{\mathfrak {m},s} /\mathcal {T}_{\mathfrak {m},s}^0 \simeq \operatorname {coker}(e \colon \mathbb {Z} \to \mathbb {Z}^I )$. We then have a commutative diagram of étale sheaves on
$\mathcal {T}_{\mathfrak {m},s} /\mathcal {T}_{\mathfrak {m},s}^0 \simeq \operatorname {coker}(e \colon \mathbb {Z} \to \mathbb {Z}^I )$. We then have a commutative diagram of étale sheaves on ![]() $(Sm/S)$
$(Sm/S)$

whose rows are exact (since ![]() $\pi _0$ is right exact). For
$\pi _0$ is right exact). For ![]() $S' /S$ smooth, and
$S' /S$ smooth, and ![]() $(\mathcal {L}, \beta = (\beta _i ))$ representing an element of
$(\mathcal {L}, \beta = (\beta _i ))$ representing an element of ![]() $\mathcal {F}^* (S' )$,
$\mathcal {F}^* (S' )$, ![]() $\beta _i (1)$ is a rational section of
$\beta _i (1)$ is a rational section of ![]() $(g_i \times \mathrm {id}_{S'} )^* \mathcal {L}$ so has a well-defined order along the special fibre
$(g_i \times \mathrm {id}_{S'} )^* \mathcal {L}$ so has a well-defined order along the special fibre ![]() $\operatorname {ord}_\mathcal {L} \beta _i (1) \in \Gamma (S' , s_* \mathbb {Z})$. If
$\operatorname {ord}_\mathcal {L} \beta _i (1) \in \Gamma (S' , s_* \mathbb {Z})$. If ![]() $(\mathcal {L}', \beta ')$ is equivalent to
$(\mathcal {L}', \beta ')$ is equivalent to ![]() $(\mathcal {L}, \beta )$, then
$(\mathcal {L}, \beta )$, then ![]() $(\operatorname {ord}_\mathcal {L} \beta _i' (1) - \operatorname {ord}_{\mathcal {L}'} \beta _i (1))_i \in \Gamma (S' , s_* (e\mathbb {Z}))$, which gives a splitting of the bottom row in the diagram (which is, therefore, also exact on the left).
$(\operatorname {ord}_\mathcal {L} \beta _i' (1) - \operatorname {ord}_{\mathcal {L}'} \beta _i (1))_i \in \Gamma (S' , s_* (e\mathbb {Z}))$, which gives a splitting of the bottom row in the diagram (which is, therefore, also exact on the left).
Example 1.17 Let us work out the simplest nontrivial example: assume that ![]() $\mathrm {char}(F ) \ne 2$, and let
$\mathrm {char}(F ) \ne 2$, and let ![]() $\mathcal {X}$ be the closed subscheme of
$\mathcal {X}$ be the closed subscheme of ![]() $\mathbb {P}^2_R$ given by the equation
$\mathbb {P}^2_R$ given by the equation ![]() $T_1 T_2 = \varpi T_0^2$. Then
$T_1 T_2 = \varpi T_0^2$. Then ![]() $X = \mathcal {X}_F$ is a smooth conic, split over
$X = \mathcal {X}_F$ is a smooth conic, split over ![]() $F$, and
$F$, and ![]() $\mathcal {X}_s$ is the line pair
$\mathcal {X}_s$ is the line pair ![]() $T_1 T_2 = 0$. Hypotheses (H1)–(H3) of § 1.3 are all satisfied. Let
$T_1 T_2 = 0$. Hypotheses (H1)–(H3) of § 1.3 are all satisfied. Let ![]() $x_0$,
$x_0$, ![]() $x_1 \in X(F ) = \mathcal {X}(S)$ be distinct points. Let
$x_1 \in X(F ) = \mathcal {X}(S)$ be distinct points. Let ![]() $\mathcal {X}_s = Y \cup Y'$, where the components are labelled in such a way that
$\mathcal {X}_s = Y \cup Y'$, where the components are labelled in such a way that ![]() $x_0$ meets
$x_0$ meets ![]() $Y'$. We consider the generalized Jacobian
$Y'$. We consider the generalized Jacobian ![]() $J_\mathfrak {m}$ with
$J_\mathfrak {m}$ with ![]() $\mathfrak {m} = (x_0 ) + (x_1 )$. The relative Picard space
$\mathfrak {m} = (x_0 ) + (x_1 )$. The relative Picard space ![]() $P = \operatorname {Pic}_{\mathcal {X}/S}$ is a scheme, and is the union of its sections over
$P = \operatorname {Pic}_{\mathcal {X}/S}$ is a scheme, and is the union of its sections over ![]() $S$. We have
$S$. We have ![]() $P (F ) = \mathbb {Z}$, generated by the class of
$P (F ) = \mathbb {Z}$, generated by the class of ![]() $\mathcal {O}_\mathcal {X} (x_0 )$, and
$\mathcal {O}_\mathcal {X} (x_0 )$, and ![]() $P (R) = P_s (k) = \mathbb {Z}^2$, generated by the classes of
$P (R) = P_s (k) = \mathbb {Z}^2$, generated by the classes of ![]() $\mathcal {O}_\mathcal {X} (Y ) \simeq \mathcal {O}_\mathcal {X} (-Y' )$ and
$\mathcal {O}_\mathcal {X} (Y ) \simeq \mathcal {O}_\mathcal {X} (-Y' )$ and ![]() $\mathcal {O}_\mathcal {X} (x_0 )$. The restriction map
$\mathcal {O}_\mathcal {X} (x_0 )$. The restriction map ![]() $P (S) \to P (F )$ is the second projection
$P (S) \to P (F )$ is the second projection ![]() $\mathbb {Z}^2 \to \mathbb {Z}$, and equals the degree map. Therefore,
$\mathbb {Z}^2 \to \mathbb {Z}$, and equals the degree map. Therefore, ![]() $P' = E$ is the ‘skyscraper scheme’
$P' = E$ is the ‘skyscraper scheme’ ![]() $s_* \mathbb {Z}$, obtained by gluing copies of
$s_* \mathbb {Z}$, obtained by gluing copies of ![]() $S$ indexed by
$S$ indexed by ![]() $\mathbb {Z}$ along their generic points, and
$\mathbb {Z}$ along their generic points, and ![]() $P' (S)$ is generated by the class of
$P' (S)$ is generated by the class of ![]() $\mathcal {O}_\mathcal {X} (Y )$.
$\mathcal {O}_\mathcal {X} (Y )$.
There is an isomorphism ![]() $\mathbb {G}_{\mathrm {m}} \xrightarrow \sim J_\mathfrak {m} = P_\Sigma ' \otimes F$, which on
$\mathbb {G}_{\mathrm {m}} \xrightarrow \sim J_\mathfrak {m} = P_\Sigma ' \otimes F$, which on ![]() $F$-points takes
$F$-points takes ![]() $a \in F^\times$ to the equivalence class of the pair
$a \in F^\times$ to the equivalence class of the pair ![]() $(\mathcal {O}_\mathcal {X} , \alpha = (\alpha _0 , \alpha _1 ))$, where
$(\mathcal {O}_\mathcal {X} , \alpha = (\alpha _0 , \alpha _1 ))$, where ![]() $\alpha _i \colon F \to x_i^* \mathcal {O}_\mathcal {X} = F$ is the identity for
$\alpha _i \colon F \to x_i^* \mathcal {O}_\mathcal {X} = F$ is the identity for ![]() $i = 0$ and multiplication by
$i = 0$ and multiplication by ![]() $a$ for
$a$ for ![]() $i = 1$. As
$i = 1$. As ![]() $x_0$ does not meet
$x_0$ does not meet ![]() $Y$ we also have
$Y$ we also have ![]() $x_0^*\mathcal {O}_\mathcal {X} (Y ) = \mathcal {O}_S$. We now have two cases.
$x_0^*\mathcal {O}_\mathcal {X} (Y ) = \mathcal {O}_S$. We now have two cases.
– If
 $x_1$ meets
$x_1$ meets  $Y'$, then
$Y'$, then  $x_1^*\mathcal {O}_\mathcal {X} (Y ) = \mathcal {O}_S$ as well. Thus, there is a canonical rigidification
$x_1^*\mathcal {O}_\mathcal {X} (Y ) = \mathcal {O}_S$ as well. Thus, there is a canonical rigidification  $(\alpha _i )$ of
$(\alpha _i )$ of  $\mathcal {O}_\mathcal {X} (Y )$ along
$\mathcal {O}_\mathcal {X} (Y )$ along  $\Sigma$, for which each
$\Sigma$, for which each  $\alpha _i$ is the identity map on
$\alpha _i$ is the identity map on  $\mathcal {O}_S$. Therefore,
$\mathcal {O}_S$. Therefore,  $P_\Sigma \simeq \mathbb {G}_{\mathrm {m}} \times P$ splits (and is not separated); likewise,
$P_\Sigma \simeq \mathbb {G}_{\mathrm {m}} \times P$ splits (and is not separated); likewise,  $P'_\Sigma \simeq \mathbb {G}_{\mathrm {m}} \times s_*\mathbb {Z}$. The pushout
$P'_\Sigma \simeq \mathbb {G}_{\mathrm {m}} \times s_*\mathbb {Z}$. The pushout  $P_\mathfrak {m}'$ is simply the product
$P_\mathfrak {m}'$ is simply the product  $\mathcal {G}_\mathrm {m} \times s_*\mathbb {Z}$.
$\mathcal {G}_\mathrm {m} \times s_*\mathbb {Z}$.– If
 $x_1$ meets
$x_1$ meets  $Y$, then
$Y$, then  $x_1^*\mathcal {O}_\mathcal {X} (Y ) = \mathcal {O}_S (s) = \varpi ^{-1}\mathcal {O}_S$. Thus, there is a bijection
$x_1^*\mathcal {O}_\mathcal {X} (Y ) = \mathcal {O}_S (s) = \varpi ^{-1}\mathcal {O}_S$. Thus, there is a bijection  $\mathbb {Z} \times R^\times \xrightarrow \sim P_\Sigma ' (S)$ which takes
$\mathbb {Z} \times R^\times \xrightarrow \sim P_\Sigma ' (S)$ which takes  $(n, a)$ to the line bundle
$(n, a)$ to the line bundle  $\mathcal {O}_\mathcal {X} (nY )$ with rigidification
$\mathcal {O}_\mathcal {X} (nY )$ with rigidification  $\alpha _0 = \mathrm {id}$,
$\alpha _0 = \mathrm {id}$,  $\alpha _1 (1) = \varpi ^{-n}$. Its composition with restriction to the generic fibre is the bijection
$\alpha _1 (1) = \varpi ^{-n}$. Its composition with restriction to the generic fibre is the bijection  $\mathbb {Z} \times R^\times \to P_\Sigma (F ) = F^\times$ given by
$\mathbb {Z} \times R^\times \to P_\Sigma (F ) = F^\times$ given by  $(n, a) \mapsto \varpi ^{-1} a$. Therefore,
$(n, a) \mapsto \varpi ^{-1} a$. Therefore,  $P_\Sigma '$ is separated, and is isomorphic to the Néron model
$P_\Sigma '$ is separated, and is isomorphic to the Néron model  $\mathcal {G}_\mathrm {m}$. The pushout
$\mathcal {G}_\mathrm {m}$. The pushout  $P_\mathfrak {m}'$ is then the tautological splitting of the extension
$P_\mathfrak {m}'$ is then the tautological splitting of the extension  $\mathbb {G}_{\mathrm {m}} \to \mathcal {G}_\mathrm {m} \to s_* \mathbb {Z}$ after pushing out through
$\mathbb {G}_{\mathrm {m}} \to \mathcal {G}_\mathrm {m} \to s_* \mathbb {Z}$ after pushing out through  $\mathbb {G}_{\mathrm {m}} \to \mathcal {G}_\mathrm {m}$, so is isomorphic to
$\mathbb {G}_{\mathrm {m}} \to \mathcal {G}_\mathrm {m}$, so is isomorphic to  $\mathcal {G}_\mathrm {m} \times s_*\mathbb {Z}$ in this case as well.
$\mathcal {G}_\mathrm {m} \times s_*\mathbb {Z}$ in this case as well.
We return to the general case. From § 1.3, ![]() $P_s^0 \cap E_s$ is finite constant and cyclic of order
$P_s^0 \cap E_s$ is finite constant and cyclic of order ![]() $d$, generated by the class of the line bundle
$d$, generated by the class of the line bundle ![]() $\mathcal {L}'$. Therefore,
$\mathcal {L}'$. Therefore, ![]() $P_{\mathfrak {m},s}^0\cap E_{\mathfrak {m},s}$ is finite constant and cyclic of order dividing
$P_{\mathfrak {m},s}^0\cap E_{\mathfrak {m},s}$ is finite constant and cyclic of order dividing ![]() $d$. Applying the results of § 1.4, we obtain the following.
$d$. Applying the results of § 1.4, we obtain the following.
Corollary 1.18 Assume that ![]() $d = 1$. Then:
$d = 1$. Then:
(a)
 $\mathcal {J}_{\mathfrak {m},s}^0 = \operatorname {Pic}^0_{(\mathcal {X}_s ,\Sigma _s )/k}$;
$\mathcal {J}_{\mathfrak {m},s}^0 = \operatorname {Pic}^0_{(\mathcal {X}_s ,\Sigma _s )/k}$;(b) if
 $k$ is perfect, there is a canonical isomorphism of
$k$ is perfect, there is a canonical isomorphism of  $\operatorname {Gal}(\bar k/k)$-modules
where the graph
$\operatorname {Gal}(\bar k/k)$-modules
where the graph \[ \operatorname{Hom}(\mathcal{J}_{\mathfrak{m},s}^{0,\mathrm{lin}}\otimes_k \bar k, \mathbb{G}_{\mathrm{m}} ) = H_1 (\widetilde\Gamma_{\mathcal{X}_{\bar s} ,\Sigma_{\bar s}} , \mathbb{Z}) \]
\[ \operatorname{Hom}(\mathcal{J}_{\mathfrak{m},s}^{0,\mathrm{lin}}\otimes_k \bar k, \mathbb{G}_{\mathrm{m}} ) = H_1 (\widetilde\Gamma_{\mathcal{X}_{\bar s} ,\Sigma_{\bar s}} , \mathbb{Z}) \]
 $\widetilde{\Gamma} _{\mathcal {X}_{\bar s} ,\Sigma _{\bar s}}$ is as in § 1.4.
$\widetilde{\Gamma} _{\mathcal {X}_{\bar s} ,\Sigma _{\bar s}}$ is as in § 1.4.
Finally, we compute the component group ![]() $\Phi (J_\mathfrak {m})$.
$\Phi (J_\mathfrak {m})$.
Theorem 1.19 Suppose that ![]() $R$ is strictly Henselian. Then
$R$ is strictly Henselian. Then ![]() $\Phi (J_\mathfrak {m})$ is canonically isomorphic to the homology of the complex
$\Phi (J_\mathfrak {m})$ is canonically isomorphic to the homology of the complex
where ![]() $a$ and
$a$ and ![]() $b$ are as in (1.3.2), and
$b$ are as in (1.3.2), and ![]() $h\colon \mathbb {Z}[C] \to \mathbb {Z}^I/e\mathbb {Z}$ is induced by the map
$h\colon \mathbb {Z}[C] \to \mathbb {Z}^I/e\mathbb {Z}$ is induced by the map
(Equivalently, ![]() $h_{ij}$ is the degree of the divisor
$h_{ij}$ is the degree of the divisor ![]() $g_i^* Y_j$ on
$g_i^* Y_j$ on ![]() $\operatorname {Spec} R_i$.)
$\operatorname {Spec} R_i$.)
Proof. By Theorem 1.16, ![]() $\Phi (J_\mathfrak {m})$ is the group of connected components of the quotient
$\Phi (J_\mathfrak {m})$ is the group of connected components of the quotient ![]() $P_{\mathfrak {m},s}'/E_{\mathfrak {m},s}$, hence is the homology of the complex
$P_{\mathfrak {m},s}'/E_{\mathfrak {m},s}$, hence is the homology of the complex ![]() $E_\mathfrak {m} (k) \to \pi _0 (P_{\mathfrak {m},s}) \xrightarrow {\deg }\mathbb {Z}$. By Theorem 1.16(d), we may rewrite this complex as (1.6.4). What remains is to identify the map
$E_\mathfrak {m} (k) \to \pi _0 (P_{\mathfrak {m},s}) \xrightarrow {\deg }\mathbb {Z}$. By Theorem 1.16(d), we may rewrite this complex as (1.6.4). What remains is to identify the map ![]() $h$. By the proof of Theorem 1.16(a),
$h$. By the proof of Theorem 1.16(a), ![]() $E_\mathfrak {m} (k)$ is generated by the equivalence class of pairs
$E_\mathfrak {m} (k)$ is generated by the equivalence class of pairs ![]() $(\mathcal {O}_\mathcal {X} (Y_j ), \beta _{\mathrm {triv}} )$, and the proof of Theorem 1.16(d) then gives the desired formula for
$(\mathcal {O}_\mathcal {X} (Y_j ), \beta _{\mathrm {triv}} )$, and the proof of Theorem 1.16(d) then gives the desired formula for ![]() $h$.
$h$.
For general ![]() $S$ we have
$S$ we have ![]() $\Sigma \times _S S^{\mathrm {sh}} = \coprod _{\tilde i \in \widetilde I} S_{\tilde i}$, where
$\Sigma \times _S S^{\mathrm {sh}} = \coprod _{\tilde i \in \widetilde I} S_{\tilde i}$, where ![]() $S_{\tilde i}$ is the spectrum of a discrete valuation ring finite over
$S_{\tilde i}$ is the spectrum of a discrete valuation ring finite over ![]() $R^{\mathrm {sh}}$. Let
$R^{\mathrm {sh}}$. Let ![]() $\widetilde C$ be the set of irreducible components of
$\widetilde C$ be the set of irreducible components of ![]() $\mathcal {X} \otimes k^\mathrm {sep}$. Then
$\mathcal {X} \otimes k^\mathrm {sep}$. Then ![]() $\operatorname {Gal}(F^{\mathrm {sep}} /F )$ acts on
$\operatorname {Gal}(F^{\mathrm {sep}} /F )$ acts on ![]() $\widetilde I$ and
$\widetilde I$ and ![]() $\widetilde C$ through its quotient
$\widetilde C$ through its quotient ![]() $\operatorname {Gal}(k^\mathrm {sep}/k)$, and the above gives a
$\operatorname {Gal}(k^\mathrm {sep}/k)$, and the above gives a ![]() $\operatorname {Gal}(k^\mathrm {sep} /k)$-equivariant isomorphism between
$\operatorname {Gal}(k^\mathrm {sep} /k)$-equivariant isomorphism between ![]() $\Phi (J_\mathfrak {m})$ and the homology of the complex
$\Phi (J_\mathfrak {m})$ and the homology of the complex
attached to ![]() $\mathcal {X} \times _S S^{\mathrm {sh}}$.
$\mathcal {X} \times _S S^{\mathrm {sh}}$.
In the semistable case we can describe both the character and component groups in terms of the reduced extended graph.
Corollary 1.20 Suppose that ![]() $\mathcal {X}\otimes R^{\mathrm {sh}}$ is semistable and
$\mathcal {X}\otimes R^{\mathrm {sh}}$ is semistable and ![]() $I=I^\mathrm {reg}$. Then we have the following.
$I=I^\mathrm {reg}$. Then we have the following.
(a) If
 $k$ is perfect, there is a canonical isomorphism of
$k$ is perfect, there is a canonical isomorphism of  $\operatorname {Gal}(\bar k/k)$-modules
where the reduced extended graph
$\operatorname {Gal}(\bar k/k)$-modules
where the reduced extended graph \[ \operatorname{Hom}(\mathcal{J}_{\mathfrak{m},s}^{0,\mathrm{lin}}\otimes_k \bar k, \mathbb{G}_{\mathrm{m}} ) = H_1 (\Gamma_{\mathcal{X}_{\bar s} ,\Sigma_{\bar s}} , \mathbb{Z}), \]
\[ \operatorname{Hom}(\mathcal{J}_{\mathfrak{m},s}^{0,\mathrm{lin}}\otimes_k \bar k, \mathbb{G}_{\mathrm{m}} ) = H_1 (\Gamma_{\mathcal{X}_{\bar s} ,\Sigma_{\bar s}} , \mathbb{Z}), \]
 $\Gamma _{\mathcal {X}_{\bar s} ,\Sigma _{\bar s}}$ is as in § 1.4.
$\Gamma _{\mathcal {X}_{\bar s} ,\Sigma _{\bar s}}$ is as in § 1.4.(b) Assume that
 $R$ is strictly Henselian. There is a canonical isomorphism
where
$R$ is strictly Henselian. There is a canonical isomorphism
where \[ \Phi(J_\mathfrak{m}) = \operatorname{coker} \big((\square, \theta^*) \colon \mathbb{Z}[C] \to \mathbb{Z}[C]_0 \oplus \mathbb{Z}^I \big), \]
\[ \Phi(J_\mathfrak{m}) = \operatorname{coker} \big((\square, \theta^*) \colon \mathbb{Z}[C] \to \mathbb{Z}[C]_0 \oplus \mathbb{Z}^I \big), \]
 $\square$ is the Laplacian of the reduced graph
$\square$ is the Laplacian of the reduced graph  $\Gamma _{\mathcal {X}_s}$, and
$\Gamma _{\mathcal {X}_s}$, and  $\theta \colon I \to C$ is the map from § 1.4.
$\theta \colon I \to C$ is the map from § 1.4.
Note that ![]() $\theta$ depends only on the labelled graph
$\theta$ depends only on the labelled graph ![]() $(\Gamma _{\mathcal {X}_s,\Sigma _s}, v_0)$. The hypothesis
$(\Gamma _{\mathcal {X}_s,\Sigma _s}, v_0)$. The hypothesis ![]() $I=I^\mathrm {reg}$ is satisfied if, for example,
$I=I^\mathrm {reg}$ is satisfied if, for example, ![]() $\{x_i\}\subset X(F^{\mathrm {sh}})$.
$\{x_i\}\subset X(F^{\mathrm {sh}})$.
Proof. Part (a) follows immediately from Corollary 1.18(b) and the fact that the geometric realizations of ![]() $\Gamma _{\mathcal {X}_s,\Sigma _s}$ and
$\Gamma _{\mathcal {X}_s,\Sigma _s}$ and ![]() $\widetilde{\Gamma} _{\mathcal {X}_s,\Sigma _s}$ are homeomorphic. For part (b), it is enough to observe that
$\widetilde{\Gamma} _{\mathcal {X}_s,\Sigma _s}$ are homeomorphic. For part (b), it is enough to observe that ![]() $(\square,\theta ^*)$ maps
$(\square,\theta ^*)$ maps ![]() $1\in \mathbb {Z}[C]$ to
$1\in \mathbb {Z}[C]$ to ![]() $(0,1)\in \mathbb {Z}[C]_0\oplus \mathbb {Z}^I$, and so the result follows from Theorem 1.19.
$(0,1)\in \mathbb {Z}[C]_0\oplus \mathbb {Z}^I$, and so the result follows from Theorem 1.19.
1.7 Description via Néron models of 1-motives [Reference SuzukiSuz19]
An alternative approach to the determination of the component group ![]() $\Phi (J_\mathfrak {m})$ is via duality and the theory of Néron models of
$\Phi (J_\mathfrak {m})$ is via duality and the theory of Néron models of ![]() $1$-motives developed in [Reference SuzukiSuz19]. We recall some of the notions and results of that paper. Recall that a
$1$-motives developed in [Reference SuzukiSuz19]. We recall some of the notions and results of that paper. Recall that a ![]() $1$-motive over
$1$-motive over ![]() $F$ is a two-term complex of group schemes over
$F$ is a two-term complex of group schemes over ![]() $F$,
$F$,
where ![]() $L$ is étale, free and finitely generated (i.e.
$L$ is étale, free and finitely generated (i.e. ![]() $L\otimes _FF^{\mathrm {sep}}\simeq \mathbb {Z}^r$), and
$L\otimes _FF^{\mathrm {sep}}\simeq \mathbb {Z}^r$), and ![]() $G/F$ is a semiabelian variety. Let
$G/F$ is a semiabelian variety. Let ![]() $T \subset G$ be its toric part, and
$T \subset G$ be its toric part, and ![]() $A=G/T$ the abelian variety quotient. We assume here that
$A=G/T$ the abelian variety quotient. We assume here that ![]() $L$ and
$L$ and ![]() $T$ split over an extension of
$T$ split over an extension of ![]() $F$ in which
$F$ in which ![]() $R$ is unramified. Then
$R$ is unramified. Then ![]() $L$ extends to a local system
$L$ extends to a local system ![]() $\Lambda$ on
$\Lambda$ on ![]() $S$. Let
$S$. Let ![]() $\mathcal {G}$ be the Néron model of
$\mathcal {G}$ be the Néron model of ![]() $G$. By the Néron property,
$G$. By the Néron property, ![]() $f$ extends to a morphism
$f$ extends to a morphism ![]() $f_S\colon \Lambda \to \mathcal {G}$ of
$f_S\colon \Lambda \to \mathcal {G}$ of ![]() $S$-group schemes and, by definition, the Néron model of
$S$-group schemes and, by definition, the Néron model of ![]() $M$ is the complex of
$M$ is the complex of ![]() $S$-group schemes
$S$-group schemes
Its component complex is the complex of ![]() $\operatorname {Gal}(k^\mathrm {sep}/k)$-modules
$\operatorname {Gal}(k^\mathrm {sep}/k)$-modules
in degrees ![]() $-1$ and
$-1$ and ![]() $0$. (In [Reference SuzukiSuz19] this complex is denoted by
$0$. (In [Reference SuzukiSuz19] this complex is denoted by ![]() $\mathcal {P}(\mathcal {M})$.)
$\mathcal {P}(\mathcal {M})$.)
Let ![]() $M'$ be the
$M'$ be the ![]() $1$-motive dual to
$1$-motive dual to ![]() $M$, so that
$M$, so that
where ![]() $L'=\operatorname {Hom}(T,\mathbb {G}_{\mathrm {m}})$ is the character group of
$L'=\operatorname {Hom}(T,\mathbb {G}_{\mathrm {m}})$ is the character group of ![]() $T$, and
$T$, and ![]() $G'$ is an extension
$G'$ is an extension ![]() $T' \to G' \to A'$, where
$T' \to G' \to A'$, where ![]() $A'$ is the dual abelian variety of
$A'$ is the dual abelian variety of ![]() $A$, and
$A$, and ![]() $T'$ is the torus with character group
$T'$ is the torus with character group ![]() $L$. Then [Reference SuzukiSuz19, Theorem B] shows that if either:
$L$. Then [Reference SuzukiSuz19, Theorem B] shows that if either:
(i)
 $A$ has semistable reduction; or
$A$ has semistable reduction; or(ii)
 $k$ is perfect;
$k$ is perfect;
there is a canonical isomorphism, in the derived category of ![]() $\operatorname {Gal}(k^\mathrm {sep}/k)$-modules, between
$\operatorname {Gal}(k^\mathrm {sep}/k)$-modules, between ![]() $\Phi (M')$ and
$\Phi (M')$ and ![]() $\mathrm {RHom}(\Phi (M),\mathbb {Z})[1]$.
$\mathrm {RHom}(\Phi (M),\mathbb {Z})[1]$.
Now let ![]() $\mathcal {X}/S$ be as in § 1.6. We will assume that
$\mathcal {X}/S$ be as in § 1.6. We will assume that ![]() $R$ is strictly Henselian. Suppose that all
$R$ is strictly Henselian. Suppose that all ![]() $n_j$ are zero (which holds, for example, if
$n_j$ are zero (which holds, for example, if ![]() $k$ is perfect), that
$k$ is perfect), that ![]() $\delta =1$, and that the points
$\delta =1$, and that the points ![]() $(x_i)_{i\in I}$ are all
$(x_i)_{i\in I}$ are all ![]() $F$-rational.
$F$-rational.
Since ![]() $J$ is autodual, the dual
$J$ is autodual, the dual ![]() $1$-motive to
$1$-motive to ![]() $J_\mathfrak {m}$ is the
$J_\mathfrak {m}$ is the ![]() $1$-motive
$1$-motive
whose component complex ![]() $\Phi (M)$ is the complex
$\Phi (M)$ is the complex ![]() $[\mathbb {Z}[I]_0 \to \Phi (J) ]$ of abelian groups, concentrated in degrees
$[\mathbb {Z}[I]_0 \to \Phi (J) ]$ of abelian groups, concentrated in degrees ![]() $-1$ and
$-1$ and ![]() $0$. Using the description (1.3.1) of
$0$. Using the description (1.3.1) of ![]() $\Phi (J)$, this is isomorphic to the complex
$\Phi (J)$, this is isomorphic to the complex ![]() $[\mathbb {Z}[I]_0 \to \mathbb {Z}^{C,0}/a(\mathbb {Z}^C) ]$.
$[\mathbb {Z}[I]_0 \to \mathbb {Z}^{C,0}/a(\mathbb {Z}^C) ]$.
As ![]() $\delta =1$, by [Reference RaynaudRay70, (8.1.2)] the complex (1.3.1) has only one nonzero homology group, namely
$\delta =1$, by [Reference RaynaudRay70, (8.1.2)] the complex (1.3.1) has only one nonzero homology group, namely ![]() $\ker (b)/\operatorname {im}(a)=\Phi (J)$, and the map
$\ker (b)/\operatorname {im}(a)=\Phi (J)$, and the map ![]() $a$ is given by the intersection pairing on the components of the special fibre. Therefore
$a$ is given by the intersection pairing on the components of the special fibre. Therefore ![]() $\Phi (M)$ is quasi-isomorphic to the following complex.
$\Phi (M)$ is quasi-isomorphic to the following complex.
Here ![]() ${}^th\colon \mathbb {Z}[I]_0 \to \mathbb {Z}^C$ is the transpose of
${}^th\colon \mathbb {Z}[I]_0 \to \mathbb {Z}^C$ is the transpose of ![]() $h$, and the term
$h$, and the term ![]() $\mathbb {Z}^C$ is in degree
$\mathbb {Z}^C$ is in degree ![]() $0$. The dual of (
$0$. The dual of (
) is the following complex.
The assumption ![]() $n_j=0$ ensures that
$n_j=0$ ensures that ![]() $a$ is symmetric, and that
$a$ is symmetric, and that ![]() $i$ and
$i$ and ![]() $b$ are transposes of one another, by (1.3.2). Assuming that one of assumptions (i) or (ii) above holds, we then recover the description of
$b$ are transposes of one another, by (1.3.2). Assuming that one of assumptions (i) or (ii) above holds, we then recover the description of ![]() $\Phi (J_\mathfrak {m})$ as the homology of (1.6.4).
$\Phi (J_\mathfrak {m})$ as the homology of (1.6.4).
1.8 Functoriality II
We will need to understand the action of correspondences on generalized Jacobians and their Néron models.
Suppose that we have two smooth geometrically connected curves ![]() $X$,
$X$, ![]() $X'$ over
$X'$ over ![]() $F$, with regular models
$F$, with regular models ![]() $\mathcal {X}$,
$\mathcal {X}$, ![]() $\mathcal {X}'$ satisfying the hypotheses of § 1.3. Let
$\mathcal {X}'$ satisfying the hypotheses of § 1.3. Let ![]() $\mathfrak {m}=\sum _{i\in I}(x_i)$,
$\mathfrak {m}=\sum _{i\in I}(x_i)$, ![]() $\mathfrak {m}'=\sum _{j\in I'}(x'_j)$, be nonzero moduli on
$\mathfrak {m}'=\sum _{j\in I'}(x'_j)$, be nonzero moduli on ![]() $X$,
$X$, ![]() $X'$. As in § 1.6 we assume that the points
$X'$. As in § 1.6 we assume that the points ![]() $x_i$,
$x_i$, ![]() $x'_j$ are distinct, and that their residue fields
$x'_j$ are distinct, and that their residue fields
are separable over ![]() $F$. Let
$F$. Let ![]() $R_i$,
$R_i$, ![]() $R'_j$ denote the integral closures of
$R'_j$ denote the integral closures of ![]() $R$ in
$R$ in ![]() $F_i$,
$F_i$, ![]() $F'_j$, and
$F'_j$, and ![]() $\Sigma =\coprod _{i\in I}\operatorname {Spec} R_i$,
$\Sigma =\coprod _{i\in I}\operatorname {Spec} R_i$, ![]() $\Sigma '=\coprod _{j\in I'}\operatorname {Spec} R_j'$. Let
$\Sigma '=\coprod _{j\in I'}\operatorname {Spec} R_j'$. Let ![]() $J_\mathfrak {m}$,
$J_\mathfrak {m}$, ![]() $J'_{\mathfrak {m}'}$ be the associated generalized Jacobians.
$J'_{\mathfrak {m}'}$ be the associated generalized Jacobians.
Let ![]() $f\colon X' \to X$ be a finite morphism such that
$f\colon X' \to X$ be a finite morphism such that ![]() $f^{-1}(\Sigma _F)=\Sigma '_F$ as sets. We write
$f^{-1}(\Sigma _F)=\Sigma '_F$ as sets. We write ![]() $f\colon I' \to I$ also for the induced surjective map on index sets. For
$f\colon I' \to I$ also for the induced surjective map on index sets. For ![]() $j\in I'$, denote by
$j\in I'$, denote by ![]() $r_j$ the ramification degree of
$r_j$ the ramification degree of ![]() $f$ at
$f$ at ![]() $x'_j$.
$x'_j$.
The discussion in § 1.5 applies, and since ![]() $f^*$,
$f^*$, ![]() $f_*$ preserve line bundles of degree zero, we obtain morphisms
$f_*$ preserve line bundles of degree zero, we obtain morphisms
By the universal Néron property, they extend uniquely to morphisms ![]() $f^*$,
$f^*$, ![]() $f_*$ of the Néron models
$f_*$ of the Néron models ![]() $\mathcal {J}_\mathfrak {m}$,
$\mathcal {J}_\mathfrak {m}$, ![]() $\mathcal {J}'_{\mathfrak {m}'}$. Let the induced homomorphisms of character groups be
$\mathcal {J}'_{\mathfrak {m}'}$. Let the induced homomorphisms of character groups be ![]() $\mathbb {X}(f^*)$,
$\mathbb {X}(f^*)$, ![]() $\mathbb {X}(f_*)$ and of component groups
$\mathbb {X}(f_*)$ and of component groups ![]() $\Phi (f^*)$,
$\Phi (f^*)$, ![]() $\Phi (f_*)$. In the next section we will need to know explicitly the restriction of these maps to the tori
$\Phi (f_*)$. In the next section we will need to know explicitly the restriction of these maps to the tori ![]() $\mathcal {T}_\mathfrak {m}$,
$\mathcal {T}_\mathfrak {m}$, ![]() $\mathcal {T}'_{\mathfrak {m}'}$. For parts (a) and (b) below, recall that we have a canonical isomorphism
$\mathcal {T}'_{\mathfrak {m}'}$. For parts (a) and (b) below, recall that we have a canonical isomorphism
and similarly for ![]() $T'_{\mathfrak {m}'}$.
$T'_{\mathfrak {m}'}$.
Proposition 1.21
(a) The map
is induced by the inclusions \begin{align*} f^* \colon T_\mathfrak{m} = \bigg(\prod_{i\in I} R_{F_i/F}\mathbb{G}_{\mathrm{m}}\bigg)/\mathbb{G}_{\mathrm{m}} \to T'_{\mathfrak{m}'} = \bigg(\prod_{j\in I'} R_{F'_j/F}\mathbb{G}_{\mathrm{m}}\bigg)/\mathbb{G}_{\mathrm{m}} \end{align*}
\begin{align*} f^* \colon T_\mathfrak{m} = \bigg(\prod_{i\in I} R_{F_i/F}\mathbb{G}_{\mathrm{m}}\bigg)/\mathbb{G}_{\mathrm{m}} \to T'_{\mathfrak{m}'} = \bigg(\prod_{j\in I'} R_{F'_j/F}\mathbb{G}_{\mathrm{m}}\bigg)/\mathbb{G}_{\mathrm{m}} \end{align*}
 $f^* \colon F_i \hookrightarrow F'_j$,
$f^* \colon F_i \hookrightarrow F'_j$,  $i=f(j)$. Its transpose is the homomorphism
given by pushforward of divisors of degree zero.
$i=f(j)$. Its transpose is the homomorphism
given by pushforward of divisors of degree zero. \[ f_* \colon \mathbb{Z}[\Sigma'(F^{\mathrm{sep}})]^{\deg=0} \to\mathbb{Z}[\Sigma(F^{\mathrm{sep}})]^{\deg=0} \]
\[ f_* \colon \mathbb{Z}[\Sigma'(F^{\mathrm{sep}})]^{\deg=0} \to\mathbb{Z}[\Sigma(F^{\mathrm{sep}})]^{\deg=0} \]
(b) The map
 $f_*\colon T'_{\mathfrak {m}'} \to T_\mathfrak {m}$ is given by the morphisms of tori, for
$f_*\colon T'_{\mathfrak {m}'} \to T_\mathfrak {m}$ is given by the morphisms of tori, for  $i=f(j)$,
Its transpose is the homomorphism
$i=f(j)$,
Its transpose is the homomorphism \begin{align*} \mathcal{R}_{F'_j/F_i}\mathbb{G}_{\mathrm{m}} & \to \mathcal{R}_{F_i/F}\mathbb{G}_{\mathrm{m}} \\ t &\mapsto (N_{F'_j/F_i}t)^{r_j}. \end{align*}
given by pullback of divisors.
\begin{align*} \mathcal{R}_{F'_j/F_i}\mathbb{G}_{\mathrm{m}} & \to \mathcal{R}_{F_i/F}\mathbb{G}_{\mathrm{m}} \\ t &\mapsto (N_{F'_j/F_i}t)^{r_j}. \end{align*}
given by pullback of divisors. \[ f^* \colon \mathbb{Z}[\Sigma(F^{\mathrm{sep}})]^{\deg=0} \to \mathbb{Z}[\Sigma'(F^{\mathrm{sep}})]^{\deg=0} \]
\[ f^* \colon \mathbb{Z}[\Sigma(F^{\mathrm{sep}})]^{\deg=0} \to \mathbb{Z}[\Sigma'(F^{\mathrm{sep}})]^{\deg=0} \]
(c) Assume that
 $R=R^{\mathrm {sh}}$. Then the induced maps between component groups
$R=R^{\mathrm {sh}}$. Then the induced maps between component groups  $\Phi (T_\mathfrak {m})$,
$\Phi (T_\mathfrak {m})$,  $\Phi (T'_{\mathfrak {m}'})$ are as follows.
$\Phi (T'_{\mathfrak {m}'})$ are as follows.

(d) Assume that
 $R=R^{\mathrm {sh}}$, and that
$R=R^{\mathrm {sh}}$, and that  $k$ is algebraically closed (so that
$k$ is algebraically closed (so that  $\Sigma (k)\simeq I$,
$\Sigma (k)\simeq I$,  $\Sigma '(k)\simeq I'$). Then the induced maps on character groups of Néron models are as follows.
$\Sigma '(k)\simeq I'$). Then the induced maps on character groups of Néron models are as follows.

Proof. For parts (a) and (b), it suffices to compute the map on character groups. The formulae are then special cases of Propositions 1.11 and 1.12 with ![]() $A=B=\Sigma ^{\mathrm {sing}}=\emptyset$,
$A=B=\Sigma ^{\mathrm {sing}}=\emptyset$, ![]() $C=\{*\}$.
$C=\{*\}$.
Combining these with Proposition 1.4 then gives the remaining parts.
Remark From parts (a) and (b) we see that if ![]() $f$,
$f$, ![]() $f'\colon X'\to X$ are finite morphisms and
$f'\colon X'\to X$ are finite morphisms and ![]() $\mathfrak {m}$ is a reduced modulus on
$\mathfrak {m}$ is a reduced modulus on ![]() $X$ which is stable under the correspondence
$X$ which is stable under the correspondence ![]() $A=f_*f^{'*}$ (in the sense of Example 1.9), then the induced endomorphism
$A=f_*f^{'*}$ (in the sense of Example 1.9), then the induced endomorphism ![]() ${}^tA$ of the character group
${}^tA$ of the character group ![]() $\operatorname {Hom}(T_\mathfrak {m}\otimes F ^{\mathrm {sep}},\mathbb {G}_{\mathrm {m}})$ equals the map
$\operatorname {Hom}(T_\mathfrak {m}\otimes F ^{\mathrm {sep}},\mathbb {G}_{\mathrm {m}})$ equals the map ![]() $D \mapsto f'_*f^*D$ on divisors of degree zero.
$D \mapsto f'_*f^*D$ on divisors of degree zero.
2. Generalized Jacobians of modular curves
2.1 Generalities on modular curves
For an integer ![]() $N\ge 1$, let
$N\ge 1$, let ![]() $X_0(N)_\mathbb {Q}$ denote the usual complete modular curve over
$X_0(N)_\mathbb {Q}$ denote the usual complete modular curve over ![]() $\mathbb {Q}$. Its non-cuspidal points parametrize pairs
$\mathbb {Q}$. Its non-cuspidal points parametrize pairs ![]() $(E,C)$, where
$(E,C)$, where ![]() $E$ is an elliptic curve (over some
$E$ is an elliptic curve (over some ![]() $\mathbb {Q}$-scheme) and
$\mathbb {Q}$-scheme) and ![]() $C\subset E$ is a subgroup scheme which is cyclic of order
$C\subset E$ is a subgroup scheme which is cyclic of order ![]() $N$. We write
$N$. We write ![]() $X_0(N)_\mathbb {Z}$ for the integral model constructed by Katz and Mazur [Reference Katz and MazurKM85, Ch. 8], which they denote
$X_0(N)_\mathbb {Z}$ for the integral model constructed by Katz and Mazur [Reference Katz and MazurKM85, Ch. 8], which they denote ![]() $\overline M([\Gamma _0(N)])$. Its non-cuspidal points parametrize pairs
$\overline M([\Gamma _0(N)])$. Its non-cuspidal points parametrize pairs ![]() $(E,C)$, where
$(E,C)$, where ![]() $C\subset E$ is a subgroup scheme of rank
$C\subset E$ is a subgroup scheme of rank ![]() $N$ which is cyclic in the sense of [Reference Katz and MazurKM85, § 6.1]; see also [Reference EdixhovenEdi90, § 1.1].
$N$ which is cyclic in the sense of [Reference Katz and MazurKM85, § 6.1]; see also [Reference EdixhovenEdi90, § 1.1].
For every prime ![]() $\ell$ we have a Hecke correspondence
$\ell$ we have a Hecke correspondence ![]() $T_\ell =v_*u^*$, where the finite morphisms
$T_\ell =v_*u^*$, where the finite morphisms ![]() $u=u_\ell$,
$u=u_\ell$, ![]() $v=v_\ell$ are given as follows.
$v=v_\ell$ are given as follows.

For ![]() $\ell \nmid N$ (respectively,
$\ell \nmid N$ (respectively, ![]() $\ell \mid N$), the morphisms
$\ell \mid N$), the morphisms ![]() $u$,
$u$, ![]() $v$ are of degree
$v$ are of degree ![]() $\ell +1$ (respectively,
$\ell +1$ (respectively, ![]() $\ell$). For
$\ell$). For ![]() $p\mid N$ we also have the Atkin–Lehner involution
$p\mid N$ we also have the Atkin–Lehner involution ![]() $W_p\colon X_0(N) \to X_0(N)$. If
$W_p\colon X_0(N) \to X_0(N)$. If ![]() $v_p(N)=r\ge 1$, then
$v_p(N)=r\ge 1$, then
When ![]() $\ell \nmid N$,
$\ell \nmid N$, ![]() $u=v\circ W_\ell$, and the correspondence
$u=v\circ W_\ell$, and the correspondence ![]() $T_\ell$ is symmetric. When
$T_\ell$ is symmetric. When ![]() $\ell \mid N$,
$\ell \mid N$, ![]() $T_\ell$ is no longer symmetric, and what we call
$T_\ell$ is no longer symmetric, and what we call ![]() $T_\ell$ is often elsewhere defined to be the transpose of
$T_\ell$ is often elsewhere defined to be the transpose of ![]() $T_\ell$ (and also often written
$T_\ell$ (and also often written ![]() $U_\ell$). We have chosen our normalizations so that the endomorphism
$U_\ell$). We have chosen our normalizations so that the endomorphism ![]() $T_\ell =v_*u^*$ of the Jacobian
$T_\ell =v_*u^*$ of the Jacobian ![]() $J_0(N)_\mathbb {Q}$ agrees with the Hecke operator in [Reference RibetRib90, p. 445] defined by ‘Picard functoriality’.
$J_0(N)_\mathbb {Q}$ agrees with the Hecke operator in [Reference RibetRib90, p. 445] defined by ‘Picard functoriality’.
Write ![]() $X_0(N)^\infty _\mathbb {Q} \subset X_0(N)_\mathbb {Q}$ for the cuspidal subscheme. It is classical that
$X_0(N)^\infty _\mathbb {Q} \subset X_0(N)_\mathbb {Q}$ for the cuspidal subscheme. It is classical that ![]() $X_0(N)^\infty _\mathbb {Q}$ is the disjoint union, over positive divisors
$X_0(N)^\infty _\mathbb {Q}$ is the disjoint union, over positive divisors ![]() $d\mid N$, of schemes
$d\mid N$, of schemes ![]() (where here
(where here ![]() $(d,N/d)$ denotes greatest common divisor). We recall (e.g. from [Reference Deligne and RapoportDR73, IV.4.11–13]) that the cusps of
$(d,N/d)$ denotes greatest common divisor). We recall (e.g. from [Reference Deligne and RapoportDR73, IV.4.11–13]) that the cusps of ![]() $X_0(N)_\mathbb {Q}$ can be conveniently described using generalized elliptic curves. Suppose that
$X_0(N)_\mathbb {Q}$ can be conveniently described using generalized elliptic curves. Suppose that ![]() $d\mid N$, and let
$d\mid N$, and let ![]() ${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$ denote the standard Néron polygon over
${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$ denote the standard Néron polygon over ![]() $\mathbb {Q}$ with
$\mathbb {Q}$ with ![]() $d$ sides [Reference Deligne and RapoportDR73, II.1.1], whose smooth locus
$d$ sides [Reference Deligne and RapoportDR73, II.1.1], whose smooth locus ![]() ${ {\rm N} {\unicode{x00E9}}{\rm r}}_d^{\mathrm {reg}}$ equals
${ {\rm N} {\unicode{x00E9}}{\rm r}}_d^{\mathrm {reg}}$ equals ![]() $\mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$. For a primitive
$\mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$. For a primitive ![]() $N$th root of unity
$N$th root of unity ![]() $\zeta _N\in \overline{\mathbb {Q}}$, let
$\zeta _N\in \overline{\mathbb {Q}}$, let ![]() $C_{d,\zeta _N}$ denote the cyclic subgroup scheme
$C_{d,\zeta _N}$ denote the cyclic subgroup scheme
Then the pair ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ determines a
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ determines a ![]() $\overline {\mathbb {Q}}$-point of
$\overline {\mathbb {Q}}$-point of ![]() $X_0(N)^\infty$. if
$X_0(N)^\infty$. if ![]() , then
, then ![]() $C_{d,\sigma \zeta _N}= C_{d,\zeta _N}$, and if
$C_{d,\sigma \zeta _N}= C_{d,\zeta _N}$, and if ![]() , then the pairs
, then the pairs ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\sigma \zeta _N}\!)$ and
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\sigma \zeta _N}\!)$ and ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N}\!)$ are isomorphic (and the isomorphism is unique if it is required to be the identity on the identity component of
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N}\!)$ are isomorphic (and the isomorphism is unique if it is required to be the identity on the identity component of ![]() ${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$). Therefore, the isomorphism class of
${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$). Therefore, the isomorphism class of ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ over
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ over ![]() $\overline {\mathbb {Q}}$ is determined by the pair
$\overline {\mathbb {Q}}$ is determined by the pair ![]() $(d,\zeta _N^{N/(d,N/d)})$ and gives rise to a closed point
$(d,\zeta _N^{N/(d,N/d)})$ and gives rise to a closed point ![]() of
of ![]() $X_0(N)^\infty _\mathbb {Q}$.
$X_0(N)^\infty _\mathbb {Q}$.
In particular, the (rational) cusps ![]() $\infty =z_{N,1}$ and
$\infty =z_{N,1}$ and ![]() $0=z_{N,N}$ correspond to the pairs
$0=z_{N,N}$ correspond to the pairs ![]() and
and ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_N,\{1\}\times \mathbb {Z}/N)$, respectively. We also know that the scheme-theoretic closure of
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_N,\{1\}\times \mathbb {Z}/N)$, respectively. We also know that the scheme-theoretic closure of ![]() $X_0(N)^\infty _\mathbb {Q}$ in
$X_0(N)^\infty _\mathbb {Q}$ in ![]() $X_0(N)_\mathbb {Z}$ is the disjoint union of copies of
$X_0(N)_\mathbb {Z}$ is the disjoint union of copies of ![]() (this follows from [Reference EdixhovenEdi90, Thm. 1.2.2.1]).
(this follows from [Reference EdixhovenEdi90, Thm. 1.2.2.1]).
Now let ![]() $\mathfrak {m}$ be a reduced modulus on
$\mathfrak {m}$ be a reduced modulus on ![]() $X_0(N)_\mathbb {Q}$, whose support is contained in
$X_0(N)_\mathbb {Q}$, whose support is contained in ![]() $X_0(N)_\mathbb {Q}^\infty$. Let
$X_0(N)_\mathbb {Q}^\infty$. Let ![]() $\ell$ be any prime such that the support of
$\ell$ be any prime such that the support of ![]() $\mathfrak {m}$ is stable under
$\mathfrak {m}$ is stable under ![]() $T_\ell$, in the sense of Example 1.9. Then
$T_\ell$, in the sense of Example 1.9. Then ![]() $T_\ell$ determines an endomorphism
$T_\ell$ determines an endomorphism ![]() $T_\ell =v_*u^*$ of
$T_\ell =v_*u^*$ of ![]() $J_\mathfrak {m}$. Let
$J_\mathfrak {m}$. Let ![]() $p\mid N$, and let
$p\mid N$, and let ![]() $\mathcal {J}_\mathfrak {m}$ be the Néron model of
$\mathcal {J}_\mathfrak {m}$ be the Néron model of ![]() $J_\mathfrak {m}$ over
$J_\mathfrak {m}$ over ![]() $\mathbb {Z}_{(p)}$. By the universal Néron property,
$\mathbb {Z}_{(p)}$. By the universal Néron property, ![]() $T_\ell$ extends to an endomorphism of
$T_\ell$ extends to an endomorphism of ![]() $\mathcal {J}_\mathfrak {m}$ and, therefore, induces endomorphisms
$\mathcal {J}_\mathfrak {m}$ and, therefore, induces endomorphisms
In order to compute these endomorphisms combinatorially, we need to compute the action of ![]() $T_\ell$ on the torus
$T_\ell$ on the torus ![]() $\mathcal {T}_\mathfrak {m}$, using the formulae of Proposition 1.21. In other words, we need to compute the restrictions of
$\mathcal {T}_\mathfrak {m}$, using the formulae of Proposition 1.21. In other words, we need to compute the restrictions of ![]() $u=u_\ell$,
$u=u_\ell$, ![]() $v=v_\ell$ to the cusps, along with the ramification degrees.
$v=v_\ell$ to the cusps, along with the ramification degrees.
Let ![]() $\zeta _{N\ell }\in \overline {\mathbb {Q}}$ be a primitive
$\zeta _{N\ell }\in \overline {\mathbb {Q}}$ be a primitive ![]() $N\ell$th root of unity, and for
$N\ell$th root of unity, and for ![]() $L\mid N\ell$,
$L\mid N\ell$, ![]() $\zeta _L=\zeta _{N\ell }^{N\ell /L}$. Let
$\zeta _L=\zeta _{N\ell }^{N\ell /L}$. Let ![]() $z=({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N\ell }}) \in X_0(N\ell )^\infty (\overline {\mathbb {Q}})$ be a cusp. Then
$z=({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N\ell }}) \in X_0(N\ell )^\infty (\overline {\mathbb {Q}})$ be a cusp. Then ![]() $u(z)\in X_0(N)^\infty (\overline {\mathbb {Q}})$ is obtained as follows: replace
$u(z)\in X_0(N)^\infty (\overline {\mathbb {Q}})$ is obtained as follows: replace ![]() $C_{d,\zeta _{N\ell }}$ by
$C_{d,\zeta _{N\ell }}$ by ![]() $\ell C _{d,\zeta _{N\ell }}=\langle (\zeta _N,\ell )\rangle \subset \mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$, and then contract any components of
$\ell C _{d,\zeta _{N\ell }}=\langle (\zeta _N,\ell )\rangle \subset \mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$, and then contract any components of ![]() ${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$ which do not meet it [Reference Deligne and RapoportDR73, IV.1.2]. Similarly, we obtain
${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$ which do not meet it [Reference Deligne and RapoportDR73, IV.1.2]. Similarly, we obtain ![]() $v(z)$ as the quotient of
$v(z)$ as the quotient of ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N\ell }})$ by the rank-
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N\ell }})$ by the rank-![]() $\ell$ group scheme
$\ell$ group scheme ![]() $NC_{d,\zeta _{N\ell }}=\langle (\zeta _\ell,N) \rangle \subset \mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$.
$NC_{d,\zeta _{N\ell }}=\langle (\zeta _\ell,N) \rangle \subset \mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$.
Explicitly, suppose that ![]() $N=M\ell ^k$,
$N=M\ell ^k$, ![]() $(\ell,M)=1$, and that
$(\ell,M)=1$, and that ![]() $d\mid N\ell$. Let
$d\mid N\ell$. Let ![]() $a$,
$a$, ![]() $b\in \mathbb {Z}$ with
$b\in \mathbb {Z}$ with ![]() $a\ell +bM=1$ and
$a\ell +bM=1$ and ![]() $a\equiv 1$ (mod
$a\equiv 1$ (mod ![]() $\ell ^k$). Then, if
$\ell ^k$). Then, if ![]() $\ell \nmid d$,
$\ell \nmid d$,
but if ![]() $\ell \mid d$, the subgroup
$\ell \mid d$, the subgroup ![]() $\langle (\zeta _N,\ell )\rangle )$ does not meet the components
$\langle (\zeta _N,\ell )\rangle )$ does not meet the components ![]() $\mathbb {G}_{\mathrm {m}}\times \{i\}$ with
$\mathbb {G}_{\mathrm {m}}\times \{i\}$ with ![]() $(i,\ell )=1$. The map
$(i,\ell )=1$. The map ![]() ${ {\rm N} {\unicode{x00E9}}{\rm r}}_d \to { {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell }$ contracting them takes
${ {\rm N} {\unicode{x00E9}}{\rm r}}_d \to { {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell }$ contracting them takes ![]() $\langle (\zeta _N,\ell )\rangle$ to
$\langle (\zeta _N,\ell )\rangle$ to ![]() $C_{d,\zeta _N}$, and so
$C_{d,\zeta _N}$, and so
 \[ u\colon ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_{N\ell}}) \mapsto \begin{cases} ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^a}) & \text{if $\ell\nmid d$} \\ ({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}) & \text{otherwise.} \end{cases} \]
\[ u\colon ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_{N\ell}}) \mapsto \begin{cases} ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^a}) & \text{if $\ell\nmid d$} \\ ({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}) & \text{otherwise.} \end{cases} \]
On closed points of ![]() $X_0(N)_\mathbb {Q}^\infty$ we then have
$X_0(N)_\mathbb {Q}^\infty$ we then have
 \begin{equation} u^{-1}(z_{N,d}) = \begin{cases} \{ z_{N\ell, d\ell} \} & \text{if $\ell | d$} \\ \{ z_{N\ell, d},\ z_{N\ell, d\ell} \} & \text{otherwise.} \end{cases} \end{equation}
\begin{equation} u^{-1}(z_{N,d}) = \begin{cases} \{ z_{N\ell, d\ell} \} & \text{if $\ell | d$} \\ \{ z_{N\ell, d},\ z_{N\ell, d\ell} \} & \text{otherwise.} \end{cases} \end{equation}
If ![]() $\ell \nmid N$, then
$\ell \nmid N$, then ![]() $u$ has degree
$u$ has degree ![]() $\ell +1$ and
$\ell +1$ and
It is well known (and follows, for example, from the Eichler–Shimura congruence relation) that ![]() $u$ is étale at
$u$ is étale at ![]() $z_{N\ell,d}$, and so has ramification degree
$z_{N\ell,d}$, and so has ramification degree ![]() $\ell$ at
$\ell$ at ![]() $z_{N\ell,d\ell }$.
$z_{N\ell,d\ell }$.
Suppose now that ![]() $k\ge 1$ and
$k\ge 1$ and ![]() $d_0 | M$,
$d_0 | M$, ![]() $d=d_0\ell ^s$. Then
$d=d_0\ell ^s$. Then ![]() $u$ has degree
$u$ has degree ![]() $\ell$ and
$\ell$ and
 \begin{align*} \deg z_{N\ell,d} &= \phi(\ell^{\min(s,k+1-s)}) \phi((d_0,M/d_0)), \\ \deg z_{N\ell,d/\ell} &= \phi(\ell^{\min(s-1,k+1-s)}) \phi((d_0,M/d_0))\quad\text{if $s\ge1$} \end{align*}
\begin{align*} \deg z_{N\ell,d} &= \phi(\ell^{\min(s,k+1-s)}) \phi((d_0,M/d_0)), \\ \deg z_{N\ell,d/\ell} &= \phi(\ell^{\min(s-1,k+1-s)}) \phi((d_0,M/d_0))\quad\text{if $s\ge1$} \end{align*}
so by (2.1.1), the ramification degree of ![]() $u$ at
$u$ at ![]() $z_{N\ell,d}$ equals
$z_{N\ell,d}$ equals
Moreover, since
the ramification degree equals ![]() $1$ also for
$1$ also for ![]() $s\in \{0,1\}$.
$s\in \{0,1\}$.
Similarly, if ![]() $d\mid N$, then the subgroup
$d\mid N$, then the subgroup ![]() $NC_{d,\zeta _{N\ell }}\subset { {\rm N} {\unicode{x00E9}}{\rm r}}_d^\mathrm {reg}=\mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$ equals
$NC_{d,\zeta _{N\ell }}\subset { {\rm N} {\unicode{x00E9}}{\rm r}}_d^\mathrm {reg}=\mathbb {G}_{\mathrm {m}}\times \mathbb {Z}/d$ equals ![]() and, therefore, is the kernel of the endomorphism
and, therefore, is the kernel of the endomorphism ![]() $(t,i)\mapsto (t^\ell,i)$ of
$(t,i)\mapsto (t^\ell,i)$ of ![]() ${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$. If
${ {\rm N} {\unicode{x00E9}}{\rm r}}_d$. If ![]() $d\mid N\ell$ but
$d\mid N\ell$ but ![]() $d\nmid N$, then
$d\nmid N$, then ![]() $NC_{d,\zeta _{N\ell }}=\langle (\zeta _\ell,N)\rangle$ is the kernel of the map
$NC_{d,\zeta _{N\ell }}=\langle (\zeta _\ell,N)\rangle$ is the kernel of the map ![]() ${ {\rm N} {\unicode{x00E9}}{\rm r}}_d\to { {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell }$,
${ {\rm N} {\unicode{x00E9}}{\rm r}}_d\to { {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell }$, ![]() $(t,i)\mapsto (t\zeta _{\ell ^k+1}^{-bi},i\text { mod }d/\ell )$, which maps
$(t,i)\mapsto (t\zeta _{\ell ^k+1}^{-bi},i\text { mod }d/\ell )$, which maps ![]() $(\zeta _{N\ell },1)$ to
$(\zeta _{N\ell },1)$ to ![]() $(\zeta _N^a,1)$ and, therefore,
$(\zeta _N^a,1)$ and, therefore,
 \[ v\colon ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_{N\ell}}) \mapsto \begin{cases}
({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N}\!) & \text{if
$d\mid N$,} \\ ({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N^a}) & \text{otherwise}.
\end{cases} \]
\[ v\colon ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_{N\ell}}) \mapsto \begin{cases}
({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N}\!) & \text{if
$d\mid N$,} \\ ({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N^a}) & \text{otherwise}.
\end{cases} \]
A similar computation as for ![]() $u$ shows that the ramification degree of
$u$ shows that the ramification degree of ![]() $v$ at
$v$ at ![]() $z_{N\ell,d}$ is
$z_{N\ell,d}$ is ![]() $1$ if
$1$ if ![]() $v_\ell (d)\ge (k+1)/2$, and
$v_\ell (d)\ge (k+1)/2$, and ![]() $\ell$ otherwise.
$\ell$ otherwise.
In particular, if ![]() $\mathfrak {m}$ is any reduced modulus supported on
$\mathfrak {m}$ is any reduced modulus supported on ![]() $X_0(N)^\infty _\mathbb {Q}$, then for every
$X_0(N)^\infty _\mathbb {Q}$, then for every ![]() $\ell \nmid N$,
$\ell \nmid N$, ![]() $\mathfrak {m}$ is stable under
$\mathfrak {m}$ is stable under ![]() $T_\ell$ (in the sense of Example 1.9) and, therefore, we obtain an endomorphism
$T_\ell$ (in the sense of Example 1.9) and, therefore, we obtain an endomorphism ![]() $T_\ell =v_*u^*$ of the generalized Jacobian
$T_\ell =v_*u^*$ of the generalized Jacobian ![]() $J_\mathfrak {m}=J_0(N)_\mathfrak {m}$. If
$J_\mathfrak {m}=J_0(N)_\mathfrak {m}$. If ![]() $\mathfrak {m}$ is the full cuspidal modulus (i.e. the reduced modulus whose support is
$\mathfrak {m}$ is the full cuspidal modulus (i.e. the reduced modulus whose support is ![]() $X_0(N)^\infty _\mathbb {Q}$) then
$X_0(N)^\infty _\mathbb {Q}$) then ![]() $\mathfrak {m}$ is stable under
$\mathfrak {m}$ is stable under ![]() $T_\ell$ for every
$T_\ell$ for every ![]() $\ell$. Using the formulae from Proposition 1.21 together with the fact that
$\ell$. Using the formulae from Proposition 1.21 together with the fact that ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ depends only on
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ depends only on ![]() $(d,\zeta _N^{N/(d,N/d)})$, we can compute the induced endomorphism
$(d,\zeta _N^{N/(d,N/d)})$, we can compute the induced endomorphism ![]() ${}^tT_\ell$ of the character group
${}^tT_\ell$ of the character group
which is the restriction of ![]() $u_*v^*$ to divisors of degree zero.
$u_*v^*$ to divisors of degree zero.
Proposition 2.1
(a) If
 $(\ell,N)=1$, then
$(\ell,N)=1$, then
 \[ {}^tT_\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N})=({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^\ell})+\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^a}). \]
\[ {}^tT_\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N})=({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^\ell})+\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^a}). \]
(b) If
 $N=M\ell ^k$ with
$N=M\ell ^k$ with  $(M,\ell )=1$ and
$(M,\ell )=1$ and  $k>0$, and
$k>0$, and  $v_\ell (d)=i$, then let
$v_\ell (d)=i$, then let  $d=d_0\ell ^i$,
$d=d_0\ell ^i$,  $e_0=(d_0,M/d_0)$,
$e_0=(d_0,M/d_0)$,  . Then
where
. Then
where \[ {}^tT_\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N})=
\begin{cases}
\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^a}\!) & i=0,\\
\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}\!) & 0< i < (k+1)/2,\\
\sum_{\sigma\in\Gamma_i}\sigma({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}\!) & (k+1)/2\le i < k ,\\
\sum_{\sigma\in\Gamma_k}\sigma({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}\!) +({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^q}\!) & i=k, \end{cases}
\]
\[ {}^tT_\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N})=
\begin{cases}
\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^a}\!) & i=0,\\
\ell({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}\!) & 0< i < (k+1)/2,\\
\sum_{\sigma\in\Gamma_i}\sigma({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}\!) & (k+1)/2\le i < k ,\\
\sum_{\sigma\in\Gamma_k}\sigma({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d/\ell},C_{d/\ell,\zeta_N}\!) +({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N^q}\!) & i=k, \end{cases}
\]
 $a$,
$a$,  $b$ are as above, and
$b$ are as above, and  $aq\equiv 1$
$aq\equiv 1$  ${\rm (mod}\ N{\rm )}$.
${\rm (mod}\ N{\rm )}$.
(In part (b) ![]() $\Gamma _i\simeq (\mathbb {Z}/\ell \mathbb {Z})^\times$ if
$\Gamma _i\simeq (\mathbb {Z}/\ell \mathbb {Z})^\times$ if ![]() $i=k$ and
$i=k$ and ![]() $\mathbb {Z}/\ell \mathbb {Z}$ otherwise, so consistent with
$\mathbb {Z}/\ell \mathbb {Z}$ otherwise, so consistent with ![]() $\deg {}^tT_\ell =\ell$.)
$\deg {}^tT_\ell =\ell$.)
Proof. First note that if ![]() $v_\ell (d)=k+1$, then
$v_\ell (d)=k+1$, then
![]() $\boxed{k=0}$ Then
$\boxed{k=0}$ Then
hence (since ![]() $q\equiv \ell$ mod
$q\equiv \ell$ mod ![]() $N$ when
$N$ when ![]() $k=0$)
$k=0$)
![]() $\boxed{k > 0}$ Then if
$\boxed{k > 0}$ Then if ![]() $v_\ell (d)<(k+1)/2$,
$v_\ell (d)<(k+1)/2$,
and applying ![]() $u_*$ to this gives
$u_*$ to this gives ![]() $\ell ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N}^a})$.
$\ell ({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N}^a})$.
If ![]() $(k+1)/2\le v_\ell (d) < k$, then the inverse image of the cusp
$(k+1)/2\le v_\ell (d) < k$, then the inverse image of the cusp ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ is the union of
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _N})$ is the union of ![]() $\ell$ cusps conjugate to
$\ell$ cusps conjugate to ![]() $({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N\ell }})$, namely
$({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta _{N\ell }})$, namely
Finally, if ![]() $v_\ell (d)=k$, then
$v_\ell (d)=k$, then
 \begin{align*} v^*({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N}) &= \sum_\sigma \sigma({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_{N\ell}}) \quad(\ell-1 \text{ terms}) \\ &\quad + ({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d\ell},C_{d\ell,\zeta_{N\ell}^q}). \end{align*}
\begin{align*} v^*({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_N}) &= \sum_\sigma \sigma({ {\rm N} {\unicode{x00E9}}{\rm r}}_d,C_{d,\zeta_{N\ell}}) \quad(\ell-1 \text{ terms}) \\ &\quad + ({ {\rm N} {\unicode{x00E9}}{\rm r}}_{d\ell},C_{d\ell,\zeta_{N\ell}^q}). \end{align*}
Applying ![]() $u_*$ to this, we get the claimed formula.
$u_*$ to this, we get the claimed formula.
Example 2.2 Set ![]() $D=(0)-(\infty )$. The following are particular cases we will need.
$D=(0)-(\infty )$. The following are particular cases we will need.
(a)
 $(\ell,N)=1$,
$(\ell,N)=1$,  . Then
. Then  ${}^tT_\ell\colon D\mapsto (\ell+1)D$.
${}^tT_\ell\colon D\mapsto (\ell+1)D$.(b)
 $N=p$ prime,
$N=p$ prime,  $\mathfrak {m}=(\infty )+(0)$. Then
$\mathfrak {m}=(\infty )+(0)$. Then  ${}^tT_p\colon D\mapsto D$.
${}^tT_p\colon D\mapsto D$.(c)
 $N=p^2$. Then there are
$N=p^2$. Then there are  $(p+1)$ elements of
$(p+1)$ elements of  $X_0(p^2)^\infty (\overline {\mathbb {Q}})$, namely
and if
$X_0(p^2)^\infty (\overline {\mathbb {Q}})$, namely
and if
 $\ell \ne p$,
and
$\ell \ne p$,
and \begin{align*} {}^tT_\ell\colon\ D & \mapsto (\ell+1)D\\ (\zeta_p)-(\infty) & \mapsto \ell(\zeta_p^{1/\ell}) +(\zeta_p^\ell) -(\ell+1)(\infty) \end{align*}
\begin{align*} {}^tT_\ell\colon\ D & \mapsto (\ell+1)D\\ (\zeta_p)-(\infty) & \mapsto \ell(\zeta_p^{1/\ell}) +(\zeta_p^\ell) -(\ell+1)(\infty) \end{align*}

2.2 Character groups
Assume that ![]() $N=pM$, with
$N=pM$, with ![]() $p>3$ prime and
$p>3$ prime and ![]() $(p,M)=1$. Let
$(p,M)=1$. Let ![]() $\mathsf {SS}_{M}$ be the set of supersingular points of
$\mathsf {SS}_{M}$ be the set of supersingular points of ![]() $X_0(M)(\overline {\mathbb {F}}_p)$, which is the set of isomorphism classes of pairs
$X_0(M)(\overline {\mathbb {F}}_p)$, which is the set of isomorphism classes of pairs ![]() $(E,C)$, where
$(E,C)$, where ![]() $E/\overline {\mathbb {F}}_p$ is a supersingular elliptic curve and
$E/\overline {\mathbb {F}}_p$ is a supersingular elliptic curve and ![]() $C\subset E$ is a cyclic subgroup scheme of order
$C\subset E$ is a cyclic subgroup scheme of order ![]() $M$.
$M$.
For ![]() $\ell \nmid M$, we have the Hecke operator
$\ell \nmid M$, we have the Hecke operator
 \begin{align*} T_\ell \colon \mathbb{Z}[\mathsf{SS}_{M}] & \to \mathbb{Z}[\mathsf{SS}_{M}] \\ (E,C) &\mapsto \sum_{D\subset E,\ \#D=\ell} (E/D,(C+D)/D). \end{align*}
\begin{align*} T_\ell \colon \mathbb{Z}[\mathsf{SS}_{M}] & \to \mathbb{Z}[\mathsf{SS}_{M}] \\ (E,C) &\mapsto \sum_{D\subset E,\ \#D=\ell} (E/D,(C+D)/D). \end{align*}
Theorem 2.3 Let ![]() $\mathfrak {m}=(\infty )+(0)$ and
$\mathfrak {m}=(\infty )+(0)$ and ![]() $J=J_0(N)$ with
$J=J_0(N)$ with ![]() $N=pM$ as above. Then there is a canonical isomorphism
$N=pM$ as above. Then there is a canonical isomorphism
taking ![]() ${}^tT_\ell$ to
${}^tT_\ell$ to ![]() $T_\ell$ for every
$T_\ell$ for every ![]() $\ell \nmid N$. Its restriction to
$\ell \nmid N$. Its restriction to ![]() $\mathbb {X}(J) \hookrightarrow \mathbb {X}(J_\mathfrak {m})$ is an isomorphism
$\mathbb {X}(J) \hookrightarrow \mathbb {X}(J_\mathfrak {m})$ is an isomorphism ![]() $\mathbb {X}(J) \xrightarrow \sim \mathbb {Z}[\mathsf {SS}_{M}]_0$.
$\mathbb {X}(J) \xrightarrow \sim \mathbb {Z}[\mathsf {SS}_{M}]_0$.
(The second isomorphism is, of course, well known: see [Reference RibetRib90, Proposition 3.1].)
Proof. We work over ![]() $S$, the strict henselization of
$S$, the strict henselization of ![]() $\operatorname {Spec} \mathbb {Z}_{(p)}$, and use the notation from § 2, so that
$\operatorname {Spec} \mathbb {Z}_{(p)}$, and use the notation from § 2, so that ![]() $k=\overline {\mathbb {F}}_p$. Let
$k=\overline {\mathbb {F}}_p$. Let ![]() $\mathcal {X}'$ denote the Deligne–Rapoport model of
$\mathcal {X}'$ denote the Deligne–Rapoport model of ![]() $X_0(N)$ over
$X_0(N)$ over ![]() $S$. Since
$S$. Since ![]() $p$ exactly divides
$p$ exactly divides ![]() $N$,
$N$, ![]() $\mathcal {X}'$ is regular apart from possible
$\mathcal {X}'$ is regular apart from possible ![]() $A_2$ or
$A_2$ or ![]() $A_3$ singularities at supersingular points in the special fibre where
$A_3$ singularities at supersingular points in the special fibre where ![]() $j=0$ or
$j=0$ or ![]() $1728$. Let
$1728$. Let ![]() $\mathcal {X} \to \mathcal {X}'$ be its minimal desingularization. The special fibre
$\mathcal {X} \to \mathcal {X}'$ be its minimal desingularization. The special fibre ![]() $\mathcal {X}'_s$ is the union of two copies of the modular curve
$\mathcal {X}'_s$ is the union of two copies of the modular curve ![]() $X_0(M)_{\overline {\mathbb {F}}_p}$ meeting transversally at the supersingular points. The cusp
$X_0(M)_{\overline {\mathbb {F}}_p}$ meeting transversally at the supersingular points. The cusp ![]() $\infty$ (respectively,
$\infty$ (respectively, ![]() $0$) meets the component of
$0$) meets the component of ![]() $\mathcal {X}'_s$ parametrizing
$\mathcal {X}'_s$ parametrizing ![]() $(E,C)$ where
$(E,C)$ where ![]() $C$ contains the kernel of Frobenius (respectively, Verschiebung). Let us refer to these as the
$C$ contains the kernel of Frobenius (respectively, Verschiebung). Let us refer to these as the ![]() $\infty$-component
$\infty$-component ![]() $Z_\infty$ and
$Z_\infty$ and ![]() $0$-component
$0$-component ![]() $Z_0$ of
$Z_0$ of ![]() $\mathcal {X}_s$.
$\mathcal {X}_s$.
First we assume that ![]() $\mathcal {X}'=\mathcal {X}$ is regular (which holds, for example, if
$\mathcal {X}'=\mathcal {X}$ is regular (which holds, for example, if ![]() $M$ is divisible by some prime
$M$ is divisible by some prime ![]() $q\equiv -1$ (mod
$q\equiv -1$ (mod ![]() $12$) or by
$12$) or by ![]() $36$; see the second table in [Reference EdixhovenEdi91, 4.1.1]). Since
$36$; see the second table in [Reference EdixhovenEdi91, 4.1.1]). Since ![]() $\mathcal {X}_s$ has an irreducible component of multiplicity one, hypotheses (H1)–(H3) of § 1.3 are satisfied. Let
$\mathcal {X}_s$ has an irreducible component of multiplicity one, hypotheses (H1)–(H3) of § 1.3 are satisfied. Let ![]() $\Sigma \to \mathcal {X}$ be the morphism induced by
$\Sigma \to \mathcal {X}$ be the morphism induced by ![]() $\mathfrak {m}$, so that
$\mathfrak {m}$, so that ![]() $\Sigma$ is the disjoint union of two sections of
$\Sigma$ is the disjoint union of two sections of ![]() $\mathcal {X}$ over
$\mathcal {X}$ over ![]() $S$. Then
$S$. Then
and since ![]() $\Sigma _s\subset \mathcal {X}^{\mathrm {reg}}_s$, by (1.4.4) we have
$\Sigma _s\subset \mathcal {X}^{\mathrm {reg}}_s$, by (1.4.4) we have
 \begin{equation} \mathbb{X}(J_\mathfrak{m}) = \ker\bigg[ \mathbb{Z}[\widetilde{\mathsf{SS}}]\oplus \mathbb{Z}[\Sigma_s] \xrightarrow{\left[\begin{smallmatrix}\psi & \theta\\ \phi & 0\end{smallmatrix}\right]} \mathbb{Z}[C] \oplus \mathbb{Z}[\mathsf{SS}] \bigg], \end{equation}
\begin{equation} \mathbb{X}(J_\mathfrak{m}) = \ker\bigg[ \mathbb{Z}[\widetilde{\mathsf{SS}}]\oplus \mathbb{Z}[\Sigma_s] \xrightarrow{\left[\begin{smallmatrix}\psi & \theta\\ \phi & 0\end{smallmatrix}\right]} \mathbb{Z}[C] \oplus \mathbb{Z}[\mathsf{SS}] \bigg], \end{equation}
where ![]() $C=\pi _0(\widetilde {\mathcal {X}_s})$,
$C=\pi _0(\widetilde {\mathcal {X}_s})$, ![]() $\mathsf {SS}=\mathsf {SS}_{M}\simeq \mathcal {X}_s^{\mathrm {sing}}$ and
$\mathsf {SS}=\mathsf {SS}_{M}\simeq \mathcal {X}_s^{\mathrm {sing}}$ and ![]() $\widetilde {\mathsf {SS}}$ is the inverse image of
$\widetilde {\mathsf {SS}}$ is the inverse image of ![]() $\mathsf {SS}$ in the normalization
$\mathsf {SS}$ in the normalization ![]() $\widetilde {\mathcal {X}_s}$ of
$\widetilde {\mathcal {X}_s}$ of ![]() $\mathcal {X}_s$.
$\mathcal {X}_s$.
The map ![]() $\theta \colon \mathbb {Z}[\Sigma _s] \to \mathbb {Z}[C]$ is a bijection since the cusps meets different components, and
$\theta \colon \mathbb {Z}[\Sigma _s] \to \mathbb {Z}[C]$ is a bijection since the cusps meets different components, and ![]() $\mathcal {X}_s$ has only ordinary double points, so the vertical maps between the three
$\mathcal {X}_s$ has only ordinary double points, so the vertical maps between the three ![]() $2$-term complexes
$2$-term complexes

are quasi-isomorphisms. Here ![]() $i$ is the map taking
$i$ is the map taking ![]() $x\in \mathsf {SS}$ to
$x\in \mathsf {SS}$ to ![]() $x^{(\infty )}-x^{(0)}$, with
$x^{(\infty )}-x^{(0)}$, with ![]() $x^{(\infty )}$,
$x^{(\infty )}$, ![]() $x^{(0)}\in \mathcal {X}_s$ being the supersingular points above
$x^{(0)}\in \mathcal {X}_s$ being the supersingular points above ![]() $x$ lying in the components containing
$x$ lying in the components containing ![]() $\infty$,
$\infty$, ![]() $0$ respectively. These quasi-isomorphisms then induce the isomorphism
$0$ respectively. These quasi-isomorphisms then induce the isomorphism ![]() $\mathbb {X}(J_\mathfrak {m})\simeq \mathbb {Z}[\mathsf {SS}]$. To get
$\mathbb {X}(J_\mathfrak {m})\simeq \mathbb {Z}[\mathsf {SS}]$. To get ![]() $\mathbb {X}(J)$ we drop the factor
$\mathbb {X}(J)$ we drop the factor ![]() $\mathbb {Z}[\Sigma _s]$ from (2.2.2), and then the kernel becomes
$\mathbb {Z}[\Sigma _s]$ from (2.2.2), and then the kernel becomes ![]() $\mathbb {Z}[\mathsf {SS}]_0$.
$\mathbb {Z}[\mathsf {SS}]_0$.
Still assuming that ![]() $\mathcal {X}'$ is regular, let
$\mathcal {X}'$ is regular, let ![]() $\ell \ne p$ be prime. Then the Deligne–Rapoport model for
$\ell \ne p$ be prime. Then the Deligne–Rapoport model for ![]() $X_0(N\ell )$ over
$X_0(N\ell )$ over ![]() $S$ is also regular. Let us denote it
$S$ is also regular. Let us denote it ![]() $\mathcal {X}^{(\ell )}$. Then maps
$\mathcal {X}^{(\ell )}$. Then maps ![]() $u,v$ extend to finite morphisms
$u,v$ extend to finite morphisms ![]() $\mathcal {X}^{(\ell )} \to \mathcal {X}$ which are therefore also flat. Therefore, the endomorphism
$\mathcal {X}^{(\ell )} \to \mathcal {X}$ which are therefore also flat. Therefore, the endomorphism ![]() $T_\ell$ of
$T_\ell$ of ![]() $\mathcal {J}_{\mathfrak {m},s}^0$ is, under the isomorphism (2.2.1), identified with the endomorphism
$\mathcal {J}_{\mathfrak {m},s}^0$ is, under the isomorphism (2.2.1), identified with the endomorphism ![]() $T_\ell =u_*v^*$ of
$T_\ell =u_*v^*$ of ![]() $\operatorname {Pic}^0_{(\mathcal {X}_s,\Sigma _s)/k}$. Now the maps
$\operatorname {Pic}^0_{(\mathcal {X}_s,\Sigma _s)/k}$. Now the maps ![]() $u$,
$u$, ![]() $v \colon \mathcal {X}^{(\ell )}_s \to \mathcal {X}_s$ map the
$v \colon \mathcal {X}^{(\ell )}_s \to \mathcal {X}_s$ map the ![]() $\infty$- and
$\infty$- and ![]() $0$-component of
$0$-component of ![]() $\mathcal {X}^{(\ell )}_s$ to the
$\mathcal {X}^{(\ell )}_s$ to the ![]() $\infty$- and
$\infty$- and ![]() $0$-component, respectively, of
$0$-component, respectively, of ![]() $\mathcal {X}_s$, and on each of these, they are just the maps
$\mathcal {X}_s$, and on each of these, they are just the maps ![]() $u$,
$u$, ![]() $v\colon X_0(M\ell ) \to X_0(M)$. Thus,
$v\colon X_0(M\ell ) \to X_0(M)$. Thus, ![]() $u_*v^*$ induces the map
$u_*v^*$ induces the map ![]() $T_\ell$ on
$T_\ell$ on ![]() $\mathbb {Z}[\mathsf {SS}_{M}]$.
$\mathbb {Z}[\mathsf {SS}_{M}]$.
In general, choose a multiple ![]() $N'=nN=pM'$ of
$N'=nN=pM'$ of ![]() $N$ with
$N$ with ![]() $(p,n)=1$ such that the Deligne–Rapoport model of
$(p,n)=1$ such that the Deligne–Rapoport model of ![]() $X_0(N')$ over
$X_0(N')$ over ![]() $S$ is regular. Let
$S$ is regular. Let ![]() $f\colon X_0(N') \to X_0(N)$ be the map
$f\colon X_0(N') \to X_0(N)$ be the map ![]() $(E,C)\mapsto (E,nC)$, and
$(E,C)\mapsto (E,nC)$, and ![]() $\mathfrak {m}'$ the reduced modulus
$\mathfrak {m}'$ the reduced modulus ![]() $f^{-1}((\infty )+(0))^{\mathrm {red}}$ on
$f^{-1}((\infty )+(0))^{\mathrm {red}}$ on ![]() $X_0(N')$. Then
$X_0(N')$. Then ![]() $f^*\colon J_0(N)_{\mathfrak {m}} \to J_0(N')_{\mathfrak {m}'}$ induces a surjection
$f^*\colon J_0(N)_{\mathfrak {m}} \to J_0(N')_{\mathfrak {m}'}$ induces a surjection

which is equivariant with respect to ![]() ${}^tT_\ell$ for all
${}^tT_\ell$ for all ![]() $\ell \nmid N'$. According to Proposition 1.11 this is induced by the map
$\ell \nmid N'$. According to Proposition 1.11 this is induced by the map ![]() $f\colon \mathsf {SS}_{M} \to \mathsf {SS}_{M}$, hence commutes with the maps
$f\colon \mathsf {SS}_{M} \to \mathsf {SS}_{M}$, hence commutes with the maps ![]() $T_\ell$ on
$T_\ell$ on ![]() $\mathbb {Z}[\mathsf {SS}_{M}]$ and
$\mathbb {Z}[\mathsf {SS}_{M}]$ and ![]() $\mathbb {Z}[\mathsf {SS}_{M}]$.
$\mathbb {Z}[\mathsf {SS}_{M}]$.
Remark Restricting to the case when ![]() $p$ exactly divides
$p$ exactly divides ![]() $N$ is rather natural, since the toric part of the special fibre of the Néron model of
$N$ is rather natural, since the toric part of the special fibre of the Néron model of ![]() $J_0(p^rM)$,
$J_0(p^rM)$, ![]() $r>1$, is a product of copies of the toric part for
$r>1$, is a product of copies of the toric part for ![]() $J_0(pM)$.
$J_0(pM)$.
In the case ![]() $N=p$ we may describe everything (including
$N=p$ we may describe everything (including ![]() $T_p$) in terms of the classical Brandt matrices, whose definition we now recall [Reference GrossGro87]. Let
$T_p$) in terms of the classical Brandt matrices, whose definition we now recall [Reference GrossGro87]. Let ![]() $\{ E_i \mid 1\le i\le h\}$ be representatives of the isomorphism classes of supersingular elliptic curves over
$\{ E_i \mid 1\le i\le h\}$ be representatives of the isomorphism classes of supersingular elliptic curves over ![]() $\overline {\mathbb {F}}_p$ (so that
$\overline {\mathbb {F}}_p$ (so that ![]() $h$ is the class number of the definite quaternion algebra
$h$ is the class number of the definite quaternion algebra ![]() $\mathrm {End}(E_i)\otimes \mathbb {Q}$). Let
$\mathrm {End}(E_i)\otimes \mathbb {Q}$). Let ![]() $\operatorname {Hom}(E_i,E_j)_n$ be the set of isogenies from
$\operatorname {Hom}(E_i,E_j)_n$ be the set of isogenies from ![]() $E_i$ to
$E_i$ to ![]() $E_j$ of degree
$E_j$ of degree ![]() $n$. Define an equivalence relation
$n$. Define an equivalence relation ![]() $\sim$ on
$\sim$ on ![]() $\operatorname {Hom}(E_i,E_j)_n$ by
$\operatorname {Hom}(E_i,E_j)_n$ by
and set ![]() $\overline {\operatorname {Hom}}(E_i,E_j)_n=\operatorname {Hom}(E_i,E_j)/\sim$. We then define the
$\overline {\operatorname {Hom}}(E_i,E_j)_n=\operatorname {Hom}(E_i,E_j)/\sim$. We then define the ![]() $h\times h$ Brandt matrix
$h\times h$ Brandt matrix ![]() $B(n)$ for
$B(n)$ for ![]() $n\geq 1$ by
$n\geq 1$ by
The matrices ![]() $B(n)$ for
$B(n)$ for ![]() $n\ge 1$ commute. They are constant row-sum matrices, with the sum of the entries in any row of
$n\ge 1$ commute. They are constant row-sum matrices, with the sum of the entries in any row of ![]() $B(n)$ equal to
$B(n)$ equal to
for ![]() $n\geq 1$.
$n\geq 1$.
Theorem 2.4 Let ![]() $N=p$ and
$N=p$ and ![]() $\mathfrak {m}=(\infty )+(0)$. The isomorphism
$\mathfrak {m}=(\infty )+(0)$. The isomorphism ![]() $\mathbb {X}(J_\mathfrak {m})\xrightarrow \sim \mathbb {Z}[\mathsf {SS}_1]$ of Theorem 2.3 takes
$\mathbb {X}(J_\mathfrak {m})\xrightarrow \sim \mathbb {Z}[\mathsf {SS}_1]$ of Theorem 2.3 takes ![]() ${}^tT_\ell$ to the transpose
${}^tT_\ell$ to the transpose ![]() ${}^tB(\ell )$ of the Brandt matrix, for every prime
${}^tB(\ell )$ of the Brandt matrix, for every prime ![]() $\ell$ (including
$\ell$ (including ![]() $\ell =p$).
$\ell =p$).
Proof. For ![]() $\ell \ne p$ this follows immediately from the definition of the Brandt matrix
$\ell \ne p$ this follows immediately from the definition of the Brandt matrix ![]() $B(\ell )$. For
$B(\ell )$. For ![]() $\ell =p$, we first note that the endomorphism
$\ell =p$, we first note that the endomorphism ![]() $T_p+W_p$ of
$T_p+W_p$ of ![]() $J_0(p)_\mathfrak {m}$ is zero. Indeed, on the quotient
$J_0(p)_\mathfrak {m}$ is zero. Indeed, on the quotient ![]() $J_0(p)$ it is zero, by [Reference RibetRib90, Proposition 3.7], and since
$J_0(p)$ it is zero, by [Reference RibetRib90, Proposition 3.7], and since ![]() $W_p$ interchanges the two cusps and
$W_p$ interchanges the two cusps and ![]() ${}^tT_p$ fixes
${}^tT_p$ fixes ![]() $(0)-(\infty )$, it is zero on the torus
$(0)-(\infty )$, it is zero on the torus ![]() $T_\mathfrak {m}=\mathbb {G}_{\mathrm {m}}\subset J_0(p)_\mathfrak {m}$. Thus, as any morphism from
$T_\mathfrak {m}=\mathbb {G}_{\mathrm {m}}\subset J_0(p)_\mathfrak {m}$. Thus, as any morphism from ![]() $J_0(p)$ to
$J_0(p)$ to ![]() $\mathbb {G}_{\mathrm {m}}$ is constant,
$\mathbb {G}_{\mathrm {m}}$ is constant, ![]() $T_p+W_p$ is zero on
$T_p+W_p$ is zero on ![]() $J_0(p)_\mathfrak {m}$. Therefore, it is enough to compute the action of
$J_0(p)_\mathfrak {m}$. Therefore, it is enough to compute the action of ![]() $W_p$ in
$W_p$ in ![]() $\mathbb {X}(J_0(p)_\mathfrak {m})$. For this, it is convenient to compute using the extended reduced graph
$\mathbb {X}(J_0(p)_\mathfrak {m})$. For this, it is convenient to compute using the extended reduced graph ![]() $\Gamma _{\mathcal {X}'_s,\Sigma }$ defined in § 1.4, with
$\Gamma _{\mathcal {X}'_s,\Sigma }$ defined in § 1.4, with ![]() $\Sigma =X_0(p)^\infty _s=\{\infty,0\}$ (where we have fixed an orientation) as follows.
$\Sigma =X_0(p)^\infty _s=\{\infty,0\}$ (where we have fixed an orientation) as follows.

As the regular model ![]() $\mathcal {X}$ is obtained by replacing the
$\mathcal {X}$ is obtained by replacing the ![]() $A_2$- and
$A_2$- and ![]() $A_3$-singularities by chains of lines, the extended graphs of
$A_3$-singularities by chains of lines, the extended graphs of ![]() $\mathcal {X}_s$ and
$\mathcal {X}_s$ and ![]() $\mathcal {X}'_s$ are homotopy equivalent, and so we may restrict to
$\mathcal {X}'_s$ are homotopy equivalent, and so we may restrict to ![]() $\mathcal {X}'_s$. On the special fibre
$\mathcal {X}'_s$. On the special fibre ![]() $\mathcal {X}_s'$,
$\mathcal {X}_s'$, ![]() $W_p$ interchanges the two irreducible components. Recall also that the supersingular points
$W_p$ interchanges the two irreducible components. Recall also that the supersingular points ![]() $\mathsf {SS}_1$ are
$\mathsf {SS}_1$ are ![]() $\mathbb {F}_{p^2}$-rational, and if
$\mathbb {F}_{p^2}$-rational, and if ![]() $x\in \mathsf {SS}_1$ is a supersingular point, corresponding to the class of a supersingular elliptic curve
$x\in \mathsf {SS}_1$ is a supersingular point, corresponding to the class of a supersingular elliptic curve ![]() $E/\overline {\mathbb {F}}_p$, then
$E/\overline {\mathbb {F}}_p$, then ![]() $W_p(x)=x^{(p)}$ is the point corresponding to
$W_p(x)=x^{(p)}$ is the point corresponding to ![]() $E^{(p)}=E/\ker (F)$. Thus, the automorphism
$E^{(p)}=E/\ker (F)$. Thus, the automorphism ![]() $W_p$ extends to an automorphism of the graph, fixing
$W_p$ extends to an automorphism of the graph, fixing ![]() $v_0$ and interchanging
$v_0$ and interchanging ![]() $Z_0$ and
$Z_0$ and ![]() $Z_\infty$, and mapping the edges labelled
$Z_\infty$, and mapping the edges labelled ![]() $E_i$ to
$E_i$ to ![]() $E_i^{(p)}$. The homology
$E_i^{(p)}$. The homology ![]() $H_1(\Gamma _{\mathcal {X}'_s,\Sigma },\mathbb {Z})$ is freely generated by the cycles
$H_1(\Gamma _{\mathcal {X}'_s,\Sigma },\mathbb {Z})$ is freely generated by the cycles ![]() $\gamma _i=(0)+(E_i)-(\infty )$, and
$\gamma _i=(0)+(E_i)-(\infty )$, and ![]() $W_p\colon \gamma _i \mapsto -\gamma _i^{(p)} = -(0)-(E_i^{(p)})+(\infty )$. Now the only element of
$W_p\colon \gamma _i \mapsto -\gamma _i^{(p)} = -(0)-(E_i^{(p)})+(\infty )$. Now the only element of ![]() $\overline {\operatorname {Hom}}(E_i,E_j)_p$ is the Frobenius
$\overline {\operatorname {Hom}}(E_i,E_j)_p$ is the Frobenius ![]() $E_i\to E_i^{(p)}=E_j$ and, therefore, the matrix of
$E_i\to E_i^{(p)}=E_j$ and, therefore, the matrix of ![]() $T_p=-W_p$ equals
$T_p=-W_p$ equals ![]() ${}^tB(p)$.
${}^tB(p)$.
2.3 Component groups
Throughout this section, we assume that ![]() $p>3$. Let
$p>3$. Let ![]() $N=p^rM$, with
$N=p^rM$, with ![]() $(p,M)=1$ and
$(p,M)=1$ and ![]() $r\ge 1$. As in the previous section, work over
$r\ge 1$. As in the previous section, work over ![]() $S$, the strict henselization of
$S$, the strict henselization of ![]() $\operatorname {Spec} \mathbb {Z}_{(p)}$. Let
$\operatorname {Spec} \mathbb {Z}_{(p)}$. Let ![]() $\mathfrak {m}$ be a reduced modulus on
$\mathfrak {m}$ be a reduced modulus on ![]() $X_0(N)$ supported at the cusps, and
$X_0(N)$ supported at the cusps, and ![]() $\mathbb {T}$ a subalgebra of the Hecke algebra
$\mathbb {T}$ a subalgebra of the Hecke algebra ![]() $\mathbb {Z}[\{T_\ell \}]$ which preserves the support of
$\mathbb {Z}[\{T_\ell \}]$ which preserves the support of ![]() $\mathfrak {m}$. Let
$\mathfrak {m}$. Let ![]() $J_\mathfrak {m}$ be the generalized Jacobian of
$J_\mathfrak {m}$ be the generalized Jacobian of ![]() $X_0(N)$ for the modulus
$X_0(N)$ for the modulus ![]() $\mathfrak {m}$. Then
$\mathfrak {m}$. Then ![]() $\mathbb {T}$ acts on
$\mathbb {T}$ acts on ![]() $J_\mathfrak {m}$, stabilizing the torus
$J_\mathfrak {m}$, stabilizing the torus ![]() $T_\mathfrak {m}$. It therefore acts on the extension of component groups
$T_\mathfrak {m}$. It therefore acts on the extension of component groups
and the action commutes with the action of ![]() $\operatorname {Gal}(\overline {\mathbb {F}}_p/\mathbb {F}_p)$. For the action of
$\operatorname {Gal}(\overline {\mathbb {F}}_p/\mathbb {F}_p)$. For the action of ![]() $\mathbb {T}$ on
$\mathbb {T}$ on ![]() $\Phi (J)$ we have the following result, proved by Edixhoven [Reference EdixhovenEdi91], generalizing Ribet [Reference RibetRib88] who treated the case of
$\Phi (J)$ we have the following result, proved by Edixhoven [Reference EdixhovenEdi91], generalizing Ribet [Reference RibetRib88] who treated the case of ![]() $N$ squarefree.
$N$ squarefree.
Theorem 2.5 For every ![]() $\ell \nmid N$,
$\ell \nmid N$, ![]() $T_\ell$ acts on
$T_\ell$ acts on ![]() $\Phi (J)$ as multiplication by
$\Phi (J)$ as multiplication by ![]() $\ell +1$.
$\ell +1$.
Corollary 2.6 Assume that ![]() $M$ is squarefree and
$M$ is squarefree and ![]() $p>3$. Then for every
$p>3$. Then for every ![]() $\ell \nmid N$,
$\ell \nmid N$, ![]() $T_\ell$ acts on
$T_\ell$ acts on ![]() $\Phi (J_\mathfrak {m})$ as multiplication by
$\Phi (J_\mathfrak {m})$ as multiplication by ![]() $\ell +1$.
$\ell +1$.
Proof. Let ![]() be a cusp, where
be a cusp, where ![]() $d\mid N$. As
$d\mid N$. As ![]() $M$ is squarefree,
$M$ is squarefree, ![]() $(d,N/d)$ is a power of
$(d,N/d)$ is a power of ![]() $p$. Therefore,
$p$. Therefore, ![]() $\operatorname {Gal}(\overline {\mathbb {Q}}/\mathbb {Q})$ acts trivially on
$\operatorname {Gal}(\overline {\mathbb {Q}}/\mathbb {Q})$ acts trivially on ![]() $\Phi (T_\mathfrak {m})$ by (1.1.5). Thus,
$\Phi (T_\mathfrak {m})$ by (1.1.5). Thus, ![]() $T_\ell$ acts on
$T_\ell$ acts on ![]() $\Phi (T_\mathfrak {m})$ as multiplication by
$\Phi (T_\mathfrak {m})$ as multiplication by ![]() $\ell +1$, and the endomorphism
$\ell +1$, and the endomorphism ![]() $T_\ell -\ell -1$ of
$T_\ell -\ell -1$ of ![]() $\Phi (J_\mathfrak {m})$ factors through a map
$\Phi (J_\mathfrak {m})$ factors through a map ![]() $\Phi (J)\to \Phi (T_\mathfrak {m})$, which is zero as
$\Phi (J)\to \Phi (T_\mathfrak {m})$, which is zero as ![]() $\Phi (J)$ is finite and
$\Phi (J)$ is finite and ![]() $\Phi (T_\mathfrak {m})$ is free.
$\Phi (T_\mathfrak {m})$ is free.
Remark Similarly, let ![]() $N$ be arbitrary, and
$N$ be arbitrary, and ![]() $\mathfrak {m}$ the reduced modulus on
$\mathfrak {m}$ the reduced modulus on ![]() $X_0(N)$ which is the sum of all the cusps. Write
$X_0(N)$ which is the sum of all the cusps. Write ![]() $T_\mathfrak {m} \to T_{p{\rm -spl}}$ for the maximal quotient which is split over
$T_\mathfrak {m} \to T_{p{\rm -spl}}$ for the maximal quotient which is split over ![]() . Let
. Let ![]() $J_{p{\rm -spl}}$ be the corresponding quotient of
$J_{p{\rm -spl}}$ be the corresponding quotient of ![]() $J_\mathfrak {m}$. Then by Corollary 1.2 the sequence of Néron models
$J_\mathfrak {m}$. Then by Corollary 1.2 the sequence of Néron models
is exact, and the same argument shows that ![]() $T_\ell =\ell +1$ on
$T_\ell =\ell +1$ on ![]() $\Phi (\mathcal {J}_{p{\rm -spl}})$.
$\Phi (\mathcal {J}_{p{\rm -spl}})$.
Now we turn to the abelian group structure of ![]() $\Phi (J_\mathfrak {m})$.
$\Phi (J_\mathfrak {m})$.
For ![]() $N=pM$,
$N=pM$, ![]() $(p,M)=1$, the structure of
$(p,M)=1$, the structure of ![]() $\Phi (J)$ was determined completely by Deligne, and described by Mazur and Rapoport in [Reference Mazur and RapoportMR77], using the description of the regular model of
$\Phi (J)$ was determined completely by Deligne, and described by Mazur and Rapoport in [Reference Mazur and RapoportMR77], using the description of the regular model of ![]() $X_0(N)$ given in [Reference Deligne and RapoportDR73]; see Table 2 on p. 174 and the calculations of § 2 in [Reference Deligne and RapoportDR73] and the corrections to their calculations made by Edixhoven [Reference EdixhovenEdi91, 4.4.1]. We recall these formulae in Corollary 2.8.
$X_0(N)$ given in [Reference Deligne and RapoportDR73]; see Table 2 on p. 174 and the calculations of § 2 in [Reference Deligne and RapoportDR73] and the corrections to their calculations made by Edixhoven [Reference EdixhovenEdi91, 4.4.1]. We recall these formulae in Corollary 2.8.
For general ![]() $N$, the minimal desingularization
$N$, the minimal desingularization ![]() $\mathcal {X} \to \mathcal {X}'$ was computed by Edixhoven [Reference EdixhovenEdi90] using the description of
$\mathcal {X} \to \mathcal {X}'$ was computed by Edixhoven [Reference EdixhovenEdi90] using the description of ![]() $\mathcal {X}'$ in [Reference Katz and MazurKM85]. Since the component of
$\mathcal {X}'$ in [Reference Katz and MazurKM85]. Since the component of ![]() $\mathcal {X}_s'$ meeting the cusp
$\mathcal {X}_s'$ meeting the cusp ![]() $\infty$ has multiplicity one,
$\infty$ has multiplicity one, ![]() $\mathcal {X}$ satisfies hypotheses (H1)–(H3). From this it is, in principle, an exercise to compute
$\mathcal {X}$ satisfies hypotheses (H1)–(H3). From this it is, in principle, an exercise to compute ![]() $\Phi (J)$ in any given case, and in [Reference EdixhovenEdi91, 4.4.2] this is done for
$\Phi (J)$ in any given case, and in [Reference EdixhovenEdi91, 4.4.2] this is done for ![]() $N=p^2$.
$N=p^2$.
We will compute ![]() $\Phi (J_\mathfrak {m})$ in various cases. First some notation: as in the previous section, let
$\Phi (J_\mathfrak {m})$ in various cases. First some notation: as in the previous section, let ![]() $\mathsf {SS}_{M}\subset X_0(M)(\overline {\mathbb {F}}_p)$ be the set of supersingular points, and
$\mathsf {SS}_{M}\subset X_0(M)(\overline {\mathbb {F}}_p)$ be the set of supersingular points, and ![]() $n=\#\mathsf {SS}_{M}$. For
$n=\#\mathsf {SS}_{M}$. For ![]() $j\in \{2,3\}$ let
$j\in \{2,3\}$ let ![]() $e_{j}$ be the number of elements
$e_{j}$ be the number of elements ![]() $(E,C)\in \mathsf {SS}_{M}$ for which
$(E,C)\in \mathsf {SS}_{M}$ for which ![]() $\#\mathrm {Aut}(E,C)=2j$.
$\#\mathrm {Aut}(E,C)=2j$.
2.3.1  $X_0(pM)$ with
$X_0(pM)$ with  $(p, M)=1$ and
$(p, M)=1$ and  $\mathfrak {m}=(\infty )+(0)$
$\mathfrak {m}=(\infty )+(0)$
Theorem 2.7 Let ![]() $N=pM$ with
$N=pM$ with ![]() $(p,M)=1$. Let
$(p,M)=1$. Let ![]() $J_\mathfrak {m}$ be the generalized Jacobian of
$J_\mathfrak {m}$ be the generalized Jacobian of ![]() $X_0(N)$ with respect to the modulus
$X_0(N)$ with respect to the modulus ![]() $\mathfrak {m}=(\infty )+(0)$. Then:
$\mathfrak {m}=(\infty )+(0)$. Then:
(a)
 $\Phi (J_\mathfrak {m}) \simeq \mathbb {Z} \oplus (\mathbb {Z}/2\mathbb {Z})^{\max (e_2-1,0)} \oplus (\mathbb {Z}/3\mathbb {Z})^{\max (e_3-1,0)}$;
$\Phi (J_\mathfrak {m}) \simeq \mathbb {Z} \oplus (\mathbb {Z}/2\mathbb {Z})^{\max (e_2-1,0)} \oplus (\mathbb {Z}/3\mathbb {Z})^{\max (e_3-1,0)}$;(b) the homomorphism
 $\Phi (T_\mathfrak {m})=\mathbb {Z} \to \Phi (J_\mathfrak {m})$ is given in terms of the isomorphism (a) by
$\Phi (T_\mathfrak {m})=\mathbb {Z} \to \Phi (J_\mathfrak {m})$ is given in terms of the isomorphism (a) by
 \[ 1\mapsto \begin{cases} n & \text{if }e_2=e_3=0, \\ (2n-e_2 ; 1,\ldots,1) & \text{if }e_2>0, e_3=0 ,\\ (3n-2_e3; 1,\ldots,1) & \text{if }e_2=0, e_3>0,\\ (6n-3e_2-4e_3;1,\ldots,1;1,\ldots,1) & \text{otherwise.} \end{cases} \]
\[ 1\mapsto \begin{cases} n & \text{if }e_2=e_3=0, \\ (2n-e_2 ; 1,\ldots,1) & \text{if }e_2>0, e_3=0 ,\\ (3n-2_e3; 1,\ldots,1) & \text{if }e_2=0, e_3>0,\\ (6n-3e_2-4e_3;1,\ldots,1;1,\ldots,1) & \text{otherwise.} \end{cases} \]
Proof. Recall that the special fibre ![]() $\mathcal {X}_s'$ of the Deligne–Rapoport model of
$\mathcal {X}_s'$ of the Deligne–Rapoport model of ![]() $X_0(N)$ is the union of two copies of
$X_0(N)$ is the union of two copies of ![]() $X_0(M)_{\overline {\mathbb {F}}_p}$, meeting tranversally at the supersingular points. The cusps
$X_0(M)_{\overline {\mathbb {F}}_p}$, meeting tranversally at the supersingular points. The cusps ![]() $\infty$ and
$\infty$ and ![]() $0$ belong to different components. The total space
$0$ belong to different components. The total space ![]() $\mathcal {X}'$ has a type
$\mathcal {X}'$ has a type ![]() $A_j$ quotient singularity at each point where
$A_j$ quotient singularity at each point where ![]() $\#\operatorname {Aut}(E,C)=2j\in \{4,6\}$. Taking their minimal resolution gives the model
$\#\operatorname {Aut}(E,C)=2j\in \{4,6\}$. Taking their minimal resolution gives the model ![]() $\mathcal {X}$. Its special fibre is obtained by replacing each crossing point which is an
$\mathcal {X}$. Its special fibre is obtained by replacing each crossing point which is an ![]() $A_j$-singularity with a chain of
$A_j$-singularity with a chain of ![]() $(j-1)$ copies of
$(j-1)$ copies of ![]() $\mathbb {P}^1$. In other words,
$\mathbb {P}^1$. In other words, ![]() $\mathcal {X}_s$ has
$\mathcal {X}_s$ has ![]() $2+e_2+2e_3$ irreducible components:
$2+e_2+2e_3$ irreducible components:
–
 $Z_\infty$ and
$Z_\infty$ and  $Z_0$, the strict transforms of the irreducible components of
$Z_0$, the strict transforms of the irreducible components of  $\mathcal {X}_s'$, isomorphic to
$\mathcal {X}_s'$, isomorphic to  $X_0(M)_{\overline {\mathbb {F}}_p}$, and labelled in such a way that the cusp
$X_0(M)_{\overline {\mathbb {F}}_p}$, and labelled in such a way that the cusp  $\alpha \in \{\infty,0\}$ belongs to
$\alpha \in \{\infty,0\}$ belongs to  $Z_\alpha$;
$Z_\alpha$;– components in the fibres of
 $\mathcal {X}_s\to \mathcal {X}_s'$ which we denote as
$\mathcal {X}_s\to \mathcal {X}_s'$ which we denote as  $E_i$ (for
$E_i$ (for  $1\le i\le e_2$) and
$1\le i\le e_2$) and  $F_{\infty,i}$,
$F_{\infty,i}$,  $F_{0,i}$ (for
$F_{0,i}$ (for  $1\le i\le e_3$), where
$1\le i\le e_3$), where  $F_{\alpha,i}$ intersects
$F_{\alpha,i}$ intersects  $Z_\alpha$.
$Z_\alpha$.
Their intersection numbers are:
–
 $(Z_\alpha.Z_\alpha )=-n$,
$(Z_\alpha.Z_\alpha )=-n$,  $(Z_\infty.Z_0)=n-e_2-e_3$;
$(Z_\infty.Z_0)=n-e_2-e_3$;–
 $(Z_\alpha.E_i)=1=(Z_\alpha.F_{\alpha,i})$;
$(Z_\alpha.E_i)=1=(Z_\alpha.F_{\alpha,i})$;– all other intersection numbers are zero.
We now use the formula for ![]() $\Phi (J_\mathfrak {m})$ from Theorem 1.19. We have
$\Phi (J_\mathfrak {m})$ from Theorem 1.19. We have ![]() $C=\pi _0(\widetilde{\mathcal{X}}_s)$, and write
$C=\pi _0(\widetilde{\mathcal{X}}_s)$, and write ![]() $Y^\vee \in \mathbb {Z}^C$ for the basis element dual to
$Y^\vee \in \mathbb {Z}^C$ for the basis element dual to ![]() $Y\in C$. We also have
$Y\in C$. We also have ![]() $I=\{\infty,0\}$, and
$I=\{\infty,0\}$, and ![]() $e$ (as in Theorem 1.19) equals
$e$ (as in Theorem 1.19) equals ![]() $(1,1)$. Therefore,
$(1,1)$. Therefore, ![]() $\mathbb {Z}^I/e\mathbb {Z} =\mathbb {Z}.V$ where
$\mathbb {Z}^I/e\mathbb {Z} =\mathbb {Z}.V$ where ![]() $V$ is the image of the dual of
$V$ is the image of the dual of ![]() $\infty$ (so that
$\infty$ (so that ![]() $-V$ is the image of the dual of
$-V$ is the image of the dual of ![]() $0$). The map
$0$). The map ![]() $h\colon \mathbb {Z}[C] \to \mathbb {Z}^I/e\mathbb {Z}$ takes
$h\colon \mathbb {Z}[C] \to \mathbb {Z}^I/e\mathbb {Z}$ takes ![]() $Z_\infty$ to
$Z_\infty$ to ![]() $V$ and
$V$ and ![]() $Z_0$ to
$Z_0$ to ![]() $-V$, and all other elements of
$-V$, and all other elements of ![]() $C$ to
$C$ to ![]() $0$. The map
$0$. The map ![]() $(a,h)\colon \mathbb {Z}[C] \to \mathbb {Z}^C\oplus \mathbb {Z}^I/e\mathbb {Z}$ is then given by the matrix
$(a,h)\colon \mathbb {Z}[C] \to \mathbb {Z}^C\oplus \mathbb {Z}^I/e\mathbb {Z}$ is then given by the matrix

As a basis for ![]() $\mathbb {Z}^{C,0}$ we take
$\mathbb {Z}^{C,0}$ we take ![]() $\overline Z=Z^\vee _\infty - Z^\vee _0$,
$\overline Z=Z^\vee _\infty - Z^\vee _0$, ![]() $\overline E_i=E^\vee _i - Z^\vee _0$,
$\overline E_i=E^\vee _i - Z^\vee _0$, ![]() $\overline F_{\alpha,i}= F^\vee _{\alpha,i}- Z^\vee _0$. Thus,
$\overline F_{\alpha,i}= F^\vee _{\alpha,i}- Z^\vee _0$. Thus, ![]() $\Phi (J_\mathfrak {m})$ is isomorphic to the quotient of the free module generated by
$\Phi (J_\mathfrak {m})$ is isomorphic to the quotient of the free module generated by ![]() $\overline Z$,
$\overline Z$, ![]() $\{\overline E_i\}$,
$\{\overline E_i\}$, ![]() $\{\overline F_{\alpha,i}\}$ and
$\{\overline F_{\alpha,i}\}$ and ![]() $V$ by the submodule of relations
$V$ by the submodule of relations
 \begin{gather*} \overline Z = 2 \overline E_i = 3\overline F_{0,i},\quad \overline F_{\infty,i} = 2\overline F_{0,i}, \\ V = n\overline Z - \sum_{i=1}^{e_2} \overline E_i - 2\sum_{i=1}^{e_3} \overline F_{0,i}. \end{gather*}
\begin{gather*} \overline Z = 2 \overline E_i = 3\overline F_{0,i},\quad \overline F_{\infty,i} = 2\overline F_{0,i}, \\ V = n\overline Z - \sum_{i=1}^{e_2} \overline E_i - 2\sum_{i=1}^{e_3} \overline F_{0,i}. \end{gather*}
If ![]() $e_2>1$, then for every
$e_2>1$, then for every ![]() $i>1$,
$i>1$, ![]() $U_i=\overline E_i-\overline E_0$ has order
$U_i=\overline E_i-\overline E_0$ has order ![]() $2$, and if
$2$, and if ![]() $e_3>1$, then
$e_3>1$, then ![]() $V_i=\overline F_{0,i}-\overline F_{0,0}$ has order
$V_i=\overline F_{0,i}-\overline F_{0,0}$ has order ![]() $3$. The subgroup generated by
$3$. The subgroup generated by ![]() $\overline Z$,
$\overline Z$, ![]() $\overline E_1$ (if
$\overline E_1$ (if ![]() $e_1\ge 1$) and
$e_1\ge 1$) and ![]() $\overline F_{1,0}$ (if
$\overline F_{1,0}$ (if ![]() $e_3\ge 1$) is infinite cyclic, with generator
$e_3\ge 1$) is infinite cyclic, with generator
 \begin{align*} \overline Z \quad &\text{if }e_2=e_3=0, \\ \overline E_1 \quad &\text{if }e_2>0,\ e_3=0, \\ \overline F_{0,1}\quad &\text{if }e_2=0,\ e_3>0,\\ \overline E_1- \overline F_{0,1}\quad&\text{otherwise}. \end{align*}
\begin{align*} \overline Z \quad &\text{if }e_2=e_3=0, \\ \overline E_1 \quad &\text{if }e_2>0,\ e_3=0, \\ \overline F_{0,1}\quad &\text{if }e_2=0,\ e_3>0,\\ \overline E_1- \overline F_{0,1}\quad&\text{otherwise}. \end{align*}
This gives the first part, and the second follows since the inclusion ![]() $\Phi (T_\mathfrak {m})=\mathbb {Z} \to \Phi (J_\mathfrak {m})$ maps
$\Phi (T_\mathfrak {m})=\mathbb {Z} \to \Phi (J_\mathfrak {m})$ maps ![]() $1$ to
$1$ to ![]() $V$.
$V$.
Since ![]() $\Phi (J)=\Phi (J_\mathfrak {m})/\Phi (T_\mathfrak {m})$, an easy computation gives the following.
$\Phi (J)=\Phi (J_\mathfrak {m})/\Phi (T_\mathfrak {m})$, an easy computation gives the following.
Corollary 2.8 ([Reference Mazur and RapoportMR77, table 2]; [Reference EdixhovenEdi91, 4.4.1])
We have
where
2.3.2  $X_0(p)$ with
$X_0(p)$ with  $\mathfrak {m}=(\infty )+(0)$
$\mathfrak {m}=(\infty )+(0)$
In the setting of Theorem 2.7, if ![]() $e_2$ and
$e_2$ and ![]() $e_3$ are at most
$e_3$ are at most ![]() $1$, then
$1$, then ![]() $\Phi (J_\mathfrak {m})$ is infinite cyclic and the map
$\Phi (J_\mathfrak {m})$ is infinite cyclic and the map ![]() $\Phi (T_\mathfrak {m})\simeq \mathbb {Z} \to \Phi (J_\mathfrak {m})$ is, up to sign, multiplication by the order of the cyclic group
$\Phi (T_\mathfrak {m})\simeq \mathbb {Z} \to \Phi (J_\mathfrak {m})$ is, up to sign, multiplication by the order of the cyclic group ![]() $\Phi (J)$. Therefore, the actions of all the Hecke operators
$\Phi (J)$. Therefore, the actions of all the Hecke operators ![]() $T_\ell$ (including for
$T_\ell$ (including for ![]() $p\mid N$) can be computed from the actions on
$p\mid N$) can be computed from the actions on ![]() $\Phi (T_\mathfrak {m})$. For example, suppose
$\Phi (T_\mathfrak {m})$. For example, suppose ![]() $N=p$. Then by Example 2.2(b), without appealing to the results of Ribet and Edixhoven we obtain the following.
$N=p$. Then by Example 2.2(b), without appealing to the results of Ribet and Edixhoven we obtain the following.
Corollary 2.9 Suppose that ![]() $N=p$ and
$N=p$ and ![]() $\mathfrak {m}=(\infty )+(0)$. Then:
$\mathfrak {m}=(\infty )+(0)$. Then:
–
 $\Phi (J_\mathfrak {m})$ is infinite cyclic;
$\Phi (J_\mathfrak {m})$ is infinite cyclic;–
 $\Phi (J)=\operatorname {coker}(\Phi (T_\mathfrak {m}) \to \Phi (J_\mathfrak {m}))$ is cyclic of order
$\Phi (J)=\operatorname {coker}(\Phi (T_\mathfrak {m}) \to \Phi (J_\mathfrak {m}))$ is cyclic of order  $n$, the numerator of
$n$, the numerator of  $(p-1)/12$;
$(p-1)/12$;– for
 $\ell \ne p$,
$\ell \ne p$,  $T_\ell =\ell +1$ on
$T_\ell =\ell +1$ on  $\Phi (J_\mathfrak {m})$, and
$\Phi (J_\mathfrak {m})$, and  $T_p=1$ on
$T_p=1$ on  $\Phi (J_\mathfrak {m})$.
$\Phi (J_\mathfrak {m})$.
2.3.3  $X_0(pM)$ with
$X_0(pM)$ with  $(p,M)=1$ and
$(p,M)=1$ and  $\mathfrak {m}$ a general cuspidal modulus
$\mathfrak {m}$ a general cuspidal modulus
Now let ![]() $\mathfrak {m}$ be any nonzero reduced modulus supported on the cusps of
$\mathfrak {m}$ be any nonzero reduced modulus supported on the cusps of ![]() $X_0(N)$, with
$X_0(N)$, with ![]() $p$ exactly dividing
$p$ exactly dividing ![]() $N$. Recall that we are working over the strict henselization
$N$. Recall that we are working over the strict henselization ![]() $R$ of
$R$ of ![]() $\mathbb {Z}_{(p)}$. Then since
$\mathbb {Z}_{(p)}$. Then since ![]() $p^2\nmid N$, all the cusps are rational over
$p^2\nmid N$, all the cusps are rational over ![]() $F$ so
$F$ so ![]() $e=(1,\ldots,1)$ and
$e=(1,\ldots,1)$ and
with ![]() $I=\mathrm {supp}(\mathfrak {m})\subset X_0(N)^\infty (\overline {\mathbb {Q}})$.
$I=\mathrm {supp}(\mathfrak {m})\subset X_0(N)^\infty (\overline {\mathbb {Q}})$.
Proposition 2.10 If the closure of the support of ![]() $\mathfrak {m}$ meets just one component of the special fibre
$\mathfrak {m}$ meets just one component of the special fibre ![]() $\mathcal {X}'_s$, then there is a canonical splitting
$\mathcal {X}'_s$, then there is a canonical splitting
Otherwise, if ![]() $x_0=\infty$,
$x_0=\infty$, ![]() $x_0\in \mathrm {supp}(\mathfrak {m})$ meet
$x_0\in \mathrm {supp}(\mathfrak {m})$ meet ![]() $Z_\infty$,
$Z_\infty$, ![]() $Z_0$, respectively, and
$Z_0$, respectively, and ![]() $\mathfrak {m}'=(x_\infty )+(x_0)$, then there is a canonical splitting
$\mathfrak {m}'=(x_\infty )+(x_0)$, then there is a canonical splitting
Proof. In the first case, we may assume that the closure of the support of ![]() $\mathfrak {m}$ meets only the component
$\mathfrak {m}$ meets only the component ![]() $Z_\infty$. If
$Z_\infty$. If ![]() $Y\in C$ and
$Y\in C$ and ![]() $Y \ne Z_\infty$, then
$Y \ne Z_\infty$, then ![]() $h(Y)=0$, but
$h(Y)=0$, but ![]() $h(Z_\infty )=(1,\ldots,1)$, so the composite
$h(Z_\infty )=(1,\ldots,1)$, so the composite ![]() $h\colon \mathbb {Z}[C]\to \mathbb {Z}^I/\mathrm {diag}(\mathbb {Z})$ is zero.
$h\colon \mathbb {Z}[C]\to \mathbb {Z}^I/\mathrm {diag}(\mathbb {Z})$ is zero.
In the second case, we have ![]() $h(Y)=0$ if
$h(Y)=0$ if ![]() $Y\notin \{Z_\infty,Z_0\}$, and
$Y\notin \{Z_\infty,Z_0\}$, and
for a suitable ordering of ![]() $I$. Therefore,
$I$. Therefore,
giving the splitting.
2.3.4  $X_0(p^2)$
$X_0(p^2)$
Finally, let us consider the curve ![]() $X_0(p^2)$,
$X_0(p^2)$, ![]() $p>3$. The Katz–Mazur model
$p>3$. The Katz–Mazur model ![]() $\mathcal {X}'$ over
$\mathcal {X}'$ over ![]() $S$ has three irreducible components in its special fibre, which we denote by
$S$ has three irreducible components in its special fibre, which we denote by ![]() $Z_i'$ (
$Z_i'$ (![]() $0\le i\le 2$). The non-supersingular non-cuspidal points of
$0\le i\le 2$). The non-supersingular non-cuspidal points of ![]() $Z_i'$ parametrize pairs
$Z_i'$ parametrize pairs ![]() $(E,C)$, where
$(E,C)$, where ![]() $E$ is an elliptic curve and
$E$ is an elliptic curve and ![]() $C$ is a cyclic (in the sense of Drinfeld) subgroup scheme of rank
$C$ is a cyclic (in the sense of Drinfeld) subgroup scheme of rank ![]() $p^2$, whose étale quotient has rank
$p^2$, whose étale quotient has rank ![]() $p^i$. The components
$p^i$. The components ![]() $Z_0'$,
$Z_0'$, ![]() $Z_2'$ have multiplicity
$Z_2'$ have multiplicity ![]() $1$, and
$1$, and ![]() $Z_1'$ has multiplicity
$Z_1'$ has multiplicity ![]() $p-1$. They meet at the supersingular points.
$p-1$. They meet at the supersingular points.
The cuspidal divisor ![]() $X_0(p^2)_\mathbb {Q}^\infty$ consists of three closed points
$X_0(p^2)_\mathbb {Q}^\infty$ consists of three closed points ![]() $\infty =z_1 = \operatorname {Spec} \mathbb {Q}$,
$\infty =z_1 = \operatorname {Spec} \mathbb {Q}$, ![]() and
and ![]() $0=z_{p^2}= \operatorname {Spec}\mathbb {Q}$, in the notation of § 2.1. For each
$0=z_{p^2}= \operatorname {Spec}\mathbb {Q}$, in the notation of § 2.1. For each ![]() $i$, the closure in
$i$, the closure in ![]() $\mathcal {X}'$ of the point
$\mathcal {X}'$ of the point ![]() $z_{p^i}$ meets the component
$z_{p^i}$ meets the component ![]() $Z_i'$ in a single point, and the completed local ring at the intersection is computed in [Reference EdixhovenEdi90, Proposition 1.2.2.1] as
$Z_i'$ in a single point, and the completed local ring at the intersection is computed in [Reference EdixhovenEdi90, Proposition 1.2.2.1] as

where ![]() $q$ is the usual parameter at infinity on the modular curve of level
$q$ is the usual parameter at infinity on the modular curve of level ![]() $1$.
$1$.
The minimal resolution ![]() $\pi \colon \mathcal {X} \to \mathcal {X}'$ is described in detail in [Reference EdixhovenEdi90, § 1.5]. We summarize the final result. Write
$\pi \colon \mathcal {X} \to \mathcal {X}'$ is described in detail in [Reference EdixhovenEdi90, § 1.5]. We summarize the final result. Write ![]() $p=12k+1+4a+6b$, with
$p=12k+1+4a+6b$, with ![]() $a$,
$a$, ![]() $b\in \{0,1\}$. We again work over the strict henselization
$b\in \{0,1\}$. We again work over the strict henselization ![]() $R$ of
$R$ of ![]() $\mathbb {Z}_{(p)}$.
$\mathbb {Z}_{(p)}$.
The Katz–Mazur model ![]() $\mathcal {X}'$ has exactly two singular points, which are the points
$\mathcal {X}'$ has exactly two singular points, which are the points ![]() $x_0$,
$x_0$, ![]() $x_{1728} \in Z_1'$ lying over the points
$x_{1728} \in Z_1'$ lying over the points ![]() $j=0$,
$j=0$, ![]() $1728$ in the curve
$1728$ in the curve ![]() $X(1)_{\overline {\mathbb {F}}_p}$. Let
$X(1)_{\overline {\mathbb {F}}_p}$. Let ![]() $E=\pi ^{-1}(x_{1728})^{\mathrm {red}}$,
$E=\pi ^{-1}(x_{1728})^{\mathrm {red}}$, ![]() $F=\pi ^{-1}(x_0)$. Then
$F=\pi ^{-1}(x_0)$. Then ![]() $E\simeq F \simeq \mathbb {P}^1$,
$E\simeq F \simeq \mathbb {P}^1$, ![]() $E$ has multiplicity
$E$ has multiplicity ![]() $(p-1+2b)/2$ and
$(p-1+2b)/2$ and ![]() $F$ has multiplicity
$F$ has multiplicity ![]() $(p-1+2a)/3$.
$(p-1+2a)/3$.
Let ![]() $Z_i$ be the reduced strict transform of
$Z_i$ be the reduced strict transform of ![]() $Z_i'$. The intersection matrix of
$Z_i'$. The intersection matrix of ![]() $\mathcal {X}_s$ is
$\mathcal {X}_s$ is

where ![]() $L=(p^2-1)/12-k$. As a basis for
$L=(p^2-1)/12-k$. As a basis for ![]() $\ker (\mathbb {Z}^C \xrightarrow {b} \mathbb {Z})$ we take
$\ker (\mathbb {Z}^C \xrightarrow {b} \mathbb {Z})$ we take ![]() $\overline Y = Y^\vee - d_Y Z^\vee _2$, for
$\overline Y = Y^\vee - d_Y Z^\vee _2$, for ![]() $Y\in \{Z_0, Z_1, E, F\}$ and where
$Y\in \{Z_0, Z_1, E, F\}$ and where ![]() $d_Y$ is the multiplicity of
$d_Y$ is the multiplicity of ![]() $Y$. (Since the residue field is perfect,
$Y$. (Since the residue field is perfect, ![]() $d_Y=\delta _Y$.)
$d_Y=\delta _Y$.)
We first consider the modulus ![]() $\mathfrak {m} = X_0(p^2)_\mathbb {Q}^\infty =\sum _{0\le i\le 2}(z_{p^i})$ of all cusps. Since the cusp
$\mathfrak {m} = X_0(p^2)_\mathbb {Q}^\infty =\sum _{0\le i\le 2}(z_{p^i})$ of all cusps. Since the cusp ![]() $z_p$ is isomorphic to
$z_p$ is isomorphic to ![]() , and the other cusps are rational,
, and the other cusps are rational, ![]() $e=(1,p-1,1)$. From the description (2.3.1) of the completed local rings at the cusps, we see that
$e=(1,p-1,1)$. From the description (2.3.1) of the completed local rings at the cusps, we see that ![]() , and the pullback of the divisor
, and the pullback of the divisor ![]() $Z_i$ to the component of
$Z_i$ to the component of ![]() $\Sigma$ which it meets has degree
$\Sigma$ which it meets has degree ![]() $1$. Therefore, the matrix
$1$. Therefore, the matrix ![]() $(h_{ij})$ giving the pairing
$(h_{ij})$ giving the pairing ![]() $C\times I\to \mathbb {Z}$ in Theorem 1.19 is
$C\times I\to \mathbb {Z}$ in Theorem 1.19 is

Let ![]() $V_i\in \mathbb {Z}^I/e\mathbb {Z}$ be the image of the
$V_i\in \mathbb {Z}^I/e\mathbb {Z}$ be the image of the ![]() $i$th basis vector (dual to
$i$th basis vector (dual to ![]() $z_{p^i}$) of
$z_{p^i}$) of ![]() $\mathbb {Z}^I$. We will take
$\mathbb {Z}^I$. We will take ![]() $\{V_0,V_1\}$ as basis for
$\{V_0,V_1\}$ as basis for ![]() $\mathbb {Z}^I/e\mathbb {Z}$.
$\mathbb {Z}^I/e\mathbb {Z}$.
Next consider the modulus ![]() $\mathfrak {m}'=(\infty )+(0)=(z_1)+(z_{p^2})$. Then
$\mathfrak {m}'=(\infty )+(0)=(z_1)+(z_{p^2})$. Then ![]() $e=(1,1)$, and the pairing
$e=(1,1)$, and the pairing ![]() $C\times I \to \mathbb {Z}$ is given by the same matrix with the
$C\times I \to \mathbb {Z}$ is given by the same matrix with the ![]() $z_p$-row deleted, and
$z_p$-row deleted, and ![]() $\mathbb {Z}^I/e\mathbb {Z}$ is generated by
$\mathbb {Z}^I/e\mathbb {Z}$ is generated by ![]() $V_0=-V_2$.
$V_0=-V_2$.
Under the isomorphism of Theorem 1.19, the image of ![]() $\mathbb {Z}^I/e\mathbb {Z}$ in the homology of the complex (1.3.1) is the subgroup
$\mathbb {Z}^I/e\mathbb {Z}$ in the homology of the complex (1.3.1) is the subgroup ![]() $\Phi (T_\mathfrak {m})$ of
$\Phi (T_\mathfrak {m})$ of ![]() $\Phi (J_\mathfrak {m})$. The analogous statement holds for
$\Phi (J_\mathfrak {m})$. The analogous statement holds for ![]() $\mathfrak {m}'$.
$\mathfrak {m}'$.
Theorem 2.11 (a) The component group ![]() $\Phi (J_\mathfrak {m})$ is isomorphic to
$\Phi (J_\mathfrak {m})$ is isomorphic to ![]() $\mathbb {Z}^2$, and (for a suitable choice of isomorphism), the image of the generators
$\mathbb {Z}^2$, and (for a suitable choice of isomorphism), the image of the generators ![]() $V_0$,
$V_0$, ![]() $V_1$ of
$V_1$ of ![]() $\Phi (T_\mathfrak {m})$ are
$\Phi (T_\mathfrak {m})$ are
(b) The component group ![]() $\Phi (J_{\mathfrak {m}'})$ is isomorphic to
$\Phi (J_{\mathfrak {m}'})$ is isomorphic to ![]() $\mathbb {Z}$, and (up to sign), the image of the generator
$\mathbb {Z}$, and (up to sign), the image of the generator ![]() $V_0$ of
$V_0$ of ![]() $\Phi (T_\mathfrak {m})$ is
$\Phi (T_\mathfrak {m})$ is ![]() $(p^2-1)/24$.
$(p^2-1)/24$.
Remark (i) From the computation in part (b) we recover the result [Reference EdixhovenEdi91, § 4.1, Proposition 2] that ![]() $\Phi (J)$ is cyclic of order
$\Phi (J)$ is cyclic of order ![]() $(p^2-1)/24$.
$(p^2-1)/24$.
(ii) In both cases the map ![]() $\Phi (T_\mathfrak {m}) \to \Phi (J_\mathfrak {m})$ is an injection of free abelian groups of the same rank, so the action of Hecke operators on
$\Phi (T_\mathfrak {m}) \to \Phi (J_\mathfrak {m})$ is an injection of free abelian groups of the same rank, so the action of Hecke operators on ![]() $\Phi (T_\mathfrak {m})$ determines that on
$\Phi (T_\mathfrak {m})$ determines that on ![]() $\Phi (J_\mathfrak {m})$ and, therefore, on the quotient
$\Phi (J_\mathfrak {m})$ and, therefore, on the quotient ![]() $\Phi (J)$, ‘by pure thought’.
$\Phi (J)$, ‘by pure thought’.
Proof. From (2.3.2) we see that ![]() $\Phi (J_\mathfrak {m})$ is generated by
$\Phi (J_\mathfrak {m})$ is generated by ![]() $\{V_0,V_1,\overline Z_0,\overline Z_1,\overline E,\overline F\}$ with relations
$\{V_0,V_1,\overline Z_0,\overline Z_1,\overline E,\overline F\}$ with relations
 \begin{gather*} V_0=L\overline Z_0 -k\overline Z_1 -b\overline E-a\overline F,\\ V_1=-k\overline Z_0 +\overline Z_1 -\overline E -\overline F,\\ b\overline Z_0 +\overline Z_1-2\overline E=0=a\overline Z_0 +\overline Z_1 -3 \overline F \end{gather*}
\begin{gather*} V_0=L\overline Z_0 -k\overline Z_1 -b\overline E-a\overline F,\\ V_1=-k\overline Z_0 +\overline Z_1 -\overline E -\overline F,\\ b\overline Z_0 +\overline Z_1-2\overline E=0=a\overline Z_0 +\overline Z_1 -3 \overline F \end{gather*}
and linear algebra then gives an isomorphism ![]() $\Phi (J_\mathfrak {m}) \xrightarrow \sim \mathbb {Z}^2$ by
$\Phi (J_\mathfrak {m}) \xrightarrow \sim \mathbb {Z}^2$ by
 \begin{align*} \overline Z_0 &\mapsto (1,0) ,\\ \overline Z_1 &\mapsto (2a-3b,6), \\ \overline E &\mapsto (a-b,3) ,\\ \overline F &\mapsto (a-b,2) ,\\ V_0 &\mapsto (L-(2k+1)a+(3k+1)b, -6k-2a-3b) ,\\ V_1 &\mapsto (-k-b,1). \end{align*}
\begin{align*} \overline Z_0 &\mapsto (1,0) ,\\ \overline Z_1 &\mapsto (2a-3b,6), \\ \overline E &\mapsto (a-b,3) ,\\ \overline F &\mapsto (a-b,2) ,\\ V_0 &\mapsto (L-(2k+1)a+(3k+1)b, -6k-2a-3b) ,\\ V_1 &\mapsto (-k-b,1). \end{align*}
This proves part (a). For part (b), we compose with the map ![]() $\mathbb {Z}^2 \xrightarrow {(1,k+b)} \mathbb {Z}$, whose kernel is the subgroup generated by
$\mathbb {Z}^2 \xrightarrow {(1,k+b)} \mathbb {Z}$, whose kernel is the subgroup generated by ![]() $V_1$, and which takes
$V_1$, and which takes ![]() $V_0$ to
$V_0$ to
Conflicts of interest
None.