2.1 Introduction
Earth’s unique status as the only life-harboring planet in the inner Solar System is often linked to its orbit being in the habitable zone that resulted in the stabilization of liquid water on its surface. However, in addition to surface liquid water, the presence of carbon and other life-essential volatile elements (LEVEs) such as nitrogen and sulfur in the surface environment is also critical for the habitability of rocky planets. Earth’s long-term equable climate and chemically habitable surface environment are therefore results of well-tuned fluxes of carbon and other LEVEs, involving the deep and the surficial Earth. Given that Earth developed into a volcano-tectonically active planet with both outgassing and ingassing mechanisms, the surface inventory of LEVEs over million- to billion-year timescales is maintained by interactions of the ocean–atmosphere system with the silicate fraction of the planet. Yet it remains uncertain how and when the initial inventory of LEVEs for the surface reservoir plus the silicate fraction (bulk silicate Earth (BSE) altogether), which set the initial boundary conditions for subsequent planet-scale volatile cycles, got established. The answers to these questions lie within Earth’s formative years – in the building blocks, in the process of Earth’s accretion, and in the early differentiation that made the major reservoirs that constitute the core, the mantle, and the crust–atmosphere.
Earth is a differentiated planet with a central metallic core and an outer shell of dominantly silicate rocks divided into the mantle and crust, which is overlain by the fluid envelope of the ocean–atmosphere system. Direct constraints on carbon and the other life-essential volatile abundance of Earth’s core are lacking (Chapter 3, this volume), although significant concentrations of carbon, sulfur, hydrogen, and nitrogen can be in Earth’s core given that the outer core is 10% lighter than pure Fe–Ni alloy liquid.Reference Birch1–Reference Poirier3 More is known about the carbon content of the present-day silicate fraction of the planet and its fluid envelope because Earth’s mantle reservoir is sampled to some extent via mantle-derived melts (e.g. Refs. Reference Javoy, Pineau and Allègre4–Reference Dasgupta and Hirschmann9 and Chapter 9, this volume). Yet the estimates of bulk mantle carbon abundance from concentrations in basalts are uncertain partly because most basalts are partially degassed and basalt generation only directly samples typically the top 100–200 km of the mantle. Nonetheless, largely based on the carbon content of basalts (e.g. C/3He, CO2/Nb, CO2/Ba, and C/40Ar ratios), the BSE abundance of carbon is estimated to be ~100–530 ppm.Reference Hirschmann and Dasgupta7, Reference Dasgupta and Hirschmann9–Reference Marty13 Among this range of estimated C budget for the BSE, most estimatesReference Hirschmann and Dasgupta7, Reference Dasgupta and Hirschmann9, Reference Bergin, Blake, Ciesla, Hirschmann and Li10–Reference Halliday12 have converged to a concentration of 90–130 ppm, and this will be used in this chapter. It can be surmised that this BSE budget of C is an end product of Earth’s accretion and early differentiation,Reference Dasgupta8, Reference Dasgupta and Walker14, Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 but the uncertainty in the C budget of BSE makes testing such hypotheses quantitatively less rigorous. Further insight could be gained, however, from C to other LEVE ratios (i.e. C/X, where X = N, S, or H; e.g. Refs. Reference Hirschmann and Dasgupta7, Reference Bergin, Blake, Ciesla, Hirschmann and Li10, Reference Hirschmann11, Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18). Specifically, these volatile ratios for the terrestrial reservoirs in general and BSE in particular could be compared with the same ratios in various planetary building blocks and evaluated against the known processes of planet formation and early differentiation.
The key questions focus on what planetary building blocks were responsible for delivering C and other associated LEVEs to Earth and when such delivery processes took place. If the C abundance and the C/X ratios of the BSE as well as the isotopic compositions of all LEVEs are similar to any of the undifferentiated meteorites, it may be concluded that such building blocks were responsible for bringing these volatiles to Earth and no postdelivery process altered their ratios (Figure 2.1). On the other hand, if the C abundance and C/X ratios of the BSE are distinct from these known building blocks, one needs to investigate whether any postdelivery processes could have altered these quantities such that the BSE LEVE geochemistry could be established. For example, if core formation processes fractionate C and/or affect the C/X ratios, then could equilibrium core formation scenarios be responsible for establishing carbon, oxygen, hydrogen, nitrogen, and sulfur in BSE (Figure 2.1)? The timing of volatile delivery is also important. If the LEVEs were delivered during the main stage of accretion, then early differentiation processes like core–mantle segregation and magma ocean (MO) degassing would have played an important role in setting up the relative budgets of the LEVEs in the primary reservoirs (Figure 2.1).Reference Dasgupta8, Reference Hirschmann11 The delivery mechanism and the timing of delivery may be intimately linked; however, less interrogation has taken place thus far regarding the delivery mechanism. For example, there is a growing recognition that following an initial period of accretion of undifferentiated planetesimals, differentiated planetary embryos with masses ranging from ~0.01 to 0.1ME (where ME is the mass of present-day Earth) were abundant in the inner Solar System;Reference Morbidelli, Lunine, O’Brien, Raymond and Walsh19 therefore, accretion of these differentiated bodies significantly contributed to the growth of larger planets like Earth.Reference Morbidelli, Lunine, O’Brien, Raymond and Walsh19, Reference O’Brien, Walsh, Morbidelli, Raymond and Mandell20 Did the impacts or merger of differentiated bodies deliver the LEVEs to the BSE and establish the C abundance and the C/X ratiosReference Li, Dasgupta, Tsuno, Monteleone and Shimizu16, Reference Tsuno, Grewal and Dasgupta17 or did post-core formation addition of undifferentiated or differentiated bodiesReference Marchi, Canup and Walker21 establish the BSE LEVE budget? And what were the relative contributions of the impacts of large differentiated and smaller undifferentiated bodies to bringing in LEVEs versus causing a depletion of LEVEs via atmospheric mass loss?Reference Schlichting and Mukhopadhyay22–Reference Ahrens24
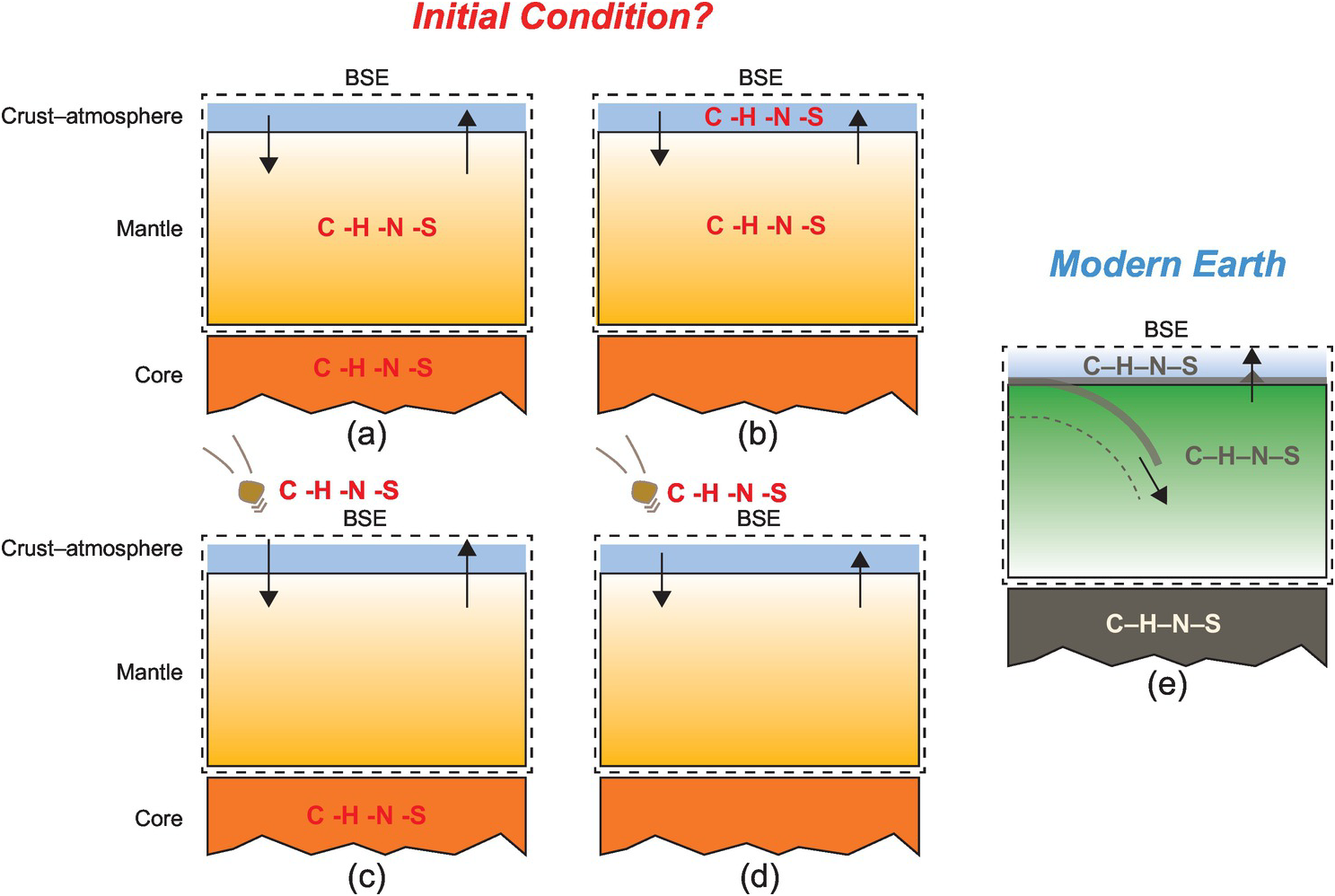
Figure 2.1 Plausible initial distributions of C, H, N, and S between Earth’s major reservoirs at the end of accretion and core formation. (a) LEVEs are available during accretion and all LEVEs are initially sequestered in the core and the MO. (b) LEVE delivery during accretion is temporally separate from the main episodes of core formation and thus the core is effectively devoid of LEVEs. (c) Available LEVEs during accretion are effectively sequestered in the core or lost to space (not shown) and the BSE acquires LEVEs via later additions. (d) Core–mantle differentiation takes place in the absence of LEVEs and LEVEs are added via late additions. These distributions eventually evolved into the setup seen in the modern world (e), where these volatile elements are thought to exchange between Earth’s mantle and the crust–ocean–atmosphere system (ingassing and outgassing) regulates the long-term habitability of the planet.
This chapter will discuss the state of the art on what is known about the origin of C relative to the other LEVEs in the BSE, highlighting open questions and gaps in knowledge. We will discuss constraints based on geochemical comparison of the potential terrestrial building blocks with Earth reservoirs and interrogate each key process of planet formation and early differentiation, such as core formation, MO crystallization, MO degassing, and atmospheric loss in shaping the absolute and relative abundances of C and the other LEVEs. The current understanding of the fractionation of C and other LEVEs during the core formation process will also be used to put constraints on the C budget of the core.
2.2 Constraints on the Compositions of Terrestrial Building Blocks
2.2.1 Constraints from Isotopes of Refractory Elements
Geochemical models based on elemental abundances and isotopic constraints predict the accretion of bulk Earth primarily from chondritic meteorites.Reference Ringwood25, Reference Anders and Ebihara26 Because elemental and isotopic fractionation trends for bulk silicate samples and chondritic meteorites have well-defined relationships, it is widely assumed that the building blocks of Earth belong to a class of primitive objects that are sampled by chondritic meteorites.Reference Allègre, Manhès and Lewin27 Close similarity of the abundances of refractory lithophile elements between the BSE and CI led to an early development of a CI model for Earth.Reference Ringwood25 Allègre et al.Reference Allègre, Manhès and Lewin27 further consolidated this model by arguing that volatile depletion trends in the BSE are matched most closely by CI chondrites. However, a distinct disparity of oxygen (second most abundant element in the BSE by mass) isotopes (i.e. 16O, 17O, and 18O) between CI chondrites and the BSE, which could not be explained by any fractionation or differentiation models,Reference Clayton, Onuma and Mayeda28, Reference Clayton29 was one of the first observed isotopic variations that challenged the CI model for Earth. Over the past decades, isotopic dissimilarity between CI chondrites and the BSE has been extended from Δ17O (deviation from a reference mass-dependent fractionation line in a triple isotope of oxygen plotReference Young30) to several radiogenic as well as non-radiogenic isotopic anomalies for a wide suite of refractory elements with contrasting geochemical behaviors: lithophile elements (ε48Ca (Ref. Reference Dauphas31), ε50Ti, μ142Nd), moderately siderophile elements (ε54Cr, ε64Ni, ε92Mo), and highly siderophile elements (HSEs; ε100Ru) (Refs. Reference Dauphas32, Reference Fischer-Gödde and Kleine33 and references therein). Interestingly, the BSE isotopic compositions for all of these elements are almost indistinguishable from enstatite chondrites (E-chondrites). This has led to the development of an E-chondrite model for Earth.Reference Dauphas32, Reference Javoy34, Reference Javoy35 Tracking the isotopic evolution of the growing BSE by taking into account the alloy–silicate partitioning behavior of several lithophile, moderately siderophile, and HSEs during core–mantle equilibration, DauphasReference Dauphas32 proposed that half of the first 60% of accreted mass was composed of E-type chondrites, while the remaining 40% was all E-type chondritic materials. However, there are a few outstanding issues with an E-chondritic model for Earth, namely: (1) the Ca/Mg ratio of the BSE (0.118Reference McDonough and Sun36) is distinctly higher than that of E-chondrites (0.080Reference Wasson and Kallemeyn37), suggesting that the BSE has an enriched refractory elemental abundance relative to E-chondrites;Reference Fitoussi, Bourdon and Wang38 (2) E-chondrites have an Mg/Si ratio that is lower than that of the BSE sampled by upper-mantle rocks,Reference Palme, O’Neill and Carlson39 which can only be explained by either incorporation of Si into the core or via an unsampled lower mantle with a low Mg/Si ratio;Reference Murakami, Ohishi, Hirao and Hirose40 and (3) δ30SiBSE is 0.3–0.4‰ higher than δ30Si of E-chondrites and aubrites.Reference Fitoussi and Bourdon41 Experimentally determined Si isotopic fractionation parametersReference Shahar42, Reference Shahar43 rule out the possibility of explaining the Si isotopic composition as well as the Mg/Si ratio of the BSE via incorporation of Si in the core if Earth was primarily accreted from E-chondrites.Reference Fitoussi and Bourdon41 Although there are studies that argue for a lower mantle or at least a portion of the lower mantle being richer in silica compared to Earth’s upper mantle,Reference Murakami, Ohishi, Hirao and Hirose40, Reference Ballmer, Houser, Hernlund, Wentzcovitch and Hirose44 such findings are debated. To circumvent these issues, Dauphas et al.Reference Dauphas, Poitrasson, Burkhardt, Kobayashi and Kurosawa45 proposed that the bulk Earth and the E-chondrites sample an isotopically similar reservoir with their subsequent chemical evolution offset by ensuing nebular fractionation and planetary differentiation processes. In summary, a large number of geochemical systematics point to the bulk Earth being made from E-chondrite-type materials, although questions on the major element and volatile element abundance mismatch remain.
2.2.2 Constraints from Isotopes of Highly Volatile Elements
In contrast to constraints from refractory elements, constraints from highly volatile elements (i.e. C, N and H (water)) paint a different picture on the potential sources of LEVEs. Although ordinary chondrites (OCs), which sample S-type asteroids in the inner belt (2.1–2.8 AU), have similar amounts of bulk water as the BSE, the D/H ratio of the BSE is not similar to that of OCs,Reference McNaughton, Borthwick, Fallick and Pillinger46 but rather is strikingly similar to that of carbonaceous chondrites, especially CI chondrites,Reference Robert, Merlivat and Javoy47 which are representative of C-type asteroids (beyond 2.8 AU) (Figure 2.2a). Similarity of 15N/14N between the BSE and CI chondrites also points toward a carbonaceous chondritic origin of volatiles on Earth (Figure 2.3b).Reference Marty13, Reference Alexander48, Reference Pearson, Sephton, Franchi, Gibson and Gilmour49 13C/12C of the BSE cannot distinguish between a chondritic or cometary origin of C (Figure 2.2b).Reference Marty, Alexander and Raymond50, Reference Sarafian, Nielsen, Marschall, McCubbin and Monteleone51 However, a clear distinction of the 15N/14N ratio of the BSE from the corresponding cometary values would necessitate C delivery by CI chondrites as well, assuming all the major volatiles (i.e. C, N, and water) were sourced from a similar parent body.
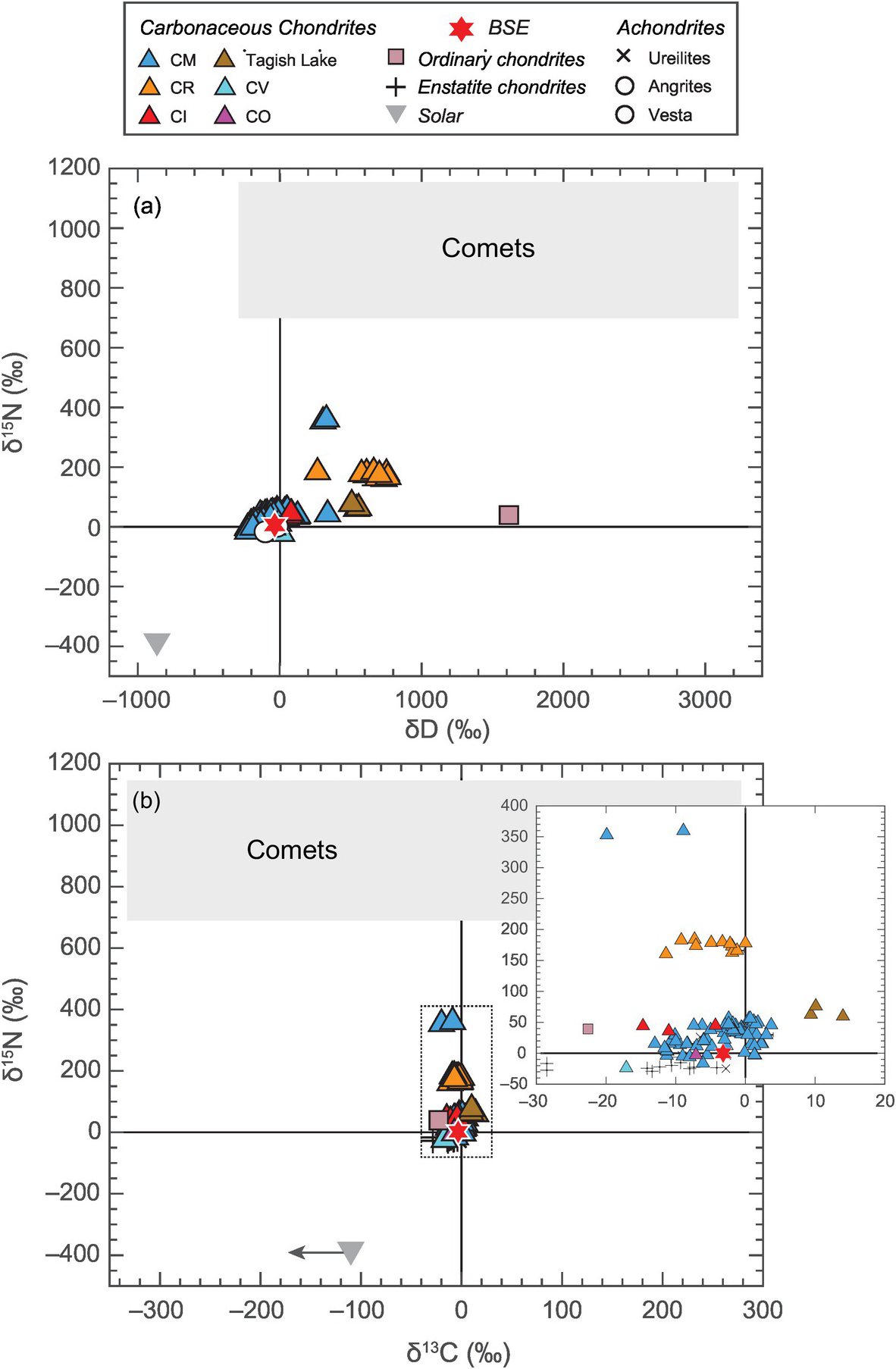
Figure 2.2 Comparison of isotopic compositions of (a) hydrogen and nitrogen and (b) carbon and nitrogen for several Solar System objects and reservoirs. The solar reservoir is depleted while the cometary reservoir is enriched in the heavier isotopes of nitrogen and hydrogen relative to all classes of meteorites as well as the BSE. Although δ13C alone cannot distinguish between the meteoritic and cometary sources, the isotopic compositions of all major LEVEs suggest that the BSE had a similar parent reservoir as carbonaceous chondrites.
Although thus far direct matching of the isotopes of C, H, and N of the BSE with undifferentiated meteorites has been the approachReference Marty and Yokochi59 to determining the source of the LEVEs on Earth, there is a growing realization that there may be fractionation of stable isotopes during early terrestrial differentiation, such as devolatilization, MO degassing, and core–mantle fractionation. Indeed, such fractionation processes may be able to reconcile some of the observed differences between the LEVE isotopic compositions of the BSE and the chondrites.Reference Wood, Li and Shahar60 For example, carbon isotopic compositions of many CI chondritic materials are distinctly lighter (δ13C, approximately –15 to –7‰Reference Marty, Alexander and Raymond50) than the average carbon isotope composition of Earth’s mantle (δ13C, approximately –5‰Reference Kerridge61, Reference Deines62). Similarly, the sulfur isotope composition of Earth’s mantle has also been argued to be non-chondritic.Reference Labidi, Cartigny and Moreira63 Graphite–Fe–carbide melt carbon isotope fractionation experimentsReference Satish-Kumar, So, Yoshino, Kato and Hiroi64 showed that 12C preferentially incorporates into the metallic phase, leaving a 13C-enriched signature in the graphite or diamond. If similar fractionation behavior applies between silicate MO and core-forming alloy liquid, then core formation could explain how Earth’s mantle evolved to have a heavier carbon isotope value compared to the chondritic building blocks.
2.2.3 Constraints from Theoretical Modeling
Because isotopic compositions of refractory elements suggest bulk Earth to be composed of materials similar to E-chondrites while volatile elements favor their delivery via CI chondritic material, the timing of admixing of C-rich material into the accreting zone of Earth becomes key. Such admixing could have taken place either during the primary stage of Earth’s growth or after the main phase of accretion. Similarly, delivery of C-bearing materials may have occurred via accretion of undifferentiated bodies similar to chondrites or via amalgamation of differentiated bodies with C abundances in relevant reservoirs of those bodies set by core–mantle differentiation and atmospheric losses.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 Theoretical models have been used to simulate the early evolution of the Solar System by accounting for dynamics of planetary accretion along with geochemical, cosmochemical, and chronological relationships between accreting and resulting bodies.Reference Walsh, Morbidelli, Raymond, O’Brien and Mandell65, Reference Raymond, O’Brien, Morbidelli and Kaib66 Constrains from Hf/W chronometry predict that Mars-sized planetary embryos were formed from mostly E-type chondritic material sourced from the inner part of the Solar System in the initial ~5 Ma.Reference Dauphas and Pourmand67 Recent advancements like pebble accretion models predict that gas giants like Jupiter also grew synchronously to their present-day mass via trapping of proto-solar nebular gas within the lifetime of the protoplanetary disk.Reference Lambrechts and Johansen68, Reference Johansen, Low, Lacerda and Bizzarro69 However, the growth of gas giants is thought to rapidly deplete the asteroid belt, which would mean minimal interaction of C-rich carbonaceous chondritic material that condensed in the outer parts of the Solar System with the growth zone of terrestrial planet accretion within 2 AU.Reference Morbidelli, Lunine, O’Brien, Raymond and Walsh19 With the consideration that the presence of giant planets in the system affects the mixing and delivery of LEVEs from the outer regions to the terrestrial planet-forming region in the disk, the migration of giant planets has been argued to be necessary to perturb the orbits of cometary and asteroid-like bodies, bringing a fraction of these to the inner regions, where they can collide with terrestrial planets, delivering additional volatile elements to the rocky planets.Reference Morbidelli, Lunine, O’Brien, Raymond and Walsh19 A specific planetary migration model, the Grand Tack scenario,Reference Morbidelli, Lunine, O’Brien, Raymond and Walsh19, Reference O’Brien, Walsh, Morbidelli, Raymond and Mandell20, Reference Walsh, Morbidelli, Raymond, O’Brien and Mandell65 postulated that the inward and outward movement of Jupiter likely repopulated the asteroid belt in the inner parts of the Solar System with C-type chondritic material. However, these models cannot constrain the net mass of volatile-rich material being delivered, as they allow for a total influx of volatile-rich material ≥0.5–2.0% of present-day Earth’s mass, assuming volatile-rich CI chondrites have water in the range of 5–10 wt.%.Reference Morbidelli, Lunine, O’Brien, Raymond and Walsh19, Reference O’Brien, Walsh, Morbidelli, Raymond and Mandell20 Delivery of a C budget that is larger than the present day in the BSE would require offsetting via later differentiation processes, while C delivery being restricted to the present-day budget of the BSE would have to be unaffected by later differentiation processes. A model such as Grand Tack does not directly constrain the relative timing of acquiring the C- and water-rich chondritic materials in the terrestrial planet-forming regions with respect to specific giant impact events. However, with the Moon formation being a specific event, similarity or a lack thereof between C and other LEVE budgets and volatile isotope signatures of Earth and Moon may shed light on when LEVE-rich materials were brought in with respect to the Moon-forming event. Little is known about the C budget of the Moon or the lunar mantle;Reference Wetzel, Hauri, Saal and Rutherford70, Reference Chi, Dasgupta, Duncan and Shimizu71 however, if water and carbon were co-delivered, the appreciable water content of lunar glasses and melt inclusionsReference Saal72, Reference Hauri, Weinreich, Saal, Rutherford and Van Orman73 and the E-chondritic nature of late veneerReference Dauphas32 can only be reconciled if volatiles were delivered to the Earth–Moon system beforeReference Saal, Hauri, Van Orman and Rutherford74, Reference Greenwood75 or during the Moon-forming impact.Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 However, if C and other LEVEs were delivered during the main stage of Earth’s accretion, then differentiation processes like core–mantle separation, as well as the delivery mechanism of volatiles – either by smaller, undifferentiated planetesimals composed of primarily CI-chondritic material or via relatively large, differentiated planetary embryos heterogeneously composed of material sourced from both inner and outer parts of the Solar System – can provide additional information on the origin of LEVEs in the BSE.
2.3 C and Other Volatiles: Abundances, Ratios, and Forms in Various Classes of Meteorites and Comparison with the BSE
The present-day BSE is estimated to be depleted in C and other highly volatile elements relative to all classes of undifferentiated meteorites by at least an order of magnitude and by as much as two orders of magnitude compared to the more primitive carbonaceous chondrites (Table 2.1).Reference Marty13 For example, carbonaceous chondrites are C rich,Reference Alexander48, Reference Alexander, McKeegan and Altwegg54, Reference Palme, Lodders, Jones, Holland and Turekian76 while enstatite and OCs are relatively C poor.Reference Alexander, McKeegan and Altwegg54, Reference Kerridge61 Among various carbonaceous chondrites, CI chondrites are the most C rich,Reference Alexander, McKeegan and Altwegg54, Reference Palme, Lodders, Jones, Holland and Turekian76–Reference Palme, Jones and Davis79 and they are also richer in other LEVEs such as N (0.19–0.32 wt.%Reference Alexander, McKeegan and Altwegg54, Reference Palme, Lodders, Jones, Holland and Turekian76, Reference Anders and Grevesse77) and H (1.55–2.02 wt.%Reference Alexander, McKeegan and Altwegg54, Reference Anders and Grevesse77) compared to other types of carbonaceous chondrites such as CV, CO, CM, and CR (Table 2.1). Severe depletion of C in the BSE relative to CI chondrites can be explained either by accretion of extremely small quantities of CI chondrites as late additions or via accretion of larger quantities of CI chondrites, but subject to subsequent loss during accretion or differentiation. Such loss of C from carbonaceous building blocks may be expected given that primary carbon is present as soluble as well as insoluble organic molecules in carbonaceous chondrites, which are expected to be unstable at the high temperatures occurring during inner-Solar System processes. Similarly, the carbonates that are products of secondary alterations in carbonaceous chondrites are also expected to volatilize during delivery and accretion in the inner-Solar systems bodies. Even though E-chondrites may have C abundances that are not much greater than that in the BSE, such concentrations are more likely to survive the delivery to the inner-Solar System bodies given their presence in the form of more refractory graphite, diamonds, and carbides.Reference Grady and Wright80 It remains unclear, however, in what form and abundance C was in E-chondrite parent bodies before thermal metamorphism. It cannot be ruled out that unprocessed E-chondritic protoliths were more C rich and may have even contained organics. Despite the survival potential of refractory C-bearing phases in E-chondrites in the inner-Solar System processes, it is generally thought that the E-chondrites had much less water than the present-day BSE,Reference Hutson and Ruzicka81 although the H budget of the BSE has significant uncertainty owing to poor constraints on the water budget of the mantle.Reference Hirschmann82
Table 2.1 C content and C/S, C/N, and C/H weight ratios of major terrestrial reservoirs and chondritic building blocks
| Reservoirs | C (wt.%) | C/S | C/N | C/H |
|---|---|---|---|---|
| Terrestrial reservoirs | ||||
| BSE | 0.011 ± 0.002 | 0.49 ± 0.14 | 40.00 ± 8.00 | 1.13 ± 0.20 |
| Mantle | 0.008 ± 0.002 | 0.36 ± 0.10 | 72.73 ± 37.72 | 2.00 ± 0.70 |
| Crust–ocean–atmosphere | 0.002 ± 0.000 | 8.89 ± 2.22 | 12.5 ± 3.22 | 0.51 ± 0.04 |
| Core | 0.50 (?) | 0.32 (?) | 85.00 (?) | 8.40 (?) |
| Carbonaceous chondrites | ||||
| CO | 0.63 ± 0.24 | 0.32 ± 0.12 | 21.74 ± 19.16 | 10.40 ± 0.00 |
| CV | 0.92 ± 0.43 | 0.42 ± 0.20 | 23.96 ± 24.16 | 10.20 ± 0.00 |
| CM | 1.89 ± 0.48 | 0.58 ± 0.15 | 21.01 ± 8.35 | 3.20 ± 0.00 |
| CI | 4.24 ± 0.77 | 0.72 ± 0.13 | 19.66 ± 11.69 | 4.80 ± 0.00 |
| Enstatite chondrites | ||||
| EH | 0.36 ± 0.13 | 0.06 ± 0.02 | 13.73 ± 7.26 | 11.00 ± 0.00 |
| EL | 0.48 ± 0.16 | 0.15 ± 0.05 | 24.43 ± 9.40 | 11.00 ± 0.00 |
| Ordinary chondrites | ||||
| H | 0.11 | 0.06 | >104.00 | 2.50 ± 0.70 |
| L | 0.09 | 0.04 | 46.10 ± 1.00 | 3.00 ± 1.00 |
| LL | 0.09 | 0.05 | 51.22 ± 1.20 | 2.60 ± 0.50 |
The mantle, the crust-ocean-atmosphere, and the BSE averages and 1σ standard deviations are from Hirschmann and DasguptaReference Hirschmann and Dasgupta7 for C/H, Bergin et al.Reference Bergin, Blake, Ciesla, Hirschmann and Li10 for C/N, and HirschmannReference Hirschmann11 for C/S. The carbonaceous chondrite data for C, H, and N are from Figure 2.3, E-chondrite C/N data are from Grady et al.Reference Grady, Wright, Carr and Pillinger52 and Alexander et al.Reference Alexander, Swan and Prombo53 OC C/N data are from Bergin et al.Reference Bergin, Blake, Ciesla, Hirschmann and Li10 and references therein. The C/S data for all chondrites are from Wasson and Kallemeyn,Reference Wasson and Kallemeyn37 and the C/H data for enstatite and OCs are from HirschmannReference Hirschmann11 and references therein. The core compositional estimates are using bulk Earth concentrations from McDonough,Reference McDonough and Carlson83 and  values are from Figure 2.5 and assuming complete core–mantle equilibration. The data for C contents are from Bergin et al.Reference Bergin, Blake, Ciesla, Hirschmann and Li10 for terrestrial reservoirs, from Alexander et al.Reference Alexander48 for carbonaceous chondrites, from Grady et al.Reference Grady, Wright, Carr and Pillinger52 for E-chondrites, and from Wasson and KallemeynReference Wasson and Kallemeyn37 for OCs.
values are from Figure 2.5 and assuming complete core–mantle equilibration. The data for C contents are from Bergin et al.Reference Bergin, Blake, Ciesla, Hirschmann and Li10 for terrestrial reservoirs, from Alexander et al.Reference Alexander48 for carbonaceous chondrites, from Grady et al.Reference Grady, Wright, Carr and Pillinger52 for E-chondrites, and from Wasson and KallemeynReference Wasson and Kallemeyn37 for OCs.
In contrast to absolute abundances, the relative abundance of C with respect to other volatile elements in the BSE (i.e. C/H, C/N and C/S) is a powerful tracer to constrain the C abundance of Earth and provides additional constraints on the processes that must have fractionated the geochemical reservoirs relative to the cosmochemical reservoirs (Figure 2.3).
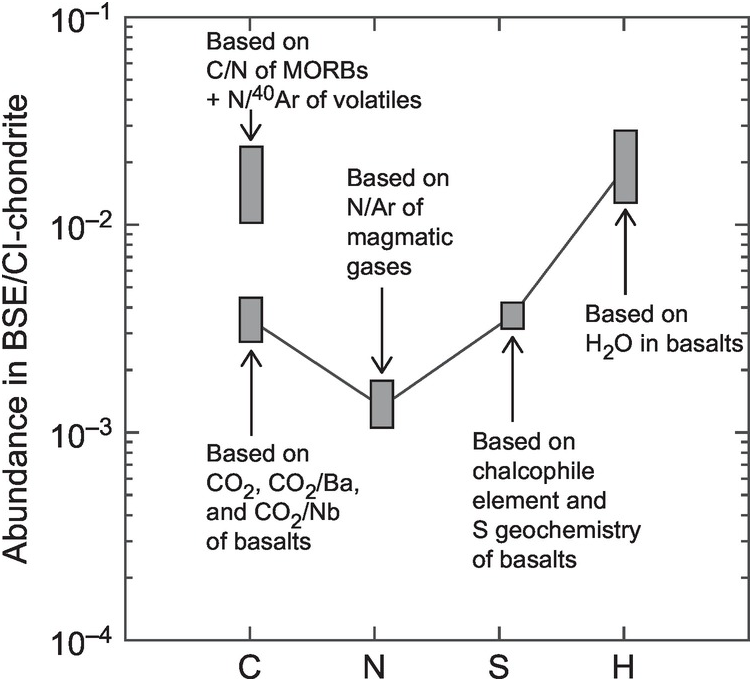
Figure 2.3 Comparison of the abundances of C, N, S, and H in the BSE normalized to their respective abundances in CI chondrites. In the BSE, C is enriched relative to N, has a similar abundance to S, and is depleted relative to H in comparison to its abundance in CI chondrites. Data from Refs. Reference Bergin, Blake, Ciesla, Hirschmann and Li10, Reference Hirschmann11, and Reference Marty13. Also noted in the figure is the main geochemical information used to estimate the BSE concentrations of the respective elements in the original studies. MORB = mid-ocean ridge basalt.
Due to the comparable 50% condensation temperatures of C and N as well as their abundances being positively correlated in various classes of chondrites, comparison of the C/N ratio of the BSE with that of the building blocks can help track the accretion and differentiation history of C in the early Earth. Recently, Bergin et al.Reference Bergin, Blake, Ciesla, Hirschmann and Li10 estimated the BSE C/N ratio to be 40 ± 8 by calculating the mantle C content using CO2/Nb and CO2/Ba ratios of possibly undegassed ocean island basalts (Figure 2.3).Reference Rosenthal, Hauri and Hirschmann84 This C/N ratio is similar to the estimate of Halliday,Reference Halliday12 but lower than the estimate of Marty.Reference Marty13 We will adopt the C/N ratio from the latest studies.Reference Hirschmann11, Reference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Dalou, Hirschmann, von der Handt, Mosenfelder and Armstrong85 The C/N ratios of volatile-rich CI and CM as well as slightly volatile-poor CO and CV chondrites are lower than the C/N ratio of the BSE by approximately a factor 2, while E-chondrites also have low C/N ratios (5–25; Figure 2.4a). Although OCs show large scatter in C/N ratios due to uncertainties in determining extremely low C and N contents, their average C/N ratios are higher than that of the BSE (Figure 2.4a). Because the average C/N ratio of all classes of chondrites lies in the range of 5–30, the superchondritic C/N ratio of the BSE has been postulated to be a legacy of either preferential incorporation of N into the core or loss of an early N-rich atmosphere.Reference Marty13 However, ureilites, a class of achondrites and assumed to be the mantle restite of an asteroidal body, are extremely C rich (average 3 wt.% C) with intergranular veins of graphite and traces of diamonds.Reference Nabiei86, Reference Kana, Masayuki and Jun-ichi87 It is interesting to note that the C/N ratio of ureilites is much higher than that of the BSE;Reference Hirschmann11, Reference Barrat, Sansjofre, Yamaguchi, Greenwood and Gillet88 therefore, if the C/N ratios of this achondrite are representative of an ureilite parent body and such a parent body significantly contributed to Earth’s accretion,Reference Schiller, Bizzarro and Fernandes89 then preferential loss of N as a necessary condition for bulk silicate reservoirs in Earth is precluded.
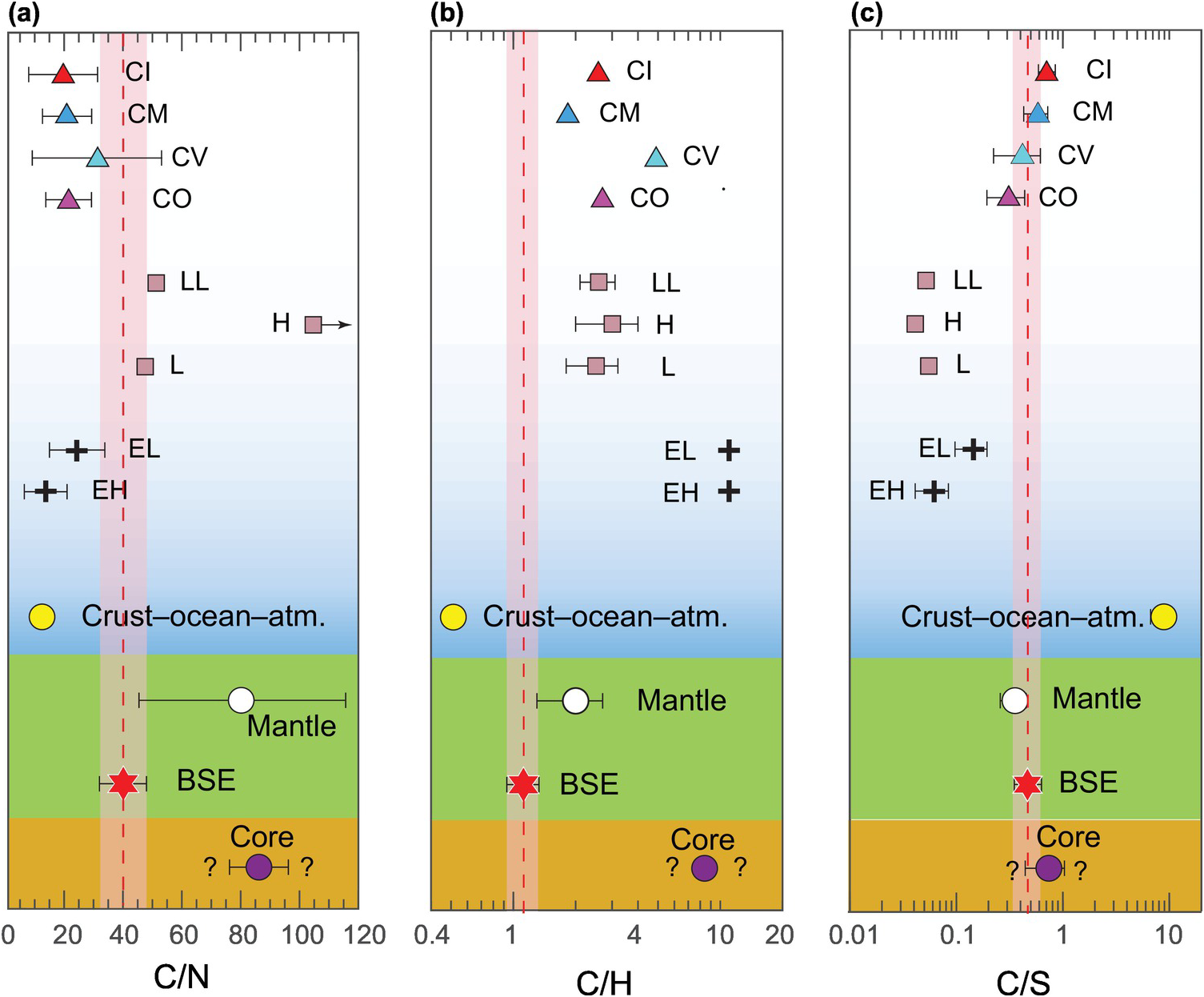
Figure 2.4 Comparison of bulk C/N (a), C/H (b), and C/S (c) weight ratios between different terrestrial and chondritic reservoirs. The data are from Table 2.1. CI = Ivuna-type Carbonaceous chondrite; CM = Mighei-type Carbonaceous chondrite; CV = Vigarano-type Carbonaceous chondrite; CO = Ornans-type Carbonaceous chondrite; LL = low total iron, low metal ordinary chondrite; H = highest total iron ordinary chondrite; L = low total iron ordinary chondrite; EL = (low enstatite) enstatite chondrite; EH = (high enstatite) enstatite chondrite.
Assuming a similar C inventory in the mantle as discussed earlier, the C/H ratio of the BSE has been estimated to be 1.13 ± 0.20.Reference Hirschmann and Dasgupta7, Reference Hirschmann11 The C/H ratio of BSE is lower than all classes of chondritic meteorites (Figure 2.4). OCs have a C/H ratio that is two to five times greater than that of the BSE, while E-chondrites, which are extremely water poor, have a 20‑times higher C/H ratio. Carbonaceous chondrites, which have the closest match to the terrestrial D/H ratio, also have a higher C/H ratio; CI and CM chondrites, which are C and water rich, have a C/H ratio that is four to six times higher; while CO and CV chondrites, which are relatively C and water poor, have a C/H ratio that is 12–15 times higher. Therefore, in contrast to a superchondritic C/N ratio, a subchondritic C/H ratio can be explained if C was preferentially incorporated into the core or lost to space relative to H during terrestrial differentiation.
Sulfur has a much higher solar nebula condensation temperature than C, N, and H; therefore, it is not a highly volatile element. Sulfur abundance in the BSE, especially in the mantle, is also better knownReference Ding and Dasgupta90–Reference Rehkämper92 relative to that of other highly volatile elements of interest (Figure 2.3). Therefore, the C/S ratio can also act as an important tracer to track the evolution of C in the early Earth. The C/S ratio of the BSE is higher than that of C-depleted E-chondrites, but it is similar to or lower than that of C-rich carbonaceous chondrites (Figure 2.4c). Therefore, a near-chondritic C/S ratio in the BSE stipulates that either both C and S showed similar loss/gain behavior during early differentiation processes or they were primarily delivered in post-differentiation processes via undifferentiated, chondritic materials.
Because the C/H ratio of the BSE is subchondritic, the C/S ratio is near-chondritic, while the C/N ratio is superchondritic, H, N, and S have widely different geochemical behaviors relative to C during core formation or MO degassing and/or they track different stages of terrestrial accretion. The following sections will explore whether there are known processes that can explain the difference between the LEVE geochemistry of the BSE and those of carbonaceous chondrites.
2.4 Establishing LEVE Budgets of the BSE After Core Formation?
2.4.1 The Role of Late Accretion
The theory of the addition of undifferentiated meteorites after the completion of metal–silicate differentiation chiefly stems from the approximately chondritic relative abundance of HSE (e.g. Re, Os, Ir, Ru, Pt, Rh, Pd, and Au) concentrations in Earth’s mantle and the BSE, plus the fact that the BSE is not as depleted of HSEs as it would have been if the entire HSE inventory of the bulk Earth was available before equilibrium core formation took place.Reference Walker93, Reference Mann, Frost, Rubie, Becker and Audétat94 Assuming that core formation originally left the silicate Earth virtually HSE free and later additions of chondritic materials elevated the HSE abundances to the present level, the chondritic mass added is estimated to be 0.5% of Earth’s mass (0.005 ME). WalkerReference Walker93 noted that this estimate may be ~1.5 times higher or a factor of four lowerReference Morgan, Walker, Brandon and Horan95 depending on the exact concentrations of HSEs in the chondritic materials being added. Willbold et al.Reference Willbold, Elliott and Moorbath96 also calculated that in order to offset the pre-late accretion 182W-excess composition of the BSE, 0.08 ME chondritic mass needs to be added. Given that many carbonaceous chondrites are rich in LEVEs, many studies have surmised that late accretion of these materials brought all of the LEVEs to the BSE.Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Albarede97–Reference Dasgupta, Chi, Shimizu, Buono and Walker99 If this was the mechanism, then the core formation would have no influence on the relative abundance of various LEVEs. Indeed, the addition of 0.0030–0.0075 ME chondritic materials with 3.48–3.65 wt.% C to the BSE would set the BSE C budget to ~100–250 ppm C (or ~360–900 ppm CO2 in the mantleReference Dasgupta8). Although this C budget may be sufficient to match even the enriched basalt source regions, as briefly discussed by Dasgupta,Reference Dasgupta8 there are several challenges in invoking CI-type carbonaceous chondrite as the chief or sole source of the BSE C and other LEVEs. Section 2.2 already discussed which elemental and isotopic compositions of the BSE are not satisfied if the BSE is chiefly made up of carbonaceous chondrites. Section 2.2 also outlined how the elemental abundance of C and the C/S ratio of the BSE can be satisfied if CI-type carbonaceous chondrite accreted to Earth after core formation was complete, but the C/N and C/H ratios and possibly δ13C and δ34S of the BSE are difficult to explain. Here, we specifically discuss what challenges exist in invoking other known meteorites as the late-accreting materials to explain the entire inventory of carbon and other LEVEs in the BSE.
Given E-chondrites (e.g. (low enstatite) enstatite chondrite (EL) and (high enstatite) enstatite chondrite (EH)) are depleted in water and also poor in C and N,Reference Grady, Wright, Carr and Pillinger52 bringing LEVEs in general and water in particular to Earth exclusively by E-chondrite is not thought to be a realistic mechanism. EH and EL chondrites also have distinctly lower C/N and C/S ratios compared to the BSE (Figure 2.4a and c). Hence, unprocessed E-chondrite, known from the studied samples, could not have brought LEVEs to Earth after core formation in the right proportions. This is at odds with recent propositions that, based on Ru isotopic composition, argued for the late veneers having E-chondritic character.Reference Dauphas32, Reference Fischer-Gödde and Kleine33 One issue in evaluating E-chondrites as plausible terrestrial building blocks based on volatile element geochemistry is that all known E-chondrites studied thus far are heavily metamorphosed; hence, before thermal metamorphism, these chondrites might have been more LEVE rich and C could have been originally organic.Reference Alexander, Fogel, Yabuta and Cody100
OCs are depleted in volatiles with respect to carbonaceous chondrites chiefly because the volatile-rich matrix volume percentage is less than that of carbonaceous chondrites.Reference Alexander, McKeegan and Altwegg54 In fact, bulk C content of most primitive OCs can be perfectly explained by its matrix material being entirely CI-type material.Reference Alexander48 OC matrices are drier, however, with bulk H of OCs falling below the concentration of what would be expected if the entire OC matrix was made up of CI-type materials.Reference Alexander, McKeegan and Altwegg54 Therefore, the C/H ratio of OCs is higher than that of the BSE (Figure 2.4b). Similarly, the C/S ratios of OCs are lower and the C/N ratios of OCs are distinctly higher compared to the estimates for the BSE (Figure 2.4a and c). Hence after core formation, OC delivery cannot be considered as the chief process of origin of Earth’s LEVEs.
Among all stony meteorites, ureilites are the only group of primitive achondrites that are rich in C and depleted in N, leading to higher C/N ratios.Reference Vdovykin101–Reference Downes103 Carbon in ureilites is also present in relatively non-labile phases (i.e. as graphites, nanodiamonds, and lonsdaleite) and hence is likely to survive high-temperature accretional processes. Primarily motivated by their high C/N ratios, recent studiesReference Hirschmann11, Reference Barrat, Sansjofre, Yamaguchi, Greenwood and Gillet88 have suggested that C-rich achondrites such as ureilites may be responsible for establishing the abundances of LEVEs in the BSE through post-core formation addition. While the C/N ratio of the BSE could be heavily shaped by the addition of a ureilite-like achondrite, the C/S ratio of ureilite is significantly higher than that estimated for the BSE. Hence, any attempt to match the C/S ratios of the BSE through addition of a ureilite-like achondrite-rich late veneer requires a very unique consideration of the composition and extent of core–mantle equilibration of proto-Earth.Reference Hirschmann11 No model of ureilite-like late-veneer addition can explain the C/N and C/S ratios simultaneously. For example, scenarios of C-rich late-silicate addition in which the superchondritic C/N ratio can be established also result in a superchondritic C/S ratio.Reference Hirschmann11
Overall, late accretion alone does not seem to account for the C budget and C to other LEVE ratios of the present-day BSE (Figure 2.5). Hence, other early Earth processes need to be considered.
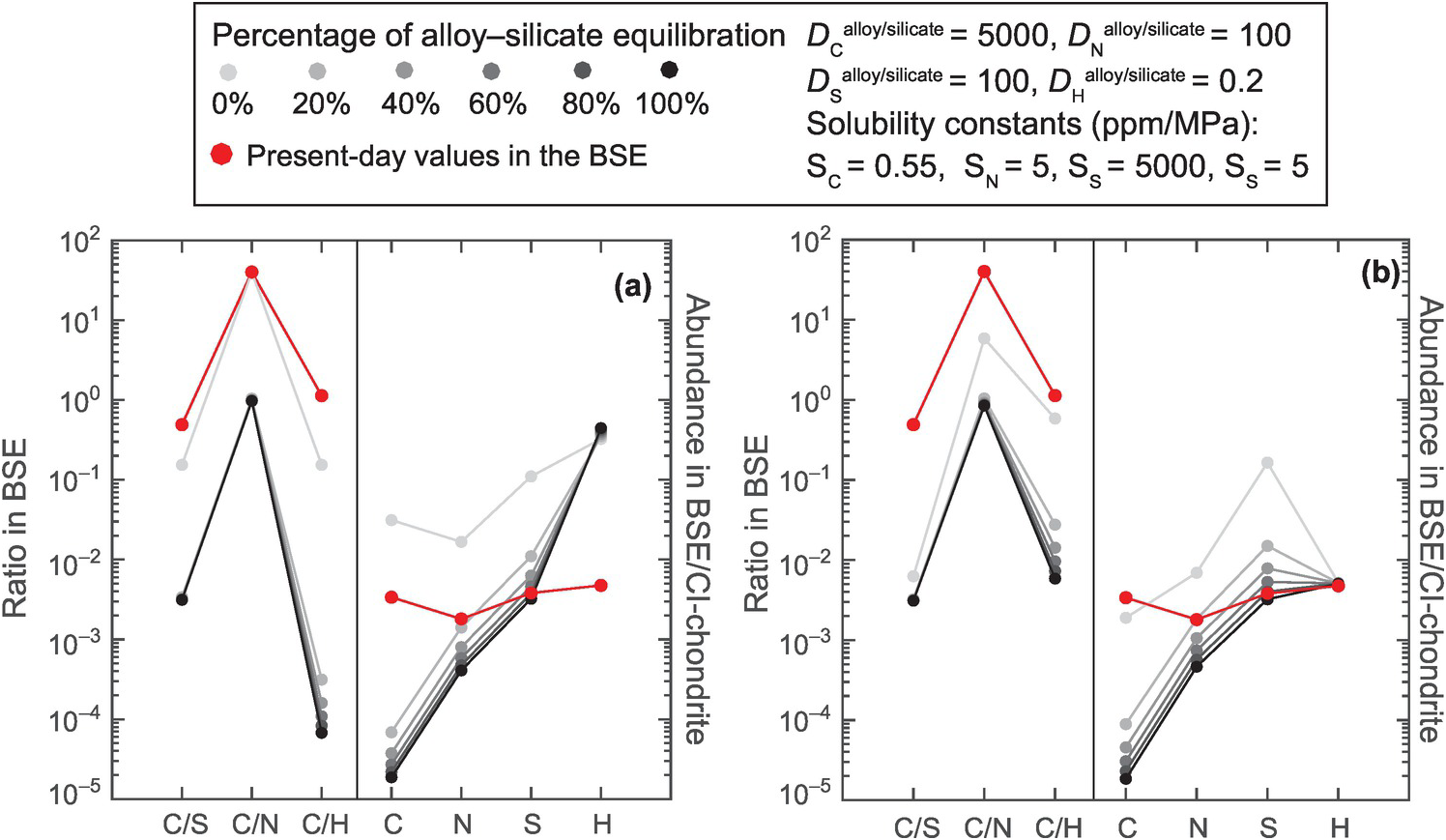
Figure 2.5 Application of alloy–silicate partition coefficients and solubilities of LEVEs in the silicate melts to examine the effect of core formation, with varying degrees of alloy–silicate equilibration, with or without loss of an early atmosphere formed via MO degassing on the remnant abundances of LEVEs in the bulk silicate reservoir. (a) LEVEs, when delivered as 0.015 ME late-accreting materials (i.e. 0% alloy–silicate equilibration), cause the volatile abundance to be higher than the present-day BSE. Core formation with increasing degrees of alloy–silicate equilibration increasingly depletes the remnant MO in all LEVEs, with C being much more depleted than other LEVEs, leading to subchondritic C/N, C/H, and C/S ratios. (b) Combining early atmospheric loss with core formation cannot offset C loss to the core due to the lower solubility of C relative to the other LEVEs in the silicate MOs. Bulk Earth volatile abundance data are from McDonough,Reference McDonough and Carlson83 while the alloy–silicate partition coefficients in a deep MO (P = 50 GPa, T = 3500 K; e.g. Siebert et al.Reference Siebert, Badro, Antonangeli and Ryerson104) for C, N, S, and H are from the parametrized relationships of Chi et al.,Reference Chi, Dasgupta, Duncan and Shimizu71 Grewal et al.,Reference Grewal, Dasgupta, Holmes, Costin and Li105 Boujibar et al.,Reference Boujibar106 and Clesi et al.,Reference Clesi107 respectively. Solubility constant data for C, N, S, and H in the silicate melt are from Armstrong et al.,Reference Armstrong, Hirschmann, Stanley, Falksen and Jacobsen108 Roskosz et al.,Reference Roskosz, Bouhifd, Jephcoat, Marty and Mysen109 O’Neill and Mavrogenes,Reference O’Neill and Mavrogenes110 and Hirschmann et al.Reference Hirschmann, Withers, Ardia and Foley111
2.4.2 The Role of Post-core Formation Sulfide Segregation
The segregation of sulfide melt has been shown to be a necessary process for explaining the HSE geochemistry of the BSE.Reference Rubie112 This would also deplete the BSE in terms of its S inventory, but owing to the low solubility of C in sulfide-rich melts (Figure 2.6a)Reference Tsuno, Grewal and Dasgupta17, Reference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Corgne, Wood and Fei113–Reference Zhang, Hastings, Von der Handt and Hirschmann116 caused by strong non-ideality of mixing between C- and S-rich components in Fe-rich alloy melts, such sulfide segregation should also elevate the C/S ratio of the BSE. Hence, if late accretion establishes a chondritic C/S ratio, sulfide segregation should alter such a ratio. N also is not compatible in S-rich Fe-alloy melts,Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 hence the S/N ratio of the BSE would also drop after sulfide melt segregation. Similarly, it is also unclear what the effects of late-stage sulfide melt segregation might be on the H budget of the BSE. If H is stored in nominally anhydrous silicate minerals in solid, post-core formation BSE, partitioning of H between segregating sulfide melts and solid silicate minerals could influence the H inventory and hence the C/H ratio of the BSE. If H partitions preferentially into sulfide liquid over relevant nominally anhydrous silicate minerals, then the C/H ratio may also increase above the chondritic value.

Figure 2.6 Experimental data showing the effects of S and Si contents in the Fe-rich alloy melt on C solubility. (a) Carbon solubility decreases monotonically with increases in sulfur content in the alloy melt. Si- and N-bearing alloys have lower C solubility for a given S content in the alloy melt. (b) Carbon solubility decreases linearly with increases in Si content in the alloy or decreases in oxygen fugacity (fO2) of silicate–alloy systems. The presence of S in the alloy does not have a major effect on carbon solubility in silicon-bearing alloys.
2.4.3 The Role of MO–Atmosphere Interactions and Atmospheric Loss
Because C and other LEVEs are atmophile elements, they were likely heavily concentrated in the proto-atmospheres at various stages of MO evolution and terrestrial accretion. Hence, it is worth considering under what circumstances silicate magma–atmosphere interactions and possible atmospheric loss through impact-driven blow-offReference Schlichting, Sari and Yalinewich23 could influence the inventory of LEVEs in the BSE. The timing of LEVE delivery is of critical importance in determining the role of silicate–atmosphere interactions (and atmospheric blow-off). For example, if a large fraction of core formation takes place before the LEVEs were available to the growing Earth,Reference O’Brien, Walsh, Morbidelli, Raymond and Mandell20, Reference Raymond, Quinn and Lunine118 then such core formation would have had negligible influence on the BSE LEVE budget, with MO–atmosphere processes being more important. On the other hand, if LEVEs were delivered throughout the terrestrial accretion history,Reference Marty13, Reference Sarafian, Nielsen, Marschall, McCubbin and Monteleone51, Reference Hallis119 then both atmosphere–MO interactions and metal–silicate equilibration could have played roles in establishing the LEVE budget of the BSE.
If the BSE C–N–S–H budgets were established chiefly by loss of proto-atmosphere overlying MO, then N needed to be lost preferentially to C and C needed to be lost preferentially to H. In other words, the proto-atmosphere overlying MO has to be N rich relative to C, C rich relative to H, and with similar abundances of C and S. Indeed, the N-depleted nature of Earth has been explained previously by loss of an N-rich atmosphere.Reference Tucker and Mukhopadhyay120 But evaluation of whether an atmosphere with a concentration of LEVEs in the order N > C~S > H can be generated overlying a silicate magma reservoir depends on the mixed-volatile solubility in shallow MO as a function of oxygen fugacity (fO2; effective partial pressure of oxygen). HirschmannReference Hirschmann11 considered a simple model evaluating the fractionation of C, N, H, and S between silicate MO, overlying atmosphere, and equilibrating core-forming liquid alloy with three distinct fO2 conditions at the MO surface (i.e. IW – 3.5 (reduced), IW – 2 (intermediate fO2), and IW + 1 (oxidized), where IW refers to the log fO2 set by equilibrium of metallic iron and iron oxide (FeO)). Among these, the most oxidizing condition is not very realistic during or soon after core formation because, for a well-mixed MO with a near-constant Fe3+/FeT ratio, the fO2 gradient is such that the shallow MO is always more reduced.Reference Kress and Carmichael121–Reference Zhang, Hirschmann, Cottrell and Withers123 Thus, if a well-mixed MO is close to equilibrium with an Fe-rich core at its base, its surface should be more reduced and therefore, for MO–atmosphere interactions, the relevant fO2 would be less than IW. The only way this may be different is if at higher pressures the fO2 gradient reverses (reduction with increasing depth) and iron disproportionation and subsequent Fe–metal segregation leads to oxidation of metal-free MO.Reference Schaefer and Elkins-Tanton124 Solubility data for most LEVEs are lacking or sparse for peridotitic or ultramafic silicate melts due to difficulty in obtaining a glass and reliable chemical analyses for such compositions.Reference Duncan, Dasgupta and Tsuno125 Based on the data available for silicic to mafic silicate liquids, for log fO2 < IW – 0.5 and with decreasing fO2, N becomes much more soluble (reaching the weight percentage level chiefly as N–H speciesReference Dalou, Hirschmann, von der Handt, Mosenfelder and Armstrong85, Reference Libourel, Marty and Humbert126, Reference Kadik127) than C (tens of ppm by weight mostly as CO32– and to some extent as C–H and C–N speciesReference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Dasgupta, Chi, Shimizu, Buono and Walker99, Reference Armstrong, Hirschmann, Stanley, Falksen and Jacobsen108, Reference Li, Dasgupta and Tsuno117, Reference Duncan, Dasgupta and Tsuno125, Reference Holloway, Pan and Gudmundsson128, Reference Li, Dasgupta and Tsuno129), with the latter mostly decreasing with decreasing fO2 and then leveling off with stabilization of C–H species. Similar to N, H also remains quite soluble in silicate melt in the form of OH– and H2O even in fairly reducing conditions such as log fO2 of IW – 1 to IW – 2, with molecular hydrogen, H2, contributing to some degree.Reference Hirschmann, Withers, Ardia and Foley111 Therefore, at log fO2 < IW – 1.5, atmospheric blow-off could lower the C/H ratio from a chondritic value, but this would result in an MO C/N ratio that is subchondritic. Similarly, S is much more soluble in mafic–ultramafic silicate melts (several thousands of ppmReference O’Neill and Mavrogenes110, Reference Ding, Hough and Dasgupta130, Reference Baker and Moretti131) compared to C and hence loss of an atmosphere would result in a residual silicate MO with a C/S ratio distinctly lower than that of chondritic value. Therefore, no condition exists where a proto-atmosphere overlying an MO can attain all of the compositional characteristics necessary to leave an MO with C/N, C/S, and C/H ratios of the modern-day BSE (Figure 2.5). Hence, late accretion of chondritic materials to an alloy-free MO followed by an atmospheric loss cannot be the chief origin of BSE LEVEs.
An alternative suggestionReference Tucker and Mukhopadhyay120 is for atmospheric loss to help define the BSE C/N and C/H ratios, but at conditions where C would be retained in the form of carbonate or bicarbonate ions either as dissolved aqueous species or in the crust, mediated by the presence of a liquid water ocean. According to this model, a superchondritic C/N ratio and a subchondritic C/H ratio could have been attained via loss of an N-rich atmosphere overlying an ocean. This mode of atmospheric loss is supported by the dynamical model of a giant impact that shows that such an impact would preferentially remove the atmosphere relative to the ocean.Reference Genda and Abe132 However, it is unclear what the water chemistry would be in these oceans, which, if they existed, is expected to be highly anoxic and thus may not sequester significant dissolved carbonates.
2.5 Establishing the Volatile Budget of the BSE through Equilibrium Accretion and MO Differentiation
The discussion on the origin of LEVEs in the BSE thus far considered building blocks and processes after the core formation was mostly complete. This approach would be appropriate if all of the LEVEs were delivered through late accretions. The discovery of a solar component (e.g. neon) in deep plume-derived magma,Reference Honda, McDougall, Patterson, Doulgeris and Clague133, Reference Sarda, Staudacher and Allègre134 however, suggests that Earth might have trapped nebular gas early within the first few millions of years of the formation of the Solar System. Indeed, the possibility of acquiring volatile elements such as primordial noble gases directly from nebular gas has been proposed in a number of studies.Reference Mizuno, Nakazawa and Hayashi135, Reference Yokochi and Marty136 Although nebular gas can persist for ∼10 Myr, its median lifetime (i.e. the time at which half of all systems lost their nebular gas disks) is ∼2.5 Myr.Reference Lynne137 Given the mean time of terrestrial accretion (i.e. the time to have grown to 50% of the final mass) is ∼11 MyrReference Yin138 while the mean accretion timescale of Mars is  Myr,Reference Dauphas and Pourmand67, Reference Tang and Dauphas139 it is likely that although the entire proto-Earth mass may not have equilibrated with the solar nebula, at least a few Mars-sized embryos that contributed to the initial proto-Earth mass likely inherited nebular volatiles. These constraints suggest that early accreting material may have been LEVE poor but likely not LEVE free. However, the LEVE compositions do not suggest direct Solar contribution to be important (Figure 2.2).
Myr,Reference Dauphas and Pourmand67, Reference Tang and Dauphas139 it is likely that although the entire proto-Earth mass may not have equilibrated with the solar nebula, at least a few Mars-sized embryos that contributed to the initial proto-Earth mass likely inherited nebular volatiles. These constraints suggest that early accreting material may have been LEVE poor but likely not LEVE free. However, the LEVE compositions do not suggest direct Solar contribution to be important (Figure 2.2).
The 182Hf/182W ratio of iron meteorites suggests metal–silicate separation in protoplanetary bodies occurred as early as ~1 Myr after the formation of the Solar System. Accordingly, core formation would influence the initial distribution of LEVEs among the planetary reservoirs.Reference Dasgupta8, Reference Hirschmann11, Reference Dasgupta and Walker14, Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16, Reference Tsuno, Grewal and Dasgupta17, Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Dalou, Hirschmann, von der Handt, Mosenfelder and Armstrong85, Reference Dasgupta, Chi, Shimizu, Buono and Walker99, Reference Li, Dasgupta and Tsuno117 Over the past decade, a significant body of research has tried to understand the fate of C and other LEVEs (S, N, and H) during core formation processes and associated alloy–silicate equilibration.Reference Dasgupta and Walker14–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Dalou, Hirschmann, von der Handt, Mosenfelder and Armstrong85, Reference Dasgupta, Chi, Shimizu, Buono and Walker99, Reference Boujibar106, Reference Roskosz, Bouhifd, Jephcoat, Marty and Mysen109, Reference Li, Dasgupta and Tsuno117, Reference Rose-Weston, Brenan, Fei, Secco and Frost140–Reference Suer, Siebert, Remusat, Menguy and Fiquet142 These investigations chiefly focused on determining the partition coefficients of LEVEs between Fe-rich alloy melts and coexisting silicate melts (i.e.  (= concentration of an element in the alloy melt divided by concentration of the same element in the equilibrium silicate melt), where x = C, N, S, etc.). If
(= concentration of an element in the alloy melt divided by concentration of the same element in the equilibrium silicate melt), where x = C, N, S, etc.). If  is >1 and if a given LEVE, x, is available during core formation, then it should be preferentially sequestered in the metallic core. On the other hand, if
is >1 and if a given LEVE, x, is available during core formation, then it should be preferentially sequestered in the metallic core. On the other hand, if  <1, the LEVE, x, present during core–mantle fractionation should preferentially concentrate in the silicate Earth.
<1, the LEVE, x, present during core–mantle fractionation should preferentially concentrate in the silicate Earth.  values provide the framework to understand how a given LEVE is expected to be distributed between the metallic and silicate portions of a differentiated planet if alloy and silicate melts equilibrated before separation.
values provide the framework to understand how a given LEVE is expected to be distributed between the metallic and silicate portions of a differentiated planet if alloy and silicate melts equilibrated before separation.
The most robust constraints available on the alloy–silicate partitioning of LEVEs are obtained through high pressure–temperature experiments. Determinations of  at high pressure–temperature exist chiefly for graphite/diamond-saturated conditions (i.e. experiments conducted in graphite capsules). Concentrations of C in Fe-rich alloy melts at graphite/diamond saturation and in the absence of any other light nonmetals show small dependence on pressure and temperature (not shown)Reference Dasgupta and Walker14, Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 and are ~5–7 wt.%. However, C solubility in Fe-rich alloy melts decreases strongly with increasing S and Si content, and at S of content 22–36 wt.% or Si content >10–12 wt.%, C solubility is <1 wt.% (Figure 2.6a and b). Carbon solubility in Fe-rich alloy melts also diminishes with increasing Ni content in the S-free or S-poor alloy.Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Tsuno and Dasgupta115, Reference Zhang, Hastings, Von der Handt and Hirschmann116, Reference Tsymbulov and Tsmekhman143 Unlike in alloy melts, C solubility in equilibrium silicate melts is tens to hundreds of ppm and mostly decreases with decreasing fO2 (Figure 2.7). The MOs of Earth and other inner-Solar System bodies are expected to be ultramafic to mafic; that is, relatively poor in silica and rich in MgO. Because of the difficulty of rapidly cooling such depolymerized silicate liquids from well-constrained high pressures–temperatures to glasses at ambient conditions, which is necessary for reliable quantitative analyses of carbon and hydrogen, C solubility data in such ultramafic–mafic liquids at core-forming reduced conditions are sparse.Reference Duncan, Dasgupta and Tsuno125 To address this, experimental studies have been conducted with a silicate melt of varying polymerization so that a meaningful extrapolation of C solubility and
at high pressure–temperature exist chiefly for graphite/diamond-saturated conditions (i.e. experiments conducted in graphite capsules). Concentrations of C in Fe-rich alloy melts at graphite/diamond saturation and in the absence of any other light nonmetals show small dependence on pressure and temperature (not shown)Reference Dasgupta and Walker14, Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 and are ~5–7 wt.%. However, C solubility in Fe-rich alloy melts decreases strongly with increasing S and Si content, and at S of content 22–36 wt.% or Si content >10–12 wt.%, C solubility is <1 wt.% (Figure 2.6a and b). Carbon solubility in Fe-rich alloy melts also diminishes with increasing Ni content in the S-free or S-poor alloy.Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Tsuno and Dasgupta115, Reference Zhang, Hastings, Von der Handt and Hirschmann116, Reference Tsymbulov and Tsmekhman143 Unlike in alloy melts, C solubility in equilibrium silicate melts is tens to hundreds of ppm and mostly decreases with decreasing fO2 (Figure 2.7). The MOs of Earth and other inner-Solar System bodies are expected to be ultramafic to mafic; that is, relatively poor in silica and rich in MgO. Because of the difficulty of rapidly cooling such depolymerized silicate liquids from well-constrained high pressures–temperatures to glasses at ambient conditions, which is necessary for reliable quantitative analyses of carbon and hydrogen, C solubility data in such ultramafic–mafic liquids at core-forming reduced conditions are sparse.Reference Duncan, Dasgupta and Tsuno125 To address this, experimental studies have been conducted with a silicate melt of varying polymerization so that a meaningful extrapolation of C solubility and  to desired silicate melt composition can be made.
to desired silicate melt composition can be made.
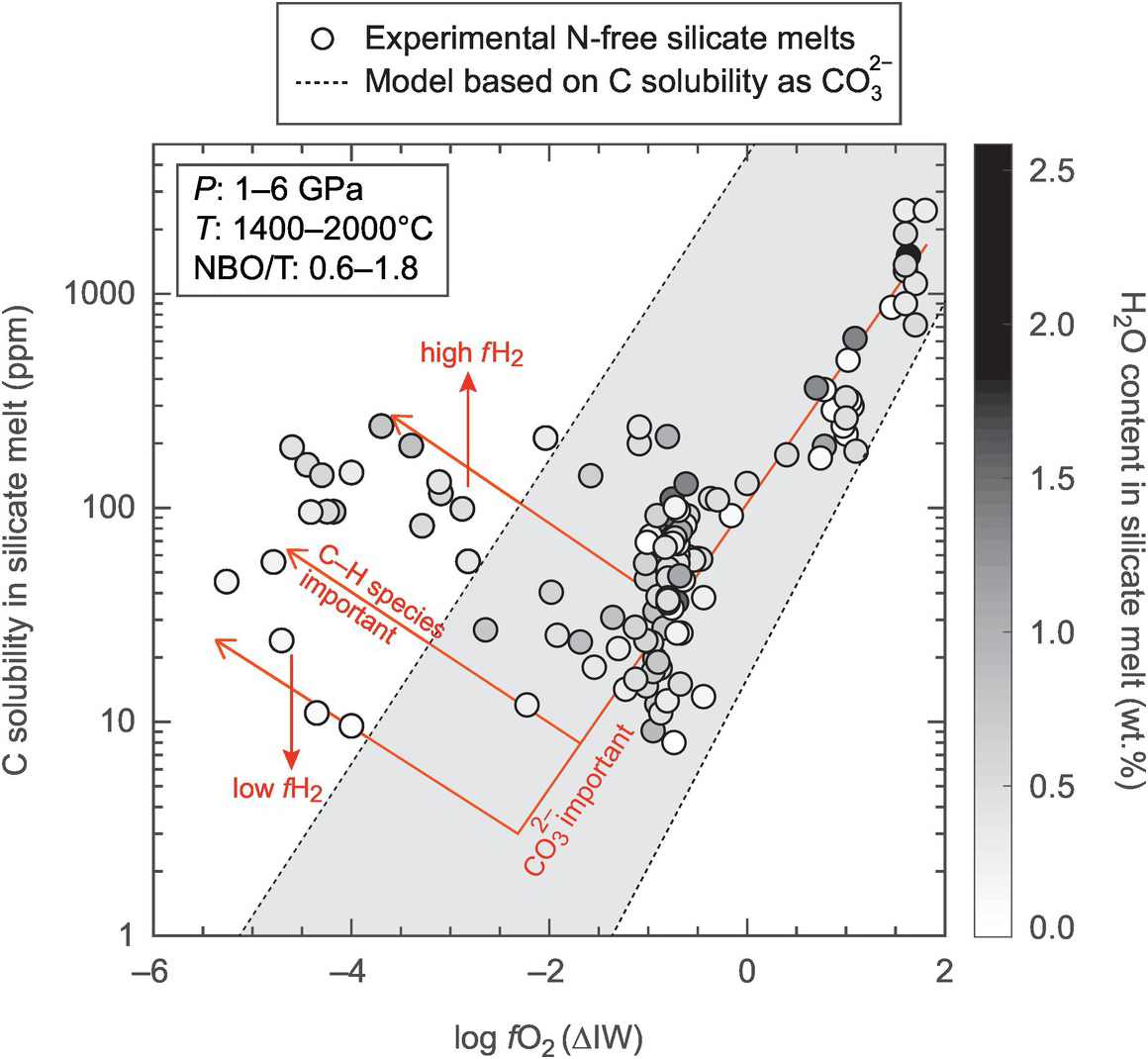
Figure 2.7 Experimental data showing the effects of fO2 and water content in the silicate melt on C solubility. Carbon solubility decreases with decreasing log fO2 until ~ΔIW of –2 to –1 followed by an increase below ~IW – 2 depending upon bulk water content in the silicate melt. This change is likely caused by the change in contributions of C as CO32− at higher fO2 and C as C–H species such as methyl groups at lower fO2. The pressure–temperature–composition (expressed as NBO/T) condition of the experimental glasses are given in the legend. The shaded region represents predicted solubility of C as CO32− at graphite saturation based on the model of Eguchi and DasguptaReference Eguchi and Dasgupta146 for the entire pressure, temperature, and XH2O space of the experimental data, while the NBO/T parameter is extrapolated for peridotite-like silicate melts (NBO/T = 2.7).
2.5.1 Carbon Speciation in MO
 and C solubility in silicate melts are affected by the incorporation mechanism of C in the silicate melt structure. Irrespective of the saturating phase such as CO2-bearing vapor or graphite/diamond, carbon can dissolve in silicate melt as molecular CO2 (CO2mol.Reference Stolper, Fine, Johnson and Newman144–Reference Duncan and Dasgupta148), as carbonate anions (CO32−Reference Duncan, Dasgupta and Tsuno125, Reference Stolper and Holloway149, Reference Pan, Holloway and Hervig150) bonded to cation modifiers, possibly as molecular CO or carbonyl,Reference Yoshioka, McCammon, Shcheka and Keppler151, Reference Wetzel, Rutherford, Jacobsen, Hauri and Saal152 and as possible C–H, C–N complexes.Reference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Li, Dasgupta and Tsuno117 For mafic–ultramafic melts, the chief species of interest is CO32−, which complexes most strongly with Ca2+ cations and also with Na+, Mg2+, and maybe K+.Reference Duncan, Dasgupta and Tsuno125, Reference Eguchi and Dasgupta146, Reference Dasgupta, Hirschmann and Smith153–Reference Ghiorso and Gualda156 Most experiments on carbon dissolution at reducing conditions employed mafic compositions of variable degrees of polymerization (i.e. tholeiitic to alkali basalts or even more silicic melts). The most common approach to extrapolating C solubility and
and C solubility in silicate melts are affected by the incorporation mechanism of C in the silicate melt structure. Irrespective of the saturating phase such as CO2-bearing vapor or graphite/diamond, carbon can dissolve in silicate melt as molecular CO2 (CO2mol.Reference Stolper, Fine, Johnson and Newman144–Reference Duncan and Dasgupta148), as carbonate anions (CO32−Reference Duncan, Dasgupta and Tsuno125, Reference Stolper and Holloway149, Reference Pan, Holloway and Hervig150) bonded to cation modifiers, possibly as molecular CO or carbonyl,Reference Yoshioka, McCammon, Shcheka and Keppler151, Reference Wetzel, Rutherford, Jacobsen, Hauri and Saal152 and as possible C–H, C–N complexes.Reference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Li, Dasgupta and Tsuno117 For mafic–ultramafic melts, the chief species of interest is CO32−, which complexes most strongly with Ca2+ cations and also with Na+, Mg2+, and maybe K+.Reference Duncan, Dasgupta and Tsuno125, Reference Eguchi and Dasgupta146, Reference Dasgupta, Hirschmann and Smith153–Reference Ghiorso and Gualda156 Most experiments on carbon dissolution at reducing conditions employed mafic compositions of variable degrees of polymerization (i.e. tholeiitic to alkali basalts or even more silicic melts). The most common approach to extrapolating C solubility and  to systems containing peridotitic compositions is to use a compositional parameter NBO/T, where “NBO” is the total concentration of non-bridging oxygen in the silicate melt and “T” is the total number of tetrahedral cations. Although this method is thought to give reasonable predictions of ultramafic melt C solubility as CO32−, Duncan et al.Reference Duncan, Dasgupta and Tsuno125 showed that the NBO/T approach may overpredict the extent of CO32− dissolution in silicate melts if an increase of NBO/T is correlated with an increase in CaO rather than MgO in melts. This is because Ca2+ cations complex with CO32− much more than Mg2+,Reference Eguchi and Dasgupta146 although peridotitic melts are still predicted to have higher CO32− dissolution capacities than basalts. Figure 2.7 shows CO32− dissolution as a function of fO2 and shallow MO conditions. Also shown in Figure 2.7 are other possible species such as C–H that may become important at low fO2.
to systems containing peridotitic compositions is to use a compositional parameter NBO/T, where “NBO” is the total concentration of non-bridging oxygen in the silicate melt and “T” is the total number of tetrahedral cations. Although this method is thought to give reasonable predictions of ultramafic melt C solubility as CO32−, Duncan et al.Reference Duncan, Dasgupta and Tsuno125 showed that the NBO/T approach may overpredict the extent of CO32− dissolution in silicate melts if an increase of NBO/T is correlated with an increase in CaO rather than MgO in melts. This is because Ca2+ cations complex with CO32− much more than Mg2+,Reference Eguchi and Dasgupta146 although peridotitic melts are still predicted to have higher CO32− dissolution capacities than basalts. Figure 2.7 shows CO32− dissolution as a function of fO2 and shallow MO conditions. Also shown in Figure 2.7 are other possible species such as C–H that may become important at low fO2.
2.5.2  and Its Impact on Carbon Distribution between BSE versus Core in Various Scenarios of Equilibrium Core Formation
and Its Impact on Carbon Distribution between BSE versus Core in Various Scenarios of Equilibrium Core Formation
Figure 2.8 provides the available data of  , showing their dependence on alloy composition and fO2 at shallow MO conditions. Shallow MO
, showing their dependence on alloy composition and fO2 at shallow MO conditions. Shallow MO  at log fO2 of IW – 2 to IW – 0.5 are in the order of ~103, with the values increasing with increasing pressure and decreasing fO2 and decreasing with increasing temperature and melt depolymerization.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16, Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Li, Dasgupta and Tsuno117 In more reducing conditions where the Si content becomes significant in the equilibrium Fe-rich alloy melts and where decreasing C dissolution as CO32− is offset to some extent by the increasing fraction of C–H complexes (Figure 2.7),
at log fO2 of IW – 2 to IW – 0.5 are in the order of ~103, with the values increasing with increasing pressure and decreasing fO2 and decreasing with increasing temperature and melt depolymerization.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16, Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Li, Dasgupta and Tsuno117 In more reducing conditions where the Si content becomes significant in the equilibrium Fe-rich alloy melts and where decreasing C dissolution as CO32− is offset to some extent by the increasing fraction of C–H complexes (Figure 2.7),  may be somewhat lower and may not monotonically increase with decreasing fO2 (Figure 2.8b).Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16, Reference Li, Dasgupta and Tsuno117 Application of empirical parameterizations of
may be somewhat lower and may not monotonically increase with decreasing fO2 (Figure 2.8b).Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16, Reference Li, Dasgupta and Tsuno117 Application of empirical parameterizations of  as a function of temperature, pressure, fO2, silicate melt composition, and alloy composition (e.g. Ni content) to conditions that many studies considered relevant for the deep terrestrial MO (e.g. pressure = 45–65 GPa, temperature = 3500–4000 K, log fO2 = IW – 2) yields values in the order of 103–104. The existing constraints on
as a function of temperature, pressure, fO2, silicate melt composition, and alloy composition (e.g. Ni content) to conditions that many studies considered relevant for the deep terrestrial MO (e.g. pressure = 45–65 GPa, temperature = 3500–4000 K, log fO2 = IW – 2) yields values in the order of 103–104. The existing constraints on  in graphite-saturated conditions therefore suggest that carbon is highly siderophile. If core formation was an equilibrium process (i.e. if the entire terrestrial core mass equilibrated with a global silicate MO), post-core formation silicate Earth would be severely depleted in carbon (≪10 ppm), with the extent of depletion being dependent upon the available bulk carbon that participates in such core–mantle fractionation.Reference Dasgupta8, Reference Tsuno, Grewal and Dasgupta17, Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Dasgupta, Chi, Shimizu, Buono and Walker99 This analysis does not imply that the core formation process was a single-stage alloy–silicate equilibration event, but rather what the C distribution between Earth’s metallic and nonmetallic portions would be for an average condition of core–mantle separation.
in graphite-saturated conditions therefore suggest that carbon is highly siderophile. If core formation was an equilibrium process (i.e. if the entire terrestrial core mass equilibrated with a global silicate MO), post-core formation silicate Earth would be severely depleted in carbon (≪10 ppm), with the extent of depletion being dependent upon the available bulk carbon that participates in such core–mantle fractionation.Reference Dasgupta8, Reference Tsuno, Grewal and Dasgupta17, Reference Chi, Dasgupta, Duncan and Shimizu71, Reference Dasgupta, Chi, Shimizu, Buono and Walker99 This analysis does not imply that the core formation process was a single-stage alloy–silicate equilibration event, but rather what the C distribution between Earth’s metallic and nonmetallic portions would be for an average condition of core–mantle separation.
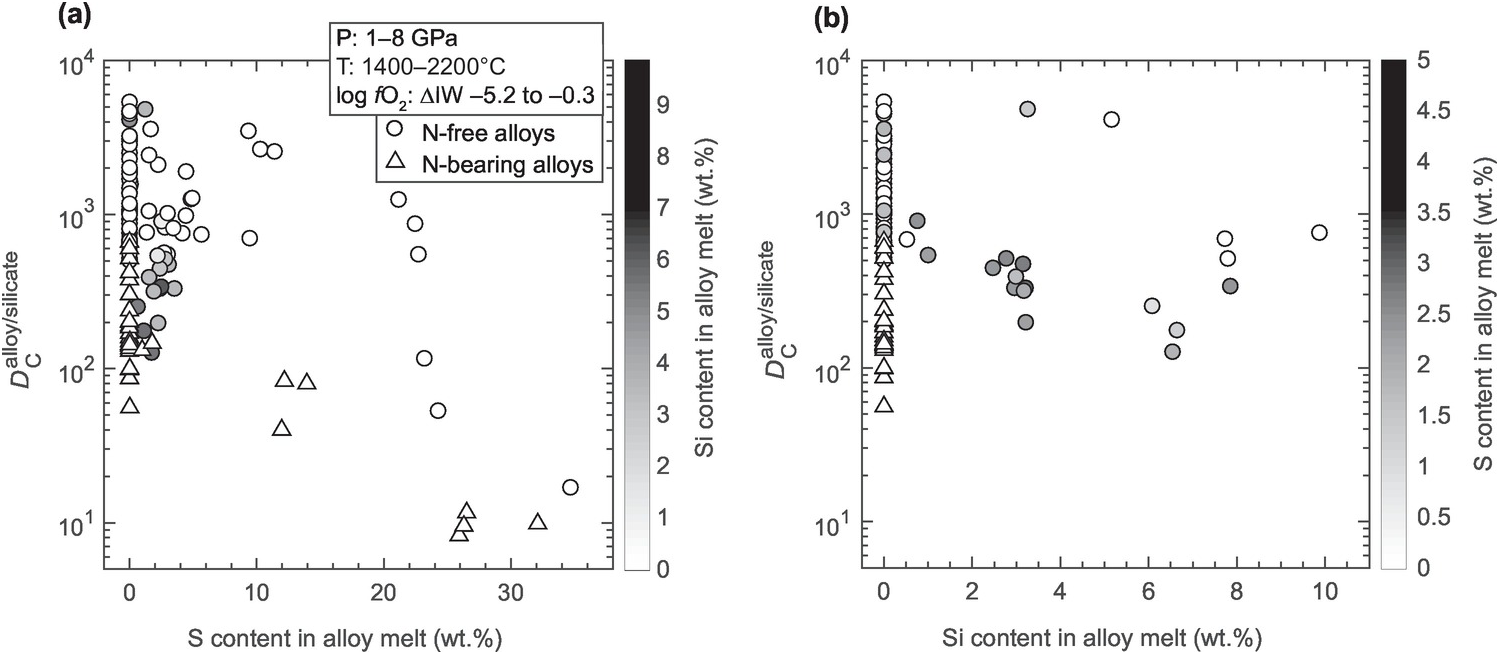
Figure 2.8 Experimental data showing the effects of S and Si in Fe-rich alloy melts on  . (a)
. (a)  decreases with increases in S content in the alloy melt. (b)
decreases with increases in S content in the alloy melt. (b)  decreases with increases in Si content in the alloy or indirect decreases in fO2 of the alloy–silicate systems. The presence of S in Si-bearing alloy melts generally decreases
decreases with increases in Si content in the alloy or indirect decreases in fO2 of the alloy–silicate systems. The presence of S in Si-bearing alloy melts generally decreases  in comparison to S-free systems.
in comparison to S-free systems.
Figure 2.9 shows more realistic scenarios of alloy–silicate equilibration and subsequent core segregation in terrestrial MO where the depth, temperature, and fO2 evolve with the extent of accretion.Reference Wade and Wood158 This style of core–mantle fractionation is described as multistage, equilibrium core formation. Competing arguments exist in the literature as to whether, with continuing accretion, proto-Earth’s MO evolved from a relatively reduced to an oxidized conditionReference Wade and Wood158, Reference Rubie159 or a relatively oxidized to a reducing condition.Reference Badro, Brodholt, Piet, Siebert and Ryerson160 Figure 2.9a therefore shows various plausible fO2 paths of MO evolution of a growing Earth and computes the change of  along those paths, following Li et al.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 It must be noted that the current data sets of
along those paths, following Li et al.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 It must be noted that the current data sets of  do not show any effects of pressure–temperature in relatively reducing conditions (e.g. log fO2 < IW – 1.5). In such reducing conditions, the controlling variables appear to be fO2, the Si content of the metal, and the water content of the silicate melt. At ~IW – 2 < log fO2 < IW, however, the key variables controlling
do not show any effects of pressure–temperature in relatively reducing conditions (e.g. log fO2 < IW – 1.5). In such reducing conditions, the controlling variables appear to be fO2, the Si content of the metal, and the water content of the silicate melt. At ~IW – 2 < log fO2 < IW, however, the key variables controlling  are pressure, temperature, fO2, and silicate melt composition. Figure 2.9b, however, shows that irrespective of MO condition,
are pressure, temperature, fO2, and silicate melt composition. Figure 2.9b, however, shows that irrespective of MO condition,  remains ≫1, and in fact deeper MO, toward the later stage of accretion, leads to even higher
remains ≫1, and in fact deeper MO, toward the later stage of accretion, leads to even higher  predictions than those experimentally measured at shallow MO conditions. Therefore, the multistage core formation model also leads to C being stripped off highly efficiently from the silicate MO, leaving behind the BSE that is <1–10 ppm for a bulk Earth with 1000 ppm C (Figure 2.9c).
predictions than those experimentally measured at shallow MO conditions. Therefore, the multistage core formation model also leads to C being stripped off highly efficiently from the silicate MO, leaving behind the BSE that is <1–10 ppm for a bulk Earth with 1000 ppm C (Figure 2.9c).
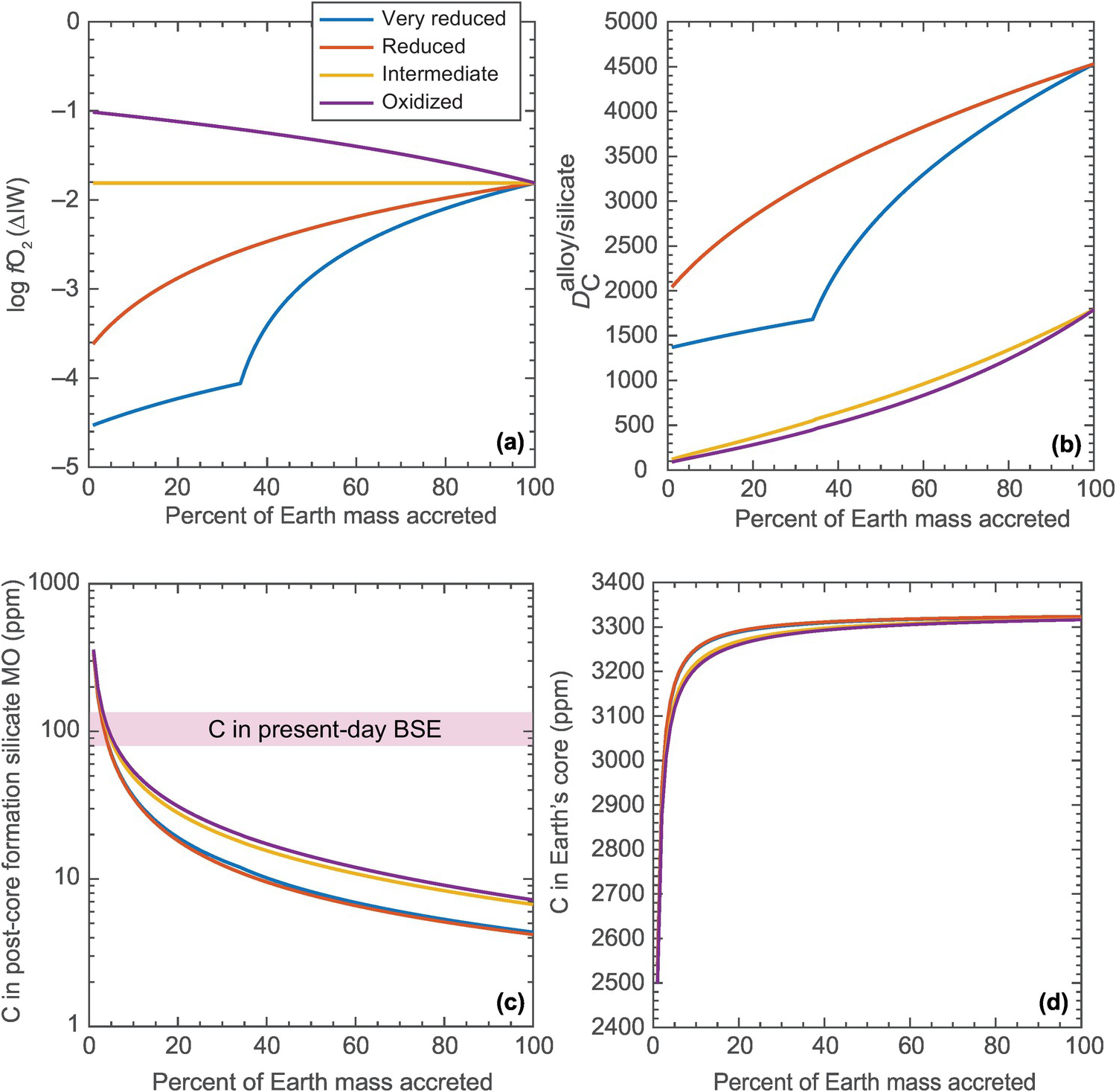
Figure 2.9 The effects of different accretion scenarios on the core–mantle partitioning behavior of carbon. (a) Four possible evolution paths for the FeO content of the mantle with its growth. The “very reduced” and “reduced” paths simulate the accretion of progressively oxidized material with time, and the “oxidized” path simulates accretion of progressively reduced material with time. All of the models converge at log fO2 of IW – 1.8, or present-day FeO content (8 wt.%) of the primitive upper mantle. (b)  at each step of accretion (i.e. accretion of 1% ME), calculated using parametrized relationships from Li et al.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 For the “very reduced” and “reduced” paths, where methyl (or alkyl) groups would be the predominant dissolved carbon species in the silicate melt, eq. (4) is chosen from Li et al.,Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 whereas for the “intermediate” and “oxidized” paths, where carbonate groups would be the predominant dissolved carbon species in the silicate melt, eq. (3) is chosen from Li et al.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 (c) Post-core formation MO resulting from a bulk system with 1000 ppm C and assuming 100% alloy–silicate equilibration at each accretional step. All of the models lead to MO with distinctly less C that those estimated for the BSE. (d) Carbon content in Earth’s core converges at ~3300 ppm at the end of all accretional models.
at each step of accretion (i.e. accretion of 1% ME), calculated using parametrized relationships from Li et al.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 For the “very reduced” and “reduced” paths, where methyl (or alkyl) groups would be the predominant dissolved carbon species in the silicate melt, eq. (4) is chosen from Li et al.,Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 whereas for the “intermediate” and “oxidized” paths, where carbonate groups would be the predominant dissolved carbon species in the silicate melt, eq. (3) is chosen from Li et al.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16 (c) Post-core formation MO resulting from a bulk system with 1000 ppm C and assuming 100% alloy–silicate equilibration at each accretional step. All of the models lead to MO with distinctly less C that those estimated for the BSE. (d) Carbon content in Earth’s core converges at ~3300 ppm at the end of all accretional models.
2.5.3 Comparison of  with Alloy–Silicate Melt Partitioning of Other LEVEs
with Alloy–Silicate Melt Partitioning of Other LEVEs
The preceding section argues that equilibrium core formation either via homogeneous or heterogeneous accretion results in a nonmetallic Earth that is too depleted in C compared to the present-day BSE. Explaining the origin of LEVEs in the BSE through equilibrium core formation is exacerbated when  is compared with the alloy–silicate partition coefficients of other LEVEs such as S, N, and H.
is compared with the alloy–silicate partition coefficients of other LEVEs such as S, N, and H.
The partition coefficient of sulfur between alloy and silicate melts,  , has been experimentally constrained in a number of studies,Reference Boujibar106, Reference Rose-Weston, Brenan, Fei, Secco and Frost140, Reference Suer, Siebert, Remusat, Menguy and Fiquet142 but only a few recent studies measured
, has been experimentally constrained in a number of studies,Reference Boujibar106, Reference Rose-Weston, Brenan, Fei, Secco and Frost140, Reference Suer, Siebert, Remusat, Menguy and Fiquet142 but only a few recent studies measured  and
and  simultaneously.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 These studies show that over the entire range of shallow MO conditions explored experimentally thus far,
simultaneously.Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 These studies show that over the entire range of shallow MO conditions explored experimentally thus far,  ≫
≫  , with
, with  /
/ varying between ~1000 and 20 as log fO2 varies from IW – 4.5 to IW – 0.5. Therefore, under any conditions of alloy–silicate equilibration, C is more siderophilic than S and equilibrium core formation leaves a subchondritic C/S ratio for the silicate MO.
varying between ~1000 and 20 as log fO2 varies from IW – 4.5 to IW – 0.5. Therefore, under any conditions of alloy–silicate equilibration, C is more siderophilic than S and equilibrium core formation leaves a subchondritic C/S ratio for the silicate MO.
Experiments also exist that constrained  .Reference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Roskosz, Bouhifd, Jephcoat, Marty and Mysen109, Reference Kadik127 Among these, the recent studies that constrain both
.Reference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Roskosz, Bouhifd, Jephcoat, Marty and Mysen109, Reference Kadik127 Among these, the recent studies that constrain both  and
and  from the same experimentsReference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Dalou, Hirschmann, von der Handt, Mosenfelder and Armstrong85 show that nitrogen is only mildly siderophile in relatively oxidizing conditions and possibly even lithophile in relatively reducing conditions (e.g. log fO2 < IW – 3). Therefore,
from the same experimentsReference Grewal, Dasgupta, Sun, Tsuno and Costin18, Reference Dalou, Hirschmann, von der Handt, Mosenfelder and Armstrong85 show that nitrogen is only mildly siderophile in relatively oxidizing conditions and possibly even lithophile in relatively reducing conditions (e.g. log fO2 < IW – 3). Therefore,  /
/ is ~6–120 at 1–7 GPa, 1400–1800°C, and fO2 of IW – 3.5 to IW – 0.5, and hence any models of equilibrium core formation would also produce a subchondritic C/N ratio for the post-core formation BSE.
is ~6–120 at 1–7 GPa, 1400–1800°C, and fO2 of IW – 3.5 to IW – 0.5, and hence any models of equilibrium core formation would also produce a subchondritic C/N ratio for the post-core formation BSE.
Alloy–silicate partitioning studies for H are limited, and two available studiesReference Clesi107, Reference Okuchi161 provide contrasting data. OkuchiReference Okuchi161 estimates the  value at a fixed pressure of 7.5 GPa and as a function of temperature, but does not provide any pressure effect. Based on the experiments of Okuchi,Reference Okuchi161 H is mildly siderophile. On the other hand, Clesi et al.Reference Clesi107 conducted experiments at 5, 10, and 20 GPa with C-rich alloy melts and measured
value at a fixed pressure of 7.5 GPa and as a function of temperature, but does not provide any pressure effect. Based on the experiments of Okuchi,Reference Okuchi161 H is mildly siderophile. On the other hand, Clesi et al.Reference Clesi107 conducted experiments at 5, 10, and 20 GPa with C-rich alloy melts and measured  of 0.04–0.77. Therefore, it remains unclear whether H is retained mostly in the core of differentiated planets or in the silicate fraction. Despite the discrepancy in the available experimental data on
of 0.04–0.77. Therefore, it remains unclear whether H is retained mostly in the core of differentiated planets or in the silicate fraction. Despite the discrepancy in the available experimental data on  , the BSE could attain a subchondritic C/H ratio via an equilibrium core formation process where much more C would be sequestered to the metallic core than H (Figure 2.4). However, if the
, the BSE could attain a subchondritic C/H ratio via an equilibrium core formation process where much more C would be sequestered to the metallic core than H (Figure 2.4). However, if the  data of Clesi et al.Reference Clesi107 are appropriate, then equilibrium core formation would lead to a BSE C/H ratio that is much lower than what is estimated for the present-day BSE.
data of Clesi et al.Reference Clesi107 are appropriate, then equilibrium core formation would lead to a BSE C/H ratio that is much lower than what is estimated for the present-day BSE.
2.6 C and Other LEVE Budgets of the BSE: A Memory of Multistage Accretion and Core Formation Process with Partial Equilibrium?
The discussion presented thus far suggests that no single process of volatile delivery such as via late accretion of any known class of meteorites or comets, through loss of an atmosphere overlying a MO,Reference Schlichting, Sari and Yalinewich23 being subjected to equilibrium core formation processes, or sulfide segregation to the coreReference Rubie112, Reference O’Neill162 can simultaneously explain carbon’s absolute as well as relative abundance compared to other LEVEs. This does not mean that these processes did not impact the volatile inventory of the BSE, and it is plausible that all of these processes acted in tandem. However, the nature of the fractionation of C with respect to H, N, and S for each of these processes is such that even if they acted together, not all of the attributes of the BSE volatile budget can be satisfied. This brings us to consider other styles of terrestrial accretion that may have been essential in establishing the LEVE budget of modern Earth.
2.6.1 Disequilibrium Core Formation
Models of protoplanetary disk dynamics, dust and planetesimal accretion, and planetary migration show that although the first 50% of proto-Earth mass growth was continuous, rapid, and completed within the first few million years of Solar System formation, the protracted growth of Earth spanning ~100 MyrReference Kleine163 involved few abrupt increases in the accreted mass via several giant impacts of Mars-sized or perhaps even larger bodies.Reference Rubie164 The final such impact is thought to be the Moon-forming giant impact.Reference Canup and Asphaug165, Reference Ćuk and Stewart166 A key aspect of accretion via these impacts is that proto-Earth collided with differentiated planetary embryos. Merger of proto-Earth with large differentiated bodies is thought to have taken place via near-disequilibrium merger of the core of the impactor with proto-Earth’s core owing to limited emulsification of the impactor’s core and the lack of complete mixing of the core with the entrained silicate melt.Reference Deguen, Olson and Cardin167, Reference Deguen, Landeau and Olson168 Therefore, core formation involving giant impacts may leave a silicate fraction with a very different LEVE budget than that predicted by equilibrium core formation models. One critical question is whether any differentiated, large impactor could bring LEVE attributes that would help proto-Earth to evolve to the present-day BSE. A full-parameter space involving not only the LEVEs but also other nonvolatile, highly siderophile, and moderately siderophile elements, major elements, and stable isotope anomalies, as well as various accretion and core formation model assumptions, is not yet explored. However, recent studiesReference Li, Dasgupta, Tsuno, Monteleone and Shimizu16–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 showed how having an S-rich or Si-rich Fe-alloy in the cores of planetary embryos allow attaining high C/N and C/S ratios in the mantles of such embryos. This would occur as the cores of these embryos reach the C solubility limit and expel graphite or diamond to the overlying silicate fraction (Figure 2.10).Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 Therefore, a merger of the silicate reservoirs of such embryos with the proto-silicate Earth reservoir could give rise to the BSE LEVE inventory. Using inverse Monte Carlo simulations, Grewal et al.Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 showed that if the merger of the impactor is in perfect disequilibrium, depending on the core size of the impactor and bulk S content, the impactor could be similar in size as Mars (~0.1 ME; Figure 2.10). It is also showed that the bulk C content of such an impactor would not need to be enriched in carbon and could have a bulk C concentration (~1000–5000 ppm C)Reference Tsuno, Grewal and Dasgupta17, Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 similar to those of E-chondrites. These model results are intriguing because these potentially circumvent the long-standing challenge of reconciling the volatile element isotope constraintsReference Sarafian, Nielsen, Marschall, McCubbin and Monteleone51, Reference Marty and Yokochi59 and constraints from the isotopic anomalies of lithophile and siderophile elementsReference Dauphas31, Reference Dauphas32 in the major building blocks of Earth. Some of these latest studies on the origins of terrestrial volatiles through late-stage accretion of a differentiated planetary embryo are also conceptually similar to models that call for the addition of a highly reduced rocky body to the growing Earth to potentially explain the superchondritic Sm/Nd and 142Nd/144Nd anomalies observed in Earth’s present mantle.Reference Wohlers and Wood169, Reference Wohlers and Wood170 The concept of bringing carbon and other LEVEs via accretion of the mantle of a differentiated embryo with little post-impact equilibration is also similar to the suggestion that Earth’s Nb/Ta may be explained by accretion of a differentiated asteroid with a reduced S-rich core that efficiently sequestered Nb.171 Grewal et al.Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 also posited that Earth’s volatile-delivering impactor may have been the Moon-forming giant impactor, given the geochemical similarity, including volatiles, between the BSE and the Moon. This is again broadly consistent with Wade and Wood,Reference Wade and Wood172 who demonstrated that near-disequilibrium accretion of a reduced planetary embryo of 0.1–0.2 ME could explain the isotopic constraints, FeO contents, and Nb/Ta and Hf/W ratios of the silicate Earth and Moon.
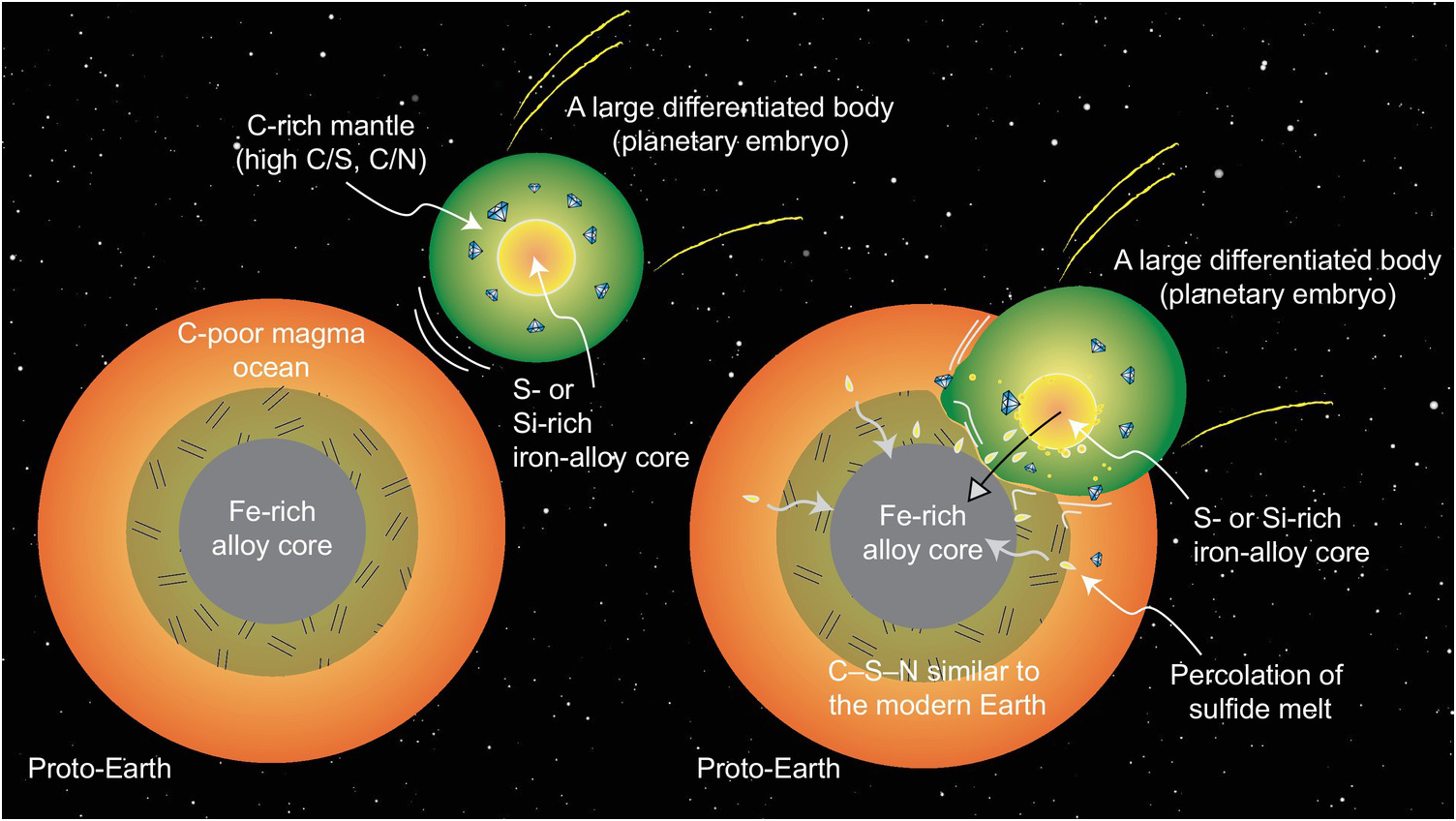
Figure 2.10 A schematic depiction of the late-stage accretion for a large rocky planet such as Earth where a large fraction of mass increase takes place via giant impacts of small planets and planetary embryos (0.1–0.2 ME).Reference Li, Dasgupta, Tsuno, Monteleone and Shimizu16–Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 This mode of accretion creates a unique possibility of establishing the LEVE inventory in the degassable portion of the rocky planets.
2.7 Carbon as a Light Element in the Core
One by-product of our discussion thus far is constraint on the concentration of C in the core. One of the main uncertainties in constraining the C budget of Earth’s core is the bulk C content in the growing Earth through time in the first ~100–120 Myr of the Solar System. It is not realistic to conceive that Earth’s building blocks and therefore the bulk C content did not change through the accretion history, but for simplicity here we assume a fixed C budget for the entire history of core formation or MO equilibration. If core formation was achieved by a single-stage equilibrium event at a deep MO, although not a physically realistic process, C content in the core as shown by DasguptaReference Dasgupta8 would be ~0.2 wt.% for a bulk Earth C content of ~730–1000 ppm. For a multistage core formation, with evolving depth–temperature–fO2 conditions of alloy–silicate equilibration, the core would finally contain ~0.34 wt.% C (Figure 2.9d). Finally, in the model where the C–N–S budget of the BSE is attained via late-stage merger of a large differentiated planetary embryo, the impactor’s S-rich core contributes ~100–700 ppm C to Earth’s core.Reference Tsuno, Grewal and Dasgupta17, Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 Therefore, depending on the volatile budget of the growing Earth leading to the giant impact, from a completely C-free proto-Earth to a proto-Earth with 1000 ppm bulk C, the final core C content would be between 700 ppm and 0.4 wt.%. The upper bound derived here is similar to the previous constraintReference Dasgupta and Walker14 placed using the mantle C abundance. Wood et al.Reference Wood, Li and Shahar60 also attempted to place constraint on the C content of Earth’s core based on the combined effects of C and S in the alloy on alloy–silicate partitioning of W and Mo, with the chief effect being W and Mo becoming more siderophile with increasing C in the alloy melt. By coupling S and C delivery in the final 13% of accretion, Wood et al.Reference Wood, Li and Shahar60 showed that in order to obtain the known Mo and W abundances of the mantle, the bulk C content of the core needs to be <1 wt.%. Badro et al.Reference Badro, Brodholt, Piet, Siebert and Ryerson160 also reached a similar conclusion that, in order to simultaneously satisfy the geochemical and geophysical constraints, Earth’s core composition cannot contain C as one of the major light elements. Therefore, all of the constraints thus far point to Earth’s core being the largest C reservoir, yet C being a minor light element in the core.
2.8 Conclusion
The origins of Earth’s LEVEs, including C, remain debated. Such debate stems in part from the uncertainty regarding the whole-Earth budget of C and other volatile elements and in part from the fate of these elements in putative planetary building blocks throughout their journey in the protoplanetary disk and planet formation process. While the abundance of each LEVE in the BSE is poorly constrained, the ratios of various LEVEs (along with their isotopic compositions) are more reliable geochemical indices to isolate key processes. Some of the key processes to consider are the accretion of undifferentiated chondritic meteorites, compound-specific condensation of the LEVEs, fractionation of the LEVEs during alloy–silicate differentiation, and MO–proto-atmosphere partitioning aided by redox-controlled solubility. Probing each of these processes in the light of the evolution of the LEVE ratios suggests that no single process or combination of processes can result in the currently estimated abundance of LEVEs in the BSE. However, a new paradigm is emerging where the late-stage growth of Earth via the impact and accretion of differentiated planetary embryos (0.1–0.2 ME) may not only explain the abundances of C–N–S, but also satisfy the broad geochemical similarity of Earth and the Moon. Despite the similarity in the arguments put forward by many recent studies that call for the accretion of one or more large planetary embryos with little post-impact equilibration of the impactor’s core with the terrestrial mantle/MO, differences remain in their details. For example, Grewal et al.Reference Grewal, Dasgupta, Sun, Tsuno and Costin18 proposed accretion of a relatively oxidized planet with an S-rich core, whereas Wade and WoodReference Wade and Wood172 called for accretion of a reduced planet with S-rich core. Future studies, therefore, will have to investigate how to reconcile these differences while fulfilling all of the geochemical constraints, both for non-volatile lithophile and siderophile elements and LEVEs. Nonetheless, it appears inevitable that a large planet like Earth’s LEVE budgets were shaped by its protracted growth history with episodes of planetesimals, planetary embryos, and planet accretion, whereas other smaller planets that grew quickly lacked some of these possible supply and modification mechanisms of key ingredients. Whatever the accretion mechanism may be, as long as mostly volatile-depleted materials accreted on Earth throughout its core formation history, C as well as N and H are going to be minor elements in the bulk core. As the search continues to find other rocky, habitable worlds beyond our Solar System, the origins of C–H–N–S on Earth provide a guiding framework.
2.9 Limits of Knowledge and Unknowns
The limits of knowledge on the origin of Earth’s C and other LEVEs derive from current unknowns about many fundamental questions regarding the formation and evolution of Earth and other rocky planets in the Solar System, as well as about the compositions and processes in Earth’s deep interior. The condensation temperature of C that dictates the formation of solid C-bearing compounds from gases is thought to be extremely low,Reference Krasnokutski173 leading to the idea that most C brought to the inner Solar System at the early stage of planet formation is largely lost from the building blocks. However, it remains unknown whether some of the refractory C-bearing phases such as graphite and carbide could have contributed to the C budget of Earth during its early growth stage.
Experimental data on alloy–silicate elemental partitioning for mixed-volatile systems, especially in conditions approaching the deep MO of Earth, are still lacking and are needed in order to refine some of the current ideas based on extrapolated values from relatively low pressure–temperature experiments. Similar experimental data are needed for volatile isotopic systems as well, which are even more restricted,Reference Li, Marty, Shcheka, Zimmermann and Keppler174, Reference Labidi175 and for many systems, such as C,Reference Satish-Kumar, So, Yoshino, Kato and Hiroi64 H, and S,Reference Labidi175 they are either nonexistent or do not extend to the pressure–temperature and compositional space directly relevant for MOs.
Acknowledgments
The authors thank many former and current members of Rice University’s experimental petrology team, including Han Chi, Yuan Li, Megan Duncan, Alexandra Holmes, Kyusei Tsuno, and James Eguchi, whose research results influenced the views expressed in this chapter. The authors thank Jonathan Tucker and coeditor Isabelle Daniel for useful reviews. This work was made possible by funding from NASA grants 80NSSC18K0828 and 80NSSC18K1314, the Deep Carbon Observatory, and a Packard Fellowship for Science and Engineering to RD.
Questions for the Classroom
1 How well do the chondritic meteorites (undifferentiated materials; i.e. mixtures or metals, sulfides, and silicates), derived from the main asteroid belt, represent the building blocks of Earth and other rocky planets and planetary embryos in the inner Solar System? In other words, should the plausible compositions of building blocks including their LEVE budgets remain restricted to the known classes of meteorites?
2 How could we improve our knowledge on the concentration of C, N, S, and H in the BSE? What other approaches can be used to determine the mantle inventory of LEVEs?
3 How can we improve our understanding of the relative contributions of giant impacts versus impacts of planetesimals on the acquisition of LEVEs for large, rocky planets?
4 What information from our knowledge on the origins of LEVEs on Earth can be applied to build a framework for exoplanetary chemical habitability?














