1. Introduction
This article aims to give a conceptual approach to unify various constructions of representations of certain Lie algebras and construct new representations of some Lie algebras using crossed homomorphisms, Lie–Rinehart algebras and Leibniz pairs.
1.1. Representations of Cartan-type Lie algebras
The representation theory of Lie algebras is of great importance due to its own overall completeness and applications in mathematics and mathematical physics. The Cartan-type Lie algebras, originally introduced and studied by Cartan, consist of four classes of infinite-dimensional simple Lie algebras of vector fields with formal power series coefficients: the Witt algebras, the divergence-free algebras, the Hamiltonian algebras and the contact algebras. The representation theory of Cartan-type Lie algebras was first studied by Rudakov [Reference Rudakov40, Reference Rudakov41]. He showed that irreducible continuous representations can be described explicitly as induced representations or quotients of induced representations. Later, Shen [Reference Shen42] studied graded modules of graded Lie algebras of Cartan type (
![]() $W^{+}_{n}, S^{+}_{n},$
and
$W^{+}_{n}, S^{+}_{n},$
and
![]() $H^{+}_{n}$
) with polynomial coefficients of positive characteristic. Larsson constructed a class of representations for the Witt algebras
$H^{+}_{n}$
) with polynomial coefficients of positive characteristic. Larsson constructed a class of representations for the Witt algebras
![]() $W_{n}$
with Laurent polynomial coefficients [Reference Larsson24]. More precisely, Shen’s modules, called mixed product, were constructed by certain monomorphism, while Larsson’s modules, named conformal fields, came from a physics background. We call the methods of constructing these modules Shen–Larsson functors. Many other authors have contributed to the theory along these approaches in the last few decades. In particular, irreducible modules with finite-dimensional weight spaces over the Virasoro algebra (universal central extension of the Lie algebra
$W_{n}$
with Laurent polynomial coefficients [Reference Larsson24]. More precisely, Shen’s modules, called mixed product, were constructed by certain monomorphism, while Larsson’s modules, named conformal fields, came from a physics background. We call the methods of constructing these modules Shen–Larsson functors. Many other authors have contributed to the theory along these approaches in the last few decades. In particular, irreducible modules with finite-dimensional weight spaces over the Virasoro algebra (universal central extension of the Lie algebra
![]() $W_{1}$
of vector fields on a circle) was classified by Mathieu in [Reference Mathieu33], while Billig and Futorny recently gave the classification of irreducible modules over the Witt algebras
$W_{1}$
of vector fields on a circle) was classified by Mathieu in [Reference Mathieu33], while Billig and Futorny recently gave the classification of irreducible modules over the Witt algebras
![]() $W_{n} \, \, (n\geq 2)$
with finite-dimensional weight spaces [Reference Billig and Futorny2]. Note that intrinsically there is a functor from the category of finite-dimensional irreducible representations of finite-dimensional simple Lie algebras to the category of representations of Cartan-type Lie algebras among these works. There should be some essential part that applies to all of those constructions (even more) of complicated modules over some classes of Lie algebras (not only Cartan-type Lie algebras) as a whole regardless of any specific feature exhibited in each particular case. From this point of view, it is no surprise that earlier results in this direction due to many authors are fragments of the general theory. We find a unifying conceptual approach generalising Shen–Larsson functors. This is one of the main purposes of the article.
$W_{n} \, \, (n\geq 2)$
with finite-dimensional weight spaces [Reference Billig and Futorny2]. Note that intrinsically there is a functor from the category of finite-dimensional irreducible representations of finite-dimensional simple Lie algebras to the category of representations of Cartan-type Lie algebras among these works. There should be some essential part that applies to all of those constructions (even more) of complicated modules over some classes of Lie algebras (not only Cartan-type Lie algebras) as a whole regardless of any specific feature exhibited in each particular case. From this point of view, it is no surprise that earlier results in this direction due to many authors are fragments of the general theory. We find a unifying conceptual approach generalising Shen–Larsson functors. This is one of the main purposes of the article.
1.2. Representations of Lie–Rinehart algebras and Leibniz pairs
Note that the abovementioned Cartan-type Lie algebras are either Lie–Rinehart algebras or Leibniz pairs.
Lie–Rinehart algebras, originally studied by Rinehart in [Reference Rinehart39] in 1963, arose from a wide variety of constructions in differential geometry and they have been introduced repeatedly into many areas under different terminologies; for example, Lie pseudoalgebras. Lie–Rinehart algebras are the underlying structures of Lie algebroids. See [Reference Mackenzie32] and references therein for more details. A Lie–Rinehart algebra is a quadruple
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
, where A is a commutative associative algebra,
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
, where A is a commutative associative algebra,
![]() $\mathcal {L}$
is an A-module,
$\mathcal {L}$
is an A-module,
![]() $[\cdot ,\cdot ]_{\mathcal {L}}$
is a Lie bracket on
$[\cdot ,\cdot ]_{\mathcal {L}}$
is a Lie bracket on
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\alpha :\mathcal {L}\to \mathsf {Der}_{\mathbb {K}}(A)$
is an A-module homomorphism with some compatibility conditions involving the Lie brackets. Lie–Rinehart algebras have been further investigated in many aspects [Reference Casas, Ladra and Pirashvili6, Reference Huebschmann19, Reference Huebschmann20, Reference Huebschmann21, Reference Mackenzie31, Reference Moerdijk and Mrčun34]. In particular, Rinehart constructed the universal enveloping algebra of a Lie–Rinehart algebra [Reference Rinehart39]. Huebschmann gave an alternative construction of the universal enveloping algebra
$\alpha :\mathcal {L}\to \mathsf {Der}_{\mathbb {K}}(A)$
is an A-module homomorphism with some compatibility conditions involving the Lie brackets. Lie–Rinehart algebras have been further investigated in many aspects [Reference Casas, Ladra and Pirashvili6, Reference Huebschmann19, Reference Huebschmann20, Reference Huebschmann21, Reference Mackenzie31, Reference Moerdijk and Mrčun34]. In particular, Rinehart constructed the universal enveloping algebra of a Lie–Rinehart algebra [Reference Rinehart39]. Huebschmann gave an alternative construction of the universal enveloping algebra
![]() $\mathcal {U}(A, \mathcal {L})$
of a Lie–Rinehart algebra
$\mathcal {U}(A, \mathcal {L})$
of a Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
via the smash product, namely,
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
via the smash product, namely,
![]() $ \mathcal {U}(A, \mathcal {L}) =(A\# U(\mathcal {L}))/J, $
where J is a certain two-sided ideal in
$ \mathcal {U}(A, \mathcal {L}) =(A\# U(\mathcal {L}))/J, $
where J is a certain two-sided ideal in
![]() $A\# U(\mathcal {L})$
, and showed that there is a one-to-one correspondence between representations of a Lie–Rinehart algebra and representations of its universal enveloping algebra [Reference Huebschmann19]. Representations of Lie–Rinehart algebras are deeply related to the theory of
$A\# U(\mathcal {L})$
, and showed that there is a one-to-one correspondence between representations of a Lie–Rinehart algebra and representations of its universal enveloping algebra [Reference Huebschmann19]. Representations of Lie–Rinehart algebras are deeply related to the theory of
![]() $\mathcal {D}$
-modules [Reference Penkov38], which are modules over the algebra
$\mathcal {D}$
-modules [Reference Penkov38], which are modules over the algebra
![]() $\mathcal {D}$
of linear differential operators on a manifold. Since the algebra
$\mathcal {D}$
of linear differential operators on a manifold. Since the algebra
![]() $\mathcal {D}$
is the universal enveloping algebra of the Lie–Rinehart algebra of vector fields, a
$\mathcal {D}$
is the universal enveloping algebra of the Lie–Rinehart algebra of vector fields, a
![]() $\mathcal {D}$
-module is the same as a module with a representation of the Lie–Rinehart algebra of vector fields. We introduce the notion of a weak representation of a Lie–Rinehart algebra. The adjoint action is naturally a weak representation of a Lie–Rinehart algebra on itself. There is a one-to-one correspondence between weak representations of a Lie–Rinehart algebra and representations of the smash product
$\mathcal {D}$
-module is the same as a module with a representation of the Lie–Rinehart algebra of vector fields. We introduce the notion of a weak representation of a Lie–Rinehart algebra. The adjoint action is naturally a weak representation of a Lie–Rinehart algebra on itself. There is a one-to-one correspondence between weak representations of a Lie–Rinehart algebra and representations of the smash product
![]() $A\# U(\mathcal {L})$
.
$A\# U(\mathcal {L})$
.
The notion of a Leibniz pair was originally introduced by Flato–Gerstenhaber–Voronov in [Reference Flato, Gerstenhaber and Voronov11], which consists of a
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $(\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}})$
and a
$(\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}})$
and a
![]() $\mathbb {K}$
-Lie algebra homomorphism
$\mathbb {K}$
-Lie algebra homomorphism
![]() $\beta :\mathcal {S}\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}(A)$
. In this article, we only consider the case that A is a commutative associative algebra. A Leibniz pair was also studied by Winter [Reference Winter47] and called a Lie algop. Leibniz pairs were further studied in [Reference Hoefel and Livernet18, Reference Kajiura and Stasheff22]. A Lie–Rinehart algebra
$\beta :\mathcal {S}\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}(A)$
. In this article, we only consider the case that A is a commutative associative algebra. A Leibniz pair was also studied by Winter [Reference Winter47] and called a Lie algop. Leibniz pairs were further studied in [Reference Hoefel and Livernet18, Reference Kajiura and Stasheff22]. A Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
naturally gives rise to a Leibniz pair by forgetting the A-module structure on
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
naturally gives rise to a Leibniz pair by forgetting the A-module structure on
![]() $\mathcal {L}$
. We introduce the notion of an admissible representation of a Leibniz pair. If
$\mathcal {L}$
. We introduce the notion of an admissible representation of a Leibniz pair. If
![]() $\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
denotes the category of weak representations of a Lie–Rinehart algebra
$\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
denotes the category of weak representations of a Lie–Rinehart algebra
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
denotes the category of admissible representations of a Leibniz pair
$\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
denotes the category of admissible representations of a Leibniz pair
![]() $\mathcal {S}$
, then we have the following category equivalence:
$\mathcal {S}$
, then we have the following category equivalence:
where the right-hand side
![]() $\mathcal {L}$
is considered as the underlying Leibniz pair of a Lie–Rinehart algebra. On the other hand, a Leibniz pair also gives rise to a Lie–Rinehart algebra
$\mathcal {L}$
is considered as the underlying Leibniz pair of a Lie–Rinehart algebra. On the other hand, a Leibniz pair also gives rise to a Lie–Rinehart algebra
![]() $\mathcal {S}\otimes _{\mathbb {K}} A$
, known as the action Lie–Rinehart algebra. We show that an admissible representation of a Leibniz pair can be naturally extended to a representation of the corresponding action Lie–Rinehart algebra. We have the following category equivalence:
$\mathcal {S}\otimes _{\mathbb {K}} A$
, known as the action Lie–Rinehart algebra. We show that an admissible representation of a Leibniz pair can be naturally extended to a representation of the corresponding action Lie–Rinehart algebra. We have the following category equivalence:
where
![]() $\mathsf {Rep}(\mathcal {S}\otimes _{\mathbb {K}} A)$
denotes the category of representations of the Lie–Rinehart algebra
$\mathsf {Rep}(\mathcal {S}\otimes _{\mathbb {K}} A)$
denotes the category of representations of the Lie–Rinehart algebra
![]() $\mathcal {S}\otimes _{\mathbb {K}} A$
. See Remark 3.34 for more details about this equivalence.
$\mathcal {S}\otimes _{\mathbb {K}} A$
. See Remark 3.34 for more details about this equivalence.
1.3. Crossed homomorphisms
The concept of a crossed homomorphism of Lie algebras was introduced in [Reference Lue30] in the study of nonabelian extensions of Lie algebras in 1966. A special class of crossed homomorphisms was recently called a differential operator of weight 1 in [Reference Guo and Keigher14, Reference Guo, Sit and Zhang15]. A flat connection
![]() $1$
-form of a trivial principle bundle is naturally a crossed homomorphism. To the best of our knowledge, this concept has not been investigated for many years, and we will use it in this article. More precisely, by using crossed homomorphisms, we show that the category of weak representations (respectively admissible representations) of Lie–Rinehart algebras (respectively Leibniz pairs) is a left module category over the monoidal category of representations of Lie algebras. In particular, we obtain bifunctors among categories of certain representations:
$1$
-form of a trivial principle bundle is naturally a crossed homomorphism. To the best of our knowledge, this concept has not been investigated for many years, and we will use it in this article. More precisely, by using crossed homomorphisms, we show that the category of weak representations (respectively admissible representations) of Lie–Rinehart algebras (respectively Leibniz pairs) is a left module category over the monoidal category of representations of Lie algebras. In particular, we obtain bifunctors among categories of certain representations:
which we call the actions of monoidal categories, generalising Shen–Larsson constructions of representations for Cartan-type Lie algebras. Our construction sheds light on some difficult classification problems in representation theory of Lie algebras.
We observe the importance of crossed homomorphisms in our above construction. To better understand crossed homomorphisms and our actions of monoidal categories, we also study deformations and cohomologies of crossed homomorphisms. The deformation of algebraic structures began with the seminal work of Gerstenhaber [Reference Gerstenhaber12, Reference Gerstenhaber13] for associative algebras, followed by its extension to Lie algebras by Nijenhuis and Richardson [Reference Nijenhuis and Richardson36]. A suitable deformation theory of an algebraic structure needs to follow a certain general principle: on one hand, for a given object with the algebraic structure, there should be a differential graded Lie algebra whose Maurer–Cartan elements characterise deformations of this object. On the other hand, there should be a suitable cohomology so that the infinitesimal of a formal deformation can be identified with a cohomology class. We successfully construct a differential graded Lie algebra such that crossed homomorphisms are characterised as Maurer–Cartan elements. The cohomology groups of crossed homomorphisms are also defined to control their linear deformations.
1.4. Outline of the article
In Section 2, we recall the concept of crossed homomorphisms between Lie algebras and show that there is a one-to-one correspondence between crossed homomorphisms and certain Lie algebra homomorphisms (Theorem 2.7). This fact is the key ingredient in our later construction of the left module category.
In Section 3, we introduce the new concepts: weak representations (respectively admissible representations) of Lie–Rinehart algebras (respectively Leibniz pairs). Using crossed homomorphisms, we show that the category of weak representations (respectively admissible representations) of Lie–Rinehart algebras (respectively Leibniz pairs) is a left module category over the monoidal category of representations of Lie algebras. In particular, the corresponding bifunctor
![]() $\mathcal {F}_{H}$
, which we call the action of monoidal categories, is established to give new representations of Lie–Rinehart algebras (respectively Leibniz pairs). See Theorems 3.26 and 3.36. This generalises and unifies various existing constructions of representations of many Lie algebras by using this new bifunctor.
$\mathcal {F}_{H}$
, which we call the action of monoidal categories, is established to give new representations of Lie–Rinehart algebras (respectively Leibniz pairs). See Theorems 3.26 and 3.36. This generalises and unifies various existing constructions of representations of many Lie algebras by using this new bifunctor.
In Section 4, to show the power of our action of monoidal categories
![]() $\mathcal {F}_{H}$
established in Section 3, we construct some examples of crossed homomorphisms in different situations using our action of monoidal categories to recover some known representations of various Lie algebras (see Subsections 4.1–4.3) and to obtain new representations of generalised Witt algebras and their Lie subalgebras (see Corollaries 4.13, 4.15, 4.16). Certainly, our action of monoidal categories will be used to other situations to give new simple representations of suitable Lie algebras.
$\mathcal {F}_{H}$
established in Section 3, we construct some examples of crossed homomorphisms in different situations using our action of monoidal categories to recover some known representations of various Lie algebras (see Subsections 4.1–4.3) and to obtain new representations of generalised Witt algebras and their Lie subalgebras (see Corollaries 4.13, 4.15, 4.16). Certainly, our action of monoidal categories will be used to other situations to give new simple representations of suitable Lie algebras.
In Section 5, we characterise crossed homomorphisms as Maurer–Cartan elements in a suitable differential graded Lie algebra and introduce the cohomology theory of crossed homomorphisms. We use the cohomology theory of crossed homomorphisms that we established to study linear deformations of crossed homomorphisms and to prove that the linear deformation
![]() ${H}_{t}:={H}+t d_{\rho _{H}} (-{H} x)$
is trivial for any Nijenhuis element x (Theorem 5.14).
${H}_{t}:={H}+t d_{\rho _{H}} (-{H} x)$
is trivial for any Nijenhuis element x (Theorem 5.14).
We conclude our article in Section 6 by asking three questions.
As usual, we denote by
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
![]() $\mathbb {Z}_{+}$
and
$\mathbb {Z}_{+}$
and
![]() $\mathbb {C}$
the sets of all integers, positive integers and complex numbers. All vector spaces are over an algebraically closed field
$\mathbb {C}$
the sets of all integers, positive integers and complex numbers. All vector spaces are over an algebraically closed field
![]() $\mathbb K$
of characteristic
$\mathbb K$
of characteristic
![]() $0$
.
$0$
.
2. Crossed homomorphisms between Lie algebras
Let
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
and
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
and
![]() $(\mathcal {\mathfrak h},[\cdot ,\cdot ]_{\mathfrak h})$
be Lie algebras. We will denote by
$(\mathcal {\mathfrak h},[\cdot ,\cdot ]_{\mathfrak h})$
be Lie algebras. We will denote by
![]() $\mathsf {Der}(\mathfrak g)$
and
$\mathsf {Der}(\mathfrak g)$
and
![]() $\mathsf {Der}(\mathfrak h)$
the Lie algebras of derivations on
$\mathsf {Der}(\mathfrak h)$
the Lie algebras of derivations on
![]() $\mathfrak g$
and
$\mathfrak g$
and
![]() $\mathfrak h$
, respectively. A Lie algebra homomorphism
$\mathfrak h$
, respectively. A Lie algebra homomorphism
![]() $\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
will be called an action of
$\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
will be called an action of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak h$
in the sequel.
$\mathfrak h$
in the sequel.
Definition 2.1 [Reference Lue30]
Let
![]() $\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
be an action of
$\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
be an action of
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
on
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
on
![]() $(\mathcal {\mathfrak h},[\cdot ,\cdot ]_{\mathfrak h})$
. A linear map
$(\mathcal {\mathfrak h},[\cdot ,\cdot ]_{\mathfrak h})$
. A linear map
![]() ${H}:\mathfrak g\to \mathfrak h$
is called a crossed homomorphism with respect to the action
${H}:\mathfrak g\to \mathfrak h$
is called a crossed homomorphism with respect to the action
![]() $\rho $
if
$\rho $
if
Remark 2.2. A crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak g$
with respect to the adjoint action is also called a differential operator of weight
$\mathfrak g$
with respect to the adjoint action is also called a differential operator of weight
![]() $1$
. See [Reference Guo and Keigher14, Reference Guo, Sit and Zhang15] for more details.
$1$
. See [Reference Guo and Keigher14, Reference Guo, Sit and Zhang15] for more details.
Example 2.3. Let P be a trivial G-principle bundle over a differential manifold M, where G is a Lie group. Let
![]() $\omega \in \Omega ^{1}(M,\mathfrak g)$
be a connection
$\omega \in \Omega ^{1}(M,\mathfrak g)$
be a connection
![]() $1$
-form, where
$1$
-form, where
![]() $\mathfrak g$
is the Lie algebra of G. Then
$\mathfrak g$
is the Lie algebra of G. Then
![]() $\omega $
is flat if and only if
$\omega $
is flat if and only if
 $d\omega +\frac {1}{2}[\omega ,\omega ]_{\mathfrak g}=0,$
which is equivalent to
$d\omega +\frac {1}{2}[\omega ,\omega ]_{\mathfrak g}=0,$
which is equivalent to
Therefore, a flat connection
![]() $1$
-form – that is,
$1$
-form – that is,
![]() $\omega \in \Omega ^{1}(M,\mathfrak g)=\mathsf {Hom}(\mathfrak X(M),\mathfrak g\otimes C^{\infty }(M))$
satisfying the above equality – is a crossed homomorphism from the Lie algebra of vector fields
$\omega \in \Omega ^{1}(M,\mathfrak g)=\mathsf {Hom}(\mathfrak X(M),\mathfrak g\otimes C^{\infty }(M))$
satisfying the above equality – is a crossed homomorphism from the Lie algebra of vector fields
![]() $\mathfrak X(M)$
to the Lie algebra
$\mathfrak X(M)$
to the Lie algebra
![]() $\mathfrak g\otimes C^{\infty }(M)$
with respect to the action
$\mathfrak g\otimes C^{\infty }(M)$
with respect to the action
![]() $\rho $
given by
$\rho $
given by
Example 2.4. If the action
![]() $\rho $
of
$\rho $
of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak h$
is zero, then any crossed homomorphism from
$\mathfrak h$
is zero, then any crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
is nothing but a Lie algebra homomorphism. If
$\mathfrak h$
is nothing but a Lie algebra homomorphism. If
![]() $\mathfrak h$
is commutative, then any crossed homomorphism from
$\mathfrak h$
is commutative, then any crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
is simply a derivation from
$\mathfrak h$
is simply a derivation from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the representation
$\mathfrak h$
with respect to the representation
![]() $(\mathfrak h;\rho )$
.
$(\mathfrak h;\rho )$
.
Definition 2.5. Let
![]() ${H}$
and
${H}$
and
![]() ${H}^{\prime }$
be crossed homomorphisms from
${H}^{\prime }$
be crossed homomorphisms from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
. A homomorphism from
$\rho $
. A homomorphism from
![]() ${H}^{\prime }$
to
${H}^{\prime }$
to
![]() ${H}$
consists of two Lie algebra homomorphisms
${H}$
consists of two Lie algebra homomorphisms
![]() $\phi _{\mathfrak g}:\mathfrak g\longrightarrow \mathfrak g$
and
$\phi _{\mathfrak g}:\mathfrak g\longrightarrow \mathfrak g$
and
![]() $\phi _{\mathfrak h}:\mathfrak h\longrightarrow \mathfrak h$
such that
$\phi _{\mathfrak h}:\mathfrak h\longrightarrow \mathfrak h$
such that
In particular, if
![]() $\phi _{\mathfrak g}$
and
$\phi _{\mathfrak g}$
and
![]() $\phi _{\mathfrak h}$
are invertible, then
$\phi _{\mathfrak h}$
are invertible, then
![]() $(\phi _{\mathfrak g},\phi _{\mathfrak h})$
is called an isomorphism from
$(\phi _{\mathfrak g},\phi _{\mathfrak h})$
is called an isomorphism from
![]() ${H}^{\prime }$
to
${H}^{\prime }$
to
![]() ${H}$
.
${H}$
.
The following result can be also found in [Reference Lue30].
Lemma 2.6. Let
![]() ${H}$
be a crossed homomorphism from
${H}$
be a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
. Define
$\rho $
. Define
![]() $\rho _{{H}}:\mathfrak g\longrightarrow \mathfrak {gl}(\mathfrak h)$
by
$\rho _{{H}}:\mathfrak g\longrightarrow \mathfrak {gl}(\mathfrak h)$
by
Then
![]() $\rho _{{H}}$
is also an action of
$\rho _{{H}}$
is also an action of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak h$
; that is,
$\mathfrak h$
; that is,
![]() $\rho _{{H}}:\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
is a Lie algebra homomorphism.
$\rho _{{H}}:\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
is a Lie algebra homomorphism.
We use
![]() $\mathfrak g\ltimes _{\rho _{{H}}}\mathfrak h $
and
$\mathfrak g\ltimes _{\rho _{{H}}}\mathfrak h $
and
![]() $\mathfrak g\ltimes _{\rho }\mathfrak h$
to denote the two semidirect products of
$\mathfrak g\ltimes _{\rho }\mathfrak h$
to denote the two semidirect products of
![]() $\mathfrak g$
and
$\mathfrak g$
and
![]() $\mathfrak h$
with respect to the actions
$\mathfrak h$
with respect to the actions
![]() $\rho _{H}$
and
$\rho _{H}$
and
![]() $\rho $
, respectively. More precisely, we have
$\rho $
, respectively. More precisely, we have
 $$ \begin{align*} ~[(x,u),(y,v)]_{\rho_{H}}&=[x,y]_{\mathfrak g}+\rho_{H}(x)v-\rho_{H}(y)u+[u,v]_{\mathfrak h},\\ ~[(x,u),(y,v)]_{\rho}&=[x,y]_{\mathfrak g}+\rho(x)v-\rho(y)u+[u,v]_{\mathfrak h}. \end{align*} $$
$$ \begin{align*} ~[(x,u),(y,v)]_{\rho_{H}}&=[x,y]_{\mathfrak g}+\rho_{H}(x)v-\rho_{H}(y)u+[u,v]_{\mathfrak h},\\ ~[(x,u),(y,v)]_{\rho}&=[x,y]_{\mathfrak g}+\rho(x)v-\rho(y)u+[u,v]_{\mathfrak h}. \end{align*} $$
Theorem 2.7. Let
![]() ${H}:\mathfrak g\to \mathfrak h$
be a linear map and
${H}:\mathfrak g\to \mathfrak h$
be a linear map and
![]() $\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
an action of
$\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
an action of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak h$
.
$\mathfrak h$
.
-
(a) Suppose that
 $\rho _{H}$
given by (4) is an action of
$\rho _{H}$
given by (4) is an action of
 $\mathfrak g$
on
$\mathfrak g$
on
 $\mathfrak h$
. Then the linear map
$\mathfrak h$
. Then the linear map
 $\hat {{H}}:\mathfrak g\ltimes _{\rho _{{H}}}\mathfrak h\longrightarrow \mathfrak g\ltimes _{\rho }\mathfrak h$
defined by (5)is a Lie algebra isomorphism if and only if H is a crossed homomorphism from
$\hat {{H}}:\mathfrak g\ltimes _{\rho _{{H}}}\mathfrak h\longrightarrow \mathfrak g\ltimes _{\rho }\mathfrak h$
defined by (5)is a Lie algebra isomorphism if and only if H is a crossed homomorphism from $$ \begin{align} \hat{{H}}(x,u):=\big(x,{H} x+u\big),\;\;\forall x\in \mathfrak g,u\in\mathfrak h, \end{align} $$
$$ \begin{align} \hat{{H}}(x,u):=\big(x,{H} x+u\big),\;\;\forall x\in \mathfrak g,u\in\mathfrak h, \end{align} $$
 $\mathfrak g$
to
$\mathfrak g$
to
 $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
 $\rho $
.
$\rho $
.
-
(b) H is a crossed homomorphism from
 $\mathfrak g$
to
$\mathfrak g$
to
 $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
 $\rho $
if and only if the map
$\rho $
if and only if the map
 $\iota _{H}:\mathfrak g\longrightarrow \mathfrak g\ltimes _{\rho }\mathfrak h$
defined by (6)is a Lie algebra homomorphism.
$\iota _{H}:\mathfrak g\longrightarrow \mathfrak g\ltimes _{\rho }\mathfrak h$
defined by (6)is a Lie algebra homomorphism. $$ \begin{align} \iota_{H}(x):=\big(x,{H} x\big),\;\;\forall x\in \mathfrak g \end{align} $$
$$ \begin{align} \iota_{H}(x):=\big(x,{H} x\big),\;\;\forall x\in \mathfrak g \end{align} $$
Proof. (a). Clearly,
![]() $\hat {{H}}$
is an invertible linear map. For all
$\hat {{H}}$
is an invertible linear map. For all
![]() $x,y\in \mathfrak g,u,v\in \mathfrak h$
, we have
$x,y\in \mathfrak g,u,v\in \mathfrak h$
, we have
 $$ \begin{align*} [\hat{{H}}(x,u),\hat{{H}}(y,v)]_{\rho}&=[(x,{H} x+u),(y,{H} y+v)]_{\rho}\\ &=([x,y]_{\mathfrak g},\rho(x)({H} y+v)-\rho(y)({H} x+u)+[{H} x+u,{H} y+v]_{\mathfrak h})\\ &=\big([x,y]_{\mathfrak g},\rho(x)v-\rho(y)u+[{H} x,v]_{\mathfrak h}-[{H} y,u]_{\mathfrak h}+[u,v]_{\mathfrak h}+[{H}x,Hy]_{\mathfrak g}\\ &\quad +\rho(x)({H} y)-\rho(y)({H} x)\big),\\ \hat{{H}}[(x,u),(y,v)]_{\rho_{{H}}}&=([x,y]_{\mathfrak g},{H}[x,y]_{\mathfrak g}+\rho_{H}(x)v-\rho_{H}(y)u +[u,v]_{\mathfrak h})\\ &=([x,y]_{\mathfrak g},{H}[x,y]_{\mathfrak g}+\rho(x)v-\rho(y)u+[{H} x,v]_{\mathfrak h}-[{H} y,u]_{\mathfrak h}+[u,v]_{\mathfrak h}). \end{align*} $$
$$ \begin{align*} [\hat{{H}}(x,u),\hat{{H}}(y,v)]_{\rho}&=[(x,{H} x+u),(y,{H} y+v)]_{\rho}\\ &=([x,y]_{\mathfrak g},\rho(x)({H} y+v)-\rho(y)({H} x+u)+[{H} x+u,{H} y+v]_{\mathfrak h})\\ &=\big([x,y]_{\mathfrak g},\rho(x)v-\rho(y)u+[{H} x,v]_{\mathfrak h}-[{H} y,u]_{\mathfrak h}+[u,v]_{\mathfrak h}+[{H}x,Hy]_{\mathfrak g}\\ &\quad +\rho(x)({H} y)-\rho(y)({H} x)\big),\\ \hat{{H}}[(x,u),(y,v)]_{\rho_{{H}}}&=([x,y]_{\mathfrak g},{H}[x,y]_{\mathfrak g}+\rho_{H}(x)v-\rho_{H}(y)u +[u,v]_{\mathfrak h})\\ &=([x,y]_{\mathfrak g},{H}[x,y]_{\mathfrak g}+\rho(x)v-\rho(y)u+[{H} x,v]_{\mathfrak h}-[{H} y,u]_{\mathfrak h}+[u,v]_{\mathfrak h}). \end{align*} $$
Thus,
 $[\hat {{H}}(x,u),\hat {{H}}(y,v)]_{\rho }=\hat {{H}}[(x,u),(y,v)]_{\rho _{{H}}}$
, if and only if (1) holds for H, which is equivalent to that H is a crossed homomorphism from
$[\hat {{H}}(x,u),\hat {{H}}(y,v)]_{\rho }=\hat {{H}}[(x,u),(y,v)]_{\rho _{{H}}}$
, if and only if (1) holds for H, which is equivalent to that H is a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
.
$\rho $
.
(b) follows from the proof of (a) by taking
![]() $u=v=0$
.
$u=v=0$
.
Remark 2.8. In fact, crossed homomorphisms correspond to split nonabelian extensions of Lie algebras. More precisely, we consider the following nonabelian extension of Lie algebras:
A section
![]() $s:\mathfrak g\,\rightarrow \, \mathfrak g\oplus \mathfrak h$
must be of the form
$s:\mathfrak g\,\rightarrow \, \mathfrak g\oplus \mathfrak h$
must be of the form
![]() $s(x)=(x,Hx), ~x\in \mathfrak g$
. Statement (b) says that s is a Lie algebra homomorphism if and only if H is a crossed homomorphism. Such an extension is called a split nonabelian extension. See [Reference Lue30] for more details.
$s(x)=(x,Hx), ~x\in \mathfrak g$
. Statement (b) says that s is a Lie algebra homomorphism if and only if H is a crossed homomorphism. Such an extension is called a split nonabelian extension. See [Reference Lue30] for more details.
3. Action of monoidal categories arising from Lie–Rinehart algebras and Leibniz pairs
In this section, first we introduce the notion of a weak representation of a Lie–Rinehart algebra and show that the category of weak representations of Lie–Rinehart algebras is a left module category over the monoidal category of representations of Lie algebras by using crossed homomorphisms. Then we introduce the notion of an admissible representation of a Leibniz pair and obtain similar results. In particular, the corresponding bifunctors are called the actions of monoidal categories for Lie–Rinehart algebras and Leibniz pairs.
3.1. Weak representations of Lie–Rinehart algebras
Let
![]() ${A}$
be a commutative associative algebra over
${A}$
be a commutative associative algebra over
![]() $\mathbb {K}$
. We denote by
$\mathbb {K}$
. We denote by
![]() $\mathsf {Der}_{\mathbb {K}}({A})$
the set of
$\mathsf {Der}_{\mathbb {K}}({A})$
the set of
![]() $\mathbb {K}$
-linear derivations of
$\mathbb {K}$
-linear derivations of
![]() ${A}$
; that is,
${A}$
; that is,
Definition 3.1 [Reference Rinehart39]
A Lie–Rinehart algebra over
![]() ${A}$
is a
${A}$
is a
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $(\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}})$
together with an
$(\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}})$
together with an
![]() ${A}$
-module structure on
${A}$
-module structure on
![]() $\mathcal {L}$
and a map
$\mathcal {L}$
and a map
![]() $\alpha :\mathcal {L}\to \mathsf {Der}_{\mathbb {K}}({A})$
(called the anchor) which is simultaneously a
$\alpha :\mathcal {L}\to \mathsf {Der}_{\mathbb {K}}({A})$
(called the anchor) which is simultaneously a
![]() $\mathbb {K}$
-Lie algebra and an
$\mathbb {K}$
-Lie algebra and an
![]() ${A}$
-module homomorphism such that
${A}$
-module homomorphism such that
We usually denote a Lie–Rinehart algebra over
![]() ${A}$
by
${A}$
by
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
or simply by
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
or simply by
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Remark 3.2. It is clear that a Lie–Rinehart algebra with
![]() $\alpha =0$
is exactly a Lie
$\alpha =0$
is exactly a Lie
![]() ${A}$
-algebra.
${A}$
-algebra.
Example 3.3.
![]() $({A},\mathsf {Der}_{\mathbb {K}}({A}),[\cdot ,\cdot ]_{C},\alpha =\textrm {Id})$
is a Lie–Rinehart algebra, where
$({A},\mathsf {Der}_{\mathbb {K}}({A}),[\cdot ,\cdot ]_{C},\alpha =\textrm {Id})$
is a Lie–Rinehart algebra, where
![]() $ [\cdot ,\cdot ]_{C}$
is the commutator bracket.
$ [\cdot ,\cdot ]_{C}$
is the commutator bracket.
Example 3.4. Let
![]() ${M}$
be an
${M}$
be an
![]() ${A}$
-module. Denote by
${A}$
-module. Denote by
![]() $\mathfrak {gl}_{A}({M})$
the set of
$\mathfrak {gl}_{A}({M})$
the set of
![]() ${A}$
-module homomorphisms from
${A}$
-module homomorphisms from
![]() ${M}$
to
${M}$
to
![]() ${M}$
. It is obvious that
${M}$
. It is obvious that
![]() $(\mathfrak {gl}_{A}({M}),[\cdot ,\cdot ]_{C})$
is a Lie
$(\mathfrak {gl}_{A}({M}),[\cdot ,\cdot ]_{C})$
is a Lie
![]() ${A}$
-algebra.
${A}$
-algebra.
Example 3.5. Let
![]() ${M}$
be an
${M}$
be an
![]() ${A}$
-module. A first-order differential operator on
${A}$
-module. A first-order differential operator on
![]() ${M}$
is a pair
${M}$
is a pair
![]() $(D,\sigma )$
, where
$(D,\sigma )$
, where
![]() $D:{M}\,\rightarrow \,{M}$
is a
$D:{M}\,\rightarrow \,{M}$
is a
![]() $\mathbb {K}$
-linear map and
$\mathbb {K}$
-linear map and
![]() $\sigma =\sigma _{D}\in \mathsf {Der}_{\mathbb {K}}({A})$
, satisfying the following compatibility condition:
$\sigma =\sigma _{D}\in \mathsf {Der}_{\mathbb {K}}({A})$
, satisfying the following compatibility condition:
Denote by
![]() $\mathfrak {D}({M})$
the set of first-order differential operators on
$\mathfrak {D}({M})$
the set of first-order differential operators on
![]() ${M}$
. It is obvious that
${M}$
. It is obvious that
![]() $\mathfrak {D}({M})$
is an
$\mathfrak {D}({M})$
is an
![]() ${A}$
-module. Define a bracket operation
${A}$
-module. Define a bracket operation
![]() $[\cdot ,\cdot ]_{C}$
on
$[\cdot ,\cdot ]_{C}$
on
![]() $\mathfrak {D}({M})$
by
$\mathfrak {D}({M})$
by
and an
![]() ${A}$
-module homomorphism
${A}$
-module homomorphism
![]() $\mathrm {Pr}:\mathfrak {D}({M})\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}({A})$
by
$\mathrm {Pr}:\mathfrak {D}({M})\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}({A})$
by
![]() $\mathrm {Pr}(D,\sigma )=\sigma $
for all
$\mathrm {Pr}(D,\sigma )=\sigma $
for all
![]() $(D,\sigma )\in \mathfrak {D}({M})$
. Then
$(D,\sigma )\in \mathfrak {D}({M})$
. Then
![]() $({A},\mathfrak {D}({M}),[\cdot ,\cdot ]_{C},\alpha =\mathrm {Pr})$
is a Lie–Rinehart algebra.
$({A},\mathfrak {D}({M}),[\cdot ,\cdot ]_{C},\alpha =\mathrm {Pr})$
is a Lie–Rinehart algebra.
Remark 3.6. Let
![]() ${M}$
be an
${M}$
be an
![]() ${A}$
-module. It is straightforward to see that we have a semidirect product commutative associative algebra
${A}$
-module. It is straightforward to see that we have a semidirect product commutative associative algebra
![]() $A\ltimes M$
, where the multiplication is given by
$A\ltimes M$
, where the multiplication is given by
Then
![]() $(D,\sigma )$
is a first-order differential operator on M if and only if
$(D,\sigma )$
is a first-order differential operator on M if and only if
![]() $(\sigma ,D)$
is a derivation on the commutative associative algebra
$(\sigma ,D)$
is a derivation on the commutative associative algebra
![]() $A\ltimes M$
. This result is the algebraic counterpart of the fact that a first-order differential operator on a vector bundle E can be viewed as a linear vector field on the dual bundle
$A\ltimes M$
. This result is the algebraic counterpart of the fact that a first-order differential operator on a vector bundle E can be viewed as a linear vector field on the dual bundle
![]() $E^{*}$
. In fact, functions on the vector bundle
$E^{*}$
. In fact, functions on the vector bundle
![]() $E^{*}\to N$
are generated by
$E^{*}\to N$
are generated by
![]() $C^{\infty }(N)$
and
$C^{\infty }(N)$
and
![]() $\Gamma (E)$
, while the latter are fibre linear functions on
$\Gamma (E)$
, while the latter are fibre linear functions on
![]() $E^{*}$
. Since a first-order differential operator maps a fibre linear function to a fibre linear function, it is viewed as a linear vector field on
$E^{*}$
. Since a first-order differential operator maps a fibre linear function to a fibre linear function, it is viewed as a linear vector field on
![]() $E^{*}.$
$E^{*}.$
Definition 3.7.
-
(i) Let
 $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
and
 $({A},\mathcal {L}^{\prime },[\cdot ,\cdot ]_{\mathcal {L}^{\prime }},\alpha ^{\prime })$
be Lie–Rinehart algebras. A Lie–Rinehart weak homomorphism is a
$({A},\mathcal {L}^{\prime },[\cdot ,\cdot ]_{\mathcal {L}^{\prime }},\alpha ^{\prime })$
be Lie–Rinehart algebras. A Lie–Rinehart weak homomorphism is a
 $\mathbb {K}$
-Lie algebra homomorphism
$\mathbb {K}$
-Lie algebra homomorphism
 $f:\mathcal {L} \to \mathcal {L}^{\prime }$
such that
$f:\mathcal {L} \to \mathcal {L}^{\prime }$
such that
 $\alpha ^{\prime }\circ f=\alpha $
.
$\alpha ^{\prime }\circ f=\alpha $
. -
(ii) A Lie–Rinehart weak homomorphism f is called a Lie–Rinehart homomorphism if f is also an
 ${A}$
-module homomorphism; that is,
${A}$
-module homomorphism; that is,
 $f(ax)=af(x)$
, for all
$f(ax)=af(x)$
, for all
 $a\in {A}$
and
$a\in {A}$
and
 $x\in \mathcal {L}.$
$x\in \mathcal {L}.$
Note that zero map from
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathcal {L}^{\prime }$
is not a Lie–Rinehart weak homomorphism if
$\mathcal {L}^{\prime }$
is not a Lie–Rinehart weak homomorphism if
![]() $\alpha \ne 0$
.
$\alpha \ne 0$
.
Proposition 3.8. Let
![]() $f_{1}:({A},\mathcal {L}_{1},[\cdot ,\cdot ]_{\mathcal {L}_{1}},\alpha _{1})\,\rightarrow \,({A},\mathcal {L}_{2},[\cdot ,\cdot ]_{\mathcal {L}_{2}},\alpha _{2})$
and
$f_{1}:({A},\mathcal {L}_{1},[\cdot ,\cdot ]_{\mathcal {L}_{1}},\alpha _{1})\,\rightarrow \,({A},\mathcal {L}_{2},[\cdot ,\cdot ]_{\mathcal {L}_{2}},\alpha _{2})$
and
![]() $f_{2}:({A},\mathcal {L}_{2},[\cdot ,\cdot ]_{\mathcal {L}_{2}},\alpha _{2}) \rightarrow \,({A},\mathcal {L}_{3},[\cdot ,\cdot ]_{\mathcal {L}_{3}},\alpha _{3})$
be two Lie–Rinehart weak homomorphisms. Then
$f_{2}:({A},\mathcal {L}_{2},[\cdot ,\cdot ]_{\mathcal {L}_{2}},\alpha _{2}) \rightarrow \,({A},\mathcal {L}_{3},[\cdot ,\cdot ]_{\mathcal {L}_{3}},\alpha _{3})$
be two Lie–Rinehart weak homomorphisms. Then
![]() $f_{2}\circ f_{1}$
is a Lie–Rinehart weak homomorphism from
$f_{2}\circ f_{1}$
is a Lie–Rinehart weak homomorphism from
![]() $({A},\mathcal {L}_{1},[\cdot ,\cdot ]_{\mathcal {L}_{1}},\alpha _{1})$
to
$({A},\mathcal {L}_{1},[\cdot ,\cdot ]_{\mathcal {L}_{1}},\alpha _{1})$
to
![]() $({A},\mathcal {L}_{3},[\cdot ,\cdot ]_{\mathcal {L}_{3}},\alpha _{3})$
.
$({A},\mathcal {L}_{3},[\cdot ,\cdot ]_{\mathcal {L}_{3}},\alpha _{3})$
.
Proof. This is easy to see.
We denote by
![]() $\mathrm {WH}(\mathcal {L},\mathcal {L}^{\prime })$
the set of weak homomorphisms from the Lie–Rinehart algebra
$\mathrm {WH}(\mathcal {L},\mathcal {L}^{\prime })$
the set of weak homomorphisms from the Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
to
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
to
![]() $({A},\mathcal {L}^{\prime },[\cdot ,\cdot ]_{\mathcal {L}^{\prime }},\alpha ^{\prime })$
. By Proposition 3.8, it is easy to see that
$({A},\mathcal {L}^{\prime },[\cdot ,\cdot ]_{\mathcal {L}^{\prime }},\alpha ^{\prime })$
. By Proposition 3.8, it is easy to see that
![]() $\mathrm {WH}(\mathcal {L},\mathcal {L})$
is a monoid.
$\mathrm {WH}(\mathcal {L},\mathcal {L})$
is a monoid.
Definition 3.9.
-
(i) A weak representation of a Lie–Rinehart algebra
 $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
on an
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
on an
 ${A}$
-module
${A}$
-module
 ${M}$
is a Lie–Rinehart weak homomorphism
${M}$
is a Lie–Rinehart weak homomorphism
 $\rho :\mathcal {L}\,\rightarrow \,\mathfrak {D}({M})$
. We denote a weak representation by
$\rho :\mathcal {L}\,\rightarrow \,\mathfrak {D}({M})$
. We denote a weak representation by
 $({M};\rho )$
.
$({M};\rho )$
. -
(ii) A weak representation
 $({M};\rho )$
is called a representation if
$({M};\rho )$
is called a representation if
 $\rho $
is also an
$\rho $
is also an
 ${A}$
-module homomorphism; that is,
${A}$
-module homomorphism; that is,
 $\rho :\mathcal {L}\,\rightarrow \,\mathfrak {D}({M})$
is a Lie–Rinehart homomorphism.
$\rho :\mathcal {L}\,\rightarrow \,\mathfrak {D}({M})$
is a Lie–Rinehart homomorphism.
Remark 3.10. A weak representation of a Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
on an
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
on an
![]() ${A}$
-module
${A}$
-module
![]() ${M}$
means a
${M}$
means a
![]() $\mathbb {K}$
-Lie algebra homomorphism
$\mathbb {K}$
-Lie algebra homomorphism
![]() $\rho :\mathcal {L}\,\rightarrow \,\mathfrak {gl}_{\mathbb {K}}({M})$
such that
$\rho :\mathcal {L}\,\rightarrow \,\mathfrak {gl}_{\mathbb {K}}({M})$
such that
that is,
![]() $(D=\rho (x),\sigma =\alpha (x))$
is a first-order differential operator on
$(D=\rho (x),\sigma =\alpha (x))$
is a first-order differential operator on
![]() ${M}$
.
${M}$
.
Remark 3.11. In [Reference Huebschmann19], Huebschmann showed that there is a one-to-one correspondence between representations of a Lie–Rinehart algebra and representations of its universal enveloping algebra
![]() $\mathcal {U}(A, \mathcal {L}) :=(A\# U(\mathcal {L}))/J$
, where J is a certain ideal of the smash product
$\mathcal {U}(A, \mathcal {L}) :=(A\# U(\mathcal {L}))/J$
, where J is a certain ideal of the smash product
![]() $A\# U(\mathcal {L})$
. More explicitly, it is known that
$A\# U(\mathcal {L})$
. More explicitly, it is known that
![]() $U(\mathcal {L})$
is a Hopf algebra and A is a
$U(\mathcal {L})$
is a Hopf algebra and A is a
![]() $U(\mathcal {L})$
-module algebra. Then the smash product
$U(\mathcal {L})$
-module algebra. Then the smash product
![]() $A\# U(\mathcal {L})$
(see [Reference Montgomery35]) is a
$A\# U(\mathcal {L})$
(see [Reference Montgomery35]) is a
![]() $\mathbb {K}$
-vector space
$\mathbb {K}$
-vector space
![]() $A\otimes U(\mathcal {L})$
with elements denoted by
$A\otimes U(\mathcal {L})$
with elements denoted by
![]() $a\#u$
and with product defined for all
$a\#u$
and with product defined for all
![]() $a,b\in A$
and
$a,b\in A$
and
![]() $u,v\in U(\mathcal {L})$
by
$u,v\in U(\mathcal {L})$
by
 $$ \begin{align*} (a\#u)(b\# v)=\sum a\alpha(u_{(1)})b\# u_{(2)}v, \end{align*} $$
$$ \begin{align*} (a\#u)(b\# v)=\sum a\alpha(u_{(1)})b\# u_{(2)}v, \end{align*} $$
where we use the standard Sweedler notation
![]() $\Delta (u)=\sum u_{(1)}\otimes u_{(2)}$
for the coproduct
$\Delta (u)=\sum u_{(1)}\otimes u_{(2)}$
for the coproduct
![]() $\Delta $
. The algebra
$\Delta $
. The algebra
![]() $A\# U(\mathcal {L})$
is also called the Massey–Peterson algebra in [Reference Huebschmann19]. It is not hard to see that there is a one-to-one correspondence between weak representations of a Lie–Rinehart algebra and representations of the smash product
$A\# U(\mathcal {L})$
is also called the Massey–Peterson algebra in [Reference Huebschmann19]. It is not hard to see that there is a one-to-one correspondence between weak representations of a Lie–Rinehart algebra and representations of the smash product
![]() $A\# U(\mathcal {L})$
.
$A\# U(\mathcal {L})$
.
Example 3.12. Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra. Define
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra. Define
![]() $\mathsf {ad}:\mathcal {L}\,\rightarrow \,\mathfrak D(\mathcal {L})$
by
$\mathsf {ad}:\mathcal {L}\,\rightarrow \,\mathfrak D(\mathcal {L})$
by
Then
![]() $\mathsf {ad}$
is a weak representation of
$\mathsf {ad}$
is a weak representation of
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $\mathcal {L}$
. Note that
$\mathcal {L}$
. Note that
![]() $\mathsf {ad}$
is generally not a representation of
$\mathsf {ad}$
is generally not a representation of
![]() $\mathcal {L}$
on itself.
$\mathcal {L}$
on itself.
Definition 3.13. Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $({M};\rho )$
and
$({M};\rho )$
and
![]() $({M}^{\prime };\rho ^{\prime })$
be two weak representations of
$({M}^{\prime };\rho ^{\prime })$
be two weak representations of
![]() $\mathcal {L}$
. An
$\mathcal {L}$
. An
![]() ${A}$
-module homomorphism
${A}$
-module homomorphism
![]() $\phi :{M}\to {M}^{\prime }$
is said to be a homomorphism of weak representations if
$\phi :{M}\to {M}^{\prime }$
is said to be a homomorphism of weak representations if
![]() $\phi \circ \rho (x)=\rho ^{\prime }(x)\circ \phi $
for all
$\phi \circ \rho (x)=\rho ^{\prime }(x)\circ \phi $
for all
![]() $x\in \mathcal {L}.$
$x\in \mathcal {L}.$
Proposition 3.14. Let
![]() $\phi :({M};\rho )\,\rightarrow \,({M}^{\prime };\rho ^{\prime })$
and
$\phi :({M};\rho )\,\rightarrow \,({M}^{\prime };\rho ^{\prime })$
and
![]() $\phi ^{\prime }:({M}^{\prime };\rho ^{\prime })\,\rightarrow \,({M^{\prime \prime }};\rho ^{\prime \prime })$
be two homomorphisms of weak representations of
$\phi ^{\prime }:({M}^{\prime };\rho ^{\prime })\,\rightarrow \,({M^{\prime \prime }};\rho ^{\prime \prime })$
be two homomorphisms of weak representations of
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() $\phi ^{\prime }\circ \phi $
is a homomorphism from
$\phi ^{\prime }\circ \phi $
is a homomorphism from
![]() $({M};\rho )$
to
$({M};\rho )$
to
![]() $({M^{\prime \prime }};\rho ^{\prime \prime })$
.
$({M^{\prime \prime }};\rho ^{\prime \prime })$
.
Proof. This is easy to see.
We usually denote by
![]() $M\stackrel {\phi }{\,\rightarrow \,}M^{\prime }$
a homomorphism between the weak representations
$M\stackrel {\phi }{\,\rightarrow \,}M^{\prime }$
a homomorphism between the weak representations
![]() $({M};\rho )$
and
$({M};\rho )$
and
![]() $({M}^{\prime };\rho ^{\prime })$
and denote by
$({M}^{\prime };\rho ^{\prime })$
and denote by
![]() $\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
the category of weak representations of a Lie–Rinehart algebra
$\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
the category of weak representations of a Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
and
![]() $\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)$
the category of representations of a
$\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)$
the category of representations of a
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
. It is obvious that the category of representations of a Lie–Rinehart algebra
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
. It is obvious that the category of representations of a Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
, denoted by
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
, denoted by
![]() $\mathsf {Rep}(\mathcal {L})$
, is a full subcategory of the category
$\mathsf {Rep}(\mathcal {L})$
, is a full subcategory of the category
![]() $\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
. Please note the subtle difference between the two categories
$\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
. Please note the subtle difference between the two categories
![]() $\mathsf {Rep}_{\mathbb {K}}(\mathcal {L})$
and
$\mathsf {Rep}_{\mathbb {K}}(\mathcal {L})$
and
![]() $\mathsf {Rep}(\mathcal {L})$
.
$\mathsf {Rep}(\mathcal {L})$
.
Definition 3.15 [Reference Casas, Ladra and Pirashvili6]
Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
be a Lie
$(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
be a Lie
![]() ${A}$
-algebra. We say that
${A}$
-algebra. We say that
![]() $\mathcal {L}$
acts on
$\mathcal {L}$
acts on
![]() $\mathcal {G}$
if a
$\mathcal {G}$
if a
![]() $\mathbb {K}$
-Lie algebra homomorphism
$\mathbb {K}$
-Lie algebra homomorphism
![]() $\rho :\mathcal {L}\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}({\mathcal {G}})$
is given such that
$\rho :\mathcal {L}\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}({\mathcal {G}})$
is given such that
Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
be a Lie
$(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
be a Lie
![]() ${A}$
-algebra on which
${A}$
-algebra on which
![]() $\mathcal {L}$
acts via
$\mathcal {L}$
acts via
![]() $\rho :\mathcal {L}\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}({\mathcal {G}})$
. On the
$\rho :\mathcal {L}\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}({\mathcal {G}})$
. On the
![]() ${A}$
-module
${A}$
-module
![]() $\mathcal {L}\oplus \mathcal {G}$
, define a bracket operation
$\mathcal {L}\oplus \mathcal {G}$
, define a bracket operation
![]() $[\cdot ,\cdot ]_{\rho }$
by
$[\cdot ,\cdot ]_{\rho }$
by
and define an
![]() ${A}$
-module homomorphism
${A}$
-module homomorphism
![]() $\tilde {\alpha }:\mathcal {L}\oplus \mathcal {G}\to \mathsf {Der}_{\mathbb {K}}({A})$
by
$\tilde {\alpha }:\mathcal {L}\oplus \mathcal {G}\to \mathsf {Der}_{\mathbb {K}}({A})$
by
Then
![]() $({A},\mathcal {L}\oplus \mathcal {G},[\cdot ,\cdot ]_{\rho },\tilde {\alpha })$
is a Lie–Rinehart algebra [Reference Casas, Ladra and Pirashvili6], which is called the semi-direct product of
$({A},\mathcal {L}\oplus \mathcal {G},[\cdot ,\cdot ]_{\rho },\tilde {\alpha })$
is a Lie–Rinehart algebra [Reference Casas, Ladra and Pirashvili6], which is called the semi-direct product of
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {G}$
and denoted by
$\mathcal {G}$
and denoted by
![]() $\mathcal {L}\ltimes _{\rho }\mathcal {G}$
.
$\mathcal {L}\ltimes _{\rho }\mathcal {G}$
.
Note that the Lie algebra
![]() $\mathcal {L}\ltimes _{\rho }\mathcal {G}$
acts on the Lie algebra
$\mathcal {L}\ltimes _{\rho }\mathcal {G}$
acts on the Lie algebra
![]() $(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
by
$(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
by
Then using Theorem 2.7 (b), we can easily verify the following result.
Proposition 3.16. With the above notations, the projection
![]() $\mathrm {Pr}:\mathcal {L}\ltimes _{\rho }\mathcal {G}\,\rightarrow \,\mathcal {G}$
is a crossed homomorphism with respect to the action
$\mathrm {Pr}:\mathcal {L}\ltimes _{\rho }\mathcal {G}\,\rightarrow \,\mathcal {G}$
is a crossed homomorphism with respect to the action
![]() $\tilde {\rho }$
.
$\tilde {\rho }$
.
3.2. Left module categories over monoidal categories
Proposition 3.17. Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $\rho $
an action of
$\rho $
an action of
![]() $\mathcal {L}$
on a Lie
$\mathcal {L}$
on a Lie
![]() ${A}$
-algebra
${A}$
-algebra
![]() $(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
. For a crossed homomorphism
$(\mathcal {G},[\cdot ,\cdot ]_{\mathcal {G}})$
. For a crossed homomorphism
![]() ${H}:\mathcal {L}\,\rightarrow \, \mathcal {G}$
between
${H}:\mathcal {L}\,\rightarrow \, \mathcal {G}$
between
![]() $\mathbb {K}$
-Lie algebras, we define a
$\mathbb {K}$
-Lie algebras, we define a
![]() $\mathbb {K}$
-linear map
$\mathbb {K}$
-linear map
![]() $\iota _{H}: \mathcal {L} \to \mathcal {L}\ltimes _{\rho }\mathcal {G}$
by
$\iota _{H}: \mathcal {L} \to \mathcal {L}\ltimes _{\rho }\mathcal {G}$
by
Then
![]() $\iota _{H}$
is a Lie–Rinehart injective weak homomorphism from
$\iota _{H}$
is a Lie–Rinehart injective weak homomorphism from
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathcal {L}\ltimes _{\rho }\mathcal {G}$
.
$\mathcal {L}\ltimes _{\rho }\mathcal {G}$
.
Proof. By Theorem 2.7 (b), we know that
![]() $\iota _{H}$
is a
$\iota _{H}$
is a
![]() $\mathbb {K}$
-Lie algebra monomorphism. Moreover, for all
$\mathbb {K}$
-Lie algebra monomorphism. Moreover, for all
![]() $x\in \mathcal {L}$
, we have
$x\in \mathcal {L}$
, we have
which implies that
![]() $\alpha =\tilde {\alpha }\circ \iota _{H}$
. Thus,
$\alpha =\tilde {\alpha }\circ \iota _{H}$
. Thus,
![]() $\iota _{H}$
is a Lie–Rinehart injective weak homomorphism.
$\iota _{H}$
is a Lie–Rinehart injective weak homomorphism.
Corollary 3.18. Let
![]() $({M};\mu )$
be a Lie–Rinehart weak representation of
$({M};\mu )$
be a Lie–Rinehart weak representation of
![]() $({A},\mathcal {L}\ltimes _{\rho }\mathcal {G},[\cdot ,\cdot ]_{\rho },\tilde {\alpha })$
and
$({A},\mathcal {L}\ltimes _{\rho }\mathcal {G},[\cdot ,\cdot ]_{\rho },\tilde {\alpha })$
and
![]() ${H}$
be a crossed homomorphism from
${H}$
be a crossed homomorphism from
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathcal {G}$
. Then
$\mathcal {G}$
. Then
![]() $({M};\mu \circ \iota _{H})$
is a Lie–Rinehart weak representation of
$({M};\mu \circ \iota _{H})$
is a Lie–Rinehart weak representation of
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
.
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
.
Proof. By Propositions 3.8 and 3.17, we deduce that
 $\mu \circ \iota _{H}:\mathcal {L}\stackrel {\iota _{H}}{\,\rightarrow \,}\mathcal {L}\ltimes _{\rho }\mathcal {G}\stackrel {\mu }{\,\rightarrow \,}\mathfrak {D}({M})$
is a Lie–Rinehart weak homomorphism.
$\mu \circ \iota _{H}:\mathcal {L}\stackrel {\iota _{H}}{\,\rightarrow \,}\mathcal {L}\ltimes _{\rho }\mathcal {G}\stackrel {\mu }{\,\rightarrow \,}\mathfrak {D}({M})$
is a Lie–Rinehart weak homomorphism.
Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
be a
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
be a
![]() $\mathbb {K}$
-Lie algebra. Then
$\mathbb {K}$
-Lie algebra. Then
![]() $\mathcal {G}=\mathfrak g\otimes _{\mathbb {K}} {A}$
is a Lie
$\mathcal {G}=\mathfrak g\otimes _{\mathbb {K}} {A}$
is a Lie
![]() ${A}$
-algebra, where the
${A}$
-algebra, where the
![]() ${A}$
-module structure and the Lie bracket
${A}$
-module structure and the Lie bracket
![]() $[\cdot ,\cdot ]_{\mathcal {G}}$
are given by
$[\cdot ,\cdot ]_{\mathcal {G}}$
are given by
Moreover, the Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
acts on the Lie
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
acts on the Lie
![]() ${A}$
-algebra
${A}$
-algebra
![]() $\mathfrak g\otimes _{\mathbb {K}} {A}$
by
$\mathfrak g\otimes _{\mathbb {K}} {A}$
by
![]() $\alpha $
as follows:
$\alpha $
as follows:
Consequently, we have the semidirect product Lie–Rinehart algebra
![]() $({A},\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}}{A}),[\cdot ,\cdot ]_{\alpha },\tilde {\alpha })$
.
$({A},\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}}{A}),[\cdot ,\cdot ]_{\alpha },\tilde {\alpha })$
.
Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $({M};\rho )$
be a Lie–Rinehart weak representation of
$({M};\rho )$
be a Lie–Rinehart weak representation of
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
. Let
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
. Let
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
be a
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
be a
![]() $\mathbb {K}$
-Lie algebra and
$\mathbb {K}$
-Lie algebra and
![]() $(V;\theta )$
be a representation of
$(V;\theta )$
be a representation of
![]() $\mathfrak g$
. Then
$\mathfrak g$
. Then
![]() ${V}\otimes _{\mathbb {K}} M$
has a natural
${V}\otimes _{\mathbb {K}} M$
has a natural
![]() ${A}$
-module structure:
${A}$
-module structure:
We define a
![]() $\mathbb {K}$
-linear map
$\mathbb {K}$
-linear map
![]() $ \rho \boxplus \theta :\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A})\,\rightarrow \,\mathfrak {gl}_{\mathbb {K}}({V}\otimes _{\mathbb {K}} M)$
by
$ \rho \boxplus \theta :\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A})\,\rightarrow \,\mathfrak {gl}_{\mathbb {K}}({V}\otimes _{\mathbb {K}} M)$
by
for all
![]() $x\in \mathcal {L},~a\in {A},~g\in \mathfrak g,~m\in {M},~v\in V$
.
$x\in \mathcal {L},~a\in {A},~g\in \mathfrak g,~m\in {M},~v\in V$
.
Lemma 3.19. With the above notations,
![]() $({V}\otimes _{\mathbb {K}} M;\rho \boxplus \theta )$
is a Lie–Rinehart weak representation of the Lie–Rinehart algebra
$({V}\otimes _{\mathbb {K}} M;\rho \boxplus \theta )$
is a Lie–Rinehart weak representation of the Lie–Rinehart algebra
![]() $({A},\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A}),[\cdot ,\cdot ]_{\alpha },\tilde {\alpha })$
.
$({A},\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A}),[\cdot ,\cdot ]_{\alpha },\tilde {\alpha })$
.
Proof. Since
![]() $\rho :\mathcal {L}\,\rightarrow \,\mathfrak {D}({M})$
and
$\rho :\mathcal {L}\,\rightarrow \,\mathfrak {D}({M})$
and
![]() $\theta :\mathfrak g\,\rightarrow \,\mathfrak {gl}(V)$
are
$\theta :\mathfrak g\,\rightarrow \,\mathfrak {gl}(V)$
are
![]() $\mathbb {K}$
-Lie algebra homomorphisms, for all
$\mathbb {K}$
-Lie algebra homomorphisms, for all
![]() $a,b\in {A},x,y\in \mathcal {L},g,h\in \mathfrak g, m\in {M},v\in V$
, we have
$a,b\in {A},x,y\in \mathcal {L},g,h\in \mathfrak g, m\in {M},v\in V$
, we have
 $$ \begin{align*} &\quad\Big([(\rho\boxplus\theta)(x,g\otimes a),(\rho\boxplus\theta)(y,h\otimes b)]_{C}-(\rho\boxplus\theta)([(x,g\otimes a),(y,h\otimes b)]_{\alpha})\Big)(v\otimes m)\\ &=(\rho\boxplus\theta)(x,g\otimes a)\Big(v\otimes \rho(y)m+\theta(h)v\otimes bm \Big)-(\rho\boxplus\theta)(y,h\otimes b)\Big(v\otimes \rho(x)m+\theta(g)v\otimes am\Big)\\ &\quad -(\rho\boxplus\theta)\Big([x,y]_{\mathcal{L}},h\otimes \alpha(x)(b)-g\otimes \alpha(y)(a)+[g,h]_{\mathfrak g}\otimes ab\Big)(v\otimes m)\\ &= v\otimes \rho(x)(\rho(y)m)+\theta(g)v\otimes a(\rho(y)m)+\theta(h)v\otimes \rho(x)(bm)+ \theta(g)(\theta(h)v)\otimes a(bm)\\ &\quad -v\otimes \rho(y)(\rho(x)m)-\theta(h)v\otimes b(\rho(x)m)-\theta(g)v\otimes \rho(y)(am)- \theta(h)(\theta(g)v)\otimes b(am)\\ &\quad -v\otimes\rho([x,y]_{\mathcal{L}})m -\theta(h)v\otimes\alpha(x)(b)m+\theta(g)v\otimes \alpha(y)(a)m-\theta([g,h]_{\mathfrak g})v\otimes (ab)m\\ &=0. \end{align*} $$
$$ \begin{align*} &\quad\Big([(\rho\boxplus\theta)(x,g\otimes a),(\rho\boxplus\theta)(y,h\otimes b)]_{C}-(\rho\boxplus\theta)([(x,g\otimes a),(y,h\otimes b)]_{\alpha})\Big)(v\otimes m)\\ &=(\rho\boxplus\theta)(x,g\otimes a)\Big(v\otimes \rho(y)m+\theta(h)v\otimes bm \Big)-(\rho\boxplus\theta)(y,h\otimes b)\Big(v\otimes \rho(x)m+\theta(g)v\otimes am\Big)\\ &\quad -(\rho\boxplus\theta)\Big([x,y]_{\mathcal{L}},h\otimes \alpha(x)(b)-g\otimes \alpha(y)(a)+[g,h]_{\mathfrak g}\otimes ab\Big)(v\otimes m)\\ &= v\otimes \rho(x)(\rho(y)m)+\theta(g)v\otimes a(\rho(y)m)+\theta(h)v\otimes \rho(x)(bm)+ \theta(g)(\theta(h)v)\otimes a(bm)\\ &\quad -v\otimes \rho(y)(\rho(x)m)-\theta(h)v\otimes b(\rho(x)m)-\theta(g)v\otimes \rho(y)(am)- \theta(h)(\theta(g)v)\otimes b(am)\\ &\quad -v\otimes\rho([x,y]_{\mathcal{L}})m -\theta(h)v\otimes\alpha(x)(b)m+\theta(g)v\otimes \alpha(y)(a)m-\theta([g,h]_{\mathfrak g})v\otimes (ab)m\\ &=0. \end{align*} $$
Therefore, we deduce that
![]() $\rho \boxplus \theta $
is a
$\rho \boxplus \theta $
is a
![]() $\mathbb {K}$
-Lie algebra homomorphism.
$\mathbb {K}$
-Lie algebra homomorphism.
Furthermore, by
![]() $\rho (x)\in \mathfrak {D}({M})$
, we have
$\rho (x)\in \mathfrak {D}({M})$
, we have
 $$ \begin{align*} (\rho\boxplus\theta)(x,g\otimes b)\Big(a(v\otimes m)\Big)&=(\rho\boxplus\theta)(x,g\otimes b)(v\otimes am)\\ &=v\otimes \rho(x)(am)+ \theta(g)v\otimes a(bm)\\ &=v\otimes \Big(a\rho(x)(m)+\alpha(x)(a)m\Big)+\theta(g)v \otimes a(bm)\\ &=a\Big( (\rho\boxplus\theta)(x,g\otimes b)(v\otimes m)\Big)+\alpha(x)(a)(v\otimes m), \end{align*} $$
$$ \begin{align*} (\rho\boxplus\theta)(x,g\otimes b)\Big(a(v\otimes m)\Big)&=(\rho\boxplus\theta)(x,g\otimes b)(v\otimes am)\\ &=v\otimes \rho(x)(am)+ \theta(g)v\otimes a(bm)\\ &=v\otimes \Big(a\rho(x)(m)+\alpha(x)(a)m\Big)+\theta(g)v \otimes a(bm)\\ &=a\Big( (\rho\boxplus\theta)(x,g\otimes b)(v\otimes m)\Big)+\alpha(x)(a)(v\otimes m), \end{align*} $$
which implies that
![]() $(\rho \boxplus \theta )(x,g\otimes b)\in \mathfrak {D}(V\otimes _{\mathbb {K}}{M})$
and
$(\rho \boxplus \theta )(x,g\otimes b)\in \mathfrak {D}(V\otimes _{\mathbb {K}}{M})$
and
![]() $\tilde {\alpha }=\mathrm {Pr}\circ (\rho \boxplus \theta )$
.
$\tilde {\alpha }=\mathrm {Pr}\circ (\rho \boxplus \theta )$
.
Therefore,
![]() $\rho \boxplus \theta :\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A})\,\rightarrow \,\mathfrak {D}(V\otimes _{\mathbb {K}}{M})$
is a Lie–Rinehart weak homomorphism.
$\rho \boxplus \theta :\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A})\,\rightarrow \,\mathfrak {D}(V\otimes _{\mathbb {K}}{M})$
is a Lie–Rinehart weak homomorphism.
Corollary 3.20. Let
![]() $({M};\rho )$
be a Lie–Rinehart representation of
$({M};\rho )$
be a Lie–Rinehart representation of
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
and
![]() $(V;\theta )$
be a representation of
$(V;\theta )$
be a representation of
![]() $\mathfrak g$
. Then
$\mathfrak g$
. Then
![]() $({V}\otimes _{\mathbb {K}} M;\rho \boxplus \theta )$
is a Lie–Rinehart representation of
$({V}\otimes _{\mathbb {K}} M;\rho \boxplus \theta )$
is a Lie–Rinehart representation of
![]() $\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A})$
.
$\mathcal {L}\ltimes _{\alpha } (\mathfrak g\otimes _{\mathbb {K}} {A})$
.
Proof. Since
![]() $\rho $
is an
$\rho $
is an
![]() ${A}$
-module homomorphism, we have
${A}$
-module homomorphism, we have
 $$ \begin{align*} &\quad \Big((\rho\boxplus\theta)(b(x,g\otimes a))-b(\rho\boxplus\theta)(x,g\otimes a)\Big)(v\otimes m)\\ &=v\otimes \rho(bx)m+\theta(g)v\otimes (ba)m-b\Big(v\otimes \rho(x)m+\theta(g)v\otimes am\Big)\\ &=0, \quad \forall a,b\in{A},~x\in\mathcal{L},~g\in\mathfrak g,~m\in{M},~v\in V. \end{align*} $$
$$ \begin{align*} &\quad \Big((\rho\boxplus\theta)(b(x,g\otimes a))-b(\rho\boxplus\theta)(x,g\otimes a)\Big)(v\otimes m)\\ &=v\otimes \rho(bx)m+\theta(g)v\otimes (ba)m-b\Big(v\otimes \rho(x)m+\theta(g)v\otimes am\Big)\\ &=0, \quad \forall a,b\in{A},~x\in\mathcal{L},~g\in\mathfrak g,~m\in{M},~v\in V. \end{align*} $$
Thus,
![]() $\rho \boxplus \theta $
is also an
$\rho \boxplus \theta $
is also an
![]() ${A}$
-module homomorphism.
${A}$
-module homomorphism.
Before we give the main result of the article, we recall the notions of a monoidal category and a left module category over a monoidal category.
Definition 3.21 [Reference Etingof, Gelaki, Nikshych and Ostrik10]
A monoidal category is a
![]() $6$
-tuple
$6$
-tuple
![]() $({\mathcal {C}},\otimes , a,\mathbf {1},l,r)$
that consists of the following data:
$({\mathcal {C}},\otimes , a,\mathbf {1},l,r)$
that consists of the following data:
-
• a category
 ${\mathcal {C}}$
;
${\mathcal {C}}$
; -
• a bifunctor
 $\otimes :{\mathcal {C}}\times {\mathcal {C}}\to {\mathcal {C}}$
called the monoidal product;
$\otimes :{\mathcal {C}}\times {\mathcal {C}}\to {\mathcal {C}}$
called the monoidal product; -
• a natural isomorphism
 $a:\otimes \circ (\otimes \times \textrm {Id}_{\mathcal {C}})\,\rightarrow \,\otimes \circ (\textrm {Id}_{\mathcal {C}}\times \otimes )$
called the associativity isomorphism;
$a:\otimes \circ (\otimes \times \textrm {Id}_{\mathcal {C}})\,\rightarrow \,\otimes \circ (\textrm {Id}_{\mathcal {C}}\times \otimes )$
called the associativity isomorphism; -
• an object
 $\mathbf {1}\in \mathrm {Ob}({\mathcal {C}})$
called the unit object;
$\mathbf {1}\in \mathrm {Ob}({\mathcal {C}})$
called the unit object; -
• a natural isomorphism
 $l:\otimes \circ (\mathbf {1}\times \textrm {Id}_{\mathcal {C}})\,\rightarrow \,\textrm {Id}_{\mathcal {C}}$
called the left unit isomorphism and a natural isomorphism
$l:\otimes \circ (\mathbf {1}\times \textrm {Id}_{\mathcal {C}})\,\rightarrow \,\textrm {Id}_{\mathcal {C}}$
called the left unit isomorphism and a natural isomorphism
 $r:\otimes \circ (\textrm {Id}_{\mathcal {C}}\times \mathbf {1})\,\rightarrow \,\textrm {Id}_{\mathcal {C}}$
called the right unit isomorphism.
$r:\otimes \circ (\textrm {Id}_{\mathcal {C}}\times \mathbf {1})\,\rightarrow \,\textrm {Id}_{\mathcal {C}}$
called the right unit isomorphism.
These data satisfy the following two axioms:
![]() $(1)$
the pentagon axiom: the pentagon diagram
$(1)$
the pentagon axiom: the pentagon diagram

commutes for all
![]() $W,X,Y,Z\in \mathrm {Ob}({\mathcal {C}})$
.
$W,X,Y,Z\in \mathrm {Ob}({\mathcal {C}})$
.
![]() $(2)$
the triangle axiom: the triangle diagram
$(2)$
the triangle axiom: the triangle diagram

commutes for all
![]() $X,Y\in \mathrm {Ob}({\mathcal {C}})$
.
$X,Y\in \mathrm {Ob}({\mathcal {C}})$
.
The monoidal category
![]() ${\mathcal {C}}$
is strict if the associativity isomorphism, left unit isomorphism and right unit isomorphism
${\mathcal {C}}$
is strict if the associativity isomorphism, left unit isomorphism and right unit isomorphism
![]() $a,l,r$
are all identities.
$a,l,r$
are all identities.
Example 3.22. Let
![]() $\mathcal {C}$
be a category and
$\mathcal {C}$
be a category and
![]() $\mathcal {E}nd(\mathcal {C})$
be the category of endofunctors (the functors from
$\mathcal {E}nd(\mathcal {C})$
be the category of endofunctors (the functors from
![]() $\mathcal {C}$
into itself). Then
$\mathcal {C}$
into itself). Then
![]() $\mathcal {E}nd(\mathcal {C})$
is a strict monoidal category with the composition of functors as the monoidal product and the identity functor as the unit object of this category.
$\mathcal {E}nd(\mathcal {C})$
is a strict monoidal category with the composition of functors as the monoidal product and the identity functor as the unit object of this category.
Example 3.23. The category of representations
![]() $\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)$
of a
$\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)$
of a
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $\mathfrak g$
is a monoidal category: the monoidal product of
$\mathfrak g$
is a monoidal category: the monoidal product of
![]() $(V_{1};\theta _{1})$
and
$(V_{1};\theta _{1})$
and
![]() $(V_{2};\theta _{2})$
is defined by
$(V_{2};\theta _{2})$
is defined by
and the unit object
![]() $\mathbf {1}$
is the 1-dimensional trivial representation
$\mathbf {1}$
is the 1-dimensional trivial representation
![]() $(\mathbb {K};0)$
of
$(\mathbb {K};0)$
of
![]() $\mathfrak g$
. Moreover, the associativity isomorphism
$\mathfrak g$
. Moreover, the associativity isomorphism
is defined by
 $$ \begin{align} a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(V_{3};\theta_{3})}\Big((v_{1}\otimes v_{2})\otimes v_{3}\Big):=v_{1}\otimes (v_{2}\otimes v_{3}),\,\,\,\,\forall v_{i}\in V_{i},~i=1,2,3, \end{align} $$
$$ \begin{align} a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(V_{3};\theta_{3})}\Big((v_{1}\otimes v_{2})\otimes v_{3}\Big):=v_{1}\otimes (v_{2}\otimes v_{3}),\,\,\,\,\forall v_{i}\in V_{i},~i=1,2,3, \end{align} $$
and the left unit isomorphism
![]() $l_{(V;\theta )}$
and the right unit isomorphism
$l_{(V;\theta )}$
and the right unit isomorphism
![]() $r_{(V;\theta )}$
are defined by
$r_{(V;\theta )}$
are defined by
Definition 3.24 [Reference Etingof, Gelaki, Nikshych and Ostrik10]
Let
![]() $({\mathcal {C}},\otimes , a,\mathbf {1},l,r)$
be a monoidal category. A left module category over
$({\mathcal {C}},\otimes , a,\mathbf {1},l,r)$
be a monoidal category. A left module category over
![]() ${\mathcal {C}}$
is a category
${\mathcal {C}}$
is a category
![]() $\mathcal {M}$
equipped with a bifunctor
$\mathcal {M}$
equipped with a bifunctor
![]() $\otimes ^{\mathcal {M}}:{\mathcal {C}}\times \mathcal {M}\,\rightarrow \,\mathcal {M}$
, a natural isomorphism
$\otimes ^{\mathcal {M}}:{\mathcal {C}}\times \mathcal {M}\,\rightarrow \,\mathcal {M}$
, a natural isomorphism
![]() $a^{\mathcal {M}}:\otimes ^{\mathcal {M}}\circ (\otimes \times \text {Id}_{\mathcal {M}})\,\rightarrow \,\otimes ^{\mathcal {M}}\circ (\text {Id}_{\mathcal {C}}\times \otimes ^{\mathcal {M}})$
and a natural isomorphism
$a^{\mathcal {M}}:\otimes ^{\mathcal {M}}\circ (\otimes \times \text {Id}_{\mathcal {M}})\,\rightarrow \,\otimes ^{\mathcal {M}}\circ (\text {Id}_{\mathcal {C}}\times \otimes ^{\mathcal {M}})$
and a natural isomorphism
![]() $l^{\mathcal {M}}:\otimes ^{\mathcal {M}}\circ (\mathbf {1}\times \textrm {Id}_{\mathcal {M}})\,\rightarrow \,\textrm {Id}_{\mathcal {M}}$
such that the pentagon diagram
$l^{\mathcal {M}}:\otimes ^{\mathcal {M}}\circ (\mathbf {1}\times \textrm {Id}_{\mathcal {M}})\,\rightarrow \,\textrm {Id}_{\mathcal {M}}$
such that the pentagon diagram

and the triangle diagram

commute for all
![]() $X,Y,Z\in \mathrm {Ob}({\mathcal {C}}),~M\in \mathrm {Ob}(\mathcal {M})$
.
$X,Y,Z\in \mathrm {Ob}({\mathcal {C}}),~M\in \mathrm {Ob}(\mathcal {M})$
.
Example 3.25. Any monoidal category
![]() $({\mathcal {C}},\otimes , a,\mathbf {1},l,r)$
is a left module category over itself. More precisely, we set
$({\mathcal {C}},\otimes , a,\mathbf {1},l,r)$
is a left module category over itself. More precisely, we set
![]() $\otimes ^{\mathcal {C}}=\otimes ,~a^{\mathcal {C}}=a,~l^{\mathcal {C}}=l$
. This left module category can be considered as a categorification of the regular representation of an associative algebra.
$\otimes ^{\mathcal {C}}=\otimes ,~a^{\mathcal {C}}=a,~l^{\mathcal {C}}=l$
. This left module category can be considered as a categorification of the regular representation of an associative algebra.
Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $\mathfrak g$
be a
$\mathfrak g$
be a
![]() $\mathbb {K}$
-Lie algebra. Let
$\mathbb {K}$
-Lie algebra. Let
![]() ${H}$
be a crossed homomorphism from the
${H}$
be a crossed homomorphism from the
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathfrak g\otimes _{\mathbb {K}}{A}$
with respect to the action
$\mathfrak g\otimes _{\mathbb {K}}{A}$
with respect to the action
![]() $\alpha $
given by (10). For all
$\alpha $
given by (10). For all
![]() $x\in \mathcal {L}$
, we set
$x\in \mathcal {L}$
, we set
![]() $Hx=\sum _{i} x_{i}^{\mathfrak g}\otimes x^{A}_{i}$
or
$Hx=\sum _{i} x_{i}^{\mathfrak g}\otimes x^{A}_{i}$
or
![]() $Hx=x_{i}^{\mathfrak g}\otimes x^{A}_{i}$
for simplicity.
$Hx=x_{i}^{\mathfrak g}\otimes x^{A}_{i}$
for simplicity.
By Corollary 3.18 and Lemma 3.19, our main theorem can be stated as follows.
Theorem 3.26. Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra and
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
be a
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
be a
![]() $\mathbb {K}$
-Lie algebra. Then any crossed homomorphism
$\mathbb {K}$
-Lie algebra. Then any crossed homomorphism
![]() $H:\mathcal {L}\,\rightarrow \,\mathfrak g\otimes _{\mathbb {K}}{A}$
induces a left module category structure of the category of weak representations
$H:\mathcal {L}\,\rightarrow \,\mathfrak g\otimes _{\mathbb {K}}{A}$
induces a left module category structure of the category of weak representations
![]() $\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
over the monoidal category
$\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
over the monoidal category
![]() $\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)$
. More precisely, the left module structure is given by
$\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)$
. More precisely, the left module structure is given by
-
• the bifunctor
 $F_{H}:\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)\times \mathsf {WRep}_{\mathbb {K}}(\mathcal {L}) \to \mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
, which is defined on the set of objects and on the set of morphisms respectively by (13)
$F_{H}:\mathsf {Rep}_{\mathbb {K}}(\mathfrak g)\times \mathsf {WRep}_{\mathbb {K}}(\mathcal {L}) \to \mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
, which is defined on the set of objects and on the set of morphisms respectively by (13) $$ \begin{align} F_{H}\Big((V;\theta),({M};\rho)\Big)&=({V}\otimes_{\mathbb{K}} M;(\rho\boxplus\theta)\circ{\iota}_{H}), \end{align} $$
(14)for
$$ \begin{align} F_{H}\Big((V;\theta),({M};\rho)\Big)&=({V}\otimes_{\mathbb{K}} M;(\rho\boxplus\theta)\circ{\iota}_{H}), \end{align} $$
(14)for $$ \begin{align} F_{H}(V\stackrel{\psi}{\,\rightarrow\,}V',M\stackrel{\phi}{\,\rightarrow\,}M')&=V\otimes M\stackrel{\psi\otimes \phi}{\,\rightarrow\,}V'\otimes M', \end{align} $$
$$ \begin{align} F_{H}(V\stackrel{\psi}{\,\rightarrow\,}V',M\stackrel{\phi}{\,\rightarrow\,}M')&=V\otimes M\stackrel{\psi\otimes \phi}{\,\rightarrow\,}V'\otimes M', \end{align} $$
 $(V;\theta ),(V^{\prime };\theta ^{\prime })\in \mathsf {Rep}_{\mathbb {K}}(\mathfrak g),~({M};\rho ),({M}^{\prime };\rho ^{\prime })\in \mathsf {WRep}_{\mathbb {K}}(\mathcal {L}),$
representation homomorphism
$(V;\theta ),(V^{\prime };\theta ^{\prime })\in \mathsf {Rep}_{\mathbb {K}}(\mathfrak g),~({M};\rho ),({M}^{\prime };\rho ^{\prime })\in \mathsf {WRep}_{\mathbb {K}}(\mathcal {L}),$
representation homomorphism
 $V\stackrel {\psi }{\,\rightarrow \,}V^{\prime }$
of the
$V\stackrel {\psi }{\,\rightarrow \,}V^{\prime }$
of the
 $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
 $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
and weak representation homomorphism
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
and weak representation homomorphism
 $M\stackrel {\phi }{\,\rightarrow \,}M^{\prime }$
of the Lie–Rinehart algebra
$M\stackrel {\phi }{\,\rightarrow \,}M^{\prime }$
of the Lie–Rinehart algebra
 $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
;
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
;
-
• the natural isomorphism
which is defined by $$ \begin{align*}a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}&:F_{H}\big((V_{1};\theta_{1})\otimes(V_{2};\theta_{2}), (M;\rho)\big)\,\\&\rightarrow\, F_{H}\Big((V_{1};\theta_{1}),F_{H}\big((V_{2};\theta_{2}), (M;\rho)\big)\Big),\\[-15pt]\end{align*} $$
(15)
$$ \begin{align*}a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}&:F_{H}\big((V_{1};\theta_{1})\otimes(V_{2};\theta_{2}), (M;\rho)\big)\,\\&\rightarrow\, F_{H}\Big((V_{1};\theta_{1}),F_{H}\big((V_{2};\theta_{2}), (M;\rho)\big)\Big),\\[-15pt]\end{align*} $$
(15) $$ \begin{align} a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}((v_{1}\otimes v_{2})\otimes m)=v_{1}\otimes (v_{2}\otimes m),\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}((v_{1}\otimes v_{2})\otimes m)=v_{1}\otimes (v_{2}\otimes m),\\[-15pt]\nonumber \end{align} $$
-
• the natural isomorphism
 $l_{({M};\rho )}:F_{H}\big ((\mathbb {K};0),({M};\rho ))\,\rightarrow \, ({M};\rho )$
, which is defined by (16)
$l_{({M};\rho )}:F_{H}\big ((\mathbb {K};0),({M};\rho ))\,\rightarrow \, ({M};\rho )$
, which is defined by (16) $$ \begin{align} l_{({M};\rho)}(k\otimes m)=km.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} l_{({M};\rho)}(k\otimes m)=km.\\[-15pt]\nonumber \end{align} $$
Proof. By Corollary 3.18 and Lemma 3.19,
![]() $({V}\otimes _{\mathbb {K}} M;(\rho \boxplus \theta )\circ \iota _{H})$
is a weak representation of
$({V}\otimes _{\mathbb {K}} M;(\rho \boxplus \theta )\circ \iota _{H})$
is a weak representation of
![]() $\mathcal {L}$
. Thus,
$\mathcal {L}$
. Thus,
![]() $F_{H}$
is well-defined on the set of objects. To see that
$F_{H}$
is well-defined on the set of objects. To see that
![]() $F_{H}$
is also well-defined on the set of morphisms, we need to show that the linear map
$F_{H}$
is also well-defined on the set of morphisms, we need to show that the linear map
![]() $\psi \otimes \phi :V\otimes M\,\rightarrow \, V^{\prime }\otimes M^{\prime }$
is indeed a homomorphism from
$\psi \otimes \phi :V\otimes M\,\rightarrow \, V^{\prime }\otimes M^{\prime }$
is indeed a homomorphism from
![]() $({V}\otimes _{\mathbb {K}} M;(\rho \boxplus \theta )\circ \iota _{H})$
to
$({V}\otimes _{\mathbb {K}} M;(\rho \boxplus \theta )\circ \iota _{H})$
to
![]() $({V}^{\prime }\otimes _{\mathbb {K}} M^{\prime };(\rho ^{\prime }\boxplus \theta ^{\prime })\circ \iota _{H})$
. In fact, for all
$({V}^{\prime }\otimes _{\mathbb {K}} M^{\prime };(\rho ^{\prime }\boxplus \theta ^{\prime })\circ \iota _{H})$
. In fact, for all
![]() $a\in A,~v\in V,~m\in M$
, we have
$a\in A,~v\in V,~m\in M$
, we have
 $$ \begin{align*} (\psi\otimes \phi)\Big(a(v\otimes m)\Big)-a\Big((\psi\otimes \phi)(v\otimes m)\Big) &=(\psi\otimes \phi)(v\otimes am)-a\Big(\psi(v)\otimes \phi(m)\Big)\\ &=\psi(v)\otimes \phi(am)\otimes -\psi(v)\otimes a\phi(m)\\ &=0.\\[-15pt] \end{align*} $$
$$ \begin{align*} (\psi\otimes \phi)\Big(a(v\otimes m)\Big)-a\Big((\psi\otimes \phi)(v\otimes m)\Big) &=(\psi\otimes \phi)(v\otimes am)-a\Big(\psi(v)\otimes \phi(m)\Big)\\ &=\psi(v)\otimes \phi(am)\otimes -\psi(v)\otimes a\phi(m)\\ &=0.\\[-15pt] \end{align*} $$
For all
![]() $x\in \mathfrak g,~v\in V$
and
$x\in \mathfrak g,~v\in V$
and
![]() $m\in M$
, we have
$m\in M$
, we have
 $$ \begin{align*} &(\psi\otimes \phi)\Big(\big((\rho\boxplus\theta)\iota_{H}(x)\big)(v\otimes m)\Big)-\Big((\rho^{\prime}\boxplus\theta^{\prime})\iota_{H}(x)\Big)\Big((\psi\otimes \phi)(v\otimes m)\Big)\\ &=(\psi\otimes \phi)\Big(\big((\rho\boxplus\theta)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\big)(v\otimes m)\Big)-\Big((\rho^{\prime}\boxplus\theta^{\prime})(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\Big)\Big(\psi(v)\otimes \phi(m)\Big)\\ &=(\psi\otimes \phi)\Big(v\otimes\rho(x)m+\theta(x_{i}^{\mathfrak g})v\otimes x_{i}^{A}m\Big)-\Big(\psi(v)\otimes \rho^{\prime}(x)\phi(m)+\theta^{\prime}(x_{i}^{\mathfrak g})\psi(v)\otimes x_{i}^{A}\phi(m)\Big)\\ &=\Big(\psi(v)\otimes\phi(\rho(x)m)+\psi(\theta(x_{i}^{\mathfrak g})v)\otimes \phi(x_{i}^{A}m)\Big)\\&\quad -\Big(\psi(v)\otimes \rho^{\prime}(x)\phi(m)+\theta^{\prime}(x_{i}^{\mathfrak g})\psi(v)\otimes x_{i}^{A}\phi(m)\Big)\\ &=0.\\[-15pt] \end{align*} $$
$$ \begin{align*} &(\psi\otimes \phi)\Big(\big((\rho\boxplus\theta)\iota_{H}(x)\big)(v\otimes m)\Big)-\Big((\rho^{\prime}\boxplus\theta^{\prime})\iota_{H}(x)\Big)\Big((\psi\otimes \phi)(v\otimes m)\Big)\\ &=(\psi\otimes \phi)\Big(\big((\rho\boxplus\theta)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\big)(v\otimes m)\Big)-\Big((\rho^{\prime}\boxplus\theta^{\prime})(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\Big)\Big(\psi(v)\otimes \phi(m)\Big)\\ &=(\psi\otimes \phi)\Big(v\otimes\rho(x)m+\theta(x_{i}^{\mathfrak g})v\otimes x_{i}^{A}m\Big)-\Big(\psi(v)\otimes \rho^{\prime}(x)\phi(m)+\theta^{\prime}(x_{i}^{\mathfrak g})\psi(v)\otimes x_{i}^{A}\phi(m)\Big)\\ &=\Big(\psi(v)\otimes\phi(\rho(x)m)+\psi(\theta(x_{i}^{\mathfrak g})v)\otimes \phi(x_{i}^{A}m)\Big)\\&\quad -\Big(\psi(v)\otimes \rho^{\prime}(x)\phi(m)+\theta^{\prime}(x_{i}^{\mathfrak g})\psi(v)\otimes x_{i}^{A}\phi(m)\Big)\\ &=0.\\[-15pt] \end{align*} $$
Thus, we obtain that
![]() $F_{H}(\psi ,\phi )=\psi \otimes \phi $
is a homomorphism of the weak representations. Moreover, by straightforward computations, we deduce that
$F_{H}(\psi ,\phi )=\psi \otimes \phi $
is a homomorphism of the weak representations. Moreover, by straightforward computations, we deduce that
![]() $F_{H}$
preserves identity morphisms and composite morphisms. Therefore,
$F_{H}$
preserves identity morphisms and composite morphisms. Therefore,
![]() $F_{H}$
is a bifunctor.
$F_{H}$
is a bifunctor.
Let
![]() $(V_{1};\theta _{1})$
and
$(V_{1};\theta _{1})$
and
![]() $(V_{2};\theta _{2})$
be representations of the
$(V_{2};\theta _{2})$
be representations of the
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $\mathfrak g$
and
$\mathfrak g$
and
![]() $({M};\rho )$
be a weak representation of the Lie–Rinehart algebra
$({M};\rho )$
be a weak representation of the Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
. For all
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
. For all
![]() $b\in A,~v_{1}\in V_{1},~v_{2}\in V_{2}$
and
$b\in A,~v_{1}\in V_{1},~v_{2}\in V_{2}$
and
![]() $m\in M$
, we have
$m\in M$
, we have
 $$ \begin{align*} &\quad a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big(b\big((v_{1}\otimes v_{2})\otimes m\big)\Big)-ba_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big((v_{1}\otimes v_{2})\otimes m\Big)\\ &=a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big((v_{1}\otimes v_{2})\otimes bm\Big)-b\Big(v_{1}\otimes (v_{2}\otimes m)\Big)\\ &=v_{1}\otimes (v_{2}\otimes bm)-v_{1}\otimes b(v_{2}\otimes m)\\ &=0. \end{align*} $$
$$ \begin{align*} &\quad a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big(b\big((v_{1}\otimes v_{2})\otimes m\big)\Big)-ba_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big((v_{1}\otimes v_{2})\otimes m\Big)\\ &=a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big((v_{1}\otimes v_{2})\otimes bm\Big)-b\Big(v_{1}\otimes (v_{2}\otimes m)\Big)\\ &=v_{1}\otimes (v_{2}\otimes bm)-v_{1}\otimes b(v_{2}\otimes m)\\ &=0. \end{align*} $$
For all
![]() $x\in \mathcal {L},~v_{1}\in V_{1},~v_{2}\in V_{2}$
and
$x\in \mathcal {L},~v_{1}\in V_{1},~v_{2}\in V_{2}$
and
![]() $m\in M$
, we have
$m\in M$
, we have
 $$ \begin{align*} &\quad a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big(\Big(\Big(\rho\boxplus\Big(\theta_{1}\otimes \text{Id}_{V_{2}}+\text{Id}_{V_{1}}\otimes \theta_{2}\Big)\Big)\iota_{H}(x)\Big)\big((v_{1}\otimes v_{2})\otimes m\big)\Big)\\ &\quad -\Big(\Big(\Big((\rho\boxplus\theta_{2})\circ\iota_{H}\Big)\boxplus\theta_{1}\Big)\iota_{H}(x)\Big)a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}((v_{1}\otimes v_{2})\otimes m)\\ &=a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big(\Big(\Big(\rho\boxplus\Big(\theta_{1}\otimes \text{Id}_{V_{2}}+\text{Id}_{V_{1}}\otimes \theta_{2}\Big)\Big)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\Big)((v_{1}\otimes v_{2})\otimes m)\Big)\\ &\quad -\Big(\Big(\Big((\rho\boxplus\theta_{2})\circ\iota_{H}\Big)\boxplus\theta_{1}\Big)\iota_{H}(x)\Big)(v_{1}\otimes (v_{2}\otimes m))\\ &=a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big((v_{1}\otimes v_{2})\otimes\rho(x)m+(\theta_{1}\otimes \text{Id}_{V_{2}}+\text{Id}_{V_{1}}\otimes \theta_{2})(x_{i}^{\mathfrak g})(v_{1}\otimes v_{2})\otimes x_{i}^{A}m\Big)\\&\quad -\Big(\Big(\Big((\rho\boxplus\theta_{2})\circ\iota_{H}\Big)\boxplus\theta_{1}\Big)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\Big)(v_{1}\otimes (v_{2}\otimes m))\\ &=v_{1}\otimes (v_{2}\otimes\rho(x)m)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes (v_{2}\otimes x_{i}^{A}m)+v_{1}\otimes (\theta_{2}(x_{i}^{\mathfrak g})v_{2}\otimes x_{i}^{A}m)\\ &\quad -\Big(v_{1}\otimes\big((\rho\boxplus\theta_{2})\iota_{H}(x)(v_{2}\otimes m)\big)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes x_{i}^{A}(v_{2}\otimes m)\Big)\\ &=v_{1}\otimes (v_{2}\otimes\rho(x)m)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes (v_{2}\otimes x_{i}^{A}m)+v_{1}\otimes (\theta_{2}(x_{i}^{\mathfrak g})v_{2}\otimes x_{i}^{A}m)\\ &\quad -\Big(v_{1}\otimes\big(v_{2}\otimes\rho(x)m+\theta_{2}(x_{i}^{\mathfrak g})v_{2}\otimes x_{i}^{A}m\big)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes (v_{2}\otimes x_{i}^{A}m)\Big)\\ &=0. \end{align*} $$
$$ \begin{align*} &\quad a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big(\Big(\Big(\rho\boxplus\Big(\theta_{1}\otimes \text{Id}_{V_{2}}+\text{Id}_{V_{1}}\otimes \theta_{2}\Big)\Big)\iota_{H}(x)\Big)\big((v_{1}\otimes v_{2})\otimes m\big)\Big)\\ &\quad -\Big(\Big(\Big((\rho\boxplus\theta_{2})\circ\iota_{H}\Big)\boxplus\theta_{1}\Big)\iota_{H}(x)\Big)a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}((v_{1}\otimes v_{2})\otimes m)\\ &=a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big(\Big(\Big(\rho\boxplus\Big(\theta_{1}\otimes \text{Id}_{V_{2}}+\text{Id}_{V_{1}}\otimes \theta_{2}\Big)\Big)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\Big)((v_{1}\otimes v_{2})\otimes m)\Big)\\ &\quad -\Big(\Big(\Big((\rho\boxplus\theta_{2})\circ\iota_{H}\Big)\boxplus\theta_{1}\Big)\iota_{H}(x)\Big)(v_{1}\otimes (v_{2}\otimes m))\\ &=a_{(V_{1};\theta_{1}),(V_{2};\theta_{2}),(M;\rho)}\Big((v_{1}\otimes v_{2})\otimes\rho(x)m+(\theta_{1}\otimes \text{Id}_{V_{2}}+\text{Id}_{V_{1}}\otimes \theta_{2})(x_{i}^{\mathfrak g})(v_{1}\otimes v_{2})\otimes x_{i}^{A}m\Big)\\&\quad -\Big(\Big(\Big((\rho\boxplus\theta_{2})\circ\iota_{H}\Big)\boxplus\theta_{1}\Big)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\Big)(v_{1}\otimes (v_{2}\otimes m))\\ &=v_{1}\otimes (v_{2}\otimes\rho(x)m)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes (v_{2}\otimes x_{i}^{A}m)+v_{1}\otimes (\theta_{2}(x_{i}^{\mathfrak g})v_{2}\otimes x_{i}^{A}m)\\ &\quad -\Big(v_{1}\otimes\big((\rho\boxplus\theta_{2})\iota_{H}(x)(v_{2}\otimes m)\big)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes x_{i}^{A}(v_{2}\otimes m)\Big)\\ &=v_{1}\otimes (v_{2}\otimes\rho(x)m)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes (v_{2}\otimes x_{i}^{A}m)+v_{1}\otimes (\theta_{2}(x_{i}^{\mathfrak g})v_{2}\otimes x_{i}^{A}m)\\ &\quad -\Big(v_{1}\otimes\big(v_{2}\otimes\rho(x)m+\theta_{2}(x_{i}^{\mathfrak g})v_{2}\otimes x_{i}^{A}m\big)+\theta_{1}(x_{i}^{\mathfrak g})v_{1}\otimes (v_{2}\otimes x_{i}^{A}m)\Big)\\ &=0. \end{align*} $$
Thus, we obtain that
![]() $a_{(V_{1};\theta _{1}),(V_{2};\theta _{2}),(M;\rho )}$
is a homomorphism of the weak representations. Moreover, by straightforward computations, we obtain that
$a_{(V_{1};\theta _{1}),(V_{2};\theta _{2}),(M;\rho )}$
is a homomorphism of the weak representations. Moreover, by straightforward computations, we obtain that
![]() $a_{(V_{1};\theta _{1}),(V_{2};\theta _{2}),(M;\rho )}$
is a natural isomorphism and satisfies the pentagon diagram in Definition 3.24.
$a_{(V_{1};\theta _{1}),(V_{2};\theta _{2}),(M;\rho )}$
is a natural isomorphism and satisfies the pentagon diagram in Definition 3.24.
Let
![]() $({M};\rho )$
be a weak representation of the Lie–Rinehart algebra
$({M};\rho )$
be a weak representation of the Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
. We have
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
. We have
 $$ \begin{align*} l_{({M};\rho)}(a(k\otimes m))&=l_{({M};\rho)}(k\otimes am)=k(am)=a(km)\\&=al_{({M};\rho)}(k\otimes m), \quad \forall a\in A,~k\in\mathbb{K}, ~m\in M. \end{align*} $$
$$ \begin{align*} l_{({M};\rho)}(a(k\otimes m))&=l_{({M};\rho)}(k\otimes am)=k(am)=a(km)\\&=al_{({M};\rho)}(k\otimes m), \quad \forall a\in A,~k\in\mathbb{K}, ~m\in M. \end{align*} $$
For all
![]() $x\in \mathcal {L},~k\in \mathbb {K}$
and
$x\in \mathcal {L},~k\in \mathbb {K}$
and
![]() $m\in M$
, we have
$m\in M$
, we have
 $$ \begin{align*} &\quad l_{({M};\rho)}\Big(\big((\rho\boxplus 0)\iota_{H}(x)\big)(k\otimes m)\Big)-\rho(x)\Big(l_{({M};\rho)}(k\otimes m)\Big)\\ &=l_{({M};\rho)}\Big(\big((\rho\boxplus 0)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\big)(k\otimes m)\Big)-\rho(x)(km) =l_{({M};\rho)}\Big(k\otimes\rho(x)m\Big)-\rho(x)(km)\\ &=k(\rho(x)m)-\rho(x)(km) =0. \end{align*} $$
$$ \begin{align*} &\quad l_{({M};\rho)}\Big(\big((\rho\boxplus 0)\iota_{H}(x)\big)(k\otimes m)\Big)-\rho(x)\Big(l_{({M};\rho)}(k\otimes m)\Big)\\ &=l_{({M};\rho)}\Big(\big((\rho\boxplus 0)(x,x_{i}^{\mathfrak g}\otimes x_{i}^{A})\big)(k\otimes m)\Big)-\rho(x)(km) =l_{({M};\rho)}\Big(k\otimes\rho(x)m\Big)-\rho(x)(km)\\ &=k(\rho(x)m)-\rho(x)(km) =0. \end{align*} $$
Thus, we deduce that
![]() $l_{({M};\rho )}$
is a homomorphism of weak representations. Moreover, by straightforward computations, we obtain that
$l_{({M};\rho )}$
is a homomorphism of weak representations. Moreover, by straightforward computations, we obtain that
![]() $l_{({M};\rho )}$
is a natural isomorphism and satisfies the triangle diagram in Definition 3.24. The proof is finished.
$l_{({M};\rho )}$
is a natural isomorphism and satisfies the triangle diagram in Definition 3.24. The proof is finished.
Since
![]() $({A};\alpha )$
is a representation of a Lie–Rinehart algebra
$({A};\alpha )$
is a representation of a Lie–Rinehart algebra
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
, which is known as the natural representation, we obtain the following result.
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
, which is known as the natural representation, we obtain the following result.
Corollary 3.27. Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra,
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra,
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
a
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
a
![]() $\mathbb {K}$
-Lie algebra and
$\mathbb {K}$
-Lie algebra and
![]() ${H}$
a crossed homomorphism from
${H}$
a crossed homomorphism from
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathfrak g\otimes _{\mathbb {K}}{A}$
. Then we have a functor
$\mathfrak g\otimes _{\mathbb {K}}{A}$
. Then we have a functor
 $$ \begin{align*}\begin{aligned} &F_{{H}}^{A}:\mathsf{Rep}_{\mathbb{K}}(\mathfrak g)\to \mathsf{WRep}_{\mathbb{K}}(\mathcal{L}),\\ & (V;\theta)\mapsto (V\otimes_{\mathbb{K}}{A}; ({\alpha}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{K}}(\mathfrak g).\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &F_{{H}}^{A}:\mathsf{Rep}_{\mathbb{K}}(\mathfrak g)\to \mathsf{WRep}_{\mathbb{K}}(\mathcal{L}),\\ & (V;\theta)\mapsto (V\otimes_{\mathbb{K}}{A}; ({\alpha}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{K}}(\mathfrak g).\end{aligned} \end{align*} $$
We can also have a very useful functor on
![]() $\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
as follows.
$\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
as follows.
Corollary 3.28. Let
![]() $({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra,
$({A},\mathcal {L},[\cdot ,\cdot ]_{\mathcal {L}},\alpha )$
be a Lie–Rinehart algebra,
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
a
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
a
![]() $\mathbb {K}$
-Lie algebra,
$\mathbb {K}$
-Lie algebra,
![]() ${H}$
a crossed homomorphism from
${H}$
a crossed homomorphism from
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathfrak g\otimes _{\mathbb {K}}{A}$
and
$\mathfrak g\otimes _{\mathbb {K}}{A}$
and
![]() $(V;\theta )$
a given representation of
$(V;\theta )$
a given representation of
![]() $\mathfrak g$
. Then we have a functor
$\mathfrak g$
. Then we have a functor
 $$ \begin{align*}\begin{aligned} &F_{H}^{\theta} :\mathsf{WRep}_{\mathbb{K}}(\mathcal{L})\to \mathsf{WRep}_{\mathbb{K}}(\mathcal{L}),\\ & ({M};\rho)\mapsto (V\otimes_{\mathbb{K}}{M} ;({\rho}\boxplus \theta)\circ\iota_{H}),\quad\forall({M};\rho)\in\mathsf{WRep}_{\mathbb{K}}(\mathcal{L}).\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &F_{H}^{\theta} :\mathsf{WRep}_{\mathbb{K}}(\mathcal{L})\to \mathsf{WRep}_{\mathbb{K}}(\mathcal{L}),\\ & ({M};\rho)\mapsto (V\otimes_{\mathbb{K}}{M} ;({\rho}\boxplus \theta)\circ\iota_{H}),\quad\forall({M};\rho)\in\mathsf{WRep}_{\mathbb{K}}(\mathcal{L}).\end{aligned} \end{align*} $$
A special but very interesting case of the above result is that
![]() $(V;\theta )=(\mathfrak g;\mathsf {ad})$
. In the next section we will show that Corollary 3.28 is a very efficient way to construct interesting modules from easy modules.
$(V;\theta )=(\mathfrak g;\mathsf {ad})$
. In the next section we will show that Corollary 3.28 is a very efficient way to construct interesting modules from easy modules.
3.3. Admissible representations of Leibniz pairs
In this subsection, we introduce the notion of an admissible representation of a Leibniz pair. In the sequel, A is always a commutative associative algebra. The notion of a Leibniz pair was originally given in [Reference Flato, Gerstenhaber and Voronov11].
Definition 3.29 [Reference Flato, Gerstenhaber and Voronov11]
A Leibniz pair consists of a
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $(\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}})$
and a
$(\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}})$
and a
![]() $\mathbb {K}$
-Lie algebra homomorphism
$\mathbb {K}$
-Lie algebra homomorphism
![]() $\beta :\mathcal {S}\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}(A)$
.
$\beta :\mathcal {S}\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}(A)$
.
We denote a Leibniz pair by
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
or simply by
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
or simply by
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Definition 3.30. An admissible representation of a Leibniz pair
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
consists of an A-module M and a
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
consists of an A-module M and a
![]() $\mathbb {K}$
-Lie algebra homomorphism
$\mathbb {K}$
-Lie algebra homomorphism
![]() $\rho :\mathcal {S}\to \mathfrak {gl}_{\mathbb {K}}(M)$
such that
$\rho :\mathcal {S}\to \mathfrak {gl}_{\mathbb {K}}(M)$
such that
Definition 3.31. Let
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair and
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair and
![]() $({M};\rho )$
and
$({M};\rho )$
and
![]() $({M}^{\prime };\rho ^{\prime })$
two admissible representations of
$({M}^{\prime };\rho ^{\prime })$
two admissible representations of
![]() $\mathcal {S}$
. An
$\mathcal {S}$
. An
![]() ${A}$
-module homomorphism
${A}$
-module homomorphism
![]() $\phi :{M}\to {M}^{\prime }$
is said to be a homomorphism of admissible representations if
$\phi :{M}\to {M}^{\prime }$
is said to be a homomorphism of admissible representations if
![]() $\phi \circ \rho (x)=\rho ^{\prime }(x)\circ \phi $
for all
$\phi \circ \rho (x)=\rho ^{\prime }(x)\circ \phi $
for all
![]() $x\in \mathcal {S}.$
$x\in \mathcal {S}.$
Admissible representations of Leibniz pairs are like weak representations of Lie–Rinehart algebras. We use
![]() $\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
to denote the category of admissible representations of
$\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
to denote the category of admissible representations of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
It is straightforward to obtain the following result.
Lemma 3.32. Let
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair, M an A-module and
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair, M an A-module and
![]() $\rho :\mathcal {S}\to \mathfrak {gl}_{\mathbb {K}}(M)$
a
$\rho :\mathcal {S}\to \mathfrak {gl}_{\mathbb {K}}(M)$
a
![]() $\mathbb {K}$
-linear map. Then
$\mathbb {K}$
-linear map. Then
![]() $(M;\rho )$
is an admissible representation of
$(M;\rho )$
is an admissible representation of
![]() $\mathcal {S}$
if and only if
$\mathcal {S}$
if and only if
 $(A\ltimes M, \mathcal {S}\oplus M,[\cdot ,\cdot ]_{\rho },\hat {\beta })$
is a Leibniz pair, where
$(A\ltimes M, \mathcal {S}\oplus M,[\cdot ,\cdot ]_{\rho },\hat {\beta })$
is a Leibniz pair, where
![]() $A\ltimes M$
is the commutative associative algebra given in Remark 3.6,
$A\ltimes M$
is the commutative associative algebra given in Remark 3.6,
![]() $[\cdot ,\cdot ]_{\rho }$
is the semidirect product Lie bracket and
$[\cdot ,\cdot ]_{\rho }$
is the semidirect product Lie bracket and
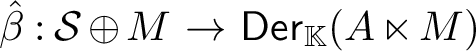 $\hat {\beta }:\mathcal {S}\oplus M\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}(A\ltimes M)$
is defined by
$\hat {\beta }:\mathcal {S}\oplus M\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}(A\ltimes M)$
is defined by
 $$ \begin{align*} \hat{\beta}(x,m)(a,n):=(\beta(x)a,\rho(x)n),\quad\forall x\in \mathcal{S}, a\in A, m,n\in M. \end{align*} $$
$$ \begin{align*} \hat{\beta}(x,m)(a,n):=(\beta(x)a,\rho(x)n),\quad\forall x\in \mathcal{S}, a\in A, m,n\in M. \end{align*} $$
It is obvious that any Lie–Rinehart algebra is a Leibniz pair. A weak representation of a Lie–Rinehart algebra is naturally an admissible representation of the underlying Leibniz pair. We have the following category equivalence:
where the right-hand side
![]() $\mathcal {L}$
is considered as a Leibniz pair.
$\mathcal {L}$
is considered as a Leibniz pair.
Conversely, given a Leibniz pair
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
, we also have an action Lie–Rinehart algebra
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
, we also have an action Lie–Rinehart algebra
![]() $(A,\mathcal {S}\otimes _{\mathbb {K}} A,[\cdot ,\cdot ],\alpha )$
, where the
$(A,\mathcal {S}\otimes _{\mathbb {K}} A,[\cdot ,\cdot ],\alpha )$
, where the
![]() ${A}$
-module structure and the
${A}$
-module structure and the
![]() $\mathbb {K}$
-Lie bracket
$\mathbb {K}$
-Lie bracket
![]() $[\cdot ,\cdot ]$
are given by
$[\cdot ,\cdot ]$
are given by
and an A-module homomorphism
![]() $\alpha :\mathcal {S}\otimes _{\mathbb {K}} A\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}({A})$
is defined by
$\alpha :\mathcal {S}\otimes _{\mathbb {K}} A\,\rightarrow \,\mathsf {Der}_{\mathbb {K}}({A})$
is defined by
![]() $ \alpha (x\otimes a):=a\beta (x) $
for all
$ \alpha (x\otimes a):=a\beta (x) $
for all
![]() $a,b\in {A},~x,y\in \mathcal {S}.$
Furthermore, we obtain the following result.
$a,b\in {A},~x,y\in \mathcal {S}.$
Furthermore, we obtain the following result.
Proposition 3.33. Let
![]() $(M;\rho )$
be an admissible representation of a Leibniz pair
$(M;\rho )$
be an admissible representation of a Leibniz pair
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
. Define
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
. Define
![]() $\overline {\rho }:\mathcal {S}\otimes _{\mathbb {K}} A\,\rightarrow \, \mathfrak {gl}_{\mathbb {K}}(M)$
by
$\overline {\rho }:\mathcal {S}\otimes _{\mathbb {K}} A\,\rightarrow \, \mathfrak {gl}_{\mathbb {K}}(M)$
by
Then
![]() $(M;\overline {\rho })$
is a representation of the Lie–Rinehart algebra
$(M;\overline {\rho })$
is a representation of the Lie–Rinehart algebra
![]() $(A,\mathcal {S}\otimes _{\mathbb {K}} A,[\cdot ,\cdot ],\alpha )$
.
$(A,\mathcal {S}\otimes _{\mathbb {K}} A,[\cdot ,\cdot ],\alpha )$
.
Proof. First, it is obvious that
![]() $ \overline {\rho }$
is an A-module homomorphism from
$ \overline {\rho }$
is an A-module homomorphism from
![]() $\mathcal {S}\otimes _{\mathbb {K}} A$
to
$\mathcal {S}\otimes _{\mathbb {K}} A$
to
![]() $\mathfrak {gl}_{\mathbb {K}}(M)$
. Then it is straightforward to deduce that
$\mathfrak {gl}_{\mathbb {K}}(M)$
. Then it is straightforward to deduce that
![]() $\overline {\rho }$
is a
$\overline {\rho }$
is a
![]() $\mathbb {K}$
-Lie algebra homomorphism. Finally, by (17), we deduce that
$\mathbb {K}$
-Lie algebra homomorphism. Finally, by (17), we deduce that
 $$ \begin{align*} \overline{\rho}(x\otimes a)(bm)=a\rho(x)(bm)=a\big(b\rho(x)m+\beta(x)(b)m\big)=b\overline{\rho}(x\otimes a)m+\alpha(x\otimes a)(b)m. \end{align*} $$
$$ \begin{align*} \overline{\rho}(x\otimes a)(bm)=a\rho(x)(bm)=a\big(b\rho(x)m+\beta(x)(b)m\big)=b\overline{\rho}(x\otimes a)m+\alpha(x\otimes a)(b)m. \end{align*} $$
Thus,
![]() $(M;\overline {\rho })$
is a representation of the Lie–Rinehart algebra
$(M;\overline {\rho })$
is a representation of the Lie–Rinehart algebra
![]() $\mathcal {S}\otimes _{\mathbb {K}} A$
.
$\mathcal {S}\otimes _{\mathbb {K}} A$
.
Remark 3.34. We have the following category equivalence if A is unital:
First, the construction of Proposition 3.33 can be easily enhanced to a functor. In fact, assume that
![]() $\phi :{M}\to {M}^{\prime }$
is a homomorphism of admissible representations of a Leibniz pair
$\phi :{M}\to {M}^{\prime }$
is a homomorphism of admissible representations of a Leibniz pair
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
; then it is straightforward to deduce that
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
; then it is straightforward to deduce that
for all
![]() $x\in \mathcal {S}, a\in A.$
Thus,
$x\in \mathcal {S}, a\in A.$
Thus,
![]() $\phi :{M}\to {M}^{\prime }$
is also a homomorphism of representations of the Lie–Rinehart algebra
$\phi :{M}\to {M}^{\prime }$
is also a homomorphism of representations of the Lie–Rinehart algebra
![]() $\mathcal {S}\otimes _{\mathbb {K}} A.$
So we obtain a functor
$\mathcal {S}\otimes _{\mathbb {K}} A.$
So we obtain a functor
![]() $P:\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})\to \mathsf {Rep}(\mathcal {S}\otimes _{\mathbb {K}} A)$
, which is defined on the sets of objects and morphisms respectively by
$P:\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})\to \mathsf {Rep}(\mathcal {S}\otimes _{\mathbb {K}} A)$
, which is defined on the sets of objects and morphisms respectively by
 $$ \begin{align*} P(M;\rho)&=(M;\overline{\rho}),\\ P(\phi:{M}\to{M}^{\prime})&=(\phi:{M}\to{M}^{\prime}). \end{align*} $$
$$ \begin{align*} P(M;\rho)&=(M;\overline{\rho}),\\ P(\phi:{M}\to{M}^{\prime})&=(\phi:{M}\to{M}^{\prime}). \end{align*} $$
Conversely, let
![]() $(M;\rho )$
be a representation of the Lie–Rinehart algebra
$(M;\rho )$
be a representation of the Lie–Rinehart algebra
![]() $\mathcal {S}\otimes _{\mathbb {K}} A.$
Define
$\mathcal {S}\otimes _{\mathbb {K}} A.$
Define
![]() $\widetilde { \rho }:\mathcal {S} \,\rightarrow \, \mathfrak {gl}_{\mathbb {K}}(M)$
by
$\widetilde { \rho }:\mathcal {S} \,\rightarrow \, \mathfrak {gl}_{\mathbb {K}}(M)$
by
Similar to the above discussion, this can also be enhanced to a functor and give the equivalence between the categories
![]() $\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
and
$\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
and
![]() $ \mathsf {Rep}(\mathcal {S}\otimes _{\mathbb {K}} A)$
.
$ \mathsf {Rep}(\mathcal {S}\otimes _{\mathbb {K}} A)$
.
Let
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair and
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair and
![]() $\mathfrak h$
be a
$\mathfrak h$
be a
![]() $\mathbb {K}$
-Lie algebra. Then
$\mathbb {K}$
-Lie algebra. Then
 $(A,\mathcal {S}\oplus (\mathfrak h\otimes _{\mathbb {K}} {A}),[\cdot ,\cdot ],\tilde {\beta })$
is a Leibniz pair, where the
$(A,\mathcal {S}\oplus (\mathfrak h\otimes _{\mathbb {K}} {A}),[\cdot ,\cdot ],\tilde {\beta })$
is a Leibniz pair, where the
![]() $\mathbb {K}$
-Lie algebra structure on
$\mathbb {K}$
-Lie algebra structure on
![]() $\mathcal {S}\oplus (\mathfrak h\otimes _{\mathbb {K}} {A})$
is given by
$\mathcal {S}\oplus (\mathfrak h\otimes _{\mathbb {K}} {A})$
is given by
 $$ \begin{align*} &[(x,g\otimes a),(y,h\otimes b)]\\&\quad =([x,y]_{\mathcal{S}},h\otimes\beta(x)(b)-g\otimes\beta(y)(a)+[g,h]_{\mathfrak h}\otimes ab),\quad \forall x,y\in \mathcal{S}, g\otimes a, h\otimes b\in\mathfrak h\otimes_{\mathbb{K}} A, \end{align*} $$
$$ \begin{align*} &[(x,g\otimes a),(y,h\otimes b)]\\&\quad =([x,y]_{\mathcal{S}},h\otimes\beta(x)(b)-g\otimes\beta(y)(a)+[g,h]_{\mathfrak h}\otimes ab),\quad \forall x,y\in \mathcal{S}, g\otimes a, h\otimes b\in\mathfrak h\otimes_{\mathbb{K}} A, \end{align*} $$
and
 $\tilde {\beta }:\mathcal {S}\oplus (\mathfrak h\otimes _{\mathbb {K}} {A})\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}(A)$
is given by
$\tilde {\beta }:\mathcal {S}\oplus (\mathfrak h\otimes _{\mathbb {K}} {A})\,\rightarrow \, \mathsf {Der}_{\mathbb {K}}(A)$
is given by
 $$ \begin{align*} \tilde{\beta}(x,g\otimes a)=\beta(x). \end{align*} $$
$$ \begin{align*} \tilde{\beta}(x,g\otimes a)=\beta(x). \end{align*} $$
Denote this Leibniz pair by
![]() $\mathcal {S}\ltimes _{\beta } (\mathfrak h\otimes _{\mathbb {K}} {A})$
.
$\mathcal {S}\ltimes _{\beta } (\mathfrak h\otimes _{\mathbb {K}} {A})$
.
Let
![]() $({M};\rho )$
be an admissible representation over
$({M};\rho )$
be an admissible representation over
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $(V;\theta )$
be a representation of a
$(V;\theta )$
be a representation of a
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $\mathfrak h$
. Then
$\mathfrak h$
. Then
![]() ${V}\otimes _{\mathbb {K}} M$
has a natural
${V}\otimes _{\mathbb {K}} M$
has a natural
![]() ${A}$
-module structure:
${A}$
-module structure:
We define a
![]() $\mathbb {K}$
-linear map
$\mathbb {K}$
-linear map
![]() $ \rho \boxplus \theta :\mathcal {S}\ltimes _{\beta } (\mathfrak h\otimes _{\mathbb {K}} {A})\,\rightarrow \,\mathfrak {gl}_{\mathbb {K}}({V}\otimes _{\mathbb {K}} M)$
by
$ \rho \boxplus \theta :\mathcal {S}\ltimes _{\beta } (\mathfrak h\otimes _{\mathbb {K}} {A})\,\rightarrow \,\mathfrak {gl}_{\mathbb {K}}({V}\otimes _{\mathbb {K}} M)$
by
Then it is straightforward to verify the following result.
Lemma 3.35. With the above notations,
![]() $({V}\otimes _{\mathbb {K}} M;\rho \boxplus \theta )$
is an admissible representation of the Leibniz pair
$({V}\otimes _{\mathbb {K}} M;\rho \boxplus \theta )$
is an admissible representation of the Leibniz pair
![]() $\mathcal {S}\ltimes _{\beta } (\mathfrak h\otimes _{\mathbb {K}} {A})$
.
$\mathcal {S}\ltimes _{\beta } (\mathfrak h\otimes _{\mathbb {K}} {A})$
.
Let
![]() ${H}$
be a crossed homomorphism from the
${H}$
be a crossed homomorphism from the
![]() $\mathbb {K}$
-Lie algebra
$\mathbb {K}$
-Lie algebra
![]() $\mathcal {S}$
to
$\mathcal {S}$
to
![]() $ \mathfrak h\otimes _{\mathbb {K}}{A}$
. Then we have the Lie algebra homomorphism
$ \mathfrak h\otimes _{\mathbb {K}}{A}$
. Then we have the Lie algebra homomorphism
 $$ \begin{align*}\begin{aligned} &\iota_{H}: \mathcal{S} \to \mathcal{S}\ltimes_{\beta} (\mathfrak h\otimes_{\mathbb{K}} {A})\\ &\iota_{H}(x)=(x,{H} x),\quad \forall x\in \mathcal{S}.\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\iota_{H}: \mathcal{S} \to \mathcal{S}\ltimes_{\beta} (\mathfrak h\otimes_{\mathbb{K}} {A})\\ &\iota_{H}(x)=(x,{H} x),\quad \forall x\in \mathcal{S}.\end{aligned} \end{align*} $$
Similar to Theorem 3.26, we have the following result.
Theorem 3.36. Any crossed homomorphism
![]() $H:\mathcal {S}\,\rightarrow \,\mathfrak h\otimes _{\mathbb {K}}{A}$
induces a left module category structure of the category of admissible representations
$H:\mathcal {S}\,\rightarrow \,\mathfrak h\otimes _{\mathbb {K}}{A}$
induces a left module category structure of the category of admissible representations
![]() $\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
over the monoidal category
$\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
over the monoidal category
![]() $\mathsf {Rep}_{\mathbb {K}}(\mathfrak h)$
,
$\mathsf {Rep}_{\mathbb {K}}(\mathfrak h)$
,
 $$ \begin{align*}\begin{aligned} &\mathcal{F}_{H}:\mathsf{Rep}_{\mathbb{K}}(\mathfrak h)\times \mathsf{ARep}_{\mathbb{K}}(\mathcal{S}) \to \mathsf{ARep}_{\mathbb{K}}(\mathcal{S})\\ &\mathcal{F}_{H}\Big((V;\theta),({M};\rho)\Big)=({V}\otimes_{\mathbb{K}} M;(\rho\boxplus\theta)\circ\iota_{H}). \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} &\mathcal{F}_{H}:\mathsf{Rep}_{\mathbb{K}}(\mathfrak h)\times \mathsf{ARep}_{\mathbb{K}}(\mathcal{S}) \to \mathsf{ARep}_{\mathbb{K}}(\mathcal{S})\\ &\mathcal{F}_{H}\Big((V;\theta),({M};\rho)\Big)=({V}\otimes_{\mathbb{K}} M;(\rho\boxplus\theta)\circ\iota_{H}). \end{aligned}\end{align*} $$
Proof. We verify that the representation
![]() $({V}\otimes _{\mathbb {K}} M;(\rho \boxplus \theta )\circ \iota _{H})$
satisfies (17). For any
$({V}\otimes _{\mathbb {K}} M;(\rho \boxplus \theta )\circ \iota _{H})$
satisfies (17). For any
![]() $x\in \mathcal {S}, a\in A, v\in V, m\in M$
. Suppose
$x\in \mathcal {S}, a\in A, v\in V, m\in M$
. Suppose
 $H(x)=Hx=\sum _{i} x_{i}^{\mathfrak h}\otimes x^{A}_{i}$
or
$H(x)=Hx=\sum _{i} x_{i}^{\mathfrak h}\otimes x^{A}_{i}$
or
 $Hx=x_{i}^{\mathfrak h}\otimes x^{A}_{i}$
for simplicity. Then
$Hx=x_{i}^{\mathfrak h}\otimes x^{A}_{i}$
for simplicity. Then
 $$ \begin{align*}\begin{aligned} ((\rho\boxplus\theta)\circ\iota_{H})(x)(a(v\otimes m)) =&(\rho\boxplus\theta) (x, x_{i}^{\mathfrak h}\otimes x^{A}_{i})(v\otimes am)\\ =&v\otimes \rho(x)(am)+ \theta(x_{i}^{\mathfrak h}) v\otimes x^{A}_{i}am\\ =&a\Big(v\otimes \rho(x)(m)+ \theta(x_{i}^{\mathfrak h}) v\otimes x^{A}_{i}m\Big)+\beta(x)(a)(v\otimes m)\\ =&a((\rho\boxplus\theta)\circ\iota_{H})(x)(v\otimes m)+\beta(x)(a)(v\otimes m).\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} ((\rho\boxplus\theta)\circ\iota_{H})(x)(a(v\otimes m)) =&(\rho\boxplus\theta) (x, x_{i}^{\mathfrak h}\otimes x^{A}_{i})(v\otimes am)\\ =&v\otimes \rho(x)(am)+ \theta(x_{i}^{\mathfrak h}) v\otimes x^{A}_{i}am\\ =&a\Big(v\otimes \rho(x)(m)+ \theta(x_{i}^{\mathfrak h}) v\otimes x^{A}_{i}m\Big)+\beta(x)(a)(v\otimes m)\\ =&a((\rho\boxplus\theta)\circ\iota_{H})(x)(v\otimes m)+\beta(x)(a)(v\otimes m).\end{aligned} \end{align*} $$
The proof is similar to Theorem 3.26, so the details will be omitted.
Since
![]() $({A};\beta )$
is an admissible representation of a Leibniz pair
$({A};\beta )$
is an admissible representation of a Leibniz pair
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
, we obtain the following result.
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
, we obtain the following result.
Corollary 3.37. Let
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair,
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair,
![]() $(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
a
$(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
a
![]() $\mathbb {K}$
-Lie algebra and
$\mathbb {K}$
-Lie algebra and
![]() ${H}$
a crossed homomorphism from
${H}$
a crossed homomorphism from
![]() $\mathcal {S}$
to
$\mathcal {S}$
to
![]() $\mathfrak h\otimes _{\mathbb {K}}{A}$
. Then we have a functor
$\mathfrak h\otimes _{\mathbb {K}}{A}$
. Then we have a functor
 $$ \begin{align*}\begin{aligned} &\mathcal{F}_{{H}}^{A}:\mathsf{Rep}_{\mathbb{K}}(\mathfrak h)\to \mathsf{ARep}_{\mathbb{K}}(\mathcal{S}),\\ & (V;\theta)\mapsto (V\otimes_{\mathbb{K}}{A}; ({\beta}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{K}}(\mathfrak h).\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\mathcal{F}_{{H}}^{A}:\mathsf{Rep}_{\mathbb{K}}(\mathfrak h)\to \mathsf{ARep}_{\mathbb{K}}(\mathcal{S}),\\ & (V;\theta)\mapsto (V\otimes_{\mathbb{K}}{A}; ({\beta}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{K}}(\mathfrak h).\end{aligned} \end{align*} $$
We can also have a very useful functor on
![]() $\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
as follows.
$\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
as follows.
Corollary 3.38. Let
![]() $(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair,
$(A,\mathcal {S},[\cdot ,\cdot ]_{\mathcal {S}},\beta )$
be a Leibniz pair,
![]() $(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
a
$(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
a
![]() $\mathbb {K}$
-Lie algebra and
$\mathbb {K}$
-Lie algebra and
![]() ${H}$
a crossed homomorphism from
${H}$
a crossed homomorphism from
![]() $\mathcal {S}$
to
$\mathcal {S}$
to
![]() $\mathfrak h\otimes _{\mathbb {K}}{A}$
and
$\mathfrak h\otimes _{\mathbb {K}}{A}$
and
![]() $(V;\theta )$
a given representation of
$(V;\theta )$
a given representation of
![]() $\mathfrak h$
. Then we have a functor
$\mathfrak h$
. Then we have a functor
 $$ \begin{align*}\begin{aligned} &\mathcal{F}_{H}^{\theta} :\mathsf{ARep}_{\mathbb{K}}(\mathcal{S})\to \mathsf{ARep}_{\mathbb{K}}(\mathcal{S}),\\ & ({M};\rho)\mapsto (V\otimes_{\mathbb{K}}{M} ;({\rho}\boxplus \theta)\circ\iota_{H}),\quad\forall({M};\rho)\in\mathsf{ARep}_{\mathbb{K}}(\mathcal{S}).\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\mathcal{F}_{H}^{\theta} :\mathsf{ARep}_{\mathbb{K}}(\mathcal{S})\to \mathsf{ARep}_{\mathbb{K}}(\mathcal{S}),\\ & ({M};\rho)\mapsto (V\otimes_{\mathbb{K}}{M} ;({\rho}\boxplus \theta)\circ\iota_{H}),\quad\forall({M};\rho)\in\mathsf{ARep}_{\mathbb{K}}(\mathcal{S}).\end{aligned} \end{align*} $$
A special but very interesting case of the above result is that
![]() $(V;\theta )=(\mathfrak h;\mathsf {ad})$
.
$(V;\theta )=(\mathfrak h;\mathsf {ad})$
.
According to Corollaries 3.27 and 3.37, the bifunctors
![]() $F_{H}$
in Theorem 3.26 and
$F_{H}$
in Theorem 3.26 and
![]() $\mathcal {F}_{H}$
given in Theorem 3.36 are the actions of monoidal categories.
$\mathcal {F}_{H}$
given in Theorem 3.36 are the actions of monoidal categories.
4. Representations of Cartan-type Lie algebras
From the definition of a crossed homomorphism we see that it is generally hard to find nontrivial crossed homomorphisms. Next, we will show some examples of crossed homomorphisms and their tremendous power in obtaining new irreducible modules via results in the previous section.
4.1. Shen–Larsson functors of Witt type
For
![]() $n\geq 1$
, recall the Witt algebra
$n\geq 1$
, recall the Witt algebra
![]() $\mathcal {W}_{n}=\mathsf {Der} (A_{n})$
over the Laurent polynomial algebra
$\mathcal {W}_{n}=\mathsf {Der} (A_{n})$
over the Laurent polynomial algebra
 $A_{n}=\mathbb {C}[x_{1}^{\pm 1}, \cdots ,x_{n}^{\pm 1}]$
, which can be interpreted as the Lie algebra of (complex-valued) polynomial vector fields on an n-dimensional torus. Let
$A_{n}=\mathbb {C}[x_{1}^{\pm 1}, \cdots ,x_{n}^{\pm 1}]$
, which can be interpreted as the Lie algebra of (complex-valued) polynomial vector fields on an n-dimensional torus. Let
 $\partial _{i}=\frac {\partial }{\partial x_{i}}$
be the partial derivation with respect to the variable
$\partial _{i}=\frac {\partial }{\partial x_{i}}$
be the partial derivation with respect to the variable
![]() $x_{i}$
for
$x_{i}$
for
![]() $i=1,2,\dots ,n$
, and denote
$i=1,2,\dots ,n$
, and denote
![]() $d_{i}=x_{i}\partial _{i}$
and
$d_{i}=x_{i}\partial _{i}$
and
![]() $x^{r}=x_{1}^{r_{1}}x_{2}^{r_{2}}\cdots x_{n}^{r_{n}}$
for
$x^{r}=x_{1}^{r_{1}}x_{2}^{r_{2}}\cdots x_{n}^{r_{n}}$
for
![]() $r=(r_{1},r_{2},\cdots , r_{n})^{T}\in \mathbb {Z}^{n}$
. Then
$r=(r_{1},r_{2},\cdots , r_{n})^{T}\in \mathbb {Z}^{n}$
. Then
with the Lie bracket
Obviously,
![]() $(A_{n},\mathcal {W}_{n}, [\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
is a Lie–Rinehart algebra. Certainly,
$(A_{n},\mathcal {W}_{n}, [\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
is a Lie–Rinehart algebra. Certainly,
![]() $ (A_{n}; \textrm {Id})$
is the natural representation of the Lie–Rinehart algebra
$ (A_{n}; \textrm {Id})$
is the natural representation of the Lie–Rinehart algebra
![]() $(A_{n},\mathcal {W}_{n}, [\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
. Let
$(A_{n},\mathcal {W}_{n}, [\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
. Let
![]() $\mathfrak g=\mathfrak {gl}_{n}$
be the Lie algebra of all
$\mathfrak g=\mathfrak {gl}_{n}$
be the Lie algebra of all
![]() $n \times n$
complex matrices. Then
$n \times n$
complex matrices. Then
![]() $\mathcal {G}=\mathfrak {gl}_{n}\otimes A_{n}$
is a Lie
$\mathcal {G}=\mathfrak {gl}_{n}\otimes A_{n}$
is a Lie
![]() $A_{n}$
-algebra. For
$A_{n}$
-algebra. For
![]() $1\leq i, j \leq n$
, we use
$1\leq i, j \leq n$
, we use
![]() $E_{ij}$
to denote the
$E_{ij}$
to denote the
![]() $n\times n$
matrix with
$n\times n$
matrix with
![]() $1$
at the
$1$
at the
![]() $(i, j)$
entry and zeros elsewhere.
$(i, j)$
entry and zeros elsewhere.
Lemma 4.1. The linear map
![]() $H:\mathcal {W}_{n}\to \mathfrak {gl}_{n}\otimes A_{n}$
defined by
$H:\mathcal {W}_{n}\to \mathfrak {gl}_{n}\otimes A_{n}$
defined by
 $$ \begin{align*} H(x^{r}d_{j})= \sum_{i=1}^{n} r_{i} E_{ij}\otimes x^{r},\quad\forall r\in \mathbb{Z}^{n}, 1\leq j\leq n \end{align*} $$
$$ \begin{align*} H(x^{r}d_{j})= \sum_{i=1}^{n} r_{i} E_{ij}\otimes x^{r},\quad\forall r\in \mathbb{Z}^{n}, 1\leq j\leq n \end{align*} $$
is a crossed homomorphism from
![]() $\mathcal {W}_{n}$
to
$\mathcal {W}_{n}$
to
![]() $\mathfrak {gl}_{n}\otimes A_{n}$
.
$\mathfrak {gl}_{n}\otimes A_{n}$
.
Proof. This follows from (2.5) in [Reference Guo, Liu, Lu and Zhao16] (or (2.3) and Lemma 2.1 in [Reference Liu, Lu and Zhao25]) and Theorem 2.7.
By Lemma 4.1 and Corollary 3.27, we obtain the following result.
Corollary 4.2. We have a functor
 $F_{{H}}^{A_{n}}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {gl}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})$
given by
$F_{{H}}^{A_{n}}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {gl}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})$
given by
 $$ \begin{align*} F_{H}^{A_{n}}(V;\theta)=(V\otimes_{\mathbb{C}}{A_{n}}; (\mathrm{Id}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{C}}(\mathfrak {gl}_{n}). \end{align*} $$
$$ \begin{align*} F_{H}^{A_{n}}(V;\theta)=(V\otimes_{\mathbb{C}}{A_{n}}; (\mathrm{Id}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{C}}(\mathfrak {gl}_{n}). \end{align*} $$
Let
 ${\mathcal {A}}_{n}=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1},\partial _{1},\cdots ,\partial _{n}]$
be the Weyl algebra, which is the universal enveloping algebra of the Lie–Rinehart algebra
${\mathcal {A}}_{n}=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1},\partial _{1},\cdots ,\partial _{n}]$
be the Weyl algebra, which is the universal enveloping algebra of the Lie–Rinehart algebra
![]() $(A_{n},\mathcal {W}_{n}, [\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
. Let
$(A_{n},\mathcal {W}_{n}, [\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
. Let
![]() $(P;\rho )$
be a representation of
$(P;\rho )$
be a representation of
![]() $\mathcal {A}_{n}$
. It is obvious that
$\mathcal {A}_{n}$
. It is obvious that
![]() $(P;\rho |_{\mathcal {W}_{n}})$
is a
$(P;\rho |_{\mathcal {W}_{n}})$
is a
![]() $\mathcal {W}_{n}$
-module. By Lemma 4.1 and Corollary 3.28, we obtain the following result.
$\mathcal {W}_{n}$
-module. By Lemma 4.1 and Corollary 3.28, we obtain the following result.
Corollary 4.3. We have a functor
![]() $F_{{H}}^{P}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {gl}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})$
given by
$F_{{H}}^{P}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {gl}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})$
given by
Remark 4.4. The functor
![]() $F_{H}^{P}$
, introduced by Liu, Lu and Zhao in [Reference Liu, Lu and Zhao25] is a generalisation of the Shen–Larsson functor of type
$F_{H}^{P}$
, introduced by Liu, Lu and Zhao in [Reference Liu, Lu and Zhao25] is a generalisation of the Shen–Larsson functor of type
![]() $(\mathcal {W}_{n},\mathfrak {gl}_{n})$
, which gives a class of new simple modules over
$(\mathcal {W}_{n},\mathfrak {gl}_{n})$
, which gives a class of new simple modules over
![]() $\mathcal {W}_{n}$
. This class of simple
$\mathcal {W}_{n}$
. This class of simple
![]() $\mathcal {W}_{n}$
-modules was used in the classification of simple
$\mathcal {W}_{n}$
-modules was used in the classification of simple
![]() $\mathcal {W}_{n}$
-modules that are finitely generated as modules over its Cartan subalgebra (see [Reference Guo, Liu, Lu and Zhao16]).
$\mathcal {W}_{n}$
-modules that are finitely generated as modules over its Cartan subalgebra (see [Reference Guo, Liu, Lu and Zhao16]).
Next we take
![]() $\mathfrak g=\mathbb {C}$
, the 1-dimensional trivial Lie algebra. Let
$\mathfrak g=\mathbb {C}$
, the 1-dimensional trivial Lie algebra. Let
 $p=(p_{1},p_{2},\cdots ,p_{n})\in \mathbb {C}[t_{1}^{\pm 1}]\times \mathbb {C}[t_{2}^{\pm 1}]\times \cdots \times \mathbb {C}[t_{n}^{\pm 1}], q\in \mathbb {C}$
. Similar to the automorphism
$p=(p_{1},p_{2},\cdots ,p_{n})\in \mathbb {C}[t_{1}^{\pm 1}]\times \mathbb {C}[t_{2}^{\pm 1}]\times \cdots \times \mathbb {C}[t_{n}^{\pm 1}], q\in \mathbb {C}$
. Similar to the automorphism
![]() $\sigma _{b}$
in Section 2 of [Reference Tan and Zhao45], we can easily see that the linear map
$\sigma _{b}$
in Section 2 of [Reference Tan and Zhao45], we can easily see that the linear map
 $$ \begin{align*}\begin{aligned} &\mathcal{W}_{n}\to \mathcal{W}_{n}\ltimes_{\text{Id}} A_{n},\\ &x^{r}d_{i}\mapsto x^{r}(d_{i}+p_{i})+q r_{i}x^{r}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} &\mathcal{W}_{n}\to \mathcal{W}_{n}\ltimes_{\text{Id}} A_{n},\\ &x^{r}d_{i}\mapsto x^{r}(d_{i}+p_{i})+q r_{i}x^{r}, \end{aligned}\end{align*} $$
is a Lie algebra homomorphism. By Theorem 2.7, we see that the linear map
 $$ \begin{align*}\begin{aligned} H_{p,q}: &\mathcal{W}_{n}\to \mathfrak g\otimes A_{n} \cong A_{n},\\ & x^{r}d_{i}\mapsto (p_{i}+q r_{i})x^{r},\quad\forall r\in \mathbb{Z}^{n}, 1\leq i\leq n, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} H_{p,q}: &\mathcal{W}_{n}\to \mathfrak g\otimes A_{n} \cong A_{n},\\ & x^{r}d_{i}\mapsto (p_{i}+q r_{i})x^{r},\quad\forall r\in \mathbb{Z}^{n}, 1\leq i\leq n, \end{aligned}\end{align*} $$
is a crossed homomorphism from
![]() $\mathcal {W}_{n}$
to
$\mathcal {W}_{n}$
to
![]() $A_{n}$
. In fact,
$A_{n}$
. In fact,
![]() $H_{p,q}\in \mathsf {Der}_{\mathbb {C}}(\mathcal {W}_{n},A_{n})$
. By Lemma 4.1 and Corollary 3.28, we obtain the following result.
$H_{p,q}\in \mathsf {Der}_{\mathbb {C}}(\mathcal {W}_{n},A_{n})$
. By Lemma 4.1 and Corollary 3.28, we obtain the following result.
Corollary 4.5. We have a functor
![]() $F_{p,q} :\mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})$
defined by
$F_{p,q} :\mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n})$
defined by
Remark 4.6. By forgetting the
![]() $A_{n}$
-module structure, the corresponding functor
$A_{n}$
-module structure, the corresponding functor
![]() $F_{p,q}$
is just the twisting functor in the
$F_{p,q}$
is just the twisting functor in the
![]() $\mathcal {W}_{n}$
-module category introduced in [Reference Lu, Guo and Zhao28, Reference Lu and Zhao29, Reference Tan and Zhao45], where a lot of new simple modules were obtained over the Virasoro algebra and
$\mathcal {W}_{n}$
-module category introduced in [Reference Lu, Guo and Zhao28, Reference Lu and Zhao29, Reference Tan and Zhao45], where a lot of new simple modules were obtained over the Virasoro algebra and
![]() $\mathcal {W}_{n}$
.
$\mathcal {W}_{n}$
.
4.2. Shen–Larsson functors of divergence zero type
In this section we assume that
![]() $n\ge 2$
. Let us recall the divergence map
$n\ge 2$
. Let us recall the divergence map
![]() $ \mathrm {div}: \mathcal {W}_{n}\to A_{n}$
with
$ \mathrm {div}: \mathcal {W}_{n}\to A_{n}$
with
![]() $ x^{r}d_{i}\mapsto r_{i}x^{r},$
for all
$ x^{r}d_{i}\mapsto r_{i}x^{r},$
for all
![]() $r\in \mathbb {Z}^{n}.$
It is well-known that
$r\in \mathbb {Z}^{n}.$
It is well-known that
is a Lie subalgebra of
![]() $\mathcal {W}_{n}$
, called the Lie algebra of divergence zero vector fields on an n-dimensional torus. Let
$\mathcal {W}_{n}$
, called the Lie algebra of divergence zero vector fields on an n-dimensional torus. Let
![]() $d_{ij}(r)=r_{j}x^{r}d_{i}-r_{i}x^{r}d_{j}$
. Then
$d_{ij}(r)=r_{j}x^{r}d_{i}-r_{i}x^{r}d_{j}$
. Then
with the Lie bracket
 $$ \begin{align*} ~[d_{k},d_{ij}(r)]_{\mathcal{W}_{n}}&=r_{k}d_{ij}(r),\\ ~[d_{ij}(r),d_{pq}(s)]_{\mathcal{W}_{n}}&=r_{j}s_{p}d_{iq}(r+s)-r_{j}s_{q}d_{ip}(r+s)-r_{i}s_{p}d_{jq}(r+s)+r_{i}s_{q}d_{jp}(r+s), \end{align*} $$
$$ \begin{align*} ~[d_{k},d_{ij}(r)]_{\mathcal{W}_{n}}&=r_{k}d_{ij}(r),\\ ~[d_{ij}(r),d_{pq}(s)]_{\mathcal{W}_{n}}&=r_{j}s_{p}d_{iq}(r+s)-r_{j}s_{q}d_{ip}(r+s)-r_{i}s_{p}d_{jq}(r+s)+r_{i}s_{q}d_{jp}(r+s), \end{align*} $$
for
![]() $r,s\in \mathbb {Z}^{N}, i,j,p,q=1,\cdots ,n$
.
$r,s\in \mathbb {Z}^{N}, i,j,p,q=1,\cdots ,n$
.
Note that
![]() $\mathcal {S}_{n}$
is not a Lie–Rinehart subalgebra since
$\mathcal {S}_{n}$
is not a Lie–Rinehart subalgebra since
![]() $\mathcal {S}_{n}$
is not an
$\mathcal {S}_{n}$
is not an
![]() $A_{n}$
-module. It is straightforward to see that
$A_{n}$
-module. It is straightforward to see that
![]() $(A_{n},\mathcal {S}_{n},[\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
is a Leibniz pair.
$(A_{n},\mathcal {S}_{n},[\cdot ,\cdot ]_{\mathcal {W}_{n}},\textrm {Id})$
is a Leibniz pair.
Recall that
![]() $\mathfrak {sl}_{n}$
is the Lie subalgebra of
$\mathfrak {sl}_{n}$
is the Lie subalgebra of
![]() $\mathfrak {gl}_{n}$
consisting of all traceless complex matrices. The restriction
$\mathfrak {gl}_{n}$
consisting of all traceless complex matrices. The restriction
![]() $H|_{\mathcal {S}_{n}}$
of the crossed homomorphism H in Lemma 4.1 is a crossed homomorphism from
$H|_{\mathcal {S}_{n}}$
of the crossed homomorphism H in Lemma 4.1 is a crossed homomorphism from
![]() $\mathcal {S}_{n}$
to
$\mathcal {S}_{n}$
to
![]() $\mathfrak {sl}_{n}\otimes A_{n}$
. By Corollary 3.37, we obtain the following result.
$\mathfrak {sl}_{n}\otimes A_{n}$
. By Corollary 3.37, we obtain the following result.
Corollary 4.7. We have a functor
 $\mathcal {F}_{{H}}^{A_{n}}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sl}_{n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {S}_{n})$
defined by
$\mathcal {F}_{{H}}^{A_{n}}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sl}_{n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {S}_{n})$
defined by
 $$ \begin{align*} \mathcal{F}_{H}^{A_{n}}(V;\theta)=(V\otimes_{\mathbb{C}}{A_{n}}; (\text{Id}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{C}}(\mathfrak {sl}_{n}). \end{align*} $$
$$ \begin{align*} \mathcal{F}_{H}^{A_{n}}(V;\theta)=(V\otimes_{\mathbb{C}}{A_{n}}; (\text{Id}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{C}}(\mathfrak {sl}_{n}). \end{align*} $$
Let
![]() $(P;\rho )$
be a representation of
$(P;\rho )$
be a representation of
![]() $\mathcal {A}_{n}$
. It follows that
$\mathcal {A}_{n}$
. It follows that
![]() $(P;\rho |_{\mathcal {S}_{n}})$
is an admissible representation of
$(P;\rho |_{\mathcal {S}_{n}})$
is an admissible representation of
![]() $\mathcal {S}_{n}$
since
$\mathcal {S}_{n}$
since
![]() $\mathcal {S}_{n}\subset \mathcal {A}_{n}$
. By Theorem 3.36, we obtain the following result.
$\mathcal {S}_{n}\subset \mathcal {A}_{n}$
. By Theorem 3.36, we obtain the following result.
Corollary 4.8. We have a functor
![]() $\mathcal {F}_{{H}}^{P}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sl}_{n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {S}_{n})$
defined by
$\mathcal {F}_{{H}}^{P}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sl}_{n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {S}_{n})$
defined by
Remark 4.9. The functor
![]() $\mathcal {F}_{H}^{P}$
was introduced in [Reference Dubsky, Guo, Yao and Zhao8] and is a generalisation of the Shen–Larsson functor of type
$\mathcal {F}_{H}^{P}$
was introduced in [Reference Dubsky, Guo, Yao and Zhao8] and is a generalisation of the Shen–Larsson functor of type
![]() $(\mathcal {S}_{n},\mathfrak {sl}_{n})$
, to give a class of new simple modules over
$(\mathcal {S}_{n},\mathfrak {sl}_{n})$
, to give a class of new simple modules over
![]() $\mathcal {S}_{n}$
.
$\mathcal {S}_{n}$
.
4.3. Shen–Larsson functors of Hamiltonian type
For
![]() $r\in \mathbb {Z}^{2n}$
, let
$r\in \mathbb {Z}^{2n}$
, let
 $$ \begin{align*} h(r) = \sum_{i=1}^{n}(r_{n+i}x^{r}\partial_{i}-r_{i}x^{r}\partial_{n+i})\in \mathcal{W}_{2n}. \end{align*} $$
$$ \begin{align*} h(r) = \sum_{i=1}^{n}(r_{n+i}x^{r}\partial_{i}-r_{i}x^{r}\partial_{n+i})\in \mathcal{W}_{2n}. \end{align*} $$
It is well-known that
![]() $ \mathcal {H}_{n}=\text {Span}_{\mathbb {C}}\{h(r)\mid r\in \mathbb {Z}^{2n}\} $
is a Lie subalgebra of
$ \mathcal {H}_{n}=\text {Span}_{\mathbb {C}}\{h(r)\mid r\in \mathbb {Z}^{2n}\} $
is a Lie subalgebra of
![]() $\mathcal {W}_{2n}$
, with
$\mathcal {W}_{2n}$
, with
 $$ \begin{align*} [h(r),h(s)]_{\mathcal{W}_{2n}}=\sum_{i=1}^{n}(r_{n+i}s_{i}-s_{n+i}r_{i})h(r+s),\quad\forall r,s\in \mathbb{Z}^{2n}.\end{align*} $$
$$ \begin{align*} [h(r),h(s)]_{\mathcal{W}_{2n}}=\sum_{i=1}^{n}(r_{n+i}s_{i}-s_{n+i}r_{i})h(r+s),\quad\forall r,s\in \mathbb{Z}^{2n}.\end{align*} $$
This Lie algebra
![]() $\mathcal {H}_{n}$
is called the Lie algebra of Hamiltonian vector fields on a
$\mathcal {H}_{n}$
is called the Lie algebra of Hamiltonian vector fields on a
![]() $2n$
-dimensional torus. Note that
$2n$
-dimensional torus. Note that
![]() $\mathcal {H}_{n}$
is not a Lie–Rinehart algebra since
$\mathcal {H}_{n}$
is not a Lie–Rinehart algebra since
![]() $\mathcal {H}_{n}$
is not an
$\mathcal {H}_{n}$
is not an
![]() $A_{2n}$
-module. It is straightforward to see that
$A_{2n}$
-module. It is straightforward to see that
![]() $(A_{n},\mathcal {H}_{n},[\cdot ,\cdot ]_{\mathcal {W}_{2n}},\textrm {Id})$
is a Leibniz pair.
$(A_{n},\mathcal {H}_{n},[\cdot ,\cdot ]_{\mathcal {W}_{2n}},\textrm {Id})$
is a Leibniz pair.
Let
![]() $\mathfrak {sp}_{2n}$
be the Lie subalgebra of
$\mathfrak {sp}_{2n}$
be the Lie subalgebra of
![]() $\mathfrak {gl}_{2n}$
consisting of all symplectic matrices. The restriction
$\mathfrak {gl}_{2n}$
consisting of all symplectic matrices. The restriction
![]() $H|_{\mathcal {H}_{n}}$
of the crossed homomorphism H in Lemma 4.1 is a linear map
$H|_{\mathcal {H}_{n}}$
of the crossed homomorphism H in Lemma 4.1 is a linear map
![]() $\mathcal {H}_{n}\to \mathfrak {sp}_{2n}\otimes A_{2n}$
given by
$\mathcal {H}_{n}\to \mathfrak {sp}_{2n}\otimes A_{2n}$
given by
 $$ \begin{align*} H(h(r))=\begin{pmatrix} r_{1}r_{n+1}&\cdots&r_{1}r_{2n}&-r_{1}r_{1}&\cdots&-r_{1}r_{n}\\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ r_{n}r_{n+1}&\cdots&r_{n}r_{2n}&-r_{n}r_{1}&\cdots&-r_{n}r_{n}\\ r_{n+1}r_{n+1}&\cdots&r_{n+1}r_{2n}&-r_{n+1}r_{1}&\cdots&-r_{n+1}r_{n}\\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ r_{2n}r_{n+1}&\cdots&r_{2n}r_{2n}&-r_{2n}r_{1}&\cdots&-r_{2n}r_{n}\\ \end{pmatrix}\otimes x^{r}\in \mathfrak{sp}_{2n}\otimes A_{2n}, \end{align*} $$
$$ \begin{align*} H(h(r))=\begin{pmatrix} r_{1}r_{n+1}&\cdots&r_{1}r_{2n}&-r_{1}r_{1}&\cdots&-r_{1}r_{n}\\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ r_{n}r_{n+1}&\cdots&r_{n}r_{2n}&-r_{n}r_{1}&\cdots&-r_{n}r_{n}\\ r_{n+1}r_{n+1}&\cdots&r_{n+1}r_{2n}&-r_{n+1}r_{1}&\cdots&-r_{n+1}r_{n}\\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ r_{2n}r_{n+1}&\cdots&r_{2n}r_{2n}&-r_{2n}r_{1}&\cdots&-r_{2n}r_{n}\\ \end{pmatrix}\otimes x^{r}\in \mathfrak{sp}_{2n}\otimes A_{2n}, \end{align*} $$
which is certainly a crossed homomorphism from
![]() $\mathcal {H}_{n}$
to
$\mathcal {H}_{n}$
to
![]() $\mathfrak {sp}_{2n}\otimes A_{2n}$
. By Corollary 3.37, we obtain the following result.
$\mathfrak {sp}_{2n}\otimes A_{2n}$
. By Corollary 3.37, we obtain the following result.
Corollary 4.10. We have a functor
 $\mathcal {F}_{{H}}^{A_{2n}}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sp}_{2n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {H}_{n})$
defined by
$\mathcal {F}_{{H}}^{A_{2n}}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sp}_{2n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {H}_{n})$
defined by
 $$ \begin{align*} \mathcal{F}_{H}^{A_{2n}}(V;\theta)=(V\otimes_{\mathbb{C}}{A_{2n}}; (\text{Id}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{C}}(\mathfrak{sp}_{2n}). \end{align*} $$
$$ \begin{align*} \mathcal{F}_{H}^{A_{2n}}(V;\theta)=(V\otimes_{\mathbb{C}}{A_{2n}}; (\text{Id}\boxplus \theta)\circ\iota_{H}),\quad\forall(V;\theta)\in \mathsf{Rep}_{\mathbb{C}}(\mathfrak{sp}_{2n}). \end{align*} $$
Remark 4.11. The functors defined in Corollaries 4.2, 4.7 and 4.10 are the well-known Shen–Larsson functors of type
![]() $(\mathcal {W}_{n},\mathfrak {gl}_{n})$
, type
$(\mathcal {W}_{n},\mathfrak {gl}_{n})$
, type
![]() $(\mathcal {S}_{n},\mathfrak {sl}_{n})$
and type
$(\mathcal {S}_{n},\mathfrak {sl}_{n})$
and type
![]() $(\mathcal {H}_{n},\mathfrak {sp}_{2n})$
, respectively. The functor of type
$(\mathcal {H}_{n},\mathfrak {sp}_{2n})$
, respectively. The functor of type
![]() $(\mathcal {W}_{n},\mathfrak {gl}_{n})$
was introduced by Shen [Reference Shen42] (over polynomial algebras) and Larsson [Reference Larsson24] (over Laurent polynomial algebras) independently in different settings. The functors of type
$(\mathcal {W}_{n},\mathfrak {gl}_{n})$
was introduced by Shen [Reference Shen42] (over polynomial algebras) and Larsson [Reference Larsson24] (over Laurent polynomial algebras) independently in different settings. The functors of type
![]() $(\mathcal {S}_{n},\mathfrak {sl}_{n})$
and
$(\mathcal {S}_{n},\mathfrak {sl}_{n})$
and
![]() $(\mathcal {H}_{n},\mathfrak {sp}_{2n})$
were introduced by Shen over polynomial algebras [Reference Shen42] and further studied in [Reference Billig and Talboom5, Reference Talboom44] over Laurent polynomial algebras. For any simple
$(\mathcal {H}_{n},\mathfrak {sp}_{2n})$
were introduced by Shen over polynomial algebras [Reference Shen42] and further studied in [Reference Billig and Talboom5, Reference Talboom44] over Laurent polynomial algebras. For any simple
![]() $\mathfrak {gl}_{n}$
-module V the simplicity of the
$\mathfrak {gl}_{n}$
-module V the simplicity of the
![]() $\mathcal {W}_{n}$
-module
$\mathcal {W}_{n}$
-module
 $F_{H}^{A_{n}}(V;\theta )$
was determined in [Reference Eswara Rao9, Reference Guo and Zhao17, Reference Liu and Zhao26]. In particular, simple
$F_{H}^{A_{n}}(V;\theta )$
was determined in [Reference Eswara Rao9, Reference Guo and Zhao17, Reference Liu and Zhao26]. In particular, simple
![]() $\mathcal {W}_{n}$
-modules of this class (with V as simple finite-dimensional
$\mathcal {W}_{n}$
-modules of this class (with V as simple finite-dimensional
![]() $\mathfrak {gl}_{n}$
-modules) are all simple Harish–Chandra
$\mathfrak {gl}_{n}$
-modules) are all simple Harish–Chandra
![]() $\mathcal {W}_{n}$
-modules [Reference Billig and Futorny2]. Note that there are still no results for
$\mathcal {W}_{n}$
-modules [Reference Billig and Futorny2]. Note that there are still no results for
![]() $\mathcal {H}_{n}$
similar to those in [Reference Eswara Rao9, Reference Guo and Zhao17, Reference Liu and Zhao26].
$\mathcal {H}_{n}$
similar to those in [Reference Eswara Rao9, Reference Guo and Zhao17, Reference Liu and Zhao26].
4.4. Actions of monoidal categories for generalised Cartan type
Let A be a commutative associative
![]() $\mathbb {C}$
-algebra and let
$\mathbb {C}$
-algebra and let
![]() $\Delta $
be a nonzero
$\Delta $
be a nonzero
![]() $\mathbb {C}$
-vector space of commuting
$\mathbb {C}$
-vector space of commuting
![]() $\mathbb {C}$
-derivations of A. Let us first recall the construction of the generalised Witt algebras from [Reference Passman37]. The tensor product
$\mathbb {C}$
-derivations of A. Let us first recall the construction of the generalised Witt algebras from [Reference Passman37]. The tensor product
![]() $A\Delta :=A\otimes _{\mathbb {C}}\Delta $
acts on A by
$A\Delta :=A\otimes _{\mathbb {C}}\Delta $
acts on A by
Since A is commutative, this gives rise to a linear transformation
![]() $ \alpha : A\Delta \to \mathsf {Der}_{\mathbb {C}}(A). $
Define a bracket
$ \alpha : A\Delta \to \mathsf {Der}_{\mathbb {C}}(A). $
Define a bracket
![]() $[\cdot ,\cdot ]_{A\Delta }$
on
$[\cdot ,\cdot ]_{A\Delta }$
on
![]() $A\Delta $
by
$A\Delta $
by
which gives a Lie algebra structure on
![]() $A\Delta $
. Then
$A\Delta $
. Then
![]() $\alpha $
is clearly an action of
$\alpha $
is clearly an action of
![]() $A\Delta $
on the commutative Lie algebra A. Assume that
$A\Delta $
on the commutative Lie algebra A. Assume that
![]() $\dim _{\mathbb {C}}\Delta <\infty $
. Then there are
$\dim _{\mathbb {C}}\Delta <\infty $
. Then there are
![]() $\partial _{1},\cdots ,\partial _{n}\in \Delta $
such that
$\partial _{1},\cdots ,\partial _{n}\in \Delta $
such that
![]() $A\Delta $
is a free A-module with basis
$A\Delta $
is a free A-module with basis
![]() $\{\partial _{1},\cdots ,\partial _{n}\}$
(see [Reference Zhao49]). We denote this Lie algebra by
$\{\partial _{1},\cdots ,\partial _{n}\}$
(see [Reference Zhao49]). We denote this Lie algebra by
![]() $\mathcal {W}_{n}(A,\Delta )$
. Note that
$\mathcal {W}_{n}(A,\Delta )$
. Note that
![]() $(A,\mathcal {W}_{n}(A,\Delta ),[\cdot ,\cdot ]_{_{A\Delta }},\alpha )$
is a Lie–Rinehart algebra.
$(A,\mathcal {W}_{n}(A,\Delta ),[\cdot ,\cdot ]_{_{A\Delta }},\alpha )$
is a Lie–Rinehart algebra.
Now we have a generalisation of Lemma 4.1.
Lemma 4.12. The linear map
![]() $H: \mathcal {W}_{n}(A,\Delta )\to \mathfrak {gl}_{n} \otimes A$
defined by
$H: \mathcal {W}_{n}(A,\Delta )\to \mathfrak {gl}_{n} \otimes A$
defined by
 $$ \begin{align*} H\left(\sum_{i=1}^{n} a_{i}\partial_{i}\right)=\sum_{i=1}^{n}\sum_{j=1}^{n} E_{ij}\otimes\partial_{i} (a_{j}),\quad a_{i}\in A \end{align*} $$
$$ \begin{align*} H\left(\sum_{i=1}^{n} a_{i}\partial_{i}\right)=\sum_{i=1}^{n}\sum_{j=1}^{n} E_{ij}\otimes\partial_{i} (a_{j}),\quad a_{i}\in A \end{align*} $$
is a crossed homomorphism from
![]() $\mathcal {W}_{n}(A,\Delta )$
to
$\mathcal {W}_{n}(A,\Delta )$
to
![]() $\mathfrak {gl}_{n} \otimes A$
.
$\mathfrak {gl}_{n} \otimes A$
.
Proof. It is straightforward but tedious to verify the above formula. We omit the details.
Similar to Corollary 4.2, by Lemma 4.12 and Theorem 3.26 we obtain the following result.
Corollary 4.13. We have a functor
![]() $F_{{H}}^{A}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {gl}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n}(A,\Delta ))$
defined by
$F_{{H}}^{A}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {gl}_{n})\to \mathsf {WRep}_{\mathbb {C}}(\mathcal {W}_{n}(A,\Delta ))$
defined by
Remark 4.14.
-
(1) If
 $A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1}]$
and
$A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1}]$
and
 $\Delta =\text {Span}_{\mathbb {C}}\{x_{1}\frac {\partial }{\partial x_{1}},\cdots , x_{n}\frac {\partial }{\partial x_{n}}\}$
,
$\Delta =\text {Span}_{\mathbb {C}}\{x_{1}\frac {\partial }{\partial x_{1}},\cdots , x_{n}\frac {\partial }{\partial x_{n}}\}$
,
 $\mathcal {W}_{n}(A,\Delta )$
is the standard Witt algebra
$\mathcal {W}_{n}(A,\Delta )$
is the standard Witt algebra
 $\mathcal {W}_{n}$
and the corresponding
$\mathcal {W}_{n}$
and the corresponding
 $F_{H}^{A}$
is the Shen–Larsson functor of type
$F_{H}^{A}$
is the Shen–Larsson functor of type
 $(\mathcal {W}_{n},\mathfrak {gl}_{n})$
.
$(\mathcal {W}_{n},\mathfrak {gl}_{n})$
. -
(2) If
 $A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1}]$
and
$A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1}]$
and
 $\bar \Delta =\text {Span}_{\mathbb {C}}\{\frac {\partial }{\partial x_{1}},\cdots , \frac {\partial }{\partial x_{n}}\}$
,
$\bar \Delta =\text {Span}_{\mathbb {C}}\{\frac {\partial }{\partial x_{1}},\cdots , \frac {\partial }{\partial x_{n}}\}$
,
 $\mathcal {W}_{n}(A,\bar \Delta )$
is also the standard Witt algebra
$\mathcal {W}_{n}(A,\bar \Delta )$
is also the standard Witt algebra
 $\mathcal {W}_{n}$
. However, the corresponding Shen–Larsson functor
$\mathcal {W}_{n}$
. However, the corresponding Shen–Larsson functor
 $\bar F_{H}^{A}$
is different from the standard
$\bar F_{H}^{A}$
is different from the standard
 $F_{H}^{A}$
except on the category of finite-dimensional
$F_{H}^{A}$
except on the category of finite-dimensional
 $\mathfrak {gl}_{n}$
-modules. This was pointed out by Liu, Lu and Zhao in [Reference Liu, Lu and Zhao25].
$\mathfrak {gl}_{n}$
-modules. This was pointed out by Liu, Lu and Zhao in [Reference Liu, Lu and Zhao25]. -
(3) If A is taken to be a polynomial algebra with finitely many variables
 $x_{i}$
together with some
$x_{i}$
together with some
 $x_{i}^{-1}$
and
$x_{i}^{-1}$
and
 $\Delta $
to be some mixed differential operators w.r.t.
$\Delta $
to be some mixed differential operators w.r.t.
 $x_{i}$
, the Lie algebra
$x_{i}$
, the Lie algebra
 $\mathcal {W}_{n}(A,\Delta )$
was introduced by Xu [Reference Xu48]. The corresponding Shen–Larsson functor
$\mathcal {W}_{n}(A,\Delta )$
was introduced by Xu [Reference Xu48]. The corresponding Shen–Larsson functor
 $F_{H}^{A}$
was introduced and studied by Zhao [Reference Zhao50], generalising Rao’s results in [Reference Eswara Rao9].
$F_{H}^{A}$
was introduced and studied by Zhao [Reference Zhao50], generalising Rao’s results in [Reference Eswara Rao9]. -
(4) Under certain finite conditions, the functor
 $F_{H}^{A}$
is the Shen–Larsson functor
$F_{H}^{A}$
is the Shen–Larsson functor
 $\mathcal {W}_{n}(A,\Delta )$
introduced and studied by Skryabin in [Reference Skryabin, Arslanov, Parshin and Shafarevich43].
$\mathcal {W}_{n}(A,\Delta )$
introduced and studied by Skryabin in [Reference Skryabin, Arslanov, Parshin and Shafarevich43]. -
(5) Let A be the coordinate ring of an irreducible affine variety and
 $\Delta $
a certain subalgebra of
$\Delta $
a certain subalgebra of
 $\mathsf {Der} (A)$
. The corresponding Shen–Larsson functor
$\mathsf {Der} (A)$
. The corresponding Shen–Larsson functor
 $F_{H}^{A}$
was introduced and studied in [Reference Billig and Futorny3, Reference Billig, Futorny and Nilsson4] to give new simple modules over
$F_{H}^{A}$
was introduced and studied in [Reference Billig and Futorny3, Reference Billig, Futorny and Nilsson4] to give new simple modules over
 $\mathcal {W}_{n}(A,\Delta )$
.
$\mathcal {W}_{n}(A,\Delta )$
.
Now let us define the divergence map
![]() $\mathrm {div}: \mathcal {W}_{n}(A,\Delta )\to A$
to be the
$\mathrm {div}: \mathcal {W}_{n}(A,\Delta )\to A$
to be the
![]() $\mathbb {C}$
-linear extension of
$\mathbb {C}$
-linear extension of
Let
![]() $ \mathcal {S}_{n}(A,\Delta )=\{w\in A\Delta \mid \text {div}(w)=0\}. $
Then
$ \mathcal {S}_{n}(A,\Delta )=\{w\in A\Delta \mid \text {div}(w)=0\}. $
Then
![]() $\mathcal {S}_{n}(A,\Delta )$
is a Lie subalgebra of
$\mathcal {S}_{n}(A,\Delta )$
is a Lie subalgebra of
![]() $\mathcal {W}_{n}(A,\Delta )$
; see [Reference Bergen and Passman1] for more details. If
$\mathcal {W}_{n}(A,\Delta )$
; see [Reference Bergen and Passman1] for more details. If
 $A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1}]$
and
$A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{n}^{\pm 1}]$
and
 $\Delta =\text {Span}_{\mathbb {C}}\{x_{1}\frac {\partial }{\partial x_{1}},\cdots , x_{n}\frac {\partial }{\partial x_{n}}\}$
,
$\Delta =\text {Span}_{\mathbb {C}}\{x_{1}\frac {\partial }{\partial x_{1}},\cdots , x_{n}\frac {\partial }{\partial x_{n}}\}$
,
![]() $\mathcal {S}_{n}(A,\Delta )$
is the Lie algebra
$\mathcal {S}_{n}(A,\Delta )$
is the Lie algebra
![]() $S_{n}$
of divergence zero vector fields on an n-dimensional torus.
$S_{n}$
of divergence zero vector fields on an n-dimensional torus.
Note that
![]() $\mathcal {S}_{n}(A,\Delta )$
is not a Lie–Rinehart subalgebra since
$\mathcal {S}_{n}(A,\Delta )$
is not a Lie–Rinehart subalgebra since
![]() $\mathcal {S}_{n}(A,\Delta )$
is not an A-module. It is straightforward to see that
$\mathcal {S}_{n}(A,\Delta )$
is not an A-module. It is straightforward to see that
![]() $(A,\mathcal {S}_{n}(A,\Delta ),[\cdot ,\cdot ]_{A\Delta },\textrm {Id})$
is a Leibniz pair.
$(A,\mathcal {S}_{n}(A,\Delta ),[\cdot ,\cdot ]_{A\Delta },\textrm {Id})$
is a Leibniz pair.
It is clear that
![]() $H|_{\mathcal {S}_{n}(A,\Delta )}$
is a crossed homomorphism from
$H|_{\mathcal {S}_{n}(A,\Delta )}$
is a crossed homomorphism from
![]() $\mathcal {S}_{n}(A,\Delta )$
to
$\mathcal {S}_{n}(A,\Delta )$
to
![]() $\mathfrak {sl}_{n} \otimes A$
. Similar to Corollary 4.5, by Lemma 4.12 and Corollary 3.37 we obtain the following result.
$\mathfrak {sl}_{n} \otimes A$
. Similar to Corollary 4.5, by Lemma 4.12 and Corollary 3.37 we obtain the following result.
Corollary 4.15. We have a functor
![]() $\mathcal {F}_{{H}}^{A}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sl}_{n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {S}_{n}(A,\Delta ))$
defined by
$\mathcal {F}_{{H}}^{A}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sl}_{n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {S}_{n}(A,\Delta ))$
defined by
Now let us define a map
![]() $D: A\to \mathcal {W}_{2n}(A,\Delta ) $
to be the linear extension of
$D: A\to \mathcal {W}_{2n}(A,\Delta ) $
to be the linear extension of
 $$ \begin{align*} D(a) = \sum_{i=1}^{n}(\partial_{i}(a)\partial_{n+i}-\partial_{n+i}(a)\partial_{i}),\quad \forall a\in A. \end{align*} $$
$$ \begin{align*} D(a) = \sum_{i=1}^{n}(\partial_{i}(a)\partial_{n+i}-\partial_{n+i}(a)\partial_{i}),\quad \forall a\in A. \end{align*} $$
Let
![]() $ \mathcal {H}_{n}(A,\Delta )=\{D(a)\mid a\in A\}. $
Then
$ \mathcal {H}_{n}(A,\Delta )=\{D(a)\mid a\in A\}. $
Then
![]() $\mathcal {H}_{n}(A,\Delta )$
is a Lie subalgebra of
$\mathcal {H}_{n}(A,\Delta )$
is a Lie subalgebra of
![]() $\mathcal {W}_{2n}(A,\Delta )$
, with
$\mathcal {W}_{2n}(A,\Delta )$
, with
 $$ \begin{align*} [D(a),D(b)]_{A\Delta}=D\left(\sum_{i=1}^{n}(\partial_{i}(a)\partial_{n+i}(b)-\partial_{n+i}(a)\partial_{i}(b))\right),\quad\forall a,b\in A. \end{align*} $$
$$ \begin{align*} [D(a),D(b)]_{A\Delta}=D\left(\sum_{i=1}^{n}(\partial_{i}(a)\partial_{n+i}(b)-\partial_{n+i}(a)\partial_{i}(b))\right),\quad\forall a,b\in A. \end{align*} $$
If
 $A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{2n}^{\pm 1}]$
and
$A=\mathbb {C}[x_{1}^{\pm 1},\cdots ,x_{2n}^{\pm 1}]$
and
 $\Delta =\text {Span}_{\mathbb {C}}\{x_{1}\frac {\partial }{\partial x_{1}},\cdots , x_{2n}\frac {\partial }{\partial x_{2n}}\}$
, then
$\Delta =\text {Span}_{\mathbb {C}}\{x_{1}\frac {\partial }{\partial x_{1}},\cdots , x_{2n}\frac {\partial }{\partial x_{2n}}\}$
, then
![]() $\mathcal {H}_{n}(A,\Delta )$
is the Lie algebra of Hamiltonian vector fields on a
$\mathcal {H}_{n}(A,\Delta )$
is the Lie algebra of Hamiltonian vector fields on a
![]() $2n$
-dimensional torus.
$2n$
-dimensional torus.
Note that
![]() $\mathcal {H}_{n}(A,\Delta )$
is not a Lie–Rinehart algebra since
$\mathcal {H}_{n}(A,\Delta )$
is not a Lie–Rinehart algebra since
![]() $\mathcal {H}_{n}(A,\Delta )$
is not an A-module. It is straightforward to see that
$\mathcal {H}_{n}(A,\Delta )$
is not an A-module. It is straightforward to see that
![]() $(A,\mathcal {H}_{n}(A,\Delta ),[\cdot ,\cdot ]_{A\Delta },\textrm {Id})$
is a Leibniz pair.
$(A,\mathcal {H}_{n}(A,\Delta ),[\cdot ,\cdot ]_{A\Delta },\textrm {Id})$
is a Leibniz pair.
The restriction
![]() $H|_{\mathcal {H}_{n}(A,\Delta )}$
of the crossed homomorphism H in Lemma 4.12 is a crossed homomorphism from
$H|_{\mathcal {H}_{n}(A,\Delta )}$
of the crossed homomorphism H in Lemma 4.12 is a crossed homomorphism from
![]() $\mathcal {H}_{n}(A,\Delta )$
to
$\mathcal {H}_{n}(A,\Delta )$
to
![]() $\mathfrak {sp}_{2n}\otimes A$
. Similar to Corollary 4.10, by Lemma 4.12 and Corollary 3.37 we obtain the following result.
$\mathfrak {sp}_{2n}\otimes A$
. Similar to Corollary 4.10, by Lemma 4.12 and Corollary 3.37 we obtain the following result.
Corollary 4.16. We have a functor
![]() $\mathcal {F}_{{H}}^{A}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sp}_{2n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {H}_{n}(A,\Delta ))$
defined by
$\mathcal {F}_{{H}}^{A}:\mathsf {Rep}_{\mathbb {C}}(\mathfrak {sp}_{2n})\to \mathsf {ARep}_{\mathbb {C}}(\mathcal {H}_{n}(A,\Delta ))$
defined by
5. Deformation and cohomologies of crossed homomorphisms
In this section, first we give the Maurer–Cartan characterisation of crossed homomorphisms of Lie algebras. In particular, we give the differential graded Lie algebra that controls deformations of crossed homomorphisms. Then we define the cohomology groups of crossed homomorphisms, which can be applied to study linear deformations of crossed homomorphisms.
5.1. The differential graded Lie algebra controlling deformations
Definition 5.1. A differential graded Lie algebra
![]() $(\mathfrak g,[\cdot ,\cdot ],d)$
is a
$(\mathfrak g,[\cdot ,\cdot ],d)$
is a
![]() $\mathbb {Z}$
-graded vector space
$\mathbb {Z}$
-graded vector space
![]() $\mathfrak g=\oplus _{i\in \mathbb {Z}}\mathfrak g_{i}$
together with a bilinear bracket
$\mathfrak g=\oplus _{i\in \mathbb {Z}}\mathfrak g_{i}$
together with a bilinear bracket
![]() $[\cdot ,\cdot ]\colon \mathfrak g\otimes \mathfrak g\to \mathfrak g$
and a linear map
$[\cdot ,\cdot ]\colon \mathfrak g\otimes \mathfrak g\to \mathfrak g$
and a linear map
![]() $d\colon \mathfrak g\to \mathfrak g$
satisfying the following conditions:
$d\colon \mathfrak g\to \mathfrak g$
satisfying the following conditions:
-
•
 $[\mathfrak g_{i},\mathfrak g_{j}]\subset \mathfrak g_{i+j}$
and
$[\mathfrak g_{i},\mathfrak g_{j}]\subset \mathfrak g_{i+j}$
and
 $[a,b]=-(-1)^{\overline {a}\overline {b}}[b,a]$
for every
$[a,b]=-(-1)^{\overline {a}\overline {b}}[b,a]$
for every
 $a,b$
homogeneous.
$a,b$
homogeneous. -
• Every
 $a,b,c$
homogeneous satisfies the Jacobi identity
$a,b,c$
homogeneous satisfies the Jacobi identity  $$ \begin{align*} [a,[b,c]]=[[a,b],c]+(-1)^{\overline{a}\overline{b}}[b,[a,c]].\end{align*} $$
$$ \begin{align*} [a,[b,c]]=[[a,b],c]+(-1)^{\overline{a}\overline{b}}[b,[a,c]].\end{align*} $$
-
•
 $d(\mathfrak g_{i})\subset \mathfrak g_{i+1}$
,
$d(\mathfrak g_{i})\subset \mathfrak g_{i+1}$
,
 $d\circ d=0$
and
$d\circ d=0$
and
 $d[a,b]=[da,b]+(-1)^{\overline {a}}[a,db]$
. The map d is called the differential of
$d[a,b]=[da,b]+(-1)^{\overline {a}}[a,db]$
. The map d is called the differential of
 $\mathfrak g$
.
$\mathfrak g$
.
We have used the notation
![]() $\bar a=i$
if
$\bar a=i$
if
![]() $a\in \mathfrak g_{i}$
.
$a\in \mathfrak g_{i}$
.
Definition 5.2 [Reference Loday and Vallette27]
Let
![]() $(\mathfrak g=\oplus _{k\in \mathbb Z}\mathfrak g_{k},[\cdot ,\cdot ],d)$
be a differential graded Lie algebra. A degree
$(\mathfrak g=\oplus _{k\in \mathbb Z}\mathfrak g_{k},[\cdot ,\cdot ],d)$
be a differential graded Lie algebra. A degree
![]() $1$
element
$1$
element
![]() $\theta \in \mathfrak g_{1}$
is called a Maurer–Cartan element of
$\theta \in \mathfrak g_{1}$
is called a Maurer–Cartan element of
![]() $\mathfrak g$
if it satisfies the following Maurer–Cartan equation:
$\mathfrak g$
if it satisfies the following Maurer–Cartan equation:
 $$ \begin{align} d \theta+\frac{1}{2}[\theta,\theta]=0. \end{align} $$
$$ \begin{align} d \theta+\frac{1}{2}[\theta,\theta]=0. \end{align} $$
Proposition 5.3 [Reference Loday and Vallette27]
Let
![]() $(\mathfrak g=\oplus _{k\in \mathbb Z}\mathfrak g_{k},[\cdot ,\cdot ],d)$
be a differential graded Lie algebra and let
$(\mathfrak g=\oplus _{k\in \mathbb Z}\mathfrak g_{k},[\cdot ,\cdot ],d)$
be a differential graded Lie algebra and let
![]() $\mu \in \mathfrak g_{1}$
be a Maurer–Cartan element. Then the map
$\mu \in \mathfrak g_{1}$
be a Maurer–Cartan element. Then the map
is a differential on the graded Lie algebra
![]() $(\mathfrak g,[\cdot ,\cdot ])$
. For any
$(\mathfrak g,[\cdot ,\cdot ])$
. For any
![]() $v\in \mathfrak g_{1}$
, the sum
$v\in \mathfrak g_{1}$
, the sum
![]() $\mu +v$
is a Maurer–Cartan element of the differential graded Lie algebra
$\mu +v$
is a Maurer–Cartan element of the differential graded Lie algebra
![]() $(\mathfrak g, [\cdot ,\cdot ],d)$
if and only if v is a Maurer–Cartan element of the differential graded Lie algebra
$(\mathfrak g, [\cdot ,\cdot ],d)$
if and only if v is a Maurer–Cartan element of the differential graded Lie algebra
![]() $(\mathfrak g, [\cdot ,\cdot ], d_{\mu })$
.
$(\mathfrak g, [\cdot ,\cdot ], d_{\mu })$
.
Let
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
and
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
and
![]() $(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
be Lie algebras and
$(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
be Lie algebras and
![]() $\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
be an action of
$\rho :\mathfrak g\,\rightarrow \,\mathsf {Der}(\mathfrak h)$
be an action of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak h$
. Consider the graded vector space
$\mathfrak h$
. Consider the graded vector space
 $$ \begin{align*}{\mathcal{C}}^{*}(\mathfrak g,\mathfrak h):=\oplus_{k\geq 0}\mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h).\end{align*} $$
$$ \begin{align*}{\mathcal{C}}^{*}(\mathfrak g,\mathfrak h):=\oplus_{k\geq 0}\mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h).\end{align*} $$
Define
![]() $d:\mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)\,\rightarrow \,\mathsf {Hom}(\wedge ^{m+1}\mathfrak g,\mathfrak h)$
by
$d:\mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)\,\rightarrow \,\mathsf {Hom}(\wedge ^{m+1}\mathfrak g,\mathfrak h)$
by
 $$ \begin{align} (df) ( x_{1},\cdots, x_{m+1} ) &=\sum_{i=1}^{m+1}(-1)^{m+i}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{m+1})\\ \nonumber&\quad +\sum_{1\le i< j\le m+1}(-1)^{m+i+j-1}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,x_{m+1}), \end{align} $$
$$ \begin{align} (df) ( x_{1},\cdots, x_{m+1} ) &=\sum_{i=1}^{m+1}(-1)^{m+i}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{m+1})\\ \nonumber&\quad +\sum_{1\le i< j\le m+1}(-1)^{m+i+j-1}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,x_{m+1}), \end{align} $$
for all
![]() $f\in \mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)$
. Define a skew-symmetric bracket operation
$f\in \mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)$
. Define a skew-symmetric bracket operation
![]() $\left [\![ \cdot ,\cdot \right ]\!] : \mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)\times \mathsf {Hom}(\wedge ^{n}\mathfrak g,\mathfrak h)\longrightarrow \mathsf {Hom}(\wedge ^{m+n}\mathfrak g,\mathfrak h)$
by
$\left [\![ \cdot ,\cdot \right ]\!] : \mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)\times \mathsf {Hom}(\wedge ^{n}\mathfrak g,\mathfrak h)\longrightarrow \mathsf {Hom}(\wedge ^{m+n}\mathfrak g,\mathfrak h)$
by
 $$ \begin{align} &\nonumber\left[\![ f_{1},f_{2}\right]\!] (x_{1},x_{2},\cdots,x_{m+n})\\ &=(-1)^{mn+1}\sum_{\sigma\in \mathbb S_{(m,n)}}(-1)^{\sigma}[f_{1}(x_{\sigma(1)},\cdots,x_{\sigma(m)}),f_{2}(x_{\sigma(m+1)},\cdots,x_{\sigma(m+n)})]_{\mathfrak h} \end{align} $$
$$ \begin{align} &\nonumber\left[\![ f_{1},f_{2}\right]\!] (x_{1},x_{2},\cdots,x_{m+n})\\ &=(-1)^{mn+1}\sum_{\sigma\in \mathbb S_{(m,n)}}(-1)^{\sigma}[f_{1}(x_{\sigma(1)},\cdots,x_{\sigma(m)}),f_{2}(x_{\sigma(m+1)},\cdots,x_{\sigma(m+n)})]_{\mathfrak h} \end{align} $$
for all
![]() $f_{1}\in \mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)$
and
$f_{1}\in \mathsf {Hom}(\wedge ^{m}\mathfrak g,\mathfrak h)$
and
![]() $f_{2}\in \mathsf {Hom}(\wedge ^{n}\mathfrak g,\mathfrak h)$
. Here
$f_{2}\in \mathsf {Hom}(\wedge ^{n}\mathfrak g,\mathfrak h)$
. Here
![]() $\mathbb S_{(m,n)}$
denotes the set of all
$\mathbb S_{(m,n)}$
denotes the set of all
![]() $(m,n)$
-shuffles.
$(m,n)$
-shuffles.
Note that for all
![]() $u,v\in \mathfrak h$
,
$u,v\in \mathfrak h$
,
![]() $\left [\![ u,v\right ]\!] =-[u,v]_{\mathfrak h}$
.
$\left [\![ u,v\right ]\!] =-[u,v]_{\mathfrak h}$
.
Proposition 5.4. With the above notations,
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d)$
is a differential graded Lie algebra. Its Maurer–Cartan elements are precisely crossed homomorphisms from
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d)$
is a differential graded Lie algebra. Its Maurer–Cartan elements are precisely crossed homomorphisms from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
.
$\rho $
.
Proof. In short, the graded Lie algebra
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
is obtained via the derived bracket [Reference Kosmann-Schwarzbach23, Reference Voronov46]. In fact, the Nijenhuis–Richardson bracket
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
is obtained via the derived bracket [Reference Kosmann-Schwarzbach23, Reference Voronov46]. In fact, the Nijenhuis–Richardson bracket
![]() $[\cdot ,\cdot ]_{\mathsf {NR}}$
associated to the direct sum vector space
$[\cdot ,\cdot ]_{\mathsf {NR}}$
associated to the direct sum vector space
![]() $\mathfrak g\oplus V$
gives rise to a graded Lie algebra
$\mathfrak g\oplus V$
gives rise to a graded Lie algebra
![]() $(\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}(\mathfrak g\oplus \mathfrak h),\mathfrak g\oplus \mathfrak h),[\cdot ,\cdot ]_{\mathsf {NR}})$
. Obviously,
$(\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}(\mathfrak g\oplus \mathfrak h),\mathfrak g\oplus \mathfrak h),[\cdot ,\cdot ]_{\mathsf {NR}})$
. Obviously,
![]() $\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
is an abelian subalgebra. We denote the Lie brackets
$\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
is an abelian subalgebra. We denote the Lie brackets
![]() $[\cdot ,\cdot ]_{\mathfrak g}$
and
$[\cdot ,\cdot ]_{\mathfrak g}$
and
![]() $[\cdot ,\cdot ]_{\mathfrak h}$
by
$[\cdot ,\cdot ]_{\mathfrak h}$
by
![]() $\mu _{\mathfrak g}$
and
$\mu _{\mathfrak g}$
and
![]() $\mu _{\mathfrak h}$
, respectively. Since
$\mu _{\mathfrak h}$
, respectively. Since
![]() $\rho $
is an action of the Lie algebra
$\rho $
is an action of the Lie algebra
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
, we deduce that
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
, we deduce that
![]() $\mu _{\mathfrak g}+\rho $
is a semidirect product Lie algebra structure on
$\mu _{\mathfrak g}+\rho $
is a semidirect product Lie algebra structure on
![]() $\mathfrak g\oplus \mathfrak h$
. Thus,
$\mathfrak g\oplus \mathfrak h$
. Thus,
![]() $\mu _{\mathfrak g}+\rho $
and
$\mu _{\mathfrak g}+\rho $
and
![]() $\mu _{\mathfrak h}$
are Maurer–Cartan elements of the graded Lie algebra
$\mu _{\mathfrak h}$
are Maurer–Cartan elements of the graded Lie algebra
![]() $({\mathcal {C}}^{*}(\mathfrak g\oplus \mathfrak h,\mathfrak g\oplus \mathfrak h),[\cdot ,\cdot ]_{\mathsf {NR}})$
. Define a differential
$({\mathcal {C}}^{*}(\mathfrak g\oplus \mathfrak h,\mathfrak g\oplus \mathfrak h),[\cdot ,\cdot ]_{\mathsf {NR}})$
. Define a differential
![]() $d_{\mu _{\mathfrak h}}$
on
$d_{\mu _{\mathfrak h}}$
on
![]() $({\mathcal {C}}^{*}(\mathfrak g\oplus \mathfrak h,\mathfrak g\oplus \mathfrak h),[\cdot ,\cdot ]_{\mathsf {NR}})$
via
$({\mathcal {C}}^{*}(\mathfrak g\oplus \mathfrak h,\mathfrak g\oplus \mathfrak h),[\cdot ,\cdot ]_{\mathsf {NR}})$
via
Further, we define the derived bracket on the graded vector space
![]() $\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
by
$\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
by
which is exactly the bracket given by (20). By
![]() $[\mu _{\mathfrak h},\mu _{\mathfrak h}]_{\mathsf {NR}}=0,$
we deduce that
$[\mu _{\mathfrak h},\mu _{\mathfrak h}]_{\mathsf {NR}}=0,$
we deduce that
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
is a graded Lie algebra.
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
is a graded Lie algebra.
Moreover, by
![]() $\mathrm {Im}\rho \subset \mathsf {Der}(\mathfrak h)$
, we have
$\mathrm {Im}\rho \subset \mathsf {Der}(\mathfrak h)$
, we have
![]() $[\mu _{\mathfrak g}+\rho ,\mu _{\mathfrak h}]_{\mathsf {NR}}=0.$
We define a linear map
$[\mu _{\mathfrak g}+\rho ,\mu _{\mathfrak h}]_{\mathsf {NR}}=0.$
We define a linear map
![]() $d=:[\mu _{\mathfrak g}+\rho ,\cdot ]_{\mathsf {NR}}$
on the graded space
$d=:[\mu _{\mathfrak g}+\rho ,\cdot ]_{\mathsf {NR}}$
on the graded space
![]() ${\mathcal {C}}^{*}(\mathfrak g\oplus \mathfrak h,\mathfrak g\oplus \mathfrak h)$
. We obtain that d is closed on the subspace
${\mathcal {C}}^{*}(\mathfrak g\oplus \mathfrak h,\mathfrak g\oplus \mathfrak h)$
. We obtain that d is closed on the subspace
![]() $\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
and is given by (19).
$\oplus _{k\geq 0}\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
and is given by (19).
By
![]() $[\mu _{\mathfrak g}+\rho ,\mu _{\mathfrak g}+\rho ]_{\mathsf {NR}}=0$
, we obtain that
$[\mu _{\mathfrak g}+\rho ,\mu _{\mathfrak g}+\rho ]_{\mathsf {NR}}=0$
, we obtain that
![]() $d\circ d=0.$
Moreover, by
$d\circ d=0.$
Moreover, by
![]() $[\mu _{\mathfrak g}+\rho ,\mu _{\mathfrak h}]_{\mathsf {NR}}=0$
, we deduce that d is a derivation of
$[\mu _{\mathfrak g}+\rho ,\mu _{\mathfrak h}]_{\mathsf {NR}}=0$
, we deduce that d is a derivation of
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
. Therefore,
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
. Therefore,
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d)$
is a differential graded Lie algebra.
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d)$
is a differential graded Lie algebra.
Finally, for a degree 1 element
![]() ${H}\in \mathsf {Hom}(\mathfrak g,\mathfrak h)$
, we have
${H}\in \mathsf {Hom}(\mathfrak g,\mathfrak h)$
, we have
 $$ \begin{align*} \big(dH+\frac{1}{2}\left[\![ {H},{H}\right]\!] \big)(x,y)=\rho(x)({H} y)-\rho(y)({H} x)-{H}[x,y]_{\mathfrak g}+[{H} x,{H} y]_{\mathfrak h}. \end{align*} $$
$$ \begin{align*} \big(dH+\frac{1}{2}\left[\![ {H},{H}\right]\!] \big)(x,y)=\rho(x)({H} y)-\rho(y)({H} x)-{H}[x,y]_{\mathfrak g}+[{H} x,{H} y]_{\mathfrak h}. \end{align*} $$
Thus, Maurer–Cartan elements are precisely crossed homomorphisms from
![]() $(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
to
$(\mathfrak g,[\cdot ,\cdot ]_{\mathfrak g})$
to
![]() $(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
with respect to the action
$(\mathfrak h,[\cdot ,\cdot ]_{\mathfrak h})$
with respect to the action
![]() $\rho $
. The proof is finished.
$\rho $
. The proof is finished.
Let
![]() ${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
![]() $\rho $
. Since
$\rho $
. Since
![]() ${H}$
is a Maurer–Cartan element of the differential graded Lie algebra
${H}$
is a Maurer–Cartan element of the differential graded Lie algebra
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d)$
by Proposition 5.4, it follows from Proposition 5.3 that
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d)$
by Proposition 5.4, it follows from Proposition 5.3 that
![]() $d_{{H}}:=d+\left [\![ {H},\cdot \right ]\!] $
is a graded derivation on the graded Lie algebra
$d_{{H}}:=d+\left [\![ {H},\cdot \right ]\!] $
is a graded derivation on the graded Lie algebra
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
satisfying
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] )$
satisfying
![]() $d^{2}_{{H}}=0$
. Therefore,
$d^{2}_{{H}}=0$
. Therefore,
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d_{{H}})$
is a differential graded Lie algebra. This differential graded Lie algebra can control deformations of crossed homomorphisms. We have obtained the following result.
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d_{{H}})$
is a differential graded Lie algebra. This differential graded Lie algebra can control deformations of crossed homomorphisms. We have obtained the following result.
Theorem 5.5. Let
![]() ${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
![]() $\rho $
. For a linear map
$\rho $
. For a linear map
![]() ${H}^{\prime }:\mathfrak g\longrightarrow \mathfrak h$
,
${H}^{\prime }:\mathfrak g\longrightarrow \mathfrak h$
,
![]() ${H}+{H}^{\prime }$
is still a crossed homomorphism from
${H}+{H}^{\prime }$
is still a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
if and only if
$\rho $
if and only if
![]() ${H}^{\prime }$
is a Maurer–Cartan element of the differential graded Lie algebra
${H}^{\prime }$
is a Maurer–Cartan element of the differential graded Lie algebra
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d_{{H}})$
.
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),\left [\![ \cdot ,\cdot \right ]\!] ,d_{{H}})$
.
5.2. Cohomologies of crossed homomorphisms
In this subsection, we define cohomologies of a crossed homomorphism, which can be used to study linear deformations in Section 5.3.
Recall that
![]() $\rho _{H}$
defined by (4) is a representation of
$\rho _{H}$
defined by (4) is a representation of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak h$
. Let
$\mathfrak h$
. Let
![]() $d_{\rho _{{H}}}: \mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)\longrightarrow \mathsf {Hom}(\wedge ^{k+1}\mathfrak g,\mathfrak h)$
be the corresponding Chevalley–Eilenberg coboundary operator. More precisely, for all
$d_{\rho _{{H}}}: \mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)\longrightarrow \mathsf {Hom}(\wedge ^{k+1}\mathfrak g,\mathfrak h)$
be the corresponding Chevalley–Eilenberg coboundary operator. More precisely, for all
![]() $f\in \mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
and
$f\in \mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
and
![]() $x_{1},\cdots ,x_{k+1}\in \mathfrak g$
, we have
$x_{1},\cdots ,x_{k+1}\in \mathfrak g$
, we have
 $$ \begin{align} &\quad d_{\rho_{{H}}} f(x_{1},\cdots,x_{k+1})\notag\\ &=\sum_{i=1}^{k+1}(-1)^{i+1}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots, x_{k+1})+\sum_{i=1}^{k+1}(-1)^{i+1}[{H} x_{i},f(x_{1},\cdots,\hat{x}_{i},\cdots, x_{k+1})]_{\mathfrak h}\\ &\quad +\sum_{1\le i<j\le k+1}(-1)^{i+j}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots, x_{k+1}). \notag \end{align} $$
$$ \begin{align} &\quad d_{\rho_{{H}}} f(x_{1},\cdots,x_{k+1})\notag\\ &=\sum_{i=1}^{k+1}(-1)^{i+1}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots, x_{k+1})+\sum_{i=1}^{k+1}(-1)^{i+1}[{H} x_{i},f(x_{1},\cdots,\hat{x}_{i},\cdots, x_{k+1})]_{\mathfrak h}\\ &\quad +\sum_{1\le i<j\le k+1}(-1)^{i+j}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots, x_{k+1}). \notag \end{align} $$
It is obvious that
![]() $u\in \mathfrak h$
is closed if and only if
$u\in \mathfrak h$
is closed if and only if
![]() $ \rho (x)u+[{H} x,u]_{\mathfrak h}=0 $
for all
$ \rho (x)u+[{H} x,u]_{\mathfrak h}=0 $
for all
![]() $x\in \mathfrak g$
, and
$x\in \mathfrak g$
, and
![]() $f\in \mathsf {Hom}(\mathfrak g,\mathfrak h)$
is closed if and only if
$f\in \mathsf {Hom}(\mathfrak g,\mathfrak h)$
is closed if and only if
Definition 5.6. Let
![]() ${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
![]() $\rho $
. Denote by
$\rho $
. Denote by
![]() ${\mathcal {C}}^{k}(\mathfrak g,\mathfrak h)=\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
and
${\mathcal {C}}^{k}(\mathfrak g,\mathfrak h)=\mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
and
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h)=\oplus _{k\geq 0}{\mathcal {C}}^{k}(\mathfrak g,\mathfrak h),d_{\rho _{{H}}})$
the above cochain complex. Denote the set of k-cocycles by
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h)=\oplus _{k\geq 0}{\mathcal {C}}^{k}(\mathfrak g,\mathfrak h),d_{\rho _{{H}}})$
the above cochain complex. Denote the set of k-cocycles by
![]() $\mathcal {Z}^{k}(\mathfrak g,\mathfrak h)$
and the set of k-coboundaries by
$\mathcal {Z}^{k}(\mathfrak g,\mathfrak h)$
and the set of k-coboundaries by
![]() $\mathcal {B}^{k}(\mathfrak g,\mathfrak h)$
. Denote by
$\mathcal {B}^{k}(\mathfrak g,\mathfrak h)$
. Denote by
the kth cohomology group, which will be taken to be the k
th cohomology group for the crossed homomorphism
![]() $ H$
.
$ H$
.
Comparing the coboundary operators
![]() $d_{\rho _{{H}}}$
given above and the operators
$d_{\rho _{{H}}}$
given above and the operators
![]() $d_{{H}}=d+\left [\![ {H},\cdot \right ]\!] $
defined by the Maurer–Cartan element
$d_{{H}}=d+\left [\![ {H},\cdot \right ]\!] $
defined by the Maurer–Cartan element
![]() ${H}$
, we have the following.
${H}$
, we have the following.
Proposition 5.7. Let
![]() ${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism. Then we have
${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism. Then we have
 $$ \begin{align*} d_{\rho_{{H}}}f=(-1)^{k-1}d_{{H}}f,\quad \forall f\in \mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h). \end{align*} $$
$$ \begin{align*} d_{\rho_{{H}}}f=(-1)^{k-1}d_{{H}}f,\quad \forall f\in \mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h). \end{align*} $$
Proof. Indeed, for all
![]() $x_{1},x_{2},\cdots ,x_{k+1}\in \mathfrak g$
and
$x_{1},x_{2},\cdots ,x_{k+1}\in \mathfrak g$
and
![]() $f\in \mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
, we have
$f\in \mathsf {Hom}(\wedge ^{k}\mathfrak g,\mathfrak h)$
, we have
 $$ \begin{align*} &(-1)^{k-1}(d_{{H}}f)(x_{1},x_{2},\cdots,x_{k+1})\\ &\quad =(-1)^{k-1}(df+\left[\![ {H},f\right]\!] )(x_{1},\cdots,x_{k+1})\\ &\quad =\sum_{i=1}^{i+1}(-1)^{i+1}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{k+1}) \nonumber \\[-14pt] \nonumber \\&\qquad +\sum_{1\le i< j\le k+1}(-1)^{i+j}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,x_{k+1})\\ &\qquad +(-1)^{k-1}(-1)^{k+1}\sum_{\sigma\in \mathbb S_{(1,k)}}(-1)^{\sigma}[{H} x_{\sigma(1)},f(x_{\sigma(2)},\cdots,x_{\sigma(k+1)})]_{\mathfrak h}\\ &\quad =\sum_{i=1}^{i+1}(-1)^{i+1}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{k+1})\\&\qquad +\sum_{1\le i< j\le k+1}(-1)^{i+j}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,x_{k+1})\\ &\qquad +\sum_{i=1}^{k+1}(-1)^{i-1}[{H} x_{i},f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{k+1})]_{\mathfrak h}\\ &\qquad =(d_{\rho_{{H}}}f)(x_{1},x_{2},\cdots,x_{k+1}), \end{align*} $$
$$ \begin{align*} &(-1)^{k-1}(d_{{H}}f)(x_{1},x_{2},\cdots,x_{k+1})\\ &\quad =(-1)^{k-1}(df+\left[\![ {H},f\right]\!] )(x_{1},\cdots,x_{k+1})\\ &\quad =\sum_{i=1}^{i+1}(-1)^{i+1}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{k+1}) \nonumber \\[-14pt] \nonumber \\&\qquad +\sum_{1\le i< j\le k+1}(-1)^{i+j}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,x_{k+1})\\ &\qquad +(-1)^{k-1}(-1)^{k+1}\sum_{\sigma\in \mathbb S_{(1,k)}}(-1)^{\sigma}[{H} x_{\sigma(1)},f(x_{\sigma(2)},\cdots,x_{\sigma(k+1)})]_{\mathfrak h}\\ &\quad =\sum_{i=1}^{i+1}(-1)^{i+1}\rho(x_{i})f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{k+1})\\&\qquad +\sum_{1\le i< j\le k+1}(-1)^{i+j}f([x_{i},x_{j}]_{\mathfrak g},x_{1},\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,x_{k+1})\\ &\qquad +\sum_{i=1}^{k+1}(-1)^{i-1}[{H} x_{i},f(x_{1},\cdots,\hat{x}_{i},\cdots,x_{k+1})]_{\mathfrak h}\\ &\qquad =(d_{\rho_{{H}}}f)(x_{1},x_{2},\cdots,x_{k+1}), \end{align*} $$
which implies that
![]() $d_{\rho _{{H}}}f=(-1)^{k-1}d_{{H}}f$
.
$d_{\rho _{{H}}}f=(-1)^{k-1}d_{{H}}f$
.
At the end of this section, we show that certain homomorphisms between crossed homomorphisms induce homomorphisms between the corresponding cohomology groups. Let
![]() ${H}$
and
${H}$
and
![]() $\widetilde {H}$
be two crossed homomorphisms from
$\widetilde {H}$
be two crossed homomorphisms from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
and
$\rho $
and
![]() $(\phi _{\mathfrak g},\phi _{\mathfrak h})$
a homomorphism from
$(\phi _{\mathfrak g},\phi _{\mathfrak h})$
a homomorphism from
![]() $\widetilde {H}$
to
$\widetilde {H}$
to
![]() ${H}$
in which
${H}$
in which
![]() $\phi _{\mathfrak g}$
is invertible. For all
$\phi _{\mathfrak g}$
is invertible. For all
![]() $k\geq 0$
, define
$k\geq 0$
, define
 $$ \begin{align*} \Phi:&\mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h)\,\rightarrow\, \mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h)\\ &f\mapsto \phi_{\mathfrak h}\circ f\circ (\phi_{\mathfrak g}^{-1})^{\otimes k}. \end{align*} $$
$$ \begin{align*} \Phi:&\mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h)\,\rightarrow\, \mathsf{Hom}(\wedge^{k}\mathfrak g,\mathfrak h)\\ &f\mapsto \phi_{\mathfrak h}\circ f\circ (\phi_{\mathfrak g}^{-1})^{\otimes k}. \end{align*} $$
Theorem 5.8. Let
![]() ${H}$
and
${H}$
and
![]() $\widetilde {H}$
be two crossed homomorphisms from
$\widetilde {H}$
be two crossed homomorphisms from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
of
$\rho $
of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak h$
and
$\mathfrak h$
and
![]() $(\phi _{\mathfrak g},\phi _{\mathfrak h})$
be a homomorphism from
$(\phi _{\mathfrak g},\phi _{\mathfrak h})$
be a homomorphism from
![]() $\widetilde {H}$
to
$\widetilde {H}$
to
![]() ${H}$
in which
${H}$
in which
![]() $\phi _{\mathfrak g}$
is invertible. Then the above
$\phi _{\mathfrak g}$
is invertible. Then the above
![]() $\Phi $
is a cochain map from the cochain complex
$\Phi $
is a cochain map from the cochain complex
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),d_{\rho _{\widetilde {H}}})$
to
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),d_{\rho _{\widetilde {H}}})$
to
![]() $({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),d_{\rho _{{H}}})$
. Consequently,
$({\mathcal {C}}^{*}(\mathfrak g,\mathfrak h),d_{\rho _{{H}}})$
. Consequently,
![]() $\Phi $
induces a homomorphism
$\Phi $
induces a homomorphism
 $\Phi _{*}: \widetilde {\mathcal {H}}^{k}(\mathfrak g,\mathfrak h)\,\rightarrow \, \mathcal {H}^{k}(\mathfrak g,\mathfrak h)$
between corresponding cohomology groups.
$\Phi _{*}: \widetilde {\mathcal {H}}^{k}(\mathfrak g,\mathfrak h)\,\rightarrow \, \mathcal {H}^{k}(\mathfrak g,\mathfrak h)$
between corresponding cohomology groups.
Proof. By the fact that
![]() $(\phi _{\mathfrak g},\phi _{\mathfrak h})$
is a homomorphism from
$(\phi _{\mathfrak g},\phi _{\mathfrak h})$
is a homomorphism from
![]() $\widetilde {H}$
to
$\widetilde {H}$
to
![]() ${H}$
, we have
${H}$
, we have
 $$ \begin{align*} &\quad (\Phi (d_{\rho_{\widetilde{{H}}}}f))(x_{1},\cdots,x_{k+1})=\phi_{\mathfrak h} (d_{\rho_{\widetilde{{H}}}}f)(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &=\sum_{i=1}^{i+1}(-1)^{i+1}\phi_{\mathfrak h}\rho(\phi_{\mathfrak g}^{-1}(x_{i}))f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &\quad +\sum_{1\le i< j\le k+1}(-1)^{i+j}\phi_{\mathfrak h} f([\phi_{\mathfrak g}^{-1} (x_{i}),\phi_{\mathfrak g}^{-1} (x_{j})]_{\mathfrak g},\phi_{\mathfrak g} {}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &\quad +\sum_{i=1}^{k+1}(-1)^{i+1}\phi_{\mathfrak h}[\widetilde{{H}} \phi_{\mathfrak g}^{-1} (x_{i}),f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1}( x_{k+1}))]_{\mathfrak h}\\ &=\sum_{i=1}^{i+1}(-1)^{i+1}\rho( x_{i})\phi_{\mathfrak h} f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1})) \nonumber \\[-14pt] \nonumber \\&\quad +\sum_{1\le i< j\le k+1}(-1)^{i+j}\phi_{\mathfrak h} f(\phi_{\mathfrak g}^{-1}[ x_{i},x_{j}]_{\mathfrak g},\phi_{\mathfrak g} {}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &\quad +\sum_{i=1}^{k+1}(-1)^{i+1}[{H} (x_{i}),\phi_{\mathfrak h} f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1}( x_{k+1}))]_{\mathfrak h}\\ &= d_{\rho_{{H}}}\Phi (f)(x_{1},\cdots,x_{k+1}), \end{align*} $$
$$ \begin{align*} &\quad (\Phi (d_{\rho_{\widetilde{{H}}}}f))(x_{1},\cdots,x_{k+1})=\phi_{\mathfrak h} (d_{\rho_{\widetilde{{H}}}}f)(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &=\sum_{i=1}^{i+1}(-1)^{i+1}\phi_{\mathfrak h}\rho(\phi_{\mathfrak g}^{-1}(x_{i}))f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &\quad +\sum_{1\le i< j\le k+1}(-1)^{i+j}\phi_{\mathfrak h} f([\phi_{\mathfrak g}^{-1} (x_{i}),\phi_{\mathfrak g}^{-1} (x_{j})]_{\mathfrak g},\phi_{\mathfrak g} {}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &\quad +\sum_{i=1}^{k+1}(-1)^{i+1}\phi_{\mathfrak h}[\widetilde{{H}} \phi_{\mathfrak g}^{-1} (x_{i}),f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1}( x_{k+1}))]_{\mathfrak h}\\ &=\sum_{i=1}^{i+1}(-1)^{i+1}\rho( x_{i})\phi_{\mathfrak h} f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1})) \nonumber \\[-14pt] \nonumber \\&\quad +\sum_{1\le i< j\le k+1}(-1)^{i+j}\phi_{\mathfrak h} f(\phi_{\mathfrak g}^{-1}[ x_{i},x_{j}]_{\mathfrak g},\phi_{\mathfrak g} {}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\hat{x}_{j},\cdots,\phi_{\mathfrak g}^{-1} (x_{k+1}))\\ &\quad +\sum_{i=1}^{k+1}(-1)^{i+1}[{H} (x_{i}),\phi_{\mathfrak h} f(\phi_{\mathfrak g}^{-1} (x_{1}),\cdots,\hat{x}_{i},\cdots,\phi_{\mathfrak g}^{-1}( x_{k+1}))]_{\mathfrak h}\\ &= d_{\rho_{{H}}}\Phi (f)(x_{1},\cdots,x_{k+1}), \end{align*} $$
which implies that
![]() $\Phi $
is a cochain map.
$\Phi $
is a cochain map.
Corollary 5.9. Let
![]() ${H}$
and
${H}$
and
![]() $\widetilde {H}$
be two isomorphic crossed homomorphisms. Then the cohomology groups
$\widetilde {H}$
be two isomorphic crossed homomorphisms. Then the cohomology groups
 $\widetilde {\mathcal {H}}^{k}(\mathfrak g,\mathfrak h)$
and
$\widetilde {\mathcal {H}}^{k}(\mathfrak g,\mathfrak h)$
and
![]() $ \mathcal {H}^{k}(\mathfrak g,\mathfrak h)$
are isomorphic for any
$ \mathcal {H}^{k}(\mathfrak g,\mathfrak h)$
are isomorphic for any
![]() $k\in \mathbb {Z}_{+}$
.
$k\in \mathbb {Z}_{+}$
.
5.3. Linear deformations of crossed homomorphisms
In this subsection, we study linear deformations of crossed homomorphisms using the cohomology theory introduced in Subsection 5.2 and show that isomorphic linear deformations are identified with the same class in the second cohomology group. We give the notion of a Nijenhuis element associated to a crossed homomorphism, which gives rise to a trivial deformation.
Definition 5.10. Let
![]() ${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
${H}:\mathfrak g\longrightarrow \mathfrak h$
be a crossed homomorphism with respect to the action
![]() $\rho $
and
$\rho $
and
![]() $\mathfrak H:\mathfrak g\longrightarrow \mathfrak h$
be a linear map. If
$\mathfrak H:\mathfrak g\longrightarrow \mathfrak h$
be a linear map. If
![]() ${H}_{t}={H}+t\mathfrak H$
is still a crossed homomorphism from
${H}_{t}={H}+t\mathfrak H$
is still a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
for all t, we say that
$\rho $
for all t, we say that
![]() $\mathfrak H$
generates a (one-parameter) linear deformation of the crossed homomorphism
$\mathfrak H$
generates a (one-parameter) linear deformation of the crossed homomorphism
![]() ${H}$
.
${H}$
.
It is direct to check that
![]() ${H}_{t}={H}+t\mathfrak H$
is a linear deformation of a crossed homomorphism
${H}_{t}={H}+t\mathfrak H$
is a linear deformation of a crossed homomorphism
![]() ${H}$
if and only if for any
${H}$
if and only if for any
![]() $x,y\in \mathfrak g$
,
$x,y\in \mathfrak g$
,
Note that Equation (23) means that
![]() $\mathfrak H$
is a 1-cocycle of the crossed homomorphism H.
$\mathfrak H$
is a 1-cocycle of the crossed homomorphism H.
Definition 5.11. Let
![]() ${H}$
be a crossed homomorphism from
${H}$
be a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
.
$\rho $
.
-
(i) Two linear deformations
 ${H}_{t}^{1}={H}+t\mathfrak H_{1}$
and
${H}_{t}^{1}={H}+t\mathfrak H_{1}$
and
 ${H}^{2}_{t}={H}+t\mathfrak H_{2}$
are said to be equivalent if there exists an
${H}^{2}_{t}={H}+t\mathfrak H_{2}$
are said to be equivalent if there exists an
 $x\in \mathfrak g$
such that
$x\in \mathfrak g$
such that
 $(\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x},\text {Id}_{\mathfrak h}+t\rho (x))$
is a homomorphism from
$(\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x},\text {Id}_{\mathfrak h}+t\rho (x))$
is a homomorphism from
 ${H}^{2}_{t}$
to
${H}^{2}_{t}$
to
 ${H}^{1}_{t}$
.
${H}^{1}_{t}$
. -
(ii) A linear deformation
 ${H}+t\mathfrak H$
of a crossed homomorphism
${H}+t\mathfrak H$
of a crossed homomorphism
 ${H}$
is said to be trivial if there exists an
${H}$
is said to be trivial if there exists an
 $x\in \mathfrak g$
such that
$x\in \mathfrak g$
such that
 $(\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x},\text {Id}_{\mathfrak h}+t\rho (x))$
is a homomorphism from
$(\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x},\text {Id}_{\mathfrak h}+t\rho (x))$
is a homomorphism from
 ${H}_{t}$
to
${H}_{t}$
to
 ${H}$
.
${H}$
.
Let
![]() $(\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x},\text {Id}_{\mathfrak h}+t\rho (x))$
be a homomorphism from
$(\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x},\text {Id}_{\mathfrak h}+t\rho (x))$
be a homomorphism from
![]() ${H}^{2}_{t}$
to
${H}^{2}_{t}$
to
![]() ${H}^{1}_{t}$
. Then
${H}^{1}_{t}$
. Then
![]() $\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x}$
and
$\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x}$
and
![]() $\text {Id}_{\mathfrak h}+t\rho (x)$
are Lie algebra endomorphisms. Thus, we have
$\text {Id}_{\mathfrak h}+t\rho (x)$
are Lie algebra endomorphisms. Thus, we have
 $$ \begin{align*} (\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})[y,z]_{\mathfrak g}&=[(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})(y),(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})(z)]_{\mathfrak g}, \;\forall y,z\in \mathfrak g,\\ (\text{Id}_{\mathfrak h}+t\rho(x))[u,v]_{\mathfrak h}&=[(\text{Id}_{\mathfrak h}+t\rho(x))(u),(\text{Id}_{\mathfrak h}+t\rho(x))(v)]_{\mathfrak h}, \;\forall u,v\in \mathfrak h, \end{align*} $$
$$ \begin{align*} (\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})[y,z]_{\mathfrak g}&=[(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})(y),(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})(z)]_{\mathfrak g}, \;\forall y,z\in \mathfrak g,\\ (\text{Id}_{\mathfrak h}+t\rho(x))[u,v]_{\mathfrak h}&=[(\text{Id}_{\mathfrak h}+t\rho(x))(u),(\text{Id}_{\mathfrak h}+t\rho(x))(v)]_{\mathfrak h}, \;\forall u,v\in \mathfrak h, \end{align*} $$
which implies that x satisfies
Then by Equation (2), we get
which implies
Finally, Equation (3) gives
which implies that x satisfies
Note that Equation (27) means that
![]() $\mathfrak H_{2}-\mathfrak H_{1}=d_{\rho _{{H}}} (-{H} x)$
. Thus, we have the following.
$\mathfrak H_{2}-\mathfrak H_{1}=d_{\rho _{{H}}} (-{H} x)$
. Thus, we have the following.
Theorem 5.12. Let
![]() ${H}$
be a crossed homomorphism from
${H}$
be a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
. If two linear deformations
$\rho $
. If two linear deformations
![]() ${H}^{1}_{t}={H}+t\mathfrak H_{1}$
and
${H}^{1}_{t}={H}+t\mathfrak H_{1}$
and
![]() ${H}^{2}_{t}={H}+t\mathfrak H_{2}$
are equivalent, then
${H}^{2}_{t}={H}+t\mathfrak H_{2}$
are equivalent, then
![]() $\mathfrak H_{1}$
and
$\mathfrak H_{1}$
and
![]() $\mathfrak H_{2}$
are in the same cohomology class of
$\mathfrak H_{2}$
are in the same cohomology class of
![]() $\mathcal {H}^{1}(\mathfrak g,\mathfrak h)=\mathcal {Z}^{1}(\mathfrak g,\mathfrak h)/\mathcal {B}^{1}(\mathfrak g,\mathfrak h)$
defined in Definition 5.6.
$\mathcal {H}^{1}(\mathfrak g,\mathfrak h)=\mathcal {Z}^{1}(\mathfrak g,\mathfrak h)/\mathcal {B}^{1}(\mathfrak g,\mathfrak h)$
defined in Definition 5.6.
Definition 5.13. Let
![]() ${H}$
be a crossed homomorphism from
${H}$
be a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
. An element
$\rho $
. An element
![]() $x\in \mathfrak g$
is called a Nijenhuis element associated to
$x\in \mathfrak g$
is called a Nijenhuis element associated to
![]() ${H}$
if x satisfies Equations (25), (26), (29) and the equation
${H}$
if x satisfies Equations (25), (26), (29) and the equation
 $$ \begin{align} \rho(x)\Big(\rho(y){H} x+[{H} y,{H} x]_{\mathfrak h}\Big)=0,\quad\forall y\in\mathfrak g. \end{align} $$
$$ \begin{align} \rho(x)\Big(\rho(y){H} x+[{H} y,{H} x]_{\mathfrak h}\Big)=0,\quad\forall y\in\mathfrak g. \end{align} $$
Denote by
![]() $\mathsf {Nij}({H})$
the set of Nijenhuis elements associated to a crossed homomorphism
$\mathsf {Nij}({H})$
the set of Nijenhuis elements associated to a crossed homomorphism
![]() ${H}$
.
${H}$
.
By Equations (25)–(29), it is obvious that a trivial linear deformation gives rise to a Nijenhuis element. The following result is in close analogy to the fact that the differential of a Nijenhuis operator on a Lie algebra generates a trivial linear deformation of the Lie algebra [Reference Dorfman7], justifying the notion of Nijenhuis elements.
Theorem 5.14. Let
![]() ${H}$
be a crossed homomorphism from
${H}$
be a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
. Then for any
$\rho $
. Then for any
![]() $x\in \mathsf {Nij}({H})$
,
$x\in \mathsf {Nij}({H})$
,
![]() ${H}_{t}:={H}+t \mathfrak H$
with
${H}_{t}:={H}+t \mathfrak H$
with
![]() $\mathfrak H:=d_{\rho _{H}} (-{H} x)$
is a linear deformation of the crossed homomorphism
$\mathfrak H:=d_{\rho _{H}} (-{H} x)$
is a linear deformation of the crossed homomorphism
![]() ${H}$
. Moreover, this deformation is trivial.
${H}$
. Moreover, this deformation is trivial.
We need the following lemma to prove this theorem.
Lemma 5.15. Let
![]() ${H}$
be a crossed homomorphism from
${H}$
be a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
. Let
$\rho $
. Let
![]() $\phi _{\mathfrak g}:\mathfrak g\longrightarrow \mathfrak g$
and
$\phi _{\mathfrak g}:\mathfrak g\longrightarrow \mathfrak g$
and
![]() $\phi _{\mathfrak h}:\mathfrak h\longrightarrow \mathfrak h$
be Lie algebra isomorphisms such that Equation (3) holds. Then
$\phi _{\mathfrak h}:\mathfrak h\longrightarrow \mathfrak h$
be Lie algebra isomorphisms such that Equation (3) holds. Then
 $\phi _{\mathfrak h}^{-1}\circ {H}\circ \phi _{\mathfrak g}$
is a crossed homomorphism from
$\phi _{\mathfrak h}^{-1}\circ {H}\circ \phi _{\mathfrak g}$
is a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
with respect to the action
$\mathfrak h$
with respect to the action
![]() $\rho $
.
$\rho $
.
Proof. It follows from straightforward computations.
The proof of Theorem 5.14
For any Nijenhuis element
![]() $x\in \mathsf {Nij}({H})$
, we define
$x\in \mathsf {Nij}({H})$
, we define
By the definition of Nijenhuis elements of
![]() ${H}$
, for any t,
${H}$
, for any t,
![]() ${H}_{t}={H}+t\mathfrak H$
satisfies
${H}_{t}={H}+t\mathfrak H$
satisfies
 $$ \begin{align*} {H}\circ \Big(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x}\Big)&=\Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big)\circ {H}_{t},\\ \Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big)\circ\rho(y)&=\rho\Big((\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})(y)\Big)\circ\Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big),\quad\forall y\in\mathfrak g. \end{align*} $$
$$ \begin{align*} {H}\circ \Big(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x}\Big)&=\Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big)\circ {H}_{t},\\ \Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big)\circ\rho(y)&=\rho\Big((\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x})(y)\Big)\circ\Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big),\quad\forall y\in\mathfrak g. \end{align*} $$
For t sufficiently small, we see that
![]() $\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x}$
and
$\text {Id}_{\mathfrak g}+t\mathsf {ad}_{x}$
and
![]() $\text {Id}_{\mathfrak h}+t\rho (x)$
are Lie algebra isomorphisms. Thus, we have
$\text {Id}_{\mathfrak h}+t\rho (x)$
are Lie algebra isomorphisms. Thus, we have
 $$ \begin{align*}{H}_{t}=\Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big)^{-1}\circ{H}\circ \Big(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x}\Big).\end{align*} $$
$$ \begin{align*}{H}_{t}=\Big(\text{Id}_{\mathfrak h}+t\rho(x)\Big)^{-1}\circ{H}\circ \Big(\text{Id}_{\mathfrak g}+t\mathsf{ad}_{x}\Big).\end{align*} $$
By Lemma 5.15, we deduce that
![]() ${H}_{t}$
is a crossed homomorphism from
${H}_{t}$
is a crossed homomorphism from
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
, for t sufficiently small. Thus,
$\mathfrak h$
, for t sufficiently small. Thus,
![]() $\mathfrak H$
given by Equation (31) satisfies the conditions (23) and (24). Therefore,
$\mathfrak H$
given by Equation (31) satisfies the conditions (23) and (24). Therefore,
![]() ${H}_{t}$
is a crossed homomorphism for all t, which means that
${H}_{t}$
is a crossed homomorphism for all t, which means that
![]() $\mathfrak H$
given by Equation (31) generates a deformation. It is straightforward to see that this deformation is trivial.
$\mathfrak H$
given by Equation (31) generates a deformation. It is straightforward to see that this deformation is trivial.
It is generally not easy to find Nijenhuis elements associated to a crossed homomorphism
![]() ${H}$
from a Lie algebra
${H}$
from a Lie algebra
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $\mathfrak h$
. Next, we give examples on some special Lie algebras where the Nijenhuis elements can be explicitly determined.
$\mathfrak h$
. Next, we give examples on some special Lie algebras where the Nijenhuis elements can be explicitly determined.
Example 5.16. Let
![]() $\mathfrak g$
be a 2-step nilpotent Lie algebra; that is,
$\mathfrak g$
be a 2-step nilpotent Lie algebra; that is,
![]() $[\mathfrak g,[\mathfrak g,\mathfrak g] ]=0$
and
$[\mathfrak g,[\mathfrak g,\mathfrak g] ]=0$
and
![]() $H:\mathfrak g\to \mathfrak g$
a crossed homomorphism with respect to the adjoint action ad of
$H:\mathfrak g\to \mathfrak g$
a crossed homomorphism with respect to the adjoint action ad of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak g$
. It is easy to see that (25), (26), (29), (30) hold for any
$\mathfrak g$
. It is easy to see that (25), (26), (29), (30) hold for any
![]() $x\in \mathfrak g$
. Therefore,
$x\in \mathfrak g$
. Therefore,
![]() $\mathsf {Nij}({H})=\mathfrak g$
for any crossed homomorphism H with respect to the adjoint action ad of
$\mathsf {Nij}({H})=\mathfrak g$
for any crossed homomorphism H with respect to the adjoint action ad of
![]() $\mathfrak g$
on
$\mathfrak g$
on
![]() $\mathfrak g$
. For example, we can take
$\mathfrak g$
. For example, we can take
![]() $\mathfrak g$
to be any Heisenberg algebra.
$\mathfrak g$
to be any Heisenberg algebra.
Example 5.17. Consider the unique
![]() $2$
-dimensional nonabelian Lie algebra on
$2$
-dimensional nonabelian Lie algebra on
![]() $\mathbb C^{2}$
. The Lie bracket is given by
$\mathbb C^{2}$
. The Lie bracket is given by
![]() $[e_{1},e_{2}]=e_{1}$
for a given basis
$[e_{1},e_{2}]=e_{1}$
for a given basis
![]() $\{e_{1},e_{2}\}$
. For a matrix
$\{e_{1},e_{2}\}$
. For a matrix
 $\left (\begin {array}{@{}cc@{}}a_{11}&a_{12}\\ a_{21}&a_{22}\end {array}\right )$
, define
$\left (\begin {array}{@{}cc@{}}a_{11}&a_{12}\\ a_{21}&a_{22}\end {array}\right )$
, define
![]() ${H}$
is a crossed homomorphism from
${H}$
is a crossed homomorphism from
![]() $\mathbb C^{2}$
to
$\mathbb C^{2}$
to
![]() $\mathbb C^{2}$
with respect to the adjoint action if and only if
$\mathbb C^{2}$
with respect to the adjoint action if and only if
By a straightforward computation, we conclude that
![]() ${H}$
is a crossed homomorphism if and only if
${H}$
is a crossed homomorphism if and only if
![]() $ a_{21}=0, ~(1+a_{11}) a_{22}=0. $
So we have the following two cases to consider.
$ a_{21}=0, ~(1+a_{11}) a_{22}=0. $
So we have the following two cases to consider.
(i) If
![]() $a_{22}=0$
, then we deduce that any
$a_{22}=0$
, then we deduce that any
 ${H}=\left (\begin {array}{@{}cc@{}}a_{11}&a_{12}\\ 0&0\end {array}\right )$
is a crossed homomorphism. In this case,
${H}=\left (\begin {array}{@{}cc@{}}a_{11}&a_{12}\\ 0&0\end {array}\right )$
is a crossed homomorphism. In this case,
![]() $x=t_{1}e_{1}+t_{2}e_{2}$
is a Nijenhuis element of
$x=t_{1}e_{1}+t_{2}e_{2}$
is a Nijenhuis element of
![]() ${H}$
if and only if
${H}$
if and only if
![]() $ t_{2}(t_{1}a_{11}+t_{2}a_{12})=0. $
Then for any
$ t_{2}(t_{1}a_{11}+t_{2}a_{12})=0. $
Then for any
![]() $t_{1}\in \mathbb C, t_{1}e_{1}$
is a Nijenhuis element for the crossed homomorphism
$t_{1}\in \mathbb C, t_{1}e_{1}$
is a Nijenhuis element for the crossed homomorphism
 ${H}=\left (\begin {array}{@{}cc@{}}a_{11}&a_{12}\\ 0&0\end {array}\right )$
.
${H}=\left (\begin {array}{@{}cc@{}}a_{11}&a_{12}\\ 0&0\end {array}\right )$
.
(ii) If
![]() $1+a_{11}=0$
, then we deduce that any
$1+a_{11}=0$
, then we deduce that any
 ${H}=\left (\begin {array}{@{}cc@{}}-1&a_{12}\\ 0&a_{22}\end {array}\right )$
is a crossed homomorphism. In this case,
${H}=\left (\begin {array}{@{}cc@{}}-1&a_{12}\\ 0&a_{22}\end {array}\right )$
is a crossed homomorphism. In this case,
![]() $x=t_{1}e_{1}+t_{2}e_{2}$
is a Nijenhuis element of
$x=t_{1}e_{1}+t_{2}e_{2}$
is a Nijenhuis element of
![]() ${H}$
if and only if
${H}$
if and only if
![]() $ t_{2}(t_{2}a_{12}-t_{1}a_{22}-t_{1})=0. $
In particular,
$ t_{2}(t_{2}a_{12}-t_{1}a_{22}-t_{1})=0. $
In particular,
![]() $e_{1}+e_{2}$
is a Nijenhuis element for the crossed homomorphism
$e_{1}+e_{2}$
is a Nijenhuis element for the crossed homomorphism
 ${H}=\left (\begin {array}{@{}cc@{}}-1&2\\ 0&1\end {array}\right )$
.
${H}=\left (\begin {array}{@{}cc@{}}-1&2\\ 0&1\end {array}\right )$
.
Example 5.18. For any crossed homomorphism H from a finite-dimensional semisimple Lie algebra
![]() $\mathfrak g$
over
$\mathfrak g$
over
![]() $\mathbb {C}$
to another Lie algebra
$\mathbb {C}$
to another Lie algebra
![]() $\mathfrak h$
with respect to any action
$\mathfrak h$
with respect to any action
![]() $\rho $
, we claim that
$\rho $
, we claim that
![]() $\mathsf {Nij}(H)=0$
.
$\mathsf {Nij}(H)=0$
.
Let
![]() $x\in \mathfrak g$
be a fixed nonzero vector and assume that
$x\in \mathfrak g$
be a fixed nonzero vector and assume that
![]() $\mathfrak g_{0}=[x, \mathfrak g]$
is abelian; that is, (25) holds. We will show that this is impossible.
$\mathfrak g_{0}=[x, \mathfrak g]$
is abelian; that is, (25) holds. We will show that this is impossible.
Denote
![]() $n=\dim \mathfrak g, \mathfrak g_{x}=\{y\in \mathfrak g:[x,y]=0\}$
. Considering the linear map
$n=\dim \mathfrak g, \mathfrak g_{x}=\{y\in \mathfrak g:[x,y]=0\}$
. Considering the linear map
![]() $\mathsf {ad}(x):\mathfrak g\to \mathfrak g$
, we see that
$\mathsf {ad}(x):\mathfrak g\to \mathfrak g$
, we see that
![]() $\dim \mathfrak g_{0}+\dim \mathfrak g_{x}=n$
. Let
$\dim \mathfrak g_{0}+\dim \mathfrak g_{x}=n$
. Let
![]() $(\cdot , \cdot )$
be a nondegenerate invariant bilinear form on
$(\cdot , \cdot )$
be a nondegenerate invariant bilinear form on
![]() $\mathfrak g$
. It is easy to see that
$\mathfrak g$
. It is easy to see that
![]() $\mathfrak g_{x}=\mathfrak g_{0}^{\perp }$
. From
$\mathfrak g_{x}=\mathfrak g_{0}^{\perp }$
. From
![]() $0=(0, \mathfrak g)=([[x, \mathfrak g], [x, \mathfrak g]], \mathfrak g)= ([x, \mathfrak g],[[x, \mathfrak g], \mathfrak g])$
we have
$0=(0, \mathfrak g)=([[x, \mathfrak g], [x, \mathfrak g]], \mathfrak g)= ([x, \mathfrak g],[[x, \mathfrak g], \mathfrak g])$
we have
We deduce that
![]() $0=[x, [[x, \mathfrak g], \mathfrak g]]=[[x, [x, \mathfrak g]], \mathfrak g]$
. Since
$0=[x, [[x, \mathfrak g], \mathfrak g]]=[[x, [x, \mathfrak g]], \mathfrak g]$
. Since
![]() $\mathfrak g$
is semisimple, we see that
$\mathfrak g$
is semisimple, we see that
![]() $[x, [x, \mathfrak g]]=0$
. Thus, x is nilpotent. From Jacobson–Morozov theorem, there are elements
$[x, [x, \mathfrak g]]=0$
. Thus, x is nilpotent. From Jacobson–Morozov theorem, there are elements
![]() $f, h\in \mathfrak {g}$
such that
$f, h\in \mathfrak {g}$
such that
We see that
![]() $[[x, h], [x, f]]= 4x\ne 0.$
So
$[[x, h], [x, f]]= 4x\ne 0.$
So
![]() $\mathfrak g_{0}$
is noncommutative, which is a contradiction. Therefore,
$\mathfrak g_{0}$
is noncommutative, which is a contradiction. Therefore,
![]() $\mathsf {Nij}(H)=0$
.
$\mathsf {Nij}(H)=0$
.
6. Conclusion
We introduce the notions of weak representations of Lie–Rinehart algebras and admissible representations of Leibniz pairs. By using crossed homomorphisms between Lie algebras, we construct two actions of the monoidal category of representations of Lie algebras on the category of weak representations of Lie–Rinehart algebras and the category of admissible representations of Leibniz pairs, respectively. In particular, the corresponding bifunctors, called the actions of monoidal categories, unify and generalise various constructions of modules over certain Cartan-type Lie algebras. New representations of some Lie algebras are also constructed using the actions of monoidal categories. To better understand crossed homomorphisms and the actions of monoidal categories, we also give a systematic study of deformations and cohomologies of crossed homomorphisms.
There are some natural questions worthy of consideration in the future:
-
(i) Whether the bifunctors
 $F_{H}$
and
$F_{H}$
and
 $\mathcal {F}_{H}$
preserve certain properties of representations. For example, when
$\mathcal {F}_{H}$
preserve certain properties of representations. For example, when
 $F_{H}(V,M) $
and
$F_{H}(V,M) $
and
 $\mathcal {F}_{H}(V,M)$
are simple if both V and M are simple.
$\mathcal {F}_{H}(V,M)$
are simple if both V and M are simple. -
(ii) For two crossed homomorphisms H and
 $H^{\prime }$
, under what conditions are the bifunctors
$H^{\prime }$
, under what conditions are the bifunctors
 $F_{H}$
and
$F_{H}$
and
 $F_{H^{\prime }}$
naturally isomorphic?
$F_{H^{\prime }}$
naturally isomorphic? -
(iii) How to classify simple objects in the categories
 $\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
and
$\mathsf {WRep}_{\mathbb {K}}(\mathcal {L})$
and
 $\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
under certain conditions.
$\mathsf {ARep}_{\mathbb {K}}(\mathcal {S})$
under certain conditions.
Acknowledgements
The authors thank L. Guo and S. Ng for help discussions on the first version of the article. The authors also thank the anonymous referees for helpful comments and suggestions. This research is supported by NSFC (11871190, 11971315, 11922110, 12001228) and NSERC (311907-2020).
Competing Interests
None.

















