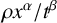1 Introduction
Menshikov and Volkov [Reference Menshikov and Volkov14] studied the time-inhomogeneous random walk
![]() $X_t\in \mathbb {R}$
,
$X_t\in \mathbb {R}$
,
![]() $t=1,2,\ldots $
, with the drift satisfying the condition
$t=1,2,\ldots $
, with the drift satisfying the condition
where
![]() $\rho>0$
,
$\rho>0$
,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
were some constants, and the meaning of the symbol ‘
$\beta $
were some constants, and the meaning of the symbol ‘
![]() $\sim $
’ was further clarified for the case studies of the paper. There were some assumptions (indicated below) and conditions on the parameters
$\sim $
’ was further clarified for the case studies of the paper. There were some assumptions (indicated below) and conditions on the parameters
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
and
$\beta $
and
![]() $\rho $
in [Reference Menshikov and Volkov14], under which the random walk was recurrent or transient. The study of this random walk was associated with urn models and random walks with vanishing drifts that have been intensively studied in the literature (see the references in [Reference Menshikov and Volkov14]), and the results obtained covered many known models from these areas.
$\rho $
in [Reference Menshikov and Volkov14], under which the random walk was recurrent or transient. The study of this random walk was associated with urn models and random walks with vanishing drifts that have been intensively studied in the literature (see the references in [Reference Menshikov and Volkov14]), and the results obtained covered many known models from these areas.
The basic assumptions, under which the study in [Reference Menshikov and Volkov14] was conducted, are quite natural:
-
(H1) uniform boundedness of jumps;
-
(H2) uniform nondegeneracy on
 $[a,\infty )$
; and
$[a,\infty )$
; and -
(H3) uniform boundedness of time to leave
 $[0,a]$
.
$[0,a]$
.
In the case when
![]() $\alpha <\beta $
, it was shown that the random walk is transient if
$\alpha <\beta $
, it was shown that the random walk is transient if
![]() $(\alpha ,\beta )$
satisfies
$(\alpha ,\beta )$
satisfies
![]() $0\leq \beta < 1, 2\beta -1 < \alpha < \beta $
and it is recurrent otherwise. In the case when
$0\leq \beta < 1, 2\beta -1 < \alpha < \beta $
and it is recurrent otherwise. In the case when
![]() ${\alpha =\beta =1}$
, the random walk started at zero is described by the equalities
${\alpha =\beta =1}$
, the random walk started at zero is described by the equalities
 $$ \begin{align} \mathsf{P}\{X_{t+1}=n\pm1~|~X_t=n\}&=\frac{1}{2}\pm\rho\frac{n}{2t}, \quad 1\leq n\leq t,\\ \mathsf{P}\{X_{t+1}=1~|~X_t=0\}&=1. \nonumber \end{align} $$
$$ \begin{align} \mathsf{P}\{X_{t+1}=n\pm1~|~X_t=n\}&=\frac{1}{2}\pm\rho\frac{n}{2t}, \quad 1\leq n\leq t,\\ \mathsf{P}\{X_{t+1}=1~|~X_t=0\}&=1. \nonumber \end{align} $$
It was shown that this random walk is transient for
![]() $\rho>1/2$
and recurrent for
$\rho>1/2$
and recurrent for
![]() $\rho <1/2$
.
$\rho <1/2$
.
Along with these cases, [Reference Menshikov and Volkov14] also discussed a number of other cases, one of which was left undecided, since the martingale methodology used there seems to be insufficient to resolve it. The boundary configurations of this case are
![]() $\alpha =2\beta -1$
and
$\alpha =2\beta -1$
and
![]() $\beta \in (0,\tfrac 12)\cup (\tfrac 12,1)$
. This motivates us to find a new approach to the problem to cover this case. With the new approach, we shall study a generalised version of (1.2):
$\beta \in (0,\tfrac 12)\cup (\tfrac 12,1)$
. This motivates us to find a new approach to the problem to cover this case. With the new approach, we shall study a generalised version of (1.2):
 $$ \begin{align} \mathsf{P}\{X_{t+1}=n\pm1~|~X_t=n\}&=\tfrac{1}{2}\pm\varphi(n,t), \quad 1\leq n\leq t,\\ \mathsf{P}\{X_{t+1}=1~|~X_t=0\}&=1,\nonumber \end{align} $$
$$ \begin{align} \mathsf{P}\{X_{t+1}=n\pm1~|~X_t=n\}&=\tfrac{1}{2}\pm\varphi(n,t), \quad 1\leq n\leq t,\\ \mathsf{P}\{X_{t+1}=1~|~X_t=0\}&=1,\nonumber \end{align} $$
for which the required assumptions will be provided later in the paper.
The random walks defined by (1.1) and (1.2) have positively biased drift. Considerations provided in [Reference Menshikov and Volkov14] implicitly assumed that the drifts considered in the random walks all vanish as
![]() $t\to \infty $
. The conditions for the parameters under which this is true were not discussed. In the analysis provided in the present paper for some particular examples, this issue is considered as well.
$t\to \infty $
. The conditions for the parameters under which this is true were not discussed. In the analysis provided in the present paper for some particular examples, this issue is considered as well.
Another possible model of random walks in
![]() $\mathbb {R}$
with positively biased drift when the random walk takes positive values and negatively biased drifts when the random walk takes negative values, closely related to that considered in [Reference Menshikov and Volkov14], is
$\mathbb {R}$
with positively biased drift when the random walk takes positive values and negatively biased drifts when the random walk takes negative values, closely related to that considered in [Reference Menshikov and Volkov14], is
where the meaning of ‘
![]() $\sim $
’ is the same as in [Reference Menshikov and Volkov14]. The study of this model is similar to that of (1.1) because of the symmetry.
$\sim $
’ is the same as in [Reference Menshikov and Volkov14]. The study of this model is similar to that of (1.1) because of the symmetry.
Since the processes described by (1.1) and (1.2) have positively biased drifts, they can be assumed to be given in
![]() $\mathbb {R}_+$
. Furthermore, the assumptions (H1), (H2) and (H3) enable us to further specify the random walks assuming that they are time-inhomogeneous processes of the birth-and-death type (or simply time-inhomogeneous birth-and-death processes). That is, we will further assume that the jumps of the random walks take the values
$\mathbb {R}_+$
. Furthermore, the assumptions (H1), (H2) and (H3) enable us to further specify the random walks assuming that they are time-inhomogeneous processes of the birth-and-death type (or simply time-inhomogeneous birth-and-death processes). That is, we will further assume that the jumps of the random walks take the values
![]() $\pm 1$
with probabilities depending on state and time, and the continuous time processes take values in
$\pm 1$
with probabilities depending on state and time, and the continuous time processes take values in
![]() $\mathbb {Z}_+$
. This will enable us to approach the model described by (1.3).
$\mathbb {Z}_+$
. This will enable us to approach the model described by (1.3).
For the study of recurrence and transience, this assumption is not restrictive. If a process of the birth-and-death type is recurrent (or transient), then there is a wide class of closely related Markov chain models satisfying the same property of recurrence (or transience respectively), the jumps of which take values in
![]() $\mathbb {Z}$
rather than in
$\mathbb {Z}$
rather than in
![]() $\{-1, 1\}$
.
$\{-1, 1\}$
.
For simplicity of explanations, consider a time-homogeneous (that is ordinary) birth-and-death process with positive birth rates
![]() $\lambda _n$
and positive death rates
$\lambda _n$
and positive death rates
![]() $\mu _n$
(with
$\mu _n$
(with
![]() $\lambda _n>\mu _n$
,
$\lambda _n>\mu _n$
,
![]() $\lambda _n+\mu _n=1$
). Observe this continuous process at the discrete times
$\lambda _n+\mu _n=1$
). Observe this continuous process at the discrete times
![]() $t=0, 1, 2,\ldots. $
At the initial time
$t=0, 1, 2,\ldots. $
At the initial time
![]() $t=0$
, the birth-and-death process is in state
$t=0$
, the birth-and-death process is in state
![]() $0$
. Up to time
$0$
. Up to time
![]() $t=1$
, a random number of births and deaths can occur, and the state of the system at
$t=1$
, a random number of births and deaths can occur, and the state of the system at
![]() $t=1$
is defined as the difference between the numbers of births and deaths before time
$t=1$
is defined as the difference between the numbers of births and deaths before time
![]() $t=1$
to be denoted by
$t=1$
to be denoted by
![]() $n_1$
. Similarly, at time
$n_1$
. Similarly, at time
![]() $t=2$
, the state of the system is denoted
$t=2$
, the state of the system is denoted
![]() $n_2$
, and so on.
$n_2$
, and so on.
Apparently, for a time-inhomogeneous birth-and-death process (that will be defined later in the paper), the construction of a Markov process with the jumps belonging to
![]() $\mathbb {Z}$
is the same. Specifically, we obtain a new Markov chain
$\mathbb {Z}$
is the same. Specifically, we obtain a new Markov chain
![]() $Y_t$
, the jumps of which belong to
$Y_t$
, the jumps of which belong to
![]() $\mathbb {Z}$
. For this newly defined Markov chain, (1.3) is rewritten as
$\mathbb {Z}$
. For this newly defined Markov chain, (1.3) is rewritten as
Condition (H1) in [Reference Menshikov and Volkov14] is restrictive. According to (H1), the jumps of a Markov chain are uniformly bounded for all t. For the model that is built above, the assumption is weaker. The jumps are not uniformly bounded, but have all moments. The only difference is that the jumps of Markov chains studied in [Reference Menshikov and Volkov14] take values in
![]() $\mathbb {R}$
, while the example below suggests the jumps belong to
$\mathbb {R}$
, while the example below suggests the jumps belong to
![]() $\mathbb {Z}$
. We think, however, that this is not crucial.
$\mathbb {Z}$
. We think, however, that this is not crucial.
Thus, the aforementioned arguments enable us to conclude that the model described by (1.3) is not less general than the model described by
under (H1).
In the present paper, we suggest a new approach to the problem on recurrence and transience for time-inhomogeneous Markov chains. By using the techniques of stochastic calculus, we provide simpler and transparent proofs of the results under general assumptions on the increments. We first derive a stochastic variant of the Chapman–Kolmogorov equations. Then we apply martingale techniques for continuous time processes and reduce the problem to the known criteria of recurrence or transience for birth-and-death processes. The stochastic variant of the Chapman–Kolmogorov equations appeared for the first time in the paper of Kogan and Liptser [Reference Kogan and Liptser11], and then it has been used in many papers (for example, [Reference Abramov1–Reference Abramov3, Reference Kogan, Liptser and Shenfild12]), the majority of which are from the area of queueing networks.
The rest of the paper is structured into four sections. In Section 2, we formulate the theorem and in Section 3, we prove it. The proof of the theorem in Section 3 consists of three parts: in Section 3.1, for a time-inhomogeneous birth-and-death process, we derive a stochastic variant of the Chapman–Kolmogorov equations and prove the convergence of the characteristics of the time-inhomogeneous birth-and-death process to the ordinary one; in Section 3.2, we recall some facts on recurrence and transience of birth-and-death processes known from the literature; in Section 3.3, we finalise the proof of the theorem. In Section 4, we provide some examples for the random walks studied in the paper. Some of the examples support the results obtained in [Reference Menshikov and Volkov14]. In Section 5, we conclude the paper.
2 Formulation of the main result
Let
![]() $X_t$
be the random walk defined by
$X_t$
be the random walk defined by
 $$ \begin{align} \mathsf{P}\{X_{t+1}=n\pm1~|~X_t=n\}&=\tfrac{1}{2}\pm\varphi(n,t), \quad 1\leq n\leq t,\\ \mathsf{P}\{X_{t+1}=1~|~X_t=0\}&=1, \nonumber \end{align} $$
$$ \begin{align} \mathsf{P}\{X_{t+1}=n\pm1~|~X_t=n\}&=\tfrac{1}{2}\pm\varphi(n,t), \quad 1\leq n\leq t,\\ \mathsf{P}\{X_{t+1}=1~|~X_t=0\}&=1, \nonumber \end{align} $$
for
![]() $t=0, 1,\ldots .$
Assume that
$t=0, 1,\ldots .$
Assume that
![]() $\varphi (n,t)$
well defines the right-hand side of (2.1) (that is, keeps the probability distributions correctly defined), and is a decreasing in t Borel function.
$\varphi (n,t)$
well defines the right-hand side of (2.1) (that is, keeps the probability distributions correctly defined), and is a decreasing in t Borel function.
Theorem 2.1. The random walk
![]() $X_t$
is recurrent if there exist
$X_t$
is recurrent if there exist
![]() $c<1$
and
$c<1$
and
![]() $n_0$
such that
$n_0$
such that
![]() $\varphi (n,n^2)\leq c/(4n)$
for all
$\varphi (n,n^2)\leq c/(4n)$
for all
![]() $n\geq n_0$
, and
$n\geq n_0$
, and
![]() $X_t$
is transient if there exist
$X_t$
is transient if there exist
![]() $c>1$
and
$c>1$
and
![]() $n_0$
such that
$n_0$
such that
![]() $\varphi (n,n^2)\geq c/(4n)$
for all
$\varphi (n,n^2)\geq c/(4n)$
for all
![]() $n\geq n_0$
.
$n\geq n_0$
.
The proof of Theorem 2.1 is given in the next section.
3 Proof of the theorem
3.1 Time-inhomogeneous birth-and-death processes
We consider a time-inhomogeneous version of the birth-and-death process
![]() $Z(\tau )$
with the instantaneous positive rates
$Z(\tau )$
with the instantaneous positive rates
![]() $\lambda _{n,\tau }$
and
$\lambda _{n,\tau }$
and
![]() $\mu _{n,\tau }$
in state n at time
$\mu _{n,\tau }$
in state n at time
![]() $\tau $
. To emphasise the continuous time process, we use
$\tau $
. To emphasise the continuous time process, we use
![]() $\tau $
as a continuous time parameter, rather than t which was a discrete time. The process
$\tau $
as a continuous time parameter, rather than t which was a discrete time. The process
![]() $Z(\tau )$
is assumed to be right-continuous with left limits. The functions
$Z(\tau )$
is assumed to be right-continuous with left limits. The functions
![]() $\lambda _{n,\tau }$
and
$\lambda _{n,\tau }$
and
![]() $\mu _{n,\tau }$
are assumed to be continuous in the variable
$\mu _{n,\tau }$
are assumed to be continuous in the variable
![]() $\tau $
with finite positive limits
$\tau $
with finite positive limits
Additionally, we assume the existence of the limits below satisfying
The system of equations for the process
![]() $Z(\tau )$
in terms of the indicators
$Z(\tau )$
in terms of the indicators
![]() $\mathsf {I}\{Z(\tau )=n\}$
is a stochastic analogue of the Chapman–Kolmogorov equations:
$\mathsf {I}\{Z(\tau )=n\}$
is a stochastic analogue of the Chapman–Kolmogorov equations:
 $$ \begin{align*} \begin{aligned} \mathsf{I}\{Z(\tau)=n\} & =\mathsf{I}\{Z(\tau-)=n+1\}\,\mathsf{I}\{\mathrm{M}_{n+1}(\tau)-\mathrm{M}_{n+1}(\tau-)=1\}\\ &\quad +\mathsf{I}\{Z(\tau-)=n-1\}\,\mathsf{I}\{\Lambda_{n-1}(\tau)-\Lambda_{n-1}(\tau-)=1\}\\ &\quad +\mathsf{I}\{Z(\tau-)=n\}\,\mathsf{I}\{\mathrm{M}_{n,}(\tau)-\mathrm{M}_{n}(\tau-)=0\} \,\mathsf{I}\{\Lambda_{n}(\tau)-\Lambda_{n}(\tau-)=0\}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathsf{I}\{Z(\tau)=n\} & =\mathsf{I}\{Z(\tau-)=n+1\}\,\mathsf{I}\{\mathrm{M}_{n+1}(\tau)-\mathrm{M}_{n+1}(\tau-)=1\}\\ &\quad +\mathsf{I}\{Z(\tau-)=n-1\}\,\mathsf{I}\{\Lambda_{n-1}(\tau)-\Lambda_{n-1}(\tau-)=1\}\\ &\quad +\mathsf{I}\{Z(\tau-)=n\}\,\mathsf{I}\{\mathrm{M}_{n,}(\tau)-\mathrm{M}_{n}(\tau-)=0\} \,\mathsf{I}\{\Lambda_{n}(\tau)-\Lambda_{n}(\tau-)=0\}, \end{aligned} \end{align*} $$
for
![]() $n=1,2,\ldots ,$
and
$n=1,2,\ldots ,$
and
 $$ \begin{align*} \begin{aligned} \mathsf{I}\{Z(\tau)=0\} & =\mathsf{I}\{Z(\tau-)=1\}\,\mathsf{I}\{\mathrm{M}_{1}(\tau)-\mathrm{M}_{1}(\tau-)=1\}\\ &\quad +\mathsf{I}\{Z(\tau-)=0\}\,\mathsf{I}\{\Lambda_{0}(\tau)-\Lambda_{0}(\tau-)=0\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathsf{I}\{Z(\tau)=0\} & =\mathsf{I}\{Z(\tau-)=1\}\,\mathsf{I}\{\mathrm{M}_{1}(\tau)-\mathrm{M}_{1}(\tau-)=1\}\\ &\quad +\mathsf{I}\{Z(\tau-)=0\}\,\mathsf{I}\{\Lambda_{0}(\tau)-\Lambda_{0}(\tau-)=0\}. \end{aligned} \end{align*} $$
Here,
![]() $Z(\tau -)$
denotes the value of the process
$Z(\tau -)$
denotes the value of the process
![]() $Z(\tau )$
immediately before the point
$Z(\tau )$
immediately before the point
![]() $\tau $
(if
$\tau $
(if
![]() $\tau $
is a point of continuity of
$\tau $
is a point of continuity of
![]() $Z(\tau )$
, then
$Z(\tau )$
, then
![]() $Z(\tau -)=Z(\tau )$
, otherwise
$Z(\tau -)=Z(\tau )$
, otherwise
![]() $|Z(\tau )-Z(\tau -)|=1$
), and
$|Z(\tau )-Z(\tau -)|=1$
), and
![]() $\Lambda _{n}(\tau )$
and
$\Lambda _{n}(\tau )$
and
![]() $\mathrm {M}_{n}(\tau )$
for each fixed n denote the time-inhomogeneous Poisson processes with the instantaneous rates
$\mathrm {M}_{n}(\tau )$
for each fixed n denote the time-inhomogeneous Poisson processes with the instantaneous rates
![]() $\lambda _{n,\tau }$
and
$\lambda _{n,\tau }$
and
![]() $\mu _{n,\tau }$
, respectively.
$\mu _{n,\tau }$
, respectively.
According to the Doob–Meyer semimartingale decomposition (see [Reference Jacod and Shiryaev9, Reference Liptser and Shiryaev13, Reference Protter15]), written here in the form of stochastic differentials,
![]() ${d}\Lambda _{n}(\tau )=\lambda _{n,\tau }d\tau +d\boldsymbol {M}_{\Lambda _{n}(\tau )}$
and
${d}\Lambda _{n}(\tau )=\lambda _{n,\tau }d\tau +d\boldsymbol {M}_{\Lambda _{n}(\tau )}$
and
![]() $d\mathrm {M}_{n}(\tau )=\mu _{n,\tau }d\tau +d\boldsymbol {M}_{\mathrm {M}_{n}(\tau )}$
. Here,
$d\mathrm {M}_{n}(\tau )=\mu _{n,\tau }d\tau +d\boldsymbol {M}_{\mathrm {M}_{n}(\tau )}$
. Here,
![]() $\lambda _{n,\tau }d\tau $
and
$\lambda _{n,\tau }d\tau $
and
![]() $\mu _{n,\tau }d\tau $
are the compensators of
$\mu _{n,\tau }d\tau $
are the compensators of
![]() $d\Lambda _{n}(\tau )$
and
$d\Lambda _{n}(\tau )$
and
![]() $d\mathrm {M}_{n}(\tau )$
, and
$d\mathrm {M}_{n}(\tau )$
, and
![]() $d\boldsymbol {M}_{\Lambda _{n}(\tau )}$
and
$d\boldsymbol {M}_{\Lambda _{n}(\tau )}$
and
![]() $d\boldsymbol {M}_{\mathrm {M}_{n}(\tau )}$
are the square integrable martingales all written in the form of stochastic differentials.
$d\boldsymbol {M}_{\mathrm {M}_{n}(\tau )}$
are the square integrable martingales all written in the form of stochastic differentials.
It is not difficult to explain that the compensators for the stochastic differentials
![]() $d\Lambda _{n}(\tau )$
and
$d\Lambda _{n}(\tau )$
and
![]() $d\mathrm {M}_{n}(\tau )$
have the forms
$d\mathrm {M}_{n}(\tau )$
have the forms
![]() $\lambda _{n,\tau }d\tau $
and
$\lambda _{n,\tau }d\tau $
and
![]() $\mu _{n,\tau }d\tau $
. The compensator of an ordinary Poisson process with rate
$\mu _{n,\tau }d\tau $
. The compensator of an ordinary Poisson process with rate
![]() $\lambda $
is known to be equal to
$\lambda $
is known to be equal to
![]() $\lambda \tau $
(see [Reference Jacod and Shiryaev9, Reference Liptser and Shiryaev13]). That is, for its stochastic differential, we have
$\lambda \tau $
(see [Reference Jacod and Shiryaev9, Reference Liptser and Shiryaev13]). That is, for its stochastic differential, we have
![]() $\lambda d\tau $
. In the case of a time-inhomogeneous Poisson process, the instantaneous rate coincides with the rate of an ordinary Poisson process given at the point
$\lambda d\tau $
. In the case of a time-inhomogeneous Poisson process, the instantaneous rate coincides with the rate of an ordinary Poisson process given at the point
![]() $\tau $
.
$\tau $
.
Using these facts, our system of equations can be rewritten as follows:
 $$ \begin{align*} \begin{aligned} d\mathsf{I}\{Z(\tau)=n\} & =\mathsf{I}\{Z(\tau-)=n+1\}\mu_{n+1,\tau}d\tau+\mathsf{I}\{Z(\tau-)=n-1\}\lambda_{n-1,\tau}d\tau\\ &\quad -\mathsf{I}\{Z(\tau-)=n\}[\lambda_{n,\tau}+\mu_{n,\tau}]d\tau +\mathsf{I}\{Z(\tau-)=n+1\}d\boldsymbol{M}_{\mathrm{M}_{n+1}(\tau)}\\ &\quad +\mathsf{I}\{Z(\tau-)=n-1\}d\boldsymbol{M}_{\Lambda_{n-1}(\tau)} -\mathsf{I}\{Z(\tau-)=n\}d[\boldsymbol{M}_{\Lambda_{n}(\tau)}+\boldsymbol{M}_{\mathrm{M}_{n}(\tau)}],\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d\mathsf{I}\{Z(\tau)=n\} & =\mathsf{I}\{Z(\tau-)=n+1\}\mu_{n+1,\tau}d\tau+\mathsf{I}\{Z(\tau-)=n-1\}\lambda_{n-1,\tau}d\tau\\ &\quad -\mathsf{I}\{Z(\tau-)=n\}[\lambda_{n,\tau}+\mu_{n,\tau}]d\tau +\mathsf{I}\{Z(\tau-)=n+1\}d\boldsymbol{M}_{\mathrm{M}_{n+1}(\tau)}\\ &\quad +\mathsf{I}\{Z(\tau-)=n-1\}d\boldsymbol{M}_{\Lambda_{n-1}(\tau)} -\mathsf{I}\{Z(\tau-)=n\}d[\boldsymbol{M}_{\Lambda_{n}(\tau)}+\boldsymbol{M}_{\mathrm{M}_{n}(\tau)}],\\ \end{aligned} \end{align*} $$
for
![]() $n=1,2,\ldots ,$
and
$n=1,2,\ldots ,$
and
 $$ \begin{align*} \begin{aligned} d\mathsf{I}\{Z(\tau)=0\} & =\mathsf{I}\{Z(\tau-)=1\}\mu_{1,\tau}d\tau-\mathsf{I}\{Z(\tau-)=0\}\lambda_{0,\tau}d\tau\\ &\quad +\mathsf{I}\{Z(\tau-)=1\}d\boldsymbol{M}_{\mathrm{M}_{1}(\tau)}-\mathsf{I}\{Z(\tau-)=0\}d\boldsymbol{M}_{\Lambda_{0}(\tau)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d\mathsf{I}\{Z(\tau)=0\} & =\mathsf{I}\{Z(\tau-)=1\}\mu_{1,\tau}d\tau-\mathsf{I}\{Z(\tau-)=0\}\lambda_{0,\tau}d\tau\\ &\quad +\mathsf{I}\{Z(\tau-)=1\}d\boldsymbol{M}_{\mathrm{M}_{1}(\tau)}-\mathsf{I}\{Z(\tau-)=0\}d\boldsymbol{M}_{\Lambda_{0}(\tau)}. \end{aligned} \end{align*} $$
Next, we rewrite the last two equations in their integral forms by taking the expectation and averaging:
 $$ \begin{align*} 0 & =\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n+1\}\mu_{n+1,\tau}d\tau \\ &\quad +\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n-1\}\lambda_{n-1,\tau}d\tau\\ &\quad -\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n\}[\lambda_{n,\tau}+\mu_{n,\tau}]d\tau \\ &\quad +\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n+1\}d\boldsymbol{M}_{\mathrm{M}_{n+1}(\tau)}\\ &\quad +\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n-1\}d\boldsymbol{M}_{\Lambda_{n-1}(\tau)}\\ &\quad -\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n\}d[\boldsymbol{M}_{\Lambda_{n}(\tau)}+\boldsymbol{M}_{\mathrm{M}_{n}(\tau)}], \end{align*} $$
$$ \begin{align*} 0 & =\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n+1\}\mu_{n+1,\tau}d\tau \\ &\quad +\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n-1\}\lambda_{n-1,\tau}d\tau\\ &\quad -\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n\}[\lambda_{n,\tau}+\mu_{n,\tau}]d\tau \\ &\quad +\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n+1\}d\boldsymbol{M}_{\mathrm{M}_{n+1}(\tau)}\\ &\quad +\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n-1\}d\boldsymbol{M}_{\Lambda_{n-1}(\tau)}\\ &\quad -\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=n\}d[\boldsymbol{M}_{\Lambda_{n}(\tau)}+\boldsymbol{M}_{\mathrm{M}_{n}(\tau)}], \end{align*} $$
for
![]() $n=1,2,\ldots ,$
and
$n=1,2,\ldots ,$
and
 $$ \begin{align*} 0=&\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=1\}\mu_{1,\tau}d\tau\\ &-\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=0\}\lambda_{0,\tau}d\tau\\ &+\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=1\}d\boldsymbol{M}_{\mathrm{M}_{1}(\tau)}\\ &-\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=0\}d\boldsymbol{M}_{\Lambda_{0}(\tau)}. \end{align*} $$
$$ \begin{align*} 0=&\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=1\}\mu_{1,\tau}d\tau\\ &-\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=0\}\lambda_{0,\tau}d\tau\\ &+\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=1\}d\boldsymbol{M}_{\mathrm{M}_{1}(\tau)}\\ &-\lim_{T\to\infty}\frac{1}{T}\mathsf{E}\int_{0}^{T}\mathsf{I}\{Z(\tau-)=0\}d\boldsymbol{M}_{\Lambda_{0}(\tau)}. \end{align*} $$
In these equations, all the terms containing an expectation over martingales (such as
![]() $\lim _{T\to \infty }T^{-1}\mathsf {E}\int _{0}^{T}\mathsf {I}\{Z(\tau -)=n-1\}d\boldsymbol {M}_{\Lambda _{n-1}(\tau )}$
) are equal to zero. From these equations, we finally arrive at the system of equations:
$\lim _{T\to \infty }T^{-1}\mathsf {E}\int _{0}^{T}\mathsf {I}\{Z(\tau -)=n-1\}d\boldsymbol {M}_{\Lambda _{n-1}(\tau )}$
) are equal to zero. From these equations, we finally arrive at the system of equations:
for
![]() $ n=1,2,\ldots ,$
and
$ n=1,2,\ldots ,$
and
where
![]() $P_n=\lim _{\tau \to \infty }\mathsf {P}\{Z(\tau )=n\}$
are the final probabilities, if they exist. It is readily seen that the system of equations for the final probabilities coincides with the standard system of equations for the ordinary birth-and-death process.
$P_n=\lim _{\tau \to \infty }\mathsf {P}\{Z(\tau )=n\}$
are the final probabilities, if they exist. It is readily seen that the system of equations for the final probabilities coincides with the standard system of equations for the ordinary birth-and-death process.
3.2 Criteria for recurrence and transience
In the proof of the theorem, we use a simplified (degenerate) version of the criteria for recurrence or transience of birth-and-death processes [Reference Abramov5], which is sufficient for the purpose of this paper. It is as follows.
Lemma 3.1. An ordinary birth-and-death process is transient if there exists
![]() $c>1$
and
$c>1$
and
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n\geq n_0$
,
$n\geq n_0$
,
and it is recurrent if there exists
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n>n_0$
,
$n>n_0$
,
 $$ \begin{align*} \frac{\lambda_{n}}{\mu_{n}}\leq1+\frac{1}{n}. \end{align*} $$
$$ \begin{align*} \frac{\lambda_{n}}{\mu_{n}}\leq1+\frac{1}{n}. \end{align*} $$
The statement of Lemma 3.1 follows immediately from the well-known Karlin–McGregor criteria [Reference Karlin and McGregor10], according to which an ordinary birth-and-death process is recurrent if and only if
 $$ \begin{align*}\sum_{n=1}^{\infty}\prod_{k=1}^{n}\frac{\mu_k}{\lambda_k}=\infty,\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty}\prod_{k=1}^{n}\frac{\mu_k}{\lambda_k}=\infty,\end{align*} $$
by application of Raabe’s convergence (divergence) test for positive series. The more general results formulated in [Reference Abramov5, Reference Abramov6] were a consequence of the extended version of the Bertrand–De Morgan test [Reference Abramov5] and Bertrand–De Morgan–Cauchy test [Reference Abramov6].
For the time-inhomogeneous birth-and-death process, the parameters of which obey (3.1)–(3.3), similar conditions apply. For transience, it is the existence of
![]() $c>1$
and
$c>1$
and
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n\geq n_0$
,
$n\geq n_0$
,
 $$ \begin{align*} \frac{\lambda_{n,\tau}}{\mu_{n,\tau}}\geq1+\frac{c}{n}. \end{align*} $$
$$ \begin{align*} \frac{\lambda_{n,\tau}}{\mu_{n,\tau}}\geq1+\frac{c}{n}. \end{align*} $$
For recurrence, it is the existence of
![]() $c<1$
and
$c<1$
and
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n\geq n_0$
,
$n\geq n_0$
,
 $$ \begin{align*} \frac{\lambda_{n,\tau}}{\mu_{n,\tau}}\leq1+\frac{c}{n}. \end{align*} $$
$$ \begin{align*} \frac{\lambda_{n,\tau}}{\mu_{n,\tau}}\leq1+\frac{c}{n}. \end{align*} $$
Here we keep in mind that
![]() $\tau \to \infty $
together with
$\tau \to \infty $
together with
![]() $n\to \infty $
with probability
$n\to \infty $
with probability
![]() $1$
.
$1$
.
3.3 The final part of the proof
To finish the proof, we adapt the criteria for recurrence and transience for the time-inhomogeneous birth-and-death process with birth rates
![]() $\lambda _{n,\tau }=1/2+\varphi (n,\tau )$
and death rates
$\lambda _{n,\tau }=1/2+\varphi (n,\tau )$
and death rates
![]() $\mu _{n,\tau }=1/2-\varphi (n,\tau )$
. The birth-and-death process is a continuous time process, while the random walk
$\mu _{n,\tau }=1/2-\varphi (n,\tau )$
. The birth-and-death process is a continuous time process, while the random walk
![]() $X_t$
we deal with in the formulation of the theorem is a discrete time process. To correctly specify our argument, we assume that we deal with the continuous càdlàg process
$X_t$
we deal with in the formulation of the theorem is a discrete time process. To correctly specify our argument, we assume that we deal with the continuous càdlàg process
![]() $Z(\tau )$
, where the moments of jumps characterise the random walk
$Z(\tau )$
, where the moments of jumps characterise the random walk
![]() $X_t$
. The meaning of t is the tth consecutive event of the Poisson processes, the parameters of which are specified at the moments of jumps, and depend on state n and discrete time t. Let
$X_t$
. The meaning of t is the tth consecutive event of the Poisson processes, the parameters of which are specified at the moments of jumps, and depend on state n and discrete time t. Let
![]() $u_t$
denote the time moment of the tth jump. It is assumed that for any
$u_t$
denote the time moment of the tth jump. It is assumed that for any
![]() $\tau $
with
$\tau $
with
![]() $u_t\leq \tau <u_{t+1}$
, the function
$u_t\leq \tau <u_{t+1}$
, the function
![]() $\varphi (n,\tau )=\varphi (n,u_t)$
, and consequently the rates of the Poisson processes are
$\varphi (n,\tau )=\varphi (n,u_t)$
, and consequently the rates of the Poisson processes are
![]() $\lambda _{n,\tau }=\lambda _{n,u_t}$
and
$\lambda _{n,\tau }=\lambda _{n,u_t}$
and
![]() $\mu _{n,\tau }=\mu _{n,u_t}$
. Notice that the rates of Poisson processes are specified such that the mean time between two jumps is equal to
$\mu _{n,\tau }=\mu _{n,u_t}$
. Notice that the rates of Poisson processes are specified such that the mean time between two jumps is equal to
![]() $1$
. It is worth noting that the replacement of the original random walk that is a discrete time process with a continuous time-inhomogeneous birth-and-death process does not change the basic property of these two stochastic processes: both of them are either recurrent or transient. The idea of such replacement is not new (see, for example, [Reference Abramov4, Reference Abramov7]).
$1$
. It is worth noting that the replacement of the original random walk that is a discrete time process with a continuous time-inhomogeneous birth-and-death process does not change the basic property of these two stochastic processes: both of them are either recurrent or transient. The idea of such replacement is not new (see, for example, [Reference Abramov4, Reference Abramov7]).
Denote by
![]() $\mathcal {F}_\tau $
the filtration of the process
$\mathcal {F}_\tau $
the filtration of the process
![]() $Z(\tau )$
. If
$Z(\tau )$
. If
![]() $\varphi (Z(\tau ),\tau )$
is a positive process vanishing in
$\varphi (Z(\tau ),\tau )$
is a positive process vanishing in
![]() $L^1$
as
$L^1$
as
![]() $\tau \to \infty $
, then denoting by
$\tau \to \infty $
, then denoting by
![]() $\triangle Z_{\tau ,\tau +\sigma }$
the increment of the process
$\triangle Z_{\tau ,\tau +\sigma }$
the increment of the process
![]() $Z(\tau )$
in the interval
$Z(\tau )$
in the interval
![]() $[\tau , \tau +\sigma )$
, for the process
$[\tau , \tau +\sigma )$
, for the process
![]() $Z^2(\tau )-\tau $
,
$Z^2(\tau )-\tau $
,
 $$ \begin{align*} \begin{aligned} \mathsf{E}[Z^2(\tau+\sigma)-(\tau+\sigma)~|~\mathcal{F}_{\tau-}]&=\mathsf{E}[(Z(\tau-)+\triangle Z_{\tau, \tau+\sigma})^2-(\tau+\sigma)~|~\mathcal{F}_{\tau-}]\\ &=Z^2(\tau-)+2\mathsf{E}(Z(\tau-)\triangle Z_{\tau, \tau+\sigma}~|~\mathcal{F}_{\tau-})-\tau\\ &=Z^2(\tau)-\tau+o(Z(\tau)), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathsf{E}[Z^2(\tau+\sigma)-(\tau+\sigma)~|~\mathcal{F}_{\tau-}]&=\mathsf{E}[(Z(\tau-)+\triangle Z_{\tau, \tau+\sigma})^2-(\tau+\sigma)~|~\mathcal{F}_{\tau-}]\\ &=Z^2(\tau-)+2\mathsf{E}(Z(\tau-)\triangle Z_{\tau, \tau+\sigma}~|~\mathcal{F}_{\tau-})-\tau\\ &=Z^2(\tau)-\tau+o(Z(\tau)), \end{aligned} \end{align*} $$
since
![]() $\mathsf {E}(Z(\tau -)\triangle Z_{t,t+s}~|~\mathcal {F}_{\tau -})=o(Z(\tau ))$
and
$\mathsf {E}(Z(\tau -)\triangle Z_{t,t+s}~|~\mathcal {F}_{\tau -})=o(Z(\tau ))$
and
![]() $\mathsf {E}(\triangle Z_{\tau ,\tau +\sigma }^2|\mathcal {F}_{\tau -})=\mathsf {E}\triangle Z_{\tau ,\tau +\sigma }^2=\sigma $
for any
$\mathsf {E}(\triangle Z_{\tau ,\tau +\sigma }^2|\mathcal {F}_{\tau -})=\mathsf {E}\triangle Z_{\tau ,\tau +\sigma }^2=\sigma $
for any
![]() $\tau $
. The last equality follows from Wald’s identity [Reference Feller8]. Specifically, we have
$\tau $
. The last equality follows from Wald’s identity [Reference Feller8]. Specifically, we have
![]() $\mathsf {E}\triangle Z_{\tau ,\tau +\sigma }^2=\mathsf {E}\sum _{i=1}^{N_\sigma }1=\sigma $
, where
$\mathsf {E}\triangle Z_{\tau ,\tau +\sigma }^2=\mathsf {E}\sum _{i=1}^{N_\sigma }1=\sigma $
, where
![]() $N_\sigma $
denotes the number of events in time
$N_\sigma $
denotes the number of events in time
![]() $\sigma $
of a Poisson process with rate
$\sigma $
of a Poisson process with rate
![]() $1$
.
$1$
.
This asymptotic relationship implies that
![]() $\varphi (Z(\tau ),\tau )\asymp \varphi (Z(\tau ),Z^2(\tau ))$
for large
$\varphi (Z(\tau ),\tau )\asymp \varphi (Z(\tau ),Z^2(\tau ))$
for large
![]() $\tau $
with probability approaching 1. It also implies that
$\tau $
with probability approaching 1. It also implies that
![]() $\varphi (X_t,t)\asymp \varphi (X_t,X_t^2)$
for large t with probability approaching
$\varphi (X_t,t)\asymp \varphi (X_t,X_t^2)$
for large t with probability approaching
![]() $1$
.
$1$
.
Then for large n,
 $$ \begin{align*} \frac{\lambda_{n,t}}{\mu_{n,t}}\asymp\frac{\lambda_{n,n^2}}{\mu_{n,n^2}}=\frac{1+2\varphi(n,n^2)}{1-2\varphi(n,n^2)}=1+4\varphi(n,n^2)+O[(\varphi(n,n^2))^2]. \end{align*} $$
$$ \begin{align*} \frac{\lambda_{n,t}}{\mu_{n,t}}\asymp\frac{\lambda_{n,n^2}}{\mu_{n,n^2}}=\frac{1+2\varphi(n,n^2)}{1-2\varphi(n,n^2)}=1+4\varphi(n,n^2)+O[(\varphi(n,n^2))^2]. \end{align*} $$
Now, application of Lemma 3.1 yields the required statement of the theorem.
4 Examples
In this section, we provide a number of examples to illustrate the main result of this paper.
Example 4.1. Let
![]() $\varphi (n,t)\asymp \rho n/(2t)$
,
$\varphi (n,t)\asymp \rho n/(2t)$
,
![]() $n\to \infty $
(see [Reference Menshikov and Volkov14]). We show that the process is recurrent if
$n\to \infty $
(see [Reference Menshikov and Volkov14]). We show that the process is recurrent if
![]() $\rho <1/2$
and it is transient if
$\rho <1/2$
and it is transient if
![]() $\rho>1/2$
. Indeed, in this case,
$\rho>1/2$
. Indeed, in this case,
![]() $\varphi (n, n^2)=\rho /(2n)$
for large n. Hence, the required statement follows from the theorem.
$\varphi (n, n^2)=\rho /(2n)$
for large n. Hence, the required statement follows from the theorem.
Let us now find the condition under which
![]() $\varphi (X_t,t)\to 0$
in
$\varphi (X_t,t)\to 0$
in
![]() $L^1$
. We have
$L^1$
. We have
From this, it is readily seen that
![]() $\mathsf {E}X_t=O(t^\rho )$
. Hence,
$\mathsf {E}X_t=O(t^\rho )$
. Hence,
![]() $\mathsf {E}X_t/t\to 0$
as
$\mathsf {E}X_t/t\to 0$
as
![]() $t\to \infty $
if and only if
$t\to \infty $
if and only if
![]() $\rho <1$
. This means that only under this condition,
$\rho <1$
. This means that only under this condition,
![]() $\varphi (X_t,t)\to 0$
in
$\varphi (X_t,t)\to 0$
in
![]() $L^1$
.
$L^1$
.
Example 4.2. Let
![]() $\varphi (n,t)\asymp n^\alpha /t^\beta $
,
$\varphi (n,t)\asymp n^\alpha /t^\beta $
,
![]() $\beta>\alpha $
,
$\beta>\alpha $
,
![]() $\beta>0$
,
$\beta>0$
,
![]() $n\to \infty $
(see [Reference Menshikov and Volkov14]). Assuming n large, for the condition of recurrence,
$n\to \infty $
(see [Reference Menshikov and Volkov14]). Assuming n large, for the condition of recurrence,
which yields
![]() $\alpha <2\beta -1$
. Keeping in mind that
$\alpha <2\beta -1$
. Keeping in mind that
![]() $\alpha <\beta $
, we obtain
$\alpha <\beta $
, we obtain
![]() $\alpha <\min \{\beta , 2\beta -1\}$
. The condition of transience is obtained similarly. It is complementary to the condition of recurrence. Namely, it is
$\alpha <\min \{\beta , 2\beta -1\}$
. The condition of transience is obtained similarly. It is complementary to the condition of recurrence. Namely, it is
![]() $0\leq \beta <1$
and
$0\leq \beta <1$
and
![]() $2\beta -1<\alpha <\beta $
.
$2\beta -1<\alpha <\beta $
.
Example 4.3. Let
![]() $\varphi (n,t)\asymp \rho n^\alpha /t^\beta $
,
$\varphi (n,t)\asymp \rho n^\alpha /t^\beta $
,
![]() $-1\leq \alpha \leq 1$
,
$-1\leq \alpha \leq 1$
,
![]() $2\beta -\alpha =1$
,
$2\beta -\alpha =1$
,
![]() $n\to \infty $
(the unsolved problem in [Reference Menshikov and Volkov14]). We have
$n\to \infty $
(the unsolved problem in [Reference Menshikov and Volkov14]). We have
![]() $\beta =(1+\alpha )/2$
and the asymptotic expression for
$\beta =(1+\alpha )/2$
and the asymptotic expression for
![]() $\varphi (n,t)$
takes the form
$\varphi (n,t)$
takes the form
For large n,
Thus, for
![]() $-1\leq \alpha \leq 1$
, the process
$-1\leq \alpha \leq 1$
, the process
![]() $X_t$
is recurrent for
$X_t$
is recurrent for
![]() $\rho <1/4$
and transient for
$\rho <1/4$
and transient for
![]() $\rho>1/4$
.
$\rho>1/4$
.
Let us now discuss the condition under which
![]() $\varphi (X_t,t)\to 0$
in
$\varphi (X_t,t)\to 0$
in
![]() $L^1$
. Here we need only consider the case of
$L^1$
. Here we need only consider the case of
![]() $\alpha =1$
, since for
$\alpha =1$
, since for
![]() $-1\leq \alpha <1$
, we obviously have the required convergence. For
$-1\leq \alpha <1$
, we obviously have the required convergence. For
![]() $\alpha =1$
, the problem reduces to the case considered in Example 4.1. Taking into account that result, we arrive at the conclusion that in the case
$\alpha =1$
, the problem reduces to the case considered in Example 4.1. Taking into account that result, we arrive at the conclusion that in the case
![]() $\alpha =1$
,
$\alpha =1$
,
![]() $\varphi (X_t,t)\to 0$
in
$\varphi (X_t,t)\to 0$
in
![]() $L^1$
if and only if
$L^1$
if and only if
![]() $\rho <1/2$
.
$\rho <1/2$
.
Example 4.4. Let
![]() $\varphi (n,t)\asymp \mathrm {e}^{\alpha n-\beta t}$
,
$\varphi (n,t)\asymp \mathrm {e}^{\alpha n-\beta t}$
,
![]() $\beta>0$
,
$\beta>0$
,
![]() $n\to \infty $
.
$n\to \infty $
.
For large n,
![]() $\varphi (n,n^2)\asymp \mathrm {e}^{\alpha n-\beta n^2}=o(1/n)$
. Hence, the process
$\varphi (n,n^2)\asymp \mathrm {e}^{\alpha n-\beta n^2}=o(1/n)$
. Hence, the process
![]() $X_t$
is recurrent.
$X_t$
is recurrent.
5 Concluding remarks
In this paper, we formulated and proved a new result for recurrence or transience of time-inhomogeneous birth-and-death processes. Compared with the earlier considerations in [Reference Menshikov and Volkov14], our achievements are as follows.
-
(1) We established simple and general criteria for recurrence or transience of time-inhomogeneous birth-and-death processes. This enables us to establish recurrence or transience of the processes in a very simple way for a wide class of processes. Our approach makes an essential difference to [Reference Menshikov and Volkov14], where special routine derivations for any particular case study were required.
-
(2) The generality of our main result enabled us to solve the open problem that was left unsolved in [Reference Menshikov and Volkov14].
-
(3) In Examples 4.1 and 4.3, we also studied the behaviour of the drift. We found the value of the parameter under which the drift was vanishing in time in the sense provided in the paper.
Acknowledgement
The author thanks all the people who helped in the preparation of this paper officially or privately.