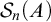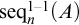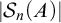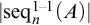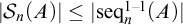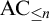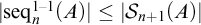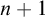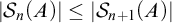THE PERMUTATIONS WITH n NON-FIXED POINTS AND THE SEQUENCES WITH LENGTH n OF A SET

Abstract

We write $\mathcal {S}_n(A)$ for the set of permutations of a set A with n non-fixed points and $\mathrm {{seq}}^{1-1}_n(A)$ for the set of one-to-one sequences of elements of A with length n where n is a natural number greater than $1$. With the Axiom of Choice, $|\mathcal {S}_n(A)|$ and $|\mathrm {{seq}}^{1-1}_n(A)|$ are equal for all infinite sets A. Among our results, we show, in ZF, that $|\mathcal {S}_n(A)|\leq |\mathrm {{seq}}^{1-1}_n(A)|$ for any infinite set A if ${\mathrm {AC}}_{\leq n}$ is assumed and this assumption cannot be removed. In the other direction, we show that $|\mathrm {{seq}}^{1-1}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any infinite set A and the subscript $n+1$ cannot be reduced to n. Moreover, we also show that “$|\mathcal {S}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any infinite set A” is not provable in ZF.

1 Introduction

The factorial $|A|!$ is the cardinality of the set of permutations of a set A. Dawson and Howard showed in [2] that, in the Zermelo–Fraenkel set theory (ZF) with the Axiom of Choice (AC), $|A|!=2^{|A|}$ for any infinite set A, where $2^{|A|}$ is the cardinality of the power set of A. They also showed that, without AC, any relationship between these cardinals cannot be concluded for an arbitrary infinite set A.

Relations between the cardinality of the set of finite sequences of elements of a set A, written $\mathrm {{seq}}(A)$ , and $2^{|A|}$ have been studied in [6, 7]. Halbeisen and Shelah showed that “ $|\mathrm {{seq}}(A)|\neq 2^{|A|}$ for any infinite set A” is the best possible result in ZF while $|\mathrm {{seq}}(A)|< 2^{|A|}$ for any infinite set A when AC is assumed. The same results also hold when $\mathrm {{seq}}(A)$ is replaced by the set of one-to-one finite sequences of elements of A, written $\mathrm {{seq}}^{1-1}(A)$ . Although, without AC, we cannot conclude any relationship between $|A|!$ and $2^{|A|}$ for an arbitrary infinite set A, it has been shown in [12] that, in ZF, relations between $|\mathrm {{seq}}(A)|$ and $|A|!$ (also $|\mathrm {{seq}}^{1-1}(A)|$ and $|A|!$ ) are exactly the same as those of $|\mathrm {{seq}}(A)|$ and $2^{|A|}$ for infinite sets A. In contrast, the main theorem in [11] showed, in ZF, that $|\mathrm {{seq}}_n(A)|<|A|!$ for any infinite set A and any natural number n, where $\mathrm {{seq}}_n(A)$ is the set of sequences of elements of A with length n, although Specker showed in [13] that “ $|\mathrm {{seq}}_2(A)|\leq 2^{|A|}$ for any infinite set A” is not provable in ZF.

In this paper, we investigate relationships between $|\mathcal {S}_n(A)|$ and $|\mathrm {{seq}}^{1-1}_n(A)|$ as well as $|\mathrm {{seq}}_n(A)|$ for infinite sets A, where $\mathcal {S}_n(A)$ is the set of permutations of A with n non-fixed points and $\mathrm {{seq}}^{1-1}_n(A)$ is the set of one-to-one sequences of elements of A with length n where n is a natural number greater than $1$ . With AC, $|\mathcal {S}_n(A)|$ , $|\mathrm {{seq}}^{1-1}_n(A)|$ , and $|\mathrm {{seq}}_n(A)|$ are equal for all infinite sets A. Among our results, we show, in ZF, that $|\mathcal {S}_n(A)|\leq |\mathrm {{seq}}^{1-1}_n(A)|$ for any infinite set A if ${\mathrm {AC}}_{\leq n}$ is assumed and this assumption cannot be removed. In the other direction, we show that $|\mathrm {{seq}}^{1-1}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any infinite set A and the subscript $n+1$ cannot be reduced to n. Moreover, we also show that “ $|\mathcal {S}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any infinite set A” is not provable in ZF.

2 Results in ZF

All proofs in this section are done in ZF. For sets A and B, $|A|=|B|$ means there is an explicit bijection from A onto B, $|A|\leq |B|$ means there is an explicit injection from A into B, and $|A|<|B|$ means $|A|\leq |B|$ but $|A|\neq |B|$ .

A set A is Dedekind infinite if $\aleph _0\leq |A|$ , otherwise A is Dedekind finite. Note that A is a Dedekind infinite set if and only if there exists a proper subset B of A such that $|A|=|B|$ .

We list the notations used in this paper below.

Notation. For a set A and a natural number n, let:

1. (1) $[A]^n=\{X\subseteq A\mid |X|=n\}$ ,

2. (2) $[A]^{\leq n}=\{X\subseteq A\mid |X|\leq n\}$ ,

3. (3) $\mathrm {{fin}} (A)= \bigcup \limits _{k\in \omega }[A]^k$ ,

4. (4) $\mathrm {{seq}}_n(A)=\{f\mid f\colon n\rightarrow A\}$ ,

5. (5) $\mathrm {{seq}}(A)=\bigcup \limits _{k\in \omega }\mathrm {{seq}}_k(A)$ ,

6. (6) $\mathrm {{seq}}^{1-1}_n(A)=\{f\in \mathrm {{seq}}_n(A)\mid f\text { is injective}\}$ ,

7. (7) $\mathrm {{seq}}^{1-1}(A)=\bigcup \limits _{k\in \omega }\mathrm {{seq}}^{1-1}_k(A)$ ,

8. (8) $\mathcal {S}(A)=\{f\colon A\rightarrow A\mid f\text { is bijective}\}$ ,

9. (9) $\mathcal {S}_n(A)=\{f\in \mathcal {S}(A)\mid |\{a\in A\mid f(a)\neq a\}|=n\}$ ,

10. (10) $\mathcal {S}_{\mathrm {{fin}}}(A)=\bigcup \limits _{k\in \omega }\mathcal {S}_k(A)$ ,

and for $\pi \in \mathcal {S}(A)$ , let $\mathrm {{m}}(\pi )=\{a\in A\mid \pi (a)\neq a\}$ ; in other words, $\mathrm {{m}}(\pi )$ collects all elements in A that $\pi $ permutes.

We write $(a_0; a_1;\ldots; a_n)$ for the cyclic permutation such that

$a_0\mapsto a_1\mapsto \cdots \mapsto a_n\mapsto a_0$ .

Throughout, n is a natural number which is greater than $1$ , unless otherwise stated.

The following weak forms of AC are relevant to our work.

• • ${\mathrm {AC}}_n$ : Every family of sets with cardinality n has a choice function.

• • ${\mathrm {AC}}_{\leq n}$ : Every family of nonempty sets with cardinality less than or equal to n has a choice function.

• • ${\mathrm {AC}}_{<\aleph _0}$ : Every family of nonempty finite sets has a choice function.

First, we give a relation between $|\mathcal {S}_n(A)|$ and $|\mathrm {{seq}}^{1-1}_n(A)|$ for an infinite set A under the weak form ${\mathrm {AC}}_{\leq n}$ . Later, we shall show in the next section that this assumption cannot be removed.

Theorem 2.1. ${\mathrm {AC}}_{\leq n}$ implies that $|\mathcal {S}_n(A)|\leq |\mathrm {{seq}}^{1-1}_n(A)|$ for every infinite set A.

Proof Let A be an infinite set. By ${\mathrm {AC}}_{\leq n}$ , we can define a linear order $<_B$ on each $B\in [A]^n$ by using a choice function for $[A]^{\leq n}.$

For each $\pi \in \mathcal {S}_n(A)$ where $\mathrm {{m}}(\pi )=\{b_1,\dots ,b_{n}\}$ and $b_1<_{\mathrm {{m}}(\pi )}\dots <_{\mathrm {{m}}(\pi )}b_{n}$ , we define $f\colon \mathcal {S}_n(A)\rightarrow \mathrm {{seq}}^{1-1}_n(A)$ by

$$\begin{align*}f(\pi)=(\pi(b_1),\dots,\pi(b_{n})).\end{align*}$$

We can see that f is an injection.

Note that if we assume ${\mathrm {AC}}_n$ and restrict the domain of f in the above proof to $\mathrm {{C}}_n(A)=\{\pi \in \mathcal {S}_n(A)\mid \pi \text { is a cyclic permutation}\}$ , then we can define an injection $g\colon \mathrm {{C}}_n(A)\to \mathrm {{seq}}^{1-1}_n(A)$ by

$$\begin{align*}g(\pi)=(\pi(b), \pi(\pi(b)),\dots,\pi^n(b)),\end{align*}$$

where b is the element chosen from $\mathrm {{m}}(\pi )$ by a choice function for $[A]^n$ . As a result, for $n\leq 3$ , the assumption of the above theorem can be weakened to ${\mathrm {AC}}_n$ .

Relations between $|\mathrm {{seq}}(A)|$ and $|\mathrm {{fin}}(A)|$ for infinite sets A have been studied in [1]. The theorem below is a result which is related to our work.

Theorem 2.2. ${\mathrm {AC}}_{\leq n}$ implies that $|\mathrm {{seq}}_n(A)|\leq |\mathrm {{fin}}(A)|$ for every infinite set A.

Proof Cf. [1, Corollary 2.2].

Thus the following corollary follows immediately from the above theorems.

Corollary 2.3. ${\mathrm {AC}}_{\leq n}$ implies that $|\mathcal {S}_n(A)|\leq |\mathrm {{fin}}(A)|$ for every infinite set A.

Theorems 2.9 and 2.10 in [10] show that if ${\mathrm {AC}}_{<\aleph _0}$ is assumed, then for any set A, $|\mathcal {S}_{\mathrm {{fin}}}(A)|\leq |\mathrm {{fin}}(A)|$ if and only if A is Dedekind infinite and this statement cannot be proved without ${\mathrm {AC}}_{<\aleph _0}$ (cf. [10, Theorem 3.2]). It is easy to see that ${\mathrm {AC}}_{<\aleph _0}$ implies $|\mathrm {{fin}}(A)|\leq |\mathrm {{seq}}^{1-1}(A)|$ for any infinite set A. Thus, under ${\mathrm {AC}}_{<\aleph _0}$ , $|\mathcal {S}_{\mathrm {{fin}}}(A)|\leq |\mathrm {{seq}}^{1-1}(A)|$ for any Dedekind infinite set A. Guozhen and Jiachen also showed in [4, Lemma 2.26] that for any linearly ordered set A, $|\mathcal {S}_{\mathrm {{fin}}}(A)|\leq |\mathrm {{seq}}^{1-1}(A)|$ and $\leq $ can be replaced by $<$ if A is Dedekind finite. Since “every set can be linearly ordered” is stronger than ${\mathrm {AC}}_{<\aleph _0}$ (cf. [9, p. 104]), we obtain a stronger result.

Theorem 2.4. ${\mathrm {AC}}_{<\aleph _0}$ implies that $|\mathcal {S}_{\mathrm {{fin}}}(A)|\leq |\mathrm {{seq}}^{1-1}(A)|$ for every infinite set A and if A is Dedekind finite, then $|\mathcal {S}_{\mathrm {{fin}}}(A)|<|\mathrm {{seq}}^{1-1}(A)|$ .

Proof Let A be an infinite set. Similarly to the proof of Theorem 2.1, under ${\mathrm {AC}}_{<\aleph _0}$ , each finite subset of A can be linearly ordered. Thus, we can define an injection $g\colon \mathcal {S}_{\mathrm {{fin}}}(A)\to \mathrm {{seq}}^{1-1}(A)$ as f in Theorem 2.1. Hence $|\mathcal {S}_{\mathrm {{fin}}}(A)|\leq |\mathrm {{seq}}^{1-1}(A)|$ . From the definition of g, we can see that for any $(b_1,\dots ,b_{n})\in \mathrm {{seq}}^{1-1}(A)$ such that $b_1$ is the least element of $\{b_1,\dots ,b_{n}\}$ , $(b_1,\dots ,b_{n})$ is not in the range of g. Thus g is not a surjection and so $\mathrm {{ran}}(g)$ is a proper subset of $\mathrm {{seq}}^{1-1}(A)$ where $|\mathcal {S}_{\mathrm {{fin}}}(A)|=|\mathrm {{ran}}(g)|$ . Suppose A is Dedekind finite. From [3, Fact 2.14], we have that $\mathrm {{seq}}^{1-1}(A)$ is also Dedekind finite. As a result, $|\mathcal {S}_{\mathrm {{fin}}}(A)|\neq |\mathrm {{seq}}^{1-1}(A)|$ . Thus $|\mathcal {S}_{\mathrm {{fin}}}(A)|<|\mathrm {{seq}}^{1-1}(A)|$ .

Next, we show relationships between $|\mathcal {S}_n(\alpha )|$ and other related cardinals when $\alpha $ is an infinite ordinal.

Theorem 2.5. For any infinite ordinal $\alpha $ , $|\alpha |\leq |\mathcal {S}_n(\alpha )|.$

Proof It is easy to see that for an infinite ordinal $\alpha $ , $f\colon \alpha \rightarrow \mathcal {S}_n(\alpha )$ defined by

$$\begin{align*}f(\beta) = \begin{cases} (\beta+1;\beta+2;\dots;\beta+n), & \text{if } \beta+n<\alpha ,\\ (k+2;k+4;\dots;k+2n), & \text{if } \beta+k=\alpha \leq \beta+n \\ \end{cases}\end{align*}$$

is an injection.

Fact 2.6. For any infinite ordinal $\alpha $ , $|\alpha |=|\mathrm {{seq}}(\alpha )|$ .

Proof Cf. [5, Theorem 5.19].

Corollary 2.7. For all infinite ordinals $\alpha $ ,

$$\begin{align*}|\alpha|=|\mathrm{{seq}}^{1-1}_n(\alpha)|=|\mathrm{{seq}}_n(\alpha)|=|\mathcal{S}_n(\alpha)|=|\mathcal{S}_{n+1}(\alpha)|.\end{align*}$$

Proof By Theorems 2.1 and 2.5, Fact 2.6, and the Cantor–Bernstein Theorem (which is provable in ZF), these bijections can be constructed.

We have shown that if ${\mathrm {AC}}_{\leq n}$ is assumed, then $|\mathcal {S}_n(A)|\leq |\mathrm {{seq}}_n(A)|$ for all infinite sets A. Now we shift our focus to the other direction. It has been shown in [4, Lemma 3.27] that for any set A with $|A|\geq 2n(n+1)$ , $|\mathrm {{seq}}_n(A)|\leq |\mathcal {S}_{\leq 2n+1}(A)|$ , where $\mathcal {S}_{\leq 2n+1}(A)$ is the set of permutations of A which move at most $2n+1$ elements of A. Now, we will show that $|\mathrm {{seq}}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any large enough finite set A and $|\mathrm {{seq}}^{1-1}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any infinite set A. First, we look at the finite case.

Theorem 2.8. Let A be a finite set with $|A|\geq 3\cdot 2^n+n.$ Then $|\mathrm {{seq}}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ .

Proof For convenience, let $|A|=a$ . Since $a\geq 3\cdot 2^n+n>2n$ , $a<2(a-n)$ and so

$$ \begin{align*} |\mathrm{{seq}}_n(A)| = a^n&<(2(a-n))^n\\ &<a\cdot(a-1)\cdot \cdots \cdot(a-(n-1))2^n \\ & \leq a\cdot(a-1)\cdot\cdots\cdot(a-n+1)\left[\frac{a-n}{3}\right] \\ & \leq a\cdot(a-1)\cdot\cdots\cdot(a-n)\left[\frac{1}{0!}-\frac{1}{1!}+\cdots+\frac{(-1)^{n+1}}{(n+1)!}\right]\\ &=\binom{a}{n+1}(n+1)!\left[\frac{1}{0!}-\frac{1}{1!}+\cdots+\frac{(-1)^{n+1}}{(n+1)!}\right]\\ &=|\mathcal{S}_{n+1}(A)| \end{align*} $$

as desired.

For the infinite case, we need some “large enough” finite set to construct an injection.

Lemma 2.9. There exists a natural number $K_n\geq 2n+1$ such that for all natural numbers $k<n$ , $k!\binom {n}{k}\binom {K_n}{k}\leq (k+1)!\binom {K_n}{k+1}$ .

Proof By straightforward computation, we can see that

$$\begin{align*}K_n=\max\{2n+1,\binom{n}{0}+0,\dots,\binom{n}{n-1}+n-1\}\end{align*}$$

satisfies the inequality.

Now we are ready for the main theorem.

Theorem 2.10. For all infinite sets A, $|\mathrm {{seq}}^{1-1}_{n}(A)|\leq |\mathcal {S}_{n+1}(A)|$ .

Proof Let A be an infinite set. By Lemma 2.9, there exists a natural number $K_n\geq 2n+1$ such that for all natural numbers $k<n$ ,

$$\begin{align*}k!\binom{n}{k}\binom{K_n}{k}\leq (k+1)!\binom{K_n}{k+1}.\end{align*}$$

Since $K_n\geq 2n+1$ , we also have that $\binom {K_n}{n}\leq \binom {K_n}{n+1}$ .

Let $X=\{x_1,x_2,\dots ,x_{K_n}\}\subseteq A$ and for each natural number $k\leq n$ , we define

$$\begin{align*}A_k=\{(a_1,\dots,a_n)\in\mathrm{{seq}}^{1-1}_n(A)\mid |\{a_1,\dots,a_n\}\cap X|=k\}.\end{align*}$$

It suffices to show that for each natural number $k\leq n$ , there exists an injection $f_k\colon A_k\rightarrow \mathcal {S}_{n+1}(A)$ where $f_0,\dots ,f_n$ have disjoint images.

First we deal with the case $k=n$ . We shall create an equivalence relation $\sim $ on $\mathrm {{seq}}^{1-1}_{n+1}(X)$ which tells us that the related sequences will generate the same cyclic permutation. The definition of $\sim $ is as follows:

For any $(a_0,\dots ,a_n),(b_0,\dots ,b_n)\in \mathrm {{seq}}^{1-1}_{n+1}(X)$ ,

$$\begin{align*}(a_0,\dots,a_n)\sim (b_0,\dots,b_n)\leftrightarrow\exists k\in\omega\forall l\in\omega,a_l=b_{l+k},\end{align*}$$

where the indices of $a_i$ and $b_i$ are considered in modulo $n+1$ . Note that

$$\begin{align*}[(a_0,\dots,a_n)]_{\sim}=[(b_0,\dots,b_n)]_{\sim}\leftrightarrow (a_0;\dots;a_n)=(b_0;\dots;b_n).\end{align*}$$

Thus $|\mathrm {{seq}}^{1-1}_{n+1}(X)/{\sim} |\leq |\mathcal {S}_{n+1}(A)|$ by mapping

$$\begin{align*}[(a_0,\dots,a_n)]_\sim \mapsto (a_0;\dots;a_n).\end{align*}$$

Since

$$ \begin{align*} |A_n|=n!\binom{K_n}{n}&\leq n!\binom{K_n}{n+1}\\&=\frac{1}{n+1}|\mathrm{{seq}}^{1-1}_{n+1}(X)|=|\mathrm{{seq}}^{1-1}_{n+1}(X)/{\sim}|, \end{align*} $$

there exists an injection $f_n\colon A_n\to \mathcal {S}_{n+1}(A)$ as desired.

Now, let $k<n$ be a natural number. We may assume that $0,1\notin A$ . We start by defining functions $n_X$ , $i_X$ , $Q_X$ , and $Q_X'$ from the same domain $\mathrm {{seq}}^{1-1}_n(A)$ as follows:

$$ \begin{align*} n_X(a_1,\dots,a_n)& =|\{a_1,\dots,a_n\}\cap X|, \\ i_X(a_1,\dots,a_n)& = (\epsilon_1,\dots,\epsilon_n), \text{where } \epsilon_i=1\text{ if } a_i\in X \text{ and}\\ & \hspace{2.8cm}\epsilon_i=0 \text{ otherwise, } \text{ for each }1\leq i\leq n, \\ Q_X(a_1,\dots,a_n) &= (a_{i_1},\ldots,a_{i_{m}}) \text{ if } \{a_1,\dots,a_n\}\cap X=\{a_{i_1},\dots,a_{i_{m}}\},\\ Q_X'(a_1,\dots,a_n) &=(a_{j_1},\ldots,a_{j_{l}}) \text{ if } \{a_1,\dots,a_n\}\setminus X=\{a_{j_1},\dots,a_{j_{l}}\}, \end{align*} $$

where the indices $i_1,\dots ,i_{m}$ and $j_1,\dots ,j_{l}$ are increasing.

Define $B_k=\{i_X(a)\mid a\in A_k\}$ . We have that

$$\begin{align*}|B_k\times \mathrm{{seq}}^{1-1}_k(X)|=k!\binom{n}{k}\binom{K_n}{k}\leq (k+1)!\binom{K_n}{k+1}=|\mathrm{{seq}}^{1-1}_{k+1}(X)|.\end{align*}$$

Hence there exists an injection $h_k\colon B_k\times \mathrm {{seq}}^{1-1}_k(X)\rightarrow \mathrm {{seq}}^{1-1}_{k+1}(X)$ .

Next, we will construct a cyclic permutation from two injective sequences of two disjoint sets.

For each $a=(a_0,\dots ,a_k)\in \mathrm {{seq}}^{1-1}_{k+1}(X)$ and $b=(b_0,\dots ,b_{n-k-1})\in \mathrm {{seq}}^{1-1}_{n-k}(A\setminus X)$ , we define the concatenation of a and b as follows:

$$\begin{align*}a^\frown b=(a_0;\dots;a_k;b_0;\dots;b_{n-k-1}).\end{align*}$$

Note that for any $a,a'\in \mathrm {{seq}}^{1-1}_{k+1}(X)$ and $b,b'\in \mathrm {{seq}}^{1-1}_{n-k}(A\setminus X)$ , if $a^\frown b=a^{\prime \frown } b',$ then $a=a'$ and $b=b'$ .

Now, we define $f_k\colon A_k\rightarrow \mathcal {S}_{n+1}(A)$ by

$$\begin{align*}f_k(a)=h_k(i_X(a),Q_X(a))^\frown Q_X'(a).\end{align*}$$

Note that $f_k$ moves exactly $k+1$ elements in X.

To show that $f_k$ is injective, let $a,b\in A_k$ be such that $f_k(a)=f_k(b)$ . Then $h_k(i_X(a),Q_X(a))=h_k(i_X(b),Q_X(b))$ and $Q_X'(a)=Q_X'(b)$ . Since $h_k$ is injective, $i_X(a)=i_X(b)$ and $Q_X(a)=Q_X(b)$ . Therefore we can retrieve the sequence a from the information $Q_X(a),Q_X'(a)$ and $i_X(a)$ as follows:

Change the $p^{\text {th}}$ occurrence of $1$ in the sequence $i_X(a)$ to $Q_X(a)(p-1)$ for each $1\leq p\leq k$ and change the $q^{\text {th}}$ occurrence of $0$ in the sequence $i_X(a)$ to $Q_X'(a)(q-1)$ for each $1\leq q\leq n-k$ . We can see that the resulting sequence is $a.$ Since the values of $i_X,Q_X,Q_X'$ at a and b are equal, we can conclude that $a=b.$ Therefore $f_k$ is injective.

Finally, since for each natural number $m\leq n$ and each $a\in A_m$ , $f_m(a)$ moves exactly $m+1$ elements in X, $f_0,\dots ,f_n$ have disjoint images. Thus $\bigcup \limits _{i=0}^{n} f_i\colon \mathrm {{seq}}^{1-1}_n(A)\rightarrow \mathcal {S}_{n+1}(A)$ is an injection.

Note that the above proof requires the choice of elements $x_1,x_2,\dots ,$ $x_{K_n}$ from A. Thus, in the absence of AC, we cannot make such choices for infinitely many n. Therefore, from the above theorem, we cannot conclude that $|\mathrm {{seq}}^{1-1}(A)|\leq |A|!$ for any infinite set A. It has been shown in [12, Theorem 3.1] that this statement is not provable in ZF as well.

From the above theorem, we have that $|\mathrm {{seq}}^{1-1}_{n}(A)|\leq |\mathcal {S}_{\mathrm {{fin}}}(A)|\leq |A|!$ for any infinite set A. From an earlier result in [11, Theorem 2.3], we know that $|\mathrm {{seq}}_{n}(A)|< |A|!$ for any infinite set A. However, Tachtsis showed in [14, Theorem 3.1] that “ $|\mathcal {S}_{\mathrm {{fin}}}(A)|< |A|!$ for any infinite set A” is not provable in ZF.

It is still questionable whether we can obtain a stronger result by replacing $\mathrm {{seq}}^{1-1}_n(A)$ in Theorem 2.10 by $\mathrm {{seq}}_n(A)$ . Guozhen and Jiachen showed in [4, Corollary 2.23] that for any set A, $|\mathrm {{seq}}(A)|= |\mathrm {{seq}}^{1-1}(A)|$ if and only if $A=\emptyset $ or A is Dedekind infinite. For the set of sequences with length n, we also have the following result.

Theorem 2.11. For any Dedekind infinite set A,

$$\begin{align*}|\mathrm{{seq}}_n(A)|= |\mathrm{{seq}}^{1-1}_{n}(A)|.\end{align*}$$

Proof Let A be a Dedekind infinite set. Without loss of generality, suppose that $A\cap (n\times n)=\emptyset $ . Since there is a canonical bijection from $A\cup (n\times n)$ onto A, it is enough to construct an injection from $\mathrm {{seq}}_n(A)$ into $\mathrm {{seq}}^{1-1}_n(A\cup (n\times n))$ .

For each $a=(a_0,\dots ,a_{n-1})\in \mathrm {{seq}}_n(A)$ and $k<n$ , let $B_{a,k}=\{l<k\mid a_l=a_k\}$ and define

$$\begin{align*}f(a)(k)= \begin{cases} a_k, & \text{if } B_{a,k}=\emptyset, \\ (\min B_{a,k},|B_{a,k}|), & \text{otherwise.} \end{cases}\end{align*}$$

Then $f\colon \mathrm {{seq}}_n(A)\rightarrow \mathrm {{seq}}^{1-1}_n(A\cup (n\times n))$ is injective as desired.

Thus the following corollary follows immediately from Theorems 2.10 and 2.11.

Corollary 2.12. For all Dedekind infinite sets A, $|\mathrm {{seq}}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ .

3 Consistency results

For relative consistency results, we shall work in permutation models which are models of ZFA, set theory with atoms. ZFA is characterized by the fact that it admits objects other than sets, called atoms (or urelements). Let A be a set of atoms and $\mathcal {G}$ be a group of permutations on A. Each $\pi \in \mathcal {G}$ is extended so that $\pi x=x$ for all pure sets x, i.e., sets whose transitive closures contain no atoms. A normal ideal I of A is a family of subsets of A such that:

1. (1) $\emptyset \in I$ ,

2. (2) if $E\in I$ and $F\subseteq E$ , then $F\in I$ ,

3. (3) if $E\in I$ and $F\in I$ , then $E\cup F\in I$ ,

4. (4) if $\pi \in \mathcal {G}$ and $E\in I$ , then $\pi [E]\in I$ ,

5. (5) for each $a\in A$ , $\{a\}\in I$ .

For each x, let $\mathrm {{fix}}_{\mathcal {G}}(x)=\{\pi \in \mathcal {G}\mid \pi y=y\text { for all }y\in x\}$ and $\mathrm {{sym}}_{\mathcal {G}}(x)=\{\pi \in \mathcal {G}\mid \pi x=x\}$ .

Let I be a normal ideal of A. A set $E\in I$ is a support of x if $\mathrm {{fix}}_{\mathcal {G}}(E)\subseteq \mathrm {{sym}}_{\mathcal {G}}(x)$ . We say x is symmetric if and only if there exists $E\in I$ such that E is a support of x. The class $\mathcal {V}=\{x\mid x \text { is symmetric and }x\subseteq \mathcal {V}\}$ consisting of all hereditarily symmetric objects is called a permutation model. Note that $x\in \mathcal {V}$ if and only if x has a support and $x\subseteq \mathcal {V}$ .

First, we use the basic Fraenkel model $\mathcal {V}_{F_0}$ which is the permutation model induced by the normal ideal $\mathrm {{fin}}(A)$ where the set of atoms A is a countably infinite set and $\mathcal {G}$ is the group of all permutations of A (for more details about the model see [9, Chapter 4]).

We have shown in Theorem 2.10 that “ $\mathrm {{seq}}^{1-1}_n(X)\leq \mathcal {S}_{n+1}(X)$ for any infinite set X” is provable in ZF. Now, we show that the subscript $n+1$ cannot be reduced to n.

Theorem 3.1. $\mathcal {V}_{F_0}\models |\mathrm {{seq}}^{1-1}_n(A)|\nleq |\mathcal {S}_n(A)|$ .

Proof Assume there is an injection $f\colon \mathrm {{seq}}^{1-1}_n(A)\rightarrow \mathcal {S}_n(A)$ with a support E. Let $M\subseteq A\backslash E$ be such that $|M|=n$ and let $u\in \mathrm {{seq}}^{1-1}_{n}(M)$ . Suppose to the contrary that there is $v\in M\setminus \mathrm {{m}}(f(u))$ . We select $w\in A\backslash (E\cup \mathrm {{m}}(f(u)))$ which is distinct from v and let $\tau =(v;w)$ . Since $\tau \in \text {fix}_{\mathcal {G}}(E\cup \mathrm {{m}}(f(u)))$ , $f(u)=\tau f(u)=(\tau f)(\tau u)=f(\tau u)$ but $\tau u\neq u$ whereas f is injective, a contradiction. Thus $M\subseteq \mathrm {{m}}(f(u))$ . Since $|M|=n=|\mathrm {{m}}(f(u))|$ , $M= \mathrm {{m}}(f(u))$ . Thus $f(s)\upharpoonright M\in \mathcal {S}_n(M)$ for all $s\in \mathrm {{seq}}^{1-1}_{n}(M)$ . Since f is an injection, $|\mathrm {{seq}}^{1-1}_{n}(M)|\leq |\mathcal {S}_n(M)|$ but $|\mathrm {{seq}}^{1-1}_{n}(M)|=n!>|\mathcal {S}_n(M)|$ , a contradiction.

Among the sets of permutations of a set with finitely many non-fixed points, it seems the size of the set with smaller number of non-fixed points is less than or equal to those with greater numbers. However, in this model, we show that such relation does not generally hold.

Theorem 3.2. $\mathcal {V}_{F_0}\models |\mathcal {S}_n(A)|\nleq |\mathcal {S}_{n+1}(A)|$ .

Proof Suppose there is an injection $f\colon \mathcal {S}_n(A)\rightarrow \mathcal {S}_{n+1}(A)$ with a support E such that $|E|\geq n$ . Let $L=|\mathcal {S}_{n+1}(E)|+1$ , $M_1,\dots ,M_L$ be distinct subsets of $A\backslash E$ with cardinality n, and $\pi _{1},\dots ,\pi _{L}$ be permutations of A such that $\mathrm {{m}}(\pi _i)= M_i$ for all $1\leq i\leq L$ .

Let $1\leq t\leq L$ . To show that $\mathrm {{m}}(f(\pi _t))\subseteq E\cup M_t$ , suppose to the contrary that there is $y\in \mathrm {{m}}(f(\pi _t))$ such that $y\not \in E\cup M_t$ . Then $y= f(\pi _t)(x)$ for some $x\in A$ such that $x\neq y$ .

Case 1. $x\in M_t$ .

Let $z\in A\backslash (E\cup M_t\cup \{y\})$ and $\sigma =(y;z)$ . Then $\sigma $ fixes $E\cup M_t$ pointwise and so $z=\sigma (y)=\sigma (f(\pi _t)(x)) = (\sigma f(\sigma \pi _t))(\sigma x) = f(\pi _t)(x)=y$ but $y\neq z$ .

Case 2. $x\in A\setminus M_t$ .

Since $|M_t|=n$ , $|\mathrm {{m}}(f(\pi _t))|=n+1$ , and $x,y\in \mathrm {{m}}(f(\pi _t)))\setminus M_t$ , there exists $r\in M_t$ such that $f(\pi _t)$ fixes r. Let $s\in A\backslash (E\cup M_t\cup \mathrm {{m}}(f(\pi _t)))$ and $\tau =(r;s)$ . Then $\tau $ fixes E and $f(\pi _t)$ fixes $\{r,s\}$ pointwise. Hence $f(\pi _t)=\tau f(\pi _t)=( \tau f)(\tau \pi _t)=f(\tau \pi _t)$ but $\tau \pi _t\neq \pi _t$ whereas f is an injection, a contradiction.

Therefore, $\mathrm {{m}}(f(\pi _t))\subseteq E\cup M_t$ . Since $|\{f(\pi _i)\mid i\in \{1,\ldots , L\}\}|=L>|\mathcal {S}_{n+1}(E)|$ , there exists $s\in \{1,\ldots , L\}$ such that $f(\pi _s)\restriction _E\notin \mathcal {S}_{n+1}(E)$ . Hence, since $|M_s|=n<n+1=|\mathrm {{m}}(f(\pi _s))|$ , there exists $w\in M_s$ such that $f(\pi _s)(w)\in E$ . Since $\pi _s$ fixes E pointwise, we have

$$\begin{align*}f(\pi_s)(w)=\pi_s (f(\pi_s)(w)) = (\pi_s f)(\pi_s \pi_s)(\pi_s w)= f(\pi_s)(\pi_s w)\end{align*}$$

but $\pi _s(w)\neq w$ whereas f is injective, a contradiction.

It follows from Theorems 2.1 and 2.10 that ${\mathrm {AC}}_{\leq n}$ implies $|\mathcal {S}_n(X)|\leq |\mathcal {S}_{n+1}(X)|$ for any infinite set X. The above theorem tells us that, in the absence of ${\mathrm {AC}}_{\leq n}$ , “ $|\mathcal {S}_n(X)|\leq |\mathcal {S}_{n+1}(X)|$ for any infinite set X” may fail. Since this statement is not provable in ZF, the condition in Theorem 2.1 cannot be removed as well. However, we shall give a model in which $|\mathcal {S}_n(X)|\nleq |\mathrm {{seq}}_n(X)|$ for some infinite set X by modifying the second Fraenkel model (see [9, Chapter 4] for more details about the model) as follows:

Let the set of atoms $A=\bigcup \{P_m\mid m\in \omega \}$ where $|P_m|=n$ for all $m\in \omega $ and all $P_m$ ’s are mutually disjoint. Let $\mathfrak {G}$ be the group of all permutations of A which fix each $P_m$ setwise, i.e., $\pi [P_m]=P_m$ for all $m\in \omega $ . Let $\mathcal {V}_{F_n}$ be the permutation model induced by the normal ideal $\mathrm {{fin}}(A)$ .

Theorem 3.3. $\mathcal {V}_{F_n}\models |\mathcal {S}_n(A)|\nleq |\mathrm {{seq}}_n(A)|$ .

Proof Assume there is an injection $f\colon \mathcal {S}_n(A)\rightarrow \mathrm {{seq}}_n(A)$ with a support $E=\bigcup \{P_m\mid m\leq k\}$ . Let $\psi $ be a permutation of A such that $\mathrm {{m}}(\psi )=P_l$ for some $l>k$ . Suppose $f(\psi )(i)\not \in E$ for some $i<n$ . Then $f(\psi )(i)\in P_t$ for some $t>k$ . Let $\pi _t$ be a permutation of A such that $\mathrm {{m}}(\pi _t)=P_t$ and if $t=l$ , let $\pi _t=\psi $ . Then $\pi _t\psi =\psi $ and $\pi _t\in \text {fix}_{\mathfrak {G}}(E)$ . Hence $\pi _t(f(\psi )(i))=(\pi _tf)(\pi _t\psi )(i)=f(\psi )(i)$ but $\pi _t$ moves all elements of $P_t$ , a contradiction. Therefore each entry of $f(\psi )$ must be in E. This leads to a contradiction since $\mathrm {{seq}}_n(E)$ is finite but $\{f(\chi )\mid \chi \in \mathcal {S}_n(A)\text { and }\mathrm {{m}}(\chi )=P_r \text { for some }r>k\}$ is infinite because f is injective.

Actually, the statement in the above theorem also holds in $\mathcal {V}_{F_0}$ . We leave this for the reader to verify.

The results from all theorems in this section can be transferred to ZF by using the Jech–Sochor First Embedding Theorem (cf. [9, Theorem 6.1]). In order to see this, we shall give a brief explanation.

A formula $\varphi (x)$ is boundable if $\mathcal {V}\models \varphi (x)\leftrightarrow \varphi ^{\mathcal {P}^{\gamma }(x)}(x)$ for some ordinal $\gamma $ . A statement is boundable if it is the existential closure of a boundable formula. From the Jech–Sochor First Embedding Theorem, we have that if a boundable statement holds in a permutation model, then it is consistent with ZF. For example, from Theorem 3.3, we have that “ $\exists X(|\mathcal {S}_n(X)|\nleq |\mathrm {{seq}}_n(X)|)$ ” holds in $\mathcal {V}_{F_n}$ . Let $\varphi (X)$ be a formula which represents “ $|\mathcal {S}_n(X)|\nleq |\mathrm {{seq}}_n(X)|$ ,” i.e., “ $\forall f(f\colon \mathcal {S}_n(X)\rightarrow \mathrm {{seq}}_n(X)\text { is not injective})$ .” We can see that $\mathcal {V}\models \varphi (X)\leftrightarrow \varphi ^{\mathcal {P}^{n+5}(X)}(X)$ . Hence $\varphi (X)$ is boundable, and so is the statement “ $\exists X(|\mathcal {S}_n(X)|\nleq |\mathrm {{seq}}_n(X)|)$ .” Therefore this statement is consistent with ZF. The results from Theorems 3.1 and 3.2 can be transferred to ZF in a similar way.

It is known that ${\mathrm {AC}}_{n}$ fails in $\mathcal {V}_{F_0}$ (cf. [8, p. 177]). Obviously, ${\mathrm {AC}}_{n}$ fails in $\mathcal {V}_{F_n}$ as well since the set of atoms of this model is Dedekind finite in the model. Since ${\mathrm {AC}}_{\leq n}$ implies ${\mathrm {AC}}_{n}$ , ${\mathrm {AC}}_{\leq n}$ fails in these models too. This fact also follows from Theorems 2.1 and 3.3.

From Theorem 2.1, $|\mathcal {S}_n(X)|\leq |\mathrm {{seq}}^{1-1}_n(X)|$ for all infinite sets X if ${\mathrm {AC}}_{\leq n}$ is assumed and the assumption can be weakened to ${\mathrm {AC}}_n$ for $n\leq 3$ . We still do not know whether, in general, it can be replaced by some weaker form of ${\mathrm {AC}}$ or not. Note that “for any infinite set X, there is an injection $f\colon \mathcal {S}_2(X)\rightarrow \mathrm {{seq}}^{1-1}_2(X)$ such that all entries of $f(\pi )$ are in $\mathrm {{m}}(\pi )$ for all $\pi \in \mathcal {S}_2(X)$ ” implies ${\mathrm {AC}}_2$ (by choosing the first entry of $f(a;b)$ from $\{a,b\}$ ). For $n=3$ , if we assume further that $f(\pi )=(x, \pi (x),\pi (\pi (x)))$ for some $x\in \mathrm {{m}}(\pi )$ (as the injection g defined in the paragraph below the proof of Theorem 2.1), then ${\mathrm {AC}}_3$ holds (by first claiming that $f(a;b;c)$ and $f(a;c;b)$ have exactly one entry that are equal and choose such entry form $\{a,b,c\}$ ). For $n>3$ , the problem becomes more complicated. These are left open for further research.