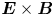Nonlinear drift-wave and energetic particle long-time behaviour in stellarators: solution of the kinetic problem

Abstract

We propose a theoretical scheme for the study of the nonlinear interaction of drift-wave-like turbulence and energetic particles in stellarators. The approach is based on gyrokinetics, and features a separation of time and scales, for electromagnetic fluctuations, inspired by linear ballooning theory. Two specific moments of the gyrokinetic equation constitute the main equations of the system, which requires a full kinetic nonlinear solution. This is found iteratively, expanding in the smallness of the bounce-average radial drift frequency, and nonlinear $\boldsymbol {E}\times \boldsymbol {B}$ drift frequency, compared with the inverse time scales of the resonantly interacting energetic particles. Our analysis is therefore valid for neoclassically optimised stellators. The resummation of all iterative and perturbative nonlinear kinetic solutions is discussed in terms of Feynman diagrams. Particular emphasis is put on the role of collisionlessly undamped large-scale structures in phase space, the kinetic equivalent of zonal flows, i.e. phase-space zonal structures, and on wave-like fluctuations generated by energetic particles.

1. Introduction

The purpose of any magnetic confinement fusion device is to access energetically favourable scenarios where fusion reactions are self-sustained by alpha particles. This has not been attained yet, but the study of energetic particle minorities, produced by auxiliary heating, gives us a glimpse of what could be the behaviour of a burning plasma.

A burning plasma is expected to be a kinetic turbulent environment in which energetic particles experience resonant interactions with fluctuating electromagnetic fields. These are believed to be faithfully described by gyrokinetic theory (Frieman & Chen 1982). Here, fluctuations are assumed to vary slowly along and strongly across the confining magnetic field, while evolving on a time scale which is slow when compared with the gyromotion, but fast when compared with the long-time behaviour of the plasma density and temperature background. Thus, within a gyrokinetic description, plasma transport properties are determined through a turbulence average (in time and space) (Frieman & Chen 1982; Abel & Cowley 2013) which allows nonlinear fluxes to act as sources in the evolution of mean quantities. Thereby, in a sense, nonlinear gyrokinetic simulations provide insight into the detailed properties of kinetic turbulence in magnetised plasmas, but do not fully characterise them from the point of view of transport, and therefore possible reactor performance, unless one knows how fluctuations, on a long time scale, impact mean quantities such as temperature and density.

Among the many approaches that one can pursue to attack the problem of turbulent transport in magnetically confined plasmas (which is naturally multiscale, and tackled with an asymptotic expansion for small Larmor radii), the one reviewed by Chen & Zonca (2019), perhaps more than others, kept the physics of fast particles at heart. In the first of a series of works there cited (Zonca et al. 2015), the question was proposed, and partially addressed, as to what would be the dominant contribution to the possible long-time behaviour of gyrokinetic fluctuations driven by wave–particle resonant interaction. By exploiting the existence of action-angle variables in axisymmetric toroidal geometry, Zonca et al. (2015) introduced a way of integrating perturbed particle orbits by using the unperturbed action-angle variables, thus capturing cumulative wave–particle resonance effects of bounce- and transit-averaged processes on unperturbed particle motion, for sufficiently small nonlinear dynamics. This approach allows one to describe several nonlinear wave–particle phenomena, such as phase locking, resonance detuning and broadening. It gives a powerful means of predicting chorus emission in planetary magnetospheres (Zonca, Tao & Chen 2021b), but it also gives the basis for the study of what the authors call phase-space zonal structures, i.e. the counterpart of zonal flows (Rosenbluth & Hinton 1998) or, more generally, zonal field structures in phase space. These are structures that are constant over magnetic flux surfaces, thus, in many circumstances, immune to collisionless Landau damping. They play a major role in the regulation of turbulence levels (Rogers, Dorland & Kotschenreuther 2000; Diamond et al. 2005).

Further advancing this line of research, Falessi & Zonca (2019) have focused on the long-time behaviour of phase-space zonal structures in axisymmetry. Their results have been successfully applied to particle-in-cell codes (Bottino et al. 2022), and completed with the evaluation of the mesoscale radial extent of fluctuations (Zonca et al. 2021a). These are evaluated as first-order corrections with a subsidiary limit of gyrokinetics that mimics the original radial envelope evaluation of ballooning modes (Connor, Hastie & Taylor 1978), Alfvèn waves (Zonca & Chen 1992, 1993) and the ion-temperature-gradient-driven modes (Romanelli & Zonca 1993).

We are starting to see the first numerical results on the behaviour of energetic particles embedded into turbulence (Biancalani et al. 2021; Di Siena et al. 2021; Carlevaro et al. 2022; Hayward-Schneider et al. 2022; Lu et al. 2023), but, to date, the aforementioned fundamental theoretical aspects have only been covered in the context of tokamak physics (Zonca et al. 2015; Chen & Zonca 2016, 2019; Falessi & Zonca 2019). A generalisation to stellarators is not straightforward mainly for two reasons. The first being that within a multiscale gyrokinetic approach in stellarators, the strong variation of the strength of the equilibrium magnetic field on flux surfaces is very likely more important than the radial variation of thermodynamic equilibrium quantities (Zocco et al. 2016; Zocco, Aleynikova & Xanthopoulos 2018a; Zocco, Plunk & Xanthopoulos 2020), the latter being the most important mesoscale effect encountered in asymmetry, and taken into account when evaluating the fluctuation radial envelope. The second problem encountered when extending the work of Falessi & Zonca (2019) to stellarators is the absence of a conserved toroidal canonical momentum, which complicates considerably the analysis.

Nevertheless, in this work, we find a way of extending to stellarators the kinetic theory first put forth by Zonca et al. (2015). Whilst realising that we are engaging with innumerable aspects of a complex endeavour, we decide to particularly focus on the kinetic solution of the problem, devising a method, given the electromagnetic fields, to solve iteratively the gyrokinetic equation while retaining the nonlinear wave–particle interaction. The method is diagrammatic, and applies not only to the physics of energetic particles, but also to the study of micro-instability-driven transport as the electrostatic ion temperature gradient at marginality (Zocco et al. 2018b), for instance, when wave–particle resonance effects are important.

This work is organised as follows. In § 2 we introduce the basic gyrokinetic equation and the equations for fluctuating fields and set up the relation between wave-like fluctuations and the underlying kinetics. In § 3 we introduce the coordinates and specify some geometric features that allow us to solve the gyrokinetic equation. In § 4 we introduce its iterative diagrammatic solution. In §§ 5 and 6 we apply the kinetic solution to the evaluation of transport due to wave-like fluctuating fields, and the phase-space zonal structure. In § 7 we conclude.

2. Nonlinear transport from finite-$\beta$ fluctuations

In this section we highlight the mathematical formulation for the study of transport from electromagnetic fluctuations. Our starting point is the evaluation of the quasi-neutrality equation and the divergence of the perturbed plasma current (Frieman et al. 1980; Tang, Connor & Hastie 1980; Qin, Tang & Rewoldt 1998; Zonca & Chen 2014; Chen & Zonca 2016; Zocco, Helander & Connor 2015; Aleynikova & Zocco 2017):

(2.1)\begin{equation} \sum_{s}q_{s}\int \,{\rm d}^{3}\boldsymbol{v}F_{0s}\frac{q_{s}\phi}{T_{0s}} =\sum_{s}q_{s}\int \,{\rm d}^{3}\boldsymbol{v}\sum_{\boldsymbol{k}} {\rm e}^{{\rm i}\boldsymbol{k}\boldsymbol{\cdot}\boldsymbol{r}}{\rm J}_{0}\left(a_{s}\right)\delta G_{s\boldsymbol{k}} \end{equation}

and

(2.2)\begin{align} B\boldsymbol{\nabla}_{{\parallel}}\frac{j_{{\parallel},\boldsymbol{k}}}{B}& ={-}\sum_{s}\frac{e_{s}^{2}}{T_{0s}}\int \,{\rm d}^{3}\boldsymbol{v}F_{0s}\left[\left(1-{\rm J}_{0}^{2}\left(a_{s}\right)\right)\frac{\partial}{\partial t}-{\rm i}\varOmega_{*,s}^{T}{\rm J}_{0}^{2}\left(a_{s}\right)\right]\phi_{\boldsymbol{k}}\nonumber\\ & \quad -\sum_{s}\frac{e_{s}^{2}}{T_{s}}\int \,{\rm d}^{3}\boldsymbol{v}F_{0s}\left(\frac{\partial}{\partial t}-{\rm i}\varOmega_{*,s}^{T}\right)4\mu B\frac{{\rm J}_{0}\left(a_{s}\right){\rm J}_{1}\left(a_{s}\right)}{a_{s}}\frac{T_{0s}}{q_{s}}\frac{\delta B_{{\parallel}\boldsymbol{k}}}{B}\nonumber\\ & \quad +{\rm i}\frac{c}{B}\hat{\boldsymbol{b}}\boldsymbol{\cdot}\boldsymbol{\boldsymbol{\kappa}\times\boldsymbol{k}} \sum_{s}\int \,{\rm d}^{3}\boldsymbol{v}m_{s}\left(\mu B+v_{{\parallel}}^{2}\right){\rm J}_{0}(a_{s})\delta G_{s\boldsymbol{k}}\nonumber\\ & \quad +\sum_{s}q_{s}\int \,{\rm d}^{3}\boldsymbol{v}{\rm J}_{0}(a_{s})\sum_{{\boldsymbol{k}}^{\prime}}\frac{c}{B}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{k}_{{\perp}}^{\prime}\times\boldsymbol{k}_{{\perp}}\left[{\rm J}_{0}(a_{s}^{\prime})\left(\phi_{\boldsymbol{k^{\prime}}}-\frac{v_{{\parallel}}}{c}A_{{\parallel}\boldsymbol{k}^{\prime}}\right)\right.\nonumber\\ & \quad+ \left.4\mu B\frac{{\rm J}_{1}(a_{s}^{\prime})}{a_{s}^{\prime}}\frac{T_{0s}}{q_{s}}\frac{\delta B_{{\parallel}\boldsymbol{k}^{\prime}}}{B}\right]\delta G_{s,\boldsymbol{k}-\boldsymbol{k}^{^{\prime}}}+B\sum_{s}\int \,{\rm d}^{3}\boldsymbol{v}\delta G_{\boldsymbol{k}}\boldsymbol{\nabla}_{{\parallel}}{\rm J}_{0}(a_{s}), \end{align}

where $F_{0s}$ is the equilibrium distribution function (taken to be Maxwellian), thus $f_{s}=F_{0s}+\delta f_{s}\equiv F_{0s}(1-q_{s}\phi (\boldsymbol {r},t)/T_{0s})+\delta G_{s}(\boldsymbol {R}_{s},\mu,\mathcal {E},t)+\mathcal {O}(\epsilon ^{2}),$ and $\delta f_{s}/F_{0s}\sim k_{\parallel }/k_{\perp }\sim \epsilon \equiv \rho _*=\rho _s/a,$ where $\rho _s$ is the Larmor radius and $a$ a macroscopic length. Here $\boldsymbol {R}_{s}=\boldsymbol {r}+\boldsymbol {v}_{\perp }\times \hat {\boldsymbol {b}}/\varOmega _{s}$ is the gyrocentre position, where $\boldsymbol {r}$ is the particle position, ${\varOmega _{s}=q_{s}B/(m_{s}c)},$ $\hat {\boldsymbol {b}}=\boldsymbol {B}/B,$ with $\boldsymbol {B}$ the equilibrium magnetic field, and $\mu =v_{\perp }^{2}/(2B),$ $\mathcal {E}=v^{2}/2$ the velocity-space coordinates. The Bessel function, ${\rm J}_{0}={\rm J}_{0}(a_{s}),$ with $a^2_{s}=2B\mu k_{\perp }^{2}/\varOmega _{s}^{2},$ relates the Fourier transform with respect to $\boldsymbol {R}_{s}$ of $\delta G_{s}$ with its Fourier transform with respect to $\boldsymbol {r}$ (velocity-space integrals in (2.1)–(2.2) are taken at constant $\boldsymbol {r}$). We also have

(2.3)\begin{equation} \varOmega_{*,s}^{T}=\frac{cT_{0s}}{Be_{s}}\hat{\boldsymbol{b}}\boldsymbol{\cdot}\boldsymbol{k}\times\frac{\boldsymbol{\nabla} F_{0s}}{F_{0s}}, \end{equation}

which takes account of diamagnetic effects, while $\boldsymbol {\kappa =}\hat {\boldsymbol {b}}\boldsymbol {\cdot }\boldsymbol {\nabla }\hat {\boldsymbol {b}}$ is the magnetic field curvature. Finally,

(2.4)\begin{equation} \frac{\delta B_{{\parallel},\boldsymbol{k}}}{B}={-}\frac{4{\rm \pi}}{c}\sum_{s}\int \,{\rm d}^{3}\boldsymbol{v}m_{s}2\mu B\frac{{\rm J}_{1}(a_{s})}{a_{s}}\delta G_{s,\boldsymbol{k}} \end{equation}

and

(2.5)\begin{equation} j_{{\parallel}\boldsymbol{k}}=\sum_{s}q_{s}\int \,{\rm d}^{3}\boldsymbol{v}v_{{\parallel}}{\rm J}_0(a_{s})\delta G_{s,\boldsymbol{k}}, \end{equation}

where $j_{\parallel }=(c/4{\rm \pi} )\hat {\boldsymbol {b}}\boldsymbol {\cdot }\boldsymbol {\nabla }\times (\boldsymbol {\nabla }\times \boldsymbol {A}).$ We take $\boldsymbol {\kappa }\approx \boldsymbol {\nabla } B/B,$ consistent with linear cancellations due to the perpendicular pressure balance (Tang et al. 1980; Hasegawa & Sato 1981; Zocco et al. 2015; Chen & Zonca 2016; Aleynikova & Zocco 2017), thus allowing us to eliminate (but not neglect!) magnetic compressibility altogether. The final term in (2.2) can be neglected in most practical applications, since the current is mostly carried by the electrons (Connor et al. 1978; Zocco et al. 2015; Aleynikova & Zocco 2017). The kinetic information is contained in the velocity-space integrals of the function $\delta G_{s}.$

The function $\delta G_{s}$ follows the nonlinear Frieman–Chen equation (Frieman & Chen 1982) for the non-adiabatic part of the perturbed distribution function, $\delta G_{s}=\delta f_{s}+F_{0s}e_{s}\phi /T_{0s}$:

(2.6)\begin{align} & \left(\frac{\partial}{\partial t}+v_{{\parallel}}\boldsymbol{\nabla}_{{\parallel}}+\boldsymbol{v}_{d,s}\boldsymbol{\cdot}\boldsymbol{\nabla}\right)\delta G_{s}\nonumber\\ & \quad= \frac{e_{s}F_{0s}}{T_{0s}}\frac{\partial}{\partial t}\left\langle \chi\right\rangle _{\boldsymbol{R}_{s}}-\frac{c}{B}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}\left\langle \chi\right\rangle _{\boldsymbol{R}_{s}}\times\boldsymbol{\nabla} F_{0_{s}}-\frac{c}{B}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}\left\langle \chi\right\rangle _{\boldsymbol{R}_{s}}\times\boldsymbol{\nabla}\delta G, \end{align}

where $\langle \chi \rangle _{\boldsymbol {R}_{s}}=\sum _{\boldsymbol {k}}\langle \chi \rangle _{\boldsymbol {R}_{s},\boldsymbol {k}}\exp {\rm i}\boldsymbol {k}\boldsymbol {\cdot }\boldsymbol {R_{s}},$ with $\langle \chi \rangle _{\boldsymbol {R}_{s},\boldsymbol {k}}={\rm J}_{0}(a_{s})(\phi _{\boldsymbol {k}}-v_{\parallel }A_{\parallel \boldsymbol {k}}/c)$ being the gyroaveraged kinetic potential, $\boldsymbol {\nabla }=\partial /\partial \boldsymbol {R}_{s},$ $\boldsymbol {v}_{d_{s}}=-v_{\parallel }\boldsymbol {b}\times \boldsymbol {\nabla }(v_{\parallel }/\varOmega _{s})$ and

(2.7)\begin{equation} \frac{c}{B}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}\chi\times\boldsymbol{\nabla}\delta G=\frac{c}{B}\left[\chi,\delta G\right]. \end{equation}

In a stellarator context, it is wise to introduce Boozer coordinates (Boozer 1981) $\boldsymbol {B}=\boldsymbol {\nabla }\psi \times \boldsymbol {\nabla }\theta +\iota \boldsymbol {\nabla }\varphi \times \boldsymbol {\nabla }\psi =G(\psi )\boldsymbol {\nabla }\varphi +I(\psi )\boldsymbol {\nabla }\theta +K(\psi,\theta,\varphi )\boldsymbol {\nabla }\psi.$ Here, the magnetic equilibrium satisfies force balance:

(2.8)\begin{equation} \frac{4{\rm \pi}}{c}{\boldsymbol J}\times{\boldsymbol B}=\frac{1}{\sqrt{g}}\left(\iota I'+G'-\iota\frac{\partial K}{\partial\theta}-\frac{\partial K}{\partial\varphi}\right)\boldsymbol{\nabla}\psi=4{\rm \pi}\boldsymbol{\nabla} p_{0}, \end{equation}

where $1/\sqrt {g}=B^{2}/(G+\iota I)\simeq B^{2}/G$ so that

(2.9)\begin{equation} \iota I^{\prime}+G^{\prime}-\iota\frac{\partial K}{\partial\theta}-\frac{\partial K}{\partial\varphi}=\frac{4{\rm \pi} G}{B^{2}}\frac{{\rm d}p_{0}}{{\rm d}\psi}, \end{equation}

and $p_{0}$ and $\boldsymbol {J}$ are the equilibrium pressure and plasma current, respectively.

It is furthermore useful to see that

(2.10)\begin{align} \boldsymbol{v}_{d}\boldsymbol{\cdot}\boldsymbol{\nabla}\delta G& ={-}v_{{\parallel}}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}\left(\frac{v_{{\parallel}}}{\varOmega}\right)\times\boldsymbol{\nabla}\delta G\nonumber\\ & ={-}\frac{v_{{\parallel}}}{\sqrt{g}B}\left\{ G\left[\left(\frac{\partial}{\partial\psi}\frac{v_{{\parallel}}}{\varOmega}\right)\frac{\partial}{\partial\theta}-\left(\frac{\partial}{\partial\theta}\frac{v_{{\parallel}}}{\varOmega}\right)\frac{\partial}{\partial\psi}\right]\right.\nonumber\\ & \quad -I\left[\left(\frac{\partial}{\partial\psi}\frac{v_{{\parallel}}}{\varOmega}\right)\frac{\partial}{\partial\varphi}-\left(\frac{\partial}{\partial\varphi}\frac{v_{{\parallel}}}{\varOmega}\right)\frac{\partial}{\partial\psi}\right]\nonumber\\ & \quad \left.+K\left[\left(\frac{\partial}{\partial\varphi}\frac{v_{{\parallel}}}{\varOmega}\right)\frac{\partial}{\partial\theta}-\left(\frac{\partial}{\partial\theta}\frac{v_{{\parallel}}}{\varOmega}\right)\frac{\partial}{\partial\varphi}\right]\right\} \delta G\nonumber\\ & \equiv{-}v_{{\parallel}}\left[\frac{v_{{\parallel}}}{\varOmega},\delta G\right]. \end{align}

2.1. Nonlinear fluctuations

Equations (2.1)–(2.2) accommodate finite-$\beta$ Alfvénic and drift-wave ballooning-like instabilities. Here we set up a model for nonlinear transport associated with balloning-type modes supported by them (Chen & Zonca 2016).

As in ballooning theory (Connor et al. 1978; Connor, Hastie & Taylor 1979), one introduces an eikonal representation for perturbed quantities (Antonsen & Lane 1980):

(2.11)\begin{equation} \delta Q(\psi,\theta,\varphi,t)=\delta\hat{Q}\left(\psi,\alpha(\theta,\varphi),\theta,t\right) \exp({{\rm i}S\left(\psi,\alpha(\theta,\varphi),t\right)}), \end{equation}

where $\alpha =\theta -\iota \varphi,$

(2.12)\begin{equation} \frac{1}{S}\frac{\partial S}{\partial t}\gg\frac{1}{\delta\hat{Q}}\frac{\partial\delta\hat{Q}}{\partial t} \end{equation}

and

(2.13)\begin{equation} \frac{1}{S}\boldsymbol{\nabla} S\gg\frac{1}{\delta\hat{Q}}\boldsymbol{\nabla}\delta\hat{Q}. \end{equation}

To leading order, (2.2) becomes a nonlinear drift-wave-ballooning equation:

(2.14)\begin{align} & B\boldsymbol{\nabla}_{{\parallel}}\frac{c}{4{\rm \pi}}k_{{\perp}}^{2}\frac{\delta\hat{A}_{{\parallel},\boldsymbol{k}}}{B}-{\rm i}\omega\sum_{s}\frac{e_{s}^{2}}{T_{s}}\int \,{\rm d}^{3}\boldsymbol{v}F_{0s}\left[1-{\rm J}_{0}^{2}\left(a_{s}\right)-\frac{\varOmega_{*,s}^{T}}{\omega}{\rm J}_{0}^{2}\left(a_{s}\right)\right]\phi_{\boldsymbol{k}}\nonumber\\ & \qquad +\frac{c}{B}\hat{\boldsymbol{b}}\boldsymbol{\cdot}\boldsymbol{\boldsymbol{\kappa}\times\boldsymbol{k}_{{\perp}}}\sum_{s}\int \,{\rm d}^{3}\boldsymbol{v}m_{s}\left(\mu B+v_{{\parallel}}^{2}\right){\rm J}_{0}(a_{s})\delta G_{s\boldsymbol{k}}\nonumber\\ & \quad ={\rm i}\,\mathcal{N}_{F,\boldsymbol{k}}, \end{align}

where $\boldsymbol {k}=\partial _{\psi }S\boldsymbol {\nabla }\psi +\partial _{\alpha }S\boldsymbol {\nabla }\alpha,$ ${\rm i}\omega =\partial _{t}S$ and $\mathcal {N}_{F}$ contains all the terms that are nonlinear in the field amplitudes:

(2.15)\begin{align} \mathcal{N}_{F,\boldsymbol{k}}& = \frac{c}{B}\sum_{\boldsymbol{k}}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{k}_{{\perp}}^{\prime}\times\boldsymbol{k}_{{\perp}}\sum_{s}q_{s}\int \,{\rm d}^{3}\boldsymbol{v}{\rm J}_{0}(a_{s}){\rm J}_{0}(a_{s}^{\prime})\hat \phi_{\boldsymbol{k^{\prime}}}\delta \hat G_{s,\boldsymbol{k}-\boldsymbol{k}^{^{\prime}}}\nonumber\\ & \quad -\frac{1}{B}\sum_{\boldsymbol{k}}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{k}_{{\perp}}^{\prime}\times\boldsymbol{k}_{{\perp}}\sum_{s}q_{s}\int \,{\rm d}^{3}\boldsymbol{v}{\rm J}_{0}(a_{s}){\rm J}_{0}(a_{s}^{\prime})\hat A_{{\parallel},\boldsymbol{k^{\prime}}}v_\parallel\delta \hat G_{s,\boldsymbol{k}-\boldsymbol{k}^{^{\prime}}}. \end{align}

In the linear limit, $\mathcal {N_{F,\boldsymbol {k}}}\rightarrow 0,$ (2.14) reduces to the equation used by Tang et al. in the study of linear kinetic ballooning modes in the intermediate-frequency regime (Tang et al. 1980; Aleynikova & Zocco 2017). Similarly, quasi-neutrality remains virtually unchanged:

(2.16)\begin{equation} n_{i}\left(\sum_{s}\frac{q_{s}}{\tau_{s}}\frac{n_{s}}{n_{i}}\right)\frac{q_{s}\delta\hat{\phi}_{\boldsymbol{k}}}{T_{0e}}=\sum_{s}\frac{q_{s}}{n_{s}}\int \,{\rm d}^{3}\boldsymbol{v}{\rm J}_{0}(a_{s})\delta\hat{G}_{s,\boldsymbol{k}}. \end{equation}

Equations (2.14)–(2.16) constitute a local eigenvalue problem for the fields $\delta \hat {A}_{{{\parallel }}}$ and $\delta \hat {\phi }$ where nonlinearities are retained.

Antonsen & Lane (1980) have proposed a way of attacking this type of eigenvalue problems, by applying a method introduced by Weinberg (1962), and further explored by Dewar & Glasser (1983). One considers, for a given radial location and a given field line, the local eigenvalue

(2.17)\begin{equation} \omega_{l}=\omega_{l}\left(\psi,\alpha,S_{\psi},S_{\alpha}\right), \end{equation}

and determines $S_{\psi }$ and $S_{\alpha }$ by solving Hamilton equations

(2.18)\begin{equation} \frac{\partial\psi}{\partial\ell}=\frac{\partial\omega_{l}}{\partial S_{\psi}},\quad \frac{\partial\alpha}{\partial\ell}=\frac{\partial\omega_{l}}{\partial S_{\alpha}} \end{equation}

and

(2.19)\begin{equation} \frac{\partial S_{\psi}}{\partial\ell}={-}\frac{\partial\omega_{l}}{\partial\psi},\quad \frac{\partial S_{\alpha}}{\partial\ell}={-}\frac{\partial\omega_{l}}{\partial\alpha}, \end{equation}

where $\ell$ parametrises the trajectories that make $\omega _{l}$ constant. This determines $S_{\psi }$ and $S_{\alpha }.$ A global eigenvalue could further be determined, but we do not proceed along these lines.

Instead, we point out that, to next order in the

(2.20)\begin{equation} \omega_{l}^{{-}1}\delta\hat{Q}^{{-}1}\partial_{t}\delta\hat{Q}\sim k_{{\perp}}^{{-}1}\delta\hat{Q}^{{-}1}\boldsymbol{\nabla}\delta\hat{Q}\ll1 \end{equation}

expansion, one obtains the equation for the global structure of field amplitudes. The outcome of this calculation is a nonlinear Schrödinger-type equation that integrates the description of finite-$\beta$ fluctuations with nonlinear wave–particle effects. Zonca et al. (2021a) have recently derived the expressions for the radial envelope of fluctuations in tokamak geometry by implementing a specific ordering between linear and nonlinear time scales. The radial envelope of fluctuations, being a higher-order perturbative quantity, will follow an equation in which corrections to the radial variation of equilibrium quantities will need to be considered. These ‘radially global’ corrections to the turbulence description supported by the gyrokinetic equation, (2.6), need to be considered extremely carefully in a stellarator, since the strong variation of the modulus of the magnetic field on the magnetic surface introduces an intermediate equilibrium scale, $\rho \ll L_B\ll R,$ which induces important ‘surface-global effects’ that have no real equivalent in axisymmetry (Zocco et al. 2016, 2020). Thus, the generalisation to non-sxisymmetry of the analysis of Zonca et al. (2021a), while conceptually unproblematic, needs its own dedicated work. We therefore dedicate the rest of the article to the kinetic side of the problem, that is, the evaluation of the function $\delta G_{s}.$

3. Kinetics

In this section we solve the kinetic equation with nonlinear wave–particle interaction in stellarators. Before proceeding, a couple of technical comments are in order.

3.1. Choice of coordinates

Let us be more precise with the choice of coordinates. We introduce

(3.1)\begin{equation} \left(\begin{array}{@{}c@{}} \theta\\ \varphi \end{array}\right)\rightarrow\left(\begin{array}{@{}c@{}} \theta_{c}\\ \alpha_{c} \end{array}\right)=\left(\begin{array}{@{}c@{}} \theta\\ \varphi-q\theta \end{array}\right), \end{equation}

where $q=\iota ^{-1},$ so that

(3.2)\begin{equation} f(\psi,\theta,\varphi)\mapsto \hat f\left(\psi,\theta_{c}(\theta),\alpha_{c}(\theta,\varphi)\right). \end{equation}

Then

(3.3)\begin{equation} \left.\frac{\partial}{\partial\theta}\right|_{\varphi}\hat f\left(\psi,\theta_{c}(\theta),\alpha_{c}(\theta,\varphi)\right)=\left(\frac{\partial}{\partial\theta_{c}}-q\frac{\partial}{\partial\alpha_{c}}\right)\hat f\left(\psi,\theta_{c},\alpha_{c}\right) \end{equation}

and

(3.4)\begin{equation} \left.\frac{\partial}{\partial\varphi}\right|_{\theta}\hat f\left(\psi,\theta_{c}(\theta),\alpha_{c}(\theta,\varphi)\right)=\frac{\partial}{\partial\alpha_{c}}\hat f\left(\psi,\theta_{c},\alpha_{c}\right). \end{equation}

The purpose of these coordinates is to reduce the parallel streaming term operator into a first-order partial derivative in one angle only:

(3.5)\begin{equation} v_{{\parallel}}\boldsymbol{\nabla}_{{\parallel}} =\frac{v_{{\parallel}}\iota}{B\sqrt{g}}\frac{\partial}{\partial\theta_{c}}, \end{equation}

as can easily be verified. Then the gyrokinetic equation reads

(3.6)\begin{align} & \frac{\partial\delta G}{\partial t}+\frac{v_{{\parallel}}\iota}{B\sqrt{g}}\frac{\partial}{\partial\theta_{c}}\delta G+\frac{v_{{\parallel}}G}{B\sqrt{g}}\left(\frac{\partial\rho_{{\parallel}}}{\partial\theta_{c}}\frac{\partial}{\partial\psi}-\frac{\partial\rho_{{\parallel}}}{\partial\psi}\frac{\partial}{\partial\theta_{c}}\right)\delta G\nonumber\\ & \qquad +\iota^{{-}1}Bv_{{\parallel}}\left(\frac{\partial\rho_{{\parallel}}}{\partial\psi}\frac{\partial}{\partial\alpha_{c}}-\frac{\partial\rho_{{\parallel}}}{\partial\alpha_{c}}\frac{\partial}{\partial\psi}\right)\delta G={-}\frac{e}{m}\frac{\partial F_{0}}{\partial\mathcal{E}}\frac{\partial}{\partial t}\chi\nonumber\\ & \qquad -\frac{c}{\sqrt{g}B^{2}}\left[G\left(\frac{\partial\chi}{\partial\psi}\frac{\partial}{\partial\theta_{c}}-\frac{\partial\chi}{\partial\theta_{c}}\frac{\partial}{\partial\psi}\right)-\iota\sqrt{g}B^{2}\left(\frac{\partial\chi}{\partial\psi}\frac{\partial}{\partial\alpha_{c}}-\frac{\partial\chi}{\partial\alpha_{c}}\frac{\partial}{\partial\psi}\right)\right]\nonumber\\ & \qquad +\frac{c}{\sqrt{g}B^{2}}\left[G\frac{\partial\chi}{\partial\theta_{c}}\frac{\partial}{\partial\psi}+\iota\sqrt{g}B^{2}\frac{\partial\chi}{\partial\alpha_{c}}\frac{\partial}{\partial\psi}\right]F_{0}, \end{align}

where we introduced $\rho _{\parallel }=v_{\parallel }/\varOmega,$ we are dropping the symbol of gyroaverage and the species index and we are working in real space. The $\boldsymbol {v}_{d}\boldsymbol {\cdot }\boldsymbol {\nabla }\theta$ term has generated the

(3.7)\begin{equation} -\frac{v_{{\parallel}}G}{B\sqrt{g}}\frac{\partial\rho_{{\parallel}}}{\partial\psi}\frac{\partial}{\partial\theta_{c}} \end{equation}

contribution, and this can be discarded if compared with the streaming term (a common approximation). However, $\partial _{\psi }\rho _{\parallel }\partial _{\theta _{c}}\sim \partial _{\theta _{c}}\rho _{\parallel }\partial _{\psi }$ so, formally, $\boldsymbol {v}_{d}\boldsymbol {\cdot }\boldsymbol {\nabla }\theta$ can be neglected for

(3.8)\begin{equation} k_{\theta_c}\frac{\partial\rho_{{\parallel}}}{\partial\psi}\ll k_{\psi}\frac{\partial\rho_{{\parallel}}}{\partial\theta_{c}}, \end{equation}

where $k_{\theta _c}$ and $k_{\psi }$ are the characteristic fast-varying wavelengths of fluctuations, which are assumed to be of the same order. The physical meaning of this statement is that finite banana width effects are caused by the poloidal variation of the equilibrium quantities that enter the definition of $\rho _{\parallel }$. We stress here that $\rho _{\parallel }$ is an equilibrium quantity. While its ‘fast’ variation might impact mode structure, it is not allowed to interfere with the gyrokinetic ordering $k_{\parallel }/k_{\perp }\ll 1$. The term $\partial \rho _{\parallel }/\partial \alpha _{c}$ is purely non-axisymmetric, and cannot be neglected if $\partial _{\theta _{c}}\rho _{\parallel }\partial _{\psi }\sim \partial _{\alpha }\rho _{\parallel }\partial _{\psi }.$ The gyrokinetic equation that we study is therefore

(3.9)\begin{align} & \frac{\partial\delta G}{\partial t}+\frac{v_{{\parallel}}\iota}{B\sqrt{g}}\frac{\partial}{\partial\theta_{c}}\delta G+\frac{v_{{\parallel}}G}{B\sqrt{g}}\frac{\partial\rho_{{\parallel}}}{\partial\theta_{c}}\frac{\partial}{\partial\psi}\delta G-\iota^{{-}1}Bv_{{\parallel}}\frac{\partial\rho_{{\parallel}}}{\partial\alpha_{c}}\frac{\partial}{\partial\psi}\delta G={-}\frac{e}{m}\frac{\partial F_{0}}{\partial\mathcal{E}}\frac{\partial}{\partial t}\chi\nonumber\\ & \qquad -\frac{c}{\sqrt{g}B^{2}}\left[G\left(\frac{\partial\chi}{\partial\psi}\frac{\partial}{\partial\theta_{c}}-\frac{\partial\chi}{\partial\theta_{c}}\frac{\partial}{\partial\psi}\right)-\iota\sqrt{g}B^{2}\left(\frac{\partial\chi}{\partial\psi}\frac{\partial}{\partial\alpha_{c}}-\frac{\partial\chi}{\partial\alpha_{c}}\frac{\partial}{\partial\psi}\right)\right]\delta G\nonumber\\ & \qquad +\frac{c}{\sqrt{g}B^{2}}\left[G\frac{\partial\chi}{\partial\theta_{c}}\frac{\partial}{\partial\psi}-\iota\sqrt{g}B^{2}\frac{\partial\chi}{\partial\alpha_{c}}\frac{\partial}{\partial\psi}\right]F_{0}, \end{align}

where we are basically assuming that equilibrium quantities vary more strongly in $\alpha$ and $\theta$ than in $\psi.$ To better understand what this approximation means, we revert to the original Boozer coordinates to obtain

(3.10)\begin{align} & \frac{\partial\delta G}{\partial t}+\frac{v_{{\parallel}}}{B\sqrt{g}}\left(\frac{\partial}{\partial\varphi}+\iota\frac{\partial}{\partial\theta}\right)\delta G+\frac{v_{{\parallel}}}{B\sqrt{g}}\left(G\frac{\partial\rho_{{\parallel}}}{\partial\theta}-I\frac{\partial\rho_{{\parallel}}}{\partial\varphi}\right)\frac{\partial}{\partial\psi}\delta G\nonumber\\ & \qquad ={-}\left\{ \frac{e}{m}\frac{\partial F_{0}}{\partial\mathcal{E}}\frac{\partial}{\partial t}\chi+\frac{c}{B}\left[\chi,\delta G\right]+\frac{c}{B}\left[\chi,F_{0}\right]\right\} . \end{align}

The terms left that are proportional to $v_{\parallel }$ are recognisable as

(3.11)\begin{equation} \frac{v_{{\parallel}}}{B\sqrt{g}}\left(\frac{\partial}{\partial\varphi}+\iota\frac{\partial}{\partial\theta}\right)\rightarrow v_{{\parallel}}\boldsymbol{\nabla}_{{\parallel}}, \end{equation}

while the last term of the first line is

(3.12)\begin{equation} \frac{v_{{\parallel}}}{B\sqrt{g}}\left(G\frac{\partial\rho_{{\parallel}}}{\partial\theta}-I\frac{\partial\rho_{{\parallel}}}{\partial\varphi}\right)\frac{\partial}{\partial\psi}\rightarrow\boldsymbol{v}_{d}\boldsymbol{\cdot}\boldsymbol{\nabla}\psi\frac{\partial}{\partial\psi}. \end{equation}

In field-following coordinates, the left-hand side of (3.10) would then be

(3.13)\begin{equation} \frac{\partial\delta G}{\partial t}+v_{{\parallel}}\boldsymbol{\nabla}_{{\parallel}}\delta G+k_{\psi}\boldsymbol{v}_{d}\boldsymbol{\cdot}\boldsymbol{\nabla}\psi \delta G. \end{equation}

One can choose the poloidal angle to be the field-following coordinate, thus accounting for a slow variation of perturbations along the field line, in the spirit of the underlying gyrokinetic ordering. However, this fact does not preclude fluctuations from being most important at short wavelengths, that is, when

(3.14)\begin{equation} k_{\psi}\sim k_{{\alpha}_c}\sim k_{{\theta}_c}\sim n/R\sim m/R\sim\rho_{i}^{{-}1}\gg 1, \end{equation}

for any set or coordinates used, where $n$ and $m$ are some poloidal and toroidal wavenumbers. This discussion is largely concerned with the influence of the strong variations of magnetic equilibrium quantities in gyrokinetics, and is specific to stellarators. Alternatively, one could state that (3.10) can be used when the radial derivatives of the fluctuating fields are much larger than any other derivative, and $\boldsymbol {v}_{d}\boldsymbol {\cdot }\boldsymbol {\nabla }\alpha _c$ does not play a role in their destabilisation.

The inclusion in (3.10) of the $\boldsymbol {v}_d \boldsymbol {\cdot } \boldsymbol {\nabla } \theta$ and $\boldsymbol {v}_d \boldsymbol {\cdot } \boldsymbol {\nabla } \varphi$ components of the magnetic drift, which would drive the toroidal branch of the ion-temperature-gradient-driven instability, would not be problematic. This could be done by simply upgrading the ordering of the radial derivatives of $\rho _{\parallel }$. However, in this work, we rely on linear drives provided by wave–particle resonant excitation, thus naturally energetic particle modes, and work with (3.10) as it is. From now on, we refer to the form of (3.9) as ‘formulation A’, and to (3.10) as ‘formulation B’. The first is more useful to treat explicitly the streaming term for the nonlinear investigation of wave–particle nonlinear interaction, the second is more practical for the study of the late-time behaviour of zonal flows in a flux tube.

4. Solution of the kinetic problem

We consider formulation B (equation (3.10)), and introduce $\delta G=\exp (-H\partial _{\psi })\delta g$, to obtain the compact form

(4.1)\begin{align} & \frac{\partial}{\partial t}\delta g+v_{{\parallel}}\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}\delta g\nonumber\\ & \qquad ={-}\bar{v}_{\psi}\frac{\partial}{\partial\psi}\delta g-{\rm e}^{{\rm i}Q}\left\{ \frac{e}{m}\frac{\partial F_{0}}{\partial\mathcal{E}}\frac{\partial}{\partial t}\chi+\frac{c}{B} \left[\chi,{\rm e}^{-{\rm i}Q}\delta g\right]+\frac{c}{B}\left[\chi,F_{0}\right]\right\} , \end{align}

where $Q=-iH\partial _{\psi }$ (this radial derivative acts on fluctuating quantities only) and $H$ solves for the magnetic differential equation

(4.2)\begin{equation} v_{{\parallel}}\boldsymbol{\nabla}_{{\parallel}}H=\frac{v_{{\parallel}}}{\sqrt{g}B}\left[G(\psi)\frac{\partial}{\partial\theta}\left(\frac{v_{{\parallel}}}{\varOmega}\right)-I(\psi)\frac{\partial}{\partial\varphi}\left(\frac{v_{{\parallel}}}{\varOmega}\right)\right]-\bar{v}_{\psi}. \end{equation}

Here $\bar {v}_{\psi }=\bar {v}_{\psi }(\mathcal {E},\psi )\equiv \overline {\boldsymbol {v}_{d}\boldsymbol {\cdot }\boldsymbol {\nabla }\psi },$ since $\overline {v_{\parallel }\boldsymbol {\nabla }_{\parallel }H}=0.$ Equation (4.1) was also derived by Sugama & Watanabe (2005), for a specific helical magnetic equilibrium. Our equation is completely general from the point of view of geometry, provided a solution to the magnetic differential equation is given. For this, see  Mishchenko, Helander & Könies (2008). Let us introduce the ‘rippling time’, $\tau,$ which satisfies the equation

(4.3)\begin{equation} \left(\frac{\partial}{\partial\varphi}+\iota\frac{\partial}{\partial\theta}\right)\tau(\theta,\varphi)=\tau_b, \end{equation}

where $\tau _{b}^{-1}=v_{\parallel }/(B\sqrt {g}).$ In these new variables, the left-hand side of (4.1) becomes

(4.4)\begin{equation} \frac{\partial}{\partial t}\delta g+v_{{\parallel}} \boldsymbol{\hat{b}\boldsymbol{\cdot}\boldsymbol{\nabla}}\delta g= \left(\frac{\partial}{\partial t}+\frac{\partial}{\partial\tau}\right)\delta g. \end{equation}

We can then introduce the ripple-bounce expansion (Sugama & Watanabe 2005):

(4.5)\begin{equation} \delta g(\tau)=\sum_{l}h_{l}{\rm e}^{{\rm i}l\omega_{b}\tau},\,\,h_{l}=T_{b}^{{-}1}\oint \,{\rm d}\tau\delta g(\tau) {\rm e}^{-{\rm i}l\omega_{b}\tau}, \end{equation}

with $\omega _{b}=2{\rm \pi} T_{b}^{-1}$ and $T_{b}=\oint \,{\rm d}\theta _{c}^{\prime }\tau _{b}(\theta _{c}^{\prime }),$ where the $\oint$ integral is from $\theta _{1}$ to $\theta _{2}$ and back to $\theta _{1},$ along a trapped particle trajectory, where $\theta _{1}$ and $\theta _{2}$ are two consecutive bounce points whose exact definition depends on the class of trapped particles considered (Sugama & Watanabe 2005; Mishchenko, Helander & Könies 2008). Then, the ripple-bounce and Laplace transforms are applied to find

(4.6)\begin{equation} \int_{0}^{\infty}\,{\rm d}t{\rm e}^{{-}pt}\frac{1}{T_{b}}\oint \,{\rm d}\tau {\rm e}^{-{\rm i}l\omega_{b}\tau}\left(\frac{\partial}{\partial t}+\frac{\partial}{\partial\tau}\right)\delta g=\left(p+{\rm i}l\omega_{b}\right)\hat{h}_{l}(p)-h_{l}(0), \end{equation}

for the first term.

All other terms in the kinetic equation are better represented by Fourier modes. We introduce

(4.7)\begin{equation} \varPhi_{mn}=\varXi_{mn}^{l}\varPhi_{l} \end{equation}

and

(4.8)\begin{equation} \varPhi_{l}=\varTheta_{l}^{mn}\varPhi_{mn}, \end{equation}

where

(4.9)\begin{equation} \varTheta_{l}^{mn}=\frac{1}{\oint\tau_{b}}\oint \,{\rm d}\tau \exp({-{\rm i}(l\tau\omega_{b}+n\varphi(\tau)-m\theta(\tau))}) \end{equation}

and

(4.10)\begin{equation} \varXi_{mn}^{l}=\int_{0}^{2{\rm \pi}}\,{\rm d}\theta\int_{0}^{2{\rm \pi}}\,{\rm d}\varphi \exp\left({{\rm i}\left(l\tau(\theta,\varphi)+n\varphi-m\theta\right)}\right). \end{equation}

We also use the radial local approximation:

(4.11)\begin{equation} \chi(\psi,\theta,\varphi,t)=\sum_{k}\varPhi_{k}(\theta,\varphi,t){\rm e}^{{\rm i}k\psi} \end{equation}

and

(4.12)\begin{equation} \delta g(\psi,\theta,\varphi,t)=\sum_{k}h_{k}(\theta,\varphi,t){\rm e}^{{\rm i}k\psi}. \end{equation}

Then, the nonlinear equation expanded in bounce harmonics is

(4.13)\begin{equation} \frac{\partial h_{k}^{l}}{\partial t}+{\rm i}l\omega_{b}h_{k}^{l}={-}{\rm i}k\bar{v}_{\psi}h_{k}^{l}-\frac{e}{m}\frac{\partial F_{0}}{\partial\mathcal{E}}q_{l^{\prime}}\frac{\partial\varPhi_{k}^{l-l^{\prime}}}{\partial t}+\frac{\partial F_{0}}{\partial\mathcal{\psi}}H_{l,l^{\prime}}\varPhi_{k}^{l^{\prime}}+\mathcal{N}_{k^{\prime}}^{ll^{\prime}l^{\prime\prime}}\varPhi_{k^{\prime}}^{l^{\prime}}h_{k-k^{\prime}}^{l^{\prime\prime}},\end{equation}

where

(4.14)\begin{align} H_{l,l^{\prime}}={\rm i}\frac{c}{\sqrt{g}B^{2}}\left(nI+mG\right)q_{l^{\prime\prime}}\varTheta_{l-l^{\prime\prime}}^{mn}\varXi_{l^{\prime}}^{mn}, \end{align}

(4.15)\begin{align} \mathcal{N}_{k^{\prime}}^{ll^{\prime}l^{\prime\prime}}=\frac{c}{\sqrt{g}B^{2}}\left(\mathcal{S}_{k^{\prime}}^{ll^{\prime}l^{\prime\prime}}+{\rm i}\mathcal{R}^{ll^{\prime}l^{\prime\prime}}kk^{\prime}\right), \end{align}

with

(4.16)\begin{equation} \mathcal{S}_{k^{\prime}}^{ll^{\prime}l^{\prime\prime}}=\left\{ G\left[k^{\prime}m^{\prime}-\left(k-k^{\prime}\right)m\right]+I\left[k^{\prime}n^{\prime}-\left(k-k^{\prime}\right)n\right]\right\} \varXi_{l^{\prime}}^{mn}\varXi_{l^{\prime\prime}}^{mn}\varTheta_{l}^{m+m^{{{\prime}}},n+n^{\prime}} \end{equation}

and

(4.17)\begin{equation} \mathcal{R}^{ll^{\prime}l^{\prime\prime}}\varPhi_{k^{\prime}}^{l^{\prime}}h_{k-k^{\prime}}^{l^{\prime\prime}}=\left(mG+nI\right)Q_{l_{\prime}}\varXi^{l^{\prime}}_{mn}\varTheta_{l}^{m+m^{\prime}+m^{\prime\prime},n+n^{\prime}+n^{\prime\prime}}\varXi_{l^{\prime\prime}}^{m^{\prime}n^{\prime}}\varXi_{l^{\prime\prime\prime}}^{m^{\prime\prime}n^{\prime\prime}}\varPhi_{k^{\prime}}^{l^{\prime\prime}}h_{k-k^{\prime}}^{l^{\prime\prime\prime}} \end{equation}

and $q_{l}$ are the coefficients of the bounce expansion of $\exp [{\rm i}Q].$ We use the Einstein convention for repeated indices.

Dynamically, for any $l,$ we choose

(4.18)\begin{equation} p\sim l\omega_{b}\gg k\bar{v}_{\psi},\omega_{\boldsymbol{E}\times\boldsymbol{B}}. \end{equation}

This means that wave–particle resonance effects are kept to all orders. However, subsidiary expansions in $p/(l \omega _b)$ are allowed. In particular, one could consider the ion sound approximation, $p \gg l\omega _{b,i}$, and derive the fluid ion-temperature-gradient-driven instability (after neglecting nonlinearities). The bounce-averaged radial drift is supposed to be small since we are not interested in unoptimised machines. Our ordering is most appropriate for turbulence driven by high-frequency resonant phenomena, such as those caused by energetic particle (or electron) instabilities, or for weak turbulence close to marginality (where resonant effects are important). Strongly driven fluid regimes would require consideration of $p\sim \omega _{\boldsymbol E \times \boldsymbol B},$ and at present we are not in the position to conclude if our solution can efficiently describe them.

Let us now introduce a perturbative nonlinear solution. In order to explore all time scales supported by our ordering, and in particular long-time turbulent behaviour, such solution must be known to all orders. We treat perturbatively the stellarator contribution and the nonlinearity, in a fashion somewhat similar to that of Al'tshu’l & Karpman (1966) for the study of nonlinear oscillations in collisionless plasmas. As already stated, the same type of treatment has proved fruitful for the study of phase-space zonal structures in tokamaks (Zonca et al. 2015; Falessi & Zonca 2019). Reverting to (4.13), we immediately realise that its solution is iterative. Indeed, after introducing the Laplace transform, we find

(4.19)\begin{equation} \left(p+{\rm i}l\omega_{b}\right)\hat{h}_{k}^{(n)l}={-}{\rm i}k\bar{v}_{\psi}\hat{h}_{k}^{(n-1)l}+\mathcal{N}_{k^{\prime}}^{ll^{\prime}l^{\prime\prime}}\int \,{\rm d}p^{\prime}\hat{\varPhi}_{k^{\prime}}^{l^{\prime}}(p^{\prime})\hat{h}_{k-k^{\prime}}^{(n-1)l^{\prime\prime}}(p-p^{\prime}), \end{equation}

where

(4.20)\begin{equation} \frac{\hat{h}_{k}^{(n+1)l}}{\hat{h}_{k}^{(n)l}}\sim \frac{\omega_{\boldsymbol{E}\times\boldsymbol{B}}}{l \omega_b}\sim \frac{k {\bar{v}}_{\psi}}{l \omega_b} \ll 1. \end{equation}

This solution has a very attractive diagrammatic interpretation. Given an $\hat {h}^{(n-1)},$ the next-order iterative solution is the creation of a new field $\hat {h}_{k}^{l,(n)}=\hat {h}_{st}^{(n)}+\hat {h}_{nl}^{(n)},$ given by two modifications of the momentum-space propagator $(p+{\rm i}l\omega _{b})^{-1},$ that is,

(4.21)\begin{equation} \hat{h}_{k}^{l,(n)}=\frac{1}{p+{\rm i}l\omega_{b}}\left\{ \text{stellarator} + \text{nonlinearity}\right\}. \end{equation}

The first term is obtained via interaction of $\hat {h}_{k}^{(n-1)}$ at the vertex $-{\rm i}k\bar {v}_{\psi }$ (resulting in the emission of the curly propagator emerging from $-{\rm i}k\bar {v}_{\psi }$ in figure 1); the other is given by the annihilation of $\hat {h}^{(n-1)}$ and $\varPhi$ (see figure 1). At each step, the full result is the sum of all the fields produced by the iteration. We analyse in more detail the nonlinearity of the first-order solution of figure 1. This is

(4.22)\begin{equation} \left(p+{\rm i}l\omega_{b}\right)\hat{h}_{nl}^{(n)}=\mathcal{N}_{k^{\prime}}^{ll^{\prime}l^{\prime\prime}}\int \,{\rm d}p^{\prime}\hat{\varPhi}_{k^{\prime}}^{l^{\prime}}(p^{\prime})\hat{h}_{k-k^{\prime}}^{(n-1)l^{\prime\prime}}(p-p^{\prime}). \end{equation}

The right-hand side is a state characterised by two momentum-like quantities $(p,k)$ and an index $l.$ This is the result of the interaction at the circular vertex of figure 1 of two incoming fields: a $\hat {\varPhi }^{l^{\prime }}$ with ‘momentum’ $(p^{\prime },k^{\prime })$ and an $\hat {h}^{(n-1)l^{\prime \prime }}$ with ‘momentum’ $(p-p^{\prime },k-k^{\prime }).$ At the vertex momenta are conserved. The interaction is integral and its action mixes bounce harmonics via the $\mathcal {N}_{k^{\prime }}^{ll^{\prime }l^{\prime \prime }}$ tensor.

Figure 1. First-order iterative solution of (4.13).

Figure 2. Second-order iterative solution of (4.13).

Perturbatively, we might write, after introducing the regularised zeroth-order solution

(4.23)\begin{equation} \tilde{h}_{k}^{(0)l}=\left(p+{\rm i}l\omega_{B}\right)\hat{h}_{k}^{(0)l}, \end{equation}

with

(4.24)\begin{equation} \hat{h}_{k}^{(0)l}=\frac{1}{p+{\rm i}l\omega_{B}}\left\{ -\frac{e}{m}\frac{\partial F_{0}}{\partial\mathcal{E}}q_{l^{\prime}}\frac{\partial\varPhi_{k}^{l-l^{\prime}}}{\partial t}+\frac{\partial F_{0}}{\partial\mathcal{\psi}}H_{l,l^{\prime}}\varPhi_{k}^{l^{\prime}}\right\} , \end{equation}

the first-order solution

(4.25)\begin{equation} \tilde{h}_{k}^{(1)l}=\frac{-{\rm i}k\bar{v}_{\psi}}{\left(p+{\rm i}l\omega_{B}\right)^{2}}\tilde{h}_{k}^{(0)l}+\frac{\mathcal{N}_{k^{\prime}}^{ll_{1}l_{2}}}{p+{\rm i}l\omega_{B}}\int \,{\rm d}p_{1}\frac{\hat{\varPhi}_{k_{1}}^{l_{1}}(p_{1})}{p-p_{1}+{\rm i}l_{2}\omega_{b}}\tilde{h}_{k-k_{1}}^{(0)l_{2}}(p-p_{1}). \end{equation}

Then, the second-order solution is

(4.26)\begin{align} & \tilde{h}_{k}^{(2)l}=\frac{-{\rm i}k\bar{v}_{\psi}}{\left(p+{\rm i}l\omega_{B}\right)}\left\{ \frac{-{\rm i}k\bar{v}_{\psi}}{\left(p+{\rm i}l\omega_{B}\right)^{2}}\tilde{h}_{k}^{(0)l}+\frac{\mathcal{N}_{k^{\prime}}^{ll_{1}l_{2}}}{p+{\rm i}l\omega_{B}}\int \,{\rm d}p_{1}\frac{\hat{\varPhi}_{k_{1}}^{l_{1}}(p_{1})}{p-p_{1}+{\rm i}l_{2}\omega_{b}}\tilde{h}_{k-k_{1}}^{(0)l_{2}}(p-p_{1})\right\}\nonumber\\ & \qquad +\frac{\mathcal{N}_{k^{\prime}}^{ll_{1}l_{2}}}{p+{\rm i}l\omega_{B}}\int \,{\rm d}p_{1}\hat{\varPhi}_{k_{1}}^{l_{1}}(p_{1})\left\{ \frac{-{\rm i}k\bar{v}_{\psi}}{\left(p-p_{1}+{\rm i}l_{2}\omega_{B}\right)^{2}}\tilde{h}_{k-k_{1}}^{(0)l_{2}}(p-p_{1})\right.\nonumber\\ & \qquad+ \left.\frac{\mathcal{N}_{k^{\prime}}^{l_{2}l_{1}l_{3}}}{p-p_{1}+{\rm i}l_{2}\omega_{B}}\int \,{\rm d}p_{2}\frac{\hat{\varPhi}_{k_{1}}^{l_{1}}(p_{2})}{p-p_{1}-p_{2}+{\rm i}l_{3}\omega_{b}}\tilde{h}_{k-k_{1}-k_{2}}^{(0)l_{3}}(p-p_{1}-p_{2})\right\} , \end{align}

and so on. Here all the poles are now expressed explicitly. For the $n$th iteration, we generate $2^{n}$ graphs. In the following we show how to exploit the newly found nonlinear solution for the transport studies introduced in § 2.

5. Wave-like fluctuations and transport

At this point, the nonlinear theory of energetic particles and drift-wave-like modes is assumed to be given as an input. This provides mode frequencies and amplitudes, as explained in § 2. Then, for all perturbations

(5.1)\begin{equation} \varPhi_{k}(\theta,\varphi,t)=\phi^{\nu}{\rm e}^{{\rm i}\omega_{\nu}t}, \end{equation}

where $\omega _{\nu }$ is the local eigenvalue (2.17) of the system of equations for the fields (2.14)–(2.16) and $\phi ^{\nu }$ solves for the nonlinear Schrödinger-type equation discussed in § 2 (notice that there is no summation for repeated indices). After applying the Laplace transform, one obtains

(5.2)\begin{equation} \hat{\varPhi}_{k}^{l}=\varTheta_{mn}^{l}\frac{\phi_{mn,k}^{\nu}}{p+{\rm i}\omega_{\nu}}\equiv\frac{\zeta_{k,\nu}^{l}}{p+{\rm i}\omega_{\nu}}, \end{equation}

and all the convolution $p$ integrals in (4.19) can be performed by applying the Cauchy theorem and evaluating the residuals. To see specific stellarator nonlinear behaviour, we need to evaluate the second-order correction $\hat {h}_{k}^{(2)l}.$ The result is the sum of four different combinations of momentum-space propagators which look like

(5.3)\begin{align} \frac{k^{2}\bar{v}_{{{\psi}}}^{2}}{\left(p+{\rm i}l\omega_{b}\right)^{3}}& \div\frac{k\bar{v}_{{{\psi}}}\mathcal{N}\zeta}{\left(p+{\rm i}l\omega_{b}\right)^{2}\left(p-p_{0}\right)}\div\frac{k\bar{v}_{{{\psi}}}\mathcal{N}\zeta}{\left(p+{\rm i}l\omega_{b}\right)\left(p-p_{0}\right)^{2}}\nonumber\\ & \div\frac{\mathcal{N}^{2}\zeta^{2}}{\left(p+{\rm i}l\omega_{b}\right)\left(p-p_{0}\right)\left(p-p_{1}\right)},\end{align}

where $p_{0}=-{\rm i}(l_{2}\omega _{b}+\omega _{\nu })$ and $p_{1}=-{\rm i}(\omega _{b}l_{3}+2\omega _{\nu }).$ How such poles generate is highlighted in Appendix B.

What is left is a sum of momentum-space propagators that combine the available vertices of the theory, the stellarator-specific $k\bar {v}_{{{\psi }}}$ and that coming from nonlinear interaction $\mathcal {N}\zeta$. The three types of second-order propagators are shown in figure 3.

Figure 3. The three types of momentum-space second-order propagators for wave-like perturbations when $-{\rm i} l \omega _b =p_0=p_1$. Signs are taken into account by arrows, and quantities are conserved at the vertices. At this order, stellarator corrections and nonlinearity interact.

Diagrammatically, the first term of (5.3) is a stellarator self-energy loop. The second and the third terms are stellarator radiative corrections to a ‘luftballon’ diagram and the last is a nonlinear self-energy.

(5.4)

 Keeping this in mind, we are able to construct all possible solutions to all orders. We notice that the sum of all the two-vertex functions in (

5.4

) gives the analogue of the radiative corrections to the electron mass in quantum electrodynamics (Peskin & Schroeder 1995) (sum à-la-Dyson). The choice of specific resonant conditions allows us to evaluate which diagram is dominant in the sum, at each order.

A physics-based choice of resonances that dominate the sum is the following. Given a pole $p_{0},$ we consider a resonant condition as $p=p_{0}+\delta p,$ with $\delta p\sim k\bar {v}_{\psi }\ll 1,$ and

(5.5)\begin{equation} k\bar{v}_{\psi}\ll\mathcal{N}\zeta\ll p_{0}. \end{equation}

That is, for a slowly evolving turbulence, and an optimised machine, we can select which diagrams enter the Dyson summation in the final transport theory.

The perturbative nonlinear approach is a useful technique that helps in gaining insight into the problem. However, an equation for the complete infinite sum is preferable. The fact that the perturbative nonlinear solution can be constructed to all orders allows us to do so.

6. Phase-space zonal structure equation

Let us then focus our attention on the component of the perturbed distribution function that contributes to a ‘redefinition’ of the equilibrium quantities, in the spirit of what was originally proposed by Zonca et al. (2015), and then derived for axisymmetric systems by Falessi & Zonca (2019). That is, we need to identify the specific component of the fluctuating distribution function which tends to have structure at the equilibrium scale and, very importantly, is not damped or suppressed by resonantly kinetic effects. Within our treatment, this is the $l=0$ bounce-harmonic component, as (4.13) shows, since here the wave–particle resonant term (the second term on the left-hand side) is absent, in total analogy with the more familiar case first studied by Rosenbluth & Hinton (1998) (which we reproduce in Appendix A). Let us then consider the infinite sum

(6.1)\begin{equation} p\sum_{n=0}^{\infty}\hat{h}_{k}^{l_{0},(n)}\equiv p\hat{H}_{k}^{l_{0}}(p)=p\left(\hat{h}_{k}^{l_{0},(0)}+\hat{h}_{k}^{l_{0},(1)}+\sum_{n\geq2}^{\infty}\hat{h}_{k}^{l_{0},(n)}\right), \end{equation}

where we notice that stellarator corrections drive the nonlinearity in the perturbed distribution function, the terms $h\,h,$ only beyond second order (see the second line of the diagram in figure 2). We then iterate the perturbative $n$th solution twice, in order to isolate the linear drive and the $\phi h^{(0)}$ ‘nonlinearity’:

(6.2)\begin{gather} (p+{\rm i} l_0\omega_b)\hat{h}_{k}^{l_{0},(n)}=\int\int\frac{{\rm d}p_{1}\,{\rm d}p_2}{p-p_{1}+{\rm i} l_0 \omega_b} \left\{ -{\rm i}k\bar{v}_{\psi}\delta_{k_{1},0}\delta_{l_2,l_0}\delta(p_{1})+\mathcal{N}_{k_{1}}^{l_{0}l_{1}l_{2}}\hat{\varPhi}_{k_{1}}^{l_{1}}(p_{1})\right\}\nonumber\\ \times \left\{ -{\rm i}(k-k_1)\bar{v}_{\psi}\delta_{k_{2},0}\delta_{l_4,0}\delta(p_{2})+\mathcal{N}_{k_{2}}^{l_{2}l_{3}l_{4}}\hat{\varPhi}_{k_{2}}^{l_{3}}(p_{2})\right\} \hat{h}_{k-(k_{1}+k_{2})}^{l_{4},(n-2)}(p-p_1-p_2). \end{gather}

Plugging this result into (6.1), we obtain

(6.3)\begin{align} p\hat{H}_{k}^{0}(p)& =p\left(\hat{h}_{k}^{0,(0)}+\hat{h}_{k}^{0,(1)}\right)\nonumber\\ & \quad+ \int\int\frac{{\rm d}p_{1}\,{\rm d}p_{2}}{p-p_{1}}\left\{ -{\rm i}k\bar{v}_{\psi}\delta_{k_{1},0}\delta_{l_{2},0}\delta(p_{1})+\mathcal{N}_{k_{1}}^{0\,l_{1}l_{2}}\hat{\varPhi}_{k_{1}}^{l_{1}}(p_{1})\right\} \nonumber\\ & \quad\times \left\{ -{\rm i}(k-k_{1})\bar{v}_{\psi}\delta_{k_{2},0}\delta_{l_{4},0}\delta(p_{2})+\mathcal{N}_{k_{2}}^{l_{2}l_{3}l_{4}}\hat{\varPhi}_{k_{2}}^{l_{3}}(p_{2})\right\} \sum_{n\geq2}\hat{h}_{k-(k_{1}+k_{2})}^{l_{4},(n-2)}(p-p_{1}-p_{2}), \end{align}

where we set $l_0=0,$ since we are interested in the zonal part of the resummed perturbed distribution function. On the other hand, $\sum _{n\geq 2}^{\infty }\hat {h}_{k-(k_{1}+k_{2})}^{l_{4},(n-2)}=\hat {H}_{k-(k_{1}+k_{2})}^{l_{4}}(p)$; thus, for $l_{0}\equiv 0,$

(6.4)\begin{align} p\hat{H}_{k}^{0}(p)& =p\left(\hat{h}_{k}^{0,(0)}+\hat{h}_{k}^{0,(1)}\right)\nonumber\\ & \quad +\int \int\frac{{\rm d}p_{1} \,{\rm d}p_2}{p-p_{1}}\left\{ -{\rm i}k\bar{v}_{\psi}\delta_{k_{1},0}\delta_{l_2,0}\delta(p_{1})+\mathcal{N}_{k_{1}}^{0\,l_{1}l_{2}}\hat{\varPhi}_{k_{1}}^{l_{1}}(p_{1})\right\}\nonumber\\ & \quad\times \left\{ -{\rm i}(k-k_1)\bar{v}_{\psi}\delta_{k_{2},0}\delta_{l_4,0}\delta(p_{2})+\mathcal{N}_{k_{2}}^{l_{2}l_{3}l_{4}}\hat{\varPhi}_{k_{2}}^{l_{3}}(p_{2})\right\} \hat{H}^{l_4}_{k-(k_{1}+k_{2})}(p-p_1-p_2). \end{align}

This is the equivalent of the Dyson equation within the Al’tshu'l–Karpman treatment (their equation 2.23), which is quadratic in the field amplitude, but linear for the phase-space zonal structure, that is, the collisionlessly undamped ($l_0=0$) bounce harmonic. Equation (6.4) determines the nonlinear distortion to the local kinetic equilibrium, and its moments describe the sought-after transport theory which embeds nonlinear wave–particle resonant interactions which dominate energetic particle physics.

7. Discussion and conclusion

In this article we have introduced a new scheme for the study of the nonlinear interaction between drift-wave-like turbulence and energetic particles in stellarator geometry. The theory is fully electromagnetic. The equations for the fluctuating fields were derived by taking moments of the gyrokinetic equation and using an ordering inspired by linear ballooning theory. We therefore describe fluctuations as strongly varying across the equilibrium magnetic field, slowly varying along it, and characterised by an envelope that encapsulates some of their global features. The solution of the nonlinear distribution function is found by applying an iterative procedure which is based of the smallness of the bounce-averaged radial drift frequency and nonlinear $\boldsymbol {E}\times \boldsymbol {B}$ frequency. The resonant wave–particle interaction is treated with a mixed bounce harmonics/Fourier expansion. We introduced a diagrammatic interpretation of the iterative solutions, which can give guidance in the resummation of all perturbative nonlinear solutions derived at each iteration. We present a second-order perturbative nonlinear solution, for the case of wave-like fluctuating perturbations, and discuss the interplay between nonlinearity and specific stellarator features. We find that a finite bounce-averaged radial drift can couple to the nonlinearity in the fields and contribute to the evolution of turbulence. Finally we extended the concept of phase-space zonal structure to stellarator geometry, deriving the equivalent of the Dyson equation as proposed by Al'tshu’l & Karpman (1966) in the theory of nonlinear electrostatic fluctuations in plasmas. The result provides the basis for transport studies in which kinetically undamped nonlinear fluctuations contribute to the redefinition of the equilibrium distribution function. This behaviour is essential for the description of transport dynamics dominated by energetic particle physics.