1. Introduction
As the contribution of renewable energy to the overall energy supply increases, the challenge of intermittency in the generation of renewable energy is leading to the need for very substantial energy storage. One solution for large-scale storage is hydrogen (![]() ${\rm H}_2$) in subsurface sedimentary formations (Heinemann et al. Reference Heinemann2021a; Krevor et al. Reference Krevor, de Coninck, Gasda, Singh Ghaleigh, de Gooyert, Hajibeygi, Juanes, Neufeld, Roberts and Swennenhuis2023). The concept is that hydrogen is injected into formations where it is trapped by an overlying impermeable cap rock, and that it remains there until needed.
${\rm H}_2$) in subsurface sedimentary formations (Heinemann et al. Reference Heinemann2021a; Krevor et al. Reference Krevor, de Coninck, Gasda, Singh Ghaleigh, de Gooyert, Hajibeygi, Juanes, Neufeld, Roberts and Swennenhuis2023). The concept is that hydrogen is injected into formations where it is trapped by an overlying impermeable cap rock, and that it remains there until needed.
There have been a number of numerical simulations regarding the injection and extraction of hydrogen in saline aquifers (e.g. Sainz-Garcia et al. Reference Sainz-Garcia, Abarca, Rubi and Grandia2017). These models have shown that since the hydrogen is much less dense and less viscous than the formation fluid, then on injection it tends to spread along the upper boundary of a layer, forming a narrow gravity-driven finger. However, on extraction, some of the water is eventually drawn back to the well, limiting the mass of hydrogen which can be recovered. On successive cycles, the mass of hydrogen in the formation gradually builds up and eventually, the mass of hydrogen that can be extracted matches that which is injected (Heinemann et al. Reference Heinemann, Scafidi, Pickup, Thaysen, Hassanpouryouzband, Wilkinson, Satterley, Booth, Edlmann and Haszeldine2021b), while there is a trapped component of hydrogen in the formation known as the cushion gas. The controls on the volume of this cushion gas, as a fraction of the volume of so-called working gas which is injected and extracted each cycle, is of important economic and practical interest.
Since hydrogen is of low viscosity and density relative to water, the motion of hydrogen in geological formations can be dominated by buoyancy forces so that it spreads below the impermeable cap-rock of a reservoir in a somewhat analogous fashion to the motion of ![]() ${\rm CO}_2$ during carbon storage (Huppert & Woods Reference Huppert and Woods1995; Barenblatt Reference Barenblatt1996; Woods Reference Woods2014). Such buoyancy-driven flows in porous media have been studied in many different contexts (Mathunjwa & Hogg Reference Mathunjwa and Hogg2007; Hesse, Orr & Tchelepi Reference Hesse, Orr and Tchelepi2008; Pegler, Huppert & Neufeld Reference Pegler, Huppert and Neufeld2013; Yu, Zheng & Stone Reference Yu, Zheng and Stone2017; Hinton & Woods Reference Hinton and Woods2018; Whelan & Woods Reference Whelan and Woods2023). Many of these models assume a sharp interface between the two immiscible fluids. This simplification is strictly valid when the buoyancy forces are much larger than capillary forces (Nordbotten & Dahle Reference Nordbotten and Dahle2011), but it provides a valuable limit to interpret the effect of buoyancy on the reservoir scale evolution of the plume for different injection rates and different injection frequency. In practice, the effect of relative permeability and capillary pressure can lead to an intermediate zone host to both hydrogen and water, and the formation of a region where there may be some capillary trapped hydrogen (Hesse et al. Reference Hesse, Orr and Tchelepi2008). However, in the present work we adopt the sharp interface simplification to build up insight into some of the fundamental controls of buoyancy on such injection–extraction cycles. The seasonal storage of heat in aquifers (Nielsen & Sørensen Reference Nielsen, Sørensen and Stryi-Hipp2016) involves the periodic injection and extraction of water with associated migration of thermal and fluid fronts through the formation (Dudfield & Woods Reference Dudfield and Woods2012, Reference Dudfield and Woods2014, Reference Dudfield and Woods2015). In the present paper, a major focus relates the ratio of working gas to cushion gas once an injection–extraction cycle reaches equilibrium. We explore the case of injection into an anticline system given that this is an ideal geological system for such storage (figure 1).
${\rm CO}_2$ during carbon storage (Huppert & Woods Reference Huppert and Woods1995; Barenblatt Reference Barenblatt1996; Woods Reference Woods2014). Such buoyancy-driven flows in porous media have been studied in many different contexts (Mathunjwa & Hogg Reference Mathunjwa and Hogg2007; Hesse, Orr & Tchelepi Reference Hesse, Orr and Tchelepi2008; Pegler, Huppert & Neufeld Reference Pegler, Huppert and Neufeld2013; Yu, Zheng & Stone Reference Yu, Zheng and Stone2017; Hinton & Woods Reference Hinton and Woods2018; Whelan & Woods Reference Whelan and Woods2023). Many of these models assume a sharp interface between the two immiscible fluids. This simplification is strictly valid when the buoyancy forces are much larger than capillary forces (Nordbotten & Dahle Reference Nordbotten and Dahle2011), but it provides a valuable limit to interpret the effect of buoyancy on the reservoir scale evolution of the plume for different injection rates and different injection frequency. In practice, the effect of relative permeability and capillary pressure can lead to an intermediate zone host to both hydrogen and water, and the formation of a region where there may be some capillary trapped hydrogen (Hesse et al. Reference Hesse, Orr and Tchelepi2008). However, in the present work we adopt the sharp interface simplification to build up insight into some of the fundamental controls of buoyancy on such injection–extraction cycles. The seasonal storage of heat in aquifers (Nielsen & Sørensen Reference Nielsen, Sørensen and Stryi-Hipp2016) involves the periodic injection and extraction of water with associated migration of thermal and fluid fronts through the formation (Dudfield & Woods Reference Dudfield and Woods2012, Reference Dudfield and Woods2014, Reference Dudfield and Woods2015). In the present paper, a major focus relates the ratio of working gas to cushion gas once an injection–extraction cycle reaches equilibrium. We explore the case of injection into an anticline system given that this is an ideal geological system for such storage (figure 1).

Figure 1. Illustration of hydrogen being injected at the crest of a brine-saturated anticline via a line source injection well. Symmetry is assumed at either side of the well.
The paper is organised as follows. In § 2 we develop a model for the gravity-driven injection and extraction of a plume of buoyant, low-viscosity hydrogen spreading into a porous layer with an inclined upper boundary. In § 3, we show that once sufficient fluid has entered the system, an equilibrium regime will develop where an equal amount of fluid is injected and extracted across each cycle. We also illustrate that the ratio of the square of the buoyancy speed to the product of the injection rate and the injection frequency leads to a key dimensionless parameter, ![]() $\beta$ (defined in the next section) which controls the dynamics of this plume. For small
$\beta$ (defined in the next section) which controls the dynamics of this plume. For small ![]() $\beta$, corresponding to fast or high-frequency injection, the thickness of the plume far from the injection well remains constant across a cycle and the fluctuations in depth and, hence, the working gas only extends to a region near the well, while for larger
$\beta$, corresponding to fast or high-frequency injection, the thickness of the plume far from the injection well remains constant across a cycle and the fluctuations in depth and, hence, the working gas only extends to a region near the well, while for larger ![]() $\beta$, corresponding to slow or low-frequency injection, the fluctuations in depth occur across the entire length of the plume from the well to the far boundary where it meets the sloping anticline. We derive scalings for the dimensions of the plume in terms of
$\beta$, corresponding to slow or low-frequency injection, the fluctuations in depth occur across the entire length of the plume from the well to the far boundary where it meets the sloping anticline. We derive scalings for the dimensions of the plume in terms of ![]() $\beta$ once the system has reached equilibrium between the volume of gas injected and extracted during one cycle. In § 4 we explore the initial transient stage of the flow before this equilibrium is reached. We examine the number of injection–extraction cycles needed to reach equilibrium as a function of
$\beta$ once the system has reached equilibrium between the volume of gas injected and extracted during one cycle. In § 4 we explore the initial transient stage of the flow before this equilibrium is reached. We examine the number of injection–extraction cycles needed to reach equilibrium as a function of ![]() $\beta$. We draw some conclusions and discuss the implications of this modelling for hydrogen storage.
$\beta$. We draw some conclusions and discuss the implications of this modelling for hydrogen storage.
2. Model
We develop a model for the flow of a buoyant incompressible current of density ![]() $\widehat {\rho _1}$ and viscosity
$\widehat {\rho _1}$ and viscosity ![]() $\hat {\mu }$ through a uniform porous medium of permeability
$\hat {\mu }$ through a uniform porous medium of permeability ![]() $\hat {k}$ and porosity
$\hat {k}$ and porosity ![]() $\phi$. We define the depth below the crest of the upper surface of the anticline to be
$\phi$. We define the depth below the crest of the upper surface of the anticline to be ![]() $\hat {b}(\hat {x})$ (see figure 2), where
$\hat {b}(\hat {x})$ (see figure 2), where ![]() $\hat {x}$ is the lateral distance from the crest. Throughout the remainder of this paper we consider the case of a shallow incline
$\hat {x}$ is the lateral distance from the crest. Throughout the remainder of this paper we consider the case of a shallow incline ![]() $\hat {b}(\hat {x}) = \hat {x} \tan \theta$. The medium is initially saturated with ambient brine of density
$\hat {b}(\hat {x}) = \hat {x} \tan \theta$. The medium is initially saturated with ambient brine of density ![]() $\widehat {\rho _2}$. The fluid is injected by a line source along the crest of the anticline with injection flux per unit length
$\widehat {\rho _2}$. The fluid is injected by a line source along the crest of the anticline with injection flux per unit length ![]() $\hat {Q}$.
$\hat {Q}$.

Figure 2. Outline of the flow of a buoyant plume of hydrogen of density ![]() $\hat {\rho }_1$, viscosity
$\hat {\rho }_1$, viscosity ![]() $\hat {\mu }$ and thickness
$\hat {\mu }$ and thickness ![]() $\hat {h}(\hat {x})$ in a porous medium of permeability
$\hat {h}(\hat {x})$ in a porous medium of permeability ![]() $\hat {k}$, porosity
$\hat {k}$, porosity ![]() $\phi$ and cap rock geometry described by
$\phi$ and cap rock geometry described by ![]() $\hat {b}(\hat {x})$, traveling with horizontal speed
$\hat {b}(\hat {x})$, traveling with horizontal speed ![]() $\hat {u}$. The coordinate system is shown with
$\hat {u}$. The coordinate system is shown with ![]() $\hat {x}$ and
$\hat {x}$ and ![]() $\hat {y}$ denoting the horizontal and vertical axes respectively. The ambient brine present has density
$\hat {y}$ denoting the horizontal and vertical axes respectively. The ambient brine present has density ![]() $\hat {\rho }_2$.
$\hat {\rho }_2$.
With a line source injection, the problem is two dimensional and it is appropriate to work in Cartesian coordinates. As a simplification, we consider the case in which the interface between the hydrogen and the water remains localised and we assume that the current lies in the region ![]() $0 < \hat {y} < \hat {h}(\hat {x},\hat {t})$ and
$0 < \hat {y} < \hat {h}(\hat {x},\hat {t})$ and ![]() $0 < \hat {x} < \hat {x}_f$, where
$0 < \hat {x} < \hat {x}_f$, where ![]() $\hat {t}$ is time (figure 2). Here,
$\hat {t}$ is time (figure 2). Here, ![]() $\hat {h}(\hat {x},\hat {t})$ is the thickness of the current while
$\hat {h}(\hat {x},\hat {t})$ is the thickness of the current while ![]() $\hat {x}_f$ is the horizontal position where the interface makes contact with the boundary, meaning
$\hat {x}_f$ is the horizontal position where the interface makes contact with the boundary, meaning ![]() $\hat {h}(\hat {x}_f, \hat {t}) = \hat {x}_f \tan \theta$. The flow is then described by Darcy's law in tandem with the incompressibility condition (Bear Reference Bear1988)
$\hat {h}(\hat {x}_f, \hat {t}) = \hat {x}_f \tan \theta$. The flow is then described by Darcy's law in tandem with the incompressibility condition (Bear Reference Bear1988)
where ![]() $\hat {p}(\hat {x},\hat {y})$ is the pressure at the point
$\hat {p}(\hat {x},\hat {y})$ is the pressure at the point ![]() $(\hat {x},\hat {y})$.
$(\hat {x},\hat {y})$.
In general the gravity current will spread out becoming long and thin ![]() $\hat {h} - \hat {b} \ll \hat {x}_f$, such that its horizontal extent is much larger than its vertical extent. From the incompressibility condition (2.1a,b), we can deduce
$\hat {h} - \hat {b} \ll \hat {x}_f$, such that its horizontal extent is much larger than its vertical extent. From the incompressibility condition (2.1a,b), we can deduce
where ![]() $\delta$ is the ratio of the characteristic vertical to horizontal length scale. From relation (2.2), it can be seen that at long time the vertical component
$\delta$ is the ratio of the characteristic vertical to horizontal length scale. From relation (2.2), it can be seen that at long time the vertical component ![]() $\hat {v}$ of the velocity
$\hat {v}$ of the velocity ![]() $\hat {\boldsymbol {u}}$ becomes negligible which then implies the pressure varies hydrostatically as given by
$\hat {\boldsymbol {u}}$ becomes negligible which then implies the pressure varies hydrostatically as given by
where ![]() $\Delta \hat {\rho } = \hat {\rho }_2 - \hat {\rho }_1$ and
$\Delta \hat {\rho } = \hat {\rho }_2 - \hat {\rho }_1$ and ![]() $\hat {P}_0( \hat {x}, \hat {t} )$ is the pressure at the fluid interface. When the aquifer has much greater depth than the thickness of the hydrogen plume, the pressure at the interface may be taken to be approximately constant (Pegler et al. Reference Pegler, Huppert and Neufeld2013)
$\hat {P}_0( \hat {x}, \hat {t} )$ is the pressure at the fluid interface. When the aquifer has much greater depth than the thickness of the hydrogen plume, the pressure at the interface may be taken to be approximately constant (Pegler et al. Reference Pegler, Huppert and Neufeld2013)
With the pressure relation (2.4), we then determine the horizontal component of the velocity ![]() $\hat {u}$ to be
$\hat {u}$ to be
where ![]() $\hat {S} = {\hat {k} \Delta \hat {\rho } \hat {g}}/{\hat {\mu }}$ is the buoyancy speed, which is the characteristic speed associated with a gravity current in a porous medium.
$\hat {S} = {\hat {k} \Delta \hat {\rho } \hat {g}}/{\hat {\mu }}$ is the buoyancy speed, which is the characteristic speed associated with a gravity current in a porous medium.
Local conservation of mass of the fluid is given by the equation
Combining this with (2.5) we find
Volume conservation (per unit length) takes the form
We also impose the condition ![]() $\hat {h}(\hat {x}_f, \hat {t}) = \hat {x}_f \tan \theta$ at the contact point. We assume the initial condition
$\hat {h}(\hat {x}_f, \hat {t}) = \hat {x}_f \tan \theta$ at the contact point. We assume the initial condition
We seek solutions to the governing equation (2.7) when there is a flux at ![]() $\hat {x}=0$ of the form (Dudfield & Woods Reference Dudfield and Woods2012)
$\hat {x}=0$ of the form (Dudfield & Woods Reference Dudfield and Woods2012)
 \begin{equation}
\hat{Q} ={-} \hat{S} \hat{h} \left.\frac{\partial \hat{h} }{\partial
\hat{x}}\right|_{\hat{x}=0} = \begin{cases} \hat{Q}_0 &
\text{if } 2n {\rm \pi}\leq \hat{\omega} \hat{t} < (2n + 1)
{\rm \pi}, \\ -\hat{Q}_0 & \text{if } (2n+1) {\rm \pi}\leq
\hat{\omega} \hat{t} < (2n + 2) {\rm \pi}\text{ and }
\hat{h}(0,\hat{t}) > 0, \\ 0 & \text{if } (2n+1) {\rm \pi}\leq
\hat{\omega} \hat{t} < (2n + 2) {\rm \pi}\text{ and }
\hat{h}(0,\hat{t}) = 0, \end{cases}
\end{equation}
\begin{equation}
\hat{Q} ={-} \hat{S} \hat{h} \left.\frac{\partial \hat{h} }{\partial
\hat{x}}\right|_{\hat{x}=0} = \begin{cases} \hat{Q}_0 &
\text{if } 2n {\rm \pi}\leq \hat{\omega} \hat{t} < (2n + 1)
{\rm \pi}, \\ -\hat{Q}_0 & \text{if } (2n+1) {\rm \pi}\leq
\hat{\omega} \hat{t} < (2n + 2) {\rm \pi}\text{ and }
\hat{h}(0,\hat{t}) > 0, \\ 0 & \text{if } (2n+1) {\rm \pi}\leq
\hat{\omega} \hat{t} < (2n + 2) {\rm \pi}\text{ and }
\hat{h}(0,\hat{t}) = 0, \end{cases}
\end{equation}
where ![]() $\hat {t}$ is time,
$\hat {t}$ is time, ![]() $\hat {Q}_0$ is the characteristic scale of the injection flux per unit length along the well,
$\hat {Q}_0$ is the characteristic scale of the injection flux per unit length along the well, ![]() $\hat {\omega }$ is a rate parameter which determines the frequency of oscillations and
$\hat {\omega }$ is a rate parameter which determines the frequency of oscillations and ![]() $n \geq 0$ is the cycle number.
$n \geq 0$ is the cycle number.
It is instructive to consider the problem in dimensionless form. To this end we define the following dimensionless variables (Pegler et al. Reference Pegler, Huppert and Neufeld2013):
 \begin{equation} x = \frac{ \tan^2(\theta) \hat{S}}{\hat{Q}_0} \hat{x} , \quad h = \frac{ \tan (\theta) \hat{S}}{\hat{Q}_0} \hat{h} , \quad t = \frac{ \tan^3 (\theta) \hat{S}^2}{\phi \hat{Q}_0} \hat{t} \quad \text{and} \quad Q = \frac{\hat{Q}}{\hat{Q}_0} . \end{equation}
\begin{equation} x = \frac{ \tan^2(\theta) \hat{S}}{\hat{Q}_0} \hat{x} , \quad h = \frac{ \tan (\theta) \hat{S}}{\hat{Q}_0} \hat{h} , \quad t = \frac{ \tan^3 (\theta) \hat{S}^2}{\phi \hat{Q}_0} \hat{t} \quad \text{and} \quad Q = \frac{\hat{Q}}{\hat{Q}_0} . \end{equation}The governing equation in non-dimensional form becomes
The flux condition at the source now has the form
 \begin{equation} Q ={-} h \left.\frac{\partial h }{\partial x} \right|_{x=0} = \begin{cases} 1 & \text{if } 2n {\rm \pi}\beta \leq t < (2n + 1) {\rm \pi}\beta ,\\ -1 & \text{if } (2n+1) {\rm \pi}\beta \leq t < (2n + 2) {\rm \pi}\beta \text{ and } h(0,t) > 0, \\ 0 & \text{if } (2n+1) {\rm \pi}\beta \leq t < (2n + 2) {\rm \pi}\beta \text{ and } h(0,t)= 0, \end{cases} \end{equation}
\begin{equation} Q ={-} h \left.\frac{\partial h }{\partial x} \right|_{x=0} = \begin{cases} 1 & \text{if } 2n {\rm \pi}\beta \leq t < (2n + 1) {\rm \pi}\beta ,\\ -1 & \text{if } (2n+1) {\rm \pi}\beta \leq t < (2n + 2) {\rm \pi}\beta \text{ and } h(0,t) > 0, \\ 0 & \text{if } (2n+1) {\rm \pi}\beta \leq t < (2n + 2) {\rm \pi}\beta \text{ and } h(0,t)= 0, \end{cases} \end{equation}while
The dimensionless group ![]() $\beta$ given by
$\beta$ given by
 \begin{equation} \beta = \frac{ \tan^3 (\theta) \hat{S}^2}{\phi \hat{Q}_0 \hat{\omega}} \end{equation}
\begin{equation} \beta = \frac{ \tan^3 (\theta) \hat{S}^2}{\phi \hat{Q}_0 \hat{\omega}} \end{equation}
measures the importance of the square of the buoyancy speed relative to the product of the injection rate and injection frequency. From relations (2.11a–d), it can be seen that for the current to be long and thin we require ![]() $\theta \ll 45^{\circ }$. During an extraction phase (
$\theta \ll 45^{\circ }$. During an extraction phase (![]() $Q < 0$) the thickness of the current at the origin may decrease to zero,
$Q < 0$) the thickness of the current at the origin may decrease to zero, ![]() $h(0,t) = 0$. This is undesirable as in such a case, the formation fluid/brine will be produced at the extraction well. If this occurs we assume the extraction of fluid is stopped for the remainder of the cycle and then we begin injection again at the start of the next cycle. In the early cycles a mismatch develops whereby more fluid is injected than extracted over a cycle, resulting in a net increase in the volume of hydrogen in the porous medium. After successive injection and extraction cycles, there is sufficient net accumulation of hydrogen that a periodic cycle develops in which the volume of fluid extracted matches the volume of fluid injected. In the next section we study this equilibrium state and then we examine the initial transient filling of the system.
$h(0,t) = 0$. This is undesirable as in such a case, the formation fluid/brine will be produced at the extraction well. If this occurs we assume the extraction of fluid is stopped for the remainder of the cycle and then we begin injection again at the start of the next cycle. In the early cycles a mismatch develops whereby more fluid is injected than extracted over a cycle, resulting in a net increase in the volume of hydrogen in the porous medium. After successive injection and extraction cycles, there is sufficient net accumulation of hydrogen that a periodic cycle develops in which the volume of fluid extracted matches the volume of fluid injected. In the next section we study this equilibrium state and then we examine the initial transient filling of the system.
3. Equilibrium states
To study the equilibrium states described at the end of the last section, we solved the system (2.12)–(2.14a,b) numerically using a finite-volume scheme (Kurganov & Tadmor Reference Kurganov and Tadmor2000; Yu et al. Reference Yu, Zheng and Stone2017). The code is run until a periodic cycle develops which we define to develop when the fractional increase of the volume of hydrogen between successive cycles is less than ![]() $10^{-4}$.
$10^{-4}$.
In figure 3, we illustrate the evolution of a hydrogen plume through a periodic cycle for five different values of ![]() $\beta$. Each plot shows the plume at four times through a cycle, namely at
$\beta$. Each plot shows the plume at four times through a cycle, namely at ![]() $t_e = 0$,
$t_e = 0$, ![]() ${{\rm \pi} \beta }/{2}$,
${{\rm \pi} \beta }/{2}$, ![]() ${\rm \pi} \beta$ and
${\rm \pi} \beta$ and ![]() ${3 {\rm \pi}\beta }/{2}$, where the period of the cycle is
${3 {\rm \pi}\beta }/{2}$, where the period of the cycle is ![]() $2 {\rm \pi}\beta$ and
$2 {\rm \pi}\beta$ and ![]() $t_e$ is the time during one injection–extraction cycle at equilibrium, meaning
$t_e$ is the time during one injection–extraction cycle at equilibrium, meaning ![]() $0 \leq t_e < 2 {\rm \pi}\beta$. It is interesting to note that in plots (a) and (b) of figure 3, a region far from the source can be observed where the thickness of the plume changes very little over the course of an injection–extraction cycle (see figure 4). We define the point where this region begins to be
$0 \leq t_e < 2 {\rm \pi}\beta$. It is interesting to note that in plots (a) and (b) of figure 3, a region far from the source can be observed where the thickness of the plume changes very little over the course of an injection–extraction cycle (see figure 4). We define the point where this region begins to be ![]() $(x^*, h^*)$. However, for larger values of
$(x^*, h^*)$. However, for larger values of ![]() $\beta$ (see figure 3c–e), it can be seen that the entire interface,
$\beta$ (see figure 3c–e), it can be seen that the entire interface, ![]() $h(x,t)$ in the region
$h(x,t)$ in the region ![]() $0 \leq x \leq x_f$, oscillates significantly over the injection–extraction cycle. This is because as the parameter
$0 \leq x \leq x_f$, oscillates significantly over the injection–extraction cycle. This is because as the parameter ![]() $\beta$ increases, the relative strength of the buoyancy speed with respect to the injection speed increases thus allowing fluid injected at the origin to be transmitted further across the porous medium during a single injection–extraction cycle. If
$\beta$ increases, the relative strength of the buoyancy speed with respect to the injection speed increases thus allowing fluid injected at the origin to be transmitted further across the porous medium during a single injection–extraction cycle. If ![]() $\beta$ is large enough then eventually these oscillations are transmitted far enough over a cycle that they reach the boundary at the leading edge of the current. We denote the critical value of
$\beta$ is large enough then eventually these oscillations are transmitted far enough over a cycle that they reach the boundary at the leading edge of the current. We denote the critical value of ![]() $\beta$ for which this phenomenon occurs to be
$\beta$ for which this phenomenon occurs to be ![]() $\beta _c$.
$\beta _c$.

Figure 3. The thickness of the plume ![]() $h$ plotted as a function of horizontal position
$h$ plotted as a function of horizontal position ![]() $x$ at a series of times during an injection–extraction cycle once the systems has reached a quasi-equilibrium. Examples are given for five values of
$x$ at a series of times during an injection–extraction cycle once the systems has reached a quasi-equilibrium. Examples are given for five values of ![]() $\beta$: (a)
$\beta$: (a) ![]() $\beta = 0.001$; (b)
$\beta = 0.001$; (b) ![]() $\beta = 0.01$; (c)
$\beta = 0.01$; (c) ![]() $\beta = 0.25$; (d)
$\beta = 0.25$; (d) ![]() $\beta = 1$; and (e)
$\beta = 1$; and (e) ![]() $\beta = 5$.
$\beta = 5$.

Figure 4. Two diagrams at different times during an injection–extraction cycle once equilibrium has been achieved showing an approximately time-independent region in the far-field. The point (![]() $x^*, h^*$) denotes the beginning of this region. The point (
$x^*, h^*$) denotes the beginning of this region. The point (![]() $x_f, h_f$) is the contact point of the current and the boundary.
$x_f, h_f$) is the contact point of the current and the boundary.
The value of ![]() $\beta _c$ may be approximated numerically by varying
$\beta _c$ may be approximated numerically by varying ![]() $\beta$ until there are noticeable oscillations at the leading edge of the current once equilibrium is reached. We define this to be when either the minimum or maximum value of the contact point
$\beta$ until there are noticeable oscillations at the leading edge of the current once equilibrium is reached. We define this to be when either the minimum or maximum value of the contact point ![]() $h_{min}$ or
$h_{min}$ or ![]() $h_{max}$ first differs from their average value
$h_{max}$ first differs from their average value ![]() $\bar {h}_f$ by
$\bar {h}_f$ by ![]() $1\,\%$ during a cycle. We have determined the approximate value to be
$1\,\%$ during a cycle. We have determined the approximate value to be ![]() $\beta _c \approx 0.05$. Similarly, we can determine approximately the time independent region
$\beta _c \approx 0.05$. Similarly, we can determine approximately the time independent region ![]() $(x^*, h^*)$ numerically by finding the closest lateral point to the source
$(x^*, h^*)$ numerically by finding the closest lateral point to the source ![]() $x^*$, where the thickness
$x^*$, where the thickness ![]() $h^*$ differs by less than
$h^*$ differs by less than ![]() $1\,\%$ of the average thickness at the leading edge
$1\,\%$ of the average thickness at the leading edge ![]() $\bar {h}_f$ during the entire cycle. When the difference is greater than
$\bar {h}_f$ during the entire cycle. When the difference is greater than ![]() $1\,\%$,
$1\,\%$, ![]() $(x^*, h^*) = (\bar {x}_f, \bar {h}_f)$
$(x^*, h^*) = (\bar {x}_f, \bar {h}_f)$
To gain insight into how this far-field region depends on the parameter ![]() $\beta$, we can develop some scalings. First, consider the regime where the oscillations near the source do not reach the boundary over the course of a cycle and the approximately time-independent region in the far-field is present. Let
$\beta$, we can develop some scalings. First, consider the regime where the oscillations near the source do not reach the boundary over the course of a cycle and the approximately time-independent region in the far-field is present. Let ![]() $\hat {L}^*$ and
$\hat {L}^*$ and ![]() $\hat {H}^*$ be the dimensional length and height scales associated with the oscillations during a cycle. The balance of mass over a cycle then requires that
$\hat {H}^*$ be the dimensional length and height scales associated with the oscillations during a cycle. The balance of mass over a cycle then requires that
where ![]() $\phi \hat {L}^*\hat {H}^*$ is a scaling for the volume associated with the oscillations. The flux in terms of
$\phi \hat {L}^*\hat {H}^*$ is a scaling for the volume associated with the oscillations. The flux in terms of ![]() $\hat {L}^*$ and
$\hat {L}^*$ and ![]() $\hat {H}^*$ is given by
$\hat {H}^*$ is given by
Combining relations (3.1) and (3.2) we can determine scalings for both ![]() $\hat {H}^*$ and
$\hat {H}^*$ and ![]() $\hat {L}^*$ finding
$\hat {L}^*$ finding
 \begin{equation} \hat{H}^* \sim \biggl( \frac{\hat{Q}_{0}^2}{\phi \hat{S} \hat{\omega}} \biggr)^{{1}/{3}} \quad \text{and}\quad \hat{L}^* \sim \biggl( \frac{ \hat{S} \hat{Q}_{0}}{\phi \hat{\omega}^2} \biggr)^{{1}/{3}}. \end{equation}
\begin{equation} \hat{H}^* \sim \biggl( \frac{\hat{Q}_{0}^2}{\phi \hat{S} \hat{\omega}} \biggr)^{{1}/{3}} \quad \text{and}\quad \hat{L}^* \sim \biggl( \frac{ \hat{S} \hat{Q}_{0}}{\phi \hat{\omega}^2} \biggr)^{{1}/{3}}. \end{equation}Writing these scalings in non-dimensional form we find
These scalings show that as ![]() $\beta$ takes progressively smaller values, the flow becomes more localised near the well, and eventually the approximation of a long and thin one-dimensional flow ceases to apply.
$\beta$ takes progressively smaller values, the flow becomes more localised near the well, and eventually the approximation of a long and thin one-dimensional flow ceases to apply.
Since the height of the time-independent region in the far-field is approximately the same as the height at the leading edge we deduce ![]() $h^* \approx h_f$ due to the time-independent approximation in the far-field, and
$h^* \approx h_f$ due to the time-independent approximation in the far-field, and ![]() $x_f = h_f$ due to the linear inclination of the cap-rock, thus
$x_f = h_f$ due to the linear inclination of the cap-rock, thus
Note from relation (3.5a,b) we see the total volume in the system obeys the following power law:
In the second equilibrium regime, when the oscillations propagate across the entire interface the flow is constrained by the boundary, ![]() $\hat {L}^* \ \tan \theta \sim \hat {H}^*$. This implies that
$\hat {L}^* \ \tan \theta \sim \hat {H}^*$. This implies that ![]() $x^* \sim x_f$. We now expect
$x^* \sim x_f$. We now expect
The corresponding scalings for ![]() $h_f$,
$h_f$, ![]() $x_f$,
$x_f$, ![]() $h^*$ and
$h^*$ and ![]() $V$ do not change from relations (3.4a,b)–(3.6) in this regime.
$V$ do not change from relations (3.4a,b)–(3.6) in this regime.
To test the validity of these scalings in figure 5, we show the variation of ![]() $\log (\bar {h}_f)$ (a),
$\log (\bar {h}_f)$ (a), ![]() $\log (\bar {V})$ (b) and
$\log (\bar {V})$ (b) and ![]() $\log (x^*)$ (c) as functions of
$\log (x^*)$ (c) as functions of ![]() $\log \beta$. Here
$\log \beta$. Here ![]() $\bar {V}$ is the average of the maximum and minimum volume values during an injection–extraction cycle at equilibrium. In (a,b) the linearity of the curves implies that
$\bar {V}$ is the average of the maximum and minimum volume values during an injection–extraction cycle at equilibrium. In (a,b) the linearity of the curves implies that ![]() $\bar {h}_f$ and
$\bar {h}_f$ and ![]() $\bar {V}$ grow consistent with relations (3.5a,b) and (3.6), respectively. In (c), linearity again implies power laws are followed whereby the far-field region beginning at
$\bar {V}$ grow consistent with relations (3.5a,b) and (3.6), respectively. In (c), linearity again implies power laws are followed whereby the far-field region beginning at ![]() $x^*$ initially grows as
$x^*$ initially grows as ![]() $\beta ^{{2}/{3}}$. However, once the oscillations reach the edge of the current denoted by the vertical dotted line in (c),
$\beta ^{{2}/{3}}$. However, once the oscillations reach the edge of the current denoted by the vertical dotted line in (c), ![]() $x^* \approx x_f$ and
$x^* \approx x_f$ and ![]() $x^*$ then grows as
$x^*$ then grows as ![]() $\beta ^{{1}/{3}}$. These results are consistent with the scalings derived in relations (3.4a,b)–(3.7). Lines of best fit are illustrated in each plot by dashed black lines with coefficients given in the caption. As mentioned earlier once an equilibrium state has been reached the volume injected
$\beta ^{{1}/{3}}$. These results are consistent with the scalings derived in relations (3.4a,b)–(3.7). Lines of best fit are illustrated in each plot by dashed black lines with coefficients given in the caption. As mentioned earlier once an equilibrium state has been reached the volume injected ![]() $V_w$ matches the volume extracted. We define the working fraction
$V_w$ matches the volume extracted. We define the working fraction ![]() $W_f$ as the ratio of the volume of working gas
$W_f$ as the ratio of the volume of working gas ![]() $V_w$ to the sum of the working gas and cushion gas
$V_w$ to the sum of the working gas and cushion gas ![]() $V_c$:
$V_c$:
where the cushion gas ![]() $V_c$ is the volume of fluid that cannot be recovered during the extraction phase (Heinemann et al. Reference Heinemann, Scafidi, Pickup, Thaysen, Hassanpouryouzband, Wilkinson, Satterley, Booth, Edlmann and Haszeldine2021b). Knowledge of how the working fraction
$V_c$ is the volume of fluid that cannot be recovered during the extraction phase (Heinemann et al. Reference Heinemann, Scafidi, Pickup, Thaysen, Hassanpouryouzband, Wilkinson, Satterley, Booth, Edlmann and Haszeldine2021b). Knowledge of how the working fraction ![]() $W_f$ varies as a function of
$W_f$ varies as a function of ![]() $\beta$ is important. In figure 6 we plot the working fraction
$\beta$ is important. In figure 6 we plot the working fraction ![]() $W_f$ as a function of
$W_f$ as a function of ![]() $\log \beta$. The larger-amplitude oscillations along the fluid interface lead to a larger volume of fluid being injected and extracted in each cycle. This results in a higher working fraction. Note that the increase of
$\log \beta$. The larger-amplitude oscillations along the fluid interface lead to a larger volume of fluid being injected and extracted in each cycle. This results in a higher working fraction. Note that the increase of ![]() $\beta$ resulting in larger working fractions implies that steepening the incline increases the working fraction. This is because of the greater constraint on the lateral extent
$\beta$ resulting in larger working fractions implies that steepening the incline increases the working fraction. This is because of the greater constraint on the lateral extent ![]() $x_f$ of the current causing greater localisation of the hydrogen plume around the source.
$x_f$ of the current causing greater localisation of the hydrogen plume around the source.

Figure 5. ![]() ${\rm Log}$–
${\rm Log}$–![]() $\log$ plots of
$\log$ plots of ![]() $\bar {h}_f$ (a),
$\bar {h}_f$ (a), ![]() $\bar {V}$ (b) and
$\bar {V}$ (b) and ![]() $x^*$ (c), as functions of varying
$x^*$ (c), as functions of varying ![]() $\beta$ (red circles). The lines of best fit (dashed black lines) are
$\beta$ (red circles). The lines of best fit (dashed black lines) are ![]() $\log \bar {h}_f = 0.34 \log \beta + 0.76$,
$\log \bar {h}_f = 0.34 \log \beta + 0.76$, ![]() $\log \bar {V} = 0.67 \log \beta + 0.74$,
$\log \bar {V} = 0.67 \log \beta + 0.74$, ![]() $\log x^* = 0.63 \log \beta + 1.70$ (
$\log x^* = 0.63 \log \beta + 1.70$ (![]() $\beta < \beta _c$) and
$\beta < \beta _c$) and ![]() $\log x^* = 0.35 \log \beta + 0.79$ (
$\log x^* = 0.35 \log \beta + 0.79$ (![]() $\beta > \beta _c$). The vertical dotted blue line in (c) denotes
$\beta > \beta _c$). The vertical dotted blue line in (c) denotes ![]() $\log \beta = \log \beta _c$. The slopes of the solid black lines indicate the theoretical predictions given by (3.4a,b)–(3.7).
$\log \beta = \log \beta _c$. The slopes of the solid black lines indicate the theoretical predictions given by (3.4a,b)–(3.7).

Figure 6. The working fraction ![]() $W_f$ plotted as a function of varying
$W_f$ plotted as a function of varying ![]() $\log \beta$.
$\log \beta$.
4. Initial transient regime
Before an equilibrium state is reached the current is in a transient state where a net increase in the volume flow of fluid occurs across a cycle due to the mismatch between the amount of fluid injected and extracted. This is because in our model if the thickness of the current at the source becomes zero, extraction is stopped to prevent brine production at the well. To understand how the parameter ![]() $\beta$ effects this transient regime, in figure 7 we show how the volume
$\beta$ effects this transient regime, in figure 7 we show how the volume ![]() $V$ varies with time for five values of
$V$ varies with time for five values of ![]() $\beta$ as the current reaches equilibrium. It can be seen that for larger values of
$\beta$ as the current reaches equilibrium. It can be seen that for larger values of ![]() $\beta$ the number of cycles needed to reach equilibrium decreases. This is due to the greater buoyancy speed which transmits fluid further into the far field and results in less localisation of fluid around the source. In turn, this causes a greater net in-flow across each cycle. As a result, the current can be supplied with the required amount of fluid to reach equilibrium over a smaller number of cycles.
$\beta$ the number of cycles needed to reach equilibrium decreases. This is due to the greater buoyancy speed which transmits fluid further into the far field and results in less localisation of fluid around the source. In turn, this causes a greater net in-flow across each cycle. As a result, the current can be supplied with the required amount of fluid to reach equilibrium over a smaller number of cycles.

Figure 7. Volume of fluid ![]() $V$ plotted as a function of varying time
$V$ plotted as a function of varying time ![]() $t$, for five values of
$t$, for five values of ![]() $\beta$: (a)
$\beta$: (a) ![]() $\beta = 0.001$, (b)
$\beta = 0.001$, (b) ![]() $\beta = 0.01$, (c)
$\beta = 0.01$, (c) ![]() $\beta = 0.25$, (d)
$\beta = 0.25$, (d) ![]() $\beta = 1$ and (e)
$\beta = 1$ and (e) ![]() $\beta = 5$. The working and cushion gas volumes have been denoted in (c).
$\beta = 5$. The working and cushion gas volumes have been denoted in (c).
To see systematically how the number of injection–extraction cycles depends on the dimensionless parameter ![]() $\beta$, in figure 8 we present a
$\beta$, in figure 8 we present a ![]() $\log \unicode{x2013}\log$ plot of the number of injection–extraction cycles
$\log \unicode{x2013}\log$ plot of the number of injection–extraction cycles ![]() $n$ required to achieve equilibrium as a function of varying
$n$ required to achieve equilibrium as a function of varying ![]() $\log \beta$. The number of cycles required to reach equilibrium
$\log \beta$. The number of cycles required to reach equilibrium ![]() $n$ rapidly decays with
$n$ rapidly decays with ![]() $\beta$ due to the greater amount of fluid injected in each cycle. Curiously this plot suggests that the number of cycles decays as a power law in
$\beta$ due to the greater amount of fluid injected in each cycle. Curiously this plot suggests that the number of cycles decays as a power law in ![]() $\beta$,
$\beta$,
Given that each cycle persists for a dimensionless time ![]() $2 {\rm \pi}\beta$, this implies that the time to reach equilibrium scales as
$2 {\rm \pi}\beta$, this implies that the time to reach equilibrium scales as

Figure 8. A ![]() $\log \unicode{x2013}\log$ plot of the number of injection–extraction cycles required to achieve equilibrium
$\log \unicode{x2013}\log$ plot of the number of injection–extraction cycles required to achieve equilibrium ![]() $n$ plotted as a function of varying
$n$ plotted as a function of varying ![]() $\beta$ (red circles). The black dashed line is the line of best fit:
$\beta$ (red circles). The black dashed line is the line of best fit: ![]() $\log n = -0.50 \log \beta + 1.33$.
$\log n = -0.50 \log \beta + 1.33$.
In the case that ![]() $\beta$ is small, there are a significant number of cycles required to reach equilibrium. Given the clear scaling laws for the total volume injected,
$\beta$ is small, there are a significant number of cycles required to reach equilibrium. Given the clear scaling laws for the total volume injected, ![]() $\beta ^{{2}/{3}}$, and the number of cycles needed to reach equilibrium, (4.1), we now explore whether there is a law for how the net flux over a cycle decays as a function of the cycle number scaled with the total number of cycles required for the system to equilibrate. If we divide the total volume
$\beta ^{{2}/{3}}$, and the number of cycles needed to reach equilibrium, (4.1), we now explore whether there is a law for how the net flux over a cycle decays as a function of the cycle number scaled with the total number of cycles required for the system to equilibrate. If we divide the total volume ![]() $\beta ^{{2}/{3}}$ (3.6) by the power law for the total number of cycles (4.1) we find a scaling for the flux per cycle. We then hypothesise that the net volume injected depends on the time at the end of the
$\beta ^{{2}/{3}}$ (3.6) by the power law for the total number of cycles (4.1) we find a scaling for the flux per cycle. We then hypothesise that the net volume injected depends on the time at the end of the ![]() $i$th cycle,
$i$th cycle, ![]() $t_i = 2{\rm \pi} \beta i$, scaled by the timescale to reach equilibrium,
$t_i = 2{\rm \pi} \beta i$, scaled by the timescale to reach equilibrium, ![]() $\beta ^{1/2}$ according to a dimensionless function
$\beta ^{1/2}$ according to a dimensionless function ![]() $f(t_i / \beta ^{1/2})$, which we assume decays to zero as
$f(t_i / \beta ^{1/2})$, which we assume decays to zero as ![]() $i \rightarrow n$, and where cycle
$i \rightarrow n$, and where cycle ![]() $i$ occurs over the time interval
$i$ occurs over the time interval ![]() $2{\rm \pi} \beta (i-1) < t < 2 {\rm \pi}\beta i$. This suggests that the injected volume on cycle
$2{\rm \pi} \beta (i-1) < t < 2 {\rm \pi}\beta i$. This suggests that the injected volume on cycle ![]() $i$,
$i$, ![]() $V^{{i}}_{{m}}$, as a function of
$V^{{i}}_{{m}}$, as a function of ![]() $\beta$ might follow a scaling law of the form:
$\beta$ might follow a scaling law of the form:
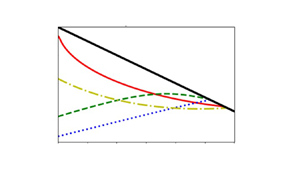
In figure 9, we now compare the relation (4.3) with the numerical data: to this end, we plot curves of the scaled net volume addition ![]() $V^{{i}}_{{m}}/\beta ^{7/6}$ as a function of
$V^{{i}}_{{m}}/\beta ^{7/6}$ as a function of ![]() $t_i/\beta ^{1/2}$. Curves are given for several values of
$t_i/\beta ^{1/2}$. Curves are given for several values of ![]() $\beta$ spanning several orders of magnitude, on both linear and logarithmic axes. The figure suggests that, to leading order, the scaled numerical data do seem follow a similar trend line, although we note that there is some scatter in the data.
$\beta$ spanning several orders of magnitude, on both linear and logarithmic axes. The figure suggests that, to leading order, the scaled numerical data do seem follow a similar trend line, although we note that there is some scatter in the data.

Figure 9. (a) Plot of ![]() $V_m \beta ^{-{7}/{6}}$ as a function of varying
$V_m \beta ^{-{7}/{6}}$ as a function of varying ![]() $t \beta ^{-{1}/{2}}$ for four values of
$t \beta ^{-{1}/{2}}$ for four values of ![]() $\beta$. The corresponding
$\beta$. The corresponding ![]() $\log \unicode{x2013}\log$ plot is presented in (b).
$\log \unicode{x2013}\log$ plot is presented in (b).
5. Conclusion
We have examined the evolution of a hydrogen plume which is periodically injected into and extracted from a porous medium with a sloping impermeable boundary. First, in § 2 we derived a simple model describing the flow in which we found a single dimensionless group ![]() $\beta$, which encodes how the dimensionless ratio of the square of the buoyancy speed to the product of the (two-dimensional) injection rate and injection frequency controls the properties of the flow. In particular, in § 3, we showed that when the system reaches equilibrium, the ratio of the volume of working gas to cushion gas increases with
$\beta$, which encodes how the dimensionless ratio of the square of the buoyancy speed to the product of the (two-dimensional) injection rate and injection frequency controls the properties of the flow. In particular, in § 3, we showed that when the system reaches equilibrium, the ratio of the volume of working gas to cushion gas increases with ![]() $\beta$. Furthermore, if
$\beta$. Furthermore, if ![]() $\beta$ is smaller than a critical value
$\beta$ is smaller than a critical value ![]() $\beta _c$, we demonstrated that a region far from the source develops in which the thickness of the plume remains approximately constant over an injection–extraction cycle. In contrast when
$\beta _c$, we demonstrated that a region far from the source develops in which the thickness of the plume remains approximately constant over an injection–extraction cycle. In contrast when ![]() $\beta > \beta _c$, oscillations of the plume extend across the entire fluid interface. Scalings were developed for the plume volume in both cases and these were verified numerically.
$\beta > \beta _c$, oscillations of the plume extend across the entire fluid interface. Scalings were developed for the plume volume in both cases and these were verified numerically.
In § 4, we examined the behaviour of the current before equilibrium is reached, showing how the volume of cushion gas grows across successive cycles until the system approaches equilibrium. Since the ratio of the cushion gas to working gas decreases with ![]() $\beta$, the number of cycles needed to reach equilibrium also decreases with increasing
$\beta$, the number of cycles needed to reach equilibrium also decreases with increasing ![]() $\beta$.
$\beta$.
The results presented in this paper are highly idealised but provide insight into some controls on the ratio of working gas to cushion gas once the system reaches equilibrium. The key dimensionless parameter ![]() $\beta$ can have a range of values in a practical case, depending on the permeability and slope of the aquifer: with typical values for
$\beta$ can have a range of values in a practical case, depending on the permeability and slope of the aquifer: with typical values for ![]() $\hat {S}$ of the order of
$\hat {S}$ of the order of ![]() $10^{-5}\unicode{x2013}10^{-6}\ {\rm m}\ {\rm s}^{-1}$, angles of slope
$10^{-5}\unicode{x2013}10^{-6}\ {\rm m}\ {\rm s}^{-1}$, angles of slope ![]() $\tan \theta$ of order
$\tan \theta$ of order ![]() $0.1\unicode{x2013}0.01$, injection rates of order
$0.1\unicode{x2013}0.01$, injection rates of order ![]() $10^{-4}\unicode{x2013}10^{-5}\ {\rm m}^2\ {\rm s}^{-1}$ and injection frequencies of
$10^{-4}\unicode{x2013}10^{-5}\ {\rm m}^2\ {\rm s}^{-1}$ and injection frequencies of ![]() $10^{-6}\unicode{x2013}10^{-7}\ {\rm s}^{-1}$, we expect
$10^{-6}\unicode{x2013}10^{-7}\ {\rm s}^{-1}$, we expect ![]() $\beta$ to have values in the range
$\beta$ to have values in the range ![]() $10^{-4}\unicode{x2013}10^{-1}$, comparable to values presented in our analysis. We are presently developing this picture to explore the effects of capillarity, residual saturation and heterogeneity on the process. The results point to the challenge of recovering stored hydrogen at high rates, corresponding to smaller values of
$10^{-4}\unicode{x2013}10^{-1}$, comparable to values presented in our analysis. We are presently developing this picture to explore the effects of capillarity, residual saturation and heterogeneity on the process. The results point to the challenge of recovering stored hydrogen at high rates, corresponding to smaller values of ![]() $\beta$, since high extraction rates can lead to low values of the working gas and early water production.
$\beta$, since high extraction rates can lead to low values of the working gas and early water production.
There are many outstanding questions raised by the present analysis, and these may form the focus of future work. In particular, it is of interest to know whether the volume of non-recoverable gas required for the system to reach equilibrium could be injected at the start of the process, rather than gradually accumulating over multiple cycles, and how the system would adjust to the periodic regime if this were the case. In addition, it would be interesting to understand how the system would behave when the injection or extraction varies irregularly over time or rate as may occur owing to the intermittency of the generation of renewable power. We also note that in this work we have assumed the hydrogen remains trapped in the formation, but there may be scenarios in which the hydrogen leaks from the formation and, if sufficient, this could affect whether the periodic injection–extraction cycles described herein can develop. Finally, we note that similar processes may influence the seasonal storage of methane in aquifers, although the viscosity and density are somewhat larger.
Declaration of interests
The authors report no conflict of interest.