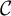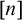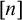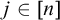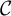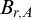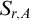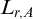EXTENSIONS AND LIMITS OF THE SPECKER–BLATTER THEOREM

Abstract

The original Specker–Blatter theorem (1983) was formulated for classes of structures $\mathcal {C}$ of one or several binary relations definable in Monadic Second Order Logic MSOL. It states that the number of such structures on the set $[n]$ is modularly C-finite (MC-finite). In previous work we extended this to structures definable in CMSOL, MSOL extended with modular counting quantifiers. The first author also showed that the Specker–Blatter theorem does not hold for one quaternary relation (2003).

If the vocabulary allows a constant symbol c, there are n possible interpretations on $[n]$ for c. We say that a constant c is hard-wired if c is always interpreted by the same element $j \in [n]$. In this paper we show:

1. (i) The Specker–Blatter theorem also holds for CMSOL when hard-wired constants are allowed. The proof method of Specker and Blatter does not work in this case.

2. (ii) The Specker–Blatter theorem does not hold already for $\mathcal {C}$ with one ternary relation definable in First Order Logic FOL. This was left open since 1983.

Using hard-wired constants allows us to show MC-finiteness of counting functions of various restricted partition functions which were not known to be MC-finite till now. Among them we have the restricted Bell numbers $B_{r,A}$, restricted Stirling numbers of the second kind $S_{r,A}$ or restricted Lah-numbers $L_{r,A}$. Here r is a non-negative integer and A is an ultimately periodic set of non-negative integers.

1. Introduction

A sequence of natural numbers $s(n)$ is C-finite if it satisfies a linear recurrence relation with constant coefficients. $s(n)$ is MC-finite if it satisfies a linear recurrence relation with constant coefficients modulo m, for each m separately. A C-finite sequence $s(n)$ must have limited growth: $s(n) \leq 2^{cn}$ for some constant c. No such bound exists for MC-finite sequences: for every monotone increasing sequence $s(n)$ the sequence $s'(n)= n! s(n)$ is MC-finite.

A typical example of a C-finite sequence is the sequence $f(n)$ of Fibonacci numbers. A typical example of an MC-finite sequence which is not C-finite is the sequence $B(n)$ of Bell numbers. The Bell number $B(n)$ counts the number of partitions of the set $[n]$ of the numbers $\{1, 2, \ldots , n\}$ . Let $Eq(n)$ be the number of equivalence relations over $[n]$ . Clearly, $B(n)= Eq(n)$ . Let $Eq_2(n)$ be the number of equivalence relations on $[n]$ with exactly two equivalence classes of the same size. $Eq_2(n)$ is not MC-finite since the value of $Eq_2(n)$ is odd iff n is an even power of $2$ , see [3].

In [24] Pfeiffer discusses counting other transitive relations besides $Eq(n)$ , in particular, partial orders $PO(n)$ , quasi-orders (aka preorders) $QO(n)$ and just transitive relations $Tr(n)$ . Using a growth argument one can see that none of these functions is C-finite. It follows directly from the Specker–Blatter theorem stated below, see Corollary 4.2, that $PO(n)$ , $QO(n)$ , and $Tr(n)$ are MC-finite. However, to the best of our knowledge, this has not been stated in the literature. This may be due to the fact that no explicit formulas for these functions are known. The Specker–Blatter theorem establishes MC-finiteness even in the absence of explicit formulas. It derives MC-finiteness solely from the assumption that $\mathcal {C}$ is definable in Monadic Second Order Logic ( $\mathrm {MSOL}$ ), or in $\mathrm {MSOL}$ augmented by modular counting quantifiers ( $\mathrm {CMSOL}$ ).

The present paper grew out of our study of modular recurrence relations for restricted partition functions [12]. We provide a short review of the Specker–Blatter theorem, and show how to extend its applicability by extending the allowed vocabulary to include constants with a fixed interpretation (“hard-wired”). The reduction allowing this extension can be made to work in the other direction. Using it we also close the gap between the Specker–Blatter theorem and its known limits, left open in [13], by constructing an $\mathrm {FOL}$ statement over a single ternary relation for which the theorem does not hold.

Formal definitions about C-finite and MC-finite sequences are given in Section 3, and more examples and details are given in Section 13.

Part I

The Specker–Blatter theorem

2. Background in logic

We generally follow the notation of [9], and assume basic knowledge of model theory as well as the logics $\mathrm {FOL}$ , $\mathrm {MSOL}$ , and $\mathrm {SOL}$ . Our vocabularies will contain no function symbols (but recall that a k-ary function can generally be simulated by a $(k+1)$ -ary relation). Standard texts for Finite Model Theory are [9, 22]. In the following, we always refer to a set $\bar R=\{R_1,\ldots ,R_{\ell _{\bar R}}\}$ of distinct binary relation symbols, a set $\bar a=\{a_1,\ldots ,a_{\ell _{\bar a}}\}$ of distinct constant symbols, and so on. By $a\in \bar a$ we mean that there exists $1\leq i\leq \ell _{\bar a}$ for which $a=a_i$ . We also use the shorthand $[n]=\{1,\ldots ,n\}$ .

Let $\tau = \bar {R} \cup \bar {a}$ be a vocabulary, i.e., a set of non-logical constants. We denote by $\mathrm {FOL}(\tau )$ the set of first order formulas with its non-logical constants in $\tau $ . If $\tau $ is clear from the context, we omit it. We denote by $\mathrm {MSOL}(\tau )$ the set of Monadic Second Order formulas, obtained from $\mathrm {FOL}(\tau )$ by allowing unary relation variables and quantification over them. The logic $\mathrm {CMSOL}$ is obtained from $\mathrm {MSOL}$ by allowing also quantification of the form $\mathrm {C}^{r,m}_x \phi (x)$ , which are interpreted by

$$ \begin{align*}\mathcal{A} \models \mathrm{C}^{r,m}_x \phi(x) \text{ iff } |\{ a \in A : \phi(a) \}| \equiv r\quad \mod{m}. \end{align*} $$

In the following we will be interested in the set of models of a logic sentence $\phi $ over a vocabulary $\tau $ whose universe is $[n]$ for any natural number n. We denote this set by

$$ \begin{align*}\mathcal{C}_{\phi}=\{\mathfrak{M}=([n],A_1,\ldots,A_m):n\in\mathbb{N},A_i\in [n]^{\rho_i},\mathfrak{M}\models\phi\}. \end{align*} $$

3. Definition of C-finite and MC-finite sequences of integers

A sequence of integers $s(n)$ is C-finite ¹ if there are constants $p, q \in \mathbb {N}$ and $c_i \in \mathbb {Z}$ , $0 \leq i \leq p-1$ such that for all $n \geq q$ the linear recurrence relation below holds for $s(n)$ :

$$ \begin{align*}s(n+p) = \sum_{i=0}^{p-1} c_i s(n+i). \end{align*} $$

A sequence of integers $s(n)$ is modular C-finite, abbreviated as MC-finite, if for every $m \in \mathbb {N}$ there are constants $p_m, q_m \in \mathbb {N}^+$ such that for every $n \geq q_m$ there is a linear recurrence relation

$$ \begin{align*}s(n+p_m) \equiv \sum_{i=0}^{p_m-1} c_{i,m} s(n+i) \bmod{m} \end{align*} $$

with constant coefficients $c_{i,m} \in \mathbb {Z}$ .

We denote by $s^m(n)$ the sequence $s(n) \bmod {m}$ . Note that the coefficients $c_{i,m}$ and both $p_m$ and $q_m$ generally do depend on m.

Proposition 3.1. The sequence $s(n)$ is MC-finite iff $s^m(n)$ is ultimately periodic for every m.

Proof MC-finiteness implies ultimate periodicity, since there is a finite number of possible sequences $s(n)\pmod {m},\ldots ,s(n+p_m-1)\, \pmod {m}$ . The converse is from [25].

Clearly, if a sequence $s(n)$ is C-finite then it is also MC-finite with $r_m=r$ and $c_{i,m}=c_i$ for all m. The converse is not true, see Section 13 below.

4. The original Specker–Blatter theorem

Let $\phi _E$ be the formula in First Order Logic ( $\mathrm {FOL}$ ) which says that $E(x,y)$ is an equivalence relation. $Eq(n)$ can be written as

$$ \begin{align*}Eq(n) = |\{ E \subseteq [n]^2 : ([n], E) \models \phi_E \}|. \end{align*} $$

$PO(n)$ , $QO(n)$ , and $Tr(n)$ can be written in a similar way.

The original Specker–Blatter theorem from 1981 [1–3, 26] gives a general criterion for certain integer sequences to be MC-finite. Let $\bar R = \{R_1, \ldots , R_{\ell _{\bar R}} \}$ be a finite set of relation symbols of arities $\rho _1,\ldots ,\rho _{\ell _{\bar R}}$ respectively, and let $\phi $ be a formula of Monadic Second Order Logic ( $\mathrm {MSOL}$ ) using relation symbols from R without free variables.

Let $f_{\phi }(n)$ be the number of ways we can interpret the relation symbols in R on $[n]$ such that the resulting structures where $A_i$ is the interpretation of $R_i$ satisfy $\phi $ . Formally

$$ \begin{align*}f_{\phi}(n)= |\{ A_i \subseteq [n]^{\rho_i}, i \leq m : ([n], A_1. \ldots, A_m) \models \phi \}|. \end{align*} $$

Theorem 4.1 (Specker–Blatter).

Let $\bar {R}$ be a finite set of binary relations and let $\phi $ be a formula of $\mathrm {MSOL}(\bar {R})$ using relation symbols in $\bar {R}$ . Then the sequence $f_{\phi }(n)$ is MC-finite.

Corollary 4.2. The sequences counting the number of partial orders $PO(n)$ , quasi-orders $QO(n$ ), and transitive relations $Tr(n)$ on $[n]$ , are MC-finite.

The idea behind the proof of the Specker–Blatter theorem consists of two parts, both of which use the assertion that $\tau = \bar {R}$ contains only binary relation symbols. Unary symbols can also be incorporated, since these can be simulated with binary symbols in a way that preserves the number of satisfying models.

The first part is combinatorial and applies to any family $\mathcal {C}$ of structures over the vocabulary $\tau $ satisfying a property that we outline below. For such a family, we let $f_{\mathcal {C}}(n)$ be the number of members of $\mathcal {C}$ whose universe is $[n]$ . In particular, $f_{\phi }(n)$ is just a shorthand for $f_{\mathcal {C}_{\phi }}(n)$ .

A pointed $\bar {R}$ -structure is an $\bar {R}$ -structure $\mathfrak {A} =([n], A_1, \ldots , A_{\mu }, a)$ with an additional distinguished point $a \in [n]$ . Given a pointed $\bar {R}$ -structure $\mathfrak {A}_1$ with universe $[n_1]$ and an $\bar {R}$ -structure $\mathfrak {A}_2$ with universe $[n_2]$ we define $\mathfrak {A} =Subst(\mathfrak {A}_1,a,\mathfrak {A}_2)$ as follows:

1. (i) The universe A of $\mathfrak {A}$ is the disjoint union of $A_1$ and $A_2$ with the point a removed. It can be assumed to be the set $[n_1+n_2-1]$ .

2. (ii) The binary relations are defined such that $\mathfrak {A}_2$ is a module in $\mathfrak {A}$ : for $u \in A_1\setminus \{a\}$ and $v \in A_2$ and $R \in \bar {R}$ , the relation $R(u,v)$ holds in $\mathfrak {A} =Subst(\mathfrak {A}_1,a,\mathfrak {A}_2)$ iff $R(u,a)$ holds in $\mathfrak {A}_1$ . For $u,v\in A_1\setminus \{a\}$ (respectively $u,v\in A_2$ ), $R(u,v)$ holds in $\mathfrak {A}$ iff it holds in $\mathfrak {A}_1$ (respectively $\mathfrak {A}_2$ ).

By using an arbitrary enumeration of all possible pointed $\bar {R}$ -structures and all possible (non-pointed) $\bar {R}$ -structures, we construct an $\mathbb {N}\times \mathbb {N}$ matrix $M_{\mathcal {C}}$ over $\{0,1\}$ , by setting for every i and j the value $M_{\mathcal {C}}(i,j)$ to be the indicator as to whether the substitution of the j’th structure in the i’th pointed structure results in a member of $\mathcal {C}$ .

The substitution rank of $\mathcal {C}$ is the rank of the matrix $M_{\mathcal {C}}$ . This is well-defined however only with respect to a specific field $\mathbb F$ . In our case, we are only interested in whether this rank is finite or infinite. Also, in our case $M_{\mathcal {C}}$ always takes values in $\{0,1\}$ , and we are only interested in finite fields (to be more precise, in finite fields and finite commutative rings). Having a finite rank in this case is characterized by having a finite number of distinct rows, ² which we codify in the following definition.

Definition 4.3. A family $\mathcal {C}$ of structures over a set of binary relations $\bar R$ is said to have finite rank if its related matrix $M_{\mathcal {C}}$ has only a finite number of distinct rows (or equivalently, a finite number of distinct columns).

The main combinatorial part of the Specker–Blatter theorem is the following.

Theorem 4.4 (Specker–Blatter, combinatorial version).

Let $\bar {R}$ be a finite set of binary relations and $\mathcal {C}$ be a class of finite $\bar {R}$ -structures whose substitution rank is finite. Then the sequence $f_{\mathcal {C}}(n)$ is MC-finite.

The above applies to an uncountable number of families $\mathcal {C}$ . Theorem 4.1 follows from it by the following proposition, which forms the second part of the original proof:

Proposition 4.5. Let $\bar {R}$ be a finite set of binary relations and $\mathcal {C}$ be a finite class of $\bar {R}$ -structures defined by an $\bar {R}$ -sentences $\phi $ in $\mathrm {MSOL}$ . Then the substitution rank of $\mathcal {C}$ is finite.

The original proof used Ehrenfeucht–Fraïssé games for $\mathrm {MSOL}$ . Alternatively, one could use the Feferman–Vaught theorem for $\mathrm {MSOL}$ . Courcelle [5, 23] proved an analogue of the Feferman–Vaught theorem for $\mathrm {CMSOL}$ . In [14, Section 14] it is shown that Proposition 4.6 still holds if $\mathrm {MSOL}$ is replaced by $\mathrm {CMSOL}$ .

Proposition 4.6. Let $\bar {R}$ be a finite set of binary relations and $\mathcal {C}$ be a class of finite $\bar {R}$ -structures defined by an $\bar {R}$ -sentence $\phi $ in $\mathrm {MSOL}$ . Then the substitution rank of $\mathcal {C}$ is finite.

When considering relations of arity higher than $2$ , the substitution operation is no longer well-defined as it is written here. As it later turned out, this is not merely a technical limitation, but an essential one.

Also, it is not clear how to handle hard-wired constants in the definition of the substitution operation. In this paper, instead of incorporating the hard-wired constants directly into the original mechanism, we show a reduction from the question of the original count to a sum of counts over other sentences that do not involve the constants. This approach turns out to be useful also in the other direction, of proving a new limit on the Specker–Blatter theorem, see Theorem 7.3.

5. Previous limitations and extensions

Limitations and extensions of the Specker–Blatter theorem have been previously discussed in [14, 16].

It is well known that Eulerian graphs and regular graphs of even degree are not definable in $\mathrm {MSOL}$ , but they are definable in $\mathrm {CMSOL}$ . In [16], the Specker–Blatter theorem was shown to hold also for $\mathrm {CMSOL}$ , as per the discussion following the statement of Proposition 4.6. Here is its statement.

Theorem 5.1 (Extended Specker–Blatter).

Let $\bar {R}$ be a finite set of binary relations and $\phi $ be a formula of $\mathrm {CMSOL}(\bar {R})$ using relation symbols in $\bar {R}$ . Then the sequence $f_{\phi }(n)$ is MC-finite.

It follows in particular that $Eul(n)$ , which counts the number of Eulerian graphs over $[n]$ (i.e., connected graphs all of whose degrees are even), is also MC-finite.

In [13] the first author showed that the Specker–Blatter theorem does not hold for quaternary relations:

Theorem 5.2 [13].

There is an $\mathrm {FOL}$ -sentence with only one quaternary relation symbol $\phi $ , such that $f_{\phi }(n)$ is not an MC-sequence.

The question of whether the Specker–Blatter theorem holds in the presence of ternary relation symbols remained open.

6. Relations of bounded degree

Definition 6.1. Let $\mathcal {A}= \langle A, \bar {R} \rangle $ be a $\tau $ -structure, where the arity of the relations is not restricted to be binary. We define a symmetric relation $E_A$ on $\mathcal {A}$ , and call $\langle A , E_A \rangle $ the Gaifman-graph of $\mathcal {A}$ .

1. (i) Let $a, b\in A$ . $(a,b) \in E_A$ iff there exist a relation $R\in \bar {R}$ and some $\bar {a}\in R$ such that both a and b appear in $\bar {a}$ (possibly with other elements of A as well).

2. (ii) For any element $a\in A$ , the degree of a is the number of elements $b\neq a$ for which $(a,b) \in E_A$ .

3. (iii) $\mathcal {A}$ is of bounded degree d if every $a\in A$ has degree at most d.

4. (iv) We say that $\mathcal {A}$ is connected if its Gaifman-graph is connected.

5. (v) For a class of structures $\mathcal {P}$ we say it is of bounded degree d (resp. connected) iff all its structures are of bounded degree d (resp. connected).

The following theorem is from [16]. Its full proof appears in [15].

Theorem 6.2. Let $\phi \in \mathrm {CMSOL}$ for $\bar {R}$ where the arity of the relations is not restricted to be binary, and all the finite models of $\phi $ are of bounded degree d. Then:

1. (i) The sequence $f_{\phi }(n)$ is MC-finite.

2. (ii) Furthermore, if additionally all the models in $\phi $ are connected, then there exists $q \in \mathbb {N}$ such that for all $n \geq q$ the sequence $f_{\phi }(n) \equiv 0 \pmod {m}$ for all m.

Recall that the substitution rank is not well defined for classes of structures with relations of arity three or more. Therefore, Theorem 4.4 cannot be applied to prove Theorem 6.2. Instead one uses an analogue of Theorem 4.4 where substitution is replaced by disjoint union.

Theorem 6.2 shows that the limitation on the arity of the relations, as stated in Theorem 5.2, does not apply if the models of $\phi $ have bounded degree.

7. Main new results

The Bell number $B(n)$ denotes the number of possible partitions of $[n]$ (or alternatively the number of possible equivalence relations over $[n]$ ), and the Stirling number of the second kind $S_k(n)$ denotes the number of possible partitions of $[n]$ into exactly k sets. In particular $B(n)=\sum _{k=1}^{\infty }S_k(n)$ . Both $B(n)$ and $S_k(n)$ (for every fixed k) can be shown to be MC-finite using the Specker–Blatter theorem.

Broder in 1984 [4] introduced the restricted Bell numbers $B_r(n)$ and the restricted Stirling numbers of the second kind $S_{k,r}(n)$ , for any fixed natural number r. Here $B_r(n)$ denotes the number of possible partitions of $[n+r]$ where all members of $[r]$ are in different parts, while correspondingly $S_{k,r}(n)$ denotes the number of possible partitions of $[n+r]$ into exactly k parts where all members of $[r]$ are in different parts (it is in particular non-zero only if $k\leq r$ ). In particular $B_r(n)=\sum _{k=1}^{n+r}S_{k,r}(n)$ . For both of these, the objects to be counted are definable in $\mathrm {FOL}$ with one binary relation and r hard-wired constants, but the Specker–Blatter theorem does not directly apply to these.

In [12] it was shown, in an ad-hoc way, how to circumvent this obstacle in the case of one equivalence relation. It followed that both $S_{k,r}(n)$ and $B_r(n)$ are MC-finite. In this paper we prove a more general theorem, applicable to all situations involving $\mathrm {CMSOL}$ sentences over binary relations and hard-wired constants:

Theorem 7.1 (Elimination of hard-wired constants).

1. (i) Let $\tau $ consist of a finite set of constant symbols $\bar {a}$ , unary relations symbols $\bar {U}$ , and binary relation symbols $\bar {R}$ . For every class $\mathcal {C}$ of $\tau $ -structures there exist classes $\mathcal {C}_1, \ldots , \mathcal {C}_r$ of $\tau '$ -structures, where $\tau '$ -contains only a finite number $r(\bar {a},\bar {U},\bar {R})$ of unary and binary relation symbols, such that

   $$ \begin{align*}f_{\mathcal{C}}(n) = \sum_{i=1}^r f_{\mathcal{C}_i}(n). \end{align*} $$
   Equality here is not modular.

2. (ii) Furthermore, if $\mathcal {C}$ is $\mathrm {FOL}$ -definable ( $\mathrm {MSOL}$ -definable, $\mathrm {CMSOL}$ -definable), so are the $\mathcal {C}_i$ .

The introduction of unary predicates is not a big change, because a unary predicate U can be easily simulated by a binary predicate $R_U$ in the following manner: Given a sentence $\phi $ , use the conjunction $\phi \wedge \forall _{x,y,z}(R_U(x,y)\leftrightarrow R_U(x,z))$ , and then in $\phi $ replace every occurrence “ $U(x)$ ” with “ $\exists _y(R_U(x,y))$ .” This allows to remove U from the vocabulary, replacing it with $R_U$ , while preserving the number of satisfying models.

The above, in conjunction with Theorem 5.1, immediately provides the following corollary.

Corollary 7.2. Let $\tau $ be a vocabulary consisting of a finite set of constant symbols $\bar {a}$ , unary relations symbols $\bar {U}$ and binary relation symbols $\bar {R}$ . For every class $\mathcal {C}$ of finite $\tau $ -structures definable in $\mathrm {CMSOL}(\tau )$ , the sequence $f_{\mathcal {C}}(n)$ is MC-finite.

The proof of Theorem 7.1 is given in Part II Section 8. The rest of Part II is devoted to extending this theorem. Section 9 contains a “many-one” version of Theorem 7.1 that uses so-called nullary (or arity zero) relations instead of a sum. This version is more “streamlined” mathematically at the cost of some conceptual opaqueness. This in turn sets the stage for Section 10, that extends Theorem 7.1 to higher arities and other logics. It is stated there as Theorem 10.1.

We have seen in Theorem 5.2 that the Specker–Blatter theorem does not hold for a single quaternary relation. The question of whether the Specker–Blatter theorem holds in the presence of a single ternary relation symbol remained open. Our second main result here answers this question. The proof is given in Part III

Theorem 7.3 (Ternary Counter-Example).

There exists an $\mathrm {FOL}$ -sentence $\phi $ with only one ternary relation symbol, such that $f_{\phi }(n)$ is not an MC-sequence.

The proof of Theorem 7.3 first produces a sentence $\psi $ which also uses one symbol for a hard-wired constant. This will be shown in Section 11. To construct $\phi $ we need a way to eliminate hard-wired constant symbols. For this we use the abovementioned Theorem 10.1, which converts $\psi $ to a sentence with a single ternary relation and a constant number of lower arity relations. In Section 12 we show how for this particular sentence we can then get rid of the added relations, leaving us with only the ternary relation.

We conclude the paper with Part IV, containing an addendum with more information about C-finite and MC-finite sequences, Section 13, and a summary with open problems in the final Section 14.

Part II

The ephemeral role of hard-coded constants

8. Proving the reduction

In this section we prove Theorem 7.1. For convenience we state it again as Theorem 8.1, and explicitly allow unary relations. While unary relations can be simulated by binary relations, explicitly allowing them streamlines the proof.

Theorem 8.1 (Reducing model counts to the case without constants).

For any class $\mathcal C$ defined by an FOL (resp. MSOL, CMSOL) sentence involving a set of constant symbols $\bar a$ , unary symbols $\bar U$ , and binary symbols $\bar R$ , there exist classes $\mathcal C_1,\ldots ,\mathcal C_r$ (where r depends on the original language), definable by FOL (resp. MSOL, CMSOL) sentences involving $\bar U'$ (which contains $\bar U$ ), $\bar R$ and no constants, satisfying $f_{\mathcal C}(n)=\sum _{i=1}^rf_{\mathcal C_i}(n)$ for all $n\in \mathbb N$ .

Later on, following similar lines, we streamline this theorem to use a single target class (a many-one reduction), and then extend to classes involving higher rank relations. The following is the immediate corollary it produces for the Specker–Blatter theorem, which is a restatement of Corollary 7.2.

Corollary 8.2 (Extended Specker–Blatter theorem).

For a class $\mathcal C$ definable in CMSOL with (hard-wired) constants, unary and binary relation symbols only, the function $f_{\mathcal C}$ is MC-finite.

Theorem 8.1 is proved by induction over the number of constants. The basis, $\ell _{\bar a}=0$ , is trivial (with $\bar U'=\bar U$ , $r=1$ , and $\mathcal C_1=\mathcal C$ ). The induction step is provided by the following.

Lemma 8.3 (Removing a single constant).

For any class $\mathcal C$ defined by an FOL (resp. MSOL, CMSOL) sentence involving a set of constant symbols $\bar a$ with $\ell _{\bar a}>0$ , unary symbols $\bar U$ and binary symbols $\bar R$ , there exist classes $\mathcal C_1,\ldots ,\mathcal C_r$ (where r depends on the original language), definable by FOL (resp. MSOL, CMSOL) sentences over the language $(\bar a',\bar U',\bar R')$ , where $\bar a'=\bar a\setminus \{a_{\ell _{\bar a}}\}$ , $\bar U'=\bar U\cup \bar I\cup \bar O$ where $\ell _{\bar I}=\ell _{\bar O}=\ell _{\bar R}$ , and $\bar R'=\bar R$ , satisfying $f_{\mathcal C}(n)=\sum _{i=1}^rf_{\mathcal C_i}(n)$ for all $n\in \mathbb N$ .

The main idea in the proof of this lemma is to encode the “interaction” of the constant $a_{\ell _{\bar a}}$ with the rest of the universe using the additional unary relations. For every $i\in [\ell _{\bar R}]$ , we will use the new relation $I_i$ to hold every $x\neq a_{\ell _{\bar a}}$ for which $(x,a)$ was in $R_i$ , and the relation $O_i$ to hold every $x\neq a_{\ell _{\bar a}}$ for which $(a,x)$ was in $R_i$ .

We cannot directly keep track whether $(a,a)$ was in $R_i$ , or whether a was in $U_i$ for $i\in [\ell _{\bar U}]$ , so we count the number of models for each of these options separately. This sets $r=2^{\ell _{\bar U}+\ell _{\bar R}}$ . Instead of a running index, we index each such option with a set $\mathfrak U\subseteq [\ell _{\bar U}]$ denoting which of the relations in $\bar U$ include the constant to be removed $a=a_{\ell _{\bar a}}$ , and a set $\mathfrak R\subseteq [\ell _{\bar R}]$ denoting which of the relations in $\bar R$ include $(a,a)$ . Using these we can define the case where a model $\mathfrak N$ over the language $(\bar a',\bar U',\bar R)$ with universe $[n+\ell _{\bar a}-1]$ corresponds (along with $\mathfrak U$ and $\mathfrak R$ ) to an “original model” $\mathfrak M$ with universe $[n+\ell _{\bar a}]$ over the original language.

Definition 8.4. Given a model $\mathfrak M$ over the language $(\bar a,\bar U,\bar R)$ with universe $[n+\ell _{\bar a}]$ , a model $\mathfrak N$ over the language $(\bar a',\bar U',\bar R)$ with universe $[n+\ell _{\bar a}-1]$ , and sets $\mathfrak U\subseteq [\ell _{\bar U}]$ and $\mathfrak R\subseteq [\ell _{\bar R}]$ , where (as always) in both models every constant $a_i$ is interpreted to be $n+i$ , we say that $(\mathfrak N,\mathfrak U,\mathfrak R)$ correspond to $\mathfrak M$ if the following hold.

• • For every $U\in \bar U$ and $x\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models U(x)$ if and only if $\mathfrak M\models U(x)$ .

• • For every $i\in [\ell _{\bar U}]$ , we have $i\in \mathfrak U$ if and only if $\mathfrak M\models U_i(a)$ .

• • For every $R\in \bar R$ and $x,y\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models R(x,y)$ if and only if $\mathfrak M\models R(x,y)$ .

• • For every $i\in [\ell _{\bar R}]$ and $x\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models I_i(x)$ if and only if $\mathfrak M\models R_i(x,a)$ .

• • For every $i\in [\ell _{\bar R}]$ and $x\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models O_i(x)$ if and only if $\mathfrak M\models R_i(a,x)$ .

• • For every $i\in [\ell _{\bar R}]$ , we have $i\in \mathfrak R$ if and only if $\mathfrak M\models R_i(a,a)$ .

It is important to note, for the purpose of counting, the following observation.

Observation 8.5. Definition 8.4 provides a bijection between the set of possible models $\mathfrak M$ over the universe $[n+\ell _{\bar a}]$ (where the constants are interpreted as in Definition 8.4) and the set of possible triples $(\mathfrak N,\mathfrak U,\mathfrak R)$ where $\mathfrak N$ is a model over $[n+\ell _{\bar a}-1]$ (where the constants are interpreted as in Definition 8.4) and $\mathfrak U\subseteq [\ell _{\bar U}]$ and $\mathfrak R\subseteq [\ell _{\bar R}]$ .

Suppose we are given an expression $\phi (\bar x)$ where $\bar x=\{x_1,\ldots ,x_{\ell _{\bar x}}\}$ is a set of variable symbols over the language $(\bar a,\bar U,\bar R)$ , as well as a set $\mathfrak U\subseteq [\ell _{\bar U}]$ and a set $\mathfrak R\subseteq [\ell _{\bar R}]$ . We will construct, by induction over the structure of $\phi $ , several expressions, where one of them will be an expression $\phi ^{\prime }_{\mathfrak U,\mathfrak R}(\bar x)$ over the language $(\bar a',\bar U',\bar R)$ . It will be constructed so that for any $\mathfrak M$ over the language $(\bar a,\bar U,\bar R)$ with universe $[n+\ell _{\bar a}]$ and $\mathfrak N$ over the language $(\bar a',\bar U',\bar R)$ with universe $[n+\ell _{\bar a}-1]$ , where $(\mathfrak N,\mathfrak U,\mathfrak R)$ correspond to $\mathfrak M$ , and any fixing of $x_1,\ldots ,x_{\ell _{\bar x}}\in [n+\ell _{\bar a}-1]$ , we will have $\mathfrak M\models \phi (\bar x)$ if and only if $\mathfrak N\models \phi ^{\prime }_{\mathfrak U,\mathfrak R}(\bar x)$ .

Lemma 8.3 then immediately follows from the case $\ell _{\bar x}=0$ (i.e., where $\phi $ is a sentence). To be precise, for a class $\mathcal C$ defined by a sentence $\phi $ over the language $(\bar a,\bar U,\bar R)$ , we obtain $f_{\mathcal C}(n)=\sum _{\mathfrak U\subseteq [\ell _{\bar U}],\mathfrak R\subseteq [\ell _{\bar R}]}f_{\mathcal C_{\mathfrak U,\mathfrak R}}(n)$ , where $\mathcal C_{\mathfrak U,\mathfrak R}$ is the class respectively defined by $\phi ^{\prime }_{\mathfrak U,\mathfrak R}(\bar x)$ over the language $(\bar a',\bar U',\bar R)$ .

To sustain the induction, the above will not be enough. This is because we need to account under the model $\mathfrak N$ also for the case where some variables are “assigned the value $a=a_{\ell _{\bar a}}$ ,” a value which does not exist in its universe (it exists only in that of $\mathfrak M$ ). We henceforth consider also a set $\mathfrak X\subseteq [\ell _{\bar x}]$ , and denote the set of variable symbols $x_{\mathfrak X}=\{x_i:i\in \mathfrak X\}$ . In our induction we will construct the expressions ${\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})}$ , where $\phi ^{\prime }_{\mathfrak U,\mathfrak R}(\bar x)$ is just the special case $\phi ^{\prime }_{\emptyset ,\mathfrak U,\mathfrak R}(\bar x)$ . With models $\mathfrak M$ and $\mathfrak N$ as above and a fixing of the variables in $\bar x\setminus x_{\mathfrak X}$ , denote by $\bar x_{\mathfrak X\to a}$ the completion of this fixing to all of $\bar x$ that is obtained by fixing $x_i$ to be equal to a for all $i\in \mathfrak X$ . We will then have $\mathfrak M\models \phi (\bar x_{\mathfrak X\to a})$ if and only if $\mathfrak N\models \phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ .

The rest of this section is concerned with the recursive definition of ${\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})}$ . There is a subsection for the base cases, a subsection for Boolean connectives, and a subsection for each class of quantifiers (first order quantifiers, counting quantifiers, and monadic second order quantifiers). In every construction we argue (at times trivially) that we keep the correspondence invariant, namely that $\mathfrak M\models \phi (\bar x_{\mathfrak X\to a})$ if and only if $\mathfrak N\models \phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ whenever $\mathfrak M$ and $(\mathfrak N,\mathfrak U,\mathfrak R)$ satisfy the correspondence condition of Definition 8.4.

8.1. The base constructions

We use the Boolean “true” and “false” statements in the following, so for formality’s sake they are also considered as atomic statements here. Clearly, if $\phi (\bar x)$ is simply the “true” statement $\top $ (respectively the “false” statement $\bot $ ), then setting $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ to $\top $ (respectively $\bot $ ) gives us the equivalent statement satisfying the correspondence invariant.

For $i\in [\ell _{\bar U}]$ and $j\in [\ell _{\bar x}]$ , let us now consider the expression $\phi (\bar x)=U_i(x_j)$ . To produce $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ , we partition to cases according to whether $j\in \mathfrak X$ . In the case where $j\notin \mathfrak X$ , we simply set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=U_i(x_j)$ as well, which clearly satisfies the invariant for any triple $(\mathfrak N,\mathfrak U,\mathfrak R)$ that is correlated with $\mathfrak M$ (recall that the “if and only if” condition in this case should hold when the value of $x_i$ is in $[n+\ell _{\bar a}-1]$ ).

Similarly, for $i\in [\ell _{\bar U}]$ and $j\in [\ell _{\bar a}-1]$ , for the expression $\phi (\bar x)=U_i(a_j)$ , we produce $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=U_i(a_j)$ , noting that in our setting the value of $a_j$ is guaranteed to be equal to $n+j\in [n+\ell _{\bar a}-1]$ .

Now consider the expression $\phi (\bar x)=U_i(x_j)$ for the case where $j\in \mathfrak X$ . Recall that in this case $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ should not depend on $x_j$ . Moreover, to preserve the invariant for corresponding sets and models, $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ should hold if and only if $U_j(a)$ holds (recall that we use the shorthand $a=a_{\ell _{\bar a}}$ throughout). We hence define $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ to be $\top $ (“true”) if $i\in \mathfrak U$ , and define it to be $\bot $ (“false”) if $i\notin \mathfrak U$ .

The remaining case for a unary relation is the expression $\phi (\bar x)=U_i(a)$ . Again, we define $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ to be $\top $ if $i\in \mathfrak U$ , and define it to be $\bot $ if $i\notin \mathfrak U$ .

We now move on to handle the atomic expressions involving a binary relation $R_i$ where $i\in [\ell _{\bar R}]$ . The first case here is the one analogous to the first case we discussed involving a unary relation. Namely, it is the case where $\phi (\bar x)=R_i(x_j,x_k)$ where both $j\notin \mathfrak X$ and $k\notin \mathfrak X$ . In this case we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=R_i(x_j,x_k)$ , and argue the same argument as above about satisfying the correspondence invariant.

Dealing with constants outside a is similar. For $j\notin \mathfrak X$ , $k\in [\ell _{\bar a}-1]$ where $\phi (\bar x)=R_i(x_j,a_k)$ we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=R_i(x_j,a_k)$ , for $j\in [\ell _{\bar a}-1]$ , $k\notin \mathfrak X$ where $\phi (\bar x)=R_i(a_j,x_k)$ we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=R_i(a_j,x_k)$ , and finally for $j,k\in [\ell _{\bar a}-1]$ where $\phi (\bar x)=R_i(a_j,a_k)$ we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=R_i(a_j,a_k)$ .

The next four cases we discuss resemble the last two cases we discussed about a unary relation. Namely, these are the cases where $\phi (\bar x)=R_i(x_j,x_k)$ with $j,k\in \mathfrak X$ , $\phi (\bar x)=R_i(x_j,a)$ or $\phi (\bar x)=R_i(a,x_j)$ with $j\in \mathfrak X$ , and $\phi (\bar x)=R_i(a,a)$ . In all these cases the resulting expression should reflect on whether $\mathfrak M\models R_i(a,a)$ , which for the corresponding $(\mathfrak N,\mathfrak U,\mathfrak R)$ is handled by the set $\mathfrak R$ . We hence set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\top $ if $i\in \mathfrak R$ , and set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\bot $ if $i\notin \mathfrak R$ .

Next we handle the cases where $\phi (\bar x)=R_i(x_j,x_k)$ with $j\notin \mathfrak X$ and $k\in \mathfrak X$ , and $\phi (\bar x)=R_i(x_j,a)$ with $j\notin \mathfrak X$ . For both these cases, for the correspondence invariant to follow we need to look at whether $\mathfrak M\models R_i(x_j,a)$ , where the value of $x_j$ is in $[n+\ell _{\bar a}-1]$ . For the corresponding $(\mathfrak N,\mathfrak U,\mathfrak R)$ this occurs if and only if $\mathfrak N\models I_i(x_j)$ , where we recall that $I_i$ is a relation from $\bar U'\setminus \bar U$ . We therefor set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=I_i(x_j)$ in these cases. Similarly, for the cases $\phi (\bar x)=R_i(a_j,x_k)$ and $\phi (\bar x)=R_i(a_j,a)$ , where $j\in [\ell _{\bar a}-1]$ and $k\in \mathfrak X$ , we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=I_i(a_j)$ .

Moving on to the remaining cases for a binary relation, we consider $\phi (\bar x)=R_i(x_k,x_j)$ with $j\notin \mathfrak X$ and $k\in \mathfrak X$ , and $\phi (\bar x)=R_i(a,x_j)$ with $j\notin \mathfrak X$ . These are analogous to the cases handled in the last paragraph, only here we use $O_i$ instead of $I_i$ . We set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=O_i(x_j)$ in these two cases. Finally, for the cases $\phi (\bar x)=R_i(x_k,a_j)$ and $\phi (\bar x)=R_i(a,a_j)$ , where $j\in [\ell _{\bar a}-1]$ and $k\in \mathfrak X$ , we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=O_i(a_j)$ .

The final atomic formula to consider is the “builtin relation” of equality. We skip all cases involving only constants (e.g., $a_i=a_j$ ), since these are equivalent to $\top $ or $\bot $ . We also skip cases that are equivalent by the symmetry of the equality relation to those that we discuss.

First, if $\phi (\bar x)$ is $x_i=x_j$ or $x_i=a_k$ for $i,j\notin \mathfrak X$ and $k\in [\ell _{\bar a}-1]$ , then since we are dealing with values that are guaranteed to be in $[n+\ell _{\bar a}-1]$ (the universe of $\mathfrak N$ ), we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ respectively to $x_i=x_j$ or $x_i=a_k$ as well (so it is “unaltered” from $\phi (\bar x)$ ).

On the other hand, if $\phi (\bar x)$ is $x_i=x_j$ or $x_i=a$ for $i,j\in \mathfrak X$ , then for the correspondence principle to hold, we need $\mathfrak N\models \phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ to hold if $\mathfrak M\models (a=a)$ . In other words, we have to set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\top $ here.

The final cases are those where $\phi (\bar x)$ is $x_i=x_j$ or $x_i=a$ for $i\notin \mathfrak X$ and $j\in \mathfrak X$ . For the correspondence principle to hold, we need $\mathfrak N\models \phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ to hold if and only if $\mathfrak M\models (x_i=a)$ . However, we make here the subtle yet important observation that this should occur for any value that $x_i$ can take from the universe of $\mathfrak N$ , which does not include a. Therefore, we can (and should) set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\bot $ in these cases.

8.2. Boolean connectives

Handling Boolean connectives is the most straightforward part of this construction. For example, suppose that we have $\phi (\bar x)=\neg \psi (\bar x)$ for some expression $\psi (\bar x)$ , for which we have already established (by the induction hypothesis) that $\mathfrak M\models \psi (\bar x_{\mathfrak X\to a})$ if and only if $\mathfrak N\models \psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ whenever $\mathfrak M$ and $(\mathfrak N,\mathfrak U,\mathfrak R)$ correspond. Here we can clearly set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\neg \psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ , and obtain that $\mathfrak M\models \phi (\bar x_{\mathfrak X\to a})$ if and only if $\mathfrak N\models \phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ whenever $\mathfrak M$ and $(\mathfrak N,\mathfrak U,\mathfrak R)$ correspond.

The same idea and analysis follow for all other Boolean connectives. For example, for the expression $\phi (\bar x)=\psi _1(\bar x)\wedge \psi _2(\bar x)$ , we set $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\psi ^{\prime }_{1,\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})\wedge \psi ^{\prime }_{2,\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ .

8.3. First order quantifiers

To deal with quantifiers over variables, we make some assumptions on the structure of our expressions that can easily be justified by the appropriate variable substitutions. Namely, we require that every quantified variable is quantified only once in the expression, and is not used at all outside the scope of the quantification. In particular, this means that the set $\mathfrak X$ that appears in the subscript of our expression cannot contain a reference to the quantified variable.

For notational convenience, when $\phi (\bar x)$ is our formula, we denote by $x=x_{\ell _{\bar x}+1}$ the quantified variable (which is not a member of $\bar x$ , the unquantified variables of this formula). So the two cases that we consider in this subsection are the existential quantification $\phi (\bar x)=\exists _x\psi (\bar x\cup \{x\})$ and the universal quantification $\phi (\bar x)=\forall _x\psi (\bar x\cup \{x\})$ , and for both of them we would like to construct a corresponding $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ where $\mathfrak X\subseteq [\ell _{\bar x}]$ .

In the existential case, we want $\mathfrak N\models \phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ to occur whenever there is at least one value of x for which $\mathfrak M\models \psi (\bar x\cup \{x\})$ . For the values of x within $[n+\ell _{\bar a}-1]$ , by the induction hypothesis, this is covered by the expression $\exists _x\psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\cup \{x\}\setminus x_{\mathfrak X})$ . However, there is one possible value of x not covered in this way, and that is the value $n+\ell _{\bar a}$ , which we identify with the constant a. But by the induction hypothesis, $\mathfrak M\models \psi (\bar x\cup \{x\})$ for $x=a$ if and only if $\mathfrak N\models \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\},\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ . The combined expression that satisfies the correspondence invariant is hence $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\exists _x\psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\vee \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\},\mathfrak U,\mathfrak R} (\bar x\setminus x_{\mathfrak X})$ .

The universal case follows an analogous argument, only here $\mathfrak M\models \psi (\bar x\cup \{x\})$ needs to hold for all values of x, those in $[n+\ell _{\bar a}-1]$ as well as the value of a. The combined expression is $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\forall _x\psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\wedge \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\},\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ .

8.4. Modular counting quantifiers

We briefly recall the definition of a modular counting quantifier. Given $\phi (\bar x)=\mathrm {C}^{r,m}_x\psi (\bar x\cup \{x\})$ , this expression is said to hold in $\mathfrak M$ for a specific assignment to the variable of $\bar x$ , if the size of the set $\{x:\mathfrak M\models \psi (\bar x\cup \{x\})\}$ is congruent to r modulo m. As with the previous subsection, we assume that the quantified variable is not used outside the quantification scope, and that no variable is quantified more than once. We again denote for notational convenience the quantified variable by $x=x_{\ell _{\bar x}+1}$ , and note that $\mathfrak X\subseteq [\ell _{\bar x}]$ cannot include a reference to x.

When working with $(\mathfrak N,\mathfrak U,\mathfrak R)$ that corresponds to $\mathfrak M$ , to obtain the original modular count, we have to count the set (satisfying the induction hypothesis) $\{x:\mathfrak N\models \psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\}$ , as well as check whether $\mathfrak N\models \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\},\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ (which if true adds $1$ to the count). This gives $(\mathrm {C}^{r-1,m}_x\!\psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\cup \{x\}\!\setminus \! x_{\mathfrak X})\wedge \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\},\mathfrak U,\mathfrak R}(\bar x\setminus \! x_{\mathfrak X}))\vee (\mathrm {C}^{r,m}_x\!\psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\cup \{x\}\!\setminus \! x_{\mathfrak X})\wedge \neg \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\},\mathfrak U,\mathfrak R}(\bar x\setminus \! x_{\mathfrak X}))$ as the combined expression for $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ .

8.5. Monadic second order quantifiers

Here we deal with quantifiers over unary relations. The cases we cover are the existential quantification $\phi (\bar x)=\exists _U\psi (\bar x)$ and the universal quantification $\phi (\bar x)=\forall _U\psi (\bar x)$ , where U is a new unary relation that does not appear in the language $(\bar a,\bar U,\bar R)$ of $\phi (\bar x)$ , while being part of the language of $\psi (\bar x)$ . As before, we assume that the quantified relation symbol U appears only in the scope of this quantification, and is not quantified anywhere else, and again denote for convenience $U=U_{\ell _{\bar U}+1}$ . In particular, when analyzing expressions of the type $\psi ^{\prime }_{\mathfrak X,\mathfrak U',\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ , we may allow $\mathfrak U'$ to contain $[\ell _{\bar U}+1]$ (the same is not allowed for the expression $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ , whose language does not contain U).

Consider now the family of possible models $\mathfrak M'$ that extend $\mathfrak M$ with an interpretation of the relation U. Now consider $(\mathfrak N',\mathfrak U',\mathfrak R')$ which correspond to $\mathfrak M'$ , in relation to $(\mathfrak N,\mathfrak U,\mathfrak R)$ which correspond to $\mathfrak M$ . Referring to Definition 8.4, every relation already appearing in $\bar U$ will have the same interpretation in $\mathfrak N$ and $\mathfrak N'$ . Also, $\mathfrak R'=\mathfrak R$ , since the binary relations are the same in the languages of both models. Additionally, from the definition, the interpretation of $U=U_{\ell _{\bar U}+1}$ in $\mathfrak N'$ is the restriction of its interpretation in $\mathfrak M'$ to $[n+\ell _{\bar a}-1]$ . As for the final ingredient $\mathfrak U'$ , for every $i\in [\ell _{\bar U}]$ , the condition on whether it is in $\mathfrak U$ or in $\mathfrak U'$ is the same. However, $\mathfrak U'$ may also include $\ell _{\bar U}+1$ according to whether $\mathfrak M'\models U(a)$ . So considering all possible models $\mathfrak M'$ , we have two possibilities. Either $\mathfrak U'=\mathfrak U$ , or $\mathfrak U'=\mathfrak U\cup \{\ell _{\bar U}+1\}$ .

We can now construct our expression that corresponds to all models extending $\mathfrak M$ . For the existential case we have $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\exists _U\psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})\vee \exists _U\psi ^{\prime }_{\mathfrak X,\mathfrak U\cup \{\ell _{\bar U}+1\},\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ , and for the universal one we have $\phi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})=\forall _U\psi ^{\prime }_{\mathfrak X,\mathfrak U,\mathfrak R}(\bar x\setminus x_{\mathfrak X})\wedge \forall _U\psi ^{\prime }_{\mathfrak X,\mathfrak U\cup \{\ell _{\bar U}+1\},\mathfrak R}(\bar x\setminus x_{\mathfrak X})$ .

9. Nullary relations and a many-one version of the reduction

Nullary relations are relations of arity zero. Formally, for a nullary relation Z, the corresponding atomic formula is $Z()$ , and a model $\mathfrak M$ over a language that includes Z interprets this formula as either true or false, that is, either $\mathfrak M\models Z()$ or $\mathfrak M\models \neg Z()$ .

Note that nullary relations can be simulated using higher arity relations. To replace a nullary relation Z in the language with a unary relation U (while preserving the model count), the logical expression under discussion should be conjuncted with “ $\forall _x\forall _y(U(x)\leftrightarrow U(y))$ ,” and then every instance of “ $Z()$ ” in the formula should be replaced with “ $\exists _xU(x)$ .”

For convenience, in the following we use explicit nullary relations in our formalism. We prove in this section a “many-one” reduction of counting with hard-wired constants to counting without them, that is, a reduction of the counting function to another counting function based on a single class, rather than a reduction to the sum of several such functions.

Theorem 9.1 (Many-one reduction to the case without constants).

For any class $\mathcal C$ defined by an FOL (resp. MSOL, CMSOL) sentence involving a set of constant symbols $\bar a$ , nullary symbols $\bar Z$ , unary symbols $\bar U$ , and binary symbols $\bar R$ , there exists a class $\mathcal C'$ definable by an FOL (resp. MSOL, CMSOL) sentence involving $\bar Z'$ , $\bar U'$ (which contain $\bar Z$ and $\bar U$ respectively), $\bar R$ and no constants, satisfying $f_{\mathcal C}(n)=f_{\mathcal C'}(n)$ for all $n\in \mathbb N$ .

Also here, the theorem follows from a single constant removal lemma, which is used for an inductive argument over $\ell _{\bar a}$ .

Lemma 9.2 (Removing a single constant in a many-one manner).

For any class $\mathcal C$ defined by an FOL (resp. MSOL, CMSOL) sentence involving a set of constant symbols $\bar a$ with $\ell _{\bar a}>0$ , nullary symbols $\bar Z$ , unary symbols $\bar U$ , and binary symbols $\bar R$ , there exists a class $\mathcal C'$ , definable by an FOL (resp. MSOL, CMSOL) sentence over the language $(\bar a',\bar Z',\bar U',\bar R')$ , where $\bar a'=\bar a\setminus \{a_{\ell _{\bar a}}\}$ , $\bar Z'=\bar Z\cup \bar S\cup \bar D$ where $\ell _{\bar S}=\ell _{\bar U}$ and $\ell _{\bar D}=\ell _{\bar R}$ , $\bar U'=\bar U\cup \bar I\cup \bar O$ where $\ell _{\bar I}=\ell _{\bar O}=\ell _{\bar R}$ , and $\bar R'=\bar R$ , satisfying $f_{\mathcal C}(n)=f_{\mathcal C'}(n)$ for all $n\in \mathbb N$ .

The main new idea in the proof of this version is to use new nullary relations to hold the information as to whether $R(a,a)$ holds for a binary relation R, or whether $U(a)$ holds for a unary relation U, while in the original version we constructed different expressions for each of these options. So, given $\phi (\bar x)$ , our inductive construction will produce the expression $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ for every possible $\mathfrak X\subseteq [\ell _{\bar x}]$ , without referring to the sets $\mathfrak U$ and $\mathfrak R$ that appeared in the proof of Lemma 8.3 and held the information about which relations contain a or $(a,a)$ .

The definition of correspondence is adapted to use the new nullary relations in the language, instead of referring to prescribed sets, in the following way.

Definition 9.3. Given a model $\mathfrak M$ over the language $(\bar a,\bar Z,\bar U,\bar R)$ with universe $[n+\ell _{\bar a}]$ , and a model $\mathfrak N$ over the language $(\bar a',\bar Z',\bar U',\bar R)$ with universe $[n+\ell _{\bar a}-1]$ , where in both models every constant $a_i$ is interpreted to be $n+i$ , we say that $\mathfrak N$ corresponds to $\mathfrak M$ if the following hold.

• • For every $Z\in \bar Z$ , we have $\mathfrak N\models Z()$ if and only if $\mathfrak M\models Z()$ .

• • For every $U\in \bar U$ and $x\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models U(x)$ if and only if $\mathfrak M\models U(x)$ .

• • For every $i\in [\ell _{\bar U}]$ , we have $\mathfrak N\models S_i()$ if and only if $\mathfrak M\models U_i(a)$ .

• • For every $R\in \bar R$ and $x,y\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models R(x,y)$ if and only if $\mathfrak M\models R(x,y)$ .

• • For every $i\in [\ell _{\bar R}]$ and $x\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models I_i(x)$ if and only if $\mathfrak M\models R_i(x,a)$ .

• • For every $i\in [\ell _{\bar R}]$ and $x\in [n+\ell _{\bar a}-1]$ , we have $\mathfrak N\models O_i(x)$ if and only if $\mathfrak M\models R_i(a,x)$ .

• • For every $i\in [\ell _{\bar R}]$ , we have $\mathfrak N\models D_i()$ if and only if $\mathfrak M\models R_i(a,a)$ .

As expected we have the immediate counterpart to Observation 8.5.

Observation 9.4. Definition 9.3 provides a bijection between the set of possible models $\mathfrak M$ over the language $(\bar a,\bar Z,\bar U,\bar R)$ with universe $[n+\ell _{\bar a}]$ , and the set of possible models $\mathfrak N$ over the language $(\bar a',\bar Z',\bar U',\bar R)$ with universe $[n+\ell _{\bar a}-1]$ (where all constants are interpreted as in Definition 9.3).

The rest of this section is concerned with the recursive definition of $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ given $\phi (\bar x)$ , satisfying the following correspondence invariant: If $\mathfrak M$ and $\mathfrak N$ correspond according to Definition 9.3, then for any fixing of the variables $\bar x\setminus x_{\mathfrak X}$ , we have $\mathfrak M\models \phi (\bar x_{\mathfrak X\to a})$ if and only if $\mathfrak N\models \phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ (we refer to Section 8 for the definitions of $\bar x\setminus x_{\mathfrak X}$ and $\bar x_{\mathfrak X\to a}$ ). The main differences between this construction and the one of Section 8 are in the handling of atomic formulas and of monadic second order quantifiers.

9.1. The base constructions

For the Boolean “true” and “false” statements, just as with Section 8.1, if $\phi (\bar x)$ is $\top $ (respectively $\bot $ ), then we also set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ to $\top $ (respectively $\bot $ ).

For the statement $\phi (\bar x)=Z_i()$ where $i\in [\ell _{\bar Z}]$ , relating to a nullary relation that was already present in the language of $\mathfrak M$ , we simply set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=Z_i()$ as well.

For the expression $\phi (\bar x)=U_i(x_j)$ where $i\in [\ell _{\bar U}]$ and $j\in [\ell _{\bar x}]$ , to produce ${\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})}$ , we again partition to cases according to whether $j\in \mathfrak X$ . In the case where $j\notin \mathfrak X$ , we again simply set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=U_i(x_j)$ to satisfy the correspondence invariant (recall that the “if and only if” condition in this case should hold when the value of $x_i$ is in $[n+\ell _{\bar a}-1]$ ).

Similarly, for $i\in [\ell _{\bar U}]$ and $j\in [\ell _{\bar a}-1]$ , for $\phi (\bar x)=U_i(a_j)$ we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=U_i(a_j)$ , noting that in our setting the value of $a_j$ is guaranteed to equal $n+j\in [n+\ell _{\bar a}-1]$ .

Returning to the expression $\phi (\bar x)=U_i(x_j)$ , for the case where $j\in \mathfrak X$ , recall that here $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ should not depend on $x_j$ , but should rather express (for the correspondence invariant to hold) whether $\mathfrak M\models U_i(a)$ . For the corresponding model $\mathfrak N$ this information is kept by the nullary relation $S_i$ . Therefore, for the invariant to hold, we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ to $S_i()$ .

The remaining case for a unary relation is the expression $\phi (\bar x)=U_i(a)$ . Also here we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ to $S_i()$ .

Moving on to the atomic expressions involving a binary relation $R_i$ where ${i\in [\ell _{\bar R}]}$ , the partition to cases is analogous to that of Section 8.1. The first case is where $\phi (\bar x)=R_i(x_j,x_k)$ where both $j\notin \mathfrak X$ and $k\notin \mathfrak X$ , for which as expected we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=R_i(x_j,x_k)$ , using very much the same argument.

Handling constants outside a is similar. For $j\notin \mathfrak X$ , $k\in [\ell _{\bar a}-1]$ where $\phi (\bar x)=R_i(x_j,a_k)$ we again set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=R_i(x_j,a_k)$ , for $j\in [\ell _{\bar a}-1]$ , $k\notin \mathfrak X$ where $\phi (\bar x)=R_i(a_j,x_k)$ we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=R_i(a_j,x_k)$ , and finally for $j,k\in [\ell _{\bar a}-1]$ where $\phi (\bar x)=R_i(a_j,a_k)$ we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=R_i(a_j,a_k)$ .

The next four cases are those that resemble the last two cases that we discussed about a unary relation. Namely, these are the cases where $\phi (\bar x)=R_i(x_j,x_k)$ with $j,k\in \mathfrak X$ , $\phi (\bar x)=R_i(x_j,a)$ or $\phi (\bar x)=R_i(a,x_j)$ with $j\in \mathfrak X$ , and $\phi (\bar x)=R_i(a,a)$ . In all these cases the resulting expression should reflect on whether $\mathfrak M\models R_i(a,a)$ , which for the corresponding $\mathfrak N$ is handled by the nullary relation $D_i$ . We hence set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=D_i()$ .

The remaining cases are handled identically to Section 8.1. For the case $\phi (\bar x)=R_i(x_j,x_k)$ where $j\notin \mathfrak X$ and $k\in \mathfrak X$ , and the case $\phi (\bar x)=R_i(x_j,a)$ where $j\notin \mathfrak X$ , for the correspondence invariant to follow we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=I_i(x_j)$ . For the similar cases $\phi (\bar x)=R_i(a_j,x_k)$ and $\phi (\bar x)=R_i(a_j,a)$ , where $j\in [\ell _{\bar a}-1]$ and $k\in \mathfrak X$ , we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=I_i(a_j)$ . For the case $\phi (\bar x)=R_i(x_k,x_j)$ where $j\notin \mathfrak X$ and $k\in \mathfrak X$ , and the case $\phi (\bar x)=R_i(a,x_j)$ where $j\notin \mathfrak X$ , we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=O_i(x_j)$ . Finally, for the cases $\phi (\bar x)=R_i(x_k,a_j)$ and $\phi (\bar x)=R_i(a,a_j)$ where $j\in [\ell _{\bar a}-1]$ and $k\in \mathfrak X$ , we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=O_i(a_j)$ .

The conversion of atomic expressions using the equality relation is completely identical to that of Section 8.1.

9.2. Boolean connectives

The handling of Boolean connectives is completely identical to that of Section 8.2, including the same straightforward arguments. For example, for the expression $\phi (\bar x)=\psi _1(\bar x)\wedge \psi _2(\bar x)$ we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\psi ^{\prime }_{1,\mathfrak X}(\bar x\setminus x_{\mathfrak X})\wedge \psi ^{\prime }_{2,\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ .

9.3. Quantifiers over variables

The handling of first order quantifiers, as well as modular counting quantifiers, is pretty much the same as that of the respective Section 8.3 and Section 8.4. In particular, we again require that every quantified variable is quantified only once in the expression, and is not used at all outside the scope of the quantification, meaning in particular that the set $\mathfrak X$ cannot contain a reference to the quantified variable.

For notational convenience, when $\phi (\bar x)$ is our formula, we again denote by ${x=x_{\ell _{\bar x}+1}}$ the quantified variable, so for example the existential quantification case is $\phi (\bar x)=\exists _x\psi (\bar x\cup \{x\})$ . For each case we will construct a corresponding $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ where $\mathfrak X\subseteq [\ell _{\bar x}]$ .

In the existential case, we want $\mathfrak N\models \phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ to occur whenever there is at least one value of x for which $\mathfrak M\models \psi (\bar x\cup \{x\})$ . If this occurs for a value of x within $[n+\ell _{\bar a}-1]$ , then by the induction hypothesis this is covered by the expression $\exists _x\psi ^{\prime }_{\mathfrak X}(\bar x\cup \{x\}\setminus x_{\mathfrak X})$ , and if the above occurs in $\mathfrak M$ for $x=a$ , then this is covered by the expression $\psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\}}(\bar x\setminus x_{\mathfrak X})$ . The combined expression that satisfies the correspondence invariant is hence $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\exists _x\psi ^{\prime }_{\mathfrak X}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\vee \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\}}(\bar x\setminus x_{\mathfrak X})$ .

The universal case follows an analogous argument, only here $\mathfrak M\models \psi (\bar x\cup \{x\})$ needs to hold for all values of x, those in $[n+\ell _{\bar a}-1]$ as well as the value a. The combined expression is hence $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\forall _x\psi ^{\prime }_{\mathfrak X}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\wedge \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\}}(\bar x\setminus x_{\mathfrak X})$ .

We now handle the modular counting quantifier case $\phi (\bar x)=\mathrm {C}^{r,m}_x\psi (\bar x\cup \{x\})$ . To obtain the original modular count for $\mathfrak M$ when working with the corresponding $\mathfrak N$ , we have to count the set (satisfying the induction hypothesis) $\{x:\mathfrak N\models \psi ^{\prime }_{\mathfrak X}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\}$ , as well as check whether $\mathfrak N\models \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\}}(\bar x\setminus x_{\mathfrak X})$ . For the complete combined expression for $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ we obtain $(\mathrm {C}^{r-1,m}_x\psi ^{\prime }_{\mathfrak X}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\wedge \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\}}(\bar x\setminus x_{\mathfrak X}))\vee (\mathrm {C}^{r,m}_x\psi ^{\prime }_{\mathfrak X}(\bar x\cup \{x\}\setminus x_{\mathfrak X})\wedge \neg \psi ^{\prime }_{\mathfrak X\cup \{\ell _{\bar x}+1\}}(\bar x\setminus x_{\mathfrak X}))$ .

9.4. Monadic second order quantifiers

We now deal with the cases of existential quantification $\phi (\bar x)=\exists _U\psi (\bar x)$ and universal quantification $\phi (\bar x)=\forall _U\psi (\bar x)$ , where U is a new unary relation that does not appear in the language $(\bar a,\bar Z,\bar U,\bar R)$ of $\phi (\bar x)$ , while being part of the language of $\psi (\bar x)$ . As before, we assume that the quantified relation symbol U appears only in the scope of this quantification, and is not quantified anywhere else, and denote for convenience $U=U_{\ell _{\bar U}+1}$ .

When preparing to analyze expressions of the type $\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ , as per the induction hypothesis for the construction of $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ , we note that just as $U_1,\ldots ,U_{\ell _{\bar U}}$ have their counterpart nullary relations $S_1,\ldots ,S_{\ell _{\bar U}}$ , we also need a new counterpart $S=S_{\ell _{\bar U}+1}$ to $U=U_{\ell _{\bar U}+1}$ . When analyzing a model $\mathfrak M'$ for $\psi (\bar x)$ , which (unlike $\mathfrak M$ ) interprets U as well, we note that the corresponding $\mathfrak N'$ must interpret both U and S, where in particular $\mathfrak N'\models S()$ if and only if $\mathfrak M'\models U(a)$ . When constructing $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ , we will need to quantify both U and S. Quantifying over S as well as U makes sure that our quantification encompasses, for the tests against the original $\psi (\bar x)$ , both U for which $U(a)$ holds and U for which $U(a)$ does not hold. Since nullary relations can be simulated by unary relations, utilizing the notion of quantification over nullary relations does not move us outside the realm of monadic second order logic.

Having discussed the role of the new relation, constructing the expressions that relate to all models corresponding to those extending $\mathfrak M$ is now simple. For the existential case we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\exists _U\exists _S\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ , and for the universal case we set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\forall _U\forall _S\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ .

10. Higher arity relations

We prove in this section an extension of Theorem 9.1 to higher arity relations, and to other logics. The less common GSOL (Guarded Second Order Logic) that appears in this statement is explained in Section 10.2.

Theorem 10.1 (Many-one reduction allowing higher arity).

For any class $\mathcal C$ defined by an FOL (resp. MSOL, CMSOL, GSOL, SOL) sentence involving a set of constant symbols $\bar a$ , and relation symbols $\bar R$ of arbitrary arities, there exists a class $\mathcal C'$ definable by an FOL (resp. MSOL, CMSOL, GSOL, SOL) sentence involving $\bar R'$ , which contains $\bar R$ , has the same maximum arity as $\bar R$ , and has no new relations of maximum arity, satisfying $f_{\mathcal C}(n)=f_{\mathcal C'}(n)$ for all $n\in \mathbb N$ .

Also here, this follows by induction of the following lemma, extending Lemma 9.2.

Lemma 10.2 (Removing a single constant with higher arities).

For any class $\mathcal C$ defined by an FOL (resp. MSOL, CMSOL, GSOL, SOL) sentence involving a set of constant symbols $\bar a$ , and relation symbols $\bar R$ of arbitrary arities, there exists a class $\mathcal C'$ , definable by an FOL (resp. MSOL, CMSOL, GSOL, SOL) sentence over the language $(\bar a',\bar R')$ , where $\bar a'=\bar a\setminus \{a_{\ell _{\bar a}}\}$ , $\bar R'$ contains $\bar R$ , has the same maximum arity as $\bar R$ , and has no new relations of maximum arity, satisfying $f_{\mathcal C}(n)=f_{\mathcal C'}(n)$ for all $n\in \mathbb N$ .

The construction is very similar to that of Section 9, and we only highlight here the differences, which are mainly in the definition of the corresponding models and the transformation of atomic relational formulas.

We first set up the language: We assume that $\bar R=\{R_1,\ldots ,R_{\ell _{\bar R}}\}$ are relation symbols whose arities are $\bar \rho =\{\rho _1,\ldots ,\rho _{\ell _{\bar R}}\}$ respectively. To construct $\bar R'$ , first every relation $R_i\in \bar R$ is replaced with $2^{\rho _i}$ relation symbols $\bar R_i=\langle R_{i,A}:A\subseteq [\rho _i]\rangle $ , where each relation $R_{i,A}$ is of arity $\rho _i-|A|$ . Note that in particular $R_{i,\emptyset }$ is identified with the original $R_i$ , and that $R_{i,[\rho _i]}$ is a nullary relation. Finally, $\bar R'$ is the union of these sets, $\bar R'=\bigcup _{i=1}^{\ell _{\bar R}}\bar R_i$ .

For some intuition of why this language is a straightforward extension of the one defined in conjunction with Definition 9.3 in Section 9, consider the case of a binary relation $R_i$ . In this case, $R_{i,\{1\}}$ is the same as $O_i$ in Section 9, $R_{i,\{2\}}$ is the same as $I_i$ there, and $R_{i,\{1,2\}}$ is the same as $D_i$ there. The following is a generalization of Definition 9.3.

Definition 10.3. Given a model $\mathfrak M$ over the language $(\bar a,\bar R)$ with universe ${[n+\ell _{\bar a}]}$ , and a model $\mathfrak N$ over the language $(\bar a',\bar R')$ with universe $[n+\ell _{\bar a}-1]$ , where in both models every constant $a_i$ is interpreted to be $n+i$ , we say that $\mathfrak N$ corresponds to $\mathfrak M$ if the following holds.

• • For every $R_i\in \bar R$ and every $\bar x=x_1,\ldots ,x_{\rho _i}\in [n+\ell _{\bar a}]$ , denoting by A the set of indexes of the variables for which $x=a=a_{\ell _{\bar a}}$ , that is $A=\{i:x_i=a\}$ , we have $\mathfrak M\models R(x_1,\ldots ,x_{\rho _i})$ if and only if $\mathfrak N\models R_{i,A}(\bar x\setminus x_A)$ , where as before we let $\bar x\setminus x_A$ denote the subsequence of variables whose indexes are not in A.

The exact analog to Observation 9.4 also holds, and we define the same correspondence invariant with respect to logic expressions. The rest of this section is concerned with the recursive definition of $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ given $\phi (\bar x)$ and $\mathfrak X\subseteq [\ell _{\bar x}]$ , satisfying the correspondence invariant.

10.1. FOL expressions and counting quantifiers

The only difference between this section and Sections 9.1–9.3 is in the construction of $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ where $\phi (\bar x)=R_i(y_1,\ldots ,y_{\rho _i})$ , and each $y_j$ is either some variable $x_{i_j}$ or some constant $a_{i_j}$ .

For this construction, we let the set A denote the indexes of all j for which $y_j$ is either some $x_i$ for $i\in \mathfrak X$ , or the constant a (but not any constant $a_{i_j}$ for $i_j<\ell _{\bar a}$ ). We denote by $\bar y\setminus y_A$ the subsequence of $\bar y=y_1,\ldots ,y_{\rho _i}$ after excluding all $y_j$ with $j\in A$ , and define $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=R_{i,A}(\bar y\setminus y_A)$ .

All other base constructions, as well as the recursive constructions for Boolean connective and quantification over variables, are identical to those of Section 9.

10.2. Second order quantifiers

We first look at the case of existential quantification $\phi (\bar x)=\exists _R\psi (\bar x)$ , where R is a new relation that does not appear in the language $(\bar a,\bar R)$ of $\phi (\bar x)$ , while being part of the language of $\psi (\bar x)$ . Again we assume that R appears only in the scope of this quantification, and is not quantified anywhere else, and denote for convenience $R=R_{\ell _{\bar R}+1}$ . We also denote by $\rho =\rho _{\ell _{\bar R}+1}$ the arity of R.

To construct $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ , just as we expanded each $R_i$ to $2^{\rho _i}$ relations for ${1\leq i\leq \ell _{\bar R}}$ , we expand the quantified relation R to a sequence of $2^{\rho }$ relations $\langle R_A:A\subseteq [\rho ]\rangle $ , where each $R_A$ is of arity $\rho -|A|$ ( $R_A$ is not part of the relations of the language of $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ , but identified with $R_{\ell _{\bar R}+1,A}$ it is part of the language of $\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ that is constructed by induction from $\psi (\bar x)$ ).

The quantification will be over all new relations, that is $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\exists _{\langle R_A:A\subseteq [\rho ]\rangle }\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ . Note that in particular for an MSOL quantification, that is when R is of arity $1$ , we will have a quantification over a unary relation $R_{\emptyset }$ and over a nullary relation $R_{\{1\}}$ , just as with the construction in Subsection 9.4.

For the case of universal quantification $\phi (\bar x)=\forall _R\psi (\bar x)$ we again define $\langle R_A:A\subseteq [\rho ]\rangle $ , and analogously set $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\forall _{\langle R_A:A\subseteq [\rho ]\rangle }\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ .

Finally, we briefly explain how to deal with guarded second order (GSOL) quantifiers. These are quantifiers over a new relation R whose arity is identical to that of an existing relation $R_i$ , where we look only at the possibilities for R that make it a subset of $R_i$ . The existential case is written $\phi (\bar x)=\exists _{R\subseteq R_i}\psi (\bar x)$ , and the universal case is written $\phi (\bar x)=\forall _{R\subseteq R_i}\psi (\bar x)$ .

We construct the relations $\langle R_A:A\subseteq [\rho ]\rangle $ , where the arity $\rho _i-|A|$ of $R_A$ is identical to that of $R_{i,A}$ in the language of $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ . We simply quantify every $R_A$ as a subset of its respective $R_{i,A}$ , so for the existential case we have $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\exists _{\langle R_A\subseteq R_{i,A}:A\subseteq [\rho ]\rangle }\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ , and for the universal case we have $\phi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})=\forall _{\langle R_A\subseteq R_{i,A}:A\subseteq [\rho ]\rangle }\psi ^{\prime }_{\mathfrak X}(\bar x\setminus x_{\mathfrak X})$ .

Part III

Ternary relations

11. An $\mathrm {FOL}$ -definable class $\mathcal {C}$ where $f_{\mathcal {C}}(n)$ is not MC-finite

In this part we negatively settle the question of whether the Specker–Blatter theorem holds for classes whose language contains only one ternary relation.

11.1. Using one hard-wired constant

We first construct a class whose language includes a single ternary relation and a single hard-wired constant. Our counterexample builds on ideas used in [13].

Theorem 11.1 (Ternary relation counterexample with a constant).

There exists an FOL sentence $\phi _{\mathcal M}$ over the language $(a,R)$ , where a is a single (hard-wired) constant and R is a single relation of arity $3$ , so that the corresponding class $\mathcal C$ satisfies $f_{\mathcal C}(n-1)=0$ for any n that is not a power of $2$ , and $f_{\mathcal C}(n-1)\equiv 1\,\pmod {2}$ for $n=2^m$ for every $m\in \mathbb {N}$ . In particular, $f_{\mathcal C}$ is not ultimately periodic modulo $2$ .

The statement uses $f_{\mathcal C}(n-1)$ instead of $f_{\mathcal C}(n)$ , but recalling the definition of $f_{\mathcal C}$ , this refers to the universe $[n-1]\cup \{a\}$ whose size is n. We explain later how to modify this class to produce a counterexample modulo other prime numbers p instead of $2$ .

By Theorem 10.1, we have the following immediate corollary that does away with the constant, at the price of adding some additional smaller arity relations.

Corollary 11.2 (Ternary counterexample without constants).

There exists an FOL sentence $\phi ^{\prime }_{\mathcal M}$ over the language $(\bar R)$ , where $\bar R$ includes one relation of arity $3$ and other relations of lower arities, so that the corresponding class $\mathcal C$ satisfies $f_{\mathcal C}(n)=0$ for every n for which $n+1$ is not a power of $2$ , and $f_{\mathcal C}(n)\equiv 1\pmod {2}$ for $n=2^m-1$ for every $m\in \mathbb {N}$ . In particular, $f_{\mathcal C}$ is not ultimately periodic modulo $2$ .

In Section 12 we show how to further reduce the language so that it includes only one ternary relation and no lower arity relations, to provide Theorem 7.3.

11.2. The first construction

The starting point of the construction is a structure that is defined over a non-constant length sequence (and hence not yet expressible in FOL) of unordered graphs. This definition follows the streamlining by Specker [27] of the original construction from [13].

Definition 11.3 (Iterated matching sequence).

Given a set V of vertices, an iterated matching sequence is a sequence of graphs over V, identified by their edge sets $\bar E=E_1,\ldots ,E_{\ell _{\bar E}}$ , satisfying the following for every $1\leq i\leq \ell _{\bar E}$ .

• • The connected components of $E_i$ are (vertex-disjoint) complete bipartite graphs.

• • The two vertex classes of every complete bipartite graph in $E_i$ as above are two connected components of $\bigcup _{j=1}^{i-1}E_j$ (for $i=1$ this means that $E_1$ is a matching).

• • Every connected component of $\bigcup _{j=1}^{i-1}E_j$ is a vertex class of some bipartite graph of $E_i$ (so in particular $E_1$ is a perfect matching).

An iterated matching sequence $\bar E$ is full if every vertex pair $u,v\in V$ (where $u\neq v$ ) appears in some $E_i$ .

The following properties of iterated matching sequences are easily provable by induction.

Observation 11.4. For an iterated matching $\bar E$ , every $E_i$ corresponds to a perfect matching over the set of connected components of $\bigcup _{j=1}^{i-1}E_j$ . Additionally, every connected component of $\bigcup _{j=1}^iE_j$ is a clique with exactly $2^i$ vertices.

The above implies that there can be a full iterated matching sequence over $[n]$ if and only if n is a power of $2$ , in which case $\ell _{\bar E}=\log _2(n)$ . Denoting the number of possible full iterated matching sequences over $[n]$ by $f_{\mathcal M}(n)$ , note the following lemma.

Lemma 11.5 (see [27]).

For every n which is not a power of $2$ we have $f_{\mathcal M}(n)=0$ , while $f_{\mathcal M}(n)\equiv 1\,\pmod {2}$ for $n=2^m$ for every $m\in \mathbb N$ .

The rest of this section concerns the construction of a sentence $\phi _{\mathcal M}$ over a language with one constant and one ternary relation, so that the corresponding class $\mathcal C$ satisfies $f_{\mathcal C}(n-1)=f_{\mathcal M}(n)$ . In the original construction utilizing a quaternary relation Q, essentially we had $(u,v,x,y)\in Q$ if $(u,v)\in E_i$ and $(x,y)\in E_{i-1}$ for some ${1<i\leq \ell _{\bar E}}$ , or $(u,v)\in E_1$ and $x=y$ . For the construction here, we only have a ternary relation R, and we encode the placement of $(u,v)$ within $\bar E$ by the set $\{w:(u,v,w)\in R\}$ . We will have to utilize the hard-wired constant a to make sure that there is exactly one way to encode every full iterated matching sequence.

11.3. Setting up and referring to an order over the vertex pairs

We simulate the structure of a full iterated matching sequence over $[n]$ (where $n\in [n]$ is identified with the constant a) by assigning “ranks” to pairs of members of $[n]$ , which we consider as vertices, where each pair $(x,y)$ is assigned the set $r_{x,y}=\{z:(x,y,z)\in R\}$ . First we need to make sure that “graphness” is satisfied, which means that $r_{x,y}$ is symmetric and is empty for loops:

$$ \begin{align*}\phi_{\mathrm{graph}}=\forall_{x,y,z}(R(x,y,z)\to(x\neq y\wedge R(y,x,z))).\end{align*} $$

Next we make sure that every two vertex pairs have ranks that are comparable by containment. This means that for every $(x_1,y_1)$ and $(x_2,y_2)$ either $r_{x_1,y_1}\subseteq r_{x_2,y_2}$ or $r_{x_2,y_2}\subseteq r_{x_1,y_1}$ :

$$ \begin{align*}\phi_{\mathrm{comp}}=\forall_{x_1,y_1,x_2,y_2}\neg\exists_{z_1,z_2}(R(x_1,y_1,z_1)\wedge\neg R(x_2,y_2,z_1)\wedge R(x_2,y_2,z_2)\wedge\neg R(x_1,y_1,z_2)).\end{align*} $$

Finally, we want every non-loop vertex pair to have a non-empty rank, and moreover for it to include the constant a. This is crucial, because a will eventually serve as an “anchor” making sure that there is only one way to assign ranks when encoding a full iterated matching sequence using the ternary relation R:

$$ \begin{align*}\phi_{\mathrm{full}}=\forall_{x,y}((x\neq y)\to R(x,y,a)).\end{align*} $$

It is a good time to sum up the full statement that sets up our pair ranks:

$$ \begin{align*}\phi_{\mathrm{rank}}=\phi_{\mathrm{graph}}\wedge\phi_{\mathrm{comp}}\wedge\phi_{\mathrm{full}}.\end{align*} $$

Whenever this statement is satisfied, we can use it to construct expressions that compare ranks. We will use the following expressions, which compare the ranks of $(x_1,y_1)$ and $(x_2,y_2)$ , when we formulate further conditions on R that will eventually force it to conform to a full iterated matching sequence. Note that conveniently, these comparison expression also work against loops (whose “rank,” the empty set, is considered to be the lowest):

$$ \begin{align*} \phi_{=}(x_1,y_1,x_2,y_2) & = \forall_z(R(x_1,y_1,z)\leftrightarrow R(x_2,y_2,z)), \\ \phi_{\leq}(x_1,y_1,x_2,y_2) & = \forall_z(R(x_1,y_1,z)\to R(x_2,y_2,z)), \\ \phi_{<}(x_1,y_1,x_2,y_2) & = \phi_{\leq}(x_1,y_1,x_2,y_2)\wedge\neg\phi_{=}(x_1,y_1,x_2,y_2). \end{align*} $$

11.4. Making the ordered pairs correspond to an iterated matching

In this subsection we consider a ternary relation R that is known to satisfy $\phi _{\mathrm {rank}}$ as defined in Section 11.3, and impose further conditions that will force it to correspond to an iterated matching sequence (which will also be full by virtue of every pair having a rank).

For every rank appearing in R, that is for every set A which is equal to $r_{x,y}$ for some $x,y\in [n]$ , we refer to the set of vertex pairs having this rank as $E_i$ , where i is the number of ranks that appear in R (including the empty set, which is the “rank” of loops) and are strictly contained in A. So in particular $E_0=\{(x,x):x\in [n]\}$ , and $E_1$ for example would be the set of vertex pairs that have the smallest non-empty set as their ranks.

We first impose the restriction that for any i, the graph defined by $\bigcup _{j=1}^iE_j$ is a transitive graph, that is a disjoint union of cliques. By Observation 11.4 this is a necessary condition for $\bar E$ to be an iterated matching sequence (note that allowing also the $0$ -ranked loops does not change the condition). This is the same as saying that for any three vertices $x,y,z$ , it cannot be the case that the rank of $(x,z)$ is larger than the maximum ranks of $(x,y)$ and $(y,z)$ :

$$ \begin{align*}\phi_{\mathrm{trans}}=\forall_{x,y,z}(\phi_{\leq}(x,z,x,y)\vee\phi_{\leq}(x,z,y,z)).\end{align*} $$

Whenever R satisfies the above, it is not hard to add the restriction that $E_i$ consists of disjoint complete bipartite graphs such that each of them connects exactly two components of $\bigcup _{j=1}^{i-1}E_j$ , with all such components being covered. First we state that if some rank A exists, that is, there exists some $(x,y)$ for which $A=r_{x,y}$ , then every vertex z is a part of an edge with such rank:

$$ \begin{align*}\phi_{\mathrm{cover}}=\forall_{x,y}\forall_z\exists_w\phi_{=}(x,y,z,w).\end{align*} $$

Then, using the prior knowledge that all connected components of both $\bigcup _{j=1}^{i-1}E_j$ and $\bigcup _{j=1}^iE_j$ are cliques, to make sure that every connected component of $E_i$ is exactly a bipartite graph encompassing two components of $\bigcup _{j=1}^{i-1}E_j$ , it is enough to state that it contains no triangles, excluding of course “triangles” of the type $(x,x,x)$ :

$$ \begin{align*}\phi_{\mathrm{part}}=\forall_{x,y,z}((x\neq y)\to\neg(\phi_{=}(x,y,y,z)\wedge\phi_{=}(x,y,x,z))).\end{align*} $$

All of the above is sufficient to guarantee that the relation R corresponds to a full iterated matching sequence. However, as things stand now there can be many relations that correspond to the same iterated matching. This occurs because we still have unwanted freedom in choosing the sets that correspond to the possible ranks. To remove this freedom, we will now require that the rank of every pair $(x,y)$ for $x\neq y$ consists of exactly one connected component of the union of all lower ranked pairs. This will be sufficient, because by $\phi _{\mathrm {full}}$ , which in particular states that for every $x\neq y$ the rank of $(x,y)$ contains the constant a, the only option would then be the one connected component that contains a.

Noting that by $\phi _{\mathrm {trans}}$ these components are cliques, it is enough to require that every member of $r_{x,y}$ is connected via a lower rank edge to a, while every vertex that is connected to a member of $r_{x,y}$ via a lower rank edge is also a member of $r_{x,y}$ . We obtain the following statement:

$$ \begin{align*} \phi_{\mathrm{anchor}}=\forall_{x,y,z}(R(x,y,z)\to(\phi_{<}(z,a,x,y)\wedge\forall_w(\phi_{<}(z,w,x,y)\to R(x,y,w)))). \end{align*} $$

The final statement that counts the number of full iterated matching sequences, and hence provides the example proving Theorem 11.1, is the following:

$$ \begin{align*} \phi_{\mathcal M}=\phi_{\mathrm{rank}}\wedge\phi_{\mathrm{trans}}\wedge\phi_{\mathrm{cover}} \wedge\phi_{\mathrm{part}}\wedge\phi_{\mathrm{anchor}}.\end{align*} $$

11.5. Adapting the example to other primes

We show here how to adapt the FOL sentence from Theorem 11.1 to provide a sequence that is not ultimately periodic modulo p for any prime number $p\geq 2$ . The analogous corollary about removing the constant also follows.

Theorem 11.6 (Ternary relation counterexample for $p\geq 2$ ).

For any prime number p, there exists an FOL sentence $\phi _{{\mathcal M}_p}$ over the language $(a,R)$ , where a is a (hard-wired) constant and R is a relation of arity $3$ , so that the corresponding class ${\mathcal C}_p$ satisfies $f_{{\mathcal C}_p}(n-1)=0$ for every n that is not a power of p, and $f_{{\mathcal C}_p}(n-1)\equiv 1\pmod {p}$ for $n=p^m$ for every $m\in \mathbb {N}$ . In particular, $f_{{\mathcal C}_p}$ is not ultimately periodic modulo p.

The construction follows the same lines as the extension from $p=2$ to $p\geq 2$ in previous works. For completeness we give some details on how it works with respect to the version of [27]. The basic idea is to use a “matching” of p-tuples instead of pairs.

Definition 11.7. A p-matching over the vertex set $[n]$ is a spanning graph, each of whose connected components is either a clique with p vertices or a single vertex. A perfect p-matching is a p-matching in which there are no single vertex components (in other words, it is a partition of $[n]$ into sets of size p).

The following is not hard to prove.

Lemma 11.8. There are no perfect p-matchings over $[n]$ unless n is a multiple of p, in which case their number is congruent to $1$ modulo p.

Proof The case where n is not a multiple of p is trivial. Otherwise, consider the number of possible partitions of the set $[p]$ into a sequence of subsets of sizes $i_1,\ldots ,i_r$ , where $\sum _{k=1}^ri_k=p$ . Note that unless $i_1=p$ (and hence $r=1$ ), the number of such partitions is divisible by $\binom {p}{i_1}$ , which is divisible by p (since p is a prime).

Denoting by $f_{M_p}(n)$ the number of perfect p-matchings over $[n]$ , we consider for any p-matching, its restriction to $[p]$ (which corresponds to a partition of $[p]$ —the reason we need to consider the partitions as sequences rather than as unordered families of sets is that we need to consider which sets in the restriction of the p-matching over $[n]\setminus [p]$ they are “attached” to). This implies that $f_{M_p}(n)\equiv f_{M_p}(n-p)\,\pmod {p}$ for every $n>p$ , allowing us to prove by induction that $f_{M_p}(n)\equiv 1\,\pmod {p}$ if p divides n.

The definition of an iterated p-matching sequence is what one would expect.

Definition 11.9 (Iterated p-matching sequence).

Given a set V of vertices, an iterated p-matching sequence is a sequence of graphs over V, identified by their edge sets $\bar E=E_1,\ldots ,E_{\ell _{\bar E}}$ , satisfying the following for every $1\leq i\leq \ell _{\bar E}$ .

• • The connected components of $E_i$ are (vertex-disjoint) complete p-partite graphs.

• • The p vertex classes of every complete p-partite graph in $E_i$ as above are p connected components of $\bigcup _{j=1}^{i-1}E_j$ (for $i=1$ this means that $E_1$ is a p-matching).

• • Every connected component of $\bigcup _{j=1}^{i-1}E_j$ is a vertex class of some p-partite graph of $E_i$ (so in particular $E_1$ is a perfect p-matching).

An iterated matching sequence $\bar E$ is full if every vertex pair $u,v\in V$ (where $u\neq v$ ) appears in some $E_i$ .

Again we have the following properties, analogous to those of iterated matching sequences.

Observation 11.10. For an iterated p-matching $\bar E$ , every $E_i$ corresponds to a perfect p-matching over the set of connected components of $\bigcup _{j=1}^{i-1}E_j$ . Additionally, every connected component of $\bigcup _{j=1}^iE_j$ is a clique with exactly $p^i$ vertices.

The above implies that there can be a full iterated matching sequence over $[n]$ if and only if n is a power of p, in which case $\ell _{\bar E}=\log _p(n)$ . Denoting the number of possible full iterated matching sequences over $[n]$ by $f_{{\mathcal M}_p}(n)$ , note the following lemma.

Lemma 11.11. For every n that is not a power of p we have $f_{\mathcal M}(n)=0$ , while for $n=p^m$ for every $m\in \mathbb N$ we have $f_{{\mathcal M}_p}(n)\equiv 1\,\pmod {p}$ .

Proof The case where n is not a power of p was already discussed above. The case $n=p^m$ is proved by induction over m using Lemma 11.8.

The construction of $\phi _{{\mathcal M}_p}$ is identical to that of $\phi _{\mathcal M}$ in Section 11.3 and Section 11.4, with the only exceptions being the replacements for $\phi _{\mathrm {cover}}$ and $\phi _{\mathrm {part}}$ .

To construct $\phi _{\mathrm {cover}_p}$ , we need to state that for every existing rank, each vertex is a part of a size p clique consisting of edges from this rank:

$$ \begin{align*}\phi_{\mathrm{cover}_p}=\forall_{x,y}\forall_{z_1}\exists_{z_2,\ldots,z_p}\bigwedge_{1\leq i<j\leq p}\phi_{=}(x,y,z_i,z_j).\end{align*} $$

To construct $\phi _{\mathrm {part}_p}$ , we need to state that no $E_i$ may contain a clique with $p+1$ vertices:

$$ \begin{align*} \phi_{\mathrm{part}_p}=\forall_{z_1,\ldots,z_{p+1}} ((z_1\neq z_2)\to\neg(\bigwedge_{1\leq i<j\leq p+1}\phi_{=}(z_1,z_2,z_i,z_j)).\end{align*} $$

The final expression is the following:

$$ \begin{align*} \phi_{{\mathcal M}_p}=\phi_{\mathrm{rank}}\wedge\phi_{\mathrm{trans}}\wedge\phi_{\mathrm{cover}_p} \wedge\phi_{\mathrm{part}_p}\wedge\phi_{\mathrm{anchor}}.\end{align*} $$

12. A class with only one ternary relation which is not MC-finite

Starting with Theorem 11.1, to remove the hard-coded constant (and arrive at Corollary 11.2) we only need to use a single invocation of Lemma 10.2. Since we started out with a single ternary relation R in the language of $\phi _{\mathcal M}$ , this leaves us with a statement $\phi ^{\prime }_{\mathcal M}$ utilizing the eight relations $R_{\emptyset },R_{\{1\}},R_{\{2\}},R_{\{3\}},R_{\{1,2\}},R_{\{2,3\}},R_{\{1,3\}},R_{\{1,2,3\}}$ . In the following we show how to remove all of these relations except the relation $R_{\emptyset }$ from the language, while keeping the model counts, which leaves us with a single ternary relation. We note that the exact same treatment will also work for the modulo p version $\phi ^{\prime }_{{\mathcal M}_p}$ .

For convenience, we let $\phi _{\mathcal M,8}$ denote $\phi ^{\prime }_{\mathcal M}$ , where “ $8$ ” is the number of relations in the language. Each time we will define an expression with a smaller number of relations, and claim that the number of satisfying models is preserved.

All throughout, we assume that $\mathfrak M$ is a model for which $\mathfrak M\models \phi _{\mathcal M}$ over the language $(a,M)$ and the universe $[n]$ (where the constant a is hard-coded to refer to n), and that $\mathfrak N$ is its corresponding model over the language of the expression $\phi _{\mathcal M,i}$ under discussion and the universe $[n-1]$ (which does not include a).

Referring to $\phi _{\mathrm {graph}}$ , which is a component of $\phi _{\mathcal M}$ , our first observation is a very easy one.

Observation 12.1. It is never the case that $\mathfrak N\models R_{\{1,2,3\}}()$ , since by $\mathfrak M\models \phi _{\mathrm {graph}}$ it is never the case that $\mathfrak M\models R(a,a,a)$ . Similarly, it is never the case that $\mathfrak N\models R_{\{1,2\}}(x)$ for any $x\in [n-1]$ (the universe of $\mathfrak N$ ), since it is never the case that $\mathfrak M\models R(a,a,x)$ .

This allows us to get rid of the nullary relation $R_{\{1,2,3\}}$ and the unary relation $R_{\{1,2\}}$ .

Definition 12.2. To construct $\phi _{\mathcal M,6}$ while preserving the model count, we replace all atomic formulas “ $R_{\{1,2,3\}}()$ ” and “ $R_{\{1,2\}}(x)$ ” (for any variable x) in $\phi _{\mathcal M,8}$ with the Boolean “false” statement $\bot $ , and remove the symbols $R_{\{1,2,3\}}$ and $R_{\{1,2\}}$ from the language of $\phi _{\mathcal M,6}$ .

We next deal with the other two unary relations, $R_{\{1,3\}}$ and $R_{\{2,3\}}$ . Here it is very important to note that the universe of $\mathfrak N$ does not include n, so in particular $\mathfrak N\models R_{\{1,3\}}(x)$ if and only if $\mathfrak M\models R(a,x,a)$ , where x is guaranteed to be unequal to a.

Observation 12.3. It is always the case that $\mathfrak N\models R_{\{1,3\}}(x)$ and $\mathfrak N\models R_{\{2,3\}}(x)$ for any x in the universe of $\mathfrak N$ , since by $\mathfrak M\models \phi _{\mathrm {full}}$ it is always the case that $\mathfrak M\models R(a,x,a)$ and $\mathfrak M\models R(x,a,a)$ .

This allows us to get rid of the two remaining unary relations.

Definition 12.4. To construct $\phi _{\mathcal M,4}$ while preserving the model count, we replace all atomic formulas “ $R_{\{1,3\}}(x)$ ” and “ $R_{\{2,3\}}(x)$ ” (for any variable x) in $\phi _{\mathcal M,6}$ with the Boolean “true” statement $\top $ , and remove the symbols $R_{\{1,3\}}$ and $R_{\{2,3\}}$ from the language of $\phi _{\mathcal M,4}$ .

We next consider the binary relation $R_{\{3\}}$ . While the truth value of $R_{\{3\}}(x,y)$ in $\mathfrak N$ depends on the actual values of x and y, it is still fully determined by $\mathfrak N$ satisfying $\phi _{\mathcal M,4}$ , or equivalently, by $\mathfrak M$ satisfying $\phi _{\mathcal M}$ , because it corresponds to the truth value of $R(x,y,a)$ in $\mathfrak M$ .

Observation 12.5. By $\mathfrak M\models \phi _{\mathrm {full}}$ and $\mathfrak M\models \phi _{\mathrm {graph}}$ , it is always the case that $\mathfrak N\models R_{\{3\}}(x,y)$ if and only if $x\neq y$ .

This allows us to remove $R_{\{3\}}$ and replace it with the equivalent expression.

Definition 12.6. To construct $\phi _{\mathcal M,3}$ while preserving the model count, we replace all atomic formulas “ $R_{\{3\}}(x,y)$ ” (for any variables x and y) in $\phi _{\mathcal M,4}$ with the expression “ $(x\neq y)$ ,” and remove the symbol $R_{\{3\}}$ from the language of $\phi _{\mathcal M,3}$ .

We now consider the two remaining binary relations, $R_{\{1\}}$ and $R_{\{2\}}$ . Their interpretation by $\mathfrak N$ can vary among different models satisfying $\phi _{\mathcal M,3}$ . However, we note that $\mathfrak N\models R_{\{1\}}(x,y)$ if and only if $\mathfrak M\models R(a,x,y)$ , and similarly ${\mathfrak N\models R_{\{2\}}(x,y)}$ if and only if $\mathfrak M\models R(x,a,y)$ . This means that $R_{\{1\}}$ and $R_{\{2\}}$ have identical interpretations.

Observation 12.7. By $\mathfrak M\models \phi _{\mathrm {graph}}$ , it is always the case that $\mathfrak N\models R_{\{1\}}(x,y)$ if and only if $\mathfrak N\models R_{\{2\}}(x,y)$ for every x and y.

This means that we can at least get rid of $R_{\{2\}}$ .

Definition 12.8. To construct $\phi _{\mathcal M,2}$ while preserving the model count, we replace all atomic formulas “ $R_{\{2\}}(x,y)$ ” (for any variables x and y) in $\phi _{\mathcal M,3}$ with “ $R_{\{1\}}(x,y)$ ,” and remove the symbol $R_{\{2\}}$ from the language of $\phi _{\mathcal M,2}$ .

For the final step we cannot replace instances of $R_{\{1\}}$ with a fixed expression. However, we can “repurpose” part of $R_{\emptyset }$ to hold the information currently held by $R_{\{1\}}$ , allowing us to create an expression over a language containing only this one ternary relation.

For this we first note (by $\phi _{\mathrm {graph}}$ ) that it is never the case that $\mathfrak M\models R(x,x,y)$ for any $x,y\in [n-1]$ , and hence it is never the case that $\mathfrak N\models R_{\emptyset }(x,x,y)$ whenever $\mathfrak N\models \phi _{\mathcal M,2}$ . For our final transformation, we need to simulate the “old” $R_{\emptyset }$ using only the truth values of $R_{\emptyset }(x,y,z)$ for $x\neq y$ , and then we can replace instances of $R_{\{1\}}$ by the truth values of $R_{\emptyset }(x,y,z)$ for $x=y$ .

This leads us to the following definition.

Definition 12.9. To construct the final $\phi _{\mathcal M,1}$ while preserving the model count, we replace all atomic formulas “ $R_{\emptyset }(x,y,z)$ ” (for any variables $x,y,z$ ) in $\phi _{\mathcal M,2}$ with “ $((x\neq y)\wedge R_{\emptyset }(x,y,z))$ ,” replace all atomic formulas “ $R_{\{1\}}(x,y)$ ” in $\phi _{\mathcal M,2}$ with “ $R_{\emptyset }(x,x,y)$ ,” and remove the symbol $R_{\{1\}}$ from the language of $\phi _{\mathcal M,1}$ .

The expression $\phi _{\mathcal M,1}$ , over the language containing only $R_{\emptyset }$ , yields the following restatement of Theorem 7.3. It is formulated modulo $2$ , although as noted above it can be extended to any prime $p\geq 2$ .

Theorem 12.10 (A sentence with a single relation).

There exists an $\mathrm {FOL}$ -sentence $\phi _{\mathcal M,1}$ over a language consisting of a single relation of arity $3$ , so that for the class $\mathcal {C}$ corresponding to $\phi _{\mathcal M,1}$ , its counting function $f_{\mathcal C}(n)$ is not ultimately periodic modulo $2$ .

Part IV

Epilogue

13. More details about C-finite and MC-finite sequences

Here are some examples for integer sequences that are C-finite, MC-finite, or neither.

Example 13.1.

1. (i) The Fibonacci sequence is C-finite.

2. (ii) If $s(n)$ is C-finite then it has at most simple exponential growth. There is $c \in \mathbb {N}^+$ such that $s(n) \leq 2^{cn}$ for all $n \in \mathbb {N}$ , see, e.g., [10, 19].

3. (iii) The Bell numbers $B(n)$ are not C-finite, but are MC-finite.

4. (iv) Let $f(n)$ be any integer sequence. The sequence $s_1(n)=2\cdot f(n)$ is ultimately periodic modulo $2$ , but not necessarily MC-finite.

5. (v) Let $g(n)$ be any integer sequence which is not almost everywhere zero. The sequence $s_2(n) = n!\cdot g(n)$ is MC-finite but not C-finite due to its growth.

6. (vi) The sequence $s_3(n)=\frac12\binom{2n}{n}$ is not MC-finite. Kummer's Theorem [20] implies that $s_3(n)$ is odd if and only if n is a power of $2$ . Direct proofs for $s_3(n)$ may also be found in [13, 26].

7. (vii) The Catalan numbers $C(n) = \frac {1}{n+1} \binom {2n}{n}$ are not MC-finite, since $C(n)$ is odd iff n is a Mersenne number, i.e., $n = 2^m-1$ for some m, see [21, Chapter 13].

8. (viii) Let p be a prime and $f(n)$ be monotone increasing. The sequence $s(n)=p\cdot f(n)+z(n)$ , where $z(n)$ is defined to equal $1$ if n is a power of p and to equal $0$ for any other n, is monotone increasing but not ultimately periodic modulo p, hence not MC-finite.

There are uncountably many MC-finite sequences, but only countably many C-finite sequences with integer coefficients, see the following Proposition 13.2.

Proposition 13.2.

1. (i) There are countably many C-finite sequences.

2. (ii) There are uncountably many monotone increasing sequences which are MC-finite, and uncountably many which are not MC-finite.

3. (iii) Almost all integer sequences (under a suitable measure) are not MC-finite.

Proof (i) follows from every C-finite sequence being completely determined by the integer r, the coefficients $m_1,\ldots ,m_r$ in its recurrence formula, and its initial values $s(1),\ldots ,s(r)$ . Hence every such sequence is determined by a finite sequence of integers, and there are countably many such sequences. (ii) follows from Example 13.1(v) and (viii). For (iii) see the discussion below.

For analyzing the notion of “almost all integer sequences,” let us first recall the definition of absolutely normal sequence.

Definition 13.3. Given a sequence $r(1),r(2),\ldots $ of members of $\mathbb {Z}_m$ , for every a and n, let us define a distribution $\mu _{a,n}$ over $(\mathbb {Z}_m)^a$ that results from drawing $i\in [n]$ uniformly and then taking the subsequence $r(i),\ldots ,r(i+a-1)$ . The sequence r is called normal if for every a the limit $\lim _{n\to \infty }\mu _{a,n}$ exists and is equal to the uniform distribution over $(\mathbb {Z}_m)^a$ .

A sequence of integers $s(1),s(2),\ldots $ is called absolutely normal if for every m, the sequence defined by $r(n)\equiv s(n)\pmod {m}$ is normal.

The sequence $s^b(n) = s(n) \bmod {b}$ can be viewed as a real number $r_b$ written in base b. A classical theorem from 1922 by E. Borel says that almost all reals are absolutely normal [10]. Also note that absolutely normal sequences cannot be MC-finite, and in fact the opposite is true.

Observation 13.4. If $s(n)$ is absolutely normal, then in particular for every m, a, and i there exist $j>i$ for which $s(j)\equiv 0\,\pmod {m}$ and $s(j+a)\equiv 1\,\pmod {m}$ , meaning that $s(n)$ is not ultimately periodic modulo m (and hence not MC-finite).

Things are less clear if we want to refer to sequences of integers since there is no “uniform over the integers” probability space. However, we can prove that if we use any “reasonable sequence of probabilities” to draw out an integer sequence it will almost always be normal.

Proposition 13.5. Suppose that $\mu _1,\mu _2,\ldots $ is a sequence of probability spaces over $\mathbb {N}$ , so that for every r and m, the probability of $\mu _n$ to draw a number equivalent to r modulo m converges to $1/m$ when n goes to infinity. Then, an integer sequence that results from independently drawing $s(n)$ using $\mu _n$ for every $n\in \mathbb {N}$ will be normal with probability $1$ .

Proof Using the notation of Definition 13.3, for fixed m and a we set $r(n)\equiv s(n)\pmod {m}$ for $n\in \mathbb {N}$ , and consider the distributions $\mu _{a,n}$ over $(\mathbb {Z}_m)^a$ . To conclude, we need to show that for every $\epsilon $ there exists $n_1$ so that the distance of $\mu _{a,n}$ from the uniform distribution is at most $\epsilon $ (in the variation distance ³ ) for every $n>n_1$ . To prove this, let $n_2$ be such that for every $n>n_2$ , the probability of $\mu _n$ to draw a number equivalent to r modulo m is in the range $1/m\pm \epsilon /2am$ . This in particular implies that for $n>n_2$ , the distribution of $(r(n),\ldots ,r(n+a-1))$ from the uniform distribution over $(\mathbb {Z}_m)^a$ is at most $\epsilon /2$ . From this it is not hard to show the existence of $n_1$ using a concentration inequality argument.

14. Conclusions and open problems

In this work we have extended the Specker–Blatter theorem to classes of $\tau $ -structures definable in $\mathrm {CMSOL}$ for vocabularies $\tau $ which contain a finite number of hard-wired constants, unary and binary relation symbols, Corollary 7.2. We have also shown that it does not hold already when $\tau $ consists of only one ternary relation symbol, Theorem 7.3. We note that in [14, 16] we have shown that for $\mathcal {C}$ definable in $\mathrm {CMSOL}$ such that all structures have degree bounded by a constant d, $S_{\mathcal {C}}(n)$ is always MC-finite. The degree of a structure $\mathcal {A}$ is defined via the Gaifman graph of $\mathcal {A}$ . With this the MC-finiteness of $S_{\mathcal {C}}(n)$ for $\mathrm {CMSOL}$ -definable classes of $\tau $ -structures as a function of $\tau $ is thoroughly understood.

Recall that a sequence of integers $s(n)$ is MC-finite if for every $m \in \mathbb {N}$ there are constants $p_m, q_m \in \mathbb {N}^+$ such that for every $n \geq q_m$ there is a linear recurrence relation

$$ \begin{align*}s(n+p_m) \equiv \sum_{i=0}^{p_m-1} c_{i,m} s(n+i) \bmod{m} \end{align*} $$

with constant coefficients $c_{i,m} \in \mathbb {Z}$ . However, the Specker–Blatter theorem gives little information on the constants $p_m$ , $q_m$ or the coefficients $c_{0,m}, \ldots , c_{p_m-1,m}$ . These in particular depend on the substitution rank of the class $\mathcal {C}$ . In fact Theorem 4.4 gives a very bad estimate of the substitution rank in the case of binary relation symbols. The constants are computable, but it is not known whether they are always computable in feasible time or whether their size is bounded by an elementary function. In the presence of constants the substitution rank is not defined. Our main Theorem 8.1 allows to eliminate the constants, and therefore gives a formula for which the substitution rank is defined. However, due to the increased complexity of the resulting formula, the estimate of the substitution rank will be even worse.

Problem 14.1. Given a sentence $\phi $ in $\mathrm {CMSOL}(\tau )$ where $\tau $ consists only of constants, unary and binary relation symbols,

1. (i) what is the time complexity of computing $p_m$ , $q_m$ and $c_{0,m}, \ldots , c_{p_m-1,m}$ ?

2. (ii) what can we say about the size of $p_m$ and $q_m$ ?

The proof of Theorem 4.4 depends on the Feferman–Vaught theorem which also holds for $\mathrm {CMSOL}(\tau )$ for any finite relational $\tau $ [11, 23]. In our context, the Feferman–Vaught theorem allows to check whether a formula of $\mathrm {CMSOL}(\tau )$ holds in $Subst({\mathfrak A}_1,a,{\mathfrak A}_2)$ by checking a sequence of $\mathrm {CMSOL}(\tau )$ -formulas in ${\mathfrak A}_1$ and ${\mathfrak A}_2$ independently. This sequence is called a reduction sequence, cf. [14]. In [7] it is shown that even for $\mathrm {FOL}(\tau )$ the size of the reduction sequences for the Feferman–Vaught theorem cannot, in general, be bounded by an elementary function.

The next problem essentially asks whether there is a way to prove Theorem 7.1 (or even a somewhat weaker statement in this vein) in a way the bypasses the use of the Feferman–Vaught theorem, and thus avoids the toll it takes on the recursion parameters.

Problem 14.2. Does there exist an elementary function $F(k)$ , so that for any sentence $\phi $ in $\mathrm {CMSOL}(\tau )$ where $\tau $ consists only of constants, unary and binary relation symbols, the size of the constants $p_m$ and $q_m$ is bounded by $F(\max \{|\phi |,m\})$ ? What if we restrict ourselves only to $\mathrm {FOL}(\tau )$ instead of $\mathrm {CMSOL}(\tau )$ ?

The Specker–Blatter theorem also applies to hereditary, monotone and minor-closed graph classes, provided they are definable using a finite set of forbidden (induced) subgraphs or minors. In the first two cases such a class is $\mathrm {FOL}$ -definable. In the case of a minor-closed class, B. Courcelle showed that it is $\mathrm {MSOL}$ -definable, see [6]. By the celebrated theorem of N. Robertson and P. Seymour [8], every minor-closed class of graphs is definable by a finite set of forbidden minors. However, there are monotone (hereditary) classes of graphs where a finite set of forbidden (induced) subgraphs does not suffice.

Problem 14.3. Are there hereditary or monotone classes of graphs $\mathcal {C}$ such that $f_{\mathcal {C}}(n)$ is not MC-finite?

An analogue question arises when we replace graphs by finite relational $\tau $ -structures. In this case one speaks of classes of $\tau $ -structures closed under substructures. Every class of finite $\tau $ -structures $\mathcal {C}$ closed under substructures can be characterized by a set of forbidden substructures. If this set is finite, $\mathcal {C}$ is again $\mathrm {FOL}$ -definable, and the Specker–Blatter theorem applies.

Problem 14.4.

1. (i) Let $\tau $ be a relational vocabulary. Are there substructure closed classes $\mathcal {C}$ of $\tau $ -structures such that $f_{\mathcal {C}}(n)$ is not MC-finite?

2. (ii) Same question when all the relations are at most binary?