Navigation Performance of the Libration Point Satellite Navigation System in Cislunar Space

Abstract

Based on the candidate architectures of the libration point satellite navigation system proposed in our previous work, a navigation performance study is conducted in this paper to verify the cislunar navigation ability of the proposed system. Using scalar satellite-to-satellite range measurement between the user and libration point navigation satellites, a virtual lunar exploration mission scenario is developed to verify the navigation performance of the candidate Earth-Moon L_1,2,4,5 four-satellite constellations. The simulation results indicate that the libration point satellite navigation system is available for cislunar navigation and the navigation accuracy of a few tens of metres can be achieved for both the trans-lunar cruise and lunar orbit phase. Besides that, it is also found that the navigation accuracy of the libration point satellite navigation system is sensitive to the orbit of the L₁ satellite. Once the L₁ navigation satellite is located in the Halo orbit or vertical Lyapunov orbit, the proposed system can present a better navigation performance in cislunar space.

1. INTRODUCTION

In the past decade, more than ten lunar exploration missions have been launched to study the natural satellite of Earth, such as the European Space Agency's (ESA's) SMART-1 mission, the National Aeronautics and Space Administration's (NASA's) GRAIL mission, and China's Chang'e missions. The renewed interest in lunar exploration gives rise to an increasing demand for a high-precision navigation system in cislunar space. As the traditional approach that is based on extensive ground tracking is onerous and inadequate in some particular circumstances, an autonomous navigation scheme for lunar explorations is preferable.

The desire for autonomous cislunar navigation is a long-standing issue that has led to numerous studies since the 1960s. Keenan and Regenhardt (1962) proposed using star occultation measurements as an aid for navigation in cislunar space. Bowers (1966), followed by Tuckness and Young (1995) demonstrated the method that adopts angular measurements between known stars and known landmarks on the Earth or Moon for trans-lunar cruise navigation. Main advantages of these solutions lie in their autonomy and robustness, however, the navigation accuracy may not satisfy the requirement of actual missions (Christian and Lightsey, 2009). Considering the specific dynamical properties of the Earth-Moon system, Farquhar (1967) first proposed the concept of using Earth-Moon libration point satellites for lunar navigation. Due to strong asymmetry of the three-body force field, a spacecraft located in the Libration Point Orbit (LPO) can track other spacecraft using crosslink range measurements and determine the absolute positions of both spacecraft simultaneously without any mathematical constraints. This linked, autonomous orbit determination method is known as Liaison navigation which was first proposed by Hill et al. (2005) and then followed by many other researchers. Parker et al. (2013) and Leonard et al. (2013) proved that by adding a single navigation satellite located around the Earth-Moon L ₁ or L ₂ libration point, the number of active ground tracking stations can be greatly reduced for a lunar exploration mission and the navigation accuracy can also be improved. Hill himself has also completed a systematic study on the autonomous orbit determination for LPOs in his PhD dissertation (Hill, 2007).

Zhang and Xu (2014) proposed a concept of using the different libration point orbits to construct the Universe Lighthouse for cislunar navigation, where some candidate libration point satellite navigation architectures are obtained based on comprehensive consideration of constellation coverage ability and autonomous orbit determination performance. As a subsequent work of the libration point satellite navigation system design, this paper is focused on navigation performance analysis in cislunar space, specifically the trans-lunar cruise and lunar orbit phase. With the aid of the extended Kalman filter, the satellite-to-satellite range tracking data between the user spacecraft and libration point navigation satellites is used to autonomously determine the orbit of the user spacecraft, and no ground-based measurements are involved in the navigation process. The navigation performance of different Earth-Moon L _1,2,4,5 four-satellite constellations are verified by numerical simulations.

The remainder of this paper is organised as follows. In Section 2, a brief review of the candidate architectures of the libration point satellite navigation system is given. After describing the mission scenario considered in this paper, the spacecraft dynamic model and observation measurements are explained in Section 3 and Section 4 gives a detailed description of the algorithm and state noise compensation method adopted in the filter process. After that, cislunar navigation simulations are performed for both the trans-lunar cruise phase and lunar orbit phase in Section 5. Finally, some brief conclusions are drawn in Section 6.

2. CANDIDATE NAVIGATION ARCHITECTURES

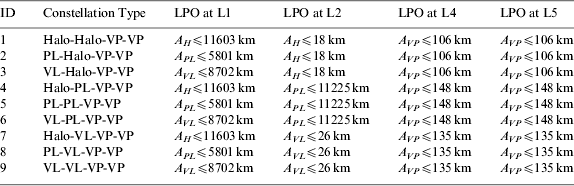
Libration point orbits around the Earth-Moon equilibrium points are promising candidates to build navigation architectures in cislunar space, which has been proved by many researchers. With the aid of the Liaison technique, the autonomy of the libration point satellite can be guaranteed and an autonomous satellite navigation system can thus be founded. An architecture analysis study was completed in our previous work and some feasible three-satellite and four-satellite navigation constellations were obtained to achieve continuous global coverage for lunar orbits, with the latter having a better coverage performance. Therefore, in the following discussions, the Earth-Moon L _1,2,4,5 four-satellite constellations are selected as the focus of the cislunar navigation performance study and the candidate four-satellite navigation architectures are listed in Table 1 (Zhang and Xu, 2014).

Table 1. Candidate navigation architectures of the Earth-Moon L _1,2,4,5 four-satellite constellation.

Candidate orbits for these navigation architectures are: Halo orbits (Halo), Planar Lyapunov orbits (PL) and Vertical Lyapunov orbits (VL) around the collinear libration points and Vertical Periodic orbits (VP) around the triangular libration points. The variables A _H, A_PL, A_VL and A _VP in the table are amplitude parameters which will be used to compute the LPOs. The construction details of these orbits can be found in Lei et al. (2013a) and Lei and Xu (2013b).

Since the autonomous orbit determination performance of the Earth-Moon L _1,2,4,5 four-satellite constellation has been verified by the Liaison technique in our previous work and it was found that the maximum position determination error in a 180 days period can be controlled within a few metres, positions of the libration point navigation satellites will be considered as known with an implicit error and their broadcast ephemeris will be used as given parameters in the navigation simulation process.

3. MISSION SCENARIOS AND MODELS

Before we start the cislunar navigation simulation, a reference mission scenario must first be developed. This section will cover a detailed description of the lunar exploration mission, as well as the spacecraft dynamic model and observation measurement model.

3.1. Design reference mission

The reference mission considered in this work mainly consists of two operation phases: a trans-lunar cruise phase and lunar orbit phase. The trans-lunar cruise departs from a LEO parking orbit with the orbital parameters given in Table 2.

Table 2. Orbital parameters of the initial LEO parking orbit.

The initial epoch of the mission is defined as 1 January 2025 UTC. By performing an approximately 3·12 km/s manoeuvre in the along-track direction, the spacecraft is inserted into the trans-lunar cruise trajectory at 1 Jan 2025 08:03:05 UTC. After approximately three days of cruise, the spacecraft reaches perilune at 4 January 2025 07:48:11 UTC with an altitude of 444 km. Then a Lunar Orbit Insertion (LOI) manoeuvre is performed to insert the spacecraft into a circular, polar lunar orbit. The magnitude of the LOI is approximately 854 m/s and the orbital parameters of the final lunar orbit are summarised in Table 3.

Table 3. Orbital parameters of the lunar orbit.

One or more trajectory correction manoeuvres may be needed to prune the trajectory and target the final nominal orbit in real missions; this is not considered here for simplicity, which will not have any significant effect on the following simulation results.

3.2. Spacecraft dynamic model

The spacecraft dynamic models of the two operation phases above are different, but both can be formulated as a perturbed two-body problem. The perturbed equation of motion can be written in a general form as

(1)$${\bi \ddot r} = - \displaystyle{\mu \over {r^3}} {\bi r} + {\bi F}_\varepsilon $$

where r is the position vector of the spacecraft, μ is the gravitational parameter of the central body and F_ε is the resultant vector of all the perturbing accelerations.

For the trans-lunar cruise phase, the motion of the spacecraft is studied in the International Celestial Reference Frame (ICRF). Perturbations considered include the non-spherical gravitation of the Earth, the third body perturbations of the Moon, the Sun and planets, and the non-gravitational perturbation due to solar radiation pressure. The non-spherical gravitational potential of the Earth can be commonly written as

(2)$$\Delta V = \displaystyle{\mu \over R}\sum\limits_{l \geqslant 2}^{} {\sum\limits_{m = 0}^l {\left( {\displaystyle{{a_e} \over R}} \right)^l {\bar P}_{lm} \left( {\sin \varphi} \right)} \left[ {{\bar C}_{lm} \cos m\lambda _G + {\bar S}_{lm} \sin m\lambda _G} \right]} $$

where a _e is the equatorial radius of the Earth, ${\bar P}_{lm} $ is the normalized associated Legendre polynomial, and ${\bar C}_{lm} $ and ${\bar S}_{lm} $ are spherical harmonics related to the non-spherical gravitational potential. In this work, the WGS84 gravity field model is adopted for the non-spherical Earth (Defense Mapping Agency, 1984). As the gravitational potential is expressed in the central body fixed frame, a coordinate transformation is also needed to convert the acceleration from the body fixed frame to the inertial frame. After considering these, the non-spherical gravitational acceleration can then be obtained by

(3)$${\bi F}_{NSP} = \left( {\displaystyle{{\partial \Delta V} \over {\partial {\bi r}}}} \right)^T = \left( {\displaystyle{{\partial {\bi R}} \over {\partial {\bi r}}}} \right)^T \left( {\displaystyle{{\partial \Delta V} \over {\partial {\bi R}}}} \right)^T $$

where (∂R/∂r)^T is the conversion from the International Terrestrial Reference Frame (ITRF) to ICRF, and the International Astronomical Union's Standards of Fundamental Astronomy (IAU SOFA) software collection can be conveniently adopted to finish this transformation (IAU SOFA Board, 2010).

The acceleration due to the third bodies can be written in a simple form as

(4)$${\bi F}_{TBP} = - \mu '\left( {\displaystyle{{\bf \Delta} \over {\Delta ^3}} + \displaystyle{{{\bi r'}} \over {r'^3}}} \right)$$

where μ′ is the gravitational parameter of the third body, here for the trans-lunar cruise, third bodies considered include the Moon, the Sun and the eight planets except the Earth. Δ is the position vector from the third body to the spacecraft, and r′ is the position vector from the Earth to the third body. The positions of these celestial bodies can be obtained from the JPL DE405 ephemerides (Standish, 1998).

As the spacecraft is far away from the Earth, influence of solar radiation pressure should also be considered. Based on a cylindrical shadow model, the acceleration due to solar radiation pressure can be written as

(5)$${\bi F}_{SRP} = vC_R \left( {\displaystyle{S \over m}} \right)\rho_{\bi e} \left( {\displaystyle{{1AU} \over {r_{\bi e}}}} \right)^2 \displaystyle{{{\bi r}_{\bi e}} \over {r_{\bi e}}} $$

where ${\bi r}_{\bi e}$ is the position vector from the Sun to the spacecraft, $\rho_{\bi e} = 4.56 \times 10^{ - 6} N/m^2 $ is the solar radiation pressure constant in the vicinity of Earth, (S/m) is the area-mass ratio of the spacecraft and C _R is the reflectivity coefficient with a value of approximately one. The eclipse factor v is determined by the following relations:

(6)$$\left\{ \matrix{\hskip-5pt Earth\,shadow: \cos \psi _1 = \left( {\displaystyle{{\bi r} \over r}} \right) \cdot \left( {\displaystyle{{{\bi r}_s} \over {r_s}}} \right) \lt 0\ \&\ \sin \psi _1 = \sqrt {1 - \cos ^2 \psi _1} \lt \displaystyle{{a_e} \over r} \cr \hskip-5pt Moon\,shadow: \cos \psi _2 = \left( {\displaystyle{{{\bi r} - {\bi r}_m} \over {\left\vert {{\bi r} - {\bi r}_m} \right\vert }}} \right) \cdot \left( {\displaystyle{{{\bi r}_s} \over {r_s}}} \right) \lt 0\ \&\ \sin \psi _2 = \sqrt {1 - \cos ^2 \psi _2} \lt \displaystyle{{a_m} \over {\left\vert {{\bi r} - {\bi r}_m} \right\vert }} } \right.$$

r_s and r_m in the above relations represent the geocentric position vector of the Sun and the Moon, while a _e and a _m are the equatorial radiuses of the Earth and the Moon, respectively. Once one of the above relations is satisfied, the eclipse factor v=0, which means the spacecraft is in the shadow of the Earth or the Moon, else v=1 meaning that the spacecraft is in sunlight.

After the spacecraft arrives at the Moon, the reference frame used to study the motion will be changed from the ICRF to the Moon-Centred Inertial (MCI) frame. The dynamical model of the spacecraft is also different from the previous phase, since the central body has been changed to the Moon. The perturbations considered are similar, but the gravitation of the Earth now becomes a third-body perturbation. Besides that, the solid tide perturbation should also be considered for the lunar orbit phase.

The lunar gravity field adopted in this work is the LP165 model (Konopliv et al., 2001). In order to obtain the conversion matrix (∂R/∂r)^T in Equation (3), a two-step transformation is considered. First is the transformation from the Moon-Centred Moon-Fixed (MCMF) frame to ICRF, which can be obtained from the lunar libration parameters as follows

(7)$${\bi R}_{MCMF} = \left[ M \right]{\bi r}_{ICRS}, \left[ M \right] = R_Z \left( \Lambda \right)R_X \left( {i_S} \right)R_Z \left( {\Omega '} \right)$$

Ω′, i _S and Λ are the Euler angles given by the JPL DE405 ephemeris. Then the conversion from the ICRF to the MCI frame can be performed by

(8)$${\bi r}_{ICRS} = \left[ N \right]^T {\bi r}_{MCI}, \left[ N \right] = R_Z \left( { - \Omega _m} \right)R_X \left( { - I_m} \right)R_Z \left( {\Omega _m} \right)R_X \left( \varepsilon \right)$$

where Ω_m is the mean longitude of the ascending node of the Moon's orbit referred to the ecliptic, I _m is the inclination of the mean lunar equator to the ecliptic and ε is the mean obliquity of the ecliptic. Values of these angles can be obtained from the Astronomical Almanac (US Nautical Almanac Office, 2013).

The tidal deformation of the Moon will cause temporal variations in the gravitational potential, which in turn will introduce perturbations in the motion of close satellites. Previous research found that the maximum term of solid tide perturbation may reach the same order of magnitude as the third-body perturbation of the Sun for a low lunar orbit (Liu and Wang, 2006). Thus it needs to be considered in the lunar orbit phase. The maximum variation of the lunar gravitational potential caused by tidal deformation can be written in the form

(9)$$\Delta V_{2,0} = \displaystyle{{\mu _e} \over {r_e^3}} \displaystyle{{k_2} \over {r^3}} P_2 \left( {\cos \varphi _e} \right)$$

where μ _e is the gravitational parameter of the Earth, r _e is the distance between the Earth and the Moon, k ₂=0.029966 is the second order Love number of the Moon and P ₂ is the second order Legendre polynomial. The lunicentric angle φ _e between the spacecraft and the Earth can be computed from the following relation,

(10)$$\cos \varphi _e = \left( {\displaystyle{{\bi r} \over r}} \right) \cdot \left( {\displaystyle{{{\bi r}_e} \over {r_e}}} \right)$$

Then the solid tide perturbation can be obtained directly by the potential gradient

(11)$${\bi F}_{STP} = \left( {\displaystyle{{\partial \Delta V_{2,0}} \over {\partial {\bi r}}}} \right)^T $$

Other perturbations like the third body perturbation and the solar radiation pressure perturbation are similar to the trans-lunar cruise phase, except the origin has been changed to the Moon and position vectors are now expressed in a Moon-centred frame.

3.3. Observation measurement model

The observation model adopted in this work is an idealised range measurement between the spacecraft and libration point navigation satellites. Once a navigation satellite is visible to the user spacecraft, idealised satellite-to-satellite range data is obtained by the user, which can be defined in the following form

(12)$$\rho = \sqrt {\left( {x - x_L} \right)^2 + \left( {y - y_L} \right)^2 + \left( {z - z_L} \right)^2} + \sigma _{bias} + \sigma _{noise} $$

where r=(x,y,z) is the position vector of the user and r_L=(x _L,y_L,z_L) is the position vector of the libration point satellite. As various errors exist in every observation measurement, two main components are considered in the above expression. One is the systematic bias σ _bias, which is related to the measurement model, and the other is a random white noise σ _noise that differs in every measurement. Both of them are drawn from Gaussian distributions with zero mean and the given standard deviations.

Noting that the position of the libration point satellite is generally expressed in the Earth-Moon barycentric synodic frame, a coordinate transformation is needed to transform it to the same reference frame as the user spacecraft. The conversion from the Earth-Moon barycentric synodic frame to the ICRF can be finished by a simple translation and rotation, given by Equation (13)

(13)$${\bi r}_L = \left[ C \right]\left( {{\bi r}\prime_{\hskip-2pt L} + \left[ {{\rm d}_{EC}, 0,0} \right]^T} \right)$$

where r′ _L is the position vector of the libration point satellite expressed in the synodic frame, d_EC is the distance between the Earth and the Earth-Moon barycentre, and [C] is a rotation matrix which can be defined by the position and velocity vectors of the Moon as follows

(14)$$\left[ C \right] = \left[ {{\bi \hat e}_1, {\bi \hat e}_2, {\bi \hat e}_3} \right], {\bi \hat e}_1 = \displaystyle{{{\bi r}_m} \over {\left\vert {{\bi r}_m} \right\vert }}, {\bi \hat e}_3 = \displaystyle{{{\bi r}_m \times {\bi \dot r}_m} \over {\left\vert {{\bi r}_m \times {\bi \dot r}_m} \right\vert }}, {\bi \hat e}_2 = {\bi \hat e}_3 \times {\bi \hat e}_1 $$

While for the conversion from the Earth-Moon barycentric synodic frame to the MCI frame, it can be finished by a similar process as

(15)$${\bi r}_L = \left[ N \right]\left[ C \right]\left( {{\bi r}\prime_{\hskip-2pt L} - \left[ {{\rm d}_{MC}, 0,0} \right]^T} \right)$$

where d_MC is the distance between the Moon and the Earth-Moon barycentre. The definitions of [N] and [C] are the same as in the previous case.

Using the nominal orbits of the user and libration point satellites, observation measurements are simulated according to the above description. Then an Extended Kalman Filter (EKF) algorithm is adopted to finish the navigation performance analysis.

4. NAVIGATION FILTER ALGORITHM

The EKF is one of the most common methods used in real-time navigation, and it is also adopted in this work. The state vector being estimated consists of the position and velocity of the spacecraft

(16)$${\bi X} = \left[ {x, y, z, \dot x, \dot y, \dot z} \right]^T $$

which is governed by a system of nonlinear differential equations, denoted by

(17)$${\bi \dot X} = F\left( {{\bi X},t} \right) + {\bi G}\left( t \right)$$

where F(X,t) is the known term that has been discussed in the previous section, G(t) is the model bias compensation and assumed to be a white noise process with

(18)$$E\left[ {{\bi G}\left( t \right)} \right] = 0\ {\rm and} \ E\left[ {{\bi G}\left( t \right){\bi G}^T \left( \tau \right)} \right] = Q\left( t \right)\delta \left( {t - \tau} \right)$$

where δ(t−τ) is the Dirac delta function, and Q is the process noise covariance matrix which will be discussed later in this section.

Since the expected value of the process noise is zero, it does not affect the orbit on average. Therefore the state estimate can be propagated as usual without consideration of the noise term. But the time update equation for the state error covariance is changed due to the presence of process noise. The modified covariance propagation formula can be obtained with the state transition matrix Φ in the following way (Montenbruck and Gill, 2000)

(19)$${\bar P}_i = \Phi \left( {t_i, t_{i - 1}} \right)P_{i - 1} \Phi ^T \left( {t_i, t_{i - 1}} \right) + \int\limits_{t_{i - 1}} ^{t_i} {\Phi \left( {t_i, \tau} \right)Q\left( \tau \right)\Phi ^T \left( {t_i, \tau} \right){\rm d}\tau} $$

the state transition matrix is obtained by integrating

(20)$${ {\rm \dot\Phi}} \left( {t,t_i} \right) = A\left( t \right)\Phi \left( {t,t_i} \right)$$

with the initial condition Φ(t _i,t_i)=I, and

(21)$$A\left( t \right) = \displaystyle{{\partial F\left( {{\bi X}^*, t} \right)} \over {\partial {\bi X}\left( t \right)}}$$

where * means the partial derivative is evaluated along the reference trajectory.

Using the observation data at time t _i, a measurement update for the state and covariance matrix can then be computed by the following relations (Tapley et al., 2004)

(22)$$K_i = \bar P_i \tilde H_i^T \left[ {\tilde H_i \bar P_i \tilde H_i^T + R_i} \right]^{ - 1} $$

(23)$${\bi \hat X}_i = {\bi X}_i^* + K_i {\bi y}_i $$

(24)$$P_i = \left[ {I - K_i \tilde H_i} \right]\bar P_i $$

where K _i is called the Kalman gain, R _i is the observation covariance matrix, y_i is the observation deviation, and $\tilde H_i $ is the observation-state mapping matrix. Here for the scalar satellite-to-satellite range data, $\tilde H_i $ is computed using the current state as

(25)$$\tilde H_i = \displaystyle{{\partial \rho \left( {{\bi X}^*, t_i} \right)} \over {\partial {\bi X}}} = \left[ {\displaystyle{{x_i^* - x_L^i} \over {\rho _i}}, \displaystyle{{y_i^* - y_L^i} \over {\rho _i}}, \displaystyle{{z_i^* - z_L^i} \over {\rho _i}}, 0, 0, 0} \right]$$

The newly updated state is then propagated forward to the time of next observation and the time and measurement updates are repeated. With regard to the above discussions, two additional remarks should be made. One is the computation of the Jacobian matrix A(t), which can be simplified due to the characteristics of the filter, and the other is the method that is adopted to determine the process noise covariance matrix Q(t).

The Jacobian matrix A(t) can cause cumbersome analytic expressions when using a complex force model. One solution to avoid this problem is using a truncated force model to compute the Jacobian matrix, by noting the gradual convergence property of the filter process. For the trans-lunar cruise phase, only the Earth point-mass gravitation is considered in the Jacobian matrix computation, which results in

(26)$$A\left( t \right) = \left[ {\matrix{ 0 & 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1 \cr { - \displaystyle{{\mu _e} \over {r^3}} + \displaystyle{{3\mu _e x^2} \over {r^5}}} & {\displaystyle{{3\mu _e xy} \over {r^5}}} & {\displaystyle{{3\mu _e xz} \over {r^5}}} & 0 & 0 & 0 \cr {\displaystyle{{3\mu _e xy} \over {r^5}}} & { - \displaystyle{{\mu _e} \over {r^3}} + \displaystyle{{3\mu _e y^2} \over {r^5}}} & {\displaystyle{{3\mu _e yz} \over {r^5}}} & 0 & 0 & 0 \cr {\displaystyle{{3\mu _e xz} \over {r^5}}} & {\displaystyle{{3\mu _e yz} \over {r^5}}} & { - \displaystyle{{\mu _e} \over {r^3}} + \displaystyle{{3\mu _e z^2} \over {r^5}}} & 0 & 0 & 0 \cr}} \right]$$

While for the Lunar orbit phase, the J ₂ term of Lunar non-spherical gravitation is added and the Jacobian matrix A(t) has the form

(27)$$A\left( t \right) = \left[ {\matrix{ 0 & 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1 \cr {c_1 + c_2 x^2} & {c_2 xy} & {c_2 xz} & 0 & 0 & 0 \cr {c_2 xy} & {c_1 + c_2 y^2} & {c_2 yz} & 0 & 0 & 0 \cr {\left( {c_2 + c_3} \right)xz} & {\left( {c_2 + c_3} \right)yz} & {c_1 + \left( {c_2 + c_3} \right)z^2} & 0 & 0 & 0 \cr}} \right]$$

With

(28)$$\eqalign{& c_1 = - \displaystyle{{\mu _m} \over {r^3}} + \displaystyle{{3J_2} \over 2}\left( {\displaystyle{{5z^2} \over {r^7}} - \displaystyle{1 \over {r^5}}} \right) \cr & c_2 = \displaystyle{{3\mu _m} \over {r^5}} + \displaystyle{{3J_2} \over 2}\left( { - \displaystyle{{35z^2} \over {r^9}} + \displaystyle{5 \over {r^7}}} \right) \cr & c_3 = \displaystyle{{15J_2 z} \over {r^7}}} $$

where μ _m is the gravitational parameter of the Moon and $J_2 = - \sqrt 5 {\bar C}_{2,0} = {\rm 2}{\rm. 03227} \times {\rm 10}^{ - 4} $.

The process noise covariance matrix Q(t) is used to compensate for the unmodelled accelerations and stop the filter from getting insensitive to further observations. The question of how to determine the process noise is complex. In this work, Q(t) is chosen as a diagonal matrix such as

(29)$$Q\left( t \right) = \left[ {\matrix{ {\sigma _x^2} & 0 & 0 & 0 & 0 & 0 \cr 0 & {\sigma _y^2} & 0 & 0 & 0 & 0 \cr 0 & 0 & {\sigma _z^2} & 0 & 0 & 0 \cr 0 & 0 & 0 & {\sigma _{\dot x}^2} & 0 & 0 \cr 0 & 0 & 0 & 0 & {\sigma _{\dot y}^2} & 0 \cr 0 & 0 & 0 & 0 & 0 & {\sigma _{\dot z}^2} \cr}} \right]$$

and it is further assumed that the velocity of the spacecraft can be considered as constant between two contiguous observations, which leads the state transition matrix Φ(t _i,τ) to be

(30)$$\Phi \left( {t_i, \tau} \right) = \left[ {\matrix{ {\bi I} & {\left( {t_i - \tau} \right){\bi I}} \cr 0 & {\bi I} \cr}} \right]$$

Then the integral in Equation (19) can be computed analytically and yields

(31)$$\eqalign{& \int\limits_{t_{i - 1}} ^{t_i} {\Phi \left( {t_i, \tau} \right)Q\left( \tau \right)\Phi ^T \left( {t_i, \tau} \right){\rm d}\tau} \cr & = \left[ {\matrix{ {\sigma _x^2 \Delta t + \sigma _{\dot x}^2 \displaystyle{{\Delta t^3} \over 3}} & 0 & 0 & {\sigma _{\dot x}^2 \displaystyle{{\Delta t^2} \over 2}} & 0 & 0 \cr 0 & {\sigma _y^2 \Delta t + \sigma _{\dot y}^2 \displaystyle{{\Delta t^3} \over 3}} & 0 & 0 & {\sigma _{\dot y}^2 \displaystyle{{\Delta t^2} \over 2}} & 0 \cr 0 & 0 & {\sigma _z^2 \Delta t + \sigma _{\dot z}^2 \displaystyle{{\Delta t^3} \over 3}} & 0 & 0 & {\sigma _{\dot z}^2 \displaystyle{{\Delta t^2} \over 2}} \cr {\sigma _{\dot x}^2 \displaystyle{{\Delta t^2} \over 2}} & 0 & 0 & {\sigma _{\dot x}^2 \Delta t} & 0 & 0 \cr 0 & {\sigma _{\dot y}^2 \displaystyle{{\Delta t^2} \over 2}} & 0 & 0 & {\sigma _{\dot y}^2 \Delta t} & 0 \cr 0 & 0 & {\sigma _{\dot z}^2 \displaystyle{{\Delta t^2} \over 2}} & 0 & 0 & {\sigma _{\dot z}^2 \Delta t} \cr}} \right]} $$

where Δt=t _i−t_{i− 1} is the observation interval, and the diagonal elements of matrix Q(t) are determined by trial and error for different circumstances.

5. NUMERICAL RESULTS OF CISLUNAR NAVIGATION SIMULATIONS

According to the mission scenarios described previously, a numerical simulation is conducted in this section to study the cislunar navigation performance of the libration point satellite navigation system.

5.1. Trans-Lunar Cruise Navigation Performance

As a starting point, the trans-lunar cruise phase is studied. Based on the dynamical model discussed earlier in Section 3, the nominal trajectory is generated for the user spacecraft. Then an observability analysis is performed for the trans-lunar cruise trajectory using the Earth-Moon L _1,2,4,5 four-satellite constellations. An illustration of the timeline of visible libration point satellites is shown in Figure 1.

Figure 1. Timeline of visible libration point satellites during the trans-lunar cruise phase. The computation is conducted for the Halo-Halo-VP-VP constellation (ID=1), while for the other constellations, the results are similar.

It can be seen from Figure 1 that the spacecraft is visible to the L ₁, L ₂, L ₄ navigation satellites for most of the trans-lunar cruise phase, while the L ₅ navigation satellite is always in the field of view for the user spacecraft. Since there is at least one available libration point satellite for the whole trans-lunar cruise trajectory, a navigation performance analysis can then be conducted. Using the nominal orbits of the libration point navigation satellites and the user, a series of satellite-to-satellite range observations are generated every 60 seconds. Considering the ephemeris error of the libration point satellites, a σ _bias=5 m systematic bias is used to corrupt the observation data. Besides that, a σ _noise=3 m white-noise error is added to compensate for the stochastic error in every range measurement.

After generating the observation data, the EKF is then employed to estimate the states of the spacecraft. The initial state used to start the filter process is computed from the true trajectory, with an initial position error in each component of 100 m and an initial velocity error in each component of 0.01 m/s. The diagonal elements of the process noise covariance matrix Q(t) are determined by trial and error and finally selected as follows for the trans-lunar cruise phase

(32)$$\eqalign{\sigma _x^2 =& 5.07 \times 10^{ - 3} {\rm m}^{\rm 2} {\rm /s}, \sigma _y^2 = 6.39 \times 10^{ - 2} {\rm m}^{\rm 2} {\rm /s}, \sigma _z^2 = 0.11{\rm m}^{\rm 2} {\rm /s} \cr \sigma _{\dot x}^2 =& 3.98 \times 10^{ - 10} {\rm m}^{\rm 2} {\rm /s}^3, \sigma _{\dot y}^2 = 5.63 \times 10^{ - 10} {\rm m}^{\rm 2} {\rm /s}^3, \sigma _{\dot z}^2 = 6.67 \times 10^{ - 10} {\rm m}^{\rm 2} {\rm /s}^3} $$

Then a trans-lunar cruise navigation simulation is conducted for the candidate Earth-Moon L _1,2,4,5 four-satellite constellations given in Table 1. The navigation results for the Halo-Halo-VP-VP constellation (ID=1) are shown in Figures 2 and 3, respectively for the position and velocity components. It can be seen from the results that the estimated position and velocity components converge quickly to the reference values. The root-mean-square (RMS) position error is 20.01 m and the RMS velocity error is 4.9 mm/s. The probability of the position estimate error falling inside the 3σ line is 97.72%, 98.17% and 98.12%, respectively for the x, y and z components, while the probability for the velocity estimate error falling inside the 3σ line is 100% for each component. In addition, from Figure 2, it can also been seen that the position estimate error in the X-direction is much smaller than the other two directions, and this may be concerned with the geometrical configuration between the libration point navigation satellites and the user spacecraft. Similar simulations are also conducted for the other candidate Earth-Moon L _1,2,4,5 four-satellite constellations and the final results are summarised in Table 4.

Figure 2. Position estimate error for the trans-lunar cruise phase using the EKF.

Figure 3. Velocity estimate error for the trans-lunar cruise phase using the EKF.

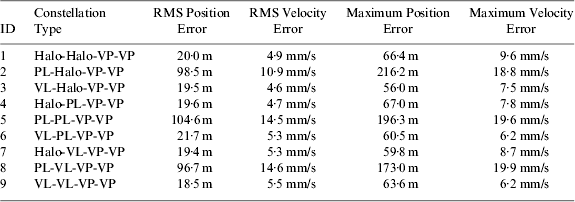
Table 4. Trans-lunar cruise navigation performance of the candidate Earth-Moon L _1,2,4,5 four-satellite constellations.

Table 4 lists the RMS position estimate error and velocity estimate error as well as the maximum position error and velocity error for all the candidate Earth-Moon L _1,2,4,5 four-satellite constellations. From the results, it can be found that the trans-lunar cruise navigation performance is directly related to the constellation architectures of the libration point satellites, especially the orbit of the L ₁ navigation satellite. When the L ₁ navigation satellite is located in the planar Lyapunov orbit (that is, the ID=2, 5, 8 constellations), the trans-lunar cruise navigation performance seems always worse than the other configurations, with the RMS position error to be about 100 m and the RMS velocity error about 10 mm/s. Once the nominal orbit of the L ₁ navigation satellite is changed to Halo orbit or vertical Lyapunov orbit (that is, the ID=1, 3, 4, 6, 7, 9 constellations), RMS state estimate error can be reduced to about 20 m and 5 mm/s, respectively, for position and velocity, and the maximum position and velocity estimate errors are also controlled within 70 m and 10 mm/s. As a result, it may be concluded that the navigation architectures with the L ₁ navigation satellite locating in Halo or vertical Lyapunov orbits are more suitable for trans-lunar cruise navigation.

5.2. Lunar Orbit Navigation Performance

After discussing the trans-lunar cruise navigation performance of the proposed system, a lunar orbit navigation simulation is conducted to further verify the navigation ability in cislunar space. As it has been proved in our previous work that the candidate Earth-Moon L _1,2,4,5 four-satellite constellations can achieve continuous global coverage for lunar orbits with arbitrary inclination and orbital altitude changing in the range of 100 km to 2000 km, the lunar orbiter considered in this work can always been tracked by the libration point satellites. An illustration of the timeline of visible navigation satellites in a seven-day period is shown in Figure 4.

Figure 4. Timeline of visible libration point satellites during the lunar orbit phase. The computation is conducted for the Halo-Halo-VP-VP constellation (ID=1), while for the other constellations, the results are similar.

It can be seen from Figure 4 that the lunar orbiter is tracked by the four libration point satellites alternately, and there are at least two visible navigation satellites in the seven-day period. For a longer time period, the results are similar and the libration point satellite navigation system is always available to a lunar orbiter. Therefore, a lunar orbit navigation simulation can be conducted. Using the nominal orbits of the user and libration point navigation satellites, a series of scalar satellite-to-satellite range data are generated every 60 seconds with the same systematic bias and white-noise error as the trans-lunar cruise case. The initial state error considered in the filter process is also 100 m and 0.01 m/s respectively for position and velocity, added to each component of the true state. The process noise covariance matrix Q(t) is determined by trial and error and the diagonal elements are finally selected as follows for the lunar orbit phase

(33)$$\eqalign{\sigma _x^2=&2.94 \times 10^{ - 4} {\rm m}^{\rm 2} {\rm /s}, \sigma _y^2 = 3.70 \times 10^{ - 3} {\rm m}^{\rm 2} {\rm /s}, \sigma _z^2 = 6.31 \times 10^{ - 3} {\rm m}^{\rm 2} {\rm /s} \cr \sigma _{\dot x}^2=&1.40 \times 10^{ - 11} {\rm m}^{\rm 2} {\rm /s}^3, \sigma _{\dot y}^2 = 1.98 \times 10^{ - 11} {\rm m}^{\rm 2} {\rm /s}^3, \sigma _{\dot z}^2 = 2.35 \times 10^{ - 11} {\rm m}^{\rm 2} {\rm /s}^3} $$

Using the observation data and initial state generated in the above way, a lunar orbit navigation simulation is then conducted for the candidate Earth-Moon L _1,2,4,5 four-satellite constellations. The navigation results for the Halo-Halo-VP-VP constellation (ID=1) are shown in Figures 5 and 6 respectively for the position and velocity components. It can be seen from the results that the filter also converges quickly to the steady state. The RMS position error is 23.35 m and the RMS velocity error is 20.3 mm/s. The probability of the position estimate error falling inside the 3σ line is 97.14%, 97.70% and 97.26% respectively for the x, y and z components, while the probability for the velocity estimate error falling inside the 3σ line is 99.65%, 99.61% and 99.65% respectively for the $\dot x$, $\dot y$ and $\dot z$ components. In addition, it can be seen from Figure 5 that the position estimate error in the Z-direction is much larger than the other two directions, which is also concerned with the geometrical configuration of the libration point satellite navigation system. Similar simulations are also conducted for the other candidate Earth-Moon L _1,2,4,5 four-satellite constellations and the final results of RMS state estimate error and maximum state estimate error are summarized in Table 5.

Figure 5. Position estimate error for the lunar orbit phase using the EKF.

Figure 6. Velocity estimate error for the lunar orbit phase using the EKF.

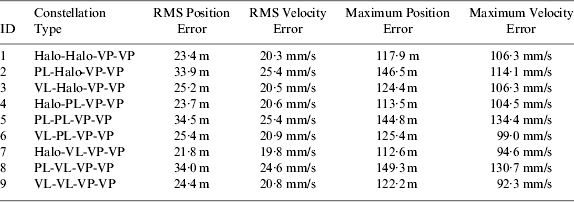
Table 5. Lunar orbit navigation performance of the candidate Earth-Moon L _1,2,4,5 four-satellite constellations.

Similar to the trans-lunar cruise phase, the lunar orbit navigation performance is also sensitive to the orbit of the L ₁ navigation satellite. When the L ₁ navigation satellite is located in the Halo orbit or vertical Lyapunov orbit (that is, the ID=1, 3, 4, 6, 7, 9 constellations), the navigation performance is always better, with the RMS position error about 23 m and the RMS velocity error about 20 mm/s. But when the orbit of the L ₁ navigation satellite is changed to the planar Lyapunov orbit (that is, the ID=2, 5, 8 constellations), the lunar orbit navigation performance gets worse, with the RMS position error about 34 m and the RMS velocity error about 25 mm/s. Besides that, the maximum state estimate error is also larger for the latter case. Therefore, we can come to the conclusion that the proper Earth-Moon L _1,2,4,5 four-satellite constellations for cislunar navigation are the ones with the L ₁ navigation satellite locating in Halo or vertical Lyapunov orbits.

6. CONCLUSIONS

In this paper, a virtual lunar exploration mission scenario is developed to verify the cislunar navigation performance of the candidate Earth-Moon L _1,2,4,5 four-satellite constellations proposed in our previous work. The results indicate that the navigation accuracy of a few tens of metres can be achieved for both the trans-lunar cruise and lunar orbit phase. In particular, the Earth-Moon L _1,2,4,5 four-satellite constellations with the L ₁ navigation satellite locating in Halo orbits or vertical Lyapunov orbits are more suitable for cislunar navigation. Consequently, the proposed libration point satellite navigation system could be available for cislunar navigation and perhaps play an important role in future lunar exploration missions. The navigation performance of our proposed libration point satellite navigation system for Mars explorations will be considered in the following work.