Experiences of early assessment to teach functional programming

Abstract

This paper reports on the experiences of using an early assessment intervention, specifically employing a Use-Modify-Create scaffold, to teach first-year undergraduate functional programming. The particular intervention that was trialled was the use of an early assessment instrument, in which students had to use code given to them, or slightly modify it, to achieve certain goals. The intended outcome was that the students would thus engage earlier with the functional language, enabling them to be better prepared for the second piece of assessment, where they create code to solve given problems. This intervention showed promise: the difference between a student’s score on the Create assignment improved by an average of 9% in the year after the intervention was implemented, a small effect.

1 Introduction

Teaching programming is seen as difficult, and indeed studies suggest that “most students who take [introductory computer science modules] do not learn the content of [them]” (Guzdial, 2015). Functional programming is a paradigm taught at many Universities and is one which students generally find difficult (Joosten et al., 1993; Chakravarty & Keller, 2004). The later stages of the COVID pandemic (namely the academic year 2021–2022) has also seen, worldwide, a lack of engagement from higher education students on their studies (Williams, 2022). Low engagement on a difficult problem (programming), especially an even more difficult subproblem (functional programming), could be deletrious to student achievement. A number of techniques have been proposed to increase student engagement, with the focus of this paper being on the use of assessment tasks. The particular assessment tasks were designed using the Use-Modify-Create (UMC) framework of Lee (Lee et al., 2011), which has been extensively studied in the context of pre-University students and computational thinking. In this paper, we report on the redesign of the summative assessment of a functional programming module, and the effects it had on student attainment, as measured by grades.

2 Background and related work

There are three strands to this current work: the use of summative assessment as an engagement tool; the utilization of a UMC paradigm in teaching; and the teaching of functional programming. All three topics have been covered in the literature, and in this section we will briefly cover the salient points related to each.

Assessment is a key part of learning and the student experience. As Ramsden (Ramsden, 2003) says, “assessment always defines the actual curriculum.” In Boud et al. (2010), it is noted that assessment is “designed to focus students,” “used to engage students,” and “plays a key role in fostering learning.” Moreover, assessment for learning should be present in curriculum design, not just as an afterthought. Holmes (2018) agrees, noting that “many students are assessment driven”, and that “assessments should be designed to help students […] to engage with their studies.” Holmes goes further, stating that increased engagement can be achieved through “careful design and development of the assessment scheme.” This sentiment is also found in Rust (2002), who notes that “students are only seriously engaging with a module […] when they are being assessed.”

It is one thing to encourage engagement, but it is better if this increased engagement leads to an improvement in grades. On this point, Knight (2010) notes that “regular engagement is associated with higher final marks.” Further, dos Santos et al. (2024) found that allowing students repeated attempts at formative quizzes meant that “many students improv[ed] from almost failing to good-to-excellent grades.” Linking the use of intermediate assessment to final marks, van Gaal & de Ridder (2013) found that students’ achievement on a final examination was better when intermediate assessment tasks were used. It is clear, then, that redesigning a module, using intermediate assessment tasks, is a fruitful avenue for investigation. The design of this intermediate assessment task must be carefully considered, however.

The UMC framework was introduced in Lee et al. (2011), to promote computational thinking. The focus of this original paper was on primary and secondary education (K-12). Most research on UMC has been on this context. For example, Lytle et al. (2019) found that 11–12-year-old students in a UMC group were able to complete tasks more quickly than those in a control group, and moreover self-reported the tasks as being easier. The authors posit that the use of the framework limits the thoughts students might have of work being “too hard.” Similarly, Franklin et al. (2020) found that, for a group of 9–14-year-olds, UMC led to engagement with the content. They found, in particular, that the “use-modify activities within the curriculum promoted student learning.” In higher education, Song (2017) found that the “use-modify-create framework […] resulted in effective learning outcomes” in the case of non-computer science pre-service teachers. The application of UMC as part of the assessment is thus motivated for higher education computer science students. How UMC is designed for the specifics of functional programming, however, needs to be examined.

Several articles give insight into the teaching experiences of academics when teaching functional programming in higher education. Joosten et al. (1993) advises that flexibility be taught: students should be able to define functions in “several different ways, for example recursively, with list comprehension, or with standard functions.” This observation was based on a five-year experiment to introduce functional programming into the first year of an undergraduate curriculum. In particular, it arose from the appreciation of students that the types and formal specification were more important than the implementation of the function itself. For Hughes (2008), the most important aspect was motivation. There should be a focus on “real programming,” allowing students to build their own interesting programs early. As he observes, students “are not a priori motivated to learn an obscure language in an obscure paradigm”; in the case of Hughes (2008), as in the module described in this paper, the language was Haskell. This view, that motivation is key for teaching computer science (not just functional programming), is found in Guzdial (2015). Learner-centered design is the idea that activities should be designed “by learning what will motivate [the student].” When specifically applied to teaching computer science students, Guzdial (2015) suggests that peer instruction, pair programming, worked examples, and games are potential ways to motivate computer science students. The work of Canou et al. (2017) focusses, like this paper, on the assessments themselves. In that paper, the context was slightly different, being a massively open online course in functional programming. The focus of Canou et al. (2017) was the development of a testing environment which would allow instant feedback on exercises, coupled with the ability for students to re-attempt exercises many times. This approach has showed great promise, with around 25% of 3,000 enrolled students (this is a MOOC) completing every exercise. Ramsey (2014) gives the experience of implementing and extending the How to Design Programs process of Felleisen et al. (2018). As noted by Ramsey, the goal was to “teach programming students how to solve problems using the computer; […] functional programming is a means, not an end.” The design process is broken down into eight steps, giving a clear scaffold for students to follow. There are also mistakes to avoid in teaching, and “where [students] do and don’t struggle in learning.” Students do not generally struggle with writing test cases but did struggle with recursion. As noted in section 3, introducing recursion effectively is one of the goals of the intervention described in this paper.

The use of flipped classrooms and blended learning, which has become widespread during the COVID pandemic, is the focus of Isomöttönen & Tirronen (2016) (although this paper pre-dates the pandemic). While promising, the authors note that their approach “requires active participation on the part of the students.” It is the lack of participation, that is, the focus of this paper. Finally, the work of Hameer & Pientka (2019), while ostensibly about the use of automatic grading to teach functional programming, contains some elements of the UMC framework. They report on requiring students to use particular higher-order functions (namely map, filter, etc.) in the solution of some problems. However, the problems themselves are still, effectively, create problems, but with a restriction on what tools can be used in creating solutions. More broadly, there is a wide body of literature on assessment practices in computer science. Becker & Quille (2019) note that, in the 50 years of the Special Interest Group on Computer Science Education (SIGSCE), there were 40 papers presented on Assessment, specifically in CS1 courses. “Learning & Assessment” is now the second most common theme for research papers (behind only “Students”), up from the seventh most common theme in the 1980s. Of particular relevance is the approach of Silva et al. (2020), where the exact timing students undertook an exam was found to have minimal increase in grades. During the COVID pandemic, many institutions moved to the asynchronous practices explored in Silva et al. (2020). ¹ Finally, the trends which interest researchers in computer science education is covered in Becker & Quille (2019).

3 Context and intervention

In this section, we describe the module, the (formative and summative) assessments, and the particular form of the intervention. The module is studied over one semester, by first-year undergraduate students (typically 18–19 years old, although a small number of mature students are enrolled). The purpose of the module is to teach the basics of discrete mathematics (propositional logic, set theory, permutations and combinations, basic probability, and basic number theory) as applied to examples from computing. In conjunction, the module also serves as an introduction to functional programming, using the language Haskell. In particular, a goal of the programming part of the module is to introduce students to recursion. There were two kinds of assessment in the module: formative (assessment for learning, i.e., that work which is optional for the student but would be beneficial to undertake) and summative (assessment of learning, i.e., that assessment which determines the final grades of the students). The intervention described in this section only affects the summative assessment.

In both years in question (academic years 2020–2021 and 2021–2022), the module was delivered online owing to COVID restrictions in place. Four hours of synchronous sessions were delivered. Pre-recorded lectures were made available to students: the recordings were of the actual lectures from academic year 2019–2020. ² Students were encouraged to watch these lectures before each synchronous session. The synchronous sessions consisted of two 2-hour blocks. In the first, there was an hour of worked mathematical examples, followed by an hour of worked Haskell examples, each set of which was related to the material that was in the pre-recorded lecture. The second 2-hour block was a practical session, where students could complete formative Haskell exercises from a workbook. Student demonstrators (students who had taken the module in previous years) were available in these sessions to aid the module leader in answering student questions. These Haskell workbook exercises did not contribute to the final module mark (i.e., were purely formative), but feedback was given to the students if they asked for help. Solutions were also provided to students to self-assess.

For the practical sessions, students could either download and install their own local version of the Haskell compiler GHC or use the version installed on the University’s application management tool, AppsAnywhere. The formative Haskell workbook exercises followed the UMC paradigm and have done since the academic year 2017–2018. In the earlier exercises, code was given to the students, and they had to answer given questions by using the code in the GHCi interactive environment. In intermediate exercises, code was supplied to students that solved a related problem to that which was given, which they could then modify to achieve the result they wanted. For example, they were provided with the function called exactlyTrueIn:

\[\begin{array}{l}\texttt{exactlyTrueIn :: Int -> [Bool] -> Bool} \\\texttt{exactlyTrueIn n bs = length (filter (==True) bs) == n }\end{array}\]

Students were then tasked with modifying this code so that it produced a function called atLeastTrueIn.

The later exercises gave students a specification for a function and asked them to create a function which met this specification. There were levels of difficulty built-in to this process: the first set of create exercises given had the required patterns in the function definition provided for them. For the last set of exercises, meanwhile, the only thing (other than the specification) provided was the intended type signature. Recall that the exercises in these practical sessions are purely formative: should a student not wish to do them, then there is no penalty applied to their final grade.

The support given for the mathematics part of the module was identical in each year. Briefly, a number of exercises were available for study, along with self-assessment tests using the Numbas system (Perfect, 2015). This systems allows instructors to create templates for mathematics questions and can support complicated grading schemes, whereby partial credit is given should a student require more information to answer a question. It has been shown to be effective for Business students (Carroll et al., 2017) and Computing students (Graham, 2020).

The intervention was the introduction of an early piece of summative coursework, the Use-Modify coursework, which carried a small number of marks. More details on this Use-Modify coursework, and the goals of the intervention, are given in Section 3.1. The summative assessment for the module in the two years (hereafter 2021 and 2022, since the module was delivered from January to May of the given year) is shown in Figure 1, with the intervention in the heavy-lined box. To pass the module, the students were required to achieve at least 30% in the maths test; at least 30% in the combined coursework scores (or just the Create coursework in 2021); and to have a weighted average of at least 40% for the maths and coursework scores. If they failed to reach the required marks, then they had to undertake reassessments to progress with their studies. Only the results of the first attempts are described in this paper.

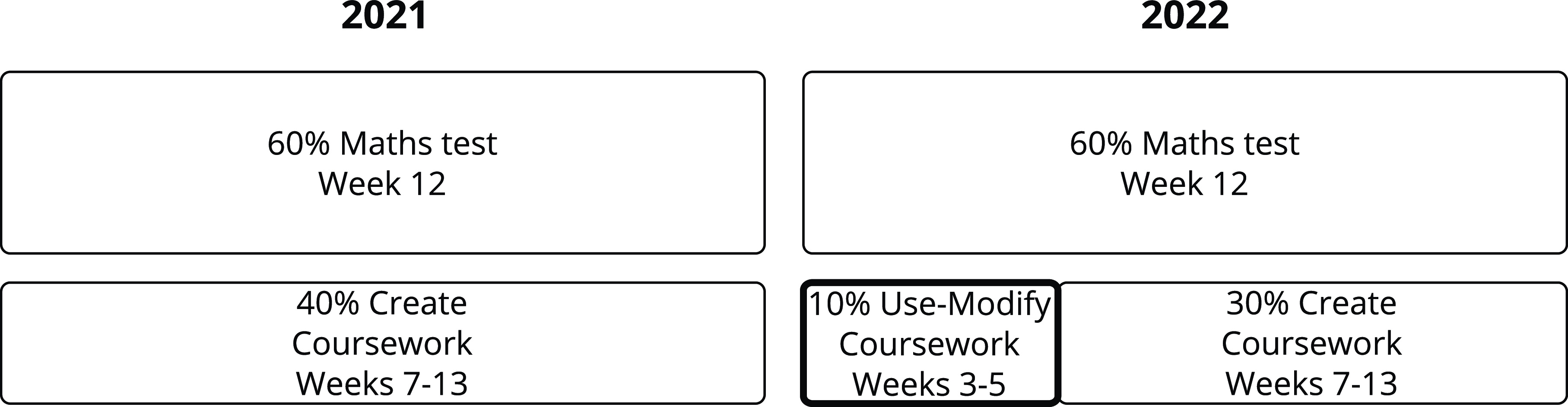
Fig. 1. Summative assessment: The difference between the two deliveries is the introduction of the Use-Modify coursework.

Both 2021 and 2022 made use of a Create coursework, which formed the large part of the coursework mark. This consisted of similar exercises to the last ones from the practical workbook: a specification for a function was given, along with a type signature and some sample input/output pairs. An example question (from 2021) is given below:

Write a function (bigUnion) which, given a list of lists $A, B, C, \ldots$ , returns the union of all of them. As an example,

\[\texttt{bigUnion [[a,b,c],[c,d,e],[f,g,c]]}\]

would return [a,b,c,d,e,f,g]. The order of the elements in your resulting list is not important. The student was also given the type signature, in the above example:

\[\texttt{bigUnion :: (Eq a) => [[a]] -> [a]}\]

and the sample input/output pairs:

\[\begin{array}{l}\texttt{bigUnion [[1,2,3],[3,4,5],[2,4,6,8]] = [1,2,3,4,5,6,8]} \\\texttt{bigUnion ["list a", "list b"] = "list ab"}\end{array} \]

along with a reminder that the order of the elements in the resulting list was not important.

For each question, there were five test cases (details on the determination of the test cases is given in Section 3.2). Students achieved marks for each test which achieved the correct answer. This allowed students freedom to implement their solution; however, they wanted and felt able to. For example, a solution using inbuilt functions (such as map, filter, and foldl) would be worth just as much as a solution which more directly used recursion and different clauses. As such, this matches the advice in Joosten et al. (1993).

In 2022, there was no requirement to achieve a particular score in either the Use-Modify coursework, or the Create coursework. All that mattered was that the combined score achieved 30%. Given the timings of the various assessments, in both years students were aware, by the time the Create coursework was due, what mark they needed in order to pass the module. For the majority of students, this score was 30% (in 2021) or slightly lower (in 2022, after having gained marks in the Use-Modify coursework). There are more details on this last point in Section 4.

3.1 Intervention

The Use-Modify coursework ³ consisted of 10 questions: five of which were questions requiring students to use code given to them, and five which required students to modify code given to them. Students were provided with a Haskell file and had to replace the definitions of functions with their own. For example, a Use question appeared in the coursework file as:

The functions q2, gB, and mP were intentionally obfuscated, as the aim of the question was to get students to use code, without necessarily needing to know how it worked. Code which produced list2 was provided at the bottom of the file. (The string itself was 300 characters long.) In a synchronous session when the coursework was handed out, it was explained that either the answer itself (in this case the space character ’ ’) could be provided, or the code which would generate it (namely q2 list2). The student solutions were then checked against the correct answer, and marks awarded if they matched.

The modify questions were of a similar format to the modify questions in the workbook. Sample output for a correct modification was provided, similar to the Create coursework. As an example, this was question 6, as it appeared in the coursework file provided to students:

If students did not wish to attempt question 6, they would just leave the code unchanged. As with the Create coursework, these solutions were marked via test cases, in this case only three. This meant students did not need to modify the code, they could create their own solution. However, the most straightforward approach was to modify the given code. The marking methodology for both the Modify and Create coursework questions is given in Section 3.2.

The goal of the intervention was to encourage engagement with the Haskell programming exercises, to ensure students were properly prepared for the Create coursework. In previous years, it was noted that a minority of students did not even begin the practical exercises until the Create coursework was handed out, and in extreme cases until not long before the Create coursework was due. Indeed, it was not unusual that students attempted to solve the Create coursework problems without having first attempted any practical exercises. This approach caused the students to struggle, especially since the practical exercises contained similar types of problems, and also developed a number of functions which would be useful in the Create coursework. In other words, using the UMC paradigm in purely formative exercises did not appear to be preparing all students for the summative Create coursework, and so an early summative assessment in the UMC paradigm was used as a summative tool as well.

3.2 Marking methodology

We briefly explain the process by which test cases were determined for both the Modify and Create questions, and how submissions were graded. As noted in Sections 3 and 3.1, student code was evaluated on specific test inputs, where the output was known. These test inputs were determined by the lecturer to cover edge cases (where the behavior of the function changes significantly) and normal-use cases. As an example of the former, where the function input was a list, then the empty list would be one of the test cases. Other edge cases were numerically based. For example, in one instance a (modify) question asks students to provide a function that “takes the numbers in a list strictly greater than 11 and less than or equal to 30, squares them, and adds 1.” One test case then involved a list which contained numbers both above and below the bounds of the question. A normal-use case, meanwhile, was a list that contained numbers that are only within the range specified.

All student submissions were tested against the same set of cases. The differences in student scores, then, should reflect only the differences in student aptitude, not the peculiarities of particular numerical inputs.

The submissions were marked automatically. A (bash) script was created that would append and prepend some needed functions (e.g., functions that would be able to check equality of lists up to re-ordering) and the test cases, and then compile and run each file. The output of running the file was a sequence of scores, written to a csv file. If the student submission failed to compile, or exceeded a two-minute time-out, ⁴ then the file moved to another folder for inspection. The students were made aware of this time-out, and it was necessary to identify non-terminating, rather than inefficient but functionally correct, code. For example, using a left-fold on an infinite list.

Each file that did not compile, or timed-out, was examined, and the problematic code identified. More often than not, it was because a student had deleted, or commented out, a function from the file as an indication of their non-attempt, rather than just leaving the placeholder code alone. Less frequently, there were issues with the student’s functions itself; in such instances, the student’s answer was commented out and replaced by the placeholder code. Students were informed before submission that this would happen. The non-compiling files were then passed through the marking script again, with further amendments made until each file compiled and executed within the time constraint.

The initial csv file with scores was now discarded, and the full set of files (all of which now compile and execute in under two minutes) were passed through the marking script again, to produce a set of scores. This process was repeated twice, and the scores from each run were checked for discrepancies. There were none, and so this set of scores formed the basis for the student grades, which are discussed in the next section.

4 Results and discussion

In this section, we present an analysis of the results of the intervention. ⁵ As noted in Section 3, two scores were recorded for each student: their score on the (unchanged) mathematics test, and their score on the equivalent pieces of Haskell coursework, that is, the Create coursework. There were 78 students who attempted both assessments in 2021 (the year before the intervention), and 40 who attempted both assessments in 2022 (the year of the intervention). The mean for each of these scores can be seen in Table 1. The data are visualized in Figure 2, using a violin plot. As can be seen, the distribution of maths scores is similar in both years, albeit with a lower mean in 2022. The Create coursework distribution, meanwhile, is more uniform in 2022, whereas there was a bias toward scores around 40 in 2021. The coursework score distribution is normal in 2021 (Shapiro–Wilk normality test, p-value $= 0.1447$ ), whereas in 2022 the distribution is not normal ( $p=0.0009$ ). Given this, it is conservative to use the non-parametric Wilcoxon test, rather than a t-test, to perform hypothesis testing.

Table 1 The p-values are for one-tailed Wilcoxon tests

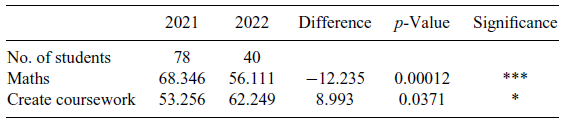
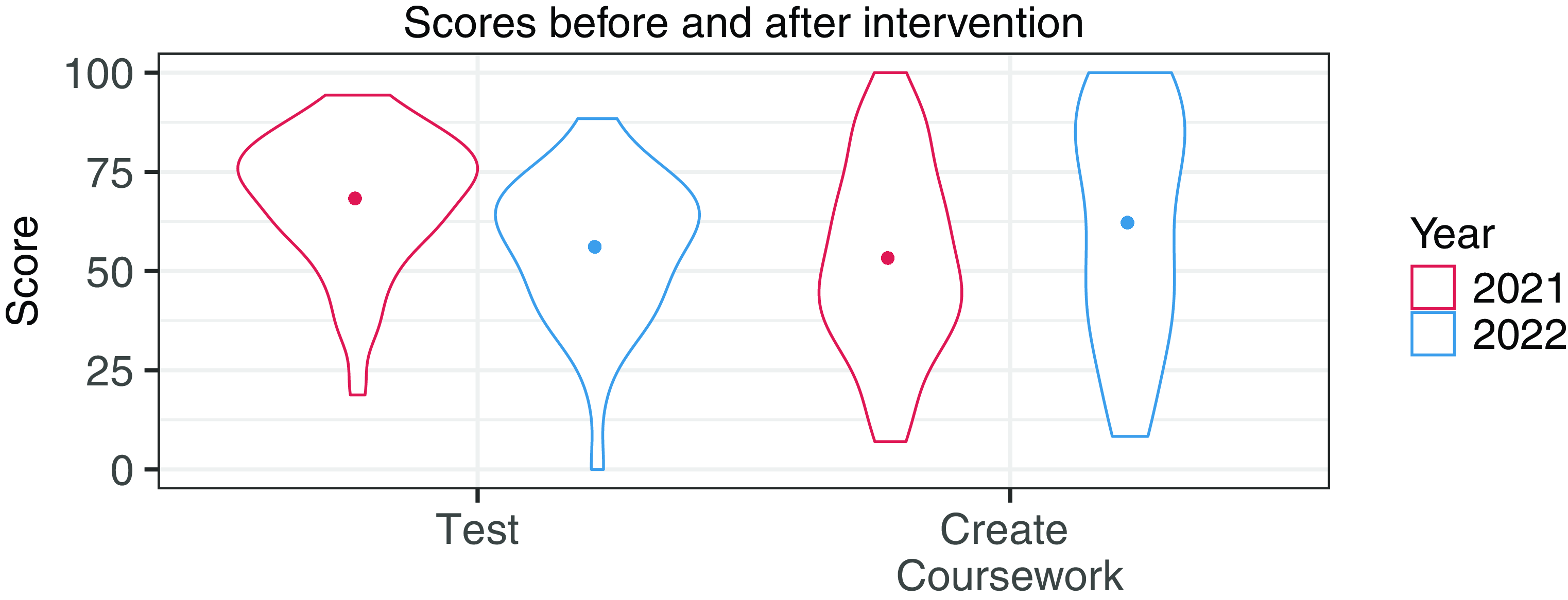
Fig. 2. The dots represent the means for each category.

We can see that maths scores declined between the years by just over 12%, which is significant. Similarly, the Create coursework scores improve by around 9%, which is significant. For the Create coursework, this yields an effect size (Wilcoxon Effect Size) of $0.164$ , which is small (Sawilowsky, 2009). In other words, the intervention appeared to have the intended effect: the students were better prepared for the Create coursework, as evidenced through better achievement on it.

The focus of this paper is on an intervention to improve Haskell engagement, as measured by scores. We now address the validity of this instrument of assessment. As noted earlier, the scores for the Create coursework are not normal. Thus, the typical measure of validity (Cronbach’s $\alpha$ ) is not applicable. Instead, we use Guttman’s $\lambda_4$ to assess validity. For these data, $\lambda_4 = 0.86$ , which demonstrates high reliability (Cohen et al., 2002). For small sample sizes (under 1,000), $\lambda_4$ has been shown to approximate the greatest lower bound well (Oosterwijk et al., 2016). 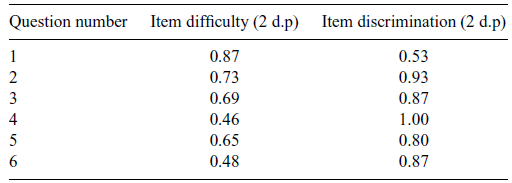Further, when the validity is above $0.8$ , $\lambda_4$ is less likely to overestimate the true validity (Benton, 2015). In addition to the validity of the whole coursework, item discrimination analysis was performed. The students in the upper and lower quartiles were identified, and their performance on each question was compared. There were six questions for students to complete. Table 2 shows the (normalized) item difficulties and the item discrimination indices. The item difficulties are simply the average score achieved by students on that question.The lowest discriminating question, question 1, is still providing good discrimination (Ebel, 1954), and the fourth question provides perfect discrimination. ⁶ With this particular question, the lowest ranking students did not attempt it. In summary, the coursework contained a reasonable range of difficulties and showed good discrimination. The first question was designed to be accessible (reflecting the difficulty score), in order that weaker students were not immediately discouraged from attempting the coursework.

Table 2 Item analysis for the Create coursework

We now examine other possible reasons for the improvement in coursework scores. As mentioned in Section 3, the module ran online in both years. Synchronous sessions were recorded in both years, too. In particular, in 2022 the recordings of both synchronous maths and Haskell example sessions from 2021 were made available to students. The 2022 students thus had a corpus of worked video examples larger than the 2021 students. ⁷ In of itself, this could explain the improved Create coursework scores. An analysis of the viewing statistics, however, shows that while the recordings from 2021 were available to the students in 2022, the later students did not avail themselves of the recordings. For example, arguably the most useful recording from 2021 is that of a extended worked example of a Create coursework question. Thirty-seven students partially viewed this recording in 2022. But, of those 37, the median viewing time for the 75 minute video was 3 minutes and 17 seconds. Only four students watched for more than 30 minutes, and only one watched the entire video.

Another possibility was that the assessments varied in difficulty between years. Both Create courseworks were prepared by the same academic, with seven years experience writing assessments on this particular module. The other pair of consecutive years which were most directly comparable with each other was 2018 and 2019. These years were both pre-COVID restrictions, and there were no substantive changes to the module between them. The Create coursework scores in these instances of the module differed by less than 1%. Further, the same internal moderator (a colleague who performs quality assurance on summative assessments before they are presented to students) did not raise any concerns about a change in difficulty between the cohorts. It is more plausible, then, that the assessments were of similar difficulty, rather than one being easier to create an increase of 9% between years.

A final possibility is that those who were not engaged in the module simply did not complete the module. In 2021, there were 78 submissions from a cohort of 88 students. Meanwhile, in 2022, there were 40 students who submitted both courseworks, from a cohort of 61. A further seven students completed the Use-Modify coursework, but not the Create coursework. It is plausible that the higher rate of completion in 2021 may have caused a poorer relative performance on the coursework. In particular, that an unengaged student still attempted all of the assessments in 2021, but the low engagement affects the coursework mark more than the test mark. The functional programming aspect, in contrast with the mathematics material, is something that very few students will have been exposed to in their pre-University education. There is then no prior knowledge to fall back on. In 2022, meanwhile, the early Use-Modify coursework may have caused these students to disengage with the module completely at an early stage, and not complete the remainder of the assessments. In other words, in this case, the early coursework has the effect of removing the least engaged students from the module. There is no evidence to suggest this is the case: other modules taken by the same cohort show a similar low completion rate in 2022 relative to 2021, and there were no changes to these modules between years.

Indeed, there may be reasons to believe that the improvement in engagement is actually more pronounced than the score difference suggests. Recall from Section 3 that the students know, by the time of the Create coursework submission deadline, what mark they need to achieve in order to pass the module. In 2021, as in years prior to that, owing to good performance on the maths test, this mark was 30% for the majority of students. It was clear from looking at marksheets for the Create coursework submissions that a number of students only even attempted around half of the coursework. In other words, they were just trying to get enough to pass the module, and, with little engagement in the Haskell material thus far, aimed only for the easiest marks. One of the concerns when introducing the Use-Modify coursework was that it could excacerbate student’s low goals: by already awarding marks it would mean that the mark needed on the Create coursework would drop. The mean score on the Use-Modify coursework was $76.2\%$ , which meant that, for most students, they only required around 16% on the Create coursework to pass the module. In light of this, that the Create coursework scores increased at all is somewhat surprising. It would appear then, that the use of early summative assessment increased engagement in the Haskell material to such an extent that students actually wanted to perform well in the Create coursework, despite them not needing to.

We must also address the fall in mathematics scores between the cohorts. There are two plausible explanations for this drop. First, that the 2022 cohort just had weaker mathematical skills relative to the 2021 cohort. The 2022 cohort, as it has progressed to second year, has had higher than usual failure rates for other modules, suggesting they are not as prepared for University study. In the UK (where the majority of the undergraduate students in the report study come from), national examinations in 2020 and 2021 were canceled, meaning that University admissions were made on the basis of high school teacher recommendations. There is some evidence that the 2022 cohort (who studied their entire final high school year under COVID restrictions) have been adversely affected by these restrictions (Azevedo et al., 2021). The 2021 cohort, meanwhile, had only one term of COVID restrictions.

Second, engagement dropped in mathematics in 2022 for some reason. As noted earlier, the 2022 cohort had lower completion rates than the 2021 cohort for their other modules, suggesting low engagement across the year as a whole. However, it could also be that the intervention aimed at increasing engagement with functional programming was successful to the extent that engagement with mathematics dropped as a result: students diverted their attention from mathematics to Haskell.

Unfortunately, owing to teaching team changes, in 2023 the mathematics part of the module was delivered by a different person than the preceding 8 years, while the functional programming part retained the same staff member. Thus, comparisons between 2022 and 2023 will have additional variances; it may not be possible to identify what explains the fall in mathematics scores from 2021 to 2022.

5 Conclusions and future work

In this paper, we presented the results of an intervention in a first-year University functional programming module. The particular intervention was the introduction of an early, low-stakes summative assessment task. The task was designed by leveraging the UMC framework: namely, the early assessment task was Use-Modify. The scores for a mathematics test and the final, Create coursework were measured for the two cohorts: before the intervention and after. The cohort after the intervention saw both an improvement in their Create coursework scores, but a drop in the mathematics test scores. This improvement in coursework suggested that the early assessment task had its intended effect: to encourage students to engage with the functional programming aspect of the module, and so were better prepared for the Create coursework.

These results are aligned with what can be found in the literature, but in the specific context of University functional programming instruction. In particular, the use of an early assessment task improved final outcomes (as seen in Van Gaal & De Ridder, 2013, for economics students) and the use of the UMC framework improved students’ learning (as seen in Franklin et al., 2020 for 9–14-year-olds). The assessment scheme in this paper also complements the literature on teaching functional programming, which has ranged from pedagogy (e.g., Isomöttönen & Tirronen, 2016) to specifics about language and syntax (e.g., Tirronen et al., 2015 and Chakravarty & Keller, 2004).

Further refinement of the assessment regime can be investigated. The initial idea was to have three separate tasks: a Use task, a Modify task, and the final Create task. However, the risk of over-assessment of students, and marking and administrative burden on staff, led to the pragmatism of the regime reported here. While it was successful, there are no guarantees that other versions may make it more effective.