Planning in BDI agents: a survey of the integration of planning algorithms and agent reasoning

Abstract

Agent programming languages have often avoided the use of automated (first principles or hierarchical) planners in favour of predefined plan/recipe libraries for computational efficiency reasons. This allows for very efficient agent reasoning cycles, but limits the autonomy and flexibility of the resulting agents, oftentimes with deleterious effects on the agent's performance. Planning agents can, for instance, synthesise a new plan to achieve a goal for which no predefined recipe worked, or plan to make viable the precondition of a recipe belonging to a goal being pursued. Recent work on integrating automated planning with belief-desire-intention (BDI)-style agent architectures has yielded a number of systems and programming languages that exploit the efficiency of standard BDI reasoning, as well as the flexibility of generating new recipes at runtime. In this paper, we survey these efforts and point out directions for future work.

1 Introduction

For a long time, agent programming languages have generally avoided the use of first principles planning approaches due to the high computational cost of generating new plans/recipes¹. Indeed, languages based on the popular belief-desire-intention (BDI) (Bratman, 1987) agent model have relied on using predefined recipes rather than on planning from scratch. This style of agent programming language has been widely used in the implementation of both academic (e.g., Bordini et al., 2007) and commercial interpreters (e.g., Busetta et al., 1999). With advances in logic-based planning algorithms (Kautz & Selman, 1996; Blum & Furst, 1997) and Hierarchical Task Network (HTN) planning (Nau et al., 1999), there has been a renewed interest in the application of planning to BDI agents. Consequently, a number of BDI architectures and agent programming languages have been proposed with the ability to use planners to either generate new recipes from scratch (e.g., Despouys & Ingrand, 1999; Meneguzzi et al., 2004b) or to guide recipe selection (e.g., Sardiña et al., 2006).

One of the key differences among BDI agent programming languages is the way in which goals are represented and processed by an agent. In one class of such languages, agent behaviour is geared towards carrying out predefined hierarchical plans under the assumption that once the plan is fully executed the agent has accomplished the associated goal. This type of agent behaviour is closely related to HTN planning (Nau et al., 1999) and typifies the notion of goals-to-do or procedural goals (Winikoff et al., 2002), widely used in agent programming languages due to its efficiency. In the other class of agent programming languages, agents reason explicitly about the state of the environment, and carry out plans to reach certain desired states. Reasoning towards achieving these goals is associated with classical STRIPS (Fikes & Nilsson, 1971), planning, and typifies the notion of goals-to-be or declarative goals (Winikoff et al., 2002). A small subset of agent languages, for example 3APL (Dastani et al., 2004), is actually capable of reasoning about goals-to-be without relying on first principles planning.

The inclusion of a planning capability substantially increases the autonomy of a BDI agent and exploits the full potential of declarative goals. For example, when there is no applicable plan for achieving a goal at hand, an agent may consider synthesising a new plan to achieve it, or to achieve some other relevant plan's precondition for the purpose of making it applicable (de Silva et al., 2009).

Planners vary significantly in the representations they use, the algorithms that solve them, and the way in which results are represented (Meneguzzi et al., 2010). Planning techniques also differ in the assumptions they make about the environment, in terms of the outcome of actions as well as the observability of the state of the world (desJardins et al., 1999). This same set of assumptions applies to the environments in which autonomous agents operate. Virtually all interpreters of BDI programming languages assume a fully observable² environment and a non-deterministic transition model³. There is, however, some initial work in bridging the gap between BDI agents and probabilistic planning techniques (Simari & Parsons, 2006).

In this paper, we survey techniques and systems aimed at integrating planning algorithms and BDI agent reasoning. We focus in particular on describing planning BDI architectures algorithmically using a common vocabulary and formalism to allow the reader to compare and contrast their inner mechanisms. Academic literature employs a variety of formalisms to describe the operation of agent architectures and programming languages, ranging from pure logic (e.g., Móra et al., 1999), specifications using formal semantics (e.g., Rao, 1996; d'Inverno et al., 1998; Hindriks et al., 1999; Sardiña & Padgham, 2011) to imperative programming languages (e.g., Walczak et al., 2006). In this paper, we follow the tradition of BDI logic (Rao, 1996) to describe a generic BDI programming language, given its wide adoption throughout the community. The semantics of this language is then given through a basic agent interpreter defined using algorithms in structured English, in the tradition of the planning literature (Ghallab et al., 2002). This allows us to examine how planning is integrated into the basic BDI interpreter, and to compare and contrast different approaches to planning in BDI systems. The paper is organised as follows. Section 2 lays out the formal foundation of planning required for the paper. In Section 3 we define an abstract agent interpreter strongly influenced by modern agent programming languages. We then follow with sections surveying architectures based on different notions of planning: Section 4 focuses on architectures integrated with declarative planners; Section 5 focuses on architectures integrated with procedural planners; and Section 6 offers insights into the potential integration of probabilistic planners into BDI agent architectures. Finally, in Section 8, we conclude the paper with future directions for research in integrating planning algorithms with BDI agents.

2 Background

In this section, we establish a common formal framework to compare the different approaches to planning within BDI agent languages. To this end, we first introduce in Section 2.1 some notation and definitions often used in the planning and agent programming literature, and then use these definitions for the formalisation of planning problems in Section 2.2.

2.1 Logic language

We use a first-order logic language consisting of an infinite set of symbols for predicates, constants, functions, and variables, obeying the usual formation rules of first-order logic. We start with the following basic definitions.

Definition 1 (Term)A term, denoted generically as τ, is a variable w, x, y, z (with or without subscripts); a constant a, b, c (with or without subscripts); or a function $$\[--><$>f({{\tau }_0},\, \ldots \,,{{\tau }_n})<$><!--$$ , where f is a n-ary function symbol applied to (possibly nested) terms $$\[--><$> {{\tau }_0},\, \ldots \,,{{\tau }_n} <$><!--$$ . □

Definition 2 (Formula)A predicate (or a first-order atomic formula), denoted as ϕ, is any construct of the form $$\[--><$> p({{\tau }_0},\, \ldots \,,{{\tau }_n}) <$><!--$$ , where p is an n-ary predicate symbol applied to terms $$\[--><$> {{\tau }_0},\, \ldots \,,{{\tau }_n} <$><!--$$ . A first-order formula Φis recursively defined as $$\[--><$> {{\rPhi }}::= \,{{\rPhi }}\, \wedge \,{{\rPhi ^{\prime}}}|\neg {{\rPhi }}|\varphi <$><!--$$ . □

We assume the usual abbreviations: $$\[--><$> {{\rPhi }}\, \vee \,{{\rPhi ^{\prime}}} <$><!--$$ stands for $$\[--><$> \neg (\neg {{\rPhi }}\, \wedge \,\neg {{\rPhi ^{\prime}}}) <$><!--$$ ; $$\[--><$> {{\rPhi }}\, \rightarrow \,{{\rPhi ^{\prime}}} <$><!--$$ stands for $$\[--><$> \neg {{\rPhi }}\, \vee \,{{\rPhi ^{\prime}}} <$><!--$$ and $$\[--><$> {{\rPhi }}\, \leftrightarrow \,{{\rPhi ^{\prime}}} <$><!--$$ stands for $$\[--><$> ({{\rPhi }}\, \rightarrow \,{{\rPhi ^{\prime}}})\, \wedge \,({{\rPhi ^{\prime}}}\, \rightarrow \,{{\rPhi }}) <$><!--$$ . Additionally, we also adopt the equivalence $$\[--><$> \{ {{{{\rPhi }}}_{\rm{1}}},\, \ldots \,,{{{{\rPhi }}}_n}\} \, \equiv \,({{{{\rPhi }}}_{\rm{1}}}\, \wedge \, \cdots \, \wedge \,{{{{\rPhi }}}_n}) <$><!--$$ and use these interchangeably. In our mechanisms we use first-order unification (Fitting, 1990), which is based on the concept of substitutions.

Definition 3 (Substitution)A substitution σ is a finite and possibly empty set of pairs $$\[--><$> \{ {{x}_1}/{{\tau }_1}, \ldots, {{x}_n}/{{\tau }_n}\} <$><!--$$ , where $$\[--><$> {{x}_1}, \ldots, {{x}_n} <$><!--$$ are distinct variables and each τ_i is a term such that $$\[--><$> {{\tau }_i}\, \ne \,{{x}_i} <$><!--$$ .□

Given an expression E and a substitution $$\[--><$> \sigma \, = \,\{ {{x}_1}/{{\tau }_1},\, \ldots, \,{{x}_n}/{{\tau }_n}\} <$><!--$$ , we use Eσ to denote the expression obtained from E by simultaneously replacing each occurrence of x_i in E with τ_i, for all $$\[--><$> i\, \in \,\{ 1,\, \ldots, \,n\} <$><!--$$ .

Unifications can be composed; that is, for any substitutions $$\[--><$> {{\sigma }_1}\, = \,\{ {{x}_1}/{{\tau }_1},\, \ldots, \,{{x}_n}/{{\tau }_n}\} <$><!--$$ and $$\[--><$> {{\sigma }_2}\, = \,\{ {{y}_1}/{{\tau ^{\prime}}_1},\, \ldots, \,{{y}_k}/{{\tau ^{\prime}}_k}\} <$><!--$$ , their composition, denoted as $$\[--><$> {{\sigma }_1}\, \cdot \,{{\sigma }_2} <$><!--$$ , is defined as $$\[--><$> \{ {{x}_1}/({{\tau }_1}{{\sigma }_2}),\, \ldots \,,{{x}_n}/({{\tau }_n}{{\sigma }_2}),{{z}_1}/({{z}_1}{{\sigma }_2}),\, \ldots \,,{{z}_m}/({{z}_m}{{\sigma }_2})\} <$><!--$$ , where $$\[--><$> \{ {{z}_1},\, \ldots, \,{{z}_m}\} <$><!--$$ are those variables in $$\[--><$> \{ {{y}_1},\, \ldots, \,{{y}_k}\} <$><!--$$ that are not in $$\[--><$> \{ {{x}_1},\, \ldots, \,{{x}_n}\} <$><!--$$ . A substitution σ is a unifier of two terms τ ₁, τ ₂, if $$\[--><$> {{\tau }_1}\sigma \, = \,{{\tau }_2}\sigma <$><!--$$ .

Definition 4 (Unify Relation)Given terms τ₁, τ₂ the relation unify $$\[--><$> ({{\tau }_1},{{\tau }_2},\sigma ) <$><!--$$ holds iff $$\[--><$> {{\tau }_1}\sigma \, = \,{{\tau }_2}\sigma <$><!--$$ for some substitution σ. Moreover, unify $$\[--><$> (p({{\tau }_0},\, \ldots \,,{{\tau }_n}),\,p({{\tau ^{\prime}}_{\!\!\!0}}, \ldots, {{\tau ^{\prime}}_{\!\!\!n}}),\sigma ) <$><!--$$ holds iff unify $$\[--><$> ({{\tau }_i},{{\tau ^{\prime}}_{\!\!\!i}},\sigma ), <$><!--$$ for all $$\[--><$> 0\,\leq \,i\,\leq \,n <$><!--$$ .□

Thus, two terms τ ₁, τ ₂ are related through the unify relation if there is a substitution σ that makes the terms syntactically equal. We assume the existence of a suitable unification algorithm that is able to find such a substitution. Specifically, we assume the implementation has the following standard properties: (i) it always terminates (possibly failing—if a unifier cannot be found); (ii) it is correct; and (iii) it has linear computational complexity.

We denote a ground predicate as $$\[--><$> \bar{\varphi } <$><!--$$ . In our algorithms, we adopt Prolog's convention (Apt, 1997) and use strings starting with a capital letter to represent variables and strings starting with a lower case letter to represent constants. We assume the availability of a sound and complete first-order inference mechanism⁴ that decides if Φ′ can be inferred from Φ, denoted as $$\[--><$> {{\rPhi }}\, \models \,{{\rPhi ^{\prime}}} <$><!--$$ . In line with the equivalence mentioned before, we sometimes treat a set of ground predicates as a formula, or more specifically, as a conjunction of ground predicates. Hence, we will sometimes use the logical entailment operator with a set of ground predicates. Moreover, we assume the existence of a mechanism to determine if a formula Φ can be inferred from a set of ground predicates, and if so, under which substitution; that is, $$\[--><$> \{ {{\bar{\varphi }}_0},\, \ldots \,,{{\bar{\varphi }}_n}\} \, \models \,{{\rPhi }}\sigma <$><!--$$ .

For simplicity of presentation, we refer to well-formed atomic formulas as atoms. Now let Σ be the infinite set of atoms and variables in this language and let Σ be any finite subset of Σ. From these sets, we define $$\[--><$> {\rm{\hat{\brSigma }}} <$><!--$$ to be a set of literals over Σ, consisting of atoms and negated atoms, as well as constants for truth ( $$\[--><$>\top<$><!--$$ ) and falsehood (⊥). We denote the logic language over Σ and the logical connectives of conjunction (∧) and negation (¬) as $$\[--><$> {{{\cal L}}_{\rm{\rSigma }}} <$><!--$$ .

2.2 Planning

Now that the preliminary formalisms have been presented we can discuss the necessary background on automated planning. Automated planning can be broadly classified into domain independent planning (also called classical planning and first principles planning) and domain dependent planning. In domain independent planning, the planner takes as input the models of all the actions available to the agent, and a planning problem specification: a description of the initial state of the world and a goal to achieve—that is, a state of affairs, all in terms of some formal language such as STRIPS (Fikes & Nilsson, 1971). States are generally represented as logic atoms denoting what is true in the world. The planner then attempts to generate a sequence of actions which, when applied to the initial state, modifies the world so that the goal state is reached. The planning problem specification is used to generate the search space over which the planning system searches for a solution, where this search space is induced by all possible instantiations of the set of operators using the Herbrand universe ⁵, derived from the symbols contained in the initial and goal state specifications. Domain-dependent planning takes as input additional domain control knowledge specifying which actions should be selected and how they should be ordered at different stages of the planning process. In this way, the planning process is more focused, resulting in plans being found faster in practice than with first principles planning. Such control knowledge, however, also restricts the space of possible plans.

2.2.1 Planning formalism

In what follows we will, for simplicity, stick to the STRIPS planning language. The input for STRIPS is an initial state and a goal state—which are both specified as sets of ground atoms—and a set of operators. An operator has a precondition encoding the conditions under which the operator can be used, and a postcondition encoding the outcome of applying the operator. Planning is concerned with sequencing actions which are obtained by instantiating operators describing state transformations.

More precisely, a state s is a finite set of ground atoms, and an initial state and a goal state are states. We define an operator o as a four-tuple 〈name(o), pre(o), del(o), add(o)〉, where (i) $$\[--><$> name(o)\, = \,act(\vec {x}) <$><!--$$ , the name of the operator, is a symbol followed by a vector of distinct variables such that all variables in pre(o), del(o) and add(o) also occur in $$\[--><$> act(\vec {x}) <$><!--$$ ; and (ii) pre(o), del(o), and add(o), called, respectively, the precondition, delete-list, and add-list, are sets of atoms. The delete-list specifies which atoms should be removed from the state of the world when the operator is applied, and the add-list specifies which atoms should be added to the state of the world when the operator is applied. An operator 〈name(o), pre(o), del(o), add(o)〉 is sometimes, for convenience, represented as a three-tuple 〈name(o), pre(o), effects(o)〉, where $$\[--><$> effects(o)\, = \,add(o)\, \cup \,\{ \neg l|l\, \in \,del(o)\} <$><!--$$ is a set of literals that combines the add-list and delete-list by treating atoms to be removed/deleted as negative literals. We use effects(o)⁺ to denote the set of positive literals in effects(o) and effects(o)⁻ to denote the set of negative literals in effects(o). Finally, an action is a ground instance of an operator.

The result of applying an action o with effects effects(o) to a state S is a new state S′ in which the positive effects effects(o)⁺ are true and the negative effects effects(o)⁻ are false.

Definition 5 (Function R)The result of applying an action o to a state specification S is described by the function $$\[--><$>R\,:\,{{2}^{{\rm{\hat{\brSigma }}}}} \,\times \,{\bar {{ {\bf O}}}}\, \rightarrow \,{{2}^{{\rm{\hat{\brSigma }}}}} <$><!--$$ , where $$\[--><$> {\bar {{ {\bf O}}}} <$><!--$$ is the set of all actions (ground operators), which is defined as ⁶

$$R(S,o)\, = \,\left\{ \matrix{ {(S\backslash effects{{{(o)}}^{\rm{ - }}} )\, \cup \,effects{{{(o)}}^ + } } \hfill & {if\,\,S\, \models \,pre\,{\rm{(}}o{\rm{)}};} \hfill \cr {undefined} \hfill & {otherwise.} \hfill \right$$

□

Definition 6 (Function Res)The result of applying a sequence of actions to a state specification is described by the function $$\[--><$> Res\,:\,{{2}^{{\rm{\hat{\rSigma }}}}} \,\times \,{{{\bar {{ {\bf O}}}}}^{\bf {{\ast}}}} \, \rightarrow \,{{2}^{{\rm{\hat{\rSigma }}}}}, <$><!--$$ which is defined inductively as

$$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!Res(S,\langle \rangle )\, = \,S$$

$$Res(S,\langle {{o}_1},{{o}_2},\, \ldots \,,{{o}_n}\rangle )\, = \,Res(R(S,{{o}_1}),\langle {{o}_2}, \ldots, {{o}_n}\rangle )$$

□

Thus, a planning problem following the STRIPS formalism comprises a domain specification, and a problem description containing the initial state and the goal state. By using the definitions introduced in this section, we define a planning instance formally in Definition 7. Here, the solution for a planning instance is a sequence of actions Δ which, when applied to the initial state specification using the Res function, results in a state specification that supports the goal state. The solution for a planning instance or plan is formally defined in Definition 8.

Definition 7 (Planning Instance)A planning instance is a tuple $$\[--><$> {\rm{\rPi }}\, = \,\langle {\rm{\brXi }},{\bf {{I}}},{\bf {{G}}}\rangle <$><!--$$ , in which:

• • $$\[--><$> \brXi \, = \,\langle {\rm{\rSigma }},{\bf {{O}}}\rangle <$><!--$$ is the domain structure, consisting of a finite set of atoms Σ and a finite set of operators O;

• • $$\[--><$> {\bf {{I}}}\, \subseteq \,{\rm{\hat{\brSigma }}} <$><!--$$ is the initial state specification; and

• • $$\[--><$> {\bf {{G}}}\, \subseteq \,{\rm{\hat{\brSigma }}} <$><!--$$ is the goal state specification.

□

Definition 8 (Plan)A sequence of actions $$\[--><$> {\rm{\rDelta }}\, = \,\langle {{o}_1},{{o}_2},\, \ldots \,,{{o}_n}\rangle <$><!--$$ is said to be a plan for a planning instance $$\[--><$> {\rm{\rPi }}\, = \,\langle {\rm{\brXi }},{\bf {{I}}},{\bf {{G}}}\rangle <$><!--$$ , or a solution for Π, if and only if $$\[--><$> Res({\bf {{I}}},{\rm{\rDelta }})\, \models \,{\bf {{G}}} <$><!--$$ ⁷. □

A planning function (or planner) is a function that takes a planning instance as its input and returns a plan for this planning instance, or failure, indicating that no plan exists for this instance. This is stated formally in Definition 9.

Definition 9 (Planning Function)A planning function is described by the function $$\[--><$> Plan\,:\,\{ {{{\rm{\rPi }}}_{\rm{1}}},\, \ldots \,,{{{\rm{\rPi }}}_n}\} \, \rightarrow \,{{{\bar {{ {\bf O}}}}}^{\bf {{\ast}}}} \, \cup \,\{ \:failure\:\}, <$><!--$$ where $$\[--><$> \{ {{{\rm{\rPi }}}_{\rm{1}}},\, \ldots \,,{{{\rm{\rPi }}}_n}\} <$><!--$$ is the set of all planning instances, which is defined as

$$Plan({\rm{\rPi }})\, = \,\left\{ {\matrix {{\rm{\rDelta }} \hfill & {{\rm{\rDelta }}\;is\,a\,plan\,for\,{\rm{\rPi }};} \hfill \cr {failure} \hfill & {otherwise.} \hfill \\\end{}} \right$$

□

We assume such a function exists. The only requirement for the result Δ of Plan(Π) is that it follows some consistency criteria (e.g., the shortest Δ). The most basic planning function is the forward search algorithm. An adapted version of the forward search algorithm (Ghallab et al., 2004, Chapter 4, page 70) is shown in Algorithm 2. The input for this algorithm is basically a planning instance, and the output is a solution for the instance. Algorithm 1 simply calls Algorithm 2 with an empty set as the last parameter, which is later used to keep track of the states visited so far during the search to avoid getting into an infinite loop (i.e., to guarantee termination)⁸. First, Algorithm 2 finds all actions that are applicable in initial state I, and saves these in the set applicable (Line 5). From this set, an action is picked arbitrarily, and the result of applying this action in state I is taken as I′ (Line 11). Next, the algorithm is recursively called with the new state I′. If the recursive call returns a plan for $$\[--><$> \langle {\bf {{I^{\prime}}}},{\bf {{G}}},{\bf {{O}}}\rangle <$><!--$$ —i.e., the goal state is eventually reached after applying some sequence of actions to I′ (Line 2)—then the result of the forward search is attached to the end of action o, and the resulting sequence returned as a solution for the planning instance. Otherwise, a different action is picked from applicable and the process is repeated. If none of the actions in applicable can be used as the first action of a sequence of actions that leads to the goal state, then failure is returned.

2.2.2 HTNs

Unlike first principles planners, which focus on bringing about states of affairs or ‘goals-to-be’, HTN planners, like BDI systems, focus on solving abstract/compound tasks or ‘goals-to-do’. Abstract tasks are solved by decomposing (refining) them repeatedly into less abstract tasks, by referring to a given library of methods, until only primitive tasks (actions) remain. Methods are supplied by the user and contain procedural control knowledge for constraining the exploration required to solve abstract tasks—an abstract task is solved by using only the tasks specified in a method associated with it.

We use the HTN definition from Kuter et al. (2009) (actually an STN from Ghallab et al., 2004, Chapter 11, pages 231–244, which is a simplified formalism useful as a first step for understanding HTNs) whereby a HTN task network is a pair $$\[--><$> {\cal H}\, = \,(T,C) <$><!--$$ where T is a finite set of tasks⁹ to be accomplished and C is a set of ordering constraints on tasks in T that together make T totally ordered. Constraints specify the order in which certain tasks must be executed and are represented by the precedes relation: $$\[--><$> {{t}_i}\, \prec \,{{t}_j} <$><!--$$ means that task t_i must be executed before t_j. Conversely, the succeeds relation represents the opposite ordering: $$\[--><$> {{t}_i}\,{\succ}\,{{t}_j} <$><!--$$ means task t_i must be executed after t_j. A task can be primitive or compound/non-primitive, with each being a predicate representing the name of the task. All tasks have preconditions as defined before, specifying a state that must be true before the task can be carried out, and primitive tasks correspond to operators in first principles planning, which thereby have effects specifying changes to the state of the world. An HTN planning domain is a pair $$\[--><$> {\cal D}\, = \,({\cal A},{\cal M}) <$><!--$$ where $$\[--><$> {\cal A} <$><!--$$ is a finite set of operators and $$\[--><$> {\cal M} <$><!--$$ is a finite set of methods. A method describes how a non-primitive task can be decomposed into subtasks. We represent methods as tuples $$\[--><$> m\, = \,(s,t,{\cal H}') <$><!--$$ , where s is a precondition, denoted by pre(m), specifying what must hold in the current state for a task t (denoted task(m)) to be refined into $$\[--><$> {\cal H}'\, = \,(T^{\prime},C^{\prime}) <$><!--$$ (denoted network(m)); this involves decomposing t into new tasks in T′ by taking into account constraints in C′.

Intuitively, given an HTN planning problem $$\[--><$>\:\;{\cal P}\: = ({d} , {\bf {{I}}},{\cal D})<$><!--$$ , where $$\[--><$> {\cal D}\, = \,({\cal A},{\cal M}) <$><!--$$ is a planning domain, d is the initial task network that needs to be solved, and I is an initial state specification as in first principles planning, the HTN planning process works as follows. First, an applicable reduction method (i.e., one whose precondition is met in the current state) is selected from $$\[--><$> {\cal M} <$><!--$$ and applied to some compound task in (the first element of) d. This will result in a new, and typically ‘more primitive’ task network d′. Then, another reduction method is applied to some compound task in d′, and this process is repeated until a task network is obtained containing only primitive tasks. At any stage during the planning process, if no applicable method can be found for a compound task, the planner essentially ‘backtracks’ and tries an alternative reduction for a compound task previously reduced.

To be more precise about the HTN planning process, we first define what a reduction is. Suppose d = (T, C) is a task network, $$\[--><$> t\, \in \,T <$><!--$$ is a compound task occurring in d, and that $$\[--><$> m\, = \,(s,t^{\prime},{\cal H}') <$><!--$$ —with $$\[--><$> {\cal H}'\, = \,(T^{\prime},C^{\prime}) <$><!--$$ —is a ground instance of some method in $$\[--><$> {\cal M} <$><!--$$ that may be used to decompose t (i.e., $$\[--><$> t^{\prime}\, = \,t\sigma <$><!--$$ ). Then, reduce(d, t, m, σ) denotes the task network resulting from decomposing task t occurring in d using method m. Informally, such decomposition involves updating both the set T in d by replacing task t with the tasks in T′, as well as the constraints C in $$\[--><$> {\cal H} <$><!--$$ to take into account constraints in C′. For example, suppose task network $$\[--><$> {\cal H} <$><!--$$ mentions a task t ₁, a task t ₂, and the constraint $$\[--><$>{{t}_1}\, \prec \,{{t}_2}<$><!--$$ . Now if a method $$\[--><$> m\, = \,({{t}_1},\{ {{t}_3},{{t}_4}\}, \{ {{t}_3}\, \prec \,{{t}_4}\} ) <$><!--$$ is applied to $$\[--><$> {\cal H} <$><!--$$ , the resulting set of constraints will be $$\[--><$> \{ {{t}_3}\, \prec \,{{t}_2},{{t}_4}\, \prec \,{{t}_2},{{t}_3}\, \prec \,{{t}_4}\} <$><!--$$ .

The HTN planning process is described in Algorithm 3 (adapted from Ghallab et al. (2004, Chapter 11, page 239)). We refer the reader to Ghallab et al. (2004) and Kuter et al. (2009) for a more detailed account of HTN planning.

Notice that, although both Algorithms 2 and 3 perform a non-deterministic search from an initial state until a certain goal condition holds, the goal condition in Algorithm 2 is an explicit world state, whereas in Algorithm 3 the goal condition is to reach a fully decomposed task network. This difference in the goal condition makes planning for HTNs significantly more practical than planning in STRIPS-like domains, since the search space is generally much smaller.

3 Agent interpreter

To show how different styles of planning can be incorporated into BDI agents, we start by defining a generic BDI interpreter, inspired by traditional implementations such as PRS (Rao & Georgeff, 1995) and the more recent Jason (Bordini et al., 2007) system. In this interpreter, an agent is defined by a set of beliefs and a set of plans or plan rules ¹⁰, with each plan rule encoding first a header stating when the plan rule is to be adopted, and then a sequence of steps that are expected to bring about a desired state of affairs. Goals are implicit, and plans intended to fulfil them are invoked whenever some triggering condition is met, notionally the moment at which this implicit goal becomes relevant. Given the terminology introduced in Section 2.2, some confusion may arise about the difference between a plan/plan rule in the context of BDI programming languages, and a plan in the context of planning systems. As we shall see below (in Definition 13) the sequence of steps associated with a BDI plan rule once fully instantiated, more closely matches the notion of a plan (from Definition 8). When there is no risk of confusion, we shall refer to BDI programming language plan rules as plans.

The main reasoning cycle of BDI agents manipulates four data structures:

• • beliefs, comprising the information known by the agent, which is regularly updated as a result of agent perception;

• • plan rules, representing the behaviours available to the agent, combined with the situations in which they are applicable;

• • goals, representing desired world states that the agent will pursue by adopting plans; and

• • intention structures, comprising a set of partially instantiated plans currently adopted by the agent.

Then, by combining all of the above entities, an agent can be formally defined as follows.

Definition 10 (Agent)An agent is a tuple 〈Ag, Ev, Bel, Plib, Int〉, where Ag is the agent identifier; Ev is a queue of events; Bel is a belief base; Plib—the plan library—is a set of plan rules; and Int—the intention structure—is a set of intentions. □

An agent is notified of changes in the environment, as well as modifications to its own data structures, through triggering events, which may trigger the adoption of plan rules. We consider two types of goal: achievement goals, denoted by an exclamation marked followed by a predicate (e.g. !move(A,B)); and test goals, denoted by a question mark followed by a predicate (e.g. ?at(Position)). Test goals are used to verify whether the predicate it mentions is true, whereas achievement goals are used to achieve a certain state of affairs. Though Rao (1996) describes goals in this type of architecture as representing world states that an agent wants to achieve, as we have discussed above, they are in practice described as intention headers used to identify groups of plan rules allocated to achieve an implicit objective. Recently, perceived events are stored in the event queue Ev in increasing order of arrival time. An event may be a belief addition or deletion, or a goal addition or deletion. Belief additions are positive ground literals (i.e., facts perceived as being true), and belief deletions are negative ground literals (i.e., facts perceived as being false)¹¹. Events form the invocation condition of a plan, as further discussed in Definition 13.

Definition 11 (Events and event-queue)Let ϕ be a predicate (cf. Definition 2). An event e is either:

1. 1. a belief addition +ϕ, whereby belief ϕ is added to the belief base;

2. 2. a belief deletion −ϕ, whereby belief ϕ is removed from the belief base;

3. 3. a goal addition +!ϕ, whereby the achievement goal !ϕ is posted to the agent;

4. 4. a goal deletion −!ϕ, whereby the achievement goal !ϕ has been dropped by the agent;

5. 5. a goal addition +?ϕ, whereby the test goal ?ϕ is posted to the agent; or

6. 6. a goal deletion −?ϕ, whereby the test goal ?ϕ has been dropped by the agent.

An event queue Ev is a sequence $$\[--><$>\left[ {\overline{{{{e}_{\rm{1}}}}}, \ldots, \overline{{{{e}_n}}} } \right] <$><!--$$ of ground events ¹². □

The belief base comprises a set of beliefs, which can be queried through an entailment relation.

Definition 12 (Beliefs and belief base)A belief is a ground first-order predicate. A belief base Bel is a finite and possibly empty set of beliefs $$\[--><$> \{ {{\bar{\varphi }}_1},\, \ldots \,,{{\bar{\varphi }}_n}\} <$><!--$$ , along with an associated logical entailment relation $$\[--><$> \models <$><!--$$ for first-order formulae.□

3.1 Plans and intentions

An agent's behaviours are encoded as plan rules that specify the means for achieving particular (implicit) goals, as well as the situations and events for which they are relevant. Plan rules contain a head describing the conditions under which a certain sequence of steps should be adopted, and a body describing the actions that the agent should carry out to accomplish the plan rule's goal. A plan rule's head contains two elements: an invocation condition, which describes when the plan rule becomes relevant as a result of a triggering event; and the context condition encoding the situations under which the plan rule is applicable, specified as a formula. Each step in a plan rule body may either be an action (causing changes to the environment) or a (sub)goal (causing the addition of a new plan from the plan library to the intention structure). Interleaving actions and subgoal invocations allows an agent to create plans using hierarchy of alternative plans, since each subgoal can be expanded using any one of a number of other plan rules whose invocation condition matches the subgoal. Finally, the plan library, defined below, stores all the plan rules available to the agent.

Definition 13 (Plan Library)A plan library Plib is a finite and possibly empty set of plan rules $$\[--><$> \{ {{{\cal P}}_1},\, \ldots, \,{{{\cal P}}_n}\} <$><!--$$ . Each plan rule $$\[--><$> {{{\cal P}}_i} <$><!--$$ is a tuple 〈t, c, bd〉 where t, the invocation condition, is an event (cf.Definition 11), indicating the event that causes the plan rule to be considered for adoption; c, the context condition, is a first-order formula (cf. Section 2.1) over the agent's belief base (with an implicit existential quantification); and bd is the plan body consisting of a finite and possibly empty sequence of steps $$\[--><$> [{{s}_0},\, \ldots, \,{{s}_n}] <$><!--$$ , where each s_i is either the invocation condition of a plan rule, or an action (cf. Definition 14).□

In Example 1, we illustrate how a plan library affects an agent's behaviour.

Example 1 (Pl) Let a plan library Pl contain the following four plan rules:

• • 〈+!move(B), at(A) ∧ ¬ same(A, B), [packBags; +!travel(A, B)]〉

• • 〈+!move(B), at(A) ∧ same(A, B), []〉

• • 〈+!travel(A, B), has(car), [drive(A, B)]〉

• • 〈+!travel(A, B), has(bike), [ride(A, B)]〉

• • 〈+!travel(A, B), $$\[--><$> \top <$><!--$$ , [walk(A, B)]〉

When an agent $$\[--><$> \langle Ag,[ + !travel(home,office)],Bel,Pl,Int\rangle <$><!--$$ (cf. Definition 10) using this plan library adopts an achievement goal to travel to a location (by generating event +!travel(home, office), it will be able to adopt one of three possible concrete plans, depending on the availability of a mode of transportation encoded in its beliefs. ▪

An agent interacts with the environment through (atomic) actions, which are invoked from within the body of plan rules to bring about desired states of affairs. An action basically consists of an action name and arguments, or more specifically, a first-order atomic formula. Thus, if walk is an action to walk from one place to another that takes two parameters, an instance of this action to walk from home to the office could be denoted by walk(home, office).

Definition 14 (Action)An action is a tuple $$\[--><$> \langle \varphi, \hslant20%\varpi, {\epsilon}\rangle <$><!--$$ , where

• • ϕ, the identifier, is a first-order predicate $$\[--><$> p({{\tau }_0},\, \ldots, \,{{\tau }_k}) <$><!--$$ where $$\[--><$> {{\tau }_0},\, \ldots, \,{{\tau }_k} <$><!--$$ are variables;

• • $$\[--><$> \hslant20%\varpi <$><!--$$ , the precondition, is a first-order formula whose free variables also occur in $$\[--><$> \varphi <$><!--$$ ;

• • ε is a set of first-order predicates representing the effects of the action. Set ε is composed of two sets, ε ⁺and ε ⁻. These sets represent new beliefs to be added to the belief base (members of ε ⁺), or beliefs to be removed from the belief base (members of ε ⁻);

• • all free variables occurring in ε must also occur in $$\[--><$> \hslant20%\varpi <$><!--$$ and $$\[--><$> \varphi <$><!--$$ .

For convenience, we refer to an action by its identifier, $$\[--><$> \varphi <$><!--$$ , and to the preconditions of an action $$\[--><$> \varphi <$><!--$$ a $$\[--><$> \hslant20%\varpi (\varphi ) <$><!--$$ and to its effects as $$\[--><$>{\epsilon}(\varphi )<$><!--$$ . We refer to the set of all possible actions as Actions.□

Hence, an agent's action as defined above is equivalent to a STRIPS-like planning operator described in Section 2.2.1. An agent's actions are stored in a library of actions $$\[--><$> {\cal A} <$><!--$$ available to the agent.

Plans that are instantiated and adopted by an agent are called intentions. When an agent adopts a certain plan as an intention, it is committing itself to executing the plan to completion. Intentions are stored in the agent's intention structure, defined below.

Definition 15 (Intentions)An intention structure Int is a finite and possibly empty set of intentions $$\[--><$> \{ in{{t}_1}, \ldots, in{{t}_n}\} <$><!--$$ . Each intention int_i is a tuple $$\[--><$> \langle \sigma, st\rangle <$><!--$$ , where σ is a substitution and st—a sequence composed of actions and invocation conditions of plan rules—is an intention stack, containing the steps remaining to be executed to achieve an intention. □

Example 2 (Intention Adoption)Let an agent be in the following state $$\[--><$> \langle Ag,\,[ + !move(office)],\,\{ at(home),\,has(car)\}, \,Pl,\{ \} \rangle <$><!--$$ with the same plan library Pl of Example 1. When this agent processes event +!move(office), this event unifies with the invocation and context conditions of the first plan rule in the plan library under substitution $$\[--><$> \sigma \, = \,\{ A/home,\,B/office\} <$><!--$$ , creating intention $$\[--><$> int\, = \,\langle \sigma, [packBags;\, + !travel(home,office)]\rangle <$><!--$$ and transitioning the agent to a state $$\[--><$> \langle Ag,[],\,\{ at{\rm{(}}home{\rm{)}},\,has{\rm{(}}car{\rm{)}}\}, \,Pl,\{ int\} \rangle . <$><!--$$ ▪

It is important to note that the intention structure may contain multiple intentions organised in a hierarchical way. Each individual intention is a stack of steps to be executed, with the next executable step being the one at the top of the stack. As an agent reacts to an event in the environment, it creates a new intention with the steps of the plan chosen to achieve the event comprising the initial stack of this intention, so their steps can be immediately executed. The steps of a plan adopted to achieve a subgoal of an existing intention are stacked on top of the steps already on the intention stack, so that its steps are executed before the rest (beginning after the subgoal) of the original intention.

3.2 Interpreter and control cycle

In this section we describe the mechanisms needed for BDI-style computational behaviour. Here, we specify a basic abstract BDI agent interpreter and subsequently extend it to incorporate different styles of planning. The abstract interpreter is shown in Algorithm 4; we describe each step in more detail below.

The first two steps are for updating events and beliefs, described in Algorithms 5 and 6. Updating events (Algorithm 5) consists of gathering all new events from the agent's sensors (Line 2) and then pushing them into the event queue (Line 3), whereas updating beliefs (Algorithm 6) consists of examining the set of events and then taking appropriate actions with the corresponding beliefs: either adding beliefs when the events are of the form $$\[--><$> + \bar{\varphi } <$><!--$$ (as shown in Line 4), or removing them when they are of the form $$\[--><$> - \bar{\varphi } <$><!--$$ (as shown in Line 5)¹³. We are not concerned here with more complex belief revision mechanisms (e.g., Gärdenfors, 2003), but such an interpreter could use them.

Example 3 (Belief Update)Let an agent be in state $$\[--><$> \langle Ag,[ + has(car),\,{\rm{ - }}at(home)],\,\{ at(home)\}, \,Pl,Int\rangle <$><!--$$ . The execution of Algorithm 6 will cause it to transition to a state $$\[--><$> \langle Ag,[ + has(car),\,{\rm{ - }}at(home)],\,\{ has(car)\}, \,Pl,\,Int\rangle <$><!--$$ . ▪

Selection of plans to deal with new events is shown in Algorithms 7 and 8, which starts by removing an event e from the event queue and checking it against the invocation condition t of each plan in the plan library (Lines 3, 4 in Algorithm 7) to generate the set of options Opt. To this end, if an event e unifies with invocation condition t of a plan $$\[--><$> {\cal P} <$><!--$$ from the plan library, via substitution σ, and the context cσ (i.e., σ applied to c) is entailed by the belief base Bel (Line 4), then the resulting substitution σ_pot and other information about the plan rule are combined into a structure and stored in Opt, as a possible option for achieving the associated goal.

Example 4 (Selecting Options)Let an agent be in the following state $$\[--><$> \langle Ag,[ + !travel(home,office)],\,\{ at(home),\,has(car)\}, \,Pl,\{ \} \rangle <$><!--$$ with the same plan library Pl of Example 1. The execution of Algorithm 7 on this agent will generate the set of options $$\[--><$>{ & Opt\, = \,\{ \langle + !travel{\rm{(}}home,\,office{\rm{)}},\,has(car),\,[drive(A,B)], \{ A/home,\,B/office\} \rangle,<$><!--$$ $$\[--><$>{ \,\langle + !travel{\rm{(}}home,\,office{\rm{)}},\top,[walk(A,B)], \cr & \{ A/home,\,B/office\} \rangle \} . \cr} <$><!--$$ ▪

After an option is chosen for execution, the substitution σ_opt that led to its selection is applied to the plan body bd (Algorithm 10), and added to the associated intention structure (Line 5), with no more plan rules selected for the new event. In the third line of Algorithm 10 (and in other algorithms where it is used), symbol int_e stands for the intention that generated event e ¹⁴. If the event is a belief update, a new intention will be created for it (Algorithm 9, Line 7); otherwise, the event is a subgoal for some existing intention and therefore the new intention is added to it (Algorithm 9, Line 5)¹⁵. If there are no options available to react to an event, two outcomes for the intention that generated the event are possible. 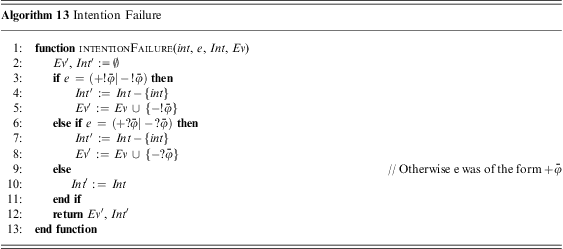For test goals of the form $$\[--><$> + ?\bar{\varphi } <$><!--$$ , even if an option (plan) to respond to that test is not available, the test goal might still succeed if the belief being tested is supported by the belief base, in which case the only change to the intention that created the event is to compose the unifier of that belief test to it (Algorithm 8, Lines 8, 9). Finally, if the event being processed is not a test goal, and there are no options to deal with it (Algorithm 8, Line 11), the intention that generated the event has failed, in which case we must deal with the failure. Algorithm 13 illustrates a possible implementation of failure handling mechanism (Bordini et al., 2007), where events denoting the failure of achievement and test goals are generated.

Example 5 (Plan Selection)Let an agent be in the following state $$\[--><$> \langle Ag,[ + !travel{\rm{(}}home,\,office{\rm{)}}],\,\{ at{\rm{(}}home{\rm{)}},\,has{\rm{(}}car{\rm{)}}\}, \,Pl,\{ \langle A/home,\,B/office\}, []\rangle \} \rangle <$><!--$$ after having executed the two steps of the intention generated in Example 2. When this agent executes Algorithm 8, Line 4 will generate the options described in Example 4. Since the set of options is non-empty, Lines 6 and 7 will execute. Assuming the algorithm selects the first option (corresponding to the plan to drive) in Line 6, Algorithms 9 and 10 will be called. Since event +!travel(home, office) was generated by the only intention in the agent state, the steps for the option to drive will be added to that intention, resulting in state $$\[--><$>{ & \langle Ag,[],\{ at{\rm{(}}home{\rm{)}},\,has{\rm{(}}car{\rm{)}}\}, \,Pl,\,\{ \langle \{ A/home,\,B/office\}, \cr & [drive(home,\,office)]\rangle \} \rangle \cr} <$><!--$$ . ▪

After a new plan is adopted, Algorithm 4 executes a step from an arbitrary intention using function executeIntention(Int, Ev), detailed in Algorithm 11, and illustrated in Figure 1. This entails selecting one intention int from the intention structure and executing the topmost step of the stack. If this step is an action it is executed immediately in the environment, and if it is a subgoal the associated event is added to the event queue.

Figure 1 Executing plan steps

One possible implementation of an action execution mechanism based on Definition 5 is shown in Algorithm 12, in which the results of an agent's actions are directly pushed back into its event queue. Consequently, Algorithm 12 ‘short circuits’ the results of an action's execution to the perception of its effects entirely within the agent. We provide such a simple implementation to provide a readily understandable function that closes the loop for the agent reasoning mechanism—in a real system actions are executed in an environment, and an agent will perceive the results of its actions through events reflecting the changes that an action brings about to this environment. Thus, although we do not deal with issues regarding the environment in this paper¹⁶, we note that the results of executing an action in most realistic multi-agent settings start to reach the agent asynchronously, possibly mixed with the results of its other actions and the actions of other agents acting concurrently in the same environment. Consequently, the complete implementation of action execution would involve a function in the agent interpreter that ultimately sends the actions executed by the agents to an implementation of the environment. Implementations of action execution can vary significantly, depending on what the underlying environment intends to model, and how the agent formalisms deal with the environment. Some agent formalisms (e.g., Sardiña et al., 2006) make assumptions about actions being atomic, and the degree to which an agent receives any feedback about the direct effects of its own actions (i.e., a new perception is the direct result of an agent's own actions, or of others). Other agent formalisms assume that the environment functions according to a stochastic transition function (Schut et al., 2002); hence the action implementation in the environment would include an element of chance. Thus if the preconditions of an action are met (Line 3), executing the action amounts to pushing the effects of the action onto the event queue (Lines 4–8).

This agent interpreter, and the processes upon which it is based, have a very low computational cost, as demonstrated by various practical implementations such as dMARS (d'Inverno et al., 2004), PRS (Ingrand et al., 1996), and Jason (Bordini & Hübner, 2006).

Now, as we have seen, multiple events may occur simultaneously in the environment, and multiple intentions may be created by an agent as a result of these events, possibly resulting in multiple plan rules becoming applicable and adopted by the agent. Hence, two execution outcomes are possible: interleaved and atomic execution. In the former, plans in different intentions alternate the execution of their steps, in which case care must be taken to ensure that no two plans that may execute simultaneously have steps that jeopardise the execution of one another (e.g., actions in one plan might invalidate the preconditions of actions in a concurrent plan).

3.3 Limitations of BDI reasoning

One shortcoming of BDI systems is that they do not incorporate a generic mechanism to do any kind of lookahead or planning (i.e., hypothetical reasoning). In general, planning is useful when (Sardiña et al., 2006): (i) important resources may be consumed by executing steps that are not necessary for a goal; (ii) steps are not reversible and may lead to situations from which the goal can no longer be solved; (iii) executing steps in the real world takes more time than deliberating about the outcome of steps (in a simulated world); and (iv) steps have side effects which are undesirable if they are not useful for the goal at hand.

Adopting intentions in traditional BDI interpreters is driven by events in the form of additions and deletions of either beliefs or goals. These events function as triggers for the adoption of plan rules in certain contexts, causing plans to be added to the intention stack from which the agent executes the plan's steps. In the process, the agent might fail to execute an atomic action or to accomplish a subgoal, resulting in the failure of the original plan's corresponding intention. On the other hand, an agent might execute a plan successfully and yet fail to bring about some result intended by the programmer. If a plan selected for the achievement of a given goal fails, the default behaviour of a traditional BDI agent is to conclude that the goal that caused the plan to be adopted is not achievable. Alternatively, modern interpreters such as JACK (Busetta et al., 1999) and Jason (Bordini et al., 2007) (among others) can try executing alternative plans (or different instantiations of the same plan rule) in the plan library until the goal is achieved, or until none of them achieve the goal. Here, the rules that allow the interpreter to search for effective alternative means to accomplish a goal, and verification of goal achievement must be explicitly encoded in the plan library by the programmer.

This control cycle (summarised in Figure 2) strongly couples plan execution to goal achievement. It also allows for situations in which the poor selection of a plan rule leads to the failure of a goal that would otherwise be achievable if the search for a plan rule was performed more intelligently. While such limitations can be mitigated through meta-level constructs that allow goal addition events to cause the execution of applicable plans in sequence (Georgeff & Ingrand, 1989; Hübner et al., 2006a), and the goal to fail only when all plans fail, in most traditional BDI interpreters goal achievement is an implicit side effect of a plan being executed successfully. Although research on declarative goals (Winikoff et al., 2002) aims to address this shortcoming from an agent programming language perspective, the problem remains that once an agent has run out of user-defined plans, the goal will fail.

Figure 2 Simplified BDI control cycle. Dashed lines represent failure recovery mechanisms

In order to address these shortcomings of BDI interpreters, as well as enable agents generate new behaviours at runtime, various planning mechanisms have been studied. The three approaches to planning that have been integrated into BDI agent systems are discussed next.

Lookahead on existing BDI plans: In this style of planning (e.g., Sardiña et al., 2006; Walczak et al., 2006), an agent is able to reason about the consequences of choosing one plan for solving a goal over another. Such reasoning can be useful for guiding the selection of plans for the purpose of avoiding negative interactions between them. For example, consider the goal of arranging a domestic holiday, which involves the subgoals of booking a (domestic) flight, ground transportation (e.g., airport shuttle) to a hotel, and hotel accommodation. Although the goal of booking a flight could be solved by selecting a plan that books the cheapest available flight, this will turn out to be a bad choice if the cheapest flight lands at a remote airport from where it is an expensive taxi ride to the hotel, and consequently not enough money is left over for accommodation. A better choice would be to book an expensive flight that lands at an airport closer to the hotel, if ground transportation is then cheap, and there is enough money left over for booking accommodation. By reasoning about the consequences of choosing one plan over another, the agent could guide its execution to avoid selecting the plan that books the cheapest flight. Such lookahead can be performed on any chosen substructures of goal-plan hierarchies; the exact substructures are determined by the programmer at design time.

Planning to find new BDI plans: The second way in which planning can be incorporated into the BDI architecture is by allowing agents to come up with new plans on the fly for handling goals (e.g., Despouys & Ingrand, 1999; Móra et al., 1999; Meneguzzi & Luck, 2007; de Silva et al., 2009). This is useful when the agent finds itself in a situation where no plan has been provided to solve a goal, but the building blocks for solving the goal are available. To find a new plan, the agent performs first principles planning, that is, it anticipates the expected outcomes of different steps so as to organise them in a manner that solves the goal at hand. To this end, the agent uses its existing repertoire of steps, specifically, some combination of basic steps (e.g., deleting a file or making a credit card payment) and the more complex ones (e.g., a high-level step for going on holiday). Similarly, to how the programmer can choose substructures of a goal-plan hierarchy when looking ahead within existing plans, when planning from first principles the programmer is able to identify the points from which first principles planning should be performed. In addition, such planning could also be done automatically on, for instance, the failure of an important goal.

Planning in a probabilistic environment: By using a deterministic model of planning, even though the languages themselves are ostensibly designed to be suitable for an uncertain world, traditional BDI agent interpreters (Georgeff et al., 1999) must rely on plan libraries designed with contingency plans in case of failures in execution. While in theory these contingency plans could be designed perfectly to take into account every conceivable failure, the agent's reasoning does not take into consideration the failures before they actually happen, as there is no model of the non-determinism associated with the failures. In order to perform this kind of proactive reasoning about failures, it is necessary to introduce a model of stochastic state transition, and an associated planning model to the BDI interpreter. The implementation of such approaches range from automatically generating contingency plans (Dearden et al., 2002) to calculating optimal policies for behaviour adoption using decision theory (e.g., using a Markov decision process (MDP); Bellman, 1957). In this way an agent adopting a plan takes into consideration not only a plan's feasibility but also its likelihood to be successful. Moreover, if the environment changes and the failure of certain plans become predictable, current BDI implementations have no mechanism to adapt its plan adoption policy to this new reality.

Unlike linear plans such as those explained in Section 2.2, contingency plans are branching structures where each branch is associated with a test on an agent's perception, leading to different sequences of actions depending on the state of the environment as the agent executes the plan. Optimal policies in MDPs consist of a function that associates the action with the highest expected reward for each state of the environment, usually taking into consideration an infinite time horizon. The two solution concepts for probabilistic planning domains are strongly related, as an optimal policy can be used to generate the tree structure corresponding to a contingency plan (Meuleau & Smith, 2003). Within the context of this paper, we can associate the creation of contingency plans as a probabilistic approach to the creation of new BDI plans, whereas optimal policies can be used as probabilistic solution to the question of selecting a plan with the best chance of success.

4 Planning with declarative planners

One of the key characteristics of traditional BDI interpreters of the type defined in Section 3 is their reliance on a library of abstract hierarchical plans. Plans in this library are selected by the efficient matching of their invocation conditions to incoming events and testing of plans’ logical context conditions against the agent's beliefs. Agents that use this model of plan adoption to react to events are said to use procedural goals (Winikoff et al., 2002), since agents are executing procedural plans under the assumption that the successful execution of a plan leads to the accomplishment of the associated implicit goal. Since the events processed by an agent have limited information about what the agent is trying to accomplish besides identifying the procedure the agent will be carrying out, this approach limits the range of responses available to an agent in case a plan selected to accomplish a procedural goal fails. Moreover, since there is no verification of the effects of a plan, it is even possible that an agent might execute a procedural plan successfully without actually accomplishing the agent's goal due to a silent failure. To address these limitations, notions of declarative goals were introduced in languages such as GOAL (Hindriks et al., 2001), CAN (Winikoff et al., 2002), 3APL (Dastani et al., 2004), 2APL (Dastani, 2008) and adapted into the Jason interpreter by Hübner et al. (2006a). Declarative goals describe a state that the agent desires to reach, rather than a task that needs to be performed, capturing more closely some of the desirable properties of goals such as the requirement for them to be persistent, possible, and unachieved. To accommodate declarative goals, the plan language (Winikoff et al., 2002) includes the construct $$\[--><$> Goal({{\phi }_s},\,P,\,{{\phi }_f}) <$><!--$$ , which intuitively states that (declarative) goal $$\[--><$> {{\phi }_s} <$><!--$$ should be achieved using (procedural) plan body P, failing if $$\[--><$> {{\phi }_f} <$><!--$$ becomes true. This entails that if program P within goal-program $$\[--><$> Goal({{\phi }_s},\,P,\,{{\phi }_f}) <$><!--$$ has completed execution but condition $$\[--><$> {{\phi }_s} <$><!--$$ is still not true, then P will be re-tried; moreover, if $$\[--><$> {{\phi }_s} <$><!--$$ becomes true during the execution of P, the goal-program will succeed immediately. In this section, we review agent architectures that rely on planning algorithms to search for solutions for goals consisting of a specific world state described as a logical formula, thereby supporting agents that use declarative goals, or a goals to be. Since, even with declarative goals, a BDI agent is still limited by the set of plans included in its plan library at design time, these architectures also let agents formulate new plans to tackle situations that were unforseen at design time.

4.1 Propice-plan

The Propice-plan (Despouys & Ingrand, 1999) framework is the combination of the IPP (Köhler et al., 1997) first principles planner and an extended version of the PRS (Ingrand et al., 1992) BDI system. It includes extensions to allow an agent to anticipate possible execution paths for its plans, as well as the ability to update the planning process in order to cope with a dynamic world. Although plan rules (called operational plans in Propice-plan, or OPs) are very similar to the ones used in PRS, they differ in that a designer specifies a plan not only in terms of a trigger, context condition, and body (see Definition 13), but also includes a specification of the expected declarative effects of the plan rule. A Propice-plan agent contains three primary modules:

1. 1. an execution module $$\[--><$>{\cal E}_m<$><!--$$ responsible for selecting plans from the plan library and executing them, similarly to the agent processes described in Section 3.2;

2. 2. an anticipation module $$\[--><$> {{{\cal A}}_m} <$><!--$$ responsible for simulating the possible outcomes of the options selected; and

3. 3. a planning module $$\[--><$> {{{\cal P}}_m} <$><!--$$ responsible for generating a new plan when the execution module fails to find an option.

The way these modules interact during plan selection is illustrated in Algorithm 14. This algorithm is somewhat similar to the original plan selection of Algorithm 8 until Line 11. It differs in that plans from the plan library are not only filtered by their trigger and context condition into Opt, but also further filtered by the anticipation module $$\[--><$> {{{\cal A}}_m} <$><!--$$ . We discuss the $$\[--><$> {{{\cal A}}_m} <$><!--$$ module in more detail in Section 5.4, but for now assume that this module takes as input a set of options Opt, containing elements of the form $$\[--><$> \langle t,c,bd,{{\sigma }_{opt}}\rangle <$><!--$$ and returns one option anticipated to be executed without failure. If such a plan cannot be found, the remainder of the algorithm (from Lines 11 to 19) uses the planning module $$\[--><$> {{{\cal P}}_m} <$><!--$$ to construct a new plan rule from scratch. Specifically, the $$\[--><$> {{{\cal P}}_m} <$><!--$$ module uses the IPP planner to obtain a new PRS plan at runtime. To formulate plans, IPP uses the plan rules of PRS (augmented with their expected declarative effects), by treating these plan rules as planning operators¹⁷. In particular, the precondition of a planning operator is taken as the context condition of the corresponding plan rule, and the postcondition of the planning operator is taken as the declarative effects of the corresponding plan rule. The goal state to plan for is the (programmer supplied) primary effect of the achievement goal that failed. Solutions found by IPP are returned to the $$\[--><$>{\cal E}_m<$><!--$$ , which executes them by mapping their actions back into ground plan rules. To this end an intention is created (Line 14) by including a test for the (ground) context condition of the plan found to ensure that when the intention is actually executed the context condition still holds. Recall from before that int_e in Algorithm 14 is the intention that generated event e.

4.2 X²-BDI

In an attempt to bridge the gap between agent logic theory and implementation (Móra et al., 1999) developed X-BDI, a logic-based agent interpreter implemented using the extended logic programming (ELP) with explicit negation formalism developed by Alferes and Pereira (1996). In turn, the ELP formalism has an implementation in Prolog that solves explicit negation using an extension of the well-founded semantics (WFS) (Alferes et al., 1995), and for which a proof of correctness exists¹⁸. X-BDI (Móra et al., 1999) is one of the first agent models to include a recognisably declarative goal semantics. An X-BDI agent is defined in terms of a set of beliefs, a set of desires, a set of intentions, and a set of time axioms, that is, as a tuple $$\[--><$> {\cal A}g\, = \,\langle {\cal B},{\cal D},{\cal I},{\cal T}\:{\rm Ax}\:\rangle <$><!--$$ . In its original implementation, X-BDI uses the time axioms of event calculus (Kowalski & Sergot 1986), which also include the description of the actions available to the agent. Beliefs are represented as a set of properties defined in a first-order language, equivalent to that of Section 2.1 and expressed in event calculus; moreover, consistency between beliefs is enforced using the revision mechanisms of ELP. However, in keeping with the algorithmic presentation style of this paper, we simplify the explanation of X-BDI and do not refer to the event calculus representation directly. Instead, we consider beliefs as ground time-stamped logical atoms. In this paper, we consider an X-BDI belief base $$\[--><$> {\cal B} <$><!--$$ as an extension of the belief base (and its entailment relation) of Definition 12 to include the notion of time, and we use $$\[--><$> {\cal B}\,{{ \models }_T}\,{{\rPhi }} <$><!--$$ to denote first-order formula Φ being entailed by the belief base at time T ¹⁹. We denote the current time as Now and denote the set of properties at time T as $$\[--><$> {{{\cal B}}_T} <$><!--$$ . Desires represent all potential goals: those that an agent might adopt, with each desire $$\[--><$> d\, = \,\langle {{P}_d},\,{{T}_d},\,T,\,b{{d}_d}\rangle <$><!--$$ consisting of a desired property P_d (which the agent desires to make true), the time T_d at which the desired property should be valid, an unbound variable T denoting the time at which the desire was committed to an intention, and a body bd_d that conditions the adoption of the desire on a (possibly empty) conjunction of beliefs. Here, bd_d is analogous to the context conditions of the plans in a procedural BDI programming language such as the one described in Section 3. We capture the essence of the intention selection process from X-BDI in Algorithm 15.

Since the desires are not necessarily mutually consistent, it might be the case that not all of them are adopted at once by the agent; moreover, the agent has to filter possible goals at every reasoning cycle. To this end, X-BDI creates two intermediate subsets of desires before committing to intentions. The first subset consists of desires whose property P_d is not believed to be true by the agent²⁰, and whose body rule is supported by the beliefs at the current time; this subset $$\[--><$> {\cal D}' <$><!--$$ is that of eligible desires (Line 2). X-BDI then selects a subset of the eligible desires that are both consistent among each other (Line 5) and possible: these are the candidate desires $$\[--><$> {{{\cal D}}_C} <$><!--$$ . A set of desires is deemed possible if there is a plan that can transform the set of beliefs so that the desired properties become true. These plans are obtained via a planning process for each element in the power set of eligible desires (Line 4). The planning problem given to the planner consists of a STRIPS domain specification $$\[--><$>{\rm{\brXi }<$><!--$$ (see Definition 7), the beliefs that are true at the current time, and the (combined) set of desired properties corresponding to element D in the power set of eligible desires (Line 8).

The set of intentions in X-BDI contains two distinct types of intention. Primary intentions are declarative goals in the sense that they represent the properties expressed as desires, which the agent has committed to achieving (Line 15). Commitment to primary intentions leads an X-BDI agent to adopt plans to achieve them. The steps of these plans comprise the relative intentions, which are analogous to procedural goals (Line 16). Thus, in X-BDI, an agent only starts acting (i.e., carrying out relative intentions) after a reasoning cycle that consists of filtering the set of desires so that a maximal subset of candidate desires is selected, and committing to these desires as primary intentions.

Unlike most of the agent architectures described in this paper, X-BDI does not include a library of fully formed plans, but rather a set of environment modification planning operators defined in event calculus analogous to those in Definition 14. So the possibility of a desire is verified by the existence of an explanation generated by logical abduction. Here, logical abduction refers to the process of generating a set of predicates (in this case, action descriptions in event calculus) that when added to the belief base entail the desired properties. Thus, in order to choose among multiple sets of candidate desires, X-BDI uses ELP constructs that allow desires to be prioritised in a logical revision process (cf., Móra et al., 1999)²¹. This type of desire selection suffered from significant inefficiencies, in particular, due to the logical abduction process required to determine if a plan is possible. In order to address this, X²-BDI (Meneguzzi et al., 2004a) improves on X-BDI by substituting the abduction process with a STRIPS planner based on Graphplan (Blum & Furst, 1997).

4.3 AgentSpeak(PL)

To further enhance the ability of an agent to respond to circumstances unforeseen at design time when achieving its goals, (Meneguzzi & Luck, 2007) has created an extended AgentSpeak(L) interpreter able to invoke a standard classical planner to create new plans at runtime. To this end, a new construct representing a declarative goal is introduced, which the designer may include at any point within a standard AgentSpeak plan. Moreover, BDI plans that can be used in the creation of new BDI plans are annotated offline with their expected effects (i.e., how the world would change if the plans were executed). Alternatively, if action descriptions (such as those from Definition 14) are available, expected effects could be extracted offline as done, for example, in Sardiña et al. (2006).

A declarative goal in AgentSpeak(PL) is a special event of the form $$\[--><$> + !goalconj([{{g}_1},\, \ldots, \,{{g}_n}]) <$><!--$$ , where $$\[--><$> {{g}_1},\, \ldots, \,{{g}_n} <$><!--$$ is a conjunction of logical literals representing what must be made true in the environment. The plan library of an AgentSpeak(PL) agent contains a special type of plan designed to be selected only if all the other standard plans to handle a declarative goal event have failed. Consequently, the computationally expensive process of planning from first principles is only used as a last resort, thereby making maximum use of standard AgentSpeak(PL) reasoning while still being able to handle situations not foreseen at design time. Enforcing the selection of the fallback plan as a last resort can be achieved in AgentSpeak-like interpreters through an appropriate Option Selection Function (Rao, 1996). In the Jason-based (Bordini et al., 2007) implementation of AgentSpeak(PL) (Meneguzzi & Luck, 2008), plan selection follows the order in which plans are added to the plan library at design time; thus the fallback plan is simply added last to the plan library. This fallback plan contains the action genplan that is associated with the planning process as follows:

$${ + !goalconj([{{g}_1},\, \ldots, \,{{g}_n}]): & true \cr & \leftarrow \;genplan([{{g}_1},\, \ldots, \,{{g}_n}]). \cr}$$

The action genplan performs three processes. First it converts the agent's plan library, beliefs, and a specified goal into a classical planning domain and problem. In this conversion, the agent's belief base is considered the initial state of a STRIPS planning problem and the declarative goal as the goal state. Each existing AgentSpeak plan is converted into a STRIPS planning operator named after the plan's invocation condition, using the plan's context condition as the operator's precondition and expected effects as the operator's effect. Second, genplan invokes the classical planner. Third, if the planner successfully generates a new plan, genplan converts the steps of the STRIPS plan into the body of a new AgentSpeak plan, pushing this new plan into the agent's intention structure. This planning approach was further extended by Meneguzzi and Luck (2008) with the addition of a method to introduce newly created plans to the agent's plan library through the generation of a minimal context condition, which ensures that the plan added to the plan library will only be invoked when it is possible to execute the plan to its completion (i.e., it assumes the downward refinement property; Bacchus & Yang, 1993). Basically, this context condition is generated by constructing a data structure similar to the planning graph from Blum and Furst (1997) using only the actions in the plan, and propagating unsatisfied preconditions from each action back to the initial level of the graph.

Although AgentSpeak(PL)'s planning capability is realised through a planning action/function implemented outside the traditional reasoning cycle, conceptually, the AgentSpeak(PL) cycle can be understood in the context of our abstract agent interpreter, as illustrated in Figure 3. Thus, the plan selection function of Algorithm 8 can be modified to represent the operational semantics of AgentSpeak(PL) by adding, after the traditional event matching mechanism, calls to the three processes used by genplan, as shown in Algorithm 16.

Figure 3 Reasoning cycle for AgentSpeak(PL)

In more detail, the traditional option selection algorithm is first invoked in Line 4. In this line the set Plib′ is an initially empty global cache of previously generated plans. If this process fails to find any options, then the desired declarative goal associated with event e, the agent's belief base Bel, and its plan library Plib are converted to a STRIPS representation in Line 11. The resulting STRIPS domain Π is then used in the invocation of a classical planner in Line 12; if it successfully generates a plan, the resulting plan is converted into the body of an AgentSpeak plan in Line 14. Before this plan can be added to the plan library, a context condition is created by the generateContext²² algorithm in Line 15. Finally, the newly created plan is added to the plan library, and then adopted as an intention.

4.4 Hybrid Planning Framework

In the Hybrid Planning Framework of de Silva et al. (2009) (hereby referred to simply as the Hybrid Planning Framework), classical planning is added to the BDI architecture with the focus being on producing plans that conform to and re-use the agent's existing procedural domain knowledge. To this end, ‘abstract plans’ are produced, which can be executed using this knowledge, where abstract plans are those that are solely made up of achievement goals. The input for such a planning process is the initial and goal states as in classical planning, along with planning operators representing achievement goals. The effects of such an operator are inferred from the hierarchical structure of the associated achievement goal, using effects of operators at the bottom of the hierarchy as a basis. The authors obtain the operator's precondition by simply taking the disjunction of the context conditions of plan rules associated with the achievement goal.

One feature of abstract plans is that, as highlighted in Kambhampati et al. (1998), the primitive plans that abstract plans produce preserve a property called user intent, which intuitively means that the primitive plan can be ‘parsed’ in terms of achievement goals whose primary/intended effects support the goal state. In addition, abstract plans also have the feature whereby they are, like typical BDI plans, flexible and robust: if a primitive step of an abstract plan happens to fail, another option may be tried to achieve the step.

The authors note, however, that producing abstract plans is not a straightforward process. The main issue is an inherent tension between producing plans that are as abstract as possible (or ‘maximally abstract’), while at the same time ensuring that actions resulting from their refinements are necessary (non-redundant) for the specific goal to be achieved. Intuitively, a higher level of abstraction implies a larger collection of tasks, thereby increasing the potential for redundant actions when the abstract plans are refined.

The authors explore the tension by first studying the notion of an ‘ideal’ abstract plan that is non-redundant while maximally abstract—a notion they identify as computationally expensive—and then defining a non-ideal but computationally feasible notion of an abstract plan in which the plan is ‘specialised’ into a new one that is non-redundant but also preserves abstraction as much as possible. More concretely, instead of improving an abstract plan by exploring all of its specialisations, the authors focus on improving the plan by exploring only the limited set of specialisations inherent in just one of its ‘decomposition traces’, and extracting a most abstract and non-redundant specialisation of the hybrid plan from this limited set.

For example, consider a Mars Rover agent that invokes a planner and obtains the abstract plan h shown in Figure 4(a)²³. Consider next the actual execution of the abstract plan, shown in Figure 4(c). Now, notice that breaking the connection after sending the results for Rock2, and then re-establishing it before sending the results for Rock3 are unnecessary/redundant steps. Such redundancy is brought about by the overly abstract task PerformSoilExperiment. What we would prefer to have is the non-redundant abstract plan h′ shown in Figure 4(b). This solution avoids the redundancy inherent in the initial solution, while still retaining a lot of the structure of the abstract plans provided by the programmer. In particular, we retain the abstract tasks Navigate and ObtainSoilResults, which lets us achieve these tasks using different refinements to that shown here, if possible and necessary. Moreover, replacing each of PerformSoilExperiment and TransmitSoilResults with a subset of their components, removes the inherent redundancy.

Figure 4 (a) A redundant abstract plan h; (b) an abstract plan h′ with redundancy (actions in bold) removed; and (c) the execution trace of h

Then, the entire process for hybrid planning (de Silva et al., 2009) involves obtaining, via classical planning, an abstract plan that achieves a required goal state given some initial state. Specifically, the steps are as follows: (i) transform achievement goals in the BDI system into abstract planning operators by ‘summarising’ the BDI hierarchy, similarly to Clement and Durfee (1999); (ii) call the classical planner of choice with the current (initial) state, the required goal state, and the abstract planning operators obtained in the first step; (iii) check the correctness of the plan obtained to ensure that a successful decomposition is possible—a necessary step due to the incompleteness of the representation used in the first transformation step; and finally, (iv) improve the plan found by extracting its non-redundant and most abstract part.

5 Planning with procedural planners

5.1 CANPlan

Considering the many similarities between BDI agent-oriented programming languages and HTN planning, Sardiña et al. (2006) formally defines how a BDI architecture can be extended with HTN planning capabilities. In this work, the authors show that the HTN process of systematically refining higher-level tasks until concrete actions are derived is analogous to the way in which a PRS-based interpreter repeatedly refines achievement goals with instantiated plans. By taking advantage of this almost direct correspondence, HTN planning is used to provide lookahead capabilities for a BDI agent, allowing it to be more ‘informed’ during plan selection. In particular, HTN planning is employed by an agent to decide which plans to instantiate and how to instantiate them in order to maximise its chances of successfully achieving goals. HTN planning does not, however, allow the agent to create new plan structures (Figure 5).

Figure 5 Summarised reasoning cycle of CANPLAN

An algorithm that illustrates the essence of the CANPlan semantics is shown in Algorithm 17²⁴. Observe that the main difference between this algorithm and Algorithm 8 is Line 5, where HTN planning is used to select a plan in set Opt for which a successful HTN decomposition of its associated intention exists, with respect to the current belief base. To this end the forwardDecomp function (Algorithm 3) is called in Algorithm 18²⁵. The inability of function forwardDecomp to find a plan is considered a failure, which is handled as in Algorithm 8. In arguments to forwardDecomp we use certain BDI entities (such as st) in place of the corresponding HTN representations, in line with the mapping shown in Table 1. Indeed, we assume the existence of a mapping function that transforms the relevant BDI entities into their corresponding HTN counterparts. We refer the reader to Sardiña et al. (2006) for the details.

Table 1 Comparison of BDI and HTN systems (Sardiña & Padgham, 2011)

Note that unlike the CANPlan semantic rules, Algorithm 17 performs HTN planning whenever a plan needs to be chosen for a goal. In CANPlan, on the other hand, HTN planning is only performed at user specified points in the plan library—hence, some goals may be refined using the standard BDI plan selection mechanism. Another difference compared to the semantics is that the algorithm does not re-plan at every step to determine if a complete, successful execution exists. Instead, the re-planning occurs only at points where goals are refined; the algorithm then executes the steps in the chosen plan until the next goal is refined. In both approaches, failure occurs in the BDI system when relevant environmental changes are detected, i.e., when the context condition in a chosen plan is no longer applicable within the BDI cycle. Consequently, environmental changes leading to failure may be detected later in the algorithm than in the semantic rules. In this sense, the algorithm seems to more closely capture the implementation discussed by Sardiña et al. (2006), which first obtains a complete HTN decomposition ‘tree’ and then executes it step by step until completion or until a failure is detected.

5.2 The LAAS-CNRS Architecture

Another system that uses an HTN-like planner to obtain a complete decomposition of a task(s) before execution is an integrated system used with (real and simulated) robots in human–robot interaction studies at the LAAS-CNRS (Alami et al., 2011). The integration combines a PRS-based robot controller with the Human-Aware Task Planner (HATP) (Alami et al., 2009) SHOP-like HTN planner. The algorithm for this approach is shown in Algorithm 19.

Goals to achieve are sent directly from the user to the PRS-based system, via a voice-based interface or an Android tablet. PRS then validates the goal (e.g., checks if the goal has already been achieved) and sends the goal, if valid, as a task for HATP to solve (Line 4). HATP first searches for a standard HTN solution—one composed of actions/primitive tasks—and then the plan found is post-processed by HATP into two semi-parallel streams of actions (Line 5): one for the agent to execute and the other for the human to execute, possibly with causal links between actions in the two streams to account for any dependencies (e.g., before executing an action the robot might have to wait for the human to execute an action that makes an object accessible to the robot). Basically, this step involves extracting a partially ordered plan from a totally ordered plan and then distinguishing actions that need to be done by a human from those that should be performed by the robot. To indicate to the human what actions he/she needs to execute the robot uses a speech synthesis module. Action execution is realised via PRS plans, which invoke functions that do more low-level geometric planning to achieve/execute the smaller steps such as robot-arm motions and gripper commands. More specifically, geometric planning is used here for things such as final object/grasp configurations and motion trajectories for the robot's arms, which takes into account constraints such as human postures, abilities, and preferences. Action execution is verified to check that their intended outcomes are satisfied, the failure of which triggers re-planning for the original goal.

5.3 Planning in Jadex

The work of Walczak et al. (2006) is another approach to merging BDI reasoning with planning capabilities, achieved through a continuous planning and execution approach implemented in the Jadex agent framework (Pokahr et al., 2005). The approach of Walczak et al. (2006) deviates significantly from traditional BDI systems in that an agent's desires are not seen as activities to be executed nor logically represented states to be achieved, but instead as inverse utility (i.e., cost) functions that assign a value to particular agent states (rather than environmental states). That is, each agent desire assigns a value to the states so that when different desires are adopted, the agent's valuation of the states changes.

Like in traditional BDI agents, goals in Jadex are specific world states that the agent is currently trying to bring about. However, unlike the logic-based representations used to specify the search space and the actions that modify the environment in the other approaches described in this paper, actions in Jadex define value-assignments to fields within objects in the Java programming language. Moreover, instead of using events to directly trigger the adoption of plans, Jadex uses an explicit representation of goals, each of which has a lifecycle consisting of the following states: option, suspended, and active. Adopted goals become options (and thus become eligible to create plans to adopt as intentions), which are then handed over to a meta-level reasoning component to manage the goal's state. This high-level view of Jadex's reasoning cycle is illustrated in Algorithm 20 and Figure 6. Given the representation of the environment state, Jadex uses a customised HTN-like planner that takes into account the agent's current goals and the functions specified by the agent's desires to refine goals into actions. This planning process takes as input a goal stack, the agent's current state, its desires, and a time deadline. Planning then consists of decomposing the goal stack into executable actions, while trying to maximise the expected utility of the resulting plan using a heuristic based on the distance from the current state to the goals and the expected utility of these goals.

Figure 6 Jadex overview (Pokahr et al., 2005)

5.4 Lookahead in Propice-plan

Similarly, to some of the systems already discussed that perform lookahead, the anticipation module $$\[--><$> {{{\cal A}}_m} <$><!--$$ of Propice-plan, introduced in Section 4.1, can also evaluate choices in advance and advise the execution module $$\[--><$> {{{\cal E}}_m} <$><!--$$ (as shown in Algorithm 14) regarding which plan choices are likely to be more cost effective (e.g., less resource intensive); moreover, the $$\[--><$> {{{\cal E}}_m} <$><!--$$ can detect unavoidable goal failures, that is, where no available options are applicable, and adapt PRS execution by ‘inserting’ instantiated plans to avoid such failure if possible. The anticipation module performs lookahead whenever there is time to do so: in the ‘blast furnace’ example domain used by Despouys and Ingrand (1999) the agent system sometimes remains idle for hours between tasks.

When performing lookahead, the $$\[--><$> {{{\cal A}}_m} <$><!--$$ simulates the hierarchical expansion of PRS plans, guided by subgoals within plan bodies. The expansion is done with respect to the current state of the agent's belief base, which is updated along the way with effects of subgoals, similarly to how the initial state of the world is updated as methods are refined in HTN planning. Whenever there is a precondition of a plan having a variable whose value is unpredictable at the time of lookahead (e.g., a variable corresponding to the temperature outside at some later time in the day), and can only be determined when the variable is bound during execution, the different possible plan instances corresponding to all potential variable assignments are accounted for during lookahead.

To avoid possible goal failures, the $$\[--><$> {{{\cal A}}_m} <$><!--$$ searches for goals that will potentially have no applicable options, before the $$\[--><$> {{{\cal E}}_m} <$><!--$$ reaches that point in the execution. The $$\[--><$> {{{\cal A}}_m} <$><!--$$ then tries to insert during execution an instantiated PRS plan whose effects will aid in the precondition holding for some plan associated with the goal. The authors state that making such minor adaptations to the execution is more efficient than immediately resorting to first principles planning, which they claim is likely to be more computationally expensive. Consequently, first principles planning is only called when all attempts at using standard PRS execution coupled with the $$\[--><$> {{{\cal A}}_m} <$><!--$$ have failed.

6 Probabilistic planning

The planning formalisms we describe in Sections 4 and 5 are based on a deterministic view of the environment. In some of these approaches actions are seen as procedures that will either succeed or fail with unknown probability²⁶. The assumption is that an action either succeeds, transitioning the environment into one particular expected state, or fails, transitioning the environment to an arbitrary state (i.e., the exact outcome of failure is not explicitly defined).

In applications where an agent needs to reason about the physical world with an explicit model of probabilistic state transition, it is necessary to consider the effect of actions in the world state differently. As opposed to the state-transition model traditionally used in previous approaches, in probabilistic approaches actions can transition to multiple other states with each of them having a certain probability associated with it. One popular formalism for modelling planning in this setting is the MDP (Bellman, 2003). This formalism assumes that the dynamics of the environment can be modelled as a markov chain, whereby the environment transitions between states stochastically, and the probability of transitioning from one state to another depends partially on the current state (and not on the history of previous states) and partially on the agent's action. Moreover, the goals of the planner are implicitly represented in a function that defines, for each state, the reward of executing a certain action.

The BDI model is not natively based on an a priori stochastic description of the environment, that is, environment models in BDI do not have an explicit representation of the probabilities with which an action can lead to particular outcome states. Modelling of the actions available for a BDI agent under the traditional HTN model used for designing an agent's plan library assumes that the agent itself does not reason about possible failures. Instead, an agent executes its plans and if an action succeeds the agent carries on with a plan, and if it fails, the agent is immediately aware of the failure, and is responsible for carrying out one or more plans to deal with this failure, a posteriori.

Environment states in stochastic models are analogous to those traditionally used to model BDI agent states (Schut et al., 2002). That is, an environment is modelled using a finite set of Boolean variables representing every possible proposition in the domain, and an environment state is a truth assignment to these variables. Moreover, Schut et al. (Schut & Wooldridge, 2001; Schut et al., 2001) suggests that components of the BDI model can be used to derive an MDP to obtain an optimal solution to a planning problem faced by the agent. By being an approximation of the optimal solution to a stochastic planning problem, BDI agents are able to plan much more efficiently than what is required to generate an optimal solution for an MDP. The tradeoff is that the actions chosen by a BDI agent are not necessarily optimal, but rather, they are based on domain knowledge provided by a designer. Thus, if a BDI agent could be translated into a MDP²⁷, the solution to this stochastic planning problem could be used by the agent to optimally choose the best plans at every possible state. Next, we review MDPs in Section 6.1, and the conversion of a traditional BDI agent into an MDP in Section 6.2.

6.1 MDPs

A state s is a truth-assignment for atoms in Σ, and a state specification S is a subset of $$\[--><$> {\rm{\hat{\rSigma }}} <$><!--$$ specifying a logic theory consisting solely of literals. S is said to be complete if, for every literal l in $$\[--><$> {\rm{{\rSigma }}} <$><!--$$ , either l or ¬l is contained in S. A state specification S describes all of the states s such that S logically supports s. For example, if we consider a language with three atoms a, b, and c, and a state specification $$\[--><$> S\, = \,\{ a,\,\neg b\} <$><!--$$ , this specification describes the states $$\[--><$> {{s}_1}\, = \,\{ a,\,\neg b,\,c\} <$><!--$$ , and $$\[--><$> {{s}_2}\, = \,\{ a,\,\neg b,\,\neg c\} <$><!--$$ . In other words, a state specification supports all states that are a model for it, so a complete state specification has only one model.

The specification formalism we use allows incomplete state specifications and first-order literals on the preconditions and effects of planning operators (incomplete state specifications can omit predicates that are not changed by an operator from its preconditions and effects, as opposed to requiring operators to include every single predicate in the language's Herbrand base)²⁸.

We consider an MDP (adapted from Shoham & Leyton-Brown, 2010) to be a tuple $$\[--><$> {\rm{\rSigma }}\, = \,(SS,\,A,\,Pr,\,R) <$><!--$$ , where SS is a finite set of states and A is a finite set of actions, Pr is a state-transition system that defines a probability distribution for each state transition so that, given $$\[--><$> s,s^{\prime}\, \in \,SS <$><!--$$ and $$\[--><$> a\, \in \,A <$><!--$$ , function $$\[--><$> P{{r}_a}(s^{\prime}|s) <$><!--$$ denotes the probability of transitioning from state s to state s′ when executing action a. R is a reward function (or utility function) that assigns a value $$\[--><$> r({{s}_i},\,{{a}_j}) <$><!--$$ to the choices of actions a_j in states s_i. The reward function is typically used to indirectly represent goal states in MDPs, making it possible to generate an optimal policy $$\[--><$> {{\pi }^\ast} <$><!--$$ that indicates the best action to take in each state. This optimal policy can be obtained through various methods that ultimately use the Bellman (1957) equations to establish the optimal choices for particular search horizons²⁹. Although we define the reward function as taking an action and a state, which might lead one to believe that the reward function only describes the desirability of taking an action, the use of an action and a state is meant to allow the calculation of the reward of a state.

6.2 Converting BDI agents to MDPs

Schut et al. (2002) provides a high-level correspondence between the theory of partially observable Markov decision processes (POMDPs) and BDI agents, suggesting that one of the key efficiency features of BDI reasoning (that of committing to intentions to restrict future reasoning) can be used in POMDP solvers in order to address their inherent intractability. POMDPs are an extension of MDPs with the addition of uncertainty on the current state of the world; hence, when an agent is making decisions about the optimal action, it has no direct way of knowing what the current state $$\[--><$> s\, \in \,SS <$><!--$$ is, but rather, an agent perceives only indirect observations $$\[--><$> o\, \in \,O <$><!--$$ that have a certain probability of being generated in each state of the world, according to a conditional probability function Ω. Thus, while an MDP is defined as a tuple $$\[--><$> \langle SS,\,A,\,O,\,Pr,\,R\rangle <$><!--$$ with SS being a set of states, A a set of actions, R a reward function, and Pr a transition function, a POMDP has additional components: a set of observations O, and an observation emission probability function Ω, making it a tuple $$\[--><$> \langle SS,\,A,\,O,\,Pr,\,\Omega, \,R\rangle <$><!--$$ . While some of the components of MDPs and BDI agents are equivalent, others require the assumption that additional information about the environment be available. Most notably, BDI agents have no explicit model of the state transitions in the environment. In order to eliminate ambiguity, we shall refer to equivalent components present in both BDI and MDP with a subscript of the corresponding model, for example, the SS_mkv symbol for the set of states from a POMDP specification, and thus represent a POMDP as $$\[--><$> \langle S{{S}_{mkv}},\,{{A}_{mkv}},\,O,\,P{{r}_{mkv}},\,\Omega, \,R\rangle <$><!--$$ . Schut et al. (2002) defines a BDI agent as a tuple $$\[--><$> \langle S{{S}_{BDI}},\,{{A}_{BDI}},\,Bel,\,Des,\,Int\rangle <$><!--$$ , where SS_BDI is the set of agent states, A_BDI is the set of actions available to the agent, Bel is the set of agent beliefs, Des is the set of desires, and Int is the set of intentions. Moreover, a BDI agent operates within an environment, such that the environment transition function $$\[--><$> {{\tau }_{bdi}} <$><!--$$ is known. They establish first the most straightforward correspondences as follows:

• • states in a POMDP are associated with world states of a BDI agent, that is, $$\[--><$> S{{S}_{mkv}}\, \equiv \,S{{S}_{BDI}} <$><!--$$ ;

• • the set of actions in a POMDP is associated with the external actions available to a BDI agent, that is, $$\[--><$> {{A}_{mkv}}\, \equiv \,{{A}_{BDI}} <$><!--$$ —however, the way in which actions change the world (i.e., the transition function) is not known to the agent; and

• • since the transition between states as a result of actions is external to the agent, it is assumed that the environment is modelled by an identical transition function so that $$\[--><$> P{{r}_{mkv}}\, \equiv \,{{\tau }_{bdi}} <$><!--$$ .

Regarding the state correspondences, Schut et al. (2002) propose associating the agent beliefs Bel to the set of observations Ω, since an agent's beliefs consist mainly of the collection of events perceived from the environment. Other equivalences are harder to establish directly, for example, the reward function R from a POMDP does not easily correspond to an agent's desires Des, since the former is usually defined in terms of state and action combinations, whereas desires are often specified as a logic variable assignment that must be reached by an agent. Nevertheless, these variable assignments do represent a preference ordering over states of the environment, and consequently, they can be used to generate a reward function with higher values for states corresponding to desires. Using these equivalences, Schut et al. (2002) compares the optimality of a BDI agent versus a POMDP-based agent modelled for the TileWorld domain, concluding that, since POMDPs examine the entire state space, an agent following a POMDP policy is guaranteed to obtain higher payoff than a BDI agent, but only in domains that are small enough to be solved by POMDP solvers. Hence, there is a tradeoff between the optimality achievable by solving a POMDP problem versus the speed achievable by the domain knowledge encoded in a BDI agent.

Simari and Parsons (2006) go into further detail in providing algorithms for bidirectional conversion between a BDI agent and an MDP, proving that they can be equivalently modelled, under the assumption that a transition function for actions in the environment is known (which is not often the case for BDI agents). The proof of the convertibility between these two formalisms is provided through two algorithms. For the MDP to BDI conversion Simari and Parsons (2006) provides an algorithm that converts an MDP policy into a BDI plan body, which Simari and Parsons (2006) call an intention plan or i-plan. The converse process is detailed by an algorithm that converts the steps of BDI plan bodies into entries of the MDP reward function. Both conversion processes rely on the assumption (common to most BDI implementations) that a plans’ successful execution leads to a high-reward (desired) state, and that the actions/steps in the plan provide a gradient of rewards to that desired state.

Thus, conversion from an optimal MDP policy consists of, for each state in the environment, finding a finite path through the policy that most likely leads to a local maximum. This local maximum is a reward state, and is commonly used as the head of a plan rule, whereas the starting state for the path is the context condition of the plan rule. Creation of this path is straightforward: since a policy specifies an action for each state in the environment, a path can be created by selecting an action; discovering the most likely resulting state from that action; and consulting the policy again until the desired state is reached. The sequence of actions in this path will comprise the body of the plan rule.

Converting a BDI agent to an MDP, on the other hand, consists of generating a reward function that reflects the gradient of increasing rewards encoded in each i-plan. For an individual plan $$\[--><$> {\cal P} <$><!--$$ with a body of length p and a base utility $$\[--><$> U({\cal P}) <$><!--$$ , assuming that the most likely state is reached after the ith action³⁰, the reward for this state is $$\[--><$> i\, \cdot \,U({\cal P}) <$><!--$$ . Converting an entire plan library involves iterating over the plans in the plan library in some fixed order (Lines 6–7 of Algorithm 21), thereby obtaining an ordered sequence of individual actions and expected states, from which the values of a reward function can be derived (Lines 8–11). Once the reward function is obtained, the resulting MDP can be solved using, for example, the value iteration algorithm (Bellman, 2003; Line 14).

6.3 Probabilistic plan selection based on learning

Singh et al. (2010) provide techniques to learn context decision trees using an agent's previous experience. Although not ostensibly developed to perform planning in a probabilistic setting, the underlying assumption for this work is that the Boolean context conditions of traditional BDI programs are not enough to ensure effective plan selection, in particular, where the environment is dynamic. As a consequence Singh et al. (2010) proposes to extend (and possibly completely supplant) the context conditions used for the selection of applicable plans with decision trees trained using data from previous executions of each plan. Basically, as an agent executes instances of the plans in its plan library in multiple environment/world configurations, it builds a model of the expected degree of success for future reference during plan selection. In more detail, the training set for the decision tree of each plan in the plan library consists of samples of the form [w, e, o], where w is the world state composed of a vector of attributes/propositions, e is the vector of parameters of the triggering event associated with the plan, and o is the outcome of executing the plan, that is, either success or failure. Here, the set of attributes included in w from the environment is a user-defined subset of the full set of attributes for the entire domain, representing the attributes that are possibly relevant to plan selection. Learning of the decision tree happens online, so that whenever a plan is executed, data associated with that execution is gathered and the tree is rebuilt.

The leaves of a decision tree then indicate the likelihood of success for a plan in a certain world state given certain parameters. However, data in the decision tree alone is not sufficient to allow an agent to make an informed decision about the best plan to select to achieve a goal, since the confidence of an agent in a tree created with very little data, intuitively, should not be very high. Thus, one of the key issues addressed by Singh et al. is the determination of when a decision tree has accumulated enough data to provide a reliable measure of the success rate for a particular plan instantiation. This problem is of particular importance, since an agent must balance the exploitation of gathered knowledge with the exploration of new data when choosing a plan in a given situation. To address this, the authors develop a confidence measure based on an analysis of sub-plan coverage. This notion of coverage is based on the fact that BDI plans are often structured as a hierarchy of subgoals, each of which can be achieved by a number of different plans; consequently, coverage is proportional to the number of these possible ways of executing a plan for which there is data available.

Using the data stored in the decision trees, as well as the confidence measure of their coverage, an agent selects a plan probabilistically using a calculated likelihood of success with respect to a set of environment attributes and parameters. The confidence $$\[--><$> {\cal C}({\cal P},\,Bel,\,n) <$><!--$$ of a plan $$\[--><$> {\cal P} <$><!--$$ is calculated using the current world state (represented by the beliefs) and the last $$\[--><$> n\,\geq \,1 <$><!--$$ executions of $$\[--><$> {\cal P} <$><!--$$ .

7 Empirical evaluation

As an attempt to obtain insights into when we could use each approach and how we could combine them, the work of de Silva and Padgham (2004) provides an empirical analysis of BDI and HTN (specifically the SHOP algorithm; Nau et al., 1999) systems under varying environmental conditions and problem sizes. The comparison is motivated by the many similarities shared between the two approaches, as highlighted in Table 2. Two concrete implementations for each type of system were chosen (specifically, JACK; Howden et al., 2001 and JSHOP—a Java implementation of the SHOP algorithm) and experiments use identical domain representations and problems for both systems, achieved with a mapping from representations used by the BDI system to those used by the HTN system, taking into account their similarities. The experiments explore time taken and memory usage in static and dynamic environments by the two systems. Their results reveal that the growth rate of the BDI system when searching for a solution in a static environment, compared to that of SHOP as the problem size increases, is linear as opposed to polynomial, which they point out as having a significant impact for large applications. Because only a single implementation of each type of system is used, however, further work is needed before any general conclusions can be drawn. The study also serves to confirm that SHOP-like HTN systems can be made to behave more like BDI systems in dynamic environments by forcing the execution of methods soon after their decomposition.

Dekker and de Silva (2006) present a simulation system of BDI-like agents equipped with a best-first planning component that uses actions available to the agent. Additionally, in this study, the user has the ability to restrict the search to a given number of planning steps. The experiments are done in a multi-agent setting involving a 21-agent (hierarchically structured) team picking up 100 objects in a randomly generated 32 × 32 grid containing 12 obstacles. The performance of the team is measured by the time it takes to pick up all the items. The authors find that, in general, performance improves when not much time is spent on planning: the best performance is reached when planning is limited to the minimum number of steps (50)—that is, when the behaviour is very close to default BDI-style reactive behaviour. However, the authors note that when the ‘thinking speed’ (the number of planning steps per time unit) is increased, planning becomes significantly more effective than default reactive behaviour, and planning for 500 steps becomes worthwhile. Although this study is done in a multi-agent context it still offers useful insights for a single-agent setting.

Despite these empirical evaluations, however, there is still a need for a thorough study of the use of HTN and first principles planning facilities in applications, and an evaluation and validation of their effectiveness and applicability of these facilities in practice³¹. For example, the types of domains in which planning from first principles is worthwhile could be explored, or one could investigate the feasibility of planning from first principles as a part of the standard BDI execution cycle, for example, whenever an applicable plan is not available, instead of letting the achievement goal fail. Intuitively, this approach is likely to be more robust in some applications since it tries to prevent the failure of achievement goals at every opportunity, rather than only at user-specified points in the BDI hierarchy as done in some of the frameworks discussed in this paper. However, this approach is also likely to be very computationally expensive, as the planner may fail to find a solution each time it is called from one level higher in the BDI hierarchy.

8 Discussion

Work on the declarative notion of goals as a means to achieve greater autonomy for an agent has been pursued by a number of researchers. In this paper we consider a number of approaches to declarative goals currently being investigated, namely those of Hübner et al. (2006b), van Riemsdijk et al. (2005), and Meneguzzi et al. (2004b). There are multiple claims as to the requirements and properties of declarative goals for an agent interpreter, and while some models involve planning from first principles to achieve such goals, other models are based on the argument that the only crucial aspect of an architecture that handles declarative goals is the specification of target world states that can be reached using a traditional procedural approach. Besides the issue of how planning can be used to aid declarative reasoning, other researchers have investigated the separate issue of using planning for adding an additional aspect of intelligence, making for more robust agent systems. Two such systems are Propice-plan (Ingrand & Despouys, 2001) and Jadex (Walczak et al., 2006). Such efforts provide insight into many practical issues that may arise from the integration of BDI architectures with AI planners, such as how to modify a planning algorithm to cope with changes in the initial state during planning (Ingrand & Despouys, 2001), and how to cope with conflicts in concurrently executing plans (Walczak et al., 2006).

Related to the work on declarative planning is the work of Kambhampati et al. (1998), motivated by the desire to combine HTN and first principles planning. In their work, first principles planning takes into account not just the primitive actions but also the (more abstract) achievement goals. The resulting ‘abstract plans’ are especially attractive in the context of BDI systems because they respect and re-use the procedural domain knowledge that is already inherent in the BDI system. According to Kambhampati et al. (1998), the primitive plans that abstract plans produce preserve a property called user intent, which they state as the property where a primitive plan can be ‘parsed’ in terms of achievement goals whose primary effects support the goal state. Another feature of abstract plans is that they are, like typical BDI plans, flexible and robust: if a primitive step of an abstract plan happens to fail, another option may be tried to achieve the step.

The work of de Silva et al. (2009) (Section 4.4) is different to Kambhampati et al. (1998) in that the former constructs abstract planning operators from a BDI plan library, and then executes the resulting hybrid plan within the framework, whereas in the latter, achievement goals are decomposed during the process of first principles planning. There are also differences in the details of the approach. Most importantly, Kambhampati et al. (1998) requires the programmer to provide effects for achievement goals, whereas de Silva et al. (2009) computes these automatically. Moreover, the former does not address the issue of the balance between abstraction and redundancy, which is explored in the latter.

Apart from the systems that combine first principles planning and BDI-like systems, there are also systems that add planning into other agent architectures. Of particular relevance to this paper are systems that combine first principles planning with the Golog (Levesque et al., 1997) action language, which has been successfully used for robot control. In Claßen et al. (2007) IndiGolog (Sardina et al., 2004)—an implementation of Golog—is extended with the FF (Hoffmann & Nebel, 2001) classical planning system. IndiGolog already supports planning from first principles via its achieve(G) procedure, where G is a goal state formula to achieve. In Claßen et al. (2007), another similar construct is added to the language, which amounts to calling the FF planner. The returned plan (if any)—a sequence of planning actions—is executed within the IndiGolog engine. The objective of this work is twofold: (i) to provide a translation from IndiGolog actions into a version of Planning Domain Definition Language (PDDL) and (ii) to show that we can improve efficiency by using the FF planner for planning as opposed to the built-in IndiGolog procedure.

Likewise, Baier et al. (2007) and Fritz et al. (2008) address the issue of planning from first principles in ConGolog—Golog with support for specifying concurrency—in a way that respects and exploits the domain control knowledge inherent in ConGolog programs similarly to Kambhampati et al. (1998) and de Silva et al. (2009). To this end, they provide a translation from a subset of the language of ConGolog into PDDL planning operators. The translation takes into account the domain control knowledge-inherent ConGolog programs. Specifically, these operators ensure that primitive solutions resulting from the planning process conform to the ConGolog programs given. Moreover, Baier et al. (2007) propose different heuristics for planning, which show how the time taken for planning can be reduced when the domain control knowledge encoded in planning operators is effectively used.

While the IxTeT-eXeC (Lemai & Ingrand, 2004) and RETSINA (Paolucci et al., 1999) systems do not perform planning from within BDI-like systems, these are still worth mentioning because they are planners that exhibit a certain element of BDI-style execution. IxTeT-eXeC is a combination of PRS and the IxTeT-eXeC (Laborie & Ghallab, 1995) planner, which allows an expressive temporal specification of planning operators. Unlike Propice-plan, IxTeT-eXeC gives more control to the planner than the BDI system. Initially, IxTeT-eXeC is given a top-level goal state to achieve by the user, which is used by the IxTeT planner to formulate a complete solution for the goal state in terms of the planning operators in the domain, which essentially correspond to leaf-level achievement goals in PRS (i.e., those handled only by plan bodies that do not mention any achievement goals). The solution is then executed by IxTeT-eXeC by sending each individual planning operator in the solution to PRS, one at a time. PRS executes a given planning operator by mapping it into the corresponding achievement goal, and then executing it using standard BDI execution mechanisms, which may involve (local) failure recovery—trying alternative leaf-level plan rules. These plan rules are composed only of primitive steps that can be directly executed by the robot. Finally, PRS sends a report back to the planner indicating the result (e.g., success or failure) of executing the achievement goal. If during the execution of a plan found by IxTeT a new goal arrives from the user, the old plan is repaired (if necessary) to take into account this new goal.

In the RETSINA (Paolucci et al., 1999) system, agents solve their top-level achievement goals by performing HTN decomposition. If the information required to decompose some lower-level achievement goal is not available at the time of planning, the agent then suspends the decomposition, locates the relevant information gathering actions in the plan being developed that would obtain the necessary information, and then executes these actions. Once the information is obtained, the decomposition of the top-level achievement goal continues. RETSINA also makes use of Rationale Based Monitoring (Veloso et al., 1998) in order to monitor conditions that are related to the plan being developed. If, while a plan is being developed, a change in the environment makes a monitored condition false, the planning process is abandoned. In comparison with the type of systems presented in this paper, RETSINA agents continuously perform HTN planning/lookahead, unless information needs to be gathered from the environment. The systems we are interested in, on the other hand, generally follow standard BDI-style execution, using the HTN planner only when useful/necessary.

9 Conclusion

Given the high computational cost of planning from first principles, it is important for the long-term efficiency of planning agent architectures to have the ability to reuse plans when similar goals need to be achieved, and to improve domain knowledge using past experiences. Although efforts towards plan reuse have been made in the planning community (Nebel & Koehler, 1995), very few BDI-based planning architectures have significant plan reuse capabilities. From the architectures surveyed in this article, only AgentSpeak(PL) (Meneguzzi & Luck, 2008) has a very basic plan reuse technique that still does not generalise to similar circumstances. Similarly, leveraging past plan executions into new domain knowledge has been the focus of recent work in generalised planning (Srivastava et al., 2009, 2011). Although the work of Singh et al. (2010) allows learning context conditions for domain-specific plans in non-deterministic environments, it lacks the ability to create new domain knowledge based on this experience.

In Table 2 we summarise the key characteristics of the architectures we have surveyed, showing, for each architecture, the type of planning algorithm employed, the type of action (or transition model), and whether the agent's plan library is dynamic or fixed. The first two items in comparison are straightforward to understand, and the plan library column refers to the types of plans that can be generated by the planner. In the architectures where the plan library is dynamic, new plan rules are found by the agent and possibly added to the agent's plan library. Conversely, in the other architectures, where the planner is used only to help optimise plan selection, new plan rules are not found and therefore the agent's plan library does not change.

Table 2 Comparison of planning architectures

From Algorithms 14 and 16 we can see that Propice-plan and AgentSpeak(PL) follow a similar approach. The main difference is that, unlike Propice-plan, AgentSpeak(PL) stores plans found for later use. There is a subtle difference in the additional test included in Propice-plan (Line 14) to determine before execution whether the context condition is still valid relative to the current state of the world. This seems unnecessary, however, since any relevant environmental changes will eventually be detected in both systems when actions or achievement goals fail. Another difference between the two systems is that in AgentSpeak(PL) the planner can be called from any point in an agent's plan (not shown in the algorithm), and hence essentially from any point in the BDI ‘hierarchy’. In Propice-plan however, planning occurs only (and always) when no options are available for solving an achievement goal (Lines 11–19).

The Hybrid Planning Framework of Section 4.4 is similar to AgentSpeak(PL) in the sense that the first principles planner can be invoked at any given programmer-selected point in the BDI ‘hierarchy’. The Hybrid Planning Framework also shares the approach adopted by Propice-plan whereby plans returned by the former (actually, post-processed versions of plans that take into account ‘desirable’ properties such as non-redundancy) are immediately executed rather than stored for later use.

The main difference between the planning and execution system of LAAS-CNRS (Section 5.2) and the CANPlan framework (Section 5.1) is that while the latter exploits HTN planning to take the right decisions at choice points—that is, to check if there is a complete successful decomposition of a plan under consideration (Line 5 of Algorithm 7), and to take a step along that successful path—the LAAS-CNRS framework uses HATP to find a plan composed of a sequence of (primitive) actions (Lines 4 and 5 of Algorithm 19), much in the same way as how architectures such as Propice-plan use a first principles planner to obtain a plan. Consequently, in the LAAS-CNRS framework the domain-knowledge encodings written for HATP do not have to match those in PRS: HATP is simply chosen as a more efficient alternative to using a first principles planner (albeit with the restriction of HTN planning where solutions are limited to those entailed by the user encodings). On the other hand, in CANPlan, the encodings used by the HTN planner have to match those in the BDI system, as HTN planning is used here to perform lookahead on the BDI hierarchy.

Overall, first principles planners seem well suited to create new BDI plan structures (de Silva et al., 2009) when a path pursued via standard BDI execution (sometimes coupled with HTN-like planning) turns out to not work, as highlighted in Algorithms 14 and 16 and discussed in Section 4.4. The domain representations used in planning are derived similarly in these three approaches: from the existing domain specification of the agent's actions, plans, and/or after analysing the agent's achievement goals. The approaches are also alike in how actions in plans found are mapped back into corresponding BDI entities. HTN-like planning, on the other hand, seems more suited to get advice on which plan instances to use when the BDI system is faced with a choice point (Sardiña et al., 2006), as shown in Lines 5 and 5 of, respectively, Algorithms 17 and 14. To this end, BDI and HTN systems either use the same domain representation (e.g., Propice-plan) or a mapping function to translate between the two representations (e.g., CANPlan). As discussed earlier, the LAAS-CNRS framework is an exception to how HTN-like planning is normally used from within a BDI system in that their HATP planner is used like how first principles planners are used to obtain plans made of primitive actions.

Direct comparison between the remaining BDI systems described in this paper is not straightforward, as they employ a different notion of plan rules and plan library in the case of X²-BDI and Jadex, or make different assumptions about the environment model in the case of the BDI ↔ MDP approach. Nevertheless, these architectures provide alternative views for the design of BDI agents that include planning, and in what follows, we attempt to relate them to more traditional BDI approaches. X²-BDI is more logic oriented, and imposes a stronger condition on the adoption of sets of desires as intentions: that of the existence of a STRIPS-based plan that can achieve the set of goals. This condition is much more expensive to verify than the context condition in traditional BDI plan rules, as it involves multiple executions of a planning algorithm in a single reasoning cycle. So, although it can be said that X²-BDI implements a more complete handling of declarative goals than traditional BDI systems (except for those in the 3APL line of interpreters (Dastani et al., 2004), it is unclear how practical this approach would be for more complex agents. Jadex is a more Java-oriented approach to programming agents, which might offer improved runtime performance, since there is no agent interpreter running the agent, but rather a Java program running directly in a virtual machine. Such design choice might ultimately come at the cost of the known theoretical properties offered by the other architectures. Finally, the approaches based on MDP planning models are relatively new, and very little experimental work has been done, but assuming a suitable stochastic model of the environment is available, they could offer optimality guarantees not yet available for traditional BDI approaches.

10 Future directions

Although efforts towards the integration of AI planning techniques into BDI agent interpreters have produced a number of results, most of which are surveyed in this paper, there is still significant scope for future work. These efforts can be divided into three distinct, yet related overall objectives. First, work towards augmenting an agent's range of behaviours by expanding the set of BDI plans available to the agent in order to cope with changes in the environment. Second, work towards improving the robustness of the BDI agents either through changes to the set existing BDI plans, or refinements in the agent's plan selection algorithm. Third, incorporating explicit social constructs into agent programming languages to facilitate development of multi-agent systems (MAS) using these languages.

Challenges in the first area include dealing with the interaction between newly generated plans and the originally designer-specified plan library, as well as the potential loss of efficiency resulting from a large number of additional rules within an agent's plan library, as indicated by Meneguzzi and Luck (2008). Since undesirable interaction between plans are likely to result in more plan/goal failures, employing learning techniques as done in the work of Singh et al. (2010) alongside systems such AgentSpeak(PL) (Meneguzzi & Luck, 2008) or Propice-plan could provide a way to learn better context decision trees to improve effectiveness of newly generated plans. Moreover, plans designed by a classical planner do not take into account contingencies that might arise during plan execution as a human designed plan library often does, thus a natural next step in BDI plan generation involves the application of contingency planners (Meuleau & Smith, 2003). In contrast to the linear nature of the output of classical planners, contingency plans consist of a tree structure where each branch of the tree contains tests for contingencies that might happen as parts of the plan are executed. Such a structure is effectively what the set of BDI plan rules stand for: sections of linear plans that are used in reaction to events in the environment or the agent itself. As such, we believe there is significant scope for further research in planning within BDI agents with the use of contingency planners. In the context of uncertain environments where a model of the uncertain actions is available, the theoretical work in the conversion of a BDI specification into an MDP representation (Simari & Parsons, 2006) can be seen as an initial step into providing a decision-theoretic method for BDI plan selection. The challenge in creating such a method lies in interpreting the solution concept of an MDP (i.e., a policy) in terms of the outcome that might result on executing an associated BDI style plan rule. Since an MDP specifies a single optimal action to take at any single state, one way to interpret a policy is to modify the agent's plan selection mechanism to choose those BDI plan rules that are in conformance with such a policy. Solution concepts that provide a promising path towards this kind of plan selection mechanism have been preliminarily studied by Tang et al. (2011). In this work, HTN plan structures are used as a probabilistic grammar in an Earley-parsing algorithm (Stolcke, 1995), which provides probability and utility values for each possible expansion of a grammar rule (or task decomposition), which could form the basis for plan selection. Work in planning with probability requires probabilistic models of the environment dynamics as well as reasoning techniques, aiming to maximise the chance of plan success, which leads to our second area for future work.

Besides expanding an agent's plan library, a key avenue of further research in BDI agent interpreters involves refinements in the plan selection process. Such improvements have often been studied in the broader context of agent meta-level reasoning, and are recognisably hard problems (Raja & Lesser, 2004) as they involve a tradeoff between agent reaction time and the optimality of an agent's decisions against its bounded resources. To this end, in architectures that employ HTN planning (such as the one described in Section 5.1) to decide ahead of time which plan decompositions are likely to be successful when certain plans are adopted, one could investigate looking ahead up to a given number of decompositions, in order to cater for domains in which there is limited time for planning. There is some initial work in this direction where the planning module is extended to take into account an additional parameter corresponding to the maximum number of steps (e.g., decompositions) up to which lookahead should be performed. Some of the theoretical and empirical results from this approach can be found in Dekker and de Silva (2006) and de Silva and Dekker (2007). Furthermore, the work in Hindriks and van Riemsdijk (2008) proposes semantics for a lookahead limit when reasoning about maintenance goals, where an agent will lookahead only up to a given number of steps when determining whether there is a path that will lead to the violation of a maintenance goal. That work might provide useful insights into developing the resource-bounded account of HTN planning.

In the Hybrid Planning Framework, one could investigate a more general approach for finding good (e.g., ‘ideal’ or ‘preferred’) hybrid solutions³². In their current framework, the authors consider redundancy as one of the underlying factors that determine whether a hybrid solution is good. While removing redundant steps is reasonable in some domains, it may be inappropriate in other domains, in particular, because HTN structures sometimes encode strong preferences from the user. For example, consider a hybrid solution containing the following sequence of tasks (Kambhampati et al., 1998): get in the bus, buy a ticket, and get out of the bus. Although it may be possible to travel by bus without buying a ticket, if this task is removed when it is redundant, we may go against a strong preference of the user that requires that task to be performed after getting into the bus and before getting out of it. To cater for strong preferences, we could use ideas (Sohrabi et al., 2009) to create a more general framework with a more flexible account in which, for instance, all HTN preferences are assumed to be strong, and a redundant task is only removed if the user has separately specified that the task is not strongly preferred. For example, while the task of buying a bus ticket may be redundant, it is not removed from a hybrid solution unless the user has specified that the task is not strongly preferred. Such specifications could be encoded as hard constraints or soft preferences, and included either within an extended version of HTN methods or as global constraints outside of methods, as done in Sohrabi et al. (2009). Taking into consideration more expressive planning frameworks introduces the possibility of employing planners to introduce new constructs in the agent programming languages themselves, which leads to our third area of future work.

Although agent programming languages are ostensibly aimed at the development of MAS, only relatively recently has there been a focus on the introduction of abstractions and mechanisms for MAS development beyond agent communication languages. One such mechanism that has been the focus of considerable attention recently consists of specifying social norms that regulate the behaviour of individual agents within a society. Here, one could employ techniques for planning with preferences (Baier et al., 2009; Sohrabi et al., 2009) to support practical implementations of norm-driven BDI agents. In norm-regulated societies, agents must plan not only to achieve their individual goals, but also to fulfil societal regulations (norms) that dictate behaviour patterns in terms of deontic modalities, such as obligations, permissions, and prohibitions. Such norms can be viewed as soft constraints, which when complied with result in some degree of benefit to the agent, and when violated result in sanctions and loss of utility. Planning under these circumstances must weigh the expected benefits of accomplishing one's goals when these can be hindered by normative stipulations. For example, an agent might decide to board a bus without a ticket (and accept a potential penalty for this action) if the action's goal of reaching a certain location within a short time frame has a very high reward. Initial work in that direction has been carried out by recent efforts in practical norm-driven BDI agents (Kollingbaum, 2005; Meneguzzi & Luck, 2009; Panagiotidi & Vázquez-Salceda, 2011).

Finally, beyond improvements in the capabilities of agent interpreters, it is clear that there is still significant work to be done in strengthening the theoretical foundations as well as evaluating the practical aspects of the agent interpreters described in this paper, as discussed in Section 7. For example, in the Hybrid Planning Framework (Section 4.4), while the authors provide a formal framework for first principles planning in BDI systems, they have not provided an operational semantics that defines the behaviour of a BDI system with an in-built first principles planner. To this end, one might need to add a construct such as $$\[--><$> Plan(\phi ) <$><!--$$ into a language such as CAN or AgentSpeak(L), with $$\[--><$> \phi <$><!--$$ being the goal state to achieve, and provide derivation rules for this module that reuse and respect the procedural domain knowledge in the plan library. The way in which the AgentSpeak(L) operational semantics is extended to incorporate a planning component (Meneguzzi & Luck, 2007; Section 4.3) might provide useful hints in this direction.