Introduction
Snowfields have a significant effect on the planetary albedo and climate. Development of satellite remote sensing of snow is of great importance, particularly for monitoring of snow age, pollution and grain sizes over difficult-to-access polar regions.
The core of the remote-sensing algorithm is the relation between measured radiative and retrieved microphysics characteristics.
The classical works on remote sensing of snow imply a snow model as a layer with large independent spherical scatterers (Reference Bohren and BarkstromBohren and Barkstrom, 1974; Reference Warren and WiscombeWarren and Wiscombe, 1980; Reference Wiscombe and WarrenWiscombe and Reference Warren and WiscombeWarren, 1980; Reference WarrenWarren, 1984). We refer to this model as model 1. Up to now all developed satellite algorithms to retrieve the snow effective grain size from measured spectral reflection characteristics have employed this snow model (Reference Grenfell, Warren and MullenGrenfell and others, 1994; Reference Hori, Aoki, Stamnes, Chen and LiHori and others, 2001; Reference Li, Stamnes, Chen and XiongLi and others, 2001). The conventional way to establish the relation between radiative and retrieved microphysics characteristics is to use Mie theory to obtain the single-scattering characteristics in terms of microphysics, and the radiative transfer theory to relate radiative properties of snow layers to the single-scattering (inherent) characteristics.
However, it follows from numerous experimental studies of optical and microphysical snow properties that a snow layer is a multiple-scattering close-packed medium with irregularly shaped non-uniform grains. A potentially more realistic snow model is a medium with non-spherical close-packed grains, which we refer to as model 2. Note that the shape of snow grains is not known a priori; moreover, there are various shapes dependent on the origin and age of snow and environment. Such a model was suggested by Reference Zege, Ivanov and KatsevZege and others (1998).
Thus, our main goal is to develop and verify an algorithm to retrieve the effective snow grain size and soot concentration, which does not imply any specific snow model or any a priori suggestions of snow grain shape, and uses the multispectral information provided by a satellite optical instrument. The first version of such an algorithm was developed by the authors in the process of a pre-launch algorithm development for the Global Imager (GLI) on board the Advanced Earth Observing Satellite (ADEOS) and was briefly characterized by Reference Zege, Ivanov and KatsevZege and others (1998). This algorithm was not deployed. At that time the habitual work with spherical particles seemed preferable.
Only now, after years of study of snow optical (Reference Aoki, Aoki, Fukabori, Hachikubo, Tachibana and NishioAoki and others, 2000, Reference T., Hachikubo and Hori2003; Reference Kokhanovsky and ZegeKokhanovsky and others, 2004, Reference Kokhanovsky, Aoki, Hachikubo, Hori and Zege2005) and microphysical properties (Reference Matzl and SchneebeliMatzl and Schneebeli, 2006; Reference Kerbrat, Pinzer, Huthwelker, Gäggeler, Ammann and SchneebeliKerbrat and others, 2008), has it become clear that the model of snow as an ensemble of independent spherical particles (model 1) was wide of the truth. Currently, we are working on verifying the algorithm to retrieve snow grain-size and pollution (SGSP) concentration from moderate-resolution imaging spectroradiometer (MODIS) data based on model 2 that are going to be immediately used for satellite snow monitoring of the Arctic region in the framework of the European integrated project DAMOCLES (Developing Arctic Modeling and Observing Capabilities for Long-term Environmental Studies).
In this paper, we present the core of this algorithm, the underlying physics, the main equations used, and estimations of accuracy without technical details.
Analytical Solutions for Inherent Optical Characteristics of Irregularly Shaped Snow Grains
The main results of snow optics considering snow as non-spherical close-packed grains of different shapes were published by Reference Zege, Ivanov and KatsevZege and others (1998) and Reference Kokhanovsky and ZegeKokhanovsky and Zege (2004). The size of the snow grains provides the applicability of geometrical optics. In the range 0.3–1.25 μm, where light attenuation along the particle size is small and the real part of the refractive index changes slightly, the particle shape affects only the phase function and the asymmetry factor g (the average cosine of the phase function). The following equations for the integral characteristics of the single scattering by non-spherical snow grains in visible and near-infrared are (Reference Zege, Ivanov and KatsevZege and others, 1998);
Reference Kokhanovsky and ZegeKokhanovsky and Zege, 2004):
Here σ e, σ a are the extinction and absorption coefficients, respectively, α = 4πχ=is the absorption coefficient of ice, χ is the imaginary part of the complex refractive index of ice, is the wavelength, C v is the volumetric particle concentration, a ef = 3hVi=4h∑i is the effective size of grains, hVi and 〈∑〉 are the average volume and cross-sectional (geometric shadow) area of snow grains, respectively, and g 0(ξ) is the average cosine of the phase function at α = 0. A factor ξ depends on the particle shape; the values ’(ξ) and g 0(ξ) depend on the shape of snow grains only. Some computations of the values φ(ξ) and g 0(ξ) for simple non-spherical particles are given by Reference Kokhanovsky and MackeKokhanovsky and Macke (1997). Data for ice crystals of different shapes with various aspect ratios (Homogeneous Hexagonal Monocrystals (HHM) model) and with air bubbles and soot inclusions and possibly with rough surfaces (Inhomogeneous Hexagonal Monocrystals (IHM) model) were obtained with codes by Reference Macke, Mishchenko and CairnsMacke and others (1996a, Reference Macke, Mueller and Raschkeb) (ray-tracing method) and by Yang and Liou (1996) (geometric-optics–integral-equation method).
It was shown by Reference Zege, Ivanov and KatsevZege and others (1998) and Reference Kokhanovsky and ZegeKokhanovsky and Zege (2004), and it is seen from Equation (3) in the next section, that the albedo of a snow layer includes only one parameter A with regard to the shape of particles:
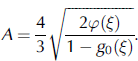
The calculation performed for spheres, prolate and oblate spheroids, fractals (the model of fractals is described by Reference Macke, Mishchenko and CairnsMacke and others, 1996a, Reference Macke, Mueller and Raschkeb) and various hexagons (plates, columns with different aspect ratio, with and without rough surfaces and inclusion) has shown that parameter A ranges approximately from 3.5 to 6.5.
The phase functions of various crystal particles computed with codes by Reference Macke, Mishchenko and CairnsMacke and others (1996a, Reference Macke, Mueller and Raschkeb) and Yang and Liou (1996) are given in Figure 1 in comparison with the phase function of spherical particles computed by a Mie code. It should be underlined that in the range of scattering angles important for satellite remote sensing (50–170˚), the spherical and non-spherical particle phase functions can differ in orders of magnitude. This feature has a deep physical meaning because of the symmetry of the sphere and is the reason why the scattering by spheres is not satisfactory to describe snow optical properties. Note that the difference between phase functions of crystals of various shapes is much less pronounced.

Fig. 1. Phase functions of spheres (solid line) and hexagon crystals: plates (dotted line) and columns (dot-dashed line). The smooth curves without halos give the phase function for plates and columns with rough surfaces.
It is very important that phase functions of large ice crystals do not depend on the wavelength in the range 0.3–1.5 μm beyond very small angles. This could be expected from the geometrical optics and it follows from the computations.
Radiative Characteristics of a Snow Layer
The snow albedo is a very important characteristic, particularly in climate problems. This is shown by a huge number of both experimental and theoretical researches devoted to studies of snow optical properties. Recent comprehensive reviews (Reference Nolin and LiangNolin and Liang, 2000; Massom and others, 2001) contain around 300 references to the subject. We present here the simplest and very accurate equations for radiative characteristics of a snow layer obtained using asymptotic solution of radiative transfer theory (Reference Yang and LiouZege and Reference Kokhanovsky and MackeKokhanovsky, 1997; Reference Zege and KokhanovskyZege and others, 1998; Reference Kokhanovsky and ZegeKokhanovsky and Zege, 2004).
It was shown that the spherical albedo R of a semi-infinite snow layer can be calculated with
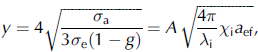
with parameter A defined by Equation (2).
The good accuracy of the simple Equation (3) was demonstrated by Zege and Reference Kokhanovsky and MackeKokhanovsky (1997) and Reference Zege, Ivanov and KatsevZege and others (1998) by comparison with both radiative transfer computation and experimental data. Moreover, it was proved by Reference Kokhanovsky and ZegeKokhanovsky and Zege (2004) that Equation (3) can be used for close-packed media with large particles, when scattering can be described in the framework of the geometrical optics enhanced by Fraunhofer diffraction. This means that Equation (3) describes the reflectance from a snow layer when the realistic model 2 is implied. This is a very important issue. This implication stays true for the radiance coefficient of a snow layer.
The radiance coefficient Ri (θ,θ 0,φ) of radiation reflected by a snow layer in the spectral channel i of the used satellite instrument (i.e. at wavelength i ) in terms of snow characteristics is the basic equation for the satellite retrieval algorithm. From the asymptotic theory (Reference Zege and KokhanovskyZege and others, 1991) it follows that
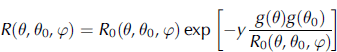
where θ and θ 0 are polar (zenith) angles of the observation and the sun, respectively, and φ is the azimuth angle.
The universal function g(θ) is of the form (Reference Zege and KokhanovskyZege and others, 1991)
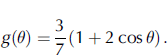
The function R 0(θ,θ 0,φ) is the radiance coefficient of the semi-infinite non-absorbing layer. As mentioned above, the phase function does not depend on the wavelength in this case and, hence, function R 0(θ,θ 0,φ) stays the same for the entire spectral range. This function is completely defined by the phase function of the medium and determined by an integral equation (Reference Zege and KokhanovskyZege and others, 1991). Figure 2 presents the function R 0(θ,θ 0,φ) computed with the integral equation for fractal and spherical particles. As seen, they differ significantly. More details about the origin, the accuracy and the range of applicability of Equations (3) and (5) can be found in Reference Zege and KokhanovskyZege and others (1991). While developing this algorithm, a new set of studies on the accuracy of the asymptotic Equations (3) and (5) with various phase functions (randomly oriented crystals of various shapes, spheres, fractals, spheroids) was calculated and showed the high accuracy for snow in the range 0.3–1.5 μm, which is exactly what is used in snow remote sensing.

Fig. 2. Radiance coefficient as a function of the sun zenith angle at the observation angle 20˚ for large spherical particles (1–3) and fractals (4–6) at σa=σ" = 0:016. The azimuth values are 0˚ (rectangles), 90˚ (ellipses) and 180˚ (triangles).
Equations for Retrieval of Effective Snow Grain Size and Soot Concentration
The operational retrieval algorithms traditionally use a lookup table (LUT) technique, with LUT developed for the spherical particles using Mie code to compute single-scattering characteristics, and radiative transfer code to compute bidirectional reflectance. By contrast, our inversion is completely analytical, based on inversion of Equation (5) appropriate for non-spherical close-packed grains.
Let us consider the soot pollution of snow. Soot particles are very fine. Their radius is smaller than 0.1 μm. The refractive index of soot is m st = n st ─ iχ st = 1:75 ─ 0:43i (WCRP, 1986) in the visible and near-infrared (near-IR) spectrum. Light scattering by such particles is extremely small. Thus, the effect of soot impurities on the value of σ e can be ignored.
The absorption coefficient of soot particles is equal to (Reference Bohren and HuffmanBohren and Huffman, 1983):
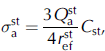
where
is the soot absorption efficiency,
is the effective radius of soot particles and C st is the soot volumetric concentration. In the following, the amount of soot pollution is characterized by the relative soot concentration C* st = C st /C V, where C st and C V are the soot and snow-grain volumetric concentrations, respectively. The absorption coefficient of polluted snow at wavelength i is then characterized by
where
The computations by Mie theory according to the Soot model (WCRP, 1986) show that in the range of interest k ⋍ 0:2.
The value of yi (Equation (4)) through Equations (1) and (8) therefore becomes:
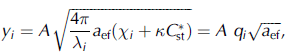
where χi is the imaginary part of the refractive index of ice at wavelength i (i.e., in the i th channel of the satellite optical
instrument), and
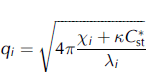
is the only value in Equation (10) that depends on wavelength.
The equation for the radiance coefficient of a polluted snow pixel in the ith spectral channel of the satellite optical instrument with wavelength i follows from Equation (5) with regard to relation (10):
We drop the arguments θ, θ 0, φ in the radiance coefficients in what follows.
Just two values, a ef and C * st, could be retrieved from satellite data using the presented algorithm. The soot concentration C * st is computed using the following equation:
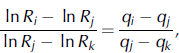
i.e. using measured data of three channels i, j, k.
Equations (11) and (13) give the algebraic equation for C * st with coefficients, given through measured Rn and known χn values (n=i,j,k). The solution is:
where
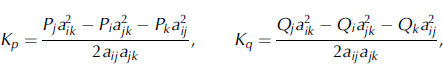
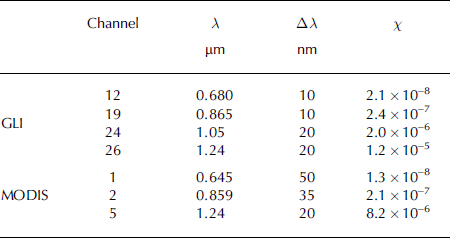
Indices i, j and k correspond to the appropriate spectral channel numbers; the χi values for the used spectral channels of GLI and MODIS are given in Table 1.
Table 1. The imaginary part of the snow refractive index χ and spectral widths Δλfor the used spectral channels of GLI and MODIS
The effective size a ef of snow grains is retrieved using the following solution of Equation (12):
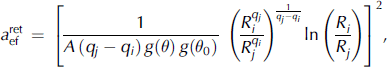
where i and j are the numbers of used spectral channels. To check the correctness of solution (20) it is enough to substitute it in Equation (12).
Equations (14–20) are a core of our algorithm to retrieve SGSP concentration. It uses data in three channels to retrieve two characteristics. The extra channel allows exclusion of the function R 0(θ, θ 0, φ) directly depending on an a priori unknown phase function (i.e. on particle shapes). This unknown requires an additional channel. The effective size a ef of snow grains is retrieved using data in two channels (one in the visible and one in the near-IR spectrum); the retrieval of soot pollution requires three channels (one in the visible and two in the near-IR spectrum). The spectral channels should be chosen with regard to the spectrum of the ice absorption. The use of four channels in the GLI algorithm (additional channel 1.05 μm in comparison with MODIS) allows one to include an additional procedure of choice between channels 24 and 26 for every pixel dependent on the value of the registered signal in these channels. Practically, this procedure optimizes the wavelength, providing maximal accuracy for the retrieval of snow parameters for each pixel.
Let us consider the retrieval with Equations (14–20). These analytical formulas give the snow effective size a ef and soot concentration
directly in terms of the measured reflectance coefficients for any shape of snow particles in a pixel without any a priori suggestions. To underline this advantage of the proposed technique over all others, let us estimate how the use of the spherical-particles snow model, for instance, in operating LUT retrievals, affects the retrieval accuracy.
Let the snowpack consist of fractals. Figure 3 gives the ratio of the retrieved value to the true value for various azimuths of observation obtained with the LUT technique (i.e. the a priori spherical-particles model while computing LUT). The accuracy of the retrieval is not satisfactory. The retrieved value of the grain size may change by an order of magnitude dependent on the geometry of the observation, especially for oblique sun angles, usually realized in polar regions. Note that these data show only the inherent inaccuracy of the conventional LUT retrieval algorithms, because no other sources of retrieval errors are included in this simulation.

Fig. 3. Ratio of the retrieved effective size to the true effective size as a function of the sun angle at an observation angle of 20˚ and different azimuth angles.
Verification of the SGSP With Computer Simulation
We have developed the very first version of a new tool, software SRS (Snow Remote Sensing), specifically to study the accuracy of various retrieval techniques for snow remote sensing. SRS software provides calculations of the bidirectional reflectance both from a snow layer and a snow– atmosphere system and simulates signals in the spectral channels of satellite optical instruments. SRS includes realistic changeable atmosphere models with stratification of all components (aerosol, gases); accurate and fast radiative transfer code; and a generator to simulate noise in the spectral channels of the optical satellite instrument. Snowfields with different snow grain sizes and shapes and soot concentrations could be included in the simulation. The optical properties are computed with Mie code for spherical grains and with the codes (Reference Macke, Mishchenko and CairnsMacke and others, 1996a, Reference Macke, Mueller and Raschkeb) for non-spherical particles (spheroids, fractals, ice crystals of different configuration, both ideal and with rough surfaces and bubbles and soot inclusions). A database of phase functions and single-scattering albedos for different grains of various shapes in the range 0.5–1.5 μm was developed and incorporated in SRS. Snow is modeled by an ensemble of randomly oriented non-spherical particles of various shapes. A snow model is specified by a snow grain shape and the relative soot concentration. The signals registered by an optical instrument on a satellite are simulated including the spectral sensitivity of spectral channels and with the simulation of random and systematic errors. These simulated data are used as input to the retrieval algorithms. We verified our SGSP algorithm using SRS computations. Retrieved values of the effective size and relative soot concentration were compared with the ‘true’ values as the input of SRS.
One of the main questions of any inverse problem is the sensitivity of the retrieved values to the error in the input. The simulations included the following parameters: effective snow size a ef = 50–1000 μm, relative soot concentration
sun angle θ 0 = 40–85˚, observation angle θ = 0–20˚ and azimuth angle = 0–180˚. The relative standard deviation (STD) of 0, 0.5, 1 and 2% for the random error of snowfield reflection coefficient measurements was considered. On the basis of the simulated and inverted data, the following conclusions are drawn:
-
Both average values and STD of the retrieved values
and a ef depend weakly on azimuth and on sun angle at θ, θ 0 < 75˚.
-
The error on the
retrieval depends strongly on the true soot concentration and on the random error of the reflection coefficient measurement. It shows a weak dependence on snow grain effective size a ef and snow grain shape. To estimate concentration with an error of less than 100%, it is necessary to measure the radiance coefficient with a random error of
with an error of less than 100%, it is necessary to measure the radiance coefficient with a random error of and 1% at
and 1% at

-
The error of the a ef retrieval depends strongly on the random error of the reflection coefficient measurement. This dependence is practically the same for snow grains of different shape. To achieve an error of the a ef retrieval of less than 20%, it is necessary to measure the radiance coefficient with a random error
and 1% at

As already underlined, the SGSP does not use any a priori estimation of the shape of snow particles. This is completely true for the retrieval of the soot concentration. But while retrieving effective size, the value of parameter A defined by Equation (2) should be specified. As mentioned, this parameter ranges approximately from 6.5 to 3.5 and stays around A = 6 for sphere and spheroids and about A = 4 for fractals. It follows from Equation (20) that without some indication of the particle shape we cannot retrieve the effective size itself, but only the value of A 2 a ef. This is not a drawback of this approach; it is a feature of the nature of snow. The physical origin of this feature is that in the common case the optical properties of irregularly shaped particles can be related to any characteristic size of particles only approximately. The snowpack reflectance does not carry information about the details of grain shape. Figure 4 shows the results of the effective snow grain-size retrieval with A = 6. This choice leads to systematic relative error of about 15–30% if an examined pixel contains spheroids, and about 50% if it consists of fractals or hexagonal crystals. Of course, this systematic shift can be decreased by a reasonable choice of parameter A. But this problem requires more experimental data on real snow structures.

Fig. 4. The average value of the retrieved effective size of snow grains ![]() marks) and the true a
ef value (solid line) vs
marks) and the true a
ef value (solid line) vs ![]() at θ= 20˚, φ = 0˚, θ
0= 40˚. The random measurement error is 1%, the parameter A = 6. Snow grain models: spheres (O), fractals (x), oblate spheroids (Δ), prolate spheroids (∇).
at θ= 20˚, φ = 0˚, θ
0= 40˚. The random measurement error is 1%, the parameter A = 6. Snow grain models: spheres (O), fractals (x), oblate spheroids (Δ), prolate spheroids (∇).
Conclusion
We presented the algorithm SGSP to retrieve snow grain size and soot pollution concentration from satellite spectral data. The underlying theory uses
-
a realistic model of snow consisting of non-spherical close-packed grains instead of the usual model with independent spherical particles;
-
the analytical solutions for the inherent optical characteristics of snow in terms of microphysical parameters obtained in the framework of geometrical optics instead of time-consuming computations;
-
the analytical asymptotic solution instead of the radiative transfer computations to relate radiative characteristics of a snow layer to its inherent optical parameters.
Note that as shapes of snow grains in a pixel are not known, any a priori model may lead to non-controlled errors in the retrieval. The main advantage of the proposed algorithm over any currently used is the rejection of any a priori model of snow particles.
The SGSP analytical retrieval (instead of the LUT technique) provides extremely fast satellite data processing.
The special software SRS that simulates the signals from a snow–atmosphere system registered in the spectral channels of satellite optical instruments was developed and briefly outlined in this paper. The first verification of the developed algorithm performance using SRS simulations was successfully carried out.
Future work will include the SGSP verification using results of a field campaign in the Arctic region in the process of DAMOCLES project execution.
Acknowledgements
At the first stage, this work was conducted as part of pre-launch algorithm development for the GLI on board ADEOS and supported by the National Space Development Agency of Japan (NASDA). The current studies are part of the European integrated project DAMOCLES. The DAMOCLES project is financed by the European Union in the 6th Framework Programme for Research and Development.




