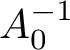1. Introduction
The theory of functional calculi forms a basis for the study of sectorial operators and semigroup generators. In particular, two functional calculi were used extensively in the research on operator semigroups and sectorial operators during the past 50 years. One of them, the Hille–Phillips (HP) functional calculus for semigroup generators, probably stemmed from the foundational monograph [Reference Hille and Phillips37], and it became an indispensable part of semigroup theory. The systematic approach to the other one, the holomorphic functional calculus for sectoral operators, was initiated by McIntosh and his collaborators in the 1980s. Though the two calculi appeared to be very useful in applications, the operator norm estimates within them are often problematic. The estimates within the HP-calculus are direct but rather crude, and the task of getting bounds within the holomorphic functional calculus is a priori cumbersome because the calculus is not, in general, a bounded Banach algebra homomorphism.
To circumvent those problems, a number of additional tools and methods appeared in the literature. In particular, the advanced notions and techniques related to bounded
![]() $H^{\infty }$
-calculus, R-boundedness, Fourier multipliers and transference were developed in depth, and one may consult [Reference Hytönen, van Neerven, Veraar and Weis38], [Reference Kunstmann and Weis41] and [Reference Haase35] for many of these function-theoretical developments. Moreover, various implications of positivity of functions and their derivatives (completely monotone, Bernstein,
$H^{\infty }$
-calculus, R-boundedness, Fourier multipliers and transference were developed in depth, and one may consult [Reference Hytönen, van Neerven, Veraar and Weis38], [Reference Kunstmann and Weis41] and [Reference Haase35] for many of these function-theoretical developments. Moreover, various implications of positivity of functions and their derivatives (completely monotone, Bernstein,
![]() $\mathcal {NP}_+$
-functions) were adjusted to the operator-theoretical setup. For clarification of the role of positivity, see [Reference Schilling, Song and Vondraček50], [Reference Gomilko and Tomilov31] and [Reference Batty, Gomilko and Tomilov6], for example.
$\mathcal {NP}_+$
-functions) were adjusted to the operator-theoretical setup. For clarification of the role of positivity, see [Reference Schilling, Song and Vondraček50], [Reference Gomilko and Tomilov31] and [Reference Batty, Gomilko and Tomilov6], for example.
Recently, in [Reference Batty, Gomilko and Tomilov7], a new functional calculus was constructed, the so-called
![]() $\mathcal B$
-calculus. First of all, the
$\mathcal B$
-calculus. First of all, the
![]() $\mathcal B$
-calculus offers a simple and efficient route to operator norm estimates for functions of semigroup generators, thus unifying a number of estimates in the literature and leading to new ones. No supplementary arguments are required and the estimates underline the strength of the calculi. Moreover, the
$\mathcal B$
-calculus offers a simple and efficient route to operator norm estimates for functions of semigroup generators, thus unifying a number of estimates in the literature and leading to new ones. No supplementary arguments are required and the estimates underline the strength of the calculi. Moreover, the
![]() $\mathcal B$
-calculus possesses all attributes of classical functional calculi, see [Reference Batty, Gomilko and Tomilov7]. When combined properly they lead to new spectral mapping theorems and generalisations of fundamentals of semigroup theory; see [Reference Batty, Gomilko and Tomilov8]. To put our results into a proper context and to use some of the
$\mathcal B$
-calculus possesses all attributes of classical functional calculi, see [Reference Batty, Gomilko and Tomilov7]. When combined properly they lead to new spectral mapping theorems and generalisations of fundamentals of semigroup theory; see [Reference Batty, Gomilko and Tomilov8]. To put our results into a proper context and to use some of the
![]() $\mathcal B$
-calculus properties in the sequel, we briefly recall the setup for the
$\mathcal B$
-calculus properties in the sequel, we briefly recall the setup for the
![]() $\mathcal B$
-calculus; see [Reference Batty, Gomilko and Tomilov7] for more details.
$\mathcal B$
-calculus; see [Reference Batty, Gomilko and Tomilov7] for more details.
Let
![]() $\mathcal B$
be the algebra of holomorphic functions on the right half-plane
$\mathcal B$
be the algebra of holomorphic functions on the right half-plane
![]() $\mathbb {C}_+$
such that
$\mathbb {C}_+$
such that
 $$ \begin{align} \|f\|_{\mathcal{B}_0}:=\int_{0}^{\infty} \sup_{\beta \in \mathbb{R} }|f'(\alpha+i\beta)| \, d\alpha <\infty. \end{align} $$
$$ \begin{align} \|f\|_{\mathcal{B}_0}:=\int_{0}^{\infty} \sup_{\beta \in \mathbb{R} }|f'(\alpha+i\beta)| \, d\alpha <\infty. \end{align} $$
These functions have been considered in some detail in [Reference Batty, Gomilko and Tomilov7] (see also [Reference Vitse53]). In particular, every
![]() $f \in \mathcal B$
belongs to
$f \in \mathcal B$
belongs to
![]() $H^{\infty }(\mathbb C_+)\cap C(\overline {\mathbb C}_+)$
, and
$H^{\infty }(\mathbb C_+)\cap C(\overline {\mathbb C}_+)$
, and
![]() $\mathcal B$
is a Banach algebra with the norm
$\mathcal B$
is a Banach algebra with the norm
Moreover, the algebra
![]() $\mathcal B$
modulo constants is isomorphic to the holomorphic Besov space
$\mathcal B$
modulo constants is isomorphic to the holomorphic Besov space
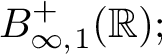 $B^{+}_{\infty ,1}(\mathbb R);$
see [Reference Batty, Gomilko and Tomilov7, Proposition 6.2]. In the setting of power bounded operators on Hilbert spaces, the unit disc counterpart of
$B^{+}_{\infty ,1}(\mathbb R);$
see [Reference Batty, Gomilko and Tomilov7, Proposition 6.2]. In the setting of power bounded operators on Hilbert spaces, the unit disc counterpart of
![]() $\mathcal B$
was employed for the study of functional calculi in [Reference Peller47].
$\mathcal B$
was employed for the study of functional calculi in [Reference Peller47].
Let A be a densely defined closed operator on a Banach space X such that
![]() $\sigma (A) \subseteq \overline {\mathbb {C}}_+$
and
$\sigma (A) \subseteq \overline {\mathbb {C}}_+$
and
 $$ \begin{align} \sup_{\alpha>0} \alpha \int_{\mathbb R} |\langle (\alpha +i\beta + A)^{-2}x, x^* \rangle| \, d\beta <\infty \end{align} $$
$$ \begin{align} \sup_{\alpha>0} \alpha \int_{\mathbb R} |\langle (\alpha +i\beta + A)^{-2}x, x^* \rangle| \, d\beta <\infty \end{align} $$
for all
![]() $x \in X$
and
$x \in X$
and
![]() $x^* \in X^*$
. This class of operators includes two substantial subclasses, namely, the negative generators of bounded
$x^* \in X^*$
. This class of operators includes two substantial subclasses, namely, the negative generators of bounded
![]() $C_0$
-semigroups on Hilbert spaces X and the negative generators of (sectorially) bounded holomorphic
$C_0$
-semigroups on Hilbert spaces X and the negative generators of (sectorially) bounded holomorphic
![]() $C_0$
-semigroups on Banach spaces X. On the other hand, every operator in the class is the negative generator of a bounded
$C_0$
-semigroups on Banach spaces X. On the other hand, every operator in the class is the negative generator of a bounded
![]() $C_0$
-semigroup.
$C_0$
-semigroup.
The study of functional calculus based on the algebra
![]() $\mathcal B$
was initiated in [Reference White57] for generators of bounded semigroups on Hilbert spaces and in [Reference Vitse53] for generators of holomorphic semigroups. These works adapted and extended the approach from [Reference Peller47] to a more demanding and involved setting of unbounded operators. Most researchers were unaware of [Reference White57] until it became accessible a few years ago. Meanwhile, the line of research put forward in [Reference White57] and [Reference Vitse53] was continued in [Reference Haase36] and [Reference Schwenninger51] proceeding in two different directions (additional related references can be found in [Reference Batty, Gomilko and Tomilov7]). In [Reference Haase36], by means of a new transference technique, counterparts of the results from [Reference Vitse53] were proved in the framework of bounded semigroups on Hilbert space and certain substantial subclasses of
$\mathcal B$
was initiated in [Reference White57] for generators of bounded semigroups on Hilbert spaces and in [Reference Vitse53] for generators of holomorphic semigroups. These works adapted and extended the approach from [Reference Peller47] to a more demanding and involved setting of unbounded operators. Most researchers were unaware of [Reference White57] until it became accessible a few years ago. Meanwhile, the line of research put forward in [Reference White57] and [Reference Vitse53] was continued in [Reference Haase36] and [Reference Schwenninger51] proceeding in two different directions (additional related references can be found in [Reference Batty, Gomilko and Tomilov7]). In [Reference Haase36], by means of a new transference technique, counterparts of the results from [Reference Vitse53] were proved in the framework of bounded semigroups on Hilbert space and certain substantial subclasses of
![]() $\mathcal B$
, and [Reference Schwenninger51] offered a number of generalisations and improvements of estimates from [Reference Vitse53]. Only [Reference Schwenninger51] and [Reference Vitse53] considered all functions in
$\mathcal B$
, and [Reference Schwenninger51] offered a number of generalisations and improvements of estimates from [Reference Vitse53]. Only [Reference Schwenninger51] and [Reference Vitse53] considered all functions in
![]() $\mathcal B$
, applied to generators of bounded holomorphic semigroups in both papers. In [Reference Batty, Gomilko and Tomilov7], we introduced a bounded
$\mathcal B$
, applied to generators of bounded holomorphic semigroups in both papers. In [Reference Batty, Gomilko and Tomilov7], we introduced a bounded
![]() $\mathcal B$
functional calculus for all operators satisfying (1.3), and we extended the theory in [Reference Batty, Gomilko and Tomilov8].
$\mathcal B$
functional calculus for all operators satisfying (1.3), and we extended the theory in [Reference Batty, Gomilko and Tomilov8].
For
![]() $f \in \mathcal {B}$
, set
$f \in \mathcal {B}$
, set
 $$ \begin{align} {\langle f(A)x, x^* \rangle} = f(\infty) \langle x, x^* \rangle - \frac{2}{\pi} \int_0^{\infty} \alpha \int_{\mathbb{R}} {f'(\alpha +i\beta)} \langle (\alpha -i\beta +A)^{-2}x, x^* \rangle \, d\beta\,d\alpha \end{align} $$
$$ \begin{align} {\langle f(A)x, x^* \rangle} = f(\infty) \langle x, x^* \rangle - \frac{2}{\pi} \int_0^{\infty} \alpha \int_{\mathbb{R}} {f'(\alpha +i\beta)} \langle (\alpha -i\beta +A)^{-2}x, x^* \rangle \, d\beta\,d\alpha \end{align} $$
for all
![]() $x \in X$
and
$x \in X$
and
![]() $x^* \in X^*$
, where
$x^* \in X^*$
, where
![]() $f(\infty ) = \lim _{\operatorname {Re}z\to \infty } f(z)$
. Using (1.3) and the definition of
$f(\infty ) = \lim _{\operatorname {Re}z\to \infty } f(z)$
. Using (1.3) and the definition of
![]() $\mathcal B$
(and the closed graph theorem), it is easy to show that
$\mathcal B$
(and the closed graph theorem), it is easy to show that
![]() $f(A)$
is a bounded linear mapping from X to
$f(A)$
is a bounded linear mapping from X to
![]() $X^{**}$
and that the linear mapping
$X^{**}$
and that the linear mapping
 $$ \begin{align*} \widetilde\Phi_A : \mathcal{B} \to \mathcal L(X,X^{**}), \qquad f \mapsto f(A), \end{align*} $$
$$ \begin{align*} \widetilde\Phi_A : \mathcal{B} \to \mathcal L(X,X^{**}), \qquad f \mapsto f(A), \end{align*} $$
is bounded.
It was discovered in [Reference Batty, Gomilko and Tomilov7] that much more is true. If A belongs to any of the classes of semigroup generators mentioned above, then the formula (1.4) defines a bounded algebra homomorphism
It is natural to call the homomorphism
![]() $\Phi _A$
the (
$\Phi _A$
the (
![]() $\mathcal {B}$
-)calculus of A. It was proved in [Reference Batty, Gomilko and Tomilov7] that
$\mathcal {B}$
-)calculus of A. It was proved in [Reference Batty, Gomilko and Tomilov7] that
![]() $\Phi _A$
possesses a number of useful properties. In particular, it admits the spectral inclusion (spectral mapping, in the case of bounded holomorphic semigroups) theorem and a convergence lemma of appropriate form. The utility of the
$\Phi _A$
possesses a number of useful properties. In particular, it admits the spectral inclusion (spectral mapping, in the case of bounded holomorphic semigroups) theorem and a convergence lemma of appropriate form. The utility of the
![]() $\mathcal B$
-calculus depends on the facts that it (strictly) extends the HP-calculus and it is compatible with the holomorphic functional calculi for sectorial and half-plane type operators.
$\mathcal B$
-calculus depends on the facts that it (strictly) extends the HP-calculus and it is compatible with the holomorphic functional calculi for sectorial and half-plane type operators.
Moreover, the
![]() $\mathcal {B}$
-calculus
$\mathcal {B}$
-calculus
![]() $\Phi _A$
is the only functional calculus that one can define for A satisfying (1.3) and for functions in
$\Phi _A$
is the only functional calculus that one can define for A satisfying (1.3) and for functions in
![]() $\mathcal {B}$
. Indeed, let A be an operator on X with dense domain, and assume that
$\mathcal {B}$
. Indeed, let A be an operator on X with dense domain, and assume that
![]() $\sigma (A) \subseteq \overline {\mathbb {C}}_+$
. A (bounded)
$\sigma (A) \subseteq \overline {\mathbb {C}}_+$
. A (bounded)
![]() $\mathcal {B}$
-calculus for A is, by definition, a bounded algebra homomorphism
$\mathcal {B}$
-calculus for A is, by definition, a bounded algebra homomorphism
![]() $\Phi : \mathcal {B} \to L(X)$
such that
$\Phi : \mathcal {B} \to L(X)$
such that
![]() $\Phi ((z+\cdot )^{-1}) = (z+A)^{-1}$
for all
$\Phi ((z+\cdot )^{-1}) = (z+A)^{-1}$
for all
![]() $z \in \mathbb {C}_+$
. As shown in [Reference Batty, Gomilko and Tomilov8], if A admits a
$z \in \mathbb {C}_+$
. As shown in [Reference Batty, Gomilko and Tomilov8], if A admits a
![]() $\mathcal B$
-calculus, then the resolvent assumption (1.3) holds, and the calculus is
$\mathcal B$
-calculus, then the resolvent assumption (1.3) holds, and the calculus is
![]() $\Phi _A$
.
$\Phi _A$
.
Though the
![]() $\mathcal B$
-calculus is optimal and unique for generators of Hilbert space semigroups, the situation is far from being so for generators of bounded holomorphic semigroups on Banach spaces (as this article will, in particular, show). Thus, using the
$\mathcal B$
-calculus is optimal and unique for generators of Hilbert space semigroups, the situation is far from being so for generators of bounded holomorphic semigroups on Banach spaces (as this article will, in particular, show). Thus, using the
![]() $\mathcal B$
-calculus ideology as a guiding principle, it is natural to try to extend it beyond the Besov algebra
$\mathcal B$
-calculus ideology as a guiding principle, it is natural to try to extend it beyond the Besov algebra
![]() $\mathcal B$
keeping all of its useful properties such as availability of good norm estimates, spectral mapping theorems, convergence lemmas, compatibility with the other calculi, etc. Moreover, it is desirable to cover all sectorial operators regardless of their sectoriality angle.
$\mathcal B$
keeping all of its useful properties such as availability of good norm estimates, spectral mapping theorems, convergence lemmas, compatibility with the other calculi, etc. Moreover, it is desirable to cover all sectorial operators regardless of their sectoriality angle.
In this article we will construct some functional calculi encompassing wider classes of functions (including some with singularities on
![]() $i\mathbb R$
) and providing finer estimates for all negative generators of (sectorially) bounded holomorphic semigroups, and eventually for all sectorial operators. Functional calculi for generators of some classes of bounded holomorphic semigroups were constructed in [Reference Galé and Pytlik28], [Reference Galé, Miana and Pytlik27], [Reference Galé and Miana25], [Reference Galé and Miana26] and [Reference Kriegler and Weis40]. However, most of the results in those papers concern sectorial operators of angle zero, and the approaches there are based on fine estimates for the corresponding semigroups rather than fine analytic properties of resolvents.
$i\mathbb R$
) and providing finer estimates for all negative generators of (sectorially) bounded holomorphic semigroups, and eventually for all sectorial operators. Functional calculi for generators of some classes of bounded holomorphic semigroups were constructed in [Reference Galé and Pytlik28], [Reference Galé, Miana and Pytlik27], [Reference Galé and Miana25], [Reference Galé and Miana26] and [Reference Kriegler and Weis40]. However, most of the results in those papers concern sectorial operators of angle zero, and the approaches there are based on fine estimates for the corresponding semigroups rather than fine analytic properties of resolvents.
Let A be a densely defined sectorial operator of sectorial angle
![]() $\theta _A \in [0,\pi )$
on a Banach space
$\theta _A \in [0,\pi )$
on a Banach space
![]() $X,$
and let
$X,$
and let
![]() $\operatorname {Sect}(\theta)$
denote the class of all sectorial operators of angle
$\operatorname {Sect}(\theta)$
denote the class of all sectorial operators of angle
![]() $\theta$
for
$\theta$
for
![]() $\theta \in [0,\pi).$
It is well-known that
$\theta \in [0,\pi).$
It is well-known that
![]() $-A$
is the generator of a (sectorially) bounded holomorphic
$-A$
is the generator of a (sectorially) bounded holomorphic
![]() $C_0$
-semigroup on X if and only if A is sectorial and
$C_0$
-semigroup on X if and only if A is sectorial and
![]() $\theta _A < \pi /2$
(we may write
$\theta _A < \pi /2$
(we may write
![]() $A \in \operatorname {Sect}(\pi /2-)$
for this class). In this article we address the question of whether the
$A \in \operatorname {Sect}(\pi /2-)$
for this class). In this article we address the question of whether the
![]() $\mathcal {B}$
-calculus for A can be extended to more functions. Because the resolvent of A satisfies the estimate
$\mathcal {B}$
-calculus for A can be extended to more functions. Because the resolvent of A satisfies the estimate
 $$ \begin{align*} M_{\psi}(A) := \sup_{z\in\Sigma_{\pi-\psi}} \|z(z+A)^{-1}\| < \infty, \end{align*} $$
$$ \begin{align*} M_{\psi}(A) := \sup_{z\in\Sigma_{\pi-\psi}} \|z(z+A)^{-1}\| < \infty, \end{align*} $$
for all
![]() $\psi \in (\theta _A,\pi )$
, a direct way to define an appropriate function algebra would be to introduce a Banach space of functions f that are holomorphic on sectors
$\psi \in (\theta _A,\pi )$
, a direct way to define an appropriate function algebra would be to introduce a Banach space of functions f that are holomorphic on sectors
![]() $\Sigma _{\psi }:=\{z\in \mathbb C: |\arg (z)| < \psi \}$
such that
$\Sigma _{\psi }:=\{z\in \mathbb C: |\arg (z)| < \psi \}$
such that
 $$ \begin{align} \|f\|_{\psi}:=\int_{\partial \Sigma_{\psi}} \frac{|f(z)|}{|z|}|dz| <\infty. \end{align} $$
$$ \begin{align} \|f\|_{\psi}:=\int_{\partial \Sigma_{\psi}} \frac{|f(z)|}{|z|}|dz| <\infty. \end{align} $$
In order to apply this to all
![]() $A \in \operatorname {Sect}(\pi /2-)$
, f should be holomorphic on
$A \in \operatorname {Sect}(\pi /2-)$
, f should be holomorphic on
![]() $\mathbb {C}_+$
and the assumption (1.5) should hold for all
$\mathbb {C}_+$
and the assumption (1.5) should hold for all
![]() $\psi \in (0,\pi /2)$
, and in order to provide an estimate that is uniform in
$\psi \in (0,\pi /2)$
, and in order to provide an estimate that is uniform in
![]() $\theta $
it is desirable to have
$\theta $
it is desirable to have
![]() $\sup _{\psi \in (0,\pi /2)} \|f\|_{\psi }<\infty $
. To our knowledge, no spaces of this type have been studied systematically in the literature, although they appear naturally in [Reference Hytönen, van Neerven, Veraar and Weis38, Appendix H2 and Chapter 10.2], [Reference Haase34, Section 6] and [Reference Haak and Haase33, Appendix C]. This class of functions is strictly included in each of the spaces
$\sup _{\psi \in (0,\pi /2)} \|f\|_{\psi }<\infty $
. To our knowledge, no spaces of this type have been studied systematically in the literature, although they appear naturally in [Reference Hytönen, van Neerven, Veraar and Weis38, Appendix H2 and Chapter 10.2], [Reference Haase34, Section 6] and [Reference Haak and Haase33, Appendix C]. This class of functions is strictly included in each of the spaces
![]() $\mathcal D_s, s>0$
(see Proposition 4.15 and a discussion following it), which we now define.
$\mathcal D_s, s>0$
(see Proposition 4.15 and a discussion following it), which we now define.
To define a functional calculus for all
![]() $A \in \operatorname {Sect}(\pi /2-)$
, we let
$A \in \operatorname {Sect}(\pi /2-)$
, we let
![]() $\mathcal {D}_s, s>-1$
, be the linear space of all holomorphic functions f on
$\mathcal {D}_s, s>-1$
, be the linear space of all holomorphic functions f on
![]() $\mathbb {C}_{+}$
such that
$\mathbb {C}_{+}$
such that
 $$ \begin{align} \|f\|_{\mathcal D_{s,0}}:= \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{|f'(\alpha +i\beta)|}{(\alpha^2+\beta^2)^{(s+1)/2}}\,d\beta\,d\alpha <\infty. \end{align} $$
$$ \begin{align} \|f\|_{\mathcal D_{s,0}}:= \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{|f'(\alpha +i\beta)|}{(\alpha^2+\beta^2)^{(s+1)/2}}\,d\beta\,d\alpha <\infty. \end{align} $$
If
![]() $f \in \mathcal D_s$
, then there exists a finite limit
$f \in \mathcal D_s$
, then there exists a finite limit
![]() $f(\infty ):=\lim _{|z|\to \infty ,\,z\in {\Sigma }_{\psi }}\,f(z)$
for all
$f(\infty ):=\lim _{|z|\to \infty ,\,z\in {\Sigma }_{\psi }}\,f(z)$
for all
![]() $\psi \in (0.\pi /2)$
.
$\psi \in (0.\pi /2)$
.
For every
![]() $s>-1$
the space
$s>-1$
the space
![]() $\mathcal D_s$
equipped with the norm
$\mathcal D_s$
equipped with the norm
is a Banach space but not an algebra. However, the spaces
![]() $\mathcal {D}_s$
increase with s, and we prove in Lemma 3.21 that
$\mathcal {D}_s$
increase with s, and we prove in Lemma 3.21 that
 $$ \begin{align*} \mathcal D_{\infty}:=\bigcup_{s>-1} \mathcal D_s \end{align*} $$
$$ \begin{align*} \mathcal D_{\infty}:=\bigcup_{s>-1} \mathcal D_s \end{align*} $$
is an algebra.
Let
![]() $f\in \mathcal {D}_{\infty }$
, so
$f\in \mathcal {D}_{\infty }$
, so
![]() $f \in \mathcal {D}_s$
for some
$f \in \mathcal {D}_s$
for some
![]() $s>-1$
, and let A be sectorial with
$s>-1$
, and let A be sectorial with
![]() $\theta _A < \pi /2$
. Define
$\theta _A < \pi /2$
. Define
 $$ \begin{align} f_{\mathcal{D}_s}(A):=f(\infty)- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} f'(\alpha+i\beta)(A+\alpha-i\beta)^{-(s+1)}\,d\beta\,d\alpha. \end{align} $$
$$ \begin{align} f_{\mathcal{D}_s}(A):=f(\infty)- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} f'(\alpha+i\beta)(A+\alpha-i\beta)^{-(s+1)}\,d\beta\,d\alpha. \end{align} $$
Then
![]() $f_{\mathcal {D}_{\sigma }}(A) = f_{\mathcal {D}_s}(A)$
whenever
$f_{\mathcal {D}_{\sigma }}(A) = f_{\mathcal {D}_s}(A)$
whenever
![]() $\sigma>s$
. The following result sets out other properties of this functional calculus. The proof will be given in Section 7.
$\sigma>s$
. The following result sets out other properties of this functional calculus. The proof will be given in Section 7.
Theorem 1.1. Let A be a densely defined closed operator on a Banach space X such that
![]() $\sigma (A) \subset \overline {\mathbb {C}}_+$
. The following are equivalent:
$\sigma (A) \subset \overline {\mathbb {C}}_+$
. The following are equivalent:
-
(i)
 $A \in {\rm Sect}(\pi /2-).$
$A \in {\rm Sect}(\pi /2-).$
-
(ii) There is an algebra homomorphism
 $\Psi _A : \mathcal {D}_{\infty } \to L(X)$
such that and
$\Psi _A : \mathcal {D}_{\infty } \to L(X)$
such that and $$ \begin{align*} \Psi_A((z+\cdot)^{-1}) = (z+A)^{-1}, \qquad z \in \mathbb{C}_+, \end{align*} $$
$$ \begin{align*} \Psi_A((z+\cdot)^{-1}) = (z+A)^{-1}, \qquad z \in \mathbb{C}_+, \end{align*} $$
 $\Psi _A$
is bounded in the sense that there exist constants
$\Psi _A$
is bounded in the sense that there exist constants
 $C_s, \, s>-1$
, such that, for every
$C_s, \, s>-1$
, such that, for every
 $f \in \mathcal D_s$
, (1.8)
$f \in \mathcal D_s$
, (1.8) $$ \begin{align} \|\Psi_A(f)\|\le C_s \|f\|_{\mathcal D_s}. \end{align} $$
$$ \begin{align} \|\Psi_A(f)\|\le C_s \|f\|_{\mathcal D_s}. \end{align} $$
When these properties hold,
![]() $\Psi _A$
is unique, and it is defined by the formula (1.7)
$\Psi _A$
is unique, and it is defined by the formula (1.7)
The homomorphism
![]() $\Psi _A$
will be called the
$\Psi _A$
will be called the
![]() ${\mathcal D}$
-calculus for A. It will be shown in Section 7 that the
${\mathcal D}$
-calculus for A. It will be shown in Section 7 that the
![]() $\mathcal {D}$
-calculus is compatible with the HP-calculus and the holomorphic calculus for sectorial operators, and a spectral mapping theorem is given in Theorem 9.3. Corollary 7.8 provides a version of this functional calculus based on the Banach algebra
$\mathcal {D}$
-calculus is compatible with the HP-calculus and the holomorphic calculus for sectorial operators, and a spectral mapping theorem is given in Theorem 9.3. Corollary 7.8 provides a version of this functional calculus based on the Banach algebra
![]() $H^{\infty }(\mathbb C_+)\cap \mathcal D_s$
for a fixed value of s.
$H^{\infty }(\mathbb C_+)\cap \mathcal D_s$
for a fixed value of s.
The
![]() $\mathcal D$
-calculus defined as above does not take into account the sectoriality angle of
$\mathcal D$
-calculus defined as above does not take into account the sectoriality angle of
![]() $A \in \text {Sect}(\pi /2-)$
. However, it can be used to construct a functional calculus that does not have this drawback. To achieve this aim we introduce the Hardy–Sobolev spaces
$A \in \text {Sect}(\pi /2-)$
. However, it can be used to construct a functional calculus that does not have this drawback. To achieve this aim we introduce the Hardy–Sobolev spaces
![]() $\mathcal {H}_{\psi }$
, on sectors
$\mathcal {H}_{\psi }$
, on sectors
![]() $\Sigma _{\psi }$
. First, for any
$\Sigma _{\psi }$
. First, for any
![]() $\psi \in (0,\pi )$
, we define the Hardy space
$\psi \in (0,\pi )$
, we define the Hardy space
![]() $H^1(\Sigma _{\psi })$
as the linear space of functions
$H^1(\Sigma _{\psi })$
as the linear space of functions
![]() $f\in \operatorname {Hol}(\Sigma _{\psi })$
such that
$f\in \operatorname {Hol}(\Sigma _{\psi })$
such that
 $$ \begin{align} \|f\|_{H^1(\Sigma_{\psi})}:=\sup_{|\varphi|< \psi}\, \int_0^{\infty} \bigl(|f(te^{i\varphi})|+ |f(te^{-i\varphi})| \bigr) \,dt <\infty. \end{align} $$
$$ \begin{align} \|f\|_{H^1(\Sigma_{\psi})}:=\sup_{|\varphi|< \psi}\, \int_0^{\infty} \bigl(|f(te^{i\varphi})|+ |f(te^{-i\varphi})| \bigr) \,dt <\infty. \end{align} $$
Note that
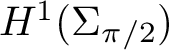 $H^1(\Sigma _{\pi /2})$
coincides with the classical Hardy space
$H^1(\Sigma _{\pi /2})$
coincides with the classical Hardy space
![]() $H^1(\mathbb C_+)$
in the right half-plane
$H^1(\mathbb C_+)$
in the right half-plane
![]() $\mathbb C_+$
. It is well-known that
$\mathbb C_+$
. It is well-known that
 $(H^1(\Sigma _{\psi }), \|\cdot \|_{H^1(\Sigma _{\psi })})$
is a Banach space, and every
$(H^1(\Sigma _{\psi }), \|\cdot \|_{H^1(\Sigma _{\psi })})$
is a Banach space, and every
![]() ${f \in H^1(\Sigma _{\psi })}$
has a boundary function on
${f \in H^1(\Sigma _{\psi })}$
has a boundary function on
![]() $\partial \Sigma _{\psi }$
. The boundary function exists as the limit of f in both an
$\partial \Sigma _{\psi }$
. The boundary function exists as the limit of f in both an
![]() $L^1$
-sense and a pointwise (almost everywhere, a.e.) sense. Moreover, the norm of f in
$L^1$
-sense and a pointwise (almost everywhere, a.e.) sense. Moreover, the norm of f in
![]() $H^1(\Sigma _{\psi })$
is attained by the
$H^1(\Sigma _{\psi })$
is attained by the
![]() $L^1$
-norm of its boundary function. See Subsection 4.1 for a succinct approach to the Hardy spaces on sectors.
$L^1$
-norm of its boundary function. See Subsection 4.1 for a succinct approach to the Hardy spaces on sectors.
The space
![]() $H^1(\Sigma _{\psi })$
induces the corresponding Hardy–Sobolev space
$H^1(\Sigma _{\psi })$
induces the corresponding Hardy–Sobolev space
![]() $\mathcal {H}_{\psi }$
on
$\mathcal {H}_{\psi }$
on
![]() $\Sigma _{\psi }$
as
$\Sigma _{\psi }$
as
 $$ \begin{align*} \mathcal{H}_{\psi}:=\left\{f \in \operatorname{Hol}(\Sigma_{\psi}): f' \in H^1(\Sigma_{\psi})\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\psi}:=\left\{f \in \operatorname{Hol}(\Sigma_{\psi}): f' \in H^1(\Sigma_{\psi})\right\}. \end{align*} $$
Any function
![]() $f \in \mathcal {H}_{\psi }$
has a finite limit
$f \in \mathcal {H}_{\psi }$
has a finite limit
![]() $f(\infty ):=\lim _{t \to \infty }f(t)$
; moreover,
$f(\infty ):=\lim _{t \to \infty }f(t)$
; moreover,
![]() $f \in H^{\infty }(\Sigma _{\psi })$
. Then
$f \in H^{\infty }(\Sigma _{\psi })$
. Then
![]() $\mathcal {H}_{\psi }$
becomes a Banach algebra in the norm
$\mathcal {H}_{\psi }$
becomes a Banach algebra in the norm
 $$ \begin{align*} \|f\|_{\mathcal{H}_{\psi}}:=\|f\|_{H^{\infty}(\Sigma_{\psi})} +\|f'\|_{H^1(\Sigma_{\psi})}, \quad f \in \mathcal{H}_{\psi}. \end{align*} $$
$$ \begin{align*} \|f\|_{\mathcal{H}_{\psi}}:=\|f\|_{H^{\infty}(\Sigma_{\psi})} +\|f'\|_{H^1(\Sigma_{\psi})}, \quad f \in \mathcal{H}_{\psi}. \end{align*} $$
The relationship between these spaces and the spaces
![]() $\mathcal D_s$
for all
$\mathcal D_s$
for all
![]() $s>-1$
is set out in Corollary 4.3 and Lemma 4.13; in particular, for each
$s>-1$
is set out in Corollary 4.3 and Lemma 4.13; in particular, for each
![]() $s>-1$
,
$s>-1$
,
![]() $\mathcal {H}_{\pi /2}$
is contained in
$\mathcal {H}_{\pi /2}$
is contained in
![]() $\mathcal {D}_s$
, and
$\mathcal {D}_s$
, and
![]() $\mathcal {D}_s$
is embedded in
$\mathcal {D}_s$
is embedded in
![]() $\mathcal {H}_{\psi }$
for
$\mathcal {H}_{\psi }$
for
![]() $\psi <\pi /2$
.
$\psi <\pi /2$
.
To make use of the angle of sectoriality of A, we can adjust the
![]() $\mathcal D$
-calculus to sectors as follows. If
$\mathcal D$
-calculus to sectors as follows. If
![]() $f\in \mathcal {H}_{\psi }$
where
$f\in \mathcal {H}_{\psi }$
where
![]() $\psi \in (\theta _A,\pi )$
,
$\psi \in (\theta _A,\pi )$
,
![]() $\gamma = \pi /(2\psi )$
and
$\gamma = \pi /(2\psi )$
and
 $f_{1/\gamma }(z):=f(z^{1/\gamma })$
, then
$f_{1/\gamma }(z):=f(z^{1/\gamma })$
, then
 $f^{\prime }_{1/\gamma }\in H^1(\mathbb {C}_{+})$
and
$f^{\prime }_{1/\gamma }\in H^1(\mathbb {C}_{+})$
and
![]() $f_{1/\gamma }(\infty )=f(\infty )$
, and hence
$f_{1/\gamma }(\infty )=f(\infty )$
, and hence
![]() $f_{1/\gamma }\in \mathcal {D}_0$
. This observation allows us to extend the
$f_{1/\gamma }\in \mathcal {D}_0$
. This observation allows us to extend the
![]() $\mathcal D$
-calculus to the class of all sectorial operators and makes the next definition (based on the
$\mathcal D$
-calculus to the class of all sectorial operators and makes the next definition (based on the
![]() $\mathcal {D}$
-calculus) natural and plausible.
$\mathcal {D}$
-calculus) natural and plausible.
If A is sectorial and
![]() $\psi \in (\theta _A,\pi )$
, define
$\psi \in (\theta _A,\pi )$
, define
 $$ \begin{align} f_{\mathcal H}(A):= f(\infty)-\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f^{\prime}_{1/\gamma}(\alpha+i\beta) (A^{\gamma}+\alpha-i\beta)^{-1}\, d\beta\,d\alpha. \end{align} $$
$$ \begin{align} f_{\mathcal H}(A):= f(\infty)-\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f^{\prime}_{1/\gamma}(\alpha+i\beta) (A^{\gamma}+\alpha-i\beta)^{-1}\, d\beta\,d\alpha. \end{align} $$
One can prove (see (8.2)) that
 $$ \begin{align} \|f_{\mathcal H}(A)\|\le |f(\infty)|+\frac{M_{\pi/2}{(A^{\gamma})}}{\pi}\|f_{1/\gamma}\|_{\mathcal{D}_{0,0}} \le |f(\infty)|+ M_{\pi/2}({A^{\gamma}}) \|f\|_{\mathcal{H}_{\psi}}. \end{align} $$
$$ \begin{align} \|f_{\mathcal H}(A)\|\le |f(\infty)|+\frac{M_{\pi/2}{(A^{\gamma})}}{\pi}\|f_{1/\gamma}\|_{\mathcal{D}_{0,0}} \le |f(\infty)|+ M_{\pi/2}({A^{\gamma}}) \|f\|_{\mathcal{H}_{\psi}}. \end{align} $$
Then (1.10) and (1.11) hold for any
![]() $\gamma \in (1,\pi /(2\psi ))$
, and the definition of
$\gamma \in (1,\pi /(2\psi ))$
, and the definition of
![]() $f_{\mathcal {H}}(A)$
does not depend on the choice of
$f_{\mathcal {H}}(A)$
does not depend on the choice of
![]() $\psi $
.
$\psi $
.
Now we are able to formalise our extension of the
![]() $\mathcal D$
-calculus as follows.
$\mathcal D$
-calculus as follows.
Theorem 1.2. Let A be a densely defined operator on a Banach space X such that
![]() $\sigma (A) \subset \overline {\Sigma }_{\theta }$
, where
$\sigma (A) \subset \overline {\Sigma }_{\theta }$
, where
![]() $\theta \in [0,\pi )$
. The following are equivalent:
$\theta \in [0,\pi )$
. The following are equivalent:
-
(i)
 $A \in \operatorname {Sect}(\theta ).$
$A \in \operatorname {Sect}(\theta ).$
-
(ii) For each
 $\psi \in (\theta ,\pi )$
, there is a bounded Banach algebra homomorphism
$\psi \in (\theta ,\pi )$
, there is a bounded Banach algebra homomorphism
 $\Upsilon _A : \mathcal {H}_{\psi } \mapsto L(X)$
such that
$\Upsilon _A : \mathcal {H}_{\psi } \mapsto L(X)$
such that
 $\Upsilon _A((z+\cdot )^{-1}) = (z+A)^{-1}, \quad z \in \Sigma _{\pi -\psi }$
.
$\Upsilon _A((z+\cdot )^{-1}) = (z+A)^{-1}, \quad z \in \Sigma _{\pi -\psi }$
.
When these properties hold, the homomorphism
![]() $\Upsilon _A$
is unique for each value of
$\Upsilon _A$
is unique for each value of
![]() $\psi $
, and it is defined by the formula (1.10):
$\psi $
, and it is defined by the formula (1.10):
The homomorphism
![]() $\Upsilon _A$
will be called the
$\Upsilon _A$
will be called the
![]() $\mathcal H$
-calculus for A.
$\mathcal H$
-calculus for A.
The
![]() $\mathcal {D}$
-calculus can be given a more succinct form, by replacing (1.10) with the somewhat more transparent formula (1.12) below, inspired by results in [Reference Boyadzhiev12].
$\mathcal {D}$
-calculus can be given a more succinct form, by replacing (1.10) with the somewhat more transparent formula (1.12) below, inspired by results in [Reference Boyadzhiev12].
Theorem 1.3. Let
![]() $A \in \operatorname {Sect}(\theta )$
,
$A \in \operatorname {Sect}(\theta )$
,
![]() $\theta < \psi < \pi $
and
$\theta < \psi < \pi $
and
![]() $\gamma =\pi /(2\psi )$
. For
$\gamma =\pi /(2\psi )$
. For
![]() $f\in \mathcal {H}_{\psi }$
, let
$f\in \mathcal {H}_{\psi }$
, let
 $$ \begin{align*} f_{\psi}(s):=\frac{f(e^{i\psi}t)+f(e^{-i\psi}t)}{2}, \quad t \ge 0. \end{align*} $$
$$ \begin{align*} f_{\psi}(s):=\frac{f(e^{i\psi}t)+f(e^{-i\psi}t)}{2}, \quad t \ge 0. \end{align*} $$
Then
 $$ \begin{align} f_{\mathcal H}(A)= f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t){\operatorname{\mathrm{arccot}}}(A^{\gamma}/t^{\gamma})\,dt \end{align} $$
$$ \begin{align} f_{\mathcal H}(A)= f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t){\operatorname{\mathrm{arccot}}}(A^{\gamma}/t^{\gamma})\,dt \end{align} $$
where the integral converges in the uniform operator topology, and
 $$ \begin{align*} \|f_{\mathcal H}(A)\|\le |f(\infty)|+ M_{\psi}(A)\|f_{\psi}'\|_{L^1(\mathbb{R}_+)} \le M_{\psi}(A) \|f\|_{\mathcal{H}_{\psi}}. \end{align*} $$
$$ \begin{align*} \|f_{\mathcal H}(A)\|\le |f(\infty)|+ M_{\psi}(A)\|f_{\psi}'\|_{L^1(\mathbb{R}_+)} \le M_{\psi}(A) \|f\|_{\mathcal{H}_{\psi}}. \end{align*} $$
Thus,
![]() $\|\Upsilon _A\| \le M_{\psi }(A)$
.
$\|\Upsilon _A\| \le M_{\psi }(A)$
.
See Subsection 8.2 for details. The
![]() $\mathcal D$
-calculus and the
$\mathcal D$
-calculus and the
![]() $\mathcal H$
-calculus possess natural properties of functional calculi such as spectral mapping theorems and convergence lemmas. These properties are studied in Section 9.
$\mathcal H$
-calculus possess natural properties of functional calculi such as spectral mapping theorems and convergence lemmas. These properties are studied in Section 9.
The strength of the constructed calculi is illustrated by several examples showing that they lead to sharper estimates than those offered by other calculi (see Section 12 for one example). Moreover, the theory developed in this article is successfully tested by deriving several significant estimates for functions of sectorial operators from the literature. In particular, in Section 10, we provide a proof of permanence of the class of sectorial operators under subordination and we revisit a few basic results from semigroup theory.
In developing the
![]() $\mathcal D$
- and
$\mathcal D$
- and
![]() $\mathcal H$
-calculi we prove a number of results of independent interest in function theory. Apart from the theory of the spaces
$\mathcal H$
-calculi we prove a number of results of independent interest in function theory. Apart from the theory of the spaces
![]() $\mathcal D_s$
and
$\mathcal D_s$
and
![]() $\mathcal {H}_{\psi }$
, their reproducing formulas and boundedness of the associated operators elaborated in this article, we emphasise the property (4.9) in Corollary 4.3 yielding isometric coincidence of spaces of Hardy type, Theorem 4.12 on Laplace representability of Hardy–Sobolev functions and Theorem 5.10 on the density of rational functions in Hardy–Sobolev spaces.
$\mathcal {H}_{\psi }$
, their reproducing formulas and boundedness of the associated operators elaborated in this article, we emphasise the property (4.9) in Corollary 4.3 yielding isometric coincidence of spaces of Hardy type, Theorem 4.12 on Laplace representability of Hardy–Sobolev functions and Theorem 5.10 on the density of rational functions in Hardy–Sobolev spaces.
Added Note: During the preparation of this article, we became aware of a paper by Arnold and Le Merdy [Reference Arnold and Le Merdy5], who considered negative generators of bounded
![]() $C_0$
-semigroups on Hilbert space. Inspired by ideas in [Reference Peller47] for the discrete case, they extended the
$C_0$
-semigroups on Hilbert space. Inspired by ideas in [Reference Peller47] for the discrete case, they extended the
![]() $\mathcal {B}$
-calculus for those operators to a strictly larger Banach algebra
$\mathcal {B}$
-calculus for those operators to a strictly larger Banach algebra
![]() $\mathcal {A}$
in which
$\mathcal {A}$
in which
![]() $\mathcal {B}$
is continuously embedded. Their extension is complementary to our extensions to the
$\mathcal {B}$
is continuously embedded. Their extension is complementary to our extensions to the
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\mathcal {H}$
-calculi for negative generators of bounded holomorphic
$\mathcal {H}$
-calculi for negative generators of bounded holomorphic
![]() $C_0$
-semigroups on Banach spaces. We are grateful to Loris Arnold for pointing out several defects in the original version of this article.
$C_0$
-semigroups on Banach spaces. We are grateful to Loris Arnold for pointing out several defects in the original version of this article.
2. Preliminaries
Notation
Throughout the article, we will use the following notation:
-
 $\mathbb {R}_+ :=[0,\infty )$
,
$\mathbb {R}_+ :=[0,\infty )$
, -
 $\mathbb {C}_+ := \{z \in \mathbb {C}: \operatorname {Re}z>0\}$
,
$\mathbb {C}_+ := \{z \in \mathbb {C}: \operatorname {Re}z>0\}$
,
 $\overline {\mathbb {C}}_+ = \{z \in \mathbb {C}: \operatorname {Re}z\ge 0\}$
,
$\overline {\mathbb {C}}_+ = \{z \in \mathbb {C}: \operatorname {Re}z\ge 0\}$
, -
 $\Sigma _{\theta } := \{z\in \mathbb {C}: z \ne 0, |\arg z|<\theta \}$
for
$\Sigma _{\theta } := \{z\in \mathbb {C}: z \ne 0, |\arg z|<\theta \}$
for
 $\theta \in (0,\pi )$
.
$\theta \in (0,\pi )$
.
For
![]() $f : \mathbb {C}_+ \to \mathbb {C}$
, we say that f has a sectorial limit at infinity if
$f : \mathbb {C}_+ \to \mathbb {C}$
, we say that f has a sectorial limit at infinity if
 $$ \begin{align*} \lim_{|z|\to\infty, z \in \Sigma_{\psi}} f(z) \end{align*} $$
$$ \begin{align*} \lim_{|z|\to\infty, z \in \Sigma_{\psi}} f(z) \end{align*} $$
exists for every
![]() $\psi \in (0,\pi /2)$
. Similarly, f has a sectorial limit at
$\psi \in (0,\pi /2)$
. Similarly, f has a sectorial limit at
![]() $0$
if
$0$
if
 $$ \begin{align*} \lim_{|z|\to0, z \in \Sigma_{\psi}} f(z) \end{align*} $$
$$ \begin{align*} \lim_{|z|\to0, z \in \Sigma_{\psi}} f(z) \end{align*} $$
exists for every
![]() $\psi \in (0,\pi /2)$
. We say that f has a half-plane limit at infinity if
$\psi \in (0,\pi /2)$
. We say that f has a half-plane limit at infinity if
 $$ \begin{align*} \lim_{\operatorname{Re}z \to \infty} f(z) \end{align*} $$
$$ \begin{align*} \lim_{\operatorname{Re}z \to \infty} f(z) \end{align*} $$
exists in
![]() $\mathbb {C}$
. We say that f has a full limit at infinity or at zero if
$\mathbb {C}$
. We say that f has a full limit at infinity or at zero if
 $$ \begin{align*} \lim_{|z| \to \infty, z\in\mathbb{C}_+} f(z) \quad \text{or} \quad \lim_{|z| \to 0, z\in\mathbb{C}_+} f(z) \end{align*} $$
$$ \begin{align*} \lim_{|z| \to \infty, z\in\mathbb{C}_+} f(z) \quad \text{or} \quad \lim_{|z| \to 0, z\in\mathbb{C}_+} f(z) \end{align*} $$
exists in
![]() $\mathbb {C}$
. The notation
$\mathbb {C}$
. The notation
![]() $f(\infty )$
and
$f(\infty )$
and
![]() $f(0)$
may denote a sectorial limit, a half-plane limit or a full limit, according to context.
$f(0)$
may denote a sectorial limit, a half-plane limit or a full limit, according to context.
For
![]() $a \in \overline {\mathbb {C}}_+$
, we define functions on
$a \in \overline {\mathbb {C}}_+$
, we define functions on
![]() $\mathbb {C}$
by
$\mathbb {C}$
by
We use the following notation for spaces of functions or measures and transforms on
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {R}_+$
:
$\mathbb {R}_+$
:
-
 $\operatorname {Hol}(\Omega )$
denotes the space of holomorphic functions on an open subset
$\operatorname {Hol}(\Omega )$
denotes the space of holomorphic functions on an open subset
 $\Omega $
of
$\Omega $
of
 $\mathbb {C}$
,
$\mathbb {C}$
,
 $H^{\infty }(\Omega )$
is the space of bounded holomorphic functions on
$H^{\infty }(\Omega )$
is the space of bounded holomorphic functions on
 $\Omega $
, and
$\Omega $
, and
 $\|f\|_{H^{\infty }(\Omega )} = \sup _{\Omega } |f(z)| $
.
$\|f\|_{H^{\infty }(\Omega )} = \sup _{\Omega } |f(z)| $
. -
 $H^p(\mathbb {C}_+), \, 1 \le p \le \infty $
, are the standard Hardy spaces on the (right) half-plane.
$H^p(\mathbb {C}_+), \, 1 \le p \le \infty $
, are the standard Hardy spaces on the (right) half-plane. -
 $M(\mathbb {R}_+)$
denotes the Banach algebra of all bounded Borel measures on
$M(\mathbb {R}_+)$
denotes the Banach algebra of all bounded Borel measures on
 $\mathbb {R}_+$
under convolution. We identify
$\mathbb {R}_+$
under convolution. We identify
 $L^1(\mathbb {R}_+)$
with a subalgebra of
$L^1(\mathbb {R}_+)$
with a subalgebra of
 $M(\mathbb {R}_+)$
in the usual way. We write
$M(\mathbb {R}_+)$
in the usual way. We write
 $\mathcal L\mu $
for the Laplace transform of
$\mathcal L\mu $
for the Laplace transform of
 $\mu \in M(\mathbb {R}_+)$
.
$\mu \in M(\mathbb {R}_+)$
. -
 $\mathcal {LM}$
is the HP algebra,
$\mathcal {LM}$
is the HP algebra,
 $\mathcal {LM} := \{\mathcal {L}\mu : \mu \in M(\mathbb {R}_+)\}$
, with the norm
$\mathcal {LM} := \{\mathcal {L}\mu : \mu \in M(\mathbb {R}_+)\}$
, with the norm
 $\|\mathcal {L}\mu \|_{\text {HP}}:= |\mu |(\mathbb {R}_+)$
, and
$\|\mathcal {L}\mu \|_{\text {HP}}:= |\mu |(\mathbb {R}_+)$
, and
 $\mathcal {L}L^1 := \{\mathcal {L} f: f \in L^1(\mathbb {R}_+)\}$
.
$\mathcal {L}L^1 := \{\mathcal {L} f: f \in L^1(\mathbb {R}_+)\}$
. -
 $dS$
denotes area measure on
$dS$
denotes area measure on
 $\mathbb {C}_+$
.
$\mathbb {C}_+$
.
For a Banach space X,
![]() $X^*$
denotes the dual space of X and
$X^*$
denotes the dual space of X and
![]() $L(X)$
denotes the space of all bounded linear operators on X. The domain, spectrum and resolvent set of an (unbounded) operator A on X are denoted by
$L(X)$
denotes the space of all bounded linear operators on X. The domain, spectrum and resolvent set of an (unbounded) operator A on X are denoted by
![]() $D(A)$
,
$D(A)$
,
![]() $\sigma (A)$
and
$\sigma (A)$
and
![]() $\rho (A)$
, respectively.
$\rho (A)$
, respectively.
If
![]() $(\mathcal {X},\|\cdot \|_{\mathcal {X}})$
and
$(\mathcal {X},\|\cdot \|_{\mathcal {X}})$
and
![]() $(\mathcal {Y},\|\cdot \|_{\mathcal {Y}})$
are normed spaces of holomorphic functions on domains
$(\mathcal {Y},\|\cdot \|_{\mathcal {Y}})$
are normed spaces of holomorphic functions on domains
![]() $\Omega _{\mathcal {X}}$
and
$\Omega _{\mathcal {X}}$
and
![]() $\Omega _{\mathcal {Y}}$
, we will use notation as follows:
$\Omega _{\mathcal {Y}}$
, we will use notation as follows:
-
 $\mathcal {Y} \overset {i}{\hookrightarrow } \mathcal {X}$
if
$\mathcal {Y} \overset {i}{\hookrightarrow } \mathcal {X}$
if
 $\Omega _{\mathcal {Y}} = \Omega _{\mathcal {X}}$
,
$\Omega _{\mathcal {Y}} = \Omega _{\mathcal {X}}$
,
 $\mathcal {Y}$
is a subset of
$\mathcal {Y}$
is a subset of
 $\mathcal {X}$
and the inclusion map is continuous;
$\mathcal {X}$
and the inclusion map is continuous; -
 $\mathcal {Y} \subset \mathcal {X}$
if
$\mathcal {Y} \subset \mathcal {X}$
if
 $\Omega _{\mathcal {Y}} = \Omega _{\mathcal {X}}$
,
$\Omega _{\mathcal {Y}} = \Omega _{\mathcal {X}}$
,
 $\mathcal {Y}$
is a subset of
$\mathcal {Y}$
is a subset of
 $\mathcal {X}$
and
$\mathcal {X}$
and
 $\mathcal {Y}$
inherits the norm from
$\mathcal {Y}$
inherits the norm from
 $\mathcal {X}$
;
$\mathcal {X}$
; -
 $\mathcal {Y} \overset {r}{\hookrightarrow } \mathcal {X}$
if
$\mathcal {Y} \overset {r}{\hookrightarrow } \mathcal {X}$
if
 $\Omega _{\mathcal {Y}} \supset \Omega _{\mathcal {X}}$
, and the restriction map
$\Omega _{\mathcal {Y}} \supset \Omega _{\mathcal {X}}$
, and the restriction map
 $f \mapsto f|_{\Omega _{\mathcal {X}}}$
is a continuous map from
$f \mapsto f|_{\Omega _{\mathcal {X}}}$
is a continuous map from
 $\mathcal {Y} \to \mathcal {X}$
.
$\mathcal {Y} \to \mathcal {X}$
.
Boundaries of all of the sectors appearing in this article will be oriented from top to bottom.
Elementary inequalities
We will need the following elementary lemma, which gives lower bounds for
![]() $|z+\lambda |$
in terms of
$|z+\lambda |$
in terms of
![]() $|z|$
and
$|z|$
and
![]() $|\lambda |$
, for z,
$|\lambda |$
, for z,
![]() $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
Lemma 2.1.
-
(i) Let
 $z=|z|e^{i\psi }$
and
$z=|z|e^{i\psi }$
and
 $\lambda =|\lambda |e^{i\varphi } \in \mathbb {C}$
, where
$\lambda =|\lambda |e^{i\varphi } \in \mathbb {C}$
, where
 $|\psi -\varphi |\le \pi $
. Then (2.1)
$|\psi -\varphi |\le \pi $
. Then (2.1) $$ \begin{align} |z+\lambda|\ge \cos\left(\frac{\psi-\varphi}{2}\right) (|z|+|\lambda|). \end{align} $$
$$ \begin{align} |z+\lambda|\ge \cos\left(\frac{\psi-\varphi}{2}\right) (|z|+|\lambda|). \end{align} $$
-
(ii) Let
 $z \in \overline {\Sigma }_{\psi }$
and
$z \in \overline {\Sigma }_{\psi }$
and
 $\lambda \in \overline {\Sigma }_{\varphi }$
, where
$\lambda \in \overline {\Sigma }_{\varphi }$
, where
 $\psi ,\varphi>0$
and
$\psi ,\varphi>0$
and
 $\varphi +\psi <\pi $
. Then (2.2)
$\varphi +\psi <\pi $
. Then (2.2) $$ \begin{align} |z+\lambda| \ge \cos\left(\frac{\psi+\varphi}{2}\right) (|z|+|\lambda|). \end{align} $$
$$ \begin{align} |z+\lambda| \ge \cos\left(\frac{\psi+\varphi}{2}\right) (|z|+|\lambda|). \end{align} $$
-
(iii) Let
 $z=|z|e^{i\psi }$
and
$z=|z|e^{i\psi }$
and
 $\lambda =|\lambda |e^{i\varphi } \in \mathbb {C}$
, where
$\lambda =|\lambda |e^{i\varphi } \in \mathbb {C}$
, where
 $|\psi |<\pi /2$
and
$|\psi |<\pi /2$
and
 $|\varphi |\le \pi /2$
. Then (2.3)and
$|\varphi |\le \pi /2$
. Then (2.3)and $$ \begin{align} |z+\lambda|\ge \cos\psi \, |\lambda| \end{align} $$
(2.4)
$$ \begin{align} |z+\lambda|\ge \cos\psi \, |\lambda| \end{align} $$
(2.4) $$ \begin{align} |z+\lambda|\ge \cos\psi\, |z|. \end{align} $$
$$ \begin{align} |z+\lambda|\ge \cos\psi\, |z|. \end{align} $$
Proof. For (2.1), we may assume that
![]() $\varphi \ge \psi $
and let
$\varphi \ge \psi $
and let
![]() $\theta := (\pi -\varphi +\psi )/2 \in [0,\pi /2]$
. By applying a rotation of
$\theta := (\pi -\varphi +\psi )/2 \in [0,\pi /2]$
. By applying a rotation of
![]() $\mathbb {C}$
we may further assume that
$\mathbb {C}$
we may further assume that
![]() $\varphi =\pi -\theta $
and
$\varphi =\pi -\theta $
and
![]() $\psi = \theta $
. Then
$\psi = \theta $
. Then
 $$ \begin{align*} |z+\lambda| \ge \operatorname{Im}z + \operatorname{Im}\lambda = \sin\theta (|z|+|\lambda|) = \cos \left(\frac{\varphi-\psi}{2}\right) (|z|+|\lambda|). \end{align*} $$
$$ \begin{align*} |z+\lambda| \ge \operatorname{Im}z + \operatorname{Im}\lambda = \sin\theta (|z|+|\lambda|) = \cos \left(\frac{\varphi-\psi}{2}\right) (|z|+|\lambda|). \end{align*} $$
The inequality (2.2) follows from (2.1), because
![]() $\psi +\varphi $
is the maximum value of
$\psi +\varphi $
is the maximum value of
![]() $|\psi '-\varphi '|$
for
$|\psi '-\varphi '|$
for
![]() $\psi '\in [-\psi ,\psi ]$
and
$\psi '\in [-\psi ,\psi ]$
and
![]() $\varphi ' \in [-\varphi ,\varphi ]$
.
$\varphi ' \in [-\varphi ,\varphi ]$
.
The inequality (2.4) is obtained by considering
![]() $\operatorname {Re}(z+\lambda )$
. For the inequality (2.3), we assume without loss of generality that
$\operatorname {Re}(z+\lambda )$
. For the inequality (2.3), we assume without loss of generality that
![]() $\sin \varphi \ge 0$
. Note that
$\sin \varphi \ge 0$
. Note that
 $$ \begin{align} |\lambda+z|^2 -|\lambda|^2\cos^2\psi &= \left(|z|+|\lambda|\cos(\varphi-\psi)\right)^2 + |\lambda|^2 \left(\sin^2\varphi - \cos^2(\varphi-\psi)\right) \\ &= |z|^2 + 2|z|\,|\lambda| \cos(\varphi-\psi) + |\lambda|^2 \sin^2 \varphi. \nonumber \end{align} $$
$$ \begin{align} |\lambda+z|^2 -|\lambda|^2\cos^2\psi &= \left(|z|+|\lambda|\cos(\varphi-\psi)\right)^2 + |\lambda|^2 \left(\sin^2\varphi - \cos^2(\varphi-\psi)\right) \\ &= |z|^2 + 2|z|\,|\lambda| \cos(\varphi-\psi) + |\lambda|^2 \sin^2 \varphi. \nonumber \end{align} $$
If
![]() $\cos (\varphi -\psi )<0$
, we have
$\cos (\varphi -\psi )<0$
, we have
Then the expression on the right-hand side of the first line of (2.5) is clearly nonnegative. If
![]() $\cos (\varphi -\psi )\ge 0$
, then the expression in the second line is clearly nonnegative. This completes the proof.
$\cos (\varphi -\psi )\ge 0$
, then the expression in the second line is clearly nonnegative. This completes the proof.
Beta function
The Beta function appears in many places in the article. It is defined for
![]() $s,t>0$
by
$s,t>0$
by
 $$ \begin{align*} B(s,t) = B(t,s) := \int_0^1 \tau^{s-1} (1-\tau)^{t-1} \, d\tau = 2 \int_0^{\pi/2} \cos^{2s-1} \psi \sin^{2t-1} \psi \, d\psi. \end{align*} $$
$$ \begin{align*} B(s,t) = B(t,s) := \int_0^1 \tau^{s-1} (1-\tau)^{t-1} \, d\tau = 2 \int_0^{\pi/2} \cos^{2s-1} \psi \sin^{2t-1} \psi \, d\psi. \end{align*} $$
In particular, for
![]() $s>-1$
we will use the relations
$s>-1$
we will use the relations
 $$ \begin{align*} B\left(\frac{s+1}{2},\frac{1}{2}\right) = \int_{-\pi/2}^{\pi/2}\cos^s\psi\,d\psi = \int_{-\infty}^{\infty} \frac{dt}{(1+t^2)^{(s+2)/2}} =\frac{\sqrt{\pi}\Gamma((s+1)/2)}{\Gamma(s/2+1)}; \end{align*} $$
$$ \begin{align*} B\left(\frac{s+1}{2},\frac{1}{2}\right) = \int_{-\pi/2}^{\pi/2}\cos^s\psi\,d\psi = \int_{-\infty}^{\infty} \frac{dt}{(1+t^2)^{(s+2)/2}} =\frac{\sqrt{\pi}\Gamma((s+1)/2)}{\Gamma(s/2+1)}; \end{align*} $$
see [Reference Prudnikov, Brychkov and Marichev48, items 2.5.3,(1) and 2.2.3,(5)]. We note also the following limit properties:
 $$ \begin{align*} \lim_{s\to -1}\,(s+1)\,B\left(\frac{s+1}{2},\frac{1}{2}\right)=2,\quad \lim_{s\to\infty}\,\sqrt{s}B\left(\frac{s+1}{2},\frac{1}{2}\right)=\sqrt{2\pi}. \end{align*} $$
$$ \begin{align*} \lim_{s\to -1}\,(s+1)\,B\left(\frac{s+1}{2},\frac{1}{2}\right)=2,\quad \lim_{s\to\infty}\,\sqrt{s}B\left(\frac{s+1}{2},\frac{1}{2}\right)=\sqrt{2\pi}. \end{align*} $$
Proof conventions
We will make extensive use of the dominated convergence theorem, often for vector-valued functions. With a few exceptions, we will not give details of the relevant dominating functions, because they are usually easily identified.
We will also use the following elementary lemma on several occasions. See [Reference Duren21, p.21, Lemma 1] for a proof.
Lemma 2.2. Let
![]() $(\Omega ,\mu )$
be a
$(\Omega ,\mu )$
be a
![]() $\sigma $
-finite measure space and
$\sigma $
-finite measure space and
![]() $(f_n)_{n\ge 1} \subset L^p(\Omega ,\mu )$
, where
$(f_n)_{n\ge 1} \subset L^p(\Omega ,\mu )$
, where
![]() $p\in [1,\infty )$
. If
$p\in [1,\infty )$
. If
![]() $f_n \to f_0$
a.e. and
$f_n \to f_0$
a.e. and
![]() $\|f_n\|_{L^p(\Omega ,\mu )} \to \|f_0\|_{L^p(\Omega ,\mu )}$
, then
$\|f_n\|_{L^p(\Omega ,\mu )} \to \|f_0\|_{L^p(\Omega ,\mu )}$
, then
![]() $\|f_n-f_0\|_{L^p(\Omega ,\mu )} \to 0$
as
$\|f_n-f_0\|_{L^p(\Omega ,\mu )} \to 0$
as
![]() $n\to \infty $
.
$n\to \infty $
.
We will use Vitali’s theorem several times, usually for holomorphic vector-valued functions. We refer to the version given in [Reference Arendt, Batty, Hieber and Neubrander4, Theorem A.5].
Let
![]() $\mathcal {X}$
be a Banach space of holomorphic functions on a domain
$\mathcal {X}$
be a Banach space of holomorphic functions on a domain
![]() $\Omega _{\mathcal {X}}$
such that the point evaluations
$\Omega _{\mathcal {X}}$
such that the point evaluations
![]() $\delta _z : f \mapsto f(z), \, z \in \Omega _{\mathcal {X}}$
, are continuous on
$\delta _z : f \mapsto f(z), \, z \in \Omega _{\mathcal {X}}$
, are continuous on
![]() $\mathcal {X}$
. Let
$\mathcal {X}$
. Let
![]() $(\Omega ,\mu )$
be either an interval in
$(\Omega ,\mu )$
be either an interval in
![]() $\mathbb {R}$
with length measure or an open set in
$\mathbb {R}$
with length measure or an open set in
![]() $\mathbb {C}$
with area measure and
$\mathbb {C}$
with area measure and
![]() $F : \Omega \to \mathcal {X}$
be a continuous function such that
$F : \Omega \to \mathcal {X}$
be a continuous function such that
![]() $\int _{\Omega } \|F(t)\|_{\mathcal {X}} \, d\mu (t) < \infty $
. Then the integral
$\int _{\Omega } \|F(t)\|_{\mathcal {X}} \, d\mu (t) < \infty $
. Then the integral
 $$ \begin{align*} G := \int_{\Omega} F(t) \, d\mu(t) \end{align*} $$
$$ \begin{align*} G := \int_{\Omega} F(t) \, d\mu(t) \end{align*} $$
exists as a Bochner integral in
![]() $\mathcal {X}$
and it can be approximated by Riemann sums. It follows that G belongs to the closed linear span of
$\mathcal {X}$
and it can be approximated by Riemann sums. It follows that G belongs to the closed linear span of
![]() $\{F(t) : t\in \Omega \}$
in
$\{F(t) : t\in \Omega \}$
in
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Now assume that
![]() $F : \Omega \to \mathcal {X}$
is locally bounded, where
$F : \Omega \to \mathcal {X}$
is locally bounded, where
![]() $\Omega $
is an open set in
$\Omega $
is an open set in
![]() $\mathbb {C}$
, and that
$\mathbb {C}$
, and that
![]() $\lambda \mapsto F(\lambda )(z)$
is holomorphic on
$\lambda \mapsto F(\lambda )(z)$
is holomorphic on
![]() $\Omega $
for all
$\Omega $
for all
![]() $z \in \Omega _{\mathcal {X}}$
. We will use the fact that
$z \in \Omega _{\mathcal {X}}$
. We will use the fact that
![]() $F: \Omega \to \mathcal {X}$
is holomorphic in the vector-valued sense, without further comment. The result at this level of generality can be seen from [Reference Arendt, Batty, Hieber and Neubrander4, Corollary A.7], using the point evaluations as separating functionals. An alternative is to show that F is continuous and then apply Morera’s theorem. If the definition of F is by an integral formula, it may also be possible to apply a standard corollary of the dominated convergence theorem that leads to an integral formula for the derivative
$F: \Omega \to \mathcal {X}$
is holomorphic in the vector-valued sense, without further comment. The result at this level of generality can be seen from [Reference Arendt, Batty, Hieber and Neubrander4, Corollary A.7], using the point evaluations as separating functionals. An alternative is to show that F is continuous and then apply Morera’s theorem. If the definition of F is by an integral formula, it may also be possible to apply a standard corollary of the dominated convergence theorem that leads to an integral formula for the derivative
![]() $F'$
.
$F'$
.
3. The Banach spaces
 $\mathcal {D}_s$
and their reproducing formulas
$\mathcal {D}_s$
and their reproducing formulas
In this section we introduce some spaces of holomorphic functions to which we will extend the
![]() $\mathcal {B}$
-calculus of operators in Section 7 onwards.
$\mathcal {B}$
-calculus of operators in Section 7 onwards.
3.1. The spaces
 $\mathcal {V}_s$
$\mathcal {V}_s$
Let
![]() $s>-1$
,
$s>-1$
,
![]() $z=\alpha +i\beta $
, and let
$z=\alpha +i\beta $
, and let
![]() $\mathcal {V}_s$
be the Banach space of (equivalence classes of) measurable functions
$\mathcal {V}_s$
be the Banach space of (equivalence classes of) measurable functions
![]() $g: \mathbb {C}_{+}\to \mathbb C$
such that the norm
$g: \mathbb {C}_{+}\to \mathbb C$
such that the norm
 $$ \begin{align} \|g\|_{\mathcal{V}_s}:&= \int_{\mathbb{C}_+} \frac{(\operatorname{Re}z)^s |g(z)|}{|z|^{s+1}} \, dS(z) \\ &= \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{|g(\alpha +i\beta)|}{(\alpha^2+\beta^2)^{(s+1)/2}}\,d\beta\,d\alpha \notag\\ &=\int_{-\pi/2}^{\pi/2}\cos^s\varphi\int_0^{\infty} |g(\rho e^{i\varphi})|\,d\rho\,d\varphi\notag \end{align} $$
$$ \begin{align} \|g\|_{\mathcal{V}_s}:&= \int_{\mathbb{C}_+} \frac{(\operatorname{Re}z)^s |g(z)|}{|z|^{s+1}} \, dS(z) \\ &= \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{|g(\alpha +i\beta)|}{(\alpha^2+\beta^2)^{(s+1)/2}}\,d\beta\,d\alpha \notag\\ &=\int_{-\pi/2}^{\pi/2}\cos^s\varphi\int_0^{\infty} |g(\rho e^{i\varphi})|\,d\rho\,d\varphi\notag \end{align} $$
is finite, where S is the area measure on
![]() $\mathbb {C}_+$
. Note that
$\mathbb {C}_+$
. Note that
and
 $$ \begin{align} \int_{\Sigma_{\psi}} \frac{|g(z)|}{|z|} \, dS(z) \le \max\left\{1,\frac{1}{\cos^s\psi}\right\} \|g\|_{\mathcal{V}_s}, \qquad g \in \mathcal{V}_s, \, \psi \in (0,\pi/2). \end{align} $$
$$ \begin{align} \int_{\Sigma_{\psi}} \frac{|g(z)|}{|z|} \, dS(z) \le \max\left\{1,\frac{1}{\cos^s\psi}\right\} \|g\|_{\mathcal{V}_s}, \qquad g \in \mathcal{V}_s, \, \psi \in (0,\pi/2). \end{align} $$
The following property of functions from
![]() $\mathcal V_s$
is an essential element in the arguments that lead to the representations for functions in
$\mathcal V_s$
is an essential element in the arguments that lead to the representations for functions in
![]() $\mathcal {V}_s$
in Proposition 3.7 and for
$\mathcal {V}_s$
in Proposition 3.7 and for
![]() $\mathcal {D}_s$
in Corollary 3.10, and eventually to the definition of a functional calculus for operators in (7.5).
$\mathcal {D}_s$
in Corollary 3.10, and eventually to the definition of a functional calculus for operators in (7.5).
Lemma 3.1. Let
![]() $g\in \mathcal {V}_s$
be holomorphic, where
$g\in \mathcal {V}_s$
be holomorphic, where
![]() $s>-1$
. For every
$s>-1$
. For every
![]() $k\ge 1$
and every
$k\ge 1$
and every
![]() $\psi \in (0,\pi /2)$
,
$\psi \in (0,\pi /2)$
,
 $$ \begin{align} \lim_{|z|\to\infty ,\;z\in \Sigma_{\psi}}\,z^k g^{(k-1)}(z)=0. \end{align} $$
$$ \begin{align} \lim_{|z|\to\infty ,\;z\in \Sigma_{\psi}}\,z^k g^{(k-1)}(z)=0. \end{align} $$
Proof. Let
![]() $g \in \mathcal V_s$
be holomorphic,
$g \in \mathcal V_s$
be holomorphic,
![]() $\psi \in (0,\pi /2)$
,
$\psi \in (0,\pi /2)$
,
![]() $\psi ' = (\pi /2 + \psi )/2$
and
$\psi ' = (\pi /2 + \psi )/2$
and
![]() $b_{\psi }={\sin ((\pi /2-\psi )/2)} = \cos \psi '$
. If
$b_{\psi }={\sin ((\pi /2-\psi )/2)} = \cos \psi '$
. If
![]() $z \in \Sigma _{\psi }$
, then
$z \in \Sigma _{\psi }$
, then
Let
![]() $r \in (0, b_{\psi }|z|)$
. By Cauchy’s integral formula for derivatives,
$r \in (0, b_{\psi }|z|)$
. By Cauchy’s integral formula for derivatives,
 $$ \begin{align*} g^{(k-1)}(z)=\frac{(k-1)!}{2\pi i}\int_{\{\lambda:\,|\lambda-z|=r\}} \frac{g(\lambda)}{(\lambda-z)^{k}}\,d\lambda. \end{align*} $$
$$ \begin{align*} g^{(k-1)}(z)=\frac{(k-1)!}{2\pi i}\int_{\{\lambda:\,|\lambda-z|=r\}} \frac{g(\lambda)}{(\lambda-z)^{k}}\,d\lambda. \end{align*} $$
Multiplying by
![]() $r^k$
and integrating with respect to r over
$r^k$
and integrating with respect to r over
![]() $(0, b_{\psi }|z|)$
gives
$(0, b_{\psi }|z|)$
gives
 $$ \begin{align*} \frac{(b_{\psi}|z|)^{k+1}}{k+1} |g^{(k-1)}(z)| \le \frac{(k-1)!}{2\pi} \int_{\{\lambda: |\lambda-z|\le b_{\psi}|z|\}} |g(\lambda)| \, dS(\lambda), \end{align*} $$
$$ \begin{align*} \frac{(b_{\psi}|z|)^{k+1}}{k+1} |g^{(k-1)}(z)| \le \frac{(k-1)!}{2\pi} \int_{\{\lambda: |\lambda-z|\le b_{\psi}|z|\}} |g(\lambda)| \, dS(\lambda), \end{align*} $$
and then
 $$ \begin{align*} |z|^k |g^{(k-1)}(z)| \le \frac{(k+1)(k-1)!(1+b_{\psi})}{2\pi b_{\psi}^{k+1}} \int_{\{\lambda\in\Sigma_{\psi'}: |\lambda|\ge (1-b_{\psi})|z|\}} \frac{|g(\lambda)|}{|\lambda|} \, dS(\lambda). \end{align*} $$
$$ \begin{align*} |z|^k |g^{(k-1)}(z)| \le \frac{(k+1)(k-1)!(1+b_{\psi})}{2\pi b_{\psi}^{k+1}} \int_{\{\lambda\in\Sigma_{\psi'}: |\lambda|\ge (1-b_{\psi})|z|\}} \frac{|g(\lambda)|}{|\lambda|} \, dS(\lambda). \end{align*} $$
It now follows from (3.3) that
![]() $|z^k g^{(k-1)}(z)| \to 0$
as
$|z^k g^{(k-1)}(z)| \to 0$
as
![]() $|z|\to \infty , \, z \in \Sigma _{\psi }$
.
$|z|\to \infty , \, z \in \Sigma _{\psi }$
.
3.2. The spaces
 $\mathcal {D}_s$
and the operators
$\mathcal {D}_s$
and the operators
 $Q_s$
$Q_s$
We now define a linear operator
![]() $Q_s$
on
$Q_s$
on
![]() $\mathcal {V}_s, \, s>-1$
. It will play a role similar to the operator Q on
$\mathcal {V}_s, \, s>-1$
. It will play a role similar to the operator Q on
![]() $\mathcal {W}$
considered in [Reference Batty, Gomilko and Tomilov8, Section 3], where
$\mathcal {W}$
considered in [Reference Batty, Gomilko and Tomilov8, Section 3], where
![]() $\mathcal {W}$
is the Banach space of all (equivalence classes of) measurable functions
$\mathcal {W}$
is the Banach space of all (equivalence classes of) measurable functions
![]() $g : \mathbb {C}_+ \to \mathbb {C}$
such that
$g : \mathbb {C}_+ \to \mathbb {C}$
such that
 $$ \begin{align} \|g\|_{\mathcal{W}} := \int_0^{\infty} \sup_{\beta\in \mathbb{R}} |g(\alpha+i\beta)| \, d\alpha < \infty. \end{align} $$
$$ \begin{align} \|g\|_{\mathcal{W}} := \int_0^{\infty} \sup_{\beta\in \mathbb{R}} |g(\alpha+i\beta)| \, d\alpha < \infty. \end{align} $$
Indeed, the definition of
![]() $Q_1$
is formally the same as the definition of Q in [Reference Batty, Gomilko and Tomilov8], but the domain
$Q_1$
is formally the same as the definition of Q in [Reference Batty, Gomilko and Tomilov8], but the domain
![]() $\mathcal {V}_1$
of
$\mathcal {V}_1$
of
![]() $Q_1$
is larger than
$Q_1$
is larger than
![]() $\mathcal {W}$
.
$\mathcal {W}$
.
For
![]() $g \in \mathcal {V}_s$
, let
$g \in \mathcal {V}_s$
, let
 $$ \begin{align} (Q_s g)(z):= - \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{g(\alpha+i\beta)}{(z+\alpha-i\beta)^{s+1}} \, d\beta\,d\alpha, \quad z\in \mathbb{C}_{+} \cup \{0\}. \end{align} $$
$$ \begin{align} (Q_s g)(z):= - \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{g(\alpha+i\beta)}{(z+\alpha-i\beta)^{s+1}} \, d\beta\,d\alpha, \quad z\in \mathbb{C}_{+} \cup \{0\}. \end{align} $$
By (2.3), the integral is absolutely convergent, and
 $$ \begin{align} |(Q_s g)(z)|\le \frac{2^s\|g\|_{\mathcal{V}_s}}{\pi \cos^{s+1}\psi}, \qquad z \in \Sigma_{\psi}, \, \psi \in (0,\pi/2). \end{align} $$
$$ \begin{align} |(Q_s g)(z)|\le \frac{2^s\|g\|_{\mathcal{V}_s}}{\pi \cos^{s+1}\psi}, \qquad z \in \Sigma_{\psi}, \, \psi \in (0,\pi/2). \end{align} $$
The dominated convergence theorem implies that
![]() $Q_s g$
is continuous on
$Q_s g$
is continuous on
![]() $\mathbb {C}_+$
, with sectorial limits at infinity and
$\mathbb {C}_+$
, with sectorial limits at infinity and
![]() $0$
:
$0$
:
 $$ \begin{align} \lim_{|z|\to\infty,\,z\in {\Sigma}_{\psi}}\,(Q_s g)(z)=0, \qquad \psi \in (0,\pi/2), \end{align} $$
$$ \begin{align} \lim_{|z|\to\infty,\,z\in {\Sigma}_{\psi}}\,(Q_s g)(z)=0, \qquad \psi \in (0,\pi/2), \end{align} $$
and
 $$ \begin{align} \lim_{|z|\to 0,\,z\in {\Sigma}_{\psi}}\,(Q_s g)(z)=(Q_s g)(0), \qquad \psi \in (0,\pi/2). \end{align} $$
$$ \begin{align} \lim_{|z|\to 0,\,z\in {\Sigma}_{\psi}}\,(Q_s g)(z)=(Q_s g)(0), \qquad \psi \in (0,\pi/2). \end{align} $$
Thus,
![]() $Q_s g$
is bounded and continuous on
$Q_s g$
is bounded and continuous on
![]() $\overline {\Sigma }_{\psi }$
for every
$\overline {\Sigma }_{\psi }$
for every
![]() $\psi \in (0,\pi /2)$
. Moreover,
$\psi \in (0,\pi /2)$
. Moreover,
![]() $Q_s g$
is holomorphic on
$Q_s g$
is holomorphic on
![]() $\mathbb {C}_+$
and
$\mathbb {C}_+$
and
 $$ \begin{align} (Q_s g)'(z) = (s+1)\frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{g(\alpha + i\beta)}{(z+\alpha-i\beta)^{s+2}}\,d\beta \, d\alpha, \qquad z\in \mathbb{C}_{+}. \end{align} $$
$$ \begin{align} (Q_s g)'(z) = (s+1)\frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{g(\alpha + i\beta)}{(z+\alpha-i\beta)^{s+2}}\,d\beta \, d\alpha, \qquad z\in \mathbb{C}_{+}. \end{align} $$
Using this, (2.3) and (2.4), we obtain that
 $$ \begin{align} |(Q_s g)'(z)|\le \frac{(s+1)2^s}{\pi\cos^{s+2}\psi \,|z|}\|g\|_{\mathcal{V}_s},\qquad z\in \Sigma_{\psi}, \end{align} $$
$$ \begin{align} |(Q_s g)'(z)|\le \frac{(s+1)2^s}{\pi\cos^{s+2}\psi \,|z|}\|g\|_{\mathcal{V}_s},\qquad z\in \Sigma_{\psi}, \end{align} $$
and
 $$ \begin{align*} |z(Q_s g)'(z)|\le \frac{(s+1)2^s}{\pi\cos^{s+2}\psi}\int_{\mathbb{C}_{+}} \frac{|z|(\operatorname{Re}\lambda)^s\,|g(\lambda)|}{|z+\overline{\lambda}||\lambda|^{s+1}}\,dS(\lambda), \qquad z\in \Sigma_{\psi}. \end{align*} $$
$$ \begin{align*} |z(Q_s g)'(z)|\le \frac{(s+1)2^s}{\pi\cos^{s+2}\psi}\int_{\mathbb{C}_{+}} \frac{|z|(\operatorname{Re}\lambda)^s\,|g(\lambda)|}{|z+\overline{\lambda}||\lambda|^{s+1}}\,dS(\lambda), \qquad z\in \Sigma_{\psi}. \end{align*} $$
Using the dominated convergence theorem again, we obtain
 $$ \begin{align} \lim_{|z|\to0,z\in\Sigma_{\psi}} z(Q_sg)'(z) = 0. \end{align} $$
$$ \begin{align} \lim_{|z|\to0,z\in\Sigma_{\psi}} z(Q_sg)'(z) = 0. \end{align} $$
We now give another formula for
![]() $Q_s$
. Let
$Q_s$
. Let
![]() $s=n+\delta>-1$
where
$s=n+\delta>-1$
where
![]() $n\in \mathbb {N}\cup \{-1,0\}$
and
$n\in \mathbb {N}\cup \{-1,0\}$
and
![]() $\delta \in [0,1)$
, and let
$\delta \in [0,1)$
, and let
 $$ \begin{align} C_s:=\int_0^{\infty}\frac{dt}{(t+1)^{n+2}t^{\delta}}= \int_0^1\frac{(1-\tau)^s}{\tau^{\delta}}\,d\tau=B(1-\delta,s+1). \end{align} $$
$$ \begin{align} C_s:=\int_0^{\infty}\frac{dt}{(t+1)^{n+2}t^{\delta}}= \int_0^1\frac{(1-\tau)^s}{\tau^{\delta}}\,d\tau=B(1-\delta,s+1). \end{align} $$
Then
 $$ \begin{align*} \int_0^{\infty} \frac{dt}{(\lambda+t)^{n+2}t^{\delta}} = \frac{C_s}{\lambda^{s+1}},\quad \lambda\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} \int_0^{\infty} \frac{dt}{(\lambda+t)^{n+2}t^{\delta}} = \frac{C_s}{\lambda^{s+1}},\quad \lambda\in \mathbb{C}_{+}. \end{align*} $$
Indeed, both sides of this equation are holomorphic functions of
![]() $\lambda \in \mathbb {C}_+$
, and they coincide for
$\lambda \in \mathbb {C}_+$
, and they coincide for
![]() $\lambda \in (0,\infty )$
, so they coincide for all
$\lambda \in (0,\infty )$
, so they coincide for all
![]() $\lambda \in \mathbb {C}_+$
, by the identity theorem for holomorphic functions. Putting
$\lambda \in \mathbb {C}_+$
, by the identity theorem for holomorphic functions. Putting
![]() $\lambda = z+\alpha -i\beta $
, we obtain
$\lambda = z+\alpha -i\beta $
, we obtain
 $$ \begin{align} (Q_s g)(z) =- \frac{2^s}{\pi C_s}\int_0^{\infty} \int_0^{\infty}\int_{-\infty}^{\infty} \frac{\alpha^s\,g(\alpha+i\beta)\,d\beta\,d\alpha}{(z+\alpha-i\beta+t)^{n+2}}\,\frac{dt}{t^{\delta}},\quad z\in \mathbb{C}_{+}. \end{align} $$
$$ \begin{align} (Q_s g)(z) =- \frac{2^s}{\pi C_s}\int_0^{\infty} \int_0^{\infty}\int_{-\infty}^{\infty} \frac{\alpha^s\,g(\alpha+i\beta)\,d\beta\,d\alpha}{(z+\alpha-i\beta+t)^{n+2}}\,\frac{dt}{t^{\delta}},\quad z\in \mathbb{C}_{+}. \end{align} $$
For
![]() $s>-1$
let
$s>-1$
let
![]() $\mathcal {D}_s$
be the linear space of all holomorphic functions f on
$\mathcal {D}_s$
be the linear space of all holomorphic functions f on
![]() $\mathbb {C}_{+}$
such that
$\mathbb {C}_{+}$
such that
equipped with the semi-norm
If
![]() $\sigma>s>-1$
, then it is immediate from (3.2) that
$\sigma>s>-1$
, then it is immediate from (3.2) that
![]() $\mathcal {D}_s \subset \mathcal {D}_{\sigma }$
. We will exhibit some functions in
$\mathcal {D}_s \subset \mathcal {D}_{\sigma }$
. We will exhibit some functions in
![]() $\mathcal {D}_s$
later in this section and in Subsection 3.3.
$\mathcal {D}_s$
later in this section and in Subsection 3.3.
In the rest of this section we will obtain a reproducing formula (3.29) for functions from
![]() $\mathcal {D}_s$
and we will describe some basic properties that will be relevant for the sequel. To this aim, we first define and study the behaviour of operators
$\mathcal {D}_s$
and we will describe some basic properties that will be relevant for the sequel. To this aim, we first define and study the behaviour of operators
![]() $Q_s$
on the scale of
$Q_s$
on the scale of
![]() $\mathcal D_s$
-spaces. Recall that in [Reference Batty, Gomilko and Tomilov8, Proposition 3.1] we showed that Q maps
$\mathcal D_s$
-spaces. Recall that in [Reference Batty, Gomilko and Tomilov8, Proposition 3.1] we showed that Q maps
![]() $\mathcal {W}$
into
$\mathcal {W}$
into
![]() $\mathcal {B}$
. However
$\mathcal {B}$
. However
![]() $Q_s$
does not map the whole of
$Q_s$
does not map the whole of
![]() $\mathcal {V}_s$
into
$\mathcal {V}_s$
into
![]() $\mathcal {D}_s$
. For
$\mathcal {D}_s$
. For
![]() $s> -1$
, a function
$s> -1$
, a function
![]() $g \in \mathcal {V}_s$
for which
$g \in \mathcal {V}_s$
for which
![]() $Q_sg \notin \mathcal {D}_s$
can be defined as follows:
$Q_sg \notin \mathcal {D}_s$
can be defined as follows:
 $$ \begin{align*} g(\rho e^{i\varphi}) &:= \left(\cos^{s+1} \varphi (\rho-\sin\varphi) \log^2 (\rho -\sin\varphi)\right)^{-1}, \\ &\quad\quad\quad \quad\quad\quad 1< \rho < 2 - \sin\varphi, \, \pi/4 < \varphi < \pi/2, \end{align*} $$
$$ \begin{align*} g(\rho e^{i\varphi}) &:= \left(\cos^{s+1} \varphi (\rho-\sin\varphi) \log^2 (\rho -\sin\varphi)\right)^{-1}, \\ &\quad\quad\quad \quad\quad\quad 1< \rho < 2 - \sin\varphi, \, \pi/4 < \varphi < \pi/2, \end{align*} $$
and
![]() $g(z)= 0$
for all other points in
$g(z)= 0$
for all other points in
![]() $\mathbb {C}_+$
. We do not give details in this article. Instead, we will show in Propositions 3.6 and 3.7 that
$\mathbb {C}_+$
. We do not give details in this article. Instead, we will show in Propositions 3.6 and 3.7 that
![]() $Q_s$
maps
$Q_s$
maps
![]() $\mathcal {V}_s$
boundedly into
$\mathcal {V}_s$
boundedly into
![]() $\mathcal {D}_{\sigma }$
for any
$\mathcal {D}_{\sigma }$
for any
![]() $\sigma>s$
, and it maps holomorphic functions in
$\sigma>s$
, and it maps holomorphic functions in
![]() $\mathcal {V}_s$
into
$\mathcal {V}_s$
into
![]() $\mathcal {D}_s$
. We need the following auxiliary lemma, which will be useful in a number of instances.
$\mathcal {D}_s$
. We need the following auxiliary lemma, which will be useful in a number of instances.
Lemma 3.2. Let
![]() $h\in L^1[0,1] \cap L^{\infty }[1/2,1]$
be a positive function. Let
$h\in L^1[0,1] \cap L^{\infty }[1/2,1]$
be a positive function. Let
![]() $s>-1$
,
$s>-1$
,
![]() $\beta>1/2$
and
$\beta>1/2$
and
 $$ \begin{align} G_{h,\beta,s}(\varphi):= \int_{-\pi/2}^{\pi/2}\cos^s\psi \int_0^1\frac{h(t)\,dt}{(t^2+2t\cos(\varphi+\psi)+1)^{\beta}}\,d\psi,\quad \varphi\in (-\pi/2,\pi/2). \end{align} $$
$$ \begin{align} G_{h,\beta,s}(\varphi):= \int_{-\pi/2}^{\pi/2}\cos^s\psi \int_0^1\frac{h(t)\,dt}{(t^2+2t\cos(\varphi+\psi)+1)^{\beta}}\,d\psi,\quad \varphi\in (-\pi/2,\pi/2). \end{align} $$
-
(a) If
 $2\beta -s-2 < 0$
, then (3.16)
$2\beta -s-2 < 0$
, then (3.16) $$ \begin{align} K_{h,\beta,s} := \sup_{|\varphi|<\pi/2}\,G_{h,\beta,s}(\varphi)<\infty. \end{align} $$
$$ \begin{align} K_{h,\beta,s} := \sup_{|\varphi|<\pi/2}\,G_{h,\beta,s}(\varphi)<\infty. \end{align} $$
-
(b) If
 $2\beta -s-2> 0$
, then (3.17)
$2\beta -s-2> 0$
, then (3.17) $$ \begin{align} \tilde{K}_{h,\beta,s} := \sup_{|\varphi|<\pi/2}\, \cos^{2\beta-s-2}\varphi \, G_{h,\beta,s}(\varphi)<\infty. \end{align} $$
$$ \begin{align} \tilde{K}_{h,\beta,s} := \sup_{|\varphi|<\pi/2}\, \cos^{2\beta-s-2}\varphi \, G_{h,\beta,s}(\varphi)<\infty. \end{align} $$
Proof. Because
![]() $G_{h,\beta ,s}(-\varphi )=G_{h,\beta ,s}(\varphi )$
, we may assume that
$G_{h,\beta ,s}(-\varphi )=G_{h,\beta ,s}(\varphi )$
, we may assume that
![]() $\varphi \in [0,\pi /2)$
. Now
$\varphi \in [0,\pi /2)$
. Now
 $$ \begin{align*} G_{h,\beta,s}(\varphi) &= \int_{-\pi/2}^{0}\cos^s\psi \int_0^1\frac{h(t)\,dt}{(t^2+2t\cos(\varphi+\psi)+1)^{\beta}}\,d\psi\\ &\hskip30pt + \int_0^{\pi/2}\cos^s\psi\int_0^1\frac{h(t)\,dt}{(t^2+2t\cos(\varphi+\psi)+1)^{\beta}}\,d\psi\\ &=: G_{h,\beta, s}^{-}(\varphi)+G_{h,\beta, s}^+(\varphi), \end{align*} $$
$$ \begin{align*} G_{h,\beta,s}(\varphi) &= \int_{-\pi/2}^{0}\cos^s\psi \int_0^1\frac{h(t)\,dt}{(t^2+2t\cos(\varphi+\psi)+1)^{\beta}}\,d\psi\\ &\hskip30pt + \int_0^{\pi/2}\cos^s\psi\int_0^1\frac{h(t)\,dt}{(t^2+2t\cos(\varphi+\psi)+1)^{\beta}}\,d\psi\\ &=: G_{h,\beta, s}^{-}(\varphi)+G_{h,\beta, s}^+(\varphi), \end{align*} $$
and we estimate these two integrals separately.
Because
![]() $\varphi \in [0,\pi /2)$
,
$\varphi \in [0,\pi /2)$
,
![]() $\beta>1/2$
and
$\beta>1/2$
and
![]() $s>-1$
, we have
$s>-1$
, we have
 $$ \begin{align*} G_{h,\beta, s}^{-}(\varphi) &\le \int_{-\pi/2}^{0}\cos^s\psi \,d\psi\int_0^1 h(t)\,dt = \frac{\|h\|_{L^1[0,1]}}{2}B\left(\frac{s+1}{2},\frac{1}{2}\right). \end{align*} $$
$$ \begin{align*} G_{h,\beta, s}^{-}(\varphi) &\le \int_{-\pi/2}^{0}\cos^s\psi \,d\psi\int_0^1 h(t)\,dt = \frac{\|h\|_{L^1[0,1]}}{2}B\left(\frac{s+1}{2},\frac{1}{2}\right). \end{align*} $$
For the second integral, note that if
![]() $\phi = \varphi +\psi \in [0, \pi )$
,
$\phi = \varphi +\psi \in [0, \pi )$
,
 $$ \begin{align*} t^2+2t\cos\phi+1\ge \begin{cases} \frac{1}{4},\quad &t\in [0,1/2], \\ (1-t)^2 + 1 + \cos\phi, \quad &t\in [1/2,1]. \end{cases} \end{align*} $$
$$ \begin{align*} t^2+2t\cos\phi+1\ge \begin{cases} \frac{1}{4},\quad &t\in [0,1/2], \\ (1-t)^2 + 1 + \cos\phi, \quad &t\in [1/2,1]. \end{cases} \end{align*} $$
Hence,
 $$ \begin{align*} &{\int_0^1\frac{h(t)}{(t^2+2t\cos\phi+1)^{\beta}}\,dt } \\ &\qquad \le 4^{\beta}\int_0^{1/2} h(t)\,dt+ \int_{1/2}^1\frac{h(t)}{((t-1)^2+(1+\cos\phi))^{\beta}}\,dt\\ &\qquad \le 4^{\beta} \|h\|_{L^1[0,1/2]}+ \|h\|_{L^{\infty}[1/2,1]}\int_0^{\infty}\frac{d\tau}{(\tau^2+ 2\cos^2(\phi/2))^{\beta}} \\ &\qquad \le \frac{C_{h,\beta}}{\cos^{2\beta-1}(\phi/2)}, \end{align*} $$
$$ \begin{align*} &{\int_0^1\frac{h(t)}{(t^2+2t\cos\phi+1)^{\beta}}\,dt } \\ &\qquad \le 4^{\beta}\int_0^{1/2} h(t)\,dt+ \int_{1/2}^1\frac{h(t)}{((t-1)^2+(1+\cos\phi))^{\beta}}\,dt\\ &\qquad \le 4^{\beta} \|h\|_{L^1[0,1/2]}+ \|h\|_{L^{\infty}[1/2,1]}\int_0^{\infty}\frac{d\tau}{(\tau^2+ 2\cos^2(\phi/2))^{\beta}} \\ &\qquad \le \frac{C_{h,\beta}}{\cos^{2\beta-1}(\phi/2)}, \end{align*} $$
for some constant
![]() $C_{h,\beta }>0$
. Replacing
$C_{h,\beta }>0$
. Replacing
![]() $\varphi $
by
$\varphi $
by
![]() $\pi /2 -\varphi $
and
$\pi /2 -\varphi $
and
![]() $\psi $
by
$\psi $
by
![]() $\pi /2-\psi $
and using
$\pi /2-\psi $
and using
 $$ \begin{align*} \omega\ge \sin \omega\ge \frac{2}{\pi}\omega,\qquad \omega\in (0,\pi/2), \end{align*} $$
$$ \begin{align*} \omega\ge \sin \omega\ge \frac{2}{\pi}\omega,\qquad \omega\in (0,\pi/2), \end{align*} $$
we infer that if
![]() $\varphi \in [0,\pi /2)$
, then
$\varphi \in [0,\pi /2)$
, then
 $$ \begin{align*} G^+_{h,\beta,s}(\pi/2-\varphi) &\le C_{h,\beta} \int_0^{\pi/2}\frac{\sin^s\psi}{\sin^{2\beta-1}((\varphi+\psi)/2)} \,d\psi\\ &\le C_{h,\beta}\pi^{2\beta-1} \int_0^{\pi/2}\frac{\psi^s}{(\varphi+\psi)^{2\beta-1}} \,d\psi. \end{align*} $$
$$ \begin{align*} G^+_{h,\beta,s}(\pi/2-\varphi) &\le C_{h,\beta} \int_0^{\pi/2}\frac{\sin^s\psi}{\sin^{2\beta-1}((\varphi+\psi)/2)} \,d\psi\\ &\le C_{h,\beta}\pi^{2\beta-1} \int_0^{\pi/2}\frac{\psi^s}{(\varphi+\psi)^{2\beta-1}} \,d\psi. \end{align*} $$
In case (a), when
![]() $2\beta -s-2 < 0$
, we have
$2\beta -s-2 < 0$
, we have
 $$ \begin{align*} \int_0^{\pi/2} \frac{\psi^s}{(\varphi+\psi)^{2\beta-1}} \,d\psi \le \int_0^{\pi/2} \psi^{s-2\beta+1} \,d\psi = \frac{\pi^{s-2\beta+2}}{(s-2\beta+2)2^{s-2\beta+2}}<\infty. \end{align*} $$
$$ \begin{align*} \int_0^{\pi/2} \frac{\psi^s}{(\varphi+\psi)^{2\beta-1}} \,d\psi \le \int_0^{\pi/2} \psi^{s-2\beta+1} \,d\psi = \frac{\pi^{s-2\beta+2}}{(s-2\beta+2)2^{s-2\beta+2}}<\infty. \end{align*} $$
In case (b), when
![]() $2\beta - s -2 > 0$
, we obtain
$2\beta - s -2 > 0$
, we obtain
 $$ \begin{align*} \int_0^{\pi/2} \frac{\psi^s}{(\varphi+\psi)^{2\beta-1}} \,d\psi \le \varphi^{s+2-2\beta} \int_0^{\infty} \frac{t^s}{(t+1)^{2\beta-1}} \,dt, \end{align*} $$
$$ \begin{align*} \int_0^{\pi/2} \frac{\psi^s}{(\varphi+\psi)^{2\beta-1}} \,d\psi \le \varphi^{s+2-2\beta} \int_0^{\infty} \frac{t^s}{(t+1)^{2\beta-1}} \,dt, \end{align*} $$
and hence
 $$ \begin{align*} \cos^{2\beta-s-2}(\pi/2-\varphi) \, G_{h,\beta,s}(\pi/2-\varphi)& \le \varphi^{2\beta-s-2} G_{h,\beta,s}(\pi/2-\varphi)\\ & \le C_{h,\beta} \pi^{2\beta-1} \int_0^{\infty} \frac{t^s}{(t+1)^{2\beta-1}} \,dt < \infty, \end{align*} $$
$$ \begin{align*} \cos^{2\beta-s-2}(\pi/2-\varphi) \, G_{h,\beta,s}(\pi/2-\varphi)& \le \varphi^{2\beta-s-2} G_{h,\beta,s}(\pi/2-\varphi)\\ & \le C_{h,\beta} \pi^{2\beta-1} \int_0^{\infty} \frac{t^s}{(t+1)^{2\beta-1}} \,dt < \infty, \end{align*} $$
for some constant
![]() $C_{h,\beta }>0$
.
$C_{h,\beta }>0$
.
Let
![]() $\mathcal {D}_{s,0}$
be the space of all functions
$\mathcal {D}_{s,0}$
be the space of all functions
![]() $f \in \mathcal {D}_s$
such that f has a sectorial limit
$f \in \mathcal {D}_s$
such that f has a sectorial limit
![]() $0$
at infinity. Then
$0$
at infinity. Then
![]() $(\mathcal {D}_{s,0}, \|\cdot \|_{\mathcal {D}_{s,0}})$
is a normed space, and we will see in Corollary 3.11 that it is a Banach space.
$(\mathcal {D}_{s,0}, \|\cdot \|_{\mathcal {D}_{s,0}})$
is a normed space, and we will see in Corollary 3.11 that it is a Banach space.
The following basic examples will play roles in several estimates later in the article. We start with the resolvent functions and their powers.
Example 3.3. Let
![]() $\lambda =|\lambda |e^{i\varphi }\in \mathbb {C}_{+}$
, and
$\lambda =|\lambda |e^{i\varphi }\in \mathbb {C}_{+}$
, and
![]() $r_{\lambda }(z)= (z+\lambda )^{-1},\; z \in \mathbb {C}_+$
. Let
$r_{\lambda }(z)= (z+\lambda )^{-1},\; z \in \mathbb {C}_+$
. Let
![]() $\gamma>0$
, and consider
$\gamma>0$
, and consider
Let
![]() $s>-1$
. Then
$s>-1$
. Then
 $$ \begin{align} \|r_{\lambda}^{\gamma}\|_{\mathcal{D}_{s,0}} &=\gamma \int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^{\infty} \frac{d\rho}{\left|\rho e^{i\psi}+ |\lambda| e^{i\varphi}\right|{}^{\gamma+1}}\,d\psi\\ &=\frac{\gamma}{|\lambda|^{\gamma}}\int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^{\infty} \frac{d\rho}{|\rho+e^{i(\varphi-\psi)}|^{\gamma+1}}\,d\psi \nonumber \\ &=\frac{\gamma}{|\lambda|^{\gamma}} \int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^1 \frac{1+t^{\gamma-1}} {(t^2+2t\cos(\varphi+\psi)+1)^{(\gamma+1)/2}}\,dt\,d\psi, \nonumber \end{align} $$
$$ \begin{align} \|r_{\lambda}^{\gamma}\|_{\mathcal{D}_{s,0}} &=\gamma \int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^{\infty} \frac{d\rho}{\left|\rho e^{i\psi}+ |\lambda| e^{i\varphi}\right|{}^{\gamma+1}}\,d\psi\\ &=\frac{\gamma}{|\lambda|^{\gamma}}\int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^{\infty} \frac{d\rho}{|\rho+e^{i(\varphi-\psi)}|^{\gamma+1}}\,d\psi \nonumber \\ &=\frac{\gamma}{|\lambda|^{\gamma}} \int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^1 \frac{1+t^{\gamma-1}} {(t^2+2t\cos(\varphi+\psi)+1)^{(\gamma+1)/2}}\,dt\,d\psi, \nonumber \end{align} $$
where we have put
![]() $t=\rho $
for
$t=\rho $
for
![]() $\rho \le 1$
and
$\rho \le 1$
and
![]() $t = \rho ^{-1}$
for
$t = \rho ^{-1}$
for
![]() $\rho>1$
. Now we apply Lemma 3.2 with
$\rho>1$
. Now we apply Lemma 3.2 with
![]() $h(t) = 1+t^{\gamma -1}$
,
$h(t) = 1+t^{\gamma -1}$
,
![]() $\beta = (\gamma +1)/2$
, so
$\beta = (\gamma +1)/2$
, so
![]() $2\beta - s -2 = \gamma -s -1$
. Thus, we obtain
$2\beta - s -2 = \gamma -s -1$
. Thus, we obtain
 $$ \begin{align} \|r_{\lambda}^{\gamma}\|_{\mathcal{D}_{s,0}} \le \begin{cases} \dfrac{\gamma K_{h,(\gamma+1)/2,s}}{|\lambda|^{\gamma}}, &s>\gamma-1>-1, \\ &\\ \dfrac{\gamma \tilde{K}_{h,(\gamma+1)/2,s}}{|\lambda|^{\gamma}\cos^{\gamma-s-1}\varphi}, &\gamma-1> s>-1. \end{cases} \end{align} $$
$$ \begin{align} \|r_{\lambda}^{\gamma}\|_{\mathcal{D}_{s,0}} \le \begin{cases} \dfrac{\gamma K_{h,(\gamma+1)/2,s}}{|\lambda|^{\gamma}}, &s>\gamma-1>-1, \\ &\\ \dfrac{\gamma \tilde{K}_{h,(\gamma+1)/2,s}}{|\lambda|^{\gamma}\cos^{\gamma-s-1}\varphi}, &\gamma-1> s>-1. \end{cases} \end{align} $$
In particular, taking
![]() $\gamma =1$
and a fixed
$\gamma =1$
and a fixed
![]() $s>0$
,
$s>0$
,
 $$ \begin{align} \|r_{\lambda}\|_{\mathcal{D}_{s,0}} = \int_{-\pi/2}^{\pi/2} \int_0^{\infty} \frac{\cos^s \psi}{|\lambda+\rho e^{i\psi}|^2} \,d\rho \,d\psi \le \frac{C_s}{|\lambda|}, \qquad\lambda \in \mathbb{C}_+. \end{align} $$
$$ \begin{align} \|r_{\lambda}\|_{\mathcal{D}_{s,0}} = \int_{-\pi/2}^{\pi/2} \int_0^{\infty} \frac{\cos^s \psi}{|\lambda+\rho e^{i\psi}|^2} \,d\rho \,d\psi \le \frac{C_s}{|\lambda|}, \qquad\lambda \in \mathbb{C}_+. \end{align} $$
This estimate will play a crucial role in the proof of Theorem 1.1.
Next we consider some functions that appear frequently in the studies of holomorphic
![]() $C_0$
-semigroups.
$C_0$
-semigroups.
Example 3.4. Let
We will show here that
![]() $f_{\nu }\in \mathcal {D}_s$
if and only if
$f_{\nu }\in \mathcal {D}_s$
if and only if
![]() $s>\nu $
. Moreover, if
$s>\nu $
. Moreover, if
![]() $s>\nu $
, then
$s>\nu $
, then
 $$ \begin{align} \|f_{\nu}\|_{\mathcal{D}_{s,0}}\le 2 B\left(\frac{s-\nu}{2},\frac{1}{2}\right)\Gamma(\nu+1). \end{align} $$
$$ \begin{align} \|f_{\nu}\|_{\mathcal{D}_{s,0}}\le 2 B\left(\frac{s-\nu}{2},\frac{1}{2}\right)\Gamma(\nu+1). \end{align} $$
This estimate will be crucial for operator estimates in Section 10.
We have
 $$ \begin{align*} f_{\nu}'(z)=e^{-z}\left(\nu{z^{\nu-1}}-z^{\nu}\right) \end{align*} $$
$$ \begin{align*} f_{\nu}'(z)=e^{-z}\left(\nu{z^{\nu-1}}-z^{\nu}\right) \end{align*} $$
and
 $$ \begin{align*} \|f_{\nu}\|_{\mathcal{D}_{s,0}}&=\int_{-\pi/2}^{\pi/2} \cos^s\varphi\int_0^{\infty} {e^{-\rho\cos\varphi}}{\rho^{\nu-1}}\left|{\rho e^{i\varphi}}-\nu\right|\,d\rho\,d\varphi\\ &=\int_{-\pi/2}^{\pi/2} \cos^{s-\nu-1}\varphi\int_0^{\infty} e^{-r}r^{\nu-1}| r e^{i\varphi}-\nu\cos\varphi|\,dr\,d\varphi. \end{align*} $$
$$ \begin{align*} \|f_{\nu}\|_{\mathcal{D}_{s,0}}&=\int_{-\pi/2}^{\pi/2} \cos^s\varphi\int_0^{\infty} {e^{-\rho\cos\varphi}}{\rho^{\nu-1}}\left|{\rho e^{i\varphi}}-\nu\right|\,d\rho\,d\varphi\\ &=\int_{-\pi/2}^{\pi/2} \cos^{s-\nu-1}\varphi\int_0^{\infty} e^{-r}r^{\nu-1}| r e^{i\varphi}-\nu\cos\varphi|\,dr\,d\varphi. \end{align*} $$
We use the estimates
If
![]() $s> \nu $
, we obtain
$s> \nu $
, we obtain
 $$ \begin{align*} \|f_{\nu}\|_{\mathcal{D}_{s,0}} &\le 2\int_0^{\pi/2} \cos^{s-\nu-1}\varphi\,d\varphi \int_0^{\infty} e^{-r} r^{\nu-1}(r+\nu) \,dr \\ &= 2 B\left(\frac{s-\nu}{2},\frac{1}{2}\right)\Gamma(\nu+1). \notag \end{align*} $$
$$ \begin{align*} \|f_{\nu}\|_{\mathcal{D}_{s,0}} &\le 2\int_0^{\pi/2} \cos^{s-\nu-1}\varphi\,d\varphi \int_0^{\infty} e^{-r} r^{\nu-1}(r+\nu) \,dr \\ &= 2 B\left(\frac{s-\nu}{2},\frac{1}{2}\right)\Gamma(\nu+1). \notag \end{align*} $$
If
![]() $s \le \nu $
, then
$s \le \nu $
, then
 $$ \begin{align*} \|f_{\nu}\|_{\mathcal{D}_{s,0}} \ge 2\int_0^{\pi/2} \cos^{s-\nu-1}\varphi \, \sin\varphi\,d\varphi \int_0^{\infty} e^{-\tau} \tau^{\nu} \,d\tau = \infty. \end{align*} $$
$$ \begin{align*} \|f_{\nu}\|_{\mathcal{D}_{s,0}} \ge 2\int_0^{\pi/2} \cos^{s-\nu-1}\varphi \, \sin\varphi\,d\varphi \int_0^{\infty} e^{-\tau} \tau^{\nu} \,d\tau = \infty. \end{align*} $$
This establishes the claims above.
Finally, we consider a function that will play an important role in our constructions of functional calculi in Section 8.
Example 3.5. The function
![]() $\operatorname {\mathrm {arccot}}$
is defined by
$\operatorname {\mathrm {arccot}}$
is defined by
 $$ \begin{align} \operatorname{\mathrm{arccot}}(z) = \frac{1}{2i} \log \left(\frac{z+i}{z-i}\right), \quad z \in \mathbb{C}_+. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{arccot}}(z) = \frac{1}{2i} \log \left(\frac{z+i}{z-i}\right), \quad z \in \mathbb{C}_+. \end{align} $$
Then
![]() $|\operatorname {Re}\operatorname {\mathrm {arccot}}(z)| \le \pi /2$
,
$|\operatorname {Re}\operatorname {\mathrm {arccot}}(z)| \le \pi /2$
,
![]() $\operatorname {\mathrm {arccot}}$
has sectorial limit
$\operatorname {\mathrm {arccot}}$
has sectorial limit
![]() $0$
at infinity and its derivative is
$0$
at infinity and its derivative is
![]() $- (z^2+1)^{-1}$
. It is easy to see that
$- (z^2+1)^{-1}$
. It is easy to see that
![]() $\operatorname {\mathrm {arccot}} \in \mathcal {D}_s$
for all
$\operatorname {\mathrm {arccot}} \in \mathcal {D}_s$
for all
![]() $s>-1$
. For
$s>-1$
. For
![]() $s = 0$
, we have
$s = 0$
, we have
 $$ \begin{align} &{\|\operatorname{\mathrm{arccot}}\|_{\mathcal{D}_{0,0}}} \\ & \ =\int_{-\pi/2}^{\pi/2}\int_0^{\infty} \frac{d\rho}{|1+\rho^2e^{2i\varphi}|}\,d\varphi =\int_0^{\infty} \int_0^{\pi}\frac{d\psi}{(\rho^4+2\rho^2\cos\psi+1)^{1/2}}\,d\rho \notag\\ & \ \le \sqrt{\pi}\int_0^{\infty} \left(\int_0^{\pi} \frac{d\psi}{\rho^4+2\rho^2\cos\psi+1}\right)^{1/2}\,d\rho = \sqrt{\pi}\int_0^{\infty} \left(\frac{\pi}{|\rho^4-1|}\right)^{1/2}\,d\rho\notag\\ & \ =\frac{\pi}{2} B(1/4,1/2) < 3 \pi.\notag \end{align} $$
$$ \begin{align} &{\|\operatorname{\mathrm{arccot}}\|_{\mathcal{D}_{0,0}}} \\ & \ =\int_{-\pi/2}^{\pi/2}\int_0^{\infty} \frac{d\rho}{|1+\rho^2e^{2i\varphi}|}\,d\varphi =\int_0^{\infty} \int_0^{\pi}\frac{d\psi}{(\rho^4+2\rho^2\cos\psi+1)^{1/2}}\,d\rho \notag\\ & \ \le \sqrt{\pi}\int_0^{\infty} \left(\int_0^{\pi} \frac{d\psi}{\rho^4+2\rho^2\cos\psi+1}\right)^{1/2}\,d\rho = \sqrt{\pi}\int_0^{\infty} \left(\frac{\pi}{|\rho^4-1|}\right)^{1/2}\,d\rho\notag\\ & \ =\frac{\pi}{2} B(1/4,1/2) < 3 \pi.\notag \end{align} $$
See [Reference Prudnikov, Brychkov and Marichev48, item 2.5.16, (38)] for the evaluation of the integral with respect to
![]() $\psi $
.
$\psi $
.
Proposition 3.6. Let
![]() $\sigma> s > -1$
. The following hold:
$\sigma> s > -1$
. The following hold:
-
(i)
 $\mathcal D_{s,0}$
is continuously embedded in
$\mathcal D_{s,0}$
is continuously embedded in
 $\mathcal {D}_{\sigma , 0}$
.
$\mathcal {D}_{\sigma , 0}$
. -
(ii) The restriction of
 $Q_{\sigma }$
to
$Q_{\sigma }$
to
 $\mathcal {V}_s$
is in
$\mathcal {V}_s$
is in
 $L(\mathcal {V}_s,\mathcal {D}_{s,0})$
.
$L(\mathcal {V}_s,\mathcal {D}_{s,0})$
. -
(iii)
 $Q_s \in L (\mathcal {V}_s, \mathcal {D}_{\sigma,0 })$
.
$Q_s \in L (\mathcal {V}_s, \mathcal {D}_{\sigma,0 })$
.
Proof. The first statement is immediate from the definitions of the spaces and (3.2).
For the second statement, let
![]() $g \in \mathcal {V}_s$
. From (3.1), (3.10) and the second case of (3.19) with
$g \in \mathcal {V}_s$
. From (3.1), (3.10) and the second case of (3.19) with
![]() $\gamma =\sigma +1$
and
$\gamma =\sigma +1$
and
![]() $h(t)=1+t^{\sigma }$
, we have
$h(t)=1+t^{\sigma }$
, we have
 $$ \begin{align*} &{\frac{\pi}{2^{\sigma}(\sigma+1)} \|Q_{\sigma}g\|_{\mathcal{D}_{s,0}}\hskip10pt}\\ & \le \int_{-\pi/2}^{\pi/2}\cos^{s}\psi \int_0^{\infty} \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} \frac{t^{\sigma+1}|g(t e^{i\varphi})|}{|\rho e^{i\psi}+t e^{-i\varphi}|^{\sigma+2}}\,d\rho\,d\varphi \,dt\,d\psi\\ & = \frac{1}{\sigma+1}\int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} t^{\sigma+1}\|r_{t e^{-i\varphi}}^{\sigma+1}\|_{\mathcal{D}_{s,0}} |g(t e^{i\varphi})|\,dt\,d\varphi \\ & \le \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} \frac{\tilde{K}_{h,(\sigma+2)/2,s}}{\cos^{\sigma-s}\varphi} |g(t e^{i\varphi})|\,dt\,d\varphi \\ & = \tilde{K}_{h,(\sigma+2)/2,s} \|g\|_{\mathcal{V}_s}. \end{align*} $$
$$ \begin{align*} &{\frac{\pi}{2^{\sigma}(\sigma+1)} \|Q_{\sigma}g\|_{\mathcal{D}_{s,0}}\hskip10pt}\\ & \le \int_{-\pi/2}^{\pi/2}\cos^{s}\psi \int_0^{\infty} \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} \frac{t^{\sigma+1}|g(t e^{i\varphi})|}{|\rho e^{i\psi}+t e^{-i\varphi}|^{\sigma+2}}\,d\rho\,d\varphi \,dt\,d\psi\\ & = \frac{1}{\sigma+1}\int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} t^{\sigma+1}\|r_{t e^{-i\varphi}}^{\sigma+1}\|_{\mathcal{D}_{s,0}} |g(t e^{i\varphi})|\,dt\,d\varphi \\ & \le \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} \frac{\tilde{K}_{h,(\sigma+2)/2,s}}{\cos^{\sigma-s}\varphi} |g(t e^{i\varphi})|\,dt\,d\varphi \\ & = \tilde{K}_{h,(\sigma+2)/2,s} \|g\|_{\mathcal{V}_s}. \end{align*} $$
This establishes the second statement.
For the third statement, the same estimation but with s and
![]() $\sigma $
interchanged and using the first case of (3.19) with
$\sigma $
interchanged and using the first case of (3.19) with
![]() $\gamma =s+1$
and
$\gamma =s+1$
and
![]() $h(t)=1+t^s$
shows that
$h(t)=1+t^s$
shows that
 $$ \begin{align*} \frac{\pi}{2^s(s+1)} \|Q_{s}g\|_{\mathcal{D}_{\sigma,0}}\le {K}_{h,(s+2)/2,\sigma} \|g\|_{\mathcal{V}_s}. \end{align*} $$
$$ \begin{align*} \frac{\pi}{2^s(s+1)} \|Q_{s}g\|_{\mathcal{D}_{\sigma,0}}\le {K}_{h,(s+2)/2,\sigma} \|g\|_{\mathcal{V}_s}. \end{align*} $$
This establishes the third statement.
For insight on why
 $\|r_{\lambda }^{\sigma +1}\|_{\mathcal {D}_{s,0}}$
appears in the proof above, we refer the reader to the proof of Theorem 5.1.
$\|r_{\lambda }^{\sigma +1}\|_{\mathcal {D}_{s,0}}$
appears in the proof above, we refer the reader to the proof of Theorem 5.1.
Proposition 3.7. Let
![]() $g \in \mathcal {V}_s$
be holomorphic, where
$g \in \mathcal {V}_s$
be holomorphic, where
![]() $s>-1$
. Then
$s>-1$
. Then
![]() $Q_s g \in \mathcal {D}_s$
and
$Q_s g \in \mathcal {D}_s$
and
![]() $(Q_s g)'= g$
.
$(Q_s g)'= g$
.
Proof. First we consider the case when
![]() $g\in \mathcal {V}_n$
, where
$g\in \mathcal {V}_n$
, where
![]() $n \in \mathbb {N}\cup \{0\}$
. Then
$n \in \mathbb {N}\cup \{0\}$
. Then
![]() $Q_n g$
is holomorphic and (3.6) holds for
$Q_n g$
is holomorphic and (3.6) holds for
![]() $s=n$
. It suffices to show that
$s=n$
. It suffices to show that
![]() $(Q_ng)' = g$
. Let
$(Q_ng)' = g$
. Let
 $$ \begin{align*} I(\alpha) &:= \int_{-\infty}^{\infty} \frac{|g(\alpha+i\beta)|}{(\alpha^2+\beta^2)^{(n+1)/2}} \,d\beta, \qquad \alpha>0,\\ J(\beta) &:= \int_0^{\infty} \frac{\alpha^n|g(\alpha+i\beta)|}{(\alpha^2+\beta^2)^{(n+1)/2}} \,d\alpha, \qquad \beta \in \mathbb{R}. \end{align*} $$
$$ \begin{align*} I(\alpha) &:= \int_{-\infty}^{\infty} \frac{|g(\alpha+i\beta)|}{(\alpha^2+\beta^2)^{(n+1)/2}} \,d\beta, \qquad \alpha>0,\\ J(\beta) &:= \int_0^{\infty} \frac{\alpha^n|g(\alpha+i\beta)|}{(\alpha^2+\beta^2)^{(n+1)/2}} \,d\alpha, \qquad \beta \in \mathbb{R}. \end{align*} $$
From (3.1) and Fubini’s theorem, we see that
 $\int _0^{\infty } \alpha ^n I(\alpha ) \, d\alpha < \infty $
. Hence,
$\int _0^{\infty } \alpha ^n I(\alpha ) \, d\alpha < \infty $
. Hence,
![]() $I(\alpha )<\infty $
for almost all
$I(\alpha )<\infty $
for almost all
![]() $\alpha>0$
and it follows that there exists a sequence
$\alpha>0$
and it follows that there exists a sequence
![]() $(\alpha _j)_{j\ge 1}$
such that
$(\alpha _j)_{j\ge 1}$
such that
 $$ \begin{align*} \lim_{j \to \infty}\alpha_j =\infty, \qquad \lim_{j\to\infty} I(\alpha_j) = 0. \end{align*} $$
$$ \begin{align*} \lim_{j \to \infty}\alpha_j =\infty, \qquad \lim_{j\to\infty} I(\alpha_j) = 0. \end{align*} $$
Similarly,
 $\int _{-\infty }^{\infty } J(\beta )\,d\beta < \infty $
, and so there exist sequences
$\int _{-\infty }^{\infty } J(\beta )\,d\beta < \infty $
, and so there exist sequences
 $(\beta _k^{\pm })_{k \ge 1}$
such that
$(\beta _k^{\pm })_{k \ge 1}$
such that
 $$ \begin{align*} \lim_{k \to \infty}\beta_k^{\pm} = \pm\infty, \qquad \lim_{k\to\infty} J(\beta_k^{\pm}) = 0. \end{align*} $$
$$ \begin{align*} \lim_{k \to \infty}\beta_k^{\pm} = \pm\infty, \qquad \lim_{k\to\infty} J(\beta_k^{\pm}) = 0. \end{align*} $$
Let
![]() $z \in \mathbb {C}_+$
be fixed. Take
$z \in \mathbb {C}_+$
be fixed. Take
![]() $\alpha>0$
with
$\alpha>0$
with
![]() $I(\alpha )<\infty $
, and let j be sufficiently large that
$I(\alpha )<\infty $
, and let j be sufficiently large that
![]() $\alpha _j> 2\alpha + \operatorname {Re}z$
and k be sufficiently large that
$\alpha _j> 2\alpha + \operatorname {Re}z$
and k be sufficiently large that
 $\beta _k^- < \operatorname {Im}z < \beta _k^+$
. We may apply the Cauchy integral formula around the rectangle with vertices
$\beta _k^- < \operatorname {Im}z < \beta _k^+$
. We may apply the Cauchy integral formula around the rectangle with vertices
 $\alpha +i\beta _k^{\pm }$
and
$\alpha +i\beta _k^{\pm }$
and
 $\alpha _j + i \beta _k^{\pm }$
, and we obtain
$\alpha _j + i \beta _k^{\pm }$
, and we obtain
 $$ \begin{align*} &{\frac{2\pi}{n!} g^{(n)}(2\alpha+z)} \\ &= \int_{\beta_k^-}^{\beta_k^+} \frac{g(\alpha_j+i\beta)}{(\alpha_j+i\beta - z -2\alpha)^{n+1}} d\beta - \int_{\beta_k^-}^{\beta_k^+} \frac{g(\alpha+i\beta)}{(\alpha+i\beta - z -2\alpha)^{n+1}} d\beta \\ &\quad -i \int_{\alpha}^{\alpha_j}\frac{g(s+i\beta_k^{-})}{(s+i\beta_k^{-}- z-2\alpha)^{n+1}}\,ds + i \int_{\alpha}^{\alpha_j}\frac{g(s+i\beta_k^{+})}{(s+i\beta_k^{+} - z -2\alpha)^{n+1}}\,ds. \end{align*} $$
$$ \begin{align*} &{\frac{2\pi}{n!} g^{(n)}(2\alpha+z)} \\ &= \int_{\beta_k^-}^{\beta_k^+} \frac{g(\alpha_j+i\beta)}{(\alpha_j+i\beta - z -2\alpha)^{n+1}} d\beta - \int_{\beta_k^-}^{\beta_k^+} \frac{g(\alpha+i\beta)}{(\alpha+i\beta - z -2\alpha)^{n+1}} d\beta \\ &\quad -i \int_{\alpha}^{\alpha_j}\frac{g(s+i\beta_k^{-})}{(s+i\beta_k^{-}- z-2\alpha)^{n+1}}\,ds + i \int_{\alpha}^{\alpha_j}\frac{g(s+i\beta_k^{+})}{(s+i\beta_k^{+} - z -2\alpha)^{n+1}}\,ds. \end{align*} $$
Letting
![]() $k \to \infty $
, we obtain
$k \to \infty $
, we obtain
 $$ \begin{align*} (-1)^n \frac{2\pi}{n!} g^{(n)}(2\alpha+z) = \int_{-\infty}^{\infty} \frac{g(\alpha+i\beta)}{(z+\alpha-i\beta)^{n+1}} \,d\beta - \int_{-\infty}^{\infty} \frac{g(\alpha_j+i\beta)}{(z+2\alpha-\alpha_j-i\beta)^{n+1}} \,d\beta. \end{align*} $$
$$ \begin{align*} (-1)^n \frac{2\pi}{n!} g^{(n)}(2\alpha+z) = \int_{-\infty}^{\infty} \frac{g(\alpha+i\beta)}{(z+\alpha-i\beta)^{n+1}} \,d\beta - \int_{-\infty}^{\infty} \frac{g(\alpha_j+i\beta)}{(z+2\alpha-\alpha_j-i\beta)^{n+1}} \,d\beta. \end{align*} $$
Letting
![]() $j \to \infty $
, we obtain
$j \to \infty $
, we obtain
 $$ \begin{align} (-1)^n \frac{2\pi}{n!} g^{(n)}(2\alpha+z) = \int_{-\infty}^{\infty} \frac{g(\alpha+i\beta)}{(z+\alpha-i\beta)^{n+1}} \,d\beta. \end{align} $$
$$ \begin{align} (-1)^n \frac{2\pi}{n!} g^{(n)}(2\alpha+z) = \int_{-\infty}^{\infty} \frac{g(\alpha+i\beta)}{(z+\alpha-i\beta)^{n+1}} \,d\beta. \end{align} $$
This holds for almost all
![]() $\alpha>0$
. Substituting this into (3.6) and then integrating by parts and using Lemma 3.1, we infer that
$\alpha>0$
. Substituting this into (3.6) and then integrating by parts and using Lemma 3.1, we infer that
 $$ \begin{align} (Q_n g)(z) &= (-1)^{n+1} \frac{2^{n+1}}{n!} \int_0^{\infty} \alpha^{n} g^{(n)}(2\alpha+z)\,d\alpha \\ &=\frac{(-1)^{n+1}}{n!}\int_0^{\infty} \alpha^n g^{(n)}(\alpha+z)\,d\alpha = - \int_0^{\infty} g(\alpha+z)\,d\alpha. \nonumber \end{align} $$
$$ \begin{align} (Q_n g)(z) &= (-1)^{n+1} \frac{2^{n+1}}{n!} \int_0^{\infty} \alpha^{n} g^{(n)}(2\alpha+z)\,d\alpha \\ &=\frac{(-1)^{n+1}}{n!}\int_0^{\infty} \alpha^n g^{(n)}(\alpha+z)\,d\alpha = - \int_0^{\infty} g(\alpha+z)\,d\alpha. \nonumber \end{align} $$
By Lemma 3.1, the integral
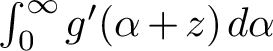 $\int _{0}^{\infty } g'(\alpha +z)\,d\alpha $
converges absolutely and uniformly for z in compact subsets of
$\int _{0}^{\infty } g'(\alpha +z)\,d\alpha $
converges absolutely and uniformly for z in compact subsets of
![]() $\mathbb {C}_+$
. So, differentiating under the integral sign we get
$\mathbb {C}_+$
. So, differentiating under the integral sign we get
![]() $(Q_n g)' = g$
.
$(Q_n g)' = g$
.
Now consider the case when
![]() $s=n+\delta>-1$
, where
$s=n+\delta>-1$
, where
![]() $n \in \mathbb {N}\cup \{-1,0\}$
,
$n \in \mathbb {N}\cup \{-1,0\}$
,
![]() $\delta \in (0,1)$
and
$\delta \in (0,1)$
and
![]() $g \in \mathcal {V}_s$
is holomorphic. Then
$g \in \mathcal {V}_s$
is holomorphic. Then
![]() $g\in \mathcal {V}_{n+1}$
,
$g\in \mathcal {V}_{n+1}$
,
![]() $n+1\in \mathbb {N}\cup \{0\}$
, and (3.24) gives
$n+1\in \mathbb {N}\cup \{0\}$
, and (3.24) gives
 $$ \begin{align*} \int_{-\infty}^{\infty} \frac{g(\alpha+i\beta)}{(z+\alpha-i\beta+t)^{n+2}} \,d\beta= (-1)^{n+1}\frac{2\pi}{(n+1)!} g^{(n+1)}(2\alpha+z+t), \end{align*} $$
$$ \begin{align*} \int_{-\infty}^{\infty} \frac{g(\alpha+i\beta)}{(z+\alpha-i\beta+t)^{n+2}} \,d\beta= (-1)^{n+1}\frac{2\pi}{(n+1)!} g^{(n+1)}(2\alpha+z+t), \end{align*} $$
for
![]() $z \in \mathbb {C}_+$
,
$z \in \mathbb {C}_+$
,
![]() $t>0$
and almost all
$t>0$
and almost all
![]() $\alpha>0$
. We obtain from (3.14) and (3.13) that
$\alpha>0$
. We obtain from (3.14) and (3.13) that
 $$ \begin{align*} C_s (Q_s g)(z) &=- \frac{2^s}{\pi}\int_0^{\infty} \int_0^{\infty}\int_{-\infty}^{\infty} \frac{\alpha^s\,g(\alpha+i\beta)\,d\beta\,d\alpha}{(z+\alpha-i\beta+t)^{n+2}}\,\frac{dt}{t^{\delta}}\\ &=(-1)^n\frac{2^{s+1}}{(n+1)!}\int_0^{\infty} \int_0^{\infty} \alpha^s g^{(n+1)}(2\alpha+z+t)\, d\alpha\,\frac{dt}{t^{\delta}}\\ &=\frac{(-1)^n}{(n+1)!}\int_0^{\infty} \int_t^{\infty} (\tau-t)^s g^{(n+1)}(\tau+z) \, d\tau\,\frac{dt}{t^{\delta}}\\ &=C_s\frac{(-1)^n}{(n+1)!}\int_0^{\infty} \tau^{n+1} \,g^{(n+1)}(\tau+z)\,d\tau. \end{align*} $$
$$ \begin{align*} C_s (Q_s g)(z) &=- \frac{2^s}{\pi}\int_0^{\infty} \int_0^{\infty}\int_{-\infty}^{\infty} \frac{\alpha^s\,g(\alpha+i\beta)\,d\beta\,d\alpha}{(z+\alpha-i\beta+t)^{n+2}}\,\frac{dt}{t^{\delta}}\\ &=(-1)^n\frac{2^{s+1}}{(n+1)!}\int_0^{\infty} \int_0^{\infty} \alpha^s g^{(n+1)}(2\alpha+z+t)\, d\alpha\,\frac{dt}{t^{\delta}}\\ &=\frac{(-1)^n}{(n+1)!}\int_0^{\infty} \int_t^{\infty} (\tau-t)^s g^{(n+1)}(\tau+z) \, d\tau\,\frac{dt}{t^{\delta}}\\ &=C_s\frac{(-1)^n}{(n+1)!}\int_0^{\infty} \tau^{n+1} \,g^{(n+1)}(\tau+z)\,d\tau. \end{align*} $$
As in (3.25), it follows that
![]() $(Q_sg)' = g$
.
$(Q_sg)' = g$
.
Corollary 3.8. If
![]() $g \in \mathcal {V}_s$
is holomorphic, then
$g \in \mathcal {V}_s$
is holomorphic, then
![]() $Q_{\sigma } g = Q_s g$
for all
$Q_{\sigma } g = Q_s g$
for all
![]() $\sigma \ge s$
.
$\sigma \ge s$
.
Remark 3.9. The proof of the property
![]() $(Q_ng)'=g', n \ge 0,$
in Proposition 3.7 uses just improper convergence of the integrals
$(Q_ng)'=g', n \ge 0,$
in Proposition 3.7 uses just improper convergence of the integrals
 $\int _{0}^{\infty } \alpha ^{k} g^{(k)}(\alpha +z)\,d\alpha $
for
$\int _{0}^{\infty } \alpha ^{k} g^{(k)}(\alpha +z)\,d\alpha $
for
![]() $0 \le k \le n-1.$
It is instructive to note that if
$0 \le k \le n-1.$
It is instructive to note that if
![]() $g \in \mathcal V_n$
is holomorphic and
$g \in \mathcal V_n$
is holomorphic and
![]() $z \in \mathbb C_+$
, then
$z \in \mathbb C_+$
, then
 $$ \begin{align} \int_{0}^{\infty} \alpha^{k} |g^{(k)}(\alpha+z)|\,d\alpha<\infty \end{align} $$
$$ \begin{align} \int_{0}^{\infty} \alpha^{k} |g^{(k)}(\alpha+z)|\,d\alpha<\infty \end{align} $$
for all
![]() $ k \ge 0.$
Indeed, if
$ k \ge 0.$
Indeed, if
![]() $g \in \mathcal V_n,$
then (3.26) holds for
$g \in \mathcal V_n,$
then (3.26) holds for
![]() $k=n$
by (3.24) and the definition of norm in
$k=n$
by (3.24) and the definition of norm in
![]() $\mathcal V_n.$
If
$\mathcal V_n.$
If
![]() $n \ge 1,$
then using Lemma 3.1, we infer that
$n \ge 1,$
then using Lemma 3.1, we infer that
 $g^{(n-1)}(\alpha +z)=-\int _{\alpha }^{\infty } g^{(n)}{(s+z)\,ds},$
and hence by Fubini’s theorem,
$g^{(n-1)}(\alpha +z)=-\int _{\alpha }^{\infty } g^{(n)}{(s+z)\,ds},$
and hence by Fubini’s theorem,
 $$ \begin{align*} \int_0^{\infty} \alpha^{n-1} |g^{(n-1)}(\alpha+z)|\,d\alpha \le \frac{1}{n} \int_0^{\infty} \alpha^n | g^{(n)}(\alpha +z)| d\alpha <\infty. \end{align*} $$
$$ \begin{align*} \int_0^{\infty} \alpha^{n-1} |g^{(n-1)}(\alpha+z)|\,d\alpha \le \frac{1}{n} \int_0^{\infty} \alpha^n | g^{(n)}(\alpha +z)| d\alpha <\infty. \end{align*} $$
Repeating this argument, we conclude that (3.26) holds also for k such that
![]() $0 \le k < n.$
If
$0 \le k < n.$
If
![]() $k>n,$
then (3.26) follows directly from (3.24) and the inclusion
$k>n,$
then (3.26) follows directly from (3.24) and the inclusion
![]() $\mathcal V_n \subset \mathcal V_k.$
$\mathcal V_n \subset \mathcal V_k.$
The following representation of functions in
![]() $\mathcal {D}_s$
has appeared in [Reference Aleksandrov2, Corollary 4.2] (see also [Reference Aleksandrov and Peller3, Lemma 3.13.2] for the case
$\mathcal {D}_s$
has appeared in [Reference Aleksandrov2, Corollary 4.2] (see also [Reference Aleksandrov and Peller3, Lemma 3.13.2] for the case
![]() $s=1$
).
$s=1$
).
Corollary 3.10. Let
![]() $f\in \mathcal {D}_s$
,
$f\in \mathcal {D}_s$
,
![]() $s>-1 $
. Then the sectorial limits
$s>-1 $
. Then the sectorial limits
 $$ \begin{align} f(\infty): =\lim_{z\to\infty ,\;z\in \Sigma_{\psi}}\,f(z), \end{align} $$
$$ \begin{align} f(\infty): =\lim_{z\to\infty ,\;z\in \Sigma_{\psi}}\,f(z), \end{align} $$
 $$ \begin{align} f(0):= \lim_{z\to 0,\;z\in \Sigma_{\psi}}\,f(z) \end{align} $$
$$ \begin{align} f(0):= \lim_{z\to 0,\;z\in \Sigma_{\psi}}\,f(z) \end{align} $$
exist in
![]() $\mathbb {C}$
for every
$\mathbb {C}$
for every
![]() $\psi \in (0,\pi /2)$
. Moreover, for all
$\psi \in (0,\pi /2)$
. Moreover, for all
![]() $z \in \mathbb {C}_{+}\cup \{0\}$
,
$z \in \mathbb {C}_{+}\cup \{0\}$
,
 $$ \begin{align} f(z)&=f(\infty)+(Q_s f')(z)\\ &=f(\infty)- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{f'(\alpha+i\beta)\,d\beta}{(z+\alpha-i\beta)^{s+1}} \, d\alpha.\notag \end{align} $$
$$ \begin{align} f(z)&=f(\infty)+(Q_s f')(z)\\ &=f(\infty)- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{f'(\alpha+i\beta)\,d\beta}{(z+\alpha-i\beta)^{s+1}} \, d\alpha.\notag \end{align} $$
With
![]() $f(0)$
defined as above,
$f(0)$
defined as above,
![]() $f \in C(\overline {\Sigma }_{\psi })$
for every
$f \in C(\overline {\Sigma }_{\psi })$
for every
![]() $\psi \in (0,\pi /2)$
.
$\psi \in (0,\pi /2)$
.
Proof. It follows from Proposition 3.7 that
![]() $(Q_s f')' = f'$
. The statements follow from (3.8) and (3.9).
$(Q_s f')' = f'$
. The statements follow from (3.8) and (3.9).
Corollary 3.11. For every
![]() $s>-1$
the space
$s>-1$
the space
![]() $\mathcal D_s$
equipped with the norm
$\mathcal D_s$
equipped with the norm
is a Banach space.
Proof. Let
![]() $s>-1$
be fixed and let
$s>-1$
be fixed and let
![]() $(f_k)_{k=1}^{\infty }$
be a Cauchy sequence in
$(f_k)_{k=1}^{\infty }$
be a Cauchy sequence in
![]() $\mathcal D_s$
. Then (3.7) and Vitali’s theorem imply that
$\mathcal D_s$
. Then (3.7) and Vitali’s theorem imply that
![]() $(Q_s f_k')_{k=1}^{\infty }$
converges uniformly on each
$(Q_s f_k')_{k=1}^{\infty }$
converges uniformly on each
![]() $\Sigma _{\psi }$
to a limit g that is holomorphic on
$\Sigma _{\psi }$
to a limit g that is holomorphic on
![]() $\mathbb {C}_+$
. Moreover,
$\mathbb {C}_+$
. Moreover,
![]() $(f_k(\infty ))_{k=1}^{\infty }$
converges to a limit
$(f_k(\infty ))_{k=1}^{\infty }$
converges to a limit
![]() $\zeta \in \mathbb {C}$
. It follows from Proposition 3.7 that
$\zeta \in \mathbb {C}$
. It follows from Proposition 3.7 that
![]() $(f_k)_{k=1}^{\infty }$
converges uniformly on
$(f_k)_{k=1}^{\infty }$
converges uniformly on
![]() $\Sigma _{\psi }$
to
$\Sigma _{\psi }$
to
![]() $f := \zeta + g$
. Then
$f := \zeta + g$
. Then
![]() $(f^{\prime }_k)_{k=1}^{\infty }$
converges pointwise on
$(f^{\prime }_k)_{k=1}^{\infty }$
converges pointwise on
![]() $\mathbb {C}_+$
to
$\mathbb {C}_+$
to
![]() $g' = f'$
. Applying Fatou’s lemma to the sequences
$g' = f'$
. Applying Fatou’s lemma to the sequences
![]() $(\|f^{\prime }_k-f^{\prime }_n\|_{\mathcal {V}_s})_{n=k}^{\infty }$
for fixed k, one sees that
$(\|f^{\prime }_k-f^{\prime }_n\|_{\mathcal {V}_s})_{n=k}^{\infty }$
for fixed k, one sees that
![]() $\|f_k' - f'\|_{\mathcal V_s} \to 0$
. So
$\|f_k' - f'\|_{\mathcal V_s} \to 0$
. So
![]() $f' \in \mathcal {V}_s$
and
$f' \in \mathcal {V}_s$
and
![]() $f \in \mathcal {D}_s$
. By (3.8),
$f \in \mathcal {D}_s$
. By (3.8),
![]() $f(\infty )=\zeta $
and so
$f(\infty )=\zeta $
and so
![]() $\|f_k - f\|_{\mathcal {D}_s} \to 0$
,
$\|f_k - f\|_{\mathcal {D}_s} \to 0$
,
![]() $k\to \infty $
.
$k\to \infty $
.
The argument used in the proof of Corollary 3.11 also provides the following corollary of Fatou type (see also Lemma 4.11).
Corollary 3.12. Let
![]() $s>-1$
and
$s>-1$
and
![]() $(f_k)_{k=1}^{\infty } \subset \mathcal D_s$
be such that
$(f_k)_{k=1}^{\infty } \subset \mathcal D_s$
be such that
![]() $\sup _{k \ge 1} \|f_k\|_{\mathcal D_s}<\infty $
and
$\sup _{k \ge 1} \|f_k\|_{\mathcal D_s}<\infty $
and
![]() $f(z)=\lim _{k \to \infty } f_k(z)$
exists for all
$f(z)=\lim _{k \to \infty } f_k(z)$
exists for all
![]() $z \in \mathbb C_+$
. Then
$z \in \mathbb C_+$
. Then
![]() $f \in \mathcal D_s$
.
$f \in \mathcal D_s$
.
Now employing (3.29), the estimates (3.7), (3.11) and (3.12) and Lemma 3.1, we obtain the following estimates.
Corollary 3.13. Let
![]() $\psi \in (0,\pi /2)$
. For all
$\psi \in (0,\pi /2)$
. For all
![]() $f\in \mathcal {D}_s$
,
$f\in \mathcal {D}_s$
,
![]() $s>-1$
,
$s>-1$
,
 $$ \begin{align*} |f(z)|\le \max\left(1,\frac{2^s}{\pi\cos^{s+1}\psi}\right)\|f\|_{\mathcal{D}_s},\qquad z\in \Sigma_{\psi}, \end{align*} $$
$$ \begin{align*} |f(z)|\le \max\left(1,\frac{2^s}{\pi\cos^{s+1}\psi}\right)\|f\|_{\mathcal{D}_s},\qquad z\in \Sigma_{\psi}, \end{align*} $$
and
 $$ \begin{align*} |f'(z)|\le \frac{(s+1)2^s}{\pi |z| \cos^{s+2}\psi}\|f'\|_{\mathcal{V}_s},\qquad z\in\Sigma_{\psi}. \end{align*} $$
$$ \begin{align*} |f'(z)|\le \frac{(s+1)2^s}{\pi |z| \cos^{s+2}\psi}\|f'\|_{\mathcal{V}_s},\qquad z\in\Sigma_{\psi}. \end{align*} $$
Moreover, f is continuous on
![]() $\Sigma _{\psi } \cup \{0\}$
and
$\Sigma _{\psi } \cup \{0\}$
and
 $$ \begin{align*} \lim_{|z|\to0, z \in \Sigma_{\psi}} z f'(z) = 0. \end{align*} $$
$$ \begin{align*} \lim_{|z|\to0, z \in \Sigma_{\psi}} z f'(z) = 0. \end{align*} $$
Remark 3.14. Corollary 3.13 implies that the point evaluation functionals
![]() $\delta _z, \, z \in \mathbb {C}_+$
, are continuous on
$\delta _z, \, z \in \mathbb {C}_+$
, are continuous on
![]() $\mathcal {D}_s, \, s>-1$
. Using (3.19) and the principle set out in Section 2, we see that the function
$\mathcal {D}_s, \, s>-1$
. Using (3.19) and the principle set out in Section 2, we see that the function
![]() $\lambda \mapsto r_{\lambda }^{\gamma }$
is holomorphic from
$\lambda \mapsto r_{\lambda }^{\gamma }$
is holomorphic from
![]() $\mathbb {C}_+$
to
$\mathbb {C}_+$
to
![]() $\mathcal {D}_s$
, for any
$\mathcal {D}_s$
, for any
![]() $s>-1$
,
$s>-1$
,
![]() $\gamma>0$
.
$\gamma>0$
.
3.3. More functions in
 $\mathcal {D}_s$
and their properties
$\mathcal {D}_s$
and their properties
In this section we give more examples of functions from
![]() $\mathcal {D}_s$
and note some additional elementary properties that will be relevant for the sequel.
$\mathcal {D}_s$
and note some additional elementary properties that will be relevant for the sequel.
Proposition 3.15. For
![]() $s> 0$
,
$s> 0$
,
 $\mathcal {B} \overset {i}{\hookrightarrow } \mathcal {D}_s$
.
$\mathcal {B} \overset {i}{\hookrightarrow } \mathcal {D}_s$
.
Proof. For
![]() $s>0$
and
$s>0$
and
![]() $f\in \mathcal {B}$
we have
$f\in \mathcal {B}$
we have
 $$ \begin{align*} \|f\|_{\mathcal{D}_{s,0}}&=|f(\infty)| +\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{|f'(\alpha+i\beta)|} {|\alpha+i\beta|^{s+1}} \,d\beta\,d\alpha \\ &\le \|f\|_{\infty} +2\int_0^{\infty} \sup_{\beta\in \mathbb{R}}\,|f'(\alpha+i\beta)|\, \int_{0}^{\infty}\frac{dt} {(t^2+1)^{(s+1)/2}}\,d\alpha\notag\\ &\le \max\{1, B(1/2,s/2)\}\|f\|_{\mathcal{B}}.\notag \end{align*} $$
$$ \begin{align*} \|f\|_{\mathcal{D}_{s,0}}&=|f(\infty)| +\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{|f'(\alpha+i\beta)|} {|\alpha+i\beta|^{s+1}} \,d\beta\,d\alpha \\ &\le \|f\|_{\infty} +2\int_0^{\infty} \sup_{\beta\in \mathbb{R}}\,|f'(\alpha+i\beta)|\, \int_{0}^{\infty}\frac{dt} {(t^2+1)^{(s+1)/2}}\,d\alpha\notag\\ &\le \max\{1, B(1/2,s/2)\}\|f\|_{\mathcal{B}}.\notag \end{align*} $$
Thus,
![]() $\mathcal {B}$
is continuously included in
$\mathcal {B}$
is continuously included in
![]() $\mathcal {D}_s$
.
$\mathcal {D}_s$
.
Remark 3.16. The representation (3.29) in Corollary 3.10 extends the reproducing formula for
![]() $\mathcal {B}$
– that is, (3.29) for
$\mathcal {B}$
– that is, (3.29) for
![]() $s=1$
– to a larger class of functions.
$s=1$
– to a larger class of functions.
Recall that
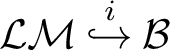 $\mathcal {LM} \overset {i}{\hookrightarrow } \mathcal {B}$
; see [Reference Batty, Gomilko and Tomilov7, Section 2.4], Thus, in view of Proposition 3.15, we have
$\mathcal {LM} \overset {i}{\hookrightarrow } \mathcal {B}$
; see [Reference Batty, Gomilko and Tomilov7, Section 2.4], Thus, in view of Proposition 3.15, we have
 $$ \begin{align*} \mathcal{LM} \overset{i}{\hookrightarrow} \mathcal{B} \overset{i}{\hookrightarrow} \mathcal{D}_s, \qquad s>0. \end{align*} $$
$$ \begin{align*} \mathcal{LM} \overset{i}{\hookrightarrow} \mathcal{B} \overset{i}{\hookrightarrow} \mathcal{D}_s, \qquad s>0. \end{align*} $$
We will show in Corollary 5.2 that
![]() $\mathcal B$
is dense in
$\mathcal B$
is dense in
![]() $\mathcal D_s$
for every
$\mathcal D_s$
for every
![]() $s>0$
, and hence
$s>0$
, and hence
![]() $\mathcal D_s$
is dense in
$\mathcal D_s$
is dense in
![]() $\mathcal D_{\sigma }$
for all
$\mathcal D_{\sigma }$
for all
![]() $\sigma> s > 0$
. On the other hand, we will show in Corollary 5.2 that
$\sigma> s > 0$
. On the other hand, we will show in Corollary 5.2 that
![]() $\mathcal {B}$
is not dense in
$\mathcal {B}$
is not dense in
![]() $\mathcal {D}^{\infty }_s$
for
$\mathcal {D}^{\infty }_s$
for
![]() $s>0$
.
$s>0$
.
For
![]() $f \in \operatorname {Hol}(\mathbb {C}_+)$
, let
$f \in \operatorname {Hol}(\mathbb {C}_+)$
, let
 $$ \begin{align*} \tilde{f}(z):=f(1/z), \qquad f_t(z): = f(tz), \qquad t>0, \quad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} \tilde{f}(z):=f(1/z), \qquad f_t(z): = f(tz), \qquad t>0, \quad z\in \mathbb{C}_{+}. \end{align*} $$
Lemma 3.17. Let
![]() $s>-1$
and
$s>-1$
and
![]() $t>0$
. Then
$t>0$
. Then
-
(i)
 $f\in \mathcal {D}_s$
if and only if
$f\in \mathcal {D}_s$
if and only if
 $\tilde {f}\in \mathcal {D}_s$
and
$\tilde {f}\in \mathcal {D}_s$
and  $$ \begin{align*} \|f-f(\infty)\|_{\mathcal{D}_s}=\|\tilde{f}- f(0)\|_{\mathcal{D}_s}. \end{align*} $$
$$ \begin{align*} \|f-f(\infty)\|_{\mathcal{D}_s}=\|\tilde{f}- f(0)\|_{\mathcal{D}_s}. \end{align*} $$
-
(ii) If f is bounded away from
 $0$
and
$0$
and
 $f \in \mathcal {D}_s$
, then
$f \in \mathcal {D}_s$
, then
 $1/f \in \mathcal {D}_s$
.
$1/f \in \mathcal {D}_s$
. -
(iii)
 $f \in \mathcal {D}_s$
if and only if
$f \in \mathcal {D}_s$
if and only if
 $f_t \in \mathcal {D}_s$
, and
$f_t \in \mathcal {D}_s$
, and
 $\|f\|_{\mathcal {D}_s} = \|f_t\|_{\mathcal {D}_s}$
.
$\|f\|_{\mathcal {D}_s} = \|f_t\|_{\mathcal {D}_s}$
.
Proof. Note that
 $$ \begin{align*} \|\tilde{f}'\|_{\mathcal{V}_s}&=\int_{-\pi/2}^{\pi/2}\cos^s\varphi\int_0^{\infty} \frac{|f'(\rho^{-1}e^{-i\varphi})|}{\rho^2}\,d\rho\,d\phi\\ &=\int_{-\pi/2}^{\pi/2}\cos^s\varphi\int_0^{\infty} |f'(r e^{i\varphi})|\,dr\,d\varphi\\ &=\|f'\|_{\mathcal{V}_s}. \end{align*} $$
$$ \begin{align*} \|\tilde{f}'\|_{\mathcal{V}_s}&=\int_{-\pi/2}^{\pi/2}\cos^s\varphi\int_0^{\infty} \frac{|f'(\rho^{-1}e^{-i\varphi})|}{\rho^2}\,d\rho\,d\phi\\ &=\int_{-\pi/2}^{\pi/2}\cos^s\varphi\int_0^{\infty} |f'(r e^{i\varphi})|\,dr\,d\varphi\\ &=\|f'\|_{\mathcal{V}_s}. \end{align*} $$
Moreover, by Corollary 3.10,
 $\tilde {f}(\infty )=f(0)$
. This proves (i). The other statements are very easy.
$\tilde {f}(\infty )=f(0)$
. This proves (i). The other statements are very easy.
Remarks 3.18. 1. Neither of the spaces
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {D}_0$
is contained in the other. Indeed, the function
$\mathcal {D}_0$
is contained in the other. Indeed, the function
![]() $e^{-z} \in \mathcal {LM} \subset \mathcal {B}$
but
$e^{-z} \in \mathcal {LM} \subset \mathcal {B}$
but
![]() $e^{-z} \not \in \mathcal D_0$
(see Example 3.4). On the other hand, there are bounded functions in
$e^{-z} \not \in \mathcal D_0$
(see Example 3.4). On the other hand, there are bounded functions in
![]() $\mathcal {D}_0$
that are not in
$\mathcal {D}_0$
that are not in
![]() $\mathcal {B}$
; for example, the function
$\mathcal {B}$
; for example, the function
![]() $\exp (\operatorname {\mathrm {arccot}} z) \in \mathcal D_0$
and is bounded but it is not in
$\exp (\operatorname {\mathrm {arccot}} z) \in \mathcal D_0$
and is bounded but it is not in
![]() $\mathcal {B}$
(see Example 3.19).
$\mathcal {B}$
(see Example 3.19).
More generally, for
![]() $\nu \ge 0$
, let
$\nu \ge 0$
, let
![]() $f_{\nu }(z) = z^{\nu } e^{-z}, \, z\in \mathbb {C}_+$
. Then
$f_{\nu }(z) = z^{\nu } e^{-z}, \, z\in \mathbb {C}_+$
. Then
![]() $f_{\nu } \in \mathcal {D}_s$
if and only if
$f_{\nu } \in \mathcal {D}_s$
if and only if
![]() $s>\nu $
(see Example 3.4). Note that if
$s>\nu $
(see Example 3.4). Note that if
![]() $\nu>0$
,
$\nu>0$
,
![]() $f_{\nu }$
is not bounded on any right half-plane. One can show that if
$f_{\nu }$
is not bounded on any right half-plane. One can show that if
![]() $f \in \mathcal {D}_{s, 0}$
, then
$f \in \mathcal {D}_{s, 0}$
, then
 $$ \begin{align*} |f(z)| \le \frac{2^s}{\pi} \|f\|_{\mathcal{D}_s,0}\left(1+\frac{4\beta^2}{\alpha^2}\right)^{(s+1)/2}, \quad z =\alpha+i\beta \in \mathbb{C}_+. \end{align*} $$
$$ \begin{align*} |f(z)| \le \frac{2^s}{\pi} \|f\|_{\mathcal{D}_s,0}\left(1+\frac{4\beta^2}{\alpha^2}\right)^{(s+1)/2}, \quad z =\alpha+i\beta \in \mathbb{C}_+. \end{align*} $$
The function
![]() $\log (1+z) e^{-z}$
is in
$\log (1+z) e^{-z}$
is in
![]() $\mathcal {D}_s, s>0$
, but is also unbounded on every right half-plane.
$\mathcal {D}_s, s>0$
, but is also unbounded on every right half-plane.
2. Because
![]() $e^{-z} \in \mathcal {D}_s$
for
$e^{-z} \in \mathcal {D}_s$
for
![]() $s>0$
, it follows from Lemma 3.17 that the functions
$s>0$
, it follows from Lemma 3.17 that the functions
![]() $e^{-t/z}$
are in
$e^{-t/z}$
are in
![]() $\mathcal D_s$
for all
$\mathcal D_s$
for all
![]() $t>0, \, s >0$
. This shows that functions
$t>0, \, s >0$
. This shows that functions
![]() $f \in \mathcal D_s$
may not have full limits at infinity or at zero. However, the properties (3.27) and (3.28) in Corollary 3.10 establish values for f at infinity and at zero as sectorial limits.
$f \in \mathcal D_s$
may not have full limits at infinity or at zero. However, the properties (3.27) and (3.28) in Corollary 3.10 establish values for f at infinity and at zero as sectorial limits.
3. The spaces
![]() $\mathcal {D}_s, \, s>-1$
, are invariant under shifts given by
$\mathcal {D}_s, \, s>-1$
, are invariant under shifts given by
Indeed, these operators form a bounded
![]() $C_0$
-semigroup on
$C_0$
-semigroup on
![]() $\mathcal {D}_s$
. See Section 11 for a proof. On the other hand,
$\mathcal {D}_s$
. See Section 11 for a proof. On the other hand,
![]() $\mathcal {D}_s$
are not invariant under the vertical shifts when
$\mathcal {D}_s$
are not invariant under the vertical shifts when
![]() $\tau \in i\mathbb {R}$
, as we see in the following example.
$\tau \in i\mathbb {R}$
, as we see in the following example.
Example 3.19. As stated in Example 3.5, the function
![]() $\operatorname {\mathrm {arccot}}$
is in
$\operatorname {\mathrm {arccot}}$
is in
![]() $\mathcal {D}_s$
for all
$\mathcal {D}_s$
for all
![]() $s>-1$
. Let
$s>-1$
. Let
Because
![]() $|\operatorname {Re}\operatorname {\mathrm {arccot}}(z)| \le \pi /2$
,
$|\operatorname {Re}\operatorname {\mathrm {arccot}}(z)| \le \pi /2$
,
![]() $\|g\|_{\infty } = \exp (\pi /2) = g(\infty )$
. For
$\|g\|_{\infty } = \exp (\pi /2) = g(\infty )$
. For
![]() $s>-1$
, we have
$s>-1$
, we have
Thus,
![]() $g \in \mathcal {D}_s$
for all
$g \in \mathcal {D}_s$
for all
![]() $s>-1$
.
$s>-1$
.
However, the boundary function of g is not continuous at
![]() $z=\pm i$
. Indeed, for a fixed
$z=\pm i$
. Indeed, for a fixed
![]() $\epsilon>0$
,
$\epsilon>0$
,
 $$ \begin{align*} \operatorname{\mathrm{arccot}} (i+i\epsilon)=\frac{1}{2i}\log\left(1+\frac{2}{\epsilon}\right); \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{arccot}} (i+i\epsilon)=\frac{1}{2i}\log\left(1+\frac{2}{\epsilon}\right); \end{align*} $$
hence,
 $$ \begin{align*} g(i+i\epsilon)=\exp{(-i\log(1+2/\epsilon)^{1/2})} \end{align*} $$
$$ \begin{align*} g(i+i\epsilon)=\exp{(-i\log(1+2/\epsilon)^{1/2})} \end{align*} $$
does not have a limit as
![]() $\epsilon \to 0+$
.
$\epsilon \to 0+$
.
Note that
![]() $g(\epsilon + i)$
does not converge as
$g(\epsilon + i)$
does not converge as
![]() $\epsilon \to 0+$
. This means that if
$\epsilon \to 0+$
. This means that if
![]() $f(z):=g(z-i)$
, then f does not have a sectorial limit at 0 and therefore does not belong to
$f(z):=g(z-i)$
, then f does not have a sectorial limit at 0 and therefore does not belong to
![]() $\mathcal {D}_s$
for any
$\mathcal {D}_s$
for any
![]() $s>-1$
. Thus,
$s>-1$
. Thus,
![]() $\mathcal {D}_s$
is not invariant under vertical shifts.
$\mathcal {D}_s$
is not invariant under vertical shifts.
3.4. Bernstein functions and
 $\mathcal {D}_s$
$\mathcal {D}_s$
Recall that a holomorphic function
![]() $g :\mathbb {C}_+ \to \mathbb {C}_+$
is a Bernstein function if it is of the form
$g :\mathbb {C}_+ \to \mathbb {C}_+$
is a Bernstein function if it is of the form
 $$ \begin{align} g(z) = a + bz + \int_{(0,\infty)} (1-e^{-zs}) \, d\mu(s), \end{align} $$
$$ \begin{align} g(z) = a + bz + \int_{(0,\infty)} (1-e^{-zs}) \, d\mu(s), \end{align} $$
where
![]() $a\ge 0$
,
$a\ge 0$
,
![]() $b\ge 0$
and
$b\ge 0$
and
![]() $\mu $
is a positive Borel measure on
$\mu $
is a positive Borel measure on
![]() $(0,\infty )$
such that
$(0,\infty )$
such that
 $\int _{(0,\infty )} \frac {s}{1+s} \,d\mu (s) < \infty $
. The following properties of Bernstein functions g will be used (these properties differ slightly from those used in [Reference Batty, Gomilko and Tomilov6]):
$\int _{(0,\infty )} \frac {s}{1+s} \,d\mu (s) < \infty $
. The following properties of Bernstein functions g will be used (these properties differ slightly from those used in [Reference Batty, Gomilko and Tomilov6]):
-
(B1) g maps
 $\Sigma _{\psi }$
into
$\Sigma _{\psi }$
into
 $\Sigma _{\psi }$
for each
$\Sigma _{\psi }$
for each
 $\psi \in [0,\pi /2]$
; see [Reference Schilling, Song and Vondraček50, Proposition 3.6] or [Reference Batty, Gomilko and Tomilov6, Proposition 2.1(1)].
$\psi \in [0,\pi /2]$
; see [Reference Schilling, Song and Vondraček50, Proposition 3.6] or [Reference Batty, Gomilko and Tomilov6, Proposition 2.1(1)]. -
(B2) g is increasing on
 $(0,\infty )$
.
$(0,\infty )$
. -
(B3) For all
 $z \in \mathbb {C}_+$
, Here the first inequality follows from taking the real parts in (3.30), and the second inequality is shown in [Reference Batty, Gomilko and Tomilov7, Section 3.5, (B3)].
$z \in \mathbb {C}_+$
, Here the first inequality follows from taking the real parts in (3.30), and the second inequality is shown in [Reference Batty, Gomilko and Tomilov7, Section 3.5, (B3)]. $$ \begin{align*} g(\operatorname{Re}z) \le \operatorname{Re}g(z) \le |g(z)|, \qquad |g'(z)| \le g'(\operatorname{Re}z). \end{align*} $$
$$ \begin{align*} g(\operatorname{Re}z) \le \operatorname{Re}g(z) \le |g(z)|, \qquad |g'(z)| \le g'(\operatorname{Re}z). \end{align*} $$
Further information on Bernstein functions can be found in [Reference Schilling, Song and Vondraček50].
Lemma 3.20. Let g be a Bernstein function,
![]() $\lambda \in \mathbb {C}_+$
, and
$\lambda \in \mathbb {C}_+$
, and
Then
![]() $f(\cdot ;\lambda ) \in \mathcal {D}_s$
for
$f(\cdot ;\lambda ) \in \mathcal {D}_s$
for
![]() $s>2$
and
$s>2$
and
 $$ \begin{align*} \|f(\cdot;\lambda)\|_{\mathcal{D}_{s,0}} \le \frac{2^s}{(s-2)|\lambda|}. \end{align*} $$
$$ \begin{align*} \|f(\cdot;\lambda)\|_{\mathcal{D}_{s,0}} \le \frac{2^s}{(s-2)|\lambda|}. \end{align*} $$
Proof. We have
 $$ \begin{align*} f'(z;\lambda)=-\frac{g'(z)}{(\lambda+g(z))^2}, \end{align*} $$
$$ \begin{align*} f'(z;\lambda)=-\frac{g'(z)}{(\lambda+g(z))^2}, \end{align*} $$
and then, for
![]() $\psi \in (-\pi /2,\pi /2)$
, using Lemma 2.1, (B2) and (B3),
$\psi \in (-\pi /2,\pi /2)$
, using Lemma 2.1, (B2) and (B3),
 $$ \begin{align*} \int_0^{\infty} |f'(\rho e^{i\psi};\lambda)|\,d\rho &=\int_0^{\infty} \frac{|g'(\rho e^{i\psi})|} {|\lambda+g(\rho e^{i\psi})|^2} \,d\rho\\ &\le \frac{1}{\cos^2((|\psi|+\pi/2)/2)} \int_0^{\infty} \frac{g'(\rho\cos\psi)} {(|\lambda|+|g(\rho e^{i\psi})|)^2} \,d\rho\\ &\le\frac{1}{\cos^2((|\psi|+\pi/2)/2)} \int_0^{\infty} \frac{g'(\rho\cos\psi)} {(|\lambda|+g(\rho\cos\psi))^2} \,d\rho\\ &\le \frac{1}{\cos^2((|\psi|+\pi/2)/2)\cos\psi} \int_0^{\infty} \frac{dt} {(|\lambda|+t)^2}\\ &= \frac{1}{\cos^2((|\psi|+\pi/2)/2)\cos\psi}\cdot \frac{1}{|\lambda|}. \end{align*} $$
$$ \begin{align*} \int_0^{\infty} |f'(\rho e^{i\psi};\lambda)|\,d\rho &=\int_0^{\infty} \frac{|g'(\rho e^{i\psi})|} {|\lambda+g(\rho e^{i\psi})|^2} \,d\rho\\ &\le \frac{1}{\cos^2((|\psi|+\pi/2)/2)} \int_0^{\infty} \frac{g'(\rho\cos\psi)} {(|\lambda|+|g(\rho e^{i\psi})|)^2} \,d\rho\\ &\le\frac{1}{\cos^2((|\psi|+\pi/2)/2)} \int_0^{\infty} \frac{g'(\rho\cos\psi)} {(|\lambda|+g(\rho\cos\psi))^2} \,d\rho\\ &\le \frac{1}{\cos^2((|\psi|+\pi/2)/2)\cos\psi} \int_0^{\infty} \frac{dt} {(|\lambda|+t)^2}\\ &= \frac{1}{\cos^2((|\psi|+\pi/2)/2)\cos\psi}\cdot \frac{1}{|\lambda|}. \end{align*} $$
If
![]() $s>2$
, then
$s>2$
, then
 $$ \begin{align*} |\lambda|\|f(\cdot;\lambda)\|_{\mathcal{D}_{s,0}} &=|\lambda|\int_{-\pi/2}^{\pi/2}\cos^s\psi \int_0^{\infty} |f'(\rho e^{i\psi};\lambda)|\,d\rho\,d\psi\\ &\le 2\int_0^{\pi/2} \frac{\cos^{s-1}\psi}{\cos^2((\psi+\pi/2)/2)}\,d\psi = 4\int_0^{\pi/2} \frac{\cos^{s-1}\psi}{1-\sin\psi} \,d\psi\\&\le 16\int_0^1(1-t^2)^{s-3}\,dt=\frac{8\sqrt{\pi} \Gamma(s-2)}{\Gamma(s-3/2)}\le \frac{16 s^{1/2}}{s-2}, \end{align*} $$
$$ \begin{align*} |\lambda|\|f(\cdot;\lambda)\|_{\mathcal{D}_{s,0}} &=|\lambda|\int_{-\pi/2}^{\pi/2}\cos^s\psi \int_0^{\infty} |f'(\rho e^{i\psi};\lambda)|\,d\rho\,d\psi\\ &\le 2\int_0^{\pi/2} \frac{\cos^{s-1}\psi}{\cos^2((\psi+\pi/2)/2)}\,d\psi = 4\int_0^{\pi/2} \frac{\cos^{s-1}\psi}{1-\sin\psi} \,d\psi\\&\le 16\int_0^1(1-t^2)^{s-3}\,dt=\frac{8\sqrt{\pi} \Gamma(s-2)}{\Gamma(s-3/2)}\le \frac{16 s^{1/2}}{s-2}, \end{align*} $$
where the latter estimate follows from Wendel’s inequality for the Gamma function [Reference Wendel56].
3.5. Algebras associated with
 $\mathcal D_s$
$\mathcal D_s$
The spaces
![]() $\mathcal {D}_s, \, s>-1$
, are not algebras, but there are some related algebras. Consider the Banach spaces
$\mathcal {D}_s, \, s>-1$
, are not algebras, but there are some related algebras. Consider the Banach spaces
![]() $\mathcal {D}_s^{\infty }:= \mathcal {D}_s\cap H^{\infty } (\mathbb {C}_{+})$
equipped with the norm
$\mathcal {D}_s^{\infty }:= \mathcal {D}_s\cap H^{\infty } (\mathbb {C}_{+})$
equipped with the norm
Thus,
![]() $\mathcal {D}_s^{\infty }$
is the space of bounded holomorphic functions on
$\mathcal {D}_s^{\infty }$
is the space of bounded holomorphic functions on
![]() $\mathbb {C}_{+}$
such that
$\mathbb {C}_{+}$
such that
 $$ \begin{align*} f(\infty):=\lim_{|z|\to\infty, z\in \Sigma_{\psi}}\,f(z) \end{align*} $$
$$ \begin{align*} f(\infty):=\lim_{|z|\to\infty, z\in \Sigma_{\psi}}\,f(z) \end{align*} $$
exists for every
![]() $\psi \in (0,\pi /2)$
, and
$\psi \in (0,\pi /2)$
, and
 $$ \begin{align*} \|f\|_{\mathcal{D}_s^{\infty}}:=\|f\|_{\infty}+\int_0^{\infty} \alpha^s \int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{(\alpha^2+\beta^2)^{(s+1)/2}}\,d\alpha\,d\beta < \infty. \end{align*} $$
$$ \begin{align*} \|f\|_{\mathcal{D}_s^{\infty}}:=\|f\|_{\infty}+\int_0^{\infty} \alpha^s \int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{(\alpha^2+\beta^2)^{(s+1)/2}}\,d\alpha\,d\beta < \infty. \end{align*} $$
Then
![]() $(\mathcal {D}_s^{\infty }, \|\cdot \|_{\mathcal {D}_s})$
is a Banach algebra and, in particular,
$(\mathcal {D}_s^{\infty }, \|\cdot \|_{\mathcal {D}_s})$
is a Banach algebra and, in particular,
By Proposition 3.15,
 $\mathcal {B}\overset {i}{\hookrightarrow } \mathcal {D}_s^{\infty }$
for
$\mathcal {B}\overset {i}{\hookrightarrow } \mathcal {D}_s^{\infty }$
for
![]() $s>0$
, and the embeddings are continuous.
$s>0$
, and the embeddings are continuous.
Example 3.19 shows that the function
![]() $g(z) := \exp (\operatorname {\mathrm {arccot}} z)$
is in
$g(z) := \exp (\operatorname {\mathrm {arccot}} z)$
is in
![]() $\mathcal {D}_s^{\infty }$
for all
$\mathcal {D}_s^{\infty }$
for all
![]() $s>-1$
, with
$s>-1$
, with
![]() $\|g\|_{\mathcal {D}_s^{\infty }} = \|g\|_{\mathcal {D}_s}$
, and consequently
$\|g\|_{\mathcal {D}_s^{\infty }} = \|g\|_{\mathcal {D}_s}$
, and consequently
![]() $\mathcal {D}_s^{\infty }$
is not invariant under vertical shifts.
$\mathcal {D}_s^{\infty }$
is not invariant under vertical shifts.
It follows from Lemma 3.17 that
 $$ \begin{align*} f\in \mathcal{D}_s^{\infty} \quad \text{if and only if}\quad \tilde{f}(z):=f(1/z)\in \mathcal{D}_s^{\infty}, \end{align*} $$
$$ \begin{align*} f\in \mathcal{D}_s^{\infty} \quad \text{if and only if}\quad \tilde{f}(z):=f(1/z)\in \mathcal{D}_s^{\infty}, \end{align*} $$
and
 $$ \begin{align*} \|f\|_{\mathcal{D}_s^{\infty}}=\|\tilde{f}\|_{\mathcal{D}_s^{\infty}}. \end{align*} $$
$$ \begin{align*} \|f\|_{\mathcal{D}_s^{\infty}}=\|\tilde{f}\|_{\mathcal{D}_s^{\infty}}. \end{align*} $$
Moreover, the spectrum of f in
![]() $\mathcal {D}_s^{\infty }$
is the closure of the range of f. In particular, the spectral radius of f is
$\mathcal {D}_s^{\infty }$
is the closure of the range of f. In particular, the spectral radius of f is
![]() $\|f\|_{\infty }$
.
$\|f\|_{\infty }$
.
Now we consider the linear space
 $$ \begin{align*} \mathcal D_{\infty}:=\bigcup_{s>-1} \mathcal{D}_s. \end{align*} $$
$$ \begin{align*} \mathcal D_{\infty}:=\bigcup_{s>-1} \mathcal{D}_s. \end{align*} $$
We will show that
![]() $\mathcal D_{\infty }$
is an algebra, which opens the way to an operator functional calculus on
$\mathcal D_{\infty }$
is an algebra, which opens the way to an operator functional calculus on
![]() $\mathcal D_{\infty }$
.
$\mathcal D_{\infty }$
.
Lemma 3.21. For
![]() $s,\sigma>-1$
, let
$s,\sigma>-1$
, let
![]() $f\in \mathcal {D}_s$
and
$f\in \mathcal {D}_s$
and
![]() $g\in \mathcal {D}_{\sigma }$
. Then
$g\in \mathcal {D}_{\sigma }$
. Then
and
 $$ \begin{align} \|h\|_{\mathcal{D}_{s+\sigma+1}} \le \left(2+\frac{2^s+2^{\sigma}}{\pi}\right)\|f\|_{\mathcal{D}_s}\,\|g\|_{\mathcal{D}_{\sigma}}. \end{align} $$
$$ \begin{align} \|h\|_{\mathcal{D}_{s+\sigma+1}} \le \left(2+\frac{2^s+2^{\sigma}}{\pi}\right)\|f\|_{\mathcal{D}_s}\,\|g\|_{\mathcal{D}_{\sigma}}. \end{align} $$
Hence,
![]() $\mathcal {D}_{\infty }$
is an algebra.
$\mathcal {D}_{\infty }$
is an algebra.
Proof. By Corollary 3.13, for
![]() $\rho>0$
and
$\rho>0$
and
![]() $|\varphi |< \pi /2$
, we have
$|\varphi |< \pi /2$
, we have
 $$ \begin{align*} |f(\rho e^{i\varphi})| &\le \left(1+\frac{2^s}{\pi\cos^{s+1}\varphi}\right)\|f\|_{\mathcal{D}_s},\\ |g(\rho e^{i\varphi})| &\le \left(1+\frac{2^{\sigma}}{\pi\cos^{\sigma+1}\varphi}\right)\|g\|_{\mathcal{D}_{\sigma}}. \end{align*} $$
$$ \begin{align*} |f(\rho e^{i\varphi})| &\le \left(1+\frac{2^s}{\pi\cos^{s+1}\varphi}\right)\|f\|_{\mathcal{D}_s},\\ |g(\rho e^{i\varphi})| &\le \left(1+\frac{2^{\sigma}}{\pi\cos^{\sigma+1}\varphi}\right)\|g\|_{\mathcal{D}_{\sigma}}. \end{align*} $$
Hence,
 $$ \begin{align*} \|h\|_{\mathcal{D}_{s+\sigma+1,0}} &= \int_{-\pi/2}^{\pi/2} \cos^{s+\sigma+1}\varphi \int_0^{\infty} \left| f'(\rho e^{i\varphi}) g(\rho e^{i\varphi}) + f(\rho e^{i\varphi}) g'(\rho e^{i\varphi})\right| \,d\rho\,d\varphi \\ &\le \left(1+\frac{2^{\sigma}}{\pi}\right)\|f\|_{\mathcal{D}_{s,0}}\,\|g\|_{\mathcal{D}_{\sigma}} +\left(1+\frac{2^s}{\pi}\right)\|f\|_{\mathcal{D}_s}\,\|g\|_{\mathcal{D}_{\sigma,0}}. \end{align*} $$
$$ \begin{align*} \|h\|_{\mathcal{D}_{s+\sigma+1,0}} &= \int_{-\pi/2}^{\pi/2} \cos^{s+\sigma+1}\varphi \int_0^{\infty} \left| f'(\rho e^{i\varphi}) g(\rho e^{i\varphi}) + f(\rho e^{i\varphi}) g'(\rho e^{i\varphi})\right| \,d\rho\,d\varphi \\ &\le \left(1+\frac{2^{\sigma}}{\pi}\right)\|f\|_{\mathcal{D}_{s,0}}\,\|g\|_{\mathcal{D}_{\sigma}} +\left(1+\frac{2^s}{\pi}\right)\|f\|_{\mathcal{D}_s}\,\|g\|_{\mathcal{D}_{\sigma,0}}. \end{align*} $$
This shows that
![]() $h \in \mathcal {D}_q$
, and (3.32) follows easily.
$h \in \mathcal {D}_q$
, and (3.32) follows easily.
3.6. Derivatives of functions in
 $\mathcal {D}_s$
$\mathcal {D}_s$
This section further clarifies the behaviour of the derivatives of functions from
![]() $\mathcal D_s$
, and Lemma 3.22 is of independent interest. Corollary 3.23 will be used in Subsection 10.3. For
$\mathcal D_s$
, and Lemma 3.22 is of independent interest. Corollary 3.23 will be used in Subsection 10.3. For
![]() $m,n \in \mathbb {N}$
, the notation
$m,n \in \mathbb {N}$
, the notation
![]() $z^mf^{(n)}$
denotes the function mapping z to
$z^mf^{(n)}$
denotes the function mapping z to
![]() $z^mf^{(n)}(z)$
. Moreover,
$z^mf^{(n)}(z)$
. Moreover,
![]() $f_t$
is the function mapping z to
$f_t$
is the function mapping z to
![]() $f(tz)$
.
$f(tz)$
.
Lemma 3.22. Let
![]() $f\in \mathcal {D}_s$
,
$f\in \mathcal {D}_s$
,
![]() $s>-1$
. Then
$s>-1$
. Then
![]() $zf'\in \mathcal {D}_{s+1}$
, and there exists
$zf'\in \mathcal {D}_{s+1}$
, and there exists
![]() $C^{\prime }_{s}$
(independent of f) such that
$C^{\prime }_{s}$
(independent of f) such that
and
 $$ \begin{align} \|f_t-f_{\tau}\|_{\mathcal{D}_{s+1}} \le \frac{C^{\prime}_s \|f\|_{\mathcal{D}_s}}{\min\{t,\tau\}} |t-\tau|, \qquad t,\tau>0. \end{align} $$
$$ \begin{align} \|f_t-f_{\tau}\|_{\mathcal{D}_{s+1}} \le \frac{C^{\prime}_s \|f\|_{\mathcal{D}_s}}{\min\{t,\tau\}} |t-\tau|, \qquad t,\tau>0. \end{align} $$
Proof. Note that
So, for (3.33), it suffices to consider
 $\|zf^{''}\|_{\mathcal V_{s+1}}$
. The argument is similar to Example 3.3 and the proof of Proposition 3.6. By Corollary 3.10, for fixed
$\|zf^{''}\|_{\mathcal V_{s+1}}$
. The argument is similar to Example 3.3 and the proof of Proposition 3.6. By Corollary 3.10, for fixed
![]() $\sigma>s$
,
$\sigma>s$
,
 $$ \begin{align*} f''(z)=-c_{\sigma} \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} \frac{\rho^{\sigma+1} f'(\rho e^{i\varphi})}{(z+\rho e^{-i\varphi})^{\sigma+3}}\,d\rho\,d\varphi,\quad z\in \mathbb{C}_{+}, \end{align*} $$
$$ \begin{align*} f''(z)=-c_{\sigma} \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_0^{\infty} \frac{\rho^{\sigma+1} f'(\rho e^{i\varphi})}{(z+\rho e^{-i\varphi})^{\sigma+3}}\,d\rho\,d\varphi,\quad z\in \mathbb{C}_{+}, \end{align*} $$
where
 $c_{\sigma }=(\sigma +1)(\sigma +2)\frac {2^{\sigma }}{\pi }$
. Then estimates similar to those in Example 3.3 and Proposition 3.6 give
$c_{\sigma }=(\sigma +1)(\sigma +2)\frac {2^{\sigma }}{\pi }$
. Then estimates similar to those in Example 3.3 and Proposition 3.6 give
 $$ \begin{align*}&{c_{\sigma}^{-1}\|zf''\|_{\mathcal{V}_{s+1}}}\\ &\ =\int_{-\pi/2}^{\pi/2}\cos^{s+1}\psi \int_0^{\infty} r \left| \int_{-\pi/2}^{\pi/2} \cos^{\sigma}\varphi \int_0^{\infty} \frac{\rho^{\sigma+1}f'(\rho e^{i\varphi})}{(r e^{i\psi}+\rho e^{-i\varphi})^{\sigma+3}}\,d\rho\,d\varphi\right| \,dr\,d\psi\\&\ \le \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_{-\pi/2}^{\pi/2} \cos^{s+1}\psi \int_{0}^{\infty}\int_0^{\infty} \frac{t |f'(\rho e^{i\varphi})|\,dt\,d\rho}{(t^2+2t\cos(\varphi+\psi)+1)^{(\sigma+3)/2}} \,d\psi\,d\varphi \\&\ = \int_{-\pi/2}^{\pi/2} \cos^{\sigma}\varphi \, G_{h,\beta,s+1}(\varphi) \int_0^{\infty} |f'(\rho e^{i\varphi})| \,d\rho\,d\varphi, \end{align*} $$
$$ \begin{align*}&{c_{\sigma}^{-1}\|zf''\|_{\mathcal{V}_{s+1}}}\\ &\ =\int_{-\pi/2}^{\pi/2}\cos^{s+1}\psi \int_0^{\infty} r \left| \int_{-\pi/2}^{\pi/2} \cos^{\sigma}\varphi \int_0^{\infty} \frac{\rho^{\sigma+1}f'(\rho e^{i\varphi})}{(r e^{i\psi}+\rho e^{-i\varphi})^{\sigma+3}}\,d\rho\,d\varphi\right| \,dr\,d\psi\\&\ \le \int_{-\pi/2}^{\pi/2} \cos^{\sigma} \varphi \int_{-\pi/2}^{\pi/2} \cos^{s+1}\psi \int_{0}^{\infty}\int_0^{\infty} \frac{t |f'(\rho e^{i\varphi})|\,dt\,d\rho}{(t^2+2t\cos(\varphi+\psi)+1)^{(\sigma+3)/2}} \,d\psi\,d\varphi \\&\ = \int_{-\pi/2}^{\pi/2} \cos^{\sigma}\varphi \, G_{h,\beta,s+1}(\varphi) \int_0^{\infty} |f'(\rho e^{i\varphi})| \,d\rho\,d\varphi, \end{align*} $$
where
![]() $h(t)=t+t^{\sigma }, \, t\in (0,1)$
,
$h(t)=t+t^{\sigma }, \, t\in (0,1)$
,
![]() $\beta = (\sigma +3)/2$
and
$\beta = (\sigma +3)/2$
and
![]() $G_{h,\beta ,s+1}(\varphi )$
is defined in (3.15), noting that
$G_{h,\beta ,s+1}(\varphi )$
is defined in (3.15), noting that
![]() $2\beta - (s+1)-2 = \sigma -s$
. Now the estimate (3.33) follows from Lemma 3.2(b).
$2\beta - (s+1)-2 = \sigma -s$
. Now the estimate (3.33) follows from Lemma 3.2(b).
For (3.34), let
![]() $g = f_{\tau } - f_t$
. Without loss, assume that
$g = f_{\tau } - f_t$
. Without loss, assume that
![]() $0 < t < \tau $
. Then
$0 < t < \tau $
. Then
 $$ \begin{align*} g'(z) = \tau f'(\tau z) - t f'(tz) = \int_t^{\tau} \left(f'(rz) + rz f''(rz)\right) \, dr = \int_t^{\tau} \frac{d}{dz} (zf'(rz)) \,dr. \end{align*} $$
$$ \begin{align*} g'(z) = \tau f'(\tau z) - t f'(tz) = \int_t^{\tau} \left(f'(rz) + rz f''(rz)\right) \, dr = \int_t^{\tau} \frac{d}{dz} (zf'(rz)) \,dr. \end{align*} $$
Hence, by Fubini’s theorem,
 $$ \begin{align*} \|g\|_{\mathcal{D}_{s+1}} &\le \int_{\mathbb{C}_+} \int_t^{\tau} \frac{(\operatorname{Re}z)^{s+1}}{|z|^{s+2}} \left|\frac{d}{dz} (zf'(rz))\right|\,dr \,dS(z)\\ &= \int_t^{\tau} \frac{\|zf'\|_{\mathcal{D}_{s+1}}}{r} \,dr \le \frac{C^{\prime}_s\|f\|_{\mathcal{D}_s}}{t} (\tau-t), \end{align*} $$
$$ \begin{align*} \|g\|_{\mathcal{D}_{s+1}} &\le \int_{\mathbb{C}_+} \int_t^{\tau} \frac{(\operatorname{Re}z)^{s+1}}{|z|^{s+2}} \left|\frac{d}{dz} (zf'(rz))\right|\,dr \,dS(z)\\ &= \int_t^{\tau} \frac{\|zf'\|_{\mathcal{D}_{s+1}}}{r} \,dr \le \frac{C^{\prime}_s\|f\|_{\mathcal{D}_s}}{t} (\tau-t), \end{align*} $$
because the
![]() $\mathcal {D}_{s+1}$
-norm is invariant under the change of variable
$\mathcal {D}_{s+1}$
-norm is invariant under the change of variable
![]() $z\mapsto rz$
(Lemma 3.17(iii)).
$z\mapsto rz$
(Lemma 3.17(iii)).
The following corollary is easily proved by induction.
Corollary 3.23. If
![]() $f \in \mathcal {D}_{\infty }$
and
$f \in \mathcal {D}_{\infty }$
and
![]() $n \in \mathbb {N}$
, then
$n \in \mathbb {N}$
, then
![]() $z^nf^{(n)} \in \mathcal {D}_{\infty }$
.
$z^nf^{(n)} \in \mathcal {D}_{\infty }$
.
Remark 3.24. Lemma 3.22 is sharp in the sense that for any
![]() $s>0$
and
$s>0$
and
![]() $\sigma \in (-1,s+1)$
, there exist functions
$\sigma \in (-1,s+1)$
, there exist functions
![]() $f \in \mathcal {D}_s$
for which
$f \in \mathcal {D}_s$
for which
![]() $zf' \notin \mathcal {D}_{\sigma }$
. For example, the function
$zf' \notin \mathcal {D}_{\sigma }$
. For example, the function
![]() $f_{\nu }(z) := z^{\nu } e^{-z}$
has these properties if
$f_{\nu }(z) := z^{\nu } e^{-z}$
has these properties if
![]() $\max \{0,\sigma -1\}<\nu < s$
. This follows directly from Example 3.4.
$\max \{0,\sigma -1\}<\nu < s$
. This follows directly from Example 3.4.
4. Hardy–Sobolev algebras on sectors
4.1.
 $H^p$
-spaces on the right half-plane and their norms
$H^p$
-spaces on the right half-plane and their norms
In this section and in Subsection 4.2 we will study the Hardy spaces
![]() $H^1(\Sigma _{\psi })$
defined on sectors
$H^1(\Sigma _{\psi })$
defined on sectors
![]() $\Sigma _{\psi }, \, \psi \in (0,\pi )$
. The properties of such spaces are similar to the properties of the classical Hardy space
$\Sigma _{\psi }, \, \psi \in (0,\pi )$
. The properties of such spaces are similar to the properties of the classical Hardy space
![]() $H^1(\mathbb {C}_+)$
, though their theory seems to be more involved. The Hardy spaces
$H^1(\mathbb {C}_+)$
, though their theory seems to be more involved. The Hardy spaces
![]() $H^p(\Sigma _{\psi })$
have been studied, mostly for
$H^p(\Sigma _{\psi })$
have been studied, mostly for
![]() $p> 1$
, but the results are scattered around various places in the literature, which is often obscure, and some proofs contain rather complicated, incomplete or vague arguments. We propose a streamlined (and probably new) approach avoiding the use of Carleson measures or log-convexity, and we obtain a new result (Corollary 4.3) on the way. The case
$p> 1$
, but the results are scattered around various places in the literature, which is often obscure, and some proofs contain rather complicated, incomplete or vague arguments. We propose a streamlined (and probably new) approach avoiding the use of Carleson measures or log-convexity, and we obtain a new result (Corollary 4.3) on the way. The case
![]() $p = 1$
does not require any significant adjustments, as we illustrate here. Standard references for the theory of Hardy spaces on the right half-plane are [Reference Duren21] and [Reference Garnett29].
$p = 1$
does not require any significant adjustments, as we illustrate here. Standard references for the theory of Hardy spaces on the right half-plane are [Reference Duren21] and [Reference Garnett29].
We set out the situation when
![]() $\psi =\pi /2$
in this section and the case of general
$\psi =\pi /2$
in this section and the case of general
![]() $\psi $
in Subsection 4.2. Although we are mainly interested in
$\psi $
in Subsection 4.2. Although we are mainly interested in
![]() $H^1$
-spaces, we present statements that are valid for
$H^1$
-spaces, we present statements that are valid for
![]() $H^p$
-spaces with
$H^p$
-spaces with
![]() $p \in [1, \infty )$
, because the arguments are the same for all such p.
$p \in [1, \infty )$
, because the arguments are the same for all such p.
Let
![]() $1\le p<\infty $
. The classical Hardy space
$1\le p<\infty $
. The classical Hardy space
![]() $H^p(\mathbb {C}_{+})$
in the right half-plane
$H^p(\mathbb {C}_{+})$
in the right half-plane
![]() $\mathbb {C}_+$
is defined as
$\mathbb {C}_+$
is defined as
 $$ \begin{align*} H^p(\mathbb{C}_{+})=\left \{g\in \mbox{Hol}(\mathbb{C}_{+}): \|g\|_{p}:=\sup_{\alpha>0}\, \left(\int_{-\infty}^{\infty} |g(\alpha+i\beta)|^p\,d\beta\right)^{1/p}<\infty \right \}. \end{align*} $$
$$ \begin{align*} H^p(\mathbb{C}_{+})=\left \{g\in \mbox{Hol}(\mathbb{C}_{+}): \|g\|_{p}:=\sup_{\alpha>0}\, \left(\int_{-\infty}^{\infty} |g(\alpha+i\beta)|^p\,d\beta\right)^{1/p}<\infty \right \}. \end{align*} $$
It is well-known that
![]() $\|\cdot \|_p$
is a norm on
$\|\cdot \|_p$
is a norm on
![]() $H^p(\mathbb C_+)$
and
$H^p(\mathbb C_+)$
and
![]() $(H^p(\mathbb {C}_+),\|\cdot \|_{p})$
is a Banach space. Moreover, for almost every
$(H^p(\mathbb {C}_+),\|\cdot \|_{p})$
is a Banach space. Moreover, for almost every
![]() $t \in \mathbb R$
there exists a sectorial limit
$t \in \mathbb R$
there exists a sectorial limit
![]() $g(it):=\lim _{z \to it} g(z)$
in
$g(it):=\lim _{z \to it} g(z)$
in
![]() $\mathbb {C}$
. For every
$\mathbb {C}$
. For every
![]() $g \in H^p(\mathbb {C}_+)$
one has
$g \in H^p(\mathbb {C}_+)$
one has
![]() $\lim _{\alpha \to 0} g(\alpha +i\cdot )= g(i\cdot )$
in
$\lim _{\alpha \to 0} g(\alpha +i\cdot )= g(i\cdot )$
in
![]() $L^p(\mathbb R)$
, and
$L^p(\mathbb R)$
, and
![]() $\|g\|_{H^p(\mathbb {C}_+)} := \|g\|_p = \|g(i\cdot )\|_{L^p(\mathbb {R})}$
.
$\|g\|_{H^p(\mathbb {C}_+)} := \|g\|_p = \|g(i\cdot )\|_{L^p(\mathbb {R})}$
.
One may also consider the normed space
![]() $(H^{p}(\Sigma _{\pi /2}), \|\cdot \|_{H^p(\Sigma _{\pi /2})})$
as the space of all
$(H^{p}(\Sigma _{\pi /2}), \|\cdot \|_{H^p(\Sigma _{\pi /2})})$
as the space of all
![]() $g\in \operatorname {Hol}(\mathbb {C}_{+})$
such that
$g\in \operatorname {Hol}(\mathbb {C}_{+})$
such that
 $$ \begin{align*}\|g\|_{H^p(\Sigma_{\pi/2})}:=\sup_{|\varphi|<\pi/2}\, \left(\int_0^{\infty} \left(|g(te^{i\varphi})|^p+ |g(te^{-i\varphi})|^p\right)\,dt\right)^{1/p}<\infty \end{align*} $$
$$ \begin{align*}\|g\|_{H^p(\Sigma_{\pi/2})}:=\sup_{|\varphi|<\pi/2}\, \left(\int_0^{\infty} \left(|g(te^{i\varphi})|^p+ |g(te^{-i\varphi})|^p\right)\,dt\right)^{1/p}<\infty \end{align*} $$
and
 $(H^{p}_{*}(\Sigma _{\pi /2}), \|\cdot \|_{H^p_{*}(\Sigma _{\pi /2})})$
as
$(H^{p}_{*}(\Sigma _{\pi /2}), \|\cdot \|_{H^p_{*}(\Sigma _{\pi /2})})$
as
 $$ \begin{align*} \left \{g\in \operatorname{Hol}(\mathbb{C}_{+}): \|g\|_{H^p_*(\Sigma_{\pi/2})}:=\sup_{|\varphi|<\pi/2}\left(\int_0^{\infty} |g(te^{i\varphi})|^p\,dt\right)^{1/p} < \infty \right\}. \end{align*} $$
$$ \begin{align*} \left \{g\in \operatorname{Hol}(\mathbb{C}_{+}): \|g\|_{H^p_*(\Sigma_{\pi/2})}:=\sup_{|\varphi|<\pi/2}\left(\int_0^{\infty} |g(te^{i\varphi})|^p\,dt\right)^{1/p} < \infty \right\}. \end{align*} $$
It is clear that
![]() $H^p(\Sigma _{\pi /2})$
and
$H^p(\Sigma _{\pi /2})$
and
![]() $H^p_*(\Sigma _{\pi /2})$
coincide as vector spaces, and
$H^p_*(\Sigma _{\pi /2})$
coincide as vector spaces, and
 $$ \begin{align*} \|g\|_{H^p_*(\Sigma_{\pi/2})} \le \|g\|_{H^p(\Sigma_{\pi/2})}\le 2^{1/p}\|g\|_{H^p_*(\Sigma_{\pi/2})}. \end{align*} $$
$$ \begin{align*} \|g\|_{H^p_*(\Sigma_{\pi/2})} \le \|g\|_{H^p(\Sigma_{\pi/2})}\le 2^{1/p}\|g\|_{H^p_*(\Sigma_{\pi/2})}. \end{align*} $$
Lemma 4.1. Let
![]() $p\in [1,\infty )$
. Then
$p\in [1,\infty )$
. Then
![]() $H^{p}(\Sigma _{\pi /2})\subset H^{p}(\mathbb {C}_{+})$
and
$H^{p}(\Sigma _{\pi /2})\subset H^{p}(\mathbb {C}_{+})$
and
Proof. Fix
![]() $p \in [1,\infty )$
. For fixed
$p \in [1,\infty )$
. For fixed
![]() $\gamma \in (1/2,1)$
define
$\gamma \in (1/2,1)$
define
 $$ \begin{align*} g_{\gamma}(z):=(\gamma z^{\gamma-1})^{1/p}g(z^{\gamma})\in \operatorname{Hol}(\Sigma_{\pi/(2\gamma)}). \end{align*} $$
$$ \begin{align*} g_{\gamma}(z):=(\gamma z^{\gamma-1})^{1/p}g(z^{\gamma})\in \operatorname{Hol}(\Sigma_{\pi/(2\gamma)}). \end{align*} $$
Note that
 $$ \begin{align} \int_0^{\infty} |g_{\gamma}(te^{i\varphi})|^p\,dt= \int_0^{\infty} |g(te^{i\gamma\varphi})|^p\,dt, \end{align} $$
$$ \begin{align} \int_0^{\infty} |g_{\gamma}(te^{i\varphi})|^p\,dt= \int_0^{\infty} |g(te^{i\gamma\varphi})|^p\,dt, \end{align} $$
and
 $$ \begin{align*} \int_{-\pi/2}^{\pi/2} \int_0^{\infty} |g_{\gamma}(te^{i\varphi})|^p\,dt \, d\varphi\le \frac{\pi}{2} \|g\|^p_{{H^{p}(\Sigma_{\pi/2})}}. \end{align*} $$
$$ \begin{align*} \int_{-\pi/2}^{\pi/2} \int_0^{\infty} |g_{\gamma}(te^{i\varphi})|^p\,dt \, d\varphi\le \frac{\pi}{2} \|g\|^p_{{H^{p}(\Sigma_{\pi/2})}}. \end{align*} $$
By Fubini’s theorem and Hölder’s inequality there exist sequences
![]() $(t_{1,n})_{n\ge 1}$
and
$(t_{1,n})_{n\ge 1}$
and
![]() $(t_{2,n})_{n\ge 1}$
such that
$(t_{2,n})_{n\ge 1}$
such that
![]() $0<t_{1,n}<t_{2,n}$
,
$0<t_{1,n}<t_{2,n}$
,
![]() $t_{1,n}\to 0$
,
$t_{1,n}\to 0$
,
![]() $t_{2,n}\to \infty $
as
$t_{2,n}\to \infty $
as
![]() $n\to \infty $
and
$n\to \infty $
and
 $$ \begin{align} \lim_{n\to\infty}\, t_{1,n} \int_{-\pi/2}^{\pi/2} |g_{\gamma} (t_{1,n}e^{i\varphi})|\,d\varphi =0, \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\, t_{1,n} \int_{-\pi/2}^{\pi/2} |g_{\gamma} (t_{1,n}e^{i\varphi})|\,d\varphi =0, \end{align} $$
 $$ \begin{align} \lim_{n\to\infty}\,\int_{-\pi/2}^{\pi/2} |g_{\gamma} (t_{2,n}e^{i\varphi})|\,d\varphi =0. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\,\int_{-\pi/2}^{\pi/2} |g_{\gamma} (t_{2,n}e^{i\varphi})|\,d\varphi =0. \end{align} $$
Let
![]() $\Omega _n:=\{z\in \mathbb {C}_{+}:\, t_{1,n}<|z|<t_{2,n}\}$
. By Cauchy’s formula,
$\Omega _n:=\{z\in \mathbb {C}_{+}:\, t_{1,n}<|z|<t_{2,n}\}$
. By Cauchy’s formula,
 $$ \begin{align} g_{\gamma}(z)=\frac{\alpha}{\pi i}\int_{\partial\Omega_n}\frac{g_{\gamma}(\lambda) }{(\lambda-z)(\lambda+\overline{z})} \,d\lambda,\quad z= \alpha+i\beta \in \Omega_n, \end{align} $$
$$ \begin{align} g_{\gamma}(z)=\frac{\alpha}{\pi i}\int_{\partial\Omega_n}\frac{g_{\gamma}(\lambda) }{(\lambda-z)(\lambda+\overline{z})} \,d\lambda,\quad z= \alpha+i\beta \in \Omega_n, \end{align} $$
for large n. Passing to the limit in (4.5) as
![]() $n \to \infty $
and using (4.2), (4.3) and (4.4), we infer that
$n \to \infty $
and using (4.2), (4.3) and (4.4), we infer that
![]() $g_{\gamma }$
satisfies the Poisson formula
$g_{\gamma }$
satisfies the Poisson formula
 $$ \begin{align} g_{\gamma}(z)=\frac{\alpha}{\pi}\int_{-\infty}^{\infty} \frac{g_{\gamma}(it)}{(t-\beta)^2+\alpha^2}\,dt. \end{align} $$
$$ \begin{align} g_{\gamma}(z)=\frac{\alpha}{\pi}\int_{-\infty}^{\infty} \frac{g_{\gamma}(it)}{(t-\beta)^2+\alpha^2}\,dt. \end{align} $$
Hence, by Young’s inequality and (4.2), for every
![]() $\alpha>0$
,
$\alpha>0$
,
Letting
![]() $\gamma \to 1$
, Fatou’s lemma implies (4.1).
$\gamma \to 1$
, Fatou’s lemma implies (4.1).
Lemma 4.2. Let
![]() $p\in [1,\infty )$
. Then
$p\in [1,\infty )$
. Then
![]() $H^{p}(\mathbb {C}_{+})\subset H^{p}(\Sigma _{\pi /2})$
and
$H^{p}(\mathbb {C}_{+})\subset H^{p}(\Sigma _{\pi /2})$
and
Proof. First let
![]() $p=2$
so that
$p=2$
so that
![]() $g\in H^2(\mathbb {C}_{+})$
. Then, by [Reference Džrbašjan22, Ch.VIII, p.508], there exists
$g\in H^2(\mathbb {C}_{+})$
. Then, by [Reference Džrbašjan22, Ch.VIII, p.508], there exists
![]() $f\in L^1(\mathbb {R}, e^{\pi |t|}\,dt)$
such that
$f\in L^1(\mathbb {R}, e^{\pi |t|}\,dt)$
such that
![]() $f \ge 0$
on
$f \ge 0$
on
![]() $\mathbb R$
, and for all
$\mathbb R$
, and for all
![]() $|\varphi |\le \pi /2$
,
$|\varphi |\le \pi /2$
,
 $$ \begin{align*} \int_0^{\infty} |g(te^{i\varphi})|^2\,dt= \int_{-\infty}^{\infty} e^{2\varphi t} f(t)\,dt. \end{align*} $$
$$ \begin{align*} \int_0^{\infty} |g(te^{i\varphi})|^2\,dt= \int_{-\infty}^{\infty} e^{2\varphi t} f(t)\,dt. \end{align*} $$
Hence,
 $$ \begin{align*} \int_0^{\infty} \bigl(|g(te^{i\varphi})|^2+|g(t e^{-i\varphi})|^2\bigr)\,dt&= 2\int_{-\infty}^{\infty} \cosh(2\varphi t)f(t)\,dt \\ \le 2\int_{-\infty}^{\infty} \cosh(\pi t)f(t)\,dt&=\int_0^{\infty} \bigl(|g(it)|^2+|g(-it)|^2 \bigr)\,dt,\notag \end{align*} $$
$$ \begin{align*} \int_0^{\infty} \bigl(|g(te^{i\varphi})|^2+|g(t e^{-i\varphi})|^2\bigr)\,dt&= 2\int_{-\infty}^{\infty} \cosh(2\varphi t)f(t)\,dt \\ \le 2\int_{-\infty}^{\infty} \cosh(\pi t)f(t)\,dt&=\int_0^{\infty} \bigl(|g(it)|^2+|g(-it)|^2 \bigr)\,dt,\notag \end{align*} $$
and (4.7) holds for
![]() $p=2$
.
$p=2$
.
Let
![]() $p\in [1,\infty ), \, p\not =2$
, be fixed and
$p\in [1,\infty ), \, p\not =2$
, be fixed and
![]() $g\in H^p(\mathbb {C}_{+})$
. Then
$g\in H^p(\mathbb {C}_{+})$
. Then
![]() $g(z)=B(z)\tilde g(z)$
,
$g(z)=B(z)\tilde g(z)$
,
![]() $z \in \mathbb C_+$
, where B is the Blaschke product associated with g and
$z \in \mathbb C_+$
, where B is the Blaschke product associated with g and
![]() $\tilde g$
has no zeros in
$\tilde g$
has no zeros in
![]() $\mathbb {C}_+$
. Then there is a well-defined holomorphic function
$\mathbb {C}_+$
. Then there is a well-defined holomorphic function
![]() $g_p(z)=[\tilde g (z)]^{p/2}$
on
$g_p(z)=[\tilde g (z)]^{p/2}$
on
![]() $\mathbb {C}_+$
and
$\mathbb {C}_+$
and
![]() $g_p \in H^2(\mathbb {C}_{+})$
. Using (4.7) for
$g_p \in H^2(\mathbb {C}_{+})$
. Using (4.7) for
![]() $p=2$
, for all
$p=2$
, for all
![]() $|\varphi |<\pi /2$
we have
$|\varphi |<\pi /2$
we have
 $$ \begin{align} \int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p\bigr)\,dt = \int_0^{\infty} \bigl(|g_p(te^{i\varphi})|^2+| g_p(te^{-i\varphi})|^2\bigr)\,dt \end{align} $$
$$ \begin{align} \int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p\bigr)\,dt = \int_0^{\infty} \bigl(|g_p(te^{i\varphi})|^2+| g_p(te^{-i\varphi})|^2\bigr)\,dt \end{align} $$
 $$\begin{align*} \le \int_{-\infty}^{\infty} |g_p(it)|^2\,dt=\int_{-\infty}^{\infty} |g(it)|^p\,dt=\|g\|_p^p, \notag \end{align*}$$
$$\begin{align*} \le \int_{-\infty}^{\infty} |g_p(it)|^2\,dt=\int_{-\infty}^{\infty} |g(it)|^p\,dt=\|g\|_p^p, \notag \end{align*}$$
and (4.7) follows.
Lemmas 4.1 and 4.2 imply the next statement.
Corollary 4.3. Let
![]() $p\in [1,\infty )$
. Then
$p\in [1,\infty )$
. Then
![]() $H^{p}(\Sigma _{\pi /2})=H^{p}(\mathbb {C}_+)$
, and for every
$H^{p}(\Sigma _{\pi /2})=H^{p}(\mathbb {C}_+)$
, and for every
![]() $g\in H^{p}(\mathbb {C}_{+})$
,
$g\in H^{p}(\mathbb {C}_{+})$
,
and
 $$ \begin{align} \|g\|_{H^{p}_{*}(\Sigma_{\pi/2})}\le \|g\|_{H^p(\mathbb{C}_+)}\le 2^{1/p}\|g\|_{H^{p}_{*}(\Sigma_{\pi/2})}. \end{align} $$
$$ \begin{align} \|g\|_{H^{p}_{*}(\Sigma_{\pi/2})}\le \|g\|_{H^p(\mathbb{C}_+)}\le 2^{1/p}\|g\|_{H^{p}_{*}(\Sigma_{\pi/2})}. \end{align} $$
Note that the two-sided estimate (4.10) was proved in [Reference Sedleckii52] and [Reference Luxemburg42] in a more complicated way (see also [Reference Akopjan1], [Reference Dilanian19], [Reference Martirosian45], [Reference von Keviczky54], [Reference von Keviczky55]). The coincidence of norms in (4.9) seems not to have been noted before. It appears to be quite useful, as we will see in the proof of Corollary 4.5.
Remark 4.4. The two-sided estimate (4.10) is sharp (and cannot be improved). Indeed, let
![]() $p\in [1,\infty )$
and let
$p\in [1,\infty )$
and let
 $$ \begin{align*} f_k(z):=\frac{1}{\pi^{1/p}(z+1+ik)^{2/p}},\qquad k\in\mathbb{N}. \end{align*} $$
$$ \begin{align*} f_k(z):=\frac{1}{\pi^{1/p}(z+1+ik)^{2/p}},\qquad k\in\mathbb{N}. \end{align*} $$
Then for all k, we have
![]() $\|f_k\|_{H^p(\mathbb {C}_{+})}=1$
and, by direct estimates,
$\|f_k\|_{H^p(\mathbb {C}_{+})}=1$
and, by direct estimates,
 $$ \begin{align*} \left( \|f_k\|_{H^p_{*}(\Sigma_{\pi/2})} \right)^p&=\int_0^{\infty} |f_k(te^{-i\pi/2})|^p\,dt\\ &=\frac{1}{\pi}\int_0^{\infty} \frac{dt}{(t-k)^2+1}\,dt =\frac{1}{2}+\frac{\arctan k}{\pi}. \end{align*} $$
$$ \begin{align*} \left( \|f_k\|_{H^p_{*}(\Sigma_{\pi/2})} \right)^p&=\int_0^{\infty} |f_k(te^{-i\pi/2})|^p\,dt\\ &=\frac{1}{\pi}\int_0^{\infty} \frac{dt}{(t-k)^2+1}\,dt =\frac{1}{2}+\frac{\arctan k}{\pi}. \end{align*} $$
Thus,
 $$ \begin{align*} \|f_0\|_{H^p(\mathbb{C}_{+})}=2^{1/p}\|f_0\|_{H^p_{*}(\Sigma_{\pi/2})} \qquad \text{and}\qquad \lim_{k\to\infty}\,\frac{\|f_k\|_{H^p_{*}(\Sigma_{\pi/2})}}{\|f_k\|_{H^p(\mathbb{C}_{+})}}=1. \end{align*} $$
$$ \begin{align*} \|f_0\|_{H^p(\mathbb{C}_{+})}=2^{1/p}\|f_0\|_{H^p_{*}(\Sigma_{\pi/2})} \qquad \text{and}\qquad \lim_{k\to\infty}\,\frac{\|f_k\|_{H^p_{*}(\Sigma_{\pi/2})}}{\|f_k\|_{H^p(\mathbb{C}_{+})}}=1. \end{align*} $$
In fact, for all
![]() $f \in \mathcal {H}^p_{*}(\Sigma _{\pi /2})$
, the norm
$f \in \mathcal {H}^p_{*}(\Sigma _{\pi /2})$
, the norm
 $\|f\|_{H^p_{*}(\Sigma _{\pi /2})}$
is attained at the boundary of
$\|f\|_{H^p_{*}(\Sigma _{\pi /2})}$
is attained at the boundary of
![]() $\Sigma _{\pi /2}$
.
$\Sigma _{\pi /2}$
.
Corollary 4.5. Let
![]() $g \in H^{p}(\Sigma _{\pi /2})$
,
$g \in H^{p}(\Sigma _{\pi /2})$
,
![]() $p\in [1,\infty )$
. Then there exist
$p\in [1,\infty )$
. Then there exist
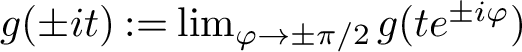 $g(\pm it):=\lim _{\varphi \to \pm \pi /2} g(te^{\pm i\varphi })$
for a.e.
$g(\pm it):=\lim _{\varphi \to \pm \pi /2} g(te^{\pm i\varphi })$
for a.e.
![]() $t \in \mathbb R_+$
,
$t \in \mathbb R_+$
,
![]() $g(\pm i \cdot ) \in L^p(\mathbb R_+)$
, and
$g(\pm i \cdot ) \in L^p(\mathbb R_+)$
, and
 $$ \begin{align} \lim_{\varphi\to\pm \pi/2}\, \int_0^{\infty} |g(te^{i\varphi})-g(\pm it)|^p\,dt=0. \end{align} $$
$$ \begin{align} \lim_{\varphi\to\pm \pi/2}\, \int_0^{\infty} |g(te^{i\varphi})-g(\pm it)|^p\,dt=0. \end{align} $$
As a consequence, for every
![]() $g \in H^p(\Sigma _{\pi /2})$
,
$g \in H^p(\Sigma _{\pi /2})$
,
Proof. Let
![]() $p \in [1,\infty )$
be fixed. By Corollary 4.3, it suffices to prove (4.11) for
$p \in [1,\infty )$
be fixed. By Corollary 4.3, it suffices to prove (4.11) for
![]() $g\in H^p(\mathbb {C}_{+})$
. If
$g\in H^p(\mathbb {C}_{+})$
. If
![]() $g\in H^p(\mathbb {C}_{+})$
, then, as recalled above, for almost all
$g\in H^p(\mathbb {C}_{+})$
, then, as recalled above, for almost all
![]() $t \in \mathbb R$
there exists a sectorial limit
$t \in \mathbb R$
there exists a sectorial limit
![]() $g(it):=\lim _{z \to it} g(z)$
, and
$g(it):=\lim _{z \to it} g(z)$
, and
![]() $g(i\cdot ) \in L^p(\mathbb {R})$
. Therefore, we also have
$g(i\cdot ) \in L^p(\mathbb {R})$
. Therefore, we also have
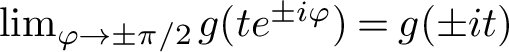 $\lim _{\varphi \to \pm \pi /2} g(te^{\pm i\varphi })=g(\pm it)$
for almost all t. Using this and Fatou’s lemma, we infer from (4.8) that
$\lim _{\varphi \to \pm \pi /2} g(te^{\pm i\varphi })=g(\pm it)$
for almost all t. Using this and Fatou’s lemma, we infer from (4.8) that
 $$ \begin{align*} \limsup_{\varphi\to \pi/2}\,&\int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p \bigr)\,dt\le \int_{-\infty}^{\infty} |g(it)|^p\,dt\\ &\le \liminf_{\varphi\to\pi/2}\,\int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p\bigr)\,dt, \end{align*} $$
$$ \begin{align*} \limsup_{\varphi\to \pi/2}\,&\int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p \bigr)\,dt\le \int_{-\infty}^{\infty} |g(it)|^p\,dt\\ &\le \liminf_{\varphi\to\pi/2}\,\int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p\bigr)\,dt, \end{align*} $$
and hence
 $$ \begin{align} \lim_{\varphi\to\pi/2}\,\int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p \bigr)\,dt= \int_{-\infty}^{\infty} |g(it)|^p\,dt. \end{align} $$
$$ \begin{align} \lim_{\varphi\to\pi/2}\,\int_0^{\infty} \bigl(|g(te^{i\varphi})|^p+|g(te^{-i\varphi})|^p \bigr)\,dt= \int_{-\infty}^{\infty} |g(it)|^p\,dt. \end{align} $$
Then, by (4.13) and Lemma 2.2, using once again the pointwise a.e. convergence of
![]() $g(te^{\pm i\varphi })$
to
$g(te^{\pm i\varphi })$
to
![]() $g(\pm it)$
as
$g(\pm it)$
as
![]() $\varphi \to \pm \pi /2$
, we obtain (4.11). Because
$\varphi \to \pm \pi /2$
, we obtain (4.11). Because
![]() $\|g\|_{H^p(\mathbb {C}_+)}=\|g(i\cdot )\|_{L^p(\mathbb R)},$
we get (4.12) as well.
$\|g\|_{H^p(\mathbb {C}_+)}=\|g(i\cdot )\|_{L^p(\mathbb R)},$
we get (4.12) as well.
For (formally) more general versions of (4.9) and (4.10), see (4.15) and (4.17).
4.2. The spaces
 $H^1(\Sigma _{\psi })$
$H^1(\Sigma _{\psi })$
Now using the results of Subsection 4.1 for
![]() $\psi =\pi /2$
, we develop basic properties of
$\psi =\pi /2$
, we develop basic properties of
![]() $H^1(\Sigma _{\psi })$
for any
$H^1(\Sigma _{\psi })$
for any
![]() $\psi \in (0,\pi )$
. Define the Hardy space
$\psi \in (0,\pi )$
. Define the Hardy space
![]() $H^1(\Sigma _{\psi })$
on the sector
$H^1(\Sigma _{\psi })$
on the sector
![]() $\Sigma _{\psi }$
to be the space of all functions
$\Sigma _{\psi }$
to be the space of all functions
![]() $f \in \operatorname {Hol}(\Sigma _{\psi })$
such that
$f \in \operatorname {Hol}(\Sigma _{\psi })$
such that
 $$ \begin{align} \|f\|_{H^1(\Sigma_{\psi})} := \sup_{|\varphi|<\psi} \int_0^{\infty} \bigl(|f(te^{i\varphi})|+ |f(te^{-i\varphi})| \bigr) \,dt <\infty. \end{align} $$
$$ \begin{align} \|f\|_{H^1(\Sigma_{\psi})} := \sup_{|\varphi|<\psi} \int_0^{\infty} \bigl(|f(te^{i\varphi})|+ |f(te^{-i\varphi})| \bigr) \,dt <\infty. \end{align} $$
We will also consider a nonsymmetric version of
![]() $H^1(\Sigma _{\psi })$
, defined as
$H^1(\Sigma _{\psi })$
, defined as
 $$ \begin{align*} H^1_{*}(\Sigma_{\psi}):=\left\{f \in \operatorname{Hol}\, (\Sigma_{\psi}): \|f\|_{H^1_{*}(\Sigma_{\psi})}:=\sup_{|\varphi|< \psi}\,\int_0^{\infty} |f(t e^{i\varphi})|\,dt<\infty\right\}. \end{align*} $$
$$ \begin{align*} H^1_{*}(\Sigma_{\psi}):=\left\{f \in \operatorname{Hol}\, (\Sigma_{\psi}): \|f\|_{H^1_{*}(\Sigma_{\psi})}:=\sup_{|\varphi|< \psi}\,\int_0^{\infty} |f(t e^{i\varphi})|\,dt<\infty\right\}. \end{align*} $$
Theorem 4.6. Let
![]() $\psi , \psi _1, \psi _2 \in (0,\pi )$
.
$\psi , \psi _1, \psi _2 \in (0,\pi )$
.
-
(i)
 $f \in H^1 (\Sigma _{\psi })$
if and only if
$f \in H^1 (\Sigma _{\psi })$
if and only if
 $f \in H^1_*(\Sigma _{\psi })$
, and then (4.15)
$f \in H^1_*(\Sigma _{\psi })$
, and then (4.15) $$ \begin{align} 2^{-1} \|f\|_{H^1(\Sigma_{\psi})} \le \|f\|_{H^1_*(\Sigma_{\psi})}\le \|f\|_{H^1(\Sigma_{\psi})}. \end{align} $$
$$ \begin{align} 2^{-1} \|f\|_{H^1(\Sigma_{\psi})} \le \|f\|_{H^1_*(\Sigma_{\psi})}\le \|f\|_{H^1(\Sigma_{\psi})}. \end{align} $$
-
(ii) For any
 $\psi _1,\psi _2 \in (0,\pi )$
, the map is an isometric isomorphism of
$\psi _1,\psi _2 \in (0,\pi )$
, the map is an isometric isomorphism of $$ \begin{align*} H^1(\Sigma_{\psi_1}) &\to H^1(\Sigma_{\psi_2})\\ f(z) &\mapsto \frac{\psi_1}{\psi_2} z^{(\psi_1/\psi_2) -1}f(z^{\psi_1/\psi_2}) \end{align*} $$
$$ \begin{align*} H^1(\Sigma_{\psi_1}) &\to H^1(\Sigma_{\psi_2})\\ f(z) &\mapsto \frac{\psi_1}{\psi_2} z^{(\psi_1/\psi_2) -1}f(z^{\psi_1/\psi_2}) \end{align*} $$
 $H^1(\Sigma _{\psi _1})$
onto
$H^1(\Sigma _{\psi _1})$
onto
 $H^1(\Sigma _{\psi _2})$
and of
$H^1(\Sigma _{\psi _2})$
and of
 $H^1_*(\Sigma _{\psi _1})$
onto
$H^1_*(\Sigma _{\psi _1})$
onto
 $H^1_*(\Sigma _{\psi _2})$
.
$H^1_*(\Sigma _{\psi _2})$
.
-
(iii) If
 $f \in H^1(\Sigma _{\psi })$
, then the limits
$f \in H^1(\Sigma _{\psi })$
, then the limits
 $f(re^{\pm i\psi }):=\lim _{\varphi \to \pm \psi } f(re^{i\varphi })$
exist a.e. and in the
$f(re^{\pm i\psi }):=\lim _{\varphi \to \pm \psi } f(re^{i\varphi })$
exist a.e. and in the
 $L^1$
-sense with respect to r. Moreover, (4.16)
$L^1$
-sense with respect to r. Moreover, (4.16) $$ \begin{align} f(z)= \frac{1}{2\pi i} \int_{\partial\Sigma_{\psi}}\,\frac{f(\lambda)}{\lambda-z} \,d\lambda, \quad z\in \Sigma_{\psi}. \end{align} $$
$$ \begin{align} f(z)= \frac{1}{2\pi i} \int_{\partial\Sigma_{\psi}}\,\frac{f(\lambda)}{\lambda-z} \,d\lambda, \quad z\in \Sigma_{\psi}. \end{align} $$
-
(iv) If
 $f \in H^1(\Sigma _{\psi })$
, then (4.17)
$f \in H^1(\Sigma _{\psi })$
, then (4.17) $$ \begin{align} \|f\|_{H^1(\Sigma_{\psi})}&=\int_{0}^{\infty}\bigl(|f(te^{i\psi})|+ |f(te^{-i\psi})| \bigr) \,dt. \end{align} $$
$$ \begin{align} \|f\|_{H^1(\Sigma_{\psi})}&=\int_{0}^{\infty}\bigl(|f(te^{i\psi})|+ |f(te^{-i\psi})| \bigr) \,dt. \end{align} $$
-
(v)
 $H^1(\Sigma _{\psi })$
and
$H^1(\Sigma _{\psi })$
and
 $H^1_*(\Sigma _{\psi })$
are Banach spaces.
$H^1_*(\Sigma _{\psi })$
are Banach spaces.
Proof. The proof of (i) is clear, and (ii) is a direct verification. For
![]() $\psi = \pi /2$
, the statements (iii) and (iv), excluding (4.16), were proved in Corollaries 4.3 and 4.5, and (v) is well-known. Then the general cases are reduced to the case when
$\psi = \pi /2$
, the statements (iii) and (iv), excluding (4.16), were proved in Corollaries 4.3 and 4.5, and (v) is well-known. Then the general cases are reduced to the case when
![]() $\psi =\pi /2$
, by means of (ii).
$\psi =\pi /2$
, by means of (ii).
The Cauchy formula (4.16) is well-known for
![]() $\psi =\pi /2$
(see, for example, [Reference Duren21, Theorem 11.8]). For general
$\psi =\pi /2$
(see, for example, [Reference Duren21, Theorem 11.8]). For general
![]() $\psi $
, we may argue similarly to the proof of Lemma 4.1, as follows.
$\psi $
, we may argue similarly to the proof of Lemma 4.1, as follows.
Because
![]() $f \in H^1(\Sigma _{\psi })$
,
$f \in H^1(\Sigma _{\psi })$
,
 $$ \begin{align*} \int_0^{\infty} \int_{-\psi}^{\psi} |f(te^{i\varphi})| \,d\varphi\,dt < \infty. \end{align*} $$
$$ \begin{align*} \int_0^{\infty} \int_{-\psi}^{\psi} |f(te^{i\varphi})| \,d\varphi\,dt < \infty. \end{align*} $$
Hence, there exist sequences
![]() $(t_{1,n})_{n\ge 1}$
and
$(t_{1,n})_{n\ge 1}$
and
![]() $(t_{2,n})_{n\ge 1}$
such that
$(t_{2,n})_{n\ge 1}$
such that
![]() $0 < t_{1,n} < t_{2,n}$
,
$0 < t_{1,n} < t_{2,n}$
,
![]() $t_{1,n} \to 0, \, t_{2,n} \to \infty $
as
$t_{1,n} \to 0, \, t_{2,n} \to \infty $
as
![]() $n\to \infty $
and
$n\to \infty $
and
 $$ \begin{align*} \lim_{n\to \infty} \int_{-\psi}^{\psi} t_{1,n} |f(t_{1,n} e^{i\varphi})| \,d\varphi = \lim_{n\to\infty} \int_{-\psi}^{\psi} |f(t_{2,n} e^{i\varphi})| \,d\varphi = 0. \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty} \int_{-\psi}^{\psi} t_{1,n} |f(t_{1,n} e^{i\varphi})| \,d\varphi = \lim_{n\to\infty} \int_{-\psi}^{\psi} |f(t_{2,n} e^{i\varphi})| \,d\varphi = 0. \end{align*} $$
By applying Cauchy’s theorem around the boundary of
 $$ \begin{align*} \left\{z \in \partial \Sigma_{\psi - n^{-1}} : t_{1,n} < |z| < t_{2,n} \right\} \end{align*} $$
$$ \begin{align*} \left\{z \in \partial \Sigma_{\psi - n^{-1}} : t_{1,n} < |z| < t_{2,n} \right\} \end{align*} $$
for large n and taking the limit, we obtain (4.16).
Remark 4.7. In addition to (4.17), it is possible to prove that
 $$ \begin{align*} \|f\|_{H^1_{*}(\Sigma_{\psi})} = \max \left(\int_{0}^{\infty}|f(te^{-i\psi})|\, dt,\int_{0}^{\infty}|f(te^{i\psi})|\,dt\right). \end{align*} $$
$$ \begin{align*} \|f\|_{H^1_{*}(\Sigma_{\psi})} = \max \left(\int_{0}^{\infty}|f(te^{-i\psi})|\, dt,\int_{0}^{\infty}|f(te^{i\psi})|\,dt\right). \end{align*} $$
This requires additional techniques, and it is not used in this article.
4.3. Functions with derivatives in
 $H^1(\Sigma _{\psi })$
$H^1(\Sigma _{\psi })$
For
![]() $\psi \in (0,\pi )$
, let us introduce the space
$\psi \in (0,\pi )$
, let us introduce the space
 $$ \begin{align*}\mathcal{H}_{\psi}:=\left\{ f \in \operatorname{Hol}(\Sigma_{\psi}): f' \in H^1 (\Sigma_{\psi})\right\}.\end{align*} $$
$$ \begin{align*}\mathcal{H}_{\psi}:=\left\{ f \in \operatorname{Hol}(\Sigma_{\psi}): f' \in H^1 (\Sigma_{\psi})\right\}.\end{align*} $$
In view of Corollary 4.3,
 $$ \begin{align}\mathcal{H}_{\pi/2} = H^{1,1}(\mathbb{C}_+):=\{f \in \operatorname{Hol}(\mathbb{C}_+): f'\in H^1(\mathbb{C}_+)\}, \end{align} $$
$$ \begin{align}\mathcal{H}_{\pi/2} = H^{1,1}(\mathbb{C}_+):=\{f \in \operatorname{Hol}(\mathbb{C}_+): f'\in H^1(\mathbb{C}_+)\}, \end{align} $$
and we may sometimes use the notation
![]() $H^{1,1}(\mathbb {C}_+)$
instead of
$H^{1,1}(\mathbb {C}_+)$
instead of
![]() $\mathcal {H}_{\pi /2}$
.
$\mathcal {H}_{\pi /2}$
.
Such function spaces are often called Hardy–Sobolev spaces, and we will also use this terminology sporadically. Spaces more general than
![]() $\mathcal {H}_{\psi }$
appear in [Reference Domelevo, Kriegler and Petermichl20]. Namely, for
$\mathcal {H}_{\psi }$
appear in [Reference Domelevo, Kriegler and Petermichl20]. Namely, for
![]() $f \in \operatorname {Hol}(\Sigma _{\psi })$
it was required in [Reference Domelevo, Kriegler and Petermichl20] that the boundary values of f exist and belong (after an appropriate ‘rescaling’) to a Besov space
$f \in \operatorname {Hol}(\Sigma _{\psi })$
it was required in [Reference Domelevo, Kriegler and Petermichl20] that the boundary values of f exist and belong (after an appropriate ‘rescaling’) to a Besov space
![]() $B^s_{\infty , 1}, \, s>0$
. One can develop a similar approach to those spaces, but we do not see much advantage in such generality within the present context.
$B^s_{\infty , 1}, \, s>0$
. One can develop a similar approach to those spaces, but we do not see much advantage in such generality within the present context.
Theorem 4.8. Let
![]() $f \in \mathcal {H}_{\psi },\, \psi \in (0,\pi )$
.
$f \in \mathcal {H}_{\psi },\, \psi \in (0,\pi )$
.
-
(i) The function f extends to a continuous bounded function on
 $\overline {\Sigma }_{\psi }$
.
$\overline {\Sigma }_{\psi }$
. -
(ii) The limit
exists. $$ \begin{align*} f(\infty):=\lim_{|z|\to \infty, z \in \Sigma_{\psi}}\,f(z) \end{align*} $$
$$ \begin{align*} f(\infty):=\lim_{|z|\to \infty, z \in \Sigma_{\psi}}\,f(z) \end{align*} $$
-
(iii) One has
(4.19)In particular, the evaluation functionals $$ \begin{align} \|f\|_{H^{\infty}(\Sigma_{\psi})} \le |f(\infty)| + \|f'\|_{H^1(\Sigma_{\psi})}. \end{align} $$
$$ \begin{align} \|f\|_{H^{\infty}(\Sigma_{\psi})} \le |f(\infty)| + \|f'\|_{H^1(\Sigma_{\psi})}. \end{align} $$
 $\delta _z,\, z\in \Sigma _{\psi }$
, are continuous on
$\delta _z,\, z\in \Sigma _{\psi }$
, are continuous on
 $\mathcal {H}_{\psi }$
.
$\mathcal {H}_{\psi }$
.
Proof. Let
![]() $\psi = \pi /2$
. Because
$\psi = \pi /2$
. Because
 $\mathcal H_{\pi /2}=H^{1,1}(\mathbb C_+) \subset \mathcal {B}$
by (4.18) and [Reference Batty, Gomilko and Tomilov7, Proposition 2.4], the statement (i) follows from [Reference Batty, Gomilko and Tomilov7, Proposition 2.2(iv)], and (ii) follows from [Reference Batty, Gomilko and Tomilov7, Proposition 2.4]. In the general case, the map
$\mathcal H_{\pi /2}=H^{1,1}(\mathbb C_+) \subset \mathcal {B}$
by (4.18) and [Reference Batty, Gomilko and Tomilov7, Proposition 2.4], the statement (i) follows from [Reference Batty, Gomilko and Tomilov7, Proposition 2.2(iv)], and (ii) follows from [Reference Batty, Gomilko and Tomilov7, Proposition 2.4]. In the general case, the map
![]() $f(z) \mapsto f(z^{2\psi /\pi })$
is an isomorphism of
$f(z) \mapsto f(z^{2\psi /\pi })$
is an isomorphism of
![]() $\mathcal {H}_{\psi }$
onto
$\mathcal {H}_{\psi }$
onto
![]() $H^{1,1}(\mathbb {C}_+)$
, by Theorem 4.6(ii), so (i) and (ii) hold for
$H^{1,1}(\mathbb {C}_+)$
, by Theorem 4.6(ii), so (i) and (ii) hold for
![]() $\mathcal {H}_{\psi }$
. The statement (iii) is easily seen.
$\mathcal {H}_{\psi }$
. The statement (iii) is easily seen.
It follows from Theorem 4.8 that
![]() $\mathcal {H}_{\psi }$
is an algebra for every
$\mathcal {H}_{\psi }$
is an algebra for every
![]() $\psi \in (0,\pi )$
. We define a norm on
$\psi \in (0,\pi )$
. We define a norm on
![]() $\mathcal {H}_{\psi }$
by
$\mathcal {H}_{\psi }$
by
 $$ \begin{align} \|f \|_{\mathcal{H}_{\psi}}:=\|f\|_{H^{\infty}(\Sigma_{\psi})}+\|f'\|_{H^1(\Sigma_{\psi})}, \qquad f \in \mathcal{H}_{\psi}. \end{align} $$
$$ \begin{align} \|f \|_{\mathcal{H}_{\psi}}:=\|f\|_{H^{\infty}(\Sigma_{\psi})}+\|f'\|_{H^1(\Sigma_{\psi})}, \qquad f \in \mathcal{H}_{\psi}. \end{align} $$
This is easily seen to be an algebra norm. Theorem 4.8(iii) shows that
 $$ \begin{align} \|f\|^{\prime}_{\mathcal{H}_{\psi}} := |f(\infty)| + \|f'\|_{H^1(\Sigma_{\psi})} \end{align} $$
$$ \begin{align} \|f\|^{\prime}_{\mathcal{H}_{\psi}} := |f(\infty)| + \|f'\|_{H^1(\Sigma_{\psi})} \end{align} $$
is an equivalent norm on
![]() $\mathcal {H}^1(\Sigma _{\psi })$
.
$\mathcal {H}^1(\Sigma _{\psi })$
.
The following lemma is simple but crucial for our theory. The completeness of the norm is a standard fact, the scale-invariance is trivial and the final isomorphism follows from Theorem 4.6(ii).
Lemma 4.9. For every
![]() $\psi \in (0,\pi )$
, the space
$\psi \in (0,\pi )$
, the space
![]() $(\mathcal {H}_{\psi }, \|\cdot \|_{\mathcal {H}_{\psi }})$
is a Banach algebra. For
$(\mathcal {H}_{\psi }, \|\cdot \|_{\mathcal {H}_{\psi }})$
is a Banach algebra. For
![]() $t>0$
, the map
$t>0$
, the map
![]() $f(z) \mapsto f(tz)$
is an isometric algebra isomorphism on
$f(z) \mapsto f(tz)$
is an isometric algebra isomorphism on
![]() $\mathcal {H}_{\psi }$
. Moreover, for any
$\mathcal {H}_{\psi }$
. Moreover, for any
![]() $\psi _1,\psi _2 \in (0,\pi )$
, the map
$\psi _1,\psi _2 \in (0,\pi )$
, the map
 $$ \begin{align*} \mathcal{H}_{\psi_1}&\to \mathcal{H}_{\psi_2}\\ f(z)&\mapsto f(z^{\psi_1/\psi_2}) \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\psi_1}&\to \mathcal{H}_{\psi_2}\\ f(z)&\mapsto f(z^{\psi_1/\psi_2}) \end{align*} $$
is an isometric algebra isomorphism.
We now give some examples of functions in
![]() $\mathcal {H}_{\psi }$
that will play important roles in subsequent sections of this article. The first example is of similar type to Example 3.3.
$\mathcal {H}_{\psi }$
that will play important roles in subsequent sections of this article. The first example is of similar type to Example 3.3.
Examples 4.10. Let
![]() $\psi \in (0,\pi)\ \text{and}\ \lambda\in \Sigma_{\pi-\varphi}, \varphi\in (\psi,\pi).$
$\psi \in (0,\pi)\ \text{and}\ \lambda\in \Sigma_{\pi-\varphi}, \varphi\in (\psi,\pi).$
-
1. Let
 $\gamma>0$
, and consider the function
$\gamma>0$
, and consider the function
 $r_{\lambda }^{\gamma }(z) = (\lambda +z)^{-\gamma }, \,z \in \Sigma _{\psi }$
. Then
$r_{\lambda }^{\gamma }(z) = (\lambda +z)^{-\gamma }, \,z \in \Sigma _{\psi }$
. Then
 $r_{\lambda }^{\gamma }\in \mathcal {H}_{\psi }$
and (4.22)where we have used Lemma 2.1. Thus,
$r_{\lambda }^{\gamma }\in \mathcal {H}_{\psi }$
and (4.22)where we have used Lemma 2.1. Thus, $$ \begin{align} \|r_{\lambda}^{\gamma}\|_{\mathcal{H}_{\psi}} = \int_{\partial\Sigma_{\psi}} \frac{\gamma |dz|}{|z+\lambda|^{\gamma+1}} \le \frac{2}{\sin^{\gamma+1} ((\varphi-\psi)/2) \,|\lambda|^{\gamma}}, \end{align} $$
$$ \begin{align} \|r_{\lambda}^{\gamma}\|_{\mathcal{H}_{\psi}} = \int_{\partial\Sigma_{\psi}} \frac{\gamma |dz|}{|z+\lambda|^{\gamma+1}} \le \frac{2}{\sin^{\gamma+1} ((\varphi-\psi)/2) \,|\lambda|^{\gamma}}, \end{align} $$
 $r_{\lambda }^{\gamma } \in \mathcal {H}_{\psi }$
, and there exists
$r_{\lambda }^{\gamma } \in \mathcal {H}_{\psi }$
, and there exists
 $C_{\varphi ,\psi ,\gamma }$
such that (4.23)In particular, if
$C_{\varphi ,\psi ,\gamma }$
such that (4.23)In particular, if $$ \begin{align} \|r_{\lambda}^{\gamma}\|^{\prime}_{\mathcal{H}_{\psi}} \le \frac{C_{\varphi,\psi,\gamma}}{|\lambda|^{\gamma}}, \qquad \lambda\in \Sigma_{\pi-\varphi}. \end{align} $$
$$ \begin{align} \|r_{\lambda}^{\gamma}\|^{\prime}_{\mathcal{H}_{\psi}} \le \frac{C_{\varphi,\psi,\gamma}}{|\lambda|^{\gamma}}, \qquad \lambda\in \Sigma_{\pi-\varphi}. \end{align} $$
 $\gamma =1$
, then (4.24)This property will be important for the proof of Lemma 5.7 and hence of Theorem 5.10, and eventually of Theorem 1.2 (see Theorem 8.2). A more general estimate will be given in Corollary 4.16.
$\gamma =1$
, then (4.24)This property will be important for the proof of Lemma 5.7 and hence of Theorem 5.10, and eventually of Theorem 1.2 (see Theorem 8.2). A more general estimate will be given in Corollary 4.16. $$ \begin{align} \|r_{\lambda}\|_{\mathcal{H}_{\psi}} \le \frac{2}{\sin^{2} ((\varphi-\psi)/2) \,|\lambda|}, \qquad \lambda \in \Sigma_{\pi-\varphi}. \end{align} $$
$$ \begin{align} \|r_{\lambda}\|_{\mathcal{H}_{\psi}} \le \frac{2}{\sin^{2} ((\varphi-\psi)/2) \,|\lambda|}, \qquad \lambda \in \Sigma_{\pi-\varphi}. \end{align} $$
-
2. Let
 $\gamma \in (0,\pi/(2\psi)), \lambda \in \Sigma_{\pi/2 -\gamma \psi},$
and
$\gamma \in (0,\pi/(2\psi)), \lambda \in \Sigma_{\pi/2 -\gamma \psi},$
and
 $e_{\gamma ,\lambda }(z) := e^{-\lambda z^{\gamma }}, \,z \in \Sigma _{\psi }$
. Then
$e_{\gamma ,\lambda }(z) := e^{-\lambda z^{\gamma }}, \,z \in \Sigma _{\psi }$
. Then
 $e_{\gamma ,\lambda } \in \mathcal {H}_{\psi }$
and
$e_{\gamma ,\lambda } \in \mathcal {H}_{\psi }$
and  $$ \begin{align*} \|e_{\gamma,\lambda}\|^{\prime}_{\mathcal{H}_{\psi}} = \|e_{1,\lambda} \|^{\prime}_{\mathcal{H}_{\gamma\psi}} \le \int_{\partial\Sigma_{\gamma \psi}} |\lambda| e^{-\operatorname{Re}\lambda z} \, |dz| \le \left(\frac{1}{\cos(\varphi+\gamma\psi)}+\frac{1}{\cos(\varphi-\gamma\psi)}\right). \end{align*} $$
$$ \begin{align*} \|e_{\gamma,\lambda}\|^{\prime}_{\mathcal{H}_{\psi}} = \|e_{1,\lambda} \|^{\prime}_{\mathcal{H}_{\gamma\psi}} \le \int_{\partial\Sigma_{\gamma \psi}} |\lambda| e^{-\operatorname{Re}\lambda z} \, |dz| \le \left(\frac{1}{\cos(\varphi+\gamma\psi)}+\frac{1}{\cos(\varphi-\gamma\psi)}\right). \end{align*} $$
More examples can be found in Subsections 4.5 and 4.6. In particular, Lemma 4.13 shows that the restriction of any function in
![]() $\mathcal {D}_{\infty }$
to
$\mathcal {D}_{\infty }$
to
![]() $\Sigma _{\psi }, \, \psi \in (0,\pi /2)$
, belongs to
$\Sigma _{\psi }, \, \psi \in (0,\pi /2)$
, belongs to
![]() $\mathcal {H}_{\psi }$
.
$\mathcal {H}_{\psi }$
.
The following lemma is a result of Fatou type closely related to Corollary 3.12.
Lemma 4.11. Let
![]() $\psi \in (0,\pi )$
and
$\psi \in (0,\pi )$
and
![]() $(f_k)_{k=1}^{\infty } \subset \mathcal {H}_{\psi }$
be such that
$(f_k)_{k=1}^{\infty } \subset \mathcal {H}_{\psi }$
be such that
![]() $\sup _{k \ge 1} \|f_k\|_{\mathcal {H}_{\psi }}<\infty $
and
$\sup _{k \ge 1} \|f_k\|_{\mathcal {H}_{\psi }}<\infty $
and
![]() $f(z):=\lim _{k \to \infty } f_k(z)$
exists for all
$f(z):=\lim _{k \to \infty } f_k(z)$
exists for all
![]() $z \in \mathbb C_+$
. Then
$z \in \mathbb C_+$
. Then
![]() $f \in \mathcal {H}_{\psi }$
.
$f \in \mathcal {H}_{\psi }$
.
Proof. By Theorem 4.8, the functions
![]() $\{f_k: k\ge 1\}$
are uniformly bounded on
$\{f_k: k\ge 1\}$
are uniformly bounded on
![]() $\Sigma _{\psi }$
. By Vitali’s theorem, f is holomorphic, and
$\Sigma _{\psi }$
. By Vitali’s theorem, f is holomorphic, and
![]() $f_k'(z) \to f'(z)$
as
$f_k'(z) \to f'(z)$
as
![]() $k \to \infty $
for each
$k \to \infty $
for each
![]() $z \in \Sigma _{\psi }$
. By Fatou’s lemma, for
$z \in \Sigma _{\psi }$
. By Fatou’s lemma, for
![]() $|\varphi | < \psi $
,
$|\varphi | < \psi $
,
 $$ \begin{align*} \int_0^{\infty} |f'(te^{i\varphi})| \,dt \le \liminf_{k\to\infty} \int_0^{\infty} |f_k'(te^{i\varphi})| \,dt \le \sup_{k\ge1} \|f_k\|_{\mathcal{H}_{\psi}}. \end{align*} $$
$$ \begin{align*} \int_0^{\infty} |f'(te^{i\varphi})| \,dt \le \liminf_{k\to\infty} \int_0^{\infty} |f_k'(te^{i\varphi})| \,dt \le \sup_{k\ge1} \|f_k\|_{\mathcal{H}_{\psi}}. \end{align*} $$
Thus,
![]() $f \in \mathcal {H}_{\psi }$
.
$f \in \mathcal {H}_{\psi }$
.
4.4. The spaces
 $H^{1,1}(\mathbb {C}_+)$
and
$H^{1,1}(\mathbb {C}_+)$
and
 $\mathcal {L} L^1$
$\mathcal {L} L^1$
In [Reference Batty, Gomilko and Tomilov7, Proposition 2.4], we showed that
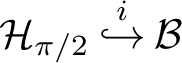 $\mathcal {H}_{\pi /2} \overset {i}{\hookrightarrow } \mathcal {B}$
. We will now show a stronger result that
$\mathcal {H}_{\pi /2} \overset {i}{\hookrightarrow } \mathcal {B}$
. We will now show a stronger result that
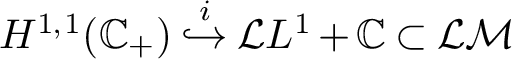 $H^{1,1}(\mathbb {C}_+) \overset {i}{\hookrightarrow } \mathcal {L} L^1 + \mathbb {C} \subset \mathcal {LM}$
, where
$H^{1,1}(\mathbb {C}_+) \overset {i}{\hookrightarrow } \mathcal {L} L^1 + \mathbb {C} \subset \mathcal {LM}$
, where
![]() $(\mathcal {LM},\|\cdot\|_{{\rm HP}})$
is the HP algebra as in Section 2. In particular, it shows that the Laplace transforms of singular measures on
$(\mathcal {LM},\|\cdot\|_{{\rm HP}})$
is the HP algebra as in Section 2. In particular, it shows that the Laplace transforms of singular measures on
![]() $(0,\infty )$
are not in
$(0,\infty )$
are not in
![]() $H^{1,1}(\mathbb {C}_+)$
, which may be of interest.
$H^{1,1}(\mathbb {C}_+)$
, which may be of interest.
Theorem 4.12. If
![]() $f\in H^{1,1}(\mathbb {C}_{+}),$
then there exists
$f\in H^{1,1}(\mathbb {C}_{+}),$
then there exists
![]() $g \in L^1(\mathbb {R}_+)$
such that
$g \in L^1(\mathbb {R}_+)$
such that
![]() $f = f(\infty ) + \mathcal {L} g$
. Moreover, there is an absolute constant C such that
$f = f(\infty ) + \mathcal {L} g$
. Moreover, there is an absolute constant C such that
Proof. Let
![]() $f\in H^{1,1}(\mathbb {C}_{+})$
and, for
$f\in H^{1,1}(\mathbb {C}_{+})$
and, for
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
 $$ \begin{align*} f_n(z) &:=f(z)-f(z+n),\qquad z \in \mathbb{C}_+, \\ g_n(t) &:= -\frac{2}{\pi} t(1-e^{-nt})\int_0^{\infty} \alpha e^{-\alpha t} \int_{-\infty}^{\infty} f'(\alpha+i\beta) e^{i\beta t}\,d\beta\,d\alpha, \quad t>0. \end{align*} $$
$$ \begin{align*} f_n(z) &:=f(z)-f(z+n),\qquad z \in \mathbb{C}_+, \\ g_n(t) &:= -\frac{2}{\pi} t(1-e^{-nt})\int_0^{\infty} \alpha e^{-\alpha t} \int_{-\infty}^{\infty} f'(\alpha+i\beta) e^{i\beta t}\,d\beta\,d\alpha, \quad t>0. \end{align*} $$
Then
![]() $f_n \in H^{1,1}(\mathbb {C}_+)$
, and
$f_n \in H^{1,1}(\mathbb {C}_+)$
, and
![]() $\|f_n\|_{H^{1,1}(\mathbb {C}_+)} \le 2\|f\|_{H^{1,1}(\mathbb {C}_+)}$
. Moreover,
$\|f_n\|_{H^{1,1}(\mathbb {C}_+)} \le 2\|f\|_{H^{1,1}(\mathbb {C}_+)}$
. Moreover,
 $$ \begin{align*} |g_n(t)| &\le \frac{2}{\pi}t(1-e^{-nt})\int_0^{\infty} \alpha e^{-\alpha t} \int_{-\infty}^{\infty} |f'(\alpha+i\beta)|\,d\beta\,d\alpha\\ &\le \frac{2}{\pi} \|f'\|_{H^1(\mathbb{C}_{+})}t(1-e^{-nt})\int_0^{\infty} \alpha e^{-\alpha t} \,d\alpha= \frac{2}{\pi}\|f'\|_{H^1(\mathbb{C}_{+})}\frac{(1-e^{-nt})}{t}\\ &\le \frac{2n}{\pi} \|f'\|_{H^1(\mathbb{C}_{+})}. \end{align*} $$
$$ \begin{align*} |g_n(t)| &\le \frac{2}{\pi}t(1-e^{-nt})\int_0^{\infty} \alpha e^{-\alpha t} \int_{-\infty}^{\infty} |f'(\alpha+i\beta)|\,d\beta\,d\alpha\\ &\le \frac{2}{\pi} \|f'\|_{H^1(\mathbb{C}_{+})}t(1-e^{-nt})\int_0^{\infty} \alpha e^{-\alpha t} \,d\alpha= \frac{2}{\pi}\|f'\|_{H^1(\mathbb{C}_{+})}\frac{(1-e^{-nt})}{t}\\ &\le \frac{2n}{\pi} \|f'\|_{H^1(\mathbb{C}_{+})}. \end{align*} $$
By the reproducing formula for
![]() $\mathcal {B}$
(see Remark 3.16 or [Reference Batty, Gomilko and Tomilov7, Proposition 2.20]) and Fubini’s theorem,
$\mathcal {B}$
(see Remark 3.16 or [Reference Batty, Gomilko and Tomilov7, Proposition 2.20]) and Fubini’s theorem,
 $$ \begin{align*} f_n(z)=&-\frac{2}{\pi}\int_0^{\infty} \alpha\int_{-\infty}^{\infty} f'(\alpha+i\beta) \left(\frac{1}{(z+\alpha-i\beta)^{2}}- \frac{1}{(z+n+\alpha-i\beta)^{2}}\right) d\beta\,d\alpha\\ =&-\frac{2}{\pi} \int_0^{\infty} \alpha \int_{-\infty}^{\infty} f'(\alpha+i\beta) \left(\int_0^{\infty} e^{-(z+\alpha-i\beta)t} t(1-e^{-nt})\,dt\right)\,d\beta\,d\alpha\\ =&-\frac{2}{\pi}\int_0^{\infty} e^{-zt} g_n(t)\,dt,\quad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} f_n(z)=&-\frac{2}{\pi}\int_0^{\infty} \alpha\int_{-\infty}^{\infty} f'(\alpha+i\beta) \left(\frac{1}{(z+\alpha-i\beta)^{2}}- \frac{1}{(z+n+\alpha-i\beta)^{2}}\right) d\beta\,d\alpha\\ =&-\frac{2}{\pi} \int_0^{\infty} \alpha \int_{-\infty}^{\infty} f'(\alpha+i\beta) \left(\int_0^{\infty} e^{-(z+\alpha-i\beta)t} t(1-e^{-nt})\,dt\right)\,d\beta\,d\alpha\\ =&-\frac{2}{\pi}\int_0^{\infty} e^{-zt} g_n(t)\,dt,\quad z\in \mathbb{C}_{+}. \end{align*} $$
It follows that
![]() $(\pi /2) f_n'$
is the Laplace transform of
$(\pi /2) f_n'$
is the Laplace transform of
![]() $t g_n(t)$
, and then
$t g_n(t)$
, and then
![]() $tg_n(t)$
is the inverse Fourier transform of
$tg_n(t)$
is the inverse Fourier transform of
![]() $(\pi /2)f_n'(i\cdot )\in L^1(\mathbb {R})$
. By Hardy’s inequality in the form of [Reference Duren21, p.198],
$(\pi /2)f_n'(i\cdot )\in L^1(\mathbb {R})$
. By Hardy’s inequality in the form of [Reference Duren21, p.198],
 $$ \begin{align} \int_0^{\infty} |g_n(t)|\,dt =\int_0^{\infty} \frac{|tg_n(t)|}{t}\,dt \le \frac{\pi}{4}\|f_n'\|_{H^1(\mathbb{C}_{+})} \le \frac{\pi}{2}\|f'\|_{H^1(\mathbb{C}_{+})}. \end{align} $$
$$ \begin{align} \int_0^{\infty} |g_n(t)|\,dt =\int_0^{\infty} \frac{|tg_n(t)|}{t}\,dt \le \frac{\pi}{4}\|f_n'\|_{H^1(\mathbb{C}_{+})} \le \frac{\pi}{2}\|f'\|_{H^1(\mathbb{C}_{+})}. \end{align} $$
Moreover,
 $$ \begin{align*} f(z)=f(\infty)+\lim_{n\to\infty} f_n(z),\qquad z\in \overline{\mathbb{C}}_{+}, \end{align*} $$
$$ \begin{align*} f(z)=f(\infty)+\lim_{n\to\infty} f_n(z),\qquad z\in \overline{\mathbb{C}}_{+}, \end{align*} $$
and then by [Reference Rudin49, Theorem 1.9.2] we infer that
![]() $f=\mathcal L (\mu)$
for some
$f=\mathcal L (\mu)$
for some
![]() $\mu \in M(\mathbb R_+),$
and (4.25) holds.
$\mu \in M(\mathbb R_+),$
and (4.25) holds.
Now let
 $$ \begin{align*} u(z) := f'(z+1)=-\int_0^{\infty} e^{-zt}e^{-t}t \, d\mu(t),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} u(z) := f'(z+1)=-\int_0^{\infty} e^{-zt}e^{-t}t \, d\mu(t),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
Because
![]() $f\in H^{\infty }(\mathbb {C}_{+})$
and
$f\in H^{\infty }(\mathbb {C}_{+})$
and
![]() $f'\in H^1(\mathbb {C}_{+})$
, we have that
$f'\in H^1(\mathbb {C}_{+})$
, we have that
![]() $u\in H^1(\mathbb {C}_+) \cap H^{\infty }(\mathbb {C}_+) \subset H^2(\mathbb {C}_{+})$
. Hence,
$u\in H^1(\mathbb {C}_+) \cap H^{\infty }(\mathbb {C}_+) \subset H^2(\mathbb {C}_{+})$
. Hence,
![]() $u = \mathcal {L} h$
for some
$u = \mathcal {L} h$
for some
![]() $h \in L^2(\mathbb {R}_+)$
, so
$h \in L^2(\mathbb {R}_+)$
, so
 $$ \begin{align*} u(z) = \int_0^{\infty} e^{-zt} h(t) \, dt, \qquad z \in \mathbb{C}_+. \end{align*} $$
$$ \begin{align*} u(z) = \int_0^{\infty} e^{-zt} h(t) \, dt, \qquad z \in \mathbb{C}_+. \end{align*} $$
From the uniqueness properties of Laplace transforms it follows that
Thus,
![]() $\mu $
is absolutely continuous on
$\mu $
is absolutely continuous on
![]() $(0,\infty )$
, with Radon–Nikodym derivative
$(0,\infty )$
, with Radon–Nikodym derivative
![]() $g.$
Because
$g.$
Because
![]() $\mu $
is a bounded measure,
$\mu $
is a bounded measure,
![]() $g \in L^1(\mathbb {R}_+)$
, and
$g \in L^1(\mathbb {R}_+)$
, and
Hence,
![]() $f = f(\infty ) + \mathcal {L} g$
.
$f = f(\infty ) + \mathcal {L} g$
.
4.5. The spaces
 $\mathcal {H}_{\psi }$
and
$\mathcal {H}_{\psi }$
and
 $\mathcal {D}_s$
$\mathcal {D}_s$
Because
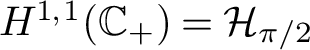 $H^{1,1}(\mathbb {C}_+) = \mathcal {H}_{\pi /2}$
(by Corollary 4.3), we have shown in Theorem 4.12 that
$H^{1,1}(\mathbb {C}_+) = \mathcal {H}_{\pi /2}$
(by Corollary 4.3), we have shown in Theorem 4.12 that
 $$ \begin{align*} \mathcal{H}_{\pi/2} \overset{i}{\hookrightarrow} \mathcal{L} L^1 + \mathbb{C} \subset \mathcal{LM} \overset{i}{\hookrightarrow} \mathcal{B} \overset{i}{\hookrightarrow} \mathcal{D}_s \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\pi/2} \overset{i}{\hookrightarrow} \mathcal{L} L^1 + \mathbb{C} \subset \mathcal{LM} \overset{i}{\hookrightarrow} \mathcal{B} \overset{i}{\hookrightarrow} \mathcal{D}_s \end{align*} $$
if
![]() $s>0$
. In the next lemma, we show that, for all
$s>0$
. In the next lemma, we show that, for all
![]() $s>-1$
,
$s>-1$
,
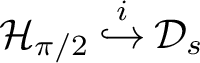 $\mathcal {H}_{\pi /2} \overset {i}{\hookrightarrow } \mathcal {D}_s$
and
$\mathcal {H}_{\pi /2} \overset {i}{\hookrightarrow } \mathcal {D}_s$
and
 $\mathcal D_s \overset {r}{\hookrightarrow } \mathcal {H}_{\psi }$
for every
$\mathcal D_s \overset {r}{\hookrightarrow } \mathcal {H}_{\psi }$
for every
![]() $\psi \in (0,\pi /2)$
. Moreover, it follows that
$\psi \in (0,\pi /2)$
. Moreover, it follows that
 $\mathcal {D}_s^{\infty } \overset {r}{\hookrightarrow } \mathcal {H}_{\psi }$
.
$\mathcal {D}_s^{\infty } \overset {r}{\hookrightarrow } \mathcal {H}_{\psi }$
.
Lemma 4.13.
-
(i) If
 $f\in \mathcal {H}_{\pi /2}$
, then
$f\in \mathcal {H}_{\pi /2}$
, then
 $f\in \mathcal {D}_s^{\infty }$
for every
$f\in \mathcal {D}_s^{\infty }$
for every
 $s>-1$
, and (4.27)
$s>-1$
, and (4.27) $$ \begin{align} \|f\|_{\mathcal D_{s,0}} &\le B\left(\frac{s+1}{2},\frac{1}{2}\right)\|f'\|_{H^1(\mathbb{C}_+)}, \\ \|f\|_{\mathcal D_{s}^{\infty} } &\le \max \left\{1, B\left(\frac{s+1}{2},\frac{1}{2}\right)\right\}\|f\|_{\mathcal{H}_{\pi/2}}. \notag \end{align} $$
$$ \begin{align} \|f\|_{\mathcal D_{s,0}} &\le B\left(\frac{s+1}{2},\frac{1}{2}\right)\|f'\|_{H^1(\mathbb{C}_+)}, \\ \|f\|_{\mathcal D_{s}^{\infty} } &\le \max \left\{1, B\left(\frac{s+1}{2},\frac{1}{2}\right)\right\}\|f\|_{\mathcal{H}_{\pi/2}}. \notag \end{align} $$
-
(ii) If
 $f\in \mathcal {D}_s$
,
$f\in \mathcal {D}_s$
,
 $s>-1$
, then
$s>-1$
, then
 $f \in \mathcal {H}_{\psi }$
for every
$f \in \mathcal {H}_{\psi }$
for every
 $\psi \in (0,\pi /2)$
, and (4.28)
$\psi \in (0,\pi /2)$
, and (4.28) $$ \begin{align} \|f'\|_{H^1(\Sigma_{\psi})}\le \frac{2^{s+1}}{\pi\cos^{s+2}(\psi/2+\pi/4)}\|f\|_{\mathcal{D}_{s,0}}. \end{align} $$
$$ \begin{align} \|f'\|_{H^1(\Sigma_{\psi})}\le \frac{2^{s+1}}{\pi\cos^{s+2}(\psi/2+\pi/4)}\|f\|_{\mathcal{D}_{s,0}}. \end{align} $$
Thus, for all
![]() $\psi \in (0,\pi /2)$
and
$\psi \in (0,\pi /2)$
and
![]() $s>-1$
, there are natural continuous embeddings
$s>-1$
, there are natural continuous embeddings
 $$ \begin{align*} \mathcal{H}_{\pi/2} \overset{i}{\hookrightarrow} \mathcal D_s \overset{r}{\hookrightarrow} \mathcal{H}_{\psi}. \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\pi/2} \overset{i}{\hookrightarrow} \mathcal D_s \overset{r}{\hookrightarrow} \mathcal{H}_{\psi}. \end{align*} $$
Note that the estimates (4.23) and (4.27) for functions
![]() $r_{\lambda }^{\gamma }$
reproduce the estimate (3.19), with different constants.
$r_{\lambda }^{\gamma }$
reproduce the estimate (3.19), with different constants.
Proof. Let
![]() $s>-1$
be fixed, and let
$s>-1$
be fixed, and let
![]() $f \in \mathcal {H}_{\pi /2}$
. Using (4.15), we have
$f \in \mathcal {H}_{\pi /2}$
. Using (4.15), we have
 $$ \begin{align*} \|f\|_{\mathcal D_{s,0}}&= \int_{-\pi/2}^{\pi/2}\cos^s\varphi \int_0^{\infty} |f'(te^{i\varphi})|\,dt\,d\varphi \\ &\le \left(\int_{-\pi/2}^{\pi/2}\cos^s\varphi\,d\varphi\right) \sup_{|\varphi|\le \pi/2}\int_0^{\infty} |f'(te^{i\varphi})|\,dt \\ &= B\left(\frac{s+1}{2},\frac{1}{2}\right)\|f'\|_{H^{1}(\mathbb{C}_+)}, \end{align*} $$
$$ \begin{align*} \|f\|_{\mathcal D_{s,0}}&= \int_{-\pi/2}^{\pi/2}\cos^s\varphi \int_0^{\infty} |f'(te^{i\varphi})|\,dt\,d\varphi \\ &\le \left(\int_{-\pi/2}^{\pi/2}\cos^s\varphi\,d\varphi\right) \sup_{|\varphi|\le \pi/2}\int_0^{\infty} |f'(te^{i\varphi})|\,dt \\ &= B\left(\frac{s+1}{2},\frac{1}{2}\right)\|f'\|_{H^{1}(\mathbb{C}_+)}, \end{align*} $$
and (i) follows.
To prove (ii), note that if
![]() $f \in \mathcal D_s$
, then by Corollary 3.10,
$f \in \mathcal D_s$
, then by Corollary 3.10,
 $$ \begin{align*} f'(z)=\frac{(s+1)2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{f'(\alpha+i\beta)}{(z+\alpha-i\beta)^{s+2}}\,d\beta\,d\alpha, \quad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} f'(z)=\frac{(s+1)2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{f'(\alpha+i\beta)}{(z+\alpha-i\beta)^{s+2}}\,d\beta\,d\alpha, \quad z\in \mathbb{C}_{+}. \end{align*} $$
Hence, using (2.1), for every
![]() $\psi \in (0,\pi /2)$
, we obtain
$\psi \in (0,\pi /2)$
, we obtain
 $$ \begin{align*} &{2^{-s}\int_0^{\infty} |f'(te^{\pm i\psi})|\,dt}\\ &\quad \le \frac{(s+1)}{\pi}\int_0^{\infty} \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{|te^{\pm i\psi}+\alpha-i\beta|^{s+2}}\,d\beta\,d\alpha\,dt\\ &\quad \le \frac{s+1}{\pi\cos^{s+2}(\psi/2+\pi/4)} \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \left( \int_0^{\infty} \frac{|f'(\alpha+i\beta)|}{(t+|\alpha+i\beta|)^{s+2}}\right) \,dt\,d\beta\,d\alpha\\ &\quad = \frac{1}{\pi\cos^{s+2}(\psi/2+\pi/4)} \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{|\alpha+i\beta|^{s+1}}\,d\beta\,d\alpha\\ &\quad =\frac{1}{\pi\cos^{s+2}(\psi/2+\pi/4)}\|f'\|_{\mathcal{V}_s}, \end{align*} $$
$$ \begin{align*} &{2^{-s}\int_0^{\infty} |f'(te^{\pm i\psi})|\,dt}\\ &\quad \le \frac{(s+1)}{\pi}\int_0^{\infty} \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{|te^{\pm i\psi}+\alpha-i\beta|^{s+2}}\,d\beta\,d\alpha\,dt\\ &\quad \le \frac{s+1}{\pi\cos^{s+2}(\psi/2+\pi/4)} \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \left( \int_0^{\infty} \frac{|f'(\alpha+i\beta)|}{(t+|\alpha+i\beta|)^{s+2}}\right) \,dt\,d\beta\,d\alpha\\ &\quad = \frac{1}{\pi\cos^{s+2}(\psi/2+\pi/4)} \int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{|\alpha+i\beta|^{s+1}}\,d\beta\,d\alpha\\ &\quad =\frac{1}{\pi\cos^{s+2}(\psi/2+\pi/4)}\|f'\|_{\mathcal{V}_s}, \end{align*} $$
and (4.28) follows.
For a function
![]() $f \in \operatorname {Hol}(\Sigma _{\psi })$
,
$f \in \operatorname {Hol}(\Sigma _{\psi })$
,
![]() $\gamma>0$
and
$\gamma>0$
and
![]() $0<\varphi \le \min \{\pi ,\psi /\gamma \}$
, define
$0<\varphi \le \min \{\pi ,\psi /\gamma \}$
, define
![]() $f_{\gamma } \in \operatorname {Hol}(\Sigma _{\varphi })$
by
$f_{\gamma } \in \operatorname {Hol}(\Sigma _{\varphi })$
by
Corollary 4.14. Let
![]() $f \in \mathcal {D}_s, \, s>-1$
, and let
$f \in \mathcal {D}_s, \, s>-1$
, and let
![]() $\gamma \in (0,1)$
. Then
$\gamma \in (0,1)$
. Then
![]() $f_{\gamma } \in \mathcal {D}_{\sigma }^{\infty } \cap \mathcal {H}_{\pi /2}$
for all
$f_{\gamma } \in \mathcal {D}_{\sigma }^{\infty } \cap \mathcal {H}_{\pi /2}$
for all
![]() $\sigma>-1$
. Moreover, for each
$\sigma>-1$
. Moreover, for each
![]() $s>-1$
and
$s>-1$
and
![]() $\sigma>-1$
, there exist constants
$\sigma>-1$
, there exist constants
![]() $C_{s,\sigma ,\gamma }$
and
$C_{s,\sigma ,\gamma }$
and
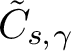 $\tilde C_{s,\gamma }$
such that
$\tilde C_{s,\gamma }$
such that
 $$ \begin{align*} \|f_{\gamma}\|_{\mathcal{D}_{\sigma}^{\infty}} \le C_{s,\sigma,\gamma} \|f\|_{\mathcal{D}_s} \quad \text{and} \quad \|f_{\gamma}\|_{\mathcal{H}_{\pi/2}} \le \tilde C_{s,\gamma} \|f\|_{\mathcal{D}_s}, \qquad f \in \mathcal{D}_s. \end{align*} $$
$$ \begin{align*} \|f_{\gamma}\|_{\mathcal{D}_{\sigma}^{\infty}} \le C_{s,\sigma,\gamma} \|f\|_{\mathcal{D}_s} \quad \text{and} \quad \|f_{\gamma}\|_{\mathcal{H}_{\pi/2}} \le \tilde C_{s,\gamma} \|f\|_{\mathcal{D}_s}, \qquad f \in \mathcal{D}_s. \end{align*} $$
Proof. Using Lemma 4.13, (i) and (ii), and Lemma 4.9, we see firstly that
![]() $f \in \mathcal {H}_{\pi \gamma /2}$
, and then
$f \in \mathcal {H}_{\pi \gamma /2}$
, and then
![]() $f_{\gamma } \in \mathcal {H}_{\pi /2} \subset \mathcal {D}_{\sigma }^{\infty }$
. Moreover, each of the embeddings from Lemma 4.13 is continuous, and the map
$f_{\gamma } \in \mathcal {H}_{\pi /2} \subset \mathcal {D}_{\sigma }^{\infty }$
. Moreover, each of the embeddings from Lemma 4.13 is continuous, and the map
![]() $f\mapsto f_\gamma\ \text{is isometric from}\ \mathcal H_{\pi\gamma/2}\ \text{to}\ \mathcal H_{\pi/2}.$
$f\mapsto f_\gamma\ \text{is isometric from}\ \mathcal H_{\pi\gamma/2}\ \text{to}\ \mathcal H_{\pi/2}.$
Now we relate the spaces
![]() $\mathcal H_{\psi }$
and
$\mathcal H_{\psi }$
and
![]() $\mathcal D_s$
to another class of spaces used in the literature on functional calculi. For
$\mathcal D_s$
to another class of spaces used in the literature on functional calculi. For
![]() $\psi \in (0,\pi )$
, let
$\psi \in (0,\pi )$
, let
 $$ \begin{align} \mathcal E_{\psi}:=\left \{f \in {\operatorname{Hol}} (\Sigma_{\psi}): \|f\|_{\psi}:=\sup_{\varphi \in (0,\psi)}\int_{\partial \Sigma_{\varphi}} \frac{|f(z)|}{|z|}|dz| <\infty\right \}. \end{align} $$
$$ \begin{align} \mathcal E_{\psi}:=\left \{f \in {\operatorname{Hol}} (\Sigma_{\psi}): \|f\|_{\psi}:=\sup_{\varphi \in (0,\psi)}\int_{\partial \Sigma_{\varphi}} \frac{|f(z)|}{|z|}|dz| <\infty\right \}. \end{align} $$
It is easy to see that
![]() $(\mathcal E_{\psi }, \|\cdot \|_{\psi })$
is a Banach space and that
$(\mathcal E_{\psi }, \|\cdot \|_{\psi })$
is a Banach space and that
Proposition 4.15. Let
![]() $f \in \mathcal E_{\psi }$
and let
$f \in \mathcal E_{\psi }$
and let
![]() $g(z):=f(z)/z$
. Then, for every
$g(z):=f(z)/z$
. Then, for every
![]() $\varphi \in (0,\psi )$
,
$\varphi \in (0,\psi )$
,
 $$ \begin{align} \|f'\|_{H^{1}(\Sigma_{\varphi})} \le \frac{1}{2\pi} \left(\frac{\pi-\psi-\varphi}{\sin(\psi+\varphi)}+ \frac{\pi-\psi+\varphi}{\sin(\psi-\varphi)}\right)\|g\|_{H^1(\Sigma_{\psi})}, \end{align} $$
$$ \begin{align} \|f'\|_{H^{1}(\Sigma_{\varphi})} \le \frac{1}{2\pi} \left(\frac{\pi-\psi-\varphi}{\sin(\psi+\varphi)}+ \frac{\pi-\psi+\varphi}{\sin(\psi-\varphi)}\right)\|g\|_{H^1(\Sigma_{\psi})}, \end{align} $$
where we set
 $\frac {0}{\sin 0}:= 1.$
Thus,
$\frac {0}{\sin 0}:= 1.$
Thus,
 $\mathcal E_{\psi } \overset {r}{\hookrightarrow } \mathcal H_{\varphi }, \, \varphi \in (0,\psi )$
, and
$\mathcal E_{\psi } \overset {r}{\hookrightarrow } \mathcal H_{\varphi }, \, \varphi \in (0,\psi )$
, and
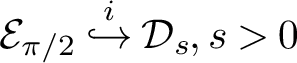 $\mathcal E_{\pi /2} \overset {i}{\hookrightarrow } \mathcal D_s,\, s>0$
.
$\mathcal E_{\pi /2} \overset {i}{\hookrightarrow } \mathcal D_s,\, s>0$
.
Proof. By Cauchy’s theorem, for every
![]() $z\in \Sigma _{\psi }$
,
$z\in \Sigma _{\psi }$
,
 $$ \begin{align*} f'(z) =\frac{1}{2\pi i}\int_{\partial\Sigma_{\psi}}\, \frac{\lambda g(\lambda)\,d\lambda}{(z-\lambda)^2}. \end{align*} $$
$$ \begin{align*} f'(z) =\frac{1}{2\pi i}\int_{\partial\Sigma_{\psi}}\, \frac{\lambda g(\lambda)\,d\lambda}{(z-\lambda)^2}. \end{align*} $$
Hence, for every
![]() $\varphi \in (0,\psi )$
, by Fubini’s theorem,
$\varphi \in (0,\psi )$
, by Fubini’s theorem,
 $$ \begin{align*} \int_0^{\infty} \left(|f'(\rho e^{i\varphi})| + |f'(\rho e^{-i\varphi})|\right)\,d\rho \le\frac{1}{2\pi} \int_{\partial\Sigma_{\psi}}|g(\lambda)| \, J(\lambda, \varphi) \, |d\lambda|, \end{align*} $$
$$ \begin{align*} \int_0^{\infty} \left(|f'(\rho e^{i\varphi})| + |f'(\rho e^{-i\varphi})|\right)\,d\rho \le\frac{1}{2\pi} \int_{\partial\Sigma_{\psi}}|g(\lambda)| \, J(\lambda, \varphi) \, |d\lambda|, \end{align*} $$
where
 $$ \begin{align*} J(\lambda, \varphi)&:= \int_0^{\infty}\left(\frac{|\lambda|}{|\rho e^{i\varphi}-\lambda|^2}+ \frac{|\lambda|}{|\rho e^{-i\varphi}-\lambda|^2}\right)\ d\rho\\ &=\int_0^{\infty}\frac{d\rho}{\rho^2-2\rho\cos(\psi+\varphi)+1} +\int_0^{\infty}\frac{d\rho}{\rho^2-2\rho\cos(\psi-\varphi)+1} \\ &=\frac{\pi-\psi-\varphi}{\sin(\psi+\varphi)}+ \frac{\pi-\psi+\varphi}{\sin(\psi-\varphi)}, \end{align*} $$
$$ \begin{align*} J(\lambda, \varphi)&:= \int_0^{\infty}\left(\frac{|\lambda|}{|\rho e^{i\varphi}-\lambda|^2}+ \frac{|\lambda|}{|\rho e^{-i\varphi}-\lambda|^2}\right)\ d\rho\\ &=\int_0^{\infty}\frac{d\rho}{\rho^2-2\rho\cos(\psi+\varphi)+1} +\int_0^{\infty}\frac{d\rho}{\rho^2-2\rho\cos(\psi-\varphi)+1} \\ &=\frac{\pi-\psi-\varphi}{\sin(\psi+\varphi)}+ \frac{\pi-\psi+\varphi}{\sin(\psi-\varphi)}, \end{align*} $$
in view of [Reference Prudnikov, Brychkov and Marichev48, item 2.2.9, (25)]. Hence,
![]() $f \in \mathcal {H}_{\varphi }$
and (4.30) follows. Thus,
$f \in \mathcal {H}_{\varphi }$
and (4.30) follows. Thus,
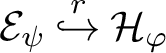 $\mathcal E_{\psi } \overset {r}{\hookrightarrow } \mathcal H_{\varphi }$
for all
$\mathcal E_{\psi } \overset {r}{\hookrightarrow } \mathcal H_{\varphi }$
for all
![]() $\varphi \in (0,\psi )$
. Recalling Lemma 4.13 and that
$\varphi \in (0,\psi )$
. Recalling Lemma 4.13 and that
 $\mathcal {H}_{\pi /2} = H^{1,1}(\mathbb C_+)$
, we have proved the inclusion
$\mathcal {H}_{\pi /2} = H^{1,1}(\mathbb C_+)$
, we have proved the inclusion
 $\mathcal E_{\pi /2} \overset {i}{\hookrightarrow } \mathcal D_s, \, s>0$
, as well.
$\mathcal E_{\pi /2} \overset {i}{\hookrightarrow } \mathcal D_s, \, s>0$
, as well.
Note that the inclusions in Proposition 4.15 are strict. Indeed, if
![]() $f(z)=z(z+1)^{-1},$
then one has
$f(z)=z(z+1)^{-1},$
then one has
![]() $f \in \mathcal H_{\psi }$
for every
$f \in \mathcal H_{\psi }$
for every
![]() $\psi \in (0,\pi )$
but
$\psi \in (0,\pi )$
but
![]() $f \notin \mathcal E_{\psi }$
for any
$f \notin \mathcal E_{\psi }$
for any
![]() $\psi \in (0,\pi )$
. Moreover, if
$\psi \in (0,\pi )$
. Moreover, if
 $$ \begin{align*} f(z)=\frac{z\,e^{-z}}{(z+1)\log^2(z+2)}, \end{align*} $$
$$ \begin{align*} f(z)=\frac{z\,e^{-z}}{(z+1)\log^2(z+2)}, \end{align*} $$
then
![]() $z^{-1}f \in H^1(\mathbb {C}_{+})$
, and
$z^{-1}f \in H^1(\mathbb {C}_{+})$
, and
![]() $f \in \mathcal {D}_0$
, but
$f \in \mathcal {D}_0$
, but
![]() $f \not \in \mathcal {D}_s$
for any
$f \not \in \mathcal {D}_s$
for any
![]() $s\in (-1,0)$
.
$s\in (-1,0)$
.
The spaces
![]() $\mathcal E_{\psi }$
are studied in [Reference Hytönen, van Neerven, Veraar and Weis38, Chapter 10]; see also [Reference Hytönen, van Neerven, Veraar and Weis38, Appendix H2], [Reference Haase34, Section 6] and [Reference Haak and Haase33, Appendix C]. To ensure the algebra property and to relate the spaces to the
$\mathcal E_{\psi }$
are studied in [Reference Hytönen, van Neerven, Veraar and Weis38, Chapter 10]; see also [Reference Hytönen, van Neerven, Veraar and Weis38, Appendix H2], [Reference Haase34, Section 6] and [Reference Haak and Haase33, Appendix C]. To ensure the algebra property and to relate the spaces to the
![]() $H^{\infty }$
-calculus, the authors considered the algebras
$H^{\infty }$
-calculus, the authors considered the algebras
![]() $H^{\infty }(\Sigma _{\psi })\cap \mathcal E_{\psi }$
. Lemma 4.15 shows that the spaces
$H^{\infty }(\Sigma _{\psi })\cap \mathcal E_{\psi }$
. Lemma 4.15 shows that the spaces
![]() $\mathcal E_{\psi }$
are fully covered within the framework of the algebras
$\mathcal E_{\psi }$
are fully covered within the framework of the algebras
![]() $\mathcal D_{\infty }$
and
$\mathcal D_{\infty }$
and
![]() $\mathcal H_{\psi }$
. These algebras will be associated to the more powerful functional calculi constructed in Corollary 7.8 and Theorem 8.2.
$\mathcal H_{\psi }$
. These algebras will be associated to the more powerful functional calculi constructed in Corollary 7.8 and Theorem 8.2.
4.6. Bernstein functions and
 $\mathcal {H}_{\psi }$
$\mathcal {H}_{\psi }$
To illustrate the relevance of the Hardy–Sobolev spaces, we show that the ‘resolvent’ of a Bernstein function belongs to an appropriate Hardy–Sobolev space. This observation will be used in Section 10 to provide a new proof of the permanence of subordination for holomorphic semigroups, one of the main results of [Reference Gomilko and Tomilov31]; see also [Reference Batty, Gomilko and Tomilov6] and [Reference Batty, Gomilko and Tomilov7].
Let g be a Bernstein function,
![]() $\psi \in (0,\pi /2)$
, and
$\psi \in (0,\pi /2)$
, and
![]() $\lambda \in \Sigma _{\pi -\psi }$
. Let
$\lambda \in \Sigma _{\pi -\psi }$
. Let
If
![]() $\lambda \in \mathbb {C}_+$
, it follows from Lemmas 3.20 and 4.13 that
$\lambda \in \mathbb {C}_+$
, it follows from Lemmas 3.20 and 4.13 that
![]() $f(\cdot , \lambda ) \in \mathcal {H}_{\psi }$
and
$f(\cdot , \lambda ) \in \mathcal {H}_{\psi }$
and
![]() $\|f(\cdot ,\lambda )\|_{\mathcal {H}_{\psi }} \le C_{\psi }/|\lambda |$
, where
$\|f(\cdot ,\lambda )\|_{\mathcal {H}_{\psi }} \le C_{\psi }/|\lambda |$
, where
![]() $C_{\psi }$
is independent of g and
$C_{\psi }$
is independent of g and
![]() $\lambda \in \mathbb {C}_+$
. In order to obtain the correct angle, we will need to extend this to
$\lambda \in \mathbb {C}_+$
. In order to obtain the correct angle, we will need to extend this to
![]() $\lambda \in \Sigma _{\pi -\varphi }$
, where
$\lambda \in \Sigma _{\pi -\varphi }$
, where
![]() $\varphi \in (\psi, \pi)$
.
$\varphi \in (\psi, \pi)$
.
Corollary 4.16. Let g be a Bernstein function,
![]() $\psi \in (0,\pi /2)$
,
$\psi \in (0,\pi /2)$
,
![]() $\varphi \in (\psi ,\pi )$
and
$\varphi \in (\psi ,\pi )$
and
![]() $\lambda \in \Sigma _{\pi -\varphi }$
. Then
$\lambda \in \Sigma _{\pi -\varphi }$
. Then
 $$ \begin{align} \|f(\cdot, \lambda)\|_{ \mathcal{H}_{\psi}} \le 2\left(\frac{1}{\sin(\min(\varphi,\pi/2))}+\frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)}\right)\frac{1}{|\lambda|}. \end{align} $$
$$ \begin{align} \|f(\cdot, \lambda)\|_{ \mathcal{H}_{\psi}} \le 2\left(\frac{1}{\sin(\min(\varphi,\pi/2))}+\frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)}\right)\frac{1}{|\lambda|}. \end{align} $$
Proof. For fixed
![]() $\psi \in (0,\pi /2)$
,
$\psi \in (0,\pi /2)$
,
![]() $\varphi \in (\psi ,\pi )$
and
$\varphi \in (\psi ,\pi )$
and
![]() $\lambda \in \Sigma _{\pi -\varphi }$
, observe that
$\lambda \in \Sigma _{\pi -\varphi }$
, observe that
 $$ \begin{align*} \|f'(\cdot,\lambda)\|_{H^1(\Sigma_{\psi})} = \int_0^{\infty} \left( \frac{|g'(te^{i\psi})|}{|\lambda+g(te^{i\psi})|^2} + \frac{|g'(te^{-i\psi})|} {|\lambda+g(te^{-i\psi})|^2} \right) \,dt. \end{align*} $$
$$ \begin{align*} \|f'(\cdot,\lambda)\|_{H^1(\Sigma_{\psi})} = \int_0^{\infty} \left( \frac{|g'(te^{i\psi})|}{|\lambda+g(te^{i\psi})|^2} + \frac{|g'(te^{-i\psi})|} {|\lambda+g(te^{-i\psi})|^2} \right) \,dt. \end{align*} $$
Using the property (B1) for Bernstein functions and (2.1), we have
Moreover, in view of (B3), for all
![]() $t \ge 0$
,
$t \ge 0$
,
Using (B2), we have
 $$ \begin{align*} \|f'(\cdot, \lambda)\|_{H^1(\Sigma_{\psi})} &\le \frac{2}{\sin^2((\varphi-\psi)/2)} \int_0^{\infty}\frac{g'(t\cos\psi)} {(|\lambda|+g(t\cos\psi ))^2} \,dt\\ &\le \frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)} \int_0^{\infty}\frac{ds} {(|\lambda|+s)^2}\\ &= \frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)}\frac{1}{|\lambda|}. \end{align*} $$
$$ \begin{align*} \|f'(\cdot, \lambda)\|_{H^1(\Sigma_{\psi})} &\le \frac{2}{\sin^2((\varphi-\psi)/2)} \int_0^{\infty}\frac{g'(t\cos\psi)} {(|\lambda|+g(t\cos\psi ))^2} \,dt\\ &\le \frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)} \int_0^{\infty}\frac{ds} {(|\lambda|+s)^2}\\ &= \frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)}\frac{1}{|\lambda|}. \end{align*} $$
Thus,
![]() $f(\cdot ,\lambda ) \in \mathcal {H}_{\psi }$
and
$f(\cdot ,\lambda ) \in \mathcal {H}_{\psi }$
and
![]() $f(\infty ,\lambda ) = (\lambda + g(\infty ))^{-1}$
. Because
$f(\infty ,\lambda ) = (\lambda + g(\infty ))^{-1}$
. Because
![]() $|\arg \lambda |<\pi -\varphi $
and
$|\arg \lambda |<\pi -\varphi $
and
![]() $g(\infty ) \in [0,\infty ]$
,
$g(\infty ) \in [0,\infty ]$
,
 $$ \begin{align} |f(\infty,\lambda)| \le \frac{1}{\sin(\min(\varphi,\pi/2))|\lambda|}. \end{align} $$
$$ \begin{align} |f(\infty,\lambda)| \le \frac{1}{\sin(\min(\varphi,\pi/2))|\lambda|}. \end{align} $$
4.7. Representations for functions in
 $\mathcal {H}_{\psi }$
$\mathcal {H}_{\psi }$
In this section we derive a reproducing formula for functions from
![]() $\mathcal {H}_{\psi }$
and obtain certain alternative representations for its kernel.
$\mathcal {H}_{\psi }$
and obtain certain alternative representations for its kernel.
Proposition 4.17. Let
![]() $f \in \mathcal {H}_{\psi }, \, \psi \in (0,\pi )$
. Let
$f \in \mathcal {H}_{\psi }, \, \psi \in (0,\pi )$
. Let
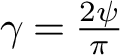 $\gamma =\frac {2\psi }{\pi }$
and
$\gamma =\frac {2\psi }{\pi }$
and
Then
 $$ \begin{align} f(z)=f(\infty)-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z^{1/\gamma}+\alpha-i\beta}\,d\beta\,d\alpha,\qquad z\in \Sigma_{\psi} \cup \{0\}. \end{align} $$
$$ \begin{align} f(z)=f(\infty)-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z^{1/\gamma}+\alpha-i\beta}\,d\beta\,d\alpha,\qquad z\in \Sigma_{\psi} \cup \{0\}. \end{align} $$
Proof. Because
![]() $f \in \mathcal {H}_{\psi }$
, Lemma 4.9 implies that
$f \in \mathcal {H}_{\psi }$
, Lemma 4.9 implies that
 $f^{\prime }_{\gamma } \in H^1(\mathbb {C}_{+})$
. Hence, by Lemma 4.13 and Theorem 4.8, we have
$f^{\prime }_{\gamma } \in H^1(\mathbb {C}_{+})$
. Hence, by Lemma 4.13 and Theorem 4.8, we have
![]() $f_{\gamma }\in \mathcal {D}_0\cap C(\overline {\mathbb C}_+)$
. Then, in view of Corollary 3.10,
$f_{\gamma }\in \mathcal {D}_0\cap C(\overline {\mathbb C}_+)$
. Then, in view of Corollary 3.10,
 $$ \begin{align*} f_{\gamma}(z)=f_{\gamma}(\infty)-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z+\alpha-i\beta}\,d\beta\,d\alpha, \qquad z\in \mathbb{C}_{+}\cup \{0\}, \end{align*} $$
$$ \begin{align*} f_{\gamma}(z)=f_{\gamma}(\infty)-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z+\alpha-i\beta}\,d\beta\,d\alpha, \qquad z\in \mathbb{C}_{+}\cup \{0\}, \end{align*} $$
and (4.34) follows.
Corollary 4.18. Let
![]() $f\in \mathcal {D}_{\infty }$
, and
$f\in \mathcal {D}_{\infty }$
, and
![]() $\gamma \in (0,1)$
. If
$\gamma \in (0,1)$
. If
![]() $f_{\gamma }$
is given by (4.33), then
$f_{\gamma }$
is given by (4.33), then
 $$ \begin{align} f(z)=f(\infty)-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z^{1/\gamma}+\alpha-i\beta}\,d\beta\,d\alpha,\quad z\in \Sigma_{\pi\gamma/2}\cup\{0\}. \end{align} $$
$$ \begin{align} f(z)=f(\infty)-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z^{1/\gamma}+\alpha-i\beta}\,d\beta\,d\alpha,\quad z\in \Sigma_{\pi\gamma/2}\cup\{0\}. \end{align} $$
The next reproducing formula for functions in
![]() $\mathcal {H}_{\psi }$
resembles [Reference Boyadzhiev12, Lemma 7.4], and it was, in fact, inspired by [Reference Boyadzhiev12, Lemma 7.4]. In particular, this formula replaces the double (area) integral in (4.34) with a line integral, it involves boundary values of
$\mathcal {H}_{\psi }$
resembles [Reference Boyadzhiev12, Lemma 7.4], and it was, in fact, inspired by [Reference Boyadzhiev12, Lemma 7.4]. In particular, this formula replaces the double (area) integral in (4.34) with a line integral, it involves boundary values of
![]() $f'$
rather than scalings of
$f'$
rather than scalings of
![]() $f'$
(such as in (4.34)), and it offers a different kernel that might sometimes be easier to deal with. The
$f'$
(such as in (4.34)), and it offers a different kernel that might sometimes be easier to deal with. The
![]() $\operatorname {\mathrm {arccot}}$
function has been defined in (3.22).
$\operatorname {\mathrm {arccot}}$
function has been defined in (3.22).
Proposition 4.19. Let
![]() $f \in \mathcal {H}_{\psi }$
,
$f \in \mathcal {H}_{\psi }$
,
![]() $\psi \in (0,\pi )$
. Let
$\psi \in (0,\pi )$
. Let
![]() $\nu =\pi /(2\psi )$
, and
$\nu =\pi /(2\psi )$
, and
 $$ \begin{align} f_{\psi}(t):=\frac{f(e^{i\psi}t)+f(e^{-i\psi}t)}{2}, \quad t>0. \end{align} $$
$$ \begin{align} f_{\psi}(t):=\frac{f(e^{i\psi}t)+f(e^{-i\psi}t)}{2}, \quad t>0. \end{align} $$
Then
 $$ \begin{align} f(z)=f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t)\, {\operatorname{\mathrm{arccot}}}(z^{\nu}/t^{\nu})\,dt,\qquad z\in \Sigma_{\psi}\cup \{0\}. \end{align} $$
$$ \begin{align} f(z)=f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t)\, {\operatorname{\mathrm{arccot}}}(z^{\nu}/t^{\nu})\,dt,\qquad z\in \Sigma_{\psi}\cup \{0\}. \end{align} $$
Proof. Because
![]() $\operatorname {\mathrm {arccot}} \lambda \in \mathcal D_0$
(see Example 3.5), (3.29) shows that
$\operatorname {\mathrm {arccot}} \lambda \in \mathcal D_0$
(see Example 3.5), (3.29) shows that
 $$ \begin{align} \operatorname{\mathrm{arccot}}(\lambda)=\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} \frac{(\lambda+u-iv)^{-1}}{(u+iv)^2+1}\,dv\, du, \quad \lambda\in \mathbb{C}_{+}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{arccot}}(\lambda)=\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} \frac{(\lambda+u-iv)^{-1}}{(u+iv)^2+1}\,dv\, du, \quad \lambda\in \mathbb{C}_{+}. \end{align} $$
Let
![]() $\gamma =1/\nu $
and
$\gamma =1/\nu $
and
![]() $f_{\gamma }$
be given by (4.33). By Proposition 4.17, for
$f_{\gamma }$
be given by (4.33). By Proposition 4.17, for
![]() $z \in \Sigma _{\psi } \cup \{0\}$
,
$z \in \Sigma _{\psi } \cup \{0\}$
,
 $$ \begin{align} f(z)-f(\infty)= -\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z^{\nu}+\alpha-i\beta}\,d\beta\,d\alpha. \end{align} $$
$$ \begin{align} f(z)-f(\infty)= -\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(\alpha+i\beta)}{z^{\nu}+\alpha-i\beta}\,d\beta\,d\alpha. \end{align} $$
It follows from Lemma 4.9 that
 $f_{\gamma }' \in H^1(\Sigma _{\pi /2}) = H^1(\mathbb {C}_+)$
, so by Cauchy’s formula for functions in
$f_{\gamma }' \in H^1(\Sigma _{\pi /2}) = H^1(\mathbb {C}_+)$
, so by Cauchy’s formula for functions in
![]() $H^1(\mathbb {C}_+)$
[Reference Duren21, Theorem 11.8], we have, for
$H^1(\mathbb {C}_+)$
[Reference Duren21, Theorem 11.8], we have, for
![]() $\lambda \in \mathbb {C}_{+}$
,
$\lambda \in \mathbb {C}_{+}$
,
 $$ \begin{align*} f_{\gamma}'(\lambda) &= \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(it)}{\lambda-it} \,dt - \frac{1}{2\pi}\int_{-\infty}^{\infty} \frac{f_{\gamma}'(it)}{\lambda+it} \,dt \\ &= \frac{i}{\pi}\int_{-\infty}^{\infty} \frac{tf_{\gamma}'(it)}{\lambda^2+t^2} \,dt\\ &=\frac{i\gamma}{\pi }\int_0^{\infty} \frac{e^{i\pi(\gamma-1)/2}f'(e^{i\pi\gamma/2}t^{\gamma})t^{\gamma} - e^{-i\pi(\gamma-1)/2}f'(e^{-i\pi\gamma/2}t^{\gamma})t^{\gamma}}{\lambda^2+t^2} \,dt\\ &=\frac{\gamma}{\pi}\int_0^{\infty} \left(e^{i\psi}f'(e^{i\psi}t^{\gamma}) +e^{-i\psi}f'(e^{-i\psi}t^{\gamma})\right)\frac{t^{\gamma}}{\lambda^2+t^2} \,dt\\ &=\frac{2}{\pi}\int_0^{\infty} \frac{f_{\psi}'(s) s^{\nu}}{\lambda^2+s^{2\nu}} \,ds. \end{align*} $$
$$ \begin{align*} f_{\gamma}'(\lambda) &= \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{f_{\gamma}'(it)}{\lambda-it} \,dt - \frac{1}{2\pi}\int_{-\infty}^{\infty} \frac{f_{\gamma}'(it)}{\lambda+it} \,dt \\ &= \frac{i}{\pi}\int_{-\infty}^{\infty} \frac{tf_{\gamma}'(it)}{\lambda^2+t^2} \,dt\\ &=\frac{i\gamma}{\pi }\int_0^{\infty} \frac{e^{i\pi(\gamma-1)/2}f'(e^{i\pi\gamma/2}t^{\gamma})t^{\gamma} - e^{-i\pi(\gamma-1)/2}f'(e^{-i\pi\gamma/2}t^{\gamma})t^{\gamma}}{\lambda^2+t^2} \,dt\\ &=\frac{\gamma}{\pi}\int_0^{\infty} \left(e^{i\psi}f'(e^{i\psi}t^{\gamma}) +e^{-i\psi}f'(e^{-i\psi}t^{\gamma})\right)\frac{t^{\gamma}}{\lambda^2+t^2} \,dt\\ &=\frac{2}{\pi}\int_0^{\infty} \frac{f_{\psi}'(s) s^{\nu}}{\lambda^2+s^{2\nu}} \,ds. \end{align*} $$
Therefore, by (4.39) and (4.38), we obtain
 $$ \begin{align*} &f(z)-f(\infty)\\ &= -\frac{2}{\pi^2}\int_0^{\infty} f^{\prime}_{\psi}(s) \left(\int_0^{\infty} \int_{-\infty}^{\infty} \frac{s^{\nu}\,d\beta\, d\alpha}{(z^{\nu}+\alpha-i\beta)((\alpha+i\beta)^2+s^{2\nu})}\right)\,ds\\ &=-\frac{2}{\pi^2}\int_0^{\infty} f^{\prime}_{\psi}(s) \left(\int_0^{\infty} \int_{-\infty}^{\infty} \frac{d\beta\, d\alpha}{((z/s)^{\nu}+\alpha-i\beta)((\alpha+i\beta)^2+1)}\right)\,ds\\ &=-\frac{2}{\pi}\int_0^{\infty} f^{\prime}_{\psi}(s)\operatorname{\mathrm{arccot}}(z^{\nu}/s^{\nu})\,ds, \end{align*} $$
$$ \begin{align*} &f(z)-f(\infty)\\ &= -\frac{2}{\pi^2}\int_0^{\infty} f^{\prime}_{\psi}(s) \left(\int_0^{\infty} \int_{-\infty}^{\infty} \frac{s^{\nu}\,d\beta\, d\alpha}{(z^{\nu}+\alpha-i\beta)((\alpha+i\beta)^2+s^{2\nu})}\right)\,ds\\ &=-\frac{2}{\pi^2}\int_0^{\infty} f^{\prime}_{\psi}(s) \left(\int_0^{\infty} \int_{-\infty}^{\infty} \frac{d\beta\, d\alpha}{((z/s)^{\nu}+\alpha-i\beta)((\alpha+i\beta)^2+1)}\right)\,ds\\ &=-\frac{2}{\pi}\int_0^{\infty} f^{\prime}_{\psi}(s)\operatorname{\mathrm{arccot}}(z^{\nu}/s^{\nu})\,ds, \end{align*} $$
so (4.37) holds for
![]() $z \in \Sigma _{\psi } \cup \{0\}$
.
$z \in \Sigma _{\psi } \cup \{0\}$
.
Proposition 4.19 motivates a more careful study of the kernel
![]() $\operatorname {\mathrm {arccot}} (z^{\nu })$
. The integral representation of this kernel will be crucial in deriving fine estimates for the
$\operatorname {\mathrm {arccot}} (z^{\nu })$
. The integral representation of this kernel will be crucial in deriving fine estimates for the
![]() $\mathcal {H}$
-calculus for operators in Subsection 8.2.
$\mathcal {H}$
-calculus for operators in Subsection 8.2.
Lemma 4.20. Let
![]() $\psi \in (0,\pi )$
and
$\psi \in (0,\pi )$
and
![]() $\nu ={\pi }/{(2\psi )}$
. Then
$\nu ={\pi }/{(2\psi )}$
. Then
 $$ \begin{align} \operatorname{\mathrm{arccot}}(z^{\nu})&=\frac{1}{2\pi}\int_0^{\infty} V_{\psi}(z,t)\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \,\frac{dt}{t}+\frac{1}{4 i}\int_{\Gamma_{\psi}}\, \frac{d\lambda}{\lambda-z},\quad z\in \Sigma_{\psi}, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{arccot}}(z^{\nu})&=\frac{1}{2\pi}\int_0^{\infty} V_{\psi}(z,t)\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \,\frac{dt}{t}+\frac{1}{4 i}\int_{\Gamma_{\psi}}\, \frac{d\lambda}{\lambda-z},\quad z\in \Sigma_{\psi}, \end{align} $$
where
 $$ \begin{align} V_{\psi}(z,t)&:=-\frac{t}{2} \left(\frac{ e^{-i\psi}} {z-t e^{-i\psi}} +\frac{ e^{i\psi}}{z-t e^{i\psi}}\right), \\ \Gamma_{\psi}&:= \{\lambda: |\lambda|=1,\,\arg\lambda \in (\psi,2\pi-\psi)\}. \notag \end{align} $$
$$ \begin{align} V_{\psi}(z,t)&:=-\frac{t}{2} \left(\frac{ e^{-i\psi}} {z-t e^{-i\psi}} +\frac{ e^{i\psi}}{z-t e^{i\psi}}\right), \\ \Gamma_{\psi}&:= \{\lambda: |\lambda|=1,\,\arg\lambda \in (\psi,2\pi-\psi)\}. \notag \end{align} $$
Proof. We have
 $$ \begin{align*} \operatorname{\mathrm{arccot}}(z^{\nu}) =\frac{1}{2i}\log\left|\frac{z^{\nu}+i}{z^{\nu}-i}\right| +\frac{1}{2}\arg\left(\frac{z^{\nu}+i} {z^{\nu}-i}\right),\qquad z\in \Sigma_{\psi}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{arccot}}(z^{\nu}) =\frac{1}{2i}\log\left|\frac{z^{\nu}+i}{z^{\nu}-i}\right| +\frac{1}{2}\arg\left(\frac{z^{\nu}+i} {z^{\nu}-i}\right),\qquad z\in \Sigma_{\psi}. \end{align*} $$
Because
![]() $\nu \psi =\pi /2$
, for every
$\nu \psi =\pi /2$
, for every
![]() $t>0, \, t\ne 1$
,
$t>0, \, t\ne 1$
,
 $$ \begin{align*} \lim_{z\in \Sigma_{\psi},\,z\to te^{i\psi}} \operatorname{\mathrm{arccot}}(z^{\nu}) =\frac{1}{2i}\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| +\frac{1}{2}\arg\left(\frac{t^{\nu}+1} {t^{\nu}-1}\right), \end{align*} $$
$$ \begin{align*} \lim_{z\in \Sigma_{\psi},\,z\to te^{i\psi}} \operatorname{\mathrm{arccot}}(z^{\nu}) =\frac{1}{2i}\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| +\frac{1}{2}\arg\left(\frac{t^{\nu}+1} {t^{\nu}-1}\right), \end{align*} $$
and
 $$ \begin{align*} \lim_{z\in \Sigma_{\psi},\,z\to te^{-i\psi}}\operatorname{\mathrm{arccot}}(z^{\nu}) =-\frac{1}{2i}\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| +\frac{1}{2}\arg\left(\frac{t^{\nu}-1} {t^{\nu}+1}\right). \end{align*} $$
$$ \begin{align*} \lim_{z\in \Sigma_{\psi},\,z\to te^{-i\psi}}\operatorname{\mathrm{arccot}}(z^{\nu}) =-\frac{1}{2i}\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| +\frac{1}{2}\arg\left(\frac{t^{\nu}-1} {t^{\nu}+1}\right). \end{align*} $$
Here,
 $$ \begin{align*} \arg\left(\frac{t^{\nu}+1} {t^{\nu}-1}\right)=\arg\left(\frac{t^{\nu}-1} {t^{\nu}+1}\right)=\pi\chi_{(0,1)}(t),\quad t>0, \, t\ne1, \end{align*} $$
$$ \begin{align*} \arg\left(\frac{t^{\nu}+1} {t^{\nu}-1}\right)=\arg\left(\frac{t^{\nu}-1} {t^{\nu}+1}\right)=\pi\chi_{(0,1)}(t),\quad t>0, \, t\ne1, \end{align*} $$
where
![]() $\chi _{[0,1]}$
is the characteristic function of
$\chi _{[0,1]}$
is the characteristic function of
![]() $(0,1)$
. So,
$(0,1)$
. So,
 $$ \begin{align} \lim_{z\in \Sigma_{\psi},\,z\to te^{\pm i\psi}} \operatorname{\mathrm{arccot}}(z^{\nu}) =\mp\frac{i}{2}\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| +\frac{\pi}{2}\chi_{[0,1]}(t). \end{align} $$
$$ \begin{align} \lim_{z\in \Sigma_{\psi},\,z\to te^{\pm i\psi}} \operatorname{\mathrm{arccot}}(z^{\nu}) =\mp\frac{i}{2}\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| +\frac{\pi}{2}\chi_{[0,1]}(t). \end{align} $$
Now fix
![]() $z \in \Sigma _{\psi }$
. Using
$z \in \Sigma _{\psi }$
. Using
![]() $\limsup _{|\lambda |\to \infty ,\,\lambda \in \mathbb {C}_{+}}\,|\lambda \operatorname {\mathrm {arccot}} \lambda |<\infty $
, it follows from Cauchy’s theorem that
$\limsup _{|\lambda |\to \infty ,\,\lambda \in \mathbb {C}_{+}}\,|\lambda \operatorname {\mathrm {arccot}} \lambda |<\infty $
, it follows from Cauchy’s theorem that
 $$ \begin{align*} \operatorname{\mathrm{arccot}}(z^{\nu})=\frac{1}{2\pi i}\int_{\partial\Sigma_{\psi}}\, \frac{\operatorname{\mathrm{arccot}}(\lambda^{\nu})}{\lambda-z}\,d\lambda, \quad \int_{\lambda\in\partial\Sigma_{\psi}, |\lambda|<1} \frac{d\lambda}{\lambda-z} = \int_{\Gamma_{\psi}} \frac{d\lambda}{\lambda-z}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{arccot}}(z^{\nu})=\frac{1}{2\pi i}\int_{\partial\Sigma_{\psi}}\, \frac{\operatorname{\mathrm{arccot}}(\lambda^{\nu})}{\lambda-z}\,d\lambda, \quad \int_{\lambda\in\partial\Sigma_{\psi}, |\lambda|<1} \frac{d\lambda}{\lambda-z} = \int_{\Gamma_{\psi}} \frac{d\lambda}{\lambda-z}. \end{align*} $$
Thus, by (4.42),
 $$ \begin{align*} \operatorname{\mathrm{arccot}}(z^{\nu}) &=\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \left(\frac{1}{t-e^{i\psi}z} +\frac{1}{t-e^{-i\psi}z}\right)\,dt +\frac{1}{4 i}\int_{\Gamma_{\psi}}\, \frac{d\lambda}{\lambda-z}\\ &=\frac{1}{2\pi}\int_0^{\infty} V_{\psi}(z,t)\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \,\frac{dt}{t}+\frac{1}{4 i}\int_{\Gamma_{\psi}}\, \frac{d\lambda}{\lambda-z}. \\[-40pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{arccot}}(z^{\nu}) &=\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \left(\frac{1}{t-e^{i\psi}z} +\frac{1}{t-e^{-i\psi}z}\right)\,dt +\frac{1}{4 i}\int_{\Gamma_{\psi}}\, \frac{d\lambda}{\lambda-z}\\ &=\frac{1}{2\pi}\int_0^{\infty} V_{\psi}(z,t)\log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \,\frac{dt}{t}+\frac{1}{4 i}\int_{\Gamma_{\psi}}\, \frac{d\lambda}{\lambda-z}. \\[-40pt] \end{align*} $$
Remark 4.21. Letting
![]() $z \to 0$
in (4.40), we obtain
$z \to 0$
in (4.40), we obtain
 $$ \begin{align*} \frac{\pi}{2} &=\frac{1}{2\pi}\int_0^{\infty} \log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \frac{dt}{t} +\frac{\pi-\psi}{2}; \end{align*} $$
$$ \begin{align*} \frac{\pi}{2} &=\frac{1}{2\pi}\int_0^{\infty} \log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \frac{dt}{t} +\frac{\pi-\psi}{2}; \end{align*} $$
hence,
 $$ \begin{align} \frac{1}{2\pi}\int_0^{\infty} \log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \frac{dt}{t}=\frac{\psi}{2}. \end{align} $$
$$ \begin{align} \frac{1}{2\pi}\int_0^{\infty} \log\left|\frac{1+t^{\nu}}{1-t^{\nu}}\right| \frac{dt}{t}=\frac{\psi}{2}. \end{align} $$
5. Dense sets in
 $\mathcal {D}_s$
and
$\mathcal {D}_s$
and
 $\mathcal {H}_{\psi }$
$\mathcal {H}_{\psi }$
In this section we establish some results concerning density and approximations in our spaces.
5.1. Dense subsets of
 $\mathcal {D}_s$
and some applications
$\mathcal {D}_s$
and some applications
Let
![]() $\mathcal {R}(\mathbb {C}_+)$
be the linear span of
$\mathcal {R}(\mathbb {C}_+)$
be the linear span of
![]() $\{r_{\lambda } : \lambda \in \mathbb {C}_+\}$
and
$\{r_{\lambda } : \lambda \in \mathbb {C}_+\}$
and
 $\widetilde {\mathcal {R}}(\mathbb {C}_+)$
be the sum of
$\widetilde {\mathcal {R}}(\mathbb {C}_+)$
be the sum of
![]() $\mathcal {R}(\mathbb {C}_+)$
and the constant functions. Using Example 4.10(1) and Lemma 4.13, we have
$\mathcal {R}(\mathbb {C}_+)$
and the constant functions. Using Example 4.10(1) and Lemma 4.13, we have
 $$ \begin{align} \mathcal{\widetilde{R}}(\mathbb{C}_+) \subset \mathcal{H}_{\pi/2} \overset{i}{\hookrightarrow} \mathcal{D}_s, \quad s>-1. \end{align} $$
$$ \begin{align} \mathcal{\widetilde{R}}(\mathbb{C}_+) \subset \mathcal{H}_{\pi/2} \overset{i}{\hookrightarrow} \mathcal{D}_s, \quad s>-1. \end{align} $$
Theorem 5.1. The space
 $$ \begin{align*} \widetilde{\mathcal{R}}(\mathbb{C}_+):=\left\{a_0 + \sum_{k=1}^n a_k(\lambda_k+z)^{-1}: n \in \mathbb N, \; a_k \in \mathbb{C}, \; \lambda_k\in \mathbb{C}_{+}\right\} \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{R}}(\mathbb{C}_+):=\left\{a_0 + \sum_{k=1}^n a_k(\lambda_k+z)^{-1}: n \in \mathbb N, \; a_k \in \mathbb{C}, \; \lambda_k\in \mathbb{C}_{+}\right\} \end{align*} $$
is dense in
![]() $\mathcal {D}_s$
for each
$\mathcal {D}_s$
for each
![]() $s>-1$
.
$s>-1$
.
Proof. Let
![]() $\mathcal {R}_{\mathcal {D}_s}(\mathbb {C}_+)$
be the closure of
$\mathcal {R}_{\mathcal {D}_s}(\mathbb {C}_+)$
be the closure of
![]() $\mathcal {R}(\mathbb {C}_+)$
in
$\mathcal {R}(\mathbb {C}_+)$
in
![]() $\mathcal {D}_{s}$
. First let
$\mathcal {D}_{s}$
. First let
![]() $s \in (-1,0)$
and
$s \in (-1,0)$
and
![]() $f \in \mathcal D_s$
. It follows from Example 3.3 and Remark 3.14 (or a direct estimate) that the function
$f \in \mathcal D_s$
. It follows from Example 3.3 and Remark 3.14 (or a direct estimate) that the function
 $$ \begin{align*} (R_f)(\lambda) := - \frac{1}{\pi} f'(\lambda) r_{\overline{\lambda}} \end{align*} $$
$$ \begin{align*} (R_f)(\lambda) := - \frac{1}{\pi} f'(\lambda) r_{\overline{\lambda}} \end{align*} $$
is continuous from
![]() $\mathbb {C}_+$
to
$\mathbb {C}_+$
to
![]() $\mathcal {D}_s$
, and it is Bochner integrable with respect to area measure S on
$\mathcal {D}_s$
, and it is Bochner integrable with respect to area measure S on
![]() $\mathbb {C}_+$
. Because point evaluations are continuous on
$\mathbb {C}_+$
. Because point evaluations are continuous on
![]() $\mathcal {D}_s$
(Remark 3.14), it follows from Corollaries 3.8 and 3.10 that
$\mathcal {D}_s$
(Remark 3.14), it follows from Corollaries 3.8 and 3.10 that
 $$ \begin{align*} Q_0 f' = \int_{\mathbb{C}_+} R_f(\lambda) \,dS(\lambda) \end{align*} $$
$$ \begin{align*} Q_0 f' = \int_{\mathbb{C}_+} R_f(\lambda) \,dS(\lambda) \end{align*} $$
as the Bochner integral of a continuous function. Hence,
![]() $Q_0 f'$
belongs to the closure in
$Q_0 f'$
belongs to the closure in
![]() $\mathcal {D}_s$
of the linear span of the range of the integrand, which is contained in
$\mathcal {D}_s$
of the linear span of the range of the integrand, which is contained in
![]() $\mathcal {R}_{\mathcal {D}_s}(\mathbb {C}_+)$
. Now
$\mathcal {R}_{\mathcal {D}_s}(\mathbb {C}_+)$
. Now
![]() $f = f(\infty ) + Q_0f',$
which is in the closure of
$f = f(\infty ) + Q_0f',$
which is in the closure of
 $\widetilde {\mathcal {R}}(\mathbb {C}_+)$
in
$\widetilde {\mathcal {R}}(\mathbb {C}_+)$
in
![]() $\mathcal {D}_s$
.
$\mathcal {D}_s$
.
If now
![]() $f\in \mathcal D_s, s \ge 0,$
then by an argument similar to the above
$f\in \mathcal D_s, s \ge 0,$
then by an argument similar to the above
![]() $f-f(\infty)$
belongs to the closed linear span of
$f-f(\infty)$
belongs to the closed linear span of
 $\{r_{\overline \lambda}^{s+2}:\lambda \in \mathbb C_+\}$
in
$\{r_{\overline \lambda}^{s+2}:\lambda \in \mathbb C_+\}$
in
![]() $\mathcal D_s.$
If
$\mathcal D_s.$
If
![]() $\lambda \in \mathbb C_+$
and
$\lambda \in \mathbb C_+$
and
![]() $\sigma \in (-1,0),$
then
$\sigma \in (-1,0),$
then
 $r_{\overline \lambda}^{s+2} \in \mathcal D_\sigma,$
so that
$r_{\overline \lambda}^{s+2} \in \mathcal D_\sigma,$
so that
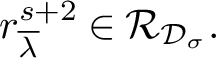 $r_{\overline \lambda}^{s+2} \in \mathcal R_{\mathcal D_\sigma}.$
Since
$r_{\overline \lambda}^{s+2} \in \mathcal R_{\mathcal D_\sigma}.$
Since
![]() $\mathcal D_\sigma \subset \mathcal D_s,$
we have
$\mathcal D_\sigma \subset \mathcal D_s,$
we have
 $r_{\overline{\lambda}}^{s+2}\in \mathcal R_{\mathcal D_s},$
and thus
$r_{\overline{\lambda}}^{s+2}\in \mathcal R_{\mathcal D_s},$
and thus
![]() $f-f(\infty) \in \mathcal{R}_{\mathcal D_s}.$
$f-f(\infty) \in \mathcal{R}_{\mathcal D_s}.$
From Proposition 3.6, we have the continuous inclusion
 $$ \begin{align*} \mathcal{D}_s \overset{i}{\hookrightarrow} \mathcal{D}_{\sigma} \quad \text{if } \sigma>s>-1, \end{align*} $$
$$ \begin{align*} \mathcal{D}_s \overset{i}{\hookrightarrow} \mathcal{D}_{\sigma} \quad \text{if } \sigma>s>-1, \end{align*} $$
and from (5.1), Theorem 4.12 and Proposition 3.15, we have
 $$ \begin{align*} \widetilde{\mathcal{R}}(\mathbb{C}_+) \subset H^{1,1}(\mathbb{C}_+) \overset{i}{\hookrightarrow} \mathcal{L} L^1 + \mathbb{C} \subset \mathcal{LM} \overset{i}{\hookrightarrow} \mathcal{B} \overset{i}{\hookrightarrow} \mathcal{D}_s^{\infty} \overset{i}{\hookrightarrow} \mathcal{D}_s \quad \text{if } s>0. \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{R}}(\mathbb{C}_+) \subset H^{1,1}(\mathbb{C}_+) \overset{i}{\hookrightarrow} \mathcal{L} L^1 + \mathbb{C} \subset \mathcal{LM} \overset{i}{\hookrightarrow} \mathcal{B} \overset{i}{\hookrightarrow} \mathcal{D}_s^{\infty} \overset{i}{\hookrightarrow} \mathcal{D}_s \quad \text{if } s>0. \end{align*} $$
Here
![]() $\mathcal {L} L^1+\mathbb {C}$
is the sum of
$\mathcal {L} L^1+\mathbb {C}$
is the sum of
![]() $\mathcal {L} L^1$
and the constant functions, and it is a closed subspace of
$\mathcal {L} L^1$
and the constant functions, and it is a closed subspace of
![]() $\mathcal {LM}$
. The following density results hold.
$\mathcal {LM}$
. The following density results hold.
Corollary 5.2.
-
1. If
 $\sigma>s>-1$
, then
$\sigma>s>-1$
, then
 $\mathcal {D}_s$
is dense in
$\mathcal {D}_s$
is dense in
 $\mathcal {D}_{\sigma }$
.
$\mathcal {D}_{\sigma }$
. -
2. For
 $s>-1$
, the spaces
$s>-1$
, the spaces
 $H^{1,1}(\mathbb {C}_+)$
and
$H^{1,1}(\mathbb {C}_+)$
and
 $\mathcal {D}_s^{\infty }$
are dense in
$\mathcal {D}_s^{\infty }$
are dense in
 $\mathcal {D}_s$
.
$\mathcal {D}_s$
. -
3. For
 $s>0$
, the spaces
$s>0$
, the spaces
 $\mathcal {L}L^1+\mathbb {C}$
,
$\mathcal {L}L^1+\mathbb {C}$
,
 $\mathcal {LM}$
and
$\mathcal {LM}$
and
 $\mathcal {B}$
are dense in
$\mathcal {B}$
are dense in
 $\mathcal {D}_s$
.
$\mathcal {D}_s$
. -
4. For
 $s>0$
, the spaces
$s>0$
, the spaces
 $\widetilde {\mathcal {R}}(\mathbb {C}_+)$
,
$\widetilde {\mathcal {R}}(\mathbb {C}_+)$
,
 $H^{1,1}(\mathbb {C}_+)$
,
$H^{1,1}(\mathbb {C}_+)$
,
 $\mathcal {L}L^1 + \mathbb {C}$
,
$\mathcal {L}L^1 + \mathbb {C}$
,
 $\mathcal {LM}$
and
$\mathcal {LM}$
and
 $\mathcal {B}$
are not dense in
$\mathcal {B}$
are not dense in
 $\mathcal {D}_s^{\infty }$
.
$\mathcal {D}_s^{\infty }$
.
Proof. The first three statements are immediate from Theorem 5.1.
Because any function in
![]() $\mathcal {B}$
extends continuously to
$\mathcal {B}$
extends continuously to
![]() $i\mathbb {R}$
, the same holds for the closure of
$i\mathbb {R}$
, the same holds for the closure of
![]() $\mathcal {B}$
in
$\mathcal {B}$
in
![]() $\mathcal {D}_s^{\infty }$
when
$\mathcal {D}_s^{\infty }$
when
![]() $s>0$
. The function
$s>0$
. The function
![]() $f(z)=e^{-1/z}\in \mathcal {D}_s^{\infty }$
for
$f(z)=e^{-1/z}\in \mathcal {D}_s^{\infty }$
for
![]() $s>0$
(see Remarks 3.18 and Example 3.4 with
$s>0$
(see Remarks 3.18 and Example 3.4 with
![]() $\nu =0$
), but f is not continuous at
$\nu =0$
), but f is not continuous at
![]() $z=0$
. This establishes the final statement.
$z=0$
. This establishes the final statement.
The function
![]() $g(z) = \exp (\operatorname {\mathrm {arccot}} z)$
considered in Example 3.19 provides another example of a function from
$g(z) = \exp (\operatorname {\mathrm {arccot}} z)$
considered in Example 3.19 provides another example of a function from
![]() $\mathcal {D}_0^{\infty }$
that is discontinuous on
$\mathcal {D}_0^{\infty }$
that is discontinuous on
![]() $i\mathbb {R}$
and so does not belong to the closure of
$i\mathbb {R}$
and so does not belong to the closure of
![]() $\mathcal {B}$
in
$\mathcal {B}$
in
![]() $\mathcal {D}^{\infty }_s$
for
$\mathcal {D}^{\infty }_s$
for
![]() $s>0$
.
$s>0$
.
In order to obtain operator norm estimates for functions
![]() $f^{(n)}$
applied to semigroup generators (see Theorem 10.3), we will need a stronger version of Corollary 3.23 on differentiability of
$f^{(n)}$
applied to semigroup generators (see Theorem 10.3), we will need a stronger version of Corollary 3.23 on differentiability of
![]() $t \to f(t\cdot )$
in the
$t \to f(t\cdot )$
in the
![]() $\mathcal{D}_s$
-norm. We first prove a lemma, and we present the stronger statement in Corollary 5.5.
$\mathcal{D}_s$
-norm. We first prove a lemma, and we present the stronger statement in Corollary 5.5.
Lemma 5.3. Let
![]() $\lambda \in \mathbb {C}_{+}$
,
$\lambda \in \mathbb {C}_{+}$
,
![]() $\tau>0$
,
$\tau>0$
,
![]() $t \in (\tau /2,2\tau )$
, and define
$t \in (\tau /2,2\tau )$
, and define
 $$ \begin{align*} g_{t,\tau,\lambda}(z):=\frac{r_{\lambda}(tz)-r_{\lambda}(\tau z)}{t-\tau}-zr_{\lambda}'(\tau z),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} g_{t,\tau,\lambda}(z):=\frac{r_{\lambda}(tz)-r_{\lambda}(\tau z)}{t-\tau}-zr_{\lambda}'(\tau z),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
Then, for every
![]() $s>-1$
,
$s>-1$
,
 $$ \begin{align} \lim_{t\to\tau}\,\|g_{t,\tau,\lambda}\|_{\mathcal{D}_s}=0. \end{align} $$
$$ \begin{align} \lim_{t\to\tau}\,\|g_{t,\tau,\lambda}\|_{\mathcal{D}_s}=0. \end{align} $$
Proof. We have
 $$ \begin{align*} g_{t,\tau,\lambda}'(z)&=\left(-\frac{t}{(tz+\lambda)^2}+ \frac{\tau}{(\tau z+\lambda)^2}\right)\frac{1}{t-\tau} +\frac{1}{(\tau z+\lambda)^2}-\frac{2\tau z}{(\tau z+\lambda)^3}\\ &= \frac{\tau t z^2 - \lambda^2}{(tz+\lambda)^2(\tau z+\lambda)^2} + \frac{\lambda-\tau z}{(\tau z+\lambda)^3} \to0, \qquad t \to \tau. \end{align*} $$
$$ \begin{align*} g_{t,\tau,\lambda}'(z)&=\left(-\frac{t}{(tz+\lambda)^2}+ \frac{\tau}{(\tau z+\lambda)^2}\right)\frac{1}{t-\tau} +\frac{1}{(\tau z+\lambda)^2}-\frac{2\tau z}{(\tau z+\lambda)^3}\\ &= \frac{\tau t z^2 - \lambda^2}{(tz+\lambda)^2(\tau z+\lambda)^2} + \frac{\lambda-\tau z}{(\tau z+\lambda)^3} \to0, \qquad t \to \tau. \end{align*} $$
Hence,
 $$ \begin{align*} |g_{t,\tau,\lambda}'(z)|\le \frac{C_{\tau,\lambda}}{1+|z|^2}, \qquad t \in (\tau/2,2\tau), \, z \in \mathbb{C}_+, \end{align*} $$
$$ \begin{align*} |g_{t,\tau,\lambda}'(z)|\le \frac{C_{\tau,\lambda}}{1+|z|^2}, \qquad t \in (\tau/2,2\tau), \, z \in \mathbb{C}_+, \end{align*} $$
for some
![]() $C_{\tau ,\lambda }$
. Because
$C_{\tau ,\lambda }$
. Because
 $$ \begin{align*} \int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^{\infty} \frac{d\rho}{1+\rho^2}\,d\psi<\infty \end{align*} $$
$$ \begin{align*} \int_{-\pi/2}^{\pi/2} \cos^s\psi\int_0^{\infty} \frac{d\rho}{1+\rho^2}\,d\psi<\infty \end{align*} $$
for any
![]() $s>-1$
, the dominated convergence theorem implies (5.2).
$s>-1$
, the dominated convergence theorem implies (5.2).
Corollary 5.4. Let
![]() $f\in \mathcal {D}_s$
,
$f\in \mathcal {D}_s$
,
![]() $s>-1$
. For
$s>-1$
. For
![]() $\tau>0$
, let
$\tau>0$
, let
![]() $zf^{\prime }_{\tau }$
denote the function mapping z to
$zf^{\prime }_{\tau }$
denote the function mapping z to
![]() $zf'(\tau z)$
. Then
$zf'(\tau z)$
. Then
 $$ \begin{align*} \lim_{t\to \tau}\left\| \frac{f_t-f_{\tau}}{t-\tau}-zf^{\prime}_{\tau}\right\|_{\mathcal{D}_{s+1}}=0. \end{align*} $$
$$ \begin{align*} \lim_{t\to \tau}\left\| \frac{f_t-f_{\tau}}{t-\tau}-zf^{\prime}_{\tau}\right\|_{\mathcal{D}_{s+1}}=0. \end{align*} $$
Proof. Let
![]() $\tau>0$
be fixed, and
$\tau>0$
be fixed, and
 $$ \begin{align*} (R_{t,\tau} f)(z) := \frac{f(t z)-f(\tau z)}{t-\tau}-zf^{\prime}_{\tau}, \qquad f \in\mathcal{D}_s, \, t>\tau/2. \end{align*} $$
$$ \begin{align*} (R_{t,\tau} f)(z) := \frac{f(t z)-f(\tau z)}{t-\tau}-zf^{\prime}_{\tau}, \qquad f \in\mathcal{D}_s, \, t>\tau/2. \end{align*} $$
By Lemma 3.22,
![]() $\{R_{t,\tau } : t> \tau /2\}$
is a bounded subset of
$\{R_{t,\tau } : t> \tau /2\}$
is a bounded subset of
![]() $L(\mathcal {D}_s,\mathcal {D}_{s+1})$
. By Lemma 5.3,
$L(\mathcal {D}_s,\mathcal {D}_{s+1})$
. By Lemma 5.3,
 $$ \begin{align*} \lim_{t\to\tau} \|R_{t,\tau}r_{\lambda}\|_{\mathcal{D}_{s+1}} = 0, \qquad \lambda \in \mathbb{C}_+. \end{align*} $$
$$ \begin{align*} \lim_{t\to\tau} \|R_{t,\tau}r_{\lambda}\|_{\mathcal{D}_{s+1}} = 0, \qquad \lambda \in \mathbb{C}_+. \end{align*} $$
Because the linear span of the functions
![]() $r_{\lambda }$
and the constants is dense in
$r_{\lambda }$
and the constants is dense in
![]() $\mathcal {D}_s$
(see Theorem 5.1), the assertion follows.
$\mathcal {D}_s$
(see Theorem 5.1), the assertion follows.
Corollary 5.5. Let
![]() $f\in \mathcal {D}_s$
,
$f\in \mathcal {D}_s$
,
![]() $s>-1$
, and let
$s>-1$
, and let
 $$ \begin{align*} G(t)(z) : = f(tz), \qquad F_n(t)(z) := z^nf^{(n)}(tz), \quad n\in \mathbb{N}, \,t>0, \, z \in \mathbb{C}_+. \end{align*} $$
$$ \begin{align*} G(t)(z) : = f(tz), \qquad F_n(t)(z) := z^nf^{(n)}(tz), \quad n\in \mathbb{N}, \,t>0, \, z \in \mathbb{C}_+. \end{align*} $$
Then G and
![]() $F_n$
map
$F_n$
map
![]() $(0,\infty )$
into
$(0,\infty )$
into
![]() $\mathcal {D}_{s+n}$
, G is n-times differentiable as a function from
$\mathcal {D}_{s+n}$
, G is n-times differentiable as a function from
![]() $(0,\infty )$
to
$(0,\infty )$
to
![]() $\mathcal {D}_{s+n}$
and
$\mathcal {D}_{s+n}$
and
Proof. Firstly,
![]() $f(tz) \in \mathcal {D}_s \subset \mathcal {D}_{s+n}$
, so G maps
$f(tz) \in \mathcal {D}_s \subset \mathcal {D}_{s+n}$
, so G maps
![]() $(0,\infty )$
into
$(0,\infty )$
into
![]() $\mathcal {D}_{s+n}$
.
$\mathcal {D}_{s+n}$
.
The proof is by induction on n. The case
![]() $n=1$
is given by Corollary 5.4. Assume that
$n=1$
is given by Corollary 5.4. Assume that
![]() $G^{(n)} = F_n$
with values in
$G^{(n)} = F_n$
with values in
![]() $\mathcal {D}_{s+n}$
, and let
$\mathcal {D}_{s+n}$
, and let
![]() $f_n(z) = z^n f^{(n)}(z)$
. Then
$f_n(z) = z^n f^{(n)}(z)$
. Then
 $$ \begin{align*} G^{(n)}(t)(z) = F_n(t)(z) = t^{-n}f_n(tz). \end{align*} $$
$$ \begin{align*} G^{(n)}(t)(z) = F_n(t)(z) = t^{-n}f_n(tz). \end{align*} $$
By Corollary 5.4 applied to
![]() $f_n\in \mathcal {D}_{s+n}$
,
$f_n\in \mathcal {D}_{s+n}$
,
![]() $G^{(n)}$
is differentiable with respect to t, when considered as a function with values in
$G^{(n)}$
is differentiable with respect to t, when considered as a function with values in
![]() $\mathcal {D}_{s+n+1}$
. Finally,
$\mathcal {D}_{s+n+1}$
. Finally,
 $$ \begin{align*} G^{(n+1)}(t)(z) = \frac{d}{dt} (z^n f^{(n)}(tz)) = z^{n+1} f^{(n+1)}(tz) = F_{n+1}(t)(z). \\[-40pt] \end{align*} $$
$$ \begin{align*} G^{(n+1)}(t)(z) = \frac{d}{dt} (z^n f^{(n)}(tz)) = z^{n+1} f^{(n+1)}(tz) = F_{n+1}(t)(z). \\[-40pt] \end{align*} $$
5.2. Approximations via change of variables
Here we consider approximations of f from
![]() $\mathcal {D}_s$
and
$\mathcal {D}_s$
and
![]() $\mathcal {H}_{\psi }$
by the functions
$\mathcal {H}_{\psi }$
by the functions
![]() $f_{\gamma }(z) = f(z^{\gamma })$
as
$f_{\gamma }(z) = f(z^{\gamma })$
as
![]() $\gamma \to 1-$
.
$\gamma \to 1-$
.
Proposition 5.6. Let
![]() $\gamma \in (0,1)$
. The following hold:
$\gamma \in (0,1)$
. The following hold:
-
1. Let
 $s>-1$
and
$s>-1$
and
 $f \in \mathcal {D}_s$
. Then(5.3)and
$f \in \mathcal {D}_s$
. Then(5.3)and $$ \begin{align} \|f_{\gamma}\|_{\mathcal{D}_s} \le \|f\|_{\mathcal{D}_s}, \end{align} $$
(5.4)
$$ \begin{align} \|f_{\gamma}\|_{\mathcal{D}_s} \le \|f\|_{\mathcal{D}_s}, \end{align} $$
(5.4) $$ \begin{align} \lim_{\gamma\to1-} \|f_{\gamma}-f\|_{\mathcal{D}_s} = 0. \end{align} $$
$$ \begin{align} \lim_{\gamma\to1-} \|f_{\gamma}-f\|_{\mathcal{D}_s} = 0. \end{align} $$
-
2. Let
 $\psi \in (0,\pi )$
and
$\psi \in (0,\pi )$
and
 $g\in \mathcal {H}_{\psi }$
. Then(5.5)
$g\in \mathcal {H}_{\psi }$
. Then(5.5) $$ \begin{align} \lim_{\gamma\to1-} \|g_{\gamma} -g\|_{\mathcal{H}_{\psi}}= 0. \end{align} $$
$$ \begin{align} \lim_{\gamma\to1-} \|g_{\gamma} -g\|_{\mathcal{H}_{\psi}}= 0. \end{align} $$
Proof. 1. First let
![]() $g \in H^{1,1}(\mathbb {C}_{+})$
. If
$g \in H^{1,1}(\mathbb {C}_{+})$
. If
![]() $0<\psi <\varphi \le \pi /2$
, then it follows from Theorem 4.6(iv) that
$0<\psi <\varphi \le \pi /2$
, then it follows from Theorem 4.6(iv) that
 $$ \begin{align} \int_0^{\infty} \left(|g'(te^{i\varphi})|+|g'(te^{-i\varphi})|\right)\,dt \ge \int_0^{\infty} \left(|g'(te^{i\psi})|+|g'(t e^{-i\psi})|\right)\,dt. \end{align} $$
$$ \begin{align} \int_0^{\infty} \left(|g'(te^{i\varphi})|+|g'(te^{-i\varphi})|\right)\,dt \ge \int_0^{\infty} \left(|g'(te^{i\psi})|+|g'(t e^{-i\psi})|\right)\,dt. \end{align} $$
Hence,
 $$ \begin{align*} \|g\|_{\mathcal{D}_s} &= |g(\infty)|+ \int_0^{\pi/2}\cos^s\varphi \int_0^{\infty} \left(|g'(te^{i\varphi})|+|g(te^{-i\varphi})|\right)\,dt\,d\varphi \\[-3pt] &\ge |g(\infty)|+ \int_0^{\pi/2}\cos^s\varphi \int_0^{\infty} \left(|g'(te^{i\gamma\varphi})|+|g'(te^{-i\gamma\varphi})|\right)\,dt\,d\varphi \\[-3pt] &= \|g_{\gamma}\|_{\mathcal{D}_s}. \end{align*} $$
$$ \begin{align*} \|g\|_{\mathcal{D}_s} &= |g(\infty)|+ \int_0^{\pi/2}\cos^s\varphi \int_0^{\infty} \left(|g'(te^{i\varphi})|+|g(te^{-i\varphi})|\right)\,dt\,d\varphi \\[-3pt] &\ge |g(\infty)|+ \int_0^{\pi/2}\cos^s\varphi \int_0^{\infty} \left(|g'(te^{i\gamma\varphi})|+|g'(te^{-i\gamma\varphi})|\right)\,dt\,d\varphi \\[-3pt] &= \|g_{\gamma}\|_{\mathcal{D}_s}. \end{align*} $$
Because
![]() $\mathcal {H}_{\pi /2}$
is dense in
$\mathcal {H}_{\pi /2}$
is dense in
![]() $\mathcal {D}_s$
(see Corollary 5.2), it follows that the map
$\mathcal {D}_s$
(see Corollary 5.2), it follows that the map
![]() $g \mapsto g_{\gamma }$
extends to a contraction on
$g \mapsto g_{\gamma }$
extends to a contraction on
![]() $\mathcal {D}_s$
, and this contraction maps f to
$\mathcal {D}_s$
, and this contraction maps f to
![]() $f_{\gamma }$
. Then (5.3) holds.
$f_{\gamma }$
. Then (5.3) holds.
Now (5.4) follows from (5.5), (5.3) and the fact that
![]() $\mathcal {H}_{\pi /2}$
is continuously and densely embedded in
$\mathcal {H}_{\pi /2}$
is continuously and densely embedded in
![]() $\mathcal {D}_s$
(see Proposition 4.13 and Corollary 5.2).
$\mathcal {D}_s$
(see Proposition 4.13 and Corollary 5.2).
2. Because the norms
![]() $\|\cdot \|_{\mathcal {H}_{\psi }}$
and
$\|\cdot \|_{\mathcal {H}_{\psi }}$
and
 $\|\cdot \|^{\prime }_{\mathcal {H}_{\psi }}$
are equivalent and
$\|\cdot \|^{\prime }_{\mathcal {H}_{\psi }}$
are equivalent and
![]() $g_{\gamma }(\infty ) = g(\infty )$
, it suffices to show that
$g_{\gamma }(\infty ) = g(\infty )$
, it suffices to show that
 $$ \begin{align*} \|g^{\prime}_{\gamma} - g'\|_{H^1(\Sigma_{\psi})} = \int_{\partial\Sigma_{\psi}} |g_{\gamma}'(z)-g'(z)| \,|dz| \to 0. \end{align*} $$
$$ \begin{align*} \|g^{\prime}_{\gamma} - g'\|_{H^1(\Sigma_{\psi})} = \int_{\partial\Sigma_{\psi}} |g_{\gamma}'(z)-g'(z)| \,|dz| \to 0. \end{align*} $$
By Lemma 4.9, we have
 $$ \begin{align*} \int_{\partial\Sigma_{\psi}}|g^{\prime}_{\gamma}(z)|\,|dz| =\int_{\partial\Sigma_{\gamma\psi}}|g'(z)|\,|dz|. \end{align*} $$
$$ \begin{align*} \int_{\partial\Sigma_{\psi}}|g^{\prime}_{\gamma}(z)|\,|dz| =\int_{\partial\Sigma_{\gamma\psi}}|g'(z)|\,|dz|. \end{align*} $$
Applying Theorem 4.6(iii) to
![]() $g'$
,
$g'$
,
 $$ \begin{align*} \lim_{\gamma\to 1-} \int_{\partial\Sigma_{\gamma\psi}}|g'(z)|\,|dz| =\int_{\partial\Sigma_{\psi}}|g'(z)|\,|dz| \end{align*} $$
$$ \begin{align*} \lim_{\gamma\to 1-} \int_{\partial\Sigma_{\gamma\psi}}|g'(z)|\,|dz| =\int_{\partial\Sigma_{\psi}}|g'(z)|\,|dz| \end{align*} $$
and
 $$ \begin{align*} \lim_{\gamma\to1-} g^{\prime}_{\gamma}(z) = g'(z), \quad \text{for almost all } z \in\partial \Sigma_{\psi}. \end{align*} $$
$$ \begin{align*} \lim_{\gamma\to1-} g^{\prime}_{\gamma}(z) = g'(z), \quad \text{for almost all } z \in\partial \Sigma_{\psi}. \end{align*} $$
5.3. Density of rational functions in
 $\mathcal {H}_{\psi }$
$\mathcal {H}_{\psi }$
In Theorem 5.1 and Corollary 5.2, we established that
 $\widetilde {\mathcal {R}}(\mathbb {C}_+)$
and several larger spaces are dense in
$\widetilde {\mathcal {R}}(\mathbb {C}_+)$
and several larger spaces are dense in
![]() $\mathcal {D}_s$
, for
$\mathcal {D}_s$
, for
![]() $s>-1$
or
$s>-1$
or
![]() $s>0$
. In particular, we noted that
$s>0$
. In particular, we noted that
![]() $H^{1,1}(\mathbb {C}_+)$
is dense in
$H^{1,1}(\mathbb {C}_+)$
is dense in
![]() $\mathcal {D}_s$
.
$\mathcal {D}_s$
.
Let
![]() $\psi \in (0,\pi )$
and
$\psi \in (0,\pi )$
and
with the norm
 $$ \begin{align*} \|f\|_{\mathcal{H}_{\psi,0}}=\|f'\|_{H^1(\Sigma_{\psi})}. \end{align*} $$
$$ \begin{align*} \|f\|_{\mathcal{H}_{\psi,0}}=\|f'\|_{H^1(\Sigma_{\psi})}. \end{align*} $$
By (4.19), this norm is equivalent to
![]() $\|\cdot \|_{\mathcal {H}_{\psi }}$
on
$\|\cdot \|_{\mathcal {H}_{\psi }}$
on
![]() $\mathcal {H}_{\psi ,0}$
.
$\mathcal {H}_{\psi ,0}$
.
Let
![]() $\psi \in (0,\pi )$
and
$\psi \in (0,\pi )$
and
![]() $\mathcal {R}(\Sigma _{\psi })$
be the linear span of
$\mathcal {R}(\Sigma _{\psi })$
be the linear span of
![]() $\{r_{\lambda } :\lambda \in \Sigma _{\pi -\psi }\}$
. Let
$\{r_{\lambda } :\lambda \in \Sigma _{\pi -\psi }\}$
. Let
![]() $\mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
be the closure of
$\mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
be the closure of
![]() $\mathcal {R}(\Sigma _{\psi })$
in
$\mathcal {R}(\Sigma _{\psi })$
in
![]() $\mathcal {H}_{\psi ,0}$
. We will prove that
$\mathcal {H}_{\psi ,0}$
. We will prove that
![]() $\mathcal {H}_{\psi ,0} = \mathcal R_{\mathcal H}(\Sigma _{\psi })$
. Thus, the rational functions that vanish at infinity and have simple poles outside
$\mathcal {H}_{\psi ,0} = \mathcal R_{\mathcal H}(\Sigma _{\psi })$
. Thus, the rational functions that vanish at infinity and have simple poles outside
![]() $\overline \Sigma _{\psi }$
are dense in
$\overline \Sigma _{\psi }$
are dense in
![]() $\mathcal {H}_{\psi }$
modulo constants. This fact may be known, but we did not find it in the literature. Our proof involves several lemmas given later and it may be of interest as a piece of function theory. The following lemma, relating to the function spaces
$\mathcal {H}_{\psi }$
modulo constants. This fact may be known, but we did not find it in the literature. Our proof involves several lemmas given later and it may be of interest as a piece of function theory. The following lemma, relating to the function spaces
![]() $\mathcal E_{\varphi }$
from Definition (4.29), is the key step in our proof.
$\mathcal E_{\varphi }$
from Definition (4.29), is the key step in our proof.
Lemma 5.7. Let
![]() $\psi \in (0,\pi )$
,
$\psi \in (0,\pi )$
,
![]() $\varphi \in (\psi ,\pi )$
and let
$\varphi \in (\psi ,\pi )$
and let
![]() $f\in H^1(\Sigma _{\varphi })$
. If
$f\in H^1(\Sigma _{\varphi })$
. If
 $$ \begin{align*} \int_{\partial\Sigma_{\varphi}}\frac{|f(\lambda)|}{|\lambda|}\,|d\lambda|<\infty, \end{align*} $$
$$ \begin{align*} \int_{\partial\Sigma_{\varphi}}\frac{|f(\lambda)|}{|\lambda|}\,|d\lambda|<\infty, \end{align*} $$
then
Proof. From (4.22) for
![]() $\gamma =1$
, the function
$\gamma =1$
, the function
![]() $F(\lambda ) := r_{\lambda }$
maps
$F(\lambda ) := r_{\lambda }$
maps
![]() $\Sigma _{\pi -\psi }$
into
$\Sigma _{\pi -\psi }$
into
![]() $\mathcal {H}_{\psi ,0}$
and is locally bounded. Moreover, F is holomorphic (see Theorem 4.8(iii) and Section 2) and its derivative is
$\mathcal {H}_{\psi ,0}$
and is locally bounded. Moreover, F is holomorphic (see Theorem 4.8(iii) and Section 2) and its derivative is
![]() $-r_{\lambda }^2$
.
$-r_{\lambda }^2$
.
The Cauchy integral formula (4.16) may be written as
 $$ \begin{align*} f(z)= \frac{1}{2\pi i} \int_{\partial\Sigma_{\varphi}} f(\lambda) F(-\lambda)(z) \,d\lambda, \quad z\in \Sigma_{\psi}. \end{align*} $$
$$ \begin{align*} f(z)= \frac{1}{2\pi i} \int_{\partial\Sigma_{\varphi}} f(\lambda) F(-\lambda)(z) \,d\lambda, \quad z\in \Sigma_{\psi}. \end{align*} $$
From (4.24), we obtain
 $$ \begin{align*} \int_{\partial\Sigma_{\varphi}} \|f(\lambda)F(-\lambda)\|_{\mathcal{H}_{\psi,0}} \,|d\lambda| \le \frac{1}{2\pi \sin^2 ((\varphi-\psi)/2) } \int_{\partial\Sigma_{\varphi}} \frac{|f(\lambda)|}{|\lambda|}\,d\lambda < \infty. \end{align*} $$
$$ \begin{align*} \int_{\partial\Sigma_{\varphi}} \|f(\lambda)F(-\lambda)\|_{\mathcal{H}_{\psi,0}} \,|d\lambda| \le \frac{1}{2\pi \sin^2 ((\varphi-\psi)/2) } \int_{\partial\Sigma_{\varphi}} \frac{|f(\lambda)|}{|\lambda|}\,d\lambda < \infty. \end{align*} $$
Thus,
 $$ \begin{align*} f = \frac{1}{2\pi i} \int_{\partial\Sigma_{\varphi}} f(\lambda)F(-\lambda) \,d\lambda \end{align*} $$
$$ \begin{align*} f = \frac{1}{2\pi i} \int_{\partial\Sigma_{\varphi}} f(\lambda)F(-\lambda) \,d\lambda \end{align*} $$
as a Bochner integral in
![]() $\mathcal {H}_{\psi ,0}$
, with continuous integrand, so it may be approximated in the
$\mathcal {H}_{\psi ,0}$
, with continuous integrand, so it may be approximated in the
![]() $\mathcal {H}_{\psi ,0}$
-norm by Riemann sums of the integrand, which lie in
$\mathcal {H}_{\psi ,0}$
-norm by Riemann sums of the integrand, which lie in
![]() $\mathcal {R}(\Sigma _{\psi })$
. Hence,
$\mathcal {R}(\Sigma _{\psi })$
. Hence,
![]() $f\in \mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
.
$f\in \mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
.
The next step in the proof is to construct a family of functions that serve as an approximate identity for
![]() $\mathcal H_{\varphi ,0}$
when restricted to any sector smaller than
$\mathcal H_{\varphi ,0}$
when restricted to any sector smaller than
![]() $\Sigma _{\varphi }$
.
$\Sigma _{\varphi }$
.
Lemma 5.8. Let
![]() $\varphi \in (0,\pi )$
and
$\varphi \in (0,\pi )$
and
![]() $\epsilon \in (0,1)$
, and let
$\epsilon \in (0,1)$
, and let
 $$ \begin{align} g_{\epsilon}(z):= \frac{2z^{\epsilon}}{1+z^{\epsilon}}(1+\epsilon z)^{-2},\qquad z\in \mathbb{C}\setminus (-\infty,0]. \end{align} $$
$$ \begin{align} g_{\epsilon}(z):= \frac{2z^{\epsilon}}{1+z^{\epsilon}}(1+\epsilon z)^{-2},\qquad z\in \mathbb{C}\setminus (-\infty,0]. \end{align} $$
Then
![]() $g_{\epsilon }\in \mathcal {H}_{\varphi ,0} \cap H^1(\Sigma _{\varphi })$
and
$g_{\epsilon }\in \mathcal {H}_{\varphi ,0} \cap H^1(\Sigma _{\varphi })$
and
 $$ \begin{align} \sup_{\epsilon \in (0,1)} \|g_{\epsilon}'\|_{H^1(\Sigma_{\varphi})} <\infty. \end{align} $$
$$ \begin{align} \sup_{\epsilon \in (0,1)} \|g_{\epsilon}'\|_{H^1(\Sigma_{\varphi})} <\infty. \end{align} $$
Moreover,
 $$ \begin{align} \lim_{\epsilon\to 0}\,g_{\epsilon}(z)=1,\quad z\in \mathbb{C}\setminus (-\infty,0], \end{align} $$
$$ \begin{align} \lim_{\epsilon\to 0}\,g_{\epsilon}(z)=1,\quad z\in \mathbb{C}\setminus (-\infty,0], \end{align} $$
and, for
![]() $0<a<b<\infty $
, there exists
$0<a<b<\infty $
, there exists
![]() $C_{\varphi ,a,b}$
such that
$C_{\varphi ,a,b}$
such that
Proof. It is clear that
![]() $g_{\epsilon } \in H^1(\Sigma _{\varphi })$
and
$g_{\epsilon } \in H^1(\Sigma _{\varphi })$
and
![]() $g_{\epsilon }(\infty )=0$
. Moreover,
$g_{\epsilon }(\infty )=0$
. Moreover,
 $$ \begin{align*} g^{\prime}_{\epsilon}(z)=\frac{2\epsilon z^{\epsilon}}{z(1+z^{\epsilon})^2(1+\epsilon z)^2}- \frac{4\epsilon z^{\epsilon}}{(1+z^{\epsilon})(1+\epsilon z)^3}. \end{align*} $$
$$ \begin{align*} g^{\prime}_{\epsilon}(z)=\frac{2\epsilon z^{\epsilon}}{z(1+z^{\epsilon})^2(1+\epsilon z)^2}- \frac{4\epsilon z^{\epsilon}}{(1+z^{\epsilon})(1+\epsilon z)^3}. \end{align*} $$
Applying Lemma 2.1, there is a constant
![]() $C_{\varphi }$
such that, for
$C_{\varphi }$
such that, for
![]() $z \in \partial \Sigma _{\varphi }$
and
$z \in \partial \Sigma _{\varphi }$
and
![]() $t=|z|$
,
$t=|z|$
,
 $$ \begin{align} |g^{\prime}_{\epsilon}(z)|\le C_{\varphi} \epsilon t^{\epsilon} \left(\frac{2}{t(1+t^{\epsilon})^2(1+\epsilon t)^2}+ \frac{4}{(1+t^{\epsilon})(1+\epsilon t)^3}\right). \end{align} $$
$$ \begin{align} |g^{\prime}_{\epsilon}(z)|\le C_{\varphi} \epsilon t^{\epsilon} \left(\frac{2}{t(1+t^{\epsilon})^2(1+\epsilon t)^2}+ \frac{4}{(1+t^{\epsilon})(1+\epsilon t)^3}\right). \end{align} $$
Hence,
 $$ \begin{align*} \|g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})} &\le 2\epsilon C_{\varphi}\int_0^{\infty} \frac{t^{\epsilon}\,dt}{t(1+t^{\epsilon})^2(1+\epsilon t)^2} + 4\epsilon C_{\varphi}\int_0^{\infty} \frac{t^{\epsilon}\,dt}{(1+t^{\epsilon})(1+\epsilon t)^3} \\ &\le 2 \epsilon C_{\varphi} \int_1^{\infty} \frac{dt}{(1+\epsilon t)^2} + 2\epsilon C_{\varphi} \int_0^1 t^{\epsilon-1}\,dt + 4 \epsilon C_{\varphi} \int_0^{\infty} \frac{dt}{(1+\epsilon t)^3} \\ &\le 6 C_{\varphi}. \end{align*} $$
$$ \begin{align*} \|g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})} &\le 2\epsilon C_{\varphi}\int_0^{\infty} \frac{t^{\epsilon}\,dt}{t(1+t^{\epsilon})^2(1+\epsilon t)^2} + 4\epsilon C_{\varphi}\int_0^{\infty} \frac{t^{\epsilon}\,dt}{(1+t^{\epsilon})(1+\epsilon t)^3} \\ &\le 2 \epsilon C_{\varphi} \int_1^{\infty} \frac{dt}{(1+\epsilon t)^2} + 2\epsilon C_{\varphi} \int_0^1 t^{\epsilon-1}\,dt + 4 \epsilon C_{\varphi} \int_0^{\infty} \frac{dt}{(1+\epsilon t)^3} \\ &\le 6 C_{\varphi}. \end{align*} $$
This yields (5.9).
The property (5.10) is straightforward, and (5.11) follows from (5.12).
Lemmas 5.7 and 5.8 enable us to show that any function
![]() $f \in \mathcal {H}_{\varphi ,0}$
, when restricted to
$f \in \mathcal {H}_{\varphi ,0}$
, when restricted to
![]() $\Sigma _{\psi }, \, \psi \in (0,\varphi )$
, can be approximated by rational functions (with simple poles) in
$\Sigma _{\psi }, \, \psi \in (0,\varphi )$
, can be approximated by rational functions (with simple poles) in
![]() $\mathcal {H}_{\psi ,0}$
.
$\mathcal {H}_{\psi ,0}$
.
Lemma 5.9. Let
![]() $\psi \in (0,\pi )$
,
$\psi \in (0,\pi )$
,
![]() $\varphi \in (\psi ,\pi )$
, and let
$\varphi \in (\psi ,\pi )$
, and let
![]() $ f\in \mathcal {H}_{\varphi ,0}. $
Then
$ f\in \mathcal {H}_{\varphi ,0}. $
Then
Proof. Assume first that
![]() $f\in H_{\varphi ,0}$
and
$f\in H_{\varphi ,0}$
and
![]() $f(0)=0$
, and let
$f(0)=0$
, and let
![]() $g_{\epsilon }$
be defined by (5.8). Then
$g_{\epsilon }$
be defined by (5.8). Then
![]() $f g_{\epsilon } \in \mathcal {H}_{\varphi ,0} \cap H^1(\Sigma _{\varphi })$
, and
$f g_{\epsilon } \in \mathcal {H}_{\varphi ,0} \cap H^1(\Sigma _{\varphi })$
, and
 $$ \begin{align*} \int_{\partial \Sigma_{\varphi}} \frac{|f(z)g_{\epsilon}(z)|}{|z|}\,|dz|<\infty. \end{align*} $$
$$ \begin{align*} \int_{\partial \Sigma_{\varphi}} \frac{|f(z)g_{\epsilon}(z)|}{|z|}\,|dz|<\infty. \end{align*} $$
By Lemma 5.7,
![]() $fg_{\epsilon } \in \mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
.
$fg_{\epsilon } \in \mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
.
Note that
 $$ \begin{align*} \|f(1-g_{\epsilon})\|_{\mathcal{H}_{\varphi,0}} \le \|f'(1-g_{\epsilon})\|_{H^1(\Sigma_{\varphi})}+ \|f g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}. \end{align*} $$
$$ \begin{align*} \|f(1-g_{\epsilon})\|_{\mathcal{H}_{\varphi,0}} \le \|f'(1-g_{\epsilon})\|_{H^1(\Sigma_{\varphi})}+ \|f g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}. \end{align*} $$
We will prove that
 $$ \begin{align} \lim_{\epsilon\to 0}\,\|f'(1-g_{\epsilon})\|_{H^1(\Sigma_{\varphi})}=0 \end{align} $$
$$ \begin{align} \lim_{\epsilon\to 0}\,\|f'(1-g_{\epsilon})\|_{H^1(\Sigma_{\varphi})}=0 \end{align} $$
and
 $$ \begin{align} \lim_{\epsilon\to 0}\,\|fg^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}=0. \end{align} $$
$$ \begin{align} \lim_{\epsilon\to 0}\,\|fg^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}=0. \end{align} $$
 $$ \begin{align*} \sup_{\epsilon\in(0,1) } \|g_{\epsilon}\|_{H^{\infty}(\Sigma_{\varphi})}\le \sup_{\epsilon \in (0,1)} \|g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}<\infty, \end{align*} $$
$$ \begin{align*} \sup_{\epsilon\in(0,1) } \|g_{\epsilon}\|_{H^{\infty}(\Sigma_{\varphi})}\le \sup_{\epsilon \in (0,1)} \|g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}<\infty, \end{align*} $$
so, using (5.10) and the dominated convergence theorem, we have
 $$ \begin{align*} \|f'(1-g_{\epsilon})\|_{H^1(\Sigma_{\varphi})}= \int_{\partial\Sigma_{\varphi}} |f'(\lambda)(1-g_{\epsilon}(\lambda))|\,|d\lambda| \to 0,\quad \epsilon\to 0. \end{align*} $$
$$ \begin{align*} \|f'(1-g_{\epsilon})\|_{H^1(\Sigma_{\varphi})}= \int_{\partial\Sigma_{\varphi}} |f'(\lambda)(1-g_{\epsilon}(\lambda))|\,|d\lambda| \to 0,\quad \epsilon\to 0. \end{align*} $$
For
![]() $0<a<b<\infty $
,
$0<a<b<\infty $
,
 $$ \begin{align*} \|f g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})} &=\int_{\partial\Sigma_{\varphi}}|f(\lambda)||g_{\epsilon}'(\lambda)|\,|d\lambda|\\ &\le \sup_{|z|>b,\,z\in\partial\Sigma_{\varphi}}\,|f(z)|\, \int_{|\lambda|>b, \,\lambda\in \partial\Sigma_{\varphi}} |g^{\prime}_{\epsilon}(\lambda)|\,|d\lambda|\\ &\hskip20pt +\sup_{|z|<a,\,z\in\partial\Sigma_{\varphi}}\,|f(z)|\, \int_{|\lambda|<a, \,\lambda\in \partial\Sigma_{\varphi}} |g^{\prime}_{\epsilon}(\lambda)|\,|d\lambda|\\ &\hskip20pt +\|f\|_{H^{\infty}(\Sigma_{\varphi})} \int_{|\lambda|\in (a,b), \,\lambda\in \partial\Sigma_{\varphi}} |g^{\prime}_{\epsilon}(\lambda)|\,|d\lambda|\\ &\le \left(\sup_{|z|>b,\,z\in\partial\Sigma_{\varphi}}\,|f(z)| +\sup_{|z|<a,\,z\in\partial\Sigma_{\varphi}}\,|f(z)|\right) \|g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}\\ &\hskip20pt +2(b-a) \|f\|_{H^{\infty}(\Sigma_{\varphi})} \sup_{|z|\in(a,b),\,z\in \partial\Sigma_{\varphi}}\,|g^{\prime}_{\epsilon}(z)|. \end{align*} $$
$$ \begin{align*} \|f g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})} &=\int_{\partial\Sigma_{\varphi}}|f(\lambda)||g_{\epsilon}'(\lambda)|\,|d\lambda|\\ &\le \sup_{|z|>b,\,z\in\partial\Sigma_{\varphi}}\,|f(z)|\, \int_{|\lambda|>b, \,\lambda\in \partial\Sigma_{\varphi}} |g^{\prime}_{\epsilon}(\lambda)|\,|d\lambda|\\ &\hskip20pt +\sup_{|z|<a,\,z\in\partial\Sigma_{\varphi}}\,|f(z)|\, \int_{|\lambda|<a, \,\lambda\in \partial\Sigma_{\varphi}} |g^{\prime}_{\epsilon}(\lambda)|\,|d\lambda|\\ &\hskip20pt +\|f\|_{H^{\infty}(\Sigma_{\varphi})} \int_{|\lambda|\in (a,b), \,\lambda\in \partial\Sigma_{\varphi}} |g^{\prime}_{\epsilon}(\lambda)|\,|d\lambda|\\ &\le \left(\sup_{|z|>b,\,z\in\partial\Sigma_{\varphi}}\,|f(z)| +\sup_{|z|<a,\,z\in\partial\Sigma_{\varphi}}\,|f(z)|\right) \|g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}\\ &\hskip20pt +2(b-a) \|f\|_{H^{\infty}(\Sigma_{\varphi})} \sup_{|z|\in(a,b),\,z\in \partial\Sigma_{\varphi}}\,|g^{\prime}_{\epsilon}(z)|. \end{align*} $$
Letting first
![]() $\epsilon \to 0$
, using (5.9)–(5.11) along with Vitali’s theorem, and then letting
$\epsilon \to 0$
, using (5.9)–(5.11) along with Vitali’s theorem, and then letting
![]() $a\to 0$
and
$a\to 0$
and
![]() $b \to \infty $
, using
$b \to \infty $
, using
![]() $f(0)=f(\infty )=0$
, we obtain
$f(0)=f(\infty )=0$
, we obtain
 $$ \begin{align*} \lim_{\epsilon\to 0}\|f g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}=0. \end{align*} $$
$$ \begin{align*} \lim_{\epsilon\to 0}\|f g^{\prime}_{\epsilon}\|_{H^1(\Sigma_{\varphi})}=0. \end{align*} $$
We have now proved the assertions (5.14) and (5.15). Thus, we obtain (5.13) under the additional assumption that
![]() $f(0)=0$
.
$f(0)=0$
.
Now let
![]() $f\in \mathcal {H}_{\varphi ,0}$
be arbitrary. Then consider
$f\in \mathcal {H}_{\varphi ,0}$
be arbitrary. Then consider
 $$ \begin{align*} f_0(z):=f(z)-2f(0)\left(\frac{1}{z+1}-\frac{1}{z+2}\right), \end{align*} $$
$$ \begin{align*} f_0(z):=f(z)-2f(0)\left(\frac{1}{z+1}-\frac{1}{z+2}\right), \end{align*} $$
and note that
 $$ \begin{align*} f_0 \in \mathcal{H}_{\varphi,0} \cap H^1(\Sigma_{\varphi}),\qquad f_0(0)=0. \end{align*} $$
$$ \begin{align*} f_0 \in \mathcal{H}_{\varphi,0} \cap H^1(\Sigma_{\varphi}),\qquad f_0(0)=0. \end{align*} $$
Then, by the above,
and hence (5.13) holds.
We now approximate functions
![]() $f \in \mathcal {H}_{\psi ,0}$
by functions from
$f \in \mathcal {H}_{\psi ,0}$
by functions from
![]() $\mathcal {H}_{\psi ',0}, \, \psi '>\psi $
, using the change of variables from Proposition 5.6.
$\mathcal {H}_{\psi ',0}, \, \psi '>\psi $
, using the change of variables from Proposition 5.6.
For
![]() $f\in \mathcal {H}_{\psi ,0}$
and
$f\in \mathcal {H}_{\psi ,0}$
and
![]() $f_{\gamma }(z) = f(z^{\gamma })$
for
$f_{\gamma }(z) = f(z^{\gamma })$
for
![]() $\gamma \in (0,1)$
, we now have
$\gamma \in (0,1)$
, we now have
 $$ \begin{align*} f_{\gamma}\in \mathcal{H}_{\varphi_{\gamma},0},\qquad \varphi_{\gamma}:=\min\{\gamma^{-1}\psi,\pi\}>\psi. \end{align*} $$
$$ \begin{align*} f_{\gamma}\in \mathcal{H}_{\varphi_{\gamma},0},\qquad \varphi_{\gamma}:=\min\{\gamma^{-1}\psi,\pi\}>\psi. \end{align*} $$
By (5.5),
 $$ \begin{align*} \lim_{\gamma\to 1-}\,\|f-f_{\gamma}\|_{\mathcal{H}_{\psi,0}}=0. \end{align*} $$
$$ \begin{align*} \lim_{\gamma\to 1-}\,\|f-f_{\gamma}\|_{\mathcal{H}_{\psi,0}}=0. \end{align*} $$
By Lemma 5.9,
![]() $f_{\gamma } \in \mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
. Thus, we obtain the following result that the rational functions with simple poles are dense in
$f_{\gamma } \in \mathcal {R}_{\mathcal {H}}(\Sigma _{\psi })$
. Thus, we obtain the following result that the rational functions with simple poles are dense in
![]() $\mathcal {H}_{\psi ,0}$
.
$\mathcal {H}_{\psi ,0}$
.
Theorem 5.10. Let
![]() $\psi \in (0,\pi )$
. Then
$\psi \in (0,\pi )$
. Then
6. Convergence Lemmas
In this section we formulate convergence lemmas for functions in
![]() $\mathcal {D}_s$
and
$\mathcal {D}_s$
and
![]() $\mathcal {H}_{\psi }$
, composed with fractional powers.
$\mathcal {H}_{\psi }$
, composed with fractional powers.
Lemma 6.1. Let
![]() $s>-1$
and
$s>-1$
and
![]() $(f_k)_{k=1}^{\infty }\subset \mathcal {D}_s$
be such that
$(f_k)_{k=1}^{\infty }\subset \mathcal {D}_s$
be such that
 $$ \begin{align*} \sup_{k \ge 1}\|f_k\|_{\mathcal{D}_s}<\infty, \end{align*} $$
$$ \begin{align*} \sup_{k \ge 1}\|f_k\|_{\mathcal{D}_s}<\infty, \end{align*} $$
and for every
![]() $z\in \mathbb {C}_{+}$
there exists
$z\in \mathbb {C}_{+}$
there exists
 $$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z). \end{align*} $$
$$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z). \end{align*} $$
Let
![]() $g\in \mathcal {D}_s$
satisfy
$g\in \mathcal {D}_s$
satisfy
For
![]() $\gamma \in (0,1)$
, let
$\gamma \in (0,1)$
, let
Then
 $$ \begin{align} \lim_{k\to\infty}\,\|(f_{k,\gamma}-f_{\gamma})g_\gamma\|_{\mathcal D_s}=0. \end{align} $$
$$ \begin{align} \lim_{k\to\infty}\,\|(f_{k,\gamma}-f_{\gamma})g_\gamma\|_{\mathcal D_s}=0. \end{align} $$
Proof. By Corollary 3.12,
![]() $f \in \mathcal D_s$
. So without loss of generality, we can assume that
$f \in \mathcal D_s$
. So without loss of generality, we can assume that
![]() $f=0$
. By Corollary 4.14,
$f=0$
. By Corollary 4.14,
![]() $g_{\gamma }$
and
$g_{\gamma }$
and
![]() $f_{k, \gamma }$
belong to the algebra
$f_{k, \gamma }$
belong to the algebra
![]() $\mathcal {D}_s^{\infty }$
, so
$\mathcal {D}_s^{\infty }$
, so
![]() $f_{k, \gamma }g_{\gamma }\in \mathcal {D}_s$
. Moreover,
$f_{k, \gamma }g_{\gamma }\in \mathcal {D}_s$
. Moreover,
 $$ \begin{align*} B:=\sup_{k \ge 1}\left(\|f_{k, \gamma}\|_{\mathcal{D}_s}+\|f_{k, \gamma}\|_{\infty}\right)< \infty. \end{align*} $$
$$ \begin{align*} B:=\sup_{k \ge 1}\left(\|f_{k, \gamma}\|_{\mathcal{D}_s}+\|f_{k, \gamma}\|_{\infty}\right)< \infty. \end{align*} $$
Let
![]() $0 < r < R < \infty $
and
$0 < r < R < \infty $
and
![]() $\Omega _{r,R} = \{z \in \mathbb {C}_+ : r \le |z| \le R\}$
. By Vitali’s theorem,
$\Omega _{r,R} = \{z \in \mathbb {C}_+ : r \le |z| \le R\}$
. By Vitali’s theorem,
 $$ \begin{align*} \lim_{k\to\infty}\,\left(|f_{k, \gamma}(z)|+|f_{k, \gamma}'(z)|\right)=0 \end{align*} $$
$$ \begin{align*} \lim_{k\to\infty}\,\left(|f_{k, \gamma}(z)|+|f_{k, \gamma}'(z)|\right)=0 \end{align*} $$
uniformly on
![]() $\Omega _{r,R}$
. Therefore, the integrals
$\Omega _{r,R}$
. Therefore, the integrals
 $$ \begin{align*} \int_{\Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,dS(z), \quad \int_{\Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,dS(z), \end{align*} $$
$$ \begin{align*} \int_{\Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,dS(z), \quad \int_{\Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,dS(z), \end{align*} $$
tend to
![]() $0$
as
$0$
as
![]() $k\ \to \infty $
. Moreover,
$k\ \to \infty $
. Moreover,
 $$ \begin{align*} \int_{\mathbb{C}_+ \setminus \Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,dS(z) \le \sup_{z \in \mathbb{C}_+ \setminus \Omega_{r,R}} |g_{\gamma}(z)| \, \|f_{k,\gamma}\|_{\mathcal{D}_s}, \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}_+ \setminus \Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,dS(z) \le \sup_{z \in \mathbb{C}_+ \setminus \Omega_{r,R}} |g_{\gamma}(z)| \, \|f_{k,\gamma}\|_{\mathcal{D}_s}, \end{align*} $$
and
 $$ \begin{align*} \int_{\mathbb{C}_+ \setminus \Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,dS(z) \le \|f_{k,\gamma}\|_{\infty} \int_{\mathbb{C}_+ \setminus\Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |g^{\prime}_{\gamma}(z)| \,dS(z). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}_+ \setminus \Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,dS(z) \le \|f_{k,\gamma}\|_{\infty} \int_{\mathbb{C}_+ \setminus\Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |g^{\prime}_{\gamma}(z)| \,dS(z). \end{align*} $$
Hence,
 $$ \begin{align*} \limsup_{k\to\infty} \| f_{k,\gamma}g_{\gamma}\|_{\mathcal{D}_s} \le B \left( \sup_{\mathbb{C}_+ \setminus \Omega_{r,R}} |g_{\gamma}(z)| + \int_{\mathbb{C}_+ \setminus \Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |g^{\prime}_{\gamma}(z)| \,dS(z) \right). \end{align*} $$
$$ \begin{align*} \limsup_{k\to\infty} \| f_{k,\gamma}g_{\gamma}\|_{\mathcal{D}_s} \le B \left( \sup_{\mathbb{C}_+ \setminus \Omega_{r,R}} |g_{\gamma}(z)| + \int_{\mathbb{C}_+ \setminus \Omega_{r,R}} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |g^{\prime}_{\gamma}(z)| \,dS(z) \right). \end{align*} $$
Letting
![]() $r\to 0$
and
$r\to 0$
and
![]() $R \to \infty $
, we obtain the assertion (6.2).
$R \to \infty $
, we obtain the assertion (6.2).
The following result is a convergence lemma for
![]() $\mathcal {H}_{\psi }$
, analogous to Lemma 6.1.
$\mathcal {H}_{\psi }$
, analogous to Lemma 6.1.
Lemma 6.2. Let
![]() $\psi \in (0,\pi )$
and
$\psi \in (0,\pi )$
and
![]() $(f_k)_{k=1}^{\infty }\subset \mathcal {H}_{\psi }$
be such that
$(f_k)_{k=1}^{\infty }\subset \mathcal {H}_{\psi }$
be such that
 $$ \begin{align*} \sup_{k \ge 1}\|f_k\|_{\mathcal{H}_{\psi}}<\infty, \end{align*} $$
$$ \begin{align*} \sup_{k \ge 1}\|f_k\|_{\mathcal{H}_{\psi}}<\infty, \end{align*} $$
and for every
![]() $z\in \mathbb {C}_{+}$
there exists
$z\in \mathbb {C}_{+}$
there exists
 $$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z). \end{align*} $$
$$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z). \end{align*} $$
Let
![]() $g\in \mathcal {H}_{\psi }$
satisfy
$g\in \mathcal {H}_{\psi }$
satisfy
For
![]() $\gamma \in (0,1)$
and
$\gamma \in (0,1)$
and
![]() $k \in \mathbb N,$
let
$k \in \mathbb N,$
let
![]() $f_{k,\gamma }$
and
$f_{k,\gamma }$
and
![]() $g_{\gamma }$
be given by (6.1). Then
$g_{\gamma }$
be given by (6.1). Then
 $$ \begin{align} \lim_{k\to\infty}\,\|(f_{k,\gamma}-f_{\gamma})g_\gamma\|_{\mathcal H_\psi}=0. \end{align} $$
$$ \begin{align} \lim_{k\to\infty}\,\|(f_{k,\gamma}-f_{\gamma})g_\gamma\|_{\mathcal H_\psi}=0. \end{align} $$
Proof. The proof is similar to Lemma 6.2.
By Lemma 4.11,
![]() $f_0 \in \mathcal H_{\psi }$
. Thus, we will assume that
$f_0 \in \mathcal H_{\psi }$
. Thus, we will assume that
![]() $f_0=0$
. Let
$f_0=0$
. Let
![]() $\gamma \in (\psi /\pi ,1)$
. By Lemma 4.9,
$\gamma \in (\psi /\pi ,1)$
. By Lemma 4.9,
![]() $g_{\gamma }$
and
$g_{\gamma }$
and
![]() $f_{k, \gamma }$
belong to the algebra
$f_{k, \gamma }$
belong to the algebra
![]() $\mathcal {H}_{\psi /\gamma } \subset \mathcal {H}_{\psi }$
, so
$\mathcal {H}_{\psi /\gamma } \subset \mathcal {H}_{\psi }$
, so
![]() $f_{k, \gamma }g_{\gamma }\in \mathcal {H}_{\psi }$
. Moreover,
$f_{k, \gamma }g_{\gamma }\in \mathcal {H}_{\psi }$
. Moreover,
 $$ \begin{align*}B:=\sup_{k \ge 1}\|f_{k,\gamma}\|_{\mathcal H_\psi}<\infty. \end{align*} $$
$$ \begin{align*}B:=\sup_{k \ge 1}\|f_{k,\gamma}\|_{\mathcal H_\psi}<\infty. \end{align*} $$
Let
![]() $0 < r < R < \infty $
and
$0 < r < R < \infty $
and
![]() $I_{r,R} = \{z \in \partial \Sigma _{\psi }: r \le |z| \le R\}$
. By Vitali’s theorem,
$I_{r,R} = \{z \in \partial \Sigma _{\psi }: r \le |z| \le R\}$
. By Vitali’s theorem,
 $$ \begin{align*} \lim_{k\to\infty}\,\left(|f_{k, \gamma}(z)|+|f_{k, \gamma}'(z)|\right)=0 \end{align*} $$
$$ \begin{align*} \lim_{k\to\infty}\,\left(|f_{k, \gamma}(z)|+|f_{k, \gamma}'(z)|\right)=0 \end{align*} $$
uniformly on
![]() $I_{r,R}$
. Therefore, the integrals
$I_{r,R}$
. Therefore, the integrals
 $$ \begin{align*} \int_{I_{r,R}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,|dz|, \quad \int_{I_{r,R}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,|dz|, \end{align*} $$
$$ \begin{align*} \int_{I_{r,R}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,|dz|, \quad \int_{I_{r,R}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,|dz|, \end{align*} $$
tend to
![]() $0$
as
$0$
as
![]() $k\ \to \infty $
. Moreover,
$k\ \to \infty $
. Moreover,
 $$ \begin{align*} \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,|dz| \le \sup_{z \in \partial\Sigma_{\psi} \setminus I_{r,R}} |g_{\gamma}(z)| \, \|f_{k,\gamma}\|_{\mathcal{H}_{\psi}}, \end{align*} $$
$$ \begin{align*} \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |f^{\prime}_{k,\gamma}(z) g_{\gamma}(z)| \,|dz| \le \sup_{z \in \partial\Sigma_{\psi} \setminus I_{r,R}} |g_{\gamma}(z)| \, \|f_{k,\gamma}\|_{\mathcal{H}_{\psi}}, \end{align*} $$
and
 $$ \begin{align*} \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,|dz| \le \|f_{k,\gamma}\|_{H^{\infty}(\Sigma_{\psi})} \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |g^{\prime}_{\gamma}(z)| \,|dz|. \end{align*} $$
$$ \begin{align*} \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |f_{k,\gamma}(z) g^{\prime}_{\gamma}(z)| \,|dz| \le \|f_{k,\gamma}\|_{H^{\infty}(\Sigma_{\psi})} \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |g^{\prime}_{\gamma}(z)| \,|dz|. \end{align*} $$
Hence,
 $$ \begin{align*} \limsup_{k\to\infty} \| f_{k,\gamma}g_{\gamma}\|_{\mathcal{H}_{\psi}} \le B \left( \sup_{\partial\Sigma_{\psi} \setminus I_{r,R}} |g_{\gamma}(z)| + \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |g^{\prime}_{\gamma}(z)| \,|dz| \right). \end{align*} $$
$$ \begin{align*} \limsup_{k\to\infty} \| f_{k,\gamma}g_{\gamma}\|_{\mathcal{H}_{\psi}} \le B \left( \sup_{\partial\Sigma_{\psi} \setminus I_{r,R}} |g_{\gamma}(z)| + \int_{\partial\Sigma_{\psi} \setminus I_{r,R}} |g^{\prime}_{\gamma}(z)| \,|dz| \right). \end{align*} $$
Letting
![]() $r\to 0$
and
$r\to 0$
and
![]() $R \to \infty $
, we obtain (6.3).
$R \to \infty $
, we obtain (6.3).
7. The
 $\mathcal D$
-calculus and its compatibility
$\mathcal D$
-calculus and its compatibility
Here we discuss functional calculus for sectorial operators A of angle less than
![]() $\pi /2$
and functions
$\pi /2$
and functions
![]() $f \in \mathcal {D}_{\infty }$
. Because f is bounded on a closed sector containing the spectrum of A (Corollary 3.10),
$f \in \mathcal {D}_{\infty }$
. Because f is bounded on a closed sector containing the spectrum of A (Corollary 3.10),
![]() $f(A)$
may be considered via the extended holomorphic (sectorial) calculus. If A is injective, then
$f(A)$
may be considered via the extended holomorphic (sectorial) calculus. If A is injective, then
![]() $f(A)$
can be defined that way as a closed operator, but we will show that
$f(A)$
can be defined that way as a closed operator, but we will show that
![]() $f(A)$
is a bounded operator when
$f(A)$
is a bounded operator when
![]() $f \in \mathcal {D}_{\infty }$
. Our methods provide estimates for
$f \in \mathcal {D}_{\infty }$
. Our methods provide estimates for
![]() $\|f(A)\|$
, and we will adapt the results in Section 8 to take account of the angle of sectoriality, by using fractional powers of operators (cf. Corollary 4.14).
$\|f(A)\|$
, and we will adapt the results in Section 8 to take account of the angle of sectoriality, by using fractional powers of operators (cf. Corollary 4.14).
Recall that a densely defined operator A on a Banach space X is sectorial of angle
![]() $\theta \in [0,\pi /2)$
if
$\theta \in [0,\pi /2)$
if
![]() $\sigma (A) \subset \overline \Sigma _{\theta }$
and, for each
$\sigma (A) \subset \overline \Sigma _{\theta }$
and, for each
![]() $\varphi \in (\theta ,\pi ]$
,
$\varphi \in (\theta ,\pi ]$
,
 $$ \begin{align} M_{\varphi}(A) := \sup \left\{\|z(z+A)^{-1}\| : z \in \Sigma_{\pi-\varphi}\right\} < \infty. \end{align} $$
$$ \begin{align} M_{\varphi}(A) := \sup \left\{\|z(z+A)^{-1}\| : z \in \Sigma_{\pi-\varphi}\right\} < \infty. \end{align} $$
The sectorial angle
![]() $\theta _A$
of A is the minimal such
$\theta _A$
of A is the minimal such
![]() $\theta $
. Note that
$\theta $
. Note that
![]() $M_{\varphi }(A)$
is a decreasing function of
$M_{\varphi }(A)$
is a decreasing function of
![]() $\varphi $
.
$\varphi $
.
Let
![]() $\operatorname {Sect}(\theta )$
stand for the class of all sectorial operators of angle
$\operatorname {Sect}(\theta )$
stand for the class of all sectorial operators of angle
![]() $\theta $
for
$\theta $
for
![]() $\theta \in [0,\pi /2)$
on Banach spaces, and denote
$\theta \in [0,\pi /2)$
on Banach spaces, and denote
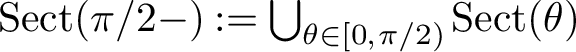 $\operatorname {Sect}(\pi /2-) := \bigcup _{\theta \in [0,\pi /2)} \operatorname {Sect}(\theta )$
. Then
$\operatorname {Sect}(\pi /2-) := \bigcup _{\theta \in [0,\pi /2)} \operatorname {Sect}(\theta )$
. Then
![]() $A \in \operatorname {Sect}(\pi /2-)$
if and only if
$A \in \operatorname {Sect}(\pi /2-)$
if and only if
![]() $-A$
generates a (sectorially) bounded holomorphic
$-A$
generates a (sectorially) bounded holomorphic
![]() $C_0$
-semigroup on X of angle
$C_0$
-semigroup on X of angle
![]() $(\pi /2)-\theta _A$
, in the sense that the semigroup has a holomorphic extension to
$(\pi /2)-\theta _A$
, in the sense that the semigroup has a holomorphic extension to
![]() $\Sigma _{(\pi /2)-\theta _A}$
that is bounded on each smaller subsector. Note that these semigroups are sometimes called sectorially bounded holomorphic semigroups in the literature. However, in this article, we will adopt the convention that bounded holomorphic semigroups are bounded on sectors. We will denote the semigroup as
$\Sigma _{(\pi /2)-\theta _A}$
that is bounded on each smaller subsector. Note that these semigroups are sometimes called sectorially bounded holomorphic semigroups in the literature. However, in this article, we will adopt the convention that bounded holomorphic semigroups are bounded on sectors. We will denote the semigroup as
![]() $(e^{-tA})_{t\ge 0}$
, and
$(e^{-tA})_{t\ge 0}$
, and
![]() $e^{-tA}$
then agrees with
$e^{-tA}$
then agrees with
![]() $e_t(A)$
defined in the HP-calculus, where
$e_t(A)$
defined in the HP-calculus, where
![]() $e_t(z) = e^{-tz}$
. One may consult [Reference Haase35] for the general theory of sectorial operators and [Reference Arendt, Batty, Hieber and Neubrander4, Section 3.7] for the theory of holomorphic semigroups.
$e_t(z) = e^{-tz}$
. One may consult [Reference Haase35] for the general theory of sectorial operators and [Reference Arendt, Batty, Hieber and Neubrander4, Section 3.7] for the theory of holomorphic semigroups.
Let A be a closed, densely defined operator on a Banach space X such that
 $$ \begin{align} \sigma(A) \subset \overline{\mathbb{C}}_+ \qquad \text{and} \qquad M_A:= M_{\pi/2}(A) = \sup_{z\in {\mathbb{C}}_{+}}\|z(z+A)^{-1}\|<\infty. \end{align} $$
$$ \begin{align} \sigma(A) \subset \overline{\mathbb{C}}_+ \qquad \text{and} \qquad M_A:= M_{\pi/2}(A) = \sup_{z\in {\mathbb{C}}_{+}}\|z(z+A)^{-1}\|<\infty. \end{align} $$
Then
![]() $\|A(z+A)^{-1}\| \le M_A+1, \,z\in \mathbb {C}_+$
, and Neumann series (see [Reference Vitse53, Lemma 1.1]) imply that
$\|A(z+A)^{-1}\| \le M_A+1, \,z\in \mathbb {C}_+$
, and Neumann series (see [Reference Vitse53, Lemma 1.1]) imply that
![]() $\sigma (A) \subset \Sigma _{\theta } \cup \{0\}$
and
$\sigma (A) \subset \Sigma _{\theta } \cup \{0\}$
and
where
So
![]() $A \in \operatorname {Sect}(\theta ) \subset \operatorname {Sect}(\pi /2-)$
. Conversely, if
$A \in \operatorname {Sect}(\theta ) \subset \operatorname {Sect}(\pi /2-)$
. Conversely, if
![]() $A \in \operatorname {Sect}(\theta )$
where
$A \in \operatorname {Sect}(\theta )$
where
![]() $\theta \in [0,\pi /2)$
, then (7.2) holds. Thus,
$\theta \in [0,\pi /2)$
, then (7.2) holds. Thus,
![]() $-A$
generates a bounded holomorphic semigroup if and only if (7.2) holds. The constant
$-A$
generates a bounded holomorphic semigroup if and only if (7.2) holds. The constant
![]() $M_A$
is a basic quantity associated with A, and we call it the sectoriality constant of A. Note that
$M_A$
is a basic quantity associated with A, and we call it the sectoriality constant of A. Note that
![]() $M_{tA} = M_A$
for all
$M_{tA} = M_A$
for all
![]() $t>0$
.
$t>0$
.
A set S of sectorial operators on the same Banach space X is uniformly sectorial of angle
![]() $\theta $
if
$\theta $
if
![]() $S \subset \operatorname {Sect}(\theta )$
and, for each
$S \subset \operatorname {Sect}(\theta )$
and, for each
![]() $\varphi \in (\theta ,\pi )$
, there exists
$\varphi \in (\theta ,\pi )$
, there exists
![]() $C_{\varphi }$
such that
$C_{\varphi }$
such that
![]() $M_{\varphi }(A) \le C_{\varphi }$
for all
$M_{\varphi }(A) \le C_{\varphi }$
for all
![]() $A \in S$
. Thus, S is uniformly sectorial of some angle
$A \in S$
. Thus, S is uniformly sectorial of some angle
![]() $\theta <\pi /2$
if and only if each
$\theta <\pi /2$
if and only if each
![]() $A \in S$
satisfies (7.2) and
$A \in S$
satisfies (7.2) and
![]() $\sup _{A \in S} M_A < \infty $
.
$\sup _{A \in S} M_A < \infty $
.
In the presentation of the
![]() $\mathcal {D}$
-calculus that follows, we assume that the reader is familiar with the holomorphic functional calculus for sectorial operators, as in [Reference Haase35], and in particular with the HP-calculus for negative generators of bounded
$\mathcal {D}$
-calculus that follows, we assume that the reader is familiar with the holomorphic functional calculus for sectorial operators, as in [Reference Haase35], and in particular with the HP-calculus for negative generators of bounded
![]() $C_0$
-semigroups. We will make extensive use of fractional powers of sectorial operators in the form
$C_0$
-semigroups. We will make extensive use of fractional powers of sectorial operators in the form
![]() $(A+z)^{-\gamma }$
where
$(A+z)^{-\gamma }$
where
![]() $\gamma>0$
. If
$\gamma>0$
. If
![]() $\gamma $
is not an integer, these operators are fractional powers that can be defined in many ways (see [Reference Martínez Carracedo and Sanz Alix44]), including using the holomorphic functional calculus (see [Reference Haase35, Chapter 3]). All of these approaches are consistent with each other. Because
$\gamma $
is not an integer, these operators are fractional powers that can be defined in many ways (see [Reference Martínez Carracedo and Sanz Alix44]), including using the holomorphic functional calculus (see [Reference Haase35, Chapter 3]). All of these approaches are consistent with each other. Because
![]() $\mathcal {D}_{\infty } = \bigcup _{n=0}^{\infty } \mathcal {D}_n$
, it is possible to define the
$\mathcal {D}_{\infty } = \bigcup _{n=0}^{\infty } \mathcal {D}_n$
, it is possible to define the
![]() $\mathcal {D}$
-calculus without using fractional powers, and this would simplify some proofs (for example, Lemma 7.1 becomes trivial, and the formulas (7.4) and (7.8) would not be needed). Thus, we could define the
$\mathcal {D}$
-calculus without using fractional powers, and this would simplify some proofs (for example, Lemma 7.1 becomes trivial, and the formulas (7.4) and (7.8) would not be needed). Thus, we could define the
![]() $\mathcal {D}$
-calculus without using fractional powers and, in particular, we could define the fractional powers
$\mathcal {D}$
-calculus without using fractional powers and, in particular, we could define the fractional powers
![]() $(z+A)^{-\gamma }$
for all
$(z+A)^{-\gamma }$
for all
![]() $\gamma> 0$
. This definition would be consistent with other definitions (see Theorem 7.4). Then we could define the
$\gamma> 0$
. This definition would be consistent with other definitions (see Theorem 7.4). Then we could define the
![]() $\mathcal {D}_s$
-calculus for all
$\mathcal {D}_s$
-calculus for all
![]() $s>-1$
in the way described below, using fractional powers in (7.5).
$s>-1$
in the way described below, using fractional powers in (7.5).
The following simple lemma for fractional powers is a version of the moment inequality applied to the sectorial operator
![]() $(A+z)^{-1}$
.
$(A+z)^{-1}$
.
Lemma 7.1. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
and
$A \in \operatorname {Sect}(\pi /2-)$
and
![]() $\gamma>0$
. Let
$\gamma>0$
. Let
![]() $\lceil \gamma \rceil $
be the ceiling function of
$\lceil \gamma \rceil $
be the ceiling function of
![]() $\gamma $
; that is, the smallest integer in
$\gamma $
; that is, the smallest integer in
![]() $[\gamma ,\infty )$
. Then
$[\gamma ,\infty )$
. Then
 $$ \begin{align*} \|(A+z)^{-\gamma}\|\le M_A^{\lceil\gamma\rceil}/|z|^{\gamma},\quad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} \|(A+z)^{-\gamma}\|\le M_A^{\lceil\gamma\rceil}/|z|^{\gamma},\quad z\in \mathbb{C}_{+}. \end{align*} $$
Proof. When
![]() $\gamma \in \mathbb {N}$
, the estimate is trivial.
$\gamma \in \mathbb {N}$
, the estimate is trivial.
Let
![]() $\gamma \in (0,1)$
. By the compatibility of our calculus with the holomorphic functional calculus for fractional powers, we may use the following standard Stieltjes formula (see [Reference Arendt, Batty, Hieber and Neubrander4, (3.52)], for example):
$\gamma \in (0,1)$
. By the compatibility of our calculus with the holomorphic functional calculus for fractional powers, we may use the following standard Stieltjes formula (see [Reference Arendt, Batty, Hieber and Neubrander4, (3.52)], for example):
 $$ \begin{align} (A+z)^{-\gamma}=\frac{\sin(\pi\gamma)}{\pi}\int_0^{\infty} t^{-\gamma}(A+z+t)^{-1}\,dt,\quad z\in \mathbb{C}_{+}. \end{align} $$
$$ \begin{align} (A+z)^{-\gamma}=\frac{\sin(\pi\gamma)}{\pi}\int_0^{\infty} t^{-\gamma}(A+z+t)^{-1}\,dt,\quad z\in \mathbb{C}_{+}. \end{align} $$
Next, let
![]() $z=\rho e^{i\varphi }\in \mathbb {C}_{+}$
. Then, using Cauchy’s theorem,
$z=\rho e^{i\varphi }\in \mathbb {C}_{+}$
. Then, using Cauchy’s theorem,
 $$ \begin{align*} (A+z)^{-\gamma}&=\frac{\sin(\pi\gamma)}{\pi}\int_0^{e^{i\varphi \infty}} w^{-\gamma}(A+\rho e^{i\varphi}+w)^{-1}\,dw\\ &=e^{i(1-\gamma )\varphi}\frac{\sin(\pi\gamma)}{\pi}\int_0^{\infty} s^{-\gamma}(A+\rho e^{i\varphi}+s e^{i\varphi})^{-1}\,ds. \end{align*} $$
$$ \begin{align*} (A+z)^{-\gamma}&=\frac{\sin(\pi\gamma)}{\pi}\int_0^{e^{i\varphi \infty}} w^{-\gamma}(A+\rho e^{i\varphi}+w)^{-1}\,dw\\ &=e^{i(1-\gamma )\varphi}\frac{\sin(\pi\gamma)}{\pi}\int_0^{\infty} s^{-\gamma}(A+\rho e^{i\varphi}+s e^{i\varphi})^{-1}\,ds. \end{align*} $$
So,
 $$ \begin{align*} \|(A+z)^{-\gamma}\|\le M_A\frac{\sin(\pi\gamma)}{\pi} \int_0^{\infty} s^{-\gamma}(\rho+s)^{-1} \,ds = \frac{M_A}{\rho^{\gamma}}. \end{align*} $$
$$ \begin{align*} \|(A+z)^{-\gamma}\|\le M_A\frac{\sin(\pi\gamma)}{\pi} \int_0^{\infty} s^{-\gamma}(\rho+s)^{-1} \,ds = \frac{M_A}{\rho^{\gamma}}. \end{align*} $$
In other cases,
![]() $\gamma = (\lceil \gamma \rceil - 1) + \delta $
where
$\gamma = (\lceil \gamma \rceil - 1) + \delta $
where
![]() $\delta \in (0,1)$
, and the estimate follows from the two previous cases.
$\delta \in (0,1)$
, and the estimate follows from the two previous cases.
Now let
![]() $s>-1$
be fixed and let
$s>-1$
be fixed and let
![]() $f\in \mathcal {D}_s$
. We define
$f\in \mathcal {D}_s$
. We define
 $$ \begin{align} f_{\mathcal{D}_s}(A):=f(\infty)- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} f'(\alpha+i\beta)(A+\alpha-i\beta)^{-(s+1)}\,d\beta\,d\alpha. \end{align} $$
$$ \begin{align} f_{\mathcal{D}_s}(A):=f(\infty)- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} f'(\alpha+i\beta)(A+\alpha-i\beta)^{-(s+1)}\,d\beta\,d\alpha. \end{align} $$
Note that when
![]() $s = 1$
and
$s = 1$
and
![]() $f \in \mathcal {B}$
, (7.5) coincides with the definition of
$f \in \mathcal {B}$
, (7.5) coincides with the definition of
![]() $f(A)$
as given by the
$f(A)$
as given by the
![]() $\mathcal {B}$
-calculus in [Reference Batty, Gomilko and Tomilov7]; cf. (1.4).
$\mathcal {B}$
-calculus in [Reference Batty, Gomilko and Tomilov7]; cf. (1.4).
This definition is valid, as the following simple proposition shows.
Proposition 7.2. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
and
$A \in \operatorname {Sect}(\pi /2-)$
and
![]() $s>-1$
.
$s>-1$
.
-
1. The map
 $f \mapsto f_{\mathcal {D}_s}(A)$
is bounded from
$f \mapsto f_{\mathcal {D}_s}(A)$
is bounded from
 $\mathcal {D}_s$
to
$\mathcal {D}_s$
to
 $L(X)$
.
$L(X)$
. -
2. For
 $f \in \mathcal {D}_s$
, (7.6)in the operator norm topology.
$f \in \mathcal {D}_s$
, (7.6)in the operator norm topology. $$ \begin{align} \lim_{\epsilon\to0+}\,f_{\mathcal D_s}(A+\epsilon) =f_{\mathcal D_s}(A), \end{align} $$
$$ \begin{align} \lim_{\epsilon\to0+}\,f_{\mathcal D_s}(A+\epsilon) =f_{\mathcal D_s}(A), \end{align} $$
Proof. Lemma 7.1 and (7.5) imply that
 $$ \begin{align} \|f_{\mathcal{D}_s}(A)\|\le |f(\infty)|+ \frac{2^s M_A^{\lceil{s+1}\rceil}}{\pi}\|f'\|_{\mathcal{V}_s}. \end{align} $$
$$ \begin{align} \|f_{\mathcal{D}_s}(A)\|\le |f(\infty)|+ \frac{2^s M_A^{\lceil{s+1}\rceil}}{\pi}\|f'\|_{\mathcal{V}_s}. \end{align} $$
Thus, the boundedness of the map
![]() $f \mapsto f_{\mathcal {D}_s}(A)$
from
$f \mapsto f_{\mathcal {D}_s}(A)$
from
![]() $\mathcal {D}_s$
to
$\mathcal {D}_s$
to
![]() $L(X)$
follows.
$L(X)$
follows.
By a standard Laplace transform representation for negative fractional powers [Reference Arendt, Batty, Hieber and Neubrander4, eqn. (3.56)],
 $$ \begin{align} (A+z)^{-(s+1)} = \frac{1}{\Gamma(s+1)} \int_0^{\infty} t^s e^{-tz} e^{-tA} \,dt, \qquad z \in \mathbb{C}_+. \end{align} $$
$$ \begin{align} (A+z)^{-(s+1)} = \frac{1}{\Gamma(s+1)} \int_0^{\infty} t^s e^{-tz} e^{-tA} \,dt, \qquad z \in \mathbb{C}_+. \end{align} $$
By the dominated convergence theorem,
![]() $z \mapsto (A+z)^{-(s+1)}$
is continuous (even holomorphic) on
$z \mapsto (A+z)^{-(s+1)}$
is continuous (even holomorphic) on
![]() $\mathbb {C}_+$
in the operator norm topology.
$\mathbb {C}_+$
in the operator norm topology.
The operators
![]() $(A+\epsilon )_{\epsilon \ge 0}$
are uniformly sectorial of angle
$(A+\epsilon )_{\epsilon \ge 0}$
are uniformly sectorial of angle
![]() $\theta $
; more precisely,
$\theta $
; more precisely,
![]() $M_{A+\epsilon } \le M_A$
[Reference Haase35, Proposition 2.1.1 f)]. By Lemma 7.1, this implies that
$M_{A+\epsilon } \le M_A$
[Reference Haase35, Proposition 2.1.1 f)]. By Lemma 7.1, this implies that
 $$ \begin{align} \|(A+\epsilon+z)^{-(s+1)}\|\le M_A^{\lceil{s+1}\rceil} |z|^{-(s+1)}, \qquad \epsilon\ge 0, \quad z\in \mathbb C_{+}. \end{align} $$
$$ \begin{align} \|(A+\epsilon+z)^{-(s+1)}\|\le M_A^{\lceil{s+1}\rceil} |z|^{-(s+1)}, \qquad \epsilon\ge 0, \quad z\in \mathbb C_{+}. \end{align} $$
Now (7.6) follows from applying (7.5) to
![]() $A+\epsilon $
, letting
$A+\epsilon $
, letting
![]() $\epsilon \to 0+$
and using the dominated convergence theorem.
$\epsilon \to 0+$
and using the dominated convergence theorem.
Remark 7.3. The property (7.6) can be compared with Corollary 11.2 where a direct proof is given that the shifts form a bounded holomorphic
![]() $C_0$
-semigroup on
$C_0$
-semigroup on
![]() $\mathcal {D}_s$
. To deduce (7.6), one also needs that if
$\mathcal {D}_s$
. To deduce (7.6), one also needs that if
![]() $f_{\epsilon }(z) = f(z+\epsilon )$
, then
$f_{\epsilon }(z) = f(z+\epsilon )$
, then
![]() $(f_{\epsilon })_{\mathcal {D}_s}(A) = f_{\mathcal {D}_s}(A+\epsilon )$
. By Theorem 5.1, it suffices that this holds for
$(f_{\epsilon })_{\mathcal {D}_s}(A) = f_{\mathcal {D}_s}(A+\epsilon )$
. By Theorem 5.1, it suffices that this holds for
![]() $f = r_{\lambda }, \, \lambda \in \mathbb {C}_+$
; that is, to show that
$f = r_{\lambda }, \, \lambda \in \mathbb {C}_+$
; that is, to show that
![]() $(r_{\lambda })_{\mathcal {D}_s}(A) = (\lambda +A)^{-1}$
. We show this in Theorem 7.6, but the argument uses (7.6).
$(r_{\lambda })_{\mathcal {D}_s}(A) = (\lambda +A)^{-1}$
. We show this in Theorem 7.6, but the argument uses (7.6).
Let
![]() $f_{\text {HP}}(A)$
stand for a function f of A defined by the HP functional calculus when f is in the HP algebra
$f_{\text {HP}}(A)$
stand for a function f of A defined by the HP functional calculus when f is in the HP algebra
![]() $\mathcal {LM}$
, and let
$\mathcal {LM}$
, and let
![]() $f_{\operatorname {Hol}}(A)$
denote a function f of A given by the holomorphic functional calculus when f is in the domain of that calculus. The following statement shows that both calculi are compatible with the
$f_{\operatorname {Hol}}(A)$
denote a function f of A given by the holomorphic functional calculus when f is in the domain of that calculus. The following statement shows that both calculi are compatible with the
![]() $\mathcal D$
-calculus and, moreover, that the definitions of
$\mathcal D$
-calculus and, moreover, that the definitions of
![]() $f_{\mathcal {D}_s}(A)$
agree for the various values of s for which
$f_{\mathcal {D}_s}(A)$
agree for the various values of s for which
![]() $f \in \mathcal {D}_s$
.
$f \in \mathcal {D}_s$
.
Theorem 7.4. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
, and let
$A \in \operatorname {Sect}(\pi /2-)$
, and let
![]() $f \in \mathcal {D}_s,\, s>-1$
.
$f \in \mathcal {D}_s,\, s>-1$
.
-
(i) If A is injective, then
(7.10) $$ \begin{align} f_{\mathcal{D}_s}(A)=f_{\text{Hol}}(A). \end{align} $$
$$ \begin{align} f_{\mathcal{D}_s}(A)=f_{\text{Hol}}(A). \end{align} $$
-
(ii) If
 $\sigma \ge s$
, then (7.11)
$\sigma \ge s$
, then (7.11) $$ \begin{align} f_{\mathcal{D}_{\sigma}}(A)=f_{\mathcal{D}_s}(A). \end{align} $$
$$ \begin{align} f_{\mathcal{D}_{\sigma}}(A)=f_{\mathcal{D}_s}(A). \end{align} $$
-
(iii) If
 $f \in \text{\rm LM} \cap \mathcal {D}_s$
, then (7.12)In particular, (7.12) holds if
$f \in \text{\rm LM} \cap \mathcal {D}_s$
, then (7.12)In particular, (7.12) holds if $$ \begin{align} f_{\mathcal{D}_s}(A)=f_{\rm HP}(A). \end{align} $$
$$ \begin{align} f_{\mathcal{D}_s}(A)=f_{\rm HP}(A). \end{align} $$
 $f \in \mathcal {LM}$
and
$f \in \mathcal {LM}$
and
 $s>0$
.
$s>0$
.
Proof. We start by proving (7.10). Assume that A is injective, and
![]() $A \in \operatorname {Sect}(\theta )$
, where
$A \in \operatorname {Sect}(\theta )$
, where
![]() $\theta \in (0, \pi /2)$
. Let
$\theta \in (0, \pi /2)$
. Let
![]() $\psi \in (\theta , \pi /2)$
. Let
$\psi \in (\theta , \pi /2)$
. Let
![]() $f \in \mathcal {D}_s, \, s>-1$
, and assume (without loss of generality) that
$f \in \mathcal {D}_s, \, s>-1$
, and assume (without loss of generality) that
![]() $f(\infty )=0$
. By the definition of the holomorphic functional calculus,
$f(\infty )=0$
. By the definition of the holomorphic functional calculus,
 $$ \begin{align*} A(1+A)^{-2}f_{\operatorname{Hol}}(A)=\frac{1}{2\pi i}\int_{\partial \Sigma_{\psi}} \frac{\lambda f(\lambda)}{(\lambda+1)^2}(\lambda-A)^{-1}\,d\lambda. \end{align*} $$
$$ \begin{align*} A(1+A)^{-2}f_{\operatorname{Hol}}(A)=\frac{1}{2\pi i}\int_{\partial \Sigma_{\psi}} \frac{\lambda f(\lambda)}{(\lambda+1)^2}(\lambda-A)^{-1}\,d\lambda. \end{align*} $$
Because
 $$ \begin{align*} f(\lambda)=-\frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{f'(\alpha+i\beta)} {(\lambda+\alpha-i\beta)^{s+1}}\,d\beta\,d\alpha,\quad \lambda\in \mathbb{C}_{+}, \end{align*} $$
$$ \begin{align*} f(\lambda)=-\frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty}\frac{f'(\alpha+i\beta)} {(\lambda+\alpha-i\beta)^{s+1}}\,d\beta\,d\alpha,\quad \lambda\in \mathbb{C}_{+}, \end{align*} $$
Fubini’s theorem and Cauchy’s theorem imply that
 $$ \begin{align*} &{A(1+A)^{-2}f_{\operatorname{Hol}}(A)} \\ &\ =- \frac{2^s}{\pi} \int_0^{\infty} \alpha^s \int_{-\infty}^{\infty} f'(\alpha+i\beta) \left(\frac{1}{2\pi i} \int_{\partial \Sigma_{\psi}}\,\frac{\lambda(\lambda-A)^{-1}}{(\lambda+1)^2(\lambda+\alpha-i\beta)^{s+1}}\,d\lambda\right) d\beta \, d\alpha\\ & \ = -\frac{2^s}{\pi}A(1+A)^{-2} \int_0^{\infty}\alpha^s \int_{-\infty}^{\infty} f'(\alpha+i\beta)(A+\alpha-i\beta)^{-(s+1)} d\beta \, d\alpha\\ & \ =A(1+A)^{-2}f_{\mathcal{D}_s}(A). \end{align*} $$
$$ \begin{align*} &{A(1+A)^{-2}f_{\operatorname{Hol}}(A)} \\ &\ =- \frac{2^s}{\pi} \int_0^{\infty} \alpha^s \int_{-\infty}^{\infty} f'(\alpha+i\beta) \left(\frac{1}{2\pi i} \int_{\partial \Sigma_{\psi}}\,\frac{\lambda(\lambda-A)^{-1}}{(\lambda+1)^2(\lambda+\alpha-i\beta)^{s+1}}\,d\lambda\right) d\beta \, d\alpha\\ & \ = -\frac{2^s}{\pi}A(1+A)^{-2} \int_0^{\infty}\alpha^s \int_{-\infty}^{\infty} f'(\alpha+i\beta)(A+\alpha-i\beta)^{-(s+1)} d\beta \, d\alpha\\ & \ =A(1+A)^{-2}f_{\mathcal{D}_s}(A). \end{align*} $$
Hence, (7.10) holds.
Now we no longer assume that A is injective. We infer by (7.10) that
for all
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $\sigma \ge s$
. Letting
$\sigma \ge s$
. Letting
![]() $\epsilon \to 0$
and using Proposition 7.2, we obtain the assertion (7.11).
$\epsilon \to 0$
and using Proposition 7.2, we obtain the assertion (7.11).
Finally, if
![]() $f\in \mathcal {LM} \cap \mathcal D_s$
for some
$f\in \mathcal {LM} \cap \mathcal D_s$
for some
![]() $s> -1$
, then
$s> -1$
, then
![]() $f\in \mathcal {B}\cap \mathcal D_s$
, and using (7.11), we have
$f\in \mathcal {B}\cap \mathcal D_s$
, and using (7.11), we have
Remark 7.5. If f has zero polynomial limits at zero and at infinity in the sense of [Reference Haase35, p. 27], then the proof above does not require the regularisation factor
![]() $\lambda (\lambda +1)^{-2}$
. Hence,
$\lambda (\lambda +1)^{-2}$
. Hence,
![]() $f_{\mathcal D}(A)=f_{\text {Hol}}(A)$
regardless of the injectivity of A. One can show that
$f_{\mathcal D}(A)=f_{\text {Hol}}(A)$
regardless of the injectivity of A. One can show that
![]() $f_{\mathcal D}(A)=f_{\text {Hol}}(A)$
even when f belongs to the extended Riesz–Dunford function class (for example,
$f_{\mathcal D}(A)=f_{\text {Hol}}(A)$
even when f belongs to the extended Riesz–Dunford function class (for example,
![]() $f(z)=e^{-tz},\, t>0$
), but we omit a discussion of this here (cf. the proof of Lemma 7.11).
$f(z)=e^{-tz},\, t>0$
), but we omit a discussion of this here (cf. the proof of Lemma 7.11).
Recall that
![]() $\mathcal D_s \subset \mathcal D_{\sigma }$
if
$\mathcal D_s \subset \mathcal D_{\sigma }$
if
![]() $-1< s \le \sigma $
, and the space
$-1< s \le \sigma $
, and the space
 $$ \begin{align*} \mathcal D_{\infty}:=\bigcup_{s>-1} \mathcal D_s \end{align*} $$
$$ \begin{align*} \mathcal D_{\infty}:=\bigcup_{s>-1} \mathcal D_s \end{align*} $$
is an algebra, by Lemma 3.21. Thus, it is a plausible and natural domain for a functional calculus, which we now define.
Theorem 7.6. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
. The formula (7.5) defines an algebra homomorphism:
$A \in \operatorname {Sect}(\pi /2-)$
. The formula (7.5) defines an algebra homomorphism:
Moreover,
-
(i)
 $\Psi _A(r_{\lambda }) = (\lambda +A)^{-1}, \quad \lambda \in \mathbb {C}_+$
.
$\Psi _A(r_{\lambda }) = (\lambda +A)^{-1}, \quad \lambda \in \mathbb {C}_+$
. -
(ii)
 $\Psi _A$
is bounded in the sense that for every
$\Psi _A$
is bounded in the sense that for every
 $s>-1$
there exists
$s>-1$
there exists
 $C_s(A)$
such that (7.13)Specifically, (7.7) holds.
$C_s(A)$
such that (7.13)Specifically, (7.7) holds. $$ \begin{align} \|\Psi_A(f)\|\le |f(\infty)| + C_s(A)\|f\|_{\mathcal D_s}, \qquad f \in \mathcal{D}_s. \end{align} $$
$$ \begin{align} \|\Psi_A(f)\|\le |f(\infty)| + C_s(A)\|f\|_{\mathcal D_s}, \qquad f \in \mathcal{D}_s. \end{align} $$
Moreover,
![]() $\Psi _A$
is the unique algebra homomorphism from
$\Psi _A$
is the unique algebra homomorphism from
![]() $\mathcal {D}_{\infty }$
to
$\mathcal {D}_{\infty }$
to
![]() $L(X)$
that satisfies (i) and (ii).
$L(X)$
that satisfies (i) and (ii).
The homomorphism
![]() $\Psi _A$
will be called the
$\Psi _A$
will be called the
![]() $\mathcal{D}$
-calculus.
$\mathcal{D}$
-calculus.
Proof. It follows from (7.11) that
![]() $\Psi _A$
is well-defined by (7.5) and from (7.10) that
$\Psi _A$
is well-defined by (7.5) and from (7.10) that
![]() $(r_{\lambda })_{\mathcal {D}_s}(A+\epsilon ) = (\lambda +\epsilon +A)^{-1}$
for
$(r_{\lambda })_{\mathcal {D}_s}(A+\epsilon ) = (\lambda +\epsilon +A)^{-1}$
for
![]() $\epsilon>0$
. Letting
$\epsilon>0$
. Letting
![]() $\epsilon \to 0$
and using (7.6) gives (i). Moreover, (7.13) is a direct consequence of Proposition 7.2.
$\epsilon \to 0$
and using (7.6) gives (i). Moreover, (7.13) is a direct consequence of Proposition 7.2.
We will now prove that
![]() $\Psi _A$
is a homomorphism. Let
$\Psi _A$
is a homomorphism. Let
![]() $f,g\in \mathcal D_{\infty }$
. Then
$f,g\in \mathcal D_{\infty }$
. Then
![]() $f\in \mathcal D_r$
and
$f\in \mathcal D_r$
and
![]() $g\in \mathcal D_t$
for some strictly positive s and t; hence,
$g\in \mathcal D_t$
for some strictly positive s and t; hence,
![]() $f g\in \mathcal D_{s+t+1}$
by Lemma 3.21. Because
$f g\in \mathcal D_{s+t+1}$
by Lemma 3.21. Because
![]() $\mathcal {LM}$
is dense in
$\mathcal {LM}$
is dense in
![]() $\mathcal D_s$
for every
$\mathcal D_s$
for every
![]() $s>0$
by Corollary 5.2, there exist
$s>0$
by Corollary 5.2, there exist
![]() $(f_n)_{n=1}^{\infty }$
and
$(f_n)_{n=1}^{\infty }$
and
![]() $(g_n)_{n=1}^{\infty }$
from
$(g_n)_{n=1}^{\infty }$
from
![]() $\mathcal {LM}$
such that
$\mathcal {LM}$
such that
and then, in view of Lemma 3.21,
![]() $f_n g_n \to f g$
in
$f_n g_n \to f g$
in
![]() $\mathcal D_{s+t+1}$
as
$\mathcal D_{s+t+1}$
as
![]() $n \to \infty $
.
$n \to \infty $
.
By the product rule for the HP-calculus and (7.12),
Passing to the limit when
![]() $n\to \infty $
and using (7.13), it follows that
$n\to \infty $
and using (7.13), it follows that
Let
![]() $\Psi : \mathcal {D}_{\infty } \to L(X)$
be an algebra homomorphism satisfying (i) and (ii). Then
$\Psi : \mathcal {D}_{\infty } \to L(X)$
be an algebra homomorphism satisfying (i) and (ii). Then
![]() $\Psi $
and
$\Psi $
and
![]() $\Psi _A$
coincide on
$\Psi _A$
coincide on
![]() $\{r_{\lambda } : \lambda \in \mathbb {C}_+\}$
. Because A is densely defined,
$\{r_{\lambda } : \lambda \in \mathbb {C}_+\}$
. Because A is densely defined,
![]() $\Psi (1)=1$
(see [Reference Batty, Gomilko and Tomilov8, Section 6, Observation (2)], so
$\Psi (1)=1$
(see [Reference Batty, Gomilko and Tomilov8, Section 6, Observation (2)], so
![]() $\Psi $
and
$\Psi $
and
![]() $\Psi _A$
coincide on the span of these functions that are dense in
$\Psi _A$
coincide on the span of these functions that are dense in
![]() $\mathcal {D}_s$
(Theorem 5.1). Because
$\mathcal {D}_s$
(Theorem 5.1). Because
![]() $\Psi $
and
$\Psi $
and
![]() $\Psi _A$
are both bounded on
$\Psi _A$
are both bounded on
![]() $\mathcal {D}_s$
, it follows that they coincide on each
$\mathcal {D}_s$
, it follows that they coincide on each
![]() $\mathcal {D}_s$
and hence on
$\mathcal {D}_s$
and hence on
![]() $\mathcal {D}_{\infty }$
.
$\mathcal {D}_{\infty }$
.
Remark 7.7. If A is an operator for which a
![]() $\mathcal {D}$
-calculus exists with the properties (i) and (ii) given in Theorem 7.6, then
$\mathcal {D}$
-calculus exists with the properties (i) and (ii) given in Theorem 7.6, then
![]() $A\in \operatorname {Sect}(\pi /2-)$
. This follows from (3.20) and the properties (i) and (ii). By combining this with Theorem 7.6, we obtain Theorem 1.1. Note also that, if (i) holds for some
$A\in \operatorname {Sect}(\pi /2-)$
. This follows from (3.20) and the properties (i) and (ii). By combining this with Theorem 7.6, we obtain Theorem 1.1. Note also that, if (i) holds for some
![]() $\lambda \in \mathbb {C}_+$
, then it holds for all
$\lambda \in \mathbb {C}_+$
, then it holds for all
![]() $\lambda \in \mathbb {C}_+$
, by the resolvent identity.
$\lambda \in \mathbb {C}_+$
, by the resolvent identity.
The Banach algebras
![]() $\mathcal {D}_s^{\infty }, \, s>-1$
, are subalgebras of
$\mathcal {D}_s^{\infty }, \, s>-1$
, are subalgebras of
![]() $\mathcal {D}_{\infty }$
, so we obtain the following corollary by restricting the
$\mathcal {D}_{\infty }$
, so we obtain the following corollary by restricting the
![]() $\mathcal {D}$
-calculus.
$\mathcal {D}$
-calculus.
Corollary 7.8. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
and
$A \in \operatorname {Sect}(\pi /2-)$
and
![]() $s>-1$
. Then there exists a bounded algebra homomorphism
$s>-1$
. Then there exists a bounded algebra homomorphism
![]() $\Psi _A^s: \mathcal D^{\infty }_s \mapsto L(X)$
such that
$\Psi _A^s: \mathcal D^{\infty }_s \mapsto L(X)$
such that
-
(i)
 $\Psi _A^s(r_{\lambda })=(\lambda +A)^{-1}, \quad \lambda \in \mathbb C_+$
.
$\Psi _A^s(r_{\lambda })=(\lambda +A)^{-1}, \quad \lambda \in \mathbb C_+$
. -
(ii)
 $\Psi ^s_A$
is bounded in the
$\Psi ^s_A$
is bounded in the
 $\mathcal {D}_s$
-norm; that is, there exists
$\mathcal {D}_s$
-norm; that is, there exists
 $C_s(A)$
such that
$C_s(A)$
such that $$ \begin{align*} \|\Psi_A(f)\|\le C_s(A) \|f\|_{\mathcal D_s}, \qquad f \in \mathcal{D}_s. \end{align*} $$
$$ \begin{align*} \|\Psi_A(f)\|\le C_s(A) \|f\|_{\mathcal D_s}, \qquad f \in \mathcal{D}_s. \end{align*} $$
Moreover,
![]() $\Psi _A^s$
is the unique algebra homomorphism from
$\Psi _A^s$
is the unique algebra homomorphism from
![]() $\mathcal {D}_s^{\infty }$
to
$\mathcal {D}_s^{\infty }$
to
![]() $L(X)$
that satisfies (i) and (ii).
$L(X)$
that satisfies (i) and (ii).
From now onwards, we will write
![]() $f_{\mathcal {D}}(A)$
instead of
$f_{\mathcal {D}}(A)$
instead of
![]() $\Psi _A(f)$
, for
$\Psi _A(f)$
, for
![]() $f \in \mathcal {D}_{\infty }$
. When
$f \in \mathcal {D}_{\infty }$
. When
![]() $f(z) = e^{-tz}$
, we will continue to use the notation
$f(z) = e^{-tz}$
, we will continue to use the notation
![]() $e^{-tA}$
for
$e^{-tA}$
for
![]() $f(A)$
, because the
$f(A)$
, because the
![]() $\mathcal D$
-calculus agrees with the HP-calculus by Theorem 7.4. So
$\mathcal D$
-calculus agrees with the HP-calculus by Theorem 7.4. So
![]() $(e^{-tA})_{t\ge 0}$
form the
$(e^{-tA})_{t\ge 0}$
form the
![]() $C_0$
-semigroup generated by
$C_0$
-semigroup generated by
![]() $-A$
, and it extends to a bounded holomorphic semigroup.
$-A$
, and it extends to a bounded holomorphic semigroup.
Let
![]() $g : \mathbb {C}_+ \to \mathbb {C}_+$
be a holomorphic function and assume that
$g : \mathbb {C}_+ \to \mathbb {C}_+$
be a holomorphic function and assume that
![]() $r_{\lambda } \circ g \in \mathcal {D}_{\infty }$
for all
$r_{\lambda } \circ g \in \mathcal {D}_{\infty }$
for all
![]() $\lambda \in \mathbb {C}_+$
. Because the functions
$\lambda \in \mathbb {C}_+$
. Because the functions
![]() $(r_{\lambda })_{\lambda \in \mathbb {C}_+}$
satisfy the resolvent identity, the operators
$(r_{\lambda })_{\lambda \in \mathbb {C}_+}$
satisfy the resolvent identity, the operators
also satisfy the resolvent identity; that is, they form a pseudo-resolvent. In particular, their kernels and their ranges are independent of
![]() $\lambda $
, and they form the resolvent of an operator B if and only if the common kernel is
$\lambda $
, and they form the resolvent of an operator B if and only if the common kernel is
![]() $\{0\}$
and the domain of B is the common range of the pseudo-resolvent (see [Reference Yosida58, Section VIII.4]).
$\{0\}$
and the domain of B is the common range of the pseudo-resolvent (see [Reference Yosida58, Section VIII.4]).
Corollary 7.9. Let
![]() $A, B \in \operatorname {Sect}(\pi /2-)$
, and let
$A, B \in \operatorname {Sect}(\pi /2-)$
, and let
![]() $g : \mathbb {C}_+ \to \mathbb {C}_+$
be holomorphic. Assume that, for each
$g : \mathbb {C}_+ \to \mathbb {C}_+$
be holomorphic. Assume that, for each
![]() $s>-1$
, there exists
$s>-1$
, there exists
![]() $\sigma>-1$
such that
$\sigma>-1$
such that
-
(a) For all
 $f \in \mathcal {D}_s$
,
$f \in \mathcal {D}_s$
,
 $f\circ g \in \mathcal {D}_{\sigma }$
, and
$f\circ g \in \mathcal {D}_{\sigma }$
, and -
(b) for all
 $\lambda \in \mathbb {C}_+$
,
$\lambda \in \mathbb {C}_+$
,
 $(r_{\lambda } \circ g)_{\mathcal {D}}(A) = (\lambda +B)^{-1}$
.
$(r_{\lambda } \circ g)_{\mathcal {D}}(A) = (\lambda +B)^{-1}$
.
Then
![]() $(f \circ g)_{\mathcal {D}}(A) = f_{\mathcal {D}}(B)$
for all
$(f \circ g)_{\mathcal {D}}(A) = f_{\mathcal {D}}(B)$
for all
![]() $f \in \mathcal {D}_{\infty }$
.
$f \in \mathcal {D}_{\infty }$
.
Proof. By assumption (a), Corollary 3.13 and the closed graph theorem,
![]() $f \mapsto f \circ g$
is a bounded map from
$f \mapsto f \circ g$
is a bounded map from
![]() $\mathcal {D}_s$
to
$\mathcal {D}_s$
to
![]() $\mathcal {D}_{\sigma }$
. Moreover, the
$\mathcal {D}_{\sigma }$
. Moreover, the
![]() $\mathcal {D}$
-calculus for A is a bounded map from
$\mathcal {D}$
-calculus for A is a bounded map from
![]() $\mathcal {D}_{\sigma }$
to
$\mathcal {D}_{\sigma }$
to
![]() $L(X)$
. Hence, the composition is a bounded map from
$L(X)$
. Hence, the composition is a bounded map from
![]() $\mathcal {D}_s$
to
$\mathcal {D}_s$
to
![]() $L(X)$
, and by assumption (b) it sends
$L(X)$
, and by assumption (b) it sends
![]() $r_{\lambda }$
to
$r_{\lambda }$
to
![]() $(\lambda +B)^{-1}$
for all
$(\lambda +B)^{-1}$
for all
![]() $\lambda \in \mathbb {C}_+$
. Moreover, the maps collectively form an algebra homomorphism from
$\lambda \in \mathbb {C}_+$
. Moreover, the maps collectively form an algebra homomorphism from
![]() $\mathcal {D}_{\infty }$
to
$\mathcal {D}_{\infty }$
to
![]() $L(X)$
. By the uniqueness in Theorem 7.6, this map is the
$L(X)$
. By the uniqueness in Theorem 7.6, this map is the
![]() $\mathcal {D}$
-calculus for B.
$\mathcal {D}$
-calculus for B.
In the context of Corollary 7.9, the operator B is sometimes written as
![]() $g(A)$
, but the precise meaning depends on the specific situation.
$g(A)$
, but the precise meaning depends on the specific situation.
There is also a version of Corollary 7.9 for fixed values of s and
![]() $\sigma $
, using the
$\sigma $
, using the
![]() $\mathcal {D}_s^{\infty }$
- and
$\mathcal {D}_s^{\infty }$
- and
![]() $\mathcal {D}_{\sigma }^{\infty }$
-calculi.
$\mathcal {D}_{\sigma }^{\infty }$
-calculi.
Examples 7.10. Examples of functions g and operators B that satisfy the conditions of Corollary 7.9 include the following:
-
1.
 $g(z) = z^{-1}$
, if A is injective (with dense range);
$g(z) = z^{-1}$
, if A is injective (with dense range);
 $\sigma =s$
,
$\sigma =s$
,
 $B=A^{-1}$
. Then
$B=A^{-1}$
. Then
 $f \circ g$
is the function
$f \circ g$
is the function
 $\tilde f \in \mathcal {D}_s$
as in Lemma 3.17. Note that
$\tilde f \in \mathcal {D}_s$
as in Lemma 3.17. Note that
 $\tilde f_{\mathcal {D}}(A)$
is defined as a bounded operator on X, even if A is not injective. If
$\tilde f_{\mathcal {D}}(A)$
is defined as a bounded operator on X, even if A is not injective. If
 $A_0$
is the restriction of A to
$A_0$
is the restriction of A to
 $X_0$
, the closure of the range of A, then
$X_0$
, the closure of the range of A, then
 $\tilde f_{\mathcal {D}}(A)$
acts as
$\tilde f_{\mathcal {D}}(A)$
acts as
 $A_0^{-1}$
on
$A_0^{-1}$
on
 $X_0$
and as the sectorial limit
$X_0$
and as the sectorial limit
 $f(\infty )$
on the kernel of A. If X is reflexive, this determines
$f(\infty )$
on the kernel of A. If X is reflexive, this determines
 $\tilde f_{\mathcal {D}}(A)$
on X.
$\tilde f_{\mathcal {D}}(A)$
on X. -
2.
 $g(z) = tz$
, where
$g(z) = tz$
, where
 $t>0$
;
$t>0$
;
 $\sigma =s$
,
$\sigma =s$
,
 $B = tA$
. See Lemma 3.17.
$B = tA$
. See Lemma 3.17. -
3.
 $g(z) = z + \eta $
, where
$g(z) = z + \eta $
, where
 $\eta \in \mathbb {C}_+$
;
$\eta \in \mathbb {C}_+$
;
 $\sigma =s$
,
$\sigma =s$
,
 $B = A +\eta $
. See Remark 7.3.
$B = A +\eta $
. See Remark 7.3. -
4.
 $g(z) = z^{\gamma }$
, where
$g(z) = z^{\gamma }$
, where
 $\gamma \in (0,1)$
;
$\gamma \in (0,1)$
;
 $s > \ - 1,\sigma >-1$
;
$s > \ - 1,\sigma >-1$
;
 $B = A^{\gamma }$
(as defined in the holomorphic functional calculus). See Corollary 4.14 for assumption (a) in Corollary 7.9 and Corollary 7.12 for assumption (b). The result also holds for
$B = A^{\gamma }$
(as defined in the holomorphic functional calculus). See Corollary 4.14 for assumption (a) in Corollary 7.9 and Corollary 7.12 for assumption (b). The result also holds for
 $\gamma \in (1, \pi /(2\theta ))$
.
$\gamma \in (1, \pi /(2\theta ))$
. -
5. Examples (2), (3) for
 $\eta \in \mathbb {R}_+$
and (4) are Bernstein functions. By Lemma 3.20,
$\eta \in \mathbb {R}_+$
and (4) are Bernstein functions. By Lemma 3.20,
 $r_{\lambda } \circ g \in \mathcal {D}_s$
for all Bernstein functions g and
$r_{\lambda } \circ g \in \mathcal {D}_s$
for all Bernstein functions g and
 $s>2$
. We will show in the proof of Theorem 10.5 that
$s>2$
. We will show in the proof of Theorem 10.5 that
 $(r_{\lambda }\circ g)_D(A) = (\lambda +g(A))^{-1}$
, where
$(r_{\lambda }\circ g)_D(A) = (\lambda +g(A))^{-1}$
, where
 $g(A)$
is a sectorial operator.
$g(A)$
is a sectorial operator.
In Example 7.10(4), we have introduced a fractional power
![]() $A^{\gamma }$
, where
$A^{\gamma }$
, where
![]() $\gamma>0$
. These operators are defined in various ways, including the extended holomorphic functional calculus. To justify the example, we need the following lemma about fractional powers, which is probably known at least in simpler form. For
$\gamma>0$
. These operators are defined in various ways, including the extended holomorphic functional calculus. To justify the example, we need the following lemma about fractional powers, which is probably known at least in simpler form. For
![]() $\gamma \in (0,1)$
and
$\gamma \in (0,1)$
and
![]() $\nu \in \mathbb {N}$
, it follows easily from a standard result [Reference Martínez Carracedo and Sanz Alix44, Proposition 5.1.4]. We give a proof that uses the holomorphic functional calculus for fractional powers as in [Reference Haase35, Section 3.1].
$\nu \in \mathbb {N}$
, it follows easily from a standard result [Reference Martínez Carracedo and Sanz Alix44, Proposition 5.1.4]. We give a proof that uses the holomorphic functional calculus for fractional powers as in [Reference Haase35, Section 3.1].
Lemma 7.11. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
,
$A \in \operatorname {Sect}(\pi /2-)$
,
![]() $\gamma \in (0,1)$
and
$\gamma \in (0,1)$
and
![]() $\nu>0$
. In the operator norm topology,
$\nu>0$
. In the operator norm topology,
 $$ \begin{align*} \lim_{\epsilon\to0+} ((A+\epsilon)^{\gamma} + z)^{-\nu} = (A^{\gamma}+z)^{-\nu}, \quad z\in \mathbb{C}_+. \end{align*} $$
$$ \begin{align*} \lim_{\epsilon\to0+} ((A+\epsilon)^{\gamma} + z)^{-\nu} = (A^{\gamma}+z)^{-\nu}, \quad z\in \mathbb{C}_+. \end{align*} $$
Proof. Let
![]() $z \in \mathbb {C}_+$
be fixed, and let
$z \in \mathbb {C}_+$
be fixed, and let
Then
![]() $f \in H^{\infty }(\mathbb {C}_+)$
and, by considering the derivative of
$f \in H^{\infty }(\mathbb {C}_+)$
and, by considering the derivative of
![]() $\mu \mapsto (\mu +z)^{-\nu }$
, we see that there exists a constant C (depending on z) such that
$\mu \mapsto (\mu +z)^{-\nu }$
, we see that there exists a constant C (depending on z) such that
Thus, f has polynomial limits at
![]() $0$
and
$0$
and
![]() $\infty $
, and so f belongs to the extended Riesz–Dunford class defined in [Reference Haase35, Lemma 2.2.3]. In other words,
$\infty $
, and so f belongs to the extended Riesz–Dunford class defined in [Reference Haase35, Lemma 2.2.3]. In other words,
has polynomial decay at
![]() $0$
and
$0$
and
![]() $\infty $
. Moreover, there exists a constant
$\infty $
. Moreover, there exists a constant
![]() $C'$
(independent of
$C'$
(independent of
![]() $\epsilon $
) such that
$\epsilon $
) such that
Let
Using the definition of the primary functional calculus [Reference Haase35, Section 2.3.1], we have
 $$ \begin{align*} f(A+\epsilon)-f(A)&= g_{\epsilon}(A)-g_0(A) + (f(\epsilon) -f(0))(I+A)^{-1}, \\ g_{\epsilon}(A)-g_0(A)&=\frac{1}{2\pi i} \int_{\Sigma_{\psi}} \left(g_{\epsilon}(\lambda)-g_0(\lambda)\right) (\lambda-A)^{-1} \,d\lambda, \end{align*} $$
$$ \begin{align*} f(A+\epsilon)-f(A)&= g_{\epsilon}(A)-g_0(A) + (f(\epsilon) -f(0))(I+A)^{-1}, \\ g_{\epsilon}(A)-g_0(A)&=\frac{1}{2\pi i} \int_{\Sigma_{\psi}} \left(g_{\epsilon}(\lambda)-g_0(\lambda)\right) (\lambda-A)^{-1} \,d\lambda, \end{align*} $$
where
![]() $\psi \in (\theta ,\pi /2)$
. By the dominated convergence theorem,
$\psi \in (\theta ,\pi /2)$
. By the dominated convergence theorem,
 $$ \begin{align*} \lim_{\epsilon \to 0+} \|(g_{\epsilon}(A) - g_0(A)\|=0. \end{align*} $$
$$ \begin{align*} \lim_{\epsilon \to 0+} \|(g_{\epsilon}(A) - g_0(A)\|=0. \end{align*} $$
The pointwise convergence of
![]() $g_{\epsilon } -g_0$
to zero is clear, and the existence of an integrable majorant follows easily from (7.14).
$g_{\epsilon } -g_0$
to zero is clear, and the existence of an integrable majorant follows easily from (7.14).
Corollary 7.12. Let
![]() $A\in \operatorname {Sect}(\pi /2-)$
and
$A\in \operatorname {Sect}(\pi /2-)$
and
![]() $\gamma \in (0,1)$
. Let
$\gamma \in (0,1)$
. Let
![]() $f \in \mathcal {D}_{\infty }$
and
$f \in \mathcal {D}_{\infty }$
and
![]() $f_{\gamma }(z) = f(z^{\gamma })$
. Then the following hold:
$f_{\gamma }(z) = f(z^{\gamma })$
. Then the following hold:
-
1. In operator norm,
 $$ \begin{align*} \lim_{\epsilon\to0+} f_{\mathcal{D}}((A+\epsilon)^{\gamma}) = f_{\mathcal{D}}(A^{\gamma}). \end{align*} $$
$$ \begin{align*} \lim_{\epsilon\to0+} f_{\mathcal{D}}((A+\epsilon)^{\gamma}) = f_{\mathcal{D}}(A^{\gamma}). \end{align*} $$
-
2.
 $(f_{\gamma })_{\mathcal {D}}(A) = f_{\mathcal {D}}(A^{\gamma })$
.
$(f_{\gamma })_{\mathcal {D}}(A) = f_{\mathcal {D}}(A^{\gamma })$
.
Proof. The proof of (1) follows from Lemma 7.11 in essentially the same way as the last paragraph of the proof of Proposition 7.2.
By Corollary 4.14,
![]() $h \in \mathcal {D}_{\infty }$
. By (7.10) and the composition theorem for the holomorphic functional calculus [Reference Haase35, Theorem 2.4.2], we have
$h \in \mathcal {D}_{\infty }$
. By (7.10) and the composition theorem for the holomorphic functional calculus [Reference Haase35, Theorem 2.4.2], we have
![]() $h_{\mathcal {D}}(A+\epsilon ) = f_{\mathcal {D}}((A+\epsilon )^{\gamma })$
. Letting
$h_{\mathcal {D}}(A+\epsilon ) = f_{\mathcal {D}}((A+\epsilon )^{\gamma })$
. Letting
![]() $\epsilon \to 0+$
and using (7.6) and (1), we obtain (2).
$\epsilon \to 0+$
and using (7.6) and (1), we obtain (2).
8. The calculus on Hardy–Sobolev algebras
Given the negative generator A of a bounded holomorphic
![]() $C_0$
-semigroup on a Banach space X, the
$C_0$
-semigroup on a Banach space X, the
![]() $\mathcal D$
-calculus allows us to extend the
$\mathcal D$
-calculus allows us to extend the
![]() $\mathcal B$
-calculus to a much larger class of functions. A drawback of the
$\mathcal B$
-calculus to a much larger class of functions. A drawback of the
![]() $\mathcal D$
-calculus is that it does not respect the sectoriality angle of A, so the results within the
$\mathcal D$
-calculus is that it does not respect the sectoriality angle of A, so the results within the
![]() $\mathcal D$
-calculus are independent of the sectoriality angle and confined to holomorphic functions on
$\mathcal D$
-calculus are independent of the sectoriality angle and confined to holomorphic functions on
![]() $\mathbb {C}_+$
. To remedy that problem, we introduce in this section a version of the
$\mathbb {C}_+$
. To remedy that problem, we introduce in this section a version of the
![]() $\mathcal D$
-calculus adjusted to an appropriate Hardy–Sobolev algebra on a sector in the right half-plane. Though the Hardy–Sobolev algebra has a ‘stronger’ norm, it appears to be an adequate substitute for
$\mathcal D$
-calculus adjusted to an appropriate Hardy–Sobolev algebra on a sector in the right half-plane. Though the Hardy–Sobolev algebra has a ‘stronger’ norm, it appears to be an adequate substitute for
![]() $\mathcal D_{\infty }$
in the setting of sectors, and it has significant applications, as we will see in Section 10.
$\mathcal D_{\infty }$
in the setting of sectors, and it has significant applications, as we will see in Section 10.
The basic idea is a very simple change of variable in the
![]() $\mathcal D$
-calculus. If
$\mathcal D$
-calculus. If
![]() $\Psi ^s_A$
is the
$\Psi ^s_A$
is the
![]() $\mathcal D_s^{\infty }$
-calculus for a sectorial operator A, then one sets
$\mathcal D_s^{\infty }$
-calculus for a sectorial operator A, then one sets
![]() $\Upsilon _A(f):= \Psi ^s_{A^{\gamma }}(f_{1/\gamma })$
for appropriate values of
$\Upsilon _A(f):= \Psi ^s_{A^{\gamma }}(f_{1/\gamma })$
for appropriate values of
![]() $\gamma $
, determined by the sectoriality angle
$\gamma $
, determined by the sectoriality angle
![]() $\theta _A$
of A. This definition does not depend on the precise choice of
$\theta _A$
of A. This definition does not depend on the precise choice of
![]() $\gamma $
, by Corollary 7.12. The definitions also agree for different
$\gamma $
, by Corollary 7.12. The definitions also agree for different
![]() $s>-1$
by Theorem 7.4(ii), and we set
$s>-1$
by Theorem 7.4(ii), and we set
![]() $s=0$
for convenience. As we will show, this eventually leads to a new calculus for Hardy–Sobolev algebras on sectors.
$s=0$
for convenience. As we will show, this eventually leads to a new calculus for Hardy–Sobolev algebras on sectors.
Throughout this section, we assume that
![]() $A\in \operatorname {Sect}(\theta )$
,
$A\in \operatorname {Sect}(\theta )$
,
![]() $0<\theta <\psi <\pi $
, and we let
$0<\theta <\psi <\pi $
, and we let
![]() $\gamma :=\pi /(2\psi )$
and, as before,
$\gamma :=\pi /(2\psi )$
and, as before,
 $$ \begin{align*} M_{\psi}(A):=\sup_{z\in \Sigma_{\pi-\psi}}\,\|z(A+z)^{-1}\|. \end{align*} $$
$$ \begin{align*} M_{\psi}(A):=\sup_{z\in \Sigma_{\pi-\psi}}\,\|z(A+z)^{-1}\|. \end{align*} $$
Then
![]() $A^{\gamma }\in \operatorname {Sect}(\pi /2-)$
, and
$A^{\gamma }\in \operatorname {Sect}(\pi /2-)$
, and
![]() $\theta _{A^{\gamma }} =\gamma \theta _A \in [\theta_A,\pi/2)$
[Reference Haase35, Proposition 3.1.2]. We are particularly interested in cases where
$\theta _{A^{\gamma }} =\gamma \theta _A \in [\theta_A,\pi/2)$
[Reference Haase35, Proposition 3.1.2]. We are particularly interested in cases where
![]() $\psi $
is close to
$\psi $
is close to
![]() $\theta $
, so that
$\theta $
, so that
![]() $\mathcal {H}_{\psi }$
is as large as possible.
$\mathcal {H}_{\psi }$
is as large as possible.
8.1. The operator
 $f(A)$
for
$f(A)$
for
 $f\in \mathcal {H}_{\psi }$
$f\in \mathcal {H}_{\psi }$
Recall from Lemmas 4.9 and 4.13(i) that if
![]() $f\in \mathcal {H}_{\psi }$
and
$f\in \mathcal {H}_{\psi }$
and
 $f_{1/\gamma }(z)=f(z^{1/\gamma }),$
then
$f_{1/\gamma }(z)=f(z^{1/\gamma }),$
then
 $$ \begin{align*} f^{\prime}_{1/\gamma}\in H^1(\mathbb{C}_{+}),\qquad f_{1/\gamma}(\infty)=f(\infty) \end{align*} $$
$$ \begin{align*} f^{\prime}_{1/\gamma}\in H^1(\mathbb{C}_{+}),\qquad f_{1/\gamma}(\infty)=f(\infty) \end{align*} $$
and, consequently,
![]() $f_{1/\gamma }\in \mathcal {D}_0$
. Together with Proposition 4.17 this motivates the following definition of the operator
$f_{1/\gamma }\in \mathcal {D}_0$
. Together with Proposition 4.17 this motivates the following definition of the operator
![]() $f_{\mathcal H}(A)$
by means of the
$f_{\mathcal H}(A)$
by means of the
![]() $\mathcal {D}$
-calculus applied to
$\mathcal {D}$
-calculus applied to
![]() $A^{\gamma }$
:
$A^{\gamma }$
:
 $$ \begin{align} f_{\mathcal H}(A):=f_{1/\gamma}(\infty)-\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f^{\prime}_{1/\gamma}(\alpha+i\beta) (A^{\gamma}+\alpha-i\beta)^{-1}\,d\beta\,d\alpha. \end{align} $$
$$ \begin{align} f_{\mathcal H}(A):=f_{1/\gamma}(\infty)-\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f^{\prime}_{1/\gamma}(\alpha+i\beta) (A^{\gamma}+\alpha-i\beta)^{-1}\,d\beta\,d\alpha. \end{align} $$
The right-hand side of (8.1) converges in the uniform operator topology, and by (7.7) and (4.27),
 $$ \begin{align} \|f_{\mathcal H}(A)\|\le |f(\infty)|+\frac{M_{A^{\gamma}}}{\pi}\|f_{1/\gamma}\|_{\mathcal{D}_{0,0}} \le |f(\infty)|+ M_{A^{\gamma}} \|f'\|_{H^1(\psi)} \le M_{A^{\gamma}} \|f\|^{\prime}_{\mathcal{H}_{\psi}}. \end{align} $$
$$ \begin{align} \|f_{\mathcal H}(A)\|\le |f(\infty)|+\frac{M_{A^{\gamma}}}{\pi}\|f_{1/\gamma}\|_{\mathcal{D}_{0,0}} \le |f(\infty)|+ M_{A^{\gamma}} \|f'\|_{H^1(\psi)} \le M_{A^{\gamma}} \|f\|^{\prime}_{\mathcal{H}_{\psi}}. \end{align} $$
If
![]() $f\in \mathcal {H}_{\psi }$
and A is injective, then
$f\in \mathcal {H}_{\psi }$
and A is injective, then
![]() $f_{\operatorname {Hol}}(A)$
can also be defined using the holomorphic functional calculus and the composition rule within it [Reference Haase35, Theorem 2.4.2]:
$f_{\operatorname {Hol}}(A)$
can also be defined using the holomorphic functional calculus and the composition rule within it [Reference Haase35, Theorem 2.4.2]:
 $$ \begin{align*} f_{\operatorname{Hol}}(A)=f_{1/\gamma,\operatorname{Hol}}(A^{\gamma}) :=\frac{1}{2\pi i}[A^{\gamma}(1+A^{\gamma})^{-2}]^{-1} \int_{\partial \Sigma_{\omega}}\,\frac{\lambda f(\lambda^{1/\gamma})}{(\lambda+1)^2}(\lambda-A^{\gamma})^{-1}\,d\lambda, \end{align*} $$
$$ \begin{align*} f_{\operatorname{Hol}}(A)=f_{1/\gamma,\operatorname{Hol}}(A^{\gamma}) :=\frac{1}{2\pi i}[A^{\gamma}(1+A^{\gamma})^{-2}]^{-1} \int_{\partial \Sigma_{\omega}}\,\frac{\lambda f(\lambda^{1/\gamma})}{(\lambda+1)^2}(\lambda-A^{\gamma})^{-1}\,d\lambda, \end{align*} $$
for
![]() $0\le\theta <\omega <\psi $
. The following proposition shows that our definition (8.1) of
$0\le\theta <\omega <\psi $
. The following proposition shows that our definition (8.1) of
![]() $f_{\mathcal H}(A)$
coincides with
$f_{\mathcal H}(A)$
coincides with
![]() $f_{\operatorname {Hol}}(A)$
when A is injective, and various other properties are easily deduced from the definition above and corresponding properties of the
$f_{\operatorname {Hol}}(A)$
when A is injective, and various other properties are easily deduced from the definition above and corresponding properties of the
![]() $\mathcal {D}$
-calculus.
$\mathcal {D}$
-calculus.
Proposition 8.1. Let
![]() $f \in \mathcal {H}_{\psi }$
and
$f \in \mathcal {H}_{\psi }$
and
![]() $A \in \operatorname {Sect}(\theta )$
, where
$A \in \operatorname {Sect}(\theta )$
, where
![]() $0 \le \theta < \psi < \pi $
.
$0 \le \theta < \psi < \pi $
.
-
(i)
 $f_{\mathcal {H}}(A)$
does not depend on the choice of
$f_{\mathcal {H}}(A)$
does not depend on the choice of
 $\psi $
.
$\psi $
. -
(ii) If
 $\nu \in (0,1)$
and
$\nu \in (0,1)$
and
 $f_{\nu }(z) = f(z^{\nu })$
, then
$f_{\nu }(z) = f(z^{\nu })$
, then
 $(f_{\nu })_{\mathcal {H}}(A) = f_{\mathcal {H}}(A^{\nu })$
.
$(f_{\nu })_{\mathcal {H}}(A) = f_{\mathcal {H}}(A^{\nu })$
. -
(iii) If
 $f \in \mathcal {D}_{\infty }$
and
$f \in \mathcal {D}_{\infty }$
and
 $\theta < \pi /2$
, then
$\theta < \pi /2$
, then
 $f_{\mathcal {H}}(A) = f_{\mathcal {D}}(A)$
.
$f_{\mathcal {H}}(A) = f_{\mathcal {D}}(A)$
. -
(iv) If A is injective, then
 $f_{\mathcal {H}}(A) = f_{\operatorname {Hol}}(A)$
.
$f_{\mathcal {H}}(A) = f_{\operatorname {Hol}}(A)$
. -
(v) In the operator norm topology,
 $\lim _{\epsilon \to 0+} f_{\mathcal {H}}(A+\epsilon ) = f_{\mathcal {H}}(A)$
.
$\lim _{\epsilon \to 0+} f_{\mathcal {H}}(A+\epsilon ) = f_{\mathcal {H}}(A)$
.
Proof. Statements (i), (ii) and (iii) follow from Corollary 7.12(ii) and Lemma 4.9. Statement (iv) follows from (iii) and Theorem 7.4(i). Statement (v) follows from Proposition 7.2.
An alternative direct proof of (iv) can be given as follows. We may assume that
![]() ${f(\infty )=0}$
. Because
${f(\infty )=0}$
. Because
![]() $f_{1/\gamma }\in \mathcal {D}_0$
, Corollary 3.10 gives
$f_{1/\gamma }\in \mathcal {D}_0$
, Corollary 3.10 gives
 $$ \begin{align*} f_{1/\gamma}(z)= -\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty}\frac{f_{1/\gamma}'(\alpha+i\beta)}{z+\alpha-i\beta}\,d\beta\,d\alpha,\qquad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} f_{1/\gamma}(z)= -\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty}\frac{f_{1/\gamma}'(\alpha+i\beta)}{z+\alpha-i\beta}\,d\beta\,d\alpha,\qquad z\in \mathbb{C}_{+}. \end{align*} $$
Using Fubini’s theorem and some basic properties of the holomorphic functional calculus, we obtain
 $$ \begin{align*} &{A^{\gamma}(1+A^{\gamma})^{-2}f_{\operatorname{Hol}}(A)}\\ &\quad =-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} f_{1/\gamma}'(\alpha+i\beta) \left(\frac{1}{2\pi i} \int_{\partial \Sigma_{\omega}}\,\frac{\lambda(\lambda-A^{\gamma})^{-1}}{(\lambda+1)^2(\lambda+\alpha-i\beta)}\,d\lambda\right) d\beta \,d\alpha\\ &\quad = -A^{\gamma}(1+A^{\gamma})^{-2}\left( \frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} f_{1/\gamma}'(\alpha+i\beta)(A^{\gamma}+\alpha-i\beta)^{-1} d\beta\, d\alpha\right)\\ &\quad =A^{\gamma}(1+A^{\gamma})^{-2}f_{\mathcal{H}}(A), \end{align*} $$
$$ \begin{align*} &{A^{\gamma}(1+A^{\gamma})^{-2}f_{\operatorname{Hol}}(A)}\\ &\quad =-\frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} f_{1/\gamma}'(\alpha+i\beta) \left(\frac{1}{2\pi i} \int_{\partial \Sigma_{\omega}}\,\frac{\lambda(\lambda-A^{\gamma})^{-1}}{(\lambda+1)^2(\lambda+\alpha-i\beta)}\,d\lambda\right) d\beta \,d\alpha\\ &\quad = -A^{\gamma}(1+A^{\gamma})^{-2}\left( \frac{1}{\pi}\int_0^{\infty} \int_{-\infty}^{\infty} f_{1/\gamma}'(\alpha+i\beta)(A^{\gamma}+\alpha-i\beta)^{-1} d\beta\, d\alpha\right)\\ &\quad =A^{\gamma}(1+A^{\gamma})^{-2}f_{\mathcal{H}}(A), \end{align*} $$
and (iv) follows.
Now we can formally define the
![]() $\mathcal H$
-calculus.
$\mathcal H$
-calculus.
Theorem 8.2. Let
![]() $A \in \operatorname {Sect}(\theta )$
, where
$A \in \operatorname {Sect}(\theta )$
, where
![]() $\theta \in [0,\pi/2)$
. For any
$\theta \in [0,\pi/2)$
. For any
![]() $\psi \in (\theta , \pi )$
the formula (8.1) defines a bounded algebra homomorphism:
$\psi \in (\theta , \pi )$
the formula (8.1) defines a bounded algebra homomorphism:
The homomorphism
![]() $\Upsilon _A$
satisfies
$\Upsilon _A$
satisfies
![]() $\Upsilon _A(r_{\lambda })=(\lambda +A)^{-1}$
for all
$\Upsilon _A(r_{\lambda })=(\lambda +A)^{-1}$
for all
![]() $\lambda \in \Sigma _{\pi -\psi }$
, and it is the unique homomorphism with these properties.
$\lambda \in \Sigma _{\pi -\psi }$
, and it is the unique homomorphism with these properties.
The homomorphism
![]() $\Upsilon _A$
will be called the
$\Upsilon _A$
will be called the
![]() $\mathcal H$
-calculus for A.
$\mathcal H$
-calculus for A.
Proof. The boundedness of
![]() $\Upsilon _A$
follows from either (8.13) or (8.2). The homomorphism property is implied by Corollary 7.8. Indeed, employing the functional calculus
$\Upsilon _A$
follows from either (8.13) or (8.2). The homomorphism property is implied by Corollary 7.8. Indeed, employing the functional calculus
![]() $\Psi ^0_A$
on
$\Psi ^0_A$
on
![]() $\mathcal D^{\infty }_0$
given by Corollary 7.8, one has
$\mathcal D^{\infty }_0$
given by Corollary 7.8, one has
 $$ \begin{align*} \Upsilon_A(fg) &= \Psi^0_A((fg)_{1/\alpha}) = \Psi^0_A(f_{1/\alpha}g_{1/\alpha}) \\ &= \Psi^0_A(f_{1/\alpha}) \Psi^0_A(g_{1/\alpha}) = \Upsilon_A(f)\Upsilon_A(g). \end{align*} $$
$$ \begin{align*} \Upsilon_A(fg) &= \Psi^0_A((fg)_{1/\alpha}) = \Psi^0_A(f_{1/\alpha}g_{1/\alpha}) \\ &= \Psi^0_A(f_{1/\alpha}) \Psi^0_A(g_{1/\alpha}) = \Upsilon_A(f)\Upsilon_A(g). \end{align*} $$
The uniqueness follows from Theorem 5.10.
Remark 8.3. If A is any operator for which there is an
![]() $\mathcal {H}_{\psi }$
-calculus as in Theorem 8.2, then
$\mathcal {H}_{\psi }$
-calculus as in Theorem 8.2, then
![]() $A \in \operatorname {Sect}(\theta )$
for some
$A \in \operatorname {Sect}(\theta )$
for some
![]() $\theta \in [0,\psi)$
. This follows from (4.24), and in combination with Theorem 8.2 this yields the proof of Theorem 1.2. If
$\theta \in [0,\psi)$
. This follows from (4.24), and in combination with Theorem 8.2 this yields the proof of Theorem 1.2. If
![]() $\Upsilon _A(r_{\lambda }) = (\lambda +A)^{-1}$
for some
$\Upsilon _A(r_{\lambda }) = (\lambda +A)^{-1}$
for some
![]() $\lambda \in \Sigma _{\pi -\psi }$
, then this holds for all
$\lambda \in \Sigma _{\pi -\psi }$
, then this holds for all
![]() $\lambda \in \Sigma _{\pi -\psi }$
, by the resolvent identity.
$\lambda \in \Sigma _{\pi -\psi }$
, by the resolvent identity.
8.2. The operator
 $\operatorname {\mathrm {arccot}}(A^{\gamma })$
and the
$\operatorname {\mathrm {arccot}}(A^{\gamma })$
and the
 $\operatorname {\mathrm {arccot}}$
formula
$\operatorname {\mathrm {arccot}}$
formula
In this section, we derive an alternative to the formula (8.1) for the
![]() $\mathcal {H}$
-calculus, in the form of an operator counterpart of Proposition 4.19 for scalar functions. In addition to its intrinsic interest, it helps us to compare our approach with the approach developed by Boyadzhiev [Reference Boyadzhiev12], as we do at the end of this section.
$\mathcal {H}$
-calculus, in the form of an operator counterpart of Proposition 4.19 for scalar functions. In addition to its intrinsic interest, it helps us to compare our approach with the approach developed by Boyadzhiev [Reference Boyadzhiev12], as we do at the end of this section.
We introduce as an operator kernel the function
 $$ \begin{align*} g(z) :=\operatorname{\mathrm{arccot}}(z) = \frac{1}{2i} \log \left(\frac{z+i}{z-i}\right), \quad z \in \mathbb{C}_+, \end{align*} $$
$$ \begin{align*} g(z) :=\operatorname{\mathrm{arccot}}(z) = \frac{1}{2i} \log \left(\frac{z+i}{z-i}\right), \quad z \in \mathbb{C}_+, \end{align*} $$
already considered in Example 3.5. Note that
![]() $g \in \mathcal {D}_0$
,
$g \in \mathcal {D}_0$
,
![]() $ g(\infty )=0$
,
$ g(\infty )=0$
,
![]() $g'(z)=-(z^2+1)^{-1}$
, and (4.38) holds:
$g'(z)=-(z^2+1)^{-1}$
, and (4.38) holds:
 $$ \begin{align*} \operatorname{\mathrm{arccot}}(z)=\frac{1}{\pi} \int_0^{\infty}\int_{-\infty}^{\infty}\frac{(z+\alpha-i\beta)^{-1}}{(\alpha+i\beta)^2+1}\,d\beta\,d\alpha\qquad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{arccot}}(z)=\frac{1}{\pi} \int_0^{\infty}\int_{-\infty}^{\infty}\frac{(z+\alpha-i\beta)^{-1}}{(\alpha+i\beta)^2+1}\,d\beta\,d\alpha\qquad z\in \mathbb{C}_{+}. \end{align*} $$
Let
![]() $A \in \operatorname {Sect}(\theta )$
, where
$A \in \operatorname {Sect}(\theta )$
, where
![]() $\theta \in [0,\pi )$
. Let
$\theta \in [0,\pi )$
. Let
![]() $\psi \in (\theta ,\pi )$
and
$\psi \in (\theta ,\pi )$
and
![]() $\gamma =\pi /(2\psi )$
. By the
$\gamma =\pi /(2\psi )$
. By the
![]() $\mathcal {D}$
-calculus in (7.5) and (7.7),
$\mathcal {D}$
-calculus in (7.5) and (7.7),
 $$ \begin{align} \operatorname{\mathrm{arccot}}(A^{\gamma}) := \operatorname{\mathrm{arccot}}_{\mathcal{D}}(A^{\gamma})=\frac{1}{\pi} \int_0^{\infty}\int_{-\infty}^{\infty}\frac{(A^{\gamma}+\alpha-i\beta)^{-1}}{(\alpha+i\beta)^2+1}\,d\beta\,d\alpha, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{arccot}}(A^{\gamma}) := \operatorname{\mathrm{arccot}}_{\mathcal{D}}(A^{\gamma})=\frac{1}{\pi} \int_0^{\infty}\int_{-\infty}^{\infty}\frac{(A^{\gamma}+\alpha-i\beta)^{-1}}{(\alpha+i\beta)^2+1}\,d\beta\,d\alpha, \end{align} $$
where the integral converges in the operator norm, and
 $$ \begin{align} \|\operatorname{\mathrm{arccot}}(A^{\gamma})\|\le\frac{M_{A^{\gamma}}}{\pi}\|\operatorname{\mathrm{arccot}} z\|_{\mathcal{D}_0} < 3M_{A^{\gamma}},\;\; M_{A^{\gamma}}:=\sup_{z\in \mathbb{C}_{+}}\,\|z(A^{\gamma}+z)^{-1}\|. \end{align} $$
$$ \begin{align} \|\operatorname{\mathrm{arccot}}(A^{\gamma})\|\le\frac{M_{A^{\gamma}}}{\pi}\|\operatorname{\mathrm{arccot}} z\|_{\mathcal{D}_0} < 3M_{A^{\gamma}},\;\; M_{A^{\gamma}}:=\sup_{z\in \mathbb{C}_{+}}\,\|z(A^{\gamma}+z)^{-1}\|. \end{align} $$
We will provide an alternative estimate for the operator
![]() $\operatorname {\mathrm {arccot}} (A^{\gamma }/s^{\gamma })$
. Following (4.40), we may formally write
$\operatorname {\mathrm {arccot}} (A^{\gamma }/s^{\gamma })$
. Following (4.40), we may formally write
 $$ \begin{align} \operatorname{\mathrm{arccot}}_{\text{int}}(A^{\gamma})&:=\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \left((t-e^{i\psi}A)^{-1} +(t-e^{-i\psi}A)^{-1}\right)\,dt\\ &\quad \ +\frac{1}{4 i}\int_{|\lambda|=1,\,\arg\lambda\in (\psi,2\pi-\psi)}\, (\lambda-A)^{-1}\,d\lambda. \notag \end{align} $$
$$ \begin{align} \operatorname{\mathrm{arccot}}_{\text{int}}(A^{\gamma})&:=\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \left((t-e^{i\psi}A)^{-1} +(t-e^{-i\psi}A)^{-1}\right)\,dt\\ &\quad \ +\frac{1}{4 i}\int_{|\lambda|=1,\,\arg\lambda\in (\psi,2\pi-\psi)}\, (\lambda-A)^{-1}\,d\lambda. \notag \end{align} $$
Lemma 8.4. Let
![]() $A \in \operatorname {Sect}(\theta )$
and
$A \in \operatorname {Sect}(\theta )$
and
![]() $\gamma = \pi /(2\psi )$
, where
$\gamma = \pi /(2\psi )$
, where
![]() $0 \le \theta < \psi < \pi $
. The operator
$0 \le \theta < \psi < \pi $
. The operator
![]() $\operatorname {\mathrm {arccot}}_{\rm int}(A^{\gamma })$
is well-defined and
$\operatorname {\mathrm {arccot}}_{\rm int}(A^{\gamma })$
is well-defined and
 $$ \begin{align} \|\operatorname{\mathrm{arccot}}_{\rm int}(A^{\gamma})\|\le M_{\psi}(A)\frac{\pi}{2}. \end{align} $$
$$ \begin{align} \|\operatorname{\mathrm{arccot}}_{\rm int}(A^{\gamma})\|\le M_{\psi}(A)\frac{\pi}{2}. \end{align} $$
Proof. Using (4.43), one notes that
 $$ \begin{align*} \|\operatorname{\mathrm{arccot}}(A^{\gamma})\|&\le \frac{M_{\psi}(A)}{2\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \,\frac{dt}{t} +\frac{M_{\psi}(A)}{4}\int_{|\lambda|=1,\; \arg \lambda\in (\psi,2\pi-\psi)}\,\frac{|d\lambda|}{|\lambda|}\\ &=M_{\psi}(A)\left(\frac{\psi}{2}+ \frac{(\pi-\psi)}{2}\right) =M_{\psi}(A)\frac{\pi}{2}. \\[-40pt] \end{align*} $$
$$ \begin{align*} \|\operatorname{\mathrm{arccot}}(A^{\gamma})\|&\le \frac{M_{\psi}(A)}{2\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \,\frac{dt}{t} +\frac{M_{\psi}(A)}{4}\int_{|\lambda|=1,\; \arg \lambda\in (\psi,2\pi-\psi)}\,\frac{|d\lambda|}{|\lambda|}\\ &=M_{\psi}(A)\left(\frac{\psi}{2}+ \frac{(\pi-\psi)}{2}\right) =M_{\psi}(A)\frac{\pi}{2}. \\[-40pt] \end{align*} $$
The next lemma shows that the formula
![]() $\operatorname {\mathrm {arccot}}_{\text {int}}(A^{\gamma })$
coincides with the definition of
$\operatorname {\mathrm {arccot}}_{\text {int}}(A^{\gamma })$
coincides with the definition of
![]() $\operatorname {\mathrm {arccot}} (A^{\gamma })$
by the
$\operatorname {\mathrm {arccot}} (A^{\gamma })$
by the
![]() $\mathcal D$
-calculus. When A is injective,
$\mathcal D$
-calculus. When A is injective,
![]() $\operatorname {\mathrm {arccot}}(A^{\gamma })$
is defined in the holomorphic functional calculus by
$\operatorname {\mathrm {arccot}}(A^{\gamma })$
is defined in the holomorphic functional calculus by
 $$ \begin{align} \operatorname{\mathrm{arccot}}_{\operatorname{Hol}}(A^{\gamma}):=\frac{1}{2\pi i}[A(1+A)^{-1}]^{-1} \int_{\partial\Sigma_{\omega}}\,\frac{\lambda\operatorname{\mathrm{arccot}}(\lambda^{\gamma})}{\lambda+1}(\lambda-A)^{-1}\,d\lambda, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{arccot}}_{\operatorname{Hol}}(A^{\gamma}):=\frac{1}{2\pi i}[A(1+A)^{-1}]^{-1} \int_{\partial\Sigma_{\omega}}\,\frac{\lambda\operatorname{\mathrm{arccot}}(\lambda^{\gamma})}{\lambda+1}(\lambda-A)^{-1}\,d\lambda, \end{align} $$
where
![]() $0\le\theta <\omega <\psi <\pi $
.
$0\le\theta <\omega <\psi <\pi $
.
Lemma 8.5. Under the assumptions above,
![]() $\operatorname {\mathrm {arccot}}_{\rm int}(A^{\gamma })=\operatorname {\mathrm {arccot}}_{\mathcal {D}}(A^{\gamma })$
. If A is injective, then
$\operatorname {\mathrm {arccot}}_{\rm int}(A^{\gamma })=\operatorname {\mathrm {arccot}}_{\mathcal {D}}(A^{\gamma })$
. If A is injective, then
![]() $\operatorname {\mathrm {arccot}}_{\rm int}(A^{\gamma })=\operatorname {\mathrm {arccot}}_{\operatorname {Hol}}(A^{\gamma })$
.
$\operatorname {\mathrm {arccot}}_{\rm int}(A^{\gamma })=\operatorname {\mathrm {arccot}}_{\operatorname {Hol}}(A^{\gamma })$
.
Proof. Assume first that A is injective. Using (8.7), (4.40) and (8.3), we obtain
 $$ \begin{align*} &{A(1+A)^{-1} \operatorname{\mathrm{arccot}}_{\text{{Hol}}} (A^{\gamma})} \\ &\ = \frac{1}{2\pi i} \int_{\partial\Sigma_{\omega}}\,\frac{z\operatorname{\mathrm{arccot}}(z^{\gamma})}{z+1}(z-A)^{-1}\,dz\\ &\ =\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \left(\frac{1}{2\pi i} \int_{\partial\Sigma_{\omega}}\,\frac{z}{z+1}(z-A)^{-1}\, V_{\psi}(z, t)\,dz \right)\,\frac{dt}{t}\\ &\qquad + \frac{1}{4i}\int_{|\lambda|=1,\,\arg \lambda\in (\psi,2\pi-\psi)}\,\left( \frac{1}{2\pi i}\int_{\partial\Sigma_{\omega}} \frac{z (z-A)^{-1}}{(z+1)(\lambda-z)} dz \right) d \lambda \\ &\ =A(A+1)^{-1}\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \left((t-e^{i\psi}A)^{-1}+(t-e^{-i\psi}A)^{-1}\right)\,dt\\ &\qquad +A(A+1)^{-1}\frac{1}{4i}\int_{|\lambda|=1,\,\arg \lambda\in (\psi,2\pi-\psi)}\, (\lambda-A)^{-1}\, d \lambda\\ &\ = A(A+1)^{-1}\operatorname{\mathrm{arccot}}_{\text{int}}(A^{\gamma}). \end{align*} $$
$$ \begin{align*} &{A(1+A)^{-1} \operatorname{\mathrm{arccot}}_{\text{{Hol}}} (A^{\gamma})} \\ &\ = \frac{1}{2\pi i} \int_{\partial\Sigma_{\omega}}\,\frac{z\operatorname{\mathrm{arccot}}(z^{\gamma})}{z+1}(z-A)^{-1}\,dz\\ &\ =\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \left(\frac{1}{2\pi i} \int_{\partial\Sigma_{\omega}}\,\frac{z}{z+1}(z-A)^{-1}\, V_{\psi}(z, t)\,dz \right)\,\frac{dt}{t}\\ &\qquad + \frac{1}{4i}\int_{|\lambda|=1,\,\arg \lambda\in (\psi,2\pi-\psi)}\,\left( \frac{1}{2\pi i}\int_{\partial\Sigma_{\omega}} \frac{z (z-A)^{-1}}{(z+1)(\lambda-z)} dz \right) d \lambda \\ &\ =A(A+1)^{-1}\frac{1}{4\pi}\int_0^{\infty} \log\left|\frac{1+t^{\gamma}}{1-t^{\gamma}}\right| \left((t-e^{i\psi}A)^{-1}+(t-e^{-i\psi}A)^{-1}\right)\,dt\\ &\qquad +A(A+1)^{-1}\frac{1}{4i}\int_{|\lambda|=1,\,\arg \lambda\in (\psi,2\pi-\psi)}\, (\lambda-A)^{-1}\, d \lambda\\ &\ = A(A+1)^{-1}\operatorname{\mathrm{arccot}}_{\text{int}}(A^{\gamma}). \end{align*} $$
Thus, the second statement holds. Moreover,
![]() $\operatorname {\mathrm {arccot}}_{\operatorname {Hol}}(A^{\gamma })=\operatorname {\mathrm {arccot}}_{\mathcal {D}}(A^{\gamma })$
, by Theorem 7.4, and the first statement follows.
$\operatorname {\mathrm {arccot}}_{\operatorname {Hol}}(A^{\gamma })=\operatorname {\mathrm {arccot}}_{\mathcal {D}}(A^{\gamma })$
, by Theorem 7.4, and the first statement follows.
If A is not injective, we have
![]() $\operatorname {\mathrm {arccot}}_{\text {int}}((A+\epsilon )^{\gamma }) = \operatorname {\mathrm {arccot}}_{\mathcal {D}}((A+\epsilon )^{\gamma })$
from the case above. When
$\operatorname {\mathrm {arccot}}_{\text {int}}((A+\epsilon )^{\gamma }) = \operatorname {\mathrm {arccot}}_{\mathcal {D}}((A+\epsilon )^{\gamma })$
from the case above. When
![]() $\epsilon \to 0+$
, the left-hand side converges in operator norm to
$\epsilon \to 0+$
, the left-hand side converges in operator norm to
![]() $\operatorname {\mathrm {arccot}}_{\text {int}}(A^{\gamma })$
by applying the dominated convergence theorem in (8.5), and the right-hand side converges to
$\operatorname {\mathrm {arccot}}_{\text {int}}(A^{\gamma })$
by applying the dominated convergence theorem in (8.5), and the right-hand side converges to
![]() $\operatorname {\mathrm {arccot}}_{\mathcal {D}}(A^{\gamma })$
by Proposition 7.2.
$\operatorname {\mathrm {arccot}}_{\mathcal {D}}(A^{\gamma })$
by Proposition 7.2.
Theorem 8.6. Let
![]() $A \in \operatorname {Sect}(\theta )$
and
$A \in \operatorname {Sect}(\theta )$
and
![]() $\gamma =\pi /(2\psi )$
, where
$\gamma =\pi /(2\psi )$
, where
![]() $0 \le \theta < \psi < \pi $
. If
$0 \le \theta < \psi < \pi $
. If
![]() $f \in \mathcal {H}_{\psi }$
and
$f \in \mathcal {H}_{\psi }$
and
![]() $f_{\psi }$
is given by (4.36), then
$f_{\psi }$
is given by (4.36), then
 $$ \begin{align} f_{\mathcal H}(A)= f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t) \,\operatorname{\mathrm{arccot}}(A^{\gamma}/t^{\gamma})\,dt, \end{align} $$
$$ \begin{align} f_{\mathcal H}(A)= f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t) \,\operatorname{\mathrm{arccot}}(A^{\gamma}/t^{\gamma})\,dt, \end{align} $$
where the integral converges in the uniform operator topology, and
 $$ \begin{align} \|f_{\mathcal H}(A)\| \le |f(\infty)| + \frac{M_{\psi}(A)}{2} \|f'\|_{H^1(\Sigma_{\psi})} \le {M_{\psi}(A)} \|f\|_{\mathcal{H}_{\psi}}. \end{align} $$
$$ \begin{align} \|f_{\mathcal H}(A)\| \le |f(\infty)| + \frac{M_{\psi}(A)}{2} \|f'\|_{H^1(\Sigma_{\psi})} \le {M_{\psi}(A)} \|f\|_{\mathcal{H}_{\psi}}. \end{align} $$
Moreover, if
![]() $f(\infty )=0$
, then
$f(\infty )=0$
, then
 $$ \begin{align} \|f_{\mathcal H}(A)\| \le \frac{M_{\psi}(A)}{2} \|f\|_{\mathcal{H}_{\psi}}. \end{align} $$
$$ \begin{align} \|f_{\mathcal H}(A)\| \le \frac{M_{\psi}(A)}{2} \|f\|_{\mathcal{H}_{\psi}}. \end{align} $$
Proof. Let
![]() $\varphi \in (\theta ,\psi )$
be fixed. Let
$\varphi \in (\theta ,\psi )$
be fixed. Let
![]() $g(z)=\operatorname {\mathrm {arccot}}(z)$
and
$g(z)=\operatorname {\mathrm {arccot}}(z)$
and
![]() $g_{\gamma }(z)=\operatorname {\mathrm {arccot}}(z^{\gamma })$
. Because
$g_{\gamma }(z)=\operatorname {\mathrm {arccot}}(z^{\gamma })$
. Because
![]() $g \in \mathcal {D}_0 \subset \mathcal {H}_{\gamma \varphi }$
, we have
$g \in \mathcal {D}_0 \subset \mathcal {H}_{\gamma \varphi }$
, we have
![]() $g_{\gamma } \in \mathcal {H}_{\varphi }$
. Let
$g_{\gamma } \in \mathcal {H}_{\varphi }$
. Let
![]() $q_t(z) = \operatorname {\mathrm {arccot}}(z^{\gamma }/t^{\gamma }), \, t>0$
. By scale-invariance (Lemma 4.9),
$q_t(z) = \operatorname {\mathrm {arccot}}(z^{\gamma }/t^{\gamma }), \, t>0$
. By scale-invariance (Lemma 4.9),
![]() $\|q_t\|_{\mathcal {H}_{\varphi }} = \|g_{\gamma }\|_{\mathcal {H}_{\varphi }}$
. It follows from Lemma 2.2 that
$\|q_t\|_{\mathcal {H}_{\varphi }} = \|g_{\gamma }\|_{\mathcal {H}_{\varphi }}$
. It follows from Lemma 2.2 that
![]() $t \mapsto q_t$
is continuous from
$t \mapsto q_t$
is continuous from
![]() $(0,\infty )$
to
$(0,\infty )$
to
![]() $\mathcal {H}_{\varphi }$
. Hence, in view of Proposition 4.19, we have
$\mathcal {H}_{\varphi }$
. Hence, in view of Proposition 4.19, we have
 $$ \begin{align} f=f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t)\, q_t \,dt, \end{align} $$
$$ \begin{align} f=f(\infty)-\frac{2}{\pi}\int_0^{\infty} f_{\psi}'(t)\, q_t \,dt, \end{align} $$
where the integral is understood as a Bochner integral in
![]() $\mathcal {H}_{\varphi }$
. Combining Proposition 8.1,(ii) and (iii) with Lemmas 8.4 and 8.5, we infer that
$\mathcal {H}_{\varphi }$
. Combining Proposition 8.1,(ii) and (iii) with Lemmas 8.4 and 8.5, we infer that
Hence, by applying the bounded operator
![]() $\Upsilon _A$
to both sides of (8.12), we obtain (8.8). The estimate (8.9) follows from (8.8) and Lemma 8.4. Given (8.9), the estimate (8.10) is direct.
$\Upsilon _A$
to both sides of (8.12), we obtain (8.8). The estimate (8.9) follows from (8.8) and Lemma 8.4. Given (8.9), the estimate (8.10) is direct.
Remarks 8.7. 1. If
![]() $M_{\psi }(A)=1$
in (8.9) – that is, if
$M_{\psi }(A)=1$
in (8.9) – that is, if
![]() $-A$
generates a holomorphic
$-A$
generates a holomorphic
![]() $C_0$
-semigroup that is contractive on
$C_0$
-semigroup that is contractive on
![]() $\Sigma _{(\pi /2)-\psi }$
– then the
$\Sigma _{(\pi /2)-\psi }$
– then the
![]() $\mathcal H$
-calculus is contractive. This seems to be a new feature that has not been present in constructions of other calculi in the literature.
$\mathcal H$
-calculus is contractive. This seems to be a new feature that has not been present in constructions of other calculi in the literature.
2. An alternative to the estimate (8.9) is
 $$ \begin{align} \|f_{\mathcal H}(A)\|\le |f(\infty)|+ 3 M_{A^{\gamma}}\|f_{\psi}'\|_{L^1(\mathbb{R}_+)}. \end{align} $$
$$ \begin{align} \|f_{\mathcal H}(A)\|\le |f(\infty)|+ 3 M_{A^{\gamma}}\|f_{\psi}'\|_{L^1(\mathbb{R}_+)}. \end{align} $$
This is obtained from (8.8), using the estimates (7.7) (with
![]() $s=0$
) and (3.23) to obtain the estimate
$s=0$
) and (3.23) to obtain the estimate
![]() $\|\operatorname {\mathrm {arccot}}(A^{\gamma })\| \le 3\pi M_{A^{\gamma }}$
. The constant
$\|\operatorname {\mathrm {arccot}}(A^{\gamma })\| \le 3\pi M_{A^{\gamma }}$
. The constant
![]() $3$
is not optimal. It is possible to provide explicit bounds for
$3$
is not optimal. It is possible to provide explicit bounds for
![]() $M_{A^{\gamma }}$
in terms of
$M_{A^{\gamma }}$
in terms of
![]() $M_A$
. However, we refrain from doing so in this article, and we refer the interested reader to [Reference Batty, Gomilko and Tomilov6, Propositions 5.1 and 5.2].
$M_A$
. However, we refrain from doing so in this article, and we refer the interested reader to [Reference Batty, Gomilko and Tomilov6, Propositions 5.1 and 5.2].
Finally, in this section we discuss the relations between [Reference Boyadzhiev12] and the present work. For
![]() $\psi \in (0,\pi )$
, as in [Reference Boyadzhiev12], let
$\psi \in (0,\pi )$
, as in [Reference Boyadzhiev12], let
 $$ \begin{align*} k_{\psi}(t) =\frac{1}{\pi^2}\log\left|\coth\left(\frac{\pi t }{4 \psi}\right) \coth\left(\frac{\pi t}{4(\pi-\psi)}\right)\right|. \end{align*} $$
$$ \begin{align*} k_{\psi}(t) =\frac{1}{\pi^2}\log\left|\coth\left(\frac{\pi t }{4 \psi}\right) \coth\left(\frac{\pi t}{4(\pi-\psi)}\right)\right|. \end{align*} $$
Note that
![]() $k_{\psi }$
is an even function on
$k_{\psi }$
is an even function on
![]() $\mathbb R\setminus \{0\}$
, and
$\mathbb R\setminus \{0\}$
, and
![]() $\|k_{\psi }\|_{L^1(\mathbb R)}=1.$
$\|k_{\psi }\|_{L^1(\mathbb R)}=1.$
For any
![]() $f \in L^{\infty } (\mathbb R_+),$
let
$f \in L^{\infty } (\mathbb R_+),$
let
 $$ \begin{align*} (f \circ k_{\psi}) (t):=\int_{0}^{\infty}f (s)k_{\psi} \left(\log (t/s) \right)\, \frac{ds}{s}, \qquad t> 0, \end{align*} $$
$$ \begin{align*} (f \circ k_{\psi}) (t):=\int_{0}^{\infty}f (s)k_{\psi} \left(\log (t/s) \right)\, \frac{ds}{s}, \qquad t> 0, \end{align*} $$
and for
![]() $A \in \operatorname {Sect}(\theta )$
,
$A \in \operatorname {Sect}(\theta )$
,
![]() $\theta \in [0,\psi )$
, define
$\theta \in [0,\psi )$
, define
 $$ \begin{align} W_{\psi}(A,t)=-\frac{A}{2}\left(e^{-i\psi} (A-e^{-i\psi}t)^{-2} + e^{i\psi}(A-e^{i\psi} t)^{-2}\right). \end{align} $$
$$ \begin{align} W_{\psi}(A,t)=-\frac{A}{2}\left(e^{-i\psi} (A-e^{-i\psi}t)^{-2} + e^{i\psi}(A-e^{i\psi} t)^{-2}\right). \end{align} $$
It was proved in [Reference Boyadzhiev12, Theorem 3.1] that if
![]() $A \in \operatorname {Sect}(\theta )$
, A has dense range and
$A \in \operatorname {Sect}(\theta )$
, A has dense range and
 $$ \begin{align} \int_{0}^{\infty}|\langle W_{\psi}(A,t)x, x^*\rangle |\, dt <\infty, \qquad x \in X,\, x^* \in X^*, \end{align} $$
$$ \begin{align} \int_{0}^{\infty}|\langle W_{\psi}(A,t)x, x^*\rangle |\, dt <\infty, \qquad x \in X,\, x^* \in X^*, \end{align} $$
then A admits a bounded
![]() $H^{\infty }(\Sigma _{\psi })$
-calculus given by
$H^{\infty }(\Sigma _{\psi })$
-calculus given by
 $$ \begin{align} \langle f(A)x, x^*\rangle=\int_{0}^{\infty}\langle W_{\psi}(A,t)x, x^*\rangle (f_{\psi} \circ k_{\psi})(t)\, dt, \quad x \in X,\, x^* \in X^*, \end{align} $$
$$ \begin{align} \langle f(A)x, x^*\rangle=\int_{0}^{\infty}\langle W_{\psi}(A,t)x, x^*\rangle (f_{\psi} \circ k_{\psi})(t)\, dt, \quad x \in X,\, x^* \in X^*, \end{align} $$
where the integral converges absolutely (in the weak sense). Conversely, if
![]() $\psi \in (\theta ,\pi )$
and
$\psi \in (\theta ,\pi )$
and
![]() $\varphi \in (\theta , \psi )$
are such that A has a bounded
$\varphi \in (\theta , \psi )$
are such that A has a bounded
![]() $H^{\infty }(\Sigma _{\varphi })$
-calculus, then (8.15) holds. (Note that in this situation A has a bounded
$H^{\infty }(\Sigma _{\varphi })$
-calculus, then (8.15) holds. (Note that in this situation A has a bounded
![]() $H^{\infty }(\Sigma _{\psi })$
-calculus given by (8.16), by the uniqueness of the calculus.) The formula (8.16) is obtained in [Reference Boyadzhiev12] by rather involved Fourier analysis, and some technical details are omitted in [Reference Boyadzhiev12].
$H^{\infty }(\Sigma _{\psi })$
-calculus given by (8.16), by the uniqueness of the calculus.) The formula (8.16) is obtained in [Reference Boyadzhiev12] by rather involved Fourier analysis, and some technical details are omitted in [Reference Boyadzhiev12].
In [Reference Boyadzhiev12, Proposition 5.1] it is observed that if
![]() $f \in H^{\infty }(\Sigma _{\psi })$
and is holomorphic in a larger sector, and
$f \in H^{\infty }(\Sigma _{\psi })$
and is holomorphic in a larger sector, and
 $f^{\prime }_{\psi } \in L^1(\mathbb R_+)$
,
$f^{\prime }_{\psi } \in L^1(\mathbb R_+)$
,
 $f^{\prime }_{\psi }(\infty )=0$
(this assumption is not relevant), then one can integrate by parts and rewrite (8.16) as
$f^{\prime }_{\psi }(\infty )=0$
(this assumption is not relevant), then one can integrate by parts and rewrite (8.16) as
 $$ \begin{align} f(A)=\int_0^{\infty} V_{\psi}(A,t) (f_{\psi}'\circ k_{\psi})(t)\,\frac{dt}{t}, \end{align} $$
$$ \begin{align} f(A)=\int_0^{\infty} V_{\psi}(A,t) (f_{\psi}'\circ k_{\psi})(t)\,\frac{dt}{t}, \end{align} $$
where
 $$ \begin{align*} V_{\psi}(A,t)=-\frac{t}{2} \left(e^{-i\psi} (A-t e^{-i\psi})^{-1} +e^{i\psi}(A-t e^{i\psi})^{-1}\right), \end{align*} $$
$$ \begin{align*} V_{\psi}(A,t)=-\frac{t}{2} \left(e^{-i\psi} (A-t e^{-i\psi})^{-1} +e^{i\psi}(A-t e^{i\psi})^{-1}\right), \end{align*} $$
and the integral converges absolutely. This formally leads to the estimate (8.9). Though our reproducing
![]() $\operatorname {\mathrm {arccot}}$
formula (8.8) was inspired by (8.17), it is not easy to put formal considerations in [Reference Boyadzhiev12] into the theory of functional calculi considered in this article. One can relate (8.17) to (8.8) and show that the formulas are essentially equivalent within the
$\operatorname {\mathrm {arccot}}$
formula (8.8) was inspired by (8.17), it is not easy to put formal considerations in [Reference Boyadzhiev12] into the theory of functional calculi considered in this article. One can relate (8.17) to (8.8) and show that the formulas are essentially equivalent within the
![]() $\mathcal H$
-calculus. This requires a number of technicalities, and we intend to communicate them elsewhere. Here we note only that
$\mathcal H$
-calculus. This requires a number of technicalities, and we intend to communicate them elsewhere. Here we note only that
 $f^{\prime }_{\psi } \in L^1(\mathbb R_+)$
and
$f^{\prime }_{\psi } \in L^1(\mathbb R_+)$
and
![]() $f \in H^{\infty }(\Sigma _{\psi })$
(for
$f \in H^{\infty }(\Sigma _{\psi })$
(for
![]() $\psi =\pi /2$
) do not imply that
$\psi =\pi /2$
) do not imply that
![]() $f \in \mathcal {H}_{\psi }$
in general, as shown by an intricate example kindly communicated to us by A. Borichev.
$f \in \mathcal {H}_{\psi }$
in general, as shown by an intricate example kindly communicated to us by A. Borichev.
9. Convergence Lemmas and Spectral Mapping Theorems
9.1. Convergence Lemmas
Given a negative semigroup generator A, a convergence lemma for the holomorphic functional calculus is a useful result allowing one to deduce the convergence of
![]() $(f_k(A))_{k=1}^{\infty }$
to
$(f_k(A))_{k=1}^{\infty }$
to
![]() $f(A)$
from rather weak assumptions on convergence of
$f(A)$
from rather weak assumptions on convergence of
![]() $(f_k)_{k=1}^{\infty }$
to f; see [Reference Cowling, Doust, McIntosh and Yagi14, Lemma 2.1], [Reference Haase35, Proposition 5.1.4] and [Reference Batty, Haase and Mubeen9, Theorem 3.1], for example.
$(f_k)_{k=1}^{\infty }$
to f; see [Reference Cowling, Doust, McIntosh and Yagi14, Lemma 2.1], [Reference Haase35, Proposition 5.1.4] and [Reference Batty, Haase and Mubeen9, Theorem 3.1], for example.
The following result is similar to a convergence lemma for the
![]() $\mathcal B$
-calculus in [Reference Batty, Gomilko and Tomilov7, Theorem 4.13 and Corollary 4.14] (see also [Reference Batty, Gomilko and Tomilov8, Section 8.1]). However, the different convergence lemmas deal with different classes of functions. To adjust the convergence lemma from [Reference Batty, Gomilko and Tomilov7] to the current setting, we apply the change of variables method used in previous sections and derive a variant of the convergence lemma for the
$\mathcal B$
-calculus in [Reference Batty, Gomilko and Tomilov7, Theorem 4.13 and Corollary 4.14] (see also [Reference Batty, Gomilko and Tomilov8, Section 8.1]). However, the different convergence lemmas deal with different classes of functions. To adjust the convergence lemma from [Reference Batty, Gomilko and Tomilov7] to the current setting, we apply the change of variables method used in previous sections and derive a variant of the convergence lemma for the
![]() $\mathcal D$
-calculus.
$\mathcal D$
-calculus.
In the following result,
![]() $f(A)$
refers to the
$f(A)$
refers to the
![]() $\mathcal {D}$
-calculus.
$\mathcal {D}$
-calculus.
Theorem 9.1. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
. Let
$A \in \operatorname {Sect}(\pi /2-)$
. Let
![]() $s>-1$
and let
$s>-1$
and let
![]() $(f_k)_{k\ge 1} \subset \mathcal {D}_s$
be such that
$(f_k)_{k\ge 1} \subset \mathcal {D}_s$
be such that
 $$ \begin{align} \sup_{k \ge 1}\|f_k\|_{\mathcal{D}_s} <\infty, \end{align} $$
$$ \begin{align} \sup_{k \ge 1}\|f_k\|_{\mathcal{D}_s} <\infty, \end{align} $$
and there exists
 $$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
Let
![]() $g\in \mathcal {D}_s$
satisfy
$g\in \mathcal {D}_s$
satisfy
Then
 $$ \begin{align} \lim_{k\to\infty}\,\|(f(A)-f_k(A))g(A)\|=0. \end{align} $$
$$ \begin{align} \lim_{k\to\infty}\,\|(f(A)-f_k(A))g(A)\|=0. \end{align} $$
In particular, if A has dense range, then
 $$ \begin{align} \lim_{k\to\infty}\,\|f(A)x-f_k(A)x\|=0, \end{align} $$
$$ \begin{align} \lim_{k\to\infty}\,\|f(A)x-f_k(A)x\|=0, \end{align} $$
for all
![]() $x\in X$
.
$x\in X$
.
Proof. By assumption, there exists
![]() $\theta \in [0,\pi /2)$
such that
$\theta \in [0,\pi /2)$
such that
![]() $A \in \operatorname {Sect}(\theta )$
. By Corollary 3.12 we have
$A \in \operatorname {Sect}(\theta )$
. By Corollary 3.12 we have
![]() $f \in \mathcal D_s$
. Thus, without loss of generality, we can assume that
$f \in \mathcal D_s$
. Thus, without loss of generality, we can assume that
![]() $f\equiv 0$
.
$f\equiv 0$
.
Let
![]() $\gamma \in (1, \pi /(2\theta ))$
. Then by Corollary 7.12, using the notation of (6.1),
$\gamma \in (1, \pi /(2\theta ))$
. Then by Corollary 7.12, using the notation of (6.1),
Because
![]() $g_{1/\gamma } \in \mathcal {D}_0^{\infty }$
,
$g_{1/\gamma } \in \mathcal {D}_0^{\infty }$
,
![]() $f_{k,1/\gamma }\in \mathcal {D}_0^{\infty }$
and
$f_{k,1/\gamma }\in \mathcal {D}_0^{\infty }$
and
![]() $f_{k,1/\gamma } g_{1/\gamma }\in \mathcal {D}_0^{\infty }$
(see Corollary 4.14) and the
$f_{k,1/\gamma } g_{1/\gamma }\in \mathcal {D}_0^{\infty }$
(see Corollary 4.14) and the
![]() $\mathcal {D}$
-calculus is an algebra homomorphism, we have
$\mathcal {D}$
-calculus is an algebra homomorphism, we have
Now (9.2) follows from Lemma 6.1 and the continuity of the
![]() $\mathcal D$
-calculus given by Proposition 7.2(1).
$\mathcal D$
-calculus given by Proposition 7.2(1).
Let
![]() $g(z)=z(1+z)^{-2}$
and note that
$g(z)=z(1+z)^{-2}$
and note that
![]() $g \in \mathcal D_s$
and g vanishes at zero and at infinity. If A has dense range, then the range of
$g \in \mathcal D_s$
and g vanishes at zero and at infinity. If A has dense range, then the range of
![]() $g(A)=A(1+A)^{-2}$
is dense as well (see [Reference Kunstmann and Weis41, Proposition 9.4], for example). Because
$g(A)=A(1+A)^{-2}$
is dense as well (see [Reference Kunstmann and Weis41, Proposition 9.4], for example). Because
![]() $\sup _{k \ge 1}\|f_k(A)\|<\infty $
, (9.2) implies (9.3).
$\sup _{k \ge 1}\|f_k(A)\|<\infty $
, (9.2) implies (9.3).
In the following result,
![]() $f(A)$
refers to the
$f(A)$
refers to the
![]() $\mathcal {H}$
-calculus.
$\mathcal {H}$
-calculus.
Theorem 9.2. Let
![]() $A \in \operatorname {Sect}(\theta ),$
and let
$A \in \operatorname {Sect}(\theta ),$
and let
![]() $\psi \in (\theta ,\pi )$
. Let
$\psi \in (\theta ,\pi )$
. Let
![]() $(f_k)_{k\ge 1} \subset \mathcal {H}_{\psi }$
be such that
$(f_k)_{k\ge 1} \subset \mathcal {H}_{\psi }$
be such that
 $$ \begin{align*} \sup_{k \ge 1}\|f_k\|_{\mathcal{H}_{\psi}} <\infty, \end{align*} $$
$$ \begin{align*} \sup_{k \ge 1}\|f_k\|_{\mathcal{H}_{\psi}} <\infty, \end{align*} $$
and there exists
 $$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
$$ \begin{align*} f(z):=\lim_{k\to\infty}\,f_k(z),\qquad z\in \mathbb{C}_{+}. \end{align*} $$
Let
![]() $g\in \mathcal {H}_{\psi }$
satisfy
$g\in \mathcal {H}_{\psi }$
satisfy
Then
 $$ \begin{align*} \lim_{k\to\infty}\,\|(f(A)-f_k(A))g(A)\|=0. \end{align*} $$
$$ \begin{align*} \lim_{k\to\infty}\,\|(f(A)-f_k(A))g(A)\|=0. \end{align*} $$
In particular, if A has dense range, then
 $$ \begin{align*} \lim_{k\to\infty}\,\|f(A)x-f_k(A)x\|=0, \end{align*} $$
$$ \begin{align*} \lim_{k\to\infty}\,\|f(A)x-f_k(A)x\|=0, \end{align*} $$
for all
![]() $x\in X$
.
$x\in X$
.
Proof. The proof is very similar to Theorem 9.1. Corollary 3.12 is replaced by Lemma 4.11, the compatibility with fractional powers follows from the definitions and Proposition 8.1(i), Corollary 4.14 is replaced by Lemma 4.9, Lemma 6.1 is replaced by Lemma 6.2 and (7.6) is replaced by Corollary 7.12.
9.2. Spectral mapping theorems
Given a semigroup generator
![]() $-A$
, a spectral mapping theorem for a functional calculus
$-A$
, a spectral mapping theorem for a functional calculus
![]() $\Xi _A$
signifies informally that
$\Xi _A$
signifies informally that
![]() $\Xi _A$
is associated to A in a ‘natural’ way. However, in general, the spectral ‘mapping’ theorem states only the inclusion
$\Xi _A$
is associated to A in a ‘natural’ way. However, in general, the spectral ‘mapping’ theorem states only the inclusion
![]() $f(\sigma (A))\subset \sigma (\Xi _A(f))$
. Equality may fail here even for functions such as
$f(\sigma (A))\subset \sigma (\Xi _A(f))$
. Equality may fail here even for functions such as
![]() $e^{-tz}$
and for rather simple operators A; see [Reference Engel and Nagel23, Section IV.3], for example. Though one may expect only the spectral inclusion as above, the equality
$e^{-tz}$
and for rather simple operators A; see [Reference Engel and Nagel23, Section IV.3], for example. Though one may expect only the spectral inclusion as above, the equality
![]() $f(\sigma (A))\cup \{f(\infty )\} = \sigma (\Xi _A(f))\cup \{f(\infty )\}$
sometimes holds if A inherits some properties of bounded operators such as strong resolvent estimates. Note that the spectral mapping theorem may not hold even for bounded operators if the functional calculus possesses only weak continuity properties, as discussed in [Reference Bercovici, Foias and Pearcy10].
$f(\sigma (A))\cup \{f(\infty )\} = \sigma (\Xi _A(f))\cup \{f(\infty )\}$
sometimes holds if A inherits some properties of bounded operators such as strong resolvent estimates. Note that the spectral mapping theorem may not hold even for bounded operators if the functional calculus possesses only weak continuity properties, as discussed in [Reference Bercovici, Foias and Pearcy10].
The following statement shows that the
![]() $\mathcal D$
-calculus possesses the standard spectral mapping properties. It is similar to [Reference Batty, Gomilko and Tomilov7, Theorem 4.17], with the addition of a statement about approximate eigenvalues. Recall that for
$\mathcal D$
-calculus possesses the standard spectral mapping properties. It is similar to [Reference Batty, Gomilko and Tomilov7, Theorem 4.17], with the addition of a statement about approximate eigenvalues. Recall that for
![]() $f \in \mathcal {D}_{\infty }$
, its values
$f \in \mathcal {D}_{\infty }$
, its values
![]() $f(\infty )$
at infnity and
$f(\infty )$
at infnity and
![]() $f(0)$
at
$f(0)$
at
![]() $0$
are defined by (3.27) and (3.28). This convention is used below.
$0$
are defined by (3.27) and (3.28). This convention is used below.
Theorem 9.3. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
,
$A \in \operatorname {Sect}(\pi /2-)$
,
![]() $f \in \mathcal D_{\infty }$
and
$f \in \mathcal D_{\infty }$
and
![]() $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
-
1. If
 $x \in D(A)$
and
$x \in D(A)$
and
 $Ax = \lambda x$
, then
$Ax = \lambda x$
, then
 $f_{\mathcal D}(A)x = f(\lambda )x$
.
$f_{\mathcal D}(A)x = f(\lambda )x$
. -
2. If
 $x^* \in D(A^*)$
and
$x^* \in D(A^*)$
and
 $A^*x^* = \lambda x^*$
, then
$A^*x^* = \lambda x^*$
, then
 $f_{\mathcal D}(A)^*x^* = f(\lambda )x^*$
.
$f_{\mathcal D}(A)^*x^* = f(\lambda )x^*$
. -
3. If
 $(x_n)_{n\ge 1}$
are unit vectors in
$(x_n)_{n\ge 1}$
are unit vectors in
 $D(A)$
and
$D(A)$
and
 $\lim _{n\to \infty }\|Ax_n - \lambda x_n\| = 0$
, then
$\lim _{n\to \infty }\|Ax_n - \lambda x_n\| = 0$
, then
 $\lim _{n\to \infty }\|f_{\mathcal {D}}(A)x_n - f(\lambda )x_n\| = 0$
.
$\lim _{n\to \infty }\|f_{\mathcal {D}}(A)x_n - f(\lambda )x_n\| = 0$
. -
4. One has
 $\sigma (f_{\mathcal D}(A)) \cup \{f(\infty )\} = f(\sigma (A)) \cup \{f(\infty )\}$
.
$\sigma (f_{\mathcal D}(A)) \cup \{f(\infty )\} = f(\sigma (A)) \cup \{f(\infty )\}$
.
Proof. The statements (1) and (2) are direct corollaries of (7.5) and the reproducing formula for the
![]() $\mathcal D_s$
-spaces given in Corollary 3.10.
$\mathcal D_s$
-spaces given in Corollary 3.10.
For (3), we use the F-product of the semigroup
![]() $(e^{-tA})_{t\ge 0}$
, as introduced in [Reference Derndinger18]. Let Y be the Banach space of all bounded sequences
$(e^{-tA})_{t\ge 0}$
, as introduced in [Reference Derndinger18]. Let Y be the Banach space of all bounded sequences
![]() $\mathbf y := (y_n)_{n\ge 1}$
in X such that
$\mathbf y := (y_n)_{n\ge 1}$
in X such that
![]() $\lim _{t\to 0+} \|e^{-tA}y_n - y_n\| = 0$
uniformly in n, where
$\lim _{t\to 0+} \|e^{-tA}y_n - y_n\| = 0$
uniformly in n, where
![]() $(e^{-tA})_{t\ge 0}$
is the bounded holomorphic
$(e^{-tA})_{t\ge 0}$
is the bounded holomorphic
![]() $C_0$
-semigroup generated by
$C_0$
-semigroup generated by
![]() $-A$
. Let Z be the closed subspace of Y consisting of the sequences
$-A$
. Let Z be the closed subspace of Y consisting of the sequences
![]() $\mathbf y$
such that
$\mathbf y$
such that
![]() $\lim _{n\to \infty } \|y_n\|=0$
, and let
$\lim _{n\to \infty } \|y_n\|=0$
, and let
 $\widetilde Y = Y/Z$
and
$\widetilde Y = Y/Z$
and
![]() $Q: Y \to \widetilde Y$
be the quotient map. Then
$Q: Y \to \widetilde Y$
be the quotient map. Then
![]() $(e^{-tA})_{t\ge 0}$
induces a bounded holomorphic
$(e^{-tA})_{t\ge 0}$
induces a bounded holomorphic
![]() $C_0$
-semigroup
$C_0$
-semigroup
 $(e^{-t\tilde A})_{t\ge 0}$
on
$(e^{-t\tilde A})_{t\ge 0}$
on
![]() $\widetilde Y$
, whose negative generator
$\widetilde Y$
, whose negative generator
![]() $\widetilde A$
is given by
$\widetilde A$
is given by
 $$ \begin{align*} D(\widetilde A) = \{Q(\mathbf y) : y_n \in D(A), (Ay_n) \in Y\}, \qquad \widetilde A(Q\mathbf y) = Q((Ay_n)). \end{align*} $$
$$ \begin{align*} D(\widetilde A) = \{Q(\mathbf y) : y_n \in D(A), (Ay_n) \in Y\}, \qquad \widetilde A(Q\mathbf y) = Q((Ay_n)). \end{align*} $$
Then
![]() $\mathbf x := (x_n) \in Y$
,
$\mathbf x := (x_n) \in Y$
,
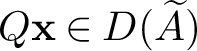 $Q\mathbf x \in D(\widetilde A)$
and
$Q\mathbf x \in D(\widetilde A)$
and
 $\widetilde A Q(\mathbf x) = \lambda Q(\mathbf x)$
. It follows from (1) that
$\widetilde A Q(\mathbf x) = \lambda Q(\mathbf x)$
. It follows from (1) that
 $f_{\mathcal {D}}(\widetilde A) Q\mathbf x = \lambda Q \mathbf x$
. However, it is very easy to see that
$f_{\mathcal {D}}(\widetilde A) Q\mathbf x = \lambda Q \mathbf x$
. However, it is very easy to see that
 $f_{\mathcal {D}}(\widetilde A) Q\mathbf x = Q((f_{\mathcal {D}}(A)x_n))$
(see [Reference Derndinger18, Theorem 1.7(i)]), and this establishes (3).
$f_{\mathcal {D}}(\widetilde A) Q\mathbf x = Q((f_{\mathcal {D}}(A)x_n))$
(see [Reference Derndinger18, Theorem 1.7(i)]), and this establishes (3).
To prove the spectral mapping theorem in (4), we follow the Banach algebra method used in [Reference Batty, Gomilko and Tomilov7] for similar purposes and inspired by [Reference Hille and Phillips37, Section 16.5] and [Reference Davies16, Section 2.2]. We may assume without loss of generality that
![]() $f(\infty )=0$
. Let
$f(\infty )=0$
. Let
![]() $\mathcal A$
be the bicommutant of
$\mathcal A$
be the bicommutant of
![]() $\{(z+A)^{-1} : -z \in \rho (A)\}$
in
$\{(z+A)^{-1} : -z \in \rho (A)\}$
in
![]() $L(X)$
, so
$L(X)$
, so
![]() $\mathcal A$
is a commutative Banach algebra and the spectrum of
$\mathcal A$
is a commutative Banach algebra and the spectrum of
![]() $f_{\mathcal {D}}(A)$
in
$f_{\mathcal {D}}(A)$
in
![]() $\mathcal {A}$
coincides with the spectrum in
$\mathcal {A}$
coincides with the spectrum in
![]() $L(X)$
. Observe that
$L(X)$
. Observe that
![]() $\sigma (A) \subset \mathbb C_+\cup \{0\}$
.
$\sigma (A) \subset \mathbb C_+\cup \{0\}$
.
Let
![]() $\chi $
be any character of
$\chi $
be any character of
![]() $\mathcal {A}$
. If
$\mathcal {A}$
. If
![]() $\chi ((1+A)^{-1})=0$
, then
$\chi ((1+A)^{-1})=0$
, then
![]() $\chi ((z+A)^{-1}) = 0$
for all
$\chi ((z+A)^{-1}) = 0$
for all
![]() $z \in \mathbb {C}_+$
, and hence
$z \in \mathbb {C}_+$
, and hence
![]() $\chi (f(A)) = 0 = f(\infty )$
. Otherwise, by the resolvent identity,
$\chi (f(A)) = 0 = f(\infty )$
. Otherwise, by the resolvent identity,
![]() $\chi ((z+A)^{-1})=(z+\lambda )^{-1}$
for some
$\chi ((z+A)^{-1})=(z+\lambda )^{-1}$
for some
![]() $\lambda \in \sigma (A)$
and all
$\lambda \in \sigma (A)$
and all
![]() $z \in \mathbb C_+$
. Let
$z \in \mathbb C_+$
. Let
![]() $s>-1$
be such that
$s>-1$
be such that
![]() $f \in \mathcal {D}_s$
. Noting that the Stieltjes representation (7.4) converges in the uniform operator topology, we infer that
$f \in \mathcal {D}_s$
. Noting that the Stieltjes representation (7.4) converges in the uniform operator topology, we infer that
![]() $\chi ((z+A)^{-(s+1)}) = (z+\lambda )^{-(s+1)}, z \in \mathbb C_+$
. Applying
$\chi ((z+A)^{-(s+1)}) = (z+\lambda )^{-(s+1)}, z \in \mathbb C_+$
. Applying
![]() $\chi $
to (7.5) gives
$\chi $
to (7.5) gives
 $$ \begin{align*} \chi (f_{\mathcal{D}}(A))=- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} f'(\alpha+i\beta)(\lambda+\alpha-i\beta)^{-(s+1)}\,d\beta\,d\alpha \end{align*} $$
$$ \begin{align*} \chi (f_{\mathcal{D}}(A))=- \frac{2^s}{\pi}\int_0^{\infty} \alpha^s\int_{-\infty}^{\infty} f'(\alpha+i\beta)(\lambda+\alpha-i\beta)^{-(s+1)}\,d\beta\,d\alpha \end{align*} $$
and then, by the reproducing formula (3.29) for
![]() $\mathcal D_s$
-functions (valid on
$\mathcal D_s$
-functions (valid on
![]() $\mathbb C_+\cup \{0\}$
), we obtain
$\mathbb C_+\cup \{0\}$
), we obtain
Hence,
![]() $\sigma (f_{\mathcal D}(A)) \cup \{0\} \subset f(\sigma (A)) \cup \{0\}$
. To prove the opposite inclusion, note that if
$\sigma (f_{\mathcal D}(A)) \cup \{0\} \subset f(\sigma (A)) \cup \{0\}$
. To prove the opposite inclusion, note that if
![]() $\lambda \in \sigma (A)$
is fixed, then there is a character
$\lambda \in \sigma (A)$
is fixed, then there is a character
![]() $\chi $
such that
$\chi $
such that
![]() $\chi ((z+A)^{-1})=(z+\lambda )^{-1}$
, so the above argument can be reversed, yielding
$\chi ((z+A)^{-1})=(z+\lambda )^{-1}$
, so the above argument can be reversed, yielding
![]() $\chi (f_{\mathcal {D}}(A))=f(\lambda )$
, thus finishing the proof.
$\chi (f_{\mathcal {D}}(A))=f(\lambda )$
, thus finishing the proof.
Next, using the same approach via Banach algebras, we prove the analogous spectral result for the
![]() $\mathcal H$
-calculus.
$\mathcal H$
-calculus.
Theorem 9.4. Let
![]() $A \in \operatorname {Sect}(\theta )$
and
$A \in \operatorname {Sect}(\theta )$
and
![]() $f \in \mathcal {H}_{\psi }$
for some
$f \in \mathcal {H}_{\psi }$
for some
![]() $\theta <\psi < \pi $
, and let
$\theta <\psi < \pi $
, and let
![]() $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
-
1. If
 $x \in D(A)$
and
$x \in D(A)$
and
 $Ax = \lambda x$
, then
$Ax = \lambda x$
, then
 $f_{\mathcal H}(A)x = f(\lambda )x$
.
$f_{\mathcal H}(A)x = f(\lambda )x$
. -
2. If
 $x^* \in D(A^*)$
and
$x^* \in D(A^*)$
and
 $A^*x^* = \lambda x^*$
, then
$A^*x^* = \lambda x^*$
, then
 $f_{\mathcal H}(A)^*x^* = f(\lambda )x^*$
.
$f_{\mathcal H}(A)^*x^* = f(\lambda )x^*$
. -
3. If
 $(x_n)_{n\ge 1}$
are unit vectors in
$(x_n)_{n\ge 1}$
are unit vectors in
 $D(A)$
and
$D(A)$
and
 $\lim _{n\to \infty }\|Ax_n - \lambda x_n\| = 0$
, then
$\lim _{n\to \infty }\|Ax_n - \lambda x_n\| = 0$
, then
 $\lim _{n\to \infty }\|f_{\mathcal {H}}(A)x_n - f(\lambda )x_n\| = 0$
.
$\lim _{n\to \infty }\|f_{\mathcal {H}}(A)x_n - f(\lambda )x_n\| = 0$
. -
4. One has
 $\sigma (f_{\mathcal H}(A)) \cup \{f(\infty )\} = f(\sigma (A)) \cup \{f(\infty )\}$
.
$\sigma (f_{\mathcal H}(A)) \cup \{f(\infty )\} = f(\sigma (A)) \cup \{f(\infty )\}$
.
Proof. The proofs of (1) and (2) are straightforward consequences of the reproducing formula (4.34). Moreover, (3) is deduced from (1) in the same way as in Theorem 9.3.
The proof of (4) is similar to the corresponding proof in Theorem 9.3, based on the formula (8.1), which converges in the uniform operator topology. Let
![]() $\gamma =\pi /(2\psi )$
. By the spectral mapping theorem for the holomorphic functional calculus [Reference Haase35, Theorem 2.7.8] or [Reference Martínez Carracedo and Sanz Alix44, Theorem 5.3.1], one has
$\gamma =\pi /(2\psi )$
. By the spectral mapping theorem for the holomorphic functional calculus [Reference Haase35, Theorem 2.7.8] or [Reference Martínez Carracedo and Sanz Alix44, Theorem 5.3.1], one has
As in the proof of Theorem 9.3, let
![]() $\mathcal A$
be the bicommutant of
$\mathcal A$
be the bicommutant of
![]() $\{(z+A)^{-1} : -z \in \rho (A)\}$
in
$\{(z+A)^{-1} : -z \in \rho (A)\}$
in
![]() $L(X)$
. Then
$L(X)$
. Then
![]() $f_{\mathcal H}(A) \in \mathcal {A}$
and the spectrum of
$f_{\mathcal H}(A) \in \mathcal {A}$
and the spectrum of
![]() $f_{\mathcal H}(A)$
in
$f_{\mathcal H}(A)$
in
![]() $\mathcal A$
coincides with the spectrum in
$\mathcal A$
coincides with the spectrum in
![]() $L(X)$
. Let
$L(X)$
. Let
![]() $\chi $
be any character of
$\chi $
be any character of
![]() $\mathcal {A}$
, and let
$\mathcal {A}$
, and let
![]() $f \in \mathcal {H}_{\psi }$
be such that
$f \in \mathcal {H}_{\psi }$
be such that
![]() $f(\infty )=0$
. If
$f(\infty )=0$
. If
![]() $\chi ((1+A^{\gamma })^{-1})=0$
, then, as above,
$\chi ((1+A^{\gamma })^{-1})=0$
, then, as above,
![]() $\chi ((z+A^{\gamma })^{-1}) = 0$
for all
$\chi ((z+A^{\gamma })^{-1}) = 0$
for all
![]() $z \in \mathbb {C}_+$
; hence,
$z \in \mathbb {C}_+$
; hence,
![]() $\chi (f_{\mathcal {H}}(A)) = 0 = f(\infty )$
. Otherwise,
$\chi (f_{\mathcal {H}}(A)) = 0 = f(\infty )$
. Otherwise,
![]() $\chi ((z+A^{\gamma })^{-1})=(\lambda ^{\gamma }+z)^{-1}$
for some
$\chi ((z+A^{\gamma })^{-1})=(\lambda ^{\gamma }+z)^{-1}$
for some
![]() $\lambda \in \sigma (A)$
and all
$\lambda \in \sigma (A)$
and all
![]() $z \in \mathbb C_+$
. Applying
$z \in \mathbb C_+$
. Applying
![]() $\chi $
to (8.1) and using the representation (4.34) for
$\chi $
to (8.1) and using the representation (4.34) for
![]() $\mathcal {H}_{\psi }$
-functions, one gets
$\mathcal {H}_{\psi }$
-functions, one gets
 $$ \begin{align*} \chi (f_{\mathcal H}(A))= -\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f^{\prime}_{1/\gamma}(t+i\beta) (\lambda^{\gamma}+t-i\beta)^{-1}\,d\beta\, dt=f(\lambda). \end{align*} $$
$$ \begin{align*} \chi (f_{\mathcal H}(A))= -\frac{1}{\pi}\int_0^{\infty}\int_{-\infty}^{\infty} f^{\prime}_{1/\gamma}(t+i\beta) (\lambda^{\gamma}+t-i\beta)^{-1}\,d\beta\, dt=f(\lambda). \end{align*} $$
Hence,
![]() $\sigma (f_{\mathcal H}(A))\cup \{0\} \subset f(\sigma (A)) \cup \{0\}$
.
$\sigma (f_{\mathcal H}(A))\cup \{0\} \subset f(\sigma (A)) \cup \{0\}$
.
On the other hand, if
![]() $\lambda \in \sigma (A)$
, then by (9.4) there is a character
$\lambda \in \sigma (A)$
, then by (9.4) there is a character
![]() $\chi $
such that
$\chi $
such that
![]() $\chi ((z+A^{\gamma })^{-1}) =(z+\lambda ^{\gamma })^{-1}$
. So using (4.34) again, we infer that
$\chi ((z+A^{\gamma })^{-1}) =(z+\lambda ^{\gamma })^{-1}$
. So using (4.34) again, we infer that
![]() $f(\lambda ) \in \sigma (f_{\mathcal H}(A))$
.
$f(\lambda ) \in \sigma (f_{\mathcal H}(A))$
.
Combining the two paragraphs above yields (4).
Our spectral mapping theorems differ from known spectral mapping theorems for the holomorphic functional calculus (see [Reference Haase34] or [Reference Haase35, Section 2.7]) in at least three respects. We do not assume that A is injective, we cover a wider class of functions including some with a mild singularity at zero (for example,
![]() $e^{-1/z}$
) and our proofs are completely different.
$e^{-1/z}$
) and our proofs are completely different.
10. Some applications to norm estimates
In this section we directly apply the
![]() $\mathcal D$
and
$\mathcal D$
and
![]() $\mathcal H$
-calculi that we have constructed to obtain some operator norm estimates. In particular, we obtain uniform bounds on the powers of Cayley transforms and on the semigroup generated by the inverse of a semigroup generator. We then compare the results to known estimates in the literature. We also revisit the theory of holomorphic
$\mathcal H$
-calculi that we have constructed to obtain some operator norm estimates. In particular, we obtain uniform bounds on the powers of Cayley transforms and on the semigroup generated by the inverse of a semigroup generator. We then compare the results to known estimates in the literature. We also revisit the theory of holomorphic
![]() $C_0$
-semigroups and obtain several basic estimates along with some slight generalisations.
$C_0$
-semigroups and obtain several basic estimates along with some slight generalisations.
10.1. Norm estimates via the
 $\mathcal D$
-calculus
$\mathcal D$
-calculus
Let
![]() $A \in \operatorname {Sect}(\pi /2 -)$
and
$A \in \operatorname {Sect}(\pi /2 -)$
and
![]() $V(A)$
be the Cayley transform
$V(A)$
be the Cayley transform
![]() $(A-I)(A+I)^{-1}$
of A. We now review several important estimates from the literature in the framework of the constructed
$(A-I)(A+I)^{-1}$
of A. We now review several important estimates from the literature in the framework of the constructed
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\mathcal {H}$
-calculi.
$\mathcal {H}$
-calculi.
Recall that
![]() $-A$
is the generator of a bounded holomorphic semigroup
$-A$
is the generator of a bounded holomorphic semigroup
![]() $(e^{-tA})_{t\ge 0}$
. Let
$(e^{-tA})_{t\ge 0}$
. Let
![]() $e_t(z) = e^{-tz}, \, t \ge 0,\,z\in \mathbb {C}_+$
. Then
$e_t(z) = e^{-tz}, \, t \ge 0,\,z\in \mathbb {C}_+$
. Then
![]() $e_t \in \mathcal {LM} \subset \mathcal {D}_{\infty }$
and
$e_t \in \mathcal {LM} \subset \mathcal {D}_{\infty }$
and
Corollary 10.1. Let
![]() $A \in \operatorname {Sect}(\pi /2 -)$
, so that (7.2) holds.
$A \in \operatorname {Sect}(\pi /2 -)$
, so that (7.2) holds.
-
(i) One has
 $$ \begin{align*} \|V(A)^n\|\le 1+32(1+(\sqrt2\pi)^{-1})M_A^2, \qquad n \in \mathbb N. \end{align*} $$
$$ \begin{align*} \|V(A)^n\|\le 1+32(1+(\sqrt2\pi)^{-1})M_A^2, \qquad n \in \mathbb N. \end{align*} $$
-
(ii) One has
 $$ \begin{align*} \|e^{-tA}\|\le 2 M_A^2, \qquad t \ge 0. \end{align*} $$
$$ \begin{align*} \|e^{-tA}\|\le 2 M_A^2, \qquad t \ge 0. \end{align*} $$
-
(iii) For every
 $\nu>0$
, one has
$\nu>0$
, one has  $$ \begin{align*} \|A^{\nu} e^{-tA}\| \le 2^{\nu+2} t^{-\nu} \Gamma(\nu+1) M_A^{\lceil\nu\rceil+2}, \qquad t>0. \end{align*} $$
$$ \begin{align*} \|A^{\nu} e^{-tA}\| \le 2^{\nu+2} t^{-\nu} \Gamma(\nu+1) M_A^{\lceil\nu\rceil+2}, \qquad t>0. \end{align*} $$
If, in addition, the inverse
![]() $A^{-1}$
exists and is densely defined, then
$A^{-1}$
exists and is densely defined, then
![]() $A^{-1}$
generates a bounded holomorphic
$A^{-1}$
generates a bounded holomorphic
![]() $C_0$
-semigroup
$C_0$
-semigroup
 $(e^{-tA^{-1}})_{t \ge 0}$
satisfying
$(e^{-tA^{-1}})_{t \ge 0}$
satisfying
 $$ \begin{align*} \|e^{-tA^{-1}}\|\le 1 + 2 M_A^2, \qquad t \ge 0, \end{align*} $$
$$ \begin{align*} \|e^{-tA^{-1}}\|\le 1 + 2 M_A^2, \qquad t \ge 0, \end{align*} $$
and, for every
![]() $\nu>0$
,
$\nu>0$
,
 $$ \begin{align*} \|A^{-\nu} e^{-tA^{-1}}\| \le 2^{\nu+2} t^{-\nu} \Gamma(\nu+1) M_A^{\lceil\nu\rceil+2}, \qquad t>0. \end{align*} $$
$$ \begin{align*} \|A^{-\nu} e^{-tA^{-1}}\| \le 2^{\nu+2} t^{-\nu} \Gamma(\nu+1) M_A^{\lceil\nu\rceil+2}, \qquad t>0. \end{align*} $$
Proof. By Lemma 12.1 and Theorem 7.6, for every
![]() $s>0$
,
$s>0$
,
 $$ \begin{align*} \|V(A)^n\|\le 1+ 2^{s+4} \pi^{-1} (B(s/2, 1/2)+2^{-s/2}) M_A^{\lceil{s}\rceil+1}, \qquad n \in \mathbb N. \end{align*} $$
$$ \begin{align*} \|V(A)^n\|\le 1+ 2^{s+4} \pi^{-1} (B(s/2, 1/2)+2^{-s/2}) M_A^{\lceil{s}\rceil+1}, \qquad n \in \mathbb N. \end{align*} $$
Setting
![]() $s=1$
we get assertion (i).
$s=1$
we get assertion (i).
By Proposition 3.15 or by Example 3.4 and Lemma 3.17(iii), the function
![]() $e^{-tz} \in \mathcal {D}_s$
for
$e^{-tz} \in \mathcal {D}_s$
for
![]() $s> 0$
and
$s> 0$
and
![]() $t>0$
, and by (3.21) and Theorem 7.6,
$t>0$
, and by (3.21) and Theorem 7.6,
 $$ \begin{align*} \|e^{-tA}\|\le 2^s \pi^{-1}B(s/2, 1/2)M_A^{\lceil{s}\rceil+1}, \qquad t \ge 0. \end{align*} $$
$$ \begin{align*} \|e^{-tA}\|\le 2^s \pi^{-1}B(s/2, 1/2)M_A^{\lceil{s}\rceil+1}, \qquad t \ge 0. \end{align*} $$
So the estimate (ii) follows by setting
![]() $s=1$
above.
$s=1$
above.
If
![]() $f_{\nu }(z):=z^{\nu } e^{-tz}$
,
$f_{\nu }(z):=z^{\nu } e^{-tz}$
,
![]() $\nu>0$
, then
$\nu>0$
, then
![]() $f_{\nu } \in \mathcal {D}_s$
if and only if
$f_{\nu } \in \mathcal {D}_s$
if and only if
![]() $s>\nu $
, and in that case
$s>\nu $
, and in that case
![]() $\|f_{\nu }\|_{\mathcal {D}_s} = 2t^{-\nu } B((s-\nu )/2,1/2) \Gamma (\nu +1)$
(see Example 3.4). Because
$\|f_{\nu }\|_{\mathcal {D}_s} = 2t^{-\nu } B((s-\nu )/2,1/2) \Gamma (\nu +1)$
(see Example 3.4). Because
![]() $f_{\nu }$
has zero polynomial limits at zero and at infinity,
$f_{\nu }$
has zero polynomial limits at zero and at infinity,
![]() $(f_{\nu })_{\mathcal D}(A)$
coincides with
$(f_{\nu })_{\mathcal D}(A)$
coincides with
![]() $A^{\nu }e^{-tA}$
as defined by the holomorphic functional calculus (see Remark 7.5). Using (3.21), it follows that, for every
$A^{\nu }e^{-tA}$
as defined by the holomorphic functional calculus (see Remark 7.5). Using (3.21), it follows that, for every
![]() $s>\nu $
,
$s>\nu $
,
 $$ \begin{align*} \|A^{\nu} e^{-tA}\|\le \frac{2^{s+1}t^{-\nu}}{\pi} B\left(\frac{s-\nu}{2},\frac{1}{2}\right)\Gamma(\nu+1) M_A^{\lceil s\rceil+1}. \end{align*} $$
$$ \begin{align*} \|A^{\nu} e^{-tA}\|\le \frac{2^{s+1}t^{-\nu}}{\pi} B\left(\frac{s-\nu}{2},\frac{1}{2}\right)\Gamma(\nu+1) M_A^{\lceil s\rceil+1}. \end{align*} $$
Setting
![]() $s=\nu +1$
, the first assertion in (iii) follows. The other two estimates are consequences of Lemma 3.17(i) and the estimates for
$s=\nu +1$
, the first assertion in (iii) follows. The other two estimates are consequences of Lemma 3.17(i) and the estimates for
![]() $e^{-tA}$
and
$e^{-tA}$
and
![]() $A^{\nu } e^{-tA}$
obtained above.
$A^{\nu } e^{-tA}$
obtained above.
The results in Corollary 10.1 are not new, and it serves as an ilustration of the utility of the
![]() $\mathcal {D}$
-calculus. We have not aimed at finding the best possible estimates, but it seems that the
$\mathcal {D}$
-calculus. We have not aimed at finding the best possible estimates, but it seems that the
![]() $\mathcal {H}$
-calculus provides bounds that are fairly precise whenever it is applicable. The power-boundedness of
$\mathcal {H}$
-calculus provides bounds that are fairly precise whenever it is applicable. The power-boundedness of
![]() $V(A)$
was shown in [Reference Crouzeix, Larsson, Piskarev and Thomée15] and [Reference Palencia46], using different methods. In [Reference Batty, Gomilko and Tomilov7, Corollary 5.9], a weaker result was shown using the
$V(A)$
was shown in [Reference Crouzeix, Larsson, Piskarev and Thomée15] and [Reference Palencia46], using different methods. In [Reference Batty, Gomilko and Tomilov7, Corollary 5.9], a weaker result was shown using the
![]() $\mathcal {B}$
-calculus (so all operators satisfying (1.3)). Corollary 10.1 shows how the
$\mathcal {B}$
-calculus (so all operators satisfying (1.3)). Corollary 10.1 shows how the
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\mathcal {H}$
-calculi can give a sharper estimate than the
$\mathcal {H}$
-calculi can give a sharper estimate than the
![]() $\mathcal {B}$
-calculus in the case of sectorial operators. Part (ii) above is one of many estimates for the bound on a bounded holomorphic semigroup in terms of its sectorial bound, and it is clearly not sharp. A careful estimation in [Reference Batty, Gomilko and Tomilov7, Lemma 4.7] of the bound obtained via the
$\mathcal {B}$
-calculus in the case of sectorial operators. Part (ii) above is one of many estimates for the bound on a bounded holomorphic semigroup in terms of its sectorial bound, and it is clearly not sharp. A careful estimation in [Reference Batty, Gomilko and Tomilov7, Lemma 4.7] of the bound obtained via the
![]() $\mathcal {B}$
-calculus gave a bound of order
$\mathcal {B}$
-calculus gave a bound of order
![]() $M_A \log M_A$
when
$M_A \log M_A$
when
![]() $M_A$
is large. See also [Reference Schwenninger51, Theorem 5.2] where the result was established for the first time. Estimates of the form given in part (iii) have been known for a long time but usually without showing the dependence on
$M_A$
is large. See also [Reference Schwenninger51, Theorem 5.2] where the result was established for the first time. Estimates of the form given in part (iii) have been known for a long time but usually without showing the dependence on
![]() $M_A$
.
$M_A$
.
Next we consider estimates similar to Corollary 10.1(iii). In Lemma 10.2 and Theorem 10.3
![]() $f(A)$
refers to the
$f(A)$
refers to the
![]() $\mathcal {D}$
-calculus.
$\mathcal {D}$
-calculus.
Lemma 10.2. Let
![]() $A\in \operatorname {Sect}(\pi /2-).$
If
$A\in \operatorname {Sect}(\pi /2-).$
If
![]() $f \in \mathcal {D}_s$
,
$f \in \mathcal {D}_s$
,
![]() $s>-1,$
and
$s>-1,$
and
![]() $n \in \mathbb {N}$
, then
$n \in \mathbb {N}$
, then
 $$ \begin{align} (z^nf^{(n)})(A)= C_{s,n} \int_0^{\infty} \alpha^s \int_{-\infty}^{\infty} f'(\alpha+i\beta)A^n (A+\alpha-i\beta)^{-(s+n+1)}\,d\beta\,d\alpha, \end{align} $$
$$ \begin{align} (z^nf^{(n)})(A)= C_{s,n} \int_0^{\infty} \alpha^s \int_{-\infty}^{\infty} f'(\alpha+i\beta)A^n (A+\alpha-i\beta)^{-(s+n+1)}\,d\beta\,d\alpha, \end{align} $$
where
 $$ \begin{align*} C_{s,n} = {(-1)}^{n+1} \frac{2^s}{\pi} \frac{\Gamma(s+n+1)}{\Gamma(s+1)}. \end{align*} $$
$$ \begin{align*} C_{s,n} = {(-1)}^{n+1} \frac{2^s}{\pi} \frac{\Gamma(s+n+1)}{\Gamma(s+1)}. \end{align*} $$
Proof. By Corollary 5.5 and the boundedness of the
![]() $\mathcal {D}_{s+n}$
-calculus,
$\mathcal {D}_{s+n}$
-calculus,
![]() $(z^nf^{(n)})(A)$
coincides with the derivative of order n of the function
$(z^nf^{(n)})(A)$
coincides with the derivative of order n of the function
![]() $t \mapsto f(tA)$
evaluated at
$t \mapsto f(tA)$
evaluated at
![]() $t=1$
. The formula (7.5) for
$t=1$
. The formula (7.5) for
![]() $f(tA) \in \mathcal D_s$
can be differentiated repeatedly with respect to t by a standard method, and putting
$f(tA) \in \mathcal D_s$
can be differentiated repeatedly with respect to t by a standard method, and putting
![]() $t=1$
then gives the formula (10.1).
$t=1$
then gives the formula (10.1).
Theorem 10.3. Let
![]() $A \in \operatorname {Sect}(\pi /2-)$
and
$A \in \operatorname {Sect}(\pi /2-)$
and
![]() $n \in \mathbb {N}$
. Let
$n \in \mathbb {N}$
. Let
![]() $f \in \mathcal {D}_{\infty }$
, and assume that
$f \in \mathcal {D}_{\infty }$
, and assume that
![]() $f^{(k)} \in \mathcal {D}_{\infty }$
for
$f^{(k)} \in \mathcal {D}_{\infty }$
for
![]() $k=1,\dots ,n$
. Then
$k=1,\dots ,n$
. Then
 $$ \begin{align} (z^nf^{(n)})(A) = A^n f^{(n)}(A). \end{align} $$
$$ \begin{align} (z^nf^{(n)})(A) = A^n f^{(n)}(A). \end{align} $$
Moreover, if
![]() $f \in \mathcal {D}_s, \, s>-1$
, then
$f \in \mathcal {D}_s, \, s>-1$
, then
 $$ \begin{align} \|t^n A^nf^{(n)}(tA)\|\le \frac{2^s\Gamma(s+n+1)}{\pi \Gamma(s+1)}(M_A+1)^n M_A^{\lceil{s}\rceil+1}\|f\|_{\mathcal{D}_s},\quad t>0. \end{align} $$
$$ \begin{align} \|t^n A^nf^{(n)}(tA)\|\le \frac{2^s\Gamma(s+n+1)}{\pi \Gamma(s+1)}(M_A+1)^n M_A^{\lceil{s}\rceil+1}\|f\|_{\mathcal{D}_s},\quad t>0. \end{align} $$
In particular, for
![]() $f(z)=e^{-z}\in \mathcal {D}_1$
,
$f(z)=e^{-z}\in \mathcal {D}_1$
,
Proof. We will prove, by induction on n, that (10.2) holds for all functions
![]() $f \in \mathcal {D}_{\infty }$
such that
$f \in \mathcal {D}_{\infty }$
such that
![]() $f^{(k)} \in \mathcal {D}_{\infty }$
for
$f^{(k)} \in \mathcal {D}_{\infty }$
for
![]() $k=1,\dots ,n$
. First, assume that
$k=1,\dots ,n$
. First, assume that
![]() $f,f' \in \mathcal {D}_{\infty }$
. Then
$f,f' \in \mathcal {D}_{\infty }$
. Then
![]() $zf' \in \mathcal D_{\infty}$
by Corollary 3.23, and
$zf' \in \mathcal D_{\infty}$
by Corollary 3.23, and
This implies that
![]() $(zf')(A) = Af'(A)$
.
$(zf')(A) = Af'(A)$
.
Now assume that, for some
![]() $n\ge 1$
,
$n\ge 1$
,
![]() $(z^kg^{(k)})(A) = A^kg^{(k)}(A)$
for
$(z^kg^{(k)})(A) = A^kg^{(k)}(A)$
for
![]() $k=1,\dots ,n$
, for all functions g such that
$k=1,\dots ,n$
, for all functions g such that
![]() $g^{(k)} \in \mathcal {D}_{\infty }$
for
$g^{(k)} \in \mathcal {D}_{\infty }$
for
![]() $k=0,\dots ,n$
. Let
$k=0,\dots ,n$
. Let
![]() $f^{(k)} \in \mathcal {D}_{\infty }$
for
$f^{(k)} \in \mathcal {D}_{\infty }$
for
![]() $k=0,1,\dots ,n+1$
. Applying the base case (
$k=0,1,\dots ,n+1$
. Applying the base case (
![]() $n=1$
) to the function
$n=1$
) to the function
![]() $z^nf^{(n)}$
(noting that this function and its first derivative are in
$z^nf^{(n)}$
(noting that this function and its first derivative are in
![]() $\mathcal {D}_{\infty }$
, by Corollary 3.23), we obtain
$\mathcal {D}_{\infty }$
, by Corollary 3.23), we obtain
 $$ \begin{align*} (z(z^nf^{(n)})')(A) = A (z^nf^{(n)})'(A). \end{align*} $$
$$ \begin{align*} (z(z^nf^{(n)})')(A) = A (z^nf^{(n)})'(A). \end{align*} $$
Then applying the inductive hypothesis with
![]() $k=n$
to the function f and with
$k=n$
to the function f and with
![]() $k=n-1$
and
$k=n-1$
and
![]() $k=n$
to the function
$k=n$
to the function
![]() $f'$
, we obtain
$f'$
, we obtain
 $$ \begin{align*} (z^{n+1}f^{(n+1)})(A) &= A \left(n(z^{n-1}f^{(n)}) + (z^nf^{(n+1)})\right)(A) - n (z^nf^{(n)})(A) \\ &= A^{n+1}f^{(n+1)}(A). \end{align*} $$
$$ \begin{align*} (z^{n+1}f^{(n+1)})(A) &= A \left(n(z^{n-1}f^{(n)}) + (z^nf^{(n+1)})\right)(A) - n (z^nf^{(n)})(A) \\ &= A^{n+1}f^{(n+1)}(A). \end{align*} $$
This completes the proof of the inductive hypothesis for all
![]() $n\in \mathbb {N}$
and hence proves (10.2)
$n\in \mathbb {N}$
and hence proves (10.2)
Because
![]() $M_A = M_{tA}$
for all
$M_A = M_{tA}$
for all
![]() $t>0$
, it suffices to prove (10.3) for
$t>0$
, it suffices to prove (10.3) for
![]() $t=1$
. From Lemmas 7.1 and 10.2, we obtain
$t=1$
. From Lemmas 7.1 and 10.2, we obtain
 $$ \begin{align*} &{\|A^n\,f^{(n)}(A)\|}\\ &\quad \le \frac{2^s\Gamma(s+n+1)}{\pi \Gamma(s+1)}(M_A+1)^n M_A^{\lceil{s}\rceil+1} \int_0^{\infty}\alpha^s\int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{|\alpha-i\beta|^{s+1}}\,d\beta\,d\alpha\\ &\quad =\frac{2^s \Gamma(s+n+1)}{\pi\Gamma(s+1)}(M_A+1)^n M_A^{\lceil{s}\rceil+1}\|f\|_{\mathcal{D}_s}. \\[-40pt] \end{align*} $$
$$ \begin{align*} &{\|A^n\,f^{(n)}(A)\|}\\ &\quad \le \frac{2^s\Gamma(s+n+1)}{\pi \Gamma(s+1)}(M_A+1)^n M_A^{\lceil{s}\rceil+1} \int_0^{\infty}\alpha^s\int_{-\infty}^{\infty} \frac{|f'(\alpha+i\beta)|}{|\alpha-i\beta|^{s+1}}\,d\beta\,d\alpha\\ &\quad =\frac{2^s \Gamma(s+n+1)}{\pi\Gamma(s+1)}(M_A+1)^n M_A^{\lceil{s}\rceil+1}\|f\|_{\mathcal{D}_s}. \\[-40pt] \end{align*} $$
Remark 10.4. In Theorem 10.3, the assumption that
![]() $f \in \mathcal {D}_{\infty }$
and
$f \in \mathcal {D}_{\infty }$
and
![]() $f^{(k)} \in \mathcal {D}_{\infty }, k=1,2,\dots ,n$
, can be replaced by the assumption that
$f^{(k)} \in \mathcal {D}_{\infty }, k=1,2,\dots ,n$
, can be replaced by the assumption that
![]() $f \in \mathcal {D}_{\infty }$
and
$f \in \mathcal {D}_{\infty }$
and
![]() $f^{(n)} \in \mathcal {D}_{\infty }$
, by using a result of Lyubich [Reference Lyubič43]. See Corollary 11.3.
$f^{(n)} \in \mathcal {D}_{\infty }$
, by using a result of Lyubich [Reference Lyubič43]. See Corollary 11.3.
10.2. Norm estimates via the
 $\mathcal {H}$
-calculus
$\mathcal {H}$
-calculus
Now we use the
![]() $\mathcal {H}$
-calculus to provide a new proof that holomorphy of operator semigroups generated by
$\mathcal {H}$
-calculus to provide a new proof that holomorphy of operator semigroups generated by
![]() $-A$
is preserved for subordinate semigroups generated by
$-A$
is preserved for subordinate semigroups generated by
![]() $-g(A)$
where g is a Bernstein function. This was proved for the first time in [Reference Gomilko and Tomilov31].
$-g(A)$
where g is a Bernstein function. This was proved for the first time in [Reference Gomilko and Tomilov31].
If
![]() $-A$
is the generator of a bounded
$-A$
is the generator of a bounded
![]() $C_0$
-semigroup
$C_0$
-semigroup
![]() $(e^{-tA})_{t \ge 0}$
on a Banach space X and g is a Bernstein function given by (3.30), then the operator
$(e^{-tA})_{t \ge 0}$
on a Banach space X and g is a Bernstein function given by (3.30), then the operator
 $$ \begin{align} g_0(A)x:=ax+bAx+\int_{(0, \infty)}\left(x-e^{-tA}x\right)\, d\mu(t), \quad x \in D(A), \end{align} $$
$$ \begin{align} g_0(A)x:=ax+bAx+\int_{(0, \infty)}\left(x-e^{-tA}x\right)\, d\mu(t), \quad x \in D(A), \end{align} $$
is closable, and
![]() $g(A)$
can be defined as the closure of
$g(A)$
can be defined as the closure of
![]() $g_0(A)$
. Thus,
$g_0(A)$
. Thus,
![]() $D(A)$
is a core for
$D(A)$
is a core for
![]() $g(A)$
, and one can prove that
$g(A)$
, and one can prove that
![]() $-g(A)$
generates a contraction
$-g(A)$
generates a contraction
![]() $C_0$
-semigroup on X. Several equivalent definitions of
$C_0$
-semigroup on X. Several equivalent definitions of
![]() $g(A)$
are possible, and we refer the reader to [Reference Schilling, Song and Vondraček50], [Reference Gomilko, Haase and Tomilov30] and [Reference Gomilko and Tomilov31]. If A is injective, then
$g(A)$
are possible, and we refer the reader to [Reference Schilling, Song and Vondraček50], [Reference Gomilko, Haase and Tomilov30] and [Reference Gomilko and Tomilov31]. If A is injective, then
![]() $g(A)$
is well-defined within the (extended) holomorphic functional calculus and is given by (10.5) as above; see Proposition 8.1 and [Reference Gomilko and Tomilov31, Propositions 3.3 and 3.6].
$g(A)$
is well-defined within the (extended) holomorphic functional calculus and is given by (10.5) as above; see Proposition 8.1 and [Reference Gomilko and Tomilov31, Propositions 3.3 and 3.6].
The next statement shows that the so-called semigroup subordination preserves the holomorphy of
![]() $C_0$
-semigroups along with the holomorphy angles. It was one of the main results of [Reference Gomilko and Tomilov31], settling a question raised by Kishimoto and Robinson [Reference Kishimoto and Robinson39]. See also [Reference Batty, Gomilko and Tomilov6] and [Reference Batty, Gomilko and Tomilov7] for generalisations and other proofs.
$C_0$
-semigroups along with the holomorphy angles. It was one of the main results of [Reference Gomilko and Tomilov31], settling a question raised by Kishimoto and Robinson [Reference Kishimoto and Robinson39]. See also [Reference Batty, Gomilko and Tomilov6] and [Reference Batty, Gomilko and Tomilov7] for generalisations and other proofs.
Theorem 10.5. Let
![]() $A \in \operatorname {Sect}(\theta )$
, where
$A \in \operatorname {Sect}(\theta )$
, where
![]() $\theta \in [0,\pi /2)$
, and let g be a Bernstein function as in (3.30). Then
$\theta \in [0,\pi /2)$
, and let g be a Bernstein function as in (3.30). Then
![]() $g(A) \in \operatorname {Sect}(\theta )$
. More precisely, for all
$g(A) \in \operatorname {Sect}(\theta )$
. More precisely, for all
![]() $\psi \in (\theta ,\pi /2)$
,
$\psi \in (\theta ,\pi /2)$
,
![]() $\varphi \in (\psi ,\pi )$
and
$\varphi \in (\psi ,\pi )$
and
![]() $\lambda \in {\Sigma }_{\pi -\varphi }$
,
$\lambda \in {\Sigma }_{\pi -\varphi }$
,
 $$ \begin{align} \|\lambda (\lambda + g(A))^{-1}\| \le 2M_{\psi} (A)\left(\frac{1}{\sin(\min(\varphi,\pi/2))}+\frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)}\right). \end{align} $$
$$ \begin{align} \|\lambda (\lambda + g(A))^{-1}\| \le 2M_{\psi} (A)\left(\frac{1}{\sin(\min(\varphi,\pi/2))}+\frac{2}{\cos\psi \sin^2((\varphi-\psi)/2)}\right). \end{align} $$
Proof. Let
![]() $\psi \in (\theta ,\pi /2)$
,
$\psi \in (\theta ,\pi /2)$
,
![]() $\varphi \in (\psi ,\pi )$
and
$\varphi \in (\psi ,\pi )$
and
![]() $\lambda \in {\Sigma }_{\pi -\varphi }$
. If
$\lambda \in {\Sigma }_{\pi -\varphi }$
. If
then by Corollary 4.16 we have
![]() $f \in \mathcal {H}_{\psi }$
. We will show that
$f \in \mathcal {H}_{\psi }$
. We will show that
![]() $f_{\mathcal {H}}(A) = (\lambda +g(A))^{-1}$
. It then follows from (8.9) and (4.31) that (10.6) holds. Because the choice of
$f_{\mathcal {H}}(A) = (\lambda +g(A))^{-1}$
. It then follows from (8.9) and (4.31) that (10.6) holds. Because the choice of
![]() $\psi \in (\theta ,\pi/2 )$
and
$\psi \in (\theta ,\pi/2 )$
and
![]() $\varphi \in (\psi ,\pi )$
is arbitrary, this shows that the operator
$\varphi \in (\psi ,\pi )$
is arbitrary, this shows that the operator
![]() $g(A)$
is sectorial of angle
$g(A)$
is sectorial of angle
![]() $\theta $
.
$\theta $
.
If A is injective, then
![]() $f(A)$
and
$f(A)$
and
![]() $\lambda + g(A)$
are consistently defined in the holomorphic functional calculus, and therefore
$\lambda + g(A)$
are consistently defined in the holomorphic functional calculus, and therefore
![]() $f_{\mathcal H}(A) = f(A) = (\lambda +g(A))^{-1}$
(see [Reference Haase35, Theorem 1.3.2f)]).
$f_{\mathcal H}(A) = f(A) = (\lambda +g(A))^{-1}$
(see [Reference Haase35, Theorem 1.3.2f)]).
When A is not injective, we follow the approach proposed in the proof of [Reference Batty, Gomilko and Tomilov6, Theorem 4.8].
Because
![]() $A+\epsilon $
is invertible, we have
$A+\epsilon $
is invertible, we have
By Proposition 8.1(v),
 $$ \begin{align} \lim_{\epsilon\to0+} \|f_{\mathcal{H}}(A+\epsilon) - f_{\mathcal{H}}(A)\|=0. \end{align} $$
$$ \begin{align} \lim_{\epsilon\to0+} \|f_{\mathcal{H}}(A+\epsilon) - f_{\mathcal{H}}(A)\|=0. \end{align} $$
Let
![]() $x \in D(A)$
. Because
$x \in D(A)$
. Because
![]() $f_{\mathcal {H}}(A+\epsilon )$
commutes with
$f_{\mathcal {H}}(A+\epsilon )$
commutes with
![]() $(1+A)^{-1}$
, we have
$(1+A)^{-1}$
, we have
![]() $f_{\mathcal {H}}(A+\epsilon )x\in D(A)$
, and by (10.5),
$f_{\mathcal {H}}(A+\epsilon )x\in D(A)$
, and by (10.5),
 $$ \begin{align*} x-(\lambda+g(A))f_{\mathcal{H}}(A+\epsilon)x =[g(A+\epsilon)-g(A)]f_{\mathcal{H}}(A+\epsilon)x\\ {\hskip30pt} =\epsilon bf_{\mathcal{H}}(A+\epsilon)x -\int_{(0,\infty)} (1-e^{-\epsilon t})e^{-tA} f_{\mathcal{H}}(A+\epsilon)x\,d\mu(t).\notag \end{align*} $$
$$ \begin{align*} x-(\lambda+g(A))f_{\mathcal{H}}(A+\epsilon)x =[g(A+\epsilon)-g(A)]f_{\mathcal{H}}(A+\epsilon)x\\ {\hskip30pt} =\epsilon bf_{\mathcal{H}}(A+\epsilon)x -\int_{(0,\infty)} (1-e^{-\epsilon t})e^{-tA} f_{\mathcal{H}}(A+\epsilon)x\,d\mu(t).\notag \end{align*} $$
It follows from (10.7) that
 $$ \begin{align*} C_{\lambda} := \sup_{\epsilon\in(0,1]} \|f_{\mathcal{H}}(A+\epsilon)\| < \infty, \end{align*} $$
$$ \begin{align*} C_{\lambda} := \sup_{\epsilon\in(0,1]} \|f_{\mathcal{H}}(A+\epsilon)\| < \infty, \end{align*} $$
and hence
 $$ \begin{align} \|x - (\lambda+g(A))f_{\mathcal{H}}(A+\epsilon)x\| &\le \epsilon b C_{\lambda}\|x\| +C_{\lambda} K_A \int_{(0,\infty)} (1-e^{-\epsilon t})\,d\mu(t)\,\|x\| \\ &\to 0,\qquad \epsilon\to 0, \notag \end{align} $$
$$ \begin{align} \|x - (\lambda+g(A))f_{\mathcal{H}}(A+\epsilon)x\| &\le \epsilon b C_{\lambda}\|x\| +C_{\lambda} K_A \int_{(0,\infty)} (1-e^{-\epsilon t})\,d\mu(t)\,\|x\| \\ &\to 0,\qquad \epsilon\to 0, \notag \end{align} $$
where
![]() $K_A := \sup _{t>0} \|e^{-tA}\|$
. Because
$K_A := \sup _{t>0} \|e^{-tA}\|$
. Because
![]() $\lambda +g(A)$
is closed, it follows firstly that
$\lambda +g(A)$
is closed, it follows firstly that
Because
![]() $D(A)$
is dense in X and
$D(A)$
is dense in X and
![]() $f_{\mathcal {H}}(A)$
is bounded, it follows secondly that
$f_{\mathcal {H}}(A)$
is bounded, it follows secondly that
Because
![]() $\lambda + g(A)$
and
$\lambda + g(A)$
and
![]() $f_{\mathcal {H}}(A)$
commute on
$f_{\mathcal {H}}(A)$
commute on
![]() $D(A)$
,
$D(A)$
,
Because
![]() $D(A)$
is a core for
$D(A)$
is a core for
![]() $g(A)$
, it follows that this holds for all
$g(A)$
, it follows that this holds for all
![]() $x \in D(g(A))$
. Thus,
$x \in D(g(A))$
. Thus,
![]() $f_{\mathcal {H}}(A)=(\lambda +g(A))^{-1}$
, as required.
$f_{\mathcal {H}}(A)=(\lambda +g(A))^{-1}$
, as required.
Remarks 10.6. 1. A new feature of Theorem 10.5 is an explicit sectoriality constant for
![]() $g(A)$
, given by the right-hand side of (10.6). This could be valuable when applying the result to families of sectorial operators. Thus, (10.6) offers an improvement over similar estimates in [Reference Batty, Gomilko and Tomilov6], [Reference Batty, Gomilko and Tomilov7] and [Reference Gomilko and Tomilov31], where the sectoriality constants for
$g(A)$
, given by the right-hand side of (10.6). This could be valuable when applying the result to families of sectorial operators. Thus, (10.6) offers an improvement over similar estimates in [Reference Batty, Gomilko and Tomilov6], [Reference Batty, Gomilko and Tomilov7] and [Reference Gomilko and Tomilov31], where the sectoriality constants for
![]() $g(A)$
are rather implicit.
$g(A)$
are rather implicit.
2. We take this opportunity to correct a parsing misprint in the proof [Reference Batty, Gomilko and Tomilov6, Theorem 4.9]. One should replace
![]() $f(A)$
with
$f(A)$
with
![]() $f(A)+z$
in the third and fourth displays in [Reference Batty, Gomilko and Tomilov6, p.932] (see (10.8) and (10.9) for similar formulas).
$f(A)+z$
in the third and fourth displays in [Reference Batty, Gomilko and Tomilov6, p.932] (see (10.8) and (10.9) for similar formulas).
Finally, as an illustration, we show how the holomorphy of
![]() $C_0$
-semigroups generated by operators
$C_0$
-semigroups generated by operators
![]() $-A^{\gamma }$
fits within the
$-A^{\gamma }$
fits within the
![]() $\mathcal {H}$
-calculus and how estimates of type similar to Corollary 10.1(ii) can be obtained from the representation of the
$\mathcal {H}$
-calculus and how estimates of type similar to Corollary 10.1(ii) can be obtained from the representation of the
![]() $\mathcal {H}$
-calculus and the function
$\mathcal {H}$
-calculus and the function
![]() $\operatorname {\mathrm {arccot}}$
, as in Theorem 8.6. The following result is similar to [Reference Boyadzhiev12, Corollary 5.2] and a generalisation of the main result in [Reference deLaubenfels17] to noninteger
$\operatorname {\mathrm {arccot}}$
, as in Theorem 8.6. The following result is similar to [Reference Boyadzhiev12, Corollary 5.2] and a generalisation of the main result in [Reference deLaubenfels17] to noninteger
![]() $\gamma $
. See also [Reference Crouzeix, Larsson, Piskarev and Thomée15, Remark 2, p.83].
$\gamma $
. See also [Reference Crouzeix, Larsson, Piskarev and Thomée15, Remark 2, p.83].
Corollary 10.7. Let
![]() $A \in \operatorname {Sect}(\theta )$
,
$A \in \operatorname {Sect}(\theta )$
,
![]() $\theta \in (0,\pi )$
and
$\theta \in (0,\pi )$
and
![]() $\gamma \in (0,\pi /(2\theta ))$
. Then
$\gamma \in (0,\pi /(2\theta ))$
. Then
![]() $(e^{-tA^{\gamma }})_{t\ge 0}$
is a bounded holomorphic
$(e^{-tA^{\gamma }})_{t\ge 0}$
is a bounded holomorphic
![]() $C_0$
-semigroup of angle
$C_0$
-semigroup of angle
![]() $(\pi /2) - \gamma \theta $
. More precisely, if
$(\pi /2) - \gamma \theta $
. More precisely, if
![]() $\psi \in (\theta ,\pi /(2\gamma ))$
and
$\psi \in (\theta ,\pi /(2\gamma ))$
and
 $\lambda = |\lambda | e^{i\varphi } \in \Sigma _{(\pi /2)-\gamma \psi }$
, then
$\lambda = |\lambda | e^{i\varphi } \in \Sigma _{(\pi /2)-\gamma \psi }$
, then
 $$ \begin{align} \|e^{-\lambda A^{\gamma}}\| \le \frac{1}{2}\left(\frac{1}{\cos(\gamma\psi+\varphi)}+\frac{1}{\cos(\gamma\psi-\varphi)}\right) M_{\gamma\psi}(A). \end{align} $$
$$ \begin{align} \|e^{-\lambda A^{\gamma}}\| \le \frac{1}{2}\left(\frac{1}{\cos(\gamma\psi+\varphi)}+\frac{1}{\cos(\gamma\psi-\varphi)}\right) M_{\gamma\psi}(A). \end{align} $$
Proof. Let
![]() $\psi \in (\theta ,\pi )$
. Because the
$\psi \in (\theta ,\pi )$
. Because the
![]() $\mathcal {H}$
-calculus
$\mathcal {H}$
-calculus
![]() $\Upsilon _A$
is a homomorphism and
$\Upsilon _A$
is a homomorphism and
![]() $\Upsilon _A(e^{-\lambda z^{\gamma }}) = e^{- \lambda A^{\gamma }}$
for every
$\Upsilon _A(e^{-\lambda z^{\gamma }}) = e^{- \lambda A^{\gamma }}$
for every
![]() $\lambda \in \Sigma _{(\pi /2)-\gamma \psi }$
, the family
$\lambda \in \Sigma _{(\pi /2)-\gamma \psi }$
, the family
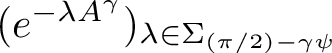 $(e^{-\lambda A^{\gamma }})_{\lambda \in \Sigma _{(\pi /2)-\gamma \psi }}$
is an operator semigroup. By Theorem 4.8 and the argument in Section 2, the map
$(e^{-\lambda A^{\gamma }})_{\lambda \in \Sigma _{(\pi /2)-\gamma \psi }}$
is an operator semigroup. By Theorem 4.8 and the argument in Section 2, the map
![]() $\lambda \mapsto e^{-\lambda z^{\gamma }}$
is holomorphic from
$\lambda \mapsto e^{-\lambda z^{\gamma }}$
is holomorphic from
![]() $\Sigma _{(\pi /2)-\gamma \psi }$
to
$\Sigma _{(\pi /2)-\gamma \psi }$
to
![]() $\mathcal {H}_{\psi }$
, so
$\mathcal {H}_{\psi }$
, so
![]() $\lambda \mapsto e^{-\lambda A^{\gamma }}$
is also holomorphic. The estimate (10.10) follows from Example 4.10(2) and (8.10), and it shows boundedness of the semigroup on each relevant sector.
$\lambda \mapsto e^{-\lambda A^{\gamma }}$
is also holomorphic. The estimate (10.10) follows from Example 4.10(2) and (8.10), and it shows boundedness of the semigroup on each relevant sector.
Note that, for
![]() $\gamma =1$
, Corollary 10.7 provides a sharper bound than Corollary 10.1(ii).
$\gamma =1$
, Corollary 10.7 provides a sharper bound than Corollary 10.1(ii).
11. Appendix: Shifts on
 $\mathcal {D}_s$
and
$\mathcal {D}_s$
and
 $\mathcal {H}_{\psi }$
$\mathcal {H}_{\psi }$
The shift semigroups on the space
![]() $\mathcal {B}$
had an important role in the study of the
$\mathcal {B}$
had an important role in the study of the
![]() $\mathcal {B}$
-calculus in [Reference Batty, Gomilko and Tomilov7] and [Reference Batty, Gomilko and Tomilov8]. Though the semigroups are not essential in this article, we think they will be important for further research, so we describe their properties on the spaces
$\mathcal {B}$
-calculus in [Reference Batty, Gomilko and Tomilov7] and [Reference Batty, Gomilko and Tomilov8]. Though the semigroups are not essential in this article, we think they will be important for further research, so we describe their properties on the spaces
![]() $\mathcal {D}_s$
and
$\mathcal {D}_s$
and
![]() $\mathcal {H}_{\psi }$
. In this appendix we prove that the shifts
$\mathcal {H}_{\psi }$
. In this appendix we prove that the shifts
![]() $(T(\tau ))_{\tau \in \mathbb {C}_+}$
given by
$(T(\tau ))_{\tau \in \mathbb {C}_+}$
given by
form a holomorphic
![]() $C_0$
-semigroup on
$C_0$
-semigroup on
![]() $\mathcal {D}_s$
for each
$\mathcal {D}_s$
for each
![]() $s>-1$
. We also show that a similar statement holds for shifts on
$s>-1$
. We also show that a similar statement holds for shifts on
![]() $\mathcal {H}_{\psi }$
for each
$\mathcal {H}_{\psi }$
for each
![]() $\psi \in (0,\pi )$
.
$\psi \in (0,\pi )$
.
We consider first the space
![]() $\mathcal {D}_s$
, and we begin by proving that the semigroup
$\mathcal {D}_s$
, and we begin by proving that the semigroup
![]() $(T(\tau ))_{\tau \in \Sigma _{\psi }}$
of operators is uniformly bounded on
$(T(\tau ))_{\tau \in \Sigma _{\psi }}$
of operators is uniformly bounded on
![]() $\mathcal {D}_s$
, for each
$\mathcal {D}_s$
, for each
![]() $s>-1$
and
$s>-1$
and
![]() $\psi \in (0,\pi /2)$
.
$\psi \in (0,\pi /2)$
.
Theorem 11.1. Let
![]() $s>-1$
,
$s>-1$
,
![]() $\psi \in (0,\pi /2)$
and
$\psi \in (0,\pi /2)$
and
![]() $a=\tan \psi $
. For all
$a=\tan \psi $
. For all
![]() $\tau \in \Sigma _{\psi }$
, we have
$\tau \in \Sigma _{\psi }$
, we have
where
 $$ \begin{align*} C_{a,s} &:= \frac{(s+1)2^{s}B((s+1)/2,1/2)}{\pi \cos\psi \cos^{s+2}(\psi/2+\pi/4)} +2^{s+1}.\end{align*} $$
$$ \begin{align*} C_{a,s} &:= \frac{(s+1)2^{s}B((s+1)/2,1/2)}{\pi \cos\psi \cos^{s+2}(\psi/2+\pi/4)} +2^{s+1}.\end{align*} $$
Proof. Let
![]() $\tau \in \Sigma _{\psi }$
and
$\tau \in \Sigma _{\psi }$
and
![]() $f \in \mathcal {D}_s$
. We have
$f \in \mathcal {D}_s$
. We have
 $$ \begin{align*} \|T(\tau)f\|_{\mathcal{D}_s}&\le |f(\infty)|+ \int_{\mathbb{C}_+} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f'(z+\tau)| \, dS(z) = |f(\infty)|+J(\tau), \end{align*} $$
$$ \begin{align*} \|T(\tau)f\|_{\mathcal{D}_s}&\le |f(\infty)|+ \int_{\mathbb{C}_+} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f'(z+\tau)| \, dS(z) = |f(\infty)|+J(\tau), \end{align*} $$
where
![]() $dS$
denotes area measure on
$dS$
denotes area measure on
![]() $\mathbb {C}_+$
and
$\mathbb {C}_+$
and
 $$ \begin{align*} J(\tau):=\int_{\operatorname{Re}z \ge \operatorname{Re}\tau} \frac{(\operatorname{Re}z-\operatorname{Re}\tau)^s} {|z-\tau|^{s+1}} |f'(z)|\,dS(z). \end{align*} $$
$$ \begin{align*} J(\tau):=\int_{\operatorname{Re}z \ge \operatorname{Re}\tau} \frac{(\operatorname{Re}z-\operatorname{Re}\tau)^s} {|z-\tau|^{s+1}} |f'(z)|\,dS(z). \end{align*} $$
Let
 $$ \begin{align*} W(\tau)&:= \left\{z\in \mathbb{C}: \operatorname{Re}z\ge \operatorname{Re}\tau,\;|z-\tau| \le |\tau| \right\},\\ W_0(\tau)&:= W(\tau)-\tau= \left\{z\in \mathbb{C}_{+}:\;|z| \le |\tau| \right\}. \end{align*} $$
$$ \begin{align*} W(\tau)&:= \left\{z\in \mathbb{C}: \operatorname{Re}z\ge \operatorname{Re}\tau,\;|z-\tau| \le |\tau| \right\},\\ W_0(\tau)&:= W(\tau)-\tau= \left\{z\in \mathbb{C}_{+}:\;|z| \le |\tau| \right\}. \end{align*} $$
If
![]() $\operatorname {Re}z \ge \operatorname {Re}\tau $
and
$\operatorname {Re}z \ge \operatorname {Re}\tau $
and
![]() $z \notin W(\tau )$
, then
$z \notin W(\tau )$
, then
![]() $|z| \le |z-\tau |+|\tau | \le 2|z-\tau |$
. Hence,
$|z| \le |z-\tau |+|\tau | \le 2|z-\tau |$
. Hence,
 $$ \begin{align} J(\tau) &\le \int_{W(\tau)} \frac{(\operatorname{Re}z - \operatorname{Re}\tau)^s}{|z-\tau|^{s+1}} |f'(z)|\,dS(z)\\ & \hskip30pt + 2^{s+1}\int_{\operatorname{Re}z \ge \operatorname{Re}\tau} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f'(z)| \,dS(z) \notag \\ &\le \max_{z\in W(\tau)}\,|f'(z)| \int_{W_0(\tau)} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}}\,dS(z) +2^{s+1}\|f'\|_{\mathcal{V}_s}.\notag \end{align} $$
$$ \begin{align} J(\tau) &\le \int_{W(\tau)} \frac{(\operatorname{Re}z - \operatorname{Re}\tau)^s}{|z-\tau|^{s+1}} |f'(z)|\,dS(z)\\ & \hskip30pt + 2^{s+1}\int_{\operatorname{Re}z \ge \operatorname{Re}\tau} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}} |f'(z)| \,dS(z) \notag \\ &\le \max_{z\in W(\tau)}\,|f'(z)| \int_{W_0(\tau)} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}}\,dS(z) +2^{s+1}\|f'\|_{\mathcal{V}_s}.\notag \end{align} $$
Moreover,
 $$ \begin{align} \int_{W_0(\tau)} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}}\,dS(z) = \int_{-\pi/2}^{\pi/2}\int_0^{|\tau|} \cos^{s}\varphi \,d\rho\,d\varphi = |\tau| B((s+1)/2,1/2). \end{align} $$
$$ \begin{align} \int_{W_0(\tau)} \frac{(\operatorname{Re}z)^s}{|z|^{s+1}}\,dS(z) = \int_{-\pi/2}^{\pi/2}\int_0^{|\tau|} \cos^{s}\varphi \,d\rho\,d\varphi = |\tau| B((s+1)/2,1/2). \end{align} $$
For
![]() $z\in W(\tau )$
, we also have
$z\in W(\tau )$
, we also have
![]() $\operatorname {Re}z \ge \operatorname {Re}\tau $
and
$\operatorname {Re}z \ge \operatorname {Re}\tau $
and
 $$ \begin{align*} |\operatorname{Im}z| \le |\operatorname{Im}\tau| + |\tau|\le \left(a + \sqrt{1+a^2}\right) \operatorname{Re}\tau. \end{align*} $$
$$ \begin{align*} |\operatorname{Im}z| \le |\operatorname{Im}\tau| + |\tau|\le \left(a + \sqrt{1+a^2}\right) \operatorname{Re}\tau. \end{align*} $$
Hence, if
 $\psi_a :=\arctan \big(a+\sqrt{1+a^2}\big)$
and
$\psi_a :=\arctan \big(a+\sqrt{1+a^2}\big)$
and
![]() $z \in \Sigma_{\psi_a}$
and
$z \in \Sigma_{\psi_a}$
and
![]() $|z|\ge \operatorname {Re}\tau $
, so by Corollary 3.13,
$|z|\ge \operatorname {Re}\tau $
, so by Corollary 3.13,
 $$ \begin{align} \max_{z\in W(\tau)}\,|f'(z)| \le \max_{z\in \Sigma_{\psi_a},\,|z|\ge \operatorname{Re}\tau}\,|f'(z)| \le \frac{(s+1)2^s}{\pi \operatorname{Re}\tau\cos^{s+2}\psi_a}\|f'\|_{\mathcal{V}_s}. \end{align} $$
$$ \begin{align} \max_{z\in W(\tau)}\,|f'(z)| \le \max_{z\in \Sigma_{\psi_a},\,|z|\ge \operatorname{Re}\tau}\,|f'(z)| \le \frac{(s+1)2^s}{\pi \operatorname{Re}\tau\cos^{s+2}\psi_a}\|f'\|_{\mathcal{V}_s}. \end{align} $$
Inserting the estimates (11.3) and (11.4) into (11.2) and using
![]() $|\tau |\le \operatorname {Re}\tau /\cos \psi $
, we obtain
$|\tau |\le \operatorname {Re}\tau /\cos \psi $
, we obtain
 $$ \begin{align*} J(\tau)\le \left( \frac{(s+1)2^s B((s+1)/2,2)}{\pi\cos\psi \cos^{s+2}\psi_a} +2^{s+1}\right) \|f'\|_{\mathcal{V}_s}. \end{align*} $$
$$ \begin{align*} J(\tau)\le \left( \frac{(s+1)2^s B((s+1)/2,2)}{\pi\cos\psi \cos^{s+2}\psi_a} +2^{s+1}\right) \|f'\|_{\mathcal{V}_s}. \end{align*} $$
Noting that
the estimate (11.1) follows.
Corollary 11.2. For any
![]() $s>-1$
, the family
$s>-1$
, the family
![]() $T:=(T(\tau ))_{\tau \in \mathbb {C}_{+}}$
is a bounded holomorphic
$T:=(T(\tau ))_{\tau \in \mathbb {C}_{+}}$
is a bounded holomorphic
![]() $C_0$
-semigroup on
$C_0$
-semigroup on
![]() $\mathcal {D}_s$
of angle
$\mathcal {D}_s$
of angle
![]() $\pi /2$
. The generator of the semigroup is
$\pi /2$
. The generator of the semigroup is
![]() $-A_{\mathcal {D}_s}$
, where
$-A_{\mathcal {D}_s}$
, where
Proof. By Theorem 11.1, T is bounded on
![]() $\Sigma _{\psi }$
for each
$\Sigma _{\psi }$
for each
![]() $\psi \in (0,\pi /2)$
, and as noted in Remark 3.14, the function
$\psi \in (0,\pi /2)$
, and as noted in Remark 3.14, the function
![]() $\lambda \mapsto r_{\lambda }$
is a holomorphic function from
$\lambda \mapsto r_{\lambda }$
is a holomorphic function from
![]() $\mathbb {C}_+$
to
$\mathbb {C}_+$
to
![]() $\mathcal {D}_s$
, so
$\mathcal {D}_s$
, so
![]() $\tau \mapsto T(\tau )r_{\lambda }$
is holomorphic. Because
$\tau \mapsto T(\tau )r_{\lambda }$
is holomorphic. Because
 $\widetilde {\mathcal {R}}(\mathbb {C}_+)$
is dense in
$\widetilde {\mathcal {R}}(\mathbb {C}_+)$
is dense in
![]() $\mathcal {D}_s$
(Theorem 5.1), it follows that T is strongly continuous on
$\mathcal {D}_s$
(Theorem 5.1), it follows that T is strongly continuous on
![]() $\Sigma _{\psi } \cup \{0\}$
and, moreover, for
$\Sigma _{\psi } \cup \{0\}$
and, moreover, for
![]() $f \in \mathcal {D}_s$
, the map
$f \in \mathcal {D}_s$
, the map
![]() $\tau \mapsto T(\tau )f$
is holomorphic on
$\tau \mapsto T(\tau )f$
is holomorphic on
![]() $\mathbb {C}_+$
.
$\mathbb {C}_+$
.
The proof of the statement about the generator is almost identical to the proof for the space
![]() $\mathcal {B}$
in [Reference Batty, Gomilko and Tomilov7, Lemma 2.6].
$\mathcal {B}$
in [Reference Batty, Gomilko and Tomilov7, Lemma 2.6].
The following corollary justifies Remark 10.4 about the assumptions in Theorem 10.3.
Corollary 11.3. Let
![]() $f \in \mathcal {D}_s$
,
$f \in \mathcal {D}_s$
,
![]() $s>-1,$
and assume that
$s>-1,$
and assume that
![]() $f^{(n)} \in \mathcal {D}_s$
for some
$f^{(n)} \in \mathcal {D}_s$
for some
![]() $n \in \mathbb {N}.$
Then
$n \in \mathbb {N}.$
Then
![]() $f^{(k)} \in \mathcal {D}_s$
for
$f^{(k)} \in \mathcal {D}_s$
for
![]() $k=1,2,\dots ,n-1$
.
$k=1,2,\dots ,n-1$
.
Proof. Consider the operator
![]() $Ag = -g'$
on
$Ag = -g'$
on
![]() $\operatorname {Hol}(\mathbb {C}_+)$
and its part
$\operatorname {Hol}(\mathbb {C}_+)$
and its part
![]() $A_{\mathcal {D}_s}$
in the subspace
$A_{\mathcal {D}_s}$
in the subspace
![]() $\mathcal {D}_s$
. The operators
$\mathcal {D}_s$
. The operators
![]() $A_{\mathcal {D}_s}+m, \, m=1,2,\dots ,n$
, are surjective on
$A_{\mathcal {D}_s}+m, \, m=1,2,\dots ,n$
, are surjective on
![]() $\mathcal {D}_s$
, and
$\mathcal {D}_s$
, and
![]() $g=0$
is the only solution in
$g=0$
is the only solution in
![]() $\mathcal {D}_s$
to
$\mathcal {D}_s$
to
![]() $\prod _{m=1}^n(A+m)g=0$
. The statement follows from [Reference Lyubič43, Theorem 1].
$\prod _{m=1}^n(A+m)g=0$
. The statement follows from [Reference Lyubič43, Theorem 1].
Remark 11.4. The space
![]() $\mathcal {B}$
is invariant under vertical shifts:
$\mathcal {B}$
is invariant under vertical shifts:
![]() $f(z) \mapsto f(z+i\sigma )$
for
$f(z) \mapsto f(z+i\sigma )$
for
![]() $\sigma \in \mathbb {R}$
. However, the spaces
$\sigma \in \mathbb {R}$
. However, the spaces
![]() $\mathcal {D}_s$
and
$\mathcal {D}_s$
and
![]() $\mathcal {D}_s^{\infty }$
are not invariant under vertical shifts. See Example 3.19.
$\mathcal {D}_s^{\infty }$
are not invariant under vertical shifts. See Example 3.19.
Now we will show that the family of shifts T also forms a bounded holomorphic
![]() $C_0$
-semigroup on
$C_0$
-semigroup on
![]() $\mathcal {H}_{\psi }$
for every
$\mathcal {H}_{\psi }$
for every
![]() $\psi \in (0,\pi )$
. If
$\psi \in (0,\pi )$
. If
![]() $\psi>\pi /2$
, then
$\psi>\pi /2$
, then
![]() $T(\tau )$
are defined for
$T(\tau )$
are defined for
![]() $\tau \in \Sigma _{\pi -\psi }$
. For this aim, we will recall the Gabriel inequality for holomorphic functions.
$\tau \in \Sigma _{\pi -\psi }$
. For this aim, we will recall the Gabriel inequality for holomorphic functions.
Let
![]() $\Omega $
be a bounded convex domain in
$\Omega $
be a bounded convex domain in
![]() $\mathbb {C}$
and let
$\mathbb {C}$
and let
![]() $\Gamma \subset \overline {\Omega }$
be a convex curve. Then there exists a universal constant
$\Gamma \subset \overline {\Omega }$
be a convex curve. Then there exists a universal constant
![]() $K>0$
(not depending on
$K>0$
(not depending on
![]() $f, \Omega $
and
$f, \Omega $
and
![]() $\Gamma $
) such that, for all
$\Gamma $
) such that, for all
![]() $f \in \operatorname {Hol}(\Omega ) \cap C(\overline \Omega )$
,
$f \in \operatorname {Hol}(\Omega ) \cap C(\overline \Omega )$
,
 $$ \begin{align} \int_{\Gamma} |f(z)|\, |dz| \le K \int_{\partial \Omega} |f(z)|\, |dz|. \end{align} $$
$$ \begin{align} \int_{\Gamma} |f(z)|\, |dz| \le K \int_{\partial \Omega} |f(z)|\, |dz|. \end{align} $$
Clearly,
![]() $K \ge 1.$
Moreover, it can be shown that if
$K \ge 1.$
Moreover, it can be shown that if
![]() $\Gamma $
is closed, then
$\Gamma $
is closed, then
![]() $2 < K < 3.7$
(see [Reference Beurling11, p.457], for example). The inequality was conjectured by J. Littlewood and first proved by Gabriel in [Reference Gabriel24, Theorem I]. It is thoroughly discussed in [Reference Beurling11, Selected Seminars, 2, 4 and 5] and [Reference Granados32, Section 5], providing simpler proofs, more general versions and additional insights.
$2 < K < 3.7$
(see [Reference Beurling11, p.457], for example). The inequality was conjectured by J. Littlewood and first proved by Gabriel in [Reference Gabriel24, Theorem I]. It is thoroughly discussed in [Reference Beurling11, Selected Seminars, 2, 4 and 5] and [Reference Granados32, Section 5], providing simpler proofs, more general versions and additional insights.
Theorem 11.5. Let
![]() $\psi \in (0,\pi )$
and
$\psi \in (0,\pi )$
and
![]() $\psi _0=\min \{\psi ,\pi -\psi \}$
. The family
$\psi _0=\min \{\psi ,\pi -\psi \}$
. The family
![]() $T=(T(\tau ))_{\tau \in \Sigma _{\psi _0}}$
is a bounded holomorphic
$T=(T(\tau ))_{\tau \in \Sigma _{\psi _0}}$
is a bounded holomorphic
![]() $C_0$
-semigroup of angle
$C_0$
-semigroup of angle
![]() $\psi _0$
on each of the spaces
$\psi _0$
on each of the spaces
![]() $\mathcal H_{\psi }$
. The generator
$\mathcal H_{\psi }$
. The generator
![]() $-A_{\mathcal H_{\psi }}$
of T on
$-A_{\mathcal H_{\psi }}$
of T on
![]() $\mathcal H_{\psi }$
is given by
$\mathcal H_{\psi }$
is given by
Proof. We will show first that the family of shifts T is uniformly bounded on
![]() $\mathcal H_{\psi }$
for every
$\mathcal H_{\psi }$
for every
![]() $\psi \in (0,\pi ).$
Then the result follows quickly by a density argument.
$\psi \in (0,\pi ).$
Then the result follows quickly by a density argument.
Let
![]() $g \in \mathcal H_{\psi }$
so that for
$g \in \mathcal H_{\psi }$
so that for
![]() $f=g'$
one has
$f=g'$
one has
![]() $f \in H^1(\Sigma _{\psi }).$
Assume first that
$f \in H^1(\Sigma _{\psi }).$
Assume first that
![]() $\psi \in (0,\pi /2]$
, and let
$\psi \in (0,\pi /2]$
, and let
![]() $\psi ' \in (0,\psi )$
and
$\psi ' \in (0,\psi )$
and
![]() $\alpha :=\sin (\psi -\psi ')$
. By the mean value inequality, for any
$\alpha :=\sin (\psi -\psi ')$
. By the mean value inequality, for any
![]() $r>0$
and
$r>0$
and
![]() $\varphi \in (-\psi ',\psi ')$
we have
$\varphi \in (-\psi ',\psi ')$
we have
 $$ \begin{align} r |f(re^{i\varphi})| &\le \frac{1}{\pi \alpha^2 r}\int_{|z-re^{i\varphi}|\le \alpha r} |f(z)| \, dS(z)\\ &\le \frac{2(1+\alpha)}{\pi \alpha^2} \int_{-\psi'}^{\psi'} \int_{(1-\alpha)r}^{(1+\alpha)r} |f(\rho e^{i\varphi})|\, d\rho\,d\varphi \notag\\ &\to 0,\notag \end{align} $$
$$ \begin{align} r |f(re^{i\varphi})| &\le \frac{1}{\pi \alpha^2 r}\int_{|z-re^{i\varphi}|\le \alpha r} |f(z)| \, dS(z)\\ &\le \frac{2(1+\alpha)}{\pi \alpha^2} \int_{-\psi'}^{\psi'} \int_{(1-\alpha)r}^{(1+\alpha)r} |f(\rho e^{i\varphi})|\, d\rho\,d\varphi \notag\\ &\to 0,\notag \end{align} $$
as
![]() $r \to 0$
or
$r \to 0$
or
![]() $r \to \infty $
, by the dominated convergence theorem.
$r \to \infty $
, by the dominated convergence theorem.
Now let
![]() $\tau \in \Sigma _{\psi }$
and
$\tau \in \Sigma _{\psi }$
and
![]() $\varphi \in (0,\psi ).$
Let
$\varphi \in (0,\psi ).$
Let
 $$ \begin{align} \Gamma_{\tau, \varphi}=\{\tau+te^{i\varphi}: t \ge 0\} \cup \{\tau+te^{-i\varphi} : t \ge 0 \}. \end{align} $$
$$ \begin{align} \Gamma_{\tau, \varphi}=\{\tau+te^{i\varphi}: t \ge 0\} \cup \{\tau+te^{-i\varphi} : t \ge 0 \}. \end{align} $$
Let
![]() $\psi>\psi'>\max (|\arg \tau |,\varphi )$
, and take
$\psi>\psi'>\max (|\arg \tau |,\varphi )$
, and take
![]() $r\in (0,1)$
such that
$r\in (0,1)$
such that
![]() $0< r <|\tau | < 1/r$
. We now apply Gabriel’s inequality (11.5) with
$0< r <|\tau | < 1/r$
. We now apply Gabriel’s inequality (11.5) with
and
We obtain
 $$ \begin{align*} &{K^{-1} \int_{\Gamma_{\tau,\varphi,r}} |f(z)|\, |dz| \le \int_{\partial\Omega_{r}} |f(z)|\, |dz|} \notag\\ &\le \int_{r}^{1/r}|f(\rho e^{i\psi'})|\, d\rho +\int_{r}^{1/r}|f(\rho e^{-i\psi'})|\, d\rho + 2 \pi r^{-1} \sup_{\varphi \in (-\psi', \psi')} |f(e^{i\varphi}/r)| \notag \\ &\quad +2 r\sin\psi' \sup_{\varphi \in (-\psi', \psi')} \left|f\left(\frac{r\cos \psi'}{\cos \varphi} e^{i\varphi}\right)\right|,\notag \end{align*} $$
$$ \begin{align*} &{K^{-1} \int_{\Gamma_{\tau,\varphi,r}} |f(z)|\, |dz| \le \int_{\partial\Omega_{r}} |f(z)|\, |dz|} \notag\\ &\le \int_{r}^{1/r}|f(\rho e^{i\psi'})|\, d\rho +\int_{r}^{1/r}|f(\rho e^{-i\psi'})|\, d\rho + 2 \pi r^{-1} \sup_{\varphi \in (-\psi', \psi')} |f(e^{i\varphi}/r)| \notag \\ &\quad +2 r\sin\psi' \sup_{\varphi \in (-\psi', \psi')} \left|f\left(\frac{r\cos \psi'}{\cos \varphi} e^{i\varphi}\right)\right|,\notag \end{align*} $$
where
![]() $K>0$
is given by (11.5).
$K>0$
is given by (11.5).
By (11.6), the last two terms converge to zero as
![]() $r \to 0.$
From Theorem 4.6(iv) it follows that
$r \to 0.$
From Theorem 4.6(iv) it follows that
 $$ \begin{align*} K^{-1} \int_{\Gamma_{\tau,\varphi}} |f(z)|\, |dz| \le \|f\|_{H^1(\Sigma_{\psi'})}\le \|f\|_{H^1(\Sigma_{\psi})}. \end{align*} $$
$$ \begin{align*} K^{-1} \int_{\Gamma_{\tau,\varphi}} |f(z)|\, |dz| \le \|f\|_{H^1(\Sigma_{\psi'})}\le \|f\|_{H^1(\Sigma_{\psi})}. \end{align*} $$
Thus, because the choice of
![]() $\varphi \in (0, \psi )$
was arbitrary, we have
$\varphi \in (0, \psi )$
was arbitrary, we have
Now we consider the case when
![]() $\psi \in (\pi /2,\pi )$
and
$\psi \in (\pi /2,\pi )$
and
![]() $\tau \in \Sigma _{\pi -\psi }.$
For
$\tau \in \Sigma _{\pi -\psi }.$
For
![]() $\varphi \in (0,\psi )$
let the path
$\varphi \in (0,\psi )$
let the path
![]() $\Gamma _{\tau , \varphi }$
be given by (11.7) and
$\Gamma _{\tau , \varphi }$
be given by (11.7) and
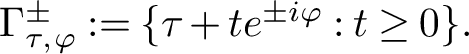 $\Gamma ^{\pm }_{\tau ,\varphi }:= \{\tau +te^{\pm i\varphi }: t \ge 0\}.$
Define the half-planes
$\Gamma ^{\pm }_{\tau ,\varphi }:= \{\tau +te^{\pm i\varphi }: t \ge 0\}.$
Define the half-planes
 $\mathbb {C}_+^{\psi }:= -ie^{i\psi } \Sigma _{\pi /2}$
and
$\mathbb {C}_+^{\psi }:= -ie^{i\psi } \Sigma _{\pi /2}$
and
 $\mathbb {C}_-^{\psi }:=ie^{-i\psi } \Sigma _{\pi /2}$
so that
$\mathbb {C}_-^{\psi }:=ie^{-i\psi } \Sigma _{\pi /2}$
so that
 $\Gamma ^{\pm }_{\tau ,\varphi }\subset \mathbb {C}_{\pm }^{\psi }.$
Letting
$\Gamma ^{\pm }_{\tau ,\varphi }\subset \mathbb {C}_{\pm }^{\psi }.$
Letting
 $\widetilde f (z):=f(-ie^{i\psi}z), z \in \Sigma_{\pi/2},$
and applying (11.8) with
$\widetilde f (z):=f(-ie^{i\psi}z), z \in \Sigma_{\pi/2},$
and applying (11.8) with
![]() $\psi =\pi /2$
,
$\psi =\pi /2$
,
 $\widetilde f\in H^1(\Sigma _{\pi /2})$
in place of f and
$\widetilde f\in H^1(\Sigma _{\pi /2})$
in place of f and
![]() $\widetilde \tau =ie^{-i\psi }\tau $
in place of
$\widetilde \tau =ie^{-i\psi }\tau $
in place of
![]() $\tau ,$
we obtain that
$\tau ,$
we obtain that
 $$ \begin{align*} K \int_{e^{i\psi}\mathbb{R}} |f(z)|\, |dz| = K \|\widetilde f\|_{H^1(\Sigma_{\pi/2})} \ge \|T(\widetilde \tau)\widetilde f\|_{H^{1}(\Sigma_{\pi/2})}\ge \int_{\Gamma^+_{\tau,\varphi}} |f(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} K \int_{e^{i\psi}\mathbb{R}} |f(z)|\, |dz| = K \|\widetilde f\|_{H^1(\Sigma_{\pi/2})} \ge \|T(\widetilde \tau)\widetilde f\|_{H^{1}(\Sigma_{\pi/2})}\ge \int_{\Gamma^+_{\tau,\varphi}} |f(z)|\, |dz|. \end{align*} $$
Similarly,
 $$ \begin{align*} K \int_{e^{-i\psi}\mathbb{R}} |f(z)|\, |dz| \ge \int_{\Gamma^-_{\tau,\varphi}} |f(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} K \int_{e^{-i\psi}\mathbb{R}} |f(z)|\, |dz| \ge \int_{\Gamma^-_{\tau,\varphi}} |f(z)|\, |dz|. \end{align*} $$
Thus, taking into account Theorem 4.6(iv), we infer that
 $$ \begin{align*} 2K\|f\|_{H^1(\Sigma_{\psi})}\ge K \left(\int_{e^{i\psi}\mathbb{R}} |f(z)|\, |dz| +\int_{e^{-i\psi}\mathbb{R}}|f(z)|\, |dz|\right) \ge \int_{\Gamma_{\tau,\varphi}} |f(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} 2K\|f\|_{H^1(\Sigma_{\psi})}\ge K \left(\int_{e^{i\psi}\mathbb{R}} |f(z)|\, |dz| +\int_{e^{-i\psi}\mathbb{R}}|f(z)|\, |dz|\right) \ge \int_{\Gamma_{\tau,\varphi}} |f(z)|\, |dz|. \end{align*} $$
Because, as above, the choice of
![]() $\varphi \in (0,\psi )$
is arbitrary, we then have
$\varphi \in (0,\psi )$
is arbitrary, we then have
if
![]() $\psi \in (\pi /2,\pi ),$
and then if
$\psi \in (\pi /2,\pi ),$
and then if
![]() $\psi \in (0,\pi )$
in view of (11.8).
$\psi \in (0,\pi )$
in view of (11.8).
Hence, for all
![]() $\tau \in \Sigma _{\psi },$
$\tau \in \Sigma _{\psi },$
A direct verification shows that
![]() $\|T(\tau )r_{\lambda }-r_{\lambda }\|_{\mathcal {H}_{\psi }} \to 0, \tau \to 0$
, for every
$\|T(\tau )r_{\lambda }-r_{\lambda }\|_{\mathcal {H}_{\psi }} \to 0, \tau \to 0$
, for every
![]() $\lambda \in \mathbb {C} \setminus \overline {\Sigma }_{\psi }$
. It now follows from (11.9) and Theorem 5.10 that
$\lambda \in \mathbb {C} \setminus \overline {\Sigma }_{\psi }$
. It now follows from (11.9) and Theorem 5.10 that
![]() $(T(\tau ))_{\tau \in \Sigma _{\psi _0}}$
is a bounded
$(T(\tau ))_{\tau \in \Sigma _{\psi _0}}$
is a bounded
![]() $C_0$
-semigroup on
$C_0$
-semigroup on
![]() $\mathcal {H}_{\psi ,0}$
and then on
$\mathcal {H}_{\psi ,0}$
and then on
![]() $\mathcal H_{\psi }$
. The holomorphy of
$\mathcal H_{\psi }$
. The holomorphy of
![]() $(T(\tau ))_{\tau \in \Sigma _{\psi _0}}$
on
$(T(\tau ))_{\tau \in \Sigma _{\psi _0}}$
on
![]() $\mathcal H_{\psi }$
follows from Theorem 4.8(iii) and the method discussed in Section 2.
$\mathcal H_{\psi }$
follows from Theorem 4.8(iii) and the method discussed in Section 2.
The claim about the generator
![]() $-A_{\mathcal H_{\psi }}$
can be justified along the lines of the proof of a similar fact for the space
$-A_{\mathcal H_{\psi }}$
can be justified along the lines of the proof of a similar fact for the space
![]() $\mathcal {B}$
in [Reference Batty, Gomilko and Tomilov7, Lemma 2.6].
$\mathcal {B}$
in [Reference Batty, Gomilko and Tomilov7, Lemma 2.6].
Remark 11.6. Following a more conventional approach, one may try to prove Theorem 11.5 by reducing the estimates to the half-plane case and applying Carleson’s embedding theorem for
![]() $H^1(\mathbb C_+)$
. However, the technical details become rather cumbersome, so we prefer to use Gabriel’s inequality allowing for a more transparent argument.
$H^1(\mathbb C_+)$
. However, the technical details become rather cumbersome, so we prefer to use Gabriel’s inequality allowing for a more transparent argument.
12. Appendix: The
 $\mathcal {D}$
-calculus vs the HP and the
$\mathcal {D}$
-calculus vs the HP and the
 $\mathcal B$
-calculi
$\mathcal B$
-calculi
It is natural to compare the strength of the
![]() $\mathcal D$
-calculus with some other functional calculi, such as the recently constructed
$\mathcal D$
-calculus with some other functional calculi, such as the recently constructed
![]() $\mathcal B$
-calculus and the well-known HP-calculus. To show the advantages of our
$\mathcal B$
-calculus and the well-known HP-calculus. To show the advantages of our
![]() $\mathcal D$
-calculus with respect to the
$\mathcal D$
-calculus with respect to the
![]() $\mathcal B$
-calculus and the HP-calculus, as an illustrative example, we consider the family of functions
$\mathcal B$
-calculus and the HP-calculus, as an illustrative example, we consider the family of functions
![]() $\{f_n: n \ge 1\}$
given by
$\{f_n: n \ge 1\}$
given by
 $$ \begin{align*} f_n(z)=\left(\frac{z-1}{z+1}\right)^n,\qquad z\in \mathbb{C}_{+},\quad n\in \mathbb{N}. \end{align*} $$
$$ \begin{align*} f_n(z)=\left(\frac{z-1}{z+1}\right)^n,\qquad z\in \mathbb{C}_{+},\quad n\in \mathbb{N}. \end{align*} $$
This family is contained in
![]() $\mathcal {LM}$
(see [Reference Batty, Gomilko and Tomilov8, Section 6]), and it arises naturally in the study of asymptotics for powers of Cayley transforms of semigroup generators. It is shown in [Reference Batty, Gomilko and Tomilov7, Lemma 3.7] and [Reference Batty, Gomilko and Tomilov8, Lemmas 5.1 and 5.2] that
$\mathcal {LM}$
(see [Reference Batty, Gomilko and Tomilov8, Section 6]), and it arises naturally in the study of asymptotics for powers of Cayley transforms of semigroup generators. It is shown in [Reference Batty, Gomilko and Tomilov7, Lemma 3.7] and [Reference Batty, Gomilko and Tomilov8, Lemmas 5.1 and 5.2] that
 $$ \begin{align*} \|f_n\|_{\mathcal{B}} \asymp \log n \qquad \text{and} \qquad \|f_n\|_{\text{HP}} \asymp n^{1/2}, \qquad n\to\infty. \end{align*} $$
$$ \begin{align*} \|f_n\|_{\mathcal{B}} \asymp \log n \qquad \text{and} \qquad \|f_n\|_{\text{HP}} \asymp n^{1/2}, \qquad n\to\infty. \end{align*} $$
We will show that the
![]() $\mathcal D$
-calculus provides sharper estimates for the corresponding operator functions. To this aim we need the next lemma.
$\mathcal D$
-calculus provides sharper estimates for the corresponding operator functions. To this aim we need the next lemma.
Lemma 12.1. For
![]() $s>0$
,
$s>0$
,
 $$ \begin{align*} \|f_n\|_{\mathcal{D}_s}\le 1+16\left(B(s/2,1/2)+2^{-s/2}\right),\qquad n\in \mathbb{N}. \end{align*} $$
$$ \begin{align*} \|f_n\|_{\mathcal{D}_s}\le 1+16\left(B(s/2,1/2)+2^{-s/2}\right),\qquad n\in \mathbb{N}. \end{align*} $$
Proof. Let
![]() $s>0$
and
$s>0$
and
![]() $n \in \mathbb N$
be fixed. We have
$n \in \mathbb N$
be fixed. We have
 $$ \begin{align*} f_n(\infty)=1,\quad f^{\prime}_n(z)=2n\frac{(z-1)^{n-1}}{(z+1)^{n+1}}, \end{align*} $$
$$ \begin{align*} f_n(\infty)=1,\quad f^{\prime}_n(z)=2n\frac{(z-1)^{n-1}}{(z+1)^{n+1}}, \end{align*} $$
and then
 $$ \begin{align*} \|f_n\|_{\mathcal{D}_s}=1+8n \int_0^{\pi/2} \cos^s\psi\int_1^{\infty} \frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi =1+8n J_n, \end{align*} $$
$$ \begin{align*} \|f_n\|_{\mathcal{D}_s}=1+8n \int_0^{\pi/2} \cos^s\psi\int_1^{\infty} \frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi =1+8n J_n, \end{align*} $$
where
 $$ \begin{align*} g_n(\rho,\psi)=\left(\frac{\rho^2-2\rho\cos\psi+1}{\rho^2+2\rho\cos\psi+1}\right)^{(n-1)/2}. \end{align*} $$
$$ \begin{align*} g_n(\rho,\psi)=\left(\frac{\rho^2-2\rho\cos\psi+1}{\rho^2+2\rho\cos\psi+1}\right)^{(n-1)/2}. \end{align*} $$
Let
![]() $J_n= J_{1, n} + J_{2,n}+J_{3,n}$
, where
$J_n= J_{1, n} + J_{2,n}+J_{3,n}$
, where
 $$ \begin{align*} J_{1,n}&=\int_0^{\pi/2} \cos^s\psi\int_2^{\infty} \frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi,\\ J_{2,n}&=\int_{\pi/4}^{\pi/2} \cos^s\psi\int_1^2\frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi,\\ J_{3,n}&=\int_0^{\pi/4}\cos^s\psi\int_1^2\frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi. \end{align*} $$
$$ \begin{align*} J_{1,n}&=\int_0^{\pi/2} \cos^s\psi\int_2^{\infty} \frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi,\\ J_{2,n}&=\int_{\pi/4}^{\pi/2} \cos^s\psi\int_1^2\frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi,\\ J_{3,n}&=\int_0^{\pi/4}\cos^s\psi\int_1^2\frac{g_n(\rho,\psi)\,d\rho}{\rho^2+2\rho\cos\psi+1}\,d\psi. \end{align*} $$
We estimate each of the summands
![]() $J_{1, n}$
,
$J_{1, n}$
,
![]() $J_{2,n}$
and
$J_{2,n}$
and
![]() $J_{3,n}$
separately. First,
$J_{3,n}$
separately. First,
 $$ \begin{align*} \frac{\partial}{\partial \rho}\,g_{n+2}(\rho,\psi)&=2(n+1)\frac{(\rho^2-1)\cos\psi}{(\rho^2+2\rho\cos\psi+1)^2}g_{n}(\rho,\psi)\\ &\ge \frac{2(n+1)}{3} \frac{\cos\psi\,g_n(\rho,\psi)}{(\rho^2+2\rho\cos\psi+1)}>0,\quad \rho>2. \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial \rho}\,g_{n+2}(\rho,\psi)&=2(n+1)\frac{(\rho^2-1)\cos\psi}{(\rho^2+2\rho\cos\psi+1)^2}g_{n}(\rho,\psi)\\ &\ge \frac{2(n+1)}{3} \frac{\cos\psi\,g_n(\rho,\psi)}{(\rho^2+2\rho\cos\psi+1)}>0,\quad \rho>2. \end{align*} $$
Hence,
 $$ \begin{align*} J_{1,n}&\le \frac{3}{2(n+1)}\int_0^{\pi/2}\cos^{s-1}\psi \int_2^{\infty} \frac{\partial}{\partial \rho}\,g_{n+2}(\rho,\psi)\,d\rho\,d\psi\\ &\le \frac{3}{2(n+1)}\int_0^{\pi/2}\cos^{s-1}\psi\,d\psi<\frac{B(s/2,1/2)}{n}. \end{align*} $$
$$ \begin{align*} J_{1,n}&\le \frac{3}{2(n+1)}\int_0^{\pi/2}\cos^{s-1}\psi \int_2^{\infty} \frac{\partial}{\partial \rho}\,g_{n+2}(\rho,\psi)\,d\rho\,d\psi\\ &\le \frac{3}{2(n+1)}\int_0^{\pi/2}\cos^{s-1}\psi\,d\psi<\frac{B(s/2,1/2)}{n}. \end{align*} $$
Next, for all
![]() $\rho \in (1,2)$
and
$\rho \in (1,2)$
and
![]() $\psi \in (\pi /4,\pi /2)$
,
$\psi \in (\pi /4,\pi /2)$
,
 $$ \begin{align*} \frac{\partial}{\partial \psi}\,g_{n+2}(\rho,\psi)&=2(n+1)\frac{\rho(\rho^2+1)\sin\psi}{(\rho^2+2\rho\cos\psi+1)^2}g_{n}(\rho,\psi)\\ &\ge \frac{(n+1)}{2} \frac{\,g_n(\rho,\psi)}{(\rho^2+2\rho\cos\psi+1)}>0, \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial \psi}\,g_{n+2}(\rho,\psi)&=2(n+1)\frac{\rho(\rho^2+1)\sin\psi}{(\rho^2+2\rho\cos\psi+1)^2}g_{n}(\rho,\psi)\\ &\ge \frac{(n+1)}{2} \frac{\,g_n(\rho,\psi)}{(\rho^2+2\rho\cos\psi+1)}>0, \end{align*} $$
so
 $$ \begin{align*} J_{2,n}&\le \frac{2}{(n+1)} \int_1^2 \int_{\pi/4}^{\pi/2}\cos^s\psi \frac{\partial}{\partial \rho}\,g_{n+2}(\rho,\psi)\,d\psi\,d\rho\\&\le -\frac{2}{(n+1)} \int_{\pi/4}^{\pi/2}(\cos^s\psi)'\,d\psi =\frac{2}{2^{s/2}(n+1)}. \end{align*} $$
$$ \begin{align*} J_{2,n}&\le \frac{2}{(n+1)} \int_1^2 \int_{\pi/4}^{\pi/2}\cos^s\psi \frac{\partial}{\partial \rho}\,g_{n+2}(\rho,\psi)\,d\psi\,d\rho\\&\le -\frac{2}{(n+1)} \int_{\pi/4}^{\pi/2}(\cos^s\psi)'\,d\psi =\frac{2}{2^{s/2}(n+1)}. \end{align*} $$
Finally, because
 $$ \begin{align*} \sup_{\rho\in (1,2),\,\psi\in (0,\pi/4)} g_n(\rho, \psi) &=g_n(2,\pi/4) =\left(\frac{5-2\sqrt{2}}{5+2\sqrt{2}}\right)^{(n-1)/2} <\frac{2}{n}, \end{align*} $$
$$ \begin{align*} \sup_{\rho\in (1,2),\,\psi\in (0,\pi/4)} g_n(\rho, \psi) &=g_n(2,\pi/4) =\left(\frac{5-2\sqrt{2}}{5+2\sqrt{2}}\right)^{(n-1)/2} <\frac{2}{n}, \end{align*} $$
we have
 $$ \begin{align*} J_{3,n}\le \frac{2}{n} \int_0^{\pi/4}\cos^s\psi\,d\psi <\frac{B(s/2,1/2)}{n}. \end{align*} $$
$$ \begin{align*} J_{3,n}\le \frac{2}{n} \int_0^{\pi/4}\cos^s\psi\,d\psi <\frac{B(s/2,1/2)}{n}. \end{align*} $$
Summing up the above estimates above, the assertion of the lemma follows.
The following corollary showing sharpness of the
![]() $\mathcal D$
-calculus is immediate.
$\mathcal D$
-calculus is immediate.
Corollary 12.2. For any
![]() $s>0$
,
$s>0$
,
 $$ \begin{align*} \frac{\|f_n\|_{\mathcal{B}}}{\|f_n\|_{\mathcal{D}_s}} \asymp \log n, \qquad \frac{\|f_n\|_{\rm HP}}{\|f_n\|_{\mathcal{D}_s}} \asymp n^{1/2}, \quad n\to\infty. \end{align*} $$
$$ \begin{align*} \frac{\|f_n\|_{\mathcal{B}}}{\|f_n\|_{\mathcal{D}_s}} \asymp \log n, \qquad \frac{\|f_n\|_{\rm HP}}{\|f_n\|_{\mathcal{D}_s}} \asymp n^{1/2}, \quad n\to\infty. \end{align*} $$
Remark 12.3. Curiously, for
![]() $s=0$
the asymptotics of
$s=0$
the asymptotics of
![]() $\|f_n\|_{\mathcal D_0}$
match those of
$\|f_n\|_{\mathcal D_0}$
match those of
![]() $\|f_n\|_{\mathcal B}$
, and one does not get any advantage using the
$\|f_n\|_{\mathcal B}$
, and one does not get any advantage using the
![]() $\mathcal D$
-calculus in this case. Specifically, one can show that, for
$\mathcal D$
-calculus in this case. Specifically, one can show that, for
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
Acknowledgements
This work was partially supported financially by a Leverhulme Trust Visiting Research Professorship and an NCN grant UMO-2017/27/B/ST1/00078 and inspirationally by the ambience of the Lamb & Flag, Oxford.