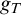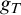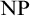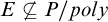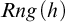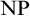1 Introduction
We investigate the old conjecture from the theory of proof complexity generatorsFootnote 1 that says that there exists a generator hard for all proof systems. Its rudimentary version can be stated without a reference to notions of the theory as follows:
-
• There exists a p-time function
 $g : {\{0,1\}^*} \rightarrow {\{0,1\}^*}$
stretching each input by one bit,
$g : {\{0,1\}^*} \rightarrow {\{0,1\}^*}$
stretching each input by one bit,
 $|g(u)| = |u| +1$
, such that the range
$|g(u)| = |u| +1$
, such that the range
 $Rng(g)$
of g intersects all infinite
$Rng(g)$
of g intersects all infinite
 ${\mbox {NP}}$
-sets.
${\mbox {NP}}$
-sets.
We present a construction of a function
![]() $g_T$
(p-time and stretching) based on provability in a first-order theory T that is able to formalize syntax of first-order logic. Function
$g_T$
(p-time and stretching) based on provability in a first-order theory T that is able to formalize syntax of first-order logic. Function
![]() $g_T$
has the property, assuming that T is sound and complete, that it intersects all infinite definable subsets of
$g_T$
has the property, assuming that T is sound and complete, that it intersects all infinite definable subsets of
![]() ${\{0,1\}^*}$
. As that is clearly absurd (since
${\{0,1\}^*}$
. As that is clearly absurd (since
![]() ${\{0,1\}^*} \setminus Rng(g_T)$
is infinite and definable) this offers a proof of Gödel’s First Incompleteness theorem. We leave it as an open problem (Problem 2.4) whether
${\{0,1\}^*} \setminus Rng(g_T)$
is infinite and definable) this offers a proof of Gödel’s First Incompleteness theorem. We leave it as an open problem (Problem 2.4) whether
![]() $g_T$
for some T satisfies the conjecture above.
$g_T$
for some T satisfies the conjecture above.
We then give a propositional version of the construction and use it to show that at least one of the following three statements has to be true:
-
1. There is no p-optimal propositional proof system.
-
2.
 $E \not \subseteq P/poly$
.
$E \not \subseteq P/poly$
. -
3. There exists function h that stretches all inputs by one bit, is computable in sub-exponential time
 $2^{O((\log n)^{\log \log n})}$
, and its range
$2^{O((\log n)^{\log \log n})}$
, and its range
 $Rng(h)$
intersects all infinite
$Rng(h)$
intersects all infinite
 ${\mbox {NP}}$
sets.
${\mbox {NP}}$
sets.
We assume that the reader is familiar with basic notions of logic and of computational and proof complexity (all can be found in [Reference Krajíček5]).
2 The construction
We take as our basic theory
![]() $S^1_2$
of Buss [Reference Buss1] (cf. [Reference Krajíček5, Section 9.3]), denoting its language simply L. The language has a canonical interpretation in the standard model
$S^1_2$
of Buss [Reference Buss1] (cf. [Reference Krajíček5, Section 9.3]), denoting its language simply L. The language has a canonical interpretation in the standard model
![]() $\mathbf{N}$
. The theory is finitely axiomatizable and formalizes smoothly syntax of first-order logic. Language L allows to define a natural syntactic hierarchy
$\mathbf{N}$
. The theory is finitely axiomatizable and formalizes smoothly syntax of first-order logic. Language L allows to define a natural syntactic hierarchy
![]() $\Sigma ^b_i$
of bounded formulas that define in
$\Sigma ^b_i$
of bounded formulas that define in
![]() $\mathbf{N}$
exactly corresponding levels
$\mathbf{N}$
exactly corresponding levels
![]() $\Sigma ^p_i$
, for
$\Sigma ^p_i$
, for
![]() $i \geq 1$
, of the polynomial time hierarchy.
$i \geq 1$
, of the polynomial time hierarchy.
An L-formula
![]() $\Psi $
will be identified with the binary string naturally encoding it and
$\Psi $
will be identified with the binary string naturally encoding it and
![]() $|\Psi |$
is the length of such a string. An L-theory T is thus a subset of
$|\Psi |$
is the length of such a string. An L-theory T is thus a subset of
![]() ${\{0,1\}^*}$
, a set of L-sentences, and it makes sense to say that it is p-time. It is well-known (and easy) that each r.e. theory has a p-time axiomatization (a simple variant of Craig’s trick; cf. [Reference Craig3]).
${\{0,1\}^*}$
, a set of L-sentences, and it makes sense to say that it is p-time. It is well-known (and easy) that each r.e. theory has a p-time axiomatization (a simple variant of Craig’s trick; cf. [Reference Craig3]).
If
![]() $u,v$
are two binary strings we denote by
$u,v$
are two binary strings we denote by
![]() $u \subseteq _e v$
the fact that u is an initial subword of v. The concatenation of u and v will be denoted simply by
$u \subseteq _e v$
the fact that u is an initial subword of v. The concatenation of u and v will be denoted simply by
![]() $uv$
. Both these relation and function are definable in
$uv$
. Both these relation and function are definable in
![]() $S^1_2$
by both
$S^1_2$
by both
![]() $\Sigma ^b_1$
and
$\Sigma ^b_1$
and
![]() $\Pi ^b_1$
formulas that are (provably in
$\Pi ^b_1$
formulas that are (provably in
![]() $S^1_2$
) equivalent. We shall assume that no formula is a proper prefix of another formula.
$S^1_2$
) equivalent. We shall assume that no formula is a proper prefix of another formula.
Let
![]() $T \supseteq S^1_2$
be a first-order theory in language L that is sound (i.e., true in
$T \supseteq S^1_2$
be a first-order theory in language L that is sound (i.e., true in
![]() $\mathbf{N}$
) and p-time. Define function
$\mathbf{N}$
) and p-time. Define function
![]() $g_T$
as follows:
$g_T$
as follows:
-
1. Given input u,
 $|u| = n$
, find an L-formula
$|u| = n$
, find an L-formula
 $\Phi \subseteq _e u$
with one free variable x such that
$\Phi \subseteq _e u$
with one free variable x such that
 $|\Phi | \le \log n$
. (It is unique if it exists.)
$|\Phi | \le \log n$
. (It is unique if it exists.)-
• If no such
 $\Phi $
exists, output
$\Phi $
exists, output
 $g_T(u) := \overline 0 \in {\{0,1\}^{n+1}}$
.
$g_T(u) := \overline 0 \in {\{0,1\}^{n+1}}$
. -
• Otherwise go to 2.
-
-
2. Put
 $c: = |\Phi |+1$
. Going through all
$c: = |\Phi |+1$
. Going through all
 $w \in {\{0,1\}^{c+1}}$
in lexicographic order, search for a T-proof of size
$w \in {\{0,1\}^{c+1}}$
in lexicographic order, search for a T-proof of size
 $\le \log n$
of the following sentence
$\le \log n$
of the following sentence
 ${\Phi ^w}$
: (1)
${\Phi ^w}$
: (1) $$ \begin{align} \exists y \forall x> y\ \Phi(x) \rightarrow \neg (w \subseteq_e x). \end{align} $$
$$ \begin{align} \exists y \forall x> y\ \Phi(x) \rightarrow \neg (w \subseteq_e x). \end{align} $$
-
• If a proof is found for all w output
 $g_T(u) := \overline 0 \in {\{0,1\}^{n+1}}$
.
$g_T(u) := \overline 0 \in {\{0,1\}^{n+1}}$
. -
• Otherwise let
 $w_0 \in {\{0,1\}^{c+1}}$
be the first such w such that no proof is found. Go to 3.
$w_0 \in {\{0,1\}^{c+1}}$
be the first such w such that no proof is found. Go to 3.
-
-
3. Output
 $g_T(u) := w_0 u_0 \in {\{0,1\}^{n+1}}$
, where
$g_T(u) := w_0 u_0 \in {\{0,1\}^{n+1}}$
, where
 $u = \Phi u_0$
.
$u = \Phi u_0$
.
Lemma 2.1. Function
![]() $g_T$
is p-time, stretches each input by one bit, and the complement of its range is infinite.
$g_T$
is p-time, stretches each input by one bit, and the complement of its range is infinite.
The infinitude of the complement of the range follows as at most half of strings in
![]() ${\{0,1\}^{n+1}}$
are in the range.
${\{0,1\}^{n+1}}$
are in the range.
Theorem 2.2. Let
![]() $A \subseteq {\{0,1\}^*}$
be an infinite L-definable set and assume that for some definition
$A \subseteq {\{0,1\}^*}$
be an infinite L-definable set and assume that for some definition
![]() $\Phi $
of A theory T proves all true sentences
$\Phi $
of A theory T proves all true sentences
![]() ${\Phi ^w}$
as in (1), for
${\Phi ^w}$
as in (1), for
![]() $w \in {\{0,1\}^{c+1}}$
where
$w \in {\{0,1\}^{c+1}}$
where
![]() $c = |\Phi |$
. Then the range of function
$c = |\Phi |$
. Then the range of function
![]() $g_T$
intersects A.
$g_T$
intersects A.
Proof Assume A and
![]() $\Phi $
satisfy the hypothesis of the theorem. As A is infinite some prefix w has to appear infinitely many times as a prefix of words in A and hence some sentence
$\Phi $
satisfy the hypothesis of the theorem. As A is infinite some prefix w has to appear infinitely many times as a prefix of words in A and hence some sentence
![]() $\Phi ^w$
is false. By the soundness of T it cannot be provable in the theory.
$\Phi ^w$
is false. By the soundness of T it cannot be provable in the theory.
Assuming that T proves all true sentences
![]() ${\Phi ^w}$
let
${\Phi ^w}$
let
![]() $\ell $
be a common upper bound to the size of some T-proofs of these true sentences. Then the algorithm computing
$\ell $
be a common upper bound to the size of some T-proofs of these true sentences. Then the algorithm computing
![]() $g_T(u)$
finds all of them if
$g_T(u)$
finds all of them if
![]() $n \geq 2^\ell $
.
$n \geq 2^\ell $
.
Putting this together, for
![]() $n \geq 2^\ell $
the algorithm finds always the same
$n \geq 2^\ell $
the algorithm finds always the same
![]() $w_0$
and this
$w_0$
and this
![]() $w_0$
does indeed show up infinitely many times in A. In particular, if
$w_0$
does indeed show up infinitely many times in A. In particular, if
![]() $v \in {\{0,1\}^{n+1}} \cap A$
is of the form
$v \in {\{0,1\}^{n+1}} \cap A$
is of the form
![]() $v = w_0 u_0$
and
$v = w_0 u_0$
and
![]() $n \geq 2^\ell $
, then
$n \geq 2^\ell $
, then
![]() $v = g_T(\Phi u_0)$
.
$v = g_T(\Phi u_0)$
.
Applying the theorem to
![]() $A := {\{0,1\}^*} \setminus Rng(g)$
(and using Lemma 2.1) yields the following version of Gödel’s First Incompleteness theorem.
$A := {\{0,1\}^*} \setminus Rng(g)$
(and using Lemma 2.1) yields the following version of Gödel’s First Incompleteness theorem.
Corollary 2.3. No sound, p-time
![]() $T \supseteq S^1_2$
is complete.
$T \supseteq S^1_2$
is complete.
Note that the argument shows that for each formula
![]() $\Phi $
defining the complement, some true sentence
$\Phi $
defining the complement, some true sentence
![]() ${\Phi ^w}$
as in (1) is unprovable in T. The complement of
${\Phi ^w}$
as in (1) is unprovable in T. The complement of
![]() $Rng(g_T)$
is in
$Rng(g_T)$
is in
![]() $\mbox {coNP}$
and that leaves room for the following problem.
$\mbox {coNP}$
and that leaves room for the following problem.
Problem 2.4. For some T as above, can each infinite
![]() ${\mbox {NP}}$
set be defined by some L-formula
${\mbox {NP}}$
set be defined by some L-formula
![]() $\Phi $
such that all true sentences
$\Phi $
such that all true sentences
![]() ${\Phi ^w}$
as in (1) are provable in T?
${\Phi ^w}$
as in (1) are provable in T?
The affirmative answer would imply by Theorem 2.2 that
![]() $Rng(g_T)$
intersects all infinite
$Rng(g_T)$
intersects all infinite
![]() ${\mbox {NP}}$
sets and hence
${\mbox {NP}}$
sets and hence
![]() $g_T$
solves the proof complexity conjecture mentioned at the beginning of the paper, and thus
$g_T$
solves the proof complexity conjecture mentioned at the beginning of the paper, and thus
![]() ${\mbox {NP}} \neq \mbox {coNP}$
. Note that, for each T, it is easy to define even as simple set as
${\mbox {NP}} \neq \mbox {coNP}$
. Note that, for each T, it is easy to define even as simple set as
by a formula
![]() $\Phi $
such that T does not prove that no string in it starts with
$\Phi $
such that T does not prove that no string in it starts with
![]() $0$
. But in the problem we do not ask if there is one definition leading to unprovability but whether all definitions of the set lead to it.
$0$
. But in the problem we do not ask if there is one definition leading to unprovability but whether all definitions of the set lead to it.
3 Down to propositional logic
The reason why the algorithm computing
![]() $g_T$
searches for T-proofs of formulas
$g_T$
searches for T-proofs of formulas
![]() ${\Phi ^w}$
rather than of
${\Phi ^w}$
rather than of
![]() $\neg {\Phi ^w}$
which may seem more natural is that
$\neg {\Phi ^w}$
which may seem more natural is that
![]() ${\mbox {NP}}$
sets can be defined by
${\mbox {NP}}$
sets can be defined by
![]() $\Sigma ^b_1$
-formulas
$\Sigma ^b_1$
-formulas
![]() $\Phi $
and for those, after substituting a witness for y,
$\Phi $
and for those, after substituting a witness for y,
![]() ${\Phi ^w}$
becomes a
${\Phi ^w}$
becomes a
![]() $\Pi ^b_1$
-formula. Hence one can apply propositional translation (cf. [Reference Cook2] or [Reference Krajíček5, Section 12.3]) and hope to take the whole argument down to propositional logic, replacing the incompleteness by lengths-of-proofs lower bounds. There are technical complications along this ideal route, but we are at least able to combine the general idea with a construction akin to that underlying [Reference Krajíček4, Th eorem 2.1]Footnote
2
and to prove the following statement.
$\Pi ^b_1$
-formula. Hence one can apply propositional translation (cf. [Reference Cook2] or [Reference Krajíček5, Section 12.3]) and hope to take the whole argument down to propositional logic, replacing the incompleteness by lengths-of-proofs lower bounds. There are technical complications along this ideal route, but we are at least able to combine the general idea with a construction akin to that underlying [Reference Krajíček4, Th eorem 2.1]Footnote
2
and to prove the following statement.
Theorem 3.1. At least one of the following three statements is true
![]() $:$
$:$
-
1. There is no p-optimal propositional proof system.
-
2.
 $E \not \subseteq P/poly$
.
$E \not \subseteq P/poly$
. -
3. There exists function h that stretches all inputs by one bit, is computable in sub-exponential time
 $2^{O((\log n)^{\log \log n})}$
, and its range
$2^{O((\log n)^{\log \log n})}$
, and its range
 $Rng(h)$
intersects all infinite
$Rng(h)$
intersects all infinite
 ${\mbox {NP}}$
sets.
${\mbox {NP}}$
sets.
Note the first statement is by [Reference Krajíček6, Th eorem 2.4] equivalent to the non-existence of a time-optimal propositional proof search algorithm.
Before starting the proof we need to recall a fact about propositional translations of
![]() $\Pi ^b_1$
-formulas. For
$\Pi ^b_1$
-formulas. For
![]() $\Phi (x) \in \Sigma ^b_1$
,
$\Phi (x) \in \Sigma ^b_1$
,
![]() $c :=|\Phi |$
and
$c :=|\Phi |$
and
![]() $w \in {\{0,1\}^{c+1}}$
, and
$w \in {\{0,1\}^{c+1}}$
, and
![]() $n \geq 1$
let
$n \geq 1$
let
![]() ${\varphi _{n,w}}$
be the canonical propositional formula expressing that
${\varphi _{n,w}}$
be the canonical propositional formula expressing that
We use the qualification canonical because the formula can be defined using the canonical propositional translation
![]() $||\dots ||^{n+1}$
(cf. [Reference Krajíček5, Section 12.3] or [Reference Cook2]) applied to
$||\dots ||^{n+1}$
(cf. [Reference Krajíček5, Section 12.3] or [Reference Cook2]) applied to
![]() ${\Phi ^w}$
after instantiating first y by
${\Phi ^w}$
after instantiating first y by
![]() $1^{(n)}$
. Formula
$1^{(n)}$
. Formula
![]() ${\varphi _{n,w}}$
has
${\varphi _{n,w}}$
has
![]() $n+1$
atoms for bits of x and
$n+1$
atoms for bits of x and
![]() $n^{O(1)}$
atoms encoding a potential witness to
$n^{O(1)}$
atoms encoding a potential witness to
![]() $\Phi (x)$
together with the p-time computation that it is correct. For any fixed
$\Phi (x)$
together with the p-time computation that it is correct. For any fixed
![]() $\Phi $
the size of
$\Phi $
the size of
![]() ${\varphi _{n,w}}$
(with
${\varphi _{n,w}}$
(with
![]() $w \in {\{0,1\}^{c+1}}$
) is polynomial in n and, in fact, the formulas are very uniform (cf. [Reference Krajíček5, Section 19.1]). We shall need only the following fact.
$w \in {\{0,1\}^{c+1}}$
) is polynomial in n and, in fact, the formulas are very uniform (cf. [Reference Krajíček5, Section 19.1]). We shall need only the following fact.
Lemma 3.2. There is an algorithm
![]() ${{\mathbf{transl}}}$
that upon receiving as inputs a
${{\mathbf{transl}}}$
that upon receiving as inputs a
![]() $\Sigma ^b_1$
-formula
$\Sigma ^b_1$
-formula
![]() $\Phi $
,
$\Phi $
,
![]() $w \in {\{0,1\}^{c+1}} $
where
$w \in {\{0,1\}^{c+1}} $
where
![]() $c := |\Phi |$
and
$c := |\Phi |$
and
![]() $1^{(n)}$
,
$1^{(n)}$
,
![]() $n \geq 1$
, outputs
$n \geq 1$
, outputs
![]() ${\varphi _{n,w}}$
such that
${\varphi _{n,w}}$
such that
is universally valid iff
![]() ${\varphi _{n,w}}$
is a tautology. In addition, for any fixed
${\varphi _{n,w}}$
is a tautology. In addition, for any fixed
![]() $\Phi $
the algorithm runs in time polynomial in n, for
$\Phi $
the algorithm runs in time polynomial in n, for
![]() $n> |\Phi |$
.
$n> |\Phi |$
.
Proof of Theorem 3.1
To prove the theorem we shall assume that statements 1) and 2) fail and (using that assumption) we construct function h satisfying statement 3). Our strategy is akin in part to that of the proof of [Reference Krajíček4, Th eorem 2.1].
For a fixed
![]() $\Phi $
assume that formulas
$\Phi $
assume that formulas
![]() ${\varphi _{n,w}}$
are valid for
${\varphi _{n,w}}$
are valid for
![]() $n \geq n_0$
. By Lemma 3.2 they are computed by
$n \geq n_0$
. By Lemma 3.2 they are computed by
![]() ${{\mathbf{transl}}}(\Phi , w, 1^{(n)})$
in p-time. Hence we can consider the pair
${{\mathbf{transl}}}(\Phi , w, 1^{(n)})$
in p-time. Hence we can consider the pair
![]() $1^{(n)}, w$
to be a proof (in an ad hoc defined proof system) of
$1^{(n)}, w$
to be a proof (in an ad hoc defined proof system) of
![]() ${\varphi _{n,w}}$
for
${\varphi _{n,w}}$
for
![]() $n \geq n_0$
$n \geq n_0$
Assuming that statement 1) fails and P is a p-optimal proof system we get a p-time function f that from
![]() $1^{(n)}, w$
,
$1^{(n)}, w$
,
![]() $n \geq n_0$
, computes a P-proof
$n \geq n_0$
, computes a P-proof
![]() $f(1^{(n)}, w)$
of
$f(1^{(n)}, w)$
of
![]() ${\varphi _{n,w}}$
. Let
${\varphi _{n,w}}$
. Let
![]() $|f(1^{(n)}, w)| \le n^\ell $
where
$|f(1^{(n)}, w)| \le n^\ell $
where
![]() $\ell $
is a constant (depending on
$\ell $
is a constant (depending on
![]() $\Phi $
). The function that from
$\Phi $
). The function that from
![]() $n,w,i$
, with
$n,w,i$
, with
![]() $i \le n^\ell $
, computes the i-th bit of
$i \le n^\ell $
, computes the i-th bit of
![]() $f(1^{(n)}, w)$
is in the computational class
$f(1^{(n)}, w)$
is in the computational class
![]() $\mbox {E}$
.
$\mbox {E}$
.
We would like to check the validity of
![]() ${\varphi _{n,w}}$
by checking the P-proof
${\varphi _{n,w}}$
by checking the P-proof
![]() $f(1^{(n)}, w)$
, but we (i.e., the algorithm that will compute h) cannot construct f from
$f(1^{(n)}, w)$
, but we (i.e., the algorithm that will compute h) cannot construct f from
![]() $\Phi $
. Here the assumption that statement 2) fails too, i.e., that
$\Phi $
. Here the assumption that statement 2) fails too, i.e., that
![]() $E \subseteq {\mbox {P}}/poly$
, will help us. By this assumption
$E \subseteq {\mbox {P}}/poly$
, will help us. By this assumption
![]() $f(1^{(n)}, w)$
is the truth-table
$f(1^{(n)}, w)$
is the truth-table
![]() ${{\mathbf{tt}}}(D)$
(i.e., the lexico-graphically ordered list of values of circuit D on all inputs) of some circuit with
${{\mathbf{tt}}}(D)$
(i.e., the lexico-graphically ordered list of values of circuit D on all inputs) of some circuit with
![]() $\log n + c + \ell \log n \le (2+\ell )\log n$
inputs and of size
$\log n + c + \ell \log n \le (2+\ell )\log n$
inputs and of size
![]() $|D| \le (\log n)^{O(\ell )}$
. In particular, for all
$|D| \le (\log n)^{O(\ell )}$
. In particular, for all
![]() $\ell $
(i.e., for all
$\ell $
(i.e., for all
![]() $\Phi \in \Sigma ^b_1$
) we haveFootnote
3
$\Phi \in \Sigma ^b_1$
) we haveFootnote
3
![]() $|D| \le (\log n)^{\log \log n}$
for
$|D| \le (\log n)^{\log \log n}$
for
![]() $n>> 1$
. Hence it is enough to look for P-proofs among
$n>> 1$
. Hence it is enough to look for P-proofs among
![]() ${{\mathbf{tt}}}(D)$
for circuits of at most this size.
${{\mathbf{tt}}}(D)$
for circuits of at most this size.
We can now define function
![]() $h_P$
in a way analogous to the definition of function
$h_P$
in a way analogous to the definition of function
![]() $g_T$
. Namely:
$g_T$
. Namely:
-
1. Given input u,
 $|u| = n$
, find a
$|u| = n$
, find a
 $\Sigma ^b_1$
-formula
$\Sigma ^b_1$
-formula
 $\Phi \subseteq _e u$
with one free variable x such that
$\Phi \subseteq _e u$
with one free variable x such that
 $|\Phi | \le \log n$
. (It is unique if it exists.)
$|\Phi | \le \log n$
. (It is unique if it exists.)-
• If no such
 $\Phi $
exists, output
$\Phi $
exists, output
 $h_P(u) := \overline 0 \in {\{0,1\}^{n+1}}$
.
$h_P(u) := \overline 0 \in {\{0,1\}^{n+1}}$
. -
• Otherwise go to 2.
-
-
2. Put
 $c: = |\Phi |+1$
. Going through all
$c: = |\Phi |+1$
. Going through all
 $w \in {\{0,1\}^{c+1}}$
in lexicographic order, do the following.Using
$w \in {\{0,1\}^{c+1}}$
in lexicographic order, do the following.Using
 ${{\mathbf{transl}}}$
compute formula
${{\mathbf{transl}}}$
compute formula
 ${\varphi _{n,w}}$
. If the computation does not halt in time
${\varphi _{n,w}}$
. If the computation does not halt in time
 $\le n^{\log n}$
stop and output
$\le n^{\log n}$
stop and output
 $h_P(u) = \overline 0 \in {\{0,1\}^{n+1}}$
. Otherwise search for a P-proof of formula
$h_P(u) = \overline 0 \in {\{0,1\}^{n+1}}$
. Otherwise search for a P-proof of formula
 ${\varphi _{n,w}}$
by going systematically through all circuits D with
${\varphi _{n,w}}$
by going systematically through all circuits D with
 $\le \log n \cdot \log \log n$
inputs and of size
$\le \log n \cdot \log \log n$
inputs and of size
 $\le (\log n)^{\log \log n}$
until some
$\le (\log n)^{\log \log n}$
until some
 ${{\mathbf{tt}}}(D)$
is a P-proof of
${{\mathbf{tt}}}(D)$
is a P-proof of
 ${\varphi _{n,w}}$
.
${\varphi _{n,w}}$
.-
• If a proof is found for all
 $w \in {\{0,1\}^{c+1}}$
output
$w \in {\{0,1\}^{c+1}}$
output
 $h_P(u) := \overline 0 \in {\{0,1\}^{n+1}}$
.
$h_P(u) := \overline 0 \in {\{0,1\}^{n+1}}$
. -
• Otherwise let
 $w_0 \in {\{0,1\}^{c+1}}$
be the first such w such that no P-proof is found. Go to 3.
$w_0 \in {\{0,1\}^{c+1}}$
be the first such w such that no P-proof is found. Go to 3.
-
-
3. Output
 $h_P(u) := w_0 u_0 \in {\{0,1\}^{n+1}}$
, where
$h_P(u) := w_0 u_0 \in {\{0,1\}^{n+1}}$
, where
 $u = \Phi u_0$
.
$u = \Phi u_0$
.
It is clear from the construction that function
![]() $h_P$
stretches each input by one bit (and hence the complement of its range is infinite) and that
$h_P$
stretches each input by one bit (and hence the complement of its range is infinite) and that
for any
![]() $\Phi (x) \in \Sigma ^b_1$
and
$\Phi (x) \in \Sigma ^b_1$
and
![]() $n>> 1$
.
$n>> 1$
.
The time needed for the computation of
![]() $h_P(u)$
is
$h_P(u)$
is
![]() $O(n)$
for step 1 and for step 2 it is bounded above by
$O(n)$
for step 1 and for step 2 it is bounded above by
The first factor bounds the number of w, the second bounds the time needed to compute
![]() ${\varphi _{n,w}}$
, the third bounds the number of circuits D, and the fourth one bounds the time needed to compute
${\varphi _{n,w}}$
, the third bounds the number of circuits D, and the fourth one bounds the time needed to compute
![]() ${{\mathbf{tt}}}(D)$
and to check whether it is a P-proof of
${{\mathbf{tt}}}(D)$
and to check whether it is a P-proof of
![]() ${\varphi _{n,w}}$
(this is p-time in
${\varphi _{n,w}}$
(this is p-time in
![]() $|{{\mathbf{tt}}}(D)|$
).
$|{{\mathbf{tt}}}(D)|$
).
Acknowledgments
Section 3 owes its existence to J. Pich (Oxford) who suggested I include some propositional version of the construction.