Remarks on labelling and determinacy

Abstract

Work by Chomsky et al. (2019) and Epstein et al. (2018) develops a third-factor principle of computational efficiency called “Determinacy”, which rules out “ambiguous” syntactic rule-applications by requiring one-to-one correspondences between the input or output of a rule and a single term in the domain of that rule. This article first adopts the concept of “Input Determinacy” articulated by Goto and Ishii (2019, 2020), who apply Determinacy specifically to the input of operations like Merge, and then proposes to extend Determinacy to the labeling procedure developed by Chomsky (2013, 2015). In particular, Input Determinacy can explain restrictions on labeling in contexts where multiple potential labels are available (labeling ambiguity), and it can also provide an explanation for Chomsky's (2013, 2015) proposal that syntactic movement of an item (“Internal Merge”) renders that item invisible to the labeling procedure.

Résumé

Les travaux de Chomsky et al. (2019) et de Epstein et al. (2018) développent un principe d'efficacité computationnelle à trois facteurs appelé « détermination », qui exclut les applications de règles syntaxiques « ambiguës » en exigeant des correspondances biunivoques entre l'entrée (‘input’) ou la sortie (‘output’) d'une règle et un terme unique dans le domaine de cette règle. Le présent article adopte d'abord le concept de détermination de l'entrée (‘Input Determinacy’) articulé par Goto et Ishii (2019, 2020), qui appliquent la détermination spécifiquement à l'entrée d'opérations comme la Fusion (‘Merge’), puis propose d'étendre la détermination à la procédure d'étiquetage développée par Chomsky (2013, 2015). En particulier, la détermination de l'entrée peut expliquer les restrictions sur l'étiquetage dans des contextes où plusieurs étiquettes potentielles sont disponibles (ambiguïté de l'étiquetage), et elle peut également fournir une explication à la proposition de Chomsky (2013, 2015) selon laquelle le mouvement syntaxique d'un élément (“Fusion interne”) rend cet élément invisible à la procédure d'étiquetage.

1. Introduction

An important goal of theoretical work from a Minimalist perspective is to identify “third-factor” constraints on syntactic rules and operations stemming from general principles of computational optimization and efficiency (Chomsky, 2001, 2005, 2008). Recent work by Chomsky et al. (2019) and Epstein et al. (2018) develops a principle of “Determinacy” whereby the input or output of a rule is required to correspond one-to-one with a single term in the domain of that rule, thereby ruling out “ambiguous” or “indeterminate” rule-applications.

The goals of this short article are threefold. The first goal is to explain the potential for a principle of Determinacy to motivate certain restrictions on syntactic rules (e.g., Merge) by reviewing proposals by Goto and Ishii (2019, 2020). The second is to apply Determinacy to the labelling procedure developed by Chomsky (2013, 2015) in order to account for restrictions on labelling in contexts where multiple potential labels are available. The third goal is to deploy Determinacy to provide an explanation for Chomsky's (2013, 2015) proposal that syntactic movement of an item renders it invisible to the labelling procedure.

In section 2, I define Determinacy and adopt a particular conception of the constraint (“input-Determinacy”) along the lines of proposals by Goto and Ishii (2019, 2020). In section 3, I extend Determinacy to the input of the labelling procedure, demonstrating how structural configurations that yield multiple potential labels can be ruled out as indeterminate. In section 4, I expand on the proposals in section 3 by applying Determinacy principles to the search procedure that precedes labelling, deploying the account of Determinacy for moved items (“copies”) in order to explain why moved items cannot enter into the labelling procedure. Section 5 concludes the paper and outlines some directions for future work.

2. Determinacy as a constraint on rules

Recent work by Epstein et al. (2018), Chomsky et al. (2019), Goto and Ishii (2019, 2020), and others develops a principle of Determinacy as a third-factor constraint on syntactic operations. Determinacy may be defined as an avoidance of “ambiguous” (Goto and Ishii 2020: 5) or “indeterminate” (Chomsky et al. 2019: 20) rule-application. Put simply, if the input or output of a particular rule does not show a one-to-one correspondence between that input/output and a term of the domain of that rule, then a “Determinacy violation” is the result.¹

To illustrate: Goto and Ishii (2019: 93) approach Determinacy as a constraint on the input of the combinatory operation Merge, which takes two objects and combines them into a single set (1a). Merge may apply recursively to its whole output, building hierarchical embedded structures (1b), and it may also select a subpart of its output, yielding syntactic movement (Internal Merge), notated with bracketed “copies” (1c) (see definitions in Chomsky 2004, 2007, 2008).

1. (1)

   1. a. Merge(X, Y) = {X, Y}

   2. b. Merge(Z, {X, Y}) = {Z, {X, Y}}

   3. c. Merge(X, {Z, {X, Y}}) = {<X₁>, {Z, {<X₂>, Y}}}²

The above authors argue that the input to Merge must be unambiguous. In other words, there must be a one-to-one correspondence between a single member of the input and a single member of the domain of Merge. In most cases, determinate inputs to Merge are automatic, since lexical items are selected from the lexicon or the workspace (=the domain of Merge) and indexed uniquely from each other. A problem arises, however, when a situation like the output of (1c) is encountered. In this case, X in the domain of Merge is indeterminate because it exists as two “copies” in that domain, notated as <X₁> and <X₂>. If X is selected for input to Merge again (e.g., in a subsequent movement step), it will be unclear which copy of X actually functions as the input, leading to a Determinacy violation.

Before continuing, it should be noted that this application of Determinacy differs from that presented by Chomsky et al. (2019) and Epstein et al. (2018). In those works, Determinacy is characterized as a constraint on the output of Merge, preventing the emergence of indeterminate structures. Goto and Ishii (2019) argue against this conception, however, on the following grounds: If Determinacy applies to the output of Merge, this means that no Merge-output may contain an indeterminate item. As a result, Internal Merge is actually blocked by output-Determinacy, since it results in a structure containing multiple copies. Chomsky et al. (2019) also identify this problem and attempt to circumvent it by including a version of the “shortest move corollary”, which states that only the structurally “highest” copy in a structure is available for further applications of Internal Merge. This has the character of a stipulation, however, given that Goto and Ishii (2019) are able to develop an account that does not require this additional constraint in order to allow Determinacy and Internal Merge to coexist.

Goto and Ishii use this version of Determinacy to capture “freezing” phenomena in English and other languages. The sentences in (2) and (3) illustrate these effects for subject phrases. Under the assumption that the sentential subject generally moves to Spec-TP in English, any attempt to extract an item from the subject fails due to a Determinacy-violation (=the Subject Condition, Chomsky 1973, Huang 1982). If, however, the subject phrase does not undergo movement, as in expletive constructions with there (3), extraction from the subject is licit (Lasnik and Park 2003, Stepanov 2007).³

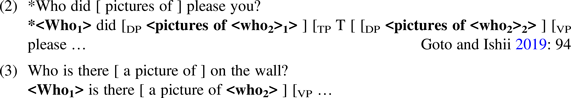
Another straightforward application of input-Determinacy is found in limits on embedded subject extraction in English with and without expletive there. In sentence (4) below, the embedded subject undergoes movement from its base position in VP to the embedded Spec-TP, but cannot move further to the matrix Spec-CP. If, however, as in sentence (5), an expletive is inserted in the embedded Spec-TP, extraction of the embedded subject to the matrix Spec-CP is much improved (examples are adapted from Moro 1997a: 126, see also Culicover 1993, Bayer and Salzmann 2013).

Goto and Ishii (2019) also successfully apply input-Determinacy to capture verb-particle constructions, constraints on vacuous topicalization, that-trace effects, and freezing effects with topics. Going forward, I adopt this conception of Determinacy as a constraint on the input of Merge, and in the next section I will extend it to another syntactic rule: the labelling procedure developed in work by Chomsky (2013, 2015).

3. Determinacy and labelling

Chomsky (2013, 2015) outlines a framework wherein the combinatory operation Merge is separated from the process of “projection” or labelling, by which the head of a syntactic object is determined. This is a break from prior conceptions of Merge, which typically incorporated projection/headedness into the combinatory operation itself (see (Chomsky, 1993, 1995), where label-projection functioned explicitly as a subpart of Merge). Instead, Chomsky (2013, 2015) describes a “labelling algorithm” which applies separately to each output of Merge, being triggered at the level of the syntactic phase.

This labelling procedure takes a single syntactic object – the output of Merge – as its input and identifies a unique label for that object according to Minimal Search (MS), another third-factor principle of minimal computation. MS requires that the least-embedded simplex item found inside a syntactic object be selected automatically as the label of that object.

Given the automatic nature of label-selection, Chomsky (2013) specifies structural configurations where labelling will be successful and configurations where labelling will fail. Example (6) shows a structure where a label cannot be found by MS, since both X and Y are equally accessible within the input set (see below for further discussion of why this would result in a labelling problem).⁴ Example (7), on the other hand, shows a structure where the input set contains X and another subset. In this case, X is found by MS and selected as label immediately, since the contents of the subset would require additional (i.e., non-minimal) search.

1. (6) Input: {X, Y}

   Label({X, Y}) = X?, Y?

2. (7) Input: {X, {…}}

   Label({X, {…}}) = X

Chomsky (2013: 43) does not go into great detail about the reason for the disallowance of labelling in (6) beyond stating that “[i]n the best case, the relevant information about [a syntactic object] will be provided by a single designated element within it […]” and that, in contexts like (6), “minimal search is ambiguous”. Importantly, it should be noted that this is by no means the first time that a property of ambiguity or symmetry has been identified as a significant factor in the evaluation of syntactic structures like (6). Chomsky (2013) in fact builds on a body of work going back to Moro's (1997a,b, 2000) Dynamic Antisymmetry, and Kayne's (1983, 1984) and Pesetsky's (1982) notions of “paths”, among other influences. The point to emphasize here is that, on further consideration, Minimal Search on its own is not necessarily the deciding factor for ruling out structures like (6) in the context of Chomsky's labelling system. In both (6) and (7), MS has, in fact, successfully identified the least embedded item(s) in the input set.

Instead, the implicit reason for failure-failure in (6) is that MS finds multiple options for labelling, and it is assumed that the ideal outcome of MS is to find a single discrete label. As a result, the labelling procedure can actually be defined by two requirements: (i) labelling must proceed according to MS, and (ii) there cannot be multiple options for labelling within a given syntactic object. The contribution of this paper to the discussion is to observe that the latter requirement has the distinct character of a Determinacy-based restriction, since it involves ambiguity: the labelling procedure is governed by a requirement that the item selected to label a syntactic object must be determinate or unambiguous in the domain of the labelling rule. The formalization of this requirement can be worked out as follows:

Application of MS to the structure in (6) finds two simplex terminals, which I have notated so far as the set {X, Y}. In order to draw out the similarity between Determinacy in the case of Goto and Ishii's proposal for copies, and Determinacy in the case of labels, however, I will now notate the output of MS as single unit α. If α is submitted as input to the labelling procedure, a Determinacy-violation will result, since α exists as two separate items (X and Y) in the domain of the labelling rule. This parallels Goto and Ishii's application of Determinacy to syntactic movement in the following way: In a context like (1c) above, if X is submitted as one of the inputs to an operation of Merge, a Determinacy-violation results since X actually exists as two separate but identical items (<X₁> and <X₂>) in the domain of Merge. Example (8) shows the relevant comparison between these two cases.

1. (8)

   1. a. X = {<X₁>, <X₂>}, X is indeterminate for Merge

   2. b. α = {X, Y}, α is indeterminate for Label

Crucially, this understanding of how Determinacy constrains the labelling procedure requires that we view the labelling procedure as “blind”: insensitive to the specific identities of the simplex items found by search, just as Merge is insensitive to the specific identities of the individual “copies” of X in (8a). The procedures of search and labelling are only concerned with finding/selecting simplex items that are determinate.

Having illustrated how a principle of Determinacy can be applied to the labelling procedure to explain why structures like {X, Y} are unlabelable, the next section addresses the question of why copies should be invisible to the labelling procedure and demonstrates that the principle of input-Determinacy can also provide an explanation in this area.

4. Explaining copy-invisibility through Determinacy

Aside from the labelling configurations in (6) and (7) above, Chomsky proposes that a non-labelable situation like (6) can also be rectified if one of the members of the input set undergoes syntactic movement, as in (1c). In this case, the remaining “copy” of the moved term is assumed to be invisible for labelling purposes due to the fact that it constitutes a “discontinuous” syntactic object (Chomsky 2013:44).

1. (9) Input: {<X>, Y}

   Label({<X>, Y}) = Y

This constitutes a third way that labelling can succeed, and Chomsky exploits the notion of movement-based labelling to elegantly unify a variety of syntactic effects, following ideas from Moro (2000), including movement of the v*P-internal subject into Spec-TP (10a), “raising-to-object” (=Spec-RP) in ECM constructions (10b), and successive-cyclic long-distance movement of phrases through Spec-CP (10c).

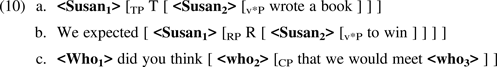
Ultimately, Chomsky's use of MS-based labelling as a motivation for certain instances of syntactic movement offers a less stipulative account of effects that were previously attributed to a purely formal EPP- or “edge-” feature. Even so, it remains unclear why precisely a “discontinuous” syntactic object should be inaccessible for label-determination. Given that a principle of Determinacy provides a means of formally distinguishing “discontinuous” (i.e., indeterminate) from “continuous” (i.e., determinate) syntactic objects, an approach that incorporates input-Determinacy is clearly desirable.

In order to build an account of how input-Determinacy explains the invisibility of copies for labelling purposes, it is necessary to consider in more detail the nature of the labelling procedure itself. Thus far, I have focused primarily on the end-result of the procedure where a label is selected, assigned, or determined for an object. It should be emphasized, however, that there is also a search procedure which precedes and directly feeds the application of labelling. This initial stage will be the focus here.

A first pass at formalizing the search procedure is to characterize it as an operation taking an object K as input and outputting the contents of K into the domain of the labelling procedure. However, the procedure employed by Chomsky (2013, 2015) requires some additional complexity. Rather than finding the immediate elements of K and terminating, Chomsky's MS also evaluates if further search is necessary. This requires not only finding the elements of K but also identifying them as simplex (i.e., a terminal element) or complex (i.e., a non-terminal element). Furthermore, search of an object K should properly be divided into two parts, given that outputs of Merge are invariably binary. In tree-theoretic terms, this means that searching K requires examination of both branches of K. With these factors in mind, I will characterize the search procedure as an operation “Search” taking two inputs,⁵ one for each branch of K (notated as K_α and K_β below), and outputting any terminal nodes found by MS on each branch. The different possible outcomes are laid out in (11) below:

1. (11)

   1. a. If K_α = X and K_β = {…}, then Search(K_α, K_β) = X

   2. b. If K_α = X and K_β = Y, then Search(K_α, K_β) = {X, Y}

In (11a), the object K is of the form {X, {…}}, as in (7) above. This means that the search procedure will only output X, ignoring the contents of K_β, since they require further search. In (11b), however, the object K is of the form {X, Y}, as in (6) above, meaning that search finds a terminal on each branch of K. The output of search in this case is the set of terminals {X, Y}. As discussed in section 2, only the output of (11a) can be successfully submitted to the labelling procedure. The output of (11b), on the other hand, is indeterminate, since it is an object that exists as multiple separate items within the domain of the labelling rule. Recall that this is what is represented by α in (8b) above.

At this point, we can consider why an item that has undergone movement in a syntactic structure would be unavailable for labelling purposes. Example (12) below shows a context where an object K contains a copy-item, K = {<X_n>, Y}, as in the VP of a sentence like What did Susan write?, where K = VP and VP consists of the set {<what>, write}. In this case, the terminal node on K_α exists as multiple copies in the derivation (i.e., <what₁>, <what₂>), making it indeterminate and prohibiting it from being submitted as input to Search. K_β, on the other hand, is fully determinate and able to serve as input, yielding Y as the output.

1. (12) If K_α = <X_n> and K_β = Y, then Search(K_β) = Y

The situation in (12) is substantively different from the situation in (11a) above. In the latter case, both inputs to Search are fully determinate, even though one of them (=K_β) does not yield a terminal element through search. In (12), K_α may not even function as an input to Search, because it is already indeterminate. The outcome in this case is the same as in (11a): the other input to Search successfully yields a terminal element that may be submitted as input to the labelling procedure.

5. Conclusion

To recap: Determinacy has potential as a third-factor principle to provide an explanation for various restrictions on syntactic rules. In particular, the notion of input-Determinacy—where each term of the input to a syntactic rule must have a one-to-one correspondence with a single term of the domain of that rule can be exploited to capture restrictions on (Internal) Merge (Goto and Ishii 2019, 2020). In this short article, I have extended input-Determinacy to explain two aspects of Chomsky's (2013, 2015) Minimal Search-based labelling system: (i) the rejection of {X, Y} structures where multiple labels are equally accessible by Minimal Search, and (ii) the invisibility of copies to the labelling procedure. In the former case, I postulate that Determinacy restricts the input to the labelling procedure itself, preventing an input that corresponds to multiple potential terminal nodes in a structure. In the latter case, Determinacy rules out the selection of a copy in the search-procedure that precedes labelling.

Further work in this area could explore the interactions between Determinacy, the search and labelling procedures, and the notion of phase-based syntax, which Goto and Ishii (2019, 2020) deploy to allow Determinacy to be circumvented in some cases. It remains to be worked out whether any aspects of labelling can be exploited in a similar fashion. An additional avenue for exploration would address the status of labelling via shared features (phi-features, Q-features, etc.), which is an important component of Chomsky's (2013, 2015) system not discussed here. In short: an alternative to moving X or Y in order to label the illicit structure {X, Y} is for X and Y to share a feature F that has been subjected to an operation AGREE that renders both features identical to each other. When MS searches into {X, Y}, it finds F on both heads, and selects F as label, circumventing the problem of ambiguous selection (Chomsky 2013: 25). Questions arise, however, in the context of a Determinacy-based system: What is the precise status of F both prior to and after AGREE? After the application of AGREE, F appears to be an item with a single identity that also exists in multiple structural positions, which is suspiciously similar to the status of items which have undergone Internal Merge.

An exploration of the precise character of AGREE would be necessary to reconcile this observation with the function of AGREE in the labelling system, and it is to be hoped that the principle of Determinacy can aid such an endeavour by providing an additional metric to evaluate different conceptions of AGREE and the status of shared features for labelling. Ultimately, appealing to a third-factor principle like Determinacy allows domain-specific stipulations (e.g., a single label is required, copies are ignored for labelling, etc.) to be reduced to one underlying constraint, in line with a Minimalist approach to understanding operations and their constraints in the language faculty.