1. INTRODUCTION
Glaciers and ice caps (hereafter referred to as glaciers) cover 132 900 km2 around the Antarctic ice sheet, representing 18% of the glacier area on Earth, excluding the ice sheets (Pfeffer and others, Reference Pfeffer2014). Despite the large extent of glaciers in the Antarctic and sub-Antarctic, very few glaciological data are available for this region. Only few estimates exist for regional extent of glacierized area in this region, which is also under-represented by long-term mass-balance data. Glaciers with continuous mass-balance measurements spanning more than 10 years include Bahía del Diablo Glacier on Vega Island, Hurd and Johnsons glaciers on Livingston Island and Bellingshausen Ice Dome on King George Island (South Shetland Islands, SSI). The mass-balance records of these small glaciers are used to represent mass changes of 2752 glaciers in the Antarctic and sub-Antarctic region, with individual areas up to 6000 km2 large (RGI Consortium, 2017). Moreover, the glaciers in this region experience distinctly different climate conditions (Cogley and others, Reference Cogley, Berthier, Donoghue and Kargel2014) and the sample of glaciers with mass balance is not representative for all subregions. The lack of data increases uncertainties in regional estimates of glacier mass changes and their projections, which are crucial for determining the impacts of melting glaciers on sea level rise and terrestrial water resources.
Surface mass-balance measurements by the glaciological method were initiated in 2009 on two small glaciers on James Ross Island (JRI) to increase the sample of glaciers with mass-balance data in the Antarctic and sub-Antarctic regions (Fig. 1). The investigated glaciers are located in the north-eastern part of the Antarctic Peninsula (AP), which experienced the second largest atmospheric warming trend across the Antarctic since the 1950s (Turner and others, Reference Turner2005). The strong warming had a remarkable impact on the regional environment including all types of ice masses. Ice shelves along the eastern coast of the AP disintegrated (e.g. Cook and Vaughan, Reference Cook and Vaughan2010 and references therein), the inland glaciers that feed the ice shelves accelerated (e.g. Fürst and others, Reference Fürst2016) and marine- and land-terminating glaciers experienced enhanced thinning and retreat (e.g. Davies and others, Reference Davies, Carrivick, Glasser, Hambrey and Smellie2012).

Fig. 1. Location of Davies Dome and Whisky Glacier on the Ulu Peninsula, north-western James Ross Island. Other ice bodies are shown in medium grey. Position of Hurd and Johnsons glaciers (H–J) and Bahía del Diablo Glacier (BD) in the inset.
The rapid atmospheric warming observed over the second half of the 20th century decelerated at the beginning of the millennium as indicated by a significant decrease in the warming trends reported from the AP region (e.g. Turner and others, Reference Turner2016). Over the 2006–15 period, the mean air temperature at the Marambio station increased at the rate of 0.017°C a−1, which has been the lowest regional warming rate since 1971 (Oliva and others, Reference Oliva2017). Ambrožová and Láska (Reference Ambrožová, Láska and Nováček2016) reported a significant decrease (0.03–0.15°C a−1) in the temperature along the AP over the 2005–15 period with the most prominent cooling at the Bibby Hill station on JRI (Fig. 2). The response of glaciers to the change in temperature trend has been reported from the northern part of the AP in a few recent studies (Oliva and others, Reference Oliva2017 and references therein), but mass-balance changes after 2011 have been analysed only for two glaciers on King George Island (Mavlyudov, Reference Mavlyudov and Kotlyakov2016; Pętlicki and others, Reference Pętlicki, Sziło, MacDonell, Vivero and Bialik2017) and one on Livingston Island (Sancho and others, Reference Sancho2017). In order to extend the regional knowledge and increase available glaciological data, we analyse surface mass-balance records from two glaciers in the northern part of JRI. Annual mass-balance measurements started on these glaciers in 2009 and preliminary results of the mass-balance programme were presented by Láska and others (Reference Láska, Nývlt, Engel and Stachoň2015). In this paper, we present and discuss surface mass-balance data collected on the investigated glaciers over the 2009–15 period.
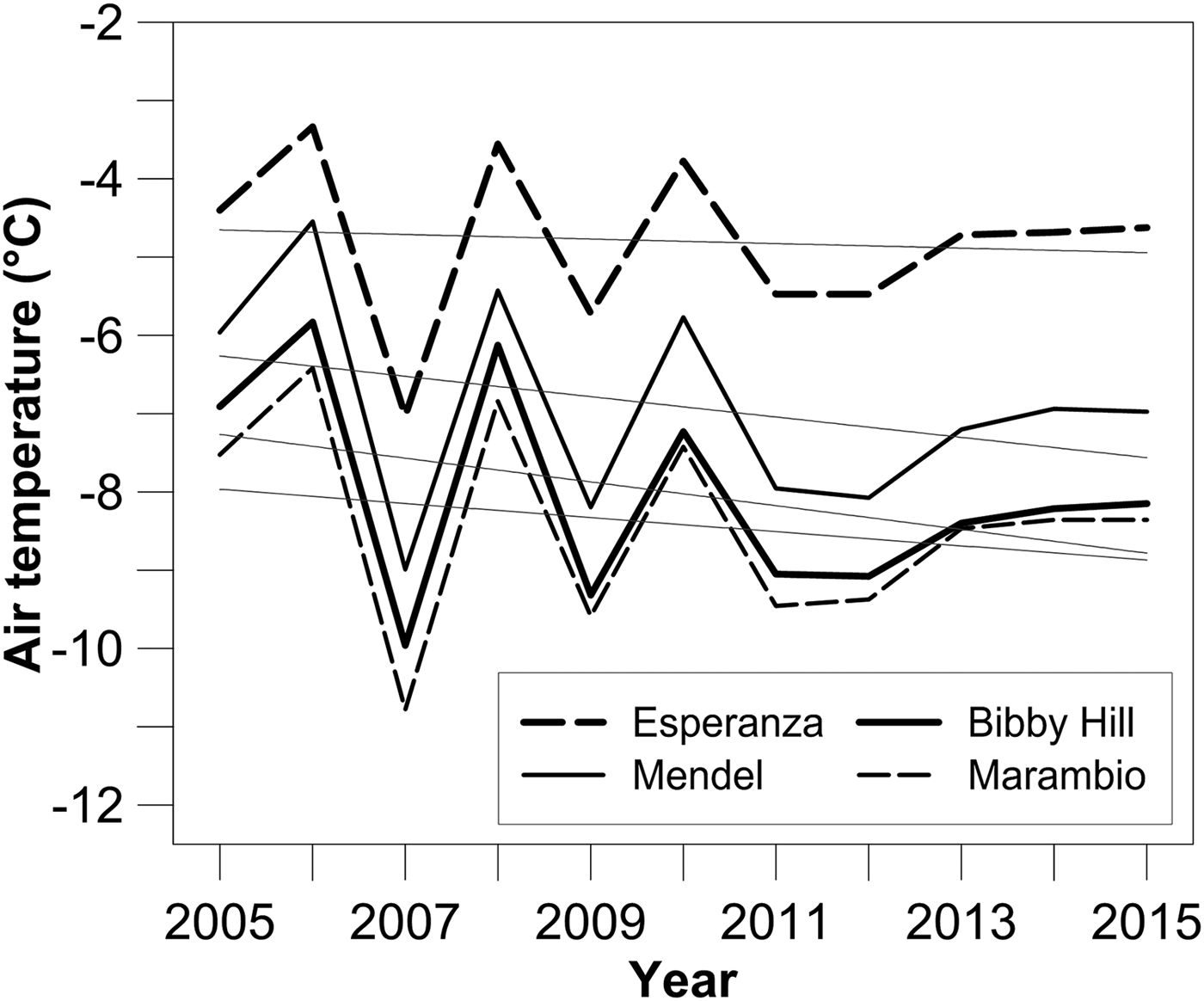
Fig. 2. Variability of mean annual air temperature completed with linear trends on meteorological stations along the north-eastern side of the Antarctic Peninsula (2005–2015). Modified from Ambrožová and Láska (Reference Ambrožová, Láska and Nováček2016).
2. STUDY AREA
The investigated glaciers are located in the northern part of JRI on the eastern side of the AP (Fig. 1). The cold climate of this region is influenced by the 1000–1800 m high orographic barrier of the Trinity Peninsula (King and others, Reference King, Turner, Marshall, Connolley, Lachlan-Cope, Domack, Leventer, Burnett, Bindschadler, Convey and Kirby2003) and the Southern Annular Mode (Marshall and others, Reference Marshall, Orr, van Lipzig and King2006). A positive trend in this annular mode increases north-westerly air flow over the AP and amplifies warming on the eastern side of the AP due to the föhn effect (Grosvenor and others, Reference Grosvenor, King, Choularton and Lachlan-Cope2014). The mean annual air temperatures (2005–15) in the northern part of JRI range from −7.0°C at sea level (Mendel Base, 10 m a.s.l.) to <−8.0°C (Bibby Hill, 375 m a.s.l.) in higher elevation areas (Ambrožová and Láska, Reference Ambrožová, Láska and Nováček2016). Positive air temperatures over the short summer season (2–3 months) cause snow and ice to melt on glaciers with large variability depending on cloudiness and solar radiation. The modelled annual precipitation is estimated between 200 and 500 mm w.e. (van Lipzig and others, Reference van Lipzig, King, Lachlan-Cope and van den Broeke2004). The distribution of snow cover is strongly influenced by the prevailing south to south-westerly winds, which effectively drift snow from flat relief and ice caps to lee-side surfaces (Zvěřina and others, Reference Zvěřina2014).
The surface of JRI is dominated by a variety of glaciers including the large Mount Haddington Ice Cap (587 km2; Rabassa and others, Reference Rabassa, Skvarca, Bertani and Mazzoni1982) in the central and southern parts of the island. Bedrock appears at the surface at the periphery of this ice cap and along the northern coast of the island. The largest glacier-free area (~180 km2) appears in the northern part of the Ulu Peninsula where glaciers cover only 10% of the land (Fig. 1). Small ice caps and land-terminating valley glaciers are the most frequent glacier systems in this area (Rabassa and others, Reference Rabassa, Skvarca, Bertani and Mazzoni1982). Because of their small volume, these glaciers are expected to have a relatively fast dynamic response to climatic oscillations and their mass balance is also considered to be a sensitive climate indicator (e.g. Allen and others, Reference Allen, Siegert and Payne2008). A land-terminating valley glacier (Whisky Glacier, cf. Chinn and Dillon, Reference Chinn and Dillon1987) and a small ice cap (Davies Dome) were selected for annual mass-balance measurements.
Whisky Glacier is a land-terminating valley glacier (63°55′–63°57′S, 57°56′–57°58′W) located between 520 and 215 m a.s.l. (Table 1). The glacier forms at the foot of the ~300 m high north-east face of Lookalike Peaks (767 m a.s.l.), which restricts snowdrift on the lee-side surfaces allowing enhanced snow accumulation on the glacier. An extensive area of debris-covered ice surrounds the western and terminal parts of the glacier, while the steep western slope of Smellie Peak (704 m a.s.l.) bounds its eastern side (Fig. 3a). The 3.2 km long glacier is gently inclined (the mean slope of 4°) to the NNE and it descends to an elevation of 215 m a.s.l. Between 1979 and 2006, the glacier retreated by ~60 m and its area decreased from 2.69 to 2.4 km2 (Engel and others, Reference Engel, Nývlt and Láska2012). The maximum thickness of ~158 m was determined by ground-penetrating radar (GPR) in the central part of the glacier where the mean annual near-surface air temperature is ~−8°C (Láska and others, Reference Láska, Nývlt, Engel and Kopačková2011). The glacier was frozen to the bed and no evidence of temperate layers was detected by GPR soundings.

Fig. 3. The location of the ablation stakes on Whisky Glacier (a) and Davies Dome (b).
Table 1. Main characteristics of Whisky Glacier and Davies Dome
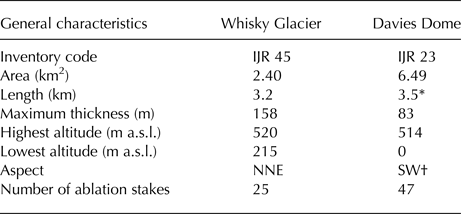
The inventory code is adopted from Rabassa and others (Reference Rabassa, Skvarca, Bertani and Mazzoni1982), the maximum thickness is determined from ground-penetrating radar survey (Engel and others, Reference Engel, Nývlt and Láska2012) and other values are derived from a digital terrain model (Czech Geological Survey, 2009)
* The distance from the highest point of the dome to an ice front measured along the central flowline of the outlet.
† The aspect of the outlet at the transition from the dome.
Davies Dome is an ice dome (63°52′–63°54′S, 58°1′–58°6′W) located ~7 km to the north-west of Whisky Glacier. The dome originates on a volcanic plateau with an elevation of 400–450 m a.s.l. The dome with a flat top at 514 m a.s.l. is elongated in the SW–NE direction being 2.3 km long. The western and northern peripheries of the dome terminate on the plateau, whereas the eastern and southern parts descend below the flat surface of the plateau (Fig. 3b). Most of the eastern margin can be found at an elevation of 210–270 m a.s.l. and only the easternmost tip descends to 170 m a.s.l. The southern part of the dome is drained into Whisky Bay where its 0.7 km wide outlet joins a much wider tidewater glacier forming a 3.3 km long ice cliff. Davies Dome was losing mass over the 1979–2006 period (Engel and others, Reference Engel, Nývlt and Láska2012) having an area of ~6.5 km2 and a maximum thickness of ~83 m in 2010 (Table 1). The mean annual near-surface air temperature on the dome is −8.8°C according to the meteorological data collected over the 2006–09 period (Láska and others, Reference Láska, Nývlt, Engel and Kopačková2011).
2.1. Methods
The mass-balance programme is based on the field measurement of height of bamboo stakes mounted on the glacier surface and the conversion of height changes to surface mass values using a zonally variable density. The surface elevation changes are measured at a fixed date once a year, which precludes determination of separate winter and summer balances. The mass-balance record from Davies Dome is also limited due to the absence of data on mass losses from a sea-terminating outlet. Therefore, we interpret the observed glacier elevation changes in terms of surface mass-balance values on Whisky Glacier and the ice dome without its outlet.
2.2. Field measurements
Field glaciological monitoring was initiated in austral summer 2005/06 on Davies Dome and it expanded to Whisky Glacier in summer 2008/09 (Nývlt and others, Reference Nývlt, Kopačková, Láska and Engel2010). The monitoring consists of ablation stake height and position measurements, which are made annually during late January. The height is measured from the top of the upright stakes to the glacier surface with 0.01 m resolution, and stake readings are eventually corrected for tilt. The location of the stakes is recorded using a differential GNSS receiver. Bamboo stakes are drilled 1–1.2 m into the glacier, which proved to be sufficient depth except for the year with the largest ablation during which the stakes melted out at the lowermost parts of the investigated glaciers. The stakes are drilled each year not only on the glacier termini but also in the highest parts of both glaciers where enhanced snow accumulation takes place.
The stake networks consist of 25 and 47 fixed locations on Whisky Glacier and Davies Dome, respectively. On Whisky Glacier, ten stakes are located along the central flowline, eight along the western parallel line and seven on the eastern side of the glacier, capturing the variability of surface mass changes across the whole glacier (Fig. 3a).The network on Davies Dome includes 44 stakes distributed over the dome and three stakes in the upper part of the glacier outlet (Fig. 3b). As ice crevasses preclude safe movement on the lower part of the outlet, the annual stake measurements are limited to the ice dome.
2.3. Surface mass-balance determination
The changes in the height of the stakes recorded with respect to the previous summer values are converted to m w.e. using the zonally variable approach (Huss, Reference Huss2013). This approach reflects variable density of the melted glacier ice in the ablation zone and snow that persists over a year in the accumulation zone. Although the density of the glacier ice may vary from 830 to 923 kg m−3 (Cuffey and Paterson, Reference Cuffey and Paterson2010), we convert the values in the ablation zone using a density of 900 kg m−3, which is recommended by Huss (Reference Huss2013) for a wide range of conditions. The density factor used for snow in the accumulation zone is more variable, ranging from 500 to 600 kg m−3 (Huss, Reference Huss2013). With respect to the density of snow reported from the AP region (Table 2), we used the value of 500 kg m−3. The uncertainty range is set to ±90 kg m−3 to cover a midrange of density values that was measured on JRI Ice Cap (Aristarain and Delmas, Reference Aristarain and Delmas1981) and Vega Island (Marinsek and Ermolin, Reference Marinsek and Ermolin2015).
Table 2. Snow density assumptions for volume to mass change conversion
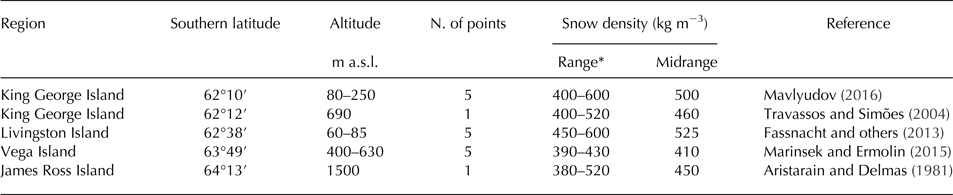
* Range of density values measured in snow pits and boreholes to a depth of <2 m.
Point balances were extrapolated over the entire glacier area, allowing the calculation of the glacier-wide average surface mass balance. As the spatial extrapolation of point data over large areas represents a considerable source of the surface mass-balance uncertainty (Huss and others, Reference Huss, Bauder and Funk2009), we first investigated and selected the most appropriate interpolation technique. We applied four appropriate techniques (inverse distance weighting, kriging, natural neighbour and the nearest neighbour; de Smith and others, Reference de Smith, Goodchild and Longley2015) to extrapolate point balance data from the year when annual surface mass balance of glaciers was close to zero. Then we compared the obtained grids using the cross-validation reports for each interpolation technique. The standard and median absolute deviations of the cross-validation residuals were taken as the main criteria for assessing the quality of the gridding methods. The cross-validation results show that the natural neighbour technique yields the lowest values of both the standard and median absolute deviations among the applied algorithm (Table 3). This technique was subsequently applied to the complete point balance dataset to generate annual surface mass-balance grids and maps of the glaciers.
Table 3. Cross-validation results for interpolation methods
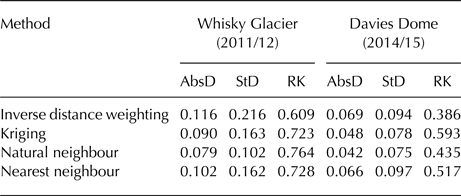
AbsD and StD: the median absolute and standard deviations of the cross-validation residuals; RK: the rank correlation between the measurements and the estimates.
Equilibrium line altitude (ELA), accumulation-area ratio (AAR) and vertical gradients in surface mass balance were determined from the annual mass-balance grids and the surface elevation data. The elevation of lines with annual zero surface mass-balance change is taken from a digital elevation model (DEM) based on aerial photographs taken in 2006. The vertical error of this DEM (0.8 m; Meixner, Reference Meixner2009) and the range of the elevation changes (−0.4 to +1.1 m; Engel and others, Reference Engel, Nývlt and Láska2012) measured on Davies Dome between 2006 and 2009 are taken into account in the estimated errors in annual mass balance described below. The accumulation area of the glaciers is determined from the annual mass-balance grids, and divided by the total glacier area to provide annual values of AAR. The surface mass-balance gradient is assessed for Whisky Glacier based on the annual mass-balance values assigned for 20 m elevation intervals. The distribution of the glacier surface area with elevation is derived from the DEM. The ratio of the mass-balance gradient in the ablation zone to the mass-balance gradient in the accumulation zone (mass-balance ratio) is determined according to the definition by Cogley and others (Reference Cogley2011), assuming each of these gradients constant and that in the accumulation zone non-zero. The mass-balance gradient is not determined for Davies Dome because of the lack of data from the lower part of its outlet. Moreover, no relation exists between the annual point mass balances and the altitude on the Dome.
Mass-balance years used in this paper refer to a fixed-date system, with the mass-balance year 2010 starting on 1 February 2009 and ending on 31 January 2010.
2.4. Error estimation
The uncertainty in the determination of the annual surface mass balance was estimated following an approach proposed by Huss and others (Reference Huss, Bauder and Funk2009). According to this approach, the uncertainty in the glaciological method arises due to local effects and spatial interpolation:
Local uncertainty (σ local) includes uncertainties in the surface mass-balance determination at the individual stakes (e.g. melt in/out of the stake, reading errors), local variations of snow density (e.g. compaction of the snow, percolation and refreezing of meltwater) and thickness changes due to snowdrift (Müller and Kappenberger, Reference Müller and Kappenberger1991). As the individual sources of uncertainty in the stake measurements and snowdrift-related thickness changes can be hardly detected, we addressed the estimate of σ local using a simplified approach. We assigned a broad range of uncertainty to the snowpack density for the accumulation area (±90 kg m−3), which should provide a sufficient interval to represent the possible magnitude of the individual sources of uncertainty. The uncertainty that results from spatial interpolation (σ int) is associated with a non-representative distribution of the stakes over the glacier surface, insufficient spatial density of the stakes and the extrapolation of the stake values to unmeasured areas (Huss and others, Reference Huss, Bauder and Funk2009). We estimated this component by the std dev. of the cross-validation residuals obtained from the interpolation of the annual surface mass-balance grids. The determined uncertainty in annual surface mass balance should be considered a lower bound because local variations in the snow thickness are not addressed. The uncertainty in cumulative surface mass balance is calculated as the std dev. for the 2009–2015 period using the root-sum-square method (Rye end others, Reference Rye, Willis, Arnold and Kohler2012). Mean values of surface mass balance, ELA and AAR for this period are reported with the standard error of the mean.
4. RESULTS
4.1. Surface mass-balance changes of the investigated glaciers
The measured data indicate a cumulative increase in the surface mass balance for the investigated glaciers over the 2009–15 period (Table 4). Whisky Glacier experienced a cumulative mass gain of 0.57 ± 0.67 m w.e. from 2009/10 to 2014/15 and its surface mass balance increased at an average rate of 0.09 ± 0.05 m w.e. a−1 (Fig. 4). The annual surface mass balance was positive except for 2011/12, when this glacier lost −0.16 ± 0.39 m w.e. a−1. In the other years of the investigated period, the annual surface mass balance ranged from 0.05 ± 0.25 to 0.23 ± 0.32 m w.e. A cumulative gain of 0.11 ± 0.37 m w.e. was observed over the 2009–15 period on Davies Dome (without its outlet), whose surface mass increased at an average rate of 0.02 ± 0.05 m w.e. a−1. The annual mass balance for the dome ranges from −0.21 ± 0.17 to 0.19 ± 0.15 m w.e.
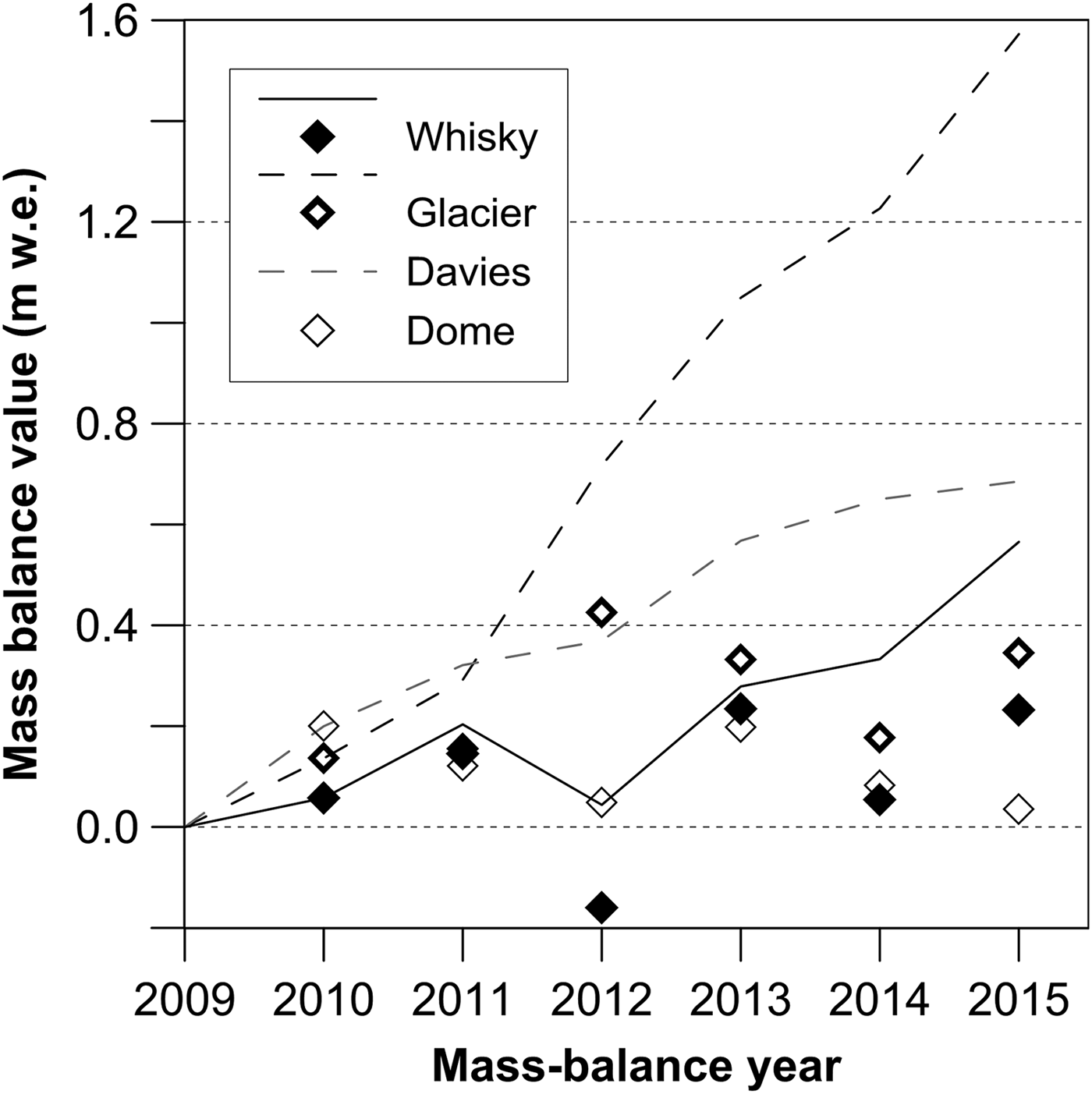
Fig. 4. Surface mass changes (relative to February 2009) of Whisky Glacier and Davies Dome over the 2009–2015 period. Diamonds and lines represent annual and cumulative values, respectively. Continuous line and solid diamonds indicate surface mass balance of Whisky Glacier, dashed lines and unfilled diamonds show surface mass gain in the accumulation zone of the glaciers.
Table 4. Surface mass-balance characteristics for Whisky Glacier and Davies Dome
The spatial distribution of the annual surface mass balance on Whisky Glacier reveals, in addition to the usual altitudinal pattern, an asymmetry along the central flowline of the glacier (Fig. 5). The elevation-related pattern is less clear in the first 2 years of the investigated period (Figs 5a, b) when the surface mass change is obscured by the lack of the stake measurements on the glacier head. The asymmetry is distinct over the whole investigated period with the most pronounced west–east increase in the surface mass in 2010/11, 2012/13 and 2014/15 (Figs 5b, d, f). Less clear asymmetry was found for 2011/12 when the difference in the surface mass balance between the western and eastern sides of the glacier only occurred in its lower part (Fig. 5c). Both the elevation and asymmetry aspects are well pronounced in the cumulative mass-balance distribution for the 2009–15 period (Fig. 6a).

Fig. 5. Spatial distribution of annual surface mass balance (in m w.e.) on Whisky Glacier during the 2009–2015 period.

Fig. 6. Cumulative surface mass balance (in m w.e.) on Whisky Glacier (a) and Davies Dome (b) over the 2009–2015 period.
The annual surface mass-balance distribution for Davies Dome is shown in Figure 7. Two different patterns of the annual mass distribution may be distinguished. Over most of the investigated period, the surface mass increases along the SW–NE transect, attaining the maximum values on the north-eastern (lee-ward) slope of the dome (Figs 7b, d–f). The loss of mass is restricted to the south-eastern margin of the dome close to the outlet where the surface mass decreases at an average of −0.1 to −0.4 m w.e. a−1. This dominant pattern is well reflected by the cumulative mass-balance distribution over the 2009–15 period, as indicated in Figure 6b. The second observed annual pattern reflects the maximum accumulation on the highest part of the dome, and a decrease in the mass gain towards the periphery of the dome at lower elevations (Figs 7a, c). A more pronounced elevation-related pattern results from the negative balance in 2011/12, when the area of mass gain was restricted to the top of the dome (Fig. 7c). The maximum measured values in this area were ~0.1 m w.e. and the area with positive surface mass balance represented <10% of the dome. Outside this area, the annual surface mass balance decreased with elevation to <−0.5 m w.e.

Fig. 7. Spatial distribution of annual surface mass balance (in m w.e.) on Davies Dome during the 2009–2015 period.
4.2. ELA, mass-balance gradient and AAR
The mean ELA for Whisky Glacier and Davies Dome over the 2009–15 period was determined to be 311 ± 16 and 393 ± 18 m, respectively (Table 4). The mean value is more representative for Whisky Glacier where four annual ELAs overlap within the mean ELA uncertainty, and three of them differ by 3–5 m from the mean (Fig. 8). Only two out of six annual ELAs differ remarkably from the mean, attaining 241 m in 2010/11 and 378 m in 2011/12. The highest ELA corresponds to the only year with negative surface mass balance on Whisky Glacier. The course of the equilibrium line obtained for this year is simple as the line crosses the glacier along a narrow 20 m elevation zone (Fig. 5c). Simple-layout equilibrium lines at Whisky Glacier correspond to the years with the elevation-dominated pattern of surface mass balance (Figs 5a, c), while more complex lines reflect asymmetry in mass accumulation along the central flowline of the glacier (Figs 5b, d–f). At Davies Dome, annual equilibrium lines are more variable in both elevation and horizontal planes. The mean annual ELAs for this glacier ranged from 323 m in 2009/10 to 464 m in 2011/12, corresponding to the years with maximum and minimum surface mass balances, respectively (Fig. 8). The layout of equilibrium lines is highly variable and complex (Fig. 7).
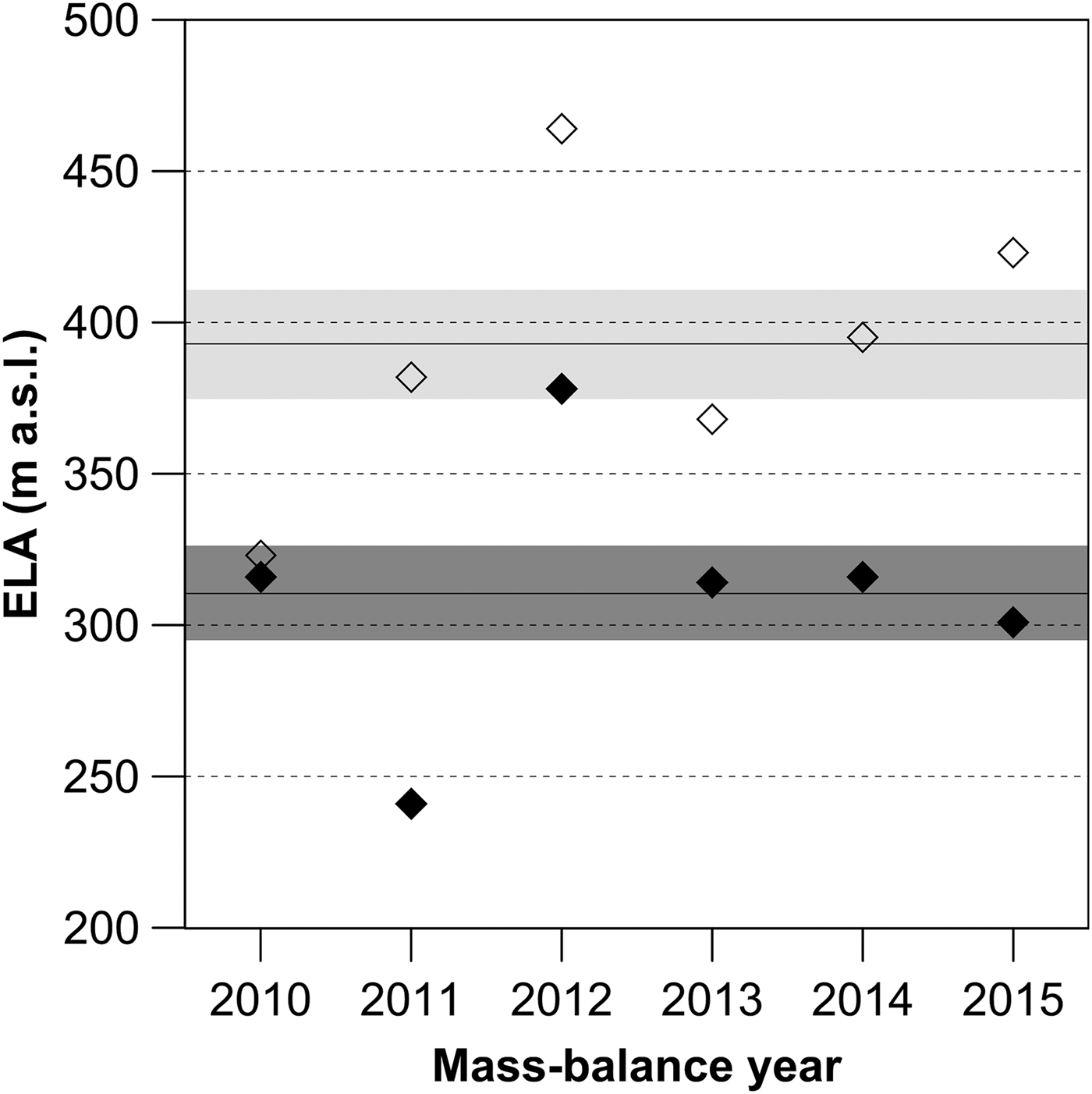
Fig. 8. Annual ELAs derived from the mass-balance surface DEM. Filled and unfilled diamonds represent the annual ELA values for Whisky Glacier and Davies Dome, respectively. Black lines in dark (Whisky Glacier) and light (Davies Dome) grey rectangles indicate the mean ELA values for the 2009–2015 period and relevant uncertainties, respectively.
The annual surface mass-balance gradient on Whisky Glacier ranged from 0.08 to 0.59 m w.e. per 100 m altitude (Table 4). The glacier had a small mass-balance gradient over most of the investigated period except for the mass-balance year 2011/12 when the highest ELA was observed. The vertical profile of the surface mass balance for that year indicates progressive ablation on the glacier surface up to 350 m a.s.l. and higher than average accumulation above 410 m a.s.l. (Fig. 9). The balance ratio of 0.82 for that year indicates slightly lower ablation gradient. A significantly higher (2.42) or lower (0.15 and 0.24) balance ratio was calculated for 2010/11, 2012/13 and 2014/15, which show no clear relation between the annual point mass balance and the altitude.

Fig. 9. Altitudinal gradient of surface mass balance on Whisky Glacier during the 2009–2015 period. Lines in bold indicate the years which show the relation between the annual point mass balance and altitude.
The mean AAR over the 2009–15 period is 0.68 ± 0.09 and 0.44 ± 0.09 for Whisky Glacier and Davies Dome, respectively. The annual AAR ranges from 0.23 to 0.96 on Whisky Glacier and from 0.08 to 0.70 on Davies Dome (Table 4). A minimum percentage of the accumulation area was observed in 2011/12, when the glaciers experienced a net mass loss and the equilibrium line was at the highest altitude over the investigated period. In the same year, the accumulation area of Davies Dome experienced only a negligible surface mass gain of 0.05 m w.e. A cumulative mass gain on the accumulation area of this glacier over the 2009–15 period was two times smaller than on Whisky Glacier accumulation area (Fig. 4).
5. DISCUSSION
5.1. Differences between the investigated glaciers
The cumulative surface mass gain observed on the investigated glaciers over the 2009–15 period is nearly three times larger for Whisky Glacier than for Davies Dome. The difference in the surface mass balance would be even more pronounced if the point balance data were available for the whole ablation area of the outlet of Davies Dome. The observed difference in the annual and cumulative surface mass values may result either from a more prominent mass loss on Davies Dome, higher accumulation on Whisky Glacier or a combination of both. The lower mean annual air temperature on Davies Dome precludes a higher melt rate on the dome, implying accumulation-related changes. Lower snowfall on Davies Dome can be also excluded, taking into account the short distance between the glaciers and a larger proportion of the dome at higher elevations compared with Whisky Glacier. The difference probably results from the snow redistribution by wind, as the changes in annual surface mass-balance distribution on both glaciers indicate. A clear elevation-related pattern in the surface mass balance was only observed in 2009/10 and 2011/12, while snowdrift-related asymmetry in the surface mass distribution on Whisky Glacier and increased mass gains on the lee-ward NE slope of Davies Dome dominated four of the six analysed years. The snowdrift pattern prevails in the surface mass-balance distribution on both glaciers for the whole investigated period, implying the dominant effect of wind on the snow redistribution and the surface mass-balance pattern. According to recent observations on Ulu Peninsula (Zvěřina and others, Reference Zvěřina2014), prevailing south to south-westerly winds play a significant role on redistribution of snow cover at the study area. The same effect was reported from SSI, where the lower accumulation rates on Hurd Glacier compared with Johnsons Glacier were attributed to snow redistribution by wind (Navarro and others, Reference Navarro, Jonsell, Corcuera and Martín-Español2013).
The uncertainty determined for the annual surface mass balance of the investigated glaciers ranges from 0.10 to 0.32 m w.e. a−1 except for the uncertainty of 0.39 m w.e. obtained for Whisky Glacier in 2011/12. All the values are well within the uncertainty range of 0.1–0.6 m w.e. reported for the glaciological method (Zemp and others, Reference Zemp, Hoelzle and Haeberli2009) but they are relatively large compared with the annual surface mass changes, as most of these are relatively small. Therefore, the interpretation of the annual surface mass balance and their comparison with the mass-balance data for other glaciers requires careful consideration of relevant uncertainties. The relatively large uncertainty results from the inter- and extrapolation of the point balance data over the glacier area. The largest uncertainty values were determined for 2011/12 when both glaciers experienced prominent surface mass decrease.
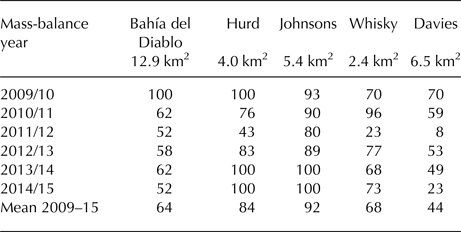
The small mass-balance gradient and a short ablation season indicate a small mass turnover of Whisky Glacier. The mass-balance ratio calculated for this land-terminating glacier are within the range of values reported for glaciers in polar regions. The values presented here for the years with significant relation between the point mass balance and the altitude range from 0.60 to 1.15, which is in agreement with the value of ~1 considered as representative for high-latitude glaciers (Ignéczi and Nagy, Reference Ignéczi and Nagy2013). These values indicate comparable accumulation and ablation gradients implying cold conditions over the elevation range of the glacier (Rea, Reference Rea2009). The low balance ratio also indicates a relatively large ablation area, which is necessary to compensate for the inputs from snowfall in the accumulation area. The mean AAR of 0.68 ± 0.09 obtained for Whisky Glacier is similar to the figure 0.65 calculated for Bahía del Diablo Glacier based on the annual data over the 2009–15 period (Table 5). The mean AAR of 0.44 determined for Davies Dome is significantly lower compared with the value reported for Whisky Glacier. Moreover, this value lies out of the range 0.5–0.8 suggested by Benn and Evans (Reference Benn and Evans2010) as typical for mid- to high-latitude glaciers. The low AAR reflects the irregular hypsometry of Davies Dome of which a substantial part (more than 40% of the surface area) is situated above 400 m a.s.l. Under such conditions, a larger ablation area or a rapid mass turnover is required to balance inputs from accumulation. The low AAR indicates an extensive ablation area, which is remarkably larger compared with the glaciers around the northern AP (Table 5).
Table 5. AAR of glaciers in the northern Antarctic Peninsula. Data from WGMS (2017) and this study.
5.2. Recent mass changes in regional context
The investigated glaciers were losing mass over the late 20th century similarly to other glaciers in the northern AP (e.g. Molina and others, Reference Molina, Navarro, Calvet, García-Sellés and Lapazaran2007). Between 1979 and 2006, the mean surface elevation of Whisky Glacier and Davies Dome decreased by 10.1 and 8.5 m, respectively (Engel and others, Reference Engel, Nývlt and Láska2012). The mean annual decrease rate of 0.3–0.4 m calculated for these glaciers is consistent with the mean surface-lowering rates reported from other parts of AP (Smith and others, Reference Smith, Vaughan, Doake and Johnson1998; Rückamp and others, Reference Rückamp, Braun, Suckro and Blindow2011). However, an order of magnitude larger lowering rate was reported for the 1990s (Ximenis and others, Reference Ximenis1999; Skvarca and De Angelis, Reference Skvarca, De Angelis, Domack, Burnett, Laventer, Conley, Kirby and Bindschadler2003) and for the beginning of the 21st century (Pritchard and others, Reference Pritchard, Arthern, Vaughan and Edwards2009; Rückamp and others, Reference Rückamp, Braun, Suckro and Blindow2011), when regional glacier mass losses culminated (Davies and others, Reference Davies, Carrivick, Glasser, Hambrey and Smellie2012). The mass loss decreased during the first decade of the 21st century, as indicated by the glaciological data from different parts of the northern AP including JRI (Davies and others, Reference Davies, Carrivick, Glasser, Hambrey and Smellie2012; Navarro and others, Reference Navarro, Jonsell, Corcuera and Martín-Español2013). The period of mass loss terminated in the mass-balance year 2008/09, after which the glaciers in the northern AP experienced a shift to mostly positive mass balances (Fig. 10). The persistence of negative mass balances until 2008/09 was also suggested for the investigated glaciers on JRI based on the 2006–09 field measurements on Davies Dome (Láska and others, Reference Láska, Nývlt, Engel and Kopačková2011).

Fig. 10. Surface mass-balance records for the glaciers around the northern Antarctic Peninsula. Data adopted from Mavlyudov (Reference Mavlyudov and Kotlyakov2016), WGMS (2017) and this study.
The first indication of the change in the mass-balance trends over the northern AP was given by Navarro and others (Reference Navarro, Jonsell, Corcuera and Martín-Español2013), who reported a shift from mostly negative to predominantly positive annual surface mass balance for Hurd and Johnsons glaciers on Livingston Island (SSI) for the mass-balance year 2009/10. The shift was confirmed subsequently based on the glaciological data from Bellingshausen Ice Dome on King George Island (SSI) (Mavlyudov, Reference Mavlyudov2014). The regional validity of the change was proved by the mass-balance record from Bahía del Diablo Glacier on Vega Island (Marinsek and Ermolin, Reference Marinsek and Ermolin2015), which represents the north-eastern part of the AP. The studies we refer to imply only 2 years with a positive mass balance, but the extended datasets for the Bellingshausen Ice Dome (Mavlyudov, Reference Mavlyudov and Kotlyakov2016), Bahía del Diablo, Hurd and Johnsons glaciers (WGMS, 2017) as well as glaciological observations on Ecology and Sphinx glaciers on King George Island (Sobota and others, Reference Sobota, Kejna and Araźny2015) indicate ongoing surface mass gains. The mass-balance data obtained for Whisky Glacier and Davies Dome correlate well with the record from the Bellingshausen Ice Dome indicating the net gain of the glaciers in the northern AP over the 2009–15 period (Fig. 10). The annual mass balance is positive except for 2011/12 when most glaciers around the northern AP experienced a surface mass loss.
We note that the recent positive mass balance observed in the region refers to the surface mass balance. For land-terminating glaciers, this is equivalent to total mass balance (neglecting subglacial mass changes). However, for glaciers and ice caps with floating or partly floating tongues, which prevail in this region, frontal ablation (the sum of iceberg calving and submarine melting at the glacier front) contributes to the mass losses and can result in negative total mass balance, as was shown by Osmanoğlu and others (Reference Osmanoğlu, Navarro, Hock, Braun and Corcuera2014) for the Livingston Island ice cap. Here, in spite of the estimated slightly positive surface mass balance of 0.06 ± 0.14 m w.e. a−1 for the period 2007–2011, the total mass balance is negative, equivalent to −0.67 ± 0.40 m w.e. a−1 over the entire ice cap area, when losses by frontal ablation are added. The similar setting of King George Island and its comparable frontal ablation estimates (Osmanoğlu and others, Reference Osmanoğlu, Braun, Hock and Navarro2013) also suggest net mass losses for its ice cap.
The changes in ELA determined for Whisky Glacier and Davies Dome over the 2009–15 period are in agreement with the ELA reported for Bahía del Diablo Glacier. The temporal changes in ELA coincide over that period except for 2009/10 when Bahía del Diablo Glacier experienced the largest mass gain since 2000 and its ELA was located much lower than on the investigated glaciers on JRI (Fig. 11). The range of ELA in subsequent years was similar for these three glaciers and the nearest mean ELA of 311 and 295 m for Whisky and Bahía del Diablo glaciers, respectively. The range of ELA on the investigated glaciers is significantly higher compared with the glaciers on SSI (Sobota and others, Reference Sobota, Kejna and Araźny2015; WGMS, 2017), and the determined changes in ELA differ between the two locations after a prominent decrease in the period between 2011/12 and 2012/13. While ELA experienced a prolonged decrease on SSI, it started to increase on the investigated glaciers and Bahía del Diablo Glacier. The observed difference in ELA probably indicates lower precipitation on JRI and Vega Island (van Lipzig and others, Reference van Lipzig, King, Lachlan-Cope and van den Broeke2004; Dethloff and others, Reference Dethloff, Glushak, Rinke and Handorf2010), where the mean annual air temperature is 4–7°C lower compared with SSI (Ambrožová and Láska, Reference Ambrožová, Láska and Nováček2016; Oliva and others, Reference Oliva2017).
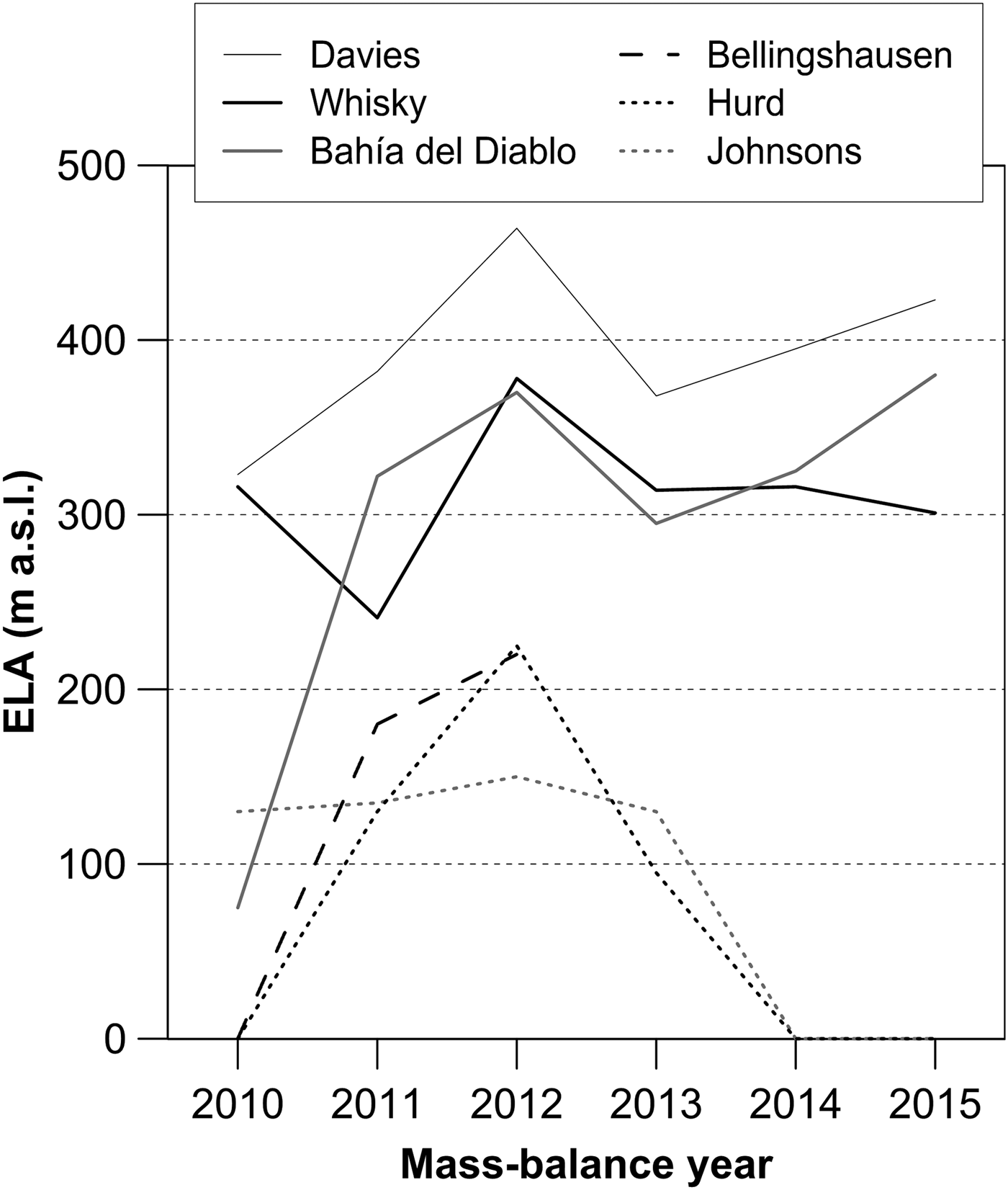
Fig. 11. ELA of the glaciers around the northern Antarctic Peninsula during the 2009–2015 period. Data from WGMS database (2017).
When interpreting mass-balance changes, it is important to include the effect of interannual climate variability. Navarro and others (Reference Navarro, Jonsell, Corcuera and Martín-Español2013) pointed out that the positive mass balances on Hurd and Johnsons glaciers may result from both increased winter accumulation and decreased summer melt, with the predominance of one or the other process depending on the year. While the increase in accumulation is related to the higher precipitation rates associated with greater cyclonic activity to the west of the AP (Turner and others, Reference Turner2016), the melt decrease can be related to the lower summer air temperature observed around the AP region over the last decade (Navarro and others, Reference Navarro, Jonsell, Corcuera and Martín-Español2013; Ambrožová and Láska, Reference Ambrožová, Láska and Nováček2016). As reported by Oliva and others (Reference Oliva2017), the mean summer temperatures decreased by 0.3–0.6°C between 1996–2005 and 2006–2015 around the mentioned glaciers. The previous studies also show that the SSI glaciers are very sensitive to air temperatures (Braun and Hock, Reference Braun and Hock2004; Jonsell and others, Reference Jonsell, Navarro, Bañón, Lapazaran and Otero2012; Abram and others, Reference Abram2013; Sobota and others, Reference Sobota, Kejna and Araźny2015; Pętlicki and others, Reference Pętlicki, Sziło, MacDonell, Vivero and Bialik2017) and the associated changes in large-scale circulation pattern (Braun and others, Reference Braun, Saurer, Vogt, Simões and Gossman2001). The reported stronger sensitivity is also related to the fact that average summer temperatures on these glaciers often fluctuate around zero, and therefore even a small temperature change may cause a rapid shift from melting to freezing conditions or vice versa.
However, it must be stressed that climate conditions on the eastern AP and JRI glaciers are different from those in the SSI region. The mean annual air temperature in the northern part of JRI is ~4°C lower than in the SSI region over 2005–2015 (Ambrožová and Láska, Reference Ambrožová, Láska and Nováček2016). These authors also reported a significant temperature decrease with the most prominent cooling (0.14°C a−1) at the elevated regions of JRI during spring and summer months. This is in agreement with the findings by van Wessem and others (Reference van Wessem2015) and Turner and others (Reference Turner2016), who attributed the cooling trend in air temperature to enhanced easterly flow across the northern Weddell Sea towards the AP and related positive trends in the sea ice cover.
Furthermore, surface mass-balance sensitivity to temperature varies according to glacier type, with maritime glaciers typically having higher sensitivity than continental glaciers (e.g. Cuffey and Paterson, Reference Cuffey and Paterson2010). We assume that the investigated glaciers in the northern JRI are therefore less sensitive to temperature than the relatively temperate region of the SSI, with a mean sensitivity between −0.6 m w.e. K−1 (Jonsell and others, Reference Jonsell, Navarro, Bañón, Lapazaran and Otero2012) and −0.1 m w.e. K−1 (Bintanja, Reference Bintanja1995). Although the impact of regional cooling in the north-eastern AP on surface mass balance has been reported recently (Marinsek and Ermolin, Reference Marinsek and Ermolin2015; Oliva and others, Reference Oliva2017), the glacial response to changes in individual climate factors remains unresolved. Besides the changes in large-scale circulation patterns (Marshall and others, Reference Marshall, Orr and Turner2013; Turner and others, Reference Turner2016), the impact of local climate factors should be considered (van Wessem and others, Reference van Wessem2015). This concerns the observed surface winds and snow cover distribution, which are affected by the orography of the AP and the northern coast of JRI. As shown by Zvěřina and others (Reference Zvěřina2014), the distribution of snow cover is strongly influenced by prevailing south to south-westerly winds, which promote intense snowdrift and snow accumulation on the lee-side surfaces and in the depressions of the northern JRI. The fact that air temperature on the northern JRI often lies below zero implies that colder and drier conditions with predominance of wind-induced snow redistribution play a major role in the positive surface mass balance of the investigated glaciers. These facts highlight the need for a more detailed study of the surface mass-balance sensitivity to changes in individual environmental factors.
6. CONCLUSIONS
The cumulative surface mass balance over the 2009–15 period was positive for the investigated glaciers on JRI. Whisky Glacier experienced a total mass gain of 0.57 ± 0.67 m w.e. and Davies Dome showed an increase in the surface mass of 0.11 ± 0.37 m w.e. over the ice dome area. Although the given surface mass balance is positive, their quoted errors are larger in magnitude, implying that the real mass balances could turn out to be slightly negative. The lower mass gain on Davies Dome results from the snowdrift on the high-elevated ice dome and snow redistribution to lee-side surfaces. The snowdrift controlled the annual pattern of the surface mass balance on both the glaciers in 4 out of the 6 years, and dominated the cumulative mass-balance distribution over the 2009–15 period. The strong influence of wind on snow redistribution and mass-balance pattern of the observed glaciers confirms the conclusions by Navarro and others (Reference Navarro, Jonsell, Corcuera and Martín-Español2013), who recognized the effect of snowdrift on the accumulation rates on the glaciers in the northern AP region.
The annual surface mass balance was positive except for 2011/12 when the investigated glaciers experienced mass loss. The observed annual changes coincide with the surface mass-balance records from Bahía del Diablo Glacier on nearby Vega Island, Bellingshausen Ice Dome on King George Island and Hurd and Johnsons glaciers on Livingston Island. The cumulative mass gain of the glaciers around the northern AP indicates a regional change from a predominantly negative surface mass balance in the first decade of the 21st century to a positive balance over the 2009–15 period. The change in the glacier mass balance follows a significant decrease in the warming rates reported from the northern AP since the end of the 20th century. The mass gain is also consistent with the regional trend of climate cooling on the eastern side of the AP. However, the climate factors for the observed mass-balance changes on the investigated glaciers require further investigation.
The annual changes in ELA and the mean ELAs determined for Whisky Glacier (311 ± 16 m a.s.l.) and Davies Dome (393 ± 18 m a.s.l.) over the 2009–15 period correspond to the values reported for Bahía del Diablo Glacier. The range of ELA on JRI and Vega Island is 200–300 m higher than those observed on the SSI. This difference probably reflects drier conditions on the eastern side of the AP compared with the relatively wet and warmer SSI. The mean AAR of 0.68 ± 0.09 determined for Whisky Glacier over the 2009–15 period is similar to the AAR 0.65 for Bahía del Diablo Glacier and well within the range of typical values for high-latitude glaciers. The significantly lower mean AAR of 0.44 ± 0.09 for Davies Dome indicates an extensive ablation area, which is much larger compared with the glaciers around the northern AP. The large ablation area implies a small mass turnover of the marine-terminating glacier. The small turnover of the investigated glaciers is also indicated by a small mass-balance gradient at ELA and a short ablation season.
ACKNOWLEDGEMENTS
We acknowledge funding from the Czech Science Foundation project GC16-14122J. Fieldwork was supported by the crew of Mendel Station financed by the Ministry of Education, Youth and Sports of the Czech Republic and the project no. LM2015078 and CZ.02.1.01/0.0/0.0/16_013/0001708. We thank Kristián Brat, Tomáš Franta, Filip Hrbáček, Tomáš Jagoš, Pavel Kapler, Jan Kavan, Pavel Ševčík, Martin Slezák, Peter Váczi, Vítězslav Vlček and Ondřej Zvěřina for research assistance in the field. We are grateful for helpful and constructive criticism and comments from Francisco Navarro and an anonymous referee.


















