Introduction
Tidal interaction with floating glaciers has been studied for many years and for many reasons. Reference HoldsworthHoldsworth (1969, Reference Holdsworth1977) analyzed the stresses set up by tidal motion in the transition region where the glacier changes from grounded to floating conditions, with a view to studying the conditions under which the fracture strength of glacier ice would be reached and iceberg calving occur.
The grounding zone, where the line of contact between glacier and bed moves forth and back with the tide, is believed to be important for the stability of the entire glacier system. In order to detect possible long-term grounding-zone migration, indicative of glacier instability, it is important to locate this zone and monitor its changing position due to tidal motion (Reference RignotRignot, 1998a, Reference Rignotb).
The synthetic-aperture radar (SAR) technique for simultaneous measurement of ice-sheet surface topography and velocity is extremely sensitive to vertical displacements in the period between the acquisition of SAR images. For floating glaciers, the effect of tidal deflections must therefore be estimated and removed from the SAR interferograms before the velocity of the glacier motion can be derived (Reference RignotRignot, 1996).
Nioghalvfjerdsfjorden Glacier
An extensive floating glacier tongue fills the entire interior of Nioghalvfjerdsfjorden (Fig. 1). The glacier drains the Greenland ice sheet via a large icefall at the west end of the fjord. The area of the drainage basin is approximately 120 000 km2, and the total accumulation in the basin amounts to about 16 km3 ice a"1 (Reference Reeh, Mayer, Miller, Thomsen and WeidickReeh and others, 1999a). The length of the glacier tongue is 80 km from west to east, and the width is 21 km halfway downstream, widening to about 30 km at the main ice front. A northern branch of the glacier, 8 km wide, drains into the fjord Dijmphna Sund west of HovgaardØ .

Fig. 1. Nioghalvfjerdsfjorden glacier. For location, see insert map in upper left corner. Surface topography is based on photogrammetric mapping from aerial photographs taken on 2 August 1978. The location of tidal GPS measurement stations (legends starting with NF), the Base camp with the fixed GPS reference point and the pressure-gauge observation site ("Syge Moster") are shown. Inclinometer observations were performed at stations NFT001, NFT002 and NFT003, and at five stations near points NF9775 and NF9776. The positions of the laser-altimeter and ice-radar profiles are shown as thick lines across the glacier. Approximate location of the upstream grounding zone is shown by the grey shading running south from the western branch of Blåsø. Islands/ice rises at the main front are denoted by A-D. Rectangular co-ordinates are Universal Transverse Mercator (UTM).
The outermost ― 6 0 km of the glacier is afloat, with an upstream grounding zone crossing the glacier from the western branch of the ice-dammed lake Blaso in the north to Lambert Land in the south. Grounding zones also occur along the side margins of the glacier and at four islands or ice rises labelled A-D in Figure 1. These obstacles divide the main front of the glacier into five sections, of which the middle three form 7–8 km long distinct ice tongues with characteristic sawtooth lateral margins. The floating part of the glacier constitutes an extremely flat ice plain, with a characteristic meltwater drainage pattern of numerous small and large rivers and shallow lakes.
Field Programme
A field programme was carried out on the glacier in the summer seasons of 1996,1997 and 1998 by the Geological Survey of Denmark and Greenland, the Danish Polar Center, the Danish Center for Remote Sensing, and the Alfred Wegener Institute for Polar and Marine Research. The study comprised observations of climate, surface mass balance, bottom melting, ice thickness, glacier dynamics and tidal movement, bathymetry and conductivity-temperature-depth measurements in the sea in front of and below the glacier. Another part of the Nioghalvfjerdsfjorden glacier project comprised collection and compilation of data to document and interpret short- and long-term variations of the glacier. This included detailed mapping of surface elevation and ice thickness by means of an airborne ice-radar and laser-altimeter survey from a small aircraft. In July 1998, about 3000 km of high-quality surface and ice-thickness profiles were flown on Nioghalvfjerdsfjorden glacier with a Greenlandair Twin Otter. The spacing between the flight tracks was about 5 km on the relatively uniform floating part of the glacier, but was decreased to about 2.5 km in the grounding zone (Christensen and others, in press).
A detailed account of the Nioghalvfjerdsfjorden glacier project is given by Reference ThomsenThomsen and others (1997). Preliminary reports on the results of the project are given by Reference Mayer, Jung-Rothenhausler, Huybrechts and Le MeurMayer and others (1999), Reference Reeh, Thompson, Higgins, Weidick and StarzerReeh and others (1999b) and Reference Thomsen, Reeh, Olesen, Starzer and BøggildThomsen and others (1999).
Figure 2, from Reference Reeh, Mayer, Miller, Thomsen and WeidickReeh and others (1999a), shows a longitudinal section along the centre line of the glacier. At the grounding line, the glacier is almost 700 m thick. Over about the first 10 km of the floating tongue, the ice thickness decreases to about 300 m, a thickness that is maintained for the following 35 km. A further decrease in ice thickness to approximately 150 m occurs over a distance of about 5 km, followed by a gradual decrease to about 70 m thickness at the front. By combining the ice-thickness variation with ice velocities calculated from repeated differential global positioning system (GPS) observations, the net balance conditions along the glacier can be estimated based on simple ice-flux modelling. Surface ablation rates on the floating glacier tongue have been measured at 0.6–1.2 mice a"1 (Reference Thomsen, Reeh, Olesen, Starzer and BøggildThomsen and others, 1999). Using these values and assuming steady state, basal melt rates are calculated that range from 30–40 m ice a"1 at the grounding line to near zero over the outermost 10–15 km of the glacier. In the main channel, basal melt rates are typically 5–10mice a"1 (Reference Thomsen, Reeh, Olesen, Starzer and BøggildThomsen and others, 1999).
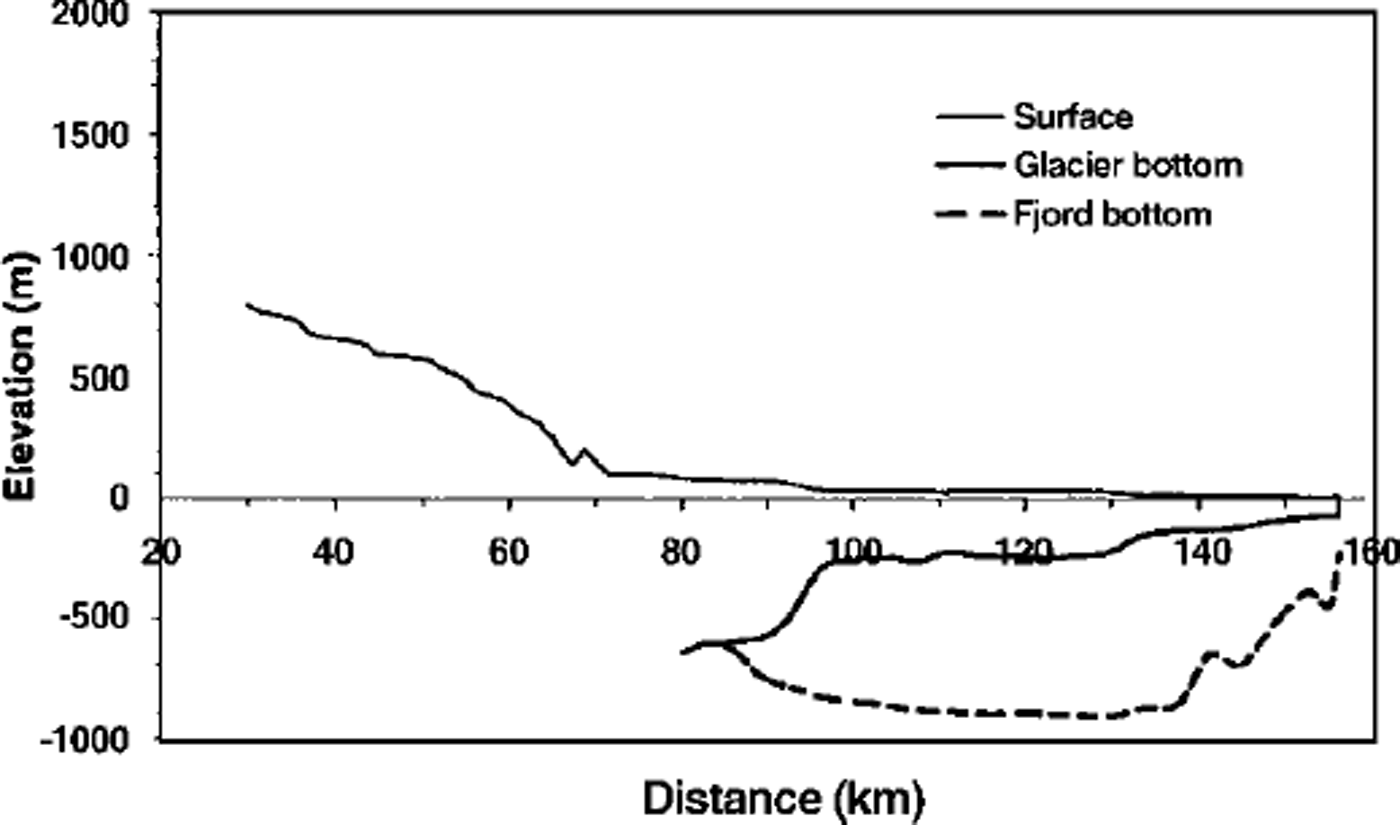
Fig. 2. Longitudinal section along the centre line of Nioghalvfjerdsfjorden glacier. The dotted line shows the fjord bottom as determined by seismic soundings. From Reference Reeh, Mayer, Miller, Thomsen and WeidickReeh and others (1999a).
The depth below sea level of the fjord bottom, as determined by seismic sounding, is 800–900 m over a large section of the profile, decreasing to about 600 m at the grounding line (Reference Mayer, Jung-Rothenhausler, Huybrechts and Le MeurMayer and others, 1999). In the openings between the islands and ice rises at the main glacier front, the sea bottom is up to 200 m below sea level. Depths along the Dijinphna Sund front of the glacier are significantly larger (up to 600 m). Although thresholds exist at the seaward end of the subglacial fjord basin, the connection between the fjord basin and the open sea is relatively free.
Observations of Tidal Motion
Tidal movement observations of the Nioghalvfjerdsfjorden glacier tongue were carried out in three different periods by simultaneous differential GPS measurements at several locations distributed on the glacier surface. The most extended GPS movement observations were performed continuously over several tidal cycles. During these periods, tiltmeter observations were performed simultaneously in a cross-profile at the northern glacier margins and in the upstream grounding zone at the head of the floating glacier tongue. A tide gauge installed in the sea immediately in front of the glacier front recorded the tide in the open sea during the field seasons. The locations of the measurement sites are shown in Figure 1.
Pressure-gauge observations in the sea
In both the 1997 and 1998 field seasons a pressure gauge with a vented transducer (±0.1% accuracy) measuring every 10 min, was installed in the open sea at the small island ˚Syge Moster"(SM) located at the very front of the glacier (see Fig. 1). Whenever the island was visited during both summer seasons, a several hundred meter open lead was observed to the north, east and south.
As the pressure-gauge site was well protected by a belt of permanent sea ice, the transducer was secured to a 7 kg iron weight and dropped into the sea onto the pebbly bottom. During the first summer, this resulted in the transducer being moved over the sea bottom by drifting sea ice on 16 August between 1710 and 1720 h when it was lifted 74 cm, and between 2040 and 2050 h when it was lowered 27 cm. The data indicate that the transducer remained stable in the intervening period, however, as consecutive measurements are at most 3 cm apart and steadily rising. Due to the consistency of the data during this 3 h 20 min long interval, the displaced data could apparently rather unambiguously be shifted ˚back in place". However, as mentioned in the section on analysis of the tidal records, the attempt at re-establishing the tidal record may not have been fully successful.
GPS observations
The most comprehensive measurement of tidal motion using GPS was undertaken in two periods: 10–11 August and 15–17 August 1997. The first period involved measurements at three points (NFT001, NFT002, NFT003) in the grounding zone at the head of the glacier, and at one point (NF0396) in the centre of the glacier, about 25 km behind the front. The second period involved six points in a cross-section about halfway down the main channel. In all cases, observations were performed as differential measurements in respect to a local reference on bedrock near Base Camp (see Fig. 1), using a recording interval of 30 s. The data were processed hour by hour using the ASHTECH GPPS software for static processing. In Figure 3, the vertical motions of the points in the cross-section are shown together with the tidal curve for Danmarkshavn (76°46’N, 18°46’W) predicted by a nine-component tidal model (personal communication from P. B. Nielsen, Royal Danish Administration of Navigation and Hydrography 1998), and used as reference. The pressure-gauge record measured in the sea at SM during the GPS recording period is also shown. All records are plotted as deviations from their mean values in the individual GPS recording periods. In order not to mask phase differences, the Danmarkshavn reference tidal series is also shown as deviations from the mean value in the recording period of the corresponding GPS record. We use the Danmarkshavn tidal series as a reference to which all our observed records of tidal motion are compared with the purpose of determining their amplitude and phase relative to each other. An alternative would be to use the observed tidal record in the sea at SM as reference. However, this record is slightly disturbed due to wave and wind action and also due to the displacement of the pressure gauge on 16 August as mentioned above. Therefore, we decided to use the ˚clean" mathematical Danmarkshavn series as reference.
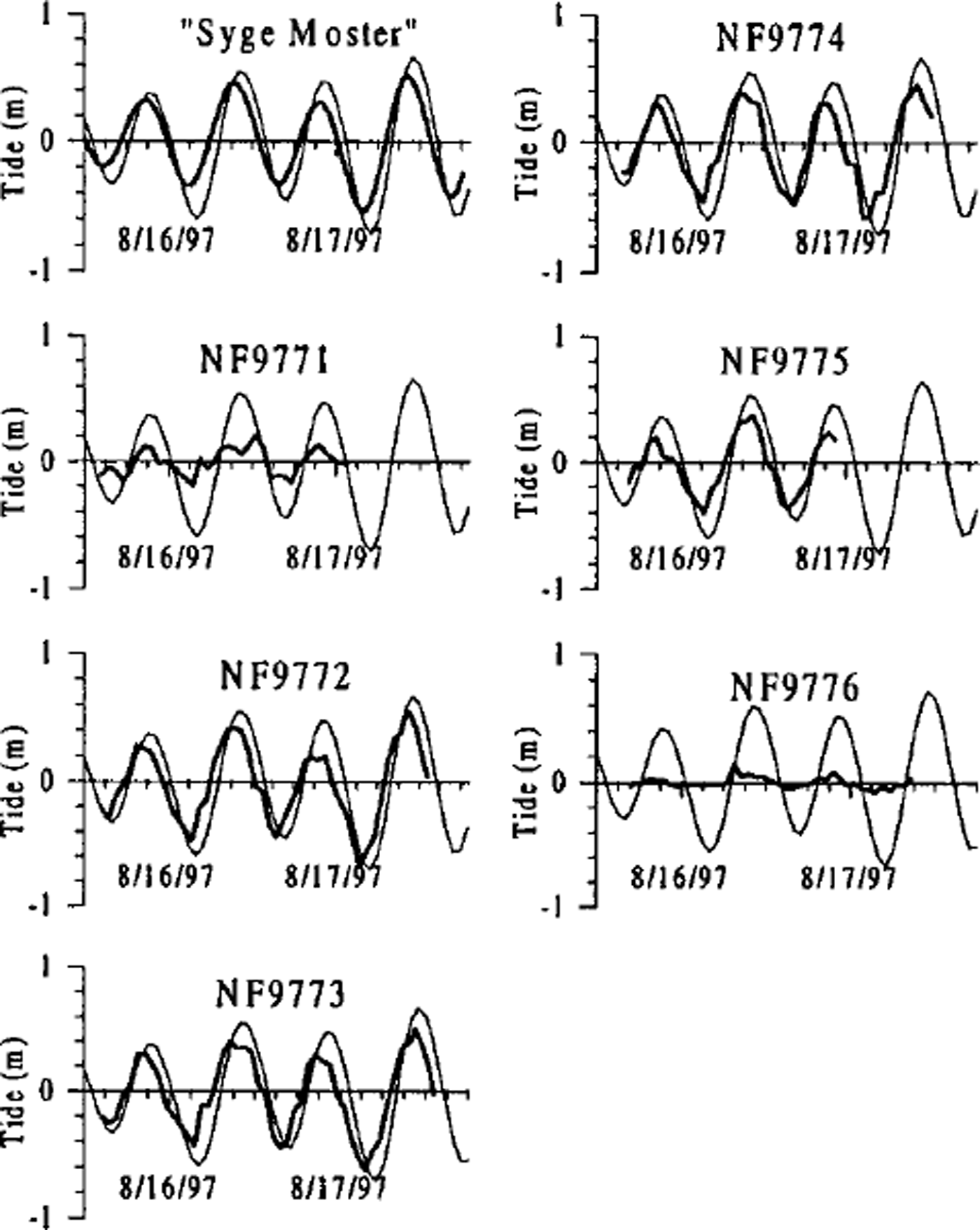
Fig. 3. Observed tide in the sea at SM and vertical motion (deflection) derived from GPS measurements of points in a cross-profile of Nioghalvfjerdsfjorden glacier, 15–18 August 1997. The location of the points in the cross-profile is shown in Figure 1. The thin curve, used as reference, is the tide for Danmarkshavn (76°46’N,18˚ 46’W) as predicted by a nine-component tidal model (Royal Danish Administration of Navigation and Hydrography, 1998).
As shown in Figure 3, all GPS records display a tidal signal, but with a significant noise contribution (5–10 cm) that must be referred to errors in the GPS measurements.
Tiltmeter observations
During two periods, the tidal influence on the glacier margins was observed using tiltmeters. These instruments measure the time-dependent tilting of the glacier surface with high resolution.
The first experiment was placed close to and parallel to the grounding line, where the glacier enters the fjord. There, three tiltmeters (NFT001, NFT002, NFT003; see Fig. 1) ran for 72–78 hours (7–10 August), recording the surface tilt every 10 min. The distance between the tiltmeters was 1.8 and 3.1 km, covering the central part of the glacier. All instrument records show a clear tidal signal, but this is disturbed, probably due to rapid ice movement in the icefall a few kilometres upstream of the measurement sites.
In the second period, five tiltmeters were placed at the northern margin of the glacier between GPS points NF9775 and NF9776 in the cross-section located about halfway between the grounding zone and the glacier front (see Fig. 1). The instruments were distributed along a 2.5 km section from the glacier margin to a prominent ice ridge (Midgardsormen) formed several kilometres upstream in a zone of intense pressure and shear, which at the location of the cross-section is afloat. In Figure 4, the tilt records of the points in the cross-section are shown together with the tidal curve for Danmarkshavn. The tilt record from AWI1 on top of Midgårdsormen, and to some extent also the record from AWI2 near Midgardsormen, are more disturbed than the tilt records from the other stations, probably reflecting focal stress and deformation anomalies at Midgardsormen.
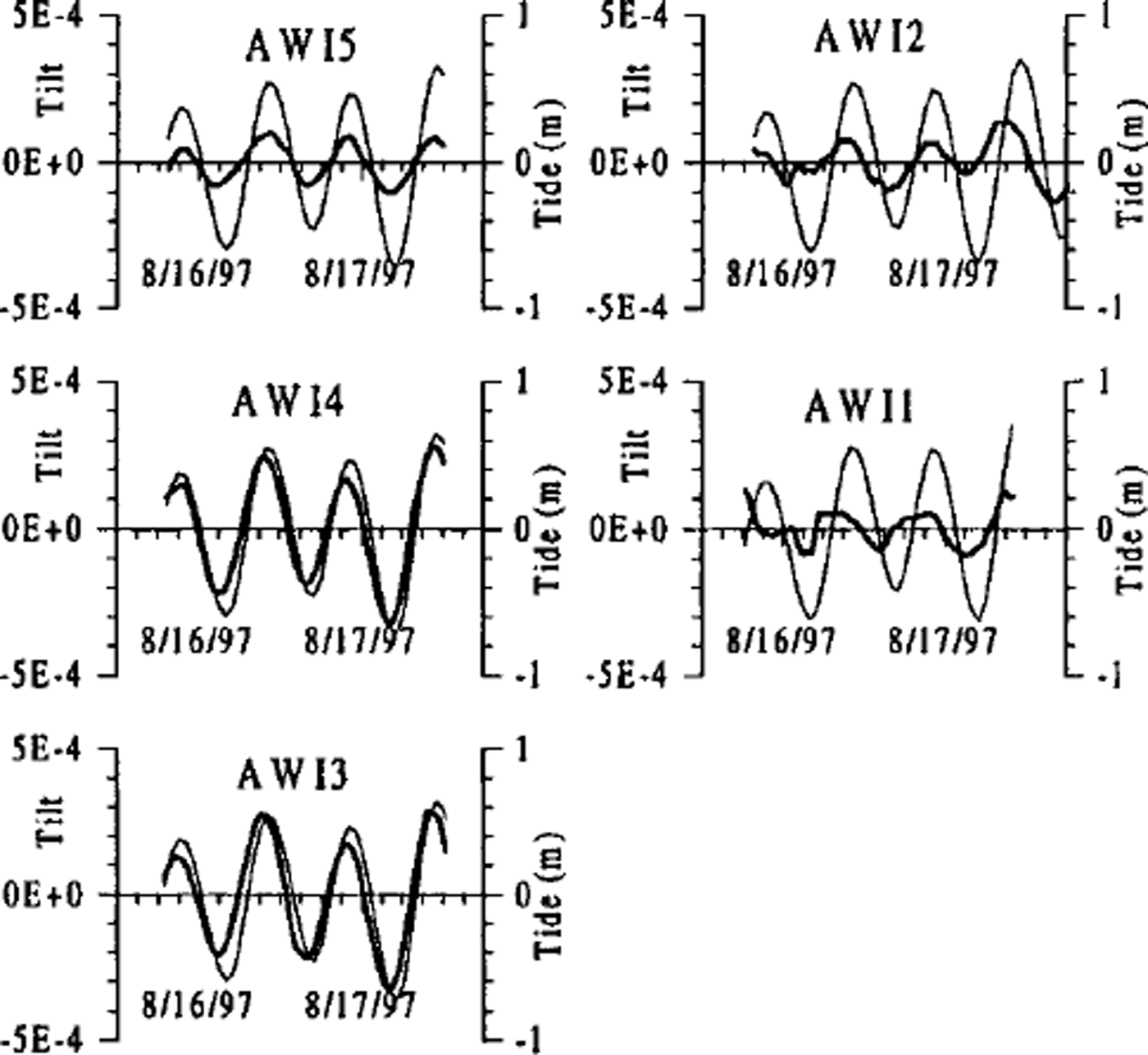
Fig. 4. Tilt measurements of points in a 2.5 km section of the near-margin part of the cross-profile of Nioghalvfjerdsfjorden glacier. The location of the points in the cross-profile is given in Table 3. The thin curve, used as reference, is the tide for Danmarkshavn (76°46’ N, 18° 46 W) as predicted by a nine-component tidal model (Royal Danish Administration of Navigation and Hydrography, 1998).
Spectral Analysis of Tidal Observations
The tidal observation records have been analyzed by cross-spectral analysis using the approach described by Reference Bendat and PiersolBendat and Piersol (1986, ch. 5, 6 and 9). Table 1 shows the phase (positive as lag) and gain factor (a measure of the amplitude) of the SM tidal record relative to the Danmarkshavn tidal series. The coherence, phase, and gain factors shown in Tables 1–3 correspond to the frequency of the basic period of the tide (about 12.5 h). The table shows that the SM record leads the Danmarkshavn tidal series by 51 ± 2 min in the period 7–11 August, and by 35 ± 15 min in the period 15–17 August. Clearly, these phases are not significantly different. Because of the problem with the displacement of the pressure gauge in the second period (see previous section) we will assume that the phase is about 50 min also in the second period. This is supported by the results of cross-spectral analysis of the two records for the 20 day period 27 July-14 August (not comprising the ˚problematic" period), which gives a phase of 48.5 ± 1.8 min, confirming that the phase difference between the two records is close to 50 mm.
Table 1. Phase (positive as lag) and gain factor (relative amplitude) of the SM tidal record relative to the Danmarkshavn tidal series
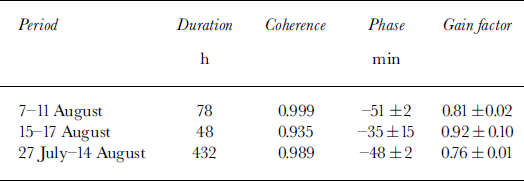
Table 2 shows the results of the cross-spectral analysis for the period 7–11 August using the SM record, which seems to be acceptable as a reference in this period. There is no significant phase difference between the deflection (GPS) records and the SM record. Moreover, the amplitudes of the deflection records are equal to or slightly less than the tidal amplitude measured at SM. On the other hand, both phases and gain factors of the tilt records show significant variations.
Table 2. Phase (positive as lag) and gain factor (amplitude) of tidal records from near the upstream grounding zone of Nioghalvfjerdsfjorden glacier relative to the SM tidal record
Table 3 shows the results of the cross-spectral analysis for the second period. Here, the Danmarkshavn tidal series is used as reference, because of the problem with the SM record in this period. The gain factors (amplitudes) of the deflection (GPS) records are, with the exception of the records from the points close to the lateral margins, about 75% of the amplitude of the Danmarkshavn tidal series, indicating amplitudes of the same order of magnitude as the focal tidal amplitude measured in the sea at SM (see Table 1). The phase of the deflection records from the central part of the glacier is about –65min. Although apparently about 15 min less than the phase of SM relative to the Danmarkshavn tidal series (see Table 1), this result, together with the results displayed in Table 2, shows that the main part of the floating glacier to a good approximation responds as a freely floating plate to the phase and amplitude of the local tide in the sea.
Table 3. Phase (positive as lag) and gain factor (amplitude) of tidal records in a cross-section of Nioghalvfjerdsfjorden glacier relative to the Danmarkshavn tidal series in the period 15–17 August 1997

Independent confirmation of this result is provided by the expected velocity of propagation c of the tidal wave in the fjord, which can be estimated from the theory of long channel waves as
where g is gravitational acceleration and D is water depth. With D ≈ 600 m, we find c ≈ 80 m s–1 ≈ 300 km h–1. The corresponding travel time of the tidal wave from the terminus to the head of the floating glacier (a 60 km distance) is therefore about 12 min, a short time as compared to the tidal period of about 12 h.
On the other hand, the deflection records from points NF9771, NF9775 and NF9776 near the glacier margin deviate from the tide in the sea with respect to both phase and amplitude. This also applies to the tilt records from the points near the glacier margin (see Table 2; Fig. 6), displaying the adjusted phases and the normalized amplitudes (gain factors) at the points in the cross-section. The data are scaled so that the phase and gain factor of the deflection record from point NF9773 in the central part of the glacier become 0 and 1.00, respectively.
Flexure Models of Floating Glaciers
Most models of tidal flexure of floating glaciers (e.g. Holds-worth, 1969; Reference Lingle, Hughes and KollmeyerLingle and others, 1981; Reference StephensonStephenson, 1984; Reference VaughanVaughan, 1994, Reference Vaughan1995) take their origin in the analysis of beams of elastic material on elastic foundations (Reference HetenyiHetenyi, 1946). Reference VaughanVaughan (1995), based on then published and unpublished tidal displacement data, concludes that the elastic-beam model with a single value of the elastic modulus 0.88 ± 0.35 GPa adequately describes almost all the data.
We also use elastic-beam theory to analyze our tidal data in the cross-section of Nioghalvfjerdsfjorden glacier where both GPS deflection data and tiltmeter data are available. The analysis is based on the detailed surface-elevation and ice-thickness profiles (Fig. 5) measured with airborne laser altimeter and ice radar in two neighbouring cross-profiles of the glacier, one located upstream, the other located downstream of the tidal observation profile (for location see Fig. 1). Instead of using the standard analytical approach presented by Reference HetenyiHetenyi (1946), which presupposes uniform ice thickness, a numerical integration procedure is chosen, which accounts for non-uniform ice-thickness variations (approximated by cubic splines fitted to the thickness data by least squares; see Fig. 6a), and which also accounts for the finite width of the glacier. The integration procedure is based on the standard Runge-Kutta method, replacing the ordinary fourth-order differential equation for the elastic deflection of a beam with a set of four first-order differential equations (Reference Press, Flannery, Teukolsky and VetterlingPress and others, 1989, p. 447). The ˚shooting method" (Reference Press, Flannery, Teukolsky and VetterlingPress and others, 1989, p. 582) is used to solve the two-point boundary-value problem arising from considering the finite width of the glacier. The procedure was checked against the analytical solution for the case of uniform ice thickness and semi-infinite glacier, resulting in insignificant deviations.
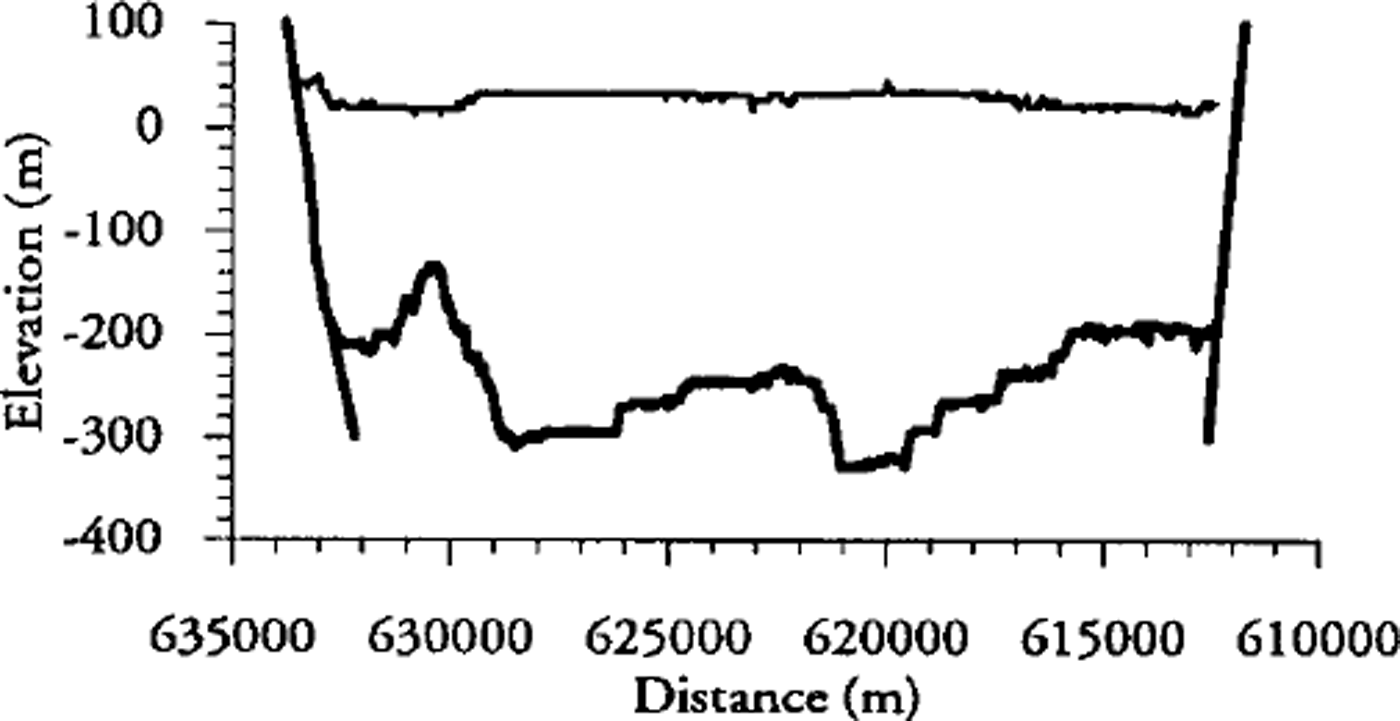
Fig. 5. Surface (thin line) and bottom (thick line) of the cross-section of Nioghalvfjerdsfjorden glacier as determined by airborne laser-altimeter and ice-radar measurements. The northwest (left) and southeast (right) rock faces bounding the glacier are also shown as thick lines.

Fig. 6. (a) Ice-thickness variation m a cross-section of Nioghalvfjerdsfjorden glacier determined by ice-radar measurements. The thick curve represents the cubic-spline approximation of the measured ice thickness used in the model calculations, (b, c) Amplitudes of relative tidal deflection and absolute tilt in the cross-section of Nioghalvfjerdsfjorden glacier as determined by an elastic-beam model. The thick lines represent results of calculations using the actually measured ice thickness. The thin lines represent results of calculations with a uniform ice thickness equal to the mean ice thickness in the profile. Measured values are marked with crosses. Standard errors of the measured deflection amplitudes are also shown. The standard error of the measured tilt amplitudes is too small to be shown, (d) Phase of the deflection and tilt measurements derived by cross-spectral analysis relative to the Danmark shavn tidal series. The phases are adjusted so that the phase of the deflection of pointNF 9773 is zero.
As model calculations with data from the two different radar profiles show only small differences, we present in the following only results from the profile located downstream. The value of the elastic modulus is set to 1.0 GPa, which is within the limits suggested by Reference VaughanVaughan (1995).
The model-predicted amplitudes of the tidal deflections and tilts are shown as thick lines in Figure 6b and c, respectively The thin lines shown in the figures represent results of a calculation with uniform ice thickness equal to the mean thickness of the glacier in the profile. Due to the relatively thin ice near the glacier margins, the regions influenced by bending are more narrow when using the actual ice thickness in the calculation instead of the mean ice thickness. The normalized amplitudes of the observed tidal deflection and tilt records are also shown in Figure 6b and c. The phases of the observed records are shown in Figure 6d.
Discussion and Conclusions
As far as the amplitudes of the deflection and tilt records are concerned, Figure 6b and c show a general agreement between model results and observations. However, there are also significant discrepancies:
The observed deflection amplitude of point NF9771 located only a few hundred metres from the southern ice margin (righthand side of the figure) deviates significantly from the model curve. Apparently, the no-slip condition used as boundary condition does not apply at this glacier margin, where the contact between glacier ice and land is an extremely steep rock slope. Some vertical sliding seems to occur either at the rock face itself or in a tidal crack near the rock wall.
Along the northern margin (lefthand side of the figure), the amplitudes of the observed deflection and tilt indicate a wider bending zone than predicted by the modelling, suggesting a suffer plate (beam) than used in the calculations. Changing the boundary condition for the beam at this margin from fixed (zero tilt) to simply supported (zero curvature) does not improve the fit between model and observations. Increasing the elastic modulus to 3 GPa (the value derived by Reference RignotRignot (1996) from fitting the tidal flexure pattern of Petermann Gletscher, North Greenland, determined by SAR interferometry, to the elastic-beam model) will bring the modelled deflection curve in closer agreement with the observations. However, the maximum value of the modelled tilt amplitudes then becomes too small, and the tilt amplitude of point AWI1 is still far too small.
Turning to the phases of our observational records, the disagreement with elastic-beam theory becomes evident. The elastic model predicts the deflection and tilt of all points to be in phase with the forcing, i.e. with the tide in the sea. Obviously this is not the case for our observations, which show systematic (and quite different) variations of the phases of the deflection and tilt records. The phase variations cannot be ascribed to differences in the arrival time of the tidal wave, which should be negligibly small within the same cross-section of the fjord.
We conclude that an elastic-beam model cannot adequately describe our data. We tentatively suggest that models of tidal bending of glaciers should use a viscoelastic approximation for glacier ice. This approximation was used in Iversen’s (1972) study of tidal bending of a glacier of a linear Maxwell material (Reference PounderPounder, 1965, p. 93). The viscoelastic-beam theory predicts more extended bending zones than the elastic theory. Also, the phase variations of the tidal deflection and tilt records are functions of the distance from the grounding fine.
The disagreement between the conclusion of earlier studies, namely, that elastic-beam theory is adequate to describe tidal flexure of glaciers, and our conclusion that it is not, results from the fact that phase information was not included in the analysis of previous workers. We use deflection and tilt data observed simultaneously at different points of the glacier over several tidal cycles, allowing us to derive both amplitude and phase information. As shown in Figure 6, the inconsistency with elastic-beam theory is most clearly demonstrated by the phase variations.
It is worth noticing that we can fit an elastic model to our deflection data by using a relatively large (compared to Vaughan’s recommendation) value of the elastic modulus (3 GPa), i.e. the same value derived from tidal deflection profiles by Reference RignotRignot (1996). This shows that phase information (probably best obtained from simultaneous tiltmeter records, extended over at least one tidal cycle, at several points in the tidal bending zone) is needed in order to distinguish between different models for tidal flexure of floating glaciers.
A comparison of our tidal deflection data with a linear viscoelastic glacier model is in progress, and will be presented elsewhere.
Acknowledgements
This work was supported by the Commission of the European Communities under contract ENV4-CT95-0124. The fieldwork benefited greatly from using the logistics platform and base camp ˚Midgardsormen" run by the Danish Polar Center near the margin of Nioghalvfjerdsfjorden glacier. Results based on Geological Survey of Denmark and Greenland (GEUS) material are published with the permission of the GEUS. Comments by A. M. Smith and an anonymous reviewer led to substantial revisions and improvements of the paper.











