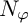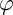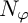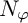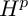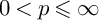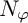1 Introduction
The theories of the Hardy, Nevanlinna, and Smirnov spaces are inextricably linked and are considered to be some of the most classical in modern complex analysis. In this paper, we study a Nevanlinna-type space
![]() $N_{\varphi }$
of analytic functions on the unit disk
$N_{\varphi }$
of analytic functions on the unit disk
![]() $\mathbb {D}$
, in the complex plane generated by a positive strongly convex nondecreasing function
$\mathbb {D}$
, in the complex plane generated by a positive strongly convex nondecreasing function
![]() $\varphi $
on
$\varphi $
on
![]() $[0, \infty )$
. These space was introduced by Rudin, and some basic information on them can be found in [Reference Rudin16]. We introduce on
$[0, \infty )$
. These space was introduced by Rudin, and some basic information on them can be found in [Reference Rudin16]. We introduce on
![]() $N_\varphi $
the linear topology given by complete, translation invariant metric. The main aim is to find a description of the topological dual space of
$N_\varphi $
the linear topology given by complete, translation invariant metric. The main aim is to find a description of the topological dual space of
![]() $N_\varphi $
for a reasonable function
$N_\varphi $
for a reasonable function
![]() $\varphi $
. To achieve that, we will describe the coefficient multipliers from
$\varphi $
. To achieve that, we will describe the coefficient multipliers from
![]() $N_\varphi $
to Hardy’s space
$N_\varphi $
to Hardy’s space
![]() $H^p$
. Finding multipliers will require some insight into the spaces
$H^p$
. Finding multipliers will require some insight into the spaces
![]() $\mathcal {H}(\Omega )$
defined by Zayed [Reference Zayed23]. We recall that, for any two spaces X and Y of analytic functions on the unit disk
$\mathcal {H}(\Omega )$
defined by Zayed [Reference Zayed23]. We recall that, for any two spaces X and Y of analytic functions on the unit disk
![]() $\mathbb {D}$
, the space of coefficient multipliers
$\mathbb {D}$
, the space of coefficient multipliers
![]() $(X,Y)$
is the completion of all sequences
$(X,Y)$
is the completion of all sequences
![]() $\{\lambda _n \}$
such that, for all
$\{\lambda _n \}$
such that, for all
![]() $f\in X$
with power series
$f\in X$
with power series
![]() $f(z)=\sum _{n=0}^\infty \widehat {f}(n) z^n$
for all
$f(z)=\sum _{n=0}^\infty \widehat {f}(n) z^n$
for all
![]() $z\in \mathbb {D}$
, function g given by
$z\in \mathbb {D}$
, function g given by
![]() $g(z):=\sum _{n=0}^\infty \lambda _n \widehat {f}(n) z^n$
for all
$g(z):=\sum _{n=0}^\infty \lambda _n \widehat {f}(n) z^n$
for all
![]() $z\in \mathbb {D}$
, is an element of Y.
$z\in \mathbb {D}$
, is an element of Y.
The starting point of our study is the so-called Nevanlinna class N defined to be the space of all functions f, analytic in the unit disk
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
 $$\begin{align*}\sup_{r\in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi} \log(1+|f(re^{i\theta})|)\,d\theta <\infty\,. \end{align*}$$
$$\begin{align*}\sup_{r\in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi} \log(1+|f(re^{i\theta})|)\,d\theta <\infty\,. \end{align*}$$
Over the years, the Nevanlinna class became one of the most classical spaces of analytic functions to consider, and it was studied in several contexts. In particular, it is known that functions from class N are quotients of two bounded analytic functions, they have radial limits almost everywhere and the embeddings
![]() $H^p\subset N$
hold for all
$H^p\subset N$
hold for all
![]() $0<p\leqslant \infty $
, where
$0<p\leqslant \infty $
, where
![]() $H^p$
is the Hardy space on the unit disk
$H^p$
is the Hardy space on the unit disk
![]() $\mathbb {D}$
(see [Reference Duren1], [Reference Garnett4]). In
$\mathbb {D}$
(see [Reference Duren1], [Reference Garnett4]). In
![]() $1929$
, Smirnov, in his work [Reference Smirnow18], considered the subspace of N containing all functions for which the family
$1929$
, Smirnov, in his work [Reference Smirnow18], considered the subspace of N containing all functions for which the family
![]() $\{\log (1+|f(re^{i\theta })|; \, r\in [0, 1)\}$
is uniformly integrable. After its inventor, this space is called the Smirnov class, and it is denoted by
$\{\log (1+|f(re^{i\theta })|; \, r\in [0, 1)\}$
is uniformly integrable. After its inventor, this space is called the Smirnov class, and it is denoted by
![]() $N^{+}$
. It took more than 40 years to find the dual of Smirnov class equipped with the natural topology. In [Reference Yanagihara22], Yanagihara found asymptotic bounds on the growth of the Taylor coefficients of a function in
$N^{+}$
. It took more than 40 years to find the dual of Smirnov class equipped with the natural topology. In [Reference Yanagihara22], Yanagihara found asymptotic bounds on the growth of the Taylor coefficients of a function in
![]() $N^{+}$
. These results are used in his paper [Reference Yanagihara21] to characterize the multipliers from
$N^{+}$
. These results are used in his paper [Reference Yanagihara21] to characterize the multipliers from
![]() $N^{+}$
into
$N^{+}$
into
![]() $H^{\infty }$
, and the dual of
$H^{\infty }$
, and the dual of
![]() $N^{+}$
. A new proof of Yanagihara’s characterization of the dual of
$N^{+}$
. A new proof of Yanagihara’s characterization of the dual of
![]() $N^{+}$
was given by McCarthy [Reference McCarthy11]. We also note that by means of solid hulls for
$N^{+}$
was given by McCarthy [Reference McCarthy11]. We also note that by means of solid hulls for
![]() $N^{+}$
, Nawrocki [Reference Nawrocki13] was able to prove Yanagihara’s result on multipliers, and simultaneously gave a description of multipliers from
$N^{+}$
, Nawrocki [Reference Nawrocki13] was able to prove Yanagihara’s result on multipliers, and simultaneously gave a description of multipliers from
![]() $N^{+}$
to other spaces of analytic functions.
$N^{+}$
to other spaces of analytic functions.
The main motivation for our work was one of the remarkable papers by Stoll, namely, [Reference Stoll20], in which Privalov’s spaces are studied. Recall that if
![]() $p\in (1, \infty )$
, then the Privalov space
$p\in (1, \infty )$
, then the Privalov space
![]() $N^p$
is defined to contain of all analytic functions on
$N^p$
is defined to contain of all analytic functions on
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
 $$\begin{align*}\sup_{r \in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi} \log^p(1+|f(re^{i\theta})|)\,d\theta <\infty\,. \end{align*}$$
$$\begin{align*}\sup_{r \in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi} \log^p(1+|f(re^{i\theta})|)\,d\theta <\infty\,. \end{align*}$$
These classes were firstly considered by Privalov in the first edition of his monograph [Reference Privalov14, p. 93], where instead of
![]() $N^p$
the symbol
$N^p$
the symbol
![]() $A_p$
is used.
$A_p$
is used.
These spaces are the natural generalization of the Nevanlinna concept. In their article, Meshtrovich and Subbotin [Reference Meshtrovich and Subbotin12] gave a description of multipliers to Hardy spaces and linear functionals for
![]() $N^p$
. The classes
$N^p$
. The classes
![]() $N^p$
are the most significant examples of more general
$N^p$
are the most significant examples of more general
![]() $N_\varphi $
spaces in which, for a given
$N_\varphi $
spaces in which, for a given
![]() $p\in (1, \infty )$
, the function
$p\in (1, \infty )$
, the function
![]() $\varphi (t)= t^p$
for all
$\varphi (t)= t^p$
for all
![]() $t\geqslant 0$
in the definition is replaced by an arbitrary strongly convex function
$t\geqslant 0$
in the definition is replaced by an arbitrary strongly convex function
![]() $\varphi $
. These, as it was mentioned above, were first introduced by Rudin [Reference Rudin16] and later were exploited also by other authors, for example, in [Reference Leśniewicz8], [Reference Stoll19], [Reference Stoll20].
$\varphi $
. These, as it was mentioned above, were first introduced by Rudin [Reference Rudin16] and later were exploited also by other authors, for example, in [Reference Leśniewicz8], [Reference Stoll19], [Reference Stoll20].
The main motivation for our work was one of the remarkable papers by Stoll, namely, [Reference Stoll20], in which Privalov’s spaces (denoted by
![]() $(\log ^{+} H)^{\alpha }$
with
$(\log ^{+} H)^{\alpha }$
with
![]() $1<\alpha <\infty $
) are studied. Let us now briefly discuss the main results of the paper. Let
$1<\alpha <\infty $
) are studied. Let us now briefly discuss the main results of the paper. Let
![]() $\varphi $
be a strongly convex function on
$\varphi $
be a strongly convex function on
![]() $\mathbb {R}_{+}:=[0, \infty ),$
that is,
$\mathbb {R}_{+}:=[0, \infty ),$
that is,
![]() $\varphi \colon \mathbb {R}_{+} \to \mathbb {R}_{+}$
is a convex, nondecreasing function with
$\varphi \colon \mathbb {R}_{+} \to \mathbb {R}_{+}$
is a convex, nondecreasing function with
![]() $\varphi (0)=0$
and
$\varphi (0)=0$
and
![]() $\varphi (t)/t\rightarrow \infty $
as
$\varphi (t)/t\rightarrow \infty $
as
![]() $t\rightarrow \infty $
. Following Rudin [Reference Rudin16], we define the space
$t\rightarrow \infty $
. Following Rudin [Reference Rudin16], we define the space
![]() $N_\varphi $
to be the space of all analytic functions in
$N_\varphi $
to be the space of all analytic functions in
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
 $$\begin{align*}\sup_{r\in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log^{+} |f(re^{i\theta})|)\,d\theta < \infty\,. \end{align*}$$
$$\begin{align*}\sup_{r\in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log^{+} |f(re^{i\theta})|)\,d\theta < \infty\,. \end{align*}$$
In §
![]() $2$
, our first goal is to define a metric on spaces
$2$
, our first goal is to define a metric on spaces
![]() $N_\varphi $
and prove preliminary results. We show that, for some special class of strongly convex functions
$N_\varphi $
and prove preliminary results. We show that, for some special class of strongly convex functions
![]() $\varphi $
,
$\varphi $
,
![]() $N_\varphi $
is an F-space, that is, a topological vector space with the topology given by complete and translation invariant metric. In §
$N_\varphi $
is an F-space, that is, a topological vector space with the topology given by complete and translation invariant metric. In §
![]() $3$
, we give a description of coefficient multipliers to Hardy spaces
$3$
, we give a description of coefficient multipliers to Hardy spaces
![]() $H^p$
. With mild assumptions on a generating function
$H^p$
. With mild assumptions on a generating function
![]() $\varphi $
, we are be able to characterize the coefficient multipliers
$\varphi $
, we are be able to characterize the coefficient multipliers
![]() $(N_\varphi ,H^p)$
,
$(N_\varphi ,H^p)$
,
![]() $p>0$
in terms of growth rate of Taylor coefficients of functions from
$p>0$
in terms of growth rate of Taylor coefficients of functions from
![]() $N_\varphi $
, as it was done in [Reference Yanagihara21], [Reference Nawrocki13] or [Reference Meshtrovich and Subbotin12] for other spaces of analytic functions on
$N_\varphi $
, as it was done in [Reference Yanagihara21], [Reference Nawrocki13] or [Reference Meshtrovich and Subbotin12] for other spaces of analytic functions on
![]() $\mathbb {D}$
. The core of this idea, which was then used by other authors, is admittedly the paper [Reference Yanagihara21] by Yanagihara. His concept of proof can be divided into two main steps. The first one is the construction of a special, bounded family consisting of analytic functions from considered space N, in which Taylor coefficients have suitable growth rate. The second step is to use information on the growth rate of coefficients in investigated space N. It was shown by Yanagihara [Reference Yanagihara22] that, if
$\mathbb {D}$
. The core of this idea, which was then used by other authors, is admittedly the paper [Reference Yanagihara21] by Yanagihara. His concept of proof can be divided into two main steps. The first one is the construction of a special, bounded family consisting of analytic functions from considered space N, in which Taylor coefficients have suitable growth rate. The second step is to use information on the growth rate of coefficients in investigated space N. It was shown by Yanagihara [Reference Yanagihara22] that, if
![]() $f\in N^{+}$
with the power series
$f\in N^{+}$
with the power series
![]() $f(z)=\sum _{k=0}^\infty \widehat {f}(k)z^k$
for all
$f(z)=\sum _{k=0}^\infty \widehat {f}(k)z^k$
for all
![]() $z\in \mathbb {D}$
, then
$z\in \mathbb {D}$
, then
![]() $\widehat {f}(k)=O(\exp [o(\sqrt {k})])$
, while for the function
$\widehat {f}(k)=O(\exp [o(\sqrt {k})])$
, while for the function
![]() $f\in N^p$
, we have that
$f\in N^p$
, we have that
![]() $\widehat {f}(k)=O(\exp [o(k^{\frac {1}{p+1}})])$
. The latter asymptotic estimate was discovered by Stoll [Reference Stoll20]. In his paper, analogously to Yanagihara for
$\widehat {f}(k)=O(\exp [o(k^{\frac {1}{p+1}})])$
. The latter asymptotic estimate was discovered by Stoll [Reference Stoll20]. In his paper, analogously to Yanagihara for
![]() $N^{+}$
, the author investigated spaces
$N^{+}$
, the author investigated spaces
![]() $F_\beta $
,
$F_\beta $
,
![]() $\beta>0$
, of all functions f analytic in
$\beta>0$
, of all functions f analytic in
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
![]() $\lim _{r\rightarrow 1-}(1-r)^\beta \log ^{+}M_{\infty }(r,f)=0$
, where
$\lim _{r\rightarrow 1-}(1-r)^\beta \log ^{+}M_{\infty }(r,f)=0$
, where
![]() $M_{\infty }(r,f):=\sup_{|z|\leqslant r}|f(z)|$
for all
$M_{\infty }(r,f):=\sup_{|z|\leqslant r}|f(z)|$
for all
![]() $r \in [0, 1)$
. Equivalently,
$r \in [0, 1)$
. Equivalently,
![]() $f\in F_\beta $
if, and only if, the condition
$f\in F_\beta $
if, and only if, the condition
 $$\begin{align*}\int_{0}^{1}M_\infty(r,f) \exp\big[-c\,(1-r)^{-\beta}\big]\,dr<\infty \end{align*}$$
$$\begin{align*}\int_{0}^{1}M_\infty(r,f) \exp\big[-c\,(1-r)^{-\beta}\big]\,dr<\infty \end{align*}$$
holds for all
![]() $c>0$
. We note that Stoll proved that, for
$c>0$
. We note that Stoll proved that, for
![]() $f\in F_\beta $
, we have
$f\in F_\beta $
, we have
![]() $\widehat {f}(n)=O(\exp [o(n^{\frac {\beta }{1+\beta }})])$
and that
$\widehat {f}(n)=O(\exp [o(n^{\frac {\beta }{1+\beta }})])$
and that
![]() $N^p\subset F_{1/p}$
which implies the desired growth rate of functions in
$N^p\subset F_{1/p}$
which implies the desired growth rate of functions in
![]() $N^p$
.
$N^p$
.
In §
![]() $3,$
we describe the growth rate of Taylor coefficients of functions in
$3,$
we describe the growth rate of Taylor coefficients of functions in
![]() $N_\varphi $
. To attain this, we find some bigger (in sense of inclusion) space for which the growth rate of Taylor coefficients of functions is known. We predict that the role of such objects can be played by the
$N_\varphi $
. To attain this, we find some bigger (in sense of inclusion) space for which the growth rate of Taylor coefficients of functions is known. We predict that the role of such objects can be played by the
![]() $\mathcal {H}(\Omega )$
spaces described by Zayed [Reference Zayed23]. These are the spaces of analytic functions on the unit disk
$\mathcal {H}(\Omega )$
spaces described by Zayed [Reference Zayed23]. These are the spaces of analytic functions on the unit disk
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
 $$\begin{align*}\int_{0}^{1} M_\infty(r,f) \exp\big[-c\,\Omega(1-r)^{-\beta}\big]\,dr<\infty\,, \end{align*}$$
$$\begin{align*}\int_{0}^{1} M_\infty(r,f) \exp\big[-c\,\Omega(1-r)^{-\beta}\big]\,dr<\infty\,, \end{align*}$$
where
![]() $\Omega $
is a positive, nonincreasing, convex, and differentiable function on
$\Omega $
is a positive, nonincreasing, convex, and differentiable function on
![]() $[0,\infty )$
, which additionally meets some requirements concerning growth rate close to the point
$[0,\infty )$
, which additionally meets some requirements concerning growth rate close to the point
![]() $0$
. It is easily seen that these are the abstract variant of spaces
$0$
. It is easily seen that these are the abstract variant of spaces
![]() $F_\beta $
. Zayed proved that, if the function
$F_\beta $
. Zayed proved that, if the function
![]() $\omega $
given by
$\omega $
given by
![]() $\omega (t):=\inf _{y>0}[\Omega (y)+ty]$
for all
$\omega (t):=\inf _{y>0}[\Omega (y)+ty]$
for all
![]() $t\geqslant 0$
satisfies some additional conditions (see [Reference Zayed23, p. 31]), then the function
$t\geqslant 0$
satisfies some additional conditions (see [Reference Zayed23, p. 31]), then the function
![]() $\Omega $
has all the properties described above, and the growth rate of Taylor coefficients of
$\Omega $
has all the properties described above, and the growth rate of Taylor coefficients of
![]() $f\in \mathcal {H}(\Omega )$
is
$f\in \mathcal {H}(\Omega )$
is
![]() $\widehat {f}(n)=O(\exp [o(\omega (n))])$
. In our work, we show that, for appropriately chosen functions
$\widehat {f}(n)=O(\exp [o(\omega (n))])$
. In our work, we show that, for appropriately chosen functions
![]() $\varphi $
, the space
$\varphi $
, the space
![]() $N_\varphi $
is a subspace of
$N_\varphi $
is a subspace of
![]() $\mathcal {H}(\Omega )$
, where
$\mathcal {H}(\Omega )$
, where
![]() $\Omega $
depends on
$\Omega $
depends on
![]() $\varphi $
and satisfies all conditions needed to exploit Zayed’s results. Then, the growth rate of Taylor coefficients of
$\varphi $
and satisfies all conditions needed to exploit Zayed’s results. Then, the growth rate of Taylor coefficients of
![]() $f \in N_\varphi $
will be given by
$f \in N_\varphi $
will be given by
![]() $\widehat {f}(n)=O(\exp [o(\omega (n))])$
, where
$\widehat {f}(n)=O(\exp [o(\omega (n))])$
, where
![]() $\omega (n)=\inf _{y>0}[\Omega (y)+ny]$
for each
$\omega (n)=\inf _{y>0}[\Omega (y)+ny]$
for each
![]() $n \geqslant 0$
.
$n \geqslant 0$
.
In §
![]() $4,$
we determine the topological dual space of
$4,$
we determine the topological dual space of
![]() $N_\varphi $
spaces. Here, as mentioned above, we will need some knowledge about the multipliers
$N_\varphi $
spaces. Here, as mentioned above, we will need some knowledge about the multipliers
![]() $(N_\varphi , H^p)$
,
$(N_\varphi , H^p)$
,
![]() $p>0$
. Our concept of proof originated in the work [Reference Duren, Romberg and Shields2] by Duren, Romberg, and Shields, who gave a description of linear functionals on
$p>0$
. Our concept of proof originated in the work [Reference Duren, Romberg and Shields2] by Duren, Romberg, and Shields, who gave a description of linear functionals on
![]() $H^p$
spaces, for
$H^p$
spaces, for
![]() $0<p<1$
. We prove that the dual space of
$0<p<1$
. We prove that the dual space of
![]() $N_\varphi $
is the same as the dual of the corresponding space
$N_\varphi $
is the same as the dual of the corresponding space
![]() $\mathcal {H}(\Omega )$
, and the following statement is true: For any linear continuous functional
$\mathcal {H}(\Omega )$
, and the following statement is true: For any linear continuous functional
![]() $L \in (N_\varphi )^{*}$
, there exists a unique function g in the disk algebra
$L \in (N_\varphi )^{*}$
, there exists a unique function g in the disk algebra
![]() $A(\mathbb {D})$
with
$A(\mathbb {D})$
with
![]() $g(z)=\sum _{n=0}^\infty \widehat {g}(n) z^n$
for all
$g(z)=\sum _{n=0}^\infty \widehat {g}(n) z^n$
for all
![]() $z\in \mathbb {D}$
, where
$z\in \mathbb {D}$
, where
![]() $\widehat {g}(n)=O(\exp [-c\,\omega (n)])$
for some
$\widehat {g}(n)=O(\exp [-c\,\omega (n)])$
for some
![]() $c>0$
and such that
$c>0$
and such that
 $$\begin{align*}L(f) = \sum_{n=0}^\infty\widehat{f}(n)\widehat{g}(n), \quad\, f\in N_{\varphi}\,, \end{align*}$$
$$\begin{align*}L(f) = \sum_{n=0}^\infty\widehat{f}(n)\widehat{g}(n), \quad\, f\in N_{\varphi}\,, \end{align*}$$
with
![]() $f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
$f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
![]() $z\in \mathbb {D}$
. Conversely, any function
$z\in \mathbb {D}$
. Conversely, any function
![]() $g\in A(\mathbb {D})$
satisfying
$g\in A(\mathbb {D})$
satisfying
![]() $\widehat {g}(n)= O(\exp [-c\,\omega (n)])$
, for some
$\widehat {g}(n)= O(\exp [-c\,\omega (n)])$
, for some
![]() $c>0$
, defines, via the foregoing expression, a continuous linear function on
$c>0$
, defines, via the foregoing expression, a continuous linear function on
![]() $N_\varphi $
.
$N_\varphi $
.
2 Definitions and preliminary results
In this section, we collect the required definitions and notation and prove some auxiliary results. The dual space of a topological linear space
![]() $X^{*}$
is the space of all continuous linear functionals on X; we denote this space by
$X^{*}$
is the space of all continuous linear functionals on X; we denote this space by
![]() $X^{*}$
. If X and Y are topological linear spaces, then
$X^{*}$
. If X and Y are topological linear spaces, then
![]() $X\hookrightarrow Y$
means that
$X\hookrightarrow Y$
means that
![]() $X \subset Y$
and the inclusion map is continuous. We write
$X \subset Y$
and the inclusion map is continuous. We write
![]() $X=Y$
whenever
$X=Y$
whenever
![]() $X\hookrightarrow Y$
and
$X\hookrightarrow Y$
and
![]() $Y\hookrightarrow X$
. Given two nonnegative functions f and g defined on the same set S, we write
$Y\hookrightarrow X$
. Given two nonnegative functions f and g defined on the same set S, we write
![]() $f \sim g$
, if there exist positive constants
$f \sim g$
, if there exist positive constants
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
such that
$\gamma _2$
such that
![]() $\gamma _1\, g(s)\leqslant f(s) \leqslant \gamma _2\, g(s)$
for all
$\gamma _1\, g(s)\leqslant f(s) \leqslant \gamma _2\, g(s)$
for all
![]() $s\in S$
.
$s\in S$
.
Let
![]() $\mathbb {D}$
be the open unit disk in the complex plane. The space of analytic functions on
$\mathbb {D}$
be the open unit disk in the complex plane. The space of analytic functions on
![]() $\mathbb {D}$
will be denoted by
$\mathbb {D}$
will be denoted by
![]() $H(\mathbb {D})$
. As usual
$H(\mathbb {D})$
. As usual
![]() $\mathbb {T}$
denotes the unit circle,
$\mathbb {T}$
denotes the unit circle,
![]() $\mathbb {T} = \{z\in \mathbb {C}; \, |z| = 1\}$
. We let m be the probability Lebesgue measure on
$\mathbb {T} = \{z\in \mathbb {C}; \, |z| = 1\}$
. We let m be the probability Lebesgue measure on
![]() $\mathbb {T}$
, and we denote by
$\mathbb {T}$
, and we denote by
![]() $L^0(\mathbb {T})$
the space of all m-measurable complex-valued almost everywhere finite functions on
$L^0(\mathbb {T})$
the space of all m-measurable complex-valued almost everywhere finite functions on
![]() $\mathbb {T}$
. In what follows, we do not distinguish functions which are equal almost everywhere. The characteristic function of a measurable set E is denoted by
$\mathbb {T}$
. In what follows, we do not distinguish functions which are equal almost everywhere. The characteristic function of a measurable set E is denoted by
![]() $\chi _E$
.
$\chi _E$
.
If a function
![]() $f\in H(\mathbb {D})$
is such that
$f\in H(\mathbb {D})$
is such that
![]() $f^{*}(e^{i\theta }) := \lim _{r\to 1-}f(re^{i\theta })$
, then
$f^{*}(e^{i\theta }) := \lim _{r\to 1-}f(re^{i\theta })$
, then
![]() $f^{*}$
is called the radial limit function of f. For
$f^{*}$
is called the radial limit function of f. For
![]() $p\in (0, \infty )$
, the Hardy space
$p\in (0, \infty )$
, the Hardy space
![]() $H^p$
consists of all
$H^p$
consists of all
![]() $f\in H(\mathbb {D})$
such that
$f\in H(\mathbb {D})$
such that
 $$\begin{align*}\|f\|_{H^p} := \sup_{r \in [0, 1)} \bigg(\frac{1}{2\pi} \int_0^{2\pi} |f(re^{i\theta})|^p\,d\theta\bigg)^{1/p} <\infty\,. \end{align*}$$
$$\begin{align*}\|f\|_{H^p} := \sup_{r \in [0, 1)} \bigg(\frac{1}{2\pi} \int_0^{2\pi} |f(re^{i\theta})|^p\,d\theta\bigg)^{1/p} <\infty\,. \end{align*}$$
The Nevanlinna class, N, consists of those functions
![]() $f \in H(\mathbb {D})$
which satisfy
$f \in H(\mathbb {D})$
which satisfy

It is a well-known fact that functions in N have radial limits. Furthermore, by subharmonicity of
![]() $\log ^{+}|f|$
for any not identically
$\log ^{+}|f|$
for any not identically
![]() $0$
holomorphic function f in
$0$
holomorphic function f in
![]() $\mathbb {D}$
, we can change the supremum in the definition of N into the limit with r tending to
$\mathbb {D}$
, we can change the supremum in the definition of N into the limit with r tending to
![]() $1-$
. We also have that
$1-$
. We also have that ![]() is a topological linear group in sense Shapiro and Shields [Reference Shapiro and Shields17], and
is a topological linear group in sense Shapiro and Shields [Reference Shapiro and Shields17], and
![]() $(N,\rho )$
is a metric space, where
$(N,\rho )$
is a metric space, where
![]() $\rho $
is given by
$\rho $
is given by
![]() $\rho (f,g):= \rule[-1pt]{1pt}{9.5pt}\hskip2pt{f-g}\hskip 2pt\rule[-1pt]{1pt}{9.5pt}$
for all
$\rho (f,g):= \rule[-1pt]{1pt}{9.5pt}\hskip2pt{f-g}\hskip 2pt\rule[-1pt]{1pt}{9.5pt}$
for all
![]() $f,g\in N$
. Note that
$f,g\in N$
. Note that
![]() $\rho $
does not generate a linear topology on N (see [Reference Shapiro and Shields17]). The largest subspace on N on which
$\rho $
does not generate a linear topology on N (see [Reference Shapiro and Shields17]). The largest subspace on N on which
![]() $\rho $
defines a linear topology is the Smirnov class, denoted by
$\rho $
defines a linear topology is the Smirnov class, denoted by
![]() $N^{+}$
. Recall that the Smirnov class
$N^{+}$
. Recall that the Smirnov class
![]() $N^{+}$
consists of all
$N^{+}$
consists of all
![]() $f\in N$
for which the family
$f\in N$
for which the family
![]() $\{\log ^{+}|f_r|;\, r\in [0, 1)\}$
is uniformly integrable, where for every
$\{\log ^{+}|f_r|;\, r\in [0, 1)\}$
is uniformly integrable, where for every
![]() $f\in H(\mathbb {D})$
and
$f\in H(\mathbb {D})$
and
![]() $r \in [0, 1)$
, we let
$r \in [0, 1)$
, we let
![]() $f_r(z):= f(rz)$
for all
$f_r(z):= f(rz)$
for all
![]() $z\in \mathbb {T}$
. It is well-known that a function
$z\in \mathbb {T}$
. It is well-known that a function
![]() $f\in N^{+}$
if, and only if,
$f\in N^{+}$
if, and only if,
 $$\begin{align*}\lim_{r\to 1-} \frac{1}{2\pi} \int_0^{2\pi} \log^{+} |f_r(e^{i\theta})| \,d\theta = \frac{1}{2\pi} \int_0^{2\pi} \log^{+}|f^{*}(e^{i\theta})|\,d\theta\,. \end{align*}$$
$$\begin{align*}\lim_{r\to 1-} \frac{1}{2\pi} \int_0^{2\pi} \log^{+} |f_r(e^{i\theta})| \,d\theta = \frac{1}{2\pi} \int_0^{2\pi} \log^{+}|f^{*}(e^{i\theta})|\,d\theta\,. \end{align*}$$
Yanagihara [Reference Yanagihara21] showed that ![]() is a Fréchet space. For more on spaces N and
is a Fréchet space. For more on spaces N and
![]() $N^{+}$
, see Duren’s book [Reference Duren1].
$N^{+}$
, see Duren’s book [Reference Duren1].
As usual by
![]() $A=A(\mathbb {D}),$
we denote the disk algebra, that is, the space of all functions holomorphic in
$A=A(\mathbb {D}),$
we denote the disk algebra, that is, the space of all functions holomorphic in
![]() $\mathbb {D}$
and continuous in
$\mathbb {D}$
and continuous in
![]() $\overline {\mathbb {D}}$
. The following proper inclusions hold for
$\overline {\mathbb {D}}$
. The following proper inclusions hold for
![]() $0<p<q\leqslant \infty $
:
$0<p<q\leqslant \infty $
:
Deep investigation of Nevanlinna and Hardy spaces and many interesting results obtained, among others, by Hardy, Littlewood, Riesz, and Nevanlinna were a motivation for some natural generalizations. Linking standard definitions of
![]() $H^p$
and N, Privalov defined spaces
$H^p$
and N, Privalov defined spaces
![]() $N^p$
,
$N^p$
,
![]() $1<p<\infty $
(see [Reference Privalov14]). For given
$1<p<\infty $
(see [Reference Privalov14]). For given
![]() $p\in (1, \infty )$
, the space
$p\in (1, \infty )$
, the space
![]() $N^p$
consists of all functions
$N^p$
consists of all functions
![]() $f \in H(\mathbb {D})$
such that
$f \in H(\mathbb {D})$
such that
 $$ \begin{align*} \sup_{r\in [0, 1)} \frac{1}{2\pi} \int_{0}^{2\pi}\log^p(1+|f(re^{i\theta})|)\,d\theta <\infty\,. \end{align*} $$
$$ \begin{align*} \sup_{r\in [0, 1)} \frac{1}{2\pi} \int_{0}^{2\pi}\log^p(1+|f(re^{i\theta})|)\,d\theta <\infty\,. \end{align*} $$
For each
![]() $q>p>1$
, the following inclusions hold:
$q>p>1$
, the following inclusions hold:
 $$\begin{align*}N^q\subsetneq N^p,\quad \bigcup_{r>0}H^r\subsetneq\bigcap_{p>1}N^p, \quad\, \bigcup_{p>1}N^p\subsetneq N^{+}\subsetneq N\,. \end{align*}$$
$$\begin{align*}N^q\subsetneq N^p,\quad \bigcup_{r>0}H^r\subsetneq\bigcap_{p>1}N^p, \quad\, \bigcup_{p>1}N^p\subsetneq N^{+}\subsetneq N\,. \end{align*}$$
We note that
![]() $f\in N^p$
if, and only if,
$f\in N^p$
if, and only if,
![]() $f \in N^{+}$
and
$f \in N^{+}$
and
![]() $\log ^{+}|f^*|\in L^p(\mathbb {T})$
(see [Reference Stoll20]). If
$\log ^{+}|f^*|\in L^p(\mathbb {T})$
(see [Reference Stoll20]). If
![]() $f\in N^p$
then, for all
$f\in N^p$
then, for all
![]() $z\in \mathbb {D}$
, we have
$z\in \mathbb {D}$
, we have
 $$\begin{align*}[\log^{+}|f(z)|]^p\leqslant \frac{1}{2\pi}\int_0^{2\pi}P(z, e^{i\theta})(\log^{+}|f^*(e^{i\theta})|)^{p}\,d\theta\,, \end{align*}$$
$$\begin{align*}[\log^{+}|f(z)|]^p\leqslant \frac{1}{2\pi}\int_0^{2\pi}P(z, e^{i\theta})(\log^{+}|f^*(e^{i\theta})|)^{p}\,d\theta\,, \end{align*}$$
and
 $$\begin{align*}\log^p(1+|f(z)|)\leqslant \frac{1}{2\pi}\int_0^{2\pi}P(z,e^{i\theta})\log^p(1+|f^*(e^{i\theta})|)\,d\theta\,, \end{align*}$$
$$\begin{align*}\log^p(1+|f(z)|)\leqslant \frac{1}{2\pi}\int_0^{2\pi}P(z,e^{i\theta})\log^p(1+|f^*(e^{i\theta})|)\,d\theta\,, \end{align*}$$
where P is the Poisson kernel defined for all
![]() $z\in \mathbb {D}$
and
$z\in \mathbb {D}$
and
![]() $\theta \in [0, 2\pi )$
by
$\theta \in [0, 2\pi )$
by
 $$\begin{align*}P(z,e^{i\theta}) =\frac{1-|z|^2}{|e^{i\theta}-z|^2}\,. \end{align*}$$
$$\begin{align*}P(z,e^{i\theta}) =\frac{1-|z|^2}{|e^{i\theta}-z|^2}\,. \end{align*}$$
Furthermore,
 $$\begin{align*}\lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}\log^p(1+|f(re^{i\theta})|)\,d\theta =\frac{1}{2\pi}\int_0^{2\pi}\log^p(1+|f^*(e^{i\theta})|)\,d\theta\,. \end{align*}$$
$$\begin{align*}\lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}\log^p(1+|f(re^{i\theta})|)\,d\theta =\frac{1}{2\pi}\int_0^{2\pi}\log^p(1+|f^*(e^{i\theta})|)\,d\theta\,. \end{align*}$$
Observe that
![]() $N^{+}$
is a “natural limit” of
$N^{+}$
is a “natural limit” of
![]() $N^p$
as
$N^p$
as
![]() $p\to 1+$
. This observation leads to the definition of a topology on
$p\to 1+$
. This observation leads to the definition of a topology on
![]() $N^p$
defined by the metric
$N^p$
defined by the metric
 $$\begin{align*}\rho_p(f,g) = \Big(\frac{1}{2\pi}\int_{-0}^{2\pi}\log^p(1+|f^{*}(e^{i\theta})-g^*(e^{i\theta})|)\, \mathit{d\theta}\Big)^{1/p}, \quad\, f, g\in N^p\,. \end{align*}$$
$$\begin{align*}\rho_p(f,g) = \Big(\frac{1}{2\pi}\int_{-0}^{2\pi}\log^p(1+|f^{*}(e^{i\theta})-g^*(e^{i\theta})|)\, \mathit{d\theta}\Big)^{1/p}, \quad\, f, g\in N^p\,. \end{align*}$$
![]() $(N^p,\rho _p)$
is an F-algebra. It is a generalization of Yanagihara’s concept for the class
$(N^p,\rho _p)$
is an F-algebra. It is a generalization of Yanagihara’s concept for the class
![]() $N^{+}$
, which can be found in [Reference Yanagihara21]. We note that, for every
$N^{+}$
, which can be found in [Reference Yanagihara21]. We note that, for every
![]() $f\in N^p$
, we have
$f\in N^p$
, we have
Our main motivation is to bring investigations on Privalov spaces to a more general setting, and find a general scheme for solving particular problems in the theory of abstract Nevanlinna classes. We will be mainly interested in problems concerning coefficient multipliers and the topological dual.
Before we will discuss in more details, these classes we point out that the study of many other important spaces of analytic functions is motivated by that fact, that for any not identically
![]() $0$
function
$0$
function
![]() $f\in H(\mathbb {D})$
and a convex nondecreasing function
$f\in H(\mathbb {D})$
and a convex nondecreasing function
![]() $\phi \colon \mathbb {R} \to [0, \infty )$
the function
$\phi \colon \mathbb {R} \to [0, \infty )$
the function
![]() $\phi (\log |f|)$
is subharmonic (we let
$\phi (\log |f|)$
is subharmonic (we let
![]() $\phi (-\infty ):= \lim _{t\to - \infty } \phi (t)=0$
and as usual it is understood that
$\phi (-\infty ):= \lim _{t\to - \infty } \phi (t)=0$
and as usual it is understood that
![]() $\log 0 := - \infty $
).
$\log 0 := - \infty $
).
Following [Reference Rudin16], a function
![]() $\phi $
defined on
$\phi $
defined on
![]() $\mathbb {R}$
is said to be strongly convex if it is nonnegative, convex, and nondecreasing with
$\mathbb {R}$
is said to be strongly convex if it is nonnegative, convex, and nondecreasing with
![]() $\phi (t)/t \to \infty $
as
$\phi (t)/t \to \infty $
as
![]() $t\to \infty $
. Let D be any domain in
$t\to \infty $
. Let D be any domain in
![]() $\mathbb {C}$
. An analytic function on D is said to be in the Hardy–Orlicz class
$\mathbb {C}$
. An analytic function on D is said to be in the Hardy–Orlicz class
![]() $H_\phi (D)$
if there exists a harmonic function h on D such that
$H_\phi (D)$
if there exists a harmonic function h on D such that
The following result will be of essential importance for us. It refers to equivalent definitions of Hardy–Orlicz class
![]() $H_{\phi }(\mathbb {D})$
on the unit disk
$H_{\phi }(\mathbb {D})$
on the unit disk
![]() $\mathbb {D}$
,
$\mathbb {D}$
,
 $$\begin{align*}H_{\phi}(\mathbb{D})= \bigg\{f\in N^{+}; \, \sup_{r\in [0, 1)} \int_0^{2\pi} \phi(\log|f(re^{i\theta})|)\,d\theta = \int_0^{2\pi} \phi(\log|f^{*}(e^{i\theta})|)\,d\theta \bigg\}\,. \end{align*}$$
$$\begin{align*}H_{\phi}(\mathbb{D})= \bigg\{f\in N^{+}; \, \sup_{r\in [0, 1)} \int_0^{2\pi} \phi(\log|f(re^{i\theta})|)\,d\theta = \int_0^{2\pi} \phi(\log|f^{*}(e^{i\theta})|)\,d\theta \bigg\}\,. \end{align*}$$
For details and the background related to Hardy–Orlicz classes, we refer to [Reference Hasumi and Kataoka5], [Reference Leśniewicz8], [Reference Rosenblum and Rovnyak15], [Reference Stoll19].
The notation and assumptions that we set down here will be used throughout the paper. We will consider only strongly convex functions on
![]() $\mathbb {R}_{+}$
, that is,
$\mathbb {R}_{+}$
, that is,
![]() $\varphi \colon \mathbb {R}_{+} \to \mathbb {R}_{+}$
such that
$\varphi \colon \mathbb {R}_{+} \to \mathbb {R}_{+}$
such that
![]() $\varphi $
is convex with
$\varphi $
is convex with
![]() $\phi (0)=0$
and
$\phi (0)=0$
and
![]() $\varphi (t)/t\rightarrow \infty $
as
$\varphi (t)/t\rightarrow \infty $
as
![]() $t\rightarrow \infty $
. The function
$t\rightarrow \infty $
. The function
![]() $\varphi $
is said to satisfy the
$\varphi $
is said to satisfy the
![]() $\Delta _2$
-condition (
$\Delta _2$
-condition (
![]() $\varphi \in (\Delta _2)$
for short), if there exists a constant
$\varphi \in (\Delta _2)$
for short), if there exists a constant
![]() $\gamma>0$
such that
$\gamma>0$
such that
![]() $\varphi (2t)\leqslant \gamma \varphi (t)$
for all
$\varphi (2t)\leqslant \gamma \varphi (t)$
for all
![]() $t>0$
. In what follows, we denote by
$t>0$
. In what follows, we denote by
![]() $\Phi _2^{sc},$
the set of all continuously differentiable strongly convex functions that satisfy
$\Phi _2^{sc},$
the set of all continuously differentiable strongly convex functions that satisfy
![]() $\Delta _2$
-condition. Examples of functions in
$\Delta _2$
-condition. Examples of functions in
![]() $\Phi _2^{sc}$
are
$\Phi _2^{sc}$
are
![]() $\varphi _p$
,
$\varphi _p$
,
![]() $1\leqslant p<\infty $
, defined by
$1\leqslant p<\infty $
, defined by
![]() $\varphi _{p}(t) = t^{p} \log (1 + t)$
for all
$\varphi _{p}(t) = t^{p} \log (1 + t)$
for all
![]() $t\geqslant 0$
.
$t\geqslant 0$
.
If
![]() $\varphi $
is a strongly convex function on
$\varphi $
is a strongly convex function on
![]() $\mathbb {R}_{+}$
, we let
$\mathbb {R}_{+}$
, we let
![]() $\phi (t):=0$
for all
$\phi (t):=0$
for all
![]() $t<0$
and
$t<0$
and
![]() $\phi (t):= \varphi (t)$
for all
$\phi (t):= \varphi (t)$
for all
![]() $t \geqslant 0$
. Then the Hardy–Orlicz class
$t \geqslant 0$
. Then the Hardy–Orlicz class
![]() $H_{\phi }(\mathbb {D})$
is called the abstract Nevanlinna class and it is denoted by
$H_{\phi }(\mathbb {D})$
is called the abstract Nevanlinna class and it is denoted by
![]() $N_\varphi $
. Following the above remarks,
$N_\varphi $
. Following the above remarks,
 $$\begin{align*}N_\varphi = \bigg\{f\in N^{+}; \,\, \sup_{r\in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi} \varphi(\log^{+} |f(re^{i\theta})|)\,d\theta <\infty\bigg\}\,. \end{align*}$$
$$\begin{align*}N_\varphi = \bigg\{f\in N^{+}; \,\, \sup_{r\in [0, 1)}\frac{1}{2\pi}\int_0^{2\pi} \varphi(\log^{+} |f(re^{i\theta})|)\,d\theta <\infty\bigg\}\,. \end{align*}$$
It follows from [Reference Rudin16] that, for all strongly convex functions
![]() $\varphi \colon \mathbb {R} \to \mathbb {R}_{+}$
, one has
$\varphi \colon \mathbb {R} \to \mathbb {R}_{+}$
, one has
where the sum is taken over all strongly convex functions
![]() $\phi \colon \mathbb {R} \to \mathbb {R}_{+}$
. Furthermore,
$\phi \colon \mathbb {R} \to \mathbb {R}_{+}$
. Furthermore,
![]() $f\in N_\varphi $
if and only if
$f\in N_\varphi $
if and only if
![]() $\varphi (\log ^{+} |f^{*}|)\in L^1(\mathbb {T})$
and, for all
$\varphi (\log ^{+} |f^{*}|)\in L^1(\mathbb {T})$
and, for all
![]() $z\in \mathbb {D},$
$z\in \mathbb {D},$
 $$ \begin{align*} \varphi(\log^{+} |f(z)|))\leqslant F(z):=\frac{1}{2\pi}\int_0^{2\pi}P(z,e^{i\theta})\varphi(\log^{+} |f^*(e^{i\theta})|)\,d\theta\,. \end{align*} $$
$$ \begin{align*} \varphi(\log^{+} |f(z)|))\leqslant F(z):=\frac{1}{2\pi}\int_0^{2\pi}P(z,e^{i\theta})\varphi(\log^{+} |f^*(e^{i\theta})|)\,d\theta\,. \end{align*} $$
Due to the inequalities
![]() $\log ^{+}|f|$
can be exchanged with
$\log ^{+}|f|$
can be exchanged with
![]() $\log (1+|f|)$
in the definition of N and
$\log (1+|f|)$
in the definition of N and
![]() $N^{+}$
. Furthermore, the
$N^{+}$
. Furthermore, the
![]() $\Delta _2$
-condition for
$\Delta _2$
-condition for
![]() $\varphi $
yields
$\varphi $
yields
 $$ \begin{align*} \varphi(\log(1+|z|))& \leqslant \varphi(\log 2+\log^+|z|) \leqslant \varphi\Big(2\Big(\frac{1}{2}\log 2+\frac{1}{2}\log^+|z|\Big)\Big)\\ & \leqslant \frac{\gamma}{2} \big(\varphi(\log 2)+\varphi(\log^+|z|)\big), \quad\, z\in\mathbb{C}\,. \end{align*} $$
$$ \begin{align*} \varphi(\log(1+|z|))& \leqslant \varphi(\log 2+\log^+|z|) \leqslant \varphi\Big(2\Big(\frac{1}{2}\log 2+\frac{1}{2}\log^+|z|\Big)\Big)\\ & \leqslant \frac{\gamma}{2} \big(\varphi(\log 2)+\varphi(\log^+|z|)\big), \quad\, z\in\mathbb{C}\,. \end{align*} $$
We conclude that, in the case
![]() $\varphi \in (\Delta _2)$
, the above inequality shows that, for every
$\varphi \in (\Delta _2)$
, the above inequality shows that, for every
![]() $f\in N_\varphi $
, we have
$f\in N_\varphi $
, we have
 $$ \begin{align*} \sup_{r\in [0, 1)}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))\,d\theta<\infty\,. \end{align*} $$
$$ \begin{align*} \sup_{r\in [0, 1)}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))\,d\theta<\infty\,. \end{align*} $$
Now, it is easy to see that the above condition allows us to define
![]() $N_{\varphi }$
in a new way. Moreover, from Theorem [Reference Stoll19, Th. 2] and the fact that
$N_{\varphi }$
in a new way. Moreover, from Theorem [Reference Stoll19, Th. 2] and the fact that
![]() $z\mapsto \log (1+|z|)$
is subharmonic in
$z\mapsto \log (1+|z|)$
is subharmonic in
![]() $\mathbb {D}$
, we deduce that, for all
$\mathbb {D}$
, we deduce that, for all
![]() $f\in N_\varphi $
, one has
$f\in N_\varphi $
, one has
 $$ \begin{align*} \varphi(\log(1+|f(z)|)) \leqslant \frac{1}{2\pi}\int_0^{2\pi}P(z, e^{i\theta})\varphi(\log(1+|f^{*}(e^{i\theta})|))\,d\theta, \quad\, z\in \mathbb{D}\,, \end{align*} $$
$$ \begin{align*} \varphi(\log(1+|f(z)|)) \leqslant \frac{1}{2\pi}\int_0^{2\pi}P(z, e^{i\theta})\varphi(\log(1+|f^{*}(e^{i\theta})|))\,d\theta, \quad\, z\in \mathbb{D}\,, \end{align*} $$
and from the properties of subharmonic functions, Fatou’s Lemma and Tonelli’s Theorem, we easily get
 $$ \begin{align*} \frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f^*(e^{i\theta})|))\,d\theta & = \lim_{r\rightarrow 1-}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))\,d\theta \\ & = \sup_{r\in [0, 1)}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))\,d\theta\,. \end{align*} $$
$$ \begin{align*} \frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f^*(e^{i\theta})|))\,d\theta & = \lim_{r\rightarrow 1-}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))\,d\theta \\ & = \sup_{r\in [0, 1)}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))\,d\theta\,. \end{align*} $$
It is now clear that we can define
![]() $N_\varphi $
as the space of all functions
$N_\varphi $
as the space of all functions
![]() $f\in N^{+}$
for which
$f\in N^{+}$
for which
 $$\begin{align*}\|f\|_\varphi :=\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f^{*}(e^{i\theta})|))\,d\theta<\infty\,. \end{align*}$$
$$\begin{align*}\|f\|_\varphi :=\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f^{*}(e^{i\theta})|))\,d\theta<\infty\,. \end{align*}$$
We note that, from the above inequality, we can derive the following useful estimate valid for all functions f in
![]() $N_\varphi $
:
$N_\varphi $
:
 $$ \begin{align*} \varphi(\log(1+|f(z)|))\leqslant \frac{1+|z|}{1-|z|}\|f\|_\varphi, \quad\, z\in \mathbb{D}\,. \end{align*} $$
$$ \begin{align*} \varphi(\log(1+|f(z)|))\leqslant \frac{1+|z|}{1-|z|}\|f\|_\varphi, \quad\, z\in \mathbb{D}\,. \end{align*} $$
In particular, this implies that, for every
![]() $f\in N_\varphi $
, we have
$f\in N_\varphi $
, we have
 $$ \begin{align*} \sup_{|z|\leqslant r} |f(z)| \leqslant\exp\bigg(\varphi^{-1}\bigg(\frac{2\|f\|_\varphi}{1-r}\bigg)\bigg)-1, \quad\, 0\leqslant r<1\,. \end{align*} $$
$$ \begin{align*} \sup_{|z|\leqslant r} |f(z)| \leqslant\exp\bigg(\varphi^{-1}\bigg(\frac{2\|f\|_\varphi}{1-r}\bigg)\bigg)-1, \quad\, 0\leqslant r<1\,. \end{align*} $$
Now, we define a topological structure on spaces
![]() $N_\varphi $
. Our goal is to define a metric for
$N_\varphi $
. Our goal is to define a metric for
![]() $N_\varphi $
, for all functions
$N_\varphi $
, for all functions
![]() $\varphi $
satisfying the conditions from the previous section. Let us begin with the following definition. Let X be a linear space. Following [Reference Kalton, Peck and Roberts6], the functional
$\varphi $
satisfying the conditions from the previous section. Let us begin with the following definition. Let X be a linear space. Following [Reference Kalton, Peck and Roberts6], the functional
![]() $\|\cdot \|\colon X\to [0,\infty )$
is called a
$\|\cdot \|\colon X\to [0,\infty )$
is called a
![]() $\Delta $
-norm on X, if it fulfills the following conditions for all x,
$\Delta $
-norm on X, if it fulfills the following conditions for all x,
![]() $y\in X$
:
$y\in X$
:
-
(i)
 $\|x\|>0$
for
$\|x\|>0$
for
 $x\neq 0$
.
$x\neq 0$
. -
(ii)
 $\|\lambda x\|\leqslant \|x\|$
for all
$\|\lambda x\|\leqslant \|x\|$
for all
 $x\in X$
and
$x\in X$
and
 $|\lambda |\leqslant 1$
.
$|\lambda |\leqslant 1$
. -
(iii) There exists a constant
 $C>0$
such that
$C>0$
such that
 $\|x+y\| \leqslant C\max \{\|x\|,\|y\|\}$
for all
$\|x+y\| \leqslant C\max \{\|x\|,\|y\|\}$
for all
 $x, y\in X$
.
$x, y\in X$
. -
(iv)
 $\lim _{\lambda \to 0}\|\lambda \,x\|=0$
for all
$\lim _{\lambda \to 0}\|\lambda \,x\|=0$
for all
 $x\in X$
.
$x\in X$
.
If
![]() $\|\cdot \|$
is a
$\|\cdot \|$
is a
![]() $\Delta $
-norm on X, it defines a metrizable topology
$\Delta $
-norm on X, it defines a metrizable topology
![]() $\tau $
on X for which
$\tau $
on X for which
forms a countable base of 0 neighborhoods. Hence, a sequence
![]() $\{x_n\}\subset X$
is convergent in
$\{x_n\}\subset X$
is convergent in
![]() $(X,\tau )$
to some element
$(X,\tau )$
to some element
![]() $x\in X$
if, and only if,
$x\in X$
if, and only if,
![]() $\|x_n-x\|\to 0$
. We note that from [Reference Kalton, Peck and Roberts6, Th. 1.2], it follows that the functional
$\|x_n-x\|\to 0$
. We note that from [Reference Kalton, Peck and Roberts6, Th. 1.2], it follows that the functional
![]() $\|\cdot \|^{*}$
defined by
$\|\cdot \|^{*}$
defined by
 $$ \begin{align*} \|x\|^{*} = \inf \bigg\{\sum_{j=1}^n\|x_j\|^{\delta}_{\varphi}; \,\,\, \sum_{j=1}^{n} x_j=x, \,\, n\in \mathbb{N} \bigg\} \end{align*} $$
$$ \begin{align*} \|x\|^{*} = \inf \bigg\{\sum_{j=1}^n\|x_j\|^{\delta}_{\varphi}; \,\,\, \sum_{j=1}^{n} x_j=x, \,\, n\in \mathbb{N} \bigg\} \end{align*} $$
is an F-norm on
![]() $N_\varphi $
satisfying condition
$N_\varphi $
satisfying condition
where
![]() $\delta>0$
is chosen such that
$\delta>0$
is chosen such that
![]() $C^\delta =2$
.
$C^\delta =2$
.
We observe that
![]() $\|\cdot \|_\varphi $
defines a
$\|\cdot \|_\varphi $
defines a
![]() $\Delta $
-norm on
$\Delta $
-norm on
![]() $N_\varphi $
. Conditions (i) and (ii) are obvious and (iii) follows by convexity and the
$N_\varphi $
. Conditions (i) and (ii) are obvious and (iii) follows by convexity and the
![]() $\Delta _2$
-condition (with constant
$\Delta _2$
-condition (with constant
![]() $\gamma $
) of
$\gamma $
) of
![]() $\varphi $
,
$\varphi $
,
 $$ \begin{align*} \|f+g\|_\varphi & \leqslant\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f^*(e^{i\theta})|)+\log(1+|g^*(e^{i\theta})|))\,d\theta\\ &\leqslant\frac{\gamma}{2}(\|f\|_\varphi+\|g\|_\varphi)\leqslant \gamma \max\big\{\|f\|_\varphi,\|g\|_\varphi\big\}\,, \end{align*} $$
$$ \begin{align*} \|f+g\|_\varphi & \leqslant\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f^*(e^{i\theta})|)+\log(1+|g^*(e^{i\theta})|))\,d\theta\\ &\leqslant\frac{\gamma}{2}(\|f\|_\varphi+\|g\|_\varphi)\leqslant \gamma \max\big\{\|f\|_\varphi,\|g\|_\varphi\big\}\,, \end{align*} $$
for all
![]() $f,g\in N_\varphi $
. Condition (iv) follows from the Lebesgue Dominated Convergence Theorem. The above mentioned remarks yield that the functional
$f,g\in N_\varphi $
. Condition (iv) follows from the Lebesgue Dominated Convergence Theorem. The above mentioned remarks yield that the functional
![]() $\|\cdot \|^*_\varphi \colon N_\varphi \to [0,\infty )$
given by the formula
$\|\cdot \|^*_\varphi \colon N_\varphi \to [0,\infty )$
given by the formula
 $$ \begin{align*} \|f\|^{*}_\varphi = \inf\bigg\{\sum_{j=1}^n\|f_j\|^\delta_\varphi; \,\,\, \sum_{j=1}^nf_j=f, \,\, n \in \mathbb{N}\bigg\} \end{align*} $$
$$ \begin{align*} \|f\|^{*}_\varphi = \inf\bigg\{\sum_{j=1}^n\|f_j\|^\delta_\varphi; \,\,\, \sum_{j=1}^nf_j=f, \,\, n \in \mathbb{N}\bigg\} \end{align*} $$
is an F-norm on
![]() $N_\varphi $
satisfying the condition
$N_\varphi $
satisfying the condition
where
![]() $\delta>0$
is chosen such that
$\delta>0$
is chosen such that
![]() $\gamma ^{\delta }=2$
.
$\gamma ^{\delta }=2$
.
It follows that
![]() $\rho _\varphi (f,g)=\|f-g\|^{*}_\varphi $
is a metric on
$\rho _\varphi (f,g)=\|f-g\|^{*}_\varphi $
is a metric on
![]() $N_\varphi $
. We can now proceed to the problem of completeness of
$N_\varphi $
. We can now proceed to the problem of completeness of
![]() $N_\varphi $
. From the above inequalities, it is also clear that topologies on
$N_\varphi $
. From the above inequalities, it is also clear that topologies on
![]() $N_\varphi $
generated by
$N_\varphi $
generated by
![]() $\|f-g\|_\varphi $
and
$\|f-g\|_\varphi $
and
![]() $\rho _\varphi (f,g)$
are equivalent. This observation will simplify our approach.
$\rho _\varphi (f,g)$
are equivalent. This observation will simplify our approach.
Using methods from [Reference Stoll20] in some generalized way, we will prove the following theorem.
Theorem 2.1. Let
![]() $\varphi \in \Phi _2^{sc}$
. The space
$\varphi \in \Phi _2^{sc}$
. The space
![]() $N_\varphi $
, with the topology given by the metric
$N_\varphi $
, with the topology given by the metric
![]() $\rho _\varphi $
, is an
$\rho _\varphi $
, is an
![]() $F-$
algebra
$F-$
algebra
![]() $($
topological vector space with the topology given by complete, translation invariant metric
$($
topological vector space with the topology given by complete, translation invariant metric
![]() $)$
. Furthermore, if
$)$
. Furthermore, if
![]() $f\in N_\varphi $
, then
$f\in N_\varphi $
, then
Before giving the proof of the above theorem, we need the following lemma.
Lemma 2.2. If
![]() $\varphi \in \Phi ^{sc}_2$
and
$\varphi \in \Phi ^{sc}_2$
and
![]() $f\in N_\varphi $
, then
$f\in N_\varphi $
, then
 $$\begin{align*}\lim_{r\rightarrow 1}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log^+|f_r(e^{i\theta})-f^{*}(e^{i\theta})|)\,d\theta =0\,. \end{align*}$$
$$\begin{align*}\lim_{r\rightarrow 1}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log^+|f_r(e^{i\theta})-f^{*}(e^{i\theta})|)\,d\theta =0\,. \end{align*}$$
Proof. From [Reference Stoll20, Th. 4], it is sufficient to show that, if
![]() $\varphi \in \Phi ^{sc}_2$
, then the inequality
$\varphi \in \Phi ^{sc}_2$
, then the inequality
is valid for some
![]() $c_1$
,
$c_1$
,
![]() $c_2>0$
and all a,
$c_2>0$
and all a,
![]() $b\geqslant 0$
. In fact, by
$b\geqslant 0$
. In fact, by
![]() $\varphi \in (\Delta _2)$
, we get that
$\varphi \in (\Delta _2)$
, we get that
 $$ \begin{align*} \varphi(\log^{+}(a+b)) & \leqslant \varphi(\log(1+a+b)) \leqslant \gamma [\varphi(\log(1+a)+\varphi(\log(1+b)] \\ &\leqslant \gamma^2[(\varphi(\log^{+}a) + \varphi(\log^{+}b) + 2\varphi(\log2))]\,.\\[-37pt] \end{align*} $$
$$ \begin{align*} \varphi(\log^{+}(a+b)) & \leqslant \varphi(\log(1+a+b)) \leqslant \gamma [\varphi(\log(1+a)+\varphi(\log(1+b)] \\ &\leqslant \gamma^2[(\varphi(\log^{+}a) + \varphi(\log^{+}b) + 2\varphi(\log2))]\,.\\[-37pt] \end{align*} $$
Proof of Theorem 2.1
The fact that
![]() $N_\varphi $
is an algebra follows from the inequality
$N_\varphi $
is an algebra follows from the inequality
We show now that
![]() $(N_\varphi , \|\cdot \|_\varphi ^{*})$
is a complete metric space. Let
$(N_\varphi , \|\cdot \|_\varphi ^{*})$
is a complete metric space. Let
![]() $\{f_n\}$
be a Cauchy sequence in
$\{f_n\}$
be a Cauchy sequence in
![]() $N_\varphi $
. Thus, there exists
$N_\varphi $
. Thus, there exists
![]() $C>0$
such
$C>0$
such
![]() $\|f_n\|_\varphi \leqslant C$
for each
$\|f_n\|_\varphi \leqslant C$
for each
![]() $n\in \mathbb {N}$
. Applying the estimate
$n\in \mathbb {N}$
. Applying the estimate
 $$\begin{align*}\sup_{|z|\leqslant r} |f(z)| \leqslant\exp\bigg(\varphi^{-1}\bigg(\frac{2\|f\|_\varphi}{1-r}\bigg)\bigg)-1, \quad\, 0\leqslant r<1\,, \end{align*}$$
$$\begin{align*}\sup_{|z|\leqslant r} |f(z)| \leqslant\exp\bigg(\varphi^{-1}\bigg(\frac{2\|f\|_\varphi}{1-r}\bigg)\bigg)-1, \quad\, 0\leqslant r<1\,, \end{align*}$$
we conclude that the sequence
![]() $\{f_n\}$
converges uniformly on any compact subset of
$\{f_n\}$
converges uniformly on any compact subset of
![]() $\mathbb {D}$
to some function f, and so from the Weierstrass theorem,
$\mathbb {D}$
to some function f, and so from the Weierstrass theorem,
![]() $f\in H(\mathbb {D})$
. Hence
$f\in H(\mathbb {D})$
. Hence
 $$\begin{align*}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))dt=\lim_{n\rightarrow\infty}\frac{1}{2\pi} \int_0^{2\pi}\varphi(\log(1+|f_n(re^{i\theta})|))\,d\theta\leqslant C\,, \end{align*}$$
$$\begin{align*}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f(re^{i\theta})|))dt=\lim_{n\rightarrow\infty}\frac{1}{2\pi} \int_0^{2\pi}\varphi(\log(1+|f_n(re^{i\theta})|))\,d\theta\leqslant C\,, \end{align*}$$
for every
![]() $0<r<1$
, so
$0<r<1$
, so
![]() $f\in N_\varphi $
(see [Reference Hasumi and Kataoka5]). We also observe that by
$f\in N_\varphi $
(see [Reference Hasumi and Kataoka5]). We also observe that by
![]() $f \in N^{+}$
one has
$f \in N^{+}$
one has
 $$ \begin{align*} \frac{1}{2\pi}&\int_0^{2\pi}\varphi(\log(1+|f_n(re^{i\theta})-f(re^{i\theta})|))\,d\theta \\ &\leqslant \lim_{m\rightarrow\infty}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f_n(re^{i\theta}) - f_m(re^{i\theta})|))\,d\theta \leqslant \lim_{m\rightarrow \infty} \|f_n-f_m\|_{\varphi}\,. \end{align*} $$
$$ \begin{align*} \frac{1}{2\pi}&\int_0^{2\pi}\varphi(\log(1+|f_n(re^{i\theta})-f(re^{i\theta})|))\,d\theta \\ &\leqslant \lim_{m\rightarrow\infty}\frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f_n(re^{i\theta}) - f_m(re^{i\theta})|))\,d\theta \leqslant \lim_{m\rightarrow \infty} \|f_n-f_m\|_{\varphi}\,. \end{align*} $$
Combining with
![]() $\lim _{r\to 1-}\frac {1}{2\pi }\int _0^{2\pi }\varphi (\log (1+|f(re^{i\theta })|))\,d\theta =\frac {1}{2\pi }\int _0^{2\pi } \varphi (\log (1+|f^*(e^{i\theta })|))\,d\theta $
, we get that
$\lim _{r\to 1-}\frac {1}{2\pi }\int _0^{2\pi }\varphi (\log (1+|f(re^{i\theta })|))\,d\theta =\frac {1}{2\pi }\int _0^{2\pi } \varphi (\log (1+|f^*(e^{i\theta })|))\,d\theta $
, we get that
This yields that
![]() $\rho _\varphi (f_n, f) \to 0$
as
$\rho _\varphi (f_n, f) \to 0$
as
![]() $n\to \infty $
. Thus, it remains to prove that
$n\to \infty $
. Thus, it remains to prove that
Since
![]() $f_r(\xi ) \to f^{*}(\xi )\ m$
-a.e. on
$f_r(\xi ) \to f^{*}(\xi )\ m$
-a.e. on
![]() $\mathbb {T}$
as
$\mathbb {T}$
as
![]() $r\rightarrow 1-$
,
$r\rightarrow 1-$
,
![]() $\varphi (\log (1+|f_r(\xi ) - f^{*}(\xi )|)) \to 0\ m$
-a.e. as
$\varphi (\log (1+|f_r(\xi ) - f^{*}(\xi )|)) \to 0\ m$
-a.e. as
![]() $r\rightarrow 1-$
. Take a sequence
$r\rightarrow 1-$
. Take a sequence
![]() $\{r_n\}$
with
$\{r_n\}$
with
![]() $r_n\rightarrow 1-$
as
$r_n\rightarrow 1-$
as
![]() $n\to \infty $
and fix
$n\to \infty $
and fix
![]() $\varepsilon>0$
. From Egorov’s theorem, there exists a set
$\varepsilon>0$
. From Egorov’s theorem, there exists a set
![]() $E\in \mathbb {T}$
such that,
$E\in \mathbb {T}$
such that,
![]() $m(\mathbb {T}\backslash E)<\varepsilon $
and
$m(\mathbb {T}\backslash E)<\varepsilon $
and
![]() $\lim _{n\to \infty } \varphi (\log (1 + |f_{r_n}(e^{i\theta }) - f^{*}(e^{i\theta })|)) = 0$
uniformly on E. Clearly,
$\lim _{n\to \infty } \varphi (\log (1 + |f_{r_n}(e^{i\theta }) - f^{*}(e^{i\theta })|)) = 0$
uniformly on E. Clearly,
In consequence, we obtain
 $$ \begin{align*} &\lim_{n\rightarrow\infty} \frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f_{r_n}(e^{i\theta})-f^{*}(e^{i\theta})|))\,d\theta\\ &=\lim_{n\rightarrow\infty}\frac{1}{2\pi}\Big(\int_E+\int_{\mathbb{T}\backslash E}\varphi(\log(1+|f_{r_n}(e^{i\theta}) -f^{*}(e^{i\theta})|))\,d\theta \Big)\\ &=\lim_{n\rightarrow\infty}\frac{1}{2\pi}\int_{\mathbb{T}\backslash E}\varphi(\log(1+|f_{r_n}(e^{i\theta}) - f^{*}(e^{i\theta})|))\,d\theta \\ & \leqslant \frac{\gamma}{2\pi}\Big[\varphi(\log 2)m(\mathbb{T}\backslash E) + \lim_{n\rightarrow\infty}\int_0^{2\pi}\varphi(\log^+|f_{r_n}(e^{i\theta}) - f^*(e^{i\theta})|)dt\Big]\,. \end{align*} $$
$$ \begin{align*} &\lim_{n\rightarrow\infty} \frac{1}{2\pi}\int_0^{2\pi}\varphi(\log(1+|f_{r_n}(e^{i\theta})-f^{*}(e^{i\theta})|))\,d\theta\\ &=\lim_{n\rightarrow\infty}\frac{1}{2\pi}\Big(\int_E+\int_{\mathbb{T}\backslash E}\varphi(\log(1+|f_{r_n}(e^{i\theta}) -f^{*}(e^{i\theta})|))\,d\theta \Big)\\ &=\lim_{n\rightarrow\infty}\frac{1}{2\pi}\int_{\mathbb{T}\backslash E}\varphi(\log(1+|f_{r_n}(e^{i\theta}) - f^{*}(e^{i\theta})|))\,d\theta \\ & \leqslant \frac{\gamma}{2\pi}\Big[\varphi(\log 2)m(\mathbb{T}\backslash E) + \lim_{n\rightarrow\infty}\int_0^{2\pi}\varphi(\log^+|f_{r_n}(e^{i\theta}) - f^*(e^{i\theta})|)dt\Big]\,. \end{align*} $$
This completes the proof by Lemma 2.2.
From now on, we will be using some standard notation, namely,
 $$\begin{align*}M_p(r,f)&:=\frac{1}{2\pi}\int_0^{2\pi}|f(re^{i\theta})|^{p}\,d\theta, \quad\, 0<p<\infty\,,\\M_\infty(r,f)&:= \sup_{\theta \in[0,2\pi)}|f(re^{i\theta})|\,. \end{align*}$$
$$\begin{align*}M_p(r,f)&:=\frac{1}{2\pi}\int_0^{2\pi}|f(re^{i\theta})|^{p}\,d\theta, \quad\, 0<p<\infty\,,\\M_\infty(r,f)&:= \sup_{\theta \in[0,2\pi)}|f(re^{i\theta})|\,. \end{align*}$$
By
![]() $F_\varphi $
, we denote the space of all functions
$F_\varphi $
, we denote the space of all functions
![]() $f\in H(\mathbb {D})$
for which
$f\in H(\mathbb {D})$
for which
The next result shows the relationship between Nevanlinna’s abstract classes and
![]() $F_\varphi $
spaces.
$F_\varphi $
spaces.
Theorem 2.3. Let
![]() $\varphi \in \Phi _2^{sc}$
. Then,
$\varphi \in \Phi _2^{sc}$
. Then,
![]() $N_\varphi \subset F_{\varphi }$
.
$N_\varphi \subset F_{\varphi }$
.
Proof. Let
![]() $f\in N_\varphi $
. Take
$f\in N_\varphi $
. Take
![]() $\varepsilon>0$
and a function
$\varepsilon>0$
and a function
![]() $g\in L^\infty (\mathbb {T})$
such that
$g\in L^\infty (\mathbb {T})$
such that
![]() $0\leqslant g \leqslant \varphi (\log ^{+}|f^{*}|) m$
-a.e. on
$0\leqslant g \leqslant \varphi (\log ^{+}|f^{*}|) m$
-a.e. on
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
 $$\begin{align*}\frac{1}{2\pi}\int_0^{2\pi}[\varphi(\log^{+}|f^{*}(e^{i\theta})|) - g(e^{i\theta})]\,d\theta \leqslant \varepsilon\,. \end{align*}$$
$$\begin{align*}\frac{1}{2\pi}\int_0^{2\pi}[\varphi(\log^{+}|f^{*}(e^{i\theta})|) - g(e^{i\theta})]\,d\theta \leqslant \varepsilon\,. \end{align*}$$
We recall that the following estimate holds:
 $$ \begin{align*} \varphi(\log^+(|f(z)|))\leqslant F(z):= \frac{1}{2\pi}\int_0^{2\pi}P(z,e^{i\theta})\varphi(\log^+(|f^*(e^{i\theta})|)\,d\theta\,. \end{align*} $$
$$ \begin{align*} \varphi(\log^+(|f(z)|))\leqslant F(z):= \frac{1}{2\pi}\int_0^{2\pi}P(z,e^{i\theta})\varphi(\log^+(|f^*(e^{i\theta})|)\,d\theta\,. \end{align*} $$
Since for all
![]() $\theta $
,
$\theta $
,
![]() $t\in [0, 2\pi )$
,
$t\in [0, 2\pi )$
,
![]() $0\leqslant r<1$
,
$0\leqslant r<1$
,
![]() $P(re^{i\theta }, e^{it})\leqslant \frac {1+r}{1-r}$
, we conclude that, for all
$P(re^{i\theta }, e^{it})\leqslant \frac {1+r}{1-r}$
, we conclude that, for all
![]() $\theta \in [0, 2\pi ),$
$\theta \in [0, 2\pi ),$
 $$ \begin{align*} |F(re^{i\theta})|& \leqslant \frac{1}{2\pi}\int_0^{2\pi}P(re^{i\theta},e^{it})[\varphi(\log^+|f^*(e^{it})|)- g(e^{it})+ g(e^{it})]\,dt\\ & \leqslant \frac{1+r}{1-r}\varepsilon + \|g\|_\infty\,. \end{align*} $$
$$ \begin{align*} |F(re^{i\theta})|& \leqslant \frac{1}{2\pi}\int_0^{2\pi}P(re^{i\theta},e^{it})[\varphi(\log^+|f^*(e^{it})|)- g(e^{it})+ g(e^{it})]\,dt\\ & \leqslant \frac{1+r}{1-r}\varepsilon + \|g\|_\infty\,. \end{align*} $$
Clearly, this implies that
![]() $(1-r)M_\infty (r,F)\leqslant (1+r)\varepsilon +\|g\|_\infty (1-r)$
. Hence
$(1-r)M_\infty (r,F)\leqslant (1+r)\varepsilon +\|g\|_\infty (1-r)$
. Hence
This combined with the above estimates yields
and this completes the proof.
Let
![]() $\varphi \in \Phi _2^{sc}$
. Then, for all
$\varphi \in \Phi _2^{sc}$
. Then, for all
![]() $t\geqslant 0$
,
$t\geqslant 0$
,
![]() $\overline {\varphi }(t):=\sup_{s>0}\frac {\varphi (st)}{\varphi (s)}$
. Note that, if a function
$\overline {\varphi }(t):=\sup_{s>0}\frac {\varphi (st)}{\varphi (s)}$
. Note that, if a function
![]() $\varphi $
satisfies the
$\varphi $
satisfies the
![]() $\Delta _2$
-condition, then
$\Delta _2$
-condition, then
![]() $\overline {\varphi }(t)<\infty $
for all
$\overline {\varphi }(t)<\infty $
for all
![]() $t\geqslant 0$
and so, for all
$t\geqslant 0$
and so, for all
![]() $t,s>0$
, we have
$t,s>0$
, we have
![]() $\varphi (st)\leqslant \overline {\varphi }(t)\varphi (s)$
.
$\varphi (st)\leqslant \overline {\varphi }(t)\varphi (s)$
.
By
![]() $F_\varphi ^{\text {int}}$
, we denote the space of all functions
$F_\varphi ^{\text {int}}$
, we denote the space of all functions
![]() $f\in H(\mathbb {D})$
, such that, for all
$f\in H(\mathbb {D})$
, such that, for all
![]() $c>0$
, we have
$c>0$
, we have
 $$ \begin{align} \|f\|_{\varphi,c}:=\int_0^1 M_\infty(r,f)\exp\Big[-c\,\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr<\infty\,. \end{align} $$
$$ \begin{align} \|f\|_{\varphi,c}:=\int_0^1 M_\infty(r,f)\exp\Big[-c\,\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr<\infty\,. \end{align} $$
Observe that
![]() $\{\|\cdot \|_{\varphi ,c}; \, c>0\}$
is a family of norms on
$\{\|\cdot \|_{\varphi ,c}; \, c>0\}$
is a family of norms on
![]() $F_\varphi ^{int}$
, thus, it means that we can define a locally convex topology on this space.
$F_\varphi ^{int}$
, thus, it means that we can define a locally convex topology on this space.
Proposition 2.4. Let
![]() $\varphi \in \Phi _2^{sc}$
. Then,
$\varphi \in \Phi _2^{sc}$
. Then,
![]() $F_\varphi \subset F_\varphi ^{\text {int}}$
.
$F_\varphi \subset F_\varphi ^{\text {int}}$
.
Proof. Fix
![]() $f\in F_\varphi $
. Then, the function
$f\in F_\varphi $
. Then, the function
![]() $g\colon [0,1)\to \mathbb {R}$
given by
$g\colon [0,1)\to \mathbb {R}$
given by
is bounded on
![]() $[0,1)$
and continuous on
$[0,1)$
and continuous on
![]() $(0,1)$
. Clearly,
$(0,1)$
. Clearly,
![]() $g(r)\to 0$
as
$g(r)\to 0$
as
![]() $r\rightarrow 1-$
and the inequality
$r\rightarrow 1-$
and the inequality
is valid for all
![]() $r\in (0,1)$
. Thus, for all
$r\in (0,1)$
. Thus, for all
![]() $c>0$
, we have
$c>0$
, we have
 $$ \begin{align*} \int_0^1M_\infty(r,f)\exp&\Big[-c\,\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]dr \\ &\leqslant\int_0^1 \exp\Big[\big(\overline{\varphi^{-1}}(g(r))-c\big)\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr\,. \end{align*} $$
$$ \begin{align*} \int_0^1M_\infty(r,f)\exp&\Big[-c\,\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]dr \\ &\leqslant\int_0^1 \exp\Big[\big(\overline{\varphi^{-1}}(g(r))-c\big)\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr\,. \end{align*} $$
From the fact that
![]() $\varphi ^{-1}\in (\Delta _2)$
, it follows that
$\varphi ^{-1}\in (\Delta _2)$
, it follows that
![]() $\overline {\varphi ^{-1}}(t)\to 0$
as
$\overline {\varphi ^{-1}}(t)\to 0$
as
![]() $t\to 0+$
. Because
$t\to 0+$
. Because
![]() $g(r)\to 0$
, so there exists
$g(r)\to 0$
, so there exists
![]() $r_0\in (0,1)$
, such that
$r_0\in (0,1)$
, such that
![]() $\overline {\varphi ^{-1}}(g(r))\leqslant c/2$
for
$\overline {\varphi ^{-1}}(g(r))\leqslant c/2$
for
![]() $r\in [r_0,1)$
. In consequence,
$r\in [r_0,1)$
. In consequence,
 $$ \begin{align*} \int_0^1\exp\Big[\big(\overline{\varphi^{-1}}(g(r))&-c\big)\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr \\ &\leqslant\int_0^{r_0}\exp\Big[\big(\overline{\varphi^{-1}}(g(r))-c\big)\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr\\ &+ \int_{r_0}^1\exp\Big[-\frac{c}{2}\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr<\infty\,, \end{align*} $$
$$ \begin{align*} \int_0^1\exp\Big[\big(\overline{\varphi^{-1}}(g(r))&-c\big)\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr \\ &\leqslant\int_0^{r_0}\exp\Big[\big(\overline{\varphi^{-1}}(g(r))-c\big)\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr\\ &+ \int_{r_0}^1\exp\Big[-\frac{c}{2}\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big]\,dr<\infty\,, \end{align*} $$
because both integrated functions on the right-hand side of inequality are bounded on the appropriate intervals.
From Theorem 2.3 and Proposition 2.4, we get the following corollary, which will become crucial in the sequel.
Corollary 2.5. Let
![]() $\varphi \in \Phi _2^{sc}$
. Then,
$\varphi \in \Phi _2^{sc}$
. Then,
![]() $N_\varphi \subset F_\varphi ^{\text {int}}$
.
$N_\varphi \subset F_\varphi ^{\text {int}}$
.
3 Multipliers form
 $N_\varphi $
to the Hardy spaces
$N_\varphi $
to the Hardy spaces
 $H^p$
$H^p$
In this section, we will be interested in describing coefficient multipliers between
![]() $N_\varphi $
and the classical Hardy spaces
$N_\varphi $
and the classical Hardy spaces
![]() $H^p$
. Let us recall that a complex sequence
$H^p$
. Let us recall that a complex sequence
![]() $\{\lambda _n\}:=\{\lambda _n\}_{n=0}^\infty $
is a multiplier from space X to Y of holomorphic functions in
$\{\lambda _n\}:=\{\lambda _n\}_{n=0}^\infty $
is a multiplier from space X to Y of holomorphic functions in
![]() $\mathbb {D}$
if, for every
$\mathbb {D}$
if, for every
![]() $f\in X$
with power series
$f\in X$
with power series
![]() $f(z)=\sum _{n=0}^\infty \widehat {f}(n) z^n$
for all
$f(z)=\sum _{n=0}^\infty \widehat {f}(n) z^n$
for all
![]() $z\in \mathbb {D}$
, we have that the function
$z\in \mathbb {D}$
, we have that the function
![]() $g(z)=\sum _{n=0}^\infty \lambda _n \widehat {f}(n) z^n$
belongs to Y. It is clear that to every multiplier
$g(z)=\sum _{n=0}^\infty \lambda _n \widehat {f}(n) z^n$
belongs to Y. It is clear that to every multiplier
![]() $\{\lambda _n\}$
, we can associate a linear operator
$\{\lambda _n\}$
, we can associate a linear operator
![]() $\Lambda \colon X\to Y$
given by the formula:
$\Lambda \colon X\to Y$
given by the formula:
 $$\begin{align*}\Lambda f(z):= \sum_{n=0}^\infty \lambda_n \widehat{f}(n) z^{n}, \quad\, z\in \mathbb{D}\,, \end{align*}$$
$$\begin{align*}\Lambda f(z):= \sum_{n=0}^\infty \lambda_n \widehat{f}(n) z^{n}, \quad\, z\in \mathbb{D}\,, \end{align*}$$
for every
![]() $f\in X$
with power series
$f\in X$
with power series
![]() $f(z)=\sum _{n=0}^\infty \widehat {f}(n) z^n$
for all
$f(z)=\sum _{n=0}^\infty \widehat {f}(n) z^n$
for all
![]() $z\in \mathbb {D}$
.
$z\in \mathbb {D}$
.
We will use the following standard fact which easily follows from the Closed Graph Theorem.
Lemma 3.1. Let X and Y be F-spaces of analytic functions in
![]() $\mathbb {D}$
, such that convergence in metric is stronger than the uniform convergence on compact subsets of
$\mathbb {D}$
, such that convergence in metric is stronger than the uniform convergence on compact subsets of
![]() $\mathbb {D}$
. Then the operator
$\mathbb {D}$
. Then the operator
![]() $\Lambda $
is continuous.
$\Lambda $
is continuous.
It can be easily seen from the previously established inequality
 $$\begin{align} \sup_{|z|\leqslant r} |f(z)| \leqslant\exp\bigg(\varphi^{-1}\bigg(\frac{2\|f\|_\varphi}{1-r}\bigg)\bigg)-1, \quad\, r\in [0, 1) \end{align} $$
$$\begin{align} \sup_{|z|\leqslant r} |f(z)| \leqslant\exp\bigg(\varphi^{-1}\bigg(\frac{2\|f\|_\varphi}{1-r}\bigg)\bigg)-1, \quad\, r\in [0, 1) \end{align} $$
that one has
![]() $N_\varphi \hookrightarrow H(\mathbb {D})$
. Since
$N_\varphi \hookrightarrow H(\mathbb {D})$
. Since
![]() $H^p \hookrightarrow H(\mathbb {D})$
for all
$H^p \hookrightarrow H(\mathbb {D})$
for all
![]() $0<p\leqslant \infty $
, it follows that
$0<p\leqslant \infty $
, it follows that
![]() $\Lambda \colon N_\varphi \to H^p$
is indeed a continuous operator.
$\Lambda \colon N_\varphi \to H^p$
is indeed a continuous operator.
Our first goal in this section is to describe a necessary condition for a sequence
![]() $\{\lambda _n\}\in \boldsymbol {\omega }$
to be a multiplier from
$\{\lambda _n\}\in \boldsymbol {\omega }$
to be a multiplier from
![]() $N_\varphi $
to
$N_\varphi $
to
![]() $H^p$
. We will start with some basic definitions and technical facts from the theory of Orlicz spaces.
$H^p$
. We will start with some basic definitions and technical facts from the theory of Orlicz spaces.
For a function
![]() $\varphi \in \Phi _2^{sc}$
, the lower (resp. upper) Matuszewska–Orlicz index
$\varphi \in \Phi _2^{sc}$
, the lower (resp. upper) Matuszewska–Orlicz index
![]() $p(\varphi )$
(resp.
$p(\varphi )$
(resp.
![]() $q(\varphi )$
) is given by the formula (see [Reference Matuszewska and Orlicz9, Reference Matuszewska and Orlicz10])
$q(\varphi )$
) is given by the formula (see [Reference Matuszewska and Orlicz9, Reference Matuszewska and Orlicz10])
 $$\begin{align*}p(\varphi)=\sup_{0<s<1}\frac{\log\overline{\varphi}(s)}{\log s} \qquad \bigg(\text{resp.} \, \, q(\varphi) =\inf_{s>1}\frac{\log\overline{\varphi}(s)}{\log s}\bigg)\,. \end{align*}$$
$$\begin{align*}p(\varphi)=\sup_{0<s<1}\frac{\log\overline{\varphi}(s)}{\log s} \qquad \bigg(\text{resp.} \, \, q(\varphi) =\inf_{s>1}\frac{\log\overline{\varphi}(s)}{\log s}\bigg)\,. \end{align*}$$
Since
![]() $\overline {\varphi }\colon [0,\infty )\to [0,\infty )$
is nondecreasing and submultiplicative, the following are true (see [Reference Krein, Petunin and Semenov7, pp. 53–54]):
$\overline {\varphi }\colon [0,\infty )\to [0,\infty )$
is nondecreasing and submultiplicative, the following are true (see [Reference Krein, Petunin and Semenov7, pp. 53–54]):
 $$\begin{align*}p(\varphi)=\lim_{s\to 0+}\frac{\log\overline{\varphi}(s)}{\log s}, \qquad q(\varphi)=\lim_{s\to\infty}\frac{\log\overline{\varphi}(s)}{\log s}\,. \end{align*}$$
$$\begin{align*}p(\varphi)=\lim_{s\to 0+}\frac{\log\overline{\varphi}(s)}{\log s}, \qquad q(\varphi)=\lim_{s\to\infty}\frac{\log\overline{\varphi}(s)}{\log s}\,. \end{align*}$$
Using the convexity of
![]() $\varphi $
, we get that
$\varphi $
, we get that
![]() $p(\varphi )\geqslant 1$
, while from
$p(\varphi )\geqslant 1$
, while from
![]() $\varphi \in (\Delta _2)$
, we have
$\varphi \in (\Delta _2)$
, we have
![]() $q(\varphi )<\infty $
. Hence
$q(\varphi )<\infty $
. Hence
![]() $1\leqslant p(\varphi )\leqslant q(\varphi )<\infty $
. From the above formulas, we obtain that for every
$1\leqslant p(\varphi )\leqslant q(\varphi )<\infty $
. From the above formulas, we obtain that for every
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $C\geqslant 1$
, such that
$C\geqslant 1$
, such that
Let us recall that a subset E of a linear topological space X is called bounded, if it is absorbed by any zero neighborhood V, that is, if there exists
![]() $\alpha _0>0$
, such that
$\alpha _0>0$
, such that
![]() $\alpha E\subset V$
for all
$\alpha E\subset V$
for all
![]() $\alpha \in \mathbb {C}$
, for which
$\alpha \in \mathbb {C}$
, for which
![]() $|\alpha | \leqslant \alpha _0$
.
$|\alpha | \leqslant \alpha _0$
.
Lemma 3.2. Let
![]() $\varphi \in \Phi _2^{sc}$
be a function such that
$\varphi \in \Phi _2^{sc}$
be a function such that
![]() $p(\varphi )>1$
, and let
$p(\varphi )>1$
, and let
![]() $\{r_n\} \subset [1/2,1)$
be a sequence such that
$\{r_n\} \subset [1/2,1)$
be a sequence such that
![]() $r_n\uparrow 1$
as
$r_n\uparrow 1$
as
![]() $n\to \infty $
. Furthermore, let
$n\to \infty $
. Furthermore, let
![]() $\{\beta _n\}\subset (0,1)$
be a sequence satisfying the condition
$\{\beta _n\}\subset (0,1)$
be a sequence satisfying the condition
 $$\begin{align*}\lim_{n\to\infty}(1-r_n)\varphi\Big(\frac{\beta_n}{1-r_n}\Big)= 0\,. \end{align*}$$
$$\begin{align*}\lim_{n\to\infty}(1-r_n)\varphi\Big(\frac{\beta_n}{1-r_n}\Big)= 0\,. \end{align*}$$
Define a sequence
![]() $\{f_n\}$
by the following formula:
$\{f_n\}$
by the following formula:
 $$\begin{align*}f_n(z)=\exp\Big(\beta_n\frac{1+r_nz}{1-r_nz}\Big), \quad\, z\in\mathbb{D}\,. \end{align*}$$
$$\begin{align*}f_n(z)=\exp\Big(\beta_n\frac{1+r_nz}{1-r_nz}\Big), \quad\, z\in\mathbb{D}\,. \end{align*}$$
Then,
![]() $\{f_{n};\, n\in \mathbb {N}\}$
is a bounded subset of
$\{f_{n};\, n\in \mathbb {N}\}$
is a bounded subset of
![]() $N_\varphi $
.
$N_\varphi $
.
Proof. We first show that
 $$ \begin{align*} C_{\varphi}:=\int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2 t^2/\pi \big)^{-1/2}\Big)\,dt <\infty\,. \end{align*} $$
$$ \begin{align*} C_{\varphi}:=\int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2 t^2/\pi \big)^{-1/2}\Big)\,dt <\infty\,. \end{align*} $$
Since
![]() $p(\varphi )>1$
, so for all
$p(\varphi )>1$
, so for all
![]() $\varepsilon \in (0,p(\varphi )-1)$
, there exists constant
$\varepsilon \in (0,p(\varphi )-1)$
, there exists constant
![]() $C=C(\varepsilon )>0$
, such that
$C=C(\varepsilon )>0$
, such that
Hence, for
![]() $p:=p(\varphi )-\varepsilon $
, we have
$p:=p(\varphi )-\varepsilon $
, we have
![]() $p>1$
and so
$p>1$
and so
 $$\begin{align*}C_{\varphi} = \int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2t^2/\pi \big)^{-1/2}\Big)\, dt\leqslant \int_{-\infty}^{\infty}\big(1+ 2 t^2/\pi \big)^{-p/2}\,dt < \infty\,. \end{align*}$$
$$\begin{align*}C_{\varphi} = \int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2t^2/\pi \big)^{-1/2}\Big)\, dt\leqslant \int_{-\infty}^{\infty}\big(1+ 2 t^2/\pi \big)^{-p/2}\,dt < \infty\,. \end{align*}$$
Let
![]() $\{\varepsilon _k\}$
and
$\{\varepsilon _k\}$
and
![]() $\{\delta _k\}$
be nonnegative sequences satisfying conditions
$\{\delta _k\}$
be nonnegative sequences satisfying conditions
![]() $\varepsilon _k\downarrow 0$
and
$\varepsilon _k\downarrow 0$
and
![]() $\delta _k\downarrow 0$
, when
$\delta _k\downarrow 0$
, when
![]() $k\to \infty $
, and additionally
$k\to \infty $
, and additionally
 $$ \begin{align*} \frac{1-r^2_k}{1-2r\cos\theta+r_k^2}\leqslant 1 \end{align*} $$
$$ \begin{align*} \frac{1-r^2_k}{1-2r\cos\theta+r_k^2}\leqslant 1 \end{align*} $$
for
![]() $|\theta |\geqslant \varepsilon _k$
and
$|\theta |\geqslant \varepsilon _k$
and
![]() $r\geqslant r_k$
,
$r\geqslant r_k$
,
![]() $k\in \mathbb {N}$
. For a given zero neighborhood,
$k\in \mathbb {N}$
. For a given zero neighborhood,
in
![]() $N_\varphi $
choose
$N_\varphi $
choose
![]() $m\in \mathbb {N}$
, such that
$m\in \mathbb {N}$
, such that
 $$ \begin{align*} \varphi(\log(1+\delta_m))+\frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_m+\frac{\gamma^2}{4\pi} C_{\varphi}\,(1-r_m)\varphi\Big(\frac{\beta_m}{1-r_m}\Big)<\eta^{1/\delta}\,, \end{align*} $$
$$ \begin{align*} \varphi(\log(1+\delta_m))+\frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_m+\frac{\gamma^2}{4\pi} C_{\varphi}\,(1-r_m)\varphi\Big(\frac{\beta_m}{1-r_m}\Big)<\eta^{1/\delta}\,, \end{align*} $$
where
![]() $\gamma $
is a
$\gamma $
is a
![]() $\Delta _2$
constant for
$\Delta _2$
constant for
![]() $\varphi $
and
$\varphi $
and
![]() $\delta =\frac {\log 2}{\log \gamma }$
. Furthermore, suppose that
$\delta =\frac {\log 2}{\log \gamma }$
. Furthermore, suppose that
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $0<\alpha _0<1$
, is chosen so that
$0<\alpha _0<1$
, is chosen so that
 $$\begin{align*}\alpha_0\exp\frac{1+r_m}{1-r_m }\leqslant \delta_{m}\,, \end{align*}$$
$$\begin{align*}\alpha_0\exp\frac{1+r_m}{1-r_m }\leqslant \delta_{m}\,, \end{align*}$$
and note that, in particular,
![]() $\alpha _0 e < \delta _m$
.
$\alpha _0 e < \delta _m$
.
Observe that for all
![]() $\theta \in [0,2\pi ]$
and each
$\theta \in [0,2\pi ]$
and each
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
 $$\begin{align*}f_{k}^{*}(e^{i\theta})=\lim_{r \to 1-}\exp\bigg(\beta_k\frac{1+r_kre^{i\theta}}{1-r_kre^{i\theta}}\bigg) =\exp\bigg(\beta_k\frac{1+r_ke^{i\theta}}{1-r_ke^{i\theta}}\bigg)\,, \end{align*}$$
$$\begin{align*}f_{k}^{*}(e^{i\theta})=\lim_{r \to 1-}\exp\bigg(\beta_k\frac{1+r_kre^{i\theta}}{1-r_kre^{i\theta}}\bigg) =\exp\bigg(\beta_k\frac{1+r_ke^{i\theta}}{1-r_ke^{i\theta}}\bigg)\,, \end{align*}$$
and hence (by
![]() $\beta _k<1$
)
$\beta _k<1$
)
 $$ \begin{align*} |f_{k}^{*}(e^{i\theta})|& = \exp \bigg(\beta_k\text{Re}\,\frac{1+r_ke^{i\theta}}{1-r_ke^{i\theta}}\bigg)\\ &= \exp\bigg(\beta_k\frac{1-r_k^2}{1-2r_k\cos \theta + r_k^2}\bigg) \leqslant \exp\bigg(\beta_k\frac{1+r_k}{1-r_k}\bigg)\,. \end{align*} $$
$$ \begin{align*} |f_{k}^{*}(e^{i\theta})|& = \exp \bigg(\beta_k\text{Re}\,\frac{1+r_ke^{i\theta}}{1-r_ke^{i\theta}}\bigg)\\ &= \exp\bigg(\beta_k\frac{1-r_k^2}{1-2r_k\cos \theta + r_k^2}\bigg) \leqslant \exp\bigg(\beta_k\frac{1+r_k}{1-r_k}\bigg)\,. \end{align*} $$
Because the function
![]() $[0,1)\ni x\mapsto \frac {1+x}{1-x}$
is increasing and
$[0,1)\ni x\mapsto \frac {1+x}{1-x}$
is increasing and
![]() $r_n\uparrow 1$
, we get that
$r_n\uparrow 1$
, we get that
 $$\begin{align*}|\alpha_0 f_k^*(e^{i\theta})|\leqslant |\alpha_0|\exp\frac{1+r_k}{1-r_k}\leqslant\delta_{m}, \quad\, k \leqslant m\,. \end{align*}$$
$$\begin{align*}|\alpha_0 f_k^*(e^{i\theta})|\leqslant |\alpha_0|\exp\frac{1+r_k}{1-r_k}\leqslant\delta_{m}, \quad\, k \leqslant m\,. \end{align*}$$
In consequence, the above estimates yields that, for all
![]() $|\alpha |\leqslant \alpha _0$
and each
$|\alpha |\leqslant \alpha _0$
and each
![]() $k\leqslant m$
, we have
$k\leqslant m$
, we have
 $$ \begin{align*} \|\alpha f_k\|_\varphi=\frac{1}{2\pi}\int_{-\pi}^{\pi}\varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta \leqslant \varphi(\log(1+\delta_m))<\eta^{1/\delta}\,. \end{align*} $$
$$ \begin{align*} \|\alpha f_k\|_\varphi=\frac{1}{2\pi}\int_{-\pi}^{\pi}\varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta \leqslant \varphi(\log(1+\delta_m))<\eta^{1/\delta}\,. \end{align*} $$
This shows that
![]() $\rho _\varphi (\alpha f_k,0) = \|\alpha f_k\|_\varphi ^\delta <\eta $
. We conclude that
$\rho _\varphi (\alpha f_k,0) = \|\alpha f_k\|_\varphi ^\delta <\eta $
. We conclude that
![]() $\alpha f_k\in V$
for each
$\alpha f_k\in V$
for each
![]() $k\leqslant m$
and all
$k\leqslant m$
and all
![]() $|\alpha |\leqslant \alpha _0$
.
$|\alpha |\leqslant \alpha _0$
.
We can now proceed to the case
![]() $k>m$
. For all
$k>m$
. For all
![]() $|\alpha |\leqslant \alpha _0$
, we have
$|\alpha |\leqslant \alpha _0$
, we have
 $$ \begin{align*} \|\alpha f_k\|_\varphi & =\frac{1}{2\pi}\int_{-\pi}^{\pi}\varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta =\frac{1}{2\pi}\int_{|\theta|\geqslant \varepsilon_k}\varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta \\[3pt] & \quad +\frac{1}{2\pi}\int_{|\theta|< \varepsilon_k} \varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta\,. \end{align*} $$
$$ \begin{align*} \|\alpha f_k\|_\varphi & =\frac{1}{2\pi}\int_{-\pi}^{\pi}\varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta =\frac{1}{2\pi}\int_{|\theta|\geqslant \varepsilon_k}\varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta \\[3pt] & \quad +\frac{1}{2\pi}\int_{|\theta|< \varepsilon_k} \varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta\,. \end{align*} $$
From the above shown inequality, one has
 $$ \begin{align*} \frac{1}{2\pi}\int_{|\theta|\geqslant \varepsilon_k} \varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta\leqslant \varphi(\log(1+\alpha_0 e)\leqslant\varphi(\log(1+\delta_m)). \end{align*} $$
$$ \begin{align*} \frac{1}{2\pi}\int_{|\theta|\geqslant \varepsilon_k} \varphi(\log(1+|\alpha f_k^*(e^{i\theta})|))\,d\theta\leqslant \varphi(\log(1+\alpha_0 e)\leqslant\varphi(\log(1+\delta_m)). \end{align*} $$
Clearly,
 $$ \begin{align*} \frac{1}{2\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log(1 & + |\alpha f_k^*(e^{i\theta})|))\,d\theta \\ &\leqslant \frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_k +\frac{\gamma}{4\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log^{+}|\alpha f_{k}^{*}(e^{i\theta})|)\,d\theta\,, \end{align*} $$
$$ \begin{align*} \frac{1}{2\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log(1 & + |\alpha f_k^*(e^{i\theta})|))\,d\theta \\ &\leqslant \frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_k +\frac{\gamma}{4\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log^{+}|\alpha f_{k}^{*}(e^{i\theta})|)\,d\theta\,, \end{align*} $$
where
![]() $\gamma $
comes from the
$\gamma $
comes from the
![]() $\Delta _2$
-condition for
$\Delta _2$
-condition for
![]() $\varphi $
.
$\varphi $
.
To estimate the second term in the sum above note that
![]() $|\sin (\theta /2)| \geqslant |\theta |/\pi $
for all
$|\sin (\theta /2)| \geqslant |\theta |/\pi $
for all
![]() $\theta \in [-\pi , \pi ]$
and
$\theta \in [-\pi , \pi ]$
and
![]() $r_k/(1-r_k)^2 \geqslant 2$
for each
$r_k/(1-r_k)^2 \geqslant 2$
for each
![]() $r_k \in [1/2, 1)$
. Hence
$r_k \in [1/2, 1)$
. Hence
 $$ \begin{align*} 1- 2 r_k \cos \theta + r_k^2 & = (1- r_k)^2 + 2 r_k(1 - \cos \theta) \\[3pt] & = (1 - r_k)^2 + 4r_k \sin^2 \Big(\frac{\theta}{2}\Big) \\[3pt] & \geqslant (1- r_k)^2\,\bigg(1 + \frac{2\theta^2}{\pi(1 - r_k)^2}\bigg)\,. \end{align*} $$
$$ \begin{align*} 1- 2 r_k \cos \theta + r_k^2 & = (1- r_k)^2 + 2 r_k(1 - \cos \theta) \\[3pt] & = (1 - r_k)^2 + 4r_k \sin^2 \Big(\frac{\theta}{2}\Big) \\[3pt] & \geqslant (1- r_k)^2\,\bigg(1 + \frac{2\theta^2}{\pi(1 - r_k)^2}\bigg)\,. \end{align*} $$
Combining this estimate with
 $$ \begin{align*} |f_{k}^{*}(e^{i\theta})| \leqslant \exp\bigg(\frac{2\beta_k}{|1- r_k e^{i\theta}|}\bigg) = \exp\Biggl(\frac{2\beta_k}{\sqrt{1-2r_k\cos \theta + r_k^2}}\Biggr)\,, \end{align*} $$
$$ \begin{align*} |f_{k}^{*}(e^{i\theta})| \leqslant \exp\bigg(\frac{2\beta_k}{|1- r_k e^{i\theta}|}\bigg) = \exp\Biggl(\frac{2\beta_k}{\sqrt{1-2r_k\cos \theta + r_k^2}}\Biggr)\,, \end{align*} $$
we obtain by
![]() $|\alpha | \leqslant \alpha _0 <1$
and
$|\alpha | \leqslant \alpha _0 <1$
and
![]() $\varphi \in (\Delta _2)$
with constant
$\varphi \in (\Delta _2)$
with constant
![]() $\gamma $
,
$\gamma $
,
 $$\begin{align*}\frac{\gamma}{4\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log^+|\alpha f_{k}^{*}(e^{i\theta})|)d\theta \leqslant \frac{\gamma^2}{4\pi}\int_{-\pi}^{\pi}\varphi\Biggl(\frac{\beta_k}{(1-r_k)\sqrt{1+\frac{2\theta^2}{\pi(1-r_k)^2}}}\Biggr)\,d\theta\,. \end{align*}$$
$$\begin{align*}\frac{\gamma}{4\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log^+|\alpha f_{k}^{*}(e^{i\theta})|)d\theta \leqslant \frac{\gamma^2}{4\pi}\int_{-\pi}^{\pi}\varphi\Biggl(\frac{\beta_k}{(1-r_k)\sqrt{1+\frac{2\theta^2}{\pi(1-r_k)^2}}}\Biggr)\,d\theta\,. \end{align*}$$
Since
![]() $\varphi (st)\leqslant \varphi (s)\overline {\varphi }(t)$
for all
$\varphi (st)\leqslant \varphi (s)\overline {\varphi }(t)$
for all
![]() $s,t>0$
, so substituting
$s,t>0$
, so substituting
![]() $t=\frac {\theta }{1-r_k}$
yields
$t=\frac {\theta }{1-r_k}$
yields
 $$ \begin{align*} \frac{\gamma}{4\pi}\int_{|\theta|< \varepsilon_k}&\varphi(\log^{+} |\alpha f_k^{*}(e^{i\theta})|)\,d\theta \\ & \leqslant\frac{\gamma^2}{4\pi}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big){\int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2t^2/\pi \big)^{-1/2}\Big)\,dt}\,. \end{align*} $$
$$ \begin{align*} \frac{\gamma}{4\pi}\int_{|\theta|< \varepsilon_k}&\varphi(\log^{+} |\alpha f_k^{*}(e^{i\theta})|)\,d\theta \\ & \leqslant\frac{\gamma^2}{4\pi}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big){\int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2t^2/\pi \big)^{-1/2}\Big)\,dt}\,. \end{align*} $$
In consequence, for all
![]() $k>m$
and
$k>m$
and
![]() $|\alpha |\leqslant \alpha _0$
,
$|\alpha |\leqslant \alpha _0$
,
 $$ \begin{align*} &\frac{1}{2\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log(1+|\alpha f_k^*(e^{i\theta}))|)\,d\theta \\ &\leqslant \frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_k + \frac{\gamma^2}{4\pi}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big){\int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2t^2/\pi \big)^{-1/2}\Big)dt}\\&\leqslant \frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_k + C_{\varphi}\, \frac{\gamma^2}{4\pi}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big)\,. \end{align*} $$
$$ \begin{align*} &\frac{1}{2\pi}\int_{|\theta|< \varepsilon_k}\varphi(\log(1+|\alpha f_k^*(e^{i\theta}))|)\,d\theta \\ &\leqslant \frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_k + \frac{\gamma^2}{4\pi}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big){\int_{-\infty}^{\infty}\overline{\varphi}\Big(\big(1+ 2t^2/\pi \big)^{-1/2}\Big)dt}\\&\leqslant \frac{\gamma}{2\pi}\varphi(\log 2)\varepsilon_k + C_{\varphi}\, \frac{\gamma^2}{4\pi}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big)\,. \end{align*} $$
Combining with the estimates above, we obtain the desired statement.
From now on, for a given
![]() $\varphi \in \Phi _2^{sc}$
, we define
$\varphi \in \Phi _2^{sc}$
, we define
![]() $h_\varphi \colon (0, \infty ) \to (0, \infty )$
by
$h_\varphi \colon (0, \infty ) \to (0, \infty )$
by
 $$\begin{align*}h_{\varphi}(y):=\varphi^{-1}\Big(\frac{1}{y}\Big), \quad\, y>0, \end{align*}$$
$$\begin{align*}h_{\varphi}(y):=\varphi^{-1}\Big(\frac{1}{y}\Big), \quad\, y>0, \end{align*}$$
and for given
![]() $t>0$
let
$t>0$
let
![]() $\widetilde {y}(t)$
be a solution of the equation
$\widetilde {y}(t)$
be a solution of the equation
![]() $h_{\varphi }(y)=ty$
, with variable being
$h_{\varphi }(y)=ty$
, with variable being
![]() $y>0$
. Furthermore, let
$y>0$
. Furthermore, let
![]() $\omega _{\varphi }(t)=\omega (t):=h_\varphi (\widetilde {y}(t))$
for all
$\omega _{\varphi }(t)=\omega (t):=h_\varphi (\widetilde {y}(t))$
for all
![]() $t>0$
. Throughout the rest of the paper, the function
$t>0$
. Throughout the rest of the paper, the function
![]() $\omega $
will be called associated with
$\omega $
will be called associated with
![]() $\varphi $
.
$\varphi $
.
In what follows, we will need the following properties of
![]() $\varphi \in \Phi _2^{sc}$
. For the sake of completeness, we include some technical details.
$\varphi \in \Phi _2^{sc}$
. For the sake of completeness, we include some technical details.
Remarks. (1) Since
![]() $\varphi ^{-1}$
is a nondecreasing function,
$\varphi ^{-1}$
is a nondecreasing function,
![]() $h_\varphi $
is nonincreasing. Clearly,
$h_\varphi $
is nonincreasing. Clearly,
![]() $\lim _{y\to \infty }h(y)=0$
and
$\lim _{y\to \infty }h(y)=0$
and
![]() $\lim _{y\to 0+}h(y)=\infty $
. Hence
$\lim _{y\to 0+}h(y)=\infty $
. Hence
![]() $\lim _{t\to \infty }\widetilde {y}(t)=0$
.
$\lim _{t\to \infty }\widetilde {y}(t)=0$
.
(2) From definition of
![]() $\omega _\varphi $
, we get that
$\omega _\varphi $
, we get that
![]() $\omega (t)=\varphi ^{-1}\big (\frac {1}{\widetilde {y}(t)}\big )$
, for all
$\omega (t)=\varphi ^{-1}\big (\frac {1}{\widetilde {y}(t)}\big )$
, for all
![]() $t>0$
. Since
$t>0$
. Since
![]() $\varphi ^{-1}\big (\frac {1}{\widetilde {y}(t)}\big )=h(\widetilde {y}(t))=t\widetilde {y}(t)$
,
$\varphi ^{-1}\big (\frac {1}{\widetilde {y}(t)}\big )=h(\widetilde {y}(t))=t\widetilde {y}(t)$
,
 $$\begin{align*}\varphi(\omega(t))\omega(t)=\frac{1}{\widetilde{y}(t)}\varphi^{-1}\Big(\frac{1}{\widetilde{y}(t)}\Big)=t, \quad\, t>0\,. \end{align*}$$
$$\begin{align*}\varphi(\omega(t))\omega(t)=\frac{1}{\widetilde{y}(t)}\varphi^{-1}\Big(\frac{1}{\widetilde{y}(t)}\Big)=t, \quad\, t>0\,. \end{align*}$$
In consequence,
![]() $\varphi (t)=\frac {\omega ^{-1}(t)}{t}$
for all
$\varphi (t)=\frac {\omega ^{-1}(t)}{t}$
for all
![]() $t> 0$
. Clearly,
$t> 0$
. Clearly,
![]() $\varphi \in \Phi _2^{sc}$
implies that
$\varphi \in \Phi _2^{sc}$
implies that
![]() $\omega $
is continuous, nondecreasing, and nonnegative function. It is easy to check that
$\omega $
is continuous, nondecreasing, and nonnegative function. It is easy to check that
![]() $\omega ^{-1}\in (\Delta _2)$
and
$\omega ^{-1}\in (\Delta _2)$
and
![]() $t^2=o(\omega ^{-1}(t))$
as
$t^2=o(\omega ^{-1}(t))$
as
![]() $t\to \infty $
.
$t\to \infty $
.
(3) If
![]() $\varphi \in \Phi _2^{sc}$
and
$\varphi \in \Phi _2^{sc}$
and
![]() $\varphi (1)\neq 1$
, then the function
$\varphi (1)\neq 1$
, then the function
![]() $\phi \in \Phi _2^{sc}$
given by
$\phi \in \Phi _2^{sc}$
given by
![]() $\phi (t):=\frac {\varphi (t)}{\varphi (1)}$
for all
$\phi (t):=\frac {\varphi (t)}{\varphi (1)}$
for all
![]() $t\geqslant 0$
, satisfies the condition
$t\geqslant 0$
, satisfies the condition
![]() $\phi (1)=1$
. Obviously,
$\phi (1)=1$
. Obviously,
![]() $N_\phi =N_\varphi $
and the topologies on both spaces are equivalent. Since
$N_\phi =N_\varphi $
and the topologies on both spaces are equivalent. Since
![]() $\phi ^{-1}(t)=\varphi ^{-1}(t\varphi (1))$
, for all
$\phi ^{-1}(t)=\varphi ^{-1}(t\varphi (1))$
, for all
![]() $t\geqslant 0$
, we have
$t\geqslant 0$
, we have
 $$\begin{align*}h_\phi(y)=\phi^{-1}\Big(\frac{1}{y}\Big)=\varphi^{-1}\Big(\frac{\varphi(1)}{y}\Big) =h_{\varphi}\Big(\frac{y}{\varphi(1)}\Big), \quad\, y>0\,. \end{align*}$$
$$\begin{align*}h_\phi(y)=\phi^{-1}\Big(\frac{1}{y}\Big)=\varphi^{-1}\Big(\frac{\varphi(1)}{y}\Big) =h_{\varphi}\Big(\frac{y}{\varphi(1)}\Big), \quad\, y>0\,. \end{align*}$$
It follows that
and the associated functions are equivalent.
We also will need the following lemma.
Lemma 3.3. Let
![]() $\varphi \in \Phi _2^{sc}$
,
$\varphi \in \Phi _2^{sc}$
,
![]() $\omega $
be the function associated with
$\omega $
be the function associated with
![]() $\varphi $
and
$\varphi $
and
![]() $h(y)=\varphi ^{-1}(\frac {1}{y})$
for all
$h(y)=\varphi ^{-1}(\frac {1}{y})$
for all
![]() $y>0$
. Then, the following conditions hold:
$y>0$
. Then, the following conditions hold:
-
(a)
 $\varphi (x)= o(\omega ^{-1}(x))$
and
$\varphi (x)= o(\omega ^{-1}(x))$
and
 $\omega (x)=o(\varphi ^{-1}(x))$
as
$\omega (x)=o(\varphi ^{-1}(x))$
as
 $x\to \infty $
.
$x\to \infty $
. -
(b)
 $\log x=o(\omega (x))$
as
$\log x=o(\omega (x))$
as
 $x\to \infty $
.
$x\to \infty $
. -
(c)
 $\log \frac {1}{x}=o(\log h(x))$
as
$\log \frac {1}{x}=o(\log h(x))$
as
 $x\to 0+$
.
$x\to 0+$
.
Proof. (a). Since
![]() $\varphi (t)=\frac {\omega ^{-1}(t)}{t}$
for
$\varphi (t)=\frac {\omega ^{-1}(t)}{t}$
for
![]() $t> 0$
,
$t> 0$
,
![]() $\varphi (x)=o(\omega ^{-1}(x))$
as
$\varphi (x)=o(\omega ^{-1}(x))$
as
![]() $x\to \infty $
. We claim that
$x\to \infty $
. We claim that
![]() $\varphi ^{-1}(x\varphi (x))/x\to \infty $
as
$\varphi ^{-1}(x\varphi (x))/x\to \infty $
as
![]() $x\to \infty $
. If we suppose the opposite, then there would exist constant
$x\to \infty $
. If we suppose the opposite, then there would exist constant
![]() $C>0$
and sequence
$C>0$
and sequence
![]() $\{x_n\}$
such that
$\{x_n\}$
such that
![]() $x_n\to \infty $
as
$x_n\to \infty $
as
![]() $n\to \infty $
and, for large enough n,
$n\to \infty $
and, for large enough n,
Since
![]() $\varphi \in (\Delta _2)$
, there exists a constant
$\varphi \in (\Delta _2)$
, there exists a constant
![]() $\gamma>0$
and a positive integer k such that
$\gamma>0$
and a positive integer k such that
![]() $C \leqslant 2^k$
and
$C \leqslant 2^k$
and
![]() $\varphi (C t)\leqslant \gamma ^k \varphi (t)$
for all
$\varphi (C t)\leqslant \gamma ^k \varphi (t)$
for all
![]() $t>0$
. Hence
$t>0$
. Hence
![]() $x_n\varphi (x_n)\leqslant \gamma ^k\varphi (x_n)$
yields that
$x_n\varphi (x_n)\leqslant \gamma ^k\varphi (x_n)$
yields that
![]() $x_n\leqslant \gamma ^k$
for each
$x_n\leqslant \gamma ^k$
for each
![]() $n\in \mathbb {N}$
. This contradiction shows that the claim is true. Combining this fact with
$n\in \mathbb {N}$
. This contradiction shows that the claim is true. Combining this fact with
![]() $\omega ^{-1}(x)=x\varphi (x)\to \infty $
as
$\omega ^{-1}(x)=x\varphi (x)\to \infty $
as
![]() $x\to \infty $
, we get that
$x\to \infty $
, we get that
 $$\begin{align*} \lim_{x\to \infty} \frac{\varphi^{-1}(x)}{\omega(x)} = \lim_{x\to \infty} \frac{\varphi^{-1}(\omega^{-1}(x))}{x} =\lim_{x\to \infty} \frac{\varphi^{-1}(x\varphi(x))}{x} = \infty\,. \end{align*}$$
$$\begin{align*} \lim_{x\to \infty} \frac{\varphi^{-1}(x)}{\omega(x)} = \lim_{x\to \infty} \frac{\varphi^{-1}(\omega^{-1}(x))}{x} =\lim_{x\to \infty} \frac{\varphi^{-1}(x\varphi(x))}{x} = \infty\,. \end{align*}$$
In consequence,
![]() $\omega (x)=o(\varphi ^{-1}(x))$
as
$\omega (x)=o(\varphi ^{-1}(x))$
as
![]() $x\to \infty $
, which proves (a).
$x\to \infty $
, which proves (a).
(b). Assume by a contradiction that there exists a constant
![]() $\gamma> 0$
, such that for every
$\gamma> 0$
, such that for every
![]() $x_0>0,$
there exists
$x_0>0,$
there exists
![]() $x>x_0$
with
$x>x_0$
with
![]() $\omega (x)\leqslant \gamma \log x$
. We claim that is not true for large enough
$\omega (x)\leqslant \gamma \log x$
. We claim that is not true for large enough
![]() $x>0$
. Otherwise, we would get that, for large enough
$x>0$
. Otherwise, we would get that, for large enough
![]() $x> e$
,
$x> e$
,
Since
![]() $\varphi \in (\Delta _2)$
, it follows that for large enough
$\varphi \in (\Delta _2)$
, it follows that for large enough
![]() $x>e$
, we get that
$x>e$
, we get that
![]() $x \leqslant c \varphi (\log x)\log x$
for some
$x \leqslant c \varphi (\log x)\log x$
for some
![]() $c>0$
. It is easy to see that
$c>0$
. It is easy to see that
![]() $\varphi \in (\Delta _2)$
yields that there are constants
$\varphi \in (\Delta _2)$
yields that there are constants
![]() $C>0$
and
$C>0$
and
![]() $\beta \geqslant 1$
such that
$\beta \geqslant 1$
such that
![]() $\varphi (x) \leqslant C x^\beta $
for all
$\varphi (x) \leqslant C x^\beta $
for all
![]() $x>0$
. Combining these estimates yields that
$x>0$
. Combining these estimates yields that
![]() $\sup_{x>e} x/\log ^{\beta +1} x <\infty $
. Since
$\sup_{x>e} x/\log ^{\beta +1} x <\infty $
. Since
![]() $x/\log ^{\beta +1} x \to \infty $
as
$x/\log ^{\beta +1} x \to \infty $
as
![]() $x\to \infty $
, we get a contradiction. This completes the proof of (b).
$x\to \infty $
, we get a contradiction. This completes the proof of (b).
To finish observe that, from (a) and (b), we get that
![]() $\log x=o(\varphi ^{-1}(x))$
as
$\log x=o(\varphi ^{-1}(x))$
as
![]() $x\to \infty $
, which is equivalent to
$x\to \infty $
, which is equivalent to
and so the statement (c) follows.
In what follows, we will use the following lemma proved by Yanagihara [Reference Yanagihara21].
Lemma 3.4. Let
![]() $0<c\leqslant 1$
, and let
$0<c\leqslant 1$
, and let
![]() $\{a_n(c)\}$
be defined by
$\{a_n(c)\}$
be defined by
 $$\begin{align*}\exp\Big(\frac{c}{2}\frac{1+z}{1-z}\Big)=\sum_{n=0}^\infty a_n(c)z^n, \quad\, z \in \mathbb{D}\,. \end{align*}$$
$$\begin{align*}\exp\Big(\frac{c}{2}\frac{1+z}{1-z}\Big)=\sum_{n=0}^\infty a_n(c)z^n, \quad\, z \in \mathbb{D}\,. \end{align*}$$
Then
![]() $a_n(c)$
satisfies the following asymptotic formula:
$a_n(c)$
satisfies the following asymptotic formula:
The following corollary is a immediate consequence of Lemma 3.4.
Corollary 3.5. If
![]() $\{c_k\}\subset (0,1]$
is a sequence such that
$\{c_k\}\subset (0,1]$
is a sequence such that
![]() $\lim _{k\to \infty } c_kk=\infty $
, then the Taylor coefficients of the function given by the formula
$\lim _{k\to \infty } c_kk=\infty $
, then the Taylor coefficients of the function given by the formula
 $$\begin{align*}\exp\Big(\frac{c_k}{2}\frac{1+z}{1-z}\Big)=\sum_{n=0}^\infty a_n(c_k)z^n, \quad\, z \in \mathbb{D}\,, \end{align*}$$
$$\begin{align*}\exp\Big(\frac{c_k}{2}\frac{1+z}{1-z}\Big)=\sum_{n=0}^\infty a_n(c_k)z^n, \quad\, z \in \mathbb{D}\,, \end{align*}$$
satisfy the condition
The following lemma is a generalization of Yanagihara’s Lemma
![]() $2.1$
from [Reference Yanagihara21], proved there for the special case
$2.1$
from [Reference Yanagihara21], proved there for the special case
![]() $\{x_k\}=\{\sqrt {k}\}$
.
$\{x_k\}=\{\sqrt {k}\}$
.
Lemma 3.6. Let
![]() $\{x_k\}\in \boldsymbol {\omega }(\mathbb {N}_0)$
be a positive and increasing sequence such that
$\{x_k\}\in \boldsymbol {\omega }(\mathbb {N}_0)$
be a positive and increasing sequence such that
![]() $x_k \to \infty $
as
$x_k \to \infty $
as
![]() $k\to \infty $
. Suppose that the complex sequence
$k\to \infty $
. Suppose that the complex sequence
![]() $\{\lambda _k\}$
satisfies the condition
$\{\lambda _k\}$
satisfies the condition
![]() $\lambda _k=O(\exp (-c_kx_k))$
for every positive sequence
$\lambda _k=O(\exp (-c_kx_k))$
for every positive sequence
![]() $\{c_k\}\in \boldsymbol {\omega }$
, such that,
$\{c_k\}\in \boldsymbol {\omega }$
, such that,
![]() $c_k\downarrow 0$
. Then, there exists
$c_k\downarrow 0$
. Then, there exists
![]() $c>0$
such that
$c>0$
such that
Proof. Clearly,
![]() $\lambda _k=O(\exp (-c_kx_k))$
yields that
$\lambda _k=O(\exp (-c_kx_k))$
yields that
![]() $\lambda _k\to 0$
and
$\lambda _k\to 0$
and
![]() $\limsup _{k\to \infty }\frac {\log |\lambda _k|}{x_k} \leqslant 0$
. It is enough to show that
$\limsup _{k\to \infty }\frac {\log |\lambda _k|}{x_k} \leqslant 0$
. It is enough to show that
![]() $\limsup _{k\to \infty }\frac {\log |\lambda _k|}{x_k}<0$
. Suppose that
$\limsup _{k\to \infty }\frac {\log |\lambda _k|}{x_k}<0$
. Suppose that
![]() $\limsup _{k\to \infty }\frac {\log |\lambda _k|}{x_k}=0$
. Then, by passing to a subsequence, if necessary, we can assume that
$\limsup _{k\to \infty }\frac {\log |\lambda _k|}{x_k}=0$
. Then, by passing to a subsequence, if necessary, we can assume that
![]() $b_k \downarrow 0$
as
$b_k \downarrow 0$
as
![]() $k\to \infty $
, where
$k\to \infty $
, where
 $$\begin{align*}b_k:=-\frac{1}{x_k}\log|\lambda_k| \downarrow 0, \quad\, k\in \mathbb{N}_0\,. \end{align*}$$
$$\begin{align*}b_k:=-\frac{1}{x_k}\log|\lambda_k| \downarrow 0, \quad\, k\in \mathbb{N}_0\,. \end{align*}$$
From our hypothesis, it follows that for every positive sequence
![]() $c=\{c_k\}\in \boldsymbol {\omega }$
with
$c=\{c_k\}\in \boldsymbol {\omega }$
with
![]() $c_k\downarrow 0$
, there exists a constant
$c_k\downarrow 0$
, there exists a constant
![]() $A(c)>0$
such that
$A(c)>0$
such that
![]() $|\lambda _k|\leqslant A(c)\exp (-c_kx_k)$
and so,
$|\lambda _k|\leqslant A(c)\exp (-c_kx_k)$
and so,
![]() $c_k x_k + \log |\lambda _k|\leqslant \log A(c)$
for each
$c_k x_k + \log |\lambda _k|\leqslant \log A(c)$
for each
![]() $k\in {\mathbb {N}_0}$
. From the definition of
$k\in {\mathbb {N}_0}$
. From the definition of
![]() $\{b_k\}$
, we have
$\{b_k\}$
, we have
![]() $\log |\lambda _k|=-b_kx_k$
. Thus, we conclude that
$\log |\lambda _k|=-b_kx_k$
. Thus, we conclude that
Now, observe that the sequence
![]() $c'=\{c_{k}'\}$
given by
$c'=\{c_{k}'\}$
given by
![]() $c_{k}'=\max \big \{2b_k,\frac {1}{\sqrt {x_k}}\big \}$
, for each
$c_{k}'=\max \big \{2b_k,\frac {1}{\sqrt {x_k}}\big \}$
, for each
![]() $k\geqslant 0$
, is decreasing and
$k\geqslant 0$
, is decreasing and
![]() $c_k'\downarrow 0$
as
$c_k'\downarrow 0$
as
![]() $k\to \infty $
(by
$k\to \infty $
(by
![]() $b_k\downarrow 0$
and
$b_k\downarrow 0$
and
![]() $x_k\uparrow \infty $
as
$x_k\uparrow \infty $
as
![]() $k\to \infty $
). Combining the above facts, now gives that there exists a constant
$k\to \infty $
). Combining the above facts, now gives that there exists a constant
![]() $A(c')>0$
such that, for each
$A(c')>0$
such that, for each
![]() $k\geqslant 0$
, we have
$k\geqslant 0$
, we have
![]() $(c_k'-b_k)x_k\leqslant \log A(c')$
. Thus, we conclude that
$(c_k'-b_k)x_k\leqslant \log A(c')$
. Thus, we conclude that
Since
![]() $x_k\to \infty $
as
$x_k\to \infty $
as
![]() $k\to \infty $
, we get a contradiction. This gives the desired conclusion.
$k\to \infty $
, we get a contradiction. This gives the desired conclusion.
We are now ready to prove the necessary condition for a sequence
![]() $\{\lambda _k\}$
to be a multiplier from
$\{\lambda _k\}$
to be a multiplier from
![]() $N_\varphi $
to
$N_\varphi $
to
![]() $H^p$
.
$H^p$
.
Theorem 3.7. Let
![]() $\varphi \in \Phi _2^{sc}$
be a function satisfying condition
$\varphi \in \Phi _2^{sc}$
be a function satisfying condition
![]() $p(\varphi )>1$
, and let
$p(\varphi )>1$
, and let
![]() $\omega $
be a function associated with
$\omega $
be a function associated with
![]() $\varphi $
. If
$\varphi $
. If
![]() $\{\lambda _k\}\in \boldsymbol {\omega }(\mathbb {N}_0)$
is a multiplier from
$\{\lambda _k\}\in \boldsymbol {\omega }(\mathbb {N}_0)$
is a multiplier from
![]() $N_\varphi $
to
$N_\varphi $
to
![]() $H^p$
for some
$H^p$
for some
![]() $p\in (0,\infty ]$
, then for some constant
$p\in (0,\infty ]$
, then for some constant
![]() $c>0$
, we have
$c>0$
, we have
Proof. From Remark (3), without loss of generality, we can assume
![]() $\varphi (1)=1$
. By Lemma 3.6, it suffices to show that, for any positive sequence
$\varphi (1)=1$
. By Lemma 3.6, it suffices to show that, for any positive sequence
![]() $\{c_k\}\in \boldsymbol {\omega }$
such that
$\{c_k\}\in \boldsymbol {\omega }$
such that
![]() $c_k\downarrow 0$
, we have
$c_k\downarrow 0$
, we have
Observe that, taking a sequence
![]() $\{c_k'\}\in \boldsymbol {\omega }$
of the form
$\{c_k'\}\in \boldsymbol {\omega }$
of the form
 $$\begin{align*}c_k'=\min\Big\{\frac{1}{2}, \max\Big\{\frac{1}{\omega(k)},c_n\Big\}\Big\}, \quad\, k\in\mathbb{N}\,, \end{align*}$$
$$\begin{align*}c_k'=\min\Big\{\frac{1}{2}, \max\Big\{\frac{1}{\omega(k)},c_n\Big\}\Big\}, \quad\, k\in\mathbb{N}\,, \end{align*}$$
we have
![]() $c_k'\downarrow 0$
. Furthermore, if we show that
$c_k'\downarrow 0$
. Furthermore, if we show that
then, for a given sequence
![]() $\{c_k\}$
as above, the formula
$\{c_k\}$
as above, the formula
![]() $\lambda _k=O(\exp [-c_k\omega (k)])$
is satisfied. This means that without loss of generality, we can assume that
$\lambda _k=O(\exp [-c_k\omega (k)])$
is satisfied. This means that without loss of generality, we can assume that
 $$\begin{align*}\frac{1}{\omega(k)}\leqslant c_k\leqslant \frac{1}{2}, \quad\, k\geqslant k_{0}\,, \end{align*}$$
$$\begin{align*}\frac{1}{\omega(k)}\leqslant c_k\leqslant \frac{1}{2}, \quad\, k\geqslant k_{0}\,, \end{align*}$$
where
![]() $k_0$
is the smallest nonnegative integer such that
$k_0$
is the smallest nonnegative integer such that
![]() $\omega (k_0)\geqslant 2$
. Choose one of such sequences
$\omega (k_0)\geqslant 2$
. Choose one of such sequences
![]() $\{c_k\}$
and let
$\{c_k\}$
and let
![]() $\{\beta _k\}$
be the sequence given by
$\{\beta _k\}$
be the sequence given by
 $$\begin{align*}\beta_k :=c_k(1-r_k)\varphi^{-1}\Big(\frac{1}{1-r_k}\Big), \quad\, k\in{\mathbb{N}_0}\,, \end{align*}$$
$$\begin{align*}\beta_k :=c_k(1-r_k)\varphi^{-1}\Big(\frac{1}{1-r_k}\Big), \quad\, k\in{\mathbb{N}_0}\,, \end{align*}$$
where
![]() $\{r_k\} \subset (0, 1)$
is a sequence such that
$\{r_k\} \subset (0, 1)$
is a sequence such that
![]() $r_k\uparrow 1$
as
$r_k\uparrow 1$
as
![]() $k\to \infty $
. The concavity of
$k\to \infty $
. The concavity of
![]() $\varphi ^{-1}$
implies that the function
$\varphi ^{-1}$
implies that the function
![]() $t\mapsto \varphi ^{-1}(t)/t$
is nonincreasing on
$t\mapsto \varphi ^{-1}(t)/t$
is nonincreasing on
![]() $(0,\infty )$
. Hence
$(0,\infty )$
. Hence
![]() $(1-r_k)\varphi ^{-1}\big (\frac {1}{1-r_k}\big )\leqslant \varphi ^{-1}(1)=1$
and so
$(1-r_k)\varphi ^{-1}\big (\frac {1}{1-r_k}\big )\leqslant \varphi ^{-1}(1)=1$
and so
![]() $\beta _k\leqslant 1/2$
for each
$\beta _k\leqslant 1/2$
for each
![]() $k\in {\mathbb {N}_0}$
. From the convexity of
$k\in {\mathbb {N}_0}$
. From the convexity of
![]() $\varphi $
, we get
$\varphi $
, we get
 $$\begin{align*}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big) =(1-r_k)\varphi\Big(c_k\varphi^{-1}\Big(\frac{1}{1-r_k}\Big)\Big)\leqslant c_k\to 0\,, \end{align*}$$
$$\begin{align*}(1-r_k)\varphi\Big(\frac{\beta_k}{1-r_k}\Big) =(1-r_k)\varphi\Big(c_k\varphi^{-1}\Big(\frac{1}{1-r_k}\Big)\Big)\leqslant c_k\to 0\,, \end{align*}$$
as
![]() $k\to \infty $
. In consequence, the sequence
$k\to \infty $
. In consequence, the sequence
![]() $\{\beta _k\}$
satisfies all of the assumptions of Lemma 3.2. Now, observe that the sequence
$\{\beta _k\}$
satisfies all of the assumptions of Lemma 3.2. Now, observe that the sequence
![]() $\{f_k\}$
(generated by
$\{f_k\}$
(generated by
![]() $\{\beta _k\}$
given above) defined in Lemma 3.2 is topologically bounded in
$\{\beta _k\}$
given above) defined in Lemma 3.2 is topologically bounded in
![]() $N_\varphi $
. Thus, from Lemma 3.1, we conclude that the sequence
$N_\varphi $
. Thus, from Lemma 3.1, we conclude that the sequence
![]() $\{\Lambda f_k\}$
is bounded in
$\{\Lambda f_k\}$
is bounded in
![]() $H^p$
. Furthermore,
$H^p$
. Furthermore,
 $$\begin{align*}\Lambda f_k(z)=\sum_{n=0}^{\infty}\lambda_n\widehat{f}_k(n)r_k^n z^n, \quad\, z \in \mathbb{D}\,, \end{align*}$$
$$\begin{align*}\Lambda f_k(z)=\sum_{n=0}^{\infty}\lambda_n\widehat{f}_k(n)r_k^n z^n, \quad\, z \in \mathbb{D}\,, \end{align*}$$
where
![]() $\widehat {f}_k(n)$
is the nth Taylor coefficient of
$\widehat {f}_k(n)$
is the nth Taylor coefficient of
![]() $\exp \big (\beta _k\frac {1+z}{1-z}\big )$
,
$\exp \big (\beta _k\frac {1+z}{1-z}\big )$
,
![]() $z\in \mathbb {D}$
. Since
$z\in \mathbb {D}$
. Since
![]() $\{\Lambda f_k\}$
is a bounded sequence in
$\{\Lambda f_k\}$
is a bounded sequence in
![]() $H^p$
there exists a constant K, such that, for all
$H^p$
there exists a constant K, such that, for all
![]() $k\in {\mathbb {N}_0}$
, the inequality
$k\in {\mathbb {N}_0}$
, the inequality
![]() $\|\Lambda f_k\|_{H^p} \leqslant K$
holds. From [Reference Duren1, Th. 6.4], it follows that there exists
$\|\Lambda f_k\|_{H^p} \leqslant K$
holds. From [Reference Duren1, Th. 6.4], it follows that there exists
![]() $C_p>0$
such that, for each
$C_p>0$
such that, for each
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $n\in {\mathbb {N}_0}$
, we have
$n\in {\mathbb {N}_0}$
, we have
 $$\begin{align} |\lambda_nf_k(n)r_k^n|\leqslant \begin{cases} K C_{p} n^{-1+\frac{1}{p}}, & \text{if} \quad\, 0<p<1\,,\\ K C_{p}, & \text{if}\quad\, 1\leqslant p\leqslant\infty\,. \end{cases} \end{align} $$
$$\begin{align} |\lambda_nf_k(n)r_k^n|\leqslant \begin{cases} K C_{p} n^{-1+\frac{1}{p}}, & \text{if} \quad\, 0<p<1\,,\\ K C_{p}, & \text{if}\quad\, 1\leqslant p\leqslant\infty\,. \end{cases} \end{align} $$
On the other hand, using notation from Lemma 3.4, we get that
 $$\begin{align*}f_k(z)=\sum_{n=0}^\infty a_n(2\beta_k)(r_kz)^n, \quad\, z \in \mathbb{D}\,. \end{align*}$$
$$\begin{align*}f_k(z)=\sum_{n=0}^\infty a_n(2\beta_k)(r_kz)^n, \quad\, z \in \mathbb{D}\,. \end{align*}$$
Now, observe that
![]() $\omega (1)=1$
(because
$\omega (1)=1$
(because
![]() $\varphi (t)=\omega ^{-1}(t)/t$
for all
$\varphi (t)=\omega ^{-1}(t)/t$
for all
![]() $t>0$
). From the assumption
$t>0$
). From the assumption
![]() $c_k\omega (k)\geqslant 1$
for
$c_k\omega (k)\geqslant 1$
for
![]() $k\geqslant k_0$
, we obtain
$k\geqslant k_0$
, we obtain
Since
![]() $c_k\downarrow 0$
and
$c_k\downarrow 0$
and
![]() $\widetilde {y}(k)=\frac {\omega (k)}{k}\downarrow 0$
as
$\widetilde {y}(k)=\frac {\omega (k)}{k}\downarrow 0$
as
![]() $k\to \infty $
, the sequence
$k\to \infty $
, the sequence
![]() $\{r_k\}$
given by
$\{r_k\}$
given by
![]() $r_k=1-c_k\widetilde {y}(k)$
for each
$r_k=1-c_k\widetilde {y}(k)$
for each
![]() $k\in {\mathbb {N}_0}$
, satisfies
$k\in {\mathbb {N}_0}$
, satisfies
![]() $r_k\in (0,1)$
and
$r_k\in (0,1)$
and
![]() $r_k\uparrow 1$
as
$r_k\uparrow 1$
as
![]() $k\to \infty $
. The function
$k\to \infty $
. The function
![]() $t\mapsto \varphi ^{-1}(t)/t$
is nonincreasing, which gives that the mapping
$t\mapsto \varphi ^{-1}(t)/t$
is nonincreasing, which gives that the mapping
![]() $t\mapsto x\varphi ^{-1}(1/x)$
is nondecreasing on
$t\mapsto x\varphi ^{-1}(1/x)$
is nondecreasing on
![]() $(0,\infty )$
. Using this observation and the above equality, we get that
$(0,\infty )$
. Using this observation and the above equality, we get that
 $$\begin{align*}\beta_k\omega(k)=c_k\,\omega(k)\,\Big[c_k\widetilde{y}(k)\varphi^{-1}\Big(\frac{1}{c_k\widetilde{y}(k)}\Big)\Big] \geqslant \frac{\varphi^{-1}(k)}{k}\,, \end{align*}$$
$$\begin{align*}\beta_k\omega(k)=c_k\,\omega(k)\,\Big[c_k\widetilde{y}(k)\varphi^{-1}\Big(\frac{1}{c_k\widetilde{y}(k)}\Big)\Big] \geqslant \frac{\varphi^{-1}(k)}{k}\,, \end{align*}$$
which is
 $$\begin{align*}k\beta_k\geqslant\frac{\varphi^{-1}(k)}{\omega(k)}, \quad k\geqslant k_{0}\,. \end{align*}$$
$$\begin{align*}k\beta_k\geqslant\frac{\varphi^{-1}(k)}{\omega(k)}, \quad k\geqslant k_{0}\,. \end{align*}$$
From Lemma 3.3(a), we know that
![]() $2k\beta _k\to \infty $
as
$2k\beta _k\to \infty $
as
![]() $k\to \infty $
. Hence, from Corollary 3.5, it follows that
$k\to \infty $
. Hence, from Corollary 3.5, it follows that
Furthermore, for each
![]() $k\in {\mathbb {N}_0}$
, we have (by
$k\in {\mathbb {N}_0}$
, we have (by
![]() $k\widetilde {y}(k)=\omega (k)$
for
$k\widetilde {y}(k)=\omega (k)$
for
![]() $k\in {\mathbb {N}_0}$
)
$k\in {\mathbb {N}_0}$
)
 $$ \begin{align*} \beta_{k}\,k& = c_{k}^2\,k\,\widetilde{y}(k) \varphi^{-1}\Big(\frac{1}{c_k\widetilde{y}(k)}\Big) = c_{k}^2\,\omega(k) \varphi^{-1}\Big(\frac{1}{c_k\widetilde{y}(k)}\Big)\\ &\geqslant c_{k}^2\,\omega(k) \varphi^{-1}\Big(\frac{1}{\widetilde{y}(k)}\Big)=c_k^2\omega^2(k)\,. \end{align*} $$
$$ \begin{align*} \beta_{k}\,k& = c_{k}^2\,k\,\widetilde{y}(k) \varphi^{-1}\Big(\frac{1}{c_k\widetilde{y}(k)}\Big) = c_{k}^2\,\omega(k) \varphi^{-1}\Big(\frac{1}{c_k\widetilde{y}(k)}\Big)\\ &\geqslant c_{k}^2\,\omega(k) \varphi^{-1}\Big(\frac{1}{\widetilde{y}(k)}\Big)=c_k^2\omega^2(k)\,. \end{align*} $$
Thus
Since
![]() $\lim _{x\to 0+}\big (1-x\big )^{-1/x}=e$
and
$\lim _{x\to 0+}\big (1-x\big )^{-1/x}=e$
and
![]() $c_k\widetilde {y}(k)\to 0$
as
$c_k\widetilde {y}(k)\to 0$
as
![]() $k\to \infty $
, we obtain
$k\to \infty $
, we obtain
Now, we apply
![]() $(**)$
for
$(**)$
for
![]() $1\leqslant p\leqslant \infty $
to get that, for some
$1\leqslant p\leqslant \infty $
to get that, for some
![]() $\gamma>0$
and for each
$\gamma>0$
and for each
![]() $k\in \mathbb {N}$
, the following estimates hold:
$k\in \mathbb {N}$
, the following estimates hold:
 $$ \begin{align*} |\lambda_k| & \leqslant \gamma (1-c_k\widetilde{y}(k))^{-k}\exp\big[-\sqrt{2\beta_kk}(1+o(1))\big] \\ & \leqslant \gamma \exp[c_k\omega(k){(1+o(1))}]\exp[-\sqrt{2}c_k\omega(k)(1+o(1))] \\ & \leqslant \gamma \exp[-(\sqrt{2}-1)c_k\omega(k)(1+o(1))]\,. \end{align*} $$
$$ \begin{align*} |\lambda_k| & \leqslant \gamma (1-c_k\widetilde{y}(k))^{-k}\exp\big[-\sqrt{2\beta_kk}(1+o(1))\big] \\ & \leqslant \gamma \exp[c_k\omega(k){(1+o(1))}]\exp[-\sqrt{2}c_k\omega(k)(1+o(1))] \\ & \leqslant \gamma \exp[-(\sqrt{2}-1)c_k\omega(k)(1+o(1))]\,. \end{align*} $$
Clearly, this gives the desired conclusion in the case
![]() $1\leqslant p<\infty $
. When
$1\leqslant p<\infty $
. When
![]() $0<p<1$
, we have
$0<p<1$
, we have
Using Lemma 3.6, we can find constants
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $\gamma _p>0$
$\gamma _p>0$
that is,
 $$\begin{align*}|\lambda_k|\leqslant \gamma_p \exp\Big(\Big(\frac{1}{p}-1\Big)\log k\Big)\exp(-\alpha \omega(k)), \quad\, k \in \mathbb{N}\,. \end{align*}$$
$$\begin{align*}|\lambda_k|\leqslant \gamma_p \exp\Big(\Big(\frac{1}{p}-1\Big)\log k\Big)\exp(-\alpha \omega(k)), \quad\, k \in \mathbb{N}\,. \end{align*}$$
From Lemma 3.3(b), it follows that
 $$\begin{align*}\lim_{k\to\infty}\frac{\log k}{\omega(k)}=0\,. \end{align*}$$
$$\begin{align*}\lim_{k\to\infty}\frac{\log k}{\omega(k)}=0\,. \end{align*}$$
Thus, there exists
![]() $k_0\in \mathbb {N}$
, such that
$k_0\in \mathbb {N}$
, such that
 $$\begin{align*}\Big(\frac{1}{p}-1\Big)\log k\leqslant \frac{a}{2}\omega(k),\quad k\geqslant k_{0}\,. \end{align*}$$
$$\begin{align*}\Big(\frac{1}{p}-1\Big)\log k\leqslant \frac{a}{2}\omega(k),\quad k\geqslant k_{0}\,. \end{align*}$$
Combining the above, we conclude that there exists
![]() $\widetilde {C}>0$
such that for
$\widetilde {C}>0$
such that for
![]() $c=\alpha /2$
, we have
$c=\alpha /2$
, we have
This completes the proof.
Now, we proceed to the investigation of sufficient conditions for the multipliers. We start with the definition of
![]() $\mathcal {H}(\omega )$
spaces given by Zayed in [Reference Zayed23]. These are the spaces of analytic functions generated by some function
$\mathcal {H}(\omega )$
spaces given by Zayed in [Reference Zayed23]. These are the spaces of analytic functions generated by some function
![]() $\omega $
. The original assumptions on
$\omega $
. The original assumptions on
![]() $\omega $
come from theory of Beurling distributions, but we will present a weaker set of conditions for which the results in [Reference Zayed23] are true. Let
$\omega $
come from theory of Beurling distributions, but we will present a weaker set of conditions for which the results in [Reference Zayed23] are true. Let
![]() $\omega \colon \mathbb {R}_{+} \to \mathbb {R}_{+}$
be a function satisfying the following conditions:
$\omega \colon \mathbb {R}_{+} \to \mathbb {R}_{+}$
be a function satisfying the following conditions:
-
(1)
 $\omega $
is concave and continuously differentiable function with
$\omega $
is concave and continuously differentiable function with
 $\omega (0)=0$
.
$\omega (0)=0$
. -
(2)
 $\omega (x)=o(x)$
as
$\omega (x)=o(x)$
as
 $x\to \infty $
.
$x\to \infty $
. -
(3)
 $\log (x)=o(\omega (x))$
as
$\log (x)=o(\omega (x))$
as
 $x\to \infty $
.
$x\to \infty $
. -
(4)
 $\omega (ax)\leqslant \delta (a)\omega (x)$
, where
$\omega (ax)\leqslant \delta (a)\omega (x)$
, where
 $a\geqslant 1$
and
$a\geqslant 1$
and
 $\delta (a)=o(a)$
as
$\delta (a)=o(a)$
as
 $a\to \infty $
.
$a\to \infty $
.
We denote the set of all functions satisfying (1)–(4) by
![]() $\boldsymbol {\Omega }$
. Observe, for every
$\boldsymbol {\Omega }$
. Observe, for every
![]() $\omega \in \boldsymbol {\Omega }$
, the function
$\omega \in \boldsymbol {\Omega }$
, the function
![]() $x\mapsto \omega (x)/x$
is decreasing on
$x\mapsto \omega (x)/x$
is decreasing on
![]() $(0, \infty )$
. Thus, for every
$(0, \infty )$
. Thus, for every
![]() $r\in [0, 1),$
there exists a unique solution x denoted by
$r\in [0, 1),$
there exists a unique solution x denoted by
![]() $\widetilde {x}(1-r)$
of the equation
$\widetilde {x}(1-r)$
of the equation
![]() $\omega (x)/x=1-r$
. In what follows, we let
$\omega (x)/x=1-r$
. In what follows, we let
For any
![]() $\omega \in \boldsymbol {\Omega }$
, we define
$\omega \in \boldsymbol {\Omega }$
, we define
![]() $H(\omega )$
to be the space of all
$H(\omega )$
to be the space of all
![]() $f\in H(\mathbb {D})$
, which for any
$f\in H(\mathbb {D})$
, which for any
![]() $c>0$
satisfies
$c>0$
satisfies
 $$ \begin{align*} \|f\|_{c}: = \int_{0}^{1} M_\infty(r,f) \exp\Big[-c\,\Omega\Big(\frac{1}{1-r}\Big)\Big]\,dr<\infty\,. \end{align*} $$
$$ \begin{align*} \|f\|_{c}: = \int_{0}^{1} M_\infty(r,f) \exp\Big[-c\,\Omega\Big(\frac{1}{1-r}\Big)\Big]\,dr<\infty\,. \end{align*} $$
Clearly, for any
![]() $c>0$
,
$c>0$
,
![]() $\|\cdot \|_c$
defines a norm in
$\|\cdot \|_c$
defines a norm in
![]() $H(\omega )$
. Furthermore, it is obvious that, any
$H(\omega )$
. Furthermore, it is obvious that, any
![]() $\varphi \in \Phi _2^{sc}$
replacing
$\varphi \in \Phi _2^{sc}$
replacing
![]() $\Omega $
with
$\Omega $
with
![]() $\varphi ^{-1}(x)$
gives the space
$\varphi ^{-1}(x)$
gives the space
![]() $F^{int}_\varphi $
. Of course, not every function
$F^{int}_\varphi $
. Of course, not every function
![]() $\varphi \in \Phi _2^{sc}$
can be represented as
$\varphi \in \Phi _2^{sc}$
can be represented as
![]() $\Omega $
for some
$\Omega $
for some
![]() $\omega $
satisfying conditions (1)–(4). In view of this observation, in what follows the following conditions on
$\omega $
satisfying conditions (1)–(4). In view of this observation, in what follows the following conditions on
![]() $\omega $
will be imposed.
$\omega $
will be imposed.
-
(i)
 $\omega $
is concave and continuously differentiable function with
$\omega $
is concave and continuously differentiable function with
 $\omega (0)=0$
.
$\omega (0)=0$
. -
(ii)
 $\omega ^{-1}$
is
$\omega ^{-1}$
is
 $2$
–strongly convex, that is,
$2$
–strongly convex, that is,
 $x^2=o(\omega ^{-1}(x))$
as
$x^2=o(\omega ^{-1}(x))$
as
 $x\to \infty $
.
$x\to \infty $
. -
(iii)
 $\omega ^{-1}\in (\Delta _2)$
.
$\omega ^{-1}\in (\Delta _2)$
. -
(iv)
 $\omega (ax)\leqslant \delta (a)\omega (x)$
, where
$\omega (ax)\leqslant \delta (a)\omega (x)$
, where
 $a\geqslant 1$
and
$a\geqslant 1$
and
 $\delta (a)=o(a)$
as
$\delta (a)=o(a)$
as
 $a\to \infty $
.
$a\to \infty $
.
If the function
![]() $\omega $
satisfies all of the above conditions, we write
$\omega $
satisfies all of the above conditions, we write
![]() $\omega \in {\boldsymbol {\widetilde {\Omega }}}$
. It can be seen that, if
$\omega \in {\boldsymbol {\widetilde {\Omega }}}$
. It can be seen that, if
![]() $\omega \in \boldsymbol {\widetilde {\Omega }}$
, then
$\omega \in \boldsymbol {\widetilde {\Omega }}$
, then
![]() $\omega \in \boldsymbol {\Omega }$
, so every function
$\omega \in \boldsymbol {\Omega }$
, so every function
![]() $\omega \in \boldsymbol {\widetilde {\Omega }}$
generates some space
$\omega \in \boldsymbol {\widetilde {\Omega }}$
generates some space
![]() $H(\omega )$
. Now, for any
$H(\omega )$
. Now, for any
![]() $\omega \in {\boldsymbol {\widetilde {\Omega }}}$
, define
$\omega \in {\boldsymbol {\widetilde {\Omega }}}$
, define
![]() $\varphi _\omega (x)\sim \frac {\omega ^{-1}(x)}{x}$
. It is equivalent to
$\varphi _\omega (x)\sim \frac {\omega ^{-1}(x)}{x}$
. It is equivalent to
![]() $\varphi _{\omega }^{-1}(\omega _{*}(x))\sim \omega (x)$
, where
$\varphi _{\omega }^{-1}(\omega _{*}(x))\sim \omega (x)$
, where
![]() $\omega _{*}(x):=\frac {x}{\omega (x)}$
, for all
$\omega _{*}(x):=\frac {x}{\omega (x)}$
, for all
![]() $x>0$
. Hence,
$x>0$
. Hence,
Since
![]() $\omega _{*}^{-1}\big (\frac {1}{1-r}\big )$
is the solution of equation
$\omega _{*}^{-1}\big (\frac {1}{1-r}\big )$
is the solution of equation
![]() $\frac {\omega (x)}{x}=1-r$
with respect to x, so
$\frac {\omega (x)}{x}=1-r$
with respect to x, so
It is also easy to see that, if
![]() $\omega \in {\boldsymbol {\widetilde {\Omega }}}$
, then
$\omega \in {\boldsymbol {\widetilde {\Omega }}}$
, then
![]() $\varphi _\omega \in \Phi _2^{sc}$
. We denote the set of all functions
$\varphi _\omega \in \Phi _2^{sc}$
. We denote the set of all functions
![]() $\varphi _\omega $
, where
$\varphi _\omega $
, where
![]() $\omega \in \boldsymbol {\widetilde {\Omega }}$
, by
$\omega \in \boldsymbol {\widetilde {\Omega }}$
, by
![]() $\Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. From previous observations, we get the following corollary.
$\Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. From previous observations, we get the following corollary.
Corollary 3.8. Let
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. Then
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. Then
![]() $F^{int}_{\varphi }=H(\omega )$
, where
$F^{int}_{\varphi }=H(\omega )$
, where
![]() $\varphi (x)\sim \frac {\omega ^{-1}(x)}{x}$
.
$\varphi (x)\sim \frac {\omega ^{-1}(x)}{x}$
.
The equality
![]() $F^{int}_{\varphi }=H(\omega )$
is an important step to give sufficient condition for the multipliers. In case of
$F^{int}_{\varphi }=H(\omega )$
is an important step to give sufficient condition for the multipliers. In case of
![]() $F^{int}_{\varphi }$
,
$F^{int}_{\varphi }$
,
![]() $\varphi \in \Phi _2^{sc}$
, there is no equivalent way to define them using growth of Taylor coefficients. But, when we impose some stricter conditions on
$\varphi \in \Phi _2^{sc}$
, there is no equivalent way to define them using growth of Taylor coefficients. But, when we impose some stricter conditions on
![]() $\varphi $
, that is,
$\varphi $
, that is,
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
(
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
(
![]() $F^{int}_{\varphi }=H(\omega )$
), it is possible to do that, as the following theorem shows. Its proof can be found in [Reference Zayed23].
$F^{int}_{\varphi }=H(\omega )$
), it is possible to do that, as the following theorem shows. Its proof can be found in [Reference Zayed23].
Theorem 3.9. Let
![]() $f\in H(\mathbb {D})$
with
$f\in H(\mathbb {D})$
with
![]() $f(z)=\sum _{n=0}^{\infty }\widehat {f}(n)z^n$
for all
$f(z)=\sum _{n=0}^{\infty }\widehat {f}(n)z^n$
for all
![]() $z\in \mathbb {D}$
. Then
$z\in \mathbb {D}$
. Then
![]() $f\in H(\omega )$
if and only if,
$f\in H(\omega )$
if and only if,
Now, we are ready to show that the condition
![]() $\lambda _k=O(\exp [-c\,\omega (k)])$
is sufficient for a sequence to be a multiplier from
$\lambda _k=O(\exp [-c\,\omega (k)])$
is sufficient for a sequence to be a multiplier from
![]() $N_\varphi $
to
$N_\varphi $
to
![]() $H^p$
, where
$H^p$
, where
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
.
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
.
Theorem 3.10. Let
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. If
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. If
![]() $\lambda _n=O(\exp (-c\,\omega (n)))$
for some
$\lambda _n=O(\exp (-c\,\omega (n)))$
for some
![]() $c>0$
, then
$c>0$
, then
![]() $\{\lambda _n\}$
is a multiplier from
$\{\lambda _n\}$
is a multiplier from
![]() $N_\varphi $
to
$N_\varphi $
to
![]() $H^p$
.
$H^p$
.
Proof. Suppose that
![]() $\lambda _n=O(\exp (-c\,\omega (n)))$
for some
$\lambda _n=O(\exp (-c\,\omega (n)))$
for some
![]() $c>0$
. If
$c>0$
. If
![]() $f\in N_\varphi $
with
$f\in N_\varphi $
with
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
, then from Theorems 2.3 and 3.9, we get that there exists
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
, then from Theorems 2.3 and 3.9, we get that there exists
![]() $C_1>0$
, such that
$C_1>0$
, such that
and
![]() $c_n\downarrow 0$
as
$c_n\downarrow 0$
as
![]() $n\to \infty $
. Let
$n\to \infty $
. Let
![]() $n_0$
be such that
$n_0$
be such that
![]() $c_k<c/2$
for each
$c_k<c/2$
for each
![]() $n\geqslant n_0$
. Then, we have
$n\geqslant n_0$
. Then, we have
for some constant
![]() $C_2>0$
. Since
$C_2>0$
. Since
![]() $\log (x)=o(\omega (x))$
as
$\log (x)=o(\omega (x))$
as
![]() $x\to \infty $
,
$x\to \infty $
,
 $$\begin{align*}\sum_{n=0}^{\infty}\exp[-c\,\omega(k)/2]<\infty\,. \end{align*}$$
$$\begin{align*}\sum_{n=0}^{\infty}\exp[-c\,\omega(k)/2]<\infty\,. \end{align*}$$
This means that
![]() $\Lambda f$
is a continuous function on
$\Lambda f$
is a continuous function on
![]() $\overline {\mathbb {D}}$
, and hence,
$\overline {\mathbb {D}}$
, and hence,
![]() $\Lambda f\in H^p$
for every
$\Lambda f\in H^p$
for every
![]() $p>0$
.
$p>0$
.
From Theorems 3.7 and 3.10, we obtain the following corollary.
Corollary 3.11. Let
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
satisfy condition
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
satisfy condition
![]() $p(\varphi )>1$
. The sequence
$p(\varphi )>1$
. The sequence
![]() $\{\lambda _n\}$
is a multiplier from
$\{\lambda _n\}$
is a multiplier from
![]() $N_\varphi $
to
$N_\varphi $
to
![]() $H^p$
if and only if
$H^p$
if and only if
![]() $\lambda _n=O(\exp (-c\,\omega (n)))$
for some
$\lambda _n=O(\exp (-c\,\omega (n)))$
for some
![]() $c>0$
.
$c>0$
.
4 Continuous linear functionals on
 $N_{\varphi }$
$N_{\varphi }$
We now proceed to the problem of finding the topological dual for the spaces
![]() $N_\varphi $
. We will start with a necessary condition true for all
$N_\varphi $
. We will start with a necessary condition true for all
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. To prove the sufficient condition, we will have to extend slightly the set of assumptions for
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. To prove the sufficient condition, we will have to extend slightly the set of assumptions for
![]() $\varphi $
, but as it will be seen, we will do it in rather natural way. We will need the following lemma.
$\varphi $
, but as it will be seen, we will do it in rather natural way. We will need the following lemma.
Lemma 4.1. Let
![]() $f\in N_\varphi $
and, for
$f\in N_\varphi $
and, for
![]() $\xi \in \mathbb {D}$
, let
$\xi \in \mathbb {D}$
, let
![]() $f_\xi (z):=f(\xi z)$
for all
$f_\xi (z):=f(\xi z)$
for all
![]() $z\in \mathbb {D}$
. Then the set
$z\in \mathbb {D}$
. Then the set
![]() $\{f_\xi; \, \xi \in \mathbb {D}\}$
is bounded in
$\{f_\xi; \, \xi \in \mathbb {D}\}$
is bounded in
![]() $N_\varphi $
.
$N_\varphi $
.
Proof. To show that a subset of
![]() $N_{\varphi }$
is bounded it is enough to apply neighborhood of zero generated by
$N_{\varphi }$
is bounded it is enough to apply neighborhood of zero generated by
![]() $\Delta $
-norm
$\Delta $
-norm
![]() $\|\cdot \|_{\varphi }$
(according to remark on page 8). Fix
$\|\cdot \|_{\varphi }$
(according to remark on page 8). Fix
![]() $f\in N_\varphi $
and let
$f\in N_\varphi $
and let
![]() $V=\big \{g\in N_\varphi ;\, \|g\|_{\varphi } <\eta \big \}$
be an arbitrary neighborhood of zero in
$V=\big \{g\in N_\varphi ;\, \|g\|_{\varphi } <\eta \big \}$
be an arbitrary neighborhood of zero in
![]() $N_\varphi $
. Since
$N_\varphi $
. Since
![]() $\|\lambda f\|_\varphi \to 0$
as
$\|\lambda f\|_\varphi \to 0$
as
![]() $\lambda \to 0$
, there exists
$\lambda \to 0$
, there exists
![]() $\alpha \in (0, 1)$
such that
$\alpha \in (0, 1)$
such that
![]() $\|\alpha f\|_\varphi <\eta $
. For fixed
$\|\alpha f\|_\varphi <\eta $
. For fixed
![]() $\theta \in [0, 2\pi )$
and
$\theta \in [0, 2\pi )$
and
![]() $r\in (0,1)$
, we consider functions
$r\in (0,1)$
, we consider functions
![]() $f_{r,\theta } \in N_\varphi $
given by
$f_{r,\theta } \in N_\varphi $
given by
![]() $f_{r,\theta }(z):=f_r(e^{i\theta }z)= f(re^{i\theta }z)$
for all
$f_{r,\theta }(z):=f_r(e^{i\theta }z)= f(re^{i\theta }z)$
for all
![]() $z\in \mathbb {D}$
. Then
$z\in \mathbb {D}$
. Then
![]() $\|\alpha f_{r, \theta }\|_\varphi = \|\alpha f_r\|_\varphi \leqslant \|\alpha f\|_\varphi $
for all
$\|\alpha f_{r, \theta }\|_\varphi = \|\alpha f_r\|_\varphi \leqslant \|\alpha f\|_\varphi $
for all
![]() $r\in (0, 1)$
and
$r\in (0, 1)$
and
![]() $\theta \in [0, 2\pi )$
. Since
$\theta \in [0, 2\pi )$
. Since
![]() $f_\xi =f_{r,\theta }$
for all
$f_\xi =f_{r,\theta }$
for all
![]() $\xi =re^{i\theta }$
, it follows that
$\xi =re^{i\theta }$
, it follows that
![]() $\{\alpha f_\xi; \, \xi \in \mathbb {D}\} \subset V$
and this completes the proof.
$\{\alpha f_\xi; \, \xi \in \mathbb {D}\} \subset V$
and this completes the proof.
Theorem 4.2. Let
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
satisfy
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
satisfy
![]() $p(\varphi )>1$
. For any continuous linear functional
$p(\varphi )>1$
. For any continuous linear functional
![]() $L \in (N_\varphi )^*$
, there exists a unique function
$L \in (N_\varphi )^*$
, there exists a unique function
![]() $g\in A(\mathbb {D})$
with
$g\in A(\mathbb {D})$
with
![]() $g(z)=\sum _{n=0}^\infty b_nz^n$
for all
$g(z)=\sum _{n=0}^\infty b_nz^n$
for all
![]() $z\in \mathbb {D}$
, for which there exists
$z\in \mathbb {D}$
, for which there exists
![]() $c>0$
such that
$c>0$
such that
![]() $b_n=O(\exp [-c\,\omega (n)])$
and
$b_n=O(\exp [-c\,\omega (n)])$
and
 $$ \begin{align*} L(f)=\lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}f(re^{i\theta})g(e^{-i\theta})\,d\theta =\sum_{n=0}^\infty \widehat{f}(n)b_n, \quad\, f \in N_{\varphi}\,, \end{align*} $$
$$ \begin{align*} L(f)=\lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}f(re^{i\theta})g(e^{-i\theta})\,d\theta =\sum_{n=0}^\infty \widehat{f}(n)b_n, \quad\, f \in N_{\varphi}\,, \end{align*} $$
where
![]() $f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
$f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
![]() $z\in \mathbb {D}$
.
$z\in \mathbb {D}$
.
Proof. Let
![]() $L \in (N_\varphi )^{*}$
and
$L \in (N_\varphi )^{*}$
and
![]() $b_n=L(z^n)$
for each
$b_n=L(z^n)$
for each
![]() $n\in {\mathbb {N}_0}$
. Since
$n\in {\mathbb {N}_0}$
. Since
![]() $\{z^{n}; \, n\in {\mathbb {N}_0}\}$
is a bounded set in
$\{z^{n}; \, n\in {\mathbb {N}_0}\}$
is a bounded set in
![]() $N_\varphi $
, it follows that
$N_\varphi $
, it follows that
![]() $\{b_n\}$
is a bounded sequence. Hence, the function g given by
$\{b_n\}$
is a bounded sequence. Hence, the function g given by
![]() $g(z):=\sum _{n=0}^\infty b_nz^n$
for all
$g(z):=\sum _{n=0}^\infty b_nz^n$
for all
![]() $z\in \mathbb {D}$
is well-defined and analytic in
$z\in \mathbb {D}$
is well-defined and analytic in
![]() $\mathbb {D}$
. Let
$\mathbb {D}$
. Let
![]() $h(\xi ) := L(f_\xi )$
, where
$h(\xi ) := L(f_\xi )$
, where
![]() $f_\xi (z)=f(\xi z)$
for all
$f_\xi (z)=f(\xi z)$
for all
![]() $\xi , z \in \mathbb {D}$
. It can be seen that for all
$\xi , z \in \mathbb {D}$
. It can be seen that for all
![]() $\xi \in \mathbb {D}$
, we get (from the continuity of L) that
$\xi \in \mathbb {D}$
, we get (from the continuity of L) that
 $$ \begin{align*} h(\xi)=L(f_\xi)=\lim_{N\to\infty} L\Big(\sum_{n=0}^N\widehat{f}(n)\xi^nz^n\Big)=\sum_{n=0}^\infty\widehat{f}(n)b_n\xi^n\,. \end{align*} $$
$$ \begin{align*} h(\xi)=L(f_\xi)=\lim_{N\to\infty} L\Big(\sum_{n=0}^N\widehat{f}(n)\xi^nz^n\Big)=\sum_{n=0}^\infty\widehat{f}(n)b_n\xi^n\,. \end{align*} $$
From Lemma 4.1,
![]() $\{f_\xi ;\, \xi \in \mathbb {D}\}$
is a bounded set in
$\{f_\xi ;\, \xi \in \mathbb {D}\}$
is a bounded set in
![]() $N_\varphi $
, so h is a bounded, analytic function in
$N_\varphi $
, so h is a bounded, analytic function in
![]() $\mathbb {D}$
. Hence,
$\mathbb {D}$
. Hence,
![]() $\{b_n\}$
is a multiplier from
$\{b_n\}$
is a multiplier from
![]() $N_\varphi $
to
$N_\varphi $
to
![]() $H^\infty $
, and therefore
$H^\infty $
, and therefore
![]() $b_n = O(\exp [-c\,\omega (n)])$
for some
$b_n = O(\exp [-c\,\omega (n)])$
for some
![]() $c>0$
. Because
$c>0$
. Because
![]() $\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
, we know that
$\varphi \in \Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
, we know that
![]() $N_\varphi \subset F_\varphi = H(\omega )$
, so by Theorem 3.9,
$N_\varphi \subset F_\varphi = H(\omega )$
, so by Theorem 3.9,
![]() $\widehat {f}(n)=O(\exp [o(\omega (n))])$
as
$\widehat {f}(n)=O(\exp [o(\omega (n))])$
as
![]() $n\to \infty $
. This shows that the series
$n\to \infty $
. This shows that the series
![]() $\sum _{n=0}^\infty \widehat {f}(n)b_n\xi ^n$
in the above formula converges for every
$\sum _{n=0}^\infty \widehat {f}(n)b_n\xi ^n$
in the above formula converges for every
![]() $\xi \in \mathbb {D}$
. Now, from the fact that
$\xi \in \mathbb {D}$
. Now, from the fact that
![]() $f_r\to f$
in
$f_r\to f$
in
![]() $N_\varphi $
as
$N_\varphi $
as
![]() $r\to 1-$
and Abel’s theorem, we conclude that
$r\to 1-$
and Abel’s theorem, we conclude that
 $$\begin{align*}L(f)=\lim_{r\to 1-} \,L(f_r)=\lim_{r\to 1-}\sum_{n=0}^\infty\widehat{f}(n)b_n r^n =\sum_{n=0}^\infty \widehat{f}(n)b_{n}\,. \end{align*}$$
$$\begin{align*}L(f)=\lim_{r\to 1-} \,L(f_r)=\lim_{r\to 1-}\sum_{n=0}^\infty\widehat{f}(n)b_n r^n =\sum_{n=0}^\infty \widehat{f}(n)b_{n}\,. \end{align*}$$
The proof of equality of the integral and the series is standard.
Now, we will proceed to the sufficient condition. From Remark (2), we know that every function
![]() $\varphi \in \Phi _2^{sc}$
can be represented in the form
$\varphi \in \Phi _2^{sc}$
can be represented in the form
![]() $\varphi (x)= \frac {\omega ^{-1}(x)}{x}$
for all
$\varphi (x)= \frac {\omega ^{-1}(x)}{x}$
for all
![]() $x>0$
, where
$x>0$
, where
![]() $\omega $
satisfies conditions (i)–(iv) from the definition of a set
$\omega $
satisfies conditions (i)–(iv) from the definition of a set
![]() $\boldsymbol {\widetilde {\Omega }}$
. If we suppose that
$\boldsymbol {\widetilde {\Omega }}$
. If we suppose that
![]() $\varphi \in \Phi _2^{sc}$
is supermultiplicative (i.e., there exists
$\varphi \in \Phi _2^{sc}$
is supermultiplicative (i.e., there exists
![]() $\gamma>0$
such that
$\gamma>0$
such that
![]() $\varphi (st)\geqslant \gamma \varphi (s) \varphi (t)$
for all
$\varphi (st)\geqslant \gamma \varphi (s) \varphi (t)$
for all
![]() $s, t>0$
), then
$s, t>0$
), then
![]() $\omega \in \boldsymbol {\widetilde {\Omega }}$
and hence
$\omega \in \boldsymbol {\widetilde {\Omega }}$
and hence
![]() $F^{int}_{\varphi }=H(\omega )$
. If we were to impose the condition that all the function
$F^{int}_{\varphi }=H(\omega )$
. If we were to impose the condition that all the function
![]() $\omega \in \boldsymbol {\widetilde {\Omega }}$
is submultiplicative (i.e., there exists
$\omega \in \boldsymbol {\widetilde {\Omega }}$
is submultiplicative (i.e., there exists
![]() $\gamma>0$
such that
$\gamma>0$
such that
![]() $\omega (st) \leqslant \gamma \omega (s)\omega (t)$
for all
$\omega (st) \leqslant \gamma \omega (s)\omega (t)$
for all
![]() $s, t>0$
), then from the above-mentioned representation of the function
$s, t>0$
), then from the above-mentioned representation of the function
![]() $\varphi \in \Phi _2^{sc}$
, it follows that
$\varphi \in \Phi _2^{sc}$
, it follows that
![]() $\varphi $
is supermultiplicative. Thus, the previously defined set
$\varphi $
is supermultiplicative. Thus, the previously defined set
![]() $\Phi _{2}^{sc}(\boldsymbol {\widetilde {\Omega }}) = \{\varphi \in \Phi _2^{sc};\, \varphi \,\, \text {is supermultiplicative}\}$
. Here, it is important to notice that we assumed something strictly weaker for
$\Phi _{2}^{sc}(\boldsymbol {\widetilde {\Omega }}) = \{\varphi \in \Phi _2^{sc};\, \varphi \,\, \text {is supermultiplicative}\}$
. Here, it is important to notice that we assumed something strictly weaker for
![]() $\omega $
(i.e., condition (iv) in
$\omega $
(i.e., condition (iv) in
![]() $\boldsymbol {\widetilde {\Omega }}$
) and thus, the right-hand side set is strictly smaller than
$\boldsymbol {\widetilde {\Omega }}$
) and thus, the right-hand side set is strictly smaller than
![]() $\Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. We will use the following result.
$\Phi _2^{sc}(\boldsymbol {\widetilde {\Omega }})$
. We will use the following result.
Theorem 4.3. Suppose that
![]() $\varphi \in \Phi _2^{sc}$
is supermultiplicative. Then, the topology of
$\varphi \in \Phi _2^{sc}$
is supermultiplicative. Then, the topology of
![]() $F^{int}_\varphi $
given by the family of seminorms
$F^{int}_\varphi $
given by the family of seminorms
![]() $\{\|\cdot \|_{F_\varphi ,c}\,;\, c>0\}$
is weaker than the topology of
$\{\|\cdot \|_{F_\varphi ,c}\,;\, c>0\}$
is weaker than the topology of
![]() $N_\varphi $
.
$N_\varphi $
.
Proof. Suppose that
![]() $\{f_n\}\subset N_\varphi $
and
$\{f_n\}\subset N_\varphi $
and
![]() $\|f_n\|_\varphi \to 0$
as
$\|f_n\|_\varphi \to 0$
as
![]() $n\to \infty $
. From the inequality
$n\to \infty $
. From the inequality
![]() $(*)$
in §2, it follows that, for every
$(*)$
in §2, it follows that, for every
![]() $r\in [0,1)$
and each
$r\in [0,1)$
and each
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
Hence,
![]() $\lim _{n\to \infty } M_\infty (r,f_n) =0$
for every
$\lim _{n\to \infty } M_\infty (r,f_n) =0$
for every
![]() $r\in [0, 1)$
.
$r\in [0, 1)$
.
Since
![]() $\varphi ^{-1}$
is submultiplicative, the above inequality yields
$\varphi ^{-1}$
is submultiplicative, the above inequality yields
Choose
![]() $c>0$
and take
$c>0$
and take
![]() $N\in \mathbb {N}$
, such that, for
$N\in \mathbb {N}$
, such that, for
![]() $n\geqslant N$
, the inequality
$n\geqslant N$
, the inequality
![]() $\varphi ^{-1}(2\|f_n\|_\varphi )\leqslant c$
holds. Then we get that, for each
$\varphi ^{-1}(2\|f_n\|_\varphi )\leqslant c$
holds. Then we get that, for each
![]() $n\geqslant N$
,
$n\geqslant N$
,
From Lebesgue’s Dominated Convergence Theorem, we obtain
 $$\begin{align*}\|f_n\|_{\varphi,c}=\int_{0}^{1} M_\infty(r,f_n) \exp\Big(-c\,\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big)\,dr\to 0\,, \end{align*}$$
$$\begin{align*}\|f_n\|_{\varphi,c}=\int_{0}^{1} M_\infty(r,f_n) \exp\Big(-c\,\varphi^{-1}\Big(\frac{1}{1-r}\Big)\Big)\,dr\to 0\,, \end{align*}$$
and so we are done.
As we observed earlier, for supermultiplicative
![]() $\varphi \in \Phi _2^{sc}$
we know that
$\varphi \in \Phi _2^{sc}$
we know that
![]() $N_\varphi \subset F^{int}_\varphi =H(\omega )$
. The following theorem can be found in [Reference Zayed23].
$N_\varphi \subset F^{int}_\varphi =H(\omega )$
. The following theorem can be found in [Reference Zayed23].
Theorem 4.4. For every functional
![]() $L\in H(\omega )^*$
, there exists a unique function
$L\in H(\omega )^*$
, there exists a unique function
![]() $g\in A(\mathbb {D})$
with
$g\in A(\mathbb {D})$
with
![]() $g(z)=\sum _{n=0}^\infty b_nz^n$
for all
$g(z)=\sum _{n=0}^\infty b_nz^n$
for all
![]() $z\in \mathbb {D}$
, where
$z\in \mathbb {D}$
, where
![]() $b_n=O(\exp [-c\,\omega (n)]),$
for some
$b_n=O(\exp [-c\,\omega (n)]),$
for some
![]() $c>0,$
and such that
$c>0,$
and such that
 $$ \begin{align*} L(f)= \lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}f(re^{i\theta})g(e^{-i\theta})\,d\theta =\sum_{n=0}^\infty \widehat{f}(n)b_n, \quad\, f\in H(\omega)\,, \end{align*} $$
$$ \begin{align*} L(f)= \lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}f(re^{i\theta})g(e^{-i\theta})\,d\theta =\sum_{n=0}^\infty \widehat{f}(n)b_n, \quad\, f\in H(\omega)\,, \end{align*} $$
where
![]() $f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
$f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
![]() $z\in \mathbb {D}$
. Conversely, every function
$z\in \mathbb {D}$
. Conversely, every function
![]() $g\in A(\mathbb {D})$
with
$g\in A(\mathbb {D})$
with
![]() $g(z)=\sum _{n=0}^\infty b_nz^n$
for all
$g(z)=\sum _{n=0}^\infty b_nz^n$
for all
![]() $z\in \mathbb {D}$
, where
$z\in \mathbb {D}$
, where
![]() $b_n=O(\exp [-c\,\omega (n)])$
for some
$b_n=O(\exp [-c\,\omega (n)])$
for some
![]() $c>0$
, defines a linear continuous functional on
$c>0$
, defines a linear continuous functional on
![]() $H(\omega )$
via the above formula.
$H(\omega )$
via the above formula.
An immediate consequence of Theorems 4.3 and 4.4 is the following result.
Theorem 4.5. Let
![]() $\varphi \in \Phi _2^{sc}$
be a supermultiplicative function. Every function
$\varphi \in \Phi _2^{sc}$
be a supermultiplicative function. Every function
![]() $g\in A(\mathbb {D})$
with power series
$g\in A(\mathbb {D})$
with power series
![]() $g(z)=\sum _{n=0}^\infty b_nz^n$
for all
$g(z)=\sum _{n=0}^\infty b_nz^n$
for all
![]() $z\in \mathbb {D}$
and
$z\in \mathbb {D}$
and
![]() $b_n=O(\exp [-c\,\omega (n)])$
for some
$b_n=O(\exp [-c\,\omega (n)])$
for some
![]() $c>0$
, defines a linear continuous functional L on
$c>0$
, defines a linear continuous functional L on
![]() $N_\varphi $
by the formula:
$N_\varphi $
by the formula:
 $$ \begin{align*} L(f)=\lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}f(re^{i\theta})g(e^{-i\theta})\,d\theta =\sum_{n=0}^\infty \widehat{f}(n)b_n, \quad\, f \in N_{\varphi}\,, \end{align*} $$
$$ \begin{align*} L(f)=\lim_{r\to 1-}\frac{1}{2\pi}\int_0^{2\pi}f(re^{i\theta})g(e^{-i\theta})\,d\theta =\sum_{n=0}^\infty \widehat{f}(n)b_n, \quad\, f \in N_{\varphi}\,, \end{align*} $$
where
![]() $f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
$f(z)=\sum _{n=0}^\infty \widehat {f}(n)z^n$
for all
![]() $z\in \mathbb {D}$
.
$z\in \mathbb {D}$
.
We conclude with a remark concerning Theorems
![]() $6$
,
$6$
,
![]() $8,$
and
$8,$
and
![]() $9$
in this section that the class of analytic functions g in
$9$
in this section that the class of analytic functions g in
![]() $\mathbb {D}$
satisfying the condition
$\mathbb {D}$
satisfying the condition
![]() $\widehat {g}(n) = O(\exp [-c\,\omega (n)])$
is known as a Gevrey-type space (the classical Gevery spaces arise when
$\widehat {g}(n) = O(\exp [-c\,\omega (n)])$
is known as a Gevrey-type space (the classical Gevery spaces arise when
![]() $\omega $
is a power function). Notice that in [Reference Dyakonov3], Dyakonov studies the problem, for which inner functions
$\omega $
is a power function). Notice that in [Reference Dyakonov3], Dyakonov studies the problem, for which inner functions
![]() $\vartheta $
and functions f in Hardy space
$\vartheta $
and functions f in Hardy space
![]() $H^2$
, the image
$H^2$
, the image
![]() $H_{\bar {\vartheta }}f$
belongs to some class X of functions in
$H_{\bar {\vartheta }}f$
belongs to some class X of functions in
![]() $L^2$
defined by smoothness conditions. Here,
$L^2$
defined by smoothness conditions. Here,
![]() $H_{\bar {\vartheta }}$
is the Hankel operator generated by the conjugate
$H_{\bar {\vartheta }}$
is the Hankel operator generated by the conjugate
![]() $\bar {\vartheta }$
of
$\bar {\vartheta }$
of
![]() $\vartheta $
. In particular, the author considers this problem when X is the Gevrey space. This space also appears as a duality result stated in Lemma
$\vartheta $
. In particular, the author considers this problem when X is the Gevrey space. This space also appears as a duality result stated in Lemma
![]() $3$
which is interesting on its own.
$3$
which is interesting on its own.
Acknowledgment
We thank the referee for helpful comments that led to improved presentation of the paper.