Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-29T12:20:17.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermohaline layering in dynamically and diffusively stable shear flows

Published online by Cambridge University Press:  16 September 2016

Timour Radko
Timour Radko*
Affiliation:
Department of Oceanography, Naval Postgraduate School, Monterey, CA 93943, USA
*
†Email address for correspondence: tradko@nps.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study we examine two-component shear flows that are stable with respect to Kelvin–Helmholtz and to double-diffusive instabilities individually. Our focus is on diffusively stratified ocean regions, where relatively warm and salty water masses are located below cool fresh ones. It is shown that such systems may be destabilized by the interplay between shear and thermohaline effects, caused by unequal molecular diffusivities of density components. 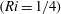Linear stability analysis suggests that parallel two-component flows can be unstable for Richardson numbers exceeding the critical value for non-dissipative systems $(Ri=1/4)$ by up to four orders of magnitude. Direct numerical simulations indicate that these instabilities transform the initially linear density stratification into a series of well-defined horizontal layers. It is hypothesized that the combined thermohaline–shear instabilities could be ultimately responsible for the widespread occurrence of thermohaline staircases in diffusively stable regions of the World Ocean.

JFM classification

Convection: Convection Convection: Double diffusive convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 805 , 25 October 2016 , pp. 147 - 170
Check for updates
Copyright
© Cambridge University Press 2016. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J. & Young, Y.-N. 2002 Stratified Kolmogorov flow. J. Fluid Mech. 450, 131–167.Google Scholar
Bebieva, Y. & Timmermans, M.-L. 2016 An examination of double-diffusive processes in a mesoscale eddy in the Arctic Ocean. J. Geophys. Res. Oceans 121, 457–475.CrossRefGoogle Scholar
Cole, S. T., Timmermans, M. L., Toole, J. M., Krishfield, R. A. & Thwaites, F. T. 2014 Ekman veering, internal waves, and turbulence observed under Arctic sea ice. J. Phys. Oceanogr. 44, 1306–1328.CrossRefGoogle Scholar
Fernando, H. J. S. 1987 The formation of layered structure when a stable salinity gradient is heated from below. J. Fluid Mech. 182, 525–541.CrossRefGoogle Scholar
Flanagan, J., Lefler, A. & Radko, T. 2013 Heat transport through diffusive interfaces. Geophys. Res. Lett. 40, 2466–2470.Google Scholar
Halle, C. & Pinkel, R. 2003 Internal wave variability in the Beaufort Sea during the winter of 1993/1994. J. Geophys. Res. 108, 3210.Google Scholar
Holyer, J. Y. 1983 Double-diffusive interleaving due to horizontal gradients. J. Fluid Mech. 137, 347–362.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid. Mech. 10, 509–512.CrossRefGoogle Scholar
Hughes, D. W. & Weiss, N. O. 1995 Double-diffusive convection with two stabilizing gradients: strange consequences of magnetic buoyancy. J. Fluid Mech. 301, 383–406.CrossRefGoogle Scholar
Kelley, D. E., Fernando, H. J. S., Gargett, A. E., Tanny, J. & Ozsoy, E. 2003 The diffusive regime of double-diffusive convection. Prog. Oceanogr. 56, 461–481.Google Scholar
Levine, M. D., Paulson, C. A. & Morison, J. H. 1985 Internal waves in the Arctic Ocean: comparison with lower-latitude observations. J. Phys. Oceanogr. 15, 800–809.Google Scholar
Merryfield, W. J. 2000 Origin of thermohaline staircases. J. Phys. Oceanogr. 30, 1046–1068.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid. Mech. 10, 496–508.CrossRefGoogle Scholar
Radko, T. 2003 A mechanism for layer formation in a double-diffusive fluid. J. Fluid Mech. 497, 365–380.Google Scholar
Radko, T. 2007 Mechanics of merging event for a series of layers in a stratified turbulent fluid. J. Fluid Mech. 577, 251–273.Google Scholar
Radko, T. 2013 Double-Diffusive Convection. p. 344. Cambridge University Press.Google Scholar
Radko, T. 2014 Applicability and failure of the flux-gradient laws in double-diffusive convection. J. Fluid Mech. 750, 33–72.Google Scholar
Radko, T., Ball, J., Colosi, J. & Flanagan, J. 2015 Double-diffusive convection in a stochastic shear. J. Phys. Oceanogr. 45, 3155–3167.Google Scholar
Radko, T., Bulters, A., Flanagan, J. & Campin, J.-M. 2014a Double-diffusive recipes. Part 1: large-scale dynamics of thermohaline staircases. J. Phys. Oceanogr. 44, 1269–1284.CrossRefGoogle Scholar
Radko, T., Flanagan, J., Stellmach, S. & Timmermans, M.-L. 2014b Double-diffusive recipes. Part 2: layer merging events. J. Phys. Oceanogr. 44, 1285–1305.Google Scholar
Radko, T. & Stern, M. E. 2011 Finescale instabilities of the double-diffusive shear flow. J. Phys. Oceanogr. 41, 571–585.Google Scholar
Richardson, L. F. 1920 The supply of energy from and to atmospheric eddies. Proc. R. Soc. Lond. A 97, 354–373.Google Scholar
Stellmach, S., Traxler, A., Garaud, P., Brummell, N. & Radko, T. 2011 Dynamics of fingering convection II: the formation of thermohaline staircases. J. Fluid Mech. 677, 554–571.Google Scholar
Stern, M. E. 1963 Joint instability of hydromagnetic fields which are separately stable. Phys. Fluids 6, 636–642.Google Scholar
Stern, M. E. 2003 Initiation of a doubly diffusive convection in a stable halocline. J. Mar. Res. 61, 211–233.Google Scholar
Stern, M. E., Radko, T. & Simeonov, J. 2001 3D salt fingers in an unbounded thermocline with application to the Central Ocean. J. Mar. Res. 59, 355–390.Google Scholar
Thorpe, S. A., Smyth, W. D. & Li, L. 2013 The effect of small viscosity and diffusivity on the marginal stability of stably stratified shear flows. J. Fluid Mech. 731, 461–476.Google Scholar
Timmermans, M.-L., Toole, J., Krishfield, R. & Winsor, P. 2008 Ice-tethered profiler observations of the double-diffusive staircase in the Canada Basin thermohaline. J. Geophys. Res. 113, C00A02.Google Scholar
Turner, J. S. 2010 The melting of ice in the Arctic Ocean: the influence of double-diffusive transport of heat from below. J. Phys. Oceanogr. 40, 249–256.CrossRefGoogle Scholar
Turner, J. S. & Stommel, H. 1964 A new case of convection in the presence of combined vertical salinity and temperature gradients. Proc. Natl Acad. Sci. 52, 49–53.Google Scholar
Veronis, G. 1965 On finite amplitude instability in thermohaline convection. J. Mar. Res. 23, 1–17.Google Scholar
Walin, G. 1964 Note on stability of water stratified by both salt and heat. Tellus 18, 389–393.Google Scholar