Monoclinic–orthorhombic first-order phase transition in K₂ZnSi₅O₁₂ leucite analogue; transition mechanism and spontaneous strain analysis

Abstract

Hydrothermally synthesised K₂ZnSi₅O₁₂ has a polymerised framework structure with the same topology as leucite (KAlSi₂O₆, tetragonal I4₁/a), which has two tetrahedrally coordinated Al³⁺ cations replaced by Zn²⁺ and Si⁴⁺. At 293 K it has a cation-ordered framework P2₁/c monoclinic structure with lattice parameters a = 13.1773(2) Å, b = 13.6106(2) Å, c = 13.0248(2) Å and β = 91.6981(9)°. This structure is isostructural with K₂MgSi₅O₁₂, the first cation-ordered leucite analogue characterised. With increasing temperature, the P2₁/c structure transforms reversibly to cation-ordered framework orthorhombic Pbca. This transition takes place over the temperature range 848−863 K where both phases coexist; there is an ~1.2% increase in unit cell volume between 843 K (P2₁/c) and 868 K (Pbca), characteristic of a first-order, displacive, ferroelastic phase transition. Spontaneous strain analysis defines the symmetry- and non-symmetry related changes and shows that the mechanism is weakly first order; the two-phase region is consistent with the mechanism being a strain-related martensitic transition.

Introduction

Leucite−pollucite crystal structures

The crystal structure of the anhydrous mineral leucite, ideally KAlSi₂O₆, consists of a three-dimensional, tetrahedrally coordinated silicate framework in which one third of the tetrahedral sites (T-sites) has Al replacing Si, with the polymerised framework consisting of linked four-, six-, and eight-membered rings of TO₄ tetrahedra. There are two types of channels in this framework structure; the larger (W) channels are occupied by extra-framework K⁺ cations, whereas the smaller (S) channels are vacant. The hydrated zeolite mineral analcime (NaAlSi₂O₆·H₂O) has a tetrahedral (Si,Al)O₄ framework structurally similar to that of leucite and most samples have been refined as cubic $Ia\bar{3}d$ (e.g. Ferraris et al., 1972) with Na in the S-sites and H₂O in the larger W-sites; analcime is the prototype (‘aristotype’) for the ideal $Ia\bar{3}d$ ANA framework structure (Baerlocher et al., 2001). At room temperature the space group of natural leucite is I4₁/a tetragonal (Mazzi et al., 1976). Most natural pollucites have Cs-rich compositions (e.g. Teertstra and Černý, 1995) in the solid-solution series pollucite (CsAlSi₂O₆) – analcime (NaAlSi₂O₆·H₂O) with Cs and H₂O located in the W-site and Na in the S channels. Natural pollucites have a cubic $Ia\bar{3}d$ (Beger, 1969) or pseudo-cubic $Ia\bar{3}d$ structure (e.g. C2/c, Kamiya et al., 2008), topologically identical to that of I4₁/a leucite. The synthetic end-member CsAlSi₂O₆ pollucite was originally reported to be $Ia\bar{3}d$ at room temperature on the basis of laboratory powder X-ray diffraction (XRD) studies (Taylor and Henderson, 1968; Torres-Martinez and West, 1989; Yanase et al., 1999), however, later papers reported a I4₁/a structure based on synchrotron powder XRD or high-resolution powder neutron-diffraction studies (Xu et al., 2002; Palmer et al., 1997). The boron analogue CsBSi₂O₆ occurs as the natural mineral kirchhoffite; this is reported to have the tetragonal space group I4₁/acd (Agakhanov et al., 2012) with the same framework topology as leucite and pollucite except that B and Si are ordered onto different T-sites which perhaps reflects their different fourfold ionic radii B³⁺ 0.11 Å and Si⁴⁺ 0.26 Å (cf. Al³⁺ 0.39 Å) (Shannon, 1976). Because of their macroscopic properties, minerals having leucite/pollucite framework structures are of technological interest with pollucites acting as potential storage materials for Cs radioisotopes in nuclear waste, while pollucites and leucites have found applications in glass ceramics and as dental porcelains (e.g. Gatta et al., 2009; Hogan and Risbud, 1991; Cesar et al., 2005). The functional property of these materials is related to the presence of channels containing large alkali cations within the framework structure, formed by six-rings of tetrahedra aligned along the crystallographic [111] direction; these are the ‘so-called’ percolation channels that are believed to control the properties of diffusion, ion conductivity and molecular sieving in zeolite-type materials and glasses (Zharadyik et al., 2020; Holakovsky et al., 2006; Jones et al., 2010). Thus, while these minerals are conventionally classified as feldspathoids (Deer et al., 1966; 2004), they also are considered to be members of the zeolite structure type (Coombs, 1997).

The general formula for leucite, pollucite and other synthetic anhydrous leucite analogues is AY ³⁺Z₂O₆, in which A is a monovalent alkali metal cation (K, Rb and Cs), Y is a trivalent cation (Al, B, Fe³⁺ and Ga) and Z is a quadrivalent cation (Si and Ge) (e.g. Taylor and Henderson, 1968; Torres-Martinez and West, 1989; Palmer et al., 1997; Martucci et al., 2011). It is also possible to have topologically equivalent leucite structures where one sixth of the T-sites is occupied by divalent cations; such dry-synthesised leucite/pollucite analogues have a general formula A ₂X ²⁺Z ₅O₁₂, in which X is a divalent cation (Be, Mg, Mn, Fe²⁺, Co, Ni, Cu, Zn and Cd) and Z is a quadrivalent tetrahedral cation (Si, Ge and Ti) (e.g. Roedder, 1951; Bayer, 1973; Torres-Martinez and West, 1989, 1984; Kohn et al., 1991, 1994; Bell et al., 1994a, 2010; Henderson et al., 1998, 2017). All of these compounds are known to occur with room-temperature crystal structures having either cubic $I\bar{4}3d$, cubic $Ia\bar{3}d$ or tetragonal I4₁/a space groups with disordered framework cation T-sites. Note that powder diffraction patterns for cubic $I\bar{4}3d$ and $Ia\bar{3}d$ for the same compound would be very similar, and our earlier work (Henderson et al., 2017) showed that refining the powder XRD data set for dry-synthesised K₂MgSi₅O₁₂ using both space groups gave very similar statistical parameters for the fit qualities; it was concluded that much higher resolution in Q on better crystallised samples would be required to resolve this situation for this disordered cubic leucite.

We have also used hydrothermal synthesis methods to obtain lower symmetry phases with a leucite/pollucite framework topology that has ordered framework T-site cations; these have the formula A ₂X ²⁺Si₅O₁₂ with K, Rb or Cs in A and Mg, Fe, Mn, Co, Ni, Cu, Zn or Cd substituting for Si in X (see Henderson et al., 2017 for a summary of such samples). Initial room temperature, laboratory powder XRD studies suggested that hydrothermally synthesised K₂MgSi₅O₁₂ had symmetry lower than tetragonal, though Kohn et al. (1991) used ²⁹Si magic-angle spinning nuclear magnetic resonance (MAS NMR), to show the presence of 10 Si peaks, which together with two tetrahedral Mg atoms, confirmed a formula with 12 T-sites in a 24 oxygen unit cell. Later multi-technique work showed that such phases are either monoclinic P2₁/c (A = K) or orthorhombic Pbca (A = Rb or Cs) at room temperature. For example, we used synchrotron powder XRD, together with electron diffraction (in a transmission electron microscope fitted with a liquid-nitrogen-cooled, double-tilt sample holder), and ²⁹Si MAS NMR, to determine the structures of P2₁/c monoclinic K₂MgSi₅O₁₂ (Bell et al., 1994a) and Pbca orthorhombic Cs₂CdSi₅O₁₂ (Bell et al., 1994b). In addition, high-resolution synchrotron and neutron powder diffraction methods were used to establish that Cs₂CuSi₅O₁₂ has a Pbca structure (Bell et al., 2010); the neutron diffraction data provided more reliable oxygen coordinates for this sample. Note that P2₁/c is a maximal, non-isomorphic sub-group of Pbca. Over the years, the data for Cs₂CdSi₅O₁₂ and K₂MgSi₅O₁₂ have provided a firm foundation for determining the structures of orthorhombic Pbca and monoclinic P2₁/c leucite analogues using either synchrotron (e.g. Bell et al., 1994a,b) or laboratory-based (e.g. Bell and Henderson, 2018) XRD methods. We have also shown recently that leucite analogues containing two different extra-framework cations with formulae RbCsX ²⁺Si₅O₁₂ (X = Mg, Ni or Cd), have Pbca orthorhombic structures with Rb and Cs ordered into separate sites (Bell and Henderson, 2019).

Hydrothermal crystallisation of framework silicates generally results in well crystallised products with narrower diffraction peaks than starting materials crystallised in air. In various papers we have reported the synthesis of both dry and hydrothermally crystallised samples from the same starting material of crushed glass or powdered gel: e.g. K₂MgSi₅O₁₂ (Bell et al., 1994a); Cs₂CuSi₅O₁₂ (Bell et al., 2010); K₂CoSi₅O₁₂ (Bell and Henderson, 2018). In the case of the apparent ‘polymorphism’ shown by K₂MgSi₅O₁₂ it was concluded earlier that the charges and sizes of Mg²⁺ (as opposed to Al³⁺) are sufficiently different from those for Si⁴⁺ to ensure that the fully-ordered monoclinic phase is formed relatively rapidly, driven by the catalytic effect of water in the hydrothermal experiment (Bell et al., 1994a; Henderson et al., 1995); Kohn et al. (1994) mainly used robust, multi-nuclear MAS NMR results to report similar suggestions for P2₁/c and Pbca leucite analogues with Mg, Zn or Cd as the divalent cation in the framework. Thus, for A ₂X ²⁺Si₅O₁₂ leucites the P2₁/c and Pbca phases are believed to be the thermodynamically more-stable forms for this compound with the cubic $Ia\bar{3}d$ phases being stranded metastable forms at room temperature and pressure (Kohn et al., 1994; Bell et al., 1994a; Henderson et al., 1995). While preparing a large sample (50 g) of cubic $Ia\bar{3}d$ K₂MgSi₅O₁₂ recently for an ongoing neutron diffraction study, one of us (CMBH) found that crystallising finely powdered starting-material glass in air at 1073 K for 5 days gave a single-phase cubic product with a very small background hump due to a residual glassy phase. This sample was reheated at 973 K for 21 days in an attempt to reduce the amount of residual glass, but this produced a second phase that could be matched to the presence of a small amount of the monoclinic polymorph. Reheating the sample at 1173 K for 11 days transformed the sample to a poorly crystallised P2₁/c monoclinic phase confirming that at these temperatures the ordered phase is indeed the thermodynamically more-stable form of K₂MgSi₅O₁₂. It seems clear that the hydrothermally crystallised low-symmetry forms of Cs₂CuSi₅O₁₂ and K₂CoSi₅O₁₂ are also more stable than their dry-crystallised cubic forms. In turn, it is likely that most of the published reports of syntheses of disordered, cubic divalent cation leucites of stoichiometry A ₂X ²⁺Si₅O₁₂ (e.g. Bayer, 1973; Torres-Martinez et al., 1984; Yanase et al., 1999) represent metastable phases.

Leucite structure, thermally driven displacive phase transitions

Phase transitions from I4₁/a (point group 4/m) tetragonal to $Ia\bar{3}d$ (point group m3m) cubic structures have been observed as the temperature increases in natural leucite and synthetic leucite analogues, and it was concluded that the phase transition in KAlSi₂O₆ leucite is second order, displacive, rapid, reversible and continuous (Taylor and Henderson, 1968; Lange et al., 1986; Palmer et al., 1989, 1997; Palmer, 1990; Carpenter et al., 1998a). Studies using XRD and differential scanning calorimetry (DSC) suggest that an intermediate I4₁/acd tetragonal phase occurs between I4₁/a and $Ia\bar{3}d$ (Lange et al., 1986; Palmer et al., 1990; Newton et al., 2008). A phase transition from $I\bar{4}3d$ cubic to $Ia\bar{3}d$ cubic has been reported in the synthetic boron-bearing leucite KBSi₂O₆ on heating (Martucci et al., 2011). The leucite analogue KGaSi₂O₆, is isostructural with KAlSi₂O₆ and also shows a I4₁/a tetragonal to $Ia\bar{3}d$ cubic phase transition over the temperature range 673–970 K but this is believed to be an unquenchable, displacive, first-order transition (Bell and Henderson, 2020). In addition, an unquenchable, displacive, first-order phase transition from P2₁/c monoclinic to Pbca orthorhombic was observed on heating the hydrothermally-synthesised, leucite analogue K₂MgSi₅O₁₂ (Redfern and Henderson, 1996). Note that the transitions for both KGaSi₂O₆ and K₂MgSi₅O₁₂ are smeared out over a range of temperatures with the low- and high-temperature polymorphs coexisting to define ‘regions of coexistence’ (Henderson and Taylor, 1982); both of these transitions show clear, positive volume discontinuities (ΔVs). Such features point to first-order phase transitions that might have martensitic mechanisms (Henderson and Taylor, 1982; Bell and Henderson, 2020). Finally, a high-temperature synchrotron powder X-ray diffraction study on Cs₂ZnSi₅O₁₂ (Bell and Henderson, 2012) showed a reversible phase transition from Pbca orthorhombic to $Pa\bar{3}$ cubic, this was the first reported leucite phase transition showing a change from ordered to disordered T-site cations.

It is clear that synthetic analogues of the leucite/pollucite group show a multiplicity of space groups (including I4₁/a, I4₁/acd, $I\bar{4}3d$, $Pa\bar{3}$, Pbca and P2₁/c); all of these are isotropy subgroups of the $Ia\bar{3}d$ aristotype (Stokes and Hatch, 1988) and can be considered to have a pseudo-cubic $Ia\bar{3}d$ structure (Henderson et al., 2017). A universal aristotype crystal structure for such phases has recently been determined by using a non-linear optimisation of the fractional coordinates (Knight and Henderson, 2019).

We have recently published room-temperature structures for P2₁/c leucite analogues having the stoichiometry K₂XSi₅O₁₂ (where X = Fe²⁺, Co and Zn) and predicted that these should show phase transitions to Pbca high-temperature polymorphs at ~700 K (Bell and Henderson, 2018). In the present paper we report high-temperature powder X-ray diffraction (HT-XRD) results for the P2₁/c K₂ZnSi₅O₁₂ leucite analogue and use calculated spontaneous strain parameters to discuss the mechanism of the phase transitions for both this sample and the equivalent K₂MgSi₅O₁₂ leucite analogue (Redfern and Henderson, 1996). In addition, we provide estimates of the heats of transition for the P2₁/c to Pbca phase transitions in two samples of monoclinic K₂ZnSi₅O₁₂ and for the equivalent K₂MgSi₅O₁₂ leucite analogue.

Experimental methods

Sample synthesis

The K₂ZnSi₅O₁₂ samples were synthesised (Henderson et al., 2016) from a stoichiometric mixture of high purity K₂CO₃, ZnO and SiO₂ (>99.9% pure). The mixture was ground under acetone for 1 hour and heated overnight in a Pt crucible at 873 K in a standard muffle furnace to break down the carbonate. It was ground again and then heated at 1373 K for 30 minutes; the resultant melt was quenched to a glass by dipping the bottom of the Pt crucible in water. The glass slug was then crushed to a fine powder (<50 μm) and this served as the starting material for synthesis under dry and water-saturated conditions. All of the KZn-leucites were prepared from this finely-ground, slightly K-poor, starting material glass (K_1.83Zn_1.00Si_5.05O₁₂, see Kohn et al., 1994). Hydrothermally synthesised sample KZS4 was prepared by heating 0.5 to 0.6 g of finely-ground glass powder plus 1 to 2 wt.% H₂O in a sealed gold capsule at 843 K in a cold-seal pressure-vessel at 50 MPa water vapour pressure for 19 days; using the same methods KZS1 was synthesised at 843 K, 50 MPa for 8 days and KZS3 at 741 K, 50 MPa for 22 days (Kohn et al., 1994). Powder XRD showed that KZS3 and KZS4 are single-phase monoclinic P2₁/c products but that KZS1 also has an impurity, disordered cubic leucite component. The monoclinic K₂MgSi₅O₁₂ (KMS2) was prepared in the same way at 873 K, 50 MPa for 7 days (Kohn et al., 1994); note that analysis of the glass starting material gave a composition of K_1.97Mg_1.01Si_5.00O₁₂, very close to the stoichiometric formula. All the hydrothermally synthesised KZS and KMS leucites were checked by laboratory XRD immediately after synthesis and found to have flat backgrounds consistent with the absence of amorphous starting material; in all cases the split peaks suggested that the symmetries were lower than cubic. In this paper we will use the names KZn-Lc and KMg-Lc for these sample compositions instead of the ideal end-member formulae.

Powder X-ray diffraction

An earlier ambient temperature study (Bell and Henderson, 2018) on hydrothermally synthesised KZn-Lc (KZS4) showed that this sample crystallised in the P2₁/c monoclinic space group with a structure identical to that of the first cation-ordered leucite analogue, hydrothermally synthesised KMg-Lc (Bell et al., 1994a); note however that the glass starting material for this sample has 1.83 K atoms per formula unit (apfu) rather than the end-member value of 2 apfu (see above). High-temperature powder XRD data were collected on this sample using an Anton Paar HTK1200N high-temperature stage mounted on a PANalytical X'Pert Pro MPD using CuKα radiation, a Ni β filter and a PIXCEL-1D area detector.

Note that when collecting XRD in this high-temperature stage the flat plate sample holder is only ~16 mm in diameter. To minimise any X-ray scattering from outside the sample the beam size defining slits and mask between the X-ray tube and the sample have to be smaller than that normally used for ambient temperature XRD measurements done in the open air. Therefore, the X-ray flux on the sample will be reduced and the resultant data quality will be poorer than normal ambient temperature measurements.

Initial high-temperature data (Run 1) were collected over the angular range 10–100°2θ for 16 temperature steps between 298 and 973 K and cell parameters after cooling the sample from 973 K to room temperature were also determined for Run 1 (Table 1). Further high-temperature data (21 temperature steps, Run 2) on the same sample were then collected from 10–80°2θ between 773 and 973 K; Run 2 experiments were carried out over smaller temperature steps than those for Run 1 to provide a more detailed study of how the phase assemblage might change through a phase transition. Run 2 cell parameters are given in Table 2. Rietveld refinements (Rietveld, 1969) using FULLPROF (Rodriguez-Carvajal, 1993) were done for both Run 1 and Run 2 data. Run 1 data up to 823 K and Run 2 data up to 843 K were single-phase-refined using the P2₁/c monoclinic cation-ordered structure of K₂ZnSi₅O₁₂ (Bell and Henderson, 2018) as a starting model. Run 1 data at 898 and 973 K and Run 2 data above 868 K were single-phase-refined using a Pbca orthorhombic cation-ordered structure isostructural with Cs₂CdSi₅O₁₂ (Bell et al., 1994b). However, this approach for P2₁/c structures gave a/c unit cell axis ratios greater than 1 while those for Pbca cells were less than 1; this clearly does not match the expected result either side of the phase transition. It is clear that the setting used for Pbca does not match that for P2₁/c and to cope with that inconsistency the highest temperature, single-phase atomic coordinates for P2₁/c were transposed to match those for the lowest temperature coordinates for a single-phase Pbca cell. These were then used as the starting model for the high temperature Pbca cells, which gave comparable results either side of the phase transition with matching cell parameters. The structural refinements were then carried out as follows.

Table 1. Variation of K₂ZnSi₅O₁₂ lattice parameters and phase proportions 294–973 K (Run 1).

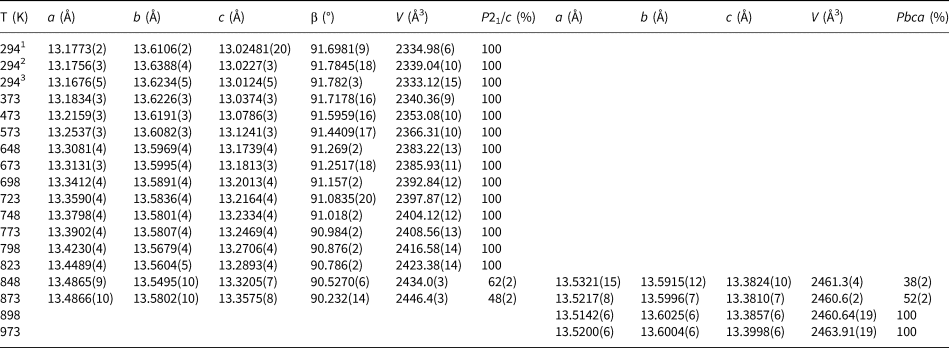
¹ Indicates original ambient temperature data (Bell and Henderson. 2018); ² indicates new data collected in furnace before heating Runs; ³ indicates new data collected in the furnace after heating.

Table 2. Variation of K₂ZnSi₅O₁₂ lattice parameters and phase proportions 773–973 K (Run 2).

Tetrahedrally coordinated Si–O distances were soft-constrained initially to 1.61(2) Å and tetrahedrally coordinated Zn–O distances were soft-constrained to 1.93(2) Å. Scale factor, zero point, background, lattice, profile, atomic coordinates and temperature-factor parameters were refined. Temperatures factors for all sites containing Si were constrained to have the same value. Temperatures factors for all sites containing O were also constrained to have the same value (though not the same as Si). For P2₁/c refinements all four K-sites were constrained to have the same temperature factor. However, for Pbca refinements the temperature factors for the two K-sites were allowed to refine freely. For P2₁/c refinements both Zn-sites were constrained to have the same temperature factor, however, for Pbca refinements there was only one Zn-site so the temperature factor for this site was allowed to refine freely.

Structural refinements for the two-phase regions were more complex. Thus, the Run 1 data at 848 K and 873 K and the Run 2 data 848–863 K were refined with two KZn-Lc phases, P2₁/c monoclinic and Pbca orthorhombic. Due to severe peak overlap no atomic coordinates or temperature factors were refined for these coexisting phases, only scale factor, zero point, background, lattice and profile parameters were refined. For the Run 1 two-phase refinements the P2₁/c coordinates and temperature factors were fixed at those from the 823 K refinement and the Pbca coordinates and temperature factors were fixed at those from the 898 K refinement; the same approach was used for Run 2 two-phase refinements. Tables 3 (Run 1) and 4 (Run 2) show the profile fitting parameters for these Rietveld refinements. Note how the R-factors and χ² parameters tend to be larger in the two-phase regions for single-phase refinements compared to those for two-phase refinements. For example, the Run 2 (Table 4) mean χ² parameter for the monoclinic stability field samples (P2₁/c) is 1.41 ± 0.03 and for the orthorhombic (Pbca) samples is 1.48 ± 0.05, compared with χ² values for P2₁/c+Pbca, P2₁/c, Pbca at 853 K of 1.49, 1.52 and 1.96 and at 863 K of 1.59, 1.80 and 1.62, respectively.

Table 4. Variation of K₂ZnSi₅O₁₂ Rietveld refinement background subtracted R-factors 773–973K (Run 2).

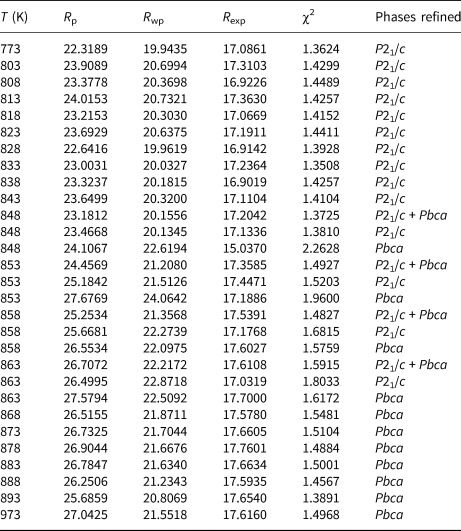
The Rietveld-refined, high-temperature data provides reliable unit cell parameters and phase proportions, and the atomic coordinates for the single-phase-field temperatures provide useful information on how the tetrahedral framework shows cooperative rotations as it expanded with increasing temperature and became more symmetrical around the large cavity cations located in the [111] channels (see later VESTA plots in Fig. 4). However, we are not able to report reliable bond distances and bond angles for the many independent T-sites and cavity-cation-sites in these framework structures. Thus, Tables 3 and 4 show R-factors of ~20 for these refinements. The R-factors for the refinement of the P2₁/c ambient temperature structure of KZn-Lc were ~1 (Bell and Henderson, 2018). This is similar to the results that we reported on our high-temperature powder XRD study on the phase transition in KGaSi₂O₆ (Bell and Henderson, 2020). For the KGaSi₂O₆ leucite sample it was possible to obtain useful atomic parameters for the low-temperature tetragonal and high-temperature cubic phases but, as mentioned above, this is more difficult for the multi-site, lower symmetry monoclinic and orthorhombic KZn-Lc polymorph data reported here. Thus, the structural interpretations and spontaneous-strain analysis reported here for KZn-Lc are based mainly on the phase stability relations and on the high-quality unit cell parameters.

Table 3. Variation of K₂ZnSi₅O₁₂ Rietveld refinement background subtracted R-factors 294−973K (Run 1).

The crystallite sizes for two samples of KZn-Lc (KZS4 and KZS3), and for the small amount of P2₁/c KMg-Lc leucite (KMS2) that was still available for study, were obtained for powder samples mounted on silicon wafers which were scanned using an Empyrean XRD with CoKα X-rays. An identical scan was done for a silicon standard to calibrate instrumental peak widths. The PANalytical HighScore Plus automatic crystallite size Rietveld program was used to obtain crystallite sizes based on the whole powder diffraction pattern, not just a few strong low-angle peaks. The estimated room-temperature crystallite sizes are given in Table 5 along with room temperature unit cell parameters for the samples studied by DSC.

Table 5. Unit cell parameters, crystallite sizes (XRD) and transition heats (DSC).

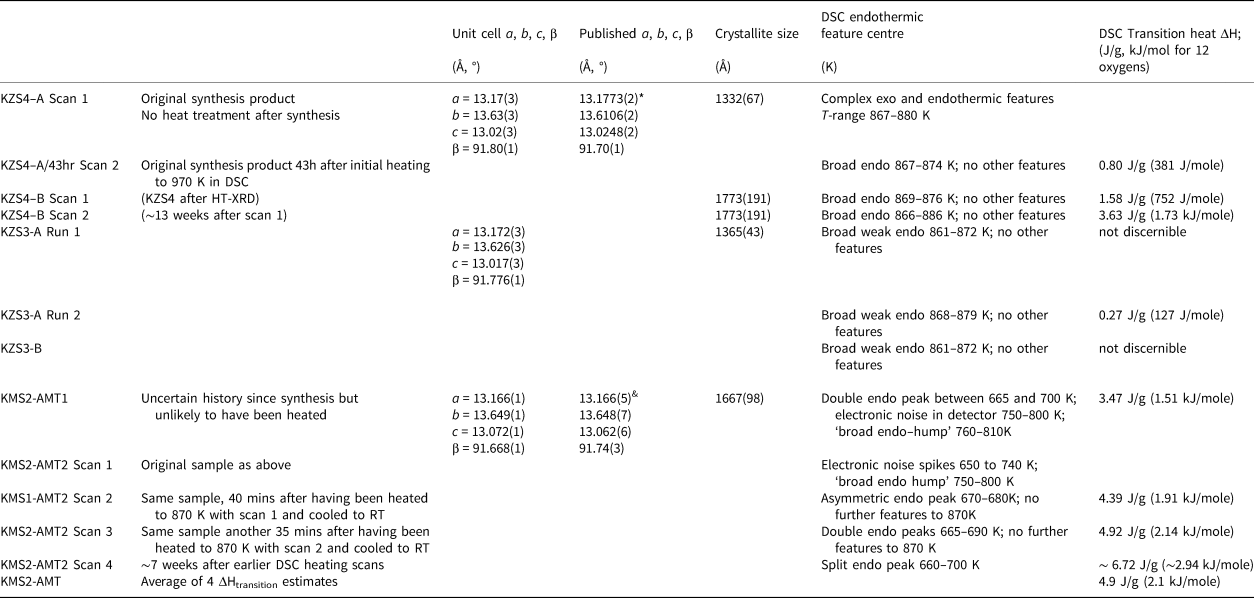
* Bell and Henderson (2018); ^& Bell et al. (1994a)

The temperature-dependent unit cell parameters for KZn-Lc reported in Table 1 were used to investigate the spontaneous strains shown by the ferroelastic monoclinic phase as it approaches the phase transition to the orthorhombic paraelastic phase. For these calculations we followed the general approach of Carpenter et al. (1998a) and that for natural leucite KAlSi₂O₆ (Palmer, 1990) where the strain for a particular unit cell parameter (x _T) at a particular temperature in the monoclinic phase is defined as (x _T – x ₀)/ x ₀, where x ₀ values are calculated by linear extrapolations of the high-temperature cell parameters for the paraelastic orthorhombic phase into the lower temperature monoclinic phase stability field. Thus a ₀, b ₀, c ₀, β₀ and V ₀ are provided for the monoclinic phases. Figure 1 shows how linear extrapolations of the KZn-Lc orthorhombic high-temperature values for a, b, c, β and V provide estimates for a ₀, b ₀, c ₀, β₀ and V ₀ at the temperatures for the Run 1 monoclinic polymorphs; note that the fitting equations used are those obtained for Run 2 (orthorhombic phase cell parameters between 868 and 973 K) as only 3 data points are available for the Run 1 data. In addition, the temperature data points chosen for the Run 2 high-temperature orthorhombic phases include only single-phase data points from above the phase transition. We also fitted the temperature variations for orthorhombic phases for averages of both Run 1 and Run 2 data; these gave different coefficients to those obtained for Run 2 data alone, though the strain parameters calculated provided overlapping data points for all parameters (except for b that shows very small changes with temperature) on the diagrams discussed in the Results. Note that the cell parameter ‘strains’ calculated will reflect errors involved in the estimation of x ₀ values with the largest errors occurring at the temperatures furthest from the phase transition. The a ₀, b ₀, c ₀ and V ₀ values for KMg-Lc were obtained in a similar way from the parameters reported in Table 1 (Redfern and Henderson, 1996); Henderson (2021) has already made a preliminary study of the spontaneous strains for the KMg-Lc data in a review of composition, thermal expansion and phase transitions in framework silicates.

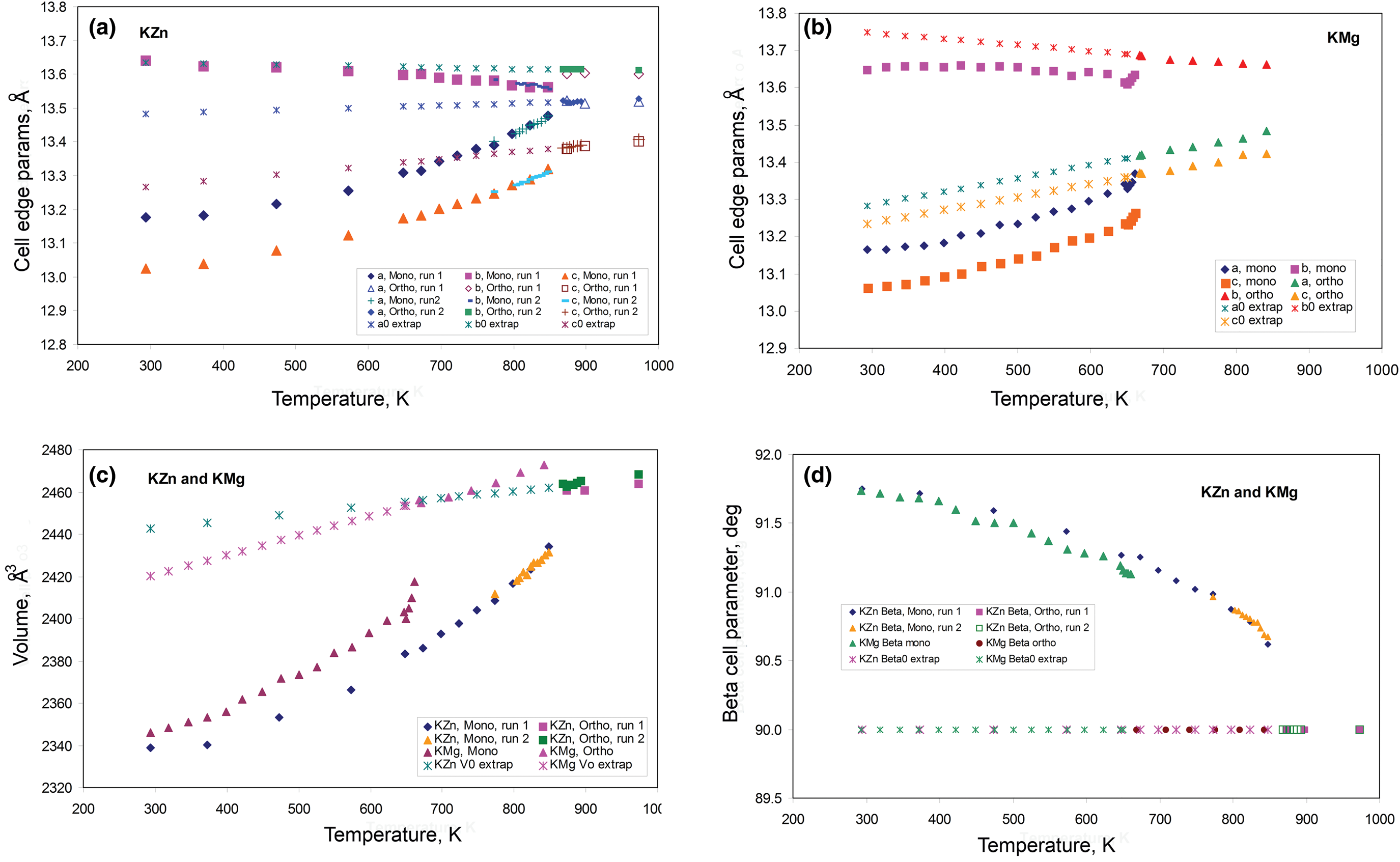
Fig. 1. Comparison of high-temperature unit cell parameters for KZS-Lc, sample KZS4 (this work) and KMg-Lc, sample KMS2 (Redfern and Henderson, 1996). (a) a, b and c cell parameters for KZS4 (Runs 1 and 2); (b) a, b and c cell parameters for KMS2; (c) V cell volumes for KZS4 (Runs 1 and 2) and KMS2; (d) β angles for KZS4 (Runs 1 and 2) and KMS2. Also shown are the high-temperature orthorhombic lattice parameters extrapolated into the monoclinic polymorph stability field; Run 2 fits are used to model these values for KZn-leucite and the published Redfern and Henderson (1996) data are used for KMg-Lc.

Thermal analysis

A Netsch STA (Simultaneous Thermal Analyzer) 409PG Luxx®) was used to collect differential thermal analysis (DTA) data on a sample of KZS4. Powder (100 mg) was loaded into an Al₂O₃ sample cup, the sample was heated at 10 K/minute over the temperature range 303–1554 K, and under a flow of air at 40 ml/minute. From the temperature difference between KZn-Lc powder and an empty Al₂O₃ sample cup a DTA trace was plotted; this showed a weak endothermic effect at ~860–870 K. A thermogravimetric analysis (TGA) scan was performed simultaneously with the DTA; this showed a weight loss of ~0.2 wt.% up to 400°C however, weight data values at higher temperatures were unreliable reflecting the very small change in mass; unfortunately, no further sample was available to assess repeatability.

A more informative thermal analysis study was subsequently carried out by differential scanning calorimetry (DSC) using a Perkin Elmer DSC8000 system. This equipment has a double furnace mode so that the heat flow change at the sample against that on the reference material is continually monitored. Samples were analysed using crimped Al capsules that were pierced with a syringe needle to allow venting; note that Al melts at 660°C (933 K) that restricts the top temperature for the DSC analyses to ~883 K. Powdered samples (20 to 30 mg, accurately weighed) were heated at a rate of 10 K/min or 20 K/min over the temperature range 523 to 883 K. The reference to the sample was an empty, crimped and pierced Al capsule. Both sample and reference were purged with nitrogen gas using a flow rate of 40 ml/minute. The instrument was calibrated for temperature and sensitivity using indium and zinc standards, and the standard procedure within the Pyris ^TM software. We found that the α–β quartz phase transition occurs at 852 K with a ΔH of 5.5 J/g compared with a suggested value of 6.0 J/g for a finely ground powder at 848 K (Ghiorso et al., 1979).

For the leucite samples studied we found that the low heat changes were difficult to discern above the baseline on the first DSC heating experiments because the samples showed complex heat effects. The temperature ranges for the thermal properties are given in Table 5 together with estimated heats of transition (ΔH_transition) determined from DSC scans following the method of Lange et al. (1986).

Powder XRD results and discussion

Thermal expansion characteristics and phase relations for KZn-Lc

The unit cell parameters for KZn-Lc (sample KZS4) at temperatures from 298 to 973 K (Run 1) are given in Table 1 and Fig. 1 shows how these refined lattice parameters vary with temperature; note that the first row gives the original unit cell parameters at room temperature (Bell and Henderson, 2018) while data in rows 2 and 3 give cell parameters determined in the heating cell before and after Run 1 heating experiments. Table 3 shows how the background subtracted R _wp, R _p, R _exp and χ² parameters from Rietveld refinements vary with temperature. For comparison, Fig. 1 also shows equivalent parameters from Redfern and Henderson (1996) for monoclinic KMg-Lc. For the KZn-Lc Run 1 data, the a and c parameters (Fig. 1a) show little significant change between 294 and 373 K but then have steadily increasing expansion rates up to ~650 K and then both show a slightly greater rate of increase up to 870 K. The b parameters initially show little significant change up to 600 K followed by a slight decrease to 870 K (Fig. 1a). At the highest temperatures the monoclinic a parameter is only slightly smaller than that for b (b/a ≈ 1.006 at ~850 K). All three cell edges then show a step up to higher values at ~870 K for the orthorhombic structures, and then only small increases up to the highest temperature studied (973 K). The β angle (Fig. 1d) shows a small decrease up to 573 K followed by a better defined and faster decrease up to 778 K and then from 898 K the orthorhombic β parameters are plotted at 90°. For Run 1, the cell volumes (Fig. 1c) show little change up to 373 K followed by steadily increasing values up to 848 K and then a step up to the volumes for the orthorhombic phases. It is clear that the monoclinic to orthorhombic transition is characterised by a small positive ΔV. On cooling, the transition is reversible returning the room-temperature cell edges to values close to, but slightly smaller than, those determined at room temperature before heating (see Table 1). This is consistent with the P2₁/c to Pbca being a displacive transition similar to that for KMg-Lc leucite (Redfern and Henderson, 1996).

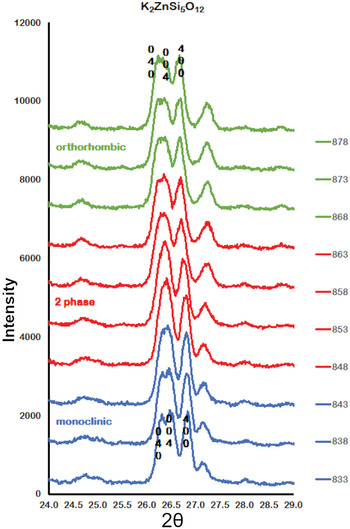
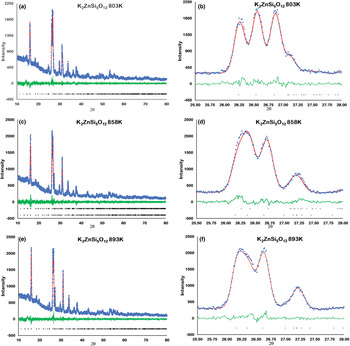
Figure 2 shows how the positions of the (004), (040) and (400) Bragg reflections in KZn-Lc move to lower 2θ values over the temperature range 833–878 K as the crystal structure transforms from P2₁/c monoclinic, through the 2-phase region, to Pbca orthorhombic. More detailed Rietveld refinement results for the KZn-Lc sample are provided in Fig. 3 and show clear differences reflecting the phase stability changes. This figure shows difference plots for XRD data collected at 803, 868 and 893 K with the full diffraction pattern given in the left-hand panels and the main (400) suite of peaks over the range 25.5 to 28.0°2θ given in the right-hand panels. Thus, at 803 K (Fig. 3a,b) only a monoclinic phase is present and the three principal axes (040, 400 and 004) are well resolved and have symmetrical shapes. The shoulder on the high angle flank of the peak at ~27°2θ is due to weaker Bragg reflections that are not part of the main (400) suite of peaks for this monoclinic phase; note the absence of a clear peak at ~27.3°2θ at this temperature. At 858 K two phases are present and the first peak in Fig. 3d is now broader than before with a shoulder ~⅔ of the way up the low 2θ flank, which can be assigned to the (040) peak for an orthorhombic phase (denoted (040)_o). The crest of this broad peak has a complex form which is explained by the existence of three overlapping Bragg reflections, namely (040)_m (m = monoclinic), (004)_o, (400)_m, in that order. Note that the Miller indices assigned here are based on the model P2₁/c and Pbca structures that have reversed a and c parameter values. The peak at ~ 26.7°2θ appears to be asymmetric, consistent with it having two components, namely (400)_o and (004)_m. There is now a clear peak at ~27.3°2θ, which is not part of the main (400) suite of peaks, consistent with the presence of an abundant orthorhombic phase in the mixture. At 893 K only an orthorhombic phase is present, but the first strong peak (Fig. 3f) is formed by the overlapping (040)_o and (004)_o reflections. The peak at ~27.3°2θ is now stronger and narrower than that at 863 K, consistent with the orthorhombic phase being the only component present above the phase transition. Even though peak overlap is more serious for the mixed phases in this ‘region of coexistence’, the Rietveld refinement gives reliable proportions for the two coexisting phases (Tables 1 and 2); indeed, the proportion of the monoclinic phase (y) decreases steadily with increasing temperature with a linear fit defined by y = –0.0357 × T (K) +31.143 (R ² = 0.96). We conclude therefore that our data for KZn-Lc show the same two-phase characteristics for the phase transition as found for the higher resolution KMg-Lc data (Redfern and Henderson, 1996); indeed the peak features for KMg-Lc in the two-phase region (figure 4, Redfern and Henderson, 1996) show exactly the same features as described above for the KZn-Lc sample.

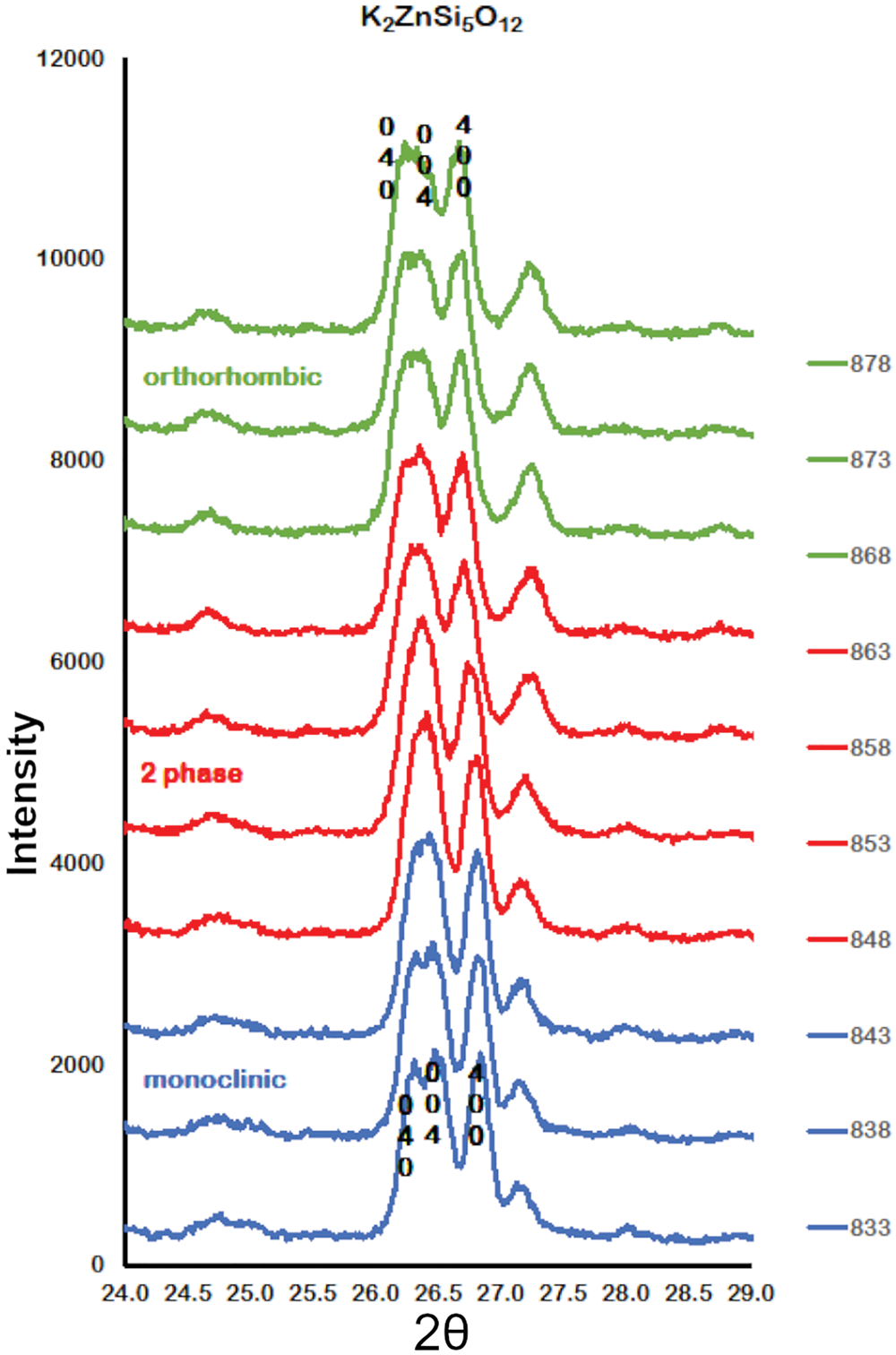
Fig. 2. Plots showing Run 2 XRD data for KZS4 from 24 to 29^o2θ over the temperature range 833 to 878 K. Monoclinic (040), (400) and (004) Bragg peaks move to lower 2θ angles through the 2-phase region into the orthorhombic phase. Monoclinic data, blue; 2-phase data, red; orthorhombic data, green.

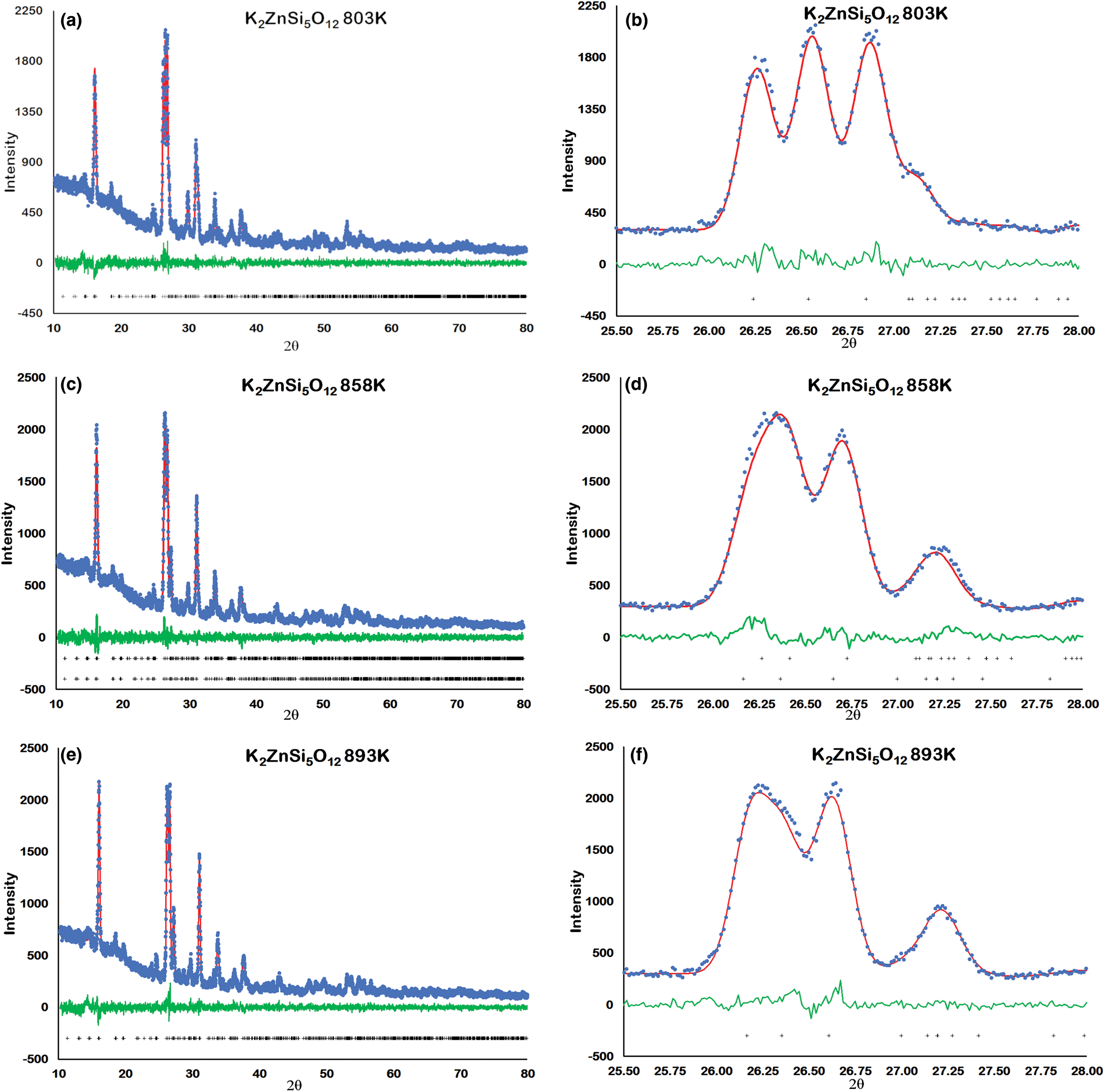
Fig. 3. Rietveld plots for KZS4 Run 2 experiments: (a) 803 K 10–80°2θ, (b) 803 K 25.5–28°2θ, (c) 858 K 10–80°2θ, (d) 858 K 25.5–28°2θ, (e) 893 K 10–80°2θ, (f) 893 K 25.5–28°2θ. Blue dots show observed data points, red lines show calculated profiles, green lines show difference between observed and calculated, black crosses show positions of Bragg reflections.

Fig. 4. VESTA plots for KZS4 looking down the [111] channel in the silicate framework structure. Purple spheres represent K⁺ cations, red spheres represent O^2– anions, green tetrahedra represent ZnO₄ units and blue tetrahedra represent SiO₄ units. (a) 773 K, monoclinic P2₁/c; (b) 843 K, monoclinic P2₁/c; (c) 868 K, orthorhombic Pbca; (d) 973 K, orthorhombic Pbca.

VESTA plots (Momma and Izumi, 2011) at temperatures chosen to demonstrate the framework changes through the phase transition are given in Fig. 4 for KZn-Lc at 773 K (monoclinic single phase), 843 K (monoclinic just below the region of coexistence), 868 K (orthorhombic just above the region of coexistence) and 973K (orthorhombic single phase); these plots show the central [111] channel of the leucite crystal structure containing K⁺ cations. Note how the central channel (effectively the cavity cation percolation channel) changes with increasing temperature due to a cooperative rotation of linked tetrahedra. This is particularly apparent over the phase transition from P2₁/c monoclinic to Pbca orthorhombic corresponding to the expansion of the unit cell over the transition. Note that this channel is more symmetrical for the orthorhombic polymorph at 973 K than for the monoclinic polymorph at 773 K reflecting a trend towards a more pseudocubic high-temperature structure (i.e. the b/c ratio at 773 K is 1.025 compared to 1.015 at 973K).

Data for the temperature dependences of the unit cell parameters for monoclinic KMg-Lc (Redfern and Henderson, 1996) are also shown here in Fig. 1b, c and d, Note that the two phase region for the KMg-Lc compound spans the temperature range from 647 to 670 K and that, for the monoclinic phases, the upturn at ~650 K for a, b, c and V, and the downturn for β, are due to the presence of the orthorhombic phase distorting the shapes of the monoclinic diffraction peaks. The unit cell expansion trends for KMg-Lc are very similar to those described here for KZn-Lc; both samples show very similar values for all parameters and similar rates of change with increasing temperature reflecting the similar sizes of the divalent Zn and Mg cations in tetrahedral coordination (0.60 and 0.57 Å, respectively; Shannon, 1976); both KZn-Lc and KMg-Lc analogue leucites have unit cell parameters b >> a > c. However, note that KMg-Lc shows a wider difference between the b versus a and c parameters at the phase transition with a b/a ratio of 1.021 compared with a value of 1.006 for KZn-Lc (cf. b/c = 1.028 and 1.017, respectively). This is clearly related to the former showing the phase transition at a much lower temperature (~650 K) compared with ~850 K for KZn-Lc (see section on ‘Characteristics of the monoclinic P2₁/c – orthorhombic Pbca transition in leucite analogues’). Redfern and Henderson (1996) pointed out that, as temperatures increased, the orthorhombic cell parameters for KMg-Lc tended to converge towards a higher symmetry structure. For example, the b/a ratio would extrapolate to 1.0 at ~1000 K. Redfern and Henderson speculated that a tetragonal phase with space group Ibca would be a possible polymorph though stressed that it would have disordered T-sites. They also suggested that leucite analogues with a ZnSi₅O₁₂ framework might show an order–disorder relationship at a phase transition. Indeed, Bell and Henderson (2012) reported such an order–disorder reversible transition in the Cs₂ZnSi₅O₁₂ leucite analogue consistent with much faster Zn–Si tetrahedral exchange kinetics than for Mg–Si (also see Kohn et al., 1994). We have shown for the monoclinic KZn-Lc leucite analogue that the b/a ratio has decreased to 1.006 at ~850 K and extrapolation of this trend for the Run 2 experiments suggests that b and a would have merged at ~873 K. If the transition to T-site ordered orthorhombic Pbca had not occurred, we speculate here that the transition might have been to a hypothetical disordered Ibca structure and ultimately to cubic disordered Ia $\bar{3}$d at an even higher temperature.

To return to known leucite analogue structures, Redfern and Henderson (1996) pointed out that the phase transition for KMg-Lc showed the coexistence of both monoclinic and orthorhombic polymorphs over a small temperature range (~25 K). For that work a Guinier X-ray camera (Huber; monochromatic CuKα₁ radiation) was used to study the KMg-Lc sample and the higher resolution of this equipment provided reliable evidence for the coexistence of two phases (see Redfern and Henderson, their figure 4). The Run 2 experiments on KZn-Lc reported here were carried out at smaller temperature steps through the phase transition than for Run 1 in order to establish if both phases coexisted over a temperature range between the beginning and end of the transition, similar to that reported for KMg-Lc; Run 2 experiments also allow a clearer temperature range for the phase transition to be established. These data are given in Tables 2 and 4 and are shown in Fig. 1 with different symbols to those for Run 1 data. It is clear that the data sets of unit cell parameters for Run 1 and Run 2 agree within experimental error. Even though the Run 1 room-temperature cell edges are smaller after the heating experiments than before, this has not affected the high-temperature physical properties of this sample (KZS4-A). Thus, for Runs 1 and 2, the a and c parameters show steady increases and b steady decreases with increasing temperature up to ~870 K (Fig. 1a). Above 870 K the orthorhombic phases all have lattice parameters displaced to higher values than the monoclinic trend; the orthorhombic lattice parameters show only a small increase with increasing temperature. Note that lattice parameters at temperatures from 848 to 863 K are shown for both the coexisting monoclinic and orthorhombic polymorphs but peak overlaps inevitably lead to less reliable parameters for the ‘mixed’ phases, especially for the orthorhombic cells (Fig. 1a); however, these cell-parameter ‘shifts’ are not random and are predictable based on the monoclinic phase having lower a, b, c and V together with higher β than the equivalent orthorhombic phase at the transition temperatures. As expected, the β angle (Fig. 1d) and volume (Fig. 1c) show clear discontinuities between the monoclinic and orthorhombic phases, with the volume trend having a positive volume discontinuity (ΔV) of ~1.2%.

Heat effects associated with the phase transition in KZn-Lc and KMg-Lc

Thermal effects observed for KZn-Lc sample

An initial DTA scan of a powdered sample of KZn-Lc (KZS4) was obtained over the temperature range 294–1281K. This scan (Fig. 5a) shows a weak endothermic feature smeared out over a temperature range from ~855 to 880 K, which can be matched clearly to the P2₁/c to Pbca phase transition observed by the high-temperature powder XRD study. In order to study the heat effects associated with the phase transition in more detail, preliminary DSC scans were carried out with a new aliquot of powdered KZS4 that had not been reheated since its original synthesis (denoted KZS4-A). The results for the temperature ranges over which thermal effects were observed and for the heats of transition observed for endothermal peaks are summarised in Table 5 and a DSC scan for key Runs are shown in Figs 5b, 5c and 5d. The first scan of the KZn-Lc sample (KZS4-A, scan 1) shows complex, sinuous undulations over the temperature ranges 834–840 K and 867–873 K that might be related to a series of exothermic and endothermic effects (see top scan in Fig. 5b). The same sample was scanned again after 43 hours at room temperature (KZS4-A scan 2; see middle scan Fig. 5b); this showed a fairly symmetrical endothermic effect over the range 867–875 K with a ΔH of 0.80 J/g (equivalent to a value of 380 J/mol on the basis of the simplest molecular formula for KZn-Lc (MW 476.04) with 12 oxygens) (Table 5). It is clear that initial heating of the sample using DSC caused some change in the sample so that the later scans with the same sample show much simpler thermal behaviour that allow the heat of the monoclinic to orthorhombic transition to be estimated from the area defined by the endothermic feature (denoted ΔH_transition). In order to assess this effect further the KZS4 sample that had been used in the HT-XRD experiments was scanned using DSC (denoted KZS4-B here). For this experiment, a clear endothermic effect over the temperature range 869–876 K is the only thermal feature present (see lower scan in Fig. 5b); this feature defines a ΔH_transition of 1.58 J/g (752 J/mole) (Table 5) though repeat scans showed significant changes in the shape of the DSC base-line leading to variable ΔH values. After 13 weeks at room temperature and following adjustments to the DSC data collection conditions, KZS4-B, scan 2 provided the highest ΔH_transition observed for this compound with a value of 3.65 J/g (1.74 kJ/mole) (Table 5, Fig. 5c).

Fig. 5. Representative DTA and DSC scans for hydrothermally synthesised monoclinic P2₁/c KZn- and KMg-leucite analogues: (a) DTA scan for KZn-Lc sample KZS4-A as-synthesised sample; (b) DSC scan for KZn-Lc sample KZS4-A as-synthesized sample; (c) DSC scan for KZS4-B, after HT-XRD studies and after one DSC heating cycle; (d) KMg-Lc sample AMT2 after three DSC heating cycles. Further information is given in Table 5 along with details of enthalpy of transition measurements.

Two other hydrothermally synthesised samples of KZn-Lc leucite were also available for study, however it was found that new powder XRD scans at room temperature for one sample (KZS1) had both ordered monoclinic and disordered cubic phases present; this sample was not studied further here. Nevertheless new powder XRD scans for the second sample (KZS3, see the section on ‘Sample synthesis’) showed that it is a single phase monoclinic analogue. Note that the room-temperature cell parameters and crystallite sizes for unheated samples of KZS4 and KZS3 are the same within experimental error (Table 5). The first DSC scan for KZS3 (KZS3-A) did not show the complicated exothermic/endothermic features of KZS4-A on the first heating; instead, it gave a very weak endothermic feature, over the temperature range 861–872 K; this feature is much weaker than those found for KZS4 and does not provide a reliable value for the transition heat. However, a second scan of sample KZS3-A gave a similar, weak endotherm from 868 to 879 K for which we have obtained a tentative transition heat of ~0.27 J/g (127 J/mole). A second sample (KZS3-B) also gave very weak heat effects at 862 to 872 K, but it is not possible to obtain a reliable estimate for its heat of transition. Although we were not able to assign a robust transition heat for the KZn-leucite KZS3, the temperature range matches that for KZS4 and clearly reflects the occurrence of the same monoclinic–orthorhombic phase transition for this compound. It is also clear that the thermal behaviour of the monoclinic KZn-Lc leucites is very sample dependent even though their room-temperature cell parameters are essentially the same and that the ΔH_transition value estimate for KZS3 is much smaller than that found for KZS4; we will consider the possible reasons for such differences below (see section ‘Possible chemical and structural controls of heat effect differences observed’).

Thermal effects observed for a KMg-Lc sample

Only one hydrothermally crystallised sample of KMg-Lc was synthesised at Manchester by CMBH, some 35 years ago, and portions of this were studied shortly after that at Warwick and Bristol (by Simon Kohn), at Cambridge (by Simon Redfern), at Daresbury and Sheffield (by AMTB), and at Manchester (by CMBH). We were keen to obtain DSC data on a sample of this compound to compare with results for KZS-Lc and only one possible small sample labelled AMT was located at Manchester however the history of usage of that sample was obscure. Further investigation using XRD at Sheffield Hallam University show this to be undoubtedly monoclinic KMg-Lc with room-temperature cell parameters matching those reported by Bell et al. (1994a) and Redfern and Henderson (1996) (Table 5). In addition the crystallite size of the original sample was found to be ~1670 Å, which shows it to be the best crystalline synthetic leucite we have studied here. Two small samples of the original, as-synthesised sample (denoted KMS2-AMT1 and KMS2-AMT2) have been scanned by DSC but the first scan of each gave complicated patterns (Table 5). The first scan for KMS2-AMT1 gave a clear double endotherm at 665 to 700 K that provides an estimate for the ΔH_transition of 3.47 J/g (1.51 kJ/mole); note that the temperature region for this heat effect is close to the region of coexistence of 646–671 K reported by Redfern and Henderson (1996). However, the region from ~750 to 800 K showed spikes of electronic-like noise superimposed on a poorly defined feature that might not be significant. Scan 1 for a new aliquot of this sample (KMS2-AMT2) showed spikes of electronic noise from 650 to 740 K and an endothermic-like feature from 750 to 840 K. We speculate that some of the other features suggest that the sample is undergoing some initial changes in composition or structure. Further heating scans were therefore carried out on sample KMS2-AMT2. Scan 2 was started 40 minutes after cooling Scan 1 to room temperature and showed a fairly narrow endothermic peak (670–680 K) giving a ΔH_transition of 4.39 J/g (1.91 kJ/mole) (Table 5). Scan 3 on the same sample was started 35 mins after scan 2 had been cooled to room temperature; this scan showed a clear double endothermic peak from 665 to 690 K and gave a ΔH_transition value of 4.92 J/g (2.14 kJ/mole) with clear baselines showing no other thermal features (Table 5). After adjustment to the baseline collection parameters a final scan (obtained 7 weeks later) gave an endothermic feature, which between 660 and 700 K defines a ΔH_transition of ~ 6.72 J/g (~ 2.94 kJ/mole) (Table 5 and Fig. 5d). The heat effects observed for the hydrothermal KMg-Lc sample occur over the same temperature conditions as the monoclinic to orthorhombic phase transition determined by HT-XRD (Redfern and Henderson, 1996) and we assign an average ΔH_transition value of 4.9 J/g (2.1 kJ/mole) to the phase transition for this compound (Table 5).

We have reported that the first heating Runs of hydrothermally synthesised KZS and KMS leucite analogues both show complex DSC patterns, which indicates that the samples are undergoing both chemical and structural changes during these initial experiments. Later scans on the same samples show simpler features with clear endotherms covering fairly wide temperature ranges; in addition, repeat heating experiments tend to show peaks having some differences in shape and in peak area, which we speculate reflect local changes that occur during the annealing and relaxation processes the samples undergo. In the following section we attempt to account for such effects.

Possible chemical and structural controls of heat effect differences observed

In a multi-nuclear MAS NMR study of leucite analogues of formula A ₂X ²⁺Si₅O₁₂ with A = K, Rb, or Cs and X = Mg, Zn or Cd, Kohn et al. (1994) commented that static ¹H NMR showed the presence of water in some hydrothermal synthesised samples; they pointed out that TGA showed that such water was lost from 100 to 600°C, though no further information was given. However, Kohn (personal communication, May 2021) has recently confirmed that ¹H NMR showed the presence of 0.5 to 2 wt.% H₂O in crystalline Mg- and Zn- leucite samples (Kohn et al., 1994). Note that the only TGA data we have been able to obtain on the KZn-leucite sample KZS4 is a 0.2 wt.% loss between room temperature and 400°C; this is lower than that reported above but no sample is available currently for a better determination. We conclude here that the water lost at the lowest temperatures would be adsorbed water (denoted H₂O^–), though that lost at the highest temperatures in the KZn- and KMg-Lc samples studied here is likely to be molecular water occupying the large cavity positions (H₂O⁺ in W-sites) within the leucite framework. Such water in analcime (NaAlSi₂O₆·H₂O) is mainly lost close to 400°C and that in wairakite (CaAl₂Si₄O₁₂·2H₂O), is mainly lost at ~400 and 550°C (Deer et al., 2004); both of these minerals have leucite-type framework structures.

Kohn et al. (1994) also used ²⁹Si MAS NMR to show that a hydrothermally synthesised KMg-Lc sample (KMS2, 600°C, 50MPa, 7 days) was characterised by the presence of 10 sharp Si peaks (10 distinct Si-sites) with a flat, low intensity background, showing that the sample is a well-crystalline, fully-ordered monoclinic P2₁/c phase. In contrast, they showed that a hydrothermal KZn-Lc sample (KZS3, see above) had 10 identifiable Si peaks of well-crystallised, ordered material superimposed on a broad hump-shaped background of more disordered material (see Kohn et al. 1994; their figure 3). Note that they comment that the powder XRD pattern for KZS3 indicates a well-crystalline monoclinic sample pointing to any disorder being on the shorter range length scale probed by MAS NMR spectroscopy.

The presence of some water in crystalline hydrothermal KMg-Lc might, therefore, account for instabilities in the DSC scan for the previously unheated sample, though the starting material glass for that sample is close to the stoichiometric end-member composition (Kohn et al., 1994). However, the fact that the starting material glass for the KZn-Lc analogue is deficient in K (see section on ‘Sample synthesis’) suggests that the vacant W-sites in some of the hydrothermal samples might well contain a significant amount of molecular water trapped within the crystalline framework. Thus, we speculate here that the complex DSC features observed in the previously unheated KZS4-A, scan 1 sample could be related to water loss mainly starting at ~500°C, which might have been accompanied by some rapid, short-range re-ordering of K in the W-sites and Si and Zn in the T-sites. Such a process could explain exothermic-like features. However, at the same time the monoclinic to orthorhombic phase transition started; that crystallographic transition together with the effects of water loss would lead to the associated endothermic features. Note that the displacive crystallographic phase transition would be fully reversible but the water loss and site-ordering features would not be reversed on cooling. We have commented earlier that slightly smaller unit cell edges were found at the end of the Run1 HT-XRD experiments on KZS4-B and we speculate here that this could be due to water loss from the W cation site leading to some framework contraction.

We have shown above that DSC heating Runs on the KZS4-A sample after 43 hours of cooling (scan 2) shows only weak endothermic effects suggesting ΔH_transition values of ~380 J/mole (Table 5, Fig. 5b). However, the sample used for the HT-XRD powder investigation of the monoclinic–orthorhombic phase transition (denoted KZS4-B here) showed a much simpler thermal behaviour with a better defined endothermic peak over a similar temperature range to that observed for KZS4-A scan 1 (Table 5, Fig. 5b) with a much larger ΔH_transition of ~750 J/mole (Table 5) though our early DSC scans showed poor reproducibility. A final scan on KZS4-B (scan 2, obtained 13 weeks later) gave a higher ΔH_transition of ~1.73 kJ/mole (Table 5, Fig. 5c). Both of the KZS4 samples show simple endothermic features over the temperature range of ~868–875 K, reflecting the occurrence of the phase transition observed by HT-XRD. However, the higher transition heat for KZS4-B would be consistent with that sample having been annealed more effectively during the HT-XRD experiments thus providing a locally better-ordered structure and a more reliable thermal analysis result. The suggestion that the KZS4 sample had become better ‘ordered’ during the HT-XRD experiments is supported by the crystallite-size estimates reported in Table 5: before high-T XRD Runs ~1330 Å and after both HT-XRD and DSC experiments, 1773 Å (Table 5). These values reflect the case that well-crystallised, ordered samples provide better powder XRD patterns resulting from the larger crystallite repeat and X-ray scattering distances. Note that naturally occurring leucite (KAlSi₂O₆) might be expected to be better crystalline than any synthetic hydrothermally-crystallised leucite and this is confirmed by the room-temperature value of 345 nm (3450 Å) reported by Bell and Henderson (2020).

The fact that hydrothermal KZS3 has a much smaller ΔH_transition than that for KZS4 must also be explained. We have shown that KZS3 has a crystallite size of ~1360 Å, within error of the unheated KZS4 sample (Table 5), though the MAS NMR data for the former sample clearly shows a much smaller proportion of a long-range-ordered monoclinic phase than for KZS4 (see above), which presumably restricts the effectiveness of any crystallographic transition and thus the size of the associated heat effect.

On the basis of the DSC data it seems clear that the transition heats in our samples are dependent on local factors in the frameworks that we do not fully understand; unfortunately, we do not have sufficient of any of the samples to study this more systematically with a program of annealing heat treatments and TGA, together with NMR, Raman or infrared spectroscopy to study the presence of water within W-sites. However, we suggest that the most reliable values for ΔH_transition are ~1.7 kJ/mole for the KZS4 sample and ~2.1 kJ/mole for the KMS2-AMT leucite. It seems likely that the best crystalline sample and most reliable ΔH_transition value is that for the KMg sample, though it is possible that none of the values represent equilibrium. Lange et al. (1986) studied the tetragonal I4₁/a to cubic Ia $\bar{3}$d phase transition in natural and synthetic K-leucite samples by DSC and reported ΔH_transition data on the basis of a 6 oxygen cell as: average of 3 natural leucites ΔH_transition = 3.37 kJ/mole; synthetic KAlSi₂O₆ 3.81 kJ/mole; synthetic KFe³⁺Si₂O₆ 2.45 kJ/mole; and synthetic Si-rich solid solution Lc_0.86Or_0.14 wt.% 2.91 kJ/mole. On a J/g basis these transition heats would be 15.5, 17.5, 9.8 and 12.7 J/g, respectively; the values we find for KMg-leucite are significantly smaller and average ~4.9 J/g. It is clear that the nature of the tetrahedral cations and their proportions would affect the transition energies, as would the perfection of the crystalline frameworks for such samples. In addition, our samples have ordered T-site frameworks while the other samples (Lange et al., 1986) will have mainly disordered Si–Al and Si–Fe frameworks. Much more sample synthesis, and high-resolution structural, spectroscopic and thermal analytical studies are required to adequately address this interesting research area, however this is not possible in the foreseeable future.

Characteristics of the monoclinic P2₁/c to orthorhombic Pbca transition in leucite analogues

The hydrothermally-synthesised KZn-Lc leucite analogue has an ambient temperature silicate framework structure in which Si and Zn cations are ordered over the framework. It has a P2₁/c monoclinic crystal structure and is isostructural with the first cation-ordered leucite analogue KMg-Lc, which was determined using integrated synchrotron powder XRD, electron diffraction, and ²⁹Si MAS NMR methods (Bell et al., 1994a). A high-temperature Guinier powder XRD study on another portion of the same KMg-Lc sample (Redfern and Henderson, 1996) showed a reversible, unquenchable ferroelastic phase transition that was initiated at ~650 K; the high-temperature form was indexed as a Pbca orthorhombic cation-ordered structure isostructural with Cs₂CdSi₅O₁₂ (Bell et al., 1994b). In that study of KMg-Lc, both monoclinic and orthorhombic polymorphs were present over a temperature range of ~25 K and the calculated unit cell volume showed a positive ΔV of ~1.6 %. Both of the features pointed to a first-order transition (Redfern and Henderson, 1996). Note that the topologically equivalent P2₁/c and Pbca structures, where the former has 12 distinct T-sites (10 Si and two M ²⁺) and the latter 6 T-sites (5 Si, 1 M ²⁺) [Bell et al., 1994a, 1994b], are permitted to show a continuous, second-order transformation (Stokes and Hatch, 1988) but the ΔV and two-phase characteristics reported for the KMg-Lc phase transition excludes this possibility. This is consistent with that transition being a reversible, non-quenchable, first-order ferroelastic phase transition.

We have already predicted that P2₁/c KZn-Lc should show a phase transition to Pbca at ~700 K (Bell and Henderson, 2018), but the high-temperature data for KZn-Lc reported here show the phase transition occurring over the temperature range 848–863 K where both monoclinic and orthorhombic phases are present. This two phase region is similar to that described for unquenchable, displacive phase transitions shown by kalsilite analogues in the SrAl₂O₄–BaAl₂O₄ system and was named the ‘region of coexistence’ (Henderson and Taylor, 1982); based on similarities shown for displacive phase transitions occurring in ZrO₂ and high-cristobalite, it was suggested that the aluminate ‘nepheline/kalsilite-type’ phase transition had properties of a strain-related martensitic transition (Henderson and Taylor, 1982; Avdeev et al., 2007; Henderson, 2021).

Two-phase regions in the I4₁/a to $Ia\bar{3}d$ displacive phase transitions have also been reported for synthetic KGaSi₂O₆ and synthetic (K,Na)[Al,Fe³⁺,Si]_3–4O_6–8 leucites and it was concluded that all these phases showed martensite-type phase transitions (Bell and Henderson, 2020); that paper included a more detailed discussion of the mechanisms of martensitic displacive phase transitions in ZrO₂, cristobalite and BaTiO₃ in the Supplementary material.

DTA and DSC measurements for KZn-Lc leucites show an endothermic heat effect smeared out over ~15 K, corresponding to the phase transition range determined by powder XRD. Figure 1 shows how the lattice parameters vary with temperature and it is clear that all these data are consistent with the P2₁/c to Pbca transition occurring over a temperature range of ~20–25 K. This is likely to be related to the effects of internal strain being mediated in a stepwise, thermally controlled fashion (see below).

KZn-Lc and KMg-Lc leucite analogues both show similar first-order phase transitions with positive ΔV values (1.2 and 1.6%, respectively), with two-phase regions smeared out over ~20–25 K; however, the phase-transition temperature for KMg-Lc is much lower than that for KZn-Lc. As the tetrahedral Zn²⁺ cation is slightly larger than that for tetrahedral Mg²⁺, the KZn-leucite should have a slightly larger framework, however, cubic disordered K, Rb and Cs leucite analogues (A ₂ZnSi₅O₁₂) invariably have smaller cell volumes than their Mg-counterparts at room temperature (Bayer, 1973; Kohn et al., 1994; Yanase et al., 1999; Henderson et al., 2017). The same is true for the ordered P2₁/c and Pbca (K, Rb and Cs)-Mg and -Zn equivalents (Kohn et al., 1994; Henderson et al., 2017; and this work). This relationship would be consistent with the larger Zn-containing frameworks being more collapsed about each central cavity cation than their Mg equivalents. This, in turn, would result in the phase transition to the higher symmetry polymorph being displaced to a higher temperature as found here. However, the starting glass material for the KZn-leucite sample shows a deficiency of K in the W-site (see above) while that for the KMg-leucite sample is within error of the stoichiometric KMg-Lc composition (Kohn et al., 1994) and this might also be a factor in influencing the actual phase-transition temperature and overall characteristics.

The spontaneous strains associated with these phase transitions are analysed in the next section.

Strains associated with the ferroelastic (P2₁/c) to paraelastic (Pbca) phase transition in KZn-Lc

We have already pointed out that T-site ordered P2₁/c and Pbca leucite analogues have the same structural topologies as the I4₁/a and $Ia\bar{3}d\;$leucite frameworks. Several detailed studies of the strains associated with the second-order ferroelastic (I4₁/a) to paraelastic ($Ia\bar{3}d$) displacive phase transition in natural leucite (KAlSi₂O₆) have been published (e.g. Palmer et al., 1989, 1997; Palmer, 1990; Carpenter et al., 1998a)_. All of these studies interpreted aspects of the phase transitions for natural leucite in terms of Landau Theory, which was developed initially for continuous second-order transformations. However, subsequent research showed that this approach could be extended to describe first-order and reconstructive phase transitions, and even to incommensurate phases (Tolédano and Tolédano, 1987; Tolédano, 2012). In the present case, as mentioned above, Group Theory shows that a phase transition from Pbca to P2₁/c is permitted to be second order as it satisfies both the Landau and Lifshitz criteria, but this does not preclude such a transition being first-order that is system dependent. A first-order transition in the Ehrenfest classification requires the first differential of the Gibbs function to be discontinuous at the phase transition, e.g. entropy or volume, which is demonstrated in KZn-Lc by the occurrence of a volume discontinuity between the orthorhombic and monoclinic phases.

The excess free energy (ΔG) at a phase transition can be defined using a simple Landau potential as:

$$\Delta G( Q ) = ( {A/2} ) ( {T\ndash T_c} ) Q^2 + ( {B/4} ) Q^4 + ( {C/6} ) Q^6$$

where Q is an order parameter, T_c is the transition temperature, T the temperatures for a series of experimental measurements, and A, B and C are coefficients defining the shape of the Q vs. T trend. For a continuous, second-order phase transition (with no ΔV) A, B and C are positive. A value of B = 0 marks the occurrence of a tricritical point and for negative B values (B < 0) the phase transition is said to be first order (e.g. Aitta, 2009); such a first-order transition will be characterised by the presence of discontinuities in symmetry-breaking and non-symmetry breaking strains, and perhaps by the occurrence of a two-phase region (e.g. also see Salje, 1990; Hayward et al., 2000; Tolédano, 2012). Redfern and Henderson (1996) have already shown for T-site ordered KMg-Lc leucite that the symmetry relations for the P2₁/c to Pbca transition satisfy the general Landau and Lifshitz criteria and that discontinuities in both the volume and the shear strain (e₁₃, see below) indicate a first-order mechanism. The spontaneous strain vs. order parameter relationships for the KMg-Lc transition show that the driving order parameter e₁₃ [effectively (–cos β*)/2] scales with the ferroelastic order parameter (Q), whereas the non-symmetry-breaking volume strain (V _ss) scales with Q ² (Redfern and Henderson 1996). Although Redfern and Henderson (1996) fitted the temperature dependence of the e₁₃ temperature dependence for KMg-Lc, and reported values determined for A/C and B/C coefficients and for T _c, we were not able to obtain robust fits for the KZn-Lc sample, reflecting the lower quality of data obtained here compared to the higher resolution Guinier camera data used by Redfern and Henderson.

Carpenter et al. (1998a) in a key paper on ferroelastic transitions gives many examples for mineral and inorganic compounds that display either second- or first-order displacive phase transitions. Other recent papers dealing with the strains associated with monoclinic–orthorhombic phase transitions involved the P2₁/n to Pnma transition in ZSM-5 zeolite (Ardit et al., 2015) and in olivenite (Tarantino et al., 2018). In these cases, and for P2₁/c to Pbca in KZn-Lc and KMg-Lc, the same point group pair mmm and 2/m is involved but note that the ZSM-5 zeolite and olivenite have many features consistent with second-order transitions in contrast to KZn-Lc and KMg-Lc. In the present work we have combined the different approaches used by Redfern and Henderson (1996), Carpenter et al. (1998a) and Ardit et al. (2015) to address the spontaneous strain relationships that reflect the changes in the structural state shown by the KZn-Lc phase transition.

Carpenter et al. (1998a) defined the components of the spontaneous strain tensor for a monoclinic–orthorhombic transition, where a ₀, b ₀, c ₀ and V ₀ are orthorhombic parameters extrapolated into the lower temperature monoclinic field. Figure 1 shows how linear extrapolations of the KZn-Lc orthorhombic high temperature values for a, b, c, β and V provide estimates for a ₀, b ₀, c ₀, β₀, and V ₀ at the temperatures for the Run 1 monoclinic polymorphs (see section on ‘Powder X-ray diffraction’). The a ₀, b ₀, c ₀ and V ₀ values for KMg-Lc were obtained in a similar way from the parameters reported in Table 1, Redfern and Henderson (1996).

The Carpenter et al. (1998a) spontaneous strain equations used here are: e₁₁ = a/a ₀ – 1 (Carpenter equation 49); e₂₂ = b/b ₀ – 1 (equation 50); e₃₃ = ((c/c ₀) sin β) – 1 (equation 51); e₁₃ = (0.5(c/c ₀)cos β) [equation 53; note that for small linear strains this has a value close to (–cos β*)/2]; e₁₂ = e₂₃ = 0 (equations 52 and 54). The linear strains e₁₁, e₂₂ and e₃₃ are non-symmetry-breaking (nsb) and scale with Q as e_ii α Q ². The shear strain e₁₃ is symmetry-breaking (sb) and scales with Q as e₁₃ α Q. The volume strain is defined as V _ss = (V – V ₀) / V ₀ (Carpenter equation 69) and there is a discontinuity, ΔV, at the transition point.

We have calculated the individual strain parameters from the measured cell parameters for KZn-Lc (this paper) and KMg-Lc (Redfern and Henderson, 1996; see also Henderson, 2021) in an Excel spreadsheet and plot the results in Fig. 6a and b. Note that the values calculated for e₁₁, e₂₂, e₃₃, and V _ss have significant uncertainties arising from the need to extrapolate orthorhombic cell parameters over wide temperatures ranges to provide a ₀, b ₀ and c ₀ for each temperature step in the monoclinic stability field, but e₁₃ is better constrained because the extrapolated β₀ term is fixed at 90°. For the KZn-Lc sample (Fig. 6a) the data for the monoclinic and orthorhombic symmetries are plotted using separate symbols. Note that we have not plotted strain data for the two-phase mixtures because overlapping Bragg peaks for the coexisting monoclinic and orthorhombic phases lead to some of their cell parameters being less reliable than for the one-phase data points. The Run 2 data plot within error of the Run 1 points and the same is true for the orthorhombic data above the phase transition though we have not included the points for monoclinic, Run 2 strains as they obscure the detailed individual trends for the monoclinic phases close to the phase transition. However, the strain trends for Runs 1 and 2 are shown separately in Figs 7 and 8 below.

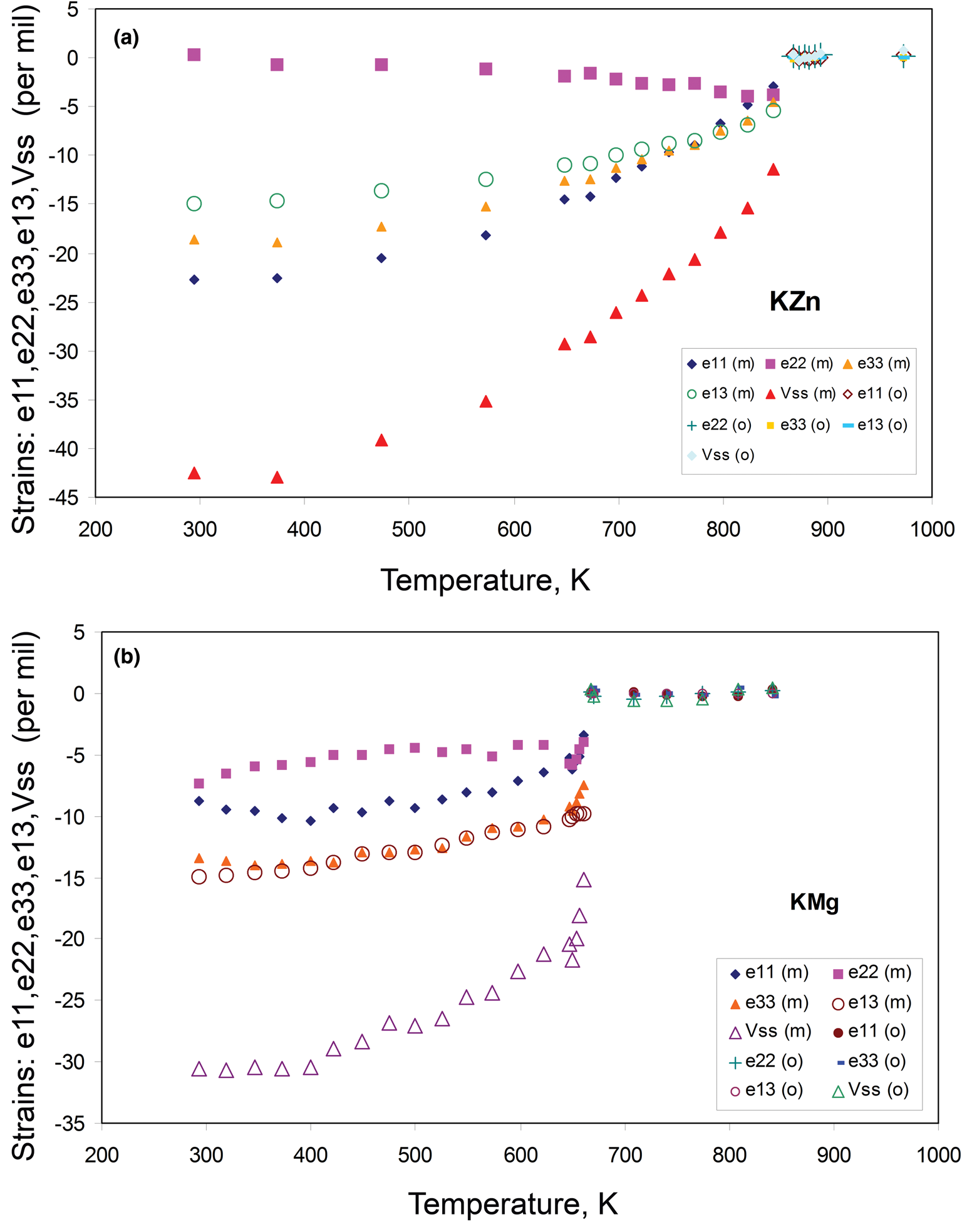
Fig. 6. Variation of calculated spontaneous strain parameters e₁₁, e₂₂, e₃₃, e₁₃, and V_ss vs. temperature: (a) KZn-Lc, sample KZS4 (this work); (b) KMg-Lc, sample KMS2 (cell parameters from Redfern and Henderson, 1996).

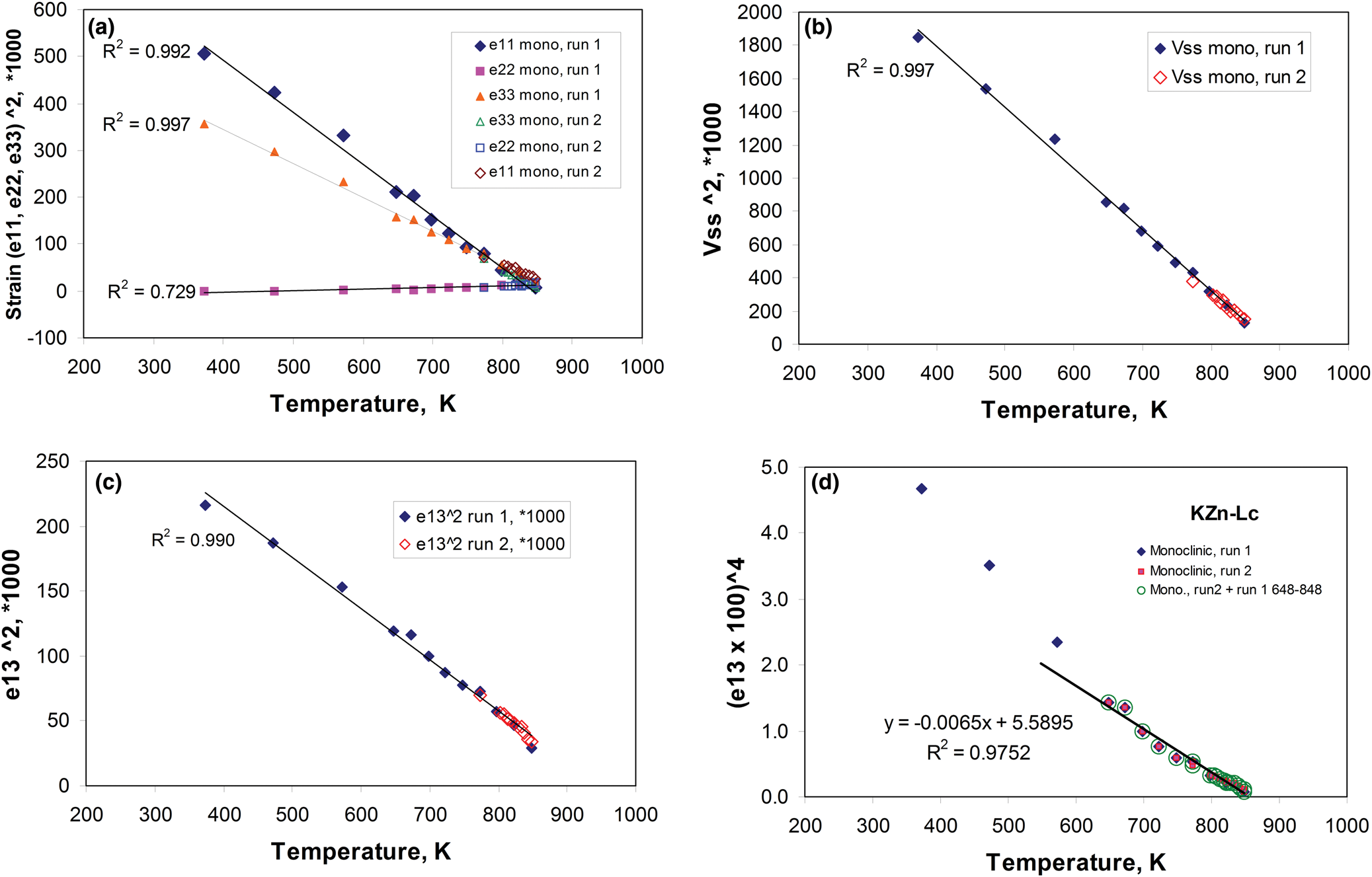
Fig. 7. Variation of strain parameters versus temperature for KZn-Lc, sample KZS4: (a) [e₁₁, e₂₂, e₃₃]² vs. T; (b) V_ss² vs. T; (c) e₁₃² vs. T; (d) e₁₃⁴ vs. T. Linear fit data are shown for strain parameters. See text for explanation.

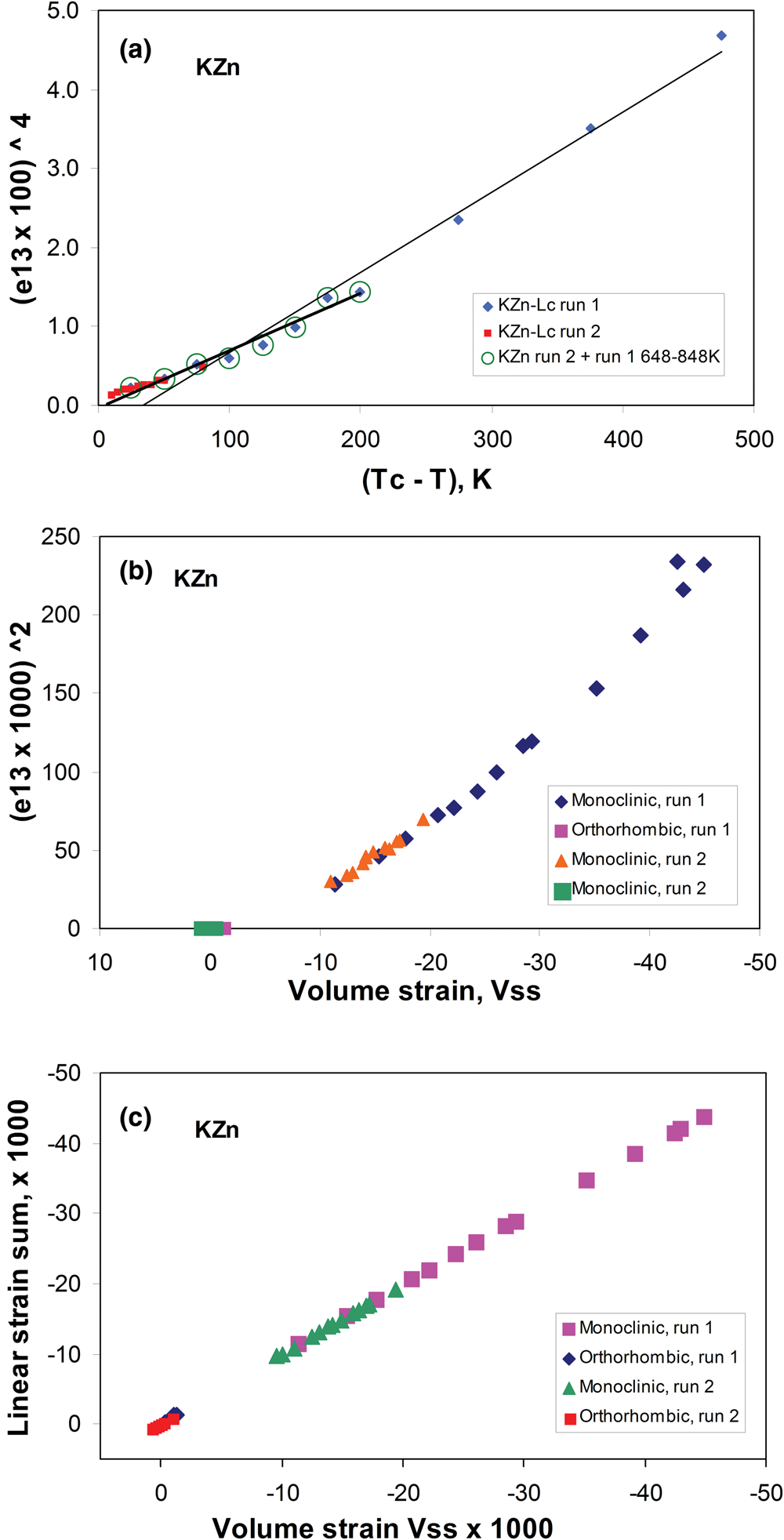
Fig. 8. Plots of spontaneous strain parameters for KZn-Lc, sample KZS4 that can be used to assess relationships between strain components and order parameters. (a) e₁₃⁴ vs. (T _c – T); (b) (e₁₃)² (e₁₃ is proportional to Q) vs. V _ss (proportional to Q ²); the line shows the linear fit obtained for Run 2 data; (c) relationship between the symmetry breaking strain (V _ss) and the sum of the non-symmetry breaking axes of the strain tensor (e₁₁ + e₂₂ + e₃₃). See text for explanation.

The spontaneous strains for e₁₁ and e₃₃ (i.e. those for the a and c axes) for the monoclinic samples start with negative values (–23‰ and –19‰, respectively) and both trends show only small changes (to less negative values) up to ~500 K, the e₁₁ then starts to change more quickly than e₃₃ with increasing temperature and the two trends cross at ~750 K to give values just below the phase transition of –3 and –5‰, respectively. The e₂₂ strains (b axis) have values close to zero and initially show little change, but then a slight fall above 650 K to ~–4‰. The e₁₃ shear strain shows little significant variation up to ~500 K (i.e. from –15 to –14‰) before decreasing to –5‰ at the transition. The volume strain shows little change up to 400 K (from –45 to –44‰) but then shows a clear, increasing rate of change with increasing temperature to a value of ~ –11‰ at the phase transition; the volume discontinuity between the monoclinic and orthorhombic strains at the transition is very clear at ~850 K in Fig. 6a. The discontinuities for the other strains are smaller but all show positive relationships between the strains for monoclinic and orthorhombic cells. For the orthorhombic data the e₁₁, e₂₂, e₃₃ and V _ss strains have very low values, scattering on the positive and negative sides of 0 reflecting experimental error, mainly error from the extrapolated i ₀ values. As expected, the e₁₃ strains plot at zero values reflecting the fact that cos90 = 0. It is clear in Fig. 6a that all of the strain parameters for the monoclinic phases show smooth, non-linear responses with increasing temperature.

The small magnitudes of discontinuities in individual strains at the transition point seen in Fig. 6a show that the orthorhombic to monoclinic transition in KZn-Lc is weakly first order. As such it is expected to be in close proximity to tricritical (Q ⁴ α (T _c – T)); approximately linear relationships between e_ii² and V _ss (α Q ⁴) vs. temperature (Fig. 7a,b) confirm that this is the case. The symmetry-breaking (e₁₃)² strain also shows a reasonable linear trend in Fig. 7c but the highest temperature points fall below this linear fit and the overall trend has a concave-down form suggesting a different behaviour for the e₁₃ strain. The plot of e₁₃⁴ vs. temperature is shown in Fig. 7d and shows some curvature though note that the higher temperature data points for Run 1 data and all of the Run 2 data show a good linear trend consistent with a relationship e₁₃ α T ^1/4 suggesting tricritical behaviour. This relationship is shown better in Fig. 8a in a plot of e₁₃⁴ vs. (T _c – T) where T _c is chosen to be the first temperature that the orthorhombic phase appears (848 K). The full data set shows a close to linear trend but the higher temperature points define a linear trend direct towards the orthorhombic phases that would plot at the origin. Thus, if the driving order parameter e₁₃ is proportional to T ^1/4 this, in turn, would be consistent with the phase transition being weakly first order, tricritical, in nature (cf. Li et al., 2013).

Figure 8b shows the relationship between e₁₃² and V _ss for KZn-Lc is non-linear although the higher temperature points do show a simpler almost-linear trend. Departures from linearity shown in Figs 7d and 8a reflect two possible internal inconsistencies: experimental error or higher order coupling effects. Absolute uncertainties in linear strains are expected to be greater than those for e₁₃ because of the necessity to extrapolate experimental data from the high-temperature orthorhombic phase field in order to estimate values for a ₀, b ₀ and c ₀ in the stability field of the monoclinic structure. In addition, the lower temperature points for the monoclinic phases tend to show very small changes reminiscent of a ‘plateau’ effect and this might explain some of the non-linear trends (see above). A partial test of the robustness of the analysis is provided by the observation that values of V _ss are essentially indistinguishable from the sum of e₁₁ + e₂₂ + e₃₃ (Fig. 8c) as required for small strains. This leaves the probability that the spontaneous strains include coupling with higher order terms in Q, as has been observed in the case of alpha–beta quartz that also has a large volume strain of up to ~5% (Carpenter et al., 1998b).

The spontaneous strains for KMg-Lc leucite have been calculated in the same way using the cell parameters from table 1 of Redfern and Henderson (1996); see also the preliminary study of strain parameters for this compound (Henderson, 2021). The e₁₁, e₃₃ and V _ss spontaneous strains for that compound (Fig. 6b) are all less negative, and that for e₂₂ is slightly more negative, than those for KZn-Lc leucite; overall the Zn-analogue clearly has a more distorted framework than the Mg form. However, for each parameter the trends are similar for the two leucite compositions. Figures 6a and 6b show distinct discontinuities for each of the strains at the transition for both KZn-Lc and KMg-Lc. These clear discontinuities and the positive ΔV are all consistent with the phase transitions being weakly first-order in character for both of these compounds.

Conclusions

High-temperature powder XRD measurements on the KZn-Lc leucite analogue show that the ambient temperature P2₁/c monoclinic cation-ordered crystal structure undergoes a phase transition to a Pbca orthorhombic cation-ordered crystal structure over the temperature range 848–863 K.

There is an ~1.2% step increase in the KZn-Lc unit cell volume over the phase transition for this phase. KZn-Lc is isostructural with KMg-Lc, which shows a similar phase transition around 650 K. The positive ΔV and the presence of two-phase regions occurring over the temperature range of the phase transition for both the Zn and Mg analogues are consistent with both transitions being first order and may have a strain-related martensite-like mechanism

The first DSC heating scans on original, as synthesised T-site-ordered leucites are, perhaps, related to loss of any water present and local structural ordering effects; nevertheless, annealed samples give ΔH values for the displacive P2₁/n to Pbca crystallographic transition for less-well-annealed KZS4 of 3.6 J/g, and for well-annealed KMS2 a value of 4.9 J/g. These values compare with values of ~15 J/g for the I4₁/a to I $a\bar{3}$d transition in well crystallised natural leucite (KAlSi₂O₆). Note that we have used J/g here rather than J/mole so as not to confuse 12 O cell values for the KZn- and KMg-Lc samples with the 6 O cell basis used for natural leucites.

Analysis of the spontaneous strains associated with the transition for KZn-Lc is shown to be similar to those reported for the KMg-Lc leucite analogue (Redfern and Henderson, 1996; Henderson, 2021). Both compounds show that the primary ferroelastic strain e₁₃ (or cos(β*)) is proportional to the driving order parameter Q while the V _ss strain is coupled to Q ².

The current work on these compounds has raised evidence of some complexities in the nature of the monoclinic to orthorhombic phase transitions in these T-site ordered KZn- and KMg-Lc P2₁/c framework structures. Structural characterisation of such low symmetry, multi-site compounds is challenging; the presence of two-phase regions at the transition, and the presence of structural water in the original samples all present problems. To address such problems it would be necessary to prepare large amounts of new, well-crystallised and stoichiometric materials that should be studied by techniques including high-resolution synchrotron X-ray or (preferably) time-of-flight neutron diffraction, multi-nuclear MAS NMR, infrared, and DSC/TGA methods. None of this would be straightforward and a new consortium would be necessary.