The Ideologies of Organized Interests and Amicus Curiae Briefs: Large-Scale, Social Network Imputation of Ideal Points

Abstract

Interest group ideology is theoretically and empirically critical in the study of American politics, yet our measurement of this key concept is lacking both in scope and time. By leveraging network science and ideal point estimation, we provide a novel measure of ideology for amicus curiae briefs and organized interests with accompanying uncertainty estimates. Our Amicus Curiae Network scores cover more than 12,000 unique groups and more than 11,000 briefs across 95 years, providing the largest and longest measure of organized interest ideologies to date. Substantively, the scores reveal that: interests before the Court are ideologically polarized, despite variance in their coalition strategies; interests that donate to campaigns are more conservative and balanced than those that do not; and amicus curiae briefs were more common from liberal organizations until the 1980s, with ideological representation virtually balanced since then.

Central to the study of American democracy is the study of factions. Among them, interest groups are both foundational and pervasive, affecting the function of every branch. There is evidence of interest group efforts on Congress (e.g., Berry 1999; Esterling 2007; Fellowes and Wolf 2004; Wawro 2001), the executive (e.g., Baumgartner et al. 2011), the Courts (e.g., Box-Steffensmeier, Christenson, and Hitt 2013; Caldeira and Wright 1988; Collins 2007), the bureaucracy (Drope and Hansen 2004; Kelleher and Yackee 2006), as well as in state and local politics (e.g., Miller 2008). Underlying these and related works are expectations about interest groups’ preferred lobbying strategies and political outcomes. Thus, core to the study of interest groups, both theoretically and empirically, is the ideology of the group. However, for the vast majority of active interests relatively little is known on this front.

While frequently implied or assumed, missing from many studies of interest group influence is an objective measure of their ideologies. Such an absence makes understanding interest group preferences at a large scale and over multiple issues, events, or periods nearly impossible. Likewise, the ability to predict political outcomes under the influence of interest groups is severely hampered. Scholars must either make (educated) guesses about interest group ideology based on in-depth knowledge, or else infer their ideological leanings from their political activity. Furthermore, complicating large-scale inferences about and from interest group activity is that the population of such interest groups is unknown. Indeed, substantial portions of those actively lobbying in the American political system do not formally register as lobbyists (LaPira and Thomas 2014). In short, many organizations, associations, and corporations actively pursue political outcomes, but do not meet the high bar to formally register and have political leanings that are generally unknown, and are therefore largely left to exert influence in the shadows.

We propose to address these deficiencies by estimating interest group ideal points for the entire population of entities engaged in a crucial form of interest group lobbying: signing amicus curiae briefs to the Supreme Court. Across nearly 100 years of activity, over 15,000 organizations from a wide range of industry sectors have signed these briefs (see, e.g., Box-Steffensmeier and Christenson 2012). By utilizing the full set of amicus-filing organizations, we expand the realm of known interest groups beyond those with histories of donating to campaigns or registering lobbying activities.

In what follows, we begin by situating our work in the context of those that have constructed related measures for interest groups, broadly construed. In doing so, we find a persistent need for a measure of this nature that is comprehensive, both in terms of time and breadth. We next introduce our methodology that couples political donation ideal points (Bonica 2014) as training labels within a network analysis of the amicus cosigning strategies of organized interests. In contrast to traditional unsupervised methods, having a set of labeled observations in our method pegs the probability of a relational tie to a known value, substantially improving the end results. Likewise, by combining insights from multiple institutions and behaviors—for example, from both campaign donations and social networks before the Court—our approach guards against a measure limited to a singular domain. We need only make the assumption that organized interests write and sign briefs in accord with their ideology.¹

However, it is important to note that by relying on ideology training labels from campaign donations (or any other measure of organized interest ideology), our scores necessarily adopt their limitations and assumptions.² To attempt to mitigate issues arising from the training labels, our approach makes use of leave-one-out cross-validation, which we also use to establish internal validity and, ultimately, as the estimated ideal points, which we call Amicus Curiae Network (ACNet) scores. These scores are unidimensional by design, which means they are low-dimensional representations of an inherently multidimensional concept, and they do not allow for the latent structure analyses or the variance-explained measures common in other ideal points.³ The scores are also derived from static ideal points and are themselves static, that is, we calculate an overall ideology score by assuming ideology for organized interests is stable across time.⁴ In sum, they, like all ideal points, have some error, but nonetheless prove a useful tool. Indeed, additional features of our approach are the ability to provide accompanying uncertainty estimates, as well as ideal points for amicus curiae briefs.⁵

We conclude by showing that the ACNet scores uncover a number of substantive insights into the behavior of organized interests before the Court. Foremost, we find that the amicus curiae cosigning network is ideologically polarized. The scores also show historically greater representation of liberal briefs that has given way to virtually equal representation since the 1980s. Finally, by comparing our measure across interest groups, we find support for the expectation that ideological extremity and campaign donations are correlated. Yet, these results only scratch the surface of insights available with a comprehensive measure of organized interest ideology. ACNet scores open the door to investigate a host of questions involving interest group influence beyond the Court and across institutional branches and levels of government, not to mention in campaigns and public opinion.

1 Ideology Scaling Based on Amicus Curiae Behavior

In recent decades, a substantial increase in lobbying activity—be it of the legislative, executive or judicial branch—points to the importance of this practice for both public officials as well as special interests. Whether it is to gain policy favors at a “low cost” (Ansolabehere, de Figueiredo, and Snyder Jr 2003), to capture legislators’ attention and efforts (e.g., Hall and Wayman 1990), or to persuade supporters and counteract the effects of opponents (e.g., Hansen 1991), interest groups direct a substantial amount of resources to influence policy outcomes. Scholars have pursued the decision of interests to lobby on particular issues and amidst competition (e.g., Gray and Lowery 1996a, b; Holyoke 2009; Leech et al. 2005) and, if so, whether to collaborate (e.g., Baumgartner et al. 2009; Hall and Deardorff 2006) and with whom (Box-Steffensmeier and Christenson 2014, 2015; Christenson and Box-Steffensmeier 2016). To further understand the objectives and degree of influence of the vast array of interest groups in our political system requires a reliable measure of their ideology.

Political science has made significant inroads to measuring ideology for a number of actors. Indeed, advances in ideal point estimation have preceded bursts of research productivity in political science, starting with the NOMINATE models (Poole and Rosenthal 1985), the most current version of which, DW-NOMINATE, relies on co-voting behavior between Members of Congress (Lewis et al. 2019), which acknowledges the fundamental network structure across legislators and bills. Subsequently scholars have developed ideal point estimates for presidents (e.g., Bertelli and Grose 2011), judges (e.g., Bailey and Maltzman 2011; Lauderdale and Clark 2012; Martin and Quinn 2001) and bureaucrats (e.g., Clinton et al. 2012). These works have made substantial contributions to understanding the political preferences and relationships of political actors and interest groups. However, there are still challenges to obtaining a wide-ranging reliable measure of interest group ideology. For instance, despite its massive contributions, the primary limitation of DW-NOMINATE is its narrow focus: only individuals who have voted on bills on the floor of Congress can be easily scaled.

Recent efforts to expand the scope of ideological scaling include Bonica (2013, 2018), who uses co-donating behavior among US citizens from campaign finance records. While this approach is able to capture information even for those unsuccessful candidates or less effective interest groups, one of the shortfalls is that not all interest groups (or their employees) make donations. Barberá (2015) scales Twitter co-followers of elected officials, candidates, and organizations. A major benefit of this study is that it allows ideal point estimates across polities for recent times, should they have a sizeable enough presence on Twitter to extract their ideological position.

Making further use of the DW-NOMINATE scores, McKay (2008) uses 72 interest groups’ expressed preferred votes on select bills to map them ideologically. In a similar vein, Crosson, Furnas, and Lorenz (2020) use interest group positions on post-2004 legislation from Maplight with roll-call votes to locate 2,646 groups in ideological space. A more direct approach is offered by Thieme (2018), who is able to estimate ideology scores for 613 state-level lobbyists in three states due to their declaration of principal lobbying positions required by law. Finally, and also utilizing amicus curiae briefs, Hansford and Depaoli (2015) estimate the ideal points of 192 of the most active organizations at the Court by linking them to justices’ ideologies who voted in the same direction as they desired on a case. Each with their own strengths and invaluable insights, we build on these advances to expand the estimation of ideal points to more interest groups—and amicus curiae briefs—and over a longer time period.

In this research, we utilize network structure and a novel imputation procedure to generate ideal point estimates for nearly all of the organizations that have signed amicus curiae briefs before the U.S. Supreme Court. Individuals, groups, and organizations lobbying the Supreme Court rely on cosigning amicus briefs to convey legal, technical, or social scientific information to the Court in support of the petitioning or responding or neither party (Collins 2008; Kearney and Merrill 2000). In the process of crafting each brief, which includes selection of content and signatories, the cosigning parties publicly declare their position toward the question being reviewed by the Court. Moreover, this coordinated declaration is an indication that the cosigning groups share an overlapping opinion and rationale on the issue at hand (Box-Steffensmeier and Christenson 2014).

In an increasingly crowded advocacy environment, these organizations are competing for a scarce resource, the attention of the justices. The level of attention afforded to each brief is strongly correlated with the quality of the brief, including factors such as the cosigners’ prestige (Bailey and Maltzman 2011; Black and Owens 2012; Caldeira and Wright 1988; Collins, Corely, and Hamner 2015; Kearney and Merrill 2000), and the quality of writing and the information provided (Collins, Corely, and Hamner 2015; Spriggs and Wahlbeck 1997), all features closely aligned with the act of conveying true preferences to the Court. As such, we have no reason to believe that amici’s expressive behavior is strategic, as there is no gain from misrepresenting their interests to persuade other groups or the justices. Regardless of which side they support, these qualities of the amicus cosigning process may make it useful for quantifying a group’s ideology.⁶

Our approach leverages this cosigning network structure more directly to expand the estimates and insights from common-space DIME scores (Bonica 2014) to the thousands of politically active organizations before the Court and other branches, the vast majority of which are without donor histories and therefore without an ideological score. In addition to being a widely used measure of ideological preferences, DIME is an independent measure based on how interest groups position themselves with respect to public officials. In contrast to measures like DW-NOMINATE, which are primarily based on voting behavior, DIME scores have been validated in a common space across institutional targets (Bonica 2019).

For our training purposes, DIME scores have advantages over other ideal points in terms of their broad institutional applications, uncertainty estimates, and number of organizations they cover. However, like any low-dimensional representation, these scores have limitations as well (see, e.g., Hill and Huber 2017). Of particular relevance to our method, DIME scores’ correlations with scores from roll-call voting within parties are weak, suggesting that one or both are imperfect measures of ideology or picking up different dimensions of the concept, and are not equally appropriate across different types of actors (Tausanovitch and Warshaw 2017). Indeed, by virtue of their work, some subsets of organizations—like tax-exempt non-profits that cannot make direct campaign contributions—do not have DIME scores, limiting the information for their ACNet scores to their political relationships. Moreover, DIME scores do not have dynamic properties; that is, they are culled from a relatively small period of time and do not change over time. By relying on DIME scores as training labels, these limitations are carried over into our estimates. Thus, as we discuss in more detail in Section 2.3 below, we perform leave-one-out cross-validation both to validate our scores and overwrite the training labels. In the Supplementary Material, we benchmark our validity tests with two simulations, show that our scores frequently have better face validity, and compare the use of DIME scores as a seed in our model with other measures of ideology.

Importantly, our estimation is not limited to groups that meet the criteria of lobbying laws at the state or federal levels, or the groups that are the most active, or only those active in recent years; it does not require groups to take positions on roll-call votes or any legislation, nor does it ask groups to express or recall their outcome preferences in subsequent interviews—and they do not have to have donated to a candidate or even tweeted. The reach here is truly broad.

2 Combining Network Science with Ideal Point Estimation

To meet the challenge of estimating ideal points for amicus-signing organizations, we leverage three sources of data: (1) the inherent network structure of amicus brief cosigning (Box-Steffensmeier and Christenson 2014), (2) accompanying case-level metadata from the Supreme Court Database (Spaeth et al. 2015); and (3) ideal point scores for a subset of amicus signers (Bonica 2012).

We begin with a database on interest groups culled from the aforementioned expressive behavior of signing amicus curiae briefs (Box-Steffensmeier and Christenson 2012; Box-Steffensmeier and Christenson 2014; Box-Steffensmeier, Christenson, and Hitt 2013). Our data consist of 14,385 amicus briefs signed by 15,376 organizations from 1917 to 2012. We structure this cosigning behavior into a bipartite (rectangular) adjacency matrix, such that for every organization the presence of (co)signing onto one or more amicus briefs is denoted with a one and zero otherwise. This matrix forms the network structure component of our data. Of these briefs, 36.3% are cosigned among two or more organizations; the average number of signers for a brief is 2.79.

Secondly, we identify 2,973 organizations in the ACNet who also occur in the DIME dataset (Bonica 2014) using both, exact matching and hand-validated fuzzy string matching (see Kaufman and Klevs 2022). These organizations act as training labels. Since all organizations who sign briefs are required to take a side in the case—that is, in support of the petitioner, respondent, or (rarely) neither—and case decisions can be measured as ideologically liberal or conservative (Spaeth et al. 2015), we have a high level of confidence in this assumption.⁷ Leveraging this homophily assumption, we use an unlabeled organization’s network proximity to those of labeled organizations to infer its ideology on the same scale as ideal point estimates from campaign donations. In the methodology section directly below, we refer to organizations whose ideal points we derive from Bonica (2014) as origin score nodes or seeds, or as the training set, and the remainder as imputed or endogenous score nodes, or the test set.

The key assumption of our method is that amicus-filing organizations cosign briefs with other organizations that share similar values or at least support the same side and nature of an argument, be it political, legal, technical, or even moral. One of the advantages of using the inherent network structure of amicus advocacy is that preferences are not only determined by who you cosign a brief with, but who those groups cosign with, and who the next set of groups cosign with in an iterative process until we reach a maximum. In our method, this iterative process potentially corrects for over time changes in behavior. While we acknowledge that the policy space does change in the period targeted in this paper, our method partially addresses this problem by putting all groups in the same space, meaning that a group’s preference is determined based on the homophily principle independent of the nature of the legal question or changes in the Court’s response.

2.1 Network Modeling and Estimation

Having built an amicus signing network of 15,376 organizations signing onto 14,385 briefs, of which 2,973 organizations are labeled, we establish a procedure for estimating ideology labels for the remaining organizations and briefs in our data.⁸ The heart of our method is an iterated weighted averaging procedure. Employing similar assumptions to Martin and Quinn 2002 in their specification of priors, we impute a set of ideal points such that each organization’s ideal point is the average of its briefs’ ideal points, and brief’s ideal point is the average of its cosigners’ ideal points. Specifically, an organization’s ideal point is the average of the ideal points of all organizations it cosigns an amicus brief with, and the ideal points of each of those organizations is the average ideal points of others it cosign an amicus brief with. This process is repeated iteratively until we recover each organization’s position in the network through convergence. And in this process, we are also able to recover the ideal points for briefs so long as they are cosigned by two or more organizations, or alternatively are signed by one group with a DIME score. One of the benefits of our network approach is that through this iterated process an organization’s ideal point is not only shaped by who it cosigns with, but also by the overall movement of other groups within the ACNet as a whole.

While many tools exist for estimating underlying or unobserved social space in networks, our simple approach offers important advantages in this context. For example, one well-established approach to learning about the similarities in nodes from only the network structure comes from latent space models (e.g., Barberá 2015; Hoff, Raftery, and Handcock 2002; Peress 2013; Ward, Ahlquist, and Rozenas 2013). Broadly speaking, these unsupervised methods utilize embedding mechanisms of “latent low-dimensional feature representations for the nodes or links in a network” (Arsov and Mirceva 2019, 1). But the costs of a completely unsupervised approach are more parameters and a reliance on functional form assumptions.⁹

Our approach improves upon these methods for our unique context by including a subset of labeled data, the DIME scores for select organizations, and in turn sheds nearly all parameterization and functional form assumptions. Our more parsimonious model has a number of critical benefits, including: reducing our reliance on functional form assumptions, reducing the computation time, allowing us to bootstrap uncertainty estimates (see the Supplementary Material), improving the quality of estimation, enabling us to estimate scores for organizations as well as briefs, and most critically, binding our ideology estimates to a commonly used, pre-existing measure.¹⁰ Nevertheless, there are a number of limitations to our current approach, including: it is unidimensional by construction, it inherits some limitations from the training label, and it does not allow for many common latent structure analyses, like the amount of variation explained.

2.2 Illustration of Iterative Weighted Average with Toy Network

To illustrate how the imputation strategy works in the iterative weighted average approach, we provide a small-scale example with a toy network.¹¹ Suppose there were three organizations in the network X, Y, and Z, who have cosigned four briefs XY1, XY2, YZ, and XYZ. X and Z are origin score nodes, meaning they have been previously assigned an ideal point. We begin with Figure 1a. In the first iteration, only nodes X and Z have scores, and so we can only calculate the scores for the four briefs; node Y receives no score since all of its briefs are unscored (Figure 1b). However, in the second iteration, the four briefs have estimated ideology scores, so we can assign Y a score based on the weighted average of the four briefs it cosigns (Figure 1c). In the third iteration, all seven nodes have been assigned scores, but the four briefs’ neighboring nodes look different: whereas before the briefs received their scores only from X and Z, now node Y also has a score, so we use node Y’s score to update the scores for the four briefs (Figure 1d). Having updated scores for X and Z, and all four briefs, in Figure 1e, we update node Y’s score. We repeat this process until the scores for all initially unscored nodes change vary little from iteration to iteration.

Figure 1 An illustration of our iterative weighted averaging procedure in five steps. Circle nodes are organizations and square nodes are briefs. Node color indicates ideology score from $-1$ (blue) to $+1$ (red). Each iteration’s updated ideology scores are indicated in green, starting with organizations X and Z on the bottom.

Although Figure 1 shows a process of ideology scores diffusing, in fact, it is more akin to a process where the weights diffuse against the exogenous scores. In Figure 1a, and in all future states, nodes X and Z weight their own exogenous score at 100%. In Figure 1b, nodes XY1 and XY2 assign 100% weight to the value of node X, node XYZ assigns 50% weight to the value of node X and 50% to the value of node Z, and node YZ assigns 100% weight to the value of node Z. In Figure 1c, node Y is equally weighted between the scores of XY1, XY2, XYZ, and YZ. Equivalently, its score is from X and from Z. In Figure 1d, the fact that now Y has a score causes an adjustment to all the other endogenous nodes. In particular, for XY1 and XY2 to have equal weight on X and Y implies that each must have a score that is from X and from Z. Similarly, other nodes have scores that are weighted combinations of X and Z.¹²

These toy calculations can be presented in a more elegant mathematical form of how the process arrives at a closed form solution.¹³ Indeed, we can show that the endogenous nodes (nodes without origin score) will ultimately have the following weights:

$$\begin{align*}\left[\begin{array}{cc} 8/13 & 5/13\\ 21/26 & 5/26\\ 21/26 & 5/26\\ 4/13 & 9/13\\ 7/13 & 6/13 \end{array}\right], \end{align*}$$

where the first column indicates the weight on node X and the second the weight on node Z. So in this matrix, the top row indicates that node Y’s final score is an average of nodes X and Z with weights $\frac {8}{13}$ and $\frac {5}{13}$ .

How do we arrive at this calculation? Suppose that the previously described weights were instead probabilities. Let the probability of moving between nodes from state $t-1$ to state t be described by a transition matrix $\mathbf {M}$ . The entries in this transition matrix are readily calculated from the network. If a node is exogenous (with an origin score), the probability of staying at that node is $1$ , so that exogenous nodes are “absorbing states.” If the node is endogenous (one without origin scores), then one has an equal chance of moving to any other node to which it is connected in a graph. Endogenous nodes are transitioning states. In the limit, the weight that each endogenous node assigns to each exogenous node is equivalent to the probability of arriving at any particular absorbing state when starting at some transitional state. Therefore, by ordering the matrix with exogenous nodes first and endogenous notes second, we can show that M will have a block matrix form like so:

$$\begin{align*}\mathbf{M}=\left[\begin{array}{cc} \mathbf{I} & 0\\ \mathbf{S} & \mathbf{Q} \end{array}\right]. \end{align*}$$

Here, $\mathbf {S}$ contains the one-step transition probabilities of a imputed score node (endogenous) to a origin score node (exogenous), and $\mathbf {Q}$ contains the transition probabilities from imputed score nodes to other imputed score nodes. After k steps, we can use block matrix multiplication to show that

$$\begin{align*}\mathbf{M^{k}=}\left[\begin{array}{cc} \mathbf{I} & 0\\ \mathbf{(I+Q+Q^{2}+\cdots+Q^{k})S} & \mathbf{Q^{k}} \end{array}\right]. \end{align*}$$

As $k\to \infty $ , the probability of being outside an absorbing state goes down with k, eventually becoming $0$ . As a result, $\lim _{k\to \infty }\mathbf {Q^{k}=}0$ . Furthermore, we have the identity $(\mathbf {I}+\mathbf {Q}+\mathbf {Q^{2}}+\cdots +\mathbf {Q^{k}}+\cdots )(\mathbf {I}-\mathbf {Q})=\mathbf {I,}$ therefore $(\mathbf {I}+\mathbf {Q}+\mathbf {Q^{2}}+\cdots +\mathbf {Q^{k}}+\cdots )\mathbf {S}=\mathbf {\left (\mathbf {\mathbf {I}-\mathbf {Q}}\right )^{-1}}\mathbf {S}$ , if $\left (\mathbf {\mathbf {I}-\mathbf {Q}}\right )$ is invertible. Since the eigenvalues of $\mathbf {Q}$ must be strictly less than $1$ for $\lim _{k\to \infty }\mathbf {Q^{k}}=0$ , the inverse of $\left (\mathbf {\mathbf {I}-\mathbf {Q}}\right )$ must exist. Therefore, we have

$$\begin{align*}\mathbf{\mathbf{M}^{\infty}=\left[\begin{array}{cc} \mathbf{I} & 0\\ \left(\mathbf{\mathbf{I}-\mathbf{Q}}\right)^{-1}\mathbf{S} & \mathbf{0} \end{array}\right]}. \end{align*}$$

Let $\tilde {\mathbf {p}}=\mathbf {M}^{\infty }\mathbf {p}$ . Then $\mathbf {M}\tilde {\mathbf {p}}=\mathbf {M\cdot M}^{\infty }\mathbf {p}=\mathbf {\mathbf {M}^{\infty }p}=\tilde {\mathbf {p}}$ , so the weighted average of cosigner property will obtain for all imputed score nodes. Furthermore, by construction, $\mathbf {(M}^{\infty }\mathbf {p})_{i}=\mathbf {p}_{i}$ for $i\le s$ .

To bring this general matrix algebra back to the example, to calculate the $5 \times 2$ matrix above, all one needs to do is order the transition matrix M appropriately and calculate $(\mathbf {I}-\mathbf {Q})^{-1}\mathbf {S}$ . Alternatively, one can also take M to very high powers. In practice, we have found it most efficient with larger matrices to avoid doing the inversion, but instead to calculate $M^2=M\times M$ , $M^4=M^2 \times M^2$ , and $M^8=M^4\times M^4$ . One gets to very high powers quickly doing this, and generally after eight or ten iterations we find that further powers do not change the values of M. In our amicus network, this example translates into a rich process where the ideal point of a node is a function of all those in its network, weighted by the number of times they have collaborated on a brief.

2.3 Validation

While our procedure for estimating ideal points has strong intuitive appeal, it is important that our outputs make intuitive sense as well, are statistically and computationally stable, and are robust to measurement error in the training labels. The scores produced by Bonica (2014) that we use as our ground truth are imperfect (Enamorado, Fifield, and Imai 2019), and we verify here that our model’s outputs show strong validity despite any noise the training labels may induce.

Ours is a leave-one-out cross-validation procedure. That is, for each training observation in our data, we temporarily withhold that organization’s ideal point from our estimation procedure, instead estimating its score as with the remaining organizations. In comparing the scores we estimate for that observation, when it is withheld to the ground truth scores we draw from DIME, we can assess the validity of our measures: if there is little deviation between our estimates and the training data, we can be confident that the estimates have strong validity.

The first set of performance statistics we consider, mean absolute deviation (MAD), is a standard target of cross-validation. In comparing the estimated ideologies for withheld organizations to DIME scores, we calculate a MAD of 0.6 (a heuristic which always guesses an ideology of 0 has a MAD of 1.00). A second performance statistic dichotomizes ideology into +1 (conservative) and –1 (liberal). When we consider only whether an organization’s ideology is less than zero or greater than zero, we find that our model estimates an organization’s ideology to be on the same side of the political spectrum as our withheld labels for 65% of organizations, and 74% for those organizations with a DIME score meaningfully different from 0.

In the Supplementary Material, we dive deeper into the model properties and validity. For example, to benchmark the accuracy measures, we conduct a pair of simulation studies on legislative cosponsorship and fully simulated networks that suggest confidence in our approach and scores at the observed and varying levels of homophily. We also benchmark our results by leveraging the fact that some organizations in the DIME database have multiple entries.¹⁴ In this exercise, our cross-validation procedure predicts DIME scores better than other DIME scores, suggesting the strength of our approach. In examining cases where our estimates and DIME scores disagree, we find many of our scores have greater face validity.¹⁵

Given evidence of strong validity resulting from the cross-validation procedure, and to ensure an internally consistent measure of ideology, we take the scores for all interest groups—regardless of whether the organization is in the training data—from our cross-validation estimates. That is, our final ideology estimates do not include raw DIME scores.¹⁶ Thus, while our scores for the organizations in the test set derive from a model trained on the full training data, our score for each organization in the training set derives from a model trained on all other organizations. This choice has an additional benefit related to mean reversion. Our iterative weighted average procedure renders our imputed nodes less overdispersed than the training nodes. By selecting our cross-validated estimates for training nodes rather than their original labels, we ensure that our training nodes and imputed nodes have equivalent mean-reversion.

3 The Ideologies of Organized Interests

Our network estimation procedure leads to new ideal points-that is, ACNet scores—for 12,549 unique interest groups and 11,731 briefs.¹⁷ We begin by displaying the ACNet scores for a small collection of benchmark organizations alongside the ideology of familiar political representatives from Bonica (2014). Figure 2 shows that Gun Owners of America and the Family Research Council are of similar conservative ideologies to former Attorney General Jeff Sessions and Senator Mitch McConnell. At the moderate level, we find Senator Joe Manchin near National Public Radio (NPR) and Hewlett Packard (HP). Interestingly, large media corporations like the NY Times and the LA Times are also shown to be moderate, with ideal points just a touch right of center, speaking to the fact that First Amendment cases do not always cut neatly along ideological lines. More liberal groups include Common Cause and the Center for Reproductive Rights, which are about as liberal as Senator Charles Schumer.

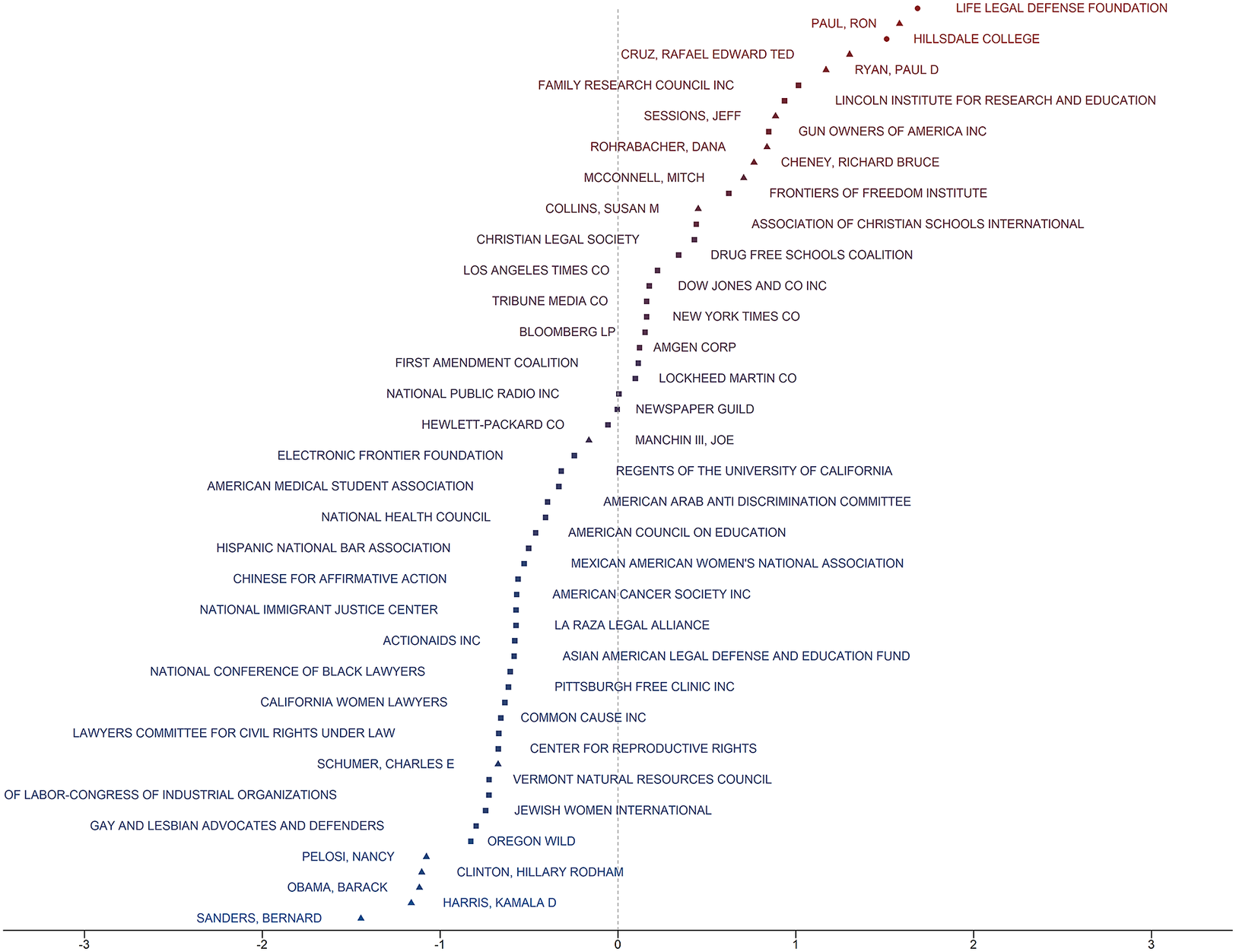
Figure 2 Ideal points of selected interest groups and political elites. Squares indicate the ACNet scores of organizations in the test set. Circles indicate the ACNet scores of organizations in the training set. Triangles indicate the DIME scores of individuals. Nodes are colored and ordered by ideology score from liberal (left and blue) to conservative (right and red).

Looking across the full range of ideology scores for all the organizations (i.e., beyond the figure), we find that the most liberal organizations are a series of law schools including Yale and Vermont, animal rights organizations such as Jews for Animal Rights, book stores like Half Price Books and Harvard Book Store Inc., and students’ or advocacy groups such as the Children’s Defense Fund of Ohio. The most conservative are corporations or corporate advocacy groups like the Ohio Valley Coal Company, hospital and healthcare provider conglomerates like Wellness Lifestyles Inc., and conservative social policy groups, like the Oklahoma Family Policy Council and the Christian Advocates Serving Evangelism.

3.1 Interest Group Coalition Strategies

ACNet scores provide a window not only into the degree of ideological heterogeneity in organized interests before the Court, but also into their coalitional strategies. Combining both their ideology and networks allows us to see whether particular interest groups work largely with other groups that are ideologically similar. For example, we might expect, given the polarization of national politics in the United States, that liberal organizations will predominantly cosign with other liberal organizations, and that conservative organizations will do the same. Alternatively, we might anticipate that the signaling value of an amicus brief signed by a bipartisan coalition of organizations would carry more weight, providing incentives for organizations to cosign broadly and across the ideological spectrum.

To this end, we graph a one-mode projection of the ties of every interest group in the data in Figure 3. Immediately evident from the graph are two dense networks in the center surrounded by several small cliques and isolates in the periphery. The coloring suggests that much like other political networks (e.g., Adamic and Glance 2005; Barberá 2015), what we see before the Court is a polarized network of two ideological communities, the conservative and the liberal. Also apparent is the larger size and increased density among the liberal organizations, whereas the conservative groups are broken into a few tighter-knit communities.

Figure 3 Amicus Curiae Network. Squares indicate organizations in the test set. Circles indicate organizations in the training set. Nodes are colored by ACNet score from liberal (blue) to conservative (red). Nodes without scores are light grey.

The periphery of the graph also conveys the relatively greater number of conservative groups working alone or in very small coalitions. However, at the center of the graph, we note the appearance of a non-trivial number of purple organizations with substantial ideological overlap. In all, the network suggests that interest group coalitions before the Court are largely but not exclusively polarized, with a small collection of groups working with both sides of the ideological spectrum.¹⁸

3.2 Ideological Heterogeneity Across Donors and Non-Donors

Our methodology uses the available ideology scores for the donor subset of amicus brief cosigners to estimate ideology for groups based on their social network. In doing so, it leverages two datasets that present us with a fundamental question about the nature of these groups: do groups that donate to campaigns look ideologically similar to those that do not? Ansolabehere, Snyder Jr, and Tripathi (2002) find a strong relationship between lobbying and campaign contributions. Interest groups active in lobbying give more equally across the ideological spectrum, while those less active appear more partisan in their giving.¹⁹ Here, we respond their call for “more careful study of the heterogeneity of groups” (152).

As aforementioned, of the 12,549 amicus brief signers for which we have estimated ACNet scores, 2,973 of the groups also have ideology scores obtained from their co-donating behavior (Bonica 2014), which means that 9,430 groups with ACNet scores are not donors, according to campaign finance records. As shown in Figure 4, the ideology distribution of both group subsets are bimodal, yet with clear differences. First, donors (green) are more evenly distributed across the ideological spectrum than the non-donors (lavender). Both have a substantial number of groups toward the ideological extremes, but in the non-donor distribution the highest peak is on the liberal side, while in the donor distribution it is on the conservative side. Second, there is a noticeable difference in the aggregate ideology scores of both groups, where donors’ average ideology is closer to zero ( $\bar {x}=-0.049; s=0.597$ ), the non-donors average ideology is more clearly liberal ( $\bar {x}=-0.219; s=0.573$ ).

Figure 4 Ideological distribution of donors and non-donors. Density plot for donor organizations is colored green. Density plot for non-donor organizations is colored lavender. Ideology scores range from liberal (left) to conservative (right).

4 The Ideologies of Amicus Curiae Briefs

Our method maintains the useful properties that an organization’s score is the average of the briefs it cosigns and a brief’s score is the average of the organizations that cosign it. As such, our approach provides an additional feature in the form of ideal point estimates for 11,731 amicus curiae briefs. These ideal points are on the same scale as the DIME scores and ACNet organization scores above, allowing for comparisons across organizations, individuals and briefs.

In Figure 5, we show the ideological distribution of amicus curiae briefs submitted for a number of prominent Supreme Court cases. Thus, each point represents a single brief on a case named above it. The x-axis refers to the ACNet score; briefs farther to the left (and bluer) are more liberal and those farther to the right (and redder) are more conservative. In terms of the y-axis, we have ordered the cases from the top with the highest mean ACNet score across the briefs (most conservative) to the bottom with the lowest mean ACNet scores (most liberal). The names of the cases that are in blue were decided by the Supreme Court in a liberal direction and those in red were in a conservative direction (as determined by Spaeth et al. (2015)).

Figure 5 The ideology of amicus curiae briefs in select U.S. Supreme Court cases. Circles indicate brief ACNet scores. Nodes are colored and ordered by ideology from liberal (blue) to conservative (red).

While only a snippet of these data, the figure provides an overall picture of the various ideological components present in each case, and how they potentially interact with each other. For instance, it is notable that for cases addressing highly controversial issues there is a high number of briefs and a greater number of briefs at the extremes of the ideological scale. For instance, in District of Columbia v. Heller, 554 U.S. 570 (2008), there were a total of 40 amicus briefs, 12 in support of the petitioner (liberal) and 28 in support of the respondent (conservative). The most liberal and most conservative amicus briefs have an ACNet score of $-1.076$ and 2.655, respectively. This wide range of ideological scores is consistent with the controversial nature of the case, especially for conservative groups such as the National Rifle Association. The figure shows a similar pattern for other highly controversial cases such as Lawrence v. Texas, 539 U.S. 558 (2003), Citizens United v. FEC, 558 U.S. 310 (2010), and NFIB v. Sebelius, 567 U.S. 519 (2012), Shelby County v. Holder, 570 U.S. 529 (2013).

In contrast, in cases addressing less controversial questions, we observe a smaller number of briefs with less extreme ideological scores. This is especially true for cases of criminal procedures such as Terry v. Ohio 392 U.S. 1 (1968) or Miranda v. Arizona 384 U.S. 436 (1966), or political questions, such as US v. Nixon, 418 U.S. 683 (1974). For instance in Terry v. Ohio, there were a total of four amicus briefs, two in support of the petitioner (liberal) and two for the respondent (conservative). In contrast to more controversial cases, the most liberal brief has a score of $-0.797$ and the score of the most conservative brief is 0.565. A similar pattern is observed for the other two cases.

4.1 The Dynamics of Brief Macro-Ideology

Having 95 years worth of amicus briefs offer the potential to gain insights from a macro and longitudinal analysis. In particular, our estimates can shed light on how the amicus curiae environment of Supreme Court decisions changed over the years, if at all. That is, are some periods more attractive targets for briefs of one ideological persuasion or the other? O’Connor and Epstein (1983) find that, between 1969 and 1980, conservative groups chose amicus briefs as their preferred method of participation in judicial proceedings at a significantly higher rate than liberal groups. However, this is not necessarily an indication that conservative groups find amicus briefs to have greater value or even file in greater number. But it does further reinforce the notion that interest groups have important heterogeneous capabilities and interests that compel further research. If we are to better understand their influence on the Courts and beyond (e.g., Collins 2008; Kearney and Merrill 2000), we need to uncover how ideology shapes interest groups’ decisions to file amicus briefs and the sides they choose during this process.

Figure 6 Brief ideology dynamics. Circles indicate the ACNet scores of briefs for Supreme Court cases decided in that year. Circles are colored and ordered by ideology score from liberal (low and blue) to conservative (high and red).

To this end, we graph the ACNet scores for each brief in our dataset in Figure 6, along with a smoothed estimate of the conditional mean and confidence interval from a generalized additive model. Doing so provides a (simple) measure of the dynamics of interest group macro-ideology before the Court that has largely escaped the discipline. In doing so, we find that the average is below zero for most of history. Filing amicus briefs is a strategy that, historically, has been employed by more liberal than conservative organizations. That is, there is a fairly consistent though small left-wing bias to amicus representation before the Court. The bias is particularly evident in the 1960s, before it shrank in the 1970s. However, since the mid-1980s, any bias has remained small to non-existent. Indeed, in the 1940s, the average ideology score of organizations that submitted an amicus brief was –0.66. By the end of our data in 2012, the ideology score of organizations that submitted an amicus brief was –0.142, a substantial change, given a standard deviation of 0.56. The volatility of the mean ideology of an amicus signing organization has also decreased over-time. Much of this decline in volatility is attributable to the increasing frequency of organizations joining amicus briefs, which has grown at roughly 6% per year since the end of the Second World War. Interestingly, this increase in activity has come at the same time the Court has taken fewer and fewer cases.

5 Discussion

Our measure of interest group ideologies opens the door to investigate a host of issues surrounding representation before the Supreme Court and beyond. This work makes three major contributions to the study of American politics. Foremost, we introduce a measure of ideology for more interest groups than ever before and across a longer timeframe. We demonstrate that the approach and scores have a high degree of validity according to a host of cross-validation tests in the manuscript and Supplementary Material, as well as simply comparing our imputed scores to those of familiar individuals and groups. Second, we make methodological and measurement contributions in extending donation based ideal points to non-donors based on social network analysis that can be applied to other substantive contexts. Finally, we provide empirical work that is central to theories in American politics and highlights the import of the measure.

By describing the dynamics of interest group macro-ideology over 95 years, we arrive at unique insights into the ideological context surrounding Supreme Court cases and issues. Interest groups before the Court are neatly, though imperfectly, polarized—that is, divided based on ideology. While they are more likely to work most closely with groups of similar ideology, few groups are entirely disconnected to ideologically different ones by virtue of either a cosigner or a case that does not fall neatly along partisan lines. Turning to campaign finance, we find support for two expectations about interest group donation behavior. While interest groups that donate to campaigns are more conservative than non-donor groups, relatively speaking they are more evenly balanced across the ideological spectrum and more moderate overall.

There are, of course, a number of caveats to consider with our approach to measuring organized interest ideology. Foremost, and like those before us, our measure is a low-dimensional representation of an inherently multidimensional concept. Organized interests take positions on various issues, politicians and events—and do so in a host of ways. By coupling donation histories with an aggregation of collaborations across issues at the Court and across time, we arrive at a comprehensive measure—but one that may not perfectly correspond to a single position at a single point in time. Our scores may also inherit limitations from the seeding ideology score. Relying on DIME scores assumes that a mapping between donors and non-donors is reasonable, though the populations are different—for example, some organizations, due to tax-exempt status, will be unable to donate to candidates, which suggests they may also lobby on different issues. However, as we show above and in the Supplementary Material, our cross-validation procedure corrects some of the issues from the training label. Moreover, as we demonstrate in the Supplementary Material, one could also begin with training labels from measures of ideology other than donations. Thus, while the resulting ACNet score undoubtedly has some error, and no one-dimensional representation is perfect, we show that it still proves useful and at least as valid as other related measures and approaches, while being far more expansive in number, time, and issue.

The ACNet scores provide an broad glimpse stretching back nearly 100 years into fundamental actors in the American democracy—and into a largely invisible web of influence in our political system. Our exposition demonstrates how the measure can shed light into the overall ideological composition of special interests in the United States and over time. Of course, such findings are only tips of the proverbial icebergs, and we hope the work here inspires a number of avenues for further research. The measure provides a sense of the ideological direction of the active population of interest groups across several decades that could be used, for example, to better understand the relationships between public and elite attitudes. The measure also opens up the ability to explore the effects of asymmetric ideological influences on elite behavior across other branches of government. Ultimately, given the vast and arguably increasing influence of special interests in American democracy, we expect future studies to benefit from this measure of interest group ideology for thousands of politically active organizations, including those that have not donated to campaigns or even formally registered as actively lobbying.