In this Corrigendum, we correct an error in Theorem 3 and its proof of [Meziani, S. & Kernane, T. (2023). Extended generator and associated martingales for M/G/1 retrial queue with classical retrial policy and general retrial times. Probability in the Engineering and Informational Sciences 37(1):206–213.].
We have confused the expectation of the residual service time ![]() $E[Y(t)]$ with the expectation of the total service time. Let S a generic random variable representing the duration of the service time of a customer in the system considered. The residual service time Y(t) at time t is given by:
$E[Y(t)]$ with the expectation of the total service time. Let S a generic random variable representing the duration of the service time of a customer in the system considered. The residual service time Y(t) at time t is given by:
Hence, from Guess et al. [Reference Guess and Proschan2]
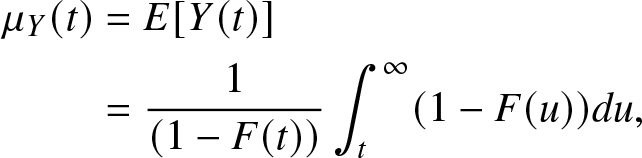 \begin{align*}
\mu_{Y}(t)&=E[Y(t)]\\
&=\frac{1}{(1-F(t))}\int_{t}^{\infty}(1-F(u))du,
\end{align*}
\begin{align*}
\mu_{Y}(t)&=E[Y(t)]\\
&=\frac{1}{(1-F(t))}\int_{t}^{\infty}(1-F(u))du,
\end{align*}where F is the distribution function of the service time.
Replace the statement of Theorem 3 with the following:
Theorem 0.1. The conditional expectation of the number of blocked customers N(t) given ![]() $ N(0)=n_{0}$ and
$ N(0)=n_{0}$ and ![]() $ Y(0)=y_{0}$
$ Y(0)=y_{0}$ ![]() $($when
$($when ![]() $ Y(t)\in \mathbb{E}_{1}\cup \partial^{*}\mathbb{E}_{1})$ is given by:
$ Y(t)\in \mathbb{E}_{1}\cup \partial^{*}\mathbb{E}_{1})$ is given by:
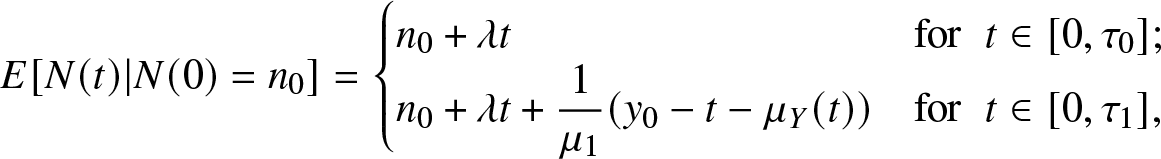 \begin{equation*}
E[N(t)|N(0)=n_{0}]= \begin{cases}
n_{0}+ \lambda t & \text{for} \;\;t \in [0,\tau_{0}];\\
n_{0}+\lambda t+\dfrac{1}{\mu_{1}} (y_{0}-t-\mu_{Y}(t)) & \text{for}\;\; t \in [0,\tau_{1}],
\end{cases}
\end{equation*}
\begin{equation*}
E[N(t)|N(0)=n_{0}]= \begin{cases}
n_{0}+ \lambda t & \text{for} \;\;t \in [0,\tau_{0}];\\
n_{0}+\lambda t+\dfrac{1}{\mu_{1}} (y_{0}-t-\mu_{Y}(t)) & \text{for}\;\; t \in [0,\tau_{1}],
\end{cases}
\end{equation*} where  $ \mu_{1}=\int\limits_{0}^{\infty}ydF(y)$ and
$ \mu_{1}=\int\limits_{0}^{\infty}ydF(y)$ and ![]() $\mu_{Y}(t)$ is the mean residual service time at time t.
$\mu_{Y}(t)$ is the mean residual service time at time t.
Proof. The equation (5.1) in the proof is replaced by:
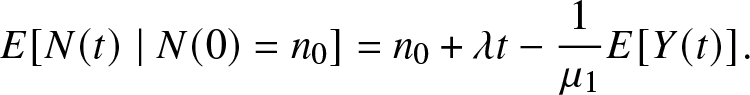 \begin{equation}
E[N(t)\mid N(0)=n_{0}]=n_{0}+\lambda t-\frac{1}{\mu_{1}}E[Y(t)].
\end{equation}
\begin{equation}
E[N(t)\mid N(0)=n_{0}]=n_{0}+\lambda t-\frac{1}{\mu_{1}}E[Y(t)].
\end{equation}Replace the mean residual service time in the proof by the following:
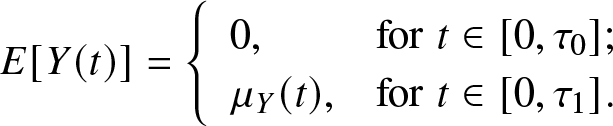 \begin{equation*}E\lbrack Y(t)\rbrack= \begin{cases}\begin{array}{ll}0,&\text{for }t\in\lbrack0,\tau_0\rbrack;\\\mu_Y(t),&\text{for }t\in\lbrack0,\tau_1\rbrack.\end{array}\end{cases}
\end{equation*}
\begin{equation*}E\lbrack Y(t)\rbrack= \begin{cases}\begin{array}{ll}0,&\text{for }t\in\lbrack0,\tau_0\rbrack;\\\mu_Y(t),&\text{for }t\in\lbrack0,\tau_1\rbrack.\end{array}\end{cases}
\end{equation*}Remark: Integrability conditions (4.7) and (4.8) in the paper can be stated without taking the expectation as in Dassios and Zhao [Reference Dassios and Zhao1], p. 817, with any consequence on the results of the paper.


