1. Introduction
To study the Pleistocene ice ages, it is desirable to use a global coupled climate–ice-sheet model. Unfortunately, a general circulation model is very expensive to run. It does not permit extensive sensitivity experiments and often its results are difficult to interpret. Therefore, an atmospheric model is needed which contains the essential feedback mechanisms that affect the growth and decay of ice sheets but it takes a much smaller amount of additional computing time and is easier to interpret. As has been suggested by Pollard (1983), Esch and Herterieh (1990) and Deblonde and Peltier (1991), these requirements seem to be met by an energy-balance climate model.
Therefore, a global, two-dimensional, vertically integrated energy-balance climate model is presented. It is solved by the spectral method in space and time. The horizontal resolution is T16 and the seasonal and semi-seasonal variations are included. The land–sea distribution and the albedo can be specified arbitrarily.
Although the model is quite similar to those of Hyde and others (1989) and Deblonde and Peltier (1991), it differs from them in three important respects. First, the model does not use observed precipitation rates which may change considerably on the time-scale of the ice ages. It rather employs a simple parameterization of the evaporation of water, transport of water vapour and its precipitation, based on the ideas of Pollard (1983), Sanberg and Oerlemans (1983) and Bowman (1985). Secondly, to reduce the computational cost, the model takes advantage of an analytically computed Fourier–Legendre representation of daily insolation. Thirdly, the coefficients which couple the spectral modes of the different fields together are evaluated recursively (Schulten and Gordan, 1975, 1976).
In the present version, the model is linear in that the sea-ice extent does not depend on temperature, To investigate its behaviour, a test case is studied which is based on the highly idealized land–sea distribution proposed by Pollard (1983). Two simple sensitivity experiments are carried out which show the effect of varying the size of an ice sheet on the global annual mean temperature.
2. Model Description
2.1. Basic equations
The vertically integrated equations of conservation of energy and humidity may be cast into the form (cf. Jentsch, 1991)


where T is the sea-level air temperature in °C and W is the amount of water vapour in an atmospheric column extending from the surface to the top of the atmosphere. The sea-level air temperature can be formally related to the vertically integrated temperature by setting

Here, ρ is taken to be a constant surface-air density over land and a constant mixed-layer density over ocean; H is the effective height of the atmosphere–ocean column considered, which may well differ from its actual height. Furthermore, ρ′ denotes the height-dependent density and T′ the height-dependent temperature of this column.
On the lefthand side of Equations (1) and (2), CT and L V W denote, respectively, the vertically integrated sensible heat of atmosphere and ocean and the vertically integrated latent heat of the atmosphere alone. Here, C ≈ c P ρH and L v play the role of inertia coefficients with c p being the specific heat at constant pressure, while L v is the latent heat of vaporization.
Following North and others (1083) and Hyde and others (1989), the thermal inertia coefficient C is given a large value C w over the ocean, a smaller value C si over sea ice and a very small value C l over land. In the first case, it is taken to represent the heat capacity of an ocean mixed layer with an average depth H w = 75 m, while in the third case it stands for the heat capacity of an atmospheric layer with effective upper boundary H a = 4.2 km. Hence, C w = 9.7 W a m−2°C−1 , C si = 0.75 W a m−2 °C−1 and C l = 0.165 W a m−2°C−1.
On the righthand side of Equations (1) and (2), F and F q denote the fluxes of heat and water vapour, and × and X q represent the diabatic terms which are given by
where R i and R 0 are the incoming and outgoing radiative fluxes at the top of the atmosphere, while E and P denote evaporation and precipitation. The latent heat of the phase change of water is V* = L v = 2.5008 × 106 J kg−1 for vaporization and L* = L s = 2.8345 × 106 J kg−1 for sublimation.
All fields in Equations (1) and (2) depend on longitude λ, latitude ϕ and time t in the year. Often μ = sin ϕ is used rather than ϕ itself
2.2. Radiation
The incoming- short-wave radiation is given by
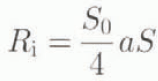
where S 0 = 1360 W m−2 is the solar constant as used by North and others (1983), a is the co-albedo (or one minus the albedo) and S determines the distribution of daily insolation at each latitude and at each time in the year (North and Coakley, 1979). Over ice-free areas, the co-albedo is taken to be a smooth function of latitude

where P n is the nth-order Legendre polynomial and the coefficients a 0 = 0.679, a 1 = 0.012 and a 2 = −0.241 are derived from present-day satellite observations (Graves and others, 1993). The discontinuous change in albedo in the presence of snow cover over land areas or sea-ice cover over ocean areas is represented by the albedo jumps ∆a sn = −0.14 and ∆a si = 0.07. Over laud, ice-covered areas, a constant value a li = 0.3 is used (Deblonde and Peltier, 1991).
According to Budyko (1969), the outgoing long-wave radiation can be parameterized as

where the constants A = 205 W m−2 and B = 1.9 W m−2°C−1 are taken From Pollard (1983) and Graves and others (1993), respectively. The term —Bγh accounts for the negative feedback of cold, elevated ice-sheet surfaces on the temperature (Bowman, 1982); γ = 6.5 K km−1 is a constant lapse rate (Pollard, 1983) and h denotes the ice-sheet surface elevation above sea level.
2.3. Heat transport
In Equation (1), the transport of heat in the atmosphere–ocean system is given by the divergence of the vertically integrated heat flux F. The explicit form of the horizontal divergence operator in spherical coordinates is

where R E = 6.37122 × 106 m is the radius of the Earth. The various kinds of heat transport are simulated by a diffusion process. Hence, they are taken to be proportional to the negative of the sea-level temperature gradient

where

is the effective diffusivity for sensible heat, K, divided by the radius of the Earth, R E . Here, the latitude-dependence of D is based on the argument that the tropical Hadley cells are much more efficient at smoothing temperature anomalies than the mid-latitude eddies (North and others, 1983). Hence, D is assumed to be three times as large at the Equator as at the poles (see Table 1). The constant k determines the degree of anisotropy of the diffusion process; in this study, it is set to 1.
2.4. Precipitation, evaporation and snow budget
The parameterization of mid-latitude precipitation and evaporation is that of Sanberg and Oerlemans (1983)
where W max is the maximum value of the moisture content W in the atmospheric column. Evaporation E is taken to depend on a characteristic time τ, which is the time-scale on which the atmosphere lends to become saturated; it is estimated as τ w = 3 d over water, τ l = 6 d over land and τ li = 30 d over ice sheets. Precipitation P is proportional to the moisture content W and consists of some background precipitation f 0 W and the upslope precipitation f 1 SW, where S is the upwind slope of the ice-sheet surface in percent. Furthermore, f 0 = 0.188 s−1 and f 1 = 0.353 s−1.
Integrating the saturation absolute humidity ρ s over an atmospheric column of height H q , using a height-dependent density ρ′ a but a constant lapse rate γ, W max can be obtained as a function of sea-level temperature T and elevation h. If one neglects the change of the latent heat of vaporization L v with pressure, one gets the
Table 1. Values, units and sources of the model parameters


where e(T 0) = 610 Pa is the saturation vapour pressure at T 0 = 0°C and R v = 46l.5 J kg−1 K−1 is the gas constant for moist air. The function Ei is the exponential integral (Press and others, 1992). The upper boundary of the atmosphere for moisture is taken in be approximately H q = 8 km high.
Assuming that the rate of change of the atmospheric latent-heat content is small compared to the net evaporation (Bowman, 1985; Chen and others, 1993), the equation of conservation of moisture Equation (2) reduces to a diagnostic relation for moisture content W, where

Now, the moisture content can be related to the temperature through the relative humidity χ, W = χW max, where χ = 0.8 is used. Approximating the flux of moisture, like that of heat, by a diffusion process, one gets

with

being the effective diffusivity for latent heat K q divided by the radius of the Earth R E . From Equations (12), (13) and (15), evaporation E and precipitation P can be obtained. The rate of snowfall or accumulation is then simply given by

where T s is the monthly sea-level temperature, corrected for height. Following Pollard (1983), the rate of snowmelt or ablation can be related to monthly surface-air temperature and insolation by

where a = 10, b = 0.2 and c = −70. Finally, the annual net snow-budget b is the difference (s – m) averaged over 1 year.
2.5. Spectral method
The method of solving Equation (2.1) is to solve directly for the steady-state seasonal cycle rather than integrate it forward in lime (North and others, 1983). This is achieved by expanding all relevant fields into truncated series of spherical harmonics in space and complex exponentials in time:

where Y lm (λ, μ) = Ρ l km (μ)e imλ and Ρ l km (μ) are the associated Legendre polynomials, normalized to one. For triangular truncation, L(m) = M and for rhombuidal truncation, L(m) = |m| + M (Washington and Parkinson, 1986). Since the fields are real, the complex-mode amplitudes satisfy the symmetry
The spatial truncation wave number M is 16 for solar forcing S and temperature response T and, to avoid aliasing, 33 for all other fields. Furthermore, the temporal truncation wave number is N = 2. Substituting the truncated series into Equation (2.1) and applying the integral operator

yields a complex system of (2N + 1)(M + 1)(M + 2)/2 linear algebraic equations for triangular truncation and of (2N + 1)(M + 1)2 ” linear algebraic equations for rhomboidal truncation, For example, the explicit form of the beat-transport term is

where the coupling coefficients
3. Numerical Implementation
All input and output fields can be represented by grid-point values on Gaussian grids, for solar forcing S and temperature response T, the number of grid points in the longitudinal direction is 64 and the number of grid points in the meridional direction is 32. For all other Melds, these numbers are 128 and 64, respectively. The transformation from physical space to spectral space is performed by a two-dimensional forward fast Fourier Transform (Press and others, 1992) and Gaussian quadrature. In the case of solar forcing, the mode amplitudes are given analytically (see Appendix A). In spectral space, the complex system of linear algebraic equations is solved by LU decomposition (Press and others, 1992). Finally, the transformation from spectral space to physical space is done by computing the sum

and performing a two-dimensional inverse Fast Fourier Transform. The grid-point values of the normalized associated Legendre polynomials are calculated using recurrence formulae (Belousov, 1962).
4. Sensitivity Analysis
For analyzing some of the model’s behaviour, a test ease with highly idealized geometry and orography is studied (Pollard, 1983). In order to capture the dominant effect of land sea distribution on climate, a continent is assumed which extends from 6° S to 74° N and covers 180° of longitude. The sea-ice lines are fixed at their present-day locations in both hemispheres and taken to be at 62° S and 66° N. South of 70° S a fixed Antarctic ice sheet is prescribed.
On the northern part of the continent, a one-dimensional ice sheet with elliptic profile

can exist. Here, h 0 is the maximum height, R is the half-width and x is the distance from the centre. The surface elevation of land not covered by an ice sheet is set to zero.
In figures 1 and 2, under modern solar forcing and without an ice sheet, the zonally integrated temperature response of the energy-balance climate model is compared

Fig. 1. Zonally averaged sea-level temperature, corrected for height, in °C, as simulated by the T16 energy-balance climate model.
with the result from the ECHAM 3 general circulation model at T42 resolution (Roeckner and others, 1992). Although the polar regions are too warm, the energy-balance climate model simulates the modern climate reasonably well, But one must bear in mind that any energy-balance climate model is tuned to modern conditions, more so than a general circulation model.
4.1. Varying maximum height
In the first sensitivity experiment, the southern-tip position of the Northern Hemisphere ice sheet is fixed at 45° N which roughly corresponds to the extent of the Laurentide ice sheet at the Last Glacial Maximum. The maximum height of the ice sheet is varied between 0 and

Fig. 2. Zonally averaged 2 m temperature in °C, as simulated by the ECHAM 3/T42 global circulation model.

Fig. 3. Global annual mean sea-level temperature versus maximum ice-sheet surface elevation. The ice sheet extends from 72° N to the fixed southern-tip position at 45° N.
6000 m. Figure 3 shows the response of the global annual mean temperature. It increases linearly with maximum height. This is expected since, according to Equation (8), the outgoing long-wave radiation decreases linearly with height. A difference in the maximum height of 1000 m corresponds roughly to a difference in global annual mean temperature of 0.3°C.
4.2. Varying southern-tip position
In the second sensitivity experiment, the maximum height of the ice sheet is taken to be
5. Discussion
An energy-balance climate model has been described which represents the vertically integrated atmosphere–ocean system. To couple it to an ice-sheet model, it has been combined with a simple parameterization of the hydrological cycle. The model includes seasonal variation and land ocean contrast. In fact, the effective-heat capacity and co-albedo fields can be specified arbitrarily. When the present, linear version of the model is coupled to an ice-sheet model, the resultant model will include both the ice-sheet–albedo feed-back and the temperature-elevation feed-back, but it will not contain the sea-ice–albedo feed-back since the sea-ice extern is not allowed to vary with temperature. This and other feed-backs, which seem to be essential for the build-up and retreat of ice sheets, are to be incorporated into future non-linear versions of the model.
First sensitivity experiments indicate that the energy-balance climate model is indeed economical and easy to understand, On an IBM RS/6000 3AT, the CPU time

Fig. 4.
Fig. 4. Global annual mean sea-level temperature versus ice-sheet size. The ice sheet extends from 72° N to the southern-tip position. Open triangles: the elevation–temperature effect is suppressed. Solid circles: the elevation–temperature effect is included. required is as follows: using the T16 (T11) truncation, the intial set-up of the model requires 56 s (9 s), white the solution for a particular seasonal cycle of sea-level temperature only takes 1.7 s (0.4 s). However, a matrix of size 765 × 765 (390 × 390), which is fairly large, must be inverted and held in memory.
6. Acknowledgements
I should like to thank A. Manschke, K. Herterich, U. Wyputta and T. Payne for useful comments and valuable advice, I acknowledge the support by the Deutsche Forschungsgemeinschaft — this is Contribution No. 114 of the Sonderforschungsbereich 261 at the University of Bremen.
Appendix A
Fourier-Legendre Amplitudes of Daily Insolation
Since the daily insolation is azimuthally symmetric, it can be represented by a truncated Fourier–Legendre series. Expressed in terms of real sines and cosines and ordinary Legendre polynomials, the distribution function S(μ, t) then reads

As outlined by North and Coakley (1979), the Fourier–Legendre amplitudes a ln and b ln can be computed analytically; North and others (1981) provided them up to L = 2 and N = 1. In order to resolve better the high latitudes where there is a long polar night or a long polar day, it is desirable to truncate the series at a higher level. It is found that the series expansion converges everywhere except on the boundary between latitudes where there is daily sunrise and sunset and latitudes where there is a long polar night or day. On this boundary, it converges only asymptotically. In this Appendix, the Fourier–Legendre amplitudes up to L = 16 and N = 4 are presented.
Table 2. Fourier–Legendre amplitudes of daily insolation for a circular orbit

In general, the distribution function S(μ, t) depends on the orbital elements eccentricity e, longitude of perihelion

where all remaining non-zero amplitudes are given by

and Table 2. Here, ε 0 = 23.45° is the present-day obliquity. The amplitudes for a general orbit can be obtained from the formulas

and

These formulae are similar to those obtained by Taylor (1984) but include the terms in e which are required for n > 2. If n = 0, then


Appendix B
Coupling Coefficients for Spectral Modes
In contrast to the spectral transform method (Machenhauer, 1979), the multiplication of two fields is also carried out in spectral space. For example, on the lefthand side of Equation (2.1), the product of temperature T and effective heat capacity C is represented by

where l 2,min = max(|l – l 1 |,m 2) and l 2,max = l + l 1 . Here, the coupling coefficients
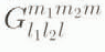

Now, the integral involving three spherical harmonies can be expressed in terms of Wigner 3j symbols

or, equivalently, in terms of Clebseh–Gordon coefficients (Messiah, 1962). Using Wigner 3j symbols, they read

For a recursive evaluation of the Wigner 3j symbols, a modified version of the algorithm by Schulten and Cordon (1975, 1976) is used. This algorithm is, at the same time, efficient and accurate even for large wave numbers.








