AIS Trajectories Simplification and Threshold Determination

Abstract

Facilitated by recent establishment of terrestrial networks and satellite constellations of Automatic Identification System (AIS) receivers, ship trajectories are becoming increasingly available and the size of recorded trajectories is getting larger. Large sets of trajectories create problems of storing, transmitting and processing data. Using appropriate methods, an accurate representation of the original trajectories can be obtained by compressing redundant information, while maintaining the main characteristic elements. In this paper, a new scheme and the implementation of the Douglas-Peucker (DP) algorithm are presented, which can simplify AIS trajectories by extracting characteristic points. As for the simplification threshold, the solo parameter of the DP algorithm, a new AIS-based minimum ship domain evaluation method is proposed and acts as criteria for simplification threshold determination. Finally, a validation is made to examine the effectiveness of the DP simplification algorithm and the rationality of the simplification threshold. The result indicates that the DP algorithm can simplify AIS trajectories effectively; the simplification threshold is scientific and reasonable.

1. INTRODUCTION

The Automatic Identification System (AIS) is an automatic tracking and self-reporting system for identifying and locating vessels by electronically exchanging data among other nearby ships, AIS base stations, and satellites. The widespread use of AIS has provided many more opportunities to trace vessel movements than ever before. Each ship makes an AIS transmission at a time interval from two seconds to six minutes, which depends on their motion (International Telecommunications Union, 2014). The authorities in charge of maritime situational awareness now routinely deal with thousands of AIS messages every second (Hammond and Peters, 2012). Consequently, the amount of information is increasingly overwhelming to human and machine operators, hence creating problems with storing, transmitting and processing. This requires a simplifying algorithm in order to compress the redundant information while retaining the main features of the information.

Receiving AIS messages from space is becoming increasingly common (Pallotta et al., 2013). This provides a cost effective solution for monitoring vessel traffic and reporting the individual positions of ships. For the limited satellite channel bandwidth, efficient data simplification is needed to transmit satellite-based AIS information effectively.

When large AIS trajectories are displayed for the observation and analysis of macroscopic traffic flow situations, the data flow may have low efficiency. A simplification algorithm that compresses redundant information is therefore needed.

To improve the speed of displaying massive AIS trajectories on the web, simplified trajectories that can accurately represent the original trajectories are needed.

The simplification of AIS trajectories is an important data pre-processing method in practical applications. It is required to both compress redundant information and to maintain the main characteristics of the original trajectory. In addition, scientific and rational criteria is needed to determine the simplification threshold.

This paper is structured as follows: Section 2 introduces line simplification theory and the overall design of AIS trajectories simplification; in Section 3, the optimal threshold is determined based on ship domain theory; Section 4 validates the effectiveness of the simplification algorithm in the determined threshold; conclusions and future work are addressed in Section 5.

2. AIS TRAJECTORIES SIMPLIFICATION

AIS trajectories are special lines with their own characteristics. Because of this, line simplification theory can be used in simplifying AIS trajectories. Line simplification algorithms have been playing important roles in map generalisation (Pallero, 2013), in 2D Digital Elevation Model (DEM) data profiles (Chen et al., 2009) as well as in cartographic generalisation (Balboa and Lopez, 2009). Several methods have been proposed to solve the problem of line simplification, such as the Visvalingam–Whyatt algorithm (Visvalingam and Whyatt, 1993), the Douglas-Peucker (DP) algorithm (Douglas and Peucker, 1973), etc. Several studies have analysed and evaluated various line simplification algorithms mathematically and perceptually and ranked the DP algorithm highly; many cartographers consider the DP algorithm to be one of the most accurate line generalisation algorithms (Jenks, 1981; White, 1985; McMaster, 1986; Cheung and Shi, 2006). Etienne et al. (2012) used the DP algorithm to simplify AIS trajectories to optimise computation time, but the detailed implementation and how to determine simplification thresholds are not available. The DP algorithm has drawbacks in having potential topological errors (Zhang et al., 2007). Although many improved DP algorithms are proposed (Bertolotto and Zhou, 2007; Chen et al., 2009; Gudmundsson et al., 2009; Pallero et al., 2013; Shi and Charlton, 2013), Zhang et al. (2014) concluded that the original DP algorithm is more suitable for simplifying AIS trajectories than the improved one by comparing the efficiency and effectiveness of these two algorithms in processing AIS trajectories.

2.1. DP Algorithm

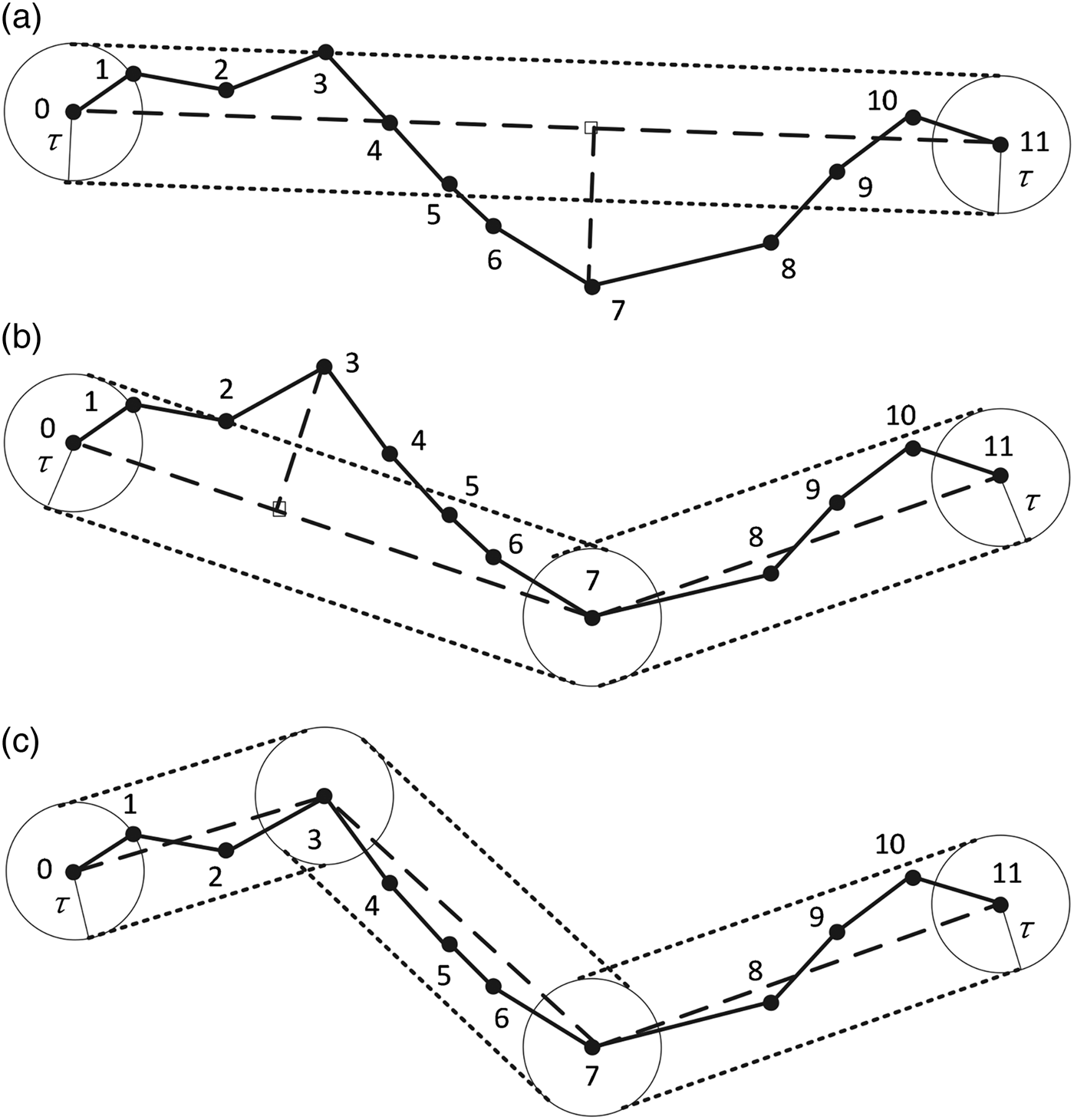
In the DP algorithm (Douglas and Peucker, 1973), line segments are used to approximate the original trajectory; the user must define tolerance τ as the threshold to simplify the line. The DP algorithm process can be summarised in Algorithm 1. The schematic plot of DP algorithm is illustrated in Figure 1. As shown, in the first step (see Figure 1 (a)), the starting point P ₀ and ending point P ₁₁ are selected to generate an approximate line. Compute the perpendicular distance of each remaining point in the original trajectory to the approximate line. Since some of the perpendicular distances are greater than the pre-defined threshold, the original trajectory is split into two sub-trajectories by selecting the split point (P ₇ in Figure 1(a)) contributing the maximum distance as the characteristic point. As a result, in the second step (see Figure 1 (b)), the original trajectory is divided into two sub-trajectories, P ₀-P₇ and P ₇-P₁₁. As shown, in the first sub-trajectory, several trajectory points have their perpendicular distances greater than the pre-defined threshold, for example, P ₃ and P ₄ in Figure 1(b). Therefore, P ₃, the most deviating trajectory point, is chosen as the characteristic point and splits the first sub-trajectory into two other sub-trajectories, P ₀-P₃ and P ₃-P₇ (see Figure 1(c)). On the other hand, in the second sub-trajectory, the perpendicular distances of all the trajectory points to the corresponding line are smaller than the threshold. Therefore, further splitting is not necessary. Trajectories are processed recursively until all the trajectory points have perpendicular distances to their corresponding approximate line within the threshold.

Figure 1. The DP algorithm; the dotted solid line represents the original trajectory and the long dash line represents the trajectory after simplification using the DP algorithm. More detailed description is in Section 2.1.

2.2. Overall Design of AIS Trajectories Simplification

The main target of a line simplification algorithm is to represent a line while reducing the number of coordinates to be stored. The results depend very much on the characteristics of the line in question. Vessels at anchor transmit their position every three minutes and increase the broadcast rate up to two seconds when manoeuvring or sailing at a high speed; every six minutes, vessels transmit other static and voyage related information. There will ususally be a lot of redundant information in the trajectories. For example,

1. (1) A vessel at anchor can be represented by the point of starting anchor time and the point of ending anchor time. The intermediate points transmitted between the time period of these two points are useless for the representation of the whole trajectories;

2. (2) A vessel sailing on a fixed course and speed can also be represented by the point of starting time and the point of ending time;

3. (3) Vessels manoeuvring in other models can also be represented by characteristic points using a simplification algorithm.

Ships generally sail on a fixed course and speed in open water. A sudden change rarely happens in the trajectories. That is to say, there is some redundant information in the original ship trajectories. Therefore, a simplification method is needed to remove the redundant points while maintaining the characteristic points.

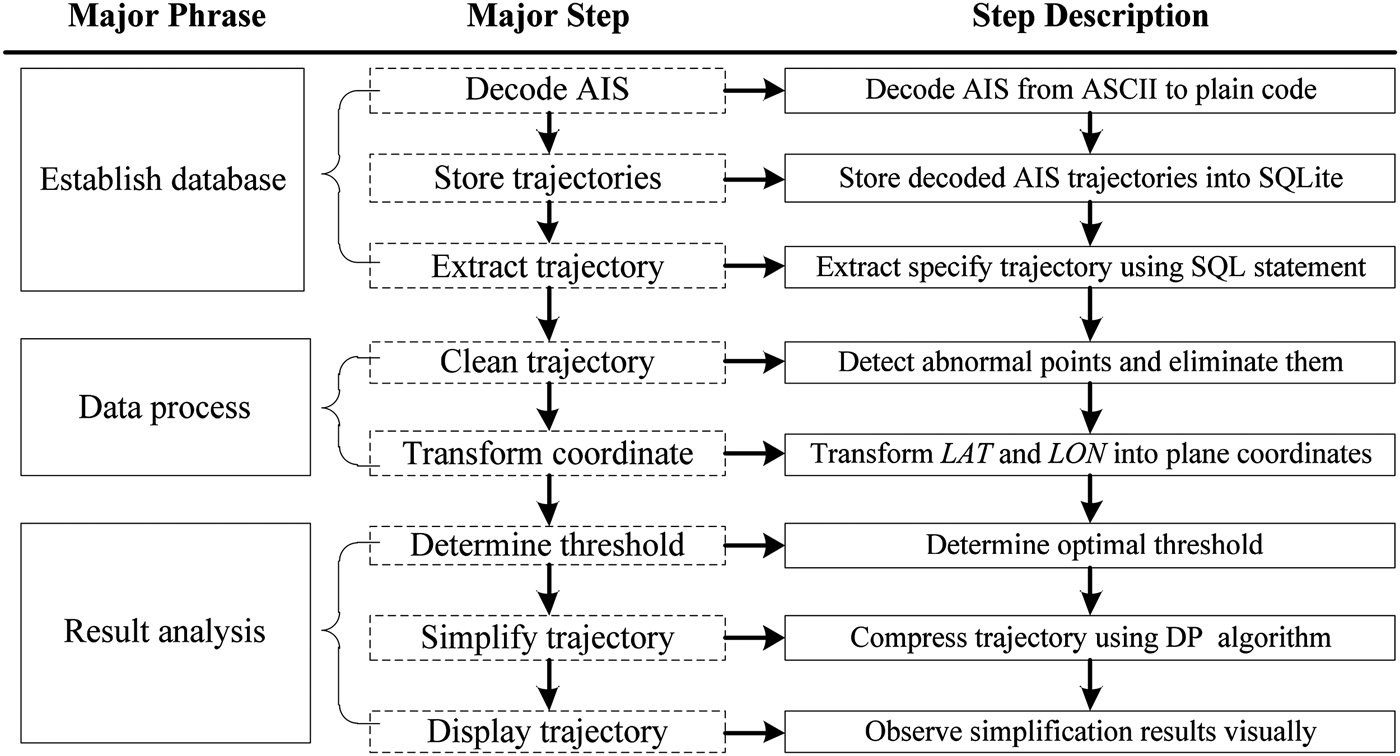
Quick storage, search and extraction of the required information from large AIS trajectory data packages is a critical requirement for simplification. AIS broadcasts information in ASCII format; the decoded AIS information is stored in the SQLite database. Each record in the SQLite database denotes a piece of information broadcast by shipborne AIS at one time instant. Trajectory simplification is based on a ship unit. While the application of the SQLite database solves the problem of fast storing and searching enormous data, frequently connecting and calling the database still reduce the process efficiency. To solve this problem, all information on one track is queried at once to avoid multiple queries and the data can be stored in a list or array container. After data cleaning and coordinate transformation, the track can be simplified using the determined threshold. The overall design of AIS trajectories simplification is illustrated in Figure 2.

Figure 2. Overall design and implementation of AIS trajectories simplification.

3. DETERMINATION OF SIMPLIFICATION THRESHOLD

In the DP algorithm, the simplification threshold is the sole parameter that needs to be determined and it determines the compression rate and deformation rate. The selection of the simplification threshold is crucial and it must be determined in a logical and scientific manner.

3.1. Simplification Threshold Evaluation Criteria

A ship domain is a free space surrounding a ship that the navigator tries to keep clear of other ships and obstacles. It is widely used as a criterion for the assessment of navigational situation. Use of the domain will control the safety of navigation as well as determining a safe trajectory of the ship (Pietrzykowski and Uriasz, 2009). In the DP algorithm, the simplification threshold means the allowed maximal perpendicular distance from the original trajectory point to the simplified trajectory line. Trajectory Belt is defined as a simplified area, trajectory centred with plus or minus threshold value τ as belt width. From Figure 1 it can be seen that all original coordinate points in the Trajectory Belt can be represented by the simplified trajectory. In order to ensure that the position of the simplified trajectory point corresponding to the original trajectory point is within the safety scope of the original trajectory point, the size of ship domain is used as the evaluation criteria for threshold determination.

Ship domain theory was first proposed by Fujii and Tanaka (1971) and formalised by Fujii et al. (1984). The shape of ship domain described by Fujii et al. (1984) is elliptical, with the ship placed in the centre of the ellipse. Two other frequently quoted definitions of ship domain are given by Goodwin (1975) and Coldwell (1983). Since then, various ship domain theories taking into account different factors have been presented (Zhao et al., 1993; Lisowski et al., 2000; Zhu et al., 2001; Szlapczynski, 2006; Wang et al., 2009; Wang, 2010). Different ship domain theories have different shapes and sizes due to differences in definitions and variations in the areas for which they are constructed. In practice, ships may be willing to accept a smaller domain in a local area with reduced space. Therefore, using empirical ship domain size as the evaluation criteria for threshold determination is not applicable. For example, the elliptical domain size of ship sailing in open water formulated by Fujii et al. (1984) is eight times ship length by 3·2 times ship length; and the size becomes six times ship length by 1·6 times ship length when a ship sails in a narrow strait. Similarly, Pietrzykowski and Uriasz (2009) make the ship domain size vary according to the different levels of safety. That is to say, the size of ship domains changes with navigational situations. Therefore, actual situations are suitable for determining the threshold of the simplification algorithm.

Hansen et al. (2013) estimated the minimum empirical ship domain that navigators actually applied using AIS trajectory data. A proposed bridge across Fehmarnbelt forms the background for their analysis of the size and shape of the ship domain. In order to allow ship navigators to pass the bridge in a comfortable and safe way, Hansen et al. (2013) take different ships in different situations into consideration. The minimum empirical ship domain is determined on the premise that a navigator feels comfortable and safe enough when passing the bridge. That is to say, it may not be the minimum in size. In the determination of the simplification threshold, only the minimum size of ship domain is needed. The method proposed by Hansen et al. (2013) is too complicated and may not be applicable in determining the minimum size of ship domain. In this paper, a new method is put forward to estimate the actual minimum ship domain based on AIS trajectories. It is not intended to establish a new ship domain theory but to evaluate the minimum size of ship domain conveniently and quickly.

3.2. Threshold Determination Algorithm

The main steps of ship domain size evaluation are as follows:

1. (1) Select AIS position reports that have the same Maritime Mobile Service Identity (MMSI). Then linearly interpolate trajectory points so that all ships are assigned to an approximate registration of the location every minute.

2. (2) Select one ship from all ships as centred ship randomly, and calculate the bearings and distances of other ships to the ship at a certain time point. Divide the distance by the ship's length (now the relative distance is obtained) for overlaying other ships' information; abandon the bearing and distance data when the relative distance is bigger than 10. Then calculate the bearings and distances of other ships to the centred ship at all other time points.

3. (3) According to the bearing and relative distance data obtained from Step (2), draw the Scatter Diagram of other ships to the centred ship, which is displaced to the centre of the coordinate centre.

4. (4) Select all other ships from all ships as centred ship, repeat Step (2) and (3). Now the scatter diagram of all ships is obtained.

5. (5) Overlay all ships' scatter diagrams obtained from Step (4), and the size of ship domain can be evaluated from it.

In order to demonstrate the ship domain size evaluation method intuitively, this method is illustrated by using sample trajectories of 962 ships collected during 11 days from 2 July 2011 to 12 July 2011 at Qiongzhou Strait AIS base station. The total number of recorded AIS position reports is 5,902,840. According to the steps defined, the Scatter Diagram of sample trajectories can be obtained (see Figure 3).

Figure 3. Scatter Diagram of centred ship to other ships according to every two ship's bearing and relative distance data. Data source and detailed procedures can be seen in Section 3.2.

In Figure 3, the coordinate centre represents vessel centre, the upward direction represents the centred ship's heading and 0^o bearing, the rightward direction represents the centred ship's beam and 90^o bearing. From Figure 3 it can be seen that other ships distribute evenly around the centred ship except the blank area around the coordinate centre. To make it clear, zooming in the centre blank area and the length of coordinate grid turns out to be one ship length. Therefore, the blank area can be seen clearly, shown as in the red rectangle in the bottom right corner of Figure 3. There are no other ships in the area that is centred in the coordinate centre and one ship length in the fore-and-aft direction and 0·8 ship length in the port and starboard direction. Based on the analysis in Section 3.1, 0·8 ship length can be chosen as the maximum simplification threshold.

4. VALIDATION OF SIMPLIFICATION ALGORITHM IN DETERMINED THRESHOLD

In order to validate the efficiency and effectiveness of simplification threshold in simplifying AIS trajectories, the DP algorithm and threshold are tested using the same sample trajectories of 962 ships. We simplify the sample trajectories using the DP algorithm with the simplification threshold set as 0·8 times ship length. The total number of original AIS position reports is 5,902,840, and 103,078 after simplifying. As a result, the compression rate is 98·25%.

4.1. Validation – From Visual Observation Perspective

In order to evaluate the efficiency and effectiveness of the DP algorithm in observing and analysing the macroscopic traffic flow situation, we imported one day of original and simplified AIS trajectories collected from Qiongzhou Strait AIS base station into an Electronic Chart Display and Information System (ECDIS) separately (see Figure 4). From Figure 4 it can be seen that the simplified trajectories can describe the macroscopic traffic flow situation almost as accurately as the original trajectories. At the same time, the simplified trajectories save storage space greatly and accelerate the speed of display and processing.

Figure 4. Import one day original and simplified AIS trajectories collected from Qiongzhou Strait AIS base station into ECDIS separately.

In order to evaluate the efficiency and effectiveness of the DP algorithm in observing and analysing microscopic traffic characteristics, we imported original and simplified trajectories of ships passing through the Strait longitudinally (see Figure 5) and latitudinally (see Figure 6) into ECDIS separately. From Figures 5 and 6 it can be seen that simplified trajectories can describe the microscopic traffic characteristics almost as accurately as the original trajectories; and the removed coordinate points can be obtained by linear interpolation.

Figure 5. Import original trajectory of ship passing through Strait longitudinal and the trajectory after simplification using DP algorithm.

Figure 6. Import original trajectory of ship passing through Strait latitudinally and the trajectory after simplification using DP algorithm.

4.2. Evaluation – From Statistical Perspective

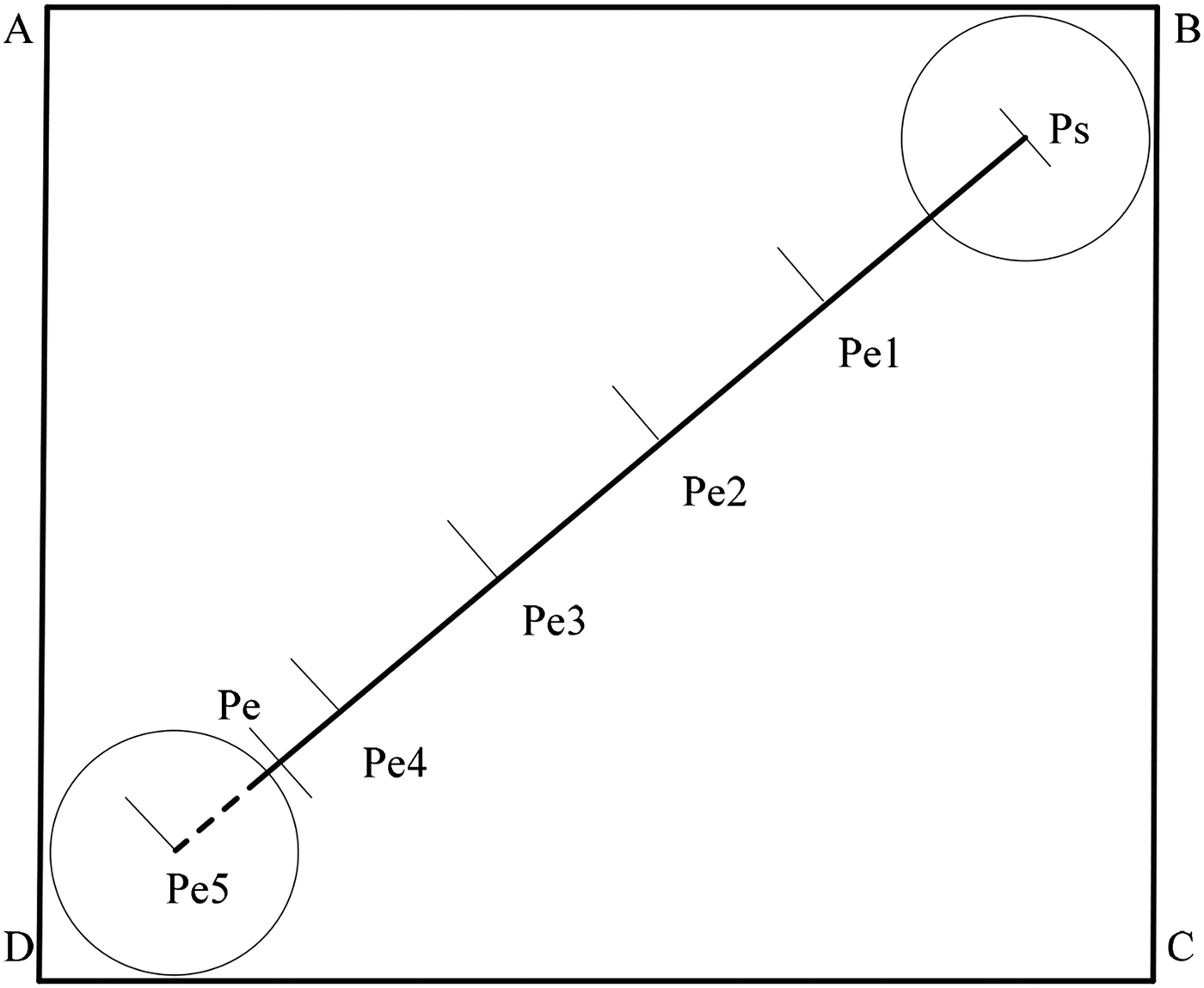
Gate Diagram is an effective measure for traffic flow situation statistics, including the total number of vessels passing through the gate, and their average speed and average length. The statistical results can be obtained by setting the position of gate and the length of sub-Gate. The schematic plot of the Gate Diagram is illustrated in Figure 7, and the detailed steps are described in Algorithm 2.

Figure 7. Schematic plot of Gate Diagram.

Figure 8. Intersection undetected cases.

4.2.1. Statistical Result

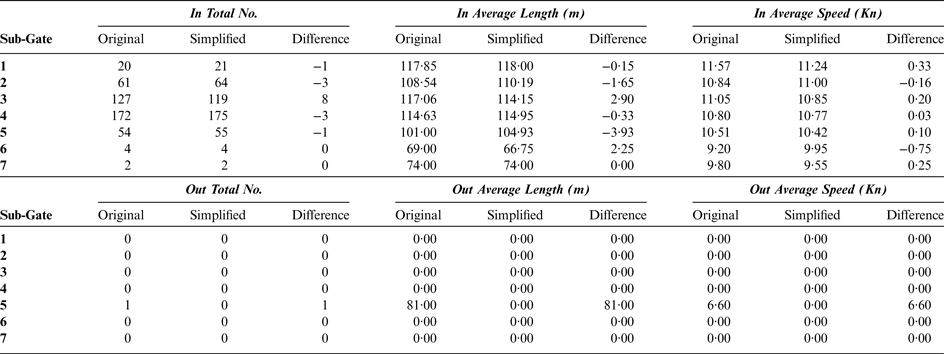
In order to evaluate the effectiveness of the DP simplification algorithm and the reasonableness of the simplification threshold, set Gate PsPe in the Traffic Separation Scheme (TSS) randomly (see Figure 9), and the length of sub-Gate is set as 0·2 nm. The Gate is divided into seven parts (from sub-Gate 1 to sub-Gate 7). The statistical results of Original trajectories' Gate Diagram and simplified trajectories' Gate Diagram are illustrated in Table 1.

Figure 9. The position of the Gate.

Table 1. The statistic results of Original trajectories' Gate Diagram and simplified trajectories' Gate Diagram.

4.2.2. Comments on Statistical Result

From Table 1 it can be seen that the differences of “In Total No.” in each sub-Gate between the original and simplified AIS trajectories is −1, −3, 8, −3, −1, 0, and 0. Also, there are some slight differences in average speed and average length. The main cause of Gate Diagram difference lies in the following three aspects:

4.2.2.1. Coordinate point error of trajectory

Take ship with MMSI of 412077250 as an example (Figure 10). The ship sailed from the left side of the figure to the right side, passed the Gate and turned back to the left. It next passed the Gate from right to left and then turned back again. The double turns in sub-Gate 5 increase the “In Total No.” of sub-Gate 5 by one, and increase “Out Total No.” by one due to the turn

back from right to left. After simplification, the DP algorithm removes the turn back point. That is why the “Out Total No.” is one in sub-Gate 5 in the original trajectories but zero in the simplified trajectories. Further research shows that the ship length is 81 m, the double turns are impossible in such reduced space and such a short time period. Therefore the turn back point may be an erroneous position due to a malfunction of the positioning system or transmission errors. In conclusion, the simplification algorithm removes the abnormal point in the original trajectory, and improves the accuracy of statistics effectively. The total number of error coordinate points in all sub-Gates is one, about 0·10% of the total.

Figure 10. Display of original and simplified trajectories passing through Gate; the original trajectory has an error point.

4.2.2.2. Coordinate point dislocation of trajectory

Trajectory coordinate point dislocation is prone to occur in the border region of the sub-Gate. Take ship with MMSI of 413355260 as an example. Its original trajectory intersected with sub-Gate 3 while its simplified trajectory intersected with sub-Gate 2 (Figure 11). The total number of dislocation ships in all sub-Gates is 27, about 2·81% of the total number. The shift between the original and simplified trajectories is within the safety limit for the simplification threshold and is determined according to the ship domain. The dislocation problem can be solved by altering the number of the sub-Gate. For example, the number of dislocation ships will be zero if the number of the sub-Gate is defined as one.

Figure 11. Display of original and simplified trajectories passing through Gate; the original and simplified trajectory intersect with a different sub-Gate.

Figure 12. Display of original trajectory passing through Gate; but one of the intersection trajectory points is outside the enclosing rectangle.

4.2.2.3. Trajectory intersection undetected

Take ship with MMSI of 412469620 as an example. Although the trajectory intersects with the Gate, one of the intersection trajectory points is in the enclosing rectangle and another is out of the enclosing rectangle. As a consequence, the trajectory is classified as non-intersecting with the Gate in statistics. Further research finds that this trajectory contained communication loss compared to normal transmission rate of the studied group of trajectories. Therefore, the intersection is still undetected though the similar situation has been considered in Step (3) of Gate Diagram statistics. The total number of intersections undetected in all sub-Gates is 1, about 0·10% of the total number. This problem can be solved by expanding the enclosing rectangle. But it comes at the expense of spending more time retrieving information. The simplified AIS trajectories have many fewer points. There is no need to improve the retrieval efficiency of intersection by setting the enclosing rectangle. Therefore, there are no intersections undetected.

All in all, although there are some differences between the original AIS trajectories' Gate Diagram and simplified AIS trajectories' Gate Diagram, the simplified AIS trajectories can still represent the original AIS trajectories accurately in a permitted error range in view that the compression rate is 98·25%.

5. CONCLUSION

AIS trajectories are sequences of position reports. Due to data quantity there are problems of transmitting, storing and processing these data when recorded trajectories become larger. In order to optimise the efficiency in practical application, trajectory simplification is needed. This paper applies the DP algorithm to simplify AIS trajectories. In addition, an AIS-based minimum ship domain evaluation approach is proposed, and the size of minimum ship domain is used as the criteria for threshold determination. The experiment results and validations in this paper show that the DP algorithm can simplify AIS trajectories effectively; the simplification threshold is scientific and reasonable.

Generally speaking, a trajectory of a ship depends on her own manoeuvring dynamics. If the ship length (L) over speed (V) ratio is big, the motion including yaw rate, as in turning or in course changing manoeuvres, is very slow. On the other hand, when L/V is small the motion is quick. While it is important to compress the redundant information in order to optimise the efficiency in transmitting, storing and processing these data, there may be certain trajectory properties to be preserved for application needs. The limitation of this paper is that the ship particulars, for example, ship length and motion characteristics, for example, ship speed, are not taken into consideration in trajectory simplification and threshold determination. Future research will take these influence factors into consideration to retain a more scientific and more satisfactory simplified trajectory.

A trajectory can be partitioned into a set of line segments according to the characteristic points obtained during simplification. Future study will focus on grouping similar line segments together into a cluster using a cluster algorithm, and providing support to route planning in order to further validate the practicability and the reliability of AIS trajectory simplification.