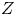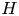Electron kinetics in a high-Z plasmoid

Abstract

The problem of the electron dynamics on a closed magnetic field line passing through a high-$Z$ plasmoid is considered. The electron kinetic equation is integrated over bounce motion and pitch angle, reducing the independent variables to a single adiabatic invariant plus time. Integration of the full Landau self-collision operator is carried out exactly, resulting in a nonlinear integro-differential operator in the new invariant. Conservation laws and the $H$ theorem of the integrated self-collision operator are proven. Numerical solutions of the integrated kinetic equation are obtained with a self-consistent quasineutral electric potential, given the initial condition of a cold plasmoid immersed in a hot ambient plasma. The fact that cold electrons are deeply trapped in a potential with a parabolic peak leads to exactly 3/4 the usual rate of collisional heating by the ambient plasma, independent of any other parameters.

1. Introduction

Plasmoids are a common feature in plasma: they are a localised excess plasma density usually associated with large spacial gradients which drive nonlinear dynamics. The excess density induces an electric potential well which serves to trap electrons. The electric field drives ions outwards along magnetic field lines, causing the plasmoid and well to expand, the expansion speed being set partly by the ion mass: heavier ions result in slower expansion. Expansion transverse to field lines also occurs, but on a much longer timescale unless extreme transverse gradients are involved.

A difficulty in understanding plasmoid dynamics is as follows: the electric potential arises due to the presence of the plasmoid, and must therefore be described in a self-consistent fashion. At the same time, the electric field and plasmoid density tend to dominate over those of the ambient plasma, precluding a linear description.

Another confounding feature is that the bounce period for an electron trapped in the well may be of the same order as, or shorter than, the electron collision timescale. Thus, a short mean-free-path description (such as the Braginskii equations) is inappropriate; electron kinetics must be considered.

The nature of the problem being kinetic, nonlinear and time-dependent, other simplifications of the system are required to gain insight. Chiefly, in strongly magnetised plasmas, a ‘1D’ description is sufficient: transverse spacial gradients are neglected. This kind of model treats the plasma independently ‘on each field line’. This 1D description is ubiquitously employed in the description of plasmoids, particularly those in the context of fuel pellet injection in magnetic confinement fusion (MCF) devices (Gurevich, Pariiskaya & Pitaevskii 1966; Mora 2003; Aleynikov et al. 2019; Arnold, Aleynikov & Helander 2021; Runov et al. 2021).

Plasmoids with high-$Z$ ions expand more slowly along field lines, owing to the larger ion mass, but also introduce strong pitch-angle scattering of electrons. Thus, a simplified description of a high-$Z$ plasmoid neglects the expansion timescale and asserts that electron pitch-angle scattering occurs on a very short timescale relative to collisions that alter electron energy. This ordering is used in the following investigation with the aim of providing an understanding of the interaction of electron kinetics and the self-consistent potential well without the additional complication of ion dynamics.

We consider ion density profiles that are symmetric and exhibit only a single peak. Figure 1 shows a schematic of the plasma density and potential.

Figure 1. Schematic of the potential well induced by excess plasma density and trapped/passing electron orbits. Here $z$ is the coordinate along the magnetic field line. The maximum electric potential is written $\phi _m$. The electron density far from the plasmoid is denoted by $n_a$.

In the kinetic problem, electron bounce motion and pitch-angle scattering, the two shortest timescales, will be integrated out. We consider a closed magnetic field line, so both trapped and passing electrons are described by the integrated kinetic equation. The conservation properties of the integrated kinetic equation will be investigated and the $H$-theorem will be proven for the integrated collision operator. Numerical studies of the system will be carried out with a self-consistent electric potential, the initial condition being a cold plasmoid immersed in a hot ambient plasma. The evolution of the system will be compared with that of two superposed Maxwellians in the absence of an electric potential.

The energy exchange between trapped and passing electrons is of particular interest, because we expect that passing electrons, which are accelerated through the potential well and spend little time in the plasmoid, exchange energy inefficiently with the trapped electrons. Conversely, we expect trapped electrons to exchange energy very efficiently with other trapped electrons. The integrated kinetic equation allows for a rigorous description of these effects.

Previous work on plasmoid dynamics in one dimension assumed the electrons to be in either global Boltzmann equilibrium (Gurevich et al. 1966; Mora 2003; Aleynikov et al. 2019; Arnold et al. 2021) or in local equilibrium with spatially dependent temperature (Runov et al. 2021). The difference in the temperatures of plasmoid electrons and ambient electrons was accounted for by introducing a collisional heating term to the equation governing plasmoid electron temperature. The heating term assumed a homogeneous ambient plasma with fixed temperature.

However, if the plasmoid is initially colder than the ambient plasma, the distribution as a whole cannot be Maxwellian. Therefore, this investigation contrasts with previous work by not assuming a Maxwellian plasmoid electron distribution function; we solve the integrated electron kinetic equation for the whole distribution function. The quenching of the ambient plasma temperature due to the presence of the cold plasmoid can be observed in such a kinetic picture, rather than the ambient temperature simply being assumed constant.

Unlike previous investigations, our kinetic description covers the effect of the potential well depth on the evolution of the plasmoid electron temperature. Further, we describe rigorously the ‘interface’ between plasmoid and ambient electrons: the region of phase-space near the passing-trapped separatrix.

2. Theory

2.1. Electron kinetic equation

Given the electron distribution function $f$, the kinetic equation in the absence of transverse motion of the guiding centre is given by

(2.1)\begin{equation} \frac{\partial f}{\partial t} + v_\parallel \frac{\partial f}{\partial z} + \frac{e}{m_e}\frac{\partial \phi}{\partial z}\frac{\partial f}{\partial v_\parallel} = C, \end{equation}

for $\phi$ the electric potential, $z$ the coordinate parallel to the magnetic field line, $v_\parallel$ the parallel velocity, $e$ the absolute electron charge, $m_e$ the electron mass and $C$ the collision operator. We split up the collision operator into self-collisions (electron–electron, ‘$e,e$’) and collisions with ions (electron–ion (species $k$), ‘$e,ik$’):

(2.2)\begin{equation} C = C_{e,e}(f) + \sum_k C_{e,ik}(f). \end{equation}

Then, we express the left-hand side of the kinetic equation in terms of energy $\mathcal {E} = m_ev^2/2 -e\phi$, magnetic moment $\mu = m_ev_\perp ^2/(2B)$ and $z$:

(2.3)\begin{equation} \frac{\partial f}{\partial t} + v_\parallel \frac{\partial f}{\partial z} - e \frac{\partial \phi}{\partial t}\frac{\partial f}{\partial \mathcal{E}} = C_{e,e}(f) + \sum_k C_{e,ik}(f). \end{equation}

This form of the kinetic equation highlights the fact that any collisionless change in electron energy is associated with explicit time variation of the electric potential. As the problem is symmetric in $z$, $f$ is an even function of $v_\parallel$, so we do not need to account for the part of $f$ that is odd in $v_\parallel$ when changing variables from $(v_\parallel, v_\perp, z, t)$ to $(\mathcal {E},\mu,z,t)$.

The self-collision operator is given by

(2.4)\begin{equation} C_{e,e}(f) = \frac{e^4 \ln \varLambda}{\varepsilon_0^2 m_e^2}\boldsymbol{\nabla}_{\boldsymbol{v}}\boldsymbol{\cdot}\left(\boldsymbol{\nabla}_{\boldsymbol{v}}\varphi f - \left(\boldsymbol{\nabla}_{\boldsymbol{v}}\boldsymbol{\nabla}_{\boldsymbol{v}} \psi\right)\boldsymbol{\nabla}_{\boldsymbol{v}}f\right) \end{equation}

(Helander & Sigmar 2002, pp. 29–30, (3.15), (3.16), (3.21)), for $\varphi$ and $\psi$ the Rosenbluth potentials

(2.5a–c)\begin{equation} \varphi ={-}\frac{1}{4 {\rm \pi}} \int \frac{f\left(\boldsymbol{v}^\prime\right)}{u}\,\mathrm{d}^3v^\prime,\quad \psi ={-}\frac{1}{8{\rm \pi}}\int u f\left(\boldsymbol{v}^\prime\right)\mathrm{d}^3v^\prime,\quad \boldsymbol{u} = \boldsymbol{v} - \boldsymbol{v}^\prime, \end{equation}

the double nabla notation being

(2.6)\begin{equation} \boldsymbol{\nabla}_{\boldsymbol{v}}\boldsymbol{\nabla}_{\boldsymbol{v}}h := \hat{\boldsymbol{v}}_i\hat{\boldsymbol{v}}_j\frac{\partial^2 h}{\partial v_i \partial v_j}. \end{equation}

We stress that henceforth the integral notation will be such that, for integration variable $\lambda$, the integrand is to the right of $\int$ and to the left of $\mathrm {d}\lambda$.

Collisions with ions are well-approximated by pitch-angle scattering against stationary charges:

(2.7)\begin{equation} C_{e,ik}(f) = \frac{e^4 \ln \varLambda}{4 {\rm \pi}\varepsilon_0^2 m_e^2} Z_k^2 n_{ik} \frac{1}{v^3}\mathcal{L}(f) \end{equation}

for Lorentz scattering operator

(2.8)\begin{equation} \mathcal{L} = \frac{1}{2\sin\theta}\frac{\partial }{\partial \theta}\left(\sin\theta \frac{\partial}{\partial \theta}\right), \end{equation}

which serves to alter only the pitch angle $\theta = \arctan {(v_\perp /v_\parallel )}$, leaving the energy of the electron unaffected. We assume no variation of $f$ in the gyroangle. In the variables $(\mathcal {E}, \mu, z)$, the Lorentz scattering operator is

(2.9)\begin{equation} \mathcal{L} = m_e v_\parallel \frac{\partial }{\partial \mu} \left(\frac{\mu v_\parallel}{B} \frac{\partial }{\partial \mu}\right), \end{equation}

indicating that anisotropy in $f$ is associated with its dependence on $\mu$.

We note that the terms proportional to $\partial f/\partial t$ and $\partial f/\partial \mathcal {E}$ on the left-hand side of (2.3) are associated with the time variation of the potential, whereas $v_\parallel (\partial f/\partial z)$ is associated with bounce motion. We seek to further simplify this kinetic equation in the context of rapid pitch-angle scattering. To this end, turning our attention first to the electron self-collision operator, we observe that in spherical coordinates (with no dependence on the gyroangle),

(2.10)\begin{gather} \boldsymbol{\nabla}_{\boldsymbol{v}} \varphi = \hat{\boldsymbol{v}} \frac{\partial \varphi}{\partial v} + \frac{\hat{\boldsymbol{\theta}}}{v} \frac{\partial \varphi}{\partial \theta}, \end{gather}

(2.11)\begin{gather}\boldsymbol{\nabla}_{\boldsymbol{v}}\boldsymbol{\nabla}_{\boldsymbol{v}} \psi = \left(I - \hat{\boldsymbol{v}}\hat{\boldsymbol{v}}\right)\frac{1}{v}\frac{\partial \psi}{\partial v} + \hat{\boldsymbol{v}}\hat{\boldsymbol{v}} \frac{\partial^2 \psi}{\partial v^2} - \frac{2\hat{\boldsymbol{\theta}}\hat{\boldsymbol{v}}}{v^2}\frac{\partial \psi}{\partial \theta} + \left(\hat{\boldsymbol{v}}\hat{\boldsymbol{\theta}} + \hat{\boldsymbol{\theta}}\hat{\boldsymbol{v}}\right)\frac{1}{v}\frac{\partial^2 \psi}{\partial \theta \partial v} + \frac{\hat{\boldsymbol{\theta}}\hat{\boldsymbol{\theta}}}{v^2}\frac{\partial^2 \psi}{\partial \theta^2}, \end{gather}

(2.12)\begin{gather}\boldsymbol{\nabla}_{\boldsymbol{v}} \boldsymbol{\cdot} \boldsymbol{F} = \frac{1}{v^2}\frac{\partial }{\partial v}\left(\boldsymbol{F}\boldsymbol{\cdot}\hat{\boldsymbol{v}}\,v^2\right) + \frac{1}{v\sin\theta}\frac{\partial }{\partial \theta}\left(\boldsymbol{F}\boldsymbol{\cdot}\hat{\boldsymbol{\theta}}\sin\theta\right), \end{gather}

which gives

(2.13)\begin{equation} C_{e,e}(f) = \frac{e^4 \ln \varLambda}{\varepsilon_0^2 m_e^2}\left\{\frac{1}{v^2}\frac{\partial }{\partial v}\left[v^2\left(\frac{\partial \varphi}{\partial v}f - \frac{\partial^2 \psi}{\partial v^2}\frac{\partial f}{\partial v}\right)\right] - \frac{2}{v^3}\frac{\partial \psi}{\partial v}\mathcal{L}(f) + R(f,\varphi,\psi)\right\} \end{equation}

for

(2.14)\begin{align} R(f,\varphi,\psi) & ={-}\frac{1}{v^3}\frac{\partial^2 \psi}{\partial \theta \partial v}\frac{\partial f}{\partial \theta} - \frac{1}{v^2} \frac{\partial }{\partial v}\left(\frac{\partial^2 \psi}{\partial \theta \partial v}\frac{\partial f}{\partial \theta}\right)\nonumber\\ & \quad +\frac{1}{v\sin\theta}\frac{\partial }{\partial \theta}\left[\sin\theta\left(\frac{1}{v}\frac{\partial \varphi}{\partial \theta}f - \left(\frac{1}{v}\frac{\partial^2 \psi}{\partial \theta \partial v} - \frac{2}{v^2}\frac{\partial \psi}{\partial \theta}\right)\frac{\partial f}{\partial v} - \frac{1}{v^3}\frac{\partial^2 \psi}{\partial \theta^2}\frac{\partial f}{\partial \theta}\right)\right], \end{align}

noting that all terms in $R$ are proportional to a $\theta$ derivate of one of the Rosenbluth potentials. Thus,

(2.15)\begin{align} C_{e,e}(f) + \sum_k C_{e,ik}(f) & = \frac{e^4 \ln \varLambda}{\varepsilon_0^2 m_e^2} \left\{\frac{1}{v^2}\frac{\partial }{\partial v}\left[v^2\left(\frac{\partial \varphi}{\partial v}f - \frac{\partial^2 \psi}{\partial v^2}\frac{\partial f}{\partial v}\right)\right]\right.\nonumber\\ & \quad \left. + \left(\frac{1}{4{\rm \pi}}\sum_k Z_k^2 n_{ik} - 2\frac{\partial \psi}{\partial v}\right)\frac{1}{v^3}\mathcal{L}(f) + R(f,\varphi,\psi)\right\}. \end{align}

In this form, collisions are split up into the following effects: energy-altering terms arising from self-collisions, pitch-angle scattering arising from self-collisions and collisions with ions, and the remainder term $R$ which is composed of terms due to angular variation of the Rosenbluth potentials.

We suppose that in the tail of the distribution function pitch-angle scattering and electron bounce motion are faster than collisions that alter energy. That is, the tail distribution follows the ordering

(2.16)\begin{equation} \left|\frac{\partial }{\partial t}\right| \sim \left|C_\mathrm{energy-altering}\right| \sim \left|C_R\right| \ll \left|v_\parallel \frac{\partial }{\partial z}\right| \sim \left|C_\mathrm{p.a.\,scattering}\right|, \end{equation}

where $C_\mathrm {p.a.\,scattering}$ is the term proportional to $\mathcal {L}$ in (2.15), $C_\mathrm {energy-altering}$ is the term proportional to $(1/v^2)(\partial /\partial v)$ and $C_R$ is the term proportional to $R$.

We correspondingly split up the distribution:

(2.17)\begin{equation} f = f_0 + f_1,\quad f_0 \gg f_1, \end{equation}

giving the lowest-order kinetic equation

(2.18)\begin{equation} v_\parallel \frac{\partial f_0}{\partial z} = v_\parallel G(\mathcal{E},\mu,z) \frac{\partial }{\partial \mu}\left(\frac{\mu v_\parallel}{v^3 B}\frac{\partial f_0}{\partial \mu}\right), \end{equation}

where

(2.19)\begin{equation} G = \frac{e^4 \ln \varLambda}{\varepsilon_0^2 m_e}\left(\frac{1}{4{\rm \pi}}\sum_k Z_k^2 n_{ik} - 2\frac{\partial \psi}{\partial v}\right). \end{equation}

Dividing through by $v_\parallel$ and orbit integrating, assuming that $f_0$ is symmetric in $z$, yields

(2.20)\begin{equation} \oint G \frac{\partial }{\partial \mu}\left(\frac{\mu v_\parallel}{v^3 B}\frac{\partial f_0}{\partial \mu}\right)\mathrm{d}z = 0. \end{equation}

As we are in the context of fast pitch-angle scattering, the above and (2.18) are solved by

(2.21)\begin{equation} \frac{\partial f_0}{\partial \mu} = \frac{\partial f_0}{\partial z} = 0. \end{equation}

However, we note that for the lowest-energy ‘core’ electrons, which are deeply trapped in the potential well, self-collisions dominate. The distribution of these electrons will be near-Maxwellian, with the distribution of Maxwellian core electrons being independent of both $z$ and $\mu$.

Therefore, (2.17) and (2.21) hold for the total distribution function labelled $f$. The kinetic equation to next order is given by

(2.22)\begin{align} \frac{\partial f_0}{\partial t} + v_\parallel \frac{\partial f_1}{\partial z} - e \frac{\partial \phi}{\partial t}\frac{\partial f_0}{\partial \mathcal{E}} & = \frac{e^4 \ln \varLambda}{\varepsilon_0^2 m_e^2} \left\{\frac{1}{v^2}\frac{\partial }{\partial v}\left[v^2\left(\frac{\partial \varphi_0}{\partial v}f_0 - \frac{\partial^2 \psi_0}{\partial v^2}\frac{\partial f_0}{\partial v}\right)\right] \right.\nonumber\\ & \quad + \left. m_e v_\parallel \left(\frac{1}{4{\rm \pi}}\sum_k Z_k^2 n_{ik} - 2\frac{\partial \psi_0}{\partial v}\right)\frac{\partial }{\partial \mu}\left(\frac{\mu v_\parallel}{v^3 B}\frac{\partial f_1}{\partial \mu}\right)\right\}, \end{align}

where we henceforth treat $f$ as the total electron distribution function. In the above, we note that $R$ vanishes in this order, and we denote $\varphi _0$ and $\psi _0$ the Rosenbluth potentials calculated from $f_0$.

Dependence upon $f_1$ can be eliminated from the above by applying the following integration to both sides:

(2.23)\begin{equation} \int^{({\mathcal{E} + e\phi_m})/{B}}_0\oint\,\frac{\cdot}{v_\parallel}\,\mathrm{d}z\,\mathrm{d}\mu, \end{equation}

which corresponds to first integrating over bounce motion, then over all possible values of $\mu$, the variable representing anisotropy, for a given energy $\mathcal {E}$.

We observe that the volume element is given by $\mathrm {d}^3v\,\mathrm {d}z = (4{\rm \pi} B)/(m_e^2v_\parallel )\,\mathrm {d}\mathcal {E}\,\mathrm {d}\mu \,\mathrm {d}z$, so the above may be interpreted as multiplying by the volume element and integrating over $z$ and $\mu$, leaving only dependence on $\mathcal {E}$. That is, the resulting kinetic equation describes how electrons may move between shells of constant energy due to adiabatic change in the potential and collisions. In essence, the zeroth moment of the kinetic equation is taken with one integration variable in momentum space and another in physical space, which is in contrast to the usual moment over all of momentum space.

Dropping the subscript from $f_0$, the resulting kinetic equation is

(2.24)\begin{equation} \frac{\partial f}{\partial t} = \left\langle C\right\rangle \end{equation}

for the integrated collision operator

(2.25)\begin{equation} \left\langle C\right\rangle = \frac{e^4 \ln \varLambda}{\varepsilon_0^2 m_e^2}\frac{\partial }{\partial K}\left[f \int^K_0 f^\prime \,\mathrm{d}K^\prime + H\frac{\partial f}{\partial K}\left(\int^K_0 f^\prime \frac{K^\prime}{H^\prime}\,\mathrm{d}K^\prime + K\int^\infty_K \frac{f^\prime}{H^\prime}\,\mathrm{d}K^\prime\right) \right], \end{equation}

where

(2.26)\begin{gather} K = \oint_s \frac{m_e^2 v^3}{3}\, \mathrm{d}z, \end{gather}

(2.27)\begin{gather}H = \frac{\partial K}{\partial \mathcal{E}} = \oint_s m_e v\,\mathrm{d}z. \end{gather}

We note that $f = f(K,t)$ in (2.24). Here $K$ is the invariant associated with electrons undergoing rapid pitch-angle scattering and bounce motion inside a slowly varying electric potential well while experiencing no energy-altering collisions. The definition of $\oint _s$ and the details of the integration procedure with its associated simplification of the kinetic equation are contained in Appendix A.

2.2. Trapped and passing electrons

Equation (2.24) expresses the fact that in the absence of collisions that alter energy, the quantity $K$ is constant for an individual electron. The fact that $K$ involves the orbit integral of $v^3$ rather than $v$ corresponds to the energy of an individual electron being equipartitioned into all three degrees of freedom by pitch-angle scattering.

At this point it is useful to make the distinction between passing and trapped electrons, and those with energy $\mathcal {E}$ above or below zero. By convention, trapped electrons are those that, when experiencing collisionless motion, are unable to escape the well; their position does not tend to infinity in infinite time. The conditions for trapped/passing electrons are

(2.28)\begin{equation} \begin{cases} \mathcal{E} < \mu B, & \mathrm{trapped,} \\ \mathcal{E} \geqslant \mu B, & \mathrm{passing.} \end{cases} \end{equation}

Consequently, bounce-averaged kinetic problems may have a separatrix at $\mathcal {E} = \mu B$.

However, the kinetic equation (2.24) has also been integrated over $\mu$, the variable responsible for anisotropy. Physically speaking, any electron with $\mathcal {E} > 0$ will experience enough pitch-angle scattering to become untrapped within any timescale present in (2.24). Conversely, electrons with $\mathcal {E} < 0$ are never able to be pitch-angle scattered such that they become passing: they simply do not have enough kinetic energy; if all their kinetic energy were in the parallel degree of freedom, their parallel speed would not equal or exceed $\sqrt {2e\phi /m_e}$.

Therefore, we introduce the terminology energy-trapped and energy-passing

(2.29)\begin{equation} \begin{cases} \mathcal{E} < 0, & \mathrm{energy-trapped,} \\ \mathcal{E} \geqslant 0, & \mathrm{energy-passing,} \end{cases} \end{equation}

in order to avoid confusion with the conventional definitions of trapped and passing.

When dealing with bounce-averaged problems on infinitely long magnetic field lines, is it very important to distinguish between trapped and passing distributions, because the bounce average of any quantity on such a field line takes on the value it has in the limit $|z|\rightarrow \infty$. This is a consequence of the orbit of a passing electron being infinitely long. Such problems have a passing–trapped separatrix, the passing distribution typically being static, with the trapped distribution equal to the passing at the separatrix to ensure continuity.

However, for closed field lines, the orbit of a passing electron is simply the whole field line. In order to account for a closed field line, it is enough to define the turning points of an orbit integral to be $\pm z_c$, where

(2.30)\begin{equation} z_c(\mathcal{E},\mu,t): \begin{cases} \mathcal{E} - \mu B(z_c,t) + e\phi(z_c,t) = 0, & \mathcal{E} < \mu B,\\ L_F/2, & \mathcal{E} \geqslant \mu B, \end{cases} \end{equation}

for connection length $L_F$. Then, electrons of all energies and magnetic moments can be considered in the bounce-integrated kinetic equation.

2.3. Alternative forms of the integrated collision operator

The integrated collision operator can be expressed directly in terms of phase-space moments of $f$:

(2.31)\begin{equation} \left\langle C\right\rangle = \frac{e^4 \ln \varLambda}{2{\rm \pi}\varepsilon_0^2} \frac{\partial }{\partial K}\left(N_Kf + H \frac{\partial f}{\partial K} \left(\frac{2}{3}E_K + K M_K\right)\right), \end{equation}

for $N_K$, $E_K$ and $M_K$ defined in Appendix B (see (B5), (B7) and (B8)). Here $N_K$ corresponds to the line-integrated density of electrons with invariant less than $K$, $E_K$ is the line-integrated kinetic energy of electrons with invariant less than $K$ and $K M_K$ is not so easily interpreted, but has the same dimensions as $E_K$ and is associated with electrons with invariant larger than $K$.

The above is a friction-diffusion form of the collision operator (namely, Rosenbluth potential form), and the contributions to each effect are somewhat intuitive: an electron with invariant $K$ experiences friction proportional to the number of electrons with invariant less than $K$, and experiences diffusion proportional to two quantities, one being the kinetic energy of electrons with invariants smaller than $K$, the other being associated with electrons with invariants larger than $K$.

The collision operator in the form (2.31) is convenient for numerical implementation and is clearly represented as a friction-diffusion operator. However, it may also be written in the form

(2.32)\begin{equation} \left\langle C\right\rangle = \frac{e^4 \ln\varLambda}{\varepsilon_0^2 m_e^2} \frac{\partial }{\partial K}\int^\infty_{{-}e\phi_m} Q\left(f^\prime \frac{\partial f}{\partial \mathcal{E}} - f \frac{\partial f^\prime}{\partial \mathcal{E}^\prime}\right)\mathrm{d}\mathcal{E}^\prime, \end{equation}

where

(2.33)\begin{equation} Q = K^\prime \varTheta\left(\mathcal{E} - \mathcal{E}^\prime\right) + K \varTheta\left(\mathcal{E}^\prime - \mathcal{E}\right) \end{equation}

for $\varTheta$ the Heaviside step function. Equation (2.32) closely resembles the Landau collision operator as presented in the original paper (Landau 1936). In this form it is clear that the integrated collision operator vanishes if the distribution is Maxwellian.

2.4. Particle conservation and the $H$ theorem

As the integrated kinetic equation was obtained from the drift kinetic equation, it must conserve particles and have an $H$ theorem. Both may be proven within the framework of the invariant $K$. Equation (2.32) provides the most convenient form for proving these properties. We write $\left \langle C\right \rangle = A (\partial I/\partial K)$ for brevity, where $A = (e^4\ln \varLambda /\varepsilon _0^2 m_e^2)$ and

(2.34)\begin{equation} I = \int^\infty_{{-}e\phi_m} Q\left(f^\prime \frac{\partial f}{\partial \mathcal{E}} - f \frac{\partial f^\prime}{\partial \mathcal{E}^\prime}\right)\mathrm{d}\mathcal{E}^\prime. \end{equation}

The line-integrated electron density (B5) is

(2.35)\begin{equation} N = \frac{2{\rm \pi}}{m_e^2}\int^\infty_0 f\,\mathrm{d}K, \end{equation}

thus,

(2.36)\begin{equation} \frac{\mathrm{d} N}{\mathrm{d} t} = \frac{2{\rm \pi} A}{m_e^2}\int^\infty_0 \frac{\partial I}{\partial K}\,\mathrm{d}K = 0, \end{equation}

proving particle conservation. The line-integrated electron entropy density is

(2.37)\begin{equation} S ={-} \frac{2{\rm \pi}}{m_e^2}\int^\infty_0 f \ln f\,\mathrm{d}K, \end{equation}

thus,

(2.38)\begin{equation} \frac{\mathrm{d} S}{\mathrm{d} t} ={-}\frac{2{\rm \pi}}{m_e^2}\int^\infty_0 \frac{\partial f}{\partial t}\left(1 + \ln f\right)\mathrm{d}K. \end{equation}

Substituting (2.24), integrating by parts and changing the integration variable to $\mathcal {E}$ yields

(2.39)\begin{equation} \frac{\mathrm{d} S}{\mathrm{d} t} = \frac{2{\rm \pi} A}{m_e^2} \int^\infty_{{-}e\phi_m}\int^\infty_{{-}e\phi_m} Q ff^\prime\left(\frac{\partial \ln f}{\partial \mathcal{E}} - \frac{\partial \ln f^\prime}{\partial \mathcal{E}^\prime}\right)\frac{\partial \ln f}{\partial \mathcal{E}}\,\mathrm{d}\mathcal{E}\,\mathrm{d}\mathcal{E}^\prime. \end{equation}

Using the fact that above expression holds when exchanging primed and unprimed terms (noting that $Q^\prime = Q$), we see that

(2.40)\begin{equation} \frac{\mathrm{d} S}{\mathrm{d} t} = \frac{{\rm \pi} A}{m_e^2} \int^\infty_{{-}e\phi_m}\int^\infty_{{-}e\phi_m} Q ff^\prime\left(\frac{\partial \ln f}{\partial \mathcal{E}} - \frac{\partial \ln f^\prime}{\partial \mathcal{E}^\prime}\right)^2\,\mathrm{d}\mathcal{E}\,\mathrm{d}\mathcal{E}^\prime \geqslant 0, \end{equation}

proving the $H$ theorem. It is also clear that the line-integrated entropy density is constant when $f$ is Maxwellian.

2.5. Generalisation to an electric–magnetic potential well

The preceding section may be generalised to include a symmetric, time-dependent magnetic field. If we include the magnetic mirror force $-\mu (\partial B/\partial z)$ in the kinetic equation (2.3), the calculation may be carried out in the same fashion as in the theory section and Appendix A (making sure not to neglect the $(z,t)$ dependence of $B$, and replacing $(\mathcal {E}+e\phi _m)/B$ with $(\mathcal {E}+e\phi _m)/(B(z=0))$ in (2.23)). We find that now the invariant $K$ has a contribution from the magnetic well:

(2.41)\begin{equation} K = \oint_s \frac{m_e^2 v^3}{3B}\,\mathrm{d}z. \end{equation}

The form of the integrated kinetic equation and integrated collision operator in terms of $K$ is identical. With regards to the conservation properties and $H$ theorem, one subtlety must be observed: the integration of particle density and entropy density must be carried out over an infinitesimal flux tube rather than over a field line. Indeed, a time-varying magnetic field changes the cross-section of the flux tube, moving the guiding centres of electrons along with the field lines, resulting in compression or expansion of the plasma due to collisionless transverse motion.

As this investigation concerns itself with parallel dynamics, the effect of magnetic field variation has been neglected, allowing us to be agnostic about the transverse profile of the plasmoid, ambient plasma and magnetic field.

3. Self-consistent electric potential

For the purpose of calculating the electric potential, there is no need to distinguish between ions of differing charges; we write $n_i = \sum _k Z_k n_{ik}$, which represents an effective density of singly charged ions. Poisson's equation formally determines the electrostatic potential:

(3.1)\begin{equation} \frac{\partial^2 \phi}{\partial z^2} + \frac{e}{\varepsilon_0}\left(n_i - n_e\right) = 0, \end{equation}

but when the Deybe length is much shorter than the length scale of interest (in our case, the plasmoid length), then the quasineutrality condition

(3.2)\begin{equation} n_e = n_i \end{equation}

is a good approximation.

4. Energy conservation

The system of the electron kinetic equation and Poisson's equation (with stationary ions) must conserve the sum of the line-integrated electron kinetic and electric field energies. The line-integrated electron energy (B6) is

(4.1)\begin{equation} W = \frac{2{\rm \pi}}{m_e^2} \int^\infty_0 \mathcal{E} f\,\mathrm{d}K, \end{equation}

thus,

(4.2)\begin{align} \frac{\mathrm{d} W}{\mathrm{d} t} & = \frac{2{\rm \pi} }{m_e^2} \int^\infty_0 \left(\left.\frac{\partial \mathcal{E}}{\partial t}\right|_Kf + A\mathcal{E}\frac{\partial I}{\partial K}\right)\mathrm{d}K\nonumber\\ & = \frac{2{\rm \pi} }{m_e^2} \int^\infty_{{-}e\phi_m} \left(-\left.\frac{\partial K}{\partial t}\right|_\mathcal{E} f + A \mathcal{E} \frac{\partial I}{\partial \mathcal{E}}\right)\mathrm{d}\mathcal{E} \nonumber\\ & ={-}\frac{2{\rm \pi} }{m_e^2} \int^\infty_{{-}e\phi_m} \left.\frac{\partial K}{\partial t}\right|_\mathcal{E} f\,\mathrm{d}\mathcal{E} - \frac{2{\rm \pi} A}{m_e^2}\int^\infty_{{-}e\phi_m} I\,\mathrm{d}\mathcal{E}. \end{align}

The former term expresses the change in electron energy due to adiabatic expansion or compression. The latter term is associated with collisions, and vanishes. To see this, we note that primed and unprimed terms in the integrand may be exchanged, and that $Q = Q^\prime$:

(4.3)\begin{align} \int^\infty_{{-}e\phi_m} I\,\mathrm{d}\mathcal{E} & = \int^\infty_{{-}e\phi_m}\int^\infty_{{-}e\phi_m} Q\left(f^\prime \frac{\partial f}{\partial \mathcal{E}} - f \frac{\partial f^\prime}{\partial \mathcal{E}^\prime}\right)\mathrm{d}\mathcal{E}^\prime \,\mathrm{d}\mathcal{E} \nonumber\\ & = \frac{1}{2} \int^\infty_{{-}e\phi_m} \int^\infty_{{-}e\phi_m} \left[ Q\left(f^\prime \frac{\partial f}{\partial \mathcal{E}} - f \frac{\partial f^\prime}{\partial \mathcal{E}^\prime}\right) +Q^\prime\left(f \frac{\partial f^\prime}{\partial \mathcal{E}^\prime} - f^\prime \frac{\partial f}{\partial \mathcal{E}}\right) \right]\mathrm{d}\mathcal{E}^\prime\,\mathrm{d}\mathcal{E}\nonumber\\ & = 0. \end{align}

Thus,

(4.4)\begin{equation} \frac{\mathrm{d} W}{\mathrm{d} t} ={-}\frac{2{\rm \pi} }{m_e^2}\int^\infty_{{-}e\phi_m} \left.\frac{\partial K}{\partial t}\right|_\mathcal{E} f\,\mathrm{d}\mathcal{E}. \end{equation}

Comparing the expression for density (B9) with the above, we find

(4.5)\begin{equation} \frac{\mathrm{d} W}{\mathrm{d} t} ={-}\int^\infty_{-\infty}n_e e \frac{\partial \phi}{\partial t}\,\mathrm{d}z, \end{equation}

where $n_e$ denotes the electron number density. As the line-integrated electron kinetic energy is given by

(4.6)\begin{equation} E = W + \int^\infty_{-\infty} e n_e \phi\,\mathrm{d}z, \end{equation}

we see that

(4.7)\begin{equation} \frac{\mathrm{d} E}{\mathrm{d} t} = \int^\infty_{-\infty}e \frac{\partial n_e}{\partial t} \phi\,\mathrm{d}z. \end{equation}

The electric potential is set by Poisson's equation (3.1), so

(4.8)\begin{equation} e \frac{\partial n_e}{\partial t} = \varepsilon_0 \frac{\partial^3 \phi}{\partial t \partial z^2} \end{equation}

(noting that $\partial n_i/\partial t = 0$). Substituting (4.8) into (4.7) and integrating by parts yields

(4.9)\begin{equation} \frac{\mathrm{d} }{\mathrm{d} t}\left(E + \int^\infty_{-\infty} \frac{\varepsilon_0}{2}\left(\frac{\partial \phi}{\partial z}\right)^2 \,\mathrm{d}z\right) = 0. \end{equation}

As the Debye length is typically extremely short compared with the size of the plasmoid, the electric field stores very little energy compared with the electrons;

(4.10)\begin{equation} \frac{\varepsilon_0\left(\dfrac{\partial \phi}{\partial z}\right)^2}{p_e} \sim \frac{\varepsilon_0\left(\dfrac{\phi_m}{L_p}\right)^2}{p_e} \sim \frac{\left(\dfrac{\varepsilon_0 T}{e^2 n_e}\right)}{L_p^2} = \left(\frac{\lambda_D}{L_p}\right)^2 \ll 1 \end{equation}

for $\lambda _D$ the Debye length, $L_p$ the plasmoid length, where $\phi _m \sim T/e$, $p_e = n_e T$ and $\partial /\partial z \sim 1/L_p$ have been assumed.

Thus, the energy balance with a short Debye length is well-approximated by

(4.11)\begin{equation} \frac{\mathrm{d} E}{\mathrm{d} t} = 0, \end{equation}

meaning that the line-integrated electron kinetic energy remains essentially constant.

5. Numerical implementation

5.1. Dimensionless scaling

For the purpose of numerics, we use a dimensionless scaling

(5.1a–e)\begin{equation} f^* = \frac{2{\rm \pi} K_m}{m_e^2}f,\quad K^* = \frac{K}{K_m},\quad H^* = \frac{H}{H_m},\quad \phi^* = \frac{\phi}{\phi_m},\quad \mathcal{E}^* = \frac{\mathcal{E}}{e\phi_m}, \end{equation}

where $K_m$ and $H_m$ are the values of $K$ and $H$ at $\mathcal {E} = 0$, respectively (their maximum values for an energy-trapped electron). The resulting kinetic equation is

(5.2)\begin{align} \frac{\partial f^*}{\partial t} & = \frac{\partial }{\partial K^*}\left[\left(K^* \frac{\mathrm{d} \ln K_m}{\mathrm{d} t} + \frac{e^4 \ln \varLambda}{2 {\rm \pi}\varepsilon_0^2 K_m}N^*_{K^*}\right)f^*\right]\nonumber\\ & \quad + \frac{\partial }{\partial K^*}\left[\frac{e^4 \ln \varLambda}{2{\rm \pi} \varepsilon_0^2 K_m}H^*\left(\frac{2}{3}E^*_{K^*} + K^*M^*_{K^*}\right)\frac{\partial f^*}{\partial K^*}\right], \end{align}

where

(5.3)\begin{equation} \left.\begin{gathered} K^* = \left. \oint_s \left(\mathcal{E}^* + \phi^*\right)^{3/2} \,\mathrm{d}z \right/ \oint_s \left(\phi^*\right)^{3/2} \mathrm{d}z, \\ K_m = \frac{2}{3} \sqrt{2m_e} \left(e\phi_m\right)^{3/2} \oint_s \left(\phi^*\right)^{3/2}\, \mathrm{d}z, \\ H^* = \left.\oint_s \left(\mathcal{E}^* + \phi^*\right)^{1/2} \,\mathrm{d}z \right/ \oint_s \left(\phi^*\right)^{1/2}\, \mathrm{d}z, \\ H_m = \sqrt{2m_e} \left(e\phi_m\right)^{1/2} \oint_s \left(\phi^*\right)^{1/2} \,\mathrm{d}z, \\ N^*_{K^*} = \int^{K^*}_0 {f^*}^\prime\,\mathrm{d}{K^*}^\prime = N_K, \\ E^*_{K^*} = \frac{3}{2}\int^{K^*}_0 {f^*}^\prime \frac{{K^*}^\prime}{{H^*}^\prime}\,\mathrm{d}{K^*}^\prime = \frac{H_m}{K_m}E_K, \\ M^*_{K^*} = \int^\infty_{K^*} {f^*}^\prime \frac{\mathrm{d}{K^*}^\prime}{{H^*}^\prime} = H_m M_K, \end{gathered}\right\} \end{equation}

and $\oint _s$ in the absence of $\mathcal {E}^*$ in the integrand corresponds to $2\int ^{\infty }_{-\infty }$.

5.2. Numerical scheme and the self-consistent electric potential

The numerical package FiPy (Guyer, Wheeler & Warren 2009) was used to solve (5.2). The solver uses explicit time-stepping, and is based on the finite-volume method, so manifestly conserves particles. Energy is not manifestly conserved, and is a significant challenge with such a nonlinear collision operator. Obtaining sufficient energy conservation typically requires a very fine $K^*$ grid, small time-stepping and multiple linear sweeps within a timestep.

Supposing that the electric potential is self-consistent at a given timestep, it is no longer self-consistent after $f^*$ has been advanced by (5.2). The new self-consistent electric potential must be found before the next timestep. Therefore, we introduce a ‘dummy’ time variable $s$ between timesteps, which is used in the procedure that finds the self-consistent potential.

As $n_i$ is specified, and $n_e(z) = g[f](\phi (z))$ for the functional $g[f]$ (namely, (B9)), we may simply invert $g[f]$ to find the $\phi$ that gives $n_e = n_i$ at each point. However, the distribution function must change if the potential changes. Therefore, any change in the potential requires solving the kinetic equation excluding the effect of collisions that alter energy:

(5.4)\begin{equation} \frac{\partial f^*}{\partial s} = \frac{\partial }{\partial K^*}\left(K^* \frac{\mathrm{d} \ln K_m}{\mathrm{d} t}f^*\right). \end{equation}

Thus, we iteratively solve for $\phi$ via inversion of $g[f]$, then update $f$ via the above equation. After many iterations, $n_e$ approaches $n_i$ and, consequently, $\phi$ approaches the self-consistent value given by quasineutrality.

5.3. Ion profile

Any symmetric single-peak ion profile may be used within the model. In this paper, we take the Gaussian profile from the self-similar plasmoid expansion in Aleynikov et al. (2019), which provides a qualitative picture for the shape of a pellet plasmoid. We choose the ion density to be this Gaussian profile plus a constant density of ambient ions:

(5.5)\begin{equation} n_i = n_a + N_{ip} \frac{1}{\sqrt{\rm \pi}}\frac{1}{L_p} \mathrm{e}^{-\left({z}/{L_p}\right)^2}, \end{equation}

where $n_i$ is the effective density of singly charged ions, $N_{ip}$ is the line-integrated density of ‘plasmoid ions’ (associated with the excess density) and $L_p$ is the length of the plasmoid. The ion profile qualitatively corresponds to that shown in figure 1.

6. Results

The plasma parameters $n_a = 2\times 10^{19}\ \mathrm {m}^{-3}$, $T_a = 2\ \mathrm {keV}$ relevant for W7-X were chosen for the numerical studies. With these parameters (given Coulomb logarithm $\ln \varLambda := 15$), the heating collision time

(6.1)\begin{equation} \tau_0 = \frac{6\sqrt{2}{\rm \pi}^{3/2}\varepsilon_0^2 m_e^{1/2} T_a^{3/2}}{n_a e^4 \ln\varLambda} \end{equation}

is approximately $100\ \mathrm {\mu } \mathrm {s}$.

Two connection lengths and two line-integrated plasmoid densities were chosen, $L_F = 50\ \mathrm {m}$, $200\ \mathrm {m}$ and $N_{ip} = 10^{21}\ \mathrm {m}^{-2}$, $10^{22}\ \mathrm {m}^{-2}$, respectively, giving four numerical runs in total.

The plasmoid length was chosen to be $L_p = 1\ \mathrm {m}$, much smaller than the connection length. The initial electron distribution was set to a Maxwellian of temperature $T = 200\ \mathrm {eV}$ in the core (energy-trapped electrons) and a Maxwellian of temperature $T_a$ in the tail (energy-passing electrons). The two Maxwellians were splined together in the region $-T \ll \mathcal {E} < 0$. A self-consistent quasineutral electric potential was used throughout.

The line-integrated densities were chosen to be representative of those found during fuel pellet injection in W7-X; the lower line-integrated density is found in the extremity of the transverse plasmoid profile, and the higher found near the core. Arnold et al. (2021, § 2) contains the corresponding analysis of how the W7-X pellet gas cloud deposits plasma on a field line, as well as estimates of line-integrated densities according to transverse gas cloud sizes observed by survey cameras (Baldzuhn et al. 2019, HFS in figure 4(2)).

In terms of analysing the problem at hand, it is important to note that the choices of $N_{ip}$ and $L_F$ lead to a variety of regimes. Namely, for $L_F = 50\ \mathrm {m}$ the ambient plasma is quenched, owing to the large deposition of material relative to the ambient plasma, but for $L_F = 200\ \mathrm {m}$ the quenching is less severe. Here $L_F = 200\ \mathrm {m}$ is approaching the limit of an infinitely long field line and leads to a visible boundary layer near $\mathcal {E} = 0$. However, for $L_F = 50\ \mathrm {m}$, the distinction between energy-passing electrons and energy-trapped electrons is less pronounced: we observe no boundary layer for this connection length.

As the plasmoid is initially much colder than the ambient plasma, we can estimate the ratio $T_\mathrm {final}/T_a$ by the dilution formula

(6.2)\begin{equation} \frac{T_\mathrm{final}}{T_a} = \frac{n_a L_F}{n_a L_F + N_{ip}}. \end{equation}

For the given $N_{ip}$, $L_F$ combinations, the ratio above may vary from $0.1$ to $0.8$, ranging from extreme quenching to minimal perturbation of the ambient temperature.

Figures 2 and 3 show the $L_F = 200\ \mathrm {m}$ runs. Figures 4 and 5 show the $L_F = 50\ \mathrm {m}$ runs. In all cases, the energy-trapped electron temperature $T$, trapped and passing electron densities $n_{t}, n_{p}$, electric potential $\phi$, and peak potential $\phi _m$ are plotted as time series. The distribution function at various times is also plotted. Here $T$ is estimated from a least-squares fit of a Maxwellian distribution to the energy-trapped distribution. For comparison, the temperature curve in the case of no potential (a homogeneous plasma) is plotted. This curve is obtained evolving the system of superposed Maxwellians of temperatures $T$ and $T_a$, respectively with line-integrated densities and kinetic energies corresponding to those of the energy-trapped and energy-passing distributions. The details are contained in Appendix C. The potential arising from the Boltzmann relation $e\phi = T \ln (n/n_a)$ is shown for comparison with $\phi$, indicating the effect of the non-Maxwellian distribution function on the self-consistent potential.

Figure 2. (a–d) Time series of the energy-trapped electron temperature $T$, trapped and passing electron densities $n_t$, $n_p$, electric potential peak $\phi _m$ and electric potential $\phi$. In (a), the final (equilibrated) temperature is given by the horizontal black dashed line. (e–h) Plots of the distribution function $f$ at various times.

Figure 3. (a–d) Time series of the energy-trapped electron temperature $T$, trapped and passing electron densities $n_t$, $n_p$, electric potential peak $\phi _m$ and electric potential $\phi$. In (a), the final (equilibrated) temperature is given by the horizontal black dashed line. (e–h) Plots of the distribution function $f$ at various times.

Figure 4. (a–d) Time series of the energy-trapped electron temperature $T$, trapped and passing electron densities $n_t$, $n_p$, electric potential peak $\phi _m$ and electric potential $\phi$. In (a), the final (equilibrated) temperature is given by the horizontal black dashed line. (e–h) Plots of the distribution function $f$ at various times.

Figure 5. (a–d) Time series of the energy-trapped electron temperature $T$, trapped and passing electron densities $n_t$, $n_p$, electric potential peak $\phi _m$ and electric potential $\phi$. In (a), the final (equilibrated) temperature is given by the horizontal black dashed line. (e–h) Plots of the distribution function $f$ at various times.

In all cases, it is evident that $T$ increases more slowly in the presence of the potential well. The well grows in height as $T$ increases. More electrons become trapped as $\phi _m$ increases. The distribution function resembles Maxwellians of different temperatures at each end of the $\mathcal {E}$ domain. They smoothly spline together in the intermediate region, with the exception of a small boundary layer formed near $\mathcal {E} = 0$. This boundary layer is only clearly visible with $L_F = 200 \mathrm {m}$. The boundary layer for the $N_{ip} = 10^{22}\ \mathrm {m}^{-2}$, $L_F = 200 \mathrm {m}$ run at $200\ \mathrm {\mu } \mathrm {s}$ is plotted in figure 6.

Figure 6. Distribution function near the boundary layer at $t = 200\ \mathrm {\mu }\mathrm {s}$ for $N_{ip} = 10^{22}\ \mathrm {m}^{-2}$ and $L_F = 200\ \mathrm {m}$.

After many collision times (several times $\tau _0$ (6.1) if the ambient plasma is not quenched), the distribution function becomes a Maxwellian of a single temperature. A limitation of the numerics is that the distribution function does not reach a perfect Maxwellian without an arbitrarily fine $K^*$ grid, explaining the small discrepancy in the final temperature in some plots despite the long evolution.

7. Discussion

The main result is that temperature equilibration between the energy-trapped and energy-passing electrons occurs more slowly than if no well is present. We also see that the distribution function is essentially Maxwellian for energy-trapped electrons. For $L_F = 200\ \mathrm {m}$, we observe a boundary-layer structure near $\mathcal {E} = 0$.

The reduced heating and essentially Maxwellian energy-trapped distribution are due in part to the change in the nature of collisions in the well, and can be explained by inspecting the friction and heating terms in the integrated collision operator. Namely, the collisional friction against the energy-trapped population experienced by energy-trapped electrons in the tail of the distribution is approximately

(7.1)\begin{equation} \left\langle C\right\rangle_\mathrm{friction} = \frac{e^4 \ln \varLambda}{2{\rm \pi}\varepsilon_0^2} \frac{1}{H} \frac{\partial }{\partial \mathcal{E}}\left(N_{\mathcal{E} = 0} f_\mathrm{tail}\right), \end{equation}

and the heating by energy-passing electrons experienced by core energy-trapped electrons is approximately

(7.2)\begin{equation} \left\langle C\right\rangle_\mathrm{heating} = \frac{e^4 \ln\varLambda}{2{\rm \pi}\varepsilon_0^2}\frac{1}{H}\frac{\partial }{\partial \mathcal{E}}\left(KM_{\mathcal{E} = 0} \frac{\partial f_\mathrm{core}}{\partial \mathcal{E}}\right). \end{equation}

Therefore, the $\mathcal {E}$-convection coefficient due to friction against the energy-trapped population is proportional to $H^{-1}$. The $\mathcal {E}$-diffusion coefficient due to heating of the energy-trapped population by the energy-passing population is proportional to $KH^{-1}$.

The strength of friction and heating in the presence of the potential may be compared with that when there is no potential. An analytical estimate for the relative strength of the heating in the well can be made by assuming that the potential is a cut-off parabola. As the coldest electrons (those with energy $\mathcal {E} \sim -e\phi _m$) are essentially confined to the peak of the potential, a cut-off parabola is a good model for understanding the dynamics of these electrons (in Aleynikov et al. (2019), the potential was modelled as a parabola for all $z$).

On a closed field line of connection length $L_F$ with no electric potential,

(7.3a,b)\begin{equation} H_F = 2\sqrt{2m_e}L_F\sqrt{\mathcal{E}+e\phi_m},\quad K_F = \tfrac{4}{3}\sqrt{2m_e}L_F\left(\mathcal{E}+e\phi_m\right)^{3/2}. \end{equation}

For a cut-off parabolic potential

(7.4)\begin{equation} e\phi = \begin{cases} e\phi_m\left(1 - \left(\dfrac{z}{L_p}\right)^2\right), & |z| < L_p, \\ 0, & |z| > L_p, \end{cases} \end{equation}

$H$ and $K$ for $\mathcal {E} < 0$ are given by

(7.5a,b)\begin{equation} H_\mathrm{par} = {\rm \pi}\sqrt{2m_e}\left(\mathcal{E}+e\phi_m\right)\frac{L_p}{\sqrt{e\phi_m}},\quad K_\mathrm{par} = \frac{1}{2}{\rm \pi}\sqrt{2m_e}\left(\mathcal{E}+e\phi_m\right)^2\frac{L_p}{\sqrt{e\phi_m}}. \end{equation}

Thus, the strengths of friction and heating in a cut-off parabolic potential well relative to those on a closed field line with no well (i.e. a homogeneous plasma) are

(7.6)\begin{gather} \mathrm{rel.\ friction} = H_\mathrm{par}^{{-}1}/H_F^{{-}1} = \frac{2}{\rm \pi}\frac{L_F}{L_p}\sqrt{\frac{e\phi}{\mathcal{E} + e\phi_m}}, \end{gather}

(7.7)\begin{gather}\mathrm{rel.\ heating} = \left.\frac{K_\mathrm{par}}{H_\mathrm{par}}\right/\frac{K_F}{H_F} = \frac{3}{4}. \end{gather}

Relative heating and friction may of course also be calculated using numerical results; these are plotted in figure 7 for the final timestep of the $N_{ip} = 10^{22}\ \mathrm {m}^{-2}$ and $L_F = 200\ \mathrm {m}$ run.

Figure 7. Friction and heating rates for energy-trapped electrons relative to a homogeneous plasma for the last timestep of the $N_{ip} = 10^{22}\ \mathrm {m}^{-2}$ and $L_F = 200\ \mathrm {m}$ run. In the relative friction plot, the width of the parabolic potential was chosen to best match the $\phi$ profile.

In essence, hot energy-trapped electrons experience very strong friction due to the fact that they are confined to the well and collide with the cold population very frequently. This explains the strongly Maxwellian energy-trapped distribution.

The relative heating is of particular interest, because it is analytically predicted to be $3/4$ in all cases, as long as the potential is parabolic near its peak. The length of the field line, the length of the plasmoid, and line-integrated plasmoid density do not affect this heating rate. This can be understood by noting that a passing electron will, in the course of its orbit, traverse the entire field line, which includes the entire plasmoid; every passing electron ‘sees’ every trapped electron on its orbit. The line-integrated plasmoid density is irrelevant to the heating by passing electrons, because the heating rate is, by definition, per electron. The mere fact that the coldest electrons are trapped in a parabolic well is responsible for the factor $3/4$.

The physical origin of the reduced heating is the acceleration of passing electrons through the well, which increases their kinetic energy but decreases their collisionality. These effects counteract each other, with the decrease in collisionality being dominant.

Although collisional heating is combined with many other effects, we find that the $3/4$ estimate is very accurate during the linear phase of heating, as plotted in figure 8.

Figure 8. Linear phase of heating in numerical runs, and a comparison with the heating in a homogeneous plasma given a collision frequency reduced to $3/4$ its usual value.

The reduction in heating and increase in friction are purely collisional effects. However, particle exchange between the energy-trapped and energy-passing distributions may also contribute to heating or cooling of the energy-trapped population. To see this, we write

(7.8)\begin{gather} n_{t} = \frac{4{\rm \pi}}{m_e^2}\int^{K_m}_{K(\mathcal{E} ={-}e\phi)} f m_e v\,\mathrm{d}K, \end{gather}

(7.9)\begin{gather}W_{K_m} = \frac{2{\rm \pi}}{m_e^2}\int^{K_m}_0 \mathcal{E} f\,\mathrm{d}K, \end{gather}

(7.10)\begin{gather}E_{K_m} = W_{K_m} + \int^\infty_{-\infty}e n_{t}\phi\,\mathrm{d}z, \end{gather}

which are the density, line-integrated energy density and line-integrated kinetic energy density of energy-trapped electrons, respectively. We find that

(7.11)\begin{equation} \frac{\mathrm{d} E_{K_m}}{\mathrm{d} t} = \int^\infty_{-\infty}e \frac{\partial n_{t}}{\partial t}\phi\,\mathrm{d}z + \frac{2{\rm \pi}}{m_e^2}\int^{K_m}_0 \mathcal{E} \left\langle C\right\rangle\mathrm{d}K, \end{equation}

so the energy-trapped distribution may gain energy collisionlessly if the energy-trapped density changes. The density can change due to electrons passing from positive to negative energies; an electron with energy $\mathcal {E} + \delta$, just above the separatrix, finds itself below the separatrix if the well increases in height by more than $\delta$. This is referred to as collisionless capture. The kinetic energy of the newly trapped electron, $e\phi$, contributes to the line-integrated kinetic energy density of energy-trapped electrons. As the energy-trapped distribution gains particles in its tail, the average electron energy will increase, consequently increasing the temperature. If instead the well becomes shallower, the inverse process occurs, causing cooling of the energy-trapped distribution due to the loss of the hottest electrons.

One remaining feature of the numerics is the boundary layer formed near $\mathcal {E} = 0$ with $L_F = 200\ \mathrm {m}$ (magnified in figure 6). Friction experienced by electrons goes as $H^{-1}$, which is plotted for $N_{ip} = 10^{22}\ \mathrm {m}^{-2}$ and $L_F = 200\ \mathrm {m}$ in figure 9. We note that friction increases rapidly as $\mathcal {E}\rightarrow 0^+$, resulting in ‘piling up’ of energy-passing electrons falling into the energy-trapped distribution. This can be understood within the parabolic-well model: energy-trapped electrons have $H \approx H_\mathrm {par}$, and energy-passing $H \approx H_F$, so we refer to (7.6) for the relative amounts of friction experienced by these electrons. The fact that relative friction is proportional to $L_F/L_p$ explains the appearance of the boundary layer when $L_F$ is large.

Figure 9. Plot of $H^{-1}$ at $t = 200\ \mathrm {\mu } \mathrm {s}$ for $N_{ip} = 10^{22}\ \mathrm {m}^{-2}$ and $L_F = 200\ \mathrm {m}$.

If we wish to consider the effect of bounce-integrated collisions of test particles with a Maxwellian, we may simply substitute a Maxwellian $f_M$ of temperature $T$ and density $n_M$ into the integral terms of the collision operator $\left \langle C\right \rangle$. Then, we obtain a collision operator with integrated Chandrasekhar functions:

(7.12)\begin{equation} \left\langle C\right\rangle(f,f_M) = \frac{n_M e^4 \ln\varLambda}{4{\rm \pi}\varepsilon_0^2 m_e^2}\frac{1}{\displaystyle v \oint_s v^\prime\,\mathrm{d}z^\prime }\frac{\partial }{\partial v}\left(2x^2 \left\langle G_F\right\rangle(x) f + \left\langle G_D\right\rangle(x) v \frac{\partial f}{\partial v}\right), \end{equation}

where $x = v/v_T$, $v^\prime = \sqrt {v^2 + (2/m_e)(e\phi ^\prime - e\phi )/T}$ for primes indicating an argument $z^\prime$, and

(7.13)\begin{gather} \left\langle G_F\right\rangle(x) = \frac{2}{x^2 \sqrt{\rm \pi}} \int^x_0 y\mathrm{e}^{{-}y^2}\oint_s y^\prime\,\mathrm{d}z^\prime \,\mathrm{d} y, \end{gather}

(7.14)\begin{gather}\left\langle G_D\right\rangle(x) = \frac{2}{3x^2\sqrt{\rm \pi}}\left(2\int^x_0 y \mathrm{e}^{{-}y^2} \oint_s \left(y^\prime\right)^3\,\mathrm{d}z^\prime \mathrm{e}^{{-}y^2}\,\mathrm{d} y + \mathrm{e}^{{-}x^2}\oint_s \left(x^\prime\right)^3\,\mathrm{d}z^\prime\right), \end{gather}

where $y^\prime = \sqrt {y^2 + (e\phi ^\prime - e\phi )/T}$ and $x^\prime = \sqrt {x^2 + (e\phi ^\prime - e\phi )/T}$. When $\phi = 0$, both $\left \langle G_F\right \rangle$ and $\left \langle G_D\right \rangle$ become the Chandrasekhar function $G(x) = (\mathrm {erf}(x)-(2/\sqrt {{\rm \pi} })x\exp (-x^2))/(2x^2)$, recovering the usual collision operator against a Maxwellian.

Velocity moments of the collision operator (7.12) could be taken to obtain a closure for a fluid system which takes into account the bounce motion of electrons, recovering the corrected heating and friction which arises due to trapped and passing orbits.

8. Conclusions and future work

Despite the seemingly complicated nature of the electron kinetic problem in a self-consistent electric potential, useful conclusions can be drawn about the effect of the potential on the heating and friction experienced by trapped electrons. Namely, owing to the facts that the potential well is deep relative to the plasmoid electron temperature and has a parabolic peak, trapped electrons experience exactly 3/4 the collisional heating by ambient electrons than if no well were present. The trapped electron distribution is also very close to Maxwellian, owing to the increased convection of hot energy-trapped electrons to the core.

As plasmoid electron heating is a consequence of collisions that alter energy, the observation of slower heating in the presence of a potential well suggests that the ordering (2.16) is strengthened by the presence of the well, so the integrated electron kinetic equation could possibly be applied to plasmoids with low-$Z$ ions. This would mean that the integrated kinetic equation may be appropriate for the electrons in the presence of the plasmoid produced during MCF fuel pellet injection. In addition, the reduced collisional heating rate could simply be implemented directly in a fluid model of the plasmoid electrons. A more rigorous approach to a fluid model involves taking moments of the integrated collision operator against a Maxwellian (7.12).

A boundary layer near $\mathcal {E} = 0$ was observed with a large connection length, the distribution resembling a lower-temperature Maxwellian for $\mathcal {E} < 0$ and a higher-temperature Maxwellian for $\mathcal {E} > 0$. Therefore, if we have a very large connection length, the model given by assuming that the distribution is two cut-off Maxwellians splined in some small region near $\mathcal {E} = 0$ could be appropriate. This would allow for simplification of the kinetic problem; only the tail of the energy-trapped electron distribution need be modelled kinetically. If the effect of the tail is insignificant, a fluid model concerning two Maxwellians would suffice.

Previous work on modelling the parallel expansion of fuel pellet plasmoids did not consider a self-consistent well, thereby overestimating the heating of plasmoid electrons (Aleynikov et al. 2019; Arnold et al. 2021; Runov et al. 2021). It was predicted that approximately 50 % of plasmoid electron heating power is transferred to ions in the form of flow velocity due to the ambipolar expansion. However, with the reduction in plasmoid electron heating, we expect an even larger transfer of energy to the ions (Runov et al. 2021), thereby increasing the plausibility of ambipolar expansion as a mechanism for an increased $T_i/T_e$ ratio after pellet injection in W7-X (Baldzuhn et al. 2019, 2020).

It should be noted that the invariant $K$ produced by the integrating procedure is constant for an electron experiencing only pitch-angle scattering and bounce motion. Therefore, the electron kinetic problem which uses the Lorentz scattering operator in place of the true collision operator can be compared with $(\partial f/\partial t)(K,t) = 0$.

Some studies of turbulent transport rely on the consideration of free energy while conserving invariants (Mackenbach, Proll & Helander 2022). For collisionless electrons, these invariants are usually chosen to be the magnetic moment and second adiabatic invariant. However, in the presence of strong pitch-angle scattering, $K$ is conserved instead: the effect of this on the minimisation of electron free energy should be investigated.