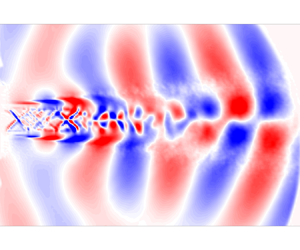
1. Introduction
It has been known since the 1960s that the shear layer in a free jet is unstable to small perturbations over a wide range of frequencies (Michalke Reference Michalke1965a). This instability is called the Kelvin–Helmholtz (K-H) instability. The presence of coherence structures (CS) generated by the K-H instability in the shear layer of a jet was identified by Michalke (Reference Michalke1965b), and was verified experimentally by Mollo-Christensen (Reference Mollo-Christensen1967) and Crow & Champagne (Reference Crow and Champagne1971) in axisymmetric jets. These flow structures are often called coherent structures, large-scale structures or instability waves, and they can be visualized experimentally around the end of the potential core of a free jet (Ho & Huerre Reference Ho and Huerre1984; Samimy, Webb & Crawley Reference Samimy, Webb and Crawley2018). The wave packet models used in the recent literature (e.g. Jordan & Colonius Reference Jordan and Colonius2013) are a mathematical representation of the growth, saturation and decay of these CS. We have used large-scale structures, rather than coherent structures, in our past publications. However, since we use LAFPAs to change the size of these structures significantly, it seems more appropriate to call them CS. The passage frequency of CS in an axisymmetric jet scales with the nozzle exit diameter (De) and velocity (Ue), St = f De/Ue, and is typically centred around St = 0.3 (Crow & Champagne Reference Crow and Champagne1971). This instability mode is called the jet column mode (JCM) or the jet preferred mode. There is another instability mode in free jets called the shear layer mode, the frequency of which scales with the shear layer momentum thickness (θ). Further details on these instabilities can be found in Samimy et al. (Reference Samimy, Webb, Esfahani and Leahy2023).
Lighthill's pioneering work (Reference Lighthill1952, Reference Lighthill1954) established a theoretical basis for the far-field (FF) noise generated by subsonic jets, and further experimental studies demonstrated that the peak FF noise is primarily generated by CS (Arndt, Long & Glauser Reference Arndt, Long and Glauser1997). Tam (Reference Tam1972, Reference Tam1975) was the first to identify noise generation mechanisms in ideally expanded supersonic jets. The CS interact with shock cells in supersonic jets operating at off-design conditions to generate broadband shock-associated noise (BBSAN) (Tam & Tanna Reference Tam and Tanna1982; Tam Reference Tam1995). The upstream travelling component of these acoustic waves perturbs the jet shear layer at the most receptive location near the nozzle exit, exciting the K-H instability and thereby generating CS (Powell Reference Powell1953). When the phase of the interference of the perturbations at the nozzle exit and the generation of CS are synchronized, a self-sustained feedback loop is established, and a high-amplitude tonal noise, called screech, is generated (Powell Reference Powell1953). Since the screech frequency is the passage frequency of CS, it is always within the JCM. The feedback process has also been attributed to guided jet modes (e.g. Tam and Hu Reference Tam and Hu1989; Nogueira & Edgington-Mitchell Reference Nogueira and Edgington-Mitchell2021). In screeching twin jets, the acoustic and flow fields of the jets can couple and significantly affect the near-field (NF) pressure fluctuations and FF noise (Raman & Taghavi Reference Raman and Taghavi1998; Kuo, Cluts & Samimy Reference Kuo, Cluts and Samimy2017; Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). Therefore, all major components of noise (mixing, BBSAN, screech) and coupling in twin jets arise due to CS and the mitigation of jet NF pressure fluctuations or FF noise, requires the development of CS to be controlled.
The foundation of active flow control using excitation of instabilities in the shear layers of jets was established in the 1960s–1980s (see Ho & Huerre Reference Ho and Huerre1984; Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). The earlier works were primarily focused on incompressible, low-speed and low Reynolds number shear layers and jets. In these works, loudspeakers were used to generate perturbations for the excitation of instabilities; however, they proved incapable of generating perturbations of sufficient amplitude for control of high-speed and high Reynolds-number flows (Kibens Reference Kibens1980). We have developed a class of plasma actuators, localized arc filament plasma actuators (LAFPAs), that can provide localized thermal perturbations with high amplitude over a wide band of frequencies for excitation of instabilities in high-speed, high Reynolds-number jets (Samimy et al. Reference Samimy, Kim, Kastner, Adamovich and Utkin2007). The frequency and phase of these actuators are controlled independently, allowing several of them to be used collectively to excite the jet shear layer or jet column mode and/or coupling in twin jets (Samimy et al. Reference Samimy, Webb and Crawley2018, Reference Samimy, Webb, Esfahani and Leahy2023). The actuators are not just used to control the development of CS in jets but also to help explore the flow physics.
The work presented in this manuscript is a continuation of our previous work involving active flow control using plasma actuators in unheated supersonic rectangular twin jets (SRTJ) (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). The focus of the current work is on exploring control of the coupling of the jets and their NF pressure/acoustics in heated SRTJ from overexpanded to design conditions. Section 2 briefly describes the experimental facility, plasma actuators and diagnostic tools and analyses. Section 3 summarizes our earlier work on unheated SRTJ and presents baseline results, including frequency scaling, screech and coupling and FF acoustics. Section 4 discusses the effects of control on coupling, NF pressure fluctuations and FF acoustics. In addition, it briefly covers the effects of coupling on NF pressure/acoustics. Finally, § 5 summarizes the conclusions of this work.
2. Experimental set-up and instrumentation
The SRTJ experimental apparatus and instrumentation used for this work is the same as the one used in Samimy et al. (Reference Samimy, Webb, Esfahani and Leahy2023). However, a heater was added to the air supply line to heat the air, and some modifications were necessary to allow the apparatus to withstand the elevated flow temperatures. A brief description of the apparatus, the heating system and the measurement tools is provided in this section. Interested readers can get more detailed information in Samimy et al. (Reference Samimy, Webb, Esfahani and Leahy2023). Figure 1 shows the SRTJ assembly, the coordinate system and major and minor axes of the SRTJ, the inner contour of one of the nozzles, and the installation of the SRTJ within the anechoic chamber at the Gas Dynamics and Turbulence Laboratory (GDTL). The wall-to-wall dimensions of the chamber are 6.2 m by 5.6 m by 3.4 m. The cut-off frequency of the anechoic chamber is 160 Hz. For acoustic measurements, all reflecting surfaces within the anechoic chamber, except the nozzles’ exit faces, were covered by acoustic foam to avoid acoustic reflection from these surfaces. Two biconic (‘military-style’), rectangular, converging–diverging nozzles with a design Mach number of 1.5 (Md = 1.5) and an aspect ratio of 2 (AR = 2) were used. The nozzle exit width (w) and height (h) of each nozzle are 24.13 mm and 12.07 mm, respectively. The area-based equivalent diameter (De) of each nozzle is 19.25 mm, and the centre-to-centre spacing between the nozzles is 43.38 mm (2.25De).

Figure 1. The SRTJ assembly (a), nozzle internal contour (b), SRTJ in anechoic chamber at GDTL (c) and NF azimuthal microphone array (d). The SRTJ coordinate system, major and minor axes, and azimuthal angle (φ) are defined in (a). The polar angle (θ) is defined in (c).
The stagnation pressure of the flow is set by a computer-controlled valve, which automatically maintains the desired nozzle pressure ratio (NPR), i.e. the ratio of jet stagnation to ambient pressure. For this work, the NPR was varied from 2.77 to 3.67 (fully expanded Mach number, Mj = 1.30 to 1.50), covering flows from the overexpanded regime to the design Mach number. This facility can deliver heated flow up to a total temperature ratio (TTR) of 2.5. An offline heating system is utilized, with a heat storage tank (HST) that is preheated prior to a run and subsequently raises the temperature of the pressurized flow passing through it. The HST is a 3.5 m (138 in.) tall by 0.3 m (12 in.) diameter cylinder containing four sets of vertically aligned rows of stainless-steel plates. Indoor laboratory air is drawn in through a blower, heated by a 15 kW Watlow heater, and sent through the HST, thus heating the stainless-steel plates to equilibrium at a set temperature. Six band heaters, consisting of four 1 kW vessel band heaters and two 0.5 kW pipe heaters on the flanges, help reduce heat loss of the hot high-pressure air to maintain the desired stagnation temperature of the jet for a longer time. The air flow capacity is sufficiently large for the experiments to run unheated flow continuously. However, the run time for heated flow (as in the current experiments) is limited and ranged from 20 to 15 min. to maintain TTR = 2 ± 0.06 for Mj = 1.3 to 1.5, respectively.
The diverging section of the converging–diverging nozzles (figure 1b) is constructed from machinable boron nitride, a ceramic material with dielectric and thermal properties which enable it to withstand the high-temperature arc generated by the LAFPAs. Each jet has six LAFPAs, three each in the top and bottom (parallel to the major axis) lips of the nozzle (figure 2). Each actuator consists of two 1-mm diameter tungsten electrodes. One is grounded while the other is connected to an in-house-built, high-voltage pulse generator. Each actuator channel is individually computer controlled, allowing a wide selection of excitation conditions (various frequencies and relative phase delays between actuators) to be implemented.

Figure 2. Plasma actuators and excitation patterns for IP (a) and OOP (b) excitation of shear layers of the two jets.
A number of excitation Strouhal numbers and two actuation patterns (schematics shown in figure 2), one for in-phase (IP) and another for out-of-phase (OOP) coupling, were used in this work. All three actuators on each nozzle lip were fired simultaneously and 180° out of phase with those on the opposing lip of the same nozzle, consistent with the natural spatial flapping mode of these rectangular twin jets (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). This pattern was used to excite the two jets either IP, figure 2(a), or OOP, figure 2(b). More detailed information on LAFPAs can be found in Samimy et al. (Reference Samimy, Webb and Crawley2018).
The boundary layer at the nozzle exit of SRTJ is very thin, as the nozzles are quite short and the boundary layer inside the nozzle develops under a favorable pressure gradient. The boundary layer thickness is estimated to be of the order of 1 mm and the momentum thickness of the order of a fraction of a millimetre, making any meaningful velocity profile measurement a major challenge. A simplified experiment (Kearney-Fischer, Kim & Samimy Reference Kearney-Fischer, Kim and Samimy2009) showed the boundary layer is fully turbulent for Reynolds numbers (based on jet diameter) above 300 000. In the current heated SRTJ experiments with TTR = 2, the lowest Reynolds number (for Mj = 1.3) was approximately 322 000; thus, the boundary layer is probably turbulent at the nozzle exit. However, compressibility effects could result in a transitional boundary layer in the lowest NPR cases.
The SRTJ flow and acoustic fields were investigated using three primary flow diagnostics: a FF microphone array (figure 1c); a NF microphone array (figure 1d); a time-resolved schlieren imaging system. The FF microphone array consists of eight Brüel and Kjær ![]() ${\textstyle{1 \over 4}}$ in. microphones (model 4939) mounted at polar angles (θ) ranging from 30° to 90° as measured from the downstream jet axes (x) and aimed at the origin of the twin jets’ coordinate system (see figure 1a). The SRTJ assembly can be rotated to locate the FF microphone array on the plane of the SRTJs’ major axis (φ = 0°) or minor axis (φ = 90°). The NF microphone array consists of an azimuthal array with four similar microphones (figure 1d). The microphones were positioned at an axial location of x/De = 0 and radially (measured normal to the twin jets’ major axis) at r/De = 2 (for microphones 1 and 2) and r/De = 4 (for microphones 3 and 4). Microphones 1 and 2 were used to measure NF pressure fluctuations in the internozzle region (z/De = 0) and along one of the jets’ minor axes (z/De = +1.125), respectively. The main purpose of microphones 1 and 2 was to measure the NF pressure fluctuations due to screech and broadband shock-associated noise radiated towards the nozzle (aircraft body in application) and the effects of coupling of the twin jets on such pressure fluctuations. Previous works in the literature have shown a significant effect of coupling on NF pressure fluctuations (Zilz & Wlezien Reference Zilz and Wlezien1990; Raman & Taghavi Reference Raman and Taghavi1998).
${\textstyle{1 \over 4}}$ in. microphones (model 4939) mounted at polar angles (θ) ranging from 30° to 90° as measured from the downstream jet axes (x) and aimed at the origin of the twin jets’ coordinate system (see figure 1a). The SRTJ assembly can be rotated to locate the FF microphone array on the plane of the SRTJs’ major axis (φ = 0°) or minor axis (φ = 90°). The NF microphone array consists of an azimuthal array with four similar microphones (figure 1d). The microphones were positioned at an axial location of x/De = 0 and radially (measured normal to the twin jets’ major axis) at r/De = 2 (for microphones 1 and 2) and r/De = 4 (for microphones 3 and 4). Microphones 1 and 2 were used to measure NF pressure fluctuations in the internozzle region (z/De = 0) and along one of the jets’ minor axes (z/De = +1.125), respectively. The main purpose of microphones 1 and 2 was to measure the NF pressure fluctuations due to screech and broadband shock-associated noise radiated towards the nozzle (aircraft body in application) and the effects of coupling of the twin jets on such pressure fluctuations. Previous works in the literature have shown a significant effect of coupling on NF pressure fluctuations (Zilz & Wlezien Reference Zilz and Wlezien1990; Raman & Taghavi Reference Raman and Taghavi1998).
Microphones 3 and 4 were used to determine the strength and mode of the jets’ coupling under various excitation conditions. To assess the coupling, the Morlet wavelet-based coherence and phase between data collected by microphones 3 and 4 were calculated. The time-averaged wavelet coherence and phase were used to determine the jets’ coupling strength and mode, respectively. While all points were used when calculating the time-averaged coherence, only those instants at which coherence magnitude was greater than 0.7 were used when calculating the time-averaged phase. The relationship between the sampling frequency and the screech frequencies of interest gives a phase resolution that varies between 15° and 20°. Additionally, the bars plotted in conjunction with time-averaged phase curves (shown in later figures) represent the circular standard deviation (![]() $S = \sqrt {2(1 - |R|)} $ for small S, where R is the vector average of all measured phase unit vectors), a measure of the temporal variation of the phase.
$S = \sqrt {2(1 - |R|)} $ for small S, where R is the vector average of all measured phase unit vectors), a measure of the temporal variation of the phase.
The schlieren images were obtained using a standard Z-type arrangement. The collimated light beam was parallel to the twin jets’ major axis (see figure 1a) and passed through both jets. This provided a good view of the CS in the major axis shear layers on the plane of the twin jets’ minor axes and allowed the LAFPAs’ effects on the CS to be documented. The results were postprocessed using Ohio Supercomputer Center resources with a spectral proper orthogonal decomposition (SPOD) (Schmidt & Colonius Reference Schmidt and Colonius2020). The calculated SPOD mode shapes and mode energy spectra at various frequencies of interest were used to assess the response of the jets to the excitation and the nature of the CS in the baseline and the excited jets.
3. Results and discussions
The focus of the current work is on heated SRTJ. Detailed experimental results with TTR = 2.0 for baseline and controlled cases were obtained for NPR from 2.77 to 3.67 (fully expanded Mach number, Mj, of 1.30 to 1.50), covering overexpanded to design flow regimes. The effects of heating on screech, coupling and NF pressure fluctuations as well as the effects of control on heated SRTJ will be presented and discussed. First, a brief summary of the results in unheated SRTJ will be presented. Then the baseline results, including screech frequency scaling, coupling and the effects of coupling on NF pressure/acoustic fluctuations, will be presented and discussed.
3.1. Summary of previous results on unheated SRTJ
Detailed experimental work using the SRTJ set-up described above was used to investigate the physics of flow and acoustics in unheated jets from overexpanded to underexpanded flow regimes. A brief summary of the findings will be presented here to put the current heated SRTJ results in context. Details of the unheated SRTJ results have been reported in Leahy et al. (Reference Leahy, Esfahani, Webb and Samimy2023) and Samimy et al. (Reference Samimy, Webb, Esfahani and Leahy2023).
Coherence and phase analyses of NF acoustics using microphones 3 and 4 (figure 1) were used to show that SRTJ were coupled at the natural screech frequency over a wide range of jet Mach numbers with various strengths and phases. The coupling was primarily OOP and IP for the overexpanded and underexpanded regimes, respectively. The temporal phase variations were more prevalent in overexpanded, lower Mj, cases but decreased as Mj increased to underexpanded cases. For moderately underexpanded Mj cases, the coupling was strong and IP at the natural screech frequency. These findings are consistent with the ‘null space’ hypothesis of Raman and Taghavi (Reference Raman and Taghavi1998). It was shown using the LAFPAs’ unique control capabilities that switching coupling from IP to OOP for an overexpanded Mj case could reduce the NF overall sound pressure level (OASPL) by nearly 14 dB in the internozzle region (Leahy et al. Reference Leahy, Esfahani, Webb and Samimy2023; Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). The findings also confirmed the significant effects of coupling on NF acoustic fluctuations where IP coupling produces significantly higher-pressure fluctuations in the internozzle region than OOP coupling (Zilz & Wlezien Reference Zilz and Wlezien1990; Raman & Taghavi Reference Raman and Taghavi1998). A surprising finding was that the coupling is nearly inconsequential to the FF radiated acoustics.
The LAFPAs demonstrated significant control authority over a wide range of jet Mach numbers, and the shear layers of these shock-containing jets responded to perturbations over a wide range of frequencies, like those in low-speed and low Reynolds-number jets (Ho & Huerre Reference Ho and Huerre1984; Samimy et al. Reference Samimy, Webb and Crawley2018). In all explored cases, the jets responded to LAFPA excitation by producing CS at the excitation frequency. By strategically introducing CS to compete with or reinforce the CS associated with the baseline screech and coupling, the LAFPAs could enhance, alter or suppress coupling, depending on the actuation phase (Webb et al. Reference Webb, Esfahani, Yoder, Leahy and Samimy2022). Two different control techniques using LAFPAs were employed to reduce the FF peak noise and OASPL in the peak mixing noise direction by up to 2 dB (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023).
3.2. Screech frequency scaling in SRTJ
For frequency scaling in a rectangular jet with a small AR, an equivalent nozzle diameter, De (the diameter of a round nozzle of equivalent cross-sectional area), can be used in lieu of the nozzle exit diameter. For supersonic jets in off-design flow regimes, fully expanded flow properties (Tam & Tanna Reference Tam and Tanna1982), such as Uj and Dj, rather than the properties at the nozzle exit, are used. There is a shortage of data in the literature from rectangular converging–diverging nozzles. In Samimy et al. (Reference Samimy, Webb, Esfahani and Leahy2023), we plotted our own screech frequency data along with the data from Karnam, Baier & Gutmark (Reference Karnam, Baier and Gutmark2020), with nearly identical SRTJ geometry and AR, over a large range of jet Mach numbers (1.3 to 1.85). The data collapsed on a single curve using St = f De/Uj, except for one data point at Mj = 1.55 (near the design Mach number of 1.5 with a relatively weak screech tone), the reason for which will be further discussed later. In this paper, we will use the fully expanded jet equivalent diameter, Dj, rather than the nozzle exit equivalent diameter, to be consistent in the use of fully expanded parameters. The change shifts the curve slightly without changing its trend. While we are using the equivalent diameter for a length scale for our AR = 2 jets, Zaman, Fagan & Upadhyay (Reference Zaman, Fagan and Upadhyay2022) showed in subsonic jet experiments that for jets of higher AR (∼>4), the nozzle exit height is a more appropriate length scale.
Tam & Tanna (Reference Tam and Tanna1982) derived an empirical equation for BBSAN in off-design supersonic jets, and Tam, Seiner & Yu (Reference Tam, Seiner and Yu1986) used the weakest link theory, recognizing the nozzle lip to be the most receptive location for the shear layer excitation, to derive a general empirical equation for the screech frequency. They showed good agreement between the experimental screech frequencies and the prediction of this empirical equation. Tam (Reference Tam1988) extended this empirical equation to rectangular jets with a large aspect ratio, as follows:
 \begin{align}St_{s} &=
\frac{{f\kern0.06em h}}{{{U_j}}} =
\frac{{\dfrac{{{U_c}}}{{{U_j}}}}}{{2(1 + {U_c}/{a_\infty
})\sqrt {M_j^2 - 1} }}{\left[ {{{\left(
{\frac{{{h_j}}}{{{w_j}}}} \right)}^2} + 1}
\right]^{1/2}}\notag\\ &\quad \times {\left\{ {\left[ {{{\left( {\frac{{1 +
\dfrac{{\gamma - 1}}{2}M_j^2}}{{1 + \dfrac{{\gamma -
1}}{2}M_d^2}}} \right)}^{(\gamma + 1)/2(\gamma -
1)}}\frac{{{M_d}}}{{{M_j}}} - 1} \right]\frac{w}{{w + h}} +
1} \right\}^{ -
1}}.\end{align}
\begin{align}St_{s} &=
\frac{{f\kern0.06em h}}{{{U_j}}} =
\frac{{\dfrac{{{U_c}}}{{{U_j}}}}}{{2(1 + {U_c}/{a_\infty
})\sqrt {M_j^2 - 1} }}{\left[ {{{\left(
{\frac{{{h_j}}}{{{w_j}}}} \right)}^2} + 1}
\right]^{1/2}}\notag\\ &\quad \times {\left\{ {\left[ {{{\left( {\frac{{1 +
\dfrac{{\gamma - 1}}{2}M_j^2}}{{1 + \dfrac{{\gamma -
1}}{2}M_d^2}}} \right)}^{(\gamma + 1)/2(\gamma -
1)}}\frac{{{M_d}}}{{{M_j}}} - 1} \right]\frac{w}{{w + h}} +
1} \right\}^{ -
1}}.\end{align}Using AR = 2, the fully expanded equivalent diameter rather than the nozzle exit height, and our design Mach number (Md = 1.5) in the current work, Tam's equation (3.1) is reduced to (3.2) below. Note that in (3.1) and (3.2), the convective velocity (Uc) of CS is an empirical parameter which is difficult to measure experimentally. Tam et al. (Reference Tam, Seiner and Yu1986) and Tam (Reference Tam1988) used Uc = 0.7Uj in their empirical prediction. Gojon, Gutmark & Mihaescu (Reference Gojon, Gutmark and Mihaescu2019) used both numerical simulations and experimental results in an AR = 2 jet with TTR = 1 to 3 and compared the screech frequency with those predicted by (3.1). They observed a good agreement by varying Uc from 0.8Uj to 0.64Uj for TTR = 1 to 3, respectively. Chen, Gojon & Mihaescu (Reference Chen, Gojon and Mihaescu2021) also utilized numerical simulation to compare with experimental results for heated rectangular jet and noticed good agreement as well,
 \begin{align}St_{s} &=
\frac{{f{D_j}}}{{{U_j}}} =
\frac{{\dfrac{{{U_c}}}{{{U_j}}}}}{{2(1 + {U_c}/{a_\infty
})\sqrt {M_j^2 - 1} }}{\left[ {{{\left(
{\frac{{{h_j}}}{{{w_j}}}} \right)}^2} + 1}
\right]^{1/2}}\notag\\ &\quad \times {\left\{ {\left[ {{{\left( {\frac{{1 +
\dfrac{{\gamma - 1}}{2}M_j^2}}{{1 + \dfrac{{\gamma -
1}}{2}{{(1.5)}^2}}}} \right)}^{(\gamma + 1)/2(\gamma -
1)}}\frac{{1.5}}{{{M_j}}} - 1} \right]\frac{2}{3} + 1}
\right\}^{ -
1}}.\end{align}
\begin{align}St_{s} &=
\frac{{f{D_j}}}{{{U_j}}} =
\frac{{\dfrac{{{U_c}}}{{{U_j}}}}}{{2(1 + {U_c}/{a_\infty
})\sqrt {M_j^2 - 1} }}{\left[ {{{\left(
{\frac{{{h_j}}}{{{w_j}}}} \right)}^2} + 1}
\right]^{1/2}}\notag\\ &\quad \times {\left\{ {\left[ {{{\left( {\frac{{1 +
\dfrac{{\gamma - 1}}{2}M_j^2}}{{1 + \dfrac{{\gamma -
1}}{2}{{(1.5)}^2}}}} \right)}^{(\gamma + 1)/2(\gamma -
1)}}\frac{{1.5}}{{{M_j}}} - 1} \right]\frac{2}{3} + 1}
\right\}^{ -
1}}.\end{align}Figure 3 shows the normalized measured screech frequency for TTR = 1 and 2 for several Mj cases (from moderately overexpanded to the design) in comparison with the empirically predicted results of Tam (Reference Tam1988) using (3.2). As reported in Gojon et al. (Reference Gojon, Gutmark and Mihaescu2019), data for different TTRs segregate into different groups but follow similar trends, and to get a good agreement between the experimental and empirically predicted results for a given TTR, Uc values in (3.2) must be adjusted. For this work, Uc = 0.73Uj and 0.70Uj were used in (3.2) for TTR = 1 and 2, respectively. The comparison is remarkable over the entire Mj range for both TTR = 1 and 2, except for Mj > 1.4 (around the design Mach number) for TTR = 2. The maximum uncertainty in measured screech Strouhal number, for the cases plotted below, was ±0.012, further highlighting this agreement. Two sets of experimental data for TTR = 1 and 2 are shown in figure 3. These data sets were acquired on different days to evaluate the repeatability of the results. While the repeatability is excellent for the TTR = 1 case, there are some day-to-day variations for the TTR = 2 cases, which only become significant at and near the fully expanded cases. Recall that (3.2) was derived by Tam (Reference Tam1988) for a typical laboratory nozzle with no shock cells at the design Mach number. This is not the case for the military-style nozzles used in the current experiments. There are two segregated sets of data (circled for clarity) for Mj = 1.45 and 1.5 (design Mach number), with only one set agreeing with the empirical predictions.

Figure 3. Comparison of normalized experimental screech frequency with the empirical predictions of Tam (Reference Tam1988) using (3.2).
In a typical converging–diverging nozzle designed in a laboratory using the method of characteristics, there are no shock cells at the design condition (i.e. ideally expanded), but they appear in off-design conditions and become stronger further from the design condition. The nozzles used in the current work with the design Mach number (Md) of 1.5 are biconic with a sharp throat, like those in applications utilizing variable geometry nozzles. Therefore, there are two shock cell systems in these jets, one originating at the nozzle throat, which exists for all Mj cases, and another due to the pressure mismatch at the nozzle exit (only present under off-design conditions). Our previously presented schlieren images at TTR = 1 (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023) clearly showed the existence of two shock systems. It is clear from the results shown in figure 3 that the screech frequency due to the pressure mismatch at the nozzle exit dominates for Mj ≤ 1.4 at TTR = 2, and the experimental and empirically predicted results agree very well. However, the dominance between the two screech frequencies at Mj = 1.45 changes from day-to-day (see also figure 4). Note that day-to-day variation does not affect the peak frequencies but does change their amplitude. Additionally, the screech frequency from the nozzle throat shock system dominates at Mj = 1.5 (design Mach number). Figure 4, the NF acoustic power spectral density (PSD) (from microphone 4, figure 1), clearly shows switching of the dominance of screech tones at Mj = 1.45 from one day to another. Finally, note that Tam's empirical equation (see (3.2)) is derived for shock cells initiated due to pressure mismatch at the nozzle exit, using a quasiperiodic shock cell system. However, these assumptions are not satisfied in the shock train generated by the nozzle sharp throat, and therefore, one set of data agrees with Tam's empirical results and the other set does not.

Figure 4. Near-field acoustic PSD for Mj = 1.45 at TTR = 2 on two different days (day 2 shifted +20 dB on plot).
3.3. Screech and coupling in heated SRTJ
In unheated SRTJ, the coupling mode was primarily OOP in the overexpanded and IP in the underexpanded flow regimes (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). The general trends observed in the heated (TTR = 2) SRTJ results (limited to overexpanded and design conditions) are similar. Figure 5 shows time-averaged coherence and phase (between microphones 3 and 4) for TTR = 2 and Mj = 1.3, 1.4 and 1.5. For the overexpanded cases, the coupling is strong and OOP with a relatively constant phase. For the design Mach number (Mj = Md = 1.5), the coupling is quite weak (figure 5c), and the phase is intermittent (as inferred from the large bars at the screech frequency), varying near IP. The data for these three cases (figure 5a–c) were acquired on the same day. The screech tones were strong and sharp for the overexpanded cases, but not sharp or strong for the design case. For the design case, the screech was supported by the shock cell system originating at the nozzle throat (as determined by the dominant screech frequency) and competing with a very weak tone from the shock system due to a minor pressure mismatch at the nozzle exit (see also figure 3). Figure 5(d) shows the coherence and phase for the design case on a different day with the same NPR and TTR (within the tolerance of the system). The screech tone (not shown) is sharper and stronger (with no change in the frequency), the competing tone is significantly diminished (again with no change in the frequency) and the coupling is strong IP.

Figure 5. Coherence and phase for TTR = 2 at Mj = 1.3 (a), 1.4 (b) and 1.5 (c); data taken on the same day and Mj = 1.5 (d), data taken on a different day.
Screech and coupling in off-design SRTJ are first- and second-order resonance phenomena, respectively. Therefore, some day-to-day variations are expected in their strength and coupling phase. However, in the heated SRTJ cases, the observed day-to-day variations have been significant. A sample variation of coherence and phase in the design Mach number case was shown in figure 5. Figure 6 shows typical variations in results for an overexpanded (Mj = 1.3) case at TTR = 2 obtained on two different days. For Case 1 (figure 6a–c), the coupling is relatively strong and IP, but the phase is quite intermittent (figure 6a). For Case 2 (figure 6d–f), the coupling is significantly weaker, and the phase is still intermittent. Scrutiny of the NF and FF PSD indicates that there are two very closely spaced screech peaks at distinct frequencies for Case 1 (see figure 6c). In contrast, Case 2 (figure 6f) clearly has a single screech peak. In the dual-peaks case, the coupling is most likely switching between the two frequencies (hence the strong coupling with significant phase variations). In the single-peak case, it is likely that the jets coupled only intermittently (hence, the weak coupling and intermittent phase).

Figure 6. Coherence and phase between two jets (a,d) and NF and FF full (b,e) and zoomed on the screech peaks (c,f) PSD for Mj = 1.3 on two different days; Case 1 (a–c); Case 2 (d–f).
The FF screech amplitude at θ = 30° is clearly higher for Case 2 than Case 1, which is true also for the NF screech amplitude measured by microphone 3. Microphone 1, which indicates the constructive or destructive interference between the feedback waves of the two jets, shows an OASPL of 156 and 152 dB (not shown) for Cases 1 and 2, respectively. This 4 dB difference in the internozzle OASPL is consistent with our unheated SRTJ results (Leahy et al. Reference Leahy, Esfahani, Webb and Samimy2023; Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023) and with the literature (Raman & Taghavi Reference Raman and Taghavi1998; Zilz & Wlezien Reference Zilz and Wlezien1990): IP coupling in SRTJ significantly increases pressure fluctuations in the internozzle region compared with OOP coupling.
The feedback loop responsible for screech in supersonic jets operating at off-design conditions has 4 main components: CS convecting in the shear layers of the jet, shock cells, upstream travelling components of BBSAN and the nozzle lip geometry. In twin jet coupling, the distance between the two jets is an additional influential factor. Comparing unheated and heated SRTJ, the strength of shock cells (which depends on NPR), the nozzle lip geometry and the distance between the two nozzles are all the same. Typical daily changes in the laboratory environment (such as temperature, humidity, etc.) are not enough to explain the differences in the jets’ behaviour in heated and unheated jets. There are three possible reasons for the larger day-to-day variations in screech (a first-order resonance phenomenon) amplitude but not frequency and in coupling (a second-order resonance phenomenon). While the TTR was kept as constant as possible (TTR = 2 ± 0.06), the small changes could play some role in day-to-day variations. The second reason is that the elevated TTR increases the convective Mach number (i.e. Mach number of CS within the jets with respect to the ambient speed of sound) and thus the compressibility level, resulting in less coherent and more three-dimensional CS (Elliott, Samimy & Arnette Reference Elliott, Samimy and Arnette1995; Kearney-Fischer, Kim & Samimy Reference Kearney-Fischer, Kim and Samimy2011; Kim, Elliott & Dutton Reference Kim, Elliott and Dutton2020). Assuming Uc = 0.7Uj, which is a typical relation used in the literature (see also figure 3 and the related discussion), the convective Mach numbers for unheated (TTR = 1) and heated (TTR = 2) Mj = 1.5 cases are 0.88 and 1.23, respectively. That is a significant change in the compressibility level which eventually leads to the onset of Mach wave radiation. Thus, less coherent and weakened CS interact less strongly with the shock cells; this produces more variations in screech and coupling strength and phase, and it results in higher sensitivity to small variations in the flow or ambient conditions. The third potential cause is again related to the increased CS convective velocity, which decreases the wavelength of the feedback waves. The smaller wavelength results in more significant changes in the interference pattern of feedback waves with minor variations in operating conditions, causing the natural coupling and even screech loop to be more susceptible to changes. Again, these findings are consistent with the ‘null space’ hypothesis of Raman & Taghavi (Reference Raman and Taghavi1998).
3.4. Far-field acoustics directivity in SRTJ
Time-averaged flow field and FF noise for axisymmetric jets are homogeneous in the azimuthal direction. For rectangular jets, the time-averaged flow field becomes axisymmetric for subsonic jets within a modest downstream distance, but it takes a significantly longer distance in supersonic rectangular jets (e.g. Zaman Reference Zaman1996). Therefore, the FF noise is often azimuthally inhomogeneous, showing significantly higher FF noise at shallow polar angles (with respect to the jet downstream axis) along the minor axis plane than along the major axis plane (Goss et al. Reference Goss, Veltin, Lee and McLaughlin2009). In twin jets, coupling and shielding could play roles in the directivity/azimuthal inhomogeneity of FF noise. However, we showed in Samimy et al. (Reference Samimy, Webb, Esfahani and Leahy2023) that while there is significant FF noise azimuthal directivity in unheated SRTJ with AR = 2 over a wide flow regime (overexpanded to underexpanded), coupling did not make any notable contribution to it. More on the well-known shielding phenomenon, where the shear layers of one jet reflect and refract acoustic waves radiated from the other jet and thereby reduce the FF noise on the twin jets’ major axis plane, can be found in Bozak & Henderson (Reference Bozak and Henderson2011) and Kuo, Cluts & Samimy (Reference Kuo, Cluts and Samimy2017).
Figure 7 shows the FF acoustic results in heated SRTJ for three different Mj cases at TTR = 2: overexpanded (Mj = 1.3 and 1.4) and the design NPR (Mj = 1.5). Figure 7(a,c,e) shows PSD at four FF microphone polar angles (measured from the downstream jet axis) from θ = 30° to 90° for both azimuthal angles of φ = 0° and 90°. Figure 7(b,d,f) shows detoned OASPL for several FF microphones from θ = 30° to 90° for both azimuthal angles of φ = 0° and 90°. As in (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023), screech tones are removed from PSD before calculating OASPL for comparison.

Figure 7. Comparison of PSD and detoned OASPL along major (φ = 0°) and minor (φ = 90°) axes for Mj = 1.3 (a,b), 1.4 (c,d) and 1.5 (e,f) for TTR = 2 at several polar angles.
A couple of observations from these FF acoustic results, and their similarities and differences with the unheated SRTJ results (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023), are as follows. First, as seen in unheated SRTJ results, the screech tones and their harmonics appear in all three cases and along both azimuthal directions, but higher amplitudes are generally seen at φ = 90°. In addition, the non-dominant screech tone, though very weak, appears in shallow angles (at 30° and 40°; figure 7e) of the Mj = 1.5 case. The two tones in the PSD, referred to as dominant and non-dominant (based on amplitude), are related to the two shock systems discussed earlier using figures 3 and 4, and they were observed only in heated jets. Second, there are significant differences between the FF PSD at the two azimuthal angles; the ranges of both Strouhal number and amplitude increase with Mj and θ. The amplitude difference with the Mj is also reflected in the FF OASPL from around θ = 35°–45°. This increased OASPL difference with the Mj seems to be related to the onset of Mach wave radiation. Such a difference did not exist in unheated SRTJ which had no potential for Mach wave radiation (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). As was discussed earlier, the shielding reduces the FF noise on the major axis plane (φ = 0°). The shielding factor is in addition to the directivity inherent to rectangular jets, namely higher FF noise at φ = 90°, as discussed earlier.
4. Effects of control on flow and acoustics
The effects of LAFPA excitation on the coupling and NF pressure fluctuations will be presented and discussed in this section, followed by a brief discussion of the effects of control on the FF acoustics. Figure 8 shows the effects of control on Mj = 1.3 at TTR = 2 for the two cases presented in figure 6, which highlighted the extent of day-to-day variations of coupling and phase in heated SRTJ. The results in figure 8(a,c,e) correspond to Case 1 (figure 6a–c), and those in figure 8(b,d,f) to Case 2 (figure 6d–f). Excitation at the natural screech frequency (Ste = Sts) with IP coupling enhances the natural tendency of SRTJ to couple IP, and results in strong IP coupling with a steady phase in both cases as expected. Excitation at the natural screech frequency (Ste = Sts) with OOP coupling results in moderately strong OOP coupling with a relatively steady phase in Case 1, but weaker coupling in Case 2. The raw NF OASPL with respect to the given baseline for both cases is increased with IP excitation, but the increase is significantly higher for Case 2 (5.5 dB) than for Case 1 (2.5 dB). In contrast, the NF OASPL for both cases is decreased with OOP excitation, but the reduction is significantly higher for Case 1 (6.5 dB) than for Case 2 (3.5 dB).
These results are qualitatively similar to our unheated SRTJ results (Leahy et al. Reference Leahy, Esfahani, Webb and Samimy2023; Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023) and consistent with the results in the literature (Raman & Taghavi Reference Raman and Taghavi1998; Zilz & Wlezien Reference Zilz and Wlezien1990). Recall that microphone 1 (figure 1d) was used to measure the NF OASPL and evaluate the constructive or destructive interference between the feedback waves of the two jets. With microphone 1 located on the minor axis (symmetry line) of the SRTJ, the interference is constructive for IP coupling (i.e. a higher OASPL) and destructive for OOP coupling (i.e. a lower OASPL). In addition, the stronger the IP or OOP coupling, the higher or lower, respectively, the OASPL. Thus, the change in OASPL from the baseline for Case 1 and 2 excited results is due to the differing baseline level/phase of coupling. In both cases, the difference between the IP and OOP coupled NF OASPL is approximately 9 dB, which is significant and consistent with the results in literature (Raman & Taghavi Reference Raman and Taghavi1998; Zilz & Wlezien Reference Zilz and Wlezien1990). The effects of excitation at Ste = Sts on other overexpanded cases are similar, so the results will not be presented.
In the controlled results discussed above, excitation at Ste = Sts was used, which clearly showed the control authority of LAFPAs, and how the nature of coupling in the closely spaced SRTJ could significantly alter the NF pressure fluctuations. Figure 9 shows the effects of IP excitation on the coherence and phase (figure 9a,b), the NF and FF screech amplitude (figure 9c,d) and the change in NF OASPL (figure 9e,f) for Mj = 1.5 (case shown in figure 5d) for two different excitation frequencies, Ste = 0.44 (figure 9a,c,e) and 0.60 (figure 9b,d,f). The first Ste is within the JCM but above Sts = 0.28. The second Ste is at the upper edge of the JCM and is the highest frequency (∼20 kHz) the LAFPAs’ current power supply can provide. Both excitation cases decouple the jets and significantly reduce both the NF and FF screech amplitude and the NF OASPL between the two jets (at microphone 1 location by 4.5 and 3 dB, respectively). While the excitation for both presented cases is IP, the OOP excitation showed similar results.

Figure 9. The effects of IP excitation on coherence and phase in SRTJ (a,b), NF and FF PSD (c,d) and NF ΔOASPL (e,f) for Mj = 1.5 case shown in figure 5(d) for two different excitation frequencies: Ste = 0.44 (a,c,e) and 0.60 (b,d,f). The FF PSD is at φ = 0°, θ = 30°, NF PSD is at microphone 3 location and ΔOASPL is at microphone 1 location.
Even though the two excitation cases presented in figure 9 provided similar results for decoupling SRTJ, the mechanisms are quite different. Ste = 0.44 (>Sts = 0.28) is within the JCM, and the excitation is expected to generate relatively strong CS, giving rise to strong interactions with the shock cells. However, the excitation period was calculated to not satisfy the phase matching criterion required to establish screech (Webb et al. Reference Webb, Esfahani, Yoder, Leahy and Samimy2022). Comparing the broad base of the natural screech (which reflects the expected variability in the flow/acoustic feedback loop (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023)) at Sts = 0.28 and the very sharp tone at Ste = 0.44 for both the NF and FF, it is clear that there was no screech tone (though the jet clearly responds to excitation) at the excitation frequency. However, the CS at the excitation frequency is expected to extract a significant amount of energy from the mean flow and thus from the natural screech loop, thereby reducing the natural screech amplitude and decoupling the jets. Increasing the excitation frequency from Ste = Sts to Ste = 0.44 produces CS that are smaller, less coherent and more numerous in comparison. Further increasing the excitation frequency to Ste = 0.60 (at the upper edge of the JCM) is expected to generate CS that are even less coherent, smaller and more numerous than those generated by Ste = 0.44 excitation. These structures are expected to develop and decay farther upstream in the shear layers of the jets, significantly limiting their interactions with the shock cells and thus significantly reducing/eliminating feedback waves. As with the Ste = 0.44 excitation, energy is drawn away from the natural screech frequency to reduce its amplitude and disrupt coupling.
The SPOD results obtained from the schlieren images for the baseline and two excited cases discussed above will be used to provide further insight to the response of the SRTJ to these excitation frequencies. Figure 10 shows the SPOD mode energy spectra for several modes and the mode 1 shape for the baseline Mj = 1.5 at TTR = 2. Figure 10(a) shows that the first mode contains approximately 95 % of the energy at Sts and approximately 37 % at 2Sts. The first mode shape (figure 10b) shows flapping (i.e. 180° out-of-phase) features in both the hydrodynamic and acoustic fields on the top and bottom sides of the shear layers. Since the baseline SRTJ are coupled IP (figure 5d), this asymmetry clearly indicates the flapping nature of the jets (previously observed in the unheated SRTJ (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). Further, the first mode shape shows three distinct hydrodynamic pressure/acoustic regions. First, the upstream-travelling feedback waves can be seen near the nozzle exit (x/De ≤ 2). Second, the nature of the waves just outside the shear layers is clearly hydrodynamic for approximately 2 < x/De < 4. Third, the nature of the waves just outside the shear layers is clearly acoustic (based on the wavefront curvature) for approximately x/De > 4. In addition, in the last region (x/De > 4), the acoustic waves appear to be an extension of the energetic features in the flow (representing CS), indicative of the presence of Mach wave radiation (Kearney-Fischer et al. Reference Kearney-Fischer, Kim and Samimy2011).

Figure 10. The SPOD mode energy spectra (a) and mode 1 shape at Sts (b) for baseline, Mj = 1.5 SRTJ.
For Mj = 1.5 at TTR = 2, excited at Ste = 0.44 (figure 9a,c), figure 11 shows the FF PSD at φ = 0°, θ = 30°, the SPOD mode energy spectra for several modes, and the mode 1 shape at Sts and at Ste = 0.44. The FF PSD shows that the screech tone has been suppressed and there are tones at Ste and its first harmonic. However, as previously mentioned, the sharp tones do not have the broad base characteristic of screech tones (due to small natural variations in the feedback timing); thus, they signify actuation noise. The SPOD mode energy shows that the first mode contains approximately 46 % of the energy at Sts and 94 % of the energy at Ste and 2Ste. The additional peaks identified as Ste–Sts and 2Ste–Sts are due to the nonlinear interaction of Sts and Ste and were also observed and discussed in previous unheated SRTJ work (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). The first mode shape at Sts shows, for both the acoustic and hydrodynamic fields, flapping (i.e. 180° out-of-phase) features on the top and bottom sides of the shear layers, similar to the baseline case (figure 10b). Also similar to the baseline results, the first mode shape shows three distinct hydrodynamic pressure/acoustic regions. However, neither the acoustic nor the hydrodynamic features are as coherent as seen in the baseline case. These results reaffirm the weakening of the natural screech loop. The first mode shape at Ste clearly shows the flapping mode and the smaller wavelength (commensurate with the difference between the excitation and baseline frequency) and that the jets are responding to the excitation. However, there are two major differences from the mode shape at Sts. First, there is no signature of upstream-travelling feedback waves, as there is no screech at Ste. Second, the hydrodynamic features just outside the shear layers have disappeared, and the entire field outside the shear layers is dominated by Mach waves; these are an extension of the hydrodynamic features, representing CS within the jet.

Figure 11. The FF PSD (a), SPOD mode energy spectra (b) and first mode shape at Sts (c) and Ste (d ) for Mj = 1.5 SRTJ excited IP at Ste = 0.44.
For brevity, the results for the excited SRTJ at Ste = 0.60 are not shown. The results are similar to those shown in figure 11, except for the reduced first SPOD mode acoustic wavelength, commensurate with the increase in the excitation frequency and the concomitant farther upstream disintegration of the smaller, less coherent CS in the shear layer.
Mach wave radiation is observed in high-supersonic (unheated or heated) and even in highly heated, high-subsonic jets. If the convection velocity of CS in a jet is supersonic with respect to the ambient, they generate Mach wave radiation. Mach wave radiation is the only component of jet noise directly generated by the convection of CS in the jet. The convective Mach number of CS is defined as the convective velocity of CS with respect to the ambient speed of sound (Mc = Uc/a). Mach wave radiation does not initiate until Mc is quite a bit higher than 1 (Papamoschou & Debiasi Reference Papamoschou and Debiasi2001). Kearney-Fischer et al. (Reference Kearney-Fischer, Kim and Samimy2011) varied the convective velocity of CS and observed that Mach wave radiation is initiated by the coalescence of NF hydrodynamic pressure fluctuations in the immediate vicinity of CS. The wavefront is curved when Uc is low but flattens as Uc is increased. Since the convective velocity of CS is continuously changing in the jets, especially in the shock-containing jets, it cannot be easily measured. Therefore, various representative Mach numbers (e.g. acoustic Mach number, convective Mach number, Oertel Mach number) have been defined and used to identify the onset of Mach wave radiation (Papamoschou & Debiasi Reference Papamoschou and Debiasi2001; Kearney-Fischer et al. Reference Kearney-Fischer, Kim and Samimy2011). Only convective Mach number will be used in this paper.
In figure 3, Uc = 0.7Uj was used in the scaling of the screech frequency for TTR = 2 SRTJ. Using this convective velocity, which provided an excellent agreement between the theoretical and experimental results, Mc changes from 1.12 to 1.23 for Mj = 1.3 to 1.5 at TTR = 2. Time-averaged schlieren images did not reveal any Mach waves in the cases explored in this work. However, one could observe some Mach waves in the instantaneous schlieren images for the Mj = 1.5 case. This is not surprising since schlieren imaging is a line-of-sight averaging technique, and the rectangular jets in the current work have a flapping mode. Therefore, the waves’ signature must survive integration over the span of the two jets to be visible in the schlieren images. Figure 12 shows conditionally averaged schlieren images for Mj = 1.3 to 1.5 when SRTJ are excited at several different frequencies. The excitation makes the CS more coherent and organized, significantly reducing any variations with time, and IP control reduces the spanwise variations. These effects collectively help to highlight the Mach waves observed in figure 12.

Figure 12. Conditionally averaged schlieren images along major axis for Mj = 1.3–1.5 excited IP at Ste = Sts (a–c) and for Mj = 1.5 excited with two different coupling modes and frequencies (d–f): Mj = 1.3, Ste = Sts (a); Mj = 1.4, Ste = Sts (b); Mj = 1.5, Ste = Sts (c); Mj = 1.5, Ste = 0.44, IP (d); Mj = 1.5, Ste = 0.44, OPP (e); Mj = 1.5, Ste = 0.60, IP (f).
The images in figure 12(a–c) are obtained using excitation at the natural screech frequencies (Sts = Ste). As can be seen, Mach waves are barely visible but weak and curved in Mj = 1.3 case. As the Mj is increased to Mj = 1.5, the waves become stronger and flatter (as observed by Kearney-Fischer et al. Reference Kearney-Fischer, Kim and Samimy2011). The observed undulation of the shear layer and the asymmetry of the waves on the top and bottom are due to the flapping nature of the jets, which was also observed in the SPOD mode shape of figures 10 and 11 as well as in the unheated SRTJ results (Samimy et al. Reference Samimy, Webb, Esfahani and Leahy2023). The images in figure 12(d–f) are obtained using excitations at two higher frequencies, Ste = 0.44 and Ste = 0.60, which were used to decouple the SRTJ (figure 9). The weakening of screech has removed the undulation of the shear layer and thus the flapping motion of the jets. In addition, as was shown in figure 11, the SRTJ responds to the excitation at these higher frequencies by generating CS, which in turn generate Mach wave radiation with a wavelength commensurate with their frequencies. The image shown in figure 12(e) is obtained using OOP excitation, generating Mach waves OOP in the two jets. The integrative nature of the schlieren technique is illustrated by the illusion that the wavelength has been halved.
For the two excitation cases discussed above (Ste = 0.44 and 0.6), one is well within the JCM, and the other is at the upper edge of the JCM. Neither is expected to provide significant FF noise mitigation, and the latter is the highest frequency that the current power supply can provide. Figure 13 shows the FF PSD at φ = 90°, θ = 30° and OASPL at φ = 90° and several polar angles from 30° to 90° for Ste = 0.44 (figure 13a,c) and 0.6 (figure 13b,d). As expected, the natural screech peak has been significantly suppressed. The former has minimal impact on the OASPL, while the latter provided a small (1 to 2 dB) noise reduction at the peak noise direction (shallow polar angles). As discussed previously, higher excitation frequency (and the production of smaller, less coherent CS) is necessary to achieve significant noise mitigation. Samimy et al. (Reference Samimy, Kearney-Fischer, Kim and Sinha2012) showed in an experimental single axisymmetric jet and Prasad & Unnikrishnan (Reference Prasad and Unnikrishnan2023) showed in a computational rectangular jet that excitation within the shear layer mode frequency range is required for a higher level of noise mitigation. With the increased frequency content of the heated SRTJ, the current power supply for LAFPAs cannot provide sufficiently high-frequency excitation to be effective for FF noise mitigation. An effort to overcome this issue is currently underway.

Figure 13. Comparison of FF PSD at φ = 90°, θ = 30° (a,b) and detoned OASPL (c,d) for baseline and two excited cases for Mj = 1.5; excited OOP at Ste = 0.44 (a,c) and at Ste = 0.60 (b,d).
5. Conclusions
Detailed experimental results of heated SRTJ with sharp-throated converging–diverging nozzles of aspect ratio 2 and a design Mach number 1.5 were presented and discussed. The total temperature ratio (TTR) was 2, and cases from overexpanded to the design Mach number (Mj = 1.3–1.5) were investigated. The work complemented our recently published work in unheated SRTJ using the same experimental facility and included both the baseline and controlled cases using LAFPAs. The results showed that the jets were coupled, primarily out-of-phase, in overexpanded cases, and that the coupling had significant effects on the NF pressure fluctuations. Specifically, NF pressure fluctuations were considerably higher for IP coupling than OOP coupling. The results also showed significantly higher FF OASPL on the minor axis plane of SRTJ. The overall trends of FF acoustic directivity, twin jets coupling and the effects of coupling on the NF pressure fluctuations are quite similar to the results in unheated SRTJ, but details are significantly different. The onset of Mach wave radiation in heated SRTJ contributed to the FF noise at the peak noise polar angles. Unlike unheated SRTJ cases, significant day-to-day variations in the coupling strength and phase were observed. The two potential reasons for this change are both related to the changes in the convective velocity of CS. First, the elevated SRTJ temperature increases the convective velocity of CS, thus increasing the screech frequency and reducing the acoustic wavelength. Reduction in the acoustic wavelength makes the closing of the screech and coupling feedback loops more sensitive to small day-to-day variations in the flow and ambient conditions. Second, the increased convective velocity increases the compressibility effects, making the CS less coherent and more three-dimensional. This then weakens the interaction of CS with the shock cells, which weakens the feedback waves in turn, again making the closing of the feedback loop more sensitive to the day-to-day variations in the experimental conditions described above.
The results also showed that heating the SRTJ has not significantly altered the LAFPAs’ control authority over the NF pressure fluctuations and FF acoustics. Three control methods were employed to change the coupling phase or reduce/suppress the coupling strength, all of which resulted in a reduction of the NF pressure fluctuations. In the first method, the excitation frequency matched the natural screech frequency (Ste = Sts), but the coupling phase was changed. In the second method, a frequency was used which was higher than the natural screech frequency (Ste > Sts, still within the JCM) but did not satisfy the feedback waves’ phase-matching criterion necessary to establish screeching/coupling. Third, a higher excitation frequency ![]() $(S{t_e} \gg S{t_s})$ which generated even smaller and less coherent CS was used. For the last case, an excitation frequency within the shear layer mode would have been desirable; however, the highest accessible frequency was only at the upper edge of the JCM. While all three cases were successful in reducing the NF pressure fluctuations, they relied on different mechanisms which were discussed in detail. However, only the third method was successful in reducing the FF noise on the minor axis plane of SRTJ at shallow polar angles, albeit by just 1 to 2 dB. Higher FF noise reduction could have been achieved by excitation at frequencies within the jet shear layer mode.
$(S{t_e} \gg S{t_s})$ which generated even smaller and less coherent CS was used. For the last case, an excitation frequency within the shear layer mode would have been desirable; however, the highest accessible frequency was only at the upper edge of the JCM. While all three cases were successful in reducing the NF pressure fluctuations, they relied on different mechanisms which were discussed in detail. However, only the third method was successful in reducing the FF noise on the minor axis plane of SRTJ at shallow polar angles, albeit by just 1 to 2 dB. Higher FF noise reduction could have been achieved by excitation at frequencies within the jet shear layer mode.
Acknowledgements
Fellowships from the Ohio State University for K.K. and N.H. and a fellowship for R.L. and a scholarship for A.Y. from the Ohio Space Grant Consortium are all greatly appreciated. The use of Ohio Supercomputer Center resources is gratefully acknowledged.
Funding
This work was sponsored by the Office of Naval Research (ONR), under grant number N00014-22-1-2227, with Dr S. Martens.
Declaration of interests
The authors report no conflict of interest.