Published online by Cambridge University Press: 07 August 2023
Stationary Poisson processes of lines in the plane are studied, whose directional distributions are concentrated on 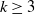 $k\geq 3$ equally spread directions. The random lines of such processes decompose the plane into a collection of random polygons, which form a so-called Poisson line tessellation. The focus of this paper is to determine the proportion of triangles in such tessellations, or equivalently, the probability that the typical cell is a triangle. As a by-product, a new deviation of Miles’s classical result for the isotropic case is obtained by an approximation argument.
$k\geq 3$ equally spread directions. The random lines of such processes decompose the plane into a collection of random polygons, which form a so-called Poisson line tessellation. The focus of this paper is to determine the proportion of triangles in such tessellations, or equivalently, the probability that the typical cell is a triangle. As a by-product, a new deviation of Miles’s classical result for the isotropic case is obtained by an approximation argument.