Hostname: page-component-6587cd75c8-vfwnz Total loading time: 0 Render date: 2025-04-24T02:16:50.976Z Has data issue: false hasContentIssue false
  • English
  • Français

On the moduli of hypersurfaces in toric orbifolds

Part of: Algebraic groups Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  14 March 2024

Dominic Bunnett Open the ORCID record for Dominic Bunnett [Opens in a new window]
Dominic Bunnett*
Affiliation:
Institut für Mathematik, TU Berlin, Germany (bunnett@math.tu-berlin.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct and study the moduli of stable hypersurfaces in toric orbifolds. Let X be a projective toric orbifold and 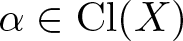$\alpha \in \operatorname{Cl}(X)$ an ample class. The moduli space is constructed as a quotient of the linear system $|\alpha|$ by $G = \operatorname{Aut}(X)$. Since the group G is non-reductive in general, we use new techniques of non-reductive geometric invariant theory. Using the A-discriminant of Gelfand, Kapranov and Zelevinsky, we prove semistability for quasismooth hypersurfaces of toric orbifolds. Further, we prove the existence of a quasi-projective moduli space of quasismooth hypersurfaces in a weighted projective space when the weighted projective space satisfies a certain condition. We also discuss how to proceed when this condition is not satisfied. We prove that the automorphism group of a quasismooth hypersurface of weighted projective space is finite excluding some low degrees.

Keywords

moduli theorygeometric invariant theorytoric varieties

MSC classification

Primary: 14J70: Hypersurfaces
Secondary: 14L24: Geometric invariant theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 2 , May 2024 , pp. 577 - 616
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arzhantsev, I., Derenthal, U., Hausen, J. and Laface, A., Cox rings. Cambridge Studies in Advanced Mathematics, (Cambridge University Press, Cambridge, 2015).Google Scholar
Asok, A. and Doran, B., On unipotent quotients and some $\mathbb{A}^1$-contractible smooth schemes, Int. Math. Res. Pap. (2), (2007), . Id/No rpm005.Google Scholar
Asok, A. and Doran, B., $\mathbb{A}^1$-homotopy groups, excision, and solvable quotients, Adv. Math. 221(4): (2009), 1144–1190.CrossRefGoogle Scholar
Bérczi, G., Doran, B., Hawes, T. and Kirwan, F., Projective completions of graded unipotent quotients. preprint, arXiv:1607.04181, 2016Jul.Google Scholar
Bérczi, G.,Doran, B.,Hawes, T. and Kirwan, F., Geometric invariant theory for graded unipotent groups and applications, J. Topol. 11(3): (2018), 826–855.CrossRefGoogle Scholar
Bérczi, G., Hawes, T., Kirwan, F. and Doran, B., Constructing quotients of algebraic varieties by linear algebraic group actions. Handbook of Group actions., Adv. Lect. Math. (ALM), 41, Volume IV, (Int. Press, Somerville, MA, 2018).Google Scholar
Bérczi, G., Jackson, J. and Kirwan, F., Variation of non-reductive geometric invariant theory. Surveys in Differential Geometry 2017. Celebrating the 50th Anniversary of the Journal of Differential Geometry, Surv. Differ. Geom., Volume 22, (Int. Press, Somerville, MA, 2018).Google Scholar
Batyrev, V. V. and Cox, D. A., On the Hodge structure of projective hypersurfaces in toric varieties, Duke Math. J. 75(2): (1994), 293–338.CrossRefGoogle Scholar
Bazhov, I., On orbits of the automorphism group on a complete toric variety, Beitr. Algebra Geom. 54(2): (2013), 471–481.CrossRefGoogle Scholar
Cox, D. A., The homogeneous coordinate ring of a toric variety, J. Algebraic Geom. 4(1): (1995), 17–50.Google Scholar
Cox, D. A., Erratum to “The homogeneous coordinate ring of a toric variety”, J. Algebraic Geom. 23(2): (2014), 393–398.CrossRefGoogle Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric varieties. Graduate Studies in Mathematics, (American Mathematical Society, Providence, RI, 2011).Google Scholar
Craw, A., Quiver representations in toric geometry. preprint, arXiv:0807.2191, 2008Jul.Google Scholar
Dolgachev, I., Weighted projective varieties, 1982, Group actions and vector fields (Vancouver, B.C. 1981). Lecture Notes in Math., Volume 956, (Springer, Berlin.Google Scholar
Dolgachev, I. V., Lectures on Invariant theory, , (Cambridge University Press, 2003).CrossRefGoogle Scholar
Doran, B. and Kirwan, F., Towards non-reductive geometric invariant theory, 2007, Pure Appl. Math. Q. 3(1): 61–105.CrossRefGoogle Scholar
Esnault, H. and Viehweg, E., Lectures on vanishing theorems. DMV Seminar, (Birkhäuser Verlag, Basel, 1992).Google Scholar
Gelfand, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants and multidimensional determinants. Modern BirkhäUser Classics, (Birkhäuser Boston, Inc, Boston, MA, 2008) Reprint of the 1994 edition.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I, Inst. Hautes ÉTudes Sci. Publ. Math. 20 (1964), .CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, (Springer-Verlag, New York-Heidelberg, 1977).Google Scholar
Hawes, T., PhD Thesis, Oxford University, 2015, Non-reductive geometric invariant theory and compactifications of enveloped quotients.Google Scholar
Iano-Fletcher, A. R., Working with weighted complete intersections. Explicit Birational Geometry of 3-folds, London Math. Soc. Lecture Note Ser., Volume 281, (Cambridge Univ. Press, Cambridge, 2000).Google Scholar
Keel, S. and Mori, S., Quotients by groupoids, Ann. of Math. (2) 145(1): (1997), 193–213.CrossRefGoogle Scholar
King, A. D., Moduli of representations of finite-dimensional algebras, 1994, Quart. J. Math. Oxford Ser. (2) 180(45): 515–530.Google Scholar
Liu, Y. and Petracci, A., On k-stability of some del pezzo surfaces of fano index 2, Bull. Lond. Math. Soc. 54(2) (2022), 517–525, arXiv 2011.05094.CrossRefGoogle Scholar
Matsumura, H. and Oort, F., Representability of group functors, and automorphisms of algebraic schemes, Invent. Math. 4 (1967), 1–25.CrossRefGoogle Scholar
Mumford, D., Fogarty, J. and Kirwan, F., Geometric invariant theory. Ergebnisse der Mathematik und Ihrer Grenzgebiete, Neue Folge, Band 34, (Springer-Verlag, Berlin-New York, 1965).Google Scholar
Odaka, Y., Spotti, C. and Sun, S., Compact moduli spaces of del Pezzo surfaces and Kähler–Einstein metrics., J. Differ. Geom. 102(1): 127–172 (English, 2016).Google Scholar
Putcha, M. S., Linear algebraic monoids. London Mathematical Society Lecture Note Series, Volume 133, (Cambridge University Press, Cambridge, 1988).Google Scholar
Stacks project authors, The stacks project 2018.Google Scholar
Tommasi, O., Rational cohomology of the moduli space of genus 4 curves, 2005, Compos. Math. 141(2): 359–384.CrossRefGoogle Scholar