2 Suite for Piano Op. 25 Varieties of Idea in Schoenberg’s earliest twelve-tone music
I will begin our exploration of the musical idea in the twelve-tone music of Schoenberg with the Suite Op. 25 for a number of reasons. First, Schoenberg himself identified it in several places as the earliest of his twelve-tone works. In his well-known essay “Composition with Twelve Tones” he calls the Suite “my first larger work in this style,”1 and in an oft-cited 1937 letter to Nicolas Slonimsky he reminisces concerning the early development of the twelve-tone approach thus:
The technique [referring to the Sonett Op. 24] is here relatively primitive, because it was one of the first works written strictly in harmony with this method, though it was not the very first – there were some movements of the “Suite for Piano” which I composed in the fall of 1921. Here I became suddenly conscious of the real meaning of my aim: unity and regularity, which unconsciously had led me this way.2
Furthermore, although Schoenberg made a number of attempts prior to the Suite’s emergence in 1921 to write pieces using the twelve-tone method in part, or using other kinds of series, some of them mentioned elsewhere in his 1937 letter, this “pre-history” of Schoenberg’s twelve-tone music has been documented and discussed with great care by other authors, most notably Ethan Haimo in Schoenberg’s Serial Odyssey.3 Thus I will refrain from revisiting it here.
However, there has been doubt expressed in the literature about whether even the Suite should be considered a thoroughgoing twelve-tone composition, or whether it too belongs with the pre-twelve-tone works. Both Jan Maegaard and Ethan Haimo claim that Schoenberg’s first awareness of the twelve-tone row (with respect to Op. 25) as a unique linear ordering, divided into two hexachords, occurred as he composed the Trio, the second-last movement to be completed, and the Gigue, which was begun just before and completed after the Trio. As Haimo puts it, the earlier-composed movements of the Suite, the Prelude, Intermezzo, Gavotte, Musette, and Menuett, are based on a “tritetrachordal polyphonic complex” – by which he means three tetrachords that together complete the aggregate, most often ordered within themselves, but not ordered between themselves, at least not to the extent that listeners can fix their attention on one ordering of the twelve tones as basic. As support for his claim, Haimo points to two indisputable facts: that the ordering between tetrachords that will eventually be used in the two last-composed movements is not seen all that often in the earlier ones, and also that Schoenberg, both in his sketches and in the first five movements, prefers retrograde forms of P4, I10, I4, and P10 (these two primes and two inversions are the only ones used in the Suite) that retrograde the pitch classes within the tetrachords but not between them.4
On the other hand, Reinhold Brinkmann describes the sketch pages leading up to the Prelude and Intermezzo of the Suite in a way that leads one to believe Schoenberg was indeed formulating a unique linear ordering of twelve notes in a step-by-step fashion through his initial sketching process, before he wrote even the first drafts for the Prelude. Brinkmann writes an exhaustive chronological account of these sketches in the critical report to the Schoenberg collected edition, as well as a more abbreviated one in an article titled “Zur Entstehung der Zwölftontechnik.”5 Both accounts take us through several stages by which Schoenberg (1) determined the content and ordering of the row’s first tetrachord, combining it initially with a pentachord and a trichord that exhaust the aggregate, (2) explored the possibility of combining the resulting complex with its transposition by tritone, (3) decided that he wanted to split the remaining eight notes of the aggregate into tetrachords, establishing the unordered content of the second and third tetrachords, (4) decided on a registral order between the tetrachords from top to bottom voices which corresponds to the eventual chronological order, and (5) established the eventual chronological order between the three tetrachords. This suggests, then, that the composer did have a unique linear ordering of all twelve tones in mind when he began the first-composed movements of the Suite, the Prelude and Intermezzo, and such an assumption underlies Martha Hyde’s analyses of the Suite, in that she accounts for various horizontal and vertical combinations of segments within and between rows in the sketches and various finished movements as “secondary harmonies,” other manifestations of the same set class as contiguous subsets of the whole twelve-tone row.6
My position with respect to the aforementioned debate could be thought of as a compromise. I believe that Schoenberg was indeed cognizant of the whole twelve-tone row as a unique linear ordering from the very onset of his work on the Suite, but that he saw that ordering as part of a spectrum of ways of presenting the row that ranged from an unordered aggregate on one end of the spectrum to complete, perfect ordering on the other end. All of the movements of the Suite can be analyzed as containing multiple choices from that spectrum, as can many of the pieces coming later in his twelve-tone output, where there is no question concerning Schoenberg’s conception of a basic twelve-tone ordering (the Piano Piece Op. 33a, which we will discuss in Chapter 5, comes to mind). To give two examples: the Prelude does include two instances of row presentations where the tetrachords are ordered between as well as within themselves – mm. 1–3, right hand, and mm. 7–8, bass voice – in addition to numerous places where the tetrachords are ordered within but not between themselves, or are ordered between but not within themselves (see P4 and I10 in mm. 15–16), or ordered neither within the tetrachord (because of vertical dyads) nor between the tetrachords. And the Gigue, which does indeed include a number of ordered row forms divided into hexachords (like mm. 34 and 36), also features row presentations that are completely de-ordered, such as those at mm. 16 or 19 (Haimo calls these instantiations of a different row, but I prefer to think of them as extreme transformations of the Suite’s source rows, for reasons that will become clear in my discussion of the Gigue’s overall processes). The Gigue also has row presentations that are ordered within but not between the tetrachords (like the first half of m. 14), and many that are ordered between but not within them (the four P and I forms that begin the movement in mm. 1–4 with their numerous vertical dyads could be heard this way).
The notion of a spectrum of approaches to row ordering fits quite well with the assertions I made in Chapter 1 about musical idea as the framework for Schoenberg’s twelve-tone music. What I plan to show is that each of the three movements I analyze, the Prelude, Menuett, and Gigue, takes a different approach to expressing the musical idea: to setting up and elaborating some sort of problem and eventually resolving it. The strict or loose row orderings, and especially the progressions from strict to loose or vice versa, often play an important role in projecting the musical idea of a movement, though there is no case in which the Idea is expressed by row ordering alone. The Prelude, as was mentioned before, suggests, obscures, and then recaptures (twice) a symmetrical pitch-class structure that arises from the “tritetrachordal complex.” The Menuett’s Idea flows out of a feature introduced initially in the Intermezzo (which was composed before it), which I call “collectional exchange.” The Menuett begins by using rhythm and register to project the content of hexachords and tetrachords of row forms other than the one in effect, it then undergoes a rotational adjustment that prevents such exchanges, and, near the end, it starts to project exchanges again despite the continuance of the adjustment. Finally, in the Gigue, the problem involves a foreign interval succession that emerges from the interval structure of the row itself, and near the end the relationship of the foreign element to the source row is highlighted. This last way of projecting the Idea looks forward to the approach Schoenberg takes in his next twelve-tone composition, the Woodwind Quintet Op. 26.
Prelude
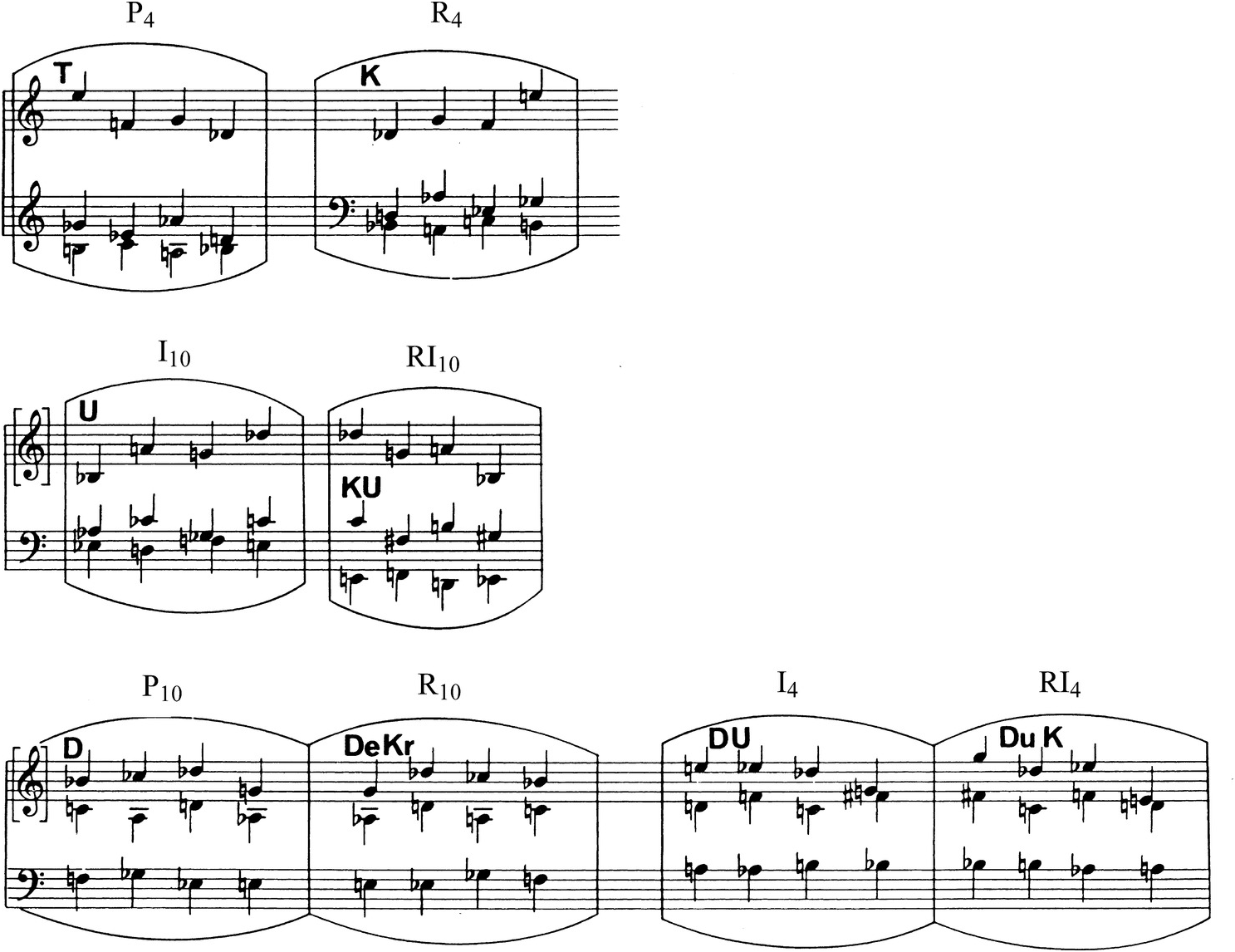
According to Maegaard and Brinkmann, Schoenberg wrote preliminary sketches and a set table for the Suite in late July of 1921 (not in the fall, as he indicated in his letter to Slonimsky), as well as the Prelude and ten measures of the Intermezzo.7 He then abandoned the work, not to pick it up again until February of 1923. Schoenberg’s 1921 set table, reproduced in Example 2.1, lays out P4, I4, P10, I10, and their retrogrades, the eight row forms that he uses exclusively in the Suite, in the form of “tritetrachordal polyphonic complexes.”
Example 2.1 Schoenberg’s set tables for the Suite Op. 25. Schoenberg PIANO SUITE OP. 25, Copyright © 1925 by Universal Edition AG, Vienna, Copyright © renewed. All rights reserved.
Each row is placed side by side with its retrograde, so that the retrograde brings back the discrete tetrachords in the same order between themselves from top to bottom as in the original, not in reverse order as a linear retrograde would. As I described above, Ethan Haimo concludes from the arrangement of this table, as well as the layout of many of the rows in the Suite itself, that such complexes form the basis for most of the movements of the Suite, as opposed to the conventional notion of linear twelve-tone row.8 But others, Reinhold Brinkmann and Martha Hyde among them, argue that Schoenberg was aware of the full linear ordering of the twelve notes from the beginning of his work on the Suite.9
I will leave the question of the source material of the Prelude – whether it should be a linear twelve-tone row or a collection of three tetrachords ordered within but not between themselves – undecided. But I want to call the reader’s attention to the set table of the Prelude for a different reason: it will help us to understand the large-scale coherence of this piece if we think of the “tritetrachordal” dispositions of these rows as basic shapes around which Schoenberg builds a musical idea. When Schoenberg divides P4 into its discrete tetrachords, aligns them vertically, and then follows them with the tetrachords of R4, reversed within but not between them, he creates a structure that is symmetrical on two levels, as Example 2.2 illustrates.
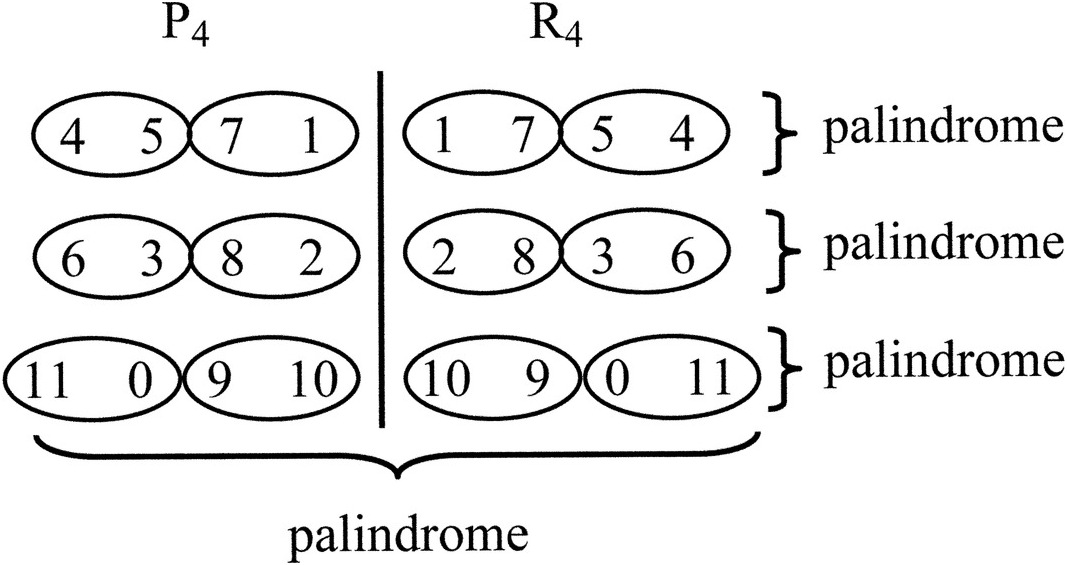
Example 2.2 Schoenberg, Prelude Op. 25: the palindromic “basic form”
The whole creates a palindrome, as does each voice, top, middle, and bottom. This palindromic structure then plays the role of an “ideal” that is hinted at yet disguised in the opening measures, striven toward in most of the piece up to a climactic point (mm. 17–19), realized (mm. 20–21), and then departed from. The Prelude thus anticipates some of Schoenberg’s later pieces, like the third choral Satire Op. 28 (discussed in Chapter 4), where a similar palindromic shape created by a combinatorial row pair is similarly hidden and then revealed, or the String Trio Op. 45 (Chapter 8), where the linear shape of the row, hidden, striven toward, and then revealed, gives rise to an Idea in much the same way.
Before taking up Schoenberg’s realization of the musical idea in this Prelude, I want to comment briefly on the form, as I will for each piece discussed in this book. See Example 2.3 for my form chart. Richard Kurth hints at hearing the Prelude as a binary form when he calls the passage after the fermata in m. 16 a “varied recapitulation of the opening measures,” and my chart places the largest division between A and A’ at that point.10 Other authors have pointed out subdivisions in the form, which my chart incorporates as subsections. Ernst Flammer calls our attention to the rest in m. 5 and the dynamic change in m. 9, and claims that the three resulting subsections create a small bar form, a larger version of the a–a–b relations between the three tetrachords of the source row (the first two tetrachords have tritones between their third and fourth notes, the third does not).11 I have indicated these same subsections as a, b, and c on my chart. In addition, a rest at the end of m. 19 and extreme dynamic changes from 
to 
at m. 20 and to 
at m. 22 divide the large A′ section into three parts, a′ (mm. 16b–19), d (mm. 20–21), and e (mm. 22–24, which serve as a coda). The small d subsection could possibly be heard as a parenthesis between a′ and e, since it interrupts an increase in dynamics, texture, and complexity of row disposition through those subsections. At the same time, mm. 20 and 21 are anything but parenthetical, because they provide the “solution” for the whole movement – clear statements of the palindromic structures toward which the piece has been striving.
Example 2.3 Schoenberg, Prelude Op. 25: form chart
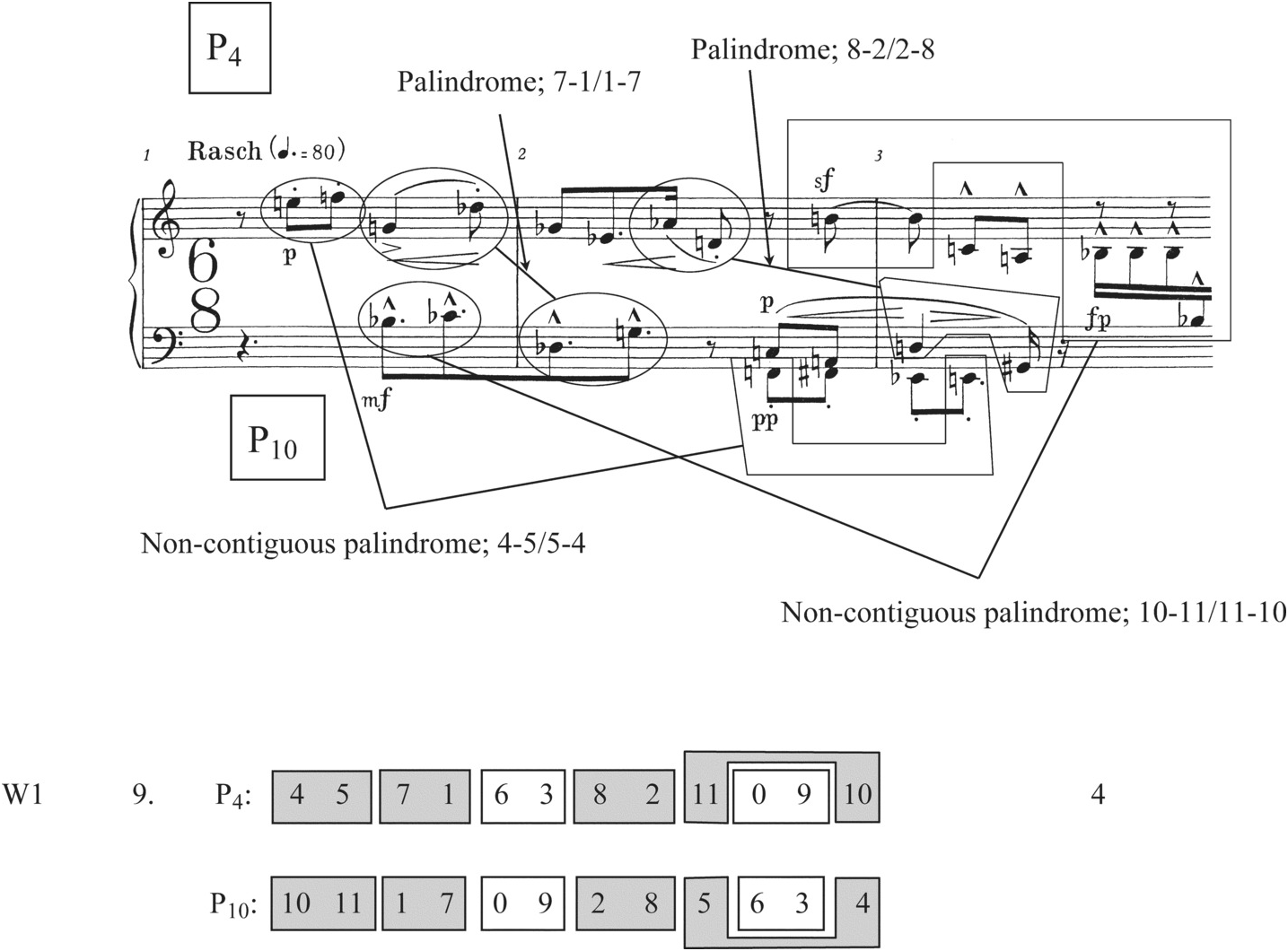
In general, the Prelude presents its row forms in pairs or triplets, taking its cue from the prime-retrograde pairs of the set table. Since Schoenberg limits himself in this movement (as well as the other movements of Op. 25) to eight row forms, P4, R4, I10, RI10, P10, R10, I4, and RI4, there are twenty-eight possible pairings of row forms available to him. He uses fifteen of these in the Prelude, as shown in Example 2.4. (Please note that the retrograde and retrograde-inverted forms in Example 2.4 follow the pattern suggested by Schoenberg’s set table: the tetrachords reverse within themselves but keep the original order between themselves.)
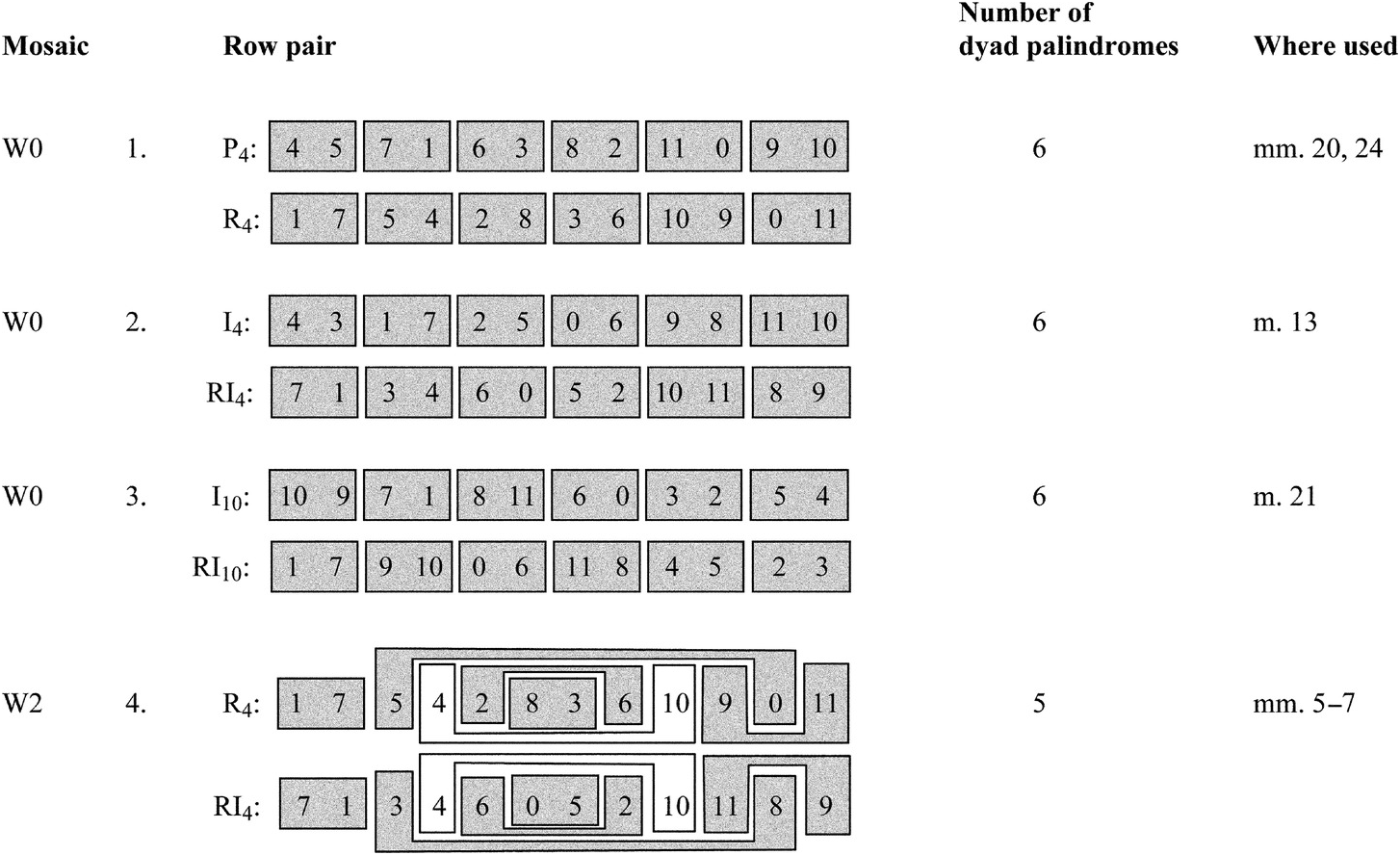
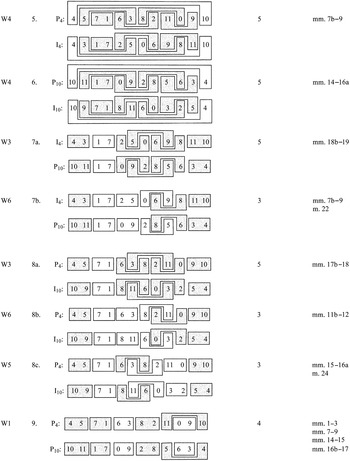
Example 2.4 Schoenberg, Prelude Op. 25: the fifteen row pairs that Schoenberg uses, together with the order-number partitions (“mosaics”) that are applied to them to create collectional invariance (palindromic dyads are indicated through shading)
Of these fifteen row pairs, thirteen have the property of “collectional invariance,” which obtains, according to Donald Martino, Andrew Mead, Richard Kurth, and others, when identical order-number partitions of two rows produce identical collections of pitch-class sets.12 In the Prelude, the collectional invariance involves reproducing the six pitch-class dyads of one row in the other, and Example 2.4 shows that certain row pairs, namely those related by retrograde, produce all six of these as palindromes, while other pairs produce only five, four, three, or two of them as palindromes (the palindromic dyads are shaded on Example 2.4). The two row pairs at the bottom of Example 2.4, which are not collectionally invariant, theoretically could present several dyad palindromes in the same manner as the rows higher on the chart (for example, in I10 and R10 the pitch classes 10 and 1 come back in reverse order). But not many of these palindromic dyads are close enough to being contiguous to be useful in a texture that would highlight them as motives within an overall segmentation into tetrachords. (This same problem occurs with the row pairs listed as having five palindromic dyads in Example 2.4. Note that Schoenberg uses each of these only once.)
The list in Example 2.4 provides Schoenberg with a repertory of collectionally invariant row pairs that are graded with respect to the number of palindromic dyads they produce. These pairs are the materials he uses to project his musical idea, which involves striving toward and then realizing an ideal shape having six dyad palindromes. The piece begins with a linear statement of P4 in the right hand placed against one of P10 in which the second and third tetrachords are aligned vertically, thus realizing row pair 9 in Example 2.4. P4 and P10 together produce four dyad palindromes, pitch classes 7–1/1–7, 4–5/5–4, 8–2/2–8, and 10–11/11–10. Two of these occur as adjacencies, 7–1/1–7 and 8–2/2–8, while the other two have pitch classes intervening between the members of one dyad. In this way P4 and P10 hint at the ideal shape (six dyad palindromes that are all contiguous) without realizing it completely. Example 2.5 is Schoenberg’s realization of this row pair: it shows that he uses slurring and metrical placement to highlight the two contiguous dyad palindromes as motives: G–D♭ at the end of m. 1 is answered by D♭–G on the downbeat of m. 2; then A♭–D going into the second dotted quarter of m. 2 is answered by D–G♯ on the downbeat of m. 3. The non-contiguous dyad palindromes, E–F in m. 1 leading to F (F♯ E♭) E in mm. 2–3, and B♭–C♭ in m. 1 leading to B (C A) B♭ in mm. 2–3, are also highlighted, through dynamics and articulation. E and F in m. 1 share staccato and p markings with F and E in mm. 2–3, while B♭ and C♭ in m. 1 share violent accents (
, 
, and 
) with B and B♭ in mm. 2–3.
Example 2.5 Schoenberg, Prelude Op. 25, mm. 1–3.
From this opening passage that hints at the movement’s basic shape but does not completely realize it, the piece immediately regresses toward a combination of rows that further obscures the work’s ultimate goal. Measures 4–5 place I10 and R10, two rows that are not collectionally invariant, side by side (see pair No. 14 in Example 2.4). The rows do share two invariant dyads, one contiguous (7–1/7–1) and the other holding order positions 4 and 7 in both rows (8–0/8–0), but neither of them reverses from one row to the other, so the possibility of dyad palindromes is limited to what one might pick up from non-contiguous, different order positions.
Schoenberg begins the small b subsection in mm. 5b–7a by placing R4 and RI4 side by side. As pair No. 4 in Example 2.4 shows, this combination gives rise to five dyad palindromes, but only three of them occur within tetrachords and only one is contiguous. Each of the three palindromes within tetrachords comes to the fore on the musical surface in a different way: see Example 2.6 for an illustration. The contiguous one, 1–7/7–1, is set as the beginnings of two identical rhythmic motives (
) that are either or accented. The other two dyad palindromes are emphasized more subtly. 2–6/6–2 forms the endpoints of overlapping rhythmic motives in mm. 6a and 6b – 7a that are similar but not identical, while 9–11/11–9 is highlighted as longer values in m. 6a and as notes on the beat in m. 6b. The general effect is of returning to a situation similar to mm. 1–3, where certain dyad palindromes are contiguous, and others are obscured by intervening notes but are still audible as beginning and ending notes of recognizable segments.
Example 2.6 Schoenberg, Prelude Op. 25, mm. 5b–7a.
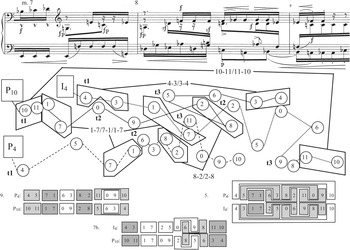
The small b subsection continues and ends in mm. 7b–9a with a passage in which three rows are presented more or less simultaneously. As Example 2.7 illustrates, P4 appears in the bass line and is the only one of the three rows to unfold itself linearly (follow the dashed line in the pitch-class map). P10 begins with it in the alto, and the solid line shows that its third tetrachord begins (on F) halfway through the performance of the second. I4 joins the mix at the end of m. 7 (see the dotted line), and also begins its third tetrachord simultaneously with the halfway point of its second (C and A in m. 9).
Example 2.7 Schoenberg, Prelude Op. 25, mm. 7b–9a.
Considering the three rows as three potential pairings, P4 with P10, P10 with I4, and P4 with I4, yields a rich crop of palindromic dyads – many of which are highlighted motivically. In general, we can hear this passage as a turn back in the direction of the ideal shape, continuing the trend of the previous measures. Most notable is the double palindrome, 1–7/7–1/1–7, created when moving from P10 through P4 to I4. Note how Schoenberg emphasizes each of the second notes of these dyad motives with a downbeat, , or marking. The 8–2/2–8 palindrome between P4 and P10 in m. 8 is less well marked, but with the accent marks on the second dyad it gives the impression of the motive growing out of the texture. Two other dyads create palindromes that span the passage, and thus are less immediately audible, but still certain features bring their relationships to the listener’s attention. 4–3/3–4 between I4 and P10 gives rise to a pitch palindrome E4–E♭4/E♭4–F♭4 that begins and ends the soprano phrase in mm. 7b–9. 10–11/11–10 between P10 and I4 does not create a pitch palindrome, but the first dyad is highlighted through wedge accents at the very beginning of the passage, and the second, coming at the end of the passage without any accompanying voices, seems to answer it.
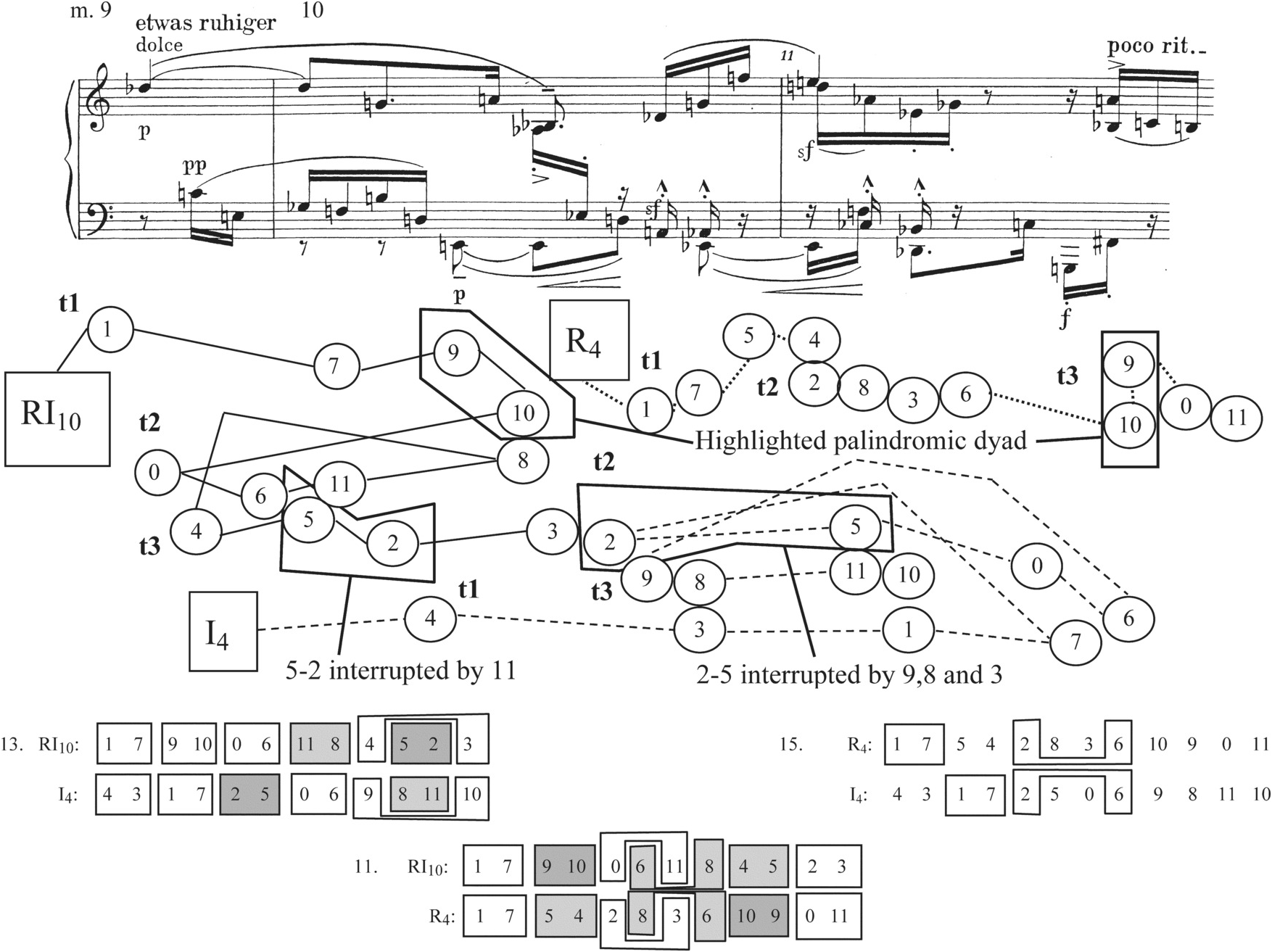
With the onset of the small c subsection in m. 9b come two passages that first back away from the ideal of six contiguous palindromic dyads, and then take a step back in the direction of that ideal. Measures 9b–11a again combine three row forms, RI10 in mm. 9b–10a followed by or overlapping with R4 and I4 in mm. 10b–11a. When these three rows are combined into pairs, as the reader can see from pairs 11, 13, and 15 in Example 2.4 (reproduced at the bottom of Example 2.8), not many dyad palindromes result. R4 and RI10 together give three; of these, only the 9–10/10–9 is strongly emphasized in the music, by pitch identity and accent (the other two palindromic dyads are hidden by octave displacement or intervening notes from another tetrachord). But Schoenberg obscures the palindromic quality of 9–10/10–9 by turning the second of them into a vertical (the A–B♭ vertical in the right hand of m. 11). As for RI10 and I4, their two palindromic dyads, 2–5/5–2 and 11–8/8–11, are made less salient by distance and intervening notes from other tetrachords (Example 2.8 illustrates how 5–2/2–5 within RI10 and I4 is so obscured). And R4 and I4 have no palindromic dyads between them, as pair 15 shows.
Example 2.8 Schoenberg, Prelude Op. 25, mm. 9b–11a.
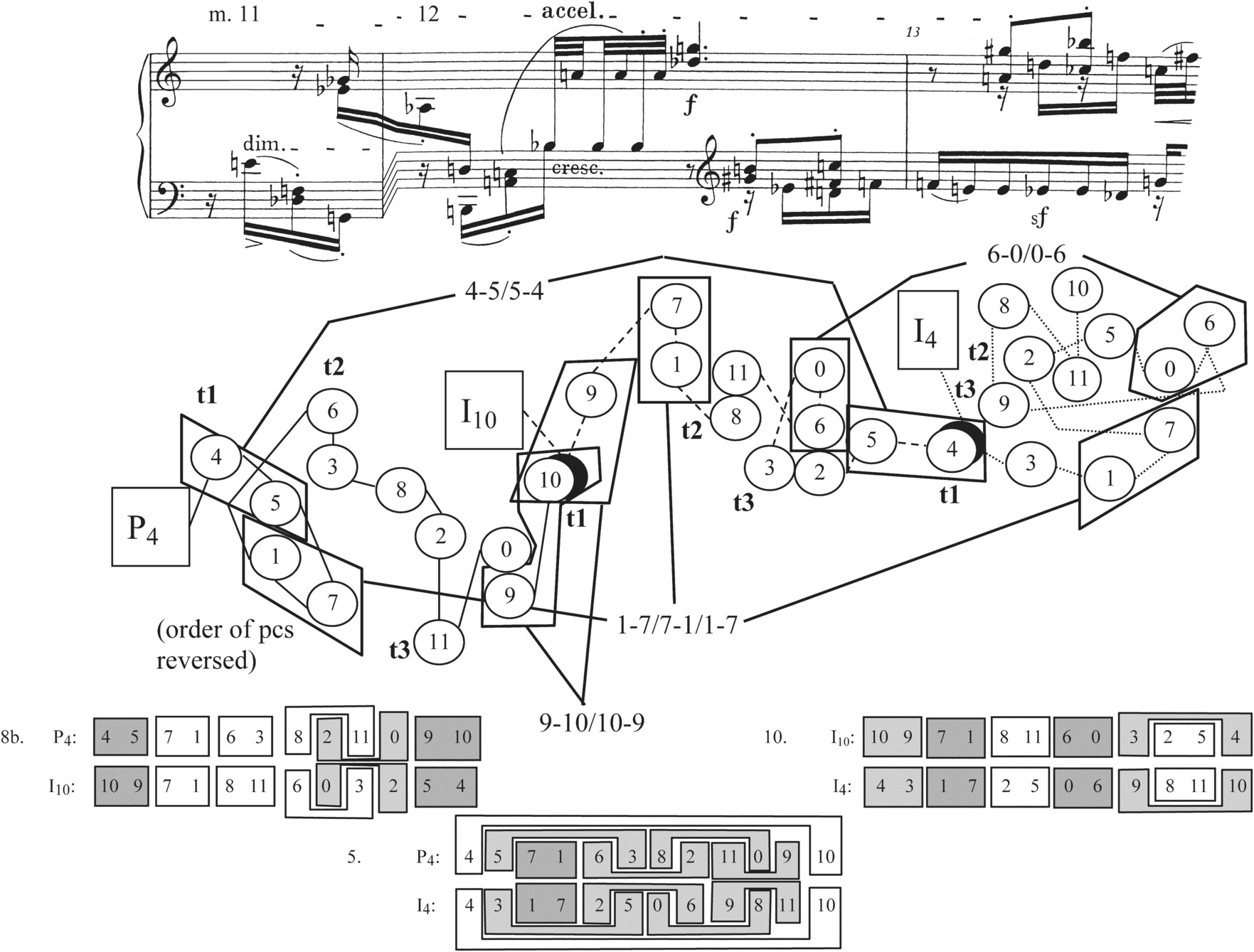
The following passage, mm. 11b–13a, represented in Example 2.9, presents, one after another, the three row forms P4, I10, and I4. Each row overlaps in one note with its neighbor(s). The row pairs P4 and I10, I10 and I4, and P4 and I4 significantly increase the numbers of dyad palindromes available to Schoenberg to bring out as motives (three, four, and five respectively; see Example 2.4, pairs 8b, 10, and 5, or the bottom of Example 2.9), and he does indeed highlight several of these. Especially notable is Schoenberg’s treatment of the dyad {1,7}. Example 2.4, pair 8b, shows that this dyad does not naturally form a palindrome between P4 and I10, but at the end of m. 11, left hand, the row order of the two pitch classes is reversed, so that 1 comes before 7. The I10 form answers this motive in the top voices of m. 12b not with <7,1> as expected but with a vertical dyad containing these pitch classes. Finally, I4 brings <1,7> back in the bass line of m. 13a. Schoenberg seems to be forgoing the palindrome that could have been available to him between P4 and I10, in favor of creating a larger, three-element palindrome spanning the whole passage: <1,7>, {1,7} as a vertical, <1,7>. The registral motion of these motives from bass to soprano to bass reinforces the pattern. Example 2.9 also illustrates three other dyad palindromes that are made salient by the musical surface.
Example 2.9 Schoenberg, Prelude Op. 25, mm. 11b–13a.
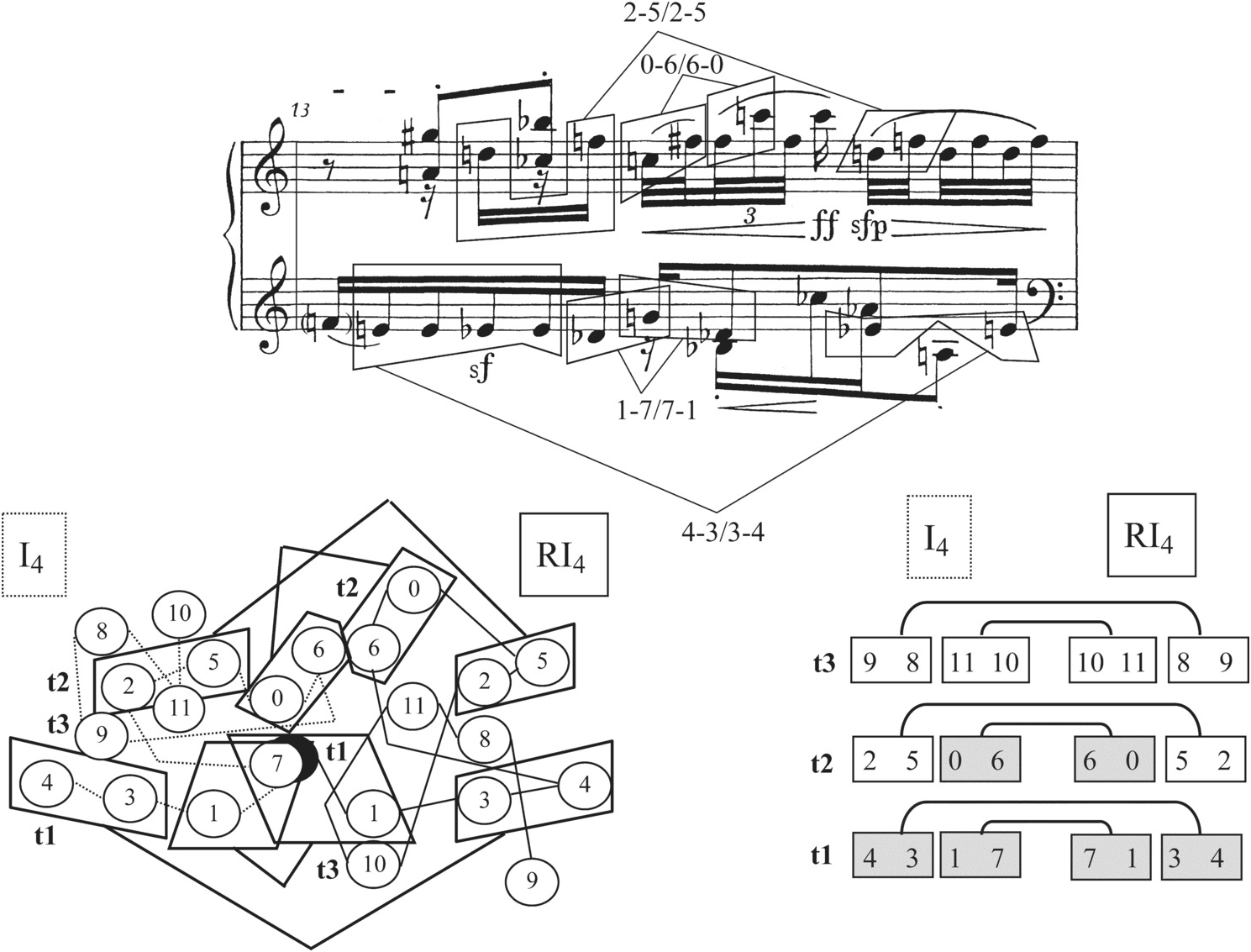
The gradual increase in palindromic motives of mm. 11b–13a over the previous measures leads toward a goal, which is reached in m. 13. For the first time in the Prelude, Schoenberg places two retrograde-related rows, I4 and RI4, side by side, with their discrete tetrachords stacked vertically. It was pointed out above that this kind of arrangement would be treated by the piece as an ultimate solution within the musical idea that embraces the whole, because it produces six contiguous palindromic dyads. But m. 13 is not near enough to the end of the work to provide a conclusive answer: that will have to wait until m. 20. Therefore, Schoenberg uses a number of different methods to obscure some of the palindromic dyads, as illustrated by Example 2.10. The example places the ideal shape of I4 and RI4, with the palindromes boxed and bracketed, and the ones that are highlighted in the music shaded, in the lower right-hand part of the page. From this comparison, the reader can see that, while certain palindromes are expressed clearly, such as 4–3/3–4, 1–7/7–1, and 0–6/6–0, another one is obscured by a reversal of order (2–5/5–2 changes to 2–5/2–5). The remaining palindromes, 9–8/8–9 and 11–10/10–11, are hidden through a combination of registral transfer from soprano to bass and changing the first dyad of each pair into a vertical (these are not circled in the example). What results from all these alterations is a musical shape closer to the ideal than anything we have heard yet, but still not perfect.
Example 2.10 Schoenberg, Prelude Op. 25, m. 13.
The next passage to consider, mm. 14–16a, has two functions. First, it provides a cadence for the first large A section in m. 16a, which Schoenberg accomplishes by rhythmic means, including the three fermatas in mm. 15 and 16. Second, it takes one step backward from m. 13’s situation in the piece’s overall quest to realize its basic shape as six dyad palindromes. This step backward will lead to the Prelude’s dynamic and registral climax in mm. 17–19, in which a complex partitioning of four row forms gives rise to palindromic structures different from the basic shape – the height of striving for the ideal without reaching it.
Example 2.11 illustrates the row forms that are used in mm. 14–16a and, at the bottom right corner of the example, some of the invariant dyads that are created thereby. Measure 14 projects P10, followed by P4 and I10 together in mm. 15 and 16a. P4 and I10 can produce a collectional invariance that yields three palindromic dyads, different from the one that was featured in mm. 11 and 12, as Example 2.4, pair 8c, shows. They are 4–5/5–4, 6–8/8–6, and 10–9/9–10. But Schoenberg’s main strategy here does not seem to be highlighting these palindromes; instead he uses both palindromic and ordered invariants to create a “balanced” relationship between P4 and I10 that Richard Kurth has already described at length.13 To summarize part of Kurth’s argument, the vertical dyads 4–5 and 3–2 of P4 in m. 15 are answered by 5–4 and 3–2 from I10 as horizontals in m. 16.14 Likewise, the offbeat dyads 10–9 and 11–0 of I10 in m. 15 are answered by the chord on the downbeat of m. 16 containing 9–10 and 11–0 from P4. The other invariant dyads between P4 and I10, 1–7/1–7 and 6–8/8–6, both overlap the two row forms in a single vertical. This exchange of directions and metrical accent qualities in mm. 15–16a overshadows the three symmetrical invariant dyads of P4 and I10, mainly because all three of the palindromes are set as verticals on at least one of the occasions when they appear.
Example 2.11 Schoenberg, Prelude Op. 25, mm. 14–16a.
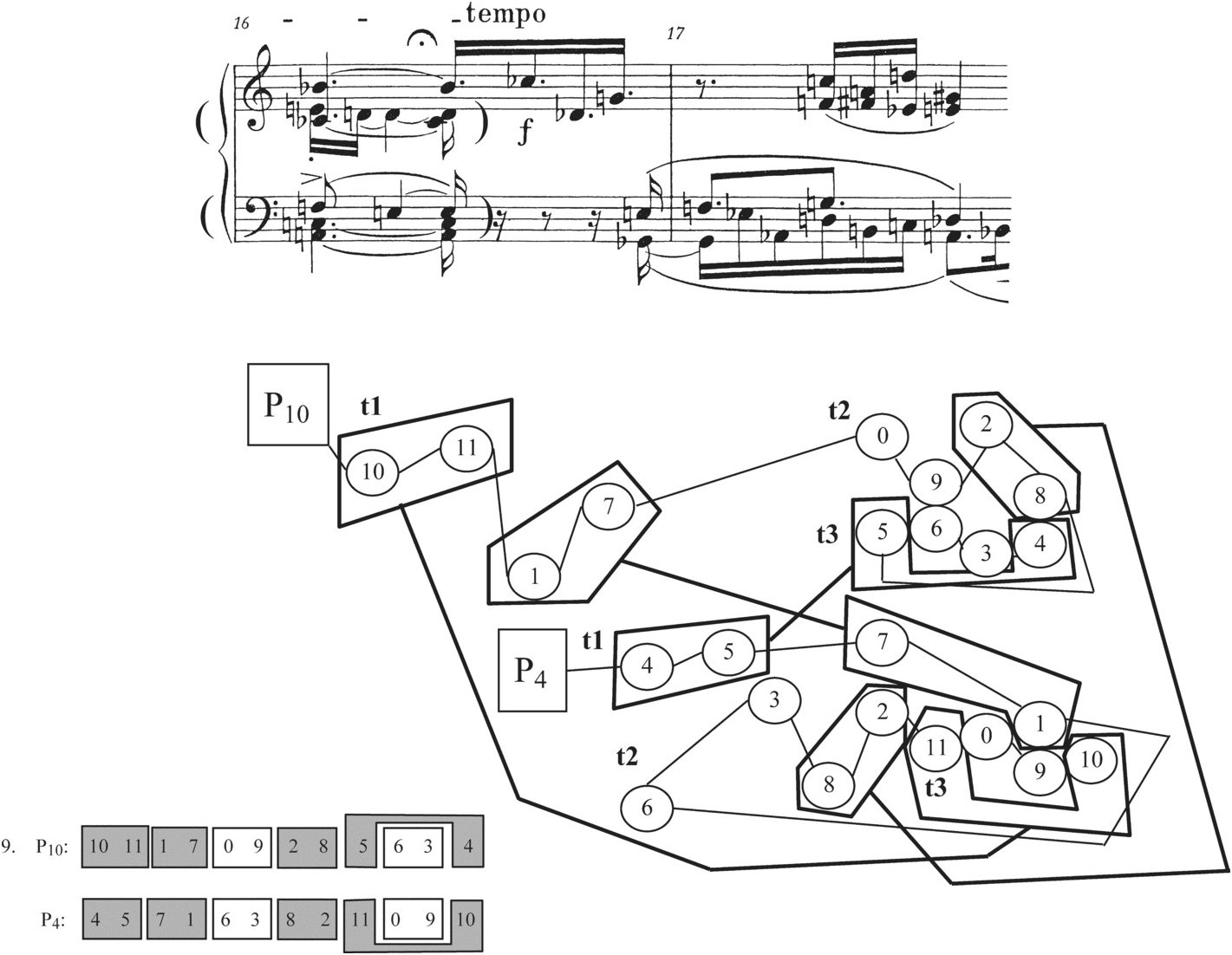
The second main section of the piece, A′, owes its label to its beginning, which is portrayed in Example 2.12. Measures 16b–17a vary the opening Grundgestalt material. P10 begins in the right hand and P4 follows in the left, and neither row is presented linearly (as P4 was in mm. 1–3). Still, the same four dyad palindromes reappear, though now not in the same order as in the Grundgestalt. We hear a sequence consisting of the first halves of 10–11/11–10, 1–7/7–1, 4–5/5–4, and 8–2/2–8, a variation of mm. 1–2’s sequence: 4–5, 1–7 together with 10–11, 8–2. Another way in which this passage is different is that the four dyad palindromes are not marked in any significant way, as they were with staccato marks, accents, and and markings in the Grundgestalt. After the clear presentations of 10–11, 1–7, and 4–5 from m. 16b to the downbeat of m. 17, the rest of the elements of the palindromic dyads seem to blur in m. 17, as the note values shorten from dotted sixteenth to sixteenth, groups of notes begin to slur together, and the texture grows to four voices. This blurring process, just as the obscuring of the dyad palindromes in mm. 15–16a did, sets the listener up for new kinds of palindromic shapes in the measures to follow.
Example 2.12 Schoenberg, Prelude Op. 25, mm. 16b–17a.
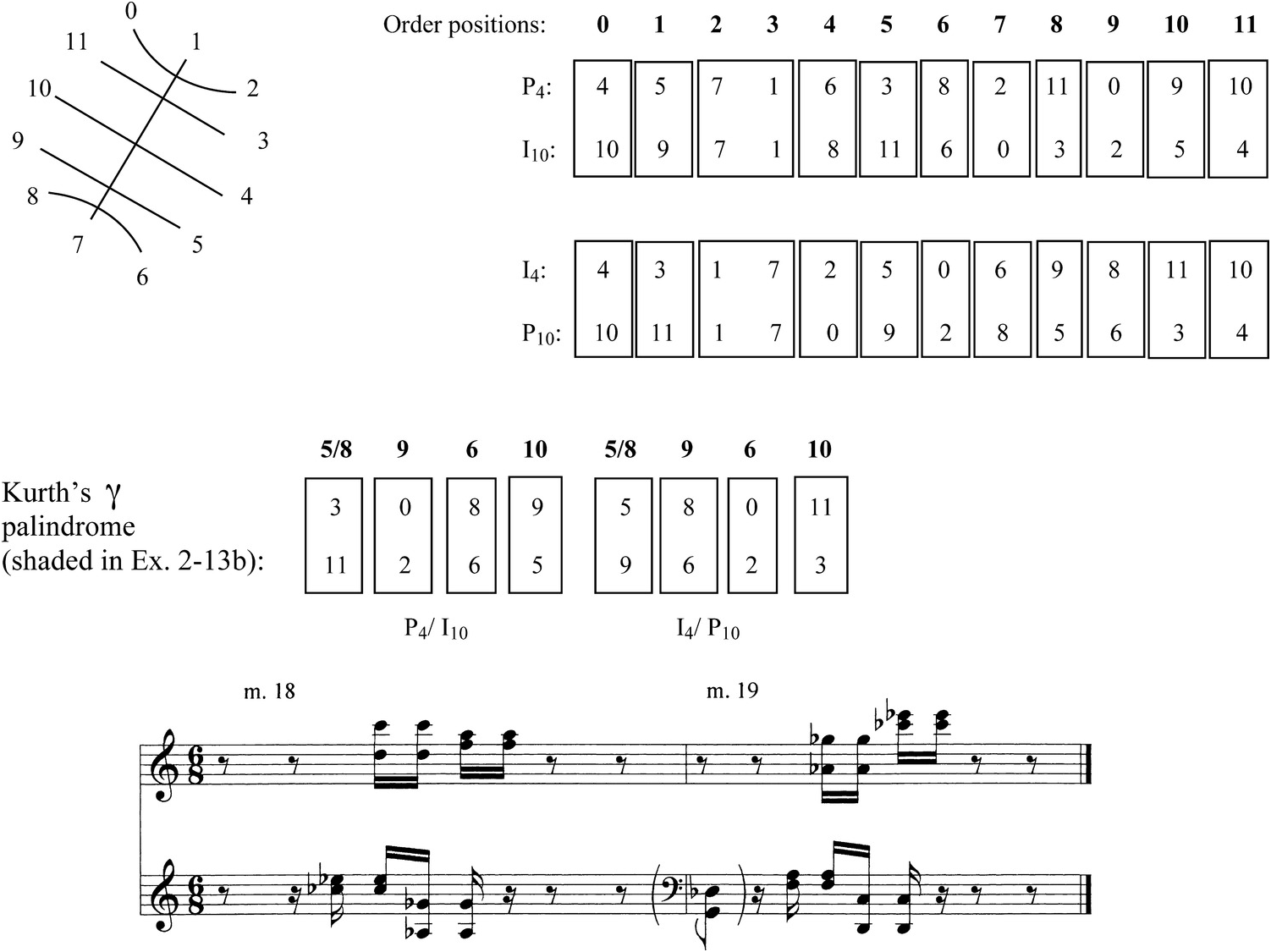
Measures 17b–19 constitute a climax for the Prelude in terms of dynamic and registral extremes, and also in terms of complexity of row-element ordering. Richard Kurth has shown that the passage adopts an ordering that not only obscures the rows as wholes, as most of the earlier passages did, but in addition makes the individual tetrachords difficult to distinguish.15 This ordering is illustrated by Example 2.13a, a reproduction of Kurth’s Figure 5. Each number in the example represents the corresponding order numbers of both rows, presented together as a vertical dyad. Parentheses indicate two order numbers of the same row which create invariant pitch classes with the corresponding order numbers in the other row, so that four order positions are presented together as a single (or repeated) vertical dyad. In mm. 17b–19, no tetrachord is completed before another enters. Furthermore, each tetrachord itself is made more difficult to distinguish by the way in which Schoenberg moves its successive members between right and left hands and from top to bottom registrally, as Example 2.13b illustrates. For an example, trace the path of the second tetrachord of P4 in mm. 17b and 18, indicated with circled pitch-class numbers ⑥, ③, ⑧, and ② in Example 2.13b. This tetrachord progresses from G♭ in the right hand’s highest register at the pickup to m. 18, to E♭ in a middle register of the left hand on the second sixteenth note of eighth-note beat 2 in m. 18. (In between, order numbers 2 and 3 from the first tetrachord have come on the downbeat of m. 18.) Next comes A♭, in the left hand’s lowest register on the second sixteenth note of beat 3 (after order positions 8 and 9 from the third tetrachord have intervened). Finally we hear D in the right hand’s middle register on the fifth beat (after order positions 10 and 11 have been heard on the two parts of the fourth beat).
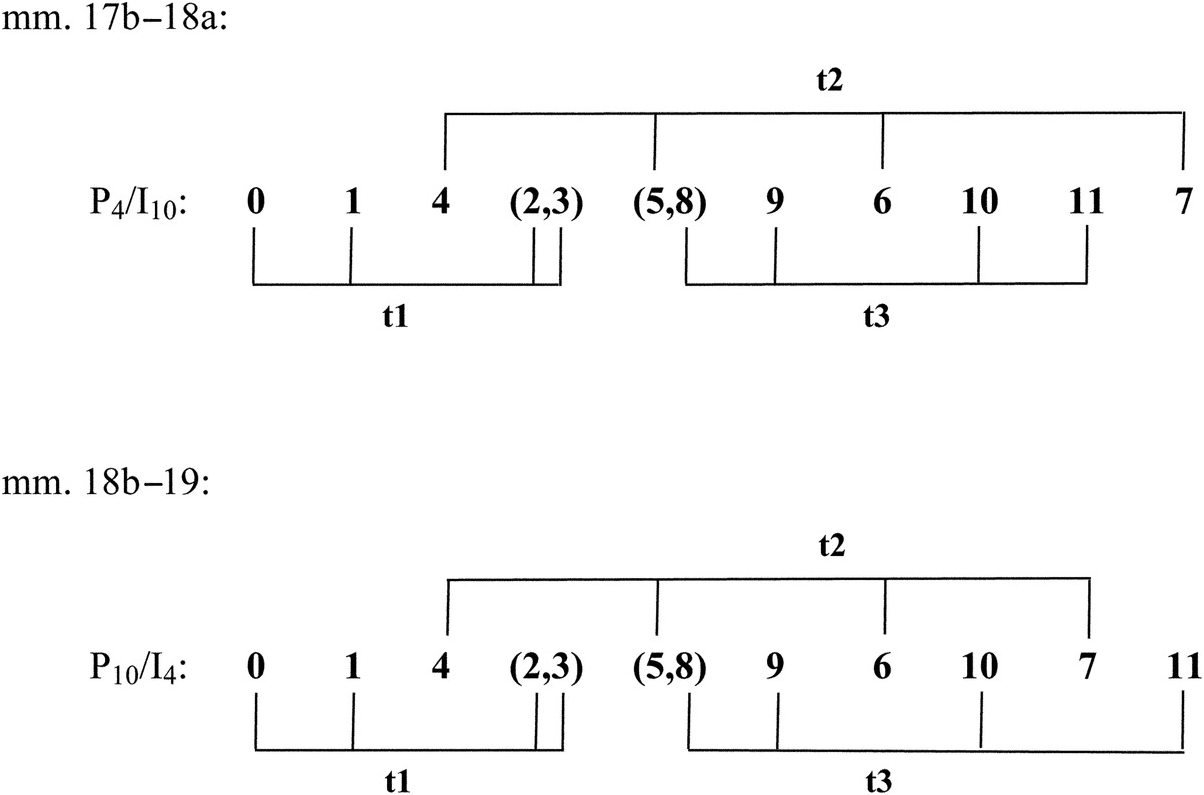
Example 2.13a Schoenberg, Prelude Op. 25, mm. 17b–19: ordering of row elements
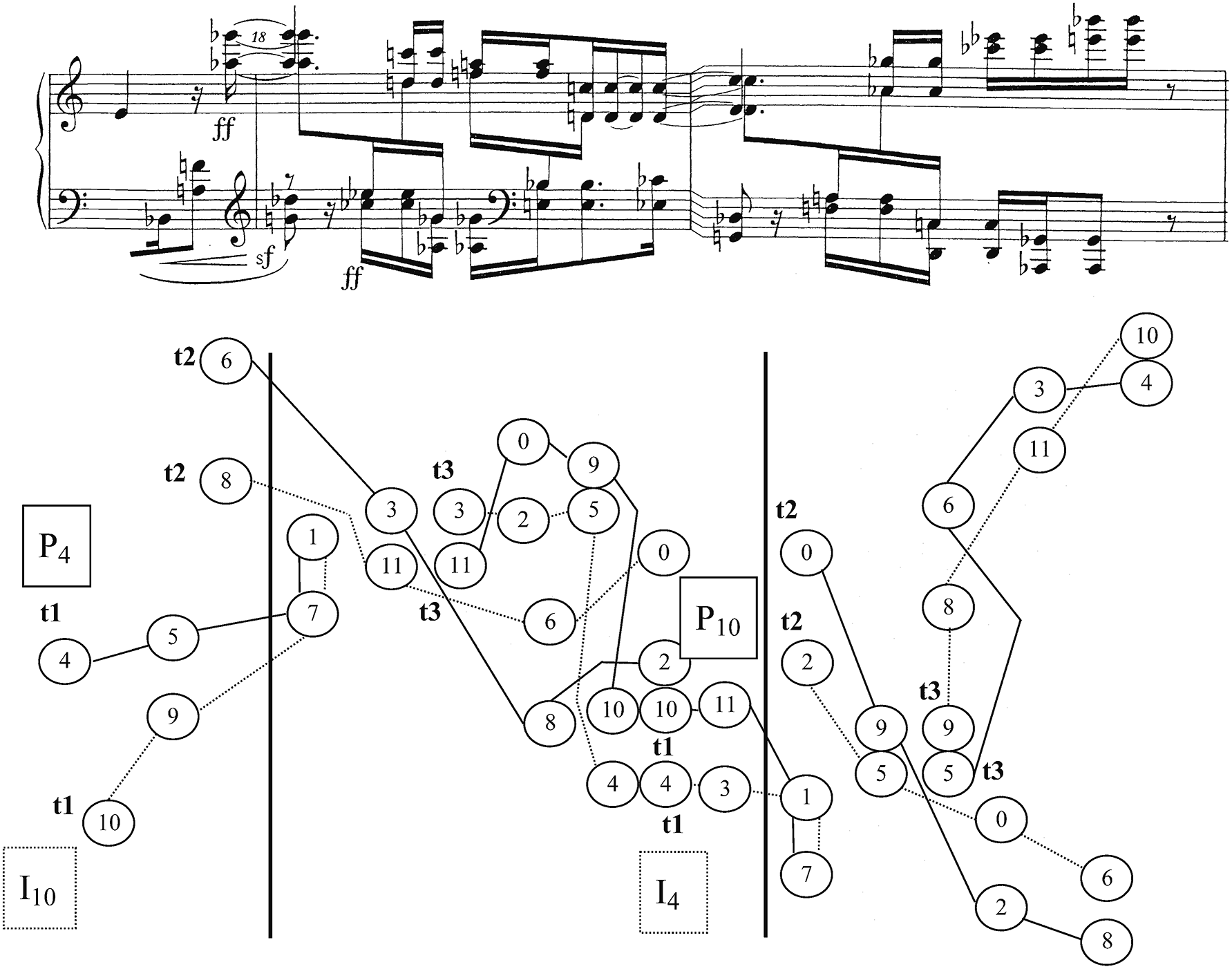
Example 2.13b Schoenberg, Prelude Op. 25, mm. 17b–19.
Schoenberg’s practice of jumbling the order between the tetrachords and disconnecting the individual pitches of the tetrachords from each other registrally has an important effect. It creates a partition of the row pairs P4/I10 and I4/P10 that forms a different sort of palindrome from the Prelude’s basic shape, but nevertheless centered on the dyad {1,7}, as the basic shape’s top tetrachord has been. This partition divides each of the row pairs into the same six vertical dyads, repeated once within the pair (portrayed at the upper right in Example 2.13c). These dyads are arranged pitch-class-symmetrically around 1 and 7, as the pitch-class clock on the upper left in Example 2.13c shows. Thus, in the climactic section, Schoenberg seems to be making an attempt to bring back the Prelude’s basic shape, but instead creates a related kind of structure. It is as if he is striving mightily to return to his Grundgestalt, but not yet finding success, making this section a climax of imbalance as well as register and dynamics.
Example 2.13c Schoenberg, Prelude Op. 25, mm. 17b–19: dyads created by partition of P4/I10 and I4/P10
My interpretation of the dramatic function of mm. 17b–19 within the whole is strengthened by other palindromic shapes within the passage that seem more audible than the underlying pitch-class symmetry around {1,7}. Kurth has highlighted three such shapes; I will focus only on what he calls the “gamma” palindrome.16 Schoenberg seems to have recognized that a certain sequence of order numbers, namely <5-and-8,9,6,10>, when applied to first P4/I10 and then I4/P10, will create a palindromic sequence of dyads (illustrated in the middle of Example 2.13c, and also shaded in Example 2.13b). This is one of the few order-number sequences that will produce such a result. The eight-dyad pitch-class palindrome that ensues is not highlighted further through pitch symmetry. But, as Kurth argues, a number of qualities draw the listener’s attention to “gamma” – its change in contour from parallel motion between the hands in m. 18 to contrary motion in m. 19, and the identical metrical position of its dyads within the two measures, not to mention the various ways in which Schoenberg highlights its midpoint, the last sixteenth of m. 18 and the downbeat of m. 19 (see the bottom of Example 2.13c for an illustration of some of gamma’s contour and rhythmic features). In this way, the role of mm. 17b–19 within the whole Prelude as a passage that – noisily and furiously – tries to get back to the basic shape, but misses the mark, is made more obvious.
After all the sound and fury, the long-awaited solution to the Prelude’s problem is introduced in m. 20, with a sudden drop in dynamics to , a shrinking of the registral compass, and a leveling-out of the rhythm. This is a quiet, innocuous setting for the piece’s conclusive passage, almost as if the answer were coming as a “still, small voice” after a great storm.17 (Schoenberg would set another piece’s conclusion in a similar way later on, that of the String Trio.) As Example 2.14 shows, m. 20 presents the basic shape for P4 and R4, which was the first line of Schoenberg’s original row table. Notice how each tetrachord stays within a relatively limited register, with only a minimum of overlapping between the top and middle tetrachords (the top tetrachord, F4–G5; the middle, D4–A♭4; the bottom, A3–C4). Measure 20 provides the “solution” in the sense that four of the six possible dyad palindromes are clearly presented as pitch mirrors; 4–5/5–4 on top, 6–3/3–6 in the middle, and 11–0/0–11 and 9–10/10–9 on the bottom. The other two dyad palindromes are represented by only one of their members, 7–1 on top and 8–2 in the middle (having the effect of making the top and middle voices incomplete palindromes as wholes). The arrangement of the bottom voice not only makes it a pitch palindrome, but also presents the third tetrachord of R4 in a shape that it has not yet taken. Pitch classes <10,9,0,11>, when spelled with German letter names, reveal a motto that has been hinted at in earlier passages – BACH. (That sequence was stated backward at mm. 2–3, 8, 12, and 17, partitioned registrally into 3 + 1 notes in m. 6, and given vertically on the downbeat of m. 16.) Here is another way in which m. 20 solves a problem posed by earlier measures.
Example 2.14 Schoenberg, Prelude Op. 25, m. 20.
Interestingly, the rhythms of the six tetrachords of P4/R4 in m. 20 are not palindromic. Instead, Schoenberg seems to be setting each tetrachord apart from its partners, by giving each a unique rhythmic pattern that repeats regularly within an overriding 3/4 meter. (The 3/4 is itself a hemiola with respect to the main meter of the piece, 6/8.) The top voice repeats 
three times, and the middle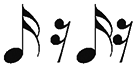 
. The bottom voice begins by repeating 
, but because of the extra pitch made necessary by its complete pitch palindrome, changes rhythm on the third beat to 
, a close relative of the former pattern.
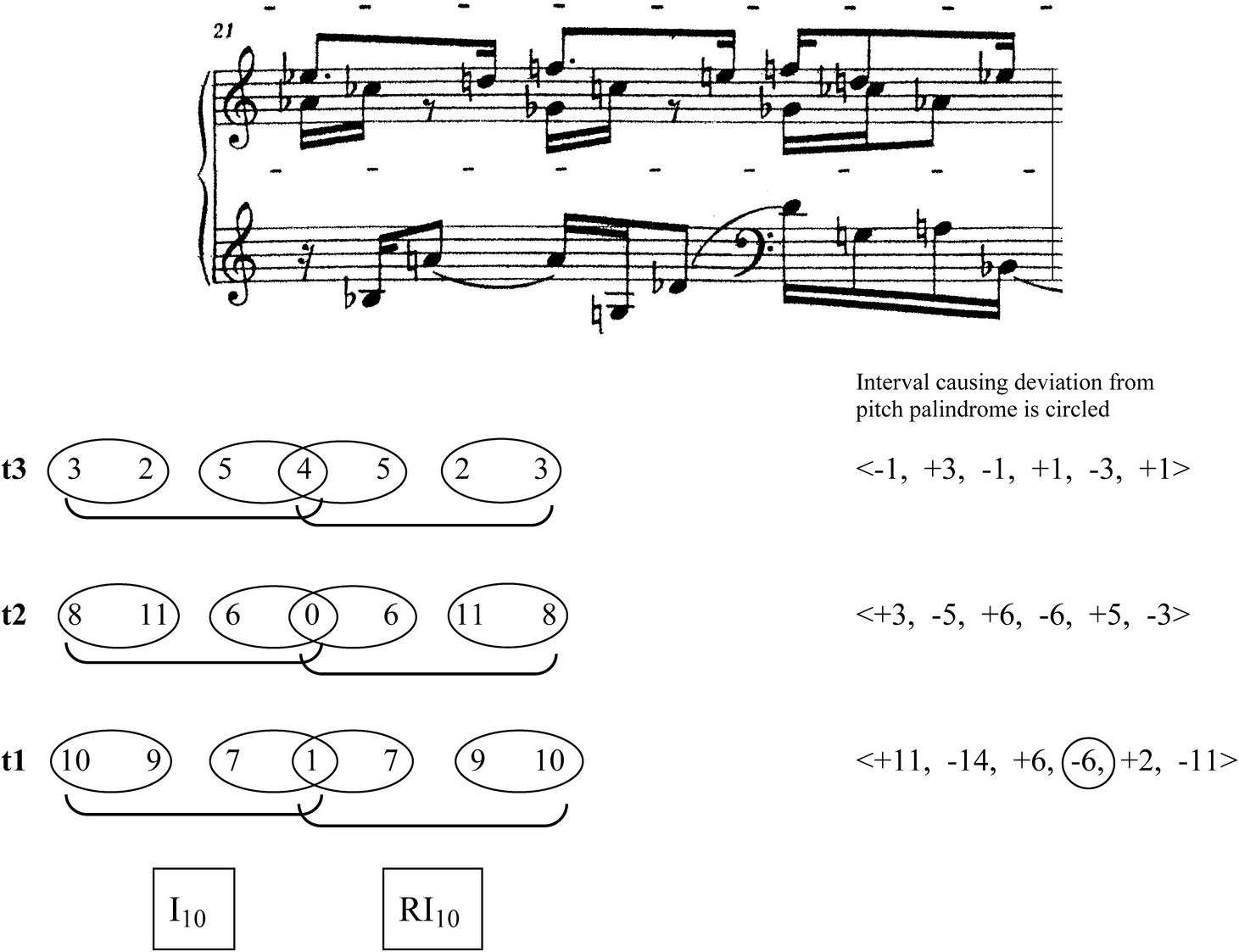
Measure 21 continues the trend of m. 20, except that now all three voices create complete palindromes within the I10/RI10 pair – with the result that all six palindromic dyads are heard clearly as pitch or pitch-class mirrors (see Example 2.15 for an illustration). The bottom voice, representing the first tetrachord in an inversion of m. 20’s registral order of voices, is a pitch-class palindrome; the middle and top voices create pitch palindromes from the second and third tetrachords respectively. Dynamically, the passage grows steadily, paralleling the closer approximation to the perfect Grundgestalt. Registrally, the three voices are again set apart from one another within limited ranges: now the bottom voice overlaps with the middle, and the top two voices are registrally distinct. Intervallically, the three voices present an inversion of the ordered pitch-interval successions of m. 20 – or, rather, what they would have been if the top two voices in m. 20 had been complete palindromes. (Consult the ordered pitch-interval strings in the bottom right-hand corners of Examples 2.14 and 2.15.) And rhythmically, each voice again repeats its own unique motto within the 3/4 framework, changing slightly on the third beat to accommodate the seventh note made necessary by each voice’s complete palindrome. The top voice takes over , which was on the bottom in m. 20. The middle voice adopts , which belonged to the top voice. And the bottom voice introduces a new rhythm, 
, and then repeats it before opening up into steady sixteenths on the third beat.
Example 2.15 Schoenberg, Prelude Op. 25, m. 21.
Measure 21 thus seems to fulfill two functions within the whole Prelude: first, it provides a solution to the piece’s overarching problem by presenting the clearest statement yet heard of the basic shape, that shape illustrated in Schoenberg’s set table sketch.18 For the first time in the piece, all six palindromic dyads are presented as pitch or pitch-class palindromes, and each of the six dyads is associated with a pair of ordered pitch intervals that mirror one another. (For example, 10–9/9–10 in the bass voice is projected by +11 and −11.) Second, m. 21 not only inverts, but develops and completes the previous measure. It satisfies this role intervallically, by transforming m. 20’s incomplete palindromes in the top and middle voices into complete ones in the middle and bottom voices, and also rhythmically, by moving m. 20’s bottom rhythm to the top, and its top rhythm to the middle.
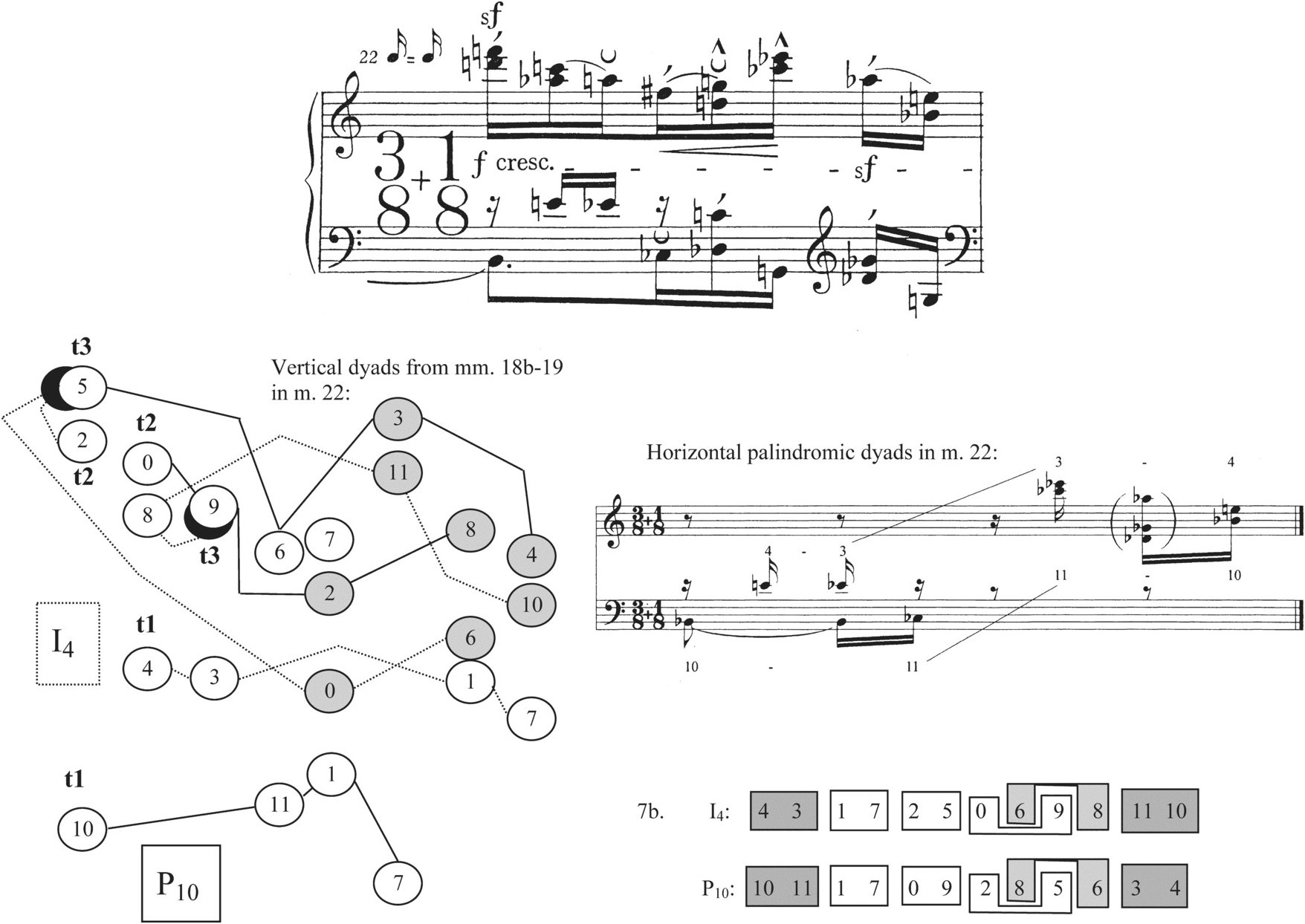
The final three measures in the Prelude are similar to ending passages in a number of Schoenberg’s other works of all three style periods, in that they return the piece’s solution to obscurity after it has just been revealed.19Example 2.16’s pitch-class map shows that m. 22 combines P10 and I4, the same pair that held sway in mm. 18b–19. Like mm. 18b–19, m. 22 combines its pair of rows in such a way that most of the individual tetrachords are indistinguishable. However, the latter passage is different from the earlier one in that it does not place as much emphasis on the vertical dyads created by corresponding order numbers. In four places, corresponding order numbers do sound as verticals (these are shaded on the pitch-class map): {0,2} formed by order position 6 in both rows on the fifth sixteenth note, {6,8} by order position 7 on the seventh sixteenth note, and two dyads that are more obvious because of their closer registral placement: {3,11} formed by order number 10 on the sixth sixteenth, and {4,10} by order number 11 on the eighth sixteenth.
Example 2.16 Schoenberg, Prelude Op. 25, m. 22.
But while these familiar verticals from the climactic section return on the last four sixteenths of m. 22, some of the horizontal palindromic dyads from earlier parts of the piece also come to the fore at other places in the measure. Specifically, 4–3/3–4 and 10–11/11–10, the dyad invariances created at order positions <0,1> and <10,11> in P10/I4, are highlighted in similar ways. As the rightmost part of Example 2.16 shows, the first part of each palindrome receives a clear statement in the left hand at the measure’s beginning, and a less clear statement (because of the intervening {A♭, G♭, D♭} chord) in the right hand at the measure’s end. It seems at least possible to hear the vertical dyads from mm. 18b–19 as coming in at the end of m. 22 and disrupting the horizontal palindromic dyads.
If m. 22 is heard as a summary of that part of the piece coming before the solution – disrupting the strivings toward the basic shape that were characteristic of mm. 1–16 with the vertical dyads that were characteristic of mm. 17–19 – then m. 23 continues the same process. This measure dissipates the horizontal palindromes even further, while the vertical dyads from the climax disappear as well. A row-count of m. 23 can be found in Example 2.17. The two rows combined here are R4 and RI10, which together account for every pitch class in the measure save the last four notes in the left hand (unattached in the example). These last four notes could be heard as an echo of the repeated 1–7, 1–7 in the initial four sixteenths of the right hand: in other words, as a motivic development (of a motive significant throughout the Prelude) that takes us beyond the influence of the twelve-tone row for a moment. Example 2.4, pair 11, shows that R4 and RI10 together create three dyad palindromes, 9–10/10–9, 5–4/4–5, and 6–8/8–6. But Schoenberg’s setting of these two rows obscures all these dyad invariances, together with the majority of the row forms’ adjacent dyads. As Example 2.17 shows, the six tetrachords from the two rows are interlocked, so that adjacent pitch classes in a tetrachord most often have a pitch class from the other row sounding in between. Where such interlocking does not occur – as in the first two sixteenths, which present adjacencies from RI10; sixteenths 3–4, which present adjacencies from R4; and sixteenths 5–6, which present an adjacency from R4 – registral shifts prevent us from hearing the dyad horizontally. In addition, Schoenberg has stacked the three tetrachords of each row more or less vertically (order positions 2, 6, and 10 are not aligned vertically in both rows). Hence, instead of the vertical dyads characteristic of mm. 17–19’s climactic passage, we hear trichords, none of which contain dyads from the earlier passage.
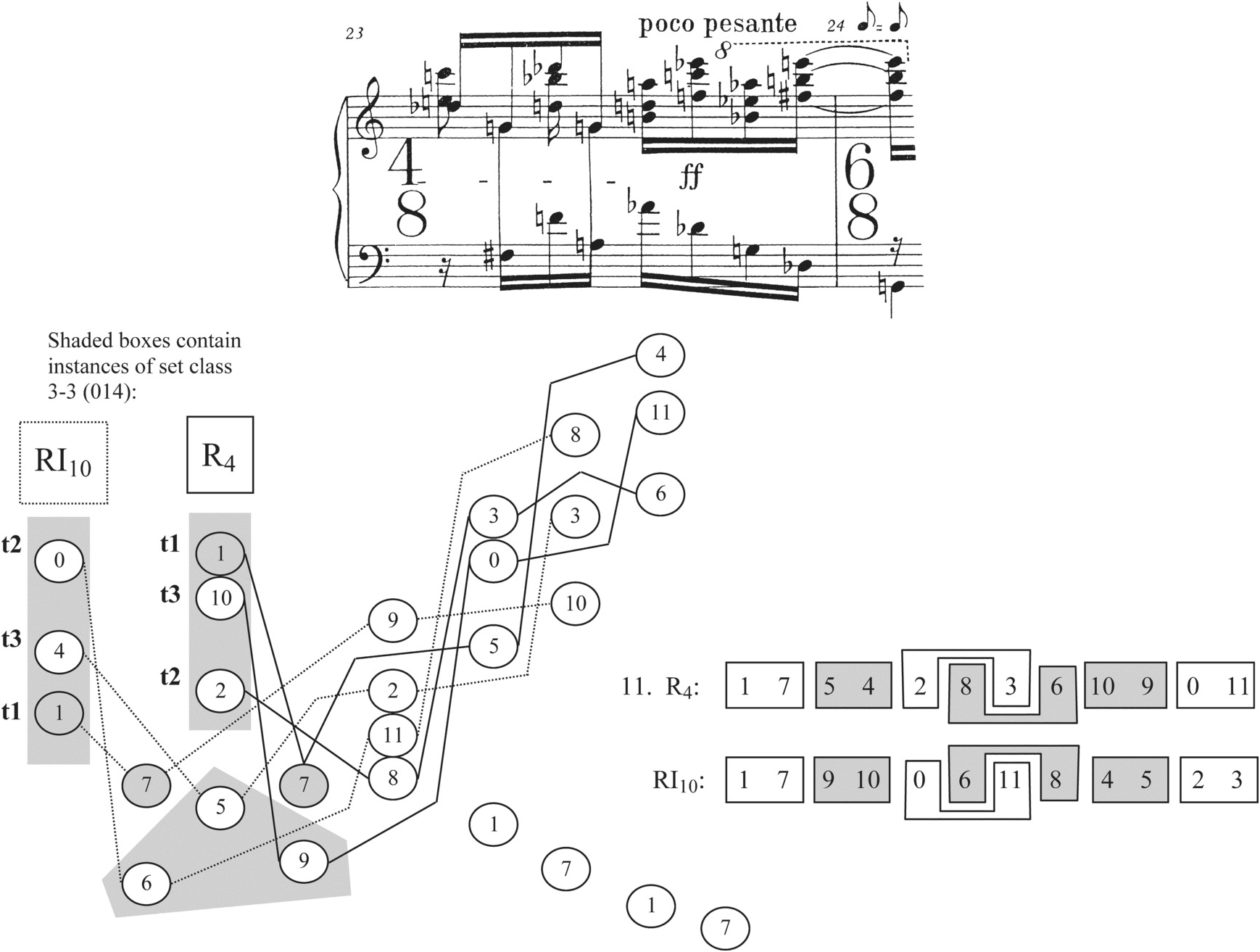
Example 2.17 Schoenberg, Prelude Op. 25, mm. 23–24a.
Thus we can hear m. 23 as dissipating the elements that were crucial in the piece’s earlier arguments. In their place, the most prominent element, at least at m. 23’s beginning, is a set class common to most of Schoenberg’s atonal and serial music: set class 3-3 (014). Instances of 3-3 are marked with shaded boxes in Example 2.17. Although 3-3 has been heard several times earlier in the Prelude (the second half of m. 1 without D♭, the downbeat of m. 3, the third to fifth sixteenths of m. 9, the final three notes of m. 9, among others), its appearances were less common in the first part of the piece, possibly because the only way it can come about is by means of non-contiguous partitioning or combining different rows. Therefore, after solving the piece’s problem in mm. 20–21, m. 23 seems preoccupied to an extent not heard before with a different, though related, element.
The final measure continues the Prelude’s journey away from the process that dominated its development in the first twenty-one measures, but at the same time recalls elements of that process, in an attempt to round off the whole. A row-count of m. 24 can be found in Example 2.18. This measure combines three rows, P4 and I10 at the beginning, and R4 following P4 in the right hand and overlapping with I10 in the left hand. P4 and R4, appearing side by side, give the composer the opportunity for six dyad palindromes, as we have already seen in m. 20. But here in m. 24, Schoenberg obscures the ideal shape by applying registral changes or changes in ordering to the palindromic dyads, or placing other pitch classes between the members of a dyad. Only 9–10/10–9 is presented in such a way that both dyads seem contiguous and clearly reverse each other; but even in that case, the right side of the palindrome, 10–9 (right hand, second and third sixteenths of the second half of m. 24), occurs as an inner voice under a more prominent motion up to G♯. An interesting case of a palindromic dyad obscured by an order change, which then comes to the fore as a repeating motive, is the last measure’s treatment of 7–1/1–7 from P4/R4. The second part of the palindrome is reversed to 7–1 on the last two sixteenths of m. 24, and hence the reversed dyad echoes 7–1 from P4 (projected as eighth-note G and triplet sixteenth C♯ on beat 3 of the 6/8). Since the 7-1 dyad of the third row, I10, is also emphasized motivically (dotted quarter G to sixteenth D♭ in the left hand in the measure’s second half), m. 24 reminds us of this motive’s importance throughout the Prelude by multiplying occurrences of it.
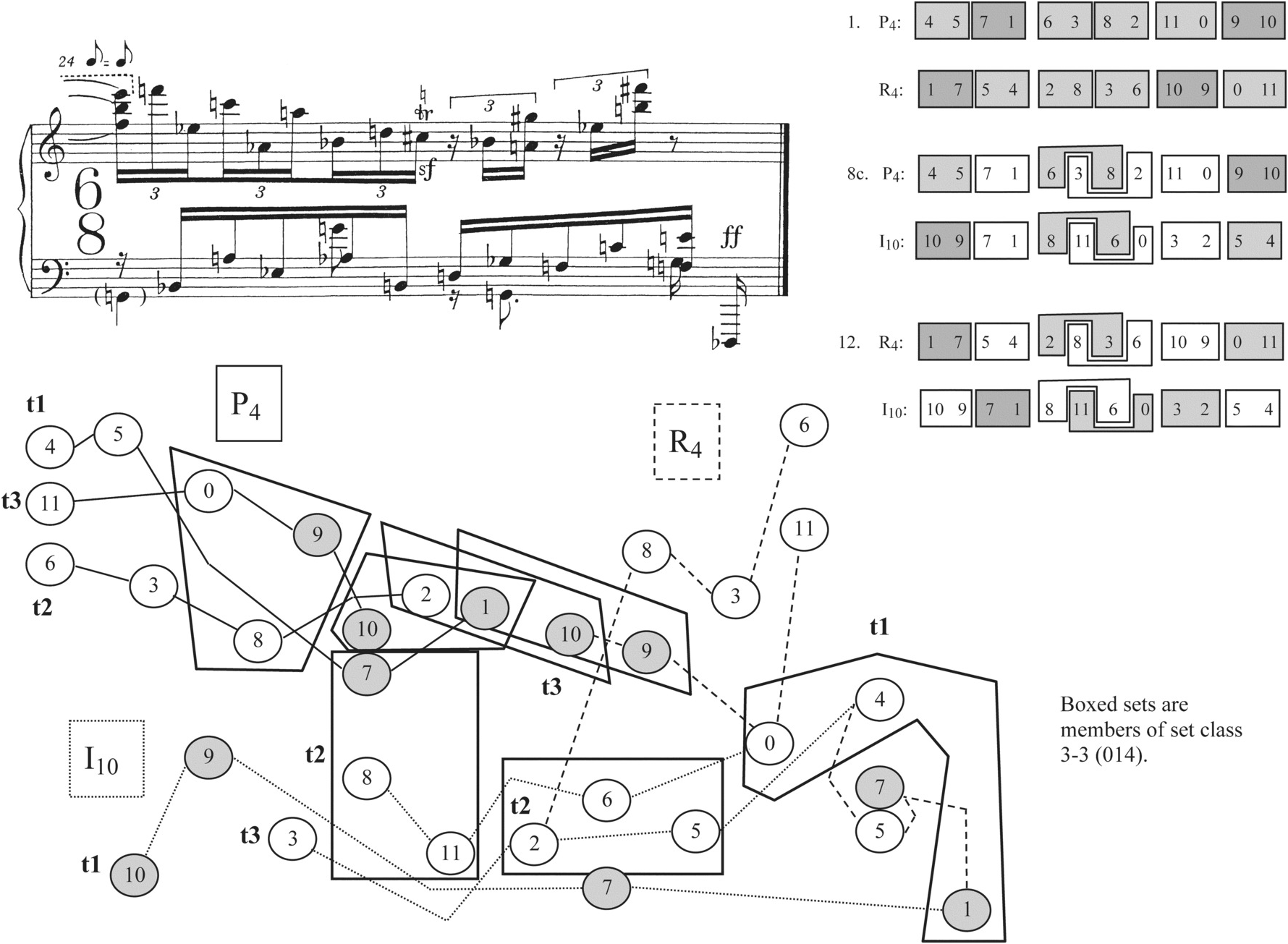
Example 2.18 Schoenberg, Prelude Op. 25, m. 24.
While recalling a few of the dyad palindromes and motives that characterized the earlier parts of the piece, m. 24 also develops certain elements that came to the fore in mm. 22 and 23. There is a saturation of trichords belonging to set class 3-3 that accounts for many of the natural segments of the passage, as well as some not-so-obvious segments. Each set class 3-3 is highlighted by a box in Example 2.18; there are seven altogether. Although that trichord has occurred a number of times earlier in the piece, and in a more concentrated manner in mm. 22 and 23, the last measure packs more set classes 3-3 into a small space than we have heard before.
To summarize, then, the Prelude Op. 25 can be heard as growing out of a process that closely resembles Schoenberg’s concept of “musical idea,” if we pay attention to the different ways in which it presents its Grundgestalt, or basic shape, from beginning to end of the piece. This shape, with its six palindromic dyads, is suggested and obscured several times in the opening measures. Then at the climax, mm. 17–19, the piece strives mightily to return to the basic shape, but succeeds only in creating other palindromic shapes, some obvious, some more subtle, that are substantially different from it. Immediately after this dynamic and registral high point, the basic shape is presented in such a way that all six of its palindromic dyads are unmistakable. But the solution is followed by a coda, mm. 22–24, which obscures the basic shape and multiplies a trichordal element significantly different from that shape’s dyadic components.
Menuett
The Menuett and its accompanying Trio share the distinction of being the most-analyzed pieces in the Suite Op. 25. A wide variety of perspectives have been brought to bear on these two short pieces, and many of them will be represented, discussed, and disputed in the paragraphs and footnotes to follow. At one point in the history of the analytical literature, writers seemed to express a “conventional wisdom” that placed a major dividing line between them: namely, the Menuett is to be understood in terms of the same partitioning into interdependent tetrachords as the earlier movements, while the Trio introduces for the first time the notion of a linear ordering of the twelve pitch classes, divided into two hexachords, the type of partition more characteristic of Schoenberg’s mature twelve-tone music. Examples of the “conventional wisdom” include Ethan Haimo’s discussion of the two pieces in Schoenberg’s Serial Odyssey and Jan Maegaard’s earlier article on the chronology of Schoenberg’s early twelve-tone music.20
A recent analysis by Stephen Peles of excerpts of the Menuett challenges the notion that logic and process in the piece can be understood only in terms of tetrachordal elements.21 Specifically, Peles uncovers (in the first two measures of the Menuett) a procedure, which I will call “collectional exchange,” operating on hexachords, as well as tetrachords. Briefly defined, collectional exchange projects the pitch-class content of the discrete subsets of some other row than the one in effect, through rhythmic and/or registral grouping. Examples of this technique appear for the first time in the Intermezzo, the Op. 25 piece that Schoenberg composed second, as well as in the Gavotte. Example 2.19 shows the tetrachord exchange that begins the Intermezzo: notice that within P4 in mm. 0–1, pitch classes 6 and 8 group together registrally in the tenor, as do pitch classes 11 and 0 in the bass.
Example 2.19 Schoenberg, Intermezzo Op. 25, mm. 0–3: phrase 1.
Now, these four pitch classes do not form a discrete tetrachord of P4, but they do form the content of the second discrete tetrachord of I10, <8,11,6,0>. Not coincidentally, the second discrete tetrachord of I10 appears immediately after, in the second part of m. 2 as the repeated figure in the right hand. Meanwhile, within I10, pitch classes 4, 5, 7, and 1 appear together in the middle and upper registers of the left hand (mm. 2b–3). This group of pitch classes cannot be found as a discrete tetrachord in I10, but they do make up the content of P4’s first tetrachord, which was highlighted as a repeated figure in the right hand of mm. 0–2a. In a sense, P4 “gives” its first tetrachord to I10, and I10 “gives” its second tetrachord to P4: a tetrachord exchange.
To return now to the opening of the Menuett, my Example 2.20a provides adaptations of Peles’s Figures 3c–e, surrounding the pertinent score excerpt. From this example, one can see that the opening statement of P4 projects the hexachords of P10 and I4 and the tetrachords of I10. (Example 2.20b shows the four source rows divided into hexachords.) The partition forming the two hexachords of P10, in reverse order, is a chronological division of P4: all the pitch classes attacked before the barline are divided from those pitch classes attacked after the barline. If we adopt a registral boundary instead (imagine a horizontal black line whose top edge touches F4 and whose bottom edge reaches to E4), the partition yields the hexachords of I4, the second hexachord above the first. And finally, if we separate the top two notes from the other four in each measure (thus creating a registral partition within a chronological one), the three tetrachords of I10 emerge. Thus, hexachordal exchange appears together with tetrachord exchange in this little passage – a situation that did not occur in the movements of Op. 25 composed earlier.
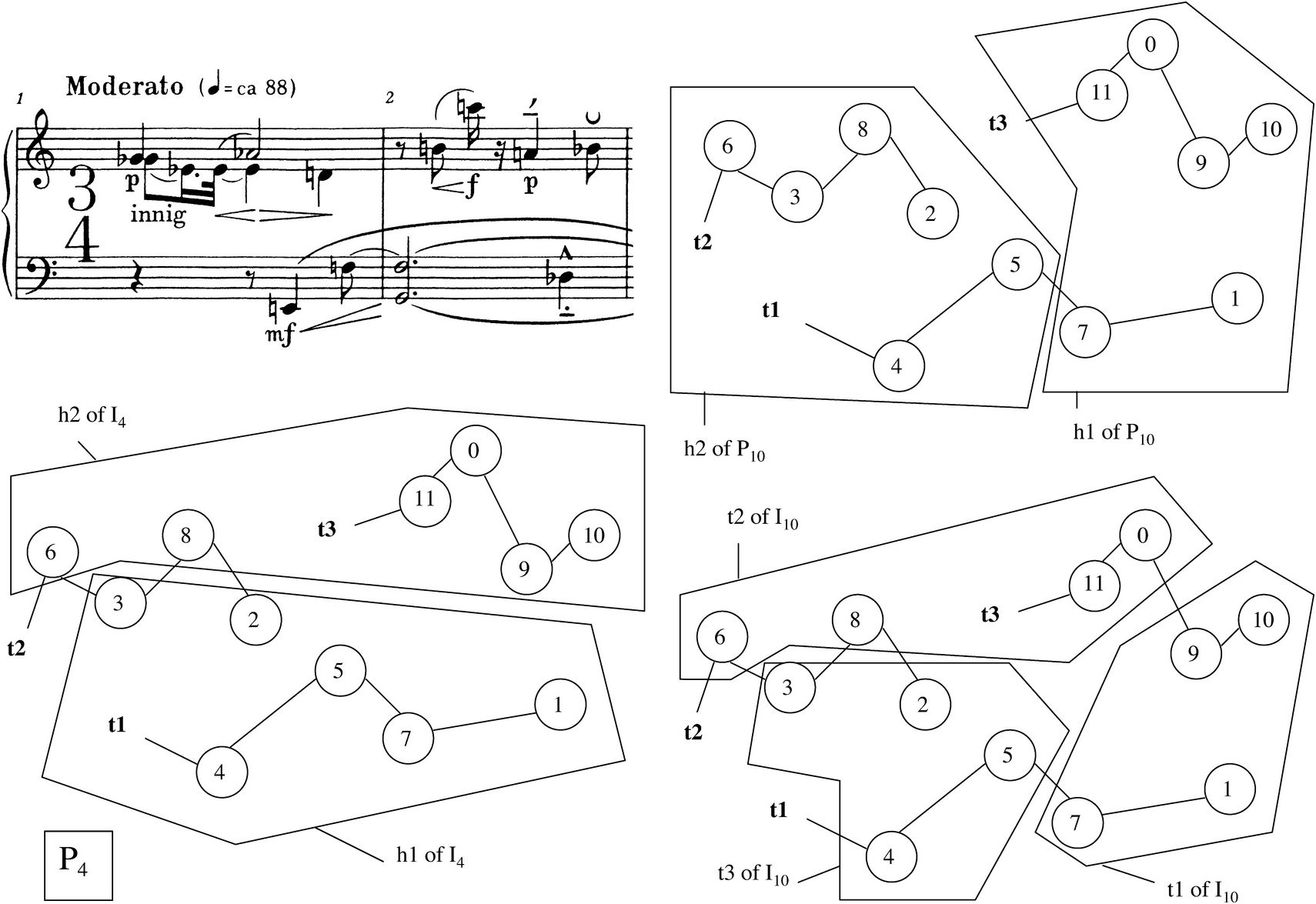
Example 2.20a Schoenberg, Menuett Op. 25, mm. 1–2, with three pitch-class maps illustrating hexachord and tetrachord exchanges (adapted from Peles, “Continuity, Reference and Implication,” Figures 3c–e).
Example 2.20b Schoenberg, Suite Op. 25: the four source rows, divided into hexachords
The main point Peles seems to make is that the opening measures of the Menuett imply all the row forms that the rest of the piece then makes use of (and, in that way, they serve as a Grundgestalt for the piece). But here I want to emphasize the fact that the procedures mm. 1–2 use to project forms P10, I4, and I10 are the same as those the Intermezzo (and Gavotte) were based on, collectional exchanges expanded to embrace the hexachord as an exchangeable unit for the first time. Later in the Menuett, certain pairs of hexachords that come about through exchange, as well as certain contiguous hexachords of the original row, are presented in ways that make the division into hexachords just as obvious as those in mm. 1–2 or more so. This leads to the Trio, where almost every row form is divided into its contiguous hexachords in an obvious way. Thus the Trio, rather than presenting a completely unheard-of way of dividing the series, should be understood as an outgrowth of exchange procedures that involved tetrachords in the Intermezzo and Gavotte and are applied to hexachords beginning with the Menuett. (The Trio will not be analyzed here, but a quick perusal of the score will demonstrate the consistency of its hexachordal partitioning.)
The basic method of my Menuett analysis, then, will be to examine the presence or absence and effects of hexachord exchange in each segment of the piece. Not surprisingly, this approach brings to light a problem on the first page of the piece that is solved later, and the “musical idea” that flows forth from mm. 1–2’s Grundgestalt occurs in stages that line up with the different sections of the Menuett’s form. My view of the form agrees with Ethan Haimo’s, John McKay’s, and Martin Boykan’s, in that it identifies three main sections: A at m. 1, B directly after the double bar at m. 12, and A′ at m. 17.22 Haimo calls this a “rounded binary,” no doubt because of the repeat sign ending the A section and the brief, five-measure length of B. I prefer to label it as ternary because mm. 17–31 reprise, extend, and develop all of the pitch and rhythmic material of mm. 1–11, rather than a condensed version of A. Whatever label we give to it, the form is the same one that was typically associated with the minuet in the common-practice period (and, as my analysis progresses, I will point out a number of ways in which Schoenberg simulates the key changes that traditionally go with this form). The musical idea lines up with the form as follows: the opening measures of A demonstrate that one row form, P4, can, through hexachord and tetrachord exchange, project the other three forms (as described above). The first two measures of B divide P10 into hexachords by means of a registral and chronological partition, but these hexachords are not the ones produced by order positions 0–5 and 6–11. Instead, Schoenberg rotates P10 to begin on order number 2, and then divides it into contiguous hexachords, so that the left hand’s hexachord constitutes order positions 2–7 (presented out of order) and the right hand has 8–1 (also out of order). Throughout the B section, the same partition of the rotated row is used, and none of the row forms divided this way (I4 in mm. 14–15, I10 in m. 16) is able to project other forms through hexachord exchange as the P4 in mm. 1–2 has done. A problem is thereby created: namely, rotation by two order positions, division into contiguous hexachords, and subsequent internal reordering seem to destroy the row’s capability for suggesting other rows through exchange, which was so crucial at the piece’s beginning. Near the beginning of A′, however, at mm. 19–20, Schoenberg introduces a form of I10 rotated by two positions in which order positions 2–7 appear in the right hand (presented out of order) and 8–1 (also out of order) in the left hand, in a rhythmic pattern reminiscent of the opening measures, and when one divides this rotated row at the barline, the partition does in fact give rise to the two contiguous hexachords of the unrotated version of I4! This shows that rotated rows can in fact suggest other rows through hexachord exchange, solving the problem. The remainder of the Menuett then produces hexachord exchanges from both rotated and unrotated rows, and at the final cadence, mm. 32–33, it shows that segments from two different row forms, both rotated by two order positions, can also be combined to produce hexachord and tetrachord exchanges. The following paragraphs will describe the process that defines the Menuett’s Idea in greater detail.
After mm. 1–2’s multidimensional demonstration of hexachord and tetrachord exchanges, the passage immediately following, mm. 3–8, seems to move away, step by step, from that ideal, obscuring it gradually in much the same way that the Prelude obscured its ideal after suggesting or presenting it. Example 2.21 depicts this, using a pitch-class map below the score. In each of the five row presentations in this passage, the hexachords of other row forms projected through exchange are marked with heavy boxes. Notice how in mm. 3–4, only one hexachord exchange is created (rather than the two of mm. 1–2), with I4. Though Schoenberg has reduced the number of exchanges, the hexachords of I4 come through clearly to the listener because of the chronological distribution of I10’s pitch classes. However, this partition is a bit less clear than the one that gave rise to P10 in mm. 1–2, because it does not line up with the barline, and because the listener has to ignore the sustained D♭ in m. 3 and the sustained B♭ and A in m. 4 to make it work.23
Example 2.21 Schoenberg, Menuett Op. 25, mm. 3–8.
The hexachord exchanges in the following measures recede yet further from the musical surface. In mm. 5–6a, P10 occurs, and this could be partitioned registrally into the hexachords of P4, were it not for the lone pitch class 11 in the tenor on the downbeat of m. 6, which belongs to the second hexachord of P4 but groups registrally with the notes of the first hexachord. This tendency toward “hexachord exchange minus one” is exacerbated in the next row, I4 in mm. 6b–7a, which produces the hexachords of I10 if the listener can somehow group the <2,5,0,6> figure of m. 6b with <3,4> on the second eighth of m. 7, and the highest pitch class, 1, on the third beat of m. 6 with the middle to low register {7,8,9,10,11} in mm. 6b–7. Measure 7b, the projection of P10 using the pitch classes of P4, presents a similar problem: the members of P10’s first hexachord are registrally proximate, but to hear the second hexachord we have to hook up pitch class 5 in the soprano on beat 2 with {2,3,4,6.8} occurring in the middle and lower register. Finally, the cadential measure, m. 8, brings forth the two hexachords of P10 through exchange, but five notes of each hexachord are separated from the other pitch class registrally: {0,1,7,9,10} in the right hand from pitch class 11 in the left hand, and {2,3,4,5,8} in the left hand from pitch class 6 in the right. There seems to be a step-by-step blurring of first the registral, and then the chronological partitions that gave rise to the multiple hexachord exchanges in mm. 1–2.
At the same time, another aspect of mm. 1–2’s structure breaks down in mm. 5–8, creating a process that we can identify as “motivic liquidation.” This term comes from Schoenberg’s Fundamentals of Musical Composition, and it refers to the procedure that he considers to be typical of opening sentence forms from Beethoven piano sonatas. In this process, a complex of motives that is introduced in the first phrase (presentation or “tonic form”) and loosely sequenced in the second phrase (repetition or “dominant form”) is then broken up increasingly into its individual motivic components during the third or “continuation” phrase, until all that remains is the “residue”: the motives with the least recognizable shape.24 According to John MacKay, mm. 1–8 in Schoenberg’s Op. 25 Menuett clearly organize themselves into a sentence form, with the first two measures constituting the presentation, mm. 3–4 the repetition, and mm. 5–8 the continuation and cadence.25 And if we look for the elements of mm. 1–2 and 3–4 in the third phrase, we find indeed that the continuation presents fewer and fewer components of the opening. In the lowest register of m. 5, we hear pitch class 5 progressing to pitch class 4, while <6,3,8,2> sounds above them in the alto register, which varies the pitch-class sequence of m. 1, but not so much as to be unrecognizable. However, if we listen for the “motivic” material of m. 2 in mm. 5b–6, the only component that comes through is <7,1> on the first quarter of m. 6. The right-hand sequence of m. 2, <11,0,9,10>, is no longer heard as a group. In the following row presentation, I4 in mm. 6b–7, the pitch classes {0,6,8,11} can be heard as a group (see the dotted enclosure on the pitch-class map), and this may enable the listener to recall m. 3’s right hand, but there is not as immediate a connection as that between mm. 1 and 5. For one reason, the order of the pitch classes has changed from <8,0,11,6> in m. 3 to <0,6,8,11> in m. 6; for another, the <0,6> and <8,11> dyads are separated into different registers so that if there is a motivic connection heard, it is experienced as a fragmentation. When we reach m. 7b, P4 is presented, so there would be the potential of recapturing the motivic complexes of mm. 1–2. Instead, Schoenberg brings back the components <6,3,8,2>, <11,0,9,10>, <4,5>, and <7,1> in different positions relative to one another (for example, <11,0,9,10> above <6,3,8,2> instead of after it); and the order of pitch classes within the components is changed, except for <4,5> and <11,0,9,10>. One might argue that <11,0,9,10> is the only component remaining from mm. 1–2 that is noticeable, so that the effect is again one of breaking off small components of larger motivic complexes. Finally, by the time we arrive at I10 in m. 8, all three tetrachords are presented in different orderings from their appearances back at mm. 3–4, and the most noticeable four-note unit is the vertical on beat 2, the second tetrachord of I4, a set that did not play any role in the presentation or repetition phrases. (At the same time, Schoenberg partitions I10 into dyads, {10,9}, {7,1}, {8,11}, {6,0}, {3,4}, {2,5}, in such a way that they could be reassembled to form the dyads of I4, creating a “dyad exchange” with a row given earlier, but not one of the two opening rows.) In mm. 5–8, the “motives” of the opening measures are first disassociated from the contexts they originally appeared in, and then disappear altogether, resembling the “liquidations” that Schoenberg described in the continuations of initial sentences in Beethoven. The whole process is dramatized by a progressive shortening of the durations that Schoenberg gives to each row statement in mm. 1–8: six beats for P4, six beats for I10, four beats for P10, three beats for I4, and two beats for P4, then expanding to three beats for I10 at the “cadence.”
A passage of three measures, mm. 9–11, a cadential extension, brings the Menuett’s A section to a close. See Example 2.22. This section brings the hexachord exchanges characteristic of the piece’s beginning, which were obscured in mm. 3–8, back up to the surface of the music. In m. 9, a chronological partition that is further divided registrally (registral boundary at C4 for the first beat, at D3 for the last two beats) produces the two hexachords of P10 within P4. In m. 10, within I4, the same partition generates the first hexachord of I10 below the registral boundaries, and would create I10’s second hexachord above them, were it not for the stray F3 at the end of the first beat in the right hand. (Visually, because the stray note is played by the right hand, the partition seems to generate an exchange just as easily as did m. 9.) And then m. 11, through a chronological partition of I10, brings forth the two hexachords of I4, but in a less obvious way because of the overlap of pitch classes 9, 10, and 5 in the middle (9 and 10 sound too early, or 5 too late, for a perfect partition). In a way, mm. 9–11 cover the same ground as the previous measures, clearly establishing a hexachord exchange and then gradually obscuring it, and making use of both registral and chronological partitions.
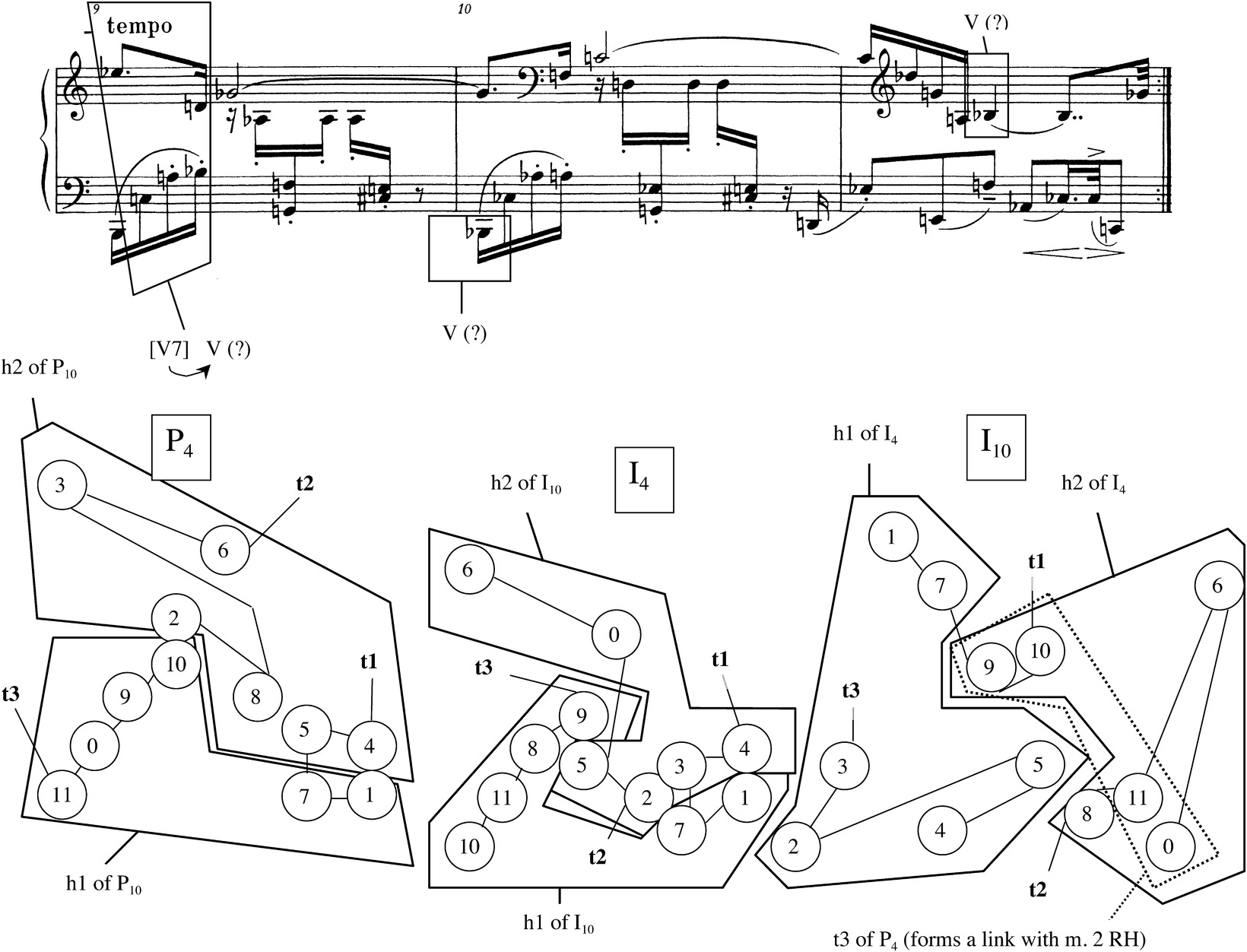
Example 2.22 Schoenberg, Menuett Op. 25, mm. 9–11.
Measures 9–11 are notable from another viewpoint, in that they place the pitch-class sequence <9,10> and pitch class 10 in prominent places. A number of writers have commented on the tonal allusions of the Menuett, including Haimo, Kurth, and MacKay.26 The latter two agree that there is an emphasis on E♭ within the twelve-tone texture in the first four measures. Kurth’s account is the most detailed, showing how exchanged and contiguous tetrachords trace a motion from <3,2,4,5> to <11,0,9,10> in mm. 1–2, going up a “perfect fifth” from “I” to “V” in other words, and how <11,0,9,10> as “V” in m. 3 returns to <4,5,2,3> as “I” in m. 4. This “tonal motion,” typical for the first two phrases of a Beethovenian sentence, is shown on the pitch-class map in the lower half of Example 2.23. As part of this motion, it is easy to pick out a sequence of half steps, one in each measure, that audibly suggests the same tonal chord progression: <E♭,D>–<A,B♭>–<A,B♭>–<D,E♭>.27 These are shown on the score excerpt in Example 2.23. When mm. 9–11 highlight pitch class 10 and <9,10> through rhythmic and metric emphases, then, as is shown on the score excerpt in Example 2.22, it is at least possible to hear the A section modulating to the dominant at its end – from E♭ to B♭. One problem with such an account of the A section is that it says nothing about the notes in between the tonal references (Kurth’s exhaustive description of mm. 1–4 is an exception, but he does not go beyond m. 4, nor does he limit himself to tonal explanations of the patterns he describes in the opening four measures). A bigger problem is that it becomes harder to find strong references to the key of E♭ in the final measures of the Menuett, where one would expect that key to be most prominent.28 Thus, in my account, the tonal hearing will have to serve as subsidiary to the description involving hexachord exchange that I offered earlier.
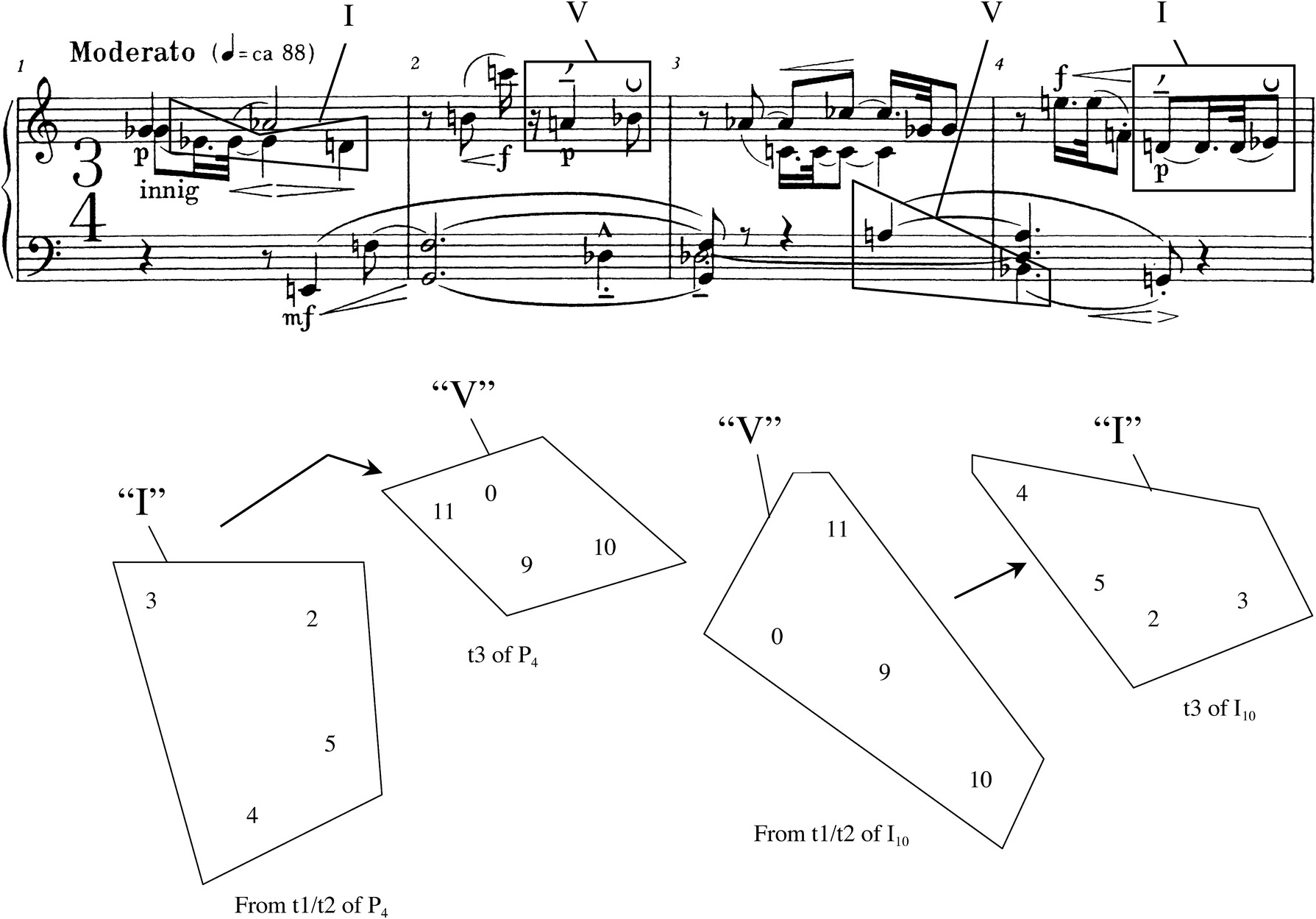
Example 2.23 Schoenberg, Menuett Op. 25, mm. 1–4: tonal allusions.
Example 2.24 illustrates mm. 12–16, which scholars have usually called the “B section.” Stephen Peles uncovers a significant intervallic relationship between the right hand of m. 12 and the opening measure: with <6,5,3,4>, t3 of P10, Schoenberg is able to produce the same pitch intervals as those of the individual voices in m. 1, which made use of t2 and half of t1 of P4. In m. 1, the ordered pitch intervals of the individual voices read (from bottom to top): <+13> from E to F, <−1> from E♭ to D, and <+2> from G♭ to A♭; in m. 12, these three pitch intervals come back in succession, all moving in opposite directions: <−13> from G♭ to F, <−2> from F to E♭, and <+1> from E♭ to F♭.29 In this way, the incipit to section B repeats important elements of the piece’s beginning, but changes an aspect of those elements (their direction), bringing to mind Bach’s practice of starting the B section of binary dance forms with the same motive that opened A, transposed to the dominant. As John MacKay, Ethan Haimo, and others have already remarked, the “dominant transposition” side of this equation is represented in two ways: by the forms of the tone row used – P10 and I4, a tritone higher than the beginning’s P4 and I10 – and by the strong emphasis on B♭ and associated pitch classes (consult the boxes on the score level in Example 2.24).30
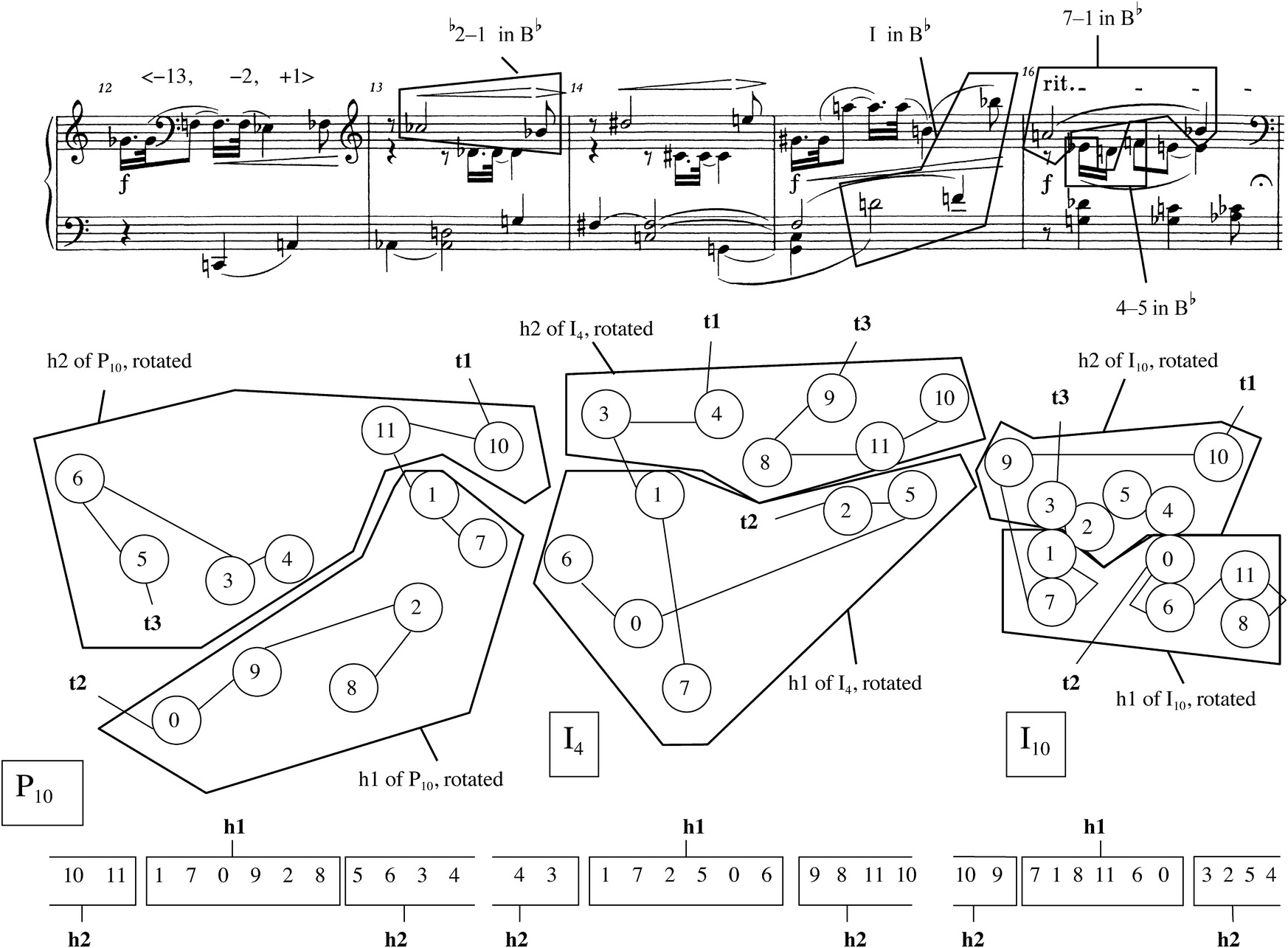
Example 2.24 Schoenberg, Menuett Op. 25, mm. 12–16 (the B section).
Hearing the right hand of m. 12 as a significant motive could inspire the listener to hook those four notes up with the <11,10> in the right hand of m. 13 to create a larger unit, a hexachord – a strategy that seems to be validated by the following measures, in which registral division of the aggregate into hexachords increasingly becomes the norm. (In addition, many of the partitions that gave rise to the hexachord exchanges of the A section were registral, so that a listener sensitive to the exchanges that Peles points out in mm. 1–2 and that I describe in mm. 3–11 will have been dividing aggregates up this way already.) But if we partition the aggregate in mm. 12–13 into six notes up and six down as indicated on the pitch-class map in Example 2.24, the resulting division of the tone row (shown at the bottom of the example) is one we have not encountered either in the Menuett or in any of the preceding pieces – a division into order positions {2,3,4,5,6,7} and {8,9,10,11,0,1}. We could characterize this new move as rotating the row forward by two order positions (which I will also refer to as a T2 rotation), and then splitting it into its discrete hexachords. As the remainder of Example 2.24 shows, I4 in mm. 14–15 and I10 in m. 16 are also split registrally in the same way, into order positions {2,3,4,5,6,7} below and {8,9,10,11,0,1} above. The registral partition seems to become clearer as the music progresses (mm. 14–15 are split at the halfway point between F♯4 and G4, and m. 16 splits between D♭4 and D4, unlike mm. 12–13, which had different splitting points for each measure).
As I mentioned earlier, the main by-product of this new rotational approach suggested by mm. 12–13 and corroborated in mm. 14–16 is that registral or chronological partitions cease to generate exchanges of hexachords with other row forms. The situation becomes dramatically obvious if one considers the pitch-class content of each of mm. 12, 13, 14, and 15. Schoenberg faithfully states six new pitch classes, half of an aggregate, in each measure – {0,3,4,5,6,9} in m. 12, {1,2,7,8,10,11} in m. 13, {0,1,3,4,6,7} in m. 14, and {2,5,8,9,10,11} in m. 15. Such a chronological partition of the aggregate is one of the devices that generated multiple exchanges with other row forms in mm. 1–2. But in mm. 12–15, not a single one of these partitioned hexachords matches a discrete hexachord of any of the basic four row forms P4, I10, I4, or P10, either unrotated or rotated by two order positions. In fact, not even the set classes formed in mm. 12–15 – 6-Z42, 6-Z13, 6-Z13, and 6-Z42 respectively – match set classes formed by the discrete hexachords of the original row forms (6-2 and 6-2) or of their T2-rotated versions (6-Z6 and 6-Z38).31 Through rotation and partition, it seems that the tone row has lost its power to project other forms of itself in different dimensions, which made it seem such a fertile Grundgestalt in mm. 1–2. This circumstance should be seen as the “problem” which the whole B section elaborates and which the A′ section will solve.
However, A′ does not solve the problem right away, as Example 2.25 illustrates. P4 returns in mm. 17–18, but it is not until I10’s entrance in mm. 19–20 that we are able to understand how a rotated and partitioned form of the row can generate a hexachord exchange with another (unrotated) row form. In mm. 17–18, there is another “almost-” hexachord exchange of the type we discussed several times in the A section. Within P4, four members of I4 cluster together through register and slurring, <4,3,7,1>, and pitch class 5 appears in a close register immediately after, but the remaining pitch class of the first hexachord of I4, pitch class 2 in the bass on the downbeat of m. 18, is registrally separate from the others. In a similar way, pitch classes <6,8> are separated registrally and chronologically from the rest of the second hexachord of I4, <11,10,0,9> in m. 18. Schoenberg’s use of <6,8> with the pitch interval +2 in the bass in m. 17 is definitely an attempt to recall the right hand’s motive from m. 1. But the A′ section’s recapitulation of m. 1 seems to break down after that, precisely because mm. 17–18 cannot create the hexachords of I4 (as mm. 1–2 did) through a registral partition.
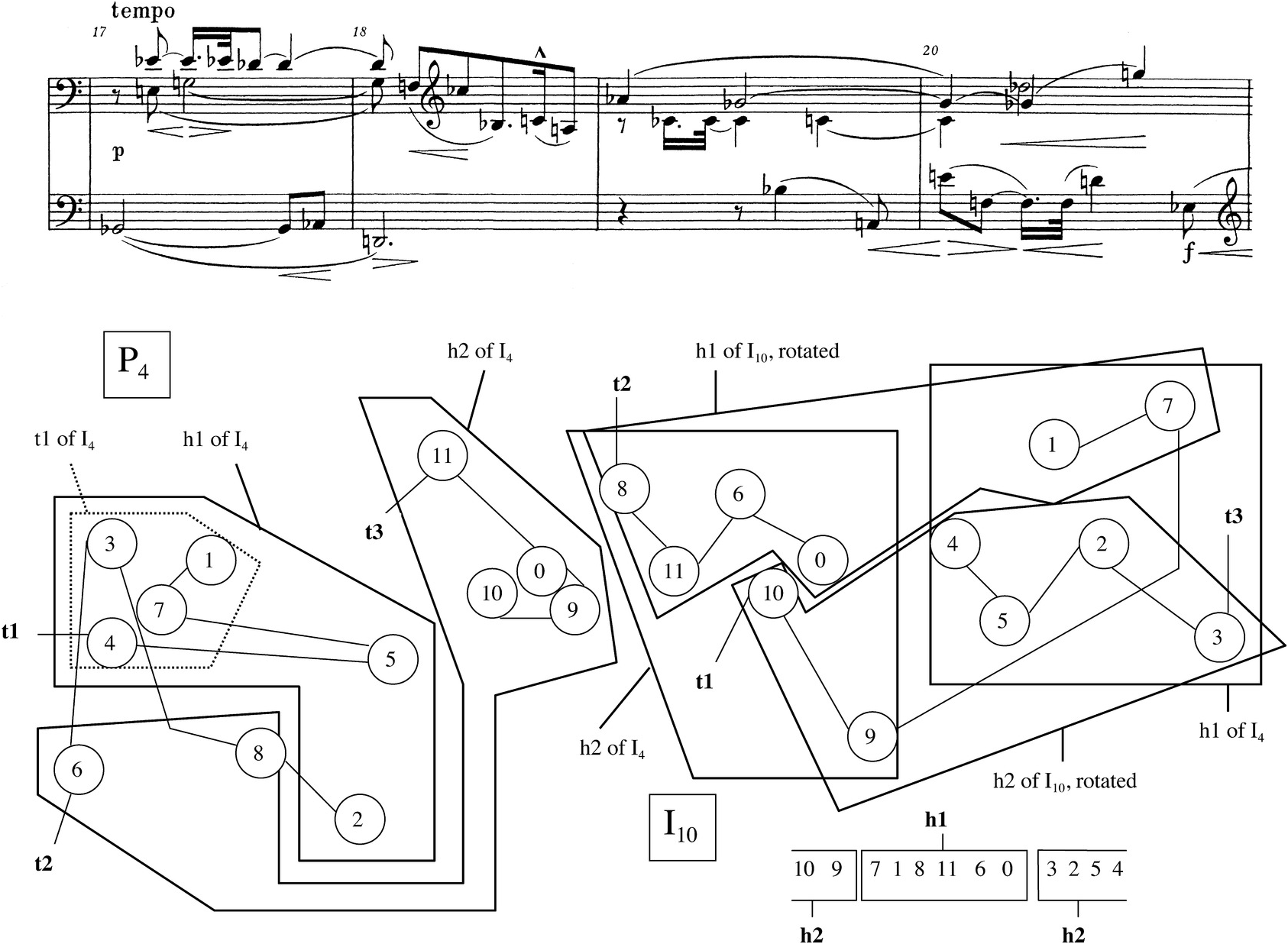
Example 2.25 Schoenberg, Menuett Op. 25, mm. 17–20 (beginning of the A′ section).
Measures 19–20, as I have suggested several times, play a crucial synthesizing role within the Menuett as a whole. Other writers have recognized the ability of these two measures to draw together a variety of pitch-class, intervallic, and rhythmic elements from the previous parts of the piece. Peles, for example, calls his reader’s attention to the fact that not until mm. 19–20 (nor at any point afterward) does Schoenberg return to a repeat of the attack rhythms of mm. 1–2. In addition, m. 19’s temporal ordering <8,11,6,10,0,9> can be derived from the temporal ordering of pitch classes in m. 1, <6,3,8,4,2,5>, by inversion followed by transposition with t = 2 (mm. 20 and 2 have no such relationship). Finally, the sequence of pitch classes in the left hand in mm. 19–20, <10,9,4,5,2,3>, when split into discrete dyads, <10,9>, <4,5>, <2,3>, generate three unordered pitch-class intervals 1, as did the three discrete dyads in the right hand of mm. 12–13, <6,5>, <3,4>, <11,10>. The connection between mm. 12–13, right hand, and mm. 19–20, left hand, is further strengthened by their two hexachords belonging to the same set class, 6-Z38 (012378).32
If we accept mm. 19 and 20, left hand, as a recapitulation of mm. 12–13, however, it becomes necessary to understand that hexachord as derived in the same way as the earlier hexachord – namely, by rotating the row, now I10, two order positions forward, and then dividing the rotated row into discrete hexachords. The process is indicated at the bottom right corner of Example 2.25. (Hearing this aggregate as divided into <10,9,4,5,2,3> on the bottom and <8,11,6,0,1,7> on top seems to justify Schoenberg’s attempts to sustain pitch classes 0 and 6 into m. 20: by sustaining those two pitch classes, he “glues” the top hexachord together.) Thus, the B section’s technique of rotation followed by division into hexachords has made a comeback – but with an important difference. Schoenberg has chronologically arranged the individual members of the two I10 hexachords, six before and six after the barline, so that the first six, {0,6,8,9,10,11}, form the second hexachord of the unrotated version of I4, and the last six, {1,2,3,4,5,7}, form I4’s first hexachord! I10 undergoes the same rotation process introduced in the B section, which was thought to have a destructive effect on the row’s ability to produce other forms of itself in different dimensions through exchange, and manages to project the hexachords of I4 through chronological partitioning anyway. The problem which arose within B is now solved near the beginning of A′.
With the solution to the Menuett’s problem coming fairly early in the movement, the question naturally arises: with what should the rest of the piece occupy itself? Schoenberg’s agenda for the remainder of the composition seems to be to bring back all of the material of the A section, with variations and extensions. He uses the same row forms as in the corresponding sections of A at the beginning and end of A′ (mostly P4 and I10, which he associated with “tonic”). In the middle of A′, the rhythmic ideas and contours of the corresponding measures of A are applied to different row forms.
Measures 21–26, which reprise and extend mm. 5–8 of A, are given in score in Example 2.26, with a pitch-class map below. Notice that, although the contours and rhythms of mm. 5–7 come back, extended and varied, in mm. 21–24, the row forms are now different: I4 (mm. 21–22a) takes the place of P10 (mm. 5–6a), P10 (mm. 22b–23a) takes the place of I4 (mm. 6b–7a), and I10 and I4 (mm. 23b–24) replace P4 (m. 7b). Measures 25 and 26 are a descending half-step sequence of m. 8’s cadence, using P10 in m. 25 and following it with I10, the original row from m. 8, in m. 26. (More will be said later about the larger significance of reordering this inversional relationship so that it sounds like a half-step transposition.) With all the changes of row, Schoenberg still manages to preserve the function of mm. 5–8 in mm. 21–26: these measures are a continuation from mm. 17–18’s presentation and 19–20’s repetition, and as such they break down the hexachord exchange ideal that mm. 19–20 so clearly presented, while at the same time carrying out a gradual liquidation process that breaks material of the preceding measures into ever-smaller fragments. Many but not all of the exchange and liquidation techniques that characterized mm. 5–8 return in mm. 21–26, and the greater length of the latter passage enables Schoenberg to add a few more motivic fragments to those of the former passage.
Example 2.26 Schoenberg, Menuett Op. 25, mm. 21–26.
The projection of I4 in mm. 21–22a departs from its model in mm. 5–6a, in that there is no attempt to create a hexachord exchange. Instead, the two hexachord groupings shown on Example 2.26’s pitch-class map (which involve registral crossing, grouping pitch class 4 in the higher register with <9,8,11,10,3> in the low register) contain contiguous hexachords of the T2 rotation of I4, similarly to the hexachord pairs of the B section. The next row form, P10 in mm. 22b–23a, does present a hexachord exchange with P4 which is defined registrally, if the listener is willing to group the low-register pitch class 10 with the high-register <0,9,8,2,11> and the high pitch classes 1 and 4 with the low <5,3,6,7>. This use of “almost-exchange” calls to mind Schoenberg’s practice throughout mm. 5–8. Measures 23b–24a, which use I10, get a little closer to the hexachord exchange ideal, especially the middle-register notes <0,10,9,8,11,6>, which bring together the second hexachord of I4. And the presentation of I4 in m. 24 also groups together in one register <7,1,9,8,11,10>, the first hexachord of I10. In mm. 23b–24a and 24, the exchanged hexachords not previously mentioned, the first hexachord of I4 and second hexachord of I10, both group together one or two pitch classes in the high register with a larger group in the low register, and hence also serve as illustrations of “almost-exchange.” The last two, cadential, measures, mm. 25 and 26, do away entirely with the notion of hexachord exchange, and instead project registrally the two hexachords 6-Z13 and 6-Z42, which, the reader will remember, were laid out chronologically in the B section. With respect to hexachord groupings, mm. 21–26 move away from the registrally defined hexachord exchange ideal of mm. 19–20, but as they do, they remind the listener of segmentations that were encountered both in the corresponding measures of the A section (mm. 5–8) and in the B section.
The liquidation process in mm. 21–26 begins and ends by following the same path as that of mm. 5–8. The ordered pitch succession <8,11,6,0> in m. 21, brought together from t2 and t3 of I4, brings back a relatively large fragment, the second tetrachord, of I10 from m. 19 in its original order. (This technique parallels exactly the tetrachord exchange involving <6,3,8,2> between m. 1 and m. 5 in the A section.) In the tetrachord’s close vicinity are the other two pitch classes that were associated with <8,11,6,0> in m. 19, pitch classes 9 and 10, although they no longer appear below the tetrachord registrally. In mm. 22b–23a, within P10, the fragment <8,2> in the right hand appears, followed closely by <3,6> in the left hand. This recalls <6,3,8,2>, the second tetrachord of P4 in m. 17, but is fragmented into dyads and with the order of one of the dyads changed. (Again, there is an exact parallel involving {0,6,8,11} in mm. 3 and 6b–7a of the A section.) In mm. 23b–24a (I10), which corresponds roughly to m. 7b, the exchanges with the presentation’s and repetition’s rows, P4 and I10, cease, and we hear only a suggestion of the first tetrachord of P10 in the top dyads of the three-note chords on the eighth notes. Measure 24, which also corresponds to m. 7b (but this time uses I4), contains three tetrachords that refer back to earlier rows, the first two of which come about through exchange: <5,4,7,1> from P4, <0,9,8,2> from P10, and <6,0,2,5> from I4. Only in the <0,9,8,2> is the order of the earlier version preserved (t2 of P10 in m. 22); in the other two tetrachords, the order is jumbled, sometimes leaving a dyad of the original intact in the interest of motivic fragmentation (the transformation from <4,7,1,5> in m. 17 to <5,4,7,1> in m. 24 is a good example). In m. 25, only one tetrachord refers back to earlier rows through exchange; the second tetrachord of P4 arises as a vertical partition within P10, in much the same way as t2 of I4 arose from I10 back in m. 8. Also similarly to m. 8, m. 25 places elements of the dyads {10,11}, {1,7}, {2,8}, {0,9}, {3,6}, and {4,5} in chronological or registral proximity to each other, suggesting the dyads of P4 within P10 (creating “dyad exchanges”). Finally, in m. 26, some (but not all) of the dyads of I10 create dyad exchanges with I4.
I mentioned above that I would consider the larger significance of Schoenberg rearranging the elements of I10 in m. 26 so that they sound like P9, a half-step transposition of P10 in m. 25. This half-step relationship between complete aggregates at the cadence is a culmination of a trend that demonstrates itself occasionally in the movements of the Suite composed earlier, in which one of the third tetrachords or one pair of tetrachords of inversion-related rows is reordered to sound like a half-step transposition of the corresponding tetrachord or pair in the other row. The reader can refer to, for instance, mm. 31–33a of the Intermezzo, where Schoenberg reverses the order of t3 of P10 to <4,3,6,5> so that it sounds a half step in pitch higher than the t3 of I10 that immediately precedes it (<3,2,5,4>). Both third tetrachords are given to the bass voice so that the relationship is more audible. Schoenberg is developing a potential relationship gradually as he progresses from piece to piece in the order in which they were composed, just as he has continued to develop collectional exchange and extend its reach as he progresses from the Intermezzo to the Menuett.
While that part of A′ shown in Example 2.26 used different row forms from the corresponding measures of A, the remainder of A′ (shown in Example 2.27) locks into the same row forms as the corresponding measures of A, after a parenthesis in m. 27. In fact, over mm. 28–31, we can hear a gradual “coming into focus” of the original A material from mm. 9–11. Measures 28 and 29 rhythmically expand m. 9, but use the same row form, P4, changing the order of appearance of pitch classes 2 and 3 and inverting the third tetrachord registrally; m. 30 uses I4, just like m. 10, keeping all the pitch classes in the same order and rhythm but still inverting the third tetrachord registrally; and m. 31 adopts the I10 of m. 11 and retains every pitch class in the original order, rhythm, and register – a “carbon copy” of the earlier measure.
Example 2.27 Schoenberg, Menuett Op. 25, mm. 27–31.
At the end of A′, then, any intended parallel with the typical use of tonic and dominant in the tonal minuet breaks down; for if the emphases on B♭ within P4, I4, and I10 in mm. 9–11 suggest a modulation to the dominant at the end of A, one would think that Schoenberg would have brought in different row forms at the end of A′ that would emphasize E♭ as tonic, or at least position the members of the same rows to emphasize E♭. But instead he brings back P4, I4, and I10 in the same order as A, and although an argument can be made that he reorders and changes the register of pitch classes in mm. 28–30 from that of mm. 9–10 to soften the “B♭-ness” of the passage, the changes do not seem to highlight E♭ in any significant way. Most writers who want to make a case for tonality in the Menuett choose not to consider the final measures; the one who does, John MacKay, has to admit that the last prominent E♭ comes in m. 24, well before the final cadence (he suggests a chromatic linear ascent to B♭ at the final cadence: a modulation?)33
From the standpoint of hexachord exchange, the role of mm. 28–31 is essentially the same as that of their counterparts in the A section: to re-establish exchange after the previous section obscured it. In mm. 28–29, a registral partition, which changes split point from C♯4 in m. 28 and the first beat of m. 29 to the halfway point between D3 and D♯3 on the second beat of m. 29, separates hexachord 2 of P10 above from hexachord 1 below. In m. 30, a registral partition with its split point at B3 on the first beat and D3 on the second two beats almost divides the aggregate into the second hexachord of I10 above and the first hexachord below. The one note that prevents a perfect registrally defined hexachord exchange, F3 on the last sixteenth of the first beat, plays a parallel role to F3 in the same location in m. 10. Measure 31, the “carbon copy” of m. 11, then replicates its chronological “almost-hexachord” exchange (pitch class 9 comes too early, and 5 too late).
The Menuett’s final cadence, mm. 31b–33, is displayed in Example 2.28. Two pitch-class maps appear below the score in the example, to show two ways in which these final measures, in the manner of a summary, recall certain properties of the row that contributed to the Menuett’s musical idea. The leftmost of the two pitch-class maps shows that each of the rows, P4 (rotated T2 and split into hexachords) in the right hand and I10 (also rotated T2 and split) in the left, is partitioned in such a way that the listener could recombine their dyads into a different row, through tetrachord exchanges.34 In the right hand, the 7-above-1 vertical on the downbeat of m. 32 could be grouped with the 10-above-11 vertical on the downbeat of m. 33 to form the first tetrachord of P10, the 2-above-8 and 9-above-0 verticals that are consecutive upper-register events could be grouped together to form P10’s second tetrachord, and the 6-above-3 in m. 31 and <4,5> in m. 32 (both associated with pickup gestures) could be heard together to form the third tetrachord of P10. (The reader should note that my assignment of P4 instead of P10 as the “true” row for this passage is based on the most chronologically proximate groupings.) In the left hand, there is less of a case for repartitioning to form tetrachord exchanges. Possibly the 0-above-6 dyad, associated with a 
rhythmic motive in m. 32, could be heard together with the left hand’s final two notes, <2,5>, also in the same rhythm, to yield the second tetrachord of I4. And the 1-above-7 and <3,4> dyads in the latter part of m. 32 also can both be heard as all or part of similar patterns (very subtly suggesting the first tetrachord of I4). The third tetrachord of I4, however, {8,9,10,11}, gives us no excuse to hear its members as a group. The significance of these tetrachord exchanges in mm. 31–33 is that all four row forms are stated or suggested, at least in part, which is almost (but not quite) a complete return to the condition at the piece’s beginning, where hexachord and tetrachord exchanges projected P10, I4, and I10 within P4.
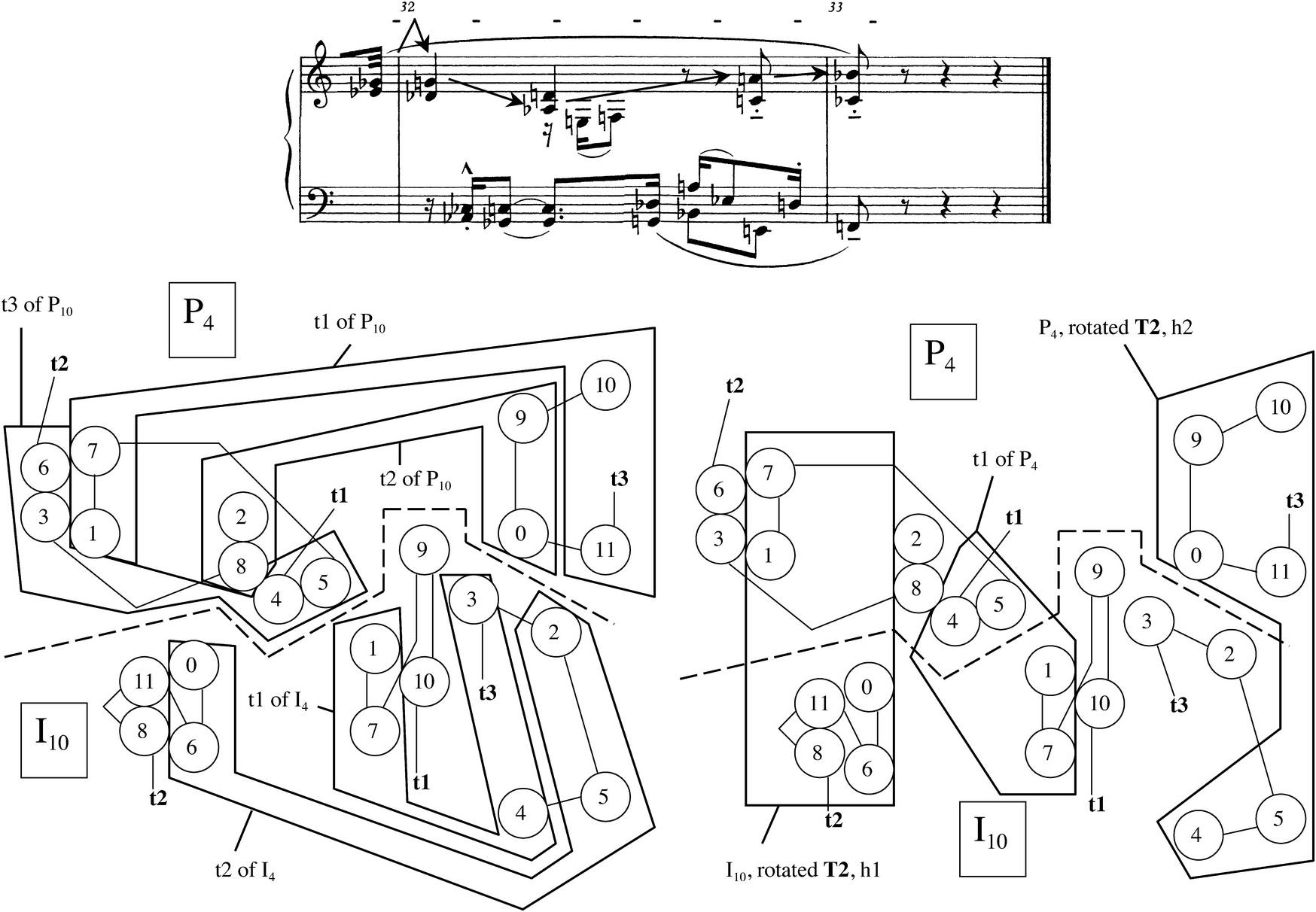
Example 2.28 Schoenberg, Menuett Op. 25, mm. 31b–33.
The rightmost pitch-class map shows that the final cadence brings the technique of exchange up to another level: for the first time in the Menuett, partitions bringing together elements from different, simultaneous row forms create hexachords and tetrachords which belong either to the rotated versions of the same two rows or to their unrotated versions.35 The first beat of m. 32, both hands, gives the first hexachord of rotated I10, and the pitches associated with the 
rhythm carrying from m. 32 into m. 33 yield the second hexachord of the rotated form of P4. Finally, the pitch classes <4,5,7,1>, appearing in order in the middle of m. 32, recall the first tetrachord of the unrotated P4. Since both rows in mm. 32–33 are T2-rotated versions, Schoenberg seems to be reminding us once more of the conclusion he reached in mm. 19–20: that rotated rows can also create hexachord exchanges. Thus the final cadence refers back not only to the Menuett’s solution but also to its opening measures: it reminds us from where the piece started and what goal it reached.
Gigue
The composition of the movement that appears last in the final version of the Suite was actually begun one day before the commencement of the Trio. According to Maegaard’s chronology, based on Schoenberg’s rather careful dating of his sketches, Schoenberg started writing the Gigue on March 2, 1923, wrote the entire Trio on March 3, 1923, and then completed the Gigue about a week after its inception (March 8, 1923).36 Because of this chronology, Maegaard argues that the Gigue may actually have been where Schoenberg hit on the notion of presenting the row as a line and dividing it into hexachords.37 (As I have suggested, those ideas, especially hexachordal division, were probably also present during his work on the Menuett from February 23, 1923 to March 3, 1923.)
The final piece in the Suite is forward-looking in another way that I think is more important, however: it presents the conflict, elaboration, and resolution of its musical idea in a way not heard before in Schoenberg’s twelve-tone music. That is, it takes a rather insignificant element from the source tone row (located at order positions 2–4 or 5–7), a 3-5 (016) trichord whose unordered pitch intervals involve some combination of a perfect fourth and tritone or perfect fifth and tritone, and repeats or develops it to the point where it de-orders and obscures the tone row, as well as destroying symmetrical patterns created from pairs of row presentations (the symmetrical patterns recall the “palindromic ideal” of the Prelude). Then, at three places in the final thirty measures, Schoenberg demonstrates ways in which clearly ordered presentations of the row can be partitioned to yield the offending motive, absorbing it back into the overall pitch structure. As we shall see in the following analysis, there are two additional ways of creating and resolving problems in the Gigue, involving appearances of the octatonic collection, as well as a contrast between horizontal and vertical symmetry that lines up with the major sections of the form.
The complete form of the Gigue is given in Example 2.29. As suggested above, it is essentially ternary, a judgment based on the repeat sign at the end of m. 25 and the return to a tempo, texture, and method of row presentation similar to those of the original at m. 47. All three main parts are further subdivided into subsections (my rationale for these subdivisions will be explained below), and elements of B are incorporated into A′ at mm. 54–55 and 69–70, making the last section a summary of all that has gone before.38 The first three subsections of A, marked a, a1, and a2 in the chart, all begin with ordered presentations of the row, which are gradually supplanted by increasingly long lines alternating ordered pitch intervals +6 and +7 or −6 and −7. Examples 2.30a and 2.30b portray the first of these, subsection a.
Example 2.29 Schoenberg, Gigue Op. 25: form chart
Example 2.30a Schoenberg, Gigue Op. 25, mm. 1–4 (subsection a).
Example 2.30b Schoenberg, Gigue Op. 25, mm. 5–9 (subsection a, continued).
The pitch-class maps in the lower halves of Examples 2.30a and 2.30b depict a gradual process, whereby lines alternating unordered pitch intervals 6 and 7 supplant patterns established at the beginning of the Gigue, in three stages. In the first stage, pairs of rows in mm. 1–2 and 3–4 create partially symmetrical shapes. Measures 1–2 balance pitch classes 10–9 with 9–10 and 4–5 with 5–4. In addition, the pitch-class successions <7,6,3,2> and <1,8,11> are carried over in identical order from m. 1 to m. 2. Measures 3–4 do not contain substantial ordered invariants, but three dyad palindromes are noticeable in this pair of measures: 4–3/3–4, 2–9/9–2, and 11–10/10–11. These shapes call to mind passages like m. 13 of the Prelude Op. 25 (refer back to Example 2.10), where certain elements were preserved across the half-measure as parts of dyad palindromes and others as ordered invariants. In addition, Schoenberg uses dynamics to guide the listener toward hearing mm. 1–2 and 3–4 as symmetrical: the notes accented by and markings (given in boldface in the pitch-class map) also form symmetrical sequences from the beginning and ending pitch classes of the four rows, <4,10,4> and <4,10,4>.
The element that will destroy these symmetries, as well as de-order the row, by the end of subsection a is already suggested in mm. 1–4, though in a subtle way. Note that the first two dyad verticals in both m. 1 and m. 2 form a tritone, followed by a perfect fifth (namely, unordered pitch intervals 6 and 7). In m. 3, the first two verticals yield a tritone followed by a perfect fourth, and in m. 4, the first and third dyad verticals are both tritones. (The pitch classes participating in these dyads are shaded on the pitch-class map.) As the pitch classes that formed symmetries such as 10 and 4 are highlighted through dynamic accent, the tritone and perfect fifth intervals just mentioned are de-emphasized with respect to stress, by placing unaccented syllable or staccato marks over almost all of them, and by putting many of them at the tail ends of slurs.39
In stage 2, from m. 5 to m. 8, the symmetrical patterns formed from pairs of rows that characterized the beginning are still present, but now in the left hand of the piano only. The left hand of mm. 5–6 contains two mirror dyads, 5–11/11–5 and 6–0/0–6; and mm. 7–8 reverse one of the previous mirrors, 11–5/5–11, and add a new one, 8–2/2–8. The pitch classes 10 and 4 that guided the listener into hearing symmetries in mm. 1–4 are still stressed in mm. 5–8, either by dynamic means or by stating them alone and repeating them. The rhythm in the left hand, mm. 5–8, at least that suggested by Schoenberg’s beaming, is actually more perfect in its symmetry than that of the preceding measures: each pair of measures groups the eighth-note attacks according to the pattern <1,3,3,2,3,3,1>.
The right hand of the piano in stage 2, however, introduces a conflicting element: successions of six pitches which project the pitch-interval succession <+6,+7,+6,+7> and its inversion, <−6,−7,−6,−7>. This element certainly can be heard as a development of the unaccented vertical dyads in mm. 1–4, but Schoenberg is now putting it forward in such a way that it begins to intrude on the listener’s consciousness (the crescendos from 
to help here, as well as the placement of the new material in the right hand) and to create conflict with the symmetries that are continuing in the left hand (the two-against-three rhythm helps here). Another way in which the introduction of <6,7> successions disrupts the previous music is with respect to row ordering: notice that order is jumbled or reversed within most tetrachords, excepting the third tetrachords, while the order between the tetrachords is preserved. Finally, the right hand in mm. 5–8 does carry over one important technique from mm. 1–4 – that is, tetrachord invariants between rows in each pair – but changes them from ordered invariants to unordered: {1,2,7,8} in mm. 5–6, {0,1,6,7} in mm. 7–8.
Measure 9 constitutes stage 3 in the subsection’s overall process. Here, the lines alternating −6 and −7 or +6 and +7 take over both hands of the piano (with some ascending intervals of the same classes dividing the triplets in the right hand). The steady eighth-note rhythm of the first four measures is completely supplanted by triplets in both hands. The row ordering is jumbled both within and between tetrachords (to the point where my labeling of m. 9 as I4 is very tentative). And, partly because of the reordering, but also because it is limited to one measure, stage 3 does not display any significant pitch-class symmetries. Thus, the a subsection supplants ordered rows, pitch-class symmetry, and eighth-note motion in mm. 1–4 with lines alternating pitch intervals 6 and 7, lack of pitch-class symmetry, and triplet-eighth-note motion in m. 9, passing through a middle stage, mm. 5–8, where both modes of organization intermix.
The three-stage model introduced in mm. 1–9 is imitated in mm. 10–16, and the second and third stages of mm. 10–16 in turn serve as a model for mm. 17–19 – which accounts for my labeling the three subsections as a, a1, and a2. Examples 2.31a, 2.31b, and 2.32 portray the latter two subsections. In Example 2.31a, we can see that the beginning stage, mm. 10–13, returns to the symmetries of mm. 1–4, now using retrograde versions of the four source rows. The symmetry seems less convincing this time, however: the experience of mm. 5–9 has apparently weakened the original pattern a little, making it necessary for Schoenberg to use tempo to distinguish mm. 10–11 and 12–13 as units. One lone mirror dyad, 10–9/9–10, marks the boundaries of mm. 10–11’s palindrome, and a repeated vertical, 4-above-5, with some emphasis put on the pitch class 4 by the upward arpeggio, locates its middle. But the pitch classes 10 on either end of mm. 10–11 are not distinguished in any particular way, except maybe through repetition in the latter case (m. 11 going into the downbeat of 12). The practice of carrying over larger invariant sets from one side of the palindrome to the other comes back in mm. 10–11; but unlike mm. 1–2, the larger invariants, {3,7,8,9,11} and {0,1,2,6,10}, are not ordered, nor do they come back in the same register; instead they take part in an exchange between upper and lower registers. Finally, the vertical elements projecting pitch intervals 6 and 5, the “disruptive” elements, are given more stress than they received in mm. 1–2 (pitch classes 6-above-1 in m. 10 and 6-above-0 in m. 11 both get accented syllable marks).
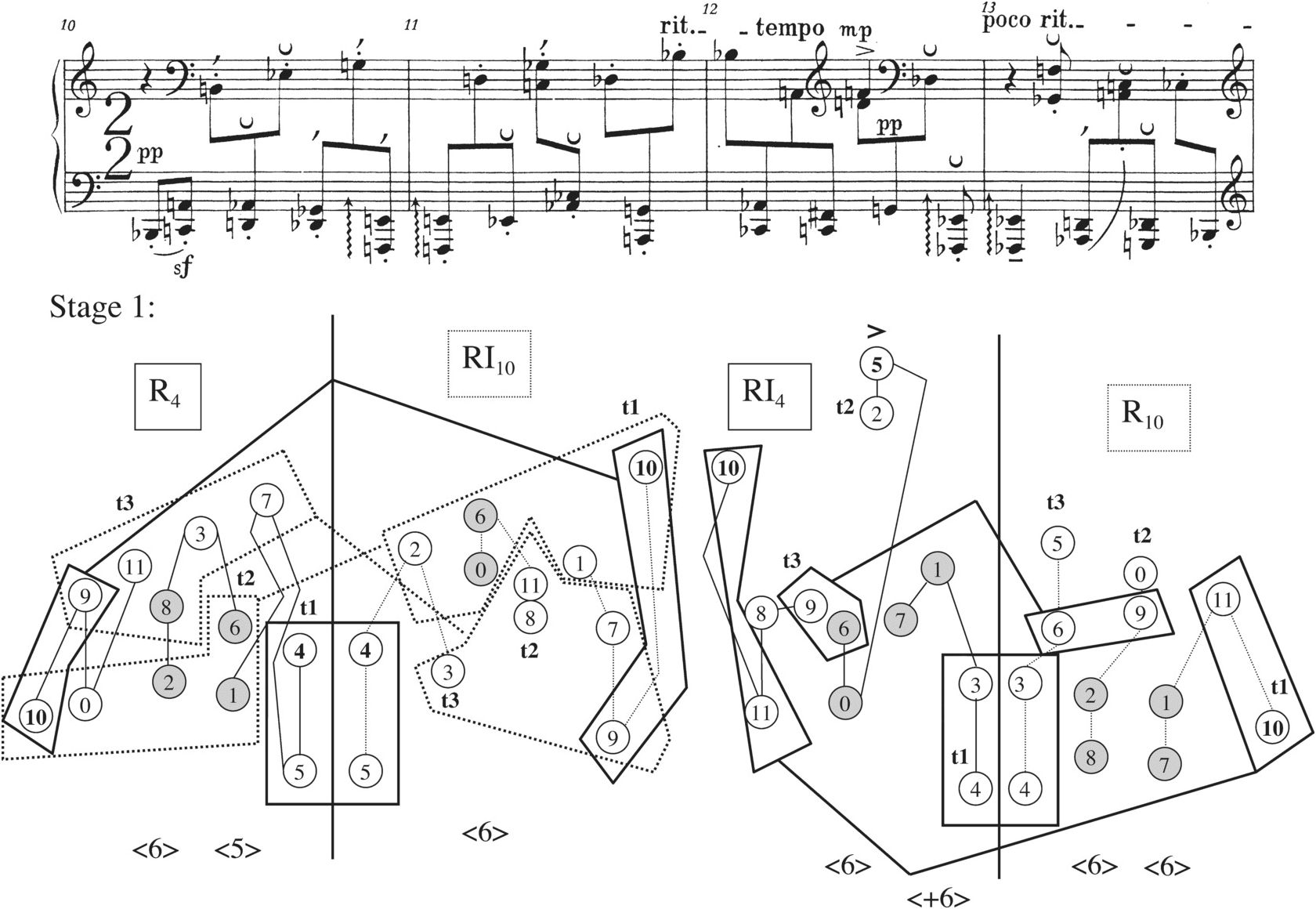
Example 2.31a Schoenberg, Gigue Op. 25, mm. 10–13 (subsection a1).
Example 2.31b Schoenberg, Gigue Op. 25, mm. 14–16 (subsection a1, continued).
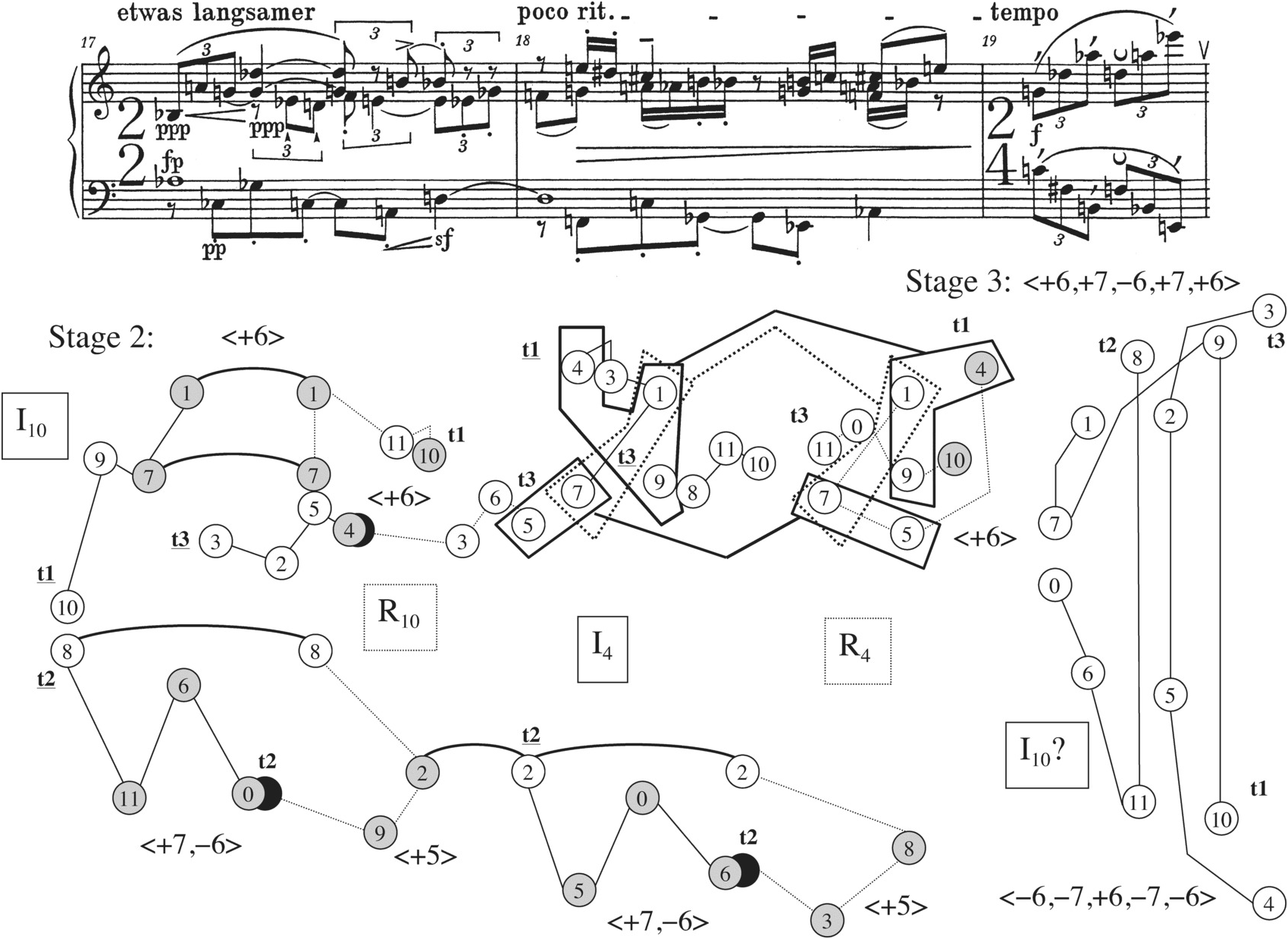
Example 2.32 Schoenberg, Gigue Op. 25, mm. 17–19 (subsection a2).
The trend of imitating stage 1 of the opening subsection continues in mm. 12–13, as Schoenberg turns his attention from larger invariants to dyad palindromes (as he did in mm. 3–4). But only two appear this time, 10–11/11–10 and 9–6/6–9 (in addition, one could hear the 3-above-4 vertical in the middle of mm. 12–13 as a palindromic dyad, though the pitch classes are not ordered). Meanwhile, one vertical tritone in m. 13, pitch classes 2-above-8, gets some stress through occurring at the beginning of a group.
Stage 2 of subsection a1 further disrupts the palindromic shapes of the first stage and brings lines alternating pitch intervals 6 and 7 to the fore, but in a way different from that in the model in mm. 5–8. In mm. 14–15, it is overlapping of row forms in anywhere from 1 to 6 pitch classes that breaks down the rhythmic correspondence of one row per measure (and one row pair per two measures) that has characterized the Gigue up to this point. (This overlapping is more clearly portrayed in Example 2.31b by using dotted lines to connect the pitch classes of alternate row forms, and underlining the labels for tetrachords in alternate rows. Pitch classes with two functions have black shading behind them.) Example 2.31b shows that RI4 begins m. 14, and then on the fourth and sixth eighth notes of that measure, two pitch classes of R10 overlap with members of RI4. This process intensifies in m. 15: the third eighth note features a pitch class 1 that serves both RI10 and R10, and the fourth eighth note contains a vertical, 3-above-11, which belongs to both R4 and RI10. The fifth eighth note introduces another vertical, 2-above-0, with both pitch classes functioning in R4 as well as RI10. Finally, pitch classes 4 and 5 on the seventh eighth note of m. 15 function in either R4 or RI10. Because of all the overlapping and Schoenberg’s repetition of pitch classes in these measures, the row-count I have just described would not be the only possibility. But it does have the advantage of placing the row overlappings in just about all the same metric locations as those where Schoenberg places accents in mm. 14–15: at either accented syllable marks, markings, or wedge accent marks. It is not far-fetched to think that he may have marked his row overlappings in such a way, especially when one considers that working out pitch overlappings between the constituent tetrachords of adjacent row forms seems to have been an important issue for him. Numerous sketches for the Suite show him experimenting with various combinations of row pairs (some involving eventually rejected versions of the source row) that enable such overlappings between tetrachords and other subsets of the rows.40
In addition to disrupting row order, the overlappings just described in stage 2 also have the effect of minimizing and skewing the symmetries and ordered invariants that were characteristic of stage 1. Only one dyad palindrome is brought out through retaining the same register for the pitch classes on both sides: the 7–1/1–7 at the beginning of m. 14 and end of m. 15. But this palindrome no longer marks the beginning and end of a pair of rows, as the palindromes in mm. 10–13 did. Instead it creates a boundary for four overlapped row forms, and the final <1,7> is obscure in its row source: it could conceivably belong to either RI10 or R4. A trichord palindrome is suggested in the left hand by the sequence <2, 6-above-3> on the first two eighths of m. 15, followed immediately by <6,3,2> on the third, fourth, and fifth eighths. But again this mirror is obscure because of the vertical dyad in its first part; and, in addition, it comes a quarter note too late to anchor a larger palindrome over mm. 14–15, as the repeated verticals 4-above-5 and 3-above-4 did in mm. 10–11 and 12–13.
On the other hand, ordered pitch-interval sequences that alternate perfect fourths and tritones become more prominent in mm. 14–15, but not by much. Actually, there is only one, in the bass at the beginning of m. 14: <−6,+5>. The pitch classes of this sequence, <6,0,5>, create the succession that will begin the right hand of stage 3, two measures later, and thus can be heard as predicting the onset of stage 3. In addition, the right hand does feature the tritone prominently at the beginning and end of mm. 14–15 (formed by the same pitches that make up the dyad palindrome described in the previous paragraph).
Even though alternations of pitch intervals 6 and 5 or 6 and 7 are not very important to the second stage of subsection a1, they return with a vengeance in stage 3, again taking place in a single measure, m. 16. The ordered pitch-interval sequence in the right hand, <−6,−7,+6,−7,−18>, almost exactly replicates the first five intervals of m. 9’s right hand, and the left hand corrects that sequence to <−6, −7,+6,−7,−6> and then inverts it to <+6,+7,−6,+7,+6>. Just as in m. 9, the onset of the alternating tritones and perfect intervals destroys order within and between the tetrachords of I4 (which is, again, a very tentative row attribution) and erases the pitch-class symmetries of the preceding music. It should be noted, however, that it does replace the said pitch class mirrors with both horizontal interval symmetries (unordered pitch intervals <6,7,6,7,6> in both hands) and vertical pitch- and pitch-class-interval symmetries (around B♭ and A, which appear at the end of the measure).
The last two stages repeat themselves again in mm. 17–19, subsection a2, which are portrayed as Example 2.32. I will not discuss these measures in too much detail, but the reader should note that stage 2 (mm. 17–18), like the corresponding sections in a and a1, features row forms placed side by side and overlapping by one or two notes. Also similar to previous stages 2 is the incomplete horizontal symmetry in m. 18, marked by heavy boxes in the pitch-class map. A third characteristic that recalls previous second stages is the prevalence of tritones, perfect fourths, and perfect fifths as melodic intervals in the bass line. These lead to another stage 3 in m. 19, which yet again pushes aside the preceding music in favor of alternating pitch intervals 6 and 7 that create their own horizontal and vertical symmetries.
The following passage in the Gigue, mm. 20–23, marked “x” in the form chart, in one way takes a substantially different direction from the music that has preceded it. Subsection x introduces a second foreign element by means of highlighting certain pitches dynamically and with note values longer than eighth notes. This element has not typically been associated with Schoenberg’s twelve-tone music by analysts; it is set class 8-28 (0134679T), the octatonic collection. Example 2.33 shows that this collection (pitch-class numbers in boldface) divides into four-note groups – and these tetrachords also belong to a set class characteristic of Stravinsky and Bartók, namely, 4-3 (0134). More typical of Schoenberg, however, are the ordered pitch-interval successions that create these two 4-3s: <−3,−1,+3> and an octave-compounded version of it, <−15,−1,+3>.41 The near-repetition of the same ordered pitch-interval succession between the highlighted notes from mm. 20–21 to 22–23 recalls the ordered pitch and pitch-class invariances across and between pairs of measures that were so prevalent in mm. 1–19. Perhaps more salient and important, however, is that the pitch-class succession of highlighted notes in mm. 20–23, <0,9,8,11,6,3,2,5>, returns in reverse as the highlighted pitches in a similar four-measure passage later in the Gigue, mm. 29–32. This creates a pitch-class palindrome larger in terms of number of measures than any we have heard, so that it is possible to speak of pitch-class symmetries as not only “supplanted” or “destroyed” but also progressively enlarged and diffused through the first part of the Gigue.
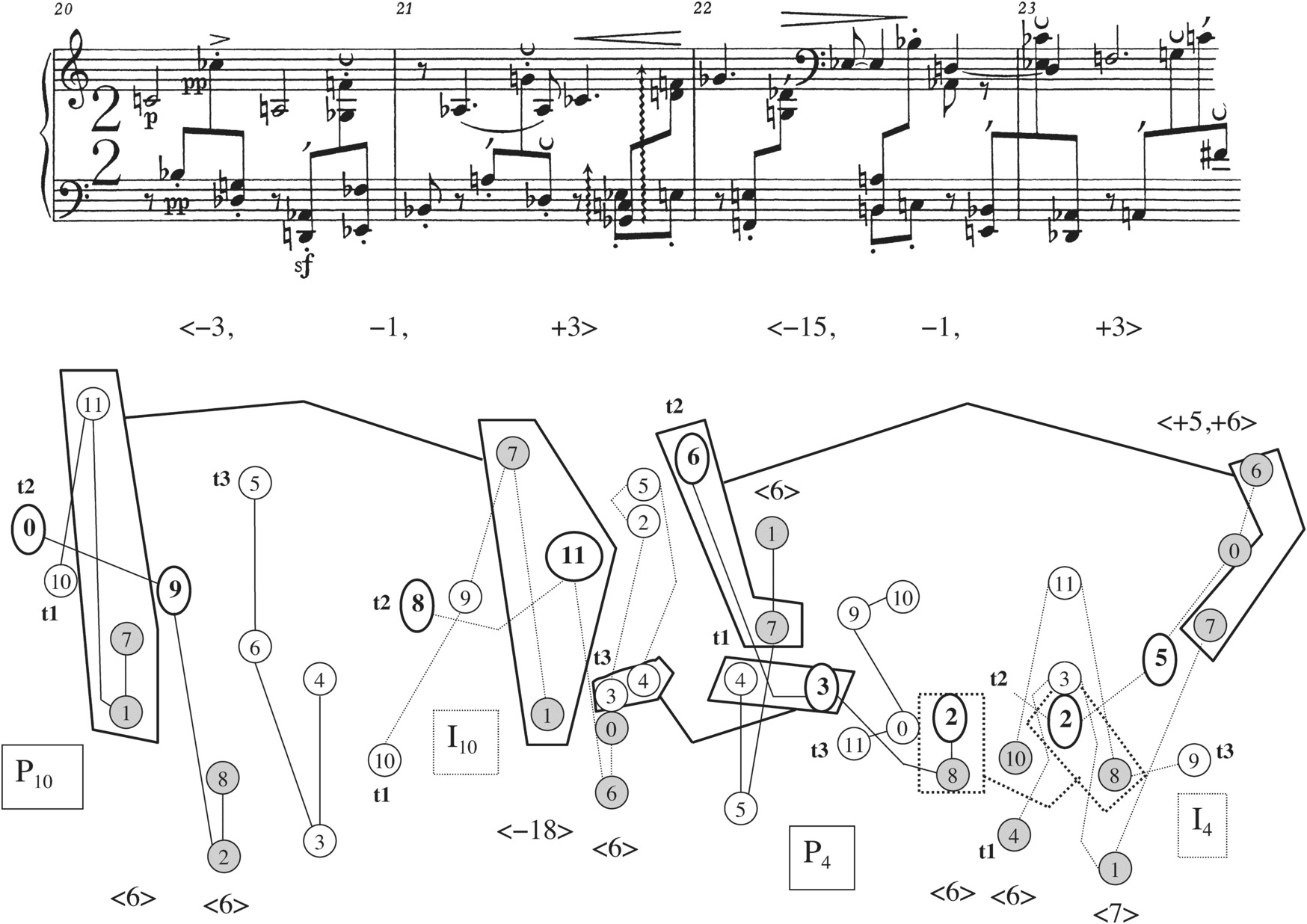
Example 2.33 Schoenberg, Gigue Op. 25, mm. 20–23 (subsection x).
The eighth-note stream that accompanies the new octatonic element in mm. 20–23, besides recalling the rhythmic groupings within similar streams in the a subsections, creates pitch-class symmetries and invariances that remind the listener of those earlier subsections. Symmetry and invariance happen on both the two- and four-measure levels. Measures 20–21 project an invariant trichord {1,7,11} partly through similar contours and partly through similar metrical placements (m. 20’s trichord appears on the third and fourth eighths, that of m. 21 on the fourth, fifth, and sixth). Measures 22–23 feature a dyad palindrome 6–7/7–6 that strongly recalls the opening measures of the movement, especially because the G♭ (in the same register and stated alone both times) begins and ends the two-measure unit, much as the B♭s and Es did at the beginning. In addition, an invariant dyad {2,8} seems to anchor the pitch-class symmetry in mm. 22–23, though the two instances of these pitch classes do not straddle the barline as they did earlier in the piece. At the four-measure level, a palindromic dyad 3–4/4–3 sits astride the barline between mm. 21 and 22. The elements of this palindrome again do not create a perfect rhythmic symmetry, but pitch classes 3 and 4 retain the same register on both sides, making the mirror noticeable. As if to strengthen its impact, Schoenberg also gives mm. 21–22 a symmetrical dynamic shape (a half-measure crescendo followed by a decrescendo of roughly the same length).
Measures 20–23 also include the alterations between tritones and perfect fourths and fifths that destroyed pitch-class symmetry in each of the a subsections, in almost exactly the same way as they were projected at the beginning of the piece. One can hear a gradual increase in emphasis on first vertical tritones and then tritones leading to perfect intervals through mm. 20–23 (consult the shaded circles in the pitch-class map in Example 2.33). The tritones gradually move from unaccented to accented positions, before appending to themselves unaccented perfect intervals. Because of the increasing salience of the tritone, we can hear subsection x as stage 1 of a fourth motion, a3, from pitch-class symmetry to lines alternating pitch intervals 6 and 7. Measures 24–25, the final measures of the A section, would then function as stages 2 and 3 in this larger motion.
In a number of ways, mm. 24–25 do indeed have the quality of stages 2 and 3. First, the passage introduces more prominent chords and lines alternating pitch intervals 6 and 7 in mm. 24 and the first two beats of 25: in the right hand, the vertical 7-above-6 repeated three times gives way to the line <+6,+7>, and then the same intervallic material appears again a tritone higher. Subsequently, on the last three beats of m. 25, the horizontal alternations of 6 and 7 take over, now not in contrary but in similar motion, both descending. By the time we reach the last part of m. 25, the identity of the row is again obscure. Like previous second stages, mm. 24–25’s stage 2 contains several dyad palindromes and invariances (see the connected boxes on Example 2.34). One of the palindromes, the more salient 2–8/8–2, hooks up with stage 3 in an interesting way: immediately after <2,8> in m. 24 comes pitch class 3 (in a right-hand triplet), and after <8,2> in m. 25 comes pitch class 9 (also part of a triplet figure in the right hand). Then the end of m. 25 sounds <9,3,8,2> in the bass, a kind of summary and bringing-together of the two prominent right-hand triplets that preceded it. Measure 9, stage 3 of subsection a, did bring back several invariant subsets from the preceding measures – consult the dotted boxes on m. 9’s pitch-class map in Example 2.30b – but it did not have a larger set that summarized the preceding measures in this way.
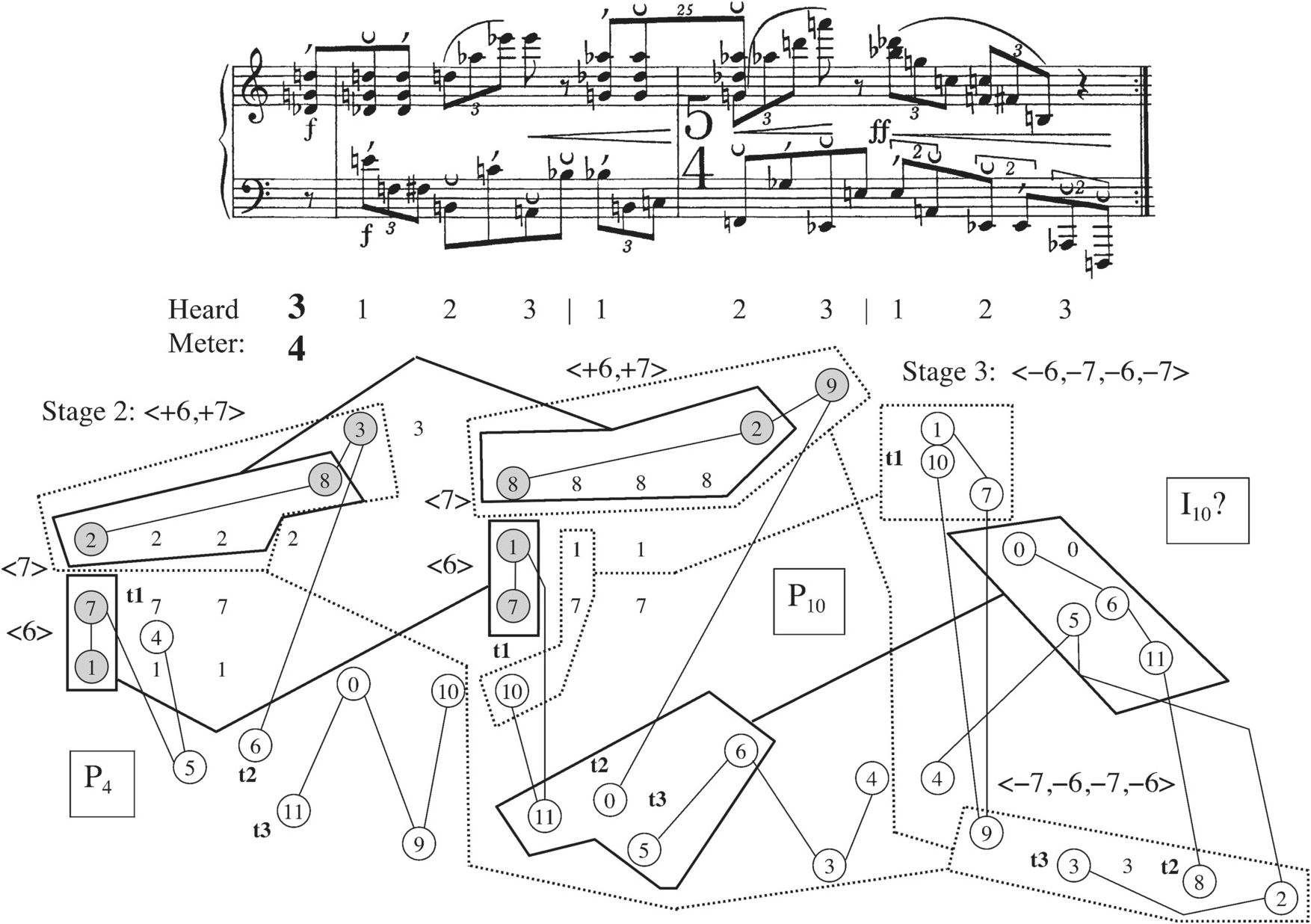
Example 2.34 Schoenberg, Gigue Op. 25, mm. 23b–25 (subsection a3, last part).
The one feature that sets mm. 24–25 off from previous manifestations of stages 2 and 3 (besides the heavier texture created by the repeating 7-above-6 verticals) is the way the stages line up with the meter. In subsection a, stage 2 fell into two neatly differentiated two-measure units, and stage 3 had its own measure. In subsection a1, stage 2 was not so carefully parsed into segments (remember, that was the passage where row overlapping was emphasized to a great degree) but stage 3 was still separated from it by a barline. (Subsection a2 returned to a more balanced segmentation of stage 2 and again separated it from stage 3.) Now, in the last two stages of what we are calling a3, there is a 2/2 measure followed by 5/4. But the sequence and rhythmic repetition between the first three beats of m. 24 and the fourth beat of m. 24 followed by the first two beats of m. 25 suggest a different meter than the notated one, which is indicated on the example between the notation and the pitch-class map: three measures of 3/4. If this alternative meter is adopted, stage 2 again contains one row in each measure, and stage 3 is again set off by a barline from its predecessor.
The onset of the large B section at m. 26 (Example 2.35) is marked by the introduction of new textures, most notably the heavily accented and closely spaced four-note chords that make their first appearance here. With new textures comes a new way of organizing the material, though one still controlled by the notion of symmetry. If the reader more closely inspects the two chords on the downbeat of m. 26 and the second eighth note of beat 4 in that same measure, he or she will recognize that they are vertically pitch-symmetrical around the axis C♯5. In addition, the left hand in m. 26, one of the few instances in the Suite of the third tetrachord of P4 actually spelled as B–A–C–H (in German letter names), almost creates a vertical pitch symmetry: had Schoenberg raised the initial B♭ an octave, he would have made the tetrachord symmetrical around B♭3/B3 (and by extension, also symmetrical around the first and last notes B♭2 and B4). The tendency toward vertical pitch symmetry continues in the right hand of m. 28, where the first eighth-note group is pitch-symmetrical around E5/F5, and the second (with the exception of G♭) is symmetrical around A4/B♭4.42 Schoenberg will continue to develop the notion of symmetry in the vertical dimension later in the Gigue, in a passage at mm. 37–39 that seems to flip over many of the elements of mm. 26–28.
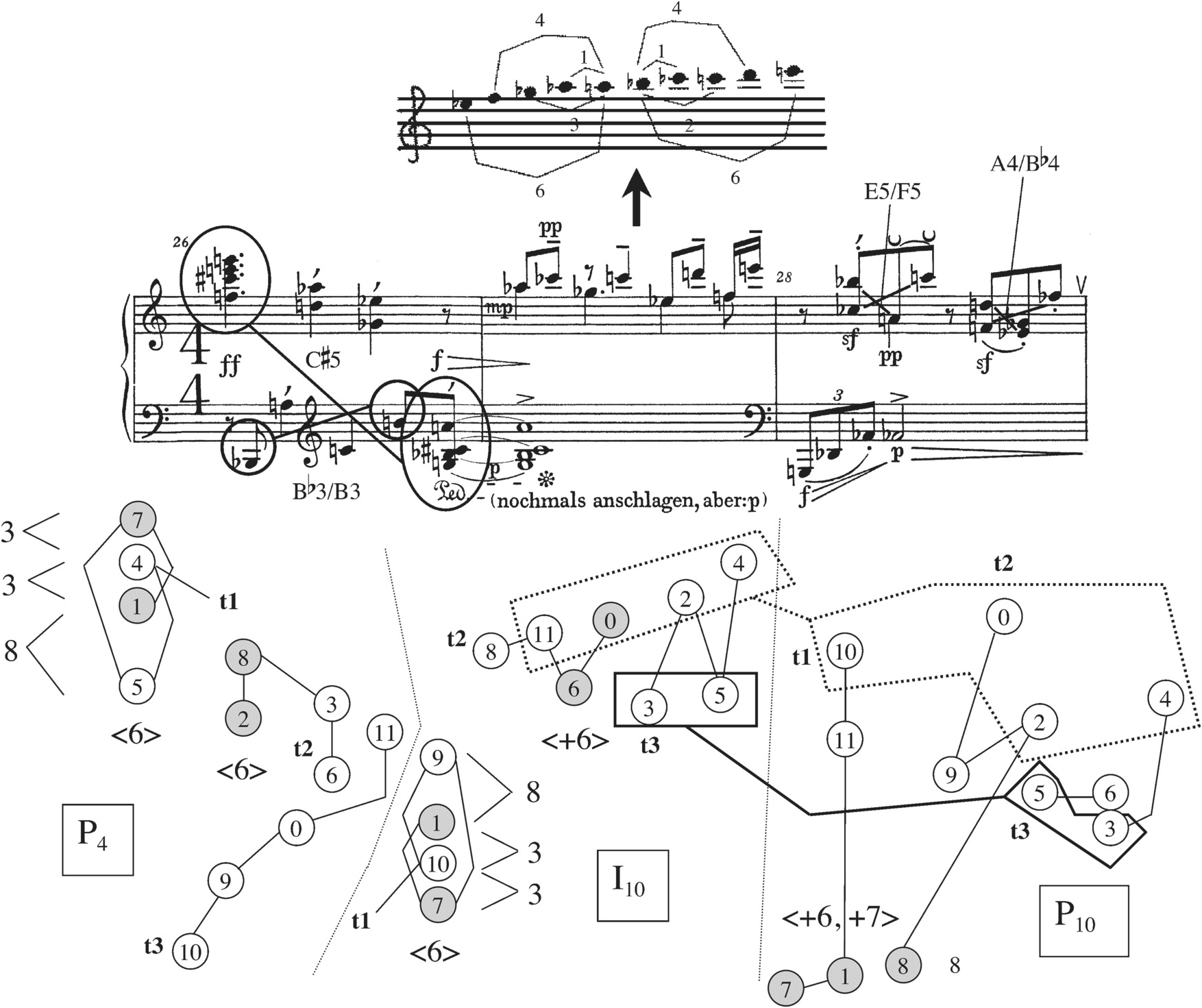
Example 2.35 Schoenberg, Gigue Op. 25, mm. 26–28 (subsection b).
The right hand of m. 27 is something of an anomaly in the context described above. An initial glance at it, with its upper voice rising and lower voice falling, seems to suggest vertical symmetry, but the pitches of the upper and lower voices do not create the same pitch intervals from a central axis. (See the registrally ascending version of m. 27’s right hand directly above the notation.) The pitches of m. 27’s right hand form an almost-symmetrical collection, <E♭5, F5, G♭5, A♭5, C♭6, C6, D6, E6>. Perhaps one explanation for this vertical asymmetry is that the right hand of m. 27 creates a palindromic dyad and an almost invariant tetrachord with the right hand of the following measure, adding horizontal symmetries to the more prevalent vertical ones. Whatever the role of m. 27’s right hand, it seems clear that the bass of the following measure, 28, has the familiar purpose (at section endings) of destroying pitch symmetry: making use of an unsymmetrical presentation of pitch intervals 6 and 7, <+6,+7>.
Measures 29–32 are called x1 because they present the reverse of the octatonic collection from mm. 20–23, completing the largest pitch-class palindrome yet heard (see the boldface pitch-class numbers on Example 2.36’s map and compare them with those in Example 2.33). This group of four measures also makes a contour palindrome with the previous passage: despite individual leaps up and down, the general shape is ascending, balancing out what was a generally descending shape in mm. 20–23. The voices that accompany this eight-note succession seem also to have the function of returning the Gigue to order, after the disruptions caused by the alternating <6,7> motives. I state this for three reasons: first, starting in m. 29, we begin to hear the three tetrachords of the row in sequence rather than simultaneously, though the sequence is reversed, t3, t2, t1. Each measure after m. 29 has one stray pitch class that overlaps into the space occupied by an adjacent tetrachord. Second, we hear two dyad palindromes and two dyad invariances that span the entire four-measure unit, characterizing it as horizontally symmetrical around the barline between mm. 30 and 31. These are 3-4/4-3 and 2-5/5-2 near the center of the mirror, 10-9/9-above-10 a little further out from the center, and the invariance 10-11/10-11 at the boundaries of the mirror. Most of these palindromes and invariances are highlighted by register or by being stated as a single line. The corresponding passage, mm. 20–23, had a few two-measure mirrors and invariances (consult Example 2.33 again), but nothing spanning the entire passage.
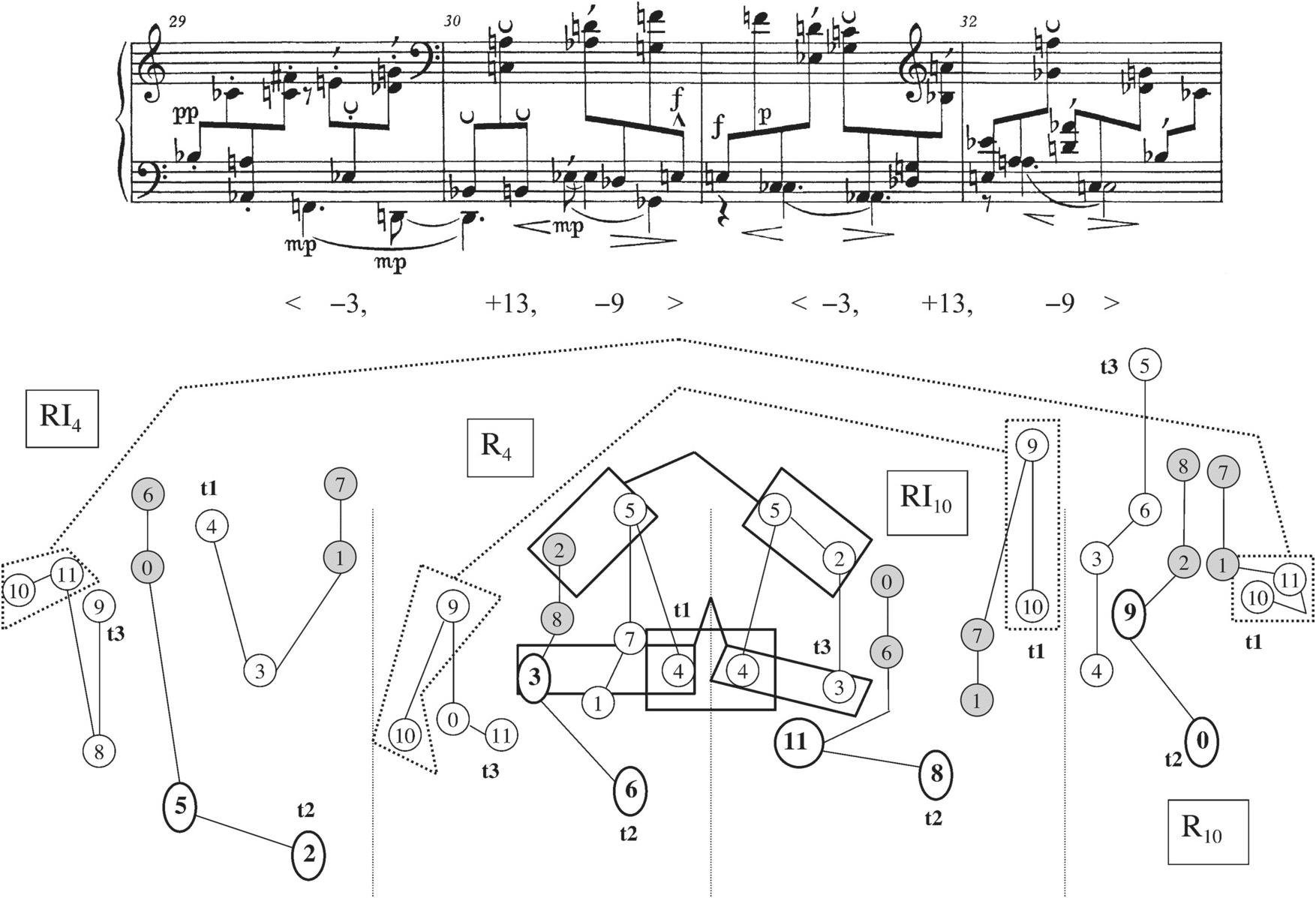
Example 2.36 Schoenberg, Gigue Op. 25, mm. 29–32 (subsection x1).
The third reason why mm. 29–32 sound more orderly is that even the vertical tritones, of which there are seven altogether, form a regular pattern with some registral symmetry (look at the shaded pitch classes and boxes on the score in Example 2.36): 6-above-0, 7-above-1 (up a half step), 2-above-8, 0-above-6, 7-above-1, 8-above-2, 7-above-1 (down a half step). This is more carefully organized (and repetitive) than the corresponding pattern of tritone verticals in mm. 20–23.
This greater emphasis on order serves a function, as is always the case with any phrase or section in Schoenberg’s music; by means of x1 he is leading into the first of several subsections in the Gigue that resolves one of the work’s problems. In Example 2.29’s form chart, mm. 33–36 (reproduced in Example 2.37) are labeled as c, because something new happens: subsection c assimilates one of the foreign elements into the larger structure of the tone row. It does this by presenting successions of intervals alternating unordered pitch intervals 6 and 7 or 6 and 5 as contiguous subsets of the row (and in one case, a non-contiguous one). Measures 33–36 constitute the first occasion since m. 13 on which we have heard a tone row stated in order, the first occasion in the movement on which rows are stated in order without incorporating multiple vertical dyads (mm. 34 and 36), and the first since m. 10 on which groups of three notes are highlighted as subsets within an ordered tone row. As has been the case with so many subsections in the Gigue, the explanation of the work’s first foreign element in mm. 33–36 happens progressively: Schoenberg first presents <−6,−7>, order positions <2,3,4> in P4, as the first part of a five-note group set off by accent and slurring in m. 33. In the following measure, there are two instances of the foreign element created contiguously, but both have features that make them less salient. In the case of <+18,−5>, order positions <2,3,4> in I10, the octave complementation and compounding and the motive’s placement at the beginning of a four-note group obscure it. With <+7,+6>, order positions <5,6,7> of I10, the foreign motive overlaps the groupings created by slurring and accents, so that its first note is separated from the other two. In m. 35, for the first time in the passage, we hear <−6,−7> set off by slurring as a motive. But the order numbers that create this motive, <2,3,6> in I4, are not contiguous. Finally in m. 36, two foreign motives appear, <−6,−7> and <+5,+6>, that are created by contiguous order numbers and highlighted by slurring and accent. The first motive brings together order numbers <2,3,4> of P10, and the latter one <5,6,7>. With this measure, Schoenberg has shown convincingly that lines alternating pitch intervals 6 and 7 or 6 and 5 can indeed be heard as part of an ordered tone row.
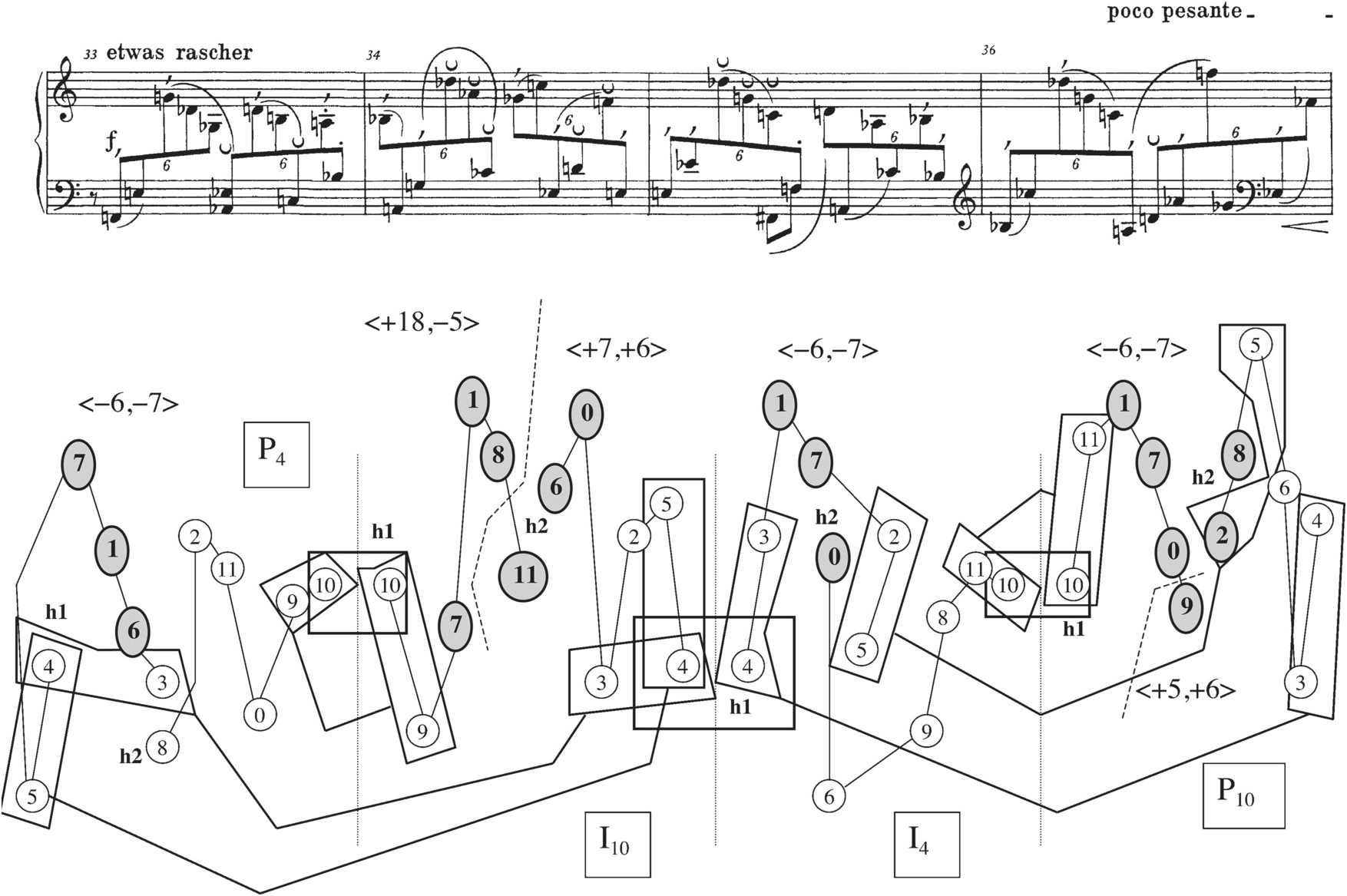
Example 2.37 Schoenberg, Gigue Op. 25, mm. 33–36 (subsection c).
But of course, the movement is only half finished at this point, so Schoenberg’s initial solution to the problem of pitch intervals {6,7} is not a conclusive one. There will be other elaborations of the same problem as well as other problems, and other solutions, in the subsequent music. The first direction he takes is to further develop the notion of vertical symmetry he introduced for the first time at m. 26. Measures 37 and 38, shown as the first two measures of Example 2.38, seem at first to be a vertical mirror of mm. 26–27, using the inversions around pitch class 4 of the rows in the previous passage, I4 and P10. As mm. 26 and 27 themselves contained a vertical mirror of their opening four-note chord, mm. 37 and 38 seem to expand the idea of vertical symmetry to the entire two-measure unit. But when comparing the notation in Example 2.38 with the strict pitch inversion of mm. 26–27 around E4 (directly below it in the example), the reader quickly recognizes that Schoenberg has made some adjustments to get to the version he uses. The two vertical tetrachords on the downbeat of m. 37 and the last eighth of that measure are revoiced, in such a way that the two chords are no longer pitch inversions of one another. The members of t2 and t3 in I4 are redistributed so that the right hand can have two voices and the left hand one, creating a similar texture to the middle of m. 26, not an inverse one. And finally, the inversion of m. 27 is transposed up one octave in m. 38, perhaps to give the entire phrase a more arch-like contour.
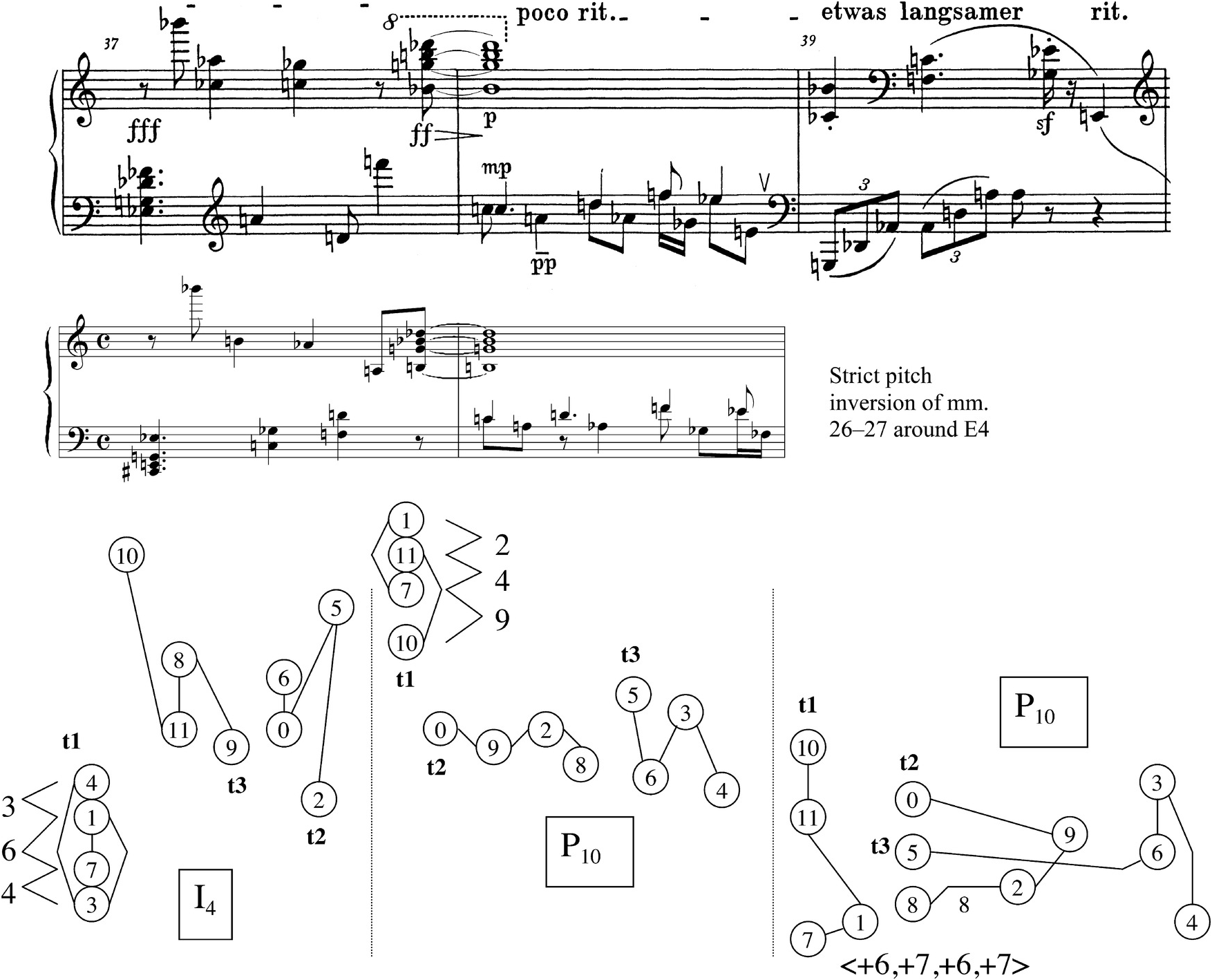
Example 2.38 Schoenberg, Gigue Op. 25, mm. 37–39 (subsection b1).
Though mm. 37–38 has undergone alterations, the eventual destiny of the passage is identical to mm. 26–28, which is the main reason why I call mm. 37–39 b1. The vertical symmetries that remain after the revoicing eventually give way to a passage in m. 39 where lines alternating pitch intervals 6 and 7 take over the bass line (just as they did in m. 28 of the original b subsection). The pitch classes that result, <7,1,8,8,2,9>, can be heard as a further outgrowth of the bass trichord of m. 28, <7,1,8>. This connection is strengthened by the retention of some of m. 28’s right-hand vertical dyads in m. 39’s right hand, 10-above-11 and 3-above-6, not to mention the carrying-over of the cross-like contour from each of m. 28’s pitch-symmetrical tetrachords to the right and left hands over all of m. 39 (right hand moves down, left hand moves up).
Measures 40–46 are called b2 because they have a similar function to the a2 subsection from mm. 17–19, though now prolonged to six measures: namely, they again bring forth the last two stages of a motion away from symmetry toward alternating <6,7> motives. However, we will see that the third stage in this subsection, in a way different from any of the a or b subsections that precede it, begins to combine some of the aspects of vertical symmetry introduced at the beginning of the B section with the inevitable lines alternating pitch intervals 6 and 7, synthesizing the diverse materials of the movement in a new way. Stage 2 of subsection b2 comprises mm. 40–42, and just like the a1 and a2 subsections that precede it, this passage uses overlapping of elements of tetrachords to obscure row forms as well as hiding palindromes and invariants between rows. The row forms labeled on Example 2.39a, P4, I4, P10, I10, P4, and P10, are in some cases no more than educated guesses.
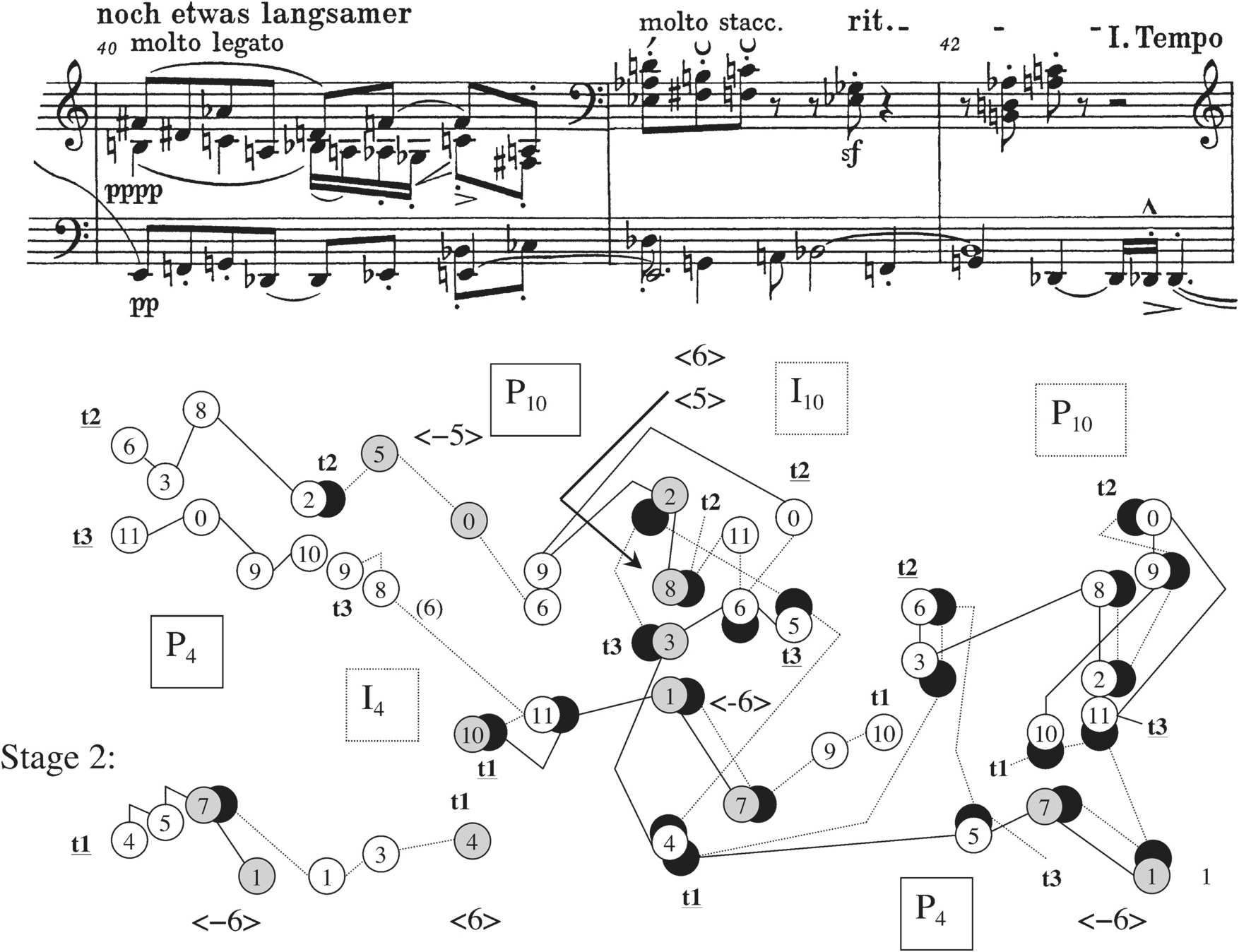
Example 2.39a Schoenberg, Gigue Op. 25, mm. 40–42 (subsection b2, stage 2).
At the same time, mm. 40–42 begin, as did the second stages in the A section, to introduce tritones and combinations of tritones and perfect fourths as prominent elements. Two verticals stand out: on the fourth beat of m. 40 a tritone in the left hand combines with a perfect fourth in the right, and the downbeat of m. 41 brings the two intervals vertically adjacent to one another in the right hand. Meanwhile, descending tritones involving pitch classes 7 and 1 sound in the bass at or near the beginning of every measure.
Stage 3a of subsection b2, which starts in m. 43 and is illustrated in Example 2.39b, introduces longer lines that alternate pitch intervals 6 and 7, as has been customary. But, as mentioned above, these lines are combined with one another in a new way: as the connected ovals superimposed over the notation of mm. 43 and 44 show, the left-hand and right-hand lines in both measures are vertically pitch-symmetrical with one another around the pitch axis E4 (B♭4 and B♭3 together – as always – can serve as alternative axes here). This is the only occasion in the piece, except for m. 19, on which the alternating <6,7> material has itself created a vertical mirror, and in that earlier instance the pitch axis was different (E/E♭). In a sense, vertical symmetry, placed around several different axes earlier in the Gigue, is now “coming home” to E and B♭ (“home” in the sense that they are the axes that the source tone rows invert around). Schoenberg seems to draw our attention to the two axes in another way as well: by ending the left-hand part in m. 43 with B♭4 and the left-hand part in m. 44 with E4. Thus one of the Gigue’s two main foreign elements (the <6,7> motive) is displayed according to a technique that was prevalent in the “contrasting” B section (vertical symmetry), to emphasize the axis pitch classes most crucial to the Suite’s four tone rows. Measures 43–44 do not explain how foreign elements derive from the tone rows, but they do bring together disparate elements and procedures of the movement in an interesting way.
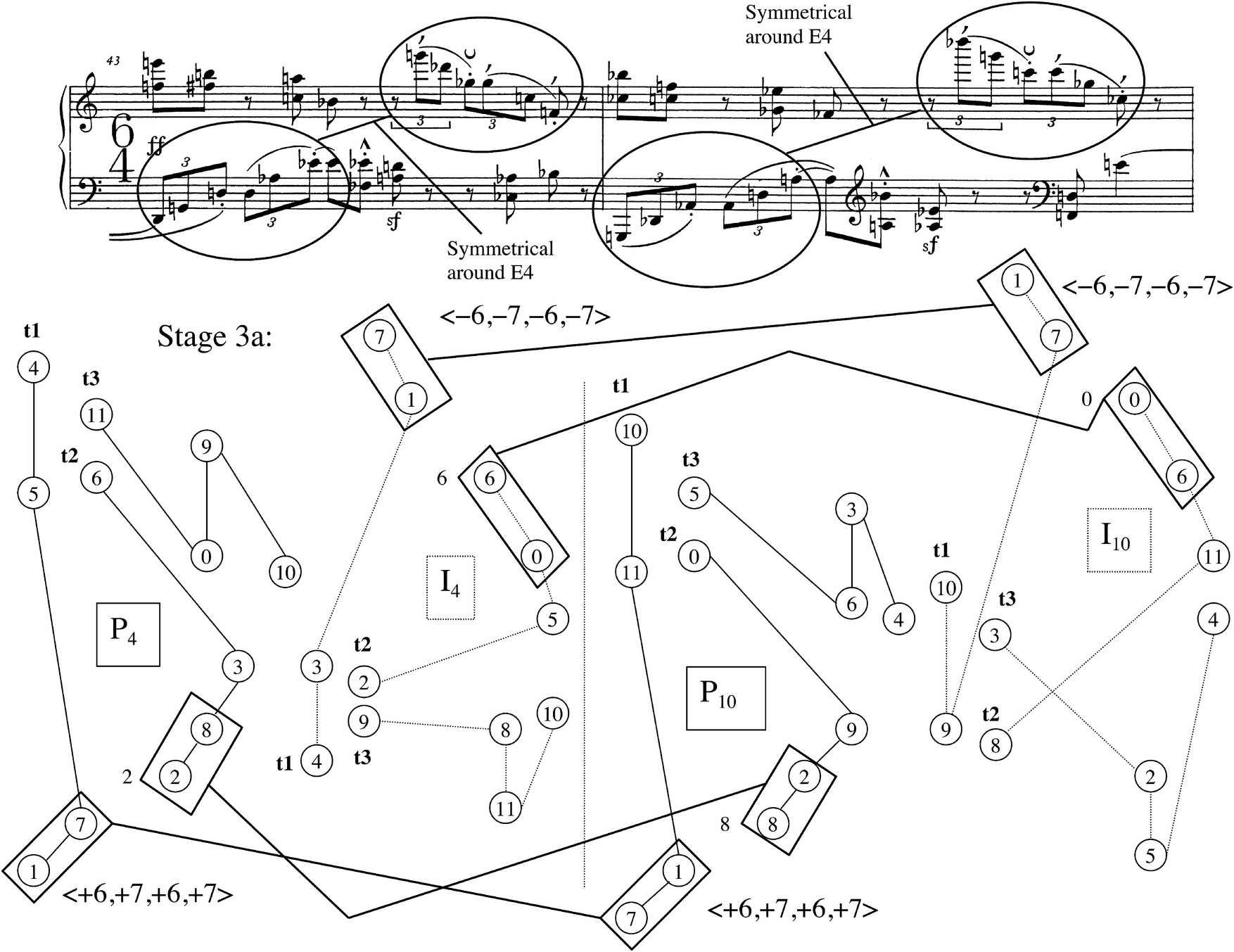
Example 2.39b Schoenberg, Gigue Op. 25, mm. 43–44 (subsection b2, stage 3, first part).
The latter part of stage 3, stage 3b (mm. 45 and 46), illustrated in Example 2.39c, first recaptures and then lets go of pitch-class symmetry in the other dimension, the horizontal one, within a context of overlapped row forms creating intervallically symmetrical alternations of pitch intervals 6 and 7 in the right hand. Measure 45 overlaps P4 and I10 in four notes, and the groups of eight notes on either side of the overlap can be split into two palindromic dyads and two dyad invariances (as the pitch-class map in m. 45 shows). The invariances 8-2/8-2 and 6-0/6-0 are perhaps easiest for the ear to pick out, because their first parts sound in outer voices. But the palindrome 4–5/5–4, which migrates from an inner voice to the bass (and is octave-complemented along the way), also has some salience. In contrast, m. 46, which overlaps P10 and I4 in three notes, has only one invariance that is not obscured by intervening pitches, 5-11/5-11.
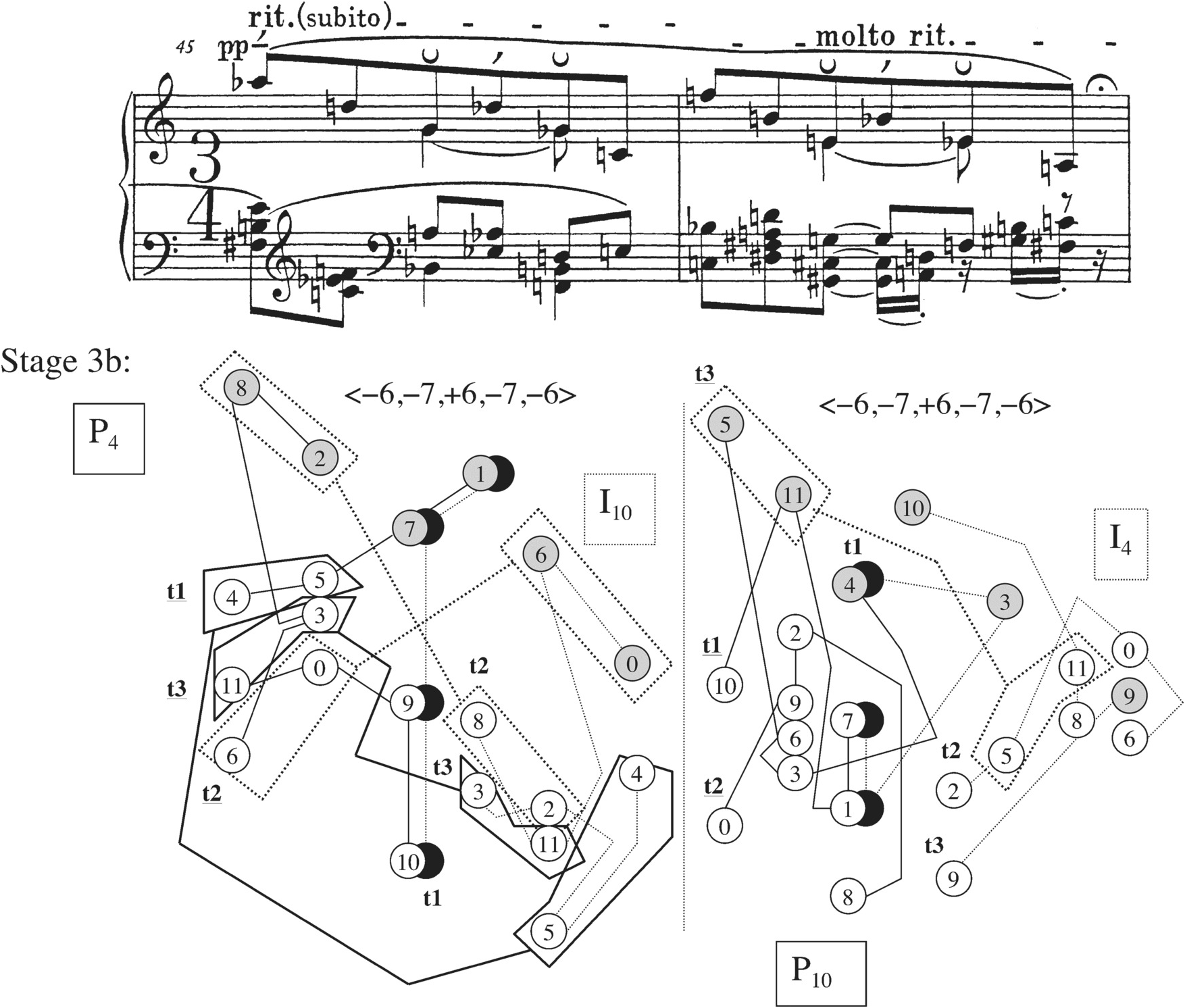
Example 2.39c Schoenberg, Gigue Op. 25, mm. 45–46 (subsection b2, last part of stage 3).
To recap our comments on section B, then, there are three subsections, b, b1, and b2, the first two of which proceed (in a similar way to their counterparts in A) from symmetry – this time vertical pitch symmetry – to an emphasis on lines alternating pitch intervals 6 and 7. The third of these subsections, b2, presents the <6,7> materials themselves in a vertically symmetrical manner, and thus contributes to the overall process of synthesis. Meanwhile, between b and b1 there is what might be described as a parenthesis, containing first the other half of the octatonic palindrome begun in section A, and second, the first of three subsections that show how the foreign <6,7> or <6,5> elements can be derived from the tone row. With m. 47 we reach the onset of the large A′ section, which emphasizes “explanatory” material even more strongly, tying up the loose ends caused by <6,7> lines and octatonic elements, and mediating the contrast between A and B sections.
Example 2.40 shows the beginning of A′, labeled as subsection a4 because, like the other three a subsections before it, it begins with passages emphasizing pitch-class and pitch symmetry and ends with pitches related by pitch intervals 6 and 5 wrecking that symmetry. Measures 47 and 48 combine R4 and R10 into a pair bounded by accented B♭3s and anchored in the middle by accented E2s, recalling the measure pairs at the movement’s beginning. Contributing to the symmetry are two dyad palindromes (one consisting of verticals, 3-above-6/6-above-3) and a dyad invariance (marked with connected boxes on Example 2.40). But probably the main feature suggesting symmetrical organization here is the contour, which opens out from B♭3 to E2 and G♭5 straddling the barline between mm. 47 and 48, and then closes back to B♭3 at the end of m. 48. This contour is closer to pitch-symmetrical than the one opening the piece in mm. 1–2, which began on E5 and ended an octave lower.
Example 2.40 Schoenberg, Gigue Op. 25, mm. 47–50 (subsection a4).
Measure 49 starts as though it wants to build another symmetrical pattern, following an accented B♭3 and rising to a repeated E4, but most of the pitch-class dyads highlighted in m. 49 do not find mirrors or invariant partners in m. 50. (There are two exceptions, 3-4/4-3 and 5-2/2-above-5, marked on the pitch-class map.) The cause of the broken symmetry is Schoenberg’s projection in m. 50 of −6 and −5 ordered pitch intervals. These intervals no longer succeed one another as parts of longer lines, but instead are placed above and below one another in separate voices. Their effect of breaking the passage’s symmetrical pattern is still the same, however.
Example 2.41 portrays the second of three c subsections in the Gigue that explains how the movement’s first foreign element, the alternating <6,7> material, is derivable from the row. In this case, the set class of many of the lines that alternated pitch intervals 6 and 7, set class 6-7 (012678), is shown to include also the initial pitch classes of each tetrachord in two ordered tone rows a tritone apart.43 This explanation happens in mm. 51–53a in the context of pitch-class symmetry, as demonstrated by the highlighted pitch class 10s and 4s and the mirrored and invariant dyads in the pitch-class map. Schoenberg highlights the first note of each tetrachord in P4 and P10 by accenting it and doubling it with a longer note value; these six pitch classes, <4,6,11,10,0,5>, if placed in normal order, {4,5,6,10,11,0}, are easily graspable as a member of set class 6-7. Though most of the set class 6-7s created by <6,7> material in the Gigue are transpositions of Schoenberg’s accented notes in mm. 51–52, there are three pitch-class successions created by alternating perfect fifths and tritones in the preceding music that duplicate the same six pitch classes. In reverse order, these are: (3) the right hand of mm. 45–46, reprised in the upper right-hand corner of Example 2.41, in the order <6,0,5,11,4,10>, (2) the left hand of m. 19, in the order <0,6,11,5,10,4>, and (1) the right hand of m. 16, presenting the ordering <6,0,5,11,4,10> again. We could say that Schoenberg’s accented pitch classes in mm. 51–52 account for previous <6,7> lines generally, and the soprano successions in mm. 45–46, 19, and 16 specifically.
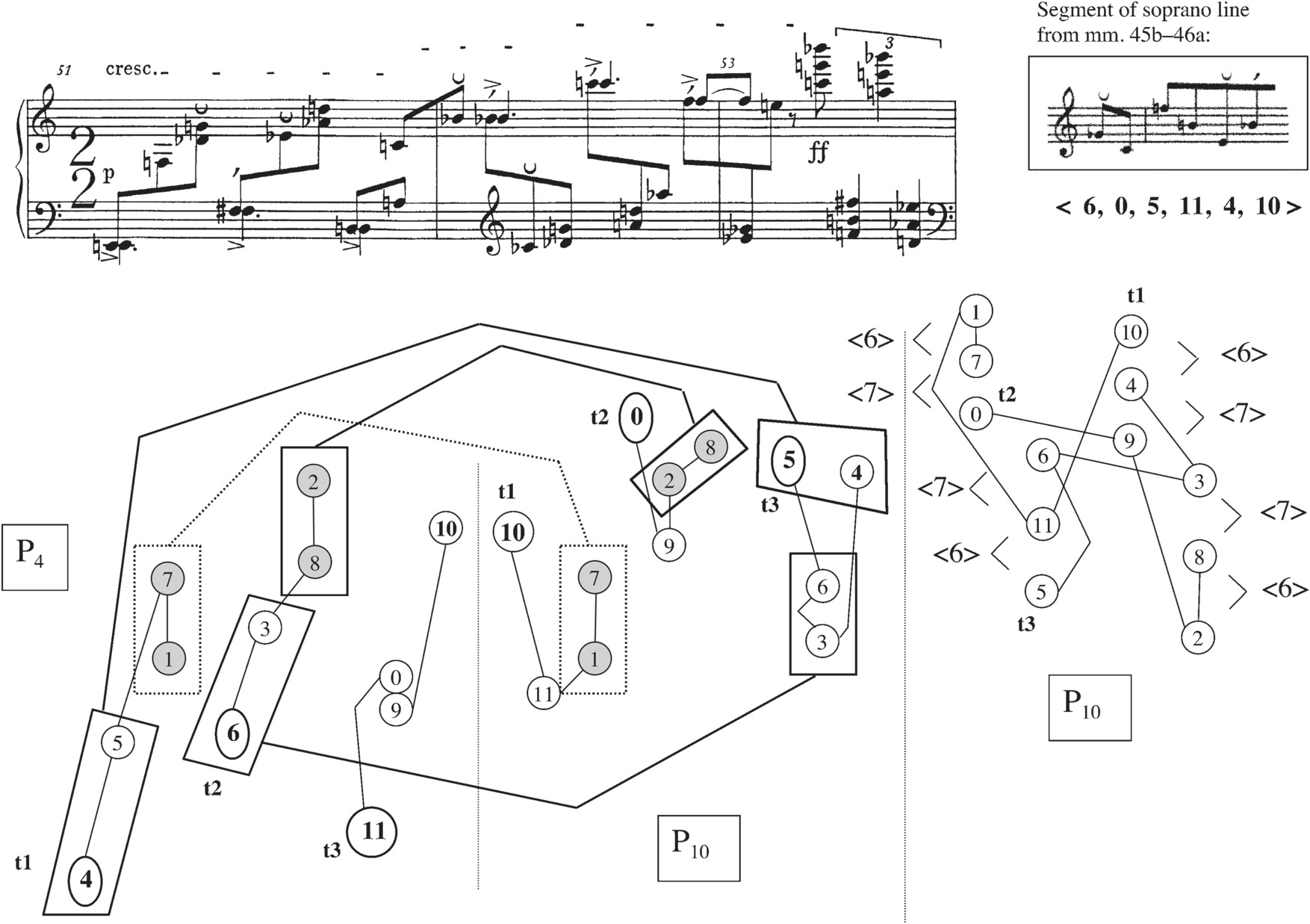
Example 2.41 Schoenberg, Gigue Op. 25, mm. 51–53 (subsection c1).
In any case, the explanation is short-lived. The last part of m. 53 gives up row ordering and horizontal symmetry to focus on two verticals (each divided into trichords) that alternate perfect fifths and tritones and, subsequently, also belong to set class 6-7. Each of these verticals is pitch-symmetrical, the first around A5 and the second around F♯5 (notice that Schoenberg has again left E and B♭ as axes of symmetry). But their relationship to the tone row is extremely obscure: my attribution of them to P10 is based more on that row’s occurrence just prior in m. 52 than on any inherent suggestion of P10 in m. 53.
In my introduction to the Gigue, I briefly mentioned a process involving subsections of the form that produces a kind of synthesis different from the others we have been discussing. The A′ section brings material from A and B together, first allowing a b subsection to succeed an a subsection, and then combining the two kinds of music together in a single subsection. Example 2.42 portrays the juxtaposition of b material in mm. 54–57a with the explanatory c1 material that preceded it immediately (mm. 51–53) and the a4 material that opened the A′ section (mm. 47–50). The vertical symmetry around a single pitch axis that characterized earlier b subsections is no longer present here (except in mm. 55–56, where the <6,7> lines take over). But there are enough textural and rhythmic similarities with earlier b music to cause the listener to make the connection, and in addition, there is an inversion in the registral placement of tetrachords between mm. 54 and 55. Like the beginning of subsection b (and section B) in m. 26, m. 54 presents t1 as a four-note chord in the high register, t2 as two quarter-note dyads following it in the right hand, and t3 as a single line working its way up from the bass. Measure 55 then places the four-note chord and the two dyads (still associated with t1 and t2) below the single line (t3). The intervals of the two four-note chords in mm. 54–55, though they are not arranged symmetrically around a center, do make a connection with previous music: they almost duplicate the interval patterns of the four-note chords at the beginning of subsection b1 in mm. 37–38, with the second chord’s intervals inverted. Counting intervals up from the bottom note, <+4,+6,+3>, <+9,+4,+2> in mm. 37–38 becomes <+4,+6,+3>, <+3,+3,+10> in mm. 54–55. Thus we can hear mm. 54–55 as themselves performing a kind of synthesis, bringing together material from two of the previous b subsections.
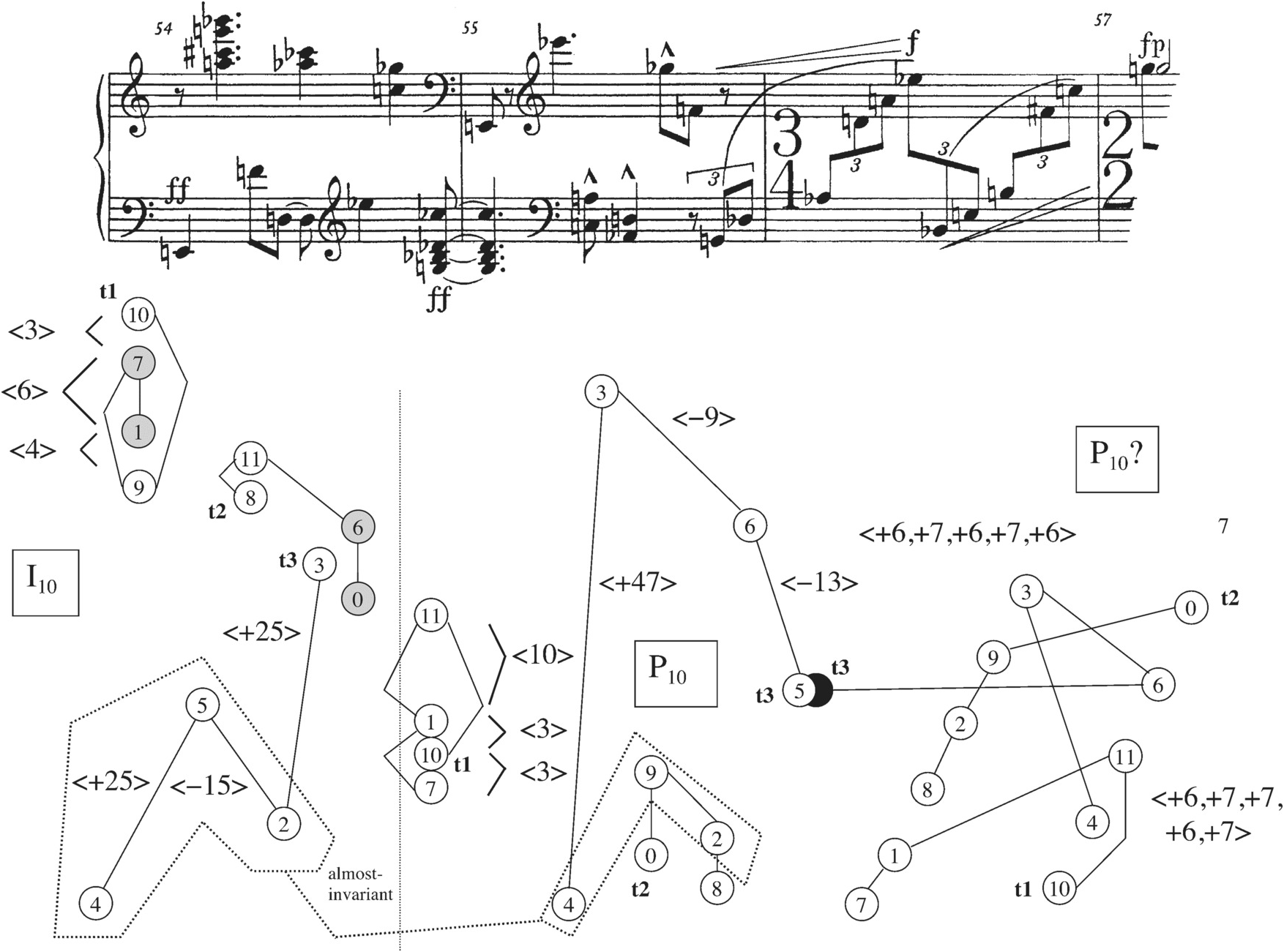
Example 2.42 Schoenberg, Gigue Op. 25, mm. 54–57a (subsection b3).
As has happened so many times before, however, this process of synthesis is rudely interrupted by the introduction of two six-note lines that both consist of +6 and +7 pitch intervals. The first one, <7,1,8,2,9,3>, is a vertically symmetrical (around B3) alternation of intervals 6 and 7 of the sort we have seen numerous times before. The second one, <10,4,11,6,0,7>, however, breaks up the alternating pattern by placing two perfect fifths together: <+6,+7,+7,+6,+7>.
I have called the music displayed in Example 2.43, mm. 57–61a, c1 rather than c2. The reason is that it most definitely has the quality of returning to the previous work of mm. 51–53 after a brief interruption. The “previous work” I am referring to is explaining the specific pitch-class collections that resulted from foreign alternations of intervals 6 and 7 earlier in the piece as derivable from the source twelve-tone rows. Measures 51–53 accounted for {4,5,6,10,11,0} as order positions {0,4,8} in P4 followed by P10. Now, in mm. 57–58, we hear {1,2,3,7,8,9} created by order positions {2,6,10} in P4 followed by P10. Then in mm. 59–60 Schoenberg explains {5,6,7,11,0,1} as order positions {2,6,10} in I10 followed by I4. The sequence of Schoenberg’s explanations is significant, because it accounts for these collections in the reverse order from which they appeared in the A section of the Gigue. As I mentioned above, mm. 51–53’s {4,5,6,10,11,0} are the pitch classes of the left hand in m. 19 and the right hand in m. 16. The collection {1,2,3,7,8,9} explained in mm. 57–58 can be found in the opposite hands at those same two places: right hand in m. 19, left hand in m. 16. Finally, the {5,6,7,11,0,1} that is accounted for in mm. 59–60 comprised the first six pitch classes of the right hand of m. 9. The introduction of foreign intervallic elements in the A section and the explanation of their resulting pitch classes as partitions of the tone row in section A′ form yet another palindrome, the largest one we have discussed, and one that corresponds to the ABA′ form of the Gigue.
Example 2.43 Schoenberg, Gigue Op. 25, mm. 57–61a (subsection c1, continued).
With all the foreign interval successions of section A accounted for (through their pitch-class collections), there are two “loose ends” yet to tie up in the remaining sixteen measures of the movement: explaining the relation of the octatonic collection, through its subsets, to the source row in its ordered form, and bringing a and b material together in a single subsection, to demonstrate features that those different kinds of material have in common. Schoenberg takes up both tasks, in the order in which I have just listed them. Measures 61–68, shown in Examples 2.44a and 2.44b, are designated x2 because their function is to account for the octatonic palindrome at mm. 20–23 and 29–32 as derivable from the twelve-tone row. The reader will remember that when the octatonic material was presented in those earlier passages, it was in the context of re-orderings of the component rows. In mm. 20–23, ordering within each tetrachord was preserved for the most part (except for the frequent use of vertical dyads), but the ordering between tetrachords was compromised greatly by overlaps. In mm. 29–32, both kinds of ordering, within and between, were altered significantly. Now, in subsection x2, Schoenberg shows that subsets of the octatonic, including but not limited to the one most prominently emphasized in the earlier passages, 4-3 (0134), can be derived through registral partitioning first from unordered presentations of the row (mm. 61–63) and then from presentations that are substantially more-ordered (mm. 63–68).
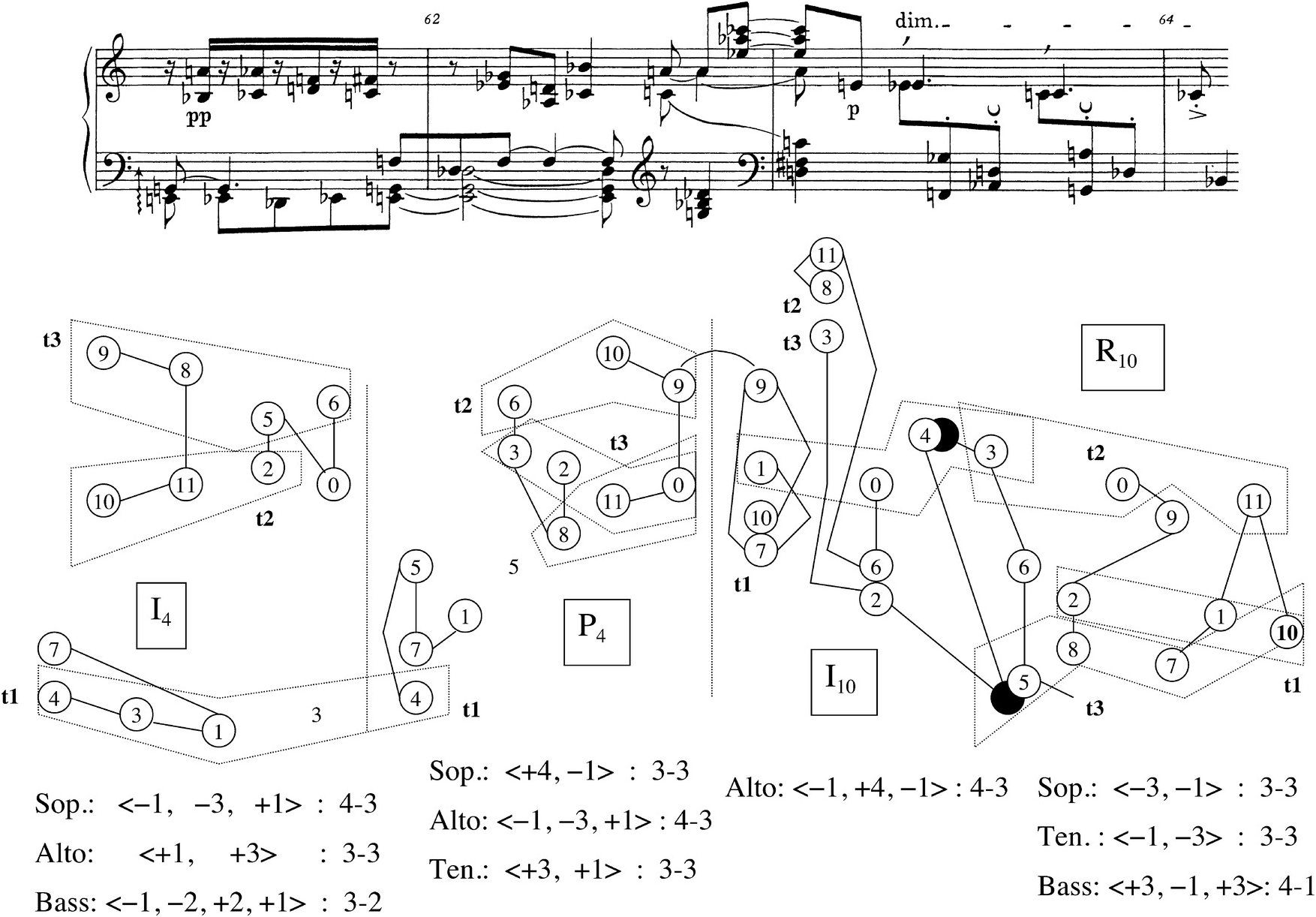
Example 2.44a Schoenberg, Gigue Op. 25, mm. 61b–64a (subsection x2, first part).
Example 2.44b Schoenberg, Gigue Op. 25, mm. 64b–68 (subsection x2, last part).
Measure 61 partitions a reordered I4 into soprano, alto and bass parts. The soprano gives a version of 4-3, <−1,−3,+1>, that involves many of the same intervals and the same general contour as 4-3’s initial appearance in mm. 20–21, <−3,−1,+3>. The alto yields 3-3 (014) as <+1,+3>, an inversion of the first part of the soprano motive, and the bass gives 3-2 (013), the other three-note subset of 4-3. Measures 61b–62a partition a P4 reordered within but not between its tetrachords into an alto 4-3 (this partition owes more to register than notation) that has the identical interval succession to its predecessor in m. 61, <−1,−3,+1>. Statements of set class 3-3 in the soprano and tenor surround it. In mm. 62b–63a, I10 is reordered within and between its tetrachords, and an alto voice yields <−1,+4,−1>, another succession belonging to 4-3.
On the second beat of m. 63, the tone rows begin to appear in order again, despite the presence of a few vertical dyads. First we hear R10, which can easily be partitioned (because of register, accent, and corresponding location in the three-note groups) into soprano and tenor voices that project descending forms of 3–3 and a bass voice that yields <+3,−1,+3>: set class 4-10 (0235), the other contiguous tetrachord subset of the octatonic scale. Following that in mm. 64b–65a and 65b–66a, P4 and I4 appear, arranged so that the upper-staff half of the pitches of I4 sound like half-step transpositions down from corresponding pitches in P4. If we focus for a moment on those six notes that sound like half-step transpositions (the second eighth note of beat 2, second eighth note of beat 3, and following downbeat in each measure), we can split them registrally into soprano and alto voices. In both measures, the soprano gives <−1,−3> and the alto <+1,+3>, which are vertically symmetrical members of set class 3-3. Meanwhile, the notes in the lowest register in both tone rows produce the interval successions <+1,−3,−13> and <−1,−3,−11>, which are both members of set class 4-3. And finally the vertical dyads that do not sound like half-step transpositions in these measures (those located on the third and fourth beats – shaded on the pitch-class map) form two members of 4-9, a non-contiguous octatonic tetrachord (these are {1,2,7,8} and {0,1,6,7}). In mm. 66b–67a and 67b–68, which use P10 and I10 respectively, Schoenberg retains the same two 4-9 tetrachords on third and fourth beats ({1,2,7,8} in m. 66, {0,1,6,7} in m. 67). And together with the latter tetrachord, he projects no fewer than four set class 3-3s in the upper, middle, and lower voices of mm. 66b–68. Thus, even though the whole octatonic collection does not seem to sound in mm. 61–68, its most salient subset, 4-3, is heard twice as a registral partition of an ordered row form, as are numerous other subsets of 8-28, most notably 3-3. (This trichord was, as we have discussed before, Schoenberg’s favorite chord during the atonal period.)
The other feature of mm. 63–68 worth remarking upon is the strong emphasis on B♭ (repeated three times by itself in the lowest register in mm. 64–66) and E (repeated nine times by itself at the end of the passage). These could be references back to the Prelude, as John Buccheri has suggested, but I prefer to think of them as reminders of the axis pitch classes that the four source rows invert around, which are also the same pitch classes that provided horizontal symmetry at the Gigue’s beginning.44
In mm. 69–72 (Example 2.45), Schoenberg presents for the second time within the A′ section material which sounds like the subsections of the contrasting B section. I believe that his purpose in doing this is to bring out various common elements that tie the a subsections (with their horizontal symmetry) and b subsections (with their vertical symmetry) together. This particular subsection, which I call b4, does not begin with vertical symmetry, however. Instead of juxtaposing inversion-related rows, Schoenberg follows P4 with P10, and the reader can see from the pitch-class map of these measures that the pitch intervals do not form a vertically symmetrical pattern in whole or in part. What makes mm. 69–70 sound like b music is the way in which he has presented the pitches of each tetrachord (t1: four-voice chord; t2: pair of dyads; t3: single line with wide leaps). In addition, m. 70 inverts the relative position of the three tetrachords, and also inverts the contours of t2 and t3, making the transpositional relationship between P4 and P10 sound at least something like an inversion.
Example 2.45 Schoenberg, Gigue Op. 25, mm. 69–72 (subsection b4).
As has been the case in previous b subsections, the opening material gives way quickly (after two measures this time) to runs alternating pitch intervals 6 and 7, which disturb the orderings of the rows. My attributions of I4 and I10 to these measures is, as before, an educated guess based on two factors: Schoenberg’s general tendency to present the four basic row forms as a group in the Gigue, and the tritone transposition between mm. 71 and 72. But there is something about these particular cascades of tritones and perfect fifths that marks them as unusual. Not only do they possess vertical symmetry both within each group (the four axes are given above the notation of mm. 71–72) and as a whole around E4/F4 (the E, of course, has recently been established as important by repetition of E3 in m. 68). But they also possess a kind of horizontal symmetry: the dyads in corresponding rhythmic positions between mm. 71 and 72 are all mirrors of each other. Thus 7–1 on the first two sextuplet eighths of m. 71 is answered in the same places in m. 72 with 1-7, and 6-0 and 0-6 are in corresponding locations, as are 5–11 and 11–5, 4–10 and 10–4, 3–9 and 9–3, 2–8 and 8–2. In this way, the symmetry characteristic of the a subsections (dyad palindromes across a barline) and the vertical symmetry characteristic of the b subsections are brought together by an element once considered to be foreign, the alternating pitch intervals 6 and 7.45
I labeled the final subsection of the piece, mm. 73–75, as a/b, because it presents features that are characteristic of both kinds of material (and incorporates one idea from the x subsections as well), but cannot in my opinion be definitively characterized as either a or b. Measure 73 splits into two halves, each five eighth notes in duration. Within each half the three tetrachords of first I10 and then P10 are distributed as they were at the beginning of each b subsection – t1 as a chord, t2 as a pair of dyads, and t3 as a single line. But now, rather than inverting the tetrachords relative to one another, Schoenberg gives them the same relative positions in both halves of the measure – t1 on the bottom, t2 and t3 intermingled in the right hand. This new distribution has several consequences. First, it enables the composer to treat the invariant trichord between the first tetrachords of I10 and P10, {1,7,10}, as a repeated diminished triad in the same register. This notion of repeating material from one row to the next reminds the listener of the ordered and unordered invariances in the a subsections. At the same time, the combinations of t2 and t3 in the right hand produce four triads, <11,3,6>, <5,8,0>, <8,0,3>, and <2,5,9> (or, if you will, B major, F minor, A♭ major, and D minor). The four divide into two pairs of triads, and each pair is vertically symmetrical around notes present in the triads, the first two around F♯ and F, the latter two around E♭ and D. If we consider the axes of symmetry themselves as a pitch-class and interval sequence, they form <6,5,3,2> or, in ordered pitch intervals, <−1,-2,-1>, that part of the octatonic collection that was featured in the x subsections, set class 4-3.
The piece’s final flourish, mm. 74–75, also merges features of subsections a and b. The ordered presentation of the dyads of P4 calls to mind other relatively ordered P4 presentations in subsections a, c, and c1. But the flourish, though it is not vertically symmetrical as a whole, has numerous segments that are, all boxed on the pitch-class map in Example 2.46. One of these vertical symmetries forms a boundary for the flourish, the F1-E2 vertical that begins it together with the B♭5-A6 vertical that ends it. It seems that dyads arranged in vertical symmetry have finally supplanted the horizontal palindromic dyads that were so prevalent at the piece’s beginning.
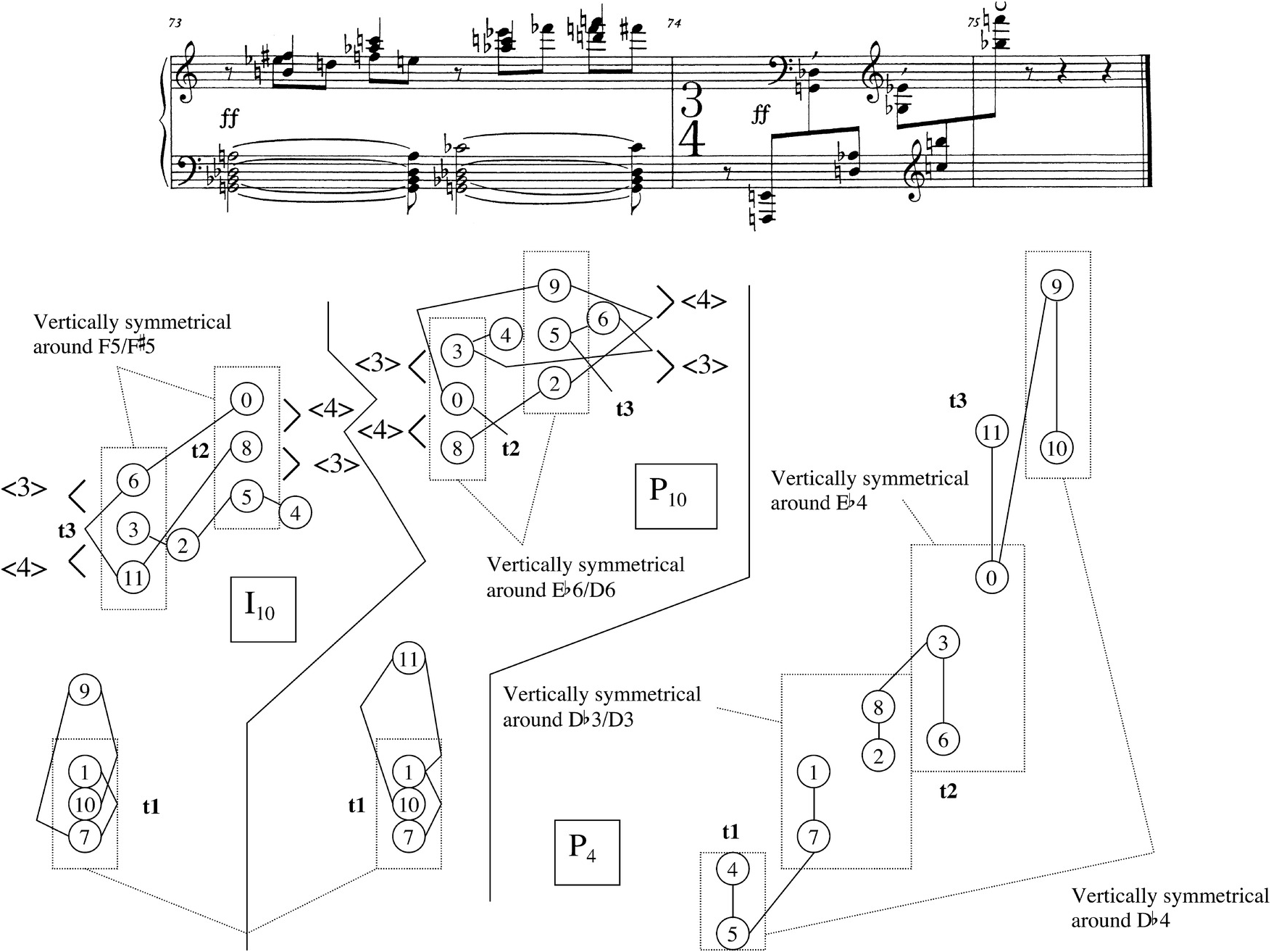
Example 2.46 Schoenberg, Gigue Op. 25, mm. 73–75 (subsection a/b).
The Gigue has long been recognized as extreme among the movements of Schoenberg’s Op. 25 Suite for its tempo, length, register, and rhythmic complexity. It is also the most complex of the movements with regard to large-scale structure, introducing not only successions of perfect fifths alternating with tritones but also an octatonic collection as “foreign” elements and re-assimilating them into the ordered presentation of the tone row, and simultaneously making a compromise in the A′ section between the horizontal pitch-class symmetries of A and the vertical interval symmetries of B. As we shall see, it is a “jumping-off spot” for Schoenberg’s later experiments with the presentation of the musical idea – but it is also an interesting and satisfying piece in itself.
1 , “Composition with Twelve Tones” (1941), in Style and Idea (1984), p. 232.
2 A transcription of the letter, dated June 3, 1937 and originally written in English, may be viewed through the correspondence database available at the website of the Arnold Schoenberg Center in Vienna, www.schoenberg.at (accessed August 4, 2013); its file name is 2892_2.jpg.
3 , Schoenberg’s Serial Odyssey: The Evolution of his Twelve-Tone Method, 1914–1928 (Oxford: Clarendon Press, 1990), pp. 42–84. presents the pre-history of Schoenberg’s twelve-tone music in a manner more friendly to the novice in “The Evolution of the Twelve-Tone Method,” in (ed.), The Arnold Schoenberg Companion (Westport, CT: Greenwood Press, 1998), pp. 101–28.
4 Haimo, Schoenberg’s Serial Odyssey, pp. 84–86 and 101–03; , “A Study in the Chronology of Op. 23–26 by Arnold Schoenberg,” Dansk aarbog for musicforskning2 (1962): 110–13.
5 Arnold Schönberg: Sämtliche Werke, section II: Klavier und Orgelmusik, series B, vol. IV: Werke für Klavier zu zwei Händen, Kritische Bericht, Skizzen, Fragmente, ed. (Mainz: B. Schott, and Vienna: Universal, 1975), pp. 67–80; , “Zur Entstehung der Zwölftontechnik,” in , , , and , eds., Bericht über den Internationalen Musikwissenschaftlichen Kongress Bonn 1970 (Kassel: Bärenreiter, 1971), pp. 284–88.
6 See, for example, her account of some of the same preliminary sketches for Op. 25 that Brinkmann discusses, in , “The Format and Function of Schoenberg’s Twelve-Tone Sketches,” Journal of the American Musicological Society36/3 (1983): 475–79, or her analyses of the Intermezzo and excerpts from various other movements of the Suite in “Musical Form and the Development of Schoenberg’s Twelve-Tone Method,” Journal of Music Theory 29/1 (Spring 1985): 85–143.
7 Arnold Schönberg: Sämtliche Werke, series B, vol. IV, p. 67. , Studien zur Entwicklung des dodekaphonen Satzes bei Arnold Schönberg, 3 vols. (Copenhagen: Wilhelm Hansen, 1972), vol. I, pp. 107–10; Maegaard, “A Study in the Chronology of Op. 23–26 by Arnold Schoenberg,” pp. 104–05.
8 Haimo, Schoenberg’s Serial Odyssey, pp. 84–89.
9 Hyde, “The Format and Function of Schoenberg’s Twelve-Tone Sketches,” pp. 470–79.
10 , “Mosaic Polyphony: Formal Balance, Imbalance and Phrase Formation in the Prelude of Schoenberg’s Suite, Op. 25,” Music Theory Spectrum14/2 (Fall 1992): 196.
11 , “Zur Schönberg-Deutung in Adornos Philosophie der neuen Musik,” Beiträge zur Musikwissenschaft32/1 (1990): 57.
12 See , “The Source Set and its Aggregate Formations,” Journal of Music Theory5/2 (Winter 1961): 224–73; , “Some Implications of the Pitch-Class/Order-Number Isomorphism Inherent in the Twelve-Tone System: Part One,” Perspectives of New Music26/2 (Summer 1988): 96–163; Kurth, “Mosaic Polyphony,” pp. 188–208.
13 Kurth, “Mosaic Polyphony,” pp. 196–99.
14 This observation necessitates understanding the E♮ in the alto on the downbeat of m. 16 as a misprint that takes the place of E♭, an interpretation that Kurth agrees with.
15 Kurth, “Mosaic Polyphony,” pp. 199–206.
16 Ibid., pp. 201–03.
17 The “still, small voice” comes from 1 Kings 19:11–13, of course. It was typical of Schoenberg to borrow topics and images from Jewish Scripture for his compositions (Moses und Aron among many others) as well as his writings (“Composition with Twelve Tones”). Perhaps the Prelude can be thought of as a subtler example of such a borrowing.
18 It should be pointed out that not every row pair in Schoenberg’s set table (Example 2.1) creates pitch or ordered interval palindromes within individual voices. The lower two voices of P4/R4 create ordered pitch-interval palindromes but not pitch palindromes (because Schoenberg transposed the second tetrachord down an octave); the lowest voice in I10/RI10 creates an ordered pitch-interval palindrome but not a pitch one (for the same reason); and the top voice of I4/RI4 creates only a pitch class palindrome (because Schoenberg has displaced two notes of its second tetrachord, G and E, by an octave). But the majority of voices do create both pitch and ordered pitch-interval mirrors, so I believe it is safe to treat that shape as a norm.
19 Several examples of twelve-tone pieces that follow a similar plan will be given in this book. For an example of an atonal piece that obscures its solution at the end, consider “Seraphita” Op. 22, No. 1, as described in my dissertation, “An Analogue to Developing Variation in a Late Atonal Song of Arnold Schoenberg” (Ph.D. dissertation, Yale University, 1991), especially pp. 219–31.
20 Haimo, Schoenberg’s Serial Odyssey, pp. 101–02; Maegaard, “A Study in the Chronology of Op. 23–26 by Arnold Schoenberg,” p. 113. Maegaard also suggests that initial work Schoenberg did on the Gigue Op. 25 before he began the Trio (during March 2–3, 1923) may have been where he first worked out the concept of dividing a linear statement of the row into hexachords. See my analysis of the Gigue, below.
21 , “Continuity, Reference and Implication: Remarks on Schoenberg’s Proverbial ‘Difficulty,’” Theory and Practice17 (1992): 35–58.
22 Haimo, Schoenberg’s Serial Odyssey, pp. 100–01; , “Series, Form and Function: Comments on the Analytical Legacy of René Leibowitz and Aspects of Tonal Form in the Twelve-Tone Music of Schoenberg and Webern,” Ex Tempore8/1 (1996): 124–26; , Silence and Slow Time (Lanham, MD: Scarecrow Press, 2004), pp. 130–36. in his review of Schoenberg’s Style and Idea, Perspectives of New Music 14–15 (Spring–Summer 1976, Fall–Winter 1976): 174–81, calls the Menuett a binary form, dividing it into mm. 1–11 and 12–33.
23 , in “Dis-Regarding Schoenberg’s Twelve-Tone Rows: An Alternative Approach to Listening and Analysis for Twelve-Tone Music,” Theory and Practice21 (1996): 98–100, reveals another way in which the first four measures of the Menuett present and then obscure or complicate a pattern. Kurth shows how the attack rhythms of t3 of P4 in m. 2 take the 
rhythm of t2 in the first measure and displace it to the right by an eighth note. The same divergence between the notated meter and its alternative (both of which can be heard) continues with the basic attack rhythms of t2 of I10 in m. 3, and t3 of I10 in m. 4.
24 Schoenberg’s definition and illustrations of sentence form, including information on the nature and role of liquidation, may be found in Schoenberg, Fundamentals of Musical Composition, pp. 20–24 and 58–81.
25 MacKay, “Series, Form and Function,” pp. 124–25.
26 Haimo, Schoenberg’s Serial Odyssey, pp. 100–01; Kurth, “Dis-Regarding Schoenberg’s Twelve-Tone Rows,” pp. 102–113; MacKay, “Series, Form and Function,” pp. 124–26.
27 Kurth, “Dis-Regarding Schoenberg’s Twelve-Tone Rows,” p. 105. Actually, this is the first of two tonal accounts that Kurth makes of the opening measures; the second groups individual notes and invariant dyads differently to suggest an A minor tonality in mm. 1–4.
28 Martin Boykan’s account of the Menuett in Silence and Slow Time shows how <9.10>, which would suggest a dominant cadence in an E♭ reading, continues to sound prominently at or near cadences for the remainder of the piece: mm. 7, 11, 16, and 31–33. Boykan does not interpret these references tonally, however, but instead limits himself to suggesting that the recurring <A, B♭> motives form part of a network of rhyming cadences which also includes <D, E♭> and variations of it. See Silence and Slow Time, pp. 133–36.
29 Peles, “Continuity, Reference and Implication,” p. 56.
30 Haimo, Schoenberg’s Serial Odyssey, pp. 100–01; MacKay, “Series, Form and Function,” p. 126. Haimo reminds the reader that Schoenberg’s labels in his set table for P4 and I10 (‘T” for “Tonika” and “U” for “Umkehrung”) connote tonic function, and his labels for P10 and I4 (“D” for “Dominante” and “DU”) connote dominant function. Refer back to my reproduction of the set table in Example 2.1.
31 It should be pointed out that 6-Z13 and 6-Z42 do contain contiguous row segments: they arise through dividing the row into order positions {5,6,7,8,9,10} and {11,0,1,2,3,4}, so the contents of mm. 12–15 could certainly be explained as “secondary harmonies” with respect to the tone row. But the connection between the specific pitch-class instances of these set classes in these four measures and the four original row forms P4, I10, I4, and P10 still seems to be a remote one.
32 Peles, “Continuity, Reference and Implication,” pp. 54–56.
33 MacKay, “Series, Form and Function,” p. 126.
34 My assertion that the two rows are rotated is based on the hexachords that result when we group the first three dyads together and separate them from the last three dyads, e.g. in the right hand, <6-above-3, 7-above-1, 2-above-8> and <4, 5, 9-above-0, 10-above-11>.
35 There was an example earlier in the piece (mm. 23–24) where dyads from consecutively appearing row forms, <3,2> from I10 and and <5,4> from I4, grouped together by virtue of their low register to form the third tetrachord of I10.
36 Maegaard, “A Study in the Chronology of Op. 23–26 by Arnold Schoenberg,” p. 105.
37 Ibid., p. 113.
38 My tripartite division agrees with John Buccheri’s outline in its large sections (except that he calls them parts I, II and III); but our viewpoints on how the large sections should be divided into subsections differ substantially. For the most part, Buccheri’s subdivisions rely on tempo and texture changes, while mine are inspired by the processes involving the development of the foreign motive 3–5 (016). See Buccheri, “An Approach to Twelve-Tone Music: Articulation of Serial Pitch Units in Piano Works of Schoenberg, Webern, Krenek, Dallapiccola, and Rochberg” (Ph.D. dissertation, Eastman School of Music, University of Rochester, 1975), pp. 95–96.
39 Martha Hyde brings out a different feature of the opening two measures of the Gigue, pointing out that the right hand of the piano projects 6-Z17 (012478) followed by 6-Z43 (012568) and the left hand gives the same two set classes in the opposite order. These hexachords are important because they can each be grouped together from three dyads shared by several of the four source rows (they are “invariant harmonies,” in other words), and Schoenberg actually creates them in such a way at the opening of the Gavotte. Thus a harmonic connection is established between openings of different movements. See Hyde, “Musical Form and the Development of Schoenberg’s Twelve-Tone Method,” pp. 120–23.
40 For an example, consider the sketch located on staves 10 and 11 of p. 27n of MS 25, located at the Arnold Schoenberg Center in Vienna and accessible from its website at www.schoenberg.at (accessed August 4, 2013). Brinkmann in his critical report for Arnold Schönberg: Sämtliche Werke, section II, series B, vol. IV, pp. 67 and 72, claims that this sketch (which he calls b6) is a precursor to the beginning of the Prelude, and the registral placement of the pitch classes in its initial P4 supports this attribution. But the sketch also divides each row registrally into tetrachords, and overlaps t3 of the initial P4 with t1 of the second form, P10, in one pitch class, 10 (bass, third beat of m. 2). One measure later, it overlaps t3 of P10 with t1 of P4 in pitch class 4 (alto, second beat of m. 3), and a measure after that, it overlaps t3 of P4 with t1 of P10 in pitch class 10 again (soprano, third beat of m. 4). This technique of chaining more than two consecutive row forms together through overlapping members of their tetrachords is hardly used in the Prelude (mm. 11–13 is an exception), but as we have seen and will see, it plays a crucial role in the Gigue.
41 I have already shown the importance to Schoenberg’s music of successions alternating unordered pitch intervals 1 and 3, as well as octave compounding (among other transformations) on interval successions, in , “Schoenberg’s Op. 22 Radio Talk and Developing Variation in Atonal Music,” Music Theory Spectrum14/2 (Fall 1992): 184–215.
42 Vertical pitch symmetry in Schoenberg’s atonal and twelve-tone music is a topic that has received a fair amount of attention in the literature, most notably ’s early article “Inversional Balance as an Organizing Force in Schoenberg’s Music and Thought,” Perspectives of New Music6/2 (Spring–Summer 1968): 1–21.
43 Places where lines or chords alternating pitch intervals 6 and 7 create set class 6-7 are: m. 9, right hand, first two beats; m. 16, each hand; m. 19, each hand; m. 45, right hand; m. 46, right hand; m. 53, second eighth note of beat 2 and first quarter of the triplet, as well as the second two quarters of the triplet; mm. 55b–56a, the first ascending six-note group; mm. 71 and 72, each of the descending six-note groups.
44 Buccheri, “An Approach to Twelve-Tone Music,” p. 110.
45 If the reader looks back through the Gigue, he or she will find that the palindromes between dyads in corresponding locations of mm. 71–72 were in fact foreshadowed by earlier instances of <6,7> material, even those instances that were described as “disruptive to horizontal symmetry.” Measure 43 presents <1,7,2,8> in the bass followed by <7,1,6,0> in the soprano, and m. 44 answers this with <7,1,8,2> in the bass followed by <1,7,0,6> in the soprano. And back in mm. 5–8, stage 2 of the original a subsection, the eighth-note triplets in the right hand presented this sequence: <1,7,2,8> in m. 5, <7,1,8,2> in m. 6, <1,7,0,6> in m. 7, and <7,1,6,0> in m. 8. The reasons why such palindromes could be described as “destructive to symmetry” are twofold: (1) they contained different pitch-class pairs from the palindromes featured at the beginnings of the a subsections, mirrors like 9–10/10–9, 11–10/10–11, 4–3/3–4, and 4–5/5–4; and (2) the horizontal symmetries created by <6,7> material were always between pitches in corresponding rhythmic locations, while the symmetries earlier in the a subsections were placed in rhythmically symmetrical locations.
