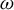1 Introduction
Contemporary high-intensity femtosecond laser facilities that are based on the chirped pulse amplification (CPA) concept[ Reference Strickland and Mourou 1 ] now reach subterawatt[ Reference Mitrofanov, Voronin, Sidorov-Biryukov, Mitryukovsky, Fedotov, Serebryannikov, Meshchankin, Shumakova, Ališauskas, Pugžlys, Panchenko, Baltuška and Zheltikov 2 ], multi-terawatt[ Reference Lozhkarev, Freidman, Ginzburg, Katin, Khazanov, Kirsanov, Luchinin, Mal'shakov, Martyanov, Palashov, Poteomkin, Sergeev, Shaykin and Yakovlev 3 – Reference Panagiotopoulos, Hastings, Kolesik, Tochitsky and Moloney 12 ] and petawatt[ Reference Jeong and Lee 13 – Reference Lureau, Matras, Chalus, Derycke, Morbieu, Radier, Casagrande, Laux, Ricaud, Rey, Pellegrina, Richard, Boudjemaa, Simon-Boisson, Baleanu, Banici, Gradinariu, Caldararu, Boisdeffre, Ghenuche, Naziru, Kolliopoulos, Neagu, Dabu, Dancus and Ursescu 20 ] power levels, with a rapid increase in their number worldwide[ Reference Yakovlev 21 – Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel 23 ]. Most of the high-power systems are near-infrared (NIR) facilities taking advantage of Ti:sapphire lasers, while others operate in the mid-IR[ Reference Mitrofanov, Voronin, Sidorov-Biryukov, Mitryukovsky, Fedotov, Serebryannikov, Meshchankin, Shumakova, Ališauskas, Pugžlys, Panchenko, Baltuška and Zheltikov 2 ] or visible[ Reference Alekseev, Ivanov, Ivanov, Losev, Mesyats, Mikheev, Panchenko, Ratakhin and Yastremskii 9 , Reference Alekseev, Ivanov, Losev, Mesyats, Mikheev, Ratakhin and Panchenko 10 ] spectral ranges. In certain cases, two-color lasers[ Reference Edwards, Fasano, Bennett, Griffith, Turley, O’Brien and Mikhailova 11 ] are advantageous for high-intensity laser–matter interaction experiments.
Tight focusing of intense femtosecond laser pulses into diffraction-limited focal spots or spots with high Strehl ratios S ≥ 0.5 and small effective radii r eff ~ 1 μm enables the transition of the laser–matter interaction to substantially relativistic regimes[ Reference Mourou, Tajima and Bulanov 24 ]. One of the important parameters in the interaction processes is the peak laser intensity on-target I 0 = a 0 2 × 1.37 × 1018 W/cm2 × (λ/μm)–2, where λ represents the laser wavelength and a 0 is a normalized vector-potential of the laser field–electron interaction. Relativistic regimes correspond to a 0 > 1.
Most of the existing high-intensity experiments have been carried out at laser intensities from I 0 ~ 1018 to 1021 W/cm2 (from a 0 ~ 1 to 30), and only a few at I 0 > 1021 W/cm2 [ Reference Nishiuchi, Dover, Hata, Sakaki, Kondo, Lowe, Miyahara, Kiriyama, Koga, Iwata, Alkhimova, Pirozhkov, Faenov, Pikuz, Sagisaka, Watanabe, Kando, Kondo, Ditter, Ettlinger, Hicks, Najmudin, Ziegler, Zeil, Schramm and Sentoku 25 – Reference Bernert, Assenbaum, Bock, Brack, Cowan, Curry, Garten, Gaus, Gauthier, Gebhardt, Göde, Glenzer, Helbig, Kluge, Kraft, Kroll, Obst-Huebl, Püschel, Rehwald, Schlenvoigt, Schoenwaelder, Schramm, Treffert, Vescovi, Ziegler and Zeil 33 ]. New regimes of laser–matter interaction require intensities I 0 ~ 1022 W/cm2 and higher, leading to efficient radiation-pressure-dominant ion acceleration at I 0 > 1022 W/cm2 [ Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima 34 , Reference Esirkepov, Yamagiwa and Tajima 35 ], radiation damping at I 0 > 3 × 1023 (μm/λ)4/3 W/cm2 [ Reference Mourou, Tajima and Bulanov 24 ] and quantum electrodynamic effects at I 0 > 6 × 1024 W/cm2 [ Reference Di Piazza, Müller, Hatsagortsyan and Keitel 36 ]. A distant goal is reaching the intensities of I 0 > 1026 W/cm2 required for optically induced vacuum breakdown[ Reference Bulanov, Mur, Narozhny, Nees and Popov 37 ]. Recently, an intensity of I 0 > 1023 W/cm2 has been experimentally demonstrated[ Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam 38 ]. Advancing laser fields to these numbers requires comprehensive control of the spatial and temporal envelope of the laser pulses[ Reference Pirozhkov, Fukuda, Nishiuchi, Kiriyama, Sagisaka, Ogura, Mori, Kishimoto, Sakaki, Dover, Kondo, Nakanii, Huang, Kanasaki and Kando 8 , Reference Nakamura, Mao, Gonsalves, Vincenti, Mittelberger, Daniels, Magana, Toth and Leemans 39 ], as well as placing the target within an extremely short Rayleigh length (~10 μm in our case), which is a consequence of using high-aperture focusing mirrors with small f-numbers to attain focal spots with r eff ~ λ. It is worth mentioning that laser–gas interactions are largely negatively affected by the focal-spot imperfections[ Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa, Tsai, Pai, Quevedo, Dyer, Gaul, Martinez, Bernstein, Borger, Spinks, Donovan, Khudik, Shvets, Ditmire and Downer 40 – Reference Pirozhkov, Esirkepov, Pikuz, Faenov, Sagisaka, Ogura, Hayashi, Kotaki, Ragozin, Neely, Koga, Fukuda, Nishikino, Imazono, Hasegawa, Kawachi, Daido, Kato, Bulanov, Kondo, Kiriyama and Kando 42 ], while laser–solid interactions are strongly influenced by laser pre-pulses and pedestals producing pre-plasmas on different timescales[ Reference Daido, Nishiuchi and Pirozhkov 43 , Reference Singh, Krupka, Istokskaia, Krasa, Guiffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha 44 ].
Common methods for target positioning include, for example, shadowgraphy, retro-focusing and direct observation of the rear side of a solid target[ Reference McKenna, Ledingham, Spencer, McCany, Singhal, Ziener, Foster, Divall, Hooker, Neely, Langley, Clarke, Norreys, Krushelnick and Clark 45 – Reference Willis, Poole, Akli, Schumacher and Freeman 47 ]. However, in the case of relatively wide and smooth mirror-like reflective tape targets, shadowgraphy cannot ensure target positioning with an accuracy of better than a few tens of micrometers[ Reference Willis, Poole, Akli, Schumacher and Freeman 47 ]. At the same time, techniques for direct observation of the target surface are most advantageous in the case of single-shot experiments or while operating low-repetition-rate laser systems that typically deliver up to several full-power shots per hour[ Reference Willis, Poole, Akli, Schumacher and Freeman 47 ]. In our case of 0.1-Hz laser operation, direct observation of the target surface for the precise target placement would be more time-consuming than using 10–20 full-power laser shots to find the best focus. The techniques we present in our paper can be used in experiments using laser systems with high repetition rates of 0.1–10 Hz, such as ALEPH[ Reference Wang, Wang, Rockwood, Luther, Hollinger, Curtis, Calvi, Menoni and Rocca 48 ] in Colorado, Astra Gemini[ Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Foster, Hancock, Hawkes, Holligan, Langley, Lester, Neely, Parry and Wyborn 49 ] in the UK, Apollon[ Reference Le Garrec, Papadopoulos, Le Blanc, Zou, Chériaux, Georges, Druon, Martin, Fréneaux, Beluze, Lebas, Mathieu and Audebert 50 ] in France, ATLAS 3000 and PFS[ Reference Kessel, Leshchenko, Jahn, Krüger, Münzer, Schwarz, Pervak, Trubetskov, Trushin, Krausz, Major and Karsch 51 ] in Munich, BELLA[ Reference Nakamura, Mao, Gonsalves, Vincenti, Mittelberger, Daniels, Magana, Toth and Leemans 39 ] in Berkeley, CoReLS[ Reference Sung, Lee, Yoo, Yoon, Lee, Yang, Son, Jang, Lee and Nam 17 ] in Republic of Korea, Diocles[ Reference Zhao, Zhang, Chen, Liu, Golovin, Banerjee, Brown, Mills, Petersen and Umstadter 52 ] in Nebraska-Lincoln, DRACO[ Reference Zeil, Kraft, Bock, Bussmann, Cowan, Kluge, Metzkes, Richter, Sauerbrey and Schramm 53 ] in Dresden, HAPLS[ Reference Condamine, Jourdain, Hernandez, Taylor, Bohlin, Fajstavr, Jeong, Kumar, Laštovička, Renner, Nakatsutsumi, Alatabi, Aldawood, Amin, Andel, Andreasson, Angelova, Antici, Bakeman and Weber 54 , Reference Borneis, Laštovička, Sokol, Jeong, Condamine, Renner, Tikhonchuk, Bohlin, Fajstavr, Hernandez, Jourdain, Kumar, Modřanský, Pokorný, Wolf, Zhai, Korn and Weber 55 ] at ELI-Beamlines in the Czech Republic, HERCULES[ Reference Yanovsky, Chvykov, Kalinchenko, Rousseau, Planchon, Matsuoka, Maksimchuk, Nees, Cheriaux, Mourou and Krushelnick 4 ] in Michigan, HF-PW at ELI-ALPS[ Reference Kühn, Dumergue, Kahaly, Mondal, Füle, Csizmadia, Farkas, Major, Várallyay, Cormier, Kalashnikov, Calegari, Devetta, Frassetto, Månsson, Poletto, Stagira, Vozzi, Nisoli, Rudawski, Maclot, Campi, Wikmark, Arnold, Heyl, Johnsson, L'Huillier, Lopez-Martens, Haessler, Bocoum, Boehle, Vernier, Iaquaniello, Skantzakis, Papadakis, Kalpouzos, Tzallas, Lépine, Charalambidis, Varjú, Osvay and Sansone 56 ] in Hungary, HPLS[ Reference Lureau, Chalus, Matras, Laux, Radier, Casagrande, Derycke, Ricaud, Rey, Morbieu, Pellegrina, Boudjemaa, Simon-Boisson, Baleanu, Banici, Gradinariu, Caldararu, Ghenuche, Naziru, Kolliopoulos, Neagu, Boisdeffre, Ursescu and Dancus 19 , Reference Lureau, Matras, Chalus, Derycke, Morbieu, Radier, Casagrande, Laux, Ricaud, Rey, Pellegrina, Richard, Boudjemaa, Simon-Boisson, Baleanu, Banici, Gradinariu, Caldararu, Boisdeffre, Ghenuche, Naziru, Kolliopoulos, Neagu, Dabu, Dancus and Ursescu 20 ] at ELI-NP in Romania, SCAPA[ Reference Jaroszynski, Ersfeld, Islam, Brunetti, Shanks, Grant, Tooley, Grant, Reboredo Gil, Lepipas, McKendrick, Cipiccia, Wiggins, Welsh, Vieux, Chen, Aniculaesei, Manahan, Anania, Noble, Yoffe, Raj, Subiel, Yang, Sheng, Hidding, Issac, Cho and Hur 57 ] at the University of Strathclyde in Glasgow, SULF[ Reference Li, Qin, Zhang, Li, Fan, Wang, Xu, Wang, Yu, Xu, Liu, Wang, Wang, Zhang, Liu, Bai, Gan, Zhang, Wang, Fan, Sun, Tang, Yao, Liang, Leng, Shen, Ji, Li and Xu 31 ] in China, VEGA[ Reference Roso 58 , Reference Roso 59 ] in Spain, as well as commercial PULSAR laser systems in Canada[ Reference Formaux, Payeur, Alexandrov, Serbanescu, Martin, Ozaki, Kudryashov and Kieffer 60 ], Italy[ Reference Gizzi, Benedetti, Cecchetti, Di Pirro, Gamucci, Gatti, Giulietti, Giulietti, Koester, Labate, Levato, Pathak and Piastra 61 ] and China[ Reference Peng, Zhang, Zhang, Tang, Zheng, Zheng, Wei, Ding, Gou, Zhou and Pei 62 ].
As the laser intensity at-focus is tremendously high, direct observation of the focal spot is difficult during the experiment. The focal spot can be measured prior to the experiment by attenuating the high-power laser beam after the amplifiers with the aid of wedges[ Reference Pirozhkov, Fukuda, Nishiuchi, Kiriyama, Sagisaka, Ogura, Mori, Kishimoto, Sakaki, Dover, Kondo, Nakanii, Huang, Kanasaki and Kando 8 ] or low-reflectivity mirrors[ Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam 38 ] with a controlled surface quality. However, when the focal spot is small and of high quality, positioning the target within the Rayleigh length becomes non-trivial, since the Rayleigh length is approximately 10 μm for a typical 1-μm focal spot and a wavelength of 0.8 μm.
Here we describe our approach to control the tight laser focusing on-target using several diagnostics during the target position scan. We show that about 10–20 full-power laser shots were required to determine the best position of the target with an accuracy of approximately 5 μm, after which we immediately started collecting data at the best in-focus target position, with no reliance on the long-term laser stability and regardless of the long-term thermal drifts, as well as without any requirements on the focal planes for the low-power and high-power shots to be coincident. The diagnostic instruments employed here covered the IR, visible, extreme ultraviolet (XUV) and X-ray spectral ranges, observing the corresponding radiation from both the front and rear sides of the target. We report on the design of the experimental setup, the methods we used and the applicability of the diagnostics for target positioning, including the dependence on the target thickness. We demonstrate target positioning within several micrometers out of the best focus, ensuring over 80% of the ideal peak laser intensity.
2 Experimental setup
The experiment was carried out in the Short-F target chamber of the J-KAREN-P laser facility[ Reference Kiriyama, Mori, Pirozhkov, Ogura, Sagisaka, Kon, Esirkepov, Hayashi, Kotaki, Kanasaki, Sakaki, Fukuda, Koga, Nishiuchi, Kando, Bulanov, Kondo, Bolton, Slezak, Vojna, Sawicka-Chyla, Jambunathan, Lucianetti and Mocek 7 , Reference Pirozhkov, Fukuda, Nishiuchi, Kiriyama, Sagisaka, Ogura, Mori, Kishimoto, Sakaki, Dover, Kondo, Nakanii, Huang, Kanasaki and Kando 8 ] at KPSI, Japan. The p-polarized laser pulses with a central wavelength of λ 0 ~ 820 nm, duration of 33 fs and energy up to 12 J were focused with an f/1.3 off-axis parabolic (OAP) mirror with a 45º deviation angle into a focal spot with an effective radius r eff ~ 1.3 μm. The laser operated at 0.1 Hz, delivering typically several hundred full-power shots per experimental day.
The top right inset in Figure 1 shows the focal-spot profile recorded with the amplified pulse at approximately 10% of the full laser power attenuated by means of wedges[ Reference Pirozhkov, Fukuda, Nishiuchi, Kiriyama, Sagisaka, Ogura, Mori, Kishimoto, Sakaki, Dover, Kondo, Nakanii, Huang, Kanasaki and Kando 8 ]. We have also recorded the full-power focal-spot profile using on-shot far-field measurements through a high-reflectivity, high-optical-quality mirror. Both approaches provided fully consistent results. The on-shot pulse spectrum and near-field profiles were also measured using a portion of the beam transmitted through this mirror. The full setup used for spectral measurements (including the mirror, wedges, filters, integrating sphere, fiber and spectrometer) was absolutely calibrated using the measured spectrum and the pulse energy after the OAP mirror. We found that the pulse energy determined by integrating this absolutely calibrated spectrum is more precise than the one obtained from the near-field profile, because the calibration factor of the near-field profile depends on the spectrum of the pulse and, thus, can vary day-to-day and even shot-to-shot.

Figure 1 Experimental scheme (not to scale). The J-KAREN-P laser pulses (Ø 280 mm, 33 fs, 10 J, λ
0 ~ 820 nm, p-polarized) were focused into an r
eff ~ 1.3 μm focal spot on a 5–20 μm stainless-steel tape target[
Reference Kondo, Nishiuchi, Sakaki, Dover, Lowe, Miyahara, Watanabe, Ziegler, Zeil, Schramm, Ditter, Hicks, Ettlinger, Najmudin, Kiriyama, Kando and Kondo
26
] mounted at a 45º incident angle. The observation direction of the back-reflection diagnostics at 1ω is shown by the red arrow. Several reflection diagnostics (1ω and 2ω imagers, 1ω–4ω fiber spectrometer) measured the reflected beam footprint on a screen mounted perpendicular to the ‘specular reflection’ direction; a three-channel flat-field XUV spectrograph (3FF) was mounted behind a hole in the screen. The first hard X-ray spectrometer, HXRS-1, was mounted 98º off the main laser pulse direction. The second hard X-ray spectrometer, HXRS-2, and an electron spectrometer (ESM) were along the direction of the main laser pulse, while the imaging XUV spectrograph was 12º off this direction. The
![]() $\vec{B}$
symbols represent dipole magnets removing electrons from HXRS-1 and HXRS-2 and dispersing electrons in the electron spectrometer ESM. Two soft X-ray spectrometers with spatial resolution (FSSR) were mounted out-of-plane on the target front (-F) and rear (-R) sides, respectively. The insets show spatial and temporal J-KAREN-P laser pulse profiles. A tape target of 20 mm width was mounted on a double-rotating-reel setup, which could be translated linearly along the laser axis with a 0.1-μm step size (the ‘+X’ denotes direction away from the OAP mirror).
$\vec{B}$
symbols represent dipole magnets removing electrons from HXRS-1 and HXRS-2 and dispersing electrons in the electron spectrometer ESM. Two soft X-ray spectrometers with spatial resolution (FSSR) were mounted out-of-plane on the target front (-F) and rear (-R) sides, respectively. The insets show spatial and temporal J-KAREN-P laser pulse profiles. A tape target of 20 mm width was mounted on a double-rotating-reel setup, which could be translated linearly along the laser axis with a 0.1-μm step size (the ‘+X’ denotes direction away from the OAP mirror).
The temporal laser pulse shape (Figure 1, bottom inset), with an effective width[ Reference Pirozhkov, Fukuda, Nishiuchi, Kiriyama, Sagisaka, Ogura, Mori, Kishimoto, Sakaki, Dover, Kondo, Nakanii, Huang, Kanasaki and Kando 8 ] of 33 fs, was measured with a commercial self-referenced spectral interferometry device (Wizzler)[ Reference Moulet, Grabielle, Cornaggia, Forget and Oksenhendler 63 ] at approximately 10% of the maximum laser power. In a separate experiment we confirmed that this method gave the same pulse duration as the full-power measurements[ Reference Lorenz, Grittani, Kondo, Kon, Liu, Sagisaka, Ogura, Nakanii, Huang, Bierwage, Namba, Ohiro, Pikuz, Koga, Chen, Kiriyama, Kando, Esirkepov, Bulanov and Pirozhkov 64 ]. The resulting peak intensity in-vacuum was up to 7 × 1021 W/cm2. The experiments presented herein were performed in a ‘medium contrast mode’ with an approximately 10–10 nanosecond laser contrast level, which was optimized for hard X-ray generation. The temporal shape of the pre-pulse at the nanosecond timescale was also measured on-shot by a fast photodiode. We have performed hydrodynamic simulations, showing that under our conditions, the pre-plasma scale length was a few micrometers and thus did not affect the optimum target position significantly, although it did affect the interaction physics. The small pre-plasma scale length can be proved indirectly by the fact that the pre-plasma was not visible on the 2ω interferometer, as it was completely inside the target shadow. The generation of high-order harmonics (HOHs) in the ‘specular reflection’ direction, which was detected by the three-channel flat-field (3FF) XUV spectrograph and is described in Section 7, also indicates a small pre-plasma scale length. More details on the laser contrast, pre-plasma, and physics of the hard X-ray generation will be presented elsewhere.
Figure 1 shows the experimental scheme: the main laser pulse, the 5-to-20-μm-thick stainless-steel (SUS) tape target[ Reference Kondo, Nishiuchi, Sakaki, Dover, Lowe, Miyahara, Watanabe, Ziegler, Zeil, Schramm, Ditter, Hicks, Ettlinger, Najmudin, Kiriyama, Kando and Kondo 26 ] mounted 45º off-normal and the diagnostics discussed herein:
-
• (front) reflected beam footprint diagnostics (at frequencies 1ω, 2ω and 3ω);
-
• (front) back-reflection diagnostics (at 1ω, the diagnostics are outside Figure 1);
-
• (rear) XUV imaging spectrograph for wavelengths 17–25 nm;
-
• (rear) magnetic electron spectrometer (ESM) for 20–100 MeV electrons;
-
• (rear) two hard X-ray spectrometers (HXRS-1 and HXRS-2) for 0.1–10 MeV photons;
-
• (front and rear) two soft X-ray focusing spectrometers with spatial resolution (FSSR-F (front) and FSSR-R (rear)) for 0.7–10 keV photons;
-
• (front) 3FF XUV spectrograph, λ = 17–34 nm.
Here (front) and (rear) correspond to the observation on the front and rear sides of the target, respectively. In the latter case, the radiation was going through the target or was generated directly on its rear side.
As electromagnetic pulses (EMPs) from high-power laser–plasma interaction are known to cause problems in electronics[ Reference Consoli, Tikhonchuk, Bardon, Bradford, Carroll, Cikhardt, Cipriani, Clarke, Cowan, Danson, Angelis, Marco, Dubois, Etchessahar, Garcia, Hillier, Honsa, Jiang, Kmetik, Krása, Li, Lubrano, McKenna, Metzkes-Ng, Poyé, Prencipe, Ra̧czka, Smith, Vrana, Woolsey, Zemaityte, Zhang, Zhang, Zielbauer and Neely 65 ], we made attempts to minimize their influence. In previous experiments we tried different motorized platforms from several companies and, finally, we found that Kohzu Precision can produce custom motorized stages and control electronics that are highly resistant to EMPs. In particular, these stages were used in our experiments for 3D target translations and rotations. EMPs did not affect our tape movement, as its control system was relatively simple and robust. At the same time, some computers and cameras related to a few diagnostics were affected by the EMPs from time to time, and had to be restarted.
Before each experiment, the initial position of the tape target was determined with an approximately 100 μm accuracy as follows. We used a focal-spot monitor consisting of an apochromatic objective lens and a high-dynamic-range charge-coupled device (CCD) camera and set a micro-needle to mark the desired focus position. The needle was positioned by illuminating it with a λ = 785 nm alignment beam (LD7 in Figure 2 of Ref. [Reference Pirozhkov, Fukuda, Nishiuchi, Kiriyama, Sagisaka, Ogura, Mori, Kishimoto, Sakaki, Dover, Kondo, Nakanii, Huang, Kanasaki and Kando8]) with an axial accuracy of a few μm, limited by the objective depth-of-focus. Then the focal-spot quality was measured as described in Ref. [Reference Pirozhkov, Fukuda, Nishiuchi, Kiriyama, Sagisaka, Ogura, Mori, Kishimoto, Sakaki, Dover, Kondo, Nakanii, Huang, Kanasaki and Kando8]. In this process, the OAP mirror was adjusted to bring the focus to the needle position, with a typical axial accuracy of better than ±5 μm, which was around a half of the Rayleigh length. Up to this point, all the positioning steps were implemented with a few-to-several-μm accuracy.
Then, an SUS tape target of 20-mm width was set to the needle position. We tried several methods (see the Appendix), but we were not able to control the target position with a better than 100-μm accuracy, since the SUS target was mirror-like reflective, wrinkle-free and non-transparent. Finally, we marked the position of the needle on the camera of a 2ω interferometer[ Reference Sagisaka, Pirozhkov, Daido, Fukumi, Li, Ogura, Yogo, Oishi, Nayuki, Fujii, Nemoto, Orimo, Nishiuchi, Hayashi, Mori, Kado, Nakamura, Noda, Choi, Sung, Ko and Lee 66 ], which observed the target along its 20-mm-long side. After removing the needle, the target orientation was adjusted by the target rotation stage to the narrowest shadow on the 2ω interferometer camera, so the tape was along the probe beam with an approximately 0.1° accuracy (therefore, the incidence angle was 45°). After that, the target was placed at the needle position with an accuracy determined by smearing of the tape image along the observation direction, caused by the defocused images of the ±10 mm tape edges, as well as the possible bending of the target edges, which was small in our case on the 100-μm scale, but may be not negligible on the required sub-10-μm scale. From this initial position, the target was shifted by 200 μm towards the OAP mirror (the negative direction in the figures). Then we irradiated the target with high-power laser pulses, performing a target position scan with 10 μm (sometimes 5 μm) steps. We note that the shot-to-shot target position variations along the laser axis were less than the depth-of-focus of the focal-spot monitor objective lens (<2 μm), and the short-term laser pointing stability was approximately 2–3 μrad, which did not affect the focusing. We stopped the scan after passing the optimum position determined consistently with several X-ray and optical diagnostics. Comparison of the final target position with the initial one determined by the interferometer revealed that the initial target position accuracy was around 50 μm.
Hereafter we describe each of the diagnostics listed above (Figure 1). For convenience, the results of all the diagnostics are given in the same section as their description. The applicability of each instrument for determination of the best in-focus target position is discussed.
3 Front-side near-infrared to visible-ultraviolet reflection diagnostics
Several NIR-to-ultraviolet (UV) diagnostics[ Reference Pirozhkov, Choi, Sung, Lee, Yu, Jeong, Kim, Hafz, Kim, Pae, Noh, Ko, Lee, Robinson, Foster, Hawkes, Streeter, Spindloe, McKenna, Carroll, Wahlström, Zepf, Adams, Dromey, Markey, Kar, Li, Xu, Nagatomo, Mori, Yogo, Kiriyama, Ogura, Sagisaka, Orimo, Nishiuchi, Sugiyama, Esirkepov, Okada, Kondo, Kanazawa, Nakai, Akutsu, Motomura, Tanoue, Shimomura, Ikegami, Daito, Kando, Kameshima, Bolton, Bulanov, Daido and Neely 67 – Reference Singh, Armstrong, Kang, Ren, Liu, Hua, Rusby, Klimo, Versaci, Zhang, Sun, Zhu, Lei, Ouyang, Lancia, Garcia, Wagner, Cowan, Zhu, Schlegel, Weber, McKenna, Neely, Tikhonchuk and Kumar 69 ] were mounted in the ‘specular reflection’ direction (90º from the laser incidence direction). Two imaging cameras observed the spatial distributions of 1ω (~700–1000 nm) and 2ω (~390–410 nm) radiation scattered from a polytetrafluoroethylene (PTFE; Teflon) screen mounted in the ‘specular reflection’ direction of the laser pulses (see Figure 1). The spectrum of the reflected beam was measured using the same PTFE screen, with a NIR-vis-UV optical fiber spectrometer (1ω–4ω) having 200–1000 nm total spectral bandwidth.
The fields of view of the two cameras, partially clipped by other instruments, are shown in Figures 2(a) and 2(b). The acceptance angles were Ω1 ≈ 80 msr and Ω2 ≈ 100 msr for the 1ω and 2ω cameras, respectively. The absolute sensitivity of the 1ω camera together with its filters was calibrated using a small portion of the main laser beam, resulting in (7.1 ± 1.5) × 10−7 J/count. The absolute sensitivity of the spectrometer with a relatively calibrated spectral response was cross-calibrated with the 1ω camera, providing an absolute calibration reference for the whole 200–1000 nm spectral region. The 2ω camera was afterwards cross-calibrated with the spectrometer. The area observed with the spectrometer (dashed ellipses in Figures 2(a) and 2(b)) had an acceptance angle of Ωs ≈ 8 msr. A typical spectrum is shown in Figure 2(c). The absolute energies could be determined for the first to third harmonics within the corresponding spectral ranges of (n ± 0.25)ω0, where n is the harmonic order. The spectrometer had low sensitivity in the λ < 200 nm spectral region, and its sensitivity calibration was unreliable there, as we used two types of commercial calibrated light sources (namely, a black-body source and a deuterium-tungsten halogen lamp) with calibration data given in the spectral range of λ > 200 nm. Thus, we did not consider the fourth harmonic signal for the target positioning goals.

Figure 2 The fields of view of the 1ω (a) and 2ω (b) cameras imaging a PTFE screen mounted perpendicular to the ‘specular reflection’ direction. The geometric center of the reflected beam is marked with white circles. The dashed ellipses denote the spectrometer observation area. (c) Typical absolutely calibrated reflected spectrum. The energy values calculated within the (n ± 0.25)ω0 spectral bandwidths (colored) are given for harmonic orders n = 1, 2, 3.
Along with the ‘specular reflection’ diagnostics, we also used 1ω back-reflection beam diagnostics. The main purpose of the back-reflection diagnostics is laser safety, as a significant portion of the laser energy can be back-reflected and consequently damage the compressor gratings and/or laser amplifiers. However, this instrument could potentially be useful for determining the best focus position in certain cases.
Figure 3 shows the normalized energy (with respect to the total pulse energy on-target) detected with all the NIR-vis-UV reflection diagnostics, including the 1ω (Figure 3(a)) and 2ω (Figure 3(b)) imagers, 1ω–4ω spectrometer (Figures 3(a)–3(c)) and the 1ω back-reflection (Figure 3(d)), recorded for the scanned target position. Here X 0 represents the best focus position, which was consistently determined by multiple diagnostics for each SUS thickness, as described in detail in Section 9. Thus, X – X 0 denotes the SUS target displacement from the best focus position.

Figure 3 Normalized energy from the four reflection beam diagnostics versus the target position X (‘–’ denotes the direction towards the OAP mirror, and X 0 corresponds to the best focus position). All values are normalized by the on-target pulse energy E 0. The plots in (a) and (b) are for the 1ω and 2ω diagnostics, respectively, where the upper data (black) are from the imagers, while the lower data (red) are integrated from the 1ω–4ω spectrometer within (1 ± 0.25)ω0 and (2 ± 0.25)ω0, correspondingly. (c) The 3ω data integrated within the (3 ± 0.25)ω0 band from the 1ω–4ω spectrometer. (d) The normalized back-reflected energy.
Figure 3(a) shows normalized energy determined from the 1ω ‘specular reflection’ diagnostics, both the 1ω imager and spectrometer signal within the (1 ± 0.25)ω0 band. The data from both instruments were in good correlation. There was a double-peak structure in the vicinity of the best focus and a gradual signal increase from both diagnostics towards X – X 0 ~ –150 μm, as the interaction probably entered the highly reflective plasma mirror regime. These multi-peak features made the 1ω diagnostics not useful for determination of the best target position.
Figure 3(b) shows the dependence of the 2ω normalized energy on X – X 0, determined from the 2ω imager (upper points) and spectrometer signal within the (2 ± 0.25)ω0 band (lower points). Both cases reveal single-peak structures that can be approximated with Lorentzian fits, giving the best focus position with approximately 4 μm discrepancy and 24 μm full width at half maximum (FWHM), indicating that 2ω ‘specular reflection’ diagnostics determine the best focus position with an approximately 12 μm accuracy.
Figure 3(c) depicts the energy of the 3ω radiation determined from the 1ω–4ω spectrometer via integration within the (3 ± 0.25)ω0 spectral band. In the 3ω case, the peak was even more prominent, with small data point fluctuations, indicating an approximately 5 μm target position accuracy.
Figure 3(d) shows the dependence of the normalized back-reflected energy on the relative target position, revealing a broad dip, instead of a peak at the X 0 position, and a broad peak at X – X 0 ≈ –100 μm. Thus, the 1ω back-reflection, along with other 1ω reflection diagnostics, was not suitable for determination of the best focus position.
4 Rear-side extreme ultraviolet spectrograph and electron spectrometer
Behind the target, three diagnostics were placed: an XUV imaging spectrograph, an ESM and HXRS-2. In this section we describe the first two instruments, while HXRS-2 will be discussed in the next section, along with the HXRS-1 diagnostics of the same type.
4.1 XUV imaging spectrograph
An XUV imaging spectrograph based on a Mo/Si aperiodic multilayer mirror (MM)[ Reference Kolachevsky, Pirozhkov and Ragozin 70 – Reference Pirozhkov and Ragozin 72 ] and a transmission diffraction grating was mounted 12º off the laser direction. The XUV acceptance angle was 3.6 msr, corresponding to an approximately 2º cone half-angle. The operating range, 17–25 nm, was defined by the multilayer structure optimized for maximum uniform reflectance in the 12.5–25 nm range[ Reference Vishnyakov, Mednikov, Pertsov, Ragozin, Reva, Ul’yanov and Shestov 73 , Reference Ragozin, Mednikov, Pertsov, Pirozhkov, Reva, Shestov, Ul’yanov and Vishnyakov 74 ] and absorption cutoff at the aluminum L2,3 edge at λ ≈ 17 nm in the optical blocking filters. Imaging spectrographs of this type are used in different forms, for example in the combination of an MM with a transmission grating[ Reference Barysheva, Garakhin, Kolesnikov, Pirozhkov, Polkovnikov, Ragozin, Shatokhin, Smertin, Svechnikov and Vishnyakov 75 ] or a varied line space (VLS) reflection grating[ Reference Vishnyakov, Kolesnikov, Kuzin, Negrov, Ragozin, Sasorov and Shatokhin 76 , Reference Shatokhin, Kolesnikov, Sasorov, Vishnyakov and Ragozin 77 ]. Such XUV spectrographs have been employed in experiments on coherent soft X-ray generation via frequency upshift of the laser pulse reflected from a relativistic ‘flying mirror’[ Reference Kando, Pirozhkov, Kawase, Esirkepov, Fukuda, Kiriyama, Okada, Daito, Kameshima, Hayashi, Kotaki, Mori, Koga, Daido, Faenov, Pikuz, Ma, Chen, Ragozin, Kawachi, Kato, Tajima and Bulanov 78 ] and via the BISER mechanism[ Reference Pirozhkov, Esirkepov, Pikuz, Faenov, Ogura, Hayashi, Kotaki, Ragozin, Neely, Kiriyama, Koga, Fukuda, Sagisaka, Nishikino, Imazono, Hasegawa, Kawachi, Bolton, Daido, Kato, Kondo, Bulanov and Kando 41 ].
A spherical aperiodic Mo/Si MM with a radius of curvature of R = 1000 mm was mounted in a geometry providing M ≈ 2.1 spatial magnification. We used two Al-based free-standing absorption filters to block the NIR-vis-UV radiation: the first filter (0.65 μm thick Al) was mounted in front of the mirror and operated in the double-pass regime, while the second filter (Al/Zr multilayer[ Reference Volodin, Gusev, Drozdov, Zuev, Klyuenkov, Lopatin, Luchin, Pestov, Salashchenko, Tsybin and Chkhalo 79 ], 0.2 μm) was in front of the CCD. A free-standing transmission diffraction grating with a groove density of 5000 lines/mm was situated 139 mm from the CCD chip.
Figure 4(a) shows a typical XUV spectrum for a 5-μm-thick SUS target close to the best focus position (X 0). The XUV spectrum contained the zeroth diffraction order and a spectrally resolved continuous first diffraction order in the 17–22 nm spectral region. The zeroth diffraction order was triple-shaped due to diffraction on the grating support structure, which was perpendicular to the dispersion direction. Each spot in the zeroth diffraction order image was elongated due to the astigmatism introduced by the spherical focusing MM operating at a small, but non-zero, incidence angle. The spectrum decay at λ > 20 nm was due to absorption of the Al/Zr multilayer filter[ Reference Volodin, Gusev, Drozdov, Zuev, Klyuenkov, Lopatin, Luchin, Pestov, Salashchenko, Tsybin and Chkhalo 79 ]. Taking the typical CCD spectral sensitivity[ Reference Vishnyakov, Kirichenko, Reva, Rizvanov, Plastinin and Kuzin 80 , Reference Vishnyakov, Shcherbakov, Pertsov, Polkovnikov, Pestov, Pariev and Chkhalo 81 ] and the spectral filter transmission into account, the total XUV radiation yield on the target rear side was estimated to be approximately (26 ± 3) × 10−10 J/sr for the 5-μm-thick SUS target and (3.8 ± 0.8)×10−10 J/sr for the 15-μm-thick SUS target.

Figure 4 (a) Typical spatially resolved XUV spectrum; λ = 0 denotes the zeroth diffraction order. (b) Dependence of the integrated zeroth order on the target position (‘–’ is towards the OAP mirror) for 5-μm- and 15-μm-thick targets, and their Lorentzian fits. (c) Dependence of the integrated ESM yield on the target position for a 15-μm-thick target. The dashed line shows the ESM noise level.
The integrated yields in the zeroth and the first diffraction orders were proportional, with a higher signal-to-noise ratio in the zeroth order. Figure 4(b) gives the dependence of the normalized integrated zeroth order signal on X – X 0 for 5 and 15 μm target thicknesses. The Lorentzian-fit curves show that the target thickness affected the precision of the target positioning: 60 μm FWHM for the 15-μm-thick target and a narrower 40 μm FWHM for the 5-μm-thick target. Deviations of the fitted peaks from the optimal target position were within approximately 5 μm for both thicknesses, meaning that the XUV imaging spectrograph provided target positioning with an approximately 20–30 μm accuracy for 5-to-15-μm targets. For 20-μm targets, the XUV signal-to-noise ratio was lower than unity, so precise target positioning was not achievable. The vertical error bars in Figure 4(b) represent solely statistical errors due to shot-to-shot signal variations.
4.2 Electron spectrometer
The magnetic ESM was mounted on the laser axis (Figure 1) 509 ± 1 mm from the target. The spectrometer consisted of a 3-mm-diameter collimator, a 100-mm-long dipole magnet with 0.95 T magnetic field, a 150-mm-long LANEX screen and an optical camera with a camera lens and a green spectral filter. The ESM covered the 20–100 MeV energy range.
The dependence of the ESM signal on X – X 0 for a 15-μm-thick target is shown in Figure 4(c); similar dependences were observed for all target thicknesses under study. The ESM signal had a broad slopped plateau within ±60 μm from the best focus, with a not-so-pronounced peak at X = +40 μm, making this instrument not suitable for precise target positioning.
5 Rear-side hard X-ray spectrometers (HXRS-1 and HXRS-2)
Two HXRSs[ Reference Armstrong 82 , Reference Rusby, Armstrong, Brenner, Clarke, McKenna and Neely 83 ] were mounted behind the target (Figure 1): HXRS-1 was 98º from the laser axis, approximately along the laser electric field direction, 1.7 m from the target, and HXRS-2 was on the laser axis, behind the ESM, 4.2 m from the target.
Each of the two HXRS instruments consisted of a linear X-ray absorption array built of 10 LYSO (Lu1.8Y0.2SiO5) scintillator crystal plates of 2 mm thickness and 10 mm × 30 mm area, with 2-mm-thick tungsten filters between each pair of plates from #4 to #9 (the numeration of the plates starts from #0). The fluorescence emitted from the LYSO array was monitored with a complementary metal oxide semiconductor (CMOS) camera. Dipole magnets (Figure 1) in front of the HXRSs prevented electrons from reaching the instruments. The scintillator sensitivity allowed for registering hard X-ray radiation with the photon energies from approximately 20 keV to 10 MeV, the best sensitivity being 0.1–2 MeV. The harder X-ray radiation was detected by deeper scintillators with higher numbers in the array. A full description of the HXRS design and data processing is given in Ref. [Reference Armstrong, Neely, Kumar, McKenna, Gray and Pirozhkov84]. In our setup the plate #9 signal was unreliable as, in addition to the X-rays coming through the other scintillators and tungsten filters in the array, its response included X-rays reflected from the walls of the experimental area. This did not affect other scintillators due to the surrounding lead shielding.
Figure 5 presents data from HXRS-1 (top) and HXRS-2 (bottom). The scintillator plate number in the array is shown next to the instrument name. The thicker the target, the stronger the recorded HXRS signal was. Figures 5(a) and 5(d) show typical scintillator plate #0 dependences for both instruments, exemplified by dependences for 10-μm-thick targets. The plots contain multi-peak structures, making this channel unsuitable for precise target positioning, although the central peak might be attributed to the best target position.

Figure 5 HXRS scintillator plate signals versus target position X (‘–’ is towards the OAP mirror, X 0 is the best focus). (a)–(c) HXRS-1 (off-axis), (d)–(f) HXRS-2 (on-axis). (a) HXRS-1 plate #0, 10-μm-thick SUS. (b) HXRS-1 plate #5, 10-μm-thick SUS. (c) HXRS-1 plate #5, 5-μm-thick SUS. (d) HXRS-2 plate #0, 10-μm-thick SUS. (e) HXRS-2 plate #3, 10-μm-thick SUS. (f) HXRS-2 plate #2, 5-μm-thick SUS. Lorentzian fits are shown, where applicable. Scintillator plate #0 was the closest to the interaction point. The error bars in all the frames are due to the CMOS camera noise.
Figures 5(b) and 5(e) show middle scintillator plate signals for 10-μm-thick targets for HXRS-1 and HXRS-2, respectively. The middle plates were most reliable for thick target positioning due to high signal-to-noise ratios and single peaks in the dependences. There was a narrow peak for the on-axis HXRS-2 (Figure 5(e), 16 μm FWHM fit), and a broad peak for the off-axis HXRS-1 (Figure 5(b), >300 μm FWHM). This shows that the target positioning precision was approximately 5 μm for the on-axis HXRS-2, while it was more than 100 μm for the off-axis HXRS-1.
Even with the thinnest 5-μm SUS target, the on-axis HXRS-2 middle scintillators were still capable of positioning the target with an approximately 5 μm accuracy (Figure 5(f)), although with a lower signal-to-noise ratio than for thicker targets. The off-axis HXRS-1 middle scintillators were not applicable for determining the best in-focus position of 5-μm SUS targets (Figure 5(c)).
6 Front-side and rear-side soft X-ray focusing spectrometers with spatial resolution
Two soft X-ray FSSRs have been assembled on both the front (FSSR-F) and rear (FSSR-R) target sides. The FSSRs were based on spherically bent mica and quartz crystals, respectively (2d = 2.36 Å in the latter case) with a curvature radius of R = 150 mm to ensure radiation focusing and high spectral resolution, up to an approximately 104 value[ Reference Faenov, Pikuz, Erko, Bryunetkin, Dyakin, Ivanenkov, Mingaleev, Pikuz, Romanova and Shelkovenko 85 – Reference Hölzer, Wehrhan, Heinisch, Förster, Pikuz, Faenov, Pikuz, Romanova and Shelkovenko 87 ].
The FSSR instruments were mounted out-of-plane, 786 and 819 mm above the horizontal plane containing the laser axis for the FSSR-F and FSSR-R instruments, respectively. FSSR-F was mounted at an in-plane angle of 8.5° ± 0.1° from the target normal and an out-of-plane angle of 17.6° ± 0.1°, with a distance from the FSSR-F crystal to the interaction point of 2600 mm. The mica crystal employed in FSSR-F gave a resolving power of λ/Δλ ~ 2500 at the central wavelength of λ 0 = 0.1875 nm in the m = 8 diffraction order corresponding to a wavelength of 1.5 nm in the first diffraction order.
FSSR-R was mounted at an in-plane angle of 10.1° ± 0.1° from the target normal and an out-of-plane angle of 23.1° ± 0.1°. The quartz crystal provided λ/Δλ ~ 3000 resolving power at a wavelength of λ 0 = 0.1812 nm in the m = 8 diffraction order, corresponding to λ = 1.45 nm in the first diffraction order. The distance from the FSSR-R crystal to the interaction point was 2045 mm.
An example of the spectrum registered with FSSR-F is shown in Figure 6(a). The spectrum covered a 1.31–1.63 nm range of wavelengths in the first diffraction order. In this spectrum, the spectral components of the other diffraction orders overlapped, thus making it possible to observe Fe Kα (λ = 0.194 nm) in the m = 8 diffraction order and Cr Kα (λ = 0.229 nm) in the m = 7 diffraction order. Most of the signals registered with the FSSR-F and FSSR-R detectors in the vicinity of the best in-focus target position were bremsstrahlung emitted from the laser–solid interaction. Spectral filters composed of 2-μm-thick C3H6 and 0.4-μm-thick Al were placed in front of the CCD camera for the FSSR instruments. An additional narrow strip of a 25-μm-thick C3H6 as a spectral filter allowed for suppressing m = 1 and m = 2 diffraction orders and thus catching the bremsstrahlung radiation in the m = 3 diffraction order.

Figure 6 (a) A typical FSSR-F spectrum recorded in the vicinity of the best in-focus target position. The spectrum covers wavelengths from 0.165 to 1.63 nm in different diffraction orders from m = 1 to m = 8. Strong characteristic lines Fe Kα (λ = 0.194 nm) and Cr Kα (λ = 0.229 nm) were observed in m = 8 and m = 7 diffraction orders, respectively. The continuous signal corresponds to bremsstrahlung. A narrow strip of a 25-μm C3H6 filter allows for observing a narrow portion of the spectrum, suppressing emission from lower diffraction orders (m = 1, m = 2). (b), (c) FSSR-F data for 15-μm SUS targets, integrated within an area without (b) and with (c) the 25-μm-thick C3H6 filter. (d), (e) FSSR-R integrated bremsstrahlung signal for 15-μm (d) and 5-μm (e) SUS targets. (f) FSSR-R Fe Kα integrated signals for 15- and 5-μm SUS targets. The black error bars correspond to statistical shot-to-shot signal variations, while the smaller colored error bars are due to CCD camera noise. Lorentzian fits are shown, where applicable.
Figures 6(b)–6(f) give the FSSR-F and FSSR-R data. Figures 6(b) and 6(c) show the FSSR-F spectrally integrated signals without a spectral filter (which was a sum of the two regions with blue shading in Figure 6(a)) and with the 25-μm C3H6 spectral filter (with violet shading in Figure 6(a)), respectively, for the 15-μm SUS target. A clear approximately 40-μm FWHM single peak occurs in both cases, assuring the best in-focus target positioning with a better than 20 μm accuracy.
Figures 6(d) and 6(e) show spectrally integrated bremsstrahlung signals (in the 1.35–1.54 nm spectral region in the first order of diffraction) from FSSR-R for 15- and 5-μm-thick targets, respectively. Multi-peak behavior was observed for the 15-μm target (Figure 6(d)), with one of the peaks (~20 μm FWHM) corresponding to the best in-focus target position. The second peak can be explained by the fact that soft X-rays can be effectively generated from large-area spots at a relatively low intensity. Since the distance between the peaks was approximately 100 μm, this can give a 10 μm accuracy if the target is put within a 50 μm range from the best focus position using other diagnostics.
Figure 6(f) shows dependences of the Fe Kα signals integrated in the 0.1925–0.1942 nm spectral region in the eighth diffraction order on X – X 0 for the 15- and 5-μm-thick SUS targets. Contrary to the previous cases, the Fe Kα signals increased when the target moved away from the best focus. Thus, the Fe Kα line was not suitable for the target positioning.
7 Three-channel flat-field spectrograph
The 3FF grazing incidence spectrograph[ Reference Neely, Chambers, Danson, Norreys, Preston, Quinn, Roper, Wark and Zepf 88 ] was mounted in the ‘specular reflection’ direction behind a hole in the screen used for the NIR-vis-UV diagnostics. The 3FF is a slit-less version of a flat-field spectrograph employing a VLS grating operating at a grazing incidence angle of 4.2º (i.e., 85.8º off-normal), designed for recording a broad spectral region of 5–90 nm[ Reference Neely, Chambers, Danson, Norreys, Preston, Quinn, Roper, Wark and Zepf 88 – Reference Ragozin, Vishnyakov, Kolesnikov, Pirozhkov and Shatokhin 90 ]. For a spatial resolution and a better signal-to-noise ratio, three gold-coated grazing incidence mirrors having shapes of elliptical cylinders were employed. The horizontal acceptance angles were slightly different for the three channels: 0.15º for the shallow-angle mirror, 0.20º for the central mirror and 0.26º for the high-deviation-angle mirror.
The VLS grating manufactured by Hitachi on a spherical substrate with R = 5649 mm had an average central groove density of 1200 lines/mm. The vertical acceptance angle of 0.087º was defined by the r = 2425 mm distance from the source to the center of the VLS grating, and by the 50 mm × 30 mm grating aperture. Thus, the acceptance angles for the three channels were 3.9×10–6, 5.2×10–6 and 7.0×10–6 sr, respectively. A single-pass 0.65-μm-thick Al filter was mounted in front of the 3FF spectrometer, defining the 17–34 nm operating spectral range.
It is well known that relativistic laser–solid interaction is an intense source of HOH generated mostly in the ‘specular reflection’ direction[ Reference Teubner and Gibbon 91 , Reference Thaury and Quéré 92 ]. However, since the harmonics’ divergence can be narrow, we did not observe them in many shots, partly due to the small acceptance angles. Also, HOH generation depends on the pre-plasma scale length[ Reference Kim, Pae, Kim, Kim, Yun, Yun, Sung, Lee, Yoon, Yu, Jeong, Nam and Lee 93 , Reference Kahaly, Monchocé, Vincenti, Dzelzainis, Dromey, Zepf, Martin and Quéré 94 ] and intensity, defined in our case by the laser contrast and X – X 0 shift.
Figure 7(a) shows a typical 3FF spectrum with HOH. Figures 7(b) and 7(c) show the dependences of the 3FF signal on X – X 0 for 10- and 15-μm-thick SUS targets, respectively. The 3FF data had an approximately 50 μm broad peak in the vicinity of the best focus, with a clear dip of the signal near the middle. There was a lower peak at X – X 0 ~ 120–140 μm. Within the main 3FF peak, the estimated dimensionless amplitude a 0 was greater than 10, reaching approximately 60 at focus. Therefore, the main HOH generation mechanism was the relativistic oscillating mirror[ Reference Bulanov, Naumova and Pegoraro 95 , Reference Lichters, Meyer-ter-Vehn and Pukhov 96 ].

Figure 7 (a) 3FF spectrum with harmonics. The upper and lower parts correspond to the shallow- and high-deviation-angle mirrors, respectively. Dashed lines show the Al filter cutoff (λ = 17 nm) in the first and second diffraction orders. (b), (c) Integrated 3FF signal versus target position for 10- and 15-μm SUS targets, respectively. The error bars correspond to shot-to-shot signal variations.
We did not observe harmonics in many shots, probably due to the small acceptance angles. Along with this, the optimum combination of the laser intensity and the pre-plasma scale length might not be satisfied in every shot. The presence of the HOH had been recorded within the ±25 μm distance from the best in-focus target position only, while the relative difference in the integrated signals from the shots with and without harmonics was around 20%.
Thus, the 3FF spectrometer can determine the best in-focus target position with an approximately 25 μm accuracy, using both the integrated 3FF signal and visual observation of harmonics. The dip in the 3FF signal close to the best focus position X 0 can be used to place the targets with an approximately 5 μm accuracy, although this result may be laser-contrast-dependent.
8 Discussion
As the laser was operated at a relatively low repetition rate of 0.1 Hz, we wanted to minimize the time spent on the search for the best target position. We used typically 10–20 shots during 3–11 minutes for the scans presented here, where the latter time was due to manual analysis of readings from many instruments operating simultaneously. All the data acquisition and saving procedures were automated, including automatic file naming with the shot number, for both facility instruments and our metrology. Further, our software automatically indicated the number of counts within our regions of interest. However, the software did not automatically plot the data versus target position figures. This was done in a separate figure plotting software, which typically took an extra 2–3 minutes for each target thickness. Obviously, this can be automated to speed up the process.
With only two or three instruments best suited for the target positioning, this time can be reduced down to 1.5–3 minutes with the same laser repetition rate. Our goal was to place the target with an accuracy of better than ±Z R, where Z R ≈ 10 μm is the Rayleigh length. We used 10 μm steps (sometimes 5 μm steps), so that the best near-focus target positions were within ±5.0 μm (or ±2.5 μm) from the ‘perfect’ position. Therefore, even in the worst case, the peak intensity on-target was higher than 0.8 (0.94) of the ideal estimated peak value of 7 × 1021 W/cm2. Assuming random defocusing within the ±5 and ±2.5 μm ranges, the intensity was 0.93 ± 0.06 and 0.98 ± 0.02 of the ideal value, respectively.
In Table 1 we summarize all the information presented in the previous sections. In most cases our scans were single-shot at each position, and the accuracy was estimated for this approach. The main limiting factors were shot-to-shot fluctuations and available experimental time. By multi-shot averaging, one can reduce the influence of the shot-to-shot fluctuations.
Table 1 Accuracy of the instruments for the best in-focus target positioning.

a Estimated accuracy was a half-step size for the clean peaks, and a half width at half maximum (HWHM) for instruments with notable data fluctuations.
The best target positioning accuracy of better than 5 μm was achieved using on-axis HXRS-2 inner scintillators and the third-order harmonic (3ω) instrument mounted in the ‘specular reflection’ direction. The 2ω, FSSR-F, FSSR-R, 3FF and XUV diagnostics provided an accuracy of approximately 10–20 μm. The instruments that were best suited for the precise target positioning goals had peaks with good symmetrical shape and low data fluctuations, which means that the accuracy was better than half width at half maximum (HWHM) and corresponded to a half-step of the scanning. On the other hand, if the data fluctuations are high enough, then the accuracy should be estimated as the HWHM of the fitted peak.
Several diagnostics, such as 1ω reflection, ESM, low X-ray photon energy plates #0 of HXRS-1 and HXRS-2 and Fe Kα yield were not suitable for determination of the best target position, since their highest signals were reached from out-of-focus large-area low-intensity interactions.
In this paper, we presented the diagnostics as useful means to find the best target position. If the main purpose of an experiment is hard X-ray generation, then our optimization with the HXRS-2 spectrometer immediately provides the best target position. At the same time, all our selected diagnostics operating at the target front and rear sides, in the optical, XUV and X-ray regions, provided the same best target positions as the hard X-ray (MeV) diagnostics, within their respective accuracy limits. In addition, this was proved for each of the target thicknesses tested. Considering a small (a few μm) pre-plasma length, it is unlikely that some other point in space, rather than the focus, would give a maximum for all the diverse diagnostics simultaneously. Thus, we conclude that the targets were placed at the best focus position.
Let us mention that we have investigated signals from many diagnostics, while most of the instruments we used in our study are not necessary at many high-power-laser facilities for the goal of best target positioning. In experiments similar to ours, given specific space constraints, an experimental team can choose two or three reliable diagnostics from the set described herein, and this should be enough for precise target positioning. Furthermore, we anticipate that by placing some of the instruments at similar but not exactly the same positions as described in this paper, using slightly different in-plane and out-of-plane angles, one can obtain similar results for the best target positioning purpose. However, this has to be proved in a separate dedicated study.
As for the types of targets that can be precisely placed at the best focus position using our method, we can highlight three important requirements:
(1) the target must be reproducibly positioned with a few micrometers accuracy;
(2) the positioning of the target before each shot should be fast, ideally faster than the laser system inverse repetition rate (for slower target positioning systems, the procedure becomes correspondingly longer; in the case of very long shot-to-shot intervals, the thermal laser stability on the extended time periods should be also tested and controlled);
(3) the targets used for the position scan should be identical or almost identical to keep the diagnostics output consistent (after that, other target types can be used, if placement to the same position is guaranteed).
We expect that any kind of target that complies with these three requirements can be precisely placed at the best focus position using our method. From our point of view, tape targets are the best for this purpose. Liquid targets can also be feasible. With the abovementioned restrictions, thin foils and nanostructured targets can also be used.
Compared to the well-established methods[ Reference McKenna, Ledingham, Spencer, McCany, Singhal, Ziener, Foster, Divall, Hooker, Neely, Langley, Clarke, Norreys, Krushelnick and Clark 45 – Reference Willis, Poole, Akli, Schumacher and Freeman 47 ], our proposed technique does not need coincidence or calculatable difference[ Reference Bahk, Rousseau, Planchon, Chvykov, Kalintchenko, Maksimchuk, Mourou and Yanovsky 97 , Reference Tiwari, Gaul, Martinez, Dyer, Gordon, Spinks, Toncian, Bowers, Jiao, Kupfer, Lisi, McCary, Roycroft, Yandow, Glenn, Donovan, Ditmire and Hegelich 98 ] between the positions of low-power and high-power focal planes. Furthermore, as the main experimental data shots immediately follow the focusing scan without changing the laser mode, moving instruments in and out or replacing filters in the laser diagnostics, the influence of long-term instabilities and thermal drifts was minimized. At the same time, our method relies on shot-to-shot reproducible laser parameters and the target position, which is relatively easily achievable with high-repetition-rate lasers and tape targets, while it can be challenging for less stable lasers or other target supply systems.
9 Conclusions
We have investigated the usefulness of 11 diagnostics (Table 1) for the best in-focus target positioning in order to have the highest on-target laser intensity in a relativistic laser–solid interaction experiment. The main challenge was to put the solid target within an extremely short Rayleigh length of approximately 10 μm. We found that several diagnostics can ensure this accuracy.
The sharpest and most reliable diagnostic instrument was the rear-side on-axis HXRS-2 made of 10 LYSO scintillator crystal plates with the best sensitivity of the inner crystals to radiation energy of 0.1–2 MeV[ Reference Armstrong 82 , Reference Rusby, Armstrong, Brenner, Clarke, McKenna and Neely 83 ]. The prominent and clean signal maxima allowed us to find the best in-focus target position with an accuracy of better than 5 μm, determined by a half step size during the target position scan.
Several other instruments were also capable of positioning the target within a comparable accuracy of approximately 5–10 μm. They were low-order harmonics (2ω, 3ω) mounted in the ‘specular reflection’ direction[ Reference Pirozhkov, Choi, Sung, Lee, Yu, Jeong, Kim, Hafz, Kim, Pae, Noh, Ko, Lee, Robinson, Foster, Hawkes, Streeter, Spindloe, McKenna, Carroll, Wahlström, Zepf, Adams, Dromey, Markey, Kar, Li, Xu, Nagatomo, Mori, Yogo, Kiriyama, Ogura, Sagisaka, Orimo, Nishiuchi, Sugiyama, Esirkepov, Okada, Kondo, Kanazawa, Nakai, Akutsu, Motomura, Tanoue, Shimomura, Ikegami, Daito, Kando, Kameshima, Bolton, Bulanov, Daido and Neely 67 – Reference Singh, Armstrong, Kang, Ren, Liu, Hua, Rusby, Klimo, Versaci, Zhang, Sun, Zhu, Lei, Ouyang, Lancia, Garcia, Wagner, Cowan, Zhu, Schlegel, Weber, McKenna, Neely, Tikhonchuk and Kumar 69 ]. At 2ω, a camera and fiber spectrometer provided consistent results.
The integrated bremsstrahlung signal over the 0.7–10 keV range (but not the Kα radiation) recorded with the rear-side FSSR-R instrument could also give an approximately 10 μm accuracy. However, the FSSR-R data had a double-peak shape with peak separation of approximately 100 μm, requiring a correct peak selection by means of other diagnostics. The front-side FSSR-F accuracy was approximately 20 μm.
The rear-side XUV spectrometer (λ = 17–22 nm) provided around 20 μm accuracy for targets with thickness of less than or equal to 10 μm. For 15-μm targets, the signal-to-noise ratio became low and the peak width increased, so the accuracy was around 30 μm. For 20-μm targets, XUV diagnostics were not applicable due to the low signal-to-noise ratio.
The ‘specular reflection’ 3FF spectrograph (17–34 nm) showed a multi-peak dependence, with approximately 30% probability of HOH registration within ±25 μm from the best focus. If the correct peak was picked by means of other diagnostics, the 3FF provided approximately 25 μm target positioning accuracy. The central peak in the dependency had a dip at the best focus position for all target thicknesses, suggesting a better, approximately 5 μm accuracy (although it may be laser-contrast-dependent).
All front-side 1ω diagnostics, as well as the rear-side ESM and off-axis HXRS-1, were not applicable for target positioning, because the estimated precision of those instruments was worse than 30 μm. We note that some of these might be used as auxiliary diagnostics to roughly place the target with an approximately 30–100 μm accuracy.
Employing the best diagnostics, we consistently performed the best in-focus target positioning with an estimated accuracy of around 5 μm and discrepancy of less than 5 μm between many instruments, resulting in the intensity on-target of at least 80% (94% for some scans) of the ideal estimate of 7 × 1021 W/cm2.
Appendix A
Here we describe the target positioning methods that we have tried, but found that they cannot provide the required approximately 10 μm accuracy.
A.1 Imaging the target surface with a focal-spot monitor
This method is often used with transparent targets using the attenuated defocused laser beam transmitted through the target. However, in our case of non-transparent stainless-steel tapes it was not usable. A variation of this method with white-light illumination from the rear side of the target required significant light power, due to the high imaging system magnification, which led to target heating and notable bending, which we confirmed by varying the illumination light power. We note that the thermal bending problem can be avoided by using a confocal microscope, which requires much lower light power; however, we did not have this technique as a facility device and decided not to implement it as a part of our experiment, because, even though this device might really help us precisely position the target at a plane coincident with the focal plane of the low-power laser beam in a mode used for the alignment, this does not guarantee that the full-power-mode beam would have focus at the same plane with the required sub-10-μm accuracy.
A.2 Imaging the edge of the non-transparent target with a focal-spot monitor
This method is often used with relatively narrow targets, when the possible errors in the target translation direction do not lead to significant defocusing. However, in our case of 20-mm-wide tapes, the direction error in the target translation by a distance of 10 mm could lead to a substantial target position mismatch. We note that narrower tapes could not be used in our case, as this increased significantly the frequency of the tape breaking under the exposure to the full-power shots, as we experienced in previous experiments. Also, any possible target edge bending may cause additional positioning errors. The final reason was the same as in the previous method. Even though the technical difficulties of this method can be potentially overcome, the target would be positioned at the low-power-mode focal plane, which is not necessarily the same as for the high-power beam.
In summary, we state that the methods described in this appendix can be used for the initial target positioning with an approximately 100 μm accuracy before the experiment. Our choice of pre-positioning the target using the interferometry line, as described in the main text, was a matter of convenience, because it also ensured alignment of the target rotation angle with an approximately 0.1° accuracy.
Acknowledgements
We acknowledge financial support from ELI-Beamlines, project Advanced Research using High Intensity Laser Produced Photons and Particles (ADONIS) (Project No. CZ.02.1.01/0.0/0.0/16_019/0000789) from the European Regional Development Fund, QST-IRI, the QST President’s Strategic Grant (Creative Research) and JSPS KAKENHI JP17F17811, JP19KK0355, JP19H00669 and JP22H01239. The authors’ thanks also go to the Czech Ministry of Education, Youth and Sports (CMEYS) for the financial support of the project number LM2023068. This work was partly supported by JSPS KAKENHI Grant No. JP23H01151.
We thank the J-KAREN-P operation group. The on-target pulse energy measurement from the absolutely calibrated spectrometer was performed in collaboration with M. Nishiuchi and N. Dover. We highly appreciate the contribution of professor David Neely who sadly passed away before this work was published; he was a colleague, mentor and friend to the authors. This work supports the ongoing diagnostic development research at the Central Laser Facility and is supported by the EPAC diagnostic work package.