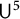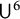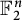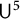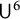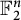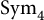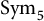1 Introduction
Let us begin by recalling the definition of Gowers uniformity norms [Reference Gowers11].
Definition 1.1 Let G be a finite abelian group. The discrete multiplicative derivative operator
![]() $\partial _a$
for shift
$\partial _a$
for shift
![]() $a \in G$
is defined by
$a \in G$
is defined by
![]() $\partial _a f(x) = f(x + a)\overline {f(x)}$
for functions
$\partial _a f(x) = f(x + a)\overline {f(x)}$
for functions
![]() $f \colon G \to \mathbb {C}$
.
$f \colon G \to \mathbb {C}$
.
Let
![]() $f \colon G \to \mathbb {C}$
be a function. The Gowers uniformity norm
$f \colon G \to \mathbb {C}$
be a function. The Gowers uniformity norm
![]() $\|f\|_{\mathsf {U}^k}$
is given by the formula
$\|f\|_{\mathsf {U}^k}$
is given by the formula

We now briefly discuss Gowers uniformity norms (the first part of the introduction of this paper is similar to that in [Reference Milićević28]). It is well known that
![]() $\|\cdot \|_{\mathsf {U}^k}$
is indeed a norm for
$\|\cdot \|_{\mathsf {U}^k}$
is indeed a norm for
![]() $k \geq 2$
. The inverse question for Gowers uniformity norms, a central problem in additive combinatorics, asks for a description of functions
$k \geq 2$
. The inverse question for Gowers uniformity norms, a central problem in additive combinatorics, asks for a description of functions
![]() $f \colon G \to \mathbb {D} = \{z \in \mathbb {C} \colon |z| \leq 1\}$
whose norm is larger than some constant
$f \colon G \to \mathbb {D} = \{z \in \mathbb {C} \colon |z| \leq 1\}$
whose norm is larger than some constant
![]() $c> 0$
. Namely, for a given finite abelian group G and the norm
$c> 0$
. Namely, for a given finite abelian group G and the norm
![]() $\|\cdot \|_{\mathsf {U}^k}$
, we seek a family
$\|\cdot \|_{\mathsf {U}^k}$
, we seek a family
![]() $\mathcal {Q}$
of functions from G to
$\mathcal {Q}$
of functions from G to
![]() $\mathbb {D}$
with the properties that:
$\mathbb {D}$
with the properties that:
-
• whenever
 $f \colon G \to \mathbb {D}$
has
$f \colon G \to \mathbb {D}$
has
 $\|f\|_{\mathsf {U}^k} \geq c$
, then we have correlation
$\|f\|_{\mathsf {U}^k} \geq c$
, then we have correlation
 $\Big |\mathop {\mathbb {E}}_{x} f(x) \overline {q(x)}\Big | \geq \Omega _{c}(1)$
for some obstruction function
$\Big |\mathop {\mathbb {E}}_{x} f(x) \overline {q(x)}\Big | \geq \Omega _{c}(1)$
for some obstruction function
 $q \in \mathcal {Q}$
, and
$q \in \mathcal {Q}$
, and -
• the family of obstructions
 $\mathcal {Q}$
is roughly minimal in the sense that if, for some obstruction function
$\mathcal {Q}$
is roughly minimal in the sense that if, for some obstruction function
 $q\in \mathcal {Q}$
, we have
$q\in \mathcal {Q}$
, we have
 $\Big | \mathop {\mathbb {E}}_{x} f(x) \overline {q(x)}\Big | \geq c$
, then
$\Big | \mathop {\mathbb {E}}_{x} f(x) \overline {q(x)}\Big | \geq c$
, then
 $\|f\|_{\mathsf {U}^k} \geq \Omega _{c}(1)$
.
$\|f\|_{\mathsf {U}^k} \geq \Omega _{c}(1)$
.
Two classes of groups for which this problem has been most intensively studied are cyclic groups of prime order (denoted
![]() $\mathbb {Z}/N\mathbb {Z}$
) and finite-dimensional vector spaces over prime fields (denoted
$\mathbb {Z}/N\mathbb {Z}$
) and finite-dimensional vector spaces over prime fields (denoted
![]() $\mathbb {F}_p^n$
). When
$\mathbb {F}_p^n$
). When
![]() $G = \mathbb {F}_p^n$
, in the so-called high characteristic case
$G = \mathbb {F}_p^n$
, in the so-called high characteristic case
![]() $p \geq k$
, Bergelson, Tao, and Ziegler [Reference Bergelson, Tao and Ziegler3] proved an inverse theorem in which they took phases of polynomials as the obstruction family. Tao and Ziegler [Reference Tao and Ziegler33] extended their results to the “low characteristic case”
$p \geq k$
, Bergelson, Tao, and Ziegler [Reference Bergelson, Tao and Ziegler3] proved an inverse theorem in which they took phases of polynomials as the obstruction family. Tao and Ziegler [Reference Tao and Ziegler33] extended their results to the “low characteristic case”
![]() $p < k$
, by proving an inverse theorem with phases of nonclassical polynomials as obstruction. We shall discuss nonclassical polynomials slightly later, but for now it is enough to mention that these arise as the solutions of the extremal problem of finding functions
$p < k$
, by proving an inverse theorem with phases of nonclassical polynomials as obstruction. We shall discuss nonclassical polynomials slightly later, but for now it is enough to mention that these arise as the solutions of the extremal problem of finding functions
![]() $f\colon \mathbb {F}_p^n \to \mathbb {D}$
with
$f\colon \mathbb {F}_p^n \to \mathbb {D}$
with
![]() $\|f\|_{\mathsf {U}^k} = 1$
. On the other hand, when
$\|f\|_{\mathsf {U}^k} = 1$
. On the other hand, when
![]() $G = \mathbb {Z}/N\mathbb {Z}$
, an inverse theorem was proved by Green, Tao, and Ziegler [Reference Green, Tao and Ziegler19] and in that setting one need the theory of nilsequences to describe obstructions. Let us also mention the theory of nilspaces, developed in papers by Szegedy [Reference Szegedy32], Camarena and Szegedy [Reference Camarena and Szegedy5] and with further improvements, generalizations, and contributions by Candela [Reference Candela6, Reference Candela7], Candela and Szegedy [Reference Candela and Szegedy9, Reference Candela and Szegedy10], and Gutman, Manners, and Varjú [Reference Gutman, Manners and Varjú20–Reference Gutman, Manners and Varjú22], which can be used to give alternative proofs of these inverse results. In particular, Candela, González-Sánchez, and Szegedy [Reference Candela, González-Sánchez and Szegedy8] were recently able to give an alternative proof the Tao–Ziegler inverse theorem.
$G = \mathbb {Z}/N\mathbb {Z}$
, an inverse theorem was proved by Green, Tao, and Ziegler [Reference Green, Tao and Ziegler19] and in that setting one need the theory of nilsequences to describe obstructions. Let us also mention the theory of nilspaces, developed in papers by Szegedy [Reference Szegedy32], Camarena and Szegedy [Reference Camarena and Szegedy5] and with further improvements, generalizations, and contributions by Candela [Reference Candela6, Reference Candela7], Candela and Szegedy [Reference Candela and Szegedy9, Reference Candela and Szegedy10], and Gutman, Manners, and Varjú [Reference Gutman, Manners and Varjú20–Reference Gutman, Manners and Varjú22], which can be used to give alternative proofs of these inverse results. In particular, Candela, González-Sánchez, and Szegedy [Reference Candela, González-Sánchez and Szegedy8] were recently able to give an alternative proof the Tao–Ziegler inverse theorem.
When it comes to the question of bounds, it should be noted that all the works above use infinitary methods or regularity lemmas and therefore give ineffective results. Effective bounds were first proved for inverse question for
![]() $\|\cdot \|_{\mathsf {U}^3}$
norm by Green and Tao [Reference Green and Tao16] for abelian groups of odd order and by Samorodnitsky when
$\|\cdot \|_{\mathsf {U}^3}$
norm by Green and Tao [Reference Green and Tao16] for abelian groups of odd order and by Samorodnitsky when
![]() $G = \mathbb {F}_2^n$
in [Reference Samorodnitsky30] (see also a recent work of Jamneshan and Tao [Reference Jamneshan and Tao23]). For
$G = \mathbb {F}_2^n$
in [Reference Samorodnitsky30] (see also a recent work of Jamneshan and Tao [Reference Jamneshan and Tao23]). For
![]() $\|\cdot \|_{\mathsf {U}^4}$
norm for the vector space case
$\|\cdot \|_{\mathsf {U}^4}$
norm for the vector space case
![]() $G = \mathbb {F}_p^n$
, quantitative bounds we obtained by Gowers and the author [Reference Gowers and Milićević12] when
$G = \mathbb {F}_p^n$
, quantitative bounds we obtained by Gowers and the author [Reference Gowers and Milićević12] when
![]() $p \geq 5$
and by Tidor [Reference Tidor34] for
$p \geq 5$
and by Tidor [Reference Tidor34] for
![]() $p < 5$
. Finally, for general values of k, quantitative bounds were achieved by Manners [Reference Manners25] in the
$p < 5$
. Finally, for general values of k, quantitative bounds were achieved by Manners [Reference Manners25] in the
![]() $G = \mathbb {Z}/N\mathbb {Z}$
setting and by Gowers and the author [Reference Gowers and Milićević13] in
$G = \mathbb {Z}/N\mathbb {Z}$
setting and by Gowers and the author [Reference Gowers and Milićević13] in
![]() $G = \mathbb {F}_p^n$
in the case of high characteristic.
$G = \mathbb {F}_p^n$
in the case of high characteristic.
The question of getting quantitative bounds in the low characteristic case in the vector space setting is still open. Nevertheless, as a part of the proof of inverse theorem in the high characteristic case [Reference Gowers and Milićević13], we have the following partial result which holds independently of the characteristic assumption.
Theorem 1.1 (Gowers and Milićević [Reference Gowers and Milićević13])
Suppose that
![]() $f \colon \mathbb {F}^n_p \to \mathbb {D}$
is a function such that
$f \colon \mathbb {F}^n_p \to \mathbb {D}$
is a function such that
![]() $\|f\|_{\mathsf {U}^{k}} \geq c$
. Then there exists a multilinear form
$\|f\|_{\mathsf {U}^{k}} \geq c$
. Then there exists a multilinear form
 $\alpha \colon \underbrace {\mathbb {F}^n_p \times \mathbb {F}^n_p \times \dots \times \mathbb {F}^n_p}_{k-1} \to \mathbb {F}_p$
such that
$\alpha \colon \underbrace {\mathbb {F}^n_p \times \mathbb {F}^n_p \times \dots \times \mathbb {F}^n_p}_{k-1} \to \mathbb {F}_p$
such that

The notation
![]() $\exp ^{(t)}$
stands for the composition of t exponentials, i.e., the tower of exponentials of height t.
$\exp ^{(t)}$
stands for the composition of t exponentials, i.e., the tower of exponentials of height t.
For the remainder of the introduction, group G stands for
![]() $\mathbb {F}_p^n$
.
$\mathbb {F}_p^n$
.
An important notion in the following discussion is that of partition rank of a multilinear form, which was introduced by Naslund in [Reference Naslund29] and which we now recall. The partition rank of a multilinear form
![]() $\alpha \colon G^d \to \mathbb {F}_p$
, denoted
$\alpha \colon G^d \to \mathbb {F}_p$
, denoted
![]() $\operatorname {prank} \alpha $
, is the least number m such that a multilinear form
$\operatorname {prank} \alpha $
, is the least number m such that a multilinear form
![]() $\alpha \colon G^d \to \mathbb {F}_p$
can be written as
$\alpha \colon G^d \to \mathbb {F}_p$
can be written as
where
![]() $\emptyset \not = I_i \subsetneq [d]$
are sets of indices, and
$\emptyset \not = I_i \subsetneq [d]$
are sets of indices, and
![]() $\beta _i \colon G^{I_i} \to \mathbb {F}_p$
and
$\beta _i \colon G^{I_i} \to \mathbb {F}_p$
and
![]() $\gamma _i \colon G^{[d] \setminus I_i} \to \mathbb {F}_p$
are multilinear forms for
$\gamma _i \colon G^{[d] \setminus I_i} \to \mathbb {F}_p$
are multilinear forms for
![]() $i \in [m]$
. One of the ways to think about this quantity is that the distance between two forms can be measured by the partition rank of their difference.
$i \in [m]$
. One of the ways to think about this quantity is that the distance between two forms can be measured by the partition rank of their difference.
The proof of high characteristic case of the inverse theorem then proceeds by studying the properties of the multilinear form
![]() $\alpha $
satisfying (1.1). As remarked in [Reference Gowers and Milićević13], it is plausible that this theorem could be used in the low characteristic case as well. For example, it turns out that condition (1.1) itself implies that
$\alpha $
satisfying (1.1). As remarked in [Reference Gowers and Milićević13], it is plausible that this theorem could be used in the low characteristic case as well. For example, it turns out that condition (1.1) itself implies that
![]() $\operatorname {prank}(\alpha - \alpha ') \leq O_c(1)$
, where
$\operatorname {prank}(\alpha - \alpha ') \leq O_c(1)$
, where
![]() $\alpha '$
is any form obtained from
$\alpha '$
is any form obtained from
![]() $\alpha $
by permuting some of its variables. This follows from the symmetry argument of Green and Tao [Reference Green and Tao16] and the inverse theorem for biased multilinear forms [Reference Janzer24, Reference Milićević26] (i.e., the so-called partition vs. analytic rank problem), and we do not need any assumptions on the characteristic of the field for this conclusion. The characteristic becomes relevant when we want to pass from an approximately symmetric multilinear form (meaning that differences
$\alpha $
by permuting some of its variables. This follows from the symmetry argument of Green and Tao [Reference Green and Tao16] and the inverse theorem for biased multilinear forms [Reference Janzer24, Reference Milićević26] (i.e., the so-called partition vs. analytic rank problem), and we do not need any assumptions on the characteristic of the field for this conclusion. The characteristic becomes relevant when we want to pass from an approximately symmetric multilinear form (meaning that differences
![]() $\alpha - \alpha '$
above are of low partition rank, rather than 0) to an exactly symmetric form (meaning that it is invariant under permutations of variables). In the high characteristic case, it is trivial to achieve this, but in the low characteristic case, this task becomes considerably harder.
$\alpha - \alpha '$
above are of low partition rank, rather than 0) to an exactly symmetric form (meaning that it is invariant under permutations of variables). In the high characteristic case, it is trivial to achieve this, but in the low characteristic case, this task becomes considerably harder.
Once that we know that there exists a symmetric multilinear form
![]() $\sigma $
such that
$\sigma $
such that
![]() $\operatorname {prank}(\alpha - \sigma )$
is small, we may deduce that (1.1) holds for
$\operatorname {prank}(\alpha - \sigma )$
is small, we may deduce that (1.1) holds for
![]() $\sigma $
in place of
$\sigma $
in place of
![]() $\alpha $
, as it turns out that (1.1) is robust under modification by forms of small partition rank. Final observation required in the high characteristic case is that symmetric multilinear forms are precisely the additive derivatives of polynomials. This fact allows us to reduce the proof to the case of the inverse theorem for
$\alpha $
, as it turns out that (1.1) is robust under modification by forms of small partition rank. Final observation required in the high characteristic case is that symmetric multilinear forms are precisely the additive derivatives of polynomials. This fact allows us to reduce the proof to the case of the inverse theorem for
![]() $\|\cdot \|_{\mathsf {U}^{k-1}}$
norm, which we assume by induction.
$\|\cdot \|_{\mathsf {U}^{k-1}}$
norm, which we assume by induction.
Note that there are two places in the argument above which rely on the fact that
![]() $p \geq k$
. The first one is the relationship between approximately symmetric and exactly symmetric multilinear forms, and the second one is the description of the additive derivatives of polynomials. Tidor [Reference Tidor34] was able to resolve these two issues for trilinear multilinear forms and carry out the strategy of elucidating the structure of multilinear form provided by Theorem 1.1 in
$p \geq k$
. The first one is the relationship between approximately symmetric and exactly symmetric multilinear forms, and the second one is the description of the additive derivatives of polynomials. Tidor [Reference Tidor34] was able to resolve these two issues for trilinear multilinear forms and carry out the strategy of elucidating the structure of multilinear form provided by Theorem 1.1 in
![]() $\mathbb {F}_2^n$
, thus proving a quantitative inverse theorem for
$\mathbb {F}_2^n$
, thus proving a quantitative inverse theorem for
![]() $\|\cdot \|_{\mathsf {U}^4}$
norm in the low characteristic case. For the first issue, it turns out that in the case of trilinear forms, approximately symmetric forms are close to exactly symmetric ones. For the second issue, we need a definition. We say that a multilinear form
$\|\cdot \|_{\mathsf {U}^4}$
norm in the low characteristic case. For the first issue, it turns out that in the case of trilinear forms, approximately symmetric forms are close to exactly symmetric ones. For the second issue, we need a definition. We say that a multilinear form
![]() $\sigma \colon G^k \to \mathbb {F}_p$
is strongly symmetric if it is symmetric and the multilinear form
$\sigma \colon G^k \to \mathbb {F}_p$
is strongly symmetric if it is symmetric and the multilinear form
![]() $(x,y_{p+1}, \dots , y_k) \mapsto \sigma (x,\dots , x, y_{p+1}, \dots , y_k)$
is also symmetric (where x occurs p times). It turns out we again have a rather satisfactory description, namely that order k additive derivatives of nonclassical polynomials of degree at most k are precisely strongly symmetric multilinear forms in k variables (this is [Reference Tidor34, Proposition 3.5]; see also [Reference Tao and Ziegler33]). Once we know that a form in (1.1) is symmetric, it is not hard to show that it is strongly symmetric using similar arguments. However, while the description of additive derivatives of nonclassical polynomials holds for all numbers of variables, it turns out that this is surprisingly not the case with approximate symmetry problem.
$(x,y_{p+1}, \dots , y_k) \mapsto \sigma (x,\dots , x, y_{p+1}, \dots , y_k)$
is also symmetric (where x occurs p times). It turns out we again have a rather satisfactory description, namely that order k additive derivatives of nonclassical polynomials of degree at most k are precisely strongly symmetric multilinear forms in k variables (this is [Reference Tidor34, Proposition 3.5]; see also [Reference Tao and Ziegler33]). Once we know that a form in (1.1) is symmetric, it is not hard to show that it is strongly symmetric using similar arguments. However, while the description of additive derivatives of nonclassical polynomials holds for all numbers of variables, it turns out that this is surprisingly not the case with approximate symmetry problem.
Theorem 1.2 [Reference Milićević28]
Given a sufficiently large positive integer n, there exists a multilinear form
![]() $\alpha \colon \mathbb {F}_2^n \times \mathbb {F}_2^n \times \mathbb {F}_2^n \times \mathbb {F}_2^n \to \mathbb {F}_2$
which is 3-approximately symmetric in the sense that
$\alpha \colon \mathbb {F}_2^n \times \mathbb {F}_2^n \times \mathbb {F}_2^n \times \mathbb {F}_2^n \to \mathbb {F}_2$
which is 3-approximately symmetric in the sense that
![]() $\operatorname {prank}(\alpha + \alpha ') \leq 3$
for any
$\operatorname {prank}(\alpha + \alpha ') \leq 3$
for any
![]() $\alpha '$
obtained from
$\alpha '$
obtained from
![]() $\alpha $
by permuting its variables, and
$\alpha $
by permuting its variables, and
![]() $\operatorname {prank}(\sigma + \alpha ) \geq \Omega (\sqrt [3]{n})$
for all symmetric multilinear forms
$\operatorname {prank}(\sigma + \alpha ) \geq \Omega (\sqrt [3]{n})$
for all symmetric multilinear forms
![]() $\sigma $
.
$\sigma $
.
With all this in mind, the main remaining obstacle in the way of the quantitative inverse theorem for uniformity norms can be formulated as follows.
Problem 1.3 Suppose that
![]() $f \colon G \to \mathbb {D}$
is a function and that
$f \colon G \to \mathbb {D}$
is a function and that
![]() $\alpha \colon G^{k} \to \mathbb {F}_p$
is a multilinear form. Assume that
$\alpha \colon G^{k} \to \mathbb {F}_p$
is a multilinear form. Assume that

Show that there exists a strongly symmetric multilinear form
![]() $\sigma \colon G^k \to \mathbb {F}_p$
such that
$\sigma \colon G^k \to \mathbb {F}_p$
such that
![]() $\operatorname {prank}(\alpha - \sigma )$
is quantitatively bounded in terms of
$\operatorname {prank}(\alpha - \sigma )$
is quantitatively bounded in terms of
![]() $k,p$
, and c.
$k,p$
, and c.
It should be noted that in a qualitative sense, this follows from the inverse theorem of Tao and Ziegler, and that, in the light of Theorem 1.2, the assumption (1.2) is essential.
Our main result in this paper is that, for
![]() $k \in \{4,5\}$
, we may overcome the additional difficulties caused by irregular behaviour of approximately symmetric forms.
$k \in \{4,5\}$
, we may overcome the additional difficulties caused by irregular behaviour of approximately symmetric forms.
Theorem 1.4 Let
![]() $k \in \{4,5\}$
, let
$k \in \{4,5\}$
, let
![]() $f \colon \mathbb {F}_2^n \to \mathbb {D}$
be a function, and let
$f \colon \mathbb {F}_2^n \to \mathbb {D}$
be a function, and let
![]() $\alpha \colon (\mathbb {F}_2^n)^k \to \mathbb {F}_2$
be a multilinear form in k variables. Suppose that
$\alpha \colon (\mathbb {F}_2^n)^k \to \mathbb {F}_2$
be a multilinear form in k variables. Suppose that

Then there exists a strongly symmetric multilinear form
![]() $\sigma \colon (\mathbb {F}_2^n)^k \to \mathbb {F}_2$
such that
$\sigma \colon (\mathbb {F}_2^n)^k \to \mathbb {F}_2$
such that
![]() $\alpha + \sigma $
has partition rank at most
$\alpha + \sigma $
has partition rank at most
![]() $O(\exp ^{(O(1))} c^{-1})$
.
$O(\exp ^{(O(1))} c^{-1})$
.
In fact, as we shall explain in the outline of the proof and in the concluding remarks, most of the arguments work for higher values of k, and the arguments of the proof of Theorem 1.4 are capable of almost proving the general case. As we shall explain in the concluding remarks, the proof breaks only for multilinear forms with very special properties (see Conjecture 7.1).
As a corollary, we deduce the quantitative inverse theorems for
![]() $\|\cdot \|_{\mathsf {U}^5}$
and
$\|\cdot \|_{\mathsf {U}^5}$
and
![]() $\|\cdot \|_{\mathsf {U}^6}$
norms in
$\|\cdot \|_{\mathsf {U}^6}$
norms in
![]() $\mathbb {F}_2^n$
.
$\mathbb {F}_2^n$
.
Corollary 1.5 Let
![]() $k \in \{5,6\}$
and let
$k \in \{5,6\}$
and let
![]() $f \colon \mathbb {F}_2^n \to \mathbb {D}$
be a function such that
$f \colon \mathbb {F}_2^n \to \mathbb {D}$
be a function such that
![]() $\|f\|_{\mathsf {U}^k} \geq c$
. Then there exists a nonclassical polynomial
$\|f\|_{\mathsf {U}^k} \geq c$
. Then there exists a nonclassical polynomial
![]() $q\colon \mathbb {F}_2^n \to \mathbb {T}$
of degree at most
$q\colon \mathbb {F}_2^n \to \mathbb {T}$
of degree at most
![]() $k - 1$
such that
$k - 1$
such that

It should also be noted that the arguments do not depend crucially on the choice of field
![]() $\mathbb {F}_2$
. This case is of principal interest in theoretical computer science, and in our case, it simplifies the notation somewhat.
$\mathbb {F}_2$
. This case is of principal interest in theoretical computer science, and in our case, it simplifies the notation somewhat.
1.1 Outline of the proof
We further specialize and write G for
![]() $\mathbb {F}_2^n$
. In the rest of the introduction, we sketch the proof of Theorem 1.4 and state other results of this paper. The overall theme is that of passing from multilinear forms with approximate algebraic properties to forms with exact versions of those properties. Mainly, these properties will be about symmetry in some set of variables.
$\mathbb {F}_2^n$
. In the rest of the introduction, we sketch the proof of Theorem 1.4 and state other results of this paper. The overall theme is that of passing from multilinear forms with approximate algebraic properties to forms with exact versions of those properties. Mainly, these properties will be about symmetry in some set of variables.
In order to state the results, we define a natural action of
![]() $\operatorname {Sym}_k$
on
$\operatorname {Sym}_k$
on
![]() $G^k$
given by permuting the coordinates, which is similar to the left regular representation of the group
$G^k$
given by permuting the coordinates, which is similar to the left regular representation of the group
![]() $\operatorname {Sym}_k$
. For a permutation
$\operatorname {Sym}_k$
. For a permutation
![]() $\pi \in \operatorname {Sym}_k$
, we misuse the notation and write
$\pi \in \operatorname {Sym}_k$
, we misuse the notation and write
![]() $\pi \colon G^k \to G^k$
for the map defined by
$\pi \colon G^k \to G^k$
for the map defined by
![]() $\pi (x_{[k]}) = (x_{\pi ^{-1}(1)}, x_{\pi ^{-1}(2)}, \dots , x_{\pi ^{-1}(k)})$
, where
$\pi (x_{[k]}) = (x_{\pi ^{-1}(1)}, x_{\pi ^{-1}(2)}, \dots , x_{\pi ^{-1}(k)})$
, where
![]() $x_{[k]}$
is the abbreviation for
$x_{[k]}$
is the abbreviation for
![]() $x_1, \dots , x_k$
. This defines an action on
$x_1, \dots , x_k$
. This defines an action on
![]() $G^k$
. Given a multilinear form
$G^k$
. Given a multilinear form
![]() $\alpha \colon G^k \to \mathbb {F}_2$
and a permutation
$\alpha \colon G^k \to \mathbb {F}_2$
and a permutation
![]() $\pi $
inducing the map
$\pi $
inducing the map
![]() $\pi \colon G^k \to G^k$
, we may compose the two maps and the composition
$\pi \colon G^k \to G^k$
, we may compose the two maps and the composition
![]() $\alpha \circ \pi $
would also be a multilinear form.
$\alpha \circ \pi $
would also be a multilinear form.
First of all, we show that if a multilinear form is approximately symmetric in the first two variables
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, then it can be made exactly symmetric in
$x_2$
, then it can be made exactly symmetric in
![]() $x_1$
and
$x_1$
and
![]() $x_2$
at the small cost. Note that this result works for any arity of the form.
$x_2$
at the small cost. Note that this result works for any arity of the form.
Theorem 1.6 Let
![]() $k \geq 2$
be an integer, and let
$k \geq 2$
be an integer, and let
![]() $\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form. Suppose that
$\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form. Suppose that
![]() $\operatorname {prank}(\alpha + \alpha \circ (1\,\,2)) \leq r$
. Then there exists a multilinear form
$\operatorname {prank}(\alpha + \alpha \circ (1\,\,2)) \leq r$
. Then there exists a multilinear form
![]() $\alpha ' \colon G^k \to \mathbb {F}_2$
such that
$\alpha ' \colon G^k \to \mathbb {F}_2$
such that
![]() $\operatorname {prank}(\alpha + \alpha ') \leq \exp ^{(O(1))}(O(r))$
and
$\operatorname {prank}(\alpha + \alpha ') \leq \exp ^{(O(1))}(O(r))$
and
![]() $\alpha '$
is symmetric in the first two variables.
$\alpha '$
is symmetric in the first two variables.
In general, it is natural to try to build up exact symmetry of an approximately symmetric form one variable at a time. Theorem 1.6 shows that the first step of such a strategy can always be carried out. On the other hand, if a multilinear form
![]() $\alpha $
is symmetric in variables
$\alpha $
is symmetric in variables
![]() $x_{[2\ell ]}$
and if
$x_{[2\ell ]}$
and if
![]() $\operatorname {prank}(\alpha + \alpha \circ (1\,\,2\ell + 1)) \leq r$
, we may easily pass to a multilinear form
$\operatorname {prank}(\alpha + \alpha \circ (1\,\,2\ell + 1)) \leq r$
, we may easily pass to a multilinear form
![]() $\alpha '$
given by
$\alpha '$
given by
which differs from
![]() $\alpha $
by partition rank at most
$\alpha $
by partition rank at most
![]() $kr$
and is exactly symmetric in
$kr$
and is exactly symmetric in
![]() $x_{[2\ell + 1]}$
. Note that the fact that
$x_{[2\ell + 1]}$
. Note that the fact that
![]() $2\ell + 1$
is odd plays a crucial role.
$2\ell + 1$
is odd plays a crucial role.
With this in mind, since our forms have at most five variables, the key question in this paper is how to pass from forms symmetric in
![]() $x_{[3]}$
to those symmetric in
$x_{[3]}$
to those symmetric in
![]() $x_{[4]}$
. Recall that in general, this is not possible for forms in four variables (counterexample in [Reference Milićević28] is actually symmetric in
$x_{[4]}$
. Recall that in general, this is not possible for forms in four variables (counterexample in [Reference Milićević28] is actually symmetric in
![]() $x_{[3]}$
). The next result shows that we may achieve this if our form has the additional property that
$x_{[3]}$
). The next result shows that we may achieve this if our form has the additional property that
![]() $\alpha (u,u,x_3,x_4)$
vanishes.
$\alpha (u,u,x_3,x_4)$
vanishes.
Theorem 1.7 Suppose that
![]() $\alpha \colon G^4 \to \mathbb {F}_2$
is a multilinear form such that:
$\alpha \colon G^4 \to \mathbb {F}_2$
is a multilinear form such that:
-
•
 $\alpha $
is symmetric in the first three variables,
$\alpha $
is symmetric in the first three variables, -
•
 $\alpha (u,u,x_3, x_4) = 0$
for all
$\alpha (u,u,x_3, x_4) = 0$
for all
 $u, x_3, x_4 \in G$
,
$u, x_3, x_4 \in G$
, -
•
 $\operatorname {prank} (\alpha + \alpha \circ (3\,\,4)) \leq r$
.
$\operatorname {prank} (\alpha + \alpha \circ (3\,\,4)) \leq r$
.
Then there exists a multilinear form
![]() $\alpha ' \colon G^4 \to \mathbb {F}_2$
such that
$\alpha ' \colon G^4 \to \mathbb {F}_2$
such that
![]() $\operatorname {prank} (\alpha + \alpha ') \leq \exp (\exp (O(r)))$
and
$\operatorname {prank} (\alpha + \alpha ') \leq \exp (\exp (O(r)))$
and
![]() $\alpha '$
is symmetric.
$\alpha '$
is symmetric.
The final result is about obtaining exact symmetry in variables
![]() $x_{[4]}$
for forms in five variables. Unlike the case of four variables, we may again achieve this without additional assumptions.
$x_{[4]}$
for forms in five variables. Unlike the case of four variables, we may again achieve this without additional assumptions.
Theorem 1.8 Suppose that
![]() $\alpha \colon G^5 \to \mathbb {F}_2$
is a multilinear form such that:
$\alpha \colon G^5 \to \mathbb {F}_2$
is a multilinear form such that:
-
•
 $\alpha $
is symmetric in the first three variables,
$\alpha $
is symmetric in the first three variables, -
•
 $\operatorname {prank} (\alpha + \alpha \circ (3\,\,4)) \leq r$
.
$\operatorname {prank} (\alpha + \alpha \circ (3\,\,4)) \leq r$
.
Then there exists a multilinear form
![]() $\alpha ' \colon G^5 \to \mathbb {F}_2$
such that
$\alpha ' \colon G^5 \to \mathbb {F}_2$
such that
![]() $\operatorname {prank} (\alpha + \alpha ') \leq \exp (\exp (O(r^{O(1)})))$
and
$\operatorname {prank} (\alpha + \alpha ') \leq \exp (\exp (O(r^{O(1)})))$
and
![]() $\alpha '$
is symmetric in the first four variables.
$\alpha '$
is symmetric in the first four variables.
A neat corollary is that in the case of five variables, we may again pass from approximately symmetric multilinear forms to those that are exactly symmetric, giving an affirmative answer to a question of Tidor [Reference Tidor34], which is surprising in the light of Theorem 1.2.
Corollary 1.9 Suppose that
![]() $\alpha \colon G^5 \to \mathbb {F}_2$
is a multilinear form such that
$\alpha \colon G^5 \to \mathbb {F}_2$
is a multilinear form such that
![]() $\operatorname {prank} (\alpha + \alpha \circ \pi ) \leq r$
holds for all permutations
$\operatorname {prank} (\alpha + \alpha \circ \pi ) \leq r$
holds for all permutations
![]() $\pi \in \operatorname {Sym}_5$
. Then there exists a symmetric multilinear form
$\pi \in \operatorname {Sym}_5$
. Then there exists a symmetric multilinear form
![]() $\alpha ' \colon G^5 \to \mathbb {F}_2$
such that
$\alpha ' \colon G^5 \to \mathbb {F}_2$
such that
![]() $\operatorname {prank} (\alpha + \alpha ') \leq \exp ^{(O(1))}(O(r^{O(1)}))$
.
$\operatorname {prank} (\alpha + \alpha ') \leq \exp ^{(O(1))}(O(r^{O(1)}))$
.
Since we have an additional condition in Theorem 1.7, we need another “approximate-to-exact” claim. We may think of a form
![]() $\alpha (x_{[k]})$
which is symmetric in
$\alpha (x_{[k]})$
which is symmetric in
![]() $x_1$
and
$x_1$
and
![]() $x_2$
such that
$x_2$
such that
![]() $\alpha (u,u,a_3, \dots , a_k) = 0 $
as being “without repeated coordinates,” since this vanishing condition is equivalent to not having monomials
$\alpha (u,u,a_3, \dots , a_k) = 0 $
as being “without repeated coordinates,” since this vanishing condition is equivalent to not having monomials
![]() $x_{1,i_1} x_{2,i_2} \dots x_{k,i_k}$
with
$x_{1,i_1} x_{2,i_2} \dots x_{k,i_k}$
with
![]() $i_1 = i_2$
present in the expansion of
$i_1 = i_2$
present in the expansion of
![]() $\alpha (x_{[k]})$
. The next theorem thus concerns forms that are “approximately without repeated coordinates.” (Symmetric multilinear forms without repeated coordinates are called classical multilinear forms [Reference Tao and Ziegler33, Reference Tidor34].)
$\alpha (x_{[k]})$
. The next theorem thus concerns forms that are “approximately without repeated coordinates.” (Symmetric multilinear forms without repeated coordinates are called classical multilinear forms [Reference Tao and Ziegler33, Reference Tidor34].)
Theorem 1.10 Let
![]() $2 \leq k \leq 5$
. Let
$2 \leq k \leq 5$
. Let
![]() $\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form which is symmetric in the first
$\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form which is symmetric in the first
![]() $m \geq 2$
variables. Suppose also that the multilinear form
$m \geq 2$
variables. Suppose also that the multilinear form
![]() $(d, a_3, \dots , a_k) \mapsto \alpha (d,d,a_3,\dots , a_k)$
has partition rank at most r. Then there exist a subspace
$(d, a_3, \dots , a_k) \mapsto \alpha (d,d,a_3,\dots , a_k)$
has partition rank at most r. Then there exist a subspace
![]() $U \leq G$
of codimension at most
$U \leq G$
of codimension at most
![]() $\exp ^{(O(1))}(O(r))$
and a multilinear form
$\exp ^{(O(1))}(O(r))$
and a multilinear form
![]() $\alpha ' \colon U^k \to \mathbb {F}_2$
, also symmetric in the first m variables such that
$\alpha ' \colon U^k \to \mathbb {F}_2$
, also symmetric in the first m variables such that
![]() $\alpha '(d,d,a_3, \dots , a_k) = 0$
for all
$\alpha '(d,d,a_3, \dots , a_k) = 0$
for all
![]() $d,a_3, \dots , a_k \in U$
and
$d,a_3, \dots , a_k \in U$
and
![]() $\operatorname {prank} (\alpha |_{U \times \cdots \times U} + \alpha ') \leq \exp (\exp (O(r^{O(1)})))$
.
$\operatorname {prank} (\alpha |_{U \times \cdots \times U} + \alpha ') \leq \exp (\exp (O(r^{O(1)})))$
.
The proof of Theorem 1.4 then proceeds by a back-and-forth argument which uses the condition (1.3) as follows: we first deduce approximate symmetry properties of
![]() $\alpha $
and then use Theorem 1.6 to replace
$\alpha $
and then use Theorem 1.6 to replace
![]() $\alpha $
by a form symmetric in
$\alpha $
by a form symmetric in
![]() $x_1$
and
$x_1$
and
![]() $x_2$
. Again, use the condition (1.3) to deduce approximate symmetry in
$x_2$
. Again, use the condition (1.3) to deduce approximate symmetry in
![]() $x_2$
and
$x_2$
and
![]() $x_3$
, and then pass to a form exactly symmetric in
$x_3$
, and then pass to a form exactly symmetric in
![]() $x_{[3]}$
, etc. each time using appropriate symmetry extension statement. The additional assumption in Theorem 1.7 makes the details of the argument more involved than this short sketch, but the overall structure of the argument is the one described.
$x_{[3]}$
, etc. each time using appropriate symmetry extension statement. The additional assumption in Theorem 1.7 makes the details of the argument more involved than this short sketch, but the overall structure of the argument is the one described.
The proofs of the “approximate-to-exact” theorems are based on an algebraic regularity method, following the overall philosophy of the approaches in [Reference Gowers and Milićević12–Reference Gowers and Milićević14, Reference Milićević28]. The proofs in this paper proceed by proving appropriate weak algebraic regularity lemmas that incorporate the additional algebraic properties of the forms in the question. Note that, despite similarity in the spirit, the previous works [Reference Gowers and Milićević12–Reference Gowers and Milićević14, Reference Milićević28] did not need such specialized lemmas. These weak algebraic regularity lemmas (Lemmas 4.1 and 5.2), coupled with multilinear algebra arguments, allow us to use the low partition rank expressions (e.g.,
![]() $\alpha + \alpha \circ (3\,\,4)$
in Theorem 1.8) to modify the given forms to the ones with exact properties (symmetric in
$\alpha + \alpha \circ (3\,\,4)$
in Theorem 1.8) to modify the given forms to the ones with exact properties (symmetric in
![]() $x_{[4]}$
in Theorem 1.8). Using the inverse theorem for biased multilinear forms (partition vs. analytic rank problem) and weak regularity lemmas rather than strong ones enables us to prove reasonable bounds in these results. We shall return to the discussion of these arguments in the concluding remarks.
$x_{[4]}$
in Theorem 1.8). Using the inverse theorem for biased multilinear forms (partition vs. analytic rank problem) and weak regularity lemmas rather than strong ones enables us to prove reasonable bounds in these results. We shall return to the discussion of these arguments in the concluding remarks.
1.2 Comparison with [Reference Tao and Ziegler33]
The proof of the inverse theorem for Gowers uniformity norms in the low characteristic by Tao and Ziegler [Reference Tao and Ziegler33] has a similar principle of deducing the full theorem from a partial result. In their case, they start from an earlier result they proved with Bergelson, saying that if
![]() $\|f\|_{\mathsf {U}^k} \geq c$
, then f correlates with the phase of a nonclassical polynomial of degree
$\|f\|_{\mathsf {U}^k} \geq c$
, then f correlates with the phase of a nonclassical polynomial of degree
![]() $d(k, p)$
, which may be larger than
$d(k, p)$
, which may be larger than
![]() $k-1$
. Thus, their remaining task is to reduce this degree to the optimal one, which is a significantly different situation to ours, where we start from Theorem 1.1, which is itself an optimal result when it comes to the degree of the obtained form
$k-1$
. Thus, their remaining task is to reduce this degree to the optimal one, which is a significantly different situation to ours, where we start from Theorem 1.1, which is itself an optimal result when it comes to the degree of the obtained form
![]() $\alpha $
, but we still have to deduce different further algebraic properties of
$\alpha $
, but we still have to deduce different further algebraic properties of
![]() $\alpha $
. Their argument also has variants of “approximate-to-exact” claims, but they primarily deal with classical symmetric multilinear forms, namely symmetric multilinear forms without monomials with multiple occurrences of the same coordinate, so there is no irregular behavior like that exhibited by approximately symmetric multilinear forms. Also, they rely on multidimensional Szemerédi theorem (see the proof of Theorem 4.1 in [Reference Tao and Ziegler33]), which, in order to be quantitative, requires the understanding of directional uniformity norms [Reference Austin1, Reference Austin2, Reference Milićević27], which is evaded in our approach.
$\alpha $
. Their argument also has variants of “approximate-to-exact” claims, but they primarily deal with classical symmetric multilinear forms, namely symmetric multilinear forms without monomials with multiple occurrences of the same coordinate, so there is no irregular behavior like that exhibited by approximately symmetric multilinear forms. Also, they rely on multidimensional Szemerédi theorem (see the proof of Theorem 4.1 in [Reference Tao and Ziegler33]), which, in order to be quantitative, requires the understanding of directional uniformity norms [Reference Austin1, Reference Austin2, Reference Milićević27], which is evaded in our approach.
2 Preliminaries
Throughout the paper, G stands for our ambient group, which is
![]() $\mathbb {F}_2^n$
for some large n.
$\mathbb {F}_2^n$
for some large n.
2.1 Notation
We use the standard expectation notation
![]() $\mathop {\mathbb {E}}_{x \in X}$
as shorthand for the average
$\mathop {\mathbb {E}}_{x \in X}$
as shorthand for the average
![]() $\frac {1}{|X|} \sum _{x \in X}$
, and when the set X is clear from the context, we simply write
$\frac {1}{|X|} \sum _{x \in X}$
, and when the set X is clear from the context, we simply write
![]() $\mathop {\mathbb {E}}_x$
. As in [Reference Gowers and Milićević13, Reference Milićević26], we use the following convention to save writing in situations where we have many indices appearing in predictable patterns. Instead of denoting a sequence of length m by
$\mathop {\mathbb {E}}_x$
. As in [Reference Gowers and Milićević13, Reference Milićević26], we use the following convention to save writing in situations where we have many indices appearing in predictable patterns. Instead of denoting a sequence of length m by
![]() $(x_1, \dots , x_m)$
, we write
$(x_1, \dots , x_m)$
, we write
![]() $x_{[m]}$
, and for
$x_{[m]}$
, and for
![]() $I\subseteq [m]$
, we write
$I\subseteq [m]$
, we write
![]() $x_I$
for the subsequence with indices in I.
$x_I$
for the subsequence with indices in I.
We extend the use of the dot product notation to any situation where we have two sequences
![]() $x=x_{[n]}$
and
$x=x_{[n]}$
and
![]() $y=y_{[n]}$
and a meaningful multiplication between elements
$y=y_{[n]}$
and a meaningful multiplication between elements
![]() $x_i y_i$
, writing
$x_i y_i$
, writing
![]() $x\cdot y$
as shorthand for the sum
$x\cdot y$
as shorthand for the sum
![]() $\sum _{i=1}^n x_i y_i$
. For example, if
$\sum _{i=1}^n x_i y_i$
. For example, if
![]() $\lambda =\lambda _{[n]}$
is a sequence of scalars, and
$\lambda =\lambda _{[n]}$
is a sequence of scalars, and
![]() $A=A_{[n]}$
is a suitable sequence of maps, then
$A=A_{[n]}$
is a suitable sequence of maps, then
![]() $\lambda \cdot A$
is the map
$\lambda \cdot A$
is the map
![]() $\sum _{i=1}^n\lambda _iA_i$
.
$\sum _{i=1}^n\lambda _iA_i$
.
Frequently, we shall consider slices of functions
![]() $f \colon G^{[k]} \to X$
, by which we mean functions of the form
$f \colon G^{[k]} \to X$
, by which we mean functions of the form
![]() $f_{x_I} \colon G^{[k] \setminus I} \to X$
that send
$f_{x_I} \colon G^{[k] \setminus I} \to X$
that send
![]() $y_{[k]\setminus I}$
to
$y_{[k]\setminus I}$
to
![]() $f(x_I, y_{[k]\setminus I})$
, for
$f(x_I, y_{[k]\setminus I})$
, for
![]() $I \subseteq [k], x_I \in G^I$
. (Here, we are writing
$I \subseteq [k], x_I \in G^I$
. (Here, we are writing
![]() $(x_I,y_{[k]\setminus I})$
not for the concatenation of the sequences
$(x_I,y_{[k]\setminus I})$
not for the concatenation of the sequences
![]() $x_I$
and
$x_I$
and
![]() $y_{[k]\setminus I}$
but for the “merged” sequence
$y_{[k]\setminus I}$
but for the “merged” sequence
![]() $z_{[n]}$
with
$z_{[n]}$
with
![]() $z_i=x_i$
when
$z_i=x_i$
when
![]() $i\in I$
and
$i\in I$
and
![]() $z_i=y_i$
otherwise.) If I is a singleton
$z_i=y_i$
otherwise.) If I is a singleton
![]() $\{i\}$
and
$\{i\}$
and
![]() $z_i\in G_i$
, then we shall write
$z_i\in G_i$
, then we shall write
![]() $S_{z_i}$
instead of
$S_{z_i}$
instead of
![]() $S_{z_{\{i\}}}$
. Sometimes, the index i will be clear from the context and it will be convenient to omit it. For example,
$S_{z_{\{i\}}}$
. Sometimes, the index i will be clear from the context and it will be convenient to omit it. For example,
![]() $f(x_{[k]\setminus \{i\}},a)$
stands for
$f(x_{[k]\setminus \{i\}},a)$
stands for
![]() $f(x_1,\dots ,x_{i-1},a,x_{i+1},\dots ,x_k)$
. If the index is not clear, we emphasize it by writing it as a superscript to the left of the corresponding variable, e.g.,
$f(x_1,\dots ,x_{i-1},a,x_{i+1},\dots ,x_k)$
. If the index is not clear, we emphasize it by writing it as a superscript to the left of the corresponding variable, e.g.,
![]() $f(x_{[k]\setminus \{i\}},{}^i\,a)$
.
$f(x_{[k]\setminus \{i\}},{}^i\,a)$
.
More generally, when
![]() $X_1, \dots , X_k$
are finite sets, Z is an arbitrary set,
$X_1, \dots , X_k$
are finite sets, Z is an arbitrary set,
![]() $f \colon X_1 \times \cdots \times X_k = X_{[k]} \to Z$
is a function,
$f \colon X_1 \times \cdots \times X_k = X_{[k]} \to Z$
is a function,
![]() $I \subsetneq [k]$
, and
$I \subsetneq [k]$
, and
![]() $x_i \in X_i$
for each
$x_i \in X_i$
for each
![]() $i \in I$
, we define a function
$i \in I$
, we define a function
![]() $f_{x_I} \colon X_{[k] \setminus I} \to Z$
, by mapping each
$f_{x_I} \colon X_{[k] \setminus I} \to Z$
, by mapping each
![]() $y_{[k] \setminus I} \in X_{[k] \setminus I}$
as
$y_{[k] \setminus I} \in X_{[k] \setminus I}$
as
![]() $f_{x_I}(y_{[k] \setminus I}) = f(x_I, y_{[k] \setminus I})$
. When the number of variables is small—for example, when we have a function
$f_{x_I}(y_{[k] \setminus I}) = f(x_I, y_{[k] \setminus I})$
. When the number of variables is small—for example, when we have a function
![]() $f(x,y)$
that depends only on two variables x and y instead of on indexed variables—we also write
$f(x,y)$
that depends only on two variables x and y instead of on indexed variables—we also write
![]() $f_x$
for the map
$f_x$
for the map
![]() $f_x(y)=f(x,y)$
.
$f_x(y)=f(x,y)$
.
Let us first recall the definition of higher-dimensional box norms. Let
![]() $X_1, \dots , X_k$
be arbitrary sets. The box norm of a function
$X_1, \dots , X_k$
be arbitrary sets. The box norm of a function
![]() $f \colon X_1 \times \cdots \times X_k \to \mathbb {C}$
(see, for example, Definition B.1 in Appendix B of [Reference Green and Tao18]) is defined by
$f \colon X_1 \times \cdots \times X_k \to \mathbb {C}$
(see, for example, Definition B.1 in Appendix B of [Reference Green and Tao18]) is defined by

The following is a well-known generalized Cauchy–Schwarz inequality for the box norm, which we refer to as the Gowers–Cauchy–Schwarz inequality.
Lemma 2.1 Let
![]() $f_I \colon X_1 \times \cdots \times X_k \to \mathbb {C}$
be a function for each
$f_I \colon X_1 \times \cdots \times X_k \to \mathbb {C}$
be a function for each
![]() $I \subseteq [k]$
. Then
$I \subseteq [k]$
. Then

The following lemma concerns quasirandomness of quadratic polynomials in the case of low characteristic.
Lemma 2.2 Suppose that
![]() $\rho _1, \dots , \rho _k \colon U \times U \to \mathbb {F}_2$
are bilinear forms such that all nonzero linear combinations of
$\rho _1, \dots , \rho _k \colon U \times U \to \mathbb {F}_2$
are bilinear forms such that all nonzero linear combinations of
![]() $\rho _i, \rho _i \circ (1\,\,2)$
have rank at least
$\rho _i, \rho _i \circ (1\,\,2)$
have rank at least
![]() $4(k + 1)$
. Then the number of solutions
$4(k + 1)$
. Then the number of solutions
![]() $u \in U$
to
$u \in U$
to
![]() $\rho _i(u,u) = 0$
, for all
$\rho _i(u,u) = 0$
, for all
![]() $i \in [k]$
, is at least
$i \in [k]$
, is at least
![]() $2^{-k-1}$
.
$2^{-k-1}$
.
Proof Let
![]() $X = \{u \in U \colon \rho _1(u,u) = \dots = \rho _k(u,u) = 0\}$
. Note that
$X = \{u \in U \colon \rho _1(u,u) = \dots = \rho _k(u,u) = 0\}$
. Note that

so we need to estimate
for nonzero
![]() $\lambda $
. Write
$\lambda $
. Write
![]() $\phi = \lambda _1 \rho _1 + \dots + \lambda _k \rho _k$
. Then
$\phi = \lambda _1 \rho _1 + \dots + \lambda _k \rho _k$
. Then

where we used the Gowers–Cauchy–Schwarz inequality in the last step. Taking 4th power and expanding, we get

However, it is a standard fact that the last expression equals
![]() $2^{-\operatorname {rank}(\phi + \phi \circ (1\,2))}$
(e.g., by Lemma 7 in [Reference Milićević28]). From assumption on forms
$2^{-\operatorname {rank}(\phi + \phi \circ (1\,2))}$
(e.g., by Lemma 7 in [Reference Milićević28]). From assumption on forms
![]() $\rho _1, \dots , \rho _k$
, we see that
$\rho _1, \dots , \rho _k$
, we see that
. The lemma now follows.
We make use of Sanders’s version of the Bogolyubov–Ruzsa lemma.
Theorem 2.3 (Corollary A.2 in [Reference Sanders31])
Suppose that
![]() $A \subseteq \mathbb {F}_2^n$
is a set of the density
$A \subseteq \mathbb {F}_2^n$
is a set of the density
![]() $\delta $
. Then there exists a subspace
$\delta $
. Then there exists a subspace
![]() $V \leq \mathbb {F}_2^n$
of codimension
$V \leq \mathbb {F}_2^n$
of codimension
![]() $O(\log ^4 (2\delta ^{-1}))$
such that
$O(\log ^4 (2\delta ^{-1}))$
such that
![]() $V \subseteq 4A$
.
$V \subseteq 4A$
.
For a multilinear form
![]() $\alpha \colon G^k \to \mathbb {F}_2$
, we have two important quantities that measure its structure. The first is the bias, defined as
$\alpha \colon G^k \to \mathbb {F}_2$
, we have two important quantities that measure its structure. The first is the bias, defined as
This quantity is closely related to the analytic rank, introduced by Gowers and Wolf [Reference Gowers and Wolf15], which is defined as
![]() $\operatorname {arank} \alpha = -\log _2 (\operatorname {bias} \alpha )$
.
$\operatorname {arank} \alpha = -\log _2 (\operatorname {bias} \alpha )$
.
The second one is the partition rank, introduced by Naslund in [Reference Naslund29], defined as the least nonnegative integer r such that there exist sets
![]() $\emptyset \not = I_i \subsetneq [k]$
and multilinear forms
$\emptyset \not = I_i \subsetneq [k]$
and multilinear forms
![]() $\beta _i \colon G^{I_i} \to \mathbb {F}_2$
and
$\beta _i \colon G^{I_i} \to \mathbb {F}_2$
and
![]() $\gamma _i \colon G^{[k] \setminus I_i} \to \mathbb {F}_2$
, where
$\gamma _i \colon G^{[k] \setminus I_i} \to \mathbb {F}_2$
, where
![]() $i \in [r]$
such that
$i \in [r]$
such that
We need the following result on the relationship between the two mentioned quantities, proved in [Reference Milićević26]. A very similar result was proved by Janzer [Reference Janzer24], and previous qualitative versions were proved by Green and Tao [Reference Green and Tao17] and by Bhowmick and Lovett [Reference Bhowmick and Lovett4], generalizing an approach of Green and Tao.
Theorem 2.4 (Inverse theorem for biased multilinear forms (the partition rank vs. the analytic rank problem) [Reference Milićević26])
For every positive integer k, there are constants
![]() $C = C_k, D = D_k> 0$
with the following property. Suppose that
$C = C_k, D = D_k> 0$
with the following property. Suppose that
![]() $\alpha \colon G^k \to \mathbb {F}_2$
is a multilinear form such that
$\alpha \colon G^k \to \mathbb {F}_2$
is a multilinear form such that
![]() $\mathop {\mathbb {E}}_{x_{[k]}} (-1)^{\alpha (x_{[k]})} \geq c$
, for some
$\mathop {\mathbb {E}}_{x_{[k]}} (-1)^{\alpha (x_{[k]})} \geq c$
, for some
![]() $c> 0$
. Then
$c> 0$
. Then
![]() $\operatorname {prank}\alpha \leq C \log _2^{D} c^{-1}$
.
$\operatorname {prank}\alpha \leq C \log _2^{D} c^{-1}$
.
The next lemma relates the partition rank of a multilinear form
![]() $\alpha $
to the partition rank of restrictions of
$\alpha $
to the partition rank of restrictions of
![]() $\alpha $
.
$\alpha $
.
Lemma 2.5 Let
![]() $\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form. Let
$\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form. Let
![]() $U \leq G$
be a subspace of codimension d. Then
$U \leq G$
be a subspace of codimension d. Then
![]() $\operatorname {prank} \alpha \leq \operatorname {prank} \alpha |_{U \times \cdots \times U} + kd$
.
$\operatorname {prank} \alpha \leq \operatorname {prank} \alpha |_{U \times \cdots \times U} + kd$
.
Proof Let
![]() $G = U \oplus \langle w_1, \dots , w_d\rangle $
. Then there exist linear maps
$G = U \oplus \langle w_1, \dots , w_d\rangle $
. Then there exist linear maps
![]() $\pi \colon G \to U$
and
$\pi \colon G \to U$
and
![]() $\phi _1, \dots , \phi _d \colon G \to \mathbb {F}_2$
such that
$\phi _1, \dots , \phi _d \colon G \to \mathbb {F}_2$
such that
![]() $x = \pi (x) + \sum _{i \in [d]} \phi _i(x) w_i$
for all
$x = \pi (x) + \sum _{i \in [d]} \phi _i(x) w_i$
for all
![]() $x \in G$
. Then
$x \in G$
. Then
 $$ \begin{align*}\alpha(x_1, \dots, x_k) = &\ \alpha(\pi(x_1) + \phi_1(x_1) w_1 + \dots + \phi_d(x_1) w_d, x_2, \dots, x_k) \\ = &\sum_{i \in [d]} \phi_i(x_1) \alpha(w_i, x_2, \dots, x_k) + \alpha(\pi(x), x_2, \dots, x_k)\\ = & \cdots\\ = & \left(\sum_{c \in [k]} \sum_{i \in [d]} \phi_i(x_c) \alpha(\pi(x_1), \dots, \pi(x_{c-1}), w_i, x_{c+1}, \dots, x_k)\right)\\ & \quad + \alpha(\pi(x_1), \dots, \pi(x_k)).\\[-34pt] \end{align*} $$
$$ \begin{align*}\alpha(x_1, \dots, x_k) = &\ \alpha(\pi(x_1) + \phi_1(x_1) w_1 + \dots + \phi_d(x_1) w_d, x_2, \dots, x_k) \\ = &\sum_{i \in [d]} \phi_i(x_1) \alpha(w_i, x_2, \dots, x_k) + \alpha(\pi(x), x_2, \dots, x_k)\\ = & \cdots\\ = & \left(\sum_{c \in [k]} \sum_{i \in [d]} \phi_i(x_c) \alpha(\pi(x_1), \dots, \pi(x_{c-1}), w_i, x_{c+1}, \dots, x_k)\right)\\ & \quad + \alpha(\pi(x_1), \dots, \pi(x_k)).\\[-34pt] \end{align*} $$
We need a variant of the above lemma which concerns forms whose restrictions are close to symmetric forms.
Corollary 2.6 Let
![]() $\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form, let
$\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form, let
![]() $U \leq G$
be a subspace of codimension d, and let
$U \leq G$
be a subspace of codimension d, and let
![]() $\sigma \colon U^k \to \mathbb {F}_2$
be a symmetric multilinear form such that
$\sigma \colon U^k \to \mathbb {F}_2$
be a symmetric multilinear form such that
![]() $\operatorname {prank}(\alpha |_{U\times \cdots \times U} + \sigma ) \leq r$
. Then there exists a symmetric multilinear form
$\operatorname {prank}(\alpha |_{U\times \cdots \times U} + \sigma ) \leq r$
. Then there exists a symmetric multilinear form
![]() $\tilde {\sigma } \colon G^k \to \mathbb {F}_2$
such that
$\tilde {\sigma } \colon G^k \to \mathbb {F}_2$
such that
![]() $\operatorname {prank}(\alpha + \tilde {\sigma }) \leq kd + r$
.
$\operatorname {prank}(\alpha + \tilde {\sigma }) \leq kd + r$
.
Proof Let the maps
![]() $\pi , \phi _1, \dots , \phi _d$
be as in the proof of the previous lemma. Define the multilinear form
$\pi , \phi _1, \dots , \phi _d$
be as in the proof of the previous lemma. Define the multilinear form
![]() $\tilde {\sigma } \colon G^k \to \mathbb {F}_2$
by
$\tilde {\sigma } \colon G^k \to \mathbb {F}_2$
by
![]() $\tilde {\sigma }(x_1, \dots , x_k) = \sigma (\pi (x_1), \dots , \pi (x_k))$
. Since
$\tilde {\sigma }(x_1, \dots , x_k) = \sigma (\pi (x_1), \dots , \pi (x_k))$
. Since
![]() $\sigma $
is symmetric on
$\sigma $
is symmetric on
![]() $U \times \cdots \times U$
, we have that
$U \times \cdots \times U$
, we have that
![]() $\tilde {\sigma }$
is symmetric. On the other hand, since
$\tilde {\sigma }$
is symmetric. On the other hand, since
![]() $\pi $
is a projection onto U, we see that
$\pi $
is a projection onto U, we see that
![]() $\tilde {\sigma }|_{U \times \cdots \times U} = \sigma $
and hence
$\tilde {\sigma }|_{U \times \cdots \times U} = \sigma $
and hence
By the previous lemma, we conclude that
![]() $\operatorname {prank}(\alpha + \tilde {\sigma }) \leq kd + r$
, as required.
$\operatorname {prank}(\alpha + \tilde {\sigma }) \leq kd + r$
, as required.
We also need a result on images of high-rank maps.
Lemma 2.7 (Lemma 2.5 in [Reference Gowers and Milićević14])
Let
![]() $\rho , \beta _1,\dots ,\beta _r \colon G^{k} \to \mathbb {F}_2$
be multilinear forms, and let
$\rho , \beta _1,\dots ,\beta _r \colon G^{k} \to \mathbb {F}_2$
be multilinear forms, and let
![]() $m \in \mathbb {N}$
be such that for all choices of
$m \in \mathbb {N}$
be such that for all choices of
![]() $\lambda \in \mathbb {F}^r_2$
,
$\lambda \in \mathbb {F}^r_2$
,
![]() $\operatorname {bias}\Big (\rho + \lambda \cdot \beta \Big ) < 2^{- k (r + m)}$
. Then, for any multilinear forms
$\operatorname {bias}\Big (\rho + \lambda \cdot \beta \Big ) < 2^{- k (r + m)}$
. Then, for any multilinear forms
![]() $\gamma _i \colon G^{I_i} \to \mathbb {F}_2$
,
$\gamma _i \colon G^{I_i} \to \mathbb {F}_2$
,
![]() $\emptyset \not = I_i \subsetneq [k]$
,
$\emptyset \not = I_i \subsetneq [k]$
,
![]() $i=1,2,\dots ,m$
, we may find
$i=1,2,\dots ,m$
, we may find
![]() $x_{[k]} \in G^{[k]}$
such that:
$x_{[k]} \in G^{[k]}$
such that:
-
•
 $\rho (x_{[k]}) = 1$
,
$\rho (x_{[k]}) = 1$
, -
•
 $(\forall i \in [r])\ \beta _i(x_{[k]}) = 0$
, and
$(\forall i \in [r])\ \beta _i(x_{[k]}) = 0$
, and -
•
 $(\forall i \in [m])\ \gamma _i(x_{I_i}) = 0$
.
$(\forall i \in [m])\ \gamma _i(x_{I_i}) = 0$
.
The following lemma is important for neglecting the low-rank differences.
Lemma 2.8 Suppose that a function
![]() $f \colon G \to \mathbb {D}$
and a multilinear form
$f \colon G \to \mathbb {D}$
and a multilinear form
![]() $\alpha \colon G^k \to \mathbb {F}_2$
satisfy
$\alpha \colon G^k \to \mathbb {F}_2$
satisfy

Let
![]() $\beta \colon G^k \to \mathbb {F}_2$
be another multilinear form such that
$\beta \colon G^k \to \mathbb {F}_2$
be another multilinear form such that
![]() $\operatorname {prank}(\alpha + \beta ) \leq r$
. Then
$\operatorname {prank}(\alpha + \beta ) \leq r$
. Then

Proof Using the notion of the large multilinear spectrum (Definition 8 in [Reference Milićević27]), and writing
![]() $c' = c^{2^{-k}}$
, we see that the condition is that
$c' = c^{2^{-k}}$
, we see that the condition is that
![]() $\alpha \in \operatorname {Spec}^{\text {ml}}_{c'} f$
. We need to show that
$\alpha \in \operatorname {Spec}^{\text {ml}}_{c'} f$
. We need to show that
![]() $\beta \in \operatorname {Spec}^{\text {ml}}_{c"} f$
for some
$\beta \in \operatorname {Spec}^{\text {ml}}_{c"} f$
for some
![]() $c" \geq 2^{-2r} c'$
. This follows from the proof of Lemma 39 in [Reference Milićević27], which has a large bias assumption instead of a low partition rank assumption.
$c" \geq 2^{-2r} c'$
. This follows from the proof of Lemma 39 in [Reference Milićević27], which has a large bias assumption instead of a low partition rank assumption.
Similarly, we are allowed to pass to arbitrary subspaces.
Lemma 2.9 Suppose that a function
![]() $f \colon G \to \mathbb {D}$
and a multilinear form
$f \colon G \to \mathbb {D}$
and a multilinear form
![]() $\alpha \colon G^k \to \mathbb {F}_2$
satisfy
$\alpha \colon G^k \to \mathbb {F}_2$
satisfy

Let
![]() $U \leq G$
be a subspace. Then there exists a function
$U \leq G$
be a subspace. Then there exists a function
![]() $\tilde {f} \colon U \to \mathbb {D}$
such that
$\tilde {f} \colon U \to \mathbb {D}$
such that

Proof Let W be a subspace such that
![]() $G = U \oplus W$
. Using this decomposition, we get
$G = U \oplus W$
. Using this decomposition, we get

By the triangle inequality, we get

By averaging, there exists a choice of
![]() $y, b_1, \dots , b_k \in W$
such that
$y, b_1, \dots , b_k \in W$
such that

We introduce additional variables
![]() $a^{\prime }_1, \dots , a^{\prime }_k \in U$
and make a change of variables where we replace x by
$a^{\prime }_1, \dots , a^{\prime }_k \in U$
and make a change of variables where we replace x by
![]() $x + a_1 + \dots + a_k$
and
$x + a_1 + \dots + a_k$
and
![]() $a_i$
by
$a_i$
by
![]() $a_i + a^{\prime }_i$
to obtain
$a_i + a^{\prime }_i$
to obtain

By the triangle inequality,

For each
![]() $x \in U$
, we may define auxiliary functions
$x \in U$
, we may define auxiliary functions
![]() $f_{I, x} \colon G^k \to \mathbb {D}$
for
$f_{I, x} \colon G^k \to \mathbb {D}$
for
![]() $I \subseteq [k]$
, each of the form
$I \subseteq [k]$
, each of the form
 $$\begin{align*}f_{I, x}(z_1, \dots, z_k) = f\Bigg(x +y + \sum_{i \in I} b_i + z_1 + \dots + z_k\Bigg) (-1)^{\alpha(z_1, \dots, z_k)} \ell_I(z_1, \dots, z_k),\end{align*}$$
$$\begin{align*}f_{I, x}(z_1, \dots, z_k) = f\Bigg(x +y + \sum_{i \in I} b_i + z_1 + \dots + z_k\Bigg) (-1)^{\alpha(z_1, \dots, z_k)} \ell_I(z_1, \dots, z_k),\end{align*}$$
where
![]() $\ell _I$
is a product of several factors, each depending on a proper subset of variables
$\ell _I$
is a product of several factors, each depending on a proper subset of variables
![]() $z_1, \dots , z_k$
, coming from terms that arise from the expansion of
$z_1, \dots , z_k$
, coming from terms that arise from the expansion of
and whose values are of modulus 1. In the new notation, we get

Using the Gowers–Cauchy–Schwarz inequality, we get
and Hőlder’s inequality implies that

Thus, there is a choice of subset
![]() $I \subseteq [k]$
such that
$I \subseteq [k]$
such that
![]() $c \leq \mathop {\mathbb {E}}_x \|f_{I, x}\|_{\square ^k}^{2^k}$
. By definition, writing
$c \leq \mathop {\mathbb {E}}_x \|f_{I, x}\|_{\square ^k}^{2^k}$
. By definition, writing
![]() $\tilde {b} = \sum _{i \in I} b_i$
and splitting
$\tilde {b} = \sum _{i \in I} b_i$
and splitting
![]() $\ell _I(z_1, \dots , z_k)$
into further factors that do not depend on a variable in
$\ell _I(z_1, \dots , z_k)$
into further factors that do not depend on a variable in
![]() $z_{[k]}$
, we have
$z_{[k]}$
, we have
for some functions
![]() $\ell _i$
with
$\ell _i$
with
![]() $|\ell _i(y_{[k] \setminus \{i\}})| = 1$
for all
$|\ell _i(y_{[k] \setminus \{i\}})| = 1$
for all
![]() $y_{[k] \setminus \{i\}}$
. Let
$y_{[k] \setminus \{i\}}$
. Let
![]() $\tilde {f} \colon U \to \mathbb {D}$
be given by
$\tilde {f} \colon U \to \mathbb {D}$
be given by
![]() $\tilde {f}(x) = f(x + y + \tilde {b})$
.
$\tilde {f}(x) = f(x + y + \tilde {b})$
.
Thus,

Another fact that we need is a combination of the symmetry argument of Green and Tao [Reference Green and Tao16] and the inverse theorem for biased multilinear forms.
Lemma 2.10 (Symmetry argument [Reference Gowers and Milićević13, Corollary 97])
Let
![]() $\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form. Suppose that
$\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form. Suppose that
for some
![]() $c> 0$
. Then, for each
$c> 0$
. Then, for each
![]() $\pi \in \operatorname {Sym}_{[k]}$
, we have
$\pi \in \operatorname {Sym}_{[k]}$
, we have
![]() $\operatorname {prank} (\alpha + \alpha \circ \pi ) \leq O\Big ((\log c^{-1})^{O(1)}\Big )$
.
$\operatorname {prank} (\alpha + \alpha \circ \pi ) \leq O\Big ((\log c^{-1})^{O(1)}\Big )$
.
Recall from the introduction that a multilinear form
![]() $\sigma \colon G^k \to \mathbb {F}_2$
is strongly symmetric if it is symmetric and the multilinear form
$\sigma \colon G^k \to \mathbb {F}_2$
is strongly symmetric if it is symmetric and the multilinear form
![]() $(x,y_3, \dots , y_k) \mapsto \sigma (x,x, y_3, \dots , y_k)$
is also symmetric. The following lemma is a crucial property of strongly symmetric multilinear forms, namely that we may lift them to higher-order strongly symmetric multilinear forms.
$(x,y_3, \dots , y_k) \mapsto \sigma (x,x, y_3, \dots , y_k)$
is also symmetric. The following lemma is a crucial property of strongly symmetric multilinear forms, namely that we may lift them to higher-order strongly symmetric multilinear forms.
Lemma 2.11 Suppose that
![]() $\sigma \colon G^k \to \mathbb {F}_2$
is a strongly symmetric multilinear form. Then there exists a strongly symmetric multilinear form
$\sigma \colon G^k \to \mathbb {F}_2$
is a strongly symmetric multilinear form. Then there exists a strongly symmetric multilinear form
![]() $\tilde {\sigma } \colon G^{k + 1} \to \mathbb {F}_2$
such that
$\tilde {\sigma } \colon G^{k + 1} \to \mathbb {F}_2$
such that
Proof Let
![]() $n = \dim G$
and fix a basis of G. Write
$n = \dim G$
and fix a basis of G. Write
![]() $\beta $
as a linear combination of monomials. Thus,
$\beta $
as a linear combination of monomials. Thus,
Define coefficients
![]() $\mu _{j_1, \dots , j_{k+1}}$
as follows: if
$\mu _{j_1, \dots , j_{k+1}}$
as follows: if
![]() $j_1, \dots , j_{k+1}$
are all distinct, then put
$j_1, \dots , j_{k+1}$
are all distinct, then put
![]() $\mu _{j_1, \dots , j_{k+1}} = 0$
, and in the other case, set
$\mu _{j_1, \dots , j_{k+1}} = 0$
, and in the other case, set
![]() $\mu _{j_1, \dots , j_{k+1}} = \lambda _{i_1, \dots , i_k}$
for any sequence
$\mu _{j_1, \dots , j_{k+1}} = \lambda _{i_1, \dots , i_k}$
for any sequence
![]() $i_1, \dots , i_k$
with the property that there is some element
$i_1, \dots , i_k$
with the property that there is some element
![]() $i_\ell $
which, if repeated, gives a permutation of the sequence
$i_\ell $
which, if repeated, gives a permutation of the sequence
![]() $j_1, \dots , j_{k+1}$
. We need to check that this is well defined. Suppose that
$j_1, \dots , j_{k+1}$
. We need to check that this is well defined. Suppose that
![]() $i^{\prime }_1, \dots , i^{\prime }_k$
is another such sequence, and that
$i^{\prime }_1, \dots , i^{\prime }_k$
is another such sequence, and that
![]() $i^{\prime }_m$
is the element that is repeated. If
$i^{\prime }_m$
is the element that is repeated. If
![]() $i^{\prime }_m = i_\ell $
, then i and
$i^{\prime }_m = i_\ell $
, then i and
![]() $i'$
are the same up to reordering, so by symmetry of
$i'$
are the same up to reordering, so by symmetry of
![]() $\sigma $
we have the equality
$\sigma $
we have the equality
![]() $\lambda _{i_1, \dots , i_k} = \lambda _{i^{\prime }_1, \dots , i^{\prime }_k}$
, as desired. On the other hand, if
$\lambda _{i_1, \dots , i_k} = \lambda _{i^{\prime }_1, \dots , i^{\prime }_k}$
, as desired. On the other hand, if
![]() $i_\ell \not = i^{\prime }_m$
, then that means that the number of times the element
$i_\ell \not = i^{\prime }_m$
, then that means that the number of times the element
![]() $i^{\prime }_m$
appears in the sequence i is one greater than the number of times it appears in the sequence
$i^{\prime }_m$
appears in the sequence i is one greater than the number of times it appears in the sequence
![]() $i'$
, and, similarly,
$i'$
, and, similarly,
![]() $i_\ell $
has one occurrence more in
$i_\ell $
has one occurrence more in
![]() $i'$
than it has in i, while other elements appear an equal number of times in both sequences. Since
$i'$
than it has in i, while other elements appear an equal number of times in both sequences. Since
![]() $\sigma $
is strongly symmetric, we again have equality
$\sigma $
is strongly symmetric, we again have equality
![]() $\lambda _{i_1, \dots , i_k} = \lambda _{i^{\prime }_1, \dots , i^{\prime }_k}$
. Coefficients
$\lambda _{i_1, \dots , i_k} = \lambda _{i^{\prime }_1, \dots , i^{\prime }_k}$
. Coefficients
![]() $\mu $
are symmetric directly from the definition, so defining
$\mu $
are symmetric directly from the definition, so defining
![]() $\tilde {\sigma }$
as
$\tilde {\sigma }$
as
produces a symmetric multilinear form. Finally,
 $$\begin{align*}&\tilde{\sigma}(x_1, x_1, x_2, \dots, x_k) = \sum_{i_1, \dots, i_k \in [n]} \mu_{i_1, i_1, \dots, i_k} x_{1\,i_1} \dots x_{k\,i_k} = \sum_{i_1, \dots, i_k \in [n]} \lambda_{i_1, i_2, \dots, i_k} x_{1\,i_1} \dots x_{k\,i_k} \\&\quad= \sigma(x_1, x_2, \dots, x_k).\end{align*}$$
$$\begin{align*}&\tilde{\sigma}(x_1, x_1, x_2, \dots, x_k) = \sum_{i_1, \dots, i_k \in [n]} \mu_{i_1, i_1, \dots, i_k} x_{1\,i_1} \dots x_{k\,i_k} = \sum_{i_1, \dots, i_k \in [n]} \lambda_{i_1, i_2, \dots, i_k} x_{1\,i_1} \dots x_{k\,i_k} \\&\quad= \sigma(x_1, x_2, \dots, x_k).\end{align*}$$
This means that
![]() $\tilde {\sigma }(x_1, x_1, x_2, \dots , x_k)$
is symmetric, and thus
$\tilde {\sigma }(x_1, x_1, x_2, \dots , x_k)$
is symmetric, and thus
![]() $\tilde {\sigma }$
is strongly symmetric.
$\tilde {\sigma }$
is strongly symmetric.
Let us now give the formal definition of nonclassical polynomials. Recall that
![]() ${G = \mathbb {F}_2^n}$
for some n. We write
${G = \mathbb {F}_2^n}$
for some n. We write
![]() $\mathbb {T}$
for the circle group
$\mathbb {T}$
for the circle group
![]() $\mathbb {R}/\mathbb {Z}$
.
$\mathbb {R}/\mathbb {Z}$
.
Definition 2.1 [Reference Tao and Ziegler33, Definition 1.2]
The discrete additive derivative operator
![]() $\Delta _a$
for shift
$\Delta _a$
for shift
![]() $a \in G$
is defined by
$a \in G$
is defined by
![]() $\Delta _a f(x) = f(x + a) - f(x)$
for functions
$\Delta _a f(x) = f(x + a) - f(x)$
for functions
![]() $f \colon G \to \mathbb {T}$
. A function
$f \colon G \to \mathbb {T}$
. A function
![]() $q \colon G \to \mathbb {T}$
is said to be a nonclassical polynomial of degree at most d if one has
$q \colon G \to \mathbb {T}$
is said to be a nonclassical polynomial of degree at most d if one has
for all
![]() $x, a_1, \dots , a_{d+1} \in G$
.
$x, a_1, \dots , a_{d+1} \in G$
.
A basic fact about nonclassical polynomials is that they have an explicit description in terms of monomials. The notation
![]() $|\cdot |_2$
stands for the map from
$|\cdot |_2$
stands for the map from
![]() $\mathbb {F}_2$
to
$\mathbb {F}_2$
to
![]() $\mathbb {R}$
which sends
$\mathbb {R}$
which sends
![]() $0$
to
$0$
to
![]() $0$
and
$0$
and
![]() $1$
to
$1$
to
![]() $1$
.
$1$
.
Lemma 2.12 [Reference Tao and Ziegler33, Lemma 1.7(iii)]
A function
![]() $q \colon \mathbb {F}_2^n \to \mathbb {T}$
is a nonclassical polynomial of degree at most d if and only if it has a representation of the form
$q \colon \mathbb {F}_2^n \to \mathbb {T}$
is a nonclassical polynomial of degree at most d if and only if it has a representation of the form
 $$\begin{align*}q(x_1, \dots, x_n) = \alpha + \sum_{\substack{0 \leq i_1, \dots, i_n \leq 1; j\geq 0\\0 < i_1 + \dots + i_n \leq d - j}} \frac{c_{i_1, \dots, i_n, j}|x_1|_2^{i_1}\dots |x_n|_2^{i_n}}{2^{j+1}} + \mathbb{Z}\end{align*}$$
$$\begin{align*}q(x_1, \dots, x_n) = \alpha + \sum_{\substack{0 \leq i_1, \dots, i_n \leq 1; j\geq 0\\0 < i_1 + \dots + i_n \leq d - j}} \frac{c_{i_1, \dots, i_n, j}|x_1|_2^{i_1}\dots |x_n|_2^{i_n}}{2^{j+1}} + \mathbb{Z}\end{align*}$$
for some coefficients
![]() $c_{i_1, \dots , i_n, j} \in \{0,1\}$
and
$c_{i_1, \dots , i_n, j} \in \{0,1\}$
and
![]() $\alpha \in \mathbb {T}$
. Furthermore, the coefficients
$\alpha \in \mathbb {T}$
. Furthermore, the coefficients
![]() $c_{i_1, \dots , i_n, j}$
and
$c_{i_1, \dots , i_n, j}$
and
![]() $\alpha $
are unique.
$\alpha $
are unique.
We do not use the lemma above in the paper, but we opted to include it for completeness. The way we obtain nonclassical polynomials in this paper is through the following result.
Lemma 2.13 (Tidor [Reference Tidor34, Proposition 3.5])
Given a strongly symmetric multilinear form
![]() $\sigma \colon G^k \to \mathbb {F}_2$
, there exists a nonclassical polynomial
$\sigma \colon G^k \to \mathbb {F}_2$
, there exists a nonclassical polynomial
![]() $q \colon G \to \mathbb {T}$
of degree at most k such that
$q \colon G \to \mathbb {T}$
of degree at most k such that
for all
![]() $a_1, \dots , a_k, x \in G$
.
$a_1, \dots , a_k, x \in G$
.
3 Properties of low partition rank decompositions
We begin our work in this section with a lemma which allows us to conclude that a low partition rank decomposition which evaluates to 0 is necessarily trivial under the appropriate assumptions.
Lemma 3.1 For given k, there exist constants
![]() $C = C_k \geq 1$
and
$C = C_k \geq 1$
and
![]() $D = D_k \geq 1$
such that the following holds. Let
$D = D_k \geq 1$
such that the following holds. Let
![]() $I_1 \cup \dots \cup I_r = [k]$
be a partition of the set
$I_1 \cup \dots \cup I_r = [k]$
be a partition of the set
![]() $[k]$
. Suppose that, for each
$[k]$
. Suppose that, for each
![]() $i \in [r]$
, we are given a multilinear map
$i \in [r]$
, we are given a multilinear map
![]() $\alpha _i \colon G^{I_i} \to \mathbb {F}_2^{d_i}$
such that for each nonzero
$\alpha _i \colon G^{I_i} \to \mathbb {F}_2^{d_i}$
such that for each nonzero
![]() $\lambda \in \mathbb {F}_2^{d_i}$
, we have
$\lambda \in \mathbb {F}_2^{d_i}$
, we have
![]() $\operatorname {prank} (\lambda \cdot \alpha _i) \geq r_i$
. Let
$\operatorname {prank} (\lambda \cdot \alpha _i) \geq r_i$
. Let
![]() $\Pi _1, \dots , \Pi _s \colon G^k \to \mathbb {F}_2$
be functions such that each
$\Pi _1, \dots , \Pi _s \colon G^k \to \mathbb {F}_2$
be functions such that each
![]() $\Pi _i(x_{[k]})$
is a product of multilinear forms of the shape
$\Pi _i(x_{[k]})$
is a product of multilinear forms of the shape
![]() $\gamma _1(x_{J_1}) \dots \gamma _t(x_{J_t})$
such that some
$\gamma _1(x_{J_1}) \dots \gamma _t(x_{J_t})$
such that some
![]() $J_i$
does not contain any of the sets
$J_i$
does not contain any of the sets
![]() $I_1, \dots , I_r$
. Suppose that there are some scalars
$I_1, \dots , I_r$
. Suppose that there are some scalars
![]() $\lambda _{i_1, \dots , i_r} \in \mathbb {F}_2$
for
$\lambda _{i_1, \dots , i_r} \in \mathbb {F}_2$
for
![]() $i_j \in [d_j]$
such that
$i_j \in [d_j]$
such that
for all
![]() $x_{[k]}$
. Provided
$x_{[k]}$
. Provided
![]() $r_i \geq C(s + d_i)^D$
for each
$r_i \geq C(s + d_i)^D$
for each
![]() $i \in [r]$
, we have
$i \in [r]$
, we have
![]() $\lambda _{i_1, \dots , i_r} = 0$
for all indices
$\lambda _{i_1, \dots , i_r} = 0$
for all indices
![]() $i_1, \dots , i_r$
.
$i_1, \dots , i_r$
.
Remark. Observe that we do not assume that factors of
![]() $\Pi _i$
have disjoint sets of variables.
$\Pi _i$
have disjoint sets of variables.
Proof Note that, for each
![]() $i \in [s]$
, we have a multilinear form
$i \in [s]$
, we have a multilinear form
![]() $\gamma _i(x_{J_i})$
that appears as a factor of
$\gamma _i(x_{J_i})$
that appears as a factor of
![]() $\Pi _i(x_{[k]})$
and
$\Pi _i(x_{[k]})$
and
![]() $J_i$
contains none of the sets
$J_i$
contains none of the sets
![]() $I_1, \dots , I_r$
. Fix indices
$I_1, \dots , I_r$
. Fix indices
![]() ${i_1 \in [d_1], \dots , i_r \in [d_r]}$
. We shall find
${i_1 \in [d_1], \dots , i_r \in [d_r]}$
. We shall find
![]() $x_{[k]}$
so that all
$x_{[k]}$
so that all
![]() $\gamma _i(x_{J_i})$
vanish (implying
$\gamma _i(x_{J_i})$
vanish (implying
![]() $\Pi _i(x_{[k]}) = 0$
),
$\Pi _i(x_{[k]}) = 0$
),
![]() $\alpha _{j, i_j}(x_{I_j}) = 1$
for each
$\alpha _{j, i_j}(x_{I_j}) = 1$
for each
![]() $j \in [r]$
and
$j \in [r]$
and
![]() $\alpha _{j, \ell }(x_{I_j}) = 0$
for each
$\alpha _{j, \ell }(x_{I_j}) = 0$
for each
![]() $j \in [r]$
and
$j \in [r]$
and
![]() $\ell \not = i_j$
. To find such an
$\ell \not = i_j$
. To find such an
![]() $x_{[k]}$
, we first find suitable
$x_{[k]}$
, we first find suitable
![]() $x_{I_1}$
, then
$x_{I_1}$
, then
![]() $x_{I_2}$
, etc. Assuming that
$x_{I_2}$
, etc. Assuming that
![]() $x_{I_1 \cup \dots \cup I_{j-1}}$
has been fixed for some
$x_{I_1 \cup \dots \cup I_{j-1}}$
has been fixed for some
![]() $j \in [r]$
, we look for
$j \in [r]$
, we look for
![]() $x_{I_j}$
such that
$x_{I_j}$
such that
![]() $\alpha _{j, i_j}(x_{I_j}) = 1$
,
$\alpha _{j, i_j}(x_{I_j}) = 1$
,
![]() $\alpha _{j, \ell }(x_{I_j}) = 0$
for
$\alpha _{j, \ell }(x_{I_j}) = 0$
for
![]() $\ell \not = i_j$
and
$\ell \not = i_j$
and
![]() $\gamma _\ell (x_{J_\ell }) = 0$
for all indices
$\gamma _\ell (x_{J_\ell }) = 0$
for all indices
![]() $\ell $
such that
$\ell $
such that
![]() $J_\ell \subseteq I_1 \cup \dots \cup I_j$
and
$J_\ell \subseteq I_1 \cup \dots \cup I_j$
and
![]() $J_\ell \cap I_j \not = \emptyset $
. By Theorem 2.4, there exist quantities
$J_\ell \cap I_j \not = \emptyset $
. By Theorem 2.4, there exist quantities
![]() $C_k, D_k$
, depending only on k, such that
$C_k, D_k$
, depending only on k, such that
![]() $\operatorname {prank} \tau \geq C t^D$
implies
$\operatorname {prank} \tau \geq C t^D$
implies
![]() $\operatorname {bias} \tau < 2^{-t}$
for all multilinear forms
$\operatorname {bias} \tau < 2^{-t}$
for all multilinear forms
![]() $\tau $
in at most k variables and all positive integers t. Thus,
$\tau $
in at most k variables and all positive integers t. Thus,
![]() $\operatorname {bias} \Big (\mu \cdot \alpha _j\Big ) < 2^{-k(d_i + s)}$
for all
$\operatorname {bias} \Big (\mu \cdot \alpha _j\Big ) < 2^{-k(d_i + s)}$
for all
![]() $\mu \not =0$
and we can find the desired
$\mu \not =0$
and we can find the desired
![]() $x_{I_j}$
using Lemma 2.7. We conclude that
$x_{I_j}$
using Lemma 2.7. We conclude that
![]() $\lambda _{i_1, \dots , i_r} = 0$
from (3.1).
$\lambda _{i_1, \dots , i_r} = 0$
from (3.1).
The following technical lemma also concerns linear combinations of multilinear forms, but is entirely linear-algebraic. It allows us to change a basis of multilinear forms to a more convenient one.
Lemma 3.2 Suppose that
![]() $I \cup J = [k]$
is a partition and that
$I \cup J = [k]$
is a partition and that
![]() $\beta _1, \dots , \beta _r \colon G^I \to \mathbb {F}_2$
and
$\beta _1, \dots , \beta _r \colon G^I \to \mathbb {F}_2$
and
![]() $\gamma _1, \dots , \gamma _r \colon G^J \to \mathbb {F}_2$
are multilinear forms. Then we may find further multilinear forms
$\gamma _1, \dots , \gamma _r \colon G^J \to \mathbb {F}_2$
are multilinear forms. Then we may find further multilinear forms
![]() $\tilde {\beta }_1, \dots , \tilde {\beta }_s \colon G^I \to \mathbb {F}_2$
and
$\tilde {\beta }_1, \dots , \tilde {\beta }_s \colon G^I \to \mathbb {F}_2$
and
![]() $\tilde {\gamma }_1, \dots , \tilde {\gamma }_s \colon G^J \to \mathbb {F}_2$
for some
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_s \colon G^J \to \mathbb {F}_2$
for some
![]() $s \leq r$
so that:
$s \leq r$
so that:
-
(i) for each
 $i \in [s]$
, the form
$i \in [s]$
, the form
 $\tilde {\beta }_i$
is a linear combination of forms
$\tilde {\beta }_i$
is a linear combination of forms
 $\beta _1, \dots , \beta _r$
and the form
$\beta _1, \dots , \beta _r$
and the form
 $\tilde {\gamma }_i$
is a linear combination of forms
$\tilde {\gamma }_i$
is a linear combination of forms
 $\gamma _1, \dots , \gamma _r$
,
$\gamma _1, \dots , \gamma _r$
, -
(ii) for all
 $x_{[k]}$
, we have
$x_{[k]}$
, we have  $$\begin{align*}\sum_{i \in [r]} \beta_i(x_I) \gamma_i(x_J) = \sum_{i \in [s]} \tilde{\beta}_i(x_I) \tilde{\gamma}_i(x_J), and\end{align*}$$
$$\begin{align*}\sum_{i \in [r]} \beta_i(x_I) \gamma_i(x_J) = \sum_{i \in [s]} \tilde{\beta}_i(x_I) \tilde{\gamma}_i(x_J), and\end{align*}$$
-
(iii) for each
 $i \in [s]$
, there exists
$i \in [s]$
, there exists
 $x_J \in G^J$
such that
$x_J \in G^J$
such that
 .
.
Proof Let
![]() $v_1, \dots , v_s \in \mathbb {F}_2^r$
be a maximal independent set of elements in
$v_1, \dots , v_s \in \mathbb {F}_2^r$
be a maximal independent set of elements in
![]() $\operatorname {Im} \gamma \subseteq \mathbb {F}_2^r$
. We may extend this sequence by
$\operatorname {Im} \gamma \subseteq \mathbb {F}_2^r$
. We may extend this sequence by
![]() $v_{s + 1}, \dots , v_r$
to obtain a basis of
$v_{s + 1}, \dots , v_r$
to obtain a basis of
![]() $\mathbb {F}_2^r$
. Let
$\mathbb {F}_2^r$
. Let
![]() $\tilde {\beta }_i = \sum _{j \in [r]} v_{i,j} \beta _j$
for each
$\tilde {\beta }_i = \sum _{j \in [r]} v_{i,j} \beta _j$
for each
![]() $i \in [r]$
. Since the matrix
$i \in [r]$
. Since the matrix
![]() $V = (v_{i,j})_{i,j \in [r]}$
is invertible, we may find its inverse
$V = (v_{i,j})_{i,j \in [r]}$
is invertible, we may find its inverse
![]() $M = (\mu _{i,j})_{i,j \in [r]}$
. Set
$M = (\mu _{i,j})_{i,j \in [r]}$
. Set
![]() $\tilde {\gamma }_i = \sum _{j \in [r]} \mu _{j,i} \gamma _j$
. Property (i) holds trivially. We claim that when
$\tilde {\gamma }_i = \sum _{j \in [r]} \mu _{j,i} \gamma _j$
. Property (i) holds trivially. We claim that when
![]() $i> s$
we have
$i> s$
we have
![]() $\tilde {\gamma }_i(x_J) = 0$
for all
$\tilde {\gamma }_i(x_J) = 0$
for all
![]() $x_J \in G^J$
. To see that, recall first that
$x_J \in G^J$
. To see that, recall first that
![]() $\gamma (x_J) \in \langle v_1, \dots , v_s \rangle $
, so there are scalars
$\gamma (x_J) \in \langle v_1, \dots , v_s \rangle $
, so there are scalars
![]() $\lambda _1, \dots , \lambda _s$
such that
$\lambda _1, \dots , \lambda _s$
such that
![]() $\gamma (x_J) = \sum _{j \in [s]} \lambda _j v_j$
.
$\gamma (x_J) = \sum _{j \in [s]} \lambda _j v_j$
.
Next, observe that

as claimed. Hence, for all
![]() $x_{[k]}$
, we have
$x_{[k]}$
, we have

proving property (ii).
For property (iii), for given
![]() $i \in [s]$
, take
$i \in [s]$
, take
![]() $x_J$
such that
$x_J$
such that
![]() $\gamma (x_J) = v_i$
. Let
$\gamma (x_J) = v_i$
. Let
![]() $j \in [s]$
. Then
$j \in [s]$
. Then
Using the multilinear forms change of basis lemma, we prove that for a given multilinear form
![]() $\phi $
of low partition rank, the lower-order forms in a decomposition of
$\phi $
of low partition rank, the lower-order forms in a decomposition of
![]() $\phi $
essentially come from
$\phi $
essentially come from
![]() $\phi $
. We want to keep track of the structure of low partition rank decomposition, and to that end, we need to define a partial order on partitions. Given two partitions
$\phi $
. We want to keep track of the structure of low partition rank decomposition, and to that end, we need to define a partial order on partitions. Given two partitions
![]() $A_1 \cup \dots \cup A_r = B_1 \cup \dots \cup B_s = [k]$
, where all sets are nonempty, we write
$A_1 \cup \dots \cup A_r = B_1 \cup \dots \cup B_s = [k]$
, where all sets are nonempty, we write
![]() $A_{[r]} \leq B_{[s]}$
if every set
$A_{[r]} \leq B_{[s]}$
if every set
![]() $B_i$
is a union of some sets among
$B_i$
is a union of some sets among
![]() $A_1, \dots , A_r$
. Thus, the trivial partition
$A_1, \dots , A_r$
. Thus, the trivial partition
![]() $\{[k]\}$
is the maximum element of this partially ordered set and
$\{[k]\}$
is the maximum element of this partially ordered set and
![]() $\{\{1\}, \dots , \{k\}\}$
is the minimum element. A set
$\{\{1\}, \dots , \{k\}\}$
is the minimum element. A set
![]() $\mathcal {P}$
of partitions of
$\mathcal {P}$
of partitions of
![]() $[k]$
is a downset if it has the property that whenever
$[k]$
is a downset if it has the property that whenever
![]() $A_{[r]} \leq B_{[s]}$
and
$A_{[r]} \leq B_{[s]}$
and
![]() $B_{[s]} \in \mathcal {P}$
, then
$B_{[s]} \in \mathcal {P}$
, then
![]() $A_{[r]} \in \mathcal {P}$
.
$A_{[r]} \in \mathcal {P}$
.
For a set of partitions
![]() $\mathcal {P}$
of the set
$\mathcal {P}$
of the set
![]() $[k]$
and a multilinear form
$[k]$
and a multilinear form
![]() $\alpha \colon G^k \to \mathbb {F}_2$
, we write
$\alpha \colon G^k \to \mathbb {F}_2$
, we write
![]() $\operatorname {prank}^{\mathcal {P}} \alpha \leq r$
if
$\operatorname {prank}^{\mathcal {P}} \alpha \leq r$
if
![]() $\alpha $
is a sum of at most r products of multilinear forms whose variable partitions belong to
$\alpha $
is a sum of at most r products of multilinear forms whose variable partitions belong to
![]() $\mathcal {P}$
. In the case when
$\mathcal {P}$
. In the case when
![]() $\mathcal {P}$
consists of all partitions except the trivial one
$\mathcal {P}$
consists of all partitions except the trivial one
![]() $\{[k]\}$
, we recover the usual notion of partition rank.
$\{[k]\}$
, we recover the usual notion of partition rank.
Proposition 3.3 Let
![]() $\phi \colon G^k \to \mathbb {F}_2$
be a multilinear form. Let
$\phi \colon G^k \to \mathbb {F}_2$
be a multilinear form. Let
![]() $\mathcal {P}$
be a downset of partitions. Suppose that
$\mathcal {P}$
be a downset of partitions. Suppose that
where each partition
![]() $\{I_{i,1}, \dots , I_{i, d_i}\}$
belongs to
$\{I_{i,1}, \dots , I_{i, d_i}\}$
belongs to
![]() $\mathcal {P}$
. Then there exists another decomposition
$\mathcal {P}$
. Then there exists another decomposition
where
![]() $r' \leq O(r^{O(1)})$
, such that each partition
$r' \leq O(r^{O(1)})$
, such that each partition
![]() $\{I^{\prime }_{i, 1}, \dots , I^{\prime }_{i, d^{\prime }_i}\}$
also belongs to
$\{I^{\prime }_{i, 1}, \dots , I^{\prime }_{i, d^{\prime }_i}\}$
also belongs to
![]() $\mathcal {P}$
and each
$\mathcal {P}$
and each
![]() $\beta ^{\prime }_{i,j}(x_{I^{\prime }_{i,j}})$
is of the shape
$\beta ^{\prime }_{i,j}(x_{I^{\prime }_{i,j}})$
is of the shape
![]() $\phi (x_{I^{\prime }_{i,j}}, y_{[k] \setminus I^{\prime }_{i,j}})$
for some fixed
$\phi (x_{I^{\prime }_{i,j}}, y_{[k] \setminus I^{\prime }_{i,j}})$
for some fixed
![]() $y_{[k] \setminus I^{\prime }_{i,j}}$
.
$y_{[k] \setminus I^{\prime }_{i,j}}$
.
Proof The proposition will follow from the next claim. In order to evade confusion with the notation for sets of partitions, we write
![]() $\mathsf {Pow} X$
for the power set of the set X.
$\mathsf {Pow} X$
for the power set of the set X.
Claim 3.4 For each nonempty downsetFootnote
1
![]() $\mathcal {U} \subseteq \mathsf {Pow}[k]$
, there exists a decomposition
$\mathcal {U} \subseteq \mathsf {Pow}[k]$
, there exists a decomposition
where
![]() $r' \leq O(r^{O(1)})$
, such that each partition
$r' \leq O(r^{O(1)})$
, such that each partition
![]() $\{I^{\prime }_{i, 1}, \dots , I^{\prime }_{i, d^{\prime }_i}\}$
belongs to
$\{I^{\prime }_{i, 1}, \dots , I^{\prime }_{i, d^{\prime }_i}\}$
belongs to
![]() $\mathcal {P}$
and if
$\mathcal {P}$
and if
![]() $I^{\prime }_{i,j} \notin \mathcal {U}$
, then
$I^{\prime }_{i,j} \notin \mathcal {U}$
, then
![]() $\beta ^{\prime }_{i,j}(x_{I^{\prime }_{i,j}})$
is of the shape
$\beta ^{\prime }_{i,j}(x_{I^{\prime }_{i,j}})$
is of the shape
![]() $\phi (x_{I^{\prime }_{i,j}}, y_{[k] \setminus I^{\prime }_{i,j}})$
for some fixed
$\phi (x_{I^{\prime }_{i,j}}, y_{[k] \setminus I^{\prime }_{i,j}})$
for some fixed
![]() $y_{[k] \setminus I^{\prime }_{i,j}}$
.
$y_{[k] \setminus I^{\prime }_{i,j}}$
.
Proof of the claim
We prove the claim by induction on
![]() $|\mathsf {Pow}[k] \setminus \mathcal {U}|$
. The base case is when
$|\mathsf {Pow}[k] \setminus \mathcal {U}|$
. The base case is when
![]() $\mathcal {U} = \mathsf {Pow}[k]$
, which makes the claim trivial. Suppose now that we have decomposition (3.2) for a given downset
$\mathcal {U} = \mathsf {Pow}[k]$
, which makes the claim trivial. Suppose now that we have decomposition (3.2) for a given downset
![]() $\mathcal {U}$
, and let
$\mathcal {U}$
, and let
![]() $I \in \mathcal {U}$
be a maximal set. Our goal is to remove I from
$I \in \mathcal {U}$
be a maximal set. Our goal is to remove I from
![]() $\mathcal {U}$
, that is to find a decomposition like that in (3.2) that has the desired properties for
$\mathcal {U}$
, that is to find a decomposition like that in (3.2) that has the desired properties for
![]() $\mathcal {U} \setminus \{I\}$
. This will prove the inductive step and thus prove the claim.
$\mathcal {U} \setminus \{I\}$
. This will prove the inductive step and thus prove the claim.
We may split the terms in decomposition (3.2) as
 $$ \begin{align}\phi(x_{[k]}) = \sum_{i \in [r_1]} \beta^{(1)}_{i, 1}(x_{I^{(1)}_{i, 1}}) \dots \beta^{(1)}_{i, d^{(1)}_i}(x_{I^{(1)}_{i, d^{(1)}_i}}) + &\sum_{i \in [r_2]} \beta^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})\nonumber\\ + &\sum_{i \in [r_3]} \beta^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}}),\end{align} $$
$$ \begin{align}\phi(x_{[k]}) = \sum_{i \in [r_1]} \beta^{(1)}_{i, 1}(x_{I^{(1)}_{i, 1}}) \dots \beta^{(1)}_{i, d^{(1)}_i}(x_{I^{(1)}_{i, d^{(1)}_i}}) + &\sum_{i \in [r_2]} \beta^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})\nonumber\\ + &\sum_{i \in [r_3]} \beta^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}}),\end{align} $$
where the terms
![]() $\beta ^{(1)}_{i, 1}(x_{I^{(1)}_{i, 1}}) \dots \beta ^{(1)}_{i, d^{(1)}_i}(x_{I^{(1)}_{i, d^{(1)}_i}})$
have the property that
$\beta ^{(1)}_{i, 1}(x_{I^{(1)}_{i, 1}}) \dots \beta ^{(1)}_{i, d^{(1)}_i}(x_{I^{(1)}_{i, d^{(1)}_i}})$
have the property that
![]() $I^{(1)}_{i, 1} = I$
for all
$I^{(1)}_{i, 1} = I$
for all
![]() $i \in [r_1]$
, the terms
$i \in [r_1]$
, the terms
![]() $\beta ^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta ^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})$
have the property that
$\beta ^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta ^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})$
have the property that
![]() $I \subsetneq I^{(2)}_{i, 1}$
for all
$I \subsetneq I^{(2)}_{i, 1}$
for all
![]() $i \in [r_2]$
, and the terms
$i \in [r_2]$
, and the terms
![]() $\beta ^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta ^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}})$
have the property that I is not contained in any of the sets
$\beta ^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta ^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}})$
have the property that I is not contained in any of the sets
![]() $I^{(3)}_{i, 1}, \dots , I^{(3)}_{i, d^{(3)}_i}$
for
$I^{(3)}_{i, 1}, \dots , I^{(3)}_{i, d^{(3)}_i}$
for
![]() $i \in [r_3]$
. For
$i \in [r_3]$
. For
![]() $i \in [r_1]$
, let
$i \in [r_1]$
, let
![]() $\gamma _i$
be the multilinear form defined by
$\gamma _i$
be the multilinear form defined by
![]() $\gamma _i(x_{[k] \setminus I}) = \beta ^{(1)}_{i, 2}(x_{I^{(1)}_{i, 2}}) \dots \beta ^{(1)}_{i, d^{(1)}_i}(x_{I^{(1)}_{i, d^{(1)}_i}})$
. Decomposition (3.3) becomes
$\gamma _i(x_{[k] \setminus I}) = \beta ^{(1)}_{i, 2}(x_{I^{(1)}_{i, 2}}) \dots \beta ^{(1)}_{i, d^{(1)}_i}(x_{I^{(1)}_{i, d^{(1)}_i}})$
. Decomposition (3.3) becomes
 $$ \begin{align*}\phi(x_{[k]}) = \sum_{i \in [r_1]} \beta^{(1)}_{i, 1}(x_I) \gamma_i(x_{[k] \setminus I}) + &\sum_{i \in [r_2]} \beta^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})\\ + &\sum_{i \in [r_3]} \beta^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}}).\end{align*} $$
$$ \begin{align*}\phi(x_{[k]}) = \sum_{i \in [r_1]} \beta^{(1)}_{i, 1}(x_I) \gamma_i(x_{[k] \setminus I}) + &\sum_{i \in [r_2]} \beta^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})\\ + &\sum_{i \in [r_3]} \beta^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}}).\end{align*} $$
Applying Lemma 3.2, we obtain a positive integer
![]() $s \leq r_1$
and multilinear forms
$s \leq r_1$
and multilinear forms
![]() $\tilde {\beta }_1, \dots , \tilde {\beta }_s \in \langle \beta ^{(1)}_{i, 1} \colon i \in [r_1]\rangle $
and
$\tilde {\beta }_1, \dots , \tilde {\beta }_s \in \langle \beta ^{(1)}_{i, 1} \colon i \in [r_1]\rangle $
and
![]() $\tilde {\gamma }_1, \dots , \tilde {\gamma }_s \in \langle \gamma _i \colon i \in [r_1]\rangle $
such that
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_s \in \langle \gamma _i \colon i \in [r_1]\rangle $
such that
 $$ \begin{align}\phi(x_{[k]}) = \sum_{i \in [s]} \tilde{\beta}_i(x_I) \tilde{\gamma}_i(x_{[k] \setminus I}) + &\sum_{i \in [r_2]} \beta^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})\nonumber\\ + &\sum_{i \in [r_3]} \beta^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}}),\end{align} $$
$$ \begin{align}\phi(x_{[k]}) = \sum_{i \in [s]} \tilde{\beta}_i(x_I) \tilde{\gamma}_i(x_{[k] \setminus I}) + &\sum_{i \in [r_2]} \beta^{(2)}_{i, 1}(x_{I^{(2)}_{i, 1}}) \dots \beta^{(2)}_{i, d^{(2)}_i}(x_{I^{(2)}_{i, d^{(2)}_i}})\nonumber\\ + &\sum_{i \in [r_3]} \beta^{(3)}_{i, 1}(x_{I^{(3)}_{i, 1}}) \dots \beta^{(3)}_{i, d^{(3)}_i}(x_{I^{(3)}_{i, d^{(3)}_i}}),\end{align} $$
and for each
![]() $i \in [s]$
, there exists
$i \in [s]$
, there exists
![]() $x_{[k] \setminus I} \in G^{[k] \setminus I}$
such that
$x_{[k] \setminus I} \in G^{[k] \setminus I}$
such that
![]() . Fix arbitrary
. Fix arbitrary
![]() $i \in [s]$
and take
$i \in [s]$
and take
![]() $y_{[k] \setminus I}$
such that
$y_{[k] \setminus I}$
such that
![]() . Evaluating decomposition (3.4) at
. Evaluating decomposition (3.4) at
![]() $(x_I, y_{[k] \setminus I})$
gives
$(x_I, y_{[k] \setminus I})$
gives
for some multilinear form
![]() $\psi $
of partition rank at most
$\psi $
of partition rank at most
![]() $r_3$
. Since the index set of arguments of the form
$r_3$
. Since the index set of arguments of the form
![]() $\beta ^{(2)}_{i, 1}$
does not belong to
$\beta ^{(2)}_{i, 1}$
does not belong to
![]() $\mathcal {U}$
, we know that
$\mathcal {U}$
, we know that
![]() $\beta ^{(2)}_{i, 1}(x_I, y_{I^{(2)}_{i, 1} \setminus I}) = \phi (x_I, z_{[k] \setminus I})$
for a suitable
$\beta ^{(2)}_{i, 1}(x_I, y_{I^{(2)}_{i, 1} \setminus I}) = \phi (x_I, z_{[k] \setminus I})$
for a suitable
![]() $z_{[k] \setminus I}$
. Replacing each
$z_{[k] \setminus I}$
. Replacing each
![]() $\tilde {\beta }_i$
with a sum of at most
$\tilde {\beta }_i$
with a sum of at most
![]() $r_2 + 1$
forms coming from slices of
$r_2 + 1$
forms coming from slices of
![]() $\phi $
and a form of partition rank at most
$\phi $
and a form of partition rank at most
![]() $r_3$
, and recalling that each
$r_3$
, and recalling that each
![]() $\tilde {\gamma }_i \in \langle \gamma _i \colon i \in [r_1]\rangle $
, we conclude that
$\tilde {\gamma }_i \in \langle \gamma _i \colon i \in [r_1]\rangle $
, we conclude that
where
![]() $r" \leq r^2_1r_2 + r^2_1r_3 + r^2_1 + r_2 + r_3 \leq O(r^{O(1)})$
, such that each partition
$r" \leq r^2_1r_2 + r^2_1r_3 + r^2_1 + r_2 + r_3 \leq O(r^{O(1)})$
, such that each partition
![]() $\{I^{\prime \prime }_{i, 1}, \dots , I^{\prime \prime }_{i, d^{\prime \prime }_i}\}$
belongs to
$\{I^{\prime \prime }_{i, 1}, \dots , I^{\prime \prime }_{i, d^{\prime \prime }_i}\}$
belongs to
![]() $\mathcal {P}$
and if
$\mathcal {P}$
and if
![]() $I^{\prime \prime }_{i,j} \notin (\mathcal {U} \setminus \{I\})$
, then
$I^{\prime \prime }_{i,j} \notin (\mathcal {U} \setminus \{I\})$
, then
![]() $\beta ^{\prime \prime }_{i,j}(x_{I^{\prime \prime }_{i,j}})$
is of the shape
$\beta ^{\prime \prime }_{i,j}(x_{I^{\prime \prime }_{i,j}})$
is of the shape
![]() $\phi (x_{I^{\prime \prime }_{i,j}}, y_{[k] \setminus I^{\prime \prime }_{i,j}})$
for some fixed
$\phi (x_{I^{\prime \prime }_{i,j}}, y_{[k] \setminus I^{\prime \prime }_{i,j}})$
for some fixed
![]() $y_{[k] \setminus I^{\prime \prime }_{i,j}}$
, completing the proof of the step of the procedure. The procedure terminates after
$y_{[k] \setminus I^{\prime \prime }_{i,j}}$
, completing the proof of the step of the procedure. The procedure terminates after
![]() $2^k - 1$
steps when the collection
$2^k - 1$
steps when the collection
![]() $\mathcal {U}$
becomes
$\mathcal {U}$
becomes
![]() $\{\emptyset \}$
.
$\{\emptyset \}$
.
Use the case
![]() $\mathcal {U} = \{\emptyset \}$
of the claim above, which is equivalent to the proposition.
$\mathcal {U} = \{\emptyset \}$
of the claim above, which is equivalent to the proposition.
4 Approximately symmetric multilinear forms
This section is devoted to the proofs of Theorems 1.6–1.8. In order to prove these theorems, we need a weak regularity lemma for multilinear forms that takes into account the symmetry properties of the given forms. Namely, we start with multilinear forms in variables
![]() $x_{[k]}$
that are symmetric in the first m variables and are interested in how far the given forms are from being symmetric in variables
$x_{[k]}$
that are symmetric in the first m variables and are interested in how far the given forms are from being symmetric in variables
![]() $x_{[m+1]}$
. The lemma allows us to express the given forms in terms of further multilinear forms that are also symmetric in the first m variables and have one of the following three additional properties:
$x_{[m+1]}$
. The lemma allows us to express the given forms in terms of further multilinear forms that are also symmetric in the first m variables and have one of the following three additional properties:
-
• Additional form
 $\alpha (x_{[k]})$
has the property that
$\alpha (x_{[k]})$
has the property that
 $\operatorname {prank} \Big (\alpha + \alpha \circ (m \,\,m+1) \Big )$
is small (this is the almost symmetric case).
$\operatorname {prank} \Big (\alpha + \alpha \circ (m \,\,m+1) \Big )$
is small (this is the almost symmetric case). -
• Additional form
 $\alpha (x_{[k]})$
has the property that
$\alpha (x_{[k]})$
has the property that
 $\operatorname {prank} \Big (\alpha + \alpha \circ (m \,\,m+1) \Big )$
is large, but
$\operatorname {prank} \Big (\alpha + \alpha \circ (m \,\,m+1) \Big )$
is large, but
 $\operatorname {prank} \Big (\sum _{i \in [m+1]} \alpha \circ (i \,\,m+1)\Big )$
is small (this is the partially symmetric case).
$\operatorname {prank} \Big (\sum _{i \in [m+1]} \alpha \circ (i \,\,m+1)\Big )$
is small (this is the partially symmetric case). -
• Additional form
 $\alpha (x_{[k]})$
has the property that the partition rank of nonzero linear combinations of forms
$\alpha (x_{[k]})$
has the property that the partition rank of nonzero linear combinations of forms
 $\alpha \circ (i \,\,m+1)$
is large (this is the asymmetric case).
$\alpha \circ (i \,\,m+1)$
is large (this is the asymmetric case).
We shall denote the forms in almost symmetric, partially symmetric, and asymmetric cases with greek letters
![]() $\sigma $
,
$\sigma $
,
![]() $\pi $
, and
$\pi $
, and
![]() $\rho $
, respectively.
$\rho $
, respectively.
For a positive quantity R, we write
![]() $\operatorname {PR}_{\leq R}$
for the collection of all multilinear forms of the partition rank at most R.
$\operatorname {PR}_{\leq R}$
for the collection of all multilinear forms of the partition rank at most R.
Lemma 4.1 Suppose that we are given some forms
![]() $\gamma _1, \dots , \gamma _r \colon G^k \to \mathbb {F}_2$
which are symmetric in the first m variables, where
$\gamma _1, \dots , \gamma _r \colon G^k \to \mathbb {F}_2$
which are symmetric in the first m variables, where
![]() $k \geq m + 1$
. Let
$k \geq m + 1$
. Let
![]() $C, D \geq 2$
be given.Footnote
2
Then there exist a positive integer
$C, D \geq 2$
be given.Footnote
2
Then there exist a positive integer
![]() $R \leq C^{D^{O_k(r)}}$
and further forms
$R \leq C^{D^{O_k(r)}}$
and further forms
![]() $\sigma _1, \dots , \sigma _s, \pi _1, \dots , \pi _q, \rho _1, \dots , \rho _t$
, where
$\sigma _1, \dots , \sigma _s, \pi _1, \dots , \pi _q, \rho _1, \dots , \rho _t$
, where
![]() $s + q + t \leq r$
, such that:
$s + q + t \leq r$
, such that:
-
(i)
 $\sigma _i, \pi _i$
, and
$\sigma _i, \pi _i$
, and
 $\rho _i$
are linear combinations of forms
$\rho _i$
are linear combinations of forms
 $\gamma _1, \dots , \gamma _r$
,
$\gamma _1, \dots , \gamma _r$
, -
(ii)
 $\operatorname {prank}\Big (\sigma _i + \sigma _i \circ (m\,\,m+1)\Big ) \leq R$
,
$\operatorname {prank}\Big (\sigma _i + \sigma _i \circ (m\,\,m+1)\Big ) \leq R$
, -
(iii)
 $\pi _i$
has the property that
$\pi _i$
has the property that
 $\operatorname {prank}\Big (\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)\Big ) \leq R$
,
$\operatorname {prank}\Big (\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)\Big ) \leq R$
, -
(iv) any linear combination of forms
 $\sigma _i$
for
$\sigma _i$
for
 $i \in [s]$
,
$i \in [s]$
,
 $\pi _i \circ (\ell \,\,m + 1)$
for
$\pi _i \circ (\ell \,\,m + 1)$
for
 $i \in [q], \ell \in [m + 1]$
and
$i \in [q], \ell \in [m + 1]$
and
 $\rho _i \circ (\ell \,\, m+1)$
for
$\rho _i \circ (\ell \,\, m+1)$
for
 $i \in [t], \ell \in [m + 1]$
has partition rank at least
$i \in [t], \ell \in [m + 1]$
has partition rank at least
 $(C(R + 2r))^D$
, unless the nonzero coefficients appear only next to the forms
$(C(R + 2r))^D$
, unless the nonzero coefficients appear only next to the forms
 $\pi _i \circ (\ell \,\,m + 1)$
and do not depend on
$\pi _i \circ (\ell \,\,m + 1)$
and do not depend on
 $\ell $
for each i, making it a linear combination of sums
$\ell $
for each i, making it a linear combination of sums
 $\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)$
for
$\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)$
for
 $i \in [q]$
, and
$i \in [q]$
, and -
(v) for all
 $j \in [r]$
, we have
$j \in [r]$
, we have  $$\begin{align*}&\gamma_j \in \langle \sigma_i \colon i \in [s]\rangle + \langle \pi_i \circ (\ell\,\,m + 1) \colon i \in [q], \ell \in [m + 1]\rangle\\&\quad + \langle \rho_i \circ (\ell\,\,m + 1) \colon i \in [t], \ell \in [m + 1]\rangle + \operatorname{PR}_{\leq R}.\end{align*}$$
$$\begin{align*}&\gamma_j \in \langle \sigma_i \colon i \in [s]\rangle + \langle \pi_i \circ (\ell\,\,m + 1) \colon i \in [q], \ell \in [m + 1]\rangle\\&\quad + \langle \rho_i \circ (\ell\,\,m + 1) \colon i \in [t], \ell \in [m + 1]\rangle + \operatorname{PR}_{\leq R}.\end{align*}$$
Remark 4.2 When
![]() $m = 1$
, we may rename the forms
$m = 1$
, we may rename the forms
![]() $\pi _{[q]}$
to
$\pi _{[q]}$
to
![]() $\sigma _{[s + 1, s + q]}$
, as conditions (ii) and (iii) become the same. In the proof of Theorems 1.7 and 1.8, we shall also make use of
$\sigma _{[s + 1, s + q]}$
, as conditions (ii) and (iii) become the same. In the proof of Theorems 1.7 and 1.8, we shall also make use of
![]() $m = 0$
case, in which case the symmetry properties of forms play no role and we end up only with forms
$m = 0$
case, in which case the symmetry properties of forms play no role and we end up only with forms
![]() $\sigma _{[s]}$
which satisfy conditions (iv) and (v).
$\sigma _{[s]}$
which satisfy conditions (iv) and (v).
Proof Let us begin by setting
![]() $s= 0$
,
$s= 0$
,
![]() $q = 0$
,
$q = 0$
,
![]() $t = r$
,
$t = r$
,
![]() $\rho _1 = \gamma _1, \dots , \rho _t = \gamma _t$
, and
$\rho _1 = \gamma _1, \dots , \rho _t = \gamma _t$
, and
![]() $R = 1$
, which satisfies all conditions except possibly the fourth. At each step, we modify the sequence of forms
$R = 1$
, which satisfies all conditions except possibly the fourth. At each step, we modify the sequence of forms
![]() $\sigma _{[s]}, \pi _{[q]}, \rho _{[t]}$
, decreasing the quantity
$\sigma _{[s]}, \pi _{[q]}, \rho _{[t]}$
, decreasing the quantity
![]() $Q = s + 10q + 100t$
and preserving all properties but the fourth. The quantity R will increase at each step as well.
$Q = s + 10q + 100t$
and preserving all properties but the fourth. The quantity R will increase at each step as well.
Suppose that at some step the fourth condition still fails. Hence, a linear combination
has partition rank at most
![]() $(C(R + 2r))^D$
and it is not a linear combination of sums
$(C(R + 2r))^D$
and it is not a linear combination of sums
![]() $\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)$
. We consider two separate cases depending on the behavior of the coefficients in the above expression.
$\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)$
. We consider two separate cases depending on the behavior of the coefficients in the above expression.
Case 1. For each
![]() $i \in [q]$
, the coefficients
$i \in [q]$
, the coefficients
![]() $\mu _{i, \ell }$
do not depend on
$\mu _{i, \ell }$
do not depend on
![]() $\ell $
, and for each
$\ell $
, and for each
![]() $i \in [t]$
, the coefficients
$i \in [t]$
, the coefficients
![]() $\nu _{i, \ell }$
do not depend on
$\nu _{i, \ell }$
do not depend on
![]() $\ell $
. By assumptions in this case, there are coefficients
$\ell $
. By assumptions in this case, there are coefficients
![]() $\mu _i$
and
$\mu _i$
and
![]() $\nu _i$
such that
$\nu _i$
such that
 $$\begin{align*}\operatorname{prank}\bigg(\sum_{i \in [s]} \lambda_i \sigma_i + \sum_{i \in [q]} \mu_i \Big(\sum_{\ell \in [m+1]} \pi_i \circ (\ell \,\, m + 1)\kern-1.2pt\Big) + \sum_{i \in [t]} \nu_{i} \Big(\sum_{\ell \in [m+1]} \rho_i \circ (\ell \,\,m + 1)\Big)\kern-1.2pt\bigg) \leq (C(R + 2r))^D.\end{align*}$$
$$\begin{align*}\operatorname{prank}\bigg(\sum_{i \in [s]} \lambda_i \sigma_i + \sum_{i \in [q]} \mu_i \Big(\sum_{\ell \in [m+1]} \pi_i \circ (\ell \,\, m + 1)\kern-1.2pt\Big) + \sum_{i \in [t]} \nu_{i} \Big(\sum_{\ell \in [m+1]} \rho_i \circ (\ell \,\,m + 1)\Big)\kern-1.2pt\bigg) \leq (C(R + 2r))^D.\end{align*}$$
If there is some
![]() $\lambda _i \not = 0$
, we may simply remove
$\lambda _i \not = 0$
, we may simply remove
![]() $\sigma _i$
from the list
$\sigma _i$
from the list
![]() $\sigma _{[s]}$
, which results in decreasing the quantity Q, noting that the fifth condition still holds as long as we replace R by
$\sigma _{[s]}$
, which results in decreasing the quantity Q, noting that the fifth condition still holds as long as we replace R by
![]() $R + (C(R + 2r))^D$
. Otherwise, assume that all
$R + (C(R + 2r))^D$
. Otherwise, assume that all
![]() $\lambda _i = 0$
. Therefore, some
$\lambda _i = 0$
. Therefore, some
![]() $\nu _j \not = 0$
. Remove
$\nu _j \not = 0$
. Remove
![]() $\rho _j$
from the list
$\rho _j$
from the list
![]() $\rho _{[t]}$
and add new form
$\rho _{[t]}$
and add new form
This decreases t by 1, increases q by 1, and thus the quantity Q decreases as well. All conditions except the fourth one are still satisfied, provided we replace R by
![]() $R + (C(R + 2r))^D$
.
$R + (C(R + 2r))^D$
.
Case 2. There exist indices
![]() $\ell , \ell ' \leq m+1$
and
$\ell , \ell ' \leq m+1$
and
![]() $i_0$
such that
$i_0$
such that
![]() $\mu _{i_0, \ell } = 1, \mu _{i_0, \ell '} = 0$
or
$\mu _{i_0, \ell } = 1, \mu _{i_0, \ell '} = 0$
or
![]() ${\nu _{i_0, \ell } = 1, \nu _{i_0, \ell '} = 0}$
. Let
${\nu _{i_0, \ell } = 1, \nu _{i_0, \ell '} = 0}$
. Let
![]() $\phi $
be the linear combination of forms in (4.1). Note that
$\phi $
be the linear combination of forms in (4.1). Note that
 $$ \begin{align}&\phi(x_{[k]}) + \phi \circ (\ell \,\,\ell')(x_{[k]}) = \sum_{i \in [s]} \lambda_i \Big(\sigma_i + \sigma_i \circ (\ell \,\,\ell')\Big) \nonumber\\&\quad+ \sum_{i \in [q] , a \in [m+1]} \mu_{i, a} \Big(\pi_i \circ (a \,\, m + 1) + \pi_i \circ (a \,\, m + 1) \circ (\ell \,\,\ell')\Big)\nonumber\\ &\quad+ \sum_{i \in [t] ,a \in [m+1]} \nu_{i, a} \Big(\rho_i \circ (a \,\,m + 1) + \rho_i \circ (a \,\,m + 1) \circ (\ell \,\,\ell')\Big)\end{align} $$
$$ \begin{align}&\phi(x_{[k]}) + \phi \circ (\ell \,\,\ell')(x_{[k]}) = \sum_{i \in [s]} \lambda_i \Big(\sigma_i + \sigma_i \circ (\ell \,\,\ell')\Big) \nonumber\\&\quad+ \sum_{i \in [q] , a \in [m+1]} \mu_{i, a} \Big(\pi_i \circ (a \,\, m + 1) + \pi_i \circ (a \,\, m + 1) \circ (\ell \,\,\ell')\Big)\nonumber\\ &\quad+ \sum_{i \in [t] ,a \in [m+1]} \nu_{i, a} \Big(\rho_i \circ (a \,\,m + 1) + \rho_i \circ (a \,\,m + 1) \circ (\ell \,\,\ell')\Big)\end{align} $$
and has partition rank at most
![]() $2(C(R + 2r))^D$
. Using the symmetry properties, we obtain
$2(C(R + 2r))^D$
. Using the symmetry properties, we obtain
 $$ \begin{align*}\operatorname{prank} \bigg(& \sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'})\Big(\pi_i \circ (\ell \,\, m + 1) + \pi_i \circ (\ell' \,\, m + 1)\Big) \\ &+ \sum_{i \in [t]}(\nu_{i, \ell} + \nu_{i, \ell'})\Big(\rho_i \circ (\ell \,\, m + 1) + \rho_i \circ (\ell' \,\, m + 1)\Big)\bigg) \leq 2(C(R + 2r))^D + sR.\end{align*} $$
$$ \begin{align*}\operatorname{prank} \bigg(& \sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'})\Big(\pi_i \circ (\ell \,\, m + 1) + \pi_i \circ (\ell' \,\, m + 1)\Big) \\ &+ \sum_{i \in [t]}(\nu_{i, \ell} + \nu_{i, \ell'})\Big(\rho_i \circ (\ell \,\, m + 1) + \rho_i \circ (\ell' \,\, m + 1)\Big)\bigg) \leq 2(C(R + 2r))^D + sR.\end{align*} $$
Define a multilinear form
![]() $\tilde {\sigma }$
as
$\tilde {\sigma }$
as
This form satisfies
![]() $\operatorname {prank} (\tilde {\sigma } \circ (\ell \,\, m + 1) + \tilde {\sigma } \circ (\ell ' \,\, m + 1)) \leq 2(C(R + 2r))^D + sR$
and is a linear combination of forms
$\operatorname {prank} (\tilde {\sigma } \circ (\ell \,\, m + 1) + \tilde {\sigma } \circ (\ell ' \,\, m + 1)) \leq 2(C(R + 2r))^D + sR$
and is a linear combination of forms
![]() $\gamma _1, \dots , \gamma _r$
. It follows that
$\gamma _1, \dots , \gamma _r$
. It follows that
![]() $\operatorname {prank} (\tilde {\sigma } + \tilde {\sigma } \circ (m \,\, m + 1)) \leq 2(C(R + 2r))^D + sR$
.
$\operatorname {prank} (\tilde {\sigma } + \tilde {\sigma } \circ (m \,\, m + 1)) \leq 2(C(R + 2r))^D + sR$
.
By assumptions in this case of the proof, we see that
![]() $\tilde {\sigma }$
is a nontrivial linear combination of the forms in (4.3). Thus, we may remove a form
$\tilde {\sigma }$
is a nontrivial linear combination of the forms in (4.3). Thus, we may remove a form
![]() $\pi _i$
or
$\pi _i$
or
![]() $\rho _i$
that appears with the nonzero coefficient in (4.3) from its list, set
$\rho _i$
that appears with the nonzero coefficient in (4.3) from its list, set
![]() $\sigma _{s+1} = \tilde {\sigma }$
, and replace R by
$\sigma _{s+1} = \tilde {\sigma }$
, and replace R by
to make sure that the fifth condition is still satisfied. As Q decreases in this case as well, the proof is complete after at most
![]() $100r$
steps (this was the initial value of the quantity Q). The bound on R is given by starting from
$100r$
steps (this was the initial value of the quantity Q). The bound on R is given by starting from
![]() $R = 1$
and replacing R by the value in (4.4) at most
$R = 1$
and replacing R by the value in (4.4) at most
![]() $100r$
times.
$100r$
times.
In fact, we can say more about the linear combinations of the additional forms in Lemma 4.1.
Observation 4.3 Let
![]() $\sigma _{[s]}, \pi _{[q]}, \rho _{[t]}, C, D, R$
be as in the previous lemma, and let
$\sigma _{[s]}, \pi _{[q]}, \rho _{[t]}, C, D, R$
be as in the previous lemma, and let
![]() $\tau $
be a multilinear form of partition rank at most R. (Recall that we assume that
$\tau $
be a multilinear form of partition rank at most R. (Recall that we assume that
![]() $C, D \geq 2$
.) Suppose that
$C, D \geq 2$
.) Suppose that
is symmetric in the first m variables. Then we have
![]() $\mu _{i, \ell } = \mu _{i, \ell '}$
and
$\mu _{i, \ell } = \mu _{i, \ell '}$
and
![]() $\nu _{i, \ell } = \nu _{i, \ell '}$
for all
$\nu _{i, \ell } = \nu _{i, \ell '}$
for all
![]() $\ell , \ell ' \in [m]$
.
$\ell , \ell ' \in [m]$
.
Moreover, if
![]() $\phi $
is symmetric in the first
$\phi $
is symmetric in the first
![]() $m+1$
variables, then
$m+1$
variables, then
for suitable scalars
![]() $\tilde {\nu }_i$
.
$\tilde {\nu }_i$
.
Proof Let
![]() $\ell , \ell ' \in [m]$
be two distinct indices. By the symmetry assumption, applying the transposition
$\ell , \ell ' \in [m]$
be two distinct indices. By the symmetry assumption, applying the transposition
![]() $(\ell \,\,\ell ')$
, we see that
$(\ell \,\,\ell ')$
, we see that
 $$ \begin{align*}0 = &\sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell \,\, m + 1) + \sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell' \,\, m + 1) \\ &+ \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell \,\, m + 1) + \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell' \,\, m + 1) + \tau + \tau \circ (\ell \,\,\ell').\end{align*} $$
$$ \begin{align*}0 = &\sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell \,\, m + 1) + \sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell' \,\, m + 1) \\ &+ \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell \,\, m + 1) + \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell' \,\, m + 1) + \tau + \tau \circ (\ell \,\,\ell').\end{align*} $$
By property (iv) (we now use the assumption that
![]() $C \geq 2$
) of the forms in the previous lemma, we have that
$C \geq 2$
) of the forms in the previous lemma, we have that
 $$ \begin{align}&\sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell \,\, m + 1) + \sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell' \,\, m + 1) \nonumber\\ &\hspace{2cm}+ \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell \,\, m + 1) + \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell' \,\, m + 1)\end{align} $$
$$ \begin{align}&\sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell \,\, m + 1) + \sum_{i \in [q]} (\mu_{i, \ell} + \mu_{i, \ell'}) \pi_i \circ (\ell' \,\, m + 1) \nonumber\\ &\hspace{2cm}+ \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell \,\, m + 1) + \sum_{i \in [t]} (\nu_{i, \ell} + \nu_{i, \ell'}) \rho_i \circ (\ell' \,\, m + 1)\end{align} $$
has to be a linear combination of sums
![]() $\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)$
. However,
$\sum _{\ell \in [m + 1]} \pi _i \circ (\ell \,\,m + 1)$
. However,
![]() $\pi _i = \pi _i \circ (m+1 \,\,m+1)$
does not appear in (4.5) for any i; hence, the displayed expression has to be zero, making
$\pi _i = \pi _i \circ (m+1 \,\,m+1)$
does not appear in (4.5) for any i; hence, the displayed expression has to be zero, making
![]() $\mu _{i, \ell } = \mu _{i, \ell '}$
and
$\mu _{i, \ell } = \mu _{i, \ell '}$
and
![]() $\nu _{i, \ell } = \nu _{i, \ell '}$
, as desired.
$\nu _{i, \ell } = \nu _{i, \ell '}$
, as desired.
Suppose now that
![]() $\phi $
is symmetric in variables
$\phi $
is symmetric in variables
![]() $x_{[m+1]}$
. Note that
$x_{[m+1]}$
. Note that
 $$ \begin{align*}\phi = &\phi \circ (m\,\,m+1) = \sum_{i \in [s]} \lambda_i \sigma_i \circ (m\,\,m+1) \\&+ \sum_{i \in [q]} \Big(\sum_{\ell \in [m-1]} \mu_{i, \ell} \pi_i \circ (\ell \,\, m + 1) + \mu_{i, m + 1} \pi_i \circ (m + 1 \,\,m) + \mu_{i, m} \pi_i\Big)\\ &+ \sum_{i \in [t]} \kern-1pt\Big(\kern-1pt\sum_{\ell \in [m-1]} \nu_{i, \ell} \rho_i \circ (\ell \,\, m \kern1.3pt{+}\kern1.3pt 1) + \nu_{i, m\kern1.3pt{+}\kern1.3pt1} \rho_i \circ (m \,\,m \kern1.3pt{+}\kern1.3pt 1) \kern1.3pt{+} \nu_{i,m} \rho_i\Big) \kern1.3pt{+}\kern1.3pt \tau\circ (m \,\,m\kern1.3pt{+}\kern1.3pt 1 ).\end{align*} $$
$$ \begin{align*}\phi = &\phi \circ (m\,\,m+1) = \sum_{i \in [s]} \lambda_i \sigma_i \circ (m\,\,m+1) \\&+ \sum_{i \in [q]} \Big(\sum_{\ell \in [m-1]} \mu_{i, \ell} \pi_i \circ (\ell \,\, m + 1) + \mu_{i, m + 1} \pi_i \circ (m + 1 \,\,m) + \mu_{i, m} \pi_i\Big)\\ &+ \sum_{i \in [t]} \kern-1pt\Big(\kern-1pt\sum_{\ell \in [m-1]} \nu_{i, \ell} \rho_i \circ (\ell \,\, m \kern1.3pt{+}\kern1.3pt 1) + \nu_{i, m\kern1.3pt{+}\kern1.3pt1} \rho_i \circ (m \,\,m \kern1.3pt{+}\kern1.3pt 1) \kern1.3pt{+} \nu_{i,m} \rho_i\Big) \kern1.3pt{+}\kern1.3pt \tau\circ (m \,\,m\kern1.3pt{+}\kern1.3pt 1 ).\end{align*} $$
Hence,
![]() $0 = \phi + \phi \circ (m\,\,m+1)$
belongs to
$0 = \phi + \phi \circ (m\,\,m+1)$
belongs to
 $$\begin{align*}&\sum_{i \in [q]} (\mu_{i, m} + \mu_{i, m + 1}) \Big(\pi_i \circ (m \,\,m+ 1) + \pi_i\Big) \\&\quad+ \sum_{i \in [t]}(\nu_{i, m} + \nu_{i, m+1}) \Big( \rho_i \circ (m \,\,m + 1) + \rho_i\Big) + \operatorname{PR}_{\leq (s + 2)R}.\end{align*}$$
$$\begin{align*}&\sum_{i \in [q]} (\mu_{i, m} + \mu_{i, m + 1}) \Big(\pi_i \circ (m \,\,m+ 1) + \pi_i\Big) \\&\quad+ \sum_{i \in [t]}(\nu_{i, m} + \nu_{i, m+1}) \Big( \rho_i \circ (m \,\,m + 1) + \rho_i\Big) + \operatorname{PR}_{\leq (s + 2)R}.\end{align*}$$
If
![]() $m = 1$
, by the remark following the previous lemma, we may assume that forms
$m = 1$
, by the remark following the previous lemma, we may assume that forms
![]() $\pi _i$
do not appear, and if
$\pi _i$
do not appear, and if
![]() $m \geq 2$
, then
$m \geq 2$
, then
![]() $\pi _i \circ (1 \,\,m+ 1)$
does not appear in the above expression. By property (iv) of Lemma 4.1 (we now use the assumption that
$\pi _i \circ (1 \,\,m+ 1)$
does not appear in the above expression. By property (iv) of Lemma 4.1 (we now use the assumption that
![]() $C \geq 2, D \geq 2$
), it follows that
$C \geq 2, D \geq 2$
), it follows that
![]() $\mu _{i, m} = \mu _{i, m + 1}$
(in the case
$\mu _{i, m} = \mu _{i, m + 1}$
(in the case
![]() $m \geq 2$
) and
$m \geq 2$
) and
![]() $\nu _{i, m} = \nu _{i, m + 1}$
. Let
$\nu _{i, m} = \nu _{i, m + 1}$
. Let
![]() $\tilde {\nu }_i = \nu _{i,1} = \dots = \nu _{i, m+1}$
. The observation follows from the property (iii) of Lemma 4.1.
$\tilde {\nu }_i = \nu _{i,1} = \dots = \nu _{i, m+1}$
. The observation follows from the property (iii) of Lemma 4.1.
4.1 Symmetry in
 $x_1$
and
$x_1$
and
 $x_2$
$x_2$
We prove Theorem 1.6 in this subsection.
Proof of Theorem 1.6
During the proof, we consider decompositions of the shape
 $$ \begin{align}&\alpha(x_1, x_2, x_3, \dots, x_k) + \alpha(x_2, x_1, x_3, \dots, x_k) = \sum_{i \in [r_1]} \beta_i(x_1, x_2, x_{I_{i}}) \beta^{\prime}_{i, 1}(z_{I^{\prime}_{i, 1}}) \cdots \beta^{\prime}_{i, d_i}(z_{I^{\prime}_{i, d_i}})\nonumber \\&\qquad+ \sum_{i \in [r_2]} \gamma_i(x_1, x_{J_{i, 1}}) \gamma^{\prime}_i(x_2, x_{J_{i, 2}})\gamma^{\prime\prime}_{i, 1}(x_{J^{\prime}_{i, 1}}) \cdots \gamma^{\prime\prime}_{i, d^{\prime}_i}(x_{J^{\prime}_{i, d^{\prime}_i}})\end{align} $$
$$ \begin{align}&\alpha(x_1, x_2, x_3, \dots, x_k) + \alpha(x_2, x_1, x_3, \dots, x_k) = \sum_{i \in [r_1]} \beta_i(x_1, x_2, x_{I_{i}}) \beta^{\prime}_{i, 1}(z_{I^{\prime}_{i, 1}}) \cdots \beta^{\prime}_{i, d_i}(z_{I^{\prime}_{i, d_i}})\nonumber \\&\qquad+ \sum_{i \in [r_2]} \gamma_i(x_1, x_{J_{i, 1}}) \gamma^{\prime}_i(x_2, x_{J_{i, 2}})\gamma^{\prime\prime}_{i, 1}(x_{J^{\prime}_{i, 1}}) \cdots \gamma^{\prime\prime}_{i, d^{\prime}_i}(x_{J^{\prime}_{i, d^{\prime}_i}})\end{align} $$
for some integers
![]() $r_1$
and
$r_1$
and
![]() $r_2$
and suitable multilinear forms where the partitions of variables in products belong to some downset of partitions
$r_2$
and suitable multilinear forms where the partitions of variables in products belong to some downset of partitions
![]() $\mathcal {P}$
. We write
$\mathcal {P}$
. We write
![]() $r' = r_1 + r_2$
, which will satisfy
$r' = r_1 + r_2$
, which will satisfy
![]() $r' \leq O(\exp ^{(O(1))}(r))$
at all times. Initially, we have
$r' \leq O(\exp ^{(O(1))}(r))$
at all times. Initially, we have
![]() $r' \leq r$
and
$r' \leq r$
and
![]() $\mathcal {P}$
contains all partitions except the trivial one
$\mathcal {P}$
contains all partitions except the trivial one
![]() $\{[k]\}$
.
$\{[k]\}$
.
The proof splits into three parts: in the first stage, we remove the
![]() $\beta _i(x_1, x_2, x_{I_{i}}) \beta ^{\prime }_{i, 1}(z_{I^{\prime }_{i, 1}}) \cdots \beta ^{\prime }_{i, d_i}(z_{I^{\prime }_{i, d_i}})$
terms, in the second, we remove the almost all of
$\beta _i(x_1, x_2, x_{I_{i}}) \beta ^{\prime }_{i, 1}(z_{I^{\prime }_{i, 1}}) \cdots \beta ^{\prime }_{i, d_i}(z_{I^{\prime }_{i, d_i}})$
terms, in the second, we remove the almost all of
![]() $ \gamma _i(x_1, x_{J_{i, 1}}) \gamma ^{\prime }_i(x_2, x_{J_{i, 2}})\gamma ^{\prime \prime }_{i, 1}(x_{J^{\prime }_{i, 1}}) \cdots \gamma ^{\prime \prime }_{i, d^{\prime }_i}(x_{J^{\prime }_{i, d^{\prime }_i}})$
terms, and in the final step, we remove remaining terms which will have linear forms in
$ \gamma _i(x_1, x_{J_{i, 1}}) \gamma ^{\prime }_i(x_2, x_{J_{i, 2}})\gamma ^{\prime \prime }_{i, 1}(x_{J^{\prime }_{i, 1}}) \cdots \gamma ^{\prime \prime }_{i, d^{\prime }_i}(x_{J^{\prime }_{i, d^{\prime }_i}})$
terms, and in the final step, we remove remaining terms which will have linear forms in
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, thereby relating
$x_2$
, thereby relating
![]() $\alpha $
to a form symmetric in the first two variables.
$\alpha $
to a form symmetric in the first two variables.
Step 1. Removing
![]() $\beta $
forms. Using Proposition 3.3, we may assume that every
$\beta $
forms. Using Proposition 3.3, we may assume that every
![]() $\beta _i$
comes from a slice of
$\beta _i$
comes from a slice of
![]() $\alpha + \alpha \circ (1\,\,2)$
. This has the cost of replacing r by
$\alpha + \alpha \circ (1\,\,2)$
. This has the cost of replacing r by
![]() $r' = O({r}^{O(1)})$
. Misusing the notation, we still write
$r' = O({r}^{O(1)})$
. Misusing the notation, we still write
![]() $r_1$
and
$r_1$
and
![]() $r_2$
for the number of products in each of the two sums. Thus, for each
$r_2$
for the number of products in each of the two sums. Thus, for each
![]() $i \in [r_1]$
, we obtain a multilinear form
$i \in [r_1]$
, we obtain a multilinear form
![]() $\tilde {\beta }_i(x_1, x_2, x_{I_{i}})$
such that
$\tilde {\beta }_i(x_1, x_2, x_{I_{i}})$
such that
![]() $\beta _i(x_1, x_2, x_{I_{i}}) = \tilde {\beta }_i(x_1, x_2, x_{I_{i}}) + \tilde {\beta }_i(x_2, x_1, x_{I_{i}})$
. Considering the multilinear form
$\beta _i(x_1, x_2, x_{I_{i}}) = \tilde {\beta }_i(x_1, x_2, x_{I_{i}}) + \tilde {\beta }_i(x_2, x_1, x_{I_{i}})$
. Considering the multilinear form
![]() $\alpha '$
defined by
$\alpha '$
defined by
we see that
![]() $\operatorname {prank}^{\mathcal {P}} (\alpha + \alpha ') \leq O({r}^{O(1)})$
and
$\operatorname {prank}^{\mathcal {P}} (\alpha + \alpha ') \leq O({r}^{O(1)})$
and
 $$ \begin{align}&\alpha'(x_1, x_2, x_3, \dots, x_k) + \alpha'(x_2, x_1, x_3, \dots, x_k) \\&\quad= \sum_{i \in [r_2]} \gamma_i(x_1, x_{J_{i, 1}}) \gamma^{\prime}_i(x_2, x_{J_{i, 2}})\gamma^{\prime\prime}_{i, 1}(x_{J^{\prime}_{i, 1}}) \cdots \gamma^{\prime\prime}_{i, d^{\prime}_i}(x_{J^{\prime}_{i, d^{\prime}_i}}).\nonumber\end{align} $$
$$ \begin{align}&\alpha'(x_1, x_2, x_3, \dots, x_k) + \alpha'(x_2, x_1, x_3, \dots, x_k) \\&\quad= \sum_{i \in [r_2]} \gamma_i(x_1, x_{J_{i, 1}}) \gamma^{\prime}_i(x_2, x_{J_{i, 2}})\gamma^{\prime\prime}_{i, 1}(x_{J^{\prime}_{i, 1}}) \cdots \gamma^{\prime\prime}_{i, d^{\prime}_i}(x_{J^{\prime}_{i, d^{\prime}_i}}).\nonumber\end{align} $$
Step 2. Removing most
![]() $\gamma $
forms. In this part of the proof, we perform another iterative procedure in which we keep track of a downset of partitions
$\gamma $
forms. In this part of the proof, we perform another iterative procedure in which we keep track of a downset of partitions
![]() $\mathcal {P}'\subseteq \mathcal {P}$
with the property that
$\mathcal {P}'\subseteq \mathcal {P}$
with the property that
![]() $1$
and
$1$
and
![]() $2$
are in different sets in every partition and swapping
$2$
are in different sets in every partition and swapping
![]() $1$
and
$1$
and
![]() $2$
results in a partition still in
$2$
results in a partition still in
![]() $\mathcal {P}'$
and we find another multilinear form
$\mathcal {P}'$
and we find another multilinear form
![]() $\alpha " \colon G^k \to \mathbb {F}_2$
such that
$\alpha " \colon G^k \to \mathbb {F}_2$
such that
![]() $\operatorname {prank}(\alpha ' + \alpha ") \leq O(\exp ^{(O(1))}(r))$
and we have an equality
$\operatorname {prank}(\alpha ' + \alpha ") \leq O(\exp ^{(O(1))}(r))$
and we have an equality
 $$ \begin{align}&\alpha"(x_1, x_2, x_3, \dots, x_k) + \alpha"(x_2, x_1, x_3, \dots, x_k) \\&\quad= \sum_{i \in [s]} \gamma_i(x_1,x_{I_i}) \gamma^{\prime}_i(x_2, x_{I^{\prime}_i}) \delta_{i, 1}(x_{J_{i,1}}) \cdots \delta_{i, d_i}(x_{J_{i,d_i}}),\nonumber\end{align} $$
$$ \begin{align}&\alpha"(x_1, x_2, x_3, \dots, x_k) + \alpha"(x_2, x_1, x_3, \dots, x_k) \\&\quad= \sum_{i \in [s]} \gamma_i(x_1,x_{I_i}) \gamma^{\prime}_i(x_2, x_{I^{\prime}_i}) \delta_{i, 1}(x_{J_{i,1}}) \cdots \delta_{i, d_i}(x_{J_{i,d_i}}),\nonumber\end{align} $$
where
![]() $s \leq O(\exp ^{(O(1))}(r))$
and each partition
$s \leq O(\exp ^{(O(1))}(r))$
and each partition
![]() $(\{1\} \cup I_i, \{2\} \cup I^{\prime }_i, J_{i,1}, \dots , J_{i, d_i})$
belongs to
$(\{1\} \cup I_i, \{2\} \cup I^{\prime }_i, J_{i,1}, \dots , J_{i, d_i})$
belongs to
![]() $\mathcal {P}'$
. (We misuse the notation as the multilinear forms
$\mathcal {P}'$
. (We misuse the notation as the multilinear forms
![]() $\gamma _i, \gamma ^{\prime }_i$
are not necessarily identical to those in the assumed decomposition (4.7) and are being modified in each step of the procedure.) Initially, we put
$\gamma _i, \gamma ^{\prime }_i$
are not necessarily identical to those in the assumed decomposition (4.7) and are being modified in each step of the procedure.) Initially, we put
![]() $\alpha " = \alpha '$
. We now describe a step in the procedure. Let
$\alpha " = \alpha '$
. We now describe a step in the procedure. Let
![]() $\Big \{\{1\} \cup I,\{2\} \cup I', J_1, \dots , J_d\Big \}$
be a maximal partition in
$\Big \{\{1\} \cup I,\{2\} \cup I', J_1, \dots , J_d\Big \}$
be a maximal partition in
![]() $\mathcal {P}'$
, where the priority is given to partitions with
$\mathcal {P}'$
, where the priority is given to partitions with
![]() $I \cup I' \not =\emptyset $
. Let
$I \cup I' \not =\emptyset $
. Let
![]() $\mathcal {P}"$
be the downset of partitions obtained by removing
$\mathcal {P}"$
be the downset of partitions obtained by removing
![]() $\Big \{\{1\} \cup I,\{2\} \cup I', J_1, \dots , J_d\Big \}$
and
$\Big \{\{1\} \cup I,\{2\} \cup I', J_1, \dots , J_d\Big \}$
and
![]() $\Big \{\{1\} \cup I',\{2\} \cup I, J_1, \dots , J_d\Big \}$
from
$\Big \{\{1\} \cup I',\{2\} \cup I, J_1, \dots , J_d\Big \}$
from
![]() $\mathcal {P}'$
. Assume first that
$\mathcal {P}'$
. Assume first that
![]() $I \cup I' \not =\emptyset $
.
$I \cup I' \not =\emptyset $
.
Before proceeding, we need to regularize the forms appearing in the expression above. We consider the following
![]() $d+2$
lists of forms:
$d+2$
lists of forms:
-
•
 $\gamma _i(u, x_I)$
for all
$\gamma _i(u, x_I)$
for all
 $i \in [s]$
such that
$i \in [s]$
such that
 $I_i = I$
and
$I_i = I$
and
 $\gamma ^{\prime }_i(u, x_I)$
for all
$\gamma ^{\prime }_i(u, x_I)$
for all
 $i \in [s]$
such that
$i \in [s]$
such that
 $I^{\prime }_i = I$
.
$I^{\prime }_i = I$
. -
•
 $\gamma _i(u, x_I)$
for all
$\gamma _i(u, x_I)$
for all
 $i \in [s]$
such that
$i \in [s]$
such that
 $I_i = I'$
and
$I_i = I'$
and
 $\gamma ^{\prime }_i(u, x_I)$
for all
$\gamma ^{\prime }_i(u, x_I)$
for all
 $i \in [s]$
such that
$i \in [s]$
such that
 $I^{\prime }_i = I'$
.
$I^{\prime }_i = I'$
. -
• For each
 $j \in [d]$
, make the list of all forms that depend on the variables
$j \in [d]$
, make the list of all forms that depend on the variables
 $x_{J_j}$
.
$x_{J_j}$
.
Let
![]() $C, D \geq 2$
be constants to be chosen later. Apply the
$C, D \geq 2$
be constants to be chosen later. Apply the
![]() $m = 0$
case of Lemma 4.1 (see Remark 4.2) to each of these lists. We thus obtain further lists of forms:
$m = 0$
case of Lemma 4.1 (see Remark 4.2) to each of these lists. We thus obtain further lists of forms:
-
•
 $\phi _i(u, x_I)$
for
$\phi _i(u, x_I)$
for
 $i \in [t_1]$
where
$i \in [t_1]$
where
 $t_1 \leq 2s$
,
$t_1 \leq 2s$
, -
•
 $\psi _i(u, x_{I'})$
for
$\psi _i(u, x_{I'})$
for
 $i \in [t_2]$
where
$i \in [t_2]$
where
 $t_2 \leq 2s$
, and
$t_2 \leq 2s$
, and -
• for each
 $j \in [d]$
, a list
$j \in [d]$
, a list
 $\mu _{j,i}(x_{J_j})$
with
$\mu _{j,i}(x_{J_j})$
with
 $i \in [q_j]$
for some
$i \in [q_j]$
for some
 $q_j \leq s$
,
$q_j \leq s$
,
and a quantity
![]() $R \leq C^{D^{O_k(s)}}$
with properties:
$R \leq C^{D^{O_k(s)}}$
with properties:
-
• each multilinear form in one of the initial
 $d+2$
lists can be expressed as a sum of a linear combination of forms in the corresponding new list and a multilinear form of partition rank at most R,
$d+2$
lists can be expressed as a sum of a linear combination of forms in the corresponding new list and a multilinear form of partition rank at most R, -
• for each of
 $d+2$
new lists, the nonzero linear combinations have partition rank at least
$d+2$
new lists, the nonzero linear combinations have partition rank at least
 $(C(R + 2s))^D$
.
$(C(R + 2s))^D$
.
Replacing the old forms by the new ones, we have scalars
![]() $\lambda _{i_1, i_2, j_1, \dots , j_d}, \lambda ^{\prime }_{i_1, i_2, j_1, \dots , j_d}$
, where
$\lambda _{i_1, i_2, j_1, \dots , j_d}, \lambda ^{\prime }_{i_1, i_2, j_1, \dots , j_d}$
, where
![]() $i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots , j_d \in [q_d]$
, and a multilinear form
$i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots , j_d \in [q_d]$
, and a multilinear form
![]() $L(x_{[k]})$
which is a sum of at most
$L(x_{[k]})$
which is a sum of at most
![]() $O(s(s + R)^k)$
products whose partitions lie in
$O(s(s + R)^k)$
products whose partitions lie in
![]() $\mathcal {P}"$
such that
$\mathcal {P}"$
such that
 $$ \begin{align}&\alpha"(x_1, x_2, x_3, \dots, x_k) + \alpha"(x_2, x_1, x_3, \dots, x_k)\nonumber\\ &\quad= \sum_{i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_1,x_{I}) \psi_{i_2}(x_2, x_{I'}) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}) \nonumber\\ &\quad+ \sum_{i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda^{\prime}_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_2,x_{I}) \psi_{i_2}(x_1, x_{I'}) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}) + L(x_{[k]}).\end{align} $$
$$ \begin{align}&\alpha"(x_1, x_2, x_3, \dots, x_k) + \alpha"(x_2, x_1, x_3, \dots, x_k)\nonumber\\ &\quad= \sum_{i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_1,x_{I}) \psi_{i_2}(x_2, x_{I'}) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}) \nonumber\\ &\quad+ \sum_{i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda^{\prime}_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_2,x_{I}) \psi_{i_2}(x_1, x_{I'}) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}) + L(x_{[k]}).\end{align} $$
Using the fact that
Lemma 3.1 implies
![]() $\lambda _{i_1, i_2, j_1, \dots , j_d} = \lambda ^{\prime }_{i_1, i_2, j_1, \dots , j_d}$
, provided C and D are sufficiently large compared only to the constants from Lemma 3.1 and k. Thus, setting
$\lambda _{i_1, i_2, j_1, \dots , j_d} = \lambda ^{\prime }_{i_1, i_2, j_1, \dots , j_d}$
, provided C and D are sufficiently large compared only to the constants from Lemma 3.1 and k. Thus, setting
 $$\begin{align*}&\alpha"'(x_{[k]}) = \alpha"(x_{[k]}) \\&\quad+ \sum_{i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_1,x_{I}) \psi_{i_2}(x_2, x_{I'}) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}),\end{align*}$$
$$\begin{align*}&\alpha"'(x_{[k]}) = \alpha"(x_{[k]}) \\&\quad+ \sum_{i_1 \in [t_1], i_2 \in [t_2], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_1,x_{I}) \psi_{i_2}(x_2, x_{I'}) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}),\end{align*}$$
it follows that
![]() $\operatorname {prank}(\alpha " + \alpha "') \leq O(\exp ^{(O(1))}(r))$
and
$\operatorname {prank}(\alpha " + \alpha "') \leq O(\exp ^{(O(1))}(r))$
and
![]() $\alpha "' + \alpha "' \circ (1\,\,2)$
satisfies (4.8) for the downset of partitions
$\alpha "' + \alpha "' \circ (1\,\,2)$
satisfies (4.8) for the downset of partitions
![]() $\mathcal {P}"$
and
$\mathcal {P}"$
and
![]() $s \leq O(\exp ^{(O(1))}(r))$
.
$s \leq O(\exp ^{(O(1))}(r))$
.
Step 3. Removing remaining forms. Let us now treat the case
![]() $I = I' = \emptyset $
. The same steps of the argument apply, except that this time the first two of the
$I = I' = \emptyset $
. The same steps of the argument apply, except that this time the first two of the
![]() $d+2$
lists of forms become the same list of linear forms
$d+2$
lists of forms become the same list of linear forms
![]() $\gamma _i(u)$
and
$\gamma _i(u)$
and
![]() $\gamma ^{\prime }_i(u)$
for
$\gamma ^{\prime }_i(u)$
for
![]() $i \in [s]$
and we may omit the list of regularized forms
$i \in [s]$
and we may omit the list of regularized forms
![]() $\psi _i$
. This time, we have that
$\psi _i$
. This time, we have that
 $$ \begin{align*}&\alpha"'(x_1, x_2, x_3, \dots, x_k) + \alpha"'(x_2, x_1, x_3, \dots, x_k)\nonumber\\ &\quad= \sum_{i \in [t_1], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_1) \phi_{i_2}(x_2) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}) + L(x_{[k]}).\end{align*} $$
$$ \begin{align*}&\alpha"'(x_1, x_2, x_3, \dots, x_k) + \alpha"'(x_2, x_1, x_3, \dots, x_k)\nonumber\\ &\quad= \sum_{i \in [t_1], j_1 \in [q_1], \dots, j_d \in [q_d]} \lambda_{i_1, i_2, j_1, \dots, j_d} \phi_{i_1}(x_1) \phi_{i_2}(x_2) \mu_{1, j_1}(x_{J_1}) \cdots \mu_{d, j_d}(x_{J_d}) + L(x_{[k]}).\end{align*} $$
Let us define the subspace
![]() $U = \{u \in G \colon (\forall i \in [t_1]) \phi _i(u) = 0\}$
, which has a codimension at most
$U = \{u \in G \colon (\forall i \in [t_1]) \phi _i(u) = 0\}$
, which has a codimension at most
![]() $O(\exp ^{(O(1))}(r))$
in G. The expression above implies that
$O(\exp ^{(O(1))}(r))$
in G. The expression above implies that
![]() $\alpha "'$
is symmetric in the first two variables on the subspace U. Let
$\alpha "'$
is symmetric in the first two variables on the subspace U. Let
![]() $\pi \colon G \to U$
be an arbitrary linear projection onto U. Set
$\pi \colon G \to U$
be an arbitrary linear projection onto U. Set
![]() $\tilde {\alpha }(x_1, \dots , x_k) = \alpha "'(\pi (x_1), \dots , \pi (x_k))$
. Then the form
$\tilde {\alpha }(x_1, \dots , x_k) = \alpha "'(\pi (x_1), \dots , \pi (x_k))$
. Then the form
![]() $\tilde {\alpha }$
is symmetric in the first two variables, and by Lemma 2.5, we have
$\tilde {\alpha }$
is symmetric in the first two variables, and by Lemma 2.5, we have
![]() $\operatorname {prank}(\alpha "' + \tilde {\alpha }) \leq k \operatorname {codim}_G U$
, implying
$\operatorname {prank}(\alpha "' + \tilde {\alpha }) \leq k \operatorname {codim}_G U$
, implying
![]() $\operatorname {prank}(\alpha + \tilde {\alpha }) \leq O(\exp ^{(O(1))}(r))$
, as desired.
$\operatorname {prank}(\alpha + \tilde {\alpha }) \leq O(\exp ^{(O(1))}(r))$
, as desired.
4.2 Symmetry in
 $x_{[4]}$
$x_{[4]}$
In this subsection, we show how to pass from a multilinear form that is symmetric in variables
![]() $x_{[3]}$
to another one which is symmetric in variables
$x_{[3]}$
to another one which is symmetric in variables
![]() $x_{[4]}$
, under suitable conditions. The main results in this subsection are Theorems 1.7 and 1.8.
$x_{[4]}$
, under suitable conditions. The main results in this subsection are Theorems 1.7 and 1.8.
Before embarking on the proof of Theorem 1.7, we note that a weaker symmetry property is sufficient to deduce the stated one.
Lemma 4.4 Let
![]() $\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form symmetric in variables
$\alpha \colon G^k \to \mathbb {F}_2$
be a multilinear form symmetric in variables
![]() $x_{[3]}$
. Let
$x_{[3]}$
. Let
![]() $\phi = \alpha + \alpha \circ (3\,\,4)$
. Then
$\phi = \alpha + \alpha \circ (3\,\,4)$
. Then
![]() $\phi $
satisfies the identity
$\phi $
satisfies the identity
Furthermore, if
![]() $\phi $
is symmetric in variables
$\phi $
is symmetric in variables
![]() $x_1$
and
$x_1$
and
![]() $x_{4}$
, then
$x_{4}$
, then
![]() $\alpha $
is in fact symmetric in variables
$\alpha $
is in fact symmetric in variables
![]() $x_{[4]}$
.
$x_{[4]}$
.
Proof Simple algebraic manipulation relying on the symmetry of
![]() $\alpha $
gives
$\alpha $
gives
 $$ \begin{align*}\phi + \phi \circ (1\,\,3) + \phi\circ(1\,\,4) =\ & \alpha + \alpha \circ (3\,\,4) + \alpha \circ (1\,\,3) + \alpha \circ (3\,\,4) \circ (1\,\,3) \\ &\hspace{4cm} + \alpha\circ(1\,\,4) + \alpha \circ (3\,\,4)\circ(1\,\,4) \\ =\ &\alpha + \alpha \circ (3\,\,4) + \alpha + \alpha \circ (1\,\,4) + \alpha\circ(1\,\,4) + \alpha \circ (3\,\,4)\\ =\ & 0.\end{align*} $$
$$ \begin{align*}\phi + \phi \circ (1\,\,3) + \phi\circ(1\,\,4) =\ & \alpha + \alpha \circ (3\,\,4) + \alpha \circ (1\,\,3) + \alpha \circ (3\,\,4) \circ (1\,\,3) \\ &\hspace{4cm} + \alpha\circ(1\,\,4) + \alpha \circ (3\,\,4)\circ(1\,\,4) \\ =\ &\alpha + \alpha \circ (3\,\,4) + \alpha + \alpha \circ (1\,\,4) + \alpha\circ(1\,\,4) + \alpha \circ (3\,\,4)\\ =\ & 0.\end{align*} $$
If
![]() $\phi $
is symmetric in variables
$\phi $
is symmetric in variables
![]() $x_1$
and
$x_1$
and
![]() $x_{4}$
, then we get
$x_{4}$
, then we get
 $$ \begin{align*}0 = \phi + \phi \circ (1\,\,3) + \phi\circ(1\,\,4) = \phi \circ (1\,\,3) =\ &\alpha \circ (1\,\,3) + \alpha \circ (3\,\,4) \circ (1\,\,3)\\ =\ &\alpha + \alpha \circ (1\,\,4).\end{align*} $$
$$ \begin{align*}0 = \phi + \phi \circ (1\,\,3) + \phi\circ(1\,\,4) = \phi \circ (1\,\,3) =\ &\alpha \circ (1\,\,3) + \alpha \circ (3\,\,4) \circ (1\,\,3)\\ =\ &\alpha + \alpha \circ (1\,\,4).\end{align*} $$
As
![]() $\alpha $
is already symmetric in variables
$\alpha $
is already symmetric in variables
![]() $x_{[3]}$
, it follows that it is symmetric in
$x_{[3]}$
, it follows that it is symmetric in
![]() $x_{[4]}$
, as required.
$x_{[4]}$
, as required.
Proof of Theorem 1.7
By assumptions, we have that
for some multilinear forms
![]() $\beta _{i, j}$
such that, for each
$\beta _{i, j}$
such that, for each
![]() $i \in [r]$
, the sets
$i \in [r]$
, the sets
![]() $I_{i,1}, \dots , I_{i,d_i}$
form a partition of
$I_{i,1}, \dots , I_{i,d_i}$
form a partition of
![]() $[4]$
, and
$[4]$
, and
![]() $d_i \geq 2$
. Notice that, for a given
$d_i \geq 2$
. Notice that, for a given
![]() $i \in [r]$
, either we have that some
$i \in [r]$
, either we have that some
![]() $I_{i,j}$
is a singleton, or we have
$I_{i,j}$
is a singleton, or we have
![]() $d_i = 2$
and both sets
$d_i = 2$
and both sets
![]() $I_{i,1}$
and
$I_{i,1}$
and
![]() $I_{i,2}$
have size 2. Let
$I_{i,2}$
have size 2. Let
![]() $\mathcal {I}$
be the set of indices
$\mathcal {I}$
be the set of indices
![]() $i \in [r]$
where we get a singleton set
$i \in [r]$
where we get a singleton set
![]() $I_{i,j(i)}$
for some
$I_{i,j(i)}$
for some
![]() $j(i) \leq d_i$
. If we set
$j(i) \leq d_i$
. If we set
![]() $U = \{u \in G \colon \beta _{i, j(i)}(u) = 0\}$
, then we have for all
$U = \{u \in G \colon \beta _{i, j(i)}(u) = 0\}$
, then we have for all
![]() $x_1, x_2, x_3, x_4 \in U$
that
$x_1, x_2, x_3, x_4 \in U$
that
holds and
![]() $|I_{i,1}| = |I_{i,2}| = 2$
for all indices i appearing in the displayed equality. Take the list of all bilinear forms appearing on the right-hand side of (4.12) and apply Lemma 4.1 to it, with parameters
$|I_{i,1}| = |I_{i,2}| = 2$
for all indices i appearing in the displayed equality. Take the list of all bilinear forms appearing on the right-hand side of (4.12) and apply Lemma 4.1 to it, with parameters
![]() $C, D$
to be chosen later (which will depend only on constants in Lemma 3.1) and
$C, D$
to be chosen later (which will depend only on constants in Lemma 3.1) and
![]() $m = 1$
. We get a positive integer
$m = 1$
. We get a positive integer
![]() $R \leq C^{D^{O(r)}}$
, bilinear forms
$R \leq C^{D^{O(r)}}$
, bilinear forms
![]() $\sigma _1, \dots , \sigma _s, \rho _1, \dots , \rho _t$
, where
$\sigma _1, \dots , \sigma _s, \rho _1, \dots , \rho _t$
, where
![]() $s + t \leq r$
, such that:
$s + t \leq r$
, such that:
-
(i) we have
 $\operatorname {rank}\Big ( \sigma _i + \sigma _i \circ (1\,\,2)\Big ) \leq R$
for all
$\operatorname {rank}\Big ( \sigma _i + \sigma _i \circ (1\,\,2)\Big ) \leq R$
for all
 $i \in [s]$
,
$i \in [s]$
, -
(ii) all nonzero linear combinations of forms
 $\sigma _1, \dots , \sigma _s, \rho _1, \dots , \rho _t$
and
$\sigma _1, \dots , \sigma _s, \rho _1, \dots , \rho _t$
and
 $ \rho _1 \circ (1\,\,2), \dots , \rho _t\circ (1\,\,2)$
have rank at least
$ \rho _1 \circ (1\,\,2), \dots , \rho _t\circ (1\,\,2)$
have rank at least
 $(C(R + 2r))^D$
, and
$(C(R + 2r))^D$
, and -
(iii) every bilinear form in the list differs from a linear combination of forms
 $\sigma _{[s]}, \rho _{[t]}$
and
$\sigma _{[s]}, \rho _{[t]}$
and
 $ \rho _{[t]} \circ (1\,\,2)$
by a bilinear form of rank at most R.
$ \rho _{[t]} \circ (1\,\,2)$
by a bilinear form of rank at most R.
Passing to a further subspace
![]() $U' \leq U$
of codimension at most
$U' \leq U$
of codimension at most
![]() $2rR$
in U, we may assume that properties (i) and (iii) are exact rather than approximate, i.e.,
$2rR$
in U, we may assume that properties (i) and (iii) are exact rather than approximate, i.e.,
![]() $\sigma _i = \sigma _i \circ (1\,\,2)$
and every bilinear form in the list equals a linear combination of the newly found forms. We may replace the bilinear forms in (4.12) with the newly found forms. This leads to equality
$\sigma _i = \sigma _i \circ (1\,\,2)$
and every bilinear form in the list equals a linear combination of the newly found forms. We may replace the bilinear forms in (4.12) with the newly found forms. This leads to equality
 $$ \begin{align}&\alpha(x_{[4]})+ \alpha \circ (3\,\,4)(x_{[4]}) \nonumber\\ &\hspace{1cm}= \sum_{\substack{i \in [s]\\(a,b,c,d) \in \mathcal{V}_1}} \lambda_{\substack{i\\a,b,c,d}} \sigma_i(x_a, x_b) \sigma_i(x_c, x_d) + \sum_{\substack{1\leq i < j \leq s\\(a,b,c,d) \in \mathcal{V}_2}} \lambda_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \sigma_j(x_c, x_d)\nonumber\\ &\hspace{2cm} + \sum_{\substack{i \in [t]\\(a,b,c,d) \in \mathcal{V}_3}} \!\mu_{\substack{i\\a,b,c,d}} \rho_i(x_a, x_b) \rho_i(x_c, x_d) + \sum_{\substack{1\leq i < j \leq t\\(a,b,c,d) \in \mathcal{V}_4}} \!\mu_{\substack{i,j\\a,b,c,d}} \rho_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\\ &\hspace{2cm} + \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d),\end{align} $$
$$ \begin{align}&\alpha(x_{[4]})+ \alpha \circ (3\,\,4)(x_{[4]}) \nonumber\\ &\hspace{1cm}= \sum_{\substack{i \in [s]\\(a,b,c,d) \in \mathcal{V}_1}} \lambda_{\substack{i\\a,b,c,d}} \sigma_i(x_a, x_b) \sigma_i(x_c, x_d) + \sum_{\substack{1\leq i < j \leq s\\(a,b,c,d) \in \mathcal{V}_2}} \lambda_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \sigma_j(x_c, x_d)\nonumber\\ &\hspace{2cm} + \sum_{\substack{i \in [t]\\(a,b,c,d) \in \mathcal{V}_3}} \!\mu_{\substack{i\\a,b,c,d}} \rho_i(x_a, x_b) \rho_i(x_c, x_d) + \sum_{\substack{1\leq i < j \leq t\\(a,b,c,d) \in \mathcal{V}_4}} \!\mu_{\substack{i,j\\a,b,c,d}} \rho_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\\ &\hspace{2cm} + \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d),\end{align} $$
for all
![]() $x_1, x_2, x_3, x_4 \in U'$
, where:
$x_1, x_2, x_3, x_4 \in U'$
, where:
-
•
 $\mathcal {V}_1 = \{(1,2,3,4), (1,3,2,4), (1,4,2,3)\}$
,
$\mathcal {V}_1 = \{(1,2,3,4), (1,3,2,4), (1,4,2,3)\}$
, -
•
 $\mathcal {V}_2 = \{(1,2,3,4), (1,3,2,4), (1,4,2,3), (2,3,1,4), (2,4,1,3), (3,4,1,2)\}$
,
$\mathcal {V}_2 = \{(1,2,3,4), (1,3,2,4), (1,4,2,3), (2,3,1,4), (2,4,1,3), (3,4,1,2)\}$
, -
•
 $\mathcal {V}_3 = \{(1,2,3,4), (2,1,3,4), (1,2,4,3), (2,1,4,3), (1,3,2,4), (3,1,2,4), (1,3,4,2), (3,1,4,2), (1,4,2,3), (4,1,2,3), (1,4,3,2), (4,1,3,2)\}$
,
$\mathcal {V}_3 = \{(1,2,3,4), (2,1,3,4), (1,2,4,3), (2,1,4,3), (1,3,2,4), (3,1,2,4), (1,3,4,2), (3,1,4,2), (1,4,2,3), (4,1,2,3), (1,4,3,2), (4,1,3,2)\}$
, -
•
 $\mathcal {V}_4 = \operatorname {Sym}_{[4]}$
, and
$\mathcal {V}_4 = \operatorname {Sym}_{[4]}$
, and -
•
 $\mathcal {V}_5 = \{(1,2,3,4),(1,2,4,3), (1,3,2,4), (1,3,4,2), (1,4,2,3), (1,4,3,2), (2,3,1,4), (2,3,4,1), (2,4,1,3), (2,4,3,1), (3,4,1,2), (3,4,2,1)\}$
.
$\mathcal {V}_5 = \{(1,2,3,4),(1,2,4,3), (1,3,2,4), (1,3,4,2), (1,4,2,3), (1,4,3,2), (2,3,1,4), (2,3,4,1), (2,4,1,3), (2,4,3,1), (3,4,1,2), (3,4,2,1)\}$
.
Write
![]() $\phi (x_{[4]}) = \alpha (x_{[4]})+ \alpha \circ (3\,\,4)(x_{[4]})$
. This form has the following properties:
$\phi (x_{[4]}) = \alpha (x_{[4]})+ \alpha \circ (3\,\,4)(x_{[4]})$
. This form has the following properties:
-
(i)
 $\phi = \phi \circ (1\,\,2)$
.
$\phi = \phi \circ (1\,\,2)$
. -
(ii)
 $\phi = \phi \circ (3\,\,4)$
.
$\phi = \phi \circ (3\,\,4)$
. -
(iii)
 $\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4) = 0$
.
$\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4) = 0$
. -
(iv)
 $\phi (u,v,u,v) = 0$
for all
$\phi (u,v,u,v) = 0$
for all
 $u,v \in U'$
.
$u,v \in U'$
.
Let us briefly explain why
![]() $\phi $
has the claimed properties. Property (i) follows from the fact that
$\phi $
has the claimed properties. Property (i) follows from the fact that
![]() $\alpha $
is symmetric in the first two variables. Property (ii) follows directly from the definition of
$\alpha $
is symmetric in the first two variables. Property (ii) follows directly from the definition of
![]() $\phi $
. Property (iii) follows from Lemma 4.4. Finally, property (iv) follows from assumptions (i) and (ii) in the statement of Theorem 1.7, namely we have
$\phi $
. Property (iii) follows from Lemma 4.4. Finally, property (iv) follows from assumptions (i) and (ii) in the statement of Theorem 1.7, namely we have
 $$ \begin{align*}\phi(u,v,u,v) =\ &\alpha(u,v,u,v) + \alpha(u,v,v,u)\hspace{2cm}(\text{definition of }\phi)\\ =\ &\alpha(u,u,v,v) + \alpha(v,v,u,u)\hspace{2cm}(\text{symmetry of }\alpha)\\ =\ &0\hspace{2cm}(\text{Theorem~1.7, assumption {(ii)}}).\end{align*} $$
$$ \begin{align*}\phi(u,v,u,v) =\ &\alpha(u,v,u,v) + \alpha(u,v,v,u)\hspace{2cm}(\text{definition of }\phi)\\ =\ &\alpha(u,u,v,v) + \alpha(v,v,u,u)\hspace{2cm}(\text{symmetry of }\alpha)\\ =\ &0\hspace{2cm}(\text{Theorem~1.7, assumption {(ii)}}).\end{align*} $$
We use these properties of
![]() $\phi $
to make
$\phi $
to make
![]() $\alpha $
symmetric in all variables. Note that applying Lemma 3.1 to the sum
$\alpha $
symmetric in all variables. Note that applying Lemma 3.1 to the sum
![]() $\phi + \phi \circ (1\,\,2)$
, which vanishes by symmetry property (i), implies that we have equality
$\phi + \phi \circ (1\,\,2)$
, which vanishes by symmetry property (i), implies that we have equality
![]() $\lambda _{\substack {i\\1,3,2,4}} = \lambda _{\substack {i\\1,4,2,3}}$
. Using Lemma 3.1 similarly for either of the symmetry properties (i) and (ii) and for other coefficients, we obtain additional equalities, such as
$\lambda _{\substack {i\\1,3,2,4}} = \lambda _{\substack {i\\1,4,2,3}}$
. Using Lemma 3.1 similarly for either of the symmetry properties (i) and (ii) and for other coefficients, we obtain additional equalities, such as
![]() $\mu _{\substack {i\\1,2,3,4}} = \mu _{\substack {i\\2,1,3,4}}$
. In the rest of the proof, we obtain further identities between coefficients, which are not direct consequences of symmetry properties (i) and (ii). We treat each of the five sums in (4.13) separately. Once we get sufficient information on relationships between different coefficients we shall be able to modify
$\mu _{\substack {i\\1,2,3,4}} = \mu _{\substack {i\\2,1,3,4}}$
. In the rest of the proof, we obtain further identities between coefficients, which are not direct consequences of symmetry properties (i) and (ii). We treat each of the five sums in (4.13) separately. Once we get sufficient information on relationships between different coefficients we shall be able to modify
![]() $\alpha $
by explicit multilinear forms of small bounded partition rank and end up with an exactly symmetric form.
$\alpha $
by explicit multilinear forms of small bounded partition rank and end up with an exactly symmetric form.
Let us also stress that the additional assumption (ii) in Theorem 1.7 that makes it possible to pass from approximately symmetric form to an exactly symmetric one is used in Step 1 and Step 2 of the proof below. More precisely, in the proof itself, we use the property (iv) of the multilinear form
![]() $\phi $
, which uses the mentioned additional property of
$\phi $
, which uses the mentioned additional property of
![]() $\alpha $
.
$\alpha $
.
Step 1. Coefficients
![]() $\lambda _{\substack {i\\a,b,c,d}}$
. Fix any
$\lambda _{\substack {i\\a,b,c,d}}$
. Fix any
![]() $i \in [s]$
. To see that
$i \in [s]$
. To see that
![]() $\lambda _{\substack {i\\1,2,3,4}} = 0$
, observethat the coefficient of
$\lambda _{\substack {i\\1,2,3,4}} = 0$
, observethat the coefficient of
![]() $\sigma _i(x_1, x_2)\sigma _i(x_3, x_4)$
in the expression
$\sigma _i(x_1, x_2)\sigma _i(x_3, x_4)$
in the expression
![]() $\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4)$
equals
$\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4)$
equals
By property (iii) of
![]() $\phi $
and Lemma 3.1, we conclude that
$\phi $
and Lemma 3.1, we conclude that
Since
![]() $\lambda _{\substack {i\\1,4,2,3}} = \lambda _{\substack {i\\1,3,2,4}}$
from discussion before this step, we finally get
$\lambda _{\substack {i\\1,4,2,3}} = \lambda _{\substack {i\\1,3,2,4}}$
from discussion before this step, we finally get
![]() $\lambda _{\substack {i\\1,2,3,4}} = 0$
.
$\lambda _{\substack {i\\1,2,3,4}} = 0$
.
Next, we show that
![]() $\lambda _{\substack {i\\1,4,2,3}} = \lambda _{\substack {i\\1,3,2,4}} = 0$
. To that end, let
$\lambda _{\substack {i\\1,4,2,3}} = \lambda _{\substack {i\\1,3,2,4}} = 0$
. To that end, let
![]() $X = \{u \in U' \colon (\forall i \in [s]) \sigma _i(u,u) = 0, (\forall i \in [t]) \rho _i(u,u) = 0\}$
. By Lemma 2.2, this set has size
$X = \{u \in U' \colon (\forall i \in [s]) \sigma _i(u,u) = 0, (\forall i \in [t]) \rho _i(u,u) = 0\}$
. By Lemma 2.2, this set has size
![]() $|X| \geq 2^{-s-t-1}|U'|$
. Since all nonzero linear combinations of forms
$|X| \geq 2^{-s-t-1}|U'|$
. Since all nonzero linear combinations of forms
![]() $\sigma _{[s]}$
,
$\sigma _{[s]}$
,
![]() $\rho _{[t]}$
and
$\rho _{[t]}$
and
![]() $\rho _{[t]}\circ (1\,\,2)$
have rank at least
$\rho _{[t]}\circ (1\,\,2)$
have rank at least
![]() $(C(R + 2r))^D - 2rR$
on
$(C(R + 2r))^D - 2rR$
on
![]() $U'$
, we may find
$U'$
, we may find
![]() $u,v \in X$
such that
$u,v \in X$
such that
![]() $\sigma _i(u,v) = 1$
,
$\sigma _i(u,v) = 1$
,
![]() $\sigma _j(u,v) = 0$
for all
$\sigma _j(u,v) = 0$
for all
![]() $j \not =i$
and
$j \not =i$
and
![]() $\rho _j(u,v) = \rho _j(v,u) = 0$
for all
$\rho _j(u,v) = \rho _j(v,u) = 0$
for all
![]() $j \in [t]$
. Putting
$j \in [t]$
. Putting
![]() $x_1 = x_3 = u, x_2 = x_4 = v$
in (4.13), we deduce that
$x_1 = x_3 = u, x_2 = x_4 = v$
in (4.13), we deduce that
as required, where we used property (iv) of
![]() $\phi $
.
$\phi $
.
Step 2. Coefficients
![]() $\mu _{\substack {i\\a,b,c,d}}$
. As remarked before the first step, from symmetry properties (i) and (ii) of
$\mu _{\substack {i\\a,b,c,d}}$
. As remarked before the first step, from symmetry properties (i) and (ii) of
![]() $\phi $
and Lemma 3.1, we have scalars
$\phi $
and Lemma 3.1, we have scalars
![]() $\overline {\mu }_i, \overline {\mu }^{\prime }_i, \overline {\mu }^{\prime \prime }_i, \overline {\mu }^{\prime \prime \prime }_i$
such that
$\overline {\mu }_i, \overline {\mu }^{\prime }_i, \overline {\mu }^{\prime \prime }_i, \overline {\mu }^{\prime \prime \prime }_i$
such that
 $$ \begin{align*}\overline{\mu}_i &= \mu_{\substack{i\\1,2,3,4}} = \mu_{\substack{i\\2,1,3,4}} = \mu_{\substack{i\\1,2,4,3}} = \mu_{\substack{i\\2,1,4,3}},\\ \overline{\mu}^{\prime}_i &= \mu_{\substack{i\\3,1,2,4}} = \mu_{\substack{i\\1,4,3,2}} = \mu_{\substack{i\\4,1,2,3}} = \mu_{\substack{i\\1,3,4,2}},\\ \overline{\mu}^{\prime\prime}_i &= \mu_{\substack{i\\1,3,2,4}} = \mu_{\substack{i\\1,4,2,3}}\,\,\text{and}\,\,\,\, \overline{\mu}^{\prime\prime\prime}_i= \mu_{\substack{i\\3,1,4,2}} = \mu_{\substack{i\\4,1, 3,2}}.\end{align*} $$
$$ \begin{align*}\overline{\mu}_i &= \mu_{\substack{i\\1,2,3,4}} = \mu_{\substack{i\\2,1,3,4}} = \mu_{\substack{i\\1,2,4,3}} = \mu_{\substack{i\\2,1,4,3}},\\ \overline{\mu}^{\prime}_i &= \mu_{\substack{i\\3,1,2,4}} = \mu_{\substack{i\\1,4,3,2}} = \mu_{\substack{i\\4,1,2,3}} = \mu_{\substack{i\\1,3,4,2}},\\ \overline{\mu}^{\prime\prime}_i &= \mu_{\substack{i\\1,3,2,4}} = \mu_{\substack{i\\1,4,2,3}}\,\,\text{and}\,\,\,\, \overline{\mu}^{\prime\prime\prime}_i= \mu_{\substack{i\\3,1,4,2}} = \mu_{\substack{i\\4,1, 3,2}}.\end{align*} $$
Fix any
![]() $i \in [t]$
. We now show that
$i \in [t]$
. We now show that
![]() $\overline {\mu }_i + \overline {\mu }^{\prime }_i + \overline {\mu }^{\prime \prime }_i = 0$
and
$\overline {\mu }_i + \overline {\mu }^{\prime }_i + \overline {\mu }^{\prime \prime }_i = 0$
and
![]() $\overline {\mu }_i + \overline {\mu }^{\prime }_i + \overline {\mu }^{\prime \prime \prime }_i = 0$
. Observe that the coefficient of
$\overline {\mu }_i + \overline {\mu }^{\prime }_i + \overline {\mu }^{\prime \prime \prime }_i = 0$
. Observe that the coefficient of
![]() $\rho _i(x_3, x_1)\rho _i(x_4, x_2)$
in the expression
$\rho _i(x_3, x_1)\rho _i(x_4, x_2)$
in the expression
![]() $\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4)$
equals
$\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4)$
equals
By Lemma 3.1, we see that
![]() $\overline {\mu }_i + \overline {\mu }^{\prime }_i + \overline {\mu }^{\prime \prime \prime }_i = 0$
. Similarly, we consider the coefficient of
$\overline {\mu }_i + \overline {\mu }^{\prime }_i + \overline {\mu }^{\prime \prime \prime }_i = 0$
. Similarly, we consider the coefficient of
![]() $\rho _i(x_1, x_3)\rho _i(x_2, x_4)$
in the expression
$\rho _i(x_1, x_3)\rho _i(x_2, x_4)$
in the expression
![]() $\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4)$
, which equals
$\phi + \phi \circ (1\,\,3) + \phi \circ (1\,\,4)$
, which equals
which vanishes by Lemma 3.1. As the last equality between coefficients in this step, we claim that
![]() $\overline {\mu }_i = \overline {\mu }^{\prime }_i$
. Let
$\overline {\mu }_i = \overline {\mu }^{\prime }_i$
. Let
![]() $X = \{u \in U' \colon (\forall i \in [s]) \sigma _i(u,u) = 0, (\forall i \in [t]) \rho _i(u,u) = 0\}$
. By Lemma 2.2, this set has size
$X = \{u \in U' \colon (\forall i \in [s]) \sigma _i(u,u) = 0, (\forall i \in [t]) \rho _i(u,u) = 0\}$
. By Lemma 2.2, this set has size
![]() $|X| \geq 2^{-s-t-1}|U'|$
. We thus have a choice of
$|X| \geq 2^{-s-t-1}|U'|$
. We thus have a choice of
![]() $u,v \in X$
such that
$u,v \in X$
such that
![]() $\rho _i(u,v) = 1$
,
$\rho _i(u,v) = 1$
,
![]() $\rho _i(v,u) = 0$
,
$\rho _i(v,u) = 0$
,
![]() $\rho _j(u,v) = \rho _j(u,v) = 0$
for
$\rho _j(u,v) = \rho _j(u,v) = 0$
for
![]() $j \not = i$
and
$j \not = i$
and
![]() $\sigma _j(u,v) = \sigma _j(v,u) = 0$
for
$\sigma _j(u,v) = \sigma _j(v,u) = 0$
for
![]() $j \in [t]$
. Then, setting
$j \in [t]$
. Then, setting
![]() $x_1 = x_3 = u, x_2 = x_4 = v$
, we get
$x_1 = x_3 = u, x_2 = x_4 = v$
, we get
 $$\begin{align*}0 = \phi(u,v,u,v) &= \sum_{(a,b,c,d) \in \mathcal{V}_3} \mu_{\substack{i\\a,b,c,d}} \rho_i(x_a, x_b) \rho_i(x_c, x_d) \\&= \overline{\mu}_i \rho_i(u,v)\rho_i(u,v) + \overline{\mu}^{\prime}_i \rho_i(u,v)\rho_i(u,v) = \overline{\mu}_i + \overline{\mu}^{\prime}_i ,\end{align*}$$
$$\begin{align*}0 = \phi(u,v,u,v) &= \sum_{(a,b,c,d) \in \mathcal{V}_3} \mu_{\substack{i\\a,b,c,d}} \rho_i(x_a, x_b) \rho_i(x_c, x_d) \\&= \overline{\mu}_i \rho_i(u,v)\rho_i(u,v) + \overline{\mu}^{\prime}_i \rho_i(u,v)\rho_i(u,v) = \overline{\mu}_i + \overline{\mu}^{\prime}_i ,\end{align*}$$
where we used property (iv) of
![]() $\phi $
. Thus, we have
$\phi $
. Thus, we have
![]() $\overline {\mu }^{\prime }_i = \overline {\mu }_i$
and
$\overline {\mu }^{\prime }_i = \overline {\mu }_i$
and
![]() $\overline {\mu }^{\prime \prime }_i = \overline {\mu }^{\prime \prime \prime }_i = 0$
.
$\overline {\mu }^{\prime \prime }_i = \overline {\mu }^{\prime \prime \prime }_i = 0$
.
Define a multilinear form
![]() $\alpha ^{(1)} \colon G^4 \to \mathbb {F}_2$
by
$\alpha ^{(1)} \colon G^4 \to \mathbb {F}_2$
by
 $$\begin{align*}\alpha^{(1)}(x_1, x_2, x_3, x_4) = \alpha(x_1, x_2, x_3, x_4) + \sum_{i \in [t]} \overline{\mu}_i \Big(\sum_{\pi \in \operatorname{Sym}_{[3]}}\rho_i(x_{\pi_1}, x_{\pi_2})\rho_i(x_{\pi_3}, x_4)\Big).\end{align*}$$
$$\begin{align*}\alpha^{(1)}(x_1, x_2, x_3, x_4) = \alpha(x_1, x_2, x_3, x_4) + \sum_{i \in [t]} \overline{\mu}_i \Big(\sum_{\pi \in \operatorname{Sym}_{[3]}}\rho_i(x_{\pi_1}, x_{\pi_2})\rho_i(x_{\pi_3}, x_4)\Big).\end{align*}$$
By our work in the first two steps, we conclude that
 $$ \begin{align}\alpha^{(1)}(x_{[4]})+ \alpha^{(1)} \circ (3\,\,4)(x_{[4]}) = &\sum_{\substack{1\leq i < j \leq s\\(a,b,c,d) \in \mathcal{V}_2}} \lambda_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \sigma_j(x_c, x_d) \\&+ \sum_{\substack{1\leq i < j \leq t\\(a,b,c,d) \in \mathcal{V}_4}} \mu_{\substack{i,j\\a,b,c,d}} \rho_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\\ & + \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\end{align} $$
$$ \begin{align}\alpha^{(1)}(x_{[4]})+ \alpha^{(1)} \circ (3\,\,4)(x_{[4]}) = &\sum_{\substack{1\leq i < j \leq s\\(a,b,c,d) \in \mathcal{V}_2}} \lambda_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \sigma_j(x_c, x_d) \\&+ \sum_{\substack{1\leq i < j \leq t\\(a,b,c,d) \in \mathcal{V}_4}} \mu_{\substack{i,j\\a,b,c,d}} \rho_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\\ & + \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\end{align} $$
holds for all
![]() $x_1, x_2, x_3, x_4 \in U'$
. Let us set
$x_1, x_2, x_3, x_4 \in U'$
. Let us set
![]() $\phi ^{(1)} = \alpha ^{(1)} + \alpha ^{(1)}\circ (3\,\,4)$
. Since
$\phi ^{(1)} = \alpha ^{(1)} + \alpha ^{(1)}\circ (3\,\,4)$
. Since
![]() $\sum _{\pi \in \operatorname {Sym}_{[3]}}\rho _i(x_{\pi _1}, x_{\pi _2})\rho _i(x_{\pi _3}, x_4)$
is symmetric in variables
$\sum _{\pi \in \operatorname {Sym}_{[3]}}\rho _i(x_{\pi _1}, x_{\pi _2})\rho _i(x_{\pi _3}, x_4)$
is symmetric in variables
![]() $x_{[3]}$
, the form
$x_{[3]}$
, the form
![]() $\phi ^{(1)}$
still satisfies symmetry conditions (i)–(iii) which we used for
$\phi ^{(1)}$
still satisfies symmetry conditions (i)–(iii) which we used for
![]() $\phi $
.
$\phi $
.
Step 3. Coefficients
![]() $\lambda _{\substack {i,j\\a,b,c,d}}$
. As discussed prior to the first step, by symmetry properties (i) and (ii) of
$\lambda _{\substack {i,j\\a,b,c,d}}$
. As discussed prior to the first step, by symmetry properties (i) and (ii) of
![]() $\phi $
and Lemma 3.1, we know that the coefficients
$\phi $
and Lemma 3.1, we know that the coefficients
![]() $\lambda _{\substack {i,j\\1,3,2,4}}, \lambda _{\substack {i,j\\1,4,2,3}}, \lambda _{\substack {i,j\\2,3,1,4}}$
, and
$\lambda _{\substack {i,j\\1,3,2,4}}, \lambda _{\substack {i,j\\1,4,2,3}}, \lambda _{\substack {i,j\\2,3,1,4}}$
, and
![]() $\lambda _{\substack {i,j\\2,4,1,3}}$
are equal. Write
$\lambda _{\substack {i,j\\2,4,1,3}}$
are equal. Write
![]() $\overline {\lambda }_{i,j}$
for this value. We show that the remaining coefficients in this step
$\overline {\lambda }_{i,j}$
for this value. We show that the remaining coefficients in this step
![]() $\lambda _{\substack {i,j\\1,2,3,4}}$
and
$\lambda _{\substack {i,j\\1,2,3,4}}$
and
![]() $\lambda _{\substack {i,j\\3,4,1,2}}$
both vanish.
$\lambda _{\substack {i,j\\3,4,1,2}}$
both vanish.
To see this, consider the coefficients of
![]() $\sigma _i(x_1, x_2)\sigma _j(x_3, x_4)$
and
$\sigma _i(x_1, x_2)\sigma _j(x_3, x_4)$
and
![]() $\sigma _i(x_3, x_4)\sigma _j(x_1, x_2)$
in
$\sigma _i(x_3, x_4)\sigma _j(x_1, x_2)$
in
![]() $\phi ^{(1)} + \phi ^{(1)} \circ (1\,\,3) + \phi ^{(1)}\circ (1\,\,4)$
. These are, respectively,
$\phi ^{(1)} + \phi ^{(1)} \circ (1\,\,3) + \phi ^{(1)}\circ (1\,\,4)$
. These are, respectively,
and
Lemma 3.1 shows that both expressions vanish, showing that
![]() $\lambda _{\substack {i,j\\1,2,3,4}} = \lambda _{\substack {i,j\\3,4,1,2}} = 0$
. Define
$\lambda _{\substack {i,j\\1,2,3,4}} = \lambda _{\substack {i,j\\3,4,1,2}} = 0$
. Define
![]() $\alpha ^{(2)} \colon G^4 \to \mathbb {F}_2$
by
$\alpha ^{(2)} \colon G^4 \to \mathbb {F}_2$
by
 $$ \begin{align*}&\alpha^{(2)}(x_1, x_2, x_3, x_4) = \alpha^{(1)}(x_1, x_2, x_3, x_4) \\ &\quad+ \sum_{\substack{i,j \in [s]\\i \not=j}} \overline{\lambda}_{i,j} \Big(\sigma_i(x_1, x_2)\sigma_j(x_3, x_4) + \sigma_i(x_2, x_3)\sigma_j(x_1, x_4)+ \sigma_i(x_3, x_1)\sigma_j(x_2, x_4)\Big).\end{align*} $$
$$ \begin{align*}&\alpha^{(2)}(x_1, x_2, x_3, x_4) = \alpha^{(1)}(x_1, x_2, x_3, x_4) \\ &\quad+ \sum_{\substack{i,j \in [s]\\i \not=j}} \overline{\lambda}_{i,j} \Big(\sigma_i(x_1, x_2)\sigma_j(x_3, x_4) + \sigma_i(x_2, x_3)\sigma_j(x_1, x_4)+ \sigma_i(x_3, x_1)\sigma_j(x_2, x_4)\Big).\end{align*} $$
Note that the additional term in the equality above is symmetric in
![]() $x_{[3]}$
on the subspace
$x_{[3]}$
on the subspace
![]() $U'$
and so is
$U'$
and so is
![]() $\alpha ^{(2)}(x_{[4]})$
. Defining
$\alpha ^{(2)}(x_{[4]})$
. Defining
![]() $\phi ^{(2)}(x_{[4]}) = \alpha ^{(2)}(x_{[4]})+ \alpha ^{(2)} \circ (3\,\,4)(x_{[4]})$
, we observe that
$\phi ^{(2)}(x_{[4]}) = \alpha ^{(2)}(x_{[4]})+ \alpha ^{(2)} \circ (3\,\,4)(x_{[4]})$
, we observe that
![]() $\phi ^{(2)}|_{U' \times \cdots \times U'}$
satisfies symmetry conditions (i)–(iii) which we used for
$\phi ^{(2)}|_{U' \times \cdots \times U'}$
satisfies symmetry conditions (i)–(iii) which we used for
![]() $\phi $
. It follows from the definition of
$\phi $
. It follows from the definition of
![]() $\alpha ^{(2)}$
that
$\alpha ^{(2)}$
that
 $$ \begin{align}\alpha^{(2)}(x_{[4]})+ \alpha^{(2)} \circ (3\,\,4)(x_{[4]}) = &\sum_{\substack{1\leq i < j \leq t\\(a,b,c,d) \in \mathcal{V}_4}} \mu_{\substack{i,j\\a,b,c,d}} \rho_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\\ &\hspace{2cm}\!\!\!\!\!\!\!\!\!\! + \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d)\end{align} $$
$$ \begin{align}\alpha^{(2)}(x_{[4]})+ \alpha^{(2)} \circ (3\,\,4)(x_{[4]}) = &\sum_{\substack{1\leq i < j \leq t\\(a,b,c,d) \in \mathcal{V}_4}} \mu_{\substack{i,j\\a,b,c,d}} \rho_i(x_a, x_b) \rho_j(x_c, x_d)\nonumber\\ &\hspace{2cm}\!\!\!\!\!\!\!\!\!\! + \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d)\end{align} $$
holds for all
![]() $x_1, x_2, x_3, x_4 \in U'$
.
$x_1, x_2, x_3, x_4 \in U'$
.
In order to simplify the notation in the remaining two steps, we introduce informal objects called places. Each symmetric form
![]() $\sigma _i$
has one place, and each asymmetric form
$\sigma _i$
has one place, and each asymmetric form
![]() $\rho _i$
has two places corresponding to the first variable and the second variable. Notice that the symmetry properties (i) and (ii) of
$\rho _i$
has two places corresponding to the first variable and the second variable. Notice that the symmetry properties (i) and (ii) of
![]() $\phi $
and Lemma 3.1 imply that the coefficients of products
$\phi $
and Lemma 3.1 imply that the coefficients of products
![]() $\rho _i(x_a, x_b) \rho _j(x_c, x_d)$
and
$\rho _i(x_a, x_b) \rho _j(x_c, x_d)$
and
![]() $\sigma _i(x_a, x_b) \rho _j(x_c, x_d)$
depend only on the choice of places for variables
$\sigma _i(x_a, x_b) \rho _j(x_c, x_d)$
depend only on the choice of places for variables
![]() $x_3$
and
$x_3$
and
![]() $x_4$
. For example, if we chose the place in
$x_4$
. For example, if we chose the place in
![]() $\sigma _i$
and a place corresponding to the second variable in
$\sigma _i$
and a place corresponding to the second variable in
![]() $\rho _j$
, then we have that products
$\rho _j$
, then we have that products
receive the same coefficient. Furthermore, our work in Step 3 could be rephrased as saying that the coefficients of products where we use two copies of the same place vanish.
Using the places terminology, we write
![]() $\lambda _{A\,\,B}$
for the coefficient received by products where
$\lambda _{A\,\,B}$
for the coefficient received by products where
![]() $x_3$
and
$x_3$
and
![]() $x_4$
are put at places A and B. In the rest of the proof, we show that
$x_4$
are put at places A and B. In the rest of the proof, we show that
for all places
![]() $A, B, C$
.
$A, B, C$
.
Step 4. Coefficients
![]() $\mu _{\substack {i,j\\a,b,c,d}}$
. Note that, in this case, the places
$\mu _{\substack {i,j\\a,b,c,d}}$
. Note that, in this case, the places
![]() $A, B$
, and C in (4.16) may assume to be distinct and furthermore that A and B belong to the form
$A, B$
, and C in (4.16) may assume to be distinct and furthermore that A and B belong to the form
![]() $\rho _i$
and C is a place in
$\rho _i$
and C is a place in
![]() $\rho _j$
(we do not assume that
$\rho _j$
(we do not assume that
![]() $i < j$
, but only that
$i < j$
, but only that
![]() $i \not =j$
). Suppose that C is the place corresponding to the first variable in
$i \not =j$
). Suppose that C is the place corresponding to the first variable in
![]() $\rho _j$
, and the other case will follow analogously. Consider the coefficient of the product
$\rho _j$
, and the other case will follow analogously. Consider the coefficient of the product
![]() $\rho _i(x_3, x_4)\rho _j(x_1, x_2)$
in
$\rho _i(x_3, x_4)\rho _j(x_1, x_2)$
in
![]() $\phi ^{(2)} + \phi ^{(2)} \circ (1\,\,3) + \phi ^{(2)}\circ (1\,\,4) = 0$
. This coefficient equals
$\phi ^{(2)} + \phi ^{(2)} \circ (1\,\,3) + \phi ^{(2)}\circ (1\,\,4) = 0$
. This coefficient equals
and vanishes, proving (4.16).
For each
![]() $i,j \in [t]$
with
$i,j \in [t]$
with
![]() $i < j$
let
$i < j$
let
![]() $\overline {\mu }_{i,j, A} = \lambda _{A\,\,D}$
,
$\overline {\mu }_{i,j, A} = \lambda _{A\,\,D}$
,
![]() $\overline {\mu }_{i,j, B} = \lambda _{B\,\,D}$
and
$\overline {\mu }_{i,j, B} = \lambda _{B\,\,D}$
and
![]() $\overline {\mu }_{i,j, C} = \lambda _{C\,\,D}$
, where
$\overline {\mu }_{i,j, C} = \lambda _{C\,\,D}$
, where
![]() $A, B, C$
, and D are, respectively, the places corresponding to the first variable in
$A, B, C$
, and D are, respectively, the places corresponding to the first variable in
![]() $\rho _i$
, the second variable in
$\rho _i$
, the second variable in
![]() $\rho _i$
, the first variable in
$\rho _i$
, the first variable in
![]() $\rho _j$
, and the second variable in
$\rho _j$
, and the second variable in
![]() $\rho _j$
. We may now define
$\rho _j$
. We may now define
![]() $\alpha ^{(3)} \colon G^4 \to \mathbb {F}_2$
by
$\alpha ^{(3)} \colon G^4 \to \mathbb {F}_2$
by
 $$ \begin{align}\alpha^{(3)}(x_1, x_2, x_3, x_4) =\alpha^{(2)}(x_1, x_2, x_3, x_4) + &\sum_{1 \leq i < j \leq t} \overline{\mu}_{i,j, A}\Big(\sum_{\pi \in \operatorname{Sym}_{[3]}} \rho_i(x_4, x_{\pi(1)}) \rho_j(x_{\pi(2)}, x_{\pi(3)})\Big)\nonumber\\ & + \sum_{1 \leq i < j \leq t} \overline{\mu}_{i,j, B}\Big(\sum_{\pi \in \operatorname{Sym}_{[3]}} \rho_i(x_{\pi(1)}, x_4) \rho_j(x_{\pi(2)}, x_{\pi(3)})\Big)\nonumber\\ & + \sum_{1 \leq i < j \leq t} \overline{\mu}_{i,j, C}\Big(\kern-1pt\sum_{\pi \in \operatorname{Sym}_{[3]}} \rho_i(x_{\pi(1)}, x_{\pi(2)}) \rho_j(x_4, x_{\pi(3)})\kern-1pt\Big).\end{align} $$
$$ \begin{align}\alpha^{(3)}(x_1, x_2, x_3, x_4) =\alpha^{(2)}(x_1, x_2, x_3, x_4) + &\sum_{1 \leq i < j \leq t} \overline{\mu}_{i,j, A}\Big(\sum_{\pi \in \operatorname{Sym}_{[3]}} \rho_i(x_4, x_{\pi(1)}) \rho_j(x_{\pi(2)}, x_{\pi(3)})\Big)\nonumber\\ & + \sum_{1 \leq i < j \leq t} \overline{\mu}_{i,j, B}\Big(\sum_{\pi \in \operatorname{Sym}_{[3]}} \rho_i(x_{\pi(1)}, x_4) \rho_j(x_{\pi(2)}, x_{\pi(3)})\Big)\nonumber\\ & + \sum_{1 \leq i < j \leq t} \overline{\mu}_{i,j, C}\Big(\kern-1pt\sum_{\pi \in \operatorname{Sym}_{[3]}} \rho_i(x_{\pi(1)}, x_{\pi(2)}) \rho_j(x_4, x_{\pi(3)})\kern-1pt\Big).\end{align} $$
It follows that
![]() $\alpha ^{(3)}|_{U'\times \cdots \times U'}$
is still symmetric in the first three variables and the form
$\alpha ^{(3)}|_{U'\times \cdots \times U'}$
is still symmetric in the first three variables and the form
![]() $\phi ^{(3)}(x_{[4]}) = \alpha ^{(3)}(x_{[4]})+ \alpha ^{(3)} \circ (3\,\,4)(x_{[4]})$
satisfies symmetry conditions (i)–(iii) which we used for
$\phi ^{(3)}(x_{[4]}) = \alpha ^{(3)}(x_{[4]})+ \alpha ^{(3)} \circ (3\,\,4)(x_{[4]})$
satisfies symmetry conditions (i)–(iii) which we used for
![]() $\phi $
on the subspace
$\phi $
on the subspace
![]() $U'$
. We claim that
$U'$
. We claim that
![]() $\phi ^{(3)}$
has simpler structure than
$\phi ^{(3)}$
has simpler structure than
![]() $\phi ^{(2)}$
.
$\phi ^{(2)}$
.
Claim 4.5 The equality
 $$ \begin{align}\alpha^{(3)}(x_{[4]})+ \alpha^{(3)} \circ (3\,\,4)(x_{[4]}) = \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d)\end{align} $$
$$ \begin{align}\alpha^{(3)}(x_{[4]})+ \alpha^{(3)} \circ (3\,\,4)(x_{[4]}) = \sum_{\substack{i \in [s],j \in [t]\\(a,b,c,d) \in \mathcal{V}_5}} \nu_{\substack{i,j\\a,b,c,d}} \sigma_i(x_a, x_b) \rho_j(x_c, x_d)\end{align} $$
holds for all
![]() $x_1, x_2, x_3, x_4 \in U'$
.
$x_1, x_2, x_3, x_4 \in U'$
.
Proof of Claim 4.5
Fix
![]() $1\leq i < j \leq t$
. Let
$1\leq i < j \leq t$
. Let
![]() $A, B, C$
, and D are, respectively, the places corresponding to the first variable in
$A, B, C$
, and D are, respectively, the places corresponding to the first variable in
![]() $\rho _i$
, the second variable in
$\rho _i$
, the second variable in
![]() $\rho _i$
, the first variable in
$\rho _i$
, the first variable in
![]() $\rho _j$
, and the second variable in
$\rho _j$
, and the second variable in
![]() $\rho _j$
. Let
$\rho _j$
. Let
![]() $(a,b,c,d) \in \mathcal {V}_4$
. Recall that the coefficient of
$(a,b,c,d) \in \mathcal {V}_4$
. Recall that the coefficient of
![]() $\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in (4.15) is
$\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in (4.15) is
![]() $\mu _{\substack {i,j\\a,b,c,d}}$
. Our goal is to show that this coefficient equals the one in the form
$\mu _{\substack {i,j\\a,b,c,d}}$
. Our goal is to show that this coefficient equals the one in the form
arising from definition (4.17). We look at different cases on places for
![]() $x_3$
and
$x_3$
and
![]() $x_4$
.
$x_4$
.
Case 1:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $A, B$
. We have
$A, B$
. We have
![]() $\{a,b\} = \{3,4\}$
and
$\{a,b\} = \{3,4\}$
and
![]() $\{c,d\} = \{1,2\}$
. The coefficient of
$\{c,d\} = \{1,2\}$
. The coefficient of
![]() $\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
equals
$\Delta (x_{[4]})$
equals
![]() $\overline {\mu }_{i,j, A} + \overline {\mu }_{i,j, B} = \lambda _{A\,\,D} + \lambda _{B\,\,D} = \lambda _{A\,\,B} = \mu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) for places
$\overline {\mu }_{i,j, A} + \overline {\mu }_{i,j, B} = \lambda _{A\,\,D} + \lambda _{B\,\,D} = \lambda _{A\,\,B} = \mu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) for places
![]() $A, B$
, and D in the second equality.
$A, B$
, and D in the second equality.
Case 2:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $A, C$
. We have
$A, C$
. We have
![]() $\{a,c\} = \{3,4\}$
and
$\{a,c\} = \{3,4\}$
and
![]() $\{b,d\} = \{1,2\}$
. The coefficient of
$\{b,d\} = \{1,2\}$
. The coefficient of
![]() $\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
equals
$\Delta (x_{[4]})$
equals
![]() $\overline {\mu }_{i,j, A} + \overline {\mu }_{i,j, C} = \lambda _{A\,\,D} + \lambda _{C\,\,D} = \lambda _{A\,\,C} = \mu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) for places
$\overline {\mu }_{i,j, A} + \overline {\mu }_{i,j, C} = \lambda _{A\,\,D} + \lambda _{C\,\,D} = \lambda _{A\,\,C} = \mu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) for places
![]() $A, C$
, and D in the second equality.
$A, C$
, and D in the second equality.
Case 3:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $A, D$
. We have
$A, D$
. We have
![]() $\{a,d\} = \{3,4\}$
and
$\{a,d\} = \{3,4\}$
and
![]() $\{b,c\} = \{1,2\}$
. The coefficient of
$\{b,c\} = \{1,2\}$
. The coefficient of
![]() $\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
equals
$\Delta (x_{[4]})$
equals
![]() $\overline {\mu }_{i,j, A} = \lambda _{A\,\,D} = \mu _{\substack {i,j\\a,b,c,d}}$
.
$\overline {\mu }_{i,j, A} = \lambda _{A\,\,D} = \mu _{\substack {i,j\\a,b,c,d}}$
.
Case 4:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $B, C$
. We have
$B, C$
. We have
![]() $\{b,c\} = \{3,4\}$
and
$\{b,c\} = \{3,4\}$
and
![]() $\{a,d\} = \{1,2\}$
. The coefficient of
$\{a,d\} = \{1,2\}$
. The coefficient of
![]() $\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
equals
$\Delta (x_{[4]})$
equals
![]() $\overline {\mu }_{i,j, B} + \overline {\mu }_{i,j, C} = \lambda _{B\,\,D} + \lambda _{C\,\,D} = \lambda _{B\,\,C} = \mu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) for places
$\overline {\mu }_{i,j, B} + \overline {\mu }_{i,j, C} = \lambda _{B\,\,D} + \lambda _{C\,\,D} = \lambda _{B\,\,C} = \mu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) for places
![]() $B, C$
, and D in the second equality.
$B, C$
, and D in the second equality.
Case 5:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $B, D$
. We have
$B, D$
. We have
![]() $\{b,d\} = \{3,4\}$
and
$\{b,d\} = \{3,4\}$
and
![]() $\{a,c\} = \{1,2\}$
. The coefficient of
$\{a,c\} = \{1,2\}$
. The coefficient of
![]() $\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
equals
$\Delta (x_{[4]})$
equals
![]() $\overline {\mu }_{i,j, B} = \lambda _{B\,\,D} = \mu _{\substack {i,j\\a,b,c,d}}$
.
$\overline {\mu }_{i,j, B} = \lambda _{B\,\,D} = \mu _{\substack {i,j\\a,b,c,d}}$
.
Case 6:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $C, D$
. We have
$C, D$
. We have
![]() $\{c,d\} = \{3,4\}$
and
$\{c,d\} = \{3,4\}$
and
![]() $\{a,b\} = \{1,2\}$
. The coefficient of
$\{a,b\} = \{1,2\}$
. The coefficient of
![]() $\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\rho _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
equals
$\Delta (x_{[4]})$
equals
![]() $\overline {\mu }_{i,j, C} = \lambda _{C\,\,D} = \mu _{\substack {i,j\\a,b,c,d}}$
.
$\overline {\mu }_{i,j, C} = \lambda _{C\,\,D} = \mu _{\substack {i,j\\a,b,c,d}}$
.
Step 5. Coefficients
![]() $\nu _{\substack {i,j\\a,b,c,d}}$
. If two of the places
$\nu _{\substack {i,j\\a,b,c,d}}$
. If two of the places
![]() $A, B$
, and C in (4.16) are the same, then without loss of the generality
$A, B$
, and C in (4.16) are the same, then without loss of the generality
![]() $A= B$
is the place in a symmetric form
$A= B$
is the place in a symmetric form
![]() $\sigma _i$
and C is one of the places in an asymmetric form
$\sigma _i$
and C is one of the places in an asymmetric form
![]() $\rho _j$
. Assume that C corresponds to the first variable in
$\rho _j$
. Assume that C corresponds to the first variable in
![]() $\rho _j$
, and the other case is similar. Equality (4.16) reduces to showing that
$\rho _j$
, and the other case is similar. Equality (4.16) reduces to showing that
![]() $\lambda _{A\,\,A} = 0$
in this case. To see this, consider the coefficient of the product
$\lambda _{A\,\,A} = 0$
in this case. To see this, consider the coefficient of the product
![]() $\sigma _i(x_3, x_4)\rho _j(x_1, x_2)$
in
$\sigma _i(x_3, x_4)\rho _j(x_1, x_2)$
in
![]() $\phi ^{(3)} + \phi ^{(3)} \circ (1\,\,3) + \phi ^{(3)}\circ (1\,\,4) = 0$
. This coefficient equals
$\phi ^{(3)} + \phi ^{(3)} \circ (1\,\,3) + \phi ^{(3)}\circ (1\,\,4) = 0$
. This coefficient equals
and vanishes, as desired.
On the other hand, if
![]() $A, B$
, and C are different, then we may assume that A is the place in
$A, B$
, and C are different, then we may assume that A is the place in
![]() $\sigma _i$
and B and C are, respectively, the first variable and the second variable in
$\sigma _i$
and B and C are, respectively, the first variable and the second variable in
![]() $\rho _j$
. This time consider the coefficient of the product
$\rho _j$
. This time consider the coefficient of the product
![]() $\sigma _i(x_3, x_2)\rho _j(x_4, x_1)$
in
$\sigma _i(x_3, x_2)\rho _j(x_4, x_1)$
in
![]() $\phi ^{(3)} + \phi ^{(3)} \circ (1\,\,3) + \phi ^{(3)}\circ (1\,\,4) = 0$
. This coefficient equals
$\phi ^{(3)} + \phi ^{(3)} \circ (1\,\,3) + \phi ^{(3)}\circ (1\,\,4) = 0$
. This coefficient equals
and vanishes, as desired.
For each
![]() $i \in [s],j \in [t]$
, let
$i \in [s],j \in [t]$
, let
![]() $\overline {\mu }_{i,j, B} = \lambda _{A\,\,B}$
and
$\overline {\mu }_{i,j, B} = \lambda _{A\,\,B}$
and
![]() $\overline {\mu }_{i,j, C} = \lambda _{A\,\,C}$
, where
$\overline {\mu }_{i,j, C} = \lambda _{A\,\,C}$
, where
![]() $A, B$
, and C are, respectively, the places corresponding to
$A, B$
, and C are, respectively, the places corresponding to
![]() $\sigma _i$
, the first variable in
$\sigma _i$
, the first variable in
![]() $\rho _j$
, and the second variable in
$\rho _j$
, and the second variable in
![]() $\rho _j$
. We may now define
$\rho _j$
. We may now define
![]() $\alpha ^{(4)} \colon G^4 \to \mathbb {F}_2$
by
$\alpha ^{(4)} \colon G^4 \to \mathbb {F}_2$
by
 $$ \begin{align*}&\alpha^{(4)}(x_1, x_2, x_3, x_4) =\alpha^{(3)}(x_1, x_2, x_3, x_4) \\ &\quad+ \sum_{i \in [s], j \in [t]} \overline{\mu}_{i,j, B}\Big(\sigma_i(x_1, x_2)\rho_j(x_4, x_3) + \sigma_i(x_2, x_3)\rho_j(x_4, x_1) + \sigma_i(x_3, x_1)\rho_j(x_4, x_2)\Big)\\ &\quad+ \sum_{i \in [s], j \in [t]} \overline{\mu}_{i,j, C}\Big(\sigma_i(x_1, x_2)\rho_j(x_3, x_4) + \sigma_i(x_2, x_3)\rho_j(x_1, x_4) + \sigma_i(x_3, x_1)\rho_j(x_2, x_4)\Big).\end{align*} $$
$$ \begin{align*}&\alpha^{(4)}(x_1, x_2, x_3, x_4) =\alpha^{(3)}(x_1, x_2, x_3, x_4) \\ &\quad+ \sum_{i \in [s], j \in [t]} \overline{\mu}_{i,j, B}\Big(\sigma_i(x_1, x_2)\rho_j(x_4, x_3) + \sigma_i(x_2, x_3)\rho_j(x_4, x_1) + \sigma_i(x_3, x_1)\rho_j(x_4, x_2)\Big)\\ &\quad+ \sum_{i \in [s], j \in [t]} \overline{\mu}_{i,j, C}\Big(\sigma_i(x_1, x_2)\rho_j(x_3, x_4) + \sigma_i(x_2, x_3)\rho_j(x_1, x_4) + \sigma_i(x_3, x_1)\rho_j(x_2, x_4)\Big).\end{align*} $$
We show that
![]() $\alpha ^{(4)}|_{U'\times \cdots \times U'}$
is symmetric.
$\alpha ^{(4)}|_{U'\times \cdots \times U'}$
is symmetric.
Claim 4.6 The form
![]() $\alpha ^{(4)}|_{U'\times \cdots \times U'}$
is symmetric.
$\alpha ^{(4)}|_{U'\times \cdots \times U'}$
is symmetric.
Proof of Claim 4.6
Let us reuse the notation
![]() $\Delta $
, this time defining it as
$\Delta $
, this time defining it as
Let
![]() $i \in [s], j \in [t]$
, and
$i \in [s], j \in [t]$
, and
![]() $(a,b,c,d) \in \mathcal {V}_5$
. We need to show that the coefficient of
$(a,b,c,d) \in \mathcal {V}_5$
. We need to show that the coefficient of
![]() $ \sigma _i(x_a, x_b) \rho _j(x_c, x_d)$
in
$ \sigma _i(x_a, x_b) \rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
equals
$\Delta (x_{[4]})$
equals
![]() $\nu _{\substack {i,j\\a,b,c,d}} $
. Let
$\nu _{\substack {i,j\\a,b,c,d}} $
. Let
![]() $A, B$
, and C be, respectively, the places corresponding to
$A, B$
, and C be, respectively, the places corresponding to
![]() $\sigma _i$
, the first variable in
$\sigma _i$
, the first variable in
![]() $\rho _j$
, and the second variable in
$\rho _j$
, and the second variable in
![]() $\rho _j$
. As in the proof of Claim 4.5, we consider the cases for the places of
$\rho _j$
. As in the proof of Claim 4.5, we consider the cases for the places of
![]() $x_3$
and
$x_3$
and
![]() $x_4$
.
$x_4$
.
Case 1:
![]() $x_3,x_4$
are both at place A. We have
$x_3,x_4$
are both at place A. We have
![]() $\{a,b\} = \{3,4\}$
and
$\{a,b\} = \{3,4\}$
and
![]() $\{c,d\} = \{1,2\}$
. The coefficient of
$\{c,d\} = \{1,2\}$
. The coefficient of
![]() $\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
vanishes, and we know that
$\Delta (x_{[4]})$
vanishes, and we know that
![]() $0 = \lambda _{A\,A} = \nu _{\substack {i,j\\a,b,c,d}}$
, as desired.
$0 = \lambda _{A\,A} = \nu _{\substack {i,j\\a,b,c,d}}$
, as desired.
Case 2:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $A, B$
. We have
$A, B$
. We have
![]() $\{b,c\} = \{3,4\}$
and
$\{b,c\} = \{3,4\}$
and
![]() $\{a,d\} = \{1,2\}$
(recalling that
$\{a,d\} = \{1,2\}$
(recalling that
![]() $\mathcal {V}_5$
is a proper subset of
$\mathcal {V}_5$
is a proper subset of
![]() $\operatorname {Sym}_{[4]}$
). The coefficient of
$\operatorname {Sym}_{[4]}$
). The coefficient of
![]() $\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
is
$\Delta (x_{[4]})$
is
![]() $\overline {\mu }_{i,j, B} = \lambda _{A\,\,B} = \nu _{\substack {i,j\\a,b,c,d}}$
.
$\overline {\mu }_{i,j, B} = \lambda _{A\,\,B} = \nu _{\substack {i,j\\a,b,c,d}}$
.
Case 3:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $A, C$
. We have
$A, C$
. We have
![]() $\{b,d\} = \{3,4\}$
and
$\{b,d\} = \{3,4\}$
and
![]() $\{a,c\} = \{1,2\}$
(again, recalling that
$\{a,c\} = \{1,2\}$
(again, recalling that
![]() $\mathcal {V}_5$
is a proper subset of
$\mathcal {V}_5$
is a proper subset of
![]() $\operatorname {Sym}_{[4]}$
). The coefficient of
$\operatorname {Sym}_{[4]}$
). The coefficient of
![]() $\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
is
$\Delta (x_{[4]})$
is
![]() $\overline {\mu }_{i,j, C} = \lambda _{A\,\,C} = \nu _{\substack {i,j\\a,b,c,d}}$
.
$\overline {\mu }_{i,j, C} = \lambda _{A\,\,C} = \nu _{\substack {i,j\\a,b,c,d}}$
.
Case 4:
![]() $x_3,x_4$
are at places
$x_3,x_4$
are at places
![]() $B, C$
. We have
$B, C$
. We have
![]() $\{c,d\} = \{3,4\}$
and
$\{c,d\} = \{3,4\}$
and
![]() $\{a,b\} = \{1,2\}$
. The coefficient of
$\{a,b\} = \{1,2\}$
. The coefficient of
![]() $\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
$\sigma _i(x_a, x_b)\rho _j(x_c, x_d)$
in
![]() $\Delta (x_{[4]})$
is
$\Delta (x_{[4]})$
is
![]() $\overline {\mu }_{i,j, B} + \overline {\mu }_{i,j, C} = \lambda _{A\,\,B} + \lambda _{A\,\,C}= \lambda _{B\,\,C}= \nu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) in the second equality.
$\overline {\mu }_{i,j, B} + \overline {\mu }_{i,j, C} = \lambda _{A\,\,B} + \lambda _{A\,\,C}= \lambda _{B\,\,C}= \nu _{\substack {i,j\\a,b,c,d}}$
, where we used (4.16) in the second equality.
We have thus obtained a multilinear form
![]() $\alpha ^{(4)}|_{U' \times \cdots \times U'}$
which is symmetric in
$\alpha ^{(4)}|_{U' \times \cdots \times U'}$
which is symmetric in
![]() $U' \times \cdots \times U'$
such that
$U' \times \cdots \times U'$
such that
![]() $\operatorname {prank}\Big ((\alpha + \alpha ^{(4)})|_{U' \times \cdots \times U'}\Big ) \leq O(r^2)$
. The claimed result follows from Corollary 2.6 (recall that
$\operatorname {prank}\Big ((\alpha + \alpha ^{(4)})|_{U' \times \cdots \times U'}\Big ) \leq O(r^2)$
. The claimed result follows from Corollary 2.6 (recall that
![]() $\operatorname {codim}_G U' \leq O(Rr)$
, which is the main contribution to the final bound). As in the proof of the previous theorem, we choose C and D depending only on the constants from Lemma 3.1 so that the partition rank condition of Lemma 3.1 holds at all times.
$\operatorname {codim}_G U' \leq O(Rr)$
, which is the main contribution to the final bound). As in the proof of the previous theorem, we choose C and D depending only on the constants from Lemma 3.1 so that the partition rank condition of Lemma 3.1 holds at all times.
As a final result in this section, we prove Theorem 1.8.
Proof of Theorem 1.8
By assumptions, we have that
where all partitions of the variables appearing above are nontrivial, that is,
![]() $d_i \geq 2$
.
$d_i \geq 2$
.
Step 1. Obtaining a decomposition with inherited properties. We begin our work by deducing some properties of the low partition rank decomposition (4.19) of
![]() $\alpha + \alpha \circ (3\,\,4)$
. Using Proposition 3.3, we may assume that every
$\alpha + \alpha \circ (3\,\,4)$
. Using Proposition 3.3, we may assume that every
![]() $\beta _{i, j}$
comes from a slice of
$\beta _{i, j}$
comes from a slice of
![]() $\alpha + \alpha \circ (3\,\,4)$
. This has the cost of replacing r by
$\alpha + \alpha \circ (3\,\,4)$
. This has the cost of replacing r by
![]() $O({r}^{O(1)})$
, which we do with a slight misuse of notation. Writing
$O({r}^{O(1)})$
, which we do with a slight misuse of notation. Writing
![]() $\beta (x_I)$
for
$\beta (x_I)$
for
![]() $\beta _{i, j}(x_{I_{i,j}})$
, we know that
$\beta _{i, j}(x_{I_{i,j}})$
, we know that
![]() $\beta (x_I) = \alpha (x_I, y_{[5] \setminus I}) + \alpha \circ (3\,\,4)(x_I, y_{[5] \setminus I})$
for some fixed
$\beta (x_I) = \alpha (x_I, y_{[5] \setminus I}) + \alpha \circ (3\,\,4)(x_I, y_{[5] \setminus I})$
for some fixed
![]() $y_{[5] \setminus I}$
. In particular, the following holds.
$y_{[5] \setminus I}$
. In particular, the following holds.
(S1) When
 $3, 4 \in I$
, then
$3, 4 \in I$
, then
 $\beta (x_I) = \alpha _{y_{[5] \setminus I}}(x_I) + \alpha _{y_{[5] \setminus I}}\circ (3\,\,4)(x_I)$
. Thus, we have the equality
$\beta (x_I) = \alpha _{y_{[5] \setminus I}}(x_I) + \alpha _{y_{[5] \setminus I}}\circ (3\,\,4)(x_I)$
. Thus, we have the equality
 $\beta = \tilde {\beta } + \tilde {\beta } \circ (3\,\,4)$
, where
$\beta = \tilde {\beta } + \tilde {\beta } \circ (3\,\,4)$
, where
 $\tilde {\beta }(x_I)$
is a multilinear form which is symmetric in the variables
$\tilde {\beta }(x_I)$
is a multilinear form which is symmetric in the variables
 $x_{I \cap [3]}$
. Therefore, replacing
$x_{I \cap [3]}$
. Therefore, replacing
 $\beta $
by
$\beta $
by
 $\tilde {\beta } + \tilde {\beta } \circ (3\,\,4)$
, we may assume that every form
$\tilde {\beta } + \tilde {\beta } \circ (3\,\,4)$
, we may assume that every form
 $\beta (x_I)$
that has
$\beta (x_I)$
that has
 $3, 4 \in I$
is either symmetric in variables
$3, 4 \in I$
is either symmetric in variables
 $x_{I \cap [3]}$
or symmetric in variables
$x_{I \cap [3]}$
or symmetric in variables
 $x_{I \cap (\{1,2,4\})}$
.
$x_{I \cap (\{1,2,4\})}$
.-
(S2) When
 $|I \cap \{3, 4\}| = 1$
, say
$|I \cap \{3, 4\}| = 1$
, say
 $\{3\} = I \cap \{3, 4\}$
, then we see that
$\{3\} = I \cap \{3, 4\}$
, then we see that
 $\beta $
is symmetric in variables
$\beta $
is symmetric in variables
 $x_{I\cap [2]}$
.
$x_{I\cap [2]}$
. (S3) When
 $3, 4 \notin I$
, then
$3, 4 \notin I$
, then
 $\beta $
is symmetric in variables
$\beta $
is symmetric in variables
 $x_{I \cap [2]}$
.
$x_{I \cap [2]}$
.
We may therefore assume that all forms in the products in (4.19) have a symmetry property described in one of (S1)–(S3).
Step 2. Simplifying the partitions. Observe that all nontrivial partitions of the set
![]() $[5]$
have either two sets which have sizes 3 and 2, or at least one set is a singleton. We refer to the former partitions as the relevant ones. In particular, each summand in (4.19) either has a relevant partition or it has a factor
$[5]$
have either two sets which have sizes 3 and 2, or at least one set is a singleton. We refer to the former partitions as the relevant ones. In particular, each summand in (4.19) either has a relevant partition or it has a factor
![]() $\gamma (x_c)$
for some linear form
$\gamma (x_c)$
for some linear form
![]() $\gamma $
. By passing to subspace defined by zero sets of such linear forms, we may assume that all partitions are in fact relevant.
$\gamma $
. By passing to subspace defined by zero sets of such linear forms, we may assume that all partitions are in fact relevant.
Step 3. Regularizing the forms. In this step, we apply our symmetry-respecting regularity lemma (Lemma 4.1).
Our goal is to remove some partitions of variables from expression (4.19). We shall first remove all relevant partitions
![]() $I_1 \cup I_2 = [5]$
such that
$I_1 \cup I_2 = [5]$
such that
![]() $|I_1| = 2$
and
$|I_1| = 2$
and
![]() $5 \in I_1$
, and second we remove all relevant partitions
$5 \in I_1$
, and second we remove all relevant partitions
![]() $I_1 \cup I_2 = [5]$
such that
$I_1 \cup I_2 = [5]$
such that
![]() $|I_1| = 3$
and
$|I_1| = 3$
and
![]() $5 \in I_1$
. Using slightly more general notation, we explain how to apply Lemma 4.1 in either of the two cases. We say that the variables
$5 \in I_1$
. Using slightly more general notation, we explain how to apply Lemma 4.1 in either of the two cases. We say that the variables
![]() $x_1, \dots , x_4$
are active and that
$x_1, \dots , x_4$
are active and that
![]() $x_5$
is the passive variable.
$x_5$
is the passive variable.
Let
![]() $(\ell _1, \ell _2) \in \{(1,3), (2,2)\}$
. The numbers
$(\ell _1, \ell _2) \in \{(1,3), (2,2)\}$
. The numbers
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
stand for the number of active variables in sets
$\ell _2$
stand for the number of active variables in sets
![]() $I_1$
and
$I_1$
and
![]() $I_2$
. We aim to remove the set
$I_2$
. We aim to remove the set
![]() $\mathcal {R}$
of all partitions
$\mathcal {R}$
of all partitions
![]() $(A_1 \cup \{5\}, A_2)$
, where
$(A_1 \cup \{5\}, A_2)$
, where
![]() $|A_i| = \ell _i$
. Write
$|A_i| = \ell _i$
. Write
![]() $P_1 = \{5\}$
and
$P_1 = \{5\}$
and
![]() $P_2 = \emptyset $
, which stand for the indices of passive variables, and make the following list. Take all forms
$P_2 = \emptyset $
, which stand for the indices of passive variables, and make the following list. Take all forms
![]() $\beta (x_{A \cup P_i})$
appearing in the decomposition (4.19) such that
$\beta (x_{A \cup P_i})$
appearing in the decomposition (4.19) such that
![]() $A \subseteq [4]$
of size
$A \subseteq [4]$
of size
![]() $|A| = \ell _i$
. By the symmetry properties S1–S3, we see that each of the chosen forms
$|A| = \ell _i$
. By the symmetry properties S1–S3, we see that each of the chosen forms
![]() $\beta $
is equal to:
$\beta $
is equal to:
-
•
 $\gamma (x_S, x_{P_i})$
where
$\gamma (x_S, x_{P_i})$
where
 $\gamma $
is symmetric in
$\gamma $
is symmetric in
 $x_S$
,
$x_S$
,
 $|S| = \ell _i$
, with
$|S| = \ell _i$
, with
 $S \subseteq [2]$
, or
$S \subseteq [2]$
, or -
•
 $\gamma (x_S, x_c, x_{P_i})$
where
$\gamma (x_S, x_c, x_{P_i})$
where
 $\gamma $
is symmetric in
$\gamma $
is symmetric in
 $x_S$
,
$x_S$
,
 $|S| = \ell _i - 1$
, with
$|S| = \ell _i - 1$
, with
 $S \subseteq [2]$
,
$S \subseteq [2]$
,
 $c \in \{3, 4\}$
, or
$c \in \{3, 4\}$
, or -
•
 $\gamma (x_S, x_c, x_{P_i})$
where
$\gamma (x_S, x_c, x_{P_i})$
where
 $\gamma $
is symmetric in
$\gamma $
is symmetric in
 $x_S$
,
$x_S$
,
 $|S| = \ell _i - 1$
, with
$|S| = \ell _i - 1$
, with
 $c \in \{3, 4\}$
,
$c \in \{3, 4\}$
,
 $S \subseteq [4] \setminus \{c\}$
.
$S \subseteq [4] \setminus \{c\}$
.
Consider all
![]() $\gamma $
above and replace variables
$\gamma $
above and replace variables
![]() $x_S$
by
$x_S$
by
![]() $z_1, \dots , z_{\ell _i}$
when
$z_1, \dots , z_{\ell _i}$
when
![]() $x_c$
does not appear, and
$x_c$
does not appear, and
![]() $x_S$
by
$x_S$
by
![]() $z_1, \dots , z_{\ell _i - 1}$
and
$z_1, \dots , z_{\ell _i - 1}$
and
![]() $x_c$
by
$x_c$
by
![]() $z_{\ell _i}$
when
$z_{\ell _i}$
when
![]() $x_c$
appears. Every form is thus symmetric in
$x_c$
appears. Every form is thus symmetric in
![]() $z_{[\ell _i - 1]}$
. Let
$z_{[\ell _i - 1]}$
. Let
![]() $C, D \geq 2$
quantities to be specified later, which will depend only on the constants in Lemma 3.1. Apply Lemma 4.1 to the list. We thus obtain integers
$C, D \geq 2$
quantities to be specified later, which will depend only on the constants in Lemma 3.1. Apply Lemma 4.1 to the list. We thus obtain integers
![]() $s,q,t$
such that
$s,q,t$
such that
![]() $s + q + t \leq r$
and multilinear forms
$s + q + t \leq r$
and multilinear forms
![]() $\sigma _{[s]}, \pi _{[q]}, \rho _{[t]}$
with properties (i)–(v) from that lemma for a parameter
$\sigma _{[s]}, \pi _{[q]}, \rho _{[t]}$
with properties (i)–(v) from that lemma for a parameter
![]() $R \leq C^{D^{O(r)}}$
. We add superscript
$R \leq C^{D^{O(r)}}$
. We add superscript
![]() $\sigma ^{i, \ell _i}_1 \dots $
to stress the dependence on i and
$\sigma ^{i, \ell _i}_1 \dots $
to stress the dependence on i and
![]() $\ell _i$
. Note that by Remark 4.2, when
$\ell _i$
. Note that by Remark 4.2, when
![]() $\ell _i = 2$
, we only have forms
$\ell _i = 2$
, we only have forms
![]() $\sigma _{[s]}$
and
$\sigma _{[s]}$
and
![]() $\rho _{[t]}$
, and when
$\rho _{[t]}$
, and when
![]() $\ell _i = 1$
, we only have forms
$\ell _i = 1$
, we only have forms
![]() $\sigma _{[s]}$
. Furthermore, since we are applying Lemma 4.1 to forms in at most three variables, low partition rank means that we may pass to a subspace where we get exact properties. Thus, by passing to a further subspace U, we may assume that forms
$\sigma _{[s]}$
. Furthermore, since we are applying Lemma 4.1 to forms in at most three variables, low partition rank means that we may pass to a subspace where we get exact properties. Thus, by passing to a further subspace U, we may assume that forms
![]() $\sigma _{[s]}$
are symmetric in their active variables. To be precise, the subspace U has a codimension at most
$\sigma _{[s]}$
are symmetric in their active variables. To be precise, the subspace U has a codimension at most
![]() $3rR + r$
inside G (recall that we have first passed to a subspace of codimension at most r in order to remove the irrelevant partitions).
$3rR + r$
inside G (recall that we have first passed to a subspace of codimension at most r in order to remove the irrelevant partitions).
Note that the forms
![]() $\pi _i$
and
$\pi _i$
and
![]() $\rho _i$
have the property that they are symmetric in the first
$\rho _i$
have the property that they are symmetric in the first
![]() $\ell _i - 1$
variables, the variables
$\ell _i - 1$
variables, the variables
![]() $x_{P_i}$
play a passive role, and
$x_{P_i}$
play a passive role, and
![]() $z_{\ell _i}$
is related to
$z_{\ell _i}$
is related to
![]() $z_{[\ell _i-1]}$
in the sense that we shall consider compositions with transpositions
$z_{[\ell _i-1]}$
in the sense that we shall consider compositions with transpositions
![]() $(a\,\,\ell _i)$
. With this in mind, we adopt the following notation. For a multilinear form
$(a\,\,\ell _i)$
. With this in mind, we adopt the following notation. For a multilinear form
![]() $\phi (z_{[\ell _i]}, x_{P_i})$
, we separate its variables as
$\phi (z_{[\ell _i]}, x_{P_i})$
, we separate its variables as
![]() $\phi (z_{[\ell _i - 1]}\,|\,z_{\ell _i}\,|\,x_{P_i})$
where the first group indicated the symmetric part, the second group has a single variable, and the third group consists of passive variables. We refer to the variable in the second group as the asymmetric variable.
$\phi (z_{[\ell _i - 1]}\,|\,z_{\ell _i}\,|\,x_{P_i})$
where the first group indicated the symmetric part, the second group has a single variable, and the third group consists of passive variables. We refer to the variable in the second group as the asymmetric variable.
Replace forms
![]() $\beta (x_I, x_{P_a})$
where
$\beta (x_I, x_{P_a})$
where
![]() $I \subseteq [4]$
,
$I \subseteq [4]$
,
![]() $|I| = \ell _a$
, by the newly found maps using property (v) of Lemma 4.1. If
$|I| = \ell _a$
, by the newly found maps using property (v) of Lemma 4.1. If
![]() $3, 4 \notin I$
, then we know that
$3, 4 \notin I$
, then we know that
![]() $\beta $
is symmetric in
$\beta $
is symmetric in
![]() $x_I$
so the second part of Observation 4.3 implies that
$x_I$
so the second part of Observation 4.3 implies that
![]() $\beta (x_I, x_{P_a})$
can be replaced by
$\beta (x_I, x_{P_a})$
can be replaced by
where
![]() $\tau (x_I, x_{P_a})$
is a multilinear form of partition rank at most
$\tau (x_I, x_{P_a})$
is a multilinear form of partition rank at most
![]() $(r+2)R$
. On the other hand, if
$(r+2)R$
. On the other hand, if
![]() $I \cap \{3, 4\} \not = \emptyset $
, take
$I \cap \{3, 4\} \not = \emptyset $
, take
![]() $c \in I\cap \{3, 4\}$
to be an index such that
$c \in I\cap \{3, 4\}$
to be an index such that
![]() $\beta $
is symmetric in
$\beta $
is symmetric in
![]() $x_{I \setminus \{c\}}$
. Properties (iii) and (v) of Lemma 4.1 and Observation 4.3 imply that
$x_{I \setminus \{c\}}$
. Properties (iii) and (v) of Lemma 4.1 and Observation 4.3 imply that
![]() $\beta (x_I, x_{P_a})$
can be replaced by
$\beta (x_I, x_{P_a})$
can be replaced by
where
![]() $\tau (x_I, x_{P_a})$
is a multilinear form of partition rank at most
$\tau (x_I, x_{P_a})$
is a multilinear form of partition rank at most
![]() $(r + 2)R$
. Hence, forms
$(r + 2)R$
. Hence, forms
![]() $\pi _i$
always appear with
$\pi _i$
always appear with
![]() $x_3$
or
$x_3$
or
![]() $x_{4}$
as the asymmetric variable.
$x_{4}$
as the asymmetric variable.
In order to express
![]() $\alpha (x_{[5]})+ \alpha \circ (3\,\,4)(x_{[5]})$
in terms of these multilinear forms, we need to set up further notation. We use richer indices than just natural numbers, of the form
$\alpha (x_{[5]})+ \alpha \circ (3\,\,4)(x_{[5]})$
in terms of these multilinear forms, we need to set up further notation. We use richer indices than just natural numbers, of the form
![]() $(i, j, \mathsf {S}, A)$
,
$(i, j, \mathsf {S}, A)$
,
![]() $(i, j, \mathsf {PS}, A, v)$
, and
$(i, j, \mathsf {PS}, A, v)$
, and
![]() $(i, j, \mathsf {AS}, A, v)$
, where
$(i, j, \mathsf {AS}, A, v)$
, where
![]() $i \in [2]$
, j is a suitable index,
$i \in [2]$
, j is a suitable index,
![]() $A \subseteq [4]$
of size
$A \subseteq [4]$
of size
![]() $|A| = \ell _i$
, letters
$|A| = \ell _i$
, letters
![]() $\mathsf {S}$
,
$\mathsf {S}$
,
![]() $\mathsf {PS}$
, and
$\mathsf {PS}$
, and
![]() $\mathsf {AS}$
indicate the type of form we take, and
$\mathsf {AS}$
indicate the type of form we take, and
![]() $v \in A$
. Using such an index
$v \in A$
. Using such an index
![]() $\boldsymbol {\mathsf {i}}$
, we define form
$\boldsymbol {\mathsf {i}}$
, we define form
![]() $\psi _{\boldsymbol {\mathsf {i}}}$
as a multilinear form in variables
$\psi _{\boldsymbol {\mathsf {i}}}$
as a multilinear form in variables
![]() $x_{A \cup P_i}$
(which are ordered by the values of indices) and
$x_{A \cup P_i}$
(which are ordered by the values of indices) and
 $$\begin{align*}\psi_{\boldsymbol{\mathsf{i}}}(x_{A \cup P_i}) = \begin{cases} \sigma^{i, \ell_i}_j (x_A, x_{P_i}), &\text{ if }\boldsymbol{\mathsf{i}} = (i, j, \mathsf{S}, A),\\ \pi^{i, \ell_i}_j (x_{A \setminus v} \,|x_v\, |\, x_{P_i}), &\text{ if }\boldsymbol{\mathsf{i}} = (i,j, \mathsf{PS}, A, v),\\ \rho^{i, \ell_i}_j (x_{A \setminus v} \,|x_v\,|\,x_{P_i}), &\text{ if }\boldsymbol{\mathsf{i}} = (i,j, \mathsf{AS}, A, v). \end{cases}\end{align*}$$
$$\begin{align*}\psi_{\boldsymbol{\mathsf{i}}}(x_{A \cup P_i}) = \begin{cases} \sigma^{i, \ell_i}_j (x_A, x_{P_i}), &\text{ if }\boldsymbol{\mathsf{i}} = (i, j, \mathsf{S}, A),\\ \pi^{i, \ell_i}_j (x_{A \setminus v} \,|x_v\, |\, x_{P_i}), &\text{ if }\boldsymbol{\mathsf{i}} = (i,j, \mathsf{PS}, A, v),\\ \rho^{i, \ell_i}_j (x_{A \setminus v} \,|x_v\,|\,x_{P_i}), &\text{ if }\boldsymbol{\mathsf{i}} = (i,j, \mathsf{AS}, A, v). \end{cases}\end{align*}$$
Let
![]() $A(\boldsymbol {\mathsf {i}})$
be the set A in the rich index
$A(\boldsymbol {\mathsf {i}})$
be the set A in the rich index
![]() $\boldsymbol {\mathsf {i}}$
. Let
$\boldsymbol {\mathsf {i}}$
. Let
![]() $\mathcal {I}$
be the set of pairs
$\mathcal {I}$
be the set of pairs
![]() $(\boldsymbol {\mathsf {i}}_1,\boldsymbol {\mathsf {i}}_2)$
such that:
$(\boldsymbol {\mathsf {i}}_1,\boldsymbol {\mathsf {i}}_2)$
such that:
-
•
 $\boldsymbol {\mathsf {i}}_1 = (1, \dots )$
and
$\boldsymbol {\mathsf {i}}_1 = (1, \dots )$
and
 $\boldsymbol {\mathsf {i}}_2 = (2, \dots )$
and
$\boldsymbol {\mathsf {i}}_2 = (2, \dots )$
and -
•
 $A(\boldsymbol {\mathsf {i}}_1) \cup A(\boldsymbol {\mathsf {i}}_2)$
is a partition of
$A(\boldsymbol {\mathsf {i}}_1) \cup A(\boldsymbol {\mathsf {i}}_2)$
is a partition of
 $[4]$
.
$[4]$
.
By our work so far, we have suitable scalars
![]() $\lambda _{\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2}$
such that
$\lambda _{\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2}$
such that
In the rest of the proof, we show how to make
![]() $\lambda _{\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2}$
vanish. More precisely, we shall find a multilinear form
$\lambda _{\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2}$
vanish. More precisely, we shall find a multilinear form
![]() $\mu (x_{[5]})$
which will be given by an appropriate linear combination of products related to those appearing on the right-hand side of (4.20) and
$\mu (x_{[5]})$
which will be given by an appropriate linear combination of products related to those appearing on the right-hand side of (4.20) and
![]() $\alpha + \mu $
will have the desired property. We refer to
$\alpha + \mu $
will have the desired property. We refer to
![]() $\mu (x_{[5]})$
as the modification term.
$\mu (x_{[5]})$
as the modification term.
To that end, we fix a pair of multilinear forms
![]() $\beta _1, \beta _2$
, where
$\beta _1, \beta _2$
, where
![]() $\beta _i$
is one of the forms in the list
$\beta _i$
is one of the forms in the list
![]() $\sigma ^{i, \ell _i}_j, \pi ^{i, \ell _i}_j, \rho ^{i, \ell _i}_j$
. We consider together all pairs of rich indices
$\sigma ^{i, \ell _i}_j, \pi ^{i, \ell _i}_j, \rho ^{i, \ell _i}_j$
. We consider together all pairs of rich indices
![]() $(\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2) \in \mathcal {I}$
that
$(\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2) \in \mathcal {I}$
that
![]() $\psi _{\boldsymbol {\mathsf {i}}_i}$
comes from
$\psi _{\boldsymbol {\mathsf {i}}_i}$
comes from
![]() $\beta _i$
for each
$\beta _i$
for each
![]() $i \in [2]$
. Our goal is to describe contribution to the modification term
$i \in [2]$
. Our goal is to describe contribution to the modification term
![]() $\mu (x_{[5]})$
coming from the choice
$\mu (x_{[5]})$
coming from the choice
![]() $\beta _1, \beta _2$
.
$\beta _1, \beta _2$
.
Note that the form
![]() $\alpha (x_{[5]})+ \alpha \circ (3\,\,4)(x_{[5]})$
is symmetric in variables
$\alpha (x_{[5]})+ \alpha \circ (3\,\,4)(x_{[5]})$
is symmetric in variables
![]() $x_{[2]}$
and in variables
$x_{[2]}$
and in variables
![]() $x_{\{3, 4\}}$
. Let
$x_{\{3, 4\}}$
. Let
![]() $\tau \in \operatorname {Sym}_{[2]} \times \operatorname {Sym}_{\{3, 4\}}$
be any permutation acting on these two sets. The fact that
$\tau \in \operatorname {Sym}_{[2]} \times \operatorname {Sym}_{\{3, 4\}}$
be any permutation acting on these two sets. The fact that
identity (4.20), properties of Lemma 4.1, and Lemma 3.1 imply the following fact.
Claim 4.7 Let
![]() $(\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2) \in \mathcal {I}$
be a rich index pair giving a product of forms
$(\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2) \in \mathcal {I}$
be a rich index pair giving a product of forms
![]() $\Pi (x_{[5]})$
, and let
$\Pi (x_{[5]})$
, and let
![]() $\tau \in \operatorname {Sym}_{[2]} \times \operatorname {Sym}_{\{3, 4\}}$
be a permutation. Let
$\tau \in \operatorname {Sym}_{[2]} \times \operatorname {Sym}_{\{3, 4\}}$
be a permutation. Let
![]() $(\boldsymbol {\mathsf {j}}_1, \boldsymbol {\mathsf {j}}_2)$
be the rich index pair corresponding to the product
$(\boldsymbol {\mathsf {j}}_1, \boldsymbol {\mathsf {j}}_2)$
be the rich index pair corresponding to the product
![]() $\Pi \circ \tau (x_{[5]})$
. Then we have
$\Pi \circ \tau (x_{[5]})$
. Then we have
![]() $\lambda _{\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2} = \lambda _{\boldsymbol {\mathsf {j}}_1, \boldsymbol {\mathsf {j}}_2}$
.
$\lambda _{\boldsymbol {\mathsf {i}}_1, \boldsymbol {\mathsf {i}}_2} = \lambda _{\boldsymbol {\mathsf {j}}_1, \boldsymbol {\mathsf {j}}_2}$
.
Step 4. Simplifying the expression—removing partially symmetric forms
![]() $\pi _i$
. Note that if the partial symmetric forms play a role, then some
$\pi _i$
. Note that if the partial symmetric forms play a role, then some
![]() $\ell _i \geq 3$
. Since we have only four active variables, there can only be one partially symmetric form present in the product.
$\ell _i \geq 3$
. Since we have only four active variables, there can only be one partially symmetric form present in the product.
Write
![]() $\phi = \alpha + \alpha \circ (3\,\,4)$
and recall that
$\phi = \alpha + \alpha \circ (3\,\,4)$
and recall that
![]() $\phi $
satisfies
$\phi $
satisfies
by Lemma 4.4.
In this step of the proof, we define a multilinear form
![]() $\tilde {\mu }(x_{[5]})$
as the sum of all terms in (4.20) that have a partially symmetric form in the product, with variable
$\tilde {\mu }(x_{[5]})$
as the sum of all terms in (4.20) that have a partially symmetric form in the product, with variable
![]() $x_{4}$
at its asymmetric place. Thus,
$x_{4}$
at its asymmetric place. Thus,
![]() $\operatorname {prank} \tilde {\mu } \leq O(r^2)$
. We then add
$\operatorname {prank} \tilde {\mu } \leq O(r^2)$
. We then add
![]() $\tilde {\mu }$
to the modification term
$\tilde {\mu }$
to the modification term
![]() $\mu $
. Let
$\mu $
. Let
![]() $P(x_{[5]})$
be the contribution of the products involving a partially symmetric form in (4.20). By Claim 4.7, we have that
$P(x_{[5]})$
be the contribution of the products involving a partially symmetric form in (4.20). By Claim 4.7, we have that
We now show that
![]() $\tilde {\mu }$
is symmetric in the first three variables.
$\tilde {\mu }$
is symmetric in the first three variables.
Recall that we fixed forms
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
. Suppose that
$\beta _2$
. Suppose that
![]() $\beta _a$
is the partially symmetric form among them, and let b be the other index in
$\beta _a$
is the partially symmetric form among them, and let b be the other index in
![]() $\{1,2\}$
. Thus,
$\{1,2\}$
. Thus,
![]() $\beta _b$
is a form among
$\beta _b$
is a form among
![]() $\sigma ^{b, \ell _b}$
and
$\sigma ^{b, \ell _b}$
and
![]() $\rho ^{b, \ell _b} \circ (c\,\,c')$
, and
$\rho ^{b, \ell _b} \circ (c\,\,c')$
, and
![]() $\beta _a$
is
$\beta _a$
is
![]() $\pi ^{a, \ell _a}_\ell $
for some index
$\pi ^{a, \ell _a}_\ell $
for some index
![]() $\ell $
. We need to show that coefficients of all products of
$\ell $
. We need to show that coefficients of all products of
![]() $\beta _a$
with
$\beta _a$
with
![]() $x_4$
as its asymmetric variable and
$x_4$
as its asymmetric variable and
![]() $\beta _b$
are the same. Observe that
$\beta _b$
are the same. Observe that
![]() $\beta _a$
has at least three active variables, as otherwise it cannot be partially symmetric. Since the partitions we consider are relevant, this implies that
$\beta _a$
has at least three active variables, as otherwise it cannot be partially symmetric. Since the partitions we consider are relevant, this implies that
![]() $P_a = \emptyset $
and
$P_a = \emptyset $
and
![]() $P_b = \{5\}$
. Hence, we need to show that the products
$P_b = \{5\}$
. Hence, we need to show that the products
 $$ \begin{align*}\Pi_1(x_{[5]}) = \pi^{a, \ell_a}_\ell(x_2, x_3 |x_4) \beta_b(x_1, x_5),\,\, &\Pi_2(x_{[5]}) = \pi^{a, \ell_a}_\ell(x_1, x_3 |x_4) \beta_b(x_2, x_5),\\ &\hspace{2cm}\Pi_3(x_{[5]}) = \pi^{a, \ell_a}_\ell(x_1, x_2 |x_4) \beta_b(x_3, x_5)\end{align*} $$
$$ \begin{align*}\Pi_1(x_{[5]}) = \pi^{a, \ell_a}_\ell(x_2, x_3 |x_4) \beta_b(x_1, x_5),\,\, &\Pi_2(x_{[5]}) = \pi^{a, \ell_a}_\ell(x_1, x_3 |x_4) \beta_b(x_2, x_5),\\ &\hspace{2cm}\Pi_3(x_{[5]}) = \pi^{a, \ell_a}_\ell(x_1, x_2 |x_4) \beta_b(x_3, x_5)\end{align*} $$
all have the same coefficient in (4.20).
Notice that coefficients of
![]() $\Pi _1(x_{[5]})$
and
$\Pi _1(x_{[5]})$
and
![]() $\Pi _2(x_{[5]})$
are the same by Claim 4.7. On the other hand, the coefficient of
$\Pi _2(x_{[5]})$
are the same by Claim 4.7. On the other hand, the coefficient of
![]() $\Pi _1(x_{[5]})$
in (4.21) is zero by Lemma 3.1. The contributing products to this coefficient from (4.20) are
$\Pi _1(x_{[5]})$
in (4.21) is zero by Lemma 3.1. The contributing products to this coefficient from (4.20) are
![]() $\Pi _1(x_{[5]})$
and
$\Pi _1(x_{[5]})$
and
![]() $\Pi _1(x_{[5]}) \circ (1 \,\,3) = \Pi _3(x_{[5]})$
(note that
$\Pi _1(x_{[5]}) \circ (1 \,\,3) = \Pi _3(x_{[5]})$
(note that
![]() $\Pi _1(x_{[5]}) \circ (1 \,\, 4)$
does not have either of
$\Pi _1(x_{[5]}) \circ (1 \,\, 4)$
does not have either of
![]() $x_{3}$
and
$x_{3}$
and
![]() $x_{4}$
at the asymmetric place, so it cannot appear in
$x_{4}$
at the asymmetric place, so it cannot appear in
![]() $\phi $
). This proves that the coefficients of products
$\phi $
). This proves that the coefficients of products
![]() $\Pi _1(x_{[5]}), \Pi _2(x_{[5]})$
, and
$\Pi _1(x_{[5]}), \Pi _2(x_{[5]})$
, and
![]() $\Pi _3(x_{[5]})$
are equal, showing that
$\Pi _3(x_{[5]})$
are equal, showing that
![]() $\tilde {\mu }$
is symmetric in
$\tilde {\mu }$
is symmetric in
![]() $x_{[3]}$
.
$x_{[3]}$
.
Step 5. Simplifying the expression—removing the remaining products. Let forms
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
now be the forms which are not partially symmetric. Similarly to the proof of Theorem 1.7, we now introduce a set of objects called places, each describing a possible position of an active variable in the product. For each symmetric form above, we have one place, and for each asymmetric form, we have two places, one for the variables is in the symmetric part of the form and another at the asymmetric position in the form. Using the symmetries in
$\beta _2$
now be the forms which are not partially symmetric. Similarly to the proof of Theorem 1.7, we now introduce a set of objects called places, each describing a possible position of an active variable in the product. For each symmetric form above, we have one place, and for each asymmetric form, we have two places, one for the variables is in the symmetric part of the form and another at the asymmetric position in the form. Using the symmetries in
![]() $x_{[2]}$
and
$x_{[2]}$
and
![]() $x_{\{3, 4\}}$
variables, we see that the coefficients of all considered products depend entirely on the choice of the places for
$x_{\{3, 4\}}$
variables, we see that the coefficients of all considered products depend entirely on the choice of the places for
![]() $x_{3}$
and
$x_{3}$
and
![]() $x_{4}$
. More precisely, by Claim 4.7, given two places A and B, we have coefficients
$x_{4}$
. More precisely, by Claim 4.7, given two places A and B, we have coefficients
![]() $\lambda _{A\,A}$
and
$\lambda _{A\,A}$
and
![]() $\lambda _{A\,B}$
such that:
$\lambda _{A\,B}$
such that:
-
• all products where
 $x_{3}$
and
$x_{3}$
and
 $x_{4}$
are at the same place A (thus both variables occur in same
$x_{4}$
are at the same place A (thus both variables occur in same
 $\sigma $
or symmetric part of the same
$\sigma $
or symmetric part of the same
 $\rho $
) get the coefficient
$\rho $
) get the coefficient
 $\lambda _{A\,A}$
,
$\lambda _{A\,A}$
, -
• all products where
 $x_{3}$
and
$x_{3}$
and
 $x_{4}$
are at places A and B which occurs at the same form (e.g.,
$x_{4}$
are at places A and B which occurs at the same form (e.g.,
 $\rho (x_1, x_{3}\,|\,x_{4})\dots $
; note that this includes both cases of
$\rho (x_1, x_{3}\,|\,x_{4})\dots $
; note that this includes both cases of
 $x_{3}$
being at A and
$x_{3}$
being at A and
 $x_{3}$
being at B) get the coefficient
$x_{3}$
being at B) get the coefficient
 $\lambda _{A\,B}$
,
$\lambda _{A\,B}$
, -
• all products where
 $x_{3}$
and
$x_{3}$
and
 $x_{4}$
are at places A and B which occurs at different forms (e.g.,
$x_{4}$
are at places A and B which occurs at different forms (e.g.,
 $\rho (x_1\,|\,x_{4}) \sigma (x_2, x_{3},x_5)$
; note that this includes both cases of
$\rho (x_1\,|\,x_{4}) \sigma (x_2, x_{3},x_5)$
; note that this includes both cases of
 $x_{3}$
being at A and
$x_{3}$
being at A and
 $x_{3}$
being at B) get the coefficient
$x_{3}$
being at B) get the coefficient
 $\lambda _{A\,B}$
. (Note that we get the same form of the coefficient
$\lambda _{A\,B}$
. (Note that we get the same form of the coefficient
 $\lambda _{A\,B}$
as in the previous case, and the difference is in the pairs of places A and B for which this case occurs.)
$\lambda _{A\,B}$
as in the previous case, and the difference is in the pairs of places A and B for which this case occurs.)
Since all partitions of variables appearing are relevant, we know that one form has three variables and the other has two variables, so we never have two copies of the same form in a product. Thus, specifying places A and B for
![]() $x_3, x_4$
essentially determines the product (up to permutation in
$x_3, x_4$
essentially determines the product (up to permutation in
![]() $\operatorname {Sym}_{\{1,2\}} \times \operatorname {Sym}_{\{3,4\}}$
, which does not affect the coefficient of the product). Our goal now is to describe a multilinear form
$\operatorname {Sym}_{\{1,2\}} \times \operatorname {Sym}_{\{3,4\}}$
, which does not affect the coefficient of the product). Our goal now is to describe a multilinear form
![]() $\tilde {\mu }(x_{[k]})$
that will be added to the modification term
$\tilde {\mu }(x_{[k]})$
that will be added to the modification term
![]() $\mu (x_{[k]})$
so that
$\mu (x_{[k]})$
so that
![]() $(\alpha + \tilde {\mu }) + (\alpha + \tilde {\mu }) \circ (3\,\,4)$
has no products of forms
$(\alpha + \tilde {\mu }) + (\alpha + \tilde {\mu }) \circ (3\,\,4)$
has no products of forms
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
.
$\beta _2$
.
We have three different cases depending on the nature of the forms: either both are symmetric, or one is symmetric and the other asymmetric, or both are asymmetric.
Symmetric case. Let the two forms be
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
with their places A and B. Without loss of generality,
$\sigma '$
with their places A and B. Without loss of generality,
![]() $\sigma $
has at least two active variables. We claim that
$\sigma $
has at least two active variables. We claim that
![]() $\lambda _{A\,A} = 0$
. Switching the roles of
$\lambda _{A\,A} = 0$
. Switching the roles of
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
if
$\sigma '$
if
![]() $\sigma '$
also has at least two active variables shows that
$\sigma '$
also has at least two active variables shows that
![]() $\lambda _{B\,B} = 0$
. To see that
$\lambda _{B\,B} = 0$
. To see that
![]() $\lambda _{A\,A}$
vanishes, consider the coefficient of product
$\lambda _{A\,A}$
vanishes, consider the coefficient of product
![]() $\sigma (x_{3}, x_1, \dots ) \sigma '(x_{4}, \dots )$
in (4.21). (Note that the positions of the remaining active variable
$\sigma (x_{3}, x_1, \dots ) \sigma '(x_{4}, \dots )$
in (4.21). (Note that the positions of the remaining active variable
![]() $x_2$
and the passive variables
$x_2$
and the passive variables
![]() $x_{P_1}$
and
$x_{P_1}$
and
![]() $x_{P_2}$
in these forms are uniquely determined, but we opt not to display them for the sake of clarity.) This coefficient vanishes, but at the same time comes from coefficients of products
$x_{P_2}$
in these forms are uniquely determined, but we opt not to display them for the sake of clarity.) This coefficient vanishes, but at the same time comes from coefficients of products
in (4.20). Thus,
giving
![]() $\lambda _{A\,A} = 0$
.
$\lambda _{A\,A} = 0$
.
We may then set
![]() $\tilde {\mu }(x_{[5]})$
to be the sum of
$\tilde {\mu }(x_{[5]})$
to be the sum of
![]() $\lambda _{A\,B} \sum _{I \in \binom {[3]}{\ell _1}} \beta _1(x_I, x_{P_1}) \beta _2(x_{[3] \setminus I}, x_{4}, x_{P_2})$
for all pairs
$\lambda _{A\,B} \sum _{I \in \binom {[3]}{\ell _1}} \beta _1(x_I, x_{P_1}) \beta _2(x_{[3] \setminus I}, x_{4}, x_{P_2})$
for all pairs
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
appearing in this case (with place A at
$\sigma '$
appearing in this case (with place A at
![]() $\sigma $
and B at
$\sigma $
and B at
![]() $\sigma '$
), where
$\sigma '$
), where
![]() $\beta _1, \beta _2$
is our initial notation for these two maps. By definition,
$\beta _1, \beta _2$
is our initial notation for these two maps. By definition,
![]() $\tilde {\mu }$
is symmetric in
$\tilde {\mu }$
is symmetric in
![]() $x_{[3]}$
and the vanishing of
$x_{[3]}$
and the vanishing of
![]() $\lambda _{C\,C}$
for the relevant places C implies that
$\lambda _{C\,C}$
for the relevant places C implies that
![]() $\tilde {\mu }(x_{[5]}) + \tilde {\mu } \circ (3\,\,4)(x_{[5]})$
equals the contribution from products of forms in this case.
$\tilde {\mu }(x_{[5]}) + \tilde {\mu } \circ (3\,\,4)(x_{[5]})$
equals the contribution from products of forms in this case.
Mixed case. Let the two forms be
![]() $\sigma $
and
$\sigma $
and
![]() $\rho $
. Let A be the place in
$\rho $
. Let A be the place in
![]() $\sigma $
, let B be the symmetric place in
$\sigma $
, let B be the symmetric place in
![]() $\rho $
, and let C be the asymmetric one. As in the previous case, we use notation for products that does not specify positions of
$\rho $
, and let C be the asymmetric one. As in the previous case, we use notation for products that does not specify positions of
![]() $x_2$
and
$x_2$
and
![]() $x_5$
for the sake of clarity, as these are uniquely determined. Considering the products
$x_5$
for the sake of clarity, as these are uniquely determined. Considering the products
![]() $\sigma (x_3, x_{4}, \dots ) \rho (x_1, \dots |\cdot )$
(which makes sense only when there are at least two active variables in
$\sigma (x_3, x_{4}, \dots ) \rho (x_1, \dots |\cdot )$
(which makes sense only when there are at least two active variables in
![]() $\sigma $
),
$\sigma $
),
![]() $\sigma (x_1, \dots ) \rho (x_3, x_{4}, \dots |\cdot )$
(which makes sense only when there are at least two variables in the symmetric part of
$\sigma (x_1, \dots ) \rho (x_3, x_{4}, \dots |\cdot )$
(which makes sense only when there are at least two variables in the symmetric part of
![]() $\rho $
), and
$\rho $
), and
![]() $\sigma (x_1, \dots ) \rho (x_3, \dots |x_{4})$
(meaning that
$\sigma (x_1, \dots ) \rho (x_3, \dots |x_{4})$
(meaning that
![]() $x_4$
is at the place C), respectively, in (4.21) gives
$x_4$
is at the place C), respectively, in (4.21) gives
thus,
We now describe the contribution
![]() $\tilde {\mu }(x_{[5]})$
to the modification term
$\tilde {\mu }(x_{[5]})$
to the modification term
![]() $\mu (x_{[5]})$
. For this choice of forms
$\mu (x_{[5]})$
. For this choice of forms
![]() $\sigma $
and
$\sigma $
and
![]() $\rho $
as
$\rho $
as
![]() $\beta _1, \beta _2$
, we add
$\beta _1, \beta _2$
, we add
![]() $\lambda _{A\,B} \Pi (x_{[5]})$
to
$\lambda _{A\,B} \Pi (x_{[5]})$
to
![]() $\tilde {\mu }(x_{[5]})$
for all products
$\tilde {\mu }(x_{[5]})$
for all products
![]() $\Pi $
of
$\Pi $
of
![]() $\sigma $
and
$\sigma $
and
![]() $\rho $
that have
$\rho $
that have
![]() $x_4$
at the symmetric place B of
$x_4$
at the symmetric place B of
![]() $\rho $
and we add
$\rho $
and we add
![]() $\lambda _{A\,C} \Pi (x_{[5]})$
to
$\lambda _{A\,C} \Pi (x_{[5]})$
to
![]() $\tilde {\mu }(x_{[5]})$
for all products
$\tilde {\mu }(x_{[5]})$
for all products
![]() $\Pi $
of
$\Pi $
of
![]() $\sigma $
and
$\sigma $
and
![]() $\rho $
that have
$\rho $
that have
![]() $x_4$
at the asymmetric place C of
$x_4$
at the asymmetric place C of
![]() $\rho $
. (Note that there are three different choices of
$\rho $
. (Note that there are three different choices of
![]() $\Pi $
for both places and both cases whether
$\Pi $
for both places and both cases whether
![]() $\sigma $
has two or three variables.) By definition,
$\sigma $
has two or three variables.) By definition,
![]() $\tilde {\mu }(x_{[5]})$
is symmetric in
$\tilde {\mu }(x_{[5]})$
is symmetric in
![]() $x_{[3]}$
. Finally, using the information on coefficients (4.22), we see that
$x_{[3]}$
. Finally, using the information on coefficients (4.22), we see that
![]() $\tilde {\mu }(x_{[5]}) + \tilde {\mu } \circ (3\,\,4)(x_{[5]})$
equals the contribution to (4.20) coming from the mixed case, as desired.
$\tilde {\mu }(x_{[5]}) + \tilde {\mu } \circ (3\,\,4)(x_{[5]})$
equals the contribution to (4.20) coming from the mixed case, as desired.
Asymmetric case. Let the two forms be
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
(in particular, this implies that both forms have two active variables). Let the symmetric places in
$\rho '$
(in particular, this implies that both forms have two active variables). Let the symmetric places in
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
be A and C, respectively, and let the asymmetric place be B and D, respectively. Looking at products
$\rho '$
be A and C, respectively, and let the asymmetric place be B and D, respectively. Looking at products
![]() $\rho (x_1, \dots | \cdot ) \rho '(x_3, \dots |x_{4}), \rho (\cdots | x_1) \rho '(x_3, \dots |x_{4}), \rho (x_3, \dots |x_{4})\rho '(x_1, \dots | \cdot )$
,
$\rho (x_1, \dots | \cdot ) \rho '(x_3, \dots |x_{4}), \rho (\cdots | x_1) \rho '(x_3, \dots |x_{4}), \rho (x_3, \dots |x_{4})\rho '(x_1, \dots | \cdot )$
,
![]() $\rho (x_3, \dots |x_{4})\rho '(\cdots |x_1)$
,
$\rho (x_3, \dots |x_{4})\rho '(\cdots |x_1)$
,
![]() $\rho (x_3, x_{4}, \dots |\cdot ) \rho '(x_1, \dots | \cdot )$
(if there are at least two variables in the symmetric part of
$\rho (x_3, x_{4}, \dots |\cdot ) \rho '(x_1, \dots | \cdot )$
(if there are at least two variables in the symmetric part of
![]() $\rho $
), and
$\rho $
), and
![]() $\rho (x_1, \dots | \cdot )\rho '(x_3, x_{4}, \dots |\cdot )$
(if there are at least two variables in the symmetric part of
$\rho (x_1, \dots | \cdot )\rho '(x_3, x_{4}, \dots |\cdot )$
(if there are at least two variables in the symmetric part of
![]() $\rho '$
) from (4.21), we deduce that
$\rho '$
) from (4.21), we deduce that
 $$ \begin{align}0 = \lambda_{C\,D} + \lambda_{A\, D} + \lambda_{A\,C} = \lambda_{C\,D} + \lambda_{B\,D} + \lambda_{B\,C} =\ &\lambda_{A\,B} + \lambda_{B\, C} + \lambda_{A\,C} = \lambda_{A\,B} +\lambda_{B\,D}+\lambda_{A\,D}\nonumber\\ =\ &\lambda_{A\,A} +\lambda_{A\,C}+\lambda_{A\,C} = \lambda_{C\,C} + \lambda_{A\,C} + \lambda_{A\,C}.\end{align} $$
$$ \begin{align}0 = \lambda_{C\,D} + \lambda_{A\, D} + \lambda_{A\,C} = \lambda_{C\,D} + \lambda_{B\,D} + \lambda_{B\,C} =\ &\lambda_{A\,B} + \lambda_{B\, C} + \lambda_{A\,C} = \lambda_{A\,B} +\lambda_{B\,D}+\lambda_{A\,D}\nonumber\\ =\ &\lambda_{A\,A} +\lambda_{A\,C}+\lambda_{A\,C} = \lambda_{C\,C} + \lambda_{A\,C} + \lambda_{A\,C}.\end{align} $$
Let us now describe the final contribution
![]() $\tilde {\mu }(x_{[5]})$
to the modification term
$\tilde {\mu }(x_{[5]})$
to the modification term
![]() $\mu (x_{[5]})$
. For this choice of forms
$\mu (x_{[5]})$
. For this choice of forms
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
as
$\rho '$
as
![]() $\beta _1, \beta _2$
, we add
$\beta _1, \beta _2$
, we add
![]() $\lambda _{A\,B} \Pi (x_{[5]})$
to
$\lambda _{A\,B} \Pi (x_{[5]})$
to
![]() $\tilde {\mu }(x_{[5]})$
for all products
$\tilde {\mu }(x_{[5]})$
for all products
![]() $\Pi $
of
$\Pi $
of
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
that have
$\rho '$
that have
![]() $x_4$
at the asymmetric place B of
$x_4$
at the asymmetric place B of
![]() $\rho $
, we add
$\rho $
, we add
![]() $\lambda _{A\,C} \Pi (x_{[5]})$
to
$\lambda _{A\,C} \Pi (x_{[5]})$
to
![]() $\tilde {\mu }(x_{[5]})$
for all products
$\tilde {\mu }(x_{[5]})$
for all products
![]() $\Pi $
of
$\Pi $
of
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
that have
$\rho '$
that have
![]() $x_4$
at the symmetric place C of
$x_4$
at the symmetric place C of
![]() $\rho '$
, and we add
$\rho '$
, and we add
![]() $\lambda _{A\,D} \Pi (x_{[5]})$
to
$\lambda _{A\,D} \Pi (x_{[5]})$
to
![]() $\tilde {\mu }(x_{[5]})$
for all products
$\tilde {\mu }(x_{[5]})$
for all products
![]() $\Pi $
of
$\Pi $
of
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
that have
$\rho '$
that have
![]() $x_4$
at the asymmetric place D of
$x_4$
at the asymmetric place D of
![]() $\rho '$
. (Note that there are six different choices of
$\rho '$
. (Note that there are six different choices of
![]() $\Pi $
for all three places and both cases whether
$\Pi $
for all three places and both cases whether
![]() $\rho $
has two or three variables.) By definition,
$\rho $
has two or three variables.) By definition,
![]() $\tilde {\mu }(x_{[5]})$
is symmetric in
$\tilde {\mu }(x_{[5]})$
is symmetric in
![]() $x_{[3]}$
. Finally, using the information on coefficients (4.23), we see that
$x_{[3]}$
. Finally, using the information on coefficients (4.23), we see that
![]() $\tilde {\mu }(x_{[5]}) + \tilde {\mu } \circ (3\,\,4)(x_{[5]})$
equals the contribution to (4.20) coming from the asymmetric case, as desired.
$\tilde {\mu }(x_{[5]}) + \tilde {\mu } \circ (3\,\,4)(x_{[5]})$
equals the contribution to (4.20) coming from the asymmetric case, as desired.
Finally, set
![]() $\tilde {\alpha } = \alpha + \mu $
. Each of the contributions to the modification term
$\tilde {\alpha } = \alpha + \mu $
. Each of the contributions to the modification term
![]() $\mu $
is symmetric in
$\mu $
is symmetric in
![]() $x_{[3]}$
and so is
$x_{[3]}$
and so is
![]() $\tilde {\alpha }$
. But we chose
$\tilde {\alpha }$
. But we chose
![]() $\mu $
so that
$\mu $
so that
![]() $\tilde {\alpha } + \tilde {\alpha } \circ (3\,\,4) = 0$
on the subspace U, so in fact
$\tilde {\alpha } + \tilde {\alpha } \circ (3\,\,4) = 0$
on the subspace U, so in fact
![]() $\tilde {\alpha }$
is symmetric in
$\tilde {\alpha }$
is symmetric in
![]() $x_{[4]}$
on U. Since
$x_{[4]}$
on U. Since
![]() $\operatorname {prank} \mu \leq O(r^2)$
, the theorem follows from Corollary 2.6 (as in the proof of the previous theorem, recall that
$\operatorname {prank} \mu \leq O(r^2)$
, the theorem follows from Corollary 2.6 (as in the proof of the previous theorem, recall that
![]() $\operatorname {codim}_G U \leq O(Rr)$
which is the main contribution to the final bound). As in the proof of Theorem 1.7, we choose C and D depending only on the constants from Lemma 3.1 so that the partition rank condition of Lemma 3.1 holds each time the lemma is applied.
$\operatorname {codim}_G U \leq O(Rr)$
which is the main contribution to the final bound). As in the proof of Theorem 1.7, we choose C and D depending only on the constants from Lemma 3.1 so that the partition rank condition of Lemma 3.1 holds each time the lemma is applied.
5 Multilinear forms which are approximately without repeated coordinates
This section is devoted to the proof of Theorem 1.10. As in the case of the previous theorems, we need a way to regularize the forms appearing in low partition rank decompositions. We need a preliminary lemma first.
Lemma 5.1 For a positive integer k, there exist constants
![]() $C = C_k, D = D_k \geq 1$
such that the following holds. Suppose that
$C = C_k, D = D_k \geq 1$
such that the following holds. Suppose that
![]() $\alpha \colon G^k \to \mathbb {F}_2$
is symmetric in the first two variables and that
$\alpha \colon G^k \to \mathbb {F}_2$
is symmetric in the first two variables and that
![]() $\alpha $
has partition rank at most r. Let
$\alpha $
has partition rank at most r. Let
![]() $\alpha ^{\times 2} \colon G^{k-1} \to \mathbb {F}_2$
be the multilinear form defined by
$\alpha ^{\times 2} \colon G^{k-1} \to \mathbb {F}_2$
be the multilinear form defined by
![]() $\alpha ^{\times 2}(d, x_{[3,k]}) = \alpha (d,d, x_{[3,k]})$
. Then
$\alpha ^{\times 2}(d, x_{[3,k]}) = \alpha (d,d, x_{[3,k]})$
. Then
![]() $\alpha ^{\times 2}$
has partition rank at most
$\alpha ^{\times 2}$
has partition rank at most
![]() $C r^{D}$
.
$C r^{D}$
.
Proof Let
for some integers
![]() $r_1, r_2 \leq r$
and suitable multilinear forms
$r_1, r_2 \leq r$
and suitable multilinear forms
![]() $\beta _i, \beta ^{\prime }_i, \gamma _i, \gamma ^{\prime }_i$
. Then we have
$\beta _i, \beta ^{\prime }_i, \gamma _i, \gamma ^{\prime }_i$
. Then we have
For each
![]() $i \in [r_2]$
, let
$i \in [r_2]$
, let
![]() $\tilde {\gamma }_i(u, y_{\tilde {J}_i})$
be the form among
$\tilde {\gamma }_i(u, y_{\tilde {J}_i})$
be the form among
![]() $\gamma _i(u, y_{J_i})$
and
$\gamma _i(u, y_{J_i})$
and
![]() $\gamma _i'(y_{u, J_i^c})$
, which does not involve variable
$\gamma _i'(y_{u, J_i^c})$
, which does not involve variable
![]() $y_3$
. In particular, we have the inclusion of varieties
$y_3$
. In particular, we have the inclusion of varieties
We thus obtain

Using the Gowers–Cauchy–Schwarz inequality, this quantity can be bounded from above by
![]() $\|(-1)^{\alpha ^{\times 2}}\|_{\square ^{k-1}} =\Big ( \operatorname {bias}( \alpha ^{\times 2})\Big )^{2^{-{k-1}}}$
. The lemma follows from Theorem 2.4.
$\|(-1)^{\alpha ^{\times 2}}\|_{\square ^{k-1}} =\Big ( \operatorname {bias}( \alpha ^{\times 2})\Big )^{2^{-{k-1}}}$
. The lemma follows from Theorem 2.4.
We may now state and prove the regularity lemma that we need.
Lemma 5.2 Let
![]() $\alpha _1, \dots \alpha _r \colon G^k \to \mathbb {F}_2$
be multilinear forms that are symmetric in the first two variables. Let
$\alpha _1, \dots \alpha _r \colon G^k \to \mathbb {F}_2$
be multilinear forms that are symmetric in the first two variables. Let
![]() $M, R_0 \geq 1$
be positive quantities. Then, we can find a positive integer R satisfying
$M, R_0 \geq 1$
be positive quantities. Then, we can find a positive integer R satisfying
![]() $R_0 \leq R \leq (2R_0 + 1)^{O(M)^{2r}}$
and subspaces
$R_0 \leq R \leq (2R_0 + 1)^{O(M)^{2r}}$
and subspaces
![]() $\Lambda \leq \Lambda ^{\times 2} \leq \mathbb {F}_2^r$
such that:
$\Lambda \leq \Lambda ^{\times 2} \leq \mathbb {F}_2^r$
such that:
-
(i) if
 $\lambda \in \Lambda $
, then
$\lambda \in \Lambda $
, then
 $\operatorname {prank} \lambda \cdot \alpha \leq R$
, and if
$\operatorname {prank} \lambda \cdot \alpha \leq R$
, and if
 $\lambda \notin \Lambda $
, then
$\lambda \notin \Lambda $
, then
 $\operatorname {prank} \lambda \cdot \alpha \geq (2R +1)^M$
, and
$\operatorname {prank} \lambda \cdot \alpha \geq (2R +1)^M$
, and -
(ii) if
 $\lambda \in \Lambda ^{\times 2}$
, then
$\lambda \in \Lambda ^{\times 2}$
, then
 $\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq R$
, and if
$\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq R$
, and if
 $\lambda \notin \Lambda ^{\times 2}$
, then
$\lambda \notin \Lambda ^{\times 2}$
, then
 $\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \geq (2R +1)^M$
.
$\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \geq (2R +1)^M$
.
Proof Let
![]() $C_i$
and
$C_i$
and
![]() $D_i$
be the constants from the previous lemma for multilinear forms in i variables, and set
$D_i$
be the constants from the previous lemma for multilinear forms in i variables, and set
![]() $C = \max _{i \in [k]} C_i, D = \max _{i \in [k]} D_i$
, which we may assume to satisfy
$C = \max _{i \in [k]} C_i, D = \max _{i \in [k]} D_i$
, which we may assume to satisfy
![]() $C, D \geq 1$
. At each step, we keep track of two subspaces
$C, D \geq 1$
. At each step, we keep track of two subspaces
![]() $\Lambda \leq \Lambda ^{\times 2} \leq \mathbb {F}_2^r$
and a quantity R such that, for each
$\Lambda \leq \Lambda ^{\times 2} \leq \mathbb {F}_2^r$
and a quantity R such that, for each
![]() $\lambda \in \Lambda $
, we have
$\lambda \in \Lambda $
, we have
![]() $\operatorname {prank} \lambda \cdot \alpha \leq R$
, and for each
$\operatorname {prank} \lambda \cdot \alpha \leq R$
, and for each
![]() $\lambda \in \Lambda ^{\times 2}$
, we have
$\lambda \in \Lambda ^{\times 2}$
, we have
![]() $\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq R$
. The procedure terminates once
$\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq R$
. The procedure terminates once
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda ^{\times 2}$
have the desired properties, that is, when we have
$\Lambda ^{\times 2}$
have the desired properties, that is, when we have
![]() $\operatorname {prank} \lambda \cdot \alpha \geq (2R +1)^M$
for each
$\operatorname {prank} \lambda \cdot \alpha \geq (2R +1)^M$
for each
![]() $\lambda \notin \Lambda $
and
$\lambda \notin \Lambda $
and
![]() $\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \geq (2R +1)^M$
for each
$\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \geq (2R +1)^M$
for each
![]() $\lambda \notin \Lambda ^{\times 2}$
. We begin by setting
$\lambda \notin \Lambda ^{\times 2}$
. We begin by setting
![]() $R = R_0$
,
$R = R_0$
,
![]() $\Lambda = \Lambda ^{\times 2} = \{0\}$
.
$\Lambda = \Lambda ^{\times 2} = \{0\}$
.
Suppose that the procedure has not yet terminated. Suppose first that, for some
![]() $\lambda \notin \Lambda $
, we have
$\lambda \notin \Lambda $
, we have
![]() $\operatorname {prank} \lambda \cdot \alpha \leq (2R +1)^M$
. By Lemma 5.1, we have
$\operatorname {prank} \lambda \cdot \alpha \leq (2R +1)^M$
. By Lemma 5.1, we have
![]() $\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq C (2R +1)^{DM}$
. Replace R by
$\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq C (2R +1)^{DM}$
. Replace R by
![]() $2C (2R +1)^{DM}$
,
$2C (2R +1)^{DM}$
,
![]() $\Lambda $
by
$\Lambda $
by
![]() $\Lambda + \langle \lambda \rangle $
, and
$\Lambda + \langle \lambda \rangle $
, and
![]() $\Lambda ^{\times 2}$
by
$\Lambda ^{\times 2}$
by
![]() $\Lambda ^{\times 2} + \langle \lambda \rangle $
. In the second case, we have
$\Lambda ^{\times 2} + \langle \lambda \rangle $
. In the second case, we have
![]() $\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq (2R +1)^M$
for some
$\operatorname {prank} \lambda \cdot \alpha ^{\times 2} \leq (2R +1)^M$
for some
![]() $\lambda \notin \Lambda ^{\times 2}$
. This time replace R by
$\lambda \notin \Lambda ^{\times 2}$
. This time replace R by
![]() $2(2R +1)^M$
and
$2(2R +1)^M$
and
![]() $\Lambda ^{\times 2}$
by
$\Lambda ^{\times 2}$
by
![]() $\Lambda ^{\times 2} + \langle \lambda \rangle $
and keep
$\Lambda ^{\times 2} + \langle \lambda \rangle $
and keep
![]() $\Lambda $
the same. The procedure thus terminates after at most
$\Lambda $
the same. The procedure thus terminates after at most
![]() $2r$
steps, and we obtain the desired subspaces.
$2r$
steps, and we obtain the desired subspaces.
Proof of Theorem 1.10
We first do the case
![]() $k = 4$
, which turns out to be rather simple. In this case,
$k = 4$
, which turns out to be rather simple. In this case,
![]() $\alpha (d,d, x_3, x_4)$
is a trilinear form of partition rank at most r, so there exists a subspace
$\alpha (d,d, x_3, x_4)$
is a trilinear form of partition rank at most r, so there exists a subspace
![]() $U \leq G$
of codimension at most r (given by the zero set of the linear forms that appear as factors in the low partition rank decomposition of
$U \leq G$
of codimension at most r (given by the zero set of the linear forms that appear as factors in the low partition rank decomposition of
![]() $\alpha (d,d, x_3, x_4)$
) such that
$\alpha (d,d, x_3, x_4)$
) such that
![]() $\alpha (d,d, x_3, x_4) = 0$
for all
$\alpha (d,d, x_3, x_4) = 0$
for all
![]() $d, x_3, x_4 \in U$
. We may take
$d, x_3, x_4 \in U$
. We may take
![]() $\alpha ' = \alpha |_{U \times \cdots \times U}$
to finish the proof in this case.
$\alpha ' = \alpha |_{U \times \cdots \times U}$
to finish the proof in this case.
Now, consider the case
![]() $k = 5$
. Suppose that
$k = 5$
. Suppose that
![]() $\alpha (x_{[m]}, y_{[m+1,5]})$
is symmetric in variables
$\alpha (x_{[m]}, y_{[m+1,5]})$
is symmetric in variables
![]() $x_{[m]}$
and that
$x_{[m]}$
and that
![]() $\alpha (d,d, x_{[3,m]}, y_{[m+1,5]})$
has partition rank at most r. Thus,
$\alpha (d,d, x_{[3,m]}, y_{[m+1,5]})$
has partition rank at most r. Thus,
holds for all
![]() $d, x_3, \dots , y_5 \in G$
, where
$d, x_3, \dots , y_5 \in G$
, where
![]() $\beta _{i, 0}$
and
$\beta _{i, 0}$
and
![]() $\beta _{i, 1}$
are suitable multilinear forms.
$\beta _{i, 1}$
are suitable multilinear forms.
We begin our proof by deducing that we may assume that every form
![]() $\beta _{i, 1}$
is symmetric in x variables and that
$\beta _{i, 1}$
is symmetric in x variables and that
![]() $\beta _{i, 0}(d, x_{I_{i, 0}}, y_{J_{i, 0}})$
equals
$\beta _{i, 0}(d, x_{I_{i, 0}}, y_{J_{i, 0}})$
equals
![]() $\tilde {\beta }(d, d, x_{I_{i, 0}}, y_{J_{i, 0}})$
for a suitable multilinear form
$\tilde {\beta }(d, d, x_{I_{i, 0}}, y_{J_{i, 0}})$
for a suitable multilinear form
![]() $\tilde {\beta }$
which is symmetric in the first
$\tilde {\beta }$
which is symmetric in the first
![]() $|I_{i, 0}| + 2$
variables. Proposition 3.3 allows us to assume that every
$|I_{i, 0}| + 2$
variables. Proposition 3.3 allows us to assume that every
![]() $\beta _{i, j}$
is a slice of the form
$\beta _{i, j}$
is a slice of the form
![]() $(d,x_{[3,m]}, y_{[m + 1, k]}) \mapsto \alpha (d,d,x_{[3,m]}, y_{[m + 1, k]})$
(and therefore has the desired properties) at the cost of replacing r by
$(d,x_{[3,m]}, y_{[m + 1, k]}) \mapsto \alpha (d,d,x_{[3,m]}, y_{[m + 1, k]})$
(and therefore has the desired properties) at the cost of replacing r by
![]() $O(r^{O(1)})$
.
$O(r^{O(1)})$
.
Furthermore, if we take all linear forms appearing in (5.1) and set U to be the subspace of codimension at most
![]() $O(r^{O(1)})$
where they vanish, we may without loss of generality assume that all forms in (5.1) are bilinear. We now consider each possible value of
$O(r^{O(1)})$
where they vanish, we may without loss of generality assume that all forms in (5.1) are bilinear. We now consider each possible value of
![]() $m \in \{2,3,4,5\}$
separately.
$m \in \{2,3,4,5\}$
separately.
Case 1:
![]() $m = 2$
. In this case, equality (5.1) becomes
$m = 2$
. In this case, equality (5.1) becomes
for some
![]() $s\leq O(r^{O(1)})$
. We know that
$s\leq O(r^{O(1)})$
. We know that
![]() $\beta _{i, 0}(d, y_{J_{i, 0}}) = \tilde {\beta }_{i, 0}(d, d, y_{J_{i, 0}})$
for a multilinear form
$\beta _{i, 0}(d, y_{J_{i, 0}}) = \tilde {\beta }_{i, 0}(d, d, y_{J_{i, 0}})$
for a multilinear form
![]() $\tilde {\beta }_{i, 0}$
which is symmetric in the first two variables. Then simply set
$\tilde {\beta }_{i, 0}$
which is symmetric in the first two variables. Then simply set
which is symmetric in
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, and satisfies
$x_2$
, and satisfies
![]() $\operatorname {prank} \sigma \leq O(r^{O(1)})$
and
$\operatorname {prank} \sigma \leq O(r^{O(1)})$
and
![]() $(\alpha + \sigma )(d,d,x_3, x_4, x_5) = 0$
for all
$(\alpha + \sigma )(d,d,x_3, x_4, x_5) = 0$
for all
![]() $d,x_3, x_4, x_5 \in U$
, as desired.
$d,x_3, x_4, x_5 \in U$
, as desired.
Case 2:
![]() $m = 3$
. In this case, equality (5.1) becomes
$m = 3$
. In this case, equality (5.1) becomes
 $$\begin{align*}&\alpha(d,d, x_3, y_4, y_5)\\&\quad = \sum_{i \in [s_1]} \beta_{i}(d, x_3) \gamma_i(y_4, y_5) + \sum_{i \in [s_2]} \beta^{\prime}_{i}(d, y_4) \gamma^{\prime}_i(x_3, y_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, y_5) \gamma^{\prime\prime}_i(x_3, y_4)\end{align*}$$
$$\begin{align*}&\alpha(d,d, x_3, y_4, y_5)\\&\quad = \sum_{i \in [s_1]} \beta_{i}(d, x_3) \gamma_i(y_4, y_5) + \sum_{i \in [s_2]} \beta^{\prime}_{i}(d, y_4) \gamma^{\prime}_i(x_3, y_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, y_5) \gamma^{\prime\prime}_i(x_3, y_4)\end{align*}$$
for some
![]() $s_1, s_2, s_3 \leq O(r^{O(1)})$
and bilinear forms
$s_1, s_2, s_3 \leq O(r^{O(1)})$
and bilinear forms
![]() $\beta _i,\dots , \gamma ^{\prime \prime }_i$
. Recall that all these forms come from slice of
$\beta _i,\dots , \gamma ^{\prime \prime }_i$
. Recall that all these forms come from slice of
![]() $\alpha $
and we have trilinear forms
$\alpha $
and we have trilinear forms
![]() $\tilde {\beta }_i(x_{[3]})$
, symmetric in
$\tilde {\beta }_i(x_{[3]})$
, symmetric in
![]() $x_{[3]}$
,
$x_{[3]}$
,
![]() $\tilde {\beta }^{\prime }_i(x_{[3]})$
, symmetric in
$\tilde {\beta }^{\prime }_i(x_{[3]})$
, symmetric in
![]() $x_{[2]}$
, and
$x_{[2]}$
, and
![]() $\tilde {\beta }^{\prime }_i(x_{[3]})$
, symmetric in
$\tilde {\beta }^{\prime }_i(x_{[3]})$
, symmetric in
![]() $x_{[2]}$
, such that
$x_{[2]}$
, such that
![]() $\beta _{i}(d, x_3) = \tilde {\beta }_i(d,d,x_3)$
,
$\beta _{i}(d, x_3) = \tilde {\beta }_i(d,d,x_3)$
,
![]() $\beta ^{\prime }_{i}(d, y_4) = \tilde {\beta }^{\prime }_i(d,d,y_4)$
, and
$\beta ^{\prime }_{i}(d, y_4) = \tilde {\beta }^{\prime }_i(d,d,y_4)$
, and
![]() $\beta _{i}"(d, y_5) = \tilde {\beta }^{\prime \prime }_i(d,d,y_5).$
Let
$\beta _{i}"(d, y_5) = \tilde {\beta }^{\prime \prime }_i(d,d,y_5).$
Let
![]() $\sigma \colon G^5 \to \mathbb {F}_2$
be the multilinear form defined as
$\sigma \colon G^5 \to \mathbb {F}_2$
be the multilinear form defined as
 $$ \begin{align*}\sigma(x_{[5]}) = &\sum_{i \in [s_1]} \tilde{\beta}_{i}(x_1, x_2, x_3) \gamma_i(x_4, x_5) \\ &+ \sum_{i \in [s_2]} \Big(\tilde{\beta}^{\prime}_{i}(x_1, x_2, x_4) \gamma^{\prime}_i(x_3, x_5) + \tilde{\beta}^{\prime}_{i}(x_1, x_3, x_4) \gamma^{\prime}_i(x_2, x_5)+ \tilde{\beta}^{\prime}_{i}(x_2, x_3, x_4) \gamma^{\prime}_i(x_1, x_5)\Big)\\ &+ \sum_{i \in [s_3]} \Big(\tilde{\beta}^{\prime\prime}_{i}(x_1, x_2, x_5) \gamma^{\prime\prime}_i(x_3, x_4) + \tilde{\beta}^{\prime\prime}_{i}(x_1, x_3, x_5) \gamma^{\prime\prime}_i(x_2, x_4)+ \tilde{\beta}^{\prime\prime}_{i}(x_2, x_3, x_5) \gamma^{\prime\prime}_i(x_1, x_4)\Big).\end{align*} $$
$$ \begin{align*}\sigma(x_{[5]}) = &\sum_{i \in [s_1]} \tilde{\beta}_{i}(x_1, x_2, x_3) \gamma_i(x_4, x_5) \\ &+ \sum_{i \in [s_2]} \Big(\tilde{\beta}^{\prime}_{i}(x_1, x_2, x_4) \gamma^{\prime}_i(x_3, x_5) + \tilde{\beta}^{\prime}_{i}(x_1, x_3, x_4) \gamma^{\prime}_i(x_2, x_5)+ \tilde{\beta}^{\prime}_{i}(x_2, x_3, x_4) \gamma^{\prime}_i(x_1, x_5)\Big)\\ &+ \sum_{i \in [s_3]} \Big(\tilde{\beta}^{\prime\prime}_{i}(x_1, x_2, x_5) \gamma^{\prime\prime}_i(x_3, x_4) + \tilde{\beta}^{\prime\prime}_{i}(x_1, x_3, x_5) \gamma^{\prime\prime}_i(x_2, x_4)+ \tilde{\beta}^{\prime\prime}_{i}(x_2, x_3, x_5) \gamma^{\prime\prime}_i(x_1, x_4)\Big).\end{align*} $$
This form is symmetric in
![]() $x_{[3]}$
, and we have
$x_{[3]}$
, and we have
![]() $\operatorname {prank} \sigma \leq O(r^{O(1)})$
and
$\operatorname {prank} \sigma \leq O(r^{O(1)})$
and
![]() $(\alpha + \sigma )(d,d,x_3, x_4, x_5) = 0$
for all
$(\alpha + \sigma )(d,d,x_3, x_4, x_5) = 0$
for all
![]() $d,x_3, x_4, x_5 \in U$
, as desired.
$d,x_3, x_4, x_5 \in U$
, as desired.
Case 3:
![]() $m = 4$
. In this case, equality (5.1) becomes
$m = 4$
. In this case, equality (5.1) becomes
 $$\begin{align*}&\alpha(d,d, x_3, x_4, y_5)\\&\quad = \sum_{i \in [s_1]} \beta_{i}(d, x_3) \gamma_i(x_4, y_5) + \sum_{i \in [s_2]} \beta^{\prime}_{i}(d, x_4) \gamma^{\prime}_i(x_3, y_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, y_5) \gamma^{\prime\prime}_i(x_3, x_4)\end{align*}$$
$$\begin{align*}&\alpha(d,d, x_3, x_4, y_5)\\&\quad = \sum_{i \in [s_1]} \beta_{i}(d, x_3) \gamma_i(x_4, y_5) + \sum_{i \in [s_2]} \beta^{\prime}_{i}(d, x_4) \gamma^{\prime}_i(x_3, y_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, y_5) \gamma^{\prime\prime}_i(x_3, x_4)\end{align*}$$
for some
![]() $s_1, s_2, s_3 \leq O(r^{O(1)})$
and bilinear forms
$s_1, s_2, s_3 \leq O(r^{O(1)})$
and bilinear forms
![]() $\beta _i,\dots , \gamma ^{\prime \prime }_i$
. Similarly to the previous case, recall that all these forms come from slice of
$\beta _i,\dots , \gamma ^{\prime \prime }_i$
. Similarly to the previous case, recall that all these forms come from slice of
![]() $\alpha $
and that we have trilinear forms
$\alpha $
and that we have trilinear forms
![]() $\tilde {\beta }_i(x_{[3]})$
, symmetric in
$\tilde {\beta }_i(x_{[3]})$
, symmetric in
![]() $x_{[3]}$
,
$x_{[3]}$
,
![]() $\tilde {\beta }^{\prime }_i(x_{[3]})$
, symmetric in
$\tilde {\beta }^{\prime }_i(x_{[3]})$
, symmetric in
![]() $x_{[3]}$
(note that this form is now symmetric in all variables in contrast to the previous case), and
$x_{[3]}$
(note that this form is now symmetric in all variables in contrast to the previous case), and
![]() $\tilde {\beta }^{\prime \prime }_i(x_{[3]})$
, symmetric in
$\tilde {\beta }^{\prime \prime }_i(x_{[3]})$
, symmetric in
![]() $x_{[2]}$
, such that
$x_{[2]}$
, such that
![]() $\beta _{i}(d, x_3) = \tilde {\beta }_i(d,d,x_3)$
,
$\beta _{i}(d, x_3) = \tilde {\beta }_i(d,d,x_3)$
,
![]() $\beta ^{\prime }_{i}(d, x_4) = \tilde {\beta }^{\prime }_i(d,d,x_4)$
and
$\beta ^{\prime }_{i}(d, x_4) = \tilde {\beta }^{\prime }_i(d,d,x_4)$
and
![]() $\beta _{i}"(d, y_5) = \tilde {\beta }^{\prime \prime }_i(d,d,y_5)$
. Also,
$\beta _{i}"(d, y_5) = \tilde {\beta }^{\prime \prime }_i(d,d,y_5)$
. Also,
![]() $\gamma ^{\prime \prime }_i(x_3, x_4)$
is symmetric for all i.
$\gamma ^{\prime \prime }_i(x_3, x_4)$
is symmetric for all i.
We now regularize some of the forms. Let
![]() $C, D \geq 2$
be two parameters to be chosen later. First, apply Lemma 4.1 (with parameters
$C, D \geq 2$
be two parameters to be chosen later. First, apply Lemma 4.1 (with parameters
![]() $C, D$
and
$C, D$
and
![]() $m = 0$
so that the symmetry properties play no role; see Remark 4.2) to the list consisting of forms
$m = 0$
so that the symmetry properties play no role; see Remark 4.2) to the list consisting of forms
![]() $\gamma _i(u,v)$
,
$\gamma _i(u,v)$
,
![]() $i \in [s_1]$
and
$i \in [s_1]$
and
![]() $\gamma ^{\prime }_i(u,v)$
,
$\gamma ^{\prime }_i(u,v)$
,
![]() $i \in [s_2]$
. We thus obtain bilinear forms
$i \in [s_2]$
. We thus obtain bilinear forms
![]() $\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
, each being a linear combination of the forms in the given list, for some
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
, each being a linear combination of the forms in the given list, for some
![]() $t \leq O(r^{O(1)})$
and some
$t \leq O(r^{O(1)})$
and some
![]() $R \leq C^{D^{O(r^{O(1)}}}$
such that:
$R \leq C^{D^{O(r^{O(1)}}}$
such that:
-
• every bilinear form in the list differs from a linear combination of forms
 $\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
by a bilinear form of rank at most R,
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
by a bilinear form of rank at most R, -
• nonzero linear combinations of
 $\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
have rank at least
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
have rank at least
 $(C(R + 2r))^{D}$
.
$(C(R + 2r))^{D}$
.
Next, apply Lemma 5.2 to the list of forms
![]() $\tilde {\beta }_i(x_{[3]})$
, for
$\tilde {\beta }_i(x_{[3]})$
, for
![]() $i \in [s_1]$
, and
$i \in [s_1]$
, and
![]() $\tilde {\beta }^{\prime }_i(x_{[3]})$
, for
$\tilde {\beta }^{\prime }_i(x_{[3]})$
, for
![]() $i \in [s_2]$
, with parameters
$i \in [s_2]$
, with parameters
![]() $M = D$
and
$M = D$
and
![]() $R_0 = r$
. We misuse the notation and still write R for the parameter produced by the lemma, which still satisfies the earlier bound
$R_0 = r$
. We misuse the notation and still write R for the parameter produced by the lemma, which still satisfies the earlier bound
![]() $R \leq C^{D^{O(r^{O(1)}}}$
. Let
$R \leq C^{D^{O(r^{O(1)}}}$
. Let
![]() $\Lambda ^{\times 2}$
be the subspaces provided by the lemma, and let
$\Lambda ^{\times 2}$
be the subspaces provided by the lemma, and let
![]() $e_1, \dots , e_q$
be a basis of an additive complement of
$e_1, \dots , e_q$
be a basis of an additive complement of
![]() $\Lambda ^{\times 2}$
in
$\Lambda ^{\times 2}$
in
![]() $\mathbb {F}_2^{s_1 + s_2}$
. Let
$\mathbb {F}_2^{s_1 + s_2}$
. Let
![]() $\tau _1, \dots , \tau _q$
be the trilinear forms given by linear combinations of the trilinear forms in the given list with coefficients corresponding to
$\tau _1, \dots , \tau _q$
be the trilinear forms given by linear combinations of the trilinear forms in the given list with coefficients corresponding to
![]() $e_1, \dots , e_q$
. Then:
$e_1, \dots , e_q$
. Then:
-
• every nonzero linear combination of
 $\tau _1, \dots , \tau _q$
has partition rank at least
$\tau _1, \dots , \tau _q$
has partition rank at least
 $(2r + 1)^D$
,
$(2r + 1)^D$
, -
• every nonzero linear combination of
 $\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
has rank at least
$\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
has rank at least
 $(2r + 1)^D$
,
$(2r + 1)^D$
, -
• every
 ${\tilde {\beta }}_i^{\times 2}$
and every
${\tilde {\beta }}_i^{\times 2}$
and every
 $\tilde {\beta }^{\prime }_i {}^{\times 2}$
differs from a linear combination of
$\tilde {\beta }^{\prime }_i {}^{\times 2}$
differs from a linear combination of
 $\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
by a bilinear form of rank at most R.
$\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
by a bilinear form of rank at most R.
Using these properties, we may pass to a further subspace
![]() $U' \leq U$
of codimension
$U' \leq U$
of codimension
![]() $\operatorname {codim}_G U' \leq O(r^{O(1)}R)$
and we may find coefficients
$\operatorname {codim}_G U' \leq O(r^{O(1)}R)$
and we may find coefficients
![]() $\lambda _{ij}, \lambda ^{\prime }_{ij}$
for
$\lambda _{ij}, \lambda ^{\prime }_{ij}$
for
![]() $i \in [q], j \in [t]$
such that
$i \in [q], j \in [t]$
such that
 $$ \begin{align*}&\alpha(d,d, x_3, x_4, y_5) = \sum_{i \in [q], j \in [t]} \lambda_{ij}\tau_i(d, d, x_3) \tilde{\gamma}_j(x_4, y_5) \\&\quad+ \sum_{i \in [q], j \in [t]} \lambda^{\prime}_{ij}\tau_i(d, d, x_4) \tilde{\gamma}_j(x_3, y_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, y_5) \gamma^{\prime\prime}_i(x_3, x_4)\end{align*} $$
$$ \begin{align*}&\alpha(d,d, x_3, x_4, y_5) = \sum_{i \in [q], j \in [t]} \lambda_{ij}\tau_i(d, d, x_3) \tilde{\gamma}_j(x_4, y_5) \\&\quad+ \sum_{i \in [q], j \in [t]} \lambda^{\prime}_{ij}\tau_i(d, d, x_4) \tilde{\gamma}_j(x_3, y_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, y_5) \gamma^{\prime\prime}_i(x_3, x_4)\end{align*} $$
holds for all
![]() $d, x_3, x_4, y_5 \in U'$
.
$d, x_3, x_4, y_5 \in U'$
.
Recall that
![]() $\alpha $
is symmetric in
$\alpha $
is symmetric in
![]() $x_{[4]}$
. Thus, for all
$x_{[4]}$
. Thus, for all
![]() $d, x_3, x_4, x_5 \in U'$
, we have
$d, x_3, x_4, x_5 \in U'$
, we have
 $$ \begin{align*}&0 = \alpha(d,d, x_3, x_4, y_5) + \alpha(d,d, x_4, x_3, y_5) \\ &\hspace{1cm}= \sum_{i \in [q], j \in [t]} \Big((\lambda_{ij} + \lambda^{\prime}_{ij})\tau_i^{\times 2}(d, x_3) \tilde{\gamma}_j(x_4, y_5) \Big) + \sum_{i \in [q], j \in [t]} \Big((\lambda^{\prime}_{ij} + \lambda_{ij})\tau_i^{\times 2}(d, x_4) \tilde{\gamma}_j(x_3, y_5)\Big).\end{align*} $$
$$ \begin{align*}&0 = \alpha(d,d, x_3, x_4, y_5) + \alpha(d,d, x_4, x_3, y_5) \\ &\hspace{1cm}= \sum_{i \in [q], j \in [t]} \Big((\lambda_{ij} + \lambda^{\prime}_{ij})\tau_i^{\times 2}(d, x_3) \tilde{\gamma}_j(x_4, y_5) \Big) + \sum_{i \in [q], j \in [t]} \Big((\lambda^{\prime}_{ij} + \lambda_{ij})\tau_i^{\times 2}(d, x_4) \tilde{\gamma}_j(x_3, y_5)\Big).\end{align*} $$
Applying Lemma 3.1 shows that
![]() $\lambda _{ij} = \lambda ^{\prime }_{ij}$
for all
$\lambda _{ij} = \lambda ^{\prime }_{ij}$
for all
![]() $i,j$
. To finish the work in this case, define
$i,j$
. To finish the work in this case, define
 $$ \begin{align*}\sigma(x_{[5]}) = \sum_{i \in [q], j \in [t]}& \lambda_{ij}\Big(\sum_{\{a,b,c\} \in \binom{[4]}{3}}\tau_{i}(x_a, x_b, x_c) \tilde{\gamma}_i(x_{[4] \setminus \{a,b,c\}}, x_5)\Big)\\ &+\sum_{i \in [s_3]} \Big(\sum_{\{a, b\} \in \binom{[4]}{2}} \tilde{\beta}^{\prime\prime}_{i}(x_a, x_b, x_5) \gamma^{\prime\prime}_i(x_{[4] \setminus \{a,b\}})\Big).\end{align*} $$
$$ \begin{align*}\sigma(x_{[5]}) = \sum_{i \in [q], j \in [t]}& \lambda_{ij}\Big(\sum_{\{a,b,c\} \in \binom{[4]}{3}}\tau_{i}(x_a, x_b, x_c) \tilde{\gamma}_i(x_{[4] \setminus \{a,b,c\}}, x_5)\Big)\\ &+\sum_{i \in [s_3]} \Big(\sum_{\{a, b\} \in \binom{[4]}{2}} \tilde{\beta}^{\prime\prime}_{i}(x_a, x_b, x_5) \gamma^{\prime\prime}_i(x_{[4] \setminus \{a,b\}})\Big).\end{align*} $$
Finally, pass to the subspace
![]() $U"$
consisting of all
$U"$
consisting of all
![]() $u \in U'$
such that all
$u \in U'$
such that all
![]() $\gamma ^{\prime \prime }_i(u,u) = 0$
(recall that these forms are symmetric). On
$\gamma ^{\prime \prime }_i(u,u) = 0$
(recall that these forms are symmetric). On
![]() $U"$
, we have that
$U"$
, we have that
![]() $(\alpha + \sigma )^{\times 2}$
vanishes, and we know that
$(\alpha + \sigma )^{\times 2}$
vanishes, and we know that
![]() $\sigma (x_{[5]})$
is symmetric in
$\sigma (x_{[5]})$
is symmetric in
![]() $x_{[4]}$
and has
$x_{[4]}$
and has
![]() $\operatorname {prank}\sigma \leq O(r^{O(1)})$
.
$\operatorname {prank}\sigma \leq O(r^{O(1)})$
.
Case 4:
![]() $m = 5$
. In this case, equality (5.1) becomes
$m = 5$
. In this case, equality (5.1) becomes
 $$\begin{align*}&\alpha(d,d, x_3, x_4, x_5) \\&\quad= \sum_{i \in [s_1]} \beta_{i}(d, x_3) \gamma_i(x_4, x_5) + \sum_{i \in [s_2]} \beta^{\prime}_{i}(d,x_4) \gamma^{\prime}_i(x_3, x_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, x_5) \gamma^{\prime\prime}_i(x_3, x_4)\end{align*}$$
$$\begin{align*}&\alpha(d,d, x_3, x_4, x_5) \\&\quad= \sum_{i \in [s_1]} \beta_{i}(d, x_3) \gamma_i(x_4, x_5) + \sum_{i \in [s_2]} \beta^{\prime}_{i}(d,x_4) \gamma^{\prime}_i(x_3, x_5) + \sum_{i \in [s_3]} \beta^{\prime\prime}_{i}(d, x_5) \gamma^{\prime\prime}_i(x_3, x_4)\end{align*}$$
for some
![]() $s_1, s_2, s_3 \leq O(r^{O(1)})$
and bilinear forms
$s_1, s_2, s_3 \leq O(r^{O(1)})$
and bilinear forms
![]() $\beta _i,\dots , \gamma ^{\prime \prime }_i$
and the forms
$\beta _i,\dots , \gamma ^{\prime \prime }_i$
and the forms
![]() $\gamma _i, \gamma ^{\prime }_i, \gamma ^{\prime \prime }_i$
are symmetric. As before, there are symmetric trilinear forms
$\gamma _i, \gamma ^{\prime }_i, \gamma ^{\prime \prime }_i$
are symmetric. As before, there are symmetric trilinear forms
![]() $\tilde {\beta }_i, \tilde {\beta }^{\prime }_i$
, and
$\tilde {\beta }_i, \tilde {\beta }^{\prime }_i$
, and
![]() $\tilde {\beta }^{\prime \prime }_i$
such that
$\tilde {\beta }^{\prime \prime }_i$
such that
![]() $\beta _i = \tilde {\beta }_i{}^{\times 2}$
, etc. We regularize the forms as in the previous case. The lists are slightly different, but the details are the same, so we are deliberately concise in order to avoid repetition.
$\beta _i = \tilde {\beta }_i{}^{\times 2}$
, etc. We regularize the forms as in the previous case. The lists are slightly different, but the details are the same, so we are deliberately concise in order to avoid repetition.
Let
![]() $C, D \geq 2$
be two parameters to be chosen later. We apply Lemma 4.1 to the list consisting of forms
$C, D \geq 2$
be two parameters to be chosen later. We apply Lemma 4.1 to the list consisting of forms
![]() $\gamma _i(u,v)$
,
$\gamma _i(u,v)$
,
![]() $i \in [s_1]$
,
$i \in [s_1]$
,
![]() $\gamma ^{\prime }_i(u,v)$
,
$\gamma ^{\prime }_i(u,v)$
,
![]() $i \in [s_2]$
, and
$i \in [s_2]$
, and
![]() $\gamma ^{\prime \prime }_i(u,v)$
,
$\gamma ^{\prime \prime }_i(u,v)$
,
![]() $i \in [s_3]$
and Lemma 5.2 to the list of forms
$i \in [s_3]$
and Lemma 5.2 to the list of forms
![]() $\tilde {\beta }_i(x_{[3]})$
,
$\tilde {\beta }_i(x_{[3]})$
,
![]() $i \in [s_1]$
,
$i \in [s_1]$
,
![]() $\tilde {\beta }^{\prime }_i(x_{[3]})$
,
$\tilde {\beta }^{\prime }_i(x_{[3]})$
,
![]() $i \in [s_2]$
, and
$i \in [s_2]$
, and
![]() $\tilde {\beta }^{\prime \prime }_i(x_{[3]})$
,
$\tilde {\beta }^{\prime \prime }_i(x_{[3]})$
,
![]() $i \in [s_3]$
. We obtain
$i \in [s_3]$
. We obtain
![]() $t, q \leq O(r^{O(1)})$
,
$t, q \leq O(r^{O(1)})$
,
![]() $R \leq C^{D^{O(r^{O(1)}}}$
, bilinear forms
$R \leq C^{D^{O(r^{O(1)}}}$
, bilinear forms
![]() $\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
and trilinear forms
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
and trilinear forms
![]() $\tau _1, \dots , \tau _q$
such that:
$\tau _1, \dots , \tau _q$
such that:
-
• every form in the list of bilinear forms differs from a linear combination of
 $\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
by a bilinear form of rank at most R,
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
by a bilinear form of rank at most R, -
• nonzero linear combinations of
 $\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
have rank at least
$\tilde {\gamma }_1, \dots , \tilde {\gamma }_t$
have rank at least
 $(C(R + 2r))^{D}$
,
$(C(R + 2r))^{D}$
, -
• each of the forms
 ${\tilde {\beta }}_i^{\times 2}$
,
${\tilde {\beta }}_i^{\times 2}$
,
 $\tilde {\beta }^{\prime }_i {}^{\times 2}$
, and
$\tilde {\beta }^{\prime }_i {}^{\times 2}$
, and
 $\tilde {\beta }^{\prime \prime }_i {}^{\times 2}$
differs from a linear combination of
$\tilde {\beta }^{\prime \prime }_i {}^{\times 2}$
differs from a linear combination of
 $\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
by a bilinear form of rank at most R,
$\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
by a bilinear form of rank at most R, -
• every nonzero linear combination of
 $\tau _1, \dots , \tau _q$
has partition rank at least
$\tau _1, \dots , \tau _q$
has partition rank at least
 $(2r + 1)^D$
,
$(2r + 1)^D$
, -
• every nonzero linear combination of
 $\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
has rank at least
$\tau _1^{\times 2}, \dots , \tau _q^{\times 2}$
has rank at least
 $(2r + 1)^D$
, and
$(2r + 1)^D$
, and -
• the newly obtained forms are symmetric.
We may now pass to a further subspace
![]() $U' \leq U$
of codimension
$U' \leq U$
of codimension
![]() $\operatorname {codim}_G U' \leq O(r^{O(1)}R)$
, and we may find coefficients
$\operatorname {codim}_G U' \leq O(r^{O(1)}R)$
, and we may find coefficients
![]() $\lambda _{ij}, \lambda ^{\prime }_{ij}, \lambda ^{\prime \prime }_{ij}$
for
$\lambda _{ij}, \lambda ^{\prime }_{ij}, \lambda ^{\prime \prime }_{ij}$
for
![]() $i \in [q], j \in [t]$
such that
$i \in [q], j \in [t]$
such that
 $$ \begin{align*}\alpha(d,d, x_3, x_4, x_5) = \sum_{i \in [q], j \in [t]} \lambda_{ij}\tau_i(d, d, x_3) \tilde{\gamma}_j(x_4, x_5)\ + &\sum_{i \in [q], j \in [t]} \lambda^{\prime}_{ij}\tau_i(d, d, x_4) \tilde{\gamma}_j(x_3, x_5)\\ + &\sum_{i \in [q], j \in [t]} \lambda^{\prime\prime}_{ij}\tau_i(d, d, x_5) \tilde{\gamma}_j(x_3, x_4)\end{align*} $$
$$ \begin{align*}\alpha(d,d, x_3, x_4, x_5) = \sum_{i \in [q], j \in [t]} \lambda_{ij}\tau_i(d, d, x_3) \tilde{\gamma}_j(x_4, x_5)\ + &\sum_{i \in [q], j \in [t]} \lambda^{\prime}_{ij}\tau_i(d, d, x_4) \tilde{\gamma}_j(x_3, x_5)\\ + &\sum_{i \in [q], j \in [t]} \lambda^{\prime\prime}_{ij}\tau_i(d, d, x_5) \tilde{\gamma}_j(x_3, x_4)\end{align*} $$
holds for all
![]() $d, x_3, x_4, x_5 \in U'$
.
$d, x_3, x_4, x_5 \in U'$
.
Recalling that
![]() $\alpha $
is symmetric and applying Lemma 3.1 to expressions
$\alpha $
is symmetric and applying Lemma 3.1 to expressions
![]() $\alpha (d,d, x_3, x_4, x_5) + \alpha (d,d, x_4, x_3, x_5)$
and
$\alpha (d,d, x_3, x_4, x_5) + \alpha (d,d, x_4, x_3, x_5)$
and
![]() $\alpha (d,d, x_3, x_4, x_5) + \alpha (d,d, x_5, x_4, x_3)$
show that
$\alpha (d,d, x_3, x_4, x_5) + \alpha (d,d, x_5, x_4, x_3)$
show that
![]() $\lambda _{ij} = \lambda ^{\prime }_{ij}= \lambda ^{\prime \prime }_{ij}$
for all
$\lambda _{ij} = \lambda ^{\prime }_{ij}= \lambda ^{\prime \prime }_{ij}$
for all
![]() $i,j$
. Let us also pass to a further subspace
$i,j$
. Let us also pass to a further subspace
![]() $U" \leq U'$
consisting of all
$U" \leq U'$
consisting of all
![]() $u \in U'$
such that
$u \in U'$
such that
![]() $\tilde {\gamma }_j(u,u) = 0$
for all
$\tilde {\gamma }_j(u,u) = 0$
for all
![]() $j \in [t]$
, whose codimension is
$j \in [t]$
, whose codimension is
![]() $\operatorname {codim}_G U" \leq O(r^{O(1)}R)$
. Finally, consider
$\operatorname {codim}_G U" \leq O(r^{O(1)}R)$
. Finally, consider
 $$ \begin{align*}\sigma(x_{[5]}) = \sum_{i \in [q], j \in [t]}& \lambda_{ij}\Big(\sum_{\{a,b,c\} \in \binom{[5]}{3}}\tau_{i}(x_a, x_b, x_c) \tilde{\gamma}_i(x_{[5] \setminus \{a,b,c\}})\Big).\end{align*} $$
$$ \begin{align*}\sigma(x_{[5]}) = \sum_{i \in [q], j \in [t]}& \lambda_{ij}\Big(\sum_{\{a,b,c\} \in \binom{[5]}{3}}\tau_{i}(x_a, x_b, x_c) \tilde{\gamma}_i(x_{[5] \setminus \{a,b,c\}})\Big).\end{align*} $$
This is a symmetric multilinear form with
![]() $\operatorname {prank} \sigma \leq O(r^{O(1)})$
and
$\operatorname {prank} \sigma \leq O(r^{O(1)})$
and
![]() $(\alpha + \sigma )^{\times 2}$
vanishes on
$(\alpha + \sigma )^{\times 2}$
vanishes on
![]() $U"$
.
$U"$
.
6 Proof of the inverse theorem
In this section, we combine Theorems 1.6–1.8 and 1.10 with other additive-combinatorial arguments in order to prove our main result.
Proof of Theorem 1.4
We prove the claim for
![]() $k \in \{4,5\}$
and assume the theorem for
$k \in \{4,5\}$
and assume the theorem for
![]() $k - 1$
. The proof will have the following structure.
$k - 1$
. The proof will have the following structure.
Step 1. We first show that whenever
(6.1)is satisfied, we may pass to a carefully chosen subspace U on which
 $\alpha $
has the additional property that the multilinear form
$\alpha $
has the additional property that the multilinear form
 $(a_2, \dots , a_k) \mapsto \alpha (u, a_2, \dots , a_k)$
is a sum of a strongly symmetric and a bounded partition rank form for each
$(a_2, \dots , a_k) \mapsto \alpha (u, a_2, \dots , a_k)$
is a sum of a strongly symmetric and a bounded partition rank form for each
 $u \in U$
.
$u \in U$
.
Step 2. Next, we prove that
 $\alpha |_{U' \times \cdots \times U'}$
is a sum of strongly symmetric and low partition rank form on a suitable subspace
$\alpha |_{U' \times \cdots \times U'}$
is a sum of strongly symmetric and low partition rank form on a suitable subspace
 $U'$
of bounded codimension.
$U'$
of bounded codimension.Step 3. Using the structure of multilinear form
 $\alpha |_{U' \times \cdots \times U'}$
, we deduce that
$\alpha |_{U' \times \cdots \times U'}$
, we deduce that
 $\alpha $
is of the desired shape.
$\alpha $
is of the desired shape.
Step 1. We formulate the work in this step as the following lemma.
Lemma 6.1 Let
![]() $V \leq G$
be a subspace, and let
$V \leq G$
be a subspace, and let
![]() $g \colon V \to \mathbb {D}$
be a function. Suppose that
$g \colon V \to \mathbb {D}$
be a function. Suppose that
Then there exists a subspace
![]() $U \leq V$
of codimension at most
$U \leq V$
of codimension at most
![]() $O(\log ^{O(1)} (2c^{-1}))$
and a function
$O(\log ^{O(1)} (2c^{-1}))$
and a function
![]() $g' \colon U \to \mathbb {D}$
such that
$g' \colon U \to \mathbb {D}$
such that
and, for any
![]() $u \in U$
, the multilinear form
$u \in U$
, the multilinear form
![]() $(a_2, \dots , a_k) \mapsto \alpha (u, a_2, \dots , a_k)$
(where
$(a_2, \dots , a_k) \mapsto \alpha (u, a_2, \dots , a_k)$
(where
![]() $a_2, \dots , a_k \in U$
) is a sum of a strongly symmetric form and a form of partition rank at most r for some
$a_2, \dots , a_k \in U$
) is a sum of a strongly symmetric form and a form of partition rank at most r for some
![]() $r \leq O(\exp ^{(O(1))} c^{-1})$
.
$r \leq O(\exp ^{(O(1))} c^{-1})$
.
Proof of Lemma 6.1
Let B be the set of all
![]() $b \in V$
such that
$b \in V$
such that
From assumption (6.2), we see that
![]() $|B| \geq \frac {c}{2}|V|$
. By Theorem 2.3,
$|B| \geq \frac {c}{2}|V|$
. By Theorem 2.3,
![]() $4B$
contains a subspace U of codimension at most
$4B$
contains a subspace U of codimension at most
![]() $O(\log ^{O(1)} (2c^{-1}))$
. Take any
$O(\log ^{O(1)} (2c^{-1}))$
. Take any
![]() $u \in U$
. In particular, since
$u \in U$
. In particular, since
![]() $U \subseteq 4B$
, u can be written as
$U \subseteq 4B$
, u can be written as
![]() $b_1 + b_2 + b_3 + b_4$
for some
$b_1 + b_2 + b_3 + b_4$
for some
![]() $b_1, b_2, b_3, b_4 \in B$
. For each
$b_1, b_2, b_3, b_4 \in B$
. For each
![]() $i \in [4]$
, we then have
$i \in [4]$
, we then have
By the induction hypothesis applied to the function
![]() $\partial _{b_i}f$
, we deduce that the multilinear form
$\partial _{b_i}f$
, we deduce that the multilinear form
![]() $(a_2, \dots , a_k) \mapsto \alpha (b_i, a_2, \dots , a_k)$
is a sum of a strongly symmetric form and a form of partition rank at most r, for some positive quantity
$(a_2, \dots , a_k) \mapsto \alpha (b_i, a_2, \dots , a_k)$
is a sum of a strongly symmetric form and a form of partition rank at most r, for some positive quantity
![]() $r \leq O(\exp ^{(O(1))} c^{-1})$
. Thus, the multilinear form
$r \leq O(\exp ^{(O(1))} c^{-1})$
. Thus, the multilinear form
![]() $(a_2, \dots , a_k) \mapsto \alpha (u, a_2, \dots , a_k)$
is a sum of a strongly symmetric form and a form of partition rank at most
$(a_2, \dots , a_k) \mapsto \alpha (u, a_2, \dots , a_k)$
is a sum of a strongly symmetric form and a form of partition rank at most
![]() $4r$
.
$4r$
.
Apply Lemma 2.9 to finish the proof.
Step 2. In this step, we show that
![]() $\alpha $
can essentially be assumed to be symmetric and to satisfy
$\alpha $
can essentially be assumed to be symmetric and to satisfy
![]() $\alpha (d,d,a_3, \dots , a_k) = 0$
. This is formulated precisely in the following claim.
$\alpha (d,d,a_3, \dots , a_k) = 0$
. This is formulated precisely in the following claim.
Claim 6.2 Assume
![]() $k \in \{4,5\}$
. Suppose that a function
$k \in \{4,5\}$
. Suppose that a function
![]() $f \colon G \to \mathbb {D}$
and a multilinear form
$f \colon G \to \mathbb {D}$
and a multilinear form
![]() $\alpha \colon G^k \to \mathbb {F}_2$
satisfy (6.1). For each
$\alpha \colon G^k \to \mathbb {F}_2$
satisfy (6.1). For each
![]() $\ell \in [2,k]$
, there exist a subspace
$\ell \in [2,k]$
, there exist a subspace
![]() $U \leq G$
of codimension at most
$U \leq G$
of codimension at most
![]() $O(\exp ^{(O(1))} c^{-1})$
, a multilinear form
$O(\exp ^{(O(1))} c^{-1})$
, a multilinear form
![]() $\beta \colon U^k \to \mathbb {F}_2$
, and a function
$\beta \colon U^k \to \mathbb {F}_2$
, and a function
![]() $g \colon U \to \mathbb {D}$
such that:
$g \colon U \to \mathbb {D}$
such that:
-
(i)
 $\beta $
is symmetric in the first
$\beta $
is symmetric in the first
 $\ell $
variables,
$\ell $
variables, -
(ii)
 $\beta (d,d,a_3, \dots , a_k) = 0$
for all
$\beta (d,d,a_3, \dots , a_k) = 0$
for all
 $d, a_3, \dots , a_k \in U$
,
$d, a_3, \dots , a_k \in U$
, -
(iii)
 $\Big |\mathop {\mathbb {E}}_{x,a_1, \dots , a_k \in U} \partial _{a_1}\dots \partial _{a_k}g(x) (-1)^{\beta (a_1, \dots , a_k)}\Big | \geq \Omega ((\exp ^{(O(1))} c^{-1})^{-1})$
, and
$\Big |\mathop {\mathbb {E}}_{x,a_1, \dots , a_k \in U} \partial _{a_1}\dots \partial _{a_k}g(x) (-1)^{\beta (a_1, \dots , a_k)}\Big | \geq \Omega ((\exp ^{(O(1))} c^{-1})^{-1})$
, and -
(iv)
 $\alpha |_{U \times \cdots \times U} = \beta + \sigma + \delta $
for a strongly symmetric multilinear form
$\alpha |_{U \times \cdots \times U} = \beta + \sigma + \delta $
for a strongly symmetric multilinear form
 $\sigma \colon U^k \to \mathbb {F}_2$
and a multilinear form
$\sigma \colon U^k \to \mathbb {F}_2$
and a multilinear form
 $\delta \colon U^k \to \mathbb {F}_2$
of partition rank at most
$\delta \colon U^k \to \mathbb {F}_2$
of partition rank at most
 $O(\exp ^{(O(1))} c^{-1})$
.
$O(\exp ^{(O(1))} c^{-1})$
.
Proof We prove the claim by induction on
![]() $\ell $
. First, we prove the base case
$\ell $
. First, we prove the base case
![]() $\ell = 2$
. By Lemma 2.10, we see that
$\ell = 2$
. By Lemma 2.10, we see that
![]() $\operatorname {prank}(\alpha + \alpha \circ (1\,\,2)) \leq O\Big ((\log c^{-1})^{O(1)}\Big )$
. Theorem 1.6 produces a multilinear form
$\operatorname {prank}(\alpha + \alpha \circ (1\,\,2)) \leq O\Big ((\log c^{-1})^{O(1)}\Big )$
. Theorem 1.6 produces a multilinear form
![]() $\beta \colon G^k \to \mathbb {F}_2$
, symmetric in the first two variables which differs from
$\beta \colon G^k \to \mathbb {F}_2$
, symmetric in the first two variables which differs from
![]() $\alpha $
by a multilinear form of partition rank at most
$\alpha $
by a multilinear form of partition rank at most
![]() $O(\exp ^{(O(1))} c^{-1})$
. This immediately gives property (iv) with
$O(\exp ^{(O(1))} c^{-1})$
. This immediately gives property (iv) with
![]() $\sigma = 0$
. Lemmas 2.8 and 2.9 imply property (iii). Note that the proof of the base case is not yet complete as we have not addressed the
$\sigma = 0$
. Lemmas 2.8 and 2.9 imply property (iii). Note that the proof of the base case is not yet complete as we have not addressed the
![]() $\beta (d,d,a_3, \dots , a_k) = 0$
property. We do this now in a more general form, which will also be used in the inductive step.
$\beta (d,d,a_3, \dots , a_k) = 0$
property. We do this now in a more general form, which will also be used in the inductive step.
Obtaining property (ii). Suppose that we are given a subspace
![]() $U \leq G$
of codimension at most
$U \leq G$
of codimension at most
![]() $O(\exp ^{(O(1))} c^{-1})$
, a multilinear form
$O(\exp ^{(O(1))} c^{-1})$
, a multilinear form
![]() $\alpha ' \colon U^k \to \mathbb {F}_2$
, and a function
$\alpha ' \colon U^k \to \mathbb {F}_2$
, and a function
![]() $g \colon U \to \mathbb {D}$
which satisfy conditions (i), (iii), and (iv) (with
$g \colon U \to \mathbb {D}$
which satisfy conditions (i), (iii), and (iv) (with
![]() $\beta $
replaced by
$\beta $
replaced by
![]() $\alpha '$
). Since
$\alpha '$
). Since
![]() $\alpha '$
satisfies property (iii), we may use Lemma 6.1 to pass to a further subspace
$\alpha '$
satisfies property (iii), we may use Lemma 6.1 to pass to a further subspace
![]() $U' \leq U$
of codimension at most
$U' \leq U$
of codimension at most
![]() $O(\exp ^{(O(1))} c^{-1})$
and to find a function
$O(\exp ^{(O(1))} c^{-1})$
and to find a function
![]() $g' \colon U' \to \mathbb {D}$
such that
$g' \colon U' \to \mathbb {D}$
such that
where
![]() $c' \geq \Omega ((\exp ^{(O(1))} c^{-1})^{-1})$
, and for any
$c' \geq \Omega ((\exp ^{(O(1))} c^{-1})^{-1})$
, and for any
![]() $u \in U'$
, the multilinear form
$u \in U'$
, the multilinear form
![]() $(a_2, \dots , a_k) \mapsto \alpha '(u, a_2, \dots , a_k)$
(where
$(a_2, \dots , a_k) \mapsto \alpha '(u, a_2, \dots , a_k)$
(where
![]() $a_2, \dots , a_k \in U'$
) is a sum of a strongly symmetric form and a form of partition rank at most r for some
$a_2, \dots , a_k \in U'$
) is a sum of a strongly symmetric form and a form of partition rank at most r for some
![]() $r \leq O(\exp ^{(O(1))} c^{-1})$
.
$r \leq O(\exp ^{(O(1))} c^{-1})$
.
By making a slight change of variables, we obtain
We may find
![]() $b \in U'$
such that
$b \in U'$
such that
However, writing
![]() $h(x) = \overline {g'(x) g'(x + b)}$
,
$h(x) = \overline {g'(x) g'(x + b)}$
,
 $$ \begin{align*}\partial_{b +d} \partial_d &\partial_{a_3} \dots \partial_{a_k} g'(x) = \partial_d \partial_{a_3} \dots \partial_{a_k} g'(x + b + d) \overline{\partial_d \partial_{a_3} \dots \partial_{a_k} g'(x)}\\ &=\partial_{a_3} \dots \partial_{a_k} g'(x + b + d + d) \overline{\partial_{a_3} \dots \partial_{a_k} g'(x + b + d)}\,\overline{\partial_{a_3} \dots \partial_{a_k} g'(x + d)} \partial_{a_3} \dots \partial_{a_k} g'(x) \\ &=\partial_{a_3} \dots \partial_{a_k} g'(x + b) \overline{\partial_{a_3} \dots \partial_{a_k} g'(x + b + d)}\,\overline{\partial_{a_3} \dots \partial_{a_k} g'(x + d)} \partial_{a_3} \dots \partial_{a_k} g'(x) \\ & = \partial_{a_3} \dots \partial_{a_k} h(x + d) \overline{\partial_{a_3} \dots \partial_{a_k} h(x)}\\ & = \partial_d \partial_{a_3} \dots \partial_{a_k} h(x),\end{align*} $$
$$ \begin{align*}\partial_{b +d} \partial_d &\partial_{a_3} \dots \partial_{a_k} g'(x) = \partial_d \partial_{a_3} \dots \partial_{a_k} g'(x + b + d) \overline{\partial_d \partial_{a_3} \dots \partial_{a_k} g'(x)}\\ &=\partial_{a_3} \dots \partial_{a_k} g'(x + b + d + d) \overline{\partial_{a_3} \dots \partial_{a_k} g'(x + b + d)}\,\overline{\partial_{a_3} \dots \partial_{a_k} g'(x + d)} \partial_{a_3} \dots \partial_{a_k} g'(x) \\ &=\partial_{a_3} \dots \partial_{a_k} g'(x + b) \overline{\partial_{a_3} \dots \partial_{a_k} g'(x + b + d)}\,\overline{\partial_{a_3} \dots \partial_{a_k} g'(x + d)} \partial_{a_3} \dots \partial_{a_k} g'(x) \\ & = \partial_{a_3} \dots \partial_{a_k} h(x + d) \overline{\partial_{a_3} \dots \partial_{a_k} h(x)}\\ & = \partial_d \partial_{a_3} \dots \partial_{a_k} h(x),\end{align*} $$
where we critically relied on the characteristic 2 assumption in the third equality. Thus,
We may apply the case
![]() $k-1$
of the theorem to the multilinear form
$k-1$
of the theorem to the multilinear form
![]() $(d, a_3, \dots , a_k) \mapsto \alpha '(b + d, d, a_3, \dots , a_k)$
(note that this is still multilinear as
$(d, a_3, \dots , a_k) \mapsto \alpha '(b + d, d, a_3, \dots , a_k)$
(note that this is still multilinear as
![]() $\alpha '$
is symmetric in the first two variables) to conclude that
$\alpha '$
is symmetric in the first two variables) to conclude that
![]() $(d, a_3, \dots , a_k) \mapsto \alpha '(b + d, d, a_3, \dots , a_k)$
is a sum of a strongly symmetric multilinear form and a multilinear form of partition rank at most
$(d, a_3, \dots , a_k) \mapsto \alpha '(b + d, d, a_3, \dots , a_k)$
is a sum of a strongly symmetric multilinear form and a multilinear form of partition rank at most
![]() $O(\exp ^{(O(1))} c^{-1})$
on subspace
$O(\exp ^{(O(1))} c^{-1})$
on subspace
![]() $U'$
. But, recall that a similar property holds for the multilinear form
$U'$
. But, recall that a similar property holds for the multilinear form
![]() $(d, a_3, \dots , a_k) \mapsto \alpha '(b, d, a_3, \dots , a_k)$
by our choice of the subspace
$(d, a_3, \dots , a_k) \mapsto \alpha '(b, d, a_3, \dots , a_k)$
by our choice of the subspace
![]() $U'$
. Thus, we conclude that there exist a strongly symmetric multilinear form
$U'$
. Thus, we conclude that there exist a strongly symmetric multilinear form
![]() $\sigma ' \colon (U')^{k-1} \to \mathbb {F}_2$
and a multilinear form
$\sigma ' \colon (U')^{k-1} \to \mathbb {F}_2$
and a multilinear form
![]() $\delta ' \colon (U')^{k-1} \to \mathbb {F}_2$
of partition rank at most
$\delta ' \colon (U')^{k-1} \to \mathbb {F}_2$
of partition rank at most
![]() $O(\exp ^{(O(1))} c^{-1})$
such that for all
$O(\exp ^{(O(1))} c^{-1})$
such that for all
![]() $d, a_3, \dots , a_k \in U'$
,
$d, a_3, \dots , a_k \in U'$
,
holds. By Lemma 2.11, there exists a strongly symmetric multilinear form
![]() $\tilde {\sigma } \colon (U')^k \to \mathbb {F}_2$
such that
$\tilde {\sigma } \colon (U')^k \to \mathbb {F}_2$
such that
Let
![]() $\tilde {\alpha } = \alpha '|_{U'\times \cdots \times U'} + \tilde {\sigma }$
, which is still symmetric in the first
$\tilde {\alpha } = \alpha '|_{U'\times \cdots \times U'} + \tilde {\sigma }$
, which is still symmetric in the first
![]() $\ell $
variables. Using Lemma 2.13, we may find phase
$\ell $
variables. Using Lemma 2.13, we may find phase
![]() $s \colon U' \to \mathbb {D}$
of a nonclassical polynomial such that
$s \colon U' \to \mathbb {D}$
of a nonclassical polynomial such that
![]() $\partial _{a_1} \dots \partial _{a_k} s(x) = (-1)^{\tilde {\sigma }(a_1, \dots , a_k)}$
for all
$\partial _{a_1} \dots \partial _{a_k} s(x) = (-1)^{\tilde {\sigma }(a_1, \dots , a_k)}$
for all
![]() $a_1, \dots , a_k, x \in U'$
. Putting
$a_1, \dots , a_k, x \in U'$
. Putting
![]() $\tilde {g}(x) = g'(x) s(x)$
, from (6.4), we obtain
$\tilde {g}(x) = g'(x) s(x)$
, from (6.4), we obtain
On the other hand, from (6.5) and (6.6), for all
![]() $d, a_3, \dots , a_k \in U'$
, we see that
$d, a_3, \dots , a_k \in U'$
, we see that
 $$ \begin{align*}&\tilde{\alpha}(d,d,a_3, \dots, a_k) = \alpha'(d,d,a_3, \dots, a_k) + \tilde{\sigma}(d,d,a_3, \dots, a_k) \\ &\quad= \sigma'(d,a_3, \dots, a_k) + \delta'(d,a_3, \dots, a_k) + \sigma'(d,a_3, \dots, a_k) = \delta'(d,a_3, \dots, a_k),\end{align*} $$
$$ \begin{align*}&\tilde{\alpha}(d,d,a_3, \dots, a_k) = \alpha'(d,d,a_3, \dots, a_k) + \tilde{\sigma}(d,d,a_3, \dots, a_k) \\ &\quad= \sigma'(d,a_3, \dots, a_k) + \delta'(d,a_3, \dots, a_k) + \sigma'(d,a_3, \dots, a_k) = \delta'(d,a_3, \dots, a_k),\end{align*} $$
which has partition rank at most
![]() $O(\exp ^{(O(1))} c^{-1})$
. By Theorem 1.10, we conclude that there exist a subspace
$O(\exp ^{(O(1))} c^{-1})$
. By Theorem 1.10, we conclude that there exist a subspace
![]() $U" \leq U'$
of codimension
$U" \leq U'$
of codimension
![]() $O(\exp ^{(O(1))} c^{-1})$
and a multilinear form
$O(\exp ^{(O(1))} c^{-1})$
and a multilinear form
![]() $\beta \colon (U")^k \to \mathbb {F}_2$
, symmetric in the first
$\beta \colon (U")^k \to \mathbb {F}_2$
, symmetric in the first
![]() $\ell $
variables, such that
$\ell $
variables, such that
![]() $\beta (d,d,a_3, \dots , a_k) = 0$
for all
$\beta (d,d,a_3, \dots , a_k) = 0$
for all
![]() $d, a_3, \dots , a_k \in U"$
and
$d, a_3, \dots , a_k \in U"$
and
![]() $\operatorname {prank}(\tilde {\alpha }|_{U" \times \cdots \times U"} + \beta ) \leq O(\exp ^{(O(1))} c^{-1})$
. Since we need to pass to further subspace
$\operatorname {prank}(\tilde {\alpha }|_{U" \times \cdots \times U"} + \beta ) \leq O(\exp ^{(O(1))} c^{-1})$
. Since we need to pass to further subspace
![]() $U"$
, we use (6.7) and apply Lemma 2.9, which provides us with a function
$U"$
, we use (6.7) and apply Lemma 2.9, which provides us with a function
![]() $h \colon U" \to \mathbb {D}$
such that
$h \colon U" \to \mathbb {D}$
such that
Since
![]() $\operatorname {prank}(\tilde {\alpha }|_{U" \times \cdots \times U"} + \beta ) \leq O(\exp ^{(O(1))} c^{-1})$
, Lemma 2.8 allows us to conclude that
$\operatorname {prank}(\tilde {\alpha }|_{U" \times \cdots \times U"} + \beta ) \leq O(\exp ^{(O(1))} c^{-1})$
, Lemma 2.8 allows us to conclude that
![]() $\beta $
satisfies property (iii) with function h on subspace
$\beta $
satisfies property (iii) with function h on subspace
![]() $U"$
. Finally, writing
$U"$
. Finally, writing
![]() $\tilde {\delta } = \tilde {\alpha }|_{U" \times \cdots \times U"} + \beta $
, we have
$\tilde {\delta } = \tilde {\alpha }|_{U" \times \cdots \times U"} + \beta $
, we have
 $$ \begin{align*}\alpha|_{U" \times\cdots\times U"} = &\alpha'|_{U" \times\cdots\times U"} + \sigma|_{U" \times\cdots\times U"} + \delta|_{U" \times\cdots\times U"} \\ = &\tilde{\alpha}|_{U" \times\cdots\times U"} + (\tilde{\sigma}|_{U" \times\cdots\times U"} + \sigma|_{U" \times\cdots\times U"}) + \delta|_{U" \times\cdots\times U"}\\ = &\beta + (\tilde{\sigma}|_{U" \times\cdots\times U"} + \sigma|_{U" \times\cdots\times U"}) + (\delta|_{U" \times\cdots\times U"} + \tilde{\delta}),\end{align*} $$
$$ \begin{align*}\alpha|_{U" \times\cdots\times U"} = &\alpha'|_{U" \times\cdots\times U"} + \sigma|_{U" \times\cdots\times U"} + \delta|_{U" \times\cdots\times U"} \\ = &\tilde{\alpha}|_{U" \times\cdots\times U"} + (\tilde{\sigma}|_{U" \times\cdots\times U"} + \sigma|_{U" \times\cdots\times U"}) + \delta|_{U" \times\cdots\times U"}\\ = &\beta + (\tilde{\sigma}|_{U" \times\cdots\times U"} + \sigma|_{U" \times\cdots\times U"}) + (\delta|_{U" \times\cdots\times U"} + \tilde{\delta}),\end{align*} $$
proving property (iv). In particular, when
![]() $\ell = 2$
, this argument allows us to complete the base case, so we now move on to proving the inductive step.
$\ell = 2$
, this argument allows us to complete the base case, so we now move on to proving the inductive step.
Inductive step. Suppose now that the claim holds for some
![]() $\ell \geq 2$
. Let
$\ell \geq 2$
. Let
![]() $U, \beta $
, and g be the relevant subspace, multilinear form, and function for
$U, \beta $
, and g be the relevant subspace, multilinear form, and function for
![]() $\ell $
. Since
$\ell $
. Since
![]() $\beta $
satisfies property (iii), we may use Lemma 2.10 to conclude that
$\beta $
satisfies property (iii), we may use Lemma 2.10 to conclude that
![]() $\operatorname {prank}(\beta + \beta \circ (1 \,\, \ell + 1)) \leq O(\exp ^{(O(1))} c^{-1})$
. When
$\operatorname {prank}(\beta + \beta \circ (1 \,\, \ell + 1)) \leq O(\exp ^{(O(1))} c^{-1})$
. When
![]() $\ell + 1$
is odd, set
$\ell + 1$
is odd, set
![]() $\beta ' = \sum _{j \in [\ell + 1]} \beta \circ (j\,\,\ell + 1)$
. If
$\beta ' = \sum _{j \in [\ell + 1]} \beta \circ (j\,\,\ell + 1)$
. If
![]() $\ell + 1$
is even, so it has to be
$\ell + 1$
is even, so it has to be
![]() $\ell + 1 = 4$
, we apply Theorem 1.7 when
$\ell + 1 = 4$
, we apply Theorem 1.7 when
![]() $k =4$
and Theorem 1.8 when
$k =4$
and Theorem 1.8 when
![]() $k =5$
. In all the described cases, we conclude that there exists a further multilinear form
$k =5$
. In all the described cases, we conclude that there exists a further multilinear form
![]() $\beta ' \colon U^k \to \mathbb {F}_2$
, symmetric in the first
$\beta ' \colon U^k \to \mathbb {F}_2$
, symmetric in the first
![]() $\ell + 1$
variables such that
$\ell + 1$
variables such that
![]() $\operatorname {prank}(\beta + \beta ') \leq O(\exp ^{(O(1))} c^{-1})$
. Using Lemma 2.8, we immediately see that
$\operatorname {prank}(\beta + \beta ') \leq O(\exp ^{(O(1))} c^{-1})$
. Using Lemma 2.8, we immediately see that
![]() $\beta '$
satisfies conditions (i), (iii), and (iv) for
$\beta '$
satisfies conditions (i), (iii), and (iv) for
![]() $\ell + 1$
. The previous part of this proof allows us to pass to a further multilinear form that satisfies property (ii) as well, completing the proof of the claim.
$\ell + 1$
. The previous part of this proof allows us to pass to a further multilinear form that satisfies property (ii) as well, completing the proof of the claim.
Step 3. We may now apply the claim above with
![]() $\ell = k$
to see that on a subspace U of codimension
$\ell = k$
to see that on a subspace U of codimension
![]() $O(\exp ^{(O(1))} c^{-1})$
we have
$O(\exp ^{(O(1))} c^{-1})$
we have
![]() $\alpha |_{U\times \cdots \times U} = \sigma + \delta $
for a strongly symmetric multilinear form
$\alpha |_{U\times \cdots \times U} = \sigma + \delta $
for a strongly symmetric multilinear form
![]() $\sigma \colon U^k \to \mathbb {F}_2$
and a multilinear form
$\sigma \colon U^k \to \mathbb {F}_2$
and a multilinear form
![]() $\delta \colon U^k \to \mathbb {F}_2$
of partition rank at most
$\delta \colon U^k \to \mathbb {F}_2$
of partition rank at most
![]() $O(\exp ^{(O(1))} c^{-1})$
. Pick any projection
$O(\exp ^{(O(1))} c^{-1})$
. Pick any projection
![]() $\pi \colon G \to U$
and define
$\pi \colon G \to U$
and define
![]() $\tilde {\sigma }, \tilde {\delta } \colon G \times \cdots \times G \to \mathbb {F}_2$
by setting
$\tilde {\sigma }, \tilde {\delta } \colon G \times \cdots \times G \to \mathbb {F}_2$
by setting
Clearly,
![]() $\tilde {\sigma }$
is strongly symmetric, while
$\tilde {\sigma }$
is strongly symmetric, while
![]() $\tilde {\delta }$
is of bounded partition rank and
$\tilde {\delta }$
is of bounded partition rank and
![]() $\tilde {\sigma }|_{U \times \cdots \times U} = \sigma $
,
$\tilde {\sigma }|_{U \times \cdots \times U} = \sigma $
,
![]() $\tilde {\delta }|_{U \times \cdots \times U} = \delta $
. Set
$\tilde {\delta }|_{U \times \cdots \times U} = \delta $
. Set
![]() $\rho = \alpha + \tilde {\sigma } + \tilde {\delta }$
, which is a multilinear form satisfying
$\rho = \alpha + \tilde {\sigma } + \tilde {\delta }$
, which is a multilinear form satisfying
![]() $\rho = 0$
on
$\rho = 0$
on
![]() $U \times \cdots \times U$
. It remains to show that such a map has low partition rank. Let
$U \times \cdots \times U$
. It remains to show that such a map has low partition rank. Let
![]() $c"$
be the density of U. Then, by Lemma 2.1,
$c"$
be the density of U. Then, by Lemma 2.1,
By Theorem 2.4, it follows that the partition rank of
![]() $\rho $
is at most
$\rho $
is at most
![]() $O(\exp ^{(O(1))} c^{-1})$
. Thus,
$O(\exp ^{(O(1))} c^{-1})$
. Thus,
completing the proof.
We may now easily deduce Corollary 1.5.
Proof of Corollary 1.5
Let
![]() $k \in \{5,6\}$
, and let
$k \in \{5,6\}$
, and let
![]() $f \colon \mathbb {F}_2^n \to \mathbb {D}$
be a function such that
$f \colon \mathbb {F}_2^n \to \mathbb {D}$
be a function such that
![]() $\|f\|_{\mathsf {U}^k} \geq c$
. By Theorem 1.1, there exists a multilinear form
$\|f\|_{\mathsf {U}^k} \geq c$
. By Theorem 1.1, there exists a multilinear form
![]() $\alpha \colon (\mathbb {F}^n_2)^{k-1} \to \mathbb {F}_2$
in
$\alpha \colon (\mathbb {F}^n_2)^{k-1} \to \mathbb {F}_2$
in
![]() $k-1$
variables such that (1.1) holds. From Theorem 1.4, we deduce that there exists a strongly symmetric multilinear form
$k-1$
variables such that (1.1) holds. From Theorem 1.4, we deduce that there exists a strongly symmetric multilinear form
![]() $\sigma \colon (\mathbb {F}_2^n)^{k-1} \to \mathbb {F}_2$
such that
$\sigma \colon (\mathbb {F}_2^n)^{k-1} \to \mathbb {F}_2$
such that
![]() $\alpha + \sigma $
has partition rank at most
$\alpha + \sigma $
has partition rank at most
![]() $O(\exp ^{(O(1))} c^{-1})$
. Lemma 2.8 allows us to replace
$O(\exp ^{(O(1))} c^{-1})$
. Lemma 2.8 allows us to replace
![]() $\alpha $
by
$\alpha $
by
![]() $\sigma $
and obtain
$\sigma $
and obtain

Using Lemma 2.13, we find a nonclassical polynomial
![]() $q \colon G \to \mathbb {T}$
of degree at most
$q \colon G \to \mathbb {T}$
of degree at most
![]() $k-1$
such that
$k-1$
such that
Hence, we get
![]() $\|f \exp (2 \pi i q)\|_{\mathsf {U}^{k-1}} \geq \Big (\exp ^{(O(1))}(O(c^{-1}))\Big )^{-1}$
, and we may now apply the lower-order inverse theorem to finish the proof.
$\|f \exp (2 \pi i q)\|_{\mathsf {U}^{k-1}} \geq \Big (\exp ^{(O(1))}(O(c^{-1}))\Big )^{-1}$
, and we may now apply the lower-order inverse theorem to finish the proof.
7 Concluding remarks
Let us now briefly return to the following question, which is central to this paper. Suppose that
![]() $\alpha \colon G^{2k} \to \mathbb {F}_2$
is a multilinear form which is symmetric in the first
$\alpha \colon G^{2k} \to \mathbb {F}_2$
is a multilinear form which is symmetric in the first
![]() $2k-1$
variables and satisfies
$2k-1$
variables and satisfies
![]() $\operatorname {prank} \Big (\alpha + \alpha \circ (2k-1 \,\,2k)\Big ) \leq r$
. Is
$\operatorname {prank} \Big (\alpha + \alpha \circ (2k-1 \,\,2k)\Big ) \leq r$
. Is
![]() $\alpha $
close to a symmetric multilinear form? While we know that the answer is negative, the arguments in the proof of Theorem 1.8 could be used to show that we may modify
$\alpha $
close to a symmetric multilinear form? While we know that the answer is negative, the arguments in the proof of Theorem 1.8 could be used to show that we may modify
![]() $\alpha $
until the low partition rank decomposition of
$\alpha $
until the low partition rank decomposition of
![]() $\alpha + \alpha \circ (2k-1 \,\,2k)$
only has products
$\alpha + \alpha \circ (2k-1 \,\,2k)$
only has products
![]() $\sigma (x_I, x_{2k-1}) \cdot \sigma (x_{[2k-2] \setminus I}, x_{2k})$
for a symmetric multilinear form
$\sigma (x_I, x_{2k-1}) \cdot \sigma (x_{[2k-2] \setminus I}, x_{2k})$
for a symmetric multilinear form
![]() $\sigma $
. In other words, using the places terminology from the proof of Theorem 1.8, we first need to make a distinction between the cases when two places A and B (not necessarily distinct) occur in the same form inside the product, having coefficient
$\sigma $
. In other words, using the places terminology from the proof of Theorem 1.8, we first need to make a distinction between the cases when two places A and B (not necessarily distinct) occur in the same form inside the product, having coefficient
![]() $\lambda ^{\text {same}}_{A\,\,B}$
, or they occur in different forms, having coefficient
$\lambda ^{\text {same}}_{A\,\,B}$
, or they occur in different forms, having coefficient
![]() $\lambda ^{\text {diff}}_{A\,\,B}$
. It turns out that we may still prove various equalities between coefficients, but the single piece of information that remains elusive is in the case when the places A and B are the same place in a symmetric form. For example, look at the product
$\lambda ^{\text {diff}}_{A\,\,B}$
. It turns out that we may still prove various equalities between coefficients, but the single piece of information that remains elusive is in the case when the places A and B are the same place in a symmetric form. For example, look at the product
![]() $\sigma (x_1, x_3, \dots , x_{2k-1})\sigma (x_2, x_4, \dots ,x_{2k})$
, where all variables with odd indices are in the first copy of
$\sigma (x_1, x_3, \dots , x_{2k-1})\sigma (x_2, x_4, \dots ,x_{2k})$
, where all variables with odd indices are in the first copy of
![]() $\sigma $
and all variables with even indices are in the second copy. This product has zero coefficient in
$\sigma $
and all variables with even indices are in the second copy. This product has zero coefficient in
![]() $\phi + \phi \circ (1\,\,2k-1) + \phi \circ (1\,\,2k)$
, where
$\phi + \phi \circ (1\,\,2k-1) + \phi \circ (1\,\,2k)$
, where
![]() $\phi = \alpha + \alpha \circ (2k-1 \,\,2k)$
, which only proves
$\phi = \alpha + \alpha \circ (2k-1 \,\,2k)$
, which only proves
![]() $\lambda ^{\text {same}}_{A\,\,A} = 0$
and says nothing about
$\lambda ^{\text {same}}_{A\,\,A} = 0$
and says nothing about
![]() $\lambda ^{\text {diff}}_{A\,\,B}$
. Of course, the reason for that is the counterexample [Reference Milićević28], which is multilinear form
$\lambda ^{\text {diff}}_{A\,\,B}$
. Of course, the reason for that is the counterexample [Reference Milićević28], which is multilinear form
![]() $\alpha \colon G^4 \to \mathbb {F}_2$
such that
$\alpha \colon G^4 \to \mathbb {F}_2$
such that
![]() $\alpha $
is symmetric in the first three variables and satisfies
$\alpha $
is symmetric in the first three variables and satisfies
for a high-rank symmetric bilinear form
![]() $\sigma $
. The arguments above actually show that the given counterexample is essentially the only way for the symmetry extension to fail. Note also that when
$\sigma $
. The arguments above actually show that the given counterexample is essentially the only way for the symmetry extension to fail. Note also that when
![]() $k =4$
, we were able to overcome this difficulty by having an additional algebraic property of
$k =4$
, we were able to overcome this difficulty by having an additional algebraic property of
![]() $\alpha $
that
$\alpha $
that
![]() $\alpha (u,u,x_3, x_4) = 0$
, which removed the problematic products of forms from
$\alpha (u,u,x_3, x_4) = 0$
, which removed the problematic products of forms from
![]() $\alpha + \alpha \circ (2k-1 \,\,2k)$
. Let us also remark that the symmetry-respecting weak regularity lemma (Lemma 4.1) holds for any number of variables.
$\alpha + \alpha \circ (2k-1 \,\,2k)$
. Let us also remark that the symmetry-respecting weak regularity lemma (Lemma 4.1) holds for any number of variables.
With this in mind, we believe that resolving the following problem, combined with arguments in this paper, should lead to a solution of Problem 1.3 and thus, paired with Theorem 1.1, to a quantitative inverse theorem for Gowers uniformity norms in low characteristic.
Conjecture 7.1 Suppose that
![]() $\alpha \colon G^{2k}\to \mathbb {F}_2$
is a multilinear form which is symmetric in the first
$\alpha \colon G^{2k}\to \mathbb {F}_2$
is a multilinear form which is symmetric in the first
![]() $2k-1$
variables such that
$2k-1$
variables such that
for a symmetric multilinear form
![]() $\sigma \colon G^k \to \mathbb {F}_2$
. Suppose that
$\sigma \colon G^k \to \mathbb {F}_2$
. Suppose that
![]() $f \colon G \to \mathbb {D}$
is a function such that
$f \colon G \to \mathbb {D}$
is a function such that
Then
![]() $\operatorname {prank} \sigma \leq \exp ^{(O_k(1))}(O_{k}(c^{-1}))$
.
$\operatorname {prank} \sigma \leq \exp ^{(O_k(1))}(O_{k}(c^{-1}))$
.
The bounds in the conjecture are chosen to be in line with other bounds in this paper, but we suspect that the conjecture holds with the bound of the shape
![]() $\operatorname {prank} \sigma \leq O_{k} (\log c^{-1})$
.
$\operatorname {prank} \sigma \leq O_{k} (\log c^{-1})$
.
Let us more generally pose the following more open-ended question.
Question 7.2 Suppose that
![]() $\alpha \colon G^{2k} \to \mathbb {F}_2$
is a multilinear form which is symmetric in the first
$\alpha \colon G^{2k} \to \mathbb {F}_2$
is a multilinear form which is symmetric in the first
![]() $2k-1$
variables and satisfies
$2k-1$
variables and satisfies
![]() $\operatorname {prank} \Big (\alpha + \alpha \circ (2k-1 \,\,2k)\Big ) \leq r$
. Under what algebraic condition on
$\operatorname {prank} \Big (\alpha + \alpha \circ (2k-1 \,\,2k)\Big ) \leq r$
. Under what algebraic condition on
![]() $\alpha $
can we guarantee to find a symmetric multilinear form
$\alpha $
can we guarantee to find a symmetric multilinear form
![]() $\alpha ' \colon G^{2k} \to \mathbb {F}_2$
which satisfies
$\alpha ' \colon G^{2k} \to \mathbb {F}_2$
which satisfies
![]() $\operatorname {prank} \Big (\alpha + \alpha '\Big ) \leq O_r(1)$
?
$\operatorname {prank} \Big (\alpha + \alpha '\Big ) \leq O_r(1)$
?
Acknowledgment
I would like to thank an anonymous referee for a thorough reading of the paper and helpful comments.