1 Introduction
Glivenko’s theorem from 1929 says that if a propositional formula
![]() ${\varphi }$
is provable in classical logic, then its double negation
${\varphi }$
is provable in classical logic, then its double negation
![]() $\neg \neg {\varphi }$
is provable in intuitionistic logic. In 1933 Gödel extended this to predicate logic, which move required to admit on the intuitionistic side the scheme of double negation shift. With Gödel’s and Gentzen’s negative translation in place of double negation, both from 1933, one can even get by with minimal logic in place of intuitionistic logic. More than one related proof translation saw the light of the day, e.g., Kolmogorov’s (1925) and Kuroda’s (1951).
$\neg \neg {\varphi }$
is provable in intuitionistic logic. In 1933 Gödel extended this to predicate logic, which move required to admit on the intuitionistic side the scheme of double negation shift. With Gödel’s and Gentzen’s negative translation in place of double negation, both from 1933, one can even get by with minimal logic in place of intuitionistic logic. More than one related proof translation saw the light of the day, e.g., Kolmogorov’s (1925) and Kuroda’s (1951).
Glivenko’s theorem thus stood right at the beginning of a fundamental change of perspective: that classical logic can be embedded into intuitionistic or even minimal logic, rather than the latter being a limited version of the former. Together with the revision of Hilbert’s Programme ascribed to Kreisel and Feferman, this has led to the much broader quest for the computational content of classical proofs, today culminating in agile areas such as dynamical algebra, formal topology, program extraction from proofs, proof analysis, proof mining and proof translations. The growing success of these approaches suggests that customary mathematics, with classical logic and set theory, might eventually prove to be much more constructive than widely thought.
In 1930 Tarski ascribed to Lindenbaum the theorem that in classical logic any given theory T equals the intersection of all the complete theories containing T. Its typical use for Gödel’s Completeness Theorem aside, this Lindenbaum Lemma is one of several theorems from that period which describe the intersection of all the ideal objects extending a given concrete object. Those intersection theorems, in their full generality recognised as forms of the Axiom of Choice (AC), are often put by contraposition as extension or separation theorems. Apart from Lindenbaum’s, prominent cases are known by the names of Artin–Schreier, Hahn–Banach, Krull and Szpilrajn. The case in algebra closest to Lindenbaum’s Lemma, however, gained prominence only in 1945, when Jacobson pointed out the relevance of the intersection of all the maximal ideals of a given ring, i.e., of what is now known as the Jacobson radical.
In the present note we follow the analogy between maximal (proper) ideals and complete (consistent) theories to carry over the Jacobson radical from ideals of commutative rings to theories of propositional calculi (Section 5.2), where it turns out to coincide with the stable closure or with the closure with respect to classical logic (Proposition 3 and Corollary 1). This prompts a variant of Lindenbaum’s Lemma that relates classical validity and intuitionistic provability (Proposition 2), and the syntactical counterpart of which happens to be Glivenko’s Theorem in the form recalled above (Theorem 2).
As a by-product we obtain a possible interpretation in logic (Theorem 3) of the axioms-as-rules conservation criterion (Theorem 1) for a multi-conclusion Scott-style entailment relation
![]() $\vdash $
over a single-conclusion one
$\vdash $
over a single-conclusion one
![]() $\rhd $
. This criterion has proved to be the common core of many a syntactical counterpart of a semantic conservation theorem corresponding to one of the aforementioned intersection theorems. Typically any such case of conservation means reduction to a special case characterised by additional axioms with (possibly empty) disjunctions in positive position. Applying the criterion means to eliminate the additional axioms for
$\rhd $
. This criterion has proved to be the common core of many a syntactical counterpart of a semantic conservation theorem corresponding to one of the aforementioned intersection theorems. Typically any such case of conservation means reduction to a special case characterised by additional axioms with (possibly empty) disjunctions in positive position. Applying the criterion means to eliminate the additional axioms for
![]() $\vdash $
by way of the corresponding disjunction elimination rules for
$\vdash $
by way of the corresponding disjunction elimination rules for
![]() $\rhd $
. The latter equally suffice for proof practice, and have proved admissible in all mathematical instances yet considered.
$\rhd $
. The latter equally suffice for proof practice, and have proved admissible in all mathematical instances yet considered.
Our interpretation of the conservation criterion in propositional logic (Theorem 3) is tantamount to Glivenko’s Theorem (Theorem 2). As for the latter, disjunction elimination plays a central role in the proof of the former, together with some notorious features of (double) negation in intuitionistic logic and of provability in classical propositional logic (Lemmas 1 and 2).
2 Preliminaries
Unless specified otherwise, we work in a suitable fragment of Aczel’s Constructive Zermelo–Fraenkel Set Theory (
![]() $\operatorname {\textbf {CZF}}$
) [Reference Aczel1–Reference Aczel and Rathjen5] based on intuitionistic first-order predicate logic. While in general the concepts of this paper are elementary and the proofs are direct anyway, we still pin down
$\operatorname {\textbf {CZF}}$
) [Reference Aczel1–Reference Aczel and Rathjen5] based on intuitionistic first-order predicate logic. While in general the concepts of this paper are elementary and the proofs are direct anyway, we still pin down
![]() $\operatorname {\textbf {CZF}}$
as metatheory if only rather for convenience’s sake; in fact much less might suffice. Likewise, when we occasionally need to invoke a fragment of the principle of Excluded Middle or even a form of the
$\operatorname {\textbf {CZF}}$
as metatheory if only rather for convenience’s sake; in fact much less might suffice. Likewise, when we occasionally need to invoke a fragment of the principle of Excluded Middle or even a form of the
![]() $\operatorname {\textrm {AC}}$
, and thus go beyond
$\operatorname {\textrm {AC}}$
, and thus go beyond
![]() $\operatorname {\textbf {CZF}}$
, we simply switch to
$\operatorname {\textbf {CZF}}$
, we simply switch to
![]() $\operatorname {\textbf {ZF}}$
and
$\operatorname {\textbf {ZF}}$
and
![]() $\operatorname {\textbf {ZFC}}$
, respectively, and indicate this accordingly.
$\operatorname {\textbf {ZFC}}$
, respectively, and indicate this accordingly.
For example, the Restricted Law of Excluded Middle (REM) is not a principle of
![]() $\operatorname {\textbf {CZF}}$
. This REM means
$\operatorname {\textbf {CZF}}$
. This REM means
![]() ${\varphi }\,\lor \,\neg {\varphi }$
for every set-theoretic formula
${\varphi }\,\lor \,\neg {\varphi }$
for every set-theoretic formula
![]() ${\varphi }$
that is, bounded in the sense that only set-bounded quantifiers of the types
${\varphi }$
that is, bounded in the sense that only set-bounded quantifiers of the types
![]() $\forall x\in y$
and
$\forall x\in y$
and
![]() $\exists x\in y$
occur in
$\exists x\in y$
occur in
![]() ${\varphi }$
. As is common in this context, negation is a defined connective:
${\varphi }$
. As is common in this context, negation is a defined connective:
![]() $\lnot {\varphi }\equiv {\varphi }\to \bot $
.
$\lnot {\varphi }\equiv {\varphi }\to \bot $
.
By a finite set we understand a set that can be written as
![]() ${a_1, \dots , a_n}$
for some
${a_1, \dots , a_n}$
for some
![]() $n \geq 0$
. Given any set S, let
$n \geq 0$
. Given any set S, let
![]() $\operatorname {\textrm {Pow}}(S)$
(respectively,
$\operatorname {\textrm {Pow}}(S)$
(respectively,
![]() $\operatorname {\textrm {Fin}}(S)$
) consist of the (finite) subsets of S. We refer to [Reference Rinaldi, Schuster and Wessel92] for further provisos to carry over to the present note.Footnote
1
$\operatorname {\textrm {Fin}}(S)$
) consist of the (finite) subsets of S. We refer to [Reference Rinaldi, Schuster and Wessel92] for further provisos to carry over to the present note.Footnote
1
Convention. By an intermediate logic we mean an intermediate propositional calculus obtained by adding to the axioms of intuitionistic logic some classically valid propositional formulas [37].
We write
![]() $\rhd $
to denote (deducibility in) any such intermediate logic in a propositional language S.
$\rhd $
to denote (deducibility in) any such intermediate logic in a propositional language S.
The subsequent properties of (double) negation are due to Brouwer for intuitionistic logic [Reference Brouwer11, Reference Brouwer12, Reference Glivenko45, Reference Troelstra109, Reference van Atten and Sundholm110] and carry over to an arbitrary
![]() $\rhd $
:
$\rhd $
:
Lemma 1. For any given intermediate logic
![]() $\rhd $
in a propositional language S,
$\rhd $
in a propositional language S,

for every
![]() $\Gamma \in \operatorname {\mathop {Pow}}(S)$
and all
$\Gamma \in \operatorname {\mathop {Pow}}(S)$
and all
![]() ${\varphi },\psi \in S$
.
${\varphi },\psi \in S$
.
We refer to [Reference Ishihara55] and [Reference Negri and von Plato77, p. 27] for a deeper discussion with earlier references of the following:
Lemma 2. Let
![]() $\vdash $
and
$\vdash $
and
![]() $\rhd $
stand for classical logic and an intermediate logic, respectively, in a propositional language S. If
$\rhd $
stand for classical logic and an intermediate logic, respectively, in a propositional language S. If
![]() $\Gamma \in \operatorname {\mathop {Pow}}(S)$
and
$\Gamma \in \operatorname {\mathop {Pow}}(S)$
and
![]() $\psi \in S$
, then
$\psi \in S$
, then
![]() $\Gamma \vdash \psi $
if and only if
$\Gamma \vdash \psi $
if and only if
![]() $\Gamma ,\Delta \rhd \psi $
for a suitable finite subset
$\Gamma ,\Delta \rhd \psi $
for a suitable finite subset
![]() $\Delta $
of
$\Delta $
of
i.e., the set of relevant instances of tertium non datur for propositional variables.
A theory of an intermediate logic
![]() $\rhd $
is a subset T of the underlying propositional language S that is, deductively closed with respect to
$\rhd $
is a subset T of the underlying propositional language S that is, deductively closed with respect to
![]() $\rhd $
:
$\rhd $
:
As usual, a theory T of
![]() $\rhd $
is
$\rhd $
is
-
— consistent if
 $\bot \notin T$
, which is to say that
$\bot \notin T$
, which is to say that
 $T\neq S$
;
$T\neq S$
; -
— complete if
 $$ \begin{align*} \forall {\varphi} \in S(T\ni {\varphi} \lor \lnot T\ni {\varphi}); \end{align*} $$
$$ \begin{align*} \forall {\varphi} \in S(T\ni {\varphi} \lor \lnot T\ni {\varphi}); \end{align*} $$
-
— stable if
 $$ \begin{align*} \forall {\varphi}\in S(T\ni \lnot\lnot{\varphi}\Rightarrow T\ni {\varphi}). \end{align*} $$
$$ \begin{align*} \forall {\varphi}\in S(T\ni \lnot\lnot{\varphi}\Rightarrow T\ni {\varphi}). \end{align*} $$
As an immediate consequence of Lemmas 1 and 2 we have the following:
Lemma 3. Let
![]() $\rhd $
be an intermediate logic in a propositional language S. The following statements are equivalent for any given subset T of S:
$\rhd $
be an intermediate logic in a propositional language S. The following statements are equivalent for any given subset T of S:
-
1. T is deductively closed with respect to classical logic.
-
2. T is a stable theory of
 $\rhd $
.
$\rhd $
. -
3. T is a theory of
 $\rhd $
that contains all instances of excluded middle
$\rhd $
that contains all instances of excluded middle
 ${\varphi }\lor \neg {\varphi }$
with
${\varphi }\lor \neg {\varphi }$
with
 ${\varphi }\in S$
.
${\varphi }\in S$
. -
4. T is a theory of
 $\rhd $
that contains all
$\rhd $
that contains all
 ${\varphi }\lor \neg {\varphi }$
where
${\varphi }\lor \neg {\varphi }$
where
 ${\varphi }$
is a propositional variable of S.
${\varphi }$
is a propositional variable of S.
In particular, if a theory T of an intermediate logic
![]() $\rhd $
is complete, then T is stable.
$\rhd $
is complete, then T is stable.
3 Entailment relations
Entailment relations, both in their single- and multi-conclusion variant, are at the heart of this note. We briefly recall the basic notions, to which end we closely follow [Reference Rinaldi, Schuster and Wessel91, Reference Rinaldi, Schuster and Wessel92].
3.1 Consequence
Let S be a set and
![]() $\rhd \subseteq \operatorname {\textrm {Pow}}(S)\times S$
. Once abstracted from the context of logical formulas, all but one of Tarski’s axioms of consequence [Reference Tarski106] can be put as
$\rhd \subseteq \operatorname {\textrm {Pow}}(S)\times S$
. Once abstracted from the context of logical formulas, all but one of Tarski’s axioms of consequence [Reference Tarski106] can be put as

where
![]() $U,V\subseteq S$
and
$U,V\subseteq S$
and
![]() $a\in S$
. These axioms also characterise a finitary covering or Stone covering in formal topology [Reference Rinaldi and Wessel95];Footnote
2
see further [Reference Ciraulo, Maietti and Sambin17, Reference Ciraulo and Sambin19, Reference Negri72, Reference Negri73, Reference Sambin97, Reference Sambin98]. The notion of consequence has allegedly been described first by Hertz [Reference Hertz49–Reference Hertz51]; see also [Reference Béziau7, Reference Legris59].
$a\in S$
. These axioms also characterise a finitary covering or Stone covering in formal topology [Reference Rinaldi and Wessel95];Footnote
2
see further [Reference Ciraulo, Maietti and Sambin17, Reference Ciraulo and Sambin19, Reference Negri72, Reference Negri73, Reference Sambin97, Reference Sambin98]. The notion of consequence has allegedly been described first by Hertz [Reference Hertz49–Reference Hertz51]; see also [Reference Béziau7, Reference Legris59].
We do not employ the one of Tarski’s axioms by which he required that S be countable. This aside, Tarski has rather characterised the set of consequences of a set of propositions, which corresponds to the algebraic closure operator
![]() $U\mapsto U^{\rhd }$
on
$U\mapsto U^{\rhd }$
on
![]() $\operatorname {\textrm {Pow}}(S)$
of a relation
$\operatorname {\textrm {Pow}}(S)$
of a relation
![]() $\rhd $
as above where
$\rhd $
as above where
3.2 Single-conclusion entailment
Rather than with Tarski’s notion, we henceforth work with its (tantamount) restriction to finite subsets, i.e., a single-conclusion entailment relation. This is, a relation
![]() $\rhd \subseteq \operatorname {\textrm {Fin}}(S)\times S$
such that
$\rhd \subseteq \operatorname {\textrm {Fin}}(S)\times S$
such that
for all finite
![]() $U,U',V,V'\subseteq S$
and
$U,U',V,V'\subseteq S$
and
![]() $a,b\in S$
, where as usual
$a,b\in S$
, where as usual
![]() $U,V\equiv U\cup V$
and
$U,V\equiv U\cup V$
and
![]() $V,b\equiv V\cup \{b\}$
. Our focus thus is on finite subsets of S, for which we henceforth reserve the letters
$V,b\equiv V\cup \{b\}$
. Our focus thus is on finite subsets of S, for which we henceforth reserve the letters
![]() $U, V, W, \ldots $
; we also sometimes write
$U, V, W, \ldots $
; we also sometimes write
![]() $a_1,\ldots ,a_n$
in place of
$a_1,\ldots ,a_n$
in place of
![]() $\{a_1,\ldots ,a_n\}$
even if
$\{a_1,\ldots ,a_n\}$
even if
![]() $n=0$
. Redefining
$n=0$
. Redefining
for arbitrary subsets T of S gives back an algebraic closure operator on
![]() $\operatorname {\textrm {Pow}}(S)$
. By writing
$\operatorname {\textrm {Pow}}(S)$
. By writing
![]() $T \rhd a$
in place of
$T \rhd a$
in place of
![]() $a \in T^{\rhd }$
, the single-conclusion entailment relations thus correspond exactly to the relations satisfying Tarski’s axioms above.
$a \in T^{\rhd }$
, the single-conclusion entailment relations thus correspond exactly to the relations satisfying Tarski’s axioms above.
3.3 Multi-conclusion entailment
Let S be a set and
![]() ${\vdash } \subseteq \operatorname {\textrm {Fin}}(S)\times \operatorname {\textrm {Fin}}(S)$
. Scott’s [Reference Scott102] axioms of entailment can be put as
${\vdash } \subseteq \operatorname {\textrm {Fin}}(S)\times \operatorname {\textrm {Fin}}(S)$
. Scott’s [Reference Scott102] axioms of entailment can be put as

for finite
![]() $U,U',V,V',W,W'\subseteq S$
and
$U,U',V,V',W,W'\subseteq S$
and
![]() $b\in S$
, where
$b\in S$
, where
![]() $U\between W$
means that U and W have an element in common [Reference Sambin97]. Any such
$U\between W$
means that U and W have an element in common [Reference Sambin97]. Any such
![]() $\vdash $
is a multi-conclusion entailment relation, where ‘multi’ includes ‘empty’. In practice,
$\vdash $
is a multi-conclusion entailment relation, where ‘multi’ includes ‘empty’. In practice,
![]() $\rhd $
and
$\rhd $
and
![]() $\vdash $
are inductively generated by the axioms of the intended models, which procedure we here take for granted [Reference Cederquist and Coquand14, Reference Coquand, Sambin, Smith and Valentini31]; see also [Reference Aczel3, Reference Rathjen87, Reference Rinaldi, Schuster and Wessel92, Reference Rinaldi and Wessel94].
$\vdash $
are inductively generated by the axioms of the intended models, which procedure we here take for granted [Reference Cederquist and Coquand14, Reference Coquand, Sambin, Smith and Valentini31]; see also [Reference Aczel3, Reference Rathjen87, Reference Rinaldi, Schuster and Wessel92, Reference Rinaldi and Wessel94].
This fairly general notion of entailment has been introduced by Scott [Reference Scott101–Reference Scott103], building on Hertz’s and Tarski’s work (see above), and of course on Gentzen’s sequent calculus [Reference Gentzen43, Reference Gentzen44]. Shoesmith and Smiley [Reference Shoesmith and Smiley104] trace multi-conclusion entailment relations back to Carnap [Reference Carnap13], and Popper apparently had related ideas [Reference Popper85, Reference Popper86].Footnote 3 Before Scott, Lorenzen had developed analogous concepts formally [Reference Lorenzen65–Reference Lorenzen68]; he even listed [Reference Lorenzen66, pp. 84–85] counterparts of the axioms (R), (T) and (M) for single- and multi-conclusion entailment [Reference Coquand, Lombardi and Neuwirth27, Reference Neuwirth81].Footnote 4 As compared with Gentzen’s and Lorenzen’s approaches, Scott’s entailment relation follow the contexts-as-sets paradigm, which has caused reservations [Reference Negri and von Plato78, Reference Negri and von Plato79]. The relevance of the notion of entailment relation to point-free topology and constructive algebra has been pointed out in [Reference Cederquist and Coquand14], and has been used very widely, e.g., in [Reference Coquand20–Reference Coquand22, Reference Coquand24, Reference Coquand and Lombardi25, Reference Coquand and Persson29, Reference Coquand and Zhang32, Reference Negri, von Plato and Coquand80, Reference Rinaldi89, Reference Rinaldi and Wessel93, Reference Schlagbauer, Schuster and Wessel100, Reference Wessel114, Reference Wessel115]. Consequence and entailment have further caught interest from various other angles [Reference Avron6, Reference Došen35, Reference Gabbay41, Reference Humberstone52–Reference Iemhoff54, Reference Payette and Schotch83, Reference Sandqvist99, Reference Shoesmith and Smiley104, Reference Wójcicki117].
4 Conservation
Again following [Reference Rinaldi, Schuster and Wessel91, Reference Rinaldi, Schuster and Wessel92], we sketch the concept of conservative extension of a multi-conclusion entailment relation
![]() $\vdash $
over a single-conclusion entailment relation
$\vdash $
over a single-conclusion entailment relation
![]() $\rhd $
on the same set S. After that we extract from [Reference Rinaldi and Schuster90]—based on [Reference Ciraulo, Rinaldi and Schuster18]—possible interpretations limited to classical logic.
$\rhd $
on the same set S. After that we extract from [Reference Rinaldi and Schuster90]—based on [Reference Ciraulo, Rinaldi and Schuster18]—possible interpretations limited to classical logic.
4.1 Conservation in syntax and semantics
Let S be a set, and let
![]() $a, b, c, \ldots $
and
$a, b, c, \ldots $
and
![]() $U, V, W, \ldots $
range over the elements of S and
$U, V, W, \ldots $
range over the elements of S and
![]() $\operatorname {\textrm {Fin}}(S)$
, respectively. Given a multi-conclusion entailment relation
$\operatorname {\textrm {Fin}}(S)$
, respectively. Given a multi-conclusion entailment relation
![]() $\vdash $
and a single-conclusion entailment relation
$\vdash $
and a single-conclusion entailment relation
![]() $\rhd $
on the same set S, we throughout assume Extension:
$\rhd $
on the same set S, we throughout assume Extension:
Of major interest to us is the converse, alias Conservation:
The trace of any given
![]() $\vdash $
is the single-conclusion entailment relation
$\vdash $
is the single-conclusion entailment relation
![]() $\rhd _{\vdash }$
defined by
$\rhd _{\vdash }$
defined by
for which
![]() $\operatorname {\textrm {Ext}}$
and
$\operatorname {\textrm {Ext}}$
and
![]() $\operatorname {\textrm {Con}}$
are tantamount to
$\operatorname {\textrm {Con}}$
are tantamount to
![]() $\rhd \subseteq \rhd _{\vdash }$
and
$\rhd \subseteq \rhd _{\vdash }$
and
![]() $\rhd \supseteq \rhd _{\vdash }$
, respectively.
$\rhd \supseteq \rhd _{\vdash }$
, respectively.
An arbitrary subset P of S is a model of
![]() $\vdash $
if
$\vdash $
if
The notion of model carries over to single-conclusion
![]() $\rhd $
in the apparent manner, such that the models of
$\rhd $
in the apparent manner, such that the models of
![]() $\rhd $
are exactly the
$\rhd $
are exactly the
![]() $P\in \operatorname {\textrm {Pow}}(S)$
which are closed under
$P\in \operatorname {\textrm {Pow}}(S)$
which are closed under
![]() $\rhd $
, i.e., for which
$\rhd $
, i.e., for which
![]() $P^\rhd =P$
. Let
$P^\rhd =P$
. Let
![]() $\operatorname {\textrm {Mod}}(\vdash )$
and
$\operatorname {\textrm {Mod}}(\vdash )$
and
![]() $\operatorname {\textrm {Mod}}(\rhd )$
consist of the models of
$\operatorname {\textrm {Mod}}(\rhd )$
consist of the models of
![]() $\vdash $
and
$\vdash $
and
![]() $\rhd $
, respectively. By Extension,
$\rhd $
, respectively. By Extension,
![]() $\operatorname {\textrm {Mod}}(\vdash )\subseteq \operatorname {\textrm {Mod}}(\rhd )$
, which in
$\operatorname {\textrm {Mod}}(\vdash )\subseteq \operatorname {\textrm {Mod}}(\rhd )$
, which in
![]() $\operatorname {\textbf {ZFC}}$
is equivalent to Extension [Reference Rinaldi, Schuster and Wessel92, Lemma 9].
$\operatorname {\textbf {ZFC}}$
is equivalent to Extension [Reference Rinaldi, Schuster and Wessel92, Lemma 9].
Now
![]() $\operatorname {\textrm {Con}}$
follows from the Generalised Krull–Lindenbaum (GKL) Lemma, viz.
$\operatorname {\textrm {Con}}$
follows from the Generalised Krull–Lindenbaum (GKL) Lemma, viz.
the converse of which holds by Extension. Again by Extension,
![]() $\operatorname {\textrm {GKL}}$
implies the Trace Completeness Theorem (TCT), viz.
$\operatorname {\textrm {GKL}}$
implies the Trace Completeness Theorem (TCT), viz.
the converse of which holds by the definition of a model of
![]() $\vdash $
. This
$\vdash $
. This
![]() $\operatorname {\textrm {TCT}} $
is a fragment of
$\operatorname {\textrm {TCT}} $
is a fragment of
![]() $\operatorname {\textrm {AC}}$
that implies REM [Reference Rinaldi, Schuster and Wessel92, Corollary 5].Footnote
5
$\operatorname {\textrm {AC}}$
that implies REM [Reference Rinaldi, Schuster and Wessel92, Corollary 5].Footnote
5
In
![]() $\operatorname {\textbf {ZFC}}$
,
$\operatorname {\textbf {ZFC}}$
,
![]() $\operatorname {\textrm {GKL}}$
and
$\operatorname {\textrm {GKL}}$
and
![]() $\operatorname {\textrm {Con}}$
are equivalent [Reference Rinaldi, Schuster and Wessel92, Theorem 6]. In
$\operatorname {\textrm {Con}}$
are equivalent [Reference Rinaldi, Schuster and Wessel92, Theorem 6]. In
![]() $\operatorname {\textbf {CZF}}$
we can make this more precise:
$\operatorname {\textbf {CZF}}$
we can make this more precise:
Remark 1. In the presence of
![]() $\operatorname {\textrm {Ext}}$
,
$\operatorname {\textrm {Ext}}$
,
![]() $\operatorname {\textrm {GKL}}$
is equivalent to the conjunction of
$\operatorname {\textrm {GKL}}$
is equivalent to the conjunction of
![]() $\operatorname {\textrm {Con}}$
and
$\operatorname {\textrm {Con}}$
and
![]() $\textrm{TCT}$
.
$\textrm{TCT}$
.
In all,
![]() $\operatorname {\textrm {GKL}}$
is semantic conservation, and Con is its syntactical counterpart.
$\operatorname {\textrm {GKL}}$
is semantic conservation, and Con is its syntactical counterpart.
4.2 Conservation in proof practice
In proof practice,
![]() $\operatorname {\textrm {GKL}}$
is useful for reductions to special cases, by making possible to use
$\operatorname {\textrm {GKL}}$
is useful for reductions to special cases, by making possible to use
![]() $\vdash $
in proofs about
$\vdash $
in proofs about
![]() $\rhd $
, but
$\rhd $
, but
![]() $\operatorname {\textrm {GKL}}$
is of semantic nature, entails REM and requires some
$\operatorname {\textrm {GKL}}$
is of semantic nature, entails REM and requires some
![]() $\operatorname {\textrm {AC}}$
. In comparison,
$\operatorname {\textrm {AC}}$
. In comparison,
![]() $\operatorname {\textrm {Con}}$
is equally sufficient for that kind of reduction, is syntactical and has elementary proofs. Many such cases are known in point-free topology such as locale theory and formal topology [Reference Cederquist and Coquand14, Reference Cederquist, Coquand and Negri15, Reference Coquand20, Reference Coquand23, Reference Mulvey and Wick-Pelletier70, Reference Mulvey and Wick-Pelletier71]; in constructive algebra, especially with dynamical methods [Reference Coquand and Lombardi26, Reference Coste, Lombardi and Roy33, Reference Lombardi61–Reference Lombardi and Quitté64, Reference Wessel116, Reference Yengui118, Reference Yengui119]; and in the proof theory of order relations [Reference Negri and von Plato78, Reference Negri, von Plato and Coquand80]. Most of those cases concern algebra at large. But what about logic? One may think of Gentzen’s classical multi-succedent sequent calculus as extending his intuitionistic single-succedent variant [Reference Gentzen43, Reference Gentzen44, Reference Negri and von Plato77, Reference Takeuti105]. As we will see, this thought goes in the right direction.
$\operatorname {\textrm {Con}}$
is equally sufficient for that kind of reduction, is syntactical and has elementary proofs. Many such cases are known in point-free topology such as locale theory and formal topology [Reference Cederquist and Coquand14, Reference Cederquist, Coquand and Negri15, Reference Coquand20, Reference Coquand23, Reference Mulvey and Wick-Pelletier70, Reference Mulvey and Wick-Pelletier71]; in constructive algebra, especially with dynamical methods [Reference Coquand and Lombardi26, Reference Coste, Lombardi and Roy33, Reference Lombardi61–Reference Lombardi and Quitté64, Reference Wessel116, Reference Yengui118, Reference Yengui119]; and in the proof theory of order relations [Reference Negri and von Plato78, Reference Negri, von Plato and Coquand80]. Most of those cases concern algebra at large. But what about logic? One may think of Gentzen’s classical multi-succedent sequent calculus as extending his intuitionistic single-succedent variant [Reference Gentzen43, Reference Gentzen44, Reference Negri and von Plato77, Reference Takeuti105]. As we will see, this thought goes in the right direction.
A typical situation is as follows: Let the single-conclusion entailment relation
![]() $\rhd $
on a set S be generated by axioms. Then the multi-conclusion entailment relation
$\rhd $
on a set S be generated by axioms. Then the multi-conclusion entailment relation
![]() $\vdash $
on the same set S is generated by the axioms of
$\vdash $
on the same set S is generated by the axioms of
![]() $\rhd $
, of course with
$\rhd $
, of course with
![]() $\vdash $
in place of
$\vdash $
in place of
![]() $\rhd $
, and by additional axioms
$\rhd $
, and by additional axioms
where
![]() $k,\ell \ge 0$
. In any such situation we say that
$k,\ell \ge 0$
. In any such situation we say that
![]() $\vdash $
extends
$\vdash $
extends
![]() $\rhd $
, and list the additional axioms if needed. This is legitimate inasmuch as if
$\rhd $
, and list the additional axioms if needed. This is legitimate inasmuch as if
![]() $\vdash $
extends
$\vdash $
extends
![]() $\rhd $
, then
$\rhd $
, then
![]() $\operatorname {\textrm {Ext}}$
is satisfied. What about
$\operatorname {\textrm {Ext}}$
is satisfied. What about
![]() $\operatorname {\textrm {Con}}$
?
$\operatorname {\textrm {Con}}$
?
The following most versatile conservation criterion [Reference Rinaldi, Schuster and Wessel91, Reference Rinaldi, Schuster and Wessel92], which in fact gathers together many of the cases of Con mentioned before, will also help to understand Con for logic:
Theorem 1. Let
![]() $\vdash $
extend
$\vdash $
extend
![]() $\rhd $
with certain additional axioms of the form
$\rhd $
with certain additional axioms of the form
where
![]() $k,\ell \ge 0$
. Then
$k,\ell \ge 0$
. Then
![]() $\vdash $
and
$\vdash $
and
![]() $\rhd $
satisfy
$\rhd $
satisfy
![]() $\operatorname {\mathop {Con}}$
if and only if
$\operatorname {\mathop {Con}}$
if and only if
 $$ \begin{align} \frac{W,b_1\rhd c \quad \cdots \quad W,b_\ell\rhd c }{W,a_1,\dots,a_k\rhd c} \end{align} $$
$$ \begin{align} \frac{W,b_1\rhd c \quad \cdots \quad W,b_\ell\rhd c }{W,a_1,\dots,a_k\rhd c} \end{align} $$
for every additional axiom (2), all
![]() $c\in S$
and every
$c\in S$
and every
![]() $W\in \operatorname {\mathop {Fin}}(S)$
.
$W\in \operatorname {\mathop {Fin}}(S)$
.
This swiftly follows [Reference Rinaldi, Schuster and Wessel92, Theorem 2] from a sandwich criterion for conservation given by Scott [Reference Scott102], and also is a corollary of cut elimination for entailment relations [Reference Rinaldi and Wessel94] as related to cut elimination in the presence of axioms [Reference Negri and von Plato76].
Quite a few instances of
![]() $\operatorname {\textrm {GKL}}$
can be classified by the two cases named Universal Krull (UK) and Universal Lindenbaum (UL) in [Reference Rinaldi, Schuster and Wessel92], for which S is a set with
$\operatorname {\textrm {GKL}}$
can be classified by the two cases named Universal Krull (UK) and Universal Lindenbaum (UL) in [Reference Rinaldi, Schuster and Wessel92], for which S is a set with
 $$\begin{align*}& \textrm{UK}: \quad \text{a distinguished element}\ e\ \text{of}\ S\ \text{and a binary operation}\ \ast\ \text{on}\ S.\\ &\textrm{UL}: \quad \text{a unary operation}\ \sim\ \text{on}\ S. \end{align*}$$
$$\begin{align*}& \textrm{UK}: \quad \text{a distinguished element}\ e\ \text{of}\ S\ \text{and a binary operation}\ \ast\ \text{on}\ S.\\ &\textrm{UL}: \quad \text{a unary operation}\ \sim\ \text{on}\ S. \end{align*}$$
The additional axioms for
![]() $\vdash $
extending
$\vdash $
extending
![]() $\rhd $
are
$\rhd $
are
 $$\begin{align*}&\textrm{UK}: \quad e \vdash \ \quad a \ast b \vdash a,b, \\ &\textrm{UL}: \quad a, {\mathop{\sim}} a \vdash \ \quad \ \vdash a, {\mathop{\sim}} a, \end{align*}$$
$$\begin{align*}&\textrm{UK}: \quad e \vdash \ \quad a \ast b \vdash a,b, \\ &\textrm{UL}: \quad a, {\mathop{\sim}} a \vdash \ \quad \ \vdash a, {\mathop{\sim}} a, \end{align*}$$
where
![]() $a,b\in S$
. The corresponding conservation criteria (Theorem 1) read
$a,b\in S$
. The corresponding conservation criteria (Theorem 1) read
 $$\begin{align*}&\textrm{UK}: \quad \frac{}{W, e \rhd c} \quad \frac{ W, a \rhd c \quad W, b \rhd c }{ W, a \ast b \rhd c }\\[5pt] &\textrm{UL}: \quad \frac{}{ W, a, {\mathop{\sim}} a \rhd c } \quad \frac{ W, a \rhd c \quad W, {\mathop{\sim}} a \rhd c }{ W \rhd c } \end{align*}$$
$$\begin{align*}&\textrm{UK}: \quad \frac{}{W, e \rhd c} \quad \frac{ W, a \rhd c \quad W, b \rhd c }{ W, a \ast b \rhd c }\\[5pt] &\textrm{UL}: \quad \frac{}{ W, a, {\mathop{\sim}} a \rhd c } \quad \frac{ W, a \rhd c \quad W, {\mathop{\sim}} a \rhd c }{ W \rhd c } \end{align*}$$
where
![]() $W\in \operatorname {\textrm {Fin}}(S)$
and
$W\in \operatorname {\textrm {Fin}}(S)$
and
![]() $a,b,c\in S$
.Footnote
6
We refer to [Reference Rinaldi, Schuster and Wessel91, Reference Rinaldi, Schuster and Wessel92] for details and references.
$a,b,c\in S$
.Footnote
6
We refer to [Reference Rinaldi, Schuster and Wessel91, Reference Rinaldi, Schuster and Wessel92] for details and references.
4.3 The case of classical logic
Building upon [Reference Ciraulo, Rinaldi and Schuster18], in [Reference Rinaldi and Schuster90] the instances of
![]() $\operatorname {\textrm {GKL}}$
in the cases UK and UL have been considered for the following data: S consists of the sentences of a logical language,
$\operatorname {\textrm {GKL}}$
in the cases UK and UL have been considered for the following data: S consists of the sentences of a logical language,
![]() $\rhd $
stands for deducibility with classical logic, e is absurdity
$\rhd $
stands for deducibility with classical logic, e is absurdity
![]() $\bot $
, the operator
$\bot $
, the operator
![]() $\ast $
is disjunction
$\ast $
is disjunction
![]() $\lor $
, and
$\lor $
, and
![]() ${\mathop {\sim }}$
is negation
${\mathop {\sim }}$
is negation
![]() $\neg $
. While the models of
$\neg $
. While the models of
![]() $\rhd $
are the stable theories of
$\rhd $
are the stable theories of
![]() $\rhd $
, the models of
$\rhd $
, the models of
![]() $\vdash $
are the complete consistent theories in S. Hence
$\vdash $
are the complete consistent theories in S. Hence
![]() $\operatorname {\textrm {GKL}}$
is Lindenbaum’s Lemma [Reference Tarski106], and Con is provable but little interesting, simply because
$\operatorname {\textrm {GKL}}$
is Lindenbaum’s Lemma [Reference Tarski106], and Con is provable but little interesting, simply because
![]() $\rhd $
is classical logic already. Let’s try to get more by relativising
$\rhd $
is classical logic already. Let’s try to get more by relativising
![]() $\rhd $
.
$\rhd $
.
Now let
![]() $\rhd $
denote (deducibility in) an intermediate logic in a propositional language S; whence the models of
$\rhd $
denote (deducibility in) an intermediate logic in a propositional language S; whence the models of
![]() $\rhd $
are the theories of
$\rhd $
are the theories of
![]() $\rhd $
.Footnote
7
Let
$\rhd $
.Footnote
7
Let
![]() $\vdash $
extend
$\vdash $
extend
![]() $\rhd $
with the following additional axioms:
$\rhd $
with the following additional axioms:
The models of
![]() $\vdash $
are exactly the complete consistent theories of
$\vdash $
are exactly the complete consistent theories of
![]() $\rhd $
, and the corresponding conservation criteria (Theorem 1) read
$\rhd $
, and the corresponding conservation criteria (Theorem 1) read
 $$ \begin{align*} \frac{}{\Gamma,\bot\rhd \psi}\qquad \frac{\Gamma, {\varphi}\rhd \psi \quad \Gamma, \lnot{\varphi}\rhd \psi}{\Gamma \rhd \psi} \end{align*} $$
$$ \begin{align*} \frac{}{\Gamma,\bot\rhd \psi}\qquad \frac{\Gamma, {\varphi}\rhd \psi \quad \Gamma, \lnot{\varphi}\rhd \psi}{\Gamma \rhd \psi} \end{align*} $$
with
![]() $\Gamma \in \operatorname {\textrm {Fin}}(S)$
and
$\Gamma \in \operatorname {\textrm {Fin}}(S)$
and
![]() ${\varphi }, \psi \in S$
. While the first criterion holds for any given intermediate logic
${\varphi }, \psi \in S$
. While the first criterion holds for any given intermediate logic
![]() $\rhd $
, the second one amounts to
$\rhd $
, the second one amounts to
![]() $\rhd $
satisfying
$\rhd $
satisfying
![]() $\rhd {\varphi }\lor \lnot {\varphi }$
, which is to say that
$\rhd {\varphi }\lor \lnot {\varphi }$
, which is to say that
![]() $\rhd $
be classical logic. Hence
$\rhd $
be classical logic. Hence
![]() $\operatorname {\textrm {Con}}$
in this case simply means that conservatively adding
$\operatorname {\textrm {Con}}$
in this case simply means that conservatively adding
![]() $\vdash {\varphi }, \lnot {\varphi }$
is equivalent to requiring
$\vdash {\varphi }, \lnot {\varphi }$
is equivalent to requiring
![]() $\rhd {\varphi }\lor \lnot {\varphi }$
. This of course is well known and of relatively little interest either. Can’t we do better?
$\rhd {\varphi }\lor \lnot {\varphi }$
. This of course is well known and of relatively little interest either. Can’t we do better?
5 Jacobson radicals
5.1 The Jacobson radical in algebra
Let
![]() $S=R$
be a commutative ring with
$S=R$
be a commutative ring with
![]() $1$
, and let
$1$
, and let
![]() $\rhd $
stand for generation in R, i.e.,
$\rhd $
stand for generation in R, i.e.,
![]() $U\rhd a$
means that a is a linear combination with coefficients from R of the elements of U. A model of
$U\rhd a$
means that a is a linear combination with coefficients from R of the elements of U. A model of
![]() $\rhd $
is nothing but an ideal of R, i.e., a subset closed under linear combination. An ideal J of R is
$\rhd $
is nothing but an ideal of R, i.e., a subset closed under linear combination. An ideal J of R is
-
— proper if
 $1\notin J$
, which is tantamount to
$1\notin J$
, which is tantamount to
 $J\neq R$
and
$J\neq R$
and -
— complete if modulo J any given
 $r\in R$
is either 0 or invertible, that is, (4)
$r\in R$
is either 0 or invertible, that is, (4) $$ \begin{align} \forall r\in R(J\ni r \lor J,r\rhd 1). \end{align} $$
$$ \begin{align} \forall r\in R(J\ni r \lor J,r\rhd 1). \end{align} $$
Every proper complete ideal is a maximal ideal, i.e., maximal among the proper ideals, and vice versa in
![]() $\operatorname {\textbf {ZF}}$
. With the current notation, the Jacobson radical of an ideal J can be defined as
$\operatorname {\textbf {ZF}}$
. With the current notation, the Jacobson radical of an ideal J can be defined as
We thus carry over to commutative rings the first-order definition of the Jacobson radical for distributive lattices [Reference Blass10, Reference Coquand, Lombardi and Quitté28, Reference Johnstone58] rather than using the more common one for commutative rings present e.g., in [Reference Lombardi and Quitté64]. The latter reads
which is to say that any given
![]() $a\in R$
belongs to
$a\in R$
belongs to
![]() $\operatorname {\textrm {Jac}}(R)$
precisely when
$\operatorname {\textrm {Jac}}(R)$
precisely when
![]() $1-ab$
is invertible modulo J for every
$1-ab$
is invertible modulo J for every
![]() $b\in R$
. We give precedence to (5) over (6) because the former, unlike the latter, can be transferred to logic without further ado (Section 5.2).
$b\in R$
. We give precedence to (5) over (6) because the former, unlike the latter, can be transferred to logic without further ado (Section 5.2).
Just as (6), the first-order definition we employ (5) is anyway equivalent in
![]() $\operatorname {\textbf {ZFC}}$
to the following more customary second-order characterisation of the Jacobson radical [Reference Jacobson57]. Although the proof is of course similar to the one with (6) in place of (5) and for maximal rather than complete ideals, see e.g., [Reference Lombardi and Quitté64], we detail this one because it carries over to logic (Proposition 2).
$\operatorname {\textbf {ZFC}}$
to the following more customary second-order characterisation of the Jacobson radical [Reference Jacobson57]. Although the proof is of course similar to the one with (6) in place of (5) and for maximal rather than complete ideals, see e.g., [Reference Lombardi and Quitté64], we detail this one because it carries over to logic (Proposition 2).
Proposition 1
 $\operatorname {\textbf {ZFC}}$
$\operatorname {\textbf {ZFC}}$
For every ideal J of a commutative ring R,
where
![]() $\operatorname {Com}_J(R)$
consists of the complete ideals
$\operatorname {Com}_J(R)$
consists of the complete ideals
![]() $\mathfrak {c}$
in R with
$\mathfrak {c}$
in R with
![]() $J\subseteq {\mathfrak {c}}$
.
$J\subseteq {\mathfrak {c}}$
.
Proof Let
![]() $a\in \operatorname {\textrm {Jac}}(J)$
, and let
$a\in \operatorname {\textrm {Jac}}(J)$
, and let
![]() $\mathfrak {c}$
be a complete ideal such that
$\mathfrak {c}$
be a complete ideal such that
![]() $\mathfrak {c}\supseteq J$
. Either
$\mathfrak {c}\supseteq J$
. Either
![]() $\mathfrak {c}\ni a$
or
$\mathfrak {c}\ni a$
or
![]() $\mathfrak {c},a\rhd 1$
. In the former case we are done. In the latter case there is
$\mathfrak {c},a\rhd 1$
. In the former case we are done. In the latter case there is
![]() $b\in R$
such that
$b\in R$
such that
![]() $\mathfrak {c}\rhd b$
(in particular,
$\mathfrak {c}\rhd b$
(in particular,
![]() $b\in \mathfrak {c}$
) and
$b\in \mathfrak {c}$
) and
![]() $a,b\rhd 1$
. Since
$a,b\rhd 1$
. Since
![]() $a\in \operatorname {\textrm {Jac}}(J)$
, we get
$a\in \operatorname {\textrm {Jac}}(J)$
, we get
![]() $J,b\rhd 1$
. As
$J,b\rhd 1$
. As
![]() $J\subseteq \mathfrak {c}$
and
$J\subseteq \mathfrak {c}$
and
![]() $b\in \mathfrak {c}$
, this implies
$b\in \mathfrak {c}$
, this implies
![]() $\mathfrak {c}\rhd 1$
. Hence
$\mathfrak {c}\rhd 1$
. Hence
![]() $\mathfrak {c}=R$
, by which again
$\mathfrak {c}=R$
, by which again
![]() $\mathfrak {c}\ni a$
.
$\mathfrak {c}\ni a$
.
Conversely, if
![]() $a\notin \operatorname {\textrm {Jac}}(J)$
, then there is
$a\notin \operatorname {\textrm {Jac}}(J)$
, then there is
![]() $b\in R$
for which
$b\in R$
for which
![]() $a,b\rhd 1$
holds but
$a,b\rhd 1$
holds but
![]() $J,b\rhd 1$
fails, and thus
$J,b\rhd 1$
fails, and thus
![]() $(J,b)^\rhd $
lacks a. Zorn’s Lemma yields an ideal
$(J,b)^\rhd $
lacks a. Zorn’s Lemma yields an ideal
![]() $\mathfrak {c}$
maximal among the ones that contain
$\mathfrak {c}$
maximal among the ones that contain
![]() $(J,b)^\rhd $
yet miss a. Any such
$(J,b)^\rhd $
yet miss a. Any such
![]() $\mathfrak {c}$
is complete: if
$\mathfrak {c}$
is complete: if
![]() $\mathfrak {c}\not \ni b$
, then
$\mathfrak {c}\not \ni b$
, then
![]() $\mathfrak {c},b\rhd a$
by maximality, and thus
$\mathfrak {c},b\rhd a$
by maximality, and thus
![]() $\mathfrak {c}, b\rhd 1$
by
$\mathfrak {c}, b\rhd 1$
by
![]() $a,b\rhd 1$
.
$a,b\rhd 1$
.
It obviously is irrelevant whether the intersection ranges over the only improper ideal R as well.
5.2 The Jacobson radical in logic
Let again
![]() $\rhd $
stand for (deducibility in) an intermediate logic in a propositional language S. That a (consistent) theory T of
$\rhd $
stand for (deducibility in) an intermediate logic in a propositional language S. That a (consistent) theory T of
![]() $\rhd $
be complete can equivalently be put as
$\rhd $
be complete can equivalently be put as
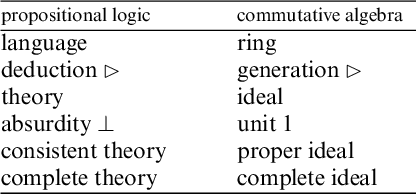
This move makes fully evident the analogy between complete ideals (4) and complete theories (7), which rests upon the following brief (and necessarily incomprehensive) dictionary:
With this at hand we translate (5) into a definition of the Jacobson radical of a theory T:
This is obviously equivalent to the following characterisation:
Mutatis mutandis the proof of Proposition 1 proves what we would like to provisionally call the Intermediate Lindenbaum Lemma:
Proposition 2
 $\operatorname {\textbf {ZFC}}$
$\operatorname {\textbf {ZFC}}$
For every theory T of an intermediate logic
![]() $\rhd $
in a propositional languageS,
$\rhd $
in a propositional languageS,
where
![]() $\operatorname {Com}_T(S)$
consists of the complete (consistent) theories C in S with
$\operatorname {Com}_T(S)$
consists of the complete (consistent) theories C in S with
![]() $T\subseteq C$
.
$T\subseteq C$
.
As for Proposition 1, it is irrelevant whether the intersection includes the only inconsistent theory S.
Since every complete theory is stable (Lemma 3), the left-hand side of
![]() $\operatorname {\textrm {ILL}}$
is as for the original Lindenbaum Lemma [Reference Tarski106] in the form
$\operatorname {\textrm {ILL}}$
is as for the original Lindenbaum Lemma [Reference Tarski106] in the form
for every stable theory T in S. Hence the left-hand side of
![]() $\operatorname {\textrm {ILL}}$
equals in
$\operatorname {\textrm {ILL}}$
equals in
![]() $\operatorname {\textbf {ZFC}}$
the classical deductive closure of T. What about the right-hand side of
$\operatorname {\textbf {ZFC}}$
the classical deductive closure of T. What about the right-hand side of
![]() $\operatorname {\textrm {ILL}}$
?
$\operatorname {\textrm {ILL}}$
?
Proposition 3. For every theory T of an intermediate logic
![]() $\rhd $
in a propositional language S,
$\rhd $
in a propositional language S,
Proof Let
![]() $\alpha \in \operatorname {\textrm {Jac}}(T)$
. Since
$\alpha \in \operatorname {\textrm {Jac}}(T)$
. Since
![]() $\alpha \rhd \neg \neg \alpha $
, we get
$\alpha \rhd \neg \neg \alpha $
, we get
![]() $T\rhd \neg \neg \alpha $
. Conversely, let
$T\rhd \neg \neg \alpha $
. Conversely, let
![]() $\alpha \in S$
be such that
$\alpha \in S$
be such that
![]() $T\ni \lnot \lnot \alpha $
. If
$T\ni \lnot \lnot \alpha $
. If
![]() $\beta \in S$
is such that
$\beta \in S$
is such that
![]() $\alpha \rhd \neg \beta $
, then
$\alpha \rhd \neg \beta $
, then
![]() $\neg \neg \alpha \rhd \neg \beta $
and thus
$\neg \neg \alpha \rhd \neg \beta $
and thus
![]() $T\rhd \neg \beta $
.
$T\rhd \neg \beta $
.
With Lemma 3 at hand we obtain the following:
Corollary 1.
![]() $\operatorname {\mathop {Jac}}(T)$
is the least stable theory of
$\operatorname {\mathop {Jac}}(T)$
is the least stable theory of
![]() $\rhd $
which contains the given theory T of
$\rhd $
which contains the given theory T of
![]() $\rhd $
; in other words,
$\rhd $
; in other words,
![]() $\operatorname {\mathop {Jac}}(T)$
equals the deductive closure of T with respect to classical logic.
$\operatorname {\mathop {Jac}}(T)$
equals the deductive closure of T with respect to classical logic.
So
![]() $\operatorname {\textrm {ILL}}$
for any intermediate logic
$\operatorname {\textrm {ILL}}$
for any intermediate logic
![]() $\rhd $
whatsoever is nothing but the original Lindenbaum Lemma!
$\rhd $
whatsoever is nothing but the original Lindenbaum Lemma!
Now let
![]() $\rhd $
be intuitionistic logic
$\rhd $
be intuitionistic logic
![]() ${\rhd _i}$
, and write
${\rhd _i}$
, and write
![]() ${\rhd _c}$
for classical logic, always in the given propositional language S. In this case and by the above, Lindenbaum’s Lemma in the form of
${\rhd _c}$
for classical logic, always in the given propositional language S. In this case and by the above, Lindenbaum’s Lemma in the form of
![]() $\operatorname {\textrm {ILL}}$
is the semantics of Glivenko’s Theorem [Reference Glivenko46], which in turn is well known as purely syntactical:
$\operatorname {\textrm {ILL}}$
is the semantics of Glivenko’s Theorem [Reference Glivenko46], which in turn is well known as purely syntactical:
Theorem 2 Glivenko 1929
Let S be a propositional language. For all
![]() $\Gamma \in \operatorname {\mathop {Fin}}(S)$
and
$\Gamma \in \operatorname {\mathop {Fin}}(S)$
and
![]() ${\varphi }\in S$
,
${\varphi }\in S$
,
For example, this follows from Corollary 1. We hasten to add that the latter rests upon Lemmas 1 and 2, which of course are the main ingredients of a very common proof of Glivenko’s theorem. Recent literature about Glivenko’s Theorem includes [Reference Espíndola36, Reference Fellin and Schuster39, Reference Galatos and Ono42, Reference Guerrieri and Naibo48, Reference Ishihara and Schwichtenberg56, Reference Litak, Polzer and Rabenstein60, Reference Negri74, Reference Negri75, Reference Ono82, Reference Pereira and Haeusler84].Footnote 8
6 Glivenko’s theorem as syntactical conservation
Once more let
![]() ${\rhd _i}$
and
${\rhd _i}$
and
![]() ${\rhd _c}$
stand for intuitionistic and classical logic in a propositional language S. For
${\rhd _c}$
stand for intuitionistic and classical logic in a propositional language S. For
![]() $\Gamma , \Delta \in \operatorname {\textrm {Fin}}(S)$
and
$\Gamma , \Delta \in \operatorname {\textrm {Fin}}(S)$
and
![]() ${\varphi }\in S$
, set
${\varphi }\in S$
, set
which defines a single- and a multi-conclusion entailment relation, respectively. Of course the trace of
![]() $\vdash _c$
is nothing but
$\vdash _c$
is nothing but
![]() ${\rhd _c}$
; so Glivenko’s Theorem (Theorem 2) can be rephrased as the following syntactical conservation:
${\rhd _c}$
; so Glivenko’s Theorem (Theorem 2) can be rephrased as the following syntactical conservation:
Theorem 3. The extension
![]() $\vdash _c$
of
$\vdash _c$
of
![]() ${\rhd _g}$
is conservative, that is,
${\rhd _g}$
is conservative, that is,
for all
![]() $\Gamma \in \operatorname {\mathop {Fin}}(S)$
and
$\Gamma \in \operatorname {\mathop {Fin}}(S)$
and
![]() ${\varphi }\in S$
.
${\varphi }\in S$
.
To see how Theorem 1 applies in this context, we now prove Theorem 3 in detail. Clearly this proof will otherwise have the main ingredients of any proof of Glivenko’s Theorem (Theorem 2). By Lemma 2,
![]() $\vdash _c$
extends
$\vdash _c$
extends
![]() ${\rhd _i}$
, and thus
${\rhd _i}$
, and thus
![]() ${\rhd _g}$
, with the following additional axioms:
${\rhd _g}$
, with the following additional axioms:
The corresponding conservation criteria (3) read
 $$ \begin{align} \frac{}{\Gamma,\bot{\rhd_g} \psi}\qquad \frac{\Gamma, {\varphi}{\rhd_g} \psi \quad \Gamma, \lnot{\varphi}{\rhd_g} \psi}{\Gamma {\rhd_g} \psi} \end{align} $$
$$ \begin{align} \frac{}{\Gamma,\bot{\rhd_g} \psi}\qquad \frac{\Gamma, {\varphi}{\rhd_g} \psi \quad \Gamma, \lnot{\varphi}{\rhd_g} \psi}{\Gamma {\rhd_g} \psi} \end{align} $$
with
![]() $\Gamma \in \operatorname {\textrm {Fin}}(S)$
and
$\Gamma \in \operatorname {\textrm {Fin}}(S)$
and
![]() ${\varphi }, \psi \in S$
.
${\varphi }, \psi \in S$
.
To prove Theorem 3, in view of Theorem 1 it thus is (necessary and) sufficient to verify (9). Writing
![]() ${\rhd _i} \lnot \lnot $
for
${\rhd _i} \lnot \lnot $
for
![]() ${\rhd _g}$
this goes as follows. Needless to say,
${\rhd _g}$
this goes as follows. Needless to say,
![]() $\Gamma ,\bot {\rhd _i} \lnot \lnot \psi $
. If both
$\Gamma ,\bot {\rhd _i} \lnot \lnot \psi $
. If both
![]() $\Gamma ,{\varphi }{\rhd _i} \lnot \lnot \psi $
and
$\Gamma ,{\varphi }{\rhd _i} \lnot \lnot \psi $
and
![]() $\Gamma ,\neg {\varphi }{\rhd _i} \lnot \lnot \psi $
, then
$\Gamma ,\neg {\varphi }{\rhd _i} \lnot \lnot \psi $
, then
![]() $\Gamma ,{\varphi }\lor \neg {\varphi }{\rhd _i} \lnot \lnot \psi $
by disjunction elimination. By Lemma 1 we get
$\Gamma ,{\varphi }\lor \neg {\varphi }{\rhd _i} \lnot \lnot \psi $
by disjunction elimination. By Lemma 1 we get
![]() $\Gamma ,\neg \neg ({\varphi }\lor \neg {\varphi }){\rhd _i} \lnot \lnot \psi $
and thus
$\Gamma ,\neg \neg ({\varphi }\lor \neg {\varphi }){\rhd _i} \lnot \lnot \psi $
and thus
![]() $\Gamma {\rhd _i} \lnot \lnot \psi $
as desired.
$\Gamma {\rhd _i} \lnot \lnot \psi $
as desired.
As the models of
![]() $\vdash _c$
are exactly the complete consistent theories, ILL for
$\vdash _c$
are exactly the complete consistent theories, ILL for
![]() $T\equiv \Gamma ^{{\rhd _i}}$
with
$T\equiv \Gamma ^{{\rhd _i}}$
with
![]() $\Gamma \in \operatorname {\textrm {Fin}}(S)$
is to
$\Gamma \in \operatorname {\textrm {Fin}}(S)$
is to
![]() $\operatorname {\textrm {Gli}}$
just as
$\operatorname {\textrm {Gli}}$
just as
![]() $\operatorname {\textrm {GKL}}$
is to
$\operatorname {\textrm {GKL}}$
is to
![]() $\operatorname {\textrm {Con}}$
for
$\operatorname {\textrm {Con}}$
for
![]() $\vdash \,\equiv \,\vdash _c$
and
$\vdash \,\equiv \,\vdash _c$
and
![]() $\rhd \equiv {\rhd _g}$
. Although
$\rhd \equiv {\rhd _g}$
. Although
![]() $\vdash _c$
equally extends
$\vdash _c$
equally extends
![]() ${\rhd _i}$
with the same additional axioms (8), and the first conservation criterion of (9) also holds for
${\rhd _i}$
with the same additional axioms (8), and the first conservation criterion of (9) also holds for
![]() ${\rhd _i}$
in place of
${\rhd _i}$
in place of
![]() ${\rhd _g}$
, this of course is not the case in general for the second one, e.g., if
${\rhd _g}$
, this of course is not the case in general for the second one, e.g., if
![]() $\psi \equiv {\varphi }\lor \lnot {\varphi }$
.
$\psi \equiv {\varphi }\lor \lnot {\varphi }$
.
We conclude by a relativised version of Glivenko’s Theorem as syntactical conservation. Let
![]() $\Gamma \subseteq \operatorname {\textrm {Fin}}(S)$
and
$\Gamma \subseteq \operatorname {\textrm {Fin}}(S)$
and
![]() $\psi \in S$
. With
$\psi \in S$
. With
![]() $\operatorname {\textrm {TND}}_0(\Gamma ,\psi )$
as in Lemma 2, for every propositional variable
$\operatorname {\textrm {TND}}_0(\Gamma ,\psi )$
as in Lemma 2, for every propositional variable
![]() ${\varphi }\in S$
consider the conservation criterion from Theorem 1 for
${\varphi }\in S$
consider the conservation criterion from Theorem 1 for
![]() $\vdash _c {\varphi },\lnot {\varphi }$
over
$\vdash _c {\varphi },\lnot {\varphi }$
over
![]() ${\rhd _i}$
:
${\rhd _i}$
:
 $$ \begin{align*} \operatorname{Cri}_{\varphi}(\Gamma,\psi):&\quad\kern-6pt \frac{\Gamma,\Delta, {\varphi}{\rhd_i} \psi \quad \Gamma,\Delta, \lnot{\varphi}{\rhd_i} \psi}{\Gamma,\Delta {\rhd_i} \psi} \kern-6pt\quad \text{or, equivalently,}\quad \kern-6pt \frac{\Gamma, \Delta,{\varphi}\lor \lnot{\varphi}{\rhd_i} \psi}{\Gamma,\Delta {\rhd_i} \psi}\\ & \quad \text{for all finite subsets}\ \Delta\ \text{of}\ \operatorname{\textrm{TND}}_0(\Gamma,\psi). \end{align*} $$
$$ \begin{align*} \operatorname{Cri}_{\varphi}(\Gamma,\psi):&\quad\kern-6pt \frac{\Gamma,\Delta, {\varphi}{\rhd_i} \psi \quad \Gamma,\Delta, \lnot{\varphi}{\rhd_i} \psi}{\Gamma,\Delta {\rhd_i} \psi} \kern-6pt\quad \text{or, equivalently,}\quad \kern-6pt \frac{\Gamma, \Delta,{\varphi}\lor \lnot{\varphi}{\rhd_i} \psi}{\Gamma,\Delta {\rhd_i} \psi}\\ & \quad \text{for all finite subsets}\ \Delta\ \text{of}\ \operatorname{\textrm{TND}}_0(\Gamma,\psi). \end{align*} $$
Proposition 4. For arbitrary but fixed
![]() $\Gamma \subseteq \operatorname {\mathop {Fin}}(S)$
and
$\Gamma \subseteq \operatorname {\mathop {Fin}}(S)$
and
![]() $\psi \in S$
, the following items are equivalent:
$\psi \in S$
, the following items are equivalent:
-
1.
 $\operatorname {Cri}_{\varphi }(\Gamma ,\psi )$
for all propositional variables
$\operatorname {Cri}_{\varphi }(\Gamma ,\psi )$
for all propositional variables
 ${\varphi }\in S$
occurring in
${\varphi }\in S$
occurring in
 $\Gamma $
or
$\Gamma $
or
 $\psi $
.
$\psi $
. -
2.
 ${\Gamma {\rhd _c} \psi }\Rightarrow {\Gamma {\rhd _i} \psi }$
, i.e.,
${\Gamma {\rhd _c} \psi }\Rightarrow {\Gamma {\rhd _i} \psi }$
, i.e.,
 $\vdash _c$
is conservative over
$\vdash _c$
is conservative over
 ${\rhd _i}$
for the given
${\rhd _i}$
for the given
 $\Gamma $
and
$\Gamma $
and
 $\psi $
.
$\psi $
.
While the first implies the second item by Lemma 2 and Theorem 1, the converse is evident.
Glivenko’s Theorem 2 is the case of the second item in which
![]() $\Gamma $
is arbitrary but
$\Gamma $
is arbitrary but
![]() $\psi $
is a negated formula, in which case the first item obtains by Lemma 1. Other cases include the one in which
$\psi $
is a negated formula, in which case the first item obtains by Lemma 1. Other cases include the one in which
![]() $\Gamma \cup \{\psi \}$
is made of negative formulas only; see e.g., [Reference David, Nour and Raffalli34, Reference Troelstra and Schwichtenberg107, Reference Troelstra and van Dalen108].
$\Gamma \cup \{\psi \}$
is made of negative formulas only; see e.g., [Reference David, Nour and Raffalli34, Reference Troelstra and Schwichtenberg107, Reference Troelstra and van Dalen108].
7 Complements
We briefly review some related observations recently made about double negation [Reference Fellin and Schuster39] in the more general context of a nucleus j in place of
![]() $\neg \neg $
.
$\neg \neg $
.
First, for any given intermediate propositional logic
![]() $\rhd $
the following are equivalent:
$\rhd $
the following are equivalent:
-
A.
 $\Gamma \vdash _c{\varphi }\Rightarrow \Gamma \rhd \neg \neg {\varphi }$
for all
$\Gamma \vdash _c{\varphi }\Rightarrow \Gamma \rhd \neg \neg {\varphi }$
for all
 $\Gamma ,{\varphi }$
and
$\Gamma ,{\varphi }$
and -
B.
 ${\varphi }\to \neg \neg \psi \rhd \neg \neg ({\varphi }\to \psi )$
for all
${\varphi }\to \neg \neg \psi \rhd \neg \neg ({\varphi }\to \psi )$
for all
 ${\varphi },\psi $
.
${\varphi },\psi $
.
Now B is well-known to hold whenever
![]() $\rhd $
is intuitionistic logic
$\rhd $
is intuitionistic logic
![]() $\rhd _i$
(see, e.g., [Reference van Dalen111, Lemma 6.2.2]), in which case A becomes Glivenko’s theorem. A posteriori B holds for any intermediate logic
$\rhd _i$
(see, e.g., [Reference van Dalen111, Lemma 6.2.2]), in which case A becomes Glivenko’s theorem. A posteriori B holds for any intermediate logic
![]() $\rhd $
whatsover, as any such
$\rhd $
whatsover, as any such
![]() $\rhd $
extends
$\rhd $
extends
![]() $\rhd _i$
.
$\rhd _i$
.
Next, if
![]() $\rhd $
is an intermediate predicate logic, then A is equivalent to B in conjunction with the double negation shift for
$\rhd $
is an intermediate predicate logic, then A is equivalent to B in conjunction with the double negation shift for
![]() $\rhd $
:
$\rhd $
:
-
C.
 $\forall x\neg \neg {\varphi }\rhd \neg \neg \forall x{\varphi }$
for all formulae
$\forall x\neg \neg {\varphi }\rhd \neg \neg \forall x{\varphi }$
for all formulae
 ${\varphi }$
.
${\varphi }$
.
Again if
![]() $\rhd $
is intuitionistic logic
$\rhd $
is intuitionistic logic
![]() $\rhd _i$
, this yields Gödel’s extension of Glivenko’s theorem [37, Reference Gödel47].
$\rhd _i$
, this yields Gödel’s extension of Glivenko’s theorem [37, Reference Gödel47].
Now C trivially holds for any existential logic, i.e., without
![]() $\forall $
altogether, for which A with
$\forall $
altogether, for which A with
![]() $\rhd _i$
as
$\rhd _i$
as
![]() $\rhd $
is [Reference Troelstra and Schwichtenberg107, Corollary to Proposition 2.3.8]. For A to hold it suffices to refrain from using the
$\rhd $
is [Reference Troelstra and Schwichtenberg107, Corollary to Proposition 2.3.8]. For A to hold it suffices to refrain from using the
![]() $\forall $
–introduction rule or right rule R
$\forall $
–introduction rule or right rule R
![]() $\forall $
, which in fact is the only rule that can cause issues in this setting [Reference Fellin and Schuster39]. To be able to avoid R
$\forall $
, which in fact is the only rule that can cause issues in this setting [Reference Fellin and Schuster39]. To be able to avoid R
![]() $\forall $
it is enough that the sequent under consideration have no positive occurrences of
$\forall $
it is enough that the sequent under consideration have no positive occurrences of
![]() $\forall $
, because derivations of such sequents by classical logic can be cleared from that rule (see, e.g., [Reference Negri74]).
$\forall $
, because derivations of such sequents by classical logic can be cleared from that rule (see, e.g., [Reference Negri74]).
Acknowledgments
The present study was carried out within the projects “A New Dawn of Intuitionism: Mathematical and Philosophical Advances” (ID 60842) funded by the John Templeton Foundation, and “Reducing complexity in algebra, logic, combinatorics—REDCOM” belonging to the programme “Ricerca Scientifica di Eccellenza 2018” of the Fondazione Cariverona. The opinions expressed in this paper are those of the authors and do not necessarily reflect the views of those foundations. An early version of the manuscript was conceived when the authors were visiting the Hausdorff Research Institute for Mathematics at Universität Bonn in 2018 during the Trimester Program “Types, Sets and Constructions.” Useful hints by Sara Negri are gratefully acknowledged. Schuster was glad for the feedback he received at the Scuola estiva di logica 2019 in Gargnano.



