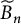In [Reference Flechsig4], Flechsig pointed out an error in [Reference Roushon6, Proposition 4.1], which was needed to deduce the Farrell–Jones isomorphism conjecture for the affine Artin groups
![]() ${\cal A}_{\widetilde B_n}$
(
${\cal A}_{\widetilde B_n}$
(
![]() $n\geq 3$
) of type
$n\geq 3$
) of type
![]() ${\widetilde B}_n$
.
${\widetilde B}_n$
.
In this note, we give an alternate argument to prove the conjecture.
Theorem 0.1 The Farrell–Jones isomorphism conjecture wreath product with finite groups (
![]() $FICwF$
) is true for
$FICwF$
) is true for
![]() ${\cal A}_{\widetilde B_n}$
(
${\cal A}_{\widetilde B_n}$
(
![]() $n\geq 3$
).
$n\geq 3$
).
Proof Consider the following hyperplane arrangement complement.
In [Reference Callegaro, Moroni and Salvetti2, Section 3], the following homeomorphism was observed. Let
![]() ${\Bbb C}^*={\Bbb C}-\{0\}$
.
${\Bbb C}^*={\Bbb C}-\{0\}$
.
 $$ \begin{align*} {\Bbb C}^*\times W&\simeq X:=\{x\in{\Bbb C}^{n+1}\ |\ x_i\neq \pm x_j,\ \text{for all}\ i\neq j; x_1\neq 0\}.\\&(\lambda, w_1,w_2,\ldots, w_n)\mapsto (\lambda, \lambda w_1,\ldots, \lambda w_n).\end{align*} $$
$$ \begin{align*} {\Bbb C}^*\times W&\simeq X:=\{x\in{\Bbb C}^{n+1}\ |\ x_i\neq \pm x_j,\ \text{for all}\ i\neq j; x_1\neq 0\}.\\&(\lambda, w_1,w_2,\ldots, w_n)\mapsto (\lambda, \lambda w_1,\ldots, \lambda w_n).\end{align*} $$
In [Reference Callegaro, Moroni and Salvetti2, Lemma 3.1], it was then proved that the hyperplane arrangement complement X is simplicial, in the sense of [Reference Deligne3].
From [Reference Huang and Osajda5], it follows that
![]() $FICwF$
is true for
$FICwF$
is true for
![]() $\pi _1(X)$
, since X is a finite real simplicial arrangement complement. Hence,
$\pi _1(X)$
, since X is a finite real simplicial arrangement complement. Hence,
![]() $FICwF$
is true for
$FICwF$
is true for
![]() $\pi _1(W)$
, as
$\pi _1(W)$
, as
![]() $\pi _1(W)$
is a subgroup of
$\pi _1(W)$
is a subgroup of
![]() $\pi _1(X)$
and
$\pi _1(X)$
and
![]() $FICwF$
has hereditary property (see [Reference Roushon6]).
$FICwF$
has hereditary property (see [Reference Roushon6]).
Next, note that there are the following two finite sheeted orbifold covering maps:
 $$ \begin{align*}W\to &PB_n(Z):=\{z\in Z^n\ |\ z_i\neq z_j,\ \text{for all}\ i\neq j\}\\&(w_1,w_2,\ldots, w_n)\mapsto (w_1^2,w_2^2,\ldots, w_n^2) \end{align*} $$
$$ \begin{align*}W\to &PB_n(Z):=\{z\in Z^n\ |\ z_i\neq z_j,\ \text{for all}\ i\neq j\}\\&(w_1,w_2,\ldots, w_n)\mapsto (w_1^2,w_2^2,\ldots, w_n^2) \end{align*} $$
and
![]() $PB_n(Z)\to B_n(Z):=PB_n(Z)/S_n$
. Here,
$PB_n(Z)\to B_n(Z):=PB_n(Z)/S_n$
. Here,
![]() $Z={\Bbb C}(1,1;2)$
(see [Reference Roushon6]) is the orbifold whose underlying space is
$Z={\Bbb C}(1,1;2)$
(see [Reference Roushon6]) is the orbifold whose underlying space is
![]() ${\Bbb C}-\{1\}$
, and
${\Bbb C}-\{1\}$
, and
![]() $0$
is an order
$0$
is an order
![]() $2$
cone point. And, the symmetric group
$2$
cone point. And, the symmetric group
![]() $S_n$
is acting on
$S_n$
is acting on
![]() $PB_n(Z)$
by permuting coordinates.
$PB_n(Z)$
by permuting coordinates.
Therefore,
![]() $\pi _1(W)$
embeds in
$\pi _1(W)$
embeds in
![]() $\pi _1^{orb}(B_n(Z))$
as a finite index subgroup. Hence,
$\pi _1^{orb}(B_n(Z))$
as a finite index subgroup. Hence,
![]() $FICwF$
is true for
$FICwF$
is true for
![]() $\pi _1^{orb}(B_n(Z))$
, since
$\pi _1^{orb}(B_n(Z))$
, since
![]() $FICwF$
passes to finite index overgroups (see [Reference Roushon6]). Next, recall that in [Reference Allcock1] Allcock showed that
$FICwF$
passes to finite index overgroups (see [Reference Roushon6]). Next, recall that in [Reference Allcock1] Allcock showed that
![]() ${\cal A}_{\widetilde B_n}$
is isomorphic to a subgroup of
${\cal A}_{\widetilde B_n}$
is isomorphic to a subgroup of
![]() $\pi _1^{orb}(B_n(Z))$
, and hence
$\pi _1^{orb}(B_n(Z))$
, and hence
![]() $FICwF$
is true for
$FICwF$
is true for
![]() ${\cal A}_{\widetilde B_n}$
by the hereditary property of
${\cal A}_{\widetilde B_n}$
by the hereditary property of
![]() $FICwF$
.
$FICwF$
.