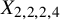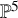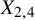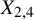1 Introduction
Stability conditions on a triangulated category were first introduced by Bridgeland in [Reference BridgelandBri07] to understand ![]() $\Pi $-stability, which was proposed by Douglas. Since then, the existence of Bridgeland stability conditions on smooth projective varieties has become a central problem. In a series of works [Reference Bayer, Macrì and TodaBMT14, Reference Bayer, Bertram, Macrì and TodaBBMT14, Reference Bayer, Macrì and StellariBMS16], a conjectural Bogomolov–Gieseker inequality is proposed to construct geometric stability conditions on threefolds. The construction is based on the double tilting technique, and the existence of geometric stability conditions relies on the conjectural Bogomolov–Gieseker inequality.
$\Pi $-stability, which was proposed by Douglas. Since then, the existence of Bridgeland stability conditions on smooth projective varieties has become a central problem. In a series of works [Reference Bayer, Macrì and TodaBMT14, Reference Bayer, Bertram, Macrì and TodaBBMT14, Reference Bayer, Macrì and StellariBMS16], a conjectural Bogomolov–Gieseker inequality is proposed to construct geometric stability conditions on threefolds. The construction is based on the double tilting technique, and the existence of geometric stability conditions relies on the conjectural Bogomolov–Gieseker inequality.
The existence of stability conditions on threefolds is only known for a limited number of examples: Fano threefolds [Reference MacrìMac14b, Reference SchmidtSch14, Reference LiLi19b, Reference PiyaratnePiy17, Reference Bernardara, Macrì, Schmidt and ZhaoBMSZ17], Abelian threefolds [Reference Maciocia and PiyaratneMP15, Reference Maciocia and PiyaratneMP16, Reference Bayer, Macrì and StellariBMS16], Kummer type threefolds [Reference Bayer, Macrì and StellariBMS16], threefolds with nef tangent bundle [Reference KosekiKos20] and product varieties of a curve with a surface [Reference LiuLiu21]. On Calabi–Yau threefolds, apart from the above examples, Li proved the existence of stability conditions on quintic threefolds [Reference LiLi19a], and Koseki proved the existence on some weighted hypersurfaces in ![]() $\mathbb {P}_{1,1,1,1,2}$ and
$\mathbb {P}_{1,1,1,1,2}$ and ![]() $\mathbb {P}_{1,1,1,1,4}$ [Reference KosekiKos22]. They both show the existence by proving that a stronger or modified Bogomolov–Gieseker inequality holds for these varieties. It is worth mentioning that the original conjectural Bogomolov–Gieseker inequality as in [Reference Bayer, Macrì and StellariBMS16] does not hold for all threefolds. In particular, counterexamples can be found in [Reference SchmidtSch17, Reference Martinez and SchmidtMS19]. However, a modified version of the Bogomolov–Gieseker inequality is sufficient to show the existence. An explanation of the construction can be found in [Reference Bayer, Macrì and StellariBMS16, Reference LiLi19a, Reference KosekiKos22].
$\mathbb {P}_{1,1,1,1,4}$ [Reference KosekiKos22]. They both show the existence by proving that a stronger or modified Bogomolov–Gieseker inequality holds for these varieties. It is worth mentioning that the original conjectural Bogomolov–Gieseker inequality as in [Reference Bayer, Macrì and StellariBMS16] does not hold for all threefolds. In particular, counterexamples can be found in [Reference SchmidtSch17, Reference Martinez and SchmidtMS19]. However, a modified version of the Bogomolov–Gieseker inequality is sufficient to show the existence. An explanation of the construction can be found in [Reference Bayer, Macrì and StellariBMS16, Reference LiLi19a, Reference KosekiKos22].
Let ![]() $X_{2,4}$ be a polarized smooth complete intersection of quadratic and quartic hypersurfaces with
$X_{2,4}$ be a polarized smooth complete intersection of quadratic and quartic hypersurfaces with ![]() $H=O_{X_{2,4}}(1)$. The main result of this paper is the following theorem ([Reference Bayer, Macrì and StellariBMS16, Conjecture 4.1]) for
$H=O_{X_{2,4}}(1)$. The main result of this paper is the following theorem ([Reference Bayer, Macrì and StellariBMS16, Conjecture 4.1]) for ![]() $X_{2,4}\subset \mathbb {P}^5$, with mild restrictions on
$X_{2,4}\subset \mathbb {P}^5$, with mild restrictions on ![]() $\alpha ,\beta $.
$\alpha ,\beta $.
Theorem 1.1 (Theorem 2.14).
Conjecture 4.1 in [Reference Bayer, Macrì and StellariBMS16] holds for ![]() $X_{2,4}$ when the parameters
$X_{2,4}$ when the parameters ![]() $(\alpha ,\beta )$ satisfy
$(\alpha ,\beta )$ satisfy ![]() $\alpha ^2+(\beta -\lfloor \beta \rfloor -\frac {1}{2})^2>\frac {1}{4}$. More precisely, assume E is
$\alpha ^2+(\beta -\lfloor \beta \rfloor -\frac {1}{2})^2>\frac {1}{4}$. More precisely, assume E is ![]() $\nu _{\alpha ,\beta ,H}$-tilt semistable for some
$\nu _{\alpha ,\beta ,H}$-tilt semistable for some ![]() $\alpha ^2+(\beta -\lfloor \beta \rfloor -\frac {1}{2})^2>\frac {1}{4}$, then the generalised Bogomolov–Gieseker inequality holds:
$\alpha ^2+(\beta -\lfloor \beta \rfloor -\frac {1}{2})^2>\frac {1}{4}$, then the generalised Bogomolov–Gieseker inequality holds:
By Theorem 1.1 and the framework in [Reference Bayer and MacrìBM14a, Reference Bayer, Bertram, Macrì and TodaBBMT14, Reference Bayer, Macrì and StellariBMS16] (see [Reference Bayer, Macrì and StellariBMS16, Theorem 8.6, Proposition 8.10]), we have
Theorem 1.2. There is a continuous family ![]() $\sigma ^{a,b}_{\alpha ,\beta ,H}=\left (Z_{\alpha ,\beta ,H}^{a,b}(X_{2,4}),\mathcal {A}^{\alpha ,\beta ,H}(X_{2,4})\right )$ of stability conditions on
$\sigma ^{a,b}_{\alpha ,\beta ,H}=\left (Z_{\alpha ,\beta ,H}^{a,b}(X_{2,4}),\mathcal {A}^{\alpha ,\beta ,H}(X_{2,4})\right )$ of stability conditions on ![]() $X_{2,4}$, parameterized by
$X_{2,4}$, parameterized by ![]() $(\alpha ,\beta ,a,b)\in \mathbb {R}_{>0}\times \mathbb {R}\times \mathbb {R}_{>0}\times \mathbb {R}$ satisfying
$(\alpha ,\beta ,a,b)\in \mathbb {R}_{>0}\times \mathbb {R}\times \mathbb {R}_{>0}\times \mathbb {R}$ satisfying
 $$ \begin{align*}\alpha^2+\left(\beta-\lfloor\beta\rfloor-\frac{1}{2}\right)^2>\frac{1}{4}\;\text{ and }\;a>\frac{\alpha^2}{6}+\frac{1}{2}|b|\alpha.\end{align*} $$
$$ \begin{align*}\alpha^2+\left(\beta-\lfloor\beta\rfloor-\frac{1}{2}\right)^2>\frac{1}{4}\;\text{ and }\;a>\frac{\alpha^2}{6}+\frac{1}{2}|b|\alpha.\end{align*} $$The detailed notation of the stability condition in the above theorem will be explained in Section 2.
The proof of Theorem 1.1 is based on a Bogomolov–Gieseker type inequality on ![]() $X_{2,4}$, the smooth projective Calabi–Yau threefold of complete intersection of quadratic and quartic hypersurfaces.
$X_{2,4}$, the smooth projective Calabi–Yau threefold of complete intersection of quadratic and quartic hypersurfaces.
Proposition 1.3 (Proposition 5.2).
Suppose F is a slope semistable sheaf on ![]() $X_{2,4}$ with
$X_{2,4}$ with ![]() $\mathop {\mathrm {ch}}\nolimits _0(F)\neq 0$, then
$\mathop {\mathrm {ch}}\nolimits _0(F)\neq 0$, then
 $$ \begin{align} \frac{H\mathop{\mathrm{ch}}\nolimits_2(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\leq \begin{cases} \left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in[0,\frac{4}{3}-\frac{\sqrt{13}}{3}]\\ \frac{5}{8}\left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{8} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{4}{3}-\frac{\sqrt{13}}{3},\frac{1}{2}]\\ \frac{5}{8}\left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{4}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{1}{2},\frac{\sqrt{13}}{3}-\frac{1}{3})\\ \left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{2} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in[\frac{\sqrt{13}}{3}-\frac{1}{3},1) \end{cases} \end{align} $$
$$ \begin{align} \frac{H\mathop{\mathrm{ch}}\nolimits_2(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\leq \begin{cases} \left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in[0,\frac{4}{3}-\frac{\sqrt{13}}{3}]\\ \frac{5}{8}\left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{8} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{4}{3}-\frac{\sqrt{13}}{3},\frac{1}{2}]\\ \frac{5}{8}\left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{4}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{1}{2},\frac{\sqrt{13}}{3}-\frac{1}{3})\\ \left(\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{2} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{ch}}\nolimits_0(F)}\in[\frac{\sqrt{13}}{3}-\frac{1}{3},1) \end{cases} \end{align} $$and for ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {ch}}\nolimits _0(F)}\in [n,n+1)$ for
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {ch}}\nolimits _0(F)}\in [n,n+1)$ for ![]() $n\in \mathbb {Z}$, we take
$n\in \mathbb {Z}$, we take ![]() $F(-nH)$ with the property
$F(-nH)$ with the property ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F(-nH))}{H^3\mathop {\mathrm {ch}}\nolimits _0(F(-nH))}\in [0,1)$.
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F(-nH))}{H^3\mathop {\mathrm {ch}}\nolimits _0(F(-nH))}\in [0,1)$.
Recall that the classical Bogomolov inequality tells us that, for a slope semistable sheaf F on ![]() $X_{2,4}$, we have
$X_{2,4}$, we have ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \frac {1}2\left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2$. From this we note that the above inequality is strictly stronger than the classical Bogomolov inequality unless
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \frac {1}2\left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2$. From this we note that the above inequality is strictly stronger than the classical Bogomolov inequality unless ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}$ takes integer values.
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}$ takes integer values.
On the other hand, as we prove the Bogomolov–Gieseker inequality for ![]() $X_{2,4}$, by applying the framework of [Reference Feyzbakhsh and ThomasFT20, Reference Feyzbakhsh and ThomasFT21, Reference Feyzbakhsh and ThomasFT22, Reference FeyzbakhshFey22b], we get explicit descriptions and properties of many enumerative invariants. In particular, let v be a numerical K-theory class of rank
$X_{2,4}$, by applying the framework of [Reference Feyzbakhsh and ThomasFT20, Reference Feyzbakhsh and ThomasFT21, Reference Feyzbakhsh and ThomasFT22, Reference FeyzbakhshFey22b], we get explicit descriptions and properties of many enumerative invariants. In particular, let v be a numerical K-theory class of rank ![]() $>0$ on
$>0$ on ![]() $X_{2,4}$. Let
$X_{2,4}$. Let ![]() $J(v)$ denote the Joyce–Song’s generalized Donaldson–Thomas invariant counting the number of Gieseker semistable sheaves. Then by [Reference Feyzbakhsh and ThomasFT22], we have
$J(v)$ denote the Joyce–Song’s generalized Donaldson–Thomas invariant counting the number of Gieseker semistable sheaves. Then by [Reference Feyzbakhsh and ThomasFT22], we have
where F is a universal polynomial in the invariants ![]() $J(\alpha _i)$ and the
$J(\alpha _i)$ and the ![]() $\alpha _i$’s are rank
$\alpha _i$’s are rank ![]() $1$ characters. By [Reference Pandharipande and PixtonPP17], MNOP conjecture holds for
$1$ characters. By [Reference Pandharipande and PixtonPP17], MNOP conjecture holds for ![]() $X_{2,4}$, and we can replace the
$X_{2,4}$, and we can replace the ![]() $J(\alpha _i)$’s by corresponding Gromov–Witten invariants.
$J(\alpha _i)$’s by corresponding Gromov–Witten invariants.
1.1 Strategy of proof
In this subsection, we explain how we prove Theorem 1.1. The general logical flow will follow [Reference LiLi19a, Reference KosekiKos22], and thus we briefly review the proof of [Reference LiLi19a]. Let ![]() $X_5$ be a smooth quintic threefold with polarization
$X_5$ be a smooth quintic threefold with polarization ![]() $H=O_{X_5}(1)$. Consider the following tower of smooth varieties:
$H=O_{X_5}(1)$. Consider the following tower of smooth varieties:
where ![]() $C_{2,2,5}$,
$C_{2,2,5}$, ![]() $S_{2,5}$ and
$S_{2,5}$ and ![]() $S_{2,2}$ are generic smooth complete intersections of
$S_{2,2}$ are generic smooth complete intersections of ![]() $(2,2,5)$,
$(2,2,5)$, ![]() $(2,5)$ and
$(2,5)$ and ![]() $(2,2)$ hypersurfaces, respectively. Then Theorem 1.1 for
$(2,2)$ hypersurfaces, respectively. Then Theorem 1.1 for ![]() $X_5$ is proved in following three steps:
$X_5$ is proved in following three steps:
1. For a stable vector bundle F on
 $C_{2,2,5}$, by pushing forward along the embedding
$C_{2,2,5}$, by pushing forward along the embedding  $C_{2,2,5}\subset S_{2,2}$, one regards F as a torsion sheaf on
$C_{2,2,5}\subset S_{2,2}$, one regards F as a torsion sheaf on  $S_{2,2}$. Then by the wall-crossing technique on the Bridgeland stability space on
$S_{2,2}$. Then by the wall-crossing technique on the Bridgeland stability space on  $S_{2,2}$ as in [Reference FeyzbakhshFey20], one gets a Clifford type inequality of F.
$S_{2,2}$ as in [Reference FeyzbakhshFey20], one gets a Clifford type inequality of F.2. Using Feyzbakhsh’s restriction theorem in [Reference FeyzbakhshFey22a], one recovers a Bogomolov–Gieseker type inequality on
 $S_{2,5}$. Using Feyzbakhsh’s restriction theorem again, a Bogomolov–Gieseker type inequality on
$S_{2,5}$. Using Feyzbakhsh’s restriction theorem again, a Bogomolov–Gieseker type inequality on  $X_5$ is obtained.
$X_5$ is obtained.3. By applying the Bogomolov–Gieseker type inequality on
 $X_5$ in step (2), one proves that
$X_5$ in step (2), one proves that  $Q_{0,0}(E)\geq 0$ for a Brill–Noether stable object E. Then by [Reference Bayer, Macrì and StellariBMS16, Theorem 5.4], one gets Theorem 1.1.
$Q_{0,0}(E)\geq 0$ for a Brill–Noether stable object E. Then by [Reference Bayer, Macrì and StellariBMS16, Theorem 5.4], one gets Theorem 1.1.
The main difference of this paper compared to [Reference LiLi19a, Reference KosekiKos22] is step (1), where we do not embed the curve ![]() $X_{2,2,2,4}$ into a del Pezzo surface but a K3 surface of Picard rank
$X_{2,2,2,4}$ into a del Pezzo surface but a K3 surface of Picard rank ![]() $1$. Unlike the proof of [Reference LiLi19a, Reference KosekiKos22], we do not have Hom vanishings of Brill–Noether semistable objects as in their cases of del Pezzo surfaces. Although a bound for global sections
$1$. Unlike the proof of [Reference LiLi19a, Reference KosekiKos22], we do not have Hom vanishings of Brill–Noether semistable objects as in their cases of del Pezzo surfaces. Although a bound for global sections ![]() $\hom (O_S,E)$ is already given in [Reference FeyzbakhshFey20], this bound is not strong enough to produce a Clifford type inequality to prove Theorem 5.5. Instead, we bound
$\hom (O_S,E)$ is already given in [Reference FeyzbakhshFey20], this bound is not strong enough to produce a Clifford type inequality to prove Theorem 5.5. Instead, we bound ![]() $\hom (O_S,E)$ directly if E is Brill–Noether semistable of negative slope or
$\hom (O_S,E)$ directly if E is Brill–Noether semistable of negative slope or ![]() $\mathop {\mathrm {ext}}\nolimits ^1(O_S,E)$ if E is Brill–Noether semistable of positive slope and then use
$\mathop {\mathrm {ext}}\nolimits ^1(O_S,E)$ if E is Brill–Noether semistable of positive slope and then use ![]() $\hom (O_S,E)=\chi (O_S,E)+\mathop {\mathrm {ext}}\nolimits ^1(O_S,E)$ to get the bound. The main technique we use is the semistability of the spherical twist of E as in Proposition 4.3. Next, we use the convex polygon trick in [Reference Feyzbakhsh and LiFL21] to get the Clifford type inequality, which is similar to [Reference LiLi19a, Section 4].
$\hom (O_S,E)=\chi (O_S,E)+\mathop {\mathrm {ext}}\nolimits ^1(O_S,E)$ to get the bound. The main technique we use is the semistability of the spherical twist of E as in Proposition 4.3. Next, we use the convex polygon trick in [Reference Feyzbakhsh and LiFL21] to get the Clifford type inequality, which is similar to [Reference LiLi19a, Section 4].
1.2 Plan of paper
The plan of this paper is the following. In Section 2, we recall basic notations, constructions and properties of stability conditions. In Section 3, with a similar method to [Reference LiLi19a], we prove Theorem 1.1 by assuming that the results in Section 5, especially Theorem 5.5, hold. This corresponds to step (3) in Section 1.1. In Section 4, we deduce a Clifford type inequality for the curve ![]() $C:=X_{2,2,2,4}$ for a slope semistable vector bundle E. The method follows the last part in Section 1.1. In Section 5, we deduce Theorem 5.5 by using the Clifford type inequality in Section 4. The proof is similar to [Reference LiLi19a]. This corresponds to step (2).
$C:=X_{2,2,2,4}$ for a slope semistable vector bundle E. The method follows the last part in Section 1.1. In Section 5, we deduce Theorem 5.5 by using the Clifford type inequality in Section 4. The proof is similar to [Reference LiLi19a]. This corresponds to step (2).
2 Introduction to Bridgeland stability
2.1 Notations of slope stability
In this section, we review notations of slope stability conditions. Let X be a smooth projective variety. The facts concerning slope stability can all be found in [Reference Huybrechts and LehnHL10].
Definition 2.1 (Slope stability).
Let F be a coherent sheaf on X, and let H be an ample divisor. The slope of F with respect to H is
 $$ \begin{align*}\mu_H(F)= \begin{cases} \frac{H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(F)}{H^n\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if }\mathop{\mathrm{ch}}\nolimits_0(F)\neq0\\ +\infty & \text{if } \mathop{\mathrm{ch}}\nolimits_0(F)=0. \end{cases} \end{align*} $$
$$ \begin{align*}\mu_H(F)= \begin{cases} \frac{H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(F)}{H^n\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if }\mathop{\mathrm{ch}}\nolimits_0(F)\neq0\\ +\infty & \text{if } \mathop{\mathrm{ch}}\nolimits_0(F)=0. \end{cases} \end{align*} $$A coherent sheaf F is said to be slope (semi)stable if for any nontrivial coherent subsheaf ![]() $E\subset F$,
$E\subset F$,
Proposition 2.2 (Harder–Narasimhan filtration).
For every coherent sheaf F, there is a filtration, called the Harder–Narasimhan filtration,
where ![]() $F_i/F_{i-1}$ is slope semistable and
$F_i/F_{i-1}$ is slope semistable and
We denote ![]() $\mu ^+(F)\;(\text {respectively}\;\mu ^-(F))$ to be the maximum (respectively minimum) slope of the HN factors of F under the slope stability function.
$\mu ^+(F)\;(\text {respectively}\;\mu ^-(F))$ to be the maximum (respectively minimum) slope of the HN factors of F under the slope stability function.
2.2 Weak stability condition and Bridgeland stability condition
Let ![]() $D^b(X)$ be the bounded derived category of coherent sheaves on X. From now on, we consider that X is of dimension
$D^b(X)$ be the bounded derived category of coherent sheaves on X. From now on, we consider that X is of dimension ![]() $2$ or
$2$ or ![]() $3$.
$3$.
Definition 2.3 (Heart of a bounded t-structure).
A full additive subcategory ![]() $\mathcal {A}\subset D^b(X)$ is called the heart of a bounded t-structure if
$\mathcal {A}\subset D^b(X)$ is called the heart of a bounded t-structure if
1.
 $\mathop {\mathrm {Hom}}\nolimits (\mathcal {A}[i],\mathcal {A}[j])=0$ if
$\mathop {\mathrm {Hom}}\nolimits (\mathcal {A}[i],\mathcal {A}[j])=0$ if  $i>j$.
$i>j$.2. For every
 $E\subset D^b(X)$, there is a chain of morphisms
$E\subset D^b(X)$, there is a chain of morphisms  $$ \begin{align*}0=E_0\xrightarrow{\phi_0}E_1\xrightarrow{\phi_1}E_2\xrightarrow{\phi_2}\ldots\xrightarrow{\phi_{n-1}}E_n=E\end{align*} $$
$$ \begin{align*}0=E_0\xrightarrow{\phi_0}E_1\xrightarrow{\phi_1}E_2\xrightarrow{\phi_2}\ldots\xrightarrow{\phi_{n-1}}E_n=E\end{align*} $$such that
 $\operatorname {\mathrm {Cone}}(\phi _i)\in \mathcal {A}[k_i]$ and
$\operatorname {\mathrm {Cone}}(\phi _i)\in \mathcal {A}[k_i]$ and  $k_0>k_1>\ldots >k_{n-1}$.
$k_0>k_1>\ldots >k_{n-1}$.
One can actually show that ![]() $\mathcal {A}$ is an abelian category.
$\mathcal {A}$ is an abelian category.
Definition 2.4 (Weak stability function).
Let ![]() $\mathcal {A}$ be an abelian category. A group homomorphism
$\mathcal {A}$ be an abelian category. A group homomorphism ![]() $Z:K_0(\mathcal {A})\rightarrow \mathbb {C}$ is called a weak stability function on
$Z:K_0(\mathcal {A})\rightarrow \mathbb {C}$ is called a weak stability function on ![]() $\mathcal {A}$ if, for
$\mathcal {A}$ if, for ![]() $E\in \mathcal {A}$, we have
$E\in \mathcal {A}$, we have ![]() $\Im (Z([E]))\geq 0$, with
$\Im (Z([E]))\geq 0$, with ![]() $\Im (Z([E]))=0\;\implies \;\Re (Z([E]))\leq 0$. The function Z is called a stability function if, moreover, for all
$\Im (Z([E]))=0\;\implies \;\Re (Z([E]))\leq 0$. The function Z is called a stability function if, moreover, for all ![]() $0\neq E\in \mathcal {A}$,
$0\neq E\in \mathcal {A}$, ![]() $\Im (Z([E]))=0\;\implies \;\Re (Z([E]))<0.$
$\Im (Z([E]))=0\;\implies \;\Re (Z([E]))<0.$
The original definition of Bridgeland stability is given by [Reference BridgelandBri07]. By [Reference BridgelandBri07, Proposition 5.3][Reference Macrì and SchmidtMS17, Lemma 5.11], a pair ![]() $\sigma =(\mathcal {A},Z)$, where
$\sigma =(\mathcal {A},Z)$, where ![]() $\mathcal {A}$ is the heart of a bounded t-structure and the function
$\mathcal {A}$ is the heart of a bounded t-structure and the function ![]() $Z:K_0(\mathcal {A})\rightarrow \mathbb {C}$ is a group homomorphism, is a Bridgeland stability condition if it satisfies the following properties:
$Z:K_0(\mathcal {A})\rightarrow \mathbb {C}$ is a group homomorphism, is a Bridgeland stability condition if it satisfies the following properties:
(1) The group homomorphism Z is a stability function. We define the slope of a nonzero object E in
 $\mathcal A$ to be
$\mathcal A$ to be  $$ \begin{align*}\nu(E):= \begin{cases} -\frac{\Re(Z([E]))}{\Im(Z([E]))} & \text{if }\Im(Z([E]))\neq0\\ +\infty & otherwise. \end{cases}\end{align*} $$
$$ \begin{align*}\nu(E):= \begin{cases} -\frac{\Re(Z([E]))}{\Im(Z([E]))} & \text{if }\Im(Z([E]))\neq0\\ +\infty & otherwise. \end{cases}\end{align*} $$An object E is called
 $\sigma $-(semi)stable if, for any nonzero proper subobject
$\sigma $-(semi)stable if, for any nonzero proper subobject  $F\subset E$, we have
$F\subset E$, we have  $\nu (F)<(\leq )\nu (E/F)$.
$\nu (F)<(\leq )\nu (E/F)$.(2) (HN filtrations) For any nonzero object
 $E\in \mathcal {A}$, we have a filtration of E, called the Harder–Narasimhan filtration:
$E\in \mathcal {A}$, we have a filtration of E, called the Harder–Narasimhan filtration:  $$ \begin{align*}0=E_0\subset E_1\subset\ldots\subset E_m=E,\end{align*} $$
$$ \begin{align*}0=E_0\subset E_1\subset\ldots\subset E_m=E,\end{align*} $$where
 $\nu (E_1/E_0)>\nu (E_2/E_1)>\ldots >\nu (E_m/E_{m-1})$ and
$\nu (E_1/E_0)>\nu (E_2/E_1)>\ldots >\nu (E_m/E_{m-1})$ and  $E_i/E_{i-1}$ are semistable.
$E_i/E_{i-1}$ are semistable.(3) (Support property) There is a constant
 $C>0$ such that, for any semistable object E, we have
$C>0$ such that, for any semistable object E, we have  $||E||\leq C\left \lvert Z([E])\right \rvert $, where
$||E||\leq C\left \lvert Z([E])\right \rvert $, where  $||\cdot ||$ is a fixed norm on
$||\cdot ||$ is a fixed norm on  $K_0(X)\otimes \mathbb {R}$.
$K_0(X)\otimes \mathbb {R}$.
The pair ![]() $\sigma $ is called a weak stability condition if in (1), we only require Z to be a weak stability function. Let
$\sigma $ is called a weak stability condition if in (1), we only require Z to be a weak stability function. Let ![]() $Stab(X)$ denote the set of all Bridgeland stability conditions on X, then Bridgeland showed that
$Stab(X)$ denote the set of all Bridgeland stability conditions on X, then Bridgeland showed that ![]() $Stab(X)$ is actually a complex manifold [Reference BridgelandBri07, Proposition 8.1]. Now, we fix a class
$Stab(X)$ is actually a complex manifold [Reference BridgelandBri07, Proposition 8.1]. Now, we fix a class ![]() $v\in K_{num}(X)$, and consider the class of
$v\in K_{num}(X)$, and consider the class of ![]() $\sigma $-semistable objects of class v when
$\sigma $-semistable objects of class v when ![]() $\sigma $ varies. Then we have a wall and chamber structure on
$\sigma $ varies. Then we have a wall and chamber structure on ![]() $Stab(X)$ based on the following proposition.
$Stab(X)$ based on the following proposition.
Proposition 2.5 [Reference BridgelandBri08, Section 9][Reference TodaTod08, Proposition 2.8][Reference Bayer and MacrìBM11, Proposition 3.3][Reference Bayer and MacrìBM14b, Proposition 2.3].
There exists a locally finite set ![]() $\mathscr {W}$ of real codimension
$\mathscr {W}$ of real codimension ![]() $1$ submanifolds with boundary in
$1$ submanifolds with boundary in ![]() $Stab(X)$ only depending on v, called walls, with the following properties:
$Stab(X)$ only depending on v, called walls, with the following properties:
1. When
 $\sigma $ varies in a chamber (connected components of
$\sigma $ varies in a chamber (connected components of  $Stab(X)\backslash (\cup _{W\in \mathscr {W}}W)$), then the sets of
$Stab(X)\backslash (\cup _{W\in \mathscr {W}}W)$), then the sets of  $\sigma $-semistable objects and
$\sigma $-semistable objects and  $\sigma $-stable objects do not change.
$\sigma $-stable objects do not change.2. When
 $\sigma $ is on a single wall
$\sigma $ is on a single wall  $W\in \mathscr {W}$, then there exists an object F such that F is unstable on the adjacent chamber of one side of the wall and semistable on the adjacent chamber on the other side of the wall.
$W\in \mathscr {W}$, then there exists an object F such that F is unstable on the adjacent chamber of one side of the wall and semistable on the adjacent chamber on the other side of the wall.
An important technique to construct weak or Bridgeland stability conditions is by tilting, which we recall now. Most of the materials here can be found in [Reference Bayer, Macrì and StellariBMS16, Reference Macrì and SchmidtMS17, Reference LiLi19a].
We define the torsion pair ![]() $(\mathcal {T}_{\beta ,H},\mathcal {F}_{\beta ,H})$ as
$(\mathcal {T}_{\beta ,H},\mathcal {F}_{\beta ,H})$ as
Definition 2.6. We let ![]() $\mathrm {Coh}^{\beta ,H}(X)\subset D^b(X)$ be the extension-closure
$\mathrm {Coh}^{\beta ,H}(X)\subset D^b(X)$ be the extension-closure
Then, by tilting, ![]() $\mathrm {Coh}^{\beta ,H}(X)$ is the heart of a bounded t-structure, in particular an abelian category. Let
$\mathrm {Coh}^{\beta ,H}(X)$ is the heart of a bounded t-structure, in particular an abelian category. Let ![]() $B\in NS(X)_{\mathbb {R}}$. We define the twisted characters as
$B\in NS(X)_{\mathbb {R}}$. We define the twisted characters as
Definition 2.7 (Tilt slope and stability).
Let ![]() $E\in \mathrm {Coh}^{\beta ,H}(X)$, we define
$E\in \mathrm {Coh}^{\beta ,H}(X)$, we define
 $$ \begin{align*}\nu_{\alpha,\beta,H}(E)= \begin{cases} \frac{H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E)-\alpha H^n\mathop{\mathrm{ch}}\nolimits_0(E)}{H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)} & \text{if }H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta,H}(E)\neq0\\ +\infty & \text{if }H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)=0. \end{cases} \end{align*} $$
$$ \begin{align*}\nu_{\alpha,\beta,H}(E)= \begin{cases} \frac{H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E)-\alpha H^n\mathop{\mathrm{ch}}\nolimits_0(E)}{H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)} & \text{if }H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta,H}(E)\neq0\\ +\infty & \text{if }H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)=0. \end{cases} \end{align*} $$An object ![]() $E\in \mathrm {Coh}^{\beta ,H}(X)$ is called
$E\in \mathrm {Coh}^{\beta ,H}(X)$ is called ![]() $\nu _{\alpha ,\beta ,H}$-tilt (semi)stable if for any nontrivial subobject
$\nu _{\alpha ,\beta ,H}$-tilt (semi)stable if for any nontrivial subobject ![]() $F\subset E$ inside
$F\subset E$ inside ![]() $\mathrm {Coh}^{\beta ,H}(X)$, we have
$\mathrm {Coh}^{\beta ,H}(X)$, we have
An object ![]() $E\in D^b(X)$ is called
$E\in D^b(X)$ is called ![]() $\nu _{\alpha ,\beta ,H}$-tilt (semi)stable if
$\nu _{\alpha ,\beta ,H}$-tilt (semi)stable if ![]() $E[n]\in \mathrm {Coh}^{\beta ,H}(X)$ is
$E[n]\in \mathrm {Coh}^{\beta ,H}(X)$ is ![]() $\nu _{\alpha ,\beta ,H}$-tilt (semi)stable for some integer n.
$\nu _{\alpha ,\beta ,H}$-tilt (semi)stable for some integer n.
Same as slope stability, ![]() $\nu _{\alpha ,\beta ,H}$-stability also admits the Harder–Narasimhan filtration property when
$\nu _{\alpha ,\beta ,H}$-stability also admits the Harder–Narasimhan filtration property when ![]() $\alpha>\frac {\beta ^2}{2}$. For an object
$\alpha>\frac {\beta ^2}{2}$. For an object ![]() $E\in \mathrm {Coh}^{\beta ,H}(X)$, we denote
$E\in \mathrm {Coh}^{\beta ,H}(X)$, we denote ![]() $\nu ^+_{\alpha ,\beta ,H}(E)$ (respectively
$\nu ^+_{\alpha ,\beta ,H}(E)$ (respectively ![]() $\nu ^-_{\alpha ,\beta ,H}(E)$) as the maximum (respectively minimum) slopes of
$\nu ^-_{\alpha ,\beta ,H}(E)$) as the maximum (respectively minimum) slopes of ![]() $\nu _{\alpha ,\beta ,H}$-HN filtration factors. We also write the central charge
$\nu _{\alpha ,\beta ,H}$-HN filtration factors. We also write the central charge
Definition 2.8. Let ![]() $E\in \mathop {\mathrm {Coh}}\nolimits ^{\beta ,H}(X)$. We define the H-discriminant of E to be
$E\in \mathop {\mathrm {Coh}}\nolimits ^{\beta ,H}(X)$. We define the H-discriminant of E to be
Theorem 2.9 [Reference BogomolovBog78], [Reference Bayer, Macrì and TodaBMT14, Theorem 7.3.1], [Reference Piyaratne and TodaPT19, Proposition 2.21].
Let E be a ![]() $\nu _{\alpha ,\beta ,H}$-semistable object for
$\nu _{\alpha ,\beta ,H}$-semistable object for ![]() $\alpha>\frac {1}{2}\beta ^2$. Then
$\alpha>\frac {1}{2}\beta ^2$. Then ![]() $\overline {\Delta }_H(E)\geq 0.$
$\overline {\Delta }_H(E)\geq 0.$
2.3 Bridgeland stability on K3 surfaces
In this section, we recall the Bridgeland stability condition on K3 surfaces. Most of this can be found in [Reference BridgelandBri08]. A review of it can be found in [Reference Feyzbakhsh and LiFL21].
Let ![]() $(S,H)$ be a polarized K3 surface with a Picard group generated by H. We use the same heart of bounded t-structure
$(S,H)$ be a polarized K3 surface with a Picard group generated by H. We use the same heart of bounded t-structure ![]() $\mathrm {Coh}^{\beta ,H}(S)$ as above and define the central charge as
$\mathrm {Coh}^{\beta ,H}(S)$ as above and define the central charge as
 $$ \begin{align*}Z_{\alpha,\beta}(E)=-\mathop{\mathrm{ch}}\nolimits_2(E)+\alpha \mathop{\mathrm{rk}}(E)+i\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(E)}{H^2}-\beta \mathop{\mathrm{rk}}(E)\right).\end{align*} $$
$$ \begin{align*}Z_{\alpha,\beta}(E)=-\mathop{\mathrm{ch}}\nolimits_2(E)+\alpha \mathop{\mathrm{rk}}(E)+i\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(E)}{H^2}-\beta \mathop{\mathrm{rk}}(E)\right).\end{align*} $$Note that this is slightly different from the central charge given above, but they give the same family of weak stability conditions. We will only use this family of stability conditions on K3 surfaces.
Now, we define a periodic function of period 1,
 $$ \begin{align*}\gamma(x)= \begin{cases} 1-x^2 & \text{if } x\in[-\frac{1}{2},\frac{1}{2}]\backslash \{0\}\\ 0 & \text{if } x=0. \end{cases}\end{align*} $$
$$ \begin{align*}\gamma(x)= \begin{cases} 1-x^2 & \text{if } x\in[-\frac{1}{2},\frac{1}{2}]\backslash \{0\}\\ 0 & \text{if } x=0. \end{cases}\end{align*} $$Let ![]() $\Gamma (x)=\frac {H^2}{2}x^2-\gamma (x)$ and
$\Gamma (x)=\frac {H^2}{2}x^2-\gamma (x)$ and ![]() $\Gamma _+$ to be the region above
$\Gamma _+$ to be the region above ![]() $\Gamma $. Then Bridgeland showed that
$\Gamma $. Then Bridgeland showed that ![]() $(\alpha ,\beta )$ with
$(\alpha ,\beta )$ with ![]() $\alpha>\Gamma (\beta )$ defines a stability condition
$\alpha>\Gamma (\beta )$ defines a stability condition ![]() $\sigma _{\alpha ,\beta }=(\mathrm {Coh}^{\beta ,H}(X),Z_{\alpha ,\beta })$ on K3 surfaces [Reference BridgelandBri08, Reference Feyzbakhsh and LiFL21] by using Theorem 2.9. The slope is defined to be
$\sigma _{\alpha ,\beta }=(\mathrm {Coh}^{\beta ,H}(X),Z_{\alpha ,\beta })$ on K3 surfaces [Reference BridgelandBri08, Reference Feyzbakhsh and LiFL21] by using Theorem 2.9. The slope is defined to be ![]() $-\frac {\Re (Z_{\alpha ,\beta })}{\Im (Z_{\alpha ,\beta })}$. If E is an object with
$-\frac {\Re (Z_{\alpha ,\beta })}{\Im (Z_{\alpha ,\beta })}$. If E is an object with ![]() $\mathop {\mathrm {rk}}(E)\neq 0$, we define
$\mathop {\mathrm {rk}}(E)\neq 0$, we define
 $$ \begin{align*}pr(E):=pr(\mathop{\mathrm{ch}}\nolimits(E))=\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(E)}{H^2\mathop{\mathrm{rk}}(E)},\frac{\mathop{\mathrm{ch}}\nolimits_2(E)}{\mathop{\mathrm{rk}}(E)}\right).\end{align*} $$
$$ \begin{align*}pr(E):=pr(\mathop{\mathrm{ch}}\nolimits(E))=\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(E)}{H^2\mathop{\mathrm{rk}}(E)},\frac{\mathop{\mathrm{ch}}\nolimits_2(E)}{\mathop{\mathrm{rk}}(E)}\right).\end{align*} $$ By abuse of notation, we also write ![]() $\Gamma $ for the graph on the plane. Then we have a description of walls.
$\Gamma $ for the graph on the plane. Then we have a description of walls.
Proposition 2.10 [Reference BridgelandBri08, Proposition 9.3].
Let ![]() $F\in D^b(X)$. Then there exists a collection of line segments (walls)
$F\in D^b(X)$. Then there exists a collection of line segments (walls) ![]() $\mathcal {W}^i_F$ in
$\mathcal {W}^i_F$ in ![]() $\Gamma _+$ with the following property:
$\Gamma _+$ with the following property:
(1) The end points are either on
 $\Gamma $ or on the vertical line segment
$\Gamma $ or on the vertical line segment  $(n,\frac {H^2}{2}n^2)$ to
$(n,\frac {H^2}{2}n^2)$ to  $\left (n,\frac {H^2}{2}n^2-1\right )$;
$\left (n,\frac {H^2}{2}n^2-1\right )$;(2) The extension of the wall passes through
 $pr(F)$ if
$pr(F)$ if  $\mathop {\mathrm {rk}}(F)\neq 0$, otherwise it has slope
$\mathop {\mathrm {rk}}(F)\neq 0$, otherwise it has slope  $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$;
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$;(3) The stability of F does not change between two consecutive walls;
(4) F is strictly
 $\sigma _{\alpha ,\beta }$-semistable (in other words semistable but not stable) if
$\sigma _{\alpha ,\beta }$-semistable (in other words semistable but not stable) if  $(\alpha ,\beta )$ is contained in one of the walls;
$(\alpha ,\beta )$ is contained in one of the walls;(5) If F is semistable on one side of the wall, then it is unstable on the other side of the wall.
The above proposition also holds if we consider a numerical class v. Then the proposition holds for potential walls, which means the walls that can happen for an object F with ![]() $v(F)=v$. The following proposition is important for us to give an upper bound for the global sections of Brill–Noether semistable objects.
$v(F)=v$. The following proposition is important for us to give an upper bound for the global sections of Brill–Noether semistable objects.
Proposition 2.11 [Reference Bayer and MacrìBM14a, Theorem 2.15(a)].
Let ![]() $Stab^\dagger (X)$ denote the connected components of
$Stab^\dagger (X)$ denote the connected components of ![]() $Stab(X)$ containing geometric stability conditions. In particular, the stability conditions
$Stab(X)$ containing geometric stability conditions. In particular, the stability conditions ![]() $\sigma _{\alpha ,\beta }$ given above are in
$\sigma _{\alpha ,\beta }$ given above are in ![]() $Stab^\dagger (X)$. Let
$Stab^\dagger (X)$. Let ![]() $v=mv_0\in H^*_{alg}(X;\mathbb {Z})$ be a Mukai vector with
$v=mv_0\in H^*_{alg}(X;\mathbb {Z})$ be a Mukai vector with ![]() $v_0$ primitive and
$v_0$ primitive and ![]() $m> 0$, and let
$m> 0$, and let ![]() $\sigma \in Stab^\dagger (X)$ be a generic stability condition with respect to v. (This means that
$\sigma \in Stab^\dagger (X)$ be a generic stability condition with respect to v. (This means that ![]() $\sigma $ is not on the wall of v.) Then the coarse moduli space
$\sigma $ is not on the wall of v.) Then the coarse moduli space ![]() $M_\sigma (v)$ is nonempty if and only if
$M_\sigma (v)$ is nonempty if and only if ![]() $v_0^2\geq -2$.
$v_0^2\geq -2$.
Now, we briefly explain how to relate ![]() $v_0^2\geq -2$ with the curve
$v_0^2\geq -2$ with the curve ![]() $\Gamma $. Let
$\Gamma $. Let ![]() $v_0=(\mathop {\mathrm {rk}},cH,s)$. If
$v_0=(\mathop {\mathrm {rk}},cH,s)$. If ![]() $cH=0$, then
$cH=0$, then ![]() $-2\mathop {\mathrm {rk}} \mathop {\mathrm {ch}}\nolimits _2-2{\mathop {\mathrm {rk}}}^2\geq -2$. This implies
$-2\mathop {\mathrm {rk}} \mathop {\mathrm {ch}}\nolimits _2-2{\mathop {\mathrm {rk}}}^2\geq -2$. This implies ![]() $\frac {\mathop {\mathrm {ch}}\nolimits _2}{\mathop {\mathrm {rk}}}\leq \frac {1}{{\mathop {\mathrm {rk}}}^2}-1\leq 0$. Now, suppose
$\frac {\mathop {\mathrm {ch}}\nolimits _2}{\mathop {\mathrm {rk}}}\leq \frac {1}{{\mathop {\mathrm {rk}}}^2}-1\leq 0$. Now, suppose ![]() $c\neq 0$. Suppose
$c\neq 0$. Suppose ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1}{H^2\mathop {\mathrm {rk}}}\in [-\frac {1}{2},\frac {1}{2}]$, then we have
$\frac {H\mathop {\mathrm {ch}}\nolimits _1}{H^2\mathop {\mathrm {rk}}}\in [-\frac {1}{2},\frac {1}{2}]$, then we have
This implies
 $$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2}{\mathop{\mathrm{rk}}}\leq\frac{H^2}{2}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1}{H^2\mathop{\mathrm{rk}}}\right)^2-1+\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1}{H^2\mathop{\mathrm{rk}}}\right)^2.\end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2}{\mathop{\mathrm{rk}}}\leq\frac{H^2}{2}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1}{H^2\mathop{\mathrm{rk}}}\right)^2-1+\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1}{H^2\mathop{\mathrm{rk}}}\right)^2.\end{align*} $$If ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1}{H^2\mathop {\mathrm {rk}}}\in [n-\frac {1}{2},n+\frac {1}{2}]\backslash \{n\}$, we have
$\frac {H\mathop {\mathrm {ch}}\nolimits _1}{H^2\mathop {\mathrm {rk}}}\in [n-\frac {1}{2},n+\frac {1}{2}]\backslash \{n\}$, we have
And thus, we get the curve ![]() $\Gamma $. So we see that, if an object is
$\Gamma $. So we see that, if an object is ![]() $\sigma $-semistable for some generic
$\sigma $-semistable for some generic ![]() $\sigma $, we have
$\sigma $, we have ![]() $\frac {\mathop {\mathrm {ch}}\nolimits _2}{\mathop {\mathrm {rk}}}\leq \Gamma \left (\frac {H\mathop {\mathrm {ch}}\nolimits _1}{H^2\mathop {\mathrm {rk}}}\right ).$ For a more detailed explanation of
$\frac {\mathop {\mathrm {ch}}\nolimits _2}{\mathop {\mathrm {rk}}}\leq \Gamma \left (\frac {H\mathop {\mathrm {ch}}\nolimits _1}{H^2\mathop {\mathrm {rk}}}\right ).$ For a more detailed explanation of ![]() $\Gamma $, we would like to ask readers to consult [Reference Lahoz and RojasLR22, Reference Lie, Li and ZhaoFLZ22] on Le Potier functions.
$\Gamma $, we would like to ask readers to consult [Reference Lahoz and RojasLR22, Reference Lie, Li and ZhaoFLZ22] on Le Potier functions.
2.4 Stability conditions on  $X_{2,4}$
$X_{2,4}$
The goal of this paper is to show that the following conjectural Bogomolov–Gieseker inequality holds when X is the complete intersection of quadratic and quartic hypersurfaces in ![]() $\mathbb {P}^5$.
$\mathbb {P}^5$.
Conjecture 2.12 [Reference Bayer, Macrì and TodaBMT14, Conjecture 2.7], [Reference Bayer, Macrì and StellariBMS16, Conjecture 4.1].
Let X be a smooth projective threefold of complete intersection of quadratic and quartic hypersurfaces in ![]() $\mathbb {P}^5$, and let H be an ample class. Assume E is
$\mathbb {P}^5$, and let H be an ample class. Assume E is ![]() $\nu _{\alpha ,\beta ,H}$-tilt semistable for some
$\nu _{\alpha ,\beta ,H}$-tilt semistable for some ![]() $\alpha>\frac {1}{2}\beta ^2$. Then
$\alpha>\frac {1}{2}\beta ^2$. Then
Remark 2.13. It was expected that Conjecture 2.12 is correct for all projective threefolds. However, this is not the case. A counterexample is given in [Reference SchmidtSch17]: The above inequality is violated in blowing up a point on ![]() $\mathbb {P}^3$. A weaker Bogomolov–Gieseker inequality is proposed and proved for all Fano threefolds; see [Reference Bernardara, Macrì, Schmidt and ZhaoBMSZ17].
$\mathbb {P}^3$. A weaker Bogomolov–Gieseker inequality is proposed and proved for all Fano threefolds; see [Reference Bernardara, Macrì, Schmidt and ZhaoBMSZ17].
In this paper, we prove the above conjecture with small restrictions on ![]() $\alpha ,\beta $.
$\alpha ,\beta $.
Theorem 2.14. Let X be a smooth projective threefold of complete intersection of quadratic and quartic hypersurfaces in ![]() $\mathbb {P}^5$, and let
$\mathbb {P}^5$, and let ![]() $H=O_X(1)$. Assume that E is
$H=O_X(1)$. Assume that E is ![]() $\nu _{\alpha ,\beta ,H}$-tilt semistable for some
$\nu _{\alpha ,\beta ,H}$-tilt semistable for some ![]() $\alpha>\frac {1}{2}\beta ^2+\frac {1}{2}(\beta -\lfloor \beta \rfloor )(\lfloor \beta \rfloor +1-\beta )$. Then
$\alpha>\frac {1}{2}\beta ^2+\frac {1}{2}(\beta -\lfloor \beta \rfloor )(\lfloor \beta \rfloor +1-\beta )$. Then ![]() $Q_{\alpha ,\beta }(E)\geq 0.$
$Q_{\alpha ,\beta }(E)\geq 0.$
Under the framework of [Reference Bayer, Macrì and TodaBMT14, Reference Bayer, Bertram, Macrì and TodaBBMT14, Reference Bayer, Macrì and StellariBMS16], we can construct a family of Bridgeland stability conditions on ![]() $X_{2,4}$. The heart
$X_{2,4}$. The heart ![]() $\mathcal {A}$ of the stability condition is constructed by ‘double-tilting’
$\mathcal {A}$ of the stability condition is constructed by ‘double-tilting’ ![]() $\mathop {\mathrm {Coh}}\nolimits (X_{2,4})$. We define the double-tilting heart
$\mathop {\mathrm {Coh}}\nolimits (X_{2,4})$. We define the double-tilting heart ![]() $\mathcal {A}^{\alpha ,\beta ,H}$ to be the extension
$\mathcal {A}^{\alpha ,\beta ,H}$ to be the extension ![]() $\langle \mathcal {T}_{\alpha ,\beta ,H},\mathcal {F}_{\alpha ,\beta ,H}[1]\rangle $, where
$\langle \mathcal {T}_{\alpha ,\beta ,H},\mathcal {F}_{\alpha ,\beta ,H}[1]\rangle $, where
We define the central charge Z on ![]() $\mathcal {A}^{\alpha ,\beta ,H}$ to be
$\mathcal {A}^{\alpha ,\beta ,H}$ to be
 $$ \begin{align*}Z^{a,b}_{\alpha,\beta,H}(E):=\left(-\mathop{\mathrm{ch}}\nolimits_3^{\beta H}(E)+bH\mathop{\mathrm{ch}}\nolimits_2^{\beta H}(E)+aH^2\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)\right)+i\left(H\mathop{\mathrm{ch}}\nolimits_2^{\beta H}(E)-\frac{\alpha^2}{2}H^3\mathop{\mathrm{rk}}(E)\right).\end{align*} $$
$$ \begin{align*}Z^{a,b}_{\alpha,\beta,H}(E):=\left(-\mathop{\mathrm{ch}}\nolimits_3^{\beta H}(E)+bH\mathop{\mathrm{ch}}\nolimits_2^{\beta H}(E)+aH^2\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)\right)+i\left(H\mathop{\mathrm{ch}}\nolimits_2^{\beta H}(E)-\frac{\alpha^2}{2}H^3\mathop{\mathrm{rk}}(E)\right).\end{align*} $$By Theorem 1.1 and the framework in [Reference Bayer, Macrì and TodaBMT14, Reference Bayer, Bertram, Macrì and TodaBBMT14, Reference Bayer, Macrì and StellariBMS16] (see [Reference Bayer, Macrì and StellariBMS16, Theorem 8.6, Proposition 8.10]), we have:
Theorem 2.15. There is a continuous family ![]() $\sigma ^{a,b}_{\alpha ,\beta ,H}=\left (Z_{\alpha ,\beta ,H}^{a,b}(X_{2,4}),\mathcal {A}^{\alpha ,\beta ,H}(X_{2,4})\right )$ of stability conditions on
$\sigma ^{a,b}_{\alpha ,\beta ,H}=\left (Z_{\alpha ,\beta ,H}^{a,b}(X_{2,4}),\mathcal {A}^{\alpha ,\beta ,H}(X_{2,4})\right )$ of stability conditions on ![]() $X_{2,4}$, parameterized by
$X_{2,4}$, parameterized by ![]() $(\alpha ,\beta ,a,b)\in \mathbb {R}_{>0}\times \mathbb {R}\times \mathbb {R}_{>0}\times \mathbb {R}$ satisfying
$(\alpha ,\beta ,a,b)\in \mathbb {R}_{>0}\times \mathbb {R}\times \mathbb {R}_{>0}\times \mathbb {R}$ satisfying
 $$ \begin{align*}\alpha^2+\left(\beta-\lfloor\beta\rfloor-\frac{1}{2}\right)^2>\frac{1}{4}\;\text{ and }\;a>\frac{\alpha^2}{6}+\frac{1}{2}|b|\alpha.\end{align*} $$
$$ \begin{align*}\alpha^2+\left(\beta-\lfloor\beta\rfloor-\frac{1}{2}\right)^2>\frac{1}{4}\;\text{ and }\;a>\frac{\alpha^2}{6}+\frac{1}{2}|b|\alpha.\end{align*} $$2.5 Useful lemmas
Now, let
 $$ \begin{align*}\text{and }\;p_H(E)=\left(\frac{H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E)}{H^n\mathop{\mathrm{ch}}\nolimits_0(E)},\frac{H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(E)}{H^n\mathop{\mathrm{ch}}\nolimits_0(E)}\right).\end{align*} $$
$$ \begin{align*}\text{and }\;p_H(E)=\left(\frac{H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E)}{H^n\mathop{\mathrm{ch}}\nolimits_0(E)},\frac{H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(E)}{H^n\mathop{\mathrm{ch}}\nolimits_0(E)}\right).\end{align*} $$Then we have the following lemma on stability conditions.
Lemma 2.16. Let E be a ![]() $\nu _{\alpha _0,\beta _0,H}$-tilt stable object in
$\nu _{\alpha _0,\beta _0,H}$-tilt stable object in ![]() $\mathop {\mathrm {Coh}}\nolimits ^{\beta _0,H}(X)$ for some
$\mathop {\mathrm {Coh}}\nolimits ^{\beta _0,H}(X)$ for some ![]() $\alpha _0>\frac {1}{2}\beta _0$. Then
$\alpha _0>\frac {1}{2}\beta _0$. Then
1. [Reference Bayer, Macrì and TodaBMT14, Corollary 3.3.3][Reference Bayer, Macrì and StellariBMS16, Appendix B] There is an open neighbourhood U of
 $(\alpha _0,\beta _0)$ such that E is
$(\alpha _0,\beta _0)$ such that E is  $\nu _{\alpha ,\beta ,H}$-tilt stable for all
$\nu _{\alpha ,\beta ,H}$-tilt stable for all  $(\alpha ,\beta )\in U$ with
$(\alpha ,\beta )\in U$ with  $\alpha>\frac {1}{2}\beta ^2$.
$\alpha>\frac {1}{2}\beta ^2$.2. [Reference MacrìMac14b, Theorem 3.1][Reference Bayer, Macrì and StellariBMS16, Lemma 4.3][Reference LiLi19a, Lemma 2.9](Bertram’s nested wall theorem) The object E is
 $\nu _{\alpha ,\beta ,H}$-tilt stable for any
$\nu _{\alpha ,\beta ,H}$-tilt stable for any  $(\alpha ,\beta )$ with
$(\alpha ,\beta )$ with  $\alpha>\frac {1}{2}\beta ^2$ on the line through
$\alpha>\frac {1}{2}\beta ^2$ on the line through  $(\alpha _0,\beta _0)$ and
$(\alpha _0,\beta _0)$ and  $p_H(E)$. More precisely, the object E is
$p_H(E)$. More precisely, the object E is  $\nu _{\alpha ,\beta ,H}$-tilt stable for
$\nu _{\alpha ,\beta ,H}$-tilt stable for  $(\alpha ,\beta )$ such that
$(\alpha ,\beta )$ such that  $$ \begin{align*}\det \begin{pmatrix} 1 & \alpha & \beta\\ 1 & \alpha_0 & \beta_0\\ H^n\mathop{\mathrm{ch}}\nolimits_0(E) & H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E) & H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(E) \end{pmatrix}=0.\end{align*} $$
$$ \begin{align*}\det \begin{pmatrix} 1 & \alpha & \beta\\ 1 & \alpha_0 & \beta_0\\ H^n\mathop{\mathrm{ch}}\nolimits_0(E) & H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E) & H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(E) \end{pmatrix}=0.\end{align*} $$The statement also holds for the semistable case. Moreover, when X is a threefold,
 $$ \begin{align*}H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)Q_{\alpha_0,\beta_0}(E)=H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta_0 H}(E)Q_{\alpha,\beta}(E).\end{align*} $$
$$ \begin{align*}H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta H}(E)Q_{\alpha_0,\beta_0}(E)=H^{n-1}\mathop{\mathrm{ch}}\nolimits_1^{\beta_0 H}(E)Q_{\alpha,\beta}(E).\end{align*} $$2’. Let F be an object in
 $\mathop {\mathrm {Coh}}\nolimits ^{\beta ,H}(X)$ such that
$\mathop {\mathrm {Coh}}\nolimits ^{\beta ,H}(X)$ such that  $p_H(F)$ is on the line through the points
$p_H(F)$ is on the line through the points  $(\alpha _0,\beta _0)$ and
$(\alpha _0,\beta _0)$ and  $p_H(E)$, then
$p_H(E)$, then  $\nu _{\alpha _0,\beta _0,H}(E)=\nu _{\alpha _0,\beta _0,H}(F)$. More precisely, the requirements on E and F are as follows: Both
$\nu _{\alpha _0,\beta _0,H}(E)=\nu _{\alpha _0,\beta _0,H}(F)$. More precisely, the requirements on E and F are as follows: Both  $\overline {v}_H(E)$ and
$\overline {v}_H(E)$ and  $\overline {v}_H(F)$ are not zero and
$\overline {v}_H(F)$ are not zero and  $$ \begin{align*}\det \begin{pmatrix} 1 & \alpha_0 & \beta_0\\ H^n\mathop{\mathrm{ch}}\nolimits_0(E) & H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E) & H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(E)\\ H^n\mathop{\mathrm{ch}}\nolimits_0(F) & H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(F) & H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(F) \end{pmatrix}=0.\end{align*} $$
$$ \begin{align*}\det \begin{pmatrix} 1 & \alpha_0 & \beta_0\\ H^n\mathop{\mathrm{ch}}\nolimits_0(E) & H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(E) & H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(E)\\ H^n\mathop{\mathrm{ch}}\nolimits_0(F) & H^{n-2}\mathop{\mathrm{ch}}\nolimits_2(F) & H^{n-1}\mathop{\mathrm{ch}}\nolimits_1(F) \end{pmatrix}=0.\end{align*} $$3. [Reference Bayer, Macrì and TodaBMT14, Corollary 3.3.3][Reference Bayer, Macrì and StellariBMS16, Appendix B] (destabilising walls) The set
 $$ \begin{align*}\left\{(\alpha,\beta)\middle|\alpha>\frac{1}{2}\beta^2\text{ and }E\text{ is strictly }\nu_{\alpha,\beta,H}\text{-semistable}\right\}\end{align*} $$
$$ \begin{align*}\left\{(\alpha,\beta)\middle|\alpha>\frac{1}{2}\beta^2\text{ and }E\text{ is strictly }\nu_{\alpha,\beta,H}\text{-semistable}\right\}\end{align*} $$is either empty or a union of lines and rays.
The following lemma is essential to the proof in the following sections.
Lemma 2.17 [Reference Bayer, Macrì and StellariBMS16, Corollary 3.10].
Let E be a strictly ![]() $\nu _{\alpha ,\beta ,H}$-tilt semistable object with finite slope. Then, for any of the Jordan–Hölder factors
$\nu _{\alpha ,\beta ,H}$-tilt semistable object with finite slope. Then, for any of the Jordan–Hölder factors ![]() $E_i$ of E, we have
$E_i$ of E, we have
The equality only holds when ![]() $\overline {\nu }_H(E_i)=\overline {\nu }_H(E)$ and
$\overline {\nu }_H(E_i)=\overline {\nu }_H(E)$ and ![]() $\overline {\Delta }_H(E)=\overline {\Delta }_H(E_i)=0$.
$\overline {\Delta }_H(E)=\overline {\Delta }_H(E_i)=0$.
One more (weak) stability condition we use is the Brill–Noether stability condition. A detailed explanation can be found in [Reference BayerBay18].
Definition 2.18. An object E is called Brill–Noether stable if there is an open subset
such that E is ![]() $\nu _{\alpha ,\beta ,H}$-tilt stable for all
$\nu _{\alpha ,\beta ,H}$-tilt stable for all ![]() $(\alpha ,\beta )\in U_{\delta }$.
$(\alpha ,\beta )\in U_{\delta }$.
We call an object E Brill–Noether semistable if there exists ![]() $\delta>0$ such that E is
$\delta>0$ such that E is ![]() $\nu _{\alpha ,0,H}$-semistable for every
$\nu _{\alpha ,0,H}$-semistable for every ![]() $0<\alpha <\delta $.
$0<\alpha <\delta $.
The Brill–Noether slope is defined by ![]() $\nu _{BN}(E)=\frac {H^{n-2}\mathop {\mathrm {ch}}\nolimits _2(E)}{H^{n-1}\mathop {\mathrm {ch}}\nolimits _1(E)}$ if
$\nu _{BN}(E)=\frac {H^{n-2}\mathop {\mathrm {ch}}\nolimits _2(E)}{H^{n-1}\mathop {\mathrm {ch}}\nolimits _1(E)}$ if ![]() $H^{n-1}\mathop {\mathrm {ch}}\nolimits _1(E)\neq 0$, and
$H^{n-1}\mathop {\mathrm {ch}}\nolimits _1(E)\neq 0$, and ![]() $+\infty $ otherwise.
$+\infty $ otherwise.
By Lemma 2.16, an object E with ![]() $H^{n-2}\mathop {\mathrm {ch}}\nolimits _2(E)\neq 0$ is Brill–Noether stable if and only if it is
$H^{n-2}\mathop {\mathrm {ch}}\nolimits _2(E)\neq 0$ is Brill–Noether stable if and only if it is ![]() $\nu _{\alpha ,\beta ,H}$-tilt stable for some
$\nu _{\alpha ,\beta ,H}$-tilt stable for some ![]() $(\alpha ,\beta )$ proportional to
$(\alpha ,\beta )$ proportional to ![]() $p_H(E)$, and a similar result holds for the Brill–Noether semistable case.
$p_H(E)$, and a similar result holds for the Brill–Noether semistable case.
The following well-known lemma will be used, and the proof can be found in [Reference LiLi19a, lemma 2.12].
Lemma 2.19 [Reference BayerBay18, Lemma 6.5].
Assume that ![]() $E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(X)$ is Brill–Noether stable. If
$E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(X)$ is Brill–Noether stable. If ![]() $\nu _{BN}(E)>0$, let
$\nu _{BN}(E)>0$, let ![]() $W\subset \mathop {\mathrm {Hom}}\nolimits (O_X,E)$ be a vector subspace and let
$W\subset \mathop {\mathrm {Hom}}\nolimits (O_X,E)$ be a vector subspace and let
where the map is the evaluation map. Then the spherical twist ![]() $\tilde {E}$ is also Brill–Noether semistable and
$\tilde {E}$ is also Brill–Noether semistable and ![]() $\tilde {E}\in \mathrm {Coh}^{0,H}(X)$.
$\tilde {E}\in \mathrm {Coh}^{0,H}(X)$.
If ![]() $\nu _{BN}(E)<0$, let
$\nu _{BN}(E)<0$, let ![]() $W'\subset \mathop {\mathrm {Hom}}\nolimits (E[-1],O_X)$ be a vector subspace and let
$W'\subset \mathop {\mathrm {Hom}}\nolimits (E[-1],O_X)$ be a vector subspace and let
where the map is the canonical map. Then the spherical twist ![]() $\tilde {E}'$ is also Brill–Noether semistable and
$\tilde {E}'$ is also Brill–Noether semistable and ![]() $\tilde {E}'\in \mathrm {Coh}^{0,H}(X)$.
$\tilde {E}'\in \mathrm {Coh}^{0,H}(X)$.
3 Proof of the main result
Let ![]() $X:=X_{2,4}\subset \mathbb {P}^5$ be a smooth complete intersection of quadratic and quartic hypersurfaces. Thus, it is a Calabi–Yau threefold by the adjunction formula. By Hirzebruch–Riemann–Roch, we have
$X:=X_{2,4}\subset \mathbb {P}^5$ be a smooth complete intersection of quadratic and quartic hypersurfaces. Thus, it is a Calabi–Yau threefold by the adjunction formula. By Hirzebruch–Riemann–Roch, we have
By the same argument as that in [Reference LiLi19a, Theorem 3.2], we get the following theorem and proposition.
Theorem 3.1 [Reference LiLi19a, Theorem 3.2], [Reference Bayer, Macrì and StellariBMS16, Theorem 5.4].
Theorem 1.1 holds if
for any Brill–Noether stable object ![]() $E\in \mathrm {Coh}^{0,H}(X)$ with
$E\in \mathrm {Coh}^{0,H}(X)$ with ![]() $\nu _{BN}(E)\in [-\frac {1}{2},\frac {1}{2}]$.
$\nu _{BN}(E)\in [-\frac {1}{2},\frac {1}{2}]$.
Proposition 3.2. The inequality ![]() $Q_{0,0}(E)\geq 0$ holds for any Brill–Noether stable object
$Q_{0,0}(E)\geq 0$ holds for any Brill–Noether stable object ![]() $E\in \mathrm {Coh}^{0,H}(X)$ with
$E\in \mathrm {Coh}^{0,H}(X)$ with ![]() $\nu _{BN}(E)\in [-\frac {1}{2},\frac {1}{2}]$.
$\nu _{BN}(E)\in [-\frac {1}{2},\frac {1}{2}]$.
The proof of this proposition depends on the positivity of the slope ![]() $\nu _{BN}(E)$. First, we consider
$\nu _{BN}(E)$. First, we consider ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$.
$\nu _{BN}(E)\in (0,\frac {1}{2}]$.
Lemma 3.3. Let ![]() $E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with
$E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$. Then we have
$\nu _{BN}(E)\in (0,\frac {1}{2}]$. Then we have
Proof. Let ![]() $E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with
$E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$. There exists
$\nu _{BN}(E)\in (0,\frac {1}{2}]$. There exists ![]() $(\alpha ,\beta )$ such that
$(\alpha ,\beta )$ such that ![]() $\alpha>\frac {1}{2}\beta ^2$,
$\alpha>\frac {1}{2}\beta ^2$, ![]() $0<\frac {\alpha }{\beta }<\nu _{BN}(E)$ and E is
$0<\frac {\alpha }{\beta }<\nu _{BN}(E)$ and E is ![]() $\nu _{\alpha ,\beta ,H}$-tilt stable. Note that
$\nu _{\alpha ,\beta ,H}$-tilt stable. Note that
By tilt stability and Serre duality, we have
for ![]() $i\geq 0$. Consider
$i\geq 0$. Consider ![]() $\tilde {E}:=\mathrm {Cone}(O_X\otimes \mathop {\mathrm {Hom}}\nolimits (O_X,E)\rightarrow E)$. By Lemma 2.19,
$\tilde {E}:=\mathrm {Cone}(O_X\otimes \mathop {\mathrm {Hom}}\nolimits (O_X,E)\rightarrow E)$. By Lemma 2.19, ![]() $\tilde {E}$ is also Brill–Noether semistable. By Theorem 5.5, the slope
$\tilde {E}$ is also Brill–Noether semistable. By Theorem 5.5, the slope ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(\tilde {E})}{H^3\mathop {\mathrm {rk}}(\tilde {E})}$ cannot be in
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(\tilde {E})}{H^3\mathop {\mathrm {rk}}(\tilde {E})}$ cannot be in ![]() $(-\frac {1}{5},0]$. Then either
$(-\frac {1}{5},0]$. Then either
 $$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(E)}{H^3(\mathrm{rk}(E)-\mathrm{hom}(O_X,E))}=\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathrm{rk}(\tilde{E})}\notin[-\frac{1}{2},-\frac{1}{5}],\end{align*} $$
$$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(E)}{H^3(\mathrm{rk}(E)-\mathrm{hom}(O_X,E))}=\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathrm{rk}(\tilde{E})}\notin[-\frac{1}{2},-\frac{1}{5}],\end{align*} $$which implies
or
 $$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathrm{rk}(\tilde{E})}\in[-\frac{1}{2},-\frac{1}{5}],\end{align*} $$
$$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathrm{rk}(\tilde{E})}\in[-\frac{1}{2},-\frac{1}{5}],\end{align*} $$which implies
As we require ![]() $E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(E)$ and
$E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(E)$ and ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$, we know that
$\nu _{BN}(E)\in (0,\frac {1}{2}]$, we know that ![]() $H\mathop {\mathrm {ch}}\nolimits _2(E)>0$ and
$H\mathop {\mathrm {ch}}\nolimits _2(E)>0$ and ![]() $H^2\mathop {\mathrm {ch}}\nolimits _1(E)>0$, and thus in both cases we always have
$H^2\mathop {\mathrm {ch}}\nolimits _1(E)>0$, and thus in both cases we always have
By slope, we have ![]() $\mathop {\mathrm {Hom}}\nolimits (O_X[1],E[j])=0$ for
$\mathop {\mathrm {Hom}}\nolimits (O_X[1],E[j])=0$ for ![]() $j\leq -1$, and combining this with equation (3.1), we have
$j\leq -1$, and combining this with equation (3.1), we have
By Hirzebruch–Riemann–Roch, we have
By multiplying with ![]() $6H^2\mathop {\mathrm {ch}}\nolimits _1(E)$ and rearranging terms, we have
$6H^2\mathop {\mathrm {ch}}\nolimits _1(E)$ and rearranging terms, we have
Lemma 3.4. For a Brill–Noether stable object ![]() $E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(X)$ with
$E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(X)$ with ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$, we have
$\nu _{BN}(E)\in (0,\frac {1}{2}]$, we have ![]() $Q_{0,0}(E)\geq 0$.
$Q_{0,0}(E)\geq 0$.
Proof. Let ![]() $E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with
$E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$. By Lemma 3.3, we have the following inequality on
$\nu _{BN}(E)\in (0,\frac {1}{2}]$. By Lemma 3.3, we have the following inequality on ![]() $Q_{0,0}$:
$Q_{0,0}$:
 $$ \begin{align} Q_{0,0}(E) & \geq 4(H\mathop{\mathrm{ch}}\nolimits_2(E))^2-6(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\mathop{\mathrm{rk}}(E)+\frac{7}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-4(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^2\mathop{\mathrm{ch}}\nolimits_1(E)) \notag \\ & = 4\left((H\mathop{\mathrm{ch}}\nolimits_2(E))-\frac{1}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\right)^2+\frac{3}{4}\left(H^2\mathop{\mathrm{ch}}\nolimits_1(E)\right)^2-\frac{3}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E)). \end{align} $$
$$ \begin{align} Q_{0,0}(E) & \geq 4(H\mathop{\mathrm{ch}}\nolimits_2(E))^2-6(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\mathop{\mathrm{rk}}(E)+\frac{7}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-4(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^2\mathop{\mathrm{ch}}\nolimits_1(E)) \notag \\ & = 4\left((H\mathop{\mathrm{ch}}\nolimits_2(E))-\frac{1}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\right)^2+\frac{3}{4}\left(H^2\mathop{\mathrm{ch}}\nolimits_1(E)\right)^2-\frac{3}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E)). \end{align} $$As we assume ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$, we have
$\nu _{BN}(E)\in (0,\frac {1}{2}]$, we have ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\notin [0,\frac {3}{7}]$ by Theorem 5.5.
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\notin [0,\frac {3}{7}]$ by Theorem 5.5.
Case 1. When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\notin [\frac {3}{7},1]$, then we have
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\notin [\frac {3}{7},1]$, then we have ![]() $H^2\mathop {\mathrm {ch}}\nolimits _1(E)>H^3\mathop {\mathrm {rk}}(E)$ and thus by inequality (3.2), we have
$H^2\mathop {\mathrm {ch}}\nolimits _1(E)>H^3\mathop {\mathrm {rk}}(E)$ and thus by inequality (3.2), we have ![]() $Q_{0,0}(E)\geq 0$.
$Q_{0,0}(E)\geq 0$.
Case 2. When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {4}{5},\frac {10}{11}]$, by Theorem 5.5, we have
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {4}{5},\frac {10}{11}]$, by Theorem 5.5, we have
Thus,
Case 3. When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {1}{2},\frac {4}{5}]$, by Theorem 5.5, we have
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {1}{2},\frac {4}{5}]$, by Theorem 5.5, we have
and thus,
 $$ \begin{align*}Q_{0,0}(E)\geq 4\left((H\mathop{\mathrm{ch}}\nolimits_2(E)-\frac{1}{8}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\right)^2\geq0.\end{align*} $$
$$ \begin{align*}Q_{0,0}(E)\geq 4\left((H\mathop{\mathrm{ch}}\nolimits_2(E)-\frac{1}{8}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\right)^2\geq0.\end{align*} $$ Case 4. When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {3}{7},\frac {1}{2}]$, by Theorem 5.5, we have
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {3}{7},\frac {1}{2}]$, by Theorem 5.5, we have
and thus we have
Case 5. When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {10}{11},1]$, we need a better bound of
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\in [\frac {10}{11},1]$, we need a better bound of ![]() $Q_{0,0}$. There are two subcases:
$Q_{0,0}$. There are two subcases:
(1) ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1(E)}\leq \frac {79}{220}$. In this case, we have
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1(E)}\leq \frac {79}{220}$. In this case, we have
 $$ \begin{align*} Q_{0,0}(E) & \geq 4(H\mathop{\mathrm{ch}}\nolimits_2(E))^2-4(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^2\mathop{\mathrm{ch}}\nolimits_1(E))+\frac{7}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-\frac{3}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))\notag \\ &\geq\frac{2,509}{3,025}(H\mathop{\mathrm{ch}}\nolimits_1(E))^2-\frac{3}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))\notag\\ &\geq\left(\frac{2,509}{3,025}\times\frac{10}{11}-\frac{3}{4}\right)(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))>0,\notag \end{align*} $$
$$ \begin{align*} Q_{0,0}(E) & \geq 4(H\mathop{\mathrm{ch}}\nolimits_2(E))^2-4(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^2\mathop{\mathrm{ch}}\nolimits_1(E))+\frac{7}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-\frac{3}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))\notag \\ &\geq\frac{2,509}{3,025}(H\mathop{\mathrm{ch}}\nolimits_1(E))^2-\frac{3}{4}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))\notag\\ &\geq\left(\frac{2,509}{3,025}\times\frac{10}{11}-\frac{3}{4}\right)(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))>0,\notag \end{align*} $$where the second inequality follows from considering ![]() $f(x)=4x^2-4x+\frac {7}{4}$ for
$f(x)=4x^2-4x+\frac {7}{4}$ for ![]() $x\leq \frac {79}{220}$, and the third inequality follows from
$x\leq \frac {79}{220}$, and the third inequality follows from ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\geq \frac {10}{11}$.
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\geq \frac {10}{11}$.
(2) ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1(E)}\geq \frac {79}{220}$. In this case, we consider the line
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1(E)}\geq \frac {79}{220}$. In this case, we consider the line ![]() $y=\frac {79}{220}x$ and the parabola
$y=\frac {79}{220}x$ and the parabola ![]() $y=\frac {5}{8}x^2-\frac {1}{8}$. They intersect at
$y=\frac {5}{8}x^2-\frac {1}{8}$. They intersect at ![]() $x=\frac {79-3\sqrt {2,374}}{275}>-\frac {1}{4}$. Then we know that in this region, we always have
$x=\frac {79-3\sqrt {2,374}}{275}>-\frac {1}{4}$. Then we know that in this region, we always have
 $$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_2(\tilde{E})}{H^3\mathop{\mathrm{rk}}(\tilde{E})}\leq-\frac{9}{32}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathop{\mathrm{rk}}(\tilde{E})}-\frac{5}{32}.\end{align*} $$
$$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_2(\tilde{E})}{H^3\mathop{\mathrm{rk}}(\tilde{E})}\leq-\frac{9}{32}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathop{\mathrm{rk}}(\tilde{E})}-\frac{5}{32}.\end{align*} $$By a similar calculation as above, we have
and thus we have
 $$ \begin{align} Q_{0,0}&\geq4(H\mathop{\mathrm{ch}}\nolimits_2(E))^2-6(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(\mathop{\mathrm{rk}}(E))+\frac{43}{20}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-\frac{24}{5}(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\notag\\ &=\frac{4}{5}(\frac{3}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^3\mathop{\mathrm{rk}}(E))-(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))) \end{align} $$
$$ \begin{align} Q_{0,0}&\geq4(H\mathop{\mathrm{ch}}\nolimits_2(E))^2-6(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(\mathop{\mathrm{rk}}(E))+\frac{43}{20}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-\frac{24}{5}(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^2\mathop{\mathrm{ch}}\nolimits_1(E))\notag\\ &=\frac{4}{5}(\frac{3}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^3\mathop{\mathrm{rk}}(E))-(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))) \end{align} $$The first term (3.3) is nonnegative since by Theorem 5.5 we have
and
 $$ \begin{align*} &\frac{3}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^3\mathop{\mathrm{rk}}(E))-(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))\\ & \quad -(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2+(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^3\mathop{\mathrm{rk}}(E))+\frac{1}{2}(H^3\mathop{\mathrm{rk}}(E))^2\\ & \quad =\frac{1}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E)-H^3\mathop{\mathrm{rk}}(E))^2\geq0. \end{align*} $$
$$ \begin{align*} &\frac{3}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2-(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^3\mathop{\mathrm{rk}}(E))-(H^2\mathop{\mathrm{ch}}\nolimits_1(E))(H^3\mathop{\mathrm{rk}}(E))\\ & \quad -(H^2\mathop{\mathrm{ch}}\nolimits_1(E))^2+(H\mathop{\mathrm{ch}}\nolimits_2(E))(H^3\mathop{\mathrm{rk}}(E))+\frac{1}{2}(H^3\mathop{\mathrm{rk}}(E))^2\\ & \quad =\frac{1}{2}(H^2\mathop{\mathrm{ch}}\nolimits_1(E)-H^3\mathop{\mathrm{rk}}(E))^2\geq0. \end{align*} $$ The second term (3.4) is also nonnegative because ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\leq 1$. The third term (3.5) is also nonnegative because by Theorem 5.5 we have
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(E)}{H^3\mathop {\mathrm {rk}}(E)}\leq 1$. The third term (3.5) is also nonnegative because by Theorem 5.5 we have ![]() $H\mathop {\mathrm {ch}}\nolimits _2(E)\leq \frac {21}{11}(H^2\mathop {\mathrm {ch}}\nolimits _1(E))-\frac {31}{22}(H^3\mathop {\mathrm {rk}}(E))$, and thus we have
$H\mathop {\mathrm {ch}}\nolimits _2(E)\leq \frac {21}{11}(H^2\mathop {\mathrm {ch}}\nolimits _1(E))-\frac {31}{22}(H^3\mathop {\mathrm {rk}}(E))$, and thus we have
Also, ![]() $H^2\mathop {\mathrm {ch}}\nolimits _1(E)-2H\mathop {\mathrm {ch}}\nolimits _2(E)\geq 0$ since we assumed
$H^2\mathop {\mathrm {ch}}\nolimits _1(E)-2H\mathop {\mathrm {ch}}\nolimits _2(E)\geq 0$ since we assumed ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1(E)}\leq \frac {1}{2}$ from the beginning.
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1(E)}\leq \frac {1}{2}$ from the beginning.
Thus, when ![]() $\nu _{BN}(E)\in (0,\frac {1}{2}]$, we have
$\nu _{BN}(E)\in (0,\frac {1}{2}]$, we have ![]() $Q_{0,0}(E)\geq 0$.
$Q_{0,0}(E)\geq 0$.
Next, we show the case ![]() $\nu _{BN}(E)\in [-\frac {1}{2},0)$. A direct proof like Lemma 3.4 is possible, but we follow an enlightening method in [Reference LiLi19a, Proposition 3.3] by considering the derived dual
$\nu _{BN}(E)\in [-\frac {1}{2},0)$. A direct proof like Lemma 3.4 is possible, but we follow an enlightening method in [Reference LiLi19a, Proposition 3.3] by considering the derived dual ![]() $\mathbb {D}(E):=E^*[1]$ to reduce to Lemma 3.4. First we recall the following proposition.
$\mathbb {D}(E):=E^*[1]$ to reduce to Lemma 3.4. First we recall the following proposition.
Proposition 3.5 [Reference Bayer, Macrì and TodaBMT14, Proposition 5.1.3(b)].
The derived dual ![]() $\mathbb {D}(E)$ fits into a distinguished triangle:
$\mathbb {D}(E)$ fits into a distinguished triangle:
where ![]() $\overline {E}$ is a Brill–Noether stable object and
$\overline {E}$ is a Brill–Noether stable object and ![]() $T_0$ is a torsion sheaf of dimension
$T_0$ is a torsion sheaf of dimension ![]() $0$.
$0$.
With this proposition, we can prove the inequality for negative slope.
Lemma 3.6. For a Brill–Noether stable object ![]() $E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(X)$ with
$E\in \mathop {\mathrm {Coh}}\nolimits ^{0,H}(X)$ with ![]() $\nu _{BN}(E)\in [-\frac {1}{2},0)$, we have
$\nu _{BN}(E)\in [-\frac {1}{2},0)$, we have ![]() $Q_{0,0}(E)\geq 0$.
$Q_{0,0}(E)\geq 0$.
Proof. Let ![]() $E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with
$E\in \mathrm {Coh}^{0,H}(X)$ be a Brill–Noether stable object with ![]() $\nu _{BN}(E)\in [-\frac {1}{2},0)$. Then
$\nu _{BN}(E)\in [-\frac {1}{2},0)$. Then ![]() $\mathbb {D}(E)$ fits into the distinguished triangle
$\mathbb {D}(E)$ fits into the distinguished triangle
for some Brill–Noether stable object ![]() $\overline {E}$ and some torsion sheaf
$\overline {E}$ and some torsion sheaf ![]() $T_0$ of dimension
$T_0$ of dimension ![]() $0$ by Proposition 3.5. The Chern characters are related by
$0$ by Proposition 3.5. The Chern characters are related by
Thus, we have ![]() $\nu _{BN}(\overline {E})\in (0,\frac {1}{2}]$. Thus, we have
$\nu _{BN}(\overline {E})\in (0,\frac {1}{2}]$. Thus, we have
Proof of Proposition 3.2.
The remaining case is when ![]() $\nu _{BN}(E)=H\mathop {\mathrm {ch}}\nolimits _2(E)=0$. To show this, we define the object
$\nu _{BN}(E)=H\mathop {\mathrm {ch}}\nolimits _2(E)=0$. To show this, we define the object ![]() $\tilde {E}$ to be
$\tilde {E}$ to be
If ![]() $\tilde {E}$ is
$\tilde {E}$ is ![]() $\nu _{\alpha ,0,H}$-tilt semistable for some
$\nu _{\alpha ,0,H}$-tilt semistable for some ![]() $\alpha>0$, then by Theorem 5.5 we have
$\alpha>0$, then by Theorem 5.5 we have
 $$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathop{\mathrm{rk}}(\tilde{E})}\notin(-\frac{1}{\sqrt{5}},0].\end{align*} $$
$$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(\tilde{E})}{H^3\mathop{\mathrm{rk}}(\tilde{E})}\notin(-\frac{1}{\sqrt{5}},0].\end{align*} $$This implies
Otherwise, for any ![]() $\delta>0$,
$\delta>0$, ![]() $\tilde {E}$ is destablised by some
$\tilde {E}$ is destablised by some ![]() $F_{\delta }$ when considering the
$F_{\delta }$ when considering the ![]() $\nu _{\delta ^2,\delta ,H}$-stability condition. We assume
$\nu _{\delta ^2,\delta ,H}$-stability condition. We assume ![]() $\delta $ is small enough such that E is
$\delta $ is small enough such that E is ![]() $\nu _{\delta ^2,\delta ,H}$-tilt stable because E is Brill–Noether stable. As
$\nu _{\delta ^2,\delta ,H}$-tilt stable because E is Brill–Noether stable. As ![]() $\mathop {\mathrm {Hom}}\nolimits (F_\delta ,\tilde {E})\neq 0$, we have
$\mathop {\mathrm {Hom}}\nolimits (F_\delta ,\tilde {E})\neq 0$, we have ![]() $\mathop {\mathrm {Hom}}\nolimits (F_{\delta },E)$ or
$\mathop {\mathrm {Hom}}\nolimits (F_{\delta },E)$ or ![]() $\mathop {\mathrm {Hom}}\nolimits (F_{\delta },O[1])$ is nonzero because
$\mathop {\mathrm {Hom}}\nolimits (F_{\delta },O[1])$ is nonzero because ![]() $\tilde {E}$ is the cone of them. Then we have
$\tilde {E}$ is the cone of them. Then we have ![]() $\nu _{\delta ^2,\delta ,H}(F_{\delta })\leq \nu _{\delta ^2,\delta ,H}(O[1])$ or
$\nu _{\delta ^2,\delta ,H}(F_{\delta })\leq \nu _{\delta ^2,\delta ,H}(O[1])$ or ![]() $\nu _{\delta ^2,\delta ,H}(F_{\delta })\leq \nu _{\delta ^2,\delta ,H}(E)$. By Theorem 5.5, when
$\nu _{\delta ^2,\delta ,H}(F_{\delta })\leq \nu _{\delta ^2,\delta ,H}(E)$. By Theorem 5.5, when ![]() $\delta <\frac {3}{7}$,
$\delta <\frac {3}{7}$,
This in total gives ![]() $\nu _{\delta ^2,\delta ,H}(F_{\delta })\leq \nu _{\delta ^2,\delta ,H}(O[1])=\delta .$ Note that the equality only holds when
$\nu _{\delta ^2,\delta ,H}(F_{\delta })\leq \nu _{\delta ^2,\delta ,H}(O[1])=\delta .$ Note that the equality only holds when ![]() $F_\delta =O_X[1]$ because both are stable, so we have
$F_\delta =O_X[1]$ because both are stable, so we have ![]() $\nu _{\delta ^2,\delta ,H}<\delta $. Now, assume
$\nu _{\delta ^2,\delta ,H}<\delta $. Now, assume ![]() $F_\delta $ has the largest slope among all destabilising objects. Then, by the above argument, the HN filtration for
$F_\delta $ has the largest slope among all destabilising objects. Then, by the above argument, the HN filtration for ![]() $\tilde {E}$ has factors
$\tilde {E}$ has factors ![]() $E_i$, with each slope smaller than
$E_i$, with each slope smaller than ![]() $\delta $. By the wall property, there is an
$\delta $. By the wall property, there is an ![]() $\alpha _i$ such that
$\alpha _i$ such that ![]() $E_i$ is
$E_i$ is ![]() $\nu _{\alpha _i,0,H}(E_i)$-tilt stable and
$\nu _{\alpha _i,0,H}(E_i)$-tilt stable and ![]() $\nu _{BN}(E_i)<\delta $. Then by Theorem 5.5,
$\nu _{BN}(E_i)<\delta $. Then by Theorem 5.5,
 $$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(E_i)}{H^3\mathop{\mathrm{rk}}(E_i)}\notin\left[\frac{4\delta-\sqrt{16\delta^2+5}}{5},0\right].\end{align*} $$
$$ \begin{align*}\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(E_i)}{H^3\mathop{\mathrm{rk}}(E_i)}\notin\left[\frac{4\delta-\sqrt{16\delta^2+5}}{5},0\right].\end{align*} $$As ![]() $\delta \rightarrow 0$, we have
$\delta \rightarrow 0$, we have
 $$ \begin{align*}\frac{H^3\mathop{\mathrm{rk}}(E_i)}{H^2\mathop{\mathrm{ch}}\nolimits_1(E_i)}\geq-\sqrt{5}.\end{align*} $$
$$ \begin{align*}\frac{H^3\mathop{\mathrm{rk}}(E_i)}{H^2\mathop{\mathrm{ch}}\nolimits_1(E_i)}\geq-\sqrt{5}.\end{align*} $$Thus, in any case, we have
Taking ![]() $\overline {E}\rightarrow \mathbb {D}(E)\rightarrow T_0[-1]$, we have
$\overline {E}\rightarrow \mathbb {D}(E)\rightarrow T_0[-1]$, we have
 $$ \begin{align*} \hom(O_X,E[2])&=\hom(E,O_X[1])=\hom(\mathbb{D}(O_X[1]),\mathbb{D}(E))=\hom(O_X,\mathbb{D}(E))\\ &=\hom(O_X,\overline{E})\leq\frac{\sqrt{5}}{8}H^2\mathop{\mathrm{ch}}\nolimits_1(E)-\mathop{\mathrm{rk}}(E), \end{align*} $$
$$ \begin{align*} \hom(O_X,E[2])&=\hom(E,O_X[1])=\hom(\mathbb{D}(O_X[1]),\mathbb{D}(E))=\hom(O_X,\mathbb{D}(E))\\ &=\hom(O_X,\overline{E})\leq\frac{\sqrt{5}}{8}H^2\mathop{\mathrm{ch}}\nolimits_1(E)-\mathop{\mathrm{rk}}(E), \end{align*} $$where the first equality is due to Serre duality and being Calabi–Yau, the second is due to duality, the third is straightforward, the fourth is due to the fact that ![]() $T_0$ is torsion of dimension
$T_0$ is torsion of dimension ![]() $0$ and the inequality is due to
$0$ and the inequality is due to ![]() $\overline {E}$ being Brill–Noether stable.
$\overline {E}$ being Brill–Noether stable.
Thus, by HRR, we have
This implies ![]() $\mathop {\mathrm {ch}}\nolimits _3(E)<0$, and we are done.
$\mathop {\mathrm {ch}}\nolimits _3(E)<0$, and we are done.
4 Clifford type inequality for curves  $X_{2,2,2,4}$
$X_{2,2,2,4}$
4.1 Bound for the wall
Let ![]() $C:=X_{2,2,2,4}\subset X_{2,2,4}\subset X_{2,4}\subset \mathbb {P}^5$ be the curve of generic smooth complete intersection of X with two quadratic hypersurfaces. By the adjunction formula, we know that the canonical bundle of C is
$C:=X_{2,2,2,4}\subset X_{2,2,4}\subset X_{2,4}\subset \mathbb {P}^5$ be the curve of generic smooth complete intersection of X with two quadratic hypersurfaces. By the adjunction formula, we know that the canonical bundle of C is ![]() $O_C((-6+2+2+2+4)H)=O_C(4H)$. Then the degree of the canonical bundle is
$O_C((-6+2+2+2+4)H)=O_C(4H)$. Then the degree of the canonical bundle is ![]() $\deg (O_C(4H))=4*2*2*2*4=128$, and thus the genus is
$\deg (O_C(4H))=4*2*2*2*4=128$, and thus the genus is ![]() $g=65$ by the formula
$g=65$ by the formula ![]() $2g-2=\deg (O_C(4H))$. Let
$2g-2=\deg (O_C(4H))$. Let ![]() $S:=X_{2,2,2}$ be a general K3 surface given as the complete intersection of three quadratic hypersurfaces containing this curve of Picard number 1, with three quadratic hypersurfaces coming from the complete intersection that gave us C, and let
$S:=X_{2,2,2}$ be a general K3 surface given as the complete intersection of three quadratic hypersurfaces containing this curve of Picard number 1, with three quadratic hypersurfaces coming from the complete intersection that gave us C, and let ![]() $\imath :C\rightarrow S$ be the embedding. Such a pair
$\imath :C\rightarrow S$ be the embedding. Such a pair ![]() $(C,S)$ always exists by [Reference Ravindra and SrinivasRS09, Theorem 1]. Let E be a slope semistable vector bundle on C with rank r and degree d. Then for sufficiently large
$(C,S)$ always exists by [Reference Ravindra and SrinivasRS09, Theorem 1]. Let E be a slope semistable vector bundle on C with rank r and degree d. Then for sufficiently large ![]() $\alpha $, the object
$\alpha $, the object ![]() $\imath _*E$ is a
$\imath _*E$ is a ![]() $\sigma _{\alpha ,0,H}$-semistable object ([Reference MaciociaMac14a, Theorem 3.11]). We would like to detect its first wall. Suppose the first wall intersects
$\sigma _{\alpha ,0,H}$-semistable object ([Reference MaciociaMac14a, Theorem 3.11]). We would like to detect its first wall. Suppose the first wall intersects ![]() $\Gamma $ at
$\Gamma $ at ![]() $(\beta _1,\Gamma (\beta _1))$ and
$(\beta _1,\Gamma (\beta _1))$ and ![]() $(\beta _2,\Gamma (\beta _2))$ (or the vertical line segments in Proposition 2.10
$(\beta _2,\Gamma (\beta _2))$ (or the vertical line segments in Proposition 2.10 ![]() $(\beta _1,\alpha _1),(\beta _2,\alpha _2)$), where
$(\beta _1,\alpha _1),(\beta _2,\alpha _2)$), where ![]() $\beta _1<\beta _2$. By Grothendieck–Riemann–Roch, we have
$\beta _1<\beta _2$. By Grothendieck–Riemann–Roch, we have
We use ![]() $\mu $ to denote the slope of E on C. In this case, the curve
$\mu $ to denote the slope of E on C. In this case, the curve ![]() $\Gamma $ (Figure 1) is
$\Gamma $ (Figure 1) is
 $$ \begin{align*} \Gamma(x)= \begin{cases} 4x^2-1+(x-n)^2 & \text{if }x\in[n-\frac{1}{2},n)\cup(n,n+\frac{1}{2}], n\in\mathbb{Z}\\ 4x^2 & \text{if }x\in\mathbb{Z}. \end{cases} \end{align*} $$
$$ \begin{align*} \Gamma(x)= \begin{cases} 4x^2-1+(x-n)^2 & \text{if }x\in[n-\frac{1}{2},n)\cup(n,n+\frac{1}{2}], n\in\mathbb{Z}\\ 4x^2 & \text{if }x\in\mathbb{Z}. \end{cases} \end{align*} $$
Figure 1 The ![]() $\Gamma $ curve (blue) intersects with positive slope line (red) and negative slope line (green).
$\Gamma $ curve (blue) intersects with positive slope line (red) and negative slope line (green).
Lemma 4.1. When ![]() $\mu \in [0,64]$, we have
$\mu \in [0,64]$, we have
1. When
 $\mu \in [0,\frac {256}{3}-\frac {32\sqrt {61}}{3})$, the object
$\mu \in [0,\frac {256}{3}-\frac {32\sqrt {61}}{3})$, the object  $\imath _*E$ is Brill–Noether semistable.
$\imath _*E$ is Brill–Noether semistable.2. When
 $\mu \in [31,32]$, then we have
$\mu \in [31,32]$, then we have  $$ \begin{align*}\beta_1\geq\frac{\mu}{32}-4\;\;\text{and}\;\;\beta_2\leq1.\end{align*} $$
$$ \begin{align*}\beta_1\geq\frac{\mu}{32}-4\;\;\text{and}\;\;\beta_2\leq1.\end{align*} $$3. When
 $\mu \in [32,33]$, then we have
$\mu \in [32,33]$, then we have  $$ \begin{align*}\beta_1\geq -3\;\;\text{and}\;\;\beta_2\leq\frac{\mu}{32}.\end{align*} $$
$$ \begin{align*}\beta_1\geq -3\;\;\text{and}\;\;\beta_2\leq\frac{\mu}{32}.\end{align*} $$4. When
 $\mu \in [63,64]$, then we have
$\mu \in [63,64]$, then we have  $$ \begin{align*}\beta_1\geq \frac{\mu}{32}-4\;\;\text{and}\;\;\beta_2\leq2.\end{align*} $$
$$ \begin{align*}\beta_1\geq \frac{\mu}{32}-4\;\;\text{and}\;\;\beta_2\leq2.\end{align*} $$5. Otherwise, we have
 $$ \begin{align*}\beta_1\geq\frac{\mu}{32}-4,\;\;\text{and}\;\; \beta_2\leq\frac{\mu}{32}.\end{align*} $$
$$ \begin{align*}\beta_1\geq\frac{\mu}{32}-4,\;\;\text{and}\;\; \beta_2\leq\frac{\mu}{32}.\end{align*} $$
Proof. The proof is similar to the proof of [Reference Feyzbakhsh and LiFL21, Lemma 3.1] and [Reference LiLi19a, Lemma 4.10]. On the wall, there is a destablising sequence ![]() $0\rightarrow F_2\rightarrow \imath _*E\rightarrow F_1\rightarrow 0.$ This sequence actually happens in the heart
$0\rightarrow F_2\rightarrow \imath _*E\rightarrow F_1\rightarrow 0.$ This sequence actually happens in the heart ![]() $\mathop {\mathrm {Coh}}\nolimits ^0(S)$. Thus, we have the following long exact sequence for cohomology sheaves:
$\mathop {\mathrm {Coh}}\nolimits ^0(S)$. Thus, we have the following long exact sequence for cohomology sheaves:
The left side is ![]() $0$ since
$0$ since ![]() $H^{-1}(\imath _*E)=0$. Now, we have two cases:
$H^{-1}(\imath _*E)=0$. Now, we have two cases: ![]() $s=0$ or
$s=0$ or ![]() $s\neq 0$.
$s\neq 0$.
Suppose ![]() $s=0$. Then
$s=0$. Then ![]() $H^{-1}(F_1)=0$ because this term is torsion-free. Since
$H^{-1}(F_1)=0$ because this term is torsion-free. Since ![]() $\imath _*E$ is supported on C, the other two supports are contained in C. Since
$\imath _*E$ is supported on C, the other two supports are contained in C. Since ![]() $F_2$ destablises
$F_2$ destablises ![]() $\imath _*E$,
$\imath _*E$, ![]() $F_2$ and
$F_2$ and ![]() $\imath _*E$ have the same tilt slope. Thus, we get
$\imath _*E$ have the same tilt slope. Thus, we get ![]() $\mathop {\mathrm {ch}}\nolimits (F_2)=k\mathop {\mathrm {ch}}\nolimits (\imath _*E)$, which contradicts the destabilising sequence being on the first wall. So this case cannot happen.
$\mathop {\mathrm {ch}}\nolimits (F_2)=k\mathop {\mathrm {ch}}\nolimits (\imath _*E)$, which contradicts the destabilising sequence being on the first wall. So this case cannot happen.
Suppose ![]() $s\neq 0$. Let
$s\neq 0$. Let ![]() $T(F_2)$ be the maximal torsion subsheaf of
$T(F_2)$ be the maximal torsion subsheaf of ![]() $F_2$. Suppose
$F_2$. Suppose ![]() $\mathop {\mathrm {ch}}\nolimits _1(T(F_2))=4tH$. Since E is of rank r, we have
$\mathop {\mathrm {ch}}\nolimits _1(T(F_2))=4tH$. Since E is of rank r, we have
From this, we get the following inequality:
By Proposition 2.10, we have ![]() $F_1$ is semistable with the same slope as
$F_1$ is semistable with the same slope as ![]() $\imath _*E$ on the wall. In particular, if
$\imath _*E$ on the wall. In particular, if ![]() $-4<\beta _1$, it is in the heart
$-4<\beta _1$, it is in the heart ![]() $\mathrm {Coh}^{\beta _1+\epsilon }$ when
$\mathrm {Coh}^{\beta _1+\epsilon }$ when ![]() $\epsilon \rightarrow 0^+$. Thus,
$\epsilon \rightarrow 0^+$. Thus,
Thus,
Suppose ![]() $\beta _1\leq -4$, then
$\beta _1\leq -4$, then ![]() $\frac {d_1}{s}\leq -4$, and thus
$\frac {d_1}{s}\leq -4$, and thus
This contradicts the assumption that ![]() $F_2/T(F_2)\in \mathop {\mathrm {Coh}}\nolimits ^0(S)$.
$F_2/T(F_2)\in \mathop {\mathrm {Coh}}\nolimits ^0(S)$.
On the other hand, by Proposition 2.10, we know that
Thus, we have that
Also, by Proposition 2.10, we know that the wall needs to have slope of ![]() $\frac {\mu }{4}-16$ by the Chern character of
$\frac {\mu }{4}-16$ by the Chern character of ![]() $\imath _*E$. However, there are two separate cases we need to consider here, where the first case is that the wall ends on
$\imath _*E$. However, there are two separate cases we need to consider here, where the first case is that the wall ends on ![]() $\Gamma $, and the second case is the wall ends at the vertical line segment from
$\Gamma $, and the second case is the wall ends at the vertical line segment from ![]() $(n,\frac {H^2}{2}n^2)$ to
$(n,\frac {H^2}{2}n^2)$ to ![]() $\left (n,\frac {H^2}{2}n^2-1\right )$. Since we want to detect the largest range of the wall, the maximum can happen when
$\left (n,\frac {H^2}{2}n^2-1\right )$. Since we want to detect the largest range of the wall, the maximum can happen when ![]() $\beta _2-\beta _1=4$. Therefore, from now on we assume that
$\beta _2-\beta _1=4$. Therefore, from now on we assume that ![]() $\beta _2-\beta _1$ is equal to
$\beta _2-\beta _1$ is equal to ![]() $4$.
$4$.
Case 1. The object ![]() $\imath _*E$ is Brill–Noether semistable. In this case, the line l intersects the y-axis below zero, where the line l is the line with slope
$\imath _*E$ is Brill–Noether semistable. In this case, the line l intersects the y-axis below zero, where the line l is the line with slope
 $$ \begin{align*}\frac{\Gamma(\beta_2)-\Gamma(\beta_1)}{\beta_2-\beta_1}=\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(\imath_*E)}{H\mathop{\mathrm{ch}}\nolimits_1(\imath_*E)}=\frac{\mu}{4}-16\end{align*} $$
$$ \begin{align*}\frac{\Gamma(\beta_2)-\Gamma(\beta_1)}{\beta_2-\beta_1}=\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(\imath_*E)}{H\mathop{\mathrm{ch}}\nolimits_1(\imath_*E)}=\frac{\mu}{4}-16\end{align*} $$and intersecting the curve at ![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2=\beta _1+4$. Then, similar to the case 2 below, we have that the line intersects
$\beta _2=\beta _1+4$. Then, similar to the case 2 below, we have that the line intersects ![]() $\Gamma $ at
$\Gamma $ at ![]() $\beta _2=\frac {\mu }{32}$ and
$\beta _2=\frac {\mu }{32}$ and ![]() $\beta _1=\frac {\mu }{32}-4$. As the slope is small in this case, we can assume
$\beta _1=\frac {\mu }{32}-4$. As the slope is small in this case, we can assume ![]() $\Gamma (x)=5x^2-1$ near
$\Gamma (x)=5x^2-1$ near ![]() $\beta _2$. Then the intersection point with the y-axis is
$\beta _2$. Then the intersection point with the y-axis is
and the requirement for ![]() $\mu $ is
$\mu $ is ![]() $t<0$, which is equivalent to
$t<0$, which is equivalent to ![]() $\mu \in [0,\frac {256}{3}-\frac {32\sqrt {61}}{3})$.
$\mu \in [0,\frac {256}{3}-\frac {32\sqrt {61}}{3})$.
Case 2. The end point is on ![]() $\Gamma $. Then we have
$\Gamma $. Then we have
 $$ \begin{align*}\frac{\Gamma(\beta_2)-\Gamma(\beta_1)}{\beta_2-\beta_1}=\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(\imath_*E)}{H\mathop{\mathrm{ch}}\nolimits_1(\imath_*E)}=\frac{\mu}{4}-16.\end{align*} $$
$$ \begin{align*}\frac{\Gamma(\beta_2)-\Gamma(\beta_1)}{\beta_2-\beta_1}=\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(\imath_*E)}{H\mathop{\mathrm{ch}}\nolimits_1(\imath_*E)}=\frac{\mu}{4}-16.\end{align*} $$Substituting ![]() $\beta _2=\beta _1+4$ and the equation of
$\beta _2=\beta _1+4$ and the equation of ![]() $\Gamma $, we have
$\Gamma $, we have
This quantity is equal to
Thus, ![]() $\beta _2=\frac {\mu }{32}$, and
$\beta _2=\frac {\mu }{32}$, and ![]() $\beta _1=\frac {\mu }{32}-4$.
$\beta _1=\frac {\mu }{32}-4$.
Case 3. The end point is on the vertical line segment from ![]() $(n,\frac {H^2}{2}n^2)$ to
$(n,\frac {H^2}{2}n^2)$ to ![]() $\left (n,\frac {H^2}{2}n^2-1\right )$. First, one notices that the slope is always negative in the range that we are considering. So the special endpoints happen when both endpoints touch the vertical wall. So we just pick
$\left (n,\frac {H^2}{2}n^2-1\right )$. First, one notices that the slope is always negative in the range that we are considering. So the special endpoints happen when both endpoints touch the vertical wall. So we just pick ![]() $\beta _1=-n$, and the endpoint has a vertical value of
$\beta _1=-n$, and the endpoint has a vertical value of ![]() $4n^2$. The corresponding
$4n^2$. The corresponding ![]() $\beta _2$ is
$\beta _2$ is ![]() $-n+4$, and the vertical minimum value is
$-n+4$, and the vertical minimum value is ![]() $4(4-n)^2-1$. By a direct calculation, we get
$4(4-n)^2-1$. By a direct calculation, we get
4.2 Upper bound of global sections
An upper bound for the global sections of semistable objects on K3 surfaces is already known in [Reference FeyzbakhshFey20]. However, we need to produce a better bound to get our final result. We will see that in some regions the two results coincide. The idea here is that we consider proper spherical twist of the object. The spherical twist of the object is semistable with respect to some generic stability condition ![]() $\sigma _{\alpha ,\beta }$ (refer to the proof of Proposition 4.3), and thus the Chern characters need to lie under the curve
$\sigma _{\alpha ,\beta }$ (refer to the proof of Proposition 4.3), and thus the Chern characters need to lie under the curve ![]() $\Gamma $. Let S be the K3 surface we mentioned at the beginning of this section, which is the complete intersection of three quadratic hypersurfaces. The following proposition is essential to the calculation.
$\Gamma $. Let S be the K3 surface we mentioned at the beginning of this section, which is the complete intersection of three quadratic hypersurfaces. The following proposition is essential to the calculation.
Proposition 4.2 [Reference FeyzbakhshFey20, Proposition 3.4].
Let X be a K3 surface. Let ![]() $E\in \mathrm {Coh}^{0,H}(X)$, then there exists
$E\in \mathrm {Coh}^{0,H}(X)$, then there exists ![]() $\epsilon>0$ such that the HN filtration for E is the same sequence with respect to all
$\epsilon>0$ such that the HN filtration for E is the same sequence with respect to all ![]() $\sigma _{\alpha ,0,H}$ for
$\sigma _{\alpha ,0,H}$ for ![]() $0<\alpha <\epsilon $ and is denoted by
$0<\alpha <\epsilon $ and is denoted by
Proposition 4.3. Let F be a ![]() $\nu _{BN}$-semistable object in
$\nu _{BN}$-semistable object in ![]() $\mathop {\mathrm {Coh}}\nolimits ^{0,H}(S)$. Then we have
$\mathop {\mathrm {Coh}}\nolimits ^{0,H}(S)$. Then we have
 $$ \begin{align} \hom(\mathcal{O}_S,F)\leq \begin{cases} \mathop{\mathrm{rk}}(F)+\frac{2}{3}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}+\frac{7}{6}\mathop{\mathrm{ch}}\nolimits_2(F)\\ -\frac{1}{6}\sqrt{\left(4\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}+\mathop{\mathrm{ch}}\nolimits_2(F)\right)^2-60\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} &\text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[\frac{11}{2},\frac{15}{2})\cup(8,\frac{97}{10}]\\ \mathop{\mathrm{rk}}(F)+\mathop{\mathrm{ch}}\nolimits_2(F)+\frac{5(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{8(H^2\mathop{\mathrm{ch}}\nolimits_2(F)+2H\mathop{\mathrm{ch}}\nolimits_1(F))} &\text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[\frac{1}{2},3)\cup(4,\frac{11}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{2}+\frac{1}{2}\sqrt{\mathop{\mathrm{ch}}\nolimits_2(F)^2+20\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{1}{2},\frac{1}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{5(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{H^2(2H\mathop{\mathrm{ch}}\nolimits_1(F)-H^2\mathop{\mathrm{ch}}\nolimits_2(F))} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{11}{2},-4)\cup(-3,-\frac{1}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{2}{3}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{1}{6}\mathop{\mathrm{ch}}\nolimits_2(F)\\-\frac{1}{6}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-4\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-60\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{97}{10},-8)\cup(-\frac{15}{2},-\frac{11}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{3}{8}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{16}\\ -\frac{1}{16}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-6\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-160\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{193}{14},-12)\cup(-\frac{35}{3},-\frac{97}{10}]\\ \mathop{\mathrm{rk}}(F)+\frac{4}{15}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{30}\\ -\frac{1}{30}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-8\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-300\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in [-\frac{107}{6},-16)\cup(-\frac{63}{4},-\frac{193}{14}]\\ \mathop{\mathrm{rk}}(F)-\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{16\mathop{\mathrm{ch}}\nolimits_2(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-4n,\frac{1-4n^2}{n}]\text{ and }n\in\mathbb{Z}_{>0} \\ \mathop{\mathrm{rk}}(F)+\mathop{\mathrm{ch}}\nolimits_2(F)+\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{16\mathop{\mathrm{ch}}\nolimits_2(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[\frac{4n^2-1}{n},4n]\text{ and }n\in\mathbb{Z}_{>0}. \end{cases} \end{align} $$
$$ \begin{align} \hom(\mathcal{O}_S,F)\leq \begin{cases} \mathop{\mathrm{rk}}(F)+\frac{2}{3}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}+\frac{7}{6}\mathop{\mathrm{ch}}\nolimits_2(F)\\ -\frac{1}{6}\sqrt{\left(4\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}+\mathop{\mathrm{ch}}\nolimits_2(F)\right)^2-60\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} &\text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[\frac{11}{2},\frac{15}{2})\cup(8,\frac{97}{10}]\\ \mathop{\mathrm{rk}}(F)+\mathop{\mathrm{ch}}\nolimits_2(F)+\frac{5(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{8(H^2\mathop{\mathrm{ch}}\nolimits_2(F)+2H\mathop{\mathrm{ch}}\nolimits_1(F))} &\text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[\frac{1}{2},3)\cup(4,\frac{11}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{2}+\frac{1}{2}\sqrt{\mathop{\mathrm{ch}}\nolimits_2(F)^2+20\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{1}{2},\frac{1}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{5(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{H^2(2H\mathop{\mathrm{ch}}\nolimits_1(F)-H^2\mathop{\mathrm{ch}}\nolimits_2(F))} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{11}{2},-4)\cup(-3,-\frac{1}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{2}{3}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{1}{6}\mathop{\mathrm{ch}}\nolimits_2(F)\\-\frac{1}{6}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-4\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-60\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if }\frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{97}{10},-8)\cup(-\frac{15}{2},-\frac{11}{2}]\\ \mathop{\mathrm{rk}}(F)+\frac{3}{8}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{16}\\ -\frac{1}{16}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-6\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-160\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-\frac{193}{14},-12)\cup(-\frac{35}{3},-\frac{97}{10}]\\ \mathop{\mathrm{rk}}(F)+\frac{4}{15}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{30}\\ -\frac{1}{30}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-8\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-300\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in [-\frac{107}{6},-16)\cup(-\frac{63}{4},-\frac{193}{14}]\\ \mathop{\mathrm{rk}}(F)-\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{16\mathop{\mathrm{ch}}\nolimits_2(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[-4n,\frac{1-4n^2}{n}]\text{ and }n\in\mathbb{Z}_{>0} \\ \mathop{\mathrm{rk}}(F)+\mathop{\mathrm{ch}}\nolimits_2(F)+\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{16\mathop{\mathrm{ch}}\nolimits_2(F)} & \text{if } \frac{H^2\mathop{\mathrm{ch}}\nolimits_2(F)}{H\mathop{\mathrm{ch}}\nolimits_1(F)}\in[\frac{4n^2-1}{n},4n]\text{ and }n\in\mathbb{Z}_{>0}. \end{cases} \end{align} $$Proof. The proof is divided into three parts, depending on the sign of ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$ and whether it is close to
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$ and whether it is close to ![]() $4n$ for some integer n.
$4n$ for some integer n.
First case. When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}>0$, and it is not inside
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}>0$, and it is not inside ![]() $[\frac {4n^2-1}{n},4n]$, we have
$[\frac {4n^2-1}{n},4n]$, we have ![]() $\nu _{BN}(O_S[1])=+\infty $. Thus,
$\nu _{BN}(O_S[1])=+\infty $. Thus,
for ![]() $i\geq 0$. On the other hand, there exists some
$i\geq 0$. On the other hand, there exists some ![]() $(\alpha ,\beta )$ on the line through
$(\alpha ,\beta )$ on the line through ![]() $0$ and
$0$ and ![]() $pr(F)$ such that
$pr(F)$ such that ![]() $\alpha>\Gamma (\beta )$. Thus,
$\alpha>\Gamma (\beta )$. Thus,
for ![]() $i\geq 0$ because
$i\geq 0$ because ![]() $O_S[1]$ and F both are
$O_S[1]$ and F both are ![]() $\sigma _{\alpha ,\beta }$-semistable of same slope by the nesting wall theorem. Thus, we have
$\sigma _{\alpha ,\beta }$-semistable of same slope by the nesting wall theorem. Thus, we have
We consider the object
Then ![]() $\tilde {F}$ is
$\tilde {F}$ is ![]() $\sigma _{\alpha ,\beta }$-semistable for
$\sigma _{\alpha ,\beta }$-semistable for ![]() $\beta <0$. We claim that
$\beta <0$. We claim that ![]() $pr(\tilde {F})$ is below the curve
$pr(\tilde {F})$ is below the curve ![]() $\Gamma $. Otherwise, suppose
$\Gamma $. Otherwise, suppose ![]() $pr(\tilde {F})$ is not below the curve
$pr(\tilde {F})$ is not below the curve ![]() $\Gamma $. Consider the HN factors
$\Gamma $. Consider the HN factors ![]() $F_i$ of
$F_i$ of ![]() $\tilde {F}$ with respect to
$\tilde {F}$ with respect to ![]() $\sigma _{\alpha ,\beta }$. Then by Lemma 2.16, the
$\sigma _{\alpha ,\beta }$. Then by Lemma 2.16, the ![]() $pr(F_i)$ are on the line passing through
$pr(F_i)$ are on the line passing through ![]() $(\alpha ,\beta )$ and
$(\alpha ,\beta )$ and ![]() $\tilde {F}$. As the segment of this line above
$\tilde {F}$. As the segment of this line above ![]() $\Gamma $ is convex, there is at least one HN factor
$\Gamma $ is convex, there is at least one HN factor ![]() $F_j$ is above
$F_j$ is above ![]() $\Gamma $. However, by Proposition 2.11,
$\Gamma $. However, by Proposition 2.11, ![]() $F_j$ cannot lie above the curve
$F_j$ cannot lie above the curve ![]() $\Gamma $. So the point
$\Gamma $. So the point ![]() $pr(\tilde {F})$ is below the curve
$pr(\tilde {F})$ is below the curve ![]() $\Gamma $. We consider the line passing through
$\Gamma $. We consider the line passing through ![]() $0$ with slope k (Figure 1), where
$0$ with slope k (Figure 1), where ![]() $k=\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$. Then it is obvious that
$k=\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$. Then it is obvious that ![]() $pr(O[1])$,
$pr(O[1])$, ![]() $pr(F)$, and
$pr(F)$, and ![]() $pr(\tilde {F}[1])$ are on this line. Let
$pr(\tilde {F}[1])$ are on this line. Let ![]() $x_0$ be the intersection point of the line with
$x_0$ be the intersection point of the line with ![]() $\Gamma $. Depending on the slope, we can solve
$\Gamma $. Depending on the slope, we can solve ![]() $x_0$ explicitly.
$x_0$ explicitly.
When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [\frac {11}{2},\frac {15}{2})\cup (8,\frac {97}{10}]$, we have
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [\frac {11}{2},\frac {15}{2})\cup (8,\frac {97}{10}]$, we have ![]() $\Gamma (x)=5x^2-4x+3$. By solving the intersection equation with the line, we have
$\Gamma (x)=5x^2-4x+3$. By solving the intersection equation with the line, we have
 $$ \begin{align*}x_0=\frac{4+k+\sqrt{((4+k)^2-60)}}{10}.\end{align*} $$
$$ \begin{align*}x_0=\frac{4+k+\sqrt{((4+k)^2-60)}}{10}.\end{align*} $$Thus, since ![]() $p_H(\tilde {F}[1])$ is below
$p_H(\tilde {F}[1])$ is below ![]() $\Gamma $, we have
$\Gamma $, we have
 $$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_1(\tilde{F}[1])}{H^2\mathop{\mathrm{rk}}(\tilde{F}[1])}\geq x_0.\end{align*} $$
$$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_1(\tilde{F}[1])}{H^2\mathop{\mathrm{rk}}(\tilde{F}[1])}\geq x_0.\end{align*} $$(The case ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(\tilde {F}[1])}{H^2\mathop {\mathrm {rk}}(\tilde {F}[1])}<0$ is also contained in this case.) Here,
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(\tilde {F}[1])}{H^2\mathop {\mathrm {rk}}(\tilde {F}[1])}<0$ is also contained in this case.) Here, ![]() $\mathop {\mathrm {ch}}\nolimits _1(\tilde {F}[1])=-\mathop {\mathrm {ch}}\nolimits _1(\tilde {F})$,
$\mathop {\mathrm {ch}}\nolimits _1(\tilde {F}[1])=-\mathop {\mathrm {ch}}\nolimits _1(\tilde {F})$, ![]() $\mathop {\mathrm {rk}}(\tilde {F}[1])=-\mathop {\mathrm {rk}}(\tilde {F})$ and
$\mathop {\mathrm {rk}}(\tilde {F}[1])=-\mathop {\mathrm {rk}}(\tilde {F})$ and ![]() $\mathop {\mathrm {rk}}(\tilde {F})=\hom (O_S,F[1])+\mathop {\mathrm {rk}}(F)>0$. This implies that
$\mathop {\mathrm {rk}}(\tilde {F})=\hom (O_S,F[1])+\mathop {\mathrm {rk}}(F)>0$. This implies that
and considering this with
we get the conclusion.
When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [\frac {1}{2},3)\cup (4,\frac {11}{2}]$, we use the same calculation method with
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [\frac {1}{2},3)\cup (4,\frac {11}{2}]$, we use the same calculation method with ![]() $\Gamma (x)=5x^2-2x$ and we get the conclusion.
$\Gamma (x)=5x^2-2x$ and we get the conclusion.
Second case. When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}<0$ and it is not inside
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}<0$ and it is not inside ![]() $[-4n,\frac {1-4n^2}{n}]$, we know that there exist some
$[-4n,\frac {1-4n^2}{n}]$, we know that there exist some ![]() $(\alpha ,\beta )$ on the line through
$(\alpha ,\beta )$ on the line through ![]() $0$ and
$0$ and ![]() $pr(F)$ with
$pr(F)$ with ![]() $\alpha>\Gamma (\beta )$ and by nesting wall theorem,
$\alpha>\Gamma (\beta )$ and by nesting wall theorem, ![]() $O[1]$ and F are
$O[1]$ and F are ![]() $\sigma _{\alpha ,\beta }$-semistable. If we consider
$\sigma _{\alpha ,\beta }$-semistable. If we consider
we get that ![]() $\tilde {F}$ is
$\tilde {F}$ is ![]() $\sigma _{\alpha ,\beta }$-semistable for
$\sigma _{\alpha ,\beta }$-semistable for ![]() $\beta>0$. By a similar argument to the first case, we know that the reduced character
$\beta>0$. By a similar argument to the first case, we know that the reduced character ![]() $pr(\tilde {F})$ is below the curve
$pr(\tilde {F})$ is below the curve ![]() $\Gamma $. Consider the line passing through
$\Gamma $. Consider the line passing through ![]() $0$ and
$0$ and ![]() $pr(F)$ (Figure 1). Then
$pr(F)$ (Figure 1). Then ![]() $pr(\tilde {F})$ is on the same line. Let
$pr(\tilde {F})$ is on the same line. Let ![]() $x_1$ be the intersection of the line and
$x_1$ be the intersection of the line and ![]() $\Gamma $ on the left-hand side. We can solve
$\Gamma $ on the left-hand side. We can solve ![]() $x_1$ explicitly depending on the slope of the line.
$x_1$ explicitly depending on the slope of the line.
When ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [-\frac {107}{6},-16)\cup (-\frac {63}{4},-\frac {193}{14}]$, let the line be
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [-\frac {107}{6},-16)\cup (-\frac {63}{4},-\frac {193}{14}]$, let the line be ![]() $y=kx$, where
$y=kx$, where ![]() $k=\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$. Recall that when
$k=\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$. Recall that when ![]() $x\in [n-\frac {1}{2},n+\frac {1}{2}]$, the curve
$x\in [n-\frac {1}{2},n+\frac {1}{2}]$, the curve ![]() $\Gamma $ has the form
$\Gamma $ has the form
 $$ \begin{align*} \Gamma(x)= \begin{cases} 4x^2-1+(x-n)^2 & \text{if }x\neq n\\ 4x^2 & \text{if }x=n. \end{cases} \end{align*} $$
$$ \begin{align*} \Gamma(x)= \begin{cases} 4x^2-1+(x-n)^2 & \text{if }x\neq n\\ 4x^2 & \text{if }x=n. \end{cases} \end{align*} $$Then by solving the equation, we get
 $$ \begin{align*}x_1=\frac{k-8-\sqrt{(8-k)^2-300}}{10}.\end{align*} $$
$$ \begin{align*}x_1=\frac{k-8-\sqrt{(8-k)^2-300}}{10}.\end{align*} $$Then we have the requirement that
 $$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_1(\tilde{F})}{H^2\mathop{\mathrm{rk}}(\tilde{F})}\leq x_1.\end{align*} $$
$$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_1(\tilde{F})}{H^2\mathop{\mathrm{rk}}(\tilde{F})}\leq x_1.\end{align*} $$This in turn tells us that
 $$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_1(\tilde{F})}{H^2x_1}\leq \mathop{\mathrm{rk}}(\tilde{F})=\mathop{\mathrm{rk}}(F)-\hom(O_S,F),\end{align*} $$
$$ \begin{align*}\frac{H\mathop{\mathrm{ch}}\nolimits_1(\tilde{F})}{H^2x_1}\leq \mathop{\mathrm{rk}}(\tilde{F})=\mathop{\mathrm{rk}}(F)-\hom(O_S,F),\end{align*} $$and then this gives
 $$ \begin{align*}\hom(O_S,F)\leq \mathop{\mathrm{rk}}(F)+\frac{4}{15}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{30}-\frac{1}{30}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-8\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-300\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2}.\end{align*} $$
$$ \begin{align*}\hom(O_S,F)\leq \mathop{\mathrm{rk}}(F)+\frac{4}{15}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}-\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{30}-\frac{1}{30}\sqrt{\left(\mathop{\mathrm{ch}}\nolimits_2(F)-8\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2-300\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2}\right)^2}.\end{align*} $$ For ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$ inside the other range, a similar calculation is done with the appropriate expression for
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}$ inside the other range, a similar calculation is done with the appropriate expression for ![]() $\Gamma $ used.
$\Gamma $ used.
Third case. When the slope ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [-4n,\frac {1-4n^2}{n}]$ or
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}\in [-4n,\frac {1-4n^2}{n}]$ or ![]() $[\frac {4n^2-1}{n},4n]$. In this case, we just use a proper spherical twist as above and use the Bogomolov inequality. If moreover
$[\frac {4n^2-1}{n},4n]$. In this case, we just use a proper spherical twist as above and use the Bogomolov inequality. If moreover ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}>0$, then we consider
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}>0$, then we consider ![]() $\tilde {F}$ as in the first case. Because
$\tilde {F}$ as in the first case. Because ![]() $\tilde {F}$ is
$\tilde {F}$ is ![]() $\sigma _{\alpha ,\beta }$-semistable for some
$\sigma _{\alpha ,\beta }$-semistable for some ![]() $(\alpha ,\beta )$, we have
$(\alpha ,\beta )$, we have
hence
 $$ \begin{align*}\mathrm{ext}^1(O_S,F)\leq \mathop{\mathrm{rk}}(F)+\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{2H^2\mathop{\mathrm{ch}}\nolimits_2(F)}+\mathop{\mathrm{ch}}\nolimits_2(F).\end{align*} $$
$$ \begin{align*}\mathrm{ext}^1(O_S,F)\leq \mathop{\mathrm{rk}}(F)+\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{2H^2\mathop{\mathrm{ch}}\nolimits_2(F)}+\mathop{\mathrm{ch}}\nolimits_2(F).\end{align*} $$If ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}<0$, we consider
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _2(F)}{H\mathop {\mathrm {ch}}\nolimits _1(F)}<0$, we consider ![]() $\tilde F$ as in the second case. Because
$\tilde F$ as in the second case. Because ![]() $\tilde {F}$ is
$\tilde {F}$ is ![]() $\sigma _{\alpha ,\beta }$-semistable for some
$\sigma _{\alpha ,\beta }$-semistable for some ![]() $(\alpha ,\beta )$, we have
$(\alpha ,\beta )$, we have
 $$ \begin{align*}\implies \hom(O_S,F)\leq \mathop{\mathrm{rk}}(F)-\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{2H^2\mathop{\mathrm{ch}}\nolimits_2(F)}.\\[-36pt]\end{align*} $$
$$ \begin{align*}\implies \hom(O_S,F)\leq \mathop{\mathrm{rk}}(F)-\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{2H^2\mathop{\mathrm{ch}}\nolimits_2(F)}.\\[-36pt]\end{align*} $$Remark 4.4. We see that the bound for the range ![]() $[-\frac {1}{2},\frac {1}{2}]$ works for all other ranges. This is the same bound given by [Reference FeyzbakhshFey20].
$[-\frac {1}{2},\frac {1}{2}]$ works for all other ranges. This is the same bound given by [Reference FeyzbakhshFey20].
Next, we would like to show some kind of convexity of the above bound. Let
 $$ \begin{align} \spadesuit(x,y)= \begin{cases} \frac{2}{3}\frac{y}{H^2}+\frac{7}{6}x -\frac{1}{6}\sqrt{\left(4\frac{y}{H^2}+x\right)^2-60\left(\frac{y}{H^2}\right)^2} &\text{if } \frac{H^2x}{y}\in[\frac{11}{2},\frac{15}{2})\cup(8,\frac{97}{10}]\\ x+\frac{5y^2}{8(H^2x+2y)} &\text{if }\frac{H^2x}{y}\in[\frac{1}{2},3)\cup(4,\frac{11}{2}]\\ \frac{x}{2}+\frac{1}{2}\sqrt{x^2+20\left(\frac{y}{H^2}\right)^2} & \text{if }\frac{H^2x}{y}\in[-\frac{1}{2},\frac{1}{2}]\\ \frac{5y^2}{H^2(2y-H^2x)} & \text{if } \frac{H^2x}{y}\in[-\frac{11}{2},-4)\cup(-3,-\frac{1}{2}]\\ \frac{2}{3}\frac{y}{H^2}-\frac{1}{6}x-\frac{1}{6}\sqrt{\left(x-4\frac{y}{H^2})^2-60(\frac{y}{H^2}\right)^2} & \text{if }\frac{H^2x}{y}\in[-\frac{97}{10},-8)\cup(-\frac{15}{2},-\frac{11}{2}]\\ \frac{3}{8}\frac{y}{H^2}-\frac{x}{16}-\frac{1}{16}\sqrt{\left(x-6\frac{y}{H^2}\right)^2-160\left(\frac{y}{H^2}\right)^2} & \text{if } \frac{H^2x}{y}\in[-\frac{193}{14},-12)\cup(-\frac{35}{3},-\frac{97}{10}]\\ \frac{4}{15}\frac{y}{H^2}-\frac{x}{30}-\frac{1}{30}\sqrt{\left(x-8\frac{y}{H^2}\right)^2-300\left(\frac{y}{H^2}\right)^2} & \text{if } \frac{H^2x}{y}\in [-\frac{107}{6},-16)\cup(-\frac{63}{4},-\frac{193}{14}]\\ -\frac{y^2}{16x} & \text{if } \frac{H^2x}{y}\in[-4n,\frac{1-4n^2}{n}]\text{ and }n\in\mathbb{Z}_{>0} \\ x+\frac{y^2}{16x} & \text{if } \frac{H^2x}{y}\in[\frac{4n^2-1}{n},4n]\text{ and }n\in\mathbb{Z}_{>0}. \end{cases} \end{align} $$
$$ \begin{align} \spadesuit(x,y)= \begin{cases} \frac{2}{3}\frac{y}{H^2}+\frac{7}{6}x -\frac{1}{6}\sqrt{\left(4\frac{y}{H^2}+x\right)^2-60\left(\frac{y}{H^2}\right)^2} &\text{if } \frac{H^2x}{y}\in[\frac{11}{2},\frac{15}{2})\cup(8,\frac{97}{10}]\\ x+\frac{5y^2}{8(H^2x+2y)} &\text{if }\frac{H^2x}{y}\in[\frac{1}{2},3)\cup(4,\frac{11}{2}]\\ \frac{x}{2}+\frac{1}{2}\sqrt{x^2+20\left(\frac{y}{H^2}\right)^2} & \text{if }\frac{H^2x}{y}\in[-\frac{1}{2},\frac{1}{2}]\\ \frac{5y^2}{H^2(2y-H^2x)} & \text{if } \frac{H^2x}{y}\in[-\frac{11}{2},-4)\cup(-3,-\frac{1}{2}]\\ \frac{2}{3}\frac{y}{H^2}-\frac{1}{6}x-\frac{1}{6}\sqrt{\left(x-4\frac{y}{H^2})^2-60(\frac{y}{H^2}\right)^2} & \text{if }\frac{H^2x}{y}\in[-\frac{97}{10},-8)\cup(-\frac{15}{2},-\frac{11}{2}]\\ \frac{3}{8}\frac{y}{H^2}-\frac{x}{16}-\frac{1}{16}\sqrt{\left(x-6\frac{y}{H^2}\right)^2-160\left(\frac{y}{H^2}\right)^2} & \text{if } \frac{H^2x}{y}\in[-\frac{193}{14},-12)\cup(-\frac{35}{3},-\frac{97}{10}]\\ \frac{4}{15}\frac{y}{H^2}-\frac{x}{30}-\frac{1}{30}\sqrt{\left(x-8\frac{y}{H^2}\right)^2-300\left(\frac{y}{H^2}\right)^2} & \text{if } \frac{H^2x}{y}\in [-\frac{107}{6},-16)\cup(-\frac{63}{4},-\frac{193}{14}]\\ -\frac{y^2}{16x} & \text{if } \frac{H^2x}{y}\in[-4n,\frac{1-4n^2}{n}]\text{ and }n\in\mathbb{Z}_{>0} \\ x+\frac{y^2}{16x} & \text{if } \frac{H^2x}{y}\in[\frac{4n^2-1}{n},4n]\text{ and }n\in\mathbb{Z}_{>0}. \end{cases} \end{align} $$Lemma 4.5. Let ![]() $O=(0,0)$ be the origin, and let
$O=(0,0)$ be the origin, and let ![]() $P=(x_p,y_p)$ and
$P=(x_p,y_p)$ and ![]() $Q=(x_q,y_q)$ be two points on the upper half plane such that
$Q=(x_q,y_q)$ be two points on the upper half plane such that ![]() $\frac {x_p}{y_p}>\frac {x_q}{y_q}$ and
$\frac {x_p}{y_p}>\frac {x_q}{y_q}$ and ![]() $y_p<y_q$. Consider a sequence of points
$y_p<y_q$. Consider a sequence of points ![]() $P_0=O,P_1,\ldots ,P_n=Q$ on the upper half plane and inside the triangle
$P_0=O,P_1,\ldots ,P_n=Q$ on the upper half plane and inside the triangle ![]() $OPQ$. In addition, assume that the points
$OPQ$. In addition, assume that the points ![]() $P_0,\ldots ,P_n$ form a convex polygon. If we consider the sum
$P_0,\ldots ,P_n$ form a convex polygon. If we consider the sum
 $$ \begin{align*}\sum_{i=0}^{n-1}\spadesuit(\overrightarrow{P_{i}P_{i+1}}),\end{align*} $$
$$ \begin{align*}\sum_{i=0}^{n-1}\spadesuit(\overrightarrow{P_{i}P_{i+1}}),\end{align*} $$it can achieve its maximum only when ![]() $n=1$ or
$n=1$ or ![]() $n=2$. When
$n=2$. When ![]() $n=2$, we can choose
$n=2$, we can choose ![]() $P_1$ on
$P_1$ on ![]() $OP$ or
$OP$ or ![]() $PQ$, unless
$PQ$, unless ![]() $\frac {x_1}{y_1}=m$, or
$\frac {x_1}{y_1}=m$, or ![]() $\frac {4m^2-1}{m}$; or
$\frac {4m^2-1}{m}$; or ![]() $\frac {x_q-x_1}{y_q-y_1}=m$ or
$\frac {x_q-x_1}{y_q-y_1}=m$ or ![]() $\frac {4m^2-1}{m}$ for some nonzero integer m.
$\frac {4m^2-1}{m}$ for some nonzero integer m.
Proof. Here, we use the trick in [Reference Feyzbakhsh and LiFL21, Section 2.2]. The first part is basically the same as in [Reference LiLi19a, Lemma 4.11], because the essence of the proof is that, in all the cases, the function is homogeneous of degree 1. This implies that we can reduce to the case ![]() $n\leq 2$. Now, we consider a triangle
$n\leq 2$. Now, we consider a triangle ![]() $OAB$, with slope
$OAB$, with slope ![]() $\frac {x(A)}{y(A)}>\frac {x(B)}{y(B)}$, such that slopes of
$\frac {x(A)}{y(A)}>\frac {x(B)}{y(B)}$, such that slopes of ![]() $\overrightarrow {OA}, \overrightarrow {OB}$, or slopes of
$\overrightarrow {OA}, \overrightarrow {OB}$, or slopes of ![]() $\overrightarrow {AB}, \overrightarrow {OB}$ fall in the same region. By calculating the derivative, we get a weak triangular inequality, that is to say
$\overrightarrow {AB}, \overrightarrow {OB}$ fall in the same region. By calculating the derivative, we get a weak triangular inequality, that is to say
Now, we consider the triangle ![]() $OP'Q$ inside the triangle
$OP'Q$ inside the triangle ![]() $OPQ$. Then by extending the line
$OPQ$. Then by extending the line ![]() $OP'$ or
$OP'$ or ![]() $QP'$, we get a new small triangle. As the function
$QP'$, we get a new small triangle. As the function ![]() $\spadesuit $ is linear when the slope is fixed, we can just consider the new small triangle. Then by the weak triangular inequality, we get the conclusion. The only thing that needs to be proven is the case in which the changing point is not equal to
$\spadesuit $ is linear when the slope is fixed, we can just consider the new small triangle. Then by the weak triangular inequality, we get the conclusion. The only thing that needs to be proven is the case in which the changing point is not equal to ![]() $\frac {4m^2-1}{m}$ or
$\frac {4m^2-1}{m}$ or ![]() $4m$. Let
$4m$. Let ![]() $P'$ be a point that does not coincide with P and the slope of
$P'$ be a point that does not coincide with P and the slope of ![]() $OP'$ (or
$OP'$ (or ![]() $P'Q$) is at the changing point not equal to
$P'Q$) is at the changing point not equal to ![]() $\frac {4m^2-1}{m}$ or
$\frac {4m^2-1}{m}$ or ![]() $4m$. Then the value
$4m$. Then the value ![]() $\spadesuit (\overrightarrow {OP'})+\spadesuit (\overrightarrow {P'Q})$ achieves the same value when the sum is calculated by the functions in different regions. Also, by the weak triangular inequality, we get the conclusion, and thus we finish the proof.
$\spadesuit (\overrightarrow {OP'})+\spadesuit (\overrightarrow {P'Q})$ achieves the same value when the sum is calculated by the functions in different regions. Also, by the weak triangular inequality, we get the conclusion, and thus we finish the proof.
With the above lemma, we can give a Clifford type inequality for the curve ![]() $C=X_{2,2,2,4}$. In the next proof, we make a change of the coordinate of
$C=X_{2,2,2,4}$. In the next proof, we make a change of the coordinate of ![]() $\spadesuit $ to be
$\spadesuit $ to be ![]() $(x',y')=(x,\frac {y}{H^2})$. By abuse of notation, we still use
$(x',y')=(x,\frac {y}{H^2})$. By abuse of notation, we still use ![]() $\spadesuit $ to denote it.
$\spadesuit $ to denote it.
Theorem 4.6. Let F be a semistable vector bundle on C of rank r, degree d and slope ![]() $\mu =\frac {d}{r}$. Then we have the following inequality (Figure 2):
$\mu =\frac {d}{r}$. Then we have the following inequality (Figure 2):
 $$ \begin{align} h^0(F)\leq \begin{cases} \frac{64r^2}{64r-d} & \text{if } \mu\in[0,\frac{256}{3}-\frac{32\sqrt{61}}{3})\\ r+\frac{5d^2}{1,024r} & \text{if } \mu\in[\frac{256}{3}-\frac{32\sqrt{61}}{3},16]\\ \frac{5d^2}{1,024r}+5r-\frac{d}{8} & \text{if } \mu\in[48,\frac{576-32\sqrt{69}}{5}]\\ d-46r & \text{if } \mu \in[\frac{576-32\sqrt{69}}{5},64]. \end{cases} \end{align} $$
$$ \begin{align} h^0(F)\leq \begin{cases} \frac{64r^2}{64r-d} & \text{if } \mu\in[0,\frac{256}{3}-\frac{32\sqrt{61}}{3})\\ r+\frac{5d^2}{1,024r} & \text{if } \mu\in[\frac{256}{3}-\frac{32\sqrt{61}}{3},16]\\ \frac{5d^2}{1,024r}+5r-\frac{d}{8} & \text{if } \mu\in[48,\frac{576-32\sqrt{69}}{5}]\\ d-46r & \text{if } \mu \in[\frac{576-32\sqrt{69}}{5},64]. \end{cases} \end{align} $$
Figure 2 The Clifford type inequality for the curve C.
Proof. If the object ![]() $\imath _*F$ is Brill–Noether semistable, then by the Bogomolov inequality, with the same argument as in Proposition 4.3, we have
$\imath _*F$ is Brill–Noether semistable, then by the Bogomolov inequality, with the same argument as in Proposition 4.3, we have
 $$ \begin{align*}h^0(F)\leq \mathop{\mathrm{rk}}(\imath_*F)-\frac{(H\mathop{\mathrm{ch}}\nolimits_1(\imath_*F))^2}{2H^2\mathop{\mathrm{ch}}\nolimits_2(\imath_*F)}= \frac{64r^2}{64r-d}.\end{align*} $$
$$ \begin{align*}h^0(F)\leq \mathop{\mathrm{rk}}(\imath_*F)-\frac{(H\mathop{\mathrm{ch}}\nolimits_1(\imath_*F))^2}{2H^2\mathop{\mathrm{ch}}\nolimits_2(\imath_*F)}= \frac{64r^2}{64r-d}.\end{align*} $$In particular, by Lemma 4.1, the bound holds for ![]() $\mu \in [0,\frac {256}{3}-\frac {32\sqrt {61}}{3})$. We may assume that there is a wall as that in Lemma 4.1 for
$\mu \in [0,\frac {256}{3}-\frac {32\sqrt {61}}{3})$. We may assume that there is a wall as that in Lemma 4.1 for ![]() $\imath _*F$ for the rest of the argument.
$\imath _*F$ for the rest of the argument.
For ![]() $\mu \in [\frac {256}{3}-\frac {32\sqrt {61}}{3},16]$, by Proposition 4.1, we know that the wall is inside the range
$\mu \in [\frac {256}{3}-\frac {32\sqrt {61}}{3},16]$, by Proposition 4.1, we know that the wall is inside the range ![]() $\frac {\mu }{32}$ and
$\frac {\mu }{32}$ and ![]() $\frac {\mu }{32}-4$. Let m be the number of HN factors of
$\frac {\mu }{32}-4$. Let m be the number of HN factors of ![]() $\imath _*F$ with respect to the Brill–Noether stability condition as that in Proposition 4.3. Then we have:
$\imath _*F$ with respect to the Brill–Noether stability condition as that in Proposition 4.3. Then we have:
 $$ \begin{align*} h^0(F)&=\hom(O_S,\imath_*F)\leq\sum_{i=0}^{m-1}\hom(O_S,F_{i+1}/F_{i})\\ &\leq\sum_{i=0}^{m-1}\mathop{\mathrm{rk}}(F_{i+1}/F_i)+\spadesuit(\mathop{\mathrm{ch}}\nolimits_2(F_{i+1}/F_i),H\mathop{\mathrm{ch}}\nolimits_1(F_{i+1}/F_i)/H^2)\\ &=\sum_{i=0}^{m-1}\spadesuit(\mathop{\mathrm{ch}}\nolimits_2(F_{i+1}/F_i),H\mathop{\mathrm{ch}}\nolimits_1(F_{i+1}/F_i)/H^2). \end{align*} $$
$$ \begin{align*} h^0(F)&=\hom(O_S,\imath_*F)\leq\sum_{i=0}^{m-1}\hom(O_S,F_{i+1}/F_{i})\\ &\leq\sum_{i=0}^{m-1}\mathop{\mathrm{rk}}(F_{i+1}/F_i)+\spadesuit(\mathop{\mathrm{ch}}\nolimits_2(F_{i+1}/F_i),H\mathop{\mathrm{ch}}\nolimits_1(F_{i+1}/F_i)/H^2)\\ &=\sum_{i=0}^{m-1}\spadesuit(\mathop{\mathrm{ch}}\nolimits_2(F_{i+1}/F_i),H\mathop{\mathrm{ch}}\nolimits_1(F_{i+1}/F_i)/H^2). \end{align*} $$On the other hand, by Lemma 4.5, we can take the number of HN factors to be less than or equal to ![]() $2$. By the explanation at the beginning for the case that
$2$. By the explanation at the beginning for the case that ![]() $\imath _*F$ is BN-semistable, we may assume that the number of the HN factors is
$\imath _*F$ is BN-semistable, we may assume that the number of the HN factors is ![]() $2$. Let
$2$. Let ![]() $Q=(d-64r,4r)$. Let P be the point such that the slope of
$Q=(d-64r,4r)$. Let P be the point such that the slope of ![]() $PQ$ is
$PQ$ is
 $$ \begin{align*}\frac{\frac{\mu}{32}-4}{\Gamma(\frac{\mu}{32}-4)}=\frac{\frac{\mu}{32}-4}{\frac{H^2}{2}(\frac{\mu}{32}-4)^2-1+(\frac{\mu}{32})^2}\end{align*} $$
$$ \begin{align*}\frac{\frac{\mu}{32}-4}{\Gamma(\frac{\mu}{32}-4)}=\frac{\frac{\mu}{32}-4}{\frac{H^2}{2}(\frac{\mu}{32}-4)^2-1+(\frac{\mu}{32})^2}\end{align*} $$and the slope of ![]() $OP$ is
$OP$ is
 $$ \begin{align*}\frac{\frac{\mu}{32}}{\Gamma(\frac{\mu}{32})}=\frac{\frac{\mu}{32}}{\frac{H^2}{2}(\frac{\mu}{32})^2-1+(\frac{\mu}{32})^2}=\frac{\frac{\mu}{32}}{5(\frac{\mu}{32})^2-1}.\end{align*} $$
$$ \begin{align*}\frac{\frac{\mu}{32}}{\Gamma(\frac{\mu}{32})}=\frac{\frac{\mu}{32}}{\frac{H^2}{2}(\frac{\mu}{32})^2-1+(\frac{\mu}{32})^2}=\frac{\frac{\mu}{32}}{5(\frac{\mu}{32})^2-1}.\end{align*} $$ By a direct calculation, the point P has the coordinate ![]() $(\frac {5d^2}{1,024r}-r,\frac {d}{32}).$ Inside this region,
$(\frac {5d^2}{1,024r}-r,\frac {d}{32}).$ Inside this region, ![]() $\left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _2}{H\mathop {\mathrm {ch}}\nolimits _1}\right )^-(\imath _*(F))\geq -\frac {63}{4}$. Also, we notice that in each case we have
$\left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _2}{H\mathop {\mathrm {ch}}\nolimits _1}\right )^-(\imath _*(F))\geq -\frac {63}{4}$. Also, we notice that in each case we have
Then, by Lemma 4.5, we get ![]() $h^0(F)\leq f_1+f_2$, where
$h^0(F)\leq f_1+f_2$, where
 $$ \begin{align*}f_1=\frac{5d^2}{2048}-\frac{r}{2}+\frac{1}{2}\left(\frac{5d^2}{1,024r}+r\right)=\frac{5d^2}{1,024r}\end{align*} $$
$$ \begin{align*}f_1=\frac{5d^2}{2048}-\frac{r}{2}+\frac{1}{2}\left(\frac{5d^2}{1,024r}+r\right)=\frac{5d^2}{1,024r}\end{align*} $$and
 $$ \begin{align*}f_2=\frac{4}{15}\left(4r-\frac{d}{32}\right)-\frac{1}{30}\left(d-64r-\frac{5d^2}{1,024r}+r\right)-\frac{\sqrt{\Delta}}{30},\end{align*} $$
$$ \begin{align*}f_2=\frac{4}{15}\left(4r-\frac{d}{32}\right)-\frac{1}{30}\left(d-64r-\frac{5d^2}{1,024r}+r\right)-\frac{\sqrt{\Delta}}{30},\end{align*} $$where
 $$ \begin{align*}\Delta=\left(d-64r-\frac{5d^2}{1,024r}+r-32r+\frac{d}{4}\right)^2-300\left(4r-\frac{d}{32}\right)^2.\end{align*} $$
$$ \begin{align*}\Delta=\left(d-64r-\frac{5d^2}{1,024r}+r-32r+\frac{d}{4}\right)^2-300\left(4r-\frac{d}{32}\right)^2.\end{align*} $$ By a direct calculation, we get ![]() $\sqrt {\Delta }=65r-\frac {5}{4}d+\frac {5d^2}{1,024r}$,
$\sqrt {\Delta }=65r-\frac {5}{4}d+\frac {5d^2}{1,024r}$, ![]() $f_2=r$, and thus we get the second inequality.
$f_2=r$, and thus we get the second inequality.
When ![]() $\mu \in [48,64]$, we let
$\mu \in [48,64]$, we let ![]() $Q=(d-64r,4r)$ and let P be the point satisfying that the slope of
$Q=(d-64r,4r)$ and let P be the point satisfying that the slope of ![]() $OP$ is
$OP$ is
 $$ \begin{align*}\frac{\frac{\mu}{32}}{\Gamma(\frac{\mu}{32})}=\frac{\frac{\mu}{32}}{\frac{H^2}{2}(\frac{\mu}{32})^2-1+(\frac{\mu}{32}-2)^2}=\frac{\frac{\mu}{32}}{4(\frac{\mu}{32})^2-1+(\frac{\mu}{32}-2)^2}\end{align*} $$
$$ \begin{align*}\frac{\frac{\mu}{32}}{\Gamma(\frac{\mu}{32})}=\frac{\frac{\mu}{32}}{\frac{H^2}{2}(\frac{\mu}{32})^2-1+(\frac{\mu}{32}-2)^2}=\frac{\frac{\mu}{32}}{4(\frac{\mu}{32})^2-1+(\frac{\mu}{32}-2)^2}\end{align*} $$and the slope of ![]() $PQ$ is
$PQ$ is
 $$ \begin{align*}\frac{\frac{\mu}{32}-4}{\Gamma(\frac{\mu}{32}-4)}=\frac{\frac{\mu}{32}-4}{\frac{H^2}{2}(\frac{\mu}{32}-4)^2-1+(\frac{\mu}{32}-2)^2}.\end{align*} $$
$$ \begin{align*}\frac{\frac{\mu}{32}-4}{\Gamma(\frac{\mu}{32}-4)}=\frac{\frac{\mu}{32}-4}{\frac{H^2}{2}(\frac{\mu}{32}-4)^2-1+(\frac{\mu}{32}-2)^2}.\end{align*} $$By a direct calculation, we get
 $$ \begin{align*}P=\left(\frac{5d^2}{1,024r}-\frac{d}{8}+3r,\frac{d}{32}\right).\end{align*} $$
$$ \begin{align*}P=\left(\frac{5d^2}{1,024r}-\frac{d}{8}+3r,\frac{d}{32}\right).\end{align*} $$Thus, we have
 $$ \begin{align*} \spadesuit(\overrightarrow{OP})&=\frac{d}{48}+\frac{7}{6}\left(\frac{5d^2}{1,024r}-\frac{d}{8}+3r\right)-\frac{1}{6}\sqrt{\left(\frac{d}{8}+\frac{5d^2}{1,024r}-\frac{d}{8}+3r\right)^2-60\left(\frac{d}{32}\right)^2}\\ &=\frac{d}{48}+\frac{7}{6}\left(\frac{5d^2}{1,024r}-\frac{d}{8}+3r\right)+\frac{1}{6}(3r-\frac{5d^2}{1,024r})=\frac{5d^2}{1,024r}+4r-\frac{d}{8}\;\; \text{and} \end{align*} $$
$$ \begin{align*} \spadesuit(\overrightarrow{OP})&=\frac{d}{48}+\frac{7}{6}\left(\frac{5d^2}{1,024r}-\frac{d}{8}+3r\right)-\frac{1}{6}\sqrt{\left(\frac{d}{8}+\frac{5d^2}{1,024r}-\frac{d}{8}+3r\right)^2-60\left(\frac{d}{32}\right)^2}\\ &=\frac{d}{48}+\frac{7}{6}\left(\frac{5d^2}{1,024r}-\frac{d}{8}+3r\right)+\frac{1}{6}(3r-\frac{5d^2}{1,024r})=\frac{5d^2}{1,024r}+4r-\frac{d}{8}\;\; \text{and} \end{align*} $$ $$ \begin{align*}\spadesuit(\overrightarrow{PQ})=\frac{8}{3}r-\frac{d}{48}-\frac{d}{6}+\frac{32}{3}r+\frac{5d^2}{6\times 1,024r}-\frac{d}{48}+\frac{r}{2}-\frac{1}{6}\sqrt{\Delta'},\end{align*} $$
$$ \begin{align*}\spadesuit(\overrightarrow{PQ})=\frac{8}{3}r-\frac{d}{48}-\frac{d}{6}+\frac{32}{3}r+\frac{5d^2}{6\times 1,024r}-\frac{d}{48}+\frac{r}{2}-\frac{1}{6}\sqrt{\Delta'},\end{align*} $$where
 $$ \begin{align*}\Delta'=\left(d-64r-\frac{5d^2}{1,024r}+\frac{d}{8}-3r-4\left(4r-\frac{d}{32}\right)\right)^2-60\left(4r-\frac{d}{32}\right)^2.\end{align*} $$
$$ \begin{align*}\Delta'=\left(d-64r-\frac{5d^2}{1,024r}+\frac{d}{8}-3r-4\left(4r-\frac{d}{32}\right)\right)^2-60\left(4r-\frac{d}{32}\right)^2.\end{align*} $$By a direct calculation, we get ![]() $\sqrt {\Delta '}=\frac {5d^2}{1,024r}-\frac {5d}{4}+77r$ and thus
$\sqrt {\Delta '}=\frac {5d^2}{1,024r}-\frac {5d}{4}+77r$ and thus ![]() $\spadesuit (\overrightarrow {OP})+\spadesuit (\overrightarrow { PQ})=\frac {5d^2}{1,024r}+5r-\frac {d}{8}$. On the other hand, we consider now a point
$\spadesuit (\overrightarrow {OP})+\spadesuit (\overrightarrow { PQ})=\frac {5d^2}{1,024r}+5r-\frac {d}{8}$. On the other hand, we consider now a point ![]() $P'$ such that the slope of
$P'$ such that the slope of ![]() $OP'$ is
$OP'$ is
and the slope of ![]() $P'Q$ is
$P'Q$ is
By a direct computation, we get ![]() $P'=(d-48r,2r)$. We also consider a point
$P'=(d-48r,2r)$. We also consider a point ![]() $P"$ on the line
$P"$ on the line ![]() $OP$ that the line
$OP$ that the line ![]() $PQ$ has slope
$PQ$ has slope ![]() $-\frac {1}{8}$. We note that both
$-\frac {1}{8}$. We note that both ![]() $P'$ and
$P'$ and ![]() $P"$ are inside
$P"$ are inside ![]() $OP"'Q$, where
$OP"'Q$, where ![]() $P"'$ is a point such that the slope of
$P"'$ is a point such that the slope of ![]() $OP"'$ is
$OP"'$ is ![]() $\frac {1}{8}$ and the slope of
$\frac {1}{8}$ and the slope of ![]() $P"'Q$ is
$P"'Q$ is ![]() $-\frac {1}{8}$. Accordingly, we get
$-\frac {1}{8}$. Accordingly, we get ![]() $P"'=(\frac {d}{2}-16r,\frac {d}{16}-2r)$, and thus
$P"'=(\frac {d}{2}-16r,\frac {d}{16}-2r)$, and thus ![]() $\spadesuit (\overrightarrow {OP"'})=d-47r$ and
$\spadesuit (\overrightarrow {OP"'})=d-47r$ and ![]() $\spadesuit (\overrightarrow {P"'Q})=r$ and so
$\spadesuit (\overrightarrow {P"'Q})=r$ and so ![]() $\spadesuit (\overrightarrow {OP"'})+\spadesuit (\overrightarrow {P"'Q})\leq d-46r$. By Lemma 4.5, we get the last two cases by considering
$\spadesuit (\overrightarrow {OP"'})+\spadesuit (\overrightarrow {P"'Q})\leq d-46r$. By Lemma 4.5, we get the last two cases by considering ![]() $\max \{d-46r, \frac {5d^2}{1,024r}+5r-\frac {d}{8}\}.$
$\max \{d-46r, \frac {5d^2}{1,024r}+5r-\frac {d}{8}\}.$
Remark 4.7. For the Brill–Noether semistable region, one can get a better Clifford type inequality by applying Lemma 4.3. One can do a more careful argument to make the break point more precise and thus get a better Clifford type inequality. But the bound above is enough for our purpose.
5 Bogomolov–Gieseker type inequality on  $X_{2,2,4}$ and
$X_{2,2,4}$ and  $X_{2,4}$
$X_{2,4}$
Now, we give a Bogomolov–Gieseker type inequality for ![]() $\mathop {\mathrm {ch}}\nolimits _2$ on
$\mathop {\mathrm {ch}}\nolimits _2$ on ![]() $S'=X_{2,2,4}$. By Hirzebruch–Riemann–Roch, we get
$S'=X_{2,2,4}$. By Hirzebruch–Riemann–Roch, we get
for a coherent sheaf E on ![]() $S'$. The following lemma is essential to the calculation.
$S'$. The following lemma is essential to the calculation.
Lemma 5.1 [Reference FeyzbakhshFey22a, Corollary 4.3], [Reference LiLi19a, Lemma 5.1].
Let ![]() $(X,H)$ be a polarized variety of dimension
$(X,H)$ be a polarized variety of dimension ![]() $n=2,3$. Let E be a coherent sheaf in
$n=2,3$. Let E be a coherent sheaf in ![]() $\mathrm {Coh}^{0,H}(X)$. Suppose there exists
$\mathrm {Coh}^{0,H}(X)$. Suppose there exists ![]() $\alpha>0$ and
$\alpha>0$ and ![]() $m\in \mathbb {Z}_{>0}$ such that
$m\in \mathbb {Z}_{>0}$ such that
1.
 $E(-mH)[1]$ is in
$E(-mH)[1]$ is in  $\mathrm {Coh}^{0,H}(X)$;
$\mathrm {Coh}^{0,H}(X)$;2. Both E and
 $E(-mH)[1]$ are
$E(-mH)[1]$ are  $\nu _{\alpha ,0,H}$-tilt stable;
$\nu _{\alpha ,0,H}$-tilt stable;3.
 $\nu _{\alpha ,0,H}(E)=\nu _{\alpha ,0,H}(E(-mH)[1]).$
$\nu _{\alpha ,0,H}(E)=\nu _{\alpha ,0,H}(E(-mH)[1]).$
Then, for a generic smooth projective irreducible subvariety ![]() $Y\in |mH|$, the restriction
$Y\in |mH|$, the restriction ![]() $E|_Y$ is
$E|_Y$ is ![]() $\mu _{H_Y}$-semistable. Moreover,
$\mu _{H_Y}$-semistable. Moreover, ![]() $\mathop {\mathrm {rk}}(E)=\mathop {\mathrm {rk}}(E|_Y)$,
$\mathop {\mathrm {rk}}(E)=\mathop {\mathrm {rk}}(E|_Y)$, ![]() $H^{n-2}_Y\mathop {\mathrm {ch}}\nolimits _1(E|_Y)=mH^{n-1}\mathop {\mathrm {ch}}\nolimits _1(E)$, and when
$H^{n-2}_Y\mathop {\mathrm {ch}}\nolimits _1(E|_Y)=mH^{n-1}\mathop {\mathrm {ch}}\nolimits _1(E)$, and when ![]() $n=3$,
$n=3$, ![]() $\mathop {\mathrm {ch}}\nolimits _2(E|_Y)=mH\mathop {\mathrm {ch}}\nolimits _2(E).$
$\mathop {\mathrm {ch}}\nolimits _2(E|_Y)=mH\mathop {\mathrm {ch}}\nolimits _2(E).$
Proposition 5.2. Suppose ![]() $F\in D^b(S')$, with
$F\in D^b(S')$, with ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in (0,1)$, is
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in (0,1)$, is ![]() $\nu _{\alpha ,0,H}$-semistable or
$\nu _{\alpha ,0,H}$-semistable or ![]() $\nu _{\alpha ',1,H}$-semistable for some
$\nu _{\alpha ',1,H}$-semistable for some ![]() $\alpha>0$ or
$\alpha>0$ or ![]() $\alpha '>\frac {1}{2}$, then we have the following Bogomolov–Gieseker type inequality (Figure 3):
$\alpha '>\frac {1}{2}$, then we have the following Bogomolov–Gieseker type inequality (Figure 3):
 $$ \begin{align} \frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq \begin{cases} \left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in(0,\frac{4}{3}-\frac{\sqrt{13}}{3}]\\ \frac{5}{8}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{8} & \text{if }\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{4}{3}-\frac{\sqrt{13}}{3},\frac{1}{2}]\\ \frac{5}{8}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{4}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{1}{2},\frac{\sqrt{13}}{3}-\frac{1}{3})\\ \left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{2} & \text{if }\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in[\frac{\sqrt{13}}{3}-\frac{1}{3},1). \end{cases} \end{align} $$
$$ \begin{align} \frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq \begin{cases} \left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in(0,\frac{4}{3}-\frac{\sqrt{13}}{3}]\\ \frac{5}{8}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{8} & \text{if }\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{4}{3}-\frac{\sqrt{13}}{3},\frac{1}{2}]\\ \frac{5}{8}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{4}\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)} & \text{if } \frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in(\frac{1}{2},\frac{\sqrt{13}}{3}-\frac{1}{3})\\ \left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{2} & \text{if }\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\in[\frac{\sqrt{13}}{3}-\frac{1}{3},1). \end{cases} \end{align} $$
Figure 3 The Bogomolov–Gieseker type inequality (blue) and the classical Bogomolov inequality (red).
Proof. The proof here is similar to [Reference LiLi19a]. We prove this by contradiction. The idea is that first to reduce to stable objects by considering Jordan–Hölder factors for ![]() $\nu _{\alpha ,0,H}$ or
$\nu _{\alpha ,0,H}$ or ![]() $\nu _{\alpha ',-1,H}$. Next, by using the Feyzbakhsh’s restriction theorem (Lemma 5.1) and the Clifford type inequality in Section 4 (Theorem 4.6), we get inequalities as in inequality (5.1) for the stable objects, and thus get the result.
$\nu _{\alpha ',-1,H}$. Next, by using the Feyzbakhsh’s restriction theorem (Lemma 5.1) and the Clifford type inequality in Section 4 (Theorem 4.6), we get inequalities as in inequality (5.1) for the stable objects, and thus get the result.
Reduce to stable objects: Suppose there is a ![]() $\nu _{\alpha ,0,H}$ or
$\nu _{\alpha ,0,H}$ or ![]() $\nu _{\alpha ',1,H}$-tilt stable object with
$\nu _{\alpha ',1,H}$-tilt stable object with ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in (0,1)$ violating the above inequality. We assume that F is an object with the minimal
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in (0,1)$ violating the above inequality. We assume that F is an object with the minimal ![]() $\overline {\Delta }_H$ of all such objects. Suppose F becomes strictly
$\overline {\Delta }_H$ of all such objects. Suppose F becomes strictly ![]() $\nu _{\alpha ,0,H}$-semistable for some
$\nu _{\alpha ,0,H}$-semistable for some ![]() $\alpha>0$ (or
$\alpha>0$ (or ![]() $\nu _{\alpha ',1,H}$ strictly semistable), then we take a Jordan–Hölder filtration. Since the inequality forms a convex curve in
$\nu _{\alpha ',1,H}$ strictly semistable), then we take a Jordan–Hölder filtration. Since the inequality forms a convex curve in ![]() $(0,\frac {1}{2}]$ and
$(0,\frac {1}{2}]$ and ![]() $[\frac {1}{2},1)$ separately, there is at least one Jordan–Hölder factor violating the inequality. For example, if
$[\frac {1}{2},1)$ separately, there is at least one Jordan–Hölder factor violating the inequality. For example, if ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in \left (0,\frac {1}{2}\right ]$ and we are considering
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in \left (0,\frac {1}{2}\right ]$ and we are considering ![]() $\nu _{\alpha ,0,H}$, then the line passing through
$\nu _{\alpha ,0,H}$, then the line passing through ![]() $(\alpha ,0)$ and
$(\alpha ,0)$ and ![]() $p_H(F)$ has the
$p_H(F)$ has the ![]() $\left (0,\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\right ]$ segment completely above the curve of the proposition. Thus, F must have a Jordan–Hölder factor
$\left (0,\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\right ]$ segment completely above the curve of the proposition. Thus, F must have a Jordan–Hölder factor ![]() $F_i$ that violates the inequality. Similarly, we can show it in the remaining cases. Finally, by Lemma 2.17, we have
$F_i$ that violates the inequality. Similarly, we can show it in the remaining cases. Finally, by Lemma 2.17, we have ![]() $\overline {\Delta }_H(F_i)<\overline {\Delta }_H(F)$, which contradicts the minimum assumption.
$\overline {\Delta }_H(F_i)<\overline {\Delta }_H(F)$, which contradicts the minimum assumption.
Now, suppose that F becomes strictly ![]() $\nu _{\alpha _0,\beta ,H}$-semistable on the vertical wall for
$\nu _{\alpha _0,\beta ,H}$-semistable on the vertical wall for ![]() $\beta =\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}$. We may assume that
$\beta =\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}$. We may assume that ![]() $F\in \mathrm {Coh}^{\beta ,H}(S')$. If all the Jordan–Hölder factors of F are torsion-free, then there is a
$F\in \mathrm {Coh}^{\beta ,H}(S')$. If all the Jordan–Hölder factors of F are torsion-free, then there is a ![]() $\nu _{\alpha ,\beta }$-stable Jordan–Hölder factor
$\nu _{\alpha ,\beta }$-stable Jordan–Hölder factor ![]() $F_i$ of F that has
$F_i$ of F that has ![]() $p_H(F)=p_H(F_i)$. By Lemma 2.17, we have
$p_H(F)=p_H(F_i)$. By Lemma 2.17, we have ![]() $\overline {\Delta }_H(F)=\overline {\Delta }_H(F_i)$. Also, by the openess of the stability conditions,
$\overline {\Delta }_H(F)=\overline {\Delta }_H(F_i)$. Also, by the openess of the stability conditions, ![]() $F_i$ is
$F_i$ is ![]() $\nu _{\alpha ,0}$ and
$\nu _{\alpha ,0}$ and ![]() $\nu _{\alpha ',1}$-stable for
$\nu _{\alpha ',1}$-stable for ![]() $\alpha $ and
$\alpha $ and ![]() $\alpha '$ large enough. If F has a torsion Jordan–Hölder factor
$\alpha '$ large enough. If F has a torsion Jordan–Hölder factor ![]() $F_0$, then the torsion factors must have
$F_0$, then the torsion factors must have ![]() $\mathop {\mathrm {ch}}\nolimits _2(F_0)\geq 0$. Since other Jordan–Hölder factors must have
$\mathop {\mathrm {ch}}\nolimits _2(F_0)\geq 0$. Since other Jordan–Hölder factors must have ![]() $0>\mathop {\mathrm {rk}}(F_i)\geq \mathop {\mathrm {rk}}(F)$ as we assume that
$0>\mathop {\mathrm {rk}}(F_i)\geq \mathop {\mathrm {rk}}(F)$ as we assume that ![]() $F\in \mathrm {Coh}^{\beta ,H}(S')$, we must have some factor
$F\in \mathrm {Coh}^{\beta ,H}(S')$, we must have some factor ![]() $F_i$ such that
$F_i$ such that ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}=\frac {H\mathop {\mathrm {ch}}\nolimits _1(F_i)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F_i)}$ and
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}=\frac {H\mathop {\mathrm {ch}}\nolimits _1(F_i)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F_i)}$ and ![]() $\frac {\mathop {\mathrm {ch}}\nolimits _2(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\leq \frac {\mathop {\mathrm {ch}}\nolimits _2(F_i)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F_i)}$. Again, by the openness of the stability conditions,
$\frac {\mathop {\mathrm {ch}}\nolimits _2(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\leq \frac {\mathop {\mathrm {ch}}\nolimits _2(F_i)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F_i)}$. Again, by the openness of the stability conditions, ![]() $F_i$ is
$F_i$ is ![]() $\nu _{\alpha ,0}$ and
$\nu _{\alpha ,0}$ and ![]() $\nu _{\alpha ',1}$-stable for
$\nu _{\alpha ',1}$-stable for ![]() $\alpha $ and
$\alpha $ and ![]() $\alpha '$ large enough. Thus, we can assume that F is
$\alpha '$ large enough. Thus, we can assume that F is ![]() $\nu _{\alpha ,0,H}$-tilt stable for all
$\nu _{\alpha ,0,H}$-tilt stable for all ![]() $\alpha>0$, and similarly for
$\alpha>0$, and similarly for ![]() $\nu _{\alpha ',1,H}$.
$\nu _{\alpha ',1,H}$.
Inequalities for stable objects: To apply the last lemma, we consider the line passing through ![]() $p_H(F):=(a,b)$ and
$p_H(F):=(a,b)$ and ![]() $p_H(F(-2H)[1]):=(a-2b+2,b-2)$. This line has the equation
$p_H(F(-2H)[1]):=(a-2b+2,b-2)$. This line has the equation
In the proper region of ![]() $(a,b)$, it will intersect at
$(a,b)$, it will intersect at ![]() $(\alpha _0,0)$ and
$(\alpha _0,0)$ and ![]() $(\alpha _1,-1)$ such that
$(\alpha _1,-1)$ such that ![]() $\alpha _0>0$ and
$\alpha _0>0$ and ![]() $\alpha _1>\frac {1}{2}$. This is equivalent to saying that
$\alpha _1>\frac {1}{2}$. This is equivalent to saying that ![]() $a>b^2-b$ and
$a>b^2-b$ and ![]() $a>b^2-\frac {1}{2}$. We see that the bound above satisfies these two conditions. Thus, we can apply the last lemma for F and we have
$a>b^2-\frac {1}{2}$. We see that the bound above satisfies these two conditions. Thus, we can apply the last lemma for F and we have ![]() $\mathop {\mathrm {rk}}(F|_C)=\mathop {\mathrm {rk}}(F)$ and
$\mathop {\mathrm {rk}}(F|_C)=\mathop {\mathrm {rk}}(F)$ and ![]() $\deg (F|_C)=2H\mathop {\mathrm {ch}}\nolimits _1(F).$
$\deg (F|_C)=2H\mathop {\mathrm {ch}}\nolimits _1(F).$
Without loss of generality, we may assume that ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\leq \frac {1}{2}$, otherwise we can take
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\leq \frac {1}{2}$, otherwise we can take ![]() $F^*(H)$, where
$F^*(H)$, where ![]() $*$ denote the dual. Then we have
$*$ denote the dual. Then we have
 $$ \begin{align*} \chi(O_{S'},F)&=\mathop{\mathrm{ch}}\nolimits_2(F)-\mathop{\mathrm{ch}}\nolimits_1(F)+20\mathop{\mathrm{ch}}\nolimits_0(F)\\ &\leq \hom(O_{S'},F)+\hom(O_{S'},F[2])\\ &=\hom(O_{S'},F)+\hom(O_{S'},F^*(2H))\\ &\leq \hom(O_C,F|_C)+\hom(O_C,F^*(2H)|_C)=:\Lambda. \end{align*} $$
$$ \begin{align*} \chi(O_{S'},F)&=\mathop{\mathrm{ch}}\nolimits_2(F)-\mathop{\mathrm{ch}}\nolimits_1(F)+20\mathop{\mathrm{ch}}\nolimits_0(F)\\ &\leq \hom(O_{S'},F)+\hom(O_{S'},F[2])\\ &=\hom(O_{S'},F)+\hom(O_{S'},F^*(2H))\\ &\leq \hom(O_C,F|_C)+\hom(O_C,F^*(2H)|_C)=:\Lambda. \end{align*} $$ Note that in this case, ![]() $\mu (F|_C)=\frac {2H\mathop {\mathrm {ch}}\nolimits _1(F)}{\mathop {\mathrm {ch}}\nolimits _0(F)}=\frac {32H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in (0,16].$
$\mu (F|_C)=\frac {2H\mathop {\mathrm {ch}}\nolimits _1(F)}{\mathop {\mathrm {ch}}\nolimits _0(F)}=\frac {32H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in (0,16].$
From now on, we let ![]() $r:=\mathop {\mathrm {ch}}\nolimits _0(F)$,
$r:=\mathop {\mathrm {ch}}\nolimits _0(F)$, ![]() $\mu =32\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}$ and
$\mu =32\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}$ and ![]() $d=\mu r$. As in the last section, we have several cases:
$d=\mu r$. As in the last section, we have several cases:
Case 1. ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in \left (0,\frac {\sqrt {69}-8}{5}\right ].$ In this region, we have
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in \left (0,\frac {\sqrt {69}-8}{5}\right ].$ In this region, we have
Therefore,
 $$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq-\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}+\frac{4}{64-32\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}}-\frac{1}{8}.\end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq-\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}+\frac{4}{64-32\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}}-\frac{1}{8}.\end{align*} $$This satisfies the bound of the proposition.
Case 2. ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in \left (\frac {\sqrt {69}-8}{5},\frac {8}{3}-\frac {\sqrt {61}}{3}\right ]$. In this region, we have
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in \left (\frac {\sqrt {69}-8}{5},\frac {8}{3}-\frac {\sqrt {61}}{3}\right ]$. In this region, we have
 $$ \begin{align*} \Lambda&\leq \frac{64r^2}{64r-d}+\frac{5}{1,024}(64-\mu)^2r+5r-\frac{1}{8}(64-\mu)r\\ &=\frac{64r^2}{64r-d}+17r-\frac{1}{2}\mu r+\frac{5\mu^2r}{1,024}. \end{align*} $$
$$ \begin{align*} \Lambda&\leq \frac{64r^2}{64r-d}+\frac{5}{1,024}(64-\mu)^2r+5r-\frac{1}{8}(64-\mu)r\\ &=\frac{64r^2}{64r-d}+17r-\frac{1}{2}\mu r+\frac{5\mu^2r}{1,024}. \end{align*} $$This implies
 $$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq\frac{5}{16}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2+\frac{4}{64-32\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}}-\frac{3}{16}.\end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq\frac{5}{16}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2+\frac{4}{64-32\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}}-\frac{3}{16}.\end{align*} $$This satisfies the bound of the proposition.
Case 3. ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in \left (\frac {8}{3}-\frac {\sqrt {61}}{3},\frac {1}{2}\right ]$. In this region, we are back to the general case.
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {ch}}\nolimits _0(F)}\in \left (\frac {8}{3}-\frac {\sqrt {61}}{3},\frac {1}{2}\right ]$. In this region, we are back to the general case.
 $$ \begin{align*} \Lambda&\leq r+\frac{5d^2}{1,024r}+\frac{5}{1,024}(64-\mu)^2r+5r-\frac{1}{8}(64-\mu)r\\ &=\frac{5}{512}\frac{32\times32\times(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)H^2}+18r-16\times\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\times \mathop{\mathrm{ch}}\nolimits_0(F)\\ &=\frac{5}{8}\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}+18\mathop{\mathrm{ch}}\nolimits_0(F)-16\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\mathop{\mathrm{ch}}\nolimits_0(F). \end{align*} $$
$$ \begin{align*} \Lambda&\leq r+\frac{5d^2}{1,024r}+\frac{5}{1,024}(64-\mu)^2r+5r-\frac{1}{8}(64-\mu)r\\ &=\frac{5}{512}\frac{32\times32\times(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)H^2}+18r-16\times\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\times \mathop{\mathrm{ch}}\nolimits_0(F)\\ &=\frac{5}{8}\frac{(H\mathop{\mathrm{ch}}\nolimits_1(F))^2}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}+18\mathop{\mathrm{ch}}\nolimits_0(F)-16\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\mathop{\mathrm{ch}}\nolimits_0(F). \end{align*} $$This implies
 $$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq\frac{5}{8}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{8}.\end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{ch}}\nolimits_2(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\leq\frac{5}{8}\left(\frac{H\mathop{\mathrm{ch}}\nolimits_1(F)}{H^2\mathop{\mathrm{ch}}\nolimits_0(F)}\right)^2-\frac{1}{8}.\end{align*} $$This satisfies the bound of the proposition.
Therefore, if ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in (0,1)$, then we have the bound of the proposition.
$\frac {H\mathop {\mathrm {ch}}\nolimits _1(F)}{H^2\mathop {\mathrm {rk}}(F)}\in (0,1)$, then we have the bound of the proposition.
Corollary 5.3. Let F be a torsion-free ![]() $\mu _H$-slope stable sheaf on
$\mu _H$-slope stable sheaf on ![]() $S'$. Then the numerical character of F satisfies the bound of Proposition 5.2.
$S'$. Then the numerical character of F satisfies the bound of Proposition 5.2.
Proof. This is because if F is ![]() $\mu _H$-slope stable, then it is
$\mu _H$-slope stable, then it is ![]() $\nu _{\alpha ,0,H}$-stable for
$\nu _{\alpha ,0,H}$-stable for ![]() $\alpha $ large enough.
$\alpha $ large enough.
Corollary 5.4. The bound in Proposition 5.2 is also true for ![]() $X_{2,4}$, where we replace
$X_{2,4}$, where we replace ![]() $\mathop {\mathrm {ch}}\nolimits _2(F)$,
$\mathop {\mathrm {ch}}\nolimits _2(F)$, ![]() $H\mathop {\mathrm {ch}}\nolimits _1(F)$ and
$H\mathop {\mathrm {ch}}\nolimits _1(F)$ and ![]() $H^2\mathop {\mathrm {rk}}(F)$ by
$H^2\mathop {\mathrm {rk}}(F)$ by ![]() $H\mathop {\mathrm {ch}}\nolimits _2(F)$,
$H\mathop {\mathrm {ch}}\nolimits _2(F)$, ![]() $H^2\mathop {\mathrm {ch}}\nolimits _1(F)$ and
$H^2\mathop {\mathrm {ch}}\nolimits _1(F)$ and ![]() $H^3\mathop {\mathrm {rk}}(F)$.
$H^3\mathop {\mathrm {rk}}(F)$.
We get the following bound, which is a little weaker but easier for calculation.
Theorem 5.5. On ![]() $X_{2,4}$, let F be a slope semistable sheaf in
$X_{2,4}$, let F be a slope semistable sheaf in ![]() $\mathrm {Coh}(X_{2,4})$ (or
$\mathrm {Coh}(X_{2,4})$ (or ![]() $\nu _{\alpha ,0,H}$-tilt semistable object for
$\nu _{\alpha ,0,H}$-tilt semistable object for ![]() $\alpha>0$, or Brill–Noether semistable). Suppose
$\alpha>0$, or Brill–Noether semistable). Suppose ![]() $\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\in [-1,1]$. Then
$\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\in [-1,1]$. Then
 $$ \begin{align} \frac{H\mathop{\mathrm{ch}}\nolimits_2(F)}{H^3\mathop{\mathrm{rk}}(F)}\leq \begin{cases} -\frac{1}{2}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert & \text{if } \left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[0,\frac{1}{5}]\\ \frac{7}{16}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{3}{16} & \text{if }\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{1}{5},\frac{1}{2}]\\ \frac{9}{16}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{1}{4} & \text{if }\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{1}{2},\frac{4}{5}]\\ \frac{51}{44}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{8}{11} & \text{if } \left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{4}{5},\frac{10}{11}]\\ \frac{21}{11}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{31}{22} & \text{if }\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{10}{11},1] \end{cases} \end{align} $$
$$ \begin{align} \frac{H\mathop{\mathrm{ch}}\nolimits_2(F)}{H^3\mathop{\mathrm{rk}}(F)}\leq \begin{cases} -\frac{1}{2}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert & \text{if } \left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[0,\frac{1}{5}]\\ \frac{7}{16}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{3}{16} & \text{if }\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{1}{5},\frac{1}{2}]\\ \frac{9}{16}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{1}{4} & \text{if }\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{1}{2},\frac{4}{5}]\\ \frac{51}{44}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{8}{11} & \text{if } \left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{4}{5},\frac{10}{11}]\\ \frac{21}{11}\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert-\frac{31}{22} & \text{if }\left\lvert\frac{H^2\mathop{\mathrm{ch}}\nolimits_1(F)}{H^3\mathop{\mathrm{rk}}(F)}\right\rvert\in[\frac{10}{11},1] \end{cases} \end{align} $$The equality can only hold when ![]() $\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in \{0,\frac {1}{5},\frac {1}{2},\frac {4}{5},\frac {1}{4},\frac {10}{11},1\}$. Moreover, when
$\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in \{0,\frac {1}{5},\frac {1}{2},\frac {4}{5},\frac {1}{4},\frac {10}{11},1\}$. Moreover, when ![]() $\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [0,\frac {1}{5}]$,
$\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [0,\frac {1}{5}]$, ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2-\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert $ holds; when
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2-\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert $ holds; when ![]() $\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [\frac {1}{5},\frac {1}{4}]$,
$\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [\frac {1}{5},\frac {1}{4}]$, ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \frac {9}{32}\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert -\frac {5}{32}$ holds; when
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \frac {9}{32}\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert -\frac {5}{32}$ holds; when ![]() $\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [\frac {1}{5},\frac {1}{2}]$,
$\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [\frac {1}{5},\frac {1}{2}]$, ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \frac {5}{8}\left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2-\frac {1}{8}$ holds and when
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \frac {5}{8}\left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2-\frac {1}{8}$ holds and when ![]() $\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [\frac {\sqrt {13}-1}{3},1]$,
$\left \lvert \frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right \rvert \in [\frac {\sqrt {13}-1}{3},1]$, ![]() $\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2-\frac {1}{2}$ holds.
$\frac {H\mathop {\mathrm {ch}}\nolimits _2(F)}{H^3\mathop {\mathrm {rk}}(F)}\leq \left (\frac {H^2\mathop {\mathrm {ch}}\nolimits _1(F)}{H^3\mathop {\mathrm {rk}}(F)}\right )^2-\frac {1}{2}$ holds.
Remark 5.6. As in [Reference LiLi19a], the method in this paper is expected to apply to other cases. A possible scheme is the following: One can start with a projective Calabi–Yau threefold X with ample divisor H, and consider a generic member ![]() $Y\in |2H|$ (or higher multiple of H), and a generic curve
$Y\in |2H|$ (or higher multiple of H), and a generic curve ![]() $C\in |2H_Y|$ (and still possible for a higher multiple of
$C\in |2H_Y|$ (and still possible for a higher multiple of ![]() $H_Y$). The essence is to have a good Bogomolov–Gieseker inequality for Y. To do this, one can embed C inside a K3 surface of Picard rank 1 (the method here) or a del Pezzo surface (as in [Reference LiLi19a, Reference KosekiKos22]), or more generally any surface for which a good
$H_Y$). The essence is to have a good Bogomolov–Gieseker inequality for Y. To do this, one can embed C inside a K3 surface of Picard rank 1 (the method here) or a del Pezzo surface (as in [Reference LiLi19a, Reference KosekiKos22]), or more generally any surface for which a good ![]() $\Gamma $-curve is known. To get a good
$\Gamma $-curve is known. To get a good ![]() $\Gamma $-curve for a surface, one can repeatedly use the method in this paper and in [Reference LiLi19a]. In particular, we expect that one can prove the Bogomolov–Gieseker inequality for
$\Gamma $-curve for a surface, one can repeatedly use the method in this paper and in [Reference LiLi19a]. In particular, we expect that one can prove the Bogomolov–Gieseker inequality for ![]() $X_{3,3}\subset \mathbb {P}^5$, the complete interesection of two generic cubics, by first restricting to the surface
$X_{3,3}\subset \mathbb {P}^5$, the complete interesection of two generic cubics, by first restricting to the surface ![]() $S_{2,3,3}$, and then using the link provided by the curve
$S_{2,3,3}$, and then using the link provided by the curve ![]() $C_{2,2,3,3}$ to the Bogomolov–Gieseker inequality of
$C_{2,2,3,3}$ to the Bogomolov–Gieseker inequality of ![]() $S_{2,2,3}$. Applying the method with the curve
$S_{2,2,3}$. Applying the method with the curve ![]() $S_{2,2,3}\supset C_{2,2,2,3}\subset S_{2,2,2}$, we get the Bogomolov–Gieseker inequality for
$S_{2,2,3}\supset C_{2,2,2,3}\subset S_{2,2,2}$, we get the Bogomolov–Gieseker inequality for ![]() $S_{2,2,3}$. Like the last remark in [Reference LiLi19a], each deformation type needs a lot of calculation.
$S_{2,2,3}$. Like the last remark in [Reference LiLi19a], each deformation type needs a lot of calculation.
Acknowledgements
The author would like to thank Dr. Chunyi Li for proposing this problem, helpful discussions and proofreading; Dr. Naoki Koseki for suggestive advice; Mr. Jesús David Fernández Caballero, Ms. Yefei Ma and Mr. Pedro Núñez for proofreading and the referees for helpful comments and references.
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
The author was supported by grants from the CSC-Warwick scholarship and Royal Society URF![]() $\backslash $R1
$\backslash $R1![]() $\backslash $201129 ‘Stability condition and application in algebraic geometry’.
$\backslash $201129 ‘Stability condition and application in algebraic geometry’.