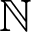1 Introduction
Throughout this paper, we let k denote a field, on which we place no further assumptions. By a graded ring, we always mean an
![]() $\mathbb {N}$
-graded ring
$\mathbb {N}$
-graded ring
 $A = \bigoplus _{n=0}^\infty A_n$
. A graded k-algebra A is locally finite if each
$A = \bigoplus _{n=0}^\infty A_n$
. A graded k-algebra A is locally finite if each
![]() $A_n$
is a finite-dimensional k-vector space, and it is connected if
$A_n$
is a finite-dimensional k-vector space, and it is connected if
![]() $A_0 = k$
.
$A_0 = k$
.
A familiar theme in noncommutative algebraic geometry is to identify a class of noncommutative algebras that are well-behaved for geometrically motivated reasons. One of the most famous such classes is that of Artin–Schelter (AS) regular algebras [Reference Artin and Schelter2], which are connected graded algebras with suitably nice projective resolutions of
![]() $k = A/A_{\geq 1}$
as a left and right A-module. This class is known to include all connected graded Auslander-regular algebras [Reference Levasseur27], and thus includes many quantum groups and related quantized algebras [Reference Brown and Goodearl9, I.15]. Another class of (not necessarily graded) algebras that has rapidly come to the forefront of such study is that of Calabi–Yau algebras [Reference Ginzburg17], which have a suitably nice resolution of A by projective bimodules. These include preprojective algebras [Reference Bocklandt5, Reference Ginzburg17] and their higher versions [Reference Amiot and Oppermann1, Reference Herschend, Iyama and Oppermann19, Reference Keller22], as well as quivers with potentials arising from dimer models [Reference Broomhead8].
$k = A/A_{\geq 1}$
as a left and right A-module. This class is known to include all connected graded Auslander-regular algebras [Reference Levasseur27], and thus includes many quantum groups and related quantized algebras [Reference Brown and Goodearl9, I.15]. Another class of (not necessarily graded) algebras that has rapidly come to the forefront of such study is that of Calabi–Yau algebras [Reference Ginzburg17], which have a suitably nice resolution of A by projective bimodules. These include preprojective algebras [Reference Bocklandt5, Reference Ginzburg17] and their higher versions [Reference Amiot and Oppermann1, Reference Herschend, Iyama and Oppermann19, Reference Keller22], as well as quivers with potentials arising from dimer models [Reference Broomhead8].
These two classes of algebras are unified by the class of twisted (or “skew”) Calabi–Yau algebras; indeed, it was shown in [Reference Reyes, Rogalski and Zhang37, Lemma 1.2] that a connected graded algebra A is twisted Calabi–Yau if and only if it is AS regular. However, many interesting examples of (graded) Calabi–Yau algebras are not connected. In this paper, we undertake a careful study of graded twisted Calabi–Yau algebras that are not necessarily connected, with the goal of explaining their relationship to a suitable generalization of AS regular algebras.
We now recall the definitions of these classes of algebras, beginning with AS regular algebras. We emphasize that in contrast to various other authors, we do not require regular algebras to have finite Gefland–Kirillov (GK)-dimension.
Definition 1.1. Let A be a connected graded algebra and let
![]() $k = A/A_{\geq 1}$
be the trivial module. Then A is AS regular of dimension d if it has graded global dimension d and satisfies
$k = A/A_{\geq 1}$
be the trivial module. Then A is AS regular of dimension d if it has graded global dimension d and satisfies
 $$ \begin{align*} {\mathrm{{Ext}}}^i_A(k,A) \cong \begin{cases} 0, & i \neq d \\ k, & i = d \end{cases} \quad \mbox{and} \quad {\mathrm{{Ext}}}^i_{A^{\mathrm{op}}}(k,A) \cong \begin{cases} 0, & i \neq d \\ k, & i = d \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^i_A(k,A) \cong \begin{cases} 0, & i \neq d \\ k, & i = d \end{cases} \quad \mbox{and} \quad {\mathrm{{Ext}}}^i_{A^{\mathrm{op}}}(k,A) \cong \begin{cases} 0, & i \neq d \\ k, & i = d \end{cases} \end{align*} $$
in
![]() $ {\mathrm {Mod-\!}} A$
and
$ {\mathrm {Mod-\!}} A$
and
![]() $A {\mathrm {\!-Mod}}$
, respectively.
$A {\mathrm {\!-Mod}}$
, respectively.
Next we recall the definition of twisted Calabi–Yau algebras. In some sources, this term refers to a twist by an automorphism as in condition (iii) below (for instance, see [Reference Bocklandt, Schedler and Wemyss6]); we will consider the more general twist by an invertible bimodule defined, for instance, in [Reference Schedler43, Definition 3.7.9]. For a k-algebra A with opposite
![]() $A^{\mathrm {op}}$
, we write
$A^{\mathrm {op}}$
, we write
![]() $A^e$
for its enveloping algebra
$A^e$
for its enveloping algebra
![]() $A \otimes _k A^{\mathrm {op}}$
. Then a k-central
$A \otimes _k A^{\mathrm {op}}$
. Then a k-central
![]() $(A, A)$
-bimodule M is also a left
$(A, A)$
-bimodule M is also a left
![]() $A^e$
-module or a right
$A^e$
-module or a right
![]() $A^e$
-module, where
$A^e$
-module, where
![]() $(a \otimes b^{\mathrm {op}}) \cdot m = amb = m \cdot (b \otimes a^{\mathrm {op}})$
. In this way we can identify the category of
$(a \otimes b^{\mathrm {op}}) \cdot m = amb = m \cdot (b \otimes a^{\mathrm {op}})$
. In this way we can identify the category of
![]() $(A, A)$
-bimodules with either
$(A, A)$
-bimodules with either
![]() $A^e {\mathrm {\!-Mod}}$
or
$A^e {\mathrm {\!-Mod}}$
or
![]() $ {\mathrm {Mod-\!}} A^e$
. Given an automorphism
$ {\mathrm {Mod-\!}} A^e$
. Given an automorphism
![]() $\mu : A \to A$
, we write
$\mu : A \to A$
, we write
![]() ${{\hspace {-0.0001pt}}}^1 A^\mu $
for the
${{\hspace {-0.0001pt}}}^1 A^\mu $
for the
![]() $(A, A)$
-bimodule structure on A where
$(A, A)$
-bimodule structure on A where
![]() $b \cdot a \cdot c = ba\mu (c)$
. Recall in addition that a left A-module M is called perfect if it has a finite length projective resolution consisting of finitely generated projective modules.
$b \cdot a \cdot c = ba\mu (c)$
. Recall in addition that a left A-module M is called perfect if it has a finite length projective resolution consisting of finitely generated projective modules.
Definition 1.2. Let A be a k-algebra. We say that:
-
(i) A is homologically smooth over k (or a homologically smooth k-algebra) if A has a resolution of finite length by finitely generated projective left
 $A^e$
-modules (i.e., if A is perfect as a left
$A^e$
-modules (i.e., if A is perfect as a left
 $A^e$
-module);
$A^e$
-module); -
(ii) A is twisted Calabi–Yau (of dimension d) if it is homologically smooth over k and if there is an invertible k-central
 $(A,A)$
-bimodule U such that as
$(A,A)$
-bimodule U such that as $$ \begin{align*} {\mathrm{{Ext}}}^i_{A^e}(A,A^e) \cong \begin{cases} 0, & i \neq d \\ U, & i = d \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^i_{A^e}(A,A^e) \cong \begin{cases} 0, & i \neq d \\ U, & i = d \end{cases} \end{align*} $$
 $(A,A)$
-bimodules, where each
$(A,A)$
-bimodules, where each
 $ {\mathrm {{Ext}}}^i_{A^e}(A,A^e)$
is considered as a right
$ {\mathrm {{Ext}}}^i_{A^e}(A,A^e)$
is considered as a right
 $A^e$
-module via the right
$A^e$
-module via the right
 $A^e$
-structure of
$A^e$
-structure of
 $A^e$
;
$A^e$
;
-
(iii) A has Nakayama automorphism
 $\,\mu $
if the isomorphism in (ii) holds with
$\,\mu $
if the isomorphism in (ii) holds with
 $U = {{\hspace {-0.0001pt}}}^1 A^\mu $
.
$U = {{\hspace {-0.0001pt}}}^1 A^\mu $
.
The use of the term “dimension” is justified in Lemma 4.4 below, where it is shown that the dimension d of a twisted Calabi–Yau algebra is equal to the projective dimension of A as a left
![]() $A^e$
-module. We call the module
$A^e$
-module. We call the module
 $U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
the Nakayama bimodule for A. It is well-known that the Nakayama automorphism of a twisted Calabi–Yau algebra, if it exists, is unique up to multiplication by an inner automorphism of A. A Calabi–Yau algebra is a twisted Calabi–Yau algebra as above for which the Nakayama bimodule is
$U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
the Nakayama bimodule for A. It is well-known that the Nakayama automorphism of a twisted Calabi–Yau algebra, if it exists, is unique up to multiplication by an inner automorphism of A. A Calabi–Yau algebra is a twisted Calabi–Yau algebra as above for which the Nakayama bimodule is
![]() $U \cong A$
; equivalently, it is a twisted Calabi–Yau algebra with an inner Nakayama automorphism.
$U \cong A$
; equivalently, it is a twisted Calabi–Yau algebra with an inner Nakayama automorphism.
The main motivation leading to the present paper is the problem of classifying twisted Calabi–Yau algebras A of dimension d (for small values of d) that are graded homomorphic images of a path algebra
![]() $kQ$
of a quiver Q, so that they are not necessarily connected. In our work with twisted Calabi–Yau algebras of dimension 2 and 3, in order to compute potential Hilbert series, it became useful to work with projective resolutions of the left module
$kQ$
of a quiver Q, so that they are not necessarily connected. In our work with twisted Calabi–Yau algebras of dimension 2 and 3, in order to compute potential Hilbert series, it became useful to work with projective resolutions of the left module
![]() $S = A/J(A)$
, rather than resolutions of the bimodule A. In the case of connected graded algebras, the aforementioned equivalence between the AS regular and twisted Calabi–Yau properties means that in order to check the twisted Calabi–Yau property, it is sufficient to compute a particular left module resolution. Thus for nonconnected algebras of the form
$S = A/J(A)$
, rather than resolutions of the bimodule A. In the case of connected graded algebras, the aforementioned equivalence between the AS regular and twisted Calabi–Yau properties means that in order to check the twisted Calabi–Yau property, it is sufficient to compute a particular left module resolution. Thus for nonconnected algebras of the form
![]() $A = kQ/I$
, we were led to wonder whether the twisted Calabi–Yau property might similarly be equivalent to a suitable generalization of the AS regular property, defined in terms of projective resolutions of S as a left or right A-module. Our main theorem, which we present as Theorem 5.15 below, will give a precise result along these lines.
$A = kQ/I$
, we were led to wonder whether the twisted Calabi–Yau property might similarly be equivalent to a suitable generalization of the AS regular property, defined in terms of projective resolutions of S as a left or right A-module. Our main theorem, which we present as Theorem 5.15 below, will give a precise result along these lines.
Another goal of this paper is to give full details of the proofs of some basic properties of homologically smooth algebras and twisted Calabi–Yau algebras, in particular the stability of these properties under common constructions, especially in the graded case. Some of these results may be folklore, but it seems useful to have them written down in one place. We begin in Section 2 with a review of preliminary results on locally finite graded algebras and their modules, including information about minimal projective resolutions, idempotent decompositions, and some isomorphisms in their derived categories of modules. Then in Sections 3 and 4, we study homological smoothness and the twisted Calabi–Yau property, respectively. In both cases, we show that these properties are stable under finite direct sum of algebras, tensor product of algebras, base field extension, and Morita equivalence. We also review several of the different “Serre duality” formulas that hold for modules over twisted Calabi–Yau algebras.
In case A is graded with
![]() $\dim _k A_0 < \infty $
, we let
$\dim _k A_0 < \infty $
, we let
![]() $J(A)$
be its graded Jacobson radical; then
$J(A)$
be its graded Jacobson radical; then
![]() $A_{\geq 1} \subseteq J(A)$
and
$A_{\geq 1} \subseteq J(A)$
and
![]() $S = A/J(A) = A_0/J(A_0)$
is a finite-dimensional semisimple algebra. In our study of homological smoothness in Section 3, we obtain the following novel characterization of homological smoothness for graded k-algebras. Recall that a k-algebra B is separable (over k) if
$S = A/J(A) = A_0/J(A_0)$
is a finite-dimensional semisimple algebra. In our study of homological smoothness in Section 3, we obtain the following novel characterization of homological smoothness for graded k-algebras. Recall that a k-algebra B is separable (over k) if
![]() $B \otimes _k K$
is semisimple for all field extensions
$B \otimes _k K$
is semisimple for all field extensions
![]() $k \subseteq K$
.
$k \subseteq K$
.
Theorem 1.3. (Theorem 3.10)
Let A be graded with
![]() $\dim _k A_0 < \infty $
as above. Then the following are equivalent:
$\dim _k A_0 < \infty $
as above. Then the following are equivalent:
-
(1) A is homologically smooth over k;
-
(2) S is separable as a k-algebra and perfect as a left (or equivalently, right) A-module.
The proof that homological smoothness implies separability of S is due to Jeremy Rickard, and we thank him for allowing us to include it here.
An important precedent for the study of generalized AS regular properties for locally finite graded algebras that are not necessarily connected was set in the work of Martinez-Villa and Solberg in [Reference Martínez-Villa30, Reference Martinéz-Villa and Solberg31] and of Minamoto and Mori in [Reference Minamoto and Mori33]; we recall these definitions in Section 5. Another possibility we would like to highlight is the following definition, which is formally similar to the original definition of AS regular algebras and tends to be one of the easier ones to work with technically.
Definition 1.4. Let A be a locally finite graded k-algebra, with
![]() $S = A/J(A)$
. We say that A is generalized AS regular of dimension d if A has graded global dimension d and there is a k-central invertible
$S = A/J(A)$
. We say that A is generalized AS regular of dimension d if A has graded global dimension d and there is a k-central invertible
![]() $(S,S)$
-bimodule V such that
$(S,S)$
-bimodule V such that
 $$ \begin{align*} {\mathrm{{Ext}}}_A^i(S, A) \cong \begin{cases} 0, & i \neq d \\ V, & i = d \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}_A^i(S, A) \cong \begin{cases} 0, & i \neq d \\ V, & i = d \end{cases} \end{align*} $$
as
![]() $(S, S)$
-bimodules.
$(S, S)$
-bimodules.
In Section 5, we show that this definition, the definition of Martinez-Villa and Solberg, and a slightly modified version of the definition of Minamoto and Mori, all give equivalent notions. Indeed, in Theorem 5.2, we show that these and even several additional slight variations are equivalent. For example, it is equivalent to require the isomorphism in Definition 1.4 to hold as right S-modules only.
Consequently, we arrive at the main theorem of the paper, which shows that the twisted Calabi–Yau condition is related to generalized AS regularity in a precise way (and often they are equivalent). Our hope is that this result will allow for an interplay between results in noncommutative Calabi–Yau geometry and the theory of AS regular algebras for algebras that are not necessarily connected.
Theorem 1.5. (Theorem 5.15)
Let A be a locally finite graded algebra, and denote
![]() $S = A_0/J(A_0)$
. Then the following are equivalent:
$S = A_0/J(A_0)$
. Then the following are equivalent:
-
(a) A is twisted Calabi–Yau of dimension d;
-
(b) A is generalized AS regular of dimension d, and S is a separable k-algebra;
-
(c) For every field extension K of k, the K-algebra
 $A \otimes K$
is generalized AS regular of dimension d.
$A \otimes K$
is generalized AS regular of dimension d.
In particular, the result above shows that if one is working over a perfect base field k (e.g., an algebraically closed field or a field of characteristic
![]() $0$
) then the twisted Calabi–Yau and generalized AS regular conditions are equivalent for locally finite graded algebras. This also recovers the equivalence [Reference Reyes, Rogalski and Zhang37, Lemma 1.2] of the two properties in the case where A is connected graded, because if A is connected then
$0$
) then the twisted Calabi–Yau and generalized AS regular conditions are equivalent for locally finite graded algebras. This also recovers the equivalence [Reference Reyes, Rogalski and Zhang37, Lemma 1.2] of the two properties in the case where A is connected graded, because if A is connected then
![]() $S \cong k$
is separable over k.
$S \cong k$
is separable over k.
The following diagram illustrates the relationships between several of the properties studied in this paper for locally finite graded k-algebras A with
![]() $S = A/J(A)$
. The implications all follow from the theorems above, with the exception of the far right arrow which follows from the proof of Theorem 5.2.
$S = A/J(A)$
. The implications all follow from the theorems above, with the exception of the far right arrow which follows from the proof of Theorem 5.2.

In the final section of the paper, Section 6, we apply our earlier results to obtain information about twisted Calabi–Yau algebras of dimension at most two. In dimension zero, we have a simple characterization of (not necessarily graded) twisted Calabi–Yau algebras as follows.
Theorem 1.6. (Theorem 4.19)
For an algebra A, the following are equivalent:
-
(a) A is twisted Calabi–Yau of dimension
 $0$
;
$0$
; -
(b) A is twisted Calabi–Yau and a finite-dimensional algebra;
-
(c) A is Calabi–Yau of dimension
 $0$
;
$0$
; -
(d) A is a separable k-algebra.
In dimension 1, we are able to characterize graded twisted Calabi–Yau algebras as certain tensor algebras and to prove that they are noetherian.
Theorem 1.7. (Theorem 6.11, Corollary 6.4)
Let A be a locally finite graded algebra, and suppose that the algebra
![]() $S = A_0/J(A_0)$
is separable. Then the following are equivalent:
$S = A_0/J(A_0)$
is separable. Then the following are equivalent:
-
(a) A is twisted Calabi–Yau of dimension
 $1$
;
$1$
; -
(b) There is an invertible, non-negatively graded, k-central
 $(S,S)$
-bimodule V such that
$(S,S)$
-bimodule V such that
 $T_S(V) \cong A$
.
$T_S(V) \cong A$
.
Furthermore, every algebra A satisfying the conditions above is noetherian.
In future work, we hope to present a fuller picture of the structure of locally finite graded twisted Calabi–Yau algebras of dimension
![]() $2$
. Here we will focus solely on the question of when such algebras have the noetherian property. In noncommutative algebraic geometry, it is generally expected that noncommutative graded algebras of a geometric nature will exhibit the best ring-theoretic properties when they have finite GK-dimension. In keeping with this theme, we prove the following.
$2$
. Here we will focus solely on the question of when such algebras have the noetherian property. In noncommutative algebraic geometry, it is generally expected that noncommutative graded algebras of a geometric nature will exhibit the best ring-theoretic properties when they have finite GK-dimension. In keeping with this theme, we prove the following.
Theorem 1.8. (Theorem 6.6)
Let A be a locally finite graded twisted Calabi–Yau algebra of dimension 2. Then A is noetherian if and only if A has finite GK-dimension.
We wish to emphasize that the proofs of the results above stating that an algebra is noetherian are all of a “structural” nature, and do not rely upon a classification of such algebras to determine that they are noetherian.
We note that while we have restricted our present study to graded algebras, it seems likely that a number of results and techniques employed here should generalize to the setting of semilocal twisted Calabi–Yau algebras A that are “locally finite” in the sense that, for the Jacobson radical J, the k-algebras
![]() $A/J^n$
are finite-dimensional for all
$A/J^n$
are finite-dimensional for all
![]() $n \geq 0$
.
$n \geq 0$
.
The companion paper [Reference Reyes and Rogalski40] focuses on the GK-dimension of locally finite graded twisted Calabi–Yau algebras. It includes fundamental results about the matrix Hilbert series of such algebras, the basic structure of the generators and relations for those of dimension 2 and 3, and techniques for distinguishing which of these algebras have finite GK-dimension. We note that the proof of Theorem 1.8 depends on a technical result from [Reference Reyes and Rogalski40].
Several routine proofs in this paper are sketched or omitted. Readers who wish to see full proofs may consult an earlier draft of this paper at arXiv:1807.10249v1.
2 Preliminaries on graded algebras and their modules
This section collects a number of preparatory results for our treatment of graded twisted Calabi–Yau algebras with the goal of improving readability of proofs in later sections. Readers who feel so inclined are encouraged to browse through the next few paragraphs on notations and conventions and then proceed directly to Section 3, referring back to these preparatory results only as needed.
In some parts, we collect known results, and in such cases, we point to proofs in the literature. In others, we provide generalizations of common arguments for connected graded algebras to locally finite algebras. While these generalizations are relatively routine, they involve some subtleties that are easily overlooked if one is accustomed to working only with connected graded algebras. We also require extensions of certain facts about modules to objects in the derived category. In such cases where proofs are not available in the literature, we include some of the shorter proofs but omit longer or more tedious ones.
We begin by discussing some conventions on rings, modules, and complexes. All rings, homomorphisms, and modules are assumed to be unital. For a ring A, we write
![]() $A {\mathrm {\!-Mod}}$
for its category of left modules and
$A {\mathrm {\!-Mod}}$
for its category of left modules and
![]() $ {\mathrm {Mod-\!}} A$
for its category of right A-modules. Letting
$ {\mathrm {Mod-\!}} A$
for its category of right A-modules. Letting
![]() $A^{\mathrm {op}}$
denote the opposite ring of A, we have
$A^{\mathrm {op}}$
denote the opposite ring of A, we have
![]() $ {\mathrm {Mod-\!}} A = A^{\mathrm {op}} {\mathrm {\!-Mod}}$
. We use the notation
$ {\mathrm {Mod-\!}} A = A^{\mathrm {op}} {\mathrm {\!-Mod}}$
. We use the notation
![]() $ {\mathrm {{Hom}}}_A(-,-)$
for Hom-sets of left A-modules, and
$ {\mathrm {{Hom}}}_A(-,-)$
for Hom-sets of left A-modules, and
![]() $ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}(-,-)$
for right modules. This will occasionally clarify any (bi)module structures induced on Hom groups in which one or both arguments are
$ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}(-,-)$
for right modules. This will occasionally clarify any (bi)module structures induced on Hom groups in which one or both arguments are
![]() $(A,A)$
-bimodules. (Recall that if
$(A,A)$
-bimodules. (Recall that if
![]() ${{\hspace {-0.0001pt}}}_A M_B$
and
${{\hspace {-0.0001pt}}}_A M_B$
and
![]() ${{\hspace {-0.0001pt}}}_A N_C$
are bimodules for rings B and C, then
${{\hspace {-0.0001pt}}}_A N_C$
are bimodules for rings B and C, then
![]() $ {\mathrm {{Hom}}}_A(M_B,N_C)$
carries an induced structure of a
$ {\mathrm {{Hom}}}_A(M_B,N_C)$
carries an induced structure of a
![]() $(B,C)$
-bimodule, which is most easily seen if one allows this
$(B,C)$
-bimodule, which is most easily seen if one allows this
![]() $ {\mathrm {{Hom}}}$
group to act on the right, opposite from the scalars. Similarly, if
$ {\mathrm {{Hom}}}$
group to act on the right, opposite from the scalars. Similarly, if
![]() ${{\hspace {-0.0001pt}}}_B P_A$
and
${{\hspace {-0.0001pt}}}_B P_A$
and
![]() ${{\hspace {-0.0001pt}}}_C Q_A$
are bimodules, then
${{\hspace {-0.0001pt}}}_C Q_A$
are bimodules, then
![]() $ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}({{\hspace {-0.0001pt}}}_B P, {{\hspace {-0.0001pt}}}_C Q)$
is a
$ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}({{\hspace {-0.0001pt}}}_B P, {{\hspace {-0.0001pt}}}_C Q)$
is a
![]() $(C,B)$
-bimodule.) If A and B are k-algebras, then all
$(C,B)$
-bimodule.) If A and B are k-algebras, then all
![]() $(A,B)$
-bimodules M considered below are assumed to be k-central (that is to say, the satisfy
$(A,B)$
-bimodules M considered below are assumed to be k-central (that is to say, the satisfy
![]() $\lambda m = m \lambda $
for every module element
$\lambda m = m \lambda $
for every module element
![]() $m \in M$
and scalar
$m \in M$
and scalar
![]() $\lambda \in k$
) unless explicitly stated otherwise.
$\lambda \in k$
) unless explicitly stated otherwise.
It will be useful to us to phrase the proofs of some of our main results in terms of derived categories, so we recall the relevant notation. Our convention is that all complexes will be cohomological complexes, as is standard when working with the derived category. Let A be a k-algebra. To indicate a complex of A-modules
we will use the notation
![]() $P^{\bullet }$
or the shorter form P. As a consequence of this cohomological notation, for modules
$P^{\bullet }$
or the shorter form P. As a consequence of this cohomological notation, for modules
![]() $M_A, L_A,$
and
$M_A, L_A,$
and
![]() ${{\hspace {-0.0001pt}}}_A N$
, we have
${{\hspace {-0.0001pt}}}_A N$
, we have
 $ {\mathrm {{Ext}}}^i_A(M,L) = H^i( {\mathrm {RHom}}_A(M,L))$
and
$ {\mathrm {{Ext}}}^i_A(M,L) = H^i( {\mathrm {RHom}}_A(M,L))$
and
 $ {\mathrm {Tor}}_i^A(M,N) = H^{-i}(M \otimes _A^L N)$
. For an abelian category
$ {\mathrm {Tor}}_i^A(M,N) = H^{-i}(M \otimes _A^L N)$
. For an abelian category
![]() $\mathcal {C}$
, we write
$\mathcal {C}$
, we write
![]() $D(\mathcal {C}), D^+(\mathcal {C}), D^-(\mathcal {C})$
, and
$D(\mathcal {C}), D^+(\mathcal {C}), D^-(\mathcal {C})$
, and
 $D^b(\mathcal {C})$
to, respectively, denote the derived categories of complexes, bounded below complexes, bounded above complexes, and bounded complexes. We also write
$D^b(\mathcal {C})$
to, respectively, denote the derived categories of complexes, bounded below complexes, bounded above complexes, and bounded complexes. We also write
![]() $D(A) = D(A {\mathrm {\!-Mod}})$
and
$D(A) = D(A {\mathrm {\!-Mod}})$
and
![]() $D(A^{\mathrm {op}}) = D( {\mathrm {Mod-\!}} A)$
, and similarly for the other derived categories. For references on derived categories and the use of
$D(A^{\mathrm {op}}) = D( {\mathrm {Mod-\!}} A)$
, and similarly for the other derived categories. For references on derived categories and the use of
![]() $ {\mathrm {RHom}}$
functors, we refer readers to [Reference Weibel49, Chapter 10] and [45, Tag 0A5W]. Given two complexes
$ {\mathrm {RHom}}$
functors, we refer readers to [Reference Weibel49, Chapter 10] and [45, Tag 0A5W]. Given two complexes
![]() $P^\bullet $
and
$P^\bullet $
and
![]() $Q^\bullet $
, we will regularly write
$Q^\bullet $
, we will regularly write
![]() $P^\bullet \cong Q^\bullet $
to denote an isomorphism in the derived category
$P^\bullet \cong Q^\bullet $
to denote an isomorphism in the derived category
![]() $D(A)$
, which is to say a quasi-isomorphism; we trust that this will not cause undue confusion, as we rarely care if two complexes are isomorphic in the (homotopy) category of complexes
$D(A)$
, which is to say a quasi-isomorphism; we trust that this will not cause undue confusion, as we rarely care if two complexes are isomorphic in the (homotopy) category of complexes
![]() $K(A)$
.
$K(A)$
.
Given a ring R, a complex of left R-modules is called perfect if it is quasi-isomorphic to a bounded complex of finitely generated projective left R-modules [45, Tag 0656]. A left R-module M is called perfect if it is perfect when considered as a complex with a single term in degree zero; this is equivalent to the existence of a projective resolution of finite length
where all
![]() $P^i$
are finitely generated.
$P^i$
are finitely generated.
2.1 Graded algebras, modules, and resolutions
We now turn to conventions and basic results on graded algebras, modules, and resolutions. Unless explicitly indicated otherwise, by a graded ring (or algebra) we mean an
![]() $\mathbb {N}$
-graded ring (or algebra). Suppose that
$\mathbb {N}$
-graded ring (or algebra). Suppose that
 $A = \bigoplus _{n=0}^\infty A_n$
is a graded algebra. We write
$A = \bigoplus _{n=0}^\infty A_n$
is a graded algebra. We write
![]() $ {\mathrm {Gr-\!}} A$
for the category of graded right A-modules, with morphisms the degree-preserving homomorphisms, which we refer to as graded homomorphisms. Similarly, we write
$ {\mathrm {Gr-\!}} A$
for the category of graded right A-modules, with morphisms the degree-preserving homomorphisms, which we refer to as graded homomorphisms. Similarly, we write
![]() $A {\mathrm {\!-Gr}}$
for the category of graded left A-modules. Given a graded module M and
$A {\mathrm {\!-Gr}}$
for the category of graded left A-modules. Given a graded module M and
![]() $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
![]() $M(n)$
will indicate the same module M with the grading shifted so that
$M(n)$
will indicate the same module M with the grading shifted so that
![]() $M(n)_m = M_{m+n}$
for all m. Given graded left A-modules M and N, let
$M(n)_m = M_{m+n}$
for all m. Given graded left A-modules M and N, let
 $ {\mathrm {{Hom}}}_A^i(M,N)$
denote the vector space of left A-module homomorphisms
$ {\mathrm {{Hom}}}_A^i(M,N)$
denote the vector space of left A-module homomorphisms
![]() $\phi \colon M \to N$
that are homogeneous of degree i (i.e.,
$\phi \colon M \to N$
that are homogeneous of degree i (i.e.,
![]() $\phi (M_n) \subseteq N_{n+i}$
). Continue to write
$\phi (M_n) \subseteq N_{n+i}$
). Continue to write
![]() $ {\mathrm {{Hom}}}_A(M,N)$
for the usual Hom in the category
$ {\mathrm {{Hom}}}_A(M,N)$
for the usual Hom in the category
![]() $A {\mathrm {\!-Mod}}$
. Then we have the graded Hom-groups
$A {\mathrm {\!-Mod}}$
. Then we have the graded Hom-groups
 $$ \begin{align*} \underline{{\mathrm{{Hom}}}}_A(M,N) = \bigoplus_{i=-\infty}^\infty {\mathrm{{Hom}}}_A^i(M,N) \subseteq {\mathrm{{Hom}}}_A(M,N). \end{align*} $$
$$ \begin{align*} \underline{{\mathrm{{Hom}}}}_A(M,N) = \bigoplus_{i=-\infty}^\infty {\mathrm{{Hom}}}_A^i(M,N) \subseteq {\mathrm{{Hom}}}_A(M,N). \end{align*} $$
It is well-known that if M and N are graded left A-modules with M finitely generated, then in fact
![]() $\underline { {\mathrm {{Hom}}}}_A(M,N) = {\mathrm {{Hom}}}_A(M,N)$
; see [Reference Năstăsescu and Van Oystaeyen35, Corollary 2.4.4], for instance. We will extend this result to the derived category in Lemma 2.4 below. We say that M is graded perfect if there is a graded projective resolution as in (2.1) with all
$\underline { {\mathrm {{Hom}}}}_A(M,N) = {\mathrm {{Hom}}}_A(M,N)$
; see [Reference Năstăsescu and Van Oystaeyen35, Corollary 2.4.4], for instance. We will extend this result to the derived category in Lemma 2.4 below. We say that M is graded perfect if there is a graded projective resolution as in (2.1) with all
![]() $P^i$
finitely generated. We denote the right derived functors of the graded Hom functor by
$P^i$
finitely generated. We denote the right derived functors of the graded Hom functor by
 $\underline { {\mathrm {{Ext}}}}^i_A = \text{R}^i\underline { {\mathrm {{Hom}}}}_A$
, and similarly we denote the total derived functor by
$\underline { {\mathrm {{Ext}}}}^i_A = \text{R}^i\underline { {\mathrm {{Hom}}}}_A$
, and similarly we denote the total derived functor by
![]() $\text{R}\underline { {\mathrm {{Hom}}}}_A$
.
$\text{R}\underline { {\mathrm {{Hom}}}}_A$
.
Given graded modules
![]() $M_A$
and
$M_A$
and
![]() ${{\hspace {-0.0001pt}}}_A N$
over the graded algebra A, we recall from [Reference Năstăsescu and van Oystaeyen34, p. 12] that the graded tensor product
${{\hspace {-0.0001pt}}}_A N$
over the graded algebra A, we recall from [Reference Năstăsescu and van Oystaeyen34, p. 12] that the graded tensor product
![]() $\,M {\mathrm {\underline {\otimes }}}_A N$
is the graded k-vector space that has the same underlying vector space as the usual tensor product
$\,M {\mathrm {\underline {\otimes }}}_A N$
is the graded k-vector space that has the same underlying vector space as the usual tensor product
![]() $M \otimes _A N$
, with the grading induced by declaring each pure tensor of the form
$M \otimes _A N$
, with the grading induced by declaring each pure tensor of the form
![]() $m \otimes n$
, where m and n are homogeneous, to be itself homogeneous of degree
$m \otimes n$
, where m and n are homogeneous, to be itself homogeneous of degree
![]() $\deg (m \otimes n) = \deg (m) + \deg (n)$
.
$\deg (m \otimes n) = \deg (m) + \deg (n)$
.
For a graded ring A, we let
![]() $J(A)$
denote its graded Jacobson radical, the intersection of its maximal homogeneous left (equivalently, right) ideals. If I is a maximal homogeneous left ideal, then
$J(A)$
denote its graded Jacobson radical, the intersection of its maximal homogeneous left (equivalently, right) ideals. If I is a maximal homogeneous left ideal, then
![]() $1 \not \in I$
; since
$1 \not \in I$
; since
![]() $1 \in A_0$
, we also have
$1 \in A_0$
, we also have
![]() $1 \not \in I_0 + A_{\geq 1} = I + A_{\geq 1}$
. By maximality,
$1 \not \in I_0 + A_{\geq 1} = I + A_{\geq 1}$
. By maximality,
![]() $A_{\geq 1} \subseteq I$
. It follows that
$A_{\geq 1} \subseteq I$
. It follows that
where
![]() $A_0$
is considered as a graded ring concentrated in degree zero, so that
$A_0$
is considered as a graded ring concentrated in degree zero, so that
![]() $J(A_0)$
is the usual Jacobson radical (see also [Reference Năstăsescu and van Oystaeyen34, Corollary II.6.5]). Thus we have
$J(A_0)$
is the usual Jacobson radical (see also [Reference Năstăsescu and van Oystaeyen34, Corollary II.6.5]). Thus we have
![]() $A/J(A) \cong A_0/J(A_0)$
as rings. Note that if
$A/J(A) \cong A_0/J(A_0)$
as rings. Note that if
![]() $A_0$
is semisimple, then
$A_0$
is semisimple, then
![]() $J(A) = A_{\geq 1}$
and
$J(A) = A_{\geq 1}$
and
![]() $A/J(A) \cong A_0$
. We always write S for the semisimple algebra
$A/J(A) \cong A_0$
. We always write S for the semisimple algebra
![]() $A/J(A)$
.
$A/J(A)$
.
We say that a graded k-algebra
 $A = \bigoplus _{n = 0}^\infty A_n$
is locally finite (elsewhere called finitely graded) if each
$A = \bigoplus _{n = 0}^\infty A_n$
is locally finite (elsewhere called finitely graded) if each
![]() $A_n$
is finite-dimensional as a k-vector space. While this will eventually be our case of interest, we are able to develop many of our results assuming only that
$A_n$
is finite-dimensional as a k-vector space. While this will eventually be our case of interest, we are able to develop many of our results assuming only that
![]() $A_0$
is finite-dimensional. If A is a graded algebra with
$A_0$
is finite-dimensional. If A is a graded algebra with
![]() $A_0$
finite-dimensional, then every left
$A_0$
finite-dimensional, then every left
![]() $A_0$
-module has a projective cover [Reference Lam25, Proposition 24.12]. From this it follows that every graded left A-module M that is bounded below (i.e.,
$A_0$
-module has a projective cover [Reference Lam25, Proposition 24.12]. From this it follows that every graded left A-module M that is bounded below (i.e.,
![]() $M_n = 0$
for
$M_n = 0$
for
![]() $n \ll 0$
) has a graded projective cover
$n \ll 0$
) has a graded projective cover
![]() $f \colon P \to M$
, in the sense that P is graded projective, f is a graded surjective morphism, and
$f \colon P \to M$
, in the sense that P is graded projective, f is a graded surjective morphism, and
![]() $\ker (f) \subseteq J(A)P$
(see also [Reference Minamoto and Mori33, p. 4064]). We define a minimal graded projective resolution of a graded left A-module to be a graded projective resolution
$\ker (f) \subseteq J(A)P$
(see also [Reference Minamoto and Mori33, p. 4064]). We define a minimal graded projective resolution of a graded left A-module to be a graded projective resolution
![]() $P^{\bullet } \to M$
such that each map
$P^{\bullet } \to M$
such that each map
![]() $d^n: P^n \to P^{n-1}$
in the complex, as well as the augmentation map
$d^n: P^n \to P^{n-1}$
in the complex, as well as the augmentation map
![]() $\epsilon : P^0 \to M$
, is a projective cover of its image. This is equivalent to the conditions
$\epsilon : P^0 \to M$
, is a projective cover of its image. This is equivalent to the conditions
![]() $\ker (d^n) \subseteq J(A) P^n$
for all
$\ker (d^n) \subseteq J(A) P^n$
for all
![]() $n \geq 1$
together with
$n \geq 1$
together with
 $\ker (\epsilon ) \subseteq J(A) P^0$
. Alternatively, this can be expressed as the conditions that
$\ker (\epsilon ) \subseteq J(A) P^0$
. Alternatively, this can be expressed as the conditions that
 $ {\mathrm {im}}(d^n) \subseteq J(A) P^{n-1}$
for all
$ {\mathrm {im}}(d^n) \subseteq J(A) P^{n-1}$
for all
![]() $n \geq 1$
.
$n \geq 1$
.
Continuing to assume that
![]() $\dim _k A_0 < \infty $
, then as in [Reference Minamoto and Mori33, Lemma 2.6], every graded projective left A-module P that is bounded below is of the form
$\dim _k A_0 < \infty $
, then as in [Reference Minamoto and Mori33, Lemma 2.6], every graded projective left A-module P that is bounded below is of the form
![]() $P \cong A \otimes _{A_0} Q$
for some graded projective left bounded left
$P \cong A \otimes _{A_0} Q$
for some graded projective left bounded left
![]() $A_0$
-module Q. Furthermore, as every projective left module over the finite-dimensional algebra
$A_0$
-module Q. Furthermore, as every projective left module over the finite-dimensional algebra
![]() $A_0$
is a direct sum of indecomposable projective modules, each isomorphic to
$A_0$
is a direct sum of indecomposable projective modules, each isomorphic to
![]() $A_0 e$
where e is a primitive idempotent [Reference Pierce36, 6.3], we have in fact
$A_0 e$
where e is a primitive idempotent [Reference Pierce36, 6.3], we have in fact
![]() $P \cong \bigoplus Ae_i(l_i)$
for some primitive idempotents
$P \cong \bigoplus Ae_i(l_i)$
for some primitive idempotents
![]() $e_i \in A_0$
and integers
$e_i \in A_0$
and integers
![]() $l_i$
.
$l_i$
.
We say that a graded module M is graded-indecomposable if one cannot write
![]() $M = M_1 \oplus M_2$
for nonzero graded submodules
$M = M_1 \oplus M_2$
for nonzero graded submodules
![]() $M_i$
. Note that if
$M_i$
. Note that if
![]() $e \in A_0$
is a primitive idempotent, then
$e \in A_0$
is a primitive idempotent, then
![]() $Ae$
is a graded-indecomposable projective. Thus every bounded below graded projective left A-module is (uniquely) a direct sum of graded-indecomposable projectives. It follows as in [Reference Minamoto and Mori33, Section 2] that any graded A-module that is bounded below has a minimal graded projective resolution whose terms are bounded below. One may check using the graded Nakayama lemma below that such a minimal resolution is unique up to (a generally nonunique) isomorphism, as expected.
$Ae$
is a graded-indecomposable projective. Thus every bounded below graded projective left A-module is (uniquely) a direct sum of graded-indecomposable projectives. It follows as in [Reference Minamoto and Mori33, Section 2] that any graded A-module that is bounded below has a minimal graded projective resolution whose terms are bounded below. One may check using the graded Nakayama lemma below that such a minimal resolution is unique up to (a generally nonunique) isomorphism, as expected.
The following graded version of Nakayama’s lemma is well-known. A proof of (1) can be found in [Reference Minamoto and Mori33, Lemma 2.1], and the derivation of (2) from (1) is standard.
Lemma 2.2. Let A be a graded k-algebra whose degree zero part
![]() $A_0$
has finite k-dimension, and let M be a bounded-below graded left A-module. Let
$A_0$
has finite k-dimension, and let M be a bounded-below graded left A-module. Let
![]() $I \subseteq A$
be a graded ideal contained in
$I \subseteq A$
be a graded ideal contained in
![]() $J(A)$
.
$J(A)$
.
-
(1) If
 $M = IM$
, then
$M = IM$
, then
 $M = 0$
.
$M = 0$
. -
(2) Any lift of a generating set of
 $M/IM$
is a generating set of M.
$M/IM$
is a generating set of M.
The following generalizes a well-known characterization of finitely generated algebras from the case where A is connected (i.e.,
![]() $A_0 = k$
).
$A_0 = k$
).
Lemma 2.3. Let A be a graded algebra with
![]() $A_0$
finite-dimensional, and denote
$A_0$
finite-dimensional, and denote
![]() $S = A/J(A)$
. Then the following are equivalent:
$S = A/J(A)$
. Then the following are equivalent:
-
(a) A is finitely generated as a k-algebra;
-
(b) S is finitely presented as a left (equivalently, right) A-module;
-
(c)
 $\dim _k J(A)/J(A)^2 < \infty $
.
$\dim _k J(A)/J(A)^2 < \infty $
.
In particular, if S is perfect as a left or right A-module, then A is a finitely generated algebra. In case the above conditions hold, A is locally finite.
Proof. For a proof in the case where A is connected, see [Reference Rogalski41, Lemma 2.1.3]. Because of the subtleties involved in extending to the case of a general graded algebra, we sketch a proof below.
Set
![]() $J = J(A)$
. The equivalence of (b) and (c) follows by considering the left (respectively, right) module presentation
$J = J(A)$
. The equivalence of (b) and (c) follows by considering the left (respectively, right) module presentation
![]() $0 \to J \to A \to S \to 0$
and applying Schanuel’s lemma along with Lemma 2.2(2) to see that S is finitely presented if and only if
$0 \to J \to A \to S \to 0$
and applying Schanuel’s lemma along with Lemma 2.2(2) to see that S is finitely presented if and only if
 $J/J^2$
is a finitely generated module over
$J/J^2$
is a finitely generated module over
![]() $A/J = S$
. Since S is finite-dimensional, this occurs if and only if
$A/J = S$
. Since S is finite-dimensional, this occurs if and only if
 $\dim _k J/J^2 < \infty $
.
$\dim _k J/J^2 < \infty $
.
To see that (c)
![]() $\implies $
(a), it suffices to fix finite-dimensional subspaces
$\implies $
(a), it suffices to fix finite-dimensional subspaces
![]() $X \subseteq A$
and
$X \subseteq A$
and
![]() $V \subseteq J$
such that
$V \subseteq J$
such that
![]() $A = X + J$
and
$A = X + J$
and
![]() $J = V + J^2$
, and to verify that
$J = V + J^2$
, and to verify that
![]() $A = X + V + V^2 + V^3 + \cdots $
so that A is finite generated. One may also show that for each graded component
$A = X + V + V^2 + V^3 + \cdots $
so that A is finite generated. One may also show that for each graded component
![]() $A_m$
, there exists
$A_m$
, there exists
![]() $r \gg 0$
such that
$r \gg 0$
such that
![]() $A_m \subseteq X + V + \cdots + V^r$
, proving that A is locally finite.
$A_m \subseteq X + V + \cdots + V^r$
, proving that A is locally finite.
To verify that (a)
![]() $\implies $
(c), begin with a finite-dimensional graded subspace W of A that generates A as a k-algebra. We may assume without loss of generality that W is an
$\implies $
(c), begin with a finite-dimensional graded subspace W of A that generates A as a k-algebra. We may assume without loss of generality that W is an
![]() $(A_0, A_0)$
-bimodule. Then writing
$(A_0, A_0)$
-bimodule. Then writing
![]() $W = A_0 + V$
for some
$W = A_0 + V$
for some
![]() $(A_0)^e$
-submodule
$(A_0)^e$
-submodule
![]() $V \subseteq A_{\geq 1}$
and verifying that
$V \subseteq A_{\geq 1}$
and verifying that
![]() $A = A_0 + V + J^2$
, one concludes that
$A = A_0 + V + J^2$
, one concludes that
 $\dim _k(J/J^2) < \infty $
.
$\dim _k(J/J^2) < \infty $
.
As mentioned earlier, if A is a graded ring and M and N are graded left A-modules with M finitely generated, then
![]() $\underline { {\mathrm {{Hom}}}}_A(M,N) = {\mathrm {{Hom}}}_A(M,N)$
. We require the following derived version of this fact.
$\underline { {\mathrm {{Hom}}}}_A(M,N) = {\mathrm {{Hom}}}_A(M,N)$
. We require the following derived version of this fact.
Lemma 2.4. Let A be a graded ring and let
![]() $M \in A {\mathrm {\!-Gr}}$
.
$M \in A {\mathrm {\!-Gr}}$
.
-
(1) M is perfect if and only if M is graded perfect.
-
(2) If
 $Q \in D^-(A {\mathrm {\!-Gr}})$
is a complex of finitely generated graded projectives and
$Q \in D^-(A {\mathrm {\!-Gr}})$
is a complex of finitely generated graded projectives and
 $N \in D(A {\mathrm {\!-Gr}})$
, then the natural map
$N \in D(A {\mathrm {\!-Gr}})$
, then the natural map
 ${\mathrm R}\underline { {\mathrm {{Hom}}}}_A(Q,N) \to {\mathrm {RHom}}_A(Q,N)$
provides a quasi-isomorphism. In particular, if
${\mathrm R}\underline { {\mathrm {{Hom}}}}_A(Q,N) \to {\mathrm {RHom}}_A(Q,N)$
provides a quasi-isomorphism. In particular, if
 $M, N \in A {\mathrm {\!-Gr}}$
with M perfect, then the natural inclusions
$M, N \in A {\mathrm {\!-Gr}}$
with M perfect, then the natural inclusions
 $\underline { {\mathrm {{Ext}}}}^i_A(M,N) \subseteq {\mathrm {{Ext}}}^i_A(M,N)$
are equalities for all
$\underline { {\mathrm {{Ext}}}}^i_A(M,N) \subseteq {\mathrm {{Ext}}}^i_A(M,N)$
are equalities for all
 $i \geq 0$
.
$i \geq 0$
.
Proof. (1) If M is graded perfect, then it is clearly perfect. Conversely, assume that M has a projective resolution of finite type, say
 $$ \begin{align*} 0 \to P^{-n} \to \cdots \to P^{-2} \overset{d^{-2}}{\longrightarrow} P^{-1} \overset{d^{-1}}{\longrightarrow} P^0 \to M \to 0, \end{align*} $$
$$ \begin{align*} 0 \to P^{-n} \to \cdots \to P^{-2} \overset{d^{-2}}{\longrightarrow} P^{-1} \overset{d^{-1}}{\longrightarrow} P^0 \to M \to 0, \end{align*} $$
so that M is quasi-isomorphic to the perfect complex
![]() $P^{\bullet }$
. Then one may construct a graded resolution
$P^{\bullet }$
. Then one may construct a graded resolution
![]() $Q^{\bullet }$
of M consisting of finitely generated graded projective modules. Because M is finitely generated, it has a finite set of homogeneous generators, and thus there is a finitely generated graded projective module
$Q^{\bullet }$
of M consisting of finitely generated graded projective modules. Because M is finitely generated, it has a finite set of homogeneous generators, and thus there is a finitely generated graded projective module
![]() $Q^0$
with a graded surjection
$Q^0$
with a graded surjection
![]() $Q^0 \twoheadrightarrow M$
. The rest of the graded resolution can now be constructed by an inductive argument, with the assistance of the generalized Schanuel’s lemma [Reference Lam24, Corollary 5.5].
$Q^0 \twoheadrightarrow M$
. The rest of the graded resolution can now be constructed by an inductive argument, with the assistance of the generalized Schanuel’s lemma [Reference Lam24, Corollary 5.5].
(2) Since Q is a bounded above complex of graded projectives,
![]() $ {\mathrm {RHom}}_A(Q, N) = {\mathrm {{Hom}}}_A(Q,N)$
and
$ {\mathrm {RHom}}_A(Q, N) = {\mathrm {{Hom}}}_A(Q,N)$
and
![]() $\text{R}\underline { {\mathrm {{Hom}}}}_A(Q,N) = \underline { {\mathrm {{Hom}}}}_A(Q,N)$
. Since each
$\text{R}\underline { {\mathrm {{Hom}}}}_A(Q,N) = \underline { {\mathrm {{Hom}}}}_A(Q,N)$
. Since each
![]() $Q^i$
is finitely generated, the inclusion
$Q^i$
is finitely generated, the inclusion
![]() $\underline { {\mathrm {{Hom}}}}_A(Q^i, N^j) \to {\mathrm {{Hom}}}_A(Q^i, N^j)$
is an equality for each
$\underline { {\mathrm {{Hom}}}}_A(Q^i, N^j) \to {\mathrm {{Hom}}}_A(Q^i, N^j)$
is an equality for each
![]() $i, j$
; it follows that the natural inclusion of complexes
$i, j$
; it follows that the natural inclusion of complexes
![]() $\underline { {\mathrm {{Hom}}}}_A(Q, N) \to {\mathrm {{Hom}}}_A(Q, N)$
is an equality as required.
$\underline { {\mathrm {{Hom}}}}_A(Q, N) \to {\mathrm {{Hom}}}_A(Q, N)$
is an equality as required.
In particular, if M is a perfect module, it is quasi-isomorphic to a bounded complex Q of finitely generated graded projectives and we have
![]() $ {\mathrm {RHom}}_A(M, N) = {\mathrm {{Hom}}}_A(Q,N)$
and
$ {\mathrm {RHom}}_A(M, N) = {\mathrm {{Hom}}}_A(Q,N)$
and
![]() $\text{R}\underline { {\mathrm {{Hom}}}}_A(M,N) = \underline { {\mathrm {{Hom}}}}_A(Q,N)$
; thus the second statement arises from the first by taking cohomology.
$\text{R}\underline { {\mathrm {{Hom}}}}_A(M,N) = \underline { {\mathrm {{Hom}}}}_A(Q,N)$
; thus the second statement arises from the first by taking cohomology.
Remark 2.5. We will often invoke the derived
![]() $ {\mathrm {{Hom}}}$
construction
$ {\mathrm {{Hom}}}$
construction
![]() $ {\mathrm {RHom}}_A(M,N)$
in the case where M and N are complexes of graded modules and M is perfect. Thanks to Lemma 2.4 and the above remarks about graded tensor products, the graded and ungraded Hom and tensor functors, as well as their corresponding derived functors, are equal in almost all cases where we are concerned. Thus unless otherwise noted, we will use the notation of the usual ungraded functors (such as
$ {\mathrm {RHom}}_A(M,N)$
in the case where M and N are complexes of graded modules and M is perfect. Thanks to Lemma 2.4 and the above remarks about graded tensor products, the graded and ungraded Hom and tensor functors, as well as their corresponding derived functors, are equal in almost all cases where we are concerned. Thus unless otherwise noted, we will use the notation of the usual ungraded functors (such as
![]() $ {\mathrm {{Hom}}}$
,
$ {\mathrm {{Hom}}}$
,
![]() $ {\mathrm {{Ext}}}$
,
$ {\mathrm {{Ext}}}$
,
![]() $-\otimes _R -$
,
$-\otimes _R -$
,
![]() $ {\mathrm {Tor}}$
, etc.) with the understanding that these objects carry a canonical grading when the arguments are graded. We trust that this slight abuse of notation will not cause confusion, and it carries the added benefit that some proofs can be written for ungraded and graded twisted Calabi–Yau algebras simultaneously; we will carefully indicate when this is not the case.
$ {\mathrm {Tor}}$
, etc.) with the understanding that these objects carry a canonical grading when the arguments are graded. We trust that this slight abuse of notation will not cause confusion, and it carries the added benefit that some proofs can be written for ungraded and graded twisted Calabi–Yau algebras simultaneously; we will carefully indicate when this is not the case.
The following generalizes a well-known argument from the setting of connected graded algebras to detect finiteness in the minimal projective resolution of a graded module.
Lemma 2.6. Let A be a graded k-algebra whose degree zero part
![]() $A_0$
has finite k-dimension, and set
$A_0$
has finite k-dimension, and set
![]() $S = A/J(A)$
. Let M be a bounded-below graded left A-module with minimal graded projective resolution
$S = A/J(A)$
. Let M be a bounded-below graded left A-module with minimal graded projective resolution
![]() $P^\bullet \to M \to 0$
. Then for every integer
$P^\bullet \to M \to 0$
. Then for every integer
![]() $i \geq 0$
we have isomorphisms of right S-modules
$i \geq 0$
we have isomorphisms of right S-modules
 $$ \begin{align*} {\mathrm{{Hom}}}_S({\mathrm{Tor}}_i^A(S,M),S) \cong {\mathrm{{Ext}}}^i_A(M,S), \end{align*} $$
$$ \begin{align*} {\mathrm{{Hom}}}_S({\mathrm{Tor}}_i^A(S,M),S) \cong {\mathrm{{Ext}}}^i_A(M,S), \end{align*} $$
and the following are equivalent:
-
(a)
 $P^{-i}$
is finitely generated (respectively, zero);
$P^{-i}$
is finitely generated (respectively, zero); -
(b) the left S-module
 $ {\mathrm {Tor}}_i^A(S, M)$
has finite k-dimension (respectively, is zero);
$ {\mathrm {Tor}}_i^A(S, M)$
has finite k-dimension (respectively, is zero); -
(c) The right S-module
 $ {\mathrm {{Ext}}}^i_A(M,S)$
has finite k-dimension (respectively, is zero).
$ {\mathrm {{Ext}}}^i_A(M,S)$
has finite k-dimension (respectively, is zero).
Proof. For notational convenience, we set
![]() $j = -i$
throughout this proof. Minimality of
$j = -i$
throughout this proof. Minimality of
![]() $P^\bullet $
implies that the boundary operators of the tensored complex
$P^\bullet $
implies that the boundary operators of the tensored complex
![]() $S \otimes _A P^\bullet $
are all zero. Setting
$S \otimes _A P^\bullet $
are all zero. Setting
![]() $J = J(A)$
, the homology modules of this complex are equal to
$J = J(A)$
, the homology modules of this complex are equal to
 $$ \begin{align*} {\mathrm{Tor}}^A_{-j}(S, M) = A/J \otimes_A P^j \cong P^j/JP^j. \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}^A_{-j}(S, M) = A/J \otimes_A P^j \cong P^j/JP^j. \end{align*} $$
Because M is bounded below, the same is true of each term
![]() $P^j$
. Similarly, because
$P^j$
. Similarly, because
![]() $P^\bullet $
is minimal, the boundary operators of
$P^\bullet $
is minimal, the boundary operators of
![]() $ {\mathrm {{Hom}}}_A(P^\bullet ,S)$
are all zero. Combining this observation with tensor-Hom adjointness yields
$ {\mathrm {{Hom}}}_A(P^\bullet ,S)$
are all zero. Combining this observation with tensor-Hom adjointness yields
 $$ \begin{align*} {\mathrm{{Ext}}}^{-j}_A(M,S) &\cong {\mathrm{{Hom}}}_A(P^j, S) \cong {\mathrm{{Hom}}}_A(P^j, {\mathrm{{Hom}}}_S(S,S)) \\ &\cong {\mathrm{{Hom}}}_S(S \otimes_A P^j, S) \cong {\mathrm{{Hom}}}_S(P^j/JP^j, S). \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^{-j}_A(M,S) &\cong {\mathrm{{Hom}}}_A(P^j, S) \cong {\mathrm{{Hom}}}_A(P^j, {\mathrm{{Hom}}}_S(S,S)) \\ &\cong {\mathrm{{Hom}}}_S(S \otimes_A P^j, S) \cong {\mathrm{{Hom}}}_S(P^j/JP^j, S). \end{align*} $$
A direct comparison of these expressions gives
 $ {\mathrm {{Hom}}}_S( {\mathrm {Tor}}_i(S,M),S) \cong {\mathrm {{Ext}}}^i_A(M,S)$
.
$ {\mathrm {{Hom}}}_S( {\mathrm {Tor}}_i(S,M),S) \cong {\mathrm {{Ext}}}^i_A(M,S)$
.
By Lemma 2.2(2), any generating set for
![]() $P^j/JP^j$
lifts to a generating set for
$P^j/JP^j$
lifts to a generating set for
![]() $P^j$
. Note that the action of A on
$P^j$
. Note that the action of A on
![]() $P^j/JP^j$
factors through the finite-dimensional algebra
$P^j/JP^j$
factors through the finite-dimensional algebra
![]() $S = A/J$
. Thus
$S = A/J$
. Thus
![]() $P^j$
is finitely generated (respectively, zero) if and only if
$P^j$
is finitely generated (respectively, zero) if and only if
 $P^j / JP^j \cong {\mathrm {Tor}}^A_{-j}(S,M)$
is finite-dimensional (respectively, zero), establishing (a)
$P^j / JP^j \cong {\mathrm {Tor}}^A_{-j}(S,M)$
is finite-dimensional (respectively, zero), establishing (a)
![]() $\iff $
(b). Because the left and right S-dual functors
$\iff $
(b). Because the left and right S-dual functors
![]() $ {\mathrm {{Hom}}}_S(-,S)$
and
$ {\mathrm {{Hom}}}_S(-,S)$
and
![]() $ {\mathrm {{Hom}}}_{S^{\mathrm {op}}}(-,S)$
restrict to inverse equivalences between finite-dimensional graded left and right S-modules, we obtain (b)
$ {\mathrm {{Hom}}}_{S^{\mathrm {op}}}(-,S)$
restrict to inverse equivalences between finite-dimensional graded left and right S-modules, we obtain (b)
![]() $\iff $
(c).
$\iff $
(c).
2.2 Idempotents and decomposition
The next few results concern idempotents and their associated decompositions. Recall that a ring is indecomposable if it is not isomorphic to a direct product of two nonzero rings, or equivalently, if it has no nontrivial central idempotents. Similarly, we say that a graded ring is graded-indecomposable if it is not isomorphic to a direct product of two graded rings; this is equivalent to the property that A has no nontrivial homogeneous central idempotents. It is useful to know that in the case of interest to us we do not need to distinguish between these.
Lemma 2.7. Let A be a graded ring. Then A is indecomposable if and only if it is graded-indecomposable.
Proof. Let
![]() $e = e_0 + e_1 + \dots + e_n$
be a idempotent, where
$e = e_0 + e_1 + \dots + e_n$
be a idempotent, where
![]() $e_i \in A_i$
, and note that
$e_i \in A_i$
, and note that
![]() $e_0$
is a homogeneous idempotent. Suppose that
$e_0$
is a homogeneous idempotent. Suppose that
![]() $e \neq 0,1$
is nontrivial; we will prove that
$e \neq 0,1$
is nontrivial; we will prove that
![]() $e_0$
is nontrivial. First suppose that
$e_0$
is nontrivial. First suppose that
![]() $e_0 = 0$
. Fix
$e_0 = 0$
. Fix
![]() $d> 0$
minimal such that
$d> 0$
minimal such that
![]() $e_d \neq 0$
. Then
$e_d \neq 0$
. Then
 $0 \neq e_d = (e^2)_d = 0$
, a contradiction. Now suppose that
$0 \neq e_d = (e^2)_d = 0$
, a contradiction. Now suppose that
![]() $e_0 = 1$
. As
$e_0 = 1$
. As
![]() $e \neq 1$
, let
$e \neq 1$
, let
![]() $d> 0$
be the minimal positive index such that
$d> 0$
be the minimal positive index such that
![]() $e_d \neq 0$
. Then
$e_d \neq 0$
. Then
 $e_d = (e^2)_d = 2e_d$
, yielding the contradiction
$e_d = (e^2)_d = 2e_d$
, yielding the contradiction
![]() $e_d = 0$
. Thus
$e_d = 0$
. Thus
![]() $e_0$
is a homogeneous nontrivial idempotent. It is also easy to see that if e is central, then so is
$e_0$
is a homogeneous nontrivial idempotent. It is also easy to see that if e is central, then so is
![]() $e_0$
. Thus if A has a nontrivial central idempotent, then it has a nontrivial homogeneous central idempotent. The converse is trivially true.
$e_0$
. Thus if A has a nontrivial central idempotent, then it has a nontrivial homogeneous central idempotent. The converse is trivially true.
We will need the following easy lemma on the interaction between idempotents and
![]() $ {\mathrm {RHom}}$
, similar to [Reference Lam25, Proposition 21.6]. Note that for an idempotent e in a ring R and a complex
$ {\mathrm {RHom}}$
, similar to [Reference Lam25, Proposition 21.6]. Note that for an idempotent e in a ring R and a complex
![]() $P \in D(R)$
, we write
$P \in D(R)$
, we write
![]() $eP$
for the complex
$eP$
for the complex
 $eR \otimes _R^L P$
, which may be obtained by multiplying all terms in the complex by e on the left. Right multiplication of a complex in
$eR \otimes _R^L P$
, which may be obtained by multiplying all terms in the complex by e on the left. Right multiplication of a complex in
![]() $D(R^{\mathrm {op}})$
by an idempotent
$D(R^{\mathrm {op}})$
by an idempotent
![]() $e \in R$
is defined similarly.
$e \in R$
is defined similarly.
Lemma 2.8. Let R, S, and T be rings. Let P be a bounded above complex of
![]() $(R, S)$
-bimodules and let Q be a complex of
$(R, S)$
-bimodules and let Q be a complex of
![]() $(R, T)$
-bimodules.
$(R, T)$
-bimodules.
-
(1) For any idempotents
 $e \in S$
,
$e \in S$
,
 $f \in T$
we have as complexes of
$f \in T$
we have as complexes of $$ \begin{align*} {\mathrm{RHom}}_R(Pe, Qf) = e {\mathrm{RHom}}_R(P,Q) f \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_R(Pe, Qf) = e {\mathrm{RHom}}_R(P,Q) f \end{align*} $$
 $(eSe, fTf)$
-bimodules.
$(eSe, fTf)$
-bimodules.
-
(2) If
 $z \in Z(R)$
is a central idempotent, then as complexes of
$z \in Z(R)$
is a central idempotent, then as complexes of $$ \begin{gather*} z {\mathrm{RHom}}_R(P, Q) = {\mathrm{RHom}}_R(P, Q) z = {\mathrm{RHom}}_R(zP, Q) = {\mathrm{RHom}}_R(P, zQ) \\ = {\mathrm{RHom}}_R(z P, zQ) = {\mathrm{RHom}}_{zR}(zP, zQ). \end{gather*} $$
$$ \begin{gather*} z {\mathrm{RHom}}_R(P, Q) = {\mathrm{RHom}}_R(P, Q) z = {\mathrm{RHom}}_R(zP, Q) = {\mathrm{RHom}}_R(P, zQ) \\ = {\mathrm{RHom}}_R(z P, zQ) = {\mathrm{RHom}}_{zR}(zP, zQ). \end{gather*} $$
 $(S, T)$
-bimodules.
$(S, T)$
-bimodules.
Further, if
![]() $R, S, T$
are graded rings,
$R, S, T$
are graded rings,
![]() $P, Q$
are complexes of graded bimodules, and
$P, Q$
are complexes of graded bimodules, and
![]() $e, f, z$
are homogeneous idempotents, the same results hold with
$e, f, z$
are homogeneous idempotents, the same results hold with
![]() $ {\mathrm {RHom}}$
replaced with
$ {\mathrm {RHom}}$
replaced with
![]() ${\mathrm R}\underline { {\mathrm {{Hom}}}}$
, as equalities of complexes of graded bimodules.
${\mathrm R}\underline { {\mathrm {{Hom}}}}$
, as equalities of complexes of graded bimodules.
Proof. (1) We prove the ungraded case; the proof in the graded case is similar. For any
![]() $(R, S)$
-bimodule M and
$(R, S)$
-bimodule M and
![]() $(R, T)$
-bimodule N, the proof that
$(R, T)$
-bimodule N, the proof that
![]() $ {\mathrm {{Hom}}}_R(Me, Nf) = e {\mathrm {{Hom}}}_R(M,N) f$
as
$ {\mathrm {{Hom}}}_R(Me, Nf) = e {\mathrm {{Hom}}}_R(M,N) f$
as
![]() $(eSe, fTf)$
-bimodules is routine. Then for any complexes
$(eSe, fTf)$
-bimodules is routine. Then for any complexes
![]() $P, Q$
as in the statement one immediately obtains
$P, Q$
as in the statement one immediately obtains
![]() $ {\mathrm {{Hom}}}_R(Pe, Qf) = e {\mathrm {{Hom}}}_R(P,Q) f$
from the definition of the total Hom complex. Considering P as a complex of
$ {\mathrm {{Hom}}}_R(Pe, Qf) = e {\mathrm {{Hom}}}_R(P,Q) f$
from the definition of the total Hom complex. Considering P as a complex of
![]() $R \otimes S^{\mathrm {op}}$
-modules, it may be replaced by a quasi-isomorphic bounded above complex of projective
$R \otimes S^{\mathrm {op}}$
-modules, it may be replaced by a quasi-isomorphic bounded above complex of projective
![]() $R \otimes S^{\mathrm {op}}$
-modules, which are also projective as left R-modules. The modules in
$R \otimes S^{\mathrm {op}}$
-modules, which are also projective as left R-modules. The modules in
![]() $Pe$
are then also projective on the left, so we get
$Pe$
are then also projective on the left, so we get
as required.
(2) Note that P is a complex of
![]() $(R, S \otimes Z(R))$
-bimodules and Q a complex of
$(R, S \otimes Z(R))$
-bimodules and Q a complex of
![]() $(R, T \otimes Z(R))$
-bimodules. Since
$(R, T \otimes Z(R))$
-bimodules. Since
![]() $Pz = zP$
and
$Pz = zP$
and
![]() $Qz = zQ$
, most of the equalities follow immediately from part (1) and the others are similarly easy.
$Qz = zQ$
, most of the equalities follow immediately from part (1) and the others are similarly easy.
Lemma 2.9. If
 $A = \bigoplus _{i=1}^n A_{(i)}$
is a direct sum of algebras, then the following hold in
$A = \bigoplus _{i=1}^n A_{(i)}$
is a direct sum of algebras, then the following hold in
![]() $D( {\mathrm {Mod-\!}} A^e)$
:
$D( {\mathrm {Mod-\!}} A^e)$
:
-
(1)
 $ {\mathrm {RHom}}_{A^e}(A_{(i)},A^e) \cong {\mathrm {RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e)$
;
$ {\mathrm {RHom}}_{A^e}(A_{(i)},A^e) \cong {\mathrm {RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e)$
; -
(2)
 $ {\mathrm {RHom}}_{A^e}(A,A^e) \cong \bigoplus _{i=1}^n {\mathrm {RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e)$
.
$ {\mathrm {RHom}}_{A^e}(A,A^e) \cong \bigoplus _{i=1}^n {\mathrm {RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e)$
.
Further, if
 $A = \bigoplus _{i=1}^n A_{(i)}$
is a direct sum of graded algebras, then the corresponding quasi-isomorphisms above hold replacing
$A = \bigoplus _{i=1}^n A_{(i)}$
is a direct sum of graded algebras, then the corresponding quasi-isomorphisms above hold replacing
![]() $ {\mathrm {RHom}}$
with
$ {\mathrm {RHom}}$
with
![]() $\text{R}\underline { {\mathrm {{Hom}}}}$
.
$\text{R}\underline { {\mathrm {{Hom}}}}$
.
Proof. Let
 $z_i \in \bigoplus _{j=1}^n A_{(j)}$
denote the element whose ith entry is the identity of
$z_i \in \bigoplus _{j=1}^n A_{(j)}$
denote the element whose ith entry is the identity of
 $A_{(i)}$
and whose other entries are zero, so that
$A_{(i)}$
and whose other entries are zero, so that
![]() $1 = \sum z_i$
is a sum of orthogonal central idempotents.
$1 = \sum z_i$
is a sum of orthogonal central idempotents.
For (1), consider the central idempotent
 $z = z_i \otimes z_i^{\mathrm {op}} \in A^e$
. Note that as a left
$z = z_i \otimes z_i^{\mathrm {op}} \in A^e$
. Note that as a left
![]() $A^e$
-module we have
$A^e$
-module we have
 $A_{(i)} = zA_{(i)}$
, and also that
$A_{(i)} = zA_{(i)}$
, and also that
 $zA^e \cong A_{(i)}^e$
as algebras and as left
$zA^e \cong A_{(i)}^e$
as algebras and as left
![]() $A^e$
-modules. Then using Lemma 2.8, we have that
$A^e$
-modules. Then using Lemma 2.8, we have that
 $$ \begin{align*} {\mathrm{RHom}}_{A^e}(A_{(i)}, A^e) &= {\mathrm{RHom}}_{A^e}(zA_{(i)}, A^e) \\ &\cong {\mathrm{RHom}}_{zA^e}(zA_{(i)}, zA^e) \\ &\cong {\mathrm{RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e). \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{A^e}(A_{(i)}, A^e) &= {\mathrm{RHom}}_{A^e}(zA_{(i)}, A^e) \\ &\cong {\mathrm{RHom}}_{zA^e}(zA_{(i)}, zA^e) \\ &\cong {\mathrm{RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e). \end{align*} $$
Since
![]() $A^e$
is a
$A^e$
is a
![]() $(A^e, A^e)$
-bimodule, the isomorphisms above hold as complexes of right
$(A^e, A^e)$
-bimodule, the isomorphisms above hold as complexes of right
![]() $A^e$
-modules.
$A^e$
-modules.
We deduce (2) as follows, where (1) is invoked in the final isomorphism:
 $$ \begin{align*} {\mathrm{RHom}}_{A^e}(A,A^e) &= {\mathrm{RHom}}_{A^e}\left( \bigoplus A_{(i)}, A^e \right) \\ &\cong \bigoplus {\mathrm{RHom}}_{A^e}(A_{(i)}, A^e) \cong \bigoplus {\mathrm{RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e). \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{A^e}(A,A^e) &= {\mathrm{RHom}}_{A^e}\left( \bigoplus A_{(i)}, A^e \right) \\ &\cong \bigoplus {\mathrm{RHom}}_{A^e}(A_{(i)}, A^e) \cong \bigoplus {\mathrm{RHom}}_{A_{(i)}^e}(A_{(i)}, A_{(i)}^e). \end{align*} $$
In case the
![]() $A_i$
are graded algebras, analogous proofs to those above, using the
$A_i$
are graded algebras, analogous proofs to those above, using the
![]() $\text{R}\underline { {\mathrm {{Hom}}}}$
version of Lemma 2.8, yield the corresponding graded isomorphisms.
$\text{R}\underline { {\mathrm {{Hom}}}}$
version of Lemma 2.8, yield the corresponding graded isomorphisms.
2.3 Invertible bimodules
Next we turn our attention to invertible bimodules over algebras and graded algebras. Note that a k-central invertible
![]() $(A,A)$
-bimodule U induces a k-linear Morita equivalence
$(A,A)$
-bimodule U induces a k-linear Morita equivalence
![]() $U \otimes _A - \colon A {\mathrm {\!-Mod}} \to A {\mathrm {\!-Mod}}$
. For this reason, a number of standard results from Morita theory (such as those in [Reference Lam24, Section 18], for instance) apply to invertible bimodules, if we impose the extra condition that the equivalences of categories are k-linear.
$U \otimes _A - \colon A {\mathrm {\!-Mod}} \to A {\mathrm {\!-Mod}}$
. For this reason, a number of standard results from Morita theory (such as those in [Reference Lam24, Section 18], for instance) apply to invertible bimodules, if we impose the extra condition that the equivalences of categories are k-linear.
Suppose that A is a graded algebra. We say that a graded
![]() $(A, A)$
-bimodule U is graded-invertible if there exists a graded bimodule V such that there are isomorphisms
$(A, A)$
-bimodule U is graded-invertible if there exists a graded bimodule V such that there are isomorphisms
![]() $U {\mathrm {\underline {\otimes }}}_A V \cong A \cong V {\mathrm {\underline {\otimes }}}_A U$
as graded bimodules. It is useful to note that a graded bimodule that is invertible in the ungraded sense is actually graded-invertible, as follows.
$U {\mathrm {\underline {\otimes }}}_A V \cong A \cong V {\mathrm {\underline {\otimes }}}_A U$
as graded bimodules. It is useful to note that a graded bimodule that is invertible in the ungraded sense is actually graded-invertible, as follows.
Lemma 2.10. Let A be a graded k-algebra, and suppose that U is an
![]() $A^e$
-module that is both graded and invertible. Then U is graded-invertible.
$A^e$
-module that is both graded and invertible. Then U is graded-invertible.
Proof. Because the bimodule U induces a Morita self-equivalence of A, it is finitely generated projective (and a generator) on each side. Thus the natural map
![]() $\underline { {\mathrm {{Hom}}}}_A(U,A) \to {\mathrm {{Hom}}}_A(U,A)$
is an isomorphism, and similarly for
$\underline { {\mathrm {{Hom}}}}_A(U,A) \to {\mathrm {{Hom}}}_A(U,A)$
is an isomorphism, and similarly for
![]() $\underline { {\mathrm {{Hom}}}}_{A^{\mathrm {op}}}(U,A)$
.
$\underline { {\mathrm {{Hom}}}}_{A^{\mathrm {op}}}(U,A)$
.
Now invertibility of U implies that the natural evaluation map
is an isomorphism of
![]() $(A, A)$
-bimodules. But this map preserves grading, so we in fact have a graded isomorphism
$(A, A)$
-bimodules. But this map preserves grading, so we in fact have a graded isomorphism
 $$ \begin{align*} \underline{{\mathrm{{Hom}}}}_{A^{\mathrm{op}}}(U,A) {\mathrm{\underline{\otimes}}}_A U \overset{\sim}{\longrightarrow} A. \end{align*} $$
$$ \begin{align*} \underline{{\mathrm{{Hom}}}}_{A^{\mathrm{op}}}(U,A) {\mathrm{\underline{\otimes}}}_A U \overset{\sim}{\longrightarrow} A. \end{align*} $$
Allowing homomorphisms of left modules to act from the right (opposite of the scalars), the evaluation map
 $U {\mathrm {\underline {\otimes }}}_A \underline { {\mathrm {{Hom}}}}_A(U,A) \to A$
is also a graded isomorphism by symmetry. From this it is straightforward to deduce that U is graded-invertible with inverse bimodule
$U {\mathrm {\underline {\otimes }}}_A \underline { {\mathrm {{Hom}}}}_A(U,A) \to A$
is also a graded isomorphism by symmetry. From this it is straightforward to deduce that U is graded-invertible with inverse bimodule
![]() $\underline { {\mathrm {{Hom}}}}_{A^{\mathrm {op}}}(U,A) \cong \underline { {\mathrm {{Hom}}}}_A(U,A)$
.
$\underline { {\mathrm {{Hom}}}}_{A^{\mathrm {op}}}(U,A) \cong \underline { {\mathrm {{Hom}}}}_A(U,A)$
.
We will make use of the following manner in which a graded-invertible bimodule interacts well with the graded Jacobson radical and semisimple quotient of a locally finite graded algebra.
Lemma 2.11. Let A be a graded algebra such that
![]() $A_0$
is finite-dimensional. Denote
$A_0$
is finite-dimensional. Denote
![]() $J = J(A)$
and
$J = J(A)$
and
![]() $S = A/J$
. If U is a graded-invertible
$S = A/J$
. If U is a graded-invertible
![]() $(A,A)$
-bimodule, then the following hold:
$(A,A)$
-bimodule, then the following hold:
-
(1)
 $S \otimes _A U \cong U \otimes _A S$
as
$S \otimes _A U \cong U \otimes _A S$
as
 $(A,A)$
-bimodules, and
$(A,A)$
-bimodules, and
 $UJ = JU$
.
$UJ = JU$
. -
(2) The bimodule
 $S \otimes _A U \cong U \otimes _A S$
, considered as a graded
$S \otimes _A U \cong U \otimes _A S$
, considered as a graded
 $(S,S)$
-bimodule is graded-invertible.
$(S,S)$
-bimodule is graded-invertible.
Proof. (1) Note that
![]() $- {\mathrm {\underline {\otimes }}}_A U$
induces an autoequivalence of the category
$- {\mathrm {\underline {\otimes }}}_A U$
induces an autoequivalence of the category
![]() $ {\mathrm {Gr-\!}} A$
, with quasi-inverse given by
$ {\mathrm {Gr-\!}} A$
, with quasi-inverse given by
 $- {\mathrm {\underline {\otimes }}}_A U^{-1}$
. Because
$- {\mathrm {\underline {\otimes }}}_A U^{-1}$
. Because
![]() $S_A$
is a semisimple graded right A-module, the same is true of
$S_A$
is a semisimple graded right A-module, the same is true of
![]() $S \otimes _A U$
. Thus
$S \otimes _A U$
. Thus
![]() $(S \otimes _A U) J = 0$
. Because
$(S \otimes _A U) J = 0$
. Because
![]() $S \otimes _A U \cong U/JU$
, this means that
$S \otimes _A U \cong U/JU$
, this means that
![]() $(U/JU) J = 0$
and thus
$(U/JU) J = 0$
and thus
![]() $UJ \subseteq JU$
. By a symmetric argument, we have
$UJ \subseteq JU$
. By a symmetric argument, we have
![]() $JU \subseteq UJ$
, giving
$JU \subseteq UJ$
, giving
![]() $UJ = JU$
. This implies that
$UJ = JU$
. This implies that
(2) Because
![]() $V = S \otimes _A U \cong U \otimes _A S$
satisfies
$V = S \otimes _A U \cong U \otimes _A S$
satisfies
![]() $JV = VJ = 0$
, we may consider it as an
$JV = VJ = 0$
, we may consider it as an
![]() $(S,S)$
-bimodule. It is easy to deduce from (1) that
$(S,S)$
-bimodule. It is easy to deduce from (1) that
![]() $U^{-1} \otimes _A S \cong S \otimes _A U^{-1}$
as well, so that this bimodule can also be considered as an
$U^{-1} \otimes _A S \cong S \otimes _A U^{-1}$
as well, so that this bimodule can also be considered as an
![]() $(S,S)$
-bimodule. We claim that
$(S,S)$
-bimodule. We claim that
![]() $V' = S \otimes _A U^{-1}$
is a graded inverse to V. Indeed,
$V' = S \otimes _A U^{-1}$
is a graded inverse to V. Indeed,
 $$ \begin{align*} V \otimes_S V' &\cong (U \otimes_A S) \otimes_S (S \otimes_A U^{-1}) \\ &\cong U \otimes_A S \otimes_A U^{-1} \\ &\cong S \otimes_A U \otimes_A U^{-1} \\ &\cong S, \end{align*} $$
$$ \begin{align*} V \otimes_S V' &\cong (U \otimes_A S) \otimes_S (S \otimes_A U^{-1}) \\ &\cong U \otimes_A S \otimes_A U^{-1} \\ &\cong S \otimes_A U \otimes_A U^{-1} \\ &\cong S, \end{align*} $$
and similarly one may compute
![]() $V' \otimes _S V \cong S$
. Thus V is graded-invertible as an
$V' \otimes _S V \cong S$
. Thus V is graded-invertible as an
![]() $(S,S)$
-bimodule.
$(S,S)$
-bimodule.
Given a graded automorphism
![]() $\sigma $
of A and an integer
$\sigma $
of A and an integer
![]() $l \in \mathbb {Z}$
, it is clear that the twisted bimodule
$l \in \mathbb {Z}$
, it is clear that the twisted bimodule
 ${{\hspace {-0.0001pt}}}^1 A^\sigma (l)$
is graded-invertible, with inverse
${{\hspace {-0.0001pt}}}^1 A^\sigma (l)$
is graded-invertible, with inverse
 ${{\hspace {-0.0001pt}}}^1 A^{\sigma ^{-1}}(-l) \cong {{\hspace {-0.0001pt}}}^\sigma A^1(-l)$
. Suppose that A is connected graded. In this case all graded projective modules are free, so if U is a graded invertible bimodule, U is free and clearly of rank
${{\hspace {-0.0001pt}}}^1 A^{\sigma ^{-1}}(-l) \cong {{\hspace {-0.0001pt}}}^\sigma A^1(-l)$
. Suppose that A is connected graded. In this case all graded projective modules are free, so if U is a graded invertible bimodule, U is free and clearly of rank
![]() $1$
on both sides; it follows that U is of the form
$1$
on both sides; it follows that U is of the form
 ${{\hspace {-0.0001pt}}}^1 A^\sigma (l)$
[Reference Minamoto and Mori33, Lemma 2.9]. However, for not necessarily connected graded algebras, an invertible bimodule need not have this form. See Example 7.1 below for one simple example. We defer more detailed results about the structure of graded invertible bimodules over graded algebras to the companion paper [Reference Reyes and Rogalski40], since such information is not needed for our results in this paper.
${{\hspace {-0.0001pt}}}^1 A^\sigma (l)$
[Reference Minamoto and Mori33, Lemma 2.9]. However, for not necessarily connected graded algebras, an invertible bimodule need not have this form. See Example 7.1 below for one simple example. We defer more detailed results about the structure of graded invertible bimodules over graded algebras to the companion paper [Reference Reyes and Rogalski40], since such information is not needed for our results in this paper.
2.4 Manipulating objects in the derived category
The final results of this section concern manipulation of objects in derived categories of modules. Part (2) of the next lemma is a slightly more general version of the lemma observed, for instance, in [Reference Yekutieli and Zhang51, Lemma 2.2].
Lemma 2.12. Fix (graded) algebras A and B. Suppose that L is a perfect complex of (graded) left A-modules, and that M is a complex of (graded) left
![]() $A \otimes B^{\mathrm {op}}$
-modules.
$A \otimes B^{\mathrm {op}}$
-modules.
-
(1) There is a natural isomorphism in the derived category of (graded) right B-modules
 $$ \begin{align*} {\mathrm{RHom}}_A(L,A) \otimes^L_A M \cong {\mathrm{RHom}}_A(L,M). \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_A(L,A) \otimes^L_A M \cong {\mathrm{RHom}}_A(L,M). \end{align*} $$
-
(2) If N is bounded above complex of left
 $B \otimes C^{\mathrm {op}}$
-modules for a (graded) algebra C, then there is an isomorphism in the derived category of (graded) right C-modules
$B \otimes C^{\mathrm {op}}$
-modules for a (graded) algebra C, then there is an isomorphism in the derived category of (graded) right C-modules  $$ \begin{align*} {\mathrm{RHom}}_A(L,M) \otimes^L_B N \cong {\mathrm{RHom}}_A(L, M \otimes^L_B N). \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_A(L,M) \otimes^L_B N \cong {\mathrm{RHom}}_A(L, M \otimes^L_B N). \end{align*} $$
Proof. Part (1) is proved, for instance, in [45, Tag 07VI], and the same proof carries over to the graded case. Then (2) follows directly from (1) because
 $$ \begin{align*}& {\mathrm{RHom}}_A(L,M) \otimes^L_B N \cong {\mathrm{RHom}}_A(L,A) \otimes^L_A M \otimes^L_B N \cong {\mathrm{RHom}}_A(L,M \otimes^L_B N).\\[-38pt]\end{align*} $$
$$ \begin{align*}& {\mathrm{RHom}}_A(L,M) \otimes^L_B N \cong {\mathrm{RHom}}_A(L,A) \otimes^L_A M \otimes^L_B N \cong {\mathrm{RHom}}_A(L,M \otimes^L_B N).\\[-38pt]\end{align*} $$
It is well-known that one can use Hochschild cohomology groups of certain bimodules to recover the “one-sided”
![]() $ {\mathrm {Tor}}$
and
$ {\mathrm {Tor}}$
and
![]() $ {\mathrm {{Ext}}}$
groups over A, for
$ {\mathrm {{Ext}}}$
groups over A, for
![]() $K_A$
,
$K_A$
,
![]() ${{\hspace {-0.0001pt}}}_A M$
, and
${{\hspace {-0.0001pt}}}_A M$
, and
![]() ${{\hspace {-0.0001pt}}}_A N$
as follows (see [Reference Cartan and Eilenberg11, Corollary IX.4.4]):
${{\hspace {-0.0001pt}}}_A N$
as follows (see [Reference Cartan and Eilenberg11, Corollary IX.4.4]):
 $$ \begin{align*} {\mathrm{Tor}}_n^A(K,N) &\cong {HH}_n(A, N \otimes K) = {\mathrm{Tor}}_n^{A^e}(A, N \otimes K), \\ \quad {\mathrm{{Ext}}}^n_A(M,N) &\cong {HH}^n(A, {\mathrm{{Hom}}}_k(M,N)) = {\mathrm{{Ext}}}^n_{A^e}(A,{\mathrm{{Hom}}}_k(M,N)). \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}_n^A(K,N) &\cong {HH}_n(A, N \otimes K) = {\mathrm{Tor}}_n^{A^e}(A, N \otimes K), \\ \quad {\mathrm{{Ext}}}^n_A(M,N) &\cong {HH}^n(A, {\mathrm{{Hom}}}_k(M,N)) = {\mathrm{{Ext}}}^n_{A^e}(A,{\mathrm{{Hom}}}_k(M,N)). \end{align*} $$
We require the following version of these identities, stated in the derived context.
Lemma 2.13. Let
![]() $A, B, C$
be (graded) algebras. Let P be a bounded above complex of (graded) left
$A, B, C$
be (graded) algebras. Let P be a bounded above complex of (graded) left
![]() $A^e$
-modules, K be a complex of (graded)
$A^e$
-modules, K be a complex of (graded)
![]() $B \otimes A^{\mathrm {op}}$
-modules, N a complex of (graded) left
$B \otimes A^{\mathrm {op}}$
-modules, N a complex of (graded) left
![]() $A \otimes C^{\mathrm {op}}$
-modules, and M a complex of (graded)
$A \otimes C^{\mathrm {op}}$
-modules, and M a complex of (graded)
![]() $A \otimes B^{\mathrm {op}}$
-modules.
$A \otimes B^{\mathrm {op}}$
-modules.
-
(1) If K and N are bounded above, then
in the derived category of (graded) $$ \begin{align*} K \otimes^L_A P \otimes^L_A N \cong P \otimes_{A^e}^L (N \otimes K) \cong (K \otimes N) \otimes^L_{A^e} P \end{align*} $$
$$ \begin{align*} K \otimes^L_A P \otimes^L_A N \cong P \otimes_{A^e}^L (N \otimes K) \cong (K \otimes N) \otimes^L_{A^e} P \end{align*} $$
 $B \otimes C^{\mathrm {op}}$
-modules.
$B \otimes C^{\mathrm {op}}$
-modules.
-
(2) If M is bounded above and N is bounded below, then
in the derived category of (graded) $$ \begin{align*} {\mathrm{RHom}}_A(P \otimes^L_A M,N) \cong {\mathrm{RHom}}_{A^e}(P, {\mathrm{{Hom}}}_k(M,N)) \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_A(P \otimes^L_A M,N) \cong {\mathrm{RHom}}_{A^e}(P, {\mathrm{{Hom}}}_k(M,N)) \end{align*} $$
 $B \otimes C^{\mathrm {op}}$
-modules.
$B \otimes C^{\mathrm {op}}$
-modules.
As usual, when
![]() $A, B, C$
are graded algebras, and
$A, B, C$
are graded algebras, and
![]() $P, K, N, M$
are graded modules, the same results hold as isomorphisms of graded modules, with
$P, K, N, M$
are graded modules, the same results hold as isomorphisms of graded modules, with
![]() $\otimes $
replaced by
$\otimes $
replaced by
![]() $ {\mathrm {\underline {\otimes }}}$
and
$ {\mathrm {\underline {\otimes }}}$
and
![]() $ {\mathrm {RHom}}$
by
$ {\mathrm {RHom}}$
by
![]() ${\mathrm R}\underline { {\mathrm {{Hom}}}}$
.
${\mathrm R}\underline { {\mathrm {{Hom}}}}$
.
The notation in part (1) needs a bit of explanation. Note that if
![]() ${{\hspace {-0.0001pt}}}_A N$
and
${{\hspace {-0.0001pt}}}_A N$
and
![]() $K_A$
are modules, then
$K_A$
are modules, then
![]() $N \otimes K$
is naturally a left
$N \otimes K$
is naturally a left
![]() $A^e$
-module via the “outer” action
$A^e$
-module via the “outer” action
![]() $(a \otimes b^{\mathrm {op}}) \cdot (n \otimes k) = an \otimes kb$
. Any left
$(a \otimes b^{\mathrm {op}}) \cdot (n \otimes k) = an \otimes kb$
. Any left
![]() $A^e$
-module is naturally also a right
$A^e$
-module is naturally also a right
![]() $A^e$
-module via the anti-automorphism
$A^e$
-module via the anti-automorphism
![]() $A^e \to A^e$
given by
$A^e \to A^e$
given by
![]() $a \otimes b^{\mathrm {op}} \mapsto b \otimes a^{\mathrm {op}}$
. When we think of
$a \otimes b^{\mathrm {op}} \mapsto b \otimes a^{\mathrm {op}}$
. When we think of
![]() $N \otimes K$
as a right
$N \otimes K$
as a right
![]() $A^e$
-module in this way, we may also write it as
$A^e$
-module in this way, we may also write it as
![]() $K \otimes N$
where the right action is the “inner” one given by
$K \otimes N$
where the right action is the “inner” one given by
![]() $(k \otimes n) \cdot (b \otimes a^{\mathrm {op}}) = kb \otimes an$
, so that the left
$(k \otimes n) \cdot (b \otimes a^{\mathrm {op}}) = kb \otimes an$
, so that the left
![]() $B \otimes C^{\mathrm {op}}$
-action is an outer action. In case N and K are complexes, we simply extend the “inner” and “outer” actions above to each term in the tensor product of complexes.
$B \otimes C^{\mathrm {op}}$
-action is an outer action. In case N and K are complexes, we simply extend the “inner” and “outer” actions above to each term in the tensor product of complexes.
We omit the proof for the sake of brevity. The argument is a straightforward computation in the derived category, carried out after replacing P by a quasi-isomorhpic bounded above complex of projective
![]() $A^e$
-modules.
$A^e$
-modules.
3 Homologically smooth algebras and global dimension
Recall from Definition 1.2(i) that a k-algebra A is homologically smooth over k if A is perfect as a left
![]() $A^e$
-module. This section is devoted to fundamental results on locally finite graded homologically smooth k-algebras.
$A^e$
-module. This section is devoted to fundamental results on locally finite graded homologically smooth k-algebras.
3.1 A characterization of homological smoothness
Our first goal will be to find an alternative characterization of homological smoothness for locally finite graded algebras.
Remark 3.1. We note (as in [Reference Lunts29, Remark 3.2]) that the “swap” algebra isomorphism
![]() $A^e = A \otimes A^{\mathrm {op}} \to A^{\mathrm {op}} \otimes A \cong (A^{\mathrm {op}})^e$
induces an equivalence between left
$A^e = A \otimes A^{\mathrm {op}} \to A^{\mathrm {op}} \otimes A \cong (A^{\mathrm {op}})^e$
induces an equivalence between left
![]() $A^e$
-modules and left
$A^e$
-modules and left
![]() $(A^{\mathrm {op}})^e$
-modules that interchanges A and
$(A^{\mathrm {op}})^e$
-modules that interchanges A and
![]() $A^{\mathrm {op}}$
and preserves perfect modules. This makes it easy to see that A is homologically smooth if and only if
$A^{\mathrm {op}}$
and preserves perfect modules. This makes it easy to see that A is homologically smooth if and only if
![]() $A^{\mathrm {op}}$
is. Thus the homologically smooth property is “left-right symmetric.”
$A^{\mathrm {op}}$
is. Thus the homologically smooth property is “left-right symmetric.”
A projective
![]() $A^e$
-module resolution of A can be used to obtain projective resolutions of every left A-module as follows.
$A^e$
-module resolution of A can be used to obtain projective resolutions of every left A-module as follows.
Lemma 3.2. Let A be a (graded) algebra.
-
(1) Let
 $P^{\bullet } \to A \to 0$
be a (graded)
$P^{\bullet } \to A \to 0$
be a (graded)
 $A^e$
-projective resolution. For any bounded above complex
$A^e$
-projective resolution. For any bounded above complex
 $N^{\bullet }$
of (graded) left A-modules,
$N^{\bullet }$
of (graded) left A-modules,
 $P \otimes _A^L N \cong N$
as complexes of (graded) left A-modules. In particular, for any (graded) left A-module M, the complex
$P \otimes _A^L N \cong N$
as complexes of (graded) left A-modules. In particular, for any (graded) left A-module M, the complex
 $P^\bullet \otimes _A M$
is a (graded) projective resolution of M.
$P^\bullet \otimes _A M$
is a (graded) projective resolution of M. -
(2) Suppose that A is homologically smooth. If N is a bounded complex of (graded) finite-dimensional left A-modules, then N is perfect.
-
(3) If A is graded and homologically smooth with
 $A_0$
finite-dimensional, then A is a finitely generated (hence locally finite) algebra.
$A_0$
finite-dimensional, then A is a finitely generated (hence locally finite) algebra.
Proof. (1) This is well known. For a proof in the case where N consists of a single nonzero module, see [Reference Ginzburg17, p. 68].
(2) Since A is homologically smooth, we may fix a perfect
![]() $A^e$
-projective resolution
$A^e$
-projective resolution
![]() $P^{\bullet }$
of A. By part (1),
$P^{\bullet }$
of A. By part (1),
![]() $P \otimes _A N$
is quasi-isomorphic to N. Because each
$P \otimes _A N$
is quasi-isomorphic to N. Because each
![]() $N^j$
is finite-dimensional and each
$N^j$
is finite-dimensional and each
![]() $P^i$
is a finitely generated projective
$P^i$
is a finitely generated projective
![]() $A^e$
-module,
$A^e$
-module,
![]() $P^i$
is a summand of some
$P^i$
is a summand of some
![]() $(A^e)^n$
, and then
$(A^e)^n$
, and then
![]() $P^i \otimes _A N^j$
is a summand of
$P^i \otimes _A N^j$
is a summand of
![]() $(A^e)^n \otimes _A N^j \cong A \otimes _k N^j$
, which is finitely generated free on the left. So
$(A^e)^n \otimes _A N^j \cong A \otimes _k N^j$
, which is finitely generated free on the left. So
![]() $P^i \otimes _A N^j$
is finitely generated projective. Thus
$P^i \otimes _A N^j$
is finitely generated projective. Thus
![]() $P \otimes _A N$
is a complex of finitely generated projective left A-modules and so N is perfect.
$P \otimes _A N$
is a complex of finitely generated projective left A-modules and so N is perfect.
(3) Let
![]() $J = J(A)$
. In this case,
$J = J(A)$
. In this case,
![]() $S = A/J$
is perfect as a left A-module by part (2), so that A is finitely generated as an algebra and locally finite according to Lemma 2.3.
$S = A/J$
is perfect as a left A-module by part (2), so that A is finitely generated as an algebra and locally finite according to Lemma 2.3.
When manipulating k-central bimodules over locally finite algebras that are not necessarily connected, it will become crucial to assume that A is separable modulo its graded Jacobson radical. Recall that a k-algebra S is said to be separable (over k) if
![]() $S \otimes K$
is semisimple for every field extension K of k. As is well-known, there are many equivalent formulations of this property, as follows.
$S \otimes K$
is semisimple for every field extension K of k. As is well-known, there are many equivalent formulations of this property, as follows.
Lemma 3.3. The following conditions are all equivalent for a k-algebra S:
-
(1)
 $S \otimes K$
is semisimple for every field extension K of k, that is, S is separable;
$S \otimes K$
is semisimple for every field extension K of k, that is, S is separable; -
(2)
 $S \otimes T$
is semisimple for every semisimple k-algebra T;
$S \otimes T$
is semisimple for every semisimple k-algebra T; -
(3) S is projective as a left
 $S^e$
-module;
$S^e$
-module; -
(4)
 $S^e$
is semisimple;
$S^e$
is semisimple; -
(5)
 $S \cong \bigoplus _{i=1}^n \mathbb {M}_{r_i}(D_i)$
for finite-dimensional division k-algebras
$S \cong \bigoplus _{i=1}^n \mathbb {M}_{r_i}(D_i)$
for finite-dimensional division k-algebras
 $D_i$
whose centers
$D_i$
whose centers
 $Z(D_i)$
are separable field extensions of k.
$Z(D_i)$
are separable field extensions of k.
Proof. See [Reference Bourbaki7, Section 13], [Reference Curtis and Reiner12, Section 71], [Reference DeMeyer and Ingraham13, Chapter II], or [Reference Weibel49, Section 9.2.1].
From the characterization of separability in part (5) above, we see that a separable algebra is necessarily finite-dimensional over k; also, if k is a perfect field (such as a field of characteristic
![]() $0$
, an algebraically closed field, or a finite field), then every finite-dimensional semisimple k-algebra is separable.
$0$
, an algebraically closed field, or a finite field), then every finite-dimensional semisimple k-algebra is separable.
For finite-dimensional algebras, the property of being homologically smooth can be seen as a higher-dimensional generalization of separability.
Lemma 3.4. For a finite-dimensional k-algebra A, the following are equivalent:
-
(a) A is homologically smooth;
-
(b)
 $ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) < \infty $
;
$ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) < \infty $
; -
(c)
 $A^e$
has finite global dimension;
$A^e$
has finite global dimension; -
(d)
 $A \otimes K$
has finite global dimension for every field extension K of k.
$A \otimes K$
has finite global dimension for every field extension K of k.
Proof. Clearly (a)
![]() $\implies $
(b); to prove the converse, assume
$\implies $
(b); to prove the converse, assume
![]() $ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = d < \infty $
. Since
$ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = d < \infty $
. Since
![]() $A^e$
is finite-dimensional and consequently noetherian, all terms in the minimal projective resolution of A in
$A^e$
is finite-dimensional and consequently noetherian, all terms in the minimal projective resolution of A in
![]() $A^e {\mathrm {\!-Mod}}$
are finitely generated. Thus (b)
$A^e {\mathrm {\!-Mod}}$
are finitely generated. Thus (b)
![]() $\implies $
(a). The equivalence of (b)–(d) is demonstrated in [Reference Buchweitz, Green, Madsen and Solberg10, p. 807].
$\implies $
(a). The equivalence of (b)–(d) is demonstrated in [Reference Buchweitz, Green, Madsen and Solberg10, p. 807].
In fact, it is known that conditions (b) and (c) above are equivalent for every k-algebra A; see [Reference Krähmer23, Corollary 2.5].
The question of whether a locally finite graded algebra is separable modulo its graded radical immediately reduces to the corresponding problem for finite-dimensional algebras, by restricting to the degree
![]() $0$
part of the algebra. The proofs of Theorem 3.6 and its supporting Lemma 3.5 were communicated to us by Jeremy Rickard. We thank him for his permission to include them here; we also thank MathOverflowFootnote
1
for providing a forum to pose the question. The following is likely a folk result, but we could not locate a suitable reference.
$0$
part of the algebra. The proofs of Theorem 3.6 and its supporting Lemma 3.5 were communicated to us by Jeremy Rickard. We thank him for his permission to include them here; we also thank MathOverflowFootnote
1
for providing a forum to pose the question. The following is likely a folk result, but we could not locate a suitable reference.
Lemma 3.5. If S is a finite-dimensional semisimple k-algebra and
![]() $K = \overline {k}$
is an algebraic closure, then
$K = \overline {k}$
is an algebraic closure, then
![]() $S \otimes K$
is a finite direct sum of matrix rings over commutative local K-algebras.
$S \otimes K$
is a finite direct sum of matrix rings over commutative local K-algebras.
Proof. Let
![]() $k^s \subseteq K$
denote the separable closure of k. By [Reference Bourbaki7, Section 12.7, Corollaire 1 to Proposition 12.8], the extension
$k^s \subseteq K$
denote the separable closure of k. By [Reference Bourbaki7, Section 12.7, Corollaire 1 to Proposition 12.8], the extension
![]() $S^s = S \otimes k^s$
is semisimple. Thus
$S^s = S \otimes k^s$
is semisimple. Thus
 $S^s \cong \bigoplus _{i=1}^n \mathbb {M}_{r_i}(D_i)$
for some finite-dimensional division
$S^s \cong \bigoplus _{i=1}^n \mathbb {M}_{r_i}(D_i)$
for some finite-dimensional division
![]() $k^s$
-algebras
$k^s$
-algebras
![]() $D_i$
. The centers
$D_i$
. The centers
![]() $L_i = Z(D_i)$
form intermediary fields
$L_i = Z(D_i)$
form intermediary fields
![]() $k^s \subseteq L_i \subseteq K$
. Since
$k^s \subseteq L_i \subseteq K$
. Since
![]() $K/k^s$
is purely inseparable, the same is true for each
$K/k^s$
is purely inseparable, the same is true for each
![]() $K/L_i$
. Thus each
$K/L_i$
. Thus each
![]() $L_i$
is separably closed and consequently has trivial Brauer group [Reference Farb and Dennis16, Corollary 4.6]. It follows that in fact
$L_i$
is separably closed and consequently has trivial Brauer group [Reference Farb and Dennis16, Corollary 4.6]. It follows that in fact
![]() $S^s \cong \bigoplus \mathbb {M}_{r_i}(L_i)$
is a sum of matrix algebras over fields. Now
$S^s \cong \bigoplus \mathbb {M}_{r_i}(L_i)$
is a sum of matrix algebras over fields. Now
 $S^K = S^s \otimes _{k^s} K \cong \bigoplus \mathbb {M}_{r_i}(L_i \otimes _{k^s} K)$
. Each ring
$S^K = S^s \otimes _{k^s} K \cong \bigoplus \mathbb {M}_{r_i}(L_i \otimes _{k^s} K)$
. Each ring
![]() $R_i = L_i \otimes _{k^s} K$
is a finite-dimensional commutative K-algebra and hence is Artinian. Then
$R_i = L_i \otimes _{k^s} K$
is a finite-dimensional commutative K-algebra and hence is Artinian. Then
![]() $R_i$
is a direct sum of finitely many commutative local K-algebras, say
$R_i$
is a direct sum of finitely many commutative local K-algebras, say
 $R_i = \bigoplus _{j=1}^{n_i} R_{ij}$
. Thus
$R_i = \bigoplus _{j=1}^{n_i} R_{ij}$
. Thus
 $S^K = \bigoplus _i \bigoplus _{j=1}^{n_i} \mathbb {M}_{r_i}( R_{ij})$
is a finite direct sum of matrix rings over commutative local K-algebras.
$S^K = \bigoplus _i \bigoplus _{j=1}^{n_i} \mathbb {M}_{r_i}( R_{ij})$
is a finite direct sum of matrix rings over commutative local K-algebras.
Theorem 3.6. (Rickard)
Let A be a finite-dimensional k-algebra. If A is homologically smooth, then
![]() $S = A/J(A)$
is separable over k.
$S = A/J(A)$
is separable over k.
Proof. Set
![]() $K = \overline {k}$
. It suffices to show that
$K = \overline {k}$
. It suffices to show that
![]() $S^K = S \otimes K$
is semisimple; see [Reference Curtis and Reiner12, Theorem 71.2] or [Reference DeMeyer and Ingraham13, Proposition II.1.8]. Thanks to Lemma 3.5 we have
$S^K = S \otimes K$
is semisimple; see [Reference Curtis and Reiner12, Theorem 71.2] or [Reference DeMeyer and Ingraham13, Proposition II.1.8]. Thanks to Lemma 3.5 we have
 $ {\mathrm {{Ext}}}^1_{S^K}(U,V) = 0$
for any nonisomorphic simple left
$ {\mathrm {{Ext}}}^1_{S^K}(U,V) = 0$
for any nonisomorphic simple left
![]() $S^K$
-modules U and V. Note that
$S^K$
-modules U and V. Note that
![]() $A^K$
has finite global dimension by Lemma 3.4. If there were a nonsplit extension of a simple left
$A^K$
has finite global dimension by Lemma 3.4. If there were a nonsplit extension of a simple left
![]() $S^K$
-module U by itself, then we would have
$S^K$
-module U by itself, then we would have
 $ {\mathrm {{Ext}}}^1_{A^K}(U,U) \neq 0$
, contradicting the no-loops conjecture [Reference Igusa20]. It follows that all extensions of simple left
$ {\mathrm {{Ext}}}^1_{A^K}(U,U) \neq 0$
, contradicting the no-loops conjecture [Reference Igusa20]. It follows that all extensions of simple left
![]() $S^K$
-modules split, making
$S^K$
-modules split, making
![]() $S^K$
semisimple.
$S^K$
semisimple.
Lemma 3.7. Let A and B be graded algebras with
![]() $A_0$
and
$A_0$
and
![]() $B_0$
are finite-dimensional, and denote
$B_0$
are finite-dimensional, and denote
![]() $S = A/J(A) = A_0/J(A_0)$
and
$S = A/J(A) = A_0/J(A_0)$
and
![]() $T = B/J(B) = B_0/J(B_0)$
. Suppose that the semisimple k-algebra S is separable. Then
$T = B/J(B) = B_0/J(B_0)$
. Suppose that the semisimple k-algebra S is separable. Then
![]() $J(A \otimes B) = A \otimes J(B) + J(A) \otimes B$
, and the natural map
$J(A \otimes B) = A \otimes J(B) + J(A) \otimes B$
, and the natural map
![]() $(A \otimes B)/J(A \otimes B) \twoheadrightarrow S \otimes _k T$
is an isomorphism.
$(A \otimes B)/J(A \otimes B) \twoheadrightarrow S \otimes _k T$
is an isomorphism.
Proof. Because
![]() $J(A \otimes B) \supseteq (A \otimes B)_{\geq 1} = A \otimes B_{\geq 1} + A_{\geq 1} \otimes B$
, we have
$J(A \otimes B) \supseteq (A \otimes B)_{\geq 1} = A \otimes B_{\geq 1} + A_{\geq 1} \otimes B$
, we have
![]() $(A \otimes B)/J(A \otimes B) \cong (A \otimes B)_0/J((A \otimes B)_0) = (A_0 \otimes B_0)/J(A_0 \otimes B_0)$
. So without loss of generality, we may replace A and B by their degree-zero parts to assume that
$(A \otimes B)/J(A \otimes B) \cong (A \otimes B)_0/J((A \otimes B)_0) = (A_0 \otimes B_0)/J(A_0 \otimes B_0)$
. So without loss of generality, we may replace A and B by their degree-zero parts to assume that
![]() $A = A_0$
and
$A = A_0$
and
![]() $B = B_0$
are finite-dimensional algebras.
$B = B_0$
are finite-dimensional algebras.
Let
![]() $J' = A \otimes J(B) + J(A) \otimes B$
. Because A and B are finite-dimensional, their respective Jacobson radicals
$J' = A \otimes J(B) + J(A) \otimes B$
. Because A and B are finite-dimensional, their respective Jacobson radicals
![]() $J(A)$
and
$J(A)$
and
![]() $J(B)$
are nilpotent ideals. It follows that
$J(B)$
are nilpotent ideals. It follows that
![]() $J'$
is a nilpotent ideal of
$J'$
is a nilpotent ideal of
![]() $A \otimes B$
, so that
$A \otimes B$
, so that
![]() $J' \subseteq J(A \otimes B)$
.
$J' \subseteq J(A \otimes B)$
.
On the other hand, if V and W are finite dimensional vector spaces with subspaces
![]() $V'$
and
$V'$
and
![]() $W',$
respectively, then it is a standard fact that
$W',$
respectively, then it is a standard fact that
![]() $V' \otimes W + V \otimes W'$
is the kernel of the natural map
$V' \otimes W + V \otimes W'$
is the kernel of the natural map
![]() $V \otimes W \to V/V' \otimes W/W'$
. Thus the kernel of the natural map
$V \otimes W \to V/V' \otimes W/W'$
. Thus the kernel of the natural map
![]() $A \otimes B \twoheadrightarrow S \otimes T$
, given by the tensor product of the natural surjections
$A \otimes B \twoheadrightarrow S \otimes T$
, given by the tensor product of the natural surjections
![]() $A \twoheadrightarrow A/J(A)$
and
$A \twoheadrightarrow A/J(A)$
and
![]() $B \twoheadrightarrow B/J(B)$
, is equal to
$B \twoheadrightarrow B/J(B)$
, is equal to
![]() $J'$
. Because S is separable and T is semisimple, the algebra
$J'$
. Because S is separable and T is semisimple, the algebra
![]() $S \otimes T \cong (A \otimes B)/J'$
is also semisimple by Lemma 3.3(2). We deduce (as in [Reference Lam25, Exercise 4.11]) that
$S \otimes T \cong (A \otimes B)/J'$
is also semisimple by Lemma 3.3(2). We deduce (as in [Reference Lam25, Exercise 4.11]) that
![]() $J(A \otimes B) \subseteq J'$
. So in fact
$J(A \otimes B) \subseteq J'$
. So in fact
![]() $J' = J(A \otimes B)$
, and the isomorphism
$J' = J(A \otimes B)$
, and the isomorphism
![]() $S \otimes T \cong (A \otimes B)/J' = (A \otimes B)/J(A \otimes B)$
follows.
$S \otimes T \cong (A \otimes B)/J' = (A \otimes B)/J(A \otimes B)$
follows.
The next lemma facilitates the passage from modules over a graded algebra A to modules over its degree zero part.
Lemma 3.8. Let A be a graded algebra with
![]() $A_0$
finite-dimensional, and let M be a non-negatively graded left A-module. If M is perfect (respectively, has
$A_0$
finite-dimensional, and let M be a non-negatively graded left A-module. If M is perfect (respectively, has
![]() $ {\mathrm {pdim}}(M) \leq d$
) over A, then
$ {\mathrm {pdim}}(M) \leq d$
) over A, then
![]() $M_0$
is perfect (respectively, has
$M_0$
is perfect (respectively, has
![]() $ {\mathrm {pdim}}(M_0) \leq d$
) as an
$ {\mathrm {pdim}}(M_0) \leq d$
) as an
![]() $A_0$
-module.
$A_0$
-module.
Proof. Let
![]() $P^{\bullet } \to M \to 0$
be a minimal projective left A-module resolution of M. Recall that every left bounded graded left projective A-module is of the form
$P^{\bullet } \to M \to 0$
be a minimal projective left A-module resolution of M. Recall that every left bounded graded left projective A-module is of the form
![]() $A \otimes _{A_0} Q$
for some graded left projective
$A \otimes _{A_0} Q$
for some graded left projective
![]() $A_0$
-module Q. Writing
$A_0$
-module Q. Writing
 $P^i = A \otimes _{A_0} Q^i$
for some graded projective
$P^i = A \otimes _{A_0} Q^i$
for some graded projective
![]() $A_0$
-modules
$A_0$
-modules
![]() $Q^i$
, because M is non-negatively graded and the resolution
$Q^i$
, because M is non-negatively graded and the resolution
![]() $P^{\bullet }$
is minimal, it easily follows that each
$P^{\bullet }$
is minimal, it easily follows that each
![]() $Q^i$
is non-negatively graded. Take the degree-zero part of the resolution of M to obtain
$Q^i$
is non-negatively graded. Take the degree-zero part of the resolution of M to obtain
![]() $P^{\bullet }_0 \to M_0 \to 0$
, which is an exact sequence of
$P^{\bullet }_0 \to M_0 \to 0$
, which is an exact sequence of
![]() $A_0$
-modules. Then
$A_0$
-modules. Then
 $P^i_0 = Q^i_0$
, which is projective over
$P^i_0 = Q^i_0$
, which is projective over
![]() $A_0$
for each i as it is a summand of
$A_0$
for each i as it is a summand of
![]() $Q^i$
. So we have a projective resolution
$Q^i$
. So we have a projective resolution
![]() $P_0^\bullet $
of M over
$P_0^\bullet $
of M over
![]() $A_0$
. If
$A_0$
. If
![]() $P^\bullet $
is perfect or has length at most d, then the same is true of the
$P^\bullet $
is perfect or has length at most d, then the same is true of the
![]() $A_0$
-resolution
$A_0$
-resolution
![]() $P_0^\bullet $
.
$P_0^\bullet $
.
Lemma 3.9. Let A be a graded algebra with
![]() $S = A/J(A)$
.
$S = A/J(A)$
.
-
(1)
 $ {\mathrm {Tor}}^A_i(S,S) \cong {\mathrm {Tor}}^{A^e}_i(S^e,A)$
as graded left
$ {\mathrm {Tor}}^A_i(S,S) \cong {\mathrm {Tor}}^{A^e}_i(S^e,A)$
as graded left
 $S^e$
-modules.
$S^e$
-modules. -
(2) If A is homologically smooth, then so is
 $A_0$
.
$A_0$
.
Proof. (1) We adapt the method of proof from the case of a connected algebra given in [Reference Yekutieli and Zhang51, Lemma 4.3(a)]. Using Lemma 2.13(1) in the second quasi-isomorphism below, we have
 $$ \begin{align*} S \otimes^L_A S \cong S \otimes^L_A (A \otimes^L_A S) \cong S^e \otimes^L_{A^e} A, \end{align*} $$
$$ \begin{align*} S \otimes^L_A S \cong S \otimes^L_A (A \otimes^L_A S) \cong S^e \otimes^L_{A^e} A, \end{align*} $$
as complexes of left
![]() $S^e$
-modules. Taking cohomology of the above yields an isomorphism
$S^e$
-modules. Taking cohomology of the above yields an isomorphism
 $ {\mathrm {Tor}}^A_i(S,S) \cong {\mathrm {Tor}}^{A^e}_i(S^e, A)$
as desired.
$ {\mathrm {Tor}}^A_i(S,S) \cong {\mathrm {Tor}}^{A^e}_i(S^e, A)$
as desired.
(2) Because A is perfect as a left
![]() $A^e$
-module, it follows from Lemma 3.8 that
$A^e$
-module, it follows from Lemma 3.8 that
![]() $A_0$
is perfect as a module over
$A_0$
is perfect as a module over
![]() $(A^e)_0 = (A_0)^e$
. Thus
$(A^e)_0 = (A_0)^e$
. Thus
![]() $A_0$
is homologically smooth.
$A_0$
is homologically smooth.
We arrive at the following alternative characterization of homological smoothness for locally finite graded algebras.
Theorem 3.10. Let A be a graded k-algebra with
![]() $A_0$
finite-dimensional, and set
$A_0$
finite-dimensional, and set
![]() $S = A/J(A) = A_0/J(A_0)$
. Then the following conditions are equivalent:
$S = A/J(A) = A_0/J(A_0)$
. Then the following conditions are equivalent:
-
(a) A is (graded) homologically smooth over k;
-
(b) S is separable over k and S is perfect as a left (respectively, right) A-module.
If the conditions hold, then A is a finitely generated (hence locally finite) algebra, and the canonical surjection
![]() $A \twoheadrightarrow S$
is split by an algebra homomorphism
$A \twoheadrightarrow S$
is split by an algebra homomorphism
![]() $S \hookrightarrow A$
.
$S \hookrightarrow A$
.
Proof. Assume (a) holds. Then S is perfect as both a left and a right A-module by Lemma 3.2(2). Next,
![]() $A_0$
is homologically smooth by Lemma 3.9(2). Now Rickard’s Theorem 3.6 implies that
$A_0$
is homologically smooth by Lemma 3.9(2). Now Rickard’s Theorem 3.6 implies that
![]() $S = A_0/J(A_0)$
is separable over k. Thus (a)
$S = A_0/J(A_0)$
is separable over k. Thus (a)
![]() $\implies $
(b).
$\implies $
(b).
Next, assume that (b) holds; we will deduce (a). Because S is separable we have
![]() $A^e/J(A^e) \cong S^e$
by Lemma 3.7. Then Lemma 3.9 (1) yields
$A^e/J(A^e) \cong S^e$
by Lemma 3.7. Then Lemma 3.9 (1) yields
 $$ \begin{align*} {\mathrm{Tor}}^A_i(A/J(A),A/J(A)) \cong {\mathrm{Tor}}^{A^e}_i(A^e/J(A^e),A). \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}^A_i(A/J(A),A/J(A)) \cong {\mathrm{Tor}}^{A^e}_i(A^e/J(A^e),A). \end{align*} $$
Applying Lemma 2.6 (and its right sided variant) for both A and
![]() $A^e$
, we have that S is perfect as a left (respectively, right) A-module if and only if the
$A^e$
, we have that S is perfect as a left (respectively, right) A-module if and only if the
![]() $ {\mathrm {Tor}}$
vector spaces above are all finite-dimensional and eventually zero for
$ {\mathrm {Tor}}$
vector spaces above are all finite-dimensional and eventually zero for
![]() $i \gg 0$
, if and only if A is perfect as a left
$i \gg 0$
, if and only if A is perfect as a left
![]() $A^e$
-module. Thus (b)
$A^e$
-module. Thus (b)
![]() $\implies $
(a).
$\implies $
(a).
If condition (b) (or equivalently condition (a)) holds, then Lemma 2.3 implies that A is a finitely generated and locally finite algebra. To establish the final claim about the splitting of
![]() $A \twoheadrightarrow S$
, simply note that this factors through the split surjection
$A \twoheadrightarrow S$
, simply note that this factors through the split surjection
![]() $A \twoheadrightarrow A_0$
via the surjection
$A \twoheadrightarrow A_0$
via the surjection
![]() $A_0 \twoheadrightarrow S$
, and that the latter is split when S is separable by a classical result of Wedderburn and Malcev [Reference Curtis and Reiner12, Theorem 72.19].
$A_0 \twoheadrightarrow S$
, and that the latter is split when S is separable by a classical result of Wedderburn and Malcev [Reference Curtis and Reiner12, Theorem 72.19].
3.2 Basic operations preserving homological smoothness
We next turn our attention to operations that preserve the property of homological smoothness. We begin with direct sums.
Proposition 3.11. For k-algebras A and B, denote
![]() $R = A \oplus B$
. Then R is homologically smooth over k if and only if both A and B are homologically smooth over k.
$R = A \oplus B$
. Then R is homologically smooth over k if and only if both A and B are homologically smooth over k.
Proof. First suppose that A and B are homologically smooth. For convenience, denote
 $A_{(1)} = A$
and
$A_{(1)} = A$
and
 $A_{(2)} = B$
. Then
$A_{(2)} = B$
. Then
 $R^e = (A_{(1)} \oplus A_{(2)}) \otimes (A_{(1)} \oplus A_{(2)})^{\mathrm {op}} = \bigoplus _{i,j\in \{1,2\}} A_{(i)} \otimes A_{(j)}^{\mathrm {op}}$
as k-algebras. Let
$R^e = (A_{(1)} \oplus A_{(2)}) \otimes (A_{(1)} \oplus A_{(2)})^{\mathrm {op}} = \bigoplus _{i,j\in \{1,2\}} A_{(i)} \otimes A_{(j)}^{\mathrm {op}}$
as k-algebras. Let
![]() $P_{(i)}$
denote a perfect left
$P_{(i)}$
denote a perfect left
 $A_{(i)}^e$
-resolution of each
$A_{(i)}^e$
-resolution of each
 $A_{(i)}$
; then it is also a perfect left
$A_{(i)}$
; then it is also a perfect left
![]() $R^e$
-resolution via the projection
$R^e$
-resolution via the projection
 $R^e \twoheadrightarrow A_{(i)} \otimes A_{(i)}^{\mathrm {op}} = A_{(i)}^e$
. Thus
$R^e \twoheadrightarrow A_{(i)} \otimes A_{(i)}^{\mathrm {op}} = A_{(i)}^e$
. Thus
![]() $P_{(1)} \oplus P_{(2)}$
is a perfect left
$P_{(1)} \oplus P_{(2)}$
is a perfect left
![]() $A^e$
-resolution of
$A^e$
-resolution of
 $A = A_{(1)} \oplus A_{(2)}$
, and so A is homologically smooth as desired.
$A = A_{(1)} \oplus A_{(2)}$
, and so A is homologically smooth as desired.
Conversely, suppose that R is homologically smooth. Consider the central idempotent
![]() $z = (1,0) \in A \oplus B = R$
. If
$z = (1,0) \in A \oplus B = R$
. If
![]() $P^{\bullet }$
is a finite resolution of R by finitely generated
$P^{\bullet }$
is a finite resolution of R by finitely generated
![]() $R^e$
-projectives, then
$R^e$
-projectives, then
![]() $(z \otimes z) P^{\bullet }$
is an
$(z \otimes z) P^{\bullet }$
is an
![]() $A^e$
-projective resolution of A with the same properties. Thus A is homologically smooth, and the same is true of B by symmetry.
$A^e$
-projective resolution of A with the same properties. Thus A is homologically smooth, and the same is true of B by symmetry.
Next we consider extension of scalars. Given a k-vector space V and a field extension K of k, we denote the scalar extension of V to a K-vector space by
![]() $V^K = V \otimes K$
. In case V is a k-algebra,
$V^K = V \otimes K$
. In case V is a k-algebra,
![]() $V^K$
becomes a K-algebra; if V is a module over a k-algebra A, then
$V^K$
becomes a K-algebra; if V is a module over a k-algebra A, then
![]() $V^K$
becomes a module over
$V^K$
becomes a module over
![]() $A^K$
in the natural way. The following basic results give the interaction between base field extension and Hom and tensor as well as their derived analogues.
$A^K$
in the natural way. The following basic results give the interaction between base field extension and Hom and tensor as well as their derived analogues.
Lemma 3.12. Let A be a k-algebra.
-
(1) Let
 $P^{\bullet }, Q^{\bullet }$
be complexes of left A-modules, with P bounded above. There is a natural map respecting any module structure obtained if P or Q is a complex of bimodules. The map
$P^{\bullet }, Q^{\bullet }$
be complexes of left A-modules, with P bounded above. There is a natural map respecting any module structure obtained if P or Q is a complex of bimodules. The map $$ \begin{align*} \Psi: {\mathrm{RHom}}_A(P,Q)^K \to {\mathrm{RHom}}_{A^K}(P^K, Q^K), \end{align*} $$
$$ \begin{align*} \Psi: {\mathrm{RHom}}_A(P,Q)^K \to {\mathrm{RHom}}_{A^K}(P^K, Q^K), \end{align*} $$
 $\Psi $
is an isomorphism if P is perfect.
$\Psi $
is an isomorphism if P is perfect.
-
(2) Let
 $P^{\bullet }$
be a bounded above complex of right A-modules, and
$P^{\bullet }$
be a bounded above complex of right A-modules, and
 $Q^{\bullet }$
a complex of left A-modules. There is a natural isomorphism which respects any module structure obtained if P or Q is a complex of bimodules.
$Q^{\bullet }$
a complex of left A-modules. There is a natural isomorphism which respects any module structure obtained if P or Q is a complex of bimodules. $$ \begin{align*} \Phi: (P \otimes^L_A Q)^K \to P^K \otimes^L_{A^K} Q^K \end{align*} $$
$$ \begin{align*} \Phi: (P \otimes^L_A Q)^K \to P^K \otimes^L_{A^K} Q^K \end{align*} $$
When A is graded, the same results hold for graded modules and complexes, with
![]() $ {\mathrm {RHom}}$
replaced by
$ {\mathrm {RHom}}$
replaced by
![]() ${\mathrm{R}}\underline { {\mathrm {{Hom}}}}$
and
${\mathrm{R}}\underline { {\mathrm {{Hom}}}}$
and
![]() $\otimes ^L$
replaced by
$\otimes ^L$
replaced by
 $ {\mathrm {\underline {\otimes }}}^L$
.
$ {\mathrm {\underline {\otimes }}}^L$
.
Proof. (1) For any
![]() $M, N \in A {\mathrm {\!-Mod}}$
there is a natural map
$M, N \in A {\mathrm {\!-Mod}}$
there is a natural map
 $\psi : {\mathrm {{Hom}}}_A(M,N)^K \to {\mathrm {{Hom}}}_{A^K}(M^K, N^K)$
which respects any bimodule structures involved. The map
$\psi : {\mathrm {{Hom}}}_A(M,N)^K \to {\mathrm {{Hom}}}_{A^K}(M^K, N^K)$
which respects any bimodule structures involved. The map
![]() $\psi $
is clearly an isomorphism when
$\psi $
is clearly an isomorphism when
![]() $M = A$
, and one can readily deduce that the same is true when M is finitely generated projective.
$M = A$
, and one can readily deduce that the same is true when M is finitely generated projective.
Since P is bounded above, we can replace it with a quasi-isomorphic bounded above complex of projective modules. Then
![]() $P^K$
is a bounded above complex of projective
$P^K$
is a bounded above complex of projective
![]() $A^K$
-modules, so
$A^K$
-modules, so
 $ {\mathrm {RHom}}_A(P, Q)^K = {\mathrm {{Hom}}}_A(P, Q)^K$
and
$ {\mathrm {RHom}}_A(P, Q)^K = {\mathrm {{Hom}}}_A(P, Q)^K$
and
 $ {\mathrm {RHom}}_{A^K}(P^K, Q^K) = {\mathrm {{Hom}}}_{A^K}(P^K, Q^K)$
. Thus one defines
$ {\mathrm {RHom}}_{A^K}(P^K, Q^K) = {\mathrm {{Hom}}}_{A^K}(P^K, Q^K)$
. Thus one defines
![]() $\Psi $
to be the map on complexes whose nth component is the natural map
$\Psi $
to be the map on complexes whose nth component is the natural map
 $$ \begin{align*}\Psi^n: \bigg[\prod_i {\mathrm{{Hom}}}_A(P^i, Q^{i+n})\bigg] \otimes K \to \prod_i {\mathrm{{Hom}}}_{A^K}(P^i \otimes K, Q^{i+n} \otimes K) \end{align*} $$
$$ \begin{align*}\Psi^n: \bigg[\prod_i {\mathrm{{Hom}}}_A(P^i, Q^{i+n})\bigg] \otimes K \to \prod_i {\mathrm{{Hom}}}_{A^K}(P^i \otimes K, Q^{i+n} \otimes K) \end{align*} $$
induced by
![]() $\psi $
. When P is perfect, we can assume that P is a bounded complex of finitely generated projectives. In this case in
$\psi $
. When P is perfect, we can assume that P is a bounded complex of finitely generated projectives. In this case in
![]() $\Psi ^n$
above, the product
$\Psi ^n$
above, the product
![]() $\prod _i$
is actually finite and each
$\prod _i$
is actually finite and each
![]() $P^i$
is finitely generated. Since tensor products commute with finite products (i.e., direct sums), we see that
$P^i$
is finitely generated. Since tensor products commute with finite products (i.e., direct sums), we see that
![]() $\Psi ^n$
is an isomorphism from the first paragraph.
$\Psi ^n$
is an isomorphism from the first paragraph.
(2) This is a similar argument as part (1), but no additional hypotheses are needed since tensor products commute with arbitrary direct sums. We leave the details to the reader.
The proofs in the graded case are the same.
We now study the behavior of homological smoothness under base field extension. In fact we have the following more general result about how perfect modules behave under extension of the base field. We do not know if part (2) of the following result also holds without the graded hypothesis.
Proposition 3.13. Let A be a k-algebra, and let K be a field extension of k.
-
(1) If M is a perfect left A-module, then
 $M^K$
is a perfect
$M^K$
is a perfect
 $A^K$
-module.
$A^K$
-module. -
(2) Suppose that A is graded with
 $\dim _k A_0 < \infty $
, and let
$\dim _k A_0 < \infty $
, and let
 $M \in A {\mathrm {\!-Gr}}$
be left bounded. Then
$M \in A {\mathrm {\!-Gr}}$
be left bounded. Then
 $M^K$
is a perfect left
$M^K$
is a perfect left
 $A^K$
-module if and only if M is perfect over A. In this case, the length of the minimal graded projective resolutions of M over A and
$A^K$
-module if and only if M is perfect over A. In this case, the length of the minimal graded projective resolutions of M over A and
 $M^K$
over
$M^K$
over
 $A^K$
are the same.
$A^K$
are the same.
Proof. (1) Let
![]() $P^{\bullet } \to M$
be a projective resolution of M as a left A-module. If M is perfect, then we can take
$P^{\bullet } \to M$
be a projective resolution of M as a left A-module. If M is perfect, then we can take
![]() $P^i$
to be finitely generated for all i and zero for
$P^i$
to be finitely generated for all i and zero for
![]() $i \ll 0$
. The functor
$i \ll 0$
. The functor
![]() $- \otimes _k K$
is exact, and is easily seen to preserve the properties of being projective and being finitely generated as a module. Then
$- \otimes _k K$
is exact, and is easily seen to preserve the properties of being projective and being finitely generated as a module. Then
 $(P^{\bullet })^K$
is an
$(P^{\bullet })^K$
is an
![]() $A^K$
-projective resolution of
$A^K$
-projective resolution of
![]() $A^K$
, for which
$A^K$
, for which
 $(P^i)^K$
is finitely generated for all i and
$(P^i)^K$
is finitely generated for all i and
![]() $0$
for
$0$
for
![]() $i \ll 0$
. Thus
$i \ll 0$
. Thus
![]() $M^K$
is perfect.
$M^K$
is perfect.
(2) By part (1), it suffices to assume that
![]() $M^K$
is perfect and prove that M is. The conditions on A and M ensure that we can take a minimal graded projective resolution
$M^K$
is perfect and prove that M is. The conditions on A and M ensure that we can take a minimal graded projective resolution
![]() $P^{\bullet } \to M$
of M as a left A-module. Similarly as above,
$P^{\bullet } \to M$
of M as a left A-module. Similarly as above,
 $(P^{\bullet })^K$
is a graded
$(P^{\bullet })^K$
is a graded
![]() $A^K$
-projective resolution of
$A^K$
-projective resolution of
![]() $M^K$
. We claim that this is also a minimal projective resolution. Suppose that
$M^K$
. We claim that this is also a minimal projective resolution. Suppose that
![]() $N, P \in A {\mathrm {\!-Gr}}$
are left bounded graded projective modules. Let
$N, P \in A {\mathrm {\!-Gr}}$
are left bounded graded projective modules. Let
![]() $f: N \to P$
be a graded A-module homomorphism with
$f: N \to P$
be a graded A-module homomorphism with
![]() $\ker f \in J(A) N$
. Then
$\ker f \in J(A) N$
. Then
![]() $f \otimes 1: N^K \to P^K$
is a graded
$f \otimes 1: N^K \to P^K$
is a graded
 $(A^K)$
-module homomorphism and clearly
$(A^K)$
-module homomorphism and clearly
![]() $\ker (f \otimes 1) = (\ker f) \otimes K$
since
$\ker (f \otimes 1) = (\ker f) \otimes K$
since
![]() $- \otimes _k K$
is exact. Recall that
$- \otimes _k K$
is exact. Recall that
![]() $J(A) = A_{\geq 1} \oplus J(A_0)$
. Clearly
$J(A) = A_{\geq 1} \oplus J(A_0)$
. Clearly
 $A_{\geq 1}^K = (A^K)_{\geq 1} \subseteq J(A^K)$
. Since
$A_{\geq 1}^K = (A^K)_{\geq 1} \subseteq J(A^K)$
. Since
![]() $J(A_0)$
is nilpotent, so is
$J(A_0)$
is nilpotent, so is
 $J(A_0)^K$
and hence
$J(A_0)^K$
and hence
 $J(A_0)^K \subseteq J(A^K)$
as well. Thus
$J(A_0)^K \subseteq J(A^K)$
as well. Thus
 $J(A)^K \subseteq J(A^K)$
. This easily extends to projective modules to prove that for any left bounded graded projective A-module Q,
$J(A)^K \subseteq J(A^K)$
. This easily extends to projective modules to prove that for any left bounded graded projective A-module Q,
 $(J(A) Q)^K \subseteq J(A^K)(Q^K)$
. Thus
$(J(A) Q)^K \subseteq J(A^K)(Q^K)$
. Thus
 $$ \begin{align*} \ker (f \otimes 1) = (\ker f) \otimes K \subseteq (J(A) N)^K \subseteq J(A^K)N^K. \end{align*} $$
$$ \begin{align*} \ker (f \otimes 1) = (\ker f) \otimes K \subseteq (J(A) N)^K \subseteq J(A^K)N^K. \end{align*} $$
Since the condition that
![]() $P^{\bullet }$
be minimal is that for each
$P^{\bullet }$
be minimal is that for each
![]() $d^i: P^i \to P^{i-1}$
we have
$d^i: P^i \to P^{i-1}$
we have
![]() $\ker d^i \subseteq J(A) P^i$
, we see that
$\ker d^i \subseteq J(A) P^i$
, we see that
 $(P^K)^{\bullet }$
is also minimal, as claimed. Now suppose that
$(P^K)^{\bullet }$
is also minimal, as claimed. Now suppose that
![]() $M^K$
is perfect. Then since
$M^K$
is perfect. Then since
![]() $M^K$
has a finite
$M^K$
has a finite
 $(A^K)$
-resolution by finitely generated projectives, the minimal graded projective resolution of
$(A^K)$
-resolution by finitely generated projectives, the minimal graded projective resolution of
![]() $M^K$
must have this property. So each
$M^K$
must have this property. So each
 $(P^i)^K$
is a finitely generated
$(P^i)^K$
is a finitely generated
![]() $A^K$
-module, with
$A^K$
-module, with
 $(P^i)^K = 0$
for
$(P^i)^K = 0$
for
![]() $i \ll 0$
. It follows that
$i \ll 0$
. It follows that
![]() $P^i = 0$
for
$P^i = 0$
for
![]() $i \ll 0$
. It is also easy to see that
$i \ll 0$
. It is also easy to see that
 $(P^i)^K$
finitely generated implies that
$(P^i)^K$
finitely generated implies that
![]() $P^i$
is a finitely generated A-module, as follows. Let
$P^i$
is a finitely generated A-module, as follows. Let
![]() $Q = P^i$
and suppose that
$Q = P^i$
and suppose that
![]() $Q = \bigcup Q_j$
is a directed union of submodules. Then
$Q = \bigcup Q_j$
is a directed union of submodules. Then
 $Q^K = \bigcup Q_j^K$
is a directed union of the extended submodules. By finite generation of
$Q^K = \bigcup Q_j^K$
is a directed union of the extended submodules. By finite generation of
![]() $Q^K$
, we have some
$Q^K$
, we have some
 $Q_j^K = Q^K$
. Thus the quotient module
$Q_j^K = Q^K$
. Thus the quotient module
 $Q^K/Q_j^K \cong (Q/Q_j)^K$
is zero. As K is faithfully flat over k we have
$Q^K/Q_j^K \cong (Q/Q_j)^K$
is zero. As K is faithfully flat over k we have
![]() $Q/Q_j = 0$
, whence
$Q/Q_j = 0$
, whence
![]() $Q = Q_j$
. Thus
$Q = Q_j$
. Thus
![]() $Q = P^i$
is finitely generated.
$Q = P^i$
is finitely generated.
We see now that M is perfect. The final statement on the lengths of the minimal projective resolutions is also clear from the proof above.
Corollary 3.14. Let A be a k-algebra, and let K be a field extension of k. If A is a homologically smooth k-algebra, then
![]() $A^K$
is a homologically smooth K-algebra. The converse holds if A is graded with
$A^K$
is a homologically smooth K-algebra. The converse holds if A is graded with
![]() $\dim _k A_0 < \infty $
.
$\dim _k A_0 < \infty $
.
Proof. Note that
![]() $(A \otimes K)^e \cong A^e \otimes K$
as (graded) K-algebras. Thus the result follows immediately from Proposition 3.13, applied to the algebra
$(A \otimes K)^e \cong A^e \otimes K$
as (graded) K-algebras. Thus the result follows immediately from Proposition 3.13, applied to the algebra
![]() $A^e$
and the module A.
$A^e$
and the module A.
Next we wish to show that homological smoothness is preserved under tensor products of algebras. For this we require the following observation.
Remark 3.15. Let R and S be k-algebras. For
![]() $M \in R {\mathrm {\!-Mod}}$
and
$M \in R {\mathrm {\!-Mod}}$
and
![]() $N \in S {\mathrm {\!-Mod}}$
, suppose that
$N \in S {\mathrm {\!-Mod}}$
, suppose that
![]() $P^\bullet $
is a projective R-module resolution of M and
$P^\bullet $
is a projective R-module resolution of M and
![]() $Q^{\bullet }$
is a projective S-module resolution of N. As we are tensoring over a field k, the Künneth formula [Reference Weibel49, Theorem 3.6.3] yields
$Q^{\bullet }$
is a projective S-module resolution of N. As we are tensoring over a field k, the Künneth formula [Reference Weibel49, Theorem 3.6.3] yields
 $H^i(X \otimes Y) \cong \bigoplus _{p+q = i} H^p(X) \otimes H^q(Y)$
for any bounded above complexes X and Y. In particular, the tensor complex
$H^i(X \otimes Y) \cong \bigoplus _{p+q = i} H^p(X) \otimes H^q(Y)$
for any bounded above complexes X and Y. In particular, the tensor complex
![]() $P \otimes Q$
forms a projective resolution of
$P \otimes Q$
forms a projective resolution of
![]() $M \otimes N$
as a left
$M \otimes N$
as a left
![]() $R \otimes S$
-module.
$R \otimes S$
-module.
Proposition 3.16. If A and B are (graded) homologically smooth k-algebras, then so is
![]() $A \otimes B$
.
$A \otimes B$
.
Proof. Denote
![]() $R = A \otimes B$
, so that
$R = A \otimes B$
, so that
![]() $R^e = A^e \otimes B^e$
. If A and B are homologically smooth, we may fix finite length resolutions
$R^e = A^e \otimes B^e$
. If A and B are homologically smooth, we may fix finite length resolutions
![]() $P^{\bullet } \to A \to 0$
and
$P^{\bullet } \to A \to 0$
and
![]() $Q^\bullet \to B \to 0$
, whose terms are finitely generated projective left modules over
$Q^\bullet \to B \to 0$
, whose terms are finitely generated projective left modules over
![]() $A^e$
and
$A^e$
and
![]() $B^e$
, respectively. By Remark 3.15, the complex
$B^e$
, respectively. By Remark 3.15, the complex
![]() $P \otimes Q$
forms a projective
$P \otimes Q$
forms a projective
![]() $R^e$
-resolution of R, from which we deduce that R is homologically smooth.
$R^e$
-resolution of R, from which we deduce that R is homologically smooth.
The final operation preserving homological smoothness that we will investigate is k-linear Morita equivalence. We say that two k-algebras are k-linearly Morita equivalent if their left module categories are equivalent via a k-linear equivalence of categories; thanks to standard Morita theory, this is clearly induced by a k-central invertible bimodule.
Proposition 3.17. If A and B are k-linearly Morita equivalent k-algebras, then A is a homologically smooth k-algebra if and only if B is.
Proof. Fix a k-central invertible
![]() $(A,B)$
-bimodule U, so that
$(A,B)$
-bimodule U, so that
![]() $U \otimes _B - \colon B {\mathrm {\!-Mod}} \to A {\mathrm {\!-Mod}}$
and
$U \otimes _B - \colon B {\mathrm {\!-Mod}} \to A {\mathrm {\!-Mod}}$
and
![]() $- \otimes _A U \colon {\mathrm {Mod-\!}} A \to {\mathrm {Mod-\!}} B$
are k-linear equivalences. Then the functor
$- \otimes _A U \colon {\mathrm {Mod-\!}} A \to {\mathrm {Mod-\!}} B$
are k-linear equivalences. Then the functor
![]() $U \otimes _B - \otimes _B U^{-1}$
gives a k-linear equivalence of categories from k-central
$U \otimes _B - \otimes _B U^{-1}$
gives a k-linear equivalence of categories from k-central
![]() $(B,B)$
-bimodules to k-central
$(B,B)$
-bimodules to k-central
![]() $(A,A)$
-bimodules; that is, we have a linear equivalence from
$(A,A)$
-bimodules; that is, we have a linear equivalence from
![]() $B^e {\mathrm {\!-Mod}}$
to
$B^e {\mathrm {\!-Mod}}$
to
![]() $A^e {\mathrm {\!-Mod}}$
. This is readily verified to preserve the tensor product of bimodules up to natural isomorphism, yielding a monoidal equivalence. In particular, the tensor units B and A correspond under the equivalence.
$A^e {\mathrm {\!-Mod}}$
. This is readily verified to preserve the tensor product of bimodules up to natural isomorphism, yielding a monoidal equivalence. In particular, the tensor units B and A correspond under the equivalence.
It follows that A has a perfect resolution in
![]() $A^e {\mathrm {\!-Mod}}$
if and only if B has a perfect resolution in
$A^e {\mathrm {\!-Mod}}$
if and only if B has a perfect resolution in
![]() $B^e {\mathrm {\!-Mod}}$
, establishing the claim.
$B^e {\mathrm {\!-Mod}}$
, establishing the claim.
3.3 Global dimension of homologically smooth algebras
We now turn our attention to the global dimension of locally finite graded algebras. Recall that the graded projective dimension of a left module M over a graded ring R, denoted
![]() $ {\mathrm {gr.pdim}}(M)$
, is the minimal (possibly infinite) length of all graded projective resolutions of M, and that the graded left global dimension of R, denoted
$ {\mathrm {gr.pdim}}(M)$
, is the minimal (possibly infinite) length of all graded projective resolutions of M, and that the graded left global dimension of R, denoted
![]() $ {\mathrm {gr.gldim}}_l(M)$
, is the supremum of
$ {\mathrm {gr.gldim}}_l(M)$
, is the supremum of
![]() $ {\mathrm {gr.pdim}}(M)$
with M ranging over all graded left R-modules.
$ {\mathrm {gr.pdim}}(M)$
with M ranging over all graded left R-modules.
The next result shows that for the graded algebras which we consider in this paper, one need not distinguish between left and right graded global dimensions, nor between graded and ungraded global dimensions.
Proposition 3.18. Let A be a graded algebra with
![]() $A_0$
finite-dimensional, and set
$A_0$
finite-dimensional, and set
![]() $S = A/J(A)$
.
$S = A/J(A)$
.
-
(1) For any graded left A-module M that is bounded below, one has
 $$ \begin{align*} {\mathrm{pdim}}(M) = {\mathrm{gr.pdim}}(M) = \sup\{n \in \mathbb{N} \mid {\mathrm{Tor}}^A_n(S,M) \neq 0\}. \end{align*} $$
$$ \begin{align*} {\mathrm{pdim}}(M) = {\mathrm{gr.pdim}}(M) = \sup\{n \in \mathbb{N} \mid {\mathrm{Tor}}^A_n(S,M) \neq 0\}. \end{align*} $$
Thus
 $ {\mathrm {gr.gldim}}_l(A) \leq {\mathrm {gldim}}_l(A)$
.
$ {\mathrm {gr.gldim}}_l(A) \leq {\mathrm {gldim}}_l(A)$
. -
(2) The left and right graded global dimensions of A are equal; in fact,
 $$ \begin{align*} {\mathrm{gr.gldim}}_l(A) = {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_A S) = {\mathrm{pdim}}(S_A) = {\mathrm{gr.gldim}}_r(A). \end{align*} $$
$$ \begin{align*} {\mathrm{gr.gldim}}_l(A) = {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_A S) = {\mathrm{pdim}}(S_A) = {\mathrm{gr.gldim}}_r(A). \end{align*} $$
-
(3) If S is a separable k-algebra, then
 $$ \begin{align*} {\mathrm{gldim}}_l(A) &= {\mathrm{gr.gldim}}_l(A) = {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_A S) = {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_{A^e} A)\\ &= {\mathrm{gldim}}_r(A) = {\mathrm{gr.gldim}}_r(A) = {\mathrm{pdim}}(S_A). \end{align*} $$
$$ \begin{align*} {\mathrm{gldim}}_l(A) &= {\mathrm{gr.gldim}}_l(A) = {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_A S) = {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_{A^e} A)\\ &= {\mathrm{gldim}}_r(A) = {\mathrm{gr.gldim}}_r(A) = {\mathrm{pdim}}(S_A). \end{align*} $$
Proof. For (1), note that
 $\sup \{n \mid {\mathrm {Tor}}^A_n(S,M) \neq 0\} \leq {\mathrm {pdim}}(M) \leq {\mathrm {gr.pdim}}(M)$
. Now let
$\sup \{n \mid {\mathrm {Tor}}^A_n(S,M) \neq 0\} \leq {\mathrm {pdim}}(M) \leq {\mathrm {gr.pdim}}(M)$
. Now let
![]() $P^\bullet \to M \to 0$
be a minimal graded projective resolution of M. Then by Lemma 2.6, we see that
$P^\bullet \to M \to 0$
be a minimal graded projective resolution of M. Then by Lemma 2.6, we see that
 $ {\mathrm {Tor}}^A_n(S,M) = 0$
if and only if the term
$ {\mathrm {Tor}}^A_n(S,M) = 0$
if and only if the term
![]() $P^{-n}$
in the complex is zero, giving
$P^{-n}$
in the complex is zero, giving
 $\sup \{n \mid {\mathrm {Tor}}^A_n(S,M) \neq 0\} = {\mathrm {gr.pdim}}(M)$
. The inequality
$\sup \{n \mid {\mathrm {Tor}}^A_n(S,M) \neq 0\} = {\mathrm {gr.pdim}}(M)$
. The inequality
![]() $ {\mathrm {gr.gldim}}_l(A) \leq {\mathrm {gldim}}_l(A)$
readily follows.
$ {\mathrm {gr.gldim}}_l(A) \leq {\mathrm {gldim}}_l(A)$
readily follows.
Part (2) follows from the results of [Reference Eilenberg14, Sections 5 and 6]. Note that similar results appear in [Reference Huishi28] and [Reference Minamoto and Mori33, Proposition 2.7].
To prove (3), we adapt the argument from the connected graded case given in [Reference Berger4]. Note that
where the first equality follows from part (2), the middle inequality from part (1), and the final inequality from Lemma 3.2. Applying (1) to the left
![]() $A^e$
-module A, along with Lemmas 3.7 and 3.9(1), we see that
$A^e$
-module A, along with Lemmas 3.7 and 3.9(1), we see that
 $$ \begin{align*} {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_{A^e} A) = \sup\{n \mid {\mathrm{Tor}}^{A^e}_n(A^e/J(A^e), A) \neq 0\} = \sup\{n \mid {\mathrm{Tor}}^A_n(S,S) \neq 0\}. \end{align*} $$
$$ \begin{align*} {\mathrm{pdim}}({{\hspace{-0.0001pt}}}_{A^e} A) = \sup\{n \mid {\mathrm{Tor}}^{A^e}_n(A^e/J(A^e), A) \neq 0\} = \sup\{n \mid {\mathrm{Tor}}^A_n(S,S) \neq 0\}. \end{align*} $$
As we saw in the proof of part (2), the quantity on the right-hand-side above is
![]() $ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_A S) = {\mathrm {pdim}}(S_A)$
. Thus we obtain
$ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_A S) = {\mathrm {pdim}}(S_A)$
. Thus we obtain
and the rest of the equalities follow by symmetry.
It is well-known that any finite-dimensional algebra A with
![]() $S = A/J(A)$
satisfies
$S = A/J(A)$
satisfies
![]() $ {\mathrm {gldim}}_l(A) = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_A S) = {\mathrm {pdim}}(S_A) = {\mathrm {gldim}}_r(A)$
; for instance, see [Reference Lam24, Corollary 5.60, Theorem 5.72]. If S is separable, then we can deduce directly from the previous proposition that this global dimension is further equal to
$ {\mathrm {gldim}}_l(A) = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_A S) = {\mathrm {pdim}}(S_A) = {\mathrm {gldim}}_r(A)$
; for instance, see [Reference Lam24, Corollary 5.60, Theorem 5.72]. If S is separable, then we can deduce directly from the previous proposition that this global dimension is further equal to
![]() $ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A)$
.
$ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A)$
.
Corollary 3.19. If A is a finite-dimensional k-algebra such that
![]() $S = A/J(A)$
is separable, then
$S = A/J(A)$
is separable, then
![]() $ {\mathrm {gldim}}(A) = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A)$
.
$ {\mathrm {gldim}}(A) = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A)$
.
Proof. Considering A as a graded algebra concentrated in degree zero, this follows immediately from Proposition 3.18(3).
The following example shows that the hypothesis that
![]() $S = A/J(A)$
is separable cannot simply be omitted in some of our previous results. It makes use of the fact that a module M over a Frobenius algebra A must have
$S = A/J(A)$
is separable cannot simply be omitted in some of our previous results. It makes use of the fact that a module M over a Frobenius algebra A must have
![]() $ {\mathrm {pdim}}(M) \in \{0,\infty \}$
. Indeed, because projective and injective A-modules coincide, any finite projective resolution of M of length greater than zero must split at the end, and therefore can be replaced with a projective resolution of shorter length.
$ {\mathrm {pdim}}(M) \in \{0,\infty \}$
. Indeed, because projective and injective A-modules coincide, any finite projective resolution of M of length greater than zero must split at the end, and therefore can be replaced with a projective resolution of shorter length.
Example 3.20. Let S be a finite-dimensional, semisimple k-algebra that is not separable. (For instance, S could be a nonseparable field extension of a nonperfect field k.) Then
![]() $S^e = S \otimes S^{\mathrm {op}}$
is a tensor product of Frobenius algebras and thus is Frobenius [Reference Lam26, Exercise 3.12]. Because S is not separable, it is not projective as a left
$S^e = S \otimes S^{\mathrm {op}}$
is a tensor product of Frobenius algebras and thus is Frobenius [Reference Lam26, Exercise 3.12]. Because S is not separable, it is not projective as a left
![]() $S^e$
-module. Because
$S^e$
-module. Because
![]() $S^e$
is Frobenius, it follows from the remark above that
$S^e$
is Frobenius, it follows from the remark above that
![]() $ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{S^e} S) = \infty $
. So S is not perfect as a left
$ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{S^e} S) = \infty $
. So S is not perfect as a left
![]() $S^e$
-module. On the other hand,
$S^e$
-module. On the other hand,
![]() $ {\mathrm {gldim}}(S) = 0$
and S is perfect as a left S-module. Taking
$ {\mathrm {gldim}}(S) = 0$
and S is perfect as a left S-module. Taking
![]() $A = S$
we see that both the implication (b)
$A = S$
we see that both the implication (b)
![]() $\implies $
(a) in Theorem 3.10 as well as part (3) of Proposition 3.18 can fail if we omit the assumption that S is separable.
$\implies $
(a) in Theorem 3.10 as well as part (3) of Proposition 3.18 can fail if we omit the assumption that S is separable.
Example 3.21. For
![]() $\mathbb {Z}$
-graded rings, not the
$\mathbb {Z}$
-graded rings, not the
![]() $\mathbb {N}$
-graded rings we are restricting to in this paper, it is easy to find examples whose graded global dimension and ungraded global dimension are different. For example, a graded division ring such as the Laurent polynomial ring
$\mathbb {N}$
-graded rings we are restricting to in this paper, it is easy to find examples whose graded global dimension and ungraded global dimension are different. For example, a graded division ring such as the Laurent polynomial ring
 $k[t, t^{-1}]$
has graded global dimension
$k[t, t^{-1}]$
has graded global dimension
![]() $0$
, but global dimension
$0$
, but global dimension
![]() $1$
. We are unaware of an
$1$
. We are unaware of an
![]() $\mathbb {N}$
-graded, locally finite algebra A whose global dimension and graded global dimension are different.
$\mathbb {N}$
-graded, locally finite algebra A whose global dimension and graded global dimension are different.
The next result provides one further characterization of finite-dimensional homologically smooth algebras, in addition to those already given in Theorem 3.10.
Corollary 3.22. Let A be a locally finite graded algebra that is left noetherian; this holds, in particular, if A is a finite-dimensional algebra with trivial grading. Then A is homologically smooth if and only if
![]() $S = A/J(A)$
is separable and A has finite global dimension.
$S = A/J(A)$
is separable and A has finite global dimension.
Proof. By Theorem 3.10, we know that A is homologically smooth if and only if S is a separable algebra and S is perfect as a left A-module. Thus it is enough to show, under the assumption that S is separable, that A has finite global dimension if and only if S is perfect. Because A is left noetherian, the finite-dimensional module
![]() ${{\hspace {-0.0001pt}}}_A S$
is perfect if and only if it has finite projective dimension. The latter holds (since S is separable) if and only if
${{\hspace {-0.0001pt}}}_A S$
is perfect if and only if it has finite projective dimension. The latter holds (since S is separable) if and only if
![]() $ {\mathrm {gldim}}(A) = {\mathrm {gr.gldim}}(A)$
is finite, thanks to Proposition 3.18, establishing the claim.
$ {\mathrm {gldim}}(A) = {\mathrm {gr.gldim}}(A)$
is finite, thanks to Proposition 3.18, establishing the claim.
It is also useful to note that the global dimension of a graded algebra bounds the global dimension of its degree
![]() $0$
part.
$0$
part.
Lemma 3.23. Let A be a graded algebra with
![]() $A_0$
finite-dimensional. If A has finite graded global dimension d, then the global dimension of
$A_0$
finite-dimensional. If A has finite graded global dimension d, then the global dimension of
![]() $A_0$
is at most d.
$A_0$
is at most d.
Proof. As in Proposition 3.18(2), the left and right graded global dimensions of A coincide, and similarly for
![]() $A_0$
. Thus it suffices to prove that
$A_0$
. Thus it suffices to prove that
![]() $ {\mathrm {gldim}}_l(A_0) \leq d$
. Given a left
$ {\mathrm {gldim}}_l(A_0) \leq d$
. Given a left
![]() $A_0$
-module M, consider it as a graded left A-module concentrated in degree zero. Because the projective dimension of M as a left A-module is at most d, it follows from Lemma 3.8 that it also has projective dimension at most d as a left
$A_0$
-module M, consider it as a graded left A-module concentrated in degree zero. Because the projective dimension of M as a left A-module is at most d, it follows from Lemma 3.8 that it also has projective dimension at most d as a left
![]() $A_0$
-module, establishing
$A_0$
-module, establishing
![]() $ {\mathrm {gldim}}_l(A_0) \leq d$
.
$ {\mathrm {gldim}}_l(A_0) \leq d$
.
Homologically smooth graded algebras need not have good ring-theoretic properties. Over a perfect field, we have seen that a locally finite graded algebra is homologically smooth if and only if
![]() ${{\hspace {-0.0001pt}}}_A S$
is a perfect module, and there are many examples of finite global dimension algebras with finite GK-dimension but bad properties. One simple such example is
${{\hspace {-0.0001pt}}}_A S$
is a perfect module, and there are many examples of finite global dimension algebras with finite GK-dimension but bad properties. One simple such example is
![]() $A = k \langle x, y \rangle /(yx)$
. This is a connected graded algebra of GK-dimension
$A = k \langle x, y \rangle /(yx)$
. This is a connected graded algebra of GK-dimension
![]() $2$
over which
$2$
over which
![]() ${{\hspace {-0.0001pt}}}_A S = A/J(A) = k$
is perfect; however, it is neither left nor right noetherian, nor is it semiprime. See [Reference Rogalski41, Example 2.1.7, Exercise 2.4.3] for details. On the other hand, twisted Calabi–Yau algebras typically have good ring-theoretic properties when they also have finite GK-dimension. The reasons for this are not yet well-understood in general, but we address the noetherian property in particular for algebras of dimension
${{\hspace {-0.0001pt}}}_A S = A/J(A) = k$
is perfect; however, it is neither left nor right noetherian, nor is it semiprime. See [Reference Rogalski41, Example 2.1.7, Exercise 2.4.3] for details. On the other hand, twisted Calabi–Yau algebras typically have good ring-theoretic properties when they also have finite GK-dimension. The reasons for this are not yet well-understood in general, but we address the noetherian property in particular for algebras of dimension
![]() $d \leq 2$
in subsequent sections of this paper.
$d \leq 2$
in subsequent sections of this paper.
4 Twisted Calabi–Yau algebras
In this section we provide some basic tools for the study of twisted Calabi–Yau algebras, as we defined in Definition 1.2.
4.1 Graded twisted Calabi–Yau algebras
Our main interest is in graded twisted Calabi–Yau algebras. The following is the natural graded analogue of the twisted Calabi–Yau condition.
Definition 4.1. Let A be an
![]() $\mathbb {N}$
-graded k-algebra. We say that:
$\mathbb {N}$
-graded k-algebra. We say that:
-
(i) A is graded homologically smooth if it is graded perfect as a left
 $A^e$
-module;
$A^e$
-module; -
(ii) A is graded twisted Calabi–Yau (of dimension d) if it is graded homologically smooth and
as graded right $$ \begin{align*} \underline{{\mathrm{{Ext}}}}^i_{A^e}(A,A^e) \cong \begin{cases} 0, & i \neq d \\ U, & i = d \end{cases} \end{align*} $$
$$ \begin{align*} \underline{{\mathrm{{Ext}}}}^i_{A^e}(A,A^e) \cong \begin{cases} 0, & i \neq d \\ U, & i = d \end{cases} \end{align*} $$
 $A^e$
-modules, for some graded-invertible bimodule U.
$A^e$
-modules, for some graded-invertible bimodule U.
Similarly as in Remark 3.1, since there is an anti-isomorphism of
![]() $A^e$
it is easy to see that A is twisted Calabi–Yau of dimension d if and only if
$A^e$
it is easy to see that A is twisted Calabi–Yau of dimension d if and only if
![]() $A^{\mathrm {op}}$
is.
$A^{\mathrm {op}}$
is.
As is turns out, the graded and ungraded versions of the twisted Calabi–Yau property are equivalent.
Theorem 4.2. Let A be a graded algebra. Then A is twisted Calabi–Yau of dimension d if and only if A is graded twisted Calabi–Yau of dimension d.
Proof. First note that by Lemma 2.4, A is homologically smooth if and only if it is graded homologically smooth, and in case either condition is satisfied the inclusions
 $\underline { {\mathrm {{Ext}}}}^i_{A^e}(A, A^e) \subseteq {\mathrm {{Ext}}}^i_{A^e}(A,A^e)$
of right
$\underline { {\mathrm {{Ext}}}}^i_{A^e}(A, A^e) \subseteq {\mathrm {{Ext}}}^i_{A^e}(A,A^e)$
of right
![]() $A^e$
-modules are equalities for all i by Lemma 2.4. For homologically smooth A, the graded bimodule
$A^e$
-modules are equalities for all i by Lemma 2.4. For homologically smooth A, the graded bimodule
 $U = {\mathrm {{Ext}}}^d_{A^e}(A, A^e)$
is invertible if and only if it is graded-invertible, by Lemma 2.10. It follows immediately that A is graded twisted Calabi–Yau algebra of dimension d if and only if it is (ungraded) twisted Calabi–Yau of dimension d.
$U = {\mathrm {{Ext}}}^d_{A^e}(A, A^e)$
is invertible if and only if it is graded-invertible, by Lemma 2.10. It follows immediately that A is graded twisted Calabi–Yau algebra of dimension d if and only if it is (ungraded) twisted Calabi–Yau of dimension d.
The following general lemma will be useful in translating from conditions involving
![]() $ {\mathrm {{Ext}}}$
to conditions in the derived category.
$ {\mathrm {{Ext}}}$
to conditions in the derived category.
Lemma 4.3. Let A be a k-algebra.
-
(1) Let
 $0 \neq M \in A {\mathrm {\!-Mod}}$
be perfect. Then
$0 \neq M \in A {\mathrm {\!-Mod}}$
be perfect. Then
 $ {\mathrm {pdim}}(M) = \max \{ i | {\mathrm {{Ext}}}^i_A(M, A) \neq 0 \}$
.
$ {\mathrm {pdim}}(M) = \max \{ i | {\mathrm {{Ext}}}^i_A(M, A) \neq 0 \}$
. -
(2) If
 $M \in A {\mathrm {\!-Mod}}$
is perfect and
$M \in A {\mathrm {\!-Mod}}$
is perfect and
 $ {\mathrm {{Ext}}}^i_A(M, A) = 0$
for
$ {\mathrm {{Ext}}}^i_A(M, A) = 0$
for
 $i \neq d$
, then setting
$i \neq d$
, then setting
 $N = {\mathrm {{Ext}}}^d_A(M, A)$
we have
$N = {\mathrm {{Ext}}}^d_A(M, A)$
we have
 $ {\mathrm {RHom}}_A(M, A) \cong N[-d]$
in
$ {\mathrm {RHom}}_A(M, A) \cong N[-d]$
in
 $D^b( {\mathrm {Mod-\!}} A)$
.
$D^b( {\mathrm {Mod-\!}} A)$
. -
(3) Suppose that A is graded with
 $\dim _k A_0 < \infty $
. If
$\dim _k A_0 < \infty $
. If
 $M \in A {\mathrm {\!-Gr}}$
is a bounded below module with
$M \in A {\mathrm {\!-Gr}}$
is a bounded below module with
 $ {\mathrm {pdim}}(M) \leq d$
,
$ {\mathrm {pdim}}(M) \leq d$
,
 $ {\mathrm {{Ext}}}^i_A(M, A) = 0$
for
$ {\mathrm {{Ext}}}^i_A(M, A) = 0$
for
 $i \neq d$
, and such that
$i \neq d$
, and such that
 $N = {\mathrm {{Ext}}}^d_A(M, A)$
satisfies
$N = {\mathrm {{Ext}}}^d_A(M, A)$
satisfies
 $\dim _k N < \infty $
, then M is perfect and part (2) applies to show
$\dim _k N < \infty $
, then M is perfect and part (2) applies to show
 $ {\mathrm {RHom}}_A(M,A) = {\mathrm{R}}\underline { {\mathrm {{Hom}}}}_A(M, A) \cong N[-d]$
in
$ {\mathrm {RHom}}_A(M,A) = {\mathrm{R}}\underline { {\mathrm {{Hom}}}}_A(M, A) \cong N[-d]$
in
 $D^b( {\mathrm {Gr-\!}} A)$
.
$D^b( {\mathrm {Gr-\!}} A)$
.
Proof. (1) This is a standard result. Assume that
![]() $M \neq 0$
. By definition, we have a finite projective resolution
$M \neq 0$
. By definition, we have a finite projective resolution
![]() $P^{\bullet } \to M$
, with all
$P^{\bullet } \to M$
, with all
![]() $P^i$
finitely generated. Let
$P^i$
finitely generated. Let
![]() $c = {\mathrm {pdim}}_{A}(M)$
. We have
$c = {\mathrm {pdim}}_{A}(M)$
. We have
 $$ \begin{align*} c = \max \{ i | {\mathrm{{Ext}}}^i_{A}(M, L) \neq 0\ \text{for some}\ A\text{-module}\ L \}. \end{align*} $$
$$ \begin{align*} c = \max \{ i | {\mathrm{{Ext}}}^i_{A}(M, L) \neq 0\ \text{for some}\ A\text{-module}\ L \}. \end{align*} $$
If F is a free A-module with a surjection onto L, from the long exact sequence we obtain
![]() $ {\mathrm {{Ext}}}^c_{A}(M, F) \neq 0$
. Since the terms
$ {\mathrm {{Ext}}}^c_{A}(M, F) \neq 0$
. Since the terms
![]() $P^i$
in the resolution of M are finitely generated, it follows from computing
$P^i$
in the resolution of M are finitely generated, it follows from computing
![]() $ {\mathrm {{Ext}}}$
with the resolution P of M that
$ {\mathrm {{Ext}}}$
with the resolution P of M that
![]() $ {\mathrm {{Ext}}}^c_A$
commutes with direct sums in the second coordinate, so that
$ {\mathrm {{Ext}}}^c_A$
commutes with direct sums in the second coordinate, so that
![]() $ {\mathrm {{Ext}}}^c_{A}(M, A) \neq 0$
. Since
$ {\mathrm {{Ext}}}^c_{A}(M, A) \neq 0$
. Since
 $ {\mathrm {{Ext}}}^i_A(M, A) = 0$
for
$ {\mathrm {{Ext}}}^i_A(M, A) = 0$
for
![]() $i \geq {\mathrm {pdim}}_A(M)$
, the result follows.
$i \geq {\mathrm {pdim}}_A(M)$
, the result follows.
(2) The result is trivial if
![]() $M = 0$
, so assume that
$M = 0$
, so assume that
![]() $M \neq 0$
. By part (1), we have
$M \neq 0$
. By part (1), we have
![]() $ {\mathrm {pdim}}(M) = d$
. Thus we can choose a projective resolution of M of the form
$ {\mathrm {pdim}}(M) = d$
. Thus we can choose a projective resolution of M of the form
![]() $P^{\bullet } \to M$
, where
$P^{\bullet } \to M$
, where
Then
![]() $ {\mathrm {RHom}}_A(M, A)= {\mathrm {{Hom}}}_A(P, A)$
is a complex which lives in complex degrees
$ {\mathrm {RHom}}_A(M, A)= {\mathrm {{Hom}}}_A(P, A)$
is a complex which lives in complex degrees
![]() $0$
to d. By assumption,
$0$
to d. By assumption,
![]() $ {\mathrm {RHom}}_A(M, A)$
has cohomology only in degree d, where the cohomology is N. It is now easy to see that there is a quasi-isomorphism
$ {\mathrm {RHom}}_A(M, A)$
has cohomology only in degree d, where the cohomology is N. It is now easy to see that there is a quasi-isomorphism
![]() $ {\mathrm {RHom}}_A(M, A) \cong N[-d]$
.
$ {\mathrm {RHom}}_A(M, A) \cong N[-d]$
.
(3) We may again assume that
![]() $M \neq 0$
. Then
$M \neq 0$
. Then
![]() $ {\mathrm {pdim}}(M) = d$
, and it follows from [Reference Minamoto and Mori33, Proposition 3.4] that M is (graded) perfect. Now
$ {\mathrm {pdim}}(M) = d$
, and it follows from [Reference Minamoto and Mori33, Proposition 3.4] that M is (graded) perfect. Now
![]() $ {\mathrm {RHom}}_A(M,A) = {\mathrm{R}}\underline { {\mathrm {{Hom}}}}_A(M,A)$
by Lemma 2.4 so that the quasi-isomorphism in part (2) automatically preserves the grading.
$ {\mathrm {RHom}}_A(M,A) = {\mathrm{R}}\underline { {\mathrm {{Hom}}}}_A(M,A)$
by Lemma 2.4 so that the quasi-isomorphism in part (2) automatically preserves the grading.
Using the preceding lemma, it is convenient to reformulate the second condition in the definition of (graded) twisted Calabi–Yau in terms of the derived category.
Lemma 4.4. A (graded) k-algebra A is twisted Calabi–Yau if and only if A is homologically smooth and
![]() $ {\mathrm {RHom}}_{A^e}(A,A^e) \cong U[-d]$
in
$ {\mathrm {RHom}}_{A^e}(A,A^e) \cong U[-d]$
in
 $D^b(A^e {\mathrm {\!-Mod}})$
(respectively, in
$D^b(A^e {\mathrm {\!-Mod}})$
(respectively, in
 $D^b(A^e {\mathrm {\!-Gr}})$
) for some (graded) invertible bimodule U. Moreover, in this case
$D^b(A^e {\mathrm {\!-Gr}})$
) for some (graded) invertible bimodule U. Moreover, in this case
![]() $d = {\mathrm {pdim}}_{A^e}(A)$
.
$d = {\mathrm {pdim}}_{A^e}(A)$
.
Proof. We prove the ungraded version; the proof in the graded case is the same. It is enough to assume that A is homologically smooth and prove that under this assumption, for an invertible bimodule U, the following conditions are equivalent:
-
(ii)
 $ {\mathrm {{Ext}}}^i_{A^e}(A,A^e) \cong \begin {cases} 0, & i \neq d \\ U, & i = d \end {cases}$
$ {\mathrm {{Ext}}}^i_{A^e}(A,A^e) \cong \begin {cases} 0, & i \neq d \\ U, & i = d \end {cases}$
-
(ii′)
 $ {\mathrm {RHom}}_{A^e}(A,A^e) \cong U[-d]$
in
$ {\mathrm {RHom}}_{A^e}(A,A^e) \cong U[-d]$
in
 $D^b(A^e {\mathrm {\!-Mod}})$
.
$D^b(A^e {\mathrm {\!-Mod}})$
.
If (ii
![]() ${}^{\prime}$
) holds, then by taking cohomology we obtain (ii). If (ii) holds, then since A is a perfect
${}^{\prime}$
) holds, then by taking cohomology we obtain (ii). If (ii) holds, then since A is a perfect
![]() $A^e$
-module we obtain (ii
$A^e$
-module we obtain (ii
![]() ${}^{\prime}$
) from Lemma 4.3(2).
${}^{\prime}$
) from Lemma 4.3(2).
The last statement follows from Lemma 4.3(1).
From now on we will use the derived category formulation of the definition of twisted Calabi–Yau without further comment.
4.2 Basic operations preserving the twisted Calabi–Yau property
Next we show that the twisted Calabi–Yau property is stable under several basic operations.
Let
![]() $Z(A)$
denote the center of an algebra A. An
$Z(A)$
denote the center of an algebra A. An
![]() $(A,A)$
-bimodule U is said to be
$(A,A)$
-bimodule U is said to be
![]() $Z(A)$
-central if, for all
$Z(A)$
-central if, for all
![]() $z \in Z(A)$
and all
$z \in Z(A)$
and all
![]() $u \in U$
, we have
$u \in U$
, we have
![]() $zu = uz$
.
$zu = uz$
.
Lemma 4.5. Let A be a twisted Calabi–Yau algebra with Nakayama bimodule U. Then U is a
![]() $Z(A)$
-central
$Z(A)$
-central
![]() $(A,A)$
-bimodule. In particular, if A has a Nakayama automorphism
$(A,A)$
-bimodule. In particular, if A has a Nakayama automorphism
![]() $\mu $
, then the restriction of
$\mu $
, then the restriction of
![]() $\mu $
to the center
$\mu $
to the center
![]() $Z(A)$
is the identity.
$Z(A)$
is the identity.
Proof. Fix
![]() $z \in Z(A)$
and denote
$z \in Z(A)$
and denote
![]() $r = z \otimes 1 - 1 \otimes z^{\mathrm {op}} \in Z(A^e)$
. Let
$r = z \otimes 1 - 1 \otimes z^{\mathrm {op}} \in Z(A^e)$
. Let
![]() $\rho _r \colon A \to A$
denote the
$\rho _r \colon A \to A$
denote the
![]() $A^e$
-module homomorphism given by (left) multiplication by r. Because A is a central
$A^e$
-module homomorphism given by (left) multiplication by r. Because A is a central
![]() $(A,A)$
-bimodule, we have
$(A,A)$
-bimodule, we have
![]() $\rho _r = 0$
. It follows from [Reference Rotman42, Proposition 6.18] that the
$\rho _r = 0$
. It follows from [Reference Rotman42, Proposition 6.18] that the
![]() $Z(A^e)$
-module endomorphism of
$Z(A^e)$
-module endomorphism of
 $ {\mathrm {{Ext}}}^i_{A^e}(A,A^e)$
given by multiplication by r is equal to
$ {\mathrm {{Ext}}}^i_{A^e}(A,A^e)$
given by multiplication by r is equal to
 $$ \begin{align*} {\mathrm{{Ext}}}^i_{A^e}(\rho_r, A^e) \colon {\mathrm{{Ext}}}^i_{A^e}(A,A^e) \to {\mathrm{{Ext}}}^i_{A^e}(A,A^e). \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^i_{A^e}(\rho_r, A^e) \colon {\mathrm{{Ext}}}^i_{A^e}(A,A^e) \to {\mathrm{{Ext}}}^i_{A^e}(A,A^e). \end{align*} $$
Because
![]() $\rho _r = 0$
, this is the zero morphism. Therefore
$\rho _r = 0$
, this is the zero morphism. Therefore
 $U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
is a central
$U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
is a central
![]() $(A,A)$
-bimodule.
$(A,A)$
-bimodule.
We will discuss a number of operations that preserve the twisted Calabi–Yau property. The first such operation is the direct sum.
Proposition 4.6. For algebras A and B, denote
![]() $R = A \oplus B$
. Then R is twisted Calabi–Yau of dimension d if and only if both A and B are twisted Calabi–Yau of dimension d, in which case the Nakayama bimodule of R is the direct sum of the Nakayama bimodules of A and B (and if A and B have Nakayama automorphisms
$R = A \oplus B$
. Then R is twisted Calabi–Yau of dimension d if and only if both A and B are twisted Calabi–Yau of dimension d, in which case the Nakayama bimodule of R is the direct sum of the Nakayama bimodules of A and B (and if A and B have Nakayama automorphisms
![]() $\mu _A$
and
$\mu _A$
and
![]() $\mu _B$
, then R has Nakayama automorphism
$\mu _B$
, then R has Nakayama automorphism
![]() $\mu _R = \mu _A \oplus \mu _B$
).
$\mu _R = \mu _A \oplus \mu _B$
).
Proof. First, suppose that both A and B are twisted Calabi–Yau of dimension d with respective Nakayama bimodules
![]() $U_1$
and
$U_1$
and
![]() $U_2$
. Then R is homologically smooth by Proposition 3.11. Note that
$U_2$
. Then R is homologically smooth by Proposition 3.11. Note that
![]() $U_1 \oplus U_2$
is an invertible
$U_1 \oplus U_2$
is an invertible
![]() $(R,R)$
-bimodule with inverse
$(R,R)$
-bimodule with inverse
 $U_1^{-1} \oplus U_2^{-1}$
. Applying Lemma 2.9 we have
$U_1^{-1} \oplus U_2^{-1}$
. Applying Lemma 2.9 we have
 $$ \begin{align*} {\mathrm{RHom}}_R(R, R^e) &\cong {\mathrm{RHom}}_{A^e}(A, A^e) \oplus {\mathrm{RHom}}_{B^e}(B, B^e) \\ &\cong U_1[-d] \oplus U_2[-d] \\ &\cong (U_1 \oplus U_2)[-d], \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_R(R, R^e) &\cong {\mathrm{RHom}}_{A^e}(A, A^e) \oplus {\mathrm{RHom}}_{B^e}(B, B^e) \\ &\cong U_1[-d] \oplus U_2[-d] \\ &\cong (U_1 \oplus U_2)[-d], \end{align*} $$
so that R is twisted Calabi–Yau of dimension d with Nakayama bimodule
![]() $U_1 \oplus U_2$
. In case
$U_1 \oplus U_2$
. In case
![]() $U_1 = {{\hspace {-0.0001pt}}}^1 A^{\mu _A}$
and
$U_1 = {{\hspace {-0.0001pt}}}^1 A^{\mu _A}$
and
![]() $U_2 = {{\hspace {-0.0001pt}}}^1 B^{\mu _B}$
for Nakayama automorphisms
$U_2 = {{\hspace {-0.0001pt}}}^1 B^{\mu _B}$
for Nakayama automorphisms
![]() $\mu _A$
and
$\mu _A$
and
![]() $\mu _B$
, then we obtain
$\mu _B$
, then we obtain
![]() $U_1 \oplus U_2 = {{\hspace {-0.0001pt}}}^1 R^{\mu _R}$
for
$U_1 \oplus U_2 = {{\hspace {-0.0001pt}}}^1 R^{\mu _R}$
for
![]() $\mu _R = \mu _A \oplus \mu _B$
.
$\mu _R = \mu _A \oplus \mu _B$
.
Conversely, suppose that R is twisted Calabi–Yau of dimension d and denote
 $U = {\mathrm {{Ext}}}^d_{R^e}(R,R^e)$
; it follows from Proposition 3.11 that both A and B are homologically smooth. Lemma 4.5 implies that the central idempotent
$U = {\mathrm {{Ext}}}^d_{R^e}(R,R^e)$
; it follows from Proposition 3.11 that both A and B are homologically smooth. Lemma 4.5 implies that the central idempotent
![]() $z_1 = (1,0) \in A \oplus B = R$
centralizes U, so that also
$z_1 = (1,0) \in A \oplus B = R$
centralizes U, so that also
![]() $U \cong U_1 \oplus U_2$
for
$U \cong U_1 \oplus U_2$
for
![]() $U_1 = z_1U$
and
$U_1 = z_1U$
and
![]() $U_2 = (1-z_1)U$
, which are, respectively, invertible bimodules over A and B. Now, using Lemma 2.8, we have for the central idempotent
$U_2 = (1-z_1)U$
, which are, respectively, invertible bimodules over A and B. Now, using Lemma 2.8, we have for the central idempotent
![]() $z = z_1 \otimes z_1^{\mathrm {op}} \in R^e$
that
$z = z_1 \otimes z_1^{\mathrm {op}} \in R^e$
that
Thus A is twisted Calabi–Yau of dimension d, and the same is true of B by symmetry.
We next show that the twisted Calabi–Yau property is a “geometric” property, being preserved under extension of scalars. (This terminology is as in [Reference Hartshorne18, Exercise II.3.15], for instance.) Recall the notation
![]() $M^K = M \otimes K$
for an A-module M.
$M^K = M \otimes K$
for an A-module M.
Proposition 4.7. Let A be a k-algebra and
![]() $K/k$
a field extension.
$K/k$
a field extension.
-
(1) If A is twisted Calabi–Yau of dimension d, then so is
 $A^K$
.
$A^K$
. -
(2) Suppose that A is graded with
 $\dim _k A_0 < \infty $
. Then
$\dim _k A_0 < \infty $
. Then
 $A^K$
is (graded) twisted Calabi–Yau of dimension d if and only if A is.
$A^K$
is (graded) twisted Calabi–Yau of dimension d if and only if A is.
Proof. (1) Suppose that A is twisted Calabi–Yau of dimension d. Then
![]() $A^K$
is homologically smooth by Corollary 3.14. Set
$A^K$
is homologically smooth by Corollary 3.14. Set
 $U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
. Then using Lemma 3.12(2), since A is perfect as an
$U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
. Then using Lemma 3.12(2), since A is perfect as an
![]() $A^e$
module we have
$A^e$
module we have
 $$ \begin{align*} {\mathrm{RHom}}_{(A^K)^e}(A^K,(A^K)^e) &\cong {\mathrm{RHom}}_{(A^e) \otimes K}(A \otimes K, (A^e) \otimes K) \\ &\cong {\mathrm{RHom}}_{A^e}(A,A^e) \otimes K \quad \\ &\cong U \otimes K[-d]. \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{(A^K)^e}(A^K,(A^K)^e) &\cong {\mathrm{RHom}}_{(A^e) \otimes K}(A \otimes K, (A^e) \otimes K) \\ &\cong {\mathrm{RHom}}_{A^e}(A,A^e) \otimes K \quad \\ &\cong U \otimes K[-d]. \end{align*} $$
It follows from taking
![]() $0$
th cohomology in Lemma 3.12(2) that
$0$
th cohomology in Lemma 3.12(2) that
 $(M \otimes _A N)^K \cong M^K \otimes _{A^K} N^K$
for any modules
$(M \otimes _A N)^K \cong M^K \otimes _{A^K} N^K$
for any modules
![]() $M \in {\mathrm {Mod-\!}} A$
and
$M \in {\mathrm {Mod-\!}} A$
and
![]() $N \in A {\mathrm {\!-Mod}}$
. In particular,
$N \in A {\mathrm {\!-Mod}}$
. In particular,
![]() $U^K$
is an invertible
$U^K$
is an invertible
![]() $A^K$
-bimodule (with inverse
$A^K$
-bimodule (with inverse
 $(U^{-1})^K$
), so that
$(U^{-1})^K$
), so that
![]() $A^K$
is twisted Calabi–Yau of dimension d.
$A^K$
is twisted Calabi–Yau of dimension d.
(2) One direction is a special case of part (1). To prove the converse, suppose that
![]() $A^K$
is twisted Calabi–Yau of dimension d. Again, Proposition 3.13 tells us that A is homologically smooth. Now the argument above shows that
$A^K$
is twisted Calabi–Yau of dimension d. Again, Proposition 3.13 tells us that A is homologically smooth. Now the argument above shows that
 $$ \begin{align*} {\mathrm{RHom}}_{(A^K)^e}(A^K,(A^K)^e) \cong {\mathrm{RHom}}_{A^e}(A,A^e) \otimes K, \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{(A^K)^e}(A^K,(A^K)^e) \cong {\mathrm{RHom}}_{A^e}(A,A^e) \otimes K, \end{align*} $$
which by assumption is isomorphic to
![]() $V[-d]$
for a graded invertible
$V[-d]$
for a graded invertible
![]() $A^K$
-bimodule V. In particular, taking cohomology we see that
$A^K$
-bimodule V. In particular, taking cohomology we see that
![]() $ {\mathrm {RHom}}_{A^e}(A, A^e) \otimes K$
has cohomology only in degree d, so the same is true of
$ {\mathrm {RHom}}_{A^e}(A, A^e) \otimes K$
has cohomology only in degree d, so the same is true of
![]() $ {\mathrm {RHom}}_{A^e}(A, A^e)$
since the functor
$ {\mathrm {RHom}}_{A^e}(A, A^e)$
since the functor
![]() $- \otimes K$
is exact. Thus we have
$- \otimes K$
is exact. Thus we have
 $ {\mathrm {{Ext}}}_{A^e}^i(A, A^e) = 0$
for
$ {\mathrm {{Ext}}}_{A^e}^i(A, A^e) = 0$
for
![]() $i \neq d$
and since A is perfect as an
$i \neq d$
and since A is perfect as an
![]() $A^e$
-module, Lemma 4.3(2) implies that
$A^e$
-module, Lemma 4.3(2) implies that
![]() $ {\mathrm {RHom}}_{A^e}(A, A^e) \cong U[-d]$
for some
$ {\mathrm {RHom}}_{A^e}(A, A^e) \cong U[-d]$
for some
![]() $(A, A)$
-bimodule U. Clearly
$(A, A)$
-bimodule U. Clearly
![]() $U \otimes K \cong V$
.
$U \otimes K \cong V$
.
Now there are natural evaluation maps of bimodules
![]() $\phi _l: U \otimes _A {\mathrm {{Hom}}}_A(U, A) \to A$
and
$\phi _l: U \otimes _A {\mathrm {{Hom}}}_A(U, A) \to A$
and
![]() $\phi _r: {\mathrm {{Hom}}}_{A^{\mathrm {op}}}(U, A) \otimes _A U \to A$
, and U is an invertible bimodule if and only if both
$\phi _r: {\mathrm {{Hom}}}_{A^{\mathrm {op}}}(U, A) \otimes _A U \to A$
, and U is an invertible bimodule if and only if both
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _r$
are bijections. Since
$\phi _r$
are bijections. Since
![]() $U^K = V$
is an invertible
$U^K = V$
is an invertible
![]() $A^K$
-module, it is finitely generated and projective on both sides, and so is certainly perfect as a left and right
$A^K$
-module, it is finitely generated and projective on both sides, and so is certainly perfect as a left and right
![]() $A^K$
-module. Then U is perfect as a left and right A-module, by Proposition 3.13(2). By taking
$A^K$
-module. Then U is perfect as a left and right A-module, by Proposition 3.13(2). By taking
![]() $0$
th cohomology in Lemma 3.12(1), we get that the natural map
$0$
th cohomology in Lemma 3.12(1), we get that the natural map
 $( {\mathrm {{Hom}}}_A(U, A))^K \to {\mathrm {{Hom}}}_{A^K}(U^K, A^K)$
is an isomorphism, and similarly on the right. Using Lemma 3.12(1)(2) again, extending the base field in
$( {\mathrm {{Hom}}}_A(U, A))^K \to {\mathrm {{Hom}}}_{A^K}(U^K, A^K)$
is an isomorphism, and similarly on the right. Using Lemma 3.12(1)(2) again, extending the base field in
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _r$
now yields the morphisms of
$\phi _r$
now yields the morphisms of
 $(A^K, A^K)$
-bimodules
$(A^K, A^K)$
-bimodules
 $U^K \otimes _{A^K} {\mathrm {{Hom}}}_{A^K}(U^K, A^K) \to A^K$
and
$U^K \otimes _{A^K} {\mathrm {{Hom}}}_{A^K}(U^K, A^K) \to A^K$
and
 $ {\mathrm {{Hom}}}_{(A^{\mathrm {op}})^K}(U^K, A^K) \otimes _{A^K} U^K \to A^K$
, which are bijections since
$ {\mathrm {{Hom}}}_{(A^{\mathrm {op}})^K}(U^K, A^K) \otimes _{A^K} U^K \to A^K$
, which are bijections since
![]() $U^K = V$
is invertible. By the exactness of base field extension,
$U^K = V$
is invertible. By the exactness of base field extension,
![]() $\phi _l$
and
$\phi _l$
and
![]() $\phi _r$
are also bijections, so that U is invertible as required. Thus A is also (graded) twisted Calabi–Yau.
$\phi _r$
are also bijections, so that U is invertible as required. Thus A is also (graded) twisted Calabi–Yau.
Note in the proof above that if A has (graded) Nakayama automorphism
![]() $\mu $
, then
$\mu $
, then
![]() $A \otimes K$
has Nakayama automorphism
$A \otimes K$
has Nakayama automorphism
![]() $\mu \otimes {\mathrm {{id}}}_K$
.
$\mu \otimes {\mathrm {{id}}}_K$
.
Another operation that preserves the twisted Calabi–Yau property is the tensor product of algebras. Before proving this we need the following technical lemma.
Lemma 4.8. Let R and S be k-algebras. For complexes
![]() $P \in D^-(R {\mathrm {\!-Mod}})$
,
$P \in D^-(R {\mathrm {\!-Mod}})$
,
![]() $N \in D(R {\mathrm {\!-Mod}})$
,
$N \in D(R {\mathrm {\!-Mod}})$
,
![]() $Q \in D^-(S {\mathrm {\!-Mod}})$
, and
$Q \in D^-(S {\mathrm {\!-Mod}})$
, and
![]() $J \in D(S {\mathrm {\!-Mod}})$
, there is a natural map of complexes of abelian groups
$J \in D(S {\mathrm {\!-Mod}})$
, there is a natural map of complexes of abelian groups
respecting any extra module structure obtained if
![]() $M, N, H$
, or J is a complex of bimodules. The map
$M, N, H$
, or J is a complex of bimodules. The map
![]() $\Phi $
is an isomorphism if P and Q are perfect.
$\Phi $
is an isomorphism if P and Q are perfect.
Proof. For left R-modules M and N and S-modules H and J, it is easy to see that there is a natural map
respecting any bimodule structures that arise. A similar argument as in the first paragraph of the proof of Lemma 3.12 shows that
![]() $\phi $
is an isomorphism in case M and H are finitely generated projective modules.
$\phi $
is an isomorphism in case M and H are finitely generated projective modules.
One may now replace P and Q by bounded above complexes of projectives and proceed in the same spirit as the proof Lemma 3.12, obtaining the desired isomorphism if P and Q are perfect. We omit the details.
Proposition 4.9. If A and B are (graded) twisted Calabi–Yau algebras of respective dimensions
![]() $d_1$
and
$d_1$
and
![]() $d_2$
, then
$d_2$
, then
![]() $A \otimes B$
is a (graded) twisted Calabi–Yau algebra of dimension
$A \otimes B$
is a (graded) twisted Calabi–Yau algebra of dimension
![]() $d_1 + d_2$
whose Nakayama bimodule is the tensor product of the Nakayama bimodules of A and B. If A and B have Nakayama automorphisms
$d_1 + d_2$
whose Nakayama bimodule is the tensor product of the Nakayama bimodules of A and B. If A and B have Nakayama automorphisms
![]() $\mu _1, \mu _2$
, respectively, then
$\mu _1, \mu _2$
, respectively, then
![]() $A \otimes B$
has Nakayama automorphism
$A \otimes B$
has Nakayama automorphism
![]() $\mu _1 \otimes \mu _2$
.
$\mu _1 \otimes \mu _2$
.
Proof. Proposition 3.16 implies that
![]() $R = A \otimes B$
is homologically smooth. Let
$R = A \otimes B$
is homologically smooth. Let
![]() $U_1$
and
$U_1$
and
![]() $U_2,$
respectively, denote the Nakayama bimodules of A and B, which are invertible bimodules and therefore projective on each side. Now applying Lemma 4.8 in the second isomorphism below, which gives an isomorphism since A is perfect over
$U_2,$
respectively, denote the Nakayama bimodules of A and B, which are invertible bimodules and therefore projective on each side. Now applying Lemma 4.8 in the second isomorphism below, which gives an isomorphism since A is perfect over
![]() $A^e$
and B is perfect over
$A^e$
and B is perfect over
![]() $B^e$
, we obtain
$B^e$
, we obtain
 $$ \begin{align*} {\mathrm{RHom}}_{R^e}(R,R^e) &\cong {\mathrm{RHom}}_{A^e \otimes B^e}(A \otimes B, A^e \otimes B^e) \\ &\cong {\mathrm{RHom}}_{A^e}(A, A^e) \otimes {\mathrm{RHom}}_{B^e}(B, B^e) \\ &\cong U_1[-d_1] \otimes U_2[-d_2] = (U_1 \otimes U_2)[-(d_1 + d_2)], \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{R^e}(R,R^e) &\cong {\mathrm{RHom}}_{A^e \otimes B^e}(A \otimes B, A^e \otimes B^e) \\ &\cong {\mathrm{RHom}}_{A^e}(A, A^e) \otimes {\mathrm{RHom}}_{B^e}(B, B^e) \\ &\cong U_1[-d_1] \otimes U_2[-d_2] = (U_1 \otimes U_2)[-(d_1 + d_2)], \end{align*} $$
where these isomorphisms hold as complexes of right
![]() $A^e$
-modules. Thus we see that A is twisted Calabi–Yau of the desired dimension, and it is easy to verify the behavior of Nakayama automorphisms from the above.
$A^e$
-modules. Thus we see that A is twisted Calabi–Yau of the desired dimension, and it is easy to verify the behavior of Nakayama automorphisms from the above.
A fundamental tool for the study of twisted Calabi–Yau algebras, and a key motivation behind their definition, is Van den Bergh duality [Reference van den Bergh47, Reference van den Bergh48]. Readers may find an excellent survey of this topic in [Reference Krähmer23]. We record the derived version of this duality below.
Lemma 4.10. Suppose A is (graded) twisted Calabi–Yau of dimension d, with
 $U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
. Then for any complex of (graded) left
$U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
. Then for any complex of (graded) left
![]() $(A^e, C)$
-bimodules M, one has a (graded) isomorphism
$(A^e, C)$
-bimodules M, one has a (graded) isomorphism
 $$ \begin{align*} {\mathrm{RHom}}_{A^e}(A,M) \cong (U \otimes^L_{A^e} M)[-d]. \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{A^e}(A,M) \cong (U \otimes^L_{A^e} M)[-d]. \end{align*} $$
as complexes of right C-modules.
Proof. This is the same as in [Reference van den Bergh47, Theorem 1], but without passing to cohomology. Beginning with Lemma 2.12, we have:
 $$ \begin{align*} {\mathrm{RHom}}_{A^e}(A,M) &\cong {\mathrm{RHom}}_{A^e}(A,A^e) \otimes^L_{A^e} M \\ &\cong U[-d] \otimes^L_{A^e} M \\ &\cong (U \otimes^L_{A^e} M)[-d].\\[-38pt] \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{A^e}(A,M) &\cong {\mathrm{RHom}}_{A^e}(A,A^e) \otimes^L_{A^e} M \\ &\cong U[-d] \otimes^L_{A^e} M \\ &\cong (U \otimes^L_{A^e} M)[-d].\\[-38pt] \end{align*} $$
Adapting Ginzburg’s observation in [Reference Ginzburg17, Remark 3.4.2], we may apply Van den Bergh duality to show that the property of being twisted Calabi–Yau of dimension d is Morita invariant, by providing an alternate characterization of such algebras.
Proposition 4.11. Let A be an algebra and let U be an invertible
![]() $(A,A)$
-bimodule. Then A is twisted Calabi–Yau of dimension d with Nakayama bimodule U if and only if A is homologically smooth and, for every algebra C and for
$(A,A)$
-bimodule. Then A is twisted Calabi–Yau of dimension d with Nakayama bimodule U if and only if A is homologically smooth and, for every algebra C and for
![]() $0 \leq i \leq d$
, one has natural isomorphisms of functors
$0 \leq i \leq d$
, one has natural isomorphisms of functors
 $$ \begin{align*} {\mathrm{Tor}}_i^{A^e}(U,-) \cong {\mathrm{{Ext}}}^{d-i}_{A^e}(A,-) \colon (A^e \otimes C^{\mathrm{op}}) {\mathrm{\!-Mod}} \to {\mathrm{Mod-\!}} C. \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}_i^{A^e}(U,-) \cong {\mathrm{{Ext}}}^{d-i}_{A^e}(A,-) \colon (A^e \otimes C^{\mathrm{op}}) {\mathrm{\!-Mod}} \to {\mathrm{Mod-\!}} C. \end{align*} $$
Consequently, the property of being twisted Calabi–Yau of dimension d is preserved under k-linear Morita equivalence.
Proof. If A is twisted Calabi–Yau of dimension d, then A is homologically smooth by definition, and satisfies the above isomorphisms by passing to cohomology in Lemma 4.10. Conversely, suppose that A is perfect as an
![]() $A^e$
-module and satisfies the isomorphisms above. Evaluating these functors at the
$A^e$
-module and satisfies the isomorphisms above. Evaluating these functors at the
![]() $(A^e,A^e)$
-bimodule
$(A^e,A^e)$
-bimodule
![]() $A^e$
yields isomorphisms
$A^e$
yields isomorphisms
 $ {\mathrm {{Ext}}}^{i}_{A^e}(A,A^e) \cong {\mathrm {Tor}}_{d-i}^{A^e}(U,A^e)$
as right
$ {\mathrm {{Ext}}}^{i}_{A^e}(A,A^e) \cong {\mathrm {Tor}}_{d-i}^{A^e}(U,A^e)$
as right
![]() $A^e$
-modules for
$A^e$
-modules for
![]() $0 \leq i \leq d$
. For
$0 \leq i \leq d$
. For
![]() $i < d$
one has
$i < d$
one has
 $$ \begin{align*} {\mathrm{{Ext}}}^i_{A^e}(A,A^e) \cong {\mathrm{Tor}}_{d-i}^{A^e}(U,A^e) = 0 \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^i_{A^e}(A,A^e) \cong {\mathrm{Tor}}_{d-i}^{A^e}(U,A^e) = 0 \end{align*} $$
by flatness of
![]() $A^e$
. For
$A^e$
. For
![]() $i = d$
we have
$i = d$
we have
 $$ \begin{align*} {\mathrm{{Ext}}}^d_{A^e}(A,A^e) \cong {\mathrm{Tor}}_0^{A^e}(U,A^e) = U \otimes_{A^e} A^e \cong U, \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^d_{A^e}(A,A^e) \cong {\mathrm{Tor}}_0^{A^e}(U,A^e) = U \otimes_{A^e} A^e \cong U, \end{align*} $$
as right
![]() $A^e$
-modules. Thus A is twisted Calabi–Yau of dimension d with Nakayama bimodule U.
$A^e$
-modules. Thus A is twisted Calabi–Yau of dimension d with Nakayama bimodule U.
Now suppose that A is twisted Calabi–Yau of dimension d with Nakayama bimodule U, and suppose that an algebra B is k-linearly Morita equivalent to A. Then B is homologically smooth by Proposition 3.17. As discussed in the proof of that proposition, a k-linear equivalence of categories
![]() $A {\mathrm {\!-Mod}} \to B {\mathrm {\!-Mod}}$
induces a monoidal k-linear equivalence
$A {\mathrm {\!-Mod}} \to B {\mathrm {\!-Mod}}$
induces a monoidal k-linear equivalence
![]() $F \colon A^e {\mathrm {\!-Mod}} \to B^e {\mathrm {\!-Mod}}$
. Because A and B are the respective tensor units, we have
$F \colon A^e {\mathrm {\!-Mod}} \to B^e {\mathrm {\!-Mod}}$
. Because A and B are the respective tensor units, we have
![]() $F(A) \cong B$
; also,
$F(A) \cong B$
; also,
![]() $V = F(U)$
must be a k-central invertible
$V = F(U)$
must be a k-central invertible
![]() $(B,B)$
-bimodule. Given an algebra C, F also induces an equivalence of categories
$(B,B)$
-bimodule. Given an algebra C, F also induces an equivalence of categories
![]() $(A^e \otimes C^{\mathrm {op}}) {\mathrm {\!-Mod}} \to (B^e \otimes C^{\mathrm {op}}) {\mathrm {\!-Mod}}$
by simply transporting the right C-action on a left
$(A^e \otimes C^{\mathrm {op}}) {\mathrm {\!-Mod}} \to (B^e \otimes C^{\mathrm {op}}) {\mathrm {\!-Mod}}$
by simply transporting the right C-action on a left
![]() $A^e$
-module X via F as an algebra morphism
$A^e$
-module X via F as an algebra morphism
![]() $C^{\mathrm {op}} \to {\mathrm {{End}}}_{A^e}(X) \to {\mathrm {{End}}}_{B^e}(F(X))$
; with a slight abuse of notation we use F to denote this equivalence as well. Now the isomorphism in the statement induces a natural isomorphism
$C^{\mathrm {op}} \to {\mathrm {{End}}}_{A^e}(X) \to {\mathrm {{End}}}_{B^e}(F(X))$
; with a slight abuse of notation we use F to denote this equivalence as well. Now the isomorphism in the statement induces a natural isomorphism
 $$ \begin{align*} {\mathrm{Tor}}_i^{A^e}(U,F^{-1}(-)) \cong {\mathrm{{Ext}}}^{d-i}_{A^e}(A,F^{-1}(-)) \colon (B^e \otimes C^{\mathrm{op}}) {\mathrm{\!-Mod}} \to {\mathrm{Mod-\!}} C. \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}_i^{A^e}(U,F^{-1}(-)) \cong {\mathrm{{Ext}}}^{d-i}_{A^e}(A,F^{-1}(-)) \colon (B^e \otimes C^{\mathrm{op}}) {\mathrm{\!-Mod}} \to {\mathrm{Mod-\!}} C. \end{align*} $$
Because F is an equivalence, it also preserves the construction of
![]() $ {\mathrm {{Ext}}}$
and
$ {\mathrm {{Ext}}}$
and
![]() $ {\mathrm {Tor}}$
spaces, so that applying F to the previous isomorphism yields a natural isomorphism of functors
$ {\mathrm {Tor}}$
spaces, so that applying F to the previous isomorphism yields a natural isomorphism of functors
 $$ \begin{align*} {\mathrm{Tor}}_i^{B^e}(V,-) \cong {\mathrm{{Ext}}}^{d-i}_{B^e}(B,-) \colon (B^e \otimes C^{\mathrm{op}}) {\mathrm{\!-Mod}} \to {\mathrm{Mod-\!}} C. \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}_i^{B^e}(V,-) \cong {\mathrm{{Ext}}}^{d-i}_{B^e}(B,-) \colon (B^e \otimes C^{\mathrm{op}}) {\mathrm{\!-Mod}} \to {\mathrm{Mod-\!}} C. \end{align*} $$
Thus B is twisted Calabi–Yau of dimension d, as desired.
4.3 Homological tools for finite-dimensional modules
This final subsection records some results that are of use for handling finite-dimensional modules over (graded) twisted Calabi–Yau algebras. It concludes with a characterization of twisted Calabi–Yau algebras of dimension 0.
The following result is a type of Serre duality formula. The idea of the next result and its corollary were extracted from the proof of [Reference Keller21, Lemma 4.1]. We will use the notation
![]() $X^* = {\mathrm {RHom}}_k(X,k) = {\mathrm {{Hom}}}_k(X,k)$
below to denote the extension of the k-dual to the derived category of k-vector spaces.
$X^* = {\mathrm {RHom}}_k(X,k) = {\mathrm {{Hom}}}_k(X,k)$
below to denote the extension of the k-dual to the derived category of k-vector spaces.
Proposition 4.12. Let A be a (graded) twisted Calabi–Yau algebra of dimension d, and set
 $U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
. Let M be a (graded)
$U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
. Let M be a (graded)
![]() $(A, B)$
-bimodule and N a (graded)
$(A, B)$
-bimodule and N a (graded)
![]() $(A, C)$
-bimodule, with M finite-dimensional. Then there are (graded) quasi-isomorphisms
$(A, C)$
-bimodule, with M finite-dimensional. Then there are (graded) quasi-isomorphisms
 $$ \begin{align*} {\mathrm{RHom}}_A(M,N) \cong M^* \otimes^L_A (U \otimes_A N)[-d] \cong (M^* \otimes_A U) \otimes^L_A N[-d], \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_A(M,N) \cong M^* \otimes^L_A (U \otimes_A N)[-d] \cong (M^* \otimes_A U) \otimes^L_A N[-d], \end{align*} $$
and, for each integer i, we have
 $$ \begin{align*} {\mathrm{{Ext}}}^i_A(M,N) \cong {\mathrm{Tor}}_{d-i}^A(M^*, U \otimes_A N) \cong {\mathrm{Tor}}_{d-i}^A(M^* \otimes_A U, N) \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^i_A(M,N) \cong {\mathrm{Tor}}_{d-i}^A(M^*, U \otimes_A N) \cong {\mathrm{Tor}}_{d-i}^A(M^* \otimes_A U, N) \end{align*} $$
as (graded)
![]() $(B, C)$
-bimodules.
$(B, C)$
-bimodules.
Proof. Because M is finite-dimensional over k, there is a natural isomorphism of
![]() $(A^e, B^{\mathrm {op}} \otimes C)$
-bimodules
$(A^e, B^{\mathrm {op}} \otimes C)$
-bimodules
![]() $ {\mathrm {{Hom}}}_k(M,N) \cong N \otimes M^*$
. Combining this observation with Lemma 2.13 and Lemma 4.10 yields
$ {\mathrm {{Hom}}}_k(M,N) \cong N \otimes M^*$
. Combining this observation with Lemma 2.13 and Lemma 4.10 yields
 $$ \begin{align*} {\mathrm{RHom}}_A(M,N) &\cong {\mathrm{RHom}}_{A^e}(A, {\mathrm{{Hom}}}_k(M,N)) \qquad ( \text{by Lemma 2.13(2)}) \\ &\cong {\mathrm{RHom}}_{A^e}(A, N \otimes M^*) \\ & \cong U \otimes^L_{A^e} (N \otimes M^*)[-d] \qquad (\text{by Lemma 4.10})\\ &\cong M^* \otimes^L_A (U \otimes^L_A N)[-d] \qquad (\text{by Lemma 2.13(1)}), \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_A(M,N) &\cong {\mathrm{RHom}}_{A^e}(A, {\mathrm{{Hom}}}_k(M,N)) \qquad ( \text{by Lemma 2.13(2)}) \\ &\cong {\mathrm{RHom}}_{A^e}(A, N \otimes M^*) \\ & \cong U \otimes^L_{A^e} (N \otimes M^*)[-d] \qquad (\text{by Lemma 4.10})\\ &\cong M^* \otimes^L_A (U \otimes^L_A N)[-d] \qquad (\text{by Lemma 2.13(1)}), \end{align*} $$
and these are quasi-isomorphisms of complexes of right
![]() $B^{\mathrm {op}} \otimes C$
-modules. By the definition of twisted Calabi–Yau, U is invertible and hence projective as both a left and a right A-module, so we obtain
$B^{\mathrm {op}} \otimes C$
-modules. By the definition of twisted Calabi–Yau, U is invertible and hence projective as both a left and a right A-module, so we obtain
 $$ \begin{align*} M^* \otimes^L_A (U \otimes_A N) \cong M^* \otimes^L_A U \otimes^L_A N \cong (M^* \otimes_A U) \otimes^L_A N. \end{align*} $$
$$ \begin{align*} M^* \otimes^L_A (U \otimes_A N) \cong M^* \otimes^L_A U \otimes^L_A N \cong (M^* \otimes_A U) \otimes^L_A N. \end{align*} $$
The isomorphisms between
![]() $ {\mathrm {{Ext}}}$
and
$ {\mathrm {{Ext}}}$
and
![]() $ {\mathrm {Tor}}$
are obtained by taking cohomology.
$ {\mathrm {Tor}}$
are obtained by taking cohomology.
The proof in the graded case is exactly the same. Note that because M is finite-dimensional and A is homologically smooth, M is perfect by Lemma 3.2. Thus in the graded case there is no difference betweeen
![]() $ {\mathrm {RHom}}_A(M,N)$
and
$ {\mathrm {RHom}}_A(M,N)$
and
![]() ${\mathrm{R}}\underline { {\mathrm {{Hom}}}}_A(M,N)$
, justifying the uniform statement of the result.
${\mathrm{R}}\underline { {\mathrm {{Hom}}}}_A(M,N)$
, justifying the uniform statement of the result.
In case both M and N above are finite-dimensional, we obtain the following, more conventional Serre duality result.
Corollary 4.13. Keeping the hypotheses of Proposition 4.12, assume additionally that N is finite-dimensional. Then we have (graded) quasi-isomorphisms
and, for each integer i,
 $$ \begin{align*} {\mathrm{{Ext}}}^i_A(M,N)^* \cong {\mathrm{{Ext}}}^{d-i}_A(U \otimes_A N, M) \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^i_A(M,N)^* \cong {\mathrm{{Ext}}}^{d-i}_A(U \otimes_A N, M) \end{align*} $$
as (graded)
![]() $(C, B)$
-bimodules.
$(C, B)$
-bimodules.
Proof. Invoking Proposition 4.12, we compute as follows:
 $$ \begin{align*} {\mathrm{RHom}}_A(M,N)^* &\cong {\mathrm{RHom}}_k({\mathrm{RHom}}_A(M,N),k) \\ &\cong {\mathrm{RHom}}_k(M^* \otimes^L_A (U \otimes_A N), k)[d] \\ &\cong {\mathrm{RHom}}_A(U \otimes_A N, {\mathrm{RHom}}_k(M^*,k))[d] \\ &\cong {\mathrm{RHom}}_A(U \otimes_AN, M)[d]. \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_A(M,N)^* &\cong {\mathrm{RHom}}_k({\mathrm{RHom}}_A(M,N),k) \\ &\cong {\mathrm{RHom}}_k(M^* \otimes^L_A (U \otimes_A N), k)[d] \\ &\cong {\mathrm{RHom}}_A(U \otimes_A N, {\mathrm{RHom}}_k(M^*,k))[d] \\ &\cong {\mathrm{RHom}}_A(U \otimes_AN, M)[d]. \end{align*} $$
As before, the isomorphism relating the
![]() $ {\mathrm {{Ext}}}$
groups is obtained by passing to cohomology.
$ {\mathrm {{Ext}}}$
groups is obtained by passing to cohomology.
Again, the same proof applies in the graded case.
We may apply the above to compute the global dimension of a twisted Calabi–Yau algebra that has a nontrivial finite-dimensional representation, including locally finite graded algebras.
Corollary 4.14. Let A be a twisted Calabi–Yau algebra of dimension d. If A has a nonzero finite-dimensional module, then
![]() $ {\mathrm {gldim}}_l(A) = {\mathrm {gldim}}_r(A) = d$
. In particular, this holds if A is graded with
$ {\mathrm {gldim}}_l(A) = {\mathrm {gldim}}_r(A) = d$
. In particular, this holds if A is graded with
![]() $\dim _k A_0 < \infty $
.
$\dim _k A_0 < \infty $
.
Proof. Recall from Lemma 4.4 that
![]() $ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = d$
, so that the left and right global dimensions of A are both at most d by Lemma 3.2(1). If A has a finite-dimensional left module
$ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = d$
, so that the left and right global dimensions of A are both at most d by Lemma 3.2(1). If A has a finite-dimensional left module
![]() $M \neq 0$
, then it also has a finite-dimensional right module
$M \neq 0$
, then it also has a finite-dimensional right module
![]() $M^* \neq 0$
. So by symmetry, it suffices to show that a finite-dimensional left A-module
$M^* \neq 0$
. So by symmetry, it suffices to show that a finite-dimensional left A-module
![]() $M \neq 0$
has projective dimension d. But this follows from Proposition 4.12, since
$M \neq 0$
has projective dimension d. But this follows from Proposition 4.12, since
 $U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
is invertible and
$U = {\mathrm {{Ext}}}^d_{A^e}(A,A^e)$
is invertible and
 $$ \begin{align*} {\mathrm{{Ext}}}^d_A(M,A) \cong {\mathrm{Tor}}_0^A(M^*, U) = M^* \otimes_A U \neq 0. \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^d_A(M,A) \cong {\mathrm{Tor}}_0^A(M^*, U) = M^* \otimes_A U \neq 0. \end{align*} $$
If A is graded with
![]() $\dim _k A_0 < \infty $
, then
$\dim _k A_0 < \infty $
, then
![]() $A_0 = A/A_{\geq 1}$
is a nonzero finite-dimensional module and the argument above applies. Alternatively, one may conclude that
$A_0 = A/A_{\geq 1}$
is a nonzero finite-dimensional module and the argument above applies. Alternatively, one may conclude that
![]() $d = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = {\mathrm {gldim}}_l(A) = {\mathrm {gldim}}_r(A)$
from Proposition 3.18(3), since
$d = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = {\mathrm {gldim}}_l(A) = {\mathrm {gldim}}_r(A)$
from Proposition 3.18(3), since
![]() $S = A/J(A)$
must be separable by Theorem 3.6.
$S = A/J(A)$
must be separable by Theorem 3.6.
The conclusion of the corollary above may fail if A has no finite-dimensional representations.
Example 4.15. For an integer
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $A_n$
denote the nth Weyl algebra over a field k of characteristic zero. Then
$A_n$
denote the nth Weyl algebra over a field k of characteristic zero. Then
![]() $A_n$
is a Calabi–Yau algebra of dimension
$A_n$
is a Calabi–Yau algebra of dimension
![]() $d = 2n$
as explained in [Reference Schedler43, Exercise 3.7.11], while the left and right global dimensions of
$d = 2n$
as explained in [Reference Schedler43, Exercise 3.7.11], while the left and right global dimensions of
![]() $A_n$
are n [Reference McConnell and Robson32, Theorem 5.8]. Furthermore, let
$A_n$
are n [Reference McConnell and Robson32, Theorem 5.8]. Furthermore, let
![]() $D_n$
denote the division algebra of quotients of
$D_n$
denote the division algebra of quotients of
![]() $A_n$
. Then
$A_n$
. Then
![]() $D_n$
is a Calabi–Yau algebra of dimension
$D_n$
is a Calabi–Yau algebra of dimension
![]() $d = 2n$
as discussed in [Reference Yekutieli and Zhang51, Example 1.9(e) and p. 115], while
$d = 2n$
as discussed in [Reference Yekutieli and Zhang51, Example 1.9(e) and p. 115], while
![]() $ {\mathrm {gldim}}(D_n) = 0$
.
$ {\mathrm {gldim}}(D_n) = 0$
.
The following standard result will be useful in the applications of the duality results above.
Lemma 4.16. Let S be a finite-dimensional semisimple k-algebra. Then S is a symmetric Frobenius algebra; that is,
![]() $S^* = {\mathrm {{Hom}}}_k(S, k) \cong S$
as
$S^* = {\mathrm {{Hom}}}_k(S, k) \cong S$
as
![]() $(S, S)$
-bimodules.
$(S, S)$
-bimodules.
Proof. See [Reference Lam24, Section 16F].
We may use the duality results above to obtain information about the socle of a graded module. For a graded left A-module M we let
![]() $ {\mathrm {soc}}(M)$
denote the graded socle of M, the largest graded semisimple submodule of M. Note that
$ {\mathrm {soc}}(M)$
denote the graded socle of M, the largest graded semisimple submodule of M. Note that
![]() $ {\mathrm {soc}}(M) = \{m \in M \mid J(A)m = 0\}$
is the annihilator in M of the graded Jacobson radical
$ {\mathrm {soc}}(M) = \{m \in M \mid J(A)m = 0\}$
is the annihilator in M of the graded Jacobson radical
![]() $J(A)$
.
$J(A)$
.
Proposition 4.17. Let A be a graded algebra with
![]() $\dim _k A_0 < \infty $
, which is a twisted Calabi–Yau k-algebra of dimension d with Nakayama bimodule U. Set
$\dim _k A_0 < \infty $
, which is a twisted Calabi–Yau k-algebra of dimension d with Nakayama bimodule U. Set
![]() $S = A/J(A)$
, and let
$S = A/J(A)$
, and let
![]() ${{\hspace {-0.0001pt}}}_A M$
be a graded left A-module. Then there is an isomorphism of graded left S-modules (hence of left A-modules)
${{\hspace {-0.0001pt}}}_A M$
be a graded left A-module. Then there is an isomorphism of graded left S-modules (hence of left A-modules)
 $$ \begin{align*} {\mathrm{Tor}}_d^A(S, M) \cong U^{-1} \otimes_A {\mathrm{soc}}(M). \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}_d^A(S, M) \cong U^{-1} \otimes_A {\mathrm{soc}}(M). \end{align*} $$
Proof. The finite-dimensional semisimple algebra S satisfies
![]() $S^* \cong S$
as an
$S^* \cong S$
as an
![]() $(S,S)$
-bimodule by Lemma 4.16, hence also as a graded left A-module. Because
$(S,S)$
-bimodule by Lemma 4.16, hence also as a graded left A-module. Because
![]() ${{\hspace {-0.0001pt}}}_A S$
is annihilated by
${{\hspace {-0.0001pt}}}_A S$
is annihilated by
![]() $J(A)$
, any graded module homomorphism
$J(A)$
, any graded module homomorphism
![]() $S \to M$
has image annihilated by
$S \to M$
has image annihilated by
![]() $J(A)$
, and therefore has image in
$J(A)$
, and therefore has image in
![]() $ {\mathrm {soc}}(M)$
. Thus we have
$ {\mathrm {soc}}(M)$
. Thus we have
![]() $ {\mathrm {{Hom}}}_A(S, M) = {\mathrm {{Hom}}}_S(S, {\mathrm {soc}}(M)) = {\mathrm {soc}}(M)$
. Now applying Proposition 4.12, we have
$ {\mathrm {{Hom}}}_A(S, M) = {\mathrm {{Hom}}}_S(S, {\mathrm {soc}}(M)) = {\mathrm {soc}}(M)$
. Now applying Proposition 4.12, we have
 $$ \begin{align*} {\mathrm{Tor}}^A_d(S_A , {{\hspace{-0.0001pt}}}_A M) &\cong {\mathrm{{Ext}}}^0_A(S^*, U^{-1} \otimes_A M) \\ &\cong {\mathrm{{Ext}}}^0_A(S, U^{-1} \otimes_A M) \\ &= {\mathrm{soc}}(U^{-1} \otimes_A M) \\ &= U^{-1} \otimes_A {\mathrm{soc}}(M) \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}^A_d(S_A , {{\hspace{-0.0001pt}}}_A M) &\cong {\mathrm{{Ext}}}^0_A(S^*, U^{-1} \otimes_A M) \\ &\cong {\mathrm{{Ext}}}^0_A(S, U^{-1} \otimes_A M) \\ &= {\mathrm{soc}}(U^{-1} \otimes_A M) \\ &= U^{-1} \otimes_A {\mathrm{soc}}(M) \end{align*} $$
as left S-modules, where we use in the last step that the graded autoequivalence
![]() $U^{-1} \otimes _A -$
must preserve the graded socle of a module.
$U^{-1} \otimes _A -$
must preserve the graded socle of a module.
In particular, it is rare for a twisted Calabi–Yau algebra to have a socle.
Corollary 4.18. Let A be a twisted Calabi–Yau algebra of dimension d.
-
(1) Suppose that A is graded with
 $\dim _k A_0 < \infty $
. If
$\dim _k A_0 < \infty $
. If
 $d> 0$
, then
$d> 0$
, then
 $ {\mathrm {soc}}(A) = 0$
.
$ {\mathrm {soc}}(A) = 0$
. -
(2) If A is a finite-dimensional algebra, then
 $d = 0$
.
$d = 0$
.
Proof. (1) Invoking Proposition 4.17 in the case where
![]() $d> 0$
yields
$d> 0$
yields
 $U^{-1} \otimes _A {\mathrm {soc}}(A) \cong {\mathrm {Tor}}^A_d(S,A) = 0$
. Because U is invertible, we obtain
$U^{-1} \otimes _A {\mathrm {soc}}(A) \cong {\mathrm {Tor}}^A_d(S,A) = 0$
. Because U is invertible, we obtain
![]() $ {\mathrm {soc}}(A) = 0$
.
$ {\mathrm {soc}}(A) = 0$
.
(2) If A is finite-dimensional, then we may consider A as a graded algebra with
![]() $A = A_0$
. Because A is artinian, its (graded) socle is nonzero. It follows from part (1) above that
$A = A_0$
. Because A is artinian, its (graded) socle is nonzero. It follows from part (1) above that
![]() $d = 0$
.
$d = 0$
.
We conclude this section by characterizing twisted Calabi–Yau algebras of dimension 0.
Theorem 4.19. For a k-algebra A, the following are equivalent:
-
(a) A is twisted Calabi–Yau of dimension 0;
-
(b) A is twisted Calabi–Yau and has finite k-dimension;
-
(c) A is Calabi–Yau of dimension 0;
-
(d) A is a separable k-algebra.
Proof. Clearly (c)
![]() $\implies $
(a). For (a)
$\implies $
(a). For (a)
![]() $\implies $
(d), note that if A is twisted Calabi–Yau of dimension 0, then
$\implies $
(d), note that if A is twisted Calabi–Yau of dimension 0, then
![]() $ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = 0$
by Lemma 4.4, making A separable by Lemma 3.3(3).
$ {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_{A^e} A) = 0$
by Lemma 4.4, making A separable by Lemma 3.3(3).
To see that (d)
![]() $\implies $
(c), suppose that A is separable. Then
$\implies $
(c), suppose that A is separable. Then
![]() ${{\hspace {-0.0001pt}}}_{A^e} A$
is projective, and so A is certainly homologically smooth. As noted earlier, Lemma 3.3(5) shows that a separable algebra must be finite-dimensional. Then we also know that
${{\hspace {-0.0001pt}}}_{A^e} A$
is projective, and so A is certainly homologically smooth. As noted earlier, Lemma 3.3(5) shows that a separable algebra must be finite-dimensional. Then we also know that
![]() $A^e$
is a finite-dimensional semisimple k-algebra, by Lemma 3.3(4). Since a separable algebra must be semisimple by definition, we have
$A^e$
is a finite-dimensional semisimple k-algebra, by Lemma 3.3(4). Since a separable algebra must be semisimple by definition, we have
![]() $A^* \cong A$
as
$A^* \cong A$
as
![]() $(A, A)$
-bimodules in Lemma 4.16. We now calculate that
$(A, A)$
-bimodules in Lemma 4.16. We now calculate that
 $$ \begin{align*} {\mathrm{{Hom}}}_{A^e}(A,A^e) &\cong {\mathrm{{Hom}}}_{A^e}(A, {\mathrm{{Hom}}}_k(A^e,k)) \\ &\cong {\mathrm{{Hom}}}_k(A^e \otimes_{A^e} A, k) \\ &\cong {\mathrm{{Hom}}}_k(A,k) \cong A \end{align*} $$
$$ \begin{align*} {\mathrm{{Hom}}}_{A^e}(A,A^e) &\cong {\mathrm{{Hom}}}_{A^e}(A, {\mathrm{{Hom}}}_k(A^e,k)) \\ &\cong {\mathrm{{Hom}}}_k(A^e \otimes_{A^e} A, k) \\ &\cong {\mathrm{{Hom}}}_k(A,k) \cong A \end{align*} $$
as right
![]() $A^e$
-modules. Furthermore,
$A^e$
-modules. Furthermore,
 $ {\mathrm {{Ext}}}_{A^e}^i(A,A^e) = 0$
for
$ {\mathrm {{Ext}}}_{A^e}^i(A,A^e) = 0$
for
![]() $i> 0$
as
$i> 0$
as
![]() ${{\hspace {-0.0001pt}}}_{A^e} A$
is projective. Thus A is Calabi–Yau of dimension 0, as desired. Since we already recalled that a separable algebra is finite-dimensional, (d)
${{\hspace {-0.0001pt}}}_{A^e} A$
is projective. Thus A is Calabi–Yau of dimension 0, as desired. Since we already recalled that a separable algebra is finite-dimensional, (d)
![]() $\implies $
(b) as well. Finally, (b)
$\implies $
(b) as well. Finally, (b)
![]() $\implies $
(a) follows from Corollary 4.18(2).
$\implies $
(a) follows from Corollary 4.18(2).
Graded twisted Calabi–Yau algebras of dimension 0 are essentially the same as (ungraded) Calabi–Yau algebras of dimension 0, since the former must be trivially graded.
Corollary 4.20. A graded algebra A is (twisted) Calabi–Yau of dimension 0 if and only if
![]() $A = A_0$
and A is separable.
$A = A_0$
and A is separable.
Proof. If
![]() $A = A_0$
is separable, then it is Calabi–Yau of dimension 0 by Theorem 4.19; because the grading of A is trivial, it is clear that A is graded twisted Calabi–Yau of dimension 0.
$A = A_0$
is separable, then it is Calabi–Yau of dimension 0 by Theorem 4.19; because the grading of A is trivial, it is clear that A is graded twisted Calabi–Yau of dimension 0.
Conversely, suppose that A is graded twisted Calabi–Yau of dimension 0. Theorem 4.2(1) shows that A is twisted Calabi–Yau of dimension 0. It follows from Theorem 4.19 that A is separable, hence a finite-dimensional semisimple k-algebra. Thus
![]() $J(A) = 0$
; because
$J(A) = 0$
; because
![]() $A_{\geq 1} \subseteq J(A)$
for an
$A_{\geq 1} \subseteq J(A)$
for an
![]() $\mathbb {N}$
-graded algebra, we obtain
$\mathbb {N}$
-graded algebra, we obtain
![]() $A = A_0$
.
$A = A_0$
.
5 AS regularity for locally finite algebras
In this section, we study the relationship between the twisted Calabi–Yau property and certain generalizations of the AS regular property for locally finite graded algebras. It was shown in [Reference Reyes, Rogalski and Zhang37, Lemma 1.2] that a connected graded algebra A is graded twisted Calabi–Yau if and only if it is AS regular (not necessarily of finite GK dimension). Several possible generalizations of AS regularity to the context of locally finite algebras have been proposed in the literature. In this section we recall some of these and show that several of the most natural generalizations are in fact equivalent. We then show that for any locally finite graded k-algebra A, under a mild technical condition (that A is separable modulo its graded Jacobson radical), these notions of regularity are further equivalent to the twisted Calabi–Yau condition.
5.1 Defining generalized AS regular algebras
For a graded algebra B, we write
![]() $B {\mathrm {\!-gr}}$
for the category of finitely generated graded left B-modules; similarly,
$B {\mathrm {\!-gr}}$
for the category of finitely generated graded left B-modules; similarly,
![]() $ {\mathrm {gr-\!}} B$
is the corresponding category of finitely generated graded right B-modules. We begin with a technical lemma that will help us to relate the different notions of regularity.
$ {\mathrm {gr-\!}} B$
is the corresponding category of finitely generated graded right B-modules. We begin with a technical lemma that will help us to relate the different notions of regularity.
Lemma 5.1. Let A be a locally finite graded k-algebra with
![]() $ {\mathrm {gr.gldim}}(A) = d$
. Let
$ {\mathrm {gr.gldim}}(A) = d$
. Let
![]() $\mathcal {X}$
be the full subcategory of
$\mathcal {X}$
be the full subcategory of
![]() $A_0 {\mathrm {\!-gr}}$
consisting of modules M such that
$A_0 {\mathrm {\!-gr}}$
consisting of modules M such that
 $ {\mathrm {{Ext}}}_A^i(M, A) = 0$
for
$ {\mathrm {{Ext}}}_A^i(M, A) = 0$
for
![]() $i \neq d$
and
$i \neq d$
and
 $ {\mathrm {{Ext}}}^d_A(M, A) \cong N$
for some
$ {\mathrm {{Ext}}}^d_A(M, A) \cong N$
for some
![]() $N \in {\mathrm {gr-\!}} A_0$
. Similarly, let
$N \in {\mathrm {gr-\!}} A_0$
. Similarly, let
![]() $\mathcal {Y}$
be the full subcategory of
$\mathcal {Y}$
be the full subcategory of
![]() $ {\mathrm {gr-\!}} A_0$
consisting of modules N such that
$ {\mathrm {gr-\!}} A_0$
consisting of modules N such that
 $ {\mathrm {{Ext}}}_{A^{\mathrm {op}}}^i(N, A) = 0$
for
$ {\mathrm {{Ext}}}_{A^{\mathrm {op}}}^i(N, A) = 0$
for
![]() $i \neq d$
and
$i \neq d$
and
 $ {\mathrm {{Ext}}}_{A^{\mathrm {op}}}^d(N, A) = M$
for some
$ {\mathrm {{Ext}}}_{A^{\mathrm {op}}}^d(N, A) = M$
for some
![]() $M \in A_0 {\mathrm {\!-gr}}$
.
$M \in A_0 {\mathrm {\!-gr}}$
.
-
(1)
 $\mathcal {X}$
can also be described as the full subcategory of
$\mathcal {X}$
can also be described as the full subcategory of
 $A_0 {\mathrm {\!-gr}}$
consisting of modules M such that
$A_0 {\mathrm {\!-gr}}$
consisting of modules M such that
 $ {\mathrm {RHom}}_A(M, A)[d] \cong N$
for some
$ {\mathrm {RHom}}_A(M, A)[d] \cong N$
for some
 $N \in {\mathrm {gr-\!}} A_0$
. Similarly,
$N \in {\mathrm {gr-\!}} A_0$
. Similarly,
 $\mathcal {Y}$
can be described as the full subcategory of
$\mathcal {Y}$
can be described as the full subcategory of
 $ {\mathrm {gr-\!}} A_0$
consisting of modules N such that
$ {\mathrm {gr-\!}} A_0$
consisting of modules N such that
 $ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A)[d] \cong M$
for some
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A)[d] \cong M$
for some
 $M \in A_0 {\mathrm {\!-gr}}$
. The objects in
$M \in A_0 {\mathrm {\!-gr}}$
. The objects in
 $\mathcal {X}$
and
$\mathcal {X}$
and
 $\mathcal {Y}$
are perfect.
$\mathcal {Y}$
are perfect. -
(2)
 $\mathcal {X}$
and
$\mathcal {X}$
and
 $\mathcal {Y}$
are closed under extensions and direct summands.
$\mathcal {Y}$
are closed under extensions and direct summands. -
(3) The functors
are mutually inverse, yielding a duality between the categories $$ \begin{align*} {\mathrm{RHom}}_A(-, A)[d] &\colon \mathcal{X}^{\mathrm{op}} \to \mathcal{Y} \quad \mbox{and} \\ {\mathrm{RHom}}_{A^{\mathrm{op}}}(-, A)[d] &\colon \mathcal{Y}^{\mathrm{op}} \to \mathcal{X} \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_A(-, A)[d] &\colon \mathcal{X}^{\mathrm{op}} \to \mathcal{Y} \quad \mbox{and} \\ {\mathrm{RHom}}_{A^{\mathrm{op}}}(-, A)[d] &\colon \mathcal{Y}^{\mathrm{op}} \to \mathcal{X} \end{align*} $$
 $\mathcal {X}$
and
$\mathcal {X}$
and
 $\mathcal {Y}$
.
$\mathcal {Y}$
.
-
(4) If
 $M \in \mathcal {X}$
is an
$M \in \mathcal {X}$
is an
 $(A_0, C)$
-bimodule for some k-algebra C, then we have an isomorphism of
$(A_0, C)$
-bimodule for some k-algebra C, then we have an isomorphism of
 $(A_0, C)$
-bimodules
$(A_0, C)$
-bimodules
 $ {\mathrm {RHom}}_{A^{\mathrm {op}}}( {\mathrm {RHom}}_A(M, A),A) \cong M$
.
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}( {\mathrm {RHom}}_A(M, A),A) \cong M$
.
Proof. (1) Since M is bounded below, we have
![]() $ {\mathrm {pdim}}(M) = {\mathrm {gr.pdim}}(M) \leq d$
by Proposition 3.18. This now follows directly from Lemma 4.3(3) and its right-sided analog.
$ {\mathrm {pdim}}(M) = {\mathrm {gr.pdim}}(M) \leq d$
by Proposition 3.18. This now follows directly from Lemma 4.3(3) and its right-sided analog.
(2) This is an easy consequence of the definitions of
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
and the long exact sequence in Ext.
$\mathcal {Y}$
and the long exact sequence in Ext.
(3) Let
![]() $M \in \mathcal {X}$
. Since M is perfect of projective dimension at most d by part (1), M is quasi-isomorphic to a complex of graded A-modules
$M \in \mathcal {X}$
. Since M is perfect of projective dimension at most d by part (1), M is quasi-isomorphic to a complex of graded A-modules
![]() $P^{\bullet }$
of the form
$P^{\bullet }$
of the form
![]() $0 \to P^{-d} \to \dots \to P^{-1} \to P^0 \to 0$
, where each
$0 \to P^{-d} \to \dots \to P^{-1} \to P^0 \to 0$
, where each
![]() $P^i$
is a finitely generated graded projective A-module. Then
$P^i$
is a finitely generated graded projective A-module. Then
![]() $N = {\mathrm {RHom}}_A(M, A)[d]$
is identified with a complex
$N = {\mathrm {RHom}}_A(M, A)[d]$
is identified with a complex
![]() $Q^\bullet $
of the form
$Q^\bullet $
of the form
![]() $0 \to Q^0 \to Q^1 \to \dots \to Q^d \to 0$
, where
$0 \to Q^0 \to Q^1 \to \dots \to Q^d \to 0$
, where
![]() $Q^i = {\mathrm {{Hom}}}_A(P^i, A)$
. Since the
$Q^i = {\mathrm {{Hom}}}_A(P^i, A)$
. Since the
![]() $P^i$
are finitely generated, it readily follows that
$P^i$
are finitely generated, it readily follows that
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}( {\mathrm {RHom}}_A(P^{\bullet },A), A)) \cong P^{\bullet }$
, which means that
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}( {\mathrm {RHom}}_A(P^{\bullet },A), A)) \cong P^{\bullet }$
, which means that
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N[-d], A) \cong M$
, or equivalently
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N[-d], A) \cong M$
, or equivalently
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A)[d] \cong M$
. Thus we have
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A)[d] \cong M$
. Thus we have
![]() $N \in \mathcal {Y}$
.
$N \in \mathcal {Y}$
.
The whole argument can be repeated starting with
![]() $N \in \mathcal {Y}$
and
$N \in \mathcal {Y}$
and
![]() $Q^\bullet $
to get that
$Q^\bullet $
to get that
![]() $M = {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A)[d]$
is in
$M = {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A)[d]$
is in
![]() $\mathcal {X}$
, with
$\mathcal {X}$
, with
![]() $ {\mathrm {RHom}}_A(M, A)[d] \cong N$
. It is now easy to see that the functors
$ {\mathrm {RHom}}_A(M, A)[d] \cong N$
. It is now easy to see that the functors
![]() $ {\mathrm {RHom}}_A(-, A)[d]$
and
$ {\mathrm {RHom}}_A(-, A)[d]$
and
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}(-, A)[d]$
yield a contravariant equivalence between
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}(-, A)[d]$
yield a contravariant equivalence between
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
as claimed.
$\mathcal {Y}$
as claimed.
(4) Given
![]() $c \in C$
, one way to calculate the left action of c on
$c \in C$
, one way to calculate the left action of c on
 $ {\mathrm {{Ext}}}^d_A(M, A)$
is as follows. Right multiplication by c on M gives a morphism
$ {\mathrm {{Ext}}}^d_A(M, A)$
is as follows. Right multiplication by c on M gives a morphism
![]() $r_c: M \to M$
in
$r_c: M \to M$
in
![]() $A {\mathrm {\!-Gr}}$
. Let
$A {\mathrm {\!-Gr}}$
. Let
![]() $P^{\bullet }$
be the graded perfect complex quasi-isomorphic to M as in part (3). Then
$P^{\bullet }$
be the graded perfect complex quasi-isomorphic to M as in part (3). Then
![]() $r_c$
lifts to a morphism of complexes
$r_c$
lifts to a morphism of complexes
![]() $\widehat {r_c}: P^{\bullet } \to P^{\bullet }$
. Applying
$\widehat {r_c}: P^{\bullet } \to P^{\bullet }$
. Applying
![]() $ {\mathrm {{Hom}}}_A( - , A)$
to the morphism of complexes, we get a morphism of complexes
$ {\mathrm {{Hom}}}_A( - , A)$
to the morphism of complexes, we get a morphism of complexes
![]() $\widehat {r_c}^*: Q^{\bullet } \to Q^{\bullet }$
where
$\widehat {r_c}^*: Q^{\bullet } \to Q^{\bullet }$
where
![]() $Q^{\bullet } = {\mathrm {{Hom}}}_A(P^{\bullet }, A)$
; then taking cohomology induces a morphism of right A-modules which is
$Q^{\bullet } = {\mathrm {{Hom}}}_A(P^{\bullet }, A)$
; then taking cohomology induces a morphism of right A-modules which is
![]() $l_c: N \to N$
, the left action of c on the Ext group
$l_c: N \to N$
, the left action of c on the Ext group
 $N = {\mathrm {{Ext}}}^d_A(M, A)$
. Of course, the analogous process on the other side shows how to calculate the right action of c on
$N = {\mathrm {{Ext}}}^d_A(M, A)$
. Of course, the analogous process on the other side shows how to calculate the right action of c on
 $ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(N, A)$
. Since applying
$ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(N, A)$
. Since applying
![]() $ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}( {\mathrm {{Hom}}}_A(-, A), A)$
to the morphism of complexes
$ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}( {\mathrm {{Hom}}}_A(-, A), A)$
to the morphism of complexes
![]() $\widehat {r_c}: P^{\bullet } \to P^{\bullet }$
gives the same morphism of complexes back, we see that the right action of c on
$\widehat {r_c}: P^{\bullet } \to P^{\bullet }$
gives the same morphism of complexes back, we see that the right action of c on
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}( {\mathrm {RHom}}_A(M, A), A)$
is the same as the original right action on M, as required.
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}( {\mathrm {RHom}}_A(M, A), A)$
is the same as the original right action on M, as required.
We now show that a number of conditions that are natural possible generalizations of the AS regular condition to the nonconnected graded case are in fact equivalent.
Theorem 5.2. Let A be a locally finite graded k-algebra with
![]() $ {\mathrm {gr.gldim}} A = d$
and let
$ {\mathrm {gr.gldim}} A = d$
and let
![]() $S = A/J$
where
$S = A/J$
where
![]() $J = J(A)$
is the graded Jacobson radical. The following conditions on A are equivalent:
$J = J(A)$
is the graded Jacobson radical. The following conditions on A are equivalent:
-
(a)
 $ {\mathrm {RHom}}_A(-, A)[d]$
gives a bijection from the set of graded simple left A-modules up to isomorphism to the set of graded simple right A-modules up to isomorphism;
$ {\mathrm {RHom}}_A(-, A)[d]$
gives a bijection from the set of graded simple left A-modules up to isomorphism to the set of graded simple right A-modules up to isomorphism; -
(b)
 $ {\mathrm {RHom}}_A(-,A)[d]$
gives a contravariant equivalence from
$ {\mathrm {RHom}}_A(-,A)[d]$
gives a contravariant equivalence from
 $A_0 {\mathrm {\!-gr}}$
to
$A_0 {\mathrm {\!-gr}}$
to
 $ {\mathrm {gr-\!}} A_0$
;
$ {\mathrm {gr-\!}} A_0$
; -
(c)
 $ {\mathrm {RHom}}_A(-,A)[d]$
gives a contravariant equivalence from
$ {\mathrm {RHom}}_A(-,A)[d]$
gives a contravariant equivalence from
 $S {\mathrm {\!-gr}}$
to
$S {\mathrm {\!-gr}}$
to
 $ {\mathrm {gr-\!}} S$
;
$ {\mathrm {gr-\!}} S$
; -
(d)
 $ {\mathrm {RHom}}_A(S,A)[d] \cong V$
as right S-modules, for some invertible graded
$ {\mathrm {RHom}}_A(S,A)[d] \cong V$
as right S-modules, for some invertible graded
 $(S,S)$
-bimodule V;
$(S,S)$
-bimodule V; -
(d′)
 $ {\mathrm {RHom}}_A(S,A)[d] \cong V$
as
$ {\mathrm {RHom}}_A(S,A)[d] \cong V$
as
 $(S, S)$
-bimodules, for some invertible graded
$(S, S)$
-bimodules, for some invertible graded
 $(S,S)$
-bimodule V;
$(S,S)$
-bimodule V; -
(e)
 $ {\mathrm {RHom}}_A(A_0, A)[d] \cong (A_0^* \otimes _{A_0} W)$
as right
$ {\mathrm {RHom}}_A(A_0, A)[d] \cong (A_0^* \otimes _{A_0} W)$
as right
 $A_0$
-modules, for some invertible graded
$A_0$
-modules, for some invertible graded
 $(A_0, A_0)$
-bimodule W;
$(A_0, A_0)$
-bimodule W; -
(e′)
 $ {\mathrm {RHom}}_A(A_0, A)[d] \cong (A_0^* \otimes _{A_0} W)$
as
$ {\mathrm {RHom}}_A(A_0, A)[d] \cong (A_0^* \otimes _{A_0} W)$
as
 $(A_0, A_0)$
-bimodules, for some invertible graded
$(A_0, A_0)$
-bimodules, for some invertible graded
 $(A_0, A_0)$
-bimodule W.
$(A_0, A_0)$
-bimodule W.
Proof. (a)
![]() $\implies $
(b): This follows from Lemma 5.1(3) if we can show that in the notation of that lemma,
$\implies $
(b): This follows from Lemma 5.1(3) if we can show that in the notation of that lemma,
![]() $\mathcal {X} = A_0 {\mathrm {\!-gr}}$
and
$\mathcal {X} = A_0 {\mathrm {\!-gr}}$
and
![]() $\mathcal {Y} = {\mathrm {gr-\!}} A_0$
. Condition (a) gives that
$\mathcal {Y} = {\mathrm {gr-\!}} A_0$
. Condition (a) gives that
![]() $M \in \mathcal {X}$
for each graded simple left module M. Now
$M \in \mathcal {X}$
for each graded simple left module M. Now
![]() $\mathcal {X}$
is closed under extensions as noted in Lemma 5.1(2). Since
$\mathcal {X}$
is closed under extensions as noted in Lemma 5.1(2). Since
![]() $A_0$
is artinian, the objects in
$A_0$
is artinian, the objects in
![]() $A_0 {\mathrm {\!-gr}}$
have finite length, so it follows that
$A_0 {\mathrm {\!-gr}}$
have finite length, so it follows that
![]() $\mathcal {X} = A_0 {\mathrm {\!-gr}}$
. By hypothesis, every graded simple right module N is of the form
$\mathcal {X} = A_0 {\mathrm {\!-gr}}$
. By hypothesis, every graded simple right module N is of the form
![]() $ {\mathrm {RHom}}_A(M, A)[d]$
for some simple graded left module M, and as saw in the proof of Lemma 5.1, this implies that
$ {\mathrm {RHom}}_A(M, A)[d]$
for some simple graded left module M, and as saw in the proof of Lemma 5.1, this implies that
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A) \cong M$
and so
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}(N, A) \cong M$
and so
![]() $N \in \mathcal {Y}$
. Since
$N \in \mathcal {Y}$
. Since
![]() $\mathcal {Y}$
is also closed under extensions, similarly we get
$\mathcal {Y}$
is also closed under extensions, similarly we get
![]() $\mathcal {Y} = {\mathrm {gr-\!}} A_0$
as required.
$\mathcal {Y} = {\mathrm {gr-\!}} A_0$
as required.
(b)
![]() $\implies $
(a): this is obvious since a contravariant equivalence of Abelian categories preserves simple modules.
$\implies $
(a): this is obvious since a contravariant equivalence of Abelian categories preserves simple modules.
(b)
![]() $\implies $
(c): This is immediate since
$\implies $
(c): This is immediate since
![]() $S {\mathrm {\!-gr}}$
is the full subcategory of semisimple objects of
$S {\mathrm {\!-gr}}$
is the full subcategory of semisimple objects of
![]() $A_0 {\mathrm {\!-gr}}$
,
$A_0 {\mathrm {\!-gr}}$
,
![]() $ {\mathrm {gr-\!}} S$
is the full subcategory of semisimple objects of
$ {\mathrm {gr-\!}} S$
is the full subcategory of semisimple objects of
![]() $ {\mathrm {gr-\!}} A_0$
, and a contravariant equivalence preserves semisimple objects.
$ {\mathrm {gr-\!}} A_0$
, and a contravariant equivalence preserves semisimple objects.
(b)
![]() $\implies $
(e): As is well known, since
$\implies $
(e): As is well known, since
![]() $A_0$
is a finite-dimensional k-algebra, the functor
$A_0$
is a finite-dimensional k-algebra, the functor
![]() $G = {\mathrm {{Hom}}}_k(-, k) = (-)^*$
gives a contravariant equivalence from
$G = {\mathrm {{Hom}}}_k(-, k) = (-)^*$
gives a contravariant equivalence from
![]() $A_0 {\mathrm {\!-gr}}$
to
$A_0 {\mathrm {\!-gr}}$
to
![]() $ {\mathrm {gr-\!}} A_0$
, with inverse
$ {\mathrm {gr-\!}} A_0$
, with inverse
 $G^{-1} = {\mathrm {{Hom}}}_k(-, k): {\mathrm {gr-\!}} A_0 \to A_0 {\mathrm {\!-gr}}$
. By (b), the functor
$G^{-1} = {\mathrm {{Hom}}}_k(-, k): {\mathrm {gr-\!}} A_0 \to A_0 {\mathrm {\!-gr}}$
. By (b), the functor
![]() $F = {\mathrm {RHom}}_A(-,A)[d]$
also gives such a contravariant equivalence. Thus
$F = {\mathrm {RHom}}_A(-,A)[d]$
also gives such a contravariant equivalence. Thus
![]() $F \circ G^{-1}: {\mathrm {gr-\!}} A_0 \to {\mathrm {gr-\!}} A_0$
is a (covariant) equivalence of categories. As such, it must be of the form
$F \circ G^{-1}: {\mathrm {gr-\!}} A_0 \to {\mathrm {gr-\!}} A_0$
is a (covariant) equivalence of categories. As such, it must be of the form
![]() $- \otimes _{A_0} W$
for some graded invertible
$- \otimes _{A_0} W$
for some graded invertible
![]() $(A_0, A_0)$
-bimodule W, by Morita theory. Applying this to the object
$(A_0, A_0)$
-bimodule W, by Morita theory. Applying this to the object
![]() $A_0^*$
, (e) follows.
$A_0^*$
, (e) follows.
(c)
![]() $\implies $
(d): This is virtually the same as the proof of (b)
$\implies $
(d): This is virtually the same as the proof of (b)
![]() $\implies $
(e), working over the ring S instead. In this case we obtain
$\implies $
(e), working over the ring S instead. In this case we obtain
![]() $ {\mathrm {RHom}}_A(S, A)[d] \cong S^* \otimes _S V$
for some invertible
$ {\mathrm {RHom}}_A(S, A)[d] \cong S^* \otimes _S V$
for some invertible
![]() $(S, S)$
-bimodule V. However, since S is semisimple, we have
$(S, S)$
-bimodule V. However, since S is semisimple, we have
![]() $S^* \cong S$
by Lemma 4.16, and so
$S^* \cong S$
by Lemma 4.16, and so
![]() $S^* \otimes _S V \cong V$
in
$S^* \otimes _S V \cong V$
in
![]() $ {\mathrm {gr-\!}} S$
.
$ {\mathrm {gr-\!}} S$
.
(d)
![]() $\implies $
(b): Suppose that
$\implies $
(b): Suppose that
![]() $ {\mathrm {RHom}}_A(S,A)[d] \cong V$
as right S-modules, where V is an invertible graded
$ {\mathrm {RHom}}_A(S,A)[d] \cong V$
as right S-modules, where V is an invertible graded
![]() $(S,S)$
-bimodule. Let
$(S,S)$
-bimodule. Let
![]() $1 = e_1+ \dots + e_n$
be a decomposition of
$1 = e_1+ \dots + e_n$
be a decomposition of
![]() $1$
as a sum of primitive orthogonal idempotents
$1$
as a sum of primitive orthogonal idempotents
![]() $e_i \in A_0$
. Then
$e_i \in A_0$
. Then
 $S = \bigoplus _{i=1}^n Se_i$
decomposes S as a direct sum of simple graded left modules. Consider the subcategories
$S = \bigoplus _{i=1}^n Se_i$
decomposes S as a direct sum of simple graded left modules. Consider the subcategories
![]() $\mathcal {X} \subseteq A_0 {\mathrm {\!-gr}}$
and
$\mathcal {X} \subseteq A_0 {\mathrm {\!-gr}}$
and
![]() $\mathcal {Y} \subseteq {\mathrm {gr-\!}} A_0$
of Lemma 5.1. By hypothesis,
$\mathcal {Y} \subseteq {\mathrm {gr-\!}} A_0$
of Lemma 5.1. By hypothesis,
![]() $S \in \mathcal {X}$
. Since
$S \in \mathcal {X}$
. Since
![]() $\mathcal {X}$
is closed under direct summands by Lemma 5.1(2), we get that all simple left
$\mathcal {X}$
is closed under direct summands by Lemma 5.1(2), we get that all simple left
![]() $A_0$
-modules are in
$A_0$
-modules are in
![]() $\mathcal {X}$
. As in the proof of Lemma 5.1, we also get
$\mathcal {X}$
. As in the proof of Lemma 5.1, we also get
![]() $V \in \mathcal {Y}$
. Since V is invertible, it must be a right generator over S, which forces it to include each indecomposable projective right S-module as a summand. This is equivalent to saying that it must contain every simple right
$V \in \mathcal {Y}$
. Since V is invertible, it must be a right generator over S, which forces it to include each indecomposable projective right S-module as a summand. This is equivalent to saying that it must contain every simple right
![]() $A_0$
-module as a direct summand. Since
$A_0$
-module as a direct summand. Since
![]() $\mathcal {Y}$
is also closed under summands, every simple right
$\mathcal {Y}$
is also closed under summands, every simple right
![]() $A_0$
-module is in
$A_0$
-module is in
![]() $\mathcal {Y}$
. Now as in the argument for (a)
$\mathcal {Y}$
. Now as in the argument for (a)
![]() $\implies $
(b), since
$\implies $
(b), since
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
are closed under extensions we get
$\mathcal {Y}$
are closed under extensions we get
![]() $\mathcal {X} = A_0 {\mathrm {\!-gr}}$
and
$\mathcal {X} = A_0 {\mathrm {\!-gr}}$
and
![]() $\mathcal {Y} = {\mathrm {gr-\!}} A_0$
and (b) follows.
$\mathcal {Y} = {\mathrm {gr-\!}} A_0$
and (b) follows.
(e)
![]() $\implies $
(b): In this case we have
$\implies $
(b): In this case we have
![]() $ {\mathrm {RHom}}_A(A_0, A)[d] \cong A_0^* \otimes _{A_0} W$
, as right
$ {\mathrm {RHom}}_A(A_0, A)[d] \cong A_0^* \otimes _{A_0} W$
, as right
![]() $A_0$
-modules, for some invertible graded
$A_0$
-modules, for some invertible graded
![]() $(A_0, A_0)$
-bimodule W. Again we consider the subcategories
$(A_0, A_0)$
-bimodule W. Again we consider the subcategories
![]() $\mathcal {X} \subseteq A_0 {\mathrm {\!-gr}}$
and
$\mathcal {X} \subseteq A_0 {\mathrm {\!-gr}}$
and
![]() $\mathcal {Y} \subseteq {\mathrm {gr-\!}} A_0$
of Lemma 5.1. In this case the hypothesis implies that
$\mathcal {Y} \subseteq {\mathrm {gr-\!}} A_0$
of Lemma 5.1. In this case the hypothesis implies that
![]() $A_0 \in \mathcal {X}$
. Since
$A_0 \in \mathcal {X}$
. Since
![]() $ {\mathrm {gr.gldim}} A = d$
, we have
$ {\mathrm {gr.gldim}} A = d$
, we have
![]() $ {\mathrm {gldim}} A_0 \leq d$
by Lemma 3.23. We claim now that every
$ {\mathrm {gldim}} A_0 \leq d$
by Lemma 3.23. We claim now that every
![]() $M \in A_0 {\mathrm {\!-gr}}$
is in
$M \in A_0 {\mathrm {\!-gr}}$
is in
![]() $\mathcal {X}$
. We prove the claim by induction on projective dimension over
$\mathcal {X}$
. We prove the claim by induction on projective dimension over
![]() $A_0$
. Since every finitely generated graded projective is a direct summand of a finite rank graded free module, and
$A_0$
. Since every finitely generated graded projective is a direct summand of a finite rank graded free module, and
![]() $\mathcal {X}$
is closed under graded shifts, direct sums and direct summands, from
$\mathcal {X}$
is closed under graded shifts, direct sums and direct summands, from
![]() $A_0 \in \mathcal {X}$
we get
$A_0 \in \mathcal {X}$
we get
![]() $P \in \mathcal {X}$
for each graded projective
$P \in \mathcal {X}$
for each graded projective
![]() $P \in A_0 {\mathrm {\!-gr}}$
. If all
$P \in A_0 {\mathrm {\!-gr}}$
. If all
![]() $M \in A_0 {\mathrm {\!-gr}}$
of projective dimension
$M \in A_0 {\mathrm {\!-gr}}$
of projective dimension
![]() $\leq e$
are in
$\leq e$
are in
![]() $\mathcal {X}$
, with
$\mathcal {X}$
, with
![]() $e < {\mathrm {gldim}} A_0$
, suppose that
$e < {\mathrm {gldim}} A_0$
, suppose that
![]() $M' \in A_0 {\mathrm {\!-gr}}$
has
$M' \in A_0 {\mathrm {\!-gr}}$
has
![]() $ {\mathrm {pdim}} M' = e +1$
. Consider the short exact sequence of graded modules
$ {\mathrm {pdim}} M' = e +1$
. Consider the short exact sequence of graded modules
![]() $0 \to K \to P \to M' \to 0$
, where
$0 \to K \to P \to M' \to 0$
, where
![]() $P \to M'$
is a projective cover of
$P \to M'$
is a projective cover of
![]() $M'$
in
$M'$
in
![]() $A_0 {\mathrm {\!-gr}}$
. Then
$A_0 {\mathrm {\!-gr}}$
. Then
![]() $ {\mathrm {pdim}} K \leq e$
and so
$ {\mathrm {pdim}} K \leq e$
and so
![]() $K \in \mathcal {X}$
; since
$K \in \mathcal {X}$
; since
![]() $P \in \mathcal {X}$
also, now the long exact sequence in Ext easily implies that
$P \in \mathcal {X}$
also, now the long exact sequence in Ext easily implies that
![]() $M' \in \mathcal {X}$
, completing the induction step. Thus
$M' \in \mathcal {X}$
, completing the induction step. Thus
![]() $\mathcal {X} = A_0 {\mathrm {\!-gr}}$
as claimed.
$\mathcal {X} = A_0 {\mathrm {\!-gr}}$
as claimed.
Now Lemma 5.1 gives an equivalence of categories
![]() $F: A_0 {\mathrm {\!-gr}} \to \mathcal {Y}$
, where
$F: A_0 {\mathrm {\!-gr}} \to \mathcal {Y}$
, where
![]() $F = {\mathrm {RHom}}_A(-, A)[d]$
. In particular,
$F = {\mathrm {RHom}}_A(-, A)[d]$
. In particular,
![]() $\mathcal {Y}$
must be an Abelian category. For any object
$\mathcal {Y}$
must be an Abelian category. For any object
![]() $N \in \mathcal {Y}$
, since it has finite length as an
$N \in \mathcal {Y}$
, since it has finite length as an
![]() $A_0$
-module, it must have finite length in the category
$A_0$
-module, it must have finite length in the category
![]() $\mathcal {Y}$
, and clearly
$\mathcal {Y}$
, and clearly
 $ {length}_{\mathcal {Y}}(N) \leq {length}_{A_0^{\mathrm {op}}}(N)$
. Now note that setting
$ {length}_{\mathcal {Y}}(N) \leq {length}_{A_0^{\mathrm {op}}}(N)$
. Now note that setting
![]() $N = F(A_0) = A_0^* \otimes _{A_0} W$
, we have
$N = F(A_0) = A_0^* \otimes _{A_0} W$
, we have
 $$ \begin{align*} {length}_{A_0}(A_0) = {length}_{A_0^{\mathrm{op}}}(A_0^*) = {length}_{A_0^{\mathrm{op}}}(N) \geq {length}_{\mathcal{Y}}(N), \end{align*} $$
$$ \begin{align*} {length}_{A_0}(A_0) = {length}_{A_0^{\mathrm{op}}}(A_0^*) = {length}_{A_0^{\mathrm{op}}}(N) \geq {length}_{\mathcal{Y}}(N), \end{align*} $$
using that taking duals preserves length, as does the autoequivalence
![]() $- \otimes _{A_0} W$
. On the other hand, since F is a contravariant equivalence, it also preserves length and so
$- \otimes _{A_0} W$
. On the other hand, since F is a contravariant equivalence, it also preserves length and so
 $ {length}_{A_0}(A_0) = {length}_{\mathcal {Y}}(N)$
. Thus all terms in the displayed equation are equal, and in particular
$ {length}_{A_0}(A_0) = {length}_{\mathcal {Y}}(N)$
. Thus all terms in the displayed equation are equal, and in particular
 $ {length}_{A_0^{\mathrm {op}}}(N) = {length}_{\mathcal {Y}}(N)$
. This means that N has the same composition series over
$ {length}_{A_0^{\mathrm {op}}}(N) = {length}_{\mathcal {Y}}(N)$
. This means that N has the same composition series over
![]() $A_0^{\mathrm {op}}$
as it does in
$A_0^{\mathrm {op}}$
as it does in
![]() $\mathcal {Y}$
, so all of the simple
$\mathcal {Y}$
, so all of the simple
![]() $\mathcal {Y}$
-objects occurring as composition factors of N are also simple over
$\mathcal {Y}$
-objects occurring as composition factors of N are also simple over
![]() $A_0^{\mathrm {op}}$
. Finally, since each of the n simple
$A_0^{\mathrm {op}}$
. Finally, since each of the n simple
![]() $A_0$
-modules up to isomorphism is a composition factor of
$A_0$
-modules up to isomorphism is a composition factor of
![]() $A_0$
, each of the n simple
$A_0$
, each of the n simple
![]() $\mathcal {Y}$
-objects is a composition factor of
$\mathcal {Y}$
-objects is a composition factor of
![]() $F(A_0) = N$
. Thus every simple
$F(A_0) = N$
. Thus every simple
![]() $\mathcal {Y}$
-object is also simple over
$\mathcal {Y}$
-object is also simple over
![]() $A_0^{\mathrm {op}}$
. Since
$A_0^{\mathrm {op}}$
. Since
![]() $A_0^{\mathrm {op}}$
also has n simple objects, we conclude that
$A_0^{\mathrm {op}}$
also has n simple objects, we conclude that
![]() $\mathcal {Y} = {\mathrm {gr-\!}} A_0$
, and (b) follows.
$\mathcal {Y} = {\mathrm {gr-\!}} A_0$
, and (b) follows.
(e
![]() ${}^{\prime}$
)
${}^{\prime}$
)
![]() $\implies $
(e) and (d
$\implies $
(e) and (d
![]() ${}^{\prime}$
)
${}^{\prime}$
)
![]() $\implies $
(d) are obvious.
$\implies $
(d) are obvious.
(e)
![]() $\implies $
(e
$\implies $
(e
![]() ${}^{\prime}$
): We have
${}^{\prime}$
): We have
![]() $ {\mathrm {RHom}}_A(A_0, A) \cong A_0^* \otimes _{A_0} W[-d]$
as right modules, for some invertible
$ {\mathrm {RHom}}_A(A_0, A) \cong A_0^* \otimes _{A_0} W[-d]$
as right modules, for some invertible
![]() $(A_0, A_0)$
-bimodule W. Let
$(A_0, A_0)$
-bimodule W. Let
 $U = {\mathrm {{Ext}}}^d_A(A_0, A)$
, which is an
$U = {\mathrm {{Ext}}}^d_A(A_0, A)$
, which is an
![]() $(A, A)$
-bimodule isomorphic on the right to
$(A, A)$
-bimodule isomorphic on the right to
![]() $A_0^* \otimes _{A_0} W$
. We know that (b) holds since (e)
$A_0^* \otimes _{A_0} W$
. We know that (b) holds since (e)
![]() $\implies $
(b). By the proof of Lemma 5.1, the inverse of the contravariant equivalence
$\implies $
(b). By the proof of Lemma 5.1, the inverse of the contravariant equivalence
![]() $ {\mathrm {RHom}}_A(-, A)[d]: A_0 {\mathrm {\!-gr}} \to {\mathrm {gr-\!}} A_0$
is
$ {\mathrm {RHom}}_A(-, A)[d]: A_0 {\mathrm {\!-gr}} \to {\mathrm {gr-\!}} A_0$
is
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}(-, A)[d]: {\mathrm {gr-\!}} A_0 \to A_0 {\mathrm {\!-gr}}$
. Moreover, taking
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}(-, A)[d]: {\mathrm {gr-\!}} A_0 \to A_0 {\mathrm {\!-gr}}$
. Moreover, taking
![]() $C = A_0$
in Lemma 5.1(4), we obtain
$C = A_0$
in Lemma 5.1(4), we obtain
 $ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(U, A) \cong A_0$
as
$ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(U, A) \cong A_0$
as
![]() $(A_0, A_0)$
-bimodules. Suppose that
$(A_0, A_0)$
-bimodules. Suppose that
![]() $x \in A_0$
satisfies
$x \in A_0$
satisfies
![]() $xU = 0$
. Inspecting the manner in which the induced right action of x on
$xU = 0$
. Inspecting the manner in which the induced right action of x on
 $ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(U, A)$
is obtained in the proof of Lemma 5.1(4), we find that right multiplication by x on
$ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(U, A)$
is obtained in the proof of Lemma 5.1(4), we find that right multiplication by x on
 $ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(U, A) \cong A_0$
is also
$ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(U, A) \cong A_0$
is also
![]() $0$
. It follows that
$0$
. It follows that
![]() $x = 1x = 0$
. So U is a torsionfree left
$x = 1x = 0$
. So U is a torsionfree left
![]() $A_0$
-module.
$A_0$
-module.
Thus U is an
![]() $(A_0, A_0)$
-bimodule that is isomorphic as a right
$(A_0, A_0)$
-bimodule that is isomorphic as a right
![]() $A_0$
-module to
$A_0$
-module to
![]() $A_0^* \otimes _{A_0} W$
, and which is torsionfree on the left. We may view the left
$A_0^* \otimes _{A_0} W$
, and which is torsionfree on the left. We may view the left
![]() $A_0$
-module structure on U as being given by an algebra homomorphism
$A_0$
-module structure on U as being given by an algebra homomorphism
Since W is invertible, clearly
![]() $ {\mathrm {{End}}}_{A^{\mathrm {op}}}(A_0^* \otimes _{A_0} W) \cong {\mathrm {{End}}}_{A^{\mathrm {op}}}(A_0^*)$
. Since
$ {\mathrm {{End}}}_{A^{\mathrm {op}}}(A_0^* \otimes _{A_0} W) \cong {\mathrm {{End}}}_{A^{\mathrm {op}}}(A_0^*)$
. Since
![]() $( - )^*$
is a contravariant equivalence
$( - )^*$
is a contravariant equivalence
![]() $A_0 {\mathrm {\!-gr}} \to {\mathrm {gr-\!}} A_0$
, we have
$A_0 {\mathrm {\!-gr}} \to {\mathrm {gr-\!}} A_0$
, we have
![]() $ {\mathrm {{End}}}_{A^{\mathrm {op}}}(A_0^*) \cong ( {\mathrm {{End}}}_{A_0}(A_0))^{\mathrm {op}} \cong ((A_0)^{\mathrm {op}})^{\mathrm {op}} \cong A_0$
. Thus the left structure of U is given by an algebra homomorphism
$ {\mathrm {{End}}}_{A^{\mathrm {op}}}(A_0^*) \cong ( {\mathrm {{End}}}_{A_0}(A_0))^{\mathrm {op}} \cong ((A_0)^{\mathrm {op}})^{\mathrm {op}} \cong A_0$
. Thus the left structure of U is given by an algebra homomorphism
![]() $\sigma : A_0 \to A_0$
, and the fact that U is torsionfree on the left implies that
$\sigma : A_0 \to A_0$
, and the fact that U is torsionfree on the left implies that
![]() $\ker \sigma = 0$
. Since
$\ker \sigma = 0$
. Since
![]() $A_0$
is a finite-dimensional algebra,
$A_0$
is a finite-dimensional algebra,
![]() $\sigma $
is an isomorphism. We conclude from this that
$\sigma $
is an isomorphism. We conclude from this that
![]() $U \cong {{\hspace {-0.0001pt}}}^{\sigma } (A_0^* \otimes _{A_0} W)$
as
$U \cong {{\hspace {-0.0001pt}}}^{\sigma } (A_0^* \otimes _{A_0} W)$
as
![]() $(A_0, A_0)$
-bimodules. This is the same as
$(A_0, A_0)$
-bimodules. This is the same as
 $^{\sigma }(A_0^*)^1 \otimes _{A_0} W$
. Now it is easy to check that
$^{\sigma }(A_0^*)^1 \otimes _{A_0} W$
. Now it is easy to check that
 $^{\sigma }(A_0^*)^1 \cong {{\hspace {-0.0001pt}}}^1(A_0^*)^{\sigma ^{-1}}$
, so our bimodule is isomorphic to
$^{\sigma }(A_0^*)^1 \cong {{\hspace {-0.0001pt}}}^1(A_0^*)^{\sigma ^{-1}}$
, so our bimodule is isomorphic to
 $A_0^* \otimes _{A_0} {{\hspace {-0.0001pt}}}^{\sigma ^{-1}}(W)^1$
. Letting
$A_0^* \otimes _{A_0} {{\hspace {-0.0001pt}}}^{\sigma ^{-1}}(W)^1$
. Letting
 $W' = {{\hspace {-0.0001pt}}}^{\sigma ^{-1}}(W)^1$
, we have that
$W' = {{\hspace {-0.0001pt}}}^{\sigma ^{-1}}(W)^1$
, we have that
![]() $U \cong A_0^* \otimes _{A_0} W'$
as
$U \cong A_0^* \otimes _{A_0} W'$
as
![]() $(A_0, A_0)$
-bimodules, where
$(A_0, A_0)$
-bimodules, where
![]() $W'$
is graded invertible. Thus (e
$W'$
is graded invertible. Thus (e
![]() ${}^{\prime}$
) holds.
${}^{\prime}$
) holds.
(d)
![]() $\implies $
(d
$\implies $
(d
![]() ${}^{\prime}$
): This is analogous to the proof of (e)
${}^{\prime}$
): This is analogous to the proof of (e)
![]() $\implies $
(e
$\implies $
(e
![]() ${}^{\prime}$
), but a bit easier since
${}^{\prime}$
), but a bit easier since
![]() $S^* \cong S$
; we leave it to the reader.
$S^* \cong S$
; we leave it to the reader.
Definition 5.3. Let A be a locally finite graded k-algebra. If A satisfies the equivalent conditions in Theorem 5.2, we say that A is a generalized AS regular algebra of dimension d, or sometimes just AS regular. If
![]() $A \otimes K$
is a (generalized) AS regular K-algebra of dimension d for all field extensions K of k, we call A geometrically AS regular of dimension d.
$A \otimes K$
is a (generalized) AS regular K-algebra of dimension d for all field extensions K of k, we call A geometrically AS regular of dimension d.
Corollary 5.4. Let A be a locally finite graded k-algebra. Then A is (geometrically) AS regular if and only if
![]() $A^{\mathrm {op}}$
is (geometrically) AS regular. In particular, all of the opposite-sided versions of the properties (a)–(e
$A^{\mathrm {op}}$
is (geometrically) AS regular. In particular, all of the opposite-sided versions of the properties (a)–(e
![]() ${}^{\prime}$
) in Theorem 5.2 are also equivalent characterizations of AS regularity.
${}^{\prime}$
) in Theorem 5.2 are also equivalent characterizations of AS regularity.
Proof. Assume that condition (b) of Theorem 5.2 holds, so
![]() $F = {\mathrm {RHom}}_A(-, A)[d]$
gives a contravariant equivalence from
$F = {\mathrm {RHom}}_A(-, A)[d]$
gives a contravariant equivalence from
![]() $A_0 {\mathrm {\!-gr}}$
to
$A_0 {\mathrm {\!-gr}}$
to
![]() $ {\mathrm {gr-\!}} A_0$
. Thus in Lemma 5.1, we must have
$ {\mathrm {gr-\!}} A_0$
. Thus in Lemma 5.1, we must have
![]() $\mathcal {X} = A_0 {\mathrm {\!-gr}}$
and
$\mathcal {X} = A_0 {\mathrm {\!-gr}}$
and
![]() $\mathcal {Y} = {\mathrm {gr-\!}} A_0$
. From the proof of the lemma, it is clear that the quasi-inverse of F is given by
$\mathcal {Y} = {\mathrm {gr-\!}} A_0$
. From the proof of the lemma, it is clear that the quasi-inverse of F is given by
![]() $G = {\mathrm {RHom}}_{A^{\mathrm {op}}}(-, A)[d]$
, so that G gives a contravariant equivalence from
$G = {\mathrm {RHom}}_{A^{\mathrm {op}}}(-, A)[d]$
, so that G gives a contravariant equivalence from
![]() $ {\mathrm {gr-\!}} A_0 \to A_0 {\mathrm {\!-gr}}$
; that is, condition (2) also holds for
$ {\mathrm {gr-\!}} A_0 \to A_0 {\mathrm {\!-gr}}$
; that is, condition (2) also holds for
![]() $A^{\mathrm {op}}$
. This shows that if A is generalized AS regular, then so is
$A^{\mathrm {op}}$
. This shows that if A is generalized AS regular, then so is
![]() $A^{\mathrm {op}}$
, and the converse is immediate. Then for every field extension
$A^{\mathrm {op}}$
, and the converse is immediate. Then for every field extension
![]() $k \subseteq K$
,
$k \subseteq K$
,
![]() $A \otimes _k K$
is generalized AS regular if and only if
$A \otimes _k K$
is generalized AS regular if and only if
![]() $(A \otimes _k K)^{\mathrm {op}} \cong A^{\mathrm {op}} \otimes _k K$
is. Thus A is geometrically AS regular if and only if
$(A \otimes _k K)^{\mathrm {op}} \cong A^{\mathrm {op}} \otimes _k K$
is. Thus A is geometrically AS regular if and only if
![]() $A^{\mathrm {op}}$
is geometrically AS regular.
$A^{\mathrm {op}}$
is geometrically AS regular.
Remark 5.5. If a locally finite graded algebra A is generalized AS regular, then it is finitely generated as a k-algebra. Indeed, as discussed in the proof of Theorem 5.2, the semisimple left A-module
![]() $S = A/J(A)$
is perfect. It follows from Lemma 2.3 that A is a finitely generated algebra.
$S = A/J(A)$
is perfect. It follows from Lemma 2.3 that A is a finitely generated algebra.
There are a few other existing generalized notions of AS regular algebras in the literature, which we now compare to Definition 5.3.
Remark 5.6. A notion of “generalized AS regular algebra” is given by Minamoto and Mori in [Reference Minamoto and Mori33, Definition 3.15] as follows: a locally finite graded algebra A is generalized AS regular of dimension d if
![]() $ {\mathrm {gldim}} A = d$
, for any simple graded left A-module M we have
$ {\mathrm {gldim}} A = d$
, for any simple graded left A-module M we have
 $ {\mathrm {{Ext}}}^i_A(M, A) =0$
for
$ {\mathrm {{Ext}}}^i_A(M, A) =0$
for
![]() $i \neq d$
, and the functors
$i \neq d$
, and the functors
 $ {\mathrm {{Ext}}}^d_A(-, A)$
and
$ {\mathrm {{Ext}}}^d_A(-, A)$
and
 $ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(-, A)$
give inverse bijections between the set of simple graded left A-modules and simple graded right A-modules. This property originated in work of Martinez-Villa for graded quotient algebras of path algebras in [Reference Martínez-Villa30] (see also his work with Solberg [Reference Martinéz-Villa and Solberg31]). Using Lemma 5.1(1), it is easy to see that this definition is equivalent to condition (a) of Theorem 5.2, except that we assume the potentially weaker condition
$ {\mathrm {{Ext}}}^d_{A^{\mathrm {op}}}(-, A)$
give inverse bijections between the set of simple graded left A-modules and simple graded right A-modules. This property originated in work of Martinez-Villa for graded quotient algebras of path algebras in [Reference Martínez-Villa30] (see also his work with Solberg [Reference Martinéz-Villa and Solberg31]). Using Lemma 5.1(1), it is easy to see that this definition is equivalent to condition (a) of Theorem 5.2, except that we assume the potentially weaker condition
![]() $ {\mathrm {gr.gldim}} A = d$
rather than
$ {\mathrm {gr.gldim}} A = d$
rather than
![]() $ {\mathrm {gldim}} A = d$
. There may in fact be no examples where these numbers are different, and as we saw in Proposition 3.18(3), they are the same if
$ {\mathrm {gldim}} A = d$
. There may in fact be no examples where these numbers are different, and as we saw in Proposition 3.18(3), they are the same if
![]() $S = A/J$
is separable. We prefer to assume the weaker condition. Morally, this shows that our definition of generalized AS regular and the one in [Reference Minamoto and Mori33, Definition 3.15] are essentially the same.
$S = A/J$
is separable. We prefer to assume the weaker condition. Morally, this shows that our definition of generalized AS regular and the one in [Reference Minamoto and Mori33, Definition 3.15] are essentially the same.
Remark 5.7. In [Reference Minamoto and Mori33], Minamoto and Mori also define a locally finite graded algebra A to be “AS regular over
![]() $A_0$
” if
$A_0$
” if
![]() $ {\mathrm {gldim}} A = d$
,
$ {\mathrm {gldim}} A = d$
,
![]() $ {\mathrm {gldim}} A_0 < \infty $
, and one has
$ {\mathrm {gldim}} A_0 < \infty $
, and one has
![]() $ {\mathrm {RHom}}_{A_0}(A_0, A)[d] \cong {{\hspace {-0.0001pt}}}^{\mu } (A_0^*)(\ell )$
as complexes of
$ {\mathrm {RHom}}_{A_0}(A_0, A)[d] \cong {{\hspace {-0.0001pt}}}^{\mu } (A_0^*)(\ell )$
as complexes of
![]() $(A, A)$
-bimodules, for some
$(A, A)$
-bimodules, for some
![]() $\ell \in \mathbb {Z}$
and automorphism
$\ell \in \mathbb {Z}$
and automorphism
![]() $\mu $
of A. See [Reference Minamoto and Mori33, Definition 3.1] and the comments following the definition. Note that Lemma 3.23 shows that the hypothesis
$\mu $
of A. See [Reference Minamoto and Mori33, Definition 3.1] and the comments following the definition. Note that Lemma 3.23 shows that the hypothesis
![]() $ {\mathrm {gldim}} A_0 < \infty $
is a consequence of
$ {\mathrm {gldim}} A_0 < \infty $
is a consequence of
![]() $ {\mathrm {gr.gldim}} A < \infty $
. Thus for A to be AS regular over
$ {\mathrm {gr.gldim}} A < \infty $
. Thus for A to be AS regular over
![]() $A_0$
of dimension d in the sense of Minamoto and Mori is equivalent to A being generalized AS regular in our sense, together with the potentially stronger condition
$A_0$
of dimension d in the sense of Minamoto and Mori is equivalent to A being generalized AS regular in our sense, together with the potentially stronger condition
![]() $ {\mathrm {gldim}} A = d$
(rather than our assumption
$ {\mathrm {gldim}} A = d$
(rather than our assumption
![]() $ {\mathrm {gr.gldim}} A = d$
) and the condition that the invertible bimodule in Theorem 5.2(e
$ {\mathrm {gr.gldim}} A = d$
) and the condition that the invertible bimodule in Theorem 5.2(e
![]() ${}^{\prime}$
) is of the particular form
${}^{\prime}$
) is of the particular form
![]() $W = {{\hspace {-0.0001pt}}}^{\mu } A_0(\ell )$
. As we discussed in the previous remark, the difference between assuming
$W = {{\hspace {-0.0001pt}}}^{\mu } A_0(\ell )$
. As we discussed in the previous remark, the difference between assuming
![]() $ {\mathrm {gldim}} A = d$
or
$ {\mathrm {gldim}} A = d$
or
![]() $ {\mathrm {gr.gldim}} A = d$
is minor and in most cases of interest irrelevant. However, it is a further restriction to assume that W has the particular form
$ {\mathrm {gr.gldim}} A = d$
is minor and in most cases of interest irrelevant. However, it is a further restriction to assume that W has the particular form
![]() ${{\hspace {-0.0001pt}}}^{\mu } A_0(\ell )$
. In Example 7.2 below, we provide an instance where the bimodule W that actually occurs for an algebra satisfying Theorem 5.2(e
${{\hspace {-0.0001pt}}}^{\mu } A_0(\ell )$
. In Example 7.2 below, we provide an instance where the bimodule W that actually occurs for an algebra satisfying Theorem 5.2(e
![]() ${}^{\prime}$
) is not of this form. Thus our notion of generalized AS regular is less restrictive than AS regularity over
${}^{\prime}$
) is not of this form. Thus our notion of generalized AS regular is less restrictive than AS regularity over
![]() $A_0$
.
$A_0$
.
Condition (b) of Theorem 5.2 was also shown by Minamoto-Mori to be a consequence of their definition of AS regularity over
![]() $A_0$
in [Reference Minamoto and Mori33, Proposition 3.5]; our theorem gives another proof of this. We also note that there is a notion of ASF-regular algebra in [Reference Minamoto and Mori33], defined in terms of graded local cohomology, which Ueyama recently showed [Reference Ueyama46, Corollary 2.11] to be equivalent for noetherian algebras A to the condition of being AS regular over
$A_0$
in [Reference Minamoto and Mori33, Proposition 3.5]; our theorem gives another proof of this. We also note that there is a notion of ASF-regular algebra in [Reference Minamoto and Mori33], defined in terms of graded local cohomology, which Ueyama recently showed [Reference Ueyama46, Corollary 2.11] to be equivalent for noetherian algebras A to the condition of being AS regular over
![]() $A_0$
. It seems possible that a suitable “invertible bimodule twist” of this property could be equivalent to the generalized AS regular property, at least for noetherian algebras, but we do not pursue that possibility here.
$A_0$
. It seems possible that a suitable “invertible bimodule twist” of this property could be equivalent to the generalized AS regular property, at least for noetherian algebras, but we do not pursue that possibility here.
We have introduced conditions (c), (d), and (d
![]() ${}^{\prime}$
) of Theorem 5.2 because we have found that certain formalisms are easier to handle over the semisimple algebra
${}^{\prime}$
) of Theorem 5.2 because we have found that certain formalisms are easier to handle over the semisimple algebra
![]() $S = A/J$
rather than over
$S = A/J$
rather than over
![]() $A_0$
as in (b), (e), (e
$A_0$
as in (b), (e), (e
![]() ${}^{\prime}$
). Thus it is useful to know that the analogous conditions defined relative to S still produce equivalent notions. For this reason we also took condition (d
${}^{\prime}$
). Thus it is useful to know that the analogous conditions defined relative to S still produce equivalent notions. For this reason we also took condition (d
![]() ${}^{\prime}$
) as the “official” definition of generalized AS regular in the introduction.
${}^{\prime}$
) as the “official” definition of generalized AS regular in the introduction.
Remark 5.8. The generalized AS regular property is preserved by k-linear graded Morita equivalence [Reference Sierra44, Section 1]. The proof of this fact is similar to that of Proposition 4.11; for instance, one can show that either condition (b) or (c) from Theorem 5.2 is preserved under a graded k-linear equivalence between graded module categories. However, we do not include the proof here. On the other hand, Example 7.2 below illustrates that the property of AS regularity over
![]() $A_0$
is not preserved under such an equivalence.
$A_0$
is not preserved under such an equivalence.
5.2 Characterizing twisted Calabi–Yau algebras
The major goal of this section is to relate the generalized AS regular property to the twisted Calabi–Yau property for locally finite graded algebras. This will be achieved in Theorem 5.15 below, where we show that the twisted Calabi–Yau property is equivalent to the geometrically AS regular property.
We require several technical lemmas in preparation for that theorem.
Lemma 5.9. Let A be a homologically smooth (graded) algebra, and let X be a finite-dimensional
![]() $(A, A)$
-bimodule.
$(A, A)$
-bimodule.
-
(1)
 $ {\mathrm {RHom}}_{A^e}(A, A^e) \otimes ^L_A X \cong {\mathrm {RHom}}_{A^{\mathrm {op}}}(X^*, A)$
as complexes of (graded)
$ {\mathrm {RHom}}_{A^e}(A, A^e) \otimes ^L_A X \cong {\mathrm {RHom}}_{A^{\mathrm {op}}}(X^*, A)$
as complexes of (graded)
 $(A, A)$
-bimodules.
$(A, A)$
-bimodules. -
(2)
 $X \otimes ^L_A {\mathrm {RHom}}_{A^e}(A, A^e) \cong {\mathrm {RHom}}_A(X^*, A)$
as complexes of (graded)
$X \otimes ^L_A {\mathrm {RHom}}_{A^e}(A, A^e) \cong {\mathrm {RHom}}_A(X^*, A)$
as complexes of (graded)
 $(A, A)$
-bimodules.
$(A, A)$
-bimodules.
Proof. We prove part (1), the proof of part (2) being symmetric. Consider the bimodule
![]() $A \otimes A$
as a left
$A \otimes A$
as a left
![]() $A^e$
-module via the “outer” structure
$A^e$
-module via the “outer” structure
![]() $(c \otimes d^{\mathrm {op}})(a_1 \otimes a_2) = ca_1 \otimes a_2 d$
and as a right
$(c \otimes d^{\mathrm {op}})(a_1 \otimes a_2) = ca_1 \otimes a_2 d$
and as a right
![]() $A^e$
-module via the “inner” structure
$A^e$
-module via the “inner” structure
![]() $(a_1 \otimes a_2)(c \otimes d^{\mathrm {op}}) = a_1 c \otimes d a_2$
. In this way, we have an isomorphism
$(a_1 \otimes a_2)(c \otimes d^{\mathrm {op}}) = a_1 c \otimes d a_2$
. In this way, we have an isomorphism
![]() $A \otimes A \cong A^e$
of
$A \otimes A \cong A^e$
of
![]() $(A^e,A^e)$
-bimodules. Restricting scalars along the natural homomorphism
$(A^e,A^e)$
-bimodules. Restricting scalars along the natural homomorphism
![]() $ {\mathrm {{id}}}_A \otimes 1 \colon A \to A \otimes A^{\mathrm {op}} = A^e$
, this makes the right
$ {\mathrm {{id}}}_A \otimes 1 \colon A \to A \otimes A^{\mathrm {op}} = A^e$
, this makes the right
![]() $A^e$
-module
$A^e$
-module
![]() $A \otimes A$
into a right A-module under the action
$A \otimes A$
into a right A-module under the action
![]() $(a_1 \otimes a_2) \cdot c = a_1 c \otimes a_2$
. Then we have the quasi-isomorphism
$(a_1 \otimes a_2) \cdot c = a_1 c \otimes a_2$
. Then we have the quasi-isomorphism
 $$ \begin{align} A^e \otimes^L_A X \cong (A \otimes A) \otimes^L_A X = (A \otimes^L_A X) \otimes A \cong X \otimes A \end{align} $$
$$ \begin{align} A^e \otimes^L_A X \cong (A \otimes A) \otimes^L_A X = (A \otimes^L_A X) \otimes A \cong X \otimes A \end{align} $$
as complexes of
![]() $(A^e, A^e)$
-bimodules.
$(A^e, A^e)$
-bimodules.
Next, we consider the
![]() $(A^e,A^e)$
-bimodule
$(A^e,A^e)$
-bimodule
![]() $X^* \otimes A$
with similar “outer” left
$X^* \otimes A$
with similar “outer” left
![]() $A^e$
-action and “inner” right
$A^e$
-action and “inner” right
![]() $A^e$
-action. We have the following quasi-isomorphisms of
$A^e$
-action. We have the following quasi-isomorphisms of
![]() $(A^e, A^e)$
-bimodules, where the first is an adjoint isomorphism:
$(A^e, A^e)$
-bimodules, where the first is an adjoint isomorphism:
 $$ \begin{align} {\mathrm{RHom}}_{A^{\mathrm{op}}}(X^* \otimes A, A) &\cong {\mathrm{RHom}}_k( X^*, {\mathrm{RHom}}_{A^{\mathrm{op}}}(A, A)) \nonumber \\ &\cong {\mathrm{RHom}}_k( X^*, A) \\ &\cong X^{**} \otimes A \cong X \otimes A. \nonumber \end{align} $$
$$ \begin{align} {\mathrm{RHom}}_{A^{\mathrm{op}}}(X^* \otimes A, A) &\cong {\mathrm{RHom}}_k( X^*, {\mathrm{RHom}}_{A^{\mathrm{op}}}(A, A)) \nonumber \\ &\cong {\mathrm{RHom}}_k( X^*, A) \\ &\cong X^{**} \otimes A \cong X \otimes A. \nonumber \end{align} $$
From Lemma 2.13(1) we further obtain quasi-isomorphisms
 $$ \begin{align} (X^* \otimes A) \otimes^L_{A^e} A \cong X^* \otimes^L_A A \otimes^L_A A \cong X^* \end{align} $$
$$ \begin{align} (X^* \otimes A) \otimes^L_{A^e} A \cong X^* \otimes^L_A A \otimes^L_A A \cong X^* \end{align} $$
as complexes of
![]() $(A, A)$
-bimodules.
$(A, A)$
-bimodules.
Finally, since A is homologically smooth, it is a perfect object in the derived category of graded left
![]() $A^e$
-modules. Thus using Lemma 2.12(2) along with the preceding observations, we have isomorphisms of
$A^e$
-modules. Thus using Lemma 2.12(2) along with the preceding observations, we have isomorphisms of
![]() $(A, A)$
-bimodules as follows:
$(A, A)$
-bimodules as follows:
 $$ \begin{align*} {\mathrm{RHom}}_{A^e}(A, A^e) \otimes^L_A X &\cong {\mathrm{RHom}}_{A^e}(A, A^e \otimes^L_A X) & \text{by Lemma 2.12(2)} \\ & \cong {\mathrm{RHom}}_{A^e}(A, X \otimes A) & \text{by (5.10)} \\ &\cong {\mathrm{RHom}}_{A^e}(A, {\mathrm{RHom}}_{A^{\mathrm{op}}}(X^* \otimes A, A)) & \text{by (5.11)} \\ &\cong {\mathrm{RHom}}_{A^{\mathrm{op}}}((X^* \otimes A) \otimes^L_{A^e} A, A) & \text{by adjointness} \\ &\cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(X^*, A). & \text{by (5.12)} \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{A^e}(A, A^e) \otimes^L_A X &\cong {\mathrm{RHom}}_{A^e}(A, A^e \otimes^L_A X) & \text{by Lemma 2.12(2)} \\ & \cong {\mathrm{RHom}}_{A^e}(A, X \otimes A) & \text{by (5.10)} \\ &\cong {\mathrm{RHom}}_{A^e}(A, {\mathrm{RHom}}_{A^{\mathrm{op}}}(X^* \otimes A, A)) & \text{by (5.11)} \\ &\cong {\mathrm{RHom}}_{A^{\mathrm{op}}}((X^* \otimes A) \otimes^L_{A^e} A, A) & \text{by adjointness} \\ &\cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(X^*, A). & \text{by (5.12)} \end{align*} $$
Note that in the first line, Lemma 2.12(2) as stated only gives an isomorphism of right A-modules. The left A-module structure comes from the right
![]() $A^{\mathrm {op}}$
structure of
$A^{\mathrm {op}}$
structure of
![]() $A^e$
, and it is easy to see that it is also preserved by the given isomorphism.
$A^e$
, and it is easy to see that it is also preserved by the given isomorphism.
In the graded case, since A is perfect as an
![]() $A^e$
-module and
$A^e$
-module and
![]() $X^*$
is perfect as a right or left A-module by Lemma 3.2, there is no difference between
$X^*$
is perfect as a right or left A-module by Lemma 3.2, there is no difference between
![]() $ {\mathrm {RHom}}$
and
$ {\mathrm {RHom}}$
and
![]() ${\mathrm{R}}\underline { {\mathrm {{Hom}}}}$
in the statement, and it is routine to see that all of the canonical isomorphisms used above preserve grading.
${\mathrm{R}}\underline { {\mathrm {{Hom}}}}$
in the statement, and it is routine to see that all of the canonical isomorphisms used above preserve grading.
Lemma 5.13. Let A be a graded algebra with
![]() $A_0$
finite-dimensional, and denote
$A_0$
finite-dimensional, and denote
![]() $J = J(A)$
and
$J = J(A)$
and
![]() $S = A/J$
. Let U be a graded k-central
$S = A/J$
. Let U be a graded k-central
![]() $(A,A)$
-bimodule such that both
$(A,A)$
-bimodule such that both
![]() ${{\hspace {-0.0001pt}}}_A U$
and
${{\hspace {-0.0001pt}}}_A U$
and
![]() $U_A$
are projective. Suppose that
$U_A$
are projective. Suppose that
![]() $(S \otimes _A U)J = 0$
and
$(S \otimes _A U)J = 0$
and
![]() $J(U \otimes _A S) = 0$
. If
$J(U \otimes _A S) = 0$
. If
![]() $V = U \otimes _A S$
is an invertible
$V = U \otimes _A S$
is an invertible
![]() $(S, S)$
-bimodule, then U is an invertible
$(S, S)$
-bimodule, then U is an invertible
![]() $(A,A)$
-bimodule.
$(A,A)$
-bimodule.
Proof. As in the proof of Lemma 2.11(1), from the hypothesis that
![]() $(S \otimes _A U)J = 0 = J(U \otimes _A S)$
we may deduce that
$(S \otimes _A U)J = 0 = J(U \otimes _A S)$
we may deduce that
![]() $UJ = JU$
and that
$UJ = JU$
and that
![]() $S \otimes _A U \cong U \otimes _A S = V$
as
$S \otimes _A U \cong U \otimes _A S = V$
as
![]() $(A, A)$
-bimodules. Since V is invertible, it is a finitely generated module over S; thus U is a finitely generated A-module by Nakayama’s lemma.
$(A, A)$
-bimodules. Since V is invertible, it is a finitely generated module over S; thus U is a finitely generated A-module by Nakayama’s lemma.
Note that, as complexes of
![]() $(A, A)$
-bimodules, we have
$(A, A)$
-bimodules, we have
 $$ \begin{align*} S \otimes_A^L {\mathrm{RHom}}_{A^{\mathrm{op}}}(U, U) &\cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(U,S \otimes^L_A U ) \\ &\cong {\mathrm{{Hom}}}_{A^{\mathrm{op}}}(U, S \otimes_A U) \\ &\cong {\mathrm{{Hom}}}_{A^{\mathrm{op}}}(S \otimes_A U, S \otimes_A U), \end{align*} $$
$$ \begin{align*} S \otimes_A^L {\mathrm{RHom}}_{A^{\mathrm{op}}}(U, U) &\cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(U,S \otimes^L_A U ) \\ &\cong {\mathrm{{Hom}}}_{A^{\mathrm{op}}}(U, S \otimes_A U) \\ &\cong {\mathrm{{Hom}}}_{A^{\mathrm{op}}}(S \otimes_A U, S \otimes_A U), \end{align*} $$
where the first isomorphism follows from Lemma 2.12 (applied to the opposite side) since
![]() $U_A$
is (finitely generated projective and hence) perfect, the second isomorphism follows from projectivity of
$U_A$
is (finitely generated projective and hence) perfect, the second isomorphism follows from projectivity of
![]() $U_A$
, and the last isomorphism holds since
$U_A$
, and the last isomorphism holds since
![]() $JU$
is in the kernel of any homomorphism
$JU$
is in the kernel of any homomorphism
![]() $U \to S \otimes _A U \cong U/JU$
. Taking
$U \to S \otimes _A U \cong U/JU$
. Taking
![]() $0$
th cohomology we obtain an isomorphism
$0$
th cohomology we obtain an isomorphism
which is given by the natural map.
Now that we know
![]() $S \otimes _A {\mathrm {{End}}}_{A^{\mathrm {op}}}(U) \cong {\mathrm {{End}}}_{S^{\mathrm {op}}}(V)$
in the natural way, we obtain a commutative diagram
$S \otimes _A {\mathrm {{End}}}_{A^{\mathrm {op}}}(U) \cong {\mathrm {{End}}}_{S^{\mathrm {op}}}(V)$
in the natural way, we obtain a commutative diagram

where
![]() $\phi (a)$
is left multiplication by a, the bottom row is formed from applying
$\phi (a)$
is left multiplication by a, the bottom row is formed from applying
![]() $S \otimes _A -$
to the top row and using the isomorphism above, and the vertical arrows are the natural quotient maps.
$S \otimes _A -$
to the top row and using the isomorphism above, and the vertical arrows are the natural quotient maps.
We claim that the projective right module
![]() $U_A$
is a generator, or equivalently, that each indecomposable graded projective of A occurs as a summand of
$U_A$
is a generator, or equivalently, that each indecomposable graded projective of A occurs as a summand of
![]() $U_A$
. Recall that the indecomposable projective graded right A-modules are the modules
$U_A$
. Recall that the indecomposable projective graded right A-modules are the modules
![]() $e_i A$
, where
$e_i A$
, where
![]() $1 = e_1 + \dots + e_n$
is a decomposition of
$1 = e_1 + \dots + e_n$
is a decomposition of
![]() $1$
as a sum of primitive orthogonal idempotents in
$1$
as a sum of primitive orthogonal idempotents in
![]() $A_0$
. Each lies over a simple S-module
$A_0$
. Each lies over a simple S-module
![]() $e_i S = e_i A \otimes _A S$
, and
$e_i S = e_i A \otimes _A S$
, and
![]() $e_i A \cong e_j A$
if and only if
$e_i A \cong e_j A$
if and only if
![]() $e_i S \cong e_j S$
. Since
$e_i S \cong e_j S$
. Since
![]() $U \otimes _A S = V$
is a generator over S, each of the distinct simple right modules up to isomorphism occurs as a summand. Thus each of the distinct indecomposable graded projective right A-modules occurs as a summand of U. So U is a progenerator on the right. Since
$U \otimes _A S = V$
is a generator over S, each of the distinct simple right modules up to isomorphism occurs as a summand. Thus each of the distinct indecomposable graded projective right A-modules occurs as a summand of U. So U is a progenerator on the right. Since
![]() $V = S \otimes _A U$
as well, by symmetry, U must also be a progenerator on the left.
$V = S \otimes _A U$
as well, by symmetry, U must also be a progenerator on the left.
Now by standard Morita theory, to see that U is invertible it suffices to show that the map
![]() $\phi $
in the diagram above is an isomorphism. Since U is a left progenerator,
$\phi $
in the diagram above is an isomorphism. Since U is a left progenerator,
![]() $_A U$
is torsionfree and so the map
$_A U$
is torsionfree and so the map
![]() $\phi $
is injective. The map
$\phi $
is injective. The map
![]() $\overline {\phi }$
is an isomorphism since V is an invertible
$\overline {\phi }$
is an isomorphism since V is an invertible
![]() $(S, S)$
-bimodule; in particular,
$(S, S)$
-bimodule; in particular,
![]() $\overline {\phi }$
is surjective. Then
$\overline {\phi }$
is surjective. Then
![]() $\phi $
is surjective by Nakayama’s lemma. Hence
$\phi $
is surjective by Nakayama’s lemma. Hence
![]() $\phi $
is an isomorphism as required.
$\phi $
is an isomorphism as required.
We need the following fact concerning minimal complexes of projectives. Similar results are well-known for complexes over certain kinds of rings but we are unaware of a reference that works in the generality we need here. If
![]() $P^{\bullet }$
is a complex of graded projective left modules over a locally finite graded algebra A with graded Jacobson radical
$P^{\bullet }$
is a complex of graded projective left modules over a locally finite graded algebra A with graded Jacobson radical
![]() $J = J(A)$
, we say P is minimal if
$J = J(A)$
, we say P is minimal if
![]() $ {\mathrm {im}} d_n \subseteq J P^{n-1}$
for all n. This is equivalent to the complex
$ {\mathrm {im}} d_n \subseteq J P^{n-1}$
for all n. This is equivalent to the complex
![]() $S \otimes _A P^{\bullet }$
having all of its differentials equal to
$S \otimes _A P^{\bullet }$
having all of its differentials equal to
![]() $0$
, where
$0$
, where
![]() $S= A/J$
. Note that if
$S= A/J$
. Note that if
![]() $P^{\bullet } \to M$
is a graded projective resolution of the module M, then it is a minimal graded projective resolution if and only if
$P^{\bullet } \to M$
is a graded projective resolution of the module M, then it is a minimal graded projective resolution if and only if
![]() $P^{\bullet }$
is a minimal complex.
$P^{\bullet }$
is a minimal complex.
Lemma 5.14. Let A be a locally finite graded algebra, with graded Jacobson radical
![]() $J = J(A)$
. Let
$J = J(A)$
. Let
![]() $S= A/J$
and assume that S is separable. Let
$S= A/J$
and assume that S is separable. Let
![]() $P^\bullet $
be a bounded complex of graded projective left A-modules, where each
$P^\bullet $
be a bounded complex of graded projective left A-modules, where each
![]() $P^i$
is left bounded and locally finite, but not necessarily finitely generated as an A-module. Then
$P^i$
is left bounded and locally finite, but not necessarily finitely generated as an A-module. Then
![]() $P^{\bullet }$
is quasi-isomorphic to a bounded minimal complex of projectives
$P^{\bullet }$
is quasi-isomorphic to a bounded minimal complex of projectives
![]() $Q^{\bullet }$
.
$Q^{\bullet }$
.
This result is well known in the connected graded case. We omit the proof, but the reader is referred to [Reference Yekutieli50, Proposition 13.2.6] for a proof of a dual version regarding minimal injective complexes.
We are now ready to relate the twisted Calabi–Yau condition to the generalized AS regular condition for locally finite graded algebras. Our arguments follow the precedent set in [Reference Yekutieli and Zhang51] and [Reference Reyes, Rogalski and Zhang37, Lemma 1.2].
Theorem 5.15. Let A be a locally finite graded k-algebra and set
![]() $S = A/J(A)$
. Then the following are equivalent:
$S = A/J(A)$
. Then the following are equivalent:
-
(a) A is graded twisted Calabi–Yau of dimension d;
-
(b) A is generalized AS regular of dimension d and S is a separable k-algebra;
-
(c) A is geometrically AS regular of dimension d.
Such an algebra has left and right global and graded global dimensions equal to d, and is a finitely generated k-algebra.
Proof. (a)
![]() $\implies $
(c): If A is graded twisted Calabi–Yau of dimension d, then any base field extension
$\implies $
(c): If A is graded twisted Calabi–Yau of dimension d, then any base field extension
![]() $A \otimes K$
is twisted Calabi–Yau over K by Proposition 4.7. Thus to establish (c), it suffices to assume that A is a locally finite twisted Calabi–Yau algebra A of dimension d and to show that A is generalized AS regular of dimension d. Let
$A \otimes K$
is twisted Calabi–Yau over K by Proposition 4.7. Thus to establish (c), it suffices to assume that A is a locally finite twisted Calabi–Yau algebra A of dimension d and to show that A is generalized AS regular of dimension d. Let
 $U = {\mathrm {{Ext}}}^d_{A^e}(A, A^e)$
, which is an invertible
$U = {\mathrm {{Ext}}}^d_{A^e}(A, A^e)$
, which is an invertible
![]() $(A, A)$
-bimodule by assumption. Recall from Lemma 4.16 that
$(A, A)$
-bimodule by assumption. Recall from Lemma 4.16 that
![]() $S \cong S^*$
. Using Proposition 4.12, we compute
$S \cong S^*$
. Using Proposition 4.12, we compute
 $$ \begin{align*} {\mathrm{{Ext}}}^i_A(S,A) \cong {\mathrm{Tor}}_{d-i}^A(S^* \otimes_A U, A) \cong {\mathrm{Tor}}_{d-i}(S \otimes_A U, A). \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^i_A(S,A) \cong {\mathrm{Tor}}_{d-i}^A(S^* \otimes_A U, A) \cong {\mathrm{Tor}}_{d-i}(S \otimes_A U, A). \end{align*} $$
This is equal to zero for
![]() $i \neq d$
because A is flat, while for
$i \neq d$
because A is flat, while for
![]() $i = d$
we have the isomorphism of graded
$i = d$
we have the isomorphism of graded
![]() $(A,A)$
-bimodules
$(A,A)$
-bimodules
 $$ \begin{align*} {\mathrm{{Ext}}}^d_A(S,A) \cong {\mathrm{Tor}}_{0}^A(S \otimes_A U, A) = S \otimes_A U. \end{align*} $$
$$ \begin{align*} {\mathrm{{Ext}}}^d_A(S,A) \cong {\mathrm{Tor}}_{0}^A(S \otimes_A U, A) = S \otimes_A U. \end{align*} $$
By Lemma 4.3, we obtain
![]() $ {\mathrm {RHom}}_A(S, A) \cong S \otimes _A U[-d]$
as complexes of graded
$ {\mathrm {RHom}}_A(S, A) \cong S \otimes _A U[-d]$
as complexes of graded
![]() $(A,A)$
-bimodules. By Lemma 2.11(2),
$(A,A)$
-bimodules. By Lemma 2.11(2),
![]() $W = S \otimes _A U$
is a graded-invertible
$W = S \otimes _A U$
is a graded-invertible
![]() $(S,S)$
-bimodule. Thus A satisfies condition (d
$(S,S)$
-bimodule. Thus A satisfies condition (d
![]() ${}^{\prime}$
) of Theorem 5.2, so A is generalized AS regular of dimension d.
${}^{\prime}$
) of Theorem 5.2, so A is generalized AS regular of dimension d.
(c)
![]() $\implies $
(b): If A is a geometrically AS regular k-algebra, then clearly it is generalized AS regular. For any field extension
$\implies $
(b): If A is a geometrically AS regular k-algebra, then clearly it is generalized AS regular. For any field extension
![]() $K/k$
, because the AS regular algebra
$K/k$
, because the AS regular algebra
![]() $A^K = A \otimes K$
has graded global dimension d, it follows from Lemma 3.23 that the finite-dimensional K-algebra
$A^K = A \otimes K$
has graded global dimension d, it follows from Lemma 3.23 that the finite-dimensional K-algebra
 $(A^K)_0 = (A_0)^K$
has finite global dimension (at most d). Lemma 3.4 implies that
$(A^K)_0 = (A_0)^K$
has finite global dimension (at most d). Lemma 3.4 implies that
![]() $A_0$
is homologically smooth over k, so that Rickard’s Theorem 3.6 implies that
$A_0$
is homologically smooth over k, so that Rickard’s Theorem 3.6 implies that
![]() $A_0/J(A_0) = A/J(A) = S$
is separable.
$A_0/J(A_0) = A/J(A) = S$
is separable.
(b)
![]() $\implies $
(a): Let A be generalized AS regular of dimension d, and assume that S is separable over k. By condition (d
$\implies $
(a): Let A be generalized AS regular of dimension d, and assume that S is separable over k. By condition (d
![]() ${}^{\prime}$
) of Theorem 5.2, there is an invertible
${}^{\prime}$
) of Theorem 5.2, there is an invertible
![]() $(S, S)$
-bimodule V such that
$(S, S)$
-bimodule V such that
![]() $ {\mathrm {RHom}}_A(S, A) \cong V[-d]$
as complexes of
$ {\mathrm {RHom}}_A(S, A) \cong V[-d]$
as complexes of
![]() $(S, S)$
-bimodules. This implies that S is perfect as a left A-module by Lemma 4.3. Then by Theorem 3.10, A is graded homologically smooth. Similarly, since we know that the opposite-sided version of condition (d
$(S, S)$
-bimodules. This implies that S is perfect as a left A-module by Lemma 4.3. Then by Theorem 3.10, A is graded homologically smooth. Similarly, since we know that the opposite-sided version of condition (d
![]() ${}^{\prime}$
) of Theorem 5.2 also holds by Corollary 5.4, we also have
${}^{\prime}$
) of Theorem 5.2 also holds by Corollary 5.4, we also have
![]() $ {\mathrm {RHom}}_{A^{\mathrm {op}}}(S, A) \cong W[-d]$
as complexes of
$ {\mathrm {RHom}}_{A^{\mathrm {op}}}(S, A) \cong W[-d]$
as complexes of
![]() $(S, S)$
-bimodules, for some invertible
$(S, S)$
-bimodules, for some invertible
![]() $(S, S)$
-bimodule W.
$(S, S)$
-bimodule W.
Now applying Lemma 5.9(1) with
![]() $X = S$
, recalling that
$X = S$
, recalling that
![]() $S \cong S^*$
by Lemma 4.16, we obtain quasi-isomorphisms
$S \cong S^*$
by Lemma 4.16, we obtain quasi-isomorphisms
 $$ \begin{align*} {\mathrm{RHom}}_{A^e}(A, A^e) \otimes_A^L S \cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(S^*, A) \cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(S, A) \cong W[-d] \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{A^e}(A, A^e) \otimes_A^L S \cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(S^*, A) \cong {\mathrm{RHom}}_{A^{\mathrm{op}}}(S, A) \cong W[-d] \end{align*} $$
as complexes of graded
![]() $(A, A)$
-bimodules. Similarly, applying Lemma 5.9(2) with
$(A, A)$
-bimodules. Similarly, applying Lemma 5.9(2) with
![]() $X = S$
yields
$X = S$
yields
 $S \otimes _A^L {\mathrm {RHom}}_{A^e}(A, A^e) \cong V[-d]$
as complexes of graded
$S \otimes _A^L {\mathrm {RHom}}_{A^e}(A, A^e) \cong V[-d]$
as complexes of graded
![]() $(A, A)$
-bimodules.
$(A, A)$
-bimodules.
Now since A is homologically smooth,
![]() $P^{\bullet } = {\mathrm {RHom}}_{A^e}(A, A^e)$
is a bounded complex, consisting of finitely generated graded projective right
$P^{\bullet } = {\mathrm {RHom}}_{A^e}(A, A^e)$
is a bounded complex, consisting of finitely generated graded projective right
![]() $A^e$
-modules. In particular, each
$A^e$
-modules. In particular, each
![]() $P^d$
is left bounded and locally finite. Now by a right-sided version of Lemma 5.14, as a complex of graded right A-modules
$P^d$
is left bounded and locally finite. Now by a right-sided version of Lemma 5.14, as a complex of graded right A-modules
![]() $P^{\bullet }$
is quasi-isomorphic to a minimal complex of graded projective right A-modules
$P^{\bullet }$
is quasi-isomorphic to a minimal complex of graded projective right A-modules
![]() $Q^{\bullet }$
. In particular, the complex
$Q^{\bullet }$
. In particular, the complex
![]() $Q^{\bullet } \otimes _A S$
has zero differentials. Since this complex is quasi-isomorphic to
$Q^{\bullet } \otimes _A S$
has zero differentials. Since this complex is quasi-isomorphic to
![]() $W[-d]$
as complexes of graded right A-modules, comparing cohomology gives
$W[-d]$
as complexes of graded right A-modules, comparing cohomology gives
![]() $Q^d \otimes _A S \cong W$
and
$Q^d \otimes _A S \cong W$
and
![]() $Q^i \otimes _A S = 0$
for
$Q^i \otimes _A S = 0$
for
![]() $i \neq d$
, so that
$i \neq d$
, so that
![]() $Q^i = 0$
for
$Q^i = 0$
for
![]() $i \neq d$
by Nakayama’s lemma. In particular,
$i \neq d$
by Nakayama’s lemma. In particular,
![]() $Q^{\bullet }$
and consequently
$Q^{\bullet }$
and consequently
![]() $ {\mathrm {RHom}}_{A^e}(A, A^e)$
have cohomology only in degree d. By Lemma 4.3,
$ {\mathrm {RHom}}_{A^e}(A, A^e)$
have cohomology only in degree d. By Lemma 4.3,
![]() $ {\mathrm {RHom}}_{A^e}(A, A^e) \cong U[-d]$
for the
$ {\mathrm {RHom}}_{A^e}(A, A^e) \cong U[-d]$
for the
![]() $(A, A)$
-bimodule
$(A, A)$
-bimodule
 $U = H^d(P^{\bullet }) = {\mathrm {{Ext}}}^d_{A^e}(A, A^e)$
. The quasi-isomorphisms above show that
$U = H^d(P^{\bullet }) = {\mathrm {{Ext}}}^d_{A^e}(A, A^e)$
. The quasi-isomorphisms above show that
![]() $U \otimes _A S \cong W$
as
$U \otimes _A S \cong W$
as
![]() $(A, A)$
-bimodules.
$(A, A)$
-bimodules.
A symmetric argument shows that
![]() $S \otimes _A U \cong V$
as
$S \otimes _A U \cong V$
as
![]() $(A, A)$
-bimodules; in particular,
$(A, A)$
-bimodules; in particular,
![]() $J(U \otimes _A S) = 0$
and
$J(U \otimes _A S) = 0$
and
![]() $(S \otimes _A U)J= 0$
. We know that U is projective as a right A-module, since
$(S \otimes _A U)J= 0$
. We know that U is projective as a right A-module, since
![]() $U \cong Q^d$
as right modules, in the notation of the previous paragraph; by symmetry, it is also projective as a left A-module. Thus the hypotheses of Lemma 5.13 hold, and we conclude that U is an invertible
$U \cong Q^d$
as right modules, in the notation of the previous paragraph; by symmetry, it is also projective as a left A-module. Thus the hypotheses of Lemma 5.13 hold, and we conclude that U is an invertible
![]() $(A, A)$
-bimodule (and, of course, that
$(A, A)$
-bimodule (and, of course, that
![]() $V \cong W$
). This establishes (a).
$V \cong W$
). This establishes (a).
Finally, if (a) holds, then since A is finitely generated as an algebra by Lemma 3.2(3), its graded and ungraded global dimensions are equal by Proposition 3.18, and these dimensions are in fact equal to d by Corollary 4.14.
Remark 5.16. If A is graded and locally finite, then the twisted Calabi–Yau property is certainly stricter than the generalized AS regular property in general. For if
![]() $A = S$
is a finite-dimensional semisimple k-algebra that is not separable, considered as a graded algebra concentrated in degree zero, then A is easily seen to be generalized AS regular; but Corollary 4.20 shows that A is not graded twisted Calabi–Yau of dimension 0, for it fails to be homologically smooth over k, as shown in Example 3.20. On the other hand, if the field k is perfect, then every finite-dimensional semisimple k-algebra is separable, which makes the twisted Calabi–Yau and generalized AS regular properties equivalent in Theorem 5.15.
$A = S$
is a finite-dimensional semisimple k-algebra that is not separable, considered as a graded algebra concentrated in degree zero, then A is easily seen to be generalized AS regular; but Corollary 4.20 shows that A is not graded twisted Calabi–Yau of dimension 0, for it fails to be homologically smooth over k, as shown in Example 3.20. On the other hand, if the field k is perfect, then every finite-dimensional semisimple k-algebra is separable, which makes the twisted Calabi–Yau and generalized AS regular properties equivalent in Theorem 5.15.
In [Reference Bocklandt5], Bocklandt takes the approach of defining Calabi–Yau algebras in terms of derived categories of finite-dimensional modules being Calabi–Yau triangulated categories [Reference Keller21]. One hopes that the statement of Theorem 5.15 could be extended to include a further equivalent condition that the derived category of finite-dimensional graded left A-modules forms a “twisted Calabi–Yau triangulated category.” An attempt to define such categories was made in [Reference Reyes, Rogalski and Zhang38], but further work to develop the theory of such categories must be done before such an equivalence can be carried out. This is partly due to the fact that [Reference Reyes, Rogalski and Zhang38] worked only in the setting of twisted Calabi–Yau algebras that possess a Nakayama automorphism. But there is still a more fundamental question of whether that definition could or should be modified to ensure uniqueness of the Nakayama autoequivalence; see [Reference Reyes, Rogalski and Zhang38, Section 2.5].
5.3 Operations preserving generalized AS regularity
We showed earlier that the tensor product of two twisted Calabi–Yau algebras is again twisted Calabi–Yau in Proposition 4.9. The analogous statement for generalized AS regular algebras is of course false; if E is a finite-dimensional nonseparable extension of k, then E is generalized AS regular of dimension
![]() $0$
, while
$0$
, while
![]() $E \otimes _k E$
has infinite global dimension and so certainly cannot be generalized AS regular. However, by analogy with the fact that the tensor product of a separable algebra with a semisimple algebra is semisimple, one might suspect that the tensor product a locally finite graded twisted CY algebra with a generalized AS regular algebra is again generalized AS regular. This is indeed the case, and can be established using a suitable adaptation of the method of proof used in Proposition 4.9.
$E \otimes _k E$
has infinite global dimension and so certainly cannot be generalized AS regular. However, by analogy with the fact that the tensor product of a separable algebra with a semisimple algebra is semisimple, one might suspect that the tensor product a locally finite graded twisted CY algebra with a generalized AS regular algebra is again generalized AS regular. This is indeed the case, and can be established using a suitable adaptation of the method of proof used in Proposition 4.9.
Proposition 5.17. Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be graded algebras. If
$A_2$
be graded algebras. If
![]() $A_1$
is generalized AS regular of dimension
$A_1$
is generalized AS regular of dimension
![]() $d_1$
and
$d_1$
and
![]() $A_2$
is twisted Calabi–Yau of dimension
$A_2$
is twisted Calabi–Yau of dimension
![]() $d_2$
, then
$d_2$
, then
![]() $A_1 \otimes A_2$
is generalized AS regular of dimension
$A_1 \otimes A_2$
is generalized AS regular of dimension
![]() $d_1 + d_2$
.
$d_1 + d_2$
.
Proof. Denote
![]() $J_i = J(A_i)$
and
$J_i = J(A_i)$
and
![]() $S_i = A_i/J_i$
for
$S_i = A_i/J_i$
for
![]() $i = 1,2$
, as well as
$i = 1,2$
, as well as
![]() $J = J(A_1 \otimes A_2)$
and
$J = J(A_1 \otimes A_2)$
and
![]() $S = (A_1 \otimes A_2)/J$
. By Theorem 5.15,
$S = (A_1 \otimes A_2)/J$
. By Theorem 5.15,
![]() $A_2$
is generalized AS regular and
$A_2$
is generalized AS regular and
![]() $S_2$
is separable. It follows from Lemma 3.7 that
$S_2$
is separable. It follows from Lemma 3.7 that
![]() $J = J_1 \otimes A_2 + A_1 \otimes J_2$
and
$J = J_1 \otimes A_2 + A_1 \otimes J_2$
and
![]() $S \cong S_1 \otimes S_2$
.
$S \cong S_1 \otimes S_2$
.
By Theorem 5.2(d), each
![]() $ {\mathrm {RHom}}_{A_i}(S_i,A)[d_i] \cong V_i$
for some invertible graded
$ {\mathrm {RHom}}_{A_i}(S_i,A)[d_i] \cong V_i$
for some invertible graded
![]() $(S_i,S_i)$
-bimodules
$(S_i,S_i)$
-bimodules
![]() $V_i$
. Note that each
$V_i$
. Note that each
![]() $S_i$
is perfect as a right
$S_i$
is perfect as a right
![]() $A_i$
-module by Lemma 5.1(1). Thus we may apply Lemma 4.8 in the following sequence of quasi-isomorphisms:
$A_i$
-module by Lemma 5.1(1). Thus we may apply Lemma 4.8 in the following sequence of quasi-isomorphisms:
 $$ \begin{align*} {\mathrm{RHom}}_{A_1 \otimes A_2}(S, A_1 \otimes A_2) &\cong {\mathrm{RHom}}_{A_1 \otimes A_2}(S_1 \otimes S_2, A_1 \otimes A_2) \\ &\cong {\mathrm{RHom}}_{A_1}(S_1, A_1) \otimes {\mathrm{RHom}}_{A_2}(S_2, A_2) \\ &\cong V_1[-d_1] \otimes V_2[-d_2] = (V_1 \otimes V_2)[-(d_1 + d_2)]. \end{align*} $$
$$ \begin{align*} {\mathrm{RHom}}_{A_1 \otimes A_2}(S, A_1 \otimes A_2) &\cong {\mathrm{RHom}}_{A_1 \otimes A_2}(S_1 \otimes S_2, A_1 \otimes A_2) \\ &\cong {\mathrm{RHom}}_{A_1}(S_1, A_1) \otimes {\mathrm{RHom}}_{A_2}(S_2, A_2) \\ &\cong V_1[-d_1] \otimes V_2[-d_2] = (V_1 \otimes V_2)[-(d_1 + d_2)]. \end{align*} $$
Since
![]() $V_1 \otimes V_2$
has inverse bimodule
$V_1 \otimes V_2$
has inverse bimodule
 $V_1^{-1} \otimes V_2^{-1}$
over
$V_1^{-1} \otimes V_2^{-1}$
over
![]() $A_1 \otimes A_2$
, we find that
$A_1 \otimes A_2$
, we find that
![]() $A_1 \otimes A_2$
is generalized AS regular of dimension
$A_1 \otimes A_2$
is generalized AS regular of dimension
![]() $d_1 + d_2$
, as desired.
$d_1 + d_2$
, as desired.
This directly applies to show, as one might expect, that generalized AS regularity is preserved when passing to polynomial rings.
Corollary 5.18. If a graded algebra A is generalized AS regular of dimension d, then
![]() $A[t]$
is generalized AS regular of dimension
$A[t]$
is generalized AS regular of dimension
![]() $d+1$
.
$d+1$
.
Proof. As it is well-known that
![]() $k[t]$
is Calabi–Yau of dimension 1 (see also Theorem 6.11 with
$k[t]$
is Calabi–Yau of dimension 1 (see also Theorem 6.11 with
![]() $S = k$
and
$S = k$
and
![]() $V = k(-1)$
), it follows from the previous proposition that
$V = k(-1)$
), it follows from the previous proposition that
![]() $A[t] \cong A \otimes k[t]$
is generalized AS regular of dimension
$A[t] \cong A \otimes k[t]$
is generalized AS regular of dimension
![]() $d+1$
.
$d+1$
.
As mentioned in Section 1 and as discussed in [Reference Minamoto and Mori33], regularity properties in the context of nonconnected locally finite graded algebras provide an avenue to connect noncommutative algebraic geometry with the study of finite-dimensional algebras. To encourage further investigation into this interesting connection, we pose the following question that is of a fundamental nature, but which remains largely open.
Question 5.19. For which finite-dimensional algebras B is there a locally finite generalized AS regular algebra A of dimension d such that
![]() $B \cong A_0$
?
$B \cong A_0$
?
While the answer for
![]() $d = 0$
is obviously the class of semisimple algebras B, we do not even know the answer in case
$d = 0$
is obviously the class of semisimple algebras B, we do not even know the answer in case
![]() $d = 1$
.
$d = 1$
.
Note that the analogous question for twisted Calabi–Yau algebras of dimension d would follow from an answer to the above by imposing the extra condition that
![]() $B/J(B)$
is separable, thanks to Theorem 5.15. In the twisted Calabi–Yau case, the answer for
$B/J(B)$
is separable, thanks to Theorem 5.15. In the twisted Calabi–Yau case, the answer for
![]() $d = 0$
is given in Theorem 4.19 and for
$d = 0$
is given in Theorem 4.19 and for
![]() $d = 1$
is given in Theorem 6.11 below. See Example 7.3 below for a class of examples A which are Calabi–Yau of dimension
$d = 1$
is given in Theorem 6.11 below. See Example 7.3 below for a class of examples A which are Calabi–Yau of dimension
![]() $2$
and have a more interesting
$2$
and have a more interesting
![]() $A_0$
.
$A_0$
.
6 Applications to algebras of dimension at most 2
In this section, we will apply the tools developed in preceding sections to the study of twisted Calabi–Yau algebras of dimension
![]() $1$
and
$1$
and
![]() $2$
. (Recall that the twisted Calabi–Yau algebras of dimension 0 are fully characterized as separable algebras by Theorem 4.19.) We will show that a locally finite graded twisted Calabi–Yau algebra A of dimension d is noetherian in case either
$2$
. (Recall that the twisted Calabi–Yau algebras of dimension 0 are fully characterized as separable algebras by Theorem 4.19.) We will show that a locally finite graded twisted Calabi–Yau algebra A of dimension d is noetherian in case either
![]() $d = 1$
, or
$d = 1$
, or
![]() $d = 2$
and A has finite GK dimension. By establishing this result before attempting any classification of low-dimensional twisted Calabi–Yau algebras, we emphasize that this result is of a structural nature, rather than by exhaustively listing all possible algebras. We then conclude with a characterization of graded twisted Calabi–Yau algebras of dimension 1 as certain tensor algebras.
$d = 2$
and A has finite GK dimension. By establishing this result before attempting any classification of low-dimensional twisted Calabi–Yau algebras, we emphasize that this result is of a structural nature, rather than by exhaustively listing all possible algebras. We then conclude with a characterization of graded twisted Calabi–Yau algebras of dimension 1 as certain tensor algebras.
6.1 The noetherian property in dimension
 $d \leq 2$
$d \leq 2$
Our approach to showing that a graded algebra is noetherian is to show that every graded noetherian module is finitely presented. This is inspired by Cohen-type arguments, using the key idea from [Reference Reyes39, Theorem 4.5].
Lemma 6.1. A graded k-algebra A is left noetherian if and only if every graded noetherian left A-module is finitely presented.
Proof. Suppose that every graded noetherian left A-module is finitely presented, and assume for contradiction that A is not left noetherian. Then there exists a graded left ideal
![]() $I \subseteq A$
that is not finitely generated; see [Reference Năstăsescu and van Oystaeyen34, II.3] or [Reference Năstăsescu and Van Oystaeyen35, Theorem 5.4.7]. Using Zorn’s lemma, we may pass to a maximal such I. Then
$I \subseteq A$
that is not finitely generated; see [Reference Năstăsescu and van Oystaeyen34, II.3] or [Reference Năstăsescu and Van Oystaeyen35, Theorem 5.4.7]. Using Zorn’s lemma, we may pass to a maximal such I. Then
![]() $A/I$
is a graded noetherian left A-module and thus is finitely presented. But then I is finitely generated (by Schanuel’s lemma, for instance), a contradiction. The converse is clear.
$A/I$
is a graded noetherian left A-module and thus is finitely presented. But then I is finitely generated (by Schanuel’s lemma, for instance), a contradiction. The converse is clear.
Now assume that A is a graded algebra of finite graded global dimension d with
![]() $\dim _k A_0 < \infty $
, and let M be a noetherian graded left module. Consider the minimal graded projective resolution of M,
$\dim _k A_0 < \infty $
, and let M be a noetherian graded left module. Consider the minimal graded projective resolution of M,
If A is to be left noetherian, then one expects all of the
![]() $P^i$
to be finitely generated. Thus a valid approach to proving that A is left noetherian would be to prove by descending induction that the
$P^i$
to be finitely generated. Thus a valid approach to proving that A is left noetherian would be to prove by descending induction that the
![]() $P^i$
are finitely generated. The next result illustrates how the twisted Calabi–Yau property takes care of the “base case” of this proposed inductive argument.
$P^i$
are finitely generated. The next result illustrates how the twisted Calabi–Yau property takes care of the “base case” of this proposed inductive argument.
Proposition 6.3. Let A be a locally finite graded twisted Calabi–Yau algebra of dimension d, and let
![]() $_A M$
be a graded left A-module. If
$_A M$
be a graded left A-module. If
![]() $ {\mathrm {soc}}(M)$
is a finitely generated module (e.g., if M is noetherian), then the term
$ {\mathrm {soc}}(M)$
is a finitely generated module (e.g., if M is noetherian), then the term
![]() $P^{-d}$
in the minimal projective resolution (6.2) of M is finitely generated.
$P^{-d}$
in the minimal projective resolution (6.2) of M is finitely generated.
Proof. Set
![]() $S = A/J(A)$
and let U be the Nakayama bimodule of A. From Proposition 4.17 we have
$S = A/J(A)$
and let U be the Nakayama bimodule of A. From Proposition 4.17 we have
 $$ \begin{align*} {\mathrm{Tor}}^A_d(S,M) \cong U^{-1} \otimes_A {\mathrm{soc}}(M). \end{align*} $$
$$ \begin{align*} {\mathrm{Tor}}^A_d(S,M) \cong U^{-1} \otimes_A {\mathrm{soc}}(M). \end{align*} $$
Because
![]() $U^{-1}$
is invertible,
$U^{-1}$
is invertible,
![]() $ {\mathrm {soc}}(M)$
is finitely generated as a module if and only if
$ {\mathrm {soc}}(M)$
is finitely generated as a module if and only if
 $U^{-1} \otimes _A {\mathrm {soc}}(M)$
is. Also, the semisimple left A-module
$U^{-1} \otimes _A {\mathrm {soc}}(M)$
is. Also, the semisimple left A-module
 $U^{-1} \otimes _A {\mathrm {soc}}(M)$
is a direct sum of simple modules over the finite-dimensional algebra
$U^{-1} \otimes _A {\mathrm {soc}}(M)$
is a direct sum of simple modules over the finite-dimensional algebra
![]() $A/J(A) = S$
, each of which is finite-dimensional. Thus
$A/J(A) = S$
, each of which is finite-dimensional. Thus
 $U^{-1} \otimes _A {\mathrm {soc}}(M)$
is finitely generated if and only if it is finite-dimensional, so that the claim follows from Lemma 2.6.
$U^{-1} \otimes _A {\mathrm {soc}}(M)$
is finitely generated if and only if it is finite-dimensional, so that the claim follows from Lemma 2.6.
This allows us to show that graded twisted Calabi–Yau algebras of dimension 1 are noetherian.
Corollary 6.4. Let A be a locally finite graded twisted Calabi–Yau algebra of dimension 1. Then A is noetherian.
Proof. Let
![]() $_A M$
be a graded noetherian left module with minimal projective resolution
$_A M$
be a graded noetherian left module with minimal projective resolution
Certainly
![]() $P^0$
is finitely generated because M is. Proposition 6.3 implies that
$P^0$
is finitely generated because M is. Proposition 6.3 implies that
![]() $P^{-1}$
is finitely generated. Hence M is finitely presented. It follows from Lemma 6.1 that A is left noetherian. By symmetry, A is also right noetherian.
$P^{-1}$
is finitely generated. Hence M is finitely presented. It follows from Lemma 6.1 that A is left noetherian. By symmetry, A is also right noetherian.
The dimension 2 case requires us to know a bit more information about the GK dimension of graded projective modules. In the companion paper [Reference Reyes and Rogalski40], we study in detail the basic properties of the Gelfand-Kirillov dimension of graded twisted Calabi–Yau algebras. There we establish the following fact.
Lemma 6.5. (See [Reference Reyes and Rogalski40, Proposition 7.4].) Let A be a graded, locally finite, twisted Calabi–Yau k-algebra of dimension 2. Suppose that
![]() $ {\mathrm {GKdim}}(A) < \infty $
. Let
$ {\mathrm {GKdim}}(A) < \infty $
. Let
 $$ \begin{align*} P_1 \overset{d_1}{\longrightarrow} P_2 \overset{d_2}{\longrightarrow} P_3 \end{align*} $$
$$ \begin{align*} P_1 \overset{d_1}{\longrightarrow} P_2 \overset{d_2}{\longrightarrow} P_3 \end{align*} $$
be an exact sequence of projectives in
![]() $ {\mathrm {Gr-\!}} A$
. If
$ {\mathrm {Gr-\!}} A$
. If
![]() $P_1$
and
$P_1$
and
![]() $P_3$
are finitely generated, then so is
$P_3$
are finitely generated, then so is
![]() $P_2$
.
$P_2$
.
We now proceed to show that graded twisted Calabi–Yau algebras of global dimension 2 with finite GK dimension are noetherian.
Theorem 6.6. Let A be a locally finite graded twisted Calabi–Yau algebra of dimension 2. Then A is noetherian if and only if it has finite GK dimension.
Proof. Assume
![]() $ {\mathrm {GKdim}}(A) < \infty $
. Let M be a noetherian graded left A-module with minimal projective resolution
$ {\mathrm {GKdim}}(A) < \infty $
. Let M be a noetherian graded left A-module with minimal projective resolution
Because M is finitely generated, so is
![]() $P^0$
. By Proposition 6.3, we see that
$P^0$
. By Proposition 6.3, we see that
![]() $P^{-2}$
is also finitely generated. Now by Lemma 6.5,
$P^{-2}$
is also finitely generated. Now by Lemma 6.5,
![]() $P^{-1}$
is finitely generated, so that M is finitely presented. Thus A is left noetherian by Lemma 6.1; by symmetry, A is also right noetherian.
$P^{-1}$
is finitely generated, so that M is finitely presented. Thus A is left noetherian by Lemma 6.1; by symmetry, A is also right noetherian.
Conversely, if A is noetherian, then
![]() $ {\mathrm {GKdim}}(A) < \infty $
by [Reference Reyes and Rogalski40, Proposition 4.4].
$ {\mathrm {GKdim}}(A) < \infty $
by [Reference Reyes and Rogalski40, Proposition 4.4].
Remark 6.7. A direct consequence of Theorem 6.6 and Proposition 4.7 is that if A is a locally finite graded twisted Calabi–Yau k-algebra of dimension
![]() $d \leq 2$
having finite GK dimension, then for every field extension
$d \leq 2$
having finite GK dimension, then for every field extension
![]() $K/k$
the algebra
$K/k$
the algebra
![]() $A \otimes K$
is noetherian. Following our earlier terminology, this property could be called “geometrically noetherian,” but the term “stably noetherian” has also been used in the literature [Reference Bell3]. This makes it tempting to posit that such algebras are in fact strongly noetherian, that is, that
$A \otimes K$
is noetherian. Following our earlier terminology, this property could be called “geometrically noetherian,” but the term “stably noetherian” has also been used in the literature [Reference Bell3]. This makes it tempting to posit that such algebras are in fact strongly noetherian, that is, that
![]() $A \otimes R$
is noetherian for all commutative noetherian k-algebras R. To this end, it would also be interesting to study graded twisted Calabi–Yau R-algebras over a general commutative ring R, under the assumption that
$A \otimes R$
is noetherian for all commutative noetherian k-algebras R. To this end, it would also be interesting to study graded twisted Calabi–Yau R-algebras over a general commutative ring R, under the assumption that
 $A = \bigoplus _{n=0}^\infty A_n$
is graded with each
$A = \bigoplus _{n=0}^\infty A_n$
is graded with each
![]() $A_n$
a finitely generated projective R-module. It seems likely that a number of results proved in the preceding sections could generalize (with suitable modification) to this general setting.
$A_n$
a finitely generated projective R-module. It seems likely that a number of results proved in the preceding sections could generalize (with suitable modification) to this general setting.
We also wonder whether the previous theorem can be extended to the ungraded case.
Question 6.8. Let A be a (not necessarily graded) twisted Calabi–Yau algebra of dimension
![]() $d \leq 2$
. If A has finite GK dimension, must A be noetherian?
$d \leq 2$
. If A has finite GK dimension, must A be noetherian?
6.2 Twisted CY-1 algebras are tensor algebras
Next, we give a structural characterization of locally finite graded twisted Calabi–Yau algebras of dimension
![]() $d=1$
as certain tensor algebras. Given a semisimple algebra S and a finite-dimensional
$d=1$
as certain tensor algebras. Given a semisimple algebra S and a finite-dimensional
![]() $(S, S)$
-bimodule V, the tensor algebra is
$(S, S)$
-bimodule V, the tensor algebra is
 $T_S(V) = \bigoplus _{n \geq 0} V^{\otimes n}$
, where
$T_S(V) = \bigoplus _{n \geq 0} V^{\otimes n}$
, where
![]() $V^{\otimes n} = V \otimes _S V \otimes _S \dots \otimes _S V$
is the n-fold tensor power over S with the usual convention
$V^{\otimes n} = V \otimes _S V \otimes _S \dots \otimes _S V$
is the n-fold tensor power over S with the usual convention
![]() $V^{\otimes 0} = S$
, and the multiplication is induced by the tensor product over S. Note that if V is positively graded, then
$V^{\otimes 0} = S$
, and the multiplication is induced by the tensor product over S. Note that if V is positively graded, then
![]() $A = T_S(V)$
is locally finite; conversely, if
$A = T_S(V)$
is locally finite; conversely, if
![]() $A = T_S(V)$
is (
$A = T_S(V)$
is (
![]() $\mathbb {N}$
)-graded and locally finite, then V must at least be non-negatively graded. In fact, it is a straightforward exercise to see that
$\mathbb {N}$
)-graded and locally finite, then V must at least be non-negatively graded. In fact, it is a straightforward exercise to see that
![]() $T_S(V)$
is non-negatively graded if and only if
$T_S(V)$
is non-negatively graded if and only if
![]() $V^{\otimes N}$
is positively graded for some
$V^{\otimes N}$
is positively graded for some
![]() $N \geq 1$
. Any graded A-module is also a graded S-module via the inclusion
$N \geq 1$
. Any graded A-module is also a graded S-module via the inclusion
![]() $S = V^{\otimes 0} \subseteq A$
. Furthermore, we claim that
$S = V^{\otimes 0} \subseteq A$
. Furthermore, we claim that
 $$ \begin{align*} J(A) = \bigoplus_{n \geq 1} V^{\otimes n} = V \otimes_S A = A \otimes_S V. \end{align*} $$
$$ \begin{align*} J(A) = \bigoplus_{n \geq 1} V^{\otimes n} = V \otimes_S A = A \otimes_S V. \end{align*} $$
Indeed, because S is semisimple and
![]() $A/(V \otimes _S A) \cong S$
, we must have
$A/(V \otimes _S A) \cong S$
, we must have
![]() $J(A) \subseteq V \otimes _S A$
. On the other hand, from
$J(A) \subseteq V \otimes _S A$
. On the other hand, from
 $V^{\otimes N} \subseteq A_{\geq 1}$
we have
$V^{\otimes N} \subseteq A_{\geq 1}$
we have
 $(V \otimes _S A)^N = V^{\otimes N} \otimes _S A \subseteq A_{\geq 1} \subseteq J(A)$
. As
$(V \otimes _S A)^N = V^{\otimes N} \otimes _S A \subseteq A_{\geq 1} \subseteq J(A)$
. As
![]() $J(A)$
is semiprime, it follows that
$J(A)$
is semiprime, it follows that
![]() $V \otimes _S A \subseteq J(A)$
, proving the desired containment.
$V \otimes _S A \subseteq J(A)$
, proving the desired containment.
We have the following technical lemma concerning the structure of
 $ {\mathrm {{Ext}}}^i_A(S, A)$
for an algebra
$ {\mathrm {{Ext}}}^i_A(S, A)$
for an algebra
![]() $A = T_S(V)$
.
$A = T_S(V)$
.
Lemma 6.9. Let S be a finite-dimensional semisimple k-algebra, let V be a non-negatively graded finite-dimensional
![]() $(S,S)$
-bimodule, and denote
$(S,S)$
-bimodule, and denote
![]() $A = T_S(V)$
. Assume that A is locally finite. Let
$A = T_S(V)$
. Assume that A is locally finite. Let
 $\widehat {V} = {\mathrm {{Hom}}}_S(V,S)$
denote the S-dual of V as a left module, and let the image of the natural right-multiplication map
$\widehat {V} = {\mathrm {{Hom}}}_S(V,S)$
denote the S-dual of V as a left module, and let the image of the natural right-multiplication map
![]() $\rho : S \to {\mathrm {{End}}}({{\hspace {-0.0001pt}}}_S V)$
be denoted by
$\rho : S \to {\mathrm {{End}}}({{\hspace {-0.0001pt}}}_S V)$
be denoted by
![]() $S'$
. Then we have the following isomorphisms of
$S'$
. Then we have the following isomorphisms of
![]() $(S,S)$
-bimodules:
$(S,S)$
-bimodules:
-
(1)
 $ {\mathrm {{Ext}}}_A^0(S,A) = {\mathrm {{Hom}}}_A(S,A) \cong {\mathrm {ann}}_r(J(A))$
.
$ {\mathrm {{Ext}}}_A^0(S,A) = {\mathrm {{Hom}}}_A(S,A) \cong {\mathrm {ann}}_r(J(A))$
. -
(2)
 $ {\mathrm {{Ext}}}_A^1(S,A) \cong \widehat {V} \oplus (( {\mathrm {{End}}}_S(V)/S') \otimes _S A)$
.
$ {\mathrm {{Ext}}}_A^1(S,A) \cong \widehat {V} \oplus (( {\mathrm {{End}}}_S(V)/S') \otimes _S A)$
.
Proof. For (1), it is clear that
![]() $ {\mathrm {{Hom}}}_A(S,A) = {\mathrm {{Hom}}}_A(A/J(A),A)$
is naturally identified with the right annihilator of
$ {\mathrm {{Hom}}}_A(S,A) = {\mathrm {{Hom}}}_A(A/J(A),A)$
is naturally identified with the right annihilator of
![]() $J(A)$
in A.
$J(A)$
in A.
We now establish (2). As a graded left A-module, we have
![]() $J(A) \cong A \otimes _S V$
, which is projective because
$J(A) \cong A \otimes _S V$
, which is projective because
![]() ${{\hspace {-0.0001pt}}}_S V$
is projective. Thus
${{\hspace {-0.0001pt}}}_S V$
is projective. Thus
![]() ${{\hspace {-0.0001pt}}}_A S$
has a graded projective resolution given by
${{\hspace {-0.0001pt}}}_A S$
has a graded projective resolution given by
In order to compute
 $ {\mathrm {{Ext}}}^1_A(S,A)$
, we apply the functor
$ {\mathrm {{Ext}}}^1_A(S,A)$
, we apply the functor
![]() $ {\mathrm {{Hom}}}_A(-,A)$
to the deleted resolution, so that we must examine
$ {\mathrm {{Hom}}}_A(-,A)$
to the deleted resolution, so that we must examine
 $$ \begin{align*} {\mathrm{{Hom}}}_A(A,A) \overset{\phi}{\longrightarrow} {\mathrm{{Hom}}}_A(J(A),A) \to 0, \end{align*} $$
$$ \begin{align*} {\mathrm{{Hom}}}_A(A,A) \overset{\phi}{\longrightarrow} {\mathrm{{Hom}}}_A(J(A),A) \to 0, \end{align*} $$
where
![]() $\phi $
is given by restriction of the right-multiplication morphisms in
$\phi $
is given by restriction of the right-multiplication morphisms in
![]() $A \cong {\mathrm {{Hom}}}_A(A,A)$
to
$A \cong {\mathrm {{Hom}}}_A(A,A)$
to
![]() $J(A)$
. Then
$J(A)$
. Then
 $ {\mathrm {{Ext}}}^1_A(S,A)$
will be the cokernel of
$ {\mathrm {{Ext}}}^1_A(S,A)$
will be the cokernel of
![]() $\phi $
.
$\phi $
.
We now have
 $$ \begin{align*} {\mathrm{{Hom}}}_A(J(A),A) & \cong {\mathrm{{Hom}}}_A(A \otimes_S V, A) \\ &\cong {\mathrm{{Hom}}}_S(V, {\mathrm{{Hom}}}_A(A ,A)) \ \ \text{(by adjointness)} \\ &\cong {\mathrm{{Hom}}}_S(V,A) \\ &\cong {\mathrm{{Hom}}}_S(V, S \oplus (V \otimes_S A) \\ &\cong {\mathrm{{Hom}}}_S(V, S) \oplus {\mathrm{{Hom}}}_S(V, V \otimes_S A) \\ &\cong {\mathrm{{Hom}}}_S(V, S) \oplus ({\mathrm{{Hom}}}_S(V, V) \otimes_S A) \ \ \text{(by Lemma 2.12)} \\ &= \widehat{V} \oplus ({\mathrm{{End}}}_S(V) \otimes_S A), \end{align*} $$
$$ \begin{align*} {\mathrm{{Hom}}}_A(J(A),A) & \cong {\mathrm{{Hom}}}_A(A \otimes_S V, A) \\ &\cong {\mathrm{{Hom}}}_S(V, {\mathrm{{Hom}}}_A(A ,A)) \ \ \text{(by adjointness)} \\ &\cong {\mathrm{{Hom}}}_S(V,A) \\ &\cong {\mathrm{{Hom}}}_S(V, S \oplus (V \otimes_S A) \\ &\cong {\mathrm{{Hom}}}_S(V, S) \oplus {\mathrm{{Hom}}}_S(V, V \otimes_S A) \\ &\cong {\mathrm{{Hom}}}_S(V, S) \oplus ({\mathrm{{Hom}}}_S(V, V) \otimes_S A) \ \ \text{(by Lemma 2.12)} \\ &= \widehat{V} \oplus ({\mathrm{{End}}}_S(V) \otimes_S A), \end{align*} $$
as
![]() $(S, S)$
-bimodules.
$(S, S)$
-bimodules.
One may verify that under this isomorphism, the morphism
corresponds to the map
 $A \cong S \otimes _S A \overset {\rho \otimes 1}{\to } {\mathrm {{End}}}_S(V) \otimes _S A$
composed with the coordinate inclusion into
$A \cong S \otimes _S A \overset {\rho \otimes 1}{\to } {\mathrm {{End}}}_S(V) \otimes _S A$
composed with the coordinate inclusion into
 $\widehat {V} \oplus ( {\mathrm {{End}}}_S(V) \otimes _S A)$
. Taking the cokernel of this map yields the desired
$\widehat {V} \oplus ( {\mathrm {{End}}}_S(V) \otimes _S A)$
. Taking the cokernel of this map yields the desired
![]() $(S,S)$
-bimodule isomorphism
$(S,S)$
-bimodule isomorphism
 $ {\mathrm {{Ext}}}^1_A(S,A) \cong \widehat {V} \oplus ( {\mathrm {{End}}}_S(V)/S') \otimes _S A$
.
$ {\mathrm {{Ext}}}^1_A(S,A) \cong \widehat {V} \oplus ( {\mathrm {{End}}}_S(V)/S') \otimes _S A$
.
This allows us to characterize those tensor algebras
![]() $T_S(V)$
as above that are generalized AS regular.
$T_S(V)$
as above that are generalized AS regular.
Theorem 6.10. Let S be a finite-dimensional semisimple k-algebra, and let
![]() $0 \neq V$
be a non-negatively graded finite-dimensional
$0 \neq V$
be a non-negatively graded finite-dimensional
![]() $(S,S)$
-bimodule such that
$(S,S)$
-bimodule such that
![]() $A = T_S(V)$
is locally finite. Then A is generalized AS regular of dimension d if and only if V is an invertible bimodule, in which case
$A = T_S(V)$
is locally finite. Then A is generalized AS regular of dimension d if and only if V is an invertible bimodule, in which case
![]() $d = 1$
.
$d = 1$
.
Proof. Suppose that A is generalized AS regular of dimension d. Since V is nonzero, we see that
 $\widehat {V} = {\mathrm {{Hom}}}_S(V, S) \neq 0$
and so
$\widehat {V} = {\mathrm {{Hom}}}_S(V, S) \neq 0$
and so
 $ {\mathrm {{Ext}}}^1_A(S, A) \neq 0$
by Lemma 6.9(2). Using condition (d) of Theorem 5.2, we see that necessarily
$ {\mathrm {{Ext}}}^1_A(S, A) \neq 0$
by Lemma 6.9(2). Using condition (d) of Theorem 5.2, we see that necessarily
![]() $d = 1$
; in addition,
$d = 1$
; in addition,
![]() $ {\mathrm {{Hom}}}_{A}(S, A) = 0$
and
$ {\mathrm {{Hom}}}_{A}(S, A) = 0$
and
 $ {\mathrm {{Ext}}}_{A}^1(S, A)$
is an invertible
$ {\mathrm {{Ext}}}_{A}^1(S, A)$
is an invertible
![]() $(S, S)$
-bimodule. By Corollary 5.4, the right-sided versions of these conditions also hold. In particular,
$(S, S)$
-bimodule. By Corollary 5.4, the right-sided versions of these conditions also hold. In particular,
![]() $ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}(S, A) = 0$
and so A has no right socle by Lemma 6.9(1). Then A has no nonzero finite-dimensional right ideals. In particular, every indecomposable graded projective left A module
$ {\mathrm {{Hom}}}_{A^{\mathrm {op}}}(S, A) = 0$
and so A has no right socle by Lemma 6.9(1). Then A has no nonzero finite-dimensional right ideals. In particular, every indecomposable graded projective left A module
![]() $e_i A$
satisfies
$e_i A$
satisfies
![]() $\dim _k e_i A = \infty $
, where
$\dim _k e_i A = \infty $
, where
![]() $1 = e_1 + \dots + e_n$
is a decomposition of
$1 = e_1 + \dots + e_n$
is a decomposition of
![]() $1$
into primitive orthogonal idempotents
$1$
into primitive orthogonal idempotents
![]() $e_i \in S$
. Any nonzero right S-module M is a direct sum of simple modules
$e_i \in S$
. Any nonzero right S-module M is a direct sum of simple modules
![]() $e_i S$
, and
$e_i S$
, and
![]() $e_i S \otimes _S A = e_i A$
. Thus
$e_i S \otimes _S A = e_i A$
. Thus
![]() $\dim _k M \otimes _S A = \infty $
as well. On the other hand,
$\dim _k M \otimes _S A = \infty $
as well. On the other hand,
 $W = {\mathrm {{Ext}}}_A^1(S, A)$
is an invertible
$W = {\mathrm {{Ext}}}_A^1(S, A)$
is an invertible
![]() $(S, S)$
-bimodule and hence since
$(S, S)$
-bimodule and hence since
![]() $\dim _k S < \infty $
, we have
$\dim _k S < \infty $
, we have
![]() $\dim _k W < \infty $
. Now Lemma 6.9(2) forces
$\dim _k W < \infty $
. Now Lemma 6.9(2) forces
![]() $ {\mathrm {{End}}}_S(V)/S' = 0$
, so that
$ {\mathrm {{End}}}_S(V)/S' = 0$
, so that
 $W = \widehat {V} = {\mathrm {{Hom}}}_S(V, S)$
is an invertible
$W = \widehat {V} = {\mathrm {{Hom}}}_S(V, S)$
is an invertible
![]() $(S, S)$
-bimodule. But then
$(S, S)$
-bimodule. But then
 $W^{-1} = {\mathrm {{Hom}}}_S(W, S) \cong V$
is also invertible.
$W^{-1} = {\mathrm {{Hom}}}_S(W, S) \cong V$
is also invertible.
Conversely, suppose that V is an invertible
![]() $(S, S)$
-bimodule. Then the natural right multiplication map
$(S, S)$
-bimodule. Then the natural right multiplication map
![]() $\rho : S \to {\mathrm {{End}}}_S(V)$
is an isomorphism. In particular, its image
$\rho : S \to {\mathrm {{End}}}_S(V)$
is an isomorphism. In particular, its image
![]() $S'$
equals
$S'$
equals
![]() $ {\mathrm {{End}}}_S(V)$
and so
$ {\mathrm {{End}}}_S(V)$
and so
![]() $ {\mathrm {{End}}}_S(V)/S' = 0$
. By Lemma 6.9(2), we have
$ {\mathrm {{End}}}_S(V)/S' = 0$
. By Lemma 6.9(2), we have
 $ {\mathrm {{Ext}}}_A^1(S, A) \cong \widehat {V} = {\mathrm {{Hom}}}_S(V, S)$
, which is an invertible
$ {\mathrm {{Ext}}}_A^1(S, A) \cong \widehat {V} = {\mathrm {{Hom}}}_S(V, S)$
, which is an invertible
![]() $(S, S)$
-bimodule isomorphic to
$(S, S)$
-bimodule isomorphic to
![]() $V^{-1}$
.
$V^{-1}$
.
Next, we have the short exact sequence
which is a graded minimal projective resolution of S, since
![]() $J(A) \cong A \otimes _S V$
is projective as noted in the proof of Lemma 6.9. Then by Proposition 3.18, we have
$J(A) \cong A \otimes _S V$
is projective as noted in the proof of Lemma 6.9. Then by Proposition 3.18, we have
![]() $ {\mathrm {gr.gldim}}(A) = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_A S) = 1$
. Applying
$ {\mathrm {gr.gldim}}(A) = {\mathrm {pdim}}({{\hspace {-0.0001pt}}}_A S) = 1$
. Applying
![]() $ {\mathrm {{Hom}}}_A(-, A)$
to the short exact sequence we obtain
$ {\mathrm {{Hom}}}_A(-, A)$
to the short exact sequence we obtain
and we claim that the map
![]() $A \cong {\mathrm {{Hom}}}_A(A,A) \to {\mathrm {{Hom}}}_A(J(A),A)$
is injective. Indeed, if the restriction of a right multiplication map
$A \cong {\mathrm {{Hom}}}_A(A,A) \to {\mathrm {{Hom}}}_A(J(A),A)$
is injective. Indeed, if the restriction of a right multiplication map
![]() $\rho _x \colon A \to A$
to
$\rho _x \colon A \to A$
to
![]() $J(A)$
is zero, then since
$J(A)$
is zero, then since
![]() $J(A) = V \otimes _S A$
we have
$J(A) = V \otimes _S A$
we have
![]() $V \otimes _S Ax = 0$
. Applying
$V \otimes _S Ax = 0$
. Applying
![]() $V^{-1} \otimes _S - $
we get
$V^{-1} \otimes _S - $
we get
![]() $Ax = 0$
and hence
$Ax = 0$
and hence
![]() $x = 0$
. This proves the claim, and thus
$x = 0$
. This proves the claim, and thus
![]() $ {\mathrm {{Hom}}}_A(S, A) = 0$
. Now since
$ {\mathrm {{Hom}}}_A(S, A) = 0$
. Now since
![]() $ {\mathrm {gr.gldim}}(A) = 1$
, we also have
$ {\mathrm {gr.gldim}}(A) = 1$
, we also have
 $ {\mathrm {{Ext}}}^i_A(S, A) = 0$
if
$ {\mathrm {{Ext}}}^i_A(S, A) = 0$
if
![]() $i> 1$
. Using Lemma 4.3(3), we find that
$i> 1$
. Using Lemma 4.3(3), we find that
 $ {\mathrm {RHom}}_A(S, A)[1] \cong V^{-1}$
is an invertible bimodule. Thus by condition (d) of Theorem 5.2, A is generalized AS regular of dimension
$ {\mathrm {RHom}}_A(S, A)[1] \cong V^{-1}$
is an invertible bimodule. Thus by condition (d) of Theorem 5.2, A is generalized AS regular of dimension
![]() $1$
.
$1$
.
We can now characterize locally finite graded twisted Calabi–Yau algebras of dimension
![]() $1$
.
$1$
.
Theorem 6.11. Let A be a graded k-algebra with
![]() $S = A/J(A)$
. Then the following are equivalent:
$S = A/J(A)$
. Then the following are equivalent:
-
(1) A is locally finite twisted Calabi–Yau of dimension
 $1$
.
$1$
. -
(2)
 $A \cong T_S(V)$
for a separable k-algebra S and an invertible, non-negatively graded
$A \cong T_S(V)$
for a separable k-algebra S and an invertible, non-negatively graded
 $(S, S)$
-bimodule V such that
$(S, S)$
-bimodule V such that
 $V^{\otimes N}$
is positively graded for some integer
$V^{\otimes N}$
is positively graded for some integer
 $N \geq 1$
.
$N \geq 1$
.
Proof.
![]() $(1) \implies (2)$
: Let
$(1) \implies (2)$
: Let
![]() $J = J(A)$
. Since A is twisted Calabi–Yau of dimension
$J = J(A)$
. Since A is twisted Calabi–Yau of dimension
![]() $1$
, Theorem 5.15 implies that A is generalized AS regular of dimension
$1$
, Theorem 5.15 implies that A is generalized AS regular of dimension
![]() $1$
and that S is separable. Then
$1$
and that S is separable. Then
![]() $S^e$
is also semisimple by Lemma 3.3(2). Thus there exists a graded left
$S^e$
is also semisimple by Lemma 3.3(2). Thus there exists a graded left
![]() $S^e$
-submodule V of J such that
$S^e$
-submodule V of J such that
 $J = V \bigoplus J^2$
as graded
$J = V \bigoplus J^2$
as graded
![]() $S^e$
-modules, that is, as graded
$S^e$
-modules, that is, as graded
![]() $(S, S)$
-bimodules. Similarly, there is a copy of
$(S, S)$
-bimodules. Similarly, there is a copy of
![]() $S \subseteq A$
such that
$S \subseteq A$
such that
![]() $S \oplus J \cong A$
as graded
$S \oplus J \cong A$
as graded
![]() $(S, S)$
-bimodules, and we use this to identify S with a graded subalgebra of A. Note that
$(S, S)$
-bimodules, and we use this to identify S with a graded subalgebra of A. Note that
 $V \cong J/J^2$
and so
$V \cong J/J^2$
and so
![]() $\dim _k V < \infty $
by Lemma 2.3 and Lemma 3.2(3). Clearly V is non-negatively graded.
$\dim _k V < \infty $
by Lemma 2.3 and Lemma 3.2(3). Clearly V is non-negatively graded.
By the universal property of the tensor algebra, there is a unique algebra homomorphism
![]() $\phi : T_S(V) \to A$
that maps S isomorphically to the given fixed copy of S in A and maps V isomorphically to the fixed complement of
$\phi : T_S(V) \to A$
that maps S isomorphically to the given fixed copy of S in A and maps V isomorphically to the fixed complement of
![]() $J^2$
in J. By the choice of V and S as graded submodules, this is a graded algebra homomorphism. By the proof of Lemma 2.3, we see that
$J^2$
in J. By the choice of V and S as graded submodules, this is a graded algebra homomorphism. By the proof of Lemma 2.3, we see that
![]() $\phi $
is surjective.
$\phi $
is surjective.
We claim that
![]() $\phi $
is an isomorphism. Indeed, denoting
$\phi $
is an isomorphism. Indeed, denoting
![]() $\phi _n = \phi \vert _{V^{\otimes n}}: V^{\otimes n} \to A$
, because
$\phi _n = \phi \vert _{V^{\otimes n}}: V^{\otimes n} \to A$
, because
![]() $\phi $
is a graded homomorphism it suffices to show by induction that each
$\phi $
is a graded homomorphism it suffices to show by induction that each
![]() $\phi _n$
is injective. This is easily verified for
$\phi _n$
is injective. This is easily verified for
![]() $n \leq 1$
by the definition of
$n \leq 1$
by the definition of
![]() $\phi $
. Now let
$\phi $
. Now let
![]() $n \geq 2$
and suppose that
$n \geq 2$
and suppose that
![]() $\phi _{n-1}$
is injective. As we saw in Theorem 6.10, the minimal projective graded left resolution of S looks like
$\phi _{n-1}$
is injective. As we saw in Theorem 6.10, the minimal projective graded left resolution of S looks like
 $$ \begin{align*} 0 \to A \otimes_S V \overset{d_1}{\to} A \to S \to 0, \end{align*} $$
$$ \begin{align*} 0 \to A \otimes_S V \overset{d_1}{\to} A \to S \to 0, \end{align*} $$
where
![]() $d_1$
is the natural multiplication map (after identifying V with a subset of A as above). Now
$d_1$
is the natural multiplication map (after identifying V with a subset of A as above). Now
![]() $\phi _n$
decomposes as the composite
$\phi _n$
decomposes as the composite
 $$ \begin{align*} V^{\otimes n} = V^{\otimes (n-1)} \otimes_S V \overset{\phi_{n-1} \otimes 1}{\to} A \otimes_S V \overset{d_1}{\to} A. \end{align*} $$
$$ \begin{align*} V^{\otimes n} = V^{\otimes (n-1)} \otimes_S V \overset{\phi_{n-1} \otimes 1}{\to} A \otimes_S V \overset{d_1}{\to} A. \end{align*} $$
Now
![]() $\phi _{n-1}$
is injective by the inductive hypothesis. Because V is a flat S-module (as S is semisimple), it follows that
$\phi _{n-1}$
is injective by the inductive hypothesis. Because V is a flat S-module (as S is semisimple), it follows that
![]() $\phi _{n-1} \otimes 1$
is injective. Thus
$\phi _{n-1} \otimes 1$
is injective. Thus
![]() $\phi _n$
is injective as desired. So we find that
$\phi _n$
is injective as desired. So we find that
![]() $\phi $
is an isomorphism.
$\phi $
is an isomorphism.
Thus
![]() $T_S(V) \cong A$
, so that that this tensor algebra is locally finite; as mentioned above, this implies that
$T_S(V) \cong A$
, so that that this tensor algebra is locally finite; as mentioned above, this implies that
![]() $V^{\otimes N}$
is positively graded for some
$V^{\otimes N}$
is positively graded for some
![]() $N \geq 1$
. Now since A is twisted Calabi–Yau of dimension
$N \geq 1$
. Now since A is twisted Calabi–Yau of dimension
![]() $1$
, Theorem 5.15 implies that it is also generalized AS regular of dimension
$1$
, Theorem 5.15 implies that it is also generalized AS regular of dimension
![]() $1$
and that S is separable. Finally, V must be invertible by Theorem 6.10.
$1$
and that S is separable. Finally, V must be invertible by Theorem 6.10.
![]() $(2) \implies (1)$
: Because
$(2) \implies (1)$
: Because
![]() $V^{\otimes N}$
is positively graded, the algebra
$V^{\otimes N}$
is positively graded, the algebra
![]() $A \cong T_S(V)$
is locally finite. The hypothesis now implies that A is generalized AS regular of dimension
$A \cong T_S(V)$
is locally finite. The hypothesis now implies that A is generalized AS regular of dimension
![]() $1$
, by Theorem 6.10. Since we also assume that S is separable, A is twisted Calabi–Yau of dimension
$1$
, by Theorem 6.10. Since we also assume that S is separable, A is twisted Calabi–Yau of dimension
![]() $1$
by Theorem 5.15.
$1$
by Theorem 5.15.
The proof of
![]() $(1) \implies (2)$
above uses separability of S in an essential way. We don’t know the answer to the following.
$(1) \implies (2)$
above uses separability of S in an essential way. We don’t know the answer to the following.
Question 6.12. If A is locally finite graded and generalized AS regular of dimension
![]() $1$
, must A be isomorphic to a tensor algebra
$1$
, must A be isomorphic to a tensor algebra
![]() $T_S(V)$
for some graded finite-dimensional
$T_S(V)$
for some graded finite-dimensional
![]() $(S, S)$
-bimodule V?
$(S, S)$
-bimodule V?
7 Examples
As mentioned earlier, a graded invertible bimodule over a locally finite graded algebra A need not have the form
![]() ${{\hspace {-0.0001pt}}}^1 A^\sigma $
. Here is a simple example.
${{\hspace {-0.0001pt}}}^1 A^\sigma $
. Here is a simple example.
Example 7.1. Let k be a field and let
![]() $A = k \oplus \mathbb {M}_2(k)$
, considered as a graded algebra with
$A = k \oplus \mathbb {M}_2(k)$
, considered as a graded algebra with
![]() $A = A_0$
. Decompose
$A = A_0$
. Decompose
![]() $1 = e_1 + e_2 + e_3$
as a sum of primitive orthogonal idempotents, where
$1 = e_1 + e_2 + e_3$
as a sum of primitive orthogonal idempotents, where
![]() $e_1 \in k$
and
$e_1 \in k$
and
![]() $e_2, e_3 \in \mathbb {M}_2(k)$
. Then
$e_2, e_3 \in \mathbb {M}_2(k)$
. Then
![]() $A e_1$
is a simple module of k-dimension
$A e_1$
is a simple module of k-dimension
![]() $1$
, and
$1$
, and
![]() $A e_2 \cong A e_3$
are simple modules of k-dimension
$A e_2 \cong A e_3$
are simple modules of k-dimension
![]() $2$
.
$2$
.
Let
![]() $U = A e_1 \oplus A e_1 \oplus A e_2$
. Then U is a projective left A-module which is obviously also a generator, so that
$U = A e_1 \oplus A e_1 \oplus A e_2$
. Then U is a projective left A-module which is obviously also a generator, so that
![]() $B = {\mathrm {{End}}}_A(U)$
is Morita equivalent to A. Since
$B = {\mathrm {{End}}}_A(U)$
is Morita equivalent to A. Since
![]() $ {\mathrm {{Hom}}}_A(A e_1, A e_2) = 0 = {\mathrm {{Hom}}}_A(A e_2, A e_1)$
we in fact have
$ {\mathrm {{Hom}}}_A(A e_1, A e_2) = 0 = {\mathrm {{Hom}}}_A(A e_2, A e_1)$
we in fact have
 $$ \begin{align*} B = {\mathrm{{End}}}_A(U) \cong {\mathrm{{End}}}_A((Ae_1)^{\oplus 2}) \oplus {\mathrm{{End}}}_A( A e_2) \cong M_2(k) \oplus k \cong A. \end{align*} $$
$$ \begin{align*} B = {\mathrm{{End}}}_A(U) \cong {\mathrm{{End}}}_A((Ae_1)^{\oplus 2}) \oplus {\mathrm{{End}}}_A( A e_2) \cong M_2(k) \oplus k \cong A. \end{align*} $$
Thus U carries the structure of a graded invertible
![]() $(A, A)$
-bimodule. On the other hand, U and A are not isomorphic as left A-modules because they have different composition factors (even different dimensions over k). Thus U cannot be of the form
$(A, A)$
-bimodule. On the other hand, U and A are not isomorphic as left A-modules because they have different composition factors (even different dimensions over k). Thus U cannot be of the form
![]() $^1 A^{\sigma }$
for any automorphism
$^1 A^{\sigma }$
for any automorphism
![]() $\sigma $
.
$\sigma $
.
We can use a similar idea as in the previous example to construct an example of a twisted Calabi–Yau algebra A whose Nakayama bimodule U is not of the form
![]() ${{\hspace {-0.0001pt}}}^1 A^\sigma $
for any automorphism
${{\hspace {-0.0001pt}}}^1 A^\sigma $
for any automorphism
![]() $\sigma $
of A.
$\sigma $
of A.
Example 7.2. Recall that if G is a finite group acting via automorphisms on an algebra A, then we can construct the skew group algebra
![]() $A \rtimes G$
: as a vector space this is
$A \rtimes G$
: as a vector space this is
![]() $A \otimes kG$
, but the multiplication is defined by
$A \otimes kG$
, but the multiplication is defined by
![]() $(a \otimes g)(b \otimes h) = ag(b) \otimes gh$
for
$(a \otimes g)(b \otimes h) = ag(b) \otimes gh$
for
![]() $a, b \in A$
and
$a, b \in A$
and
![]() $g, h \in G$
. When A is locally finite graded and G acts by graded automorphisms, then
$g, h \in G$
. When A is locally finite graded and G acts by graded automorphisms, then
![]() $A \rtimes G$
is again locally finite graded, where the elements of G have degree
$A \rtimes G$
is again locally finite graded, where the elements of G have degree
![]() $0$
.
$0$
.
Assume that k has characteristic not equal to
![]() $2$
. Let
$2$
. Let
![]() $A = k[x,y] \rtimes \mathbb {Z}_2$
, where the nonidentity element of
$A = k[x,y] \rtimes \mathbb {Z}_2$
, where the nonidentity element of
![]() $\mathbb {Z}_2$
acts via the automorphism
$\mathbb {Z}_2$
acts via the automorphism
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha (x) = x, \alpha (y) = -y$
. The structure of A can be seen to be a quiver algebra modulo certain relations using the McKay correspondence; we refer readers to [Reference Bocklandt, Schedler and Wemyss6, Corollary 4.1] for details. It is known that
$\alpha (x) = x, \alpha (y) = -y$
. The structure of A can be seen to be a quiver algebra modulo certain relations using the McKay correspondence; we refer readers to [Reference Bocklandt, Schedler and Wemyss6, Corollary 4.1] for details. It is known that
![]() $A = kQ/I$
, where Q is the McKay quiver of the action; in this case Q has two vertices, one loop
$A = kQ/I$
, where Q is the McKay quiver of the action; in this case Q has two vertices, one loop
![]() $x_i$
at each vertex i, an arrow
$x_i$
at each vertex i, an arrow
![]() $y_1$
from vertex 1 to vertex 2, and an arrow
$y_1$
from vertex 1 to vertex 2, and an arrow
![]() $y_2$
from vertex 2 to vertex 1. The ideal I is generated by
$y_2$
from vertex 2 to vertex 1. The ideal I is generated by
![]() $x_1 y_1 - y_2 x_1$
and
$x_1 y_1 - y_2 x_1$
and
![]() $x_2 y_2 - y_1 x_2$
, where we compose arrows from left to right. We also have
$x_2 y_2 - y_1 x_2$
, where we compose arrows from left to right. We also have
![]() $A_0 = ke_1 + ke_2$
where
$A_0 = ke_1 + ke_2$
where
![]() $e_1$
and
$e_1$
and
![]() $e_2$
are the trivial paths. By [Reference Reyes, Rogalski and Zhang37, Theorem 4.1], A is twisted Calabi–Yau of dimension
$e_2$
are the trivial paths. By [Reference Reyes, Rogalski and Zhang37, Theorem 4.1], A is twisted Calabi–Yau of dimension
![]() $2$
(the term skew Calabi–Yau is used there), and its Nakayama bimodule is
$2$
(the term skew Calabi–Yau is used there), and its Nakayama bimodule is
 $U = {{\hspace {-0.0001pt}}}^1 A^{\mu }(2)$
, where the Nakayama automorphism
$U = {{\hspace {-0.0001pt}}}^1 A^{\mu }(2)$
, where the Nakayama automorphism
![]() $\mu $
is also calculated by that result. Explicitly,
$\mu $
is also calculated by that result. Explicitly,
![]() $\mu $
acts trivially on x and y, while
$\mu $
acts trivially on x and y, while
![]() $\mu (g) = {hdet}(g) g$
for
$\mu (g) = {hdet}(g) g$
for
![]() $g \in \mathbb {Z}_2$
. Here,
$g \in \mathbb {Z}_2$
. Here,
![]() $ {hdet}(g)$
is simply the determinant of the action of g on
$ {hdet}(g)$
is simply the determinant of the action of g on
![]() $kx + ky$
. Thus if
$kx + ky$
. Thus if
![]() $\mathbb {Z}_2 = \{1, a\}$
then
$\mathbb {Z}_2 = \{1, a\}$
then
![]() $\mu (a) = -a$
. Since
$\mu (a) = -a$
. Since
![]() $e_1 = (1 + a)/2$
and
$e_1 = (1 + a)/2$
and
![]() $e_2 = (1-a)/2$
, we see that
$e_2 = (1-a)/2$
, we see that
![]() $\mu $
switches the two idempotents in
$\mu $
switches the two idempotents in
![]() $A_0$
.
$A_0$
.
Now let
![]() $M_2(A)$
be the 2 by 2 matrix ring over A. By Proposition 4.11 and its proof, we have that
$M_2(A)$
be the 2 by 2 matrix ring over A. By Proposition 4.11 and its proof, we have that
![]() $M_2(A)$
is twisted Calabi–Yau with Nakayama bimodule
$M_2(A)$
is twisted Calabi–Yau with Nakayama bimodule
![]() $M_2(U)$
. Write
$M_2(U)$
. Write
![]() $1 = f_1 + f_2 + f_ 3 + f_4$
as a sum of primitive orthogonal idempotents in
$1 = f_1 + f_2 + f_ 3 + f_4$
as a sum of primitive orthogonal idempotents in
![]() $M_2(A)$
, where
$M_2(A)$
, where
 $$ \begin{align*} f_1 = \begin{pmatrix} e_1 & 0 \\ 0 & 0 \end{pmatrix}, \ f_2 = \begin{pmatrix} e_2 & 0 \\ 0 & 0 \end{pmatrix}, \ f_3 = \begin{pmatrix} 0 & 0 \\ 0 & e_1 \end{pmatrix}, \ f_4 = \begin{pmatrix} 0 & 0 \\ 0 & e_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} f_1 = \begin{pmatrix} e_1 & 0 \\ 0 & 0 \end{pmatrix}, \ f_2 = \begin{pmatrix} e_2 & 0 \\ 0 & 0 \end{pmatrix}, \ f_3 = \begin{pmatrix} 0 & 0 \\ 0 & e_1 \end{pmatrix}, \ f_4 = \begin{pmatrix} 0 & 0 \\ 0 & e_2 \end{pmatrix}. \end{align*} $$
Then
![]() $f_1 M_2(A) \cong f_3 M_2(A) $
and
$f_1 M_2(A) \cong f_3 M_2(A) $
and
![]() $f_2 M_2(A) \cong f_4 M_2(A)$
as right
$f_2 M_2(A) \cong f_4 M_2(A)$
as right
![]() $M_2(A)$
-modules. Thus the idempotent
$M_2(A)$
-modules. Thus the idempotent
![]() $g = f_1 + f_2 + f_3$
is full, so that the algebra
$g = f_1 + f_2 + f_3$
is full, so that the algebra
![]() $B = g M_2(A) g$
is Morita equivalent to A. By Proposition 4.11 and its proof, B is also twisted Calabi–Yau of dimension
$B = g M_2(A) g$
is Morita equivalent to A. By Proposition 4.11 and its proof, B is also twisted Calabi–Yau of dimension
![]() $2$
with Nakayama bimodule
$2$
with Nakayama bimodule
![]() $V = g M_2(U) g$
.
$V = g M_2(U) g$
.
Consider the right B-module structure of V. Note that the Morita equivalence
![]() $M \mapsto Mg$
from graded right
$M \mapsto Mg$
from graded right
![]() $M_2(A)$
-modules to graded right B-modules sends
$M_2(A)$
-modules to graded right B-modules sends
![]() $gM_2(U)$
to V. We have
$gM_2(U)$
to V. We have
![]() $gM_2(U) = f_1 M_2(U) \oplus f_2 M_2(U) \oplus f_3 M_2(U)$
, where
$gM_2(U) = f_1 M_2(U) \oplus f_2 M_2(U) \oplus f_3 M_2(U)$
, where
![]() $f_1 M_2(U) \cong (e_1 U, e_1 U) \cong f_3 M_2(U)$
, and
$f_1 M_2(U) \cong (e_1 U, e_1 U) \cong f_3 M_2(U)$
, and
![]() $f_2 M_2(U) \cong (e_2U, e_2 U)$
, as modules given by row vectors. Moreover, as (ungraded) right A-modules, we have
$f_2 M_2(U) \cong (e_2U, e_2 U)$
, as modules given by row vectors. Moreover, as (ungraded) right A-modules, we have
![]() $e_1 U = (e_1 A)^{\mu }$
; since
$e_1 U = (e_1 A)^{\mu }$
; since
![]() $\mu $
switches the idempotents it is easy to see that in fact
$\mu $
switches the idempotents it is easy to see that in fact
![]() $e_1 U \cong e_2 A$
as right modules. Similarly,
$e_1 U \cong e_2 A$
as right modules. Similarly,
![]() $e_2 U \cong e_1 A$
. Thus in fact the right
$e_2 U \cong e_1 A$
. Thus in fact the right
![]() $M_2(A)$
-module
$M_2(A)$
-module
![]() $g M_2(U)$
is, up to isomorphism, a direct sum of 2 copies of
$g M_2(U)$
is, up to isomorphism, a direct sum of 2 copies of
![]() $(e_2 A, e_2 A)$
and one copy of
$(e_2 A, e_2 A)$
and one copy of
![]() $(e_1 A, e_1 A)$
. On the other hand,
$(e_1 A, e_1 A)$
. On the other hand,
![]() $gM_2(A)$
is, up to isomorphism, a direct sum of 1 copy of
$gM_2(A)$
is, up to isomorphism, a direct sum of 1 copy of
![]() $(e_2 A, e_2 A)$
and 2 copies of
$(e_2 A, e_2 A)$
and 2 copies of
![]() $(e_1 A, e_1 A)$
. These same properties pass via the Morita equivalence to the ring B; and so B has two indecomposable projective right modules P and Q up to isomorphism, such that
$(e_1 A, e_1 A)$
. These same properties pass via the Morita equivalence to the ring B; and so B has two indecomposable projective right modules P and Q up to isomorphism, such that
![]() $B \cong P^{\oplus 2} \oplus Q$
and
$B \cong P^{\oplus 2} \oplus Q$
and
![]() $V \cong P \oplus Q^{\oplus 2}$
. So V is not a free right B-module and hence it cannot be of the form
$V \cong P \oplus Q^{\oplus 2}$
. So V is not a free right B-module and hence it cannot be of the form
![]() ${{\hspace {-0.0001pt}}}^1 B^{\sigma }$
for an automorphism
${{\hspace {-0.0001pt}}}^1 B^{\sigma }$
for an automorphism
![]() $\sigma $
.
$\sigma $
.
The previous example also shows that there really is a difference between the twisted Calabi–Yau property for locally finite graded algebras A and AS regularity over
![]() $A_0$
as defined by Minamoto and Mori (see Remark 5.7). For if B is the algebra constructed in the example, then since B is twisted Calabi–Yau it is also generalized AS regular. Considering condition (e
$A_0$
as defined by Minamoto and Mori (see Remark 5.7). For if B is the algebra constructed in the example, then since B is twisted Calabi–Yau it is also generalized AS regular. Considering condition (e
![]() ${}^{\prime}$
) in Theorem 5.2, we have
${}^{\prime}$
) in Theorem 5.2, we have
![]() $ {\mathrm {RHom}}_B(B_0, B)[2] \cong (B_0^* \otimes _{B_0} W)$
as
$ {\mathrm {RHom}}_B(B_0, B)[2] \cong (B_0^* \otimes _{B_0} W)$
as
![]() $(B_0, B_0)$
-bimodules, for some invertible graded
$(B_0, B_0)$
-bimodules, for some invertible graded
![]() $(B_0, B_0)$
-bimodule W. By the proof of Theorem 5.15, if V is the Nakayama bimodule of B then we have
$(B_0, B_0)$
-bimodule W. By the proof of Theorem 5.15, if V is the Nakayama bimodule of B then we have
![]() $W = B/B_{\geq 1} \otimes V$
. Since V is not a free B-module on the right, it is easy to see that W is not a free
$W = B/B_{\geq 1} \otimes V$
. Since V is not a free B-module on the right, it is easy to see that W is not a free
![]() $B_0$
-module on the right, and hence W is not of the form
$B_0$
-module on the right, and hence W is not of the form
 ${{\hspace {-0.0001pt}}}^1 B_0^{\sigma }$
. As mentioned in Remark 5.8, this also shows that the property of AS regularity over
${{\hspace {-0.0001pt}}}^1 B_0^{\sigma }$
. As mentioned in Remark 5.8, this also shows that the property of AS regularity over
![]() $A_0$
is not preserved under Morita equivalence, since B is Morita equivalent to the algebra
$A_0$
is not preserved under Morita equivalence, since B is Morita equivalent to the algebra
![]() $A = k[x,y] \rtimes \mathbb {Z}_2$
above and A is AS regular over
$A = k[x,y] \rtimes \mathbb {Z}_2$
above and A is AS regular over
![]() $A_0$
with
$A_0$
with
 $W = A/A_{\geq 1} \otimes _A U \cong {{\hspace {-0.0001pt}}}^1 A_0^\mu (2)$
.
$W = A/A_{\geq 1} \otimes _A U \cong {{\hspace {-0.0001pt}}}^1 A_0^\mu (2)$
.
Throughout the paper we have allowed arbitrary locally finite graded algebras A, without any assumption on the structure of
![]() $A_0$
. The most common examples of (twisted) Calabi–Yau algebras occur as
$A_0$
. The most common examples of (twisted) Calabi–Yau algebras occur as
![]() $A = kQ/I$
for a finite quiver Q, where the relations generating I come from taking derivatives of a superpotential; see, for example, [Reference Bocklandt, Schedler and Wemyss6]. In these examples, A has a natural grading where the arrows in Q have degree
$A = kQ/I$
for a finite quiver Q, where the relations generating I come from taking derivatives of a superpotential; see, for example, [Reference Bocklandt, Schedler and Wemyss6]. In these examples, A has a natural grading where the arrows in Q have degree
![]() $1$
, and hence
$1$
, and hence
![]() $A_0 \cong k^{\oplus n}$
is semisimple, where n is the number of vertices in the quiver. In many cases, however, it is possible to grade Q in a different manner so that the arrows have degrees possibly different from
$A_0 \cong k^{\oplus n}$
is semisimple, where n is the number of vertices in the quiver. In many cases, however, it is possible to grade Q in a different manner so that the arrows have degrees possibly different from
![]() $1$
, in a way that is compatible with the relations. Choosing some arrows to have degree
$1$
, in a way that is compatible with the relations. Choosing some arrows to have degree
![]() $0$
, one obtains examples with more interesting
$0$
, one obtains examples with more interesting
![]() $A_0$
. The following is one special case.
$A_0$
. The following is one special case.
Example 7.3. Let Q be a finite connected quiver. Let
![]() $\overline {Q}$
be the double of Q, obtained by adding an arrow
$\overline {Q}$
be the double of Q, obtained by adding an arrow
![]() $\alpha ^*$
in the opposite direction for each arrow
$\alpha ^*$
in the opposite direction for each arrow
![]() $\alpha $
in Q. The corresponding preprojective algebra is
$\alpha $
in Q. The corresponding preprojective algebra is
 $A = k\overline {Q}/(r)$
, where
$A = k\overline {Q}/(r)$
, where
![]() $r = \sum _{\alpha } \alpha \alpha ^* - \alpha ^* \alpha $
, the sum over all arrows
$r = \sum _{\alpha } \alpha \alpha ^* - \alpha ^* \alpha $
, the sum over all arrows
![]() $\alpha $
. As long as Q is not a Dynkin quiver, it is known that A is Calabi–Yau of dimension
$\alpha $
. As long as Q is not a Dynkin quiver, it is known that A is Calabi–Yau of dimension
![]() $2$
. This follows because the matrix Hilbert series of A is as expected [Reference Etingof and Eu15, Theorem 3.4.1], [Reference Reyes and Rogalski40, Lemma 7.6].
$2$
. This follows because the matrix Hilbert series of A is as expected [Reference Etingof and Eu15, Theorem 3.4.1], [Reference Reyes and Rogalski40, Lemma 7.6].
If one regrades A by choosing all nonstarred arrows to have degree
![]() $0$
, then the relation r is still homogeneous (now of degree
$0$
, then the relation r is still homogeneous (now of degree
![]() $1$
), so A obtains a different grading where
$1$
), so A obtains a different grading where
![]() $A_0 \cong kQ$
. In case Q has no oriented cycles, this regraded A is still locally finite, and consequently it is still (graded) Calabi–Yau since this property does not depend on the grading thanks to Theorem 4.2. Thus for connected quivers Q that are not Dynkin and have no oriented cycles, the preprojective algebra A regraded with nonstarred arrows having degree
$A_0 \cong kQ$
. In case Q has no oriented cycles, this regraded A is still locally finite, and consequently it is still (graded) Calabi–Yau since this property does not depend on the grading thanks to Theorem 4.2. Thus for connected quivers Q that are not Dynkin and have no oriented cycles, the preprojective algebra A regraded with nonstarred arrows having degree
![]() $0$
gives a locally finite graded Calabi–Yau algebra with
$0$
gives a locally finite graded Calabi–Yau algebra with
![]() $A_0 = kQ$
.
$A_0 = kQ$
.
Acknowledgments
We would like to thank James Zhang for helpful conversations and Stephan Weispfenning for helpful comments about earlier drafts of this paper. We are particularly grateful to Jeremy Rickard for allowing us to use his ideas in the proof of Theorem 1.3. Finally, we thank the referees for their careful reading of this paper, providing a number of suggestions that have improved the readability of this paper as well as interesting suggestions for future problems.