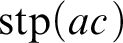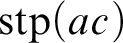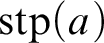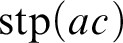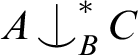0. Introduction and background
Given a complete theory T, the notion of the Lascar (Galois) group
![]() $\operatorname {Gal}_{\operatorname {L}}(T)$
was introduced by D. Lascar (see [Reference Casanovas, Lascar, Pillay and Ziegler2]). The Lascar group only depends on the theory and it is a quasi-compact topological group with respect to a quotient topology of a certain Stone type space over a model ([Reference Casanovas, Lascar, Pillay and Ziegler2] or [Reference Ziegler and Tent13]). More recently, the notions of the relativized Lascar groups were introduced in [Reference Dobrowolski, Kim and Lee3] (and studied also in [Reference Krupiński, Newelski and Simon11] in the context of topological dynamics). Namely, given a type-definable set X in a large saturated model of the theory T, we consider the group of automorphisms restricted to the set X quotiented by the group of restricted automorphisms fixing the Lascar types of the sequences from X of length
$\operatorname {Gal}_{\operatorname {L}}(T)$
was introduced by D. Lascar (see [Reference Casanovas, Lascar, Pillay and Ziegler2]). The Lascar group only depends on the theory and it is a quasi-compact topological group with respect to a quotient topology of a certain Stone type space over a model ([Reference Casanovas, Lascar, Pillay and Ziegler2] or [Reference Ziegler and Tent13]). More recently, the notions of the relativized Lascar groups were introduced in [Reference Dobrowolski, Kim and Lee3] (and studied also in [Reference Krupiński, Newelski and Simon11] in the context of topological dynamics). Namely, given a type-definable set X in a large saturated model of the theory T, we consider the group of automorphisms restricted to the set X quotiented by the group of restricted automorphisms fixing the Lascar types of the sequences from X of length
![]() $\lambda $
. The relativized Lascar groups also only depend on T, on the type that defines X, and on the cardinal
$\lambda $
. The relativized Lascar groups also only depend on T, on the type that defines X, and on the cardinal
![]() $\lambda $
. These groups are endowed with the quasi-compact quotient topologies induced by the canonical surjective maps from
$\lambda $
. These groups are endowed with the quasi-compact quotient topologies induced by the canonical surjective maps from
![]() $\operatorname {Gal}_{\operatorname {L}}(T)$
to the relativized Lascar groups.
$\operatorname {Gal}_{\operatorname {L}}(T)$
to the relativized Lascar groups.
This paper continues the study started in [Reference Dobrowolski, Kim and Lee3], where a connection between the relativized Lascar groups of a strong type and the first homology group of the strong type was established. If T is G-compact (for example when T is simple), then the relativized Lascar group of a strong type is compact and connected, and we use compact group theory to obtain results presented here.
A common theme for the results in this paper is the connection between group theoretic properties of the Lascar group of a strong type and the model theoretic properties of the type. In Section 1, we use the fact that any compact connected group is divisible to show that any strong type p in a simple theory has a property we call divisible amalgamation. The property would follow from the Independence Theorem if p was a Lascar type, but here p is only assumed to be a strong type. Moreover, we give amalgamation criteria for when the Lascar group of the strong type of a model is abelian, and for when the strong type of a model is a Lascar type.
In Section 2, we study morphisms between the relativized Lascar groups. The main goal is to understand the connection between the Lascar group of
![]() $\operatorname {stp}(a)$
, for some tuple a, and the Lascar group of
$\operatorname {stp}(a)$
, for some tuple a, and the Lascar group of
![]() $\operatorname {stp}(\operatorname {acl}(a))$
or
$\operatorname {stp}(\operatorname {acl}(a))$
or
![]() $\operatorname {stp}(ac)$
, for a finite tuple
$\operatorname {stp}(ac)$
, for a finite tuple
![]() $c\in \operatorname {acl}(a)$
. We prove that if T is G-compact, then for a finite tuple c algebraic over a, the restriction map from a Lascar group of
$c\in \operatorname {acl}(a)$
. We prove that if T is G-compact, then for a finite tuple c algebraic over a, the restriction map from a Lascar group of
![]() $\operatorname {stp}(ac)$
to that of
$\operatorname {stp}(ac)$
to that of
![]() $\operatorname {stp}(a)$
is a covering map. In addition, if the Lascar group of
$\operatorname {stp}(a)$
is a covering map. In addition, if the Lascar group of
![]() $\operatorname {stp}(ac)$
is abelian then this group is isomorphic to that of
$\operatorname {stp}(ac)$
is abelian then this group is isomorphic to that of
![]() $\operatorname {stp}(a)$
as topological groups. In order to achieve this, we separately prove a purely compact group theoretical result that any compact connected abelian group is isomorphic to its quotient by a finite subgroup. We also give an example showing that the abelianity of the relativized Lascar group is essential in the isomorphism result.
$\operatorname {stp}(a)$
as topological groups. In order to achieve this, we separately prove a purely compact group theoretical result that any compact connected abelian group is isomorphic to its quotient by a finite subgroup. We also give an example showing that the abelianity of the relativized Lascar group is essential in the isomorphism result.
In Section 3, we mainly present three counterexamples: a non-G-compact theory where
![]() $\operatorname {stp}(a)$
is a Lascar type but
$\operatorname {stp}(a)$
is a Lascar type but
![]() $\operatorname {stp}(\operatorname {acl}(a))$
is not a Lascar type; an example showing that in the above-mentioned isomorphism result in Section 2, the tuple c being finite is essential; and an example answering a question raised in [Reference Kim and Lee10], namely a Lie group structure example where an RN-pattern minimal 2-chain is not equivalent to a Lascar pattern 2-chain having the same boundary.
$\operatorname {stp}(\operatorname {acl}(a))$
is not a Lascar type; an example showing that in the above-mentioned isomorphism result in Section 2, the tuple c being finite is essential; and an example answering a question raised in [Reference Kim and Lee10], namely a Lie group structure example where an RN-pattern minimal 2-chain is not equivalent to a Lascar pattern 2-chain having the same boundary.
Let us remark that the results of Section 2 and the supplementary examples from Sections 3.1 and 3.2 do not make any use of the homology groups
![]() $H_1(p)$
, so a reader interested only in these results is advised to skip from Fact 0.4 to Section 2.
$H_1(p)$
, so a reader interested only in these results is advised to skip from Fact 0.4 to Section 2.
In the remaining part of this section we recall the definitions and terminology of basic notions, which, unless said otherwise, we use throughout this note. We work in a large saturated model
![]() ${\mathcal M}(={\mathcal M}^{\operatorname {eq}})$
of a complete theory T, and we use the standard notation. So
${\mathcal M}(={\mathcal M}^{\operatorname {eq}})$
of a complete theory T, and we use the standard notation. So
![]() $A, B,\dots $
and
$A, B,\dots $
and
![]() $M,N,\dots $
are small subsets and elementary submodels of
$M,N,\dots $
are small subsets and elementary submodels of
![]() ${\mathcal M}$
, respectively. Lower-case letters
${\mathcal M}$
, respectively. Lower-case letters
![]() $a,b,\dots $
will denote tuples of elements from
$a,b,\dots $
will denote tuples of elements from
![]() ${\mathcal M}$
, possibly infinite. We will explicitly specify when a tuple is assumed to be finite.
${\mathcal M}$
, possibly infinite. We will explicitly specify when a tuple is assumed to be finite.
To simplify the notation, we state the results for types over the empty set (rather than over
![]() $\operatorname {acl}(\emptyset )$
). This does not reduce the generality because, after naming a parameter set, we assume for the rest that
$\operatorname {acl}(\emptyset )$
). This does not reduce the generality because, after naming a parameter set, we assume for the rest that
![]() $\operatorname {dcl}(\emptyset )(=\operatorname {dcl}^{\operatorname {eq}}(\emptyset ))=\operatorname {acl}(\emptyset )(=\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
. We fix a complete strong type
$\operatorname {dcl}(\emptyset )(=\operatorname {dcl}^{\operatorname {eq}}(\emptyset ))=\operatorname {acl}(\emptyset )(=\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
. We fix a complete strong type
![]() $p(x)\in S(\emptyset )$
with possibly infinite arity of x. For tuples
$p(x)\in S(\emptyset )$
with possibly infinite arity of x. For tuples
![]() $a,b$
, we write
$a,b$
, we write
![]() $a\equiv _Ab$
(
$a\equiv _Ab$
(
![]() $a\equiv ^s_Ab$
, resp.) to mean that they have the same (strong, resp.) type over A. Note that
$a\equiv ^s_Ab$
, resp.) to mean that they have the same (strong, resp.) type over A. Note that
![]() $a\equiv ^s_Ab$
if and only if
$a\equiv ^s_Ab$
if and only if
![]() $a\equiv _{\operatorname {acl}(A)}b$
.
$a\equiv _{\operatorname {acl}(A)}b$
.
Let us recall the definitions of the Lascar groups and types. These are well-known notions in model theory. In particular, the Lascar group depends only on T and is a quasi-compact group under the topology introduced in [Reference Casanovas, Lascar, Pillay and Ziegler2] or [Reference Ziegler and Tent13]. Moreover, due to our assumption
![]() $\operatorname {dcl}(\emptyset )=\operatorname {acl}(\emptyset )$
, the group is connected as well. Recall that a topological space is compact if it is quasi-compact and Hausdorff.
$\operatorname {dcl}(\emptyset )=\operatorname {acl}(\emptyset )$
, the group is connected as well. Recall that a topological space is compact if it is quasi-compact and Hausdorff.
-
•
 $\operatorname {Autf}({\mathcal M})$
is the normal subgroup of
$\operatorname {Autf}({\mathcal M})$
is the normal subgroup of
 $\operatorname {Aut}({\mathcal M})$
generated by
$\operatorname {Aut}({\mathcal M})$
generated by  $$ \begin{align*}\{f \in \operatorname{Aut}({\mathcal M}) \mid f \mbox{ fixes some model } M \prec {\mathcal M} \mbox{ pointwise}\}.\end{align*} $$
$$ \begin{align*}\{f \in \operatorname{Aut}({\mathcal M}) \mid f \mbox{ fixes some model } M \prec {\mathcal M} \mbox{ pointwise}\}.\end{align*} $$
-
• For tuples
 $a,b \in {\mathcal M}$
, we say they have the same Lascar type, written
$a,b \in {\mathcal M}$
, we say they have the same Lascar type, written
 $a\equiv ^Lb$
or
$a\equiv ^Lb$
or
 $\operatorname {Ltp}(a)=\operatorname {Ltp}(b)$
, if there is
$\operatorname {Ltp}(a)=\operatorname {Ltp}(b)$
, if there is
 $f\in \operatorname {Autf}({\mathcal M}) $
such that
$f\in \operatorname {Autf}({\mathcal M}) $
such that
 $f(a)=b$
. We say
$f(a)=b$
. We say
 $a,b$
have the same KP(Kim–Pillay)-type (write
$a,b$
have the same KP(Kim–Pillay)-type (write
 $a\equiv ^{KP} b$
) if they are in the same class of any bounded
$a\equiv ^{KP} b$
) if they are in the same class of any bounded
 $\emptyset $
-type-definable equivalence relation.
$\emptyset $
-type-definable equivalence relation. -
• The group
 $\operatorname {Gal}_{\operatorname {L}}(T):=\operatorname {Aut}({\mathcal M})/\operatorname {Autf}({\mathcal M})$
is called the Lascar (
Galois
) group of T.
$\operatorname {Gal}_{\operatorname {L}}(T):=\operatorname {Aut}({\mathcal M})/\operatorname {Autf}({\mathcal M})$
is called the Lascar (
Galois
) group of T. -
• We say T is G-compact if
 $\operatorname {Gal}_{\operatorname {L}}(T)$
is compact; equivalently
$\operatorname {Gal}_{\operatorname {L}}(T)$
is compact; equivalently
 $\{\mbox {id}\}$
is closed in
$\{\mbox {id}\}$
is closed in
 $\operatorname {Gal}_{\operatorname {L}}(T)$
; also equivalently
$\operatorname {Gal}_{\operatorname {L}}(T)$
; also equivalently
 $a\equiv ^L b$
iff
$a\equiv ^L b$
iff
 $a\equiv ^{KP} b$
for any (possibly infinite) tuples
$a\equiv ^{KP} b$
for any (possibly infinite) tuples
 $a,b$
from
$a,b$
from
 ${\mathcal M}$
[Reference Kim8].
${\mathcal M}$
[Reference Kim8].
Note that the above is the definition of “G-compactness over
![]() $\emptyset $
,” but for convenience throughout this paper we omit “over
$\emptyset $
,” but for convenience throughout this paper we omit “over
![]() $\emptyset $
.”
$\emptyset $
.”
Fact 0.2. For tuples
![]() $a,b$
, we have
$a,b$
, we have
![]() $a\equiv ^L b$
if and only if the Lascar distance between a and b is finite, i.e., there are finitely many indiscernible sequences
$a\equiv ^L b$
if and only if the Lascar distance between a and b is finite, i.e., there are finitely many indiscernible sequences
![]() $I_1,\ldots , I_n$
, and tuples
$I_1,\ldots , I_n$
, and tuples
![]() $a=a_0, a_1,\ldots , a_n=b$
such that each of
$a=a_0, a_1,\ldots , a_n=b$
such that each of
![]() $a_{i-1}I_i$
and
$a_{i-1}I_i$
and
![]() $a_iI_i$
is an indiscernible sequence for
$a_iI_i$
is an indiscernible sequence for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
Now let us recall, mainly from [Reference Dobrowolski, Kim and Lee3], the definitions of various relativized Lascar groups of p and related facts.
-
•
 $\operatorname {Aut}(p):=\{ f \restriction p({\mathcal M}) \mid f\in \operatorname {Aut}({\mathcal M})\}$
;
$\operatorname {Aut}(p):=\{ f \restriction p({\mathcal M}) \mid f\in \operatorname {Aut}({\mathcal M})\}$
; -
• for a cardinal
 $\lambda> 0$
,
$\lambda> 0$
,
 $\operatorname {Autf}^{\lambda }(p)=\operatorname {Autf}_{\operatorname {fix}}^{\lambda }(p):=$
$\operatorname {Autf}^{\lambda }(p)=\operatorname {Autf}_{\operatorname {fix}}^{\lambda }(p):=$
 $$ \begin{align*}\{\sigma\in \operatorname{Aut}(p)\mid \mbox{ for any } \bar{a}=(a_i)_{i< \lambda} \mbox{ with } a_i\models p, \ \bar{a}\equiv^L \sigma(\bar{a}) \};\end{align*} $$
$$ \begin{align*}\{\sigma\in \operatorname{Aut}(p)\mid \mbox{ for any } \bar{a}=(a_i)_{i< \lambda} \mbox{ with } a_i\models p, \ \bar{a}\equiv^L \sigma(\bar{a}) \};\end{align*} $$
-
•
 $\operatorname {Autf}_{\operatorname {fix}}(p):=$
and
$\operatorname {Autf}_{\operatorname {fix}}(p):=$
and $$ \begin{align*}\{\sigma\in \operatorname{Aut}(p) \mid \bar{a}\equiv^L \sigma(\bar{a})\mbox{ where } \bar{a} \mbox{ is some enumeration of } p({\mathcal M}) \};\end{align*} $$
$$ \begin{align*}\{\sigma\in \operatorname{Aut}(p) \mid \bar{a}\equiv^L \sigma(\bar{a})\mbox{ where } \bar{a} \mbox{ is some enumeration of } p({\mathcal M}) \};\end{align*} $$
 $\operatorname {Autf}_{\operatorname {res}}(p):=\{ f \restriction p({\mathcal M}) \mid f\in \operatorname {Autf}({\mathcal M})\}$
.
$\operatorname {Autf}_{\operatorname {res}}(p):=\{ f \restriction p({\mathcal M}) \mid f\in \operatorname {Autf}({\mathcal M})\}$
.
Notice that
 $\operatorname {Autf}^{\lambda }(p)$
,
$\operatorname {Autf}^{\lambda }(p)$
,
![]() $\operatorname {Autf}_{\operatorname {fix}}(p)$
, and
$\operatorname {Autf}_{\operatorname {fix}}(p)$
, and
![]() $\operatorname {Autf}_{\operatorname {res}}(p)$
are normal subgroups of
$\operatorname {Autf}_{\operatorname {res}}(p)$
are normal subgroups of
![]() $\operatorname {Aut}(p)$
.
$\operatorname {Aut}(p)$
.
-
•
 $\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}, \lambda }(p):=\operatorname {Aut}(p)/\operatorname {Autf}^{\lambda }(p)$
;Footnote
1
$\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}, \lambda }(p):=\operatorname {Aut}(p)/\operatorname {Autf}^{\lambda }(p)$
;Footnote
1
-
•
 $\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}}(p):=\operatorname {Aut}(p)/\operatorname {Autf}_{\operatorname {fix}}(p)$
, and
$\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}}(p):=\operatorname {Aut}(p)/\operatorname {Autf}_{\operatorname {fix}}(p)$
, and
 $\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p):=\operatorname {Aut}(p)/\operatorname {Autf}_{\operatorname {res}}(p)$
.
$\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p):=\operatorname {Aut}(p)/\operatorname {Autf}_{\operatorname {res}}(p)$
.
We will give an example (in Example 2.3) where
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
and
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
and
 $\operatorname {Gal}_{\operatorname {L}}^2(p)$
are distinct. In [Reference Dobrowolski, Kim and Lee3, Remark 3.4], a canonical topology on each of the above groups was defined. With these topologies, they become quotients of the topological group
$\operatorname {Gal}_{\operatorname {L}}^2(p)$
are distinct. In [Reference Dobrowolski, Kim and Lee3, Remark 3.4], a canonical topology on each of the above groups was defined. With these topologies, they become quotients of the topological group
![]() $\operatorname {Gal}_{\operatorname {L}}(T)$
.
$\operatorname {Gal}_{\operatorname {L}}(T)$
.
Fact 0.4 [Reference Dobrowolski, Kim and Lee3]
![]() $\operatorname {Autf}^{\omega }(p)=\operatorname {Autf}_{\operatorname {fix}}(p)$
, and, for each
$\operatorname {Autf}^{\omega }(p)=\operatorname {Autf}_{\operatorname {fix}}(p)$
, and, for each
![]() $\lambda (\leq \omega )$
,
$\lambda (\leq \omega )$
,
 $\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
does not depend on the choice of a monster model, and is a quasi-compact connected topological group. Hence, if T is G-compact,
$\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
does not depend on the choice of a monster model, and is a quasi-compact connected topological group. Hence, if T is G-compact,
 $\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
is a compact connected group.
$\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
is a compact connected group.
If
![]() $p(x)$
is a type of a model, then
$p(x)$
is a type of a model, then
 $\operatorname {Autf}^1(p)=\operatorname {Autf}_{\operatorname {fix}}(p)=\operatorname {Autf}_{\operatorname {res}}(p)$
,
$\operatorname {Autf}^1(p)=\operatorname {Autf}_{\operatorname {fix}}(p)=\operatorname {Autf}_{\operatorname {res}}(p)$
,
 $\operatorname {Gal}_{\operatorname {L}}^1(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}}(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p)\cong \operatorname {Gal}_{\operatorname {L}}(T)$
. The abelianization of
$\operatorname {Gal}_{\operatorname {L}}^1(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}}(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p)\cong \operatorname {Gal}_{\operatorname {L}}(T)$
. The abelianization of
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
(i.e., the group
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
(i.e., the group
 $\operatorname {Gal}_{\operatorname {L}}^1(p)/(\operatorname {Gal}_{\operatorname {L}}^1(p))'$
) is isomorphic to the first homology group
$\operatorname {Gal}_{\operatorname {L}}^1(p)/(\operatorname {Gal}_{\operatorname {L}}^1(p))'$
) is isomorphic to the first homology group
![]() $H_1(p)$
.
$H_1(p)$
.
The last statement in the above fact explains the connection between the relativized Lascar group and the model theoretic homology group
![]() $H_1$
of the type. Let us recall now the key definitions in the homology theory in model theory. We fix a ternary automorphism-invariant relation
$H_1$
of the type. Let us recall now the key definitions in the homology theory in model theory. We fix a ternary automorphism-invariant relation
![]() between small sets of
between small sets of
![]() ${\mathcal M}$
satisfying
${\mathcal M}$
satisfying
-
• finite character: for any sets
 $A,B,$
and C, we have
$A,B,$
and C, we have
 iff
iff
 for any finite tuples
for any finite tuples
 $a\in A$
and
$a\in A$
and
 $b\in B$
;
$b\in B$
; -
• normality: for any sets A, B, and C, if
 , then
, then
 ;
; -
• symmetry: for any sets
 $A,B,$
and C, we have
$A,B,$
and C, we have
 iff
iff
 ;
; -
• transitivity:
 iff
iff
 and
and
 , for any sets A and
, for any sets A and
 $B\subseteq C\subseteq D$
;
$B\subseteq C\subseteq D$
; -
• extension: for any sets A and
 $B\subseteq C$
, there is
$B\subseteq C$
, there is
 $A'\equiv _BA$
such that
$A'\equiv _BA$
such that
 .
.
Throughout this paper we call the above axioms the basic 5 axioms. We say that A is
![]() $*$
-independent from B over C if
$*$
-independent from B over C if
 . Notice that there is at least one such relation for any theory, namely, the trivial independence relation given by: For any sets
. Notice that there is at least one such relation for any theory, namely, the trivial independence relation given by: For any sets
![]() $A,B,C$
, put
$A,B,C$
, put
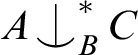 . Of course there is a non-trivial such relation when T is simple or rosy, given by forking or thorn-forking, respectively.
. Of course there is a non-trivial such relation when T is simple or rosy, given by forking or thorn-forking, respectively.
Notation 0.5. Let s be an arbitrary finite set of natural numbers. Given any subset
![]() $X\subseteq {\mathcal P}(s)$
, we may view X as a category where for any
$X\subseteq {\mathcal P}(s)$
, we may view X as a category where for any
![]() $u, v \in X$
,
$u, v \in X$
,
![]() $\operatorname {Mor}(u,v)$
consists of a single morphism
$\operatorname {Mor}(u,v)$
consists of a single morphism
![]() $\iota _{u,v}$
if
$\iota _{u,v}$
if
![]() $u\subseteq v$
, and
$u\subseteq v$
, and
![]() $\operatorname {Mor}(u,v)=\emptyset $
otherwise. If
$\operatorname {Mor}(u,v)=\emptyset $
otherwise. If
![]() $f\colon X \rightarrow {\mathcal C}_0$
is any functor into some category
$f\colon X \rightarrow {\mathcal C}_0$
is any functor into some category
![]() ${\mathcal C}_0$
, then for any
${\mathcal C}_0$
, then for any
![]() $u, v\in X$
with
$u, v\in X$
with
![]() $u \subseteq v$
, we let
$u \subseteq v$
, we let
![]() $f^u_v$
denote the morphism
$f^u_v$
denote the morphism
![]() $f(\iota _{u,v})\in \operatorname {Mor}_{{\mathcal C}_0}(f(u),f(v))$
. We shall call
$f(\iota _{u,v})\in \operatorname {Mor}_{{\mathcal C}_0}(f(u),f(v))$
. We shall call
![]() $X\subseteq {\mathcal P}(s)$
downward closed if for any
$X\subseteq {\mathcal P}(s)$
downward closed if for any
![]() $u, v\in {\mathcal P}(s)$
, if
$u, v\in {\mathcal P}(s)$
, if
![]() $u\subseteq v$
and
$u\subseteq v$
and
![]() $v\in X$
then
$v\in X$
then
![]() $u\in X$
. Note that if X is non-empty and downward closed then it has
$u\in X$
. Note that if X is non-empty and downward closed then it has
![]() $\emptyset \subseteq \omega $
as an object.
$\emptyset \subseteq \omega $
as an object.
We use now
![]() ${\mathcal C}$
to denote the category whose objects are the small subsets of
${\mathcal C}$
to denote the category whose objects are the small subsets of
![]() ${\mathcal M}$
, and whose morphisms are elementary maps. For a functor
${\mathcal M}$
, and whose morphisms are elementary maps. For a functor
![]() $f:X\to {\mathcal C}$
and objects
$f:X\to {\mathcal C}$
and objects
![]() $u\subseteq v$
of X,
$u\subseteq v$
of X,
![]() $f^u_v(u)$
denotes the set
$f^u_v(u)$
denotes the set
![]() $f^u_v(f(u))(\subseteq f(v))$
.
$f^u_v(f(u))(\subseteq f(v))$
.
Definition 0.6. By a
![]() $*$
-independent functor in p, we mean a functor f from some non-empty downward closed
$*$
-independent functor in p, we mean a functor f from some non-empty downward closed
![]() $X\subseteq {\mathcal P}(s)$
, viewed as a category as above, into
$X\subseteq {\mathcal P}(s)$
, viewed as a category as above, into
![]() ${\mathcal C}$
satisfying the following:
${\mathcal C}$
satisfying the following:
-
(1) If
 $\{ i \}\subseteq \omega $
is an object in X, then
$\{ i \}\subseteq \omega $
is an object in X, then
 $f(\{ i \})$
is of the form
$f(\{ i \})$
is of the form
 $\operatorname {acl}(Cb)$
where
$\operatorname {acl}(Cb)$
where
 $b\models p$
,
$b\models p$
,
 $C=\operatorname {acl}(C)=f^{\emptyset }_{\{ i \}}(\emptyset )$
, and
$C=\operatorname {acl}(C)=f^{\emptyset }_{\{ i \}}(\emptyset )$
, and
 .
. -
(2) Whenever
 $u(\neq \emptyset )\subseteq \omega $
is an object in X, we have and
$u(\neq \emptyset )\subseteq \omega $
is an object in X, we have and $$ \begin{align*} f( u) = \operatorname{acl} \left( \bigcup_{i\in u} f^{\{ i \}}_u(\{ i \}) \right) \end{align*} $$
$$ \begin{align*} f( u) = \operatorname{acl} \left( \bigcup_{i\in u} f^{\{ i \}}_u(\{ i \}) \right) \end{align*} $$
 $\{f^{\{i\}}_u(\{i\})|\ i\in u \}$
is
$\{f^{\{i\}}_u(\{i\})|\ i\in u \}$
is
 $*$
-independent over
$*$
-independent over
 $f^\emptyset _u(\emptyset )$
.
$f^\emptyset _u(\emptyset )$
.
We let
![]() ${\mathcal A}^*_p$
denote the family of all
${\mathcal A}^*_p$
denote the family of all
![]() $*$
-independent functors in p.
$*$
-independent functors in p.
A
![]() $*$
-independent functor f is called a
$*$
-independent functor f is called a
![]() $*$
-independent n-simplex in p if
$*$
-independent n-simplex in p if
![]() $f(\emptyset )=\emptyset $
, our named algebraically closed set, and
$f(\emptyset )=\emptyset $
, our named algebraically closed set, and
![]() $\operatorname {dom}(f)={\mathcal P}(s)$
with
$\operatorname {dom}(f)={\mathcal P}(s)$
with
![]() $s\subseteq \omega $
and
$s\subseteq \omega $
and
![]() $|s|=n+1$
. We call s the support of f and denote it by
$|s|=n+1$
. We call s the support of f and denote it by
![]() $\operatorname {supp}(f)$
.
$\operatorname {supp}(f)$
.
In the rest we may call a
![]() $*$
-independent n-simplex in p just an n-simplex of p, as far as no confusion arises.
$*$
-independent n-simplex in p just an n-simplex of p, as far as no confusion arises.
Definition 0.7. Let
![]() $n\geq 0$
. We define:
$n\geq 0$
. We define:
 $$ \begin{align*} &S_n({\mathcal A}^*_p):= \{\, f\in {\mathcal A}^*_p \mid f\ \mbox{is an}\ n\mbox{-simplex of}\ p\, \},\\ &C_n({\mathcal A}^*_p): = \mbox{the free abelian group generated by}\ S_n({\mathcal A}^*_p). \end{align*} $$
$$ \begin{align*} &S_n({\mathcal A}^*_p):= \{\, f\in {\mathcal A}^*_p \mid f\ \mbox{is an}\ n\mbox{-simplex of}\ p\, \},\\ &C_n({\mathcal A}^*_p): = \mbox{the free abelian group generated by}\ S_n({\mathcal A}^*_p). \end{align*} $$
An element of
 $C_n({\mathcal A}^*_p)$
is called an n-chain of p. The support of a chain c, denoted by
$C_n({\mathcal A}^*_p)$
is called an n-chain of p. The support of a chain c, denoted by
![]() $\operatorname {supp}(c)$
, is the union of the supports of all the simplices that appear in c with a non-zero coefficient. Now for
$\operatorname {supp}(c)$
, is the union of the supports of all the simplices that appear in c with a non-zero coefficient. Now for
![]() $n\geq 1$
and each
$n\geq 1$
and each
![]() $i=0, \ldots , n$
, we define a group homomorphism
$i=0, \ldots , n$
, we define a group homomorphism
 $$ \begin{align*} \partial^i_n\colon C_n({\mathcal A}^*_p) \rightarrow C_{n-1}({\mathcal A}^*_p) \end{align*} $$
$$ \begin{align*} \partial^i_n\colon C_n({\mathcal A}^*_p) \rightarrow C_{n-1}({\mathcal A}^*_p) \end{align*} $$
by putting, for any n-simplex
![]() $f\colon {\mathcal P}(s) \rightarrow {\mathcal C}$
in
$f\colon {\mathcal P}(s) \rightarrow {\mathcal C}$
in
 $S_n({\mathcal A}^*_p)$
where
$S_n({\mathcal A}^*_p)$
where
![]() $s = \{ s_0 <\cdots < s_n \}\subseteq \omega $
,
$s = \{ s_0 <\cdots < s_n \}\subseteq \omega $
,
and then extending linearly to all n-chains in
 $C_n({\mathcal A}^*_p)$
. Then we define the boundary map
$C_n({\mathcal A}^*_p)$
. Then we define the boundary map
 $$ \begin{align*} \partial_n\colon C_n({\mathcal A}^*_p)\rightarrow C_{n-1}({\mathcal A}^*_p) \end{align*} $$
$$ \begin{align*} \partial_n\colon C_n({\mathcal A}^*_p)\rightarrow C_{n-1}({\mathcal A}^*_p) \end{align*} $$
by
 $$ \begin{align*} \partial_n(c):=\sum_{0\leq i\leq n}(-1)^i \partial_n^i(c). \end{align*} $$
$$ \begin{align*} \partial_n(c):=\sum_{0\leq i\leq n}(-1)^i \partial_n^i(c). \end{align*} $$
We shall often refer to
![]() $\partial _n(c)$
as the boundary of c. Next, we define:
$\partial _n(c)$
as the boundary of c. Next, we define:
 $$ \begin{align*} &Z_n({\mathcal A}^*_p):= \operatorname{Ker} \, \partial_n,\\ & B_n({\mathcal A}^*_p):= \operatorname{Im} \, \partial_{n+1}. \end{align*} $$
$$ \begin{align*} &Z_n({\mathcal A}^*_p):= \operatorname{Ker} \, \partial_n,\\ & B_n({\mathcal A}^*_p):= \operatorname{Im} \, \partial_{n+1}. \end{align*} $$
The elements of
 $Z_n({\mathcal A}^*_p)$
and
$Z_n({\mathcal A}^*_p)$
and
 $B_n({\mathcal A}^*_p)$
are called n-cycles and n-boundaries in p, respectively. It is straightforward to check that
$B_n({\mathcal A}^*_p)$
are called n-cycles and n-boundaries in p, respectively. It is straightforward to check that
![]() $ \partial _{n}\circ \partial _{n+1} =0.$
Hence we can now define the group
$ \partial _{n}\circ \partial _{n+1} =0.$
Hence we can now define the group
 $$ \begin{align*} H^*_n(p):= Z_n({\mathcal A}^*_p)/B_n({\mathcal A}^*_p) \end{align*} $$
$$ \begin{align*} H^*_n(p):= Z_n({\mathcal A}^*_p)/B_n({\mathcal A}^*_p) \end{align*} $$
called the nth
![]() $*$
-homology group of p.
$*$
-homology group of p.
-
(1) For
 $c\in Z_n({\mathcal A}^*_p)$
,
$c\in Z_n({\mathcal A}^*_p)$
,
 $[c]$
denotes the homology class of c in
$[c]$
denotes the homology class of c in
 $H^*_n(p)$
.
$H^*_n(p)$
. -
(2) When n is clear from the context, we shall often omit it in
 $\partial ^i_n$
and in
$\partial ^i_n$
and in
 $\partial _n$
, writing simply
$\partial _n$
, writing simply
 $\partial ^i$
and
$\partial ^i$
and
 $\partial $
.
$\partial $
.
Definition 0.9. A
![]() $1$
-chain
$1$
-chain
 $c\in C_1({\mathcal A}^*_p)$
is called a
$c\in C_1({\mathcal A}^*_p)$
is called a
![]() $1$
-
$1$
-
![]() $*$
-shell (or just a
$*$
-shell (or just a
![]() $1$
-shell) in p if it is of the form
$1$
-shell) in p if it is of the form
where
![]() $f_i$
’s are
$f_i$
’s are
![]() $1$
-simplices of p satisfying
$1$
-simplices of p satisfying
 $$ \begin{align*} \partial^i f_j = \partial^{j-1} f_i \quad \mbox{whenever}\ 0\leq i < j \leq 2. \end{align*} $$
$$ \begin{align*} \partial^i f_j = \partial^{j-1} f_i \quad \mbox{whenever}\ 0\leq i < j \leq 2. \end{align*} $$
Hence, for
![]() $\operatorname {supp}(c)=\{n_0< n_1< n_2\}$
and
$\operatorname {supp}(c)=\{n_0< n_1< n_2\}$
and
![]() $ k\in \{0,1, 2\}$
, it follows that
$ k\in \{0,1, 2\}$
, it follows that
Notice that the boundary of any
![]() $2$
-simplex is a
$2$
-simplex is a
![]() $1$
-shell. Recall that a notion of an amenable collection of functors into a category is introduced in [Reference Goodrick, Kim, Kolesnikov, Jang, Kim, Lee and Yie5]. Due to the 5 axioms of
$1$
-shell. Recall that a notion of an amenable collection of functors into a category is introduced in [Reference Goodrick, Kim, Kolesnikov, Jang, Kim, Lee and Yie5]. Due to the 5 axioms of
![]() , it easily follows that
, it easily follows that
![]() ${\mathcal A}^*_p$
forms such a collection of functors into
${\mathcal A}^*_p$
forms such a collection of functors into
![]() ${\mathcal C}$
. Hence the following corresponding fact holds.
${\mathcal C}$
. Hence the following corresponding fact holds.
Fact 0.10 [Reference Goodrick, Kim, Kolesnikov, Jang, Kim, Lee and Yie5] or [Reference Dobrowolski, Kim and Lee3]
We now recall basic notions and results that appeared in [Reference Dobrowolski, Kim and Lee3]. For the rest of this section we assume that p is the strong type of an algebraically closed set.
-
(1) Let
 $f:{\mathcal P}(s)\to {\mathcal C}$
be an n-simplex of p. For
$f:{\mathcal P}(s)\to {\mathcal C}$
be an n-simplex of p. For
 $u\subseteq s$
with
$u\subseteq s$
with
 $u = \{ i_0 <\cdots < i_k \}$
, we shall write
$u = \{ i_0 <\cdots < i_k \}$
, we shall write
 $f(u)=[a_0 \ldots a_k]_u$
, where each
$f(u)=[a_0 \ldots a_k]_u$
, where each
 $a_j\models p$
is an algebraically closed tuple as assumed above, if
$a_j\models p$
is an algebraically closed tuple as assumed above, if
 $f(u)=\operatorname {acl}(a_0\ldots a_k)$
, and
$f(u)=\operatorname {acl}(a_0\ldots a_k)$
, and
 $\operatorname {acl}(a_j)=f^{ \{ i_j \} } _u (\{i_j\})$
. So,
$\operatorname {acl}(a_j)=f^{ \{ i_j \} } _u (\{i_j\})$
. So,
 $\{a_0,\ldots ,a_k\}$
is
$\{a_0,\ldots ,a_k\}$
is
 $*$
-independent. Of course, if we write
$*$
-independent. Of course, if we write
 $f(u)\equiv [b_0 \ldots b_k]_u$
, then it means that there is an automorphism sending
$f(u)\equiv [b_0 \ldots b_k]_u$
, then it means that there is an automorphism sending
 $a_0\ldots a_k$
to
$a_0\ldots a_k$
to
 $b_0\ldots b_k$
.
$b_0\ldots b_k$
. -
(2) Let
 $s=fv_{12}-f_{02}+f_{01}$
be a 1-
$s=fv_{12}-f_{02}+f_{01}$
be a 1-
 $*$
-shell in p such that
$*$
-shell in p such that
 $\operatorname {supp}(f_{ij})=\{n_i,n_j\}$
with
$\operatorname {supp}(f_{ij})=\{n_i,n_j\}$
with
 $n_i< n_j$
for
$n_i< n_j$
for
 $0\le i< j \le 2$
. Clearly there is a quadruple
$0\le i< j \le 2$
. Clearly there is a quadruple
 $(a_0,a_1,a_2,a_3)$
of realizations of p such that
$(a_0,a_1,a_2,a_3)$
of realizations of p such that
 $f_{01}(\{n_0,n_1\})\equiv [a_0 a_1]_{\{n_0,n_1\}}$
,
$f_{01}(\{n_0,n_1\})\equiv [a_0 a_1]_{\{n_0,n_1\}}$
,
 $f_{12}(\{n_1,n_2\})\equiv [a_1 a_2]_{\{n_1,n_2\}}$
, and
$f_{12}(\{n_1,n_2\})\equiv [a_1 a_2]_{\{n_1,n_2\}}$
, and
 $f_{02}(\{n_0,n_2\})\equiv [a_3 a_2]_{\{n_0,n_2\}}$
. We call this quadruple a representation of s. For any such representation of s, call
$f_{02}(\{n_0,n_2\})\equiv [a_3 a_2]_{\{n_0,n_2\}}$
. We call this quadruple a representation of s. For any such representation of s, call
 $a_0$
an initial point,
$a_0$
an initial point,
 $a_3$
a terminal point, and
$a_3$
a terminal point, and
 $(a_0,a_3)$
an endpoint pair of the representation.
$(a_0,a_3)$
an endpoint pair of the representation.
We summarize some properties of endpoint pairs of
![]() $1$
-shells. We define an equivalence relation
$1$
-shells. We define an equivalence relation
![]() $\sim ^*$
on the set of pairs of realizations p as follows: For
$\sim ^*$
on the set of pairs of realizations p as follows: For
![]() $a,a',b,b'\models p$
,
$a,a',b,b'\models p$
,
![]() $(a,b)\sim ^*(a',b')$
if two pairs
$(a,b)\sim ^*(a',b')$
if two pairs
![]() $(a,b)$
and
$(a,b)$
and
![]() $(a',b')$
are endpoint pairs of
$(a',b')$
are endpoint pairs of
![]() $1$
-shells s and
$1$
-shells s and
![]() $s'$
respectively such that
$s'$
respectively such that
![]() $[s]=[s']\in H^*_1(p)$
. We write
$[s]=[s']\in H^*_1(p)$
. We write
![]() ${\mathcal E}^*=p({\mathcal M})\times p({\mathcal M})/\sim ^*$
. We denote the class of
${\mathcal E}^*=p({\mathcal M})\times p({\mathcal M})/\sim ^*$
. We denote the class of
![]() $(a,b)\in p({\mathcal M})\times p({\mathcal M})$
by
$(a,b)\in p({\mathcal M})\times p({\mathcal M})$
by
![]() $[a,b]$
. Now, define a binary operation
$[a,b]$
. Now, define a binary operation
![]() $+_{{\mathcal E}^*}$
on
$+_{{\mathcal E}^*}$
on
![]() ${\mathcal E}^*$
as follows: For
${\mathcal E}^*$
as follows: For
![]() $[a,b],[b',c']\in {\mathcal E}^*$
,
$[a,b],[b',c']\in {\mathcal E}^*$
,
![]() $[a,b]+_{{\mathcal E}^*} [b',c']=[a,c]$
, where
$[a,b]+_{{\mathcal E}^*} [b',c']=[a,c]$
, where
![]() $bc\equiv b'c'$
.
$bc\equiv b'c'$
.
Fact 0.12. The operation
![]() $+_{{\mathcal E}^*}$
is well-defined, and the pair
$+_{{\mathcal E}^*}$
is well-defined, and the pair
![]() $({\mathcal E}^*,+_{{\mathcal E}^*})$
forms an abelian group which is isomorphic to
$({\mathcal E}^*,+_{{\mathcal E}^*})$
forms an abelian group which is isomorphic to
![]() $H^*_1(p)$
. More specifically, for
$H^*_1(p)$
. More specifically, for
![]() $a,b,c\models p$
and
$a,b,c\models p$
and
![]() $\sigma \in \operatorname {Aut}({\mathcal M})$
, we have:
$\sigma \in \operatorname {Aut}({\mathcal M})$
, we have:
-
•
 $[a,b]+[b,c]=[a,c];$
$[a,b]+[b,c]=[a,c];$
-
•
 $[a,a]$
is the identity element;
$[a,a]$
is the identity element; -
•
 $-[a,b]=[b,a];$
$-[a,b]=[b,a];$
-
•
 $\sigma ([a,b]):=[\sigma (a),\sigma (b)]=[a,b];$
and
$\sigma ([a,b]):=[\sigma (a),\sigma (b)]=[a,b];$
and -
•
 $f:{\mathcal E}^*\to H^*_1(p)$
sending
$f:{\mathcal E}^*\to H^*_1(p)$
sending
 $[a,b]\mapsto [s]$
, where
$[a,b]\mapsto [s]$
, where
 $(a,b)$
is an endpoint pair of s, is a group isomorphism.
$(a,b)$
is an endpoint pair of s, is a group isomorphism.
We identify
![]() ${\mathcal E}^*$
and
${\mathcal E}^*$
and
![]() $H^*_1(p)$
.
$H^*_1(p)$
.
Fact 0.13.
![]() $H_1^*(p)$
is isomorphic to
$H_1^*(p)$
is isomorphic to
![]() $G/N$
where
$G/N$
where
![]() $G:=\operatorname {Aut}(p)$
and N is the normal subgroup of G consisting of all automorphisms fixing setwise all orbits of elements of
$G:=\operatorname {Aut}(p)$
and N is the normal subgroup of G consisting of all automorphisms fixing setwise all orbits of elements of
![]() $p({\mathcal M})$
under the action of
$p({\mathcal M})$
under the action of
![]() $G'$
(so
$G'$
(so
![]() $G/N$
does not depend on the choice of a monster model). Hence
$G/N$
does not depend on the choice of a monster model). Hence
![]() $H_1^*(p)$
does not depend on the choice of
$H_1^*(p)$
does not depend on the choice of
![]() and we write
and we write
![]() $H_1(p)$
for
$H_1(p)$
for
![]() $H_1^*(p)$
.
$H_1^*(p)$
.
Fact 0.14. Let p be the fixed strong type of an algebraically closed set.
-
(1) Let
 be an independence relation satisfying the 5 basic axioms. Let
be an independence relation satisfying the 5 basic axioms. Let
 $a,b \models p$
. Then the following are equivalent.
$a,b \models p$
. Then the following are equivalent.-
(a)
 $[a,b]=0$
in
$[a,b]=0$
in
 $H_1(p);$
$H_1(p);$
-
(b) There is a balanced-chain-walk from a to b, i.e., there are some
 $n\geq 0$
and a finite sequence
$n\geq 0$
and a finite sequence
 $(d_i)_{0\le i\le 2n+2}$
of realizations of p satisfying the following conditions:
$(d_i)_{0\le i\le 2n+2}$
of realizations of p satisfying the following conditions:-
(i)
 $d_0=a$
, and
$d_0=a$
, and
 $d_{2n+2}=b;$
$d_{2n+2}=b;$
-
(ii)
 $\{d_{j},d_{j+1}\}$
is
$\{d_{j},d_{j+1}\}$
is
 $*$
-independent for each
$*$
-independent for each
 $j\le 2n+1;$
and
$j\le 2n+1;$
and -
(iii) there is a bijection
such that $$ \begin{align*}\sigma:\{0,1,\ldots,n\}\to\{0,1,\ldots,n\}\end{align*} $$
$$ \begin{align*}\sigma:\{0,1,\ldots,n\}\to\{0,1,\ldots,n\}\end{align*} $$
 $d_{2i} d_{2i+1}\equiv d_{2\sigma (i)+2}d_{2\sigma (i)+1}$
for
$d_{2i} d_{2i+1}\equiv d_{2\sigma (i)+2}d_{2\sigma (i)+1}$
for
 $ i \le n;$
$ i \le n;$
-
-
(c) There are some
 $n\geq 0$
and finite sequences
$n\geq 0$
and finite sequences
 $(d_i:0\le i\le n)$
,
$(d_i:0\le i\le n)$
,
 $(d^j_i: i< n,\ 1\le j\le 3)$
of realizations of p such that
$(d^j_i: i< n,\ 1\le j\le 3)$
of realizations of p such that
 $d_0=a$
,
$d_0=a$
,
 $d_n=b$
, and for each
$d_n=b$
, and for each
 $i< n$
,
$i< n$
,
 $d_id^1_i\equiv d^3_id^2_i$
,
$d_id^1_i\equiv d^3_id^2_i$
,
 $d^1_id^2_i\equiv d_{i+1}d^3_i$
.
$d^1_id^2_i\equiv d_{i+1}d^3_i$
. -
(d)
 $h(a)=b$
for some h in the commutator subgroup of
$h(a)=b$
for some h in the commutator subgroup of
 $\operatorname {Aut}(p)$
.
$\operatorname {Aut}(p)$
.
 $a\equiv ^L b$
then
$a\equiv ^L b$
then
 $[a,b]=0\in H_1(p)$
.
$[a,b]=0\in H_1(p)$
.
-
-
(2) The following are equivalent.
-
(a)
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian;
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian; -
(b) For all
 $a,b \models p$
,
$a,b \models p$
,
 $[a,b]=0$
in
$[a,b]=0$
in
 $H_1(p)$
if and only if
$H_1(p)$
if and only if
 $a \equiv ^L b$
.
$a \equiv ^L b$
.
-
-
(3) p is a Lascar type (i.e.,
 $a\equiv ^Lb$
for any
$a\equiv ^Lb$
for any
 $a,b\models p)$
if and only if
$a,b\models p)$
if and only if
 $H_1(p)$
is trivial and
$H_1(p)$
is trivial and
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian.
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian.
Remark 0.15. (1) Assume that
![]() $p(x)$
is the type of a small model. Then for any
$p(x)$
is the type of a small model. Then for any
![]() $M, N\models p$
, the equivalence classes of (equality of) Lascar types of M and N are interdefinable: Let
$M, N\models p$
, the equivalence classes of (equality of) Lascar types of M and N are interdefinable: Let
![]() $M\equiv ^L M'$
and
$M\equiv ^L M'$
and
![]() $MN\equiv M'N'$
. It suffices to show that
$MN\equiv M'N'$
. It suffices to show that
![]() $N\equiv ^L N'$
. Now there is
$N\equiv ^L N'$
. Now there is
![]() $f\in \operatorname {Autf}({\mathcal M})$
such that
$f\in \operatorname {Autf}({\mathcal M})$
such that
![]() $f(M')=M$
. Let
$f(M')=M$
. Let
![]() $N'':=f(N')$
so that
$N'':=f(N')$
so that
![]() $N''\equiv ^LN'$
and
$N''\equiv ^LN'$
and
![]() $MN\equiv MN''$
. Hence
$MN\equiv MN''$
. Hence
![]() $N\equiv _{M}N''$
and
$N\equiv _{M}N''$
and
![]() $N\equiv ^L N''\equiv ^L N'$
as wanted. When p is a type of any tuple we will see that the same holds if
$N\equiv ^L N''\equiv ^L N'$
as wanted. When p is a type of any tuple we will see that the same holds if
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian (Remark 1.10).
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian (Remark 1.10).
(2) Notice that for tuples
![]() $a,b\models p$
, we have:
$a,b\models p$
, we have:
-
(**) there is a commutator f in
 $\operatorname {Aut}(p)$
such that
$\operatorname {Aut}(p)$
such that
 $f(a)=b$
if and only if there are
$f(a)=b$
if and only if there are
 $d^1,d^2,d^3\models p$
such that
$d^1,d^2,d^3\models p$
such that
 $ad^1\equiv d^3d^2$
and
$ad^1\equiv d^3d^2$
and
 $bd^3\equiv d^1d^2$
.
$bd^3\equiv d^1d^2$
.
Now we recall the following fact of compact group theory by M. Gotô from [Reference Hofmann and Morris6, Theorem 9.2]: Assume
![]() $(F,\cdot )$
is a compact connected topological group. Then
$(F,\cdot )$
is a compact connected topological group. Then
![]() $F'$
, the commutator subgroup of F, is simply the set of commutators in F, i.e.,
$F'$
, the commutator subgroup of F, is simply the set of commutators in F, i.e.,
 $$ \begin{align*}F'=\{ f\cdot g \cdot f^{-1}\cdot g^{-1}\mid f,g \in F\}.\end{align*} $$
$$ \begin{align*}F'=\{ f\cdot g \cdot f^{-1}\cdot g^{-1}\mid f,g \in F\}.\end{align*} $$
It follows that
![]() $F'$
is a closed subgroup of F, and both
$F'$
is a closed subgroup of F, and both
![]() $F'$
and
$F'$
and
![]() $F/F'$
are compact connected groups as well.
$F/F'$
are compact connected groups as well.
Due to the theorem we newly observe here that if T is G-compact then in Fact 0.14(1)(c), we can choose
![]() $n=1$
: If the equivalent conditions in Fact 0.14(1) hold, then we have that
$n=1$
: If the equivalent conditions in Fact 0.14(1) hold, then we have that
![]() $h(a)=b$
for some h in the commutator subgroup of
$h(a)=b$
for some h in the commutator subgroup of
![]() $\operatorname {Aut}(p)$
. Now, as T is G-compact, we get by Gotô’s Theorem that h is a commutator in
$\operatorname {Aut}(p)$
. Now, as T is G-compact, we get by Gotô’s Theorem that h is a commutator in
![]() $\operatorname {Aut}(p)$
, so, by
$\operatorname {Aut}(p)$
, so, by
![]() $(**)$
, there are
$(**)$
, there are
![]() $d^1,d^2,d^3\models p$
such that
$d^1,d^2,d^3\models p$
such that
![]() $bd^3\equiv d^1d^2$
.
$bd^3\equiv d^1d^2$
.
1. Amalgamation properties of strong types in simple theories
Note that if T is simple then since T is G-compact, each
 $\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
is a compact (i.e., quasi-compact and Hausdorff) connected group, so it is divisible (see [Reference Hofmann and Morris6, Theorem 9.35]). In this section we assume T is simple (except Remark 1.10 and Example 1.11), and the independence is nonforking independence. It is still an open question whether the strong type p is necessarily a Lascar type. If so, then the following theorem follows easily by the
$\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
is a compact (i.e., quasi-compact and Hausdorff) connected group, so it is divisible (see [Reference Hofmann and Morris6, Theorem 9.35]). In this section we assume T is simple (except Remark 1.10 and Example 1.11), and the independence is nonforking independence. It is still an open question whether the strong type p is necessarily a Lascar type. If so, then the following theorem follows easily by the
![]() $3$
-amalgamation of Lascar types in simple theories. But regardless of the answer to the question, p has the following amalgamation property. We do not assume here that a realization of p is algebraically closed.
$3$
-amalgamation of Lascar types in simple theories. But regardless of the answer to the question, p has the following amalgamation property. We do not assume here that a realization of p is algebraically closed.
Theorem 1.1 (Divisible amalgamation)
Let p be a strong type in a simple theory. Let
![]() $a,b\models p$
and
$a,b\models p$
and
![]() . Then for each
. Then for each
![]() $n\geq 1$
, there are independent
$n\geq 1$
, there are independent
![]() $a=a_0,a_1,\ldots ,a_n=b$
such that
$a=a_0,a_1,\ldots ,a_n=b$
such that
![]() $a_0a_1\equiv a_ia_{i+1}$
for every
$a_0a_1\equiv a_ia_{i+1}$
for every
![]() $i< n$
.
$i< n$
.
Proof Clearly we can assume
![]() $n>1$
. Note that there is
$n>1$
. Note that there is
![]() $f \in \operatorname {Aut}(p)$
such that
$f \in \operatorname {Aut}(p)$
such that
![]() $b=f(a)$
. Then since
$b=f(a)$
. Then since
 $G:=\operatorname {Gal}_{\operatorname {L}}^1(p)$
is divisible, there is
$G:=\operatorname {Gal}_{\operatorname {L}}^1(p)$
is divisible, there is
![]() $h \in \operatorname {Aut}(p)$
such that
$h \in \operatorname {Aut}(p)$
such that
![]() $[h]^n=[f]$
(in G). Put
$[h]^n=[f]$
(in G). Put
![]() $c=h(a)$
. Now there is
$c=h(a)$
. Now there is
![]() $c_1\equiv ^L c$
such that
$c_1\equiv ^L c$
such that
![]() . Then there is
. Then there is
 $h' \in \operatorname {Autf}^1(p)$
such that
$h' \in \operatorname {Autf}^1(p)$
such that
![]() $h'(c)=c_1$
. Let
$h'(c)=c_1$
. Let
![]() $g=h'\circ h$
. Then
$g=h'\circ h$
. Then
![]() $[g]=[h]$
so
$[g]=[h]$
so
![]() $[g]^n=[f]$
too, and
$[g]^n=[f]$
too, and
![]() $g(a)=c_1$
.
$g(a)=c_1$
.
Claim. We can find additional elements
![]() $c_2,\ldots ,c_n$
such that
$c_2,\ldots ,c_n$
such that
![]() $\{a=c_0,c_1,\ldots ,c_n,b\}$
is independent, and for each
$\{a=c_0,c_1,\ldots ,c_n,b\}$
is independent, and for each
![]() $1\leq m\leq n$
,
$1\leq m\leq n$
,
![]() $c_0c_1\equiv c_{m-1}c_{m}$
and there is
$c_0c_1\equiv c_{m-1}c_{m}$
and there is
![]() $h_m\in \operatorname {Aut}(p)$
such that
$h_m\in \operatorname {Aut}(p)$
such that
![]() $[h_m]=[g]^m$
in G, and
$[h_m]=[g]^m$
in G, and
![]() $h_m(a)=c_m$
.
$h_m(a)=c_m$
.
Proof of the Claim For an induction hypothesis, assume for
![]() $1\leq m< n$
we have found
$1\leq m< n$
we have found
![]() $a=c_0,c_1,\ldots , c_m$
such that
$a=c_0,c_1,\ldots , c_m$
such that
![]() $\{c_0,c_1,\ldots ,c_m,b\}$
is independent and
$\{c_0,c_1,\ldots ,c_m,b\}$
is independent and
![]() $c_0c_1\equiv c_{i-1}c_{i}$
for all
$c_0c_1\equiv c_{i-1}c_{i}$
for all
![]() $1\leq i\leq m$
and there is
$1\leq i\leq m$
and there is
![]() $h_m\in \operatorname {Aut}(p)$
such that
$h_m\in \operatorname {Aut}(p)$
such that
![]() $[h_m]=[g]^m$
in G, and
$[h_m]=[g]^m$
in G, and
![]() $h_m(c_0)=c_m$
.
$h_m(c_0)=c_m$
.
Notice now that then
![]() $c^{\prime }_m:=g^m(a)\equiv ^L h_m(a)=c_m$
. Put
$c^{\prime }_m:=g^m(a)\equiv ^L h_m(a)=c_m$
. Put
 $c^{\prime }_{m+1}:=g(c^{\prime }_m)=g^{m+1}(a)$
. Then there is
$c^{\prime }_{m+1}:=g(c^{\prime }_m)=g^{m+1}(a)$
. Then there is
![]() $c_{m+1}$
such that
$c_{m+1}$
such that
 $c_mc_{m+1}\equiv ^L c^{\prime }_mc^{\prime }_{m+1}$
, and
$c_mc_{m+1}\equiv ^L c^{\prime }_mc^{\prime }_{m+1}$
, and
![]() $\{c_0,c_1,\ldots ,c_{m+1},b\}$
is independent. Since
$\{c_0,c_1,\ldots ,c_{m+1},b\}$
is independent. Since
 $c_{m+1}\equiv ^L c^{\prime }_{m+1}$
, there is
$c_{m+1}\equiv ^L c^{\prime }_{m+1}$
, there is
 $h'' \in \operatorname {Autf}^1(p)$
, such that
$h'' \in \operatorname {Autf}^1(p)$
, such that
 $h''(c^{\prime }_{m+1})=c_{m+1}$
and so for
$h''(c^{\prime }_{m+1})=c_{m+1}$
and so for
![]() $h_{m+1}:=h''\circ g^{m+1}$
, we have
$h_{m+1}:=h''\circ g^{m+1}$
, we have
![]() $h_{m+1}(a)=c_{m+1}$
and
$h_{m+1}(a)=c_{m+1}$
and
![]() $[g]^{m+1}= [h_{m+1}]$
in G. Moreover the equality of types
$[g]^{m+1}= [h_{m+1}]$
in G. Moreover the equality of types
![]() $c_mc_{m+1}\equiv c^{\prime }_mc^{\prime }_{m+1} \equiv c_0c_1$
is witnessed by
$c_mc_{m+1}\equiv c^{\prime }_mc^{\prime }_{m+1} \equiv c_0c_1$
is witnessed by
![]() $g^m$
. Hence the claim is proved.
$g^m$
. Hence the claim is proved.
Notice that
![]() $ c_n=h_n(a)$
with
$ c_n=h_n(a)$
with
![]() $[h_n]=[g]^n=[f]$
. Hence
$[h_n]=[g]^n=[f]$
. Hence
![]() $c_n\equiv ^L b=f(a)$
. Then, by
$c_n\equiv ^L b=f(a)$
. Then, by
![]() $3$
-amalgamation, we find
$3$
-amalgamation, we find
![]() $b' \models \operatorname {tp}(b/a) \cup \operatorname {tp}(c_n/c_1\dots c_{n-1})$
with
$b' \models \operatorname {tp}(b/a) \cup \operatorname {tp}(c_n/c_1\dots c_{n-1})$
with
![]() . Then the automorphic images of
. Then the automorphic images of
![]() $c_1\dots c_{n-1}$
(rename them as
$c_1\dots c_{n-1}$
(rename them as
![]() $a_1\ldots a_{n-1}$
) under a map sending
$a_1\ldots a_{n-1}$
) under a map sending
![]() $b'$
to b over a satisfy the conditions of the theorem.⊣
$b'$
to b over a satisfy the conditions of the theorem.⊣
Now we assume that p is the type of an algebraically closed tuple. For
![]() $a,a'\models p$
, we have a better description of
$a,a'\models p$
, we have a better description of
![]() $[a,a']=0$
in
$[a,a']=0$
in
![]() $H_1(p).$
$H_1(p).$
Proposition 1.2. For
![]() $a,a'\models p$
, the following are equivalent.
$a,a'\models p$
, the following are equivalent.
-
(1)
 $[a,a']=0$
in
$[a,a']=0$
in
 $H_1(p)$
, equivalently there is h in the commutator subgroup of
$H_1(p)$
, equivalently there is h in the commutator subgroup of
 $\operatorname {Aut}(p)$
such that
$\operatorname {Aut}(p)$
such that
 $h(a)=a'$
.
$h(a)=a'$
. -
(2) There are
 $b,c,d\models p$
such that each of
$b,c,d\models p$
such that each of
 $\{a,b,c,d\}$
,
$\{a,b,c,d\}$
,
 $\{a', b,c,d\}$
is independent, and
$\{a', b,c,d\}$
is independent, and
 $ab\equiv cd$
,
$ab\equiv cd$
,
 $bd\equiv a'c$
.
$bd\equiv a'c$
.
Proof (1)
![]() $\Rightarrow $
(2) Since T is G-compact, by Remark 0.15(2) there are
$\Rightarrow $
(2) Since T is G-compact, by Remark 0.15(2) there are
![]() $b',c',d'\models p$
such that
$b',c',d'\models p$
such that
![]() $ab'\equiv c'd'$
and
$ab'\equiv c'd'$
and
![]() $b'd'\equiv a'c'$
. Now there is
$b'd'\equiv a'c'$
. Now there is
![]() $b\equiv ^L b'$
such that
$b\equiv ^L b'$
such that
![]() . Hence, by
. Hence, by
![]() $3$
-amalgamation, there is
$3$
-amalgamation, there is
![]() $d_0\equiv ^L d'$
such that
$d_0\equiv ^L d'$
such that
![]() $d_0\models \operatorname {tp}(d'/b) \cup \operatorname {tp}(d''/b')$
and
$d_0\models \operatorname {tp}(d'/b) \cup \operatorname {tp}(d''/b')$
and
![]() , where
, where
![]() $d''b'\equiv d'b$
and
$d''b'\equiv d'b$
and
![]() $d''\equiv ^L d'\equiv ^L d_0$
. By extension there is no harm in assuming that
$d''\equiv ^L d'\equiv ^L d_0$
. By extension there is no harm in assuming that
![]() .
.
Now since
![]() $a'c'\equiv b'd'$
, there are
$a'c'\equiv b'd'$
, there are
![]() $a''c$
such that
$a''c$
such that
![]() $b'd'bd_0\equiv a'c'a''c$
. Hence,
$b'd'bd_0\equiv a'c'a''c$
. Hence,
![]() $c\equiv ^L c'$
,
$c\equiv ^L c'$
,
![]() $a''\equiv ^L a'$
, and
$a''\equiv ^L a'$
, and
![]() . Again by extension, we can further assume that
. Again by extension, we can further assume that
![]() . Moreover, since
. Moreover, since
![]() $ab'\equiv c'd'$
, there is
$ab'\equiv c'd'$
, there is
![]() $d_1\equiv ^L d'$
such that
$d_1\equiv ^L d'$
such that
![]() $ab'b\equiv c'd'd_1$
. Then since
$ab'b\equiv c'd'd_1$
. Then since
![]() with
with
![]() $c\equiv ^Lc$
, and
$c\equiv ^Lc$
, and
![]() , again by
, again by
![]() $3$
-amalgamation we can assume that
$3$
-amalgamation we can assume that
![]() $c'd_1\equiv cd_1$
and
$c'd_1\equiv cd_1$
and
![]() .
.
Now the situation is that
![]() ,
,
![]() , and
, and
![]() . Moreover,
. Moreover,
![]() $d_0\equiv ^L d'\equiv ^L d_1$
. Hence, by
$d_0\equiv ^L d'\equiv ^L d_1$
. Hence, by
![]() $3$
-amalgamation, we have
$3$
-amalgamation, we have
![]() $d\models \operatorname {tp}(d_0/aa'b)\cup \operatorname {tp}(d_1/c)$
and
$d\models \operatorname {tp}(d_0/aa'b)\cup \operatorname {tp}(d_1/c)$
and
![]() . Therefore, each of
. Therefore, each of
![]() $\{a,b,c,d\}$
,
$\{a,b,c,d\}$
,
![]() $\{a', b,c,d\}$
is independent. Moreover, due to above combinations
$\{a', b,c,d\}$
is independent. Moreover, due to above combinations
and
as wanted.
(2)
![]() $\Rightarrow $
(1) Clear by Remark 0.15(2).⊣
$\Rightarrow $
(1) Clear by Remark 0.15(2).⊣
From now until Theorem 1.8, we assume that
![]() $p(x)$
is the (
strong
) type of a small model, and all tuples
$p(x)$
is the (
strong
) type of a small model, and all tuples
![]() $a,b,c,\dots $
realize p, so all are universes of models. Hence, by Fact 0.4,
$a,b,c,\dots $
realize p, so all are universes of models. Hence, by Fact 0.4,
 $\operatorname {Autf}^1(p)=\operatorname {Autf}_{\operatorname {fix}}(p)$
and
$\operatorname {Autf}^1(p)=\operatorname {Autf}_{\operatorname {fix}}(p)$
and
 $(\operatorname {Gal}_{\operatorname {L}}(T)\cong )\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}}(p)=\operatorname {Gal}_{\operatorname {L}}^{1}(p)$
, which we simply write
$(\operatorname {Gal}_{\operatorname {L}}(T)\cong )\operatorname {Gal}_{\operatorname {L}}^{\operatorname {fix}}(p)=\operatorname {Gal}_{\operatorname {L}}^{1}(p)$
, which we simply write
![]() $\operatorname {Autf}(p)$
and
$\operatorname {Autf}(p)$
and
![]() $\operatorname {Gal}_{\operatorname {L}}(p)$
, respectively. Moreover,
$\operatorname {Gal}_{\operatorname {L}}(p)$
, respectively. Moreover,
![]() $H_1(p)\cong \operatorname {Gal}_{\operatorname {L}}(p)/(\operatorname {Gal}_{\operatorname {L}}(p))'$
and hence it is a compact connected (so divisible) abelian group.
$H_1(p)\cong \operatorname {Gal}_{\operatorname {L}}(p)/(\operatorname {Gal}_{\operatorname {L}}(p))'$
and hence it is a compact connected (so divisible) abelian group.
Definition 1.3. Let
![]() $r(x,y), s(x,y)$
be types completing
$r(x,y), s(x,y)$
be types completing
![]() .
.
-
(1) We say p has abelian (or commutative) amalgamation of r and s, if there are independent
 $a,b,c,d\models p$
such that
$a,b,c,d\models p$
such that
 $ab,cd\models r$
and
$ab,cd\models r$
and
 $ac, bd\models s$
.We say p has abelian amalgamation if it has abelian amalgamation for any such completions r and s.
$ac, bd\models s$
.We say p has abelian amalgamation if it has abelian amalgamation for any such completions r and s. -
(2) We say p has reversible amalgamation of r and s if there are independent
 $a,b,c,d\models p$
such that
$a,b,c,d\models p$
such that
 $ab,dc\models r$
and
$ab,dc\models r$
and
 $ac, db\models s$
.We say p has reversible amalgamation if it has reversible amalgamation for any such completions r and s.
$ac, db\models s$
.We say p has reversible amalgamation if it has reversible amalgamation for any such completions r and s.
Lemma 1.4. The following are equivalent.
-
(1) The type p has abelian amalgamation.
-
(2) Let
 $r(x,y), s(x,y)$
be any types completing
$r(x,y), s(x,y)$
be any types completing
 , and let
, and let
 $a,b,c\models p$
be independent such that
$a,b,c\models p$
be independent such that
 $ac\models s$
and
$ac\models s$
and
 $ab\models r$
. Then there is
$ab\models r$
. Then there is
 $d\models p $
independent from
$d\models p $
independent from
 $abc$
such that
$abc$
such that
 $cd\models r$
and
$cd\models r$
and
 $bd \models s$
.
$bd \models s$
.
Proof (1)
![]() $\Rightarrow $
(2) By (1), there are
$\Rightarrow $
(2) By (1), there are
![]() $b_0, d_0\models p$
such that
$b_0, d_0\models p$
such that
![]() $\{a,c,b_0,d_0\}$
is independent,
$\{a,c,b_0,d_0\}$
is independent,
![]() $ab_0,cd_0\models r$
, and
$ab_0,cd_0\models r$
, and
![]() $ac, b_0d_0\models s$
. Hence, there is
$ac, b_0d_0\models s$
. Hence, there is
![]() $d_1$
such that
$d_1$
such that
![]() $abd_1\equiv ab_0d_0$
. Now by
$abd_1\equiv ab_0d_0$
. Now by
![]() $3$
-amalgamation over the model a, there is
$3$
-amalgamation over the model a, there is
such that
![]() $\{a,b,c,d\}$
is independent. Moreover,
$\{a,b,c,d\}$
is independent. Moreover,
![]() $cd\equiv cd_0\models r$
and
$cd\equiv cd_0\models r$
and
![]() $bd\equiv bd_1\equiv b_0d_0 \models s$
, as desired.
$bd\equiv bd_1\equiv b_0d_0 \models s$
, as desired.
(2)
![]() $\Rightarrow $
(1) Clear.⊣
$\Rightarrow $
(1) Clear.⊣
By the same proof we obtain the following too.
Lemma 1.5. The following are equivalent.
-
(1) The type p has reversible amalgamation.
-
(2) Let
 $r(x,y), s(x,y)$
be any types completing
$r(x,y), s(x,y)$
be any types completing
 , and let
, and let
 $a,b,c\models p$
be independent such that
$a,b,c\models p$
be independent such that
 $ac\models s$
and
$ac\models s$
and
 $ab\models r$
. Then there is
$ab\models r$
. Then there is
 $d\models p $
independent from
$d\models p $
independent from
 $abc$
such that
$abc$
such that
 $dc\models r$
and
$dc\models r$
and
 $db \models s$
.
$db \models s$
.
Theorem 1.6. The following are equivalent.
-
(1)
 $ \operatorname {Gal}_{\operatorname {L}}(p)(\cong \operatorname {Gal}_{\operatorname {L}}(T))$
is abelian.
$ \operatorname {Gal}_{\operatorname {L}}(p)(\cong \operatorname {Gal}_{\operatorname {L}}(T))$
is abelian. -
(2) p has abelian amalgamation.
Proof (1)
![]() $\Rightarrow $
(2) Assume (1). Thus for
$\Rightarrow $
(2) Assume (1). Thus for
![]() $G:=\operatorname {Aut}(p)$
, we have
$G:=\operatorname {Aut}(p)$
, we have
![]() $G'\leq \operatorname {Autf}(p)$
. Now let
$G'\leq \operatorname {Autf}(p)$
. Now let
![]() $r(x,y)$
and
$r(x,y)$
and
![]() $s(x,y)$
be some complete types containing
$s(x,y)$
be some complete types containing
![]() . There are independent
. There are independent
![]() $a,a', b,d,c\models p$
such that
$a,a', b,d,c\models p$
such that
![]() $ab,cd\models r$
and
$ab,cd\models r$
and
![]() $bd, a'c\models s$
. Hence there is a commutator
$bd, a'c\models s$
. Hence there is a commutator
![]() $f\in G'\leq \operatorname {Autf}(p)$
such that
$f\in G'\leq \operatorname {Autf}(p)$
such that
![]() $f(a)=a'$
, so
$f(a)=a'$
, so
![]() $a\equiv ^L a'$
. Then by
$a\equiv ^L a'$
. Then by
![]() $3$
-amalgamation of
$3$
-amalgamation of
![]() $\operatorname {Lstp}(a)$
, there is
$\operatorname {Lstp}(a)$
, there is
such that
![]() $\{a_0,b,c,d\}$
is independent,
$\{a_0,b,c,d\}$
is independent,
![]() $a_0b\equiv ab\models r$
, and
$a_0b\equiv ab\models r$
, and
![]() $a_0c\equiv a'c\models s$
. Therefore p has commutative amalgamation.
$a_0c\equiv a'c\models s$
. Therefore p has commutative amalgamation.
(2)
![]() $\Rightarrow $
(1) To show (1), due to Fact 0.14(2) it is enough to prove that if
$\Rightarrow $
(1) To show (1), due to Fact 0.14(2) it is enough to prove that if
![]() $a,a'\models p$
and
$a,a'\models p$
and
![]() $[a,a']=0\in H_1(p)$
(
$[a,a']=0\in H_1(p)$
(
![]() $\dagger $
), then
$\dagger $
), then
![]() $a\equiv ^L a'$
. Now assume (2) and (
$a\equiv ^L a'$
. Now assume (2) and (
![]() $\dagger $
). Thus, by Proposition 1.2, there are
$\dagger $
). Thus, by Proposition 1.2, there are
![]() $b,c,d\models p$
such that each of the sets
$b,c,d\models p$
such that each of the sets
![]() $\{a,b,c,d\}$
and
$\{a,b,c,d\}$
and
![]() $\{a', b,c,d\}$
is independent,
$\{a', b,c,d\}$
is independent,
![]() $ab\equiv cd$
, and
$ab\equiv cd$
, and
![]() $bd\equiv a'c$
. Now by Lemma 1.4 and extension there is
$bd\equiv a'c$
. Now by Lemma 1.4 and extension there is
![]() $c'\models p$
such that
$c'\models p$
such that
![]() and
and
![]() $ac'\equiv bd\equiv a'c$
and
$ac'\equiv bd\equiv a'c$
and
![]() $c'd\equiv ab\equiv cd$
. Then, since d is a model, we have
$c'd\equiv ab\equiv cd$
. Then, since d is a model, we have
![]() $c \equiv ^L c'$
, and there is
$c \equiv ^L c'$
, and there is
![]() $a''$
such that
$a''$
such that
![]() $a'c\equiv _da''c'$
, so
$a'c\equiv _da''c'$
, so
![]() $a\equiv ^L a''$
and
$a\equiv ^L a''$
and
![]() $a''\equiv _{c'}a$
. Since
$a''\equiv _{c'}a$
. Since
![]() $c'$
is a model as well, we conclude that
$c'$
is a model as well, we conclude that
![]() $a'\equiv ^L a''\equiv ^L a$
.⊣
$a'\equiv ^L a''\equiv ^L a$
.⊣
A proof similar to that of the above Theorem 1.6 (2)
![]() $\Rightarrow $
(1) applying Fact 0.14(1)(b) gives the following as well.
$\Rightarrow $
(1) applying Fact 0.14(1)(b) gives the following as well.
Proposition 1.7. If p has reversible amalgamation, then
![]() $\operatorname {Gal}_{\operatorname {L}}(p)$
is abelian (equivalently, p has abelian amalgamation).
$\operatorname {Gal}_{\operatorname {L}}(p)$
is abelian (equivalently, p has abelian amalgamation).
Proof Assume that p has reversible amalgamation, and
![]() $[a,b]=0\in H_1(p)$
for
$[a,b]=0\in H_1(p)$
for
![]() $a,b\models p$
(
$a,b\models p$
(
![]() $\dagger $
). As before it is enough to prove that
$\dagger $
). As before it is enough to prove that
![]() $a\equiv ^L b$
. It follows from the extension axiom for Lascar types together with Fact 0.14(1)(b), there are
$a\equiv ^L b$
. It follows from the extension axiom for Lascar types together with Fact 0.14(1)(b), there are
![]() $b'\equiv ^L b$
and a finite independent sequence
$b'\equiv ^L b$
and a finite independent sequence
![]() $(d_i)_{0\le i\le 2n+2}$
of realizations of p satisfying the following conditions:
$(d_i)_{0\le i\le 2n+2}$
of realizations of p satisfying the following conditions:
-
(i)
 $d_0=a$
,
$d_0=a$
,
 $d_{2n+2}=b'$
; and
$d_{2n+2}=b'$
; and -
(ii) there is a bijection
such that $$ \begin{align*}\sigma:\{0,1,\ldots,n\}\to\{0,1,\ldots,n\}\end{align*} $$
$$ \begin{align*}\sigma:\{0,1,\ldots,n\}\to\{0,1,\ldots,n\}\end{align*} $$
 $d_{2i} d_{2i+1}\equiv d_{2\sigma (i)+2}d_{2\sigma (i)+1}$
for
$d_{2i} d_{2i+1}\equiv d_{2\sigma (i)+2}d_{2\sigma (i)+1}$
for
 $ i \le n$
.
$ i \le n$
.
In other words, there is an independent balanced chain-walk from a to
![]() $b'$
, and it suffices to prove
$b'$
, and it suffices to prove
![]() $a\equiv ^L b'$
. Notice that, by reversible amalgamation, condition (2) of Lemma 1.5 implies that in the above chain-walk two adjacent edges can be swapped with sign reversed (i.e., for say
$a\equiv ^L b'$
. Notice that, by reversible amalgamation, condition (2) of Lemma 1.5 implies that in the above chain-walk two adjacent edges can be swapped with sign reversed (i.e., for say
![]() $d_jd_{j+1}$
and
$d_jd_{j+1}$
and
![]() $d_{j+1}d_{j+2}$
there is
$d_{j+1}d_{j+2}$
there is
 such that
such that
 $d_jd^{\prime }_{j+1}\equiv d_{j+2}d_{j+1}$
and
$d_jd^{\prime }_{j+1}\equiv d_{j+2}d_{j+1}$
and
 $d^{\prime }_{j+1}d_{j+2}\equiv d_{j+1}d_{j}$
). By iterating this process one can transfer the chain-walk to another balanced chain-walk
$d^{\prime }_{j+1}d_{j+2}\equiv d_{j+1}d_{j}$
). By iterating this process one can transfer the chain-walk to another balanced chain-walk
![]() $(d^{\prime }_i)_{0\le i\le 2n+2}$
from a to
$(d^{\prime }_i)_{0\le i\le 2n+2}$
from a to
![]() $b'$
such that the walk has a Lascar pattern, i.e., the bijection
$b'$
such that the walk has a Lascar pattern, i.e., the bijection
![]() $\sigma $
for the new walk is the identity map. Hence it follows
$\sigma $
for the new walk is the identity map. Hence it follows
 $d^{\prime }_{2i}\equiv _{d^{\prime }_{2i+1}} d^{\prime }_{2i+2}$
for
$d^{\prime }_{2i}\equiv _{d^{\prime }_{2i+1}} d^{\prime }_{2i+2}$
for
![]() $i\leq n$
, and since each
$i\leq n$
, and since each
![]() $d^{\prime }_{2i+1}$
is a model, we have
$d^{\prime }_{2i+1}$
is a model, we have
![]() $a=d^{\prime }_0\equiv ^Lb'$
, as wanted.⊣
$a=d^{\prime }_0\equiv ^Lb'$
, as wanted.⊣
A stronger consequence is obtained.
Theorem 1.8. The strong type p is a Lascar type if and only if p has reversible amalgamation.
Proof (
![]() $\Rightarrow $
) It follows from
$\Rightarrow $
) It follows from
![]() $3$
-amalgamation of Lascar strong types.
$3$
-amalgamation of Lascar strong types.
(
![]() $\Leftarrow $
) Assume p has reversible amalgamation. Due to Fact 0.14(3) and Proposition 1.7, it suffices to show
$\Leftarrow $
) Assume p has reversible amalgamation. Due to Fact 0.14(3) and Proposition 1.7, it suffices to show
![]() $H_1(p)$
is trivial. Let an arbitrary
$H_1(p)$
is trivial. Let an arbitrary
![]() $[s]\in H_1(p)$
be given, and let
$[s]\in H_1(p)$
be given, and let
![]() $[a,b']=[s]$
for
$[a,b']=[s]$
for
![]() $a,b'\models p$
. Then, for any
$a,b'\models p$
. Then, for any
![]() $b\equiv ^L b'$
with
$b\equiv ^L b'$
with
![]() , we have
, we have
![]() $[a,b]=[a,b']+[b',b]=[s]+0=[s]$
. Similarly, for
$[a,b]=[a,b']+[b',b]=[s]+0=[s]$
. Similarly, for
![]() $c\equiv ^L b$
with
$c\equiv ^L b$
with
![]() , we have
, we have
![]() $[b,c]=0$
in
$[b,c]=0$
in
![]() $H_1(p)$
. Now reversible amalgamation (or Lemma 1.5) says that
$H_1(p)$
. Now reversible amalgamation (or Lemma 1.5) says that
![]() $[s]=[a,b]+[b,c]=[c,b]+[b,a]=-[s]$
. Hence
$[s]=[a,b]+[b,c]=[c,b]+[b,a]=-[s]$
. Hence
![]() $[s]+[s]=0$
. Since
$[s]+[s]=0$
. Since
![]() $H_1(p)$
is compact and connected so divisible, any element in
$H_1(p)$
is compact and connected so divisible, any element in
![]() $H_1(p)$
is divisible by
$H_1(p)$
is divisible by
![]() $2$
. Therefore,
$2$
. Therefore,
![]() $H_1(p)=0$
by what we have just proved.⊣
$H_1(p)=0$
by what we have just proved.⊣
Question 1.9. Can the same results hold if p is the type of an algebraically closed tuple (not necessarily a model) in a simple theory? The answer to this question is yes if any two Lascar equivalence classes in p are interdefinable, since essentially this property (Remark 0.15(1)) implied the results in this section when p is the type of a model. At least we can show the following remark.
Remark 1.10. Let T be any theory, and let a realization of p be any tuple. If
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian then any two Lascar equivalence classes in p are interdefinable: Let
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian then any two Lascar equivalence classes in p are interdefinable: Let
![]() $a,b\models p$
, and
$a,b\models p$
, and
![]() $f\in \operatorname {Aut}(p)$
. Assume
$f\in \operatorname {Aut}(p)$
. Assume
![]() $f(a)\equiv ^L a$
. We want to show the same holds for b. Now there is
$f(a)\equiv ^L a$
. We want to show the same holds for b. Now there is
![]() $g\in \operatorname {Aut}(p)$
such that
$g\in \operatorname {Aut}(p)$
such that
![]() $g(a)=b$
. Since
$g(a)=b$
. Since
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian, we have
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian, we have
![]() $f(b)=f(g(a))\equiv ^L g(f(a))\equiv ^L g(a)=b$
.
$f(b)=f(g(a))\equiv ^L g(f(a))\equiv ^L g(a)=b$
.
Notice that
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is the group of automorphic permutations of the Lascar classes in p. Hence, if
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is the group of automorphic permutations of the Lascar classes in p. Hence, if
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian, then
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is abelian, then
 $f/\operatorname {Autf}^1(p)\in \operatorname {Gal}_{\operatorname {L}}^1(p)$
is determined by the pair of Lascar classes of c and
$f/\operatorname {Autf}^1(p)\in \operatorname {Gal}_{\operatorname {L}}^1(p)$
is determined by the pair of Lascar classes of c and
![]() $f(c)$
for some (any)
$f(c)$
for some (any)
![]() $c\models p$
.
$c\models p$
.
Example 1.11. Let
![]() $({\mathcal M},<)$
be a monster model of
$({\mathcal M},<)$
be a monster model of
![]() $\operatorname {Th}({\mathbb Q},<)$
. Then thorn-independence
$\operatorname {Th}({\mathbb Q},<)$
. Then thorn-independence
![]() in
in
![]() ${\mathcal M}$
coincides with
${\mathcal M}$
coincides with
![]() $\operatorname {acl}$
-independence. We can also consider a notion of reversible amalgamation using thorn independence instead of nonforking independence. Note that the Lascar group of
$\operatorname {acl}$
-independence. We can also consider a notion of reversible amalgamation using thorn independence instead of nonforking independence. Note that the Lascar group of
![]() $\operatorname {Th}({\mathcal M})$
is trivial because of o-minimality, but the reversible amalgamation for
$\operatorname {Th}({\mathcal M})$
is trivial because of o-minimality, but the reversible amalgamation for
![]() fails.
fails.
Let p be the unique
![]() $1$
-type over
$1$
-type over
![]() $\emptyset (=\operatorname {acl}(\emptyset ))$
. Consider two types
$\emptyset (=\operatorname {acl}(\emptyset ))$
. Consider two types
![]() $r(x,y)=\{x< y\}$
and
$r(x,y)=\{x< y\}$
and
![]() $s(x,y)=\{y< x\}$
completing
$s(x,y)=\{y< x\}$
completing
![]() . Then p has no reversible amalgamation of r and s. Suppose
. Then p has no reversible amalgamation of r and s. Suppose
![]() $a,b,c,d\models p$
such that
$a,b,c,d\models p$
such that
![]() $ab,dc\models r$
and
$ab,dc\models r$
and
![]() $ac,db\models s$
. Then
$ac,db\models s$
. Then
![]() $a< b< d< c < a$
, and there are no such elements. Thus, a type of a model does not have reversible amalgamation either.
$a< b< d< c < a$
, and there are no such elements. Thus, a type of a model does not have reversible amalgamation either.
2. Relativized Lascar Galois groups and algebraicity
As mentioned in the introduction, this section does not make any use of the homology groups and thus can be read independently from Section 1. Recall that throughout we assume that
![]() $\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
. In Remark 1.8 from [Reference Dobrowolski, Kim and Lee3] it was noticed that if
$\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
. In Remark 1.8 from [Reference Dobrowolski, Kim and Lee3] it was noticed that if
![]() $\operatorname {tp}(a)$
is a Lascar type, and a finite tuple c is algebraic over a then
$\operatorname {tp}(a)$
is a Lascar type, and a finite tuple c is algebraic over a then
![]() $\operatorname {tp}(ac)$
is also a Lascar type, and hence if additionally T is G-compact then
$\operatorname {tp}(ac)$
is also a Lascar type, and hence if additionally T is G-compact then
![]() $\operatorname {tp}(\operatorname {acl}(a))$
is also a Lascar type. In other words, if
$\operatorname {tp}(\operatorname {acl}(a))$
is also a Lascar type. In other words, if
 $\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(a))$
is trivial, then
$\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(a))$
is trivial, then
 $\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(\operatorname {acl}(a))$
is trivial when T is G-compact. It seems natural to ask whether, more generally,
$\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(\operatorname {acl}(a))$
is trivial when T is G-compact. It seems natural to ask whether, more generally,
 $\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(a))$
and
$\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(a))$
and
 $\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(\operatorname {acl}(a))$
must be always isomorphic in a G-compact T. In general, the answer turns out to be negative (see Section 3), but we obtain some positive results if, instead of looking at
$\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(\operatorname {acl}(a))$
must be always isomorphic in a G-compact T. In general, the answer turns out to be negative (see Section 3), but we obtain some positive results if, instead of looking at
![]() $\operatorname {acl}(a)$
, we add only a finite part of it to a.
$\operatorname {acl}(a)$
, we add only a finite part of it to a.
Remark 2.1. The only properties of Lascar equivalence
![]() $\equiv ^L$
in G-compact theories used in this section are that it is a bounded
$\equiv ^L$
in G-compact theories used in this section are that it is a bounded
![]() $\emptyset $
-type definable equivalence relation and that for any compatible tuples a and b with
$\emptyset $
-type definable equivalence relation and that for any compatible tuples a and b with
![]() $a\equiv ^L b$
we also have
$a\equiv ^L b$
we also have
![]() $a_0\equiv b_0$
for all corresponding subtuples
$a_0\equiv b_0$
for all corresponding subtuples
![]() $a_0\subseteq a$
and
$a_0\subseteq a$
and
![]() $b_0\subseteq b$
. As KP-equivalence
$b_0\subseteq b$
. As KP-equivalence
![]() $\equiv ^{KP}$
has these properties in any theory, all the main results of this section: Theorem 2.6, Corollary 2.9, Propositions 2.12 and 2.14, and Corollaries 2.16 and 2.20 hold without the G-compactness assumption if we replace the Lascar equivalence by KP-equivalence, and relativized Lascar groups
$\equiv ^{KP}$
has these properties in any theory, all the main results of this section: Theorem 2.6, Corollary 2.9, Propositions 2.12 and 2.14, and Corollaries 2.16 and 2.20 hold without the G-compactness assumption if we replace the Lascar equivalence by KP-equivalence, and relativized Lascar groups
 $\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
by relativized Kim–Pillay groups
$\operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
by relativized Kim–Pillay groups
 $\operatorname {Gal}_{\operatorname {KP}}^{\lambda }(p):=\operatorname {Aut}(p)/\operatorname {Autf}^{\lambda }_{\operatorname {KP}}(p)$
, where
$\operatorname {Gal}_{\operatorname {KP}}^{\lambda }(p):=\operatorname {Aut}(p)/\operatorname {Autf}^{\lambda }_{\operatorname {KP}}(p)$
, where
 $\operatorname {Autf}^{\lambda }_{\operatorname {KP}}(p)$
is defined as the group of automorphisms in
$\operatorname {Autf}^{\lambda }_{\operatorname {KP}}(p)$
is defined as the group of automorphisms in
![]() $\operatorname {Aut}(p)$
fixing the KP-type of any
$\operatorname {Aut}(p)$
fixing the KP-type of any
![]() $\lambda $
-many realizations of p.
$\lambda $
-many realizations of p.
For the whole Section 2, we fix the following notation.
Notation 2.2. Assume that
![]() $p=\operatorname {tp}(a)$
and
$p=\operatorname {tp}(a)$
and
![]() $\bar {p}=\operatorname {tp}(ac)$
, where
$\bar {p}=\operatorname {tp}(ac)$
, where
![]() $c\subseteq \operatorname {acl}(a)$
is finite. Consider the natural projection
$c\subseteq \operatorname {acl}(a)$
is finite. Consider the natural projection
 $\pi _{\lambda }:\operatorname {Gal}_{\operatorname {L}}^{\lambda }(\bar {p})\to \operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
, and put
$\pi _{\lambda }:\operatorname {Gal}_{\operatorname {L}}^{\lambda }(\bar {p})\to \operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
, and put
![]() $ \pi :=\pi _1$
. We denote the kernel of
$ \pi :=\pi _1$
. We denote the kernel of
![]() $\pi $
by K. Denote by E the relation of being Lascar-equivalent (formally, E depends on the length of tuples on which we consider it). Let
$\pi $
by K. Denote by E the relation of being Lascar-equivalent (formally, E depends on the length of tuples on which we consider it). Let
![]() $ac_1,\dots ,ac_{N}$
be a tuple of representatives of all E-classes in
$ac_1,\dots ,ac_{N}$
be a tuple of representatives of all E-classes in
![]() $\bar {p}$
in which the first coordinate is equal to a (so
$\bar {p}$
in which the first coordinate is equal to a (so
![]() $N\leq $
the number of realizations of
$N\leq $
the number of realizations of
![]() $\operatorname {tp} (c/a)$
), and for any
$\operatorname {tp} (c/a)$
), and for any
![]() $a'\models p$
, let
$a'\models p$
, let
 $a'c^{a'}_1,\dots ,a'c^{a'}_{N}$
be its conjugate by an automorphism sending a to
$a'c^{a'}_1,\dots ,a'c^{a'}_{N}$
be its conjugate by an automorphism sending a to
![]() $a'$
.
$a'$
.
Example 2.3. We give an example of a structure and a type p such that
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
and
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
and
 $\operatorname {Gal}_{\operatorname {L}}^2(p)$
are distinct. Let
$\operatorname {Gal}_{\operatorname {L}}^2(p)$
are distinct. Let
![]() $\mathbb {C}=\mathbb {R}\times \mathbb {R}$
be a Euclidean plane. Let
$\mathbb {C}=\mathbb {R}\times \mathbb {R}$
be a Euclidean plane. Let
 $\Lambda =\{r\pi \mid r\in \mathbb {Q}\cap (0,\frac {1}{2}]\}$
. For
$\Lambda =\{r\pi \mid r\in \mathbb {Q}\cap (0,\frac {1}{2}]\}$
. For
![]() $q\in \Lambda $
, define
$q\in \Lambda $
, define
![]() $R_q(xy, zw)$
on
$R_q(xy, zw)$
on
![]() $\mathbb {C}^4$
such that
$\mathbb {C}^4$
such that
![]() $R_q(ab, cd)$
iff
$R_q(ab, cd)$
iff
![]() $a\ne b$
,
$a\ne b$
,
![]() $c\ne d$
, and either the lines
$c\ne d$
, and either the lines
![]() $L(ab)$
containing
$L(ab)$
containing
![]() $a,b$
and
$a,b$
and
![]() $L(cd)$
are parallel, or the smaller angle between
$L(cd)$
are parallel, or the smaller angle between
![]() $L(ab)$
and
$L(ab)$
and
![]() $L(cd)$
is
$L(cd)$
is
![]() $\leq q$
. Also define a family of ternary relations
$\leq q$
. Also define a family of ternary relations
![]() $S_r(x,y,z)$
, for
$S_r(x,y,z)$
, for
![]() $r\in \mathbb {Q}^+$
, so that
$r\in \mathbb {Q}^+$
, so that
![]() $S_r(a,b,c)$
if and only if
$S_r(a,b,c)$
if and only if
![]() $|ab|< r|ac|$
.
$|ab|< r|ac|$
.
Consider a model
 $M=(\mathbb {C}; R_q(xy,zw); S_r(x,y,z))_{q\in \Lambda ,r\in \mathbb Q^+}$
. Then
$M=(\mathbb {C}; R_q(xy,zw); S_r(x,y,z))_{q\in \Lambda ,r\in \mathbb Q^+}$
. Then
 $F(xy,zw):=\bigwedge _{q\in \Lambda }R_q(xy,zw)$
is an
$F(xy,zw):=\bigwedge _{q\in \Lambda }R_q(xy,zw)$
is an
![]() $\emptyset $
-type-definable bounded equivalence relation in
$\emptyset $
-type-definable bounded equivalence relation in
![]() $T=\mbox {Th}(M)$
, and each class corresponds to a class of lines whose slopes are infinitesimally close.
$T=\mbox {Th}(M)$
, and each class corresponds to a class of lines whose slopes are infinitesimally close.
Let
![]() $\mathcal R$
be a sufficiently saturated model of the reals,
$\mathcal R$
be a sufficiently saturated model of the reals,
![]() $\mathcal {C}=\mathcal R^2$
,
$\mathcal {C}=\mathcal R^2$
,
![]() $N\models T$
, a a finite tuple in N, and
$N\models T$
, a a finite tuple in N, and
![]() $c\in N$
an element. Then for any
$c\in N$
an element. Then for any
![]() $b\in \mathcal {C}$
that has the same quantifier-free type as a there is
$b\in \mathcal {C}$
that has the same quantifier-free type as a there is
![]() $d\in \mathcal {C}$
such that
$d\in \mathcal {C}$
such that
![]() $ac$
and
$ac$
and
![]() $bd$
have the same quantifier-free type.
$bd$
have the same quantifier-free type.
Let p be the unique complete
![]() $1$
-type over
$1$
-type over
![]() $\emptyset $
. Indeed p is a Lascar type, so
$\emptyset $
. Indeed p is a Lascar type, so
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is trivial. On the other hand, a rotation of
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is trivial. On the other hand, a rotation of
![]() $\mathcal {C}$
around a point in
$\mathcal {C}$
around a point in
![]() $\mathbb {C}$
belongs to
$\mathbb {C}$
belongs to
 $\operatorname {Autf}^1(p)$
but does not belong to
$\operatorname {Autf}^1(p)$
but does not belong to
 $\operatorname {Autf}^2(p)$
. One can show that
$\operatorname {Autf}^2(p)$
. One can show that
 $\operatorname {Gal}_{\operatorname {L}}^2(p)$
is a circle group, and T is G-compact (see Definition 0.1 and Fact 0.2).
$\operatorname {Gal}_{\operatorname {L}}^2(p)$
is a circle group, and T is G-compact (see Definition 0.1 and Fact 0.2).
In fact for any
![]() $n>0$
, and any finite
$n>0$
, and any finite
![]() $a_{< n}=a_0\dots a_{n-1}$
and
$a_{< n}=a_0\dots a_{n-1}$
and
![]() $b_{< n}=b_0\dots b_{n-1}$
(
$b_{< n}=b_0\dots b_{n-1}$
(
![]() $a_j, b_j\in \mathcal {C}^1$
), the following are equivalent:
$a_j, b_j\in \mathcal {C}^1$
), the following are equivalent:
-
(1)
 $a_{< n}\equiv ^L b_{<n}$
.
$a_{< n}\equiv ^L b_{<n}$
. -
(2)
 $F(a_ia_j,b_ib_j)$
for
$F(a_ia_j,b_ib_j)$
for
 $i< j< n$
.
$i< j< n$
. -
(3) There is
 $I=( c^i_{< n}\mid i< \omega )$
such that both
$I=( c^i_{< n}\mid i< \omega )$
such that both
 $a_{< n}I$
and
$a_{< n}I$
and
 $b_{< n}I$
are indiscernibles.
$b_{< n}I$
are indiscernibles.
It is enough to show
![]() $(2)\Rightarrow (3)$
. We write
$(2)\Rightarrow (3)$
. We write
![]() $a_{ij}=a_ia_j$
for
$a_{ij}=a_ia_j$
for
![]() $i,j< n$
. We say that
$i,j< n$
. We say that
![]() $a_0$
,
$a_0$
,
![]() $a_1$
, and
$a_1$
, and
![]() $a_2$
are collinear if
$a_2$
are collinear if
![]() $F(a_{ij},a_{ik})$
for
$F(a_{ij},a_{ik})$
for
![]() $\{i,j,k\}=\{0,1,2\}$
. Suppose
$\{i,j,k\}=\{0,1,2\}$
. Suppose
![]() $F(a_{ij}, b_{ij})$
for all
$F(a_{ij}, b_{ij})$
for all
![]() $i<j<n$
. Then there is
$i<j<n$
. Then there is
![]() $d\in \mathcal {C}$
such that
$d\in \mathcal {C}$
such that
![]() $d,a_i,b_i$
are collinear for each
$d,a_i,b_i$
are collinear for each
![]() $i< n$
. (Even when
$i< n$
. (Even when
![]() $F(a_ib_i, a_jb_j)$
holds for each
$F(a_ib_i, a_jb_j)$
holds for each
![]() $i< j< n$
, there still is such
$i< j< n$
, there still is such
![]() $d\in {\mathcal M}$
, by compactness.) In other words, there is a perspective point d for the sets
$d\in {\mathcal M}$
, by compactness.) In other words, there is a perspective point d for the sets
![]() $a_{< n}$
and
$a_{< n}$
and
![]() $b_{< n}$
in
$b_{< n}$
in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Let
![]() $N\prec \mathcal R$
be a small elementary substructure containing all coordinates of the points
$N\prec \mathcal R$
be a small elementary substructure containing all coordinates of the points
![]() $a_{< n}\cup b_{< n}$
. Consider a complete type
$a_{< n}\cup b_{< n}$
. Consider a complete type
![]() $p_{\infty }(x)=\{x>a:a\in N\}$
over N in the ordered ring language. Let
$p_{\infty }(x)=\{x>a:a\in N\}$
over N in the ordered ring language. Let
![]() $\{\alpha _i\mid i<\omega \}$
be a Morley sequence of realizations
$\{\alpha _i\mid i<\omega \}$
be a Morley sequence of realizations
![]() $p_{\infty }$
such that
$p_{\infty }$
such that
![]() $\operatorname {tp}(\alpha _i/N\alpha _{< i})$
is an heir extension of
$\operatorname {tp}(\alpha _i/N\alpha _{< i})$
is an heir extension of
![]() $p_{\infty }$
so that
$p_{\infty }$
so that
![]() $\alpha _i$
is infinite with respect to
$\alpha _i$
is infinite with respect to
![]() $\operatorname {dcl}(N\alpha _{< i})$
. Now, we can take I to be the sequence of scaled by
$\operatorname {dcl}(N\alpha _{< i})$
. Now, we can take I to be the sequence of scaled by
![]() $\alpha _i$
copies of
$\alpha _i$
copies of
![]() $a_{< n}$
relative to the point d:
$a_{< n}$
relative to the point d:
 $c^i_{j} = \alpha _i(a_j-d)+d$
.
$c^i_{j} = \alpha _i(a_j-d)+d$
.
Let us recall basic definitions and facts on covering maps between topological groups (see for example [Reference Hofmann and Morris6]).
-
• Let
 $X, Y$
be topological spaces, and let
$X, Y$
be topological spaces, and let
 $f:X\to Y$
be a continuous surjective map. We call f a (
k-
)
covering map if for each
$f:X\to Y$
be a continuous surjective map. We call f a (
k-
)
covering map if for each
 $y\in Y$
there is an open set V containing y such that
$y\in Y$
there is an open set V containing y such that
 $f^{-1}(V)$
is a union of (k-many) disjoint open sets in X, and f induces a homeomorphism between each such open set and V. We call f a local homeomorphism if for any
$f^{-1}(V)$
is a union of (k-many) disjoint open sets in X, and f induces a homeomorphism between each such open set and V. We call f a local homeomorphism if for any
 $x\in X$
, there is an open set U containing x such that
$x\in X$
, there is an open set U containing x such that
 $f\restriction U:U\to f(U)$
is a homeomorphism. Obviously a covering map is a local homeomorphism. Conversely, if both X and Y are compact, then a local homeomorphism is a covering map. We call X a covering space of Y if there is a covering map from X to Y.
$f\restriction U:U\to f(U)$
is a homeomorphism. Obviously a covering map is a local homeomorphism. Conversely, if both X and Y are compact, then a local homeomorphism is a covering map. We call X a covering space of Y if there is a covering map from X to Y. -
• Let G be topological group, and let H be a normal subgroup of G such that
 $G/H$
with its quotient topology is also a topological group, and the projection map
$G/H$
with its quotient topology is also a topological group, and the projection map
 $\mbox {pr}: G\to G/H$
is an open continuous homomorphism. Recall that
$\mbox {pr}: G\to G/H$
is an open continuous homomorphism. Recall that
 $\mbox {pr}$
is a covering map if and only if H is a discrete subgroup. If G is compact, then H is discrete if and only if H is finite, and hence iff
$\mbox {pr}$
is a covering map if and only if H is a discrete subgroup. If G is compact, then H is discrete if and only if H is finite, and hence iff
 $\mbox {pr}$
is a covering map.Assume F is another topological group and
$\mbox {pr}$
is a covering map.Assume F is another topological group and
 $f:G\to F$
is a continuous surjective homomorphism. If G is compact and F is Hausdorff, then f induces an isomorphism between the compact topological groups
$f:G\to F$
is a continuous surjective homomorphism. If G is compact and F is Hausdorff, then f induces an isomorphism between the compact topological groups
 $G/\operatorname {Ker}(f)$
and F.
$G/\operatorname {Ker}(f)$
and F. -
• Assume T is G-compact. By the above,
 $\pi _{\lambda }$
is a covering homomorphism iff the kernel of
$\pi _{\lambda }$
is a covering homomorphism iff the kernel of
 $\pi _{\lambda }$
is finite. In particular, we shall show that
$\pi _{\lambda }$
is finite. In particular, we shall show that
 $\pi =\pi _1$
is a covering homomorphism (Corollary 2.9).
$\pi =\pi _1$
is a covering homomorphism (Corollary 2.9).
If T is G-compact then the Lascar equivalence E is
![]() $\emptyset $
-type-definable (see [Reference Kim7, Proposition 20]), and we can assume any formula
$\emptyset $
-type-definable (see [Reference Kim7, Proposition 20]), and we can assume any formula
![]() $\varphi $
in E is symmetric (i.e.,
$\varphi $
in E is symmetric (i.e.,
![]() $\varphi (\bar z,\bar w)\models \varphi (\bar w,\bar z)$
).
$\varphi (\bar z,\bar w)\models \varphi (\bar w,\bar z)$
).
Lemma 2.5. Assume T is G-compact. There is a formula
![]() $\alpha (xy,x'y')\in E(xy,x'y')$
such that if
$\alpha (xy,x'y')\in E(xy,x'y')$
such that if
![]() $\bar p(xy)\wedge \bar p(x'y') \wedge \alpha (xy,x'y')\wedge E(x,x')$
holds then
$\bar p(xy)\wedge \bar p(x'y') \wedge \alpha (xy,x'y')\wedge E(x,x')$
holds then
![]() $\models E(xy,x'y').$
$\models E(xy,x'y').$
Proof Notice that the type
 $$ \begin{align*}E(xy,x'y')\wedge\exists zwz'w'\equiv xyx'y' \left(\bigvee_{ 1\leq i\ne j\leq N} (E(zw,ac_i)\wedge E(z'w',ac_j))\right)\end{align*} $$
$$ \begin{align*}E(xy,x'y')\wedge\exists zwz'w'\equiv xyx'y' \left(\bigvee_{ 1\leq i\ne j\leq N} (E(zw,ac_i)\wedge E(z'w',ac_j))\right)\end{align*} $$
is inconsistent, and choose
![]() $\alpha (xy,x'y')\in E(xy,x'y')$
so that the type
$\alpha (xy,x'y')\in E(xy,x'y')$
so that the type
 $$ \begin{align*}\alpha(xy,x'y')\wedge\exists zwz'w'\equiv xyx'y' \left(\bigvee_{1\leq i\ne j\leq N} (E(zw,ac_i)\wedge E(z'w',ac_j))\right)\end{align*} $$
$$ \begin{align*}\alpha(xy,x'y')\wedge\exists zwz'w'\equiv xyx'y' \left(\bigvee_{1\leq i\ne j\leq N} (E(zw,ac_i)\wedge E(z'w',ac_j))\right)\end{align*} $$
is inconsistent. Now, if
![]() $\bar p(xy)\wedge \bar p(x'y') \wedge \alpha (xy,x'y')\wedge E(x,x')$
holds, then we can find
$\bar p(xy)\wedge \bar p(x'y') \wedge \alpha (xy,x'y')\wedge E(x,x')$
holds, then we can find
![]() $c'a'c''$
such that
$c'a'c''$
such that
![]() $ac'a'c'' \equiv xyx'y'$
, and then
$ac'a'c'' \equiv xyx'y'$
, and then
![]() $a'\equiv ^L a$
so
$a'\equiv ^L a$
so
![]() $a'c'' \equiv ^L ac_i$
for some i, and also
$a'c'' \equiv ^L ac_i$
for some i, and also
![]() $ac' \equiv ^L ac_j$
for some j, but, by the choice of
$ac' \equiv ^L ac_j$
for some j, but, by the choice of
![]() $\alpha $
,
$\alpha $
,
![]() $i=j$
so
$i=j$
so
![]() $ac'\equiv ^L a'c''$
, so
$ac'\equiv ^L a'c''$
, so
![]() $xy \equiv ^L x'y'$
.⊣
$xy \equiv ^L x'y'$
.⊣
The following theorem and its proof will use the setting described in Notation 2.2.
Theorem 2.6. If T is G-compact, then K is finite.
Proof Assume T is G-compact. Since E is transitive, there is
![]() $\phi (xy,x'y')\in E(xy,x'y')$
such that
$\phi (xy,x'y')\in E(xy,x'y')$
such that
where
![]() $\alpha \in E$
is the formula given by Lemma 2.5.
$\alpha \in E$
is the formula given by Lemma 2.5.
Let
![]() $(a_{\ell })_{\ell \in I}$
be a small set of representatives of E-classes of realizations of p. For any
$(a_{\ell })_{\ell \in I}$
be a small set of representatives of E-classes of realizations of p. For any
![]() $a'c'\models \bar {p}$
, there are
$a'c'\models \bar {p}$
, there are
![]() $\ell \in I$
and
$\ell \in I$
and
![]() $1\leq j\leq N$
such that
$1\leq j\leq N$
such that
 $\models E(a'c',a_{\ell }c_j^{a_{\ell }})$
, so
$\models E(a'c',a_{\ell }c_j^{a_{\ell }})$
, so
 $\models \phi (a'c',a_{\ell }c_j^{a_{\ell }})$
. Hence, by compactness, there are
$\models \phi (a'c',a_{\ell }c_j^{a_{\ell }})$
. Hence, by compactness, there are
![]() $a_0,\dots ,a_k\models p$
such that
$a_0,\dots ,a_k\models p$
such that
 $$ \begin{align*}\bar{p}(xy) \vdash \bigvee\{ \phi(xy,a_ic^{a_i}_j)\mid i\leq k;\ 1\leq j\leq N \}\ \ (**).\end{align*} $$
$$ \begin{align*}\bar{p}(xy) \vdash \bigvee\{ \phi(xy,a_ic^{a_i}_j)\mid i\leq k;\ 1\leq j\leq N \}\ \ (**).\end{align*} $$
Claim 2.7. Let
 $f/\operatorname {Autf}^1(\bar {p})\in K$
. For each
$f/\operatorname {Autf}^1(\bar {p})\in K$
. For each
 $a_ic_j^{a_i}$
chosen above, there is a unique
$a_ic_j^{a_i}$
chosen above, there is a unique
 $a_ic^{a_i}_{j'}$
with
$a_ic^{a_i}_{j'}$
with
![]() $ 1\leq j'\leq N$
such that
$ 1\leq j'\leq N$
such that
 $\phi (f(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
holds. Such a
$\phi (f(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
holds. Such a
![]() $j'$
does not depend on the choice of a representative of
$j'$
does not depend on the choice of a representative of
 $f/\operatorname {Autf}^1(\bar {p})$
.
$f/\operatorname {Autf}^1(\bar {p})$
.
Proof Notice that
 $f/\operatorname {Autf}^1(\bar {p})\in K$
implies
$f/\operatorname {Autf}^1(\bar {p})\in K$
implies
![]() $E(f(a_i),a_i)$
, so
$E(f(a_i),a_i)$
, so
 $E(f(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
holds for some
$E(f(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
holds for some
![]() $j'$
. Now if
$j'$
. Now if
 $\phi (f(a_ic^{a_i}_j), a_ic^{a_i}_{j''})$
holds as well, then due to
$\phi (f(a_ic^{a_i}_j), a_ic^{a_i}_{j''})$
holds as well, then due to
![]() $(*)$
(with the symmetry of the formulas) and Lemma 2.5, we must have
$(*)$
(with the symmetry of the formulas) and Lemma 2.5, we must have
![]() $j'=j''$
. The second statement of the claim follows similarly.⊣
$j'=j''$
. The second statement of the claim follows similarly.⊣
Claim 2.8. Let
 $f/\operatorname {Autf}^1(\bar {p})$
,
$f/\operatorname {Autf}^1(\bar {p})$
,
 $g/\operatorname {Autf}^1(\bar {p})\in K$
. Assume that the permutations of tuples
$g/\operatorname {Autf}^1(\bar {p})\in K$
. Assume that the permutations of tuples
 $a_ic_j^{a_i}$
by f and g described in the claim above are the same. Then
$a_ic_j^{a_i}$
by f and g described in the claim above are the same. Then
 $f/\operatorname {Autf}^1(\bar {p})=g/\operatorname {Autf}^1(\bar {p})$
.
$f/\operatorname {Autf}^1(\bar {p})=g/\operatorname {Autf}^1(\bar {p})$
.
Proof Let
![]() $a'c'\models \bar p$
. By
$a'c'\models \bar p$
. By
![]() $(**)$
, there is some
$(**)$
, there is some
 $a_ic_j^{a_i}$
such that
$a_ic_j^{a_i}$
such that
 $\phi (a'c', a_ic_j^{a_i})$
holds. Hence,
$\phi (a'c', a_ic_j^{a_i})$
holds. Hence,
 $\phi (f(a'c'), f(a_ic_j^{a_i}))$
and
$\phi (f(a'c'), f(a_ic_j^{a_i}))$
and
 $\phi (g(a'c'), g(a_ic_j^{a_i}))$
hold. Moreover, by the previous claim with our assumption, there is
$\phi (g(a'c'), g(a_ic_j^{a_i}))$
hold. Moreover, by the previous claim with our assumption, there is
![]() $ j'\leq N$
such that
$ j'\leq N$
such that
 $\phi (f(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
and
$\phi (f(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
and
 $\phi (g(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
hold.
$\phi (g(a_ic^{a_i}_j), a_ic^{a_i}_{j'})$
hold.
Then, again due to
![]() $(*)$
and Lemma 2.5,
$(*)$
and Lemma 2.5,
 $f(a_ic^{a_i}_j)\equiv ^L g(a_ic^{a_i}_j)$
since
$f(a_ic^{a_i}_j)\equiv ^L g(a_ic^{a_i}_j)$
since
![]() $f(a_i)\equiv ^Lg(a_i)\equiv ^L a_i$
. Hence, there is
$f(a_i)\equiv ^Lg(a_i)\equiv ^L a_i$
. Hence, there is
 $h\in \operatorname {Autf}^1(\bar p)$
such that
$h\in \operatorname {Autf}^1(\bar p)$
such that
 $f(a_ic^{a_i}_j)=hg(a_ic^{a_i}_j)$
. Now by
$f(a_ic^{a_i}_j)=hg(a_ic^{a_i}_j)$
. Now by
![]() $(*)$
again,
$(*)$
again,
![]() $\alpha (f(a'c'), hg(a'c'))$
holds, and, since
$\alpha (f(a'c'), hg(a'c'))$
holds, and, since
![]() $f(a')\equiv ^Lhg(a')\equiv ^L a'$
, we have
$f(a')\equiv ^Lhg(a')\equiv ^L a'$
, we have
![]() $f(a'c')\equiv ^L hg(a'c')\equiv ^L g(a'c')$
. We conclude that
$f(a'c')\equiv ^L hg(a'c')\equiv ^L g(a'c')$
. We conclude that
 $f/\operatorname {Autf}^1(\bar {p})=g/\operatorname {Autf}^1(\bar {p})$
.⊣
$f/\operatorname {Autf}^1(\bar {p})=g/\operatorname {Autf}^1(\bar {p})$
.⊣
As there are only finitely many permutations of
 $a_ic_j^{a_i}$
(
$a_ic_j^{a_i}$
(
![]() $i\leq k$
,
$i\leq k$
,
![]() $ 1\leq j\leq N$
), K is finite.⊣
$ 1\leq j\leq N$
), K is finite.⊣
By Remark 2.4, we have the following.
Corollary 2.9. If T is G-compact then
 $\pi :\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {p})\to \operatorname {Gal}_{\operatorname {L}}^{1}(p)$
is a covering homomorphism.
$\pi :\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {p})\to \operatorname {Gal}_{\operatorname {L}}^{1}(p)$
is a covering homomorphism.
Example 2.10. Consider the following model:
 $$ \begin{align*}M=((M_1,S_1,\{g^1_n\mid 0< n\}),(M_2,S_2,\{g^2_n\mid 0< n\}),\delta),\end{align*} $$
$$ \begin{align*}M=((M_1,S_1,\{g^1_n\mid 0< n\}),(M_2,S_2,\{g^2_n\mid 0< n\}),\delta),\end{align*} $$
a 2-sorted structure. Here
![]() $M_1, M_2$
are disjoint unit circles. For
$M_1, M_2$
are disjoint unit circles. For
![]() $i=1,2$
,
$i=1,2$
,
![]() $S_i$
is a ternary relation on
$S_i$
is a ternary relation on
![]() $M_i$
such that
$M_i$
such that
![]() $S_i(a,b,c)$
holds iff
$S_i(a,b,c)$
holds iff
![]() $a,b,c$
are distinct and b comes before c going clockwise around
$a,b,c$
are distinct and b comes before c going clockwise around
![]() $M_i$
from a; and
$M_i$
from a; and
![]() $g^i_n$
is the clockwise rotation of
$g^i_n$
is the clockwise rotation of
![]() $M_i$
by
$M_i$
by
![]() $\frac {2\pi }{n}$
-radians. The map
$\frac {2\pi }{n}$
-radians. The map
![]() $\delta :M_1\to M_2$
is a double covering, i.e., if we identify each
$\delta :M_1\to M_2$
is a double covering, i.e., if we identify each
![]() $M_i$
as the unit circle in
$M_i$
as the unit circle in
![]() $xy$
-plane centered at
$xy$
-plane centered at
![]() $0$
, then
$0$
, then
![]() $\delta $
is given by
$\delta $
is given by
![]() $(\cos t, \sin t)\mapsto (\cos 2t,\sin 2t).$
By arguments similar to those described in [Reference Dobrowolski, Kim and Lee3] for
$(\cos t, \sin t)\mapsto (\cos 2t,\sin 2t).$
By arguments similar to those described in [Reference Dobrowolski, Kim and Lee3] for
![]() $M_i$
, it follows that
$M_i$
, it follows that
![]() $T=\operatorname {Th}(M)$
is G-compact, and, in T,
$T=\operatorname {Th}(M)$
is G-compact, and, in T,
![]() $\emptyset =\operatorname {acl}^{\operatorname {eq}}(\emptyset )$
. Let
$\emptyset =\operatorname {acl}^{\operatorname {eq}}(\emptyset )$
. Let
![]() ${\mathcal M}_1,{\mathcal M}_2$
be saturated models of
${\mathcal M}_1,{\mathcal M}_2$
be saturated models of
![]() $M_1,M_2$
respectively. For any
$M_1,M_2$
respectively. For any
![]() $a_i,a^{\prime }_i\in {\mathcal M}_i$
, we have
$a_i,a^{\prime }_i\in {\mathcal M}_i$
, we have
![]() $a_i\equiv a^{\prime }_i$
; and
$a_i\equiv a^{\prime }_i$
; and
![]() $a_i\equiv ^La^{\prime }_i$
iff they are infinitesimally close. Now, given
$a_i\equiv ^La^{\prime }_i$
iff they are infinitesimally close. Now, given
![]() $a\in M_2$
, there are two antipodal
$a\in M_2$
, there are two antipodal
![]() $c_1,c_2\in M_1$
such that
$c_1,c_2\in M_1$
such that
![]() $\delta (c_i)=a$
. Then
$\delta (c_i)=a$
. Then
![]() $c_i\in \operatorname {acl}(a)$
and
$c_i\in \operatorname {acl}(a)$
and
![]() $ac_1\equiv ac_2$
, but
$ac_1\equiv ac_2$
, but
![]() $ac_1\not \equiv ^L ac_2$
. For
$ac_1\not \equiv ^L ac_2$
. For
![]() $p=\operatorname {tp}(a)$
and
$p=\operatorname {tp}(a)$
and
![]() $\bar p=\operatorname {tp}(ac_1)$
,
$\bar p=\operatorname {tp}(ac_1)$
,
 $\pi :\operatorname {Gal}_{\operatorname {L}}^{1}(\bar p)\to \operatorname {Gal}_{\operatorname {L}}^{1}(p)$
is a 2-covering homomorphism of circle groups. Notice that for any
$\pi :\operatorname {Gal}_{\operatorname {L}}^{1}(\bar p)\to \operatorname {Gal}_{\operatorname {L}}^{1}(p)$
is a 2-covering homomorphism of circle groups. Notice that for any
![]() $n>2$
,
$n>2$
,
 $$ \begin{align*}\delta(y)=x \wedge \delta(y')=x' \wedge (S_1(y,y',g_n^1(y)) \vee S_1(y',y,g_n^1(y')))\end{align*} $$
$$ \begin{align*}\delta(y)=x \wedge \delta(y')=x' \wedge (S_1(y,y',g_n^1(y)) \vee S_1(y',y,g_n^1(y')))\end{align*} $$
serves as the formula
![]() $\alpha (xy,x'y')$
in Lemma 2.5.
$\alpha (xy,x'y')$
in Lemma 2.5.
Question 2.11. If T is G-compact, then is the kernel of the projection
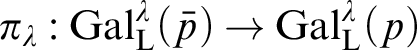 $\pi _{\lambda }:\operatorname {Gal}_{\operatorname {L}}^{\lambda }(\bar {p})\to \operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
finite as well for
$\pi _{\lambda }:\operatorname {Gal}_{\operatorname {L}}^{\lambda }(\bar {p})\to \operatorname {Gal}_{\operatorname {L}}^{\lambda }(p)$
finite as well for
![]() $\lambda>1$
? Is T being G-compact essential in Theorem 2.6?
$\lambda>1$
? Is T being G-compact essential in Theorem 2.6?
We have a partial answer to the second question above. Namely, we also get that K is finite when we replace the assumption of G-compactness by abelianity of
 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
.
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
.
Proposition 2.12. If
 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
is abelian, then
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
is abelian, then
![]() $|K|=N$
.
$|K|=N$
.
Proof If
 $f/\operatorname {Autf}^1(\bar {p})\in K$
, then
$f/\operatorname {Autf}^1(\bar {p})\in K$
, then
![]() $f(a)\equiv ^L a$
, so there is another representative
$f(a)\equiv ^L a$
, so there is another representative
![]() $f'$
fixing a. Now, since
$f'$
fixing a. Now, since
 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
is abelian, by Remark 1.10, the class of an automorphism
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
is abelian, by Remark 1.10, the class of an automorphism
![]() $f'$
fixing a depends only on the Lascar type of
$f'$
fixing a depends only on the Lascar type of
![]() $f'(ac)=af'(c)$
for which, due to our choice, there are exactly N possibilities.⊣
$f'(ac)=af'(c)$
for which, due to our choice, there are exactly N possibilities.⊣
We will investigate the epimorphism
![]() $\pi $
further assuming the theory T satisfies, in addition to G-compactness, some other nice hypotheses, obtaining better versions of Theorem 2.6 in these cases.
$\pi $
further assuming the theory T satisfies, in addition to G-compactness, some other nice hypotheses, obtaining better versions of Theorem 2.6 in these cases.
-
(1) Let X be an
 $\emptyset $
-type-definable set, and let F be a bounded
$\emptyset $
-type-definable set, and let F be a bounded
 $\emptyset $
-type-definable equivalence relation on X. Recall the logic topology on
$\emptyset $
-type-definable equivalence relation on X. Recall the logic topology on
 $X/F$
: A subset of
$X/F$
: A subset of
 $X/F$
is closed if and only if its pre-image in X is type-definable over some parameters. It follows that
$X/F$
is closed if and only if its pre-image in X is type-definable over some parameters. It follows that
 $X/F$
is compact with the logic topology.
$X/F$
is compact with the logic topology. -
(2) Assume T is G-compact. By the natural embedding,
 $G:=\operatorname {Gal}_{\operatorname {L}}^1(p)$
can be considered as a subgroup of
$G:=\operatorname {Gal}_{\operatorname {L}}^1(p)$
can be considered as a subgroup of
 $\operatorname {Homeo}(p({\mathcal M})/E)$
, where
$\operatorname {Homeo}(p({\mathcal M})/E)$
, where
 $p({\mathcal M})/E$
is equipped with the logic topology. Moreover, for
$p({\mathcal M})/E$
is equipped with the logic topology. Moreover, for
 $x:=a/E$
and
$x:=a/E$
and
 $G_x:=\{ g\in G\mid g. x= x\}$
(the stabilizer subgroup of G at x), we have that
$G_x:=\{ g\in G\mid g. x= x\}$
(the stabilizer subgroup of G at x), we have that
 $G/G_x$
as a homogeneous coset space with the quotient topology and
$G/G_x$
as a homogeneous coset space with the quotient topology and
 $p({\mathcal M})/E$
with the logic topology are homeomorphic. Needless to say, analogous facts hold for
$p({\mathcal M})/E$
with the logic topology are homeomorphic. Needless to say, analogous facts hold for
 $\bar p$
.
$\bar p$
. -
(3) Let
 $X,Y$
be topological spaces. Recall that if X is path-connected then so is any quotient space of X. Moreover, if X is a connected covering space of Y, then X is path-connected if and only if Y is.
$X,Y$
be topological spaces. Recall that if X is path-connected then so is any quotient space of X. Moreover, if X is a connected covering space of Y, then X is path-connected if and only if Y is. -
(4) Given a covering map
 $\delta :X\to Y$
, the unique path-lifting property says that for any
$\delta :X\to Y$
, the unique path-lifting property says that for any
 $x_0\in X$
,
$x_0\in X$
,
 $y_0\in Y$
with
$y_0\in Y$
with
 $\delta (x_0)=y_0$
, and any path
$\delta (x_0)=y_0$
, and any path
 $\gamma $
in Y starting at
$\gamma $
in Y starting at
 $y_0$
(i.e.,
$y_0$
(i.e.,
 $\gamma :[0,1]\to Y$
is continuous and
$\gamma :[0,1]\to Y$
is continuous and
 $\gamma (0)=y_0$
), there is a unique path
$\gamma (0)=y_0$
), there is a unique path
 $\gamma '$
starting at
$\gamma '$
starting at
 $x_0$
such that
$x_0$
such that
 $\delta \circ \gamma '=\gamma $
.
$\delta \circ \gamma '=\gamma $
.
Proposition 2.14. Assume T is G-compact and consider the canonical restriction map
![]() $\delta :\bar {p}({\mathcal M})/E\to p({\mathcal M})/E$
of compact spaces
$\delta :\bar {p}({\mathcal M})/E\to p({\mathcal M})/E$
of compact spaces
![]() $\bar {p}({\mathcal M})/E$
,
$\bar {p}({\mathcal M})/E$
,
![]() $p({\mathcal M})/E$
equipped with the logic topology. Then
$p({\mathcal M})/E$
equipped with the logic topology. Then
![]() $\delta $
is an N-covering map.
$\delta $
is an N-covering map.
Proof Choose
![]() $\phi $
as in the proof of Theorem 2.6 and fix
$\phi $
as in the proof of Theorem 2.6 and fix
![]() $a'c'\models \bar {p}$
. Define
$a'c'\models \bar {p}$
. Define
![]() $D:=\bar {p}({\mathcal M})\backslash \{a''c''/E:a''c''\models \bar {p}\ \wedge \neg \phi (a''c'',a'c')\}$
. Then D is an open neighborhood of
$D:=\bar {p}({\mathcal M})\backslash \{a''c''/E:a''c''\models \bar {p}\ \wedge \neg \phi (a''c'',a'c')\}$
. Then D is an open neighborhood of
![]() $a'c'/E$
in
$a'c'/E$
in
![]() $\bar {p}({\mathcal M})/E$
. To show that
$\bar {p}({\mathcal M})/E$
. To show that
![]() $\delta $
is a covering map, by Remark 2.4, it is enough to see that
$\delta $
is a covering map, by Remark 2.4, it is enough to see that
![]() $\delta $
is injective on D. So choose two pairs
$\delta $
is injective on D. So choose two pairs
![]() $a^0c^0,a^1c^1 \models \bar {p}$
such that
$a^0c^0,a^1c^1 \models \bar {p}$
such that
![]() $a^0c^0/E,a^1c^1/E \in D$
and
$a^0c^0/E,a^1c^1/E \in D$
and
![]() $\delta (a^0c^0/E)=\delta (a^1c^1/E)$
. Then, by the first condition,
$\delta (a^0c^0/E)=\delta (a^1c^1/E)$
. Then, by the first condition,
![]() $\models \phi (a^0c^0,a'c')\wedge \phi (a^1c^1,a'c')$
, and, by the second one,
$\models \phi (a^0c^0,a'c')\wedge \phi (a^1c^1,a'c')$
, and, by the second one,
![]() $E(a^0,a^1)$
. We conclude by the choice of
$E(a^0,a^1)$
. We conclude by the choice of
![]() $\phi $
that
$\phi $
that
![]() $a^0c^0/E=a^1c^1/E$
. By our choice of N, we have that
$a^0c^0/E=a^1c^1/E$
. By our choice of N, we have that
![]() $\delta $
is N-covering map.⊣
$\delta $
is N-covering map.⊣
Observe the following remark on covering maps.
Remark 2.15. Given topological spaces
![]() $X,Y$
, suppose that
$X,Y$
, suppose that
![]() $\delta :X\to Y$
is a k-covering. Put
$\delta :X\to Y$
is a k-covering. Put
![]() $F:=\{f\in \operatorname {Homeo}(X): \delta \circ f=\delta \}$
.
$F:=\{f\in \operatorname {Homeo}(X): \delta \circ f=\delta \}$
.
-
(1) If Y is path-connected, then
 $|F|\leq k!$
and this bound is optimal.
$|F|\leq k!$
and this bound is optimal. -
(2) If X is path-connected (thus so is Y), then
 $|F|\le k$
.
$|F|\le k$
.
Proof We prove (1) first. It is enough to show that if
![]() $f(\in F)$
fixes some fiber
$f(\in F)$
fixes some fiber
![]() $\delta ^{-1}(y)$
with
$\delta ^{-1}(y)$
with
![]() $y\in Y$
pointwise
$y\in Y$
pointwise
![]() $(*)$
, then f is identity. Fix
$(*)$
, then f is identity. Fix
![]() $x'\in X$
and let
$x'\in X$
and let
![]() $y'=\delta (x')$
. Now there is a path
$y'=\delta (x')$
. Now there is a path
![]() $\alpha $
from y to
$\alpha $
from y to
![]() $y'$
. Then, by the unique path-lifting property, there is a unique path
$y'$
. Then, by the unique path-lifting property, there is a unique path
![]() $\beta $
starting at x, say, and ending at
$\beta $
starting at x, say, and ending at
![]() $x'$
such that
$x'$
such that
![]() $\delta \circ \beta =\alpha $
. Hence,
$\delta \circ \beta =\alpha $
. Hence,
![]() $\delta (x)=y$
. Now, since
$\delta (x)=y$
. Now, since
![]() $f\in F$
, we have
$f\in F$
, we have
![]() $\delta \circ (f\circ \beta )=\delta \circ \beta =\alpha $
too. Moreover due to
$\delta \circ (f\circ \beta )=\delta \circ \beta =\alpha $
too. Moreover due to
![]() $(*)$
,
$(*)$
,
![]() $f(x)=x$
and by the uniqueness, we have
$f(x)=x$
and by the uniqueness, we have
![]() $f\circ \beta =\beta $
, so
$f\circ \beta =\beta $
, so
![]() $f(x')=x'$
. Therefore f is the identity map as desired.
$f(x')=x'$
. Therefore f is the identity map as desired.
To see that the bound is optimal, consider
 $X=\bigcup _{1\le i\le k} (i-1,i)$
and
$X=\bigcup _{1\le i\le k} (i-1,i)$
and
![]() $Y=(0,1)$
. Define a covering map
$Y=(0,1)$
. Define a covering map
![]() $\delta :X\rightarrow Y, x\mapsto x-\lfloor x\rfloor $
, where
$\delta :X\rightarrow Y, x\mapsto x-\lfloor x\rfloor $
, where
![]() $\lfloor x\rfloor $
is the greatest integer which is less than or equal to x. Then, each permutation on
$\lfloor x\rfloor $
is the greatest integer which is less than or equal to x. Then, each permutation on
![]() $\{1,\ldots , k\}$
induces a homeomorphism of X fixing each fibers of
$\{1,\ldots , k\}$
induces a homeomorphism of X fixing each fibers of
![]() $\delta $
and in this case,
$\delta $
and in this case,
![]() $|F|=k!$
.
$|F|=k!$
.
For (2), it is enough to show that if
![]() $f\in F$
fixes a point x in X, then f is the identity. Suppose
$f\in F$
fixes a point x in X, then f is the identity. Suppose
![]() $f\in F$
fixes
$f\in F$
fixes
![]() $x\in X$
. If X is path-connected, then for each
$x\in X$
. If X is path-connected, then for each
![]() $x'\in X$
, there is a unique path
$x'\in X$
, there is a unique path
![]() $\beta $
from x to
$\beta $
from x to
![]() $x'$
due to the unique path-lifting property, so f is the identity by a similar argument as in the proof of (1).⊣
$x'$
due to the unique path-lifting property, so f is the identity by a similar argument as in the proof of (1).⊣
Recall that, by Fact 0.4, the topological group
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is connected (due to our assumption
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is connected (due to our assumption
![]() $\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
). By Remarks 2.13(2)(3) and 2.15 and Proposition 2.14, we immediately get the following:
$\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
). By Remarks 2.13(2)(3) and 2.15 and Proposition 2.14, we immediately get the following:
Corollary 2.16. Assume T is G-compact. If
![]() $\bar {p}({\mathcal M})/E$
or
$\bar {p}({\mathcal M})/E$
or
![]() $p({\mathcal M})/E$
is path-connected—each of which holds if
$p({\mathcal M})/E$
is path-connected—each of which holds if
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
is path-connected, for example a (connected) Lie group—then
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
is path-connected, for example a (connected) Lie group—then
![]() $|K|=N$
.
$|K|=N$
.
Now we show a purely compact abelian group theoretical result, which implies Corollary 2.20. Gleason–Yamabe Theorem [Reference Yamabe12, Theorem 5′] states that every locally compact group G is a generalized Lie group, i.e., for every neighbourhood U of the identity there is an open group
![]() $G_1$
of G and a compact normal subgroup C of
$G_1$
of G and a compact normal subgroup C of
![]() $G_1$
such that
$G_1$
such that
![]() $C\subseteq U$
and
$C\subseteq U$
and
![]() $G_1/C$
is a Lie group [Reference Gleason4, Definition 1.4]. Note that if additionally G is connected, then its only open subgroup is G itself, so the above gives the following folklore fact:
$G_1/C$
is a Lie group [Reference Gleason4, Definition 1.4]. Note that if additionally G is connected, then its only open subgroup is G itself, so the above gives the following folklore fact:
Fact 2.17. Every locally compact connected group is an inverse limit of Lie groups.
Lemma 2.18. Let G be an abelian compact connected topological group, and let F be a finite subgroup of G. Then G and
![]() $G/F$
are isomorphic as topological groups.
$G/F$
are isomorphic as topological groups.
Proof Recall that given a finite group F and a prime number q dividing the order of F, there is a subgroup of F of order q. Hence, we can assume that F has a prime order q (applying the prime order case and quotienting out finitely many times to obtain the conclusion for any finite F).
By Fact 2.17 we can present G as
![]() $\mathop {\lim }_{\longleftarrow I} G_i$
with some directed system
$\mathop {\lim }_{\longleftarrow I} G_i$
with some directed system
![]() $(I,\le )$
and continuous homomorphisms
$(I,\le )$
and continuous homomorphisms
![]() $f_{i,j}:G_i\to G_j$
for
$f_{i,j}:G_i\to G_j$
for
![]() $j\leq i\in I$
, where each
$j\leq i\in I$
, where each
![]() $G_i$
is an abelian connected Lie group, hence a torus. We can assume each
$G_i$
is an abelian connected Lie group, hence a torus. We can assume each
![]() $f_{i,j}$
is surjective. Since F has a prime order, it is generated by a single element, say
$f_{i,j}$
is surjective. Since F has a prime order, it is generated by a single element, say
![]() $a=(a_i)_{i\in I}$
. Also, replacing I by
$a=(a_i)_{i\in I}$
. Also, replacing I by
![]() $I_{i_0}:=\{i\in I|\ i_0\le i\}$
for an appropriate
$I_{i_0}:=\{i\in I|\ i_0\le i\}$
for an appropriate
![]() $i_0$
, we can assume that I has the least element
$i_0$
, we can assume that I has the least element
![]() $i_0$
, and that each
$i_0$
, and that each
![]() $F_i$
(i.e., the projection of F onto the ith coordinate) has order q. We have that
$F_i$
(i.e., the projection of F onto the ith coordinate) has order q. We have that
 $$ \begin{align*}G/F=\lim_{\longleftarrow I} H_i,\end{align*} $$
$$ \begin{align*}G/F=\lim_{\longleftarrow I} H_i,\end{align*} $$
where
![]() $H_i=G_i/F_i$
, with maps
$H_i=G_i/F_i$
, with maps
![]() $k_{i,j}:H_i\to H_j$
induced by
$k_{i,j}:H_i\to H_j$
induced by
![]() $f_{i,j}$
. Moreover, for each
$f_{i,j}$
. Moreover, for each
![]() $i\in I$
, we let
$i\in I$
, we let
![]() $S_i$
be the unique one-dimensional subtorus of
$S_i$
be the unique one-dimensional subtorus of
![]() $G_i$
containing
$G_i$
containing
![]() $a_i$
.
$a_i$
.
Claim 2.19. We can find subtori
![]() $T_i< G_i$
,
$T_i< G_i$
,
![]() $i\in I$
, such that:
$i\in I$
, such that:
-
(1)
 $G_i$
is the direct sum of
$G_i$
is the direct sum of
 $T_i$
and
$T_i$
and
 $S_i$
(in other words,
$S_i$
(in other words,
 $T_i$
intersects
$T_i$
intersects
 $S_i$
trivially, and
$S_i$
trivially, and
 $G_i=T_i+S_i$
), and
$G_i=T_i+S_i$
), and -
(2)
 $f_{i,j}[T_i]\subseteq T_j$
for each
$f_{i,j}[T_i]\subseteq T_j$
for each
 $j\le i$
.
$j\le i$
.
Proof For
![]() $i=i_0$
, we choose any torus
$i=i_0$
, we choose any torus
![]() $T_{i_0}$
such that
$T_{i_0}$
such that
![]() $G_{i_0}=T_{i_0}\oplus S_{i_0}$
(we can do this just because
$G_{i_0}=T_{i_0}\oplus S_{i_0}$
(we can do this just because
![]() $S_{i_0}$
is a subtorus of
$S_{i_0}$
is a subtorus of
![]() $G_{i_0}$
).
$G_{i_0}$
).
Now, take any other
![]() $i\in I$
. Put
$i\in I$
. Put
 $V_i=f_{i,i_0}^{-1}[T_{i_0}]$
. Since both
$V_i=f_{i,i_0}^{-1}[T_{i_0}]$
. Since both
![]() $a_i$
and
$a_i$
and
![]() $a_{i_0}$
have order q and
$a_{i_0}$
have order q and
![]() $f_{i,i_0}(a_i)=a_{i_0}$
, the map
$f_{i,i_0}(a_i)=a_{i_0}$
, the map
![]() $f_{i,i_0}$
maps
$f_{i,i_0}$
maps
![]() $S_i$
isomorphically onto
$S_i$
isomorphically onto
![]() $S_{i_0}$
. Hence,
$S_{i_0}$
. Hence,
![]() $S_i\cap V_i=\{e\}$
(if x was a nontrivial element in the intersection, then
$S_i\cap V_i=\{e\}$
(if x was a nontrivial element in the intersection, then
![]() $f_{i,i_0}(x)$
would be a nontrivial element in
$f_{i,i_0}(x)$
would be a nontrivial element in
![]() $T_{i_0}\cap S_{i_0}$
). Also, for any
$T_{i_0}\cap S_{i_0}$
). Also, for any
![]() $x\in G_i$
, there are
$x\in G_i$
, there are
![]() $y\in T_{i_0}$
and
$y\in T_{i_0}$
and
![]() $z\in S_{i_0}$
such that
$z\in S_{i_0}$
such that
![]() $f_{i,i_0}(x)=y+z$
, so choosing
$f_{i,i_0}(x)=y+z$
, so choosing
![]() $w\in S_{i}$
such that
$w\in S_{i}$
such that
![]() $f_{i,i_0}(w)=z$
, we get that
$f_{i,i_0}(w)=z$
, we get that
![]() $f_{i,i_0}(x-w)=y\in T_{i_0}$
and
$f_{i,i_0}(x-w)=y\in T_{i_0}$
and
![]() $x\in S_i+V_i$
. Hence,
$x\in S_i+V_i$
. Hence,
![]() $G_i$
is the direct sum of
$G_i$
is the direct sum of
![]() $S_i$
and
$S_i$
and
![]() $V_i$
. Note that
$V_i$
. Note that
![]() $V_i$
is a closed (so compact) subgroup of
$V_i$
is a closed (so compact) subgroup of
![]() $G_i$
.
$G_i$
.
Now let
![]() $T_i$
be the identity component of the group
$T_i$
be the identity component of the group
![]() $V_i$
. Then
$V_i$
. Then
![]() $T_i$
is a torus of the same dimension as
$T_i$
is a torus of the same dimension as
![]() $V_i$
intersecting
$V_i$
intersecting
![]() $S_i$
trivially, so
$S_i$
trivially, so
![]() $\operatorname {dim}(T_i+S_i)=\operatorname {dim}(G_i)$
. Hence, by the connectedness of
$\operatorname {dim}(T_i+S_i)=\operatorname {dim}(G_i)$
. Hence, by the connectedness of
![]() $G_i$
, we get that
$G_i$
, we get that
![]() $G_i=T_i\oplus S_i$
.
$G_i=T_i\oplus S_i$
.
To see that
![]() $f_{i,j}[T_i]\subseteq T_j$
for
$f_{i,j}[T_i]\subseteq T_j$
for
![]() $j\le i$
, notice first that
$j\le i$
, notice first that
![]() $f_{i,j}[T_i]\subseteq V_j$
. Now, since
$f_{i,j}[T_i]\subseteq V_j$
. Now, since
![]() $f_{i,j}$
is continuous and
$f_{i,j}$
is continuous and
![]() $T_i$
is connected,
$T_i$
is connected,
![]() $f_{i,j}[T_i]$
is a connected subgroup of
$f_{i,j}[T_i]$
is a connected subgroup of
![]() $G_j$
, so it must be contained in the connected component
$G_j$
, so it must be contained in the connected component
![]() $T_j$
of
$T_j$
of
![]() $V_j$
. This gives the claim.⊣
$V_j$
. This gives the claim.⊣
Now we will define isomorphisms
![]() $g_i$
from
$g_i$
from
![]() $H_i$
to
$H_i$
to
![]() $G_i$
such that, for
$G_i$
such that, for
![]() $j< i$
,
$j< i$
,
(Recall that
![]() $k_{i,j}:H_i\to H_j$
is the map induced by
$k_{i,j}:H_i\to H_j$
is the map induced by
![]() $f_{i,j}$
.) Clearly, we can write
$f_{i,j}$
.) Clearly, we can write
![]() $H_i=G_i/F_i$
as
$H_i=G_i/F_i$
as
![]() $T_i\oplus (S_i/\langle a_i\rangle )$
. We define
$T_i\oplus (S_i/\langle a_i\rangle )$
. We define
![]() $g_{i}$
to be the identity map on
$g_{i}$
to be the identity map on
![]() $T_i$
, and to be equal to the map
$T_i$
, and to be equal to the map
![]() $\alpha _q:S_i/\langle a_i\rangle \to S_i$
induced by multiplication by q of representatives modulo
$\alpha _q:S_i/\langle a_i\rangle \to S_i$
induced by multiplication by q of representatives modulo
![]() $\langle a_i\rangle $
on
$\langle a_i\rangle $
on
![]() $S_i/\langle a_i\rangle $
, and extend additively to a map from
$S_i/\langle a_i\rangle $
, and extend additively to a map from
![]() $H_i=T_i\oplus (S_i/\langle a_i\rangle )$
to
$H_i=T_i\oplus (S_i/\langle a_i\rangle )$
to
![]() $T_i \oplus S_i=G_i$
. To check
$T_i \oplus S_i=G_i$
. To check
![]() $(*)$
, notice that, for
$(*)$
, notice that, for
![]() $x\in T_i$
, both
$x\in T_i$
, both
![]() $f_{i,j}g_i(x)$
and
$f_{i,j}g_i(x)$
and
![]() $g_jk_{i,j}(x)$
are equal to
$g_jk_{i,j}(x)$
are equal to
![]() $f_{i,j}(x)$
, and for
$f_{i,j}(x)$
, and for
![]() $y/\langle a_i\rangle \in S_i/\langle a_i\rangle $
, we have that
$y/\langle a_i\rangle \in S_i/\langle a_i\rangle $
, we have that
![]() $f_{i,j}g_i(y/\langle a_i\rangle )$
and
$f_{i,j}g_i(y/\langle a_i\rangle )$
and
![]() $g_jk_{i,j}(y/\langle a_i\rangle )$
are both equal to
$g_jk_{i,j}(y/\langle a_i\rangle )$
are both equal to
![]() $qf_{i,j}(y)/\mathbb {Z}$
, where
$qf_{i,j}(y)/\mathbb {Z}$
, where
![]() $S_j=(\mathbb {R},+)/\mathbb {Z}$
.
$S_j=(\mathbb {R},+)/\mathbb {Z}$
.
Now, the system of isomorphisms
![]() $g_i$
induces an isomorphism of topological groups G and
$g_i$
induces an isomorphism of topological groups G and
![]() $G/F$
.⊣
$G/F$
.⊣
Corollary 2.20. Suppose T is G-compact, and
 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
is abelian. Then,
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
is abelian. Then,
 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
and
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
and
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
are isomorphic as topological groups.
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
are isomorphic as topological groups.
Proof By Proposition 2.12 or Theorem 2.6, K is finite; hence, by Lemma 2.18, the compact connected group
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
isomorphic to
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
isomorphic to
 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})/K$
must be isomorphic to
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})/K$
must be isomorphic to
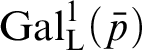 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
as well.⊣
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {p})$
as well.⊣
Finally, we observe that Corollary 2.20 does not generalize to the non-abelian case.
Proposition 2.21. Let G be a connected compact Lie group, and N a finite normal subgroup of G. Then, one can find types
![]() $p=\operatorname {tp}(a)$
and
$p=\operatorname {tp}(a)$
and
![]() $\bar p=\operatorname {tp}(ac)$
(with
$\bar p=\operatorname {tp}(ac)$
(with
![]() $c\in \operatorname {acl}(a)$
finite) in some G-compact theory T with
$c\in \operatorname {acl}(a)$
finite) in some G-compact theory T with
![]() $\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
(in
$\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
(in
![]() $T^{\operatorname {eq}}$
so that
$T^{\operatorname {eq}}$
so that
 $G=\operatorname {Gal}_{\operatorname {L}}^1(\bar p)$
and
$G=\operatorname {Gal}_{\operatorname {L}}^1(\bar p)$
and
 $G/N=\operatorname {Gal}_{\operatorname {L}}^1(p)$
. The same holds for the groups
$G/N=\operatorname {Gal}_{\operatorname {L}}^1(p)$
. The same holds for the groups
![]() $\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}$
and
$\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}$
and
 $\operatorname {Gal}_{\operatorname {L}}^{\lambda }$
for any
$\operatorname {Gal}_{\operatorname {L}}^{\lambda }$
for any
![]() $\lambda $
.
$\lambda $
.
If we take
![]() $G = SO(4,\mathbb {R})$
,
$G = SO(4,\mathbb {R})$
,
![]() $N = Z(G) = \{I, -I\}$
, then
$N = Z(G) = \{I, -I\}$
, then
![]() $G/N = PSO(4,\mathbb {R})$
and
$G/N = PSO(4,\mathbb {R})$
and
![]() $Z(G/N)$
is trivial, so G and
$Z(G/N)$
is trivial, so G and
![]() $G/N$
are not isomorphic.Footnote
2
$G/N$
are not isomorphic.Footnote
2
Proof The Lie group G is definable in some o-minimal expansion
![]() ${\mathcal R}$
of the ordered field of real numbers (see for example the discussion preceding Fact 1.1 in [Reference Barriga and Onshuus1]), and (using elimination of imaginaries for o-minimal expansions of
${\mathcal R}$
of the ordered field of real numbers (see for example the discussion preceding Fact 1.1 in [Reference Barriga and Onshuus1]), and (using elimination of imaginaries for o-minimal expansions of
![]() $\mathbb {R}$
) we identify
$\mathbb {R}$
) we identify
![]() ${\mathcal R}$
with
${\mathcal R}$
with
![]() ${\mathcal R}^{eq}$
. Put
${\mathcal R}^{eq}$
. Put
![]() $H:=G/N$
. We can assume that
$H:=G/N$
. We can assume that
![]() $N\subseteq \operatorname {dcl}(\emptyset )=\operatorname {acl}(\emptyset )$
, so H is
$N\subseteq \operatorname {dcl}(\emptyset )=\operatorname {acl}(\emptyset )$
, so H is
![]() $0$
-definable. We consider a structure
$0$
-definable. We consider a structure
![]() ${\mathcal M}=({\mathcal R},X,Y)$
, where
${\mathcal M}=({\mathcal R},X,Y)$
, where
![]() ${\mathcal R}$
comes with its original structure, X and Y are sets equipped with a regular G-action and a regular
${\mathcal R}$
comes with its original structure, X and Y are sets equipped with a regular G-action and a regular
![]() $G/N$
-action, respectively (both denoted by
$G/N$
-action, respectively (both denoted by
![]() $\cdot $
), and we add to the language the map
$\cdot $
), and we add to the language the map
![]() $\pi :X\to Y$
, defined as follows: fix any elements
$\pi :X\to Y$
, defined as follows: fix any elements
![]() $x_0\in X$
and
$x_0\in X$
and
![]() $y_0\in Y$
, and, for any
$y_0\in Y$
, and, for any
![]() $g \in G$
, we set
$g \in G$
, we set
![]() $\pi (g\cdot x_0):=gN\cdot y_0$
. Put
$\pi (g\cdot x_0):=gN\cdot y_0$
. Put
![]() $T=\operatorname {Th}({\mathcal M})$
.
$T=\operatorname {Th}({\mathcal M})$
.
Note that
![]() ${\mathcal M}=({\mathcal R},X,Y)$
is
${\mathcal M}=({\mathcal R},X,Y)$
is
![]() $0$
-interpretable in the structure
$0$
-interpretable in the structure
![]() $({\mathcal R},X)$
, so every automorphism of
$({\mathcal R},X)$
, so every automorphism of
![]() $({\mathcal R},X)$
extends to an automorphism of
$({\mathcal R},X)$
extends to an automorphism of
![]() ${\mathcal M}$
. Moreover, this extension is unique, as
${\mathcal M}$
. Moreover, this extension is unique, as
![]() $Y\subseteq \operatorname {dcl}(X)$
. The same holds for the saturated extension
$Y\subseteq \operatorname {dcl}(X)$
. The same holds for the saturated extension
![]() ${\mathcal M}^*=({\mathcal R}^*,X^*,Y^*)$
, hence, by [Reference Ziegler and Tent13, Chapter 7], every automorphism of
${\mathcal M}^*=({\mathcal R}^*,X^*,Y^*)$
, hence, by [Reference Ziegler and Tent13, Chapter 7], every automorphism of
![]() ${\mathcal M}^*$
is of the form
${\mathcal M}^*$
is of the form
![]() $\bar {g}\bar {\phi }$
, where
$\bar {g}\bar {\phi }$
, where
![]() $g\in G^*$
and
$g\in G^*$
and
![]() $\phi \in \operatorname {Aut}({\mathcal R}^*)$
(using the notation from [Reference Ziegler and Tent13], and identifying an automorphism of
$\phi \in \operatorname {Aut}({\mathcal R}^*)$
(using the notation from [Reference Ziegler and Tent13], and identifying an automorphism of
![]() $({\mathcal R}^*,X^*)$
with its unique extension to
$({\mathcal R}^*,X^*)$
with its unique extension to
![]() ${\mathcal M}^*$
), and
${\mathcal M}^*$
), and
![]() $\operatorname {Gal}_{\operatorname {L}}(T)=G$
.
$\operatorname {Gal}_{\operatorname {L}}(T)=G$
.
Let q and p be the unique (strong) types of the sorts
![]() $X^*$
and
$X^*$
and
![]() $Y^*$
, respectively. It follows from [Reference Ziegler and Tent13] that an automorphism
$Y^*$
, respectively. It follows from [Reference Ziegler and Tent13] that an automorphism
![]() $\bar {g}\bar {\phi }$
is Lascar-strong iff
$\bar {g}\bar {\phi }$
is Lascar-strong iff
![]() $g\in G^*_{\inf }$
(the group of infinitesimals of
$g\in G^*_{\inf }$
(the group of infinitesimals of
![]() $G^*$
). It follows that two elements
$G^*$
). It follows that two elements
![]() $x,y\in X^*$
have the same Lascar type iff there is
$x,y\in X^*$
have the same Lascar type iff there is
![]() $g\in G^*_{\inf }$
such that
$g\in G^*_{\inf }$
such that
![]() $g\cdot x=y$
, and two elements
$g\cdot x=y$
, and two elements
![]() $w,u\in Y$
have the same Lascar type iff there is
$w,u\in Y$
have the same Lascar type iff there is
![]() $g\in G^*_{\inf }$
and
$g\in G^*_{\inf }$
and
![]() $n\in N$
such that
$n\in N$
such that
![]() $(gn)\cdot w=u$
. As all automorphism of the form
$(gn)\cdot w=u$
. As all automorphism of the form
![]() $\bar {\phi }$
move any
$\bar {\phi }$
move any
![]() $x\in X^{*}$
to its translate by some element of
$x\in X^{*}$
to its translate by some element of
![]() $G^{*}_{\inf }$
, we conclude easily that
$G^{*}_{\inf }$
, we conclude easily that
 $$ \begin{align*}\operatorname{Autf}^1(q)=\operatorname{Autf}^{\operatorname{res}}(q)=\{\bar{g}\bar{\phi}:g \in G^*_{\inf}, \phi\in \operatorname{Aut}(R^*)\}\end{align*} $$
$$ \begin{align*}\operatorname{Autf}^1(q)=\operatorname{Autf}^{\operatorname{res}}(q)=\{\bar{g}\bar{\phi}:g \in G^*_{\inf}, \phi\in \operatorname{Aut}(R^*)\}\end{align*} $$
and
 $$ \begin{align*}\operatorname{Autf}^1(p)=\operatorname{Autf}^{\operatorname{res}}(p)=\{\bar{g}\bar{\phi}:g \in G^*_{\inf}N, \phi\in \operatorname{Aut}(R^*)\}.\end{align*} $$
$$ \begin{align*}\operatorname{Autf}^1(p)=\operatorname{Autf}^{\operatorname{res}}(p)=\{\bar{g}\bar{\phi}:g \in G^*_{\inf}N, \phi\in \operatorname{Aut}(R^*)\}.\end{align*} $$
Hence, the map
is an isomorphism
 $G\to \operatorname {Gal}_{\operatorname {L}}^1(q)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(q)$
, and the map
$G\to \operatorname {Gal}_{\operatorname {L}}^1(q)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(q)$
, and the map
is an epimorphism
 $G\to \operatorname {Gal}_{\operatorname {L}}^1(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p)$
with kernel N, so
$G\to \operatorname {Gal}_{\operatorname {L}}^1(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p)$
with kernel N, so
 $\operatorname {Gal}_{\operatorname {L}}^1(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p)=G/N=H$
.
$\operatorname {Gal}_{\operatorname {L}}^1(p)=\operatorname {Gal}_{\operatorname {L}}^{\operatorname {res}}(p)=G/N=H$
.
Now, if we take
![]() $c\models q$
and
$c\models q$
and
![]() $a=\pi (c)\models p$
and
$a=\pi (c)\models p$
and
![]() $\bar {p}=\operatorname {tp}(ac)$
, then
$\bar {p}=\operatorname {tp}(ac)$
, then
![]() $c\in \operatorname {acl}(a)$
(as the fibers of
$c\in \operatorname {acl}(a)$
(as the fibers of
![]() $\pi $
are finite), but the Lascar-Galois groups of p are isomorphic to H, and we see (as
$\pi $
are finite), but the Lascar-Galois groups of p are isomorphic to H, and we see (as
![]() $ac$
is interdefinable with c) that those of
$ac$
is interdefinable with c) that those of
![]() $\bar {p}$
are isomorphic to G.
$\bar {p}$
are isomorphic to G.
Finally, since
![]() $\operatorname {Gal}_{\operatorname {L}}(T)=G$
is connected, its connected component
$\operatorname {Gal}_{\operatorname {L}}(T)=G$
is connected, its connected component
 $\operatorname {Gal}_{\operatorname {L}}^0(T)$
is the same as G, so we get by Theorem 21 from [Reference Ziegler and Tent13] that all algebraic imaginaries are fixed by all automorphisms over
$\operatorname {Gal}_{\operatorname {L}}^0(T)$
is the same as G, so we get by Theorem 21 from [Reference Ziegler and Tent13] that all algebraic imaginaries are fixed by all automorphisms over
![]() $\emptyset $
, hence
$\emptyset $
, hence
![]() $\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
.⊣
$\operatorname {acl}(\emptyset )=\operatorname {dcl}(\emptyset )$
.⊣
We will see in Theorem 3.7 that, in a non-G-compact T, some
![]() $\operatorname {tp}(\operatorname {acl}(a)/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
fails to be a Lascar type while
$\operatorname {tp}(\operatorname {acl}(a)/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
fails to be a Lascar type while
![]() $\operatorname {tp}(a/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
is a Lascar type. We will also see in Proposition 3.10 that, even in a G-compact theory,
$\operatorname {tp}(a/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
is a Lascar type. We will also see in Proposition 3.10 that, even in a G-compact theory,
 $\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(\operatorname {acl}(a)/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
may be abelian but not isomorphic to
$\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(\operatorname {acl}(a)/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
may be abelian but not isomorphic to
 $\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(a/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
.
$\operatorname {Gal}_{\operatorname {L}}^1(\operatorname {tp}(a/\operatorname {acl}^{\operatorname {eq}}(\emptyset ))$
.
3. Examples
The starting point of the study in Section 2 was the result observed in [Reference Dobrowolski, Kim and Lee3] that in a G-compact T if
![]() $\operatorname {stp}(a)$
is a Lascar type, then so is
$\operatorname {stp}(a)$
is a Lascar type, then so is
![]() $\operatorname {stp}(\operatorname {acl}(a))$
. In this section we give an example showing that T being G-compact is essential in the result. Moreover, it is natural to ask whether all the hypotheses are essential in Corollary 2.20. In Example 2.21, we have already seen that the abelianity assumption cannot be removed, and we present in this section an example showing that the assumption that c is finite cannot be removed either. Lastly, we find a Lie group structure example answering a question raised in [Reference Kim and Lee10], which asks whether there exists an RN-pattern minimal 2-chain not equivalent to a Lascar pattern 2-chain having the same boundary.
$\operatorname {stp}(\operatorname {acl}(a))$
. In this section we give an example showing that T being G-compact is essential in the result. Moreover, it is natural to ask whether all the hypotheses are essential in Corollary 2.20. In Example 2.21, we have already seen that the abelianity assumption cannot be removed, and we present in this section an example showing that the assumption that c is finite cannot be removed either. Lastly, we find a Lie group structure example answering a question raised in [Reference Kim and Lee10], which asks whether there exists an RN-pattern minimal 2-chain not equivalent to a Lascar pattern 2-chain having the same boundary.
We now explain preliminary examples. Throughout this section we will use
![]() ${\mathcal M}$
,
${\mathcal M}$
,
![]() ${\mathcal N}$
, …to denote some models which need not be saturated. For a positive integer n, consider a structure
${\mathcal N}$
, …to denote some models which need not be saturated. For a positive integer n, consider a structure
![]() ${\mathcal M}_{1,n}=(M;S,g_n)$
, where M is a unit circle; S is a ternary relation on M such that
${\mathcal M}_{1,n}=(M;S,g_n)$
, where M is a unit circle; S is a ternary relation on M such that
![]() $S(a,b,c)$
holds if and only if
$S(a,b,c)$
holds if and only if
![]() $a,b,c$
are distinct and b comes before c going around the circle clockwise starting at a; and
$a,b,c$
are distinct and b comes before c going around the circle clockwise starting at a; and
![]() $g_n=\sigma _{1/n}$
, where
$g_n=\sigma _{1/n}$
, where
![]() $\sigma _r$
is the clockwise rotation by
$\sigma _r$
is the clockwise rotation by
![]() $2\pi r$
-radians.
$2\pi r$
-radians.
For
![]() $p=\operatorname {tp}(a)$
, we will denote
$p=\operatorname {tp}(a)$
, we will denote
![]() $\operatorname {tp}(\operatorname {acl}(a))$
by
$\operatorname {tp}(\operatorname {acl}(a))$
by
![]() $\bar {\bar {p}}$
.
$\bar {\bar {p}}$
.
Fact 3.1 [Reference Casanovas, Lascar, Pillay and Ziegler2]
-
(1)
 $\operatorname {Th}({\mathcal M}_{1,n})$
has a unique 1-complete type
$\operatorname {Th}({\mathcal M}_{1,n})$
has a unique 1-complete type
 $p_n(x)$
over
$p_n(x)$
over
 $\emptyset $
, which is isolated by the formula
$\emptyset $
, which is isolated by the formula
 $x=x$
.
$x=x$
. -
(2)
 $\operatorname {Th}({\mathcal M}_{1,n})$
is
$\operatorname {Th}({\mathcal M}_{1,n})$
is
 $\aleph _0$
-categorical and has quantifier elimination.
$\aleph _0$
-categorical and has quantifier elimination. -
(3) For any subset
 $A\subseteq M_n$
,
$A\subseteq M_n$
,
 $\operatorname {acl}(A)=\operatorname {dcl}(A)=\bigcup _{0\le i< n} g_n^i(A)$
(in the home sort), where
$\operatorname {acl}(A)=\operatorname {dcl}(A)=\bigcup _{0\le i< n} g_n^i(A)$
(in the home sort), where
 $g_n^i=\underbrace {g_n \circ \cdots \circ g_n}_{i~\text {times}}$
.
$g_n^i=\underbrace {g_n \circ \cdots \circ g_n}_{i~\text {times}}$
. -
(4) The unique complete 1-type
 $p_n$
is also a Lascar type.
$p_n$
is also a Lascar type.
3.1. Non-
 $G$
-compact theory with
$G$
-compact theory with
 $p$
Lascar type but
$p$
Lascar type but
 $\bar {\bar {p}}$
not Lascar type
$\bar {\bar {p}}$
not Lascar type
We give an example of non-G-compact theory which has a Lascar strong type
![]() $\operatorname {tp}(a)$
but
$\operatorname {tp}(a)$
but
![]() $\operatorname {tp}(\operatorname {acl}(a))$
is not a Lascar strong type. Let
$\operatorname {tp}(\operatorname {acl}(a))$
is not a Lascar strong type. Let
![]() ${\mathcal M}=(M_i,S_i,g_i,\pi _i)_{i\ge 1}$
be a multi-sorted structure where
${\mathcal M}=(M_i,S_i,g_i,\pi _i)_{i\ge 1}$
be a multi-sorted structure where
![]() ${\mathcal M}_{1,i}=(M_i,S_i,g_i)$
(as introduced in Fact 3.1, but of course
${\mathcal M}_{1,i}=(M_i,S_i,g_i)$
(as introduced in Fact 3.1, but of course
![]() $M_i$
and
$M_i$
and
![]() $M_j$
are disjoint for
$M_j$
are disjoint for
![]() $i\ne j$
) and
$i\ne j$
) and
![]() $\pi _i:\ M_i\rightarrow M_1$
sending
$\pi _i:\ M_i\rightarrow M_1$
sending
![]() $x\mapsto x^i$
for each
$x\mapsto x^i$
for each
![]() $i\ge 1$
(if we identify each
$i\ge 1$
(if we identify each
![]() $M_i$
with the unit circle in the complex plane). For each
$M_i$
with the unit circle in the complex plane). For each
![]() $n\ge 1$
, let
$n\ge 1$
, let
![]() ${\mathcal M}_{\le n}=(M_i,S_i,g_i,\pi _i)_{1\leq i\le n}$
. Let
${\mathcal M}_{\le n}=(M_i,S_i,g_i,\pi _i)_{1\leq i\le n}$
. Let
![]() $T=\operatorname {Th}({\mathcal M})$
,
$T=\operatorname {Th}({\mathcal M})$
,
![]() $T_i=\operatorname {Th}({\mathcal M}_{1,i})$
, and
$T_i=\operatorname {Th}({\mathcal M}_{1,i})$
, and
![]() $T_{\le n}=\operatorname {Th}({\mathcal M}_{\le n})$
.
$T_{\le n}=\operatorname {Th}({\mathcal M}_{\le n})$
.
Remark 3.2. Both T and
![]() $T_{\le n}$
are
$T_{\le n}$
are
![]() $\aleph _0$
-categorical.
$\aleph _0$
-categorical.
Remark 3.3. Let
![]() ${\mathcal N}=(N_i,\ldots )$
be a model of T. For
${\mathcal N}=(N_i,\ldots )$
be a model of T. For
![]() $A\subseteq {\mathcal N}$
, define
$A\subseteq {\mathcal N}$
, define
 $A_1:=\mathop {\bigcup }_{i\ge 1} \pi _i(\mathop {\bigcup }_{j\le i} g_i^j(A\cap N_i) )$
, and
$A_1:=\mathop {\bigcup }_{i\ge 1} \pi _i(\mathop {\bigcup }_{j\le i} g_i^j(A\cap N_i) )$
, and
 $\operatorname {cl}(A)=\bigcup _{i\ge 1}\pi _i^{-1}[A_1].$
$\operatorname {cl}(A)=\bigcup _{i\ge 1}\pi _i^{-1}[A_1].$
-
(1)
 $\operatorname {cl}(A)$
is the smallest substructure containing A.
$\operatorname {cl}(A)$
is the smallest substructure containing A. -
(2) For
 $B,C\subseteq {\mathcal N}$
algebraically closed, if
$B,C\subseteq {\mathcal N}$
algebraically closed, if
 $B_1=C_1$
, then
$B_1=C_1$
, then
 $B=C$
.
$B=C$
.
Fact 3.4 [Reference Dobrowolski, Kim and Lee3, Theorem 5.5]
Let T be
![]() $\aleph _0$
-categorical and let
$\aleph _0$
-categorical and let
![]() ${\mathcal M}=(M,\ldots )$
be a saturated model of T. Suppose that if
${\mathcal M}=(M,\ldots )$
be a saturated model of T. Suppose that if
![]() $X\subseteq M^1$
is definable over each of two algebraically closed sets
$X\subseteq M^1$
is definable over each of two algebraically closed sets
![]() $A_0$
and
$A_0$
and
![]() $A_1$
, then X is definable over
$A_1$
, then X is definable over
![]() $B:=A_0\cap A_1$
.
$B:=A_0\cap A_1$
.
Then, for any subset Y of
![]() $M^n$
, if Y is both
$M^n$
, if Y is both
![]() $A_0$
-definable and
$A_0$
-definable and
![]() $A_1$
-definable, then it is B-definable. Furthermore, in this case, T has weak elimination of imaginaries.
$A_1$
-definable, then it is B-definable. Furthermore, in this case, T has weak elimination of imaginaries.
-
(1) Both T and
 $T_{\le n}$
,
$T_{\le n}$
,
 $n\ge 1$
, have quantifier elimination.
$n\ge 1$
, have quantifier elimination. -
(2) Both T and
 $T_{\le n}$
,
$T_{\le n}$
,
 $n\ge 1$
, weakly eliminate imaginaries.
$n\ge 1$
, weakly eliminate imaginaries.
Proof
![]() $(1)$
Here we prove that T has quantifier elimination. By a similar reason, each
$(1)$
Here we prove that T has quantifier elimination. By a similar reason, each
![]() $T_{\le n}$
has also quantifier elimination. Let
$T_{\le n}$
has also quantifier elimination. Let
![]() ${\mathcal N}_1=(N_{i}^1,\ldots )$
and
${\mathcal N}_1=(N_{i}^1,\ldots )$
and
![]() ${\mathcal N}_2=(N_{i}^2,\ldots )$
be models of T. Take some finite
${\mathcal N}_2=(N_{i}^2,\ldots )$
be models of T. Take some finite
![]() $A\subseteq {\mathcal N}_1$
, and let
$A\subseteq {\mathcal N}_1$
, and let
![]() $f: \operatorname {cl}(A) \rightarrow {\mathcal N}_2$
be a partial embedding. Take
$f: \operatorname {cl}(A) \rightarrow {\mathcal N}_2$
be a partial embedding. Take
![]() $a\in {\mathcal N}_1$
arbitrary. It is enough to show that there is a partial embedding
$a\in {\mathcal N}_1$
arbitrary. It is enough to show that there is a partial embedding
![]() $g :\operatorname {cl}(Aa)\rightarrow {\mathcal N}_2$
extending f. By Remark 3.3(1), we may assume that
$g :\operatorname {cl}(Aa)\rightarrow {\mathcal N}_2$
extending f. By Remark 3.3(1), we may assume that
![]() $A=A_1\subset N_1^1$
. Suppose
$A=A_1\subset N_1^1$
. Suppose
![]() $a\in N_i^1$
. Let
$a\in N_i^1$
. Let
![]() $a_1=\pi _i(a)$
. If
$a_1=\pi _i(a)$
. If
![]() $a_1\in A$
, then
$a_1\in A$
, then
![]() $a\in \operatorname {acl}(A)$
, and we are done. Without loss of generality, we may assume that
$a\in \operatorname {acl}(A)$
, and we are done. Without loss of generality, we may assume that
![]() $a_1\not \in A$
. Since
$a_1\not \in A$
. Since
![]() $T_1$
has quantifier elimination, we can pick
$T_1$
has quantifier elimination, we can pick
![]() $b_1\in N_{1}^2$
such that
$b_1\in N_{1}^2$
such that
 $b_1\models \operatorname {tp}_{T_1}(a_1/A)$
. Let
$b_1\models \operatorname {tp}_{T_1}(a_1/A)$
. Let
![]() $A_i=\pi _i^{-1}[A]\subseteq N_i^1$
, which is finite, and let
$A_i=\pi _i^{-1}[A]\subseteq N_i^1$
, which is finite, and let
![]() $\bar {a}_i=(a_i^1,\ldots ,a_i^i)$
be an enumeration of
$\bar {a}_i=(a_i^1,\ldots ,a_i^i)$
be an enumeration of
![]() $\pi _i^{-1}(a_1)$
. Since each
$\pi _i^{-1}(a_1)$
. Since each
![]() $T_i$
has quantifier elimination, we can pick an enumeration
$T_i$
has quantifier elimination, we can pick an enumeration
 $\bar {b}_i=(b_i^1,\ldots ,b_i^i)$
of
$\bar {b}_i=(b_i^1,\ldots ,b_i^i)$
of
![]() $\pi _i^{-1}(b_1)$
such that
$\pi _i^{-1}(b_1)$
such that
 $\bar {b}_i\models \operatorname {tp}_{T_i}(\bar {a}_i/A_i)$
. Note that
$\bar {b}_i\models \operatorname {tp}_{T_i}(\bar {a}_i/A_i)$
. Note that
 $\operatorname {cl}(Aa)=\operatorname {cl}(A)\cup \mathop {\bigcup }_{i\ge 1} \pi _i^{-1}(a_1)$
. Consider a map
$\operatorname {cl}(Aa)=\operatorname {cl}(A)\cup \mathop {\bigcup }_{i\ge 1} \pi _i^{-1}(a_1)$
. Consider a map
 $g=f\cup \{(a_i^j,b_i^j)|\ 1\le i,1\le j\le i\}$
. For each i,
$g=f\cup \{(a_i^j,b_i^j)|\ 1\le i,1\le j\le i\}$
. For each i,
 $g\restriction _{N_i^1}$
is a partial embedding to
$g\restriction _{N_i^1}$
is a partial embedding to
![]() $N_i^2$
, and for each
$N_i^2$
, and for each
![]() $j\le i$
,
$j\le i$
,
 $b_1=\pi _i(b_i^j)=\pi _i(g(a_i^j))$
. Therefore
$b_1=\pi _i(b_i^j)=\pi _i(g(a_i^j))$
. Therefore
![]() $g:\operatorname {cl}(Aa)\rightarrow {\mathcal N}_2$
is a partial embedding extending f, and we are done. As a consequence,
$g:\operatorname {cl}(Aa)\rightarrow {\mathcal N}_2$
is a partial embedding extending f, and we are done. As a consequence,
![]() $\operatorname {acl}(A)=\operatorname {cl}(A)$
for each A.
$\operatorname {acl}(A)=\operatorname {cl}(A)$
for each A.
![]() $(2)$
We first show that each
$(2)$
We first show that each
![]() $T_{\le n}$
weakly eliminates imaginaries. We consider
$T_{\le n}$
weakly eliminates imaginaries. We consider
![]() ${\mathcal M}_{\le n}$
as
${\mathcal M}_{\le n}$
as
 ${\mathcal M}_{\le n}'=(M',S',g',\pi ')$
, where
${\mathcal M}_{\le n}'=(M',S',g',\pi ')$
, where
![]() $M'=M_1\cup \cdots \cup M_n$
,
$M'=M_1\cup \cdots \cup M_n$
,
![]() $ S'=S_1\cup \cdots \cup S_n$
,
$ S'=S_1\cup \cdots \cup S_n$
,
![]() $g'=g_1\cup \cdots \cup g_n$
, and
$g'=g_1\cup \cdots \cup g_n$
, and
![]() $\pi '=\pi _1\cup \cdots \cup \pi _n$
. Let
$\pi '=\pi _1\cup \cdots \cup \pi _n$
. Let
 $T_{\le n}'=\operatorname {Th}({\mathcal M}_{\le n}')$
. It is enough to show that
$T_{\le n}'=\operatorname {Th}({\mathcal M}_{\le n}')$
. It is enough to show that
 $T_{\le n}'$
weakly eliminates imaginaries. Note that
$T_{\le n}'$
weakly eliminates imaginaries. Note that
 $T_{\le n}'$
is
$T_{\le n}'$
is
![]() $\aleph _0$
-categorical. Let
$\aleph _0$
-categorical. Let
![]() ${\mathcal N}=(N(=N_1\cup \cdots \cup N_n),\ldots )$
be a saturated model of
${\mathcal N}=(N(=N_1\cup \cdots \cup N_n),\ldots )$
be a saturated model of
 $T_{\le n}'$
. By Fact 3.4, it is enough to show that a subset X of
$T_{\le n}'$
. By Fact 3.4, it is enough to show that a subset X of
![]() $N^1$
which is both A-definable and B-definable, where A and B are algebraically closed, is also definable over
$N^1$
which is both A-definable and B-definable, where A and B are algebraically closed, is also definable over
![]() $C=A\cap B$
. Let
$C=A\cap B$
. Let
![]() $A_i$
,
$A_i$
,
![]() $B_i$
, and
$B_i$
, and
![]() $C_i$
denote the intersections of A, B, and C, respectively, with
$C_i$
denote the intersections of A, B, and C, respectively, with
![]() $N_i$
,
$N_i$
,
![]() $1\le i \le n$
. Note that
$1\le i \le n$
. Note that
![]() $C_i=A_i\cap B_i$
for each
$C_i=A_i\cap B_i$
for each
![]() $1\le i\le n$
and
$1\le i\le n$
and
![]() $C=\operatorname {acl}(C_1)$
. We may assume that
$C=\operatorname {acl}(C_1)$
. We may assume that
![]() $X\subseteq N_{i}$
for some
$X\subseteq N_{i}$
for some
![]() $1\le i\le n$
by taking
$1\le i\le n$
by taking
![]() $X\cap N_{i}$
. By quantifier elimination, X is definable over
$X\cap N_{i}$
. By quantifier elimination, X is definable over
![]() $A_{i}$
and
$A_{i}$
and
![]() $B_{i}$
. Then from the proof of [Reference Kim, Kim and Lee9, Theorem 4.3(1)], X is definable over
$B_{i}$
. Then from the proof of [Reference Kim, Kim and Lee9, Theorem 4.3(1)], X is definable over
![]() $C_{i}=A_{i}\cap B_{i}$
and clearly over
$C_{i}=A_{i}\cap B_{i}$
and clearly over
![]() $C=\operatorname {acl}(C_i)$
. Thus
$C=\operatorname {acl}(C_i)$
. Thus
 $T_{\le n}'$
weakly eliminates imaginaries and so does
$T_{\le n}'$
weakly eliminates imaginaries and so does
![]() $T_{\le n}$
.
$T_{\le n}$
.
Let
![]() ${\mathcal M}'$
be a saturated model of T and let
${\mathcal M}'$
be a saturated model of T and let
 ${\mathcal M}_{\le n}'$
be the saturated structure corresponding to
${\mathcal M}_{\le n}'$
be the saturated structure corresponding to
![]() ${\mathcal M}_{\le n}$
. By Remark 3.3(1) and quantifier elimination, there is no strictly decreasing chain of algebraically closures of finite sets in
${\mathcal M}_{\le n}$
. By Remark 3.3(1) and quantifier elimination, there is no strictly decreasing chain of algebraically closures of finite sets in
![]() ${\mathcal M}'$
. Since
${\mathcal M}'$
. Since
![]() ${\mathcal M}'=\bigcup _n {\mathcal M}_{\le n}$
, by the same reasoning as in the proof of [Reference Dobrowolski, Kim and Lee3, Theorem 5.9], we conclude that T weakly eliminates imaginaries.⊣
${\mathcal M}'=\bigcup _n {\mathcal M}_{\le n}$
, by the same reasoning as in the proof of [Reference Dobrowolski, Kim and Lee3, Theorem 5.9], we conclude that T weakly eliminates imaginaries.⊣
Let
![]() ${\mathcal N}=(N_i,\ldots )$
be a saturated model of T. By Proposition 3.5,
${\mathcal N}=(N_i,\ldots )$
be a saturated model of T. By Proposition 3.5,
![]() $\operatorname {acl}^{\operatorname {eq}}(\emptyset )=\emptyset $
. Let
$\operatorname {acl}^{\operatorname {eq}}(\emptyset )=\emptyset $
. Let
![]() $a\in N_1^1$
, and consider strong types
$a\in N_1^1$
, and consider strong types
![]() $p:=\operatorname {tp}(a)$
(isolated by
$p:=\operatorname {tp}(a)$
(isolated by
![]() $x=x$
) and
$x=x$
) and
![]() $\bar {\bar {p}}:=\operatorname {tp}(\operatorname {acl}(a))$
.
$\bar {\bar {p}}:=\operatorname {tp}(\operatorname {acl}(a))$
.
Fact 3.6 [Reference Casanovas, Lascar, Pillay and Ziegler2]
For
![]() $a\neq b\in N_n$
, a and b have the same type over some elementary substructure of
$a\neq b\in N_n$
, a and b have the same type over some elementary substructure of
![]() $N_n$
if and only if
$N_n$
if and only if
![]() $N_n\models S_n(a,b,g_n(a))\wedge S_n(g_n^{-1}(a),b,a)$
. So there are
$N_n\models S_n(a,b,g_n(a))\wedge S_n(g_n^{-1}(a),b,a)$
. So there are
![]() $a,b\in N_n$
whose Lascar distance is at least
$a,b\in N_n$
whose Lascar distance is at least
![]() $n/2$
.
$n/2$
.
Theorem 3.7. The type p is a Lascar strong type but
![]() $\bar {\bar {p}}$
is not a Lascar strong type.
$\bar {\bar {p}}$
is not a Lascar strong type.
Proof By Fact 3.6, p is a Lascar strong type. Take
![]() $a,b\in N_1$
which are Lascar equivalent. Let
$a,b\in N_1$
which are Lascar equivalent. Let
![]() $\bar {a}_i=(a_i^1,\ldots ,a_i^i)$
and
$\bar {a}_i=(a_i^1,\ldots ,a_i^i)$
and
 $\bar {b}_i=(b_i^1,\ldots ,b_i^i)$
be enumerations of
$\bar {b}_i=(b_i^1,\ldots ,b_i^i)$
be enumerations of
![]() $\pi _i^{-1}(a)$
and
$\pi _i^{-1}(a)$
and
![]() $\pi _i^{-1}(b)$
. Denote
$\pi _i^{-1}(b)$
. Denote
 $\sigma _i(a_i)=(a_i^{\sigma (1)},\ldots ,a_i^{\sigma (i)})$
for each permutation
$\sigma _i(a_i)=(a_i^{\sigma (1)},\ldots ,a_i^{\sigma (i)})$
for each permutation
![]() $\sigma \in S_i$
. Let
$\sigma \in S_i$
. Let
![]() $\tau _i$
be the permutation of
$\tau _i$
be the permutation of
![]() $\{1,2,\ldots , i\}$
sending j to
$\{1,2,\ldots , i\}$
sending j to
![]() $j+1$
for
$j+1$
for
![]() $j< i$
and i to
$j< i$
and i to
![]() $1$
. Then
$1$
. Then
 $(a_1,\tau _2^{k_2}(\bar {a}_2),\tau _3^{k_3}(\bar {a}_3),\ldots )\models \bar {\bar {p}}$
for arbitrary
$(a_1,\tau _2^{k_2}(\bar {a}_2),\tau _3^{k_3}(\bar {a}_3),\ldots )\models \bar {\bar {p}}$
for arbitrary
![]() $k_2,k_3,\ldots (*)$
. For each i, there are
$k_2,k_3,\ldots (*)$
. For each i, there are
![]() $a_i\in \pi _i^{-1}(a_1)$
and
$a_i\in \pi _i^{-1}(a_1)$
and
![]() $b_i\in \pi _i^{-1}(b_1)$
whose Lascar distance is at least
$b_i\in \pi _i^{-1}(b_1)$
whose Lascar distance is at least
![]() $i/2$
. So, by
$i/2$
. So, by
![]() $(*)$
,
$(*)$
,
![]() $\bar {\bar {p}}$
is not a Lascar strong type.⊣
$\bar {\bar {p}}$
is not a Lascar strong type.⊣
3.2. A
 $G$
-compact theory with
$G$
-compact theory with
 $\operatorname {Gal}_{\operatorname {L}}^1(\bar {\bar {p}})$
abelian and not isomorphic to
$\operatorname {Gal}_{\operatorname {L}}^1(\bar {\bar {p}})$
abelian and not isomorphic to
 $\operatorname {Gal}_{\operatorname {L}}^1(p)$
$\operatorname {Gal}_{\operatorname {L}}^1(p)$
We will use the symbols
![]() $\sigma _r$
,
$\sigma _r$
,
![]() $g_n$
, and
$g_n$
, and
![]() $(M_i, S_i)$
defined in the previous subsection. Put
$(M_i, S_i)$
defined in the previous subsection. Put
 $\widetilde {{\mathcal M}}=\widetilde {{\mathcal M}}_1=(M_1,S_1,g_{1,n})_{n\geq 1}$
, where
$\widetilde {{\mathcal M}}=\widetilde {{\mathcal M}}_1=(M_1,S_1,g_{1,n})_{n\geq 1}$
, where
![]() $g_{1,n}$
is the same rotation as
$g_{1,n}$
is the same rotation as
![]() $g_n$
on the unit circle
$g_n$
on the unit circle
![]() $M_1=S^1$
. We define a multi-sorted structure
$M_1=S^1$
. We define a multi-sorted structure
 $$ \begin{align*}{\mathcal M}'=((\widetilde{{\mathcal M}}_k),\delta_k)_{k\geq 1},\end{align*} $$
$$ \begin{align*}{\mathcal M}'=((\widetilde{{\mathcal M}}_k),\delta_k)_{k\geq 1},\end{align*} $$
where each
 $\widetilde {{\mathcal M}}_k:= (M_k=\{x_{(k)}:x \in S^1\},S_k,g_{k,n})_{n\geq 1}$
is a copy of
$\widetilde {{\mathcal M}}_k:= (M_k=\{x_{(k)}:x \in S^1\},S_k,g_{k,n})_{n\geq 1}$
is a copy of
![]() $\widetilde {{\mathcal M}}_1$
(again
$\widetilde {{\mathcal M}}_1$
(again
![]() $g_{k,n}$
is the same rotation as
$g_{k,n}$
is the same rotation as
![]() $g_n$
on
$g_n$
on
![]() $M_k$
, and we may omit k in
$M_k$
, and we may omit k in
![]() $S_k$
and
$S_k$
and
![]() $g_{k,n}$
), and
$g_{k,n}$
), and
 $\delta _k:\widetilde {{\mathcal M}}_{k+1}\to \widetilde {{\mathcal M}}_k$
is given by
$\delta _k:\widetilde {{\mathcal M}}_{k+1}\to \widetilde {{\mathcal M}}_k$
is given by
 $\delta _k (x_{(k+1)})=x^2_{(k)}$
. Put
$\delta _k (x_{(k+1)})=x^2_{(k)}$
. Put
![]() $T'=\operatorname {Th}({\mathcal M}')$
.
$T'=\operatorname {Th}({\mathcal M}')$
.
Lemma 3.8.
![]() $T'$
admits quantifier elimination.
$T'$
admits quantifier elimination.
Proof It is enough to prove quantifier elimination for the restriction of
![]() ${\mathcal M}'$
to finitely many sorts
${\mathcal M}'$
to finitely many sorts
 $\widetilde {{\mathcal M}}_{\leq k}$
for each k, but such a restriction is quantifier-free interpretable in the structure
$\widetilde {{\mathcal M}}_{\leq k}$
for each k, but such a restriction is quantifier-free interpretable in the structure
![]() ${\mathcal M}'$
for some n, which is known to admit quantifier elimination [Reference Dobrowolski, Kim and Lee3, Theorem 5.8].⊣
${\mathcal M}'$
for some n, which is known to admit quantifier elimination [Reference Dobrowolski, Kim and Lee3, Theorem 5.8].⊣
Using quantifier elimination, it is easy to check that two (possibly infinite) tuples have the same Lascar type if and only if their corresponding coordinates are infinitesimally close (in the same sort), and S induces corresponding partial orders on the tuples. As this is a type-definable condition, we get that
![]() $T'$
is G-compact.
$T'$
is G-compact.
By Theorem 5.9 from [Reference Dobrowolski, Kim and Lee3],
![]() $\widetilde {{\mathcal M}}$
, and hence also any
$\widetilde {{\mathcal M}}$
, and hence also any
 $\widetilde {{\mathcal M}}_{\leq k}$
, weakly eliminates imaginaries. Hence, we get:
$\widetilde {{\mathcal M}}_{\leq k}$
, weakly eliminates imaginaries. Hence, we get:
Remark 3.9.
![]() $T'$
weakly eliminates imaginaries.
$T'$
weakly eliminates imaginaries.
By Lemma 3.8, one easily gets that
![]() $\operatorname {acl}_{T'}(\emptyset )=\emptyset $
in the home-sort; hence, by Remark 3.9,
$\operatorname {acl}_{T'}(\emptyset )=\emptyset $
in the home-sort; hence, by Remark 3.9,
 $\operatorname {acl}_{T'}^{\operatorname {eq}}(\emptyset )=\emptyset $
. Now, let p be the (unique) type of an element
$\operatorname {acl}_{T'}^{\operatorname {eq}}(\emptyset )=\emptyset $
. Now, let p be the (unique) type of an element
![]() $a\in \widetilde {{\mathcal M}}$
. Then
$a\in \widetilde {{\mathcal M}}$
. Then
 $\operatorname {Gal}_{\operatorname {L}}^1(p)\cong \operatorname {Gal}_{\operatorname {L}}(\operatorname {Th}(\widetilde {{\mathcal M}}))\cong S^1$
. On the other hand, for
$\operatorname {Gal}_{\operatorname {L}}^1(p)\cong \operatorname {Gal}_{\operatorname {L}}(\operatorname {Th}(\widetilde {{\mathcal M}}))\cong S^1$
. On the other hand, for
![]() $\bar {\bar {p}}=\operatorname {tp}(\operatorname {acl}(a))$
, we have:
$\bar {\bar {p}}=\operatorname {tp}(\operatorname {acl}(a))$
, we have:
Proposition 3.10.
 $\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
is isomorphic to the
$\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
is isomorphic to the
![]() $2$
-solenoid
$2$
-solenoid
 $G:=\varprojlim _i \mathbb {R}/2^i\mathbb {Z}$
(the projections in the inverse limit are the natural quotient maps). Hence,
$G:=\varprojlim _i \mathbb {R}/2^i\mathbb {Z}$
(the projections in the inverse limit are the natural quotient maps). Hence,
 $\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
is abelian and non-isomorphic to
$\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
is abelian and non-isomorphic to
 $\operatorname {Gal}_{\operatorname {L}}^{1}(p)$
.
$\operatorname {Gal}_{\operatorname {L}}^{1}(p)$
.
Proof Consider the homomorphism
 $\phi :G=\varprojlim _i \mathbb {R}/2^i\mathbb {Z}\to \operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
sending a sequence
$\phi :G=\varprojlim _i \mathbb {R}/2^i\mathbb {Z}\to \operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
sending a sequence
![]() $(r_i/2^i\mathbb {Z})_i$
to the class induced by the automorphism
$(r_i/2^i\mathbb {Z})_i$
to the class induced by the automorphism
![]() $f_{(r_i)_i}$
(defined on a monster model of
$f_{(r_i)_i}$
(defined on a monster model of
![]() $T'$
) equal to
$T'$
) equal to
![]() $\sigma _{r_i/2^i}$
on
$\sigma _{r_i/2^i}$
on
![]() $\widetilde {{\mathcal M}}_{i}$
for each i. If
$\widetilde {{\mathcal M}}_{i}$
for each i. If
![]() $r_i\notin 2^i\mathbb {Z}$
, then
$r_i\notin 2^i\mathbb {Z}$
, then
![]() $f_{(r_i)_i}$
does not preserve the Lascar types of elements of
$f_{(r_i)_i}$
does not preserve the Lascar types of elements of
![]() $\widetilde {{\mathcal M}}_{i}$
, hence
$\widetilde {{\mathcal M}}_{i}$
, hence
![]() $\operatorname {Ker}(\phi )=\{0\}$
. It remains to check that
$\operatorname {Ker}(\phi )=\{0\}$
. It remains to check that
![]() $\phi $
is surjective. Consider a class in
$\phi $
is surjective. Consider a class in
 $\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
induced by an automorphism f. As all elements of
$\operatorname {Gal}_{\operatorname {L}}^{1}(\bar {\bar {p}})$
induced by an automorphism f. As all elements of
![]() $ \widetilde {{\mathcal M}}_{1}$
have the same Lascar type, we may assume that
$ \widetilde {{\mathcal M}}_{1}$
have the same Lascar type, we may assume that
![]() $f(a)=a$
for some
$f(a)=a$
for some
![]() $a\in \widetilde {{\mathcal M}}_{1}$
(by composing f with a strong automorphism sending
$a\in \widetilde {{\mathcal M}}_{1}$
(by composing f with a strong automorphism sending
![]() $f(a)$
to a). Now, for each i, as f commutes with
$f(a)$
to a). Now, for each i, as f commutes with
![]() $\delta _1\delta _2\dots \delta _{i-1}$
, it must preserve
$\delta _1\delta _2\dots \delta _{i-1}$
, it must preserve
 $\operatorname {acl}(a)\cap \widetilde {{\mathcal M}}_{i}$
setwise. Hence, there is
$\operatorname {acl}(a)\cap \widetilde {{\mathcal M}}_{i}$
setwise. Hence, there is
![]() $r_i$
such that on
$r_i$
such that on
 $\operatorname {acl}(a)\cap \widetilde {{\mathcal M}}_{i}$
, f is equal to
$\operatorname {acl}(a)\cap \widetilde {{\mathcal M}}_{i}$
, f is equal to
![]() $\sigma _{r_i/2^i}$
. Then f and
$\sigma _{r_i/2^i}$
. Then f and
![]() $f_{(r_i)_i}$
have infinitesimally close values on every element of the monster model, so
$f_{(r_i)_i}$
have infinitesimally close values on every element of the monster model, so
 $f^{-1}f_{(r_i)_i}$
is Lascar strong and
$f^{-1}f_{(r_i)_i}$
is Lascar strong and
 $\phi (f_{(r_i)_i})$
is equal to the class induced by f.⊣
$\phi (f_{(r_i)_i})$
is equal to the class induced by f.⊣
3.3. RN but not a Lascar pattern
 $2$
-chain
$2$
-chain
Let p be a strong type of an algebraically closed set. In [Reference Kim, Kim and Lee9], it was shown that any
![]() $2$
-chain in p with
$2$
-chain in p with
![]() $1$
-shell boundary can be reduced to a
$1$
-shell boundary can be reduced to a
![]() $2$
-chain having an RN-pattern or an NR-pattern.Footnote
3
Also for
$2$
-chain having an RN-pattern or an NR-pattern.Footnote
3
Also for
![]() $a,b\models p$
, if
$a,b\models p$
, if
![]() $a\equiv ^L b$
, then
$a\equiv ^L b$
, then
![]() $(a,b)$
is an endpoint pair of a
$(a,b)$
is an endpoint pair of a
![]() $1$
-shell which is the boundary of a
$1$
-shell which is the boundary of a
![]() $2$
-chain having a Lascar pattern, a kind of an RN-pattern. In [Reference Kim and Lee10, Question 4.5], it was asked whether all minimal
$2$
-chain having a Lascar pattern, a kind of an RN-pattern. In [Reference Kim and Lee10, Question 4.5], it was asked whether all minimal
![]() $2$
-chains having an RN-pattern with
$2$
-chains having an RN-pattern with
![]() $1$
-shell boundary should be equivalent to one having a Lascar pattern. It was also noticed that if there is a counterexample, then its length should be at least
$1$
-shell boundary should be equivalent to one having a Lascar pattern. It was also noticed that if there is a counterexample, then its length should be at least
![]() $7$
.
$7$
.
In this subsection, we assume the reader has some familiarity with the notions described in [Reference Kim, Kim and Lee9, Reference Kim and Lee10], and we work with the trivial independence to define independent functors in a strong type (see Definition 0.6), and corresponding
![]() $1$
-shells and
$1$
-shells and
![]() $2$
-chains. We now give descriptions of
$2$
-chains. We now give descriptions of
![]() $2$
-chains having an RN- or a Lascar pattern in terms of balanced walks, rather than original definitions. For more combinatorial descriptions for RN- or Lascar pattern
$2$
-chains having an RN- or a Lascar pattern in terms of balanced walks, rather than original definitions. For more combinatorial descriptions for RN- or Lascar pattern
![]() $2$
-chains, see [Reference Kim and Lee10].
$2$
-chains, see [Reference Kim and Lee10].
Remark/Definition 3.11. Let
![]() $a,b\models p$
. For
$a,b\models p$
. For
![]() $n\ge 1$
, a balanced edge-walk of length
$n\ge 1$
, a balanced edge-walk of length
![]() $2n$
from a to b is simply a balanced chain-walk of length
$2n$
from a to b is simply a balanced chain-walk of length
![]() $2n$
from a to b in Fact 0.14
(1)(b) with the trivial independence (so (1)(b)(ii) is removed), that is, a finite sequence
$2n$
from a to b in Fact 0.14
(1)(b) with the trivial independence (so (1)(b)(ii) is removed), that is, a finite sequence
![]() $(d_i)_{0\le i\le 2n}$
of realizations of p satisfying the following conditions:
$(d_i)_{0\le i\le 2n}$
of realizations of p satisfying the following conditions:
-
(1)
 $d_0=a$
, and
$d_0=a$
, and
 $d_{2n}=b;$
and
$d_{2n}=b;$
and -
(2) there is a bijection
such that $$ \begin{align*}\sigma:\{0,1,\ldots,n-1\}\to\{0,1,\ldots,n-1\}\end{align*} $$
$$ \begin{align*}\sigma:\{0,1,\ldots,n-1\}\to\{0,1,\ldots,n-1\}\end{align*} $$
 $d_{2i} d_{2i+1}\equiv d_{2\sigma (i)+2}d_{2\sigma (i)+1}$
for
$d_{2i} d_{2i+1}\equiv d_{2\sigma (i)+2}d_{2\sigma (i)+1}$
for
 $ i < n$
.
$ i < n$
.
With the trivial independence, a balanced edge-walk of length
![]() $2n$
from a to b induces a
$2n$
from a to b induces a
![]() $2$
-chain of length
$2$
-chain of length
![]() $2n+1$
(having the
$2n+1$
(having the
![]() $1$
-shell boundary whose endpoint pair is
$1$
-shell boundary whose endpoint pair is
![]() $(a,b)$
), which is a chain-walk (cf., the proof of [Reference Dobrowolski, Kim and Lee3, Theorem 4.2]). Such an induced
$(a,b)$
), which is a chain-walk (cf., the proof of [Reference Dobrowolski, Kim and Lee3, Theorem 4.2]). Such an induced
![]() $2$
-chain need not be unique but it is unique up to the first homology class.
$2$
-chain need not be unique but it is unique up to the first homology class.
In particular, given a minimal
![]() $2$
-chain
$2$
-chain
![]() $\alpha $
of length
$\alpha $
of length
![]() $2n+1$
with the
$2n+1$
with the
![]() $1$
-shell boundary s,
$1$
-shell boundary s,
![]() $\alpha $
is equivalent to a Lascar pattern
$\alpha $
is equivalent to a Lascar pattern
![]() $2$
-chain if and only if
$2$
-chain if and only if
![]() $\alpha $
is equivalent to a chain-walk induced by a balanced edge-walk of length
$\alpha $
is equivalent to a chain-walk induced by a balanced edge-walk of length
![]() $2n$
from a to b with
$2n$
from a to b with
![]() $\sigma =\operatorname {id}$
such that
$\sigma =\operatorname {id}$
such that
![]() $[a,b]=[s]\in H_1(p)$
.
$[a,b]=[s]\in H_1(p)$
.
Fact 3.12 [Reference Dobrowolski, Kim and Lee3, Reference Kim and Lee10]
Let
![]() $\alpha $
be a minimal
$\alpha $
be a minimal
![]() $2$
-chain of length
$2$
-chain of length
![]() $2n+1 (n\geq 1)$
in p with the boundary
$2n+1 (n\geq 1)$
in p with the boundary
![]() $s=g_{12} -g_{02} + g_{01}$
such that
$s=g_{12} -g_{02} + g_{01}$
such that
![]() $\operatorname {supp}(g_{ij})=\{i,j\}$
. Then the following are equivalent.
$\operatorname {supp}(g_{ij})=\{i,j\}$
. Then the following are equivalent.
-
(1) The
 $2$
-chain
$2$
-chain
 $\alpha $
has an RN-pattern.
$\alpha $
has an RN-pattern. -
(2) The
 $2$
-chain
$2$
-chain
 $\alpha $
is equivalent to a
$\alpha $
is equivalent to a
 $2$
-chain which is a chain-walk of
$2$
-chain which is a chain-walk of $$ \begin{align*}\alpha'=\mathop{\sum}\limits_{i=0}^{2n} (-1)^i f_i,\end{align*} $$
$$ \begin{align*}\alpha'=\mathop{\sum}\limits_{i=0}^{2n} (-1)^i f_i,\end{align*} $$
 $2$
-simplices from
$2$
-simplices from
 $g_{01}$
to
$g_{01}$
to
 $-g_{02}$
such that
$-g_{02}$
such that
 $\partial ^2 f_{0}=g_{01}$
,
$\partial ^2 f_{0}=g_{01}$
,
 $\partial ^0 f_{2n}=g_{12}$
,
$\partial ^0 f_{2n}=g_{12}$
,
 $\partial ^1(f_{2n})=-g_{02}$
, and
$\partial ^1(f_{2n})=-g_{02}$
, and
 $\operatorname {supp}(\alpha ')=3=\{0,1,2\}$
.
$\operatorname {supp}(\alpha ')=3=\{0,1,2\}$
.
-
(3) There are an endpoint pair
 $(a,b)$
of s, and a balanced-edge-walk of length
$(a,b)$
of s, and a balanced-edge-walk of length
 $2n$
from a to b which induces a
$2n$
from a to b which induces a
 $2$
-chain equivalent to
$2$
-chain equivalent to
 $\alpha $
.
$\alpha $
.
In this subsection we will give a minimal
![]() $2$
-chain example (with 1-shell boundary) having an RN-pattern but not equivalent to that having a Lascar pattern. The example will have length
$2$
-chain example (with 1-shell boundary) having an RN-pattern but not equivalent to that having a Lascar pattern. The example will have length
![]() $7$
. We start with preparatory constructions. Let G be a connected compact Lie group definable in
$7$
. We start with preparatory constructions. Let G be a connected compact Lie group definable in
![]() ${\mathbb R}$
in the ordered ring language. Let X be a set equipped with a regular G-action. Let
${\mathbb R}$
in the ordered ring language. Let X be a set equipped with a regular G-action. Let
![]() ${\mathcal M}_2=({\mathcal R},X,\cdot )$
be a two sorted structure, where
${\mathcal M}_2=({\mathcal R},X,\cdot )$
be a two sorted structure, where
![]() ${\mathcal R}$
is the field of real numbers with a named finite set of elements over which G is definable. Let
${\mathcal R}$
is the field of real numbers with a named finite set of elements over which G is definable. Let
![]() ${\mathcal N}_n=({\mathcal M}_{1,n}, {\mathcal M}_2)$
, and there is no interaction between
${\mathcal N}_n=({\mathcal M}_{1,n}, {\mathcal M}_2)$
, and there is no interaction between
![]() ${\mathcal M}_{1,n}$
and
${\mathcal M}_{1,n}$
and
![]() ${\mathcal M}_2$
.
${\mathcal M}_2$
.
Let
 ${\mathcal N}_n^*=({\mathcal M}_{1,n}^*,{\mathcal M}_2^*)$
be a saturated model of
${\mathcal N}_n^*=({\mathcal M}_{1,n}^*,{\mathcal M}_2^*)$
be a saturated model of
![]() $\operatorname {Th}({\mathcal M}_n)$
such that
$\operatorname {Th}({\mathcal M}_n)$
such that
 ${\mathcal M}_{1,n}^*=(M^*,S,g_n)$
and
${\mathcal M}_{1,n}^*=(M^*,S,g_n)$
and
![]() ${\mathcal M}_2^*=({\mathcal R}^*,X^*,\cdot )$
are saturated models of
${\mathcal M}_2^*=({\mathcal R}^*,X^*,\cdot )$
are saturated models of
![]() $\operatorname {Th}({\mathcal M}_{1,n})$
and
$\operatorname {Th}({\mathcal M}_{1,n})$
and
![]() $\operatorname {Th}({\mathcal M}_2)$
respectively. Since there are no other interactions between
$\operatorname {Th}({\mathcal M}_2)$
respectively. Since there are no other interactions between
![]() ${\mathcal M}_{1,n}^*$
and
${\mathcal M}_{1,n}^*$
and
![]() ${\mathcal M}_2^*$
, we have that
${\mathcal M}_2^*$
, we have that
-
•
 $\operatorname {Aut}({\mathcal N}_n^*)=\operatorname {Aut}({\mathcal M}_{1,n}^*)\times \operatorname {Aut}({\mathcal M}_2^*)$
.
$\operatorname {Aut}({\mathcal N}_n^*)=\operatorname {Aut}({\mathcal M}_{1,n}^*)\times \operatorname {Aut}({\mathcal M}_2^*)$
. -
• For
 $a\in {\mathcal M}_{1,n}^*$
and
$a\in {\mathcal M}_{1,n}^*$
and
 $b\in {\mathcal M}_2^*$
,
$b\in {\mathcal M}_2^*$
,
 $\operatorname {acl}(ab)=\operatorname {acl}_{{\mathcal M}_{1,n}}(a)\cup \operatorname {acl}_{{\mathcal M}_2}(b)$
, where
$\operatorname {acl}(ab)=\operatorname {acl}_{{\mathcal M}_{1,n}}(a)\cup \operatorname {acl}_{{\mathcal M}_2}(b)$
, where
 $\operatorname {acl}_{{\mathcal M}_{1,n}}$
and
$\operatorname {acl}_{{\mathcal M}_{1,n}}$
and
 $\operatorname {acl}_{{\mathcal M}_2}$
are the algebraic closures taken in
$\operatorname {acl}_{{\mathcal M}_2}$
are the algebraic closures taken in
 ${\mathcal M}_{1,n}^*$
and
${\mathcal M}_{1,n}^*$
and
 ${\mathcal M}_2^*$
respectively.
${\mathcal M}_2^*$
respectively. -
• For
 $a\in {\mathcal M}_{1,n}^*$
and
$a\in {\mathcal M}_{1,n}^*$
and
 $b\in {\mathcal M}_2^*$
,
$b\in {\mathcal M}_2^*$
,
 $\operatorname {tp}(ab)=\operatorname {tp}_{{\mathcal M}_{1,n}}(a)\cup \operatorname {tp}_{{\mathcal M}_2}(b)$
where
$\operatorname {tp}(ab)=\operatorname {tp}_{{\mathcal M}_{1,n}}(a)\cup \operatorname {tp}_{{\mathcal M}_2}(b)$
where
 $\operatorname {tp}_{{\mathcal M}_{1,n}}(a)$
and
$\operatorname {tp}_{{\mathcal M}_{1,n}}(a)$
and
 $\operatorname {tp}_{{\mathcal M}_2}(b)$
are complete types in
$\operatorname {tp}_{{\mathcal M}_2}(b)$
are complete types in
 ${\mathcal M}_{1,n}^*$
and
${\mathcal M}_{1,n}^*$
and
 ${\mathcal M}_2^*$
respectively.
${\mathcal M}_2^*$
respectively.
First, let us recall a fact on minimal lengths of
![]() $1$
-shells in
$1$
-shells in
![]() $p_n$
from [Reference Kim, Kim and Lee9].
$p_n$
from [Reference Kim, Kim and Lee9].
Definition 3.13. Let
![]() ${\mathcal A}$
be a non-trivial amenable collection and let s be a
${\mathcal A}$
be a non-trivial amenable collection and let s be a
![]() $1$
-shell. Define
$1$
-shell. Define
If s is not the boundary of any
![]() $2$
-chain, define
$2$
-chain, define
![]() $B(s) := - \infty $
.
$B(s) := - \infty $
.
Fact 3.14. For
![]() $n\ge 7$
, there is a
$n\ge 7$
, there is a
![]() $1$
-shell s in
$1$
-shell s in
![]() $p_n$
such that
$p_n$
such that
![]() $B(s)=7$
.
$B(s)=7$
.
Note that in [Reference Kim, Kim and Lee9], the authors considered
![]() $1$
-shells and
$1$
-shells and
![]() $2$
-chains defined under
$2$
-chains defined under
![]() $\operatorname {acl}$
-independence for Fact 3.14. By similar methods as in the proofs, it is not hard to see that the same Fact 3.14 holds for
$\operatorname {acl}$
-independence for Fact 3.14. By similar methods as in the proofs, it is not hard to see that the same Fact 3.14 holds for
![]() $1$
-shells and
$1$
-shells and
![]() $2$
-chains defined under the trivial independence as in this subsection.
$2$
-chains defined under the trivial independence as in this subsection.
Next, let us recall some facts about
![]() ${\mathcal M}_2^*$
from [Reference Ziegler and Tent13]. Let
${\mathcal M}_2^*$
from [Reference Ziegler and Tent13]. Let
![]() $G^*$
be the extension of G in
$G^*$
be the extension of G in
![]() ${\mathcal R}^*$
. Let
${\mathcal R}^*$
. Let
![]() $\mu $
be the normal subgroup of infinitesimals in
$\mu $
be the normal subgroup of infinitesimals in
![]() $G^*$
. We fix a base point
$G^*$
. We fix a base point
![]() $x_0\in X^*$
so that for
$x_0\in X^*$
so that for
![]() $x\in X^*$
there is a unique element
$x\in X^*$
there is a unique element
![]() $h\in G^*$
with
$h\in G^*$
with
![]() $x=h\cdot x_0$
.
$x=h\cdot x_0$
.
-
(1) Each
 $\phi \in \operatorname {Aut}({\mathcal R}^*)$
is extended to
$\phi \in \operatorname {Aut}({\mathcal R}^*)$
is extended to
 $\operatorname {Aut}({\mathcal M}^*_2)$
defined by
$\operatorname {Aut}({\mathcal M}^*_2)$
defined by
 $\bar {\phi }(h\cdot x_0):=\phi (h)\cdot x_0$
. An automorphism which fixes
$\bar {\phi }(h\cdot x_0):=\phi (h)\cdot x_0$
. An automorphism which fixes
 ${\mathcal R}^*$
pointwise is of the form
${\mathcal R}^*$
pointwise is of the form
 $\bar {g}$
for some
$\bar {g}$
for some
 $g\in G^*$
, where
$g\in G^*$
, where
 $\bar {g}(h\cdot x_0)=(hg^{-1})\cdot x_0$
, and the commutation rule is given by
$\bar {g}(h\cdot x_0)=(hg^{-1})\cdot x_0$
, and the commutation rule is given by
 $\bar {\phi }\bar {g}=\overline {\phi (g)}\bar {\phi }$
. So we have
$\bar {\phi }\bar {g}=\overline {\phi (g)}\bar {\phi }$
. So we have
 $\operatorname {Aut}({\mathcal M}^*_2)=\operatorname {Aut}({\mathcal R}^*)\ltimes G^*$
.
$\operatorname {Aut}({\mathcal M}^*_2)=\operatorname {Aut}({\mathcal R}^*)\ltimes G^*$
. -
(2) An automorphism
 $\Phi =\bar {\phi }\bar {g}$
is a strong automorphism if and only if g is an infinitesimal. So the Lascar Galois group of
$\Phi =\bar {\phi }\bar {g}$
is a strong automorphism if and only if g is an infinitesimal. So the Lascar Galois group of
 $\operatorname {Th}({\mathcal M}_2)$
is isomorphic to G.
$\operatorname {Th}({\mathcal M}_2)$
is isomorphic to G. -
(3)
 $\mu =\{h^{-1}\phi (h)|\ h\in G^*,\ \phi \in \operatorname {Aut}({\mathcal R}^*)\}$
.
$\mu =\{h^{-1}\phi (h)|\ h\in G^*,\ \phi \in \operatorname {Aut}({\mathcal R}^*)\}$
.
We note that in
![]() $X^*$
, there is a unique
$X^*$
, there is a unique
![]() $1$
-type over
$1$
-type over
![]() $\emptyset $
and it is also a strong type over
$\emptyset $
and it is also a strong type over
![]() $\emptyset $
.
$\emptyset $
.
Proposition 3.16. For any
![]() $x\in X$
,
$x\in X$
,
![]() $x\equiv x_0$
and
$x\equiv x_0$
and
![]() $\operatorname {tp}(x_0)=\operatorname {stp}(x_0)$
.
$\operatorname {tp}(x_0)=\operatorname {stp}(x_0)$
.
Proof Suppose there are
![]() $x,x'\in X^*$
with
$x,x'\in X^*$
with
![]() $\operatorname {stp}(x)\neq \operatorname {stp}(x')$
. Then there is an
$\operatorname {stp}(x)\neq \operatorname {stp}(x')$
. Then there is an
![]() $\emptyset $
-definable finite equivalence relation E on
$\emptyset $
-definable finite equivalence relation E on
![]() $X^*$
such that
$X^*$
such that
![]() $\neg E(x,x')$
. Define
$\neg E(x,x')$
. Define
![]() $H:=\{g\in G^*|\ E(x,g\cdot x)\}$
. Since E is
$H:=\{g\in G^*|\ E(x,g\cdot x)\}$
. Since E is
![]() $\emptyset $
-definable, H is
$\emptyset $
-definable, H is
![]() $\emptyset $
-definable subgroup of
$\emptyset $
-definable subgroup of
![]() $G^*$
, and it is proper. We claim that
$G^*$
, and it is proper. We claim that
![]() $[G^*:H]$
is finite. Note that
$[G^*:H]$
is finite. Note that
![]() $gg^{-1}\in H$
if and only if
$gg^{-1}\in H$
if and only if
![]() $E(g\cdot x,g'\cdot x)$
. So the map sending
$E(g\cdot x,g'\cdot x)$
. So the map sending
![]() $gH\in G^*/H\mapsto g(x)E\in X^*/E$
is a bijection because
$gH\in G^*/H\mapsto g(x)E\in X^*/E$
is a bijection because
![]() $G^*$
acts on
$G^*$
acts on
![]() $X^*$
transitively. Since
$X^*$
transitively. Since
![]() $X^*/E$
is finite, so is
$X^*/E$
is finite, so is
![]() $G^*/H$
, contradicting the connectedness of G.⊣
$G^*/H$
, contradicting the connectedness of G.⊣
Let
![]() $\operatorname {acl}_{{\mathcal R}^*}^{\operatorname {eq}}(\emptyset )$
be the algebraic closure of
$\operatorname {acl}_{{\mathcal R}^*}^{\operatorname {eq}}(\emptyset )$
be the algebraic closure of
![]() $\emptyset $
in
$\emptyset $
in
![]() $({\mathcal R}^*)^{\operatorname {eq}}$
. For
$({\mathcal R}^*)^{\operatorname {eq}}$
. For
![]() $x\in X^*$
,
$x\in X^*$
,
![]() $\operatorname {acl}^{\operatorname {eq}}(x)=\{x\}\cup \operatorname {acl}_{{\mathcal R}^*}^{\operatorname {eq}}(\emptyset )$
. From Proposition 3.16, we have that
$\operatorname {acl}^{\operatorname {eq}}(x)=\{x\}\cup \operatorname {acl}_{{\mathcal R}^*}^{\operatorname {eq}}(\emptyset )$
. From Proposition 3.16, we have that
![]() $\operatorname {tp}(x)\models \operatorname {stp}(\operatorname {acl}^{\operatorname {eq}}(x))$
. So we say
$\operatorname {tp}(x)\models \operatorname {stp}(\operatorname {acl}^{\operatorname {eq}}(x))$
. So we say
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are endpoints if
$x_2$
are endpoints if
![]() $\operatorname {acl}^{\operatorname {eq}}(x_1)$
and
$\operatorname {acl}^{\operatorname {eq}}(x_1)$
and
![]() $\operatorname {acl}^{\operatorname {eq}}(x_2)$
are endpoints of a
$\operatorname {acl}^{\operatorname {eq}}(x_2)$
are endpoints of a
![]() $1$
-shell in
$1$
-shell in
![]() $p:=\operatorname {stp}(\operatorname {acl}^{\operatorname {eq}}(x))$
.
$p:=\operatorname {stp}(\operatorname {acl}^{\operatorname {eq}}(x))$
.
Lemma 3.17. For
![]() $x_1, x_2, x_3\in X^*$
, if
$x_1, x_2, x_3\in X^*$
, if
![]() $x_1x_2\equiv x_3x_2$
, then there is
$x_1x_2\equiv x_3x_2$
, then there is
![]() $h\in \mu $
such that
$h\in \mu $
such that
![]() $\bar {h}(x_1)=x_3$
.
$\bar {h}(x_1)=x_3$
.
Proof Let
![]() $x_1,x_2,x_3\in X^*$
be such that
$x_1,x_2,x_3\in X^*$
be such that
![]() $x_1x_2\equiv x_3x_2$
. Let
$x_1x_2\equiv x_3x_2$
. Let
![]() $h_1,h_2,h_3\in G^*$
be such that
$h_1,h_2,h_3\in G^*$
be such that
![]() $x_i=h_i\cdot x_0$
. It is enough to show that
$x_i=h_i\cdot x_0$
. It is enough to show that
![]() $h_3h_1^{-1}\in \mu $
.
$h_3h_1^{-1}\in \mu $
.
Take
![]() $\phi \in \operatorname {Aut}({\mathcal R}^*)$
and
$\phi \in \operatorname {Aut}({\mathcal R}^*)$
and
![]() $g\in G^*$
such that
$g\in G^*$
such that
![]() $\bar g \bar \phi (x_1x_2)=x_3x_2$
. Then we have
$\bar g \bar \phi (x_1x_2)=x_3x_2$
. Then we have
 $$ \begin{align*} \bar g \bar \phi(x_1x_2) &=\bar g((\phi(h_1)\cdot x_0) (\phi(h_2) \cdot x_0))\\ &=(\phi(h_1)g^{-1}\cdot x_0)(\phi(h_2)g^{-1}\cdot x_0)\\ &=(h_3\cdot x_0)(h_2\cdot x_0). \end{align*} $$
$$ \begin{align*} \bar g \bar \phi(x_1x_2) &=\bar g((\phi(h_1)\cdot x_0) (\phi(h_2) \cdot x_0))\\ &=(\phi(h_1)g^{-1}\cdot x_0)(\phi(h_2)g^{-1}\cdot x_0)\\ &=(h_3\cdot x_0)(h_2\cdot x_0). \end{align*} $$
By the regularity of the action of
![]() $G^*$
, we have
$G^*$
, we have
![]() $\phi (h_1)g^{-1}=h_3$
and
$\phi (h_1)g^{-1}=h_3$
and
![]() $\phi (h_2)g^{-1}=h_2$
, and so
$\phi (h_2)g^{-1}=h_2$
, and so
![]() $g=h_2^{-1}\phi (h_2)\in \mu $
. And
$g=h_2^{-1}\phi (h_2)\in \mu $
. And
![]() $h_3h_1^{-1}=\phi (h_1)g^{-1}h_1^{-1}=\phi (h_1)h_1^{-1}=\operatorname {id}$
modulo
$h_3h_1^{-1}=\phi (h_1)g^{-1}h_1^{-1}=\phi (h_1)h_1^{-1}=\operatorname {id}$
modulo
![]() $\mu $
because
$\mu $
because
![]() $\mu $
is a normal subgroup of
$\mu $
is a normal subgroup of
![]() $G^*$
. Thus
$G^*$
. Thus
![]() $h_3h_1^{-1}\in \mu $
.⊣
$h_3h_1^{-1}\in \mu $
.⊣
Theorem 3.18. For
![]() $x_1,x_2\in X^*$
, the following are equivalent:
$x_1,x_2\in X^*$
, the following are equivalent:
-
(1)
 $x_1\equiv ^{L}x_2$
.
$x_1\equiv ^{L}x_2$
. -
(2) There is
 $h\in \mu $
such that
$h\in \mu $
such that
 $\overline h(x_1)=x_2$
.
$\overline h(x_1)=x_2$
. -
(3)
 $x_1$
and
$x_1$
and
 $x_2$
are endpoints of a
$x_2$
are endpoints of a
 $1$
-shell which is the boundary of a
$1$
-shell which is the boundary of a
 $2$
-chain in p having a Lascar pattern.
$2$
-chain in p having a Lascar pattern.
Proof
![]() $(1) \Leftrightarrow (2)$
was proved in [Reference Ziegler and Tent13] and
$(1) \Leftrightarrow (2)$
was proved in [Reference Ziegler and Tent13] and
![]() $(1)\Rightarrow (3)$
was proved in [Reference Kim, Kim and Lee9]. It is enough to show
$(1)\Rightarrow (3)$
was proved in [Reference Kim, Kim and Lee9]. It is enough to show
![]() $(3)\Rightarrow (2)$
. By definition of Lascar pattern 2-chain (in [Reference Kim, Kim and Lee9]) and Lemma 3.17,
$(3)\Rightarrow (2)$
. By definition of Lascar pattern 2-chain (in [Reference Kim, Kim and Lee9]) and Lemma 3.17,
![]() $(3)\Rightarrow (2)$
is also true.⊣
$(3)\Rightarrow (2)$
is also true.⊣
Now we give a promised example of a minimal
![]() $2$
-chain having an RN-pattern but not equivalent to one having a Lascar pattern. Denote
$2$
-chain having an RN-pattern but not equivalent to one having a Lascar pattern. Denote
![]() $[g,h]=ghg^{-1}h^{-1}$
. Consider
$[g,h]=ghg^{-1}h^{-1}$
. Consider
![]() ${\mathcal N}_n^*$
for some
${\mathcal N}_n^*$
for some
![]() $n\ge 7$
and let
$n\ge 7$
and let
![]() $q=\operatorname {tp}(ab)$
for
$q=\operatorname {tp}(ab)$
for
![]() $a\models p$
and
$a\models p$
and
![]() $b\models p_n$
, which is a strong type.
$b\models p_n$
, which is a strong type.
Theorem 3.19. Suppose G is not abelian. Then there is a minimal
![]() $2$
-chain in q which has an RN-pattern but not equivalent to any Lascar pattern 2-chain.
$2$
-chain in q which has an RN-pattern but not equivalent to any Lascar pattern 2-chain.
Proof Suppose G is not abelian. We can choose
![]() $g_1, g_2, g_3\in G$
such that
$g_1, g_2, g_3\in G$
such that
![]() $[(g_3g_2)^{-1},(g_2g_1))]\neq \operatorname {id}$
. Let
$[(g_3g_2)^{-1},(g_2g_1))]\neq \operatorname {id}$
. Let
![]() $h_1:=g_1$
,
$h_1:=g_1$
,
![]() $h_2:=g_2$
,
$h_2:=g_2$
,
![]() $h_3:=g_3$
,
$h_3:=g_3$
,
![]() $h_4:=h_1^{-1}[h_1,(h_3h_2)]$
,
$h_4:=h_1^{-1}[h_1,(h_3h_2)]$
,
![]() $h_5:=h_2^{-1}[h_2,(h_4h_3)]$
, and
$h_5:=h_2^{-1}[h_2,(h_4h_3)]$
, and
 $h_6:=h_3^{-1}[h_3,(h_5h_4)]$
. Set
$h_6:=h_3^{-1}[h_3,(h_5h_4)]$
. Set
![]() $x_i=(h_i h_{i-1}\cdots h_1)^{-1}\cdot x_0$
for
$x_i=(h_i h_{i-1}\cdots h_1)^{-1}\cdot x_0$
for
![]() $1\le i\le 6$
. Consider a
$1\le i\le 6$
. Consider a
![]() $1$
-shell
$1$
-shell
![]() $s=f_{01}+f_{12}-f_{02}$
, where
$s=f_{01}+f_{12}-f_{02}$
, where
![]() $f_{01}(\{01\})\equiv [x_0 x_0]$
,
$f_{01}(\{01\})\equiv [x_0 x_0]$
,
![]() $s=f_{12}(\{1,2\})=[x_0 x_0]$
, and
$s=f_{12}(\{1,2\})=[x_0 x_0]$
, and
![]() $f_{02}(\{0,2\})\equiv [x_6 x_0]$
, and its endpoints are
$f_{02}(\{0,2\})\equiv [x_6 x_0]$
, and its endpoints are
![]() $x_0$
and
$x_0$
and
![]() $x_6$
. Let
$x_6$
. Let
![]() $f_i=h_ih_{i-1}\cdots h_1\in G\subseteq G^*$
for
$f_i=h_ih_{i-1}\cdots h_1\in G\subseteq G^*$
for
![]() $1\le i\le 6$
. Then we have that
$1\le i\le 6$
. Then we have that
-
•
 $f_4=f_3f_1^{-1}$
;
$f_4=f_3f_1^{-1}$
; -
•
 $f_5f_1^{-1}=f_4f_2^{-1}$
; and
$f_5f_1^{-1}=f_4f_2^{-1}$
; and -
•
 $f_6f_2^{-1}=f_5f_3^{-1}$
.
$f_6f_2^{-1}=f_5f_3^{-1}$
.
This implies
![]() $\bar f_4(x_0x_1)=x_4x_3$
,
$\bar f_4(x_0x_1)=x_4x_3$
,
 $\overline {f_5f_1^{-1}}(x_1x_2)=x_5x_4$
, and
$\overline {f_5f_1^{-1}}(x_1x_2)=x_5x_4$
, and
 $\overline {f_6f_2^{-1}}(x_2x_3)=x_6x_5$
. Then we have that
$\overline {f_6f_2^{-1}}(x_2x_3)=x_6x_5$
. Then we have that
![]() $x_0x_1\equiv x_4x_3$
,
$x_0x_1\equiv x_4x_3$
,
![]() $x_1x_2\equiv x_6x_5$
, and
$x_1x_2\equiv x_6x_5$
, and
![]() $x_2x_3\equiv x_5x_4$
.
$x_2x_3\equiv x_5x_4$
.

This gives a
![]() $2$
-chain
$2$
-chain
![]() $\alpha $
of length
$\alpha $
of length
![]() $7$
having the
$7$
having the
![]() $1$
-shell boundary s. Note that
$1$
-shell boundary s. Note that
 $$ \begin{align*} f_6&= (h_6h_5h_4h_3)h_2h_1\\ &=(h_5h_4)h_2h_1\\ &=(h_4h_3h_2^{-1}h_3^{-1})h_2h_1\\ &=(h_4h_3)(h_2^{-1}h_3^{-1})(h_2h_1)\\ &=(h_3h_2)(h_2h_1)^{-1}(h_2^{-1}h_3^{-1})(h_2h_1)\\ &=[(h_3h_2),(h_2h_1)^{-1}]\neq \operatorname{id}, \end{align*} $$
$$ \begin{align*} f_6&= (h_6h_5h_4h_3)h_2h_1\\ &=(h_5h_4)h_2h_1\\ &=(h_4h_3h_2^{-1}h_3^{-1})h_2h_1\\ &=(h_4h_3)(h_2^{-1}h_3^{-1})(h_2h_1)\\ &=(h_3h_2)(h_2h_1)^{-1}(h_2^{-1}h_3^{-1})(h_2h_1)\\ &=[(h_3h_2),(h_2h_1)^{-1}]\neq \operatorname{id}, \end{align*} $$
and
![]() $f_6\notin \mu $
. By Theorem 3.18, s is not the boundary of
$f_6\notin \mu $
. By Theorem 3.18, s is not the boundary of
![]() $2$
-chain with a Lascar pattern and
$2$
-chain with a Lascar pattern and
![]() $B(s)\le 7$
.
$B(s)\le 7$
.
Let
![]() $b,b'\models p_n$
where
$b,b'\models p_n$
where
![]() $(b,b')$
is an endpoint pair of a
$(b,b')$
is an endpoint pair of a
![]() $1$
-shell
$1$
-shell
![]() $s'$
of
$s'$
of
![]() $p_n$
such that
$p_n$
such that
![]() $B(s')=7$
in
$B(s')=7$
in
![]() ${\mathcal M}_{1,n}$
. Let
${\mathcal M}_{1,n}$
. Let
![]() $\alpha '$
be a minimal
$\alpha '$
be a minimal
![]() $2$
-chain with an RN-pattern having the
$2$
-chain with an RN-pattern having the
![]() $1$
-shell boundary
$1$
-shell boundary
![]() $s'$
of length
$s'$
of length
![]() $7$
. Note that we can take such a
$7$
. Note that we can take such a
![]() $2$
-chain because
$2$
-chain because
![]() $p_n$
is a Lascar type. Consider
$p_n$
is a Lascar type. Consider
![]() $a=(x_0,b),a'=(x_6,b')\models q$
. Let
$a=(x_0,b),a'=(x_6,b')\models q$
. Let
![]() $s''$
be a
$s''$
be a
![]() $1$
-shell induced from s and
$1$
-shell induced from s and
![]() $s'$
with an endpoint pair
$s'$
with an endpoint pair
![]() $(a,a')$
. Consider a
$(a,a')$
. Consider a
![]() $2$
-chain
$2$
-chain
![]() $\alpha ''$
in q induced from
$\alpha ''$
in q induced from
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
, which does not a Lascar pattern and has length
$\alpha '$
, which does not a Lascar pattern and has length
![]() $7$
. We claim that
$7$
. We claim that
![]() $\alpha ''$
is minimal. Since
$\alpha ''$
is minimal. Since
![]() $B(s)\le 7$
and
$B(s)\le 7$
and
![]() $B(s')=7$
, we have that
$B(s')=7$
, we have that
![]() $B(s'')=7$
and so
$B(s'')=7$
and so
![]() $\alpha ''$
is minimal. By the construction of
$\alpha ''$
is minimal. By the construction of
![]() $\alpha ''$
, it has an RN-pattern. Therefore, the minimal
$\alpha ''$
, it has an RN-pattern. Therefore, the minimal
![]() $2$
-chain
$2$
-chain
![]() $\alpha ''$
has an RN-pattern but is not equivalent to a Lascar pattern
$\alpha ''$
has an RN-pattern but is not equivalent to a Lascar pattern
![]() $2$
-chain.⊣
$2$
-chain.⊣
Acknowledgments
The first author was supported by European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 705410. The second and fourth authors were supported by an NRF of Korea grant 2018R1D1A1A02085584 and Samsung Science Technology Foundation under Project Number SSTF-BA1301-03, respectively.