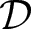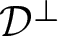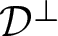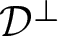1. Introduction
Pseudo-Riemannian manifolds (or metrics) in dimensions ![]() $n\ge4$ with parallel Weyl tensor W are often called conformally symmetric [Reference Chaki and Gupta1]. One speaks of ECS manifolds/metrics [Reference Derdzinski, Roter, Dillen and Van de Woestyne4] when, in addition, the metric is neither conformally flat nor locally symmetric, ‘ECS’ being short for essentially conformally symmetric.
$n\ge4$ with parallel Weyl tensor W are often called conformally symmetric [Reference Chaki and Gupta1]. One speaks of ECS manifolds/metrics [Reference Derdzinski, Roter, Dillen and Van de Woestyne4] when, in addition, the metric is neither conformally flat nor locally symmetric, ‘ECS’ being short for essentially conformally symmetric.
ECS metrics exist in every dimension ![]() $n\ge4$, as shown by Roter [Reference Roter17, Corollary 3], who also proved that they are all indefinite [Reference Derdziński and Roter3, Theorem 2]. The local structure of all ECS metrics is described in [Reference Derdzinski and Roter6].
$n\ge4$, as shown by Roter [Reference Roter17, Corollary 3], who also proved that they are all indefinite [Reference Derdziński and Roter3, Theorem 2]. The local structure of all ECS metrics is described in [Reference Derdzinski and Roter6].
Given an ECS manifold ![]() $(M,\mathtt{g})$, we define its rank [Reference Derdzinski and Terek8] to be the rank
$(M,\mathtt{g})$, we define its rank [Reference Derdzinski and Terek8] to be the rank ![]() $d\in\{1,2\}$ of its Olszak distribution
$d\in\{1,2\}$ of its Olszak distribution ![]() $\mathcal{D}$, which is a null parallel distribution on M discovered by Olszak [Reference Olszak16]. The sections of
$\mathcal{D}$, which is a null parallel distribution on M discovered by Olszak [Reference Olszak16]. The sections of ![]() $\mathcal{D}$ are the vector fields v having the property that
$\mathcal{D}$ are the vector fields v having the property that ![]() $\mathtt{g}(v,\cdot)\wedge[W(v^{\prime}, v^{\prime \prime},\cdot,\cdot)]=0$ for all vector fields
$\mathtt{g}(v,\cdot)\wedge[W(v^{\prime}, v^{\prime \prime},\cdot,\cdot)]=0$ for all vector fields ![]() $v^{\prime},v^{\prime \prime}$. Every Lorentzian ECS manifold has rank one, as the Lorentzian signature limits the ranks of null distributions to at most 1. For more details, see [Reference Derdzinski and Roter6, p. 119].
$v^{\prime},v^{\prime \prime}$. Every Lorentzian ECS manifold has rank one, as the Lorentzian signature limits the ranks of null distributions to at most 1. For more details, see [Reference Derdzinski and Roter6, p. 119].
Compact rank-one ECS manifolds are known to exist in all dimensions ![]() $n\ge5$, where they represent all indefinite metric signatures [Reference Derdzinski and Roter7, Reference Derdzinski and Terek8]. There are also non-compact locally homogeneous ECS manifolds [Reference Derdziński2] of every dimension
$n\ge5$, where they represent all indefinite metric signatures [Reference Derdzinski and Roter7, Reference Derdzinski and Terek8]. There are also non-compact locally homogeneous ECS manifolds [Reference Derdziński2] of every dimension ![]() $n\ge4$. More recently, in [Reference Derdzinski and Terek10], we constructed examples of compact locally homogeneous ECS manifolds of all odd dimensions
$n\ge4$. More recently, in [Reference Derdzinski and Terek10], we constructed examples of compact locally homogeneous ECS manifolds of all odd dimensions ![]() $n\ge5$.
$n\ge5$.
Our main result can be phrased as follows.
Theorem A. Every non-locally homogeneous compact rank-one ECS manifold with transversally orientable distribution ![]() $\mathcal{D}^\perp$ is diffeomorphic to a bundle over the circle in such a way that the fibres coincide with the leaves of
$\mathcal{D}^\perp$ is diffeomorphic to a bundle over the circle in such a way that the fibres coincide with the leaves of ![]() $\mathcal{D}^\perp$. This conclusion remains valid in the locally homogeneous case, as long as
$\mathcal{D}^\perp$. This conclusion remains valid in the locally homogeneous case, as long as ![]() $\mathcal{D}^\perp$ is assumed to have at least one compact leaf.
$\mathcal{D}^\perp$ is assumed to have at least one compact leaf.
The assertion of Theorem A obviously implies that the leaves of ![]() $\mathcal{D}^\perp$ are all compact and mutually diffeomorphic. Note that transversal orientability of
$\mathcal{D}^\perp$ are all compact and mutually diffeomorphic. Note that transversal orientability of ![]() $\mathcal{D}^\perp$ can always be achieved by replacing the manifold in question, if necessary, with a twofold isometric covering.
$\mathcal{D}^\perp$ can always be achieved by replacing the manifold in question, if necessary, with a twofold isometric covering.
Theorem A generalizes Theorem B of [Reference Derdzinski and Roter5] from the Lorentzian case to any indefinite metric signature. The assumption in [Reference Derdzinski and Roter5, Theorem B] does not include rank one or exclude local homogeneity, since a Lorentzian ECS manifold necessarily has rank one (see above) and cannot be locally homogeneous (Remark 7.4). The Appendix explains how our proof of Theorem A differs from that used for [Reference Derdzinski and Roter5, Theorem B].
The examples of [Reference Derdzinski and Terek10], mentioned earlier, show that the final clause of Theorem A is non-vacuous, at least in odd dimensions.
Triviality of the pullback to ![]() $\mathrm{I\!R}$ of a bundle over S 1 makes the next result an obvious consequence of Theorem A except when
$\mathrm{I\!R}$ of a bundle over S 1 makes the next result an obvious consequence of Theorem A except when  $(\widehat{M},\mathtt{g})$ is locally homogeneous.
$(\widehat{M},\mathtt{g})$ is locally homogeneous.
Theorem B. The leaves of ![]() $\mathcal{D}^\perp$ in the pseudo-Riemannian universal covering space
$\mathcal{D}^\perp$ in the pseudo-Riemannian universal covering space  $(\widehat{M},\mathtt{g})$ of any compact rank-one ECS manifold are the factor manifolds of a global product decomposition of
$(\widehat{M},\mathtt{g})$ of any compact rank-one ECS manifold are the factor manifolds of a global product decomposition of ![]() $\widehat{M}$. More precisely, every leaf L of
$\widehat{M}$. More precisely, every leaf L of ![]() $\mathcal{D}^\perp$ in
$\mathcal{D}^\perp$ in ![]() $\widehat{M}$ is simply connected, and
$\widehat{M}$ is simply connected, and ![]() $\widehat{M}$ is diffeomorphic to
$\widehat{M}$ is diffeomorphic to ![]() $\mathrm{I\!R}\times L$.
$\mathrm{I\!R}\times L$.
We prove both theorems in § 11.
2. Outline of the main argument
We fix a compact rank-one ECS manifold ![]() $(M,\mathtt{g})$ of dimension
$(M,\mathtt{g})$ of dimension ![]() $n\ge4$, and denote by
$n\ge4$, and denote by  $\,(\widehat{M},\mathtt{g})\,$ its pseudo-Riemannian universal covering and by
$\,(\widehat{M},\mathtt{g})\,$ its pseudo-Riemannian universal covering and by  $\pi:\widehat{M}\to M=\widehat{M}/\Gamma$ the covering projection. Here
$\pi:\widehat{M}\to M=\widehat{M}/\Gamma$ the covering projection. Here ![]() $\Gamma\approx\pi_1 M$ is a group of isometries of
$\Gamma\approx\pi_1 M$ is a group of isometries of  $(\widehat{M},\mathtt{g})$ acting on
$(\widehat{M},\mathtt{g})$ acting on ![]() $\widehat{M}$ freely and properly discontinuously. Also,
$\widehat{M}$ freely and properly discontinuously. Also, ![]() $\mathcal{D}$ stands for the Olszak distribution (see the Introduction), with the same symbols
$\mathcal{D}$ stands for the Olszak distribution (see the Introduction), with the same symbols ![]() $\mathcal{D}$ and
$\mathcal{D}$ and ![]() $\mathcal{V}=\mathcal{D}^\perp$ denoting objects in
$\mathcal{V}=\mathcal{D}^\perp$ denoting objects in ![]() $\widehat{M}$ and their projections onto M. According to Equations (6.3)–(6.7), on
$\widehat{M}$ and their projections onto M. According to Equations (6.3)–(6.7), on ![]() $\widehat{M}$ there exists a function t with a parallel gradient
$\widehat{M}$ there exists a function t with a parallel gradient ![]() $\nabla t$ spanning
$\nabla t$ spanning ![]() $\mathcal{D}$, so that
$\mathcal{D}$, so that ![]() $\mathcal{D}^\perp = \mathrm{Ker}\,{\rm d}t$, and the Ricci tensor of
$\mathcal{D}^\perp = \mathrm{Ker}\,{\rm d}t$, and the Ricci tensor of  $(\widehat{M},\mathtt{g})$ equals
$(\widehat{M},\mathtt{g})$ equals ![]() $(2-n)f(t)\,{\rm d}t\otimes {\rm d}t$, where
$(2-n)f(t)\,{\rm d}t\otimes {\rm d}t$, where  $f:\widehat{M}\to\mathrm{I\!R}$ is locally a function of t. If a C 1 function
$f:\widehat{M}\to\mathrm{I\!R}$ is locally a function of t. If a C 1 function  $\chi:\widehat{M}\to\mathrm{I\!R}$ is locally a function of t, one may define its t-derivative
$\chi:\widehat{M}\to\mathrm{I\!R}$ is locally a function of t, one may define its t-derivative  $\dot\chi:\widehat{M}\to\mathrm{I\!R}$ by
$\dot\chi:\widehat{M}\to\mathrm{I\!R}$ by ![]() $d\chi=\dot\chi\,{\rm d}t$. It easily follows – cf. Equation (6.8) – that
$d\chi=\dot\chi\,{\rm d}t$. It easily follows – cf. Equation (6.8) – that
 \begin{equation}
\begin{array}{l}
\mathrm{the\ action\ of\ }\Gamma \mathrm{\ multiplies\ }\nabla t
\textrm{
by non-zero constants,}\\
\mathrm{implying\ }\Gamma \textrm{-invariance of both
}|f|^{1/2}\,{\rm d}t\mathrm{\ and }|\dot f|^{1/3}\,{\rm d}t.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\mathrm{the\ action\ of\ }\Gamma \mathrm{\ multiplies\ }\nabla t
\textrm{
by non-zero constants,}\\
\mathrm{implying\ }\Gamma \textrm{-invariance of both
}|f|^{1/2}\,{\rm d}t\mathrm{\ and }|\dot f|^{1/3}\,{\rm d}t.
\end{array}
\end{equation} We now assume transversal orientability of ![]() $\mathcal{V}$ and proceed to summarize the steps, leading to the main conclusion of Theorem A: that, unless
$\mathcal{V}$ and proceed to summarize the steps, leading to the main conclusion of Theorem A: that, unless ![]() $\mathtt{g}$ is locally homogeneous,
$\mathtt{g}$ is locally homogeneous, ![]() $\mathcal{V}=\mathcal{D}^\perp$ must be the vertical distribution of a fibration
$\mathcal{V}=\mathcal{D}^\perp$ must be the vertical distribution of a fibration ![]() $M\to S^1$.
$M\to S^1$.
This is achieved by showing that ![]() $\mathcal{V}$, in addition to being a transversally orientable codimension-one foliation on the compact manifold M, also has what we call property (4.1): for every compact leaf L of
$\mathcal{V}$, in addition to being a transversally orientable codimension-one foliation on the compact manifold M, also has what we call property (4.1): for every compact leaf L of ![]() $\mathcal{V}$, the nearby leaves are either all non-compact – with the exception of L – or they are all compact and there exists a product-like
$\mathcal{V}$, the nearby leaves are either all non-compact – with the exception of L – or they are all compact and there exists a product-like ![]() $\mathcal{V}$-saturated tubular neighbourhood of L in M. Furthermore, some compact leaf of
$\mathcal{V}$-saturated tubular neighbourhood of L in M. Furthermore, some compact leaf of ![]() $\mathcal{V}$ then realizes the second case in the either–or clause of Equation (4.1).
$\mathcal{V}$ then realizes the second case in the either–or clause of Equation (4.1).
The reason why the main claim in Theorem A follows from the two conditions italicized above is that, even within the general context of foliations, with no reference to ECS geometry, these conditions imply that all leaves of ![]() $\mathcal{V}$ are compact, which forces M to be a bundle over the circle (Theorem 4.1).
$\mathcal{V}$ are compact, which forces M to be a bundle over the circle (Theorem 4.1).
Returning to our ECS case, we prove property (4.1) for ![]() $\mathcal{V}=\mathcal{D}^\perp$ by first observing, in § 10, that the rank-one Olszak distribution
$\mathcal{V}=\mathcal{D}^\perp$ by first observing, in § 10, that the rank-one Olszak distribution ![]() $\mathcal{D}$ on
$\mathcal{D}$ on ![]() $\widehat{M}$ is spanned by the parallel gradient
$\widehat{M}$ is spanned by the parallel gradient ![]() $\nabla t$, and so the Levi-Civita connection of the compact ECS manifold
$\nabla t$, and so the Levi-Civita connection of the compact ECS manifold ![]() $(M,\mathtt{g})$ induces flat linear connections both in
$(M,\mathtt{g})$ induces flat linear connections both in ![]() $\mathcal{D}$ (over M) and in the line bundle
$\mathcal{D}$ (over M) and in the line bundle ![]() $\mathcal{D}_{L}^*$ over any leaf L of
$\mathcal{D}_{L}^*$ over any leaf L of ![]() $\mathcal{D}^\perp$, dual to the line bundle
$\mathcal{D}^\perp$, dual to the line bundle ![]() $\mathcal{D}_L $ arising as the restriction of
$\mathcal{D}_L $ arising as the restriction of ![]() $\mathcal{D}$ to L. At the same time,
$\mathcal{D}$ to L. At the same time, ![]() $\mathcal{D}_{L}^*$ is canonically isomorphic to the normal bundle of L in M. Assuming compactness of L, we then show in Theorem 10.1 (see the next paragraph) that, under a suitable diffeomorphic identification Ψ of a neighbourhood U of L in M with a neighbourhood Uʹ of the zero section L in the line bundle
$\mathcal{D}_{L}^*$ is canonically isomorphic to the normal bundle of L in M. Assuming compactness of L, we then show in Theorem 10.1 (see the next paragraph) that, under a suitable diffeomorphic identification Ψ of a neighbourhood U of L in M with a neighbourhood Uʹ of the zero section L in the line bundle ![]() $\mathcal{D}_{L}^*$, the distribution
$\mathcal{D}_{L}^*$, the distribution ![]() $\mathcal{D}^\perp$ on U corresponds to the restriction to Uʹ of the horizontal distribution of the flat linear connection in
$\mathcal{D}^\perp$ on U corresponds to the restriction to Uʹ of the horizontal distribution of the flat linear connection in ![]() $\mathcal{D}_{L}^*$, mentioned above. By Equation (2.1), the holonomy group HL of the latter connection consists of multiplications by positive real constants (‘non-zero’ in Equation (2.1) becoming ‘positive’ due to transversal orientability of
$\mathcal{D}_{L}^*$, mentioned above. By Equation (2.1), the holonomy group HL of the latter connection consists of multiplications by positive real constants (‘non-zero’ in Equation (2.1) becoming ‘positive’ due to transversal orientability of ![]() $\mathcal{V}=\mathcal{D}^\perp$), and the dichotomy required in Equation (4.1) comes from the obvious fact that HL is either infinite or trivial.
$\mathcal{V}=\mathcal{D}^\perp$), and the dichotomy required in Equation (4.1) comes from the obvious fact that HL is either infinite or trivial.
The identification ![]() $\Psi:U\to U^{\prime}$, given by formula (10.2), uses a fixed smooth vector field on M, nowhere tangent to
$\Psi:U\to U^{\prime}$, given by formula (10.2), uses a fixed smooth vector field on M, nowhere tangent to ![]() $\mathcal{D}^\perp$, to provide the curve segments forming the fibres of the tubular neighbourhood U, and along these segments, pulled back to
$\mathcal{D}^\perp$, to provide the curve segments forming the fibres of the tubular neighbourhood U, and along these segments, pulled back to ![]() $\widehat{M}$, we define Ψ so that it sends local t-levels to local sections parallel relative to the flat linear connection. Due to Equation (2.1), this construction is Γ-equivariant, and hence projects into M.
$\widehat{M}$, we define Ψ so that it sends local t-levels to local sections parallel relative to the flat linear connection. Due to Equation (2.1), this construction is Γ-equivariant, and hence projects into M.
Finally, still in the ECS case, we establish the second option of property (4.1) for some compact leaf of ![]() $\mathcal{V}=\mathcal{D}^\perp$ by considering, in § 8, the vector space
$\mathcal{V}=\mathcal{D}^\perp$ by considering, in § 8, the vector space ![]() $\mathcal{F}$ of all continuous functions
$\mathcal{F}$ of all continuous functions  $\chi:\widehat{M}\to\mathrm{I\!R}$ such that the 1-form
$\chi:\widehat{M}\to\mathrm{I\!R}$ such that the 1-form ![]() $\chi\,{\rm d}t$ is closed (i.e., locally exact) and projectable onto M, with the linear operator
$\chi\,{\rm d}t$ is closed (i.e., locally exact) and projectable onto M, with the linear operator ![]() $P:\mathcal{F}\to H^1(M,\mathrm{I\!R})$ sending χ to the cohomology class of the projected 1-form on M.
$P:\mathcal{F}\to H^1(M,\mathrm{I\!R})$ sending χ to the cohomology class of the projected 1-form on M.
First, let ![]() $\dim\mathcal{F}=m \lt \infty$. By Equation (2.1),
$\dim\mathcal{F}=m \lt \infty$. By Equation (2.1), ![]() $|f|^{1/2},|\dot f|^{1/3}\in\mathcal{F}$, and
$|f|^{1/2},|\dot f|^{1/3}\in\mathcal{F}$, and ![]() $\mathcal{F}$ is closed under the m-argument operation assigning
$\mathcal{F}$ is closed under the m-argument operation assigning ![]() $|\psi_1 \cdots\psi_m |^{1/m}$ to
$|\psi_1 \cdots\psi_m |^{1/m}$ to ![]() $\psi_1 ,\ldots,\psi_m $. Simple set-theoretical reasons then cause
$\psi_1 ,\ldots,\psi_m $. Simple set-theoretical reasons then cause ![]() $|\dot f|^{1/3}$ to be a constant multiple of
$|\dot f|^{1/3}$ to be a constant multiple of ![]() $|f|^{1/2}$ (see the proof of Theorem 9.1). This makes f globally a function of t, of the form
$|f|^{1/2}$ (see the proof of Theorem 9.1). This makes f globally a function of t, of the form ![]() $f=\varepsilon(t-b)^{-2}$ with real constants
$f=\varepsilon(t-b)^{-2}$ with real constants ![]() $\varepsilon\ne0$ and b, which combined with a result from algebraic geometry – Whitney’s theorem – implies local homogeneity of
$\varepsilon\ne0$ and b, which combined with a result from algebraic geometry – Whitney’s theorem – implies local homogeneity of ![]() $\mathtt{g}$ (a precise cross-reference being Lemma 7.1 invoked in the proof of Theorem 7.3).
$\mathtt{g}$ (a precise cross-reference being Lemma 7.1 invoked in the proof of Theorem 7.3).
On the other hand, when ![]() $\mathcal{F}$ is infinite-dimensional, P must be non-injective due to compactness of M and, given any
$\mathcal{F}$ is infinite-dimensional, P must be non-injective due to compactness of M and, given any ![]() $\chi\in\mathcal{F}\smallsetminus\{0\}$ with
$\chi\in\mathcal{F}\smallsetminus\{0\}$ with ![]() $P\chi=0$, we see that
$P\chi=0$, we see that ![]() $\chi\,{\rm d}t$ projects onto an exact 1-form on M, and hence onto
$\chi\,{\rm d}t$ projects onto an exact 1-form on M, and hence onto ![]() ${\rm d}\mu$ for some (non-constant) C 1 function
${\rm d}\mu$ for some (non-constant) C 1 function ![]() $\mu:M\to\mathrm{I\!R}$. As
$\mu:M\to\mathrm{I\!R}$. As ![]() $\mathcal{D}^\perp=\mathrm{Ker}\,{\rm d}t$ on
$\mathcal{D}^\perp=\mathrm{Ker}\,{\rm d}t$ on ![]() $\widehat{M}$, this µ is constant along
$\widehat{M}$, this µ is constant along ![]() $\mathcal{D}^\perp$.
$\mathcal{D}^\perp$.
Even though µ is only guaranteed to be of class C 1, Sard’s theorem still applies (Remark 9.2), and any connected component L of a regular level of µ clearly realizes the second case of Equation (4.1).
3. Preliminaries
Manifolds are (usually) connected, pseudo-Riemannian metrics and vector fields are assumed ![]() $C^\infty$-differentiable, while functions may be of lower regularity. The terms ‘foliation’ and (integrable) ‘distribution’ will be used interchangeably; by their ‘leaves’, we always mean maximal connected integral manifolds.
$C^\infty$-differentiable, while functions may be of lower regularity. The terms ‘foliation’ and (integrable) ‘distribution’ will be used interchangeably; by their ‘leaves’, we always mean maximal connected integral manifolds.
The following four facts will be used in § 4, 7 and 9.
Remark 3.1. Let points ![]() $x,x^{\prime}$ of codimension-one submanifolds
$x,x^{\prime}$ of codimension-one submanifolds ![]() $L,L^{\prime}$ of a manifold M be joined by an integral curve Cx of a complete
$L,L^{\prime}$ of a manifold M be joined by an integral curve Cx of a complete ![]() $C^\infty$ vector field v on M, which is transverse to L at x and to Lʹ at xʹ. Then Cx belongs to a smooth variation
$C^\infty$ vector field v on M, which is transverse to L at x and to Lʹ at xʹ. Then Cx belongs to a smooth variation  $\widetilde U\ni y\mapsto C_y $ of integral curves of v, parametrized by a neighbourhood
$\widetilde U\ni y\mapsto C_y $ of integral curves of v, parametrized by a neighbourhood ![]() $\widetilde U$ of x in M such that, for some neighbourhoods
$\widetilde U$ of x in M such that, for some neighbourhoods ![]() $U,U^{\prime}$ of x in L and xʹ in Lʹ with
$U,U^{\prime}$ of x in L and xʹ in Lʹ with ![]() $U\subseteq\widetilde U$, each Cy joins
$U\subseteq\widetilde U$, each Cy joins ![]() $y\in\widetilde U$ to a point
$y\in\widetilde U$ to a point ![]() $y^{\prime}\in U^{\prime}$ and the resulting mapping
$y^{\prime}\in U^{\prime}$ and the resulting mapping ![]() $y\mapsto y^{\prime}$ is a submersion
$y\mapsto y^{\prime}$ is a submersion ![]() $\widetilde U\to U^{\prime}$, while its restriction to U is a diffeomorphism
$\widetilde U\to U^{\prime}$, while its restriction to U is a diffeomorphism ![]() $U\to U^{\prime}$. The word ‘smooth’ also applies here to the domain intervals of the integral curves.
$U\to U^{\prime}$. The word ‘smooth’ also applies here to the domain intervals of the integral curves.
Namely, let ![]() $\mathrm{I\!R}\times M\ni(\tau,y)\mapsto\phi(\tau,y)\in M$ be the flow of v, so that Cx is parametrized by
$\mathrm{I\!R}\times M\ni(\tau,y)\mapsto\phi(\tau,y)\in M$ be the flow of v, so that Cx is parametrized by ![]() $[0,\tau_* ]\ni\tau\mapsto\phi(\tau,x)$. We now fix a neighbourhood
$[0,\tau_* ]\ni\tau\mapsto\phi(\tau,x)$. We now fix a neighbourhood ![]() $\widetilde U^{\prime}$ of xʹ in M and a
$\widetilde U^{\prime}$ of xʹ in M and a ![]() $C^\infty$ function
$C^\infty$ function ![]() $\theta:\widetilde U^{\prime}\to\mathrm{I\!R}$ with
$\theta:\widetilde U^{\prime}\to\mathrm{I\!R}$ with  $L^{\prime}\cap\widetilde U^{\prime}=\theta^{-1}(0)$, having 0 as a regular value. The equation
$L^{\prime}\cap\widetilde U^{\prime}=\theta^{-1}(0)$, having 0 as a regular value. The equation ![]() $\theta(\phi(\tau,y))=0$, imposed on
$\theta(\phi(\tau,y))=0$, imposed on  $(\tau,y)\in\mathrm{I\!R}\times\widetilde U$, is satisfied when
$(\tau,y)\in\mathrm{I\!R}\times\widetilde U$, is satisfied when ![]() $(\tau,y)=(\tau_* ,x)$. The implicit function theorem [Reference Lang12, p. 18] applied to this equation yields a
$(\tau,y)=(\tau_* ,x)$. The implicit function theorem [Reference Lang12, p. 18] applied to this equation yields a ![]() $C^\infty$ function
$C^\infty$ function ![]() $y\mapsto\tau(y)$, defined near x in M, with
$y\mapsto\tau(y)$, defined near x in M, with ![]() $\theta(\phi(\tau(y),y))=0$ and
$\theta(\phi(\tau(y),y))=0$ and ![]() $\tau(x)=\tau_* $. Consequently,
$\tau(x)=\tau_* $. Consequently, ![]() $y^{\prime}=\phi(\tau(y),y)$ lies in Lʹ. The submersion/diffeomorphism property of the mapping
$y^{\prime}=\phi(\tau(y),y)$ lies in Lʹ. The submersion/diffeomorphism property of the mapping ![]() $\widetilde U\to U^{\prime}$ or
$\widetilde U\to U^{\prime}$ or ![]() $U\to U^{\prime}$ arising in this way, with
$U\to U^{\prime}$ arising in this way, with ![]() $U=L\cap\widetilde U$, is immediate since
$U=L\cap\widetilde U$, is immediate since ![]() $\widetilde U\to U^{\prime}$ has a right inverse
$\widetilde U\to U^{\prime}$ has a right inverse ![]() $U^{\prime}\to U$ obtained by using the same principle for −v instead of v.
$U^{\prime}\to U$ obtained by using the same principle for −v instead of v.
Remark 3.2. For a (possibly disconnected) codimension-one submanifold L of a manifold M and the flow ![]() $\mathrm{I\!R}\times M\ni(\tau,x)\mapsto\phi(\tau,x)\in M$ of a complete
$\mathrm{I\!R}\times M\ni(\tau,x)\mapsto\phi(\tau,x)\in M$ of a complete ![]() $C^\infty$ vector field on M, which is nowhere tangent to L, the restriction
$C^\infty$ vector field on M, which is nowhere tangent to L, the restriction ![]() $\phi:\mathrm{I\!R}\times L\to M$ is locally diffeomorphic (a codimension-zero immersion). If, in addition, L is also compact,
$\phi:\mathrm{I\!R}\times L\to M$ is locally diffeomorphic (a codimension-zero immersion). If, in addition, L is also compact, ![]() $\phi:(-\varepsilon,\varepsilon)\times L\to M$ is an embedding for all ɛ > 0 close to 0.
$\phi:(-\varepsilon,\varepsilon)\times L\to M$ is an embedding for all ɛ > 0 close to 0.
In fact, the first claim follows, since ![]() $\phi:\mathrm{I\!R}\times L\to M$ has smooth local inverses as an easy consequence of Remark 3.1. Next, if the embedding assertion failed, there would exist two termwise distinct sequences in
$\phi:\mathrm{I\!R}\times L\to M$ has smooth local inverses as an easy consequence of Remark 3.1. Next, if the embedding assertion failed, there would exist two termwise distinct sequences in ![]() $\mathrm{I\!R}\times L$ having the
$\mathrm{I\!R}\times L$ having the ![]() $\mathrm{I\!R}$ components tending to 0, with the same sequence of ϕ-values. Since L is now compact, so are
$\mathrm{I\!R}$ components tending to 0, with the same sequence of ϕ-values. Since L is now compact, so are ![]() $\phi([-\varepsilon,\varepsilon]\times L)$ for all ɛ > 0, and hence both sequences have subsequences converging to the same limit
$\phi([-\varepsilon,\varepsilon]\times L)$ for all ɛ > 0, and hence both sequences have subsequences converging to the same limit ![]() $x\in L$. Injectivity of our mapping on a neighbourhood of
$x\in L$. Injectivity of our mapping on a neighbourhood of ![]() $(0,x)$ now leads to a contradiction.
$(0,x)$ now leads to a contradiction.
By an m-argument operation Π in the following lemma, we mean any mapping associating, with any ordered m-tuple ![]() $(\psi_1 ,\ldots,\psi_m )$ of functions
$(\psi_1 ,\ldots,\psi_m )$ of functions ![]() $X\to\mathrm{I\!R}$, a function
$X\to\mathrm{I\!R}$, a function ![]() $\Pi(\psi_1 ,\ldots,\psi_m ):X\to\mathrm{I\!R}$.
$\Pi(\psi_1 ,\ldots,\psi_m ):X\to\mathrm{I\!R}$.
Lemma 3.3. Let a vector space ![]() $\mathcal{F}$ of functions
$\mathcal{F}$ of functions ![]() $X\to\mathrm{I\!R}$ on a set X have a positive finite dimension m. If X is closed both under the absolute-value operation
$X\to\mathrm{I\!R}$ on a set X have a positive finite dimension m. If X is closed both under the absolute-value operation ![]() $\psi\mapsto|\psi|$ and under some m-argument operation Π sending any
$\psi\mapsto|\psi|$ and under some m-argument operation Π sending any ![]() $\psi_1 ,\ldots,\psi_m $ to a non-negative function
$\psi_1 ,\ldots,\psi_m $ to a non-negative function ![]() $\Pi(\psi_1 ,\ldots,\psi_m )$, which has the same zeros as the product
$\Pi(\psi_1 ,\ldots,\psi_m )$, which has the same zeros as the product ![]() $\psi_1, \ldots,\psi_m $, then there exists a proper subset X 0 of X, a partition
$\psi_1, \ldots,\psi_m $, then there exists a proper subset X 0 of X, a partition ![]() $\{X_j \}_{j=1}^m$ of
$\{X_j \}_{j=1}^m$ of ![]() $X\smallsetminus X_0 $ and a basis
$X\smallsetminus X_0 $ and a basis ![]() $\chi_1 ,\ldots,\chi_m $ of
$\chi_1 ,\ldots,\chi_m $ of ![]() $\mathcal{F}$ such that
$\mathcal{F}$ such that ![]() $\chi_j \gt 0$ on Xj and
$\chi_j \gt 0$ on Xj and ![]() $\chi_j =0$ on
$\chi_j =0$ on ![]() $X\smallsetminus X_j $ for every
$X\smallsetminus X_j $ for every ![]() $j=1,\ldots,m$. In other words, some basis
$j=1,\ldots,m$. In other words, some basis ![]() $\chi_1 ,\ldots,\chi_m $ of
$\chi_1 ,\ldots,\chi_m $ of ![]() $\mathcal{F}$ consists of non-negative functions with pairwise disjoint supports, the word ‘support’ meaning here the complement of the zero set.
$\mathcal{F}$ consists of non-negative functions with pairwise disjoint supports, the word ‘support’ meaning here the complement of the zero set.
Proof. Choose ![]() $x_1 ,\ldots,x_m \in X$ with the m evaluations
$x_1 ,\ldots,x_m \in X$ with the m evaluations ![]() $\delta_{x_j}$ forming a basis of the dual space
$\delta_{x_j}$ forming a basis of the dual space ![]() $\mathcal{F}^*$, so that some
$\mathcal{F}^*$, so that some ![]() $\sigma_1 ,\ldots,\sigma_m \in\mathcal{F}$ have
$\sigma_1 ,\ldots,\sigma_m \in\mathcal{F}$ have ![]() $\sigma_j (x_i ) \lt 0 \lt \sigma_j (x_j )$ whenever
$\sigma_j (x_i ) \lt 0 \lt \sigma_j (x_j )$ whenever ![]() $i\ne j$. The positive-part and negative-part operations
$i\ne j$. The positive-part and negative-part operations ![]() $( )^\pm:\mathcal{F}\to\mathcal{F}$ are given by
$( )^\pm:\mathcal{F}\to\mathcal{F}$ are given by ![]() $\sigma^\pm=(|\sigma|\pm\sigma)/2$. We set
$\sigma^\pm=(|\sigma|\pm\sigma)/2$. We set ![]() $\chi_j =
\Pi(\widetilde\sigma_1 ,\ldots,\widetilde\sigma_m )$, where
$\chi_j =
\Pi(\widetilde\sigma_1 ,\ldots,\widetilde\sigma_m )$, where  $\widetilde\sigma_j =\sigma_j^+$ and
$\widetilde\sigma_j =\sigma_j^+$ and ![]() $\widetilde\sigma_i =\sigma_i^-$ for
$\widetilde\sigma_i =\sigma_i^-$ for ![]() $i\ne j$. The supports
$i\ne j$. The supports  $X_j =\chi_j^{-1}((0,\infty))$ are non-empty (as
$X_j =\chi_j^{-1}((0,\infty))$ are non-empty (as ![]() $x_j \in X_j $) and pairwise disjoint (since, if
$x_j \in X_j $) and pairwise disjoint (since, if ![]() $i\ne j$, one has
$i\ne j$, one has ![]() $\sigma_i \lt 0 \lt \sigma_j $ on Xj), which trivially implies linear independence of
$\sigma_i \lt 0 \lt \sigma_j $ on Xj), which trivially implies linear independence of ![]() $\chi_1 ,\ldots,\chi_m $. Our claim thus follows if we declare X 0 to be
$\chi_1 ,\ldots,\chi_m $. Our claim thus follows if we declare X 0 to be  $X\smallsetminus\bigcup_{j=1}^mX_j $, that is, the simultaneous zero set of
$X\smallsetminus\bigcup_{j=1}^mX_j $, that is, the simultaneous zero set of ![]() $\chi_1 ,\dots,\chi_m $.
$\chi_1 ,\dots,\chi_m $.
Remark 3.4. A locally diffeomorphic ![]() $C^\infty$ mapping from a compact manifold into a connected one is necessarily surjective, and so the latter manifold must be compact as well. In fact, the image of the mapping is both compact and open. (We do not need the well-known stronger conclusion that the mapping is then also a covering projection.)
$C^\infty$ mapping from a compact manifold into a connected one is necessarily surjective, and so the latter manifold must be compact as well. In fact, the image of the mapping is both compact and open. (We do not need the well-known stronger conclusion that the mapping is then also a covering projection.)
Remark 3.5. A non-empty proper subset K of ![]() $(0,\infty)$, different from
$(0,\infty)$, different from ![]() $\{1\}$, and closed under the mappings
$\{1\}$, and closed under the mappings ![]() $q\mapsto q^r$ for all
$q\mapsto q^r$ for all ![]() $r\in\mathsf{Z\hskip-4ptZ}$, must have infinitely many connected components: if
$r\in\mathsf{Z\hskip-4ptZ}$, must have infinitely many connected components: if ![]() $q\in(1,\infty)\smallsetminus K$ is fixed, choosing a connected component Kr of each non-empty intersection
$q\in(1,\infty)\smallsetminus K$ is fixed, choosing a connected component Kr of each non-empty intersection ![]() $K\cap(q^r,q^{r+1})$,
$K\cap(q^r,q^{r+1})$, ![]() $r\in\mathsf{Z\hskip-4ptZ}$, we obtain, due to unboundedness of K, an infinite family of such components Kr.
$r\in\mathsf{Z\hskip-4ptZ}$, we obtain, due to unboundedness of K, an infinite family of such components Kr.
4. Codimension-one foliations
The results of this section are the most crucial steps in proving Theorem A.
Here is a property of a codimension-one foliation ![]() $\mathcal{V}$ on a manifold M:
$\mathcal{V}$ on a manifold M:
 \begin{equation}
\begin{array}{l}
\mathrm{every\ compact\ leaf\ } L\mathrm{\ of\
}\mathcal{V}\mathrm{\ has\ a\ neighbourhood\
} U\mathrm{\ in\ }M\mathrm{\ such\ that}\\
\mathrm{the\ leaves\ of\ }\mathcal{V}\mathrm{\
intersecting\ }U\smallsetminus L\textrm{ are
either
all non-compact, or}\\
\mathrm{they\ are\ all\ compact\ and\ some\ neighbourhood\
of\ } L\mathrm{\ in\ } M\mathrm{\ is\ a\ union}\\
\mathrm{of\ compact\ leaves\ of\ }\mathcal{V}\mathrm{\
and\ may\ be\ diffeomorphically\ identified}\\
\mathrm{with\ }\mathrm{I\!R}\times L\mathrm{\ so\ as\ to\ make\
}\mathcal{V}\mathrm{\ appear\ as\ the\
}L\mathrm{\ factor\ foliation.}
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\mathrm{every\ compact\ leaf\ } L\mathrm{\ of\
}\mathcal{V}\mathrm{\ has\ a\ neighbourhood\
} U\mathrm{\ in\ }M\mathrm{\ such\ that}\\
\mathrm{the\ leaves\ of\ }\mathcal{V}\mathrm{\
intersecting\ }U\smallsetminus L\textrm{ are
either
all non-compact, or}\\
\mathrm{they\ are\ all\ compact\ and\ some\ neighbourhood\
of\ } L\mathrm{\ in\ } M\mathrm{\ is\ a\ union}\\
\mathrm{of\ compact\ leaves\ of\ }\mathcal{V}\mathrm{\
and\ may\ be\ diffeomorphically\ identified}\\
\mathrm{with\ }\mathrm{I\!R}\times L\mathrm{\ so\ as\ to\ make\
}\mathcal{V}\mathrm{\ appear\ as\ the\
}L\mathrm{\ factor\ foliation.}
\end{array}
\end{equation} The final clause of property (4.1) means that some diffeomorphism of a neighbourhood of L in M onto ![]() $\mathrm{I\!R}\times L$ pushes
$\mathrm{I\!R}\times L$ pushes ![]() $\mathcal{V}$ forward onto the L factor foliation of
$\mathcal{V}$ forward onto the L factor foliation of ![]() $\mathrm{I\!R}\times L$, which has the leaves
$\mathrm{I\!R}\times L$, which has the leaves ![]() $\{\tau\}\times L$, for
$\{\tau\}\times L$, for ![]() $\tau\in\mathrm{I\!R}$.
$\tau\in\mathrm{I\!R}$.
Theorem 4.1. Let a transversally-orientable codimension-one foliation ![]() $\mathcal{V}$ on a compact manifold M satisfy condition (4.1). If, in addition, some compact leaf L of
$\mathcal{V}$ on a compact manifold M satisfy condition (4.1). If, in addition, some compact leaf L of ![]() $\mathcal{V}$ realizes the second possibility in property (4.1), so as to have a product-like
$\mathcal{V}$ realizes the second possibility in property (4.1), so as to have a product-like ![]() $\mathcal{V}$-saturated neighbourhood in M formed by compact leaves, then the leaves of
$\mathcal{V}$-saturated neighbourhood in M formed by compact leaves, then the leaves of ![]() $\mathcal{V}$ are all compact and they constitute the fibres of a bundle projection
$\mathcal{V}$ are all compact and they constitute the fibres of a bundle projection ![]() $M\to S^1$.
$M\to S^1$.
Proof. Transversal orientability of ![]() $\mathcal{V}$ allows us to fix a
$\mathcal{V}$ allows us to fix a ![]() $C^\infty$ vector field v on M, nowhere tangent to
$C^\infty$ vector field v on M, nowhere tangent to ![]() $\mathcal{V}$. We also fix a compact leaf L of
$\mathcal{V}$. We also fix a compact leaf L of ![]() $\mathcal{V}$ satisfying the second option in the either–or clause of property (4.1). With
$\mathcal{V}$ satisfying the second option in the either–or clause of property (4.1). With ![]() $\mathrm{I\!R}\times M\ni(\tau,x)\mapsto\phi(\tau,x)\in M$ denoting the flow of v and z a given point of L, the ‘second option’ guarantees the existence of an open interval
$\mathrm{I\!R}\times M\ni(\tau,x)\mapsto\phi(\tau,x)\in M$ denoting the flow of v and z a given point of L, the ‘second option’ guarantees the existence of an open interval ![]() $(a^{\prime},b^{\prime})$ containing 0 such that, for all
$(a^{\prime},b^{\prime})$ containing 0 such that, for all ![]() $\tau\in(a^{\prime},b^{\prime})$, the leaf
$\tau\in(a^{\prime},b^{\prime})$, the leaf ![]() $L_{\phi(\tau,z)} $ of
$L_{\phi(\tau,z)} $ of ![]() $\mathcal{V}$ passing through
$\mathcal{V}$ passing through ![]() $\phi(\tau,z)$ is compact. Let (a, b) be the maximal open interval with this property (i.e., the union of all such intervals).
$\phi(\tau,z)$ is compact. Let (a, b) be the maximal open interval with this property (i.e., the union of all such intervals).
All ![]() $L_{\phi(\tau,z)} $ with
$L_{\phi(\tau,z)} $ with ![]() $\tau\in(a,b)$ satisfy the second option in condition (4.1), as their compactness obviously precludes the first one. The resulting product structure of a neighbourhood of each
$\tau\in(a,b)$ satisfy the second option in condition (4.1), as their compactness obviously precludes the first one. The resulting product structure of a neighbourhood of each ![]() $L_{\phi(\tau,z)} $ has three immediate consequences. First, the set
$L_{\phi(\tau,z)} $ has three immediate consequences. First, the set ![]() $E=\{(\tau,y)\in(a,b)\times M:y\in L_{\phi(\tau,z)} \}$ is open in
$E=\{(\tau,y)\in(a,b)\times M:y\in L_{\phi(\tau,z)} \}$ is open in ![]() $(a,b)\times M$. Second, the mapping
$(a,b)\times M$. Second, the mapping ![]() $E\ni(\tau,y)\mapsto\tau\in(a,b)$ constitutes a bundle projection. Finally,
$E\ni(\tau,y)\mapsto\tau\in(a,b)$ constitutes a bundle projection. Finally,
The pullback of v under this last mapping is a vector field on the total space E of the bundle in (b), transverse to the fibres, so that it spans a nonlinear connection (horizontal distribution) in E.
For any fixed ![]() $x\in L$, let
$x\in L$, let ![]() $(a,b)\ni\tau\mapsto(\tau,\lambda(\tau,x))
\in E$ be the horizontal lift, relative to this connection, of the curve
$(a,b)\ni\tau\mapsto(\tau,\lambda(\tau,x))
\in E$ be the horizontal lift, relative to this connection, of the curve ![]() $\tau\mapsto\tau$ in the base manifold (a, b), with the initial value
$\tau\mapsto\tau$ in the base manifold (a, b), with the initial value ![]() $(0,x)$ at τ = 0. Such a horizontal lift clearly exists on some neighbourhood (c, d) of 0 in (a, b), as it constitutes a solution to an ordinary differential equation. Compactness of the fibres
$(0,x)$ at τ = 0. Such a horizontal lift clearly exists on some neighbourhood (c, d) of 0 in (a, b), as it constitutes a solution to an ordinary differential equation. Compactness of the fibres ![]() $E_{\tau} =\{\tau\}\times L_{\phi(\tau,z)} $ guarantees in turn that the maximal such (c, d) equals (a, b). Namely, if we had c > a, or d < b, a neighbourhood of Ec or Ed in E forming a union of horizontal curves would have the property that a horizontal lift entering it can be extended so as to reach Ec or Ed and beyond, contrary to maximality of (c, d).
$E_{\tau} =\{\tau\}\times L_{\phi(\tau,z)} $ guarantees in turn that the maximal such (c, d) equals (a, b). Namely, if we had c > a, or d < b, a neighbourhood of Ec or Ed in E forming a union of horizontal curves would have the property that a horizontal lift entering it can be extended so as to reach Ec or Ed and beyond, contrary to maximality of (c, d).
Note that ![]() $(a,b)\ni\tau\mapsto\lambda(\tau,x)$, for any given
$(a,b)\ni\tau\mapsto\lambda(\tau,x)$, for any given ![]() $x\in L$, is a reparametrization of the integral curve
$x\in L$, is a reparametrization of the integral curve ![]() $\tau\mapsto\phi(\tau,x)$ of v. Thus, for any
$\tau\mapsto\phi(\tau,x)$ of v. Thus, for any ![]() $(\tau,x)\in(a,b)\times L$,
$(\tau,x)\in(a,b)\times L$,
passing through x for τ = 0 and, for some ![]() $C^\infty$ function
$C^\infty$ function ![]() $\sigma:(a,b)\times L\to\mathrm{I\!R}$,
$\sigma:(a,b)\times L\to\mathrm{I\!R}$,
whenever ![]() $(\tau,x)\in(a,b)\times L$. Also,
$(\tau,x)\in(a,b)\times L$. Also,
![]() ${\rm d}[\sigma(\tau,x)]/{\rm d}\tau$ being positive as it is non-zero everywhere and
${\rm d}[\sigma(\tau,x)]/{\rm d}\tau$ being positive as it is non-zero everywhere and ![]() $\sigma(\tau,z)=\tau$.
$\sigma(\tau,z)=\tau$.
We now proceed to establish the following conclusion:
We will achieve this by deriving a contradiction from the assumption that
First, ![]() $\lambda(\tau,x)\in L_{\phi(\tau,z)} $ by Equations (4.4)–(4.5), so that Equations (4.7) and (4.3) give
$\lambda(\tau,x)\in L_{\phi(\tau,z)} $ by Equations (4.4)–(4.5), so that Equations (4.7) and (4.3) give
Positivity of ![]() ${\rm d}[\sigma(\tau,x)]/{\rm d}\tau$ – see Equation (4.5) – implies, whenever
${\rm d}[\sigma(\tau,x)]/{\rm d}\tau$ – see Equation (4.5) – implies, whenever ![]() $x\in L$, that
$x\in L$, that ![]() $\sigma(\tau,x)$ has a limit
$\sigma(\tau,x)$ has a limit ![]() $\sigma(b,x)\le\infty$ as
$\sigma(b,x)\le\infty$ as ![]() $\tau\to b$. As a further consequence of Equation (4.7),
$\tau\to b$. As a further consequence of Equation (4.7), ![]() $\sigma(b,x) \lt \infty$ for every
$\sigma(b,x) \lt \infty$ for every ![]() $x\in L$ (and so, by Equation (4.5),
$x\in L$ (and so, by Equation (4.5), ![]() $b=\sigma(b,z) \lt \infty$). Otherwise, we may fix
$b=\sigma(b,z) \lt \infty$). Otherwise, we may fix ![]() $x\in L$ and a strictly increasing sequence
$x\in L$ and a strictly increasing sequence ![]() $\tau_j \gt a$ with
$\tau_j \gt a$ with ![]() $\tau_j \to b$ and
$\tau_j \to b$ and ![]() $\sigma(\tau_j ,x)\to\infty$ as
$\sigma(\tau_j ,x)\to\infty$ as ![]() $j\to\infty$. The sequence
$j\to\infty$. The sequence ![]() $\lambda(\tau_j ,x)=\phi(\sigma(\tau_j ,x),x)$ lies in the single integral curve Cx and, passing to a subsequence, we may assume that it converges to some point
$\lambda(\tau_j ,x)=\phi(\sigma(\tau_j ,x),x)$ lies in the single integral curve Cx and, passing to a subsequence, we may assume that it converges to some point ![]() $y\in M$, which has a neighbourhood in M forming a union of ‘short’ unparametrized segments of integral curves of v intersecting a neighbourhood of y in the leaf Ly. Since
$y\in M$, which has a neighbourhood in M forming a union of ‘short’ unparametrized segments of integral curves of v intersecting a neighbourhood of y in the leaf Ly. Since ![]() $\lambda(\tau_j ,x)\to y$ while its parameter
$\lambda(\tau_j ,x)\to y$ while its parameter ![]() $\sigma(\tau_j ,x)$ increases towards an infinite limit and, due to Equations (4.7)–(4.8),
$\sigma(\tau_j ,x)$ increases towards an infinite limit and, due to Equations (4.7)–(4.8), ![]() $(a,b)\ni\tau\mapsto\lambda(\tau,x)$ is injective, Cx must contain infinitely many of the ‘short’ integral-curve segments and, as a result, intersect some leaves
$(a,b)\ni\tau\mapsto\lambda(\tau,x)$ is injective, Cx must contain infinitely many of the ‘short’ integral-curve segments and, as a result, intersect some leaves ![]() $L_{\phi(\tau,z)} $, with
$L_{\phi(\tau,z)} $, with ![]() $\tau=\tau_j $, at infinitely many points, contrary to Equation (4.8). Thus,
$\tau=\tau_j $, at infinitely many points, contrary to Equation (4.8). Thus, ![]() $\sigma(b,x) \lt \infty$ whenever
$\sigma(b,x) \lt \infty$ whenever ![]() $x\in L$.
$x\in L$.
Next, let us set ![]() $\lambda(b,x)=\phi(\sigma(b,x),x)$ and denote by
$\lambda(b,x)=\phi(\sigma(b,x),x)$ and denote by ![]() $L_{b,x} =L_{\lambda(b,x)} $ the leaf of
$L_{b,x} =L_{\lambda(b,x)} $ the leaf of ![]() $\mathcal{V}$ through
$\mathcal{V}$ through ![]() $\lambda(b,x)$. Now
$\lambda(b,x)$. Now
and ![]() $L\ni x\mapsto\sigma(b,x)$ is
$L\ni x\mapsto\sigma(b,x)$ is ![]() $C^\infty$-differentiable. In fact, given
$C^\infty$-differentiable. In fact, given ![]() $x\in L$, the integral curve (4.3) joins x to
$x\in L$, the integral curve (4.3) joins x to ![]() $\lambda(b,x)\in L_{b,x} $. Remark 3.1 applied to our L and
$\lambda(b,x)\in L_{b,x} $. Remark 3.1 applied to our L and ![]() $L^{\prime}=L_{b,x} $ yields a smooth variation of integral curves Cy of v, for all points y from a neighbourhood U of x in L, with each Cy joining y to a point in
$L^{\prime}=L_{b,x} $ yields a smooth variation of integral curves Cy of v, for all points y from a neighbourhood U of x in L, with each Cy joining y to a point in ![]() $L_{b,x} $. Each of these Cy is parametrized by
$L_{b,x} $. Each of these Cy is parametrized by ![]() $\tau\mapsto\phi(\tau,x)$ with τ ranging over an interval
$\tau\mapsto\phi(\tau,x)$ with τ ranging over an interval ![]() $[0,\tau_* ]$, where
$[0,\tau_* ]$, where ![]() $\tau_* $ depends on y. As before,
$\tau_* $ depends on y. As before, ![]() $\lambda(b,x)$ has a neighbourhood in M constituting a union of ‘short’ unparametrized integral-curve segments intersecting a neighbourhood of
$\lambda(b,x)$ has a neighbourhood in M constituting a union of ‘short’ unparametrized integral-curve segments intersecting a neighbourhood of ![]() $\lambda(b,x)$ in
$\lambda(b,x)$ in ![]() $L_{b,x} $. One of these segments, the one passing through
$L_{b,x} $. One of these segments, the one passing through ![]() $\lambda(b,x)$, contains the portion
$\lambda(b,x)$, contains the portion ![]() $\{\lambda(\tau,x):b-\varepsilon\le\tau\le b\}$ of Cx, with some ɛ > 0. The third equality of Equation (4.5) along with Equation (4.8) for
$\{\lambda(\tau,x):b-\varepsilon\le\tau\le b\}$ of Cx, with some ɛ > 0. The third equality of Equation (4.5) along with Equation (4.8) for ![]() $y\in L$ near x (rather than x itself) show that each nearby Cy similarly contains
$y\in L$ near x (rather than x itself) show that each nearby Cy similarly contains ![]() $\{\lambda(\tau,y):b-\varepsilon\le\tau \lt b\}$ and hence also the limit
$\{\lambda(\tau,y):b-\varepsilon\le\tau \lt b\}$ and hence also the limit ![]() $\lambda(b,x)$. However, by Equation (4.8), all
$\lambda(b,x)$. However, by Equation (4.8), all ![]() $\lambda(\tau,y)$ lie in
$\lambda(\tau,y)$ lie in ![]() $L_{\phi(\tau,z)} $, just as
$L_{\phi(\tau,z)} $, just as ![]() $\lambda(\tau,x)$ does, and so
$\lambda(\tau,x)$ does, and so ![]() $\lambda(b,y)\in L_{b,x} $, which gives
$\lambda(b,y)\in L_{b,x} $, which gives ![]() $L_{b,y} =L_{b,x} $ and thus proves Equation (4.9). At the same time, Remark 3.1 yields smoothness of the mapping
$L_{b,y} =L_{b,x} $ and thus proves Equation (4.9). At the same time, Remark 3.1 yields smoothness of the mapping ![]() $L\ni y\mapsto\sigma(b,y)$.
$L\ni y\mapsto\sigma(b,y)$.
Since the leaf L is connected, local constancy in assertion (4.9) amounts to constancy, so that ![]() $L_{\lambda(b,x)} =L_{\phi(b,z)} $ for all
$L_{\lambda(b,x)} =L_{\phi(b,z)} $ for all ![]() $x\in L$. Thus, for every
$x\in L$. Thus, for every ![]() $x\in L$, the integral curve
$x\in L$, the integral curve ![]() $[0,\sigma(b,x)]\ni\tau\mapsto\phi(\tau,x)\in M$ joins x to the point
$[0,\sigma(b,x)]\ni\tau\mapsto\phi(\tau,x)\in M$ joins x to the point ![]() $\lambda(b,x)$ in
$\lambda(b,x)$ in ![]() $L_{\phi(b,z)} $. Remark 3.1 also implies that the mapping
$L_{\phi(b,z)} $. Remark 3.1 also implies that the mapping ![]() $L\ni x\mapsto\lambda(b,x)\in L_{\phi(b,z)} $ is locally diffeomorphic. Compactness of L and Remark 3.4 now yield compactness of
$L\ni x\mapsto\lambda(b,x)\in L_{\phi(b,z)} $ is locally diffeomorphic. Compactness of L and Remark 3.4 now yield compactness of ![]() $L_{\phi(b,z)} $ along with the second possibility in Equation (4.1), for
$L_{\phi(b,z)} $ along with the second possibility in Equation (4.1), for ![]() $L_{\phi(b,z)} $, since the first one is precluded by compactness of the nearby leaves
$L_{\phi(b,z)} $, since the first one is precluded by compactness of the nearby leaves ![]() $L_{\phi(\tau,z)} $ with
$L_{\phi(\tau,z)} $ with ![]() $a \lt \tau \lt b$. This in turn also implies compactness of
$a \lt \tau \lt b$. This in turn also implies compactness of ![]() $L_{\phi(\tau,z)} $ for
$L_{\phi(\tau,z)} $ for ![]() $\tau\ge b$, close to b, contradicting maximality of (a, b) and, consequently, proving Equation (4.6).
$\tau\ge b$, close to b, contradicting maximality of (a, b) and, consequently, proving Equation (4.6).
Let us now fix ![]() $c,d$ with the property (4.6). The image, under the mapping in Equation (4.2), of the set
$c,d$ with the property (4.6). The image, under the mapping in Equation (4.2), of the set ![]() $E_{[c,d]}
=\{(\tau,y)\in[c,d]\times M:y\in L_{\phi(\tau,z)} \}$ is then clearly compact, but also open in M. In fact, it suffices to verify that
$E_{[c,d]}
=\{(\tau,y)\in[c,d]\times M:y\in L_{\phi(\tau,z)} \}$ is then clearly compact, but also open in M. In fact, it suffices to verify that ![]() $L_{\phi(c,z)} $ is contained in the interior of this image – which trivially follows since the image contains both kinds of sufficiently small one-sided neighbourhoods of
$L_{\phi(c,z)} $ is contained in the interior of this image – which trivially follows since the image contains both kinds of sufficiently small one-sided neighbourhoods of ![]() $L_{\phi(c,z)}=L_{\phi(d,z)} $ in M. The image thus coincides with M, which proves that all leaves of
$L_{\phi(c,z)}=L_{\phi(d,z)} $ in M. The image thus coincides with M, which proves that all leaves of ![]() $\mathcal{V}$ are compact.
$\mathcal{V}$ are compact.
Therefore, there exists a bundle projection ![]() $M\to S^1$ with the leaves of
$M\to S^1$ with the leaves of ![]() $\mathcal{V}$ serving as the fibres [Reference Moerdijk and Mrčun15, Exercise 2.29(3)(i) on p. 49].
$\mathcal{V}$ serving as the fibres [Reference Moerdijk and Mrčun15, Exercise 2.29(3)(i) on p. 49].
5. Rank-one ECS metrics
Let the data ![]() $f,I,n,V,\langle\cdot,\cdot\rangle,A$ consist of
$f,I,n,V,\langle\cdot,\cdot\rangle,A$ consist of
 \begin{equation}
\begin{array}{l}
\mathrm{a}\ {\textrm {non-constant}\ }C^\infty\mathrm{\ function\
}f:I\to\mathrm{I\!R}\mathrm{\ on\ an\ open\ interval}\\
I\subseteq\mathrm{I\!R}\mathrm{,\ an\ integer\ }n\ge4\mathrm{,\ a\ real\
vector\ space\ }V\mathrm{\ of\ dimension}\\
n-2\mathrm{,\ a\ } \textrm{pseudo-Euclidean}\
\mathrm{inner\ product\ }\langle\cdot,\cdot\rangle\mathrm{\ on\ }V\mathrm{,\
and\ a}\ \textrm{non-zero}, \\
\mathrm{ traceless,\
}\langle\cdot,\cdot\rangle \textrm{-self-adjoint linear
endomorphism }A\mathrm{ of }V.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\mathrm{a}\ {\textrm {non-constant}\ }C^\infty\mathrm{\ function\
}f:I\to\mathrm{I\!R}\mathrm{\ on\ an\ open\ interval}\\
I\subseteq\mathrm{I\!R}\mathrm{,\ an\ integer\ }n\ge4\mathrm{,\ a\ real\
vector\ space\ }V\mathrm{\ of\ dimension}\\
n-2\mathrm{,\ a\ } \textrm{pseudo-Euclidean}\
\mathrm{inner\ product\ }\langle\cdot,\cdot\rangle\mathrm{\ on\ }V\mathrm{,\
and\ a}\ \textrm{non-zero}, \\
\mathrm{ traceless,\
}\langle\cdot,\cdot\rangle \textrm{-self-adjoint linear
endomorphism }A\mathrm{ of }V.
\end{array}
\end{equation}Following [Reference Roter17], one then defines a rank-one ECS metric [Reference Derdzinski and Roter6, Theorem 4.1]
on the n-dimensional manifold ![]() $I\times\mathrm{I\!R}\times V$. The products of differentials denote here symmetric products,
$I\times\mathrm{I\!R}\times V$. The products of differentials denote here symmetric products, ![]() $t,s$ are the Cartesian coordinates on
$t,s$ are the Cartesian coordinates on ![]() $I\times\mathrm{I\!R}$ treated, with the aid of the projection
$I\times\mathrm{I\!R}$ treated, with the aid of the projection ![]() $I\times\mathrm{I\!R}\times V\to I\times\mathrm{I\!R}$, as functions on
$I\times\mathrm{I\!R}\times V\to I\times\mathrm{I\!R}$, as functions on ![]() $I\times\mathrm{I\!R}\times V$, and δ is the pullback to
$I\times\mathrm{I\!R}\times V$, and δ is the pullback to ![]() $I\times\mathrm{I\!R}\times V$ of the flat pseudo-Riemannian metric on V corresponding to the inner product
$I\times\mathrm{I\!R}\times V$ of the flat pseudo-Riemannian metric on V corresponding to the inner product ![]() $\langle\cdot,\cdot\rangle$. Finally,
$\langle\cdot,\cdot\rangle$. Finally, ![]() $\kappa:I\times\mathrm{I\!R}\times V\to\mathrm{I\!R}$ is the function given by
$\kappa:I\times\mathrm{I\!R}\times V\to\mathrm{I\!R}$ is the function given by
If we let ![]() $i,j$ range over
$i,j$ range over ![]() $2,\dots,n-1$, fix linear coordinates x i on V and use them, along with
$2,\dots,n-1$, fix linear coordinates x i on V and use them, along with ![]() $x^1=t$ on I and
$x^1=t$ on I and ![]() $x^n=s/2$ on
$x^n=s/2$ on ![]() $\mathrm{I\!R}$, to form a global coordinate system on
$\mathrm{I\!R}$, to form a global coordinate system on ![]() $I\times\mathrm{I\!R}\times V$, then the possibly non-zero components of the metric
$I\times\mathrm{I\!R}\times V$, then the possibly non-zero components of the metric ![]() $\mathtt{g}$ and the Levi-Civita connection
$\mathtt{g}$ and the Levi-Civita connection ![]() $\nabla$ are [Reference Roter17, p. 93] those algebraically related to
$\nabla$ are [Reference Roter17, p. 93] those algebraically related to
 \begin{equation}
\begin{array}{l}
g_{11} =\kappa,\quad g_{1n} =g_{n1} =1 \quad
\mathrm{and\ (constants)\ }g_{ij} ,\\
\Gamma_{11}^{ n}=\partial_1 \kappa/2,\quad
\Gamma_{11}^{ i}=-g^{ij}\partial_j \kappa/2,\quad
\Gamma_{1i}^{ n}=\partial_i \kappa/2.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
g_{11} =\kappa,\quad g_{1n} =g_{n1} =1 \quad
\mathrm{and\ (constants)\ }g_{ij} ,\\
\Gamma_{11}^{ n}=\partial_1 \kappa/2,\quad
\Gamma_{11}^{ i}=-g^{ij}\partial_j \kappa/2,\quad
\Gamma_{1i}^{ n}=\partial_i \kappa/2.
\end{array}
\end{equation}Remark 5.1. Conversely [Reference Derdzinski and Roter6, Theorem 4.1], in any n-dimensional rank-one ECS manifold, some neighbourhood of any given point is isometric to an open subset of a manifold of type (5.2), where one has Equation (5.1) with one possible exception: f may be constant. More precisely, ![]() ${\rm d}f/{\rm d}t=0$ precisely at those points at which the covariant derivative
${\rm d}f/{\rm d}t=0$ precisely at those points at which the covariant derivative ![]() $\nabla R$ of the curvature tensor vanishes. Thus, if f is constant on a subinterval Iʹ of I, the metric (5.2) will have
$\nabla R$ of the curvature tensor vanishes. Thus, if f is constant on a subinterval Iʹ of I, the metric (5.2) will have ![]() $\nabla R=0$ on
$\nabla R=0$ on ![]() $I^{\prime}\times\mathrm{I\!R}\times V$.
$I^{\prime}\times\mathrm{I\!R}\times V$.
In other words, a rank-one ECS manifold may have locally symmetric open submanifolds, and then the function f appearing in the local-coordinate form of [Reference Derdzinski and Roter6, Theorem 4.1] is constant.
6. Assumptions and notation
Our ![]() $(M,\mathtt{g})$ is always a rank-one ECS manifold, often compact, and
$(M,\mathtt{g})$ is always a rank-one ECS manifold, often compact, and  $(\widehat{M},\mathtt{g})$ denotes its pseudo-Riemannian universal covering space, which leads to
$(\widehat{M},\mathtt{g})$ denotes its pseudo-Riemannian universal covering space, which leads to
 \begin{equation}
\mathrm{the\ universal\ covering\ projection\
}\pi:\widehat{M}\to M=\widehat{M}/\Gamma,
\end{equation}
\begin{equation}
\mathrm{the\ universal\ covering\ projection\
}\pi:\widehat{M}\to M=\widehat{M}/\Gamma,
\end{equation} ![]() $\Gamma\approx\pi_1 M$ being a group of isometries of
$\Gamma\approx\pi_1 M$ being a group of isometries of  $(\widehat{M},\mathtt{g})$ acting on
$(\widehat{M},\mathtt{g})$ acting on ![]() $\widehat{M}$ freely and properly discontinuously. Most of the time, the same symbols will stand for objects in
$\widehat{M}$ freely and properly discontinuously. Most of the time, the same symbols will stand for objects in ![]() $\widehat{M}$ and their projections in M, such as the metric
$\widehat{M}$ and their projections in M, such as the metric ![]() $\mathtt{g}$, and the (rank-one) Olszak distribution
$\mathtt{g}$, and the (rank-one) Olszak distribution ![]() $\mathcal{D}$ described in the Introduction. In any rank-one ECS manifold, the distribution
$\mathcal{D}$ described in the Introduction. In any rank-one ECS manifold, the distribution ![]() $\mathcal{D}$, being parallel, carries a linear connection induced by the Levi-Civita connection of
$\mathcal{D}$, being parallel, carries a linear connection induced by the Levi-Civita connection of ![]() $\mathtt{g}$, and this induced connection is flat since, locally,
$\mathtt{g}$, and this induced connection is flat since, locally, ![]() $\mathcal{D}$ is spanned by the parallel gradient
$\mathcal{D}$ is spanned by the parallel gradient ![]() $\nabla t$ of the coordinate function t appearing in Equation (5.2) – see [Reference Derdzinski and Terek8, the lines following formula (3.6)]. (As stated in Remark 5.1, Equation (5.2) is a general local description of all rank-one ECS metrics.) Simple connectivity of
$\nabla t$ of the coordinate function t appearing in Equation (5.2) – see [Reference Derdzinski and Terek8, the lines following formula (3.6)]. (As stated in Remark 5.1, Equation (5.2) is a general local description of all rank-one ECS metrics.) Simple connectivity of ![]() $\widehat{M}$ allows us to choose a global parallel vector field w on
$\widehat{M}$ allows us to choose a global parallel vector field w on ![]() $\widehat{M}$ spanning
$\widehat{M}$ spanning ![]() $\mathcal{D}$, and then the 1-form
$\mathcal{D}$, and then the 1-form ![]() $\mathtt{g}(w,\cdot)$, being parallel, is closed, and hence exact, so that we may also fix a
$\mathtt{g}(w,\cdot)$, being parallel, is closed, and hence exact, so that we may also fix a ![]() $C^\infty$ function
$C^\infty$ function ![]() $t:\widehat{M}\to\mathrm{I\!R}$ with
$t:\widehat{M}\to\mathrm{I\!R}$ with ![]() ${\rm d}t=\mathtt{g}(w,\cdot)$. This determines t uniquely up to affine substitutions, that is, replacements of t by qt + p with
${\rm d}t=\mathtt{g}(w,\cdot)$. This determines t uniquely up to affine substitutions, that is, replacements of t by qt + p with ![]() $q,p\in\mathrm{I\!R}$ and q > 0. Positivity of q reflects the fact that we always assume transversal orientability of the orthogonal complement
$q,p\in\mathrm{I\!R}$ and q > 0. Positivity of q reflects the fact that we always assume transversal orientability of the orthogonal complement ![]() $\mathcal{D}^\perp$, which can be achieved by replacing
$\mathcal{D}^\perp$, which can be achieved by replacing ![]() $(M,\mathtt{g})$ with a twofold isometric covering and amounts to requiring that Γ be a subgroup of the group
$(M,\mathtt{g})$ with a twofold isometric covering and amounts to requiring that Γ be a subgroup of the group  $\mathrm{Iso}^+(\widehat{M},\mathtt{g})$ of all self-isometries of
$\mathrm{Iso}^+(\widehat{M},\mathtt{g})$ of all self-isometries of  $(\widehat{M},\mathtt{g})$ preserving a fixed transversal orientation of
$(\widehat{M},\mathtt{g})$ preserving a fixed transversal orientation of ![]() $\mathcal{D}^\perp$. Thus, for every
$\mathcal{D}^\perp$. Thus, for every  $\gamma\in\mathrm{Iso}^+(\widehat{M},\mathtt{g})$,
$\gamma\in\mathrm{Iso}^+(\widehat{M},\mathtt{g})$,
The assignment ![]() $\gamma\mapsto q$ is a group homomorphism
$\gamma\mapsto q$ is a group homomorphism  $\mathrm{Iso}^+(\widehat{M},\mathtt{g})\to(0,\infty)$, and we refer to q as the q-image of γ. Summarizing,
$\mathrm{Iso}^+(\widehat{M},\mathtt{g})\to(0,\infty)$, and we refer to q as the q-image of γ. Summarizing,
 \begin{equation}
w=\nabla t\mathrm{\ is\ a\ parallel\ vector\ field\ on\
}\widehat{M}\mathrm{,\ spanning\ }\mathcal{D}\mathrm{,\ and\
}{\rm d}t=\mathtt{g}(w,\cdot\,).
\end{equation}
\begin{equation}
w=\nabla t\mathrm{\ is\ a\ parallel\ vector\ field\ on\
}\widehat{M}\mathrm{,\ spanning\ }\mathcal{D}\mathrm{,\ and\
}{\rm d}t=\mathtt{g}(w,\cdot\,).
\end{equation}As a consequence of Equation (6.3),
Since Equation (5.2) remains unchanged when t and s are replaced by qt + p and ![]() $q^{-1} s$,
$q^{-1} s$,
cf. Remark 5.1. According to [Reference Roter17, p. 93], where the curvature tensor has the sign opposite to ours, the metric (5.2) has the Ricci tensor ![]() $\mathrm{Ric}=(2-n)f(t)\,{\rm d}t\otimes {\rm d}t$, for
$\mathrm{Ric}=(2-n)f(t)\,{\rm d}t\otimes {\rm d}t$, for ![]() $n=\dim M$. Therefore, by Remark 5.1, with our t chosen as above,
$n=\dim M$. Therefore, by Remark 5.1, with our t chosen as above,
 \begin{equation}
\mathrm{on\ }(\widehat{M},\mathtt{g})\mathrm{\ one\ has\ }\mathrm{Ric}
=(2-n)f \,{\rm d}t\otimes {\rm d}t
\end{equation}
\begin{equation}
\mathrm{on\ }(\widehat{M},\mathtt{g})\mathrm{\ one\ has\ }\mathrm{Ric}
=(2-n)f \,{\rm d}t\otimes {\rm d}t
\end{equation}for a unique (non-constant) function  $f:\widehat{M}\to\mathrm{I\!R}$ and, again by Remark 5.1,
$f:\widehat{M}\to\mathrm{I\!R}$ and, again by Remark 5.1,
Changing the notational convention so as to absorb the factor ![]() $2-n$ into the function f does not seem to be a good option, since the inverse of that factor then would have to appear in Equation (5.3). Also, the word ‘locally’ in Equation (6.7) cannot in general be skipped: it means that f is constant on the connected components of the level sets of t, and the level sets themselves may be disconnected.
$2-n$ into the function f does not seem to be a good option, since the inverse of that factor then would have to appear in Equation (5.3). Also, the word ‘locally’ in Equation (6.7) cannot in general be skipped: it means that f is constant on the connected components of the level sets of t, and the level sets themselves may be disconnected.
If  $\chi:\widehat{M}\to\mathrm{I\!R}$ is of class C 1 and, locally, a function of t (which amounts to
$\chi:\widehat{M}\to\mathrm{I\!R}$ is of class C 1 and, locally, a function of t (which amounts to ![]() ${\rm d}\chi$ being a functional multiple of
${\rm d}\chi$ being a functional multiple of ![]() ${\rm d}t$), we define the derivative
${\rm d}t$), we define the derivative  $\dot\chi:\widehat{M}\to\mathrm{I\!R}$ by
$\dot\chi:\widehat{M}\to\mathrm{I\!R}$ by ![]() ${\rm d}\chi=\dot\chi\, {\rm d}t$, so that, in terms of a local expression of
${\rm d}\chi=\dot\chi\, {\rm d}t$, so that, in terms of a local expression of ![]() $\mathtt{g}$ in Equations (5.2)–(5.4),
$\mathtt{g}$ in Equations (5.2)–(5.4), ![]() $\dot\chi={\rm d}\chi/{\rm d}t$. For f in Equations (6.6)–(6.7), any
$\dot\chi={\rm d}\chi/{\rm d}t$. For f in Equations (6.6)–(6.7), any ![]() $\gamma\in\Gamma$, any C 1 function
$\gamma\in\Gamma$, any C 1 function  $\chi:\widehat{M}\to\mathrm{I\!R}$, which is locally a function of t, and
$\chi:\widehat{M}\to\mathrm{I\!R}$, which is locally a function of t, and ![]() $q,p,a\in\mathrm{I\!R}$ with q > 0,
$q,p,a\in\mathrm{I\!R}$ with q > 0,
 \begin{equation}
\begin{array}{l}
\mathrm{if\ \ }\,t\circ\gamma=qt+p\mathrm{,\ \ then\ \ }\gamma^*\,{\rm d}t
=q\,{\rm d}t\mathrm{\ \ and\ \ }\,f\circ\gamma=q^{-2}f,\\
\mathrm{if\ \ }\chi\circ\gamma=q^a\chi\mathrm{,\ \ then\
}\,\dot\chi\circ\gamma=q^{a-1}\chi,
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\mathrm{if\ \ }\,t\circ\gamma=qt+p\mathrm{,\ \ then\ \ }\gamma^*\,{\rm d}t
=q\,{\rm d}t\mathrm{\ \ and\ \ }\,f\circ\gamma=q^{-2}f,\\
\mathrm{if\ \ }\chi\circ\gamma=q^a\chi\mathrm{,\ \ then\
}\,\dot\chi\circ\gamma=q^{a-1}\chi,
\end{array}
\end{equation}which is clear from Equation (6.6) and the fact that the pullback of differential forms commutes with exterior differentiation. By Equations (6.3) and (6.8), for any  $\gamma\in\mathrm{Iso}^+(\widehat{M},\mathtt{g})$,
$\gamma\in\mathrm{Iso}^+(\widehat{M},\mathtt{g})$,
Let us point out that the choices of t and w made above are convenient but not canonical, and so, rather than being preserved by isometries, t and w are transformed by them via Equations (6.8) and (6.9).
7. Local homogeneity
We adopt here the assumptions and notation of §6. First, note that
or else the curvature and Weyl tensors would coincide, implying local symmetry.
Just as was the case with ![]() $\mathcal{D}$, the distribution
$\mathcal{D}$, the distribution ![]() $\mathcal{D}^\perp$ is parallel, and so it inherits a linear connection from the Levi-Civita connection
$\mathcal{D}^\perp$ is parallel, and so it inherits a linear connection from the Levi-Civita connection ![]() $\nabla$ of
$\nabla$ of ![]() $\mathtt{g}$. As
$\mathtt{g}$. As ![]() $\mathcal{D}\subseteq\mathcal{D}^\perp$, a natural connection arises in the quotient bundle
$\mathcal{D}\subseteq\mathcal{D}^\perp$, a natural connection arises in the quotient bundle ![]() $\mathcal{E}=\mathcal{D}^\perp/\mathcal{D}$ over
$\mathcal{E}=\mathcal{D}^\perp/\mathcal{D}$ over ![]() $\widehat{M}$, or M, and
$\widehat{M}$, or M, and
This was established in [Reference Derdzinski and Roter6, Lemma 2.2-f], but we need to justify it here, again, to draw additional conclusions. Namely, by Equations (5.4) and (6.3), the coordinate vector field ![]() $\partial_n =w=\nabla t$, spanning
$\partial_n =w=\nabla t$, spanning ![]() $\mathcal{D}$, is parallel, while
$\mathcal{D}$, is parallel, while ![]() $\partial_n $ and
$\partial_n $ and ![]() $\partial_i $, for
$\partial_i $, for ![]() $i,j=2,\ldots,n-1$, span
$i,j=2,\ldots,n-1$, span ![]() $\mathcal{D}^\perp$. Now Equation (7.2) follows since, in Equation (5.4),
$\mathcal{D}^\perp$. Now Equation (7.2) follows since, in Equation (5.4), ![]() $\Gamma_{1n}^{\bullet}=\Gamma_{1i}^{\bullet}
=\Gamma_{in}^{\bullet}=\Gamma_{ij}^{\bullet}
=\Gamma_{nn}^{\bullet}=\Gamma_{ni}^{\bullet}=0$, with
$\Gamma_{1n}^{\bullet}=\Gamma_{1i}^{\bullet}
=\Gamma_{in}^{\bullet}=\Gamma_{ij}^{\bullet}
=\Gamma_{nn}^{\bullet}=\Gamma_{ni}^{\bullet}=0$, with ![]() $\bullet$ denoting any index other than n, so that
$\bullet$ denoting any index other than n, so that ![]() $\partial_i $,
$\partial_i $, ![]() $i=2,\ldots,n-1$, project onto parallel local trivializing sections of
$i=2,\ldots,n-1$, project onto parallel local trivializing sections of ![]() $\mathcal{E}$. As
$\mathcal{E}$. As ![]() $\partial_i $ are also constant vector fields on the space V in Equations (5.1)–(5.2), we may identify V with the space of parallel sections of
$\partial_i $ are also constant vector fields on the space V in Equations (5.1)–(5.2), we may identify V with the space of parallel sections of ![]() $\mathcal{E}$, defined on the coordinate domain. The parallel vector-bundle morphism
$\mathcal{E}$, defined on the coordinate domain. The parallel vector-bundle morphism ![]() $[\mathcal{D}^*]^{\otimes2}
\to\mathcal{E}^{\otimes2}$, over any rank-one ECS manifold, defined in [Reference Derdzinski and Roter5, formula (6)] (where it was denoted by Φ, and built from the Weyl tensor W, cf. the Appendix), is easily seen to be valued in
$[\mathcal{D}^*]^{\otimes2}
\to\mathcal{E}^{\otimes2}$, over any rank-one ECS manifold, defined in [Reference Derdzinski and Roter5, formula (6)] (where it was denoted by Φ, and built from the Weyl tensor W, cf. the Appendix), is easily seen to be valued in ![]() $\mathcal{E}^{\odot2}$. Let the parallel section ξ of the line bundle
$\mathcal{E}^{\odot2}$. Let the parallel section ξ of the line bundle ![]() $\mathcal{D}^*$ over
$\mathcal{D}^*$ over ![]() $\widehat{M}$ be
$\widehat{M}$ be
for the trivializing parallel section w of ![]() $\mathcal{D}$ appearing in Equation (6.3). Thus, over
$\mathcal{D}$ appearing in Equation (6.3). Thus, over ![]() $\widehat{M}$, the morphism
$\widehat{M}$, the morphism ![]() $[\mathcal{D}^*]^{\otimes2}\to\mathcal{E}^{\otimes2}$ sends
$[\mathcal{D}^*]^{\otimes2}\to\mathcal{E}^{\otimes2}$ sends ![]() $\xi\otimes\xi$ to a parallel section of
$\xi\otimes\xi$ to a parallel section of ![]() $\mathcal{E}^{\odot2}$, which may also be treated as a parallel vector-bundle endomorphism of
$\mathcal{E}^{\odot2}$, which may also be treated as a parallel vector-bundle endomorphism of ![]() $\mathcal{E}$, due to the presence in
$\mathcal{E}$, due to the presence in ![]() $\mathcal{E}$ of the parallel fibre metric induced by
$\mathcal{E}$ of the parallel fibre metric induced by ![]() $\mathtt{g}$. This last endomorphism acts on local parallel sections of
$\mathtt{g}$. This last endomorphism acts on local parallel sections of ![]() $\mathcal{E}$ and, when the space of these sections is identified with V (see above), it becomes the endomorphism
$\mathcal{E}$ and, when the space of these sections is identified with V (see above), it becomes the endomorphism ![]() $A:V\to V$ of Equation (5.1). (One sees this comparing formula (6) in [Reference Derdzinski and Roter5] with the expression, in [Reference Roter17, p. 93], for the only possibly non-zero essential component
$A:V\to V$ of Equation (5.1). (One sees this comparing formula (6) in [Reference Derdzinski and Roter5] with the expression, in [Reference Roter17, p. 93], for the only possibly non-zero essential component ![]() $W_{1i1 j} $ of the Weyl tensor W.) We will therefore use the symbols V and
$W_{1i1 j} $ of the Weyl tensor W.) We will therefore use the symbols V and ![]() $A:V\to V$ for the space of parallel sections of
$A:V\to V$ for the space of parallel sections of ![]() $\mathcal{E}$ over
$\mathcal{E}$ over ![]() $\widehat{M}$ and for the endomorphism just described. Note that, due to simple connectivity of
$\widehat{M}$ and for the endomorphism just described. Note that, due to simple connectivity of ![]() $\widehat{M}$ and Equation (7.2), the bundle
$\widehat{M}$ and Equation (7.2), the bundle ![]() $\mathcal{E}$ is trivialized by global parallel sections.
$\mathcal{E}$ is trivialized by global parallel sections.
By Equations (6.2) and (6.9), any  $\gamma\in\mathrm{Iso}^+(\widehat{M},\mathtt{g})$ pulls w, or ξ appearing in Equation (7.3), back to qw or, respectively,
$\gamma\in\mathrm{Iso}^+(\widehat{M},\mathtt{g})$ pulls w, or ξ appearing in Equation (7.3), back to qw or, respectively, ![]() $q^{-1}\xi$, for some
$q^{-1}\xi$, for some ![]() $q\in(0,\infty)$. Since
$q\in(0,\infty)$. Since ![]() $A:V\to V$ as interpreted above was the image of
$A:V\to V$ as interpreted above was the image of ![]() $\xi\otimes\xi$ under a natural vector-bundle morphism, the isometry in question pulls A back to
$\xi\otimes\xi$ under a natural vector-bundle morphism, the isometry in question pulls A back to ![]() $q^{-2} A$, while it also acts as a linear isometry B of the space V of parallel sections. In terms of push-forwards rather than pullbacks,
$q^{-2} A$, while it also acts as a linear isometry B of the space V of parallel sections. In terms of push-forwards rather than pullbacks,
Lemma 7.1. Let A be a non-zero linear endomorphism of a pseudo-Euclidean vector space V. If, for some ![]() $q\in(0,\infty)\smallsetminus\{1\}$ there exists a linear isometry B of V satisfying Equation (7.4) then, with our fixed A, such B exists for every
$q\in(0,\infty)\smallsetminus\{1\}$ there exists a linear isometry B of V satisfying Equation (7.4) then, with our fixed A, such B exists for every ![]() $q\in(0,\infty)$.
$q\in(0,\infty)$.
Proof. For the space ![]() $\mathrm{End}\ V$ of all linear endomorphisms V → V, the formula
$\mathrm{End}\ V$ of all linear endomorphisms V → V, the formula ![]() $\mathcal{J}=\{(q,B)\in\mathrm{I\!R}\times\mathrm{End}\ V:(BB^*,B AB^*)
=(\mathrm{Id},q^2 A)\}$ defines an algebraic variety
$\mathcal{J}=\{(q,B)\in\mathrm{I\!R}\times\mathrm{End}\ V:(BB^*,B AB^*)
=(\mathrm{Id},q^2 A)\}$ defines an algebraic variety ![]() $\mathcal{J}\subseteq\mathrm{I\!R}\times\mathrm{End}\,V$. By Whitney’s classical result [Reference Whitney18, Theorem 3],
$\mathcal{J}\subseteq\mathrm{I\!R}\times\mathrm{End}\,V$. By Whitney’s classical result [Reference Whitney18, Theorem 3], ![]() $\mathcal{J}$ has finitely many connected components, and hence so does the intersection
$\mathcal{J}$ has finitely many connected components, and hence so does the intersection ![]() $K=K^{\prime}\cap(0,\infty)$ for the image Kʹ of
$K=K^{\prime}\cap(0,\infty)$ for the image Kʹ of ![]() $\mathcal{J}$ under the projection
$\mathcal{J}$ under the projection ![]() $(q,B)\mapsto q$. As
$(q,B)\mapsto q$. As ![]() $q^r\in K$ whenever
$q^r\in K$ whenever ![]() $q\in K$ and
$q\in K$ and ![]() $r\in\mathsf{Z\hskip-4ptZ}$, Remark 3.5 now gives
$r\in\mathsf{Z\hskip-4ptZ}$, Remark 3.5 now gives ![]() $K=(0,\infty)$.
$K=(0,\infty)$.
We have the following immediate consequence of the conclusion (7.1):
 \begin{equation}
\mathrm{local\ homogeneity\ of\ }(M,\mathtt{g})\mathrm{\ or\
}(\widehat{M},\mathtt{g})\mathrm{\ implies\ that\ }\mathrm{Ric}\ne0\mathrm{\
everywhere.}
\end{equation}
\begin{equation}
\mathrm{local\ homogeneity\ of\ }(M,\mathtt{g})\mathrm{\ or\
}(\widehat{M},\mathtt{g})\mathrm{\ implies\ that\ }\mathrm{Ric}\ne0\mathrm{\
everywhere.}
\end{equation} If ![]() $\mathrm{Ric}\ne0$ everywhere, it follows from Equations (6.6)–(6.8) that
$\mathrm{Ric}\ne0$ everywhere, it follows from Equations (6.6)–(6.8) that
 \begin{equation}
|f|^{1/2}\,{\rm d}t\mathrm{\ is\ a\ closed\ }\Gamma{\textrm -}\mathrm{invariant\
}C^\infty\ 1{\textrm -}\mathrm{form\ without\ zeros\ on\ }\widehat{M}.
\end{equation}
\begin{equation}
|f|^{1/2}\,{\rm d}t\mathrm{\ is\ a\ closed\ }\Gamma{\textrm -}\mathrm{invariant\
}C^\infty\ 1{\textrm -}\mathrm{form\ without\ zeros\ on\ }\widehat{M}.
\end{equation} Closedness is here due to Equation (6.7). Thus, in view of Equation (6.3), the ![]() $C^\infty$ vector field
$C^\infty$ vector field ![]() $w^{\prime}=|f|^{1/2} w$ is π-projectable onto a vector field without zeros on
$w^{\prime}=|f|^{1/2} w$ is π-projectable onto a vector field without zeros on  $M=\widehat{M}/\Gamma$, also denoted by wʹ and, from Equations (6.3), (6.4) and (6.7),
$M=\widehat{M}/\Gamma$, also denoted by wʹ and, from Equations (6.3), (6.4) and (6.7),
Lemma 7.2. Let  $(\widehat{M},\mathtt{g})$ be the pseudo-Riemannian universal covering space of a compact rank-one ECS manifold. If
$(\widehat{M},\mathtt{g})$ be the pseudo-Riemannian universal covering space of a compact rank-one ECS manifold. If ![]() $\widehat{M}$ admits a closed Γ-invariant
$\widehat{M}$ admits a closed Γ-invariant ![]() $C^\infty$ 1-form without zeros, which is a functional multiple of
$C^\infty$ 1-form without zeros, which is a functional multiple of ![]() ${\rm d}t$, for the function
${\rm d}t$, for the function ![]() $t:\widehat{M}\to\mathrm{I\!R}$ introduced in §6, then the leaves of
$t:\widehat{M}\to\mathrm{I\!R}$ introduced in §6, then the leaves of ![]() $\mathcal{D}^\perp$ in
$\mathcal{D}^\perp$ in ![]() $\widehat{M}$ are the factor manifolds of a global product decomposition of
$\widehat{M}$ are the factor manifolds of a global product decomposition of ![]() $\widehat{M}$ and coincide with the levels of t.
$\widehat{M}$ and coincide with the levels of t.
Proof. Up to a change of sign, the 1-form in question may be expressed as ![]() $\psi\,{\rm d}t$, where
$\psi\,{\rm d}t$, where  $\psi:\widehat{M}\to(0,\infty)$ is locally a function of t. Choosing
$\psi:\widehat{M}\to(0,\infty)$ is locally a function of t. Choosing  $\chi:\widehat{M}\to\mathrm{I\!R}$ with
$\chi:\widehat{M}\to\mathrm{I\!R}$ with ![]() ${\rm d}\chi=\psi\,{\rm d}t$, and denoting by
${\rm d}\chi=\psi\,{\rm d}t$, and denoting by ![]() $D\chi$ the h-gradient of χ, where h is the π-pullback of a Riemannian metric on M, we see that
$D\chi$ the h-gradient of χ, where h is the π-pullback of a Riemannian metric on M, we see that ![]() $D\chi$ and
$D\chi$ and ![]() $u=D\chi/[h(D\chi,D\chi)]$ are both non-zero everywhere and complete (the latter since
$u=D\chi/[h(D\chi,D\chi)]$ are both non-zero everywhere and complete (the latter since ![]() ${\rm d}\chi=h(D\chi,\cdot)$, with
${\rm d}\chi=h(D\chi,\cdot)$, with ![]() ${\rm d}\chi$ and h both π-projectable onto M). By Equation (6.4), the (possibly disconnected) levels of χ are unions of leaves of
${\rm d}\chi$ and h both π-projectable onto M). By Equation (6.4), the (possibly disconnected) levels of χ are unions of leaves of ![]() $\mathcal{D}^\perp$.
$\mathcal{D}^\perp$.
We now use Milnor’s argument [Reference Milnor14, p. 12] involving the flow ![]() $(\tau,x)\mapsto\phi(\tau,x)$ of u. Remark 3.2 may be applied to a fixed (possibly disconnected) level L of χ and the restriction of the flow ϕ to
$(\tau,x)\mapsto\phi(\tau,x)$ of u. Remark 3.2 may be applied to a fixed (possibly disconnected) level L of χ and the restriction of the flow ϕ to ![]() $\mathrm{I\!R}\times L$. The restriction is not only locally diffeomorphic, but bijective as well, since
$\mathrm{I\!R}\times L$. The restriction is not only locally diffeomorphic, but bijective as well, since ![]() $d_u\chi=1$ and so the parameter τ of each integral curve differs from χ by a constant. Since
$d_u\chi=1$ and so the parameter τ of each integral curve differs from χ by a constant. Since ![]() $\mathrm{I\!R}\times L$, diffeomorphic to
$\mathrm{I\!R}\times L$, diffeomorphic to ![]() $\widehat{M}$, must be connected, the assertion follows, the levels of t being the same as those of χ (and thus equal to the leaves of
$\widehat{M}$, must be connected, the assertion follows, the levels of t being the same as those of χ (and thus equal to the leaves of ![]() $\mathcal{D}^\perp$) due to positivity of
$\mathcal{D}^\perp$) due to positivity of ![]() $\psi={\rm d}\chi/{\rm d}t$.
$\psi={\rm d}\chi/{\rm d}t$.
Theorem 7.3. Let  $\widehat{M},\mathtt{g},\Gamma,f,t,
( )\dot{\phantom o}= {\rm d}/{\rm d}t$ and
$\widehat{M},\mathtt{g},\Gamma,f,t,
( )\dot{\phantom o}= {\rm d}/{\rm d}t$ and  $M=\widehat{M}/\Gamma$ be as in §6. If M is compact, the following three conditions are mutually equivalent.
$M=\widehat{M}/\Gamma$ be as in §6. If M is compact, the following three conditions are mutually equivalent.
(i)
 $(\widehat{M},\mathtt{g})$, or
$(\widehat{M},\mathtt{g})$, or  $(M,\mathtt{g})$, is locally homogeneous.
$(M,\mathtt{g})$, is locally homogeneous.(ii)
 $f\ne0$ everywhere and
$f\ne0$ everywhere and  $(|f|^{-1/2})\ddot{\phantom o}=0$.
$(|f|^{-1/2})\ddot{\phantom o}=0$.(iii)
 $(|f|^{-1/2})\ddot{\phantom o}=0$ wherever
$(|f|^{-1/2})\ddot{\phantom o}=0$ wherever  $f\ne0$.
$f\ne0$.
Proof. First, (i) yields ![]() $f\ne0$ everywhere due to Equations (7.5) and (6.6). By Remark 5.1,
$f\ne0$ everywhere due to Equations (7.5) and (6.6). By Remark 5.1, ![]() $\mathtt{g}$ has, locally, the form (5.4) on some coordinate domain U, and then, as shown in [Reference Derdzinski and Terek8, formula (3.3)], the existence of a Killing field v on U with an everywhere-non-zero component in the t coordinate direction (which follows from local homogeneity) gives
$\mathtt{g}$ has, locally, the form (5.4) on some coordinate domain U, and then, as shown in [Reference Derdzinski and Terek8, formula (3.3)], the existence of a Killing field v on U with an everywhere-non-zero component in the t coordinate direction (which follows from local homogeneity) gives ![]() $(|f|^{-1/2})\ddot{\phantom o}=0$ on U, that is, (ii), while (ii) trivially leads to (iii). Assuming (iii), we now obtain (ii):
$(|f|^{-1/2})\ddot{\phantom o}=0$ on U, that is, (ii), while (ii) trivially leads to (iii). Assuming (iii), we now obtain (ii): ![]() $f\ne0$ everywhere, since otherwise we could choose local coordinates as above around a boundary point of the zero set of f, with t ranging over an open interval Iʹ. (By Equations (6.6) and (7.1),
$f\ne0$ everywhere, since otherwise we could choose local coordinates as above around a boundary point of the zero set of f, with t ranging over an open interval Iʹ. (By Equations (6.6) and (7.1), ![]() $f\ne0$ somewhere.) A maximal open subinterval Iʹʹ of Iʹ with
$f\ne0$ somewhere.) A maximal open subinterval Iʹʹ of Iʹ with ![]() $|f| \gt 0$ on Iʹʹ must equal Iʹ, or else Iʹʹ would have a finite endpoint lying in Iʹ, at which
$|f| \gt 0$ on Iʹʹ must equal Iʹ, or else Iʹʹ would have a finite endpoint lying in Iʹ, at which ![]() $|f|^{-1/2}$, being a linear function, would have a finite limit, contrary to vanishing of f at the endpoint due to maximality of Iʹʹ. This contradiction shows that the zero set of f has no boundary points, proving (ii).
$|f|^{-1/2}$, being a linear function, would have a finite limit, contrary to vanishing of f at the endpoint due to maximality of Iʹʹ. This contradiction shows that the zero set of f has no boundary points, proving (ii).
Suppose now that (ii) holds. According to Equation (7.6), the 1-form ![]() $|f|^{1/2}\,{\rm d}t$ satisfies the assumption, and hence the assertion, of Lemma 7.2, so that the levels of t are connected. We may thus drop the word ‘locally’ in Equation (6.7) and, with
$|f|^{1/2}\,{\rm d}t$ satisfies the assumption, and hence the assertion, of Lemma 7.2, so that the levels of t are connected. We may thus drop the word ‘locally’ in Equation (6.7) and, with ![]() $I\subseteq\mathrm{I\!R}$ denoting the range of t, view f as a function
$I\subseteq\mathrm{I\!R}$ denoting the range of t, view f as a function ![]() $f:I\to\mathrm{I\!R}$ which, since
$f:I\to\mathrm{I\!R}$ which, since ![]() $(|f|^{-1/2})\ddot{\phantom o}=0$ and f is non-constant (Remark 5.1), has the form
$(|f|^{-1/2})\ddot{\phantom o}=0$ and f is non-constant (Remark 5.1), has the form ![]() $f(t)=\varepsilon(t-b)^{-2}$ for some real constants
$f(t)=\varepsilon(t-b)^{-2}$ for some real constants ![]() $\varepsilon\ne0$ and b. Thus,
$\varepsilon\ne0$ and b. Thus, ![]() $I\subseteq(-\infty,b)$ or
$I\subseteq(-\infty,b)$ or ![]() $I\subseteq(b,\infty)$. Now Equation (6.2) leads to a homomorphism
$I\subseteq(b,\infty)$. Now Equation (6.2) leads to a homomorphism ![]() $\Gamma\ni\gamma\mapsto(q,p)\in\mathrm{Af{}f}^+(\mathrm{I\!R})$ into the group of increasing affine transformations of
$\Gamma\ni\gamma\mapsto(q,p)\in\mathrm{Af{}f}^+(\mathrm{I\!R})$ into the group of increasing affine transformations of ![]() $\mathrm{I\!R}$ mapping I onto itself. As
$\mathrm{I\!R}$ mapping I onto itself. As ![]() $I\subseteq(-\infty,b)$ or
$I\subseteq(-\infty,b)$ or ![]() $I\subseteq(b,\infty)$, the image of this homomorphism cannot contain a non-trivial translation and must be infinite (or else it would be trivial, causing t to descend to a function without critical points on the compact manifold
$I\subseteq(b,\infty)$, the image of this homomorphism cannot contain a non-trivial translation and must be infinite (or else it would be trivial, causing t to descend to a function without critical points on the compact manifold  $M=\widehat{M}/\Gamma$). Consequently, some
$M=\widehat{M}/\Gamma$). Consequently, some ![]() $\gamma\in\Gamma$ has
$\gamma\in\Gamma$ has ![]() $q\in(0,\infty)\smallsetminus\{1\}$ in Equation (6.2). Then Equation (7.4) and Lemma 7.1 imply that
$q\in(0,\infty)\smallsetminus\{1\}$ in Equation (6.2). Then Equation (7.4) and Lemma 7.1 imply that
 \begin{equation}
\begin{array}{l}
\mathrm{for\ every\ }q\in(0,\infty)\smallsetminus\{1\}\mathrm{\ there\
exists\ a\ linear}\\
\langle\cdot,\cdot\rangle\ \mathrm{isometry\ }B:V\to V\mathrm{\ with\
}B AB^{-1}=q^2 A,
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\mathrm{for\ every\ }q\in(0,\infty)\smallsetminus\{1\}\mathrm{\ there\
exists\ a\ linear}\\
\langle\cdot,\cdot\rangle\ \mathrm{isometry\ }B:V\to V\mathrm{\ with\
}B AB^{-1}=q^2 A,
\end{array}
\end{equation}where ![]() $A,V$ and
$A,V$ and ![]() $\langle\cdot,\cdot\rangle$ are a part of the data (5.1) representing the metric
$\langle\cdot,\cdot\rangle$ are a part of the data (5.1) representing the metric ![]() $\mathtt{g}$ in suitable coordinates around any point of
$\mathtt{g}$ in suitable coordinates around any point of ![]() $\widehat{M}$. (See the lines preceding Equation (7.4).) Also, instead of
$\widehat{M}$. (See the lines preceding Equation (7.4).) Also, instead of ![]() $f(t)=\varepsilon(t-b)^{-2}$, we may require that f have the form
$f(t)=\varepsilon(t-b)^{-2}$, we may require that f have the form
as we are free to modify our choice of t via the affine substitution replacing t by ![]() $|t-b|$. (The equality
$|t-b|$. (The equality ![]() $I=(0,\infty)$, rather than just the inclusion
$I=(0,\infty)$, rather than just the inclusion ![]() $I\subseteq(0,\infty)$, follows since an infinite group of increasing affine transformations maps I onto itself.)
$I\subseteq(0,\infty)$, follows since an infinite group of increasing affine transformations maps I onto itself.)
Local homogeneity of ![]() $\mathtt{g}$ now follows: by Equation (7.9), the local-coordinate expression (5.4) of
$\mathtt{g}$ now follows: by Equation (7.9), the local-coordinate expression (5.4) of ![]() $\mathtt{g}$ amounts to that of the metric g P in [Reference Derdziński2, top of p. 170], with our coordinate
$\mathtt{g}$ amounts to that of the metric g P in [Reference Derdziński2, top of p. 170], with our coordinate ![]() $x^1=t$ denoted there by u 1. Our Equation (7.8) now becomes formula (10) in [Reference Derdziński2, p. 172] which, as stated there, guarantees homogeneity of the metric g P on
$x^1=t$ denoted there by u 1. Our Equation (7.8) now becomes formula (10) in [Reference Derdziński2, p. 172] which, as stated there, guarantees homogeneity of the metric g P on ![]() $I\times\mathrm{I\!R}\times V$, for
$I\times\mathrm{I\!R}\times V$, for ![]() $I=(0,\infty)$ and
$I=(0,\infty)$ and ![]() $V=\mathrm{I\!R}^{n-2}$.
$V=\mathrm{I\!R}^{n-2}$.
We have thus shown that (ii) implies (i), completing the proof.
Remark 7.4. A Lorentzian ECS manifold must have rank one (see the Introduction) and is never locally homogeneous: Equation (7.4) with ![]() $q\ne\pm1$ implies nilpotency of A, while in the Lorentzian case, the fibre metric in
$q\ne\pm1$ implies nilpotency of A, while in the Lorentzian case, the fibre metric in ![]() $\mathcal{E}$ induced by
$\mathcal{E}$ induced by ![]() $\mathtt{g}$, which corresponds to
$\mathtt{g}$, which corresponds to ![]() $\langle\cdot,\cdot\rangle$ in (5.1), is positive definite, and so the non-zero
$\langle\cdot,\cdot\rangle$ in (5.1), is positive definite, and so the non-zero ![]() $\langle\cdot,\cdot\rangle$-self-adjoint linear endomorphism
$\langle\cdot,\cdot\rangle$-self-adjoint linear endomorphism ![]() $A:V\to V$, being diagonalizable, cannot be nilpotent.
$A:V\to V$, being diagonalizable, cannot be nilpotent.
8. Function spaces and the first real cohomology
We refer to a continuous 1-form ζ on a manifold M as closed if it is locally exact in the sense that every point of M has a neighbourhood U with ![]() $\zeta=d\psi$ on U for some C 1 function
$\zeta=d\psi$ on U for some C 1 function ![]() $\psi:U\to\mathrm{I\!R}$.
$\psi:U\to\mathrm{I\!R}$.
Due to the universal coefficient theorem [Reference Lee13, p. 378, Theorem 13.43], for any manifold M, one has an isomorphic identification ![]() $H^1(M,\mathrm{I\!R})=\mathrm{Hom}(\pi_1 M,\mathrm{I\!R})$.
$H^1(M,\mathrm{I\!R})=\mathrm{Hom}(\pi_1 M,\mathrm{I\!R})$.
As in the case of smooth 1-forms, a closed continuous 1-form ζ on M thus gives rise to the cohomology class ![]() $\mathsf{[}\zeta\mathsf{]}\in H^1(M,\mathrm{I\!R})$, which, as a homomorphism
$\mathsf{[}\zeta\mathsf{]}\in H^1(M,\mathrm{I\!R})$, which, as a homomorphism ![]() $\pi_1 M\to\mathrm{I\!R}$, assigns to each homotopy class of piecewise C 1 loops at a fixed base point the integral of ζ over a representative loop. Clearly,
$\pi_1 M\to\mathrm{I\!R}$, assigns to each homotopy class of piecewise C 1 loops at a fixed base point the integral of ζ over a representative loop. Clearly, ![]() $\mathsf{[}\zeta\mathsf{]}=0$ if and only if
$\mathsf{[}\zeta\mathsf{]}=0$ if and only if ![]() $\zeta={\rm d}\psi$ for some C 1 function
$\zeta={\rm d}\psi$ for some C 1 function ![]() $\psi:M\to\mathrm{I\!R}$.
$\psi:M\to\mathrm{I\!R}$.
The following lemma uses the notation  $\pi,\widehat{M},t,f,\Gamma$ introduced in §6.
$\pi,\widehat{M},t,f,\Gamma$ introduced in §6.
Lemma 8.1. Let ![]() $\mathcal{F}$ be the real vector space formed by all continuous functions
$\mathcal{F}$ be the real vector space formed by all continuous functions  $\chi:\widehat{M}\to\mathrm{I\!R}$ such that the 1-form
$\chi:\widehat{M}\to\mathrm{I\!R}$ such that the 1-form ![]() $\chi\,{\rm d}t$ is closed and
$\chi\,{\rm d}t$ is closed and
Then ![]() $|f|^{1/2}\in\mathcal{F}$ and
$|f|^{1/2}\in\mathcal{F}$ and ![]() $|\dot f|^{1/3}\in\mathcal{F}$. Furthermore, if
$|\dot f|^{1/3}\in\mathcal{F}$. Furthermore, if ![]() $\chi\in\mathcal{F}$, then the 1-form
$\chi\in\mathcal{F}$, then the 1-form ![]() $\chi\,{\rm d}t$ is Γ-invariant, and hence π-projectable onto a closed 1-form on
$\chi\,{\rm d}t$ is Γ-invariant, and hence π-projectable onto a closed 1-form on  $M=\widehat{M}/\Gamma$, also denoted by
$M=\widehat{M}/\Gamma$, also denoted by ![]() $\chi\,{\rm d}t$, which gives rise to a linear operator
$\chi\,{\rm d}t$, which gives rise to a linear operator
9. Existence of special functions
Theorem 9.1. Let ![]() $(M,\mathtt{g})$ be a compact rank-one ECS manifold such that
$(M,\mathtt{g})$ be a compact rank-one ECS manifold such that ![]() $\mathcal{D}^\perp$ is transversally orientable. If
$\mathcal{D}^\perp$ is transversally orientable. If ![]() $(M,\mathtt{g})$ is not locally homogeneous, then there exists a non-constant C 1 function
$(M,\mathtt{g})$ is not locally homogeneous, then there exists a non-constant C 1 function ![]() $\mu:M\to\mathrm{I\!R}$, constant along
$\mu:M\to\mathrm{I\!R}$, constant along ![]() $\mathcal{D}^\perp$.
$\mathcal{D}^\perp$.
Proof. We will show that, for ![]() $\mathcal{F}$ defined in Lemma 8.1, either
$\mathcal{F}$ defined in Lemma 8.1, either ![]() $\dim\mathcal{F} \lt \infty$ and
$\dim\mathcal{F} \lt \infty$ and ![]() $(M,\mathtt{g})$ is locally homogeneous, or
$(M,\mathtt{g})$ is locally homogeneous, or ![]() $\dim\mathcal{F}=\infty$ and such µ exists.
$\dim\mathcal{F}=\infty$ and such µ exists.
First, let ![]() $\dim\mathcal{F} \lt \infty$. In this case, even without using compactness of M, we can apply Lemma 3.3 to X = M, our vector space
$\dim\mathcal{F} \lt \infty$. In this case, even without using compactness of M, we can apply Lemma 3.3 to X = M, our vector space ![]() $\mathcal{F}$, and the m-argument operation Π sending
$\mathcal{F}$, and the m-argument operation Π sending ![]() $\psi_1 ,\dots,\psi_m $ to the product of powers of the absolute values
$\psi_1 ,\dots,\psi_m $ to the product of powers of the absolute values ![]() $|\psi_1 |,\dots,|\psi_m |$ with any fixed positive exponents adding up to 1 (for instance, the geometric mean of the absolute values). As
$|\psi_1 |,\dots,|\psi_m |$ with any fixed positive exponents adding up to 1 (for instance, the geometric mean of the absolute values). As ![]() $|f|^{1/2},|\dot f|^{1/3}$ lie in
$|f|^{1/2},|\dot f|^{1/3}$ lie in ![]() $\mathcal{F}$ (see Lemma 8.1), on each of the open sets
$\mathcal{F}$ (see Lemma 8.1), on each of the open sets ![]() $X_j \subseteq M$ obtained in Lemma 3.3,
$X_j \subseteq M$ obtained in Lemma 3.3, ![]() $|f|^{1/2}$ and
$|f|^{1/2}$ and ![]() $|\dot f|^{1/3}$ are constant multiples of the jth function χj from the basis
$|\dot f|^{1/3}$ are constant multiples of the jth function χj from the basis ![]() $\chi_1 ,\dots,\chi_m $ of
$\chi_1 ,\dots,\chi_m $ of ![]() $\mathcal{F}$, which clearly gives
$\mathcal{F}$, which clearly gives ![]() $(|f|^{-1/2})\ddot{\phantom o}=0$ wherever
$(|f|^{-1/2})\ddot{\phantom o}=0$ wherever ![]() $f\ne0$. (Note that
$f\ne0$. (Note that ![]() $|f|^{1/2}$, being a linear combination of the functions
$|f|^{1/2}$, being a linear combination of the functions ![]() $\chi_1 ,\dots,\chi_m $, vanishes on their simultaneous zero set
$\chi_1 ,\dots,\chi_m $, vanishes on their simultaneous zero set  $X\smallsetminus\bigcup_{j=1}^mX_j $.) Local homogeneity is now immediate from Theorem 7.3.
$X\smallsetminus\bigcup_{j=1}^mX_j $.) Local homogeneity is now immediate from Theorem 7.3.
Finally, suppose that ![]() $\dim\mathcal{F}=\infty$. Due to compactness of M, Equation (8.2) is non-injective and we may fix
$\dim\mathcal{F}=\infty$. Due to compactness of M, Equation (8.2) is non-injective and we may fix ![]() $\chi\in\mathcal{F}\smallsetminus\{0\}$ lying in its kernel, so that
$\chi\in\mathcal{F}\smallsetminus\{0\}$ lying in its kernel, so that ![]() $\chi\,{\rm d}t$ treated as a 1-form on M equals
$\chi\,{\rm d}t$ treated as a 1-form on M equals ![]() ${\rm d}\mu$ for some (non-constant) C 1 function
${\rm d}\mu$ for some (non-constant) C 1 function ![]() $\mu:M\to\mathrm{I\!R}$. By Equation (6.4), this completes the proof.
$\mu:M\to\mathrm{I\!R}$. By Equation (6.4), this completes the proof.
Remark 9.2. Sard’s theorem [Reference Hirsch11, Theorem 1.3 on p. 69] normally applies to C k mappings from an n-manifold into an m-manifold, with ![]() $k\ge\mathrm{max}(n-m+1,1)$, guaranteeing that the critical values form a set of zero measure. In our case, even though
$k\ge\mathrm{max}(n-m+1,1)$, guaranteeing that the critical values form a set of zero measure. In our case, even though ![]() $\mu:M\to\mathrm{I\!R}$ is only of class C 1, and M can have any dimension
$\mu:M\to\mathrm{I\!R}$ is only of class C 1, and M can have any dimension ![]() $n\ge4$, the same conclusion remains valid, and so, due to compactness of M,
$n\ge4$, the same conclusion remains valid, and so, due to compactness of M,
![]() $\mu(M)$ being the range of µ. In fact, Equation (6.3) gives
$\mu(M)$ being the range of µ. In fact, Equation (6.3) gives ![]() ${\rm d}t\ne0$ everywhere in
${\rm d}t\ne0$ everywhere in ![]() $\widehat{M}$, and so M is covered by finitely many connected open sets U each of which can be diffeomorphically identified with an open set
$\widehat{M}$, and so M is covered by finitely many connected open sets U each of which can be diffeomorphically identified with an open set ![]() $\widehat{U}\subseteq\widehat{M}$ such that the levels of
$\widehat{U}\subseteq\widehat{M}$ such that the levels of ![]() $t:\widehat{U}\to\mathrm{I\!R}$ are all connected. This turns µ restricted to U into a function of t, allowing us to use Sard’s theorem as stated above for
$t:\widehat{U}\to\mathrm{I\!R}$ are all connected. This turns µ restricted to U into a function of t, allowing us to use Sard’s theorem as stated above for ![]() $k=n=m=1$.
$k=n=m=1$.
10. Holonomy of compact leaves
Let ![]() $(M,\mathtt{g})$ be a rank-one ECS manifold. Its rank-one Olszak distribution
$(M,\mathtt{g})$ be a rank-one ECS manifold. Its rank-one Olszak distribution ![]() $\mathcal{D}$ (see the Introduction), being parallel, carries a linear connection induced from the Levi-Civita connection of
$\mathcal{D}$ (see the Introduction), being parallel, carries a linear connection induced from the Levi-Civita connection of ![]() $\mathtt{g}$, and this connection is flat since, locally,
$\mathtt{g}$, and this connection is flat since, locally, ![]() $\mathcal{D}$ is spanned by the parallel gradient
$\mathcal{D}$ is spanned by the parallel gradient ![]() $\nabla t$, cf. Equation (6.3).
$\nabla t$, cf. Equation (6.3).
For any leaf L of ![]() $\mathcal{D}^\perp$, this flat connection gives rise to one in the line bundle
$\mathcal{D}^\perp$, this flat connection gives rise to one in the line bundle ![]() $\mathcal{D}_L $ arising as the restriction of
$\mathcal{D}_L $ arising as the restriction of ![]() $\mathcal{D}$ to L and, consequently, also to what we call
$\mathcal{D}$ to L and, consequently, also to what we call
Note that ![]() $\mathcal{D}_{L}^*$ is canonically isomorphic to the normal bundle of L in M, since
$\mathcal{D}_{L}^*$ is canonically isomorphic to the normal bundle of L in M, since ![]() $\mathcal{D}$ is isomorphic to the dual of
$\mathcal{D}$ is isomorphic to the dual of ![]() $T M/\mathcal{D}^\perp$, via the isomorphism assigning to
$T M/\mathcal{D}^\perp$, via the isomorphism assigning to ![]() $v\in\mathcal{D}_x $, at any
$v\in\mathcal{D}_x $, at any ![]() $x\in M$, the linear functional
$x\in M$, the linear functional ![]() $\mathtt{g}_x (v,\cdot):{T_x M}\to\mathrm{I\!R}$, vanishing on
$\mathtt{g}_x (v,\cdot):{T_x M}\to\mathrm{I\!R}$, vanishing on ![]() $\mathcal{D}_x^\perp$.
$\mathcal{D}_x^\perp$.
The next result remains valid without transversal orientability of ![]() $\mathcal{D}^\perp$ or compactness of M. We make these assumptions here just to simplify the discussion.
$\mathcal{D}^\perp$ or compactness of M. We make these assumptions here just to simplify the discussion.
Theorem 10.1. Let L be a compact leaf of ![]() $\mathcal{D}^\perp$ in a compact rank-one ECS manifold
$\mathcal{D}^\perp$ in a compact rank-one ECS manifold ![]() $(M,\mathtt{g})$. If
$(M,\mathtt{g})$. If ![]() $\mathcal{D}^\perp$ is transversally orientable, then some neighbourhood U of L in M can be diffeomorphically identified with a neighbourhood Uʹ of the zero section L in the line bundle
$\mathcal{D}^\perp$ is transversally orientable, then some neighbourhood U of L in M can be diffeomorphically identified with a neighbourhood Uʹ of the zero section L in the line bundle ![]() $\mathcal{D}_{L}^*$ so as to make the distribution
$\mathcal{D}_{L}^*$ so as to make the distribution ![]() $\mathcal{D}^\perp$ on U correspond to the restriction to Uʹ of the horizontal distribution of the flat connection in
$\mathcal{D}^\perp$ on U correspond to the restriction to Uʹ of the horizontal distribution of the flat connection in ![]() $\mathcal{D}_{L}^*$.
$\mathcal{D}_{L}^*$.
Proof. Let ![]() $U=\phi((-\varepsilon,\varepsilon)\times L)$ for the flow ϕ of a fixed
$U=\phi((-\varepsilon,\varepsilon)\times L)$ for the flow ϕ of a fixed ![]() $C^\infty$ vector field v on M, which is nowhere tangent to
$C^\infty$ vector field v on M, which is nowhere tangent to ![]() $\mathcal{D}^\perp$, and for ɛ chosen as in Remark 3.2. We define the required diffeomorphism
$\mathcal{D}^\perp$, and for ɛ chosen as in Remark 3.2. We define the required diffeomorphism ![]() $\Psi:U\to U^{\prime}$ by declaring how
$\Psi:U\to U^{\prime}$ by declaring how ![]() $\Psi(\phi(\tau,x))$ depends on
$\Psi(\phi(\tau,x))$ depends on ![]() $(\tau,x)\in(-\varepsilon,\varepsilon)\times L$, cf. Remark 3.2. For any point
$(\tau,x)\in(-\varepsilon,\varepsilon)\times L$, cf. Remark 3.2. For any point ![]() $y\in\pi^{-1}(x)$, with π as in Equation (6.1), the flow
$y\in\pi^{-1}(x)$, with π as in Equation (6.1), the flow ![]() $\hat\phi$ of the vector field
$\hat\phi$ of the vector field ![]() $\hat v$ on
$\hat v$ on ![]() $\widehat{M}$ projecting under π onto v, and the parallel section ξ of the line bundle
$\widehat{M}$ projecting under π onto v, and the parallel section ξ of the line bundle ![]() $\mathcal{D}^*$ over
$\mathcal{D}^*$ over ![]() $\widehat{M}$ appearing in Equation (7.3), we set
$\widehat{M}$ appearing in Equation (7.3), we set
 \begin{equation}
\Psi(\phi(\tau,x))
=[ t(\hat\phi(\tau,y))-t(y)]\xi_y \circ(d\pi_y )^{-1}
\in \mathcal{D}_{ x}^*\subseteq\,\mathcal{D}_{L}^*.
\end{equation}
\begin{equation}
\Psi(\phi(\tau,x))
=[ t(\hat\phi(\tau,y))-t(y)]\xi_y \circ(d\pi_y )^{-1}
\in \mathcal{D}_{ x}^*\subseteq\,\mathcal{D}_{L}^*.
\end{equation} Here ![]() $\xi_y \in\mathcal{D}_{ y}^*$ is a linear functional on
$\xi_y \in\mathcal{D}_{ y}^*$ is a linear functional on  $\mathcal{D}_{ y} \subseteq{T_y \widehat{M}}$, and we compose it with the inverse of the isomorphism
$\mathcal{D}_{ y} \subseteq{T_y \widehat{M}}$, and we compose it with the inverse of the isomorphism  $d\pi_y :{T_y \widehat{M}}\to{T_x M}$, so that the result is a functional on
$d\pi_y :{T_y \widehat{M}}\to{T_x M}$, so that the result is a functional on ![]() $\mathcal{D}_{ x} \subseteq{T_x M}$, which we then multiply by the scalar
$\mathcal{D}_{ x} \subseteq{T_x M}$, which we then multiply by the scalar  $t(\hat\phi(\tau,y))-t(y)$. The fibres
$t(\hat\phi(\tau,y))-t(y)$. The fibres ![]() $\mathcal{D}_{ x}$ of the line bundle
$\mathcal{D}_{ x}$ of the line bundle ![]() $\mathcal{D}_{L}^*$ over L are treated here as pairwise disjoint subsets of the total space, also denoted by
$\mathcal{D}_{L}^*$ over L are treated here as pairwise disjoint subsets of the total space, also denoted by ![]() $\mathcal{D}_{L}^*$.
$\mathcal{D}_{L}^*$.
First, Equation (10.2) does not depend on the choice of ![]() $y\in\pi^{-1}(x)$. In fact, replacing y by
$y\in\pi^{-1}(x)$. In fact, replacing y by ![]() $\gamma(y)$, with
$\gamma(y)$, with ![]() $\gamma\in\Gamma$, cf. Equation (6.1), we get the same right-hand side in Equation (10.2), since
$\gamma\in\Gamma$, cf. Equation (6.1), we get the same right-hand side in Equation (10.2), since
 \begin{equation*}
t(\hat\phi(\tau,\gamma(y)))- t(\gamma(y))
= q[ t(\hat\phi(\tau,y))- t(y)],\
\xi_{\gamma(y)} \circ(d\pi_{\gamma(y)} )^{-1}
= q^{-1}\xi_y \circ(d\pi_y )^{-1}
\end{equation*}
\begin{equation*}
t(\hat\phi(\tau,\gamma(y)))- t(\gamma(y))
= q[ t(\hat\phi(\tau,y))- t(y)],\
\xi_{\gamma(y)} \circ(d\pi_{\gamma(y)} )^{-1}
= q^{-1}\xi_y \circ(d\pi_y )^{-1}
\end{equation*}for some real q > 0. Namely, as γ leaves ![]() $\hat v$ invariant,
$\hat v$ invariant,  $\hat\phi(\tau,\gamma(y))=\gamma(\hat\phi(\tau,y))$, and so the relation
$\hat\phi(\tau,\gamma(y))=\gamma(\hat\phi(\tau,y))$, and so the relation ![]() $t\circ\gamma=qt+p$ in Equation (6.2) yields the first equality displayed above. At the same time, Equations (6.9) and (7.3) give
$t\circ\gamma=qt+p$ in Equation (6.2) yields the first equality displayed above. At the same time, Equations (6.9) and (7.3) give ![]() $q^{-1}\xi=\gamma^*\xi$, which, since
$q^{-1}\xi=\gamma^*\xi$, which, since ![]() $\pi=\pi\circ\gamma$, leads to
$\pi=\pi\circ\gamma$, leads to  $q^{-1}\xi_y =\xi_{\gamma(y)} \circ d\gamma_y$ and
$q^{-1}\xi_y =\xi_{\gamma(y)} \circ d\gamma_y$ and ![]() $d\pi_y =d\pi_{\gamma(y)} \circ d\gamma_y $, so that
$d\pi_y =d\pi_{\gamma(y)} \circ d\gamma_y $, so that  $q^{-1}\xi_y \circ(d\pi_y )^{-1}
=\xi_{\gamma(y)} \circ(d\pi_{\gamma(y)} )^{-1}$.
$q^{-1}\xi_y \circ(d\pi_y )^{-1}
=\xi_{\gamma(y)} \circ(d\pi_{\gamma(y)} )^{-1}$.
Smoothness of Ψ is obvious if one uses y depending on x via a local inverse of π. Also, Ψ is a fibre-preserving mapping from ![]() $U=\phi((-\varepsilon,\varepsilon)\times L)$ (viewed, when identified with
$U=\phi((-\varepsilon,\varepsilon)\times L)$ (viewed, when identified with ![]() $(-\varepsilon,\varepsilon)\times L$, as a trivial bundle with one-dimensional fibres) into the line bundle
$(-\varepsilon,\varepsilon)\times L$, as a trivial bundle with one-dimensional fibres) into the line bundle ![]() $\mathcal{D}_{L}^*$, operating as the identity on the base manifold L and constituting an embedding of each fibre separately: by Equation (6.4),
$\mathcal{D}_{L}^*$, operating as the identity on the base manifold L and constituting an embedding of each fibre separately: by Equation (6.4),  $| {\rm d}[ t(\hat\phi(\tau,y))]/{\rm d}t| \gt 0$. This makes Ψ itself an embedding.
$| {\rm d}[ t(\hat\phi(\tau,y))]/{\rm d}t| \gt 0$. This makes Ψ itself an embedding.
Finally, with y near ![]() $y_* $ smoothly depending on
$y_* $ smoothly depending on ![]() $x\in L$ near some fixed
$x\in L$ near some fixed ![]() $x_* $ as before,
$x_* $ as before, ![]() $t(y)=t(y_* )$ is constant, by Equation (6.4). Requiring that an assignment
$t(y)=t(y_* )$ is constant, by Equation (6.4). Requiring that an assignment ![]() $y\mapsto\tau(y)$ give
$y\mapsto\tau(y)$ give  $t(\hat\phi(\tau(y),y))=t_* $ for a constant
$t(\hat\phi(\tau(y),y))=t_* $ for a constant ![]() $t_* $ near
$t_* $ near ![]() $t(y_* )$, and so
$t(y_* )$, and so  $y\mapsto\lambda(y)=\hat\phi(\tau(y),y)$ sends a neighbourhood of
$y\mapsto\lambda(y)=\hat\phi(\tau(y),y)$ sends a neighbourhood of ![]() $y_* $ in the leaf Ly into a single leaf, yields (Remark 3.1) a diffeomorphism λ between neighbourhoods of
$y_* $ in the leaf Ly into a single leaf, yields (Remark 3.1) a diffeomorphism λ between neighbourhoods of ![]() $y_* $ and
$y_* $ and ![]() $\lambda(y_* )$ in the two leaves. By Equation (10.2),
$\lambda(y_* )$ in the two leaves. By Equation (10.2), ![]() $\Psi(\pi(\lambda(y)))
=[ t_* -t(y_* )]\xi_y \circ(d\pi_y )^{-1}$ which, due to constancy of
$\Psi(\pi(\lambda(y)))
=[ t_* -t(y_* )]\xi_y \circ(d\pi_y )^{-1}$ which, due to constancy of ![]() $t_* -t(y_* )$, is a parallel local section of
$t_* -t(y_* )$, is a parallel local section of ![]() $\mathcal{D}_{L}^*$. This completes the proof.
$\mathcal{D}_{L}^*$. This completes the proof.
The holonomy representation of Equation (10.1) assigns to each ![]() $x\in L$ and each homotopy class of piecewise C 1 loops at x in L a linear automorphism of the line
$x\in L$ and each homotopy class of piecewise C 1 loops at x in L a linear automorphism of the line ![]() $\mathcal{D}_x $, that is, the multiplication by some
$\mathcal{D}_x $, that is, the multiplication by some ![]() $q\in\mathrm{I\!R}\smallsetminus\{0\}$. Since this is a multiple of the identity, the holonomy group HL of the flat connection (10.1) in the line bundle
$q\in\mathrm{I\!R}\smallsetminus\{0\}$. Since this is a multiple of the identity, the holonomy group HL of the flat connection (10.1) in the line bundle ![]() $\mathcal{D}_{L}^*$ over L, formed by all these q, does not depend on x. Obviously,
$\mathcal{D}_{L}^*$ over L, formed by all these q, does not depend on x. Obviously,
Theorem 10.2. In any rank-one ECS manifold ![]() $(M,\mathtt{g})$ such that
$(M,\mathtt{g})$ such that ![]() $\mathcal{D}^\perp$ is transversally orientable, condition (4.1) holds for
$\mathcal{D}^\perp$ is transversally orientable, condition (4.1) holds for ![]() $\mathcal{V}=\mathcal{D}^\perp$. In addition, the two possibilities named in Equation (4.1) correspond precisely to the two cases of Equation (10.3).
$\mathcal{V}=\mathcal{D}^\perp$. In addition, the two possibilities named in Equation (4.1) correspond precisely to the two cases of Equation (10.3).
Proof. Theorem 10.1 allows us to treat some neighbourhood Uʹ of the zero section L in the line bundle ![]() $\mathcal{D}_{L}^*$ as a neighbourhood of L in M.
$\mathcal{D}_{L}^*$ as a neighbourhood of L in M.
Any fixed fibre metric in the line bundle ![]() $\mathcal{D}_{L}^*$ gives rise to the norm function
$\mathcal{D}_{L}^*$ gives rise to the norm function ![]() $N:\mathcal{D}_{L}^*\to[0,\infty)$ on the total space
$N:\mathcal{D}_{L}^*\to[0,\infty)$ on the total space ![]() $\mathcal{D}_{L}^*$ and to radius ɛ interval sub-bundles
$\mathcal{D}_{L}^*$ and to radius ɛ interval sub-bundles ![]() $U_\varepsilon =N^{-1}([0,\varepsilon))
\subseteq\mathcal{D}_{L}^*$, where ɛ > 0. As L is compact,
$U_\varepsilon =N^{-1}([0,\varepsilon))
\subseteq\mathcal{D}_{L}^*$, where ɛ > 0. As L is compact, ![]() $U_\varepsilon \subseteq U^{\prime}$ for ɛ near 0, which turns Uɛ into a neighbourhood of L in M, and is expressed as
$U_\varepsilon \subseteq U^{\prime}$ for ɛ near 0, which turns Uɛ into a neighbourhood of L in M, and is expressed as ![]() $U_\varepsilon \subseteq M$.
$U_\varepsilon \subseteq M$.
First let HL be trivial. The total space of ![]() $\mathcal{D}_{L}^*$ is thus the union of global parallel sections obtained from one such section (on which the norm function N has some maximum value r > 0) via multiplication by constants
$\mathcal{D}_{L}^*$ is thus the union of global parallel sections obtained from one such section (on which the norm function N has some maximum value r > 0) via multiplication by constants ![]() $a\ne0$. If
$a\ne0$. If ![]() $| a|\in(0,\varepsilon/r)$, the resulting parallel sections are thus contained in
$| a|\in(0,\varepsilon/r)$, the resulting parallel sections are thus contained in ![]() $U_\varepsilon \subseteq M$, and hence constitute compact leaves of
$U_\varepsilon \subseteq M$, and hence constitute compact leaves of ![]() $\mathcal{D}^\perp$. This is the second option in the either–or clause of Equation (4.1).
$\mathcal{D}^\perp$. This is the second option in the either–or clause of Equation (4.1).
Next, let HL be infinite. We fix ![]() $q\in H_L \cap(0,1)$ and, for any
$q\in H_L \cap(0,1)$ and, for any ![]() $x\in L$, choose a piecewise C 1 loop λx at x in L such that the parallel transport along λx in the line bundle
$x\in L$, choose a piecewise C 1 loop λx at x in L such that the parallel transport along λx in the line bundle ![]() $\mathcal{D}_{L}^*$ equals the multiplication by q in the line
$\mathcal{D}_{L}^*$ equals the multiplication by q in the line ![]() $\mathcal{D}_{x}^*$. For any
$\mathcal{D}_{x}^*$. For any ![]() $u\in\mathcal{D}_{x}^*\cap U_\varepsilon $, the horizontal lift
$u\in\mathcal{D}_{x}^*\cap U_\varepsilon $, the horizontal lift ![]() $\widetilde{\lambda}_x $ of λx with the initial point u has the terminal point qu. Treating
$\widetilde{\lambda}_x $ of λx with the initial point u has the terminal point qu. Treating ![]() $\widetilde{\lambda}_x $ as a compact subset of the total space
$\widetilde{\lambda}_x $ as a compact subset of the total space ![]() $\mathcal{D}_{L}^*$, on which the norm function N has some maximum value
$\mathcal{D}_{L}^*$, on which the norm function N has some maximum value ![]() $r_x \gt 0$, we may form the union
$r_x \gt 0$, we may form the union  $Q_x =\bigcup_{i=k}^\infty q^i\widetilde{\lambda}_x $ for the least integer
$Q_x =\bigcup_{i=k}^\infty q^i\widetilde{\lambda}_x $ for the least integer ![]() $k\ge0$ with
$k\ge0$ with ![]() $q^kr_x \lt \varepsilon$. Thus,
$q^kr_x \lt \varepsilon$. Thus, ![]() $Q_x \subseteq U_\varepsilon $ is a union of piecewise C 1 horizontal curves in the total space
$Q_x \subseteq U_\varepsilon $ is a union of piecewise C 1 horizontal curves in the total space ![]() $\mathcal{D}_{L}^*$, joined end-to-end, and the same is true for aQx whenever
$\mathcal{D}_{L}^*$, joined end-to-end, and the same is true for aQx whenever ![]() $a\in(-1,1)\smallsetminus\{0\}$ which, as
$a\in(-1,1)\smallsetminus\{0\}$ which, as ![]() $U_\varepsilon \subseteq M$, makes aQx a subset of a leaf
$U_\varepsilon \subseteq M$, makes aQx a subset of a leaf ![]() $L_{(a)} $ of
$L_{(a)} $ of ![]() $\mathcal{D}^\perp$ with
$\mathcal{D}^\perp$ with ![]() $L_{(a)} \subseteq U_\varepsilon \smallsetminus L$. Each
$L_{(a)} \subseteq U_\varepsilon \smallsetminus L$. Each ![]() $L_{(a)} $ contains the sequence
$L_{(a)} $ contains the sequence ![]() $aq^i u$, with integers
$aq^i u$, with integers ![]() $i\ge k$, and
$i\ge k$, and ![]() $aq^i u$ converges as
$aq^i u$ converges as ![]() $i\to\infty$ to
$i\to\infty$ to ![]() $x\in L$ (the zero vector in the line
$x\in L$ (the zero vector in the line ![]() $\mathcal{D}_{x}^*$), so that the leaves
$\mathcal{D}_{x}^*$), so that the leaves ![]() $L_{(a)} $ are all non-compact. At the same time,
$L_{(a)} $ are all non-compact. At the same time,  $aq^k u\in L_{(a)} $, with our fixed k and all
$aq^k u\in L_{(a)} $, with our fixed k and all ![]() $a\in(-1,1)\smallsetminus\{0\}$. Such
$a\in(-1,1)\smallsetminus\{0\}$. Such ![]() $aq^k u$ form a neighbourhood of 0, with 0 itself removed, in the line
$aq^k u$ form a neighbourhood of 0, with 0 itself removed, in the line ![]() $\mathcal{D}_{x}^*$. Thus, in the portion of the radius ɛ interval bundle Uɛ over a neighbourhood of x in L on which
$\mathcal{D}_{x}^*$. Thus, in the portion of the radius ɛ interval bundle Uɛ over a neighbourhood of x in L on which ![]() $\mathcal{D}_{L}^*$ has a non-zero parallel section, the products of this parallel section by all real numbers sufficiently close to 0 fill a neighbourhood U(x) of x in M, and the leaves of
$\mathcal{D}_{L}^*$ has a non-zero parallel section, the products of this parallel section by all real numbers sufficiently close to 0 fill a neighbourhood U(x) of x in M, and the leaves of ![]() $\mathcal{D}^\perp$ intersecting
$\mathcal{D}^\perp$ intersecting ![]() $U(x)\smallsetminus L$ are all non-compact. Compactness of L allows us to choose finitely many
$U(x)\smallsetminus L$ are all non-compact. Compactness of L allows us to choose finitely many ![]() $x\in L$ such that L is contained in the union U of the corresponding sets U(x), which yields the first option in the either–or clause of Equation (4.1).
$x\in L$ such that L is contained in the union U of the corresponding sets U(x), which yields the first option in the either–or clause of Equation (4.1).
11. Proofs of Theorems A and B
To establish Theorem A, fix a compact rank-one ECS manifold ![]() $(M,\mathtt{g})$. Passing to a two-fold isometric covering of
$(M,\mathtt{g})$. Passing to a two-fold isometric covering of ![]() $(M,\mathtt{g})$, if necessary, we may also assume transversal orientability of
$(M,\mathtt{g})$, if necessary, we may also assume transversal orientability of ![]() $\mathcal{D}^\perp$. Theorem 10.2 now implies Equation (4.1) for
$\mathcal{D}^\perp$. Theorem 10.2 now implies Equation (4.1) for ![]() $\mathcal{V}=\mathcal{D}^\perp$.
$\mathcal{V}=\mathcal{D}^\perp$.
In addition, under the hypotheses of Theorem A, there exists a compact leaf L of ![]() $\mathcal{D}^\perp$ realizing the second possibility in Equation (4.1), the one where some product-like neighbourhood of L in M is a union of compact leaves of
$\mathcal{D}^\perp$ realizing the second possibility in Equation (4.1), the one where some product-like neighbourhood of L in M is a union of compact leaves of ![]() $\mathcal{D}^\perp$.
$\mathcal{D}^\perp$.
To prove this, note that either ![]() $(M,\mathtt{g})$ is locally homogeneous and
$(M,\mathtt{g})$ is locally homogeneous and ![]() $\mathcal{D}^\perp$ has a compact leaf or
$\mathcal{D}^\perp$ has a compact leaf or ![]() $(M,\mathtt{g})$ is not locally homogeneous.
$(M,\mathtt{g})$ is not locally homogeneous.
In the latter case, Theorem 9.1 allows us to choose a non-constant C 1 function ![]() $\mu:M\to\mathrm{I\!R}$, constant along
$\mu:M\to\mathrm{I\!R}$, constant along ![]() $\mathcal{D}^\perp$, and Remark 9.2 implies Equation (9.1). Letting
$\mathcal{D}^\perp$, and Remark 9.2 implies Equation (9.1). Letting ![]() $\mu(x)$ be a regular value of µ and fixing a one-dimensional submanifold of M containing x and transverse to
$\mu(x)$ be a regular value of µ and fixing a one-dimensional submanifold of M containing x and transverse to ![]() $\mathcal{D}^\perp$, we see that for every point y in this submanifold lying sufficiently close to x, the connected component, containing y, of the µ-preimage of
$\mathcal{D}^\perp$, we see that for every point y in this submanifold lying sufficiently close to x, the connected component, containing y, of the µ-preimage of ![]() $\mu(y)$ is a compact leaf of
$\mu(y)$ is a compact leaf of ![]() $\mathcal{D}^\perp$. This causes L to satisfy the second option in Equation (4.1) by obviously precluding the first one.
$\mathcal{D}^\perp$. This causes L to satisfy the second option in Equation (4.1) by obviously precluding the first one.
Consider now the former case: local homogeneity along with the existence of a compact leaf L. By Equations (7.5) and (7.7), the line bundle ![]() $\mathcal{D}_{L}^*$ with the connection (10.1) has the global parallel section wʹ and, consequently, its holonomy group HL is trivial. This leads again, via Theorem 10.2, to the second option in Equation (4.1).
$\mathcal{D}_{L}^*$ with the connection (10.1) has the global parallel section wʹ and, consequently, its holonomy group HL is trivial. This leads again, via Theorem 10.2, to the second option in Equation (4.1).
Theorem A is now immediate from Theorem 4.1 applied to ![]() $\mathcal{V}=\mathcal{D}^\perp$.
$\mathcal{V}=\mathcal{D}^\perp$.
As pointed out in the Introduction, Theorem B trivially follows from Theorem A except when  $(\widehat{M},\mathtt{g})$ is locally homogeneous. On the other hand, in the locally homogeneous case, Equations (7.5) and (7.6) imply that
$(\widehat{M},\mathtt{g})$ is locally homogeneous. On the other hand, in the locally homogeneous case, Equations (7.5) and (7.6) imply that ![]() $|f|^{1/2}\,{\rm d}t$ is a closed Γ-invariant
$|f|^{1/2}\,{\rm d}t$ is a closed Γ-invariant ![]() $C^\infty$ 1-form without zeros on
$C^\infty$ 1-form without zeros on ![]() $\widehat{M}$. Theorem B is now obvious from Lemma 7.2.
$\widehat{M}$. Theorem B is now obvious from Lemma 7.2.
12. Further consequences
Let  $(\widehat{M},\mathtt{g})$ be the pseudo-Riemannian universal covering space of a compact rank-one ECS manifold
$(\widehat{M},\mathtt{g})$ be the pseudo-Riemannian universal covering space of a compact rank-one ECS manifold ![]() $(M,\mathtt{g})$, with the Olszak distribution
$(M,\mathtt{g})$, with the Olszak distribution ![]() $\mathcal{D}$, and the universal covering projection
$\mathcal{D}$, and the universal covering projection  $\pi:\widehat{M}\to M=\widehat{M}/\Gamma$, cf. Equation (6.1). As in §6, we assume transversal orientability of the orthogonal complement
$\pi:\widehat{M}\to M=\widehat{M}/\Gamma$, cf. Equation (6.1). As in §6, we assume transversal orientability of the orthogonal complement ![]() $\mathcal{D}^\perp$.
$\mathcal{D}^\perp$.
For future reference, we state here three consequences of the above assumptions.
First, ![]() $\widehat{M}$ admits a smooth positive function
$\widehat{M}$ admits a smooth positive function  $\psi:\widehat{M}\to(0,\infty)$ for which the 1-form
$\psi:\widehat{M}\to(0,\infty)$ for which the 1-form ![]() $\psi\,{\rm d}t$ is both Γ-invariant (in other words, π-projectable onto M) and closed (which amounts to requiring that ψ be, locally, a function of t).
$\psi\,{\rm d}t$ is both Γ-invariant (in other words, π-projectable onto M) and closed (which amounts to requiring that ψ be, locally, a function of t).
In fact, in the locally homogeneous case (or, more generally, when ![]() $\mathrm{Ric}\ne0$ everywhere), Equation (7.6) allows us to choose
$\mathrm{Ric}\ne0$ everywhere), Equation (7.6) allows us to choose ![]() $\psi=|f|^{1/2}$.
$\psi=|f|^{1/2}$.
If ![]() $(M,\mathtt{g})$ is not locally homogeneous,
$(M,\mathtt{g})$ is not locally homogeneous, ![]() $\mathcal{D}^\perp$, on M, is the vertical distribution of a fibration
$\mathcal{D}^\perp$, on M, is the vertical distribution of a fibration ![]() $M\to S^1$. (This is Theorem A.) We obtain our
$M\to S^1$. (This is Theorem A.) We obtain our ![]() $\psi\,{\rm d}t$, or its opposite, by pulling back from S 1 to M a smooth 1-form without zeros.
$\psi\,{\rm d}t$, or its opposite, by pulling back from S 1 to M a smooth 1-form without zeros.
Second, the parallel vector field ![]() $w=\nabla t$ on
$w=\nabla t$ on ![]() $\widehat{M}$, spanning
$\widehat{M}$, spanning ![]() $\mathcal{D}$, which appears in Equation (6.3), is complete. Namely, for
$\mathcal{D}$, which appears in Equation (6.3), is complete. Namely, for  $\psi:\widehat{M}\to(0,\infty)$ as above, Γ-invariance of
$\psi:\widehat{M}\to(0,\infty)$ as above, Γ-invariance of ![]() $\psi\,{\rm d}t$ implies the same for
$\psi\,{\rm d}t$ implies the same for ![]() $\psi w$ (since
$\psi w$ (since ![]() $w=\nabla t$, that is,
$w=\nabla t$, that is, ![]() ${\rm d}t=\mathtt{g}(w,\cdot)$). Completeness of
${\rm d}t=\mathtt{g}(w,\cdot)$). Completeness of ![]() $\psi w$ now follows due to its resulting π-projectability onto the compact manifold M. However, our ψ is, locally, a function of t and, by Equation (6.4),
$\psi w$ now follows due to its resulting π-projectability onto the compact manifold M. However, our ψ is, locally, a function of t and, by Equation (6.4), ![]() $\mathcal{D}^\perp=\mathrm{Ker}\,{\rm d}t$ on
$\mathcal{D}^\perp=\mathrm{Ker}\,{\rm d}t$ on ![]() $\widehat{M}$. This makes ψ constant along every leaf of
$\widehat{M}$. This makes ψ constant along every leaf of ![]() $\mathcal{D}^\perp$ and w tangent to the leaf. The integral curves of
$\mathcal{D}^\perp$ and w tangent to the leaf. The integral curves of ![]() $\psi w$ are thus affine reparametrizations of those of w, and so w is complete as well.
$\psi w$ are thus affine reparametrizations of those of w, and so w is complete as well.
Finally, the levels of ![]() $t:\widehat{M}\to\mathrm{I\!R}$ are all connected and coincide with the leaves of
$t:\widehat{M}\to\mathrm{I\!R}$ are all connected and coincide with the leaves of ![]() $\mathcal{D}^\perp$ in
$\mathcal{D}^\perp$ in ![]() $\widehat{M}$. Thus, if
$\widehat{M}$. Thus, if  $\chi:\widehat{M}\to\mathrm{I\!R}$ is locally a function of t, it must also be one globally, in the sense of being a composite of t with some function
$\chi:\widehat{M}\to\mathrm{I\!R}$ is locally a function of t, it must also be one globally, in the sense of being a composite of t with some function  $t(\widehat{M})\to\mathrm{I\!R}$, which applies, in particular, to
$t(\widehat{M})\to\mathrm{I\!R}$, which applies, in particular, to ![]() $\chi=f$ appearing in Equations (6.6)–(6.7).
$\chi=f$ appearing in Equations (6.6)–(6.7).
To see this, use Theorem B: the leaves of ![]() $\mathcal{D}^\perp$ in
$\mathcal{D}^\perp$ in ![]() $\widehat{M}$ are the factor manifolds of a global product decomposition of
$\widehat{M}$ are the factor manifolds of a global product decomposition of ![]() $\widehat{M}$, some open interval
$\widehat{M}$, some open interval ![]() $I^{\prime}\subseteq\mathrm{I\!R}$ being the one-dimensional factor. The leaves are thus connected, and
$I^{\prime}\subseteq\mathrm{I\!R}$ being the one-dimensional factor. The leaves are thus connected, and ![]() $t:\widehat{M}\to\mathrm{I\!R}$, constant along them due to Equation (6.4), and having a non-zero parallel gradient – see Equation (6.3) – descends to a strictly monotone function
$t:\widehat{M}\to\mathrm{I\!R}$, constant along them due to Equation (6.4), and having a non-zero parallel gradient – see Equation (6.3) – descends to a strictly monotone function ![]() $I^{\prime}\to\mathrm{I\!R}$, the levels of which thus are single points. This makes the levels of t equal to single leaves of
$I^{\prime}\to\mathrm{I\!R}$, the levels of which thus are single points. This makes the levels of t equal to single leaves of ![]() $\mathcal{D}^\perp$, and hence connected.
$\mathcal{D}^\perp$, and hence connected.
Acknowledgements
The authors greatly appreciate suggestions made by the anonymous referee, which allowed us to considerably improve the exposition.
Competing interests
The authors declare none.
Appendix: The Lorentzian case
From now on we always assume transversal orientability of ![]() $\mathcal{D}^\perp$ for the Olszak distribution
$\mathcal{D}^\perp$ for the Olszak distribution ![]() $\mathcal{D}$ of the ECS manifold
$\mathcal{D}$ of the ECS manifold ![]() $(M,\mathtt{g})$ in question, which makes
$(M,\mathtt{g})$ in question, which makes ![]() $\mathcal{D}$ a trivial line bundle over M.
$\mathcal{D}$ a trivial line bundle over M.
The purpose of this section is to inform the reader how the proof of Theorem A differs from that for Lorentzian ECS manifolds in [Reference Derdzinski and Roter5], and specifically what issues arise in higher signatures and how they are dealt with. We already explained in the Introduction why Theorem B of the paper [Reference Derdzinski and Roter5] – the Lorentzian case of our Theorem A – does not require assuming rank one or excluding local homogeneity.
Let us begin by outlining the proof of [Reference Derdzinski and Roter5, Theorem B], given in [Reference Derdzinski and Roter5]. First – as we pointed out in the lines following Equation (6.1), and in Equation (7.2) – in any rank-one ECS manifold ![]() $(M,\mathtt{g})$, the Levi-Civita connection
$(M,\mathtt{g})$, the Levi-Civita connection ![]() $\nabla$ induces natural flat connections both in the Olszak distribution
$\nabla$ induces natural flat connections both in the Olszak distribution ![]() $\mathcal{D}$ and in the quotient bundle
$\mathcal{D}$ and in the quotient bundle ![]() $\mathcal{E}=\mathcal{D}^\perp/\mathcal{D}$ over M, while – see [Reference Derdzinski and Roter5, Sect.4] – the Weyl tensor W leads to a vector-bundle morphism
$\mathcal{E}=\mathcal{D}^\perp/\mathcal{D}$ over M, while – see [Reference Derdzinski and Roter5, Sect.4] – the Weyl tensor W leads to a vector-bundle morphism ![]() $\Phi:(\mathcal{D}^*)^{\otimes2}\to(\mathcal{E}^*){}^{\otimes2}$ with
$\Phi:(\mathcal{D}^*)^{\otimes2}\to(\mathcal{E}^*){}^{\otimes2}$ with ![]() $\Phi_x (\lambda\otimes\lambda^{\prime}):\mathcal{E}_x
\times\mathcal{E}_x \to\mathrm{I\!R}$, for any
$\Phi_x (\lambda\otimes\lambda^{\prime}):\mathcal{E}_x
\times\mathcal{E}_x \to\mathrm{I\!R}$, for any ![]() $x\in M$ and
$x\in M$ and ![]() $\lambda,\lambda^{\prime}\in\mathcal{D}_{x}^*$, equal to the symmetric bilinear form sending the cosets
$\lambda,\lambda^{\prime}\in\mathcal{D}_{x}^*$, equal to the symmetric bilinear form sending the cosets ![]() $v+\mathcal{D}_x $ and
$v+\mathcal{D}_x $ and ![]() $v^{\prime}+\mathcal{D}_x $ of vectors
$v^{\prime}+\mathcal{D}_x $ of vectors ![]() $v,v^{\prime}\in\mathcal{D}_{ x}^{\perp}$ to
$v,v^{\prime}\in\mathcal{D}_{ x}^{\perp}$ to ![]() $W_x (v,u,u^{\prime},v^{\prime})$, where
$W_x (v,u,u^{\prime},v^{\prime})$, where ![]() $u,u^{\prime}\in{T_x M}$ are any vectors with
$u,u^{\prime}\in{T_x M}$ are any vectors with ![]() $\lambda=g_x (u,\cdot)$ and
$\lambda=g_x (u,\cdot)$ and ![]() $\lambda^{\prime}=g_x (u^{\prime},\cdot)$ on
$\lambda^{\prime}=g_x (u^{\prime},\cdot)$ on ![]() $\mathcal{D}_x $. As observed in [Reference Derdzinski and Roter5, Sect.4], the morphism Φ is well-defined, parallel relative to natural flat the connections in the bundles involved and nonzero (which makes it injective) at every point
$\mathcal{D}_x $. As observed in [Reference Derdzinski and Roter5, Sect.4], the morphism Φ is well-defined, parallel relative to natural flat the connections in the bundles involved and nonzero (which makes it injective) at every point ![]() $x\in M$. So far, the metric signature of
$x\in M$. So far, the metric signature of ![]() $\mathtt{g}$ was arbitrary: but when it is Lorentzian, the fibre metric in
$\mathtt{g}$ was arbitrary: but when it is Lorentzian, the fibre metric in ![]() $\mathcal{E}=\mathcal{D}^\perp/\mathcal{D}$ induced by
$\mathcal{E}=\mathcal{D}^\perp/\mathcal{D}$ induced by ![]() $\mathtt{g}$ is positive definite, leading, via injectivity of Φ, to a parallel fibre norm
$\mathtt{g}$ is positive definite, leading, via injectivity of Φ, to a parallel fibre norm ![]() $| |$ in the line bundle
$| |$ in the line bundle ![]() $\mathcal{D}$. Cf. [Reference Derdzinski and Roter5, the end of Sect.4]. This proves [Reference Derdzinski and Roter5, Theorem D]: for the Olszak distribution
$\mathcal{D}$. Cf. [Reference Derdzinski and Roter5, the end of Sect.4]. This proves [Reference Derdzinski and Roter5, Theorem D]: for the Olszak distribution ![]() $\mathcal{D}$ of any Lorentzian ECS manifold, it follows (from transversal orientability of
$\mathcal{D}$ of any Lorentzian ECS manifold, it follows (from transversal orientability of ![]() $\mathcal{D}^\perp$) that
$\mathcal{D}^\perp$) that
(a)
 $\mathcal{D}$ is spanned by a global parallel section w, namely, one with
$\mathcal{D}$ is spanned by a global parallel section w, namely, one with  $|w|=1$.
$|w|=1$.
We can now paraphrase the remainder of the proof of [Reference Derdzinski and Roter5, Theorem B], which consists of the paragraph preceding [Reference Derdzinski and Roter5, Remark 5.1], followed by [Reference Derdzinski and Roter5, Lemma 1.2], and instead of assuming the Lorentzian signature, use only (a); the symbols ![]() $\xi,u,\rho,\phi$ and
$\xi,u,\rho,\phi$ and ![]() $\psi=\theta$ of [Reference Derdzinski and Roter5] correspond to our
$\psi=\theta$ of [Reference Derdzinski and Roter5] correspond to our ![]() ${\rm d}t,w,\mathrm{Ric},(2-n)\dot f$ and
${\rm d}t,w,\mathrm{Ric},(2-n)\dot f$ and ![]() $(2-n)f$. On the pseudo-Riemannian universal covering space
$(2-n)f$. On the pseudo-Riemannian universal covering space  $(\widehat{M},\mathtt{g})$ of
$(\widehat{M},\mathtt{g})$ of ![]() $(M,\mathtt{g})$, the pullback of w with (a), still denoted by w, equals
$(M,\mathtt{g})$, the pullback of w with (a), still denoted by w, equals ![]() $\nabla t$, and
$\nabla t$, and  $M=\widehat{M}/\Gamma$, as in Equations (6.3) and (6.1). Milnor’s argument [Reference Milnor14, p. 12] is used in [Reference Derdzinski and Roter5, proof of Lemma 1.2] to show that the levels of t in
$M=\widehat{M}/\Gamma$, as in Equations (6.3) and (6.1). Milnor’s argument [Reference Milnor14, p. 12] is used in [Reference Derdzinski and Roter5, proof of Lemma 1.2] to show that the levels of t in ![]() $\widehat{M}$ are connected: the word ‘locally’ in Equation (6.7) may be skipped. Due to Γ-invariance of
$\widehat{M}$ are connected: the word ‘locally’ in Equation (6.7) may be skipped. Due to Γ-invariance of ![]() $w=\nabla t$, one has Equation (6.2) with q = 1, and the first line of Equation (6.8) gives periodicity of f as a function of t (since a non-trivial element of Γ must thus have
$w=\nabla t$, one has Equation (6.2) with q = 1, and the first line of Equation (6.8) gives periodicity of f as a function of t (since a non-trivial element of Γ must thus have ![]() $p\ne0$). Non-constancy of f, cf. Equation (6.6), implies that the values of p arising from Γ form a cyclic subgroup of
$p\ne0$). Non-constancy of f, cf. Equation (6.6), implies that the values of p arising from Γ form a cyclic subgroup of ![]() $\mathrm{I\!R}$ with a unique generator c > 0. Thus,
$\mathrm{I\!R}$ with a unique generator c > 0. Thus,
(b)
 $t:\widehat{M}\to\mathrm{I\!R}$ descends to a bundle projection
$t:\widehat{M}\to\mathrm{I\!R}$ descends to a bundle projection  $M\to\mathrm{I\!R}/c\mathsf{Z\hskip-4ptZ}=S^1$,
$M\to\mathrm{I\!R}/c\mathsf{Z\hskip-4ptZ}=S^1$,
which completes the proof of [Reference Derdzinski and Roter5, Theorem B].
As we already pointed out, the above proof remains valid if the Lorentzian hypothesis is replaced by the weaker condition (a), transversal orientability of ![]() $\mathcal{D}^\perp$ being always assumed. However, a compact rank-one ECS manifold does not have to be translational in the sense of satisfying (a) – in other words,
$\mathcal{D}^\perp$ being always assumed. However, a compact rank-one ECS manifold does not have to be translational in the sense of satisfying (a) – in other words, ![]() $q\ne1$ may occur in Equation (6.8), and then
$q\ne1$ may occur in Equation (6.8), and then  $M=\widehat{M}/\Gamma$, with its ECS metric, is referred to as dilational. The existence of dilational-type compact rank-one ECS manifolds, including locally homogeneous ones, was established quite recently in [Reference Derdzinski and Terek10, Theorems 6.1 and B.1] – and for them, instead of (b), one gets the different conclusion (c) appearing below.
$M=\widehat{M}/\Gamma$, with its ECS metric, is referred to as dilational. The existence of dilational-type compact rank-one ECS manifolds, including locally homogeneous ones, was established quite recently in [Reference Derdzinski and Terek10, Theorems 6.1 and B.1] – and for them, instead of (b), one gets the different conclusion (c) appearing below.
Compared to the above derivation of (b), the path leading to our proof of Theorem A is rather indirect, and we outline it here by briefly summarizing, in the following five sentences, the five paragraphs (or two-paragraph parts) of Section 2 that begin with the phrases ‘This is achieved’, ‘Returning’, ‘Finally’, ‘First’ and ‘On the other hand’. Namely, we start by showing that ![]() $\mathcal{D}^\perp$ satisfies condition (4.1). To derive Equation (4.1) for
$\mathcal{D}^\perp$ satisfies condition (4.1). To derive Equation (4.1) for ![]() $\mathcal{D}^\perp$, we use the fact that – since in
$\mathcal{D}^\perp$, we use the fact that – since in ![]() $\widehat{M}$ the leaves of
$\widehat{M}$ the leaves of ![]() $\mathcal{D}^\perp$ are the connected components of levels of t and
$\mathcal{D}^\perp$ are the connected components of levels of t and ![]() ${\rm d}t$ is parallel – the leaf holonomy of any compact leaf of
${\rm d}t$ is parallel – the leaf holonomy of any compact leaf of ![]() $\mathcal{D}^\perp$ may be diffeomorphically identified with its normal-connection holonomy. Next, we introduce a vector space
$\mathcal{D}^\perp$ may be diffeomorphically identified with its normal-connection holonomy. Next, we introduce a vector space ![]() $\mathcal{F}$ of functions
$\mathcal{F}$ of functions ![]() $\widehat{M}\to\mathrm{I\!R}$, obviously having either a finite or an infinite dimension. The former italicized case implies local homogeneity. The latter one causes a natural linear operator
$\widehat{M}\to\mathrm{I\!R}$, obviously having either a finite or an infinite dimension. The former italicized case implies local homogeneity. The latter one causes a natural linear operator ![]() $\mathcal{F}\to H^1(M,\mathrm{I\!R})$ to be non-injective and a non-trivial function lying in its kernel leads, via Sard’s theorem, to a compact leaf of
$\mathcal{F}\to H^1(M,\mathrm{I\!R})$ to be non-injective and a non-trivial function lying in its kernel leads, via Sard’s theorem, to a compact leaf of ![]() $\mathcal{D}^\perp$, satisfying the second option in the either–or clause of Equation (4.1), thus implying compactness of all leaves of
$\mathcal{D}^\perp$, satisfying the second option in the either–or clause of Equation (4.1), thus implying compactness of all leaves of ![]() $\mathcal{D}^\perp$ and the conclusion that they form the fibres of a bundle projection
$\mathcal{D}^\perp$ and the conclusion that they form the fibres of a bundle projection ![]() $M\to S^1$.
$M\to S^1$.
A final remark: our proof of Theorem A does eventually lead to a conclusion analogous to (b), but different from it – namely, in the dilational case, unless ![]() $(M,\mathtt{g})$ is locally homogeneous, with
$(M,\mathtt{g})$ is locally homogeneous, with ![]() $\mathcal{D}^\perp$ still assumed transversally orientable,
$\mathcal{D}^\perp$ still assumed transversally orientable,
(c)
 $\tau:\widehat{M}\to\mathrm{I\!R}$ descends to a bundle projection
$\tau:\widehat{M}\to\mathrm{I\!R}$ descends to a bundle projection  $M\to\mathrm{I\!R}/\mathsf{Z\hskip-4ptZ}=S^1$.
$M\to\mathrm{I\!R}/\mathsf{Z\hskip-4ptZ}=S^1$.
Here our choice of t has been modified by an affine substitution so that the range  $t(\widehat{M})$ equals
$t(\widehat{M})$ equals ![]() $(0,\infty)$, and
$(0,\infty)$, and ![]() $\tau=(\log t)/(\log q)$ with suitably chosen
$\tau=(\log t)/(\log q)$ with suitably chosen ![]() $q\in(0,\infty)\smallsetminus\{1\}$. Cf. [Reference Derdzinski and Terek9, the first proof paragraph of Theorem 2.3].
$q\in(0,\infty)\smallsetminus\{1\}$. Cf. [Reference Derdzinski and Terek9, the first proof paragraph of Theorem 2.3].