Theoretical considerations, laboratory experiments, and inclinometer data support a value [Inline 1] for the exponent of the flow law relating stress and strain-rate in polar ice at low stresses (Reference Pimienta and DuvalPimienta and Duval, 1987). But a value of 3 was deduced from ice-shelf data by Reference Jezek, Alley and ThomasJezek and others (1985). The effect of longitudinal stresses, the development of preferred crystal orientations, or experimental errors explain these discrepancies.
One way of identifying deformation processes of ceramics is to analyze densification rates during isostatic pressure. In polar regions, ice particles sinter under the driving force of the pressure due to the weight of particles deposited on top of them. The final stage of pressure sintering corresponds to the densification of ice with closed spherical pores, i.e. after close-off. At this stage, densification is determined by the creep of the thick spherical shell surrounding each bubble. Surface tensions are too small to influence the sintering process. The densification rate by power-law creep and by diffusion can be calculated by using models given by Reference Arzt, Ashby and EasterlingArtz and others (1983). Figure 1 shows the evolution of the effective pressure at Byrd Station (Antarctica) below the close-off depth. The power-law creep model was used with n = 3 and n = 1. A good fit of the experimental results given by Reference GowGow (1968) was obtained by taking successively n = 3 and n = 1. On the other hand, the densification rates deduced from the diffusion model are about one order of magnitude lower than experimental values. The quasi-Newtonian behaviour of polar ice at low stresses is therefore supported by this analysis.
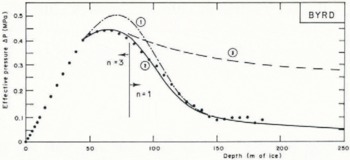
Fig. 1. Variation of effective pressure with depth. Curves 1 and 3 were respectively calculated with = I and n = 3. Curve 2 was calculated by taking successively n = 3 and n = 1. Experimental points are from Reference GowGow (1968).
Evidence of grain-boundary migration in polar ice from the surface down to bedrock is discussed. Grain growth, driven by grain-boundary energy, is observed in the first 100 m of ice sheets. At Byrd Station, grain growth ceases at 450 m, whereas it is still observed, at least, down to a depth of 2000 m at Vostok. Strain energy must be sufficiently small so as not to inhibit this migration process. In the last 100 m above bedrock, a recrystallization regime involving rapid migration of grain boundaries is observed, if the ice temperature is above ≈–10°C. Multi-maxima fabrics are associated with this form of migration recrystallization. At Byrd Station, this regime is observed only below 1800 m. Between these two zones, grain boundaries migrate slowly and grain refinement is achieved via progressive sub-grain rotation. This recrystallization regime is also driven by strain energy and is termed rotation recrystallization (Reference Wilson, Hobbs and HeardWilson, 1986). The greater part of ice sheets are involved in this form of recrystallization process.
Both grain-growth and rotation-recrystallization processes are associated with dislocation glide. The rotation of c-axes by basal glide appears to be the main mechanism for the formation of fabrics in polar ice (Reference Pimienta, Duval and Ya. Lipenkov.Pimienta and others, 1987).
Finally, it is shown that dislocation glide is the only mode of deformation in polar ice.



