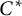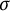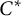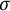1 Introduction
A
![]() $^*$
-algebra is a unital associative algebra
$^*$
-algebra is a unital associative algebra
![]() $\mathcal {A}$
over the field of complex numbers that is endowed with an antilinear involution
$\mathcal {A}$
over the field of complex numbers that is endowed with an antilinear involution
![]() $ {\,\cdot \,} ^*$
of
$ {\,\cdot \,} ^*$
of
![]() $\mathcal {A}$
fulfilling
$\mathcal {A}$
fulfilling
![]() $(ab)^* = b^*a^*$
for all
$(ab)^* = b^*a^*$
for all
![]() $a,b\in \mathcal {A}$
. Note that
$a,b\in \mathcal {A}$
. Note that
![]() $^*$
-algebras are always assumed to have a unit which is denoted by
$^*$
-algebras are always assumed to have a unit which is denoted by
![]() . A
. A
![]() $C^*$
-algebra is a
$C^*$
-algebra is a
![]() $^*$
-algebra that is complete with respect to a norm
$^*$
-algebra that is complete with respect to a norm
![]() ${\lVert { {\,\cdot \,} } \rVert }$
on
${\lVert { {\,\cdot \,} } \rVert }$
on
![]() $\mathcal {A}$
that fulfils
$\mathcal {A}$
that fulfils
![]() ${\lVert {ab} \rVert } \le {\lVert {a} \rVert } {\lVert {b} \rVert }$
for all
${\lVert {ab} \rVert } \le {\lVert {a} \rVert } {\lVert {b} \rVert }$
for all
![]() $a,b\in \mathcal {A}$
and
$a,b\in \mathcal {A}$
and
![]() ${\lVert {a^*a} \rVert } = {\lVert {a} \rVert }^2$
for all
${\lVert {a^*a} \rVert } = {\lVert {a} \rVert }^2$
for all
![]() $a\in \mathcal {A}$
.
$a\in \mathcal {A}$
.
The Gelfand–Naimark representation theorems [Reference Gelfand and Neumark6, Theorem 1 and Lemma 1] are cornerstones of the theory of
![]() $C^*$
-algebras and—together with the well-behaved spectral theory—make
$C^*$
-algebras and—together with the well-behaved spectral theory—make
![]() $C^*$
-algebras important tools in mathematical physics. In their simplest form, these two theorems state that all
$C^*$
-algebras important tools in mathematical physics. In their simplest form, these two theorems state that all
![]() $C^*$
-algebras have a faithful representation as
$C^*$
-algebras have a faithful representation as
![]() $^*$
-algebras of bounded operators on a Hilbert space, and that all commutative
$^*$
-algebras of bounded operators on a Hilbert space, and that all commutative
![]() $C^*$
-algebras have a faithful representation as
$C^*$
-algebras have a faithful representation as
![]() $^*$
-algebras of bounded complex-valued functions. This allows to interpret
$^*$
-algebras of bounded complex-valued functions. This allows to interpret
![]() $C^*$
-algebras as algebras of observables of physical systems: of quantum systems in general, and in the commutative case of classical systems. From this point of view, the perplexing differences between the description of quantum systems by means of operators on a Hilbert space, and of classical systems by functions on a smooth manifold, are just artifacts of the choice of two different ways to represent the observable algebras. Consequently, the problem of quantization, i.e., of finding a somehow suitable quantum system to a given classical one, can be formulated in a mathematically precise way, e.g., as finding deformations of commutative
$C^*$
-algebras as algebras of observables of physical systems: of quantum systems in general, and in the commutative case of classical systems. From this point of view, the perplexing differences between the description of quantum systems by means of operators on a Hilbert space, and of classical systems by functions on a smooth manifold, are just artifacts of the choice of two different ways to represent the observable algebras. Consequently, the problem of quantization, i.e., of finding a somehow suitable quantum system to a given classical one, can be formulated in a mathematically precise way, e.g., as finding deformations of commutative
![]() $C^*$
-algebras to noncommutative ones in the sense of [Reference Rieffel10].
$C^*$
-algebras to noncommutative ones in the sense of [Reference Rieffel10].
However, the restriction of the Gelfand–Naimark theorems to
![]() $C^*$
-algebras is unfortunate. While there obviously exist many interesting examples of
$C^*$
-algebras is unfortunate. While there obviously exist many interesting examples of
![]() $^*$
-algebras of functions or operators that are not
$^*$
-algebras of functions or operators that are not
![]() $C^*$
-algebras, and for which an abstract description might be desirable, the main motivation for generalizing the Gelfand–Naimark theorems might again come from physics: It is well known that some of the most basic
$C^*$
-algebras, and for which an abstract description might be desirable, the main motivation for generalizing the Gelfand–Naimark theorems might again come from physics: It is well known that some of the most basic
![]() $^*$
-algebras of observables that a (physics-)student gets to know in a course on quantum mechanics are far away from being
$^*$
-algebras of observables that a (physics-)student gets to know in a course on quantum mechanics are far away from being
![]() $C^*$
-algebras: If
$C^*$
-algebras: If
![]() $\mathcal {A}$
is a complex associative algebra with unit
$\mathcal {A}$
is a complex associative algebra with unit
![]() and
and
![]() $P,Q\in \mathcal {A}$
fulfil the canonical commutation relation
$P,Q\in \mathcal {A}$
fulfil the canonical commutation relation
![]() with
with
![]() $\lambda \in \mathbb{C}\setminus \{0\}$
, then the n-fold commutator of P with
$\lambda \in \mathbb{C}\setminus \{0\}$
, then the n-fold commutator of P with
![]() $Q^n$
fulfils the identity
$Q^n$
fulfils the identity
![]() for all
for all
![]() $n\in \mathbb{N}$
. Consequently, there cannot exist a nontrivial submultiplicative seminorm
$n\in \mathbb{N}$
. Consequently, there cannot exist a nontrivial submultiplicative seminorm
![]() ${\lVert { {\,\cdot \,} } \rVert }$
on
${\lVert { {\,\cdot \,} } \rVert }$
on
![]() $\mathcal {A}$
, because submultiplicativity would imply at most exponential growth with n of
$\mathcal {A}$
, because submultiplicativity would imply at most exponential growth with n of
![]() ${\lVert { [P,[P,\dots [P,Q^n]\dots ]] } \rVert }$
. This rules out any possibility to embed
${\lVert { [P,[P,\dots [P,Q^n]\dots ]] } \rVert }$
. This rules out any possibility to embed
![]() $\mathcal {A}$
in a
$\mathcal {A}$
in a
![]() $C^*$
-algebra, and also in many weaker types of topological
$C^*$
-algebra, and also in many weaker types of topological
![]() $^*$
-algebras like pro-
$^*$
-algebras like pro-
![]() $C^*$
-algebras, for which one can prove rather direct generalizations of the Gelfand–Naimark theorems. Note that faithful representations of
$C^*$
-algebras, for which one can prove rather direct generalizations of the Gelfand–Naimark theorems. Note that faithful representations of
![]() $^*$
-algebras of canonical commutation relations are well known and can be given, e.g., by differential operators. The problem is not to find faithful representations, but to find a sufficiently large class of
$^*$
-algebras of canonical commutation relations are well known and can be given, e.g., by differential operators. The problem is not to find faithful representations, but to find a sufficiently large class of
![]() $^*$
-algebras for which the existence of such faithful representations can be proved by general arguments.
$^*$
-algebras for which the existence of such faithful representations can be proved by general arguments.
This note gives a solution by focusing not so much on topological properties, but on order properties of
![]() $^*$
-algebras. This is motivated by [Reference Cimprič5], where it was shown that a suitable order on the Hermitian elements of a
$^*$
-algebras. This is motivated by [Reference Cimprič5], where it was shown that a suitable order on the Hermitian elements of a
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
allows to construct a
$\mathcal {A}$
allows to construct a
![]() $C^*$
-seminorm on the “bounded” elements of
$C^*$
-seminorm on the “bounded” elements of
![]() $\mathcal {A}$
, and by [Reference Schötz13], where the continuous calculus and the spectral theory of
$\mathcal {A}$
, and by [Reference Schötz13], where the continuous calculus and the spectral theory of
![]() $C^*$
-algebras have been extended to certain ordered
$C^*$
-algebras have been extended to certain ordered
![]() $^*$
-algebras. In Section 2, some basic definitions and results, mainly from locally convex analysis, are recapitulated. The general idea then is to follow the classical approach from [Reference Kadison8]: Section 3 develops the main result for ordered vector spaces, namely Theorem 3.7, which guarantees that on
$^*$
-algebras. In Section 2, some basic definitions and results, mainly from locally convex analysis, are recapitulated. The general idea then is to follow the classical approach from [Reference Kadison8]: Section 3 develops the main result for ordered vector spaces, namely Theorem 3.7, which guarantees that on
![]() $\sigma $
-bounded Archimedean ordered vector spaces, there exist many (extremal) positive linear functionals, and which considerably generalizes the result from [Reference Kadison8]. Here, an ordered vector space is called “
$\sigma $
-bounded Archimedean ordered vector spaces, there exist many (extremal) positive linear functionals, and which considerably generalizes the result from [Reference Kadison8]. Here, an ordered vector space is called “
![]() $\sigma $
-bounded” essentially if it contains an increasing sequence of positive elements that eventually becomes greater than every fixed element. Theorem 4.9 shows that every
$\sigma $
-bounded” essentially if it contains an increasing sequence of positive elements that eventually becomes greater than every fixed element. Theorem 4.9 shows that every
![]() $\sigma $
-bounded closed ordered
$\sigma $
-bounded closed ordered
![]() $^*$
-algebra can be represented faithfully as operators on a (pre-) Hilbert space, and Theorem 4.24 shows that in the commutative case, such algebras also admit a faithful representation as functions if an additional regularity condition (which is clearly necessary) is fulfilled.
$^*$
-algebra can be represented faithfully as operators on a (pre-) Hilbert space, and Theorem 4.24 shows that in the commutative case, such algebras also admit a faithful representation as functions if an additional regularity condition (which is clearly necessary) is fulfilled.
2 Preliminaries
The natural numbers are
![]() and
and
![]() , and the fields of real and complex numbers are denoted by
, and the fields of real and complex numbers are denoted by
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $\mathbb{C}$
, respectively. If X and Y are partially ordered sets (i.e., sets together with a reflexive, transitive, and antisymmetric relation
$\mathbb{C}$
, respectively. If X and Y are partially ordered sets (i.e., sets together with a reflexive, transitive, and antisymmetric relation
![]() $\le $
), then a map
$\le $
), then a map
![]() $\Phi \colon X \to Y$
is called increasing if
$\Phi \colon X \to Y$
is called increasing if
![]() $\Phi (x) \le \Phi (x')$
holds for all
$\Phi (x) \le \Phi (x')$
holds for all
![]() $x,x'\in X$
with
$x,x'\in X$
with
![]() $x\le x'$
. It is called an order embedding if it is increasing and if additionally
$x\le x'$
. It is called an order embedding if it is increasing and if additionally
![]() $x\le x'$
holds for all
$x\le x'$
holds for all
![]() $x,x'\in X$
for which
$x,x'\in X$
for which
![]() $\Phi (x) \le \Phi (x')$
. Note that an order embedding is injective. A partially ordered set X is called directed if, for all
$\Phi (x) \le \Phi (x')$
. Note that an order embedding is injective. A partially ordered set X is called directed if, for all
![]() $x,x' \in X$
, there exists a
$x,x' \in X$
, there exists a
![]() $y\in X$
such that
$y\in X$
such that
![]() $x\le y$
and
$x\le y$
and
![]() $x'\le y$
. Similarly, a subset S of a partially ordered set X is called directed if it is directed with respect to the order inherited from X. For two vector spaces V and W over the same field of scalars
$x'\le y$
. Similarly, a subset S of a partially ordered set X is called directed if it is directed with respect to the order inherited from X. For two vector spaces V and W over the same field of scalars
![]() $\mathbb{F}$
, the vector space of all linear maps from V to W is denoted by
$\mathbb{F}$
, the vector space of all linear maps from V to W is denoted by
![]() $\mathcal {L}(V,W)$
. In the special case that
$\mathcal {L}(V,W)$
. In the special case that
![]() $W = \mathbb{F}$
, we write
$W = \mathbb{F}$
, we write
![]() , the elements of
, the elements of
![]() $V^*$
are called linear functionals on V, and the evaluation of a linear functional
$V^*$
are called linear functionals on V, and the evaluation of a linear functional
![]() $\omega \in V^*$
on a vector
$\omega \in V^*$
on a vector
![]() $v\in V$
is denoted by means of the bilinear dual pairing
$v\in V$
is denoted by means of the bilinear dual pairing
![]() ${\langle \,{ {\,\cdot \,} } \,,\, { {\,\cdot \,} }\,\rangle } \colon V^*\times V \to \mathbb{F}$
,
${\langle \,{ {\,\cdot \,} } \,,\, { {\,\cdot \,} }\,\rangle } \colon V^*\times V \to \mathbb{F}$
,
![]() $(\omega ,v) \mapsto {\langle \,{\omega } \,,\, {v}\,\rangle }$
.
$(\omega ,v) \mapsto {\langle \,{\omega } \,,\, {v}\,\rangle }$
.
The main technical tools needed in the following are some basic theorems from locally convex analysis. A filter on a set X is a nonempty set
![]() $\mathcal {F}$
of subsets of X with the following two properties:
$\mathcal {F}$
of subsets of X with the following two properties:
-
• If
 $S,T \in \mathcal {F}$
, then
$S,T \in \mathcal {F}$
, then
 $S\cap T \in \mathcal {F}$
.
$S\cap T \in \mathcal {F}$
. -
• If
 $S \in \mathcal {F}$
and if a subset T of X fulfils
$S \in \mathcal {F}$
and if a subset T of X fulfils
 $T\supseteq S$
, then
$T\supseteq S$
, then
 $T\in \mathcal {F}$
.
$T\in \mathcal {F}$
.
Similarly, a basis of a filter on X is a nonempty set
![]() $\mathcal {E}$
of subsets of X such that for all
$\mathcal {E}$
of subsets of X such that for all
![]() $S,T\in \mathcal {E}$
, there exists an
$S,T\in \mathcal {E}$
, there exists an
![]() $R\in \mathcal {E}$
with
$R\in \mathcal {E}$
with
![]() $R\subseteq S\cap T$
. In this case,
$R\subseteq S\cap T$
. In this case,
is a filter on X, called the filter generated by
![]() $\mathcal {E}$
. A (real) topological vector space is a real vector space V endowed with a (not necessarily Hausdorff) topology under which addition
$\mathcal {E}$
. A (real) topological vector space is a real vector space V endowed with a (not necessarily Hausdorff) topology under which addition
![]() $V\times V \to V$
as well as scalar multiplication
$V\times V \to V$
as well as scalar multiplication
![]() $\mathbb{R} \times V \to V$
are continuous. Then it follows from the continuity of addition that a subset U of V is a neighborhood of a vector
$\mathbb{R} \times V \to V$
are continuous. Then it follows from the continuity of addition that a subset U of V is a neighborhood of a vector
![]() $v\in V$
if and only if
$v\in V$
if and only if
![]() is a neighborhood of
is a neighborhood of
![]() $0$
, so the topology of V is completely described by the
$0$
, so the topology of V is completely described by the
![]() $0$
-neighborhoods. The set
$0$
-neighborhoods. The set
![]() $\mathcal {N}_0$
of all
$\mathcal {N}_0$
of all
![]() $0$
-neighborhoods of V is a filter on V, and
$0$
-neighborhoods of V is a filter on V, and
![]() $\mathcal {N}_{0,\mathrm {conv}}$
, the set of all convex
$\mathcal {N}_{0,\mathrm {conv}}$
, the set of all convex
![]() $0$
-neighborhoods of V, is a basis of a filter on V. In general,
$0$
-neighborhoods of V, is a basis of a filter on V. In general,
![]() ${\langle \!\langle \,{\mathcal {N}_{0,\mathrm {conv}}}\,\rangle \!\rangle _{\mathrm {fltr}}} \subseteq \mathcal {N}_0$
holds, and V is called a (real) locally convex vector space if even
${\langle \!\langle \,{\mathcal {N}_{0,\mathrm {conv}}}\,\rangle \!\rangle _{\mathrm {fltr}}} \subseteq \mathcal {N}_0$
holds, and V is called a (real) locally convex vector space if even
![]() ${\langle \!\langle \,{\mathcal {N}_{0,\mathrm {conv}}}\,\rangle \!\rangle _{\mathrm {fltr}}} = \mathcal {N}_0$
, i.e., if the filter of
${\langle \!\langle \,{\mathcal {N}_{0,\mathrm {conv}}}\,\rangle \!\rangle _{\mathrm {fltr}}} = \mathcal {N}_0$
, i.e., if the filter of
![]() $0$
-neighborhoods of V is generated by the convex
$0$
-neighborhoods of V is generated by the convex
![]() $0$
-neighborhoods. A locally convex topology on V is a topology with which V becomes a locally convex vector space.
$0$
-neighborhoods. A locally convex topology on V is a topology with which V becomes a locally convex vector space.
There is an easy procedure to construct locally convex topologies on a real vector space V: A subset S of V is called absorbing if, for every
![]() $v\in V$
, there is a
$v\in V$
, there is a
![]() $\lambda \in {]0,\infty [}$
such that
$\lambda \in {]0,\infty [}$
such that
![]() $\lambda v \in S$
, and it is called balanced if
$\lambda v \in S$
, and it is called balanced if
![]() $\lambda s \in S$
for all
$\lambda s \in S$
for all
![]() $s\in S$
and all
$s\in S$
and all
![]() $\lambda \in {[-1,1]}$
. If
$\lambda \in {[-1,1]}$
. If
![]() $\mathcal {N}_{0,\mathrm {abc}}$
is a basis of a filter on V consisting of only absorbing balanced convex subsets of V, then its generated filter
$\mathcal {N}_{0,\mathrm {abc}}$
is a basis of a filter on V consisting of only absorbing balanced convex subsets of V, then its generated filter
![]() ${\langle \!\langle \,{\mathcal {N}_{0,\mathrm {abc}}}\,\rangle \!\rangle _{\mathrm {fltr}}}$
is the filter of
${\langle \!\langle \,{\mathcal {N}_{0,\mathrm {abc}}}\,\rangle \!\rangle _{\mathrm {fltr}}}$
is the filter of
![]() $0$
-neighborhoods of a locally convex topology on V. Note that every absorbing balanced convex subset S of V yields a seminorm
$0$
-neighborhoods of a locally convex topology on V. Note that every absorbing balanced convex subset S of V yields a seminorm
![]() ${\lVert { {\,\cdot \,} } \rVert }_{S}$
on V by setting
${\lVert { {\,\cdot \,} } \rVert }_{S}$
on V by setting
![]() for all
for all
![]() $v\in V$
, which is the Minkowski functional of S. Conversely, for every seminorm
$v\in V$
, which is the Minkowski functional of S. Conversely, for every seminorm
![]() ${\lVert { {\,\cdot \,} } \rVert }$
on V, the unit ball
${\lVert { {\,\cdot \,} } \rVert }$
on V, the unit ball
![]() is an absorbing balanced convex subset of V whose Minkowski functional is again the original seminorm
is an absorbing balanced convex subset of V whose Minkowski functional is again the original seminorm
![]() ${\lVert { {\,\cdot \,} } \rVert }$
. However, the map from absorbing balanced convex subsets of V to seminorms on V is only surjective, but not injective in general. Because of this, there is more freedom in describing locally convex vector spaces via a basis of the filter of
${\lVert { {\,\cdot \,} } \rVert }$
. However, the map from absorbing balanced convex subsets of V to seminorms on V is only surjective, but not injective in general. Because of this, there is more freedom in describing locally convex vector spaces via a basis of the filter of
![]() $0$
-neighborhoods than via the corresponding seminorms.
$0$
-neighborhoods than via the corresponding seminorms.
An important example of Hausdorff locally convex vector spaces is the dual space
![]() $V^*$
of an arbitrary real vector space V with the weak-
$V^*$
of an arbitrary real vector space V with the weak-
![]() $^*$
-topology, i.e., with the weakest topology on
$^*$
-topology, i.e., with the weakest topology on
![]() $V^*$
under which all the evaluation maps
$V^*$
under which all the evaluation maps
![]() $V^* \ni \omega \mapsto {\langle \,{\omega } \,,\, {v}\,\rangle } \in \mathbb{R}$
with vectors
$V^* \ni \omega \mapsto {\langle \,{\omega } \,,\, {v}\,\rangle } \in \mathbb{R}$
with vectors
![]() $v\in V$
are continuous. This is the locally convex topology whose filter of
$v\in V$
are continuous. This is the locally convex topology whose filter of
![]() $0$
-neighborhoods is generated by the intersections of unit balls of finitely many seminorms of the form
$0$
-neighborhoods is generated by the intersections of unit balls of finitely many seminorms of the form
![]() $V^* \ni \omega \mapsto {\lvert {{\langle \,{\omega } \,,\, {v}\,\rangle }} \rvert } \in {[0,\infty [}$
with
$V^* \ni \omega \mapsto {\lvert {{\langle \,{\omega } \,,\, {v}\,\rangle }} \rvert } \in {[0,\infty [}$
with
![]() $v\in V$
.
$v\in V$
.
The following classical theorems will be crucial for the various representation theorems. As usual, for such results, their proofs typically make use of the axiom of choice.
Theorem 2.1 (Hahn–Banach)
Let V be a (real) locally convex vector space, let C be a closed and convex subset of V, and let
![]() $v \in V\setminus C$
. Then there exists a continuous linear functional
$v \in V\setminus C$
. Then there exists a continuous linear functional
![]() $\omega $
on V such that the inequality
$\omega $
on V such that the inequality
![]() ${\langle \,{\omega } \,,\, {c}\,\rangle } \ge 1+{\langle \,{\omega } \,,\, {v}\,\rangle }$
holds for all
${\langle \,{\omega } \,,\, {c}\,\rangle } \ge 1+{\langle \,{\omega } \,,\, {v}\,\rangle }$
holds for all
![]() $c\in C$
.
$c\in C$
.
Theorem 2.2 (Banach–Alaoglu)
Let V be a real vector space, and let U be an absorbing subset of V, then
is a convex subset of
![]() $V^*$
and compact in the weak-
$V^*$
and compact in the weak-
![]() $^*$
-topology.
$^*$
-topology.
If C is a convex subset of a real vector space V, then an extreme point of C is an element
![]() $e\in C$
with the following property: Whenever
$e\in C$
with the following property: Whenever
![]() $e = \lambda c_1 + (1-\lambda ) c_2$
holds for some
$e = \lambda c_1 + (1-\lambda ) c_2$
holds for some
![]() $c_1,c_2\in C$
and
$c_1,c_2\in C$
and
![]() $\lambda \in {]0,1[}$
, then
$\lambda \in {]0,1[}$
, then
![]() $e=c_1 = c_2$
. The set of all extreme points of C will be denoted by
$e=c_1 = c_2$
. The set of all extreme points of C will be denoted by
![]() $\mathrm {ex}(C)$
. Moreover, if V is a locally convex vector space and S a nonempty subset of V, then
$\mathrm {ex}(C)$
. Moreover, if V is a locally convex vector space and S a nonempty subset of V, then
![]() ${\langle \!\langle \,{S}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
will denote the closed convex hull of S, i.e., the closure of the convex hull of S, or equivalently, the intersection of all closed convex subsets of V which contain S. In the special case that V is a real vector space and S a nonempty subset of
${\langle \!\langle \,{S}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
will denote the closed convex hull of S, i.e., the closure of the convex hull of S, or equivalently, the intersection of all closed convex subsets of V which contain S. In the special case that V is a real vector space and S a nonempty subset of
![]() $V^*$
, then
$V^*$
, then
![]() ${\langle \!\langle \,{S}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
is understood to be the closed convex hull of S with respect to the weak-
${\langle \!\langle \,{S}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
is understood to be the closed convex hull of S with respect to the weak-
![]() $^*$
-topology and
$^*$
-topology and
holds. This can be seen either by elementary linear algebra or as a consequence of the Hahn–Banach Theorem and the fact that all weak-
![]() $^*$
-continuous linear functionals on
$^*$
-continuous linear functionals on
![]() $V^*$
can be expressed as maps
$V^*$
can be expressed as maps
![]() $V^* \ni \omega \mapsto {\langle \,{\omega } \,,\, {v}\,\rangle } \in \mathbb{R}$
with a suitable vector
$V^* \ni \omega \mapsto {\langle \,{\omega } \,,\, {v}\,\rangle } \in \mathbb{R}$
with a suitable vector
![]() $v\in V$
.
$v\in V$
.
Theorem 2.3 (Krein–Milman)
Let V be a real vector space, and let K be a weak-
![]() $^*$
-compact and convex subset of
$^*$
-compact and convex subset of
![]() $V^*$
, then
$V^*$
, then
![]() $K = {\langle \!\langle \,{\mathrm {ex}(K)}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
.
$K = {\langle \!\langle \,{\mathrm {ex}(K)}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
.
The tools needed to prove the generalized Gelfand–Naimark theorems are essentially results about the existence of many (extremal) positive linear functionals on ordered vector spaces.
An ordered vector space is a real vector space V endowed with a partial order
![]() $\le $
such that the conditions
$\le $
such that the conditions
hold for all
![]() $u,v,w\in V$
with
$u,v,w\in V$
with
![]() $v\le w$
and all
$v\le w$
and all
![]() $\lambda \in {[0,\infty [}$
. Then
$\lambda \in {[0,\infty [}$
. Then
![]() is the set of positive elements of V, which uniquely determines the order on V because
is the set of positive elements of V, which uniquely determines the order on V because
![]() $v \le w$
is equivalent to
$v \le w$
is equivalent to
![]() $w-v\in V^+$
for all
$w-v\in V^+$
for all
![]() $v,w\in V$
. An ordered vector space V is called Archimedean if it has the following property: Whenever
$v,w\in V$
. An ordered vector space V is called Archimedean if it has the following property: Whenever
![]() $v\le \epsilon w$
holds for two vectors
$v\le \epsilon w$
holds for two vectors
![]() $v\in V$
,
$v\in V$
,
![]() $w\in V^+$
, and all
$w\in V^+$
, and all
![]() $\epsilon \in {]0,\infty [}$
, then
$\epsilon \in {]0,\infty [}$
, then
![]() $v\le 0$
. Note also that an ordered vector space V is directed if and only if every
$v\le 0$
. Note also that an ordered vector space V is directed if and only if every
![]() $v\in V$
can be decomposed as
$v\in V$
can be decomposed as
![]() $v = v_{(+)} - v_{(-)}$
with
$v = v_{(+)} - v_{(-)}$
with
![]() $v_{(+)}, v_{(-)} \in V^+$
. Of course, such a decomposition is not uniquely determined in general.
$v_{(+)}, v_{(-)} \in V^+$
. Of course, such a decomposition is not uniquely determined in general.
If V and W are ordered vector spaces, then a linear map
![]() $\Phi \colon V\to W$
is increasing if and only if
$\Phi \colon V\to W$
is increasing if and only if
![]() $\Phi (v) \in W^+$
for all
$\Phi (v) \in W^+$
for all
![]() $v\in V^+$
. We write
$v\in V^+$
. We write
![]() $\mathcal {L}(V,W)^+$
for the set of all increasing linear maps from V to W. If V is directed, then there actually exists a (unique) partial order on
$\mathcal {L}(V,W)^+$
for the set of all increasing linear maps from V to W. If V is directed, then there actually exists a (unique) partial order on
![]() $\mathcal {L}(V,W)$
such that
$\mathcal {L}(V,W)$
such that
![]() $\mathcal {L}(V,W)$
becomes an ordered vector space whose positive elements are precisely the increasing linear functions. However, for simplicity, a linear map
$\mathcal {L}(V,W)$
becomes an ordered vector space whose positive elements are precisely the increasing linear functions. However, for simplicity, a linear map
![]() $\Phi \colon V \to W$
will always be called positive if it is increasing, also in the case that V is not necessarily directed. Note that a positive linear map
$\Phi \colon V \to W$
will always be called positive if it is increasing, also in the case that V is not necessarily directed. Note that a positive linear map
![]() $\Phi \colon V\to W$
is an order embedding if and only if
$\Phi \colon V\to W$
is an order embedding if and only if
![]() $\Phi (v) \in W\setminus W^+$
for all
$\Phi (v) \in W\setminus W^+$
for all
![]() $v\in V \setminus V^+$
. The case that
$v\in V \setminus V^+$
. The case that
![]() $W=\mathbb{R}$
will be especially interesting: Then the set of positive linear functionals is denoted by
$W=\mathbb{R}$
will be especially interesting: Then the set of positive linear functionals is denoted by
If V is directed, then
![]() $V^*$
is an ordered vector space itself and a positive linear functional
$V^*$
is an ordered vector space itself and a positive linear functional
![]() $\omega $
on V is said to be extremal if, for every
$\omega $
on V is said to be extremal if, for every
![]() $\rho \in V^{*,+}$
with
$\rho \in V^{*,+}$
with
![]() $\rho \le \omega $
, there is an
$\rho \le \omega $
, there is an
![]() $\mu \in {[0,1]}$
such that
$\mu \in {[0,1]}$
such that
![]() $\rho = \mu \omega $
. The set of all extremal positive linear functionals on V will then be denoted by
$\rho = \mu \omega $
. The set of all extremal positive linear functionals on V will then be denoted by
![]() $V^{*,+,\mathrm {ex}}$
, and one can check that
$V^{*,+,\mathrm {ex}}$
, and one can check that
![]() $0\in V^{*,+,\mathrm {ex}}$
and
$0\in V^{*,+,\mathrm {ex}}$
and
![]() $\lambda \omega \in V^{*,+,\mathrm {ex}}$
for all
$\lambda \omega \in V^{*,+,\mathrm {ex}}$
for all
![]() $\omega \in V^{*,+,\mathrm {ex}}$
and all
$\omega \in V^{*,+,\mathrm {ex}}$
and all
![]() $\lambda \in {]0,\infty [}$
. Note that this definition of extremal positive linear functionals only makes sense on a directed ordered vector space V because it refers to the partial order on
$\lambda \in {]0,\infty [}$
. Note that this definition of extremal positive linear functionals only makes sense on a directed ordered vector space V because it refers to the partial order on
![]() $V^*$
. There is an extension theorem for (extremal) positive linear functionals from a sufficiently large linear subspace of a directed ordered vector space to the whole space (see [Reference Schmüdgen12, Lemma 1.3.2] for details)
$V^*$
. There is an extension theorem for (extremal) positive linear functionals from a sufficiently large linear subspace of a directed ordered vector space to the whole space (see [Reference Schmüdgen12, Lemma 1.3.2] for details)
Theorem 2.4 (Extension theorem)
Let V be a directed ordered vector space, and let S be a linear subspace of V with the property that for every
![]() $v\in V$
, there exists an
$v\in V$
, there exists an
![]() $s\in S$
such that
$s\in S$
such that
![]() $0\le s$
and
$0\le s$
and
![]() $v\le s$
. Then S with the order inherited from V is a directed ordered vector space, and for every
$v\le s$
. Then S with the order inherited from V is a directed ordered vector space, and for every
![]() $\tilde {\omega } \in S^{*,+}$
, there exists an
$\tilde {\omega } \in S^{*,+}$
, there exists an
![]() $\omega \in V^{*,+}$
that extends
$\omega \in V^{*,+}$
that extends
![]() $\tilde {\omega }$
, i.e., that fulfils
$\tilde {\omega }$
, i.e., that fulfils
![]() ${\langle \,{\omega } \,,\, {s}\,\rangle } = {\langle \,{\tilde {\omega }} \,,\, {s}\,\rangle }$
for all
${\langle \,{\omega } \,,\, {s}\,\rangle } = {\langle \,{\tilde {\omega }} \,,\, {s}\,\rangle }$
for all
![]() $s\in S$
. Moreover, in the case that
$s\in S$
. Moreover, in the case that
![]() $\tilde {\omega } \in S^{*,+,\mathrm {ex}}$
, there even exists
$\tilde {\omega } \in S^{*,+,\mathrm {ex}}$
, there even exists
![]() $\omega \in V^{*,+,\mathrm {ex}}$
that extends
$\omega \in V^{*,+,\mathrm {ex}}$
that extends
![]() $\tilde {\omega }$
.
$\tilde {\omega }$
.
The question of existence of many (extremal) positive linear functionals is nontrivial in general. More precisely, one asks whether or not the following two properties are fulfilled.
Definition 2.1 Let V be an ordered vector space, then we say that the order on V is induced by its positive linear functionals if, for all
![]() $v \in V\setminus V^+$
, there is an
$v \in V\setminus V^+$
, there is an
![]() $\omega \in V^{*,+}$
such that
$\omega \in V^{*,+}$
such that
![]() ${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
.
${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
.
Definition 2.2 Let V be a directed ordered vector space, then we say that the order on V is induced by its extremal positive linear functionals if, for all
![]() $v \in V\setminus V^+$
, there is an
$v \in V\setminus V^+$
, there is an
![]() $\omega \in V^{*,+,\mathrm {ex}}$
such that
$\omega \in V^{*,+,\mathrm {ex}}$
such that
![]() ${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
.
${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
.
These two conditions are equivalent to demanding that, for every
![]() $v\in V$
, the inequality
$v\in V$
, the inequality
![]() $0 \le v$
holds if and only if
$0 \le v$
holds if and only if
![]() $0\le {\langle \,{\omega } \,,\, {v}\,\rangle }$
for all
$0\le {\langle \,{\omega } \,,\, {v}\,\rangle }$
for all
![]() $\omega \in V^{*,+}$
or for all
$\omega \in V^{*,+}$
or for all
![]() $\omega \in V^{*,+, \mathrm {ex}}$
, respectively.
$\omega \in V^{*,+, \mathrm {ex}}$
, respectively.
We will see shortly that the above conditions of existence of “many” (extremal) positive linear functionals are closely related to the properties of certain locally convex topologies: Given two elements
![]() $\ell $
and u of an ordered vector space V, then the order interval between
$\ell $
and u of an ordered vector space V, then the order interval between
![]() $\ell $
and u is defined as
$\ell $
and u is defined as
![]() . Moreover, a subset S of V is called saturated if
. Moreover, a subset S of V is called saturated if
![]() $[\ell , u] \subseteq S$
is fulfilled for all
$[\ell , u] \subseteq S$
is fulfilled for all
![]() $\ell , u\in S$
with
$\ell , u\in S$
with
![]() $\ell \le u$
. For example, every order interval is saturated. It is not hard to see that the intersection of finitely many (or arbitrarily many) saturated subsets of an ordered vector space V is again saturated. As a consequence, the set of all absorbing balanced convex and saturated subsets of V is a basis of the filter of
$\ell \le u$
. For example, every order interval is saturated. It is not hard to see that the intersection of finitely many (or arbitrarily many) saturated subsets of an ordered vector space V is again saturated. As a consequence, the set of all absorbing balanced convex and saturated subsets of V is a basis of the filter of
![]() $0$
-neighborhoods of a locally convex topology.
$0$
-neighborhoods of a locally convex topology.
Definition 2.3 Let V be an ordered vector space, then the normal topology on V is the locally convex topology whose filter of
![]() $0$
-neighborhoods is generated by the absorbing balanced convex and saturated subsets of V.
$0$
-neighborhoods is generated by the absorbing balanced convex and saturated subsets of V.
This topology is not unknown in the theory of ordered vector spaces and
![]() $^*$
-algebras. For example, the normal topology is essentially the topology
$^*$
-algebras. For example, the normal topology is essentially the topology
![]() $\tau _n$
in [Reference Schmüdgen12, Section 1.5].
$\tau _n$
in [Reference Schmüdgen12, Section 1.5].
3 Existence of extremal positive linear functionals
Lemma 3.1 is a standard application of the Hahn–Banach theorem, and a proof is given for convenience of the reader.
Lemma 3.1 Let V be an ordered vector space, and assume that there is a locally convex topology
![]() $\tau $
on V such that
$\tau $
on V such that
![]() $V^+$
is closed with respect to
$V^+$
is closed with respect to
![]() $\tau $
. Then, for every
$\tau $
. Then, for every
![]() $v\in V \setminus V^+$
, there exists a positive linear functional
$v\in V \setminus V^+$
, there exists a positive linear functional
![]() $\omega $
on V that fulfils
$\omega $
on V that fulfils
![]() ${\langle \,{\omega } \,,\, {v}\,\rangle }< 0$
and that is continuous with respect to
${\langle \,{\omega } \,,\, {v}\,\rangle }< 0$
and that is continuous with respect to
![]() $\tau $
.
$\tau $
.
Proof As
![]() $V^+$
is convex and closed with respect to
$V^+$
is convex and closed with respect to
![]() $\tau $
, the Hahn-Banach theorem implies that, for every
$\tau $
, the Hahn-Banach theorem implies that, for every
![]() $v\in V\setminus V^+$
, there exists a linear functional
$v\in V\setminus V^+$
, there exists a linear functional
![]() $\omega \in V^*$
that fulfils
$\omega \in V^*$
that fulfils
![]() ${\langle \,{\omega } \,,\, {c}\,\rangle } \ge 1+ {\langle \,{\omega } \,,\, {v}\,\rangle }$
for all
${\langle \,{\omega } \,,\, {c}\,\rangle } \ge 1+ {\langle \,{\omega } \,,\, {v}\,\rangle }$
for all
![]() $c\in V^+$
and that is continuous with respect to
$c\in V^+$
and that is continuous with respect to
![]() $\tau $
. From
$\tau $
. From
![]() $0\in V^+$
, it follows that
$0\in V^+$
, it follows that
![]() $-1 \ge {\langle \,{\omega } \,,\, {v}\,\rangle }$
. Moreover,
$-1 \ge {\langle \,{\omega } \,,\, {v}\,\rangle }$
. Moreover,
![]() ${\langle \,{\omega } \,,\, {c}\,\rangle } \ge 0$
holds for all
${\langle \,{\omega } \,,\, {c}\,\rangle } \ge 0$
holds for all
![]() $c\in V^+$
, and hence
$c\in V^+$
, and hence
![]() $\omega \in V^{*,+}$
: Indeed, if there was some
$\omega \in V^{*,+}$
: Indeed, if there was some
![]() $c\in V^+$
with
$c\in V^+$
with
![]() ${\langle \,{\omega } \,,\, {c}\,\rangle }<0$
, then
${\langle \,{\omega } \,,\, {c}\,\rangle }<0$
, then
![]() ${\langle \,{\omega } \,,\, {\lambda c}\,\rangle } = {\langle \,{\omega } \,,\, {v}\,\rangle }$
with
${\langle \,{\omega } \,,\, {\lambda c}\,\rangle } = {\langle \,{\omega } \,,\, {v}\,\rangle }$
with
![]() , which yields a contradiction because
, which yields a contradiction because
![]() $\lambda \in {]0,\infty [}$
by construction, and hence
$\lambda \in {]0,\infty [}$
by construction, and hence
![]() $\lambda c\in V^+$
.
$\lambda c\in V^+$
.
Proposition 3.2 Let V be an ordered vector space, then the order on V is induced by its positive linear functionals if and only if
![]() $V^+$
is closed in V with respect to the normal topology.
$V^+$
is closed in V with respect to the normal topology.
Proof If
![]() $V^+$
is closed in V with respect to the normal topology, then the order on V is induced by its positive linear functionals as an immediate consequence of Lemma 3.1. Conversely, assume that the order on V is induced by its positive linear functionals, and let
$V^+$
is closed in V with respect to the normal topology, then the order on V is induced by its positive linear functionals as an immediate consequence of Lemma 3.1. Conversely, assume that the order on V is induced by its positive linear functionals, and let
![]() $v\in V\setminus V^+$
be given. Then there exists
$v\in V\setminus V^+$
be given. Then there exists
![]() $\omega \in V^{*,+}$
such that
$\omega \in V^{*,+}$
such that
![]() ${\langle \,{\omega } \,,\, {v}\,\rangle }=-1$
and
${\langle \,{\omega } \,,\, {v}\,\rangle }=-1$
and
![]() is an absorbing balanced convex and saturated subset of V, so
is an absorbing balanced convex and saturated subset of V, so
![]() $v+U$
is a neighborhood of v with respect to the normal topology. Moreover, application of
$v+U$
is a neighborhood of v with respect to the normal topology. Moreover, application of
![]() $\omega $
shows that
$\omega $
shows that
![]() $(v+U) \cap V^+ = \emptyset $
holds, so
$(v+U) \cap V^+ = \emptyset $
holds, so
![]() $V^+$
is closed.
$V^+$
is closed.
For finding a sufficient condition under which the order of a directed ordered vector space is induced by its extremal positive linear functionals, it will be helpful to be able to decompose a positive linear functional into extremal ones. We follow essentially the argument of [Reference Schmüdgen12, Lemmas 12.4.3 and 12.4.4].
Proposition 3.3 Let V be a directed ordered vector space, and let U be an absorbing balanced and directed subset of V. Write K for the set of all those
![]() $\omega \in V^{*,+}$
that fulfil
$\omega \in V^{*,+}$
that fulfil
![]() ${\langle \,{\omega } \,,\, {u}\,\rangle } \le 1$
for all
${\langle \,{\omega } \,,\, {u}\,\rangle } \le 1$
for all
![]() $u\in U$
, then K is weak-
$u\in U$
, then K is weak-
![]() $^*$
-compact and
$^*$
-compact and
![]() $K = {\langle \!\langle \,{K\cap V^{*,+,\mathrm {ex}}}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
.
$K = {\langle \!\langle \,{K\cap V^{*,+,\mathrm {ex}}}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
.
Proof First, note that
![]() $K = U^\circ \cap V^{*,+}$
with
$K = U^\circ \cap V^{*,+}$
with
![]() $U^\circ $
like in (2.2) because U is balanced. As
$U^\circ $
like in (2.2) because U is balanced. As
![]() $U^\circ $
is convex and weak-
$U^\circ $
is convex and weak-
![]() $^*$
-compact by the Banach–Alaoglu theorem, and as
$^*$
-compact by the Banach–Alaoglu theorem, and as
![]() $V^{*,+}$
is convex and weak-
$V^{*,+}$
is convex and weak-
![]() $^*$
-closed in
$^*$
-closed in
![]() $V^*$
, it follows that K is also convex and weak-
$V^*$
, it follows that K is also convex and weak-
![]() $^*$
-compact. The Krein–Milman theorem then shows that
$^*$
-compact. The Krein–Milman theorem then shows that
![]() $K = {\langle \!\langle \,{\mathrm {ex}(K)}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
.
$K = {\langle \!\langle \,{\mathrm {ex}(K)}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
.
In order to complete the proof, it is sufficient to show that
![]() $\mathrm {ex}(K) \subseteq V^{*,+,\mathrm {ex}}$
. Denote the linear span of K in
$\mathrm {ex}(K) \subseteq V^{*,+,\mathrm {ex}}$
. Denote the linear span of K in
![]() $V^*$
by W. Then the map
$V^*$
by W. Then the map
![]() $h \colon W \to {[0,\infty [}$
$h \colon W \to {[0,\infty [}$
is a seminorm on W and
![]() $K = {\{\,{\omega \in W\cap V^{*,+}} \; |\; {h(\omega ) \le 1}\,\}}$
. Moreover, as U is balanced and directed,
$K = {\{\,{\omega \in W\cap V^{*,+}} \; |\; {h(\omega ) \le 1}\,\}}$
. Moreover, as U is balanced and directed,
![]() $h(\omega + \omega ') \ge h(\omega ) + h(\omega ')$
, hence
$h(\omega + \omega ') \ge h(\omega ) + h(\omega ')$
, hence
![]() $h(\omega + \omega ') = h(\omega ) + h(\omega ')$
, holds for all
$h(\omega + \omega ') = h(\omega ) + h(\omega ')$
, holds for all
![]() $\omega ,\omega ' \in W \cap V^{*,+}$
.
$\omega ,\omega ' \in W \cap V^{*,+}$
.
Now, let
![]() $\omega \in \mathrm {ex}(K)$
be given. If
$\omega \in \mathrm {ex}(K)$
be given. If
![]() $h(\omega ) = 0$
, then
$h(\omega ) = 0$
, then
![]() $\omega = 0$
because U is absorbing, so
$\omega = 0$
because U is absorbing, so
![]() $\omega \in V^{*,+,\mathrm {ex}}$
is trivially fulfilled. Otherwise,
$\omega \in V^{*,+,\mathrm {ex}}$
is trivially fulfilled. Otherwise,
![]() $h(\omega ) = 1$
because on the one hand,
$h(\omega ) = 1$
because on the one hand,
![]() $h(\omega ) \le 1$
is clear, and on the other,
$h(\omega ) \le 1$
is clear, and on the other,
![]() $\omega = h(\omega ) \big ( h(\omega )^{-1} \omega \big ) + \big (1-h(\omega )\big ) 0$
is a representation of
$\omega = h(\omega ) \big ( h(\omega )^{-1} \omega \big ) + \big (1-h(\omega )\big ) 0$
is a representation of
![]() $\omega $
as a convex combination of the two elements
$\omega $
as a convex combination of the two elements
![]() $h(\omega )^{-1} \omega $
and
$h(\omega )^{-1} \omega $
and
![]() $0$
of K, which excludes the possibility that
$0$
of K, which excludes the possibility that
![]() $h(\omega ) \in {]0,1[}$
. In this second case that
$h(\omega ) \in {]0,1[}$
. In this second case that
![]() $h(\omega )=1$
, consider some
$h(\omega )=1$
, consider some
![]() $\rho \in V^{*,+}$
that fulfils
$\rho \in V^{*,+}$
that fulfils
![]() $\rho \le \omega $
. Then, for all
$\rho \le \omega $
. Then, for all
![]() $u\in U$
, there exists
$u\in U$
, there exists
![]() $v \in U \cap V^+$
such that
$v \in U \cap V^+$
such that
![]() $u \le v$
because U is directed, and hence
$u \le v$
because U is directed, and hence
![]() ${\langle \,{\rho } \,,\, {u}\,\rangle } \le {\langle \,{\rho } \,,\, {v}\,\rangle } \le {\langle \,{\omega } \,,\, {v}\,\rangle }\le 1$
. This means
${\langle \,{\rho } \,,\, {u}\,\rangle } \le {\langle \,{\rho } \,,\, {v}\,\rangle } \le {\langle \,{\omega } \,,\, {v}\,\rangle }\le 1$
. This means
![]() $\rho \in K$
, and the same estimate with
$\rho \in K$
, and the same estimate with
![]() $\omega - \rho $
in place of
$\omega - \rho $
in place of
![]() $\rho $
shows that
$\rho $
shows that
![]() $\omega -\rho \in K$
as well. If
$\omega -\rho \in K$
as well. If
![]() $h(\rho ) = 0$
or
$h(\rho ) = 0$
or
![]() $h(\omega -\rho ) = 0$
, then
$h(\omega -\rho ) = 0$
, then
![]() $\rho = \mu \omega $
with
$\rho = \mu \omega $
with
![]() $\mu = 0$
or
$\mu = 0$
or
![]() $\mu = 1$
, respectively. Otherwise,
$\mu = 1$
, respectively. Otherwise,
![]() $\omega = h(\rho ) \big ( h(\rho )^{-1} \rho \big ) + h(\omega -\rho ) \big ( h(\omega -\rho )^{-1} (\omega -\rho ) \big )$
is a representation of
$\omega = h(\rho ) \big ( h(\rho )^{-1} \rho \big ) + h(\omega -\rho ) \big ( h(\omega -\rho )^{-1} (\omega -\rho ) \big )$
is a representation of
![]() $\omega $
as a nontrivial convex combination of the two elements
$\omega $
as a nontrivial convex combination of the two elements
![]() $h(\rho )^{-1} \rho $
and
$h(\rho )^{-1} \rho $
and
![]() $h(\omega -\rho )^{-1} (\omega -\rho )$
of K; therefore,
$h(\omega -\rho )^{-1} (\omega -\rho )$
of K; therefore,
![]() $\rho = \mu \omega $
with
$\rho = \mu \omega $
with
![]() $\mu = h(\rho )$
. We conclude that
$\mu = h(\rho )$
. We conclude that
![]() $\omega \in V^{*,+,\mathrm {ex}}$
in this case as well.
$\omega \in V^{*,+,\mathrm {ex}}$
in this case as well.
Corollary 3.4 Let V be a directed ordered vector space. If there exists a locally convex topology
![]() $\tau $
on V whose filter of
$\tau $
on V whose filter of
![]() $0$
-neighborhoods has a basis consisting of absorbing balanced convex and saturated as well as directed subsets of V and with respect to which
$0$
-neighborhoods has a basis consisting of absorbing balanced convex and saturated as well as directed subsets of V and with respect to which
![]() $V^+$
is closed, then the order on V is induced by its extremal positive linear functionals.
$V^+$
is closed, then the order on V is induced by its extremal positive linear functionals.
Proof Given
![]() $v\in V\setminus V^+$
, then Lemma 3.1 shows that there exists a positive linear functional
$v\in V\setminus V^+$
, then Lemma 3.1 shows that there exists a positive linear functional
![]() $\omega $
on V such that
$\omega $
on V such that
![]() ${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
and that is continuous with respect to
${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
and that is continuous with respect to
![]() $\tau $
. Continuity of
$\tau $
. Continuity of
![]() $\omega $
implies that there exists an absorbing balanced convex and saturated as well as directed subset U of V such that
$\omega $
implies that there exists an absorbing balanced convex and saturated as well as directed subset U of V such that
![]() ${\lvert {{\langle \,{\omega } \,,\, {u}\,\rangle }} \rvert } \le 1$
for all
${\lvert {{\langle \,{\omega } \,,\, {u}\,\rangle }} \rvert } \le 1$
for all
![]() $u\in U$
. Define the set
$u\in U$
. Define the set
![]() like in Proposition 3.3, then
like in Proposition 3.3, then
![]() $\omega \in K = {\langle \!\langle \,{K\cap V^{*,+,\mathrm {ex}}}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
, and equation (2.3) shows that there necessarily exists a
$\omega \in K = {\langle \!\langle \,{K\cap V^{*,+,\mathrm {ex}}}\,\rangle \!\rangle _{\mathrm {cl\text {-}conv}}}$
, and equation (2.3) shows that there necessarily exists a
![]() $\rho \in K\cap V^{*,+,\mathrm {ex}}$
that also fulfils
$\rho \in K\cap V^{*,+,\mathrm {ex}}$
that also fulfils
![]() ${\langle \,{\rho } \,,\, {v} \,\rangle } < 0$
.
${\langle \,{\rho } \,,\, {v} \,\rangle } < 0$
.
There is a rather large class of ordered vector spaces for which the normal topology cannot only be described explicitly, but also allows to apply Corollary 3.4.
Definition 3.1 An ordered vector space V is said to be
![]() $\sigma $
-bounded if there exists an increasing sequence
$\sigma $
-bounded if there exists an increasing sequence
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
in
$(\hat {v}_n)_{n\in \mathbb{N}}$
in
![]() $V^+$
with the property that, for all
$V^+$
with the property that, for all
![]() $v\in V$
, there is an
$v\in V$
, there is an
![]() $n\in \mathbb{N}$
such that
$n\in \mathbb{N}$
such that
![]() $-\hat {v}_n \le v \le \hat {v}_n$
holds. Such a sequence will be called a dominating sequence.
$-\hat {v}_n \le v \le \hat {v}_n$
holds. Such a sequence will be called a dominating sequence.
Note that being
![]() $\sigma $
-bounded can be seen as the combination of two properties: First, it is required that V is directed, and then, additionally, that there exists an increasing sequence
$\sigma $
-bounded can be seen as the combination of two properties: First, it is required that V is directed, and then, additionally, that there exists an increasing sequence
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
in
$(\hat {v}_n)_{n\in \mathbb{N}}$
in
![]() $V^+$
which has the property that, for every
$V^+$
which has the property that, for every
![]() $v\in V^+$
, there exists an
$v\in V^+$
, there exists an
![]() $n\in \mathbb{N}$
such that
$n\in \mathbb{N}$
such that
![]() $v\le \hat {v}_n$
.
$v\le \hat {v}_n$
.
Definition 3.2 Let V be a
![]() $\sigma $
-bounded ordered vector space with a dominating sequence
$\sigma $
-bounded ordered vector space with a dominating sequence
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
, and let
$(\hat {v}_n)_{n\in \mathbb{N}}$
, and let
![]() $(\delta _n)_{n\in \mathbb{N}}$
be a sequence in
$(\delta _n)_{n\in \mathbb{N}}$
be a sequence in
![]() ${]0,\infty [}$
. Then the subset
${]0,\infty [}$
. Then the subset
![]() $U_\delta $
of V is defined as the union of increasing order intervals
$U_\delta $
of V is defined as the union of increasing order intervals
Of course,
![]() $U_\delta $
depends not only on the sequence
$U_\delta $
depends not only on the sequence
![]() $(\delta _n)_{n\in \mathbb{N}}$
, but also on the choice of the dominating sequence
$(\delta _n)_{n\in \mathbb{N}}$
, but also on the choice of the dominating sequence
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
and of V itself, which will always be clear from the context.
$(\hat {v}_n)_{n\in \mathbb{N}}$
and of V itself, which will always be clear from the context.
Proposition 3.5 Let V be a
![]() $\sigma $
-bounded ordered vector space with a dominating sequence
$\sigma $
-bounded ordered vector space with a dominating sequence
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
, and let
$(\hat {v}_n)_{n\in \mathbb{N}}$
, and let
![]() $(\delta _n)_{n\in \mathbb{N}}$
be a sequence in
$(\delta _n)_{n\in \mathbb{N}}$
be a sequence in
![]() ${]0,\infty [}$
. Then
${]0,\infty [}$
. Then
![]() $U_\delta $
is an absorbing balanced convex and saturated as well as directed subset of V.
$U_\delta $
is an absorbing balanced convex and saturated as well as directed subset of V.
Proof Given
![]() $v\in V$
, then there exists
$v\in V$
, then there exists
![]() $n\in \mathbb{N}$
such that
$n\in \mathbb{N}$
such that
![]() $-\hat {v}_n \le v \le \hat {v}_n$
and therefore
$-\hat {v}_n \le v \le \hat {v}_n$
and therefore
![]() $\delta _n v \in U_\delta $
. So
$\delta _n v \in U_\delta $
. So
![]() $U_\delta $
is absorbing. Every order interval in V of the form
$U_\delta $
is absorbing. Every order interval in V of the form
![]() $[-w,w]$
with
$[-w,w]$
with
![]() $w\in V^+$
clearly is balanced, convex, saturated, and directed. As
$w\in V^+$
clearly is balanced, convex, saturated, and directed. As
![]() $U_\delta $
is the union of an increasing sequence of such sets, it is balanced, convex, saturated, and directed itself.
$U_\delta $
is the union of an increasing sequence of such sets, it is balanced, convex, saturated, and directed itself.
Proposition 3.6 Let V be a
![]() $\sigma $
-bounded ordered vector space, and let
$\sigma $
-bounded ordered vector space, and let
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
be a dominating sequence in V. Then the set of all
$(\hat {v}_n)_{n\in \mathbb{N}}$
be a dominating sequence in V. Then the set of all
![]() $U_\delta $
with
$U_\delta $
with
![]() $(\delta _n)_{n\in \mathbb{N}}$
a sequence in
$(\delta _n)_{n\in \mathbb{N}}$
a sequence in
![]() ${]0,\infty [}$
is a basis of the filter of
${]0,\infty [}$
is a basis of the filter of
![]() $0$
-neighborhoods of the normal topology on V.
$0$
-neighborhoods of the normal topology on V.
Proof Proposition 3.5 already shows that such a set
![]() $U_\delta $
is a
$U_\delta $
is a
![]() $0$
-neighborhood of the normal topology on V for every sequence
$0$
-neighborhood of the normal topology on V for every sequence
![]() $(\delta _n)_{n\in \mathbb{N}}$
in
$(\delta _n)_{n\in \mathbb{N}}$
in
![]() ${]0,\infty [}$
.
${]0,\infty [}$
.
Conversely, if S is a
![]() $0$
-neighborhood of the normal topology on V, then there exists a sequence
$0$
-neighborhood of the normal topology on V, then there exists a sequence
![]() $(\delta _n)_{n\in \mathbb{N}}$
in
$(\delta _n)_{n\in \mathbb{N}}$
in
![]() ${]0,\infty [}$
such that
${]0,\infty [}$
such that
![]() $U_\delta \subseteq S$
, which can be constructed as follows: Let
$U_\delta \subseteq S$
, which can be constructed as follows: Let
![]() $S'$
be an absorbing balanced convex and saturated subset of V such that
$S'$
be an absorbing balanced convex and saturated subset of V such that
![]() $S'\subseteq S$
. For every
$S'\subseteq S$
. For every
![]() $n\in \mathbb{N}$
, there exists
$n\in \mathbb{N}$
, there exists
![]() $\epsilon _n \in {]0,\infty [}$
such that
$\epsilon _n \in {]0,\infty [}$
such that
![]() $\epsilon _n \hat {v}_n \in S'$
because
$\epsilon _n \hat {v}_n \in S'$
because
![]() $S'$
is absorbing, and we can define
$S'$
is absorbing, and we can define
![]() for all
for all
![]() $n\in \mathbb{N}$
. Then
$n\in \mathbb{N}$
. Then
![]() $\sum _{n=1}^N \delta _n \hat {v}_n = \sum _{n=1}^N 2^{-n} \epsilon _n \hat {v}_n \in S'$
for all
$\sum _{n=1}^N \delta _n \hat {v}_n = \sum _{n=1}^N 2^{-n} \epsilon _n \hat {v}_n \in S'$
for all
![]() $N\in \mathbb{N}$
because
$N\in \mathbb{N}$
because
![]() $S'$
is balanced and convex. Consequently,
$S'$
is balanced and convex. Consequently,
![]() $\big [-\sum _{n=1}^N \delta _n \hat {v}_n,\sum _{n=1}^N \delta _n \hat {v}_n \big ] \subseteq S' \subseteq S$
for all
$\big [-\sum _{n=1}^N \delta _n \hat {v}_n,\sum _{n=1}^N \delta _n \hat {v}_n \big ] \subseteq S' \subseteq S$
for all
![]() $N \in \mathbb{N}$
because
$N \in \mathbb{N}$
because
![]() $S'$
is also saturated, so
$S'$
is also saturated, so
![]() $U_\delta \subseteq S$
.
$U_\delta \subseteq S$
.
The above description of the normal topology on a
![]() $\sigma $
-bounded ordered vector space has essentially already been given in [Reference Schmüdgen12, Propositions 4.1.2 and 4.1.3] and has also been applied indirectly to the decomposition of positive linear functionals into extremal ones in [Reference Schmüdgen12, Theorem 12.4.7]. Even though these results where stated for
$\sigma $
-bounded ordered vector space has essentially already been given in [Reference Schmüdgen12, Propositions 4.1.2 and 4.1.3] and has also been applied indirectly to the decomposition of positive linear functionals into extremal ones in [Reference Schmüdgen12, Theorem 12.4.7]. Even though these results where stated for
![]() $O^*$
-algebras or
$O^*$
-algebras or
![]() $^*$
-algebras, their above generalization to ordered vector spaces does not require any new techniques. Combining them with a completely order-theoretic characterization of those
$^*$
-algebras, their above generalization to ordered vector spaces does not require any new techniques. Combining them with a completely order-theoretic characterization of those
![]() $\sigma $
-bounded ordered vector spaces, whose set of positive elements is closed, gives our first important result.
$\sigma $
-bounded ordered vector spaces, whose set of positive elements is closed, gives our first important result.
Theorem 3.7 Let V be a
![]() $\sigma $
-bounded ordered vector space, then the following are equivalent:
$\sigma $
-bounded ordered vector space, then the following are equivalent:
-
(1) V is Archimedean.
-
(2)
 $V^+$
is closed in V with respect to the normal topology.
$V^+$
is closed in V with respect to the normal topology. -
(3) The order on V is induced by its extremal positive linear functionals.
-
(4) The order on V is induced by its positive linear functionals.
Proof Let
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
be a dominating sequence of V, which exists by assumption.
$(\hat {v}_n)_{n\in \mathbb{N}}$
be a dominating sequence of V, which exists by assumption.
First, consider the case that V is Archimedean. In order to prove the implication (1)
![]() $\Longrightarrow $
(2), we have to show that
$\Longrightarrow $
(2), we have to show that
![]() $V\setminus V^+$
is open with respect to the normal topology on V. Given
$V\setminus V^+$
is open with respect to the normal topology on V. Given
![]() $v\in V\setminus V^+$
, then construct recursively a sequence
$v\in V\setminus V^+$
, then construct recursively a sequence
![]() $(w_n)_{n\in \mathbb{N}_0}$
in
$(w_n)_{n\in \mathbb{N}_0}$
in
![]() $V\setminus V^+$
and a sequence
$V\setminus V^+$
and a sequence
![]() $(\delta _n)_{n\in \mathbb{N}}$
in
$(\delta _n)_{n\in \mathbb{N}}$
in
![]() ${]0,\infty [}$
as follows: Set
${]0,\infty [}$
as follows: Set
![]() . If
. If
![]() $w_{n-1}$
has been defined for some
$w_{n-1}$
has been defined for some
![]() $n\in \mathbb{N}$
, then choose
$n\in \mathbb{N}$
, then choose
![]() $\delta _n \in {]0,\infty [}$
such that
$\delta _n \in {]0,\infty [}$
such that
![]() $-w_{n-1} \le \delta _n \hat {v}_n$
does not hold, i.e., such that
$-w_{n-1} \le \delta _n \hat {v}_n$
does not hold, i.e., such that
![]() $w_{n-1} + \delta _n \hat {v}_n \in V\setminus V^+$
, and set
$w_{n-1} + \delta _n \hat {v}_n \in V\setminus V^+$
, and set
![]() . Note that such a
. Note that such a
![]() $\delta _n$
exists because
$\delta _n$
exists because
![]() $w_{n-1} \in V\setminus V^+$
and because V is Archimedean by assumption. From the construction of the sequence
$w_{n-1} \in V\setminus V^+$
and because V is Archimedean by assumption. From the construction of the sequence
![]() $(\delta _n)_{n\in \mathbb{N}}$
, it follows that
$(\delta _n)_{n\in \mathbb{N}}$
, it follows that
![]() $v+U_\delta \subseteq V\setminus V^+$
: Indeed, for every
$v+U_\delta \subseteq V\setminus V^+$
: Indeed, for every
![]() $x \in v+U_\delta $
, there exists
$x \in v+U_\delta $
, there exists
![]() $N\in \mathbb{N}$
such that
$N\in \mathbb{N}$
such that
![]() $x \le v+\sum _{n=1}^N \delta _n \hat {v}_n = w_N \in V\setminus V^+$
, and hence
$x \le v+\sum _{n=1}^N \delta _n \hat {v}_n = w_N \in V\setminus V^+$
, and hence
![]() $x \in V\setminus V^+$
. Proposition 3.6 now shows that
$x \in V\setminus V^+$
. Proposition 3.6 now shows that
![]() $V\setminus V^+$
is a neighborhood of v with respect to the normal topology on V.
$V\setminus V^+$
is a neighborhood of v with respect to the normal topology on V.
The implication (2)
![]() $\Longrightarrow $
(3) is just an application of Corollary 3.4 using that all the subsets
$\Longrightarrow $
(3) is just an application of Corollary 3.4 using that all the subsets
![]() $U_\delta $
of V with
$U_\delta $
of V with
![]() $(\delta _n)_{n\in \mathbb{N}}$
a sequence in
$(\delta _n)_{n\in \mathbb{N}}$
a sequence in
![]() ${]0,\infty [}$
are absorbing balanced convex and saturated as well as directed by Proposition 3.5 and form a basis of the filter of
${]0,\infty [}$
are absorbing balanced convex and saturated as well as directed by Proposition 3.5 and form a basis of the filter of
![]() $0$
-neighborhoods of the normal topology on the
$0$
-neighborhoods of the normal topology on the
![]() $\sigma $
-bounded ordered vector space V by Proposition 3.6.
$\sigma $
-bounded ordered vector space V by Proposition 3.6.
Finally, the implication (3)
![]() $\Longrightarrow $
(4) is trivial, and in order to prove (4)
$\Longrightarrow $
(4) is trivial, and in order to prove (4)
![]() $\Longrightarrow $
(1), assume that the order on V is induced by its positive linear functionals and let
$\Longrightarrow $
(1), assume that the order on V is induced by its positive linear functionals and let
![]() $v\in V$
and
$v\in V$
and
![]() $w\in V^+$
be given such that
$w\in V^+$
be given such that
![]() $v\le \epsilon w$
for all
$v\le \epsilon w$
for all
![]() $\epsilon \in {]0,\infty [}$
. Then it follows that
$\epsilon \in {]0,\infty [}$
. Then it follows that
![]() ${\langle \,{\rho } \,,\, {v}\,\rangle } \le 0$
holds for all
${\langle \,{\rho } \,,\, {v}\,\rangle } \le 0$
holds for all
![]() $\rho \in V^{*,+}$
because
$\rho \in V^{*,+}$
because
![]() $\mathbb{R}$
is Archimedean, and therefore
$\mathbb{R}$
is Archimedean, and therefore
![]() $v\le 0$
.
$v\le 0$
.
One special class of
![]() $\sigma $
-bounded ordered vector spaces are ordered vector spaces V with a strong order unit e, i.e., an element
$\sigma $
-bounded ordered vector spaces are ordered vector spaces V with a strong order unit e, i.e., an element
![]() $e\in V^+$
with the property that, for all
$e\in V^+$
with the property that, for all
![]() $v\in V$
, there exists
$v\in V$
, there exists
![]() $\lambda \in {[0,\infty [}$
such that
$\lambda \in {[0,\infty [}$
such that
![]() $v \le \lambda e$
. In this case,
$v \le \lambda e$
. In this case,
![]() $(ne)_{n\in \mathbb{N}}$
is a dominating sequence, and the existence of positive linear functionals on Archimedean ordered vector spaces with a strong order unit was already proved in [Reference Kadison8, Lemma 2.5]. Theorem 3.7 generalizes this classical result to
$(ne)_{n\in \mathbb{N}}$
is a dominating sequence, and the existence of positive linear functionals on Archimedean ordered vector spaces with a strong order unit was already proved in [Reference Kadison8, Lemma 2.5]. Theorem 3.7 generalizes this classical result to
![]() $\sigma $
-bounded ordered vector spaces and applies the decomposition of positive linear functionals into extremal ones from [Reference Schmüdgen12, Theorem 12.4.7].
$\sigma $
-bounded ordered vector spaces and applies the decomposition of positive linear functionals into extremal ones from [Reference Schmüdgen12, Theorem 12.4.7].
It should be unnecessary to point out that there are many examples of important
![]() $\sigma $
-bounded ordered vector spaces which do not have a strong order unit. These can be as ordinary as the space of real-valued polynomial functions on
$\sigma $
-bounded ordered vector spaces which do not have a strong order unit. These can be as ordinary as the space of real-valued polynomial functions on
![]() $\mathbb{R}$
with the pointwise order.
$\mathbb{R}$
with the pointwise order.
Before closing this section, we prove a new representation theorem for ordered vector spaces. Given any set X, then
![]() $\mathbb{R}^X$
denotes the ordered vector space of all
$\mathbb{R}^X$
denotes the ordered vector space of all
![]() $\mathbb{R}$
-valued functions on X with the pointwise operations and the pointwise order. As a consequence of Theorem 3.7, we obtain the following corollary.
$\mathbb{R}$
-valued functions on X with the pointwise operations and the pointwise order. As a consequence of Theorem 3.7, we obtain the following corollary.
Corollary 3.8 Let V be an Archimedean
![]() $\sigma $
-bounded ordered vector space, then the map
$\sigma $
-bounded ordered vector space, then the map
![]() $\pi \colon V \to \mathbb{R}^{V^{*,+,\mathrm {ex}}}$
,
$\pi \colon V \to \mathbb{R}^{V^{*,+,\mathrm {ex}}}$
,
![]() $v\mapsto \pi (v)$
with
$v\mapsto \pi (v)$
with
![]() $\pi (v) \colon V^{*,+,\mathrm {ex}} \to \mathbb{R}$
,
$\pi (v) \colon V^{*,+,\mathrm {ex}} \to \mathbb{R}$
,
is linear and an order embedding.
Proof It is easily checked that
![]() $\pi $
is linear and increasing. Given
$\pi $
is linear and increasing. Given
![]() $v \in V \setminus V^+$
, then there exists
$v \in V \setminus V^+$
, then there exists
![]() $\omega \in V^{*,+,\mathrm {ex}}$
such that
$\omega \in V^{*,+,\mathrm {ex}}$
such that
![]() ${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
because the order on V is induced by its extremal positive linear functionals by Theorem 3.7, so
${\langle \,{\omega } \,,\, {v}\,\rangle } < 0$
because the order on V is induced by its extremal positive linear functionals by Theorem 3.7, so
![]() $\pi (v)(\omega ) < 0$
, which means that
$\pi (v)(\omega ) < 0$
, which means that
![]() $\pi (v) \in \mathbb{R}^{V^{*,+,\mathrm {ex}}} \setminus (\mathbb{R}^{V^{*,+,\mathrm {ex}}})^+$
. This shows that
$\pi (v) \in \mathbb{R}^{V^{*,+,\mathrm {ex}}} \setminus (\mathbb{R}^{V^{*,+,\mathrm {ex}}})^+$
. This shows that
![]() $\pi $
is an order embedding.
$\pi $
is an order embedding.
If V is a Riesz space, i.e., an ordered vector space in which all finite infima and suprema exist, then Corollary 3.8 essentially is the representation theorem for Riesz spaces from [Reference Buskes and van Rooij4]: One can show that, in this case, the extremal positive linear functionals on V are Riesz morphisms, i.e., compatible with finite infima and suprema, so that the representation
![]() $\pi $
from (3.2) is also a Riesz morphism. We will not discuss the details here, but rather turn our attention in the next section to the case that V is an ordered vector space that carries a multiplication.
$\pi $
from (3.2) is also a Riesz morphism. We will not discuss the details here, but rather turn our attention in the next section to the case that V is an ordered vector space that carries a multiplication.
4 Representation of ordered
 $^*$
-algebras
$^*$
-algebras
We now come to the main section, which develops the generalized Gelfand–Naimark theorems for ordered
![]() $^*$
-algebras. The definition of
$^*$
-algebras. The definition of
![]() $^*$
-algebras has already been given in the introduction. An element a of a
$^*$
-algebras has already been given in the introduction. An element a of a
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
is called Hermitian if
$\mathcal {A}$
is called Hermitian if
![]() $a=a^*$
and the real linear subspace of all Hermitian elements in
$a=a^*$
and the real linear subspace of all Hermitian elements in
![]() $\mathcal {A}$
is denoted by
$\mathcal {A}$
is denoted by
![]() $\mathcal {A}_{\mathrm {H}}$
. An ordered
$\mathcal {A}_{\mathrm {H}}$
. An ordered
![]() $^*$
-algebra is a
$^*$
-algebra is a
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
together with a partial order
$\mathcal {A}$
together with a partial order
![]() $\le $
on
$\le $
on
![]() $\mathcal {A}_{\mathrm {H}}$
such that
$\mathcal {A}_{\mathrm {H}}$
such that
![]() $\mathcal {A}_{\mathrm {H}}$
becomes an ordered vector space fulfilling
$\mathcal {A}_{\mathrm {H}}$
becomes an ordered vector space fulfilling
![]() and
and
![]() $a^*b\,a \in \mathcal {A}_{\mathrm {H}}^+$
for all
$a^*b\,a \in \mathcal {A}_{\mathrm {H}}^+$
for all
![]() $a\in \mathcal {A}$
,
$a\in \mathcal {A}$
,
![]() $b\in \mathcal {A}^+_{\mathrm {H}}$
. This ordered vector space of Hermitian elements is automatically directed because
$b\in \mathcal {A}^+_{\mathrm {H}}$
. This ordered vector space of Hermitian elements is automatically directed because
![]() and
and
![]() hold for all
hold for all
![]() $a\in \mathcal {A}_{\mathrm {H}}$
. A unital
$a\in \mathcal {A}_{\mathrm {H}}$
. A unital
![]() $^*$
-subalgebra
$^*$
-subalgebra
![]() $\mathcal {B}$
of an ordered
$\mathcal {B}$
of an ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
, i.e., a linear subspace
$\mathcal {A}$
, i.e., a linear subspace
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $\mathcal {A}$
fulfilling
$\mathcal {A}$
fulfilling
![]() as well as
as well as
![]() $b^* \in \mathcal {B}$
and
$b^* \in \mathcal {B}$
and
![]() $bb' \in \mathcal {B}$
for all
$bb' \in \mathcal {B}$
for all
![]() $b,b'\in \mathcal {B}$
, is again an ordered
$b,b'\in \mathcal {B}$
, is again an ordered
![]() $^*$
-algebra with the order on
$^*$
-algebra with the order on
![]() $\mathcal {B}_{\mathrm {H}}$
inherited from
$\mathcal {B}_{\mathrm {H}}$
inherited from
![]() $\mathcal {A}_{\mathrm {H}}$
. Ordered
$\mathcal {A}_{\mathrm {H}}$
. Ordered
![]() $^*$
-algebras have already been used for understanding representations of
$^*$
-algebras have already been used for understanding representations of
![]() $^*$
-algebras, e.g., in [Reference Powers9] or [Reference Schmüdgen12]. The set of positive Hermitian elements of an ordered
$^*$
-algebras, e.g., in [Reference Powers9] or [Reference Schmüdgen12]. The set of positive Hermitian elements of an ordered
![]() $^*$
-algebra is an “m-admissible cone” in the language of [Reference Schmüdgen12], or a “quadratic module” in the language of (noncommutative) real algebraic geometry.
$^*$
-algebra is an “m-admissible cone” in the language of [Reference Schmüdgen12], or a “quadratic module” in the language of (noncommutative) real algebraic geometry.
An ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
is called
$\mathcal {A}$
is called
![]() $\sigma $
-bounded if the ordered vector space
$\sigma $
-bounded if the ordered vector space
![]() $\mathcal {A}_{\mathrm {H}}$
is
$\mathcal {A}_{\mathrm {H}}$
is
![]() $\sigma $
-bounded. Similarly, an ordered
$\sigma $
-bounded. Similarly, an ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
is said to be closed if
$\mathcal {A}$
is said to be closed if
![]() $\mathcal {A}_{\mathrm {H}}$
is an Archimedean ordered vector space. Note that this is not a topological property but rather an order property; only for
$\mathcal {A}_{\mathrm {H}}$
is an Archimedean ordered vector space. Note that this is not a topological property but rather an order property; only for
![]() $\sigma $
-bounded ordered
$\sigma $
-bounded ordered
![]() $^*$
-algebras, it follows from Theorem 3.7 that
$^*$
-algebras, it follows from Theorem 3.7 that
![]() $\mathcal {A}$
is closed as an ordered
$\mathcal {A}$
is closed as an ordered
![]() $^*$
-algebra if and only if the quadratic module
$^*$
-algebra if and only if the quadratic module
![]() $\mathcal {A}^+_{\mathrm {H}}$
is closed in
$\mathcal {A}^+_{\mathrm {H}}$
is closed in
![]() $\mathcal {A}_{\mathrm {H}}$
with respect to a certain locally convex topology. Note also that this property is not at all related to the notion of Archimedean quadratic modules in real algebraic geometry. It is unfortunate that the term “Archimedean” is being used in several different ways. Because of this, the term “Archimedean” should be avoided in the context of ordered
$\mathcal {A}_{\mathrm {H}}$
with respect to a certain locally convex topology. Note also that this property is not at all related to the notion of Archimedean quadratic modules in real algebraic geometry. It is unfortunate that the term “Archimedean” is being used in several different ways. Because of this, the term “Archimedean” should be avoided in the context of ordered
![]() $^*$
-algebras. There are some important examples of ordered
$^*$
-algebras. There are some important examples of ordered
![]() $^*$
-algebras that will be relevant in the following, and these also illustrate that the notion of ordered
$^*$
-algebras that will be relevant in the following, and these also illustrate that the notion of ordered
![]() $^*$
-algebras used here is rather minimalistic.
$^*$
-algebras used here is rather minimalistic.
Example 4.1 For every set X, the space
![]() $\mathbb{C}^X$
of all complex-valued functions on X with the pointwise operations and the pointwise order on the Hermitian (i.e., real-valued) functions is a commutative, closed, and ordered
$\mathbb{C}^X$
of all complex-valued functions on X with the pointwise operations and the pointwise order on the Hermitian (i.e., real-valued) functions is a commutative, closed, and ordered
![]() $^*$
-algebra.
$^*$
-algebra.
Example 4.2 If
![]() $\mathcal {D}$
is a pre-Hilbert space, i.e., a complex vector space endowed with an inner product
$\mathcal {D}$
is a pre-Hilbert space, i.e., a complex vector space endowed with an inner product
![]() ${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }$
, antilinear in the first and linear in the second argument, then we write
${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }$
, antilinear in the first and linear in the second argument, then we write
![]() $\mathcal {L}^*(\mathcal {D})$
for the
$\mathcal {L}^*(\mathcal {D})$
for the
![]() $^*$
-algebra of all linear endomorphisms a of
$^*$
-algebra of all linear endomorphisms a of
![]() $\mathcal {D}$
that are adjointable in the algebraic sense, i.e., for which there exists a (necessarily unique) linear endomorphism
$\mathcal {D}$
that are adjointable in the algebraic sense, i.e., for which there exists a (necessarily unique) linear endomorphism
![]() $a^*$
of
$a^*$
of
![]() $\mathcal {D}$
such that
$\mathcal {D}$
such that
![]() ${\langle \,{\phi } \,|\, {a(\psi )}\,\rangle } = {\langle \,{a^*(\phi )} \,|\, {\psi }\,\rangle }$
holds for all
${\langle \,{\phi } \,|\, {a(\psi )}\,\rangle } = {\langle \,{a^*(\phi )} \,|\, {\psi }\,\rangle }$
holds for all
![]() $\phi ,\psi \in \mathcal {D}$
. An element a of
$\phi ,\psi \in \mathcal {D}$
. An element a of
![]() $\mathcal {L}^*(\mathcal {D})$
is Hermitian if and only if
$\mathcal {L}^*(\mathcal {D})$
is Hermitian if and only if
![]() ${\langle \,{\phi } \,|\, {a(\phi )}\,\rangle } \in \mathbb{R}$
for all
${\langle \,{\phi } \,|\, {a(\phi )}\,\rangle } \in \mathbb{R}$
for all
![]() $\phi \in \mathcal {D}$
and
$\phi \in \mathcal {D}$
and
![]() $\mathcal {L}^*(\mathcal {D})_{\mathrm {H}}$
will always be endowed with the usual partial order of operators, i.e., given
$\mathcal {L}^*(\mathcal {D})_{\mathrm {H}}$
will always be endowed with the usual partial order of operators, i.e., given
![]() $a\in \mathcal {L}^*(\mathcal {D})_{\mathrm {H}}$
, then a is positive if and only if
$a\in \mathcal {L}^*(\mathcal {D})_{\mathrm {H}}$
, then a is positive if and only if
![]() ${\langle \,{\phi } \,|\, {a(\phi )}\,\rangle } \ge 0$
for all
${\langle \,{\phi } \,|\, {a(\phi )}\,\rangle } \ge 0$
for all
![]() $\phi \in \mathcal {D}$
. This way,
$\phi \in \mathcal {D}$
. This way,
![]() $\mathcal {L}^*(\mathcal {D})$
becomes a closed ordered
$\mathcal {L}^*(\mathcal {D})$
becomes a closed ordered
![]() $^*$
-algebra which is not commutative in general. Unital
$^*$
-algebra which is not commutative in general. Unital
![]() $^*$
-subalgebras of
$^*$
-subalgebras of
![]() $\mathcal {L}^*(\mathcal {D})$
are called
$\mathcal {L}^*(\mathcal {D})$
are called
![]() $O^*$
-algebras (see, e.g., [Reference Schmüdgen12]).
$O^*$
-algebras (see, e.g., [Reference Schmüdgen12]).
Example 4.3 A
![]() $\Phi $
-algebra is an Archimedean ordered vector space
$\Phi $
-algebra is an Archimedean ordered vector space
![]() $\mathcal {R}$
in which the supremum
$\mathcal {R}$
in which the supremum
![]() and the infimum
and the infimum
![]() of any two elements
of any two elements
![]() $r,s \in \mathcal {R}$
exist, and that is endowed with a bilinear product that turns
$r,s \in \mathcal {R}$
exist, and that is endowed with a bilinear product that turns
![]() $\mathcal {R}$
into an associative, commutative, and unital real algebra with the properties that
$\mathcal {R}$
into an associative, commutative, and unital real algebra with the properties that
![]() $rs \in \mathcal {R}^+$
for all
$rs \in \mathcal {R}^+$
for all
![]() $r,s\in \mathcal {R}^+$
and
$r,s\in \mathcal {R}^+$
and
![]() $rs=0$
for all
$rs=0$
for all
![]() $r,s \in \mathcal {R}$
with
$r,s \in \mathcal {R}$
with
![]() $r\wedge s = 0$
. With
$r\wedge s = 0$
. With
![]() , it follows from the properties of
, it follows from the properties of
![]() $\vee $
and
$\vee $
and
![]() $\wedge $
that
$\wedge $
that
![]() $({\lvert {r} \rvert }-r)\wedge ({\lvert {r} \rvert }+r) = {\lvert {r} \rvert }+((-r)\wedge r) = {\lvert {r} \rvert } -{\lvert {r} \rvert } = 0$
, so
$({\lvert {r} \rvert }-r)\wedge ({\lvert {r} \rvert }+r) = {\lvert {r} \rvert }+((-r)\wedge r) = {\lvert {r} \rvert } -{\lvert {r} \rvert } = 0$
, so
![]() ${\lvert {r} \rvert }^2 - r^2 = ({\lvert {r} \rvert }-r)({\lvert {r} \rvert }+r) = 0$
, i.e.,
${\lvert {r} \rvert }^2 - r^2 = ({\lvert {r} \rvert }-r)({\lvert {r} \rvert }+r) = 0$
, i.e.,
![]() $r^2 = {\lvert {r} \rvert }^2 \ge 0$
for all
$r^2 = {\lvert {r} \rvert }^2 \ge 0$
for all
![]() $r\in \mathcal {R}$
. The complexification
$r\in \mathcal {R}$
. The complexification
![]() of such a
of such a
![]() $\Phi $
-algebra
$\Phi $
-algebra
![]() $\mathcal {R}$
is therefore a commutative, closed, and ordered
$\mathcal {R}$
is therefore a commutative, closed, and ordered
![]() $^*$
-algebra whose real linear subspace of Hermitian elements is
$^*$
-algebra whose real linear subspace of Hermitian elements is
![]() $\mathcal {A}_{\mathrm {H}} \cong \mathcal {R}$
. For
$\mathcal {A}_{\mathrm {H}} \cong \mathcal {R}$
. For
![]() $\Phi $
-algebras, there exists, e.g., a representation theorem by means of functions with values in the extended real line
$\Phi $
-algebras, there exists, e.g., a representation theorem by means of functions with values in the extended real line
![]() $[-\infty ,\infty ]$
(see [Reference Henriksen and Johnson7]). In Theorem 4.24, we will prove a representation theorem by means of
$[-\infty ,\infty ]$
(see [Reference Henriksen and Johnson7]). In Theorem 4.24, we will prove a representation theorem by means of
![]() $\mathbb{R}$
-valued functions under the additional assumption of
$\mathbb{R}$
-valued functions under the additional assumption of
![]() $\sigma $
-boundedness.
$\sigma $
-boundedness.
Example 4.4 If
![]() $\mathcal {A}$
is a
$\mathcal {A}$
is a
![]() $C^*$
-algebra, then its Hermitian elements can be endowed with a partial order that turns
$C^*$
-algebra, then its Hermitian elements can be endowed with a partial order that turns
![]() $\mathcal {A}$
into a closed ordered
$\mathcal {A}$
into a closed ordered
![]() $^*$
-algebra in which the positive Hermitian elements are precisely those Hermitian ones whose spectrum is a subset of
$^*$
-algebra in which the positive Hermitian elements are precisely those Hermitian ones whose spectrum is a subset of
![]() ${[0,\infty [}$
. This is a well known, but nontrivial result in the theory of
${[0,\infty [}$
. This is a well known, but nontrivial result in the theory of
![]() $C^*$
-algebras. Showing, e.g., that the sum of two positive Hermitian elements is again a positive Hermitian element required some considerable effort in the original proof of the (noncommutative) representation theorem for
$C^*$
-algebras. Showing, e.g., that the sum of two positive Hermitian elements is again a positive Hermitian element required some considerable effort in the original proof of the (noncommutative) representation theorem for
![]() $C^*$
-algebras in [Reference Gelfand and Neumark6]. Moreover, in a
$C^*$
-algebras in [Reference Gelfand and Neumark6]. Moreover, in a
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {A}$
, the unit
$\mathcal {A}$
, the unit
![]() is a strong order unit of
is a strong order unit of
![]() $\mathcal {A}_{\mathrm {H}}$
, i.e., for every
$\mathcal {A}_{\mathrm {H}}$
, i.e., for every
![]() $a\in \mathcal {A}_{\mathrm {H}}$
, there exists a
$a\in \mathcal {A}_{\mathrm {H}}$
, there exists a
![]() $\lambda \in {[0,\infty [}$
such that
$\lambda \in {[0,\infty [}$
such that
![]() (see also the discussion under Theorem 3.7).
(see also the discussion under Theorem 3.7).
Example 4.5 Let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $^*$
-algebra, and define the set
$^*$
-algebra, and define the set
of algebraically positive elements in
![]() $\mathcal {A}$
. If
$\mathcal {A}$
. If
![]() $\mathcal {A}^{++}_{\mathrm {H}}$
does not contain a real linear subspace of
$\mathcal {A}^{++}_{\mathrm {H}}$
does not contain a real linear subspace of
![]() $\mathcal {A}_{\mathrm {H}}$
in addition to the trivial one
$\mathcal {A}_{\mathrm {H}}$
in addition to the trivial one
![]() $\{0\}$
, then
$\{0\}$
, then
![]() $\mathcal {A}$
can be turned into an ordered
$\mathcal {A}$
can be turned into an ordered
![]() $^*$
-algebra such that
$^*$
-algebra such that
![]() $\mathcal {A}^+_{\mathrm {H}} = \mathcal {A}^{++}_{\mathrm {H}}$
. Otherwise, i.e., if there is
$\mathcal {A}^+_{\mathrm {H}} = \mathcal {A}^{++}_{\mathrm {H}}$
. Otherwise, i.e., if there is
![]() $a\in \mathcal {A}_{\mathrm {H}} \setminus \{0\}$
such that both a and
$a\in \mathcal {A}_{\mathrm {H}} \setminus \{0\}$
such that both a and
![]() $-a$
are algebraically positive, there is no possibility to turn
$-a$
are algebraically positive, there is no possibility to turn
![]() $\mathcal {A}$
into an ordered
$\mathcal {A}$
into an ordered
![]() $^*$
-algebra. So the existence of a suitable order on a
$^*$
-algebra. So the existence of a suitable order on a
![]() $^*$
-algebra (especially the antisymmetry of the order) is a nontrivial condition. We will see that this, together with two or three further conditions, allows to prove representation theorems similar to, but more general than those known for
$^*$
-algebra (especially the antisymmetry of the order) is a nontrivial condition. We will see that this, together with two or three further conditions, allows to prove representation theorems similar to, but more general than those known for
![]() $C^*$
-algebras.
$C^*$
-algebras.
Note also that there are many different types of ordered algebras that have been examined in the last decades. Motivations to do so can be rather divers, e.g., generalizing results for ordered vector spaces (especially Riesz spaces) to ordered algebras, generalizing results from (commutative) real algebraic geometry to the noncommutative case, or studying operator algebras by purely algebraic means. Consequently, one can find conflicting definitions in the literature.
Example 4.6 The definition of
![]() $O^*$
-algebras used in [Reference Albeverio, Ayupov and Dadakhodjayev1] is different from the one of Example 4.2. In fact, the notion of complex
$O^*$
-algebras used in [Reference Albeverio, Ayupov and Dadakhodjayev1] is different from the one of Example 4.2. In fact, the notion of complex
![]() $O^*$
-algebras used there is a special case of the ordered
$O^*$
-algebras used there is a special case of the ordered
![]() $^*$
-algebras here, requiring also existence and good behavior of certain suprema and infima of algebra elements (the stability of the set of positive Hermitian elements under conjugations
$^*$
-algebras here, requiring also existence and good behavior of certain suprema and infima of algebra elements (the stability of the set of positive Hermitian elements under conjugations
![]() $a \mapsto b^*a\,b$
with arbitrary algebra elements b is a nontrivial consequence of their axioms of
$a \mapsto b^*a\,b$
with arbitrary algebra elements b is a nontrivial consequence of their axioms of
![]() $O^*$
-algebras; see the remark under Theorem 2.2). In [Reference Albeverio, Ayupov and Dadakhodjayev1, Theorem 5.5], a representation theorem is proved that makes use of these infima and suprema. In contrast to this, Theorems 4.24 and 4.9 here are based on Theorem 3.7, and therefore require
$O^*$
-algebras; see the remark under Theorem 2.2). In [Reference Albeverio, Ayupov and Dadakhodjayev1, Theorem 5.5], a representation theorem is proved that makes use of these infima and suprema. In contrast to this, Theorems 4.24 and 4.9 here are based on Theorem 3.7, and therefore require
![]() $\sigma $
-boundedness instead.
$\sigma $
-boundedness instead.
If
![]() $\mathcal {A}$
is a
$\mathcal {A}$
is a
![]() $^*$
-algebra, then its complex dual vector space
$^*$
-algebra, then its complex dual vector space
![]() $\mathcal {A}^*$
carries an antilinear involution
$\mathcal {A}^*$
carries an antilinear involution
![]() $ {\,\cdot \,} ^* \colon \mathcal {A}^* \to \mathcal {A}^*$
,
$ {\,\cdot \,} ^* \colon \mathcal {A}^* \to \mathcal {A}^*$
,
![]() $\omega \mapsto \omega ^*$
, given by
$\omega \mapsto \omega ^*$
, given by
![]() for all
for all
![]() $a\in \mathcal {A}$
. We say again that an element
$a\in \mathcal {A}$
. We say again that an element
![]() $\omega \in \mathcal {A}^*$
is Hermitian if
$\omega \in \mathcal {A}^*$
is Hermitian if
![]() $\omega ^*=\omega $
and write
$\omega ^*=\omega $
and write
![]() $\mathcal {A}_{\mathrm {H}}^*$
for the set of all Hermitian linear functionals on
$\mathcal {A}_{\mathrm {H}}^*$
for the set of all Hermitian linear functionals on
![]() $\mathcal {A}$
, which is a real linear subspace of
$\mathcal {A}$
, which is a real linear subspace of
![]() $\mathcal {A}^*$
. Note that a linear functional
$\mathcal {A}^*$
. Note that a linear functional
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {A}$
is Hermitian if and only if
$\mathcal {A}$
is Hermitian if and only if
![]() ${\langle \,{\omega } \,,\, {a}\,\rangle } \in \mathbb{R}$
holds for all
${\langle \,{\omega } \,,\, {a}\,\rangle } \in \mathbb{R}$
holds for all
![]() $a\in \mathcal {A}_{\mathrm {H}}$
. Thus, every
$a\in \mathcal {A}_{\mathrm {H}}$
. Thus, every
![]() $\omega \in \mathcal {A}^*_{\mathrm {H}}$
can be restricted to an
$\omega \in \mathcal {A}^*_{\mathrm {H}}$
can be restricted to an
![]() $\mathbb{R}$
-linear functional on
$\mathbb{R}$
-linear functional on
![]() $\mathcal {A}_{\mathrm {H}}$
, and one can check that this restriction describes an
$\mathcal {A}_{\mathrm {H}}$
, and one can check that this restriction describes an
![]() $\mathbb{R}$
-linear isomorphism between the vector spaces
$\mathbb{R}$
-linear isomorphism between the vector spaces
![]() $\mathcal {A}^*_{\mathrm {H}}$
and
$\mathcal {A}^*_{\mathrm {H}}$
and
![]() $(\mathcal {A}_{\mathrm {H}})^*$
. An (extremal) positive Hermitian linear functional on an ordered
$(\mathcal {A}_{\mathrm {H}})^*$
. An (extremal) positive Hermitian linear functional on an ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
is then defined as a Hermitian linear functional on
$\mathcal {A}$
is then defined as a Hermitian linear functional on
![]() $\mathcal {A}$
whose restriction to a (real) linear functional on the ordered vector space
$\mathcal {A}$
whose restriction to a (real) linear functional on the ordered vector space
![]() $\mathcal {A}_{\mathrm {H}}$
is an (extremal) positive linear functional. The sets of these (extremal) positive Hermitian linear functionals are denoted by
$\mathcal {A}_{\mathrm {H}}$
is an (extremal) positive linear functional. The sets of these (extremal) positive Hermitian linear functionals are denoted by
![]() $\mathcal {A}^{*,+}_{\mathrm {H}}$
and
$\mathcal {A}^{*,+}_{\mathrm {H}}$
and
![]() $\mathcal {A}^{*,+,\mathrm {ex}}_{\mathrm {H}}$
, respectively, and we say that the order on
$\mathcal {A}^{*,+,\mathrm {ex}}_{\mathrm {H}}$
, respectively, and we say that the order on
![]() $\mathcal {A}$
is induced by its (extremal) positive Hermitian linear functionals if the order on
$\mathcal {A}$
is induced by its (extremal) positive Hermitian linear functionals if the order on
![]() $\mathcal {A}_{\mathrm {H}}$
is induced by its (extremal) positive linear functionals. Note that positivity of a Hermitian linear functional
$\mathcal {A}_{\mathrm {H}}$
is induced by its (extremal) positive linear functionals. Note that positivity of a Hermitian linear functional
![]() $\omega $
on an ordered
$\omega $
on an ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
is in general a stronger condition than just the requirement that
$\mathcal {A}$
is in general a stronger condition than just the requirement that
![]() ${\langle \,{\omega } \,,\, {a^*a}\,\rangle } \ge 0$
for all
${\langle \,{\omega } \,,\, {a^*a}\,\rangle } \ge 0$
for all
![]() $a\in \mathcal {A}$
, which is used quite often in the literature when linear functionals on general
$a\in \mathcal {A}$
, which is used quite often in the literature when linear functionals on general
![]() $^*$
-algebras are discussed. However, if
$^*$
-algebras are discussed. However, if
![]() $\mathcal {A}$
is an ordered
$\mathcal {A}$
is an ordered
![]() $^*$
-algebra in which only the algebraically positive Hermitian linear functionals are positive, i.e., if
$^*$
-algebra in which only the algebraically positive Hermitian linear functionals are positive, i.e., if
![]() $\mathcal {A}$
is of the type of Example 4.5, then
$\mathcal {A}$
is of the type of Example 4.5, then
![]() ${\langle \,{\omega } \,,\, {a^*a}\,\rangle } \ge 0$
for all
${\langle \,{\omega } \,,\, {a^*a}\,\rangle } \ge 0$
for all
![]() $a\in \mathcal {A}$
is also sufficient for a Hermitian linear functional
$a\in \mathcal {A}$
is also sufficient for a Hermitian linear functional
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {A}$
to be positive.
$\mathcal {A}$
to be positive.
Positive Hermitian linear functionals on an ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
have some nice properties: Given
$\mathcal {A}$
have some nice properties: Given
![]() $\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
and
$\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
and
![]() $a,b\in \mathcal {A}$
, then the Cauchy–Schwarz inequality
$a,b\in \mathcal {A}$
, then the Cauchy–Schwarz inequality
holds, as well as
in the special case that
![]() . This has an important consequence: If a positive Hermitian linear functional
. This has an important consequence: If a positive Hermitian linear functional
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {A}$
fulfils
$\mathcal {A}$
fulfils
![]() , then
, then
![]() $\omega = 0$
. A state on
$\omega = 0$
. A state on
![]() $\mathcal {A}$
is a positive Hermitian linear functional
$\mathcal {A}$
is a positive Hermitian linear functional
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {A}$
that fulfils
$\mathcal {A}$
that fulfils
![]() . So every
. So every
![]() $\tilde {\omega } \in \mathcal {A}^{*,+}_{\mathrm {H}} \setminus \{0\}$
is a multiple of a unique state
$\tilde {\omega } \in \mathcal {A}^{*,+}_{\mathrm {H}} \setminus \{0\}$
is a multiple of a unique state
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {A}$
, namely of
$\mathcal {A}$
, namely of
![]() . The set of all states on
. The set of all states on
![]() $\mathcal {A}$
will be denoted by
$\mathcal {A}$
will be denoted by
![]() $\mathcal {S}(\mathcal {A})$
and is clearly a convex (possibly empty) subset of the real vector space
$\mathcal {S}(\mathcal {A})$
and is clearly a convex (possibly empty) subset of the real vector space
![]() $\mathcal {A}^*_{\mathrm {H}}$
. Again, note that by this definition, states are positive on whole
$\mathcal {A}^*_{\mathrm {H}}$
. Again, note that by this definition, states are positive on whole
![]() $\mathcal {A}^+_{\mathrm {H}}$
, not just on squares.
$\mathcal {A}^+_{\mathrm {H}}$
, not just on squares.
A map
![]() $\Phi \colon \mathcal {A} \to \mathcal {B}$
between two
$\Phi \colon \mathcal {A} \to \mathcal {B}$
between two
![]() $^*$
-algebras is said to be multiplicative if
$^*$
-algebras is said to be multiplicative if
![]() $\Phi (aa') = \Phi (a) \Phi (a')$
holds for all
$\Phi (aa') = \Phi (a) \Phi (a')$
holds for all
![]() $a,a' \in \mathcal {A}$
. Furthermore, it is called a unital
$a,a' \in \mathcal {A}$
. Furthermore, it is called a unital
![]() $^*$
-homomorphism if it is linear and multiplicative, maps the unit of
$^*$
-homomorphism if it is linear and multiplicative, maps the unit of
![]() $\mathcal {A}$
to the unit of
$\mathcal {A}$
to the unit of
![]() $\mathcal {B}$
and fulfils
$\mathcal {B}$
and fulfils
![]() $\Phi (a^*) = \Phi (a)^*$
for all
$\Phi (a^*) = \Phi (a)^*$
for all
![]() $a\in \mathcal {A}$
. This last condition is equivalent to
$a\in \mathcal {A}$
. This last condition is equivalent to
![]() $\Phi (a) \in \mathcal {B}_{\mathrm {H}}$
for all
$\Phi (a) \in \mathcal {B}_{\mathrm {H}}$
for all
![]() $a\in \mathcal {A}_{\mathrm {H}}$
. If
$a\in \mathcal {A}_{\mathrm {H}}$
. If
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are ordered
$\mathcal {B}$
are ordered
![]() $^*$
-algebras, then such a unital
$^*$
-algebras, then such a unital
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\Phi $
is called positive or an order embedding if its restriction to an
$\Phi $
is called positive or an order embedding if its restriction to an
![]() $\mathbb{R}$
-linear map between the ordered vector spaces
$\mathbb{R}$
-linear map between the ordered vector spaces
![]() $\mathcal {A}_{\mathrm {H}}$
and
$\mathcal {A}_{\mathrm {H}}$
and
![]() $\mathcal {B}_{\mathrm {H}}$
is positive or an order embedding, respectively.
$\mathcal {B}_{\mathrm {H}}$
is positive or an order embedding, respectively.
For ordered
![]() $^*$
-algebras, we are going to discuss two different types of representations, which correspond to the first two examples mentioned above.
$^*$
-algebras, we are going to discuss two different types of representations, which correspond to the first two examples mentioned above.
Definition 4.1 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra. Then a representation as functions of
$^*$
-algebra. Then a representation as functions of
![]() $\mathcal {A}$
is a tuple
$\mathcal {A}$
is a tuple
![]() $(X, \pi )$
of a set X and a positive unital
$(X, \pi )$
of a set X and a positive unital
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\pi \colon \mathcal {A} \to \mathbb{C}^X$
. Similarly, a representation as operators of
$\pi \colon \mathcal {A} \to \mathbb{C}^X$
. Similarly, a representation as operators of
![]() $\mathcal {A}$
is a tuple
$\mathcal {A}$
is a tuple
![]() $(\mathcal {D}, \pi )$
of a pre-Hilbert space
$(\mathcal {D}, \pi )$
of a pre-Hilbert space
![]() $\mathcal {D}$
and a positive unital
$\mathcal {D}$
and a positive unital
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\pi \colon \mathcal {A} \to \mathcal {L}^*(\mathcal {D})$
. Moreover, such a representation (as functions or as operators) is called faithful if
$\pi \colon \mathcal {A} \to \mathcal {L}^*(\mathcal {D})$
. Moreover, such a representation (as functions or as operators) is called faithful if
![]() $\pi $
is an order embedding.
$\pi $
is an order embedding.
Of course, representations as functions are especially interesting for commutative ordered
![]() $^*$
-algebras. As we will see, the existence of faithful representations of an ordered
$^*$
-algebras. As we will see, the existence of faithful representations of an ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
is closely linked to the question of whether or not the order on
$\mathcal {A}$
is closely linked to the question of whether or not the order on
![]() $\mathcal {A}$
is induced by its (extremal) positive Hermitian linear functionals.
$\mathcal {A}$
is induced by its (extremal) positive Hermitian linear functionals.
4.1 Representation as operators
The well-known construction of the Gelfand–Naimark–Segal (GNS) representation yields a representation as operators of an ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
out of any positive Hermitian linear functional.
$\mathcal {A}$
out of any positive Hermitian linear functional.
Proposition 4.7 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra, and let
$^*$
-algebra, and let
![]() $\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
. Then the map
$\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
. Then the map
![]() ${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_\omega \colon \mathcal {A} \times \mathcal {A} \to \mathbb{C}$
,
${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_\omega \colon \mathcal {A} \times \mathcal {A} \to \mathbb{C}$
,
is sesquilinear (antilinear in the first, and linear in the second argument) and fulfils
![]() $\overline {{{\langle \,{a} \,|\, {b}\,\rangle }_\omega }} = {\langle \,{b} \,|\, {a}\,\rangle }_\omega $
as well as
$\overline {{{\langle \,{a} \,|\, {b}\,\rangle }_\omega }} = {\langle \,{b} \,|\, {a}\,\rangle }_\omega $
as well as
![]() ${\langle \,{a} \,|\, {a}\,\rangle }_\omega \in {[0,\infty [}$
for all
${\langle \,{a} \,|\, {a}\,\rangle }_\omega \in {[0,\infty [}$
for all
![]() $a,b\in \mathcal {A}$
. Write
$a,b\in \mathcal {A}$
. Write
![]() ${{\lVert { {\,\cdot \,} } \rVert }_{\omega }}$
for the corresponding seminorm on
${{\lVert { {\,\cdot \,} } \rVert }_{\omega }}$
for the corresponding seminorm on
![]() $\mathcal {A}$
, defined as
$\mathcal {A}$
, defined as
![]() for all
for all
![]() $a\in \mathcal {A}$
, and write
$a\in \mathcal {A}$
, and write
![]() for its kernel. Then
for its kernel. Then
![]() ${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_\omega $
remains well defined on the quotient vector space
${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_\omega $
remains well defined on the quotient vector space
![]() $\mathcal {A} / \mathrm {ker}{{\lVert { {\,\cdot \,} } \rVert }_{\omega }}$
on which it describes an inner product. Now, write
$\mathcal {A} / \mathrm {ker}{{\lVert { {\,\cdot \,} } \rVert }_{\omega }}$
on which it describes an inner product. Now, write
![]() $\mathcal {D}_\omega $
for the pre-Hilbert space of
$\mathcal {D}_\omega $
for the pre-Hilbert space of
![]() $\mathcal {A} / \mathrm {ker}{{\lVert { {\,\cdot \,} } \rVert }_{{\omega }}}$
with inner product
$\mathcal {A} / \mathrm {ker}{{\lVert { {\,\cdot \,} } \rVert }_{{\omega }}}$
with inner product
![]() ${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_\omega $
, and
${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_\omega $
, and
![]() $[b]_\omega \in \mathcal {A} / \mathrm {ker}{{\lVert { {\,\cdot \,} } \rVert }_{\omega }}$
for the equivalence class of an element
$[b]_\omega \in \mathcal {A} / \mathrm {ker}{{\lVert { {\,\cdot \,} } \rVert }_{\omega }}$
for the equivalence class of an element
![]() $b\in \mathcal {A}$
. Then, for every
$b\in \mathcal {A}$
. Then, for every
![]() $a\in \mathcal {A}$
, the map
$a\in \mathcal {A}$
, the map
![]() $\pi _\omega (a) \colon \mathcal {D}_\omega \to \mathcal {D}_\omega $
,
$\pi _\omega (a) \colon \mathcal {D}_\omega \to \mathcal {D}_\omega $
,
is a well-defined linear endomorphism of
![]() $\mathcal {D}_\omega $
, it is adjointable with adjoint
$\mathcal {D}_\omega $
, it is adjointable with adjoint
![]() $\pi _\omega (a^*)$
, and the resulting map
$\pi _\omega (a^*)$
, and the resulting map
![]() $\mathcal {A} \ni a \mapsto \pi _\omega (a) \in \mathcal {L}^*(\mathcal {D}_\omega )$
is a positive unital
$\mathcal {A} \ni a \mapsto \pi _\omega (a) \in \mathcal {L}^*(\mathcal {D}_\omega )$
is a positive unital
![]() $^*$
-homomorphism. Altogether,
$^*$
-homomorphism. Altogether,
![]() $\big (\mathcal {D}_\omega ,\pi _\omega \big )$
is a representation as operators of the ordered
$\big (\mathcal {D}_\omega ,\pi _\omega \big )$
is a representation as operators of the ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof The only detail which is not completely part of the classical GNS construction for
![]() $^*$
-algebras as described, e.g., in [Reference Schmüdgen12, Section 8.6], is the observation that
$^*$
-algebras as described, e.g., in [Reference Schmüdgen12, Section 8.6], is the observation that
![]() $\pi _\omega $
is not only a unital
$\pi _\omega $
is not only a unital
![]() $^*$
-homomorphism, but also positive, because
$^*$
-homomorphism, but also positive, because
![]() ${\langle \,{[b]_\omega } \,|\, {\pi _\omega (a)\,[b]_\omega }\,\rangle } = {\langle \,{\omega } \,,\, {b^*a\,b}\,\rangle } \ge 0$
for all
${\langle \,{[b]_\omega } \,|\, {\pi _\omega (a)\,[b]_\omega }\,\rangle } = {\langle \,{\omega } \,,\, {b^*a\,b}\,\rangle } \ge 0$
for all
![]() $a\in \mathcal {A}^+_{\mathrm {H}}$
.
$a\in \mathcal {A}^+_{\mathrm {H}}$
.
Definition 4.2 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra, and let
$^*$
-algebra, and let
![]() $\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
, then the representation as operators
$\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
, then the representation as operators
![]() $\big ( \mathcal {D}_\omega , \pi _\omega \big )$
from Proposition 4.7 is called the GNS representation of
$\big ( \mathcal {D}_\omega , \pi _\omega \big )$
from Proposition 4.7 is called the GNS representation of
![]() $\mathcal {A}$
with respect to
$\mathcal {A}$
with respect to
![]() $\omega $
.
$\omega $
.
The problem of existence of representations as operators of ordered
![]() $^*$
-algebras can be treated completely analogous to the case of general
$^*$
-algebras can be treated completely analogous to the case of general
![]() $^*$
-algebras:
$^*$
-algebras:
Proposition 4.8 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra, then there exists a faithful representation as operators of
$^*$
-algebra, then there exists a faithful representation as operators of
![]() $\mathcal {A}$
if and only if the order on
$\mathcal {A}$
if and only if the order on
![]() $\mathcal {A}$
is induced by its positive Hermitian linear functionals.
$\mathcal {A}$
is induced by its positive Hermitian linear functionals.
Proof Assume that there exists a faithful representation as operators
![]() $(\mathcal {D},\pi )$
of
$(\mathcal {D},\pi )$
of
![]() $\mathcal {A}$
. Given
$\mathcal {A}$
. Given
![]() $a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
, then there exists
$a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
, then there exists
![]() $\phi \in \mathcal {D}$
such that
$\phi \in \mathcal {D}$
such that
![]() ${\langle \,{\phi } \,|\, {\pi (a)(\phi )}\,\rangle } < 0$
. However,
${\langle \,{\phi } \,|\, {\pi (a)(\phi )}\,\rangle } < 0$
. However,
![]() $\mathcal {A} \ni b \mapsto {\langle \,{\phi } \,|\, {\pi (b)(\phi )}\,\rangle } \in \mathbb{C}$
is a positive Hermitian linear functional. So we conclude that the order on
$\mathcal {A} \ni b \mapsto {\langle \,{\phi } \,|\, {\pi (b)(\phi )}\,\rangle } \in \mathbb{C}$
is a positive Hermitian linear functional. So we conclude that the order on
![]() $\mathcal {A}$
is induced by its positive Hermitian linear functionals.
$\mathcal {A}$
is induced by its positive Hermitian linear functionals.
Conversely, assume that the order on
![]() $\mathcal {A}$
is induced by its positive Hermitian linear functionals. Using the GNS representations of
$\mathcal {A}$
is induced by its positive Hermitian linear functionals. Using the GNS representations of
![]() $\mathcal {A}$
, define the orthogonal sum of pre-Hilbert spaces
$\mathcal {A}$
, define the orthogonal sum of pre-Hilbert spaces
with inner product denoted by
![]() ${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_{\mathrm {tot}}$
, as well as for every element
${\langle \,{ {\,\cdot \,} } \,|\, { {\,\cdot \,} }\,\rangle }_{\mathrm {tot}}$
, as well as for every element
![]() $a\in \mathcal {A}$
the linear endomorphism
$a\in \mathcal {A}$
the linear endomorphism
of
![]() $\mathcal {D}_{\mathrm {tot}}$
, i.e.,
$\mathcal {D}_{\mathrm {tot}}$
, i.e.,
. Then it is easy to check that
![]() $\pi _{\mathrm {tot}}(a)$
is adjointable with adjoint
$\pi _{\mathrm {tot}}(a)$
is adjointable with adjoint
![]() $\pi _{\mathrm {tot}}(a^*)$
and that the resulting map
$\pi _{\mathrm {tot}}(a^*)$
and that the resulting map
![]() $\pi _{\mathrm {tot}} \colon \mathcal {A} \to \mathcal {L}^*\big ( \mathcal {D}_{\mathrm {tot}} \big )$
,
$\pi _{\mathrm {tot}} \colon \mathcal {A} \to \mathcal {L}^*\big ( \mathcal {D}_{\mathrm {tot}} \big )$
,
![]() $a\mapsto \pi _{\mathrm {tot}}(a)$
is a positive unital
$a\mapsto \pi _{\mathrm {tot}}(a)$
is a positive unital
![]() $^*$
-homomorphism. Moreover,
$^*$
-homomorphism. Moreover,
![]() $\pi _{\mathrm {tot}}$
is an order embedding: Indeed, for every
$\pi _{\mathrm {tot}}$
is an order embedding: Indeed, for every
![]() $a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
, there exists an
$a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
, there exists an
![]() $\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
such that
$\omega \in \mathcal {A}^{*,+}_{\mathrm {H}}$
such that
![]() ${\langle \,{\omega } \,,\, {a}\,\rangle } < 0$
and thus
${\langle \,{\omega } \,,\, {a}\,\rangle } < 0$
and thus
. It follows that
![]() $\big ( \mathcal {D}_{\mathrm {tot}}, \pi _{\mathrm {tot}} \big )$
is a faithful representation as operators.
$\big ( \mathcal {D}_{\mathrm {tot}}, \pi _{\mathrm {tot}} \big )$
is a faithful representation as operators.
Application of Theorem 3.7 to Proposition 4.8 immediately yields the following generalization of the (noncommutative) Gelfand–Naimark theorem.
Theorem 4.9 Let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $\sigma $
-bounded ordered
$\sigma $
-bounded ordered
![]() $^*$
-algebra, then
$^*$
-algebra, then
![]() $\mathcal {A}$
has a faithful representation as operators if and only if
$\mathcal {A}$
has a faithful representation as operators if and only if
![]() $\mathcal {A}$
is closed.
$\mathcal {A}$
is closed.
The original (noncommutative) Gelfand–Naimark theorem is essentially the special case of this Theorem 4.9 for ordered
![]() $^*$
-algebras
$^*$
-algebras
![]() $\mathcal {A}$
in which the multiplicative unit
$\mathcal {A}$
in which the multiplicative unit
![]() is also a strong order unit. As discussed under Theorem 3.7,
is also a strong order unit. As discussed under Theorem 3.7,
![]() $\mathcal {A}$
is automatically
$\mathcal {A}$
is automatically
![]() $\sigma $
-bounded in this case. Note also that the image of a
$\sigma $
-bounded in this case. Note also that the image of a
![]() $\sigma $
-bounded ordered
$\sigma $
-bounded ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
under a faithful representation as operators is an
$\mathcal {A}$
under a faithful representation as operators is an
![]() $O^*$
-algebra with metrizable graph topology in the language of [Reference Schmüdgen12], which, conversely, are always
$O^*$
-algebra with metrizable graph topology in the language of [Reference Schmüdgen12], which, conversely, are always
![]() $\sigma $
-bounded. So Theorem 4.9 yields an order-theoretic characterization of the
$\sigma $
-bounded. So Theorem 4.9 yields an order-theoretic characterization of the
![]() $O^*$
-algebras with metrizable graph topology. This goes in a similar direction as [Reference Schmüdgen11], where a topological characterization of a large class of
$O^*$
-algebras with metrizable graph topology. This goes in a similar direction as [Reference Schmüdgen11], where a topological characterization of a large class of
![]() $O^*$
-algebras has been given.
$O^*$
-algebras has been given.
Despite being valid only in the
![]() $\sigma $
-bounded case, Theorem 4.9 still implies that, heuristically, every closed ordered
$\sigma $
-bounded case, Theorem 4.9 still implies that, heuristically, every closed ordered
![]() $^*$
-algebra “behaves essentially like an
$^*$
-algebra “behaves essentially like an
![]() $O^*$
-algebra”. In order to make this more precise, we need the following lemma.
$O^*$
-algebra”. In order to make this more precise, we need the following lemma.
Lemma 4.10 Let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $^*$
-algebra that is generated by a countable subset of
$^*$
-algebra that is generated by a countable subset of
![]() $\mathcal {A}$
. If
$\mathcal {A}$
. If
![]() $\mathcal {A}_{\mathrm {H}}$
is endowed with any partial order
$\mathcal {A}_{\mathrm {H}}$
is endowed with any partial order
![]() $\le $
such that
$\le $
such that
![]() $\mathcal {A}$
becomes an ordered
$\mathcal {A}$
becomes an ordered
![]() $^*$
-algebra, then
$^*$
-algebra, then
![]() $\mathcal {A}$
with this order is
$\mathcal {A}$
with this order is
![]() $\sigma $
-bounded.
$\sigma $
-bounded.
Proof As
![]() $\mathcal {A}$
is generated by a countable subset, it has at most countable dimension, so there exists a sequence
$\mathcal {A}$
is generated by a countable subset, it has at most countable dimension, so there exists a sequence
![]() $(a_n)_{n\in \mathbb{N}}$
in
$(a_n)_{n\in \mathbb{N}}$
in
![]() $\mathcal {A}_{\mathrm {H}}$
such that the
$\mathcal {A}_{\mathrm {H}}$
such that the
![]() $\mathbb{R}$
-linear span of
$\mathbb{R}$
-linear span of
![]() ${\{\,{a_n} \;|\; {n\in \mathbb{N}}\,\}}$
is whole
${\{\,{a_n} \;|\; {n\in \mathbb{N}}\,\}}$
is whole
![]() $\mathcal {A}_{\mathrm {H}}$
. Moreover, from
$\mathcal {A}_{\mathrm {H}}$
. Moreover, from
![]() , it follows that
, it follows that
![]() for all
for all
![]() $n\in \mathbb{N}$
. So define the increasing sequence
$n\in \mathbb{N}$
. So define the increasing sequence
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
in
$(\hat {v}_n)_{n\in \mathbb{N}}$
in
![]() $\mathcal {A}_{\mathrm {H}}^+$
as
$\mathcal {A}_{\mathrm {H}}^+$
as
![]() , then
, then
![]() $(\hat {v}_n)_{n\in \mathbb{N}}$
is a dominating sequence because for every
$(\hat {v}_n)_{n\in \mathbb{N}}$
is a dominating sequence because for every
![]() $b \in \mathcal {A}_{\mathrm {H}}$
there exists an
$b \in \mathcal {A}_{\mathrm {H}}$
there exists an
![]() $n\in \mathbb{N}$
such that b can be expressed as
$n\in \mathbb{N}$
such that b can be expressed as
![]() $b = \sum _{k=1}^n 2\beta _n a_n$
with coefficients
$b = \sum _{k=1}^n 2\beta _n a_n$
with coefficients
![]() $\beta _1,\dots ,\beta _n \in [{-n},n]$
, and hence
$\beta _1,\dots ,\beta _n \in [{-n},n]$
, and hence
![]() $b \le \hat {v}_n$
.
$b \le \hat {v}_n$
.
Proposition 4.11 Let
![]() $\mathcal {A}$
be a closed ordered
$\mathcal {A}$
be a closed ordered
![]() $^*$
-algebra, and let
$^*$
-algebra, and let
![]() $(a_n)_{n\in \mathbb{N}}$
be any sequence in
$(a_n)_{n\in \mathbb{N}}$
be any sequence in
![]() $\mathcal {A}$
. Then the unital
$\mathcal {A}$
. Then the unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $\mathcal {A}$
that is generated by
$\mathcal {A}$
that is generated by
![]() ${\{\,{a_n} \;|\; {n \in \mathbb{N}}\,\}}$
has a faithful representation as operators.
${\{\,{a_n} \;|\; {n \in \mathbb{N}}\,\}}$
has a faithful representation as operators.
4.2 Representation as functions
A slight modification of the well-known Gelfand transformation yields a representation as functions of any ordered
![]() $^*$
-algebra.
$^*$
-algebra.
Definition 4.3 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra, then the set of all multiplicative states on
$^*$
-algebra, then the set of all multiplicative states on
![]() $\mathcal {A}$
, i.e., of all positive unital
$\mathcal {A}$
, i.e., of all positive unital
![]() $^*$
-homomorphisms from
$^*$
-homomorphisms from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathbb{C}$
, will be denoted by
$\mathbb{C}$
, will be denoted by
![]() $\mathcal {S}_{\mathrm {m}}(\mathcal {A})$
.
$\mathcal {S}_{\mathrm {m}}(\mathcal {A})$
.
Proposition 4.12 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra. Then the map
$^*$
-algebra. Then the map
![]() $\pi _{\mathrm {Gelfand}} \colon \mathcal {A} \to \mathbb{C}^{\mathcal {S}_{\mathrm {m}}(\mathcal {A})}$
,
$\pi _{\mathrm {Gelfand}} \colon \mathcal {A} \to \mathbb{C}^{\mathcal {S}_{\mathrm {m}}(\mathcal {A})}$
,
![]() $a \mapsto \pi _{\mathrm {Gelfand}}(a)$
with
$a \mapsto \pi _{\mathrm {Gelfand}}(a)$
with
![]() $\pi _{\mathrm {Gelfand}}(a) \colon \mathcal {S}_{\mathrm {m}}(\mathcal {A}) \to \mathbb{C}$
,
$\pi _{\mathrm {Gelfand}}(a) \colon \mathcal {S}_{\mathrm {m}}(\mathcal {A}) \to \mathbb{C}$
,
is a positive unital
![]() $^*$
-homomorphism and
$^*$
-homomorphism and
![]() $\big ( \mathcal {S}_{\mathrm {m}}(\mathcal {A}), \pi _{\mathrm {Gelfand}} \big )$
is a representation as functions of
$\big ( \mathcal {S}_{\mathrm {m}}(\mathcal {A}), \pi _{\mathrm {Gelfand}} \big )$
is a representation as functions of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof Immediate consequence of the properties of the elements in
![]() $\mathcal {S}_{\mathrm {m}}(\mathcal {A})$
.
$\mathcal {S}_{\mathrm {m}}(\mathcal {A})$
.
In order to guarantee the existence of many multiplicative states, we have to examine states which are at the same time extremal positive Hermitian linear functionals.
Definition 4.4 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra. Then a state
$^*$
-algebra. Then a state
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {A}$
is called pure if
$\mathcal {A}$
is called pure if
![]() $\omega $
is also an extremal positive Hermitian linear functional on
$\omega $
is also an extremal positive Hermitian linear functional on
![]() $\mathcal {A}$
. The set of all pure states on
$\mathcal {A}$
. The set of all pure states on
![]() $\mathcal {A}$
will be denoted by
$\mathcal {A}$
will be denoted by
![]() .
.
The above definition of pure states is equivalent to the more common one as extreme points of the convex set of states.
Proposition 4.13 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra, then
$^*$
-algebra, then
![]() $\mathcal {S}_{\mathrm {p}}(\mathcal {A}) = \mathrm {ex}\big ( \mathcal {S}(\mathcal {A})\big )$
.
$\mathcal {S}_{\mathrm {p}}(\mathcal {A}) = \mathrm {ex}\big ( \mathcal {S}(\mathcal {A})\big )$
.
Proof If
![]() $\omega $
is an extreme point of
$\omega $
is an extreme point of
![]() $\mathcal {S}(\mathcal {A})$
, then it is also an extremal positive Hermitian linear functional, hence a pure state: Indeed, given
$\mathcal {S}(\mathcal {A})$
, then it is also an extremal positive Hermitian linear functional, hence a pure state: Indeed, given
![]() $\rho \in \mathcal {A}^{*,+}_{\mathrm {H}}$
such that
$\rho \in \mathcal {A}^{*,+}_{\mathrm {H}}$
such that
![]() $\rho \le \omega $
, then, as a consequence of the Cauchy–Schwarz inequality, either both
$\rho \le \omega $
, then, as a consequence of the Cauchy–Schwarz inequality, either both
and
are in
![]() ${]0,1[}$
, or
${]0,1[}$
, or
![]() $\rho = \mu \omega $
with
$\rho = \mu \omega $
with
![]() $\mu \in \{0,1\}$
. In the former case,
$\mu \in \{0,1\}$
. In the former case,
is a representation of
![]() $\omega $
as a nontrivial convex combination of two elements of
$\omega $
as a nontrivial convex combination of two elements of
![]() $\mathcal {S}(\mathcal {A})$
, which implies that
$\mathcal {S}(\mathcal {A})$
, which implies that
![]() $\rho = \mu \omega $
with
$\rho = \mu \omega $
with
.
Conversely, if
![]() $\omega $
is pure state on
$\omega $
is pure state on
![]() $\mathcal {A}$
, then it is an extreme point of
$\mathcal {A}$
, then it is an extreme point of
![]() $\mathcal {S}(\mathcal {A})$
: If
$\mathcal {S}(\mathcal {A})$
: If
![]() $\omega = \lambda \rho + (1-\lambda )\rho '$
with
$\omega = \lambda \rho + (1-\lambda )\rho '$
with
![]() $\rho ,\rho ' \in \mathcal {S}(\mathcal {A})$
and
$\rho ,\rho ' \in \mathcal {S}(\mathcal {A})$
and
![]() $\lambda \in {]0,1[}$
, then
$\lambda \in {]0,1[}$
, then
![]() $\lambda \rho \le \omega $
and
$\lambda \rho \le \omega $
and
![]() $(1-\lambda ) \rho ' \le \omega $
. Consequently, there are
$(1-\lambda ) \rho ' \le \omega $
. Consequently, there are
![]() $\mu ,\mu '\in {[0,1]}$
such that
$\mu ,\mu '\in {[0,1]}$
such that
![]() $\lambda \rho = \mu \omega $
and
$\lambda \rho = \mu \omega $
and
![]() $(1-\lambda ) \rho ' = \mu '\omega $
. Evaluation on
$(1-\lambda ) \rho ' = \mu '\omega $
. Evaluation on
![]() shows that
shows that
![]() $\lambda = \mu $
and
$\lambda = \mu $
and
![]() $(1-\lambda ) = \mu '$
, and hence
$(1-\lambda ) = \mu '$
, and hence
![]() $\rho = \omega = \rho '$
.
$\rho = \omega = \rho '$
.
The sets of pure states and of multiplicative states on an ordered
![]() $^*$
-algebra are closely related. In order to see this, the following concept will be helpful.
$^*$
-algebra are closely related. In order to see this, the following concept will be helpful.
Definition 4.5 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra, let
$^*$
-algebra, let
![]() $\omega $
be a state on
$\omega $
be a state on
![]() $\mathcal {A}$
, and let
$\mathcal {A}$
, and let
![]() $a\in \mathcal {A}$
. The variance of
$a\in \mathcal {A}$
. The variance of
![]() $\omega $
on a is defined as
$\omega $
on a is defined as
Note that
![]() $\mathrm {Var}_\omega (a) \in {[0,\infty [}$
and that
$\mathrm {Var}_\omega (a) \in {[0,\infty [}$
and that
![]() $\mathrm {Var}_\omega (a) = {\langle \,{\omega } \,,\, {a^*a}\,\rangle } - {\lvert {{\langle \,{\omega } \,,\, {a}\,\rangle }} \rvert }^2$
holds for every state
$\mathrm {Var}_\omega (a) = {\langle \,{\omega } \,,\, {a^*a}\,\rangle } - {\lvert {{\langle \,{\omega } \,,\, {a}\,\rangle }} \rvert }^2$
holds for every state
![]() $\omega $
on every ordered
$\omega $
on every ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
and all
$\mathcal {A}$
and all
![]() $a\in \mathcal {A}$
.
$a\in \mathcal {A}$
.
Proposition 4.14 If
![]() $\mathcal {A}$
is an ordered
$\mathcal {A}$
is an ordered
![]() $^*$
-algebra and
$^*$
-algebra and
![]() $\omega $
is a multiplicative state on
$\omega $
is a multiplicative state on
![]() $\mathcal {A}$
, then
$\mathcal {A}$
, then
![]() $\omega $
is a pure state on
$\omega $
is a pure state on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof By Proposition 4.13, the pure states are precisely the extreme points of the set of all states. So assume that
![]() $\rho ,\rho ' \in \mathcal {S}(\mathcal {A})$
and
$\rho ,\rho ' \in \mathcal {S}(\mathcal {A})$
and
![]() $\lambda \in {]0,1[}$
fulfil
$\lambda \in {]0,1[}$
fulfil
![]() $\omega = \lambda \rho + (1-\lambda )\rho '$
, then one can check that the identity
$\omega = \lambda \rho + (1-\lambda )\rho '$
, then one can check that the identity
holds for all
![]() $a\in \mathcal {A}$
. Moreover,
$a\in \mathcal {A}$
. Moreover,
![]() $\mathrm {Var}_\omega (a) = 0$
because
$\mathrm {Var}_\omega (a) = 0$
because
![]() $\omega $
is multiplicative. It follows that
$\omega $
is multiplicative. It follows that
![]() ${\lvert {{\langle \,{\rho -\rho '} \,,\, {a}\,\rangle }} \rvert }^2 = 0$
for all
${\lvert {{\langle \,{\rho -\rho '} \,,\, {a}\,\rangle }} \rvert }^2 = 0$
for all
![]() $a\in \mathcal {A}$
because
$a\in \mathcal {A}$
because
![]() $\mathrm {Var}_{\rho }(a)$
and
$\mathrm {Var}_{\rho }(a)$
and
![]() $\mathrm {Var}_{\rho '}(a)$
are nonnegative, so
$\mathrm {Var}_{\rho '}(a)$
are nonnegative, so
![]() $\rho = \rho ' = \omega $
.
$\rho = \rho ' = \omega $
.
In order to be able to obtain a converse statement, we need some more assumptions.
Definition 4.6 An ordered
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathcal {A}$
is called radical if it has the following property: Whenever
$\mathcal {A}$
is called radical if it has the following property: Whenever
![]() $a, b \in \mathcal {A}_{\mathrm {H}}$
commute and fulfil
$a, b \in \mathcal {A}_{\mathrm {H}}$
commute and fulfil
![]() and
and
![]() $0 \le ab$
, then
$0 \le ab$
, then
![]() $0 \le b$
.
$0 \le b$
.
There are some important examples of radical commutative ordered
![]() $^*$
-algebras.
$^*$
-algebras.
Proposition 4.15 Let
![]() $\mathcal {A}$
be a commutative ordered
$\mathcal {A}$
be a commutative ordered
![]() $^*$
-algebra. If
$^*$
-algebra. If
![]() $\mathcal {A}$
has a faithful representation as functions, then
$\mathcal {A}$
has a faithful representation as functions, then
![]() $\mathcal {A}$
is radical and closed.
$\mathcal {A}$
is radical and closed.
Proof Let
![]() $(X,\pi )$
be a faithful represent as functions of
$(X,\pi )$
be a faithful represent as functions of
![]() $\mathcal {A}$
. It is easy to check that
$\mathcal {A}$
. It is easy to check that
![]() $\mathbb{C}^X$
is radical and closed, essentially because
$\mathbb{C}^X$
is radical and closed, essentially because
![]() $\mathbb{C}$
is radical and closed. Using that
$\mathbb{C}$
is radical and closed. Using that
![]() $\pi \colon \mathcal {A} \to \mathbb{C}^X$
is a positive unital
$\pi \colon \mathcal {A} \to \mathbb{C}^X$
is a positive unital
![]() $^*$
-homomorphism and an order embedding, it follows immediately that
$^*$
-homomorphism and an order embedding, it follows immediately that
![]() $\mathcal {A}$
has to be radical and closed as well.
$\mathcal {A}$
has to be radical and closed as well.
Proposition 4.16 Let
![]() be the complexification of a
be the complexification of a
![]() $\Phi $
-algebra
$\Phi $
-algebra
![]() $\mathcal {R}$
, then
$\mathcal {R}$
, then
![]() $\mathcal {A}$
is a radical and closed commutative ordered
$\mathcal {A}$
is a radical and closed commutative ordered
![]() $^*$
-algebra.
$^*$
-algebra.
Proof As discussed in Example 4.3,
![]() $\mathcal {A}$
is a closed commutative ordered
$\mathcal {A}$
is a closed commutative ordered
![]() $^*$
-algebra. Consider
$^*$
-algebra. Consider
![]() $a, b \in \mathcal {A}_{\mathrm {H}}$
such that
$a, b \in \mathcal {A}_{\mathrm {H}}$
such that
![]() and
and
![]() $0 \le ab$
. We can express b as the difference
$0 \le ab$
. We can express b as the difference
![]() $b = b_+ -b_-$
of its positive and negative components,
$b = b_+ -b_-$
of its positive and negative components,
![]() , and
, and
![]() . From
. From
![]() $b_+ \wedge b_- = 0$
, it follows that
$b_+ \wedge b_- = 0$
, it follows that
![]() $b_+ b_- = 0$
. As
$b_+ b_- = 0$
. As
![]() $\mathcal {A}^+_{\mathrm {H}}$
is closed under products by definition of
$\mathcal {A}^+_{\mathrm {H}}$
is closed under products by definition of
![]() $\Phi $
-algebras, multiplication with
$\Phi $
-algebras, multiplication with
![]() $b_-$
yields
$b_-$
yields
![]() $0 \le b_-\,ab = - b_-\,a\,b_- \le 0$
, so
$0 \le b_-\,ab = - b_-\,a\,b_- \le 0$
, so
![]() $b_-\,a\,b_- = 0$
. From
$b_-\,a\,b_- = 0$
. From
![]() , it now follows that
, it now follows that
![]() $0 \le (b_-)^2 \le b_-\,a\,b_- = 0$
, so
$0 \le (b_-)^2 \le b_-\,a\,b_- = 0$
, so
![]() $(b_-)^2 = 0$
. As a consequence,
$(b_-)^2 = 0$
. As a consequence,
![]() , and hence
, and hence
![]() for all
for all
![]() $\epsilon \in {]0,\infty [}$
, which implies that
$\epsilon \in {]0,\infty [}$
, which implies that
![]() $b_- \le 0$
because
$b_- \le 0$
because
![]() $\mathcal {A}$
is closed by assumption. This finally shows that
$\mathcal {A}$
is closed by assumption. This finally shows that
![]() $b = b_+-b_- \ge 0$
.
$b = b_+-b_- \ge 0$
.
It is also worthwhile to mention an important nonexample.
Example 4.17 Consider the
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathbb{C}[x,y]$
of complex polynomials in two variables x and y with the
$\mathbb{C}[x,y]$
of complex polynomials in two variables x and y with the
![]() $^*$
-involution given by complex conjugation of coefficients, and thus
$^*$
-involution given by complex conjugation of coefficients, and thus
![]() $\mathbb{C}[x,y]_{\mathrm {H}} \cong \mathbb{R}[x,y]$
. On
$\mathbb{C}[x,y]_{\mathrm {H}} \cong \mathbb{R}[x,y]$
. On
![]() $\mathbb{C}[x,y]_{\mathrm {H}}$
, choose the partial order that turns
$\mathbb{C}[x,y]_{\mathrm {H}}$
, choose the partial order that turns
![]() $\mathbb{C}[x,y]$
into an ordered
$\mathbb{C}[x,y]$
into an ordered
![]() $^*$
-algebra with cone of positive elements given by sums of Hermitian squares, i.e.,
$^*$
-algebra with cone of positive elements given by sums of Hermitian squares, i.e.,
Note that
![]() $\mathbb{C}[x,y]_{\mathrm {H}}^+ \cap (- \mathbb{C}[x,y]_{\mathrm {H}}^+) = \{0\}$
because every sum of Hermitian squares of polynomials is pointwise positive on
$\mathbb{C}[x,y]_{\mathrm {H}}^+ \cap (- \mathbb{C}[x,y]_{\mathrm {H}}^+) = \{0\}$
because every sum of Hermitian squares of polynomials is pointwise positive on
![]() $\mathbb{R}^2$
. Moreover, the product of two elements of
$\mathbb{R}^2$
. Moreover, the product of two elements of
![]() $\mathbb{C}[x,y]_{\mathrm {H}}^+$
is again in
$\mathbb{C}[x,y]_{\mathrm {H}}^+$
is again in
![]() $\mathbb{C}[x,y]_{\mathrm {H}}^+$
. It is well known that there exist polynomials
$\mathbb{C}[x,y]_{\mathrm {H}}^+$
. It is well known that there exist polynomials
![]() $p \in \mathbb{C}[x,y]_{\mathrm {H}} \setminus \mathbb{C}[x,y]_{\mathrm {H}}^+$
that are pointwise positive on
$p \in \mathbb{C}[x,y]_{\mathrm {H}} \setminus \mathbb{C}[x,y]_{\mathrm {H}}^+$
that are pointwise positive on
![]() $\mathbb{R}^2$
. An explicit example from [Reference Berg, Christensen and Jensen2] is
$\mathbb{R}^2$
. An explicit example from [Reference Berg, Christensen and Jensen2] is
Now, consider
, then
As
, we conclude that
![]() $\mathbb{C}[x,y]$
(with this choice for the order) is not a radical ordered
$\mathbb{C}[x,y]$
(with this choice for the order) is not a radical ordered
![]() $^*$
-algebra and especially does not have a faithful representation as functions due to Proposition 4.15. Closer inspection shows that this is indeed because of the existence of ill-behaved pure states (see, e.g., [Reference Schmüdgen12, Corollary 11.6.4] and the discussion there for details).
$^*$
-algebra and especially does not have a faithful representation as functions due to Proposition 4.15. Closer inspection shows that this is indeed because of the existence of ill-behaved pure states (see, e.g., [Reference Schmüdgen12, Corollary 11.6.4] and the discussion there for details).
We proceed with examining the relation between pure states and multiplicative states.
Lemma 4.18 Let
![]() $\mathcal {A}$
be an ordered
$\mathcal {A}$
be an ordered
![]() $^*$
-algebra, let
$^*$
-algebra, let
![]() $\omega $
be a state on
$\omega $
be a state on
![]() $\mathcal {A}$
, and let
$\mathcal {A}$
, and let
![]() $a\in \mathcal {A}$
with
$a\in \mathcal {A}$
with
![]() $\mathrm {Var}_\omega (a) = 0$
, then
$\mathrm {Var}_\omega (a) = 0$
, then
hold for all
![]() $b\in \mathcal {A}$
. A state
$b\in \mathcal {A}$
. A state
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {A}$
thus is multiplicative if (and only if)
$\mathcal {A}$
thus is multiplicative if (and only if)
![]() $\mathrm {Var}_\omega (a) = 0$
for all
$\mathrm {Var}_\omega (a) = 0$
for all
![]() $a\in \mathcal {A}$
.
$a\in \mathcal {A}$
.
Proof The Cauchy–Schwarz inequality yields

for all
![]() $a,b\in \mathcal {A}$
. If
$a,b\in \mathcal {A}$
. If
![]() $\mathrm {Var}_\omega (a) = 0$
, then this implies that (4.7) holds.
$\mathrm {Var}_\omega (a) = 0$
, then this implies that (4.7) holds.
Lemma 4.19 Let
![]() $\mathcal {A}$
be a commutative ordered
$\mathcal {A}$
be a commutative ordered
![]() $^*$
-algebra, and let
$^*$
-algebra, and let
![]() $\omega \in \mathcal {S}(\mathcal {A})$
, then the subset
$\omega \in \mathcal {S}(\mathcal {A})$
, then the subset
![]() ${\big \{\,{a\in \mathcal {A}} \;\big |\; {\mathrm {Var}_\omega (a)=0}\,\big \}}$
of
${\big \{\,{a\in \mathcal {A}} \;\big |\; {\mathrm {Var}_\omega (a)=0}\,\big \}}$
of
![]() $\mathcal {A}$
is a unital
$\mathcal {A}$
is a unital
![]() $^*$
-subalgebra and this is the largest (with respect to inclusion) unital
$^*$
-subalgebra and this is the largest (with respect to inclusion) unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $\mathcal {A}$
on which the restriction of
$\mathcal {A}$
on which the restriction of
![]() $\omega $
is multiplicative. In the special case that
$\omega $
is multiplicative. In the special case that
![]() holds for all
holds for all
![]() $a\in \mathcal {A}_{\mathrm {H}}$
, it follows that
$a\in \mathcal {A}_{\mathrm {H}}$
, it follows that
![]() $\omega $
is multiplicative on whole
$\omega $
is multiplicative on whole
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof First assume that
![]() $\omega $
is an arbitrary state on
$\omega $
is an arbitrary state on
![]() $\mathcal {A}$
. Then it is easy to check that
$\mathcal {A}$
. Then it is easy to check that
![]() $\mathrm {Var}_\omega (\lambda a) = {\lvert {\lambda } \rvert }^2 \mathrm {Var}_\omega (a)$
and also (using the commutativity of
$\mathrm {Var}_\omega (\lambda a) = {\lvert {\lambda } \rvert }^2 \mathrm {Var}_\omega (a)$
and also (using the commutativity of
![]() $\mathcal {A}$
)
$\mathcal {A}$
)
![]() $\mathrm {Var}_\omega (a^*) = \mathrm {Var}_\omega (a)$
hold for all
$\mathrm {Var}_\omega (a^*) = \mathrm {Var}_\omega (a)$
hold for all
![]() $a\in \mathcal {A}$
and all
$a\in \mathcal {A}$
and all
![]() $\lambda \in \mathbb{C}$
. Moreover, if
$\lambda \in \mathbb{C}$
. Moreover, if
![]() $a,b\in \mathcal {A}$
fulfil
$a,b\in \mathcal {A}$
fulfil
![]() $\mathrm {Var}_\omega (a) = \mathrm {Var}_\omega (b) = 0$
, then one can check with the help of Lemma 4.18 that
$\mathrm {Var}_\omega (a) = \mathrm {Var}_\omega (b) = 0$
, then one can check with the help of Lemma 4.18 that
and
As
![]() is clearly fulfilled as well, one sees that
is clearly fulfilled as well, one sees that
![]() ${\{\,{a\in \mathcal {A}} \;|\; {\mathrm {Var}_\omega (a)=0}\,\}}$
is a unital
${\{\,{a\in \mathcal {A}} \;|\; {\mathrm {Var}_\omega (a)=0}\,\}}$
is a unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $\mathcal {A}$
. From Lemma 4.18, it also follows that the restriction of
$\mathcal {A}$
. From Lemma 4.18, it also follows that the restriction of
![]() $\omega $
to
$\omega $
to
![]() ${\{\,{a\in \mathcal {A}} \;|\; {\mathrm {Var}_\omega (a)=0}\,\}}$
is multiplicative. Conversely, if
${\{\,{a\in \mathcal {A}} \;|\; {\mathrm {Var}_\omega (a)=0}\,\}}$
is multiplicative. Conversely, if
![]() $\mathcal {B}$
is another unital
$\mathcal {B}$
is another unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $\mathcal {A}$
such that the restriction of
$\mathcal {A}$
such that the restriction of
![]() $\omega $
to
$\omega $
to
![]() $\mathcal {B}$
is multiplicative, then it follows that
$\mathcal {B}$
is multiplicative, then it follows that
![]() $\mathrm {Var}_\omega (b) = {\langle \,{\omega } \,,\, {b^*b}\,\rangle } - {\lvert {{\langle \,{\omega } \,,\, {b}\,\rangle }} \rvert }^2 = 0$
for all
$\mathrm {Var}_\omega (b) = {\langle \,{\omega } \,,\, {b^*b}\,\rangle } - {\lvert {{\langle \,{\omega } \,,\, {b}\,\rangle }} \rvert }^2 = 0$
for all
![]() $b\in \mathcal {B}$
and therefore the inclusion
$b\in \mathcal {B}$
and therefore the inclusion
![]() $\mathcal {B} \subseteq {\{\,{a\in \mathcal {A}} \;|\; {\mathrm {Var}_\omega (a)=0}\,\}}$
holds.
$\mathcal {B} \subseteq {\{\,{a\in \mathcal {A}} \;|\; {\mathrm {Var}_\omega (a)=0}\,\}}$
holds.
Now, assume that
![]() holds for all
holds for all
![]() $a\in \mathcal {A}_{\mathrm {H}}$
. As
$a\in \mathcal {A}_{\mathrm {H}}$
. As
![]() holds for all
holds for all
![]() $b\in \mathcal {A}_{\mathrm {H}}$
, it follows from
$b\in \mathcal {A}_{\mathrm {H}}$
, it follows from
![]() that
that
![]() $\mathrm {Var}_\omega (b) = 0$
for all
$\mathrm {Var}_\omega (b) = 0$
for all
![]() $b\in \mathcal {A}_{\mathrm {H}}$
, and hence
$b\in \mathcal {A}_{\mathrm {H}}$
, and hence
![]() $\mathrm {Var}_\omega (c) = 0$
for all
$\mathrm {Var}_\omega (c) = 0$
for all
![]() $c\in \mathcal {A}$
because
$c\in \mathcal {A}$
because
![]() $c = c_r+\mathrm {i} c_i$
with
$c = c_r+\mathrm {i} c_i$
with
![]() and
and
![]() . Application of Lemma 4.18 shows that
. Application of Lemma 4.18 shows that
![]() $\omega $
is multiplicative on whole
$\omega $
is multiplicative on whole
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Theorem 4.20 Let
![]() $\mathcal {A}$
be a radical commutative ordered
$\mathcal {A}$
be a radical commutative ordered
![]() $^*$
-algebra, then
$^*$
-algebra, then
![]() $\mathcal {S}_{\mathrm {p}}(\mathcal {A}) = \mathcal {S}_{\mathrm {m}}(\mathcal {A})$
, i.e., a state on
$\mathcal {S}_{\mathrm {p}}(\mathcal {A}) = \mathcal {S}_{\mathrm {m}}(\mathcal {A})$
, i.e., a state on
![]() $\mathcal {A}$
is a pure state if and only if it is multiplicative.
$\mathcal {A}$
is a pure state if and only if it is multiplicative.
Proof Let
![]() $\mathcal {\omega }$
be a state on
$\mathcal {\omega }$
be a state on
![]() $\mathcal {A}$
. If
$\mathcal {A}$
. If
![]() $\omega $
is multiplicative, then Proposition 4.14 shows that
$\omega $
is multiplicative, then Proposition 4.14 shows that
![]() $\omega $
is also a pure state. Conversely, if
$\omega $
is also a pure state. Conversely, if
![]() $\omega $
is a pure state, then it remains to show that the identity
$\omega $
is a pure state, then it remains to show that the identity
![]() holds for all
holds for all
![]() $a\in \mathcal {A}_{\mathrm {H}}$
, which, by Lemma 4.19, already implies that
$a\in \mathcal {A}_{\mathrm {H}}$
, which, by Lemma 4.19, already implies that
![]() $\omega $
is multiplicative.
$\omega $
is multiplicative.
So let
![]() $a\in \mathcal {A}_{\mathrm {H}}$
be given and define the subset
$a\in \mathcal {A}_{\mathrm {H}}$
be given and define the subset
of
![]() $\mathcal {A}_{\mathrm {H}}$
. It is clear that
$\mathcal {A}_{\mathrm {H}}$
. It is clear that
![]() $S_a$
is a (real) linear subspace of
$S_a$
is a (real) linear subspace of
![]() $\mathcal {A}_{\mathrm {H}}$
. If
$\mathcal {A}_{\mathrm {H}}$
. If
with
![]() $b,b' \in \mathcal {A}_{\mathrm {H}}$
, then
$b,b' \in \mathcal {A}_{\mathrm {H}}$
, then
![]() $b-b'=0$
because
$b-b'=0$
because
and because
![]() $\mathcal {A}$
is radical. So every element of
$\mathcal {A}$
is radical. So every element of
![]() $S_a$
is of the form
$S_a$
is of the form
with a unique
![]() $b\in \mathcal {A}_{\mathrm {H}}$
and the map
$b\in \mathcal {A}_{\mathrm {H}}$
and the map
![]() $\tilde {\rho } \colon S_{a} \to \mathbb{R}$
,
$\tilde {\rho } \colon S_{a} \to \mathbb{R}$
,
is well defined and is clearly
![]() $\mathbb{R}$
-linear. Moreover, for every
$\mathbb{R}$
-linear. Moreover, for every
![]() $c\in \mathcal {A}_{\mathrm {H}}$
, there exists an element
$c\in \mathcal {A}_{\mathrm {H}}$
, there exists an element
with
![]() $b\in \mathcal {A}_{\mathrm {H}}$
such that
$b\in \mathcal {A}_{\mathrm {H}}$
such that
and
, e.g.,
. Using again that
![]() $\mathcal {A}$
is radical one sees that
$\mathcal {A}$
is radical one sees that
![]() $\tilde {\rho }$
is positive with respect to the order on
$\tilde {\rho }$
is positive with respect to the order on
![]() $S_a$
inherited from
$S_a$
inherited from
![]() $\mathcal {A}_{\mathrm {H}}$
, so the extension theorem for positive linear functionals applies and shows that there exists a positive linear functional
$\mathcal {A}_{\mathrm {H}}$
, so the extension theorem for positive linear functionals applies and shows that there exists a positive linear functional
![]() $\rho $
on
$\rho $
on
![]() $\mathcal {A}_{\mathrm {H}}$
fulfilling
$\mathcal {A}_{\mathrm {H}}$
fulfilling
for all
![]() $b\in \mathcal {A}_{\mathrm {H}}$
. Using the isomorphism between
$b\in \mathcal {A}_{\mathrm {H}}$
. Using the isomorphism between
![]() $(\mathcal {A}_{\mathrm {H}})^*$
and
$(\mathcal {A}_{\mathrm {H}})^*$
and
![]() $\mathcal {A}_{\mathrm {H}}^*$
, we can also treat
$\mathcal {A}_{\mathrm {H}}^*$
, we can also treat
![]() $\rho $
as a positive Hermitian linear functional on
$\rho $
as a positive Hermitian linear functional on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
As
holds for all
![]() $b\in \mathcal {A}_{\mathrm {H}}$
, it follows that
$b\in \mathcal {A}_{\mathrm {H}}$
, it follows that
![]() $\rho \le \omega $
, and hence there exists
$\rho \le \omega $
, and hence there exists
![]() $\mu \in {[0,1]}$
such that
$\mu \in {[0,1]}$
such that
![]() $\rho = \mu \omega $
because
$\rho = \mu \omega $
because
![]() $\omega $
is a pure state by assumption. From evaluation on
$\omega $
is a pure state by assumption. From evaluation on
and
, one gets
and
which yields
![]() $\mu \neq 0$
and
$\mu \neq 0$
and
as well as
, and thus
.
Similar results about the relation between pure and multiplicative states on certain
![]() $^*$
-algebras have already occurred before, e.g., [Reference Bucy and Maltese3, Theorem 2] for Banach
$^*$
-algebras have already occurred before, e.g., [Reference Bucy and Maltese3, Theorem 2] for Banach
![]() $^*$
-algebras or [Reference Schmüdgen12, Proposition 11.3.9] for general
$^*$
-algebras or [Reference Schmüdgen12, Proposition 11.3.9] for general
![]() $^*$
-algebras endowed with a special choice of a (pre-)order.
$^*$
-algebras endowed with a special choice of a (pre-)order.
Corollary 4.21 Let X be a set, and let
![]() $\mathcal {A}$
be a unital
$\mathcal {A}$
be a unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $\mathbb{C}^X$
, endowed with the pointwise order inherited from
$\mathbb{C}^X$
, endowed with the pointwise order inherited from
![]() $\mathbb{C}^X$
, then the pure states on
$\mathbb{C}^X$
, then the pure states on
![]() $\mathcal {A}$
are precisely the multiplicative ones.
$\mathcal {A}$
are precisely the multiplicative ones.
Note, however, that there might be more multiplicative states on
![]() $\mathcal {A}$
than just evaluation functionals at points of X.
$\mathcal {A}$
than just evaluation functionals at points of X.
Corollary 4.22 Let
![]() $\mathcal {A}$
be a radical commutative ordered
$\mathcal {A}$
be a radical commutative ordered
![]() $^*$
-algebra, then
$^*$
-algebra, then
and the set
![]() $\mathcal {A}^{*,+,\mathrm {ex}}_{\mathrm {H}}$
of extremal positive Hermitian linear functionals on
$\mathcal {A}^{*,+,\mathrm {ex}}_{\mathrm {H}}$
of extremal positive Hermitian linear functionals on
![]() $\mathcal {A}$
is weak-
$\mathcal {A}$
is weak-
![]() $^*$
-closed in
$^*$
-closed in
![]() $\mathcal {A}_{\mathrm {H}}^*$
.
$\mathcal {A}_{\mathrm {H}}^*$
.
Proof Let
![]() $\omega $
be a positive Hermitian linear functional on
$\omega $
be a positive Hermitian linear functional on
![]() $\mathcal {A}$
. Then either
$\mathcal {A}$
. Then either
![]() $\omega = 0$
, in which case
$\omega = 0$
, in which case
![]() $\omega \in \mathcal {A}^{*,+,\mathrm {ex}}_{\mathrm {H}}$
and
$\omega \in \mathcal {A}^{*,+,\mathrm {ex}}_{\mathrm {H}}$
and
![]() for all
for all
![]() $a\in \mathcal {A}$
hold, or
$a\in \mathcal {A}$
hold, or
![]() . In this second case,
. In this second case,
![]() is a state on
is a state on
![]() $\mathcal {A}$
and the following chain of equivalences holds:
$\mathcal {A}$
and the following chain of equivalences holds:
![]() $\omega $
is an extremal positive Hermitian linear functional if and only if
$\omega $
is an extremal positive Hermitian linear functional if and only if
![]() $\tilde {\omega }$
is a pure state, which is equivalent to
$\tilde {\omega }$
is a pure state, which is equivalent to
![]() $\tilde {\omega }$
being multiplicative by Theorem 4.20, and Lemma 4.18 shows that this holds if and only if
$\tilde {\omega }$
being multiplicative by Theorem 4.20, and Lemma 4.18 shows that this holds if and only if
![]() $\mathrm {Var}_{\tilde {\omega }}(a) = 0$
for all
$\mathrm {Var}_{\tilde {\omega }}(a) = 0$
for all
![]() $a\in \mathcal {A}$
. As
$a\in \mathcal {A}$
. As
![]() , identity (4.8) is proved.
, identity (4.8) is proved.
Finally, as
![]() $\mathcal {A}^{*,+}_{\mathrm {H}}$
is weak-
$\mathcal {A}^{*,+}_{\mathrm {H}}$
is weak-
![]() $^*$
-closed in
$^*$
-closed in
![]() $\mathcal {A}^*_{\mathrm {H}}$
and as
$\mathcal {A}^*_{\mathrm {H}}$
and as
![]() is a weak-
is a weak-
![]() $^*$
-continuous function, one sees that the right-hand side of (4.8) is weak-
$^*$
-continuous function, one sees that the right-hand side of (4.8) is weak-
![]() $^*$
-closed in
$^*$
-closed in
![]() $\mathcal {A}^*_{\mathrm {H}}$
.
$\mathcal {A}^*_{\mathrm {H}}$
.
Corollary 4.23 Let
![]() $\mathcal {A}$
be a radical commutative ordered
$\mathcal {A}$
be a radical commutative ordered
![]() $^*$
-algebra, then the following are equivalent:
$^*$
-algebra, then the following are equivalent:
-
(1) The Gelfand transformation
 $\big ( \mathcal {S}_{\mathrm {m}}(\mathcal {A}), \pi _{\mathrm {Gelfand}} \big )$
of
$\big ( \mathcal {S}_{\mathrm {m}}(\mathcal {A}), \pi _{\mathrm {Gelfand}} \big )$
of
 $\mathcal {A}$
discussed in Proposition 4.12 is a faithful representation as functions.
$\mathcal {A}$
discussed in Proposition 4.12 is a faithful representation as functions. -
(2) There exists a faithful representation as functions of
 $\mathcal {A}$
.
$\mathcal {A}$
. -
(3) The order on
 $\mathcal {A}$
is induced by its extremal positive Hermitian linear functionals.
$\mathcal {A}$
is induced by its extremal positive Hermitian linear functionals.
Proof The implication (1)
![]() $\Longrightarrow $
(2) is trivial.
$\Longrightarrow $
(2) is trivial.
Assume that there exists a faithful representation as functions
![]() $(X,\pi )$
of
$(X,\pi )$
of
![]() $\mathcal {A}$
, and let
$\mathcal {A}$
, and let
![]() $a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
be given. Then there exists
$a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
be given. Then there exists
![]() $x\in X$
fulfilling
$x\in X$
fulfilling
![]() $\pi (a)(x) < 0$
. However, the linear functional
$\pi (a)(x) < 0$
. However, the linear functional
![]() $\mathcal {A} \ni b \mapsto \pi (b)(x) \in \mathbb{C}$
is a multiplicative state, hence a pure state by Proposition 4.14, and thus especially an extremal positive Hermitian linear functional on
$\mathcal {A} \ni b \mapsto \pi (b)(x) \in \mathbb{C}$
is a multiplicative state, hence a pure state by Proposition 4.14, and thus especially an extremal positive Hermitian linear functional on
![]() $\mathcal {A}$
. This proves the implication (2)
$\mathcal {A}$
. This proves the implication (2)
![]() $\Longrightarrow $
(3).
$\Longrightarrow $
(3).
Finally, if the order on
![]() $\mathcal {A}$
is induced by its extremal positive Hermitian linear functionals, then for every
$\mathcal {A}$
is induced by its extremal positive Hermitian linear functionals, then for every
![]() $a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
, there exists an extremal positive Hermitian linear functional
$a\in \mathcal {A}_{\mathrm {H}} \setminus \mathcal {A}_{\mathrm {H}}^+$
, there exists an extremal positive Hermitian linear functional
![]() $\tilde {\omega }$
on
$\tilde {\omega }$
on
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() ${\langle \,{\tilde {\omega }} \,,\, {a}\,\rangle } < 0$
. From
${\langle \,{\tilde {\omega }} \,,\, {a}\,\rangle } < 0$
. From
![]() $\tilde {\omega } \neq 0$
, it follows that
$\tilde {\omega } \neq 0$
, it follows that
![]() and therefore
and therefore
![]() is a well-defined pure state on
is a well-defined pure state on
![]() $\mathcal {A}$
, hence also a multiplicative state by Theorem 4.20. So we see that
$\mathcal {A}$
, hence also a multiplicative state by Theorem 4.20. So we see that
![]() $\pi _{\mathrm {Gelfand}}(a)$
cannot be positive because
$\pi _{\mathrm {Gelfand}}(a)$
cannot be positive because
![]() $\pi _{\mathrm {Gelfand}}(a)(\omega ) < 0$
, and conclude that the Gelfand transformation of
$\pi _{\mathrm {Gelfand}}(a)(\omega ) < 0$
, and conclude that the Gelfand transformation of
![]() $\mathcal {A}$
is faithful, i.e., (3)
$\mathcal {A}$
is faithful, i.e., (3)
![]() $\Longrightarrow $
(1) holds.
$\Longrightarrow $
(1) holds.
There are some representation theorems for commutative
![]() $^*$
-algebras endowed with a locally convex topology defined by submultiplicative seminorms, i.e., seminorms fulfilling the estimate
$^*$
-algebras endowed with a locally convex topology defined by submultiplicative seminorms, i.e., seminorms fulfilling the estimate
![]() ${\lVert {ab} \rVert } \le {\lVert {a} \rVert } {\lVert {b} \rVert }$
for all elements a and b of the algebra. One example is of course the commutative Gelfand–Naimark theorem. However, for radical commutative ordered
${\lVert {ab} \rVert } \le {\lVert {a} \rVert } {\lVert {b} \rVert }$
for all elements a and b of the algebra. One example is of course the commutative Gelfand–Naimark theorem. However, for radical commutative ordered
![]() $^*$
-algebras, Corollary 4.23 combined with Corollary 3.4 yields an approach using a rather different type of locally convex topologies.
$^*$
-algebras, Corollary 4.23 combined with Corollary 3.4 yields an approach using a rather different type of locally convex topologies.
Application of Theorem 3.7 to Corollary 4.23 immediately yields the following generalization of the commutative Gelfand–Naimark theorem.
Theorem 4.24 Let
![]() $\mathcal {A}$
be a
$\mathcal {A}$
be a
![]() $\sigma $
-bounded radical commutative ordered
$\sigma $
-bounded radical commutative ordered
![]() $^*$
-algebra, then
$^*$
-algebra, then
![]() $\mathcal {A}$
has a faithful representation as functions if and only if
$\mathcal {A}$
has a faithful representation as functions if and only if
![]() $\mathcal {A}$
is closed.
$\mathcal {A}$
is closed.
Like before, this implies that, heuristically, every closed radical commutative ordered
![]() $^*$
-algebra “behaves essentially like a
$^*$
-algebra “behaves essentially like a
![]() $^*$
-algebra of functions.”
$^*$
-algebra of functions.”
Corollary 4.25 Let
![]() $\mathcal {A}$
be a closed radical commutative ordered
$\mathcal {A}$
be a closed radical commutative ordered
![]() $^*$
-algebra, and let
$^*$
-algebra, and let
![]() $(a_n)_{n\in \mathbb{N}}$
be any sequence in
$(a_n)_{n\in \mathbb{N}}$
be any sequence in
![]() $\mathcal {A}$
. Then the unital
$\mathcal {A}$
. Then the unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $\mathcal {A}$
that is generated by
$\mathcal {A}$
that is generated by
![]() ${\{\,{a_n} \;|\; {n \in \mathbb{N}}\,\}}$
has a faithful representation as functions.
${\{\,{a_n} \;|\; {n \in \mathbb{N}}\,\}}$
has a faithful representation as functions.
Proof By Lemma 4.10, the unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $\mathcal {A}$
that is generated by
$\mathcal {A}$
that is generated by
![]() ${\{\,{a_n} \;|\; {n \in \mathbb{N}}\,\}}$
is
${\{\,{a_n} \;|\; {n \in \mathbb{N}}\,\}}$
is
![]() $\sigma $
-bounded, so Theorem 4.24 applies.
$\sigma $
-bounded, so Theorem 4.24 applies.
Theorems 4.9 and 4.24 allow to develop a theory of
![]() $^*$
-algebras of (possibly unbounded) operators in a representation-independent way. While the assumption of being
$^*$
-algebras of (possibly unbounded) operators in a representation-independent way. While the assumption of being
![]() $\sigma $
-bounded might be replaced by others, e.g., the existence of a well-behaved locally convex topology, the property of being radical is necessary for a commutative ordered
$\sigma $
-bounded might be replaced by others, e.g., the existence of a well-behaved locally convex topology, the property of being radical is necessary for a commutative ordered
![]() $^*$
-algebra to have a faithful representation as functions (see Proposition 4.15).
$^*$
-algebra to have a faithful representation as functions (see Proposition 4.15).
Acknowledgment
I would like to thank Profs. K. Schmüdgen and G. Buskes, and the anonymous referee, for some helpful discussions and comments on earlier versions of the manuscript.