Association between covariates and disease occurrence in the presence of diagnostic error

Summary

Identification of covariates associated with disease is a key part of epidemiological research. Yet, while adjustment for imperfect diagnostic accuracy is well established when estimating disease prevalence, similar adjustment when estimating covariate effects is far less common, although of important practical relevance due to the sensitivity of such analyses to misclassification error. Case-study data exploring evidence for seasonal differences in Salmonella prevalence using serological testing is presented, in addition simulated data with known properties are analysed. It is demonstrated that: (i) adjusting for misclassification error in models comprising continuous covariates can have a very substantial impact on the resulting conclusions which can then be drawn from any analyses; and (ii) incorporating prior knowledge through Bayesian estimation can provide potentially more informative assessments of covariates while removing the assumption of perfect diagnostic accuracy. The method presented is widely applicable and easily generalized to many types of epidemiological studies.

INTRODUCTION

A primary objective of many epidemiological studies is to test hypothesized relationships, for example between specific covariates of interest and some response variable, denoting say the presence of, or exposure to, a pathogen or parasite [1–5]. If, however, the method of diagnosis used to classify subjects as disease positive (negative) suffers from imperfect sensitivity and/or specificity then the observed response variable is an estimate of the diagnosis positive fraction of subjects in the study population – typically referred to as apparent prevalence. In contrast, what is actually desired is an estimate of the disease positive fraction – the true prevalence. Moreover, analyses of diseases which have low prevalence represent a particular challenge because even when using a diagnostic with very high specificity, false positives may be more numerous than true positives.

A complication in performing any data analyses is that the true prevalence in a study with an imperfect diagnostic is not directly observed, but rather contained latently within the data collected. The analytical challenge for the epidemiologist is to release this latent information, and thus enable estimation of the effects of the covariates of interest, after adjusting for diagnostic misclassification. Analytical approaches for misclassification in regression models in epidemiology were introduced some years ago [6–8]; however, the use of such approaches is far from common practice.

It is intuitively obvious that additional uncertainty must be introduced into any analyses when an imperfect rather than gold-standard test is used, and thus a resulting reduction in statistical power. What may be surprising in practice is just how large an impact this may have on the conclusions which can then be drawn from any analyses. This is the key message of this article, i.e. that misclassification error, can and should, always be investigated to ensure scientifically credible conclusions of regression analyses involving imperfect diagnostics. The impact of an imperfect diagnostic is first examined using simulated data, followed by analyses which explore temporal (seasonal) fluctuations in Salmonella prevalence in farmed pigs. Salmonella is zoonotic, and one of the main risks from this pathogen to humans is through the consumption of pork products which accounts for up to 20% of human salmonellosis cases found in some European countries, and it remains the second highest (regarding occurrence) in the list of human zoonotic diseases across the European Union [9–12]. Frequentist and Bayesian estimations are both considered and viewed as complementary approaches.

There exists an extensive literature on the study and development of methods for analysing results from imperfect diagnostic tests, both from frequentist and Bayesian perspectives [13–17]. Adopting a no-gold standard (NGS) approach does, however, come with numerous caveats [15], and unlike many other statistical estimation methods the results of model fitting are not generally testable against the observed data, as the variables being estimated are latent. It is, however, very difficult to argue that an NGS approach should not at least be considered whenever study results are based on a diagnostic which is not known to be a gold-standard test against the specific study population. This is particularly relevant in analyses focused on estimation of the effect of covariates, particularly continuous covariates, as the true functional relationship between the response variable and covariates is generally unknown and hence needs to be estimated from the observed data. Any additional variance in the response variable due to misclassification error may considerably affect the accuracy with which any functional form can be estimated, with the danger of attributing erroneous covariates to a particular disease status.

Model identifiability, i.e. are there sufficient degrees of freedom available given a particular study design to estimate latent variables, is a particular challenge in analyses concerned with imperfect diagnostic testing [18]. In theory, it is highly desirable that a model is identifiable as otherwise some parameters may be entirely redundant, in which case they should arguably be removed from any model. For example, in a binomial distribution it is possible to formulate the parameter p, the probability of observing a subject with disease as p=S _e π+(1−S _p )(1−π), where S _e and S _p are the sensitivity and specificity of the diagnostic test used, respectively, and π the true disease prevalence within the population. The terms p and π here are the apparent prevalence and true prevalence, respectively. The goodness of fit to observed data will only depend on the value of p, and no matter what combination of values are chosen for S _e , S _p , π they cannot improve the goodness of fit to the data, and hence cannot be uniquely estimated.

Much of the existing methodological NGS literature focuses on the problem of prevalence estimation using multiple imperfect tests applied to single or multiple study populations to ensure model identifiability [13]. In practice, however, it may be that for a model to be identifiable biologically untenable assumptions may be required, which is, at least in part, a practical reason for choosing a Bayesian estimation approach where identifiability is much less of a concern as prior information can be used to avoid this issue. For epidemiological studies which utilize only a single diagnostic test, which is common particularly in larger scale studies, estimation of the latent prevalence of disease is still possible but requires alternative approaches [5, 19].

In terms of previous methodological approaches to misclassification in regression models, log-linear analyses where information on error rates is provided through the availability of supplementary information, and logistic regression approaches with examples using discrete covariates have been available for many years [6, 7, 20]. However, the uptake of such approaches in practice has been very limited with a paucity of studies, particularly temporal and/or spatial studies which are a key aspect of zoonotic epidemiological research [21].

This article describes how to estimate the effects of covariates in relation to the unobserved ‘true’ prevalence in a population when an imperfect diagnostic test is used, and explores the resulting impact on the precision of the parameters of interest. In the analyses presented, the simplest case of a single continuous covariate is considered which is both sufficient for illustrative purposes, and also epidemiologically relevant in a zoonotic context as demonstrated in the later section Salmonella case study. Models with both continuous and discrete covariates and using multiple imperfect tests are deferred to the Discussion. Of related interest is using frequentist and Bayesian estimations as complementary approaches, with the former assisting with issues of parameter stability and robustness, while the latter allows for the incorporation of valuable prior information which can be used to decrease variance/increase power.

METHODS

While Bayesian approaches to imperfect diagnostic test estimation are widespread [22], and increasingly accessible through software which implements efficient Markov chain Monte Carlo (MCMC) estimation such as WinBUGS and JAGS [23], a maximum-likelihood (ML) approach is considered alongside Bayesian estimation. An advantage of using ML estimation is that issues and difficulties around model identifiability are, generally speaking, more immediately recognizable compared to a Bayesian approach where the influence of the prior information used can be sufficient to mask a model which would be unidentifiable given the observed data alone. This is practically relevant because if a model is unidentifiable in a ML context, then in a Bayesian analyses – while WinBUGS/JAGS will probably have no problem in producing parameter estimates – any results may be very highly sensitive to the prior information used (e.g. from expert opinion) which may be undesirable.

Latent variable logistic regression

A binomial regression model with a logit link function between the latent true prevalence and covariates associated with disease occurrence can be defined as follows; for covariate pattern i,

(1)

with q _i the probability that a subject with the ith covariate pattern tests positive (apparent prevalence) and π _i the probability that a subject with the ith covariate pattern is disease positive (true prevalence), where the latter is parameterized as a function of covariates β. The transposed vector x _i ^T represents the ith row of the design matrix X, i.e. the combination of model parameters which will be used to estimate the ith covariate pattern. The parameters S _e and S _p are, respectively, the sensitivity and specificity of the diagnostic used. When S _e =1 and S _p =1 then the model reverts to the classical logistic regression model where q _i =π _i (note that when S _e <1 or S _p <1 then q _i does not have a logit link function).

The key aspect in fitting the model in equation (1) to data is the complication that the π _i s are latent parameters. The expectation maximization (EM) algorithm is a standard approach for ML estimation in the presence of unobserved variables [15, 24]. Technical implementation details of an EM algorithm for a latent variable logistic regression model can be found in the Supplementary material (available online) along with suitable R code. Model fits were assessed both visually against the data and also more formally using the ML ratio test and Akaike's Information Criterion (AIC) metric.

Later, Bayesian estimation is applied to the same form of model using MCMC via JAGS and all computer code is again provided as Supplementary material to allow easy replication of the results presented. As is good practice in Bayesian analyses a large number of different chains were run from many different initial starting points and of different lengths, including some very long runs of many millions of iterations. Trace plots for individual parameters and deviances were compared and examined to identify signs of poor behaviour such as very slow mixing, and also to assess convergence along with the use of the usual Gelman & Rubin convergence diagnostic [25].

Simulated data

Analysing simulated data where the true parameters are known with certainty provides a means of investigating the behaviour and utility of latent variable approaches. We consider the case of a single covariate where the logit of the (mean) true prevalence is modelled by a straight line where x _i ^T comprises of (1, x _1,i ), and β ^T =(β₀, β₁), hence logit(π _i )=β₀ +x _1,i β₁. In the simulated data β₀=−2, β₁=10 with x _1,i taking 24 equally spaced values from 0·2 to 0·4 and S _e =0·7 and S _p =0·9. The simulated data were created in a straightforward fashion by first generating the (linear and deterministic) mean on a logit scale, inverting to the probability scale (i.e. true prevalence π _i ), then creating an apparent probability (q _i ) for each covariate pattern. Finally, Bernoulli observations were generated, e.g. coin tosses where ‘heads’ and ‘tails’ are replaced with diagnosis positive or diagnostic negative, where q _i is the probability of observing a diagnosis positive observation at covariate pattern i.

Of primary interest is exploring the impact of allowing additional variance into the regression relationship as a result of diagnostic test error. To this end two different sample sizes were considered, first with n=100 independent Bernoulli observations for each covariate pattern, e.g. for each value of x _1,i , and then a larger dataset with n=2000 Bernoulli observations per covariate pattern. This gives a total of 2400 and 48 000 individual diagnostic test results, respectively. These are deliberately large sample sizes – if the impact of misclassification error is appreciable in such relatively large sample sizes then it is reasonable to expect this to be larger in smaller datasets. Moreover, while 2400 test results might be large relative to certain types of human epidemiological studies, this is small relative to data collection in certain zoonotic contexts, e.g. the later Salmonella case study in farmed pigs has over 8000 observations, and in general food safety and meat inspection data can comprise very large numbers of observations. Each simulated dataset provides a potential maximum of 24 degrees of freedom (d.f.) and fitting a standard logistic regression model (where S _e =S _p =1) requires 2 d.f. For the latent variable model to be identifiable it requires that the data contain sufficient additional information to also allow for S _e and S _p to be estimated.

Two different sets of prior distributions are considered when modelling this data, first, where S _e and S _p have independent Beta distributions, specifically β(1, 1) (equivalent to uniform on 0, 1), and with β₀ and β₁ having diffuse independent normal priors with mean zero and variance 1000. Next, the priors for S _e and S _p are made more informative using β(70, 30) and β(90, 10), respectively, where these have means of 0·7 and 0·9 and roughly equate to a total prior weighting of 100 Bernoulli observations (in a simple conjugate model with a binomial density – and equal to about 1·2% of the weight of the observed data).

Model identifiability and parameter estimation

Two aspects are of particular interest, first is the latent variable model identifiable. Assessing the identifiability of any given model in a formal mathematical setting is challenging [18] and still largely an open question. However, this can be assessed relatively easily empirically. If the algorithm used to estimate the model parameters produces different estimates, e.g. starting the algorithm from different starting points gives different estimates but which have identical maximum log-likelihood values, then that is strong evidence that the likelihood is at least in parts completely flat, and hence the model is not identifiable. Note that in practice some allowance may need to be made for numerical approximation errors in whatever algorithms are used. Even if the maximal log-likelihood values are not identical but only very similar (for different parameter estimates), then a similar issue exists since this suggests that the standard errors for at least some of the model parameters are likely be very large, and therefore give results which will not be statistically significant.

Assuming a model is identifiable, the second aspect of particular interest is estimating the uncertainty in the parameter(s) of interest, in the case of the simulated data given above this is, β₁, the covariate associated with the presence of disease. To estimate confidence intervals profile likelihood is used [26] in all (non-Bayesian) analyses presented. Profile likelihood is a method for estimating confidence intervals in the presence of ‘nuisance parameters’, for example, to estimate a confidence interval for β₁ we need to also take into account the uncertainty in the other unknown parameters in the model, e.g. β₀, S _p , S _e .

In the context of estimating a confidence interval for β₁ then β₀, S _p , S _e can be considered as nuisance variables, similarly when estimating β₀ then β₁, S _p , S _e become nuisance variables. We consider confidence interval estimation for β₁. First, we plot the log-likelihood function for the latent variable logistic regression model over a range of values for β₁, where for each value of β₁ the maximum possible value of the log-likelihood function is used (allowing the nuisance parameters to take any values in their range) – this is called the profile likelihood for β₁. Figure 1(c, d) shows profile likelihood functions for β₁ constructed in this way. A (1−α) confidence interval for β₁, where for example α=0·05 gives a 95% confidence interval (95% CI), is found by drawing a horizontal line at a value of below the maximum value of the profile likelihood function where is the (1−α) quantile of the χ² probability distribution with d degrees of freedom. For a confidence interval for a single parameter then d=1, for a joint confidence interval of two parameters then d=2 and so on. Therefore, a 95% CI for β₁ is given by where a horizontal line crosses the profile likelihood function for β₁ at a distance below the maximum value of this function (Fig. 1 c, d). It is also possible to estimate joint 95% CIs in an analogous fashion, in the two-parameter case this interval (or region) is now defined by a horizontal cross-section across a profile likelihood surface (see Fig. 2).

Fig. 1. Analysis of simulated data. (a, b) Raw data with corresponding fitted trend lines assuming the diagnostic test used was a gold-standard test [apparent prevalence (dashed line), true prevalence (solid line)] as a function of the covariate. As expected there is considerable difference between apparent and true prevalence. (a) n=100 per covariate pattern, test positive (T+) and true prevalence (D+); (b) n=2000 per covariate pattern. (c, d) Estimates for the slope parameters in panels (a) and (b). 95% confidence intervals (defined as where the horizontal lines cross the profile likelihood) show there is great uncertainty in the slope when the test is not a gold standard and this is still considerable even for the much larger sample size. (c) n=100 per covariate pattern; (d) n=2000 per covariate pattern.

Fig. 2. Profile likelihood surface for S _e and S _p estimated from Salmonella data. There is great uncertainty in the estimate of S _e but relatively less in S _p . The MLE is (S _e , S _p )=(0·99, 0·907) with the critical value defining a 95% confidence set within this surface at −2904·61 (outside the limits shown).

Salmonella case study data

Data comprising ELISA serological test results for exposure to Salmonella from 8028 individual finishing pigs destined for human consumption in the UK were analysed. Visual inspection of the data suggests considerable seasonal fluctuations in Salmonella prevalence, with a strong peak in late summer and rapid decline during the winter months for the two years (2008 and 2009) for which data were available. Salmonella seasonal variation has been observed before, and is potentially associated with an increase of the proliferation of bacteria in the farm environment during the warmer months and an increase in Salmonella shedding by infected pigs resulting from heat stress [9, 27]. This is directly relevant to human health as it implies that the risk of Salmonella in pork products may be greater during the warmer months, which may have implications for risk assessment strategies designed to minimize Salmonella entering the food chain. A particular question of interest is whether analyses using standard binomial logistic regression (assuming the ELISA is a gold-standard test) support seasonal variation in prevalence, and what is the impact of removing this unsupported assumption through fitting a latent variable logistic regression model. Robust estimates of sensitivity and specificity of the ELISA used when applied to the relevant UK pig population are unavailable.

RESULTS

Simulated data

Figure 1(a, b) shows the simulated data along with corresponding fitted trend lines assuming the diagnostic test used was a gold-standard test, and the true prevalence in the population as a function of the covariate. Figure 1(c, d) contains the profile likelihood for β₁ and corresponding confidence intervals for the effect of this covariate. The latent variable model is identifiable with a unique solution of (β₀, β₁, S _e , S _p )=(−1·38, 7·48, 0·76, 0·999 997) with maximum log-likelihood of −1635·02 for n=100, and (β₀, β₁, S _e , S _p )=(−2·12, 11·54, 0·68, 0·953) with maximum log-likelihood of −32 657·91 for n=2000. For the standard regression model the maximum log-likelihood values are −1635·11 and −32 670·38, respectively, for n=100 and n=2000; note that these are not the same as those in the latent variable model as S _e and S _p are not implicitly contained within the parametrization of the standard model. While the ML solutions are unique, the likelihood surface is relatively flat resulting in comparatively low parameter precision, as can be seen in the wide confidence intervals for β₁ (Fig. 1 c, d, Table 1); in contrast, 95% CIs for β₁ in the gold-standard model are relatively very precise. It is instructive to compare results using Bayesian estimation with the ML results. Table 1 shows 95% CIs for β₁ using 2·5% and 97·5% quantiles.

Table 1. Analysis of simulated data [95% confidence intervals for slope parameter (β1) by sample size and model type]

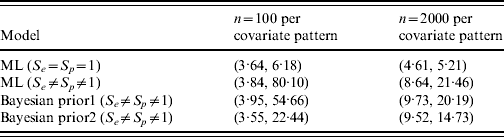
ML, Maximum-likelihood model.

Prior 1 is β(1, 1) on both S _e and S _p ; prior 2 is β(70, 30) and β(90, 10) for S _e and S _p , respectively.

Salmonella case study

Figure 3 a shows the observed data – the apparent prevalence of finishing pigs for Salmonella split by calendar month, along with the best-fit regression line using a standard binomial regression model. Polynomials in month (as a dummy variable 1–12) of increasing order were considered and both the ML ratio test and AIC strongly support a cubic relationship as the best-fitting model (AIC for orders 0–4: 5831·861, 5815·318, 5814·606, 5811·872, 5813·813). Treating the test as a gold standard, and considering the relatively narrow range of (cubic) trajectories which fit within the 95% prediction limits for the conditional mean (Fig. 3 a), suggests that the magnitude of this change in prevalence is potentially worthy of further epidemiological investigation.

Fig. 3. (a) Analysis of Salmonella data. There are great differences between true and apparent prevalence. Total sample size of 8028 pigs, apparent prevalence (T+), latent true prevalence (D+). (b) After accounting for the impact of the imperfect test it is not possible to draw any conclusions as to seasonal changes in true prevalence. Range of trajectories corresponds to the joint 95% confidence set for S _e and S _p .

We now consider instead that the ELISA has not been shown to be a gold standard against this specific study population, and moreover, suppose than no reliable information is available in respect of likely true and false positive rates against the study population. Using ML estimation to fit a cubic polynomial latent variable model gives the maximum-likelihood point estimate (MLE) (β₀, β₁, β₂, β₃, S _e , S _p )=(−5·98, 0·0033, 0·12, −0·0091, 0·99, 0·907), the true prevalence estimate (Fig. 3 a) is clearly well outside the 95% range of trajectories for the gold-standard equivalent (maximum log-likelihood is −2901·61, with −2901·94 in the gold-standard model).

The existing range of gold-standard prevalence trajectories need to be adjusted to take into account the implicitly estimated sensitivity and specificity of the Salmonella ELISA. Figure 3 b shows cubic polynomial trajectories where each of these corresponds uniquely to a point in the joint 95% confidence set for the sensitivity and specificity (S _e , S _p ). Once this additional uncertainty has been included, not only does the MLE in the standard binomial model appear strongly biased relative to the ‘true’ prevalence MLE, but the additional uncertainty introduced due to ignorance of likely prior distributions for (S _e , S _p ) is so large that in practical terms it is impossible to draw any substantive conclusions as to the relationship between calendar month and Salmonella prevalence.

Figure 2 shows an estimate of the joint (profile) likelihood surface for (S _e , S _p ). The critical value – the value of the profile likelihood surface at the cross-section required to produce a joint 95% confidence set for (S _e , S _p ) – is −2904·61, and as is clear from the contour plot that while it is not completely flat, and hence strictly speaking the model is identifiable, it is so flat that this results in the very wide range of trajectories for the monthly prevalence estimates shown in Figure 3 b (the Supplementary online material contains an additional contour plot with wider ranges).

Given the very wide range of uncertainty in the ML estimation it is instructive to investigate how much this could be reduced by the introduction of prior information, for example sourced from a smaller scale study on the same target population whose aim was estimation of diagnostic accuracy. Figure 4 shows results from using Bayesian estimation with prior distributions for S _e and S _p of β(99, 1) and β(99, 1), respectively, with β _i for i=0, 1, 2, 3 having diffuse independent normal priors with mean zero and variance 1000. These are highly informative priors with low variance and very high accuracy for both sensitivity and specificity. Not surprisingly, the variance in trajectories for the true prevalence in the Bayesian model is extremely smaller than in the ML model (with unknown S _e and S _p ), but still rather larger than the gold-standard ML model (Fig. 4 c).

Fig. 4. Bayesian estimation of Salmonella data using extremely strong priors of β(99, 1), close to perfect accuracy, for S _e and S _p . There still exists a very large amount of uncertainty in estimates of true prevalence over time and much more than assuming a gold-standard test. (a) Prior and posterior densities for S _e . (b) Prior and posterior densities for S _p . (c) Range of trajectories corresponding to the top 95% of log-likelihood values sampled during Markov chain estimation of the Bayesian latent variable model. The trajectory estimate with highest posterior log-likelihood is also shown.

As a practically important footnote, estimating the Bayesian model required some care. In a Bayesian analyses the usual objective is to estimate probability distributions for each parameter of interest (which can then provide, for example confidence intervals), which are a combination of the data available and prior knowledge. The key part of this estimation process when using WinBUGS/JAGS is that they attempt to describe (e.g. map) a possibly very complex surface which defines the joint probability distribution for all parameters in the model. They do this by effectively ‘walking’ around this landscape taking different sized steps, depending on the specific algorithm used. During this process it is possible to get ‘trapped’ in a particular area of the surface and therefore the map of the landscape it produces will be at best incomplete, if not entirely unreliable. In the Salmonella analyses many different ‘walks’ (Markov chains) were performed from different initial starting points in the landscape, and for varying numbers of steps which is generally considered good practice in MCMC analyses. About half of the chains appeared to get trapped indefinitely sampling around a mode with log-likelihood of about −2915, whereas other chains sampled around a mode with log-likelihood of about −2902, the latter corresponding to the ML analyses. Some chains eventually reached the ML mode but some did not even after many millions of iterations (steps). The ML analyses was valuable in assessing whether the results from the Bayesian estimation procedure were robust (technical note: chains sampling from the node at −2915 had values of about 1·0 for the usual Gelman & Rubin convergence diagnostic [25] indicating convergence, and similarly for the chains sampling around the ML node). Summary outputs and diagnostics can be found in the Supplementary material (online).

DISCUSSION

There are two key results from the analyses presented. First, that even a relatively small margin of misclassification error in the response variable in regression models can considerably increase the variance of the estimated functional relationship. Second, the methods presented for adjusting for misclassification error in regression models are relatively straightforward, especially in a Bayesian context via MCMC, e.g using either WinBUGS or JAGS (JAGS code is provided with the Supplementary material). As illustrated with the case study analyses, however, performing appropriate diagnostics and examining issues such as sensitivity to priors are then of crucial importance. The key practical implication of the work presented is that some form of adjustment for misclassification error should be considered in any study unless there is overwhelming biological evidence that the diagnostic used is error free.

The methods presented here have particular application to the study of rare diseases in populations. Although highly specific diagnostic tests may be developed, the specificity is often <1·0. This results in poor positive predictive values of the tests as the frequency of false positives in the population may exceed that of true positives. Consequently, there is a substantial risk of making inappropriate conclusions on covariates associated with disease presence as they may be substantially influenced by covariates associated with individuals who test false positive. For example a population study of human cystic echinococcosis, a highly pathogenic parasitic disease caused by Echinococus granulosus, in Kazakhstan reported an estimated prevalence of 0·011 [28]. As part of the study the population was tested with an ELISA using cyst fluid antigens isolated from E. granulosus. This test had a specificity of 0·990 but the positive predictive value was just 0·382. Hence using standard logistic regression to evaluate covariates in the population associated with infection status, using positive test results from this ELISA is likely to produce substantial errors.

Only polynomial models in a single continuous covariate have been considered; however, the methods demonstrated are equally applicable to richer forms of regression models, e.g. with more complex variance structure, and also potentially comprising both continuous and discrete covariates. Models to identify temporal or spatial correlations with disease are particularly obvious candidates. Model identifiability is again a consideration as this is likely to become more difficult and challenging the more complex the model considered for a given dataset (see Supplementary material for a brief discussion). Also of relevance is available sample size; in the simulated data example the sample sizes used were relatively large, yet the variance in the regression coefficients was still considerable. This again, suggests that some form of informative prior may be of significant benefit even in larger studies.